Tóm tắt Chương 3.Đo lường rủi ro môn Quản trị rủi ro tài chính

8/20/21&
ĐO&LƯỜNG&RỦI&RO& BA, August 2021 Contents&
1.#Giới thiệu các thước đo rủi ro#
2.#Lý thuyết xác xuất#
3.#Các thươc đo rủi ro tài sản# 4.#Value at risk# 2&
Một số thuật ngữ cơ bản&
• Duration: Thời gian đáo hạn bình quân • Variance: Phư n ơ g sai
• Standard deviation: độ lệch chuẩn
• Capital asset pricing model: mô hình định giá tài sản vốn • Value at Risk: VaR
• Correlation variance: Hiệp phương sai
• Correlation coefficient: Hệ số tương quan
• Portfolio: Danh mục đầu tư
• Capital market line: Đường thị trư n ờ g vốn
• Securities market line: Đường thị trư n ờ g chứng khoán 1& 8/20/21&
Sự phát triển của các phương pháp đo lường rủi ro& Năm
Phương pháp đo lường rủi ro TK18 Lý thuyết xác suất 1938
Thời lượng của trái phiếu (Duration) 1952
Phân tích trung bình và Phương sai của Markowitz 1963
Mô hình định giá tài sản vốn (CAPM) của Sharpe 1966 Mô hình đa nhân tố 1973
Mô hình định giá quyền chọn Black- Scholes 1988
Tài sản theo trọng số rủi ro đối với NHTM 1993 Value at risk 1997
Thước đo tín nhiệm, Rủi ro tín dụng 1998
Sự kết hợp của rủi ro tín dụng và rủi ro thị trường 1998
Phân bổ ngân quỹ cho rủi ro !
Sự phát triển của các phương pháp đo lường rủi ro& • 1938: Macaulay là ngư i ờ đầu tiê n đề xuất phương pháp
đánh giá rủi ro của lãi suất trái phiếu thông qua thước
đo thờ i lượng trái phiế u (Duration).
• 1952: Markowitz mở đường cho phương pháp phân tíc h
quan hệ rủi ro- lãi suất qua mô hình phân tích trung bình và phươ ng sai.
• 1963: William Sharpe mở ra bước ngoặt cho sự phát
triển của thị trường tà
i chính với mô hình nghiên cứu về định gi
á tài sản vốn (CAPM), trong đó ông đã nhấn mạnh rằng bet a c
ó thể dùng để đo lường rủi ro của một tà i sản
trong mối tương quan với cá c tà i sản khác trong DMĐT
Sự phát triển của các phương pháp đo lường rủi ro&
• 1966: Fama và French đã đưa ra mô hình b nhân t a ố, cho rằng tỷ suất sinh lợi c a m ủ t ộ danh m c
ụ đầu tư hoặc một c phi ổ ếu
riêng biệt phụ thuộc vào 3 yếu tố đó là: yếu tố thị trường,
yếu tố quy mô công ty và yếu tố t s ỷ ố gi á trị sổ sách trên gi á trị t hị t
rường vốn chủ sở hữu • 1998:
– Mô hình bốn nhân tố đưa thêm vào m t nhân t ộ ố g i ọ là
“xung lượng thị trường”…
– Mô hình tám nhân tố đưa thêm vào mô hình bốn nhân tố
các nhân tố: lợi suất c phi ổ
ếu, lợi suất dòng tiền, chênh
lệch kỳ hạn và khả năng vỡ nợ.
– Mô hình mười nhân tố đưa thêm nhân tố beta - (nhân tố
dựa trên thu nhập chứng khoán tích lũy theo thời kỳ 12
đến 60 tháng trước đó). 2& 8/20/21&
Sự phát triển của các phương pháp đo lường rủi ro&
• 1973: mô hình Black Scholes về định gi á quyền ch n ọ được giới thiệu, c
ác thước đo rủi ro quyền chọn cũng đượ c đưa ra như: – Delta đo lường độ nhạy củ ộ
a m t quyền chọn với một sự thay i đổ nh trong ỏ gi á trị c a ủ tài sản cơ sở;
– Gamma đo lường bi độ ến n độ g c a delta ủ đối với một sự thay i trong đổ gi á trị tài sản cơ sở; – Vega phản án m h ức biến động gi c á a ủ quyền ch n khi ọ c ó một sự thay i v
đổ ề mức độ biến động (volatility) gi á tài sản cơ sở;
– Theta đo lường mức thay độ i c đổ a ủ gi á quyền ch n khi ọ thời gia t n ới ngày đá h o ạn g ả i m đi một ngày
(1) Lý thuyết xác suất& • Phân tíc
h xác suất cụ thể hóa mức phân bổ xác suất cho
mỗi rủi ro và xem xét ảnh!hưởng của rủi ro tác động đến toàn bộ dự án. • Đâ
y là phương pháp phân tíc
h định lượng thường sử
dụng trong phân tích rủi ro, đặc biệt sử dụng kỹ thuật lấy mẫu.
• Phương pháp này dựa vào sự tín h toá n ngẫu nhiên cá c gi á trị trong cá
c phân phối xác suất nhất định, được mô tả!dưới dạng ư c
ớ lượng là tối thiểu, trun g bình và tối đa.
• Kết quả là sự kết hợp của tất cả các giá trị được lựa chọn
cho mỗi mức rủi ro. Sự tín h toá
n này được lặp lại một số
lần khá lớn để nhận được phân bố xác suất kết quả dự án.! Phân phối chuẩn& 3& 8/20/21&
(2)&Đo&lường&biến&động&giá&Tp&
Mức biến động giá Thời gian Tg đáo hạn đáo hạn đ ề Độ lồi bq i u bình quân chỉnh 10
Thời&gian&đáo&hạn&bình&quân&
- Macaulay Duration (D) = f(F, C, n, r)
- Thời gian cần thiết để thu hồi vốn đầu tư vào trái phiếu 11 =
Công&thức&Macaulay&duraUon&
Để xác định sự thay đổi xấp xỉ của giá trái phiếu đối với một sự thay đổi
nhỏ của lãi suất, lấy đạo hàm cấp 1 của phương trình trên theo lãi suất 12 4& 8/20/21&
Công&thức&Macaulay&duraUon& t w = 1 ( + ) t [ r CF t ] P T D t wt = ∑ × t=1 13 Macaulay&duraUon&
Là thời gian đáo hạn bình quân gia quyền của các khoản thu
nhập bằng tiền từ trái phiếu, với quyền số là hiện giá của
chúng. Dùng để đo biến động giá trái phiếu khi lãi suất thị trường thay đổi.
% mức biến động giá trái phiếu 14 Ví&dụ#
Tính thời gian đáo hạn bình quân của một trái phiếu có kỳ hạn 2 năm, lãi suất
danh nghĩa 8%/năm, một năm trả lãi 2 lần, mệnh giá $1,000, lãi suất chiết khấu 10%. 8%
Time Payment PV of CF Weight C1 X C4 Bond years (10%) .5 40 38.095 .0395 .0197 1 40 36.281 .0376 .0376 1.5 40 34.553 .0358 .0537 2.0 1040 855.611 .8871 1.7742 sum 964.540 1.000 1.8852 5& 8/20/21& Modified duration ΔP/P = - D* x Δr 16
Đặc điểm của duration
1. D của trái phiếu zéro coupon cũng chính là kỳ hạn của TP
2. Nếu thời gian cho tới khi đáo hạn và YTM không đổi, D của t
p và độ nhạy cảm của nó sẽ
cao hơn khi l/s cuống phiếu thấp hơn
3. Nếu l/s cuống phiếu không đổi, D và độ nhạy
cảm l/s của tp sẽ tăng cùng với thời gian cho tới khi đáo hạn
4. Nếu các yếu tố khác không thay đổi, D của t p trả
lãi sẽ cao hơn khi YTM của trái phiếu thấp hơn
5. D của trái phiếu vĩnh viễn = (1+y)/y 17
(3) Đo lường biến động giá cổ phiếu& Trái tức/ Lãi/lỗ vốn& Cổ tức& 6& 8/20/21&
Tỷ suất sinh lời trong kỳ đầu tư&
Tỷ suất sinh lời kỳ vọng&
Đo lường rủi ro theo tỷ suất sinh lời kỳ đầu tư& 7& 8/20/21&
Đo lường rủi ro theo tỷ suất sinh lời kỳ vọng&
Thước đo tương đối của rủi ro - CV&
(4) Đo lường rủi ro DMĐT
MỨC SINH LỜI CỦA DANH MỤC ĐẦU TƯ Công thức
E(r ) = w E(r ) + w E(r ) + … … + w E(r ) P 1 1 2 2 n n
Hay E(r ) = ∑w E(r ) p i i Trong ®ã: w : Tỷ tr ng ọ
đầu tư vào tài sản thứ i i
E(r ): Tỷ suất sinh lời c a tài s ủ ản thứ i i 8& 8/20/21&
Phương sai của danh mục đầu tư Trong đó: σ
= độ lệch chuẩn của danh mục đầu tư port
w = tỷ trọng của tài sản i trong danh mục đầu tư i
σ2 = phương sai mức sinh lời của tài sản i i
Cov = hệ số tích sai giữa mức sinh lời của tài sản i và j i j &
Hệ số tích sai của mức sinh lời (Covariance of returns) • Công thức: Cov (r ,r ) = σ = ∑
∑ P [r i - E(r )][r i - E(r )] A B AB i A A B B
• Tích sai là một hệ số đo lường về mối
tương quan giữa mức độ biến động rủi ro
của 2 chứng khoán khác nhau
– Cov > 0: Lợi suất hay giá của hai CK Biến động cùng chiều
– Cov < 0: Lợi suất hay giảm giá của hai CK
biến động ngược chiều 26&
Hệ số tương quan - Correlation coefficient • C«ng thøc: ρ Cov(r ,r ) 1 2 (r1,r2) = σ σ 1 2 • (-1 ≤ ρ ≤ 1)
• ρ < 0: Phản ánh sự biến động ngược chiều của hai chứng khoán
• ρ = +1: Hai chứng khoán có dao động hoàn toàn giống nhau
• ρ = -1: Hai chứng khoán có quan hệ hoàn toàn ngược chiều
• ρ = 0: Hai chứng khoán không có quan hệ tương quan với nhau 9& 8/20/21&
Hiệu quả của đa dạng hóa&
Danh mục đầu tư gồm hai chứng khoán A và B E(R ) = w R + w R P A A B B
σ 2 = w 2 σ 2 + w 2 σ 2 + 2w w Cov(r r ) P A A B B A B A, B
– ρ = 1: đa dạng hoá DMĐT không có ý nghĩa
– ρ = -1: đa dạng hoá DMĐT đạt hiệu quả cao nhất – ρ = 0 28&
Hiệu quả của đa dạng hóa
Danh mục đầu tư gồm nhiều tài sản 10& 8/20/21& Gi¶i thÝch b»ng ma trËn CK 1 2 3 … n … . 1 w 2 σ 2 w w cov(R ,R ) w w cov(R ,R ) w w cov(R ,R ) 1 1 1 2 1 2 1 3 1 3 1 N 1 N 2 w w cov(R ,R ) w 2 σ 2 w w cov(R ,R ) w w cov(R ,R ) 2 1 2 1 2 2 2 3 2 3 2 N 2 N 3 w w cov(R ,R ) w w cov(R ,R ) w 2 σ 2 w w cov(R ,R ) 3 1 3 1 3 2 3 2 3 3 3 N 3 N … ……………… …………… …………… … …………….. …. … n
w w cov(R ,R ) w w cov(R ,R ) w w cov(R ,R ) w 2 2 N 1 N 1 N 2 N 2 N 3 N 3 n σn Hiệu&quả&Đ &
a dạng&hóa&DMĐT& 32&
&Mô hình định giá tài sản vốn&
• Cốt lõi của lý thuyết kinh tế tài chính hiện đại
• Harry Markowitz là người đặt nền móng đầu tiên (1952)
• 1964: William Sharpe, John Lintner và Jan Mossin phát triển tiếp
– Xây dựng mô hình dự đoán mối quan hệ giữa rủi
ro và tỷ suất sinh lời kỳ vọng 11& 8/20/21&
RỦI RO HỆ THỐNG VÀ PHI HỆ THỐNG 34&
• Các chứn khoán ri g
êng lẻ tác động như thế nào đến rủi ro danh mục – Rủi r
o của một danh mục đa
đ dạng hoá tốt phụ thuộc vào rủi r o
thị trường của các chứng khoán trong danh mục • Rủi r o thị trườn g được đo l đ ườn b g ằn B g eta
– Nếu muốn biết một chứng khoán riêng lẻ góp phần vào danh mục đa đ dạn
g hoá thì cần phải đo đ lườn g rủi r o thị trườn g của
chứng khoán bằng cách đo
đ lường độ nhạy cảm của chứng khoán
đó (ß) đối vói biến độn g của thị trườn g 8/20/21& HÖ sè beta 35& Mô hình CAPM
• Víi β j =δj/δm, ®"êng CML: 36&
E(Rj) = R + (E(R ) – R ) β F M F j
Là phương trình định giá tài sản v n, ố thể hiện m i ố quan hệ giữa r i ủ ro và lợi nhuận k ỳ v ng ọ c a
ủ từng chứng khoán riêng lẻ – β = 0: E(Rj) = R j F – β = 1: E(Rj) = E(R j M) 12& 8/20/21& Ý nghĩa của beta 37&
• Beta là hệ số đo lường mức độ biến động lợi nhuận
của một cổ phiếu so với mức biến động lợi nhuận của
danh mục cổ phiếu thị trường • Beta >1
– Beta = 1 (danh mục thị trường) – Beta < 1
• Beta được xem là phương pháp đo lường mức rủi ro
tương đối của một chứng khoán
• Có một mối quan hệ tuyến tính giữa mức sinh lời và
rủi ro, beta càng cao thì mức sinh lời kỳ vọng càng cao và ngược lại. Ý nghĩa của beta • VÝ dô: Beta E(R) Cæ phiÕu A 1.5 12% Cæ phiÕu B 2 10%
• CAPM: một cổ phiếu có beta cao được kỳ vọng mang lại mức
sinh lời cao bởi vì độ rủi ro cao. Tuy nhiên, không có nghĩa cổ
phiếu có beta cao luôn mang lại mức sinh lời cao hơn cổ phiếu có beta thấp hơn.
• Nhưng trong một thời gian dài, mức sinh lời trung bình của cổ
phiếu có beta cao thường mang lại mức sinh lời cao hơn cổ phiếu có beta thấp. 38&
(5) Giá trị rủi ro - Value at Risk&
• VaR là một phương pháp đo lường dựa trên khả năng (xác suất) t
hua lỗ tiềm ẩn trong một côn g ty, một quỹ đầu
tư, một danh mục, một gia o dịc h hay một chiến lư c ợ . • VaR là việc ư c ớ tín
h khoản thua lỗ (theo đơn vị tiền tệ)
mà chúng ta kỳ vọng mức lỗ này sẽ bị vư t ợ qua tại một
mức xác suất nhất định được đưa ra trước trong một khoảng thời gia n nhất định.
• VaR đo lường mức thua lỗ tối thiểu
• VaR mang tính thời điểm, do vậy cá c gi á trị Va R không thể so sánh một các
h trực tiếp trừ khi chúng được tính
toán trong những khoảng thời gia n đều nhau 13& 8/20/21&
Các yếu tố trong đo lường VaR&
• Mức xác suất: thường được lựa chọn là 0.05 hoặc 0.01
(tương ứng với mức độ tin cậy tương ứng là 95% hoặc 99%).
• Giai đoạn tính: VaR thường được đo lường theo từng
ngày, nhưng cũng hay được dùng trong một khoảng thời gian dài hơn
• Lựa chọn kỹ thuật sử dụng: nhận dạng những đặc điểm
phân bố xác suất của những khoản tỷ suất sinh lời của danh mục
– Phương pháp giải tích (phương sai – hiệp phương sai)
– Phương pháp lịch sử (Historical method)
– Phương pháp mô phỏng Monte Carlo
(1)&Phương pháp giải tích&
• Giả định: Tỷ suất sinh lời theo phân phối chuẩn
– Tỷ suất sinh lời kỳ vọng – Độ lệch chuẩn
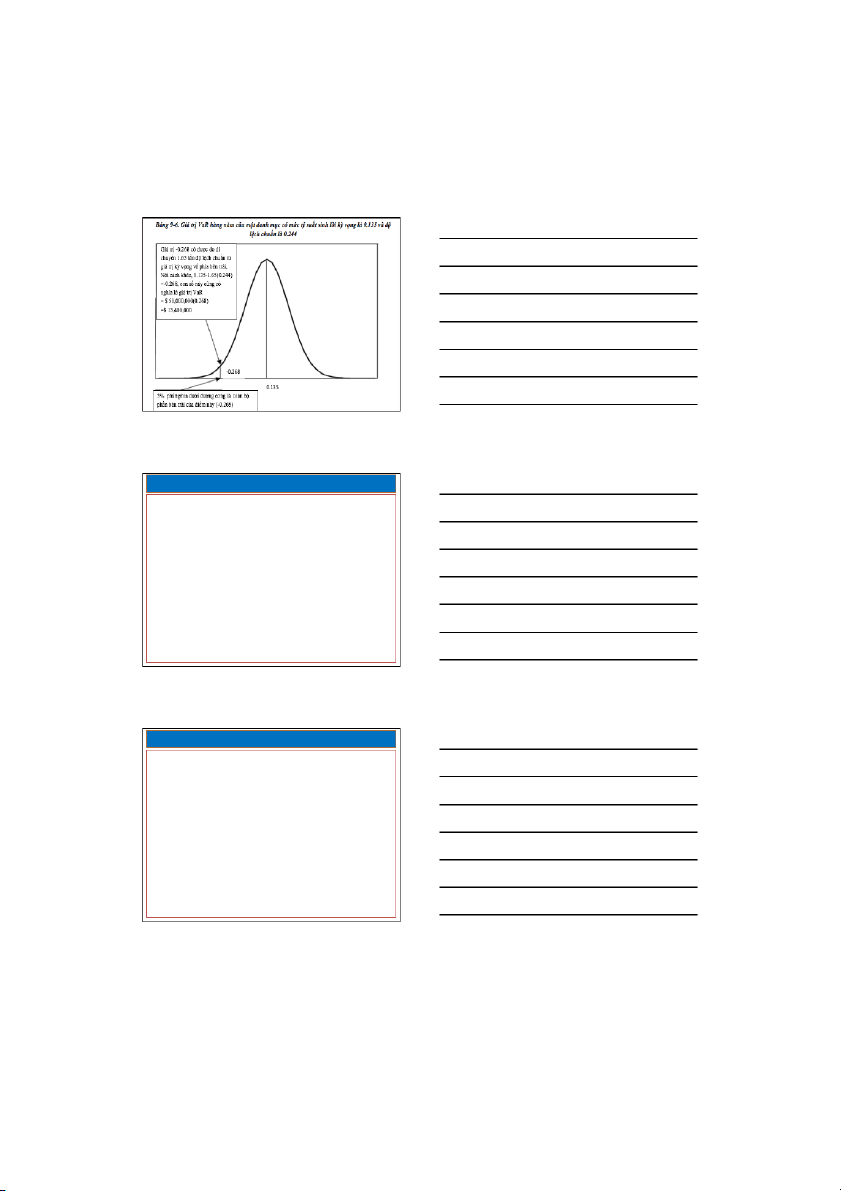
• Mức tỷ suất sinh lời kỳ vọng µP và độ lệ ẩ σP ch chu n , của cá
c vị thế trên được tín h toá n như sau: – µP = wS. µS + wN . µN
– σP =( w 2. σ 2 + w 2. σ 2 + 2. ρ σ S S N N . w . . S wN S. σN) 1/2 S&P 500 NASDAQ DMĐT hỗ hợp
• Ví dụ: Tỷ trọng đầu tư (w) 0.75 0.25 1.00
Tỷ suất sinh lời kỳ vọng hàng năm (µ) 0.12 0.18 0.135* Độ lệch chuẩn (σ) 0.20 0.40 0.244** Hệ số tương quan (ρ) 0.90 ! Ví dụ&
* Tỷ suất sinh lời kỳ vọng của danh mục
µP = wS. µS + wN . µN = 0.75(0.12)+0.25(0.18) = 0.135 ** Độ lệc h chuẩn của danh mục
σP = (w 2. σ 2 + w 2. σ 2 + 2. ρ . w σ S S N N S. wN. S. σN )1/2
=[ (0.75)2 (0.20)2 + (0.25)2 (0.40)2 + 2(0.90)(0.75) (0.25)(0.20)(0.40)]1/2 = 0.05951/2 = 0.244 14& 8/20/21&
Ưu, nhược điểm của VaR&
• Phương pháp tính đơn giản
• Không chính xác nếu áp dụng với trường hợp tỷ suất
sinh lời lệch chuẩn (Skewness)
• Giả định phân phối chuẩn không phù hợp với những danh mục c ó bao gồm cả cá
c hợp đồng quyền chọn
– Việc phân phối tỷ suất sinh lời với những danh mục
hợp đồng quyền chọn thường khác xa với phân phối chuẩn thông thường
(2)&Phương pháp lịch sử& • Phương pháp lịc
h sử thỉnh thoảng cũng được gọi là
phương pháp mô phỏng lịc h sử (the historical situmulation method).
• Mục đích sử dụng là để ứng dụng những sự thay đổi về
giá lịch sử- giá quá khứ so với danh mục hiện tại
• Không bị hạn chế trong việc sử dụng phân phối chuẩn, đơn thuần c ỉ h thu t ậ h p cá
c dữ liệu lịch sử và xác định
mức tỷ suất sinh lời có 5% hoặc 1% trong tổng số các dữ
liệu tỷ suất sinh lời đan
g được nghiên cứu ở mức thấp hơn mức này. 15& 8/20/21& Ví dụ&
• Xem xét danh mục đầu tư gồm 75% vốn được phân bổ
đầu tư vào S&P500 và 25% được đầu tư vào c ỉ h số tổng hợp NASDAQ. • Năm đan
g được nghiên cứu gồm c ó 248 mức tỷ suất
sinh lời. Có 5% trong tổng số 248 dữ liệu này nằm ở
phần đuôi thấp hơn của phân phối chuẩn nghĩa là c ó
khoảng 12 quan sát về tỷ suấ tỷ suất sinh lời sẽ nhỏ hơn
giá trị VaR ước lượng.
• Tỷ suất sinh lời thấp nhất- mức sinh lời thứ 12 là
-0.0294. Với một danh mục trị gi á 50 triệu $, thì gi á trị VaR một ngày c
ó thể là 0.0294(50 triệu $)= 1.47 triệu $ Tỷ#suất#sinh#lờ # i hàn # g ngà # y tron #
g quá#khứ#của#một#dan # h mục#đầ # u tư#
75%#vốn#vào#chỉ#số#S&P#500#và#25%#vào#NASDAQ&& ưu, nhược điểm& • Không c ó tham số- nonparametric
• Bất lợi của mô hình là phụ thuộc hoàn toà n vào những
sự kiện trong quá khứ, và bất cứ sự phân phối nào chiếm ưu t ế h trong quá khứ c ó t ể h sẽ không nắm g ữ i được vị thế này trong tương lai. 16& 8/20/21&
(3)&Phương pháp mô phỏng Monte Carlo&
• Phương pháp mô phỏng Monte Carlo sử dụng một phân
phối xác suất cho mỗi biến số tỷ suất lợi tức và một cơ
chế kỹ thuật để cho các giá trị thu nhập một cách ngẫu nhiên tù y theo từng phân phối.
• Phương pháp mô phỏng Monte Carlo cho ra những kết
quả ngẫu nhiên, vì vậy chúng ta c ó t ể h kiểm tra xem liệu
điều gì xảy ra dẫn tới việc sinh ra một nhóm rủi ro.
• Sau đó tập hợp lại những tỷ suất sinh lời vào một phân phối giản lư c
ợ từ phân phối mà chúng ta c ó thể xác định
giá trị nào/mức nào tương ứng với 5% trong tổng số
các kết quả tỷ suất sinh lời nằm ở phía đuôi dưới của
đường phân phối chuẩn .
• Sử dụng con số này cùn g với gi
á trị danh mục để tín h ra giá trị VaR. Ví dụ&
• Danh mục 50 triệu đô trong đó có 75% vốn đầu tư vào S&P 500 và 25% cò
n lại đầu tư vào chỉ số tổng hợp NASDAQ.
• Giả định rằng danh mục này sẽ c
ó tỷ suất sinh lời kỳ vọng hàng
năm là 13.5% và độ lệch chuẩn la 24.4% .
• Sử dụng một hệ thống xuất dữ liệu số ngẫu nhiên để xuất ra một loạt cá c gi á t ị r ngẫu nhiên. – Giả sử gi
á trị đầu tiên mà hệ thống cho ra là tỷ suất sinh lời
-21.87% tương đương với gi
á trị danh mục 39.07 triệu đô vào cuối năm..
– Tỷ suất sinh lời ngẫu nhiên thứ hai được sinh ra là -4.79%, tương đương với gi
á trị danh mục 47.61 triệu đô.
– Tỷ suất sinh lời ngẫn nhiên thứ ba được cho ra là 31.38%, gi á
trị danh mục tương ứng là 65.79 triệu đô.
• Các thu nhập/ tỷ suất sinh lời ngẫu nhiên là hoàn toà n độc lập,
không liên tiếp nhau. Do đó mỗi mức thu nhập thể hiện một tỷ
suất sinh lời liên quan tới gi
á trị danh mục ban đầu là 50 triệu $
các#giá#trị#được#mô#phỏng#sau#một#năm#với#danh#mụ #
c đầu#tư#75%#vốn#vào#
S&P500#và#25%#vào#NASDAQ& 17& 8/20/21& Ví dụ& • Để tì
m được điểm ở phần đuôi dưới của mô hình phân
phối chuẩn mà 5% trong tổng số cá c kết quả c ó gi á trị
vượt quá điểm này (5% của 300 kết quả =15 kết quả),
chúng ta phân loại dữ liệu và tì
m kết quả thấp nhất thứ
15, tương ứng với nó là gi
á trị danh mục ở mức 34.25
triệu đô, tương đương với khoản lỗ 15.75 triệu đô. Giá trị này ca
o hơn VaR hàng năm đã ước lượng được theo phương pháp giải tíc h (13.4 triệu đô). Hai gi á trị này c ó thể là g ố
i ng nhau(hoặc gần như vậy) nếu chúng đã sử
dụng một mẫu có kích thước đủ lớn trong phương pháp
mô phỏng Monte Carlo để mẫu VaR c ó thể hội tụ về gi á
trị VaR phổ biến thực sự.
ƯU, NHƯỢC ĐIỂM CỦA VAR&
• Về mặt ngắn hạn thì VaR đưa ra ước lượng về những khoản
lỗ tiềm năng và những nhà quản lý lâu năm dễ dàng hiểu
được vấn đề này. Nhiều cơ quan quản lý, giám sát co iVa R
như một công cụ đo lư n ờ g r i ro và m ủ t s ộ ố thì yêu cầu cá c
định chế tài chính phải đưa ra thông tin về Va trong R cá c báo cá c o ủa họ.
• Nhiều công ty sử dụng VaR như là m t ph ộ ương pháp đo lường mức r độ i ro c ủ a v ủ ốn đầu tư c a h ủ . ọ • VaR c
ó thể khó ước lượng và với những phương pháp ước
lượng khác nhau có thể cho ra những kết quả về giá trị VaR khác nhau
• VaR của những vị thế đơn lẻ không kết hợp lại theo m t ộ
cách đơn giản để thành VaR danh mục, và như ậ v y, người ta
cho rằng nó cho thấy một phức tran không h đầy v đủ ề cá c mức r độ i ro t ủ ổng thể
• Một ước lượng VaR chính xác cũng có thể là rất khó xác định đố
i với những cấu trúc phức tạp.
Mở rộng và bổ sung VaR&
• Incremental VaR đo lường tác động của tỷ suất sinh lời của một tà i sản tới gi
á trị VaR của một danh mục bằng
việc đo lường chênh lệc
h giữa VaR danh mục khi chứa
một tài sản cụ thể với VaR của danh mục không có tài sản đó . • VaR mở rộng:
– cashflow at risk –CFAR: dòng tiền â m tối thiểu –
cashflow loss mà chúng ta kỳ vọng là sẽ bị vư t ợ quá trong một gia
i đoạn nhất định với một xác suất được đưa ra trước.
– earnings at risk- EAR: được xác định tương tự như
CFAR nhưng đo lường rủi ro đối với khoản lợi nhuận kế toán. 18&