Tóm tắt Môn Kinh tế kinh doanh | Đại học Ngoại Thương

lOMoAR cPSD| 58540065
CHƯƠNG 1: TỔNG QUAN VỀ MÔN HỌC VÀ CẤU TRÚC DOANH NGHIỆP
I. CÁC VẤN ĐỀ CƠ BẢN CỦA KINH TẾ KINH DOANH
KTH kinh doanh là môn khoa học vận dụng các lý thuyết kinh tế học và các công
cụ của khoa học ra quyết định vào việc phân bổ, sử dụng các nguồn lực khan hiếm của 1 tổ chức.
II. TỔNG QUAN VỀ DOANH NGHIỆP
III. CẤU TRÚC THỊ TRƯỜNG VÀ QUYẾT ĐỊNH KINH DOANH
3.1. Hãng chấp nhận giá và hãng đặt giá - Hãng chấp nhận giá:
+ Không thể đặt giá cho sản phẩm của mình.
+ Giá được xác định trên thị trường hoàn toàn do cung và cầu thị trường quyết định. - Hãng đặt giá:
+ Có thể đặt giá cho sản phẩm của mình.
+ Có sức mạnh thị trường (tức là có thể tăng giá mà không mất toàn bộ khách hàng).
3.2. Khái niệm thị trường
3.3. Cấu trúc thị trường
3.3.1. Thị trường cạnh tranh hoàn hảo - Có
số lượng lớn các doanh nghiệp hoạt động.
- Sản phẩm hàng hóa là đồng nhất.
- Không có rào cản gia nhập thị trường.
3.3.2. Thị trường độc quyền thuần túy
- Có một hãng duy nhất trên thị trường.
- Không có sản phẩm thay thế gần gũi.
- Được bảo vệ bởi các rào cản gia nhập thị trường.
VD: Xăng dầu, điện, nước,...
3.3.3. Cạnh tranh độc quyền lOMoAR cPSD| 58540065
- Có số lượng lớn các doanh nghiệp hoạt động.
- Sản phẩm hàng hóa khác biệt.
- Không có rào cản gia nhập thị trường.
⇒ Cạnh tranh bằng SP khác biệt, đưa ra các mức giá khác nhau.
VD: Đồ điện tử, bánh Pizza, các mặt hàng tiêu dùng (dầu gội, bột giặc, sữa tắm,...)
3.3.4. Độc quyền nhóm
- Một số ít các doanh nghiệp sản xuất toàn bộ hoặc phần lớn sản lượng của thị trường.
- Các hãng phụ thuộc lẫn nhau: hành động của bất kỳ doanh nghiệp nào
trên thị trường cũng có ảnh hưởng lớn đến sản lượng bán ra và lợi nhuận của các doanh nghiệp khác.
VD: Hàng không (3 hãng), Viễn thông (6 hãng).
IV. CUNG, CẦU VÀ CÂN BẰNG THỊ TRƯỜNG 4.1. Cầu
4.1.1. Khái niệm
4.1.2. Hàm cầu tổng quát
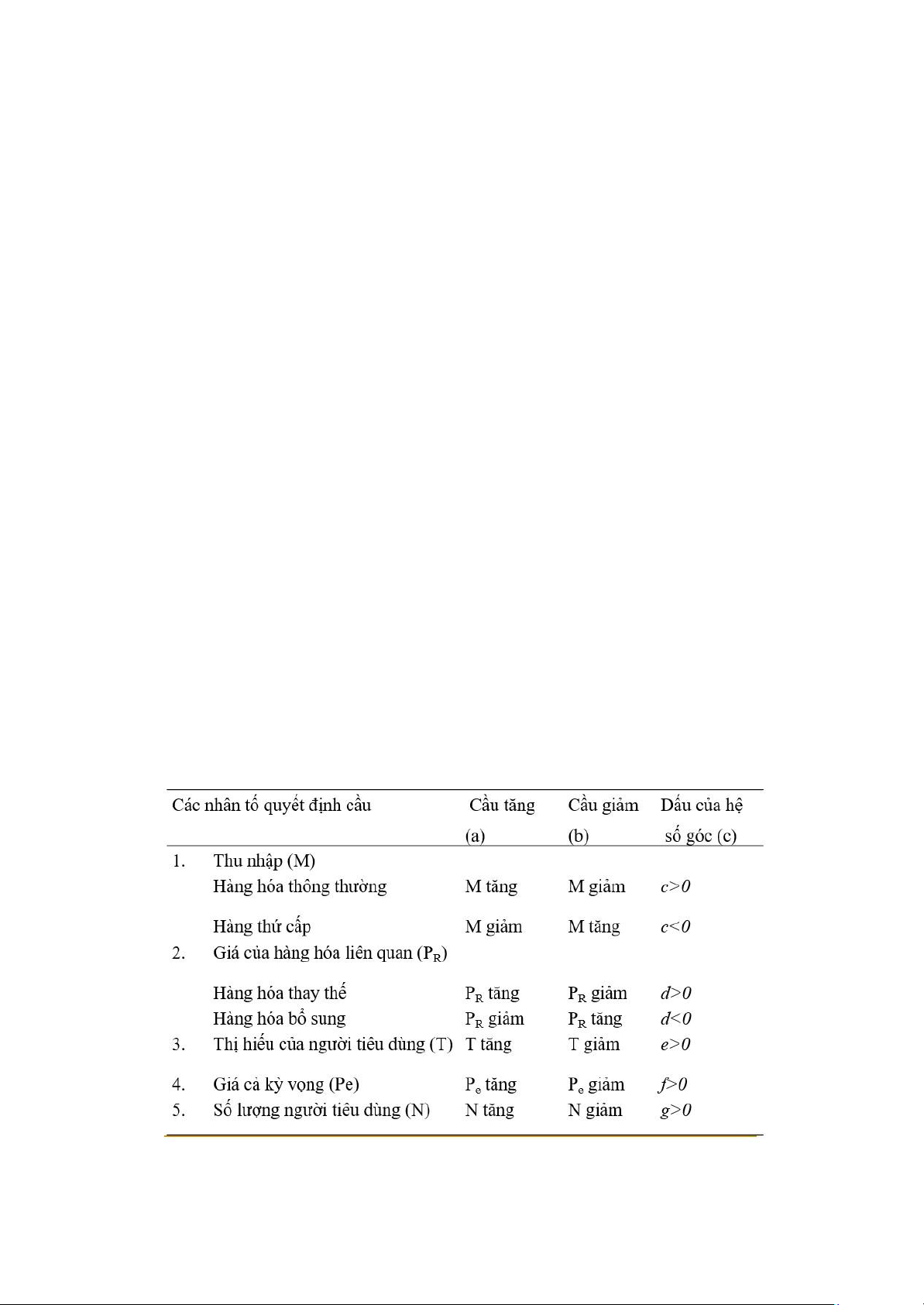
Qd = f (P, M, PR, T, Pe, N) = a + bP + cM + dPR + eT + fPe + gN
4.1.3. Hàm cầu lOMoAR cPSD| 58540065 Qd = f(P)
- Luật cầu: Lượng cầu tăng khi giá giảm và lượng cầu giảm khi giá tăng,
các yếu tố khác là không đổi. ⇒ ΔQd/ΔP phải mang dấu âm.
4.1.4. Hàm cầu ngược
- Hàm cầu ngược: Hàm cầu khi giá được thể hiện dưới dạng hàm của lượng cầu: P = f(Qd).
4.1.5. Đường cầu
- Sự thay đổi trong lượng cầu: + P thay đổi.
+ Gây ra sự di chuyển (trượt dọc) trên đường cầu
- Sự thay đổi trong cầu:
+ Các yếu tố ngoài P (M, PR, T, PE, N) thay đổi.
+ Đường cầu dịch chuyển song song sang phải hoặc sang trái. 4.2. Cung
4.2.1. Khái niệm
4.2.2. Hàm cung tổng quát
Qs = f (P, PI, Pr, T, Pe, F) = h + kP + lPI + mPr + nT + rPe + sF
4.2.3. Hàm cung
Qs = g (P, P’I, P’r, T’, Pe’, F’) = g (P)
4.2.4. Hàm cung ngược lOMoAR cPSD| 58540065
Hàm cung khi giá được thể hiện dưới dạng hàm của lượng cung: P = f(Qs).
4.2.5. Đường cung
- Sự thay đổi của lượng cung: + P thay đổi.
+ Gây ra sự di chuyển (trượt dọc) theo đường cung.
- Sự thay đổi của cung:
+ Các yếu tố ngoài P (PI, PR, T, PE, F) thay đổi.
+ Đường cung dịch chuyển song song sang phải hoặc sang trái.
4.3. Cân bằng thị trường
4.3.1. Giá và lượng cân bằng
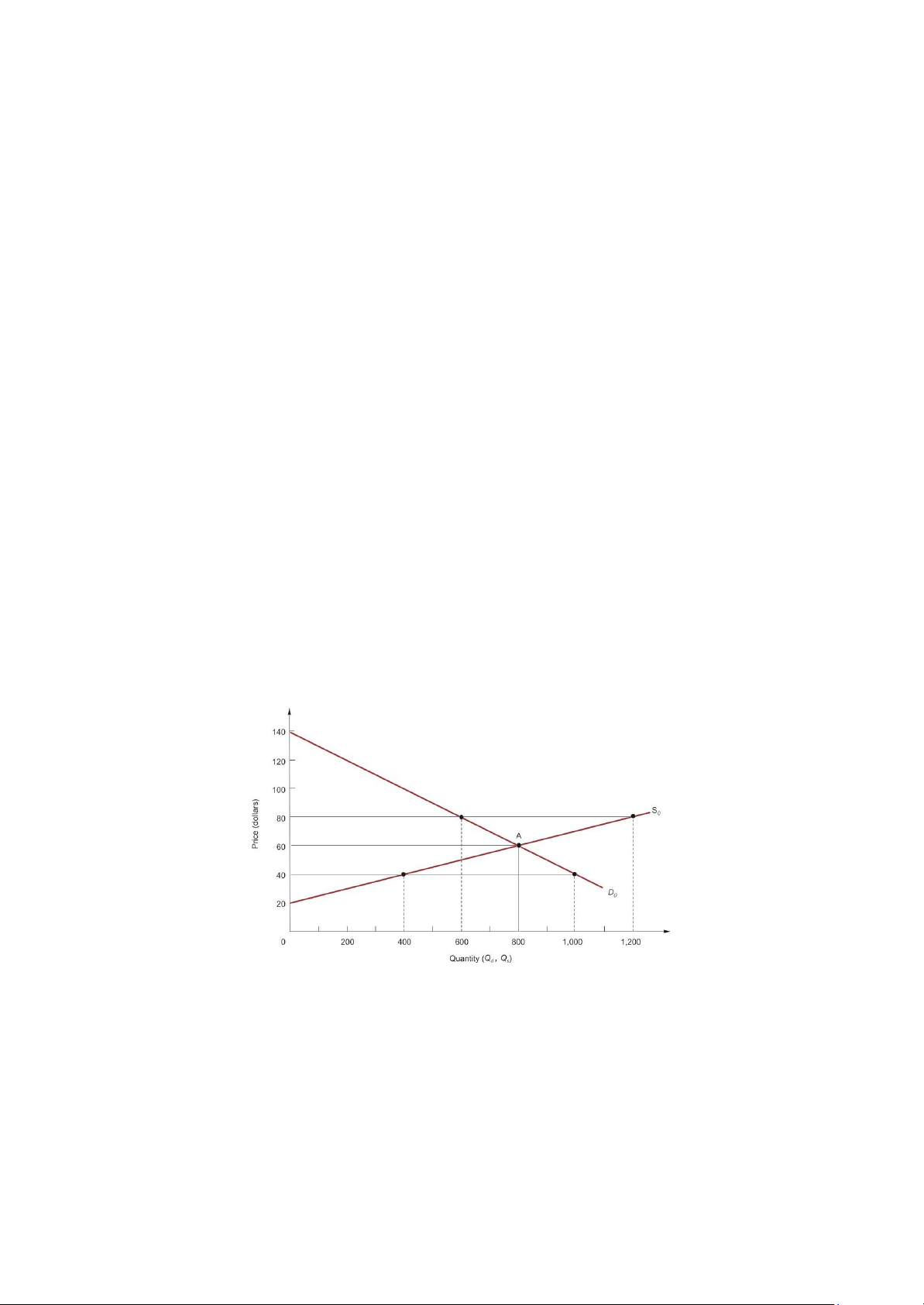
- Giá và lượng cân bằng được xác định tại giao điểm giữa đường cung và đường cầu:
+ Tại điểm giao nhau Qd = Qs.
+ Người tiêu dùng có thể mua được tất cả hàng hóa mà họ muốn.
+ Nhà sản xuất bán hết được toàn bộ số hàng mà họ muốn bán.
4.3.2. Tình trạng mất cân bằng
- Dư cầu (thiếu hụt): Xảy ra khi lượng cầu lớn hơn lượng cung
(lượng cung khan hiếm trong khi nhu cầu rất lớn).
- Dư cung (dư thừa): Xảy ra khi lượng cung lớn hơn lượng cầu (hàng
hóa rất nhiều nhưng thiếu người mua). lOMoAR cPSD| 58540065
4.3.2. Sự thay đổi trạng thái cân bằng Cầu (D) Không đổi Tăng Giảm Không đổi P, Q không đổi Q↑, P↑ Q↓, P↓ Cung (S) Tăng P↓, Q↑ P↑↓, Q↑ P↓, Q↑↓ Giảm P↑, Q↓ P↑, Q↑↓ P↑↓, Q↓
V. PHÂN TÍCH CẬN BIÊN CHO CÁC QUYẾT ĐỊNH TỐI ƯU 5.1. Định nghĩa
- Với một quy mô cố định cho trước, ta sẽ thay đổi các biến đầu vào sao cho hàm
mục tiêu tốt nhất có thể (theo hướng tối đa hoặc tối thiểu hóa tùy TH):
+ Đứng trên góc độ doanh thu/lợi nhuận, cần tối đa hóa hàm mục tiêu.
+ Đứng trên góc độ giá thành hay chi phí sản phẩm, cần tối thiểu hóa hàm mục tiêu.
5.2. Lợi ích ròng (Net benefit - NB)
- Là hiệu số của tổng lợi ích (TB) và tổng chi phí (TC) thực hiện hoạt động đó. NB = TB - TC
- Mức độ tối ưu của hoạt động: Mức hoạt động mà tại đó lợi ích
ròng được tối đa hoá. lOMoAR cPSD| 58540065
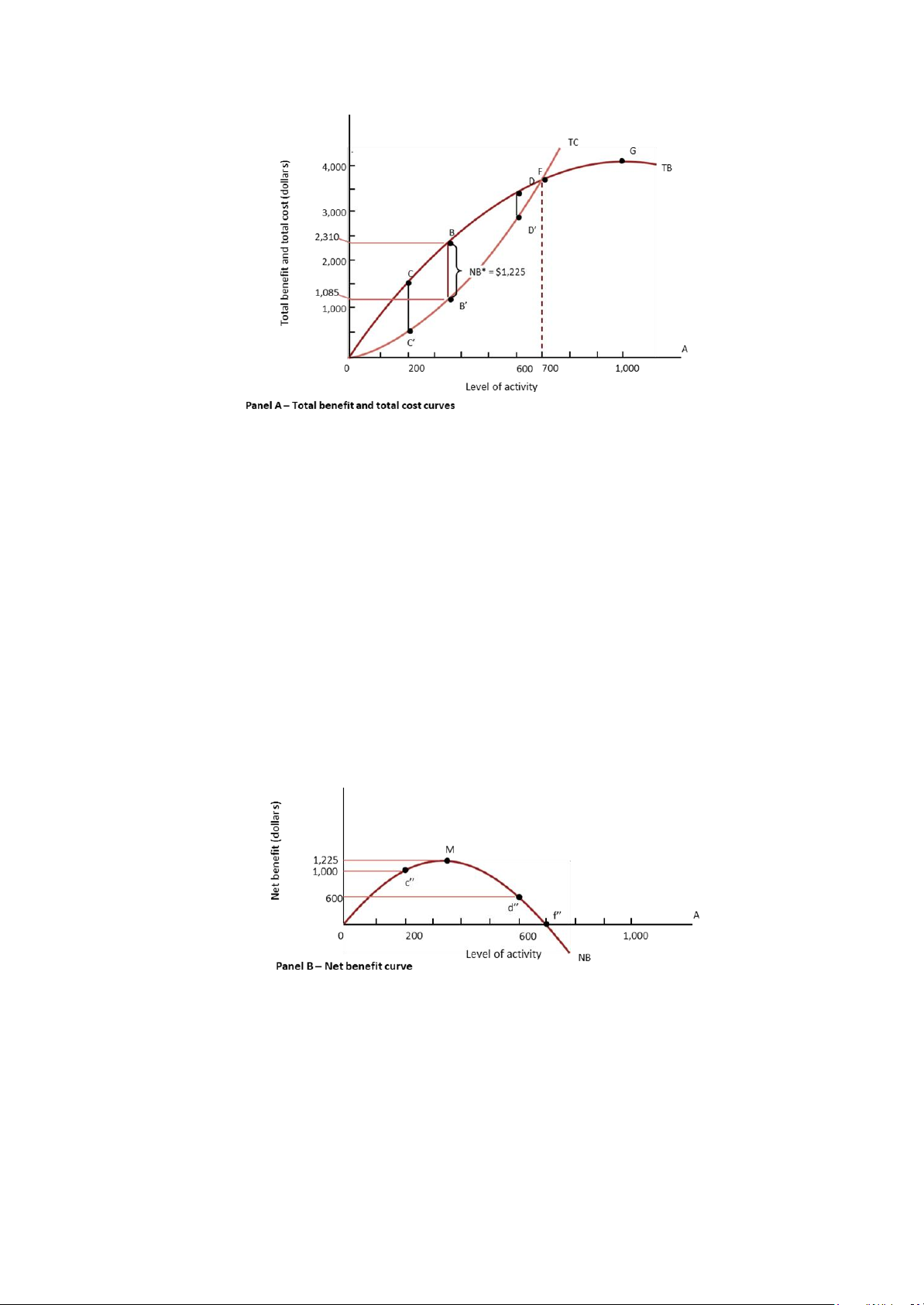
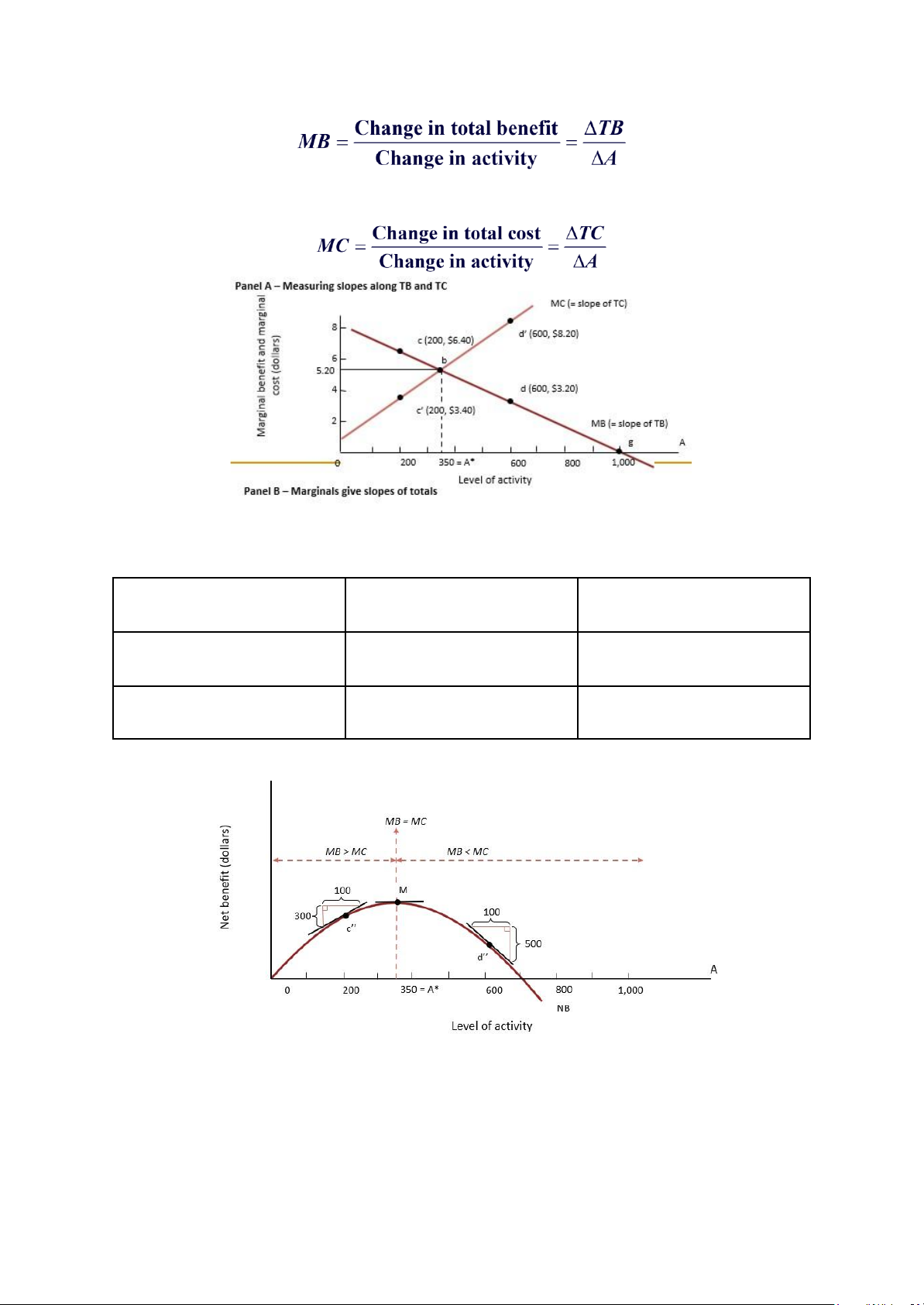
* Mô tả đồ thị:
- Tổng chi phí: có chiều hướng tăng đến vô cùng khi tăng hoạt động.
- Tổng lợi ích: chỉ tăng đến một mức nhất định sẽ giảm xuống vì quy
luật lợi ích cận biên giảm dần.
- Chênh lệch giữa tổng lợi ích và tổng chi phí là lợi nhuận. Đoạn BB’
được xem là khoảng cách chênh lệch cao nhất ứng với NB max.
- Những điểm dễ gây nhầm:
+ NB max không phải đạt được ở điểm mà TB và TC.
+ Điểm G là điểm có tổng lợi ích lớn nhất chứ không phải điểm có NB lớn nhất.
* Mô tả đồ thị:
- Trước điểm M, NB sẽ tăng khi tăng hoạt động. Sau M, tăng hoạt động
làm NB giảm. Tại M, NB đạt cực đại. 5.3. Lợi
ích cận biên và chi phí cận biên - Lợi ích cận biên (MB): lOMoAR cPSD| 58540065 - Chi phí cận biên (MC):
* Mô tả đồ thị: Điểm cắt giữa MB và MC là mức tối đa của 1 hoạt động, tại đó MB = MC. MB > MC MB < MC Tăng hoạt động NB tăng NB giảm Giảm hoạt động NB giảm NB tăng
5.4. Tìm mức tối ưu của hoạt động
- Điểm M được xác định bằng cách cho MB = MC. Trước điểm M là khoảng MB
> MC và nên tăng hoạt động. Sau điểm M, nên giảm hoạt động.
5.5. Chi phí chìm, chi phí cố định và chi phí bình quân lOMoAR cPSD| 58540065
5.5.1. Chi phí chìm
- Chi phí đã được thanh toán và không thể lấy lại cho dù có thực hiện
hoạt động tiếp theo nữa hay không.
VD: Chi phí xây dựng, thiết kế video quảng cáo,...
5.5.2. Chi phí cố định
- Chi phí liên tục và phải thanh toán cho dù đang thực hiện bất cứ mức
hoạt động nào. (Kiểu gì cũng phải trả dù có hoạt động hay không)
VD: Chi phí trả tiền quảng cáo “phát video vào một khung giờ cố định
trong thời gian 1 tháng”. >< Chi phí quảng cáo trả theo số lần phát (phát càng nhiều trả càng nhiều)
5.5.3. Chi phí cố định bình quân
- Chi phí cho mỗi đơn vị hoạt động, được tính bằng thương số giữa tổng
chi phí cố định và số đơn vị hoạt động.
⇒ Những chi phí này không tác động đến MC và do vậy không tác động đến quyết định tối ưu.
5.6. Tối ưu hóa có ràng buộc
5.6.1. Bài toán tối ưu hóa có ràng buộc
- Lợi ích cận biên trên mỗi đơn vị tiền tệ (MB/P): phản ánh lợi nhuận
tăng thêm trên một đơn vị chi ra cho hoạt động đó.
- Tối đa hóa hoặc tối thiểu hóa hàm mục tiêu khi có điều kiện ràng buộc đạt được khi:
+ Lợi ích cận biên của mỗi đơn vị tiền được chi tiêu cho tất cả
các hoạt động là bằng nhau:
+ Điều kiện ràng buộc được thỏa mãn.
5.6.2. Phương pháp thế
- Phương pháp này gồm 2 bước:
+ Tìm ra được một trong nhiều biến quyết định thỏa mãn nhất. lOMoAR cPSD| 58540065
+ Thay giá trị của biến này vào hàm mục tiêu.
VD: Giả sử một hãng sản xuất với 2 dây chuyền lắp ráp tự động và hoạt động
với hàm tổng chi phí có dạng TC(x, y) = 3x2 + 6y2 - xy, trong đó x = sản lượng đầu ra
của dây chuyền thứ nhất và y = sản lượng đầu ra của dây chuyền thứ 2. Các nhà quản
lý cần phải quyết định phương pháp kết hợp x và y sao cho tốn ít chi phí nhất, với điều
kiện rằng tổng đầu ra phải là 20 đơn vị. ⇒ x = 13, y = 7
5.6.3. Phương pháp nhân tử Lagrange lOMoAR cPSD| 58540065
VI. CÁC KỸ THUẬT ƯỚC LƯỢNG CƠ BẢN
6.1. Hàm cầu tổng quát
Qd = a + bP + cM + dPR + eT + fPe + gN
- Cần ước lượng các tham số a, b, c, d, e, f, g.
- Sử dụng phương pháp phân tích hồi quy: Là kỹ thuật thống kê
nhằm ước lượng giá trị các tham số của một phương trình và kiểm định ý nghĩa thống kê.
6.2. Mô hình hồi quy tuyến tính đơn
- Khi xem xét mối quan hệ tương quan với nhau, giữa X và Y, chúng
ta phải mô hình hóa nó, sẽ có 2 dạng:
+ Tuyến tính (PT đường thẳng).
+ Phi tuyến (PT đường cong: hàm bậc 2, 3, hàm số mũ, hàm log).
- Mô hình hồi quy tuyến tính đơn chỉ ra mối quan hệ giữa biến phụ
thuộc Y với một biến độc lập (biến giải thích) X.
Y = a + bX (a: hệ số chặn; b: hệ số góc)
- VD: Biểu diễn đường cầu theo P, giả định các yếu tố khác không đổi, PT đường cầu sẽ có dạng: Q = a + bP
+ a đo lường ảnh hưởng của các yếu tố khác ngoài giá.
+ b đo lường mức độ ảnh hưởng của giá đối với cầu của mặt hàng đó. lOMoAR cPSD| 58540065
6.3. Hàm hồi quy tổng thể
- Giả sử biến phụ thuộc Y chỉ phụ thuộc vào một biến giải thích X.
- Hàm hồi quy tổng thể: E(Y/Xi) = f(Xi)
- Hàm hồi quy tổng thể dạng tuyến tính:
E(Y/Xi) = a + bXi/𝑌 = 𝐴 + 𝐵𝑋
6.4. Sai số ngẫu nhiên
- Xét giá trị Yi thuộc (Y/Xi), thông thường Yi ≠ E(Y/Xi). Sai số ngẫu
nhiên (SSNN): ui = Yi – E(Y/Xi).
- Bản chất của SSNN: đại diện cho tất cả những yếu tố không phải
biến giải thích nhưng cũng tác động tới biến phụ thuộc.
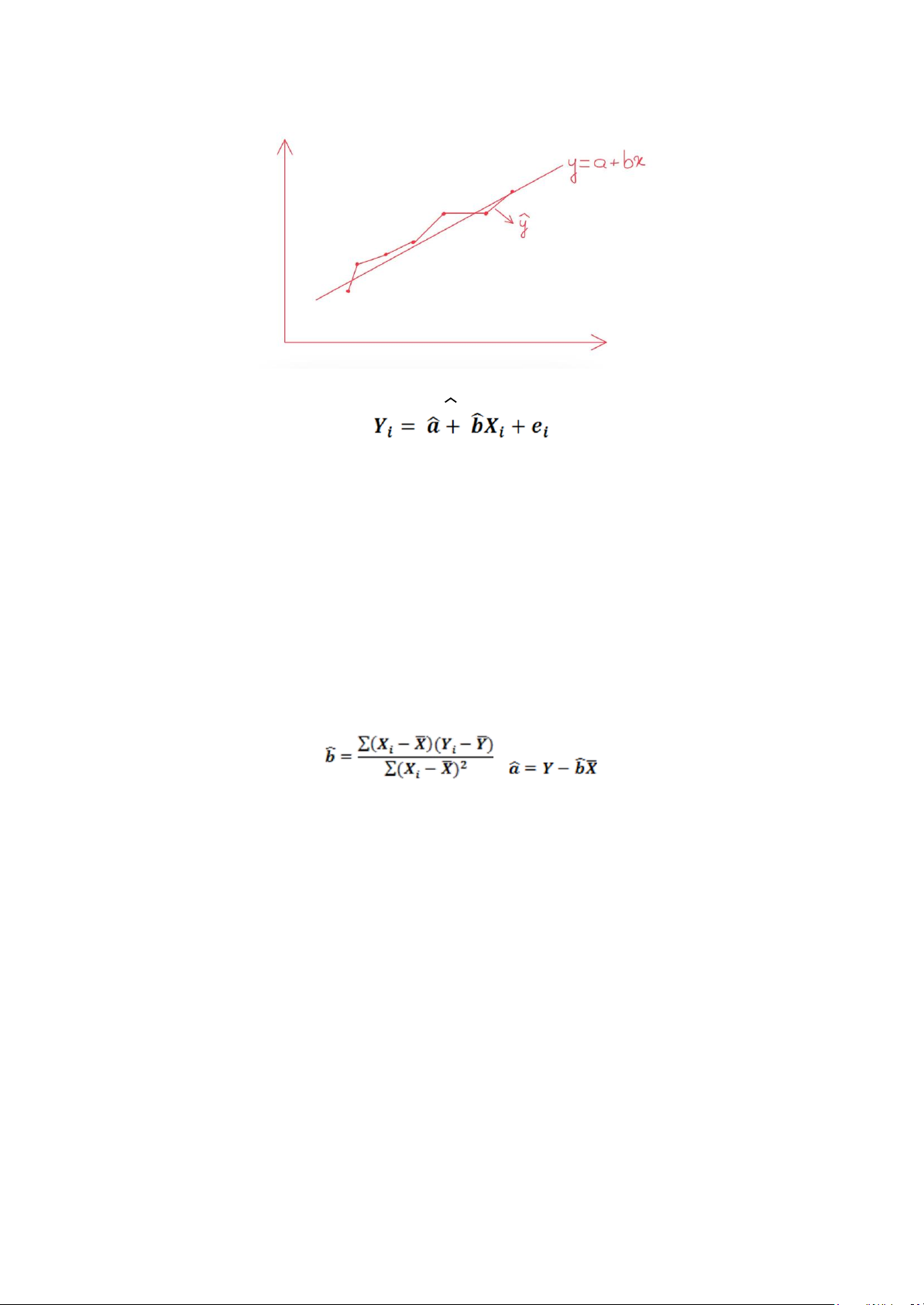
6.5. Mô hình hồi quy tổng thể Yi = a + bXi + ui (i = 1,N)
6.6. Hàm hồi quy mẫu và mô hình hồi quy mẫu -
Do không biết toàn bộ tổng thể nên phải ước lượng các tham số
của hàm hồi quy tổng thể thông qua mẫu ngẫu nhiên. -
Hàm hồi quy mẫu có dạng: / 𝑦 = 𝑎 + 𝑏𝑥 - Chú ý:
+ Vì có vô số mẫu ngẫu nhiên nên có vô số giá trị của a (mũ) và b (mũ)
⇒ a (mũ) và b (mũ) là các biến ngẫu nhiên.
+ Với một mẫu cụ thể kích thước n, a (mũ) và b (mũ) sẽ là con số cụ thể. -
Phần dư: Là phần chênh lệch giữa giá trị ước lượng và giá trị thực tế của Y
(bản chất giống SSNN ui) - Mô hình hồi quy mẫu: lOMoAR cPSD| 58540065
6.7. Phương pháp bình phương nhỏ nhất - Đi tìm các tham số:
+ Tìm a, b sao cho ∑ (𝑦 − 𝑦)2min (PP OLS - PP bình phương nhỏ nhất)
- Xác định các tham số ước lượng bằng cách lựa chọn giá trị của a và b sao cho
tổng bình phương các phần dư là nhỏ nhất. ;
6.8. Kiểm định ý nghĩa thống kê
6.8.1. Thực hiện kiểm định t lOMoAR cPSD| 58540065
6.8.2. Sử dụng p-value
- Các tham số ước lượng được coi là có ý nghĩa về mặt thống kê nếu giá
trị p-value của nó nhỏ hơn mức ý nghĩa cho phép cao nhất.
- P-value cho biết mức ý nghĩa chính xác (hoặc tối thiểu) của một tham số ước lượng.
6.9. Hệ số xác định R2 - Công thức tính R2 lOMoAR cPSD| 58540065
- R2 được gọi là hệ số xác định, đo lượng tỷ lệ phần trăm sự biến
động của biến phụ thuộc được giải thích bởi hàm hồi quy (bởi các biến giải
thích) (𝑅2 = 0. 89 có nghĩa là sự biến động của biến độc lập giải thích được
89% sự biến động của biến phụ thuộc.)
6.10. Kiểm định về sự thích hợp của mô hình
6.11. Hệ số tương quan r
- Nếu như mối liên hệ của biến nguyên nhân và biến kết quả là tuyến tính, để
đánh giá mối liên hệ giữa các biến, sử dụng hệ số tương quan: r (1 biến độc lập) hay hệ
số tương quan bội (nhiều biến độc lập).
𝑟 = 𝑏 δδ𝑦𝑥 , dấu phụ thuộc vào 𝑏, |𝑟| ≤ 1
0 < 𝑅 = δ𝑦𝑥 < 1 (HSTQ bội, tương tự với tỷ số tương quan) - Nếu như mốiδ
liên hệ của biến nguyên nhân và biến kết quả là phi tuyến, để
đánh giá mối liên hệ giữa các biến, sử dụng tỷ số tương quan.
⇒ Càng gần 1, MLH giữa X và Y ngày càng chặt chẽ; càng gần 0 thì MLH lỏng lẻo. lOMoAR cPSD| 58540065 6.12. Hồi quy bội
- Mô hình hồi quy bội: Mô hình có nhiều hơn một biến giải thích.
- Hệ số của mỗi biến giải thích là số đo độ biến động của biến phụ
thuộc Y được giải thích bởi sự biến động của biến giải thích đó, khi các biến
giải thích khác cố định.
- Sử dụng kiểm định t, kiểm định F và hệ số xác định R2 để phân tích
sự phù hợp của hàm hồi quy.
6.13. Mô hình hồi quy phi tuyến tính
- Mô hình hồi quy bậc hai: Y = a + bX + cX2 - Tạo biến mới Z: Z = X2 -
Thay vào mô hình ban đầu ta có: Y = a + bX + cZ 6.14. Kết luận
- Các tham số Beta là những tham số khi ước lượng để xem xét mối
liên hệ giữa các biến khác nhau trong mô hình hồi quy. Cần lưu ý:
+ Dấu của các tham số hồi quy có phù hợp với kỳ vọng của mình hay không?
+ Các tham số hồi quy này có ý nghĩa thống kê không?
+ Mối tương quan giữa các biến nguyên nhân và biến kết quả nó như thế nào? lOMoAR cPSD| 58540065
- Các tham số cần lưu ý:
+ Hệ số tương quan r/Tỷ số tương quan nếu đó là liên hệ phi tuyến.
+ Sự phù hợp của mô hình.
- Trong nghiên cứu, nếu đó là liên hệ tuyến tính thì hệ số tương quan
chính là hệ số xác định. Liên hệ phi tuyến thì khác.
- Hồi quy tuyến tính bội có vấn đề: Phương trình được đưa vào nhiều
biến nguyên nhân. Do đó, sẽ có 2 loại hệ số tương quan:
+ Hệ số tương quan riêng: Đo lường ảnh hưởng của từng biến nguyên
nhân tới biến kết quả. B mũ i.Độ lệch tiêu chuẩn của XY/Độ lệch tiêu chuẩn của Y. ⇒
Tính cho từng biến tác động một.
+ Hệ số tương quan chung: Đo lường ảnh hưởng của tất cả biến nguyên
nhân tới biến kết quả.
- Đối với các hàm hồi quy phi tuyến, dùng kỹ thuật đổi biến ⇒ Tạo biến mới.
+ VD: Y = a + bX + cX2, ta đặt M = X, N = X2. Khi đó, từ phương trình
bậc 2 cũ, ta hồi quy tham số của mô hình tuyến tính đa biến: Y = a + bM + cN.
+ Đối với hàm có số mũ, ta biến đổi bằng cách lấy ln hai vế rồi mới
dùng kỹ thuật đổi biến như trên để đưa về tuyến tính đa biến. lOMoAR cPSD| 58540065
CHƯƠNG 2: MỤC TIÊU KINH DOANH VÀ CÁC LÝ THUYẾT VỀ DOANH NGHIỆP
I. MỤC TIÊU KINH DOANH CỦA DOANH NGHIỆP
1.1. Đo lường và tối đa hóa lợi nhuận KT
- Chi phí cơ hội của việc sử dụng nguồn lực: Là toàn bộ phí tổn mà doanh nghiệp
phải gánh chịu để có thể sử dụng các nguồn lực nhằm sản xuất ra hàng hóa hay dịch vụ.
1.2. Tổng chi phí kinh tế
1.2.1. Chi phí hiện
- Khoản trả bằng tiền cho việc sử dụng các nguồn lực do TT cung cấp.
1.2.2. Chi phí ẩn
- Chi phí cơ hội không thể hiện bằng tiền của việc sử dụng các nguồn
lực do chủ sở hữu cung cấp. - Các dạng chi phí ẩn:
+ Chi phí cơ hội của vốn góp bằng tiền của chủ sở hữu.
+ Chi phí cơ hội của việc sử dụng tài sản vốn (đất đai, nhà
xưởng) của chủ sở hữu.
+ Chi phí cơ hội của thời gian mà chủ sở hữu doanh nghiệp dành
cho việc quản lý kinh doanh.
1.2.3. Tổng chi phí kinh tế
Chi phí thực của việc sử dụng các nguồn lực được cung cấp bởi thị trường
(Các khoản phải trả cho chủ sở hữu các nguồn lực) +
Chi phí ẩn của việc sử dụng các nguồn lực được cung cấp bởi chủ sở hữu
(Các khoản thu bị mất đi khi không đưa các nguồn lực của chủ sở hữu vào thị trường) =
Tổng chi phí kinh tế
(Tổng chi phí cơ hội của việc sử dụng cả 02 nguồn lực)
1.3. Lợi nhuận KT và lợi nhuận kế toán lOMoAR cPSD| 58540065
- LN Kinh tế = Tổng doanh thu – chi phí kinh tế = Tổng doanh thu
– chi phí hiện – chi phí ẩn.
- LN Kế toán = Tổng doanh thu – chi phí hiện.
1.4. Tối đa hóa giá trị doanh nghiệp -
Dưới góc độ tối đa hóa giá trị, cần tính được giá trị của DN trong
1 khoảng thời gian nhất định nào đó. - Giá trị doanh nghiệp:
+ Là mức giá mà người mua phải trả để mua doanh nghiệp.
+ Bằng giá trị hiện tại của lợi nhuận kỳ vọng trong tương lai. -
Phí rủi ro (risk premium): (Nickname khác: Phần bù rủi ro)
+ Phần tính thêm nhằm bù đắp cho sự rủi ro của việc không biết trước
giá trị tương lai của lợi nhuận.
+ Sự không chắc chắn về lợi nhuận tương lai càng lớn → phí rủi ro càng
lớn → giá trị của doanh nghiệp giảm -
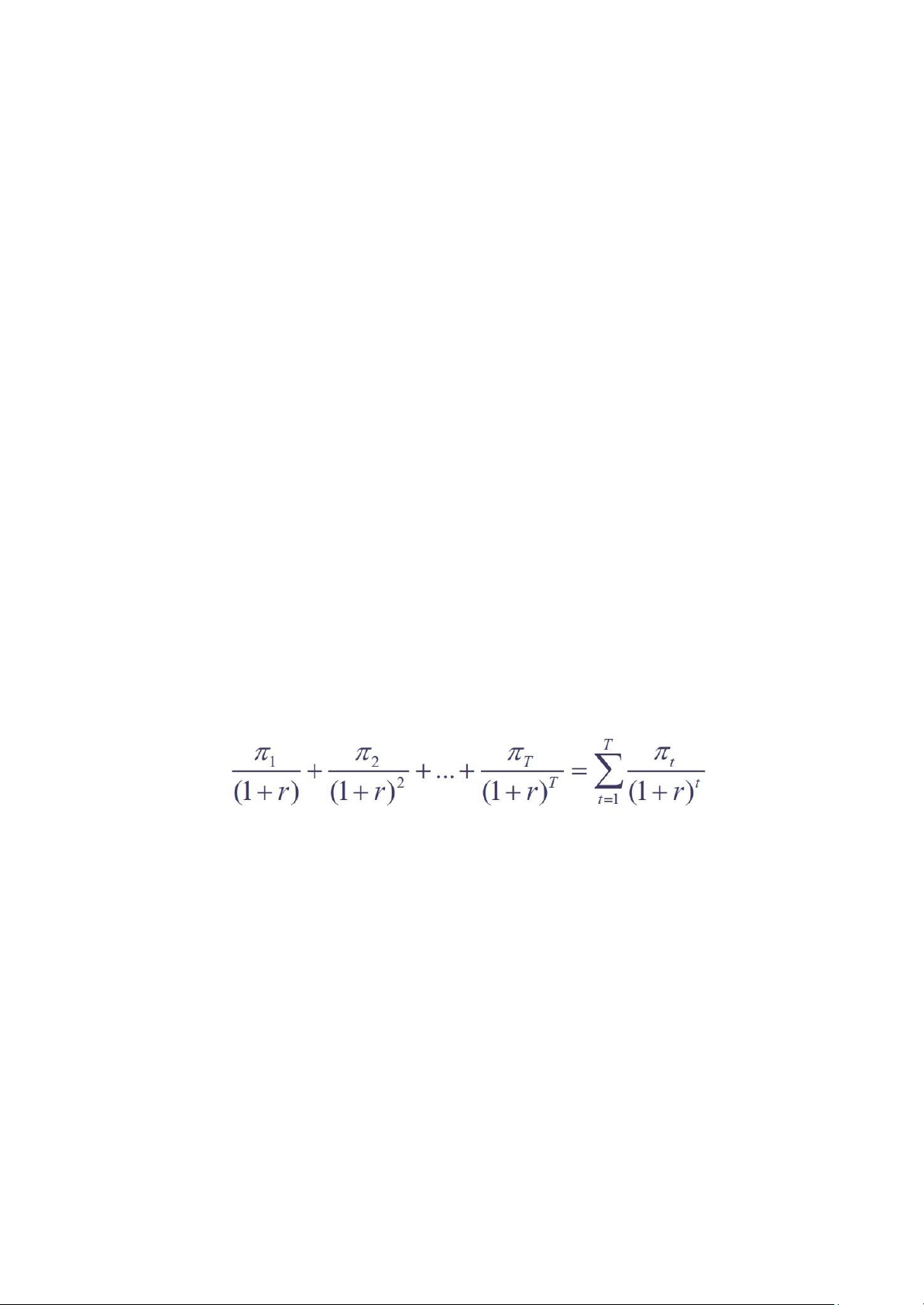
Công thức: Giá trị DN = Giá trị hiện tại của lợi nhuận kỳ vọng trong tương lai
(liên quan đến công thức tính giá trị hiện tại của dòng tiền) - Trong đó:
+ t là lợi nhuận kinh tế ước tính sẽ thu được trong khoảng thời gian t
+ r là tỷ lệ khấu trừ được điều chỉnh theo rủi ro
+ T là số năm tồn tại của một doanh nghiệp
II. LÝ THUYẾT VỀ HÀNH VI VÀ TRÁCH NHIỆM XÃ HỘI CỦA DOANH NGHIỆP
2.1. Trách nhiệm xã hội của doanh nghiệp (CSR) lOMoAR cPSD| 58540065
- CSR: Các doanh nghiệp tích hợp các mối quan tâm của xã hội và môi trường
vào hoạt động kinh doanh của mình - có sự tương tác với các bên liên quan trên cơ sở
tự nguyện ((European Commission, 2001)
2.2. Hành vi của các hãng
- Quyết định về sản lượng và định giá sản phẩm của doanh nghiệp phụ thuộc vào
cấu trúc thị trường hiện tại mà doanh nghiệp đang hoạt động, tức là phụ thuộc vào “mức
độ kiểm soát giá của doanh nghiệp”.
III. CÁC QUYẾT ĐỊNH TRONG THỊ TRƯỜNG CẠNH TRANH HOÀN HẢO
3.1. Đặc điểm của hãng CTHH -
Hãng CTHH là những người chấp nhận giá. -
Tất cả các hãng sản xuất một loại hàng hoá đồng nhất hay được
tiêu chuẩn hoá hoàn hảo. -
Việc gia nhập và rút lui khỏi thị trường cạnh tranh hoàn hảo không bị hạn chế.
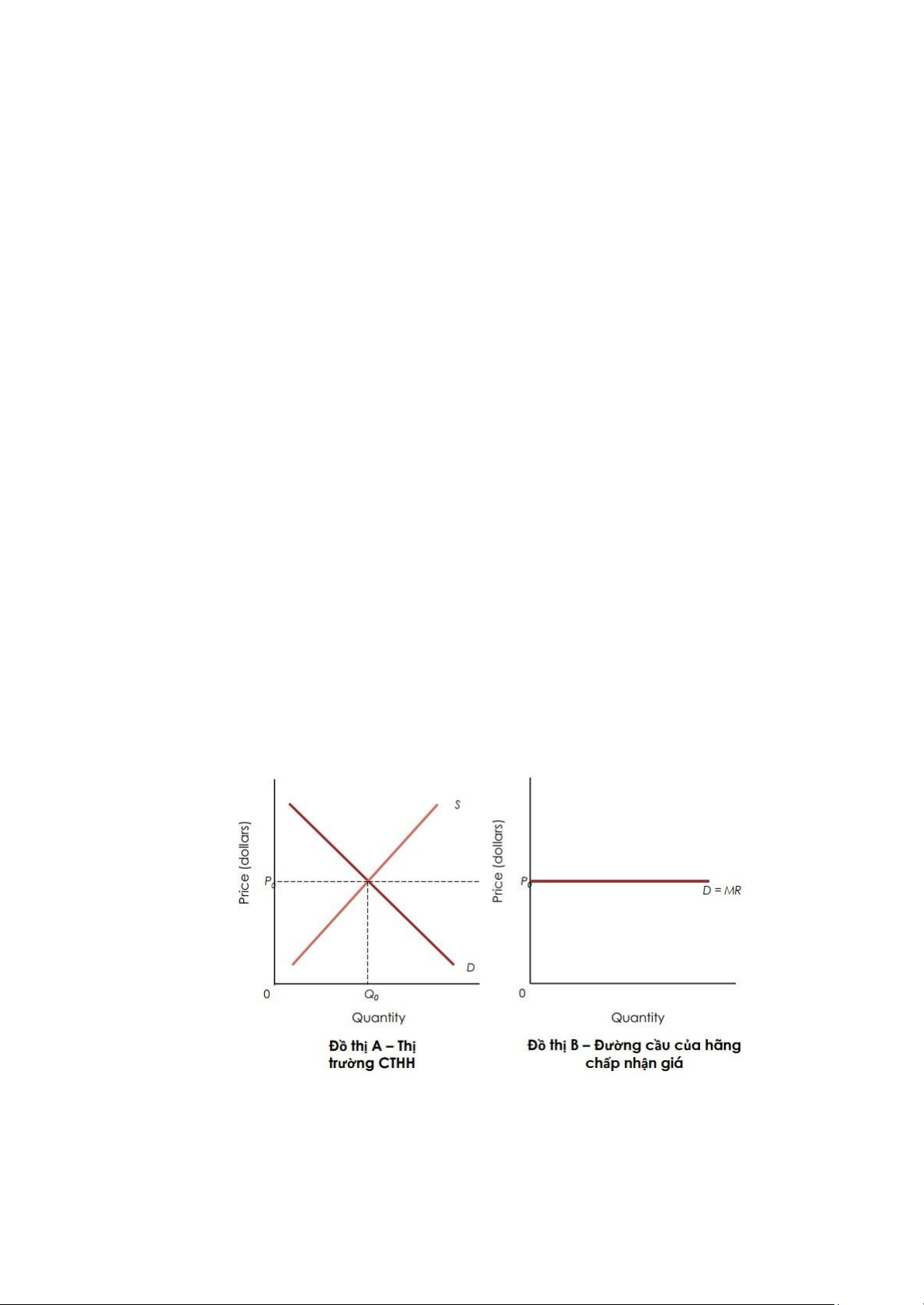
3.2. Đường cầu của hãng chấp nhận giá
- Đối với hãng CTHH, đường giá chính là đường cầu và là đường DT cận biên; cầu hoàn toàn co giãn.
3.3. Tối đa hóa lợi nhuận trong ngắn hạn lOMoAR cPSD| 58540065
3.3.1. Tối đa hóa lợi nhuận
- Hãng sẽ quyết định mức SL là bao nhiêu để tối đa hóa lợi nhuận? + Giá do TT quyết định.
+ Với mỗi mức SL khác nhau thì các hãng sẽ có chi phí SX khác nhau.
- Đối với TT cạnh tranh HH, DN sẽ sản xuất tại MR = MC = P của thị trường.
- P > ATCmin: DN có lợi nhuận dương nên SX để tối đa hóa LN.
3.3.2. Tối thiểu hóa lỗ
- Nếu AVCmin ≤ P ≤ ATCmin: DN tiếp tục SX để tối thiểu hóa lỗ:
+ P = AVCmin: DN tiếp tục sản xuất để thực hiện trách nhiệm XH (người
LĐ có việc làm,...) và đỡ mất các chi phí hoạt động lại.
- Nếu P < AVCmin: DN đóng cửa.
3.3.3. Lợi nhuận trung bình
3.3.4. Quyết định sản xuất ngắn hạn
3.3.5. Sự không liên quan của chi phí cố định
3.4. Đường cung ngắn hạn
- Đường cung ngắn hạn đối với hãng chấp nhận giá.
+ Là một phần đường chi phí cận biên nằm trên điểm AVCmin (do DN
tiếp tục sản xuất khi P > AVCmin).
+ Khi mức giá P < AVCmin, lượng cung bằng 0.
- Đường cung ngắn hạn đối với ngành cạnh tranh hoàn hảo:
+ Là tổng theo chiều ngang đường cung của tất cả các hãng trong ngành
(cộng theo phương nằm ngang).
+ Luôn có độ dốc dương.
3.5. Cân bằng cạnh tranh dài hạn
- Tất cả các hãng thực hiện mức sản lượng tối đa hóa lợi nhuận (P = LMC).
- Do thị trường CTHH không có rào cản gia nhập thị trường nên:
Khi ngành có lợi nhuận kinh tế dương sẽ thu hút thêm hãng mới gia nhập ngành và ngược lại.