Tổng hợp bài tập môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh Tế Quốc Dân

TRƯỜNG ĐẠI HỌC KINH TẾ QUỐC DÂN
TỔNG HỢP BÀI TẬP MÔN THỐNG KÊ TRONG KINH
TẾ VÀ KINH DOANH NHÓM 6 Nhóm trưởng :
Thành viên nhóm : : Lớp : Giảng viên : Hà Nội, 2024
Bảng phân công nhóm Họ và tên Mã sinh viên Công việc Trịnh Thu Phương 11218289 - Phân công bài tập
- Tổng hợp bài tập đã làm
- Làm bài: 18/tr37, 27/tr273, 27/tr519 Phạm Phương Thảo 11225952
- Làm bài: 82/tr91, 70/tr310, 10/tr505 Đỗ Bùi Minh Tuấn 11216060
- Làm bài: 32/tr69, 59/tr309, 28/tr519 Phùng Thiên Quang 11232954
- Tổng hợp bài tập đã làm - Làm bài: 26/tr67, 26/tr342 Nguyễn Trung Quân 11232956
- Làm bài: 26/tr43, 14/tr403, 29/tr565 Nguyễn Lâm Khoa 11234376
- Làm bài: 26/tr43, 23/tr481, 29/tr519, 11/tr539 1 Mục lục
Câu 18 trang 37:.................................................................................................................3
Câu 32 trang 69:.................................................................................................................6
Câu 82 trang 91:.................................................................................................................7
Câu 26 trang 67:.................................................................................................................9
Câu 26 trang 43:.................................................................................................................9
Câu 27 trang 273:.............................................................................................................14
Câu 59 trang 309..............................................................................................................16
Câu 70 trang 310:.............................................................................................................18
Câu 26 trang 342:.............................................................................................................20
Câu 14 trang 403:.............................................................................................................21
Câu 23 trang 481:.............................................................................................................22
Câu 10 trang 505..............................................................................................................28
Câu 27 trang 519:.............................................................................................................29
Câu 28 trang 519:.............................................................................................................30
Câu 29 trang 519:.............................................................................................................30
Câu 11 trang 539:.............................................................................................................31
Câu 29 trang 565..............................................................................................................35 2 Câu
18 trang 37: Đúng
Một cửa hàng trực tuyến khảo sát về thời gian chờ của khách (tính từ lúc khách đặt đế
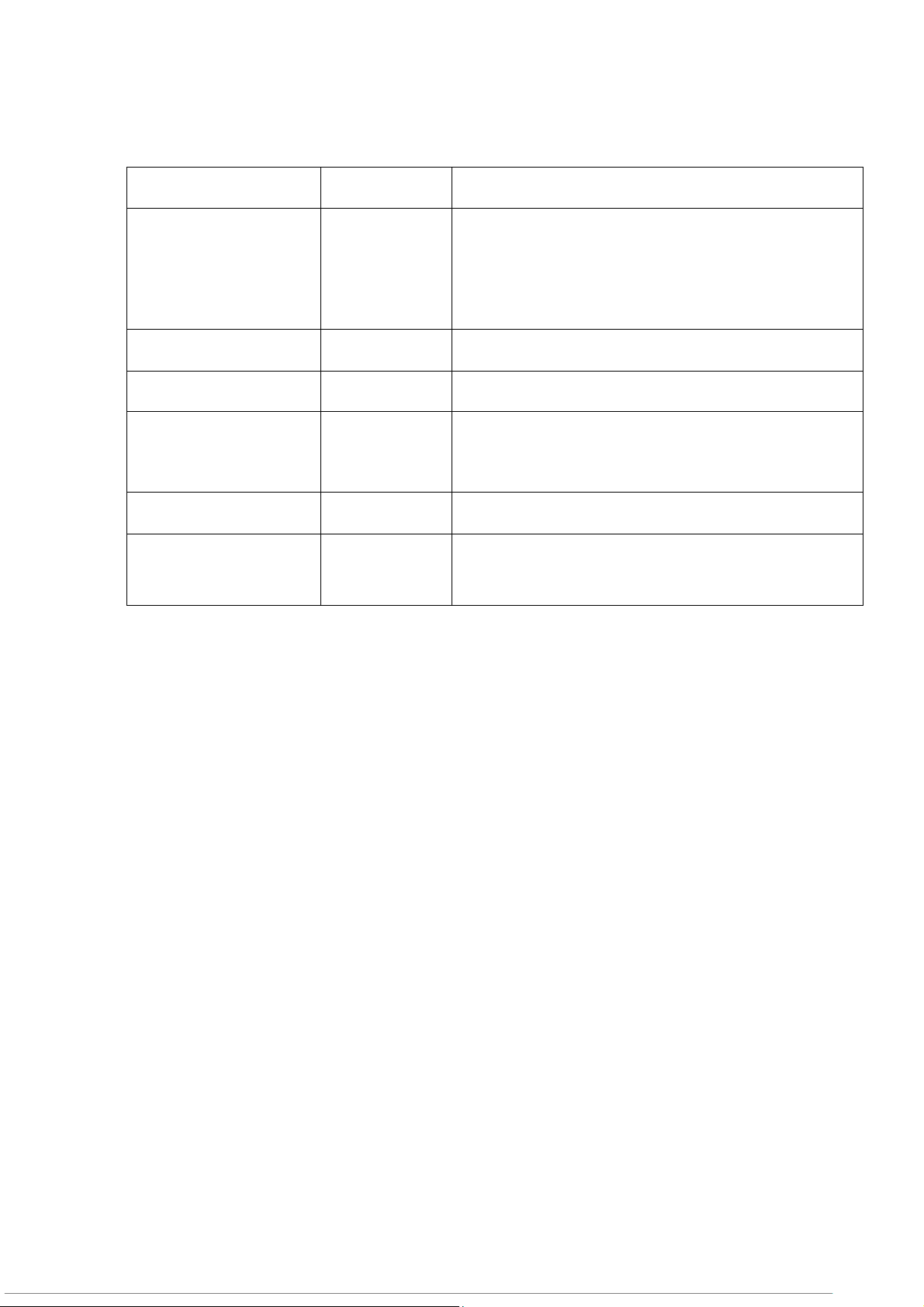
khi nhận hàng). Kết quả được như bảng sau Thời gian chờ (ngày) Tần số Từ 0 đến dưới 5 6 Từ 5 đến dưới 10 7 Từ 10 đến dưới 15 12 Từ 15 đến dưới 20 8 Từ 20 đến dưới 25 7 Tổng 40
a. Có bao nhiêu đơn hàng được khảo sát?
b. Trị số giữa của tố đầu tiên là bao nhiêu?
c. Trong đa giác tần số, toạ độ của điểm đầu tiên là bao nhiêu?
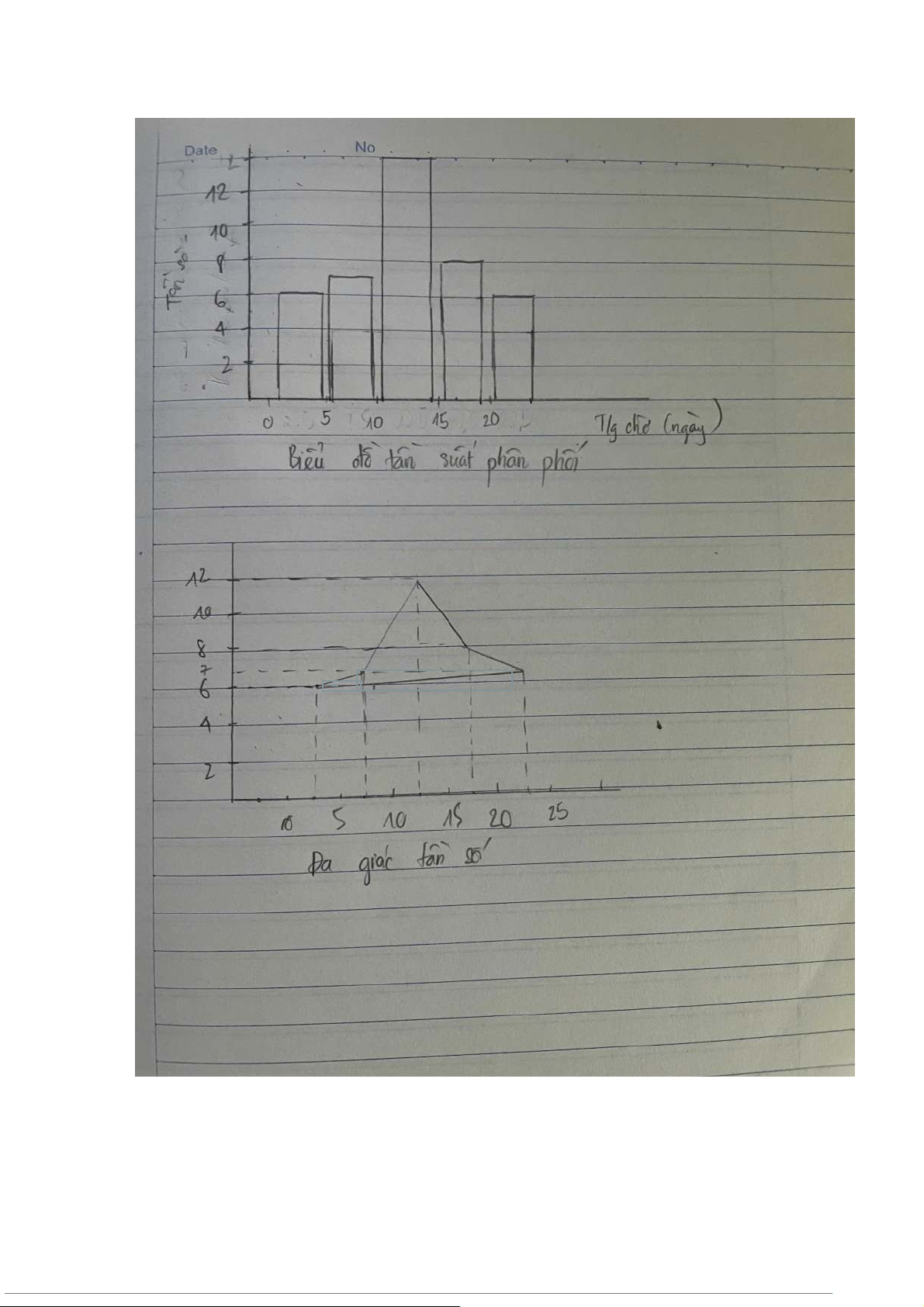
d. Vẽ biểu đồ tần số phân phối e. Vẽ đa giác tần số
f. Nhận xét về thời gian chờ của khách hàng dựa trên hai biểu đồ trên. Bài làm
a. Có bao nhiêu đơn hàng được khảo sát?
Để biết số lượng đơn hàng được khảo sát, ta cộng các tần số trong bảng: 6+7+12+8+ 7 = 40
Kết luận: Có 40 đơn hàng được khảo sát.
b. Trị số giữa của tổ đầu tiên là bao nhiêu?
Trị số giữa của tổ đầu tiên (từ 0 đến dưới 5) được tính bằng cách lấy trung bình của h giới hạn: (0 + 5) / 2 =2.5
Kết luận: Trị số giữa của tổ đầu tiên là 2.5 ngày.
c. Trong đa giác tần số, tọa độ của điểm đầu tiên là bao nhiêu? 3
Để xác định tọa độ của điểm đầu tiên trong đa giác tần số, chúng ta cần biết trị số giữ
của tổ và tần số tương ứng. Tọa độ sẽ là:
• Trị số giữa: 2.5 (đã tính ở câu b) Tần số: 6 (theo bảng)
Vậy tọa độ của điểm đầu tiên trong đa giác tần số là (2.5, 6).
d. Vẽ biểu đồ tần số phân phối
Trục hoành: Biểu thị các trị số giữa của các tổ (lớp), lần lượt là 2.5, 7.5, 12.5, 17.5, 22
(tính theo trung bình của các giới hạn tổ).
• Trục tung: Biểu thị tần số tương ứng của các tổ, lần lượt là 6, 7, 12, 8, 7. e. Vẽ đa giác tần số
1. Trị số giữa cho mỗi tổ là: Tổ 1: (0 + 5) / 2 = 2.5 Tổ 2: (5 + 10) / 2 =7.5 Tổ 3: (10 + 15) / 2 = 12.5 Tổ 4: (15 + 20) / 2 = 17.5 Tổ 5: (20 + 25) / 2 = 22.5
2. Tọa độ của các điểm là:
(2.5, 6), (7.5, 7), (12.5, 12), (17.5, 8), (22.5, 7) 4
f. Nhận xét về thời gian chờ của khách dựa vào hai biểu đồ trên Dựa vào bảng tần số biểu đồ: 5
• Thời gian chờ phổ biến nhất là từ 10 đến dưới 15 ngày, với tần số cao nhất là 12.
Đa số khách hàng nhận hàng trong khoảng 5 đến 20 ngày, với tổng số khách hàng tron
khoảng này là 27 (chiếm 67.5% số lượng đơn hàng).
• Một số ít đơn hàng có thời gian chờ lâu hơn (trên 20 ngày) hoặc ngắn hơn (dưới 5 ngày).
Kết luận: Thời gian chờ trung bình của khách hàng thường tập trung vào khoảng 10 đến
dưới 15 ngày, cho thấy đây là thời gian giao hàng khá ổn định đối với phần lớn đơn h Câu
32 trang 69: Đúng
JetBlue Airways là hãng hàng không giá rẻ của Mỹ, có trụ sở ở thành phố New York v
cơ sở chính ở sân bay quốc tế John F. Kennedy. Doanh thu của JetBlue's năm 2002 đạt
635.2 triệu đô-la. Đến năm 2017, doanh thu chạm mốc 7,015.0 triệu đô-la. Tính tốc độ
tăng trung bình hàng năm về doanh thu trong giai đoạn trên? Bài làm:
Công thức tính tốc độ tăng trưởng trung bình hàng năm (CAGR):
Với các số liệu trong đề bài, ta có:
Doanh thu năm 2002 (Giá trị ban đầu): 635.2 triệu đô-la
Doanh thu năm 2017 (Giá trị cuối cùng): 7015 triệu đô-la
Số năm: 2017 - 2002 = 15 năm
Thay vào công thức: ≈ 0.1737 hay 17.37%
=> Tốc độ tăng trưởng trung bình hàng năm (CAGR) là khoảng 17.37% Câu 82
trang 91: Đúng 6
Trận Derby Kentucky được tổ chức vào thứ Bảy đầu tiên của tháng Năm tại Churchill
Downs ở Louisville, Kentucky. Cuộc đua được chia theo hai cự ly: 1 mile và 1/4 mile.
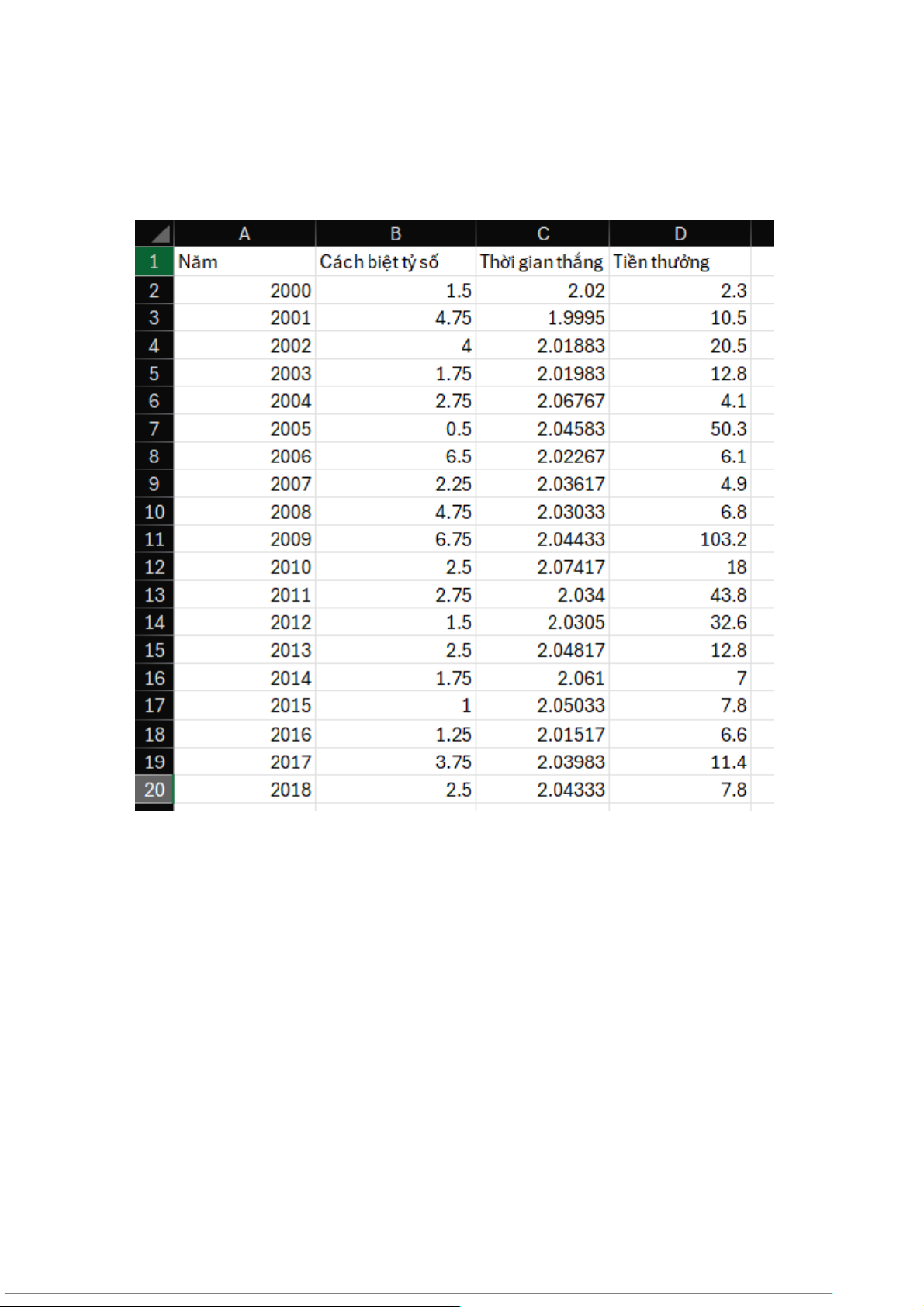
Bảng kết quả dưới đây cho biết thông tin về những người thắng cuộc, cách biệt tỷ số,
gian thắng của họ và tiền thưởng khi đặt cược $2.
a. Tính trung bình và trung vị đối với "thời gian thẳng" và "tiền thưởng".
b. Xác định khoảng biến thiên và độ lệch chuẩn đối với biến "thời gian thắng" và "tien thudng".
c. Xét biến "cách biệt tỷ số", thang đo nào đã được sử dụng? Mức độ trung tâm nà
là phù hợp nhất với biến này? Bài làm:
Sử dụng Excel: Data Analysis cho thời gian thắng và tiền thưởng ta được kết quả như sau: 7 a.
Trung bình thời gian thắng (Mean): 2.036929474
Trung vị thời gian thắng (Median): 2.03617
Nhận xét: Có 50% số thời gian thắng là từ 2.03 trở lên
Trung bình tiền thưởng: 19.43684211
Trung vị tiền thưởng: 10.5
Nhận xét: Có 50% số tiền thưởng là từ 10.5 trở lên b
Khoảng biến thiên thời gian thắng (Range): 0.07467
Nhận xét: Thời gian thắng nhanh nhất chênh với chậm nhất là 0.07467
Độ lệch chuẩn thời gian thắng (Standard Deviation): 0.0189721
Khoảng biến thiên tiền thưởng: 100.9
Nhận xét: Tiền thưởng cao nhất chênh với thấp nhất là 100.9
Độ lệch chuẩn tiền thưởng: 24.3121417 8 c
Biến cách biệt tỷ số sử dụng thang đo khoảng
Mức độ trung tâm phù hợp nhất: Trung vị hoặc phân vị, trong một số trường hợp có th
dùng trung bình tùy thuộc vào mục đích sử dụng số liệu. Câu
26 trang 67: Đúng
Andrews and Associates là tổ chức chuyên tư vấn về luật doanh nghiệp. Họ tính phí the
một giờ như sau: $100 để nghiên cứu một vụ việc, $75 để tư vấn và $200 để viết báo
Tuần trước, một trong những cộng sự đã dành 10 giờ để tư vấn với khách hàng, 10 giờ
nghiên cứu và 20 giờ để viết báo cáo. Tính phí trung bình một giờ của các dịch vụ ph lý. Bài làm
Chi phí trung bình 1 giờ của các dịch vụ pháp lý là: Ctb= =143.75 $/h Câu
26 trang 43: Đúng 9
a, Đay là loại biến gì? Biến trên sử dụng thang đo nào
b, Cây dựng bảng tần số phản ánh tình hình giao hàng của tháng trước
c, Xây dựng bảng tần suất phản ánh tình hình giao hàng của tháng trước
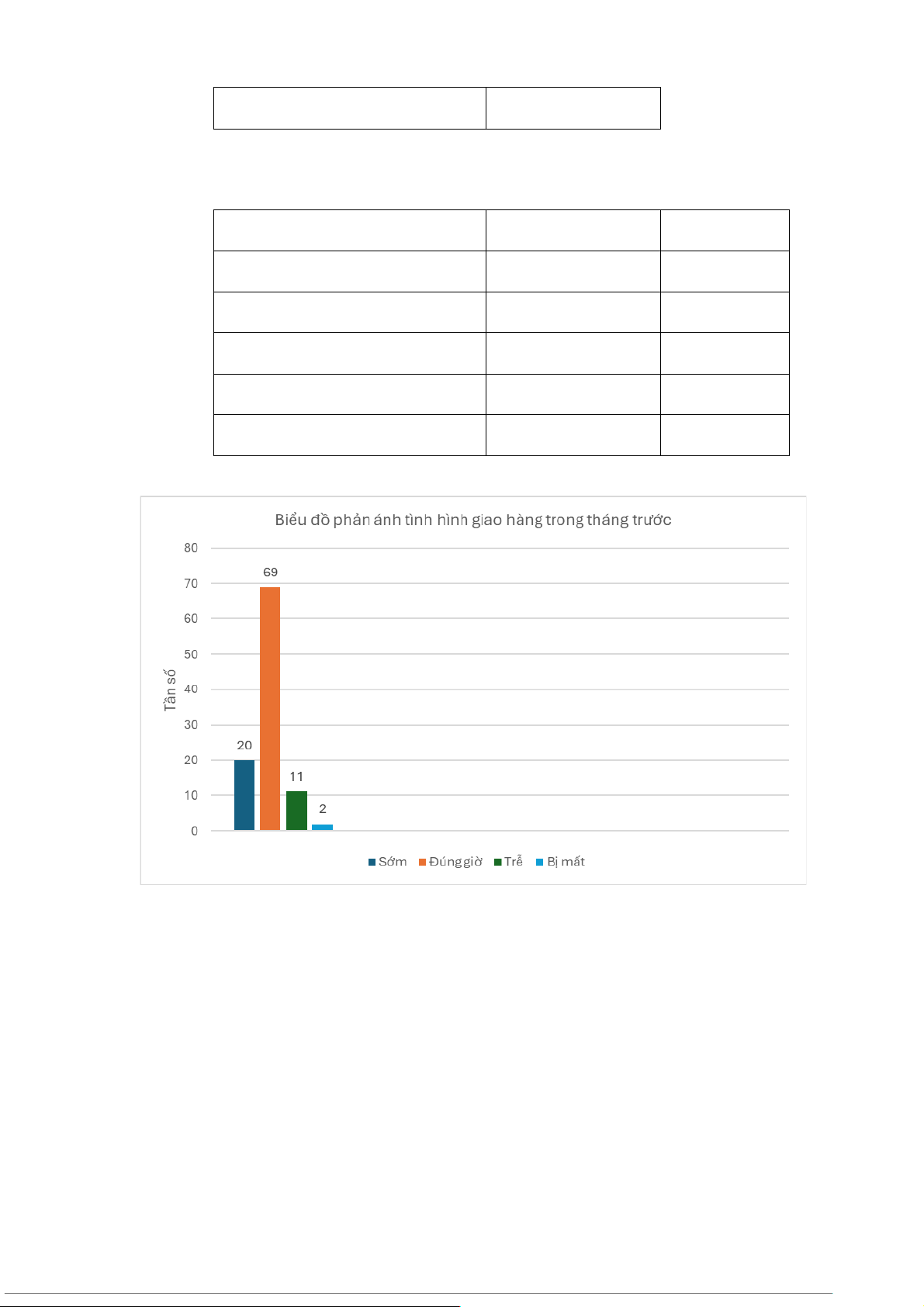
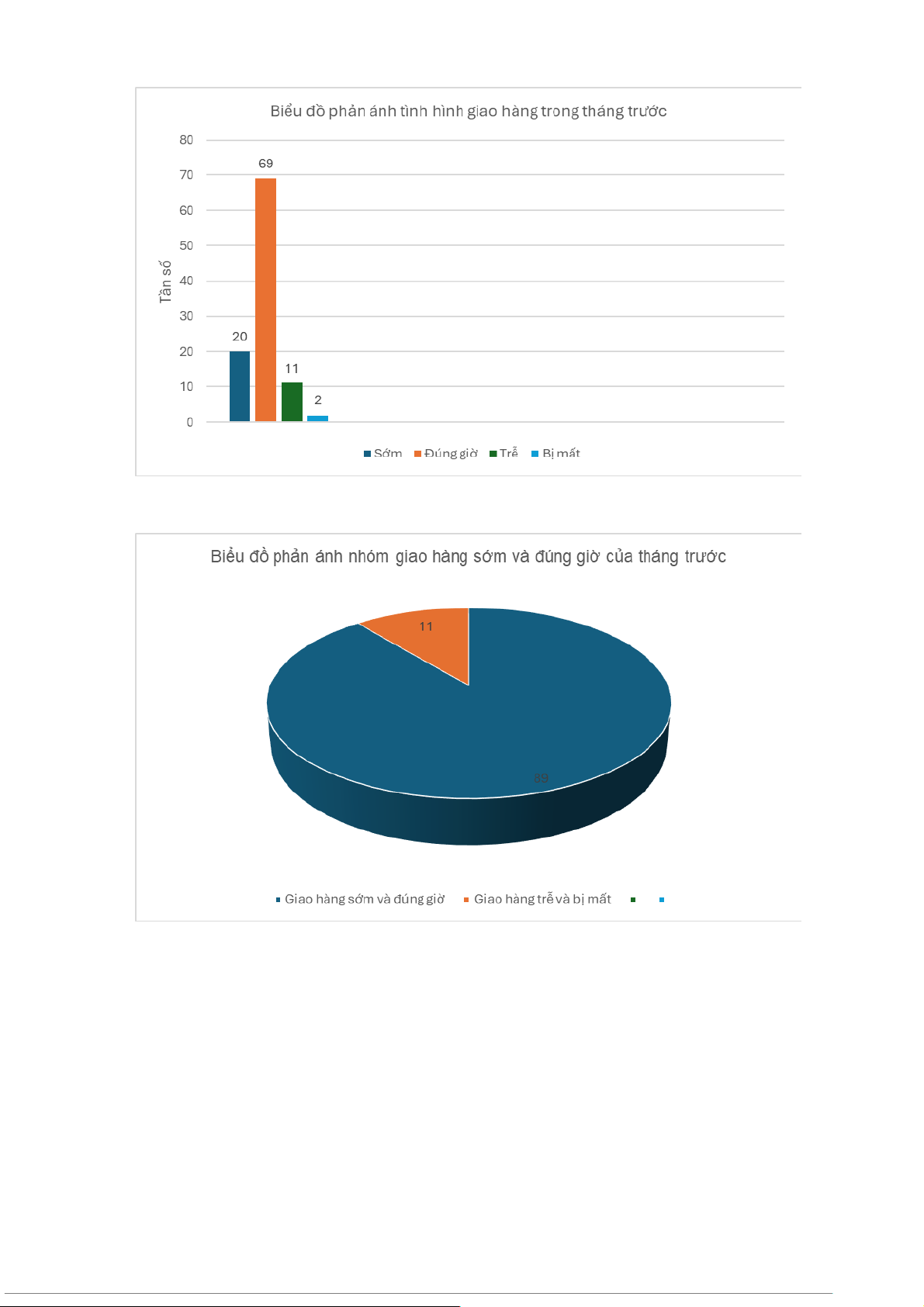
d, Vẽ biểu đồ hình cột phản ánh tình hình giao hàng của tháng trước
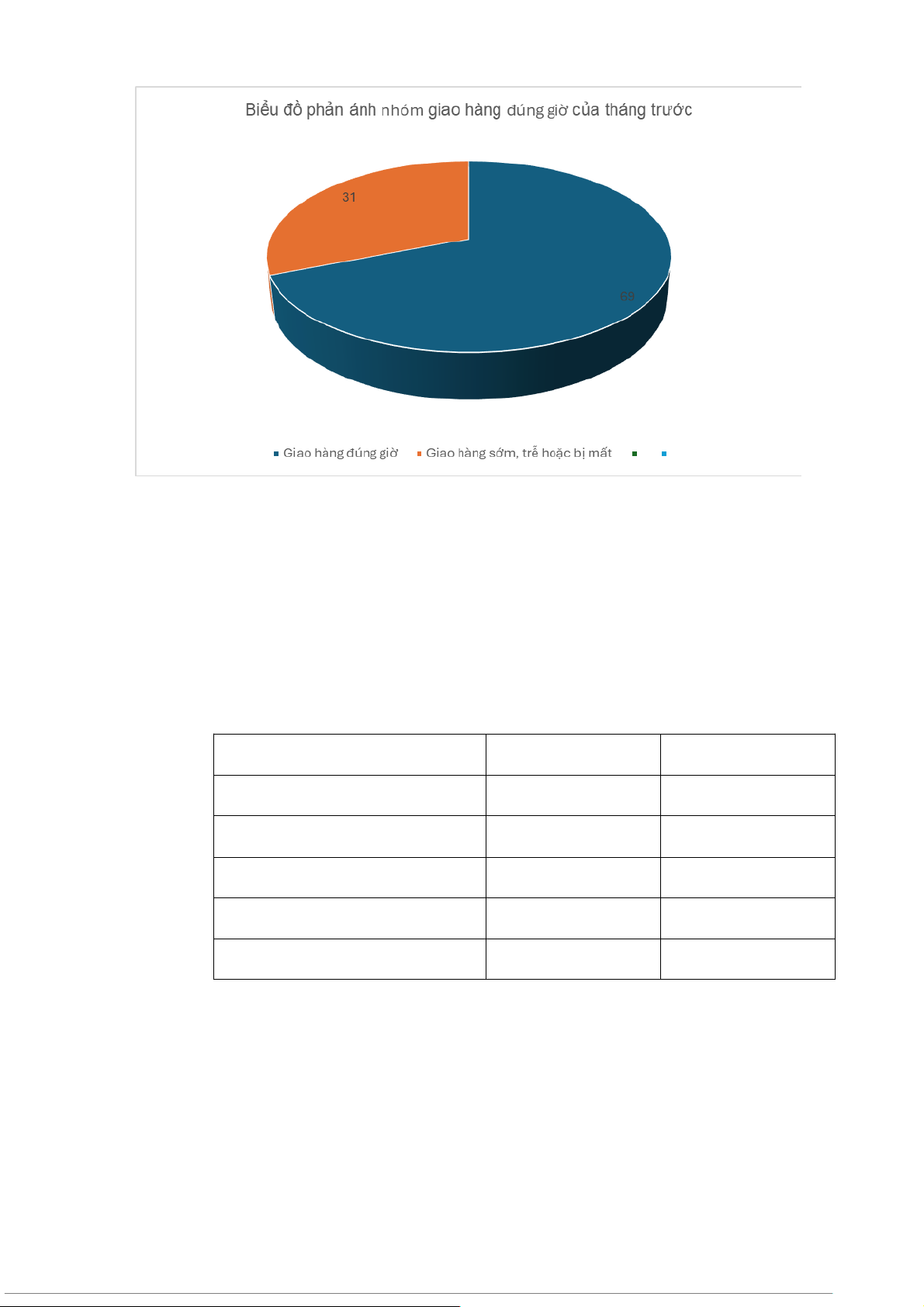
e, Vẽ biểu đồ hình tròn phản ánh tình hình giao hàng đúng giờ của tháng trước
f, Viết một bản báo cáo, trong đó, bao gồm bảng, đồ thị thích hợp và đưa ra nhận xét.
Trên cơ sở đó, so sánh với mục tiêu đã đặt ra của Speedy Swift Bài làm
a, Là biến định tính. Biến này sử dụng thang đo thứ bậc. b, Bảng tần số: Tần số Sớm 20 Đúng giờ 69 Trễ 9 Bị mất 2 10 Tổng 100 c, Bảng tần suất Tần số Tần suất (%) Sớm 20 20 Đúng giờ 69 69 Trễ 9 9 Bị mất 2 2 Tổng 100 100 d, e, 11 f, Báo cáo
Về tình hình giao hàng của Speedy Swift trong tháng trước
I . Bảng thống kê phản ánh tần số và tần suất: Tần số Tần suất (%) Sớm 20 20 Đúng giờ 69 69 Trễ 9 9 Bị mất 2 2 Tổng 100 100
II . Đồ thị phản ánh tình hình giao hàng của tháng trước: 12 III. Nhận xét 1. Tình hình giao hàng
Tổng tỉ lệ giao hàng sớm và đúng giờ trong tháng là 89%
Tỉ lệ giao hàng đúng giờ chiếm cao nhất trong tháng là 69%.
Tỉ lệ giao hàng sớm hơn dự kiến là 20%, cho thấy khả năng giao hàng vượt
thời gian đạt mức khá ổn. 13
Tỉ lệ giao hàng trễ và bị mất đơn lần lượt là 9% và 2% cho thấy công ty cò
một số khuyết điểm gây ảnh hưởng đến chất lượng dịch vụ.
2. So sánh với mục tiêu của công ty
Mục tiêu của Speedy Swift là 99.9% đơn hàng phải được giao đúng giờ hoặc
sớm. Tuy nhiên, tổng tỷ lệ giao hàng đúng giờ và sớm trong tháng trước chỉ đạt 89%.
Với 11% đơn hàng giao bị trễ, công ty chưa đạt được mục tiêu đề ra. Điều này
cho thấy công ty cần có sự cải thiện để đạt được độ chính xác cao hơn trong tương lai. Câu
27 trang 273: Đúng
Giả sử giáo viên thống kê cho 6 bài kiểm tra trong một học kỳ. Điểm các bài thi của
như sau: 79, 64, 84, 82, 92 và 77. Giáo viên quyết định chọn ngẫu nhiên 2 bài thi và
điểm trung bình của 2 bài này làm điểm trung bình môn học của bạn.
a. Tính trung bình của tổng thể
b. Có thể lấy được bao nhiêu mẫu từ tổng thể trên?
c. Liệt kê tất cả các mẫu và tính giá trị trung bình của các mẫu này.
d. Tính trung bình của các trung bình mẫu và so sánh với trung bình của tổng thể
e. Bạn có thích cách tính điểm này không? Kết quả sẽ thế nào nếu bỏ điểm thấp nh
ra khỏi tổng thể? Viết mô tả ngắn gọn Bài làm
a. Tính trung bình của tổng thể
Điểm các bài thi là: 79, 64, 84, 92, 77, 82.
- Tổng điểm của 5 bài thi:
Tổng điểm ∑ = 79 + 64 + 84 + 82+ 92+77=478
- Số lượng bài thi = 6
- Trung bình của tổng thể: µ= 478/6 = 79.67
Vậy trung bình của tổng thể là 79.67
b. Có thể lấy được bao nhiêu mẫu có thể từ tổng thể trên? 14
Khi chọn 2 bài thi từ 6 bài thi, chúng ta sẽ sử dụng công thức kết hợp để tính số mẫu thể.
Số mẫu có thể được tính bằng công thức: Trong đó:
n là số lượng phần tử trong tổng thể (5 bài thi),
k là số lượng phần tử trong mẫu (2 bài thi). Áp dụng vào bài toán:
Vậy số lượng mẫu có thể từ tổng thể là . 15
c. Liệt kê tất cả các mẫu và tính giá trị trung bình của các mẫu này
Các điểm bài thi là: 79, 64, 84, 82, 92, 77.
d. Tính trung bình của các trung bình mẫu và so sánh với trung bình của tổng t
Trung bình của các trung bình mẫu: µx= 15 = 79.67 µ = 79.67
Vì vậy trung bình của các trung bình mẫu bằng trung bình tổng thể
e. Bạn có thích cách tính điểm này không? Kết quả sẽ thế nào nếu bỏ điểm thấ
nhất ra khỏi tổng thể? Viết mô tả ngắn gọn
Việc tính điểm trung bình cho tất cả các bài thi là một cách công bằng, nhưng có thể
không phản ánh đúng khả năng thực sự của học sinh trong một vài trường hợp. Điểm
thấp nhất đôi khi có thể là một ngoại lệ do các yếu tố bên ngoài (ví dụ: học sinh bị b
hoặc gặp khó khăn cá nhân trong ngày thi).
Nếu bỏ điểm thấp nhất (64) ra khỏi tổng thể, kết quả sẽ thay đổi như sau:
Tính trung bình mới:
Danh sách điểm sau khi loại bỏ: 79, 84, 82, 92, 77. Trung bình mới sẽ là: =
Như vậy, trung bình mới là 82.8, cao hơn trung bình cũ (79.67). Điều này cho thấy việ
bỏ điểm thấp nhất có thể làm tăng trung bình tổng thể, nhưng cũng có thể không hoàn
toàn công bằng vì nó loại bỏ một phần dữ liệu. Câu
59 trang 309.
Dựa vào kết quả điều tra 50 cư dân Mỹ, American Film Institute thấy rằng thời
xem phim trung bình của 1 người Mỹ là 78 giờ với độ lệch chuẩn là 9 giờ.
a. Xác định khoảng tin cậy 95% cho thời gian xem phim trung bình (giờ) của cư dân M
b. Với độ tin cậy 90% và phạm vi sai số là 1.0 giờ, hãy xác định cỡ mẫu để ước lượn
thời gian xem phim trung bình của cư dân Mỹ. Bài làm
Câu a: Xác định khoảng tin cậy 95%
Bước 1: Công thức tính khoảng tin cậy
Khoảng tin cậy = X trung bình ± t a/2 x σ/√(n) 16 Trong đó:
X trung bình = 78 (giờ) là trung bình mẫu
t(a/2) = 1.96 là hệ số Z tương ứng với mức tin cậy 95%
Độ lệch chuẩn (σ) = 9 (giờ) là độ lệch chuẩn
Cỡ mẫu (n) = 50 là cỡ mẫu
Bước 2: Tính độ lệch chuẩn chuẩn hóa của mẫu Công thức = σ/√(n) Thay số vào công thức:
Công thức = 9/√(50) = 9/7.071 = 1.27
Do đó, độ lệch chuẩn chuẩn hóa của mẫu là 1.27.
Bước 3: Tính khoảng tin cậy
Khoảng tin cậy = X trung bình ± t a/2 x σ/√(n) Thay số vào công thức:
Công thức = 78 ± 1.96 x 1.27 = 78 ± 2.49 Kết quả:
Khoảng tin cậy = 78 - 2.49 đến 78 + 2.49
Khoảng tin cậy = 75.51 giờ đến 80.49 giờ
=> Khoảng tin cậy 95% cho thời gian xem phim trung bình của cư dân Mỹ là từ 75.51 giờ đến 80.49 giờ.
Câu b: Xác định cỡ mẫu để ước lượng thời gian xem phim trung bình với độ ti
90% và sai số 1.0 giờ
Bước 1: Công thức tính cỡ mẫu Công thức cỡ mẫu Trong đó: 17
Za/2 = 1.645 là hệ số Z tương ứng với mức tin cậy 90%
Độ lệch chuẩn (σ) = 9 (giờ) là độ lệch chuẩn
Sai số = 1.0 (giờ) là sai số cho phép
Bước 2: Thay số vào công thức Công thức cỡ mẫu = = 219.14
Bước 3: Làm tròn cỡ mẫu
Vì cỡ mẫu phải là một số nguyên, nên làm tròn lên = 220
=> Để đạt được độ tin cậy 90% với sai số 1.0 giờ, cỡ mẫu cần thiết là 220 người. Câu 70
trang 310:
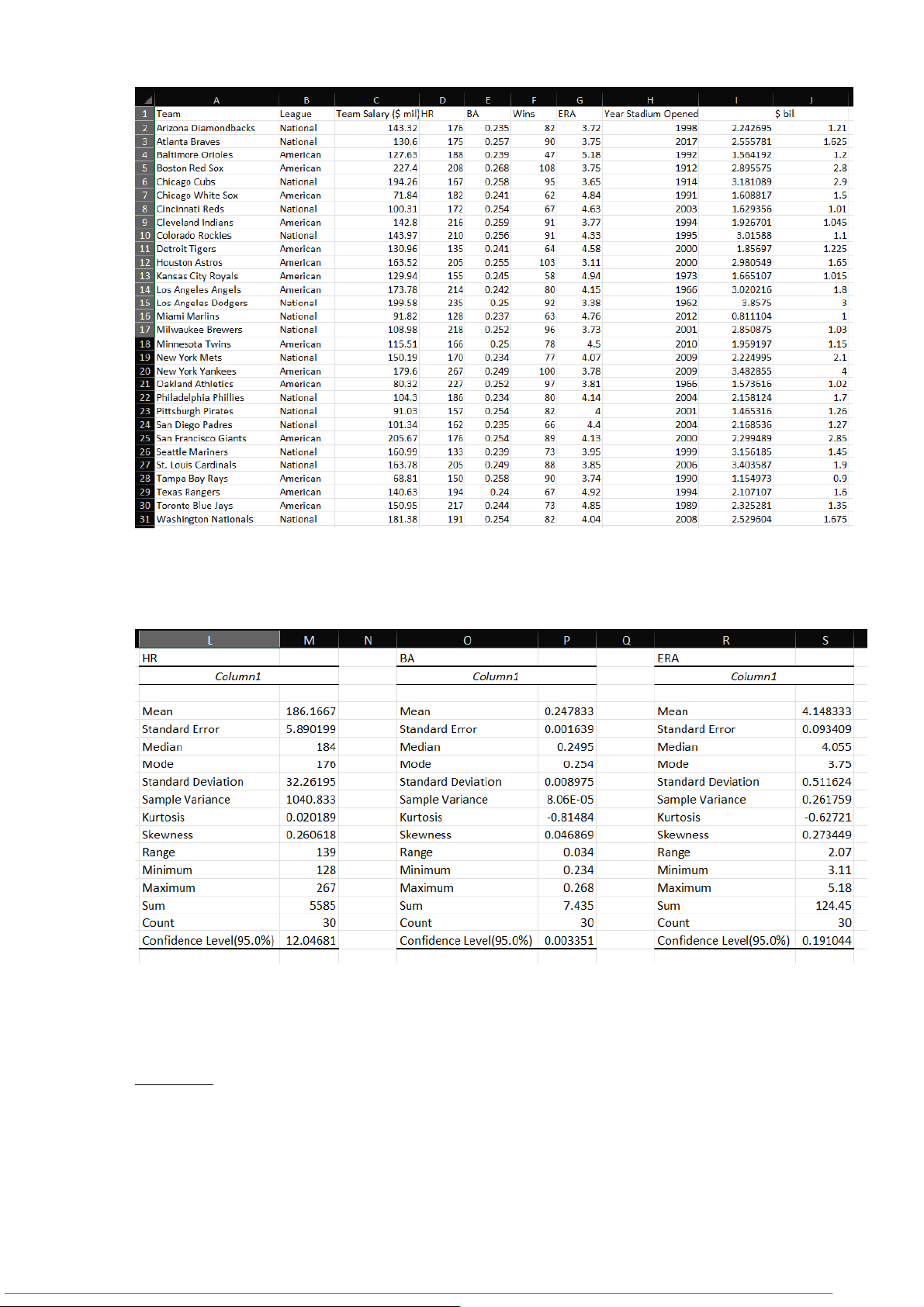
Căn cứ vào dữ liệu bóng chày năm 2018 (2018_Baseball xisx), giả sử đây là đữ liệu m xác định:
a. Khoảng tin cậy 95% về số lần ghi điểm trực tiếp trung bình (HR) của mỗi đội.
b. Khoảng tin cậy 95% về hệ số đánh bóng trung bình (BA) của mỗi đội.
c. Khoảng tin cậy 95% về số lần chạy giành được điểm trên 9 hiệp (ERA) của mỗi đội. 18 Bài làm:
Sử dụng Data Analysis trong Excel cho cột HR, BA và ERA ta được kết quả như sau:
a. Khoảng tin cậy 95% về số lần ghi điểm trực tiếp trung bình (HR) của mỗi đội là
(186.1667-12.0468; 186.1667+12.0468) = (174.1199; 198.2135)
Nhận xét: Với mức ý nghĩa 5% thì HR nằm trong khoảng (174.1199; 198.2135)
b. Khoảng tin cậy 95% về hệ số đánh bóng trung bình (BA) của mỗi đội là: 19