Bài tập/Kiểm tra thường kỳ #1 Đề số: Họ và tên: MSSV: Lớp:
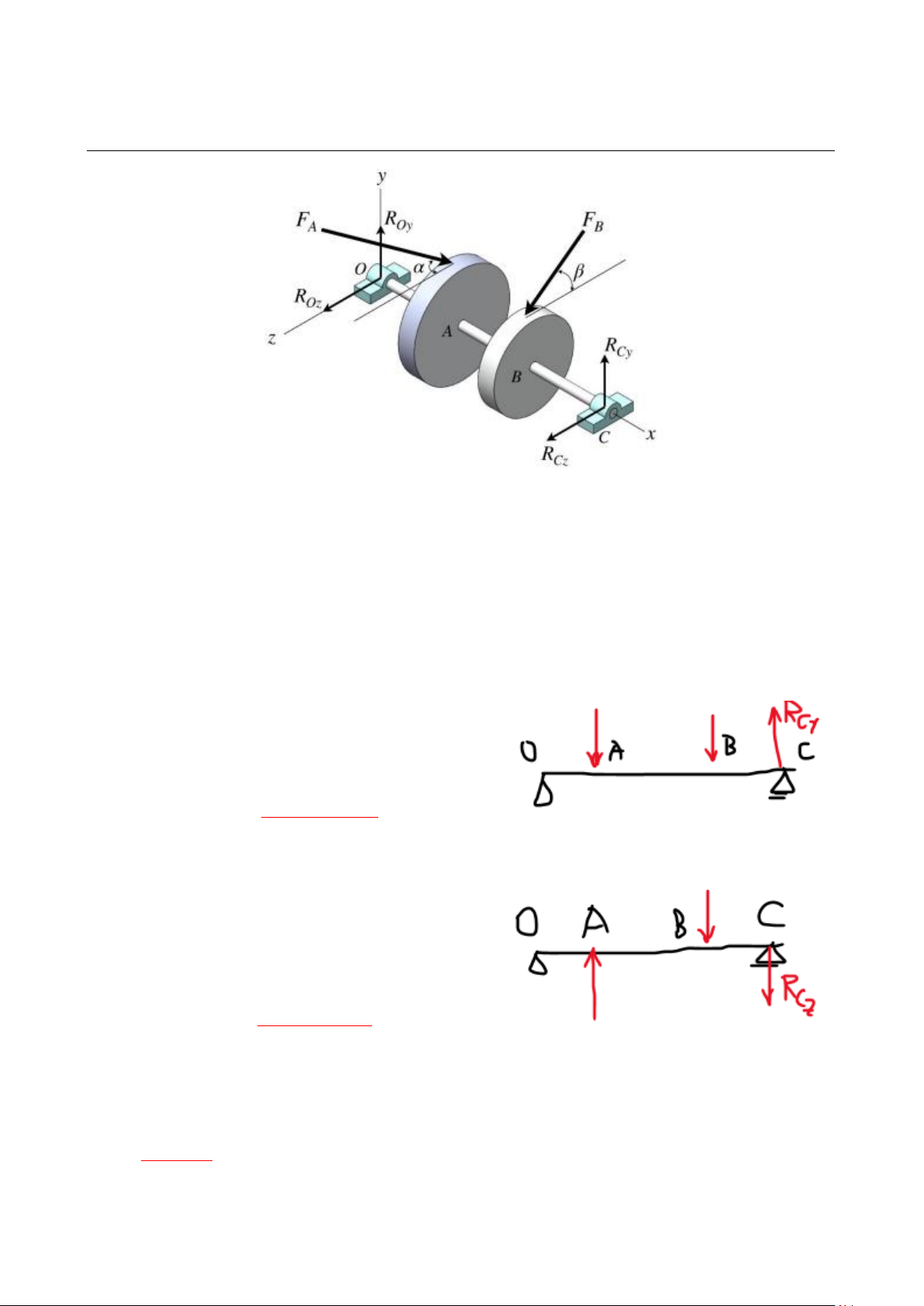
Trục trung gian của hộp giảm tốc hai cấp làm bằng thép có các đặc trưng (MPa) như sau: σb=730;
σch=400. Trên trục lắp các bánh răng bị dẫn B và bánh răng dẫn A, chịu các lực pháp tuyến FA và FB
với α=20,8o và β=19,76o. Biết lực FA=3730N; đường kính các bánh răng dA=175mm và dB=385mm;
các khoảng cách OA=140; AB=95; BC=275 (mm). Xác định:
Câu 1. Độ lớn lực FB (N)
Cân bằng mômen xoắn: 𝐹𝐴. 𝑐𝑜𝑠α. 𝑑𝐴/2 = 𝐹𝐵. 𝑐𝑜𝑠β. 𝑑𝐵/2, suy ra 𝐹𝐵 = 𝐹𝐴. cosα. 𝑑𝐴/(𝑑𝐵. cosβ). Thay
số tính được FB = 1684,12 ≈ 1684N
Câu 2. Độ lớn phản lực RCY (N)
Lập sơ đồ tính cho mặt phẳng xOy và cân bằng mômen tại O, tính được Rcy:
𝐴𝑦. 𝑂𝐴 + 𝐵𝑦. 𝑂𝐵 𝑅𝐶𝑦 = 𝑂𝐶
trong đó Ay = FA. sinα; By = FB. sinβ
hay số tính được: Rcy = 625,96 ≈ 626N
Câu 3. Độ lớn phản lực RCZ (N)
Lập sơ đồ tính cho mặt phẳng xOy và cân bằng mômen tại O, tính được Rcy: 𝐴 𝑅
𝑧. 𝑂𝐴 − 𝐵𝑧. 𝑂𝐵 𝐶𝑧 = 𝑂𝐶
trong đó Az = FA. cosα; Bz = FB. cosβ
Thay số tính được: Rcz = 226,87 ≈ 227N
Câu 4. Độ lớn mômen uốn tổng tại A (Nm) M = √𝑀2 2
𝑦 + 𝑀𝑧 với My và Mz lần lượt là mômen uốn trong XZ và XY
Bỏ qua quy ước dấu của mômen, có thể tính các đại lượng My và Mx theo sơ đồ dưới đây.
Để tính My => xét các lực trong mặt phẳng XZ và cân bằng mômen My tại vị trí mặt cắt
=> 𝑀𝑦 = −𝑅𝐶𝑧. 𝑥 − 𝐵𝑧. (𝑥 − 𝐵𝐶). Thay x =AC sẽ được mômen My tại A.
Tương tự, xét các lực trong mặt phẳng XY => => 𝑀𝑧 = 𝑅𝐶𝑦. x − 𝐵𝑦. (𝑥 − 𝐵𝐶). Thay x = AC sẽ được mômen Mz tại A.
Thay số tính được: MyA = -234561 Nmm; MzA = 177530 Nmm và MA = 294169 Nmm ≈ 294,2 Nm
Chú ý: kết quả có thể lệch khoảng ± 0,5 do việc làm tròn tại các bước trung gian.
Câu 5. Độ lớn mômen uốn tổng tại B (Nm)
Sử dụng phương pháp mặt cắt tương tự như câu 4 (cắt qua điểm nằm trong đoạn BC, xét nửa bên
phải) => tính được My và Mz:
𝑀𝑦𝐵 = −𝑅𝐶𝑧. 𝐵𝐶 và 𝑀𝑧𝐵 = 𝑅𝐶𝑦. 𝐵𝐶
Thay số tính được: MyB = -52425 Nmm; MzB = 172150 Nmm và MB = 183119 Nmm ≈ 183,1 Nm
Chú ý: kết quả có thể lệch khoảng ± 0,5 do việc làm tròn tại các bước trung gian.
Câu 6. Hệ số an toàn theo độ bền tĩnh của tiết diện có momen lớn nhất trên trục, sử dụng thuyết
bền thế năng biến đổi hình dáng (thuyết bền 4) nếu đường kính tại tiết diện này bằng 45mm
Mômen lớn nhất trên trục Mmax = max{ MA; MB} đã tính trên đây => Mmax ≈ 294,2.103 Nmm.
Mômen xoắn tại tiết diện A và B: 𝑇 = 𝐹𝐴. 𝑐𝑜𝑠α. 𝑑𝐴/2 = 305104 Nmm.
Tiết diện d = 45mm nên mômen chống uốn 𝑊𝑢 = π. 𝑑3/32 = 8946 mm3; momen chống xoắn 𝑊𝑜 = π. 𝑑3/16 = 17892 mm3.
Ứng suất uốn: σ = 𝑀/𝑊𝑢 = 32,88 MPa
Ứng suất xoắn: τ = 𝑇/𝑊𝑜 = 17,05 MPa
Ứng suất tương đương: σ𝑡đ = √σ2 + 3τ2 = 44,2 MPa
Hệ số an toàn: 𝑠 = σ𝑔ℎ/σ𝑡đ = σ𝑐ℎ/σ𝑡đ = 400/44,2 ≈ 9,05 --------------- Câu 7--10
Đường cong mỏi của mẫu thử bằng thép có giới hạn mỏi dài hạn 320MPa, số chu trình cơ sở 7x106
và số mũ (bậc) đường cong mỏi bằng 6. Trục quay 10 vòng/ph được làm từ vật liệu này và tiết diện
nguy hiểm nhất trên trục có đường kính d=20mm; hệ số tập trung ứng suất Kσ=1,2; hệ số ảnh hưởng
của kích thước εσ=0,9; mômen uốn danh nghĩa có chiều không đổi với giá trị M=2,6x105 Nmm. Xác định các thông số sau:
Câu 7. Giới hạn mỏi dài hạn (MPa) của chi tiết trục tại tiết diện đã cho. Đáp sô: 240
Câu 8. Biên độ ứng suất uốn tại tiết diện đã cho khi chịu mômen uốn danh nghĩa M. Đáp sô: 331
Câu 9. Tuổi thọ của trục, tính bằng số vòng quay, khi trục làm việc ở chế độ tải trọng thay đổi: 30%
thời gian với tải trọng 0,9M, 70% thời gian với tải 0,7M. Đáp sô: 6380.103
Câu 10. Biết trục đã làm việc 1200 giờ theo chế độ tải trọng ở câu c), đánh giá xem trục có còn dùng
được không và nếu dùng được thì khi chịu mômen 0,8M và tốc độ quay như trước tuổi thọ còn
lại (tính bằng giờ) của trục? Đáp sô: 5737 Gợi ý:
7) σ𝑟𝑘 ≈ σ−1. β. ϵσ/𝐾σ
8) σ𝑎 = σ𝑚𝑎𝑥 = M/𝑊𝑢 = 32M/(π. 𝑑3)
9) Gọi L là tuổi thọ của trục (tính bằng số chu trình ứng suất = số vòng quay) => trục làm việc ở chế
độ sau (với σa đã tính ở câu 8):
+ ở mức ứng suất σ1 = 0,9. σ𝑎 trong 𝑛1 = 0,3. 𝐿 chu trình
+ ở mức ứng suất σ2 = 0,7. σ𝑎 trong 𝑛2 = 0,7. 𝐿 chu trình
Theo thuyết Palmgren – Miner: n1/N1 + n2/N2 = 1, thay n1, n2 tính theo L trên đây =>
𝐿. (0,3/𝑁1 + 0,7/𝑁2) = 1 , từ đó tính được tuổi thọ 𝐿 = 1/(0,3/𝑁1 + 0,7/𝑁2)
Các đại lượng (1/N1) và (1/N2) tính từ phương trình đường cong mỏi theo:
+ Khi σ𝑖 < σ𝑟𝑘: 1/𝑁𝑖 = 0 (tức là 𝑁𝑖 = ∞)
+ Khi Khi σ𝑖 ≥ σ𝑟𝑘: 1/𝑁𝑖 = (σ𝑖/σ𝑟𝑘)𝑚/𝑁0
10) Đã biết mỗi phút trục quay n=10 vòng => trong 1200 giờ đã quay được n1+n2 = 60.1200.n =
60.1200.10 = 70.103 vòng. Theo kết quả câu c), số vòng quay đã thực hiện ít hơn tuổi thọ tính toán
(L=6380.103 vòng) nên trục chưa hỏng.
Gọi n3 là tuổi thọ còn lại (tính bằng số vòng quay) khi trục tiếp tục làm việc ở mức ứng suất σ3 =
0,8. σ𝑎 thì n3 có thể xác định như sau:
+ Nếu σ3 < σ𝑟𝑘: 𝑛3 = ∞
+ Nếu σ3 ≥ σ𝑟𝑘: 1/𝑁3 = (σ3/σ𝑟𝑘)𝑚/𝑁0 và theo Palmgren – Miner suy ra n1/N1 + n2/N2 + n3/N3= 1.
Với đại lượng 𝑛1/𝑁1 + 𝑛2/𝑁2 = 𝐿. (0,3/𝑁1 + 0,7/𝑁2) đã tính ở câu c) dễ dàng tính được n3.
Từ số vòng quay n3 => quy đổi ra số giờ: 𝐿ℎ3 = 𝑛3/(60. 𝑛). ⧠
Bài tập/Kiểm tra thường kỳ #2 Đề số: Họ và tên: MSSV: Lớp:
Bảng 1: Kích thước bulông tiêu chuẩn (d1 = đường kính chân ren; d0 = d với bulông lắp không khe hở) Ký hiệu M5 M6 M8
M10 M12 M14 M16 M18 M20 M22 M24 M27 M30 d1, mm
4,02 4,77 6,47 8,16 9,85 11,6 13,6 14,9 16,9 18,9 20,3 23,3 25,7
Câu 1. Mối ghép ren sử dụng z=4 bulông không được siết chặt, chịu lực tổng F = 42x103N. Biết ứng suất kéo
cho phép của bulông là [σ] = 175MPa. Kích thước tối thiếu của bulông là: Giải:
Tải trọng tác động lên mỗi bulông: 𝑃 = 𝐹/𝑧 = 42.10 /4 = 10500𝑁 Đường kính chân ren: . 𝑑 ≥ = = 8,74 .[ ] .
Tra bảng 1, với d1 trong bảng ≥ d1 đã tính => bulông M12
Câu 2. Hai tấm thép có ứng suất dập cho phép [σdt] = 92 MPa, dày lần lượt là s1=12mm và s2=7mm, được
ghép chồng bằng z=6 bulông kiểu không có khe hở để chịu lực ngang tổng F=20x103N. Ứng suất cắt và dập
cho phép của bulông lần lượt là [τ] 59MPa và [σdb]=138MPa. Kích thước tối thiểu của bulông là: Giải:
Tải trọng tác động lên mỗi bulông: 𝑃 = 𝐹/𝑧 = 20.10 /6 = 3333,33𝑁
Đường kính thân bulông theo độ bền cắt: : . , 𝑑 ≥ = = 8,48 .[ ] .
Tra bảng với d0 ≈ d > d0 đã tính => bulông M10.
Kiểm tra độ bền dập: Do ứng suất dập cho phép của bulông lớn hơn của tấm nên chỉ cần kiểm tra cho các
tấm ghép. Chiều dày tính toán s = min{s1; s2; d0) = min{12; 7; 10} = 7. Điều kiện bền: σ = 𝑃/𝐴 =
𝑃/(𝑠. 𝑑 ) ≤ [σ ]. Thay số tính được σd = 47,62MPa < [σdt] = 92 MPa => đủ bền. Vậy M10 đảm bảo cả độ bền cắt và dập.
Chú ý: Nếu điều kiện bền dập không đảm bảo => tăng đường kính bulông lên và kiểm tra lại độ bền dập cho
đến khi đảm bảo đủ bền
Câu 3. Hai tấm được ghép chồng lên nhau bằng bulông M22 có ứng suất kéo cho phép [σ]=120MPa để chịu
lực ngang tổng F=430x103N. Biết hệ số ma sát giữa các tấm ghép f=0,697 và lực siết vừa đủ để đạt hệ số an
toàn chống trượt k=1,9. Số bulông ít nhất là: Giải:
Tải trọng tác động lên mỗi bulông: 𝑃 = 1000𝐹/𝑧(𝑁)
Lực siết cần thiết: 𝑉 = 𝑘𝑃/(𝑖𝑓) = 1000𝑘𝐹/(𝑖𝑓𝑧) Điều kiện bền: . , . . , . /( ) σ = = ≤ [σ] . . Suy ra: . , . z ≥ . . . .[ ]
Với M22 tra được d1=18,9; số bề mặt ma sát i=1 và các số liệu đã cho => z ≥ 45,26 => chọn z = 46.
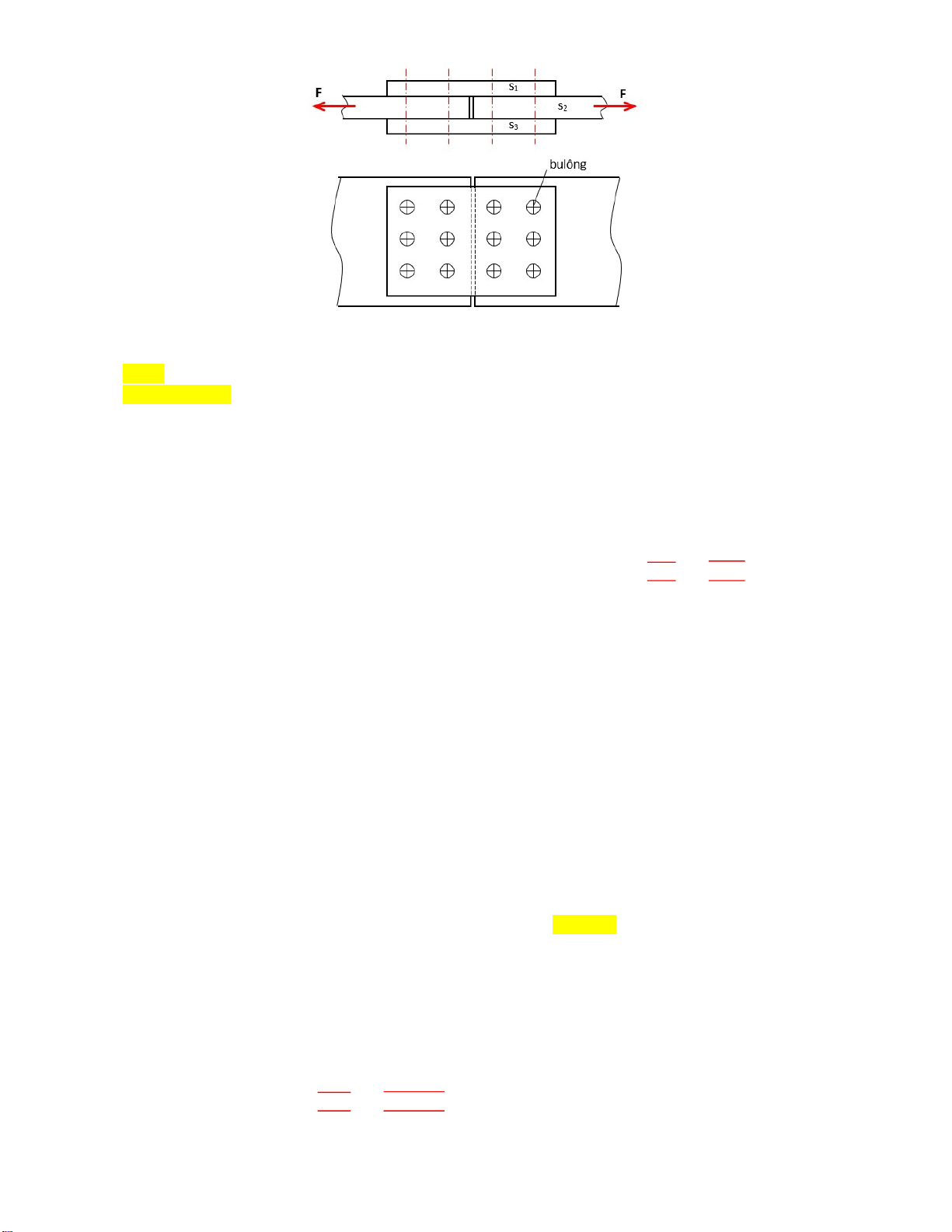
Hình 1 – Mối ghép bulông
Câu 4. Các tấm thép có ứng suất dập cho phép [σdt]=98MPa, được ghép chồng bằng bulông trong mối ghép
không có khe hở để chịu lực ngang tổng F=7.5x103N như Hình 1. Chiều dày các tấm ốp s1=s3=13mm, các
tấm giữa s2=15mm. Bulông có ứng suất cắt và dập cho phép lần lượt là [τ]=78MPa và [σdb]=118MPa. Kích
thước tối thiểu của bulông là: Giải:
Thực tế đây là 2 mối ghép như nhau, mỗi mối ghép gồm z=6 bulông.
Tải trọng tác động lên mỗi bulông: 𝑃 = 1000𝐹/𝑧 = 1000.7,5/6 = 1250(𝑁)
Đường kính thân bulông theo độ bền cắt, chú ý số tiết diện chịu cắt i=2 : . 𝑑 ≥ = = 3,19 .[ ] .
Tra bảng với d0 ≈ d > d0 đã tính => bulông M5.
Kiểm tra độ bền dập: Do ứng suất dập cho phép của bulông lớn hơn của tấm nên chỉ cần kiểm tra cho các
tấm ghép. Với tấm giữa, lực tác dụng = P, chiều dày tính toán s = min{s2, d0) = min{15; 5} = 5, còn với các
tấm ốp lực tác dụng sẽ là P' = P/2 và chiều dày tính toán s' = min{s1, d0} = min{13; 5} = 5.
Điều kiện bền của tấm giữa: σ = 𝑃/𝐴 = 𝑃/(𝑠. 𝑑 ) ≤ [σ ]. Thay số tính được σd = 50MPa < [σdt] = 98 MPa => đủ bền.
Đối với các tấm ốp: do s' và d0 giống như tấm giữa nhưng P' = P/2 nên dễ dàng suy ra σ'd = 25MPa < [σdt] = 98 MPa => đủ bền.
Vậy M5 đảm bảo cả độ bền cắt và dập.
Chú ý: Nếu điều kiện bền dập không đảm bảo => tăng đường kính bulông lên và kiểm tra lại độ bền dập cho
đến khi đảm bảo đủ bền
Câu 5. Với kết cấu mối ghép như Hình 1 nhưng sử dụng mối ghép có khe hở và tổng lực ngang F=153x103N.
Bulông có ứng suất kéo cho phép bằng 145MPa, hệ số ma sát giữa các tấm bằng 0.594 và các bulông được
siết vừa đủ để đạt hệ số an toàn chống trượt 2. Kích thước tối thiểu của bulông là: Giải:
Tải trọng tác động lên mỗi bulông: 𝑃 = 1000𝐹/𝑧 = 1000.153/6 = 25500(𝑁)
Lực siết cần thiết: 𝑉 = 𝑘𝑃/(𝑖𝑓) = 2.1250/(2.0,594) = 42929 N Đường kính chân ren: . , . , . 𝑑 ≥ = = 22,13 .[ ] .
Tra bảng 1, với d1 trong bảng ≥ d1 đã tính => bulông M27
Câu 6. Nắp nồi hơi chịu áp suất p=0.8 N/mm2 có đường kính D=320mm được ghép chặt với thân nồi hơi
bằng z=10 bulông. Tỉ lệ độ cứng của bulông và thân nồi hơi là 0.32. Hệ số an toàn chống tách hở là k=1.8.
Ứng suất kéo cho phép của bulông là [σ]=165 MPa. Kích thước tối thiểu của bulông là: Giải:
Lực tác động lên nắp nồi hơi: Q = p.Anắp = p.π.D2/4 = 0,8.π.3202/4 ≈ 64400N
Lực dọc tác động tại mỗi vị trí lắp bulông: F = Q/z = 64399.82/10 = 6440N
Lực siết cần thiết để chống tách hở (với hệ số an toàn k): /
𝑉 = 𝑘(1 − χ). 𝐹, trong đó χ = = = / ,
= 0,242. Thay số tính được V = 9763N , Đường kính chân ren: .( , . ) .( , . , . ) 𝑑 ≥ = = 10,49 .[ ] .
Tra bảng 1, với d1 trong bảng ≥ d1 đã tính => bulông M14 ---------------
Bulông M24 được siết chặt với lực siết 64x103N và hệ số ngoại lực χ=0.32. Trong quá trình làm việc tại vị trí
ghép này có thêm tải trọng tác động theo phương dọc trục bulông thay đổi theo chu kỳ từ 3.4x103N đến
23.8x103N. Xác định các đại lượng ứng suất sau trong bulông (MPa):
Câu 7. Ứng suất kéo lớn nhất:
Đường kính chân ren của bulông M24: tra bảng 1 => d1 = 20,3.
Bulông chịu tải trọng kéo tổng P = V + χ.F, suy ra Pmin = 65088 N; Pmax = 71616 N. Ứng suất kéo: . σ = .
Thay P = Pmax tính được σmax = 221,3
Câu 8. Ứng suất kéo trung bình:
Thay P = Pmin tính được σmin = 201,1
Từ đó tính được ứng suất trung bình: σm = 0,5.(σmax + σmin) = 211,2 MPa
Câu 9. Biên độ ứng suất kéo:
Biên độ ứng suất: σa = 0,5.(σmax - σmin) = 10,1 MPa --------------- Hình 2
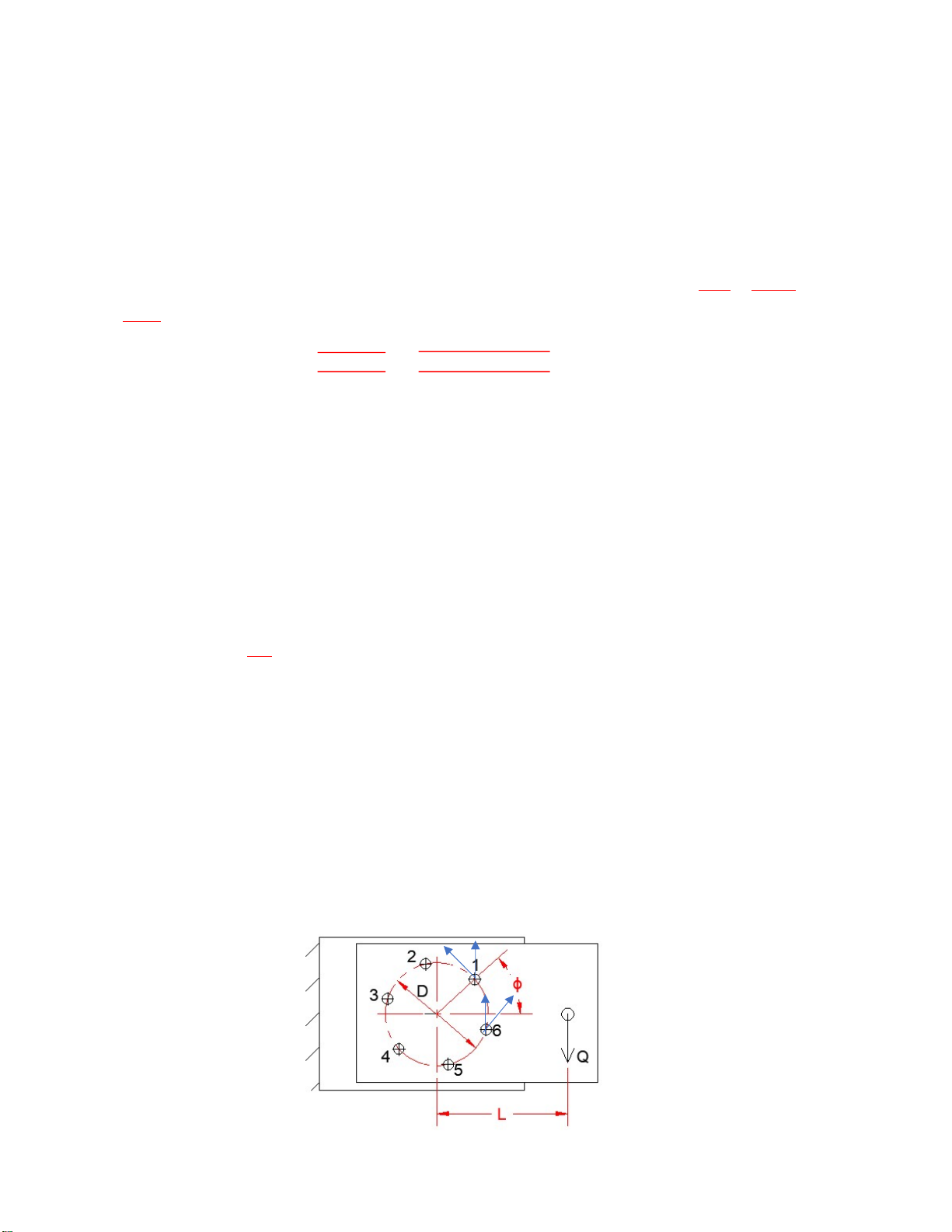
Câu 10. Mối ghép gồm 6 bulông phân bố đều trên đường tròn đường kính D=290mm, góc φ=10 độ, chịu lực
Q=6000N đặt cách tâm vòng tròn khoảng cách L=290mm như Hình 2. Kích thước bulông phải được tính
toán lựa chọn theo vị trí lắp nào sau đây:
Chuyển lực Q về tâm mối ghép C được lực P=Q và mômen M=Q. Phân tích lực tác động lên các bulông do
lực P và mômen M được: FPi = P/z = P/6 F 2 Mi = M.ri/ Σri
trong đó, ri là khoảng cách từ tâm C đến các điểm i. Các khoảng cách này bằng nhau và bằng D/2.
Do đó, độ lớn các lực tác động lên các vị trí bulông FPi như nhau và FMi cũng như nhau. Vì vậy lực tổng hợp
F⃗ = F ⃗ + F ⃗ sẽ lớn nhất khi góc giữa các véc tơ thành phần nhỏ nhất.
Nhìn trên hình minh họa (phản lực tại các vị trí lắp bulông), với số liệu đã cho ∠1C6 = 360/6 = 60o, góc ∠1Cx
= φ = 10o nên có thể thấy các điểm có góc tạo bởi hai véc tơ lực trên đây sẽ nhỏ hơn cả tại các điểm 1 hoặc
6. Do ∠6Cx = 50 độ lớn hơn ∠1Cx = 10 độ nên vị trí 1 sẽ chịu tải lớn nhất nên chỉ cần tính cho bulông tại vị trí này. --- Hết ---
Bài tập/Kiểm tra thường kỳ #3 Đề số: Họ và tên: MSSV: Lớp:
Cho sơ đồ bố trí bộ truyền đai như Hình 1, biết góc ôm α1 ≥ 143o; tỉ
số truyền u  2,01; đường kính bánh đai nhỏ d1 = 200mm; hệ số trượt
lấy bằng 0,025. Khe hở giữa các bánh đai Δ ≥ 255mm. Xác định các
thông số sau để bộ truyền có kích thước nhỏ gọn nhất:
Dãy tiêu chuẩn đường kính bánh đai (mm): 100; 112; 125; 140; 150;
160; 180; 200; 224; 250; 280; 300; 315; 355; 400; 450; 500; 560; 630;
710; 800; 900; 1000; 1120; 1250; 1400; 1600; 2000…
Chiều dài tiêu chuẩn của dây đai (mm): 400, 450, 500, 560, 630, 710, Hình 1
800, 900, 1000, 1120, 1250, 1400, 1600, 1800, 2000, 2240, 2500,
2800, 3150, 3550, 4000,…
Câu 1. Đường kính bánh đai lớn d2 (mm) với sai lệch tỉ số truyền ít nhất so với giá trị đã cho
Đường kính bánh đai bị dẫn: trước tiên tính sơ bộ theo công thức 𝑑2 = 𝑑1. 𝑢. (1 − ε), với ε là hệ số
trượt, sau đó chọn gần với số đã cho trong dãy tiêu chuẩn.
Thay số tính được d2 = 200.2,01.(1-0,025) = 391,95 => chọn d2 = 400 mm.
Câu 2. Khoảng cách tâm a sơ bộ đáp ứng các yêu cầu đã cho (mm)
Do các đường kính bánh đai đã xác định nên bộ truyền nhỏ gọn nhất khi khoảng cách trục nhỏ nhất,
nhưng khoảng cách này phải đáp ứng cả 2 điều kiện:
1) từ khe hở Δ suy ra a ≥ a1 = (𝑑1/2 + 𝑑2/2) + Δ và
2) từ α1 = 180𝑜 − 57𝑜. (𝑑2 − 𝑑1)/𝑎 ≥ α𝑚𝑖𝑛 suy ra 𝑎 ≥ a2 = 57. (𝑑2 − 𝑑1)/(180𝑜 − α𝑜)
Từ đó thay số tính được a ≥ max{a1; a2} = max{555; 308,1} => a = 555 mm.
Câu 3. Chiều dài dây đai theo dãy tiêu chuẩn (mm) 𝑑 (𝑑
Chiều dài dây đai tính theo công thức: 𝐿 ≈ 2𝑎 + 𝜋 1+𝑑2 + 2−𝑑1)2. Với khoảng cách trục a ≥ 555 thay 2 4𝑎
số tính được L ≥ 2070,5mm. Theo dãy tiêu chuẩn chọn L = 2240mm.
Câu 4. Giá trị lực Fr (N) tác dụng lên trục lắp các bánh đai, biết lực căng ban đầu F0=830N và góc ôm
vẫn giữ nguyên giá trị đã cho.
Thay số được Fr ≈ 1574 N --------
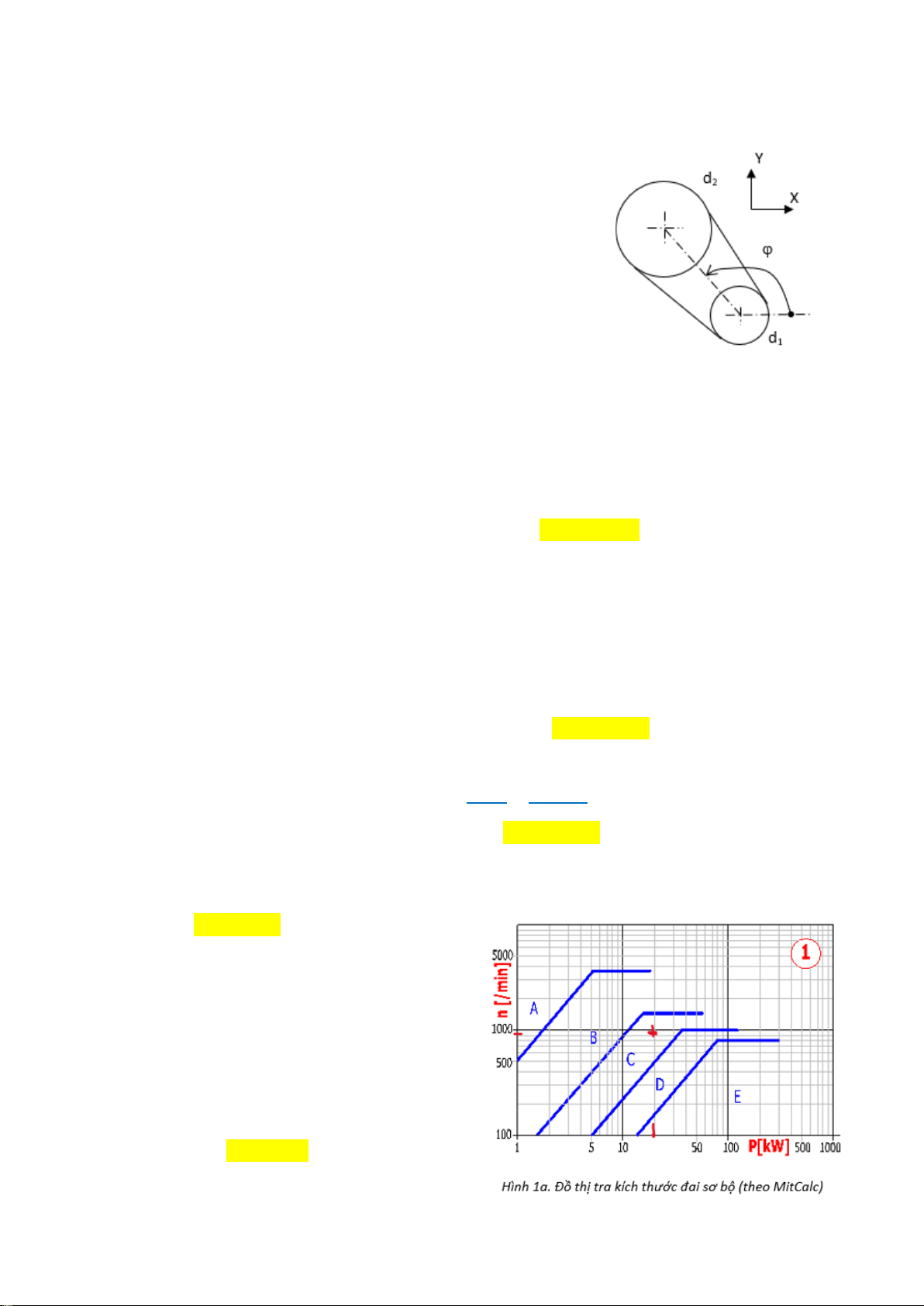
Câu 5. Khi thiết kế bộ truyền đai thang với công
suất cần truyền là P1=20kW và số vòng quay
bánh dẫn là 900v/ph thì tiết diện đai sơ bộ nên chọn là:
Đây là câu đơn giản nhất: chỉ việc tra từ đồ thị đã
cho., với n = 900; P = 20 KW sẽ được tiết diện đai
sơ bộ nên dùng là tiết diện C.
Sơ đồ bộ truyền xích như Hình 2 với tỉ số truyền dự kiến u  2,2; công
suất P1 = 4kW; số vòng quay n1 = 245v/ph và góc ϕ = 120o. Xích 2 dãy
có bước 44,45mm, không sử dụng các má xích chuyển tiếp, số mắt
xích đảm bảo điều kiện ≥ 33 lần bước xích. Số răng đĩa xích chọn lẻ
để tăng độ mòn đều của răng và z1 ≥ 17. Hệ số sử dụng 𝐾 =
𝐾đ𝐾𝑎𝐾𝑜𝐾𝑐𝐾đ𝑐𝐾𝑏𝑡 = 1,81.
Số vòng quay của bộ truyền xích thử nghiệm n01 (v/ph) lấy trong dãy
sau: 50, 200, 400, 600, 800, 1000, 1200, 1600.
Với điều kiện bộ truyền được thiết kế có kích thước nhỏ nhất, hãy Hình 2
xác định các thông số sau:
Câu 6. Số răng đĩa xích bị dẫn z2 (với sai lệch tỉ số truyền và kích thước nhỏ nhất)
Áp dụng công thức 𝑧1 ≈ 29 − 2. u để tính z1, sau đó làm tròn về số lẻ gần nhất ≥ 17 (lý do chọn số lẻ
vì số mắt xích chẵn để có thể nối thành vòng kín mà không sử dụng mắt chuyển tiếp), do vậy mà xích
và răng đĩa mòn đều hơn).
Với số liệu đã cho tính được z1 = 29 – 2. 2,2 = 24,6; do đó chọn z1c = 23. Số răng đĩa 2 tính từ số răng
z1c đã chọn theo công thức 𝑧2 = 𝑢. 𝑧1𝑐 và cũng làm tròn về số lẻ. Với z1c=25; u=2,2 tính được z2=55; do đó chọn z2c=55.
Câu 7. Công suất tính toán Pt (kW) trên mỗi dãy xích 𝑃 Áp dụng công thức 𝑃 1.𝐾𝑛.𝐾𝑧.𝐾 𝑡 = , trong đó: 𝐾𝑑
K = hệ số sử dụng, đã cho 1,81;
Kn = n01/n1 = 200 / 245 (n01 = 200 là số vòng quay thử nghiệm, gần nhất với n1 đã cho)
Kz = z01/z1 = 25/25 (z01 = 25 là số răng đĩa xích thử nghiệm)
Kd – hệ số tính đến số dãy xích, tra bảng (xem Phụ lục); xích 2 dãy => Kd = 1,7.
Thay số tính được Pt ≈ 3,48 kW.
Câu 8. Chiều dài xích (mm)
Áp dụng công thức 𝐿 = 𝑥. 𝑝, trong đó p là bước xích, còn x là số mắt xích tính theo công thức sau đây,
nhưng phải làm tròn lên về số chẵn (để đảm bảo a/p ≥ giá trị cho trước và để có thể nối thành vòng
kín vì không dùng má xích chuyển tiếp) 2𝑎 𝑧 (𝑧 x = + 1 + 𝑧2 + 2 − 𝑧1)2𝑝 𝑝 2 4𝜋2𝑎
Thay số tính được x = 106,69 => chọn x = 108 và tính được L = 108x44,45 = 4800,6. Vậy L ≈ 4801 mm.
Câu 9. Khi bị mòn, nếu bước xích tăng thêm một lượng Δp=0,021mm thì đường kính qua tâm con lăn
của xích trên đĩa xích bị dẫn sẽ tăng thêm bao nhiêu mm?
Áp dụng công thức Δ𝑑2 = Δ𝑝/𝑠𝑖𝑛(π/z2), thay số tính được Δd2 ≈ 0,368 mm.
Câu 10. Lực hướng tâm Fr (N) tác dụng lên trục đĩa xích dẫn.
Áp dụng công thức nên 𝐹𝑟 = 6.107. 𝑃1k/(𝑧1𝑛1𝑝), với k là hệ số phụ thuộc góc nghiêng đường nối tâm
các đĩa xích so với phương ngang (xem Phụ lục). Góc nghiêng β này tính theo góc ϕ đã cho như sau:
+ khi 0o ≤ ϕ ≤ 90o thì β = ϕ
+ khi 90o <ϕ ≤ 180o thì β = 90 - ϕ
Với ϕ = 120o => β = 180 – 120 = 60o, do đó tra được k = 1,05, từ đó tính được Fr ≈ 926 N. Phụ lục
1) Hệ số tính đến ảnh hưởng của số dãy xích Số dãy 1 2 3 4 Kd 1 1,7 2,5 3
2) Hệ số tính đến ảnh hưởng của vị trí bộ truyền khi tính lực tác dụng lên trục (β là góc nghiêng
đường nối tâm đĩa xích so với phương ngang, 0 ≤ β ≤ 90 độ) Góc β, độ 0 ≤ β ≤ 40 40 < β ≤ 90 Hệ số k 1,15 1,05 --- Hết ---