Tổng hợp câu hỏi lý thuyết môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

Câu hỏi tự luận VẬT LÍ ĐẠI CƯƠNG II
CHƯƠNG 1: TRƯỜNG TĨNH ĐIỆN
Câu 1: Điện trường là gì? Nêu định nghĩa và ý nghĩa của vector cường độ điện
trường. Trình bày công thức xác định vector cường độ điện trường gây bởi điện
tích điểm, hệ điện tích điểm và của vật mang điện.
Định nghĩa điện trường:
- Xung quanh mỗi một điện tích tồn tại một môi trường vật chất đặc biệt
bao quanh nó gọi là điện trường.
- Đặc điểm của điện trường là tác dụng lực điện lên điện tích khi đặt vào trong điện trường.
- Tương tác giữa các điện tích được thể hiện như sau: mỗi một điện tích
gây ra xung quanh nó một điện trường. Điện trường của điện tích này tác
dụng lên điện trường của điện tích kia một lực điện.
Nêu định nghĩa và ý nghĩa của vector cường độ điện trường
Giả sử ta đặt một điện tích tại một điểm M nào đó trong điện trường, qo
sẽ bị điện trường tác dụng một lực  . qo F
Tỉ số F không phụ thuộc vào qo mà phụ thuộc vào vị trí điểm M, nghĩa là qo
tại mỗi điểm M thì tỉ số  = F = const E qo
 : vector cường độ điện trường E
E: cường độ điện trường
Nếu chọn = +1 thì  =  nghĩa là : vector cường độ điện trường tai một điểm q0 E F
là một đại lượng vector bằng lực tác dụng của điện trường lên một đơn vị điện
tích dương tại điểm đó
 đặc trưng cho điện trường về phương diện tác dụng lực tại điểm đang xét. E
Công thức xác định vector cường độ điện trường gây ra bởi điện tích điểm
Ta có : lực tác dụng lên điện tích .q . q0 lên bằng: r2. q0 F=1   r 4πε ε0 r
( : bán kính vector hướng từ điện tích q tới điểm M) r = .qr2. 1    ( 1) E= F r q0 4πε ε0 r
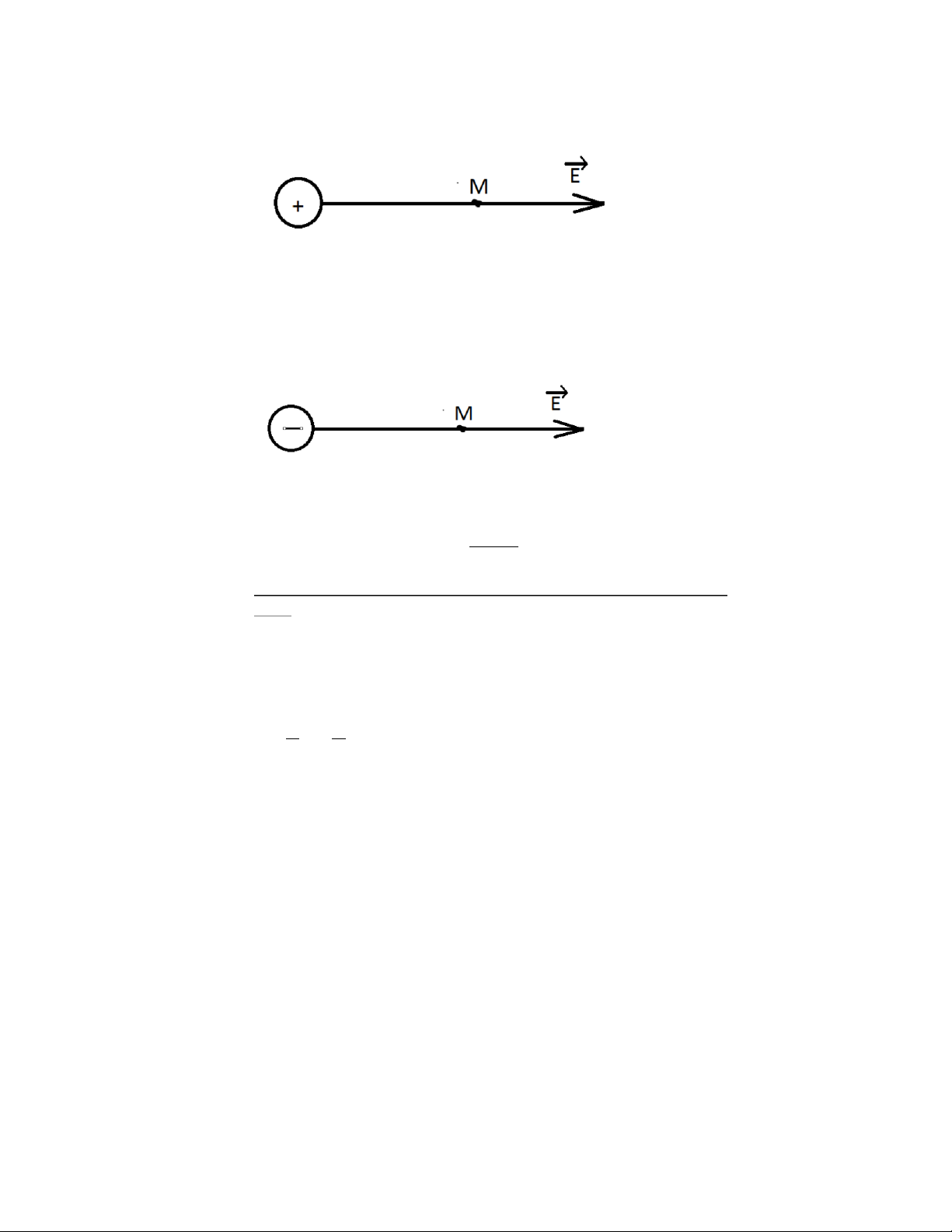
Từ (1) nhận thấy rằng :
q > 0 => E cùng hướng với r => E hướng ra xa điện tích q
q < 0 =>E ngược hướng với r => E hướng vào điện tích q
Cường độ điện trường tại điểm M tỉ lệ thuận với độ lớn của q và tỉ lệ
nghịch với bình phương khoảng cách từ điểm đang xét đến q. E = |q| 4πε ε0r2
Công thức xác định vector cường độ điện trường gây ra bởi hệ điện tích điểm:
Xét một hệ điện tích điểm q1, q2, q3, … , qnđược phân bố liên tục trong không gian.
Đặt tại M một điện tích thử q0. Ta có: n
F=∑ Fi ( Fi là lực tác dụng của qi lên q0 ) i=1  n F  F i E= =∑ q0 i= q 1 0
Nhưng Ei=Fi chính là vector cường độ điện trường gây ra bởi qitại M
Vector cường độ điện trường gây ra bởi một hệ điện tích điểm bằng tổng
các vector cường độ điện trường gây ra bởi từng điện tích điểm của hệ.
( Nguyên lí chồng chất điện trường )
Công thức xác định vector cường độ điện trường gây ra bởi một vật mang điện.
Chia vật mang điện thành nhiều phần nhỏ sao cho điện tích dq mang trên
mỗi phần đó có thể coi là điện tích điểm.
Gọi dE là vector cường độ điện trường gây ra bởi điện tích dq tại một
điểm M cách dq một khoảng r, r là bán kính vector hướng từ dq tới M.
Vector cường độ điện trường do vật mang điện gây ra tại điểm M ❑ ❑1  .dq d  r E=∫ d  E=∫
4π ε0 ε r2r toànbộ toànbộ vật vật
Câu 2: Xác định vector cddt gây bởi lưỡng cực điện tại điểm M thuộc trung
trực và cách tâm O khoảng r khá lớn. Nêu định nghĩa và ý nghĩa của moment lưỡng cực điện. 1. Lưỡng cực điện
Định nghĩa lưỡng cực điện:
Lưỡng cực điện là một hệ 2 điện tích điểm có độ lớn bằng nhau nhưng
trái dấu +q và –q (q > 0) cách nhau một đoạn l rất nhỏ so với khoảng
cách từ lưỡng cực điện tới những điểm đang xét của trường. Để đặc
trưng cho tính chất điện ca lưỡng cực điện, người ta dùng đại lượng
vector momen lưỡng cực điện hay momen điện của lưỡng cực, kí hiệu là Pe.
Pe=q l
l: là vector hướng từ -q đến +q
l : có độ lớn bằng khoảng cách từ -q đến +q. Xác định
E tại M thuộc đường trung trực cách O một khoảng h khá lớn.
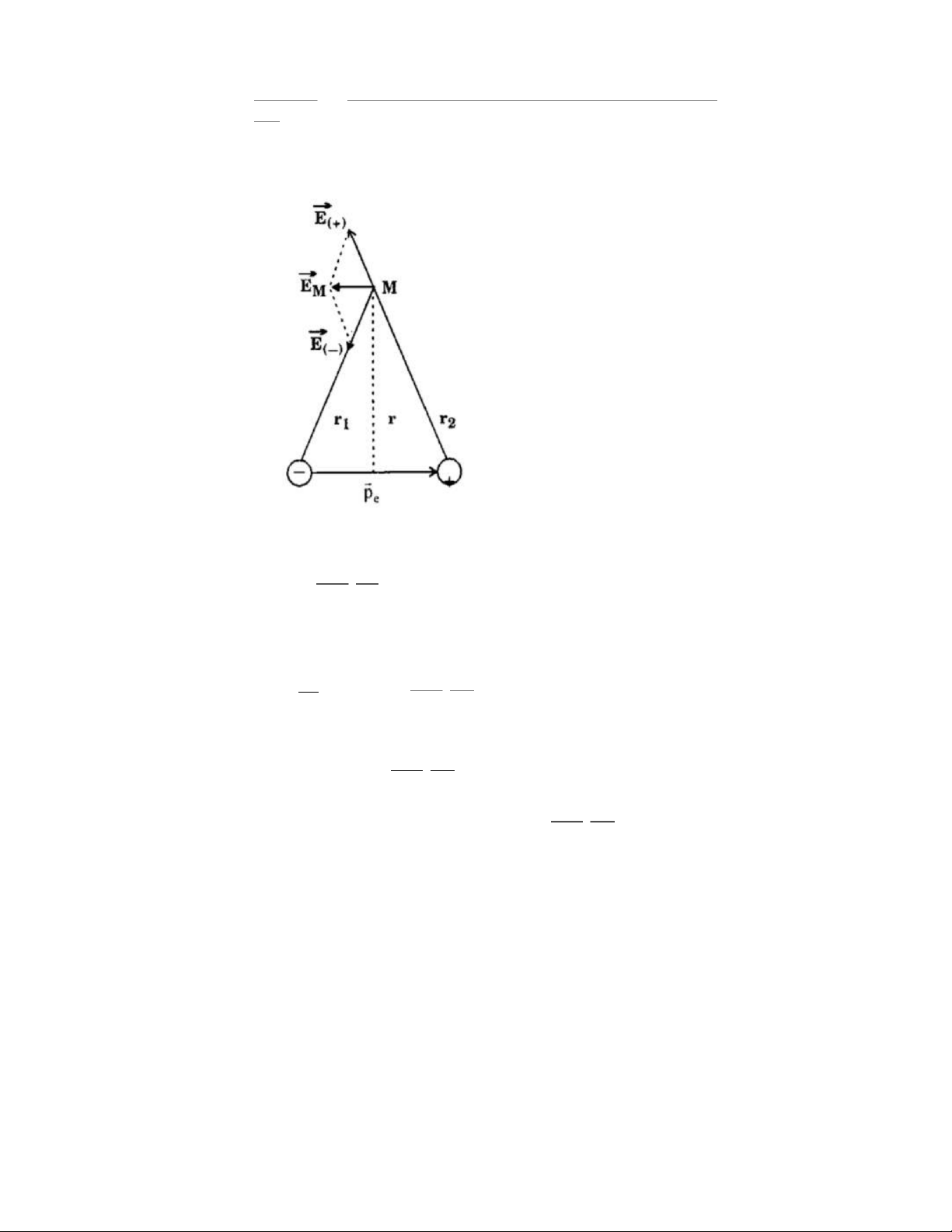
Theo nguyên lí chồng chất điện trường, vector cường độ điện trường E
gây ra bởi lưỡng cực tại M bằng tổng vector cường độ điện trường gây ra
bởi –q và +q của lưỡng cực.
E= E1+ E2
E1 , E2 hướng như hình vẽ, r1=r2 E .q 1=E2=1 4π ε 2 0 εr 1
Theo quy tắc tổng hợp vector => E song song, ngược chiều với l E = 2.E1.cosα l 1 .ql Cos α = => E = 2r 3 1 4π ε0 ε r1
Vì h ≫ l nên r1 h 1 .Pe
Mà ql = Pe => E = 4π ε 3 0 ε r1 Pe
Do E song song, ngược chiều với l nên E=1 . 4π ε 3 0 ε r1
Ý nghĩa của Pe: Biết vector momen điện Peta có thể xác định được vector
cường độ điện trường do lưỡng cực gây ra. Do đó, ta nói vector momen
điện đặc trưng cho tính chất điện của lưỡng cực điện.
2. Tính cường độ điện trường gây ra bởi dòng điện tròn:
–Tại tâm O: chia dây thành những phần tử mang điện tích dq, tại phần tử
điện tích A gây ra tại O một điện trường EA, ta có thể cho một phần tử điện
tích B đối xứng với A qua O, gây ra tại O một điện trường, vector cường độ
điện trường do phần tử B gây ra tại O là EB
 EA, EB cùng độ lớn nhưng ngược chiều.
 EA + EB = 0
Tương tự cho các phần tử điện khác
Áp dụng nguyên lí chồng chất điện trường n E  O=∑ Ei=  0 => EO=0 i=1 -Tại M
Chia dây thành những phần tử mang điện dq nhỏ.
Ứng với mỗi phần tử điện tích A, ta có thể chọn được một phần tử điện
tích B đối xứng với A qua O. Phần tử điện tích B sẽ có điện tích dq cách M mội khoảng r’ = AM.
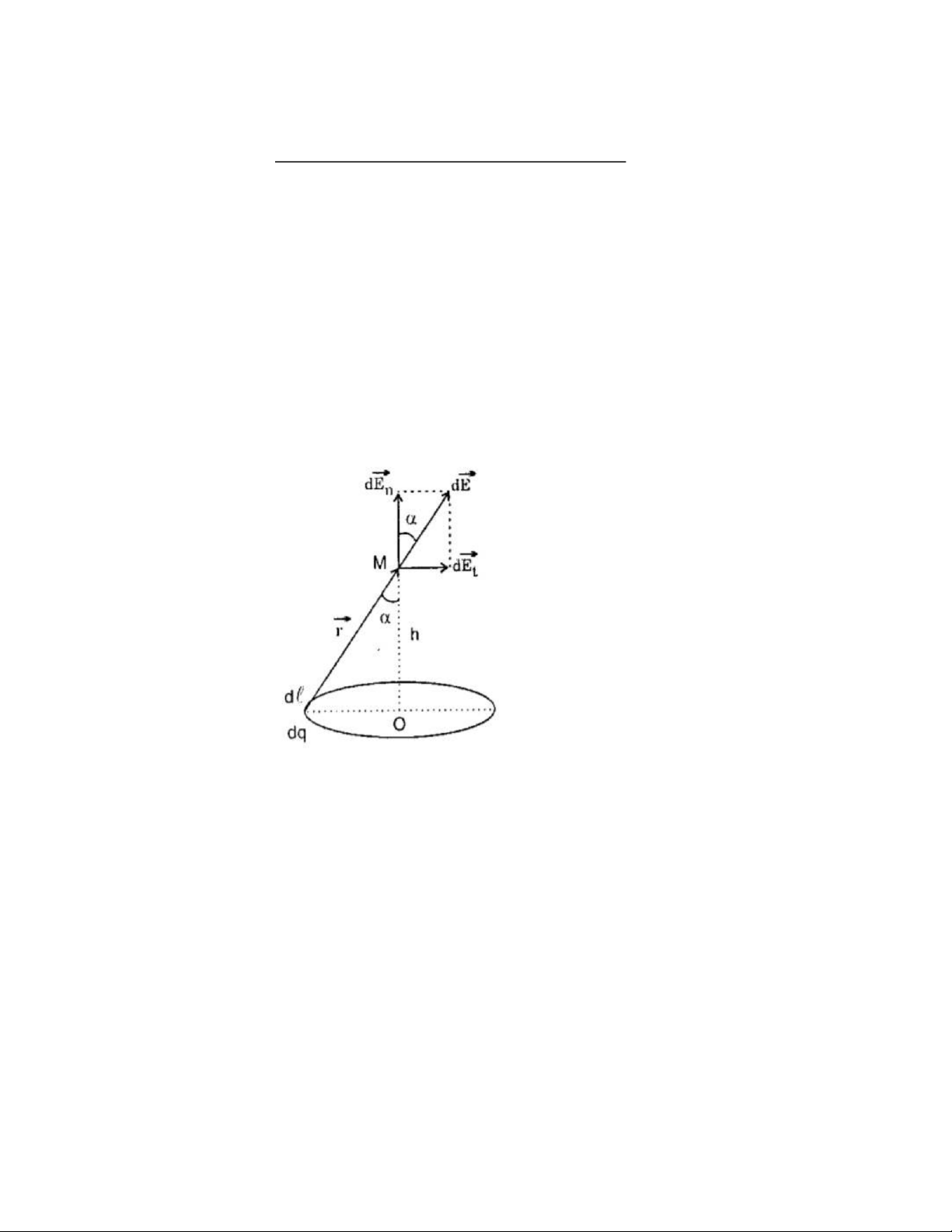
Do đối xứng nên dE1, dE2 đối xứng qua OM => dE1=dE2
Cường độ điện trường tổng hợp tại M:
dE = dE1+ dE2 => dE = 2 dE1 cos α
cos α=hr=h√h2+r2 hh h . dq dE = 2+r2.dq √ 4π ε 4π ε
0.(h2+r2 ) = 0(h2+r2)3/2
Áp dụng nguyên lí chồng chất điện trường: Qh . dq
4π ε0(h2+r2)3/2=hQ EM=∫dE=∫
4π ε 0.(h2+r2)3/2 0 Câu
3 : Phát biểu, viết biểu thức của định lý O-G trong điện trường, ý nghĩa. Áp
dụng tính cddt gây bởi một mặt phẳng vô hạn tích điện đều có mật độ điện mặt
là σ. Từ đó suy ra cddt trong tụ điện phẳng tích điện.
1. Định lí Ostrogradski Gauss:
Điện thông qua 1 mặt kín bằng tổng đại số các điện tích chứa trong mặt kín ấy. ❑ n θ  m=∫ D .d S=∑ qi S i=1
∑qi Là phép lấy tổng đại số các điện tích chứa trong mặt kín S
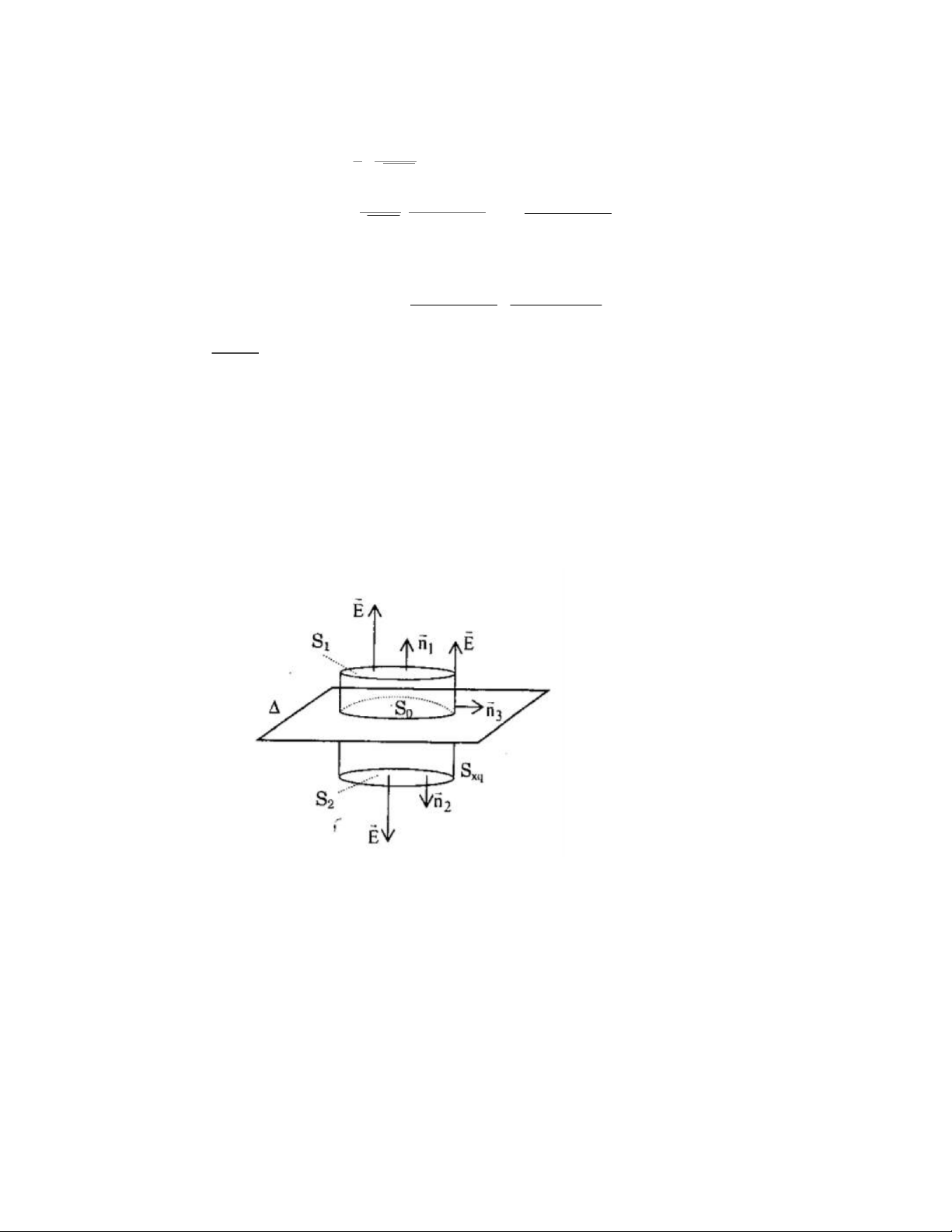
2. Vẽ qua M một mặt trụ kín ( hình vẽ ), mặt trụ có đường sinh vuông góc
mặt phẳng, 2 đáy song song, bằng nhau và cách đều mặt phẳng.
Thông lượng cảm ứng điện qua mặt trụ kín bằng: ❑ ❑ ❑ ∅    e=∫
D1n1d s+∫
D2 n2d s+∫
D3 n3d s mặt bên mặt đáy mặt đáy ❑ ❑ = ∫ D D 2ds+∫ 3ds mặt bên mặt đáy
Do D2, D3 không đổi trên 2 đáy σ
 ∅e=D1∆ S1+D2∆ S2 = 2D ∆ S = Q => D = σ E =  2 2ε ε0
3. Trong tụ điện phẳng tích điện đều
D1 , D2 lần lượt là vector cảm ứng điện do từng mặt gây ra
Vector cảm ứng điện do 2 mặt phẳng mang điện gây ra
D = D1 + D2 ( Theo nguyên lí chồng chất điện trường )
D1 , D2 có phương vuông góc với mặt phẳng mang điện, có độ lớn
D1=D2=σ2
D1 , D2 cùng chiều => D có phương vuông góc với 2 mặt phẳng. D σ
D =D1 + D2 = σ => E = = ε ε0 ε ε0 Câu
4 : CMR điện trường tinh gây bởi 1 điện tích điểm là trường thế. Viết biểu
thức lưu số của vector cddt và ý nghĩa.
Công của lực tĩnh điện trong chuyển dời vô cùng nhỏ ds bằng: q0.q q0. q
dA = F . ds=q 4 0.  E . sd hay dA =
r. ds = πε ε0r2ds . cosα ( α=¿ 4πε ε0r3
Từ hình vẽ ta thấy ds.cosα = dr, do đó: q0. q
dA = 4πε ε0r2dr
Công của lực tĩnh điện trong sự dịch chuyển điện tích q0 từ M tới N là: Nq0. q A 4
- q0. q
MN=∫ πε ε0r2dr = q0.q 4 4 M πε ε0rM πε ε0rN
Công của lực tĩnh điện trong sự dịch chuyển điện tích q0trong
điện trường tĩnh của một điện tích điểm không phụ thuộc vào
dạng đường cong dịch chuyển mà phụ thuộc vào vị trí điểm đầu
và điểm cuối của chuyển dời.
Lưu số của vector cường độ điện trường dọc theo đường cong kín bằng 0.
A = ∮. E dl = 0 (1) Ý nghĩa:
oĐiện trường tĩnh là một trường thế, các đường sức của chúng
không khép kín trong không gian. Câu
5 : Nêu định nghĩa và ý nghĩa của điện thế. Viết công thức tính điện thế tại
1 điểm trong điện trường gây bởi 1 điện tích điểm và trong điện trường gây bởi
1 vật tích điện có điện tích phân bố liên tục.
Định nghĩa điện thế:
Tỉ số W/qo không phụ thuộc vào độ lớn của điện tích q0 mà chỉ phụ thuộc
vào độ lớn của các điện tích gây ra điện trường và vào vị trí điểm đang
xét trong điện trường. Vì vậy, có thể dùng tỉ số đó để đặc trưng cho điện
trường tại điểm đang xét. V = W/q0
V được gọi là điện thế của điện trường tại điểm đang xét.
Điện thế gây ra bởi một điện tích điểm q tại điểm cách nó một khoảng là r V = q 4πɛ ɛ0r
Điện thế gây ra bởi một vật tích điện có điện tích phân bố liên tục.
V = ∫dV =∫14πε ε0rdq
r: khoảng cách từ vật đến điểm đang xét Ý nghĩa: ∞
VM = ∫E ds : Điện thế tại một điểm M bất kì trong điện trường. M
AMN=(V¿¿M−VN)¿ q0
 VM−VN = AMN q0
Nếu q0= +1 => VM−VN = AMN
Hiệu điện thế giữa hai điểm M và N trong điện trường là một đại lượng
về trị số = công của lực tĩnh điện trong sự dịch chuyển 1 đơn vị diện tích
+ từ M đến N.VM - V∞ = AM ∞
Nếu lấy q0 = +1 đơn vị điện tích và chọn N ở xa vô cùng thì
Điện thế tại 1 điêm trong điện trường là một đại lượng về trị số bằng công
của lực tĩnh điện trong dịch chuyển 1 đơn vị điện tích dương từ M đến vô cùng. Câu
6 : Phát biểu và viết biểu thức của định lý O-G trong điện trường. Ý nghĩa
là định lý. Áp dụng tính cddt gây bởi mặt trụ dài vô hạn tích điện đều với mật
độ điện mặt là σ, bán kính tiết diện ngang là R, tại điểm M cách trục của trụ
một khoảng là r > R (M nằm ngoài mặt trụ)
1. – Định lí Ostragradski Gauss trong điện trường:
Điện thông qua 1 mặt kín bằng tổng đại số các điện tích chứa trong mặt kín ấy. ❑ n θ  m=∫ D .d S=∑ qi S i=1
∑q Là phép lấy tổng đại số các điện tích chứa trong mặt kín S i
2. Dựng mặt trụ ( S ) cùng trục ∆ với mặt trụ đã cho, đường sinh song song
với ∆và ∆ vuông góc với 2 đáy , M ϵ ( S )
Áp dụng định lí Ostragradski Gauss
Thông lượng cảm ứng điện từ qua ( S ) ❑ ❑ ❑ ∅    e=∫
Dnd s=∫ Dnd s+∫ Dnd s mặt trụ mặt 2mặt đáy ❑
Tại 2 mặt đáy ( Dn;d s ) = π => ∫ Dnd s=0 2 2mặt đáy ❑ ❑ ❑  ∅  e=∫
Dnd s = ∫ Dnds = ∫ Dds mặt bên mặt bên mặt bên ❑ D ∫ ds = σ.2πRl mặt bên
D.2πrl = σ.2πRl(l: độ dài mặt trụ ). D = σR π σR E =
( Q = λl = σ2πRl ¿ ε ε0r
Câu 7: Thiết lập công thức liên hệ giữa vector cddt và điện thế. Từ đó suy ra
công thức tính HĐT giữa 2 bản cực của một tụ điện phẳng tích điện đều với mật
độ điện mặt là σ và khoảng cách giữa 2 bản cực là d.
Xét 2 điểm M, N rất gần nhau trong điện trường E. Giả sử điện thế tại
M,N lân lượt là V, V+ dV (dV> 0)
dA = qoE ds d s= MN Mặt khác:
dA = qo[V – (V +dV)] = -qodV
 E ds=−dV =¿E=−dV d s
Vì dV > 0 nên E ds=E . dscosα <0hay cosα <0;α=
E ( ,ds)
Do đó α là góc tù véc tơ cường độ điện trường luôn luôn hướng theo 
chiều giảm của điện thế.
Hình chiếu của vector cường độ điện trường trên 1 phương nào
đó về trị số bằng độ giảm điện thế trên 1 đơn vị dài của phương đó.
Ex, Ey, Ez là hình chiếu của E lên Ox, Oy, Oz. Ex=−∂ V x ; Ey= ∂−∂ y V ; Ez=−∂V ∂ z E=Ex 
i+Ey j+Ez 
k=− (i. ∂ V
∂ x +j. ∂V ∂ y +
k . ∂V)=−∂ V x=− gradV ∂ z ∂ 
Công thức hiệu điện thế giữa 2 bản cực của tụ điện phẳng : σd U = ε ε0
CHƯƠNG II: VẬT DẪN Câu 1:
Phát biểu điều kiện cân bằng tĩnh điện của một vật dẫn mang điện?
Trình bày các tính chất của một vật dẫn cân bằng tĩnh điện.
Điều kiện cân bằng tĩnh điện:
-Vector cường độ điện trường bên trong vật bằng 0. : Etrong=0
-Thành phần tiếp tuyến Et của vector cường độ điện trường tại mọi
điểm trên vật dẫn bằng 0 . Et=0; E=En
Tính chất của vật dẫn cân bằng tĩnh điện:
-Vật dẫn cân bằng tĩnh điện là một khối đẳng thế. Mặt vât dẫn là một mặt đẳng thế.
-Giả sử truyền cho vật một điện tích q nào đó. Khi vật dẫn đã ở trạng
thái cân bằng tĩnh điện, ta có thể coi rằng điện tích q chỉ được phân bố
trên bề mặt vật dẫn, bên trong vật dẫn điện tích bằng 0.
-Đối với vật dẫn rỗng đã ở trạng thái cân bằng tĩnh điện, điện trường
của vật rỗng và trong thành của vật rỗng bằng không. Câu 2:
Trình bày các vấn đề sau:
a) Hiện tượng điện hưởng là gì? Phát biểu định lý các phần tử tương ứng
b) Định nghĩa tụ điện? Tìm biểu thức điện dung của tụ điện phẳng?
a) Hiện tượng các điện tích cảm ứng xuất hiện trên vật dẫn ( lúc đầu
không mang điện) khi đặt trong điện trường ngoài gọi là hiện tượng điện hưởng.
Định lí các phần tử tương ứng:
Điện tích cảm ứng trên các phần tử tương ứng có độ lớn bằng nhau và trái dấu.
b) Tụ điện là một hệ 2 vật dẫn A, B sao cho vật dẫn B được bao bọc hoàn
toàn bên trong vật dẫn A (A, B thường được gọi là 2 cốt hoặc 2 bản tụ
điện ). A, B ở trạng thái điện hưởng toàn phần.
Tụ điện phẳng có hai bản cùng diện tích S, cách nhau 1 khoảng d.
Nếu d rất nhỏ so với kích thước mỗi bản, ta có thể coi điện trường
giữa hai bản tụ là điện trường gây bởi 2 mặt phẳng song song vô hạn tích điện đều.
V1−V2=dσ =dQ
ε ε0 ε ε0S  C=Q =ε ε0S V1−V2 d
Câu 3: Trình bày thế năng tương tác giữa hai điện tích điểm, năng lượng của
hệ điện tích điểm, năng lượng của vật dẫn mang điện?
Thế năng tương tác giữa 2 điện tích điểm:
2 điện tích điểm q1, q2 đặt cách nhau một khoảng r thì thế năng tương tác
của q1 trong điện trường q2 bằng thế năng tương tác của q2 trong điện trường q1. W .q1. q2 t=1
= 12.(q1V1+q2V2) 4π ε0 εr
Năng lượng của hệ điện tích điểm: n W = 12∑ qiVi i=1
Năng lượng của vật dẫn cô lập:
Chia vật dẫn thành những điện tích điểm dq
Năng lượng của vật dẫn đó là: W = 12∫Vdq
Đối với vật cân bằng điện tích, V = const: q W = 1 2
2V∫dq = 12qV =1 2 C
(q = CV , C: điện dung vật dẫn)
Tính cường độ điện trường tại điểm M nằm bên trong mặt cầu (S ) tích điện Q, bán kính R
Áp dụng định lí O – G: ❑ θ  m=∫ D . d
S=D.4π r2=ρV Cảvật Q .43π r3 4 E = 3π R 3 ρV 4π ε 4π ε 0ε r2=Qr 0ε r2= 4π ε 0ε R3
Câu 4: Tính năng lượng điện trường của tụ điện phẳng tích điện? Suy ra công
thức mật độ năng lượng điện trường và năng lượng của một điện trường bất kì?
CHƯƠNG III: ĐIỆN MÔI
Câu 1: Thế nào là hiện tượng phân cực điện môi? Định nghĩa vector phân cực
điện môi? Tìm mối liên hệ giữa vector phân cực điện môi và mật độ điện tích
liên kết trên bề mặt điện môi?
-Hiện tượng trên thanh điện môi đặt trong điện trường có xuất hiện
điện tích gọi là hiện tượng phân cực điện môi.
-Giả sử trong thể tích của khổi điện môi đồng chất có n phân tử điện
môi. Gọi Pe là vector momen điện của phần tử thứ i.
Vector phân cực điện môi là một đại lượng đo bằng tổng momen điện
của các phần tử có trong 1 đơn vị V của khối điện môi. n ∑ Pei  i=1 Pe= ∆V
-Mối liên hệ giữa vector phân cực điện môi và mật độ điện tích liên kết trên bề mặt điện môi: σ=Pe. n
Mật độ điện tích liên kết xuất hiện trên mặt giới hạn của khổi điện môi
có giá trị bằng hình chiếu của vector phân cực điện môi trên pháp
tuyến của mặt giới hạn đó.
Câu 2: Viết CT tính vector cddt tổng hợp và vector cảm ứng điện trong chất
điện môi đồng chất và đẳng hướng? Thế nào là hiệu ứng áp điện thuận và nghịch?
-Giả sử ta có một điện trường đều Eo giữa 2 mặt phẳng song song vô
hạn, mang điện đều nhưng trái dấu, chất điện môi được lấp đầy
khoảng không gian giữa hai mặt phẳng.
Trên các mặt giới hạn xuất hiện điện tích liên kết. Điện tích liên kết
gây ra điện trường phụ E’
Theo nguyên lí chồng chất điện trường, vector cường độ điện trường E
tại một điểm bất kì bằng: E= E0 + E'
Chiếu lên phương E0 : E = E0−E' E'=σ ε0
Mặt khác: σ'=Pe.n = ε0χeE E’ = χe. E E0 E0 E = = 1+χeE ɛ
Vector cảm ứng điện theo định nghĩa: D=ɛ0ɛ E với = ɛ 1+χe
Do đó: : D=ɛ   0
E+¿ ɛ0χe E Mà ɛ  
0χe E=Pe nên 
D=ɛ0 E+Pe
-Hiệu ứng áp điện thuận:
Khi nén hoặc kéo dãn mẫu tinh thể điện môi theo những phương đặc
biệt trong tinh thể thì trên các mặt giới hạn của tinh thể có xuất hiện
những điện tích trái dấu, tương tự như những điện tích trong hiện tượng phân cực điện.
-Hiệu ứng áp điện nghịch:
Nếu ta đặt lên hai mặt của một tinh thể một hiệu điện thế thì nó sẽ bị
dãn hoặc nén. Nếu hiệu điện thế này là một hiệu điện thế xoay chiều
thì bản tinh thể sẽ bị dãn, nén liên tiếp và dao động theo tần số của
hiệu điện thế xoay chiều.
CHƯƠNG IV: TỪ TRƯỜNG KHÔNG ĐỔI
Câu 1: Trình bày các vấn đề sau
a) Dạng vi phân của định luật Ohm?
b) Khái niệm nguồn điện, thiết lập biểu thức suất điện động của nguồn điện
a) Dạng vi phân của định luật Ohm: tr114
b) Nguồn điện là nguồn tạo ra trường lực lạ tác dụng lên hạt điện dương một
lực đưa hạt điện dương chạy ngược chiều trường tĩnh (lập luận tương tự
đối với các hạt điện âm)
Thiết lập biểu thức suất điện động của nguồn điện: tr116
Câu 2: Phát biểu và viết biểu thức của định luật Bios – Savart – Laplace. Minh
họa bằng hình vẽ. Áp dụng tính cảm ứng từ gây bởi dòng điện thẳng tại điểm M
cách dòng điện một khoảng là r. Xét trường hợp dòng điện thẳng dài vô hạn
1. Định luật Bio – Xava – Laplace (tr130)
Vector cảm ứng điện từ d B do một phần tử dòng điện Id l gây ra tại điểm
M, cách phần tử một khoảng r là một vector có: - Gốc tại M
- Phương vuông góc với mặt phẳng chứa phần tử dòng điện Id l và điểm M.
- Chiều sao cho vector dl, r, dB theo thứ tự hợp thành một tam diện thuận
c) Độ lớn dB (cảm ứng từ) xác định bởi công thức: dB = μ0 4 μ π.Idlsinθ r2 2. Áp dụng : tr133
Câu 3: Tính cảm ứng từ gây bởi dòng điện tròn có cường độ I, bán kính R, tại
điểm M nằm trên trục của dòng điện, cách tâm O một khoảng h. Từ đó đưa ra
moment từ của dòng điện kín và xét 2 trường hợp giới hạn khi M trùng với tâm
O của dòng điện (h=0) và khi M ở rất xa dòng điện (h>>R) tr135
Câu 4: Phát biểu và viết biểu thức của định lý Ampere về lưu số của vector
cường độ từ trường. Ý nghĩa của định lý. Áp dụng công thức của định lý trên để
tính cảm ứng từ trong lòng cuộn dây dẫn hình xuyến và ống dây điện thẳng dài vô hạn
-Phát biểu: Lưu số của vector cường độ từ trường dọc theo một đường
cong kín (C) bất kì (một vòng) bằng tổng đại số cường độ của các
dòng điện xuyên qua diện tích giới hạn bởi đường cong đó: ❑ n
∮ H dl=∑ Ii (C) i=1
-Ý nghĩa: từ trường không phải là một trường thế mà là một trường
xoáy, đường sức từ trường khép kín trong không gian. -Áp dụng: tr152
Câu 5: Cho hạt điện có điện tích q, khối lượng m, bay vào một từ trường đều
cảm ứng từ B theo phương vuông góc với đường sức từ trường với vận tốc v.
Tìm phương trình chuyển động và phương trình quỹ đạo của hạt điện? tr163
CHƯƠNG V: HIỆN TƯỢNG CẢM ỨNG ĐIỆN TỪ
Câu 1: Trình bày hiện tượng cảm ứng điện từ? Phát biểu định luật Lenz về
chiều của dòng điện cảm ứng? Thiết lập biểu thức suất điện động cảm ứng.
-Khi từ thông gửi qua một mạch kín thay đổi thì trong mạch điện xuất
hiện một dòng điện (dòng điện cảm ứng) => hiện tượng cảm ứng điện từ.
-Định luật Lenz về chiều của dòng điện cảm ứng: Dòng điện cảm ứng
phải có chiều sao cho từ trường do nó sinh ra có tác dụng chống lại
nguyên nhân đã sinh ra nó.
-Biểu thức suất điện động cảm ứng (tr173): Suất điện động cảm ứng
luôn luôn bằng về trị số, nhưng trái dấu với tốc độ biến thiên của từ
thông gửi qua diện tích của mạch điện. EC=−d ϕm dt
Câu 2: Hiện tượng tự cảm là gì? Thiết lập biểu thức tính suất điện động tự cảm
và biểu thức tính độ tự cảm của ống dây thẳng dài vô hạn. Nêu một ví dụ thực
tế ứng dụng hiện tượng tự cảm.
-Hiện tượng tự cảm: Khi làm thay đổi cường độ dòng điện trong một
mạch điện để từ thông do chính dòng điện đó gửi qua diện tích của
mạch thay đổi thì trong mạch cũng xuất hiện dòng điện cảm ứng.
Dòng điện này do sự cảm ứng của dòng trong mạch sinh ra nên được
gọi là dòng điện tự cảm và hiện tượng này gọi là hiện tượng tự cảm.
-Thiết lập biểu thức tính suất điện động tự cảm (tr180)
-VD: Ứng dụng của hiện tượng tự cảm trong tôi kim loại ở lớp bề mặt.
Nhiều chi tiết máy như biên, trục máy, bánh răng khía.. cần đạt yêu
cầu kĩ thuật là : bề mặt phải thật cứng bên trong vẫn còn độ dẻo thích
hợp, do đó, cho dòng điện cao tần chạy qua một cuộn dây điện bên
trong có đặt chi tiết máy cần tôi. Dòng điện cao tần sinh ra trong chi
tiết máy, những dòng điện cảm ứng biến đổi với tần số cao tần. Do
hiện tượng tự cảm, những dòng điện này chỉ chạy ở lớp bề mặt của chi
tiết máy. Khi lớp bề mặt này đã được nung đỏ đến mức cần thiết, ta
nhúng chi tiết máy vào nước tôi và như vậy, ta được một lớp mặt
ngoài cứng còn bên trong chi tiết máy vẫn dẻo.
Câu 3: Tìm biểu thức tính năng lượng từ trường của ống dây điện thẳng dài, từ
đó suy ra năng lượng của từ trường bất kỳ. tr188
CHƯƠNG VII: TRƯỜNG ĐIỆN TỪ
Câu 1: Phát biểu luận điểm I của Maxwell. Phân biệt giữa điện trường tĩnh và
điện trường xoáy về nguồn gốc phát sinh và tính chất cơ bản. Thiết lập phương
trình Maxwell – Faraday dạng tích phân?
-Luận điểm 1 của Maxwell: Bất kì một từ trường nào biến đổi theo thời
gian cũng sinh ra một điện trường xoáy.
-Phân biệt điện trường tĩnh và điện trường xoáy:
oĐiện trường tĩnh: có đường sức là các đường cong hở, công của
điện trường tĩnh trong sự dịch chuyển hạt điện theo đường cong kín bằng 0.
oĐiện trường xoáy: có đường sức là các đường cong kín, công
của điện trường trong sự dịch chuyển hạt điện theo đường cong kín khác 0. -Thiết lập: tr224
Câu 2: Phát biểu luận điểm II của Maxwell. Khái niệm dòng điện dịch. So sánh
dòng điện dịch và dòng điện dẫn. Thiết lập phương trình Maxwell – Ampere dạng tích phân?
-Luận điểm 2 của Maxwell: Bất kì 1 điện trường nào biến đổi theo thời
gian cũng sinh ra một từ trường.
-Dòng điện dịch: là dòng điện tương đương với điện trường biến đổi
theo thời gian về phương diện sinh ra từ trường.
-Dòng điện dẫn: là dòng chuyển dời có hường của các hạt mang điện. Dòng điện dịch Dòng điện dẫn
Tương đương với điện trường
Là dòng chuyển dời có hường
biến đổi theo thời gian về của các hạt mang điện
phương diện sinh ra từ trường tồn tại trong chân không Không gây tỏa nhiệt Gây tỏa nhiệt Jun Len-xơ
Không chịu tác dụng của từ
Chịu tác dụng của từ trường bên trường bên ngoài ngoài
Sinh ra từ trường, điện trường Sinh ra từ trường
thay đổi, sinh ra từ trường thay đổi theo thời gian
-Thiết lập công thức Maxwell – Ampere dạng tích phân: tr229
CHƯƠNG BỔ SUNG: TRÌNH BÀY
Câu 1: Thế nào là chất thuận từ, chất nghịch từ, chất sắt từ, vector từ độ j. Xác
định công thức tính từ trường tổng hợp trong lòng các chất thuận từ trong môi
trường đồng tính, đẳng hướng.
-Chất thuận từ: những chất này khi bị từ hóa sẽ sinh ra một từ trường
phụ B' hướng cùng chiều với từ trường ban đầu Bo . Do đó, từ trường
tổng hợp B trong thuận từ lớn hơn từ trường ban đầu Bo.
-Chất nghịch từ: những chất này khi bị từ hóa sẽ sinh ra một từ trường
phụ B' hướng cùng ngược với từ trường ban đầu Bo. Do đó, từ trường
tổng hợp B trong thuận từ nhỏ hơn từ trường ban đầu Bo.
-Sắt từ: từ trường phụ B' do sắt từ bị từ hóa sinh ra cùng hướng cùng
chiều với từ trường ban đầu Bo . Từ trường phụ B' có thể lớn hơn hơn
từ trường ban đầu Bo hàng chục nghìn lần còn từ trường phụ B' của
nghịch từ và thuận từ rất nhỏ so với từ trường ban đầu Bo.
-Vector từ độ j: tr201 -Công thức: tr208
Câu 2: Mạch RC
Câu 3: Mạch từ, hiệu ứng Hốp-kin-sơn tr154
Câu 4: Bộ lọc vận tốc, hiệu ứng Hall
Câu 5: Định luật Kiefhoff tr120
Câu 6: Phương pháp ảnh điện tr80