Tổng hợp công thức Hình học 12

CÁC KHỐI ĐA DIỆN ĐỀU Hình vuông cạnh a
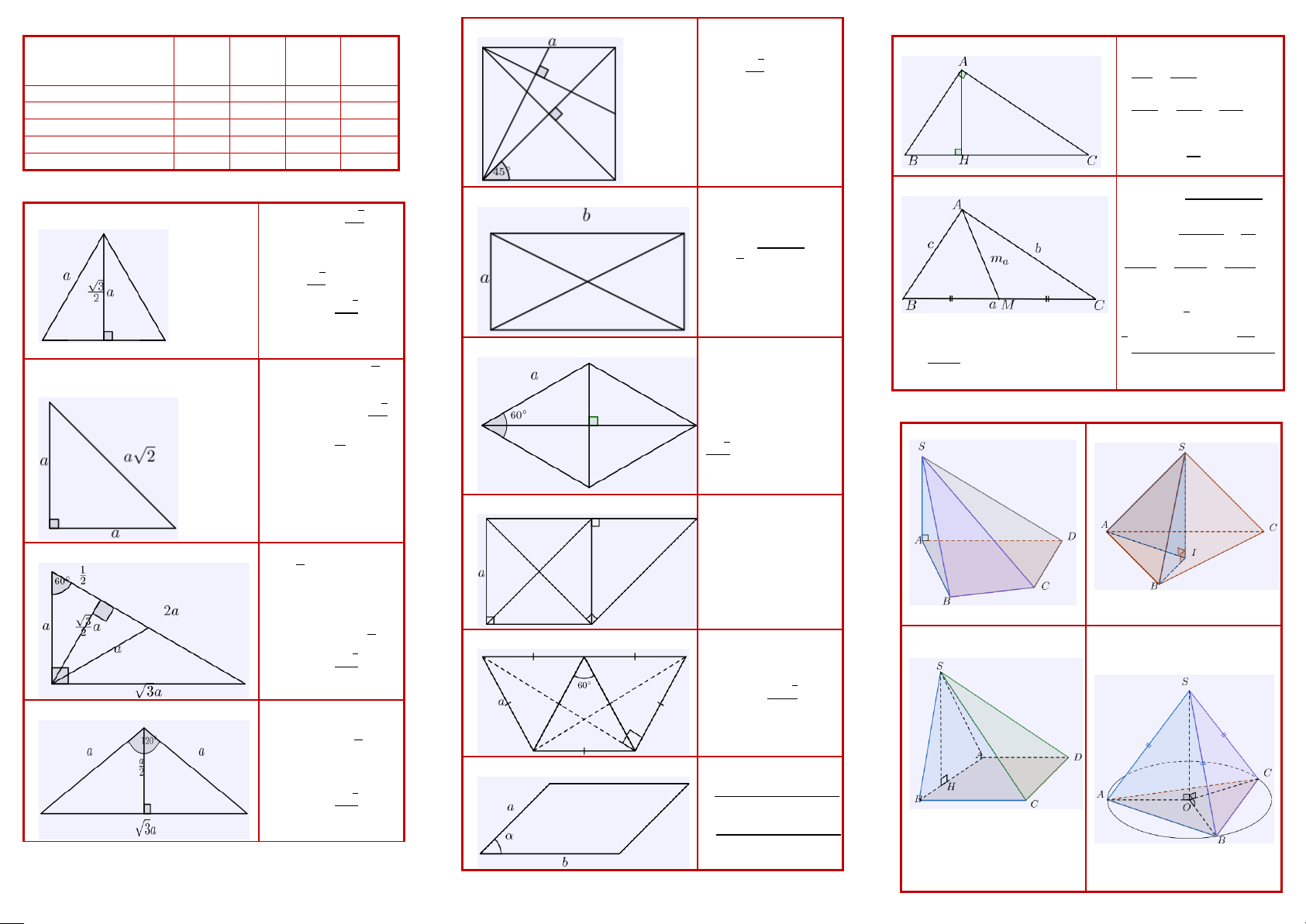
HỆ THỨC LƯỢNG TRONG TAM GIÁC Tên (m mặt) Loại Số Số Số mp
Diện tích: 𝒂𝒂𝟐𝟐 Tam giác vuông
𝑩𝑩𝑩𝑩. 𝑩𝑩𝑩𝑩 = 𝑩𝑩𝑨𝑨𝟐𝟐 {p;q} đỉnh cạnh đối
𝑩𝑩𝑩𝑩 𝑩𝑩𝑨𝑨𝟐𝟐 =mp/q =mp/2 xứng
𝑹𝑹đ = 𝒂𝒂√𝟐𝟐 𝟐𝟐 Tứ diện đều {3;3} 4 6 6
𝑩𝑩𝑩𝑩 = 𝑩𝑩𝑩𝑩𝟐𝟐 𝟏𝟏 𝟏𝟏 𝟏𝟏 Hình lập phương {4;3} 8 12 9 Bát diện đều {3;4} 6 12 9
𝑨𝑨𝑩𝑩𝟐𝟐 = 𝑨𝑨𝑩𝑩𝟐𝟐 + 𝑨𝑨𝑩𝑩𝟐𝟐
Thập nhị (12) mặt đều {5;3} 20 30 15
𝑨𝑨𝑩𝑩. 𝑨𝑨𝑩𝑩 = 𝑨𝑨𝑩𝑩. 𝑩𝑩𝑩𝑩
Nhị thập (20) mặt đều {3;5} 12 30 15
𝐭𝐭𝐭𝐭𝐬𝐬 𝑩𝑩 = 𝑨𝑨𝑩𝑩 , v.v... 𝑨𝑨𝑩𝑩
CÁC LOẠI ĐÁY THƯỜNG GẶP Tam giác thường
Đáy là hình chữ nhật
𝒃𝒃𝟐𝟐 + 𝒄𝒄𝟐𝟐 − 𝒂𝒂𝟐𝟐 𝒂𝒂 × 𝒃𝒃 Diện tích: ab
𝐜𝐜𝐜𝐜𝐬𝐬 𝑨𝑨 =
Tam giác đều cạnh a 𝟐𝟐𝒃𝒃𝒄𝒄
Đường cao: 𝒂𝒂√𝟑𝟑
Bán kính đường tròn
𝒃𝒃𝟐𝟐 + 𝒄𝒄𝟐𝟐 𝒂𝒂𝟐𝟐 𝟐𝟐 ngoại tiếp: 𝒎𝒎𝟐𝟐 = Bán kính đường 𝟏𝟏 𝒂𝒂 𝟐𝟐 − 𝟒𝟒 tròn ngoại tiếp: � 𝒂𝒂 𝒃𝒃 𝒄𝒄
𝟐𝟐 𝒂𝒂𝟐𝟐 + 𝒃𝒃𝟐𝟐 𝑹𝑹
𝐬𝐬𝐬𝐬𝐬𝐬 𝑨𝑨 = 𝐬𝐬𝐬𝐬𝐬𝐬 𝑩𝑩 = 𝐬𝐬𝐬𝐬𝐬𝐬 𝑩𝑩
đ = 𝒂𝒂√𝟑𝟑 Th 𝟑𝟑 Th
= 𝟐𝟐𝑹𝑹đ
Diện tích: 𝒂𝒂𝟐𝟐√𝟑𝟑
Diện tích: 𝟏𝟏 𝒂𝒂.𝒉𝒉 𝟒𝟒 𝒂𝒂 = ầy ầ
𝒓𝒓: bán kính đường tròng nội tiếp. 𝟐𝟐 y L
𝟏𝟏 𝒃𝒃𝒄𝒄𝐬𝐬𝐬𝐬𝐬𝐬 𝑨𝑨 = 𝒑𝒑.𝒓𝒓 = 𝒂𝒂𝒃𝒃𝒄𝒄 = L
Hình thoi có góc 𝟔𝟔𝟎𝟎𝒐𝒐 Hình ghép của hai
𝑹𝑹đ: Bán kính đường tròn ngoại tiếp 𝟐𝟐 𝟒𝟒𝑹𝑹đ
Tam giác vuông cân cạnh bên bằng
�𝒑𝒑(𝒑𝒑 − 𝒂𝒂)(𝒑𝒑 − 𝒃𝒃)(𝒑𝒑 − 𝒄𝒄) Cạnh huyền: tam giác đều.
𝒑𝒑 = 𝒂𝒂+𝒃𝒃+𝒄𝒄: nửa chu vi 𝒂𝒂√𝟐𝟐 𝟐𝟐 ụ ụ a c T Hình ghép của hai Bán kính đường c T tam giác cân 120.
tròn ngoại tiếp: 𝒂𝒂√𝟐𝟐
Diện tích bằng ½ tích
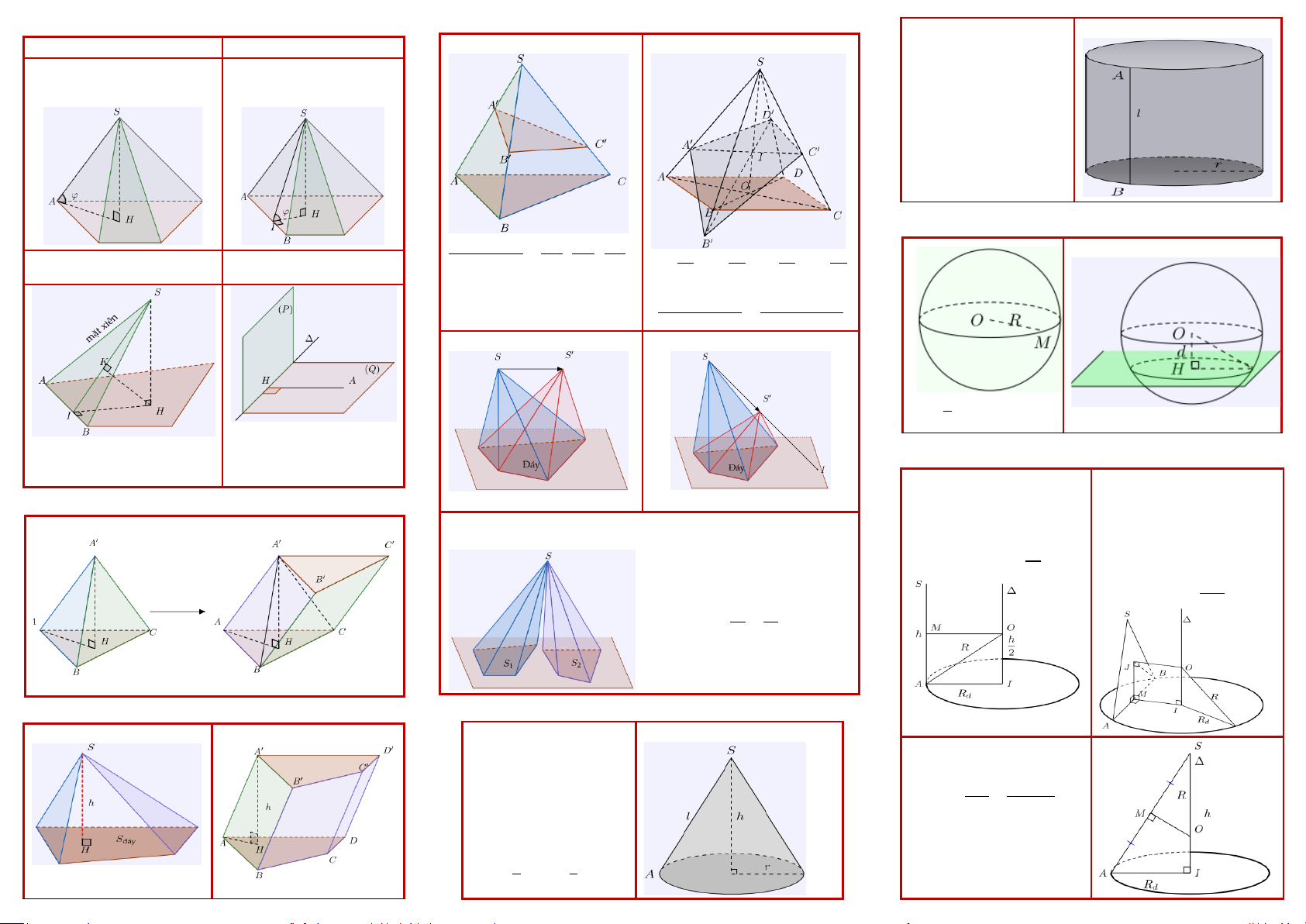
CÁC TRƯỜNG HỢP HÌNH CHÓP THƯỜNG GẶP 𝟐𝟐 rí r hai đường chéo = í
Cạnh bên vuông đáy T T
Hai mặt cùng vuông với đáy
Diện tích: 𝒂𝒂𝟐𝟐 𝟐𝟐
𝒂𝒂𝟐𝟐√𝟑𝟑. u 𝟐𝟐 y u ê y n ên
Hình thang vuông đặc biệt Ghép bởi 1 hình – – vuông và 1 tam giác 0 0 vuông cân. 9 9
Tam giác vuông 𝟔𝟔𝟎𝟎𝒐𝒐 Tỉ lệ 3 cạnh: 72
Ghép bởi 2 tam giác 72
𝟏𝟏: √𝟑𝟑: 𝟐𝟐 vuông cân. 1 1 Bán kính đường 77 77
tròn ngoại tiếp: 𝒂𝒂
Đường cao là giao tuyến của 71 71
Đường cao là cạnh bên đó.
Đường cao ứng với 7 hai mặt đó. 7
cạnh huyền: 𝒂𝒂√𝟑𝟑/𝟐𝟐
Nửa lục giác đều Là 3 tam giác đều
Mặt bên vuông với đáy
Các cạnh bên bằng nhau ghép lại.
(cạnh bên cùng tạo với đáy
Diện tích: 𝒂𝒂𝟐𝟐√𝟑𝟑 góc bằng nhau). 𝟐𝟐 𝑹𝑹đ = 𝒂𝒂
Diện tích: 𝟑𝟑𝒂𝒂𝟐𝟐√𝟑𝟑
Tam giác cân có đỉnh 𝟏𝟏𝟐𝟐𝟎𝟎𝒐𝒐
Đường cao = ½ cạnh 𝟒𝟒 bên. Đường chéo vuông
góc với cạnh bên.
Cạnh đáy = √𝟑𝟑 cạnh bên. Hình bình hành
Diện tích: 𝒂𝒂𝒃𝒃 𝐬𝐬𝐬𝐬𝐬𝐬 𝜶𝜶 𝑹𝑹đ = 𝒂𝒂
Đường chéo ngắn:
Diện tích: 𝒂𝒂𝟐𝟐√𝟑𝟑
√𝒂𝒂𝟐𝟐 + 𝒃𝒃𝟐𝟐 − 𝟐𝟐𝒂𝒂𝒃𝒃 𝐜𝐜𝐜𝐜𝐬𝐬 𝜶𝜶 𝟒𝟒 Đường chéo dài
Đường cao là đường cao hạ
từ đỉnh S của tam giác mặt
�𝒂𝒂𝟐𝟐 + 𝒃𝒃𝟐𝟐 + 𝟐𝟐𝒂𝒂𝒃𝒃 𝐜𝐜𝐜𝐜𝐬𝐬 𝜶𝜶 bên đó.
Chân đường cao trùng với
tâm đường tròn ngoại tiếp đáy.
GÓC CƠ BẢN VÀ KHOẢNG CÁCH CƠ BẢN TỈ SỐ THỂ TÍCH - Thiết diện qua trục: Khối trụ
Góc giữa cạnh bên và đáy
Góc giữa mặt bên và đáy Chóp tam giác
Chóp hình bình hành
Hình chữ nhật 𝟐𝟐𝒓𝒓 × 𝒉𝒉
Kẻ từ chân đường cao tới giao Kẻ từ chân đường cao tới - Thiết diện song song
điểm của cạnh bên với đáy.
giao tuyến của mặt bên với
trục là HCN: dây cung × 𝒉𝒉 Nối với S đáy. Nối với S
- Quan hệ: 𝒉𝒉 = 𝒍𝒍
- Diện tích xq: 𝑺𝑺𝒙𝒙𝒙𝒙 = 𝟐𝟐𝝅𝝅𝒓𝒓𝒍𝒍 - Diện tích toàn phần:
𝑺𝑺𝒕𝒕𝒑𝒑 = 𝟐𝟐𝝅𝝅𝒓𝒓𝒍𝒍 + 𝟐𝟐𝝅𝝅𝒓𝒓𝟐𝟐 - Thể tích
𝑽𝑽 = 𝑺𝑺đ. 𝒉𝒉 = 𝝅𝝅𝒓𝒓𝟐𝟐𝒉𝒉 KHỐI CẦU
𝑽𝑽(𝑺𝑺. 𝑨𝑨′𝑩𝑩′𝑩𝑩′) 𝑺𝑺𝑨𝑨′ 𝑺𝑺𝑩𝑩′ 𝑺𝑺𝑩𝑩′
Mặt phẳng cắt (S) theo đtr (H;r)
Khoảng cách từ chân đường
Khoảng cách từ điểm thuộc
𝑽𝑽(𝑺𝑺. 𝑨𝑨𝑩𝑩𝑩𝑩) = 𝑺𝑺𝑨𝑨 ⋅ 𝑺𝑺𝑩𝑩 ⋅ 𝑺𝑺𝑩𝑩
𝒂𝒂 = 𝑺𝑺𝑨𝑨 ; 𝒃𝒃 = 𝑺𝑺𝑩𝑩 ; 𝒄𝒄 = 𝑺𝑺𝑩𝑩 ; 𝒅𝒅 = 𝑺𝑺𝑺𝑺
cao đến mặt xiên.
đáy đến mặt thẳng đứng. 𝑺𝑺𝑨𝑨′ 𝑺𝑺𝑩𝑩′ 𝑺𝑺𝑩𝑩′ 𝑺𝑺𝑺𝑺′
Có: 𝒂𝒂 + 𝒄𝒄 = 𝒃𝒃 + 𝒅𝒅 Th
𝑽𝑽(𝑺𝑺𝑨𝑨′𝑩𝑩′𝑩𝑩′𝑺𝑺′) 𝒂𝒂 + 𝒃𝒃 + 𝒄𝒄 + 𝒅𝒅 Th
𝑽𝑽(𝑺𝑺𝑨𝑨𝑩𝑩𝑩𝑩𝑺𝑺) =
𝟒𝟒𝒂𝒂𝒃𝒃𝒄𝒄𝒅𝒅 ầy L ầ
Dịch chuyển đinh song song
Dịch đỉnh không song song y L ụ ụ c T c T 𝟒𝟒 𝑽𝑽 = 𝟐𝟐
𝑹𝑹𝟐𝟐 = 𝒓𝒓𝟐𝟐 + 𝒅𝒅
𝟑𝟑 𝝅𝝅𝑹𝑹𝟑𝟑; 𝑺𝑺 = 𝟒𝟒𝝅𝝅𝑹𝑹𝟐𝟐 �𝑶𝑶;(𝑷𝑷)� r rí Kẻ vuông hai nhát: í
Từ điểm đó kẻ vuông góc T T
- Kẻ HI vuông với giao tuyến.
với giao tuyến của mặt đó
BA CÔNG THỨC BÁN KÍNH MẶT CẦU NGOẠI TIẾP
- Kẻ HK vuông góc với SI với đáy. u u y y
Chóp hoặc lăng trụ có cạnh
Chóp hoặc lăng trụ có mặt ê ê KHỐI LĂNG TRỤ n 𝑽𝑽 ′
bên vuông góc với đáy
bên vuông với đáy 𝑺𝑺 = 𝑽𝑽 n 𝑺𝑺
𝑽𝑽𝑺𝑺/𝑽𝑽𝑺𝑺′ = 𝑺𝑺𝑺𝑺/𝑺𝑺′𝑺𝑺 𝑹𝑹 𝑹𝑹 –
Tách khối chóp ra khỏi lăng trụ –
Dịch chuyển đáy: Khi thấy đáy nằm trong một mặt phẳng có thể
đ: Là bán kính đường tròn
𝒃𝒃: là bán kính đường tròn 0 mở rộng. ngoại tiếp đáy.
ngoại tiếp mặt bên. 0 9 9 𝒉𝒉𝟐𝟐
𝑮𝑮𝑮𝑮: Là giao tuyến của mặt 72 72
𝑹𝑹𝟐𝟐 = 𝑹𝑹𝟐𝟐đ + 𝟒𝟒 bên và đáy. 1 1 𝑮𝑮𝑮𝑮𝟐𝟐 77 77
𝑹𝑹𝟐𝟐 = 𝑹𝑹𝟐𝟐 𝟐𝟐 đ + 𝑹𝑹𝒃𝒃 − 71 𝑽𝑽 𝟒𝟒 𝟏𝟏 𝑺𝑺𝟏𝟏 71 7 𝑽𝑽 = 𝟐𝟐 𝑺𝑺𝟐𝟐 7
Làm việc với lăng trụ chỉ cần làm việc với hình chóp.
THỂ TÍCH KHỐI CHÓP VÀ LĂNG TRỤ
KHỐI NÓN VÀ KHỐI TRỤ
Thể tích khối chóp
Thể tích lăng trụ
- Thiết diện qua trục: 𝑺𝑺𝑨𝑨𝑩𝑩 Khối nón
- Góc ở đỉnh: 𝑨𝑨𝑺𝑺𝑩𝑩 �
Chóp có cạnh bên bằng nhau
- Quan hệ: 𝒍𝒍𝟐𝟐 = 𝒉𝒉𝟐𝟐 + 𝒓𝒓𝟐𝟐 (nón) - Diện tích xq: 𝑺𝑺
𝑺𝑺𝑨𝑨𝟐𝟐 𝒉𝒉𝟐𝟐 + 𝑹𝑹𝟐𝟐
𝒙𝒙𝒙𝒙 = 𝝅𝝅. 𝒓𝒓. 𝒍𝒍 𝑹𝑹 = đ - Diện tích toàn phần: 𝟐𝟐𝒉𝒉 = 𝟐𝟐𝒉𝒉 𝑺𝑺
Cạnh bên bình chia hai lần
𝒕𝒕𝒑𝒑 = 𝝅𝝅𝒓𝒓𝒍𝒍 + 𝝅𝝅𝒓𝒓𝟐𝟐 đường cao. - Thể tích 𝟏𝟏 𝟏𝟏
𝑽𝑽 = 𝟏𝟏/𝟑𝟑. 𝑺𝑺đ. 𝒉𝒉 𝑽𝑽 = 𝑽𝑽 = 𝑺𝑺
𝟑𝟑 𝑺𝑺đ. 𝒉𝒉 = 𝟑𝟑 𝝅𝝅𝒓𝒓𝟐𝟐𝒉𝒉 đ. 𝒉𝒉
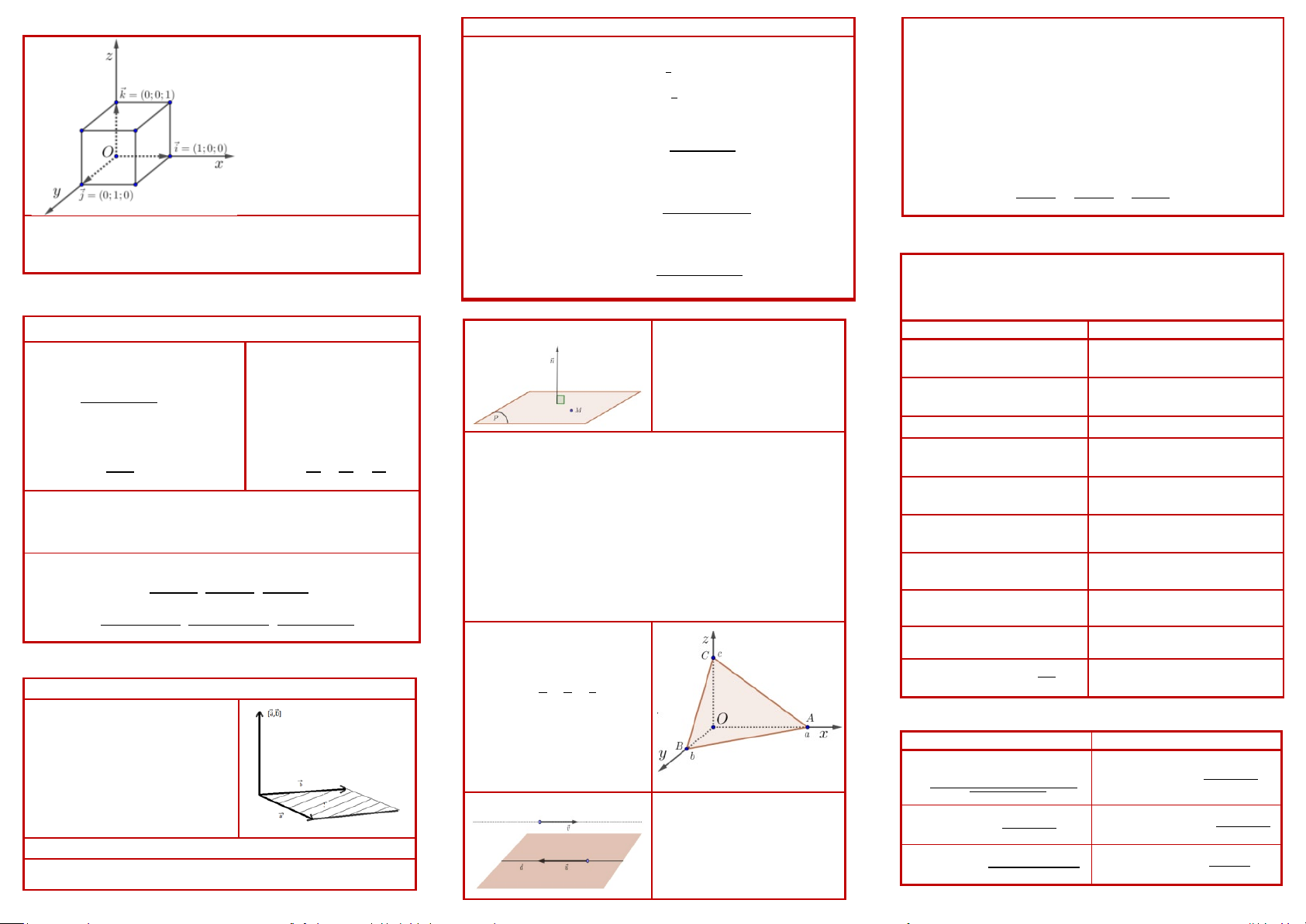
TỌA ĐỘ VECTOR VÀ ĐIỂM TRONG KHÔNG GIAN
Ứng dụng tích có hướng của hai vector
Đường thẳng (d) xác định bởi cặp (𝑨𝑨, 𝒒𝒒�⃗) (ký hiệu
- 3 vector đơn vị: 𝒊𝒊⃗, 𝒋𝒋⃗, 𝒌𝒌�⃗ độ
Điều kiện 𝒂𝒂�⃗ , 𝒃𝒃�⃗, 𝒄𝒄�⃗ đồng phẳng: �𝒂𝒂�⃗, 𝒃𝒃�⃗�. 𝒄𝒄�⃗ = 𝟎𝟎
(𝒅𝒅)~(𝑨𝑨, 𝒒𝒒�⃗)) nghĩa là:
dài 1 và đôi một vuông Diện tích tam giác ���⃗ ���⃗ góc.
𝐀𝐀𝑩𝑩𝑩𝑩: 𝑺𝑺𝑨𝑨𝑩𝑩𝑩𝑩 = 𝟏𝟏 ��𝑨𝑨𝑩𝑩, 𝑨𝑨𝑩𝑩�� 𝟐𝟐
�𝒙𝒙𝒒𝒒𝒂𝒂 𝑨𝑨(𝒙𝒙𝟎𝟎; 𝒚𝒚𝟎𝟎; 𝒛𝒛𝟎𝟎)
𝒒𝒒�⃗ = (𝒂𝒂; 𝒃𝒃; 𝒄𝒄)
- Trục Oz: trục cao.
Thể tích tứ diện 𝑨𝑨𝑩𝑩𝑩𝑩𝑺𝑺: 𝑽𝑽𝑨𝑨𝑩𝑩𝑩𝑩𝑺𝑺 = 𝟏𝟏 ��𝑨𝑨��𝑩𝑩
��⃗, 𝑨𝑨��𝑩𝑩�⃗�. 𝑨𝑨��𝑺𝑺 ��⃗� 𝟔𝟔
Phương trình tham số: - Tọa độ vector:
Khoảng cách từ 𝑴𝑴 đến đường phẳng (AB):
𝒙𝒙 = 𝒙𝒙𝟎𝟎 + 𝒂𝒂𝒕𝒕
𝒂𝒂�⃗ = (𝒙𝒙; 𝒚𝒚; 𝒛𝒛) ⇔ ��𝑨𝑨��𝑩𝑩
��⃗, 𝑨𝑨��𝑴𝑴 ��⃗��
�𝒚𝒚 = 𝒚𝒚𝟎𝟎 + 𝒃𝒃𝒕𝒕 (𝒕𝒕 ∈ ℝ )
𝒂𝒂�⃗ = 𝒙𝒙 𝒊𝒊⃗ + 𝒚𝒚 𝒋𝒋⃗ + 𝒛𝒛 𝒌𝒌�⃗
𝒅𝒅�𝑴𝑴, (𝑨𝑨𝑩𝑩)� = 𝒛𝒛 = 𝒛𝒛 �𝑨𝑨��𝑩𝑩 ��⃗� 𝟎𝟎 + 𝒄𝒄𝒕𝒕
- Tọa độ của điểm 𝑨𝑨 chính
Phương trình chính tắc khi Khoảng cách từ
𝒂𝒂𝒃𝒃𝒄𝒄 ≠ 𝟎𝟎:
𝑴𝑴 đến mặt phẳng (𝑨𝑨𝑩𝑩𝑩𝑩):
là tọa độ 𝑶𝑶 ��𝑨𝑨 ��⃗.
𝒙𝒙 − 𝒙𝒙𝟎𝟎 𝒚𝒚 − 𝒚𝒚𝟎𝟎 𝒛𝒛 − 𝒛𝒛𝟎𝟎 ��𝑨𝑨��𝑩𝑩
��⃗, 𝑨𝑨��𝑩𝑩�⃗�. 𝑨𝑨��𝑴𝑴 ��⃗�
𝒅𝒅�𝑴𝑴, (𝑨𝑨𝑩𝑩𝑩𝑩)� = 𝒂𝒂 = 𝒃𝒃 = 𝒄𝒄
Cho 𝑨𝑨(𝒂𝒂; 𝒃𝒃; 𝒄𝒄). Tọa độ hình chiếu vuông góc của 𝑨𝑨 lên: ��𝑨𝑨��𝑩𝑩
��⃗, 𝑨𝑨��𝑩𝑩�⃗��
𝑶𝑶𝒙𝒙: là (𝒂𝒂; 𝟎𝟎; 𝟎𝟎) 𝑶𝑶𝒚𝒚: là (𝟎𝟎; 𝒃𝒃; 𝟎𝟎) 𝑶𝑶𝒛𝒛: là (𝟎𝟎; 𝟎𝟎; 𝒄𝒄)
Khoảng cách hai đường chéo nhau 𝑨𝑨𝑩𝑩, 𝑩𝑩𝑺𝑺:
VỊ TRÍ TƯƠNG ĐỐI
(𝑶𝑶𝒙𝒙𝒚𝒚): là (𝒂𝒂; 𝒃𝒃; 𝟎𝟎) (𝑶𝑶𝒙𝒙𝒛𝒛): là (𝒂𝒂; 𝟎𝟎; 𝒄𝒄) (𝑶𝑶𝒚𝒚𝒛𝒛): là (𝟎𝟎; 𝒃𝒃; 𝒄𝒄) ��𝑨𝑨��𝑩𝑩
��⃗, 𝑩𝑩𝑺𝑺�. 𝑨𝑨��𝑩𝑩�⃗�
Cho các đường 𝒅𝒅𝟏𝟏~(𝑨𝑨𝟏𝟏, 𝒒𝒒�𝟏𝟏�⃗), 𝒅𝒅𝟐𝟐~(𝑨𝑨𝟐𝟐, 𝒒𝒒�𝟐𝟐�⃗), 𝒅𝒅~(𝑨𝑨, 𝒒𝒒�⃗)
𝒅𝒅(𝑨𝑨𝑩𝑩, 𝑩𝑩𝑺𝑺) = ��𝑨𝑨��𝑩𝑩
��⃗, 𝑩𝑩��𝑺𝑺 ��⃗�� Cho các mặt phẳng Th Th
CÔNG THỨC TỌA ĐỘ PHÉP TOÁN
(𝑷𝑷)~(𝑩𝑩, 𝒏𝒏�⃗), (𝑷𝑷 ��⃗), (𝑷𝑷 ��⃗)
PHƯƠNG TRÌNH MẶT PHẲNG – ĐƯỜNG THẲNG
𝟏𝟏)~(𝑩𝑩𝟏𝟏, 𝒏𝒏𝟏𝟏
𝟐𝟐)~(𝑩𝑩𝟐𝟐, 𝒏𝒏𝟐𝟐
Cho 𝒂𝒂�⃗ = (𝒙𝒙 ầ ầ
𝟏𝟏; 𝒚𝒚𝟏𝟏; 𝒛𝒛𝟏𝟏) và 𝒃𝒃
�⃗ = (𝒙𝒙𝟐𝟐;𝒚𝒚𝟐𝟐;𝒛𝒛𝟐𝟐) y L
Vector pháp tuyến 𝒏𝒏�⃗
Chọn 1 vector pháp tuyến Vị trí Điều kiện y L
𝒂𝒂�⃗ ± 𝒃𝒃�⃗ = (𝒙𝒙
- Nếu biết 𝒏𝒏�⃗ ∥ 𝒂𝒂�⃗:
��⃗ ∥ 𝒒𝒒��⃗
𝟏𝟏 ± 𝒙𝒙𝟐𝟐; 𝒚𝒚𝟏𝟏 ± 𝒚𝒚𝟐𝟐; 𝒛𝒛𝟏𝟏 ± 𝒅𝒅 𝟐𝟐 𝒛𝒛
𝒙𝒙𝟏𝟏 = 𝒙𝒙𝟐𝟐
𝟏𝟏 ≡ 𝒅𝒅𝟐𝟐 ⇔ �𝒒𝒒𝟏𝟏 𝑨𝑨 𝟐𝟐)
Chọn 𝒏𝒏�⃗ = 𝒂𝒂�⃗ 𝟏𝟏 ∈ 𝒅𝒅𝟐𝟐 ụ ụ
𝒌𝒌 𝒂𝒂�⃗ = (𝒌𝒌𝒙𝒙
𝒂𝒂�⃗ = 𝒃𝒃�⃗ ⇔ �𝒚𝒚𝟏𝟏 = 𝒚𝒚𝟐𝟐
𝟏𝟏; 𝒌𝒌𝒚𝒚𝟏𝟏; 𝒌𝒌𝒛𝒛𝟏𝟏) 𝒛𝒛 c T
- Nếu biết 𝒏𝒏�⃗ ⊥ 𝒂𝒂�⃗ và 𝒏𝒏�⃗ ⊥ 𝒃𝒃�⃗: c T
��⃗ ∥ 𝒒𝒒�𝟐𝟐�⃗ 𝟏𝟏 = 𝒛𝒛𝟐𝟐
𝒅𝒅𝟏𝟏 ∥ 𝒅𝒅𝟐𝟐 ⇔ �𝒒𝒒𝟏𝟏 𝑨𝑨
|𝒂𝒂�⃗| = �𝒙𝒙𝟐𝟐 𝟐𝟐 𝟐𝟐 𝒙𝒙 Chọn 𝟏𝟏 ∉ 𝒅𝒅𝟐𝟐
𝟏𝟏 + 𝒚𝒚𝟏𝟏 + 𝒛𝒛𝟏𝟏
𝟏𝟏 = 𝒌𝒌𝒙𝒙𝟐𝟐
𝒏𝒏�⃗ ∥ �𝒂𝒂�⃗, 𝒃𝒃�⃗�
𝒂𝒂�⃗ ∥ 𝒃𝒃�⃗ ⇔ �𝒚𝒚 r r 𝒅𝒅
��⃗ ⊥ 𝒒𝒒��⃗
𝟏𝟏 = 𝒌𝒌𝒚𝒚𝟐𝟐
𝟏𝟏 ⊥ 𝒅𝒅𝟐𝟐 ⇔ 𝒒𝒒𝟏𝟏 𝟐𝟐 í í
𝒂𝒂�⃗ ⋅ 𝒃𝒃�⃗ = 𝒙𝒙 T
Mặt phẳng (P) xác định bởi cặp ( T
𝟏𝟏𝒙𝒙𝟐𝟐 + 𝒚𝒚𝟏𝟏𝒚𝒚𝟐𝟐 + 𝒛𝒛𝟏𝟏 𝒛𝒛𝟐𝟐 𝒛𝒛
𝑨𝑨, 𝒏𝒏�⃗) (ký hiệu (𝑷𝑷)~(𝑨𝑨, 𝒏𝒏�⃗))
𝟏𝟏 = 𝒌𝒌𝒛𝒛𝟐𝟐
��⃗ ∥ 𝒏𝒏��⃗ 𝒙𝒙 𝒚𝒚 𝒛𝒛 nghĩa là (𝑷𝑷 𝟐𝟐
𝟏𝟏) ≡ (𝑷𝑷𝟐𝟐) ⇔ � 𝒏𝒏𝟏𝟏
𝐜𝐜𝐜𝐜𝐬𝐬�𝒂𝒂�⃗, 𝒃𝒃�⃗� = 𝒂𝒂�⃗⋅𝒃𝒃�⃗
⇔ 𝟏𝟏 = 𝟏𝟏 = 𝟏𝟏 u u
𝑩𝑩𝟏𝟏 ∈ (𝑷𝑷𝟐𝟐)
|𝒂𝒂�⃗|⋅�𝒃𝒃�⃗� 𝒙𝒙 y y 𝟐𝟐
𝒚𝒚𝟐𝟐 𝒛𝒛𝟐𝟐 ê
�𝒙𝒙𝒒𝒒𝒂𝒂 𝑨𝑨(𝒙𝒙𝟎𝟎; 𝒚𝒚𝟎𝟎; 𝒛𝒛𝟎𝟎) ê
��⃗ ∥ 𝒏𝒏��⃗ Cho 𝑨𝑨(𝒙𝒙 ( n n 𝑷𝑷 𝟐𝟐
𝑨𝑨; 𝒚𝒚𝑨𝑨; 𝒛𝒛𝑨𝑨); 𝑩𝑩(𝒙𝒙𝑩𝑩; 𝒚𝒚𝑩𝑩; 𝒛𝒛𝑩𝑩); 𝑩𝑩(𝒙𝒙𝑩𝑩; 𝒚𝒚𝑩𝑩; 𝒛𝒛𝑩𝑩).
𝒏𝒏�⃗ = (𝒂𝒂; 𝒃𝒃; 𝒄𝒄)
𝟏𝟏) ∥ (𝑷𝑷𝟐𝟐) ⇔ � 𝒏𝒏𝟏𝟏 𝑩𝑩 𝑴𝑴(𝒙𝒙
𝟏𝟏 ∉ (𝑷𝑷𝟐𝟐)
𝑴𝑴; 𝒚𝒚𝑴𝑴; 𝒛𝒛𝑴𝑴) là trung điểm của 𝐀𝐀𝑩𝑩. – Phương trình: – 𝑮𝑮(𝒙𝒙
𝑮𝑮; 𝒚𝒚𝑮𝑮; 𝒛𝒛𝑮𝑮) là trọng tâm tam giác 𝑨𝑨𝑩𝑩𝑩𝑩. 0 𝒂𝒂(𝒙𝒙 − 𝒙𝒙 0
𝟎𝟎) + 𝒃𝒃(𝒚𝒚 − 𝒚𝒚𝟎𝟎) + 𝒄𝒄(𝒛𝒛 − 𝒛𝒛𝟎𝟎) = 𝟎𝟎
(𝑷𝑷𝟏𝟏) ⊥ (𝑷𝑷𝟐𝟐)
⇔ 𝒏𝒏�⃗ ⊥ 𝒏𝒏�𝟐𝟐�⃗ 9
Ngược lại, mặt phẳng có dạng 9 72 72 𝑨𝑨��𝑩𝑩
��⃗ = (𝒙𝒙𝑩𝑩 − 𝒙𝒙𝑨𝑨; 𝒚𝒚𝑩𝑩 − 𝒚𝒚𝑨𝑨; 𝒛𝒛𝑩𝑩 − 𝒛𝒛𝑨𝑨)
𝒅𝒅 ∥ (𝑷𝑷)
⇔ � 𝒒𝒒�⃗ ⊥ 𝒏𝒏�⃗ 𝒙𝒙 𝒚𝒚 𝒛𝒛
𝒂𝒂𝒙𝒙 + 𝒃𝒃𝒚𝒚 + 𝒄𝒄𝒛𝒛 + 𝒅𝒅 = 𝟎𝟎 1 1
𝑨𝑨 ∉ (𝑷𝑷)
𝑴𝑴 � 𝑨𝑨 + 𝒙𝒙𝑩𝑩 𝑨𝑨 + 𝒚𝒚𝑩𝑩 𝑨𝑨 + 𝒛𝒛𝑩𝑩 77
Thì có một vector pháp tuyến là 77 𝟐𝟐 ; 𝟐𝟐 ; 𝟐𝟐 �
𝒏𝒏�⃗ = (𝒂𝒂; 𝒃𝒃; 𝒄𝒄) và thay 𝒙𝒙, 𝒚𝒚 bởi 𝒙𝒙 𝒚𝒚 𝒛𝒛 71
hai số bất kỳ rồi giải ra 𝒛𝒛 ta được điểm 𝑨𝑨 ∈ (𝑷𝑷). 71
𝒅𝒅 ⊂ (𝑷𝑷)
⇔ � 𝒒𝒒�⃗ ⊥ 𝒏𝒏�⃗
𝑮𝑮 � 𝑨𝑨 + 𝒙𝒙𝑩𝑩 + 𝒙𝒙𝑩𝑩 𝑨𝑨 + 𝒚𝒚𝑩𝑩 + 𝒚𝒚𝑩𝑩 𝑨𝑨 + 𝒛𝒛𝑩𝑩 + 𝒛𝒛𝑩𝑩
𝑨𝑨 ∈ (𝑷𝑷) 𝟑𝟑 ; 𝟑𝟑 ; 𝟑𝟑 � 7
Phương trình mặt chắn: 7
𝑨𝑨(𝒂𝒂; 𝟎𝟎; 𝟎𝟎), 𝑩𝑩(𝟎𝟎; 𝒃𝒃; 𝟎𝟎),
𝒅𝒅 ⊥ (𝑷𝑷)
⇔ 𝒒𝒒�⃗ ∥ 𝒏𝒏�⃗
TÍCH CÓ HƯỚNG CỦA HAI VECTOR - ỨNG DỤNG
𝑩𝑩(𝟎𝟎; 𝟎𝟎; 𝒄𝒄).
Đường hoặc mặt cắt 𝒅𝒅
- Tham số điểm cắt 𝑴𝑴(𝒕𝒕). Định nghĩa 𝒙𝒙 𝒚𝒚 𝒛𝒛 (𝑨𝑨𝑩𝑩𝑩𝑩): thỏa mãn (*)
- Từ (*) giải PT ẩn 𝒕𝒕.
𝒂𝒂 + 𝒃𝒃 + 𝒄𝒄 = 𝟏𝟏
�𝒂𝒂�⃗, 𝒃𝒃�⃗� = 1 vec tơ có:
Với 𝒂𝒂𝒃𝒃𝒄𝒄 ≠ 𝟎𝟎
KHOẢNG CÁCH VÀ GÓC
+ Hướng vuông góc với cả 𝒂𝒂�⃗ và 𝒃𝒃�⃗ . Khoảng cách Góc + Độ lớn:
𝒅𝒅�𝑴𝑴, (𝑷𝑷)�
��𝒂𝒂�⃗, 𝒃𝒃�⃗�� = |𝒂𝒂�⃗|�𝒃𝒃�⃗�. 𝐬𝐬𝐬𝐬𝐬𝐬�𝒂𝒂�⃗, 𝒃𝒃�⃗� |𝒂𝒂 𝒙𝒙
|𝒒𝒒�𝟏𝟏�⃗. 𝒒𝒒�𝟐𝟐�⃗|
𝑴𝑴 + 𝒃𝒃𝒚𝒚𝑴𝑴 + 𝒄𝒄𝒛𝒛𝑴𝑴 + 𝒅𝒅|
+ Độ lớn bằng độ lớn diện tích =
𝐜𝐜𝐜𝐜𝐬𝐬(𝒅𝒅𝟏𝟏, 𝒅𝒅𝟐𝟐) = |𝒒𝒒�𝟏𝟏�⃗|.|𝒒𝒒�𝟐𝟐�⃗|
hình bình hành hai cạnh là hai
Vector chỉ phương 𝒒𝒒�⃗
Chọn 1 vector pháp tuyến
√𝒂𝒂𝟐𝟐 + 𝒃𝒃𝟐𝟐 + 𝒄𝒄𝟐𝟐
��𝒒𝒒�⃗, 𝑨𝑨��𝑴𝑴 ��⃗��
|𝒏𝒏��⃗. 𝒏𝒏��⃗|
vector 𝒂𝒂�⃗ và 𝒃𝒃�⃗
- Nếu biết 𝒒𝒒�⃗ ∥ 𝒂𝒂�⃗: 𝒅𝒅(𝑴𝑴, 𝒅𝒅) =
𝐜𝐜𝐜𝐜𝐬𝐬�(𝑷𝑷 𝟏𝟏 𝟐𝟐 |𝒒𝒒�⃗|
𝟏𝟏), (𝑷𝑷𝟐𝟐)� = |𝒏𝒏��⃗|. |𝒏𝒏��⃗|
Công thức tọa độ
Chọn 𝒒𝒒�⃗ = 𝒂𝒂�⃗ 𝟏𝟏 𝟐𝟐 �����⃗ 𝒚𝒚 𝒛𝒛 𝒙𝒙 | - Nếu biết
�[𝒒𝒒�𝟏𝟏�⃗, 𝒒𝒒�𝟐𝟐�⃗]. 𝑨𝑨𝟏𝟏𝑨𝑨𝟐𝟐� 𝒒𝒒�⃗. 𝒏𝒏|
�𝒂𝒂�⃗ , 𝒃𝒃�⃗� = �� 𝟏𝟏 𝒛𝒛𝟏𝟏 𝟏𝟏 𝒙𝒙𝟏𝟏 𝟏𝟏 𝒚𝒚𝟏𝟏
𝒒𝒒�⃗ ⊥ 𝒂𝒂�⃗ và 𝒒𝒒�⃗ ⊥ 𝒃𝒃�⃗:
𝒅𝒅(𝒅𝒅𝟏𝟏, 𝒅𝒅𝟐𝟐) =
𝐬𝐬𝐬𝐬𝐬𝐬�𝒅𝒅, (𝑷𝑷)� = 𝒚𝒚 � ; � � ; � ��
|[𝒒𝒒��⃗, 𝒒𝒒��⃗]| |𝒒𝒒�⃗|. |𝒏𝒏| 𝟐𝟐
𝒛𝒛𝟐𝟐 𝒛𝒛𝟐𝟐 𝒙𝒙𝟐𝟐 𝒙𝒙𝟐𝟐 𝒚𝒚𝟐𝟐
Chọn 𝒒𝒒�⃗ ∥ �𝒂𝒂�⃗,𝒃𝒃�⃗� 𝟏𝟏 𝟐𝟐 MẶT CẦU
DỊCH CHUYỂN KHOẢNG CÁCH VÀ DÙNG THỂ TÍCH
Mặt cầu (S) tâm 𝑺𝑺(𝒙𝒙
TỈ SỐ THỂ TÍCH LĂNG TRỤ
𝟎𝟎; 𝒚𝒚𝟎𝟎; 𝒛𝒛𝟎𝟎), bán kính 𝑹𝑹:
(𝒙𝒙 − 𝒙𝒙𝟎𝟎)𝟐𝟐 + (𝒚𝒚 − 𝒚𝒚𝟎𝟎)𝟐𝟐 + (𝒛𝒛 − 𝒛𝒛𝟎𝟎)𝟐𝟐 = 𝑹𝑹𝟐𝟐 Đặt Đặt
Ngược lại, mặt cầu (S) có phương trình:
𝒂𝒂 = 𝑨𝑨𝟏𝟏𝑨𝑨′; 𝒃𝒃 = 𝑩𝑩𝟏𝟏𝑩𝑩′; 𝒄𝒄 = 𝑩𝑩𝟏𝟏𝑩𝑩′ 𝒂𝒂 = 𝑨𝑨𝟏𝟏𝑨𝑨′; 𝒃𝒃 = 𝑩𝑩𝟏𝟏𝑩𝑩′; 𝒄𝒄 = 𝑩𝑩𝟏𝟏𝑩𝑩′;..
𝒙𝒙𝟐𝟐 + 𝒚𝒚𝟐𝟐 + 𝒛𝒛𝟐𝟐 + 𝟐𝟐𝒂𝒂𝒙𝒙 + 𝟐𝟐𝒃𝒃𝒚𝒚 + 𝟐𝟐𝒄𝒄𝒛𝒛 + 𝒅𝒅 = 𝟎𝟎 𝑨𝑨𝑨𝑨′ 𝑩𝑩𝑩𝑩′ 𝑩𝑩𝑩𝑩′ 𝑨𝑨𝑨𝑨′ 𝑩𝑩𝑩𝑩′ 𝑩𝑩𝑩𝑩′
Với điều kiện 𝒂𝒂𝟐𝟐 + 𝒃𝒃𝟐𝟐 + 𝒄𝒄𝟐𝟐 − 𝒅𝒅 > 𝟎𝟎 thì có:
tâm 𝑺𝑺(−𝒂𝒂; −𝒃𝒃; −𝒄𝒄) và bán kính 𝑹𝑹 = √𝒂𝒂𝟐𝟐 + 𝒃𝒃𝟐𝟐 + 𝒄𝒄𝟐𝟐 − 𝒅𝒅
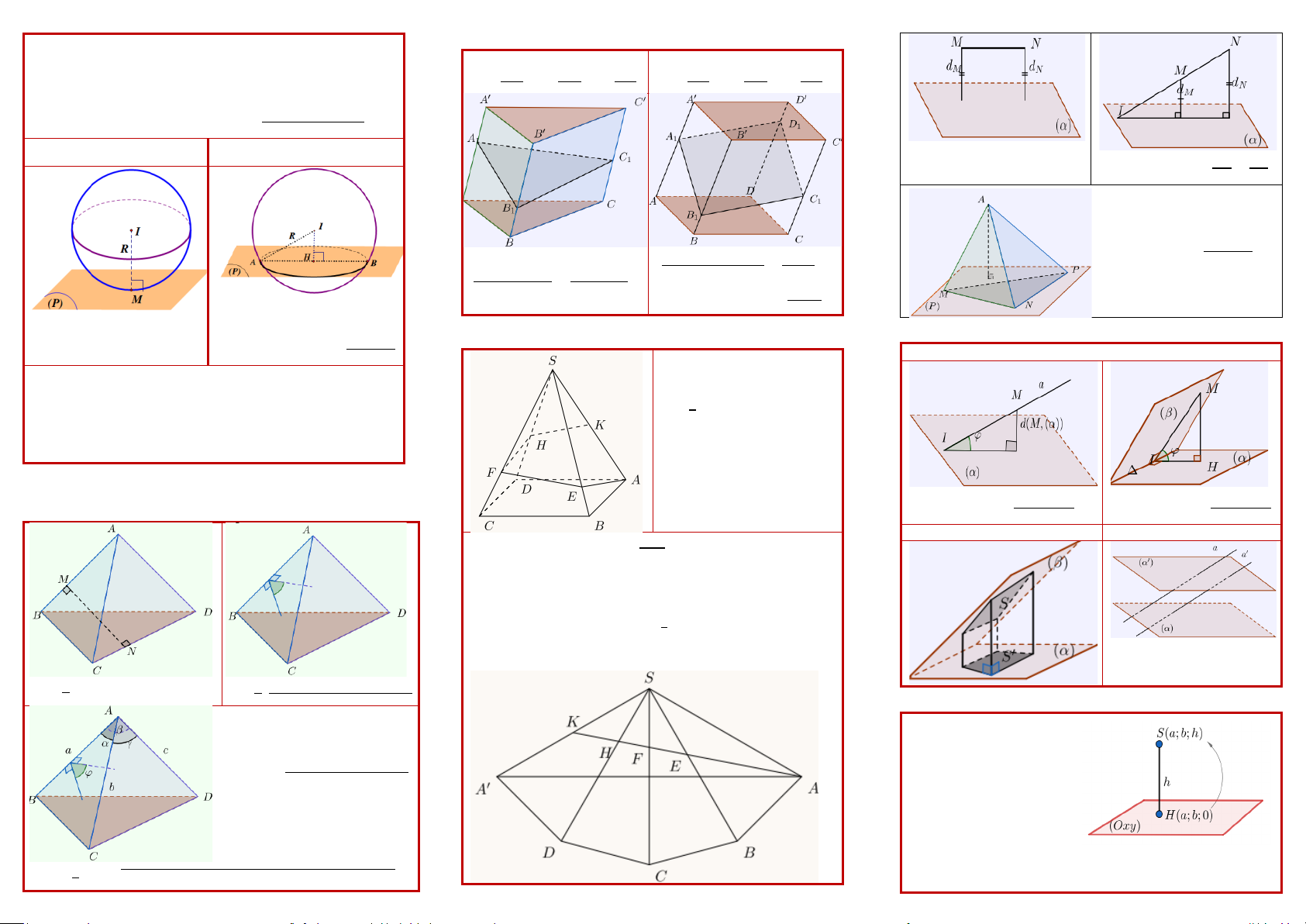
Mặt cầu (S) tiếp xúc mp(P) Mặt cầu (S) cắt mp(P)
𝑴𝑴𝑴𝑴 ∥ (𝜶𝜶 ) ⇒ 𝒅𝒅
𝒅𝒅𝑴𝑴 𝑺𝑺𝑴𝑴
𝑴𝑴 = 𝒅𝒅𝑴𝑴
𝑴𝑴𝑴𝑴 ∩ (𝜶𝜶 ) = 𝑺𝑺 ⇒ 𝒅𝒅 = 𝑴𝑴 𝑺𝑺𝑴𝑴
𝟑𝟑𝑽𝑽𝑨𝑨𝑴𝑴𝑴𝑴𝑷𝑷 𝑽𝑽
𝒅𝒅�𝑨𝑨, (𝑷𝑷)� =
𝑨𝑨′𝑩𝑩′𝑩𝑩′𝑺𝑺′.𝑨𝑨 𝒂𝒂 + 𝒄𝒄 𝑺𝑺 𝑽𝑽
𝟏𝟏𝑩𝑩𝟏𝟏𝑩𝑩𝟏𝟏𝑺𝑺𝟏𝟏 = 𝑴𝑴𝑴𝑴𝑷𝑷
𝑨𝑨′𝑩𝑩′𝑩𝑩′.𝑨𝑨 𝒂𝒂 + 𝒃𝒃 + 𝒄𝒄
𝟏𝟏𝑩𝑩𝟏𝟏𝑩𝑩𝟏𝟏
𝑽𝑽𝑨𝑨𝑩𝑩𝑩𝑩𝑺𝑺.𝑨𝑨′𝑩𝑩′𝑩𝑩′𝑺𝑺′ 𝟐𝟐 Th Th 𝑽𝑽 =
𝑨𝑨𝑩𝑩𝑩𝑩.𝑨𝑨′𝑩𝑩′𝑩𝑩′ 𝟑𝟑 𝒃𝒃 + 𝒅𝒅
- ĐK: 𝒅𝒅�𝑺𝑺, (𝑷𝑷)� < 𝑹𝑹. = ầ 𝟐𝟐 ầ
- ĐK: 𝒅𝒅�𝑺𝑺, (𝑷𝑷)� = 𝑹𝑹
- Thiết diện là đường tròn y L y L
- Tiếp điểm là hình chiếu
tâm 𝑩𝑩 là hình chiếu của 𝑺𝑺 lên
PHƯƠNG PHÁP TRẢI PHẲNG TÌM QUÃNG ĐƯỜNG MIN TÍNH GÓC NÂNG CAO
của 𝑺𝑺 lên (P).
(P) và bán kính 𝒓𝒓 = √𝑹𝑹𝟐𝟐 − 𝒅𝒅𝟐𝟐
Dùng khoảng cách từ điểm M bất kỳ ụ ụ Chú ý: c
Hình chóp 𝒏𝒏 giác đều có các c T
- Tương tự đối với vị trí của mặt cầu và đường thẳng. Chỉ
góc ở đỉnh của mặt bên là Tr
khác trường hợp đường cắt mặt cầu sẽ là một dây cung.
𝜶𝜶 < 𝝅𝝅. r
- Vị trí tương đối của hai mặt cầu tương tự vị trí tương đối 𝒏𝒏 í Tu í T
của hai đường tròn ở THCS. Chỉ khác khi cắt nhau thì thiết
Gọi 𝑲𝑲 là trung điểm 𝑺𝑺𝑨𝑨. Tìm
diện là đường tròn.
quãng đường ngắn nhất đi từ u
𝑨𝑨 đến 𝑲𝑲 mà phải đi qua 4 yê y
mặt bên của hình chóp. ê
MỘT SỐ VẤN ĐỀ NÂNG CAO n n
𝒅𝒅�𝑴𝑴, (𝜶𝜶)�
𝒅𝒅�𝑴𝑴, (𝜶𝜶)� – –
CÁC CÔNG THỨC TÍNH THỂ TÍCH TÚ DIỆN
𝐬𝐬𝐬𝐬𝐬𝐬�𝒂𝒂, (𝜶𝜶)� =
𝐬𝐬𝐬𝐬𝐬𝐬�(𝜶𝜶), (𝜷𝜷)� = 0 𝑴𝑴𝑺𝑺 𝒅𝒅(𝑴𝑴, 𝚫𝚫) 0 9 Giải
Diện tích hình chiếu
Dich chuyển song song 72 972
Trải phẳng 4 mặt bên của hình chóp. Chú ý 𝑨𝑨′ là bản sao
177 của 𝑨𝑨. 177
Quãng đường ngắn nhất là 𝑨𝑨𝑲𝑲 trong 𝚫𝚫𝑺𝑺𝑲𝑲𝑨𝑨. 71 71
Tính 𝑨𝑨𝑲𝑲 sử dụng định lý hàm số cos trong tam giác 𝑺𝑺𝑲𝑲𝑨𝑨 với 7 7 𝑨𝑨𝑺𝑺𝑲𝑲
� = 𝒏𝒏𝜶𝜶, hai cạnh bên là 𝒍𝒍 và 𝒍𝒍, với 𝒍𝒍 là cạnh bên hình 𝟐𝟐 chóp.
Khi dịch chuyển đường
hay mặt song song thì góc 𝟏𝟏 𝟐𝟐 𝑺𝑺 không đổi. 𝑽𝑽 =
𝑨𝑨𝑩𝑩𝑩𝑩. 𝑺𝑺𝑨𝑨𝑩𝑩𝑺𝑺. 𝐬𝐬𝐬𝐬𝐬𝐬(𝑨𝑨𝑩𝑩𝑩𝑩, 𝑨𝑨𝑩𝑩𝑺𝑺)
𝟔𝟔 𝑨𝑨𝑩𝑩. 𝑩𝑩𝑺𝑺. 𝑴𝑴𝑴𝑴. 𝐬𝐬𝐬𝐬𝐬𝐬(𝑨𝑨𝑩𝑩, 𝑩𝑩𝑺𝑺) 𝑽𝑽 = 𝟑𝟑. 𝑨𝑨𝑩𝑩
NGUYÊN TẮC TỌA ĐỘ HÓA HÌNH KHÔNG GIAN
Công thức tính góc nhị diện
biết 3 góc ở tam diện:
Chọn 𝑶𝑶𝒙𝒙 và 𝑶𝑶𝒚𝒚 là hai
đường vuông góc ở đáy:
𝐜𝐜𝐜𝐜𝐬𝐬 𝜸𝜸 − 𝐜𝐜𝐜𝐜𝐬𝐬 𝜶𝜶 . 𝐜𝐜𝐜𝐜𝐬𝐬 𝜷𝜷
- Sẵn có với tam giác
𝐜𝐜𝐜𝐜𝐬𝐬 𝝋𝝋 =
vuông, hình chữ nhật,
𝐬𝐬𝐬𝐬𝐬𝐬 𝜶𝜶 . 𝐬𝐬𝐬𝐬𝐬𝐬 𝜷𝜷 vuông, thoi.
- Kẻ trung tuyến với tam giác đều.
- Như thế mới dễ xác định
tọa độ các điểm ở đáy. 𝟏𝟏
Không cần kẻ 𝑶𝑶𝒛𝒛 vì cao độ chính là chiều cao 𝒉𝒉 của hình 𝑽𝑽 =
𝟔𝟔 . 𝒂𝒂𝒃𝒃𝒄𝒄. �𝟏𝟏 − 𝐜𝐜𝐜𝐜𝐬𝐬𝟐𝟐 𝜶𝜶 − 𝐜𝐜𝐜𝐜𝐬𝐬𝟐𝟐 𝜷𝜷 − 𝐜𝐜𝐜𝐜𝐬𝐬𝟐𝟐 𝜸𝜸 + 𝟐𝟐 𝐜𝐜𝐜𝐜𝐬𝐬 𝜶𝜶 𝐜𝐜𝐜𝐜𝐬𝐬 𝜷𝜷 𝐜𝐜𝐜𝐜𝐬𝐬 𝜸𝜸
- Tọa độ S suy ra từ tọa độ H