
















Preview text:
TỔNG HỢP ĐỀ TRẮC NGHIỆM VẬT LÝ ĐẠI CƯƠNG 2
Câu 1: Tại đỉnh của một tam giác đều cạnh
a có ba điện tích điểm q . Ta cần phải đặt tại tâm G của tam giác
một điện tích ' bằng nao nhiêu để toàn bộ hệ ở trạng thái cân bằng q q3q3q q A.q' . B. ' q . C. ' q . D. ' q . 3 3 3 3 Giải
Theo đề bài ta có:q1
q2q3q
Giả sử q q q1, 2, 3 đặt tại 3 đỉnh A B C,, k q q. . kq2
Lực đẩy do q1 tác dụng lên q2 là F12 a1 22
a2 F ( với a là độ dài cạnh tam giác)
Lực đẩy do q3 tác dụng lên q2 là F32 k q q.a3 22. kqa22 F
Hợp lực do q1 và q3 tác dụng lên q2 là hợp lực của F12 và F32
Ta thấy lực này có hướng là tia phân giác của góc đối đỉnh với góc ABC và độ lớn là F2 F. 3 ( độ lớn tính
bằng định lý cos trong tam giác )
Để q2 nằm cân bằng thì lực do q0 tác dụng lên q2 phải có độ lớn bằng
3.F và có hướng ngược lại q0 tích
điện âm và nằm trên tia phân giác góc B
Tương tự khi xét điều kiện cân bằng của q3 sẽ thấy q0 phải nằm trên tia phân giác góc C q0 nằm tại tâm tam giác ABC
k q. 0 .q2 k q 3 0 q . Ta có F02 2 2 a a 3 k q. 2 3 k q q 3 0q q
Để q2 cân bằng thì F02
F2 a2a2 0 3
Câu 2: Một electron bay vào khoảng không gian giữa hai bản của một tụ điện phẳng. Mật độ điện tích trên bản tụ là . Cường độ điện trường giữa hai
bản tụ là E . Trong không gian giữa hai
bản tụ có từ trường đều Bvuông góc với
điện trường E . Electron chuyển động
thẳng vuông góc với cả điện trường E lẫn từ
trường B . Thời gian electron đi được
quãng đường 1 bên trong tụ . là . C. B.0l A. B 0B B l 0lB 0 . l
TUẤN TEO TÓP – BEST LÝ TTQ
VIỆN VẬT LÝ KỸ THUẬT – ĐẠI HỌC BÁCH KHOA HÀ NỘI D.. Giải E v E
Điện trường trong tụ là 0 . Để electron chuyển động thẳng, tốc độ v của nó phải thỏa mãn B 0B . t l 0Bl
Thời gian electron đi được
quãng đường l là v
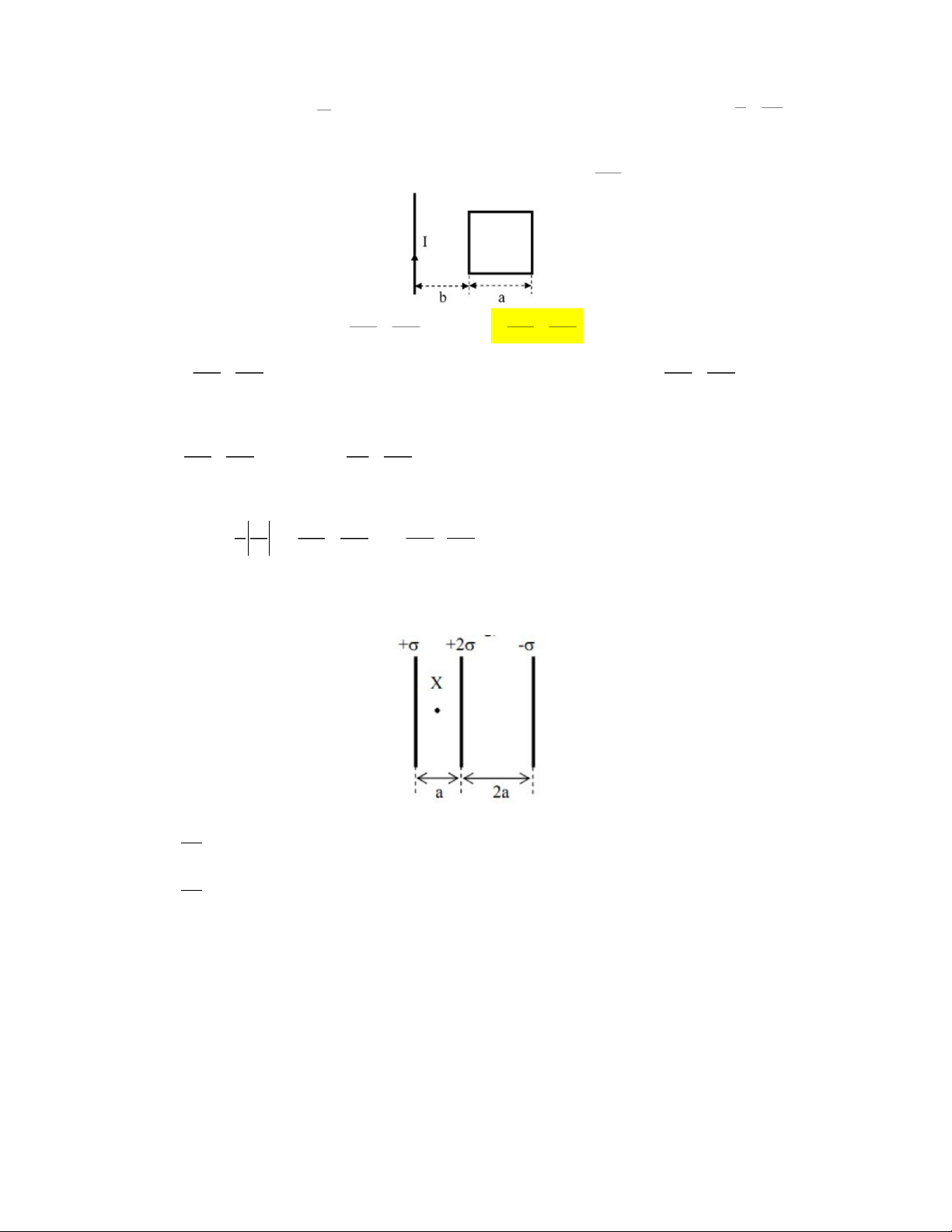
Câu 3: Một dây dẫn thẳng dài
vô hạn có dòng điện cường độ I
được đặt cách khung dây dẫn hình vuông có cạnh a một khoảng
b. Dây dẫn nằm trong mặt
phẳng của khung dây và song
song với một cạnh khung dây
(xem hình vẽ). Điện trở của khung
là R Cường độ dòng điện trong .
dây thẳng giảm dần đến 0 trong
thời gian t .Điện tích chạy qua
tiết diện ngang của dây dẫn tại 0Ia b a . C.0 Ia b a .
một điểm trên khung dây trong ln t ln thời gian t là 2 R 2 R b
A. 0Iblnba t .
B. D.0Iblnba t . 2 b b 2R b Giải
Nếu cường độ dòng diện trong dây dẫn thẳng là I thì từ thông qua điện tích giới hạn bởi khung dây là 0Ia ln ab , do đó d
dI 0a ln ab 2 b2 b
Điện lượng qua tiết diện ngang của dây trong thời gian t được cho bởi biểu thức: t tI
Q 0 Idt R dt 0 1 d
dt 20aRln abb dI 0
20aIRln abb
Câu 4: Ba bản phẳng rộng vô hạn được đặt song song với nhau như hình vẽ. Các bản tích điện với mặt độ điện
tích bề mặt lần lượt là , 2 và . Điện trường tổng cộng tại điểm X là (0 là hằng số điện môi của chân không) A.
, hướng sang phải. 20 B. , hướng sang trái. 20
TUẤN TEO TÓP – BEST LÝ TTQ
VIỆN VẬT LÝ KỸ THUẬT – ĐẠI HỌC BÁCH KHOA HÀ NỘI 4 C. , hướng sang trái. 20 D.0 . Giải
Điện trường gây bởi bản phẳng rộng vô hạn tại điểm bất kỳ bên ngoài bản có độ lớn 1 , trong đó 1 là mật độ
20 điện tích bề mặt của bản phẳng. Điện trường gây bới hai bản tích điện và
có độ lớn bằng điện
trường gây bởi bản tích điện 2 nhưng ngược chiều. Do đó điện trường t ổng cộng bằng 0.
Câu 5: Một electrôn được bắn thẳng đến tâm của một bản kim loại rộng có điện tích âm dư với mật độ điện tích mặt 2.10
6 C m/ 2. Nếu động năng ban đầu của điện tử bằng 100eV và nếu nó dừng (do lực đẩy tĩnh điện) ngay
khi đạt đến bản, thì nó phải được bắn cách bản bao nhiêu?
A.8,86mm .
B.4,43mm .
C.0,886mm.
D.0,443mm . Giải 12eU U 2Wd
Động năng của electron thu được là W d mv 2e Mặt khác, ta có: U
E d.U2W d W 2 2.1,6.10 .100.1.8,86.10 19
12 E 0 d E
e0 ed0 19 .2.106 0,000886m 0,886mm 1,6.10
Câu 6: Hai bản kim loại lớn có diện tích 1,0m
2 nằm đối diện nhau. Chúng cách nhau 5,0cm và có điện tích bằng
nhau nhưng trái dấu ở trên các mặt trong của chúng. Nếu cường độ điện trường ở giữa hai bản bằng 55V m/ thì
độ lớn của các điện tích trên các bản bằng bao nhiêu? Bỏ qua các hiệu ứng mép A.0,443.10 10 C.
B.0,443.109 C.
C.0,487.109 C.
D.0,487.1010 C. Giải
Hiệu điện thế giữa hai bản: U
E d. 55.5.102 2,75V
Điện dung của tụ điện được xác định theo công thức: C 0S d
Điện tích trên các bản là: Q CU d0S .U 1.8,86.105.10212 .1.2,75
0,487.1010C
Câu 7: Một điện tích điểm tạo một điện thông 750Vm đi qua một mặt Gauss hình cầu có bán kính bằng
10cm và có tâm nằm ở điện tích. Nếu bán kính của mặt Gauss tăng gấp đôi thì điện thông qua mặt đó bằng bao nhiêu?
TUẤN TEO TÓP – BEST LÝ TTQ
VIỆN VẬT LÝ KỸ THUẬT – ĐẠI HỌC BÁCH KHOA HÀ NỘI A.Tăng 4 lần. B. Không đổi. C.Tăng 2 lần. D. Giảm 2 lần. Giải
Điệm thông: E (hay thông lượng của véctơ
E gửi qua diện tích ) là đại lượ S
ng vô hướng xác định bởi: E
En S E Scos
Với: S : phần tử diện tích đủ nhỏ trong điện trường E :
véc tơ cường độ điện trường tại điểm thuộc S
n : véc tơ pháp tuyển của S Theo bài ra, ta có: 12 EE E S cosE S cos 12
EE.4.4 R cosR cos .. 122 12
EE RR122 2RR112 1 41E 2 2 2 42E
Câu 8: Một đĩa kim loại bán kính R
30cm quay quanh trục của nó với vận tốc góc 1200v ph/ . Lực quán
tính li tâm sẽ làm một số hạt điện tử văng về phía mép đĩa. Hiệu điện thế xuất hiện giữa tâm đĩa và một điểm
trên mép đĩa nhận giá trị nào? A.4,038.10 9 V .
B.3,038.109 V .
C.5,038.109 V .
D.2,038.109 V . Giải
Khi không có từ trường, các electron bị văng ra mép đĩa do lực quán tính li tâm. Do đó, giữa tâm và mép đĩa
xuất hiện một hiệu điện thế. Lúc hiệu điện thế ổn định, lực điện chính bằng lực hướng tâm của các electron. eEr m E r 2 r U Edr R
me 2 r dr. m22 2eR
9,1.102.1,6.1031. 40 192 .0,32
4,038.109V m 2r e0
Câu 9: Hai điện tích điểm q1 và q2 (q1 0 và q1 4q2 ) đặt tại hai điểm P và Q cách nhau một khoảng l
13cm trong không khí. Điểm M có cường độ điện trường bằng 0 cách q1 là
A.25,7cm. B.26,0cm. C.25,4cm. D.26,9cm. Giải
Các lực td lên điểm M q 3:
+ Lực tĩnh điện q1 td: F13
TUẤN TEO TÓP – BEST LÝ TTQ
VIỆN VẬT LÝ KỸ THUẬT – ĐẠI HỌC BÁCH KHOA HÀ NỘI L + ực tĩnh đi ện 2 q td: 23 F Điều kiện cân b ằng: 0F F F F F F 13 23 13 23 13 23 Mà . qq 12 0
nên 3 q nằm ngoài đo ạn PQ 23 13 . qq1. qq 2 PM q1 1 Ta có: 2 2 13 F 2 23 F k PM k QM QM q QM PM 2 Theo bài ra, ta có: QM PM 13 2
Từ 1 và 2 PM 26 cmQM ; cm 13
Câu 10: Cho ba quả cầu kim loại giống hệt nhau A B C, , . Hai quả cầu A và B tích điện bằng nhau, đặt cách
nhau một khoảng lớn hơn rất nhiều so với kích thước của chúng. Lực tác dụng giữa hai quả cầu là F Quả cầu . C
không tích điện. Người ta cho quả cầu C tiếp xúc với quả cầu A, sau đó cho tiếp xúc với quả cầu B, rồi cuối
cùng đưa C ra rất xa A và B Bây giờ lực tĩnh điện giữa . A và B là . F 3F A. . B . . C. . D. . 8 2 416 Giải
Lúc đầu, điện tích của quả cầu A và B bằng nhau và bằng . Cho quả cầu q
C tiếp xúc với quả cầu A, điện tích q
của quả cầu A bằng điện tích của quả cầu C và bằng
. Cho quả cầu C tiếp xúc với quả cầu B, điện tích của 2 3 3 q F
quả cầu B và C và bằng
. Do đó, lực tác dụng tương hỗ giữa quả cầu A và B bây giờ là 4 8
Câu 11: Hai tụ điện phẳng giống nhau có diện tích mỗi bản là và khoảng cách giữa các bản là S , giữa các bản d
là không khí. Tích điện cho hai tụ đến hiệu điện thế U rồi nối các bản tụ mang điện cùng dấu với nhau bằng dây
dẫn có điện trở không đáng kể. Nếu các bản tụ của một tụ dịch lại gần với với tốc độ v và các bản của tụ còn lại
dịch ra xa nhau cũng với tốc độ v thì dòng điện chạy trong dây dẫn là: A. B. 0 2S vU
20dS2 vU . C. 0dS vU . D. 20dS vU . . d Giải
Tổng điện tích 2 tụ: q1 q2 q 2 2C U0 1 với C0 0 S . d
Khi các bản tụ dịch chuyển thì C 1 d2
d vt q1
CU1 1 d vt 2 do U1 U2U
C2d1d vt q2C U2 2 vt d
TUẤN TEO TÓP – BEST LÝ TTQ
VIỆN VẬT LÝ KỸ THUẬT – ĐẠI HỌC BÁCH KHOA HÀ NỘI Từ và 1 suy ra: 2
q2 d dvt C U0 Idqdt2 d02 S vU. Câu 12: Một quả cầu điện môi bán kính R, tích điện với mật độ diện tích đồng nhất, tác A.. B.7 dụng lực F1 lên 9. C.3. D.7. điện R
tích q đặt tại điểm P cách tâm quả cầu một khoảng 2R. Tạo một lỗ hổng hình cầu bán kính . quả cầu có lỗ 2 F2 bằng: hổng
tác dụng lực F2 lên điện tích cũng đặt tại điểm q P Tỷ số . F1 Giải R
Gọi Q là điện tích của quả cầu và F là lực gây bởi quả cầu bán kính tích điện trái dấu với Q có cùng mật 2
độ và nằm tại vị trí lỗ hổng thì
F2 F1F. Ta có: Qq Q q' 4 R 2 F2
k 4R2 k R 3 2 , trong đó Q' 3 2 2 7Qq F27 F2 36 k R2 F1 9
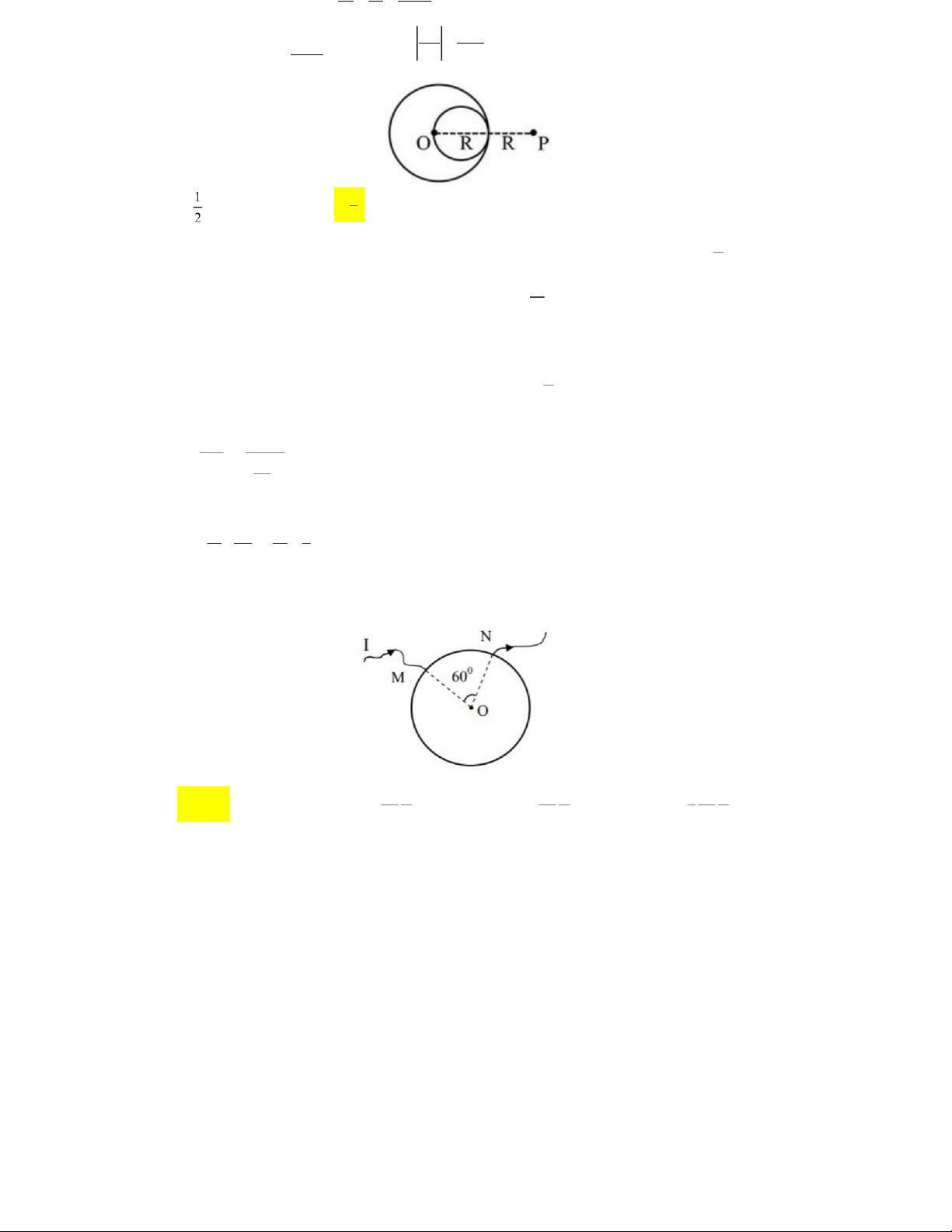
Câu 13: Cho một vòng dây dẫn tròn đồng chất, tiết diện đều, tâm O bán kính R .Dòng điện cường độ I đi vào
vòng dây tại điểm M và ra tại điểm N Góc .
MON 600 . Cảm ứng từ tại tâm vòng dây có độ lớn 5. I I I A B .0 . B.0 BR 5 . C. BR D. BR 4 0 5 . 0 2 62 Giải
TUẤN TEO TÓP – BEST LÝ TTQ
VIỆN VẬT LÝ KỸ THUẬT – ĐẠI HỌC BÁCH KHOA HÀ NỘI
Theo định luật Biot – Savart, cảm ứng từ Bi tại tâm vòng dây gây bởi dòng điện trong cung tròn i có độ lớn tỷ lệ
với cường độ dòng diện Ii và chiều dài Li của cung: Bi ~ I Li i .
Mặt khác, cường độ dòng điện Ii tỷ lệ nghịch với điện trở của cung dây , tức là tỷ lệ nghịch với chiều dài cung.
Như vậy, cảm ứng từ gây bởi dòng điện trong hai cung M N1 và M N2 không phụ thuộc vào độ dài của cung, do
đó có độ lớn như nhau, nhưng có chiều ngược nhau. Vậy cảm ứng từ tổng cộng tại tâm vòng dây bằng 0.
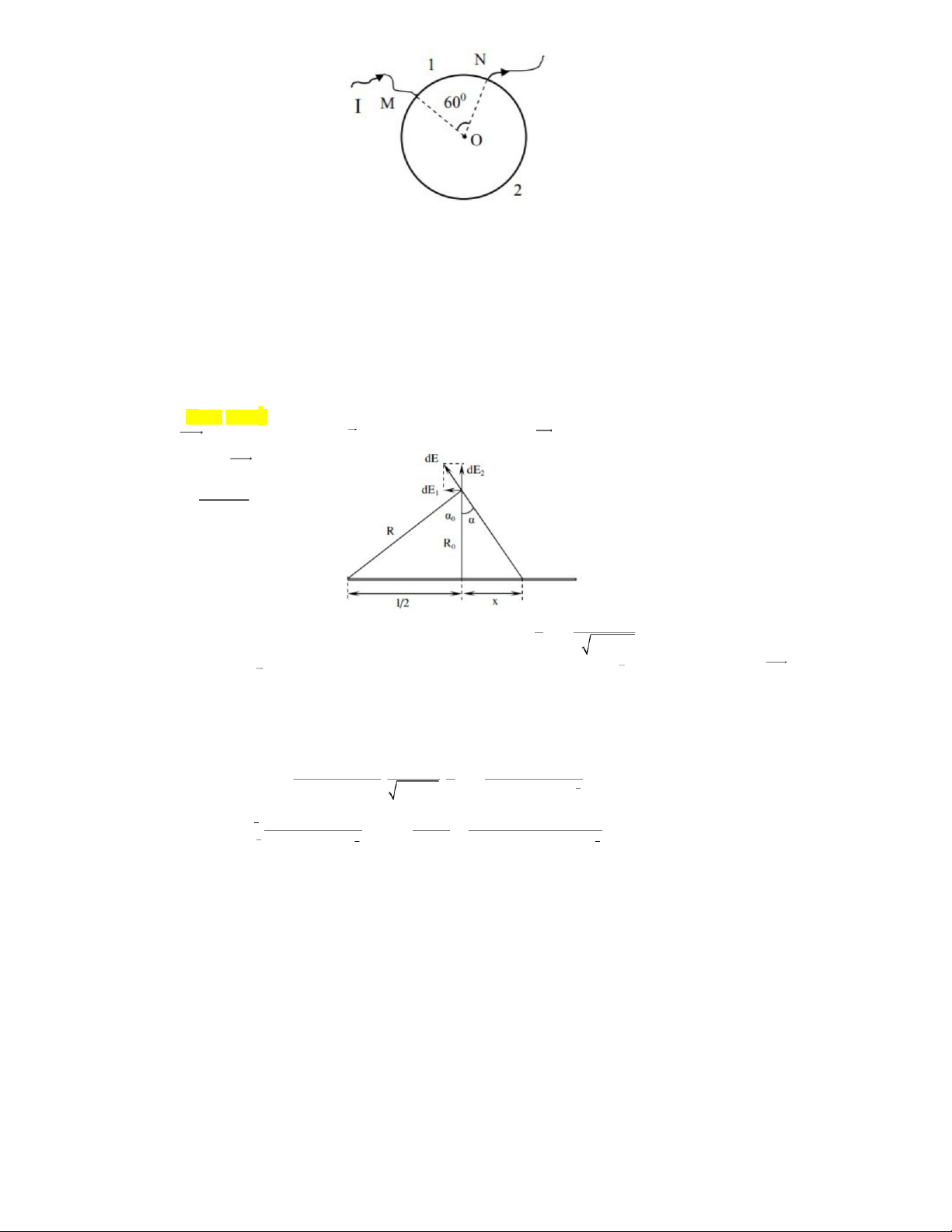
Câu 14: Một thanh mảnh mang điện tích q 2.10 7 C được phân bố đều trên thanh, gọi E là cường độ điện
trường tại một điểm cách hai đầu của thanh một đoạn R 300cm và cách tâm của thanh một đoạnR0 10 cm . Tìm E A.6.10 V m/. C.4,5.10 3 3V m/ . B.4.103 V m/.
D.6,7.103V m/. Giải q q Chia thanh thành nh ững đoạn nhỏ . dx Chúng có đi ện tích là: dq dx 2 0 2 dx R lR 2
Xét điện trường dE gây ra do đo ạ n dx gây ra t
ại điểm đang xét. Ta có th
ể tách dE thành hai thành ph ầ n x dE
và dEy . Điện trường tổng cộng E là tổng tất cả các điện trường dE đó. Do tính đối xứng nên tổng tất cả các
thành phần dEy bằng 0. Ta có: 0 3 0 dq R 1 xdx 22.2 dx 2 2 2 2 . . 4 0 2 4 0 40. r R x R x lR xl q qR 00 0 0 qR 23 0 0 qR R 0 dE dx d xxRtan l 00 22 cos 4 .R. 0l Rtan l
TUẤN TEO TÓP – BEST LÝ TTQ
VIỆN VẬT LÝ KỸ THUẬT – ĐẠI HỌC BÁCH KHOA HÀ NỘI
4l R 2x2
q0q02q q l q E4lR 0
cos d40 0lR sin0 40 0lR 2 0 0 0 0lR .2R 40RR0 6.10 Thay số: E 4 .1.8,86.10 2.10712
.3.0,1 3 V m/
Câu 15: Hai dây dẫn dài cách nhau d mang cùng dòng điện I nhưng trái chiều nhau như cho trên hình vẽ. Xác
định độ lớn của từ trường tổng cộng tại điểm P cách đều hai dây: 0id 2id D. A . C. .2 0 R 20idd2. B . 24R2 d2 2 d2. 4R 02idd 2. Giải
Gọi B B1, 2 lần lượt là cảm ứng từ do dòng điện I1 và I2 gây ra tại P . Áp dụng quy tắc bàn tay phải xác định
được chiều B B1, 2 như hình vẽ Ta có: B1 B2 0 . I 4 r d I 2
Theo hình vẽ, ta có: r R2 B1 B2 0 2 4 2 d 4 R 4
Cảm ứng từ tổng hợp tại P B: B1B2
Áp dụng nguyên lý chồng chất, ta được: B 2B cos1.
TUẤN TEO TÓP – BEST LÝ TTQ
VIỆN VẬT LÝ KỸ THUẬT – ĐẠI HỌC BÁCH KHOA HÀ NỘI d d d Theo hình v ẽ, ta có: 2224 cos r r d 2 2 R 0 I d 0 0 2 Id Id B R dd 1 2.44 Bcos 2. 2 2. . 2 2 2 2 d R 2 R 24 d R 4 4 4
Câu 16: Hai quả cầu nhỏ giống nhau tích điện q1 và q2 có giá trị bằng nhau và đặt trong không khí. Khi khoảng
cách giữa chúng là r 1
4cm thì chúng hút nhau với một lực F1 27.103N. Cho 2 quả cầu tiếp xúc với nhau rồi
tách chúng ra một khoảng r
2 3cm thì chúng đẩy nhau một lực F2 103N. Tính q1 và q2 A.q 1 8.108C;q2 6.108C .
B.q1 6.108C;q2 8.108C . C.q C
1 8.108C;q2 6.108C .
D.q1 6.108 ;q2 8.108C . Giải
Ban đầu khi chưa tiếp xúc hai quả cầu hút nhau với một lực F 1 27.103N. N q qF r 27.10 .0,049.10 Ta có: 1 2. 1 1k. 2 3 9 2 4,8.1015 q q1 2. F1 k q qr1 22. 27.103 4,8.10 1 15 (vì hai 1
điện tích q q1, 2hút nhau nên chúng trái dấu nhau) Sau khi tiếp xúc hai quả cầu
đẩy nhau một lực F 2 103 N q'1 q '2 q1 q2 2 Ta có: F2 k q. r' . ' 1 q 2
2 103Nq' . '1 q 2 F r2 2k. 2 10 .0,03 9.1039 2 1016
q' . '1 q 2 1016 (do hai điện tích 2
q ' ,1 q '2 đẩy nhau nên chúng cùng dấu nhau) 2 Mà q '1 q '2
q1 q 2 2
q '12 1016
q1 2 q2 1016
q1 q2 2.10 2 8 q 1
8.108 C q2 6.10 Từ và 1
2 , ta có hệ phương trình: qq q .
1 2q4,8.102.10815 q8.108C(giả sử q1 q2 ) 1 2 1 8 C q 2 6.108 C
Câu 17: So sánh các tương tác hấp dẫn và tĩnh điện giữa hai electron, biểu thức đúng là 2 2 2 e 2 A. m G k . TU
O TÓP – BEST LÝ TTQ
VIỆN VẬT LÝ KỸ THUẬT – ĐẠI HỌC BÁCH KHOA HÀ NỘI B. me ln Gk . C. meln Gk . D. m ke G . Giải ke2
Theo công thức của định luật Culông và định luật vạn vật hấp dẫn, ta có: F1 r2 2
F2 Gmr2 FF1 Gmke22 me 2 Gk 2
Câu 18: Một dây cáp đồng trục có các dòng điện cùng cường độ i chạy ngược chiều nhau ở lõi bên trong và vỏ
bên ngoài (xem hình vẽ). Độ lớn của cảm ứng từ tại điểm P bên ngoài dây cáp cách trục của dây cáp một khoảng r là A.0. B.0i .
C.2 2c02i 2 r . D.2 2 02i 2 r b. 2 rc b 2 rc b 2r Giải
Xét đường tròn bán kính r trong mặt phẳng vuông góc với trục dây cáp và có tâm nằm trên trục của dây. Áp
dụng địn lý Ampe về dòng toàn phần, do đối xứng của dây, ta có: Bdl. B dl 2
rB 0I
k 0, trong đó lấy tổng đại số các dòng điện đi xuyên qua diện tích hình tròn. C C k Vậy B 0
Câu 19: Một vòng dây tròn bán kính R được tích điện với mật độ đều . Độ lớn của cường độ điện trường tại
điểm nằm trên trục của vòng dây và các tâm vòng dây một khoảng R là A. B. k. k.
C.2k. D. k. 2R 2R R R Giải
Xét 2 đoạn dây rất nhỏ chiều dài dl nằm đối xứng qua tâm vòng dây. Điện trường do 2 đoạn dây này gây ra tại
điểm đang xét hướng dọc theo trục đối xứng của vòng dây và có độ lớn:
TUẤN TEO TÓP – BEST LÝ TTQ
VIỆN VẬT LÝ KỸ THUẬT – ĐẠI HỌC BÁCH KHOA HÀ NỘI dE 2
k dl2R2 cos450 k dl2R2
Lấy tổng theo toàn bộ vòng dây ta được: E
k2R2R 2kR
Câu 20: Một dây dẫn hình trụ bán kính R
2 gồm lõi có bán kính R R12
2R1, điện trở suất 1 và vỏ là phần
còn lại có điện trở suất 2 2 1. Dòng điện có cường độ I chạy trong dây dẫn đó. Cảm ứng từ điểm cách
trục của dây một khoảng r 1,5R1 có độ lớn: A. 0,75 0,65 0I . C. 0,85 B. 0I . 0,950I . . 0I R13R1 Giải 3R1
Dòng điện gồm I1 chạy trong lõi và I2 chạy trong vỏ: I
I I và I1 2 S1
2 1R22I1 2 I 1 2 I S2 . 1
1R22 R12 3I2 53 I 2 5 r 2 R12
Dòng diện chạy trong phần dây giới hạn bởi bán kính r là I I 1I
. 2R2 R12 0,65I 2 0,650I
Áp dụng định lý Ampe: B.2
r 0I ' B 3R1
Câu 21: Một mặt hình bán cầu tích điện đều với mật độ điện mặt 10
9 C m/ 2 Xác định cường độ điện .
trường tại tâm O của bán cầu A. . B. . C. 2 . D. . 0 2 00 Giải 4 0
TUẤN TEO TÓP – BEST LÝ TTQ
VIỆN VẬT LÝ KỸ THUẬT – ĐẠI HỌC BÁCH KHOA HÀ NỘI
Chia bán cầu thành những đới cầu có bề rộng (tính theo phương t dh
rục của nó). Đới cầu được tích điện tích:
dQ .2 r dh
h. 2. .r dhh 2R dh.
( với là góc giữa mặt đới cầu và trục đối xứng của
đới cầu.) cosrh R
Điện trường dE do đới cầu gây ra tại O có hướng như hình vẽ và có độ lớn bằng: dE 3 4 rh .dQ
h.2420R dhR.3 2h2 0h R. 2R h h
Lấy tích phân theo h từ 0 đến R, ta có: E dE 0 20R2 dh 20R2 2 0 40
Câu 22: Xét thanh thẳng AB có chiều dài l, mật độ điện dài Xác định cường độ điện trường do thanh gây ra .
tại một điểm M nằm trên đường kéo dài của thanh và cách đầu B của thanh một khoảng r
D. lnl r
A.kl .
B. kr . C. k
1r r 1l . r . k r Giải
Ta đi xét trường hợp tổng quát: nếu gọi khoảng cách từ điểm M đến trục dây dẫn thứ nhất là x thì cường độ 1
l với là mật độ điện dài
điện trường tại M là: E 2
x l x
20x l x 0 dU Edx U Edx 2 0 l r 1x l1x
2lrr 2
l r
dx lnxln l xln Mặt khác: r00 r
Câu 23: Hai quả cầu mang điện có bán kính và khối lượng bằng nhau được treo ở hai đầu sợi dây có chiều dài
bằng nhau. Người ta nhúng chúng vào một chất điện môi (dầu) có khối lượng riêng 1 và hằng số điện môi .
Hỏi khối lượng riêng của quả cầu phải
bằng bao nhiêu để góc giữa các sợi dây trong không khí và chất điện môi là như nhau? A. B. 1.
1. C. 1 1. D . 1 1. 1 1 Giải
TUẤN TEO TÓP – BEST LÝ TTQ
VIỆN VẬT LÝ KỸ THUẬT – ĐẠI HỌC BÁCH KHOA HÀ NỘI q0
Do các quả cầu là giống nhau nên điện tích mỗi quả cầu nhận được là: q1 q2 2
Hai quả cầu cân bằng khi: P FdT0
Theo hình vẽ, ta có: tg FP d với P mg và Fd kq qr1 22
4 2 . l sinkq022 tgq02
P q02 kq02 4 .16 0 l sin22 . P64 .16 0 l sin22
.tg16 .l sin22 .tg
Đối với quả cầu đặt trong không khí thì: P 64 1 0 q202 2.tg 1 1 .16l sin 1
Khi nhúng các quả cầu vào dầu hoả, mỗi quả cầu sẽ chịu thêm tác dụng của lực đẩy Acsimét P1 hướng ngược
chiều với trọng lực. Do đó, bằng tính toán tương tự bài trên, ta thu được: P P q02 2
1 642 0l sin2. 2 2.tg 2
Mặt khác: P mg Vg P ; 1 0Vg 3 Từ 1, 2 , 3 ,
ta có: PPP1
1..sinsin22 1..tgtg 12 0 2 2
2.sin2 2.tg 2 0. 2
.sin .2tg 2 1.sin2 1.tg 1 2 .sin .2tg Thay 0 1, 2 ; 1 1, ta có: 1. 2
.tg 2 2 sin22 1.tg 1 1 sinsin22 21..tgtg 12 .sin 2
Với điều kiện góc lệch giữa các sợi dây trong không khí và chất điện môi là như nhau hay: 1 2sin2
1.tg 1 sin2 2.tg 2
TUẤN TEO TÓP – BEST LÝ TTQ
VIỆN VẬT LÝ KỸ THUẬT – ĐẠI HỌC BÁCH KHOA HÀ NỘI
Biểu thức trở thành 1 1
Câu 24: Cho một vành bán kính R nhiễm điện đều với điện tích tổng cộng là Q
0 . Thế tĩnh điện tại điểm P
trên trục đối xứng của vành và cách tâm vành khoảng x là Q Q Qx Qx A. . B. . D. . 4 2 2 . C. 2 2 3 0x 4 R x 40 R x 4 2 2 2 0 R x 0 Giải 1 Khi x
, có thể xem vành tích điện như một điện tích điểm.
Vì vậy, thế tĩnh điện tại điểm P tỷ lệ với x khi x
. Đáp án B thỏa mãn điều kiện này .
Câu 25: Một khung dây dẫn hình vuông đặt trong từ trường đều B, mặt phẳng của khung dây vuông góc với
phương từ trường như trong hình vẽ. Khi dạng khung dây này được chuyển đều sang hình tròn trong cùng mặt
phẳng, trong khung dây có dòng điện hay không?
A. Có dòng điện theo chiều kim đồng hồ. B. Không có dòng điện.
C. Có dòng điện ngược chiều kim đồng hồ.
D. Không có kết luận gì. Giải
Hình tròn có diện tích lớn hơn hình vuông có cùng chu vi. Vì vậy, trong thời gian biến đổi khung hình vuông
thành khung hình tròn, từ thông qua diện tích khung tăng lên, trong khung xuất hiện dòng điện cảm ứng. Theo
định luật Lenz, dòng điện cảm ứng sinh ra từ trường ngược chiều với từ trường B Do đó, dòng điện cảm ứng có .
chiều theo chiều kim đồng hồ.
Câu 26: Xác định lực tác dụng lên một điện tích điểm q .10
9 C đặt ở tâm nửa vòng xuyến bán kính r0
5cm tích điện đều với điện tích Q 3.10 7 C (đặt trong chân không) A.2,01.10 3N.
B.1,14.103N .
C.3,15.103N.
D.1,83.103N . Giải
TUẤN TEO TÓP – BEST LÝ TTQ
VIỆN VẬT LÝ KỸ THUẬT – ĐẠI HỌC BÁCH KHOA HÀ NỘI
Ta chia nửa vòng xuyến thành những phần tử dl mang điện tích dQ. Chúng tác dụng lên điện tích q lực dF. áp
dụng nguyên lý chồng chất lực, ta có: F x
dFsin; Fy dFcos; nua vong xuyen nua vong xuyen dQ q.Q Qq Ta có: dF
4r2 với dQ r0 dl dl; r d0
dF 420 0r2 d 0 0
Do tính đối xứng, ta thấy ngay F y 0, nên F F x 2 4Qq2 0 0r2cos d
2Qq2 0 0r2 2 .1.8,86.103.10 2 ..10 7 .0 12 9 ,052 1,14.103N 2
Câu 27: Một hạt bụi mang một điện tích q C 2 1,7.1016
ở cách một dây dẫn thẳng một khoảng 0,4cm và ở gần
đường trung trực của dây dẫn ấy. Đoạn dây dẫn này dài 150cm, mang điện tíchq 1
2.107 C. Xác định lực tác
dụng lên hạt bụi. Giả thiết rằng q1 được phân bố đều trên sợi dây và sự có mặt của q2không ảnh hưởng gì đến sự phân bố đó. A.2,01.10 10 N.
B.1,14.1010 N.
C.1,24.1010 N . D.1010 N. Giải
Xét mặt Gaox là mặt trụ đáy tròn bán kính R0 có trục trùng với sợi dây, chiều cao h h 1 ở vùng giữa sợi dây
và cách sợi dây một khoảng R0 1, ta có thể coi điện trường trên mặt trụ là đều. Sử dụng định lý Otxtrôgratxki- q01. q h1 E q1
Gaox, ta có: E.2R h0. 0 0
l20 0R l q q 1 2. 1,7.1016.2.10710 10N
Lực điện tác dụng lên hạt bụi là: F E q. 2 2R l 2 .1.8,86.10 12.4.10 .1,53 0 0
Câu 28: Tính công cần thiết để dịch chuyển một điện tích q .10
7 C từ một điểm M cách quả cầu tích điện
bán kính r 1cm một khoảng
R 10cm ra xa vô cực. Biết quả cầu có mật độ điện m ặt 10 11C m/ 2 A.2,97.10 7 J.
B.3,42.107 J.
C.3,78.107 J.
D.4,20.107 J.
TUẤN TEO TÓP – BEST LÝ TTQ
VIỆN VẬT LÝ KỸ THUẬT – ĐẠI HỌC BÁCH KHOA HÀ NỘI Giải
Công của lực tĩnh điện khi dịch chuyển điện tích là: A q V. A VB Q Q qQ Vậy A
q. (do R2 ) 40R 4 1 0R2 40R1 4q.4
rr2 R
. qrr 2R
10 . .10 .0,011.8,86.107 13 712.0,112 3,42.107 J 0 0
Câu 29: Một điện tích điểm q .10
9 C nằm cách một sợi dây dài tích điện đều một khoảng r1 4cm; dưới
tác dụng của điện trường do sợi dây gây ra, điện tích dịch chuyển theo hướng đ ờng ƣ
sức điện trường đến khoảng cách r 2
2cm; khi đó lực điện trường thực hiện một công A
50.107 J . Tính mật độ điện dài của dây A. 6.10 7 C m/2.
B. 7.107 C m/2.
C.8.107 C m/2.
D.9.107 C m/2. Giải Ta có: dA q dV. q Edr . q . dr 20r Lấy tích phân r2 AdA
2q0 r1 drr
2q0 lnr lnr 2 1
2q0 ln rr12
Vậy mật độ điện dài của dây là 2
0rA2 .1.8,86.10 .50.10 12
7 6.107 C m/2 12 4 9 . 3 qln 2 .10 ln r2
Câu 30: Có một điện tích điểm q đặt tại tâm O của hai đường tròn đồng tâm bán kính r và R . Qua tâm O ta
vẽ một đường thẳng cắt hai đường tròn tại các điểm A B C D, , , . Tính công của lực điện trường khi dịch
chuyển một điện tích q0 từ B đến C và từ A đến D A. A
BC 0, AAD 0.
B. ABC 0, AAD 0 .
C. ABC 0, AAD 0 .
D. ABC 0, AAD 0 . Giải
TUẤN TEO TÓP – BEST L
VIỆN VẬT LÝ KỸ THUẬT
– ĐẠI HỌC BÁCH KHOA q HÀ NỘI V V A D 40R Từ hình vẽ, ta có:
VB VC q 40r
Công của lực điện trường khi dịch chuyển điện tích q0 từ B đến C và từ A đến D là bằng không: A
BC q V0 B VC 0; AAD q V0 A VD 0
Câu 31: Một mặt phẳng tích điện đều với mật độ .
Tại khoảng giữa của mặt có một lỗ hổng bán kính a nhỏ
so với kích thước của mặt. Tính cường độ điện trường tại một điểm nằm trên đường thẳng vuông góc với mặt
phẳng và đi qua tâm lỗ hổng, cách tâm đó một đoạn b. A.. B. . C. . D. . 2 2 2 20 1 ba20 1 ba0 1 ba 0 1 ba 2 Giải
Ta có thể coi mặt phẳng tích điện có lỗ hổng không tích điện như một mặt phẳng tích điện đều mật độ và
một đĩa bán kính a nằm tại vị trí lỗ tích điện đều với mật độ .
+ Điện trường do mặt phẳng tích điện đều gây ra tại điểm đang xét là: E1 2
0 + Điện trường do đĩa gây ra tại điểm đang xét là:
Chia đĩa thành từng dải vành khăn có bề rộng dr .
Xét dải vành khăn có bán kính r r
a. Vành khăn có điện
tích tổng cộng: dQ .2 r dr.
Chia vành khăn thành các điện tích điểm
. Chúng gây ra điện trường dq
dE tại A . Theo định lý chồng chất điện
trường, điện trường tại A bằng tổng tất cả các giá trị dE đó. Điện trường dE có thể phân thành hai thành phần dE1 và dE2 dE
. Do tính đối xứng nên tổng các thành phần 1 bằng không. Vậy: dE r dE2 dEcos, với là góc giữa dE và OA
TUẤN TEO TÓP – BEST LÝ TTQ
VIỆN VẬT LÝ KỸ THUẬT – ĐẠI HỌC BÁCH KHOA HÀ NỘI 3 dE r
40 dqr2 b2. r2bb2
40 rb2 b232 .dQ 20br. .2r 2 drb
2 Điện trường do cả đĩa gây ra tại A là: a b b . rdr 1 1 a 1 2 E 2 dE b r a r 32 2 10 0 2 02 0 2 2 2 0 r b b 2
+ Điện trường do mặt phẳng và đĩa gây ra cùng phương và ngược chiều nên: E
E1 E2 2 2 0 1 ba
Câu 32: Tính điện thế tại một điểm trên trục của một đĩa tròn mang điện tích đều và cách tâm đĩa một khoảng
h . Đĩa có bán kính R, mật độ điện mặt . A . R2 h 2 h.
B. R2 h2 h.
C. R2 h2 h.
D. R2 h2 h. 202000 Giải
Chia đĩa thành những phần tử hình vành khăn bán kính x, bề rộng dx. Phần tử vành khăn mang điện tích dq . dS .2 . xdx. dq 2 xdx xdx Điện thế
x do hình vành khăn gây là: h 0 x h 0dV x h 2 0 2 2 2 2 2 4 4 2
Điện thế do cả đĩa gây ra: 2 2 R R h 2 2 2 2 xdx t h dt R h h 2 R h 2 2 2 2 0 0 tx h h 0 00 4 2 x h t 4 2 2 2
Câu 33: Giữa hai dây dẫn hình trụ song song cách nhau một khoảng l 20
cm người ta đặt một hiệu điện thế U
4000V . Bán kính tiết diện mỗi dây là r 2mm. Hãy xác định cường độ điện trường tại trung điểm của
khoảng cách giữa 2 sợi dây biết rằng các dây dẫn đặt trong không khí.
A.3680V m/ .
B.8700V m/ .
C.3780V m/ .
D.7560V m/. Giải
Ta đi xét trường hợp tổng quát: nếu gọi khoảng cách từ điểm M đến trục dây dẫn thứ nhất là x thì cường độ 1
l với là mật độ điện dài
điện trường tại M là: E 2
x l x
20x l x 0 dU Edx U Edx 2 l r llr l r 1 1
TUẤN TEO TÓP – BEST LÝ TTQ
VIỆN VẬT LÝ KỸ THUẬT – ĐẠI HỌC BÁCH KHOA HÀ NỘI Mặt khác: 0
r x xdx 2 0 lnxln l xr 20 ln r Mật độ điện dài 0U ln l r r l
Thế vào biểu thức cường độ điện trường và thay x , ta có: 2
A 1l. U 0 2U 2.4000
8704V / m
20 2l .l 2l
lnl r r
l ln. l r r 0,2.ln 2
Câu 34: Cho một quả cầu tích điện đều với mật độ điện khối ,bán kính . T a
ính hiệu điện thế giữa hai điểm a
cách tâm lần lượt là và . 2 a a2a 2 a2 A. . B.. C . . D. a2 . 0 4 0 2 0 Giải 80
Xét mặt Gaox đồng tâm với khối cầu bán kínhr r a
. Do tính đối xứng nên điện trường trên mặt này là như
nhau và vuông góc với mặt cầu. Theo định lý Otstrogratxki-Gaox: 4 3 E.4r2 q r . 3 E r 00 3 0 a
a rr r2 a 3a2 a2
Từ đó, ta có: Va2 Va a Edr a 30dr 30 2 a 30 . 8 80 2 22
Câu 35: Một hình bán cầu tích điện đều, mật độ điện mặt là 1.10
9 C m/ 2. Tính cường độ điện trường tại
tâm O của bán cầu.
A.58,22V m/.
B.48,22V m/.
C.38,22V m/.
D.28,22V m/. Giải
TUẤN TEO TÓP – BEST LÝ TTQ
VIỆN VẬT LÝ KỸ THUẬT – ĐẠI HỌC BÁCH KHOA HÀ NỘI
Chia bán cầu thành những đới cầu có bề rộng (tính theo phương t dh
rục của nó). Đới cầu được tích điện tích:
dQ .2 r dh
h. 2. .r dhh 2R dh.
( với là góc giữa mặt đới cầu và trục đối xứng của
đới cầu.) cosrh R
Điện trường dE do đới cầu gây ra tại O có hướng như hình vẽ và có độ lớn bằng:
h h.2R dh dE . dQ . 40 3 3 2 2h2R 4 0 rh .h h2 R R
Lấy tích phân theo h từ 0 đến R, ta có: E dE
20R2 dh 20R2 2 0 40 0 1.109
Vậy cường độ điện trường tại tâm O của bán cầu là: E 40 4.1.8,86.1012 28,22V m/
Câu 36: Một vòng dây dẫn bán kính R tích điện đều với điện tích Q . Tính điện thế tại tâm vòng tròn, điện thế
tại điểm M nằm trên trục của vòng dây cách tâm O một đoạn h Q Q Q Q A.V
O 2;VM 2h2 . B V
. O 20 ;VM 40 R2 h2 . 0 4 0 R Q Q Q Q D.V
O 40 ;VM C.V
O 0 ;VM 40 R2 4
R2 h2 . h2 . 0 4 Giải
Chia vòng dây thành những đoạn vô cùng nhỏ dl mang điện tích dq . Điện thế do điện tích dq gây ra tại điểm dq
M trên trục vòng dây, cách tâm của vòng dây một đoạn là: h dV 2 2 2R 0h dq Q 2 2 2 2
Điện thế do cả vòng gây ra tại 4 4 M là: V dV 0 R h 0 R h Q
TUẤN TEO TÓP – BEST LÝ TTQ




