Tổng hợp Hóa Keo: Đặc điểm, Đối tượng & Hiện tượng Bề mặt | Hóa học môi trường | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Hà Nội
Hóa keo nghiên cứu các hệ phân tán dị thể, nghĩa là được cấu tạo từ 2 tướng trở lên, một trong hai tướng phải ở trạng thái chia nhỏ. Tướng phân tán có bề mặt riêng nhỏ, các quá trình hóa học và vật lí xảy ra trên bề mặt của hệ keo. Về mặt động học, độ bền của hệ vững tập hợp của các hệ phân tán được xác định bởi mối tương quan giữa lực hút và lực đẩy phân tử. ➢ Tóm lại, hóa keo là khoa học vê các quá trình hình thành và phá hủy các hệ phân tán. Tài liệu được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Hóa học môi trường 10 tài liệu
Trường: Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Hà Nội 0.9 K tài liệu
Tác giả:
Preview text:
CHƯƠNG 1: HỆ PHÂN TÁN VÀ ĐỐI TƯỢNG CỦA HÓA LÝ HỌC CÁC HỆ PHÂN TÁN.
I. ĐẶC ĐIỂM CỦA CÁC HỆ PHÂN TÁN
Hóa keo khảo sát những hệ phân tán dị thể đặc biệt gọi chung là hệ thống keo.
Đặc điểm của dung dịch keo:
- Khả năng phan tán ánh sáng.
- Khuếch tán chậm và có khả năng thẩm tích (khả năng lọc được bằng màng bán thẩm).
- Không bền vững tập hợp.
- Thường có hiện tượng điện di.
➢ Từ tất cả đặc điểm trên cho thấy hệ keo là một hệ dị thể và thường mang điện tích. II. ĐỐI T Ợ Ư NG CỦA HÓA KEO
Hóa keo nghiên cứu các hệ phân tán dị thể, nghĩa là được cấu tạo từ 2 tướng trở lên,
một trong hai tướng phải ở trạng thái chia nhỏ. Tướng phân tán có bề mặt riêng nhỏ,
các quá trình hóa học và vật lí xảy ra trên bề mặt của hệ keo.
Về mặt động học, độ bền của hệ vững tập hợp của các hệ phân tán được xác định
bởi mối tương quan giữa lực hút và lực đẩy phân tử.
➢ Tóm lại, hóa keo là khoa học vê các quá trình hình thành và phá hủy các hệ phân tán. III. ĐỘ PHÂN TÁN 𝑙 Độ phân tán: D = 𝑎 Trong đó:
a là kích thức hạt (đối với hạt hình cầu là đường kính d, hạt hình lập
phương là chiều dài cạnh l). Công thức bề mặ 𝑆 t riêng: Sr = 12 𝑉1 Trong đó:
S12 bề mặt phân cách tướng 1 và tướng 2
V1 thể tích tướng phân tán Với hạt hình cầ 4𝜋𝑟2 u: Sr = 4 = 3 = 6 3𝜋𝑟3 𝑟 𝑎
Với hạt hình lập phương: Sr= 6𝑙2 = 6 𝑙3 𝑙 IV.
PHÂN LOẠI CÁC HỆ PHÂN TÁN
1. Phân loại theo độ phân tán TÊN HỆ KÍCH THƯỚC HẠT (cm)
Hệ phân tán thô (huyền phù, nhũ tương) 104
Hệ phân tán trung bình (khói…) 10−4- 10−5
Hệ phân tán cao (hệ keo điển hình) 10−5- 10−7 Dung dịch phân tử <10−7
Khác biệt giữa hệ phân tán thô và hệ phân tán keo: HỆ PHÂN TÁN THÔ HỆ PHÂN TÁN KEO
Tướng phân tán sa lắng nhanh dưới ảnh Có tính bền vững sa lắng
hưởng của trọng trường
Tướng phân tán không lọt được giấy lọc Tướng phân tán qua được giấy lọc thường thường
nhưng bị giấy siêu lọc giữ lại
Có thể quan sát được bằng kính hiển v Không qua sát được bằng kính hiển vi thường thường
2. Phân loại theo trạng thái tập hợp TT TƯỚNG MÔI KÝ TÊN HỆ PHÂN TÁN TRƯỜNG HIỆU PHÂN TÁN 1 Khí Khí K/K Hệ đồng thể 2 Lỏng Khí L/K Keo khí (mây, sương mù) 3 Rắn Khí R/K Keo khí (bụi, khói) 4 Khí Lỏng K/L Nhủ tương khí (bọt) 5 Lỏng Lỏng L/L Nhủ tương 6 Rắn Lỏng R/L Sol, huyền phù 7 Khí Rắn K/R Bọt sốp 8 Lỏng Rắn L/R
Nhủ tương rắn, gel sốp 9 Rắn Rắn R/R Keo rắn, hợp kim
3. Phân loại theo tương tác giữa tướng phân tán và môi trường phân tán. TÊN HỆ
TƯƠNG TÁC GIỮA TƯỚNG PHÂN TÁN VÀ MÔI TRƯỜNG PHÂN TÁN Keo ưa lỏng Khá lớn (Lyophylles) Keo kỵ lỏng Yếu (Lyophobes)
4. Phân loại theo tương tác giữa các hạt
- Hệ phân tán tự do: các hạt tồn tại độc lập với nhau
- Hệ phân tán liên kết: các hạt liên kết với nhau bằng lực phân tử. V. Ý NGHĨA
- Có ý nghĩa to lớn trong nền kỹ thuật hiện đại: Vũ trụ, mây và sương mù, đất, quá
trình sống trong cơ thể động vật, gốm sứ, cao su, xà phòng, nhuộm vải sợi, thuộc da
- Trong công nghiệp thực phẩm. - Trong hóa dược.
CHƯƠNG 2: CÁC HIỆN TƯỢNG BỀ MẶT – SỰ HẤP PHỤ
A. CÁC HIỆN TƯỢNG BỀ MẶT
I. SỨC CĂNG BỀ MẶT:
Xét một khố chất lỏng có: phân tử A nằm trong long chất lỏng và phân tử B
nằm ở gần bề mặt ranh giới phân chia tướng lỏng – khí
• Nằm trong lòng khối chất lỏng. Phân tử A
• Lực hút giữa các phân tử hình cầu tác dụng
hướng theo mọi phía và cân bằng nhau.
• → Lực tương tác tổng hợp bằng 0 • Nằm gần mặt thoáng.
• Lực tương hỗ tác dụng theo mọi phía không thể Phân tử B cân bằng nhau.
• Chịu một hợp lực hướng vào bên trong lòng chất
lỏng gọi là nội áp (nội áp càng tăng khi B càng gần mặt thoáng).
Muốn làm tăng bề mặt (thể tích không đổi) cần phải thực hiện một công chống lại nội áp
(đưa các phân tử lên lớp bề mặt thoáng).
Trong điều kiện đẳng nhiệt, thuận nghịch, công bằng độ tăng của năng lượng dư bề mặt
dGs, tỷ lệ với độ tang diện tích tiế xúc: W = dGs = 𝜎. 𝑑𝑠 (1)
Trong đó: 𝜎 là sức căng bề mặt
𝑑𝑠 là độ tăng diện tích tiếp xúc
Khi 𝒅𝒔 = 1 ➔ dGs
= 𝝈; nên có thể nói 𝜎 là năng lượng tạo ra một đơn vị bề mặt .
Khi 𝒅𝒔 ≠ 1. Ví dụ: nhúng khung hình vuông vào dung dịch xà phòng rồi rút ra: 𝑑𝑠 = 2.l. dh (2)
Trong đó: l là chiều dài khung hình
dh là khi dịch chuyển khung hình một đoạn
Công thực hiện quá trình đó là: W = fdh (3)
f: lực tác dụng lên khung hình W = dGs = Từ (1) và (2) →
𝜎. 𝑑𝑠 = 2. 𝜎.ldh (4) Từ (3) và (4) → 𝜎 𝑓 = 2𝑙
Đổi đơn vị: erg, cm-2 = dyn.cm.cm-2 = dyn.cm-1
Giá trị sức căng bề mặt phụ thuộc vào:
Bản chất mỗi chất, khi tương tác giữa các phân tử của chất càng lớn → công để để
thắng lực gây nên nội áp càng lớn → sức căng bề mặt càng lớn.
Bản chất của chất tiếp xúc vì lực tương tác phân tử giữa hai tướng.
II. Hiện tượng thấm ướt:
- Năng lượng bề mặt của một chất phụ thuộc:
+ Bản chất của chính chất đó.
+ Tính chất của chất tiếp xúc với nó.
- Trường hợp: 3 chất tiếp xúc nhau (rắn, lỏng, khí) toàn hệ có cấu hình sao cho thế
năng toàn phần là cực tiểu => xác định mức độ t ấ
h m ướt vật rắn này hay vật rắn
khác bởi chất lỏng + giải thích hiện tượng bằng tác dụng của SCBM.
VD: Giọt chất lỏng tiếp xúc với tướng rắn và khí. 𝜎 𝐿𝐾
Chu vi giọt chất lỏng là giới hạn của 3 môi trườ
ng: lỏng, không khí, rắn, tạo
thành từng cặp phân cách:
+ Lỏng – không khí (𝜎𝐿𝐾) + Không khí – rắn ( 𝜑 𝜎𝑅𝐾) 𝜎𝑅𝐾
+ Lỏng – rắn (𝜎𝑅𝐿) 𝜎𝑅𝐿
- Điều kiện xảy ra quá trình thấm ướt: NĂNG LƯỢNG TỰ DO của hệ GIẢM (NLTD
giảm càng nhiều →quá trình thấm ướt càng tốt . - Độ t ấ
h m ướt được đo bằng góc thấm ướt (𝜑).
Quá trình: Khi thấm ướt các phân tử trong giọt chất lỏng chuyển động lan trên bề mặt
của tướng rắn theo khuynh hướng thay thế bề mặt tiếp xúc R-K có SCBM lớn (𝜎𝑅𝐾) bằng
bề mặt tiếp xúc R-L có SCBM nhỏ (𝜎𝑅𝐿)→hệ giảm SCBM; khi cân bằng được thiết lập→quá
trình dừng lại, tại biên giới 3 tướng có cân bằng lực: 𝝈
𝒄𝒐𝒔𝜽 = 𝑹𝑲 − 𝝈𝑹𝑳 𝝈 𝑳𝑲
• 𝜃 = 0 ↔ 𝑐𝑜𝑠𝜃 = 1 ∶ 𝑡ℎấ𝑚 ướ𝑡 ℎ𝑜à𝑛 𝑡𝑜à𝑛
• 𝜃 = 180𝑜 ↔ 𝑐𝑜𝑠𝜃 = −1 ∶ ℎ𝑜à𝑛 𝑡𝑜à𝑛 𝑘ℎô𝑛𝑔 𝑡ℎấ𝑚 ướ𝑡
𝑐𝑜𝑠𝜃 càng lớn thì chất lỏng thấm ướt bề mặt rắn càng tốt (Để: 𝑐𝑜𝑠𝜃 ↑ → 𝜎𝑅𝐾 ↑ →
𝜎𝑅𝐿 & 𝜎𝐿𝐾 ↓).
Bề mặt thấm ướt tốt (𝑐𝑜𝑠𝜃 > 0): bề mặt ưa lỏng, trái lại bề mặt (𝑐𝑜𝑠𝜃 <
0): 𝑏ề 𝑚ặ𝑡 𝑘ỵ 𝑙ỏ𝑛𝑔.
- Có thể chuyển một bề mặt kỵ lỏng sang ưa lỏng và ngược ạ
l i (vd: tạo một lớp hấp
phụ trên bề mặt rắn để thay đổi SCBM giữ R và L. Nếu SCBM mới nhỏ đi→hệ thấm
ướt tốt hơn→bề mặt ưa lỏng hơn và ngược lại).
- Ứng dụng hiện tượng thấm ướt bề mặt: trong tuyển nổi quặng, trong việc bảo vệ
keo và nhũ tương, trong kỹ thuật nhuộm... B. SỰ HẤP PHỤ:
I. Một số khái niệm và định nghĩa: 1. Định nghĩa:
Định nghĩa - Sự hấp phụ (adsorption) là hiện tượng thay đổi nồng độ của chất ở trên ranh giới pha so với trong lòng của pha.
- Một định nghĩa khác: Mọi quá trình tập trung chất lên bề mặt phân chia tướng được gọi là sự hấp phụ.
Phụ thuộc - Bản chất chất hấp phụ (adsorbent) và chất bị hấp thụ (adsorbate).
- Nhiệt độ, nồng độ dung dịch (pha lỏng), áp suất (pha khí). Lực tương
- Có nhiều dạng lực tương tác giữa phân tử bị hấp thụ với bề mặt chất rắn: từ những lực tác
yếu không phân cực (Val der Waals) cho đến lực liên kết hóa học mạnh.
2. Phân loại hấp phụ: gồm 2 loại: hấp phụ vật lý và hấp phụ hóa học. HẤP PHỤ VẬT LÝ HẤP PHỤ HÓA HỌC Loại liên kết
- Lực tương tác vật lý (liên kết Val der
- Liên kết hóa học, có sự trao đổi
Waals), không có sự trao đổi điện tử. điện tử. Nhiệt hấp phụ - Vài Kcal/mol. - Vài chục Kcal/mol. NL hoạt hóa - Không quan trọng. - Quan trọng. Khoảng to hấp phụ - Nhiệt độ thấp.
- Ưu đãi ở nhiệt độ cao. Số lớp hấp phụ - Nhiều lớp. - Một lớp. Tính đặc thù
- Ít phụ thuộc vào bản chất của bề mặt .
- Có tính đặc thù, có tính chọn lọc
- Phụ thuộc vào điều kiện to, áp suất.
cao, sự hấp phụ chỉ diễn ra khi có sự
tạo thành liên kết hóa học. Tính thuận nghịch - Có tính thuận nghịch.
- Thường bất thuận nghịch.
- Quá trình giải hấp phụ khó (sản
phẩm giải hấp phụ bị biến đổi thành phần hóa học).
II. SỰ HẤP PHỤ KHÍ VÀ HƠI TRÊN CHẤT HẤP PHỤ RẮN:
- Sự hấp phụ của chất khí vào bề mặt chất rắn → là dạng đơn giản nhất → có thể xảy ra khi chất bị
hấp phụ chỉ gồm 1 cấu tử → quá trình không phức tạp hóa khi có cấu tử thứ 2.
1. Độ hấp phụ x:
- Lượng khí bay hơi (mol) bị hấp thụ trong 1 đơn vị khối lượng. Đơn vị: mol/gam hoặc mmol/gam.
- Lượng chất bị hấp phụ tính cho một đơn vị diện tích bề mặt chất hấp phụ. Đơn vị: mol/cm2 hoặc mmol/cm2.
- Ngoài ra, còn sử dụng đại lượng thể tích ở đktc: 𝑉 = 𝑥 (cm3/g) 22.400
- Đường cong biểu diễn sự thay đổi của độ hấp phụ theo nồng độ hoặc áp suất cân bằng của chất
hấp phụ ở nhiệt độ (áp suất) không đổi → đường đẳng nhiệt (áp) hấp phụ → đường đẳng nhiệt được sử dụng nhiều nhất.
2. Phương trình hấp phụ đẳng nhiệt Freunlich: → chỉ thích hợp trong khoảng áp suất trung bình.
- Đường đẳng nhiệt hấp phụ gần với dạng parabol → Freunlich đề nghị phương trình thực nghiệm: 1
𝑥 = 𝑏. 𝑝𝑛. Trong đó, x: độ hấp phụ; p: áp suất cân bằng trên chất hấp phụ; b, n: là các hằng số thực nghiệm.
- Từ phương trình trên → có thể rút ra phương trình đường thẳng: 1
𝑙𝑜𝑔𝑥 = 𝑙𝑜𝑔𝑏 + 𝑛𝑙𝑜𝑔𝑝
→ xây dựng đồ thị (trục tung log x, trục hoành log p), ta có thể xác định hằng số b và 1/n.
Dạng phương trình cũng có thể sử dụng trong trường hợp hấp phụ các chất trên bề mặt phân chia
lỏng - rắn (thay p bằng C).
3. Phương trình hấp phụ đẳng nhiệt Langmuir: → chưa thật hoàn chỉnh đối với việc mô tả sự hấp
phụ trên ranh giới phụ. Là cơ sở cần thiết để hiểu rõ tất cả các thuyết khác.
- Phương trình đẳng nhiệt Langmuir được xây dựng dựa trên những cơ sở giả thuyết sau (lý thuyết hấp phụ đơn lớp):
+ Các phần tử bị hấp phụ (adsorbate) liên kết với những vị trí nhất định trên bề mặt chất hấp phụ (adsorbent).
+ Bề mặt hấp phụ có trường lực hóa trị chưa bão hòa → hình thành những trung tâm hấp phụ (tâm liên kết).
+ Lực hấp phụ có bán kính nhỏ → mỗi tâm liên kết chỉ có thể nhận 1 phần tử bị hấp phụ → hấp phụ đơn lớp.
+ Năng lượng ở các tâm hấp phụ đều bằng nhau → không phụ thuộc sự hiện diện hay không của các
phần tử bị hấp phụ ở các tâm khác → chỉ tương tác với bề mặt chất hấp phụ.
+ Sự hấp phụ là thuận nghịch → phân tử bị hấp phụ chỉ bị giữ trên bề mặt chất hấp thụ 1 thời gian
nhất định → đứt ra và chuyển vào tướng khí → phân tử khác lại bị hấp thụ vào.
- Bằng con đường động học, Langmuir đã đưa ra phương trình hấp phụ đẳng nhiệt:
+ Tốc độ hấp phụ: 𝑉 ↓ = 𝑘1. 𝑝. (1 − 𝜃), tỉ lệ với p và (1 − 𝜃).
Trong đó: p: áp suất khí; 𝜽: phần bề mặt bị phân tử khí chiếm; (𝟏 − 𝜽): phần bề mặt còn trống.
+ Tốc độ phản ứng hấp phụ: 𝑉 ↑ = 𝑘2. 𝜃, tỉ lệ với phần bề mặt bị che phủ (bị chiếm).
+ Khi cân bằng hấp phụ được hình thành: 𝑽 ↓ = 𝑽 ↑
Ta có: 𝜃 = 𝑘1.𝑝 . Đặ𝑡 𝐴 = 𝑘1 ; 𝜃 = 𝑥 : 𝑘2+𝑘1.𝑝 𝑘2 𝑥𝑚
𝑉ớ𝑖 𝒙, 𝒙𝒎 ∶ độ ℎấ𝑝 𝑝ℎụ 𝑡ạ𝑖 1 𝑡ℎờ𝑖 đ𝑖ể𝑚 𝑣à độ ℎấ𝑝 𝑝ℎụ 𝑐ự𝑐 đạ𝑖. 𝑝
𝑇ℎì 𝑥 = 𝑥𝑚 𝐴 + 𝑝 → 𝒙 𝒕ỉ 𝒍ệ 𝒃ậ𝒄 𝒏𝒉ấ𝒕 𝒗ớ𝒊 𝒑.
Khi 𝒑 ≪ 𝟏 → 𝒙 = 𝒙𝒎 𝒑 ; 𝒑 ≫ 𝟏 → 𝒙 = 𝒙 𝑨 𝒎
Để xác định A và x ể
m, có th chuyển về dạng phương trình đường thẳng: 𝑝 𝐴 1
𝑦 = 𝑎𝑥 + 𝑏 → 𝑥 = 𝑥 + .𝑝 𝑚 𝑥𝑚
4. Phương trình hấp phụ BET (Brunuauer-Emmelt-Teller):
- Lớp hấp phụ đa phân tử → đường hấp phụ đẳng nhiệt dạng hình chữ S.
- Những cơ sở chính của phương trình BET là:
+ Bề mặt chất hấp phụ là đồng nhất → mọi vị trí đều tương đương nhau.
+ Các phân tử hấp thụ trong lớp đầu tiên đều có tính cục bộ → không thể chuyển động tự do.
+ Không có sự giới hạn về số lớp hấp phụ, không có sự tương tác giữa các phân tử đã bị hấp phụ.
+ Lớp đầu tiên → hình thành do tương tác Val der Waals với bề mặt rắn → có năng lượng khác với các lớp bên trong.
+ Các lớp tiếp theo → hình thành do sự ngưng tụ khí, nhiệt hấp thụ (năng lượng) ở lớp thứ 2 và tất
cả các lớp tiếp theo giống nhau.
- Phương trình BET có dạ 𝑝 ng: = 1 + 𝐶−1. 𝑝 𝑉(𝑝𝑜−𝑝) 𝑉𝑚𝐶 𝑉𝑚𝐶 𝑝𝑜 Trong đó: p ấ
o: áp suất hơi bão hòa; V: thể tích khí hấp phụ ở áp su t p. V ể ị ấ ụ ở ớ ứ ớp đơn phân tử
m: th tích khí b h p ph l p th nhất (l ). ∆𝑞
C: thừa số năng lượng (𝐶 = 𝑒𝑅𝑇, ∆𝑞: hiệu số nhiệt hấp phụ khí trong lớp đơn phân tử và nhiệt hóa lỏng).
- Phương trình BET được sử dụng để xác định bề mặt chất hấp phụ: 𝑆𝑜 = 𝑉𝑚.𝑁.𝑊𝑚 𝑉𝑜
Trong đó: N: số Avogadro; W ề ớ ử đơn.
m: b mặt chiếm 1 phân tử ở l p phân t V ể ủ ở đktc
o: th tích c a 1 mol khí (22.400 cm3/mol).
5. Hiện tượng mao quản:
- Khi chất hấp phụ là xốp → đường hấp phụ đẳng nhiệt cũng có dạng hình chữ S → do sự ngưng tụ hơi của c ấ
h t bị hấp phụ trong mao quản của chất ấ
h p phụ xốp → diễn ra theo sau sự hấp phụ → gọi
là sự ngưng tụ mao quản.
- Do kết quả sự hấp phụ → màng mỏng chất bị hấp phụ hình thành trên thành mao quản hẹp →
chất bị hấp phụ thấm ướt vào thành mao quản → mặt cong lõm trong các mao quản hẹp → hơi chất
bị hấp phụ bắt đầu ngưng tụ → áp suất p cân bằng ở bề mặt cong lõm < áp suất po hơi bão hòa trên bề mặt phẳng.
III. SỰ HẤP PHỤ TRÊN RANH GIỚI DUNG DỊCH LỎNG – KHÍ:
1. Phương trình hấp phụ Gibbs: Γ 1 𝑑𝜎 𝐶 = −𝑅𝑇 . 𝑑𝐶
Với: 𝚪: biến thiên nồng độ chất trong lớp bề mặt, hay độ hấp phụ, mol/cm2.
C: nồng độ cân bằng trong dung dịch lỏng, mol/l.
𝝈: sức căng bề mặt, N/cm2.
2. Các chất hoạt động bề mặt:
- Từ phương trình Gibbs ta có các trường hợp sau:
+ Gọi 𝜎, 𝜎𝑐: là sức căng bề mặt của dung môi tinh chất và dung môi có nồng độ C. TRƯỜNG HỢP ĐẶC ĐIỂM
𝑑𝜎 > 0, Γ < 0 (𝜎
Sức căng bề mặt ↑ khi nồng độ chất tan ↑ → sự hấp phụ âm 𝑑𝐶 𝑐 > 𝜎𝑜) - .
- Là trường hợp của dung dịch các chất điện ly.
- Các ion tương tác mạnh với các phân tử của dung môi (solvat hóa)
→ bị kéo sâu vào trong thể tích của hệ → mật độ chất tan ở bề mặt < trong thể tích. 𝑑𝜎 = 0, Γ = 0 (𝜎
Sự phân bố chất tan ở lớp bề mặt
trong thể tích là như nhau → chất 𝑑𝐶 𝑐 = 𝜎𝑜) - và
không hoạt động bề mặt.
𝑑𝜎 < 0, Γ > 0 (𝜎
Sức căng bề mặt ↓ khi nồng độ chất tan ↑ → sự hấp phụ dương. 𝑑𝐶 𝑐 < 𝜎𝑜) -
- Chất tan là chất hoạt động bề mặt → do có cấu trúc nội tại của phân tử những chất đó.
- Nồng độ chất tan ở lớp bề mặt > trong thể tích.
❖ Cấu trúc phân tử của chất HĐBM gồm 2 phần:
- Gốc không phân cực: dãy hidrocarbon R
- Nhóm định chức phân cực: -OH, -COOH, -NO2, -NH2, …
- Chất HĐBM là những acid hay baz hữu cơ, các dẫn xuất halogen, … Gốc kỵ nước hidrocarbon
được đẩy vào môi trường không phân cực, còn nhóm ưa nước nằm trong môi trường nước. 3. Qui tắc Traube:
- Năm 1884, Traube đưa ra qui tắc thực nghiệm:
Tính HĐBM của các acid hữu cơ no trong nước trong 1 dãy đồng đẳng tăng lên theo số
cacbon, trung bình cho mỗi cacbon tăng từ 3 đến 3,5 lần.
- Qui tắc Traube chỉ đúng cho trường hợp dung môi là nước (môi trường rất phân cực). Với dung
môi không phân cực thì tính hòa tan của chất HĐBM sẽ tăng và làm giảm tính HĐBM.
IV. SỰ HẤP PHỤ TRÊN RANH GIỚI LỎNG – RẰN:
1. Sự hấp phụ phân tử:
- Lượng chất bị hấp phụ x (mmol/g) được tính từ công thức: (𝐶 𝑥 = 𝑜 − 𝐶1)𝑉 𝑚 . 100
Trong đó: CO, C1: nồng độ ban đầu và cân bằng của chất bị hấp phụ (mol/l).
V: thể tích trong đó xảy ra sự hấp phụ (l).
m: lượng chất hấp phụ (g).
- Sự hấp phụ trên ranh giới lỏng - rắn có thể được biểu diễn bằng các đường đẳng nhiệt hấp phụ Langmuir hay Freundlich.
- Sự hấp phụ phân tử chịu ảnh hưởng của các yếu tố sau:
➢ Ảnh hưởng của dung môi: giữa dung môi và chất tan thường có sự cạnh tranh hấp phụ lên bề
mặt rắn. Cấu tử nào có SCBM nhỏ hơn sẽ ưu tiên hấp phụ.
➢ Ảnh hưởng của tính chất chất hấp phụ: bề mặt phân cực sẽ hấp phụ tốt chất bị hấp phụ phân cực và ngược lại.
➢ Anh hưởng của tính chất chất bị hấp phụ
- Quy tắc Rebinder: chất chỉ hấp phụ lên ranh giới pha khi sự hiện diện của nó trong lớp bề mặt
làm cân bằng độ phân cực của hai pha.
- Hiện tượng hấp phụ phân tử có ý nghĩa rất lớn vì nó diễn ra trong cơ thể động vật và trong nhiều
quá trình kỹ thuật khác như: sắc ký, làm sạch chất lỏng, …
2. Sự hấp phụ các chất điện ly:
- Các ion trong dung dịch là những phần tử tích điện, cho nên sự hấp phụ các ion là quá trình diễn
ra sự phân bố lại điện tích.
- Do tương tác tĩnh điện các ion trái dấu được hút đến gần lớp bề mặt phân chia tướng và hình thành lớp điện kép.
a) Hấp phụ chọn lọc:
Các ion chất điện ly được hấp phụ ưu tiên theo những tính chất sau:
- Bề mặt chất hấp phụ có điện tích xác định nên chỉ hấp phụ các ion tích điện trái dấu với nó.
- Khả năng hấp phụ phụ thuộc bản chất các ion:
▪ Đối với ion cùng hóa trị, ion nào có bán kính lớn nhất sẽ có khả năng hấp phụ cao nhất:
VD: Khả năng hấp phụ của các ion cùng hóa trị. Li+ < Na+ < K+ + < Rb < Cs+
Mg2+ < Ca2+ < Sr2+ < Ba2+ Cl- < Br- < NO - - - 3 < I < CNS
▪ Đối với các ion có hóa trị khác nhau, ion nào có hóa trị càng cao (điện tích lớn) càng dễ bị hấp phụ.
K+ < Ca2+ < Al3+ < Th4+
Trong hóa keo, vấn đề quan trọng là sự hấp phụ các ion trong dung dịch lên bề mặt tinh thể
bằng lực hóa học để hình thành hệ keo.
b) Hấp phụ trao đổi:
- Trong hấp phụ trao đổi, chất hấp phụ hấp phụ một lượng ion xác định nào đó từ dung dịch và
đồng thời đẩy một lượng tương đương các ion khác có cùng điện tích vào dung dịch
- Sự hấp phụ trao đổi có một số đặc điểm sau:
➢ Có tính chọn lọc cao: sự trao đổi chỉ xảy ra với những loại ion xác định tùy thuộc bản chất chất
hấp phụ và ion bị hấp phụ
+ Chất hấp phụ acid (SiO2, SnO2, ...) có khả năng trao đổi với cation.
+ Chất hấp phụ baz (Fe2O3, Al2O3, …) có khả năng trao đổi với anion.
➢ Quá trình không phải luôn luôn là thuận nghịch.
➢ Sự trao đổi có tốc độ nhỏ, nhất là đối với các ion nằm sâu trong chất hấp phụ.
➢ Nếu sự trao đổi diễn ra với sự tham gia của ion H+ hay OH- thì pH của môi trường sẽ thay đổi.
- Sự hấp phụ trao đổi có ý nghĩa rất lớn trong việc nghiên cứu đất, trong sinh vật học cũng như trong kỹ thuật.
▪ Trao đổi các ion K+, NH + với các ion Ca2+ 2+ trong hạt keo đất. 4 , Mg
▪ Xử lý nước cứng (có các ion Ca2+, Mg2+) bằng phương pháp trao đổi ion, sử dụng nhựa trao đổi ion cationit:
2 cationit Na+ + Ca2+ → (cationit) + + 2Ca2 + 2Na
▪ Tách các chất điện ly ra khỏi nước biển:
cationit H+ + anionit OH- + Na+ + Cl- → cationit Na+ + anionit Cl- + H2O
Nhựa trao đổi ion có thể tái sinh bằng cách xử lý với acid và baz.
CHƯƠNG 3: TÍNH CHẤT QUANG HỌC CUẢ HỆ PHÂN TÁN
I. SỰ PHÂN TÁN ÁNH SÁNG:
• Cường độ ánh sáng phân tán theo hướng khác nhau thì khác nhau.
a là kích thước của hạt; λ là bước sóng của tia sáng
a > λ: Ánh sáng sẽ phản xạ dưới những góc xác định a < λ : Nhiễu xạ a << λ : C ờng ư
độ ánh sáng phân tán theo hướng 0 và 180 là mạnh nhất
Nếu hạt tương đối lướng nhưng vẫn nhỏ hơn λ : ánh sáng phân tán theo hướng tia
tới 180 là lớn nhất.
• Ánh sáng phân tán thường phân cực
a << λ: không phân cực theo góc 0 và 180, phân cực hoàn toàn theo góc 90
a < λ : phân cực hoàn toàn theo góc khác 90
Phương trình Rayleigh: Ipt = 24𝜋3( 𝑛12−𝑛22 ) × 𝑣2𝑉 𝐼 𝑛 𝑜 12−2𝑛22 𝜆4
Từ phương trình Rayleigh rút ra kết luận như sau:
1. Khi các hạt có kích thước nhất định cường độ ánh sáng tỉ lệ thuận với nồng độ
sol, nhưng nồng độ rất lớn thì ánh sáng sẽ bị phân tán nhiều lần
2. Cường độ ánh sáng phân tán (Ipt) tỉ lệ thuận với bình phương thể tích hạt; khi
nồng độ trọng lượng không đổi, độ phân tán D của sol càng cao thìcường độ ánh sáng phân tán càng yếu
VD: Ban đầu Ipt = kV𝑣2𝐼0 khi nồng độ trọng lượng không đổi, thể tích bị chia nhỏ giảm x lần 𝑣 I’pt = kxV( )2 𝑥 𝐾𝑣2𝑉 I = 𝐼 => cường độ ả ầ 𝑥 𝑜
ánh sáng phân tán gi m x l n
Trong đó: v là nồng độ hạt V thể tích mỗi hạt
λo bước sóng ánh sáng tới
Io cường độ ánh sáng tới
3. Chiết suất của tướng phân tán và môi trường phân tán lệch nhau nhiều thì Ipt càng lớn.
4. Ipt tỉ lệ nghịch với λ4 nên trong ánh sáng trắng thì những tia có bước sóng ngắn
(xanh, tím) phân tán mạnh nhất
II. SỰ HẤP THỤ ÁNH SÁNG:
Sự hấp thụ ánh sáng đơn sắc của hệ keo tuân thủ theo định luận Beer – Lambert: I = Ioe-KlC Trong đó: I cường độ tia ló Io cường độ tia tới
l chiều dày lớp ánh sáng mà dung dịch đi qua C nồng độ chất tan k hệ số hấp thu
Ngoài ra phương trình còn được dùng dưới dạng: 𝐼
D = ln 𝑜 𝑘𝑐𝑙 trong đó:
D là độ hấp thu hay mật độ quang củ dung dịch 𝐼 𝐼
𝑜 là độ truyền suất tương đối 𝐼
K phụ thuộc vào bản chất của hệ và bước sóng ánh sáng nhưng không phụ thuoovj vào nồng độ của hệ.
K = K1 + K2 Trong đó: K1 là hệ số hấp thu thuần túy, phụ thuộc vào ánh sáng tới
K2 hệ số hấp thu giả, phụ thuộc vào bước sóng và độ phân tán
III. DỤNG CỤ QUANG HỌC DÙNG NGHIÊN CỨU KEO: 1. Kính siêu vi
Thực tế không quang sát được kích thước và hình dạng hạt nhưng các thông số có
thể xác định một cách gián tiếp
Ví dụ: hệ keo có nồng độ khối lượng C (g/cm3), thể tích V, đếm được n hạt. Khối l ợ ư ng 1 hạ 𝐶𝑉 t: m = 𝑛 3
Hạt hình cầu có tỉ trọng γ m = 4 𝜋 𝑟3𝛾 => r = √ 3𝐶𝑉 3 4𝜋𝛾𝑛
2. Kính hiển vi điện tử :
Đo trực tiếp được kích thước và hình dạng của hạt, nhưng không cho khả năng
nghiên cứu trạng thái động học của hệ keo khí, keo lỏng và quá trình biến đổi của sự phân tán.
CHƯƠNG 4: TÍNH CHẤT ĐỘNG HỌC PHÂN TỬ CỦA HỆ KEO
I. CHUYỂN ĐỘNG NHIỆT
Phân tử khí hay lỏng có 3 loại chuyển động: tịnh tiến, quay và dao động. Trong
chuyển động tịnh tiến số dao động va chạm giữa các phân tử là rất lớn dẫn đến vô số
trật tự trong chuyển động.
Thí nghiệm: nhà sinh vật học người Anh, Brown khi quan sát huyền phù bằng kính
hiển vi phát hiện rằng: các hạt phấn hoa không ngừng chuyển động hỗn loạn và cường
độ chuyển động không bị giảm theo thời gian. Sự chuyển động đó được gọi là chuyển động Brown.
Như đã biết (trong sách ghi chứ không học làm sao biết), hạt keo hình cầu có kích
thước lớn hơn phân tử nếu ở trong dung dịch, nó sẽ bị các phân tử của môi trường phân
tán, do chuyển động nhiệt va đập từ các hướng khác nhau. Đối với hạt:
Kích thước > 5𝜇, các va chạm từ các hướng có thể bù trừ cho nhau (về lực), nên hạt gần như đứng im.
Kích thước < 5𝜇, số va chạm từ các hướng không đều làm cho các hạt chuyển
động hỗn loạn về các hướng theo một quỹ đạo phức tạp.
Nếu các phân tử môi trường phân tán va đập vào hạt keo theo hướng không thẳng
góc thì có thể làm cho hạt chuyển động quay.
Để tính toán người ta dung đại lượng dịch chuyển bình phương trung bình của hạt: Ở đây, l à h ì n h c h i ế u c ủ a n h ữ n g chuyển dịch của hạt
trên trục x tỏng những khoảng thời gian bằng nhau, n là số lần mà ta nhìn thấy hình chiếu. II. SỰ KHUẾCH TÁN
1. Các định luật Fick
Khuếch tán là quá trình tự san bằng nồng độ trong hệ. Quá trình đó tự xảy ra trong
hệ do ảnh hưởng của chuyển động nhiệt và chỉ xảy ra khi hệ có nồng độ đầu không đồng đều. Định luật Fick 1
Lượng chất m chuyển qua tiết diện s (đặt vuông góc với chiều khuếch tán), thì sẽ
tỷ lệ thuận với S, khoảng thời gian khuếch tán t và gradient nồng độ theo khoảng cách dC/dx. 𝑑𝐶 dm= -D 𝑆𝑑𝑡 𝑑𝑋
Với định nghĩ dòng khuếch tán i: trong đó i là hàm số của x và t vì gradien nồng
độ dC/dx phụ thuộc vào x và t: 𝑑𝑚 i = = −𝐷 𝑑𝐶 𝑆𝑑𝑡 𝑑𝑥
Nếu trong trường hợp gradient nồng độ không đổi theo thờ gian thì i cũng sẽ
không đổi theo thời gian và trong hệ sẽ thiết lập một trạng thái dừng ta có 𝑑𝐶
𝑚 = −𝐷 𝑑𝑥 𝑆𝑡 Định luật Fick 2:
Khi sự khuếch tán không xảy ra ở trạng thái dừng thì i là hàm số của x và t:
Với dC/dt là độ giảm nồng độ chất tan trong thể tích hình trụ: 𝑑𝐶 𝑑2𝐶 𝑑𝑡 = 𝐷 𝑑𝑥2
2. Phương trình Einstein Với hạt hình cầu: 𝑘𝑇 𝐷 = 6𝜋.𝜂.𝑟
Ta thấy hệ số khuếch tán D tỷ lệ thuận với nhiệt độ T, tỷ lệ nghịch với độ nhớt 𝜂
và kích thước hạt. Vì kích thước hạt keo lớn hơn kích thước phân tử rất nh ề i u, do
đó các dung dịch keo có hệ số khuếch tán nhỏ. r: bán kính hạt keo. 4 M = 𝜋. 𝑟3. 𝛾. 𝑁 3 N: hằng số Avogado M: trọng lượng hạt
𝛾: tỉ trọng của tướng phân tán
3. Phương trình Einstein – Smolukhopsky 𝑅𝑇2𝑡 ∆= √𝑁6𝜋𝜂𝑛
III. Áp suất thẩm thấu của dung dịch keo:
Hiện tượng thẩm thấu:
- Nguyên nhân: sự chuyển động hỗn loạn của các hạt trong dung dịch.
- Hiện tượng thẩm thấu trong dung dịch keo tương tự trong dung dịch thật, chỉ
khác nhau về mặt định lượng.
- Hiện tượng thẩm thấu: Khi ngăn cách 2 dung dịch có nồng độ khác nhau bởi
màng bán thấm sẽ có dòng dung môi di chuyển từ phía dd có nồng độ thấp sang
phía dd có nồng độ cao hơn → san bằng nồng độ ở 2 phía màng (việc chuyển các
phân tử dung môi sẽ tiếp tục cho đến khi đạt được trạng thái cân bằng).
Áp suất thẩm thấu:
- Áp suất thẩm thấu IL: Dòng dung môi sẽ ngưng lưu chuyển, khi tạo được một
gradien áp suất cần thiết chống lại, áp suất này cân bằng với áp suất thủy tinh tương ứng.
- Lý giải hiện tượng:
+ Theo quan điểm nhiệt động: chiều tăng entropi của quá trình.
+ theo quan điểm động học: số dư của va chạm của các phân tử dung môi lên màng từ phía dd loãng.
- Ở dung dịch lý tưởng: pt Van’t Hoff ấ ẩ ấ IL ILdd : áp su t th m th u dd =CRT C: nồng độ thể tích -
Ở dung dịch keo: nồng độ t ớ
ư ng phân tán được dùng là nồng độ hạt (số hạt
trong đ.vị thể tích và nồng độ k/l hạt Cd) →(𝑪𝒅 = 𝒗) 𝑵
Phương trình áp suất thẩm thấu: 𝒗 ILk = 𝑹𝑻 = 𝑪 𝑵 𝒅𝑹𝑻
- Đặc điểm của áp suất thẩm thấu trong dd keo:
+ Hệ keo không bền vững nhiệt động nên khi để lâu, nồng độ hạt có thể giảm do
hiện tượng keo tưởng => Áp suất thẩm thấu của hệ keo thường bị giảm theo t/g.
+ Ở điều kiện giống nhau về nhiệt động, nồng độ khối lượng, hệ keo luôn cho áp
suất nhỏ hơn nhiều so với dd thật.
VD: 2 hệ cùng nồng độ khối lượng, ở cùng 𝝅 ạ ố ạ 𝟏 𝒗𝟏
nhiệt độ nhưng do t o thành s h t khác nhau
(v1 ≠ v2), áp suất thẩm thấu 2 hệ tỷ lệ với nhau: 𝝅 = 𝟐 𝒗𝟐
→ Kích thước hạt càng nhỏ (càng có nhiều hạt) → 𝝅 càng lớn.
→Dung dịch thật (chứa các phân tử kích thước rất nhỏ) so với dung dịch keo →
𝝅𝒅𝒅 𝒕𝒉ậ𝒕 > 𝝅𝒌𝒆𝒐.
IV. Sự sa lắng và cân bằng sa lắng
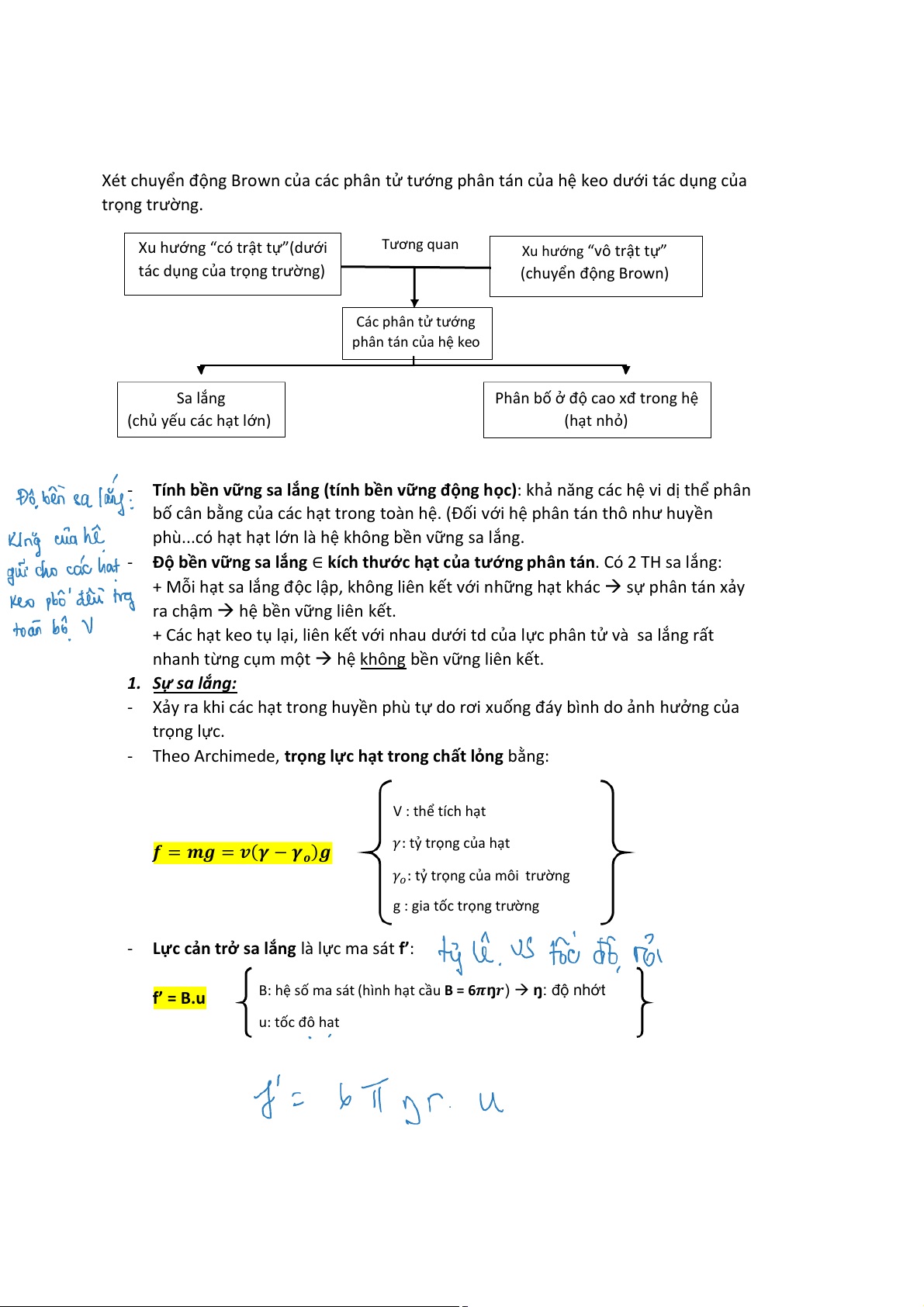
Xét chuyển động Brown của các phân tử tướng phân tán của hệ keo dưới tác dụng của trọng trường.
Xu hướng “có trật tự”(dưới Tương quan
Xu hướng “vô trật tự” ụ ủ ọng trườ tác d ng c a tr ng) (chuyển động Brown) Các phân tử tướng phân tán của hệ keo Sa lắng
Phân bố ở độ cao xđ trong hệ
(chủ yếu các hạt lớn) (hạt nhỏ)
- Tính bền vững sa lắng (tính bền vững động học): khả năng các hệ vi dị thể phân
bố cân bằng của các hạt trong toàn hệ. (Đối với hệ phân tán thô như huyền
phù...có hạt hạt lớn là hệ không bền vững sa lắng.
- Độ bền vững sa lắng ∈ kích thước hạt của tướng phân tán. Có 2 TH sa lắng:
+ Mỗi hạt sa lắng độc lập, không liên kết với những hạt khác → sự phân tán xảy
ra chậm → hệ bền vững liên kết .
+ Các hạt keo tụ lại, liên kết với nhau dưới td của lực phân tử và sa lắng rất
nhanh từng cụm một → hệ không bền vững liên kết. 1. Sự sa lắng:
- Xảy ra khi các hạt trong huyền phù tự do rơi xuống đáy bình do ảnh hưởng của trọng lực.
- Theo Archimede, trọng lực hạt trong chất ỏ l ng bằng: V : thể tích hạt
𝒇 = 𝒎𝒈 = 𝒗(𝜸 − 𝜸
𝛾: tỷ trọng của hạt 𝒐)𝒈
𝛾𝑜: tỷ trọng của môi trường
g : gia tốc trọng trường
- Lực cản trở sa lắng là lực ma sát f : ’ f’ = B.u ệ ố ạ
B: h s ma sát (hình h t cầu B = 6𝝅ŋ𝒓) → ŋ: độ nhớt u: tốc độ hạt
→Lúc đầu hạt rơi nhanh (do u còn nhỏ f>f’), nhưng u tăng dần làm f’ tăng đến khi
bằng giá trị của trọng lực.
Lúc đó, hạt sa lắng với tốc độ đều: f=f’ 𝒗(𝜸 − 𝜸𝒐)𝒈 = 𝑩. 𝒖 Với hạt hình cầ 𝟒 u: 𝝅𝒓𝟑(𝜸 − 𝜸 𝟑
𝒐)𝒈 = 𝟔. 𝝁. ŋ. 𝒓. 𝒖
Tốc độ sa lắng của hạt: 𝒖 = 𝒅𝒙 = 𝟐𝒓𝟐 (𝜸 − 𝜸 → (*) 𝒅𝒕 √ 𝟗.ŋ.𝒖 𝟗ŋ 𝒐)𝒈
𝒓 = 𝟐(𝜸−𝜸𝒐)𝒈
*Lưu ý: phương trình trên chỉ thích hợp cho những huyền phù có kích thước 5 -
100𝝁 (vì với những hạt này, t/g đạt được tốc độ sa lắng không đổi rất nhỏ →
không ảnh hưởng kết quả). Các hạt có:
+ r > 100𝝁 : sa lắng rất nhanh.
+ r < 5𝝁 : dễ thiết lập cân bằng phân bố.
2. Phân tích sa lắng biết được kích thước hạt. Hệ đơn phân tán Hệ đa phân tán
Kích thước các loại hạt Bé nhất Lớn nhất và trung bình
Tốc độ sa lắng của hạt Như nhau Không đều nhau Lượng chất sa lắng Phải xác định tốc (p) tỷ lệ thuận với độ tích lũy hạt, tức thời gian (t). thiết lập sự phụ thuộc lượng chất 𝒉 ắ ờ 𝒖 = sa l ng vào th i 𝒕 gian, p=f(t) => đồ h: quãng đường đi của thị hàm này gọi là hạt. đường cong sa
*Thế gtrị u vào (*) => r. lắng.
(tham khảo đồ thị sách trang 72)
Thực tế, phép phân tích sa lắng được tiến hành dựa trên cơ sở xác định tốc độ chất chứa trên đĩa cân.
Điều kiện giới hạn sử dụng phương pháp phân tích sa lắng:
- Phương trình cơ bản dùng trong phương pháp này chỉ đúng cho trường hợp các
hạt hình cầu. Nếu hạt không phải hình cầu, ta chỉ tính được bán kính tương đương của nó.