





















Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI HỌC SINH GIỎI CẤP TRƯỜNG VĨNH YÊN NĂM HỌC 2022-2023 Môn thi: TOÁN 7 ĐỀ CHÍNH THỨC
Thời gian: 120 phút (không kể thời gian giaođề)
(Đề thi gồm có 01 trang)
Câu 1. (4 điểm) a) Thực hiện phép tính: 12 5 6 2 10 3 5 2 2 .3 4 .9 5 .7 25 .49 A 6 3 9 3 2 4 5 125.7 5 .14 2 .3 8 .3 b) Tính 100 99 98 2 S 2
2 2 .... 2 2 c) Chứng tỏ: 1 2 3 2019 ... 0,75 2 3 2019 3 3 3 3
Câu 2. (4 điểm)
a b c
b c a
c a b
a) Cho a, b, c là ba số thực khác 0, thoả mãn : và a+b+c 0 c a b b a c
Hãy tính giá trị của biểu thức: B 1 1 1 . a c b
b) Ba lớp 7A, 7B, 7C cùng mua một số gói tăm từ thiện, lúc đầu số gói tăm dự định chia cho ba lớp
tỉ lệ với 5,6,7 nhưng sau đó chia theo tỉ lệ 4,5,6 nên có một lớp nhận nhiều hơn dự định 4 gói. Tính
tổng số gói tăm mà ba lớp đã mua. x y z
c) Cho ba số x,y, z tỉ lệ với 3,4,5. Tính 2017 2018 2019 P
2017x 2018y 2019z
Câu 3. (4 điểm)
a) Tìm giá trị nhỏ nhất của biểu thức A = 2x 2 2x 2013 với x là số nguyên.
b) Tìm nghiệm nguyên dương của phương trình x y z xyz .
Câu 4. (6 điểm)
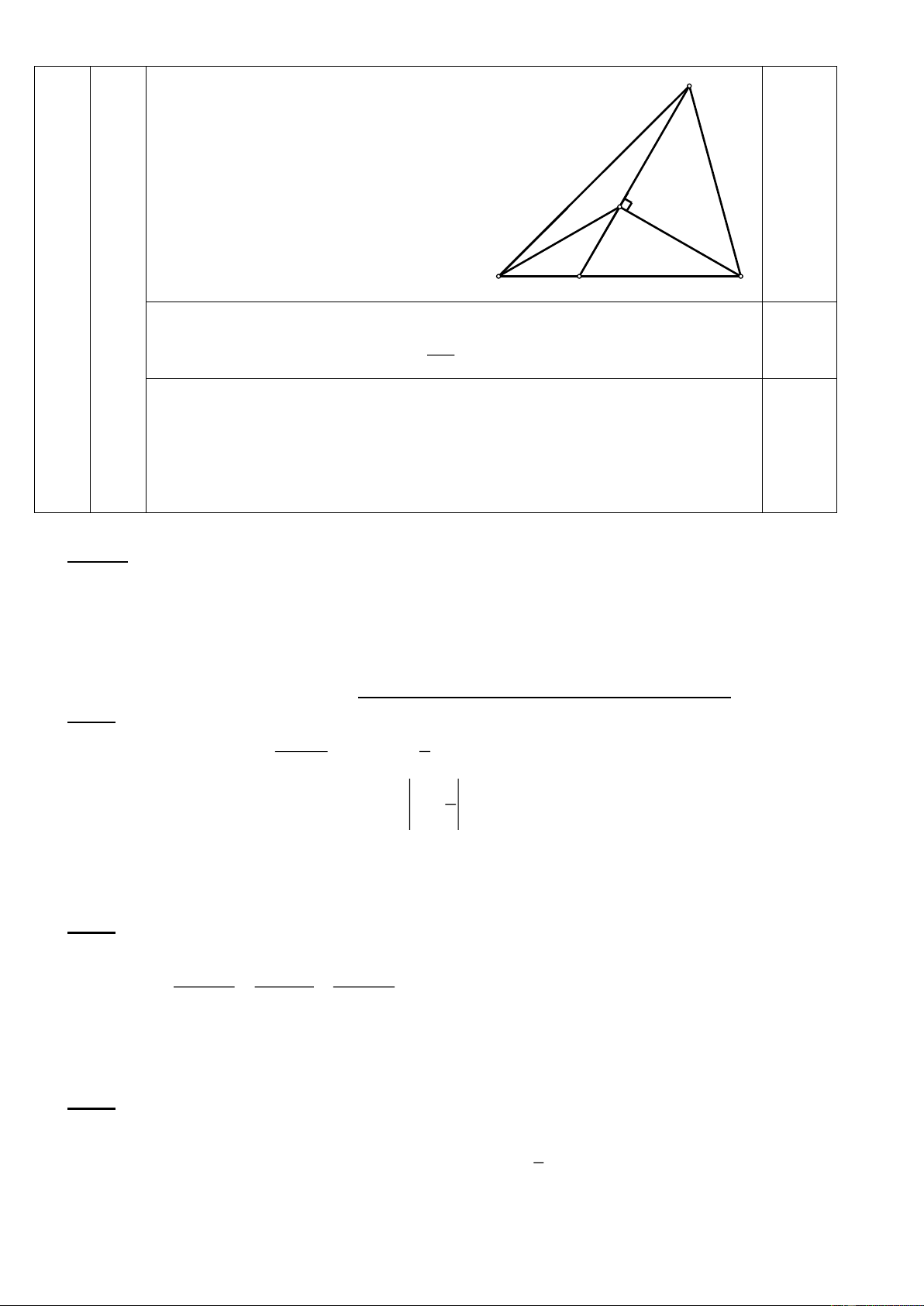
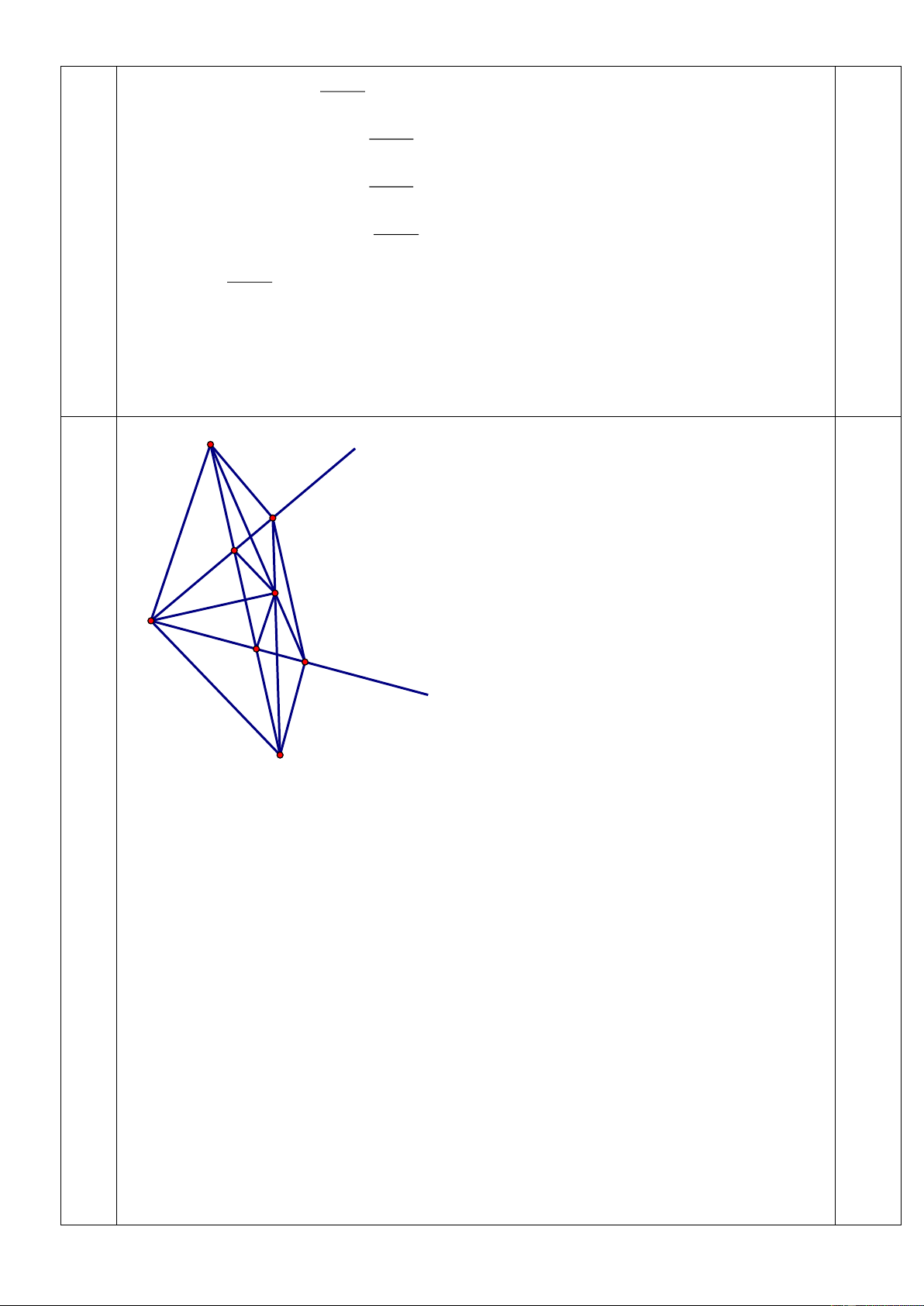
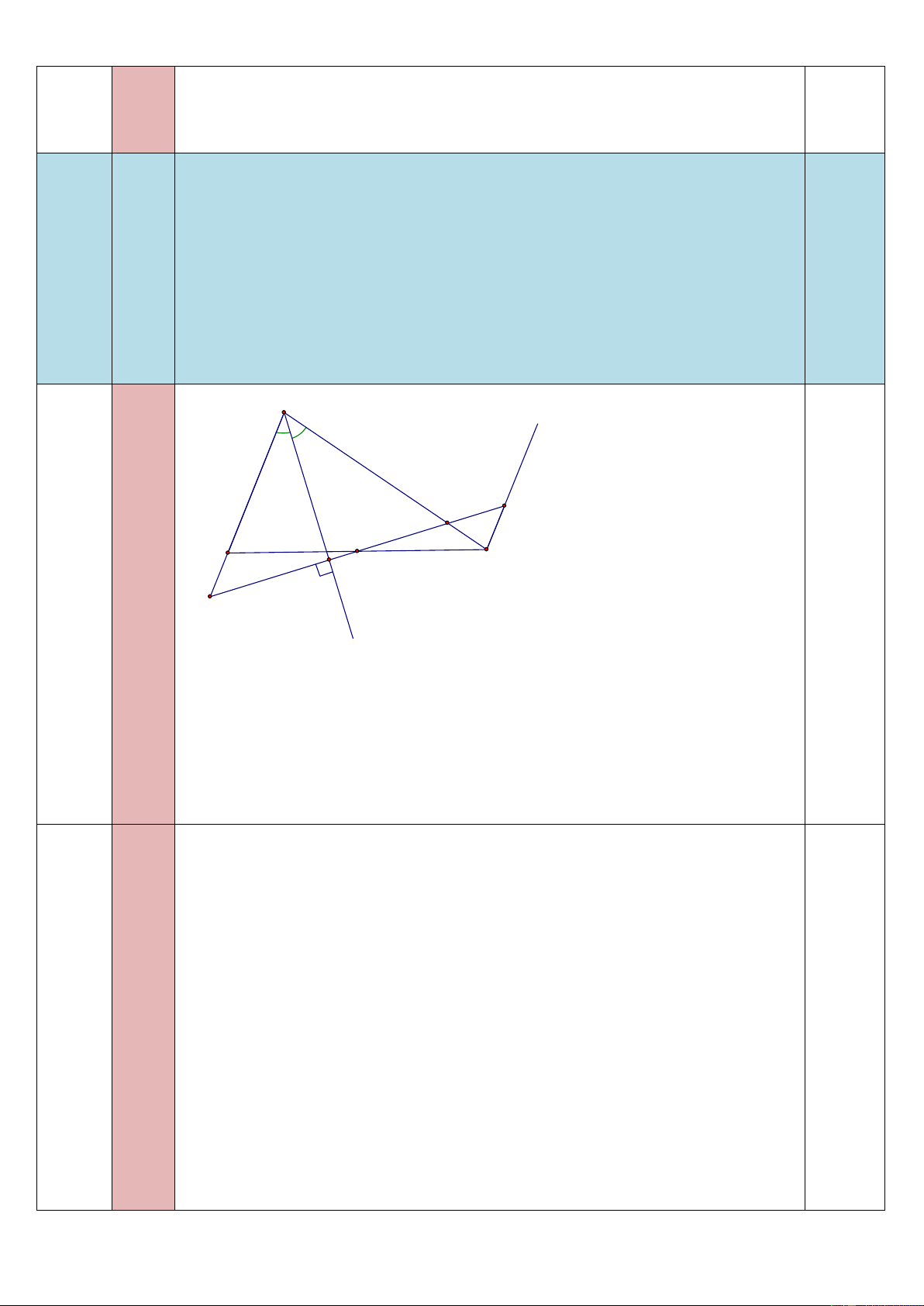
Cho tam giác ABC có AB < AC. Trên tia đối của tia CA lấy điểm D sao cho CD = AB. Gọi P,Q là
trung điểm của AD, BC, và I là giao điểm các đường vuông góc với AD và BC tại P và Q.
a) Chứng minh ∆AIB = ∆DIC
b) Chứng minh AI là tia phân giác của góc BAC. 1
c) Kẻ IE vuông góc với AB, chứng minh AE AD . 2
Câu 5. (2 điểm) Cho biết xyz=1 x y z Tính giá trị A = xy x 1 yz y 1 xz z 1
Giám thị coi thi không giải thích gì thêm - SBD:.......................
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐÁP ÁN ĐỀ THI HỌC SINH GIỎI CẤP TRƯỜNG VĨNH YÊN NĂM HỌC 2022-2023 Môn thi: TOÁN 7 ĐỀ CHÍNH THỨC
( Đáp án gồm có 03 trang) Câu Phần Nội dung Điểm a 12 5 6 2 10 3 5 2 2 .3 4 .9 5 .7 25 .49 2đ A 2 .36 8 .3 125.73 9 3 2 4 5 5 .14 Câu 1 (4 điểm) 10 12 5 12 4 10 3 4 2 .3 2 .3 5 .7 5 .7 12 6 12 5 9 3 9 3 3 2 .3 2 .3 5 .7 5 .2 .7 0,5 12 4 2 .3 .3 10 3 1 5 .7 .1 7 12 5 2 .3 .3 9 3 1 5 .7 . 3 1 2 0,5 12 4 10 3 2 .3 .2 5 .7 . 6 1 10 7 12 5 9 3 2 .3 .4 5 .7 .9 6 3 2 1 b
S =(-3)0+(-3)1 + (-3)2+(-3)3+...+ (-3)2015. 0.5 2đ
-3S = (-3).[(-3)0+(-3)1+(-3)2 + ....+(-3)2015] 0.5
= (-3)1+ (-3)2+ ....+(-3)2016]
-3S – S = [(-3)1 + (-3)2+...+(-3)2016]-(3)0-(-3)1-...-(-3)2015. 0.5 -4S = (-3)2016 -1. 2016 ( 3 ) 1 2016 2016 3 1 1 3 0.5 S = 4 = 4 4 +Vì a+b+c 0 a
Theo tính chất dãy tỉ số bằng nhau ,ta có: 1,5 đ
a b c
b c a
c a b
= a b c b c a c a b = 1 0.5 c a b
a b c Câu 2
a b c
b c a
c a b ( 4 điểm ) mà 1 1 1 = 2 c a b 0.5 => a b b c c a =2 c a b 0.5 Vậy B = b a c b a c a b c 1 1 1 ( )( )( ) =8 a c b a c b b
Gọi tổng số gói tăm 3 lớp cùng mua là x ( x là số tự nhiên khác 0) 1,5 đ
Số gói tăm dự định chia cho 3 lớp 7A, 7B, 7C lúc đầu lần lượt là: a, b, c a b c
a b c x 5x 6x x 7x Ta có: a ; b ;c (1) 5 6 7 18 18 18 18 3 18 0.5
Số gói tăm sau đó chia cho 3 lớp lần lượt là a’, b’, c’, ta có: , , , , , , a b c a b c x 4x 5x x 6x , , , a ;b ;c (2) 4 5 6 15 15 15 15 3 15
So sánh (1) và (2) ta có: a > a’; b=b’; c < c’ nên lớp 7C nhận nhiều hơn lúc đầu 0.5 Vây: c’ – 6x 7x x c = 4 hay 4 4 x 360 15 18 90
Vậy số gói tăm 3 lớp đã mua là 360 gói. 0.5 c 5z 6 y 6x 4z 4 y 5x Từ 1 đ 4 5 6 20z 24 y 30x 20z 24 y 30x => 0.5 16 25 36 =>10z = 12y = 15x x y z 3x 2 y 5z => => và 3x – 2y + 5z = 96 4 5 6 12 10 30
Giải ra ta được x = 12; y = 15; z = 18 0.5 0.5
1) Ta có: A 2x 2 2x 2013 2x 2 2013 2x a 2đ
2x 2 2013 2x 2011 0.5 Câu 3 (4 điểm) Dấu “=” xảy ra khi 2013 (2x 2)(2013 2x) 0 1 x 0.5 2 KL:…….. 0.5 b
2) Vì x,y,z nguyên dương nên ta giả sử 1 2đ x y z 0.25 1 1 1 1 1 1 3 0.5 Theo bài ra 1 = + + + + = yz yx zx 2 x 2 x 2 x 2 x => x 2 3 => x = 1
Thay vào đầu bài ta có 1 y z yz => y – yz + 1 + z = 0
=> y(1-z) - ( 1- z) + 2 =0 => (y-1) (z - 1) = 2
TH1: y -1 = 1 => y =2 và z -1 = 2 => z =3 0.5 0.25
TH2: y -1 = 2 => y =3 và z -1 = 1 => z =2 0.25
Vậy có hai cặp nghiệp nguyên thỏa mãn (1,2,3); (1,3,2) 0.25 A P C B 0,5 Câu 4 E (6 điểm ) D I a Ta có IB = IC, IA = ID 1 2đ Lại có AB = CD (gt) 0,5
Do đó ∆AIB = ∆DIC (c.c.c) 0,5 b CM: DAI = D 0,5
1,5đ ∆AIB = ∆DIC (câu a), suy ra BAI = D 0,5 Do đó DAI = BAI. 0,5
Vậy AI là tia phân giác của góc BAC c
Kẻ IE AB, ta có ∆AIE = ∆AIP 0,5 => AE = AP 0,5 2đ
Mà AP = ½ AD (vì P là trung điểm AD) 0,5 1 Suy ra AE AD 0,5 2 Câu 5 𝑥 𝑦 𝑧 xz xyz z ( 2 điểm ) + + = 𝑥𝑦+𝑥+1 𝑦𝑧+𝑦+1 𝑥𝑧+𝑧+1 2
xyz xz z
xyz xyz xz xz z 1 1 xz xyz z xyz xz 1 = 1 1 1 xz z z 1 xz xz z 1 xyz xz 1
Lưu ý .Học sinh có cách giải khác đúng vẫn cho điểm tối đa.
PHÒNG GD & ĐT DIỄN CHÂU
KỲ THI CHỌN HỌC SINH GIỎI TRƯỜNG VÒNG 1 LIÊN TRƯỜNG THCS NĂM HỌC 2022-2023 ĐỀ CHÍNH THỨC MÔN THI: TOÁN 7
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
Câu 1. (4,5 điểm)
1. Tính giá trị biểu thức: 2 3 4 5 4 3 5 1 1 1 a) : : ; b) . 6 .
3 1 : ( 1 7 11 11 7 11 11 3 3 3 2 2 1 1 0, 4 0,25 2022 c) 9 11 3 5 : 7 7 1 2023 1,4 1 0,875 0, 7 9 11 6
Câu 2. (4,0 điểm) x x a) Tìm x biết: 2 2 .3 3 99 ; 1+3y 1+5y 1+7y b) Tìm x, y biết: ; 12 5x 4x
c) Tìm số tự nhiên x, y biết: 2 2
7(x 2023) 23 y
Câu 3. (4,5 điểm)
a) Cho p là số nguyên tố lớn hơn 3, biết p + 2 cũng là số nguyên tố. Chứng tỏ rằng p + 1 chia hết cho 6. x 1
b) Tìm số nguyên x để biểu thức sau đạt giá trị lớn nhất, tìm giá trị lớn nhất đó: P 2x2 .
c) Một trường THCS có ba lớp 7, tổng số học sinh hai lớp 7A, 7B là 85 em, Nếu
chuyển 10 học sinh từ lớp 7A sang lớp 7C thì số học sinh ba lớp 7A, 7B, 7C tỉ lệ
thuận với 7;8;9. Hỏi lúc đầu mỗi lớp có bao nhiêu học sinh?
Câu 4.(7,0 điểm)
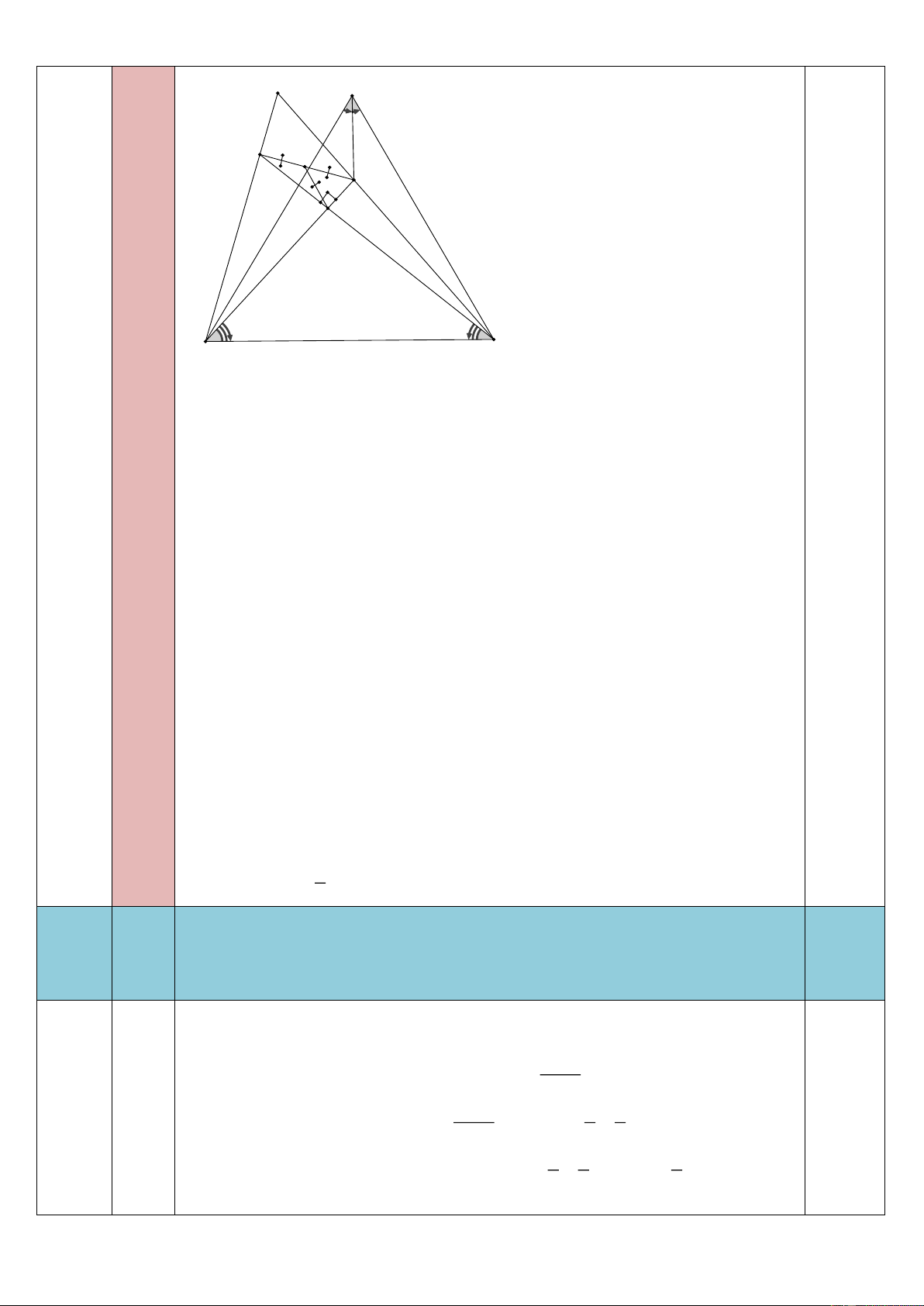
1. Cho tam giác ABC cân tại A. Trên cạnh BC lấy điểm D, trên tia đối của CB lấy
điểm E sao cho BD = CE. Các đường thẳng vuông góc với BC kẻ từ D và E cắt AB và AC
lần lượt ở M và N. Chứng minh rằng: a) BM = CN. b) BC < MN.
c) Đường thẳng vuông góc với MN tại giao điểm của MN và BC luôn luôn đi qua một
điểm cố định khi D thay đổi trên cạnh BC
2. Cho tam giác ABC có góc B bằng 450 , góc C bằng 1200. Trên tia đối của tia CB
lấy điểm D sao cho CD = 2CB . Tính góc ADB
--------------HẾT--------------
Giám thị không giải thích gì thêm
Họ và tên thí sinh...............................................................SBD:.............
HƯỚNG DẪN CHẤM ĐỀ THI HỌC SINH TRƯỜNG MÔN TOÁN LỚP 7 NĂM HỌC 2022-2023
( Hướng dẫn chấm này có 04 trang ) Câu Ý Nội dung Điểm 1 a
1. Tính giá trị biểu thức: 1,5 4,5 1,5 3 4 5 4 3 5 đ a) : : ; 7 11 11 7 11 11 3 4 5 4 3 5 3 4 4 3 5 0,5 : : ( ) : 7 11 11 7 11 11 7 11 7 11 11 3 4 4 3 5 1 5 0,5 ( ) : ( 1 ) : 7 7 11 11 11 11 11 1 0 11 0,5 . 2 11 5 b 2 1,5 1 1 1 1,5 b) . 6 .
3 1 : ( 1 3 3 3 2 1 1 1 1 4 0.5 6. 3. 1
: ( 1) 6. 11 : ( ) 3 3 3 9 3 1 4 2 3 0.5
6. 11 : ( ) ( 2).( ) 9 3 3 4 8 3 0.5 .( ) 2 3 4 c 2 2 1 1 1,5 0, 4 0,25 1,5 2022 c) 9 11 3 5 : 7 7 1 2023 1,4 1 0,875 0, 7 9 11 6 2 2 2 1 1 1 0,5 2022 5 9 11 3 4 5 : 7 7 7 7 7 7 2023 5 9 11 6 8 10 1 1 1 1 1 1 0,5 2 5 9 11 3 4 5 2022 :
1 1 1 7 1 1 1 2023 7
5 9 11 2 3 4 5 2 2 2022 0.5 : 0 7 7 2023 2 a x x 1,0 2. a) Tìm x biết: 2 2 .3 3 99 ; 4,0 1,0 x x2 x x2 0.25 2 .3 3 99 2.3 3 99 đ x 2 3 (2 3 ) 99 0.25
3 .x11 99 3x 9 x 2 0.5 b 1+3y 1+5y 1+7y 1,5 b) Tìm x, y biết: ; 1,5 12 5x 4x
Áp dụng tính chất dãy tỷ số bằng nhau ta có: 1+3y 1+5y 1+7y 1 7y 1 5y 2y 1 5y 1 3y 2y 12 5x 4x 4x 5x x 5x 12 5x 12 0,5 2 y 2 y => x 5x 12
TH1: y = 0, thay vào=> không thỏa mãn 0,5
TH2: y 0 x 5x -12 x=2
Thay x = 2 vào trên ta được:1 3y 2y y 12 2 1 =>1+ 3y = -12y=> y = 15 Vậy x = 2, y = 1 thoả mãn đề bài. 0,5 15 c
c) Tìm số tự nhiên x, y biết: 2 2
7(x 2023) 23 y 1,5
1,5 Vì x, y là các số tự nhiên nên 2
(x 2023) , y 2 là các số chính phương 0,5 nên không âm nên 2 23 y 23 2
0 7(x 2023) 23 2 0.5 Do đó (x 2023) 0 x 2023 2 (x 2023) 1 x 2024
+ Với x = 2023 thì không có giá trị của y tự nhiên thỏa mãn. 0.25 + Với x =2024 thì 2
y 16 y 4 . Vậy (x;y) =(2024;4) 0.25 3 a
a) Cho p là số nguyên tố lớn hơn 3. Biết p + 2 cũng là số nguyên tố. 1,5 4,5
1,5 Chứng tỏ rằng p + 1 chia hết cho 6. đ
Vì p là số nguyên tố lớn hơn 3 nên p lẻ, do đó p + 1 chẵn 0,5 => (p + 1) 2 (1)
Cũng do p là số nguyên tố lớn hơn 3 nên p = 3k + 1 hoặc p = 3k + 2 0,25 (k N)
Nếu p = 3k + 1 thì p +2 = 3k +3 = 3(k + 1) 3 0,25
=> p + 2 không là số nguyên tố nên p = 3k + 1 không xảy ra.
Do đó p = 3k + 2 => p + 1 = 3k + 3 = 3(k +1) 3 (2) 0,25
Vì (2;3) = 1 nên từ (1) và (2) ta có (p + 1) 6 0,25 b
b) Tìm số nguyên x để biểu thức sau đạt giá trị lớn nhất, tìm giá trị lớn 1.5 1,5 nhất đó x 1 : P . 2x 2 x 1 (x 1) 2 1 2 P 0.5 2x 2 2(x 1) 2 x 1 Để 2 P a m x a
m x x-1 >0 và nhỏ nhất (x nguyên) x 2 0.5 x-1 1 2 3 P a m x x 2 0.5 2 2 1 2 b
c) Một trường THCS có ba lớp 7, tổng số học sinh hai lớp 7A, 7B là
85 em, Nếu chuyển 10 học sinh từ lớp 7A sang lớp 7C thì số học 1,5
sinh ba lớp 7A, 7B, 7C tỉ lệ thuận với 7;8;9. Hỏi lúc đầu mỗi lớp có 1,5 bao nhiêu học sinh?
Gọi số học sinh của lớp 7A, 7B, 7C lần lượt là x, y, z (học sinh) ( *
x, y, z N , x 10 0,25
Theo bài ra ta có x y 85 (1) 0.25
Nếu chuyển 10 học sinh từ lớp 7A sang lớp 7C thì số học sinh ba
lớp 7A, 7B, 7C tỉ lệ thuận với 7;8;9 nên ta có: 0,25 x 10 y z 10 (2) 7 8 9
Áp dụng tính chất dãy tỉ số bằng nhau ta có: 0,25 x 10 y z 10 (x 10) y 85 10 5 7 8 9 7 8 15
Suy ra x 45, y 40, z 35 (Thỏa mãn điều kiện) 0.25
Vậy số học sinh của lớp 7A, 7B, 7C lần lượt là 45, 40, 35 học sinh. 0,25 4
1. Cho tam giác ABC cân tại A. Trên cạnh BC lấy điểm D, trên tia 6,0 7,0
đối của CB lấy điểm E sao cho BD = CE. Các đường thẳng vuông đ
góc với BC kẻ từ D và E cắt AB và AC lần lượt ở M và N. Chứng minh rằng: a) BM = CN. b) BC < MN.
c) Đường thẳng vuông góc với MN tại giao điểm của MN và
BC luôn luôn đi qua một điểm cố định khi D thay đổi trên cạnh BC a Xét ∆MDB và ∆NEC có: 0 2,0 MDB NEC( 90 ) 0.5 BD = CE (gt) 0.25
MBD NCE( ACB) 0.75
=>∆MDB = ∆NEC (g.c.g)=> BM = CN (hai cạnh tương ứng) 0.5 b
Ta có BC=BD+DC; DE=DC+CE, mà BD=CE(gt) 1.0 => BC=DE
2.0 Gọi I là giao điểm của MN và BC ta có DE=DI+IE1.0
giữa đường vuông góc và đường xiên)=>BCc
Gọi H là chân đường vuông góc kẻ từ A xuống BC.
=> AH vừa là đường cao vừa là đường phân giác của tam giác cân ABC. 2.0 0,25
Gọi O là giao điểm của AH với đường thẳng vuông góc với MN kẻ từ I. ∆OAB = ∆OAC (c.g.c) 0,25
OBA OCA (cặp góc tương ứng) (*)
OC = OB (cặp cạnh tương ứng) (1) 0,25 ∆MDI = ∆NEI (g.c.g) 0,25
IM = IN (cặp cạnh tương ứng) (2) ∆OIM = ∆OIN (c.g.c) 0,25
OM = ON (cặp cạnh tương ứng) (3)
Từ (1), (2) và (3)=> ∆OBM = ∆OCN (c.c.c) 0,25
OBM OCN (cặp góc tương ứng) (**)
Từ (*) và (**) suy ra OCA OCN =900, do đó OC AC. 0,25
=> điểm O cố định. Vậy đường thẳng vuông góc với MN tại giao điểm
của MN và BC luôn luôn đi qua một điểm cố định khi D thay đổi trên 0,25 cạnh BC
2. Cho tam giác ABC có góc B bằng 450 , góc C bằng 1200. Trên tia
đối của tia CB lấy điểm D sao cho CD = 2CB . Tính góc ADB 1.0 2. A 1,0 đ H B C D
KÎ DH Vu«ng gãc víi AC v× 0 0
ACD 60 CDH 30 CD
Từ đó chứng minh được CH = CH = BC 2 0,5 Tam gi¸c BCH c©n t¹i C 0 0
CBH 30 ABH 15 Mµ 0
ABH 15 nªn tam gi¸c AHB c©n t¹i H
Do ®ã tam gi¸c AHD vu«ng c©n t¹i H VËy 0 0 0
ADB 45 30 75 ADB = 450+300=750 0,5 Lưu ý:
- Nếu học sinh không vẽ hình bài 4 hoặc vẽ sai thì không chấm bài 4.
- Nếu học sinh làm cách khác đúng thì vẫn cho điểm tương ứng với từng phần.
PHÒNG GD ĐT THÀNH PHỐ
ĐỀ KHẢO SÁT HỌC SINH GIỎI
TRƯỜNG THCS TRẦN LÃM NĂM HỌC: 2021- 2022 MÔN : TOÁN 7
Thời gian làm bài : 120 phút ( không kể giao đề)
Bài 1(4,0 điểm) x - 3 Cho biểu thức: A = 7 8 với x¹ 2x - 3 2
1. Tính giá trị của biểu thức A biết 1 x + - 2 = -1 3
2. Tìm các giá trị nguyên của x để biểu thức A có giá trị lớn nhất. Tìm giá trị lớn nhất đó.
Bài 2 ( 4,0 điểm)
1. Tìm x ; y; z thỏa mãn các điều kiện sau: 6x - 4z 5z - 6y 4y - 5x = = và 3x – 2y + 5z = 96 5 4 6
2. Lớp 7A có 52 học sinh chia làm ba tổ. Nếu tổ một bớt đi 1 học sinh, tổ hai bớt đi 2
học sinh, tổ ba thêm vào 3 học sinh thì số học sinh tổ một, hai, ba tỉ lệ nghịch với 3;4;2.
Tìm số học sinh của mỗi tổ.
Bài 3(4,0 điểm)
Cho hàm số y = m|x| + 2x ( Với m là hằng số cho trước).
1. Xác định m biết đồ thị hàm số đi qua điểm A( 1 - ;1). 2
2. Vẽ đồ thị hàm số với m vừa tìm được.
Bài 4(6,0 điểm)
Cho tam giác ABC vuông cân tại A. Gọi M,N lần lượt là trung điểm của AB,AC. Kẻ NH
vuông góc CM tại H, HE vuông góc AB tại E, AK vuông góc CM tại K, AQ vuông góc HN tại Q. · 1. Tính BKH ?
2. Chứng minh tam giác ABH cân.
3. Chứng minh HM là phân giác của · BHE .
Bài 5(2,0 điểm)
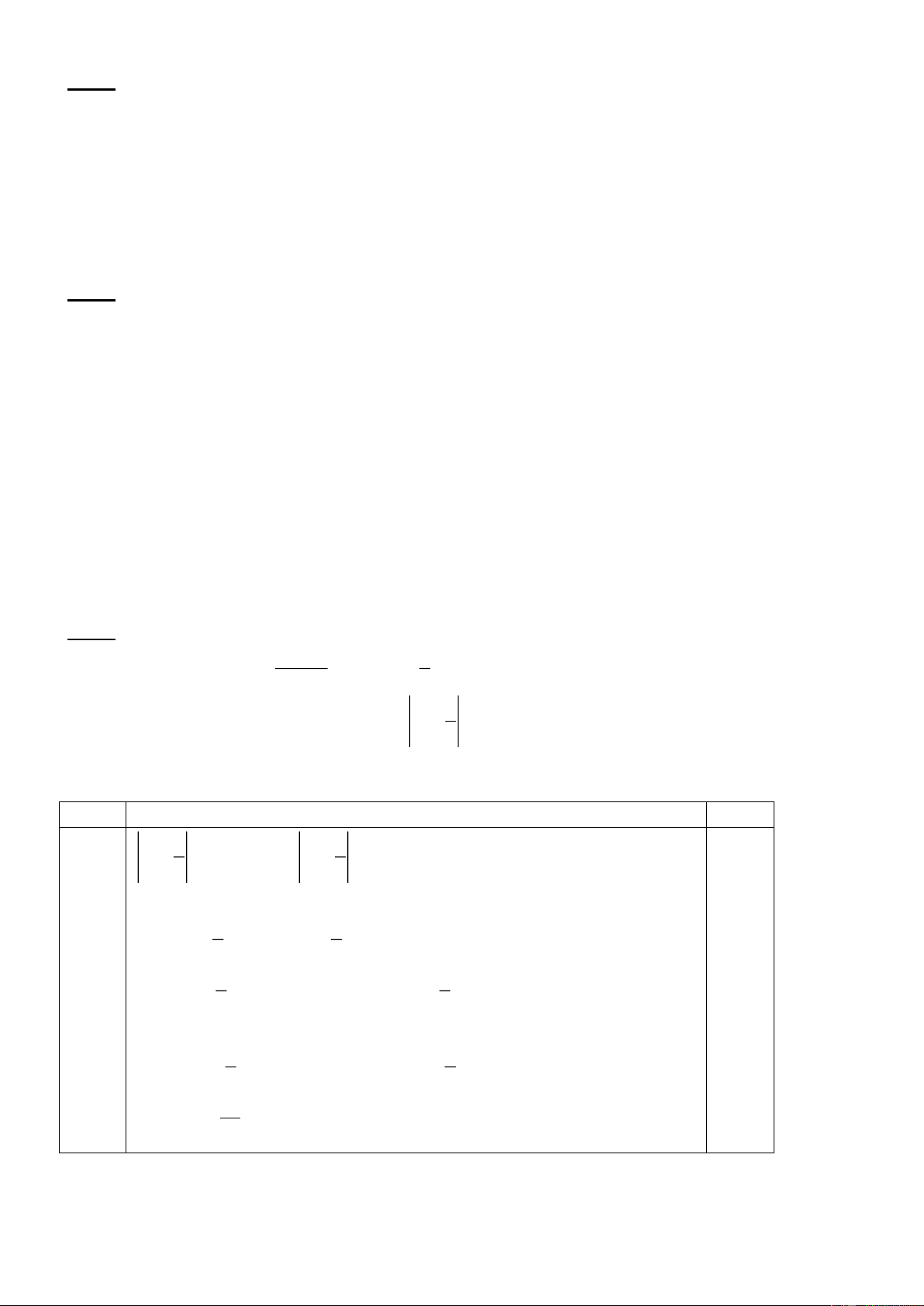
Từ một điểm I tùy ý trong tam giác ABC kẻ IM, IN, IP lần lượt vuông góc với BC, CA,
AB. Chứng minh rằng : AN2 + BP2 + CM2 = AP2 + BM2 + CN2 ---------Hết---------
Họ và tên thí sinh.................................................. Số báo danh.......................
PHÒNG GD ĐT THÀNH PHỐ
BIỂU ĐIỂM CHẤM MÔN: TOÁN 7
TRƯỜNG THCS TRẦN LÃM
HỌC SINH GIỎI THÀNH PHỐ
NĂM HỌC : 2021- 2022
Bài 1(4,0 điểm) x - 3 Cho biểu thức: A = 7 8 với x¹ 2x - 3 2
1. Tính giá trị của biểu thức A biết 1 x + - 2 = -1 3
2. Tìm các giá trị nguyên của x để biểu thức A có giá trị lớn nhất. Tìm giá trị lớn nhất đó. Câu Đáp án Điểm 1 1 x + - 2 = -1 => x + = 1 0,25 3 3 2 0,25 => x = hoặc x = 4 - 3 3 3 1
Với x = 2 thỏa mãn điều kiện x¹
thay vào biểu thức A tính 0,75 3 2 được A = 2 Với x = 4 3 - thỏa mãn điều kiện x¹
thay vào biểu thức A tính 3 2 0,75 được A = 52 17 7 21 5 (2x - 3) - 8 + 7x - 8 7 A= = 2 2 = + 2 0,5 2x - 3 2x - 3 2 2x - 3 5
A lớn nhất khi 2 lớn nhất 0,25 2x - 3 5 2 2
lớn nhất khi (2x – 3) là số nguyên dương nhỏ nhất 0,5 2x - 3 Vậy 2x – 0,25 3 = 1 => x= 2 5
Thay x=2 vào biểu thức A = 7 2 + = 6 0,25 2 2x - 3
KL : Với giá trị nguyên x= 2 giá trị lớn nhất của biểu thức A 0,25 bằng 6
Bài 2 ( 4,0 điểm)
1. Tìm x ; y; z thỏa mãn các điều kiện sau: 6x - 4z 5z - 6y 4y - 5x = = và 3x – 2y + 5z = 96 5 4 6
2. Lớp 7A có 52 học sinh chia làm ba tổ. Nếu tổ một bớt đi 1 học sinh, tổ hai bớt đi 2
học sinh, tổ ba thêm vào 3 học sinh thì số học sinh tổ một, hai, ba tỉ lệ nghịch với 3;4;2.
Tìm số học sinh của mỗi tổ. Câu Đáp án Điểm 6x - 4z 5z - 6y 4y - 5x 5(6x - 4z ) 4(5z - 6y) 6(4y - 5x ) = = = = = 0,5 5 4 6 25 16 36 30x - 20z 20z - 24y 24y - 30x = = = 0,5 25 16 36
30x - 20z + 20z - 24y + 24y - 30x = = 0 0,25 1 25 + 16 + 36
=> 6x = 4z, 5z = 6y,4y = 5x 0,25 x y z 3x 2y 5z
3x - 2y + 5z 96 => = = = = = = = = 3 0,25 4 5 6 12 10 30 12 - 10 + 30 32 0,25 => x= 12; y= 15; z=18
Gọi số học sinh tổ một, tổ hai ,tổ ba của lớp 7A lần lượt là x,y,z 0,5 (x,y,z Î N*; x,y,z < 52)
*Lớp 7A có 52 học sinh => x+y+z = 52 0,25
*Nếu tổ một bớt đi 1 học sinh, tổ hai bớt đi 2 học sinh , tổ ba 0,25 2
thêm vào 3 học sinh thì số học sinh tổ một ,hai, ba tỉ lệ nghịch với 3;4;2.
Nên ta có 3.( x-1) = 4.(y-2) = 2.(z+3) 0,25 3(x - 1) 4(y - 2) 2(z + 3) x - 1 y - 2 z + 3 = = = = = 0,5 12 12 12 4 3 6 x + y + z 52 = = = 4 13 13
=> x = 17,y= 14, z= 21 (Thỏa mãn điều kiện) 0,25 KL ....
Bài 3(4,0 điểm)
Cho hàm số y = m|x| + 2x ( Với m là hằng số cho trước).
1. Xác định m biết đồ thị hàm số đi qua điểm A( 1 - ;1). 2
2. Vẽ đồ thị hàm số với m vừa tìm được. Câu Đáp án Điểm
Xác định m biết đồ thị hàm số đi qua điểm A( 1 - ; 1). 0,75 2
Vì đồ thị hàm số đi qua điểm A( 1 1 - ; 1), thay x =- , y = 1 vào 0,25 1 2 2 công thức ta có: 1= m.| 1 1 - |+2.(- ) =>....=> m= 4 2 2 KL.... 0,25
Với m = 4 hàm số có dạng y = 4.|x| + 2x
=> y = 4x+2x = 6x với x³ 0 ; y = -4x+2x = - 2x với x£ 0 0,5
* Vẽ đồ thị hàm số y= 6x với x³ 0 0,5
- Đồ thị hàm số đi qua gốc tọa độ O(0;0)
- Cho x =1 => y = 6 => điểm B(1; 6) Î đồ thị hàm số
* Vẽ đồ thị hàm số y= - 2x với x£ 0 0,5
- Đồ thị hàm số đi qua gốc tọa độ O(0;0)
- Cho x = -1 => y = 2 => C( - 1; 2) Î đồ thị hàm số 2 1 y y = 6x ( x 0 ) 6 0,25 y = - 2x B ( x 0 ) C 2 O -1 1 x
KL: Vậy đths là tập hợp các điểm Î tia OB, OC như hình vẽ.
Bài 4(6,0 điểm)
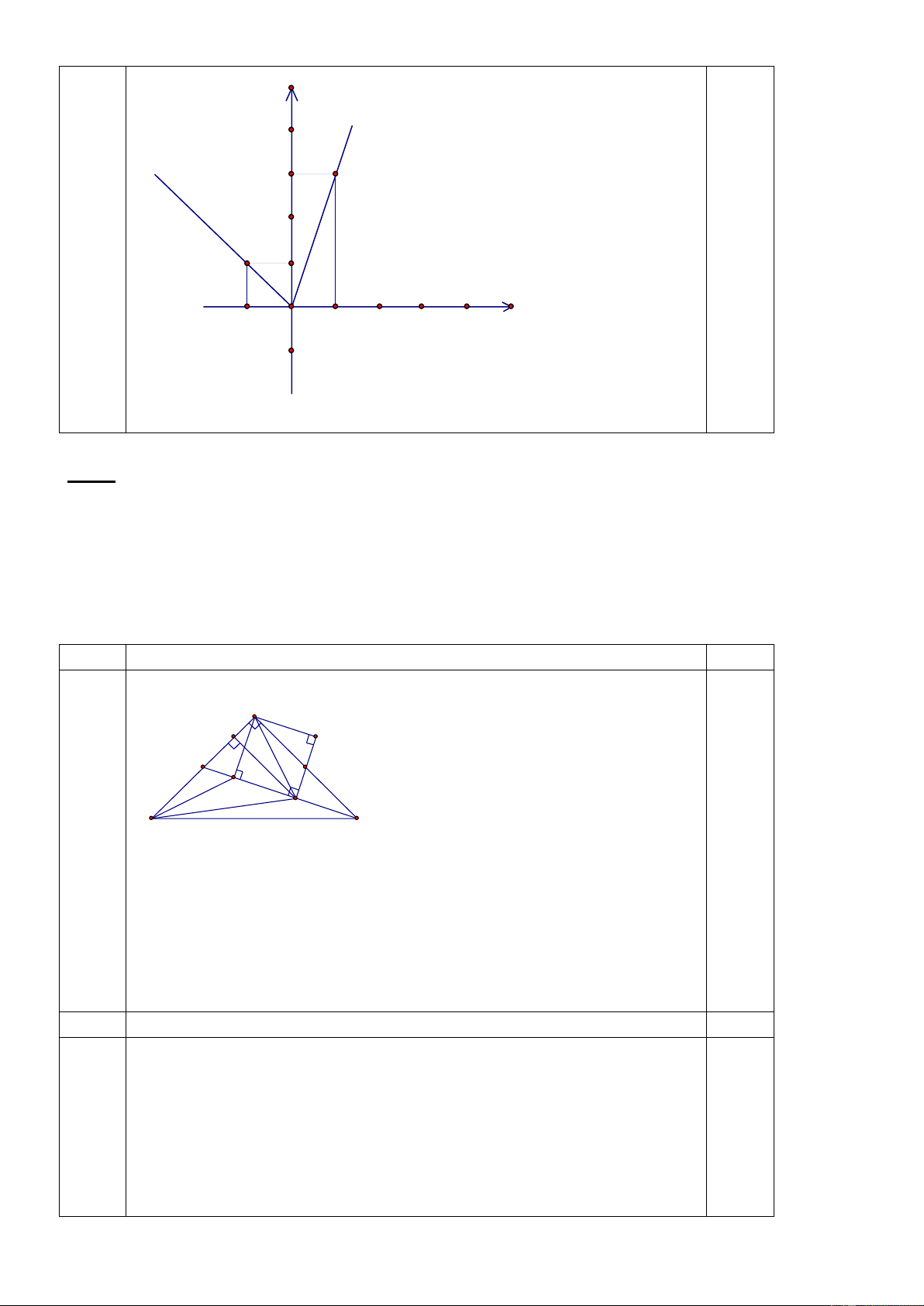
Cho tam giác ABC vuông cân tại A. Gọi M,N lần lượt là trung điểm của AB,AC. Kẻ NH
vuông góc CM tại H, HE vuông góc AB tại E, AK vuông góc CM tại K, AQ vuông góc HN tại Q. · 1. Tính BKH ?
2. Chứng minh tam giác ABH cân.
3. Chứng minh HM là phân giác của · BHE . Câu Đáp án Điểm VÏ h×nh, ghi GT- KL ®óng A E Q I M N K H B C 1 0, 5
C/m D AKM = D AQN D (ch+ gn) => AQ = AK
D AQH = D HKA (gcg) => AQ = KH 0, 5 => AQ = KH · 0, 5
=> D AKH vuông cân tại K => ·
A HK = 450 = A KH · · C/m
D AHC = D BKA( gcg) => A HC = A KB = 900 + 450 = 1350 · · · 0,25
BKH = A KB => BKH = 3600 - 900 -1350 = 1350 0,25 2
C/m D BKA = D BKH (cgc) => BA = BH => D BAH cân tại B 2
Tam giác vuông AEI và tam giác vuông HKI có: · ·
A IE = KIH ( đđỉnh) 0,5 · · => 0,5 EA I = KHI 3 · ·
Mà BA K = BHK ( hai góc tương ứng) 0,5 · ·
=> BHK = KHI , tia HM nằm giữa hai tia HA và HB nên HM là tia phân giác của · A HB 0,5
Bài 5(2,0 điểm)
Từ một điểm I tùy ý trong tam giác ABC kẻ IM, IN, IP lần lượt vuông góc với BC, CA,
AB. Chứng minh rằng : AN2 + BP2 + CM2 = AP2 + BM2 + CN2 Bài 5 2,0điểm A N P I B C M
Áp dụng định lí Pitago vào tam giác vuông NIA và NIC ta có : 0,5
AN2 = AI2 - IN2; CN2 = IC2 - IN2 0,5
=> CN2 – AN2 = IC2 –AI2 (1) Tương tự ta có : AP2 0,25 – BP2 = AI2 – IB2 (2) MB2 –CM2= IB2 - IC2 (3) 0,25
Từ (1) (2) (3) => AN2 + BP2 +CM2 = AP2+ BM2+CN2 0,5
Lưu ý : Nếu học sinh có cách làm khác đúng vẫn cho điểm tối đa.
Phßng gi¸o dôc vµ ®µo
kú thi häc sinh giái cÊp tr-êng t¹o n¨m häc 2022 - 2023
M«n: to¸n – khèi 7 NGƯỜI RA ĐỀ
Thêi gian lµm bµi: 120 phót (kh«ng kÓ thêi gian giao TRỊNH ĐỊNH HÂN ®Ò) ®Ò BµI Câu 1: (4 điểm)
1.Tính bằng cách hợp lí: 1 1 1 1 1 1 A ..... 100 100.99 99.98 98.97 3.2 2.1
2. Cho tỉ lệ thức: a c a b c d .Chứng minh rằng: 2 3 2 3 b d 2a 3b 2c 3d
(giả thiết các tỉ lệ thức đều có nghĩa) Câu 2: (4 điểm) x 1 x 2 x 3 x 4 1. Tìm x biết 2022 2021 2020 2019
2. Cho đa thức A x 2023 2022 2021 2020 x 2023x 2023x 2023x ... 2023x 1 .
Tính giá trị của đa thức A x tại x 2022 . Câu 3: (4 điểm)
1. Tìm hai số nguyên tố a và b biết: 2a3 – b2 = 2.( 4a - b)
2. Cho a, b là các số nguyên dương sao cho a 9 và b 2011 chia hết cho 6. Chứng minh
rằng 4a a b chia hết cho 6. Câu 4: (1 điểm) Cho a, ,
b c là độ dài ba cạnh của một tam giác
Chứng minh rằng: a2 + b2 + c2 < 2(ab + bc + ca)
Câu 5: (5 điểm) Cho tam giác ABC cân tại A và có cả ba góc đều là góc nhọn
1.Về phía ngoài của tam giác vẽ tam giác ABE vuông cân ở B. Gọi H là trung điểm BC,
trên tia đối của tia AH lấy điểm I sao cho AI B .
C Chứng minh hai tam giác ABI và BEC
bằng nhau và BI CE
2.Phân giác của các góc ABC, BDC cắt AC, BC lần lượt tại D, M.Phân giác của góc BDA cắt 1
BC tại N. Chứng minh BD MN 2
Câu 6: (2 điểm) Tìm tất cả các số nguyên dương n để:
A = 2n + 3n + 4n là một số chính phương.
H-íng dÉn chÊm m«n to¸n khèi 7 Biểu Câu Đáp án điểm
1.Tính bằng cách hợp lí: 1 1 1 1 1 1 1.1) A ..... 100 100.99 99.98 98.97 3.2 2.1 1 1 1 1 1 1 A ..... 0,5 100 100.99 99.98 98.97 3.2 2.1 1 1 1 1 1 1 A ..... 100 1.2 2.3 97.98 98.99 99.100 0,5 1 1 1 1 1 1 1 1 1 1 0,5 1 A 1 ..... 100 2 2 3 97 98 98 99 99 100 (4 điểm) 0,5 1 1 49 A 1 100 100 50
2. Giả thiết các tỉ lệ thức đều có nghĩa, từ a c a b 2a 3b 0,5 b d c d 2c 3d
Áp dụng tính chất dãy tỉ số bằng nhau, ta có: 2a 3b 2a 2c 2a 3b 2a 3b 2c 3d 1 2c 3d 2c 3d 2c 3d 2a 3b 2c 3d 0,5 Vậy: nếu a c 2a 3b 2c 3d . thì b d 2a 3b 2c 3d 𝒙−𝟏 𝒙−𝟐 𝒙−𝟑 𝒙−𝟒 1. + = + 𝟐𝟎𝟐𝟐 𝟐𝟎𝟐𝟏 𝟐𝟎𝟐𝟎 𝟐𝟎𝟏𝟗 𝑥−1 𝑥−2 𝑥−3 𝑥−4 - 1+ - 1 = - 1 + - 1 0,5 2022 2021 2020 2019 𝑥−2023 𝑥−2023 𝑥−2023 𝑥−2023 0,5 + = + 2022 2021 2020 2019 0,25 1 1 1 1 (x – 2023)( + - - ) = 0 2022 2021 2020 2019 1 1 1 1 0,5 Do + - - khác 0 2022 2021 2020 2019 nên x- 2023=0 =>x=2023 0,25 Vậy x = 2023 2
2. Cho đa thức A x 2023 2022 2021 2020 x 2023x 2023x 2023x
... 2023x 1 . (4
điểm) Tính giá trị của đa thức A x tại x 2022 . A x 2023 x 2022 x 2021 x 2020 2022 1 2022 1 2022 1 x ... 2022 1 x 1 0,5
Thay x 2022 vào biểu thức trên có: 0,5 A x 2023 x x 2022 x x 2021 x x 2020 1 1 1 x ... x 1 x 1 A x 2023 2023 2022 2022 2021 2021 2020 2 x x x x x x x
... x x 1 0,5 Thì
A x x 1
Tại x 2022 thì A2022 2022 1 2021 0,25 Vậy: A = 2021 0,25
1. Tìm số nguyên tố a và b biết:
2a3 – b2 = 2.( 4a - b)
Ta có VP = 2.( 4a - b) là số chẵn 0,25
Nên VT = 2a3 – b2 là số chẵn 0,25
Mà 2a2 là số chẵn nên b2 phải là số chẵn 0,5
Mà b là số nguyên tố nên b =2 Từ đó ta có: 2a 0,5 3 – 8a = 0 Suy ra a = 0; a = -2, a = 2 0,25
Mà a là số nguyên tố nên a = 2 0,25 Vậy a=b=2 3 (4 điểm)
2. Cho a, b là các số nguyên dương sao cho a 9 và b 2011 chia hết cho 6. Chứng minh rằng
4a a b chia hết cho 6. 0,25
Ta có: a là số nguyên dương nên 4a chia cho 3 dư 1 4a 2 chia hết cho 3 0,25
Mà 4a 2 chia hết cho 2
Suy ra: 4a 2 chia hết cho 6 vì 2,3 1 0,25 0,5
Vì 4a 2 ; a 9 ; b 2011; 2022 chia hết cho 6 0,5
4a 4a a b
2 a 11 b 2009 2022 6
Vậy với a, b là số nguyên dương sao cho a 9 và b 2011 chia hết cho 6 thì 0,25
4a a b chia hết cho 6. 2. Cho a, ,
b c là độ dài ba cạnh của một tam giác
Chứng minh rằng: a2 + b2 + c2 < 2(ab + bc + ca)
Theo BĐT tam giác ta có: a + b > c Suy ra ac + bc > c2 0,25
Tương tự: b + c > a Suy ra ab + ac > a 2
c + a > b Suy ra bc + ab > b2 0,5 4
Nên: a2 + b2 + c2 < 2(ab + bc + ca) 0,25 (1 điểm) I A D E C F N M B H 1)
1 Xét hai tam giác AIB và BCE có: AI BC ; BE BA 0,5
Góc IAB là góc ngoài của ABH nên: 0
IAB ABH AHB ABH 90 0 0,5
Ta có: EBC EBA ABC ABC 90 IAB EBC 5 Do đó: A BI B EC( . c g.c) 0,5 (5 điểm) Do ABI BEC
AIB BCE 0,5
Trong tam giác vuông IHB vuông tại H có: 0
AIB IBH 90 Do đó: 0,5 0
BCE IBH 90
Vậy CE vuông góc với BI 2)
2. Do tính chất của đường phân giác, ta có: DM DN 0,5
Gọi F là trung điểm của MN.Ta có: FM FD FN
Tam giác FDM cân tại F nên FMD MDF
FMD MBD BDM (góc ngoài của tam giác) 0,5
MBD CDM MBD CDF (1)
Ta có: MCD CDF CFD (2) 0,5
Do tam giác ABC cân tại A nên MCD 2MBD (3)
Từ (1), (2), (3) MBD DFC hay tam giác DBF cân tại D. 0,5 Do đó: 1 BD DF MN 0,5 2
Tìm tất cả các số nguyên dương n để:
A = 2n + 3n + 4n là một số chính phương.
Ta xét các trường hợp sau:
TH1: Nếu n = 1 thì B = 9 thỏa mãn 0,5
TH2: xét n > 1 thì 2n > 2 nên 2n + 4n chia hết cho 4.
Mà 3n thì chia cho 4 có số dư là 1 hay (-1) tương ứng với n chẵn hoặc lẻ. 0,5 6
Mà một số chính phương chia cho 4 thì dư 0 hoặc 1 (2
Do (3,4) = 1 nên để A là số chính phương thì 3n phải chia 4 dư 1 điểm)
Nên n là số chẵn.
Với n là số chẵn thì n= 2k ( k là số nguyên dương) 0,5
Khi đó: 2n = 22k =4k sẽ chia cho 3 dư 1 Lại có 3n chia hết cho 3
Nên: A = 2n + 3n + 4n chia cho 4 dư 2 ( Vô lí) 0,5
Vì A là số chính phương thì chia cho 3 phải dư 0 hoặc 1
Vậy n = 1 Thì A là số chính phương 0,5 PHÒNG GD&ĐT SƠN TỊNH
ĐỀ THI HSG CẤP TRƯỜNG
TRƯỜNG THCS TỊNH BẮC MÔN: TOÁN 7 NĂM HỌC 2022-2023
(Thời gian làm bài: 120 phút không kể thời gian giao đề) 4 2 10 .8116.15
Câu 1. (2,0 điểm) Rút gọn biểu thức sau: A 4 4 .675 x y z
Câu 2. (2,0 điểm) Tìm ba số x, y, z thỏa mãn: và 2 2 x 2 2 y 3 2 z 10 0 . 3 4 5
Câu 3. (2,0 điểm) Cho các số x, y thỏa mãn (x - 2)4 + (2y - 1)2018 0 .
Tính giá trị của biểu thức M = 11x2y + 4xy2.
Câu 4. (4,0 điểm)
a) Tìm tất cả các cặp số nguyên x, y sao cho: x - 2xy +2 y = 0.
b) Tìm giá trị nhỏ nhất của M x 5 x 6 x 2020 27 2x
Câu 5. (2,0 điểm) Tìm giá trị lớn nhất của biểu thức Q =
(với x là số nguyên). 12 x
Câu 6. (6,0 điểm)
Cho xOy nhọn. Trên tia Ox lấy A, trên tia Oy lấy B sao cho OA OB . Vẽ ra phía ngoài
xOy hai đoạn thẳng AM và BN sao cho AM BN , AM Ox và BN Oy . a) Chứng minh: OM = ON
b) Chứng minh AMB BNA
c) MN cắt Ox tại E, MN cắt Oy tại F. Gọi I là giao điểm của AN và BM. Chứng
minh OI là đường trung trực của là tam giác cân.
Câu 7. (2 điểm) Cho ba số x, y, z thoả mãn 0 x y z 1. x y z Chứng minh: 2 yz 1 xz 1 xy 1
-------------HẾT------------
Cán bộ coi thi không giải thích gì thêm!
Họ và tên thí sinh: .................................... Số báo danh: ...............Phòng thi: ....... PHÒNG GD&ĐT SƠN TỊNH HƯỚNG DẪN CHẤM
TRƯỜNG THCS TỊNH BẮC
ĐỀ THI HSG CẤP TRƯỜNG MÔN: TOÁN 7 NĂM HỌC 2022-2023 Hướng dẫn chung:
- Học sinh giải theo cách khác mà đúng, đảm bảo tính lôgic, khoa học thì giám khảo vẫn cho điểm tối đa.
- Câu hình học, học sinh không vẽ hình hoặc vẽ hình sai phần nào không chấm điểm phần đó. Câu Nội dung Điểm 4 2 10 .8116.15 4 4 4 4 2 2 2 .5 3 . 2 3 . 5 . A = 0,5 4 4 .675 8 3 2 2 .3 .5 1 4 2 2 2 2 2 .3 .5 5 ( .3 ) 1 225 1 = = (2đ) 0,5 8 3 2 2 .3 .5 4 2 .3 224 25.7 14 = = = 0,5 4 2 .3 24.3 3 0,5 0,5 Từ x y z ta suy ra: 0,5 2 3 4 5 (2đ) 2 2 2 x y z 2 2 x 2 2 y 3 2 z 2 2 x 2 2 y 3 2 z 100 4 9 16 25 18 32 75 25 25 x 6 y 0,5 2 x 8 36 x 2 10
Suy ra: y 64
( Vì x, y, z cùng dấu) x 6 2 z 100 y 8 0,5 z 10
KL: Có hai bộ (x; y; z) thỏa mãn là : (6; 8 ;10) và (-6; -8;-10)
Vì (x - 2)4 0; (2y – 1) 2018 0 với mọi x, y nên 0,25
(x - 2)4 + (2y – 1) 2014 0 với mọi x, y. 0,25
Mà theo đề bài : (x - 2)4 + (2y – 1) 2014 0 3
Suy ra (x - 2)4 + (2y – 1) 2014 = 0 0,25
(2đ) Hay: (x - 2)4 = 0 và (2y – 1) 2018 = 0 0,25 1 suy ra x = 2, y = 0,25 2
Khi đó tính được: M = 24. 0,25 0,5
a) Tìm tất cả các cặp số nguyên x, y sao cho: x - 2xy +2 y = 0. Ta có: x - 2xy + 2y = 0. x(1 – 2y) + 2y = 0
(2 y-1) + x(1 – 2y) = -1 0,5 (x-1)(1 – 2y) = -1 Ta có: -1 = 1.(-1 ) Ta có bảng: 0,25 x-1 1 -1 0,75 1 – -1 1 2y x 2 0 0,5 y 1 0 4 0,25
(4đ) Vậy (x;y) {(2;1);(0;0)}
b) Tìm giá trị nhỏ nhất của M x 5 x 6 x 2020 0,25
Ta có . a a ; a 0, a
. Dấu bằng xảy ra khi a=0;
a a, a
. Dấu bằng xảy ra khi a 0 1,0
x 5 6 x x 2020 Vì 6 x 6 , x x
; x 5 0, ;
x x 2020 x 2020, x 0,25
Nên M 6 x 0 x 2020, x
M 2026, x 6 x 0 6 x Dấu bằng xảy ra x 5 0 x 5 x 5 0,25 x 2020 0 x 2 020
Vậy GTNN của M=2026 tại x=5 5 27 2x 3 Ta có: Q = = 2+ . 0,25 (2đ) 12 x 12 x 3
Suy ra Q lớn nhất khi lớn nhất 0,25 12 x * Nếu x > 12 thì 3 12 x 0 0 . 0,25 12 x * Nếu x < 12 thì 3 12 x 0 0 . 0,25 12 x
Từ 2 trường hợp trên suy ra 3 lớn nhất khi 12-x>0 12 x 0,25
Vì phân số 3 có tử và mẫu là các số nguyên dương, tử không đổi nên phân 12 x
số có giá trị lớn nhất khi mẫu là số nguyên dương nhỏ nhất. 0,25
Hay 12 x 1 x 11
Suy ra A có giá trị lớn nhất là 5 khi x =11 0,25 0,25 M x A 0,5 E I O F B y N a) Xét OAM và OBN 6
(6đ) Có OA = OB; AM = BN; OAM OBN 0,5
=> OAM = OBN (c.g.c) => OM = ON 0,5 b) Xét OMB và ONA 0,5
Có OA = OB; OM = ON; MOB NOA OMB = ONA (c.g.c) 0,5 => MB = NA
Chứng minh AMB = BNA (c.c.c) 0,5
=> AMB BNA
c) Theo câu b có IAB cân tại I => IA = IB 0,5
=> OIA = OIB (c.c.c) 0,5
=> EOI FOI
Chứng minh được OEM = OFN (g.c.g) 0,5 => OE = OF
=> OIE = OIF (c.g.c) => IE = IF 0,5 0,5 0,5
Vì 0 x y z 1 x - 1 0, y - 1 0 (x - 1) (y - 1) 0 1 1 z z xy + 1 x + y (1) xy+1 x+y xy+1 x+y 0,5 Chứng minh tương tự x x y y 0,5 : (2) ; (3) yz+1 y+z xz+1 x+z
Cộng từng vế của (1) (2) (3) ta có : x y z x y z 0,5 + + + + (4) yz+1 xz+1 xy+1 y+z x+z x+y 7 (2đ) x x+x x 2x Mà y+z x+y+z y+z x+y+z 2y z 2z
Chứng minh tương tự y ; x+z x+y+z x+y x+y+z x y z 2(x+y+z) + + 2 (5) y+z x+z x+y x+y+z 0,5 Từ (4) (5) đpcm ----------Hết--------- ĐỀ THI THAM KHẢO
ĐỀ THI HỌC SINH GIỎI MÔN TOÁN 7 ĐỀ SỐ 28
NĂM HỌC: 2022 – 2023
Thời gian làm bài: 150 phút Bài 1: (4,0 điểm)
1) Thực hiện phép tính sau: 36 13 18 6 2 .3 4 .9 7 . 5 10 3 5 2 25 .49 a) A 2 .312 16 .3 125.73 5 9. 14 3 3 9 12 10 5 5 3 3 155 0,9 b) 7 11 23 5 13 B 26 13 13 7 3 403 0, 2 7 11 23 91 10
2) Tìm giá trị của biểu thức P= 28a2b- 9ab2 với a, b thỏa mãn
(a -3)2022 +(3b +1)2024 0 Bài 2: (4,0 điểm) a c 2 2 b a b a 1) Cho . Chứng minh rằng: c b 2 2 a c a 1+3y 1+5y 1+7y 2) Tìm x, y biết 12 5x 4x
3) Trường THCS CVA dự định trao quà tết cho học sinh nghèo ba khối 6; 7; 8 tỉ lệ
với 3; 4; 5. nhưng sau đó vì số học sinh các khối được nhận quà thay đổi nên
chia lại tỉ lệ với 2; 3; 4. Như vậy có một khối nhận được nhiều hơn so với dự
định là 1 xuất quà. Tính tổng số xuất quà mà nhà trường đã phân chia cho các khối. Bài 3: (4,0 điểm)
1) Cho x, y là các số nguyên dương thỏa mãn x2 + y2 – x chia hết cho xy.
Chứng minh rằng: x là số chính phương
2) Tìm các cặp số nguyên x, y thoả mãn: x2 + xy + 3x + 2y = 1 Bài 4: (6,0 điểm)
1) Cho tam giác ABC có AB < AC. Gọi M là trung điểm của BC, từ M kẻ đường thẳng
vuông góc với tia phân giác của góc BAC tại N và cắt tia AB tại E và cắt tia AC tại F. Chứng minh rằng: a) AE = AF; b) BE = CF 2) Cho tam giác ABC có 0 0
ABC 70 , ACB 50 . Trên cạnh AC lấy điểm M sao cho 0
ABM 20 . Trên cạnh AB lấy điểm N sao cho 0
ACN 10 .Gọi P là giao điểm của BM và
CN. Chứng minh rằng MN = 2PM. Bài 5: (2,0 điểm)
Cho các số không âm a, b, c thỏa mãn : a +3c =2021 và a+2b =2022
Tìm giá trị lớn nhất của biểu thức P = a+ b +c.
= = = = = = = = = = HẾT = = = = = = = = = =
HƯỚNG DẪN CHẤM ĐỀ HSG TOÁN 7 NĂM HỌC 2022-2023 Câu Ý Nội dung Điểm Bài 1: Phần đề bài 4đ 4đ
1) Thực hiện phép tính sau: 36 13 18 6 2 .3 4 .9 7 . 5 10 3 5 2 25 .49 a) A 2 .312 16 .3 125.73 5 9. 14 3 3 9 12 10 5 5 3 3 155 0,9 b) 7 11 23 5 13 B 26 13 13 7 3 403 0, 2 7 11 23 91 10
2) Tìm giá trị của biểu thức P= 28a2b- 9ab2 với a, b thỏa mãn
(a -3)2022 +(3b +1)2024 0 1a 36 13 18 6 2 .3 4 .9 7 . 5 10 3 5 2 1đ 25 .49 A 2 .312 16 .3 125.73 5 9. 14 3 3 9 12 10 36 13 36 12 10 3 4 2 .3 2 .3 5 .7 5 .7 36 12 36 12 9 3 9 3 3 0.25 2 .3 2 .3 5 .7 5 .2 .7 36 12 2 .3 .3 10 3 1 5 .7 .1 7 36 12 9 3 2.2 .3 5 .7 . 3 1 2 10 3 5 .7 . 6 1 0.5 9 3 5 .7 .9 1 0 7 1 0.25 3 3 1b 1đ 10 5 5 3 3 2 1 1 1 1 3 155 0,9 5 31 3 7 11 23 5 13 7 11 23 5 13 10 B 26 13 13 7 3 0.75 2 1 1 1 1 3 403 0, 2 13 31 7 11 23 91 10 7 11 23 5 13 10 5 3 4 3 13 13 0.25 2
Ta có : (a -3)2 0 với mọi a, (3b +1)100 0 với mọi b 2đ
suy ra (a -3)2022 +(3b +1)2024 0 với mọi a, b do đó từ 0.5
(a -3)2022 +(3b +1)2024 0 suy ra (a -3)2022 =0 và (3b +1)2024 =0 1 suy ra a=3, b= 0.5 3 1
Thay a=3, b= vào biểu thức ta có: 3 2 1 1 P= 28a2b- 9ab2 = 2 28.3 . 9.3. 84 3 81 1.0 3 3 Bài 2: Phần đề bài 4đ 4đ a c 2 2 b a b a 1) Cho . Chứng minh rằng: c b 2 2 a c a 1+3y 1+5y 1+7y 2) Tìm x, y biết 12 5x 4x
3) Trường THCS CVA dự định trao quà tết cho học sinh nghèo
ba khối 6; 7; 8 tỉ lệ với 3; 4; 5. nhưng sau đó vì số học sinh
các khối được nhận quà thay đổi nên chia lại tỉ lệ với 2; 3; 4.
Như vậy có một khối nhận được nhiều hơn so với dự định là
1 xuất quà. Tính tổng số xuất quà mà nhà trường đã phân chia cho các khối. 1 a c 2 2 2 a c a ab
a a b 2 2 a b c b 1đ Từ 2 c ab khi đó 0.5 c b 2 2 2 b c b ab
b b a 2 2 b a c a 2 2 2 2 2 2 b c b b c b b a b a Từ 1 1 2 2 2 2 2 2 a c a a c a a c a 2 2 Vậy b a b a 2 2 0.5 a c a 2 * Điều kiện: x khác 0 1đ
- Ta thấy y = 0 không thoả mãn yêu cầu đề bài. 0.25 - Nếu y khác 0
Áp dụng tính chất dãy tỉ số bằng nhau. 1+3y 1+5y 1+7y 1 7y 1 5y 2y 1 5y 1 3y 2y 12 5x 4x 4x 5x x 5x 12 5x 12 2 y 2 y => x 5x 12 => -x = 5x -12
=> x = 2. Thay x = 2 vào dãy trên ta được. 0.25 1 3y 2 y y 12 2 =>1+ 3y = -12y 0.25 => 1 = -15y 1 => y = 15
Vậy x = 2, y = 1 thoả mãn 0.25 15 3.
3) Gọi tổng số xuất quà ba khối nhận được là x( x∈N*) 2đ
Số xuất quà dự định trao cho ba khối 6, 7,8 lần lượt là a, b, c a b c
a b c x x x 5 (a,b,c ∈N*) ta có:
a ,b ,c x (1) 0.75 3 4 5 3 4 5 12 4 3 12
Số xuất quà sau đó trao cho ba khối lớp 6, 7,8 lần lượt là m, n, p m n p
m n p x 2 x 4 (m, n, p∈N*)ta có:
m x,n ,p x (2) 0.5 2 3 4 2 3 4 9 9 3 9
So sánh (1) và (2) ta có a>m, b=n, c
0.25 đầu suy ra p-c =1 4 5 1 suy ra x x 1
x 1 x 36 9 12 36
Vậy số quà của ba khối 6, 7,8 là 36 xuất. 0.5 Bài 3: Phần đề bài 4đ (4đ)
1) Cho x, y là các số nguyên dương thỏa mãn x2 + y2 – x chia hết cho xy.
Chứng minh rằng: x là số chính phương
2) Tìm các cặp số nguyên x, y thoả mãn: x2 + xy + 3x + 2y = 1 1
1) 1) Đặt (x, y) =d, ta có: x = dm, y = dn, với m, n là các số 2đ
nguyên dương nguyên tố cùng nhau. Theo đề bài cho ta có: 0.25 2 2 2 2 2 2 2
x y x xy d m d n dm d mn 0.25 m d 1 0.75 2 2
dm dn m dmn 2 dn m 2
Vì (m,n)=1 nên (m, n2) = 1 nên từ (2) ta có: d m (3) 0.5
Từ (1) và (3) ta có: m = d
Vậy x = dm = d2 là số chính phương (đpcm) 0.25 2 2) Ta có: 2
x xy 3x 2y 1 x 2 x y 1 3 0.5 2đ
Do x, y nguyên x 2; x y 1 nguyên
Mà 3 1.3 3.1 3 . 1 1 . 3 1.25
Vậy nghiệm nguyên dương
;x y của phương trình là: 1 ;3,1; 1 , 3 ; 1 , 5 ;3 0.25 Bài 4: Phần đề bài 6đ (6đ)
1) Cho tam giác ABC có AB < AC. Gọi M là trung điểm của BC, từ
M kẻ đường thẳng vuông góc với tia phân giác của góc BAC tại N và
cắt tia AB tại E và cắt tia AC tại F. Chứng minh rằng: a) AE = AF; b) BE = CF 2) Cho tam giác ABC có 0 0
ABC 70 , ACB 50 . Trên cạnh AC lấy điểm M sao cho 0
ABM 20 . Trên cạnh AB lấy điểm N sao cho 0 ACN 10
.Gọi P là giao điểm của BM và CN. Chứng minh rằng MN = 2PM. 1a A 2đ x K F 1 2 M B C N E
- Xét ANE và ANF có :
EAN FAN ( Vì AN là phân giác) AN cạnh chung (gt) 0 ANE ANF( 90 )
Suy ra : ANE = ANF (g – c - g) 2.0
AE = AF (2 cạnh tương ứng) 1b b) 2đ
- Từ C kẻ tia Cx // AB, cắt tia EF tại K
- Xét BME và CMK có : MB = MC (gt)
BME CMK (đối đỉnh)
BEM CKM (so le trong)
Suy ra: BME = CMK (g – c - g) 1.0
BE = CK (2 cạnh tương ứng) (1)
- Vì AE = AF nên tam giác AEF cân tại A, suy ra: E F 1 Mà:
F F (đối đỉnh) và E K (so le trong) 1 2
Suy ra: F K 2
tam giác CFK cân tại C CF = CK (2)
Từ (1) và (2) suy ra: BE = CF (đpcm) 1.0 2 A Q 2đ N I M P 10° 10° 10° 10° 400 500 C B
Dựng tam giác đều BCQ ( Q, A cùng nằm trên nửa mặt phẳng bờ BC)
Từ giả thiết bài toán có 0 MBC MCB 50 0.5 Suy ra M BC cân tại M
=> MB = MC, kết hợp với QB = QC có Q MB Q MC(c.c.c) 0.5 dẫn đến 0 MQC MQB 30 (1) vì 0 0 NBC 70 , NCB 40 nên 0 BNC 70 từ đó C NB cân tại C 0.5
CN = CB= CQ. Xét hai tam giác CMN và CMQ có CN=CQ, CM chung 0 NCM QCM 10 do đó C MN C MQ (c.g.c) Từ (1) có 0 MNC MQC 30 (2)
Cũng từ giả thiết bài ra ta thấy M
NP vuông cân tại P; gọi I là trung điểm của MN thì do 0
MNC 30 ( theo (2) ) suy ra MIP đều 1 0.5
=> PM = IM = MN, hay MN = 2PM ( đpcm) 2 Bài 5: Phần đề bài 2đ 2đ
Cho các số không âm a, b, c thỏa mãn : a +3c =2021 và a+2b =2022
Tìm giá trị lớn nhất của biểu thức P = a+ b +c.
Ta có : a +3c =2021 (1) và a+2b =2022 (2) Từ (1) suy ra a =2021- 3c 0.5 Lấy (2) trừ (1) ta có: 2b 3c 1 -3c =1 suy ra b = 0.5 2 3c 1 1 1 Ta có: P = a +b+c= 2021 -3c+ +c = 2021 - c 2 2 2 0.75
vì a, b, c là các số không âm nên P = 1 1 1 2021 - c 2021 2 2 2
Vậy P có giá trị lớn nhất bằng 1 0.25 2021 khi c =0. 2 Tổng 12 20điểm
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC SINH GIỎI
TRƯỜNG TH&THCS …. Năm học 2022 - 2023 Môn: Toán 7
Thời gian làm bài: 120 phút
(Đề kiểm tra gồm 01 trang) Bài 1. (4,0 điểm)
a) Tính giá trị của biểu thức sau: 2 2 2 2 1 3 5 7 ... 49 A ... . 4.9 9.14 14.19 44.49 623 1 1 1 1 1 b) Cho B 1 . 1 . 1 ... 1
. Hãy so sánh B với . 2 2 2 2 2 3 4 100 2
Bài 2. (3,0 điểm) a) Tìm x, biết:
x x 3 x x 13 4 4 0
b) Cho a, b, c là ba số thực khác 0, thoả mãn điều kiện:
a b 2023c
b c 2023a
c a 2023b . Hãy tính giá trị của biểu thức c a b b a c C 1 1 1 . a c b Bài 3. (3,0 điểm)
a) Cho các số thực x, y, z thỏa mãn (x – 1)2022 + (2y – 1)2022 + |x + 2y – z|2023 = 0. Chứng minh rằng x = y. z. b) Cho biểu thức 99 98 97 96
P x 100x 100x 100x ... 100x 1 . Tính giá trị biểu thức P với x = 99. Bài 4. (3,0 điểm)
a) Một đội công nhân có 38 người, được chia thành ba nhóm I, II, III. Nếu thêm 2 người
vào nhóm I, thêm 3 người vào nhóm II và bớt 4 người của nhóm III thì số công nhân của
ba nhóm I, II, III tỉ lệ nghịch với các số 4; 3; 2. Tìm số công nhân của mỗi nhóm.
b) Tìm giá trị lớn nhất của biểu thức sau 2 2 K= 3x - 2y - 4y - 6x - x + y - 5 Bài 5. ( 6,0 điểm)
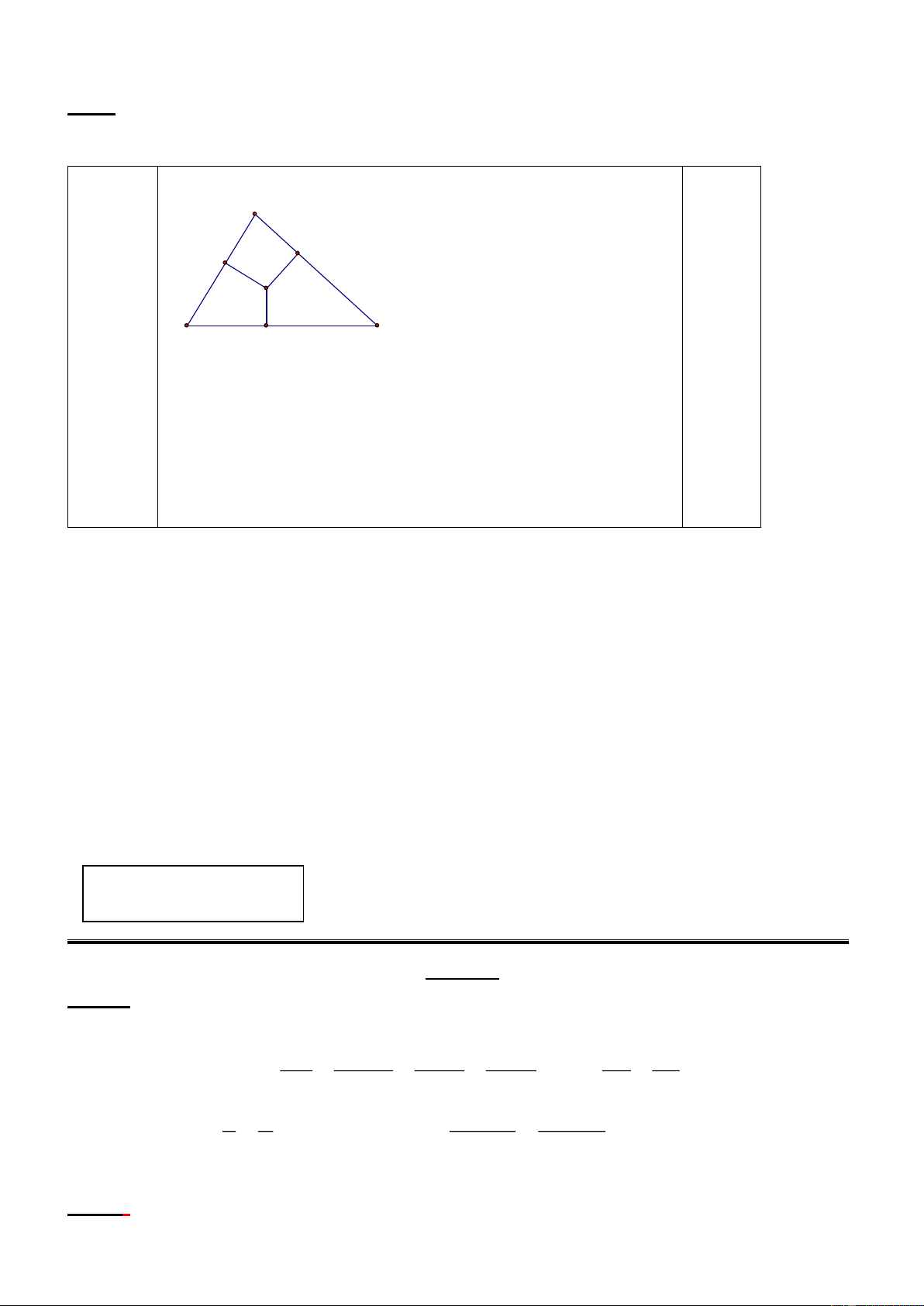
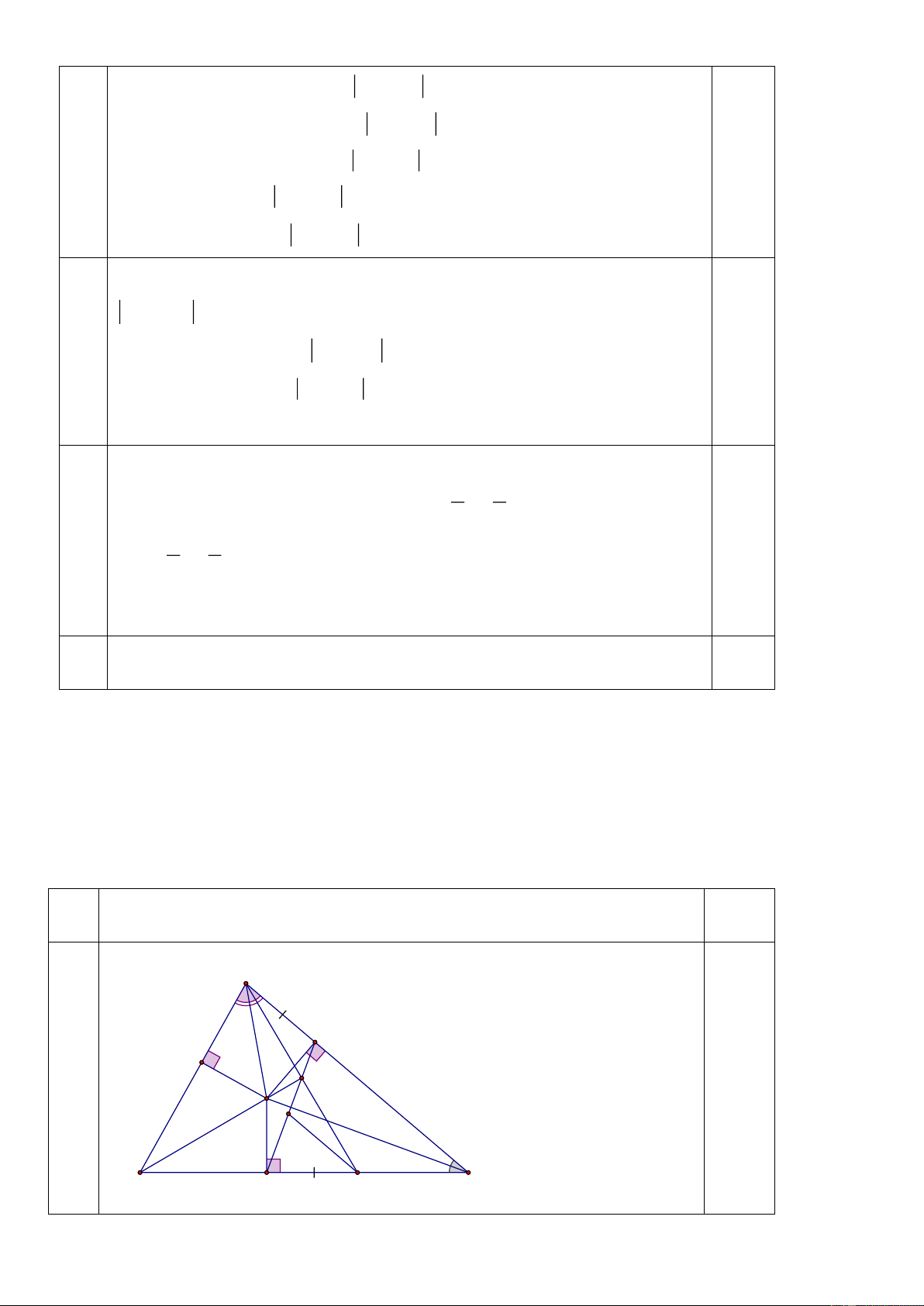
Cho tam giác ABC có 3 góc nhọn, AB < AC < BC. Các tia phân giác của góc A và góc
C cắt nhau tại O. Từ O kẻ OF vuông góc với BC, OH vuông góc với AC (F thuộc BC, H
thuộc AC). Lấy điểm I trên đoạn FC sao cho FI = AH. Gọi K là giao điểm của FH và AI.
a) Chứng minh tam giác FCH cân ; b) Chứng minh AK = KI ;
c) Chứng minh 3 điểm B, O, K thẳng hàng.
Bài 6. (1,0 điểm) Cho a, b, c, d là các số dương. Tìm giá trị nhỏ nhất của biểu thức
E x a x b x c x d .
-------------------Hết------------------
Họ và tên thí sinh:.........................................................Số báo danh:................
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA CHỌN
HỌC SINH GIỎI HUYỆN
Môn Toán 7. Năm học 2022 – 2023 Bài 1. (4,0 điểm)
a) Tính giá trị của biểu thức sau: 2 2 2 2
1 3 5 7 ... 49 A ... . 4.9 9.14 14.19 44.49 623 1 1 1 1 1 b) Cho B 1 . 1 . 1 ... 1
. Hãy so sánh B với . 2 2 2 2 2 3 4 100 2 Biểu Bài Nội dung điểm 1 2 2 2 2
1 3 5 7 ... 49 Ta có A ... . 4.9 9.14 14.19 44.49 623 2 2 2 2
2 (1 3 5 7 ... 49) ... . 4.9 9.14 14.19 44.49 623 0,25 2 2 2 2 * ... 4.9 9.14 14.19 44.49 2 5 5 5 5 . ... 0,25 5 4.9 9.14 14.19 44.49 2 1 1 1 1 1 1 1 1 . ... 5 4 9 9 14 14 19 44 49 2 1 1 . 5 4 49 0,25 2 45 . 5 4.49 9 98 0,25
* 1 3 5 7 ... 49 (có 25 số hạng) 49 1 .25 0,25 2 25.25 625 0,25 Do đó 2 2 2 2
2 (1 3 5 7 ... 49) A ... . 4.9 9.14 14.19 44.49 623 9 2 625 . 98 623 9 6 23 . 98 623 9 0,25 98 Vậy 9 A 98 0,25
b) B là tích của 99 số âm, do đó: 0,25 1 1 1 1 B 1 1 1 .... 1 2 4 9 16 100 0,25 1.3 2.4 3.5 99.101 B . . ... 0,25 2 2 2 2 2 3 4 100
1.2.3.4...98.99 3.4.5....100.101 B . 0,25 2.3.4...99.100 2.3.4....99.100 1 101 B . 100 2 0,25 101 B 200 0,25 101 100 1 1 Vì nên B 200 200 2 2 0,25 1 B . Vậy 1 B 2 2 0,25 Bài 2. (3,0 điểm) a) Tìm x, biết:
x x 3 x x 13 4 4 0
b) Cho a, b, c là ba số thực khác 0, thoả mãn điều kiện:
a b 2023c
b c 2023a
c a 2023b . Hãy tính giá trị của biểu thức c a b b a c C 1 1 1 . a c b Biểu Bài Nội dung điểm a)
x x 3 x x 13 4 4 0 0,25 2 x 3 10
x 4 1 x 4 0 x x 3 4
0 hoặc x 10 1 4 0 0,25
x x 3 4 0 0,25
x 4 0 (Điều kiện x + 3 0) 0,25 x 4 x 10 1 4 0 x 10 4 1
x 4 1 hoặc x 4 1 0,25
x 5 hoặc x 3 Vậy x = 3, x = 4, x = 5. 0,25
b) Ta có a b 2023c b c 2023a c a 2023b c a b
a b 2023c
b c 2023a
c a 2023b 2024 2024 2024 c a b
a b c
b c a
c a b 0,25 c a b
+ Nếu a+b+c 0 thì a = b = c. 0,25 b a c 0,25 C 1 1 1 2.2.2 8 a c b
+ Nếu a+b+c = 0 thì a + b = -c; a + c = -b; b + c = -a 0,25 b a c C 1 1 1 a c b
a b a c c b
a c b (a).( b ).(c) . a . b c 0,25 1 Vậy C = 8 hoặc C = -1 0,25
Bài 3. (3,0 điểm)
a) Cho các số thực x, y, z thỏa mãn (x – 1)2022 + (2y – 1)2022 + |x + 2y – z|2023 = 0. Chứng minh rằng x = y. z. b) Cho biểu thức 99 98 97 96
P x 100x 100x 100x ... 100x 1 . Tính giá trị biểu thức P với x = 99. Biểu Bài Nội dung điểm
a) Ta có: (x – 1)2022 0 x (2y – 1)2020 0 y 0,25
|x + 2y – z|2023 0 x, y, z
(x – 1)2022 + (2y – 1)2022 + |x + 2y – z|2023 0 x, y, z 3 0,25
Mà (x – 1)2022 + (2y – 1)2022 + |x + 2y – z|2022 = 0 nên dấu x – 2022 1 0 "=" xảy ra khi 2y – 2022 1 0 0,25 2023 x 2y – z 0 x 1 x 1 1 1 y y 2 2 1 z 1 2. – 2 z 0 2 0,5
x = y.z (đều bằng 1) (đpcm) 0,25 b) 99 98 97 96
P x 100x 100x 100x ... 100x 1 99 98 98 97 99 96 96
P x 99x x 99x x 99x x ... 99x x 1 0,25 98 97 96
P x (x 99) x (x 99) x (x 99) ... x(x 99) (x1) 0,25 98 97 96
P (x 99)(x x
x ... x) (x1) 0,25 Với x = 99, ta có: 98 97 96
P (99 99)(99 99 99 ... 99) (99 1) 0,25 98 0,25 Vậy P = 98 với x = 99 0,25 Bài 4. (3,0 điểm)
a) Một đội công nhân có 38 người, được chia thành ba nhóm I, II, III. Nếu thêm 2 người
vào nhóm I, thêm 3 người vào nhóm II và bớt 4 người của nhóm III thì số công nhân của
ba nhóm I, II, III tỉ lệ nghịch với các số 4; 3; 2. Tìm số công nhân của mỗi nhóm.
b) Tìm giá trị lớn nhất của biểu thức sau 2 2 K= 3x - 2y - 4y - 6x - x + y - 5 Biểu Bài Nội dung điểm
a) Gọi số công nhân của ba nhóm I, II, III lần lượt là x, y, z (người) 0,25
(x, y, z N* và x, y, z < 38).
Vì đội công nhân có 38 người x + y + z = 38. 0,25
Nếu thêm 2 người vào nhóm I, thêm 3 người vào nhóm II và bớt 4
người của nhóm III thì số công nhân của ba nhóm I, II, III tỉ lệ 0,25
nghịch với các số 4; 3; 2 4
4(x + 2) = 3(y + 3) = 2(z -4) 4x + 2 3y + 3 2z - 4 x + 2 y + 3 z - 4 = = = = = 12 12 12 3 4 6 0,25 x + 2 + y + 3+ z - 4 x + y + z +1 39 = = = = 3 0,25 3+ 4 + 6 13 13
Tìm được x=7, y = 9, z = 22 (thỏa mãn x, y, z N* và x, y, z < 38)
Vậy số công nhân của ba nhóm I, II, III lần lượt là 7, 9, 22 (người) 0,25 b) Ta có 2 2 K = 3x - 2y - 4y - 6x - x + y - 5 2 2
= 3x - 2y - 4.2y - 3x - x + y - 5 0,25 2 2 3x - 2y - 4. 3x - 2y - x + y - 5 2 = - 3. 3x - 2y - x + y - 5 0,25 2 = - 3. 3x - 2y + x + y - 5 Ta có 2 3. 3x - 2y
0 với mọi giá trị của x, y
x + y - 5 0 với mọi giá trị của x, y Do đó 2 3. 3x - 2y
+ x + y - 5 0 với mọi giá trị của x, y 0,25 Nên 2 - 3. 3x - 2y + x + y - 5 0
với mọi giá trị của x, y
Hay K ≤ 0 với mọi giá trị của x, y 0,25
Dấu ‘‘ = ’’ xảy ra khi và chỉ khi 3x - 2y 0 và x + y - 5 0 (1) + Với x y 3x - 2y = 0 thì 3x = 2y = 2 3 0,25 Đặt x y =
= k . Khi đó x = 2k ; y = 3k 2 3
Thay x = 2k và y = 3k vào (1) ta được
2k + 3k - 5 = 0 5k = 5 k = 1
Với k = 1 thì x = 2 ; y = 3 0,25
Vậy giá trị lớn nhất của biểu thức K là 0 khi và chỉ khi x = 2; y = 3 Bài 5. ( 6,0 điểm)
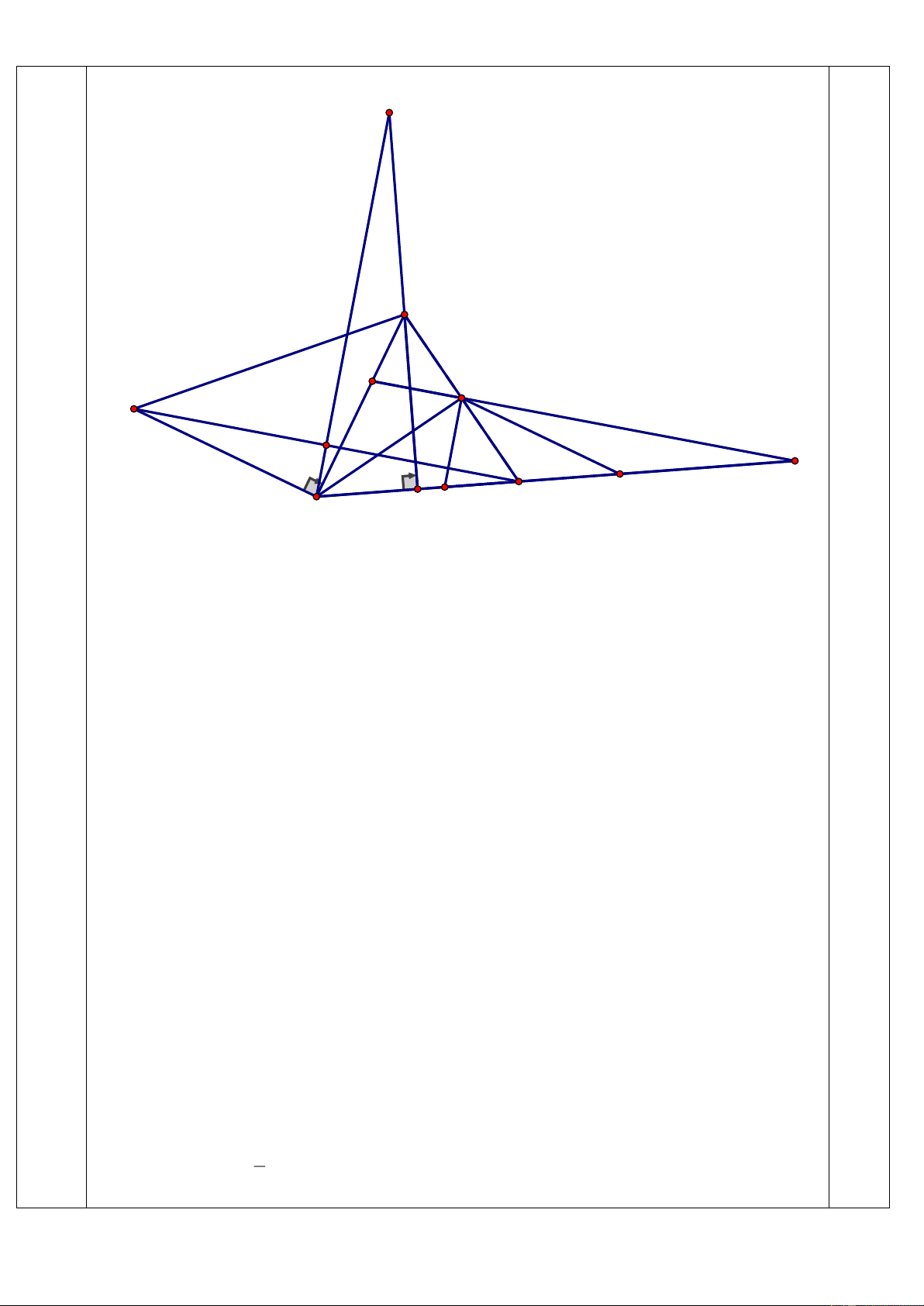
Cho tam giác ABC có 3 góc nhọn, AB < AC < BC. Các tia phân giác của góc A và góc
C cắt nhau tại O. Từ O kẻ OF vuông góc với BC, OH vuông góc với AC (F thuộc BC, H
thuộc AC). Lấy điểm I trên đoạn FC sao cho FI = AH. Gọi K là giao điểm của FH và AI.
a) Chứng minh tam giác FCH cân ; b) Chứng minh AK = KI ;
c) Chứng minh 3 điểm B, O, K thẳng hàng. Biểu Bài Nội dung điểm A H E 5 O K G B C F I Chứng minh:
Ta có CHO = CFO = 0
90 ( vì OH AC ; OF BC ) 0,25 + Xét C
HO vuông tại H và C
FO vuông tại F có : 0,25 OC chung; 0,25 a
HCO = FCO (vì CO là tia phân giác C ) 0,25 Vậy C HO = C
FO(cạnh huyền – góc nhọn) 0,25
CH = CF (2 cạnh tương ứng của hai tam giác bằng nhau) 0,25 Vậy F
CH cân tại C (tam giác có 2 cạnh bằng nhau) 0,5
+ Qua I vẽ IG //AC (G FH) 0,25 Ta có F
CH cân tại C (cm trên)
CHF CFH (2 góc ở đáy của tam giác cân) (1) 0,25
Mà CHF FGI (hai góc đồng vị, IG // AC) (2) 0,25
Từ (1),(2) CFH FGI hay IFG IGF Vậy I FG cân tại I 0,25
FI = GI (hai cạnh bên của tam giác cân ) Mặt khác FI = AH 0,25 b
Nên GI = AH (cùng bằng FI )
Lại có: IGK AHK (hai góc so le trong, IG // AC) 0,25
HAK = GIK (hai góc so le trong, IG // AC)
Xét AHK và I GK có:
IGK AHK (cm trên) GI = AH (cm trên)
HAK GIK (cm trên) 0,25
Vậy AHK = I GK ( g.c.g)
AK = KI (2 cạnh tương ứng của 2 tam giác bằng nhau) 0,25 Vẽ OE AB tại E 0,25 + Xét O
AE vuông tại E và O
AH vuông tại H có : OA chung;
OAE OAH (vì AO là tia phân giác A ) Vậy O AE = O
AH ( cạnh huyền – góc nhọn) 0,25
OE = OH (2 cạnh tương ứng của 2 tam giác bằng nhau)
Lại có OH = OF (vì C HO = C FO) Do đó OE = OF 0,25 c + Xét O
BE vuông tại E và O
BF vuông tại F có : OB chung; OE = OF (cm trên) Vậy O BE = O
BF (cạnh huyền – cạnh góc vuông)
OBE OBF (hai góc tương ứng của hai tam giác bằng nhau)
Mà tia BO nằm giữa hai tia BE, BF
BO là tia phân giác của 0,25
EBF hay BO là tia phân giác của ABC (*)
Ta có BA = BE + AE; BI = BF + FI; BE = BF (vì O BE = O BF ); AE = AH (vì O AE = O
AH ); AH = FI (giả thiết) 0,25 Do đó BA = BI Nối B với K Xét BKA và BKI có: BA = BI (cm trên ) KA = KI (cm trên ) BK là cạnh chung Vậy BKA = BKI ( c.c.c) 0,25
Suy ra ABK IBK (hai góc tương ứng của hai tam giác bằng nhau)
Mà tia BK nằm giữa hai tia BA, BC Do đó 0,25
BK là tia phân giác của ABC (* *)
Từ (*) và (* *) suy ra tia BK và tia BO trùng nhau
Hay B, O, K là 3 điểm thẳng hàng 0,25
Bài 6. (1,0 điểm) Cho a, b, c, d là các số dương. Tìm giá trị nhỏ nhất của biểu thức:
E x a x b x c x d Biểu Bài Nội dung điểm
Không mất tính tổng quát, giả sử a b c d. Áp dụng BĐT
a b a b , dấu bằng xảy ra khi và chỉ khi ab ≥ 0 ta có: 0,25
x a x d x a d x x a d x d a (1) 0,25 6
x b x c x b c x x b c x c b (2)
Suy ra E ≥ c + d – a – b. Dấu “=” xảy ra khi và chỉ khi dấu “=” ở (1) và 0,25
(2) xảy ra (x – a)(d – x) ≥ 0 và (x – b)(c – x) ≥ 0 a x d và b x
c. Do đó minE = c + d –a – b b x c. 0,25




