TOP 10 đề thi thử QG môn Toán 2020 -Tập 6 (có đáp án)

Trang 1

ĐỀ 51

ĐỀ THI THỬ THPT QUỐC GIA 2020

MÔN TOÁN

Thời gian: 90 phút

Câu 1. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hai mặt bên (SAB) và (SAC) cùng

vuông góc với đáy và SB =

3a

. Tính thể tích khối chóp S.ABC.

A.

3

6

3

a

B.

3

6

12

a

C.

3

6

3

a

D.

3

26

9

a

Câu 2. Cho hàm số y = f (x) thỏa mãn f(0) = 1, f'(x) liên tục trên R và

3

0

'( ) 9f x dx =



. Giá trị của f(3) là

A. 6 B. 3 C. 10 D. 9

Câu 3. Cho a, b là các số dương tùy ý, khi đó ln (a + ab) bằng

A.

ln .ln(ab)a

B.

ln ln(1 )ab++

C.

ln

ln(1 )

a

b+

D.

ln lna ab+

Câu 4.Họ nguyên hàm của hàm số

1

()

23

fx

x

=

+

là

A.

2

1

(2 3)

C

x

+

B.

2

3

(2 3)

C

x

−+

+

C.

1

ln 2 3

2

xC− + +

D.

1

ln 2 3

2

xC++

Câu 5. Bất phương trình

2

11

28

xx−









có tập nghiệm là (a; b). Khi đó giá trị của b - a là

A. 4 B. -4 C. 2 D. -2

Câu 6. Trong hệ tọa độ Oxyz, cho đường thẳng

122

:

1 2 3

x y z

d

− − +

==

−

. Phương trình nào sau đây là

phương trình tham số của d?

A.

1

2

23

x

yt

zt

=





=−





= − +



B.

1

22

13

x

yt

zt

=





=+





=+



C.

1

22

23

xt

yt

zt

=+





=−





= − +



D.

1

2

13

x

yt

zt

=





=+





=−



Câu 7. Tìm số phức liên hợp của số phức

(3 1)z i i=+

A.

3zi=+

B.

3zi= − +

C.

3zi=−

D.

3zi= − −

Câu 8. Viết phương trình mặt phẳng (P) đi qua điểm A (0; -1; 2), song song với trục Ox và vuông góc

với mặt phẳng (Q) : x + 2y - 2z +1 = 0.

A. (P) : 2y + 2z - 1 = 0 B. (P) : y + z - 1 = 0 C. (P) : y - z + 3 = 0 D. (P) : 2x + z - 2 = 0

Câu 9. Số phức z thỏa mãn z = 5 - 8i có phần ảo là

A. -8 B. 8 C. 5 D. -8i

Câu 10. Cho hàm số y = x

3

- 3x

2

+ 2. Đồ thị hàm số có điểm cực đại là

A. (2; -2) B. (0; -2) C. (0; 2) D. (2; 2)

Câu 11. Đường cong trong hình bên là đồ thị của một hàm số trong bốn

hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số

đó là hàm số nào?

A. y = x

4

– x

2

+ 1 B. y = – x

2

+ x - 1

Trang 2

C. y = -x

3

+ 3x + 1 D. y = x

3

- 3x + 1

Câu 12. Cho điểm A (1; 2; 3) và hai mặt phẳng (P) :2x + 2y + z +1 = 0, (Q) : 2x - y + 2z - 1 = 0. Phương

trình đường thẳng d đi qua A song song với cả (P) và (Q) là

A.

1 2 3

1 1 4

x y z− − −

==

−

B.

1 2 3

1 2 6

x y z− − −

==

−

C.

1 2 3

1 6 2

x y z− − −

==

D.

1 2 3

5 2 6

x y z− − −

==

−−

Câu 13. Cho cấp số cộng (u

n

) có u

1

= -5 và d = 3. Mệnh đề nào sau đây đúng?

A. u

15

= 45 B. u

13

= 31 C. u

10

= 35 D. u

15

= 34

Câu 14. Trong hệ tọa độ Oxyz, cho hai điểm A(1; 2; 3), B(-1; 4; 1). Phương trình mặt cầu đường kính AB

là

A. ( x+1)

2

+ (y - 4)

2

+ (z - 1)

2

= 12 B. (x - 1)

2

+ (y - 2)

2

+ (z - 3)

2

= 12

C. x

2

+ (y - 3)

2

+ (z - 2)

2

= 3 D. x

2

+ (y - 3)

2

+ (z - 2)

2

= 12

Câu 15. Số giao điểm của đường thẳng y = x + 2 và đường cong y = x

3

+ 2 là

A. 1 B. 0 C. 3 D. 2

Câu 16. Tính chiều cao h của hình trụ biết chiều cao h bằng bán kính đáy và thể tích của khối trụ đó là 8

A.

2h =

B.

22h =

C.

3

32h =

D.

3

4h =

Câu 17. Phương trình z

2

+ 2z + 10 = 0 có hai nghiệm là z

1

, z

2

. Giá trị của

12

zz−

là

A. 4 B. 3 C. 6 D. 2

Câu 18. Hàm số y = f (x) có đạo hàm f '(x) = (x - 1)

2

(x -3) với mọi x . Phát biểu nào sau đây đúng?

A. Hàm số có 1 điểm cực đại. B. Hàm số không có điểm cực trị.

C. Hàm số có hai điểm cực trị. D. Hàm số có đúng một điểm cực trị.

Câu 19. Giá trị của biểu thức

3

1

log 4

2

9

bằng

A. 2 B. 4 C. 3 D. 16

Câu 20. Tập xác định của hàm số

( )

2

log 2y x x=−

là

A.

( ) ( )

;0 2;−  +

B.

 

0;2

C.

(

 

)

;0 2;−  +

D.

( )

0;2

Câu 21.Cho hàm số

2

()

1

xm

y f x

x

+

==

−

. Tính tổng các giá trị của tham số m để

 

2;3

max ( ) min ( ) 2

x

f x f x



−=

A. -4 B. -2 C. -1 D. -3

Câu 22. Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = 2a, AD =

3a

, cạnh bên SA vuông góc

với mặt phẳng đáy, góc giữa SD và mặt phẳng đáy là 30

o

. Diện tích mặt cầu ngoại tiếp hình chóp là

A.

2

8 a



B.

2

8

3

a



C.

2

4 a



D.

2

4

3

a



Câu 23. Cho các đường thẳng

1

11

:

1 2 1

x y z

d

−+

==

−

và

2

23

:

1 2 2

x y z

d

−+

==

. Viết phương trình đường

thẳng  đi qua A (1; 0; 2), cắt d

1

và vuông góc với d

2

.

A.

12

2 2 1

x y z−−

==

−

B.

12

4 1 1

x y z−−

==

−−

C.

12

2 3 4

x y z−−

==

−

D.

12

2 2 1

x y z−−

==

−

Trang 3

Câu 24. Cho hình nón đỉnh S có đáy là đường tròn tâm O, bán kính R. Trên đường tròn (O) lấy hai

điểm A, B sao cho tam giác OAB vuông. Biết diện tích tam giác SAB bằng

2

2R

, thể tích hình nón đã

cho bằng

A.

3

14

2

R

V



=

B.

3

14

6

R

V



=

C.

3

14

12

R

V



=

D.

3

14

3

R

V



=

Câu 25. Cho mặt phẳng (Q): x - y + 2z - 2 = 0. Viết phương trình mặt phẳng (P) song song với mặt

phẳng (Q), đồng thời cắt các trục Ox, Oy lần lượt tại các điểm M, N sao cho

22MN =

.

A. (P): x - y + 2z + 2 = 0 B. (P): x - y + 2z = 0

C. (P): x - y + 2z ± 2 = 0 D. (P): x - y + 2z - 2 = 0

Câu 26. Cho hình lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng a, góc giữa mặt phẳng (A'BC ) và

mặt phẳng ( ABC ) bằng 45

o

. Thể tích của khối lăng trụ ABC.A'B'C' bằng

A.

3

8

a

B.

3

2

a

C.

3

4

a

D.

3

8

a

Câu 27. Tích tất cả các nghiệm của phương trình

2

21

35

xx−+

=

là

A. 1 B.

3

2 log 5−

C.

3

log 45−

D.

3

log 5

Câu 28. Cho hàm số f(x) liên tục trên R và

8

2

( ) 10f x dx =



. Tính

3

1

3

(3 1)

2

I f x dx=−



A. 30 B. 10 C. 20 D. 5

Câu 29. Cho hàm số

2xm

y

xm

−

=

+

. Với giá trị nào của m thì hai đường tiệm cận của đồ thị hàm số cùng

với hai trục tọa độ tạo thành hình vuông.

A. m = -2 B. m  2 C. m = 2 D.

2

m

=





=−



Câu 30. Trong hệ tọa độ Oxyz, lập phương trình đường thẳng vuông góc chung  của hai đường thẳng

1

1 3 2

:

1 1 2

x y z

d

− − −

==

−

và

2

3

:

13

xt

d y t

zt

=−





=





= − −



A.

2 2 4

1 3 2

x y z− − −

==

−−

B.

3 1 2

1 1 1

x y z− + −

==

−

C.

1 3 2

3 1 1

x y z− − −

==

−

D.

1

1 6 1

x y z +

==

Câu 31. Có bao nhiêu số phức thỏa mãn z

2

- 2018z = 2019 |z|

2

?

A. Vô số B. 2 C. 1 D. 0

Câu 32. Biết

23

1

ln

e

I x xdx ae b= = +



với a,b là các số hữu tỉ. Giá trị của 9(a + b) bằng

A. 3 B. 10 C. 9 D. 6

Câu 33. Cho đa giác đều có 20 cạnh. Có bao nhiêu hình chữ nhật (không phải là hình vuông), có các đỉnh

là đỉnh của đa giác đều đã cho?

A. 45 B. 35 C. 40 D. 50

Câu 34.Cho hàm số y = x

4

- 2mx

2

+ 3m - 2 (với m là tham số). Có bao nhiêu giá trị của tham số m để các

điểm cực trị của đồ thị hàm số đều nằm trên các trục tọa độ?

A. 2 B. 0 C. 3 D. 1

Trang 4

Câu 35. Cho đường thẳng

1 2 2

:

1 2 1

x y z

d

− − −

==

−

và điểm A (1; 2; 1). Tìm bán kính của mặt cầu có

tâm I nằm trên d, đi qua A và tiếp xúc với mặt phẳng (P): x - 2y + 2z + 1 = 0

A. R = 2 B. R = 4 C. R = 1 D. R = 3

Câu 36. Cho hình trụ có trục OO' và có bán kính đáy bằng 4. Một mặt phẳng song song với trục OO' và

cách OO' một khoảng bằng 2 cắt hình trụ theo thiết diện là một hình vuông. Diện tích xung quanh của

hình trụ đã cho bằng

A.

26 3



B.

83



C.

16 3



D.

32 3



Câu 37. Cho đường thẳng

1 2 2

:

3 2 2

x y z

d

+ − −

==

−

. Viết phương trình mặt cầu tâm I (1; 2; -1) cắt d tại các

điểm A, B sao cho

23AB =

A. (x – 1)

2

+ (y – 2)

2

+ (z + 1)

2

= 25 B. (x – 1)

2

+ (y – 2)

2

+ (z + 1)

2

= 4

C. (x – 1)

2

+ (y – 2)

2

+ (z + 1)

2

= 9 D. (x – 1)

2

+ (y – 2)

2

+ (z + 1)

2

= 16

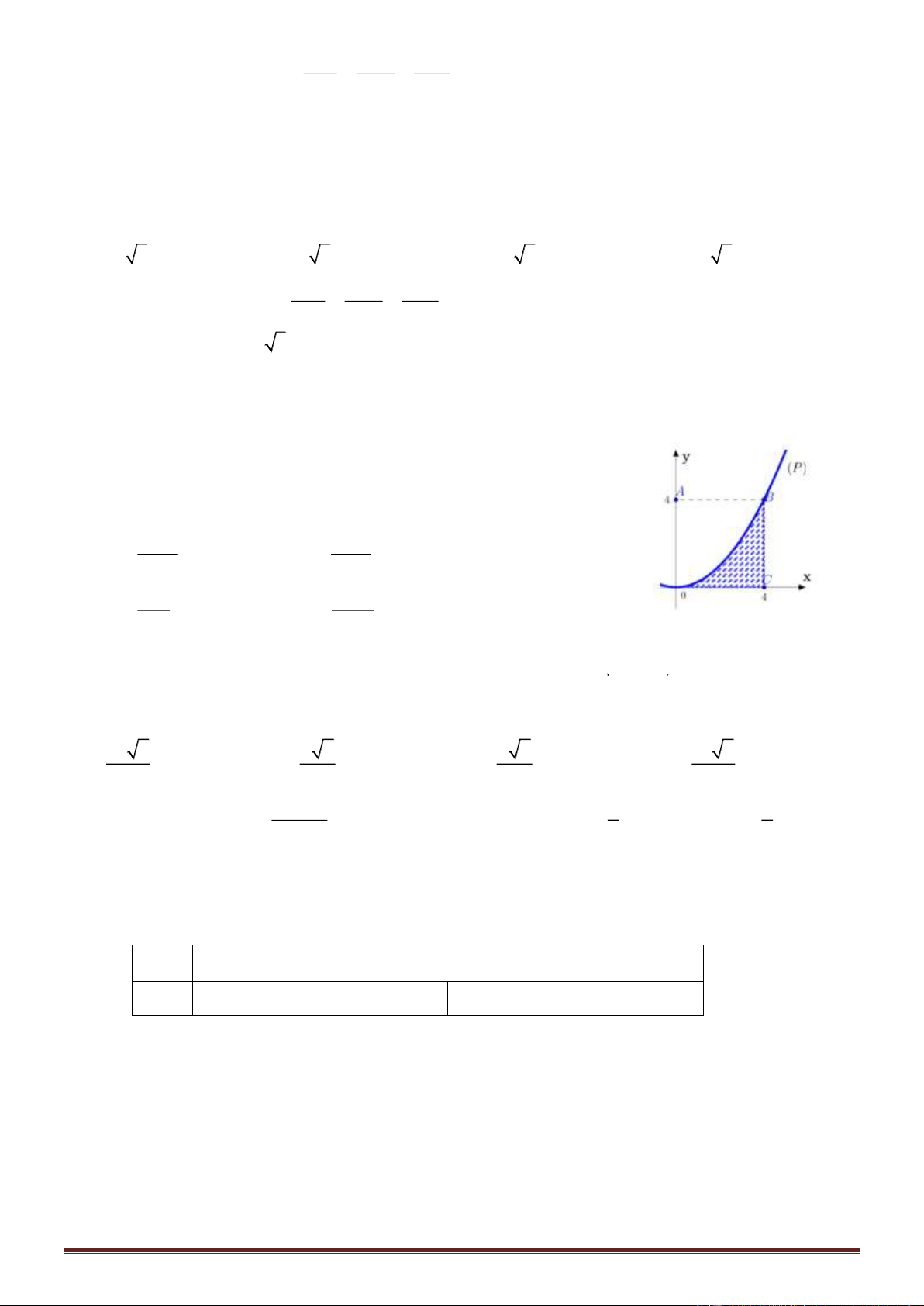
Câu 38. Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần

bởi đường parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch

(như hình vẽ). Tính thể tích V của khối tròn xoay khi cho phần S quay

quanh trục Ox

A.

128

5

V



=

B.

128

3

V



=

C.

64

5

V



=

D.

256

5

V



=

Câu 39. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân có AB = BC = a. Cạnh bên SA

vuông góc với đáy, SBA = 60°. Gọi M là điểm nằm trên AC sao cho

2AC CM=

. Tính khoảng cách giữa

SM và AB.

A.

67

7

a

B.

7

a

C.

7

21

a

D.

37

7

a

Câu 40. Phương trình

( )

2

3

2

21

log 3 8 5

1

x

xx

x

−

= − +

−

có hai nghiệm là a và

a

b

(với a,b  N* và

a

b

là phân số

tối giản). Giá trị của b là

A. 1 B. 4 C. 2 D. 3

Câu 41. Cho hàm số y = f(x) liên tục trên R và có bảng xét dấu của đạo hàm như sau:

x

- -1 1 3 +

f'(x)

- 0 +

+ 0 -

Có bao nhiêu giá trị nguyên của tham số m để hàm số g (x) = f (x + m) đồng biến trên khoảng (0; 2).

A. 3 B. 4 C. 2 D. 1

Câu 42. Cho A (1; 4; 2), B (-1; 2; 4), đường thẳng

54

: 2 2

4

xt

d y t

zt

=−





=+





=+



và điểm M thuộc d. Tìm giá trị nhỏ nhất

của diện tích tam giác AMB

Trang 5

A.

23

B.

22

C.

32

D.

62

Câu 43. Cho phương trình

2

33

log log 3 0x x m− + − =

. Tìm tất cả các giá trị nguyên của tham số m

để phương trình đã cho có hai nghiệm phân biệt x

1

< x

2

thỏa mãn x

2

– 81x

1

< 0

A. 4 B. 5 C. 3 D. 6

Câu 44. Cho hai số phức z

1

, z

2

khác 0 thỏa mãn

1

2

z

là số thuần ảo và

12

10zz−=

. Giá trị lớn của

12

zz+

bằng

A. 10 B.

10 2

C.

10 3

D. 20

Câu 45. Cho hàm số y = f (x) liên tục trên R có đồ thị như hình

vẽ. Biết trên (-; -3)(2; +) thì f'(x) > 0. Số nghiệm nguyên

thuộc (-10; 10) của bất phương trình [f (x) + x - 1](x

2

- x - 6) > 0

là

A. 9 B. 10

C. 8 D. 7

Câu 46. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, hình chiếu vuông góc của đỉnh

S trên mặt phẳng (ABC) là một điểm nằm trên đoạn thẳng BC. Mặt phẳng (SAB) tạo với (SBC) một góc

60

0

và mặt phẳng (SAC) tạo với (SBC) một góc  thỏa mãn

2

cos

4



=

. Gọi  là góc tạo bởi SA và mặt

phẳng (ABC). Tính tan

A.

3

B.

2

C.

1

2

D.

3

Câu 47. Cho hàm số y = f (x) có đồ thị (C), biết tiếp tuyến của đồ thị (C) tại điểm có hoành độ

x = 0 là đường thẳng y = 3x - 3. Giá trị của

0

3

lim

(3 ) 5 (4 ) 4 (7 )

x

f x f x f x

→

−+

A.

1

10

B.

3

31

C.

3

25

D.

1

11

Câu 48. Cho hàm số y = f(x) liên tục trên R sao cho

 

0;10

max ( ) (2) 4

x

f x f



==

. Xét hàm số

32

( ) ( ) 2g x f x x x x m= + − + +

. Giá trị của tham số m để

 

0;2

maxg( ) 8

x



=

là

A. 5 B. 4 C. -1 D. 3

Câu 49. Cho đa thức bậc bốn y = f (x) đạt cực trị tại x = 1 và x = 2. Biết

0

2 '( )

lim 2

2

x

x f x

x

→

+

=

. Tích phân

1

0

'( )f x dx



A.

3

2

B.

1

4

C.

3

4

D. 1

Câu 50. Cho hàm số f(x) = x

5

+ 3x

3

- 4m. Có bao nhiêu giá trị nguyên của tham số m để phương trình

( )

3

()f f x m x m+ = −

có nghiệm thuộc [1; 2]?

A. 15 B. 16 C. 17 D. 18

Trang 6

----------- HẾT ----------

Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.

ĐÁP ÁN

1-B

2-C

3-B

4-D

5-A

6-C

7-D

8-B

9-A

10.C

11-D

12-D

13-B

14-C

15-C

16-A

17-C

18-D

19-B

20-A

21-A

22-A

23-C

24-B

25-A

26-A

27-C

28-D

29-D

30-A

31-B

32-A

33-C

34-A

35-D

36-D

37-D

38-D

39-D

40-D

41-A

42-C

43.C

44-B

45-C

46-C

47-D

48-D

49-B

50-B

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1.

Phương pháp

Sử dụng định lý Pytago để tính chiều cao hình chóp

Sử dụng công thức tính thể tích khối chóp có diện tích đáy S và chiều cao h là V =

1

3

h.S

Cách giải:

Vì

( ) ( )

( ) ( ) ( )

( ) ( )

SAB ABC

SAC ABC SA ABC

SAB SAC SA

⊥





⊥  ⊥





=



Xét tam giác vuông SAB có

2 2 2 2

32SA SB AB a a a= − = − =

Diện tích tam giác ABC là

2

3

4

ABC

a

S =

Thể tích khối chóp là

23

.

1 1 3 6

. . 2.

3 3 4 12

S ABC ABC

aa

V SAS a= = =

Chọn B.

Câu 2.

Phương pháp

Sử dụng công thức tích phân

'( ) ( ) (a)

b

a

f x dx f b f=−



Cách giải:

Ta có:

3

0

'( ) 9 (3) (0) f(3) 9 f(0) 9 1 10f x dx f f= = −  = + = + =



Chọn C

Câu 3.

Phương pháp

Sử dụng công thức log

a

(bc) = log

a

b + log

a

c (0 < a  1; b, c > 0 )

Cách giải:

Ta có ln( a + ab ) = ln( a (1 + b )) = lna + ln(1 + b )

Chọn B.

Trang 7

Câu 4.

Phương pháp

Sử dụng công thức nguyên hàm

11

lndx ax b C

ax b a

= + +

+



Cách giải:

Ta có:

11

( ) ln 2 3

2 3 2

f x dx dx x C

x

= = + +

+



Chọn D.

Câu 5.

Phương pháp

Đưa về giải bất phương trình có cơ số 0 < a < 1 :

()

( ) log

fx

a

a b f x b  

Cách giải:

Ta có

2

1

2

22

1 1 1

2 log

2 8 8

2 3 2 3 0 1 3

xx

x x x x x

−



  − 





 −   − −   −  

Tập nghiệm của bất phương trình S = (-1; 3)  a = -1; b = 3 nên b - a = 4.

Chọn A.

Chú ý :

Một số em không đổi dấu bất phương trình dẫn đến không ra đáp án.

Câu 6.

Phương pháp

Tìm VTCP của d và điểm đi qua, từ đó suy ra phương trình tham số.

Cách giải:

Đường thẳng

122

:

1 2 3

x y z

d

− − +

==

−

đi qua A(1; 2; -2) và nhận

(1; 2;3)u =−

làm VTCP

 d:

1

22

23

xt

yt

zt

=+





=−





= − +



Chọn C.

Câu 7.

Phương pháp

Số phức liên hợp của số phức z = a + bi (a, b  R) là

z a bi=−

Cách giải:

Ta có

2

(3 1) 3i 3z i i i i= + = + = − +

Số phức liên hợp của z là

3zi= − −

Chọn D.

Câu 8.

Phương pháp

Trang 8

(P) // Ox và (P) ⊥ (Q) thì

()

( ) ( )

P

PQ

ni

nn



⊥





⊥





Cách giải:

Gọi

()P

n

là VTPT của (P). Do (P) // Ox và (P) ⊥ (Q) nên

()

( ) ( )

P

PQ

ni

nn



⊥





⊥





.

Ox có VTPT

( )

1;0;0i =

và (Q) : x + 2y - 2z + l = 0 có VTPT

( )

()

1;2; 2

Q

n =−

Có

( )

()

, 0;2;2

Q

in



=



nên chọn

( )

(P)

0;1;1n =

.

(P) đi qua A(0; -1; 2) và nhận

( )

(P)

0;1;1n =

làm VTPT nên

(P) : 0(x - 0) +1(y +1) +1(z - 2) = 0  y + z - 1 = 0.

Chọn B.

Câu 9.

Phương pháp

Số phức z = a + bi (a, b  R) có phần thực là a và phần ảo là b.

Cách giải:

Phần ảo của số phức z = 5 – 8i là -8.

Chọn A.

Câu 10.

Phương pháp

- Tính y' và tìm nghiệm của y' = 0 .

- Lập bảng biến thiên của hàm số suy ra điểm cực đại của đồ thị hàm số.

Cách giải:

Ta có :

2

0

' 3 6 0

2

x

y x x

x

=



= − = 



=



Bảng biến thiên :

x

- 0 2 +

y'

0 0

y

2 +

- -2

Vậy điểm cực đại của đồ thị hàm số là (0; 2) .

Chọn C.

Câu 11.

Phương pháp

Sử dụng cách đọc đồ thị hàm đa thức bậc ba và trùng phương bậc bốn.

Cách giải:

Từ hình dáng đồ thị ta thấy hình vẽ là đồ thị của hàm đa thức bậc ba nên loại đáp án A, B.

Lại từ hình vẽ ta thấy

lim ; lim

xx→− →+

= − = +

nên chỉ có đáp án D thỏa mãn.

Trang 9

Chọn D.

Câu 12.

Phương pháp

Đường thẳng d song song với cả (P) và (Q) thì

()

(Q)

dP

d

un



⊥





⊥





Cách giải:

(P): 2x + 2y + z + 1 = 0 

()

(2;2;1)

P

n =

là VTPT của (P).

(Q): 2x - y + 2z - 1 = 0 

(Q)

(2; 1;2)n =−

là VTPTcủa (Q).

Gọi

d

u

là VTCP của đường thẳng d.

Đường thẳng d song song với cả (P) và (Q) thì

()

(Q)

dP

d

un



⊥





⊥





Có

( )

( ) ( )

, 5; 2; 6

PQ

nn



= − −



nên chọn

(5; 2; 6)

d

u = − −

d đi qua A (1; 2; 3) và nhận

(5; 2; 6)

d

u = − −

làm VTCP nên

1 2 3

5 2 6

x y z− − −

==

−−

Chọn D.

Câu 13.

Phương pháp

Cấp số cộng có số hạng đầu u

1

và công sai d thì có số hạng thứ n là u

n

= u

1

+ (n - 1)d

Cách giải:

Ta có u

1

= -5; d = 3 nên u

15

= u

1

+ 14d = 37 ; u

13

= u

1

+ 12d = 31; u

10

= u

1

+ 9d = 22 nên A, C, D sai, B

đúng.

Chọn B.

Câu 14.

Phương pháp

Mặt cầu đường kính AB có tâm là trung điểm AB và bán kính

2

AB

R =

.

Cách giải:

Ta có: A(1; 2; 3), B(-1; 4; 1)  I(0; 3; 2) là trung điểm AB và

12 2 3AB ==

Mặt cầu (S) đường kính AB có tâm I(0; 3; 2) và bán kính

3

2

AB

R ==

 (S) :(x - 0)

2

+ (y - 3)

2

+ (z - 2)

2

= 3 hay (S): x

2

+ (y - 3)

2

+ (z - 2)

2

= 3 .

Chọn C.

Câu 15.

Phương pháp

Số giao điểm của hai đồ thị hàm số f (x) và g (x) là số nghiệm của phương trình f (x) = g(x).

Cách giải:

Xét phương trình hoành độ giao điểm:

Trang 10

3 3 2

0

2 2 0 ( 1) 0 1

1

x

x x x x x x x

x

=





+ = +  − =  − =  =



=−



Suy ra số giao điểm của hai đồ thị y = x + 2; y = x

3

+ 2 là 3 giao điểm.

Chọn C.

Câu 16.

Phương pháp

Sử dụng công thức tính thể tích khối trụ V = R

2

h .

Cách giải:

Ta có: V = R

2

h  8 = .h

2

.h  h = 2.

Chọn A.

Câu 17.

Phương pháp

Giải phương trình tìm z

1

, z

2



12

zz−

Số phức

z x yi=+

(x; y  R) có mô đun

22

z x y=+

Cách giải:

Ta có

( ) ( )

22

1 3 1 3

2 10 0 1 9 1 9

1 3 1 3

z i z i

z z z z i

z i z i

+ = = − +



+ + =  + = −  + =  



+ = − = − −



Suy ra

( )

12

1 3 1 3 6 36 6z z i i i− = − + − − − = = =

Chọn C.

Câu 18.

Phương pháp:

Tìm nghiệm của đạo hàm và suy ra các điểm cực trị:

+) Các điểm làm cho đạo hàm đổi dấu từ âm sang dương là điểm cực tiểu.

+) Các điểm làm cho đạo hàm đổi dấu từ dương sang âm là điểm cực đại.

Cách giải:

Ta có:

1

'( ) 0

3

x

fx

x

=



=



=



'( ) 0 3f x x  

và

'( ) 0 3f x x  

nên đạo hàm f'(x) đổi dấu từ âm sang dương qua điểm x = 3.

Vậy hàm số chỉ có duy nhất một điểm cực trị, chính là điểm cực tiểu x = 3 .

Chọn D.

Câu 19.

Phương pháp

Sử dụng công thức

( )

log

.

; 0 1; 0

a

n

b

m n m

a a a b a b= =   

Cách giải:

Ta có

3

log 4

11

log 4

22

9 9 3 4.



= = =





Chọn B.

Trang 11

Câu 20.

Phương pháp:

Hàm số

log ( )

a

y f x=

xác định nếu f (x) xác định và f (x) > 0 .

Cách giải:

Hàm số

( )

2

log 2y x x=−

xác định nếu

2

2 0 .

0

x

xx

x





−  







Vậy TXĐ : D = (-; 0)  (2; +).

Chọn A.

Câu 21.

Phương pháp:

+) Tính y'.

+) Xác định các giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên (2; 3).

Cách giải:

ĐK : x  1. Ta có

( )

2

'

1

m

y

x

−−

=

−

TH1:

' 0 2 0 2y m m − −    −

suy ra hàm số đã cho đồng biến trên từng khoảng (-; 1)  (1; +)

nên hàm số đông biến trên (2; 3)

Suy ra

 

2;3

6

max (3) ;min (2) 4

2

m

y y y y m

+

= = = = +

Từ ycbt ta có

( )

6

2 4 2 ( )

4 2 2 4

2 4 6 ( )

2

m

m m ktm

mm

m m tm

+

+ = =



− + =  − − =  



+ = − = −



TH1 :

' 0 2 0 2y m m − −    −

suy ra hàm số đã cho nghịch biến trên từng khoảng xác định

(-; 1)  (1; +) nên hàm số nghịch biến trên (2; 3).

Suy ra

 

2;3

6

min (3) ;max (2) 4

2

m

y y y y m

+

= = = = +

Từ ycbt ta có

6

2 4 2 ( )

4 2 2 4

2 4 6 ( )

2

m

m m tm

mm

m m ktm

+

+ = =



+ − =  + =  



+ = − = −



Vậy m = 2; m = -6 nên tổng các giá trị của m là 2 + (-6) = -4.

Chọn A.

Câu 22.

Phương pháp

- Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp.

- Tính diện tích theo công thức S = 4R

2

.

Cách giải:

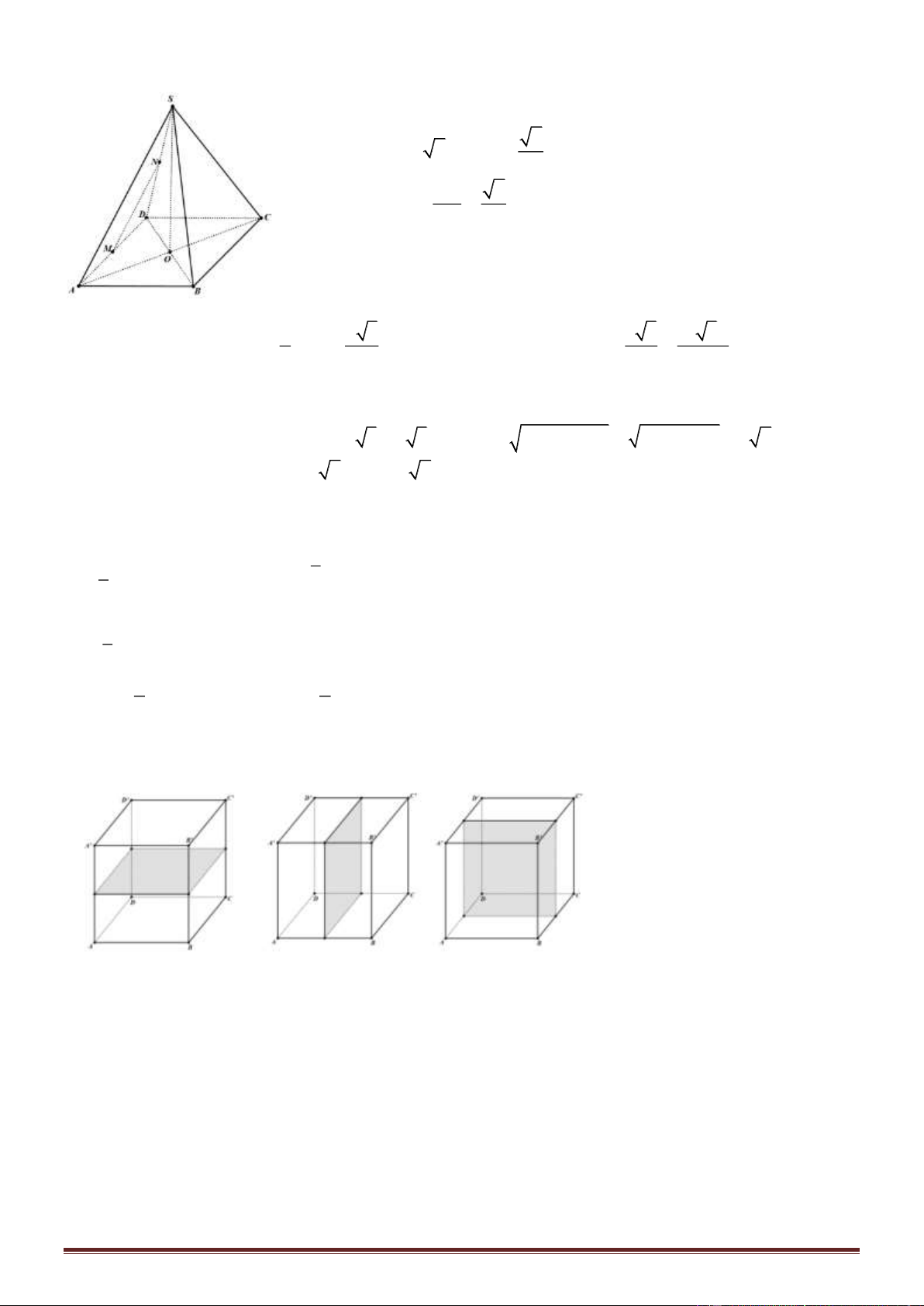
Gọi O = AC  BD.

Qua O dựng đường thẳng d vuông góc với đáy. Mặt phẳng trung trục của

SA cắt d tại I.

Khi đó I là tâm mặt cầu ngoại tiếp hình chóp.

Do SA ⊥ (ABCD) nên góc giữa SD và đáy bằng SDA = 30°.

Trang 12

Tam giác SAD vuông tại A có

0

3, 30AD a SDA==

( )

0

2 2 2 2

22

2

2 2 2 2

3

tan30 3.

3

1 1 1 1 7

; 3 4

2 2 2 2 2 7

7

2 4 4 2 8

44

SA AD a a

aa

AH AS AO AC AD DC a a

aa

AI AO OI a S AI a a

  

 = = =

 = = = = + = + =

 = + = + =  = = =

Chọn A.

Chú ý khi giải: Các em cũng có thể sử dụng ngay công thức tính bán kính mặt cầu ngoại tiếp hình chóp

có cạnh bên vuông góc đáy, đó là

2

4

h

Rr=+

, với R là bán kính mặt cầu ngoại tiếp hình chóp, r là bán

kính đường tròn ngoại tiếp đa giác đáy, h là độ dài cạnh bên vuông góc đáy.

Câu 23.

Phương pháp

+) Gọi M là giao điểm của  và d

1

, biểu diễn tọa độ M theo tham số t.

+) Từ đề bài suy ra

.0

d

AM u =

từ đó tìm được t, suy ra

AM

.

+) Viết phương trình đường thẳng  đi qua A (1; 0; 2) và nhận

AM

làm VTCP.

Cách giải:

Đường thẳng

11

1

11

: : 1 2

1 2 1

xt

x y z

d d y t

zt

=+



−+



= =  = − +



−



=−



Đường thẳng

2

23

:

1 2 2

x y z

d

−+

==

có 1 VTCP là

( )

2

1;2;2

d

u =

Gọi giao điểm của  với đường thẳng d

1

là M (1+t; -1 + 2t; -t)

Vì  đi qua A(1; 0; 2) nên

( )

; 1 2 ; 2AM t t t= − + − −

là 1 VTCP của 

Vì

22

2

.0

dd

d AM u AM u ⊥  ⊥  =

( ) ( )

1. 2. 1 2 2. 2 0 3 6 0 2t t t t t + − + + − − =  − =  =

Suy ra

( )

2;3; 4AM =−

Phương trình đường thẳng  đi qua A(1; 0; 2) và nhận

( )

2;3; 4AM =−

làm VTCP là

12

2 3 4

x y z−−

==

−

Chọn C.

Câu 24.

Phương pháp

- Gọi H là trung điểm AB.

- Tính SO suy ra thể tích

2

1

.

3

V r h



=

Cách giải:

Gọi H là trung điểm của AB ta có OH ⊥ AB, SH ⊥ AB .

Trang 13

Tam giác OAB vuông tại O

12

2, .

22

R

AB R OH AB = = =

Tam giác SAB có

2

22

2 2 .

2

SAB

S

R

S R SH R

AB

R

=  = = =

2

2 2 2

2 14

4.

42

RR

SO SH OH R = − = − =

Thể tích khối nón

3

22

1 1 14 14

. . .

3 3 2 6

RR

V OA SO R





= = =

Chọn B.

Câu 25.

Phương pháp

Mặt phẳng (P) song song với mặt phẳng (Q): ax + by + cz + d = 0 có phương trình ax + by + cz + d' = 0

(d  d')

Từ đề bài suy ra tọa độ điểm M, N từ đó thay tọa độ M, N vào phương trình mặt phẳng (P) và sử dụng

định lý Pytago để tìm được d'

Cách giải:

Vì (P) / / (Q) nên phương trình mặt phẳng (P): x - y + 2z + d = 0 (d  -2) có VTPT

( )

1; 1;2n =−

Vì M  Ox; N  Oy nên

( ) ( )

;0;0 , 0;y ;0

MN

M x N

mà M,N  (P) nên ta có

0

MM

x d x d+ =  = −

và

0

NN

y d d y− + =  =

Hay

( ) ( )

;0;0 , 0; ;0 ;M d N d OM d ON d−  = =

Lại có tam giác OMN vuông tại O nên

2 2 2 2 2

2 ( )

2 8 4

2 ( )

d tm

MN OM ON d d

d ktm

=



= +  =  = 



=−



Suy ra phương trình mặt phẳng (P): x - y + 2z + 2 = 0.

Chọn A.

Câu 26.

Phương pháp:

- Xác định góc 45

0

(góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng mà cùng vuông góc với giao

tuyến).

- Tính chiều cao, diện tích đáy và suy ra thể tích theo công thức V = Bh với B là diện tích đáy, h là chiều

cao.

Cách giải:

Gọi M là trung điểm của BC  AM ⊥ BC và A'M ⊥ BC (tam giác A'BC cân).

Mà ( A'BC)  (ABC) = BC nên góc giữa hai mặt phẳng (A'BC) và (ABC) bằng

góc giữa AM và A'M hay A'MA = 45

0

Tam giác ABC đều cạnh a nên

3

.

2

a

AM =

Trang 14

Tam giác AMA' có A = 90

0

,

3

2

a

AM =

và A'MA = 45

0

nên

0

3

AA' tan45 .

2

a

AM AM= = =

Thể tích khối lăng trụ:

22

3 3 3

AA' . .

4 2 8

ABC

a a a

VS= = =

Chọn A.

Câu 27.

Phương pháp:

Sử dụng

(x) ( )

( ) ( ).log

f g x

a

a b f x g x b=  =

với 0 < a  1; b > 0.

Sử dụng hệ thức Vi-ét để tính tích các nghiệm.

Cách giải:

Ta có

( )

22

2 1 2 1 2

3 3 3

3 5 log 3 log 5 2 1 log 5

x x x x

xx

− + − +

=  =  − = +

2

33

.log 5 2 log 5 0xx − − − =

Nhận thấy

( )

3

1. 2 log 5 0ac = − − 

nên phương trình có hai nghiệm phân biệt trái dấu x

1

; x

2

.

Theo hệ thức Vi-et ta có

( )

1 2 3 3 3 3 3

. 2 log 5 log 9 log 5 log 9.5 log 45xx= − − = − − = − = −

Chọn C.

Câu 28.

Phương pháp:

Sử dụng phương pháp đổi biến tính tích phân.

Cách giải:

Đặt

3 1 3

3

dt

t x dt dx dx= −  =  =

Đổi cận

1 2, 3 8.x t x t=  = =  =

Khi đó

3 8 8

1 2 2

3 3 ( ) 1 1

(3 1) ( ) .10 5.

2 2 3 2 2

ft

I f x dx dt f t dt= − = = = =

  

Chọn D.

Câu 29.

Phương pháp:

Đồ thị hàm số

ax b d

yx

cx d c

+



=  −



+



nhận đường thẳng

a

y

c

=

làm TCĐ và nhận đường thẳng

d

x

c

=−

làm TCN.

Từ YCBT suy ra

ac

cd

=−

từ đó ta tìm được m.

Cách giải:

Xét hàm số

2xm

y

xm

−

=

−

với x  m

Điều kiện để đồ thị hàm số có 2 tiệm cận là m  0

Đồ thị hàm số nhận y = 2 làm TCĐ và x = m làm TCN

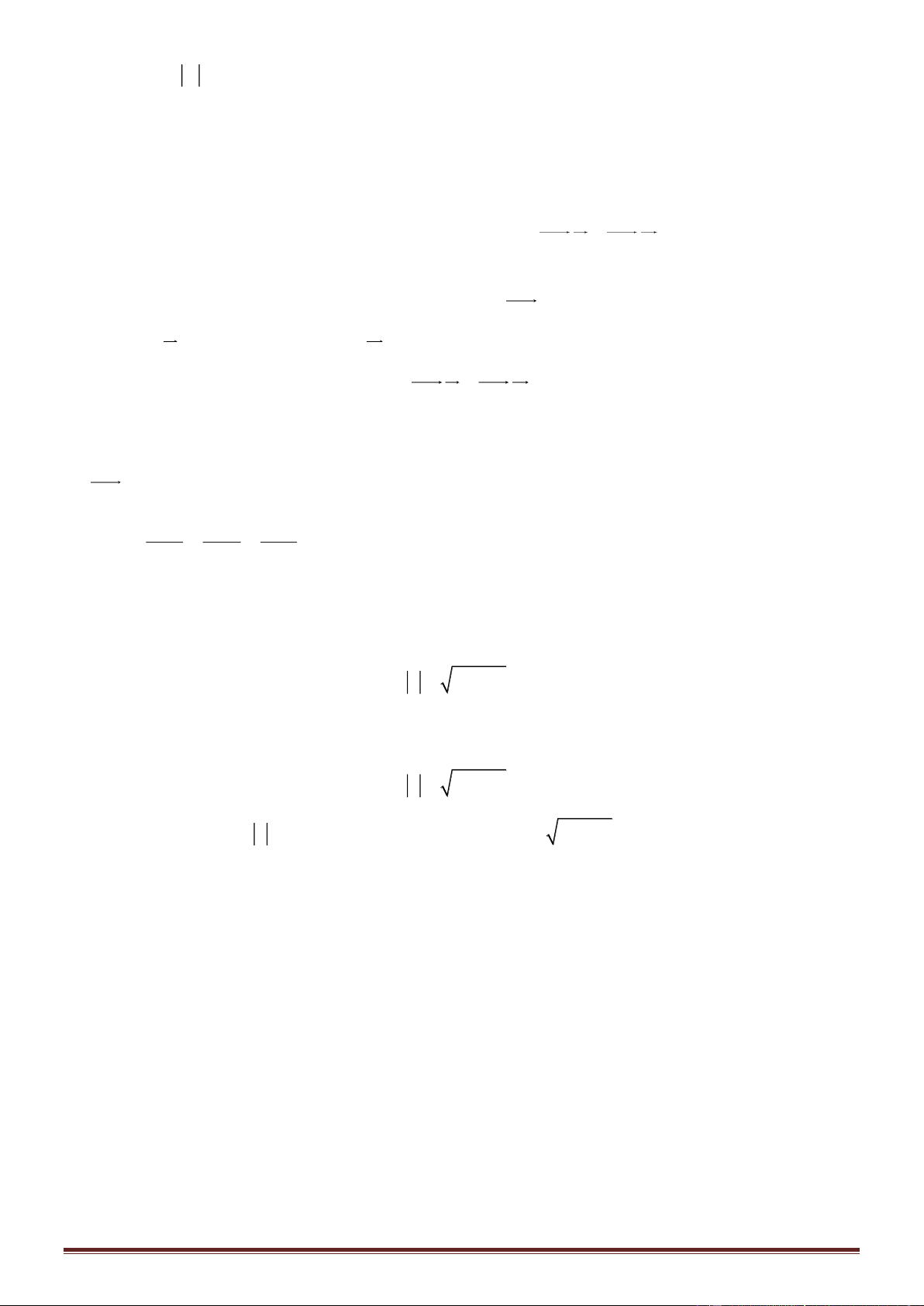
Trang 15

Từ ycbt suy ra

2

m

=



=



=−



Chọn D.

Câu 30.

Phương pháp:

- Gọi tọa độ hai điểm M, N theo tham số của hai đường thẳng, với MN là đường vuông góc chung.

- MN là đoạn vuông góc chung của hai đường thẳng d

1

, d

2

thì

12

. . 0MN u MN u==

Cách giải:

Ta có

( ) ( ) ( )

12

1 ;3 ;2 2 , 3 '; '; 1 3 ' 3 ' 1 ; ' 3 ; 3 3 ' 2M t t t d N t t t d MN t t t t t t+ − +  − − −   = − − − − + − − −

d

1

có VTCP

( )

1

1; 1;2u =−

, d

2

có VTCP

( )

2

3;1; 3u = − −

MN là đoạn vuông góc chung của d

1

và d

2



12

. . 0MN u MN u==

  

1( 3 ' 1 ) 1( ' 3 ) 2( 3 3 ' 2 ) 0 10 ' 6 4 0 ' 1

3( 3 ' 1 ) 1( ' 3 ) 3( 3 3 ' 2 ) 0 19 ' 10 9 0 1

t t t t t t t t t

− − − − − + + − − − = − − − = = −

  

− − − − + − + − − − − = + + = =

( )

1; 3; 2MN = − −

và M(2; 2; 4)

Vậy

2 2 4

:

1 3 2

x y z

MN

− − −

==

−−

Chọn A.

Câu 31.

Phương pháp:

Gọi số phức z = x + yi (x; y  R) thì mô đun

22

z x y=+

Từ đó biến đổi đưa về hai số phức bằng nhau thì phần thực bằng nhau và phần ảo bằng nhau.

Cách giải:

Gọi số phức z = x + yi (x; y  R) thì mô đun

22

z x y=+

Ta có

( ) ( )

(

)

2

2 2 2

2018 2019 2018 2019z z z x yi x yi x y− =  + − + = +

( )

2 2 2 2

22

2 2018 2018 2019 2019

2018 2020 2018 2 2018 0

0

2 2018 0

1009

2018 2018 2018 0

x xyi y x yi x y

x y x xy y i

y

xy y

x

x y x

 + − − − = +

 + + − − =



=



−=







=







+ + =





+ + =



Với

( )

2

0

0 2018 2018 0 2018 1 0

1

x

y x x x x

x

=



=  + =  + = 



=−



Suy ra z = 0; z = -1

Với

2 2 2 2

1009 2018.1009 2020 2018.1009 0 2020 2018.1009 2018.1009x y y=  + + =  = − −

(vô nghiệm

vì VT không âm và VP âm)

Vậy có 2 số phức thỏa mãn đề bài.

Chọn B.

Câu 32.

Trang 16

Phương pháp:

- Sử dụng tích phân từng phần, đặt

2

lnux

dx x dx

=





=



.

- Tính tích phân đã cho tìm a, b và kết luận.

Cách giải:

Đặt

23

1

ln

3

du dx

ux

x

dx x dx x

v



=



=









=





=





( )

3 3 3 3 3 3 3 3

2

11

1 1 1 1 2 1

ln . .

11

3 3 3 3 3 3 3 3 9 9 3 9

21

, 9 3.

99

ee

x x e e x e e e

ee

I x dx x dx

x

a b a b

   

 = − = − = − = − + = +

   

   

 = =  + =



Chọn A.

Câu 33.

Phương pháp:

Đa giác đều có n cạnh (với n chẵn) thì luôn tồn tại đường chéo là đường kính của đường tròn ngoại tiếp.

Từ đó sử dụng kiến thức về tổ hợp để tính toán.

Cách giải:

Số hình vuông tạo thành từ các đỉnh của đa giác đều 20 cạnh là 20: 4 = 5 hình

vuông (do hình vuông có 4 cạnh bằng nhau và 4 góc bằng nhau)

Vì đa giác đều có 20 đỉnh nên có 10 cặp đỉnh đối diện hay có 10 đường chéo

đi qua tâm đường tròn ngoại tiếp.

Cứ mỗi 2 đường chéo đi qua tâm đường tròn ngoại tiếp tạo thành một hình

chữ nhật nên số hình chữ nhật tạo thành là

2

10

C

hình trong đó có cả những

hình chữ nhật là hình vuông.

Số hình chữ nhật không phải hình vuông tạo thành là

2

10

5 40C −=

hình.

Chọn C.

Câu 34.

Phương pháp:

- Tính y', tìm điều kiện để y' = 0 có ba nghiệm phân biệt.

- Tìm điều kiện để các điểm cực trị nằm trên các trục tọa độ và kết luận.

Cách giải:

Ta có :

32

2

0

' 4 4 0 4 ( ) 0

x

y x mx x x m

xm

=



= − =  − = 



=



Để đồ thị hàm số có 3 điểm cực trị thì y' = 0 có ba nghiệm phân biệt  m > 0.

Khi đó đồ thị hàm số có các điểm cực trị là

( )

( ) ( )

22

0;3 2 , ; 3 2 , ; 3 2 .A m B m m m C m m m− − + − − − + −

Dễ thấy A  Oy nên bài toán thỏa khi B, C  Ox

2

3 2 0

1

m

mm

m

=



 − + − = 



=



(thỏa mãn)

Vậy có 2 giá trị của m thỏa mãn bài toán.

Trang 17

Chọn A.

Câu 35.

Phương pháp:

+ Từ đề bài suy ra IA = d (I; (P))

+ Sử dụng công thức khoảng cách từ I (x

0

; y

0

; z

0

) đến mặt phẳng (P) : ax + by + cz + d = 0 là

( )

0 0 0

2 2 2

;( )

ax by cz d

d I P

abc

+ + +

=

++

Cách giải:

Đường thẳng

1

1 2 2

: : 2 2

1 2 1

2

xt

x y z

d d y t

zt

=+



− − −



= =  = −



−



=+



Vì

( )

1 ;2 2 ;2I d I t t t  + − +

Lại có mặt cầu đi qua A (1; 2; 1) và tiếp xúc với mặt phẳng (P) : x - 2y + 2z +1 = 0 nên bán kính mặt cầu

R = IA = d (I; (P ))

Lại có

( ) ( )

2

2 2 2

1 2(2 2 ) 2(2 ) 1 7 2

4 1 16 2 1; ;( )

3

1 ( 2) 2

t t t t

IA t t t t t d I P

+ − − + + + +

= + + − − = + + = =

+ − +

Từ đó ta có

( )

2

72

;( ) 6 2 1

3

t

IA d I P t t

+

=  + +

( )

( ) ( )

22

9 6 2 1 7 2 5 10 5 0 5 1 0 1t t t t t t t + + = +  = + =  − =  =

Suy ra

( )

7.1 2

;( ) 3

3

R d I P

+

= = =

Chọn D.

Câu 36.

Phương pháp:

Tính chiều cao hình trụ và tính diện tích xung quanh theo công thức S

xq

= 2Rh.

Cách giải:

Ta có : OHA vuông tại H có

22

2, 4 2 3.OH OA AH OA OH= =  = − =

Thiết diện là hình vuông có cạnh

2 2.2 3 4 3 ' 4 3.AH h OO= =  = =

Diện tích xung quanh

2 2 .4.4 3 32 3.S Rh

  

= = =

Chọn D.

Câu 37.

Phương pháp:

+ Sử dụng khoảng cách từ điểm I đến đường thẳng d đi qua M và có VTCP

u

là

;IM u

d

u





=

+ Sử dụng định lý Pytago để tính bán kính mặt cầu

+ Mặt cầu tâm I (a; b; c) và bán kính R có phương trình (x - a)

2

+ (y - b)

2

+ (z - c)

2

= R

Cách giải:

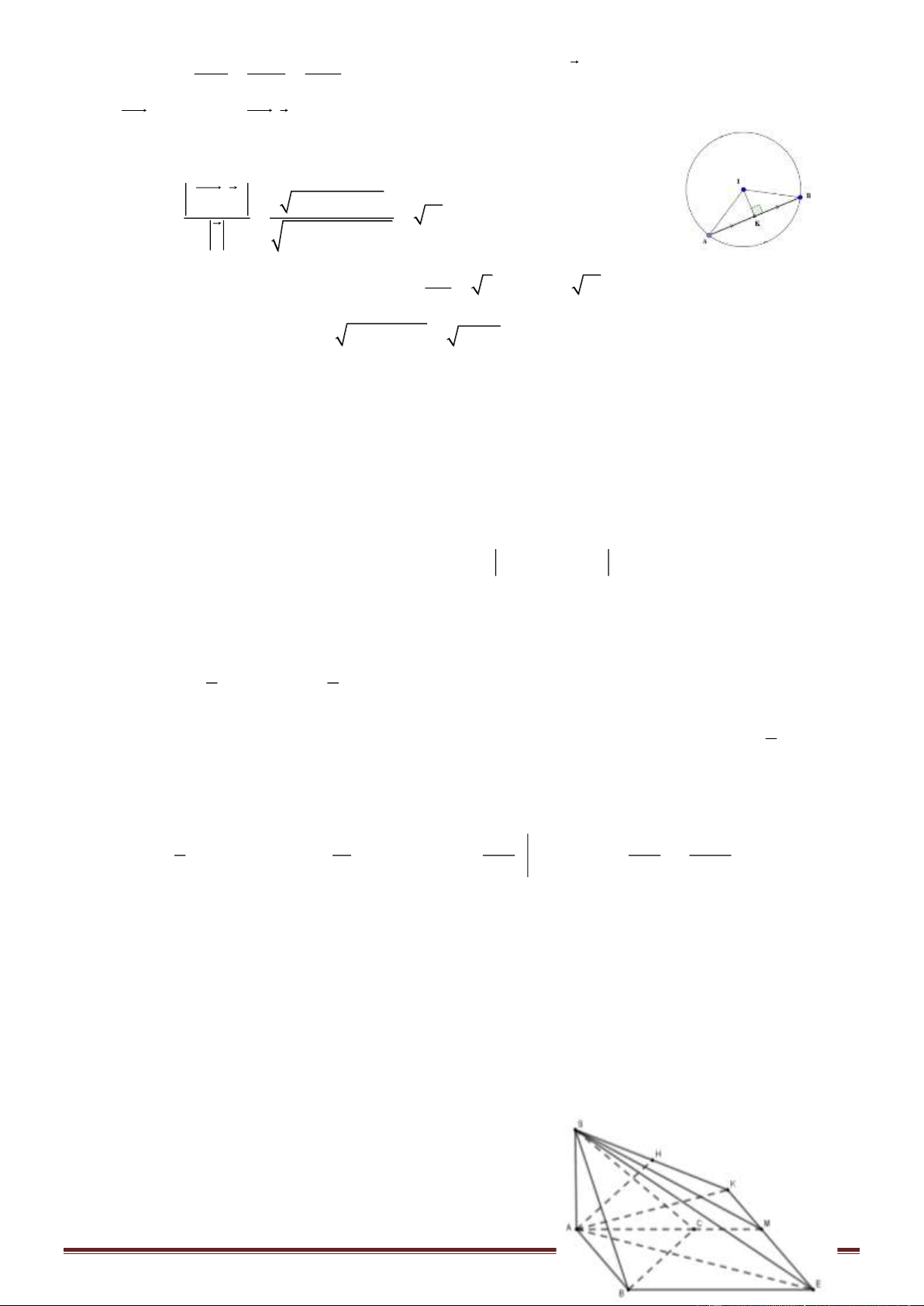
Trang 18

Đường thẳng

1 2 2

:

3 2 2

x y z

d

+ − −

==

−

đi qua M (-1; 2; 2) có VTCP

( )

3; 2;2u =−

Suy ra

( ) ( )

2;0;3 ; ; 6;13;4IM IM u



= − =



Khoảng cách h từ tâm I đến đường thẳng d là

( )

2 2 2

2

22

;

6 13 4

;( ) 13

3 2 2

IM u

h d I d

u



++



= = = =

+ − +

Gọi K là trung điểm dây AB

; 3; 13

2

AB

IK AB KB IK h ⊥ = = = =

Xét tam giác IKB vuông tại K

22

13 3 4IB KB IK= + = + =

Phương trình mặt cầu tâm I (1; 2; -1) và bán kính R = IB = 4 là (x - 1)

2

+ (y - 2)

2

+ (z + 1)

2

= 16

Chọn D.

Câu 38.

Phương pháp:

- Viết phương trình parabol.

- Sử dụng công thức tính thể tích khối tròn xoay khi quay hình phẳng (H) giới hạn bởi các đồ thị

y = f(x), y = g(x), các đường thẳng x = a, x = b là

( ) ( )

22

.

b

a

V f x g x dx



=−



Cách giải:

Phương trình parabol (P) có dạng y = ax

2

đi qua điểm B(4; 4)

2

1

4 .4

4

aa =  =

nên

( )

2

1

:.

4

P y x=

Gọi (H) là phần diện tích hình phẳng giới hạn bởi đường thẳng y = 4, đồ thị hàm số

2

1

4

yx=

, đường

thẳng x = 0.

Khi đó thể tích khối tròn xoay tạo thành khi quay (H) quanh Ox là:

2

44

55

2 2 4

00

1 1 4 256

4

4 16 16 16.4

0

4 16 16.5 16.5 5

x

V x dx x dx x



   



   

= − = − = − = − =



   

   



   





Chọn D.

Câu 39.

Phương pháp:

+ Sử dụng d (a; b ) = d (a; (P)) = d (A; (P)) với b  (P), a // (P), A  a để đưa về tìm khoảng cách giữa

điểm A và mặt phẳng (P) sao cho AB // ( P ).

+ Sử dụng định lý Pytago và hệ thức lượng trong tam giác vuông để tính toán.

Cách giải:

Trong (ABC), qua M kẻ đường thẳng song song với AB, qua B

kẻ đường thẳng song song với AM . Hai đường thẳng này cắt

nhau tại E ta được tứ giác ABEM là hình bình hành.

Vì ME / / AB  AB / / ( SME)

 d (AB; SM ) = d ( AB; (SME)) = d (A; (SME))

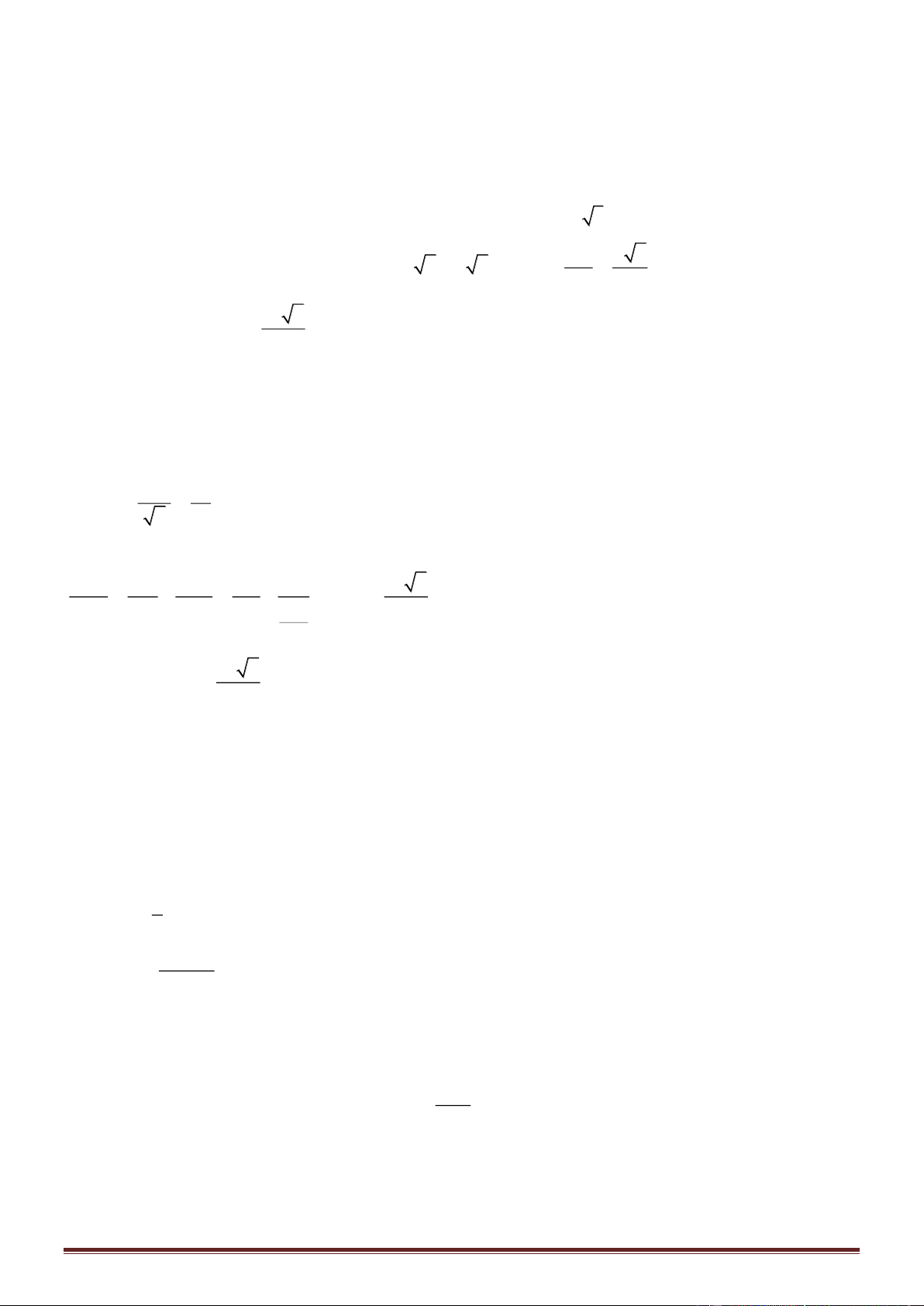
Trang 19

Từ A trong mặt phẳng (ABEM) kẻ AK ⊥ ME , lại có

ME ⊥ SA (do SA ⊥ (ABEM ))  EK ⊥ (SAK)

Trong (SAK) kẻ AH ⊥ SK tại H

Ta có AH ⊥ SK; EK ⊥ AH (do EK ⊥ (SAK))  AH ⊥ (SKE) tại H.

Từ đó d(AB; SM ) = d(A; (SME )) = AH

+ Xét tam giác SBA vuông tại A có

0

.tan .tan60 3.SA AB SBA a a= = =

+ Lại có ABC vuông cân tại B nên

2

22

AC a

AC AB a CM= =  = =

Do đó

32

2

a

AM AC CM= + =

+ ABC vuông cân tại B nên ACB = 45°  CBE = ACB = 45° (hai góc so le trong)

Từ đó ABE = ABC + CBE = 90° + 45° = 135° , suy ra AME = 135° (hai góc đối hình bình hành)

Nên tam giác AME là tam giác tù nên K năm ngoài đoạn ME.

Ta có KMA = 180° - AME = 45° mà tam giác AMK vuông tại K nên tam giác AMK vuông cân tại K

3

2

AM a

AK = =

+ Xét tam giác SAK vuông tại A có đường cao AH, ta có

2

2 2 2 2

1 1 1 1 1 3 7

9

37

4

a

AH

a

AH SA AK a

= + = +  =

Vậy

( )

37

;.

7

a

d AB SM =

Chọn D.

Câu 40.

Phương pháp:

- Biến đổi phương trình về dạng f (u) = f (v) với u, v là các biểu thức ẩn x .

- Sử dụng phương pháp hàm đặc trưng, xét hàm y = f (t) suy ra mối quan hệ u, v.

Cách giải:

Điều kiện:

1

1.

2

x

Khi đó

( )

2 2 2

3 3 3

2

21

log 3 8 5 log (2 1) log ( 1) 3( 1) (2 1) 1

1

x

x x x x x x

x

−

= − +  − − − = − − − +

−

( )

22

3 3 3

22

33

log 2 1 (2 1) 3( 1) log ( 1) log 3

log 2 1 (2 1) 3( 1) log 3( 1) (*)

x x x x

 − + − = − + − +



 − + − = − + −



Xét hàm

3

( ) logy f t t t= = +

với t > 0 có

1

'( ) 1 0, 0

ln3

f t t

t

= +   

Do đó hàm số y = f(t) đồng biến trên (0; +).

Phương trình (*) là

( )

2

(2 1) 3( 1) 2 1 3 1f x f x x x− = −  − = −

Trang 20

( )

22

2

2 1 3 2 1 3 8 4 0 ( ).

2

3

x

x x x x x tm

x

=





 − = − +  − + = 

=





Vậy phương trình có nghiệm 2 và

2

3

nên a = 2, b = 3.

Chọn D.

Câu 41.

Phương pháp:

Đặt t = x + m từ đó lập luận để f (t) đồng biến trên (m; 2 + m) .

Lưu ý: Nếu f'(x) > 0 trên (a; b) thì hàm số f (x) đồng biến trên (a; b)

Cách giải:

Đặt t = x + m. Để g(x) đồng biến trên (0; 2) thì hàm số f (x + m) hay f (t) đồng biến trên (m; 2 + m)

Từ BBT và theo đề bài f(x) liên tục trên R thì ta có f(x) đồng biến trên (-1; 3)

Nên để f (t) đồng biến trên (m; 2 + m) thì

(m; 2+m)  [-1; 3]  1  m < m + 2  3  -1  m  1 mà m  Z  m  {-1; 0; 1}

Chọn A.

Câu 42.

Phương pháp:

- Gọi tọa độ điểm M thuộc đường thẳng d .

- Tính diện tích tam giác MAB và đánh giá GTNN của của diện tích.

Công thức tính diện tích:

1

,

2

MAB

S MA MB



=



Cách giải:

Gọi M(5 - 4t; 2 + 2t; 4 + t)  d

( ) ( )

( )

( ) ( ) ( )

( )

2 2 2

22

2

4 4 ;2 2 ; 2 , 6 4 ; 2 ;

, 6 ; 6 12; 12 12

, 36 36 2 144 1 6 8 16 10 6 8 1 2

1

, 3 8 1 2 3 2.

2

MAB

MA t t t MB t t t

MA MB t t t

MA MB t t t t t t

S MA MB t

 = − + − − − = − + − −



 = − − + − +





 = + − + − = − + = − +





 = = − + 



Dấu “=” xảy ra khi t = 1  M (1; 4; 5).

Vậy diện tích tam giác MAB nhỏ nhất bằng

32

khi M (1; 4; 5).

Chọn C.

Câu 43.

Phương pháp:

+ Tìm ĐK.

+ Đặt

3

log xt=

từ đó đưa về phương trình bậc hai ẩn t.

+ Biến đổi yêu cầu bài toán để sử dụng được hệ thức Vi-ét.

Cách giải:

Đk: x > 0

Đặt

3

log xt=

ta có phương trình t

2

- 4t + m - 3 = 0 (*)

Trang 21

Để phương trình đã cho có hai nghiệm phân biệt x

1

< x

2

thì phương trình (*) có hai nghiệm phân biệt

t

1

< t

2

Hay ' = 2

2

- (m - 3) = 7 - m > 0  m < 7

Theo hệ thức Vi-et ta có

12

4

.3

tt

t t m

+=





=−



Ta có

12

1 3 1 1 2 3 2 2

log 3 ; log 3

tt

t x x t x x=  = =  =

Khi đó

2

2 1 1

4

2 1 2 1 2 1

81 0 3 81.3 0 3 3 4 4

t

t t t

x x t t t t

+

−   −      +  − 

Suy ra

( )

2

22

2 1 2 1 1 2

( ) 16 4 16 ( 4) 4( 3) 16 3 0 3t t t t t t m m m−   + −   − − −   −   

Từ đó 3 < m < 7 mà m  Z nên m  {4; 5; 6}.

Vậy có 3 giá trị của m thỏa mãn đề bài.

Chọn C.

Câu 44.

Phương pháp:

- Viết z

1

= kiz

2

(k  R), thay vào đẳng thức bài cho tìm

21

,zz

theo k .

- Tìm GTLN của

12

zz+

và kết luận.

Cách giải:

Ta có :

1

2

z

là số thuần ảo nên ta viết lại

1

12

2

z

ki z kiz

z

=  =

Khi đó

( )

1 2 2 2 2 2

2

10 10

10 10 1 10

1

z z kiz z z ki z

ki

k

− =  − =  − + =  = =

−+

+

( )

1 2 1 2

2

22

10 1

10

..

1

11

k

z ki z k z z

k

kk

+

 = =  + = =

+

++

Xét

( )

2 2 2 2

2

10( 1)

( ) 10( 1) 1 100( 1) 1

1

t

y f t t y t t y t

t

+

= =  + = +  + = +

+

( ) ( )

2 2 2 2 2 2 2

100 2 1 100 100 0t t y t y y t y + + = +  − + − =

Phương trình có nghiệm

( ) ( )

2

2 2 2 2

' 100 100 200 0 10 2 10 2y y y y = − − = −   −  

Vậy

max 10 2y =

khi t = 1 hay k = ±1.

Chọn B.

Câu 45.

Phương pháp:

Chia hai trường hợp để giải bất phương trình

Sử dụng hình vẽ và sự tương giao của hai đồ thị hàm số y = f (x) và y = g (x) để xét dấu biểu thức

f (x) – g (x).

Trên (a; b) mà đồ thị hàm số y = f (x) nằm phía trên đồ thị hàm số y = g (x) thì f (x) - g (x) > 0 .

Cách giải:

Ta có

 

( )

2

( ) 1 6 0(*)f x x x x+ − − − 

Trang 22

TH1:

2

60

3

( ) 1 0

( ) 1

x

xx

x

f x x

  −







− − 











+ − 





−



Đường thẳng y = 1 – x đi qua các điểm (-3; 4); (-1; 2); (0; 1); (2; -l) như hình vẽ và giao với đồ thị hàm số

y = f (x) tại 4 điểm như trên.

Từ đồ thị hàm số thì ta thấy

31

( ) 1

2

x

f x x

x

−   −



 − 







Kết hợp điều kiện

2

3

x

−









thì ta có

32

(1)

3

x

−   −









TH2:



2

23

60

( ) 1

( ) 1 0

x

xx

f x x

−  



− − 





−

+ − 



Từ đồ thị hàm số thì ta thấy

3

( ) 1

12

x

f x x

x

−



 − 



−  



kết hợp với

-2 < x < 3 ta được -1 < x < 2. (2)

Từ (1) và (2) ta có

32

12

3

x

−   −





−  







mà x  (-10;10) và x  Z nên x  {0;1;4;5;6;7;8;9}

Nhận thấy tại x = 0 thì f (0) = 1  f (x) + x - 1 = f (1) - 1 = 0  VT của (*) bằng 0 nên x = 0 không thỏa

mãn BPT.

Có 7 giá trị x thỏa mãn đề bài.

Chọn D.

Câu 46.

Phương pháp:

Gắn hệ trục tọa độ, sử dụng các công thức góc giữa hai mặt phẳng, góc giữa đường thẳng và mặt phẳng

rồi tính toán.

Cách giải:

Gọi O là trung điểm của BC, qua O kẻ tia Oz cắt SC tại M .

Gắn hệ trục tạo độ như hình vẽ, ở đó O(0; 0; 0 ), A(1; 0; 0), C(0; 1; 0 ),

B(0; -1; 0 ), S(0; m; n )

( ) ( ) ( )

1; 1;0 , 1;1;0 , 1; ;nAB AC AS m = − − = − = −

Mặt phẳng (SBC) : x = 0 có VTPT

( )

1;0;0i =

Mặt phẳng (SAC) có VTPT

( )

1

, ; ; 1n AC AS n n m



= = − +



Mặt phẳng (SAB) có VTPT

( )

2

, ; ; 1n AB AS n n m



= = − − −



( ) ( )

( )

( ) ( )

2

0

22

2

22

2 2 2

1

22

2

1

.

1

60

2

.

2 1 2 1

4 2 1 2 1 (1)

.

2

4 4 2 1 6 1 (2)

4

.

21

ni

nn

cos

ni

n m n m

n n m n m

ni

n

cos n n m n m

ni

nm



−−

= =  =

+ − − + − −

 = + − −  = − −

= = =  = + −  = −

+ − +

Trang 23

Từ (1) và (2) suy ra

( ) ( )

22

2 3 2 3

3 1 1

23

mn

mm

m

n



= − + = −

+ = −  



= − −



=+



(

)

(

)

( )

2

0; 2 3; 2 3

2 3, 1 2 3 2 2 3

0; 2 3;0

2 3, 1 2 3 2 2 3

1

tan .

2

S

SH AH

H

SH AH

SH

AH





− + −







− − +







= − = + − + = −

−+







−−



= + = + − − = +



 = =

Chọn C.

Câu 47.

Phương pháp:

Sử dụng phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại M(x

0

; y

0

) là

0 0 0

'( )( )y f x x x y= − +

Sử dụng định nghĩa đạo hàm của f(x) tại x

0

là

0

( ) ( )

'( ) lim

xx

f x f x

fx

xx

→

−

=

−

từ đó biến đổi để tính giới hạn.

Cách giải:

Vì tiếp tuyến tại điểm có hoành độ x = 0 là đường thẳng y = 3x – 3.

Nên



'(0) 3

(0) 3

f

=

=−

Suy ra

00

( ) (0) ( ) 3

lim 3 lim 3

0

xx

f x f f x

xx

→→

−−

=  =

−

Từ đó suy ra

0 0 0

(3 ) 3 (4 ) 3 (7 ) 3

lim 3;lim 3;lim 3

3 4 7

x x x

f x f x f x

xxx

→ → →

−−−

===

Ta có:

( ) ( )

0

3

lim

(3 ) 5 (4 ) 4 (7 )

3

lim

(3 ) 3 5 (4 ) 3 4 (7 ) 3

3

lim

(4 ) 3 (7 ) 3

(3 ) 3

54

3

lim

(4 ) 3 (7 ) 3

(3 ) 3

3. 5.4 4.7

31

.

3.3 5.4.3 4.7.3 11

x

f x f x f x

x

f x f x f x

f x f x

fx

x x x

f x f x

fx

x x x

→

−+

=

− − − + −

=

−−

−

−+

=

−−

−

−+

==

−+

Chọn D.

Câu 48.

Phương pháp:

Tìm GTLN của hàm số y = f (x

3

+ x) và y = -x

2

+ 2x + m trên đoạn [0; 2] và suy ra đáp số.

Cách giải:

Trang 24

Xét g (x) = f (x

3

+ x) - x

2

+ 2x + m trên [0; 2] ta có:

Với mọi x  [0;2] thì x

3

+ x  [0;10] nên

 

3

0;2

max ( ) 4f x x+=

xảy ra khi

3

2 1.x x x+ =  =

Lại có

( )

2

2 1 1 1x x m m x m− + + = + − −  +

nên

( )

2

21max x x m m− + + = +

xảy ra khi x = 1.

Do đó

 

0;2

max ( ) (1) 4 1 5g x g m m= = + + = +

Bài toán thỏa khi 5 + m = 8  m = 3.

Chọn D.

Câu 49.

Phương pháp:

Từ giả thiết biến đổi để có f'(0 ) = 0

Từ đó tìm được hàm f'(x) và tính tích phân.

Cách giải:

Ta có

0

2 '( )

lim 2

2

x

x f x

x

→

+

=

mà

0

lim2 0

x

→

=

nên

( )

00

lim 2 '( ) 0 lim '( ) 0 '(0) 0

xx

x f x f x f

→→

+ =  =  =

(vì nếu

( )

0

lim 2 '( ) 0

x

x f x

→

+

thì

0

2 '( )

lim 2

2

x

x f x

x

→

+

=  

)

Từ đó x = 0; x = 1; x = 2 là ba cực trị của hàm số đã cho. Hay phương trình f'(x) = 0 có ba nghiệm x = 0;

x = 1; x = 2

Vì f(x) là hàm đa thức bậc 4 nên ta giả sử hàm

( )( )

'( ) . 1 2f x m x x x= − −

Từ đề bài ta có

( )( ) ( )( )

00

2 1 2 2 1 2

22

lim 2 lim 2 2 1

2 2 2

xx

x mx x x m x x

m

x

→→

+ − − + − −

+

=  =  =  =

Nên

( )( )

32

'( ) 1 2 3 2f x x x x x x x= − − = − +

Từ đó

( )

11

32

00

1

'( ) 3 2 .

4

f x dx x x x dx= − + =



Chọn B.

Câu 50.

Phương pháp:

- Đặt

3

( ) mf x u+=

đưa về phương trình g (w) = g (v) với w, v là các biểu thức ẩn x, u .

- Sử dụng phương pháp hàm đặc trưng, xét hàm y = g (x) suy ra mối quan hệ x, t.

Cách giải:

Đặt

3

( ) m ( )f x u f x m u+ =  + =

3

3 3 3 3

3

()

( ) ( ) ( ) ( )

()

f u x m

f u f x x u f u u f x x

f x u m



=−

  − = −  + = +



=−



Xét hàm

3 5 3 3 5 3

( ) ( ) 3 4 4 4g x f x x x x m x x x m= + = + − + = + −

có

 

42

'( ) 5 12 0, 1;2g x x x x= +   

Do đó y = g (x) đồng biến trên [1; 2].

33

3

3 5 3 3 5 3

( ) u ( ) ( )

( ) 3 4 2 3

f u f x x u x f x m x

f x m x x x m m x x x m

 + = +  =  + =

 + =  + − + =  + =

Xét hàm

53

h( ) 2x x x=+

trên [1; 2] có

 

42

h'( ) 5 6 0, 1;2x x x x= +   

Trang 25

 h(x) đồng biến trên [1;2]  h(1)  h(x)  h(2)  3  h (x)  48 .

Phương trình h(x) = 3m có nghiệm thuộc [1; 2]  3  3m  48  1  m  16

Vậy có 16 giá trị nguyên của m thỏa mãn bài toán.

Chọn B.

ĐỀ 52

ĐỀ THI THỬ THPT QUỐC GIA 2020

MÔN TOÁN

Thời gian: 90 phút

Câu 1: Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại B,

0

, 45AB a ACB=  =

, cạnh bên SA

vuông góc với mặt phẳng đáy.góc

0

60SBA =

.Tính thể tích V của khối chóp S.ABC

A.

3

9

a

V =

B.

=

3

a3

V

6

C.

3

43

a

V =

D.

3

18

a

V =

Câu 2: Trong các hàm số sau, hàm số đồng biến trên là

A.

42

31y x x= + −

B.

32

y x 3x 6x 2= − + +

C.

42

y x 3x 5= − −

D.

3 2x

y

x1

−

=

+

Câu 3: Cho hàm số phù hợp với bảng biến thiên sau. Mệnh đề nào đúng?

x

−

-1 0 1

+

'y

+ 0 - - 0 +

y

11

-1 5

A. Hàm số đồng biến trên khoảng

( ) ( )

; 1 1;− −  +

và nghịch biến trên

( ) ( )

1;0 0;1−

B. Hàm số đồng biến trên hai khoảng

( ) ( )

; 1 ; 11;− − +

và nghịch biến trên

( )

1;11−

C. Hàm số đồng biến trên hai khoảng

( ) ( )

; 1 ; 1;− − +

và nghịch biến trên khoảng

( )

1;1−

D. Hàm số đồng

biến trên hai khoảng

( ) ( )

; 1 ; 1;− − +

và nghịch biến trên hai khoảng

( ) ( )

1;0 ; 0;1−

Câu 4: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có AB=2a,

AA' 3a=

. Tính thể tích khối lăng trụ

ABC.A’B’C’ A.

3

a

B. 3

3

a

C.

3

4

a

D.

3

4

a

Câu 5: Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, AB=BC=a và

0

120ABC=

. Cạnh bên SA

vuông góc với mặt phẳng đáy và SA=2a. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.ABC

A.

2

5

a

B.

2a

C.

5a

D.

2

4

a

Câu 6: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB=AA’=a, AC=2a. Khoảng cách từ điểm D đến mặt phẳng

( )

'ACD

là A.

3

a

B.

5

a

C.

10

5

a

D.

a 21

7

Trang 26

Câu 7: Nếu cạnh của một hình lập phương tăng lên gấp 3 lần thì thể tích của hình lập phương đó tăng lên bao nhiêu

lần? A. 27 B. 9 C. 6 D. 4

Câu 8: Cho hình chóp S.ABCD có đáy hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a. Gọi M và N

lần lượt là trung điểm của AD và SD. Số đo góc

( )

,MN SC

bằng A.

0

45

B.

0

30

C.

0

90

D.

0

60

Câu 9: Cho hình trụ có diện tích toàn phần là

8



và có thiết diện cắt bởi mặt phẳng qua trục là hình vuông. Tính

thể tích khối trụ? A.

4

9



B.

6

9



C.

16 3

9



D.

6

12



Câu 10: Mệnh đề nào sau đây là đúng?

A. Hàm số

( )

y f x=

đồng biến trên khoảng

( )

;ab

khi và chỉ khi

( )

'0fx

( )

;x a b

B. Nếu

( )

'0fx

( )

;x a b

thì hàm số

( )

y f x=

đồng biến trên

( )

;ab

C. Hàm số

( )

y f x=

đồng biến trên khoảng

( )

;ab

khi và chỉ khi

( )

'0fx

( )

;x a b

D. Nếu

( )

'0fx

( )

;x a b

thì hàm số

( )

y f x=

đồng biến trên khoảng

( )

;ab

Câu 11: Cho hình hộp đứng

1 1 1 1

.ABCD A BC D

có đáy ABCD là hình vuông cạnh 2a, đường thẳng

1

DB

tạo với

mặt phẳng

( )

11

BCC B

góc

0

30

. Tính thể tích khối hộp

1 1 1 1

.ABCD A BC D

A.

3

a3

B.

3

a2

3

C.

3

8a 2

D.

3

a

Câu 12: Đồ thị trong hình bên là đồ thị của hàm số nào trong các hàm số sau

A.

3

31y x x= − +

B.

42

21y x x= − +

C.

3

31y x x= − + −

D.

32

2 3 1y x x= − +

Câu 13: Trong các đường thẳng sau, đường thẳng nào là đường thẳng đi qua điểm

( )

3;0A

và tiếp xúc với đồ thị hàm số

3

1

3

y x x= − +

?

A.

27

y y x

55

= = +

B.

39

yx

44

= − +

C.

y 6x 18=−

D.

y 6x 18= − +

Câu 14: Với a là số thực dương bất kì, mệnh đề nào dưới đây là đúng?

A.

ln3a ln3 lna=+

B.

a1

ln lna

33

=

C.

5

1

lna lna

5

=

D.

( )

ln 3 a ln3 lna+ = +

Câu 15: Hình lập phương có tất cả bao nhiêu mặt phẳng đối xứng? A. 3 B. 9 C. 6 D. 4

Câu 16: Giá trị cực tiểu của hàm số

32

3 9 2y x x x= − − +

là A. -25 B. 3 C. 7 D. -20

Câu 17: Trong các mệnh đề sau, mệnh đề nào đúng?

A.

1 sin2 cos2 2 2cos .cos

4

x x x x





+ − = +





B.

( )

1 sin2 cos2 2cos sin cosx x x x x+ − = −

C.

1 sin2 cos2 2 2sin .cos

4

x x x x





+ − = −





D.

1 sin2 cos2 2cos .cos

4

x x x x





+ − = −





Câu 18: Trong các hàm số sau, hàm số nào nghịch biến trên ?

A.

5

logyx=

B.

1

2

y log x=

C.

x

2

y

3

−



=





D.

x

e

y

3



=





Câu 19: Gọi E là tập hợp các số tự nhiên gồm 3 chữ số phân biệt từ các chữ số 1, 2, 3, 4, 5. Chọn ngẫu nhiên 2 số

khác nhau từ tập hợp E. Tính xác suất để 2 số được chọn có đúng 1 số có chữ số 5.

A.

7

22

B.

5

63

C.

144

295

D.

132

271

Trang 27

Câu 20:

0

11

lim

x

→

−−

bằng A.

1

2

−

B.

1

2

C.

+

D.

0

Câu 21: Khoảng cách từ điểm

( )

3; 4M −

đến đường thẳng

:3 4 1 0xy − − =

bằng A.

8

5

B.

24

5

C. 5 D.

7

5

Câu 22: Cho các số thực dương a,b thỏa mãn

log ,loga x b y==

. Tính

( )

23

logP a b=

A.

6P xy=

B.

23

p x y=

C.

23

P x y=+

D.

23P x y=+

Câu 23: Trong khoảng

( )

;



−

, phương trình

6 2 6

sin 3sin cos cos 1x x x x+ + =

có

A. 4 nghiệm B. 1 nghiệm C. 3 nghiệm D. 2 nghiệm

Câu 24: Tập xác định của hàm số

( )

3

2yx=−

là A.

 

\2

B. C.

( )

;2−

D.



(

;2−

Câu 25: Tính thể tích

V

của khối nón có bán kính đáy bằng 3 và chiều cao bằng 6

A.

18V



=

B.

54V



=

C.

108V



=

D.

36V



=

Câu 26: Cho hàm số

2

23

ln 2

x

yx= − +

.Mệnh đề nào sau đây sai?

A. Hàm số đồng biến trên

( )

0;+

B. Hàm số có giá trị cực tiểu là

2

1

ln2

y =+

C. Hàm số nghịch biến trên khoảng

( )

;0−

D. Hàm số đạt cực trị tại

1x =

Câu 27: Trong các số tự nhiên từ 100 đến 999 có bao nhiêu số mà các chữ số của nó tăng dần hoặc giảm dần.

A. 168 B.204 C. 216 D. 120

Câu 28: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

( )

42

2 4 3f x x x= − + +

trên đoạn

 

0;2

lần lượt là:

A. 6 và -12 B. 6 và -13 C. 5 và -13 D. 6 và -31

Câu 29: Gía trị của

m

để phương trình

42

8 3 4 0x x m− + − =

có 4 nghiệm thực phân biệt là:

A.

13

4

m−  

3

4

B.

−  

13 3

m

44

C.



3

m

4

D.

13

4

m −

Câu 30: Tổng các nghiệm của phương trình

( )

2

1

2

log 5 7 0xx− + =

bằng A. 6 B. 7 C. 13 D. 5

Câu 31: Trong các mệnh đều sau, mệnh đề nào sai?

A. Một đường thẳng và một mặt phẳng (không chứa đường thẳng đã cho) cùng vuông góc với một đường thẳng thì

song song với nhau.

B. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

C. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

D. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song với nhau.

Câu 32: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh a và

( )

SA ABCD⊥

. Biết

6

3

a

SA =

.

Tính góc giữa

SC

và

( )

ABCD

A.

30

B.

60

C.

75

D.

45

Câu 33: Phương trình

2

2 2 8

23

x x x− + −

=

có một nghiệm dạng

log 4

a

xb=−

với

a

,

b

là các số nguyên dương thuộc

khoảng

( )

1;5

. Khi đó

2ab+

bằng A. 6 B.14 C.9 D. 7

Câu 34: Các đường tiệm cận của đồ thị hàm số

21

1

x

y

x

+

=

−

là

A.

1; 2xy= = −

B.

1; 2xy==

C.

1; 0xy==

D.

1; 2xy= − =

Câu 35: Tập nghiệm của phương trình

( )

2

22

log 1 log 2xx−=

là

Trang 28

A.

12

2

S



+



=







B.

 

12S =+

C.

 

1 2;1 2S = + −

D.

 

2;4S =

Câu 36: Hàm số

( )

fx

có đạo hàm

( ) ( ) ( )

3

2

' 1 2f x x x x= + +

. Số cực trị của hàm số là

A.0 B. 1 C.2 D. 3

Câu 37: Số hạng không chứa x trong khai triển

( )

5

3

2

1

P x x

x



=−





( )

0x 

là số hạng thứ

A. 3 B. 6 C. 4 D. 5

Câu 38: Cho x, y là những số thực thỏa mãn

22

1x xy y− + =

. Gọi

M

và

m

lần lượt là giá trị lớn nhất và giá trị

nhỏ nhất của

44

22

1

xy

P

xy

++

=

++

. Giá trị của

15A M m=+

là

A.

17 2 6A =−

B.

17 6A =−

C.

17 6A =+

D.

17 2 6A =+

Câu 39: Cho biểu thức

22

2xy

P

xy

=

+

với

,xy

khác 0. Giá trị nhỏ nhất của

P

bằng A. -2 B. 0 C. -1

D. 1

Câu 40: Cho khai triển

( )

2

0 1 2

1 2 ...

n

x a a x a x a x+ = + + + +

( )

*

n

và các hệ số thỏa mãn

1

0

... 4096

22

n

a

a + + + =

. Hệ số lớn nhất là A. 126720 B. 1293600 C. 729 D. 924

Câu 41: Có bao nhiêu giá trị nguyên dương của tham số m để hàm số

( )

2

ln 1

2

x

y mx x= − + −

đồng biến trên

khoảng

( )

1; +

? A. 4 B. 1 C. 3 D. 2

Câu 42: Hàm số

2

3

x

y

xm

−

=

+−

đồng biến trên khoảng

( )

0;+

khi A.

1m 

B.

1m =

C.

3m 

D.

1m 

Câu 43: Cho hàm số

( )

1

ln2018 ln

x

fx

x

+



=−





.Tính

( ) ( ) ( ) ( )

' 1 ' 2 ' 3 ... ' 2017S f f f f= + + + +

A.

4035

2018

B. 2017 C.

2016

2017

D.

2017

2018

Câu 44: Cho hai vectơ

a

và

b

khác vecto không và thảo mãn

u a b=+

vuông góc với vecto

23v a b=−

và

53m a b=−

vuông góc với

27n a b= − +

. Tính góc tạo bởi hai vecto

a

và

b

A.

0

60

B.

0

45

C.

0

90

D.

0

30

Câu 45: Tập hợp các gia trị của m để hàm số

( )

32

1

6 2 11

3

y x x m x= − + − +

có hai điểm cực trị trái dấu là

A.

( )

;38−

B.

( )

;2−

C.

( ;2]−

D.

( )

2;38

Câu 46: Khi sản xuất vỏ lon sữa bò hình trụ, các nhà thiết kế đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ hộp

ít nhất (diện tích toàn phần của lon nhỏ nhất). Bán kính đáy của vỏ lon là bao nhiêu khi muốn thể tích của lon là

314

3

cm

.A.

3

314

r cm

4

=



B.

3

r 942 2=

cm C.

3

314

r

2

=



cm D.

3

314

r =



cm

Câu 47: Tập hợp các giá trị m để hàm số

2

62

2

mx x

y

x

+−

=

+

có tiệm cận đứng là:

A.

7

2







B. C.

7

\

2



−





D.

7

\

2







Câu 48: Một người gửi 50 triệu đồng vào ngân hàng với lãi suất

0

8,4 /

năm. Biết rằng nếu không rút tiền ra khỏi

ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập làm vốn ban đầu để tính lãi cho năm tiếp theo. Hỏi sau ít

nhất bao nhiêu năm, người đó được lĩnh số tiền không ít hơn 80 triệu đồng (cả vốn ban đầu lẫn lãi), biết rằng trong

suốt thời gian gửi tiền người đó không rút tiền và lãi suất không thay đổi?

Trang 29

A. 4 năm B.7 năm C. 5 năm D. 6 năm

Câu 49: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn

 

0;2018

để hệ phương trình

0

1

x y m

xy y

− + =







+=





có

nghiệm? A. 2016 B. 2018 C. 2019 D. 2017

Câu 50: Tìm tất cả các giá trị của tham số m để phương trình

( ) ( )

2 2 2

2 2 1 2 4 2

9.9 2 1 15 4 2 5 0

x x x x x x

mm

− − + − +

− + + − =

có 2 nghiệm thực phân biệt.

A.

1

2

m

B.

36

2

m

+



hoặc

36

2

m

−



C.

1m 

hoặc

1

2

m 

D.

3 6 3 6

22

m

−+



LỜI GIẢI CHI TIẾT

1-B

2-B

3-D

4-B

5-B

6-D

7-A

8-C

9-C

10-D

11-C

12-A

13-D

14-A

15-B

16-A

17-C

18-D

19-C

20-A

21-B

22-D

23-C

24-C

25-A

26-A

27-B

28-C

29-A

30-D

31-D

32-A

33-D

34-B

35-B

36-C

37-C

38-A

39-C

40-A

41-C

42-C

43-D

44-B

45-B

46-C

47-D

48-D

49-B

50-A

Câu 1: Đáp án B.

SAB

vuông tại A có

0

60SBA=

nên

3SA a=

ABC

vuông cân tại B nên

2

11

.

22

ABC

S AB AC a



==

.Do đó

23

.

1 1 1 3

. . 3 .

3 3 2 6

S ABC ABC

V SAS a a a



= = =

Câu 2: Đáp án B

Hàm số

32

3 6 2y x x x= − + +

có

( )

2

' 3 6 6 3 1 3 0y x x x x= − + = − +   

nên hàm số này đồng biến trên

Câu 3: Đáp án D

Câu 4: Đáp án B.

( )

2

22

33

. . 2 3

44

ABC

S AB a a= = =

.Do đó

23

. ' 3 . 3 3V S AA a a a= = =

Câu 5: Đáp án B.Dựng tam giác đều IAB (I và C cùng phía bờ AB). Ta có

0 0 0

120 60 60IBC = − =

và IB=BC nên

IBC

đều, IA=IB=IC=a

Qua I dựng đường thẳng song song với SA, cắt đường trung trực của SA tại O thì

O là tâm mặt cầu ngoại tiếp hình chóp.Gọi M là trung điểm của SA.

Ta có OM=IA=a;

2

SA

AM a==

nên

22

2OA OM MA a= + =

2Ra=

Câu 6: Đáp án D.

2 2 2 2

43BC AC AB a a a= − = − =

Do đó

3 ; 'DA a DC DD a= = =

Tứ diện DACD’ vuông tại D nên ta có:

2 2 2 2 2 2 2 2

1 1 1 1 1 1 1 7

' 3 3h DA DC DD a a a a

= + + = + + =

3 21

77

h a a = =

Câu 7: Đáp án A.

( )

3

33

' 3 3 . 27V a a V= = =

Trang 30

Câu 8: Đáp án C.MN là đường trung bình của tam giác DAS nên

//MN SA

.

Gọi O là tâm của hình vuông ABCD, vì SA=SC=SB=SD nên

( )

SO ABCD⊥

Có

2

AC AO=  =

nên

0

2

sin 45

2

AO

ASO ASO

SA

= =   =

nên

0

90ASC=

Câu 9: Đáp án C.Gọi bán kính đường tròn đáy là r. Vì thiết diện cắt bởi

mặt phẳng qua trục là hình vuông nên chiều cao hình trụ là 2r. Ta có

2 2 2

2 2 2 2 2 .2 6

tp d xq

S S S r rh r r r r

    

= + = + = + =

Theo đề bài:

2 2 2 3

4 2 3 8 3 16 3

8 ; .2 2 2 .

3 3 9 9

tp

S r r V r h r r r



    

=  =  = = = = = =

Câu 10: Đáp án D

Câu 11: Đáp án C.Hình chiếu vuông góc của D xuống mặt phẳng

( )

11

BCC B

là điểm C. Theo đề bài, ta có

0

1

30DB C=

.

0 2 2 2 2

1 1 1

.cot30 2 3 2 3 12 4 2 2BC DC a a BB BC BC a a a= = =  = − = − =

Do đó

1 1 1 1

23

.1

. 2 2 .4 8 2

ABCD A B C D ABCD

V S BB a a a= = =

Câu 12: Đáp án A

Câu 13: Đáp án D.Giả sử phương trình đường thẳng đó là

( )

3y k x=−

. Đường thẳng tiếp xúc với đồ thị hàm số

3

1

3

y x x=+

thì phương trình

( )

3

2

1

33

3

x x k x

xk



− + = −







− + =



có nghiệm. Từ

2

3xk− + =

, thế vào phương trình đầu, ta

có

( )

3 2 3 3 2

1

3 3 3 9 3 3 3 9

3

x x x x x x x x x− + = − + −  − + = − + + −

3

2

x = −

hoặc

3x =

. Do đó

3

4

k =

hoặc

6k =−

Câu 14: Đáp án A

Câu 15: Đáp án B.Hình lập phương có tất cả 9 mặt đối xứng gồm:

3 mặt phẳng chia hình lập phương thành 2 khối hộp hình chữ nhật.

6 mặt phẳng chia hình lập phương thành 2 khối lăng trụ tam giác.

Trang 31

Câu 16: Đáp án A.

( )

( )( )

22

' 3 6 9 3 2 3 3 1 3y x x x x x x= − − = − − = + −

, từ đó

3

CT

x =

nên

( )

3 25.

CT

yy= = −

Câu 17: Đáp án C.

2

1 sin2 cos2 2sin cos 2sin 2sin (sin cos ) 2 2sin .cos

4

x x x x x x x x x x





+ − = + = + = −





Câu 18: Đáp án D (chú ý rằng

1

3

e



)

Câu 19: Đáp án C. Số phần tử của tập hợp E:

3

5

60EA==

(phần tử).

Không gian mẫu:

( )

2

60

1770.nC = =

Số số thuộc E không có chữ số 5 là:

2

4

.3! 36C =

(số).

Số trường hợp thỏa mãn là:

36.24 864.=

Xác suất cần tính:

864 144

.

1770 295

P ==

Câu 20: Đáp án A.

( )

0 0 0

11

1 1 1 1

lim lim lim

2

11

x x x

x

→ → →

−−

− − −

= = = −

−+

.

Câu 21: Đáp án B.

( )

2

3.3 4 4 1

24

5

34

M

d



− − −

==

+−

.

Câu 22: Đáp án D.

( ) ( ) ( )

2 3 2 3

log log log 2log 3log 2 3a b a b a b x y= + = + = +

.

Câu 23: Đáp án C.Ta có

( ) ( )

6 6 2 2 2 2 2 2 2 2

sin cos sin cos 3sin cos sin cos 1 3sin cos .x x x x x x x x x x+ = + − + = −

Do đó phương trình tương đương với:

( )

2 2 2 2

cos 0

3sin cos 3sin cos 0 sin cos 1 cos 0

cos 1

x

x x x x x x x

x

=



− =  − = 



=



Vẽ đường tròn đơn vị ra, ta thấy phương trình có 3 nghiệm trên

( )

;



−

,

;0;

22





−





Câu 24: Đáp án C.Hàm số xác định khi và chỉ khi

2 0 2xx−   

.

Câu 25: Đáp án A.

22

11

.3 .6 18 .

33

V r h

  

= = =

Câu 26: Đáp án A.

( )

' 2 2, 0;1 , ' 0

x

y x y= −   

nên hàm số nghịch biến trên

( )

0;1

.

Câu 27: Đáp án B.Với ba chữ số khác nhau thuộc tập hợp

 

1;2;3;4;5;6;7;8;9

, ta viết được 2 số có 3 chữ số

theo thứ tự tăng dần hoặc giảm dần (

abc

với

abc

hoặc

abc

), có

3

9

2. 168C =

số

Trang 32

Với 2 chữ số khác nhau thuộc tập hợp

 

1;2;3;4;5;6;7;8;9

và 1 chữ số 0, ta viết được 1 số theo thứ tự tăng dần

hoặc giảm dần (

0ab

với

0ab

), có

2

9

36C =

số.Vậy có tất cả

168 36 204+=

(số).

Câu 28: Đáp án C.

( )

( )( )

32

' 8 8 8 1 8 1 1f x x x x x x x x= − + = − − = − − +

Xét

( ) ( )

0 3, 1 5ff==

và

( )

2 13f =−

.

Câu 29: Đáp án A.Đặt

2

xt=

, phương trình tương đương với

2

8 3 4 0t t m− + − =

(1)

Để phương trình có 4 nghiệm phân biệt thì (1) có nghiệm t dương phân biệt

16 3 4 0

'0

13 3

3

3 4 0

44

4

m

− + 









   −  



−









.

Câu 30: Đáp án D

Phương trình tương đương với

2

5 7 0xx− + =

, tổng các nghiệm của phương trình này là 5 (theo định lý Vi-et).

Câu 31: Đáp án D

Câu 32: Đáp án A.Góc giữa SC và (ABCD) là

;SCA

6

3

tan

3

2

a

SA

SCA

SC

a

= = =

nên

0

30SCA=

.

Câu 33: Đáp án D.Phương trình tương đương với

( ) ( ) ( )( )

2

33

3

2

2 log 2 2 8 2 log 2 2 4

log 2 4

x

x x x x x x

x

=



− = + −  − = − + 



=−



Vậy

3; 2ab==

nên

27ab+=

.

Câu 34: Đáp án B

Câu 35: Đáp án B.

( )

22

2

22

1 2 2 1 0

log 1 log 2 1 2

00

x x x x

x x x

xx



− = − − =

− =    = +







.

Câu 36: Đáp án C.Hàm số có 2 điểm cực trị là

1x =−

và

2x =−

. Chú ý rằng

( )

' 0 0f =

nhưng

( )

'fx

không đổi

dấu khi qua điểm

0x =

nên

0x =

không là cực trị của hàm số.

Câu 37: Đáp án C.

( )

55

5

3 2 15 5

55

00

. 1 . 1 .

kk

k k k

kk

P x C x x C x

−

−−

==

= − = −



. Số hạng không chứa

x

ứng với

3k =

, số hạng này là số hạng thứ 4.

Câu 38: Đáp án A.Đặt

2xy t+=

, ta có

22

11x y xy t+ = + = −

( ) ( )

2

22

0 2 1 2 2 3x y x y xy t t t−   +   −  −  

( ) ( )

2

22

5

0 2 0 1 2 2 0

3

x y x y xy t t t+   + +   − + −   

Các dấu bằng đều xảy ra nên

5

;3

3

t









.Ta có

( )

22

1 2 2 2x y xy t t+ + = + = + − =

;

( )

( ) ( )

2

22

4 4 2 2 2 2 2

1 2 1 1 2 2 1 6 6x y x y x y t t t t+ + = + − + = − − − + = − + −

Do đó

6

6Pt

t

= − + −

; xét hàm

( )

6

6f t t

t

= − − +

có

( )

( )( )

22

66

6

'1

tt

ft

tt

−+

= − + =

( )

5 11

; 3 1; 6 6 2 6

3 15

f f f



= = = −





. Do đó

5

;3

3

11

min ; max 6 2 6

15

m P M P







= = = = −

15 17 2 6A M m= + = −

.

Trang 33

Câu 39: Đáp án C.

( )

2

2 2 2 2

2

1 1 0

xy

P

x y x y

+

+ = + = 

++

nên

1P −

. Dấu bằng xảy ra khi và chỉ khi

0xy= − 

.

Câu 40: Đáp án A.Bước 1: Tìm n

Cách 1: Từ

( )

2

0 1 2

1 2 ...

n

x a a x a x a x+ = + + + +

, thay

1

2

x =

vào, ta được:

( )

0 1 2

2

1 1 1

1 1 ... 4096 12.

2 2 2

n

a a a a n+ = + + + + =  =

Cách 2:

( )

0

1 2 2 . .2 ( 0;1;2;...; )

n

k k k k k

n k n

k

x C x a C k n

=

+ =  = =



.Theo đề bài

00

4096 4096

2

nn

k

n

k

kk

a

C

==

=  =



Chú ý rằng

( )

0

2 1 1

n

nk

n

k

C

=

= + =



, do đó

12

2 2 12

n

n=  =

. Vậy

12

.2

kk

k

aC=

Bước 2: Tìm hệ số lớn nhất.

12

0 12

1; 2aa==

. Xét

,1 11ii  

, ta có:

( )

1 1 1 1 1

1 12 12 12 12

.2 .2 2 2

i i i i i i i

ii

a a C C C C

− − − − −

−

− = − = −

( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )

11

1

12! 12! 2 .12! 2 1 2 .12! 26 3

2 . 2. .

! 12 ! 1 ! 13 ! 1 !. 12 ! 13 1 !. 12 ! 13

ii

i

i i i i i i i i i i i i

−−

−



−



= − = − =



− − − − − − − − −



Do đó

11

26

26 3 0 8; 26 3 0 9

3

i i i i

a a i i i a a i i

−−

  −        −   

Vậy

0 1 2 7 8

...a a a a a    

và

8 9 10 11 12

a a a a a   

nên hệ số lớn nhất là

88

8 12

.2 126720aC==

.

Nhận xét: Với bài toán này giá trị n khá nhỏ (n = 12) nên hoàn toàn có thể thử bằng máy tính bởi chức năng

TABLE, nhập hàm

( )

12

.2

xx

f x C=

. START x= 0, END x = 12 và STEP 1.

Câu 41: Đáp án C.Hàm số luôn xác định trên

( )

1; +

, có

11

'

11

y x m x m

xx

= − + = + −

−−

Với

1x

, áp dụng BĐT AM-GM:

( )

1 1 1

1 1 2 1 1 3

1 1 1

x m x m x m m

x x x

+ − = − + − +  − − + = − +

− − −

Dấu bằng xảy ra khi và chỉ khi

2x =

(thỏa mãn)

Vậy

( )

1;

min ' 3ym

+

=−

, hàm số đồng biến trên

( )

1; +

khi và chỉ khi

'0y 

( )

1;

1; min ' 0 3 0 3x y m m

+

  +    −   

. Mà

 

1;2;3mm

+

  

.

Câu 42: Đáp án C.

( ) ( )

22

3 2 1

'

33

mm

y

x m x m

− + −

==

+ − + −

. Hàm số đồng biến trên

( )

0;+

khi và chỉ khi

( )

10

1

3

3 0 0;

30

m

x m x

m

−









  



+ −    +

−





Câu 43: Đáp án D .

( )

2

1 1 1 1

'.

1 1 1

x

fx

x x x x x x



= − − = = −



+ + +



Do đó

1 1 1 1 1 1 1 1 1 2017

... 1

1 2 2 3 3 4 2017 2018 2018 2018

S = − + − + − + + − = − =

Câu 44: Đáp án B.

( )( )

22

. 0 2 3 0 2 3 .u v a b a b a b a b=  + − =  − =

(1)

( )( )

22

. 0 5 3 2 7 0 10 21 41 .m n a b a b a b ab=  − − + =  + =

(2)

Từ (1) và (2) suy ra

2

2 2 2

2 2 . 2 2a b a b a b b b=  =  = =

Trang 34

Từ (1) ta lại có

2 2 2

1

. 2.2 3 .

2

a b b b b a b= − = =

. Do đó

( )

.1

cos ;

2

.

ab

==

nên góc hợp bởi hai vecto

bằng

0

45

Câu 45: Đáp án B.

( )

2

' 12 2y x x m= − + −

. Hàm số có hai điểm cực trị trái dấu khi và chỉ khi

2 0 2mm−   

Câu 46: Đáp án C.Gọi bán kính đáy của vỏ lon là x(cm)

( )

0x 

Theo đề bài, thể tích của lon là

3

314cm

nên chiều cao của lon là

2

314

h

x



=

Diện tích toàn phần của lon:

22

314

2 2 2 2

toanphan day xungquanh

S S S x xh x

x

  





= + = + = +





Áp dụng BĐT AM-GM:

22

2

33

314 314 314 314

3 2 .3

2 2 2 2

toanphan

xS

xx



   

   

+ +   

   

   

Dấu bằng xảy ra khi và chỉ khi

2

3

314 314

22

xx

x



=  =

Câu 47: Đáp án D.Hàm số

2

62

2

mx x

y

x

+−

=

+

có tiệm cận đứng khi và chỉ khi phương trình

2

6 2 0mx x+ − =

không có nghiệm

( ) ( )

2

7

2 . 2 6. 2 2 0 4 14 0

2

x m m m= −  − + − −   −   

Câu 48: Đáp án D.Số tiền người đó thu được sau n năm:

( ) ( )

0

1 50 1 8,4

nn

P A r= + = +

(triệu đồng)

1,084

88

80 1,084 log 5,83

55

n

P    

Câu 49: Đáp án B.

( )

2

1

12

11

1

xy y

xy y y

xy y xy y

y

=−



= − +



+ =  = −  









(1)

Nếu y=0, hiển nhiên không thỏa mãn hệ: Nếu

1

2

0,(1)

2

1

xy

y



= − +













Thế vào

0x y m− + =

, ta có

11

2 0 2y y m m

yy

− + − + =  = −

(2)

Để hệ có nghiệm thì (2) có nghiệm

 

( ;1]\ 0y −

. Xét hàm

( )

1

fy

y

=

có

( )

2

1

'0fy

y

= − 

với mọi

 

( ;1]\ 0y −

nên ta có bảng biến thiên hàm

( )

fy

như sau:

y

−

0 1

( )

'fy

- -

( )

fy

0

+

−

1

Trang 35

Dựa vào bảng biến thiên trên, ta thấy (2) có nghiệm

 

( ;1]\ 0y −

khi và chỉ khi

2 0 2

2 1 1

mm

−  







−  



.

Mà

m

và

 

0;2018m

nên

 

0;1;3;4;5;6;...;2018m

Câu 50: Đáp án A.

( ) ( )

2 2 2

2 2 1 2 4 2

9.9 2 1 15 4 2 5 0

x x x x x x

mm

− − + − +

− + + − =

( ) ( )

( )

(

)

( )

( ) ( )

( )

(

)

2 2 2

2 2 2 2

2 1 2 1 2 4 2

22

1 1 1 1

9 2 1 15 4 2 5 0

3 2 1 3 .5 4 2 5 0

x x x x x x

x x x x

mm

− + − + − +

− − − −

 − + + − =

( )

22

2

11

33

2 1 4 2 0

55

xx

mm

−−



   



 − + + − =

   



   



(1)

Đặt

( )

( ) ( )( )

2

1

2

3

,(1) 2 1 4 2 0 2 2 1 0

21

5

x

t

t t m t m t t m

tm

−

=





=  − + + − =  − − + = 





=−





Chú ý rằng với

( )

2

1

2

3

5

3

2 2 1 log 2

5

x

tx

−



=  =  − =





, mà

3

5

log 2 0

và

( )

2

10x −

nên phương trình này

vô nghiệm

Do đó

( )

2

1

3

(1) 2 1

5

x

m

−



 = −





(2)

Xét hàm

( )

2

1

3

5

x

fx

−



=





có

( )

( ) ( )

2

1

33

' .ln .2 1 , ' 0 1

55

x

f x x f x x

−

   

= − =  =

   

   

Bảng biến thiên hàm số

( )

fx

x

−

1

+

t

+ 0 -

't

1

0 0

Dựa vào bảng biến thiên hàm

( )

fx

, ta thấy để phương trình (1) có 2 nghiệm thực

x

phân biệt thì phương trình

(2) phải có duy nhất 1 nghiệm thuộc khoảng

( )

0;1

, nghiệm còn lại (nếu có) khác 1. Số nghiệm của (2) là số giao

điểm của đồ thị hàm số

( )

2

1

3

5

x

y

−



=





và đường thẳng

21ym=−

nên điều kiện của m thỏa mãn là

1

0 2 1 1 1

2

mm −    

ĐỀ 53

ĐỀ THI THỬ THPT QUỐC GIA 2020

MÔN TOÁN

Thời gian: 90 phút

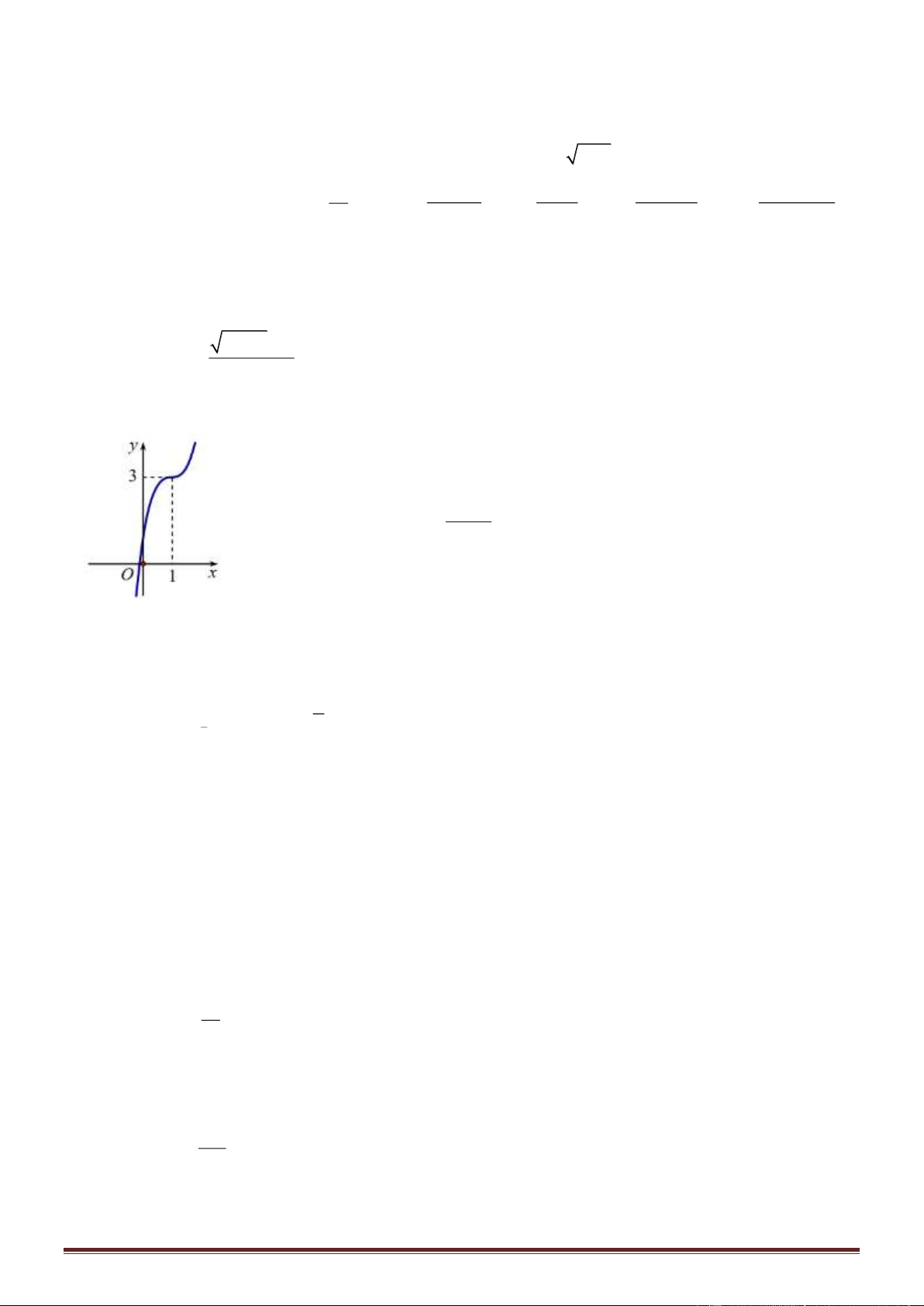
Trang 36

Câu 1.Hàm số

32

35y x x= − +

đồng biến trên khoảng nào dưới đây?

A.

(0;2)

B.

(0; )+

C.

( ;2)−

.

D.

( ,0)−

và

(2; )+

Câu 2.Trong các dãy số sau đây, dãy số nào là một cấp số cộng?

A.

2

1, 1

n

u n n= + 

. B.

2 , 1

n

un=

. C.

1, 1

n

u n n= + 

. D.

2 3, 1

n

u n n= − 

.

Câu 3.Hàm số có đạo hàm bằng

2

1

2x

x

+

là:A.

3

22x

y

x

−

=

.B.

3

1x

y

x

+

=

.C.

3

33xx

y

x

+

=

.D.

3

51xx

y

x

+−

=

.

Câu 4.Nếu hàm số

()y f x=

có đạo hàm tại

0

x

thì phương trình tiếp tuyến của đồ thị hàm số tại điểm

( )

00

;M x f x

là A.

( ) ( )

00

()y f x x x f x



= − +

.

B.

( ) ( )

00

()y f x x x f x



= − −

.

C.

( )( ) ( )

0 0 0

y f x x x f x



= − +

.

D.

( )( ) ( )

0 0 0

y f x x x f x



= − −

Câu 5.Giới hạn

2

22

lim

2

x

→

+−

−

bằng A.

−

. B. 1. C.

+

. D.

1−

Câu 6.Cho tập S có 20 phần tử. Số tập con gồm 3 phần tử của S. A.

3

20

A

. B.

3

20

C

. C.

60

. D.

3

20

.

Câu 7.Đường cong ở hình dưới là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào?

A.

32

2 6 1y x x x= − + +

B.

32

2 6 6 1y x x x= − + +

C.

32

2 6 6 1y x x x= − − +

D.

32

2 6 6 1y x x x= − − − +

Câu 8.Đồ thị hàm số

23

1

x

y

x

−

=

−

có các đường tiệm cận đứng và tiệm cận ngang lần

lượt là: A.

1x =

và

2y =

. B.

2x =

và

1y =

.

C.

1x =

và

3y =−

. D.

1x =−

và

2y =

.

Câu 9.Có

7

bông hồng đỏ,

8

bông hồng vàng và

10

bông hồng trắng, các bông hồng khác nhau từng đôi một.

Hỏi có bao nhiêu cách lấy

3

bông hồng có đủ ba màu. A.

319

. B.

3014

. C.

310

. D.

560

.

Câu 10.Xét các số thực

a

,

b

thỏa mãn

1ab

. Tìm giá trị nhỏ nhất

min

P

của biểu thức

( )

22

log 3log



=+





ba

b

a

Pa

b

. A.

min

19=P

B.

min

13=P

C.

min

14=P

D.

min

15=P

Câu 11.Trong các khẳng định sau, khẳng định nào là khẳng định sai?

A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

B. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì cũng vuông góc với

đường thẳng còn lại.

C. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

D. Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đó) cùng vuông góc với một đường

thẳng thì song song với nhau.

Câu 12.Cho hình chóp

SABC

có đáy

ABC

là tam giác vuông tại

,B SA

vuông góc với mặt phẳng

( ),ABC AH

là đường cao trong tam giác

SAB

Trong các khẳng định sau, khẳng định nào là khẳng định sai?

A.

AH AC⊥

. B.

AH BC⊥

. C.

SA BC⊥

. D.

AH SC⊥

Câu 13.Cho hàm số

3

2

32

3

x

yx= + −

có đồ thị là (C). Viết phương trình tiếp tuyến với đồ thị (C) biết tiếp tuyến có hệ số góc

9k =−

. A.

16 9( 3)yx+ = − +

. B.

9( 3)yx= − +

. C.

16 9( 3)yx− = − −

. D.

16 9( 3)yx− = − +

.

Câu 14.Cho tứ diện

SABC

có các cạnh

,,SA SB SC

đôi một vuông góc với nhau. Biết

3 , 4 , 5SA a SB a SC a= = =

Tính theo a thể tích V của khối tứ diện

SABC

A.

3

20Va=

B.

3

10Va=

C.

3

5

2

a

V =

. D.

3

5Va=

Câu 15.Trong các mệnh đề sau, mệnh đề nào đúng?

A. Tứ diện có bốn cạnh bằng nhau là tứ diện đều. B. Hình chóp tam giác đều là tứ diện đều.

C. Tứ diện có bốn mặt là bốn tam giác đều là tứ diện đều. D. Tứ diện có đáy là tam giác đều là tứ diện đều.

Trang 37

Câu 16.Hàm số

2sin 1

1 cos

x

y

x

+

=

−

xác định khi A.

2

xk



+

. B.

xk





. C.

2xk





. D.

2

xk



+

Câu 17.Cho hàm số

()y f x=

đồng biến trên khoảng

( ; )ab

Mệnh đề nào sau đây sai?

A. Hàm số

( 1)y f x=+

đồng biến trên khoảng

( ; )ab

. B. Hàm số

( ) 1y f x= − +

nghịch biến trên khoảng

( ; )ab

.

C. Hàm số

( ) 1y f x=+

đồng biến trên khoảng

( ; )ab

.

D. Hàm số

( ) 1y f x= − −

nghịch biến trên khoảng

( ; )ab

Câu 18.Đạo hàm của hàm số

3

sin 4

2

yx





=−





là: A.

4cos4x−

.B.

4cos4x

. C.

4sin4x

. D.

4sin4x−

Câu 19.Phương trình:

cos 0xm−=

vô nghiệm khi

m

là:A.

11m−  

.B.

1m 

.C.

1m −

. D.

1

m







−



.

Câu 20.Cho hình chóp

SABC

có

A



,

B



lần lượt là trung điểm của

SA

,

SB

. Gọi

1

V

,

2

V

lần lượt là thể tích của

khối chóp

SA B C



và

SABC

. Tính tỉ số

1

2

V

. A.

1

8

. B.

1

4

. C.

1

2

. D.

1

3

.

Câu 21.Với các số thực dương

x

,

y

tùy ý, đặt

3

log x



=

,

3

log y



=

. Mệnh đề nào dưới đây đúng?

A.

3

27

log 9

2

x

y







=−





B.

3

27

log

2

x

y







=+





C.

3

27

log 9

2

x

y







=+





D.

3

27

log

2

x

y







=−





Câu 22.Cho đường thẳng Để phép tịnh tiến theo biến đường thẳng thành chính nó thì

phải là véc tơ nào sau đây: A.

B.

C. D.

Câu 23.Hàm số nào sau đây đạt cực tiểu tai điểm

0x =

A.

3

2yx=+

. B.

2

1yx=+

. C.

3

1y x x= − + −

. D.

32

32y x x= − +

.

Câu 24.Cho hàm số xác định trên và có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng?

A. Hàm số đồng biến trên mỗi khoảng

( 1;0)−

và

(1; )+

.

B. Hàm số đồng biến trên mỗi khoảng

( , 1)− −

và

(0;1)

.

C. Hàm số nghịch biến trên khoảng

( 1;1)−

.

D. Hàm số nghịch biến trên mỗi khoảng

( 1;0)−

và

( )

1; +

.

Câu 25.Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

,a SA

vuông góc với mặt đáy ,

2SA a=

. Tính theo a thể tích khối chóp

.S ABC

A.

3

a

. B.

3

6

a

. C.

3

4

a

. D.

3

2

5

a

Câu 26.Cho hàm số có đạo hàm trên R và có đồ thị như hình vẽ.

Xét hàm số

( )

2

−= xfxg

. Mệnh đề nào sau đây sai?

A. Hàm số nghịch biến trên .

B. Hàm số đồng biến trên .

C. Hàm số nghịch biến trên .

D. Hàm số nghịch biến trên .

Câu 27.Tìm tất cả các giá trị của tham số

m

để hàm số

1mx

y

xm

+

=

+

đồng biến

trên khoảng

(2; )+

A.

21m−   −

hoặc

1m 

. B.

1m −

hoặc

1m 

.

C.

11m−  

. D.

1m −

hoặc

1m 

.

:2 1 0.d x y− + =

v

d

v

( )

1;2 .v =−

( )

2; 1 .v =−

( )

1;2 .v =

( )

2;1 .v =

( )

=y f x

( )

ABCD

y = f (x)

y = f '(x)

g(x)

(0;2)

g(x)

(2;+¥)

g(x)

(-¥;-2)

g(x)

(-1;0)

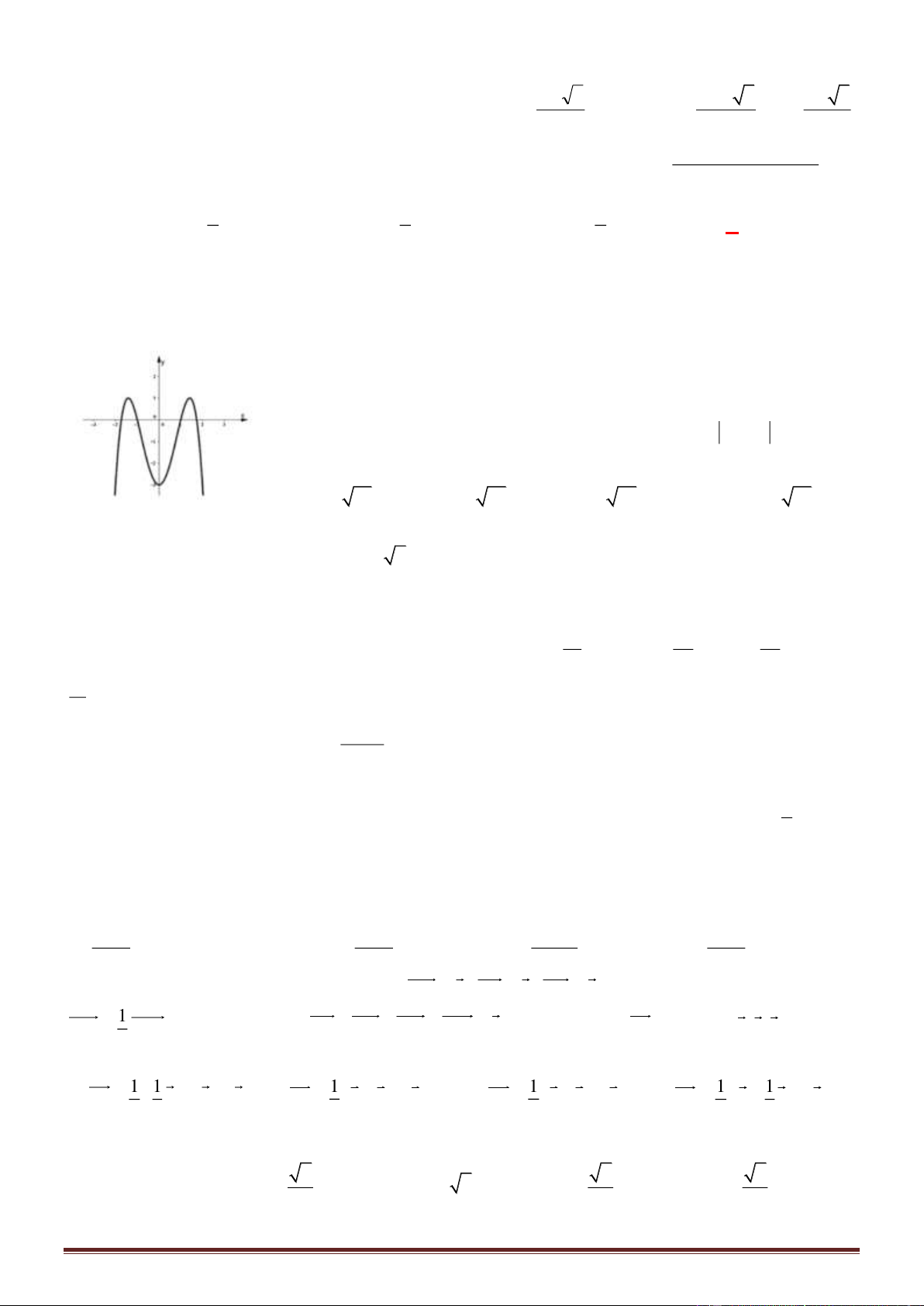
Trang 38

Câu 28.Cho cấp số nhân

( )

n

u

cố công bội

q

và

1

0u 

. Điểu kiện của

q

để cấp số nhân

( )

n

u

có ba số hạng liên

tiếp là độ dài ba cạnh của một tam giác là : A.

0 q 1

B.

2

51

1

+

 q

C.

1q 

. D.

1 5 1 5

22

q

− + +



Câu 29.Cho

, xy

là các số thực lớn hơn

1

thoả mãn

+=

22

96x y xy

. Tính

( )

++

=

+

12 12

12

1 log log

2log 3

xy

M

xy

.

A.

=

1

2

M

. B.

=

1

3

M

. C.

=

1

4

M

. D.

= 1M

Câu 30.Tính tổng

A. . B. . C. . D.

Câu 31.Cho hàm số có đồ thị như hình vẽ. Mệnh đề nào dưới đây đúng ?

A.

0, 0, 0a b c  

. B.

0, 0, 0abc  

.

C.

0, 0, 0a b c  

. D.

0, 0, 0a b c  

Câu 32.Gọi S là tập các giá trị dương của tham số

m

sao cho hàm số

32

3 27 3 2y x mx x m= − + + −

đạt cực trị tại

12

,xx

thỏa mãn

12

5xx−

. Biết

(



;S a b=

. Tính

2T b a=−

.

A.

51 6T =+

. B.

61 3T =+

. C.

61 3T =−

. D.

51 6T =−

.

Câu 33.Cho hình hộp

ABCDABC D

   

có tất cả các mặt là hình vuông cạnh

a

. Các điểm

,MN

lần lượt nằm trên

,AD DB



sao cho

;(0 2)AM DN x x a= =  

. Khi

x

thay đổi, đường thẳng

MN

luôn song song với mặt

phẳng cố định nào sau đây? A.

( )

CB D



. B.

( )

A BC



. C.

( )

AD C



D.

( )

BAC



Câu 34.Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 4 tấm thẻ từ hộp đó. Gọi P là xác

suất để tổng các số ghi trên 4 tấm thẻ ấy là một số lẻ. Khi đó P bằng: A.

1

12

. B.

16

33

. C.

10

33

. D.

2

11

Câu 35.Cho hàm số có đồ thị

21

( ):

1

x

Cy

x

+

=

−

. Gọi

M

là điểm bất kì thuộc đồ thị

()C

. Gọi tiếp tuyến của đồ thị

()C

tại

M

cắt các tiệm cận của

()C

tại hai điểm

P

và

Q

. Gọi

G

là trọng tâm tam giác

IPQ

(với

I

là giao

điểm của hai đường tiệm cận của

()C

). Diện tích tam giác

GPQ

là A.

2

. B.

4

. C.

2

3

.

D.

1

Câu 36.Cho khối hộp

ABCDABC D

   

có thể tích bằng

2018

. Gọi

M

là trung điểm của cạnh

AB

. Mặt phẳng

( )

MB D



chia khối chóp

ABCDABC D

   

thành hai khối đa diện. Tính thể tích phần khối đa diện chứa đỉnh

A

A.

5045

6

. B.

7063

6

C.

10090

17

. D.

7063

12

.

Câu 37.Cho lăng trụ tam giác . Đặt . Gọi là điểm thuộc sao cho

, điểm thỏa mãn . Biểu diễn véc tơ

qua véc tơ . Trong

các khẳng định sau, khẳng định nào là khẳng định đúng?

A. . B. . C. . D. .

Câu 38.Cho hình chóp

SABC

có

1, 2, 3SA SB SC= = =

và

60 , 120 , 90ASB BSC CSA=  =  = 

. Tính thể tích

khối chóp

.S ABC

. A.

2

. B.

2

. C.

2

6

. D.

2

4

.

Câu 39.Cho

a

và

b

là hai số thực dương thỏa mãn

3

8ab =

. Giá trị của

22

log 3logab+

bằng

0 1 2000

2000 2000 2000

2 ... 2001S C C C= + + +

2000

1000.2

2000

2001.2

2000

2000.2

2000

1001.2

42

y ax bx c= + +

. ' ' 'ABC A B C

' , ,AA a AB b AC c= = =

I

'CC

1

''

3

C I C C=

G

' ' ' 0GB GA GB GC+ + + =

IG

,,abc

11

23

43

IG a b c



= + −





( )

1

2

3

IG a b c= + +

( )

1

2

4

IG a c b= + −

11

2

43

IG b c a



= + −





Trang 39

A.

8

. B.

6

. C.

2

. D.

3

.

Câu 40.Tìm tất cả các giá trị thực của tham số

731

sao cho phương trình

2

4

3 1 1 2 1x m x x− + + = −

có hai nghiệm thực phân biệt.

A.

31m

. B.

1

2

3

m−  

. C.

1

4

m−  

. D.

1

0

3

m

.

Câu 41.Nghiệm của phương trình

44

3

sin cos cos sin 3 0

4 4 2

x x x x



   

+ + −  − − =

   

   

là

A.

,

3

x k k



= + 

. B.

2,

3

x k k



= + 

. C.

2,

4

x k k



= + 

. D.

,

4

x k k



= + 

Câu 42.Cho dãy số

( )

n

u

xác định bởi

*

2 2 2

1 3 2 1

,

n

un

n n n

−

= + ++ 

. Giá trị của

lim

n

u

bằng

A.

0

. B.

+

. C.

−

. D.

1

Câu 43.Cho hình chóp

SABCD

có đáy là hình thang vuông tại

1

và

B

.

,2AB BC a AD a= = =

. Biết

SA

vuông

góc với đáy

()ABCD

và

SA a=

. Gọi

,MN

lần lượt là trung điểm

,SB CD

. Tính sin góc giữa đường thẳng

MN

và mặt phẳng

()SAC

A.

5

. B.

55

10

. C.

35

10

. D.

25

5

Câu 44. Cho hai số thực x, y thay đổi thỏa mãn điều kiện

22

2xy+=

. Gọi M, m lần lượt là giá trị lớn nhất và

giá trị nhỏ nhất của biểu thức

( )

33

23P x y xy= + −

. Giá trị của của M + m bằng A.

4−

. B.

1

2

−

.C.

6−

. D.

1 4 2−

.

Câu 45.Đường dây điện KV kéo từ trạm phát ( điểm ) trong đất liền ra đảo ( điểm ). Biết khoảng cách

ngắn nhất từ đến là km, khoảng cách từ đến là km,

mỗi km dây điện dưới nước chi phí là triệu đồng, chi phí mỗi km dây

điện trên bờ là triệu đồng. Hỏi điểm cách bao nhiêu km để mắc

dây điện từ đến rồi từ đến chi phí thấp nhất? (Đoạn trên

bờ, đoạn dưới nước )

A.

50 (km)

. B.

60

(km). C.

55

(km). D.

45

(km).

Câu 46.Tập hợp các giá trị của

m

để hàm số

4 3 2

3 4 12 1y x x x m= − − + −

có

T

điểm cực trị là:

A.

(0;6)

. B.

(6;33)

. C.

(1;33)

. D.

(1;6)

.

Câu 47.Tính tổng tất cả các nghiệm của phương trình

23

2

cos cos 1

cos2 tan

cos

xx

x

−−

−=

trên đoạn

[1;70]

A.

188



. B.

263



. C.

363



. D.

365



Câu 48.Cho hàm số

32

25y x x x= − + +

có đồ thị là

( )

C

. Trong các tiếp tuyến của

( )

C

, tiếp tuyến có hệ số góc

nhỏ nhất, thì hệ số góc của tiếp tuyến đó là

A.

4

3

. B.

5

3

. C.

2

3

. D.

1

3

.

Câu 49.Cho hàm số

2

1

23

x

y

mx x

−

=

−+

. Có tất cả bao nhiêu giá trị

m

để đồ thị hàm số có đúng hai đường tiệm

cận.

A. 2. B. 3. C. 0. D. 1

Câu 50:Cho hàm số

2

()

1

x

fx

x

=

−

. Đạo hàm cấp 2018 của hàm số

()fx

là:

A.

2013

(2018)

2013

2018!

()

(1 )

x

fx

x

=

−

. B.

(2018)

219

2018!

()

(1 )

fx

x

=

−

.

110

A

C

B

60

A

B

100

60

G

A

G

C

AB

GC

Trang 40

C.

(2018)

2019

2018!

()

(1 )

fx

x

=−

−

. D.

2013

(2018)

2013

2018!

()

(1 )

x

fx

x

=

−

LỜI GIẢI

Câu 1: Chọn D.TXĐ: D = R

xxy 63'

2

−=

;







=

=

2

0

0'

x

y

Từ bảng biến thiên suy ra hàm số đồng biến trên các khoảng

( ;0)−

và

(2; )+

.

Câu 2: Chọn D.Phương án A có

1 2 3

2, 5, 10u u u= = =

nên không phải cấp số cộng.

Phương án B có

1 2 3

2, 4, 8u u u= = =

nên không phải cấp số cộng.

Phương án C có

1 2 3

2, 3, 2u u u= = =

nên không phải cấp số cộng.

Bằng phương pháp loại trừ, ta chọn đáp án D

Chú ý: - Cách khác: Xét dãy số (u

n

) với

2 3, 1

n

u n n= − 

( ) ( )

*

1

,23212 Nnnnuu

nn

=−−−=−

+

Nên (u

n

) là cấp số cộng với u

1

= - 1 và công sai d = 2.

- Có thể sử dụng kết quả: Số hạng tổng quát của mọi cấp số cộng (u

n

) có công sai a đều có dạng u

n

= an +

b, với n là số tự nhiên khác 0. Nên thấy ngay

2 3, 1

n

u n n= − 

là cấp số cộng với công sai d = 2.

Câu 3: Chọn D.Ta có

2

3

2

4'

2

22

x

xy

x

y +=−=

−

=

2

3

1

2'

11

x

xy

x

y −=+=

+

=

;

0,6'0,33

33

2

3

=+=

+

= xxyxx

x

xx

y

3

2

5 1 1 1

52

xx

y x y x

x x x



+−

= = + −  = +

nên chọn đáp án D.

Chú ý: Khi học sinh đã học nguyên hàm thì đối với câu hỏi này, cách nhanh nhất là tìm họ các nguyên

hàm của hàm số đề cho.

Câu 4: Chọn C.Theo ý nghĩa hình học của đạo hàm, tiếp tuyến của đồ thị hàm số y = f(x) tại

( )

00

;M x f x

có hệ số góc là

( )

0

'fx

. Suy ra phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại

điểm

( )

00

;M x f x

là:

( )( ) ( )

0 0 0

y f x x x f x



= − +

.

Câu 5: Chọn B.Chia cả tử và mẫu cho

0x 

ta được:

2

22

1

2 2 1 0 0

lim lim 1

2

2 1 0

1

xx

x

xx

x

→− →+

+−

+ − + −

= = =

−−

−

Câu 6: Chọn B.Mỗi tập con gồm 3 phần tử của S là một tổ hợp chập 3 của 20 phần tử thuộc S và ngược

lại. Nên số các tập con gồm 3 phần tử của S bằng số các tổ hợp chập 3 của 20 phần tử thuộc S và bằng

3

20

C

.

Trang 41

Câu 7: Chọn B.Ta thấy đồ thị hàm số đi qua điểm

( )

1;3 .I

Lần lượt thay tọa độ điểm I vào các biểu thức

hàm số ở các đáp án, cho ta đáp án

.B

Câu 8: Chọn A.Ta có

23

lim 2

1

x

→

−

=

−

nên

2y =

là tiệm cận ngang (2 bên).

−=

−

+

→

1

32

lim

1

x

,

+=

−

→

1

32

lim

1

x

nên

1x =

là tiệm cận đứng (2 bên).

Câu 9: Chọn D.Có 3 loại hoa khác nhau, chọn 3 bông đủ ba màu nên dùng quy tắc nhân.

- Chọn một bông hồng đỏ có 7 cách. - Chọn một bông hồng vàng có 8 cách.- Chọn một bông hồng trắng

có 10 cách.

Theo quy tắc nhân có 7.8.10 = 560 cách.

Câu 10:Chọn D.Với điều kiện đề bài, ta có

( )

2

log 3log 2log 3log 4 log . 3log



       

= + = + = +

       



       

   

a a a

bb

b

bb

a a a a

P a a b

b b b b

2

4 1 log 3log

a

b

a

b





= + +









Đặt

log 0=

a

b

tb

(vì

1ab

), ta có

( ) ( )

2

33

4 1 4 48= + = + =+ + +P t t

t

t ft

t

.

Ta có

( )

2

32

2 2 2

2 1 4 3

3 8 3

( ) 8

6

8

++−



= + − = =

+−

t

tt

t

f t t

t t t

Vậy

( )

1

0

2



=  =f t t

. Khảo sát hàm số, ta có

min

1

15

2



=





=P f

.

Câu 11: Chọn A.

Hình ảnh minh họa hai mặt phẳng

()P

và

()Q

cùng vuông góc với mặt

phẳng

()R

nhưng không song song với nhau.

Câu 12: Chọn A. Do

()SA ABC SA BC⊥  ⊥

nên C đúng.

Ta có:

()

BC SA

BC SAB BC AH

BC AB gt

⊥



 ⊥  ⊥



⊥



nên B đúng.

Mà:

SB AH⊥

Từ (1),(2) suy ra:

()AH SBC⊥



AH SC⊥

nên D đúng.

Vậy A sai.

Câu 13: Chọn D.Gọi

( )

00

:A x y

là tọa độ tiếp điểm. Ta có:

3

2

( ) 3 2

3

x

y f x x= = + −

.

Tiếp tuyến với đồ thị (C) tại A có hệ số góc

9k =−

.

( )

0

9fx



 = −

2

00

69xx + = −

00

3 16xy = −  =

Phương trình tiếp tuyến của độ thị tại tiếp điểm

( )

00

:A x y

là:

( ) ( )

0 0 0

.y y f x x x



− = −

16 9( 3)yx − = − +

.

Câu 14: Chọn B.

Có

( )

SBCSA

SBSA

SCSA

⊥







⊥

3

.

105.4.3.

6

1

..

6

1

.

3

1

aaaaSCSBSASSAV

SBCABCS

====



Câu 15: Chọn C.

Theo định nghĩa, tứ diện đều là tứ diện có 4 mặt là 4 tam giác đều nên đáp án đúng là C

Chú ý. Có thể nhấn mạnh: Tứ diện đều có 6 cạnh bằng nhau. Đáp án A, D sai vì chưa đủ điều kiện 6

cạnh bằng nhau. Đáp án B sai vì tồn tại hình chóp tam giác đều có độ dài cạnh bên khác độ dài cạnh đáy.

Trang 42

Câu 16: Chọn C.Hàm số xác định khi và chỉ khi

1 cos 0x−

cos 1x

2xk





với

k 

.

Câu 17: Chọn A.

Theo giả thiết ta có

( ) ( )

baxxf ,,0' 

, (dấu bằng xảy ra tại hữu hạn điểm thuộc (a;

b)).

Trên khoảng (a; b)

- Hàm số y = f(x) + 1 có đạo hàm bằng f’(x) nên C đúng.

- Các hàm số y = - f(x) + 1 và y = - f(x ) - 1 có đạo hàm bằng - f’(x) nên B, D đúng.

Do đó A sai

Câu 18: Chọn C.Ta có

3

sin 4 sin 4

22

y x x





   

= − = + −

   

   

sin 4 cos4

2

xx





= − − = −







( cos4 ) 4sin4y x x



= − =

.

Câu 19: Chọn D.Phương trình:

cos 0 cosx m x m− =  =

Vì

1 cos 1x−  

,

x

nên phương trình trên vô nghiệm

1

m









−



Câu 20: Chọn B.

.

1 1 1

..

2 2 4

S A B C

S ABC

V

SA SB

V SA SB



= = =

.

Câu 21:Chọn D.

3

27

log

x

y







27 27

3

log 3log

2

xy=−

33

1

log log

22

xy





= − = −

.

Câu 22: Chọn C.Phép tịnh tiến theo biến đường thẳng thành chính nó khi và chỉ khi

0=v

hoặc

là một vectơ chỉ phương của . Từ phương trình đường thẳng d, ta thấy

( )

2;1v

là một vectơ chỉ phương

của nên chọn đáp án C.

Câu 23: Chọn B.•

32

2 3 0,y x y x x



= +  =   

nên hàm số không có điểm cực trị.

•

1

2

+= xy



y’ = 2x, y’’ = 2. . Vì

( )









=

00"

00'

y

nên hàm số đạt cực tiểu tại x = 0 , chọn B.

•

13'1

23

+−=++−= xyxxy

. Vì y’(0) = 1 nên hàm số không đạt cực trị tại x = 0, loại C

•

3 2 2

0

3 2 3 6 0

2

x

y x x y x x

x



=



= − +  = − = 



=



, y” = 6x - 6.

Vì

( )









=

00"

00'

y

nên hàm đạt cực đại tại điểm

0x =

, loại D

Chú ý: Có thể lập bảng biến thiên của các hàm số để tìm đáp án.

Câu 24: Chọn A

.Dựa vào đồ thị hàm số ta thấy hàm số đồng biến trên các

khoảng

( 1;0)−

và

(1; )+

.

Câu 25: Chọn A.Ta có:

3

2

1 1 1

2

3 3 2 3

SABC ABC

a

V S SA a a



= =   =





.

Lời bình: Có thể cho 1 đáp án nhiễu là

3

2

3

a

vì có thể học sinh cần rút kinh

nghiệm khi hấp tấp đọc đề nhanh thành tính theo a thể tích khối chóp

..S ABCD

Câu 26: Chọn D.Ta có

( )

2

−= xfxg

;

( )

xxfxg 2.2''

2

−=

B'

A'

C

B

A

S

v

d

v

d

a

2a

D

A

B

C

S

Trang 43

( )







−=

=

−=

=









=−

−=−

=









=−

=

=

2

1

0

22

12

0

02'

0

0'

2

x

xf

x

xg

Ta có

( ) ( )

07'.63' = fg

, g’(x) đổi dấu qua các nghiệm đơn hoặc bội lẻ, không đổi dấu qua các nghiệm bội

chẵn nên ta có bảng xét dấu g’(x):

x

−

-2 -1 0 1 2

+

g’(x)

- 0 + 0 + 0 - 0 - 0 +

Suy ra đáp án là D.

Câu 27: Chọn A.TXĐ:

\{ }Dm=−

;

2

1

()

m

y

xm



−

=

+

Hàm số

1mx

y

xm

+

=

+

đồng biến trên khoảng

(2; )+

( )

2

10

2;

m



−





−  +





( )

+ ;2,0' xy

2

( ; 1) (1; ) ( ; 1) (1; )

10

22

2

mm

m

mm

m

 − −  +  − −  +



−



  

  

−   −

−





[ 2; 1) (1; )m  − −  +

.

Câu 28: Chọn D.Giả sử ba số hạng liên tiếp là

12

1 1 1

,,

n n n

u q u q u q

++

. Ba số hạng này là độ dài ba cạnh của

một tam giác



21

2

1 1 1

1 2 2

1 1 1

2

12

1 1 1

0

10

1 5 1 5

0 1 0

22

10

0

n n n

u q u q u q

qq

u q u q u q q q q

qq

u q u q u q

++



+ − 

− + 



− + +



+ −   + −    





+ − 





.

Câu 29: Lời giải.Chọn D.Ta có

( )

+ =  − =  =

2

22

9 6 3 0 3x y xy x y x y

.

Khi đó

( )

++

= = = =

+

2

12 12 12 12

22

12

1 log log log 12 log 36

1

2log 3

log 36

log 3

x y xy y

M

xy

y

xy

.

Câu 30: Chọn D.Cách 1:Ta có: . Áp dụng vào S

.

Cách 2:Ta có : ( 1+x)

2000

= + x + x

2

+ x

3

+ …+ x

2000

Nhân cả hai vế với x ta có :x( 1+x)

2000

= x + x

2

+ x

3

+ x

4

+ …+ x

2001

Lấy đạo hàm hai vế ta có :( 1+x)

2000

+ 2000x(1+x)

1999

= + 2 x + 3 x

2

+ 4 x

3

+ …+

2001 x

2000

(*)

Thay x=1 vào (*) ta được :1001.2

2000

= + 2 + 3 +…+ 2001

Cách 3

.Ta có

2000

1999

2000

1

2000

0

2000

.2001.2000....2 CCCCS ++++=

, (1)

Hay

0

2000

1

2000

1999

2000

2....2000.2001 CCCCS ++++=

2000

1999

2000

1

2000

0

2000

2....2000.2001 CCCCS ++++=

, (2)

Cộng vế với vế của (1) và (2) ta được

2000

1999

2000

1

2000

0

2000

.2002.2002....2002.20022 CCCCS ++++=

1

2000 1999

. 2000. , 1,2000

kk

k C C k

−

=  =

( ) ( ) ( )

0 1 2000 1 2 2000 2000 0 1 1999

2000 2000 2000 2000 2000 2000 1999 1999 1999

... 2 ... 2000 2 2000 ...S C C C C C C C C C= + + + + + + = + + + +

2000 1999 2000

2 2000.2 1001.2= + =

0

2000

C

1

2000

C

2

2000

C

3

2000

C

2000

C

0

2000

C

1

2000

C

2

2000

C

3

2000

C

2000

C

0

2000

C

1

2000

C

2

2000

C

3

2000

C

2000

C

0

2000

C

1

2000

C

2

2000

C

2000

C

Trang 44

( )

20002000

2000

1999

2000

1

2000

0

2000

2.1001....1001 =++++= CCCCS

Câu 31: Chọn C- Dựa vào hình dạng đồ thị suy ra

0a 

- Hàm số có 3 điểm cực trị nên

00ab b  

- Giao điểm với trục tung nằm dưới trục hoành nên

0c 

.

Câu 32: Chọn C.+) Ta có

2

3 6 27y x mx



= − +

,

2

0 2 9 0y x mx



=  − + =

(1)

+) Theo giả thiết hàm số đạt cực trị tại

12

,xx



phương trình

(1)

có

2

nghiệm phân biệt

0



  

2

3

90

3

m





 −  



−



(*)

+) Với điều kiện (*) thì phương trình

(1)

có

2

nghiệm

12

,xx

, theo Vi-ét ta có:

12

2

9

x x m

xx

+=





=



+) Ta lại có

12

5xx−

( ) ( )

22

1 2 1 2 1 2

25 4 25 0x x x x x x −   + − − 

2

61 61

4 61 0

22

mm −   −  

(**)

+) Kết hợp (*), (**) và điều kiện

m

dương ta được:

61

3

2

m

3

2 61 3

61

2

a

T b a

b

=





  = − = −



=





.

Câu 33: Chọn B. * Sử dụng định lí Ta-lét đảo.

Ta có

2

AM DN x

AD DB

a





==





nên

AM MD AD

DN NB DB



==

.

Áp dụng định lí Ta-lét đảo, ta có

,,AD MN BD



lần lượt nằm trên ba mặt

phẳng song song.

M

song song với mặt phẳng

()P

chứa

BD



và song

song với

AD

.

Nên

( )

//MN BCD A



hay

( )

//MN A BC



* Sử dụng định lí Ta-lét.Vì

//AD A D



nên tồn tại

()P

là mặt phẳng qua

AD

và song song với mp

( )

A D CB



()Q

là mặt phẳng qua

M

và song song với mp

( )

A D CB



. Giả sử

()Q

cắt

DB

tại

N

Theo định lí Ta-lét ta có:

( )

AM DN

AD DB



=



Mà các mặt của hình hộp là hình vuông cạnh

a

nên

2AD DB a



==

Từ

( )



ta có

AM DN



=

DN DN



=

NN





()MQ

( )

( ) / /Q A D CB



suy ra

M

luôn song song với mặt phẳng cố định

( )

A D CB



hay

( )

A BC



Câu 34: Chọn B.Số phần tử của không gian mẫu là:

4

11

||C=

Trong 11 tấm thẻ được đánh số từ 1 đến 11 có 6 tấm thẻ được ghi số lẻ và 5 tấm thẻ được ghi số chẵn.

Gọi

A

là biến cố: “Tổng các số ghi trên 4 tấm thẻ là một số lẻ”.

TH1: Chọn 4 tấm thẻ gồm 1 tấm thẻ được ghi số lẻ và 3 tấm thẻ được ghi số chẵn

→

Có

13

65

60CC =

(cách)

TH2: Chọn 4 tấm thẻ gồm 3 tấm thẻ được ghi số lẻ và 1 tấm thẻ được ghi số chẵn

→

Có

31

65

100CC =

(cách)

Vậy số phần tử của

1

là:

| | 60 100 160A = + =

| | 160 16

()

| | 330 33

A

PA = = =



Trang 45

Câu 35: Chọn A.

2

3

( 1)

y

x



−

=

−

. Giả sử

( )

21

;

1

a

M a C

a

+







−



.

Phương trình tiếp tuyến tại điểm

M

là

2

3 2 1

: ( )

( 1) 1

a

d y x a

aa

−+

= − +

−−

Đồ thị

()C

có hai tiệm cận có phương trình lần lượt là

1

:1dx=

;

2

:2dy=

cắt

( )

1

d

tại điểm

24

1;

1

a

P

a

+





−



;

d

cắt

2

d

tại điểm

(2 1;2)Qa−

,

1

d

cắt

2

d

tại điểm

(1;2)I

.

6

; 2 1

1

IP IQ a

a

= = −

−

;Ta có

11

36

GPQ IPQ

S S IPIQ==

16

2| 1| 2

6 | 1|

a

= − =

−

.

Câu 36: Chọn D.

+) Gọi

BM AA E



=

;

ED AD N



=

.

Ta có M là trung điểm của AB

M

là trung điểm là

EB



N

là trung điểm của

ED



và

AD

+) Ta có

.

1

..

8

E AMN

E A B D

V

EA EM EN

V EA EB ED

  

==



. . . .

7 7 1 7 7063

.2. .

8 8 2 24 12

AMN A B D E A B D A A B D ABCD A B C D

V V V V

            

 = = = =

Câu 37: Chọn A. Từ suy ra

Ta có

; .Do đó

.

Câu 38: Chọn A.Trên cạnh

SB

,

SC

lần lượt lấy các điểm

,MN

thỏa mãn

1SM SN==

Ta có

1, 2, 3AM AN MN= = =

→

tam giác

AMN

vuông tại

A

Hình chóp

.S AMN

có

1SA SM SN= = =

→

hình chiếu của

S

trên

()AMN

là tâm

I

của đường tròn

ngoại tiếp tam giác

AMN

, ta có

I

là trung điểm của

MN

.Trong

22

1

,

2

SIM SI SN IN = − =

.

1 1 2 2

3 2 2 12

S AM

V =   =

.Ta có

,

1

6

SAM

S ABC

V

SM SN

V SB SC

=  =

→

.

2

S ABC

V =

.

Câu 39:Chọn D.

( )

33

2 2 2 2 2 2

log 3log log log log log 8 3a b a b ab+ = + = = =

.

Câu 40: Chọn D.Điều kiện

1x 

.Ta có phương trình

2

4

3 1 1 2 1x m x x− + + = −

4

11

32

11

xx

m

xx

−−

 + =

++

d

N

M

E

D

C

B

A

D'

C'

B'

A'

' ' ' 0GB GA GB GC+ + + =

( )

1

' ' '

4

IG IB IA IB IC= + + +

2

3

IB IC CB a b c= + = − + −

11

' ' ' ' ' ' '

33

IA IC C A CC A C a c= + = − = −

1

' ' ' '

3

IB IC C B a b c= + = + −

1

'

3

IC a=

1 2 1 1 1 1 1

23

4 3 3 3 3 4 3

IG a b c a c a b c a a b c

   

= − + − + − + + − + = + −

   

   

Trang 46

Bảng biến thiên:

Đặt

44

12

1 0 1

11

x

tt

xx

−

= = −   

++

.

Phương trình trở thành:

2

32m t t= − +

(1).Nhận xét: Mỗi

giá trị của

[0;1)t

cho ta

1

nghiệm

[1; )x +

.

Do đó phương trình đã cho có 2 nghiệm thực phân biệt



phương trình (1) có

2

nghiệm phân biệt t

[0;1)

.

Từ bảng biến thiên suy ra

1

0

3

m

Câu 41: Chọn D.Phương trình đã cho tương đương với

22

1 1 1 3

1 sin 2 sin2 sin 2 0

2 2 2 2

x x x

   

− + − + − =

   

   

2

11

sin 2 sin2 1 0

22

xx + − =

sin 2 1

sin 2 2( )

x

x VN

=







=−



Với

sin2 1 2 2

2

x x k



=  = +

,

4

x k k



 = + 

.

Câu 42: Chọn D.Ta có

2 2 2

1 3 2 1

n

u

n n n

−

= + ++

2

1 3 (2 1)n

n

+ ++ −

=

2

(1 (2 1))

2

1

nn

n

+−







==

Vậy

lim lim1 1

n

u ==

.

Câu 43: Chọn C. Ta gọi

,EF

lần lượt là trung điểm của

SC AB

=

.

Ta có

//ME NF

( do cùng song song với

BC

. Nên tứ giác

MENF

là hình thang,và

/

()

MF ISA

MF ABCD

SA ABCD



⊥



⊥



hay tứ giác

MENF

là hình thang vuông tại

,MF

Gọi

,K NF AC I EK M=  = 

thì

()I MN SAC=

Ta có:

()

NC AC

NC SAC

NC SA

⊥



⊥



⊥



hay

E

là hình chiếu vuông góc

của

N

lên

()SAC

Từ đó ta có được, góc giữa

MN

và

()SAC

là góc giữa

MN

và

CI

Suy ra, gọi

Q

là góc giữa

MN

và

()SAC

thì

sin

CN

IN



=

12

D

22

a

NC C==

;

2

3

IN KN

IN MN

M ME

= =  =

22

2 10

33

a

MF FN= + =

.Vậy

35

sin

10

CN

IN



==

.

Câu 44: Chọn B.

( ) ( )

3 3 2 2

2 3 2( ) 3P x y xy x y x y xy xy= + − = + + − −

2( )(2 ) 3x y xy xy= + − −

(do

22

2xy+=

)

Đặt

xyt+=

. Ta có

22

()

2 1 1

22

x y t

x y xy

+

+ =  = − = −

Từ

2

22

( ) 4 4 1 2 2

2

t

x y xy t t



+    −  −  





22

32

3

( ) 2 2 1 3 1 6 3

2 2 2

tt

P f t t t t t



   

= = − − − − = − − + +



   

   



Xét

()ft

trên

[ 2;2]−

.Ta có

2

1 [ 2;2]

( ) 3 3 6, ( ) 0

2 [ 2;2]

t

f t t t f t

t



=  −



= − − + = 



= −  −



.

t

0

1/3

1

0

1/3

–1

Trang 47

Bảng biến thiên

Từ bảng biến thiên ta có

13

max max ( ) ;min min ( ) 7

2

P f t P f t= = = = −

Lời bình: Có thể thay bbt thay bằng

Ta có

13

1 [ 2;2]; 2 [ 2;2]; (0) 7; (1) ; (2) 1

2

t t f f f=  − = −  − = − = =

suy ra kết luận.

Bài tương tự.Cho các số thực không âm x, y thay đổi và thỏa mãn

1xy+=

. Tìm giá trị lớn nhất và giá trị

nhỏ nhất của biểu thức

( )( )

22

4 3 4 3 25S x y y x xy= + + +

Lời giải.

( )( ) ( )

2 2 2 2 3 3

4 3 4 3 25 16 12 34S x y y x xy x y x y xy= + + + = + + +

2 2 3

16 12 ( ) 3 ( ) 34x y x y xy x y xy



= + + − + +



22

16 12(1 3 ) 34x y xy xy= + − +

22

16 2 12x y xy= − +

Đặt t = x.y, vì x, y  0 và x + y = 1 nên

1

0

4

t

. Khi đó

2

( ) 16 2 12S f t t t= = − +

.

Xét

()ft

trên

1

0;

4







;

11

( ) 32 2; ( ) 0 0;

16 4

f t t f t t





= − =  = 





S(0) = 12;

1

4

S



=





25

2

;

1

16

s



=





191

16

.

25

Max

2

S =

khi x = y =

1

2

và

191

min

16

S =

khi

23

4

23

4

x

y



+

=





−



=





hoặc

23

4

23

4

x

y



−

=





+



=





.

Câu 45: Chọn C.Đặt

GB x=

(km),

0 100x

2

3600GC x = +

(km). Số tiền cần để mắc dây điện

từ

4

đến

G

rồi từ

G

đến

E

là:

2

( ) 60(100 ) 100 3600f x x x= − + +

(triệu đồng)

Cách 1:

2

100

( ) 60

3600

x

fx

x



=−

+

;

2

( ) 0 100 60 3600f x x x



=  = +

2

0 100

5 3 3600

x

xx











=+





45x=

Vậy

()fx

đạt giá trị nhỏ nhất tại

45x =

55GA=

km.

Cách 2: Dùng casio sử dụng MODE 7 được

()fx

đạt giá trị nhỏ nhất tại

45x =

55GA=

km.

Câu 46: Chọn D.Xét hàm số

4 3 2

( ) 3 4 12 1f x x x x m= − − + −

,

Có

( )

+=

+→

xf

x

lim

,

( )

+=

−→

xf

x

lim

;

( )

3 2 2

( ) 12 12 24 12 2f x x x x x x x



= − − = − −

;

0

( ) 0 1

2

x

f x x

x



=





=  = −



=



.

Bảng biến thiên:

Trang 48

Từ bảng biến thiên, ta có hàm số

()y f x=

có

T

điểm cực trị



đồ thị hàm số

()y f x=

cắt

Ox

tại

4

điểm phân biệt

6 0 1 1 6m m m −   −   

.

Câu 47: Chọn C.ĐK:

cos 0x 

Khi đó, phương trình

( ) ( )

2 2 2 2 3

2cos 1 cos 1 cos cos cos 1x x x x x −  − − = − −

4 3 2

2cos cos cos 0x x x + − =

2

2cos cos 1 0xx + − =

(vì

cos 0x 

)

1

2

3

2

cos 1

2

1

3

cos

2

3

xk

x

xk

x

xk









=+

=−





  = +



=





= − +



Vì

[1;70]x

nên

1 2 3

0 ; 10;1 11k k k   

Áp dụng công thức tính tổng 11 số hạng đầu tiên của một cấp số cộng, ta có

( )







3632.11

3

2

32

11

2.10

332

11

2.10

2

11

=

























+−+













+−+

























++++=S

.

(Lưu ý: Tất cả các nghiệm này không có nghiệm nào trùng nhau. Và giả như phương trình có một số họ

nghiệm trùng nhau thì tổng các nghiệm trên đoạn [1; 70] vẫn không thay đổi vì đề không yêu cầu tính

tổng các nghiệm phân biệt ).

Câu 48: Chọn B.+)Gọi

( )

00

; ( )M x y C

và



là tiếp tuyến của

( )

C

tại

M

.

+)

2

3 2 2y x x



= − + 

hệ số góc của



là

2

00

3 2 2k x x= − +

.

+) Ta có

2

00

2 1 5

3

3 9 3

k x x



= − + +





2

00

1 5 5

3,

3 3 3

xx



= − +  





.

5

min

3

k=

, đạt được khi

0

1

3

x =

.

Câu 49: Chọn B.Nhận xét:

+

2

( ) 2 3f x mx x= − +

có bậc

1

nên đồ thị hàm số luôn có 1 tiệm cận ngang.

+ Do đó: Yêu cầu bài toán

9

đồ thị hàm số có đúng 1 tiệm cận đứng.

+

0m =

, đồ thị hàm số có 1 tiệm cận đứng là đường thẳng

3

2

x =



m = 0 thỏa bài toán.

+

0m 

, đồ thị hàm số có đúng 1 tiệm cận đứng khi và chỉ khi phương trình mx

2

- 2x + 3 = 0 có nghiệm

kép hoặc nhận x = 1 làm nghiệm







−=

=









=

=



1

3

1

0)1(

0

m

f

+ KL:

1

0; ; 1

3

m



−





.

Câu 50: Chọn B.Ta có

1

( ) 1

1

f x x

x

= − − −

−

;

( )

2

1

1'

−

+−=

x

xf

;

( )

( ) ( )

33

1

!2

1

1.2

"

−

−=

−

−=

xx

xf

Trang 49

( )

( ) ( )

44

3

1

!3

1

1.2.3

−

=

−

=

xx

xf

;

( )

( ) ( )

55

4

1

!4

1

1.2.3.4

−

−=

−

−=

xx

xf

....

Suy ra:

(2018)

2019 2019

2018! 2018!

()

( 1) (1 )

fx

xx

−

==

−−

Chú ý: Có thể dùng phương pháp quy nạp toán học chứng minh được

( )

( ) ( )

( )

*

1

,

1

!

1 Nn

x

n

xf

n



−

−=

+

ĐỀ 54

ĐỀ THI THỬ THPT QUỐC GIA 2020

MÔN TOÁN

Thời gian: 90 phút

Câu 1: Hàm số

3

3y x x=−

có giá trị cực đại bằng

A.

1.

B.

2.−

C.

1.−

D.

2.

Câu 2: Thể tích của khối cầu tiếp xúc với tất cả các cạnh của hình lập phương cạnh

22

bằng

A.

32

3





B.

64 2

3





C.

256

3





D.

8 6.



Câu 3: Diện tích toàn phần của hình trụ có thiết diện qua trục là hình vuông cạnh a bằng

A.

2

.a



B.

2

2.a



C.

2

a





D.

2

3

2

a





Câu 4: Cho hàm số

21

2

x

y

x

−

=

−

. Khẳng định nào sau đây đúng?

A. Hàm số nghịch biến trên khoảng

1

;.

2



+





B. Hàm số nghịch biến trên khoảng

( )

2; .+

C. Hàm số đồng biến trên khoảng

( )

2; .+

D. Hàm số đồng biến trên khoảng

1

;.

2



+





Câu 5: Cho khối chóp

.S ABC

có ba cạnh

,,SA SB SC

cùng có độ dài bằng a và vuông góc với nhau từng đôi

một. Thể tích của khối chóp

.S ABC

bằng A.

3

2

a



B. .

3

a



C.

3

6

a



D.

3

.a

Câu 6: Trong không gian, cho hai điểm phân biệt

,AB

cố định. Xét điểm

M

di động luôn nhìn đoạn

AB

dưới

một góc vuông. Hỏi điểm

M

thuộc mặt nào trong các mặt sau?

A. Mặt cầu. B. Mặt nón. C. Mặt trụ. D. Mặt phẳng.

Câu 7: Tập nghiệm S của bất phương trình

( ) ( )

11

22

log 3 2 log 4xx−  −

là

A.

3

;4

2

S



=





B.

2

;3

3

S



=





C.

3

;

2

S



= − 





D.

23

;

32

S



=





Câu 8: Cho hàm số

2

log .yx=

Xét các phát biểu

(1) Hàm số

2

logyx=

đồng biến trên khoảng

( )

0; .+

(2) Hàm số

2

logyx=

có một điểm cực tiểu.

(3) Đồ thị hàm số

2

logyx=

có tiệm cận.

Số phát biểu đúng là A. 3. B. 0. C. 1. D. 2.

Trang 50

Câu 9: Tính đạo hàm của hàm số

.

ex

y x e=+

A.

.ln .

ex

y x x e



=+

B.

( )

11

.

ex

y x x e

−−



=+

C.

( )

11

.

xe

y e e x

−−



=+

D.

.ln .y e x x



=+

Câu 10: Cho hàm số

( )

y f x=

có đồ thị như hình vẽ .

Hàm số

( )

y f x=

là

A.

42

4 4.y x x= − +

B.

31

2

x

y

x

−

=

+

C.

32

3.y x x= − +

D.

32

3.y x x=−

Câu 11: Một hình đa diện có ít nhất bao nhiêu đỉnh? A. 6. B. 3. C. 5. D. 4.

Câu 12: Cho phương trình

( )

2

5

log 1 1xx+ + =

. Khẳng định nào sau đây đúng?

A. Phương trình có 2 nghiệm trái dấu. B. Phương trình có một nghiệm bằng 0 và một nghiệm âm.

C. Phương trình có 2 nghiệm âm. D. Phương trình vô nghiệm.

Câu 13: Số giao điểm của đồ thị hàm số

3

41y x x= − +

và đường thẳng

:1d y x=+

bằng

A.

1.

B.

4.

C.

3.

D.

2.

Câu 14: Phương trình

1

42

2

( ) 4x =

có bao nhiêu nghiệm thực? A. vô số. B.

3.

C.

2.

D.

1.

Câu 15: Các tiệm cận của đồ thị hàm số

21

1

x

y

x

+

=

−

là

A.

1, 1.xy= = −

B.

1, 2.xy==

C.

2, 1.xy==

D.

1

, 1.

2

xy= − =

Câu 16: Cho biểu thức

2

1

2

log log 4

a

Aa=+

với

0, 1.aa

Khẳng định nào sau đây đúng?

A.

1 2 .Aa=+

B.

4 2 .Aa=+

C.

1 2 .Aa=−

D.

4 2 .Aa=−

Câu 17: Đồ thị hàm số

2

21

4

x

y

x

+

=

−

có bao nhiêu tiệm cận? A.

4.

B.

1.

C.

3.

D.

2.

Câu 18: Cho

1

3

. , 0.P a a a=

Khẳng định nào sau đây đúng? A.

11

3

.Pa=

B.

2

3

.Pa=

C.

2

.Pa=

D.

1

9

.Pa=

Câu 19: Bất phương trình

1 2 3

22

xx

ee

−+

   



   

   

có nghiệm làA.

4.x −

B.

4.x −

C.

4.x −

D.

4.x −

Câu 20: Hàm số

2

y x x=−

nghịch biến trên khoảngA.

1

;.

2



−





B.

( )

0;1 .

C.

( )

;0 .−

D.

( )

1; .+

Câu 21: Cho hàm số

( )

y f x=

liên tục trên và có bảng biến thiên như hình vẽ

Trang 51

Khẳng định nào sau đây đúng?

A. Hàm số

( )

y f x=

nghịch biến trên một đoạn có độ dài bằng 1.

B. Giá trị lớn nhất của hàm số

( )

y f x=

trên bằng

0.

C. Hàm số

( )

y f x=

chỉ có một cực trị.

D. Giá trị nhỏ nhất của hàm số

( )

y f x=

trên bằng

1.−

Câu 22: Khối mười hai mặt đều (hình vẽ dưới đây) là khối đa diện đều loại

A.

 

3;4 .

B.

 

3;5 .

C.

 

5;3 .

D.

 

4;3 .

Câu 23: Cho hàm số

2

33

.

1

xx

y

x

−+

=

−

Gọi

,Mm

lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên

đoạn

1

1; .

2



−





Tính tích

..Mm

A.

1

.

2

−

B.

21

.

2

C.

3.−

D.

0.

Câu 24: Cho hình lăng trụ tứ giác đều có cạnh đáy bằng

a

và cạnh bên bằng

2.a

Diện tích xung quanh của hình

lăng trụ đã cho bằng A.

2

8.a

B.

2

10 .a

C.

2

9.a

D.

2

4.a

Câu 25: Số giao điểm của đồ thị hàm số

2

1

1 2 3

3

y x x x



= − − +





với trục hoành là

A.

4

. B.

3

. C.

5

. D.

1

.

Câu 26: Tổng tất cả các nghiệm của phương trình

1

4 3.2 8 0

xx+

− + =

bằng

A.

6.

B.

3.

C.

2

1 log 3.−

D.

2

1 log 3.+

Câu 27: Hàm số nào sau đây có giá trị nhỏ nhất trên đoạn

 

0;2

bằng

2?−

A.

2 2.

x

y =−

B.

3

10.yx=−

C.

2 2.yx= + −

D.

2

.

1

x

y

x

−

=

+

Câu 28: Cắt một khối nón bởi mặt phẳng đi qua trục của nó, ta được một tam giác vuông cân có diện tích bằng 8.

Khẳng định nào sau đây sai?

A. Khối nón có diện tích đáy bằng

8.



B. Khối nón có diện tích xung quanh bằng

16 2.



C. Khối nón có độ dài đường sinh bằng

4.

D. Khối nón có thể tích bằng

16 2

3





Câu 29: Cho hàm số

( )

y f x=

có đồ thị như hình vẽ

Trang 52

Khẳng định nào sau đây đúng?

A. Hàm số đồng biến trên khoảng

( )

1; .− +

B. Hàm số nghịch biến trên khoảng

( )

1;0 .−

C. Hàm số đồng biến trên khoảng

( )

1; .+

D. Hàm số nghịch biến trên khoảng

( )

1; .− +

Câu 30: Thể tích của khối bát diện đều cạnh

a

bằng A.

3

22a

. B.

3

2

6

a



C.

3

22

3

a



D.

3

2

3

a



Câu 31: Cho các hàm số

log , log

ab

y x y x==

và

x

yc=

(với a, b, c là các số dương khác 1) có đồ thị như

hình vẽ.Khẳng định nào sau đây đúng?

A.

.bac

B.

.c b a

C.

.abc

D.

.c a b

Câu 32: Phương trình

3.9 7.6 2.4 0

x x x

− + =

có hai nghiệm

12

,.xx

Tổng

12

xx+

bằng

A.

1.

B.

1.−

C.

3

2

7

log .

3

D.

7

.

3

Câu 33: Cho hàm số

4

3x

y

x

+

=

có giá trị cực đại

1

y

và giá trị cực tiểu

2

.y

Giá trị của

12

S y y=−

bằng

A.

0.S =

B.

8.S =

C.

8.S =−

D.

2.S =−

Câu 34: Cho mặt nón có chiều cao

6,h =

bán kính đáy

3.r =

Hình lập phương

. ' ' ' 'ABCD A B C D

đặt trong

mặt nón sao cho trục của mặt nón đi qua tâm hai đáy của hình lập phương, một đáy của hình lập phương nằm trong

cùng một mặt phẳng với đáy của hình trụ, các đỉnh của đáy còn lại thuộc các đường sinh của hình nón. Độ dài

đường chéo của hình lập phương bằng A.

( )

6 3 2 1 .−

B.

3 3.

C.

36

2



D.

( )

6 2 1 .−

Câu 35: Đồ thị của hàm số nào sau đây có ba tiệm cận?

A.

1

y

x

=

B.

2

x

y

xx

=

−

C.

2

1

x

y

x

=

−

D.

2

x

y

xx

=

−

Câu 36: Gọi giá trị nhỏ nhất, giá trị lớn nhất của hàm số

.lny x x=

trên đoạn

2

1

;e

e







lần lượt là

m

và

.M

Tích

.Mm

bằng A.

2

e

−



B.

1.−

C.

2.e

D.

1.

Câu 37: Cho tứ diện ABCD có

AB x=

thay đổi, tất cả các cạnh còn lại có độ dài

.a

Tính khoảng cách giữa hai

đường thẳng AB và CD trong trường hợp thể tích của khối tứ diện ABCD lớn nhất.

A.

6

3

a



B.

6

4

a



C.

3

4

a



D.

3

a



Câu 38: Phương trình

2 1 2

1 2 2 1

xx

e e x x

+

− = − + +

có nghiệm trong khoảng nào sau đây?

y

x

-1

2

1

O

1

Trang 53

A.

5

2;

2







. B.

3

;2

2







. C.

3

1;

2







. D.

1

;1

2







.

Câu 39: Tìm tất cả các giá trị thực của tham số m để hàm số

3

3y x x m= − +

có giá trị cực đại và giá trị cực tiểu

trái dấu.

A.

2 2.m−  

B.

 

2;2 .m−

C.

2m −

hoặc

2.m 

D.

.m

Câu 40: Bạn Nam làm một cái máng thoát nước mưa, mặt cắt là hình thang cân có độ dài hai cạnh bên và

cạnh đáy đều bằng 20cm, thành máng nghiêng với mặt đất một góc



(

00

0 90





). Bạn Nam phải nghiêng thành máng một góc trong

khoảng nào sau đây để lượng nước mưa thoát được là nhiều nhất?

A.

)

oo

50 ;70 .





B.

)

oo

10 ;30 .





C.

)

oo

30 ;50 .





D.

)

oo

70 ;90 .





Câu 41: Cho phương trình

( )

4

2

4 16

log 4 4 log 4 0x x x m− + + + − =

. Tìm tất cả các giá trị của tham số thực m

để phương trình đã cho có 4 nghiệm phân biệt.

A.

m

B.

22

2log 3 2log 3m−  

C.

2

2log 3.m −

D.

2

2log 3.m 

Câu 42: Theo thống kê dân số năm 2017, mật độ dân số của Việt Nam là 308 người/km

2

và mức tăng trưởng dân

số là 1.03% / năm. Với mức tăng trưởng như vậy, tới năm bao nhiêu mật độ dân số Việt Nam đạt 340 người/km

2

?

A. Năm 2028. B. Năm 2025. C. Năm 2027. D. Năm 2026.

Câu 43: Cho hàm số

23

2

x

y

x

+

=

−

có đồ thị

( )

.C

Có bao nhiêu giá trị thực của tham số

m

để đường thẳng

2y x m=+

cắt đồ thị

( )

C

tại hai điểm phân biệt mà tiếp tuyến của

( )

C

tại hai điểm đó song song với nhau?

A. vô số. B. 1. C. 0. D. 2.

Câu 44: Một khối gỗ hình hộp chữ nhật có chiều dài, chiều rộng và chiều cao lần lượt là

30cm, 20cm

và

30cm

(như hình vẽ).Một con kiến xuất phát từ điểm A muốn tới điểm B thì

quãng đường ngắn nhất nó phải đi dài bao nhiêu cm?

A.

10 34 cm.

B.

30 10 14 cm.+

C.

10 22 cm.

D.

20 30 2 cm.+

Câu 45: Cho hình chóp tam giác đều

.S ABC

với

6, 3.SA AB==

Diện tích của mặt cầu có tâm

A

và tiếp xúc

với mặt phẳng

()SBC

bằng A.

108

5





B.

54

5





C.

60 .



D.

18 .



Câu 46: Cho hình chóp

.S ABCD

có đáy là hình thang vuông tại

A

và

,B

2,AB BC==

4;AD =

mặt bên

SAD

nằm trong mặt phẳng vuông góc với đáy và có diện tích bằng 6. Thể tích khối

.S BCD

bằng

A.

1.

B.

6.

C.

18.

D.

2.

Câu 47: Phương trình

3

22

30x x m− − =

(với m là tham số thực) có nhiều nhất bao nhiêu nghiệm phân biệt?

A. 3 nghiệm. B. 4 nghiệm. C. 2 nghiệm. D. 6 nghiệm.

Trang 54

Câu 48: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

2,a

()SA ABCD⊥

và

.SA a=

Gọi E là

trung điểm của cạnh

.AB

Diện tích mặt cầu ngoại tiếp hình chóp

.S BCE

bằng

A.

2

12 .a



B.

2

11 .a



C.

2

14 .a



D.

2

8.a



Câu 49: Cho hàm số

( )

y f x=

và

( )

y g x=

có đồ thị lần lượt như hình vẽ

-2 -1.5 -1 -0.5 0.5 1 1.5 2

-2

-1.5

-1

-0.5

0.5

1

1.5

2

x

y

y=f(x)

-2 -1.5 -1 -0.5 0.5 1 1.5 2

-2

-1.5

-1

-0.5

0.5

1

1.5

2

x

y

y=g (x)

Đồ thị hàm số

( ) ( )

.y f x g x=

là đồ thị nào sau đây?

A.

-2 -1.5 -1 -0.5 0.5 1 1.5 2 2.5

-1

1

2

3

x

y

B.

-2 -1.5 -1 -0.5 0.5 1 1.5 2 2.5

-3

-2.5

-2

-1.5

-1

-0.5

0.5

1

1.5

x

y

C.

-2 -1.5 -1 -0.5 0.5 1 1.5 2 2.5

-3

-2.5

-2

-1.5

-1

-0.5

0.5

1

1.5

x

y

D.

-2 -1.5 -1 -0.5 0.5 1 1.5 2 2.5

-2

-1.5

-1

-0.5

0.5

1

1.5

2

2.5

x

y

Câu 50: Biết rằng phương trình

2 1 2 1 1 2

5 .5 4.5

x x x x

m

+ − − −

−=

có nghiệm khi và chỉ khi

 

;,m a b

với m là tham

số. Giá trị của

ba−

bằng A.

9

5



B.

9.

C.

1.

D.

1

5



----------- HẾT ----------

Trang 55

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1:Chọn D.

2

1

3 3 0

1

x

yx

x

=





= − = 



=−



Lập BBT, ta suy ra hàm số đạt cực đại tại

1x =−

và giá trị cực đại bằng

2

Câu 2.Chọn A. Gọi O là giao các đường chéo của hình lập phương

Gọi

H

là trung điểm của cạnh

AA



. Ta có

1

2

OH AC==

. Vậy

mặt cầu tiếp xúc với 12 cạnh của hình lập phương là mặt cầu có tâm O

là trung điểm của đường chéo

AC



và bán kính

2R OH==

3

4 32

.2

33

V



 = =

.

Câu 3.Chọn D .Ta có hình trụ có thiết diện qua trục là hình vuông cạnh anên

,

2

a

l a r==

2

22

3

2 2 2 . 2

2 2 2

tp

aa

S rl r a a

    



 = + = + =





.

Câu 4.Chọn B.Ta có

( )

2

3

' 0, 2

2

yx

x

−

=   

−

nên hàm số nghịch biến trên

( )

;2−

và

( )

2; .+

Câu 5.Chọn C .Ta có

3

.

1 1 1

. . . . . .

3 3 2 6

S ABC ABC

a

V SA S a a a= = =

Câu 6.Chọn A .Ta có

90AMB =

nên M luôn thuộc mặt cầu tâm O là trung điểm của

AB

.

Câu 7.Chọn D .Điều kiện

2

;4

3

4

x









  













.

Khi đó .

Kết hợp điều kiện suy ra tập nghiệm bất phương trình là .

Câu 8.Chọn D .Tập xác định:

( )

0;D = +

.

( )

1

0, 0;

ln2

yx

x



=    +

nên hàm số

2

logyx=

đồng biến trên khoảng

( )

0;+

và hàm số

2

logyx=

không có điểm cực tiểu.

0

lim

x

y

+

→

= −

nên đồ thị hàm số

2

logyx=

có tiệm cận đứng là

0x =

.

3 2 0

40

x

−





−



( ) ( )

11

22

3

log 3 2 log 4 3 2 4

2

x x x x x−  −  −  −  

23

;

32

S



=





A

B

C

D

A

’

B

’

C

’

D

’

O

Trang 56

Câu 9.Chọn C .Ta có

( )

1 1 1

.

e x e x

y e x e e x e

− − −



= + = +

.

Câu10.Chọn D.Từ hình dáng đồ thị ta thấy đồ thị hàm số là đồ thị hàm bậc

3

nên loại

; AB

. Có hình dáng đồ thị hướng lên trên. Vậy đồ thị là đồ thị hàm

32

3y x x=−

.

Câu 11.Chọn D.Trong không gian tồn tại

4

điểm không đồng phẳng nên hình đa diện có

ít nhất

4

đỉnh.

Câu 12.Chọn A.

( )

2

5

log 1 1xx+ + =

( )

2

1 0 d

40

15

x x l

xx



+ + 



  + − =



+ + =





Phương trình

2

40xx+ − =

có

.0ac

nên phương trình đã cho có hai nghiệm trái dấu.

Câu13.Chọn C.Hoành độ giao điểm của đồ thị hàm số

3

41y x x= − +

và đường thẳng

:1d y x=+

là nghiệm của phương trình:

3

0

4 1 1 5

5

x

x x x x

x

=





− + = +  =



=−



Câu 14.Chọn C.ĐK:

0x

.

( )

1

2

4 2 2 2 2

2

( ) 4 4 4

2

x

x x x

x

=



=  =  = 



=−



Câu 15.Chọn B.Ta có

11

2 1 2 1

lim , lim

11

xx

−+

→→

++

=− =+ 

−−



Đồ thị hàm số có đường tiệm cận đứng là

1x =

21

lim 2

1

x

→

+

=

−

đồ thị hàm số có đường tiệm cận ngang là:

2y=

Câu16.Chọn D.Ta có

2

1

2

log log 4

a

Aa=+

11

2

log log 4

a

−

=+

2

4log log 4

a

aa=−

42a=−

.

Câu17. Chọn C.Ta có

lim 0

x

y

→

=

nên đồ thị hàm số nhận đường thẳng

0y =

làm TCN.

Và

2

lim

x

y

+

→

= −

;

( )

2

lim

x

y

−

→−

= +

nên đồ thị hàm số nhận hai đường thẳng

2x =

và

2x =−

làm TCĐ.

Vậy đồ thị hàm số đã cho có ba đường tiệm cận.

Câu 18.Chọn B.Với

0a 

, ta có

1

3

.P a a=

11

33

.aa=

2

3

a=

.

Câu 19.Chọn B.Ta có:

1 2 3

22

xx

ee

−+

   



   

   

1 2 3 4x x x −  +   −

.

Câu 20.Chọn C..+ TXĐ:

( ) ( )

;0 1;D = −  +

.

+

2

21

2

x

y

xx

−



=

−

;

1

0

2

yx



=  =

(loại). +

( )

0, ;0yx



   −

.

Nên hàm số nghịch biến trên khoảng

( )

;0−

.

Câu 21.Chọn A.+ Hàm số không có giá trị lớn nhất và giá trị nhỏ nhất trên .

+ Hàm số có 2 điểm cực trị.

+ Hàm số nghịch biến trên khoảng

( )

0;1

có độ dài bằng 1.

Câu 22.Chọn C.Theo định nghĩa: khối mười hai mặt đều là khối đa diện đều loại

 

5;3

.

Câu 23.Chọn B.

( )

2

1

xx

y

x

−



=

−

.

0y



=

2

20xx − =

1

0 1;

2

1

2 1;

2

x





=  −















=  −









.

Trang 57

( )

7

1

2

y − = −

;

( )

03y =−

;

17

22

y



=−





. Giá trị lớn nhất của hàm số là

3M =−

.

Giá trị nhỏ nhất của hàm số là

7

2

m =−

. Vậy: tích

7 21

. 3.

22

Mm



= − − =





.

Câu 24.Chọn A.

2

ADD A ABB A BCC B CDD C

S S S S a

       

= = = =

.Vậy

4

xq ADD A

SS



=

2

4.2a=

2

8a=

.

Câu 25.Chọn B.Xét phương trình hoành độ

( )

22

2

10

1

10

11

1 2 3 0 2 3 0 0 3

1

33

2 3 0

3

1

2 3 0 0

3

x

x x x x x x x

xx

x

x x x





−=

=



 − =







− − + =   − + =   =





− + =





=−







+ + = 



Vậy đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt.

Câu 26.Chọn B.

1

2 4 2

4 3.2 8 0 4 6.2 8 0

1

22

x

x x x x

x

+



==



− + =  − + =  



=



Vậy tổng các nghiệm của phương trình

1

4 3.2 8 0

xx+

− + =

bằng

3

.

Câu 27.Chọn D.Ta có

( )

2

23

'0

1

x

yy

x

−

=  = 

+

.Vậy

 

( )

0;2

min 0 2yy= = −

.

Câu 28.Chọn B.Gọi

,,r l h

thứ tự là bán kính đáy, độ dài đường sinh, chiều cao của khối

nón. Ta có:

2

8 4; 2 2

2

ll

l r h=  = = = =

.Diện tích xung quanh của khối nón là

. . 8 2rl



=

.

Câu 29.Chọn C

Câu 30.Chọn D.Chiều cao của khối chóp tứ giác đều có các cạnh đều bằng

a

là:

2

22

aa

ha



= − =





Thể tích khối bát diện đều cạnh

a

là:

3

2

12

2. . .

33

2

aa

Va==

.

Câu31.Chọn ATừ hình vẽ, ta có

01c

,

1, 1ab

và

ab

nên

1 ab

.

Do đó

01c a b   

.

Câu 32.Chọn B.Ta có

2

33

3.9 7.6 2.4 0 3. 7. 2 0

22

xx

x x x

   

− + =  − + =

   

   

.

Suy ra

1 2 1 2

12

3 3 3 2

.1

2 2 2 3

x x x x

xx

+

     

= =  + = −

     

     

.

Trang 58

Câu 33.Chọn C.Ta có

4

32

2

3 3 3

3

x

y x y x

x x x

+



= = +  = −

.

2

3

0 3 0 1y x x

x



=  − =  = 

.

3

6

6yx

x



=+

.

(1) 12 0y



=

nên

1x =

là điểm cực tiểu. Suy ra

2

(1) 4yy==

.

( 1) 12 0y



− = − 

nên

1x =−

là điểm cực tiểu. Suy ra

1

( 1) 4yy= − = −

.

Do đó

12

4 4 8S y y= − = − − = −

.

Câu 35.Chọn A.Gọi

x

là cạnh của hình lập phương

( )

0x 

.

Xét tam giác

SOP

có

//O A OP



.

Suy ra

2

6

2

63

x

SO O A x

SO OP

  

−

=  =

.

6 2 6 2 6x x x − =  = −

Vậy đường chéo của hình lập phương là

( )

6 3 2 1−

Câu 36.Chọn D.Tập xác định

( )  

0; \ 2D = +

.

2

lim 0

2

x

xx

→+

=

−

, suy ra tiệm cận ngang

0y =

.

( )

2

0 0 0

1

lim lim lim

22

2

x x x

xx

x x x x

xx

+ + +

→ → →

= = = −

−−

−

, tiệm cận đứng

0x =

.

2

lim

2

x

xx

+

→

= +

−

, suy ra tiệm cận đứng

2x =

.

Câu 36.Chọn B.Tập xác định

( )

0;D = +

.

( )

1

' ln 1 0 0;y x x

e

= + =  =  +

.Ta có

( )

22

1 1 1 2

; ; f f f e e

e e e e

   

= − = − =

   

   

.

Suy ra

1

; m M e

e

= − =

.Vậy

.1Mm=−

.

Câu 37.Chọn B. Gọi E và F lần lượt là trung điểm của AB và CD. Ta chứng minh được

( )

CD ABF⊥

.

Trang 59

Dựng

AH BF⊥

( )

AH BCD⊥

. Do tam giác ACD đều cạnh bằng

a

nên đường cao

3

2

AF a=

.Ta có

( )

1

.

3

ABCD

V AH dt BCD=

mà

( )

2

3

4

dt BCD a=

nên thể tích

ABCD

V

lớn nhất khi và chỉ khi AH lớn nhất. Do

AH FH⊥

nên

AH AF

. Vậy

ABCD

V

lớn nhất khi tam giác

H F AF BF  ⊥

.

Khi đó khoảng cách giữa AB và CD là

6

EF=

4

2

AF a

=

.

Câu38.Chọn A .Sử dụng máy tính được nghiệm trong khoảng

5

2;

2







.

Câu 39.Chọn A .Ta có

2

D

' 3 3 0 1 2, 2

C CT

y x x y m y m= − =  =   = + = −

. Từ đó giá trị cực

đại và giá trị cực tiểu trái dấu

2

4 0 2 2mm −  −  

.

Câu 40.Chọn A.Máng nước có dạng hình lăng trụ , đáy là hình thang cân có thể tích :

.V B h=

Máng nước thoát được nhiều nước nhất nếu đáy hình thang có diện tích lớn nhất.

Ta có : Chiều cao của hình thang :

20.sinh



=

và

20.cosCM



=

.

Đáy lớn của hình thang :

( )

20 2. 20cos 20 40.cosCD



= + = +

.

Diện tích hình thang :

( ) ( ) ( )

( )

2

11

. 20 20 40.cos .20sin 400 1 cos .sin 1600.

22

1

t

S AB CD h

t

   

= + = + + = + =





+

.

Với

tan

2

t



=

và

01t

.

Xét hàm số :

( )

42

22

3 2 1

11

t t t

f t f t

tt

− − +



=  =

++

;

( ) ( )

1

0 0;1

3

f t t



=  = 

.

Bảng xét dấu :

t

0

1

3

1

( )

ft



+

0

−

( )

ft

Vậy

( )

ft

đạt giá trị lớn nhất tại

0

11

tan 60

2

33

t



=  =  =

.

Suy ra : diện tích hình thang lớn nhất

0

60



=

.

Câu 41.Chọn D.Ta có :

( )

( ) ( ) ( ) ( )

2

4 2 4

2

4 16 4

4

log 4 4 log 4 0 log 2 log 4 0 *x x x m x x m− + + + − =  − + + − =

Trang 60

Điều kiện :

2 0 2

4 0 4

xx

−  







+   −



.

Khi đó :

( ) ( ) ( )

( ) ( )

22

4 4 4

* log 2 log 4 0 log 2 8 2 8 4

m

x x m x x m x x − + + − =  + − =  + − =

( ) ( )

( )

22

2 8 2 2 8 2 **

mm

x x x x + − =  + − =

.

Xét hàm số

( )

2

28f x x x= + −

.

( )

22f x x



 = +

.

( )

01f x x



=  = −

.

Bảng biến thiên

x

−

1−

+

( )

fx



−

0

+

( )

2

28f x x x= + −

+

0

9−

0

+

Từ đó suy ra bảng biến thiên của hàm số :

( )

2

28f x x x= − −

x

−

1−

+

( )

fx



−

0

+

( )

2

28f x x x= + −

+

0

9

0

+

Để phương trình

( )

**

có

4

nghiệm phân biệt thì

2

0 2 9 2log 3

m

m   

.

Vậy

( )

2

;2log 3m −

thỏa yêu cầu bài toán.

Câu 42.Chọn C.Theo công thức tăng trưởng dân số :

.

ni

S Ae=

.

Ta có :

.1.03% .1.03%

85

ln

85

77

340 308.e e 9.6

77 1.03%

nn

n







=  =  = 

(năm )

Câu 43.Chọn B.Phương trình hoành độ giao điểm:

23

2

x

xm

x

+

=+

−

( ) ( )

2

2 6 2 3 0 *

2

x m x m

x



+ − − − =













.

Do

( )

2

*

2

4 60 0,

2.2 6 2 2 3 0

m m m

mm



 = + +  





+ − − − 





nên đường thẳng

:2d y x m=+

luôn cắt đồ thị

( )

C

tại hai điểm phân biệt

(Giả sử hoành độ giao điểm lần lượt là

12

,xx

). Ta có:

( )

2

7

2

y

x

−



=

−

Theo yêu cầu bài toán:

( ) ( )

12

22

12

77

22

y x y x

xx

−−



=  =

−−

Trang 61

( )

22

1 2 1 2

40x x x x − − − =

( )( )

1 2 1 2

40x x x x − + − =

12

6

4 4 2

2

xx

m

x x m

=







−



+ =  =  = −



Loại

12

xx=

(Không xảy ra do yêu cầu bài toán đường thẳng phải cắt đồ thị

( )

C

tại hai điểm phân biệt).

Từ đó ta tìm được duy nhất một giá trị của

m

.

Câu 44.Chọn A . Giả sử đường đi của con kiến là A-C-B ( hình vẽ ).

Đặt

 

; 0;30CE x x=

. Độ dài đường đi

( )

2

2 2 2

30 20 30y AC CB x x= + = + + + − 

( ) ( )

22

30 20 30 50 30 10 34xx+ + + − = + =

Dấu bằng khi

( )

20. 30. 30 18x x x= −  =

cm

.

Câu 45.Chọn A . Gọi

O

là tâm đáy. Ta có:

( )

SO ABC⊥

và

( )

2

3. 3

63

3

SO



= − =





Dựng

OK SM⊥

. Suy ra

( )

OK SBC⊥

;

3. 3 3

62

OM ==

( )

22

3

.3

. 15

4

;

3

5

3

4

OM SO

d O SBC OK

OM SO

= = = =

+

( )

,

d A SBC

AM

OM

d O SBC

=

.

Suy ra:

( )

15 3 15

, . 3.

55

AM

R d A SBC OK

OM

= = = =

Diện tích mặt cầu:

2

3 15 108

44

55

SR







= = =





.

Câu 46. Chọn D.Gọi

H

là hình chiếu vuông góc của

S

lên

AD

. Suy ra,

( ) ( )

.SH ABCD SH BCD⊥  ⊥

2.

2.6

3.

4

ACD

S

SH

AD

= = =

Gọi

I

là trung điểm của

AD

nên

1

.2.2 2.

2

BCD ICD

SS= = =

Thể tích

.S BCD

là:

.

1

.2.3 2.

3

S BCD

V ==

Câu 47.Chọn A.

3 3 2

2 2 2

3 0 3x x m x x m− − =  − =

( )

*

Số nghiệm phương trình

( )

*

bằng số giao điểm của đồ thị hàm số

32

3y x x=−

và

2

ym=

.

Đồ thị hàm số

32

3y x x=−

là:

30

cm

30 -

x

30

cm

20

cm

A

F

G

B

D

E

C

H

O

M

N

A

C

B

S

K

2

I

A

B

C

S

D

H

Trang 62

TH1:

( )

*

có

2

nghiệm

2

4

0

m



=−

  







.

TH2:

( )

*

có

4

nghiệm

2

40m−  

(Vô lý) .

TH3:

( )

*

có

3

nghiệm

2

00mm =  =

.

Do đó phương trình

3

22

30x x m− − =

có nhiều nhất

3

nghiệm thực.

Câu 48.Chọn C. - Dựng trục đường tròn ngoại tiếp

BCE

(Đường thẳng

d

qua trung điểm

J

của

EC

và vuông

góc với mp

( )

BCE

).

- Dựng tâm

K

của đường tròn ngoại tiếp

SBE

, dựng trục đường tròn

ngoại tiếp

SBE

(Đường thẳng

d



qua tâm

K

và vuông góc với

( )

mp SEB

).

Gọi

I d d



=

. Suy ra

I

là tâm mặt cầu ngoại tiếp hình chóp

.S BCE

.

- Bán kính mặt cầu ngoại tiếp

.S BCE

là:

22

R IC IJ JC= = +

.

- Do

IKHJ

là hình chữ nhật nên

IJ HK=

.

Do

K

là tâm đường tròn ngoại tiếp

SBE

nên ta có

2BKE BSE=

( Góc ở tâm có số đo gấp hai lần góc nội tiếp

cùng chắn cung

BE

).

HKE BSE



 = =

.cot .cot

2

a

KH EH



 = =

.

SAE

vuông cân tại

A

nên

0

45SEA ASE==

2

tan 2

a

BSA

a

==

.Mà

0

45BSA



=−

( )

0

tan 1 1

tan tan 45

3

1 tan

BSA



−

= − = =

+

cot 3



=

.

3

.cot .3

22

aa

KH EH



 = = =

;

22

45

2 2 2

EC a a a

JC

+

= = =

2

3 5 14

2 2 2

aa

Ra



= + =





.

2 2 2

14

4. . 4. . 14

4

mc

S R a a

  

 = = =

.

Câu 49.Chọn C.Theo giả thiết ta có .Khi

0x 

thì

( )

( ) ( )

0

.0

0

gx

y f x g x

fx







 = 









Và khi

0x 

thì

( )

( ) ( )

0

.0

0

gx

y f x g x

fx







 = 









.Trong

4

đáp án ta thấy có đáp án C thỏa mãn.

Câu 50.Chọn A..Điều kiện:

1

.

2

x 

Phương trình đã cho tương đương :

( )

1 2 1 2

5 5 .5 4 0 1

x x x x

m

+ − − − −

− − =

.

Đặt

12

5 , 0

xx

tt

+−

=

..Phương trình đã cho trở thành:

( )

2

5

4 0 4 5 2

m

t t t m

t

− − =  − =

x

y

-4

-2

2

O

1

2a

a

d'

d

I

K

H

J

E

D

A

B

C

S

K

H

B

E

S

Trang 63

Xét

1

( ) 1 2 ,

2

f x x x x= + −  

.

Với

1

2

x 

, ta có:

( ) ( )

1

1 0 1 2 1 0

12

f x f x x x

x



= −  =  − =  =

−

Lập bảng biến thiên ta được

( ) 1.fx

Do đó

05t

Để phương trình

( )

1

có nghiệm thì

( )

2

phải có nghiệm trên khoảng

(



0;5

.

Xét hàm số:

( ) ( ) ( ) ( )

2

4 ; 0 5 2 4 0 2f t t t t f t t f t t



= −    = −  =  =

.

Bảng biến thiên:

Từ bảng biến thiên ta được

4

4 5 5 1

5

mm−    −  

9

5

ba − =

.

ĐỀ 55

ĐỀ THI THỬ THPT QUỐC GIA 2020

MÔN TOÁN

Thời gian: 90 phút

Câu 1: Giá trị lớn nhất của hàm số y = 2x + 3x - 1 trên đoạn

1

;1

2



−





A.

1

;1

2

max 4y



−





=

B.

1

;1

2

max 6y



−





=

C.

1

;1

2

max 3y



−





=

D.

1

;1

2

max 5y



−





=

Câu 2: Xét các mệnh đề sau, mệnh đề nào là mệnh đề đúng?

A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thì song song với nhau.

B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

C. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song songvới nhau.

D. Hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì song song với nhau.

Câu 3: Một hình trụ có bán kính đáy , r = a độ dài đường sinh . l = 2a Diện tích toàn phần của hình trụ này là:

A. 2



a

2

. B. 4



a

2

. C.6



a

2

. D. 5



a

2

.

Câu 4: Có bao nhiêu phép tịnh tiến biến một đường thẳng thành chính nó?

A. 1 B. 2 C. Không có D. Vô số

Câu 5: Tập nghiệm của bất phương trình

21

3 27

x−



là:A.

( )

3; +

B.

1

;

3



+





C.

1

;

2



+





D.

( )

2;+

Câu 6: Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập số thực

?

0

1

2

−

x

y



y

0

−

+

1

2

−

0

5

2

t

( )

ft



( )

ft

0

−

+

4−

5

0

Trang 64

A.

1

2

logyx=

B.

3

x

y





=





C.

2

x

y

e



=





D.

( )

2

4

log 2 1yx



=+

Câu 7: Cho hàm số có f đạo hàm trên khoảng I. Xét các mệnh đề sau:

(I). Nếu , thì hàm f (x)  0 x I số nghịch biến trên I

(II). Nếu , f (x)  0 x I (dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I ) thì hàm số nghịch biến trên I

(III). Nếu , thì hàm f ( x)  0 x I số nghịch biến trên khoảng I

(IV). Nếu , f (x)  0 x I và f (x) = 0 tại vô số điểm trên thì hàm I số không f thể nghịch biến trên khoảng I

Trong các mệnh đề trên. Mệnh đề nào đúng, mệnh đề nào sai?

A. I, II và IV đúng, còn III sai. B. I, II, III và IV đúng.

C. I và II đúng, còn III và IV sai. D. I, II và III đúng, còn IV sai.

Câu 8: Một nhóm có 10 người, cần chọn ra ban đại diện gồm 3 người. Số cách chọn là: A.240 B.

3

10

A

C.

3

10

C

D.360.

Câu 9: Trong mặt phẳng tọa độ cho Oxy bốn điểm A(3;−5), B(−3;3) ,C(−1;−2) ,D(5;−10). Hỏi G

1

;3

3



−





là trọng

tâm của tam giác nào dưới đây? A.ABC. B. BCD. C.ACD.

D.ABD

Câu 10: Tập xác định của hàm số

( )

1

5

1yx=−

là: A.

( )

0;+

B.



1;



+



C.

( )

1; +

D.

Câu 11: Trong các hàm số sau, hàm số nào là hàm số chẵn. A. y = tan x B.y = sin x C.y = cos x D.y =

cot x

Câu 12: Gọi là d tiếp tuyến tại điểm cực đại của đồ thị hàm số . Mệnh đề nào dưới đây y = x

3

− 3x

2

+ 2 đúng?

A. d có hệ số góc dương. B. d song song với đường thẳng x = 3

C. d có hệ số góc âm. D. d song song với đường thẳng y = 3.

Câu 13: Hình lập phương có mấy mặt phẳng đối xứng ? A. 6 B. 8

C. 9 D. 7

Câu 14: Trong các dãy số sau, dãy nào là cấp số cộng:

A.

1

3

n

u

+

=

B.

2

1

n

u

n

=

+

C.

2

1

n

un=+

D.

52

3

n

u

−

=

Câu 15: Cho dãy số

( )

1

5

:

n

nn

u

u u n

+

=





=+



. Số 20 là số hạng thứ mấy trong dãy?A. 5 B. 6. C. 9

D. 10

Câu 16: A và B là hai điểm thuộc hai nhánh khác nhau của đồ thị hàm số

2

x

y

x

=

−

. Khi đó độ dài đoạn AB ngắn

nhất bằng A.

42

B. 4 C. 2

D.

22

Câu 17: Cho hình lăng trụ đều ABC.A



B



C



. Biết mặt phẳng (A¢BC) tạo với mặt phẳng (ABC) một góc 30° và tam

giác có A¢BC diện tích bằng Tính thể tích khối lăng trụ 8a

2

. ABC.A



B



C



.A.

3

83a

B.

3

8a

C.

3

83

3

a

D.

3

8

3

a

Câu 18: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. là M một điểm thuộc đoạn SB( M khác S và B).

Mặt phẳng ( ADM ) cắt hình chóp S.ABCD theo thiết diện là

A. Hình bình hành. B. Tam giác C. Hình chữ nhật. D. Hình thang

Câu 19: Hàm số nào sau đây có đồ thị như hình bên?

Trang 65

A. y = −x

4

+ 4x

2

+ 3 B. y = −x

4

+ 2x

2

+ 3 C. y = (x

2

- 2)

2

-1 D. y = (x

2

+ 2)

2

-1

Câu 20: Tìm tập xác định của hàm số

( )

2

1

log 5

y

x

=

−

A.(−;5) \4. B. (5;+). C. (−;5). D. 5;+)

Câu 21: Cắt hình trụ (T) bằng một mặt phẳng đi qua trục được thiết diện là một

hình chữ nhật có diện tích bằng 30cm

2

và chu vi bằng 26cm . Biết chiều dài của

hình chữ nhật lớn hơn đường kính mặt đáy của hình trụ (T). Diện tích toàn phần

của (T) là: A.

( )

2

23 cm



B.

( )

2

23

2

cm



C.

( )

2

69

2

cm



D.

( )

2

69 cm



Câu 22: Cho log

12

3 = a . Tính log

24

18 theo a A.

31

3

a

−

B.

31

3

a

+

−

C.

31

3

a

+

D.

31

3

a

−

+

Câu 23: Hệ số của số hạng chứa x

6

trong khai triển nhị thức

12

3

x



−





(với

0x 

) là:

A.

220

729

−

B.

6

220

729

x

C.

6

220

729

x

−

D.

220

729

Câu 24: Khối nón có bán kính (N) đáy bằng và 3 diện tích xung quanh bằng . Tính 15 thể tích V của khối nón (N)

A.V = 36 B.V = 60 C.V = 20 D.V =12

Câu 25: Cho tứ diện ABCD có AB = AC, DB = DC. Khẳng định nào sau đây là đúng?

A. AB ⊥ BC B.CD ⊥ ( ABD) C.BC ⊥ AD D.AB ⊥ (ABC)

Câu 26: Cho phương trình

3

2 sin

44

xx



   

− = +

   

   

. Tính tổng các nghiệm thuộc khoảng

( )

0;



của phương

trình trên. A.

7

2



B.



C.

3

2



D.

4



Câu 27: Hàm số nào trong bốn hàm số được liệt kê dưới đây không có cực trị?

A.

23

2

x

y

x

−

=

+

B.

4

yx=

C.

3

y x x= − +

D.

2yx=+

Câu 28: Có bao nhiêu tiếp tuyến của đồ thị hàm số

23

2

x

y

x

−

=

+

đi qua giao điểm hai đường tiệm cận?

A. 1. B. Không có. C. Vô số. D. 2.

Câu 29: Trong mặt phẳng tọa độ Oxy cho tam giác ABC có D(3;4), E (6;1), F (7;3) lần lượt là trung điểm các cạnh

AB, BC,CA. Tính tổng tung độ của ba đỉnh tam giác ABC A.

16

3

B.

8

3

C. 8 D. 16

Câu 30: Cho hình chóp có S.ABC đáy ABC là tam giác vuông cân, BA = BC =a,

0

90SAB SCB==

biết khoảng

cách từ A đến mặt phẳng (SBC) bằng

3

2

a

. Góc giữa SC và mặt phẳng (ABC)là: A.

6



B. arccos

3

4

C.

3



D.

4



Câu 31: Cho hàm số

42

1

3

4

y x x=−

có đồ thị (C) . Có bao nhiêu điểm A thuộc (C) sao cho tiếp tuyến của (C) tại A

cắt (C) tại hai điểm phân biệt M (x

1

; y

1

) N (x

2

; y

2

) ( M ,N khác A ) thỏa mãn

( )

1 2 1 2

5y y x x− = −

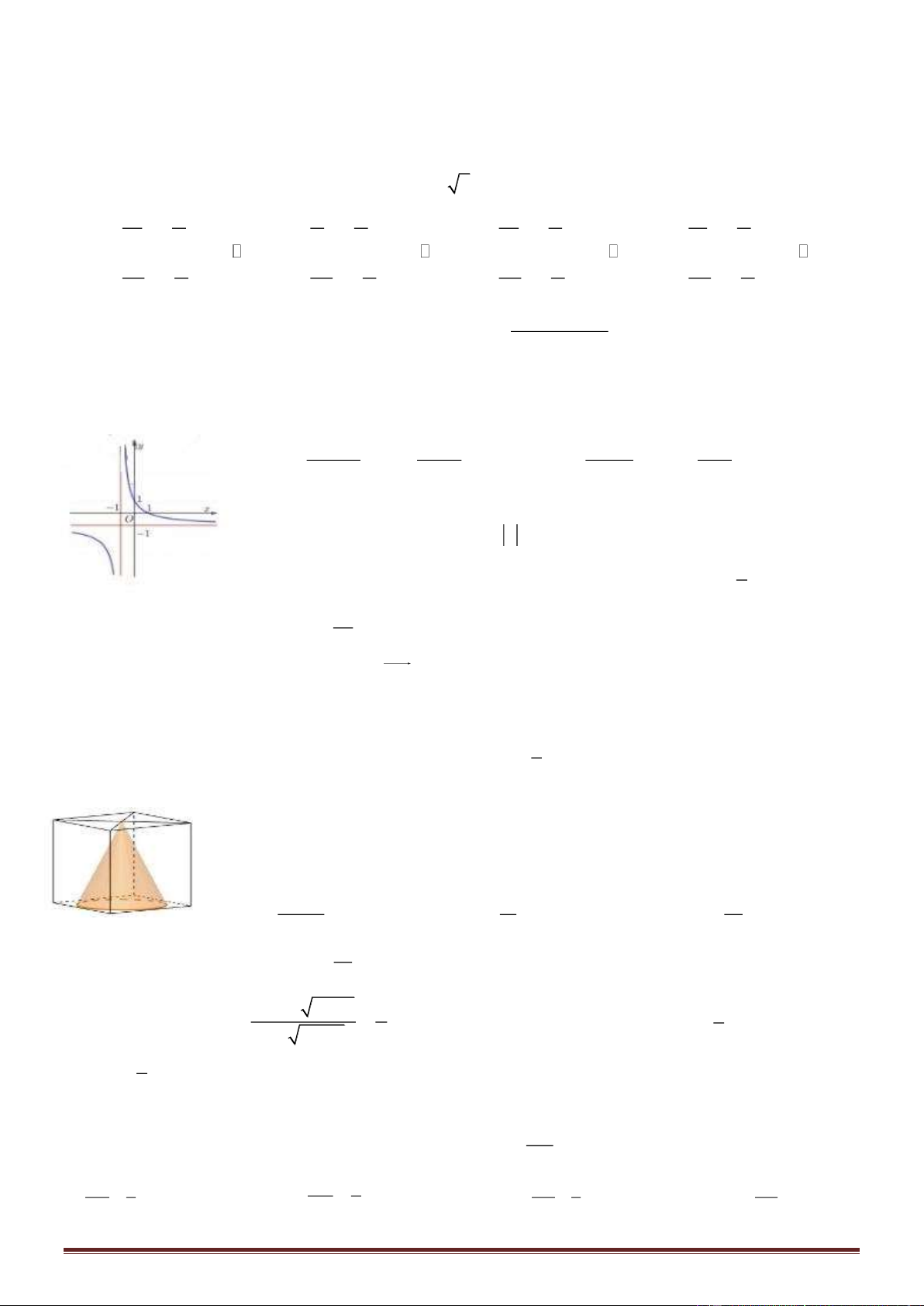
Trang 66

A. 1. B. 2 . C. 0 . D. 3 .

Câu 32: Giả sử đồ thị hàm số

( )

2 4 2 2

1 2 1y m x mx m= + − + +

có 3 điểm cực trị là A, B ,C mà x

A

 x

B

 x

C

. Khi

quay tam giác ABC quanh cạnh AC ta được một khối tròn xoay. Giá trị của m để thể tích của khối tròn xoay đó lớn

nhất thuộc khoảng nào trong các khoảng dưới đây: A. (4;6) B. (2;4) C. (−2;0)

D. (0;2)

Câu 33: Giải phương trình

8.cos2 .sin2 .cos4 2x x x =−

A.

( )

32 4

3

32 4

xk

k

xk





=+







=+





B.

( )

88

3

88

xk

k

xk





=+







=+





C.

( )

32 4

5

32 4

xk

k

xk





=+







=+





D.

( )

16 8

3

16 8

xk

k

xk





=+







=+





Câu 34: Tìm tất cả các giá trị thực của tham số m để hàm số

2

log 2

log 1

mx

y

xm

−

=

−−

nghịch biến trên (4;+) .

A. m  −2 hoặc m 1. B. m  −2 hoặc m =1. C. m  −2 hoặc m =1.

D. m  −2.

Câu 35: Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?

A.

21

x

y

x

−+

=

+

B.

1

x

y

x

−+

=

+

C.

2

21

x

y

x

−+

=

+

D.

1

x

y

x

−

=

+

Câu 36: Cho hàm số

( ) ( ) ( )

32

2 1 3 2y f x x m x m x= = − + + − +

. Tìm tất cả các giá

trị của tham số m để hàm số

( )

y f x=

có 3 điểm cực trị.

A. m  3. B. m  3. C.

1

2

m−

D.

1

3

2

m

−



Câu 37: Có bao nhiêu số tự nhiên có 3 chữ số

abc

cho a, b, c là độ dài 3 cạnh của một tam giác cân.

A. 45. B. 216. C. 81. D. 165.

Câu 38: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A −3;0 ,B 3;0 và C 2;6 . Gọi H a; b; là trực tâm của

tam giác ABC. Tính 6ab A. 10 B.

5

3

C. 60

D. 6

Câu 39: Một chiếc thùng đựng nước có hình của một khối lập phương chứa đầy nước .

Đặt vào trong thùng đó một khối có dạng nón sao cho đỉnh trùng với tâm một mặt của lập

phương, đáy khối nón tiếp xúc với các cạnh của mặt đối diện. Tính tỉ số thể tích của lượng

nước trào ra ngoài và lượng nước còn lại ở trong thùng.

A.

12



−

B.

1

11

C.

12



D.

11

12

Câu 40: Cho giới hạn

3

1 5 1

lim

43

x

x x a

b

xx

→

+ − +

=

−−

(phân số tối giản). Giá trị của T = 2a− b là: A.

1

9

B.

1−

C.10. D.

9

8

Câu 41: Cho tứ diện ABCD. Gọi K, L lần lượt là trung điểm của AB và BC, N là điểm thuộc đoạn CD sao cho CN =

2ND. Gọi P là giao điểm của AD với mặt phẳng (KLN). Tính tỷ số

PA

PD

A.

1

2

PA

PD

=

B.

2

3

PA

PD

=

C.

3

2

PA

PD

=

D.

2

PA

PD

=

Trang 67

Câu 42: Tìm số nghiệm của phương trình log

2

x + log

2

(x -1) = 2 A. 0 B. 1 C. 3

D. 2

Câu 43: Hàm số

( )

2

ln 1y x mx= + +

xác định với mọi giá trị của x khi

A.

2

m

−









B. m >2 C. − 2 m  2 D. m < 2

Câu 44: Trong một lớp có (2n +3 ) học sinh gồm An, Bình, Chi cùng 2n học sinh khác . Khi xếp tùy ý các học sinh

này vào dãy ghế được đánh số từ 1 đến (2n +3 ) , mỗi học sinh ngồi một ghế thì xác xuất để số ghế của An, Bình,

Chi theo thứ tự lập thành cấp số cộng la

17

1155

. Số học sinh của lớp là:A. 27. B. 25. C. 45. D. 35.

Câu 45: Cho một khối lập phương có cạnh bằng a. Tính theo a thể tích của khối bát diện đều có các đỉnh là tâm

các mặt của khối lập phương. A.

3

4

a

B.

3

6

a

C.

3

12

a

D.

3

8

a

Câu 46: Đồ thị hàm số

( )

y f x=

đối xứng với đồ thị của hàm số

( )

0; 1

x

y a a a=  

qua điểm I (1;1).Giá trị

của

biểu thức

1

2 log

2018

a

f



+





bằng A. 2016 . B. −2016 . C. 2020 . D.

−2020 .

Câu 47: Tìm tất cả các giá trị thực của tham số m để hàm số

32

sin 3cos sin 1y x x m x= − − −

đồng biến trên đoạn

3

;

2









A. m  −3 . B. m  0 . C. m  −3 . D. m  0

.

Câu 48: Một cái phễu có dạng hình nón chiều cao của phễu là 30cm. Người ta đổ

một lượng nước vào phễu sao cho chiều cao của cột nước trong phễu bằng 15cm.

(Hình H

1

). Nếu bịt kín miệng phễu rồi lật ngược phễu lên (hình H

2

) thì chiều cao

của cột nước trong phễu gần bằng với giá trị nào sau đây?

A. 1,553 (cm). B. 1,306 (cm). C. 1,233 (cm). D. 15 (cm)

Câu 49: Hàm số

( )

2

log 4 2

xx

ym= − +

có tập xác định là thì

A.

1

4

m 

B.

0m 

C.

1

4

m 

D.

1

4

m 

Câu 50: Cho hình thang vuông ABCD với đường cao AB = 2a , các cạnh đáy AD = a và BC = 3a . Gọi M là điểm

trên đoạn AC sao cho

AM k AC=

. Tìm k để BM ⊥ CD A.

4

9

B.

3

7

C.

1

3

D.

2

5

HƯỚNG DẪN GIẢI ĐỀ 04

ĐÁP ÁN

1-A

2-C

3-C

4-D

5-D

6-C

7-C

8-C

9-B

10-C

11-C

12-D

13-D

14-D

15-B

16-B

17-A

18-D

19-C

20-A

21-C

22-B

23-A

24-D

25-C

26-B

27-A

28-B

29-C

30-C

31-B

32-B

33-C

34-D

35-B

36-A

37-D

38-A

39-A

40-C

41-D

42-B

43-C

44-D

45-B

46-B

47-B

48-B

49-D

50-D

LỜI GIẢI CHI TIẾT

Câu 1: Đáp án A.Tập xác định: D

=

.Hàm số

32

2 3 1y x x= + −

liên tục và có đạo hàm trên đoạn

1

;1

2



−





.

Trang 68

Đạo hàm:

2

' 6 6y x x=+

.Xét

2

1

0 ;1

2

' 0 6 6 0

1

1 ;1

2

x

y x x

x





=  −









=  + = 





= −  −









Ta có:

( ) ( )

11

; 0 1; 1 4

22

y y y



− = − = − =





.Vậy

1

;1

2

max 4y



−





=

Câu 2: Đáp án C. “Hai mặt phẳng cùng vuông góc với một mặt phẳng thì song song với nhau”

và mệnh đề “Hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì song song

với nhau” là mệnh đề sai, ví dụ trong hình lập phương trên ta có (C

1

B

1

BC) và (D

1

B

1

BD)

cùng vuông góc với (ABCD) nhưng 2 mặt phẳng đó lại cắt nhau.

“Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau” là

mệnh đề sai ví dụ như trong hình lập phương trên ta có A

1

B

1

và C

1

B

1

cùng vuông góc với B

1

B

nhưng A

1

B

1

⊥

C

1

B

1

“Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau” là

mệnh đề đúng .

Câu 3: Đáp án C.

22

2 2 2 .2 6

tp d xq

S S S a a a a

  

= + = + =

Câu 4: Đáp án D.Có vô số phép tịnh tiến biến một đường thẳng thành chính nó. Đó là các phép tịnh tiến có véc tơ

tịnh tiến là véc tơ không hoặc véc tơ tịnh tiến là véc tơ chỉ phương của đường thẳng đó.

Câu 5: Đáp án D.

2 1 2 1 3

3 27 3 3 2 1 3 2

xx

−−

    −   

Vậy tập nghiệm của bất phương trình là (2;

+

)

Câu 6:Đáp án C.Hàm số

2

x

y

e



=





là hàm số mũ, có cơ số 0 < a

2

1

e

=

nên hàm sốnghịch biến trên tập số thực

Câu 7: Đáp án C.Câu III sai vì thiếu dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I

Câu IV sai vì có thể vô số điểm trên I xuất hiện rời rạc thì vẫn có thể nghịch biến trên khoảng I

Câu 8: Đáp án C.+ Số cách chọn ra 3 người vào ban đại diện trong 10 người là :

3

10

C

(không phân biệt thứ tự).

Câu 9: Đáp án B.Ta thấy

( ) ( )

2; 5 , 8; 13BC BD= − = −

nên chúng không cùng phương B,C,D là 3 đỉnh của một

tam giác.Mặt khác, ta lại có:

3 1 5 1

3 3 3

3 2 10

3

33

B C D

x x x

y y y

++

− − +



==





++

−−



= = −





Vậy

1

;3

3

G



−





là trọng tâm của tam giác BCD

Câu 10: Đáp ánC.Hàm số y = x



với  không nguyên xác định khi . x  0

Điều kiện xác định của hàm số

( )

1

5

1yx=−

là x -1 > 0 hay x > 1.Vậy tập xác định:

( )

1;D = +

Câu 11: Đáp án C.Hàm số y = tan x, y = sin x, y = cot x là các hàm số lẻ.Hàm số y = cos x là hàm số chẵn

Câu 12: Đáp án D.Ta có

2

02

' 3 6 , ' 0

22

xy

y x x y

xy

=  =



= − = 



=  = −



Bảng biến thiên

Từ bảng biến thiên ta suy ra đồ thị hàm số có điểm cực đại là (0;2)

Phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm(0;2) là

( ) ( )

0 0 2 2y x y d= − +  =

Do đó song song d với đường thẳng y = 3.

Trắc nghiệm: Hàm số đã cho có đạo hàm tại mọi điểm và tại

điểm cực trị có y ' = 0 nên tiếp tuyến d của đồ thị hàm số tại điểm

cực đại (hoặc tại điểm cực tiểu) là đường thẳng song song trục

hoặc trùng Ox,từ đó Chọn D.

Câu 13: Đáp án là D

Trang 69

Câu 14: Đáp án là D.Ta có dãy u

n

là cấp số cộng khi

1

,*

nn

u u d n

+

− =  

với là hằng số.

Bằng cách tính 3 số hạng đầu của các dãy số ta dự đoán đáp án D.

Xét hiệu

1nn

uu

+

−

( )

5 1 2

5 2 5

,*

3 3 3

n

+−

−

= − =  

Vậy dãy

52

3

n

u

−

=

là cấp số cộng.

Câu 15: Đáp án là B.

1 2 3 4 5 6

5, 6, 8, 11, 16, 20u u u u u u= = = = = =

.Vậy số là 20 số hạng thứ 6 .

Câu 16: Đáp án là B. Hàm số

2

x

y

x

=

−

có đồ thị ( C ) như hình vẽ. Gọi A

;

2

a





−



và

;

2

b

Bb

b





−



là hai điểm thuộc hai nhánh của

( )( )

2C a b

.Ta có:

( )( )

;;

2 2 2 2

b a b a

AB b a b a

b a b a



−



= − − = −



− − − −



Áp dụng BĐT Côsi ta có:

( )( )

( )

2

22

4

ba

−

− − 

Suy ra:

( )

( )( )

( )

2

22

2

22

64

16

22

ba

AB b a b a

ba

−

= − +  − + 

−

−−





4AB

. Dấu bằng xảy ra khi và chỉ khi

22a =−

và

22b =+

.Vậy

min

4AB =

Câu 17: Đáp án A.Gọi là trung M điểm của BC.Chứng minh được BC

⊥

(AA'M) . Do đó góc giữa hai mặt phẳng

và

(A'BC) mặt phẳng

( )

ABC

là góc

0

' 30A MA =

.Đặt AB = x

Tam giác là hình ABC chiếu của tam giác A'BC lên mặt phẳng

( )

02

' ' '

03

. ' ' '

.cos30 4 3 4 2a 3

'

tan30 ' 2a; '. 8 3

ABC A B C

ABC A B C ABC

ABC S S a x a AM

AA

AA V AA S a

AM

 = =  =  =

=  = = =

Câu 18: Đáp án D. Ta có là M một điểm thuộc đoạn SB với M khác . S và B

Trang 70

Suy ra

( ) ( )

( )

( ) ( )

/ / / /

//

M ADM SBC

AD ADM

ADM SBC Mx BC AD

BC SBC

AD BC











  =









Gọi N = Mx



SC thì (ADM ) cắt hình chóp theo S.ABCD thiết diện là tứ giác . Vì

AMND. Vì MN // AD và MN với AD không bằng nhau nên tứ giác là hình thang.

Câu 19: Đáp án C.Dựa vào hình dạng của đồ thị hàm số

42

y ax bx c= + +

suy ra hệ số a > 0 -> loại A,B.

Và hàm số có 3 điểm cực trị => a.b < 0

( )

2

21yx = − −

Câu 20: Đáp án A.Điều kiện xác định của hàm số là

( )

2

50

55

log 5 0

5 1 4

x

xx

x

xx

−











  

−

−  







Vậy tập xác định của hàm số là D =

( )  

;5 \ 4−

Câu 21: Đáp án C. Gọi h,r lần lượt là đường cao và bán kính đáy của hình trụ (T ) Thiết diện của mặt phẳng và

hình trụ là hình (T ) chữ nhật ABCD. Khi đó theo giả thiết ta có

( )

22

.2 30 15

2 13

2 2 26

ABCD

h r h r

S h r hr

hr

C h r









= =  =





+=

= + =



( )

2

22

13 2 13 2

2 15 15 0

53

3

10

2

h r h r

rr

r h l

r h tm











 = −  = −





− + − =

=  =













=  =









Vậy

( )

2

22

3 3 69

2 2 2 2 . .10 2

2 2 2

tp xq

S S S rh r cm



   



= + = + = + =





Câu 22: Đáp án B.Ta có:

( ) ( )

2 2 2 2

12 2

22

2 2 2

log 3 log 3 log 3 log 3

2

log 3 log 3

log 12 2 log 3 1

log 2 .3 log 2 log 3

a

= = = = =  =

+−

+

Ta có:

( )

2

22

24

2

22

2

1 2.

log 2.3

log 18 1 2log 3

31

1

log 18

2

log 24 3 log 3 3

log 2 .3

3

1

a

+

−

= = = = =

+−

+

−

.Vậy

24

31

log 18

3

a

+

=

−

Câu 23: Đáp án A.Số hạng tổng quát trong khai triển

12

3

x



−





là

( ) ( )

12

12 2 2 12

12 12

3

1 .3 . , 12

3

kk

k

k k k k

x

T C C x k k

x

−

−−

   

= − = −  

   

   

.T chứa

6

2 12 6 9x k k − =  =

Vậy hệ số cần tìm là :

( )

9

96

12

220

1 .3

729

C

−

−=

Trang 71

Câu 24: Đáp án DTa có

15

5

3

xq

S

S rl l

r





=  = = =

Chiều cao

22

25 9 4h l r= − = − =

;

22

11

.3 .4 12

33

V r h

  

= = =

Câu 25: Đáp án C.Gọi I là trung điểm BC.Có Suy ra là trung AB = AC,

IB = IC. Suy ra là trung AI trực của BC . Nên BC

⊥

AI.Tương tự BC

⊥

DI.Suy ra BC

⊥

(AID) Suy ra . BC

⊥

AD Chọn C

Câu 26: Đáp án B

Ta có:

( )

3

2

22

3

44

sin 2 sin

2

3

44

22

63

44

xk

x x k

xk

x x k









=+

− = + +





   



− = +   



   



=+

   



− = − − +







+ Xét

( )

2x k k



= + 

Do

1

0 0 2 0

2

x k k

   

    +   −  

Vì

k 

nên không có giá trị k

+ Xét

( )

2

63

x k k



= + 

Do

2 1 5

00

6 3 4 4

x k k



    +   −  

. Vì

k 

nên hai giá trị k là k = 0 ; k = 1

Với k = 0

6

x



=

Với

5

1

6

kx



=  =

Do đó trên khoảng

( )

0;



phương trình đã cho có hai nghiệm

6

x



=

và

5

6

x



=

Vậy tổng các nghiệm của phương trình đã cho trong khoảng

( )

0;



là:

6



+

5

6



=



Câu 27: Đáp án A.+ Hàm số

23

2

x

y

x

−

=

+

.Tập xác định:

( ) ( )

; 2 2;D = − −  − +

Có

( )

2

7

'0

2

y x D

x

=   

+

=> hàm số luôn đồng biến trên từng khoảng xác định =>hàm số không có cực trị.

Các hàm số khác dễ dàng chứng minh được y’ có nghiệm và đổi dấu qua các nghiệm. Riêng hàm số cuối y’ không

xác định tại -2 nhưng hàm số xác định trên R và y’ đổi dấu qua -2 do đó có hàm số có điểm cực trị x = -2.

Câu 28: Đáp án B.Đồ thị hàm số nhận đường thẳng

2

d

x

c

= − = −

làm 2 tiệm cận đứng.

Đồ thị hàm số nhận đường thẳng

2

a

y

c

==

làm 2 tiệm cận ngang.Vậy là giao I (-2;2) điểm của hai đường tiệm

cận.

TXĐ: D = ;

( )

2

7

'

2

y

x

=

+

.Gọi tiếp tuyến tại

( )

00

;M x y

của đồ thị hàm số

23

2

x

y

x

−

=

+

có dạng:

( ) ( )

0 0 0

: ' .y y x x x y = − +

hay

( )

0

2

0

23

7

:.

2

x

y x x

x

−

 = − +

+

Vì



đi qua

( )

0

2

0

23

7

2;2 2 . 2

2

x

Ix

x

−

−  = − − +

+

Trang 72

( )

00

0

2

0 0 0

0

2 3 2 3

77

2 . 2 2

2 2 2

2

xx

x

x x x

x

−−

 = + +  = +

+ + +

+

0

2 10

2 4 10

2

x

−

 =  = −

+

trình vô

nghiệm.Vậy không tồn tại tiếp tuyến nào của đồ thị hàm số

23

2

x

y

x

−

=

+

mà đi qua giao điểm của hai tiệm cận.

Câu 29: Đáp án là C.Ta có

( )

2 2.4 8

2 2.3 6 2 8 6 2 16

2 2.1 2

A B D

A C F A B C

B C E

y y y

y y y y y y

y y y

+ = = =





+ = = =  + + = + + =





+ = = =



=>

A B C

yyy++

= 8

Câu 30: Đáp án là C. Gọi là hình D chiếu vuông góc của S lên ( ABC). H chiếu vuông góc của D lên SC.

Khi đó:

( )

AB SA

AB SAD AB AD

AB SD

⊥



 ⊥  ⊥



⊥



( )

BC SC

BC SDC BC DC

BC SD

⊥



 ⊥  ⊥



⊥



=> ABCD là hình vuông và CD = a .Ta có:

( )

3

/ / / /

2

A SBC D SBC

a

AD BC SBC d d DH DH  = =  =

Vì là hình DC chiếu vuông góc của SC lên mặt phẳng là góc ( ABCD) nên

SCD

là góc giữa đường thẳng SC và

(ABC).

3

sin

23

DH

SCD SCD

DC



= =  =

Câu 31: Đáp án B.

3

'6y x x=−

.Gọi

42

0 0 0

1

;3

4

A x x x



−





là tọa độ tiếp điểm của tiếp tuyến tại A. Phương trình

tiếp tuyến tại A là đường thẳng (d) có phương trình:

( )

3 4 2

0 0 0 0 0

1

63

4

y x x x x x x= − − + −

Phương trình hoành độ giao điểm của (d) và (C) là:

( )

3 4 2 4 2

0 0 0 0 0

11

6 3 3

44

x x x x x x x x− − + − = −

( )

2

22

0 0 0

2 3 12 0x x x x x x − + + − =

( )

0

2

00

0

2 3 12 0 2

xx

x x x x

−=







+ + − =



(d) cắt (C) tại hai điểm phân biệt khác A khi và chỉ chi phương trình (2) có hai

nghiệm phân biệt khác x

0

( )

0

2

3

66

x









−  





Khi đó, phương trình (2) có hai nghiệm phân biệt x

1,

x

2

và (d) cắt (C) tại hai điểm phân biệt M (x

1

; y

1

), N(x

2

; y

2

)

trong đó:

( )

3 4 2

1 0 0 1 0 0 0

1

63

4

y x x x x x x= − − + −

( )

3 4 2

2 0 0 2 0 0 0

1

63

4

y x x x x x x= − − + −

( )

3

1 2 0 0 1 2

6y y x x x x − = − −

Từ giả thiết ta suy ra:

( )

( ) ( )

33

0 0 1 2 1 2 0 0

6 5 6 5x x x x x x x x− − = −  − =

(vi

12

xx

)

0

1

1 21

2

1 21

2

x



=−



−−



=



−+



=





Kết hợp với điều kiện (3) có hai giá trị thỏa mãn x

0

yêu cầu bài toán là

0

1

1 21

2

x

=−





−+



=





Trang 73

Câu 32: Đáp án là B

( ) ( )

2 3 2 2

' 4 1 4 4 1y m x mx x m x m



= + − = + −



( )

22

2

0

' 0 4 1 0 0

1

x

y x m x m m

m

x

m

=







+ =  + − =  





=



+



+ Với thì m > 0 đồ thị hàm số có 3 điểm cực trị (với

A B C

xxx

) là:

( )

22

2 2 2

2 2 2 2

; 1 ; 0; 1 ; ; 1

1 1 1 1

m m m m

A m B m C m

m m m m

   

− − + + + − + +

   

+ + + +

   

+ Quay thì



ABC quanh AC được khối tròn xoay có thể tích là:

( )

29

2

5

22

2

1 2 2 2

2. . . .

3 3 3 1 1 3

1

m m m

V r h BI IC

mm

m

   



= = = =



++



+

+ Xét hàm số

( )

9

5

2

1

m

fx

m

=

+

Có:

( )

( ) ( )

82

6

2

9

; ' 0 3 0

1

mm

f x f x m m

m

−

= =  = 

+

Ta có BBT:

Câu 33: Đáp án C :

8.cos2 .sin2 .cos4 2 4.sin4 .cos4 2 2.sin8 2x x x x x x= −  = −  = −

( ) ( )

82

2

32 4

4

sin8

55

2

82

4 32 4

xk

x k k

x k x k





  





= − +



−

 =    



= + = +





Câu 34: Đáp án D.Đặt

2

logtx=

.Ta có

( ) ( )

4; 2;xt +   +

.Hàm số được viết lại

( )

2

1

mt

y

tm

−

=

−−

Vì

2

logtx=

đồng biến trên

( )

0;+

nên yêu cầu bài toán



(1) nghịch biến trên

( )

2;+

( )

2

1 2 0

2

1

12

1

m

mm

m

  −



− + + 







    −







+











Câu 35: Đáp án B.Từ đồ thị của hàm số đã cho ta có:

Tiệm cận đứng của đồ thị hàm số là đường thằng có phương trình x = -1

Tiệm cận ngang của đồ thị hàm số là đường thằng có phương trình y = -1

Đồ thị hàm số đi qua các điểm (1;0) và (0;1).Suy ra hàm số cần tìm là

1

x

y

x

−+

=

+

Câu 36: Đáp án A.Hàm số

( ) ( )

32

2 1 3 2y x m x m x= − + + − +

TXĐ:

( ) ( )

2

' 3 2 2 1 3y x m x m= − + + −

Hàm số

( )

y f x=

có ba điểm cực trị khi và chỉ khi phương trình có hai y’ = 0 nghiệm x

1

, x

2

thỏa mãn

12

0xx

Trường hợp 1: Phương trình y’= 0 có hai nghiệm

12

0xx

( )

3 3 0 3mm −   

Trường hợp 2: Phương trình y’= 0 có hai nghiệm

12

0xx=

.Có

( )

' 0 0 3ym=  =

Trang 74

Với m = 3 thì

2

0

' 3 14 ; ' 0

14

0

3

x

y x x y

x

=





= − = 



=



(thỏa mãn)

Vậy với

3m 

thì hàm số

( )

y f x=

có ba điểm cực trị.

Câu 37: Đáp án D

TH1: là a,b,c độ dài 3 cạnh của một tam giác đều Trường hợp này có 9 số thỏa mãn yêu cầu bài toán.

TH2 : là a,b,c độ dài 3 cạnh của một tam giác cân và không đều. Không làm mất tính tổng quát, giả sử a = b

*) a = b > c

+ a = b = 2



c =1. + a = b = 3



c =1,2. + a = b = 4



c =1,2,3.

...........

+ a = b = 9



c = 1, 2,3,...,8



Có : 1+ 2 + 3+…+ 8 = 36 số thỏa bài toán.

*) a = b < c

Do

2

c

a b c a c+    

9

9 9 5,6,7,8; 8 4 8 5,6,7

2

7

7 7 4,5,6; 6 3 6 4,5

2

53

5 4 3,4; 4 2 4 3; 3 3 2

22

c a a c a a

c a a c a a c a a

+ =     = + =     =

+ =     = + =     = + =     =

+ c = 2,1 không có a tương ứng.



Có : 4+ 3+ 3+ 2 + 2 +1+1 = 16 số thỏa bài toán.



Trong trường hợp

a b c=

, có: 36 +16 = 52 số thỏa mãn.

Tương tự, mỗi trường hợp

,b c a c a b=  = 

đều có 52 số thỏa mãn.

Theo quy tắc cộng ta có: 9 + 52.3 = 165 số thỏa mãn yêu cầu bài toán bài toán.

Câu 38: Đáp án A. Đường thẳng AH đi qua

( )

3;0A −

và nhận

( )

1;6BC =−

làm véctơ pháp tuyến. Suy ra

phương trình đường thẳng AH là:

6 3 0xy− + =

Đường thẳng BH đi qua

( )

3;0B

và nhận

( )

5;6AC =

làm véctơ pháp tuyến. Suy ra phương trình đường thẳng BH

là:

5 6 15 0xy− − =

Ta có

H AH BH=  

Tọa độ H là nghiệm của hệ

6 3 0

5

2;

5 6 15 0

6

xy

H

xy

− + =











+ − =





Do đó

5

2; 6 10

6

a b ab= =  =

Câu 39: Đáp án A.Coi khối lập phương có cạnh 1. Thể tích khối lập

phường là V = 1

Từ giả thiết ta suy ra khối nón có chiều cao , bán kính h = 1 đáy

1

2

r =

Thể tích lượng nước trào ra ngoài là thể tích V

1

của khối nón.Ta có:

2

1

1 1 1

. .1

3 3 4 12

V r h





= = =

Thể tích lượng nước còn lại trong thùng là:

21

12

1

12 12

V V V



−

= − = − =

.Do đó:

1

2

12

V



=

−

Câu 40: Đáp án C.

( )

( )( )

2

33

3 4 3

1 5 1

lim lim

43

4 3 1 5 1

xx

x x x x

xx

x x x x

→→

− + −

+ − +

=

−−

− + + + +

( )

3

43

3. 3 3

9

lim

2. 4 4 8

1 1 5 1

x

x x x

→

+−

+

= = =

+

+ + + +

.Vậy T = 2a - b = 10

Câu 41: Đáp án D. Giả sử

LN BD I=

Nối K với I cắt AD tại

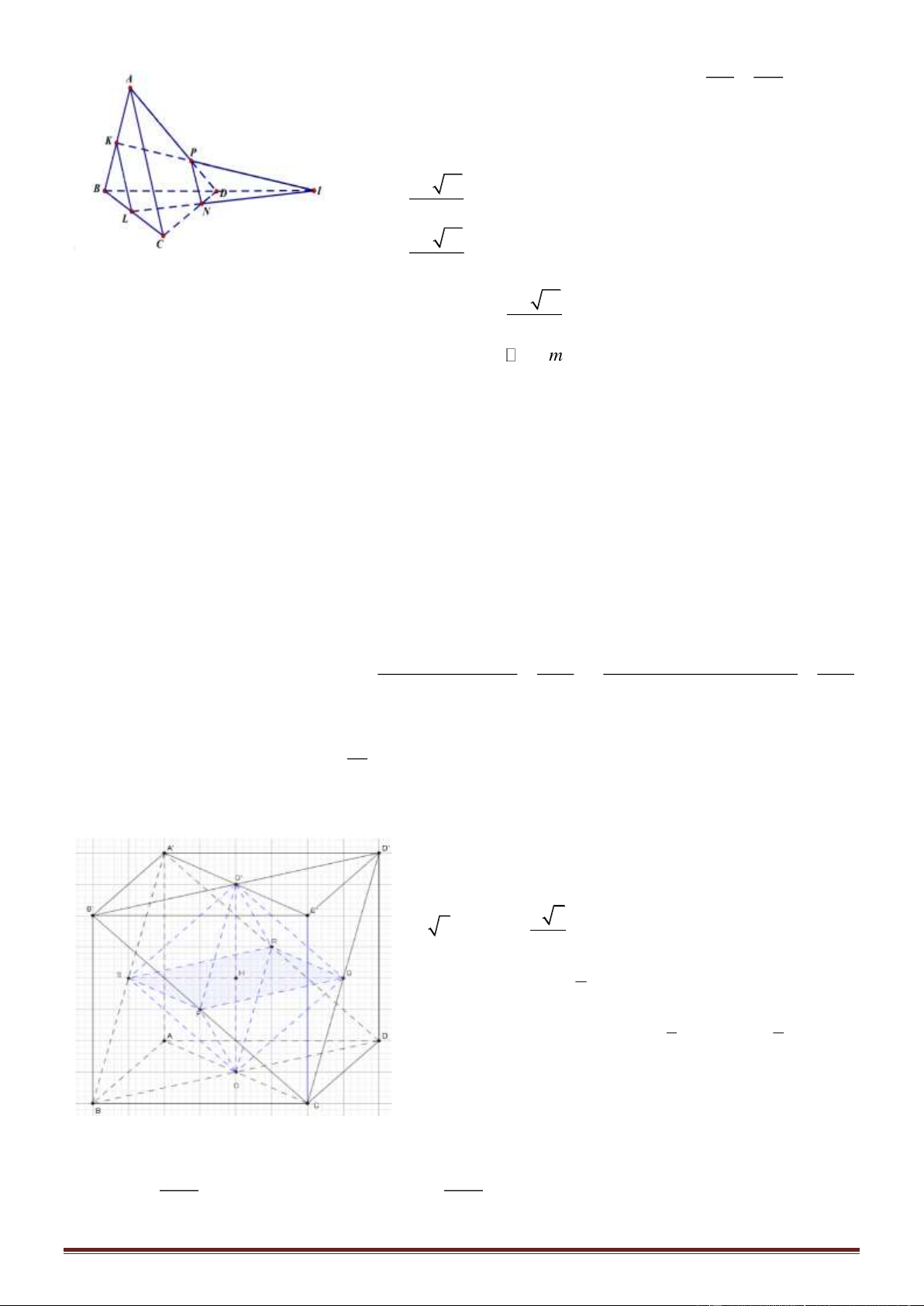
Trang 75

Suy ra

( )

KLN AD P=

.Ta có: KL // AC Suy ra:

2

PA NC

PD ND

==

Câu

42: Đáp án B.Điều kiện: x > 1.Ta có:

( )

22

log log 1 2xx+ − =

( ) ( )

2

1 2 1 2 4 0log x x x x x x − =  − =  − − =





1 17

2

1 17

2

x



−

=







+

=





Đối chiếu với điều kiện ta được nghiệm của phương trình là

1 17

2

x

+

=

Câu 43: Đáp án C.Yêu cầu bài toán

22

1 0, 4 0 2 2x mx x m m + +     −   −  

Câu 44: Đáp án D.Số cách các xếp học sinh vào ghế là

( )

2 3 !n +

Nhận xét rằng nếu ba số tự nhiên a, b, c lập thành một cấp số cộng thì a + c = 2b nên a + c là số chẵn. Như vậy a, c

phải cùng chẵn hoặc cùng lẻ.

Từ 1 đến 2n + 3 có n + 1 số chẵn và n + 2 số lẻ.

Muốn có một cách xếp học sinh thỏa số ghế của An, Bình, Chi theo thứ tự lập thành một cấp số cộng ta sẽ tiến

hành như sau:

Bước 1: chọn hai ghế có số thứ tự cùng chẵn hoặc cùng lẻ rồi xếp An và Chi vào, sau đó xếp Bình vào ghế chính

giữa. Bước này có

22

12nn

AA

++

+

cách.

Bước 2: xếp chỗ cho 2n học sinh còn lại. Bước này có

( )

2!n

Như vậy số cách xếp thỏa yêu cầu này là

( )

22

12

. 2 !

nn

A A n

++

+

Ta có phương trình

( )

( ) ( )( )

22

12

. 2 !

1 1 2

17 17

2 3 ! 1155 2 1 2 2 2 3 1155

nn

A A n

n n n n

++

+

+ + + +

=  =

+ + + + +

2

16

68 1019 1104 0

69

68

n

nn

n

=





 − − = 



=−



Vậy số học sinh của lớp là 35.

Câu 45: Đáp án là B.

Giả sử hình lập phương có ABCD.A’B’C’D’ cạnh bằng và tâm

các a mặt là P,Q, R, S,O,O’ như hình vẽ.

Ta có là PQ đường trung bình của tam giác đều B’CD’ cạnh

2a

nên

2

a

PQ =

Do đó

22

1

2

PQRS

S PQ a==

và

OO' a=

.

Vậy thể tích bát diện cần tìm là

3

11

.'

36

PQRS

V S OO a==

(đvtt)

Câu 46: Đáp án là B.Gọi là (C) đồ thị hàm số

( )

1

;

x

y a C=

là đồ thị hàm số

( )

y f x=

.

( )

1

11

2 log ; 2 log

2018 2018

a M M a

M y C y f

   

+   = +

   

   

Trang 76

Gọi N đối xứng với M qua

( )

1;1I

1

log ;2

2018

aM

Ny



 − −





Do đồ thị (C

1

) đối xứng qua

( )

1;1I

nên

( )

1

log ;2

2018

aM

N y C



− − 





( )

1

log

2018

2 2 2018 2016

a

M M M

N C y a y y

−

  − =  − =  = −

.Vậy

1

2 log 2016

2018

a

f



+ = −





Câu 47: Đáp án là B.Ta có:

( ) ( )

32

sin 3sin sin 4 1y f x x x m x= = + − −

Đặt t = sin x , do

 

3

; 1;0

2

xt





   −





.Hàm số (1) trở thành

( ) ( )

32

3 4 2y g t t t mt= = + − −

Hàm số (1) đồng biến trên

3

;

2









khi và chỉ khi hàm số (2) nghịch biến trên

 

1;0−

( )

 

' 0, 1;0g t t    −

(

( )

'0gt=

tại hữu hạn điểm)

Hàm số

( )

32

34y g t t t mt= = + − −

trên

 

1;0−

ta có:

( )

2

' 3 6g t t t m= + −

Suy ra:

( )

   

2

' 0 , 1;0 3 6 0 1;0g t t t t m t  −  + −    −

 

2

3 6 , 1;0t t m t +    −

.Xét hàm số

( )

2

36y h t t t= = +

trên đoạn

 

1;0−

Ta có

( )

 

( )

' 6 6 0, 1;0h t t t h t= +    

đồng biến trên

 

1;0−

;

( )

 

( )

1;0

max 0 0h t h

−

==

Tức

( )

 

( )

 

1;0

' 0, 1;0 max 1;0g t t h t m t   −     −

.Do đó có

0m 

Hàm số (1) đồng biến trên

3

;

2









khi và chỉ khi

 

0;m +

Câu 48: Đáp án B. Phễu có dạng hình nón, gọi là E đỉnh, đáy là đường tròn tâm O ,

bán kính OA chiều cao OE = 30cm

Gọi là V thể tích của khối nón có đỉnh E đáy là đường tròn tâm O ,

bán kính OA.Ta có

22

1

. . 10

3

V OA OE OA



==

Gọi là trung M điểm của đoạn , là trung OE, N điểm của đoạn

EA.Khi đổ nước vào phễu chiều cao của cột nước là EM =15cm.

Gọi V

1

là thể tích của khối nón có đỉnh E , đáy là đường tròn tâm M

, bán kính MN .

=>Thể tích nước là

2 2 2

11

1 5 1

. . 5 . .

3 4 8

V MN EM MN OA V V

  

= = =  =

Khi bịt kín miệng phễu rồi lật ngược phễu lên, chiều cao của cột nước là OP

Gọi V

2

là thể tích của khối nón có đỉnh E , đáy là đường tròn tâm P , bán kính PQ

Ta có

( )

2

1

2

1

..

7 7 7 . 7

3

1

8 2 8 8 OA .O 8

.OA .O

3

PQ PE

V

PQ PE

V V V

E

V



= − =  =  =  =

Ta có

PEQ

vuông tại P và

OEA

vuông O tại có

OEA PEQ=

PEQ

và

OEA

đồng dạng

PQ PE

OA OE

=

Do đó

( )

3

33

7 7 7

1

8 2 2

PE PE OE OP

OE OE OE

−



 =  =  =





Trang 77

33

77

1 30 1 1,306

22

OP OE

   

 = − = − 

   

   

Câu 49: Đáp án là D.Điều kiện xác định:

4 2 0

xx

m− + 

Hàm số đã cho có tập xác định là

( )

4 2 0, 4 2 , *

x x x x

m x m x − +      − +  

Đặt

( )

2 , 0

x

tt=

.Khi đó (*) trở thành

( )

2

0;

, 0 maxm t t t m f t

+

 − +    

với

( )

2

,0f t t t t= − + 

Ta có:

( ) ( )

1

' 2 1, ' 0

2

f t t f t t= − + =  =

Bảng biến thiên của hàm số

( )

2

,0f t t t t= − + 

Từ BBT ta thấy

( )

0;

1

max

4

ft

+

=

đạt được khi

1

2

t =

.Vậy

( )

0;

1

max

4

m f t m

+

  

Câu 50: Đáp án D.Chọn hệ trục tọa độ như hình vẽ sao cho gốc tọa độ trùng với điểm B, điểm A thuộc trục Oy và

điểm C thuộc trục Ox

Theo bài ra ta có B(0;0), A(0;2), C(3;0), D(1;2).Khi đó

( )

3; 2AC =−

.

Phương trình tham số của đường thẳng AC là

3

22

xt

yt

=





=−



Gọi

( )

3 ;2 2M AC M t t  −

. Ta có

( )

3 ;2 2BM t t=−

và

( )

2; 2DC =−

. Để BM ⊥ DC thì

2 6 6

. 0 6 4 4 0 ;

5 5 5

BM DC t t t M



=  − + =  = 





Khi đó

6 4 52

;

5 5 5

AM AM

−



=  =





và

( )

3; 2 13AC AC−  =

Vì

AM k AC=

và

,AM AC

cùng chiều

52 2

5

5 13

AM

k

AC

 = = =

ĐỀ 56

ĐỀ THI THỬ THPT QUỐC GIA 2020

MÔN TOÁN

Thời gian: 90 phút

Câu 1:Tính giới hạn

21

lim

32

n

+

. A.

2

3

. B.

3

2

. C.

1

2

. D.

0

.

Câu 2. Cho hàm số

( )

y f x=

có bảng biến thiên như hình vẽ bên. Mệnh đề nào dưới đây đúng?

Trang 78

A.

0

CT

y =

. B.

max 5y =

. C.

5

CÐ

y =

. D.

min 4y =

.

Câu 3:Cho hình chóp tam giác

.S ABC

có thể tích bằng

8

. Gọi

M

,

N

,

P

lần lượt là trung điểm các cạnh

AB

,

BC

,

CA

. Tính thể tích khối chóp

.S MNP

. A.

3

. B.

6

. C.

2

. D.

4

.

Câu 4:Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông. Mặt bên

SAB

là tam giác đều có đường cao

SH

vuông góc với

( )

ABCD

. Gọi



là góc giữa

BD

và

( )

SAD

. Tính

sin



.

A.

6

sin

4



=

. B.

1

sin

2



=

. C.

3

sin

2



=

. D.

10

sin

4



=

.

Câu 5: Cho hình lập phương

.ABCD A B C D

   

có cạnh bằng

2

. Tính khoảng cách giữa hai mặt phẳng

( )

AB D



và

( )

BC D



. A.

3

. B.

3

. C.

3

2

. D.

2

3

.

Câu 6:Đồ thị hàm số nào trong bốn hàm số liệt kê ở bốn phương án A, B, C, D dưới đây, có đúng một cực trị?

A.

32

3y x x x= − +

. B.

42

23y x x= + −

. C.

3

45y x x= − − +

. D.

23

1

x

y

x

−

=

+

.

Câu 7: Phương trình tiếp tuyến của đồ thị hàm số

3

2 5 1y x x= + +

tại điểm có tung độ bằng

1

là

A.

20xy+ − =

. B.

5 1 0xy− + =

. C.

10xy+ − =

. D.

5 1 0xy+ + =

.

Câu 8:Cho hàm số

( )

2

4

khi 2

2

3 khi 2

x

fx

x

m m x



−





=

−





+=



. Tìm

m

để hàm số liên tục tại

0

2x =

.

A.

0m =

hoặc

1m =

. B.

1m =

hoặc

4m =−

. C.

4m =−

hoặc

1m =−

. D.

0m =

hoặc

4m =−

.

Câu 9. Tìm

1

32

lim

1

x

→

+−

−

. A.

1−

. B.

2

3

. C.

1

4

. D.

5

4

.

Câu 10:Tính thể tích

V

của khối lập phương

.ABCD A B C D

   

biết

3AC a



=

.

A.

3

Va=

. B.

3

4

a

V =

. C.

3

36

4

a

V =

. D.

3

33Va=

.

Câu 11:Khối đa diện đều loại

 

4; 3

có bao nhiêu mặt? A.

4

. B.

7

. C.

8

. D.

6

.

Câu 12:Tính đạo hàm của hàm số

( )

2

21y x x= − +

.

A.

2

2 2 1

1

xx

y

x

−−



=

+

. B.

2

2 2 1

1

xx

y

x

++



=

+

. C.

2

2 2 1

1

xx

y

x

−+



=

−

. D.

2

2 2 1

1

xx

y

x

−+



=

+

.

Câu 13:Tìm số đường tiệm cận của đồ thị hàm số

2

2 1 3 1xx

y

xx

+ − +

=

−

. A.

2

. B.

1

. C.

0

. D.

3

.

Câu 14:Lăng trụ tam giác đều

.ABC A B C

  

có cạnh đáy bằng

4

và diện tích tam giác

A BC



bằng

8

. Tính thể

tích khối lăng trụ đó. A.

83

. B.

63

. C.

43

. D.

23

.

Trang 79

Câu 15:Cho lăng trụ tam giác

.ABC A B C

  

có đáy

ABC

là tam giác đều cạnh

2a

. Hình chiếu của

A



lên mặt

phẳng

( )

ABC

trùng với trọng tâm tam giác

ABC

. Biết góc giữa cạnh bên và mặt đáy bằng

60

. Tính thể tích

khối lăng trụ

.ABC A B C

  

. A.

3

4

a

. B.

3

43a

. C.

3

23a

. D.

3

2

a

.

Câu 16:Cho khối hộp

.ABCD A B C D

   

. Gọi

,M

,N

P

lần lượt là trung điểm của

,AB

AD

và

AA



. Tính tỉ số

thể tích

k

của khối chóp

.AMNP

và khối hộp đã cho. A.

1

12

k =

. B.

1

48

k =

. C.

1

8

k =

. D.

1

24

k =

.

Câu 17:Cho hình chóp

.S ABCD

đáy

ABCD

là hình chữ nhật,

AB a=

,

2AD a=

. Cạnh bên

SA

vuông góc với

đáy

( )

ABCD

,

2SA a=

. Tính

tan

của góc giữa hai mặt phẳng

( )

SBD

và

( )

ABCD

.

A.

1

5

. B.

2

5

. C.

5

. D.

5

2

.

Câu 18:Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số

21

1

x

y

x

−

=

+

.

A.

1

,

2

x =

1y =−

. B.

1,x =

2y =−

. C.

1,x =−

2y =

. D.

1,x =−

1

2

y =

.

Câu 19:Cho hàm số

( )

fx

có đạo hàm

( ) ( ) ( ) ( )

23

1 1 2f x x x x



= + − −

. Hỏi hàm số đồng biến trên khoảng nào

dưới đây? A.

( )

2;+

. B.

( )

1;2

. C.

( )

;1− −

. D.

( )

1;1−

.

Câu 20:Gọi

,M

n

theo thứ tự là giá trị lớn nhất và giá trị nhỏ nhất của hàm số

2

3

1

x

y

x

+

=

−

trên đoạn

 

2;0−

. Tính

P M m=+

. A.

1P =

. B.

5P =−

. C.

13

3

P =−

. D.

3P =−

.

Câu 21:Vật thể nào trong các vật thể sau không phải khối đa diện?

A. B. C. D.

Câu 22:Hàm số nào dưới đây đồng biến trên khoảng

( )

;− +

?

A.

3

3y x x= − −

. B.

1

2

x

y

x

−

=

−

. C.

1

3

x

y

x

+

=

+

. D.

3

3y x x=+

.

Câu 23:Tìm tất cả các phương trình tiếp tuyến của đồ thị hàm số

21

1

x

y

x

+

=

−

song song với đường thẳng

3 15yx= − +

.

A.

31yx= − +

,

37yx= − −

.B.

31yx= − −

,

3 11yx= − +

.C.

31yx= − −

.D.

3 11yx= − +

,

35yx= − +

.

Câu 24:Cho hình lập phương

.ABCD A B C D

   

. Khẳng định nào sau đây là khẳng định sai?

A. Góc giữa hai đường thẳng

BD



và

AA



bằng

60

. B. Góc giữa hai đường thẳng

AC

và

BD



bằng

90

.

C. Góc giữa hai đường thẳng

AD

và

BC



bằng

45

. D. Góc giữa hai đường thẳng

BD

và

AC



bằng

90

.

Trang 80

Câu 25:Tìm giá trị nhỏ nhất của hàm số

2

yx

x

=+

trên khoảng

( )

0;+

A. không tồn tại. B.

( )

0;

min 3y

+

=

.

C.

( )

0;

min 1y

+

=

. D.

( )

0;

min 1y

+

=−

.

Câu 26:Cho đồ thị hàm

( )

y f x=

như hình vẽ. Số điểm cực trị của đồ thị

hàm số là:

A.

4

. B.

3

. C.

5

. D.

2

.

Câu 27:Cho hàm số

( )

y f x=

có bảng biến thiên như hình dưới. Hỏi đồ thị hàm số

( )

y f x=

có bao nhiêu

đường tiệm cận:

A.

3

. B.

4

. C.

2

. D.

1

.

Câu 28:Tính độ dài cạnh bên của khối lăng trụ đứng có thể tích

V

và diện tích đáy bằng

S

:

A.

V

S

=

. B.

2

V

S

=

. C.

V

S

=

. D.

3V

S

=

.

Câu 29:Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật,

AB a=

,

2AD a=

. Tam giác

SAB

cân tại

S

và nằm trong mặt phẳng vuông góc với đáy. Đường thẳng

SC

tạo với đáy một góc

60

. Khi đó thể tích của khối

chóp

.S ABCD

bằng A.

3

17

3

a

. B.

3

17

3

a

. C.

3

17

9

a

. D.

3

17

6

a

.

Câu 30:Tính đạo hàm của hàm số

tan

4

yx





=−





:

A.

2

1

cos

4

y

x





=−



−





. B.

2

1

cos

4

y

x





=



−





. C.

2

1

sin

4

y

x





=



−





. D.

2

1

sin

4

y

x





=−



−





.

Câu 31:Hình đa diện nào sau đây không có mặt phẳng đối xứng?

A. Hình lăng trụ lục giác đều. B. Hình lăng trụ tam giác. C. Hình chóp tứ giác đều. D. Hình lập phương.

Câu 32:Số giao điểm của đồ thị hai hàm số

2

31y x x= − −

và

3

1yx=−

là

A.

1

. B.

0

. C.

2

. D.

3

.

O

x

y

2−

2

4

6

Trang 81

Câu 33:Để hàm số

2

1x mx

y

xm

++

=

+

đạt cực đại tại

2x =

thì

m

thuộc khoảng nào?

A.

( )

2; 4

. B.

( )

0; 2

. C.

( )

4; 2−−

. D.

( )

2; 0−

.

Câu 34:Đường cong hình bên là đồ thị của hàm số nào trong bốn hàm số sau đây?

A.

32

3

1

2

y x x= + +

. B.

32

3

1

2

y x x= − − +

.

C.

32

2 3 1y x x= − − +

. D.

32

2 3 1y x x= + +

.

Câu 35:Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

B

,

AB a=

,

cạnh bên

SA

vuông góc với mặt đáy và

2SA a=

. Gọi

M

là trung điểm của

AB

.

Tính khoảng cách

d

giữa hai đường thẳng

SM

và

BC

.

A.

3

2

a

d =

. B.

2

3

a

d =

. C.

3

a

d =

. D.

2

a

d =

.

Câu 36:Cho hàm số

( )

32

1 3 1y x m x x= − + + +

, với

m

là tham số. Gọi

S

là tập hợp các giá trị nguyên của

m

để hàm số đồng biến trên khoảng

( )

;− +

. Tìm số phần tử của

S

. A.

7

. B.

6

. C. Vô số. D.

5

.

Câu 37:Tìm tất cả các giá trị của tham số

m

để đồ thị hàm số

2

1

x

y

x mx

−

=

−+

có hai đường tiệm cận đứng.

A.

( ) ( )

5

; 2 2; \

2

m



 − −  +





. B.

(

 

)

; 2 2;m − −  +

.C.

( ) ( )

; 2 2;m − −  +

. D.

5

2

m 

.

Câu 38:Cho hàm số

1

x

y

x

+

=

−

và đường thẳng

2y x m= − +

. Tìm giá trị của

m

để đồ thị hai hàm số đã cho cắt

nhau tại hai điểm

A

,

B

phân biệt, đồng thời trung điểm của đoạn thẳng

AB

có hoành độ bằng

5

2

.

A.

9m =−

. B.

9m =

. C.

8m =

. D.

10m =

.

Câu 39:Biết rằng hàm số

( )

42

y f x ax bx c= = + +

có đồ thị là đường cong trong hình vẽ bên dưới.

f(x)=2x^4-4x^2+1

f(x)=-1

x(t)=-1 , y(t)=t

x(t)=1 , y(t)=t

x

y

O

-

Tính giá trị

( )

f a b c++

. A.

( )

2f a b c+ + = −

. B.

( )

2f a b c+ + =

.

C.

( )

1f a b c+ + = −

. D.

( )

1f a b c+ + =

.

Câu 40:Cho hình chóp

.S ABC

có đáy

ABC

là một tam giác vuông tại

A

,

2BC a=

,

60ABC =

. Gọi

M

là trung điểm

BC

. Biết

39

3

a

SA SB SM= = =

. Tính khoảng cách

d

từ đỉnh

S

đến mặt phẳng

( )

ABC

. A.

3da=

. B.

da=

. C.

2da=

. D.

4da=

.

Câu 41:Có hai tiếp tuyến của đồ thị hàm số

( )

32

1

x

yC

x

−

=

−

đi qua điểm

( )

9;0A

. Tích hệ số góc của hai tiếp

tuyến đó bằng A.

3

.

8

−

B.

3

.

8

C.

9

.

64

D.

9

.

64

−

Câu 42:Cho hàm số

32

y ax bx cx d= + + +

có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?

1−

2

1

x

y

O

Trang 82

A.

0, 0, 0, 0.a b c d  = 

B.

0, 0, 0, 0.a b c d  = 

C.

0, 0, 0, 0.a b c d   

. D.

0, 0, 0, 0.a b c d   

.

Câu 43:Một chuyển động xác định bởi phương trình

( )

32

3 9 2S t t t t= − − +

.

Trong đó

t

được tính bằng giây,

S

được tính bằng mét. Khẳng định nào sau đây

đúng?

A. Vận tốc của chuyển động bằng

0

khi

0st =

hoặc

2s.t =

B. Gia tốc của chuyển động tại thời điểm

3st =

là

2

12 m/s

.

C. Gia tốc của chuyển động bằng

2

0 m/s

khi

0st =

.

D. Vận tốc của chuyển động tại thời điểm

2st =

là

18m/s.v =

Câu 44:Tìm tập hợp tất cả các giá trị thực của tham số

m

để phương trình

42

2 3 0x x m− − + =

có đúng hai

nghiệm thực. A.

( )  

;3 4 .− 

B.

( )

;3 .−

C.

  ( )

4 3; .−  − + 

D.

( )

3; .− +

Câu 45:Cho hàm số

( )

32

3 1 1y x x m x= − + + +

có đồ thị

( )

m

C

, với

m

là tham số. Tìm tất cả các giá trị thực của

tham số

m

để đường thẳng

:1d y x=+

cắt đồ thị

( )

m

C

tại ba điểm phân biệt

( )

0;1P

,

M

,

N

sao cho tam giác

OMN

vuông tại

O

với

O

là gốc tọa độ. A.

2.m =−

B.

6.m =−

C.

3.m =−

D.

7

.

2

m =−

Câu 46:Một công ty muốn thiết kế một loại hộp có dạng hình hộp chữ nhật, có đáy là hình vuông, sao cho thể tích

khối hộp được tạo thành là

3

8 dm

và diện tích toàn phần là nhỏ nhất. Tìm độ dài cạnh đáy của mỗi hộp được thiết

kế.

A.

3

2 2 dm

. B.

2 dm

. C.

4 dm

. D.

2 2 dm

.

Câu 47:Cho tứ diện

ABCD

có

5AB CD==

,

10AC BD==

,

13AD BC==

. Tính thể tích tứ diện đã cho.

A.

5 26

. B.

5 26

6

. C.

4

. D.

2

.

Câu 48:Cho hàm số

( )

y f x=

liên tục trên đoạn

 

2;2−

và có đồ thị là đường

cong như trong hình vẽ.

Hỏi phương trình

( )

11fx−=

có bao nhiêu nghiệm phân biệt trên đoạn

 

2;2−

? A.

4

. B.

5

. C.

3

. D.

6

.

Câu 49:Cho

x

,

y

là các số thực thỏa mãn

1 2 2x y x y+ = − + +

. Gọi

M

,

m

lần lượt là giá trị lớn nhất và

nhỏ nhất của

( )( )

22

2 1 1 8 4P x y x y x y= + + + + + − −

. Tình giá trị

Mm+

. A.

41

. B.

44

. C.

42

.

D.

43

.

Câu 50:Tìm tất cả các giá trị thực của

m

để hàm số

( ) ( )

22

1 1 siny m m x m m x= + + + − +

luôn đồng biến trên

( )

0;2



. A.

0m 

. B.

0m 

. C.

0m 

. D.

0m 

.

HƯỚNG DẪN GIẢI

Câu 1:Chọn A .Ta có

1

2

2 1 2

lim lim

2

3 2 3

3

n

+

==

+

.

Trang 83

Câu 2.Chọn C.Dựa vào bảng biến thiên ta thấy hàm số đạt cực đại tại

1x =

,

5

CÐ

y =

; đạt cực tiểu tại

0x =

,

4

CT

y =

; hàm số không có giá trị lớn nhất và giá

trị nhỏ nhất.

Câu 3:Chọn C . Gọi

h

là chiều cao hình chóp

.S ABC

.

Ta có

.

1

.8

3

S ABC ABC

V h S==

.

Mặt khác

1

4

MNP ABC

SS=

và

.

1

.

3

S MNP MNP

V h S=

.Suy ra

.

8

2

44

S ABC

S MNP

V

V = = =

.

Câu 4:Chọn A . Gọi

I

là trung điểm

SA

. Ta có

BI SA⊥

và

BI AD⊥

(do

AD AB⊥

và

AD SH⊥

).

Do đó

( )

BI SAD⊥

. Khi đó: Hình chiếu của

BD

lên

( )

SAD

là

ID

,

góc giữa

BD

và

( )

SAD

là

BDI



=

.

Đặt

AB a=

. Ta có

3

2

a

BI =

;

2BD a=

.

Xét tam giác

BID

vuông tại

I

có

3

6

2

sin

4

2

a

BI

BD

a



= = =

.

Câu 5:Chọn D . Ta có

//B D BD



và

//AB DC



. Suy ra

( ) ( )

//AB D BC D

  

.

Gọi

O

,

O



lần lượt là tâm hình vuông

ABCD

và

A B C D

   

. Kẻ

OH AO



⊥

.

Ta có

B D OO

  

⊥

và

B D AC



⊥

nên

B D OH



⊥

.

Do đó

( )

OH AB D



⊥

. Suy ra

( ) ( )

( )

,,d ABD BC D d O AB D OH

    

==

.

Xét tam giác

OAO



vuông tại

O

có

2OO



=

,

11

2 2 2

22

OA AC= = =

.

Suy ra

22

. 2. 2 2

4 2 3

OO OA

OH

OO OA



= = =

+



+

.

Cách khác: Sử dụng công thức nhanh

( ) ( )

( )

1 1 2

, 2 3

33

3

d AB D BC D A C

   

= = =

.

Câu 6:Chọn B.Ta có đồ thị hàm số

32

y ax bx cx d= + + +

với

0a 

luôn có hai hoặc không có cực trị.

Đồ thị hàm số

ax b

y

cx d

+

=

+

với

0ad bc−

không có cực trị.

Câu 7:Chọn B.Ta có

2

65yx



=+

.Gọi

( )

00

;xy

là tọa độ tiếp điểm.

Theo giả thiết có

0

1y =

suy ra

3

00

2 5 1 1xx+ + =

0

0x=

.Hệ số góc của tiếp tuyến là

( )

05ky



==

.

Vây phương trình tiếp tuyến cần tìm là

( )

5 0 1yx= − +

hay

5 1 0xy− + =

.

Câu 8:Chọn B.Tập xác định

D =

. Ta có

( )

2

lim

x

fx

→

2

4

lim

2

x

→

−

=

−

( )

2

lim 2

x

→

=+

2 2 4= + =

.

Hàm số đã cho liên tục tại

0

2x =

khi và chỉ khi

( ) ( )

2

lim 2

x

f x f

→

=

2

43mm = +

2

3 4 0mm + − =

1

4

m

=







=−



.

P

N

M

C

B

A

S

I

α

H

D

C

B

A

S

H

O'

O

D'

C'

B'

A'

D

C

B

A

Trang 84

Câu 9.Chọn C.Ta có

1

32

lim

1

x

→

+−

−

( )( )

( )

1

3 2 3 2

lim

1 3 2

x

xx

→

+ − + +

=

− + +

( )

1

34

lim

1 3 2

x

xx

→

+−

=

− + +

( )

1

lim

32

x

→

=

++

11

4

1 3 2

==

++

.

Câu 10:Chọn A.Ta có

3AC AB



=

33AB a=

AB a=

.

Do đó thể tích

V

của khối lập phương

.ABCD A B C D

   

là

3

Va=

.

Câu 11:Chọn D.Khối đa diện đều loại

 

4; 3

là hình lập phương nên có sáu mặt.

Câu 12:Chọn D.Ta có

( ) ( )

(

)

( )

2

2 2 2

22

2

2 2 1

2 1 2 1 1

11

xx

y x x x x x

xx

−



−+



= − + + − + = + + =

++

.

Câu 13:Chọn A.Ta có : Vì

2 3 4

2

2 1 3 1

lim lim 0

1

xx

x x x x

xx

x

→+ →+

+ − +

==

−



đường thẳng

0y =

là tiệm cận ngang của đồ thị hàm số.

Vì

( )

2

0 0 0

2

0 0 0

4

2 1 3 1 4 1 1

lim lim lim

12

1 2 1 3 1 1 2 1 3 1

4

2 1 3 1 4 1 1

lim lim lim

12

1 2 1 3 1 1 2 1 3 1

x x x

xx

x x x

xx

x x x x x x x

xx

x x x

xx

x x x x x x x

+ + +

− − −

→ → →



+

+ − + +



= = = −

−

 − + + + − + + +





+



+ − + +

= = = −



−

− + + + − + + +





nên đường thẳng

0x =

không là tiệm cận đứng của đồ thị hàm số.

Vì

( ) ( )

11

2 1 3 1 2 1 3 1

lim ; lim

11

xx

x x x x

+−

→→

+ − + + − +

= + = −

−−

nên đường thẳng

1x =

là tiệm cận đứng của đồ thị

hàm số. Vậy đồ thị hàm số có hai đường tiệm cận

Câu 14:Chọn A. Do

ABC

đều ,

4BC =

nên

2

43

4

ABC

S



==

.

Gọi

H

là trung điểm

BC

43

23

2

AH = =

.

Khi đó,

AH



là đường cao của

A BC





.

Theo giả thiết, ta có.

1 16 16

. . 8 4

24

A BC

S A H BC A H

BC







= =  = = =

.

Trong tam giác vuông

A AH



, ta có

2

22

43

16 2

2

A A A H AH





= − = − =





.

Vậy

.

. 2.4 3 8 3

ABC A B C ABC

V A AS

  





= = =

Câu 15:Chọn C. Gọi

H

là trung điểm cạnh

BC

và

G

là trọng tâm tam giác

ABC

.

Trang 85

Ta có

2 2 2 3 2 3

.

3 3 2 3

aa

AG AH= = =

. Do

( )

A G ABC A AG



⊥

là góc

giữa cạnh bên và mặt phẳng đáy.

Theo giả thiết, ta có:

60A AG



=

.Trong tam giác vuông

A GA



, ta có:

23

.tan . 3 2

3

a

A G AG A AG a



= = =

.

Vậy

( )

2

3

.

23

. 2 . 2 3

4

ABC A B C ABC

a

V A G S a a

  





= = =

.

Câu 16:Chọn B

Cách 1 : Ta có:

( )

1 1 1 1

.

4 4 2 8

1

;;

2

AMN ABD ABCD ABCD

S S S S

d P AMN d A ABCD



= = =









=





.

Suy ra:

( )

1 1 1 1

. . ; . . ;

3 3 8 2

AMN ABCD

S d P AMN S d A ABCD



=

..

1

48

A MNP ABCD A B C D

VV

   

=

. Vậy

1

48

k =

.

Bổ sung cách 2.Ta có

1

8

1

48

6

AMNP

ABDA

AMNP

ABDA

ABCDA B C D

V

AM AN AP

V AB AD AA

V

k

V



   



==







 = =





=





Câu 17:Chọn C . Kẻ

AH BD⊥

,

( )

H BD

(1).

( )

BD SA SA ABCD

BD AH



⊥⊥





⊥





( )

BD SAH⊥

BD SH⊥

(2).

Và:

( ) ( )

SBD ABCD BD=

(3).

Từ (1) (2) và (3) suy ra: góc giữa hai mặt phẳng

( )

SBD

và

( )

ABCD

là

SHA

.

Xét

ABD

vuông tại

A

:

222

1 1 1

AH AB AD

=+

22

11

4aa

=+

2

5

4a

=

2

5

a

AH=

.Xét

SAH

vuông tại

A

:

tan 5

SA

SHA

AH

==

.

Câu 18:Chọn C.Ta có : Vì

1

2

21

lim lim 2

1

xx

x

→ →

−

==

+

nên đường thẳng

2y =

là tiệm cận ngang của đồ thị hàm

số

Vì

1

21

lim

1

x

+

→−

−

= −

+

,

1

21

lim

1

x

−

→−

−

= +

+

nên đường thẳng

1x =−

là tiệm cân đứng của đồ thị hàm số

Câu 19:Chọn B .

( )

'0fx=

1

2

x

=−





=



=



.

P

N

M

A

D

B

C

A'

D'

B'

C'

2a

a

2a

A

D

B

C

S

H

Trang 86

BBT:

Dựa vào BBT, ta thấy hàm số đồng biến trên khoảng

( )

1;2

.

Câu 20:Chọn B.

( )

2

23

'0

1

xx

y

x

−−

==

−

 

1 2;0

3 2;0

x



= −  −





=  −





.

( )

7

2

3

y − = −

,

( )

12y − = −

,

( )

03y =−

.

 

2;0

max 2

min 3

My

my

−

= = −









= = −





5P M m = + = −

.

Câu 21:Chọn C.Dựa vào định nghĩa khối đa diện : Khối đa diện được giới hạn hữu hạn bởi đa giác thoả mãn điều

kiện :

1.Hai đa giác bất kì không có điểm chung, hoặc có 1 điểm chung hoặc có chung 1 cạnh.

2.Mỗi cạnh của đa giác là cạnh chung của đúng 2 đa giác.

Khối đa diện trong hình C vi phạm điều kiện thứ 2 : có 1 cạnh là cạnh chung của 4 đa giác.

Câu 22:Chọn D.Hàm số

1

3

x

y

x

+

=

+

đồng biến trên từng khoảng xác định không thỏa

Hàm số

1

2

x

y

x

−

=

−

nghịch biến trên từng khoảng xác định không thỏa

Hàm số

3

3y x x= − −

có

2

3 3 0y x y



= − −  =

vô nghiệm và

10a = − 

, suy ra hàm số nghịch biến trên

( )

;− +

Với

2

10

' 3 3 0( )

a

y x PTVN

=





= + =



thì hàm số

3

3y x x=+

đồng biến trên khoảng

( )

;− +

.

Câu 23:Chọn B.Gọi

( )

00

;,M x y

0

1x 

là tiếp điểm

( )

2

3

1

y

x



=−

−

Đồ thị hàm số song song với

3 15yx= − +

nên ta có

( )

0

3fx



=−

( )

2

0

3

1x

 − = −

−

0

2

x

=







=



Với

0

0x =

0

1y = −



phương trình tiếp tuyến là:

31yx= − −

Với

0

2x =

0

5y=



phương trình tiếp tuyến là:

3 11yx= − +

.

Câu 24:Chọn A. Ta có

( )

, 90B D AA

  

=

(vì

( )

AA A B C D

    

⊥

nên khẳng định Góc giữa hai đường thẳng

BD



và

AA



bằng

60

là sai

B đúng vì

//

A C B D

AC B D

BD B D

   

⊥





⊥







C đúng vì

//A D B C



nên góc giữa

AD

và

BC



là góc giữa

AD

và

AD



và là góc

45

o

ADA



=

D đúng vì

//

A C B D

A C BD

BD B D

   

⊥





⊥







+

0

1

x

y'

y

1

2

+

0

∞

Trang 87

Câu 25:Chọn B.Ta có:

0

lim

x

y

+

→

= +

;

lim

x

y

→+

= +

.

2

2yx

x



=−

;

0y



=

1x=

Bảng biến thiên

Vậy

( )

0;

min 3y

+

=

.

Câu 26:Chọn C.Đồ thị hàm số có 5 điểm cực trị.

Chú ý, tại các điểm mà đồ thị có dạng “nhọn” thì đó vẫn là điểm cực trị của đồ thị hàm số.

Câu 27:Chọn A .Từ bảng biến thiên, ta được:

lim 3

x

y

→+

=

suy ra đồ thị hàm số có TCN

3y =

.

( )

1

lim

x

y

+

→−

= +

;

1

lim

x

−

→

= +

suy ra đồ thị hàm số có hai đường tiệm cận đứng

1; 1xx= = −

Vậy đồ thị hàm số

( )

y f x=

có 3 đường tiệm cận.

Câu 28:Chọn C.Cạnh bên cũng là đường cao của lăng trụ đứng. Ta có:

.

V

VS

S

=  =

.

Câu 29:Chọn A . Gọi

H

là trung điểm

AB

.Ta có tam giác

SAB

cân tại

S

SH AB⊥

Mà

( ) ( )

SAB ABCD

SAB ABCD AB

⊥







=





nên

( )

SH ABCD⊥

.

HC

là hình chiếu vuông góc của

SC

lên mặt phẳng

( )

ABCD

.

( )

(

)

( )

, , 60SC ABCD SC HC SCH = = = 

.

Mặt khác .Tam giác

HBC

vuông tại

B

có

22

17

2

a

HC BH BC= + =

Tam giác

SHC

vuông tại

H

có

17

.tan60 . 3

2

a

SH HC=  =

.

Khi đó thể tích khối chóp

.S ABCD

là

.

1

.

3

S ABCD ABCD

V S SH=

, với

2

ABCD

Sa=

Vậy

3

2

1 17 17

.2 . . 3

32

3

aa

Va==

.

Câu 30:Chọn A .

22

11

.

4

cos cos

44

yx

xx











= − = −



   



−−

   

   

Câu 31:Chọn B

Câu 32:Chọn A.Phương trình hoành độ giao điểm

3 2 3 2

1 3 1 3 0x x x x x x− = − −  − + =

+

∞

3

+

∞

+

∞

y

y'

x

+

1

-

0

S

A

B

C

D

H

60

Trang 88

( )

2

1 11

3 0 0 0

24

x x x x x x





 − + =  − + =  =











.Vậy đồ thị hai hàm số có

1

điểm chung.

Câu 33:Chọn C.Tập xác định

 

\Dm=−

.

( )

22

2

21

,

x mx m

y x m

xm

+ + −



=   −

+

Điều kiện cần :Để hàm số đạt cực đại tại

2x =

thì

( )

2

1

2 0 4 3 0

3

m

y m m

m

=−





=  + + = 



=−



Điều kiện đủ : Với

1m =−

, ta có

( )

2

,1

1

xx

yx

x

−



=  

−

;

2

0

x

y

x

=





=



=



Bảng biến thiên

Dựa vào bảng biến thiên ta thấy hàm số đạt cực tiểu tại

21xm=  = −

không thoả mãn ycbt.

Với

3m =−

, ta có

( )

2

68

,3

3

xx

yx

x

−+



=  

−

;

4

0

2

x

y

x

=





=



=



Bảng biến thiên

Dựa vào bảng biến thiên ta thấy hàm số đạt cực tiểu tại

23xm=  = −

thoả mãn ycbt.Vậy

( )

3 4; 2m = −  − −

.

Câu 34:Chọn D.Dựa vào đồ thị hàm số ta thấy



0a 

loại B, C.  Khi

1x =−

thì

2y =

Chọn D

Câu 35:Chọn B . Gọi

N

là trung điểm

AC

.Ta có

( )

//

MN BC

BC SMN

MN SMN















( ) ( )

( )

, , , ,d SM BC d BC SMN d B SMN d A SMN = = =

(vì

M

là trung

điểm

AB

).Mặt khác

( )

MN AB

MN SAB

MN SA

⊥



⊥



⊥



;

( )

( ) ( )

SMN SAB

MN SMN

SMN SAB SM

⊥









=





Trong mặt phẳng

( )

SAB

, kẻ

( ) ( )

( )

,AH SM AH SMN AH d A SMN⊥  ⊥  =

Tam giác

SAM

vuông tại

A

có

2 2 2

1 1 1 2

3

a

AH

AH SA AM

= +  =

.Vậy

( )

2

,

3

a

d SM BC =

.

Câu 36:Chọn A.Tập xác định

D =

.

( )

2

3 2 1 3y x m x



= − + +

.

Hàm số đã cho đồng biến trên

( )

;− +

0,yx



   

( Dấu

'' ''=

chỉ xảy ra tại hữu hạn điểm trên )

S

A

B

C

M

N

H

Trang 89

ĐK:

( )

2

1 9 0 4 2mm+ −   −  

.Suy ra có

7

giá trị nguyên của

m

.

Câu 37:Chọn AĐồ thị hàm số có hai đường tiệm cận đứng



phương trình

2

10x mx− + =

có hai nghiệm phân

biệt khác

2

40

2

2 2 1 0

5

2

m

  −









 = − 











− + 













.

Câu 38:Chọn B.Phương trình hoành độ giao điểm:

( ) ( )

2

1

2 2 1 1 0, 1

1

x

x m x m x m x

x

+

= − +  − + + + = 

−

.

Đồ thị hai hàm số cắt nhau tại hai điểm phân biệt



phương trình

( )

2

2 1 1 0x m x m− + + + =

có hai nghiệm phân

biệt khác

1

.ĐK:

( )

2

6 7 0

1

7

2.1 1 .1 1 0

mm

m

mm



 = − − 

−













− + + + 







(*).

Khi đó, gọi

12

,xx

lần lượt là hoành độ của điểm

A

và

B

. Theo Viet :

12

1

2

1

2

m

xx

m

xx

+



+=





+



=





Tọa độ

( )

11

;2A x x m−+

,

( )

22

;2B x x m−+

.Tọa độ trung điểm của đoạn thẳng

AB

là

12

;

2

xx

I x x m

+



− − +





Ta cần có

12

5 1 5

9

2 2 4 2

xx

m

+

=  =  =

(thỏa (*)).

Câu 39:Chọn C.Ta có

3

42y ax bx



=+

.Từ đồ thị, ta có hệ phương trình:

( )

01

1

1 2 0 2

4

11

fc

c

f a b a

b

f a b c

==



=







 = + =  =





=−

 = + + = −



.

Suy ra

( )

42

2 4 1f x x x= − +

( ) ( )

11f a b c f + + = − = −

.

Câu 40:Chọn C.

Trong

ABC

có

.cos60AB BC a=  =

ABM

đều và

SA SB SM==

nên hình chiếu của

S

lên

( )

ABC

trùng với điểm

H

là

trọng tâm của

ABM

d SH=

.

Trong

ABM

có

2 3 3

.

3 2 3

aa

HM ==

.Suy ra

22

39 3

2

99

aa

SH SM HM a= − = − =

.

Câu 41:Chọn C.TXĐ

 

\ 1 .

( )

2

1

y

x

−



=

−

Đường thẳng

d

đi qua điểm

( )

9;0A

với hệ số góc

k

có phương trình

( )

9y k x=−

.

Đường thẳng

d

tiếp xúc với đồ thị

( )

C

khi và chỉ khi hệ phương trình sau có nghiệm

( ) ( )

( )

2

32

91

1

2

1

x

kx

x

k

x

−



=−



−





−



=

−





2a

H

N

M

A

B

C

S

Trang 90

Thế

( )

2

vào

( )

1

, ta có

( )

( ) ( )( )

2

1

3 2 1

. 9 3 2 1 9 3 4 7 0

7

1

3

x

x x x x x x

x

=−



−−



= −  − − = −  − − = 



−

=

−



Do đó tích hệ số góc của hai tiếp tuyến đó bằng

( )

22

7 1 1 9

1 . . .

3 64

11

7

1

3

yy

−−





− = =





−−



−





Cách 2.

( )

2

1

y

x

−



=

−

.Gọi

0

x

là hoành độ tiếp điểm của tiếp tuyến kẻ từ

A

( )

0

1x 

.

Phương trình tiếp tuyến là:

( )

0

2

0

32

1

x

y x x

x

−

= − +

−

.

Tiếp tuyến qua

A

( )

( )( )

0

00

0 0 0

2

0

1

9 3 2

0 9 3 2 1 0

7

1

3

x

xx

x x x

x

=−



−−



 + =  − + − − = 



−

=

−





.

Hai hệ số góc của hai tiếp tuyến kẻ từ

A

là

( )

79

1.

3 64

yy





−=





.

Câu 42:Chọn A.

32

y ax bx cx d= + + +

;

( )

2

' 3 2f x ax bx c= + +

.

Cho

0x =

, ta có

( )

0 0.fd=

Từ hình dáng đồ thị ta thấy

0a 

Đồ thị hàm số có điểm cực đại và cực tiểu, suy ra

( )

'0fx=

có hai nghiệm phân biệt, từ đồ thị có hoành độ hai

điểm cực trị không âm do đó

12

0

2

00

3

0

3

a

b

x x b

a

c

xx

a













+ = −   





=





==





Câu 43:Chọn B.Vận tốc của chuyển động tại thời điểm

t

có phương trình là

( ) ( )

2

3 6 9.v t S t t t



= = − −

Gia tốc của chuyển động tại thời điểm

t

có phương trình là

( ) ( )

6 6.a t v t t



= = −

Tại thời điểm

3st =

ta có

( )

2

3 6.3 6 12 m/s .a = − =

Câu 44:Chọn A .Đặt

2

0xt=

, phương trình

42

2 3 0x x m− − + =

( )

1

trở thành

2

2 3 0t t m− − + =

( )

2

Để phương trình

( )

1

có đúng hai nghiệm thực thì phương trình

( )

2

có đúng một nghiệm

0.t 

TH1:

12

0 3 0 3.t t m m   −   

TH2:

12

0 tt=

.Đk:

12

0

4 0 4

10

mm

tt



=



 − =  =



= = 



Kết luận:

( )  

;3 4 .m − 

Trang 91

Cách 2: Phương trình

42

2 3 0x x m− − + =

có đúng hai nghiệm thực



Đồ thị

hàm số

42

23y x x= − −

và đường thẳng

ym=−

có hai điểm chung phân

biệt.Đồ thị hàm số

42

23y x x= − −

:

Ycbt

44

33

mm

− = − =







−  − 



.

Câu 45:Chọn AHoành độ giao điểm là nghiệm của phương trình

( ) ( )

( )

3 2 3 2 2

2

0

3 1 1 1 3 0 * 3 0

3 0.

x

x x m x x x x mx x x x m

x x m

=



− + + + = +  − + =  − + = 



− + =



Phương trình

( )

*

có ba nghiệm phân biệt khi và chỉ khi phương trình

2

30x x m− + =

có hai nghiệm phân biệt

khác

0

hay

0 9 4 0

9

0.

0 3.0 0 0

4

m

mm

 − 



   



− +  



Gọi

12

,xx

là hai nghiệm phân biệt của phương trình

2

30x x m− + =

.Theo Viet

12

3xx

x x m

+=





=



Tọa độ

( ) ( )

1 1 2 2

; 1 , ; 1M x x N x x++

. Khi đó tam giác

OMN

vuông tại

O

khi và chỉ khi

( )( ) ( )

1 2 1 2 1 2 1 2

. 0 1 1 0 2 1 0 3 2 1 0 2. TmđkOM ON x x x x x x x x m m=  + + + =  + + + =  + + =  = −

Câu 46:Chọn B.Gọi

,,abc

(

, , 0abc

,đơn vị

dm

) lần lượt là chiều dài, chiều rộng và chiều cao của khối hộp

chữ nhật.Khi đó, thể tích khối hộp là

8V abc==

; diện tích toàn phần là

( )

2

tp

S ab bc ca= + +

.

Có

( )

3

2 2.3 . . 24

tp

S ab bc ca abbcca= + +  =

.Dấu bằng xảy ra khi

2abc= = =

.

Câu 47:Chọn D.Lồng khối tứ diện

ABCD

vào một khối tứ diện

AMNP

sao cho

,,B C D

lần lượt là trung điểm

,,MN NP PM

như hình vẽ.Dễ dàng ta có khối

AMNP

có

,,AM AN AP

đôi

một vuông góc và

2 5;MN =

2 10;NP =

2 13AD =

.

Suy ra

4; 2; 6AM AN AP= = =

, nên thể tích

1

. . 8

6

AMNP

V AM AN AP==

.Mà

1

2

4

ABCD AMNP

VV==

.

Câu 48:Chọn B.Đồ thị hàm số

( )

1y f x=−

là tịnh tiến đồ thị hàm số

( )

y f x=

xuống dưới 1 đơn vị.

Đồ thị hàm số

( )

1y f x=−

được suy ra từ đồ thị hàm số

( )

1y f x=−

bằng

cách giữ nguyên phần đồ thị trên trục hoành; lấy đối xứng qua trục

Ox

phần đồ

thị nằm dưới trục hoành.

Ta được đồ thị hàm số

( )

1y f x=−

như hình vẽ:

Phương trình

( )

11fx−=

là phương trình hoành độ giao điểm của đồ thị hàm số

( )

1y f x=−

và đường thẳng

1y =

.

Dựa vào đồ thị, phương trình đã cho có 5 nghiệm phân biệt trên

 

2;2−

.

Câu 49:Chọn D.Đk:

1; 1xy  −

. Đặt

t x y=+

;

0t 

.

Có

( ) ( )

1 2 2 1 2. 1 3 3x y x y x y x y x y− + + = − + +  +  +  +

.

Vậy

2

3 3 0 0 3t t t t t  −    

.

Trang 92

( ) ( ) ( )

2

2 2 8 4P x y x y x y= + + + + + − +

nên

2

2 2 8 4P t t t= + + + −

4

22

4

Pt

t



= + −

−

.

( )

0 2 2 4 4P t t



=  + − =

 

0

1 2 2 0;3

t

=







=  





.

( )

0 18;P =

( )

3 25P =

.Suy ra

25; 18Mm==

43Mm + =

.

Câu 50:Chọn B.

( )

22

1 1 cosy m m m m x



= + + + − +

.

Hàm số đồng biến trên

( )

0;2



( )

0, 0;2yx





   

.

( )

22

1 1 cos 0m m m m x + + + − + 

( )

0;2x





2

1

cos

1

mm

x

mm

++

  −

−+

( )

0;2x





ĐK:

2

1

mm

++

−  −

−+

22

11m m m m − +  + +

0m

ĐỀ 57

ĐỀ THI THỬ THPT QUỐC GIA 2020

MÔN TOÁN

Thời gian: 90 phút

Câu 1: Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với

đáy, SA = a. Tính thể tích khối chóp S.ABC. A.

3

.

12

a

V =

B.

3

.

4

a

V =

C.

3

.

4

a

V =

D.

3

.

12

a

V =

Câu 2: Giá trị cực tiểu của hàm số

3

1

3

y x x= − + −

là: A.

5

.

3

−

B.

1

.

3

−

C.

1.−

D. 1.

Câu 3: Cho khối chóp có đáy hình vuông cạnh a và chiều cao bằng 2a. Thể tích của khối chóp đã cho

bằng:

A.

3

4.a

B.

3

2

.

3

a

C.

3

2.a

D.

3

4

.

3

a

Câu 4: Số đường tiệm cận của đồ thị hàm số

2

1

x

y

x

=

−

nằm

bên phải trục tung là: A. 2. B. 3. C. 4.

D. 1.

Câu 5: Đường cong trong hình vẽ là đồ thị của hàm số nào

trong bốn hàm số sau:

A.

22

.

1

x

y

x

−+

=

+

B.

2

.

2

x

y

x

−+

=

+

C.

22

.

1

x

y

x

−

=

+

D.

2

.

1

x

y

x

−

=

+

Câu 6: Thể tích của khối lăng trụ có khoảng cách giữa môt

đường

thẳng bất kỳ của đáy này tới một đường thẳng bất kỳ của đáy kia bằng

h

và diện tích của đáy bằng

B

là:

A.

1

.

6

V Bh=

B.

1

.

3

V Bh=

C.

1

.

2

V Bh=

D.

.V Bh=

Trang 93

Câu 7: Một vật chuyển động theo quy luật

23

1

10 ,

3

S t t=−

với t (giây) là khoảng thời gian tính từ lúc vật

bắt đầu chuyển động và S (m) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng

thời gian 15 giây, kể từ khi vật bắt đầu chuyển động vận tốc

( )

/v m s

của vật đạt giá trị lớn nhất tại thời

điểm

( )

ts

bằng:

A. 8 (s). B. 20 (s). C. 10 (s). D. 15 (s).

Câu 8: Cho khối tứ diện

OABC

có

,,OA OB OC

đôi một vuông góc và

, , .OA a OB b OC c= = =

Thể tích

khối tứ diện

.O ABC

được tính theo công thức nào sau đây:A.

1

.

6

V abc=

B.

1

.

3

V abc=

C.

1

.

2

V abc=

D.

3.V abc=

Câu 9: Khối hộp chữ nhật

.ABCD A B C D

   

có độ dài các cạnh lần lượt là 2a, 3a và 4a. Thể tích khối hộp

.ABCD A B C D

   

là: A.

3

20 .Va=

B.

3

24 .Va=

C.

3

.Va=

D.

3

18 .Va=

Câu 10: Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số

32

2 3 12 10y x x x= − − +

trên đoạn

 

3;3−

là:

A.

1.−

B. 18. C.

18.−

D. 7.

Câu 11: Tọa độ tâm đối xứng của đồ thị hàm số

2

21

x

y

x

−

=

−

là:A.

1

;2 .

2



−





B.

11

;.

22







C.

1

; 1 .

2



−





D.

11

;.

22



−





Câu 12: Cho hàm số

42

2 2 1.y x mx m= − + − +

Với gái trị nào của m thì đồ thị hàm số có 3 điểm cực trị?

A.

0.m 

B.

0.m =

C.

0.m 

D.

0.m 

Câu 13: Cho hàm số

31

.

2

x

y

x

−

=

−+

Khẳng định nào sau đây là

đúng?

A. Hàm số luôn nghịch biến trên

.

B. Hàm số luôn nghịch biến trên từng khoảng xác định.

C. Hàm số luôn đồng biến trên các khoảng

( )

;2−

và

( )

2; .− +

D. Hàm số luôn nghịch biến trên các khoảng

( )

;2− −

và

( )

2; .− +

Câu 14: Cho hàm số

( )

42

,0y ax bx c a= + + 

có đồ thị như hình vẽ. Hàm số đã cho nghịch biến trên bao

nhiêu khoảng? A. 2. B. 4. C.

3.

D. 1.

Câu 15: Cho hình chóp

.S ABCD

có đáy là hình thang vuông tại A và D. SA vuông góc với mặt phẳng

đáy

( )

ABCD

;

2 ; .AB a AC CD a= = =

Mặt phẳng

( )

P

đi qua CD và trọng tâm G của tam giác

SAB

cắt

các cạnh SA, SB lần lượt tại M và N. Tính thể tích khối chóp

.S CDMN

theo thể tích khối chóp

..S ABCD

A.

..

14

.

27

S CDMN S ABCD

VV=

B.

..

4

.

27

S CDMN S ABCD

VV=

C.

..

10

.

27

S CDMN S ABCD

VV=

D.

.

2

S ABCD

S CDMN

V

V =

Câu 16: Gọi

12

,mm

là các giá trị của

m

để hệ phương trình

( )

2 2 2

2 1 0

2 4 5

y x y

x x y y m

 − − − =





− + − + =





có đúng 4

nghiệm nguyên.

Trang 94

Khi đó

22

2

1

mm+

bằng: A. 10. B. 9. C. 20. D. 4.

Câu 17: Cho hàm số

()y f x=

có đồ thị nhưu hình bên. Giá trị lớn nhất của

hàm số này trên đoạn

 

1;2−

bằng: A. 5. B. 2. C. 1. D. Không

xác định.

Câu 18: Cho hàm số

()y f x=

xác định trên và có bảng xét dấu đạo hàm

như sau:

x

−

1

x

2

x

3

x

+

y



−

0 + ||

−

0 +

Khi đó số điểm cực trị của đồ thị hàm số

()y f x=

là:A. 3. B. 2. C. 4. D. 1.

Câu 19: Hình nào dưới đây là đồ thị hàm số

32

3 4?y x x= − +

Câu 20: Lập phương trình tiếp tuyến với đồ thị hàm số

()y f x=

thỏa mãn

( ) ( )

23

1 2 1f x x f x+ = − −

tại

điểm có hoành độ x = 1? A.

16

.

77

yx= − −

B.

16

.

77

yx= − +

C.

16

.

77

yx=−

D.

16

77

yx=+

Câu 21: Cho hàm số

( )

3 2 2

11

2 4 4 3 1

32

y x m x m m x= − + + + + +

(m là tham số). Tìm để hàm số đạt cực

đại tại

0

2?x =

A.

1.m =

B.

2.m =−

C.

1.m =−

D.

2.m =

Câu 22: Cho khối đa diện đều. Khẳng định nào sau đây sai?

A. Số đỉnh của khối lập phương bằng 8. B. Số mặt của khối tứ diện đều bằng 4.

C. Khối bát diện đầu là loại

 

4;3 .

D. Số cạnh của khối bát diện đều bằng 12.

Câu 23: Đồ thị hàm số nào sau đây có 3 điểm cực trị?

A.

42

2 3.y x x= + −

B.

4 3 2

1 1 1

3.

4 3 2

y x x x x= − − + +

C.

2

1 4.yx= − −

D.

3

1.yx=−

Câu 24: Cho khối chóp

.S ABC

có thể tích

.V

Nếu giữu nguyên chiều cao và tăng các đáy lên 3 lần thì

thể tích khối chóp thu được là: A.

3.V

B.

6.V

C.

9.V

D.

12 .V

Câu 25: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật.

,2AB a BC a==

cạnh bên SA vuông

góc với đáy và

2.SA a=

Tính thể tích khối chóp

.?S ABCD

A.

3

23

.

3

a

B.

3

22

.

3

a

C.

3

2 2.a

D.

3

2.a

Câu 26: Cho hàm số

()y f x=

có bảng biến thiên dưới đây. Mệnh đề nào sau đây là đúng?

x

−

2−

0 2

+

()fx



+ 0

−

||

−

0 +

()fx

4−

+

−

4

Trang 95

A. Hàm số đạt cực tiểu tại

4.x =

B. Đồ thị hàm số có đường tiệm cận ngang. C.

Hàm số có

4.

CD

y =

D. Đồ thị hàm số có một tiệm cận đứng là đường thẳng

0.x =

Câu 27: Cho khối chóp tứ giác đều

.S ABCD

có đáy

ABCD

là hình vuông cạnh

3cm. Cạnh bên tạo với đáy

0

60

. Thể tích (cm

3

) của khối chóp đó là:

A.

32

.

2

B.

96

.

2

C.

93

.

2

D.

36

.

2

Câu 28: Hãy xác định

,ab

để hàm số

2 ax

y

xb

−

=

+

có đồ thị như hình vẽ:

A.

1; 2.ab= = −

B.

2.ab==

C.

1; 2.ab= − = −

D.

2.ab= = −

Câu 29: Cho hàm số

42

y ax bx c= + +

có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?

A.

0, 0, 0.abc  

B.

0, 0, 0.a b c  

C.

0, 0, 0.a b c  

D.

0, 0, 0.a b c  

Câu 30: Cho hàm số

32

y ax bx cx d= + + +

có đồ thị như hình bên. Mệnh đề nào dưới đây là đúng?

A.

0, 0, 0, 0.a b c d   

B.

0, 0, 0, 0.a b c d   

C.

0, 0, 0, 0.a b c d   

D.

0, 0, 0, 0.a b c d   

Câu 31: Cho hình chóp tứ giác đều

.S ABCD

có cạnh đáy bằng

,a

cạnh bên hợp với mặt đáy một góc 60

0

. Tính theo

a

thể tích khối chóp

.S ABCD

.

A.

3

6

.

6

a

V =

B.

3

6

.

2

a

V =

C.

3

6

.

3

a

V =

D.

3

.

3

a

V =

Câu 32: Cho lăng trụ đứng

.ABC A B C

  

có đáy là

ABC

vuông tại B,

0

, 60 ,AB a BAC==

3.AA a



=

Thể tích khối lăng trụ là: A.

3

.

2

a

B.

3

2

.

3

a

C.

3

.

3

a

D.

3

.

9

a

Câu 33: Cho hàm số

3

2

32

3

x

yx= + −

có đồ thị là

( )

.C

Viết phương trình tiếp tuyến với đồ thị

( )

C

biết

tiếp tuyến có hệ số góc

9.k =−

A.

( )

16 9 3 .yx+ = − +

B.

( )

9 3 .yx= − +

C.

( )

16 9 3 .yx− = − −

D.

( )

16 9 3 .yx− = − +

Câu 34: Cho hàm số

()y f x=

liên tục trên D và có giá trị lớn nhất, gái trị nhỏ nhất trên D. Khi đó bất

phương trình

()f x m

có nghiệm khi và chỉ khi:

A.

( ) .

D

Max f x m

B.

( ) .

D

Max f x m

C.

1

( ) ( ) .

2

DD

Max f x Min f x m



−



D.

( ) .

D

Min f x m

Câu 35: Cho hình hộp

.ABCD A B C D

   

có đáy

ABCD

là hình thoi cạnh

0

. 120a BCD =

,

7

.

2

AA a



=

Hình

chiếu vuông góc của

A



lên mạt phẳng

( )

ABCD

trung với giao điểm của

AC

và

.BD

Tính theo

a

thể

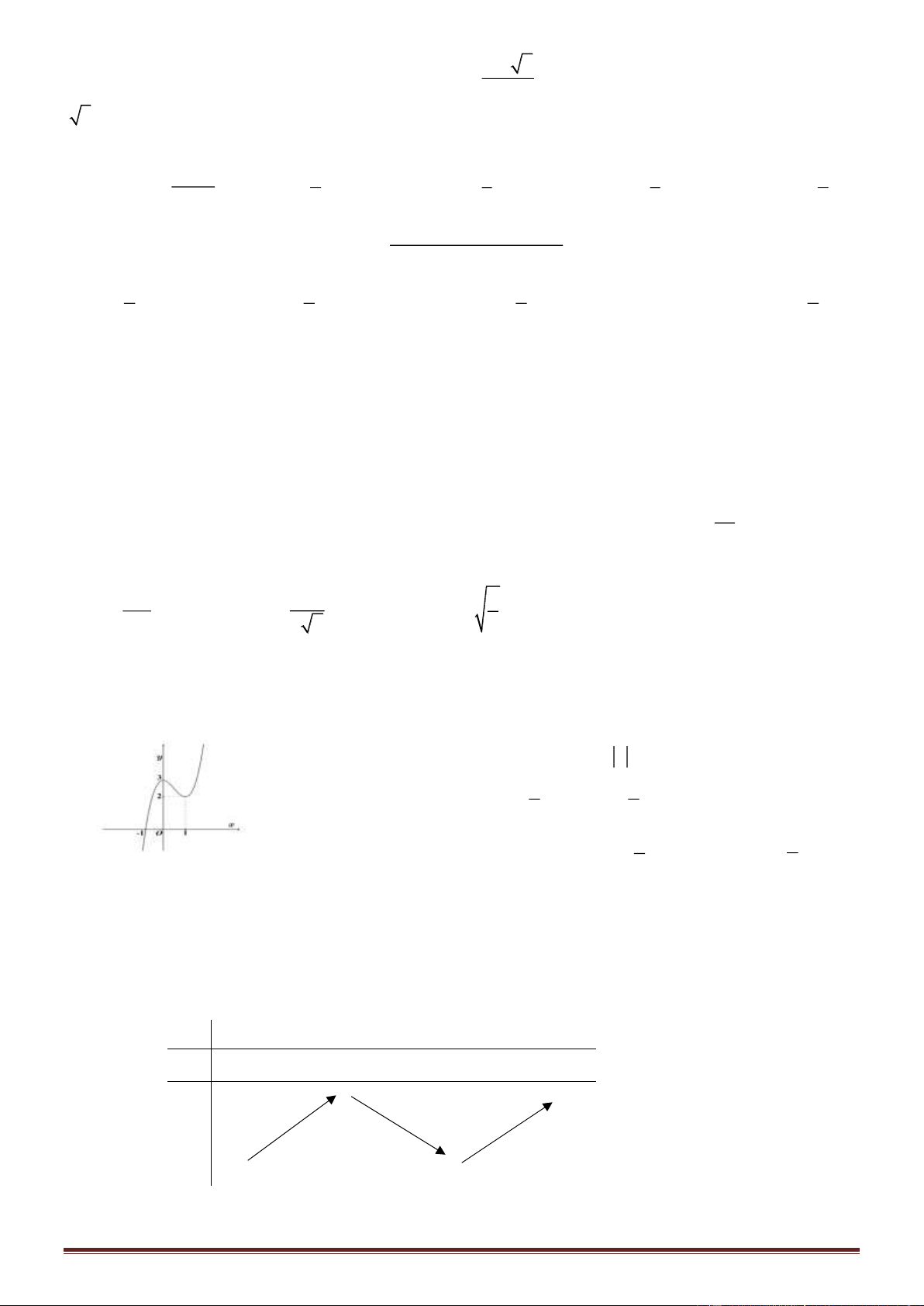
Trang 96

tích khối hộp

.ABCD A B C D

   

? A.

3

3.a

B.

3

46

.

3

a

C.

3

2.a

D.

3

3.a

Câu 36: Cho tứ diện

MNPQ

. Gọi

;;I J K

lần lượt là trung điểm các cạnh

; ; .MN MP MQ

Tỉ số thể tích

MIJK

MNPQ

V

bằng: A.

1

.

4

B.

1

.

3

C.

1

.

8

D.

1

.

6

Câu 37: Xác định

m

để đồ thị hàm số

( )

22

1

2 1 2

x

y

x m x m

−

=

+ − + −

có đúng hai đường tiệm cận đứng.

A.

3

.

2

m 

B.

3

; 1.

2

mm − 

C.

3

; 1; 3.

2

m m m −   −

D.

3

.

2

m −

Câu 38: Hàm số

()fx

có đạo hàm

( )

2

( ) 2 .f x x x



=+

Phát biểu nào sau đây là đúng?

A. Hàm số đồng biến trên khoảng

( )

2; .− +

B. Hàm số nghịch biến trên các khoảng

( )

;2− −

và

( )

0; .+

C.Hàm số đồng biến trên các khoảng

( )

;2− −

và

( )

0; .+

D. Hàm số nghịch biến trên khoảng

( )

2;0 .−

Câu 39: Cho hình lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác đều cạnh a,

3

.

2

a

AA



=

Biết rằng hình

chiếu vuông góc của

A



lên

( )

ABC

là trung điểm

.BC

Tính thể tích

V

của lăng trụ đó.

A.

3

2

.

3

a

V =

B.

3

.

42

a

V =

C.

3

.

2

Va=

D.

3

.Va=

Câu 40: Cho hàm số

42

42y x x= − −

có đồ thị

( )

C

và đồ thị

( )

2

: 1 .P y x=−

Số giao điểm của

( )

P

và

đồ thị

( )

C

là: A. 1. B. 4. C. 2. D. 3.

Câu 41: Cho hàm số

()y f x=

có đồ thị như hình vẽ bên:

Điều kiện của

m

để phương trình

( )

f x m=

có 4 nghiệm phân biệt

1 2 3 4

, , ,x x x x

thỏa mãn

1 2 3 4

11

22

x x x x −    

là:

A.

( )

2;3 .m

B.

 

2;3 .m

C.

)

5

;3 .

2

m









D.

5

2; .

2

m















Câu 42: Cho hàm số

3

3 1.y x x= − −

Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên khoảng

( )

;.− +

B. Hàm số nghịch biến trên khoảng

( )

1;1 .−

C. Hàm số nghịch biến trên khoảng

( )

; 1 .− −

D. Hàm số đồng biến trên khoảng

( )

0;1 .

Câu 43: Cho hàm số

()y f x=

có bảng biến thiên như sau:

x

−

2−

2

+

y



+ 0

−

0 +

y

3

+

−

0

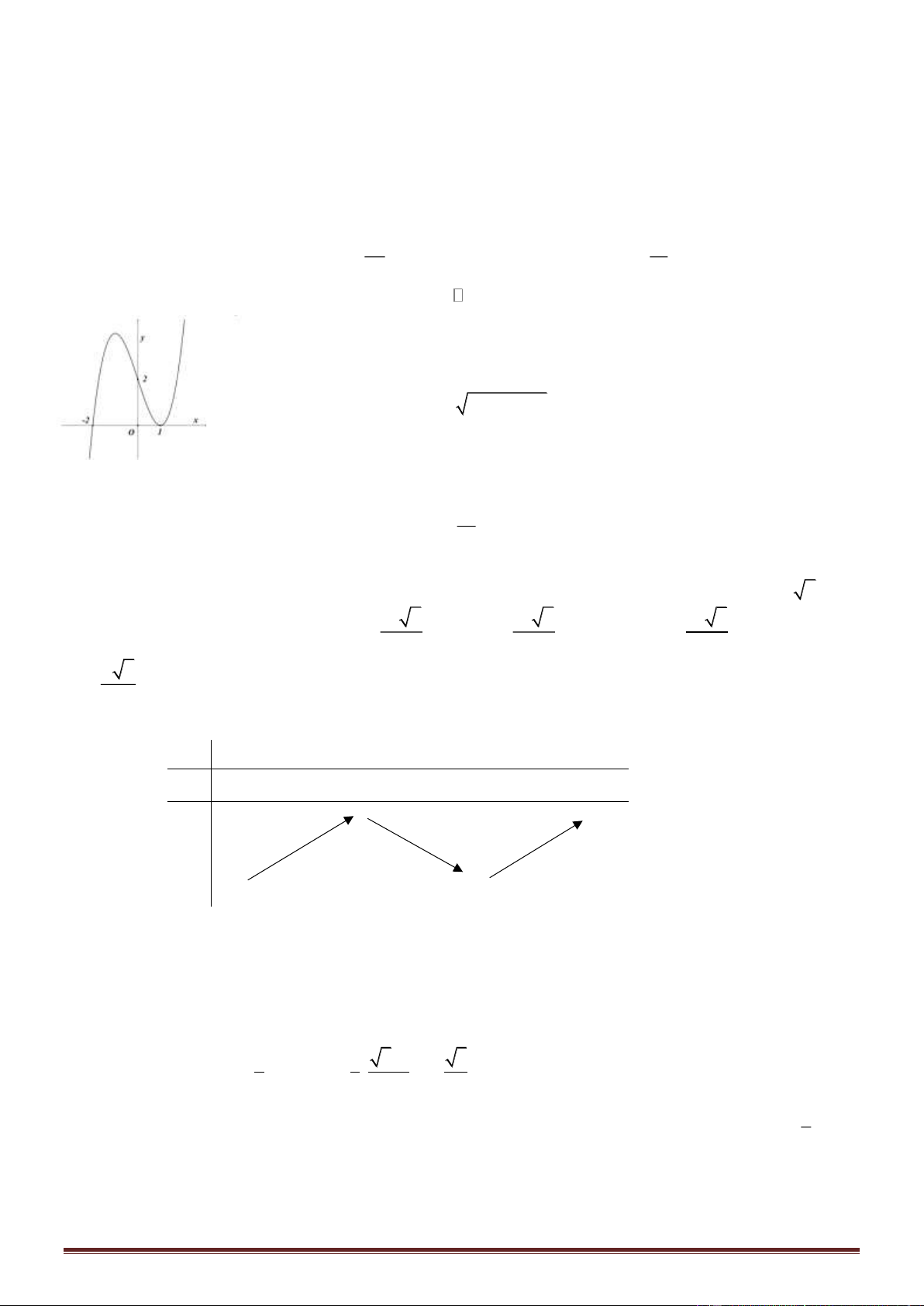
Trang 97

Mệnh đề nào dưới đây là đúng? A. Hàm số đạt cực đại tại

3.x =

B. Hàm số đạt cực tiểu tại

2.x =−

C. Hàm số có

3.

CD

y =

D. Hàm số nghịch biến trên các khoảng

( )

;2− −

và

( )

2; .+

Câu 44: Tổng diện tích các mặt của một hình lập phương bằng 54. Thể tích của khôi lập phương là:

A. 15. B. 27. C. 18. D. 21.

Câu 45: Một xưởng sản xuất những thùng bằng kẽm hình hộp chữ nhật không có nắp và có các kích

thước

,,x y z

(dm). Biết tỉ số hai cạnh đáy là

: 1:3xy=

và thể tích của hộp bằng 18

3

( ).dm

Để tốn ít vật

liệu nhất thì tổng

x y z++

bằng? A.

26

.

3

B. 10. C.

19

.

2

D. 26.

Câu 46: Cho hàm số

()y f x=

được xác định trên và hàm số

()y f x



=

có đồ thị như hình vẽ.

Tìm khoảng nghịch biến của hàm số

( )

2

3?y f x=−

A.

( )

;1− −

và

( )

0;1 .

B.

( )

1;0 .−

C.

( )

1;0 .−

D.

( )

1;1 .−

Câu 47: Cho hàm số

2

20y x x= − −

. Mệnh đề nào dưới đây là sai?

A. Hàm số nghịch biến trên khoảng

( )

;4 .−

B. Hàm số đạt cực đại tại

5.x =

C. Hàm số đồng biến trên khoảng

( )

5; .+

D. Hàm số không có cực trị.

Câu 48: Tìm tất cả các giá trị của m để hàm số

( ) ( )

3

2

1 2 1 2

3

x

y m x m x= − − + − +

đồng biến trên tập xác

định của nó là: A.

1 3.m

B.

1.m 

C.

1 3.m

D.

3.m 

Câu 49: Cho hình lăng trụ đứng

.ABC A B C

  

có đáy là tam giác đều cạnh a. Cạnh bên

2AA a



=

. Thể

tích khối lăng trụ

.ABC A B C

  

là: A.

3

6

.

4

a

V =

B.

3

6

.

2

a

V =

C.

3

6

.

12

a

V =

D.

6

.

4

a

V =

Câu 50: Cho hàm số

()y f x=

có bảng biến thiên như sau:

x

−

1−

3

+

y



+ 0

−

0 +

y

4

+

−

2−

Số nghiệm của phương trình

2 ( ) 1 0fx+=

là: A. 0. B. 3. C. 1.

D. 2.

HƯỚNG DẪN GIẢI

Câu 1: Chọn A.

2

3

.

1 1 3 3

. . . .

3 3 4 12

S ABC ABC

a

V S SA a a



= = =

Câu 2: Chọn A.

2

1

1 0 ; 2

1

x

y x y x

x

=



 

= − + =  = −



=−



. Vì

( ) ( )

1 0 1yy

 

−  

nên

( )

5

1.

3

CT

yy= − = −

Trang 98

Nhận xét: Khi giải toán trắc nghiệm, thực ra không cần tính

y



. Hãy nhớ rằng

đồ thị hàm số bậc ba có 3 điểm cực trị và hệ số a < 0 có hình dạng như hình vẽ

bên dưới.

Qua đó có thể thấy điểm cực tiểu của đồ thị hàm số là điểm cực trị bên trái, hay

nói cách khác là điểm cực trị có hoành độ nhỏ hơn (nghiệm bé hơn của phương

trình

0y



=

).

Câu 3: Chọn B.

23

12

.2

33

V a a a==

Câu 4: Chọn D.Hàm số này có 2 đường tiệm cận đứng là

1; 1xx= − =

, đường

nằm bên phái trục tung chỉ có đường

1.x =

Câu 5: Chọn A.Nhìn vào đồ thị hàm số ta thấy:

Đồ thị hàm số có đường tiệm cận đứng

1,x =−

loại phương án B.

Đồ thị hàm số có đường tiệm cận ngang

2,y =−

loại phương án C,D.

Câu 6: Chọn D.Giả thiết khoảng cách giữa một đường thẳng bất kỳ của đáy này tới một đường thẳng bất

kỳ của đáy kia bằng

h

cho ta thông tin chiều cao của lăng trụ bằng

,h

vì 2 đáy song song với nhau. Do

đó

.V Bh=

Câu 7: Chọn C.

( ) ( )

2

22

20 20 100 100 100 10 100v s t t t t t t



= = − = − + − + = − − 

Dấu bằng xảy ra khi và chỉ khi

10 (s)t =

Câu 8: Chọn A.

Câu 9: Chọn B.

3

.

2 .3 .4 24 .

ABCD A B C D

V a a a a

   

==

Câu 10: Chọn C.

( )( )

2

6 6 12 6 1 2 ,y x x x x



= − − = + −

hàm số liên tục trên

( )

3;3−

( ) ( ) ( ) ( )

3 35; 1 17; 1 3; 3 1.y y y y− = − − = = − =

Do đó

   

3;3 3;3

17; 35Max Min

−−

= = −

nên tổng

   

3;3 3;3

17 35 18.Max Min

−−

+ = − = −

Câu 11: Chọn B.Tâm đối xứng của đồ thị hàm số này là giao điểm của 2 đường tiệm cận

11

: ; .

22

I







Câu 12: Chọn D.

( )

32

4 4 4 .y x mx x x m



= − + = − −

Đồ thị hàm số có 3 điểm cực trị khi và chỉ khi phương

trình

0y



=

có 3 nghiệm phân biệt

0.m

Câu 13: Chọn B.

( ) ( )

22

3 1 6 2 4

0.

2

22

x

yy

x

xx

− − + −



=  = = 

−

−−

Câu 14: Chọn A.Có 2 khoảng nghịch biến của đồ thị hàm số là

( )

;1− −

và

( )

0;1 .

Câu 15: Chọn A. Gọi K là trung điểm của AB.

( )

/ / / / / /DC AB DC mp SAB DC MN

Do đó

2

.

3

SM SN SG

SA SB SK

===

Vì

2 2.

ABD DCB

AB CD S S



=  =

Do đó

.

. . .

.

4 2 4 8

. . . .

9 3 9 27

S DMN

S DMN S ABCD S ABCD

S DAB

V

SM SN

V V V

V SA SB

= =  = =

.

2

3

S DCN

S DCB

V

SN

V SD

==

nên

. . . .

2 2 1 2

..

3 3 3 9

S DCN S DCB S ABCD S ABCD

V V V V= = =

Do đó

. . .

8 2 14

27 9 27

S CDMN S ABCD S ABCD

V V V



= + =





Câu 16: Chọn C.Hệ đã cho tương đương với

( )( )

( ) ( )

22

2

2 1 3

21

yx

y x m

− − =







− + − =





Trang 99

Hệ có nghiệm nguyên

( )

00

;xy

thì

( )

 

0

3

1 1; 3 .xU−  =  

Nếu

( )

2

0

11x −=

thì

( )

2

0

2 9 10ym− =  =

;Nếu

( )

2

0

19x −=

thì

( )

2

0

2 1 10ym− =  =

Do đó

22

1 2 1 2

10, 10 20.m m m m= − =  + =

Câu 17: Chọn A.Dựa vào đồ thị hàm số

()y f x=

, rõ ràng

 

1;2

( ) 5.max f x

−

=

Câu 18: Chọn A.Tại các điểm

1 2 3

, , ,x x x

hàm số

()y f x=

xác định và hàm số

()y f x



=

không xác định

hoặc bằng 0, ngoài ra hàm số

()y f x



=

còn đổi dấu qua các điểm đó nên hàm số

()y f x=

có 3 điểm cực

trị.

Câu 19: Chọn C.Hệ số a > 0, loại phương án A và D.

Đồ thị hàm số cắt trục tung tại điểm (0;4), loại phương án B.

Câu 20: Chọn A.Phương tình tiếp tuyến của đồ thị hàm số tại điểm

1: (1).( 1) (1)x y f x f



= = − +

Từ

23

(1 2 ) (1 ),f x x f x+ = − −

thay

0x =

vào, ta có

23

(1) 0

(1) (1)

(1) 1

f

ff

f

=



= − 



=−



Lấy đạo hàm hai vế:

2 (1 2 ). (1 2 ).2 1 3 (1 ). (1 ).( 1)f x f x f x f x



+ + = − − − −

2

4 (1 2 ). (1 2 ) 1 3 (1 ). (1 )f x f x f x f x



 + + = + − −

Thay

0x =

vào, ta có:

2

4. (1). (1) 1 3. (1). (1) (1).f f f f



=+

Nếu

(1) 0, (1) 0 = 1f =

(vô lý)

Nếu

1

(1) 1, (1) -4 (1) 1 3 (1) (1) .

7

f f f f

  

= −  = +  = −

Do đó phương trình tiếp tuyến:

( )

1 1 6

1 1 .

7 7 7

y x x= − − − = − −

Câu 21: Chọn A.

( )

( ) ( )( ) ( )( )

2 2 2

2 4 4 3 2 4 1 3 1 3 .y x m x m m x m x m m x m x m



= − + + + + = − + + + + = − − − −

1

0

3

xm

y

xm

=+





=



=+



Hệ số a > 0 nên hàm số đạt cực đại tại điểm nghiệm của

y



nhỏ hơn, tức là

1

CD

xm=+

. Ta có

1 2 1.mm+ =  =

Câu 22: Chọn C.Khối bát diện đều là loại

 

3;4 .

Câu 23: Chọn C.Chú ý rằng hàm số

42

y ax bx c= + +

có ba điểm cực trị khi và chỉ khi

0ab 

, phương

án A sai.

Hàm số

4 3 2

1 1 1

3

4 3 2

y x x x x= − − + +

có

( ) ( )

2

32

1 1 1y x x x x x



= − − + = − +

có 1 điểm cực trị

Hàm số

3

1yx=−

có 1 điểm cực trị vì hàm số

( )

3

1yx=−

đơn điệu trên R.

Hàm số

2

14yx= − −

có số điểm cực trị là 3 điểm, đó là

1; 1; 0x x x= − = =

Câu 24: Chọn C.Các đáy được tăng lên 3 lần thì diện tích tăng lên 9 lần.

1

.

3

d

V S h=

tăng lên 9 lần.

Câu 25: Chọn B.

2 2 3

.

1 1 2 2

. .2 2 . . . 2.2 .

3 3 3

ABCD S ABCD ABCD

S AB BC a a a V SAS a a a= = =  = = =

Câu 26: Chọn D.

0

lim .

x

+

→

= +

Câu 27: Chọn B.Gọi H là tâm của hình vuông ABCD thì

( )

SH mp ABCD⊥

3

2.

AB HA=  =

Do đó

0

3 3 6

.tan60 . 3 .

2

SH AH= = =

Trang 100

23

.

1 1 3 6 9 6

. . .3 ( )

3 3 2 2

S ABCD ABCD

V SH S cm= = =

Câu 28: Chọn C.Đồ thị hàm số có đường tiệm cận đứng

2x =

nên

2 0 2.bb+ =  = −

Đồ thị hàm số cắt trục hoành tại điểm

2

;0

a







nên

2

21a

a

= −  = −

Câu 29: Chọn B.Dễ thấy

lim

x

y

→+

= +

nên a > 0.Đồ thị hàm số có 3 điểm cực trị nên

00ab b  

Đồ thị hàm số cắt trục tung tại điểm (0;c) có tung độ dương nên c > 0.

Câu 30: Chọn D.Dễ thấy

lim

x

y

→+

= +

nên a > 0.

2

3 2 , 0y ax bx c y



= + + =

có 2 nghiệm phân biệt là 2 và 7 nên

2

27

3

2.7

3

b

a

c

a



+ = −







=





Vì a > 0 nên b < 0, c > 0.

Câu 31: Chọn A.Gọi H là tâm của hình vuông ABCD thì

( )

SH mp ABCD⊥

2

a

AB a HA=  =

. Do đó

0

6

.tan60 . 3 .

2

aa

SH AH= = =

( )

2 3 3

.

1 1 6 6

..

3 3 2 6

S ABCD ABCD

a

V SH S a a cm= = =

Câu 32: Chọn A.

ABC

vuông tại B nên

02

1 1 3

.tan60 3 . . 3 .

2 2 2

ABC

BC AB a S AB BC a a a



= =  = = =

23

.

33

. 3. .

22

ABC A B C ABC

V AA S a a a

  





= = =

Câu 33: Chọn D.

22

6 , 9 6 9 3y x x y x x x



= + = −  + = −  = −

Phương trình tiếp tuyến của

( )

C

tại điểm

( )( ) ( ) ( )

3: 3 3 3 9 3 16x y y x y x



= − = − + + − = − + +

Câu 34: Chọn A.Phương trình này có nghiệm khi và chỉ khi

()

D

Max f x m

Câu 35: Chọn A.

22

33

2 2.

42

ABCD ABC

S S a a



= = =

;

2 2 2 2

1 49 1

2 3 .

2 2 4 4

a

AH AC A H A A AH a a a



= =  = − = − =

23

.

3

. 2 3 . 3 .

2

ABCD A B C D ABCD

V A H S a a a

   



= = =

Câu 36: Chọn C.

1 1 1 1

. . . . .

2 2 2 8

MIJK

MNPQ

V

MI MJ MK

V MN MP MQ

= = =

Câu 37:Chọn C.Đồ thị hàm số

( )

22

1

2 1 2

x

y

x m x m

−

=

+ − + −

có đúng hai đường tiệm cận đứng khi và chỉ

khi phương trình

( )

22

2 1 2 0x m x m+ − + − =

có 2 nghiệm phân biệt khác 1. Điều này xảy ra khi và chỉ

khi

( )

2

3

2 3 0

1 2 0

2

2 3 0

(1) 1 2 2 2 0

1; 3.

m

mm

m

mm

f m m

mm





− + 

 = − − − 









  

+ − 



= + − + − 





  −



Trang 101

Câu 38: Chọn A.

( ) 0 2.f x x



   −

Câu 39: Chọn B.

2

3

4

ABC

Sa



=

;

2 2 2 2

9 3 6

4 4 2

A H AA AH a a a



= − = − =

;

23

.

6 3 3 2

. . .

2 4 8

ABC A B C ABC

V A H S a a a

  



= = =

Câu 40: Chọn C.Phương trình hoành độ giao điểm

4 2 2 4 2

4 2 1 3 3 0x x x x x− − = −  − − =

, phương trình này có đúng hai

nghiệm.

Câu 41: Chọn C.Đồ thị hàm số

( )

y f x=

được vẽ như hình bên.

Đồ thị hàm số có điểm uốn là trung điểm của 2 đường cực trị

15

;

22

I







Số nghiệm của phương trình

( )

f x m=

là số giao điểm của đồ thị hàm số

( )

y f x=

và đường thẳng

.ym=

Để phương trình có 4 nghiệm thỏa mãn

điều kiện đề bài thì

5

3.

2

m

Câu 42: Chọn B.

( )( )

2

3 3 3 1 1 ; 0 1 1.y x x x y x



= − = − +   −  

Câu 43: Chọn C.

Câu 44: Chọn B.Gọi cạnh của hình lập phương là

a

, theo đề bài ra

2

6 54 3.aa=  =

Do đó

3

27.Va==

Câu 45: Chọn C.Đáy có kích thước là

,3 .xx

Chiều cao là

z

nên thể tích thùng là

22

3 18 6.V x z x z= =  =

Để tốn ít vật liệu nhât thì diện tich sản xuất phải nhỏ nhất.

( )

22

3 . 2 6 3 8S x z x x x xz= + + = +

2 2 2 2

3

6 48 24 24 24 24

3 8. 3 3 3 3 . . 36.x x x x

x x x x x x

= + = + = + +  =

Dấu bằng xảy ra khi và chỉ khi

2

24

3 2.xx

x

=  =

Khi đó

2

63

3 6; .

2

y x z

x

= = = =

3 19

2 6 .

22

x y z+ + = + + =

Câu 46: Chọn A.

22

( 3) 2 . ( 3).y f x y x f x



= −  = −

Nếu x > 0, ta có

( )

2 2 2

0 3 0 3 2 1 0 1.y f x x x x



  −   −  −     

Hàm số nghich biến trên

(0;1).

Nếu x < 0, ta có

( )

2 2 2

0 3 0 3 2 1 1.y f x x x x



  −   −  −     −

Hàm số nghcihj biến trên

( )

; 1 .− −

Câu 47: Chọn B.

( )( )

2

5

20 4 5 0

4

x

x x x x

x





− − = + +  



−



TXĐ:

 

)

(

; 4 5; .D = − −  +

2

21

, 0 5, 0 4.

2 20

x

y y x y x

xx

−

  

=       −

−−

Hàm số không có cực trị,

Nhận xét: Nhiều bạn sẽ cho rằng hàm số này có cực trị tại x = 5, vì không tồn tại đạo hàm tại x = 5 nhưng

hàm số vẫn xác định tại x = 5.Chưa đủ,

y



còn phải đổi dấu khi x đi qua 5. Tuy nhiên trong trường hợp

này, hàm số không xác định khi

( )

4;5x−

nên x = 5 không là điểm cực trị.

Trang 102

Câu 48: Chọn C.

( ) ( )

2

2 1 2 1 ,y x m x m



= − − + −

hàm số đồng biến trên

0yx



   

( ) ( ) ( )( )

2

1 2 1 0 1 3 0 1 3.m m m m m



  = − − −   − −    

Câu 49: Chọn A..

2

3

,

4

ABC

Sa=

do đó

23

.

36

. 2 .

44

ABC A B C

V a a a

  

==

Câu 50: Chọn B.

1

2 ( ) 1 0 ( ) .

2

f x f x+ =  = −

Dựa vào bảng biến thiên, ta thấy đồ thị hàm số

()y f x=

cắt đường thẳng

1

2

y =−

tại 3 điểm phân biệt.

ĐỀ 58

ĐỀ THI THỬ THPT QUỐC GIA 2020

MÔN TOÁN

Thời gian: 90 phút

Câu 1.Cho cấp số cộng

( )

n

u

có

1

2u =−

và công sai

3d =

. Tìm số hạng

10

u

.

A.

9

10

2.3u =−

. B.

10

25u =

. C.

10

28u =

. D.

10

29u =−

.

Câu 2.Cho các số thực dương

x

,

y

. Tìm giá trị lớn nhất của biểu thức

(

)

2

3

22

4

xy

P

x x y

=

++

A.

max 1P =

. B.

1

max

10

P =

. C.

1

max

8

P =

. D.

1

max

2

P =

.

Câu 3.Cho khối tứ diện

ABCD

có thể tích bằng

V

, thể tích của khối đa diện có đỉnh là trung điểm các cạnh của

tứ diện

ABCD

bằng

V



. Tính tỉ số

V



. A.

1

2

V



=

. B.

1

8

V



=

. C.

1

4

V



=

. D.

3

4

V



=

.

Câu 4.Hình nào dưới đây không phải là hình đa diện?

A. Hình 4. B. Hình 1. C. Hình 2. D. Hình 3.

Câu 5.Gọi

( )

P

là đường Parabol qua ba điểm cực trị của đồ thị hàm số

4 2 2

1

4

y x mx m= − +

. Gọi

0

m

là giá trị để

( )

P

đi qua điểm

( )

2; 24A

. Hỏi

0

m

thuộc khoảng nào dưới đây?

A.

( )

10; 15

. B.

( )

6; 1−

. C.

( )

2; 10−

. D.

( )

8; 2−

.

Câu 6.Có bao nhiêu giá trị nguyên của tham số

m

để hàm số

3

2

61y x x m x= − + −

có

5

điểm cực trị.

A.

11

. B.

15

. C.

6

. D.

8

.

Câu 7.Đường cong trong hình bên là đồ thị của một hàm số nào dưới đây.

A.

42

23y x x= − − −

. B.

42

23y x x= + −

.

C.

42

3y x x= − −

. D.

42

23y x x= − −

.

Câu 8.Cho lăng trụ tam giác đều

.ABC A B C

  

có cạnh đáy bằng

a

góc giữa đường thẳng

AC



và mặt phẳng đáy bằng

60

. Tính thể tích khối lăng trụ

.ABC A B C

  

theo

.a

A.

3

4

a

. B.

3

12

a

. C.

3

4

a

. D.

3

4

a

.

Hình 1

Hình 2

Hình 3

Hình 4

O

x

y

1

1−

3−

2−

2

Trang 103

Câu 9.Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh bằng

1

. Tam giác

SAB

đều và nằm trong mặt

phẳng vuông góc với mặt đáy

( )

ABCD

. Tính khoảng cách từ

B

đến

( )

.SCD

A.

1

. B.

21

3

. C.

2

. D.

21

7

.

Câu 10.Giải phương trình

sin 1

2

x

=

.

A.

4,x k k



= + 

. B.

2,x k k



=

. C.

2,x k k



= + 

. D.

2,

2

x k k



= + 

.

Câu 11.Chọn khẳng định sai. Trong một khối đa diện

A. mỗi đỉnh là đỉnh chung của ít nhất 3 mặt. C. mỗi cạnh của một khối đa diện là cạnh chung của đúng 2 mặt.

B. mỗi mặt có ít nhất 3 cạnh. D. hai mặt bất kì luôn có ít nhất một điểm chung.

Câu 12.Có 10 tấm bìa ghi 10 chữ “NƠI”, “NÀO”, “CÓ”, “Ý”, “CHÍ”, “NƠI”, “ĐÓ”, “CÓ”, “CON”, “ĐƯỜNG”.

Một người xếp ngẫu nhiên 10 tấm bìa cạnh nhau. Tính xác suất để xếp các tấm bìa được dòng chữ “ NƠI NÀO CÓ

Ý CHÍ NƠI ĐÓ CÓ CON ĐƯỜNG”.

A.

1

40320

. B.

1

10

. C.

1

3628800

. D.

1

907200

.

Câu 13.Tìm tất cả các giá trị

m

để hàm số

( )

32

2 1 2

3

m

y x mx m x= − + − −

nghịch biến trên tập xác định của nó.

A.

0m 

. B.

1m −

. C.

2m 

. D.

0m 

.

Câu 14.Cho hàm số

( )

3 1 khi 0

1 2 1

khi 0

x a x

fx

x

+ − 





=



+−







. Tìm tất cả giá trị của

a

để hàm số đã cho liên tục trên

.

A.

1a =

. B.

3a =

. C.

2a =

. D.

4a =

.

Câu 15.Tìm số đường tiệm cận của đồ thị hàm số

2

21

1

x

y

x

−

=

+

. A.

0

. B.

2

. C.

1

. D.

3

.

Câu 16.Gọi

a

là giá trị nhỏ nhất của

( )

3 3 3 3

log 2.log 3.log 4...log

9

n

fn=

với

n

và

2n 

. Hỏi có bao

nhiêu giá trị của

n

để

( )

f n a=

. A. 2 B. 4 C. 1 D. vô số

Câu 17.Trong các hàm số sau hàm số nào là hàm số chẵn?

A.

1 sinyx=−

. B.

sinyx=

. C.

cos

3

yx





=+





. D.

sin cosy x x=+

.

Câu 18.Cho tứ diện

ABCD

và các điểm

M

,

N

xác định bởi

23AM AB AC=−

;

DN DB xDC=+

. Tìm

x

để các véc tơ

AD

,

BC

,

MN

đồng phẳng. A.

1x =−

. B.

3x =−

. C.

2x =−

. D.

2x =

.

Câu 19.Cho khối chóp tam giác đều

.S ABC

có cạnh đáy bằng

a

,

3SA a=

. Tính thể tích

V

của khối chóp

.S ABC

. A.

3

35

24

a

V =

. B.

3

6

a

V =

. C.

3

2

6

a

V =

. D.

3

2

a

V =

.

Câu 20.Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông tại

A

với

AB a=

,

2BC a=

. Điểm

H

thuộc

cạnh

AC

sao cho

1

3

CH CA=

,

SH

là đường cao hình chóp

.S ABC

và

6

3

a

SH =

. Gọi

I

là trung điểm

BC

.

Tính diện tích thiết diện của hình chóp với mặt phẳng đi qua

H

và vuông góc với

AI

.

A.

2

3

a

. B.

2

6

a

. C.

2

3

a

. D.

2

3

6

a

.

Câu 21.Cho hàm số

( )

y f x=

có đồ thị

( )

y f x



=

cắt trục

Ox

tại ba điểm có hoành độ

abc

như hình vẽ.

Trang 104

Khẳng định nào dưới đây có thể xảy ra?

A.

( ) ( ) ( )

f a f b f c

. B.

( ) ( ) ( )

f b f a f c

.

C.

( ) ( ) ( )

f c f a f b

. D.

( ) ( ) ( )

f c f b f a

Câu 22.Cho một tấm nhôm hình vuông cạnh

( )

1m

như hình vẽ dưới đây. Người ta cắt phần tô đậm của tấm nhôm

rồi

gập thành một hình chóp tứ giác đều có cạnh đáy bằng

( )

mx

, sao

cho bốn đỉnh của hình vuông gập lại thành đỉnh của hình chóp. Tìm

giá trị của

x

để khối chóp nhận được có thể tích lớn nhất.

A.

2

4

x =

. B.

2

3

x =

. C.

22

5

x =

. D.

1

2

x =

Câu 23.Cho hàm số

42

1y x x= − +

. Mệnh đề nào dưới đây đúng?

A. Hàm số có

1

điểm cực đại và

2

điểm cực tiểu. B. Hàm số có

2

điểm cực đại và

1

điểm cực tiểu.

C. Hàm số có

1

điểm cực trị. D. Hàm số có

2

điểm cực trị.

Câu 24.Một lô hàng gồm

30

sản phẩm tốt và

10

sản phẩm xấu. Lấy ngẫu nhiên

3

sản phẩm. Tính xác suất để

3

sản phẩm lấy ra có ít nhất một sản phẩm tốt. A.

135

988

. B.

3

247

. C.

244

247

. D.

15

26

Câu 25.Đa diện đều loại

 

5,3

có tên gọi nào dưới đây?

A. Tứ diện đều. B. Lập phương. C. Hai mươi mặt đều. D. Mười hai mặt đều

Câu 26.Cho hàm số

3

3.y x x=−

Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên khoảng

( )

;1− −

và nghịch biến trên khoảng

( )

1; +

.

B. Hàm số đồng biến trên khoảng

( ; ).− +

C. Hàm số nghịch biến trên khoảng

( )

;1− −

và đồng biến trên khoảng

( )

1; +

D. Hàm số nghịch biến trên khoảng

( )

1;1−

.

Câu 27.Cho dãy số

( )

n

u

được xác định bởi

( )

1

3

.

2 1 2

nn

u

n u nu n

+

=







+ = + +





Tính

lim .

n

u

A.

lim 1.

n

u =

B.

lim 4.

n

u =

C.

lim 3.

n

u =

D.

lim 0.

n

u =

Câu 28.Tìm giá trị nhỏ nhất của hàm số

2cos sin 1.

2

x

yx= + +

A.

1 2 3.−

B.

2 5 3

.

2

−

C.

1.−

D.

2 3 3

.

2

−

Câu 29.Có

5

nhà toán học nam,

3

nhà toán học nữ và

4

nhà vật lý nam. Lập một đoàn công tác gồm

3

người cần

có cả nam và nữ, có cả nhà toán học và vật lý thì có bao nhiêu cách. A.

120.

B.

90.

C.

80.

D.

220.

Câu 30.Cho hàm số

( )

2

11y x x x= − +

có đồ thị

( )

C

. Mệnh đề nào dưới đây đúng?

A.

( )

C

cắt trục hoành tại

3

điểm phân biệt. B.

( )

C

không cắt trục hoành.

C.

( )

C

cắt trục hoành tại

2

điểm phân biệt. D.

( )

C

cắt trục hoành tại

1

điểm.

Câu 31.Với

,2nn

và thỏa mãn

2 2 2 2

2 3 4

1 1 1 1 9

...

5

n

C C C C

+ + + + =

. Tính giá trị của biểu thức

( )

53

2

4!

nn

CC

P

n

+

=

−

.

A.

61

90

. B.

59

90

. C.

29

45

. D.

53

90

.

Câu 32.Tứ diện đều có bao nhiêu mặt phẳng đối xứng? A.

2

. B.

3

. C.

6

. D.

9

.

O

x

y

a

b

c

Trang 105

Câu 33.Tìm số điểm cực trị của hàm số

( )

y f x=

biết

( )

2018

2

12f x x x x



= − +

. A.

2

. B.

3

C.

4

.

D.

1

.

Câu 34.Cho đồ thị hàm số

( )

23

:

1

x

Cy

x

−+

=

−

. Viết phương trình tiếp tuyến của đồ thị

( )

C

tại giao điểm của

( )

C

và đường thẳng

3yx=−

. A.

3yx= − +

và

1yx= − −

. B.

3yx= − −

và

1yx= − +

.

C.

3yx=−

và

1yx=+

. D.

3yx= − +

và

1yx= − +

.

Câu 35.Gọi

K

là tập hợp tất cả các giá trị của tham số

m

để phương trình

sin2 2sin 2

4

x x m





+ + − =





có

đúng hai nghiệm thuộc khoảng

3

0;

4









. Hỏi

K

là tập con của tập hợp nào dưới đây?

A.

22

;

22



−









. B.

( )

1 2; 2−

. C.

2

2;

2



−





. D.

2

;2

2



−









.

Câu 36.Cho lăng trụ

.ABC A B C

  

có các mặt bên là hình vuông cạnh

a

. Gọi

D

,

E

lần lượt là trung điểm các

cạnh

BC

,

AC



. Tính khoảng cách giữa hai đường thẳng

AB



và

DE

theo

a

.A.

3

a

. B.

3

4

a

. C.

3

2

a

.

D.

3a

.

Câu 37.Tìm hệ số của số hạng chứa

6

x

trong khai triển

( )

8

3

1xx−

A.

28−

B.

70

C.

56−

. D.

56

.

Câu 38.Các thành phố

A

,

B

,

C

được nối với nhau bởi các con đường như hình vẽ. Hỏi có bao nhiêu cách đi từ

thành phố

A

đến thành phố

C

mà qua thành phố

B

chỉ một lần?

A.

8

. B.

12

. C.

6

. D.

4

.

Câu 39.Tìm số đường tiệm cận của đồ thị hàm số

1

4 3 1 3 5

x

y

xx

−

=

+ − −

A.

3

. B.

0

. C.

1

. D.

2

.

Câu 40.Tìm giá trị nhỏ nhất của hàm số

1

yx

x

=−

trên

 

1;3

A.

9

. B.

2

. C.

28

. D.

0

.

Câu 41.Cho khối chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

,

SA

vuông góc với mặt phẳng

( )

ABCD

.

Góc giữa mặt phẳng

( )

SBC

và

( )

ABCD

bằng

45

. Gọi

,MN

lần lượt là trung điểm

,AB AD

. Tính thể tích

khối chóp

.S CDMN

theo

a

. A.

3

5

8

a

. B.

3

8

a

. C.

3

5

24

a

. D.

3

a

.

Câu 42.Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số

2

1

xx

y

x

+

=

−

A.

22yx= − −

. B.

22yx=+

. C.

22yx=−

. D.

22yx= − +

.

Câu 43.Tìm cực đại của hàm số

2

1y x x=−

. A.

1

2

B.

1

2

−

. C.

1

2

−

. D.

1

2

.

Câu 44.Trong trò chơi “Chiếc nón kỳ diệu” chiếc kim của bánh xe có thể dừng lại ở một trong

6

vị trí với khả

năng như nhau. Tính xác suất để trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trí khác

nhau.

A.

5

36

. B.

5

9

. C.

5

54

. D.

1

36

.

Câu 45.Cho hình chóp

.S ABCD

có cạnh

SA x=

còn tất cả các cạnh khác có độ dài bằng

2

. Tính thể tích

V

lớn

nhất của khối chóp

.S ABCD

. A.

1V =

B.

1

2

V =

. C.

3V =

. D.

2V =

.

A

B

C

Trang 106

Câu 46.Giải phương trình

cos 3sin

0

2sin 1

xx

x

−

=

−

.

A.

5

2 , .

6

x k k



= − + 

B.

5

,.

6

x k k



= − + 

C.

2 , .

6

x k k



= + 

D.

,.

6

x k k



= + 

Câu 47.Cho hình lăng trụ đứng

.ABC A B C

  

, đáy

ABC

là tam giác vuông tại

A

, cạnh

AA



hợp với

BC



một

góc

60

và khoảng cách giữa chúng bằng

,a

2B C a



=

. Thể tích của khối lăng trụ

.ABC A B C

  

theo

:a

A.

3

.

2

a

B.

3

.

2

a

C.

3

.

4

a

D.

3

.

4

a

Câu 48.Cho hình chóp

.S ABC

có đáy là tam giác đều cạnh

a

, mặt phẳng

( )

SAB

vuông góc với mặt phẳng

( )

ABC

và tam giác

SAB

vuông cân tại

S

. Tính thể tích khối chóp

.S ABC

theo

a

.

A.

3

12

a

. B.

3

24

a

. C.

3

a

. D.

3

4

a

.

Câu 49.Cho hàm số

( )

y f x=

xác định, liên tục trên và có bảng biến thiên như hình vẽ

Mệnh đề nào dưới đây đúng?

A. Hàm số chỉ có giá trị nhỏ nhất không có giá trị lớn nhất. B. Hàm số có một điểm cực trị.

C. Hàm số có hai điểm cực trị. D. Hàm số có giá trị lớn nhất bằng

2

và giá trị nhỏ nhất bằng

3.−

Câu 50.Cho hình chóp

.S ABC

có

AB AC=

,

SAC SAB=

. Tính số đo của góc giữa hai đường thẳng

SA

và

.BC

A.

45

. B.

60

. C.

30

. D.

90

.

HƯỚNG DẪN GIẢI

Câu 1.Chọn B. Ta có

10 1

9u u d=+

2 9.3 25= − + =

.

Câu 2.Chọn C.

(

)

2

33

2

22

4

1 1 4

y

xy

x

P

x x y

y

x







==



++





++





( )

,0xy  

.

Đặt

2

14

y

t

x



=+





,

1t 

. Khi đó biểu thức trở thành

( )

2

3

1

t

Pt

t

−

=

+

với

1t 

.

( )

2

4

23

03

1

tt

P t t

t

− + +



= =  =

+

.

Bảng biến thiên:

Trang 107

Vậy

( )

1

max 3

8

PP==

.

Câu 3.Chọn A. Ta có

1

..

8

AEJF AEJF

ABCD

VV

AE AJ AF

V V AB AC AD

= = =

.

Tương tự:

1

8

BIGE

V

=

,

1

8

CIHJ

V

=

,

1

8

DHGF

V

=

.Vậy:

1

1 4.

8

V



=−

1

2

=

.

Câu 4.Chọn D.Hình 3 không phải là hình đa diện, vì tồn tại hai cạnh của đa

giác đáy không phải là cạnh chung của hai mặt của hình.

Câu 5.Chọn C. Tập xác định

D =

.

3

'2y x mx=−

.

Vì

2

0

'

2

0

x

y

x m

=



=



=





nên hàm số đã cho có ba điểm cực trị khi và chỉ khi phương trình

0y



=

có ba nghiệm

phân biệt. Điều này tương đương

0m 

.Khi đó tọa độ ba điểm cực trị là:

( )

2

0; ,Am

( )

2 ;0 ,Bm

( )

2 ;0Cm−

.

Nhận xét: Parabol

( )

P

đi qua ba điểm

,A

,B

C

có dạng

2

y ax b=+

(vì hai điểm

B

và

C

đối xứng qua trục

tung). Suy ra

( )

P

có phương trình là

22

1

2

y mx m= − +

.

Vì

( )

P

đi qua

( )

2; 24A

nên

2

2 24 0mm− − =

6

4

m

=







=−



0

6mm = =

(thỏa điều kiện

0m 

).

Câu 6.Chọn A.Hàm số

3

2

61y x x m x= − + −

có

5

điểm cực trị khi hàm số

32

61y x x mx= − + −

có hai điểm

cực trị có hoành độ dương



phương trình

2

3 12 0y x x m



= − + =

có hai nghiệm dương phân biệt.

Điều kiện:

0 36 3 0

0 0 0 12

0 4 0

m

P m m

S



  − 





     









.Vì

m

nguyên nên có

11

giá trị

m

thỏa yêu cầu bài toán.

Câu 7.Chọn D. Từ đồ thị ta có: Hàm số có

3

điểm cực trị nên loại A, B.

Hàm số có

1x =

là điểm cực trị nên Chọn D.

Câu 8.Chọn A. Vì

( )

AA ABC



⊥

nên góc giữa đường thẳng

AC



và mặt phẳng đáy

là

60A CA



=

.

tan60 3.AA a a



 =  =

Vậy

.

23

33

. 3 .

44

ABC A B C

aa

Va

  

==

Câu 9.Chọn D. Gọi

H

,

M

lần lượt là trung điểm của

AB

và

CD

suy ra

1HM =

,

3

2

SH =

và

7

2

SM =

.

A

B

C

A



B



C



60

A

B

C

D

E

F

I

H

G

J

Trang 108

Vì tam giác

SAB

đều và nằm trong mặt phẳng vuông góc với đáy

( )

ABCD

nên

( )

SH ABCD⊥

.

Cách 1:

.

1 1 3 3

..

3 2 2 12

S BCD

V ==

.

Khoảng cách từ

B

đến

( )

SCD

là

( )

.

3

21

,

7

17

.1.

3

4

22

S BCD

SCD

V

d B SCD

S



= = =

.

Cách 2: Vì

//CAB D

nên

( )

//AB SCD

. Do đó

( )

;;d B SCD d H SCD HK==

với

HK SM⊥

trong

SHM

.Ta có:

2 2 2

111

HK SH HM

=+

21

7

HK=

.

Câu 10.Chọn A.Ta có

sin 1 2 4 ,

2 2 2

xx

k x k k



  

=  = +  = + 

.

Vậy nghiệm của phương trình là

, .4x k k



= + 

Câu 11.Chọn D. Hình lập phương, hình hộp có các mặt song song với nhau.

Câu 12.Chọn D.Số phần tử của không gian mẫu là

( )

10!n  =

Gọi

A

là biến cố xếp các tấm bìa được dòng chữ “NƠI NÀO CÓ Ý CHÍ NƠI ĐÓ CÓ CON ĐƯỜNG”.

Chú ý rằng có hai chữ “NƠI” và hai chữ “CÓ”, nên để tính

( )

nA

, ta làm như sau:

-Có

1

2

C

cách chọn một chữ “NƠI” và đặt vào đầu câu

-Có

1

2

C

cách chọn một chữ “CÓ” và đặt vào vị trí thứ ba

-Các vị trí còn lại chỉ có một cách đặt chữ

Vậy

( )

11

22

.14.n A C C ==

, nên

( )

4 4 1

.

10! 3628800 907200

PA= = =

Câu 13.Chọn A.Tập xác định

D =

Trường hợp

1

:

0m =

.Hàm số trở thành

2yx= − +

nghịch biến trên

0m=

thỏa mãn.

Trường hợp

2

:

0m 

.

2

2 2 1y mx mx m



= − + −

Hàm số nghịch biến trên tập xác định

0,yx



   

.(Dấu

''=

xảy ra tại hữu hạn điểm trên )

ĐK:

0

m 











( )

2

0

2 1 0

m

m m m











− − 





2

0

m

mm









− + 



0

1

0

m







  

















.

Kết hợp cả

2

trường hợp ta được

0m 

Câu 14.Chọn C. Tập xác định

D =

.Ta có: Hàm số liên tục trên các khoảng

( )

;0−

và

( )

0;+

.

( ) ( )

00

lim lim 3 1 1.

xx

f x x a a

−−

→→

= + − = −

( )

0 0 0

1 2 1 2

lim lim lim 1.

1 2 1

x x x

x

fx

x

+ + +

→ → →

+−

= = =

++

;

( )

0 1.fa=−

Hàm số liên tục trên



Hàm số liên tục tại điểm

0 1 1 2.x a a=  − =  =

Câu 15.Chọn C. Tập xác định

D =

.Đồ thị hàm số không có tiệm cận đứng.

Vì

lim 0

x

y

→

=

Tiệm cận ngang của đồ thị hàm số là đường thẳng

0.y =

Vậy đồ thị hàm số có một đường tiệm cận.

Câu 16.Chọn A.

( )

9 9 9 9

3 3 3 3

log 2.log 3.log 4...log

1

log 2.log 3.log 4...log

99

n

f n n==

Ta có:- Nếu

( )

9 9 9 9 9

88

3 3 3 3 3

1

2 3 0 log 1 log 2.log 3.log 4...log 3

9

n k f n n f      = 

S

A

B

C

D

M

H

K

Trang 109

- Nếu

( ) ( ) ( )

9

9 9 8 9 8

3

3 3 3 .log 3 3n f f f=  = =

- Nếu

( )

( ) ( ) ( )

9 9 9

9 9 9 9

3 3 3

3 log 1 3 .log 3 1 ...log 3n n f n f n f    = + 

Từ đó suy ra

( )

( ) ( )

98

3 3Min f n f f==

.

Câu 17.Chọn B. TXĐ:

D =

.

:x D x D x D    − 

( )

1

Ta có

( ) ( ) ( ) ( ) ( )

sin sin sinf x x x x f x− = − = − = =

( )

2

.

Từ

( )

1

và

( )

2

suy ra hàm số

sinyx=

là hàm chẵn.

Câu 18.Chọn C. Ta có

( )

32MN MA AD DN AC AB AD DB xDC= + + = − + + +

.

( )

3 3 2 2AD DC AD DB AD DB xDC= + − − + + +

( ) ( )

2 3 2 3AD DB x DC AD BC CD x DC= − + + = + + + +

( )

22AD BC x DC= + + +

.

Ba véc tơ

AD

,

BC

,

MN

đồng phẳng khi và chỉ khi

2 0 2xx+ =  = −

.

Câu 19.Chọn C. Gọi

M

là trung điểm của

BC

.

O

là chân đường cao hạ từ

S

xuống mặt phẳng

( )

ABC

.

Ta có

2

3 3 3

;

4 2 3

ABC

a a a

S AM AO= =  =

.

Xét tam giác vuông

SAO

có

22

26

3

a

SO SA AO= − =

.

Vậy

23

.

1 3 2 6 2

..

3 4 3 6

S ABC

a a a

V ==

.

Câu 20.Chọn B. Cách 1: Gọi

( )



là mặt phẳng đi qua

H

và vuông góc với

AI

.

Vì

( )

,SH ABC⊥

( )

AI ABC

nên

( )

SH





.

Ta có

AI AB BI a= = =

nên

ABI

là tam giác đều. Gọi

M

là trung điểm

AI

, ta được

( )

1BM AI⊥

. Từ đây suy ra

( )

// BM



(vì cùng vuông góc

AI

).Trong

( )

ABC

dựng

//HN BM

với

N BC

, ta suy ra

( ) ( )

ABC HN



=

.

Từ đó, thiết diện của mặt phẳng

( )



và hình chóp là

SHN

.

Xét

ABP

vuông có:

2 2 3

cos30

cos30 3

3

1 2 3 3

sin30

.

2 3 3

AB a a

AB

BP

AP

aa

AP

BP



= = =

=













=

==





.

Dễ thấy

3AC a=

3

33

AC a

CH = =

. Vậy

H

là trung điểm của

CP

HN

là đường trung bình của

CBP

hay

NI

13

23

a

HN BP = =

.

Xét tam giác vuông

( )

90SHN H =

:

2

1 1 6 3 2

.

2 2 3 3 6

SHN

a a a

S HS HN= = =

.

Cách 2: Tam giác

ABI

đều

30IAH = 

.Áp dụng định lí côsin trong

AHI

có

3

a

IH =

S

A

B

C

IN

P

H

M

S

A

B

C

M

O

Trang 110

Vậy

2

22

4

3

a

AH

a

HI

AI a



=



=





=





suy ra

AIH

vuông đỉnh

I

hay

HI AI⊥

. Phần tiếp theo giống cách 1.

Câu 21.Chọn C.

Cách 1. Dùng bảng biến thiên kết hợp các phương án để loại trừ.

Từ đồ thị của

( )

y f x



=

ta có bảng biến thiên như sau

Từ bảng biến thiên ta có

( ) ( ) ( ) ( )

,f a f b f c f b

(

( )

fb

là số nhỏ nhất) nên phương án C có thể xảy ra.

Cách 2. Dùng diện tích hình phẳng

Đồ thị của hàm số

( )

y f x



=

liên tục trên các đoạn

 

;ab

và

 

;bc

, lại có

( )

fx

là một nguyên hàm của

( )

fx



.

Do đó diện tích của hình phẳng giới hạn bởi các đường:

( )

0

y f x

y

xa

xb



=





=





=



=



là:

( ) ( ) ( ) ( ) ( )

1

dd

bb

b

a

aa

S f x x f x x f x f a f b



= = − = − = −



.Vì

( ) ( )

1

0S f a f b  

( )

1

Tương tự: diện tích của hình phẳng giới hạn bởi các đường:

( )

0

y f x

y

xb

xc



=





=





=



=



là:

( ) ( ) ( ) ( ) ( )

2

dd

cc

c

b

bb

S f x x f x x f x f c f b



= = = = −



.

( ) ( )

2

0S f c f b  

( )

2

.

Mặt khác, dựa vào hình vẽ ta có:

( ) ( ) ( ) ( ) ( ) ( )

12

S S f a f b f c f b f a f c  −  −  

( )

3

.

Từ

( ) ( ) ( )

1 , 2 , 3

suy ra

( ) ( ) ( )

f c f a f b

.

Câu 22.Chọn C. Từ hình vuông ban đầu ta tính được

11

2

,

22

xx

OM S M S O OM

−

= = − =

. (

02x

)

Khi gấp thành hình chóp

.S ABCD

thì

1

SS

nên ta có

1

SM S M=

. Từ đó

22

2 2 2

2

x

SO SM OM

−

= − =

.

(Điều kiện

2

0

2

x

)

Thể tích khối chóp

.S ABCD

:

2 4 5

.

1 1 1

. 2 2 2 2 2 2

3 6 6

S ABCD ABCD

V S SO x x x x= = − = −

.

S

A

B

D

M

O

1

S

C

A

B

C

D

O

x

M

Trang 111

Ta thấy

SABCD

V

lớn nhất khi

( )

45

2 2 2 ,f x x x=−

2

0

2

x

đạt giá trị lớn nhất

Bảng biến thiên

Ta có

( )

3 4 3

8 10 2 2 4 5 2f x x x x x



= − = −

;

( )

0

22

5

x

fx

x

=







=



=





Vậy:

.S ABCD

V

lớn nhất khi và chỉ khi

22

5

x =

Câu 23.Chọn A.Ta có

3

42y x x



=−

;

0

2

x

y

x

=







=



=





Ta có bảng biến thiên sau

Vậy: hàm số có hai điểm cực tiểu và một điểm cực

đại.Nhận xét: Có thể giải nhanh bài toán như sau

Hàm số đã cho là hàm trùng phương có

0, 0ab

nên

có hai điểm cực tiểu và một điểm cực đại.

Câu 24.Chọn C.Chọn ra ba sản phẩm tùy ý có

3

40

9880C =

cách chọn.Do đó

( )

9880n =

.Gọi

A

là

biến cố có ít nhất

1

sản phẩm tốt. Khi đó

A

là biến cố 3

sản phẩm không có sản phẩm tốt.

( )

3

10

120n A C==

.

Vậy xác suất cần tìm là

( )

120 244

1 1 1

9880 247

nA

AA

n

= − = − = − =



PP

.

Câu 25.Chọn D.

Câu 26. Chọn D.Ta có

2

3 3 0 1y x x



= − =  = 

.Bảng biến thiên

Dựa vào bảng biến thiên ta chọn đáp án D.

Câu 27.Chọn A.Ta có

1

2

(*)

2 2 2 2

nn

uu

nn

+

=+

++

Đặt

a lim ,

n

u=

trong biểu thức

(*)

cho

n → +

ta được

11

1 lim .

22

n

a a a u= +  = =

❖Chú ý: Để chặt chẽ hơn ta có thể lập luận như sau:

Sử dụng quy nạp toán học, ta chứng minh được

1

n

u 

với mọi

*n

, nên dãy

( )

n

u

bị chặn dưới.

Khi đó ta cũng có

1

..

22

.

2 2 2 2 2 2 2 2

n

nn n

n

nu nu

nn

u u u

n n n n

+

++

= +  + =

+ + + +

nên dãy

( )

n

u

là dãy giảm.

Vậy, dãy

( )

n

u

có giới hạn (Học sinh cần chú ý tính chất: một dãy giảm và bị chặn dưới, hoặc tăng và bị chặn trên,

thì có giới hạn).Đặt

lim ,

n

au=

trong biểu thức

(*)

cho

n → +

ta được

11

1 lim .

22

n

a a a u= +  = =

Trang 112

Câu 28. Chọn D. Nhận xét: Hàm số tuần hoàn với chu kì

4T



=

nên ta chỉ cần tìm GTLN, GTNN của hàm số

trên

 

2 ;2



−

.Ta có

sin cos

2

x

yx



= − +

;

2

sin 1

2

0 sin 1 2sin 0

1

2 2 3

sin

5

22

3

x

xx

yx

x







=−



=−





=  − + − =   =



=







=



(do

 

2 ;2x



−

)

( ) ( ) ( )

2 2cos sin 2 1 1y

  

− = − + − + = −

;

( ) ( ) ( )

2 2cos sin 2 1 1y

  

= + + = −

( ) ( )

2cos sin 1 1

2

y







− = − + − + =





;

3 2 3 3

2cos sin 1 3 1

3 6 3 2 2

y

  

+

     

= + + = + + =

     

     

5 5 5 3 2 3 3

2cos sin 1 3 1

3 6 3 2 2

y

  

−

     

= + + = − − + =

     

     

.Vậy

5 2 3 3

min .

32

yy



−



==





Câu 29.Chọn B. Ta có các trường hợp sau:

TH1: Chọn được

1

nhà vật lý nam, hai nhà toán học nữ có

12

43

12CC =

cách chọn.

TH2: Chọn được

1

nhà vật lý nam, một nhà toán học nữ và một nhà toán học nam có

1 1 1

4 3 5

60C C C =

cách chọn.

TH3: Chọn được

2

nhà vật lý nam, một nhà toán học nữ có

21

43

18CC =

cách chọn.

Vậy, có

12 60 18 90+ + =

cách chọn thỏa yêu cầu bài toán.

Câu 30.Chọn C. Phương trình hoành độ giao điểm của đồ thị

( )

C

với trục

:Ox

( )

2

0

1 1 0

1

x

x x x C

x

=



− + =  



=



cắt

Ox

tại hai điểm phân biệt.

Câu 31.Chọn B.Ta có

2 2 2 2

2 3 4

1 1 1 1 9

...

5

n

C C C C

+ + + + =



( )

2 !2!

0!2! 1!2! 2!2! 9

...

2! 3! 4! ! 5

n

−

+ + + + =



( )

1 1 1 1 9

2! ...

1.2 2.3 3.4 1 5nn



+ + + + =



−





1 1 1 1 1 1 1 9

2! 1 ...

2 2 3 3 4 1 5nn



− + − + − + + − =



−





1 9 1 1

2! 1

5 10nn



− =  =







10n =

.

( )

53

2

4!

nn

CC

P

n

+

=

−

53

10 12

6!

CC+

=

59

90

=

Câu 32.Chọn C. Gọi

M

,

N

,

P

,

Q

,

R

,

S

lần lượt là trung điểm các cạnh

AB

,

BC

,

CA

,

AD

,

DC

,

BD

2

Các mặt phẳng đối xứng của tứ diện đều

ABCD

là:

( )

ABR

,

( )

BCQ

,

( )

CAS

,

( )

ADN

,

( )

DCM

,

( )

BDP

.

Vậy tứ diện đều có

6

mặt phẳng đối xứng.

Câu 33.Chọn B. Ta thấy phương trình

( )

0fx



=

có

3

nghiệm phân biệt là

0, 1, 1x x x= = = −

và

( )

fx



liên

tục đổi dấu qua

3

nghiệm đó nên hàm số có

3

điểm cực

trị.

Câu 34.Chọn B.Ta có

23

1

x

y

x

−+

=

−

( )

2

1

y

x

−



=

−

1x

Trang 113

Hoành độ giao điểm của đường thẳng

3yx=−

và đồ thị

( )

23

:

1

x

Cy

x

−+

=

−

là nghiệm phương

trình:

23

3

1

x

−+

=−

−

( )

1



2

20xx−=



0

2

x

=





=



Với

03xy=  = −

,

( )

01y



=−

, phương trình tiếp tuyến tại giao điểm

( )

0; 3A −

là

3yx= − −

Với

21xy=  = −

,

( )

21y



=−

, phương trình tiếp tuyến tại giao điểm

( )

2; 1B −

là

1yx= − +

.

Câu 35.Chọn C.Cách 1: Đặt

2sin sinx cos

4

t x x





= + = +





,

2; 2t



−



.

Suy ra

2

1 sin2tx=+



2

3t t m+ − =

.Xét hàm số

( )

2

3y f t t t= = + −

,

2; 2t



−



( )

21f t t



=+

;

( )

0ft



=



1

2

t =−

2; 2



−



Phương trình

sin2 2sin 2

4

x x m





+ + − =





có đúng hai nghiệm thuộc khoảng

3

0;

4











Phương trình

2

3t t m+ − =

có đúng một nghiệm

( )

1; 2t 

Dựa vào bảng biến thiên ta thấy

( )

1; 2 1K = − −



2

2;

2



−





Cách 2 : Xét hàm số

( )

sin2 2sin 2

4

f x x x





= + + −





với

3

0;

4

x











.

Ta có

( )

2cos2 2 cos

4

f x x x







= + +





, vậy

( )

0 2cos2 2 cos 0

4

f x x x







=  + + =





( )

22

3

0;

cos sin 0

44

2 cos sin cos sin 0

2 cos sin 1 0

2 2sin 1 0 *

4

x

xx

x x x

xx

x









=





−=







 − + − =  



+ + =







+ + =













Vì trong khoảng

3

0;

4









thì

sin

4

0x









+

nên phương trình

( )

*

vô nghiệm trên

3

0;

4









. Lập bảng biến

thiên

Vậy để phương trình đã cho có hai nghiệm phân biệt trên khoảng

3

0;

4









thì

( )

2

2;1; 2

2

1m



−



−



−









.

Trang 114

Câu 36.Chọn B. Gọi

I

là trung điểm của

AB

. Khi đó

3

,

2

a

CI =

( )

CI ABB A



⊥

Gọi

H

là trung điểm của

IB

. Vì

//DH CI

nên

( )

DH ABB A



⊥

Vì

// //

1

2

ID AC A E











==





nên tứ giác

AEDI



là hình bình hành, suy ra

( )

//DE A I ABB A

  

. Ta có

( )

//DE ABB A



.Vậy

( ) ( )

( )

3

,,

24

CI a

d AB DE d D ABB A DH

  

= = = =

Câu 37.Chọn C- Số hạng tổng quát của khai triển là:

( ) ( )

33

88

.1

kk

k k k

x C x C x

+

− = −

- Số hạng chứa

6

x

: khi

3 6 3kk+ =  =

- KL: hệ số cần tìm là

( )

3

8

1 56C − = −

.

Câu 38.Chọn A.Hai giai đoạn- Chọn đường từ

A

đến

B

: có 4 cách- Chọn đường từ

B

đến

C

: có 2 cách

KL: vậy theo quy tắc nhân có tất cả

4 2 8=

cách

Câu 39.Chọn D.Ta có

4 3 1 3 5 0 4 3 1 3 5x x x x+ − − =  + = +

( ) ( )

2

5

3 5 0

1

3

16 3 1 3 5

9 18 9 0

x

xx



+



−



   =



+ = +





− + =



.TXĐ:

 

1

; \ 1

3

D



= − + 







- Tìm TCĐ:

( )

2

11

1 4 3 1 3 5

lim lim

91

xx

x x x

y

x

−−

→→

− + + +

=

−−

( )

1

4 3 1 3 5

lim

91

x

xx

x

−

→

+ + +

= = +

−−

Vậy đồ thị hàm số có

1

tiệm cận đứng. - Tìm TCN: Xét

11

lim lim

3

4 3 1 3 5

xx

x

y

xx

→+ →+

−−

==

+ − −

.

Vậy đồ thị hàm số có

1

tiệm cận ngang là

1

3

y =−

.KL: Đồ thị của hàm số có

2

tiệm cận.

Câu 40.Chọn D.

 

\0D =

.

2

1

10y

x



= + 

nên hàm số tăng trên từng khoảng xác định

( )

;0−

và

( )

0;+

;

do đó tăng trên

 

1;3

. Vậy

 

( )

1;3

min 1 0yy==

.

Câu 41.Chọn C. Ta có

( ) ( )

SBC ABCD BC=

,

( )

BC SAB BC SB⊥  ⊥

,

AB BC⊥

nên góc giữa mặt phẳng

( )

SBC

và

( )

ABCD

là

SBA

.

Do đó

0

tan45SA AB a==

.

Mặt khác

2 2 2

2

5

8 4 8

MNDC ABCD AMN BMC

a a a

S S S S a= − − = − − =

.

Vậy

23

.

1 1 5 5

. . . .

3 3 8 24

S CDMN CDMN

aa

V S SA a= = =

.

Câu 42.Chọn B.

( )

2

22

1

xx

y

x

−−



=

−

,

1 3 4 2 3

0

1 3 4 2 3

xy

y

xy



= +  = +



=



= −  = −





Vậy đồ thị hàm số có hai điểm cực trị là

( )

1 3;4 2 3A ++

và

( )

1 3;4 2 3B −−

. Đường thẳng qua hai điểm

cực trị có vectơ chỉ phương là

( )

2 3;4 3BA =

nên có vectơ pháp tuyến là

( )

2; 1−

. Suy ra phương trình đường

thẳng đi qua hai điểm cực trị là

2 2 0xy−+=

hay

22yx=+

.

S

A

B

C

D

N

M

A

B

C

A



B



C



E

D

H

I

Trang 115

*Cách khác: Đường thẳng qua hai điểm cực trị có phương trình là

( )

2

22

1

xx

yx

x



+

= = +



−

.

Câu 43.Chọn D.Tập xác định là

 

1;1−

.Ta có

2

22

12

1

11

xx

y x x

xx

−−



= − + =

−−

;

2

0

2

yx



=  = 

Bảng biến thiên

Ta thấy cực đại của hàm số là

1

2

.

Câu 44.Chọn B.Số phần tử của không gian mẫu là

( )

1 1 1 3

666

6n C C C = =

Gọi A là biến cố “trong ba lần quay, chiếc kim của bánh xe

dừng lại ở ba vị trí khác nhau”

Số phần tử thuận lợi cho biến cố

A

là

( )

1 1 1

6 5 4

n A C C C=

Vậy xác suất của biến cố

A

là

( )

1 1 1

6 5 4

111

666

5

9

nA

C C C

A

n C C C

= = =



P

Câu 45.Chọn D. Gọi

O

là giao điểm của

AC

và

BD

. Ta có:

BAD BSD BCD =  = 

nên

AO SO CO==

1

2

SO AC=

SAC

vuông tại

S

.Do đó:

2 2 2

4AC SA SC x= + = +

22

4 12

4

42

xx

OD AD AO

+−

 = − = − =

2

12BD x = −

,

0 2 3x

. Ta thấy:

( )

BD AC

BD SAC

BD SO

⊥



⊥



⊥



Trong

SAC

hạ

SH AC⊥

. Khi đó:

( )

SH AC

SH ABCD

SH BD

⊥



⊥



⊥



2 2 2

1 1 1

SH SA SC

=+

2 2 2

. 2.

4

SA AC x

SH

SA SC x

 = =

++

2 2 2

.

2

1 1 2 1

. 4. 12 . . . 12

3 2 3

4

S ABCD

x

V x x x x

x

 = + − = −

+

22

1 12

2

32

xx+−

=

Dấu

""=

xảy ra khi

22

12 6x x x= −  =

.

Câu 46. Chọn A. Điều kiện

2

1

6

sin , .

5

2

6

xk





+



  





+





Với điều kiện trên ta có

13

cos 3sin 0 cos sin 0.

22

x x x x− =  − =

os 0 ,

3 3 2 6

c x x l x l l

   





 + =  + = +  = + 





Đối chiếu với điều kiện ta có nghiệm của phương trình là

5

2 , .

6

x k k



= − + 

Câu 47.Chọn B. Vì

//CC AA



nên góc giữa

AA



và

BC



là góc giữa

'CC

và

BC



và là góc

o

60B CC



=

0

S

A

B

C

D

O

H

a

x

Trang 116

Trong

B C C





:

o

3

sin60

.2 3

2

'

1

cos60

' .2

'

2

BC

B C a a

BC

CC

CC a a

BC





=



==













=

==





Gọi

H

là hình chiếu của

A

lên

BC

, khi đó

( ) ( )

,.AH BCC B d AA B C AH a

   

⊥  = =

3

.

1 1 3

. . . 3. .

2 2 2

ABC A B C ABC

a

V S AA AH BC AA a a a

  







= = = =





Câu 48.Chọn B. Gọi

H

là trung điểm của

AB

. Khi đó:

( ) ( )

( )

SH AB

SAB ABC SH ABC

SAB ABC AB



⊥



⊥  ⊥





=



Vì

SAB

vuông tại

S

nên

1

22

a

SH AB==

.Vậy

23

.

1 1 3 3

. . . .

3 3 4 2 24

S ABC ABC

a a a

V S SH



= = =

Câu 49.Chọn C.Tại

0x =

và

1x =

ta có

y



đổi dấu và

y

tồn tại nên hàm số đã cho có

hai điểm cực trị.

Câu 50. Chọn D. Cách 1:Ta có

( )

. . . . . .cos . .cos 0.AS BC AS AC AB AS AC AS AB AS AC SAC AS AB SAB= − = − = − =

Do đó số đo của góc giữa hai đường thẳng

SA

và

BC

bằng

90 .

Cách 2: Vì

AB AC=

,

SAC SAB=

nên

SAC SAB=

, suy ra

SB SC=

, nên hai tam

giác

ABC

và

SBC

là tam giác cân. Gọi

H

là trung điểm

BC

, ta có

( )

AH BC

SAH BC

SH BC

⊥



⊥



⊥



. Vậy

SA BC⊥

.

ĐỀ 59

ĐỀ THI THỬ THPT QUỐC GIA 2020

MÔN TOÁN

Thời gian: 90 phút

Câu 1.Giá trị lớn nhất của hàm số

3

35y x x= − +

trên đoạn

3

0;

2







là:

A.

3

. B.

5

. C.

7

. D.

31

8

.

Câu 2.Biết đồ thị hàm số

21

3

x

y

x

−

=

+

cắt trục

,Ox Oy

lần lượt tại hai điểm phân biệt

,AB

. Tính diện tích

S

của

tam giác

OAB

. A.

1

12

S =

. B.

1

6

S =

. C.

3S =

. D.

6S =

.

Câu 3.Đường cong trong hình bên là đồ thị của một trong bốn hàm số nào sau đây?

A.

42

2.y x x= − +

B.

42

2.y x x=−

C.

2

2.y x x= − +

D.

32

2 1.y x x x= + − −

S

A

B

C

H

S

A

B

C

H

A

C

B

A



C



B



H

Trang 117

Câu 4.Rút gọn biểu thức

1

6

3

.P x x=

với

0x 

.

A.

2

Px=

. B.

Px=

. C.

1

8

Px=

. D.

2

9

Px=

.

Câu 5.Cho

33

02

( )d , ( )d .f x x a f x x b==



Khi đó

2

0

( )df x x



bằng:

A.

ab−−

. B.

ba−

. C.

ab+

. D.

ab−

.

Câu 6.Cho hàm số

( )

y f x=

có đạo hàm

( )

2 2 3

( 2) ( 2)f x x x x



= − +

,

x

. Số điểm cực trị của hàm số là

A.

1

. B.

2

. C.

3

. D.

4

.

Câu 7.Trong không gian với hệ tọa độ Oxyz, cho

(1;2; 3), ( 3;2;9)AB−−

. Mặt phẳng trung trực của đoạn thẳng

AB

có phương trình là A.

3 10 0xz+ + =

. B.

4 12 10 0xz− + − =

. C.

3 10 0xy− + =

. D.

3 10 0xz− + =

.

Câu 8.Cho

, 0; , 1a b a b

và

,xy

là hai số thực dương. Trong các mệnh đề dưới đây, mệnh đề nào sai?

A.

( )

log log log

a a a

xy x y=+

. B.

log .log log

b a b

a x x=

. C.

11

log

a

xx

=

. D.

log log log

a a a

x

xy

y

=−

.

Câu 9.Biết đồ thị

()C

của hàm số

2

23

1

xx

y

x

−+

=

−

có hai điểm cực trị. Đường thẳng đi qua hai điểm cực trị của

đồ thị

()C

cắt trục hoành tại điểm

M

có hoành độ

M

x

bằngA.

12

M

x =−

. B.

2

M

x =−

. C.

1

M

x =

.D.

12

M

x =+

.

Câu 10.Cho tứ diện

.O ABC

có

,,OA OB OC

đôi một vuông góc với nhau. Gọi

H

là hình chiếu của

O

trên mặt

phẳng

()ABC

. Mệnh đề nào sau đây đúng? A.

H

là trọng tâm tam giác

ABC

. B.

H

là trung điểm của

BC

.

C.

H

là trực tâm của tam giác

ABC

. D.

H

là trung điểm của

AC

.

Câu 11.Cho hình chóp đều

.S ABCD

có tất cả các cạnh đều bằng

a

. Gọi

M

và

N

lần lượt là trung điểm của

AD

và

SD

. Số đo của góc giữa hai đường thẳng

MN

và

SC

bằng A.

45

. B.

60

. C.

30

. D.

90

.

Câu 12.Cho hàm số

2

23

3

xx

y



++



=





. Tìm khẳng định đúng ?

A. Hàm số luôn đồng biến trên . B. Hàm số luôn nghịch biến trên

.

C. Hàm số luôn nghịch biến trên khoảng

( )

;1− −

.

D. Hàm số luôn đồng biến trên khoảng

( )

;1− −

.

Câu 13.Cho hàm số

xa

y

bx c

−

=

+

có đồ thị như hình vẽ bên.

Tính giá trị của biểu thức

P a b c= + +

A.

3P =−

. B.

1P =

. C.

5P =

D.

2P =

.

Câu 14.Tổng tất cả các nghiệm thực của phương trình

( ) ( )

2

44

2log 3 log 5 0xx− + − =

là:

A.

8

. B.

82+

. C.

82−

. D.

42+

.

Câu 15.Tìm tập nghiệm của bất phương trình

13

2017 2017

2018 2018

xx− − +

   



   

   

.

Trang 118

A.

( )

2;+

. B.

( )

;2−

. C.



)

2;+

. D.

(



;2−

.

Câu 16.Một người gửi tiết kiệm vào ngân hàng 200 triệu đồng theo thể thức lãi kép (tức là tiền lãi được cộng vào

vốn của kỳ kế tiếp). Ban đầu người đó gửi với kỳ hạn 3 tháng, lãi suất

2,1%

/kỳ hạn, sau 2 năm người đó thay đổi

phương thức gửi, chuyển thành kỳ hạn 1 tháng với lãi suất

0,65%

/tháng. Tính tổng số tiền lãi nhận được (làm tròn

đến nghìn đồng) sau 5 năm. A.

98217000

đồng. B.

98215000

đồng. C.

98562000

đồng.

D.

98560000

đồng.

Câu 17.Trong không gian với hệ tọa độ Oxyz, gọi

H

hình chiếu vuông góc của

(2;0;1)M

lên đường thẳng

12

:

1 2 1

x y z−−

 = =

. Tìm tọa độ điểm

H

.

A.

(2;2;3)H

. B.

(0; 2;1)H −

. C.

(1;0;2)H

. D.

( 1; 4;0)H −−

.

Câu 18.Biết đồ thị

( )

C

ở hình bên là đồ thị hàm số

(a 0;a 1).

x

ya=  

Gọi

( )

C



là

đường đối xứng với

( )

C

qua đường thẳng

yx=

. Hỏi

( )

C



là đồ thị của hàm số nào

dưới đây.

A.

1

2

logyx=

. B.

2

x

y =

. C.

1

2

x

y



=





. D.

2

logyx=

.

Câu 19.Cho hàm số

()y f x=

xác định trên

 

\1

, liên tục trên mỗi khoảng xác định và có bảng biến thiên như

hình

bên. Tìm tập hợp tất cả các giá trị thực của tham số

m

sao

cho phương trình

( )

f x m=

có ba nghiệm thực phân biệt.

A.

(

2; 1



−−



. B.

( )

2; 1−−

. C.

(



1;1−

. D.

( )

1;1−

.

Câu 20.Cho hình chóp

.S ABCD

, đáy

ABCD

là hình

vuông cạnh

a

,

SA

vuông góc với mặt phẳng

()ABCD

;

,MN

là hai điểm nằm trên hai cạnh

,BC CD

. Đặt

BM x=

,

DN y=

,

(0 , )x y a

. Hệ thức liên hệ giữa

x

và

y

để hai mặt

phẳng

()SAM

và

()SMN

vuông góc với nhau là:

A.

22

( 2 )x a a x y+ = +

. B.

22

()x a a x y+ = +

. C.

22

2 ( )x a a x y+ = +

. D.

22

2 ( )x a a x y+ = +

.

Câu 21.Tập xác định của hàm số

tan cos

2

yx





=





là A.

 

\ 0 .R

B.

 

\ 0; .R



C.

\.

2

Rk









D.

 

\.Rk



Câu 22.Giải phương trình

2

2sin 3sin2 3+=xx

.

A.

.

3

xk



= − +

B.

.

3

xk



=+

C.

2

2.

3

xk



=+

D.

.

4

xk



=+

Câu 23.Khối mười hai mặt đều có bao nhiêu cạnh ?

A.

30

cạnh. B.

12

cạnh. C.

16

cạnh. D.

20

cạnh.

Câu 24.Một đám vi khuẩn tại ngày thứ

x

có số lượng là

( )

Nx

. Biết rằng

( )

2000

1

N' x =

+x

và lúc đầu số lượng vi khuẩn là

5000

con. Vậy ngày thứ

12

số

lượng vi khuẩn (sau khi làm tròn) là bao nhiêu con? A.

10130

. B.

5130

. C.

5154

. D.

10132

.

Trang 119

Câu 25.Tìm hệ số của số hạng chứa

9

x

trong khai triển nhị thức Newton

11

(1 2 )(3 )xx++

.

A.

4620.

B.

1380.

C.

9405.

D.

2890.

Câu 26.Trong không gian với hệ tọa độ Oxyz, cho điểm

(1; 2;3)I −

. Phương trình mặt cầu tâm I và tiếp xúc với

trục Oy là:

A.

2 2 2

( 1) ( 2) ( 3) 10x y z− + + + − =

. B.

2 2 2

( 1) ( 2) ( 3) 9.x y z− + + + − =

C.

2 2 2

( 1) ( 2) ( 3) 8.x y z− + + + − =

D.

2 2 2

( 1) ( 2) ( 3) 16.x y z− + + + − =

Câu 27.Gọi A là tập các số tự nhiên có

6

chữ số đôi một khác nhau được tạo ra từ các chữ số

0,1,2,3,4,5

. Từ A

chọn ngẫu nhiên một số. Tính xác suất để số được chọn có chữ số

3

và chữ số

4

đứng cạnh nhau.

A.

4

.

25

B.

4

.

15

C.

8

.

25

D.

2

.

15

Câu 28.Cho hàm số

2

3

x

y

x

−

=

+

. Tìm khẳng định đúng.

A. Hàm số xác định trên

 

\3R

. B. Hàm số đồng biến trên

 

\3R −

.

C. Hàm số nghịch biến trên mỗi khoảng xác định. D. Hàm số đồng biến trên mỗi khoảng xác định.

Câu 29.Hình trụ (T) được sinh ra khi quay hình chữ nhật ABCD quanh cạnh AB. Biết

22AC a=

và

0

45ACB =

. Diện tích toàn phần

tp

S

của hình trụ (T) là:

A.

2

16 .

tp

Sa



=

B.

2

10 .

tp

Sa



=

C.

2

12 .

tp

Sa



=

D.

2

8.

tp

Sa



=

Câu 30.Cho

( )

2

1

12f x xdx+=



. Khi đó

5

2

()I f x dx=



bằng:A.

2.

B.

1.

C.

1.−

D.

4.

Câu 31.Tìm nguyên hàm

cosI x xdx=



.

A.

2

sin

2

x

I x C=+

. B.

sin cosI x x x C= + +

. C.

sin cosI x x x C= − +

. D.

2

cos

2

x

I x C=+

.

Câu 32.Biết

( )

2 1 1

b

a

x dx−=



. Khẳng định nào sau đây đúng?

A.

1ba−=

. B.

22

1a b a b− = − +

. C.

22

1b a b a− = − +

. D.

1ab−=

.

Câu 33.Một giải thi đấu bóng đá quốc gia có

16

đội thi đấu vòng tròn

2

lượt tính điểm.(Hai đội bất kỳ đều thi đấu

với nhau đúng

2

trận). Sau mỗi trận đấu, đội thắng được

3

điểm, đội thua

0

điểm; nếu hòa mỗi đội được

1

điểm.

Sau giải đấu, ban tổ chức thống kê được

80

trận hòa. Hỏi tổng số điểm của tất cả các đội đội sau giải đấu bằng bao

nhiêu?

A.

720

. B.

560

. C.

280

. D.

640

.

Câu 34.Số nghiệm thực của phương trình

sin2 1 0x+=

trên đoạn

3

;10

2





−





làA.

12

. B.

11

. C.

20

.

D.

21

.

Câu 35.Thể tích của khối cầu ngoại tiếp bát diện đều có cạnh bằng

a

là

A.

3

a



. B.

3

2

6

a



. C.

3

2

3

a



. D.

3

82

3

a



.

Câu 36.Trong không gian với hệ tọa độ

Oxyz

, cho điểm

( )

2;1;0M

và đường thẳng

11

:

2 1 1

x y z

d

−+

==

−

. Phương trình của đường thẳng



đi qua điểm

M

, cắt và vuông góc với đường thẳng

d

là:

A.

21

1 4 2

x y z−−

==

−−

. B.

21

1 4 2

x y z−−

==

−−

. C.

21

1 3 2

x y z−−

==

−−

. D.

21

3 4 2

x y z− − +

==

− − −

.

Trang 120

Câu 37.Trong không gian với hệ tọa độ

Oxyz

, cho điểm

( )

1;2;3M

. Gọi

( )

P

là mặt phẳng đi qua điểm

M

và

cách gốc tọa độ

O

một khoảng lớn nhất, mặt phẳng

( )

P

cắt các trục tọa độ tại các điểm

,,A B C

. Tính thể tích

khối chóp

.O ABC

. A.

1372

9

. B.

686

9

. C.

524

3

. D.

343

9

.

Câu 38.Số các giá trị thực của tham số

m

đề phương trình

( ) ( )

( )

2

sin 1 2cos 2 1 cos 0x x m x m− − + + =

có đúng

4

nghiệm thực thuộc đoạn

 

0;2



là: A.

1

. B.

2

. C.

3

. D. Vô số.

Câu 39.Tổng số các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số

4

2

16

x

y

x

+

=

−

là:

A.

3

. B.

0

. C.

2

. D.

1

.

Câu 40.Tập tất cả các giá trị của tham số

m

để hàm số

( )

ln cos 2 1y x mx= + − +

đồng biến trên là:

A.

1

;

3



− −







. B.

1

;

3



− −







. C.

1

;

3



− +







. D.

1

;

3



− +







.

Câu 41.Cho hình chóp đều

.S ABC

có đáy là tam giác đều cạnh

a

. Gọi

E

,

F

lần lượt là trung điểm các cạnh

SB

,

SC

. Biết mặt phẳng

( )

AEF

vuông góc với mặt phẳng

( )

SBC

. Tính thể tích khối chóp

.S ABC

.

A.

3

5

24

a

. B.

3

5

8

a

. C.

3

24

a

. D.

3

6

12

a

.

Câu 42.Xét hàm số

( )

fx

liên tục trên đoạn

 

0;1

và thỏa mãn

( ) ( )

2

2 3 1 1f x f x x+ − = −

. Tính

( )

1

0

df x x



.

A.

4



. B.

6



. C.

20



. D.

16



.

Câu 43.Diện tích toàn phần của hình nón có khoảng cách từ tâm của đáy đến đường sinh bằng

3

và thiết diện

qua trục là tam giác đều bằng A.

16



. B.

8



. C.

20



. D.

12



.

Câu 44.Cho đa giác đều

100

đỉnh nội tiếp một đường tròn. Số tam giác tù được tạo thành từ

3

trong

100

đỉnh của

đa giác là A.

44100

. B.

78400

. C.

117600

. D.

58800

.

Câu 45.Cho hình chóp

.S ABCD

có các cạnh bên bằng nhau và bằng

2a

, đáy là hình chữ nhật

ABCD

có

2,AB a AD a==

. Gọi

K

là điểm thuộc

BC

sao cho

3 2 0BK CK+=

. Tính khoảng cách giữa hai đường thẳng

AD

và

SK

. A.

2 165

15

a

. B.

165

15

a

. C.

2 135

15

a

. D.

135

15

a

.

Câu 46.Xét phương trình

32

10ax x bx− + − =

với

,ab

là các số thực,

0,a a b

sao cho các nghiệm đều là số

thực dương. Tìm giá trị nhỏ nhất của biểu thức

( )

2

5 3 2a ab

P

a b a

−+

=

−

. A.

15 3

. B.

82

. C.

11 6

.

D.

12 3

.

Câu 47.Cho tham số thực

a

. Biết phương trình

2

xx

e e cosax

−

−=

có

5

nghiệm thực phân biệt. Hỏi phương trình

24

xx

e e cosax

−

+ = +

có bao nhiêu nghiệm thực phân biệt. A.

5

. B.

6

. C.

10

. D.

11

.

Trang 121

Câu 48.Cho hàm số

( )

y f x=

liên tục trên . Đồ thị hàm số

( )

'y f x=

như

hình vẽ dưới. Đặt

( ) ( ) ( )

2

21g x f x x= − +

. Mệnh đề nào dưới đây đúng ?

A.

 

( ) ( )

3;3

1Min g x g

−

=

. B.

 

( ) ( )

3;3

1Max g x g

−

=

.

C.

 

( ) ( )

3;3

3Max g x g

−

=

. D. Không tồn tại giá trị nhỏ nhất của

( )

gx

trên

 

3;3−

.

Câu 49.Cho khối chóp

.S ABCD

có đáy là hình bình hành

ABCD

. Gọi

M

,

N

,

P

,

Q

lần lượt là trọng tâm các tam giác

SAB

,

SBC

,

SCD

,

SDA

. Biết

thể tích khối chóp

.S MNPQ

là

V

, khi đó thể tích của khối chóp

.S ABCD

là:

A.

27

4

V

. B.

2

9

2

V







. C.

9

4

V

. D.

81

8

V

.

Câu 50.Cho khối lăng trụ đứng

.ABC A B C

  

có đáy là tam giác vuông

ABC

vuông tại

A

,

AC a=

,

60ACB =

. Đường thẳng

BC



tạo với mặt phẳng

( )

A C CA



góc

30

. Tính thể tích khối lăng trụ đã cho.

A.

3

23a

. B.

3

6a

. C.

3

2

a

. D.

3

a

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1.Chọn B.Xét hàm số

3

y x 3x 5= − +

trên đoạn

3

0;

2







2

33yx



=−

.

( )

1

0

1

xN

y

xL

=





=



=−





Tính

( ) ( )

3 31

0 5; 1 3;

28

y y y



= = =





.

3

0;

2

max 5y







=

.

Câu 2.Chọn A.

1

0 2 1 0

2

y x x=  − =  =

1

;0

2

A









.

1

0

3

xy=  = −

1

0;

3

B



−





Ta có

11

;

23

OA OB==

.

11

..

2 12

OAB

S OAOB



==

.

Câu 3. Chọn D.Đây là đồ thị hàm số bậc bốn trùng phương, hệ số

0a 

. Chọn A.

Câu 4.Chọn B.

1 1 1

1

6

3 3 6

2

..P x x x x x x= = = =

.

Câu 5.Chọn A.Ta có:

3 2 3

0 0 2

( )d ( )d ( )df x x f x x f x x=+

  

2 3 3

0 0 2

( )d ( )d ( )df x x f x x f x x a b = − = −

  

.

Câu 6.Chọn C

Câu 7.Chọn C.Ta có trung điểm

( )

1; 2; 3I −

cỉa

AB

,

( ) ( )

4; 0;12 4 1; 0; 3 .AB = − = − −

Mặt phẳng trung trực;

3 10 0.xz− + =

Câu 8.Chọn C.C sai. Vì

1

log log .

aa

x

=−

O

1

3

x

2

4

2−

3−

y

Trang 122

Câu 9.Chọn C.Ta có

: 2 2d y x=−

là đường thẳng đi qua hai điểm cực trị

của đồ thị

( )

.C

Và do đó

d

cắt

Ox

tại điểm

( )

1; 0 .M

Câu 10.Chọn C.Ta có

( )

.

AB OC

AB SAI

AB OH

⊥



⊥



⊥



(với

I

là chân đường

cao kẻ

C

của

).ABC

Suy ra

.AB AH⊥

Tương tự, ta chứng minh được

.BC AH⊥

Vậy

ABC

Câu 11.Chọn D.Ta có

//MN SA

nên góc giữa

MN

và

SC

bằng góc giữa

SA

và

SC

và bằng

ASC

(vì tam giác

SAC

cân tại

S

).

Lại có

;2SA SC a AC a= = =

suy ra

90ASC =

.

Câu 12.Chọn D.

( )

2

23

33

.ln . 2 1

xx

yx



++

   



=+

   

   

.Do

3

ln 0











và

2

23

3

0

xx

x



++



  





nên

( )

0 ; 1yx



   − −

.

Câu 13.Chọn A.Dựa vào đồ thị hàm số ta thấy đồ thị hàm số có tiệm cận ngang

11yb=  =

;

Đồ thị hàm số có tiệm cận đứng

22xc=  = −

.

Đồ thị hàm số đi qua điểm

( )

0; 1 2Aa−  = −

.Vậy

2 1 2 3P a b c= + + = − + − = −

.

Câu 14.Chọn B.Điều kiện xác định:

3x 

và

5x 

.

Khi đó ta có:

( ) ( ) ( ) ( )

2 2 2

4 4 4 4

2log 3 log 5 0 log 3 log 5 0x x x x− + − =  − + − =

.

( ) ( ) ( )( )

( )( )

2

22

4

3 5 1

log 3 5 0 3 5 1

3 5 1

xx

x x x x

xx



− − =



 − − =  − − = 





− − = −





( )

2

42

8 14 0

42

8 16 0

4

x

xx

xL

xx

x



=+





−+=

  = −



−+=





=





.Vậy

12

4 2 4 8 2T x x= + = + + = +

.

Câu 15.Chọn B.Ta có:

13

2017 2017

1 3 2 4 2

2018 2018

xx

x x x x

− − +

   

  −  − +    

   

   

.

Vậy tập nghiệm của bất phương trình là:

( )

;2−

.

Câu 16.Chọn A.Hai năm đầu người đó gửi với kỳ hạn 3 tháng và 3 năm sau gửi với kỳ hạn 1 tháng nên ta có số

tiền người đó nhận được sau 5 năm là:

( ) ( )

8 36

6

5

200.10 . 1 0,021 . 1 0,0065 298217000P = + + 

đồng.

Vậy số tiền lãi người đó nhận được sau 5 năm là:

298217000 200000000 98217000−=

đồng.

Câu 17.Chọn C.Ta có

H 

( )

1 ;2 ;2H t t t + +

,

t 

và

( )

1;2 ; 1MH t t t= − +

,

( )

1;2;1u



=

.

Vì

H

là hình chiếu của

M

lên

( )

.0MH u



  =

( )

1 2 2 1 0t t t − + + + =

0t=

.Vậy

( )

1;0;2H

.

Câu 18.Chọn D.Ta có

( ) ( )

1;2AC

1

22aa =  =

. Vậy đồ thị hàm số

( )

C

là:

2

x

y =

.

Suy ra đồ thị hàm số đối xứng với đồ thị hàm số

2

x

y =

qua đường thẳng

yx=

là

2

logyx=

.

I

H

C

B

A

O

N

M

O

C

A

D

S

Trang 123

Câu 19.Chọn B.Số nghiệm của phương trình

( )

f x m=

là số giao điểm của đồ thị hàm số

( )

y f x=

và đường

thẳng

ym=

.Dựa vào BBT để phương trình

( )

f x m=

có ba nghiệm thực phân biệt



đường thẳng

ym=

cắt

đồ thị hàm số

( )

y f x=

tại 3 điểm phân biệt

21m −   −

.

Câu 20.Chọn B.

Xét hệ trục tọa độ

Axyz

như hình vẽ có

( )

0;0;0A

,

( )

0;0;Sz

,

( )

; ;0M x a

,

( )

; ;0N a y

Có

( )

0;0;AS z=

,

( )

; ;0AM x a=

( )

( ) ( )

; ;0 ; ;0

SAM

n az xz z a x = − = −

Và

( )

;;SM x a z=−

,

( )

;;SN a y z=−

( )

2

;;

SMN

n zy az xz az xy a = − − −

Để mặt phẳng

()SAM

và

()SMN

vuông góc với nhau

( ) ( )

.0

SAM SMN

nn=

( ) ( )

0az y a xz x a − − + − =

22

0ay a x xa − + + − =

( )

22

x a a x y + = +

.

Câu 21.Chọn D. ĐK:

( )

cos cos 0 cos cos 1 2 cos 1

2 2 2

x x k x k x x k k

  





   +   +      





Câu 22.Chọn B.

2

2sin 3sin2 3+=xx

1 cos2 3sin2 3xx − + =

3sin2 cos2 2xx − =

31

sin2 cos2 1

22

xx − =

sin 2 1

6

x





 − =





22

62

xk





 − = +

( )

3

x k k



 = + 

Câu 23.Chọn A.

Câu 24.Chọn A.

( ) ( )

d =



12

0

'N x x N x

( ) ( )

2000

12 - 0d N N=

+



12

0

1

x

( ) ( )

2000

12 0N d N = +

+



12

0

1

x

( )

2000. ln N 0= + +

12

0

1 x

= 2000.ln13+500

10130

Câu 25.Chọn C.Số hạng tổng quát trong khai triển trên là:

11

1 11

(1 2 ). 3

k k k

k

T x C x

−

+

=+

( )

11 11 1

11 11

3 2 3 ,0 11 .

k k k k k k

C x C x k k

− − +

= +   

Hệ số của số hạng chứa

9

x

trong khai triển là

9 2 8 3

11 11

3 2 3 9405.CC+=

Câu 26.Chọn A.Bán kính mặt cầu

22

1 3 10R = + =

Phương trình mặt cầu

2 2 2

( 1) ( 2) ( 3) 10x y z− + + + − =

.

Câu 27.Chọn C.Không gian mẫu

6! 1.5.4.3.2.1 600 = − =

.

Coi chữ số

3

và chữ số

4

đứng cạnh nhau là một vị trí.

Từ đó

4

chữ số còn lại được lấy ra từ các số

0;1;2;5

.Gọi số cần tìm là

abcde

.

Khi đó

a

có bốn cách chọn,

b

có bốn cách chọn,

c

có ba cách chọn,

d

có hai cách chọn,

e

có một cách chọn.

Đồng thời có

2

cách xếp chữ số

3

và chữ số

4

đứng cạnh nhau nên số phần tử của A là

4.4.3.2.2 192=

.

Xác suất

( )

192 8

600 25

PA==

.

Câu 28.Chọn D.TXĐ:

( ) ( )

; 3 3;− −  − +

y

x

B

A

D

C

S

M

N

z

x

y

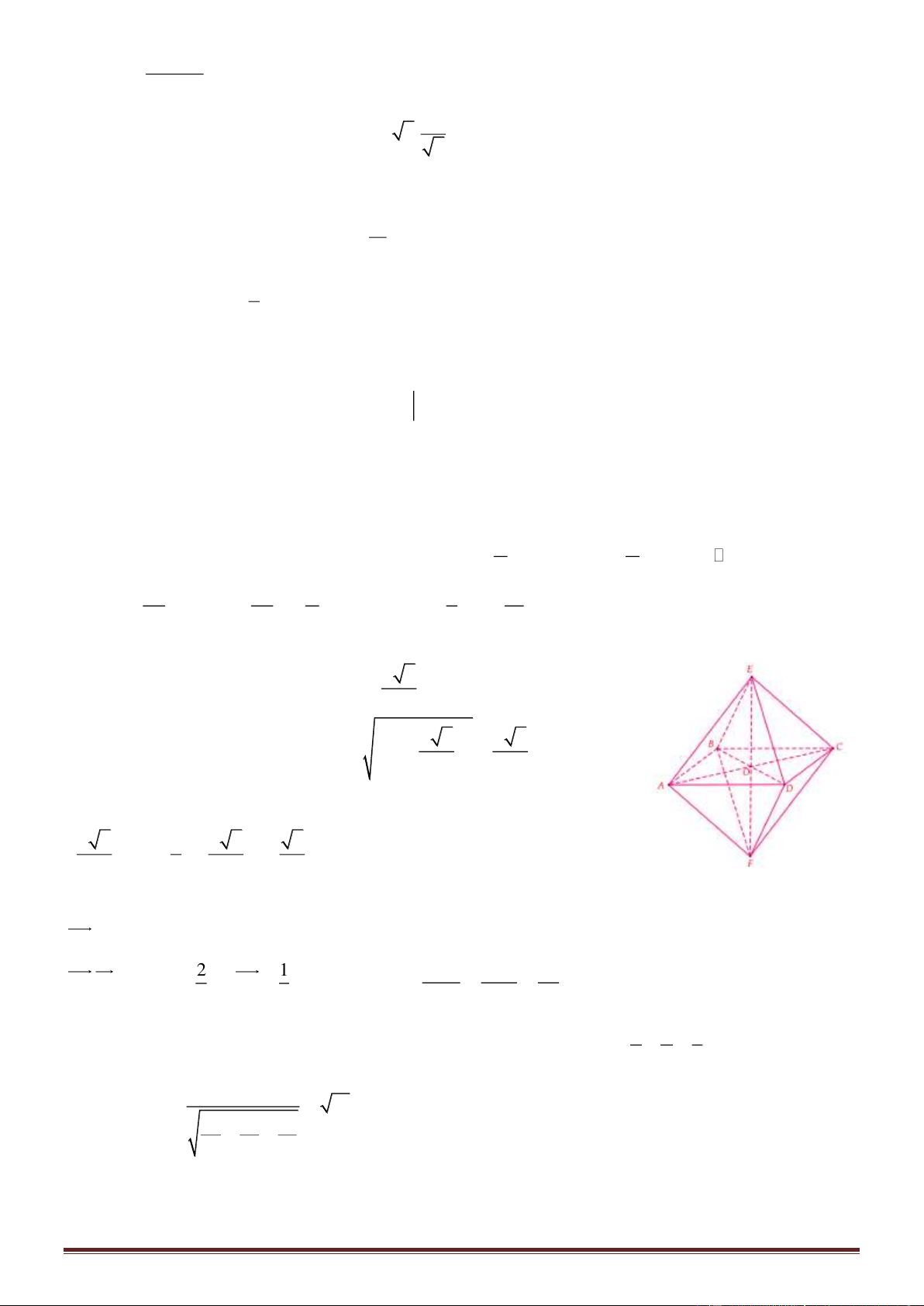
Trang 124

Ta có

( )

2

5

0

3

y

x



=

+

nên hàm số đồng biến trên mỗi khoảng xác định.

Câu 29.Chọn A.Ta có

1

.sin45 2 2. 2

2

AB AC a a BC=  = = =

Hình trụ tạo thành có bán kính đáy

2a

và chiều cao

2a

nên

( )

2

2 .2 .2 2 2 16

tp

S a a a a

  

= + =

.

Câu 30.Chọn D.Ta đặt

2

1

2

dt

x t xdx+ =  =

1 2; 2 5x t x t=  = =  =

Khi đó

( )

( ) ( ) ( )

2 5 5 5

2

1 2 2 2

1

1 2 4

2

f x xdx f t dt f t dt f x dx+ = =  = =

   

.

Câu 31.Chọn B.Ta có

( )

cos sin sin sin sin cosI x xdx x x dx x x xdx x x x C



= = = − = + +

  

Câu 32.Chọn C.Tính

( )

2 2 2

21

b

a

I x dx x x b b a a= − = − = − − +



. Theo giả thiết

1I =

nên ta có phương

trình:

2 2 2 2

11b b a a b a b a− − + =  − = − +

.

Câu 33.Chọn D.Số trận đấu của giải đấu là

2

16

.2 240C =

. Số trận hòa là

80 

số trận thắng là

240 80 160−=

.

Suy ra số điểm của tất cả các trận đấu là

160.3 80.2 640+=

.

Câu 34.Chọn ATa có phương trình

( )

sin2 1 0 2 2

24

x x k x k k



+ =  = − +  = − + 

.

Do

3 3 5 41

;10 10

2 2 4 4 4

x k k

  



 −  −  − +   −  





, suy ra

1...10k =−

.

Vậy có

12

nghiệm.

Câu 35.Chọn C.Ta có

2

a

OD OA OB OC= = = =

.

Xét tam giác vuông

EOD

tại

O

, ta có

2

22

aa

OE a OF



= − = =





.

Suy ra

O

là tâm khối cầu ngoại tiếp và bán kính

3

2

2 4 2 2

2 3 2 3

aa

R V a





=  = =





.

Câu 36.Chọn A.Gọi

I

là hình chiếu của

M

trên

d

( )

1 2 ; 1 ;I t t t + − + −

( )

2 1; 2;MI t t t = − − −

( )

21

. 0 1; 4; 2

33

d

MI u t MI =  =  = − −

21

:.

1 4 2

x y z−−

  = =

−−

Câu 37.Chọn B.Gọi

( ) ( ) ( )

;0;0 , 0; ;0 , 0;0;A a B b C c

. Ta có phương trình

( )

:1

x y z

P

a b c

+ + =

.

( )

2 2 2

1

, 14

1 1 1

d O P

abc

 = 

++

.Dấu

'' ''=

xảy ra khi

23a b c==

.

Trang 125

Mà

( )

23

1 2 3

1

a b c

MP

abc

==









+ + =





14

7

14

3

a

b

c





=



=





=



.Khi đó

.

1 686

69

O ABC

V abc==

.

Câu 38.Chọn B.Ta có

( ) ( )

( )

2

sin 1 2cos 2 1 cos 0x x m x m− − + + =

( )

2

sin 1

2cos 2 1 cos 0

x

x m x m

=







− + + =



.

sin 1 2

2

x x k



=  = +

 

0;2

2

x



 = 

Để phương trình đã cho có đúng

4

nghiệm thực thuộc đoạn

 

0;2



thì phương trình

( )

2

2cos 2 1 cos 0x m x m− + + =

có đúng 3 nghiệm thực thuộc đoạn

 

0;2



.

Ta có

( )

2

1

cos

2cos 2 1 cos 0

2

cos

x

x m x m

xm



=



− + + = 



=



.

 

2

15

3

cos ; 0;2

2 3 3

2

3

xk

xx

xk









=+





=    









= − +





.

Khi đó yêu cầu bài toán



cos xm=

có đúng một nghiệm khác

5

;;

3 2 3

  







và thuộc

 

0;2



 

1;0 .m  −

Câu 39.Chọn D.Điều kiện:

22x−  



đồ thị hàm số không có tiệm cận ngang.

Ta có

2

lim 0;

x

y

+

→−

=

2

lim

x

y

−

→

= +



đồ thị hàm số có một tiệm cận đứng.

Câu 40.Chọn B.Ta có

sin

0,

cos 2

x

y m x

x



= −   

+

sin

,

cos 2

x

mx

x

   

+

( )

1

min

3

m f x  = −

.

Câu 41.Chọn D.Do

SAB SAC = 

nên

AE AF=

. Gọi

I

là trung điểm

EF

nên

AI EF⊥

.

( ) ( )

AEF SBC⊥

nên

( )

AI SBC⊥

. Gọi

M

là trung điểm

BC

thì

AI SM⊥

và

I

là trung điểm

SM

.

Đặt

SA x=

. Ta có

..AI SM SH AM=

với

2

4

a

SM x=−

,

3

2

a

AM =

;

2 2 2 2

2 2 2

3 1 13

4 4 4 16 4

a a a x

AI AM IM x



= − = − − = −





;

2

2 2 2

3

a

SH SA AH x= − = −

.

Ta có phương trình:

2 2 2 2

22

13 3

..

16 4 4 3 2

a x a a a

xx− − = −

( )

2 2 2

2 2 2 2

3

13 4 4

.

16 4 4

x a a

a x x a

−

   

−−

=

   

   

4 2 2 4

16 8 3 0x a x a − − =

2

3

4

a

x=

3

2

a

x=

.Vậy

15

6

a

SH =

nên

23

1 15 3 5

..

3 6 4 24

a a a

V ==

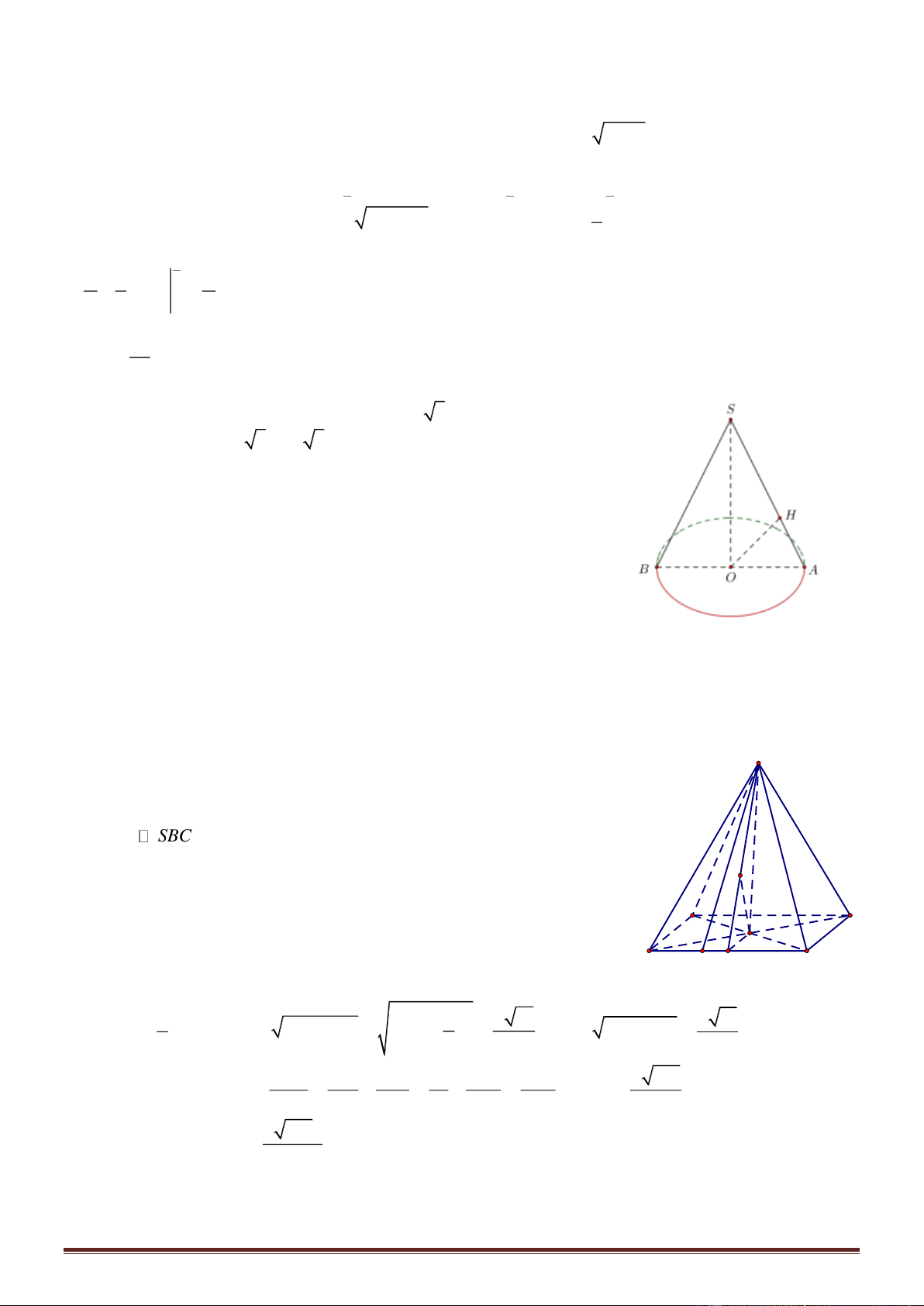
Trang 126

Câu 42.Chọn C.Đặt

( )

1

0

dI f x x=



.Đặt

1tx=−

ddtx = −

. Ta có

( ) ( )

01

10

1 d 1 dI f t t f x x= − − = −



.

Khi đó

( ) ( )

11

00

5 2 d 3 1 dI f x x f x x= + −



( ) ( )

1

0

2 3 1 df x f x x= + −







1

2

0

1dxx=−



.

Đặt

sinxt=

d cos dx t t=

nên

2

0

5 1 sin .cos dI t t t



=−



( )

22

2

00

1

cos d 1 cos2 d

2

t t t t



= = +



2

0

1

sin2

4 4 4

t





= + =

.

Vậy

20

I



=

.

Câu 43.Chọn D.Đặt

2AB x=

, ta có

OA x=

,

3SO x=

,

2SA x=

..OH SA SOOA=

2

2 3 3xx=

2x=

.

Diện tích toàn phần là

( ) ( )

.2 4 2 12

tp

S r l r

  

= + = + =

.

Câu 44.Chọn C.Đánh số các đỉnh là

1 2 100

, ,...,A A A

.

Xét đường chéo

1 51

AA

của đa giác là đường kính của đường tròn ngoại tiếp

đa giác đều chia đường tròn ra làm

2

phần mỗi phần có

49

điểm từ

2

A

đến

50

A

và

52

A

đến

100

A

. Khi đó, mỗi tam giác có dạng

1 ij

A A A

là tam

giác tù nếu

i

A

và

j

A

cùng nằm trong nửa đường tròn chứa điểm

1

A

tính theo chiều kim đồng hồ nên

i

A

,

j

A

là hai điểm tùy ý được lấy từ

49

điểm

2

A

,

3

A

đến

50

A

. Vậy có

2

49

1176C =

tam giác tù.Vì đa giác có

100

đỉnh nên số tam giác tù là

1176.100 117600=

tam giác tù.

Câu 45.Chọn A.Gọi

O

là hình chiếu của

S

lên

( )

ABCD

mà

SA SB SC SD OA OB OC OD= = =  = = =

.

Vậy

O

là tâm của hình chữ nhật

ABCD

.

Ta có:

( )

( ) ( )

( )

,,

AD SBC

d AD SK d AD SBC

SK SBC





=









.

( )

, 2 ,d A SBC d O SBC==

Gọi

I

là trung điểm của

BC

OI BC⊥

mà

( )

SO BC BC SOI⊥  ⊥

.

Trong

( )

SOI

kẻ

( ) ( )

( )

,OH SI OH SBC d O SBC OH⊥  ⊥  =

.

Ta có:

1

2

OI AB a==

,

2

2 2 2

15

4

22

aa

SI SB BI a



= − = − =





,

22

11

2

a

SO SI OI= − =

.

Xét tam giác vuông

SOI

có

2 2 2 2 2 2

1 1 1 1 4 15 165

11 11 15

a

OH

OH OI SO a a a

= + = + =  =

.

Vậy

( )

2 165

,2

15

a

d AD SK OH==

.

Câu 46.Chọn D.Giả sử ba nghiệm dương (kể cả nghiệm bội) của phương trình là

,,x y z

theo vi-ét, ta có:

I

O

D

A

B

C

S

K

H

Trang 127

1

x y z

a

b

xy yz zx

a

xyz

a



+ + =



++=





=





0, 0ab  

.Áp dụng BĐT AM – GM ta có:

3

3x y z xyz+ + 

3

1 1 1

30

33

a

aa

    

và

( ) ( )

2

3x y z xy yz zx+ +  + +

2

1 3 1

3

b

a a a

   

.Xem

P

là hàm số với ẩn

b

, ta có:

( )

2 2 2

22

3 5 2 2 1

0

a a a

Pb

a b a a b a

− + − +



= = 

−−

( ) ( )

( )

2

3

3 5 1

1

33

a

P b P f a

a a a

+



  = =



−



.

Xét hàm số

( )

2

3

3 5 1

3

a

fa

aa

+

=

−

trên nửa khoảng

1

0;

33









,

( )

4 3 2

2

3

135 90 42 3 1

0 0;

33

3

a a a

f a a

aa

− + −





=   







−

. (vì

42

5 14

135 0; 42 0

27 9

aa−  − 

)

( )

1

0;

33

1

min 12 3

33

f a f











 = =





. Vậy

min

12 3P =

khi

1

,3

33

ab==

.

Câu 47.Chọn C.

( )

2

22

2 4 2 2 1 4

2

xx

x x x x

ax

e e cosax e e cosax e e cos

−

−−



+ = +  − + = +  − =





( )

22

2 s 1

2

2 s 2

2

xx

ax

e e co

ax

e e co

−





−=















− = −









Phương trình

( )

1

có

5

nghiệm phân biệt.

( )

22

2

xx

ax

e e cos

−



 − = −





,

phương trình này cũng có

5

nghiệm phân biệt khác

5

nghiệm phương trình

( )

1

.

Vậy phương trình

24

xx

e e cosax

−

− = +

có

10

nghiệm phân biệt.

Câu 48.Chọn B.Ta có:

( ) ( ) ( )

' 2 ' 2 1g x f x x= − +

;

( ) ( ) ( )

' 0 ' 1 1g x f x x=  = +

.

Quan sát đồ thị ta thấy đường thẳng

1yx=+

cắt đồ thị hàm

số

( )

'y f x=

tại ba điểm phân biệt có hoành độ lần lượt là

3;1;3−

. Do đó

( )

3

11

3

x

=−





=



=



.Vậy

 

( ) ( )

3;3

1Max g x g

−

=

.

Bảng biến thiên

Câu 49.Chọn A.Ta có

( )

,

2

3

,

d S MNPQ

SM

SI

d S ABCD

==

.

Mặt khác gọi

ABCD

SS=

ta có

1 1 1

.

4 2 8

DEJ

BDA

S



==

1

16

DEJ

SS



=

.

Tương tự ta có

1

4

JAI

DAB

S



=

1

8

JAI

S



=

.Suy ra

1 1 1

1 4. 2.

16 8 2

HKIJ

S S S





= − + =









.

F

E

J

Q

P

H

N

K

M

I

O

D

S

A

B

C

Trang 128

Mà

2

24

39

MNPQ

HKIJ

S



==





2

9

MNPQ ABCD

SS=

. Suy ra

( )

.

1

,.

3

S ABCD

V d S ABCD S=

( )

1 3 9 27

. , .

3 2 2 4

d S MNPQ S V==

.

Câu 50.Chọn B.Ta có

3AB a=

, dễ thấy góc giữa dường thẳng

BC



tạo với mặt

phẳng

( )

A C CA



là góc

30BC A



=

. Suy ra

3

tan30

a

AC

=



3AC a



=

22C C a



=

.Vậy

.

1

2 2 . . 3

2

ABC A B C

V a a a

  

=

3

6a=

.

BẢNG ĐÁP ÁN

1.B

2.A

3.D

4.B

5.A

6.C

7.C

8.C

9.C

10.C

11.D

12.D

13.A

14.B

15.B

16.A

17.C

18.D

19.B

20.B

21.D

22.B

23.A

24.A

25.C

26.A

27.C

28.D

29.A

30.D

31.B

32.C

33.D

34.A

35.C

36.A

37.B

38.B

39.D

40.B

41.D

42.C

43.D

44.C

45.A

46.D

47.C

48.B

49.A

50.B

www.thuvienhoclieu.com

ĐỀ 60

ĐỀ THI THỬ THPT QUỐC GIA 2020

MÔN TOÁN

Thời gian: 90 phút

Câu 1. Cho hàm số có đồ thị như hình vẽ. Giá trị cực đại của hàm số bằng:

A.

1.−

B.

2−

C. 1. D. 0.

Câu 2. Cho số dương a và

, mn

. Mệnh đề nào sau đây đúng?

A.

..

−

=

m n m n

a a a

B.

( )

..=

n

m n m

a a a

C.

..

+

=

m n m n

a a a

D.

..=

m n mn

a a a

Câu 3. Một mặt cầu có đường kính bằng a có diện tích S bằng bao nhiêu?

A.

2

4

.

3

=



a

S

B.

2

.

3

=



a

S

C.

2

.=



Sa

D.

2

4.=



Sa

Câu 4. Cho số phức

2 5 .=+zi

Điểm biểu diễn số phức z trong mặt phẳng Oxy có tọa độ là:

A. (5;2) B. (2;5) C.

( 2;5)−

D.

(2; 5)−

30

60

a

A'

B'

C

B

A

C'

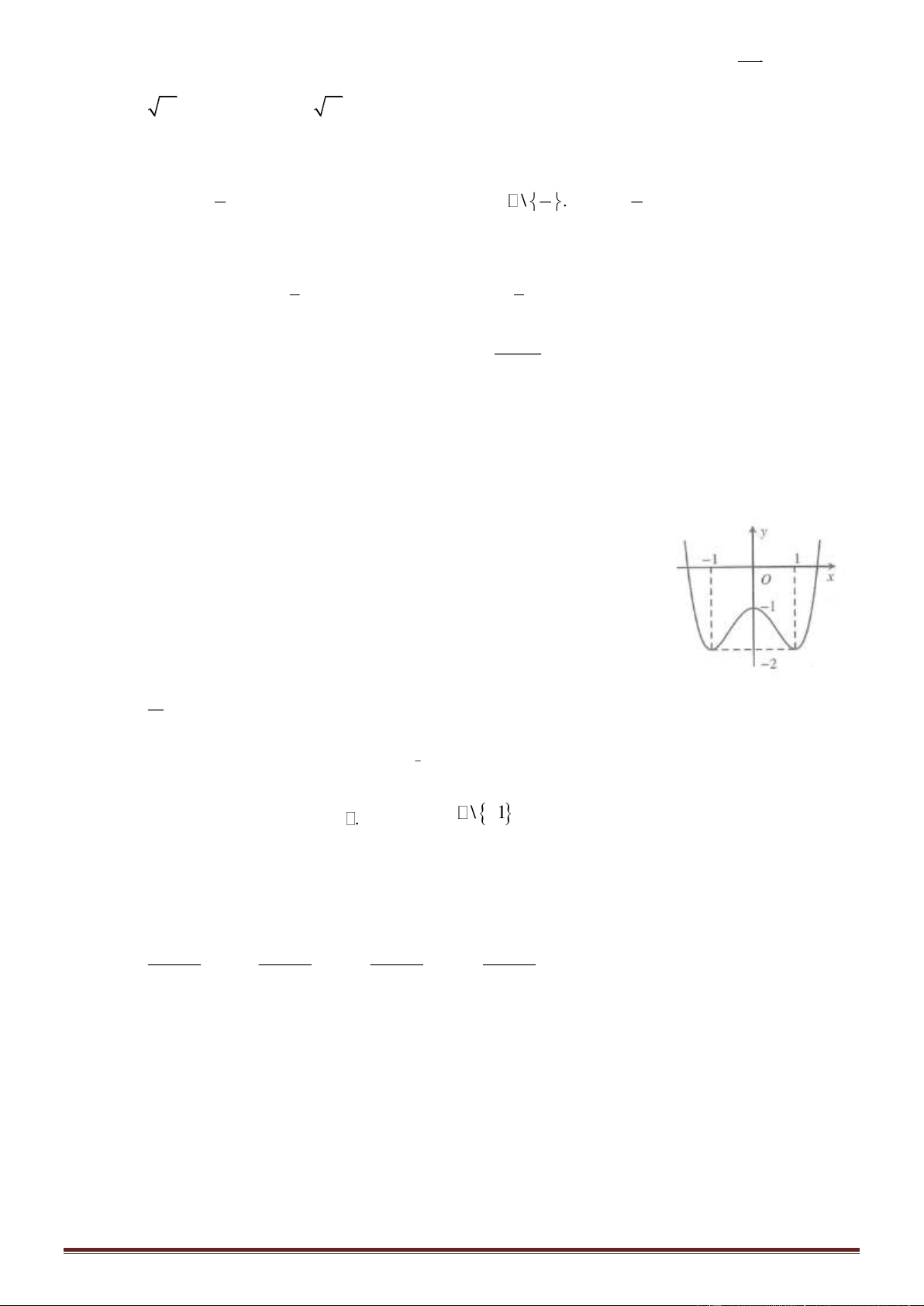
Trang 129

Câu 5. Trong không gian Oxyz cho hai điểm

( ) ( )

2;3;4 3;0;1 .A và B

Khi đó độ dài véctơ

AB

là.

A.

19.

B. 19. C.

13.

D. 13.

Câu 6. Với giá trị nào của x thì biểu thức

( )

2

21B log x=−

xác định?

A.

1

;.

2

x



 −





B.

( )

1; .x − +

C.

1

\.

2

x









D.

1

;.

2

x



 +





Câu 7. Cho khối nón có bán kính đáy là r, chiều cao h . Thể tích V của khối nón đó là:

A.

2

.V r h



=

B.

2

1

.

3

V r h=

C.

2

.V r h=

D.

2

1

.

3

V r h



=

Câu 8. Tìm đường tiệm cận ngang của đồ thị hàm số

22

.

1

x

y

x

−

=

+

A.

1.x =−

B.

2.x =−

C.

2.y =

D.

2.y =−

Câu 9. Cho hàm số có đồ thị như hình vẽ. Hàm số đã cho đồng biến trên

khoảng nào dưới đây?

A.

( )

1;0 .−

B.

( )

1;1 .−

C.

( )

1; .− +

D.

( )

0;1

Câu 10. Số tập hợp con có 3 phần tử của một tập hợp có 7 phần tử là.

A.

7!

3!

B. 21. C.

3

7

A

D.

3

7

.C

Câu 11. Tập xác định D của hàm số

1

3

()1yx=+

là.

A.

( )

; 1 .D = − −

B.

.D =

C.

 

\1D =−

D.

( )

1;− +

Câu 12. Hình bát diện đều có bao nhiêu đỉnh?

A. 10. B. 8. C. 12. D. 6.

Câu 13. Đạo hàm của hàm số

2

)53(y ln x=−

là:

A.

2

6

.

35x −

B.

2

53

x

x−

C.

2

6

.

35

x

x −

D.

2

6

.

35

x

x −

−

Câu 14. Cho số phức

5 4 .zi=−

Số phức đối của z có tọa độ điểm biểu diễn là.

A.

( )

5; 4−−

B.

( )

5;4

C.

( )

5;4−

D.

( )

5; 4−

Câu 15. Cho

( ) ( )

22

11

2 2 8.f x dx và g x dx==



Khi đó

( ) ( )

2

1

f x g x dx+







bằng.

A. 6. B. 10. C. 18. D. 0.

Câu 16. Họ nguyên hàm của hàm số

( )

2

3f x x=+

là

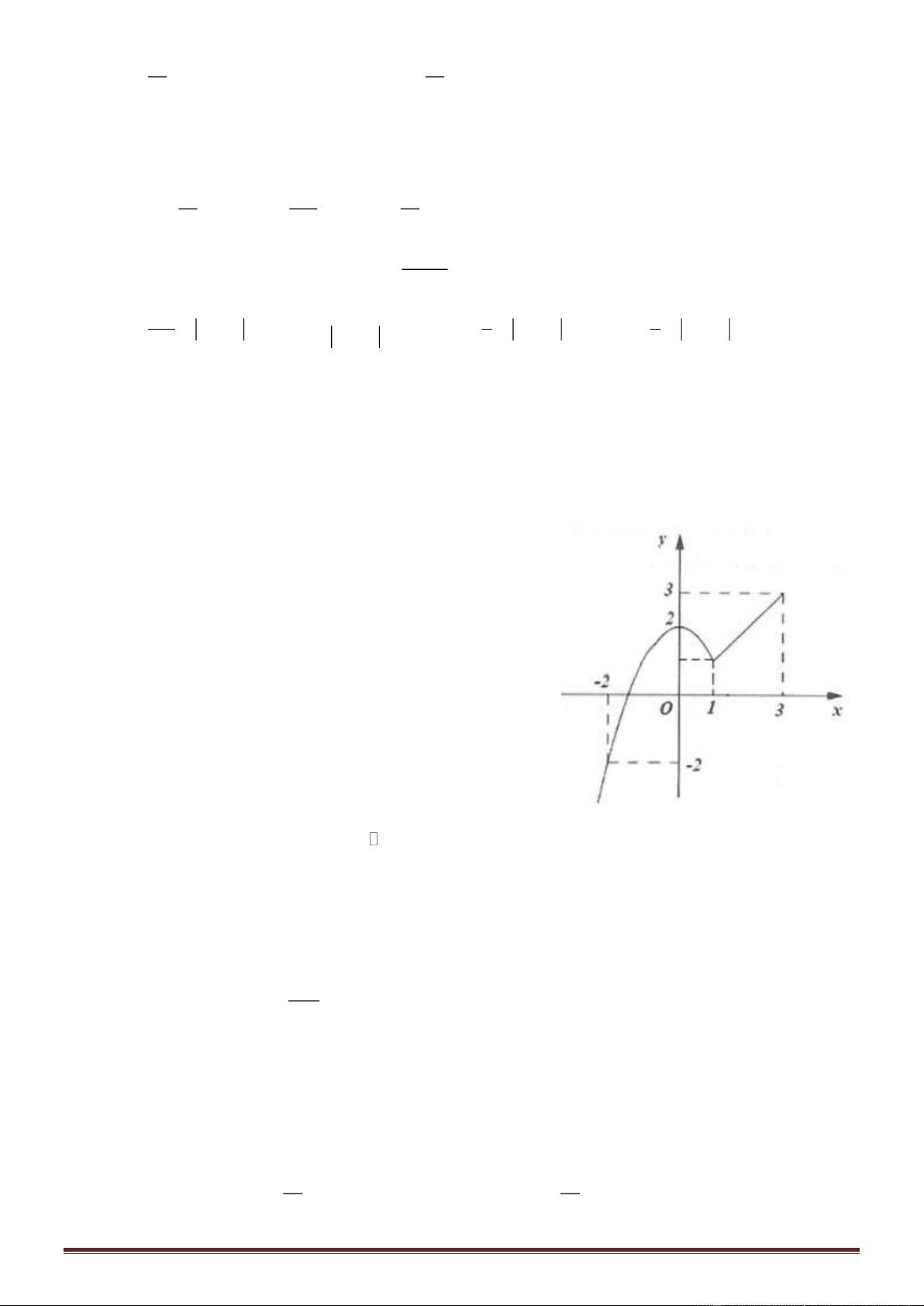
Trang 130

A.

3

3.

3

x

xC++

B.

3

3.x x C++

C.

3

3.

2

x

xC++

D.

2

3.xC++

Câu 17. Cho S.ABCD có đáy ABCD là hình vuông cạnh a . Biết

( )

.SA ABCD và SA a⊥=

Tính thể tích

của khối chóp S.ABCD.

A.

3

.

3

a

V =

B.

2

3

.

2

a

V =

C.

3

.

6

a

V =

D.

3

.Va=

Câu 18. Họ nguyên hàm của hàm số

( )

1

54

fx

x

=

+

là

A.

1

ln 5 4 .

ln5

xC++

B.

ln 5 4 .xC++

C.

.

1

ln 5

5

4xC++

D.

.

1

ln 5

5

4xC++

Câu 19. Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc,

4 , 5 , 3 .AB cm AC cm AD cm= = =

Thể

tích khối tứ diện ABCD bằng.

A. 15 cm3 B. 10 cm3 C. 60 cm3 D. 20 cm3

Câu 20. Số nghiệm của phương trình

2

2 7 5

21

xx−+

=

là:

A. 1 B. 0 C. 3 D. 2

Câu 21. Cho hàm số

( )

 

, 2;3y f x x=  −

có đồ thị như hình vẽ.

Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm

số

( )

fx

trên đoạn

 

2;3 .−

Giá trị của

S M m=+

là:

A. 6 B. 3

C. 5 D. 1

Câu 22. Tập xác định của hàm số

2sinyx=

là.

A.

 

0;2

B.

 

2;2−

C. D.

 

1;1−

Câu 23. Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng?

A. 9. B. 6. C. 4. D. 3.

Câu 24. Cắt một khối trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh

bằng a . Tính diện tích xung quanh S của khối trụ đó.

A.

2

2.Sa



=

B.

2

.

2

a

S



=

C.

2

.Sa



=

D.

2

4.Sa



=

Câu 25. Điểm cực tiểu của đồ thị hàm số

3

35y x x= − +

là điểm:

A.

( )

1;3 .M

B.

( )

1;7 .N −

C.

( )

3;1Q

D.

( )

7; 1P −

Câu 26. Kết quả tính

2 )ln( 1x x dx−



bằng:

A.

( )

2

1 ln 1 .

2

x

xx C− − ++−

B.

( )

2

1 ln 1 .

2

x

xx C− − + +−

Trang 131

C.

( )

2

.ln

2

1

x

xxx C−− −+

D.

( )

2

ln 11.

2

x

xCx x−− − − +

Câu 27. Tìm tất cả các giá trị thực của tham số m để phương trình

4 .2 1 0

x x

m− +=

có hai nghiệm

12

;xx

thỏa

12

1:xx+=

A.

2.m 

B.

m

C.

2; 2.mm  −

D.

0.m =

Câu 28. Phương trình

cos2 2cos 3 0xx+ − =

có bao nhiêu nghiệm trong khoảng

( )

0;2019

?

A. 1009. B. 1010. C. 320. D. 321.

Câu 29. Trong không gian Oxyz, cho mặt phẳng

( )

: 2 2 10 0.P x y z+ + − =

Phương trình mặt phẳng (Q)

song song với (P) và khoảng cách giữa hai mặt phẳng (P) và (Q) bằng

7

3

là:

A.

2 2 3 0; 2 2 17 0.x y z x y z+ + − = + + − =

B.

2 2 3 0; 2 2 17 0.x y z x y z+ + + = + + + =

C.

2 2 3 0; 2 2 17 0.x y z x y z+ + + = + + − =

D.

2 2 3 0; 2 2 17 0.x y z x y z+ + − = + + + =

Câu 30. Cho hàm số

( )

y f x=

có đạo hàm trên là

( )( )( )

4

.( 2 1 5) 3f x x x x



= + − +

. Hàm số đã cho có

tất cả bao nhiêu điểm cực trị?

A. 2 B. 1 C. 4 D. 3

Câu 31. Biết

3

0

ln2 ln3,

3

4 2 1

xa

dx b c

x

= + +

++



trong đó a, b, c là các số nguyên. Tính

.T a b c= + +

A.

1.T =

B.

4.T =

C.

3.T =

D.

6.T =

Câu 32. Cho hình chóp S.ABCD đáy là hình thoi tâm O và

( )

6

,,

3

a

SO ABCD SO⊥=

.BC SB a==

Số

đo góc giữa hai mặt phẳng (SBC) và (SCD) là:

A. 90o B. 60o C. 30o D. 45o

Câu 33. Gọi

12

;zz

là các nghiệm của phương trình

2

2 3 0.zz− + =

Mô-đun của

34

12

.zz

bằng:

A. 81. B. 16. C.

27 3.

D.

8 2.

Câu 34. Có bao nhiêu số nguyên m để phương trình

3

x

x me+=

có 2 nghiệm phân biệt?

A. 7. B. 6. C. 5. D. Vô số.

Câu 35. Trong không gian Oxyz, cho mặt phẳng

( )

: 3 0P x y z+ + − =

và đường thẳng

12

:.

1 2 1

x y z

d

+−

==

−

Đường thẳng d' đối xứng với d qua mặt phẳng (P) có phương trình là:

A.

1 1 1

.

1 2 7

x y z− − −

==

−

B.

1 1 1

.

1 2 7

x y z+ + +

==

−

C.

1 1 1

.

1 2 7

x y z− − −

==

D.

1 1 1

.

1 2 7

x y z+ + +

==

Trang 132

Câu 36. Cho tập

 

0;1;2;3;4;5;6 .A=

Xác suất để lập được số tự nhiên gồm 5 chữ số khác nhau lấy từ các

phần tử của tập A sao cho số đó chia hết cho 5 và các chữ số 1, 2, 3 luôn có mặt cạnh bằng nhau là:

A.

1

40

B.

11

360

C.

11

420

D.

1

.

45

Câu 37. Cho hình thang ABCD có

90 , , 2 .A B AB BC a AD a= =  = = =

Tính thể tích khối nón tròn xoay

sinh ra khi quay quanh hình thang ABCD xung quanh trục CD.

A.

3

7

12

a



B.

3

72

12

a



C.

3

72

6

a



D.

3

7

6

a



Câu 38. Cho hàm số

( )

y f x=

có đạo hàm liên tục trên , hàm số

( )

y f x



=

có đồ thị như hình vẽ. Số điểm cực trị của hàm số

( )

1y f x=−

là:

A. 3 B. 0

C. 1 D. 2

Câu 39. Ông A có 200 triệu đồng gửi tiết kiệm tại ngân hàng với kì hạn 1 tháng so với lãi suất 0,6% /1

tháng được trả vào cuối kì. Sau mỗi kì hạn ông đến tất toán cả gổc lẫn lãi, rút ra 4 triệu đồng để tiêu dùng,

số tiền còn lại ông gửi vào ngân hàng theo phương thức trên (phương thức giao dịch và lãi suất không

thay đổi trong suốt quá trình gửi). Sau đúng 1 năm (đúng 12 kì hạn) kể từ ngày gửi, ông A tất toán và rút

ra toàn bộ số tiền nói trên ở ngân hàng, số tiền đó là bao nhiêu? (làm tròn đến nghìn đồng).

A. 169234 (nghìn đồng). B. 165288 (nghìn đồng).

C. 168269 (nghìn đồng). D. 165269 (nghìn đồng).

Câu 40. Cho hàm số

( )

y f x=

liên tục trên đoạn [1; 3], thỏa mãn

( ) ( )

 

4 , 1;3f x f x x− =  

và

( )

3

1

2.xf x dx =−



Giá trị

( )

3

1

2 f x dx



bằng:

A. 2. B. 1. C.

2−

D.

1.−

Câu 41. Cho

( )

fx

mà đồ thị hàm số

( )

y f x



=

như hình bên đây.

Hàm số

( )

2

12y f x x x= − + −

đồng biến trên khoảng?

A.

( )

1;2

B.

( )

1;0−

C.

( )

0;1

D.

( )

2; 1−−

Trang 133

Câu 42. Cho hình lăng trụ đều ABC.A'B'C' có tất cả các cạnh bằng 1. Gọi E, F lần lượt là trung điểm của

AA' và BB'; đường thẳng CE cắt đường thẳng C'A' tại E', đường thẳng CF cắt đường thẳng C'B' tại F'.

Thể tích khối đa diện EFA'B’E'F' bằng:

A.

3

.

12

B.

3

.

2

C.

3

.

3

D.

3

.

6

Câu 43. Cho một bảng ô vuông

33

. Điền ngẫu nhiên các số 1,2, 3, 4, 5, 6, 7, 8, 9 vào bảng trên (mỗi ô

chỉ điền một số). Gọi A là biến cố: “mồi hàng, mỗi cột bất kì đều có ít nhất một số lẻ”. Xác suất của biến

cố A bằng:

A.

( )

5

.

7

PA=

B.

( )

1

.

3

PA=

C.

( )

1

.

56

PA=

D.

( )

10

.

21

PA=

Câu 44. Cho hình chóp S.ABCD có đáy là hình vuông cạnh

3,a

mặt bên SAB là tam giác đều và nằm

trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp S.ABCD là:

A.

3

93

.

2

a

B.

3

.

2

a

C.

3

.

3

a

D.

3

.

2

a

Câu 45. Tìm tất cả các giá trị thực của tham số m để phương trình

0()cos2 2 1 cos 1x m x m− + + + =

có

nghiệm trên khoảng

3

;?

22









A.

1 0.m−  

B.

1 0.m−  

C.

1 0.m−  

D.

1

1.

2

m−  

Câu 46. Có 4 hành khách bước lên một đoàn tàu gồm 4 toa. Mỗi hành khách độc lập với nhau và chọn

ngẫu nhiên một toa. Tính xác suất để 1 toa có 3 người, 1 toa có 1 người, 2 toa còn lại không có ai.

A.

1

4

B.

3

.

4

C.

13

.

16

D.

3

16

Câu 47. Giá trị của

32

2

0

11

lim

x

xx

x

→

+ + −

bằng.

A. 1. B.

1

.

2

C.

1−

D. 0.

Câu 48. Cho hàm số

( )

3 2

()2()2 1 2.xf x x m m x−−= − + +

Tìm tất cả các giá trị của tham số để hàm số

( )

y f x=

có 5 cực trị:

A.

5

2.

4

m−  

B.

5

2.

4

m−  

C.

5

2.

4

m

D.

5

2.

4

m

Trang 134

Câu 49. Để giá trị lớn nhất của hàm số

3

2 3 4y x x m= − − +

đạt giá trị nhỏ nhất thỏa mãn:

A.

3

.

2

m =

B.

1

2

m =

C.

4

.

3

m =

D.

5

.

3

m =

Câu 50. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,

17

,

2

a

SD =

hình chiếu vuông góc

H của S trên mặt phẳng (ABCD) là trung điểm của đoạn AB. Gọi K là trung điểm của đoạn AD (tham

khảo hình vẽ). Khoảng cách giữa hai đuờng HK và SD theo a là :

A.

3

.

5

a

B.

3

.

45

a

C.

3

.

15

a

D.

3

.

25

a

Trang 135

Đáp án

1-A

2-C

3-C

4-B

5-A

6-D

7-D

8-D

9-A

10-D

11-D

12-D

13-C

14-C

15-A

16-A

17-A

18-C

19-B

20-D

21-D

22-C

23-C

24-C

25-A

26-D

27-A

28-D

29-A

30-A

31-A

32-A

33-C

34-A

35-A

36-B

37-C

38-D

39-D

40-D

41-A

42-D

43-A

44-D

45-A

46-D

47-B

48-C

49-A

50-A

LỜI GIẢI CHI TIẾT

Câu 1: Đáp án A

Dựa vào đồ thị ta có:

1

CD

y =−

khi

0.

CD

x =

Câu 2: Đáp án C

Sử dụng công thức:

. .

m n m n

a a a

+

=

Mệnh đề đúng:

..

m n m n

a a a

+

=

Câu 3: Đáp án C

Sử dụng công thức tính diện tích mặt cầu bán kính r là

2

4.Sr



=

Câu 4: Đáp án B

Số phức

() ,z a bi a b= + 

có điểm biểu diễn số phức trong mặt phẳng Oxy là (a;b). Điểm biểu diễn số

phức z trong mặt phẳng Oxy có tọa độ là:

( )

2;5 .

Câu 5: Đáp án A

( ) ( ) ( )

2

1; 3; 3 1 3 3 19AB AB= − −  = + − =−+

Câu 6: Đáp án D

Để biểu thức

2

()log 2 1Bx=−

xác định thì

1

2 1 0 .

2

xx−   

Câu 7: Đáp án D

Thể tích khối nón có bán kính đáy R và chiều cao h:

2

1

.

3

V R h



=

Câu 8: Đáp án D

Sử dụng: đồ thị hàm số

ax b

y

cx d

+

=

+

nhận đường thẳng

a

y

c

=

làm đường tiệm cận ngang và đường thẳng

d

x

c

=−

làm đường tiệm cận đứng.

Ta có:

22

lim 2 2.

1

x

y

x

→+

−

= −  = −

+

là tiệm cận ngang của đồ thị hàm số.

Câu 9: Đáp án A

Hàm số đồng biến trên

( ) ( )

1;0 1;và− +

Hàm số nghịch biến trên

( ) ( )

; 1 0;1và− −

Trang 136

Câu 10: Đáp án D

Số tập con gồm k phần tử của tập hợp gồm n phân tử là:

k

n

C

tập hợp.

Số tập con gồm 3 phần tử của tập hợp gồm 7 phân tử là:

3

7

C

tập hợp.

Câu 11: Đáp án D

Hàm số

1

3

()1yx=+

xác định khi

1 0 1.xx+    −

Câu 12: Đáp án D

Nhìn hình vẽ.

Hình bát diện đều có 6 đỉnh.

Câu 13: Đáp án C

Sử dụng công thức tính đạo hàm

( )

ln

u



=

( )

2

22

66

ln 5 3 .

5 3 3 5

xx

x

xx

−





−=



− −

=



Câu 14: Đáp án C

Số phức đối của z là

5 4 .zi=−

Câu 15: Đáp án A

( ) ( ) ( ) ( )

2 2 2

1 1 1

2 4 6f x dx và g x dx x g x dxf= =  +





=

  

Câu 16: Đáp án A

( )

3

2

3.3

3

x

x Cdx x+ ++=



Câu 17: Đáp án A

Ta có:

3

2

11

. . .

3 3 3

SABCD ABCD

a

V SA S a a= = =

Câu 18: Đáp án C

Ta có:

5

l

5

4.

4

n

1

5

dx

x

xC= ++

+



Câu 19: Đáp án B

Thể tích của tứ diện có các cạnh đôi một vuông góc và các cạnh

đó có độ dài lần lượt là a, b, c là

1

.

6

V abc=

Tứ diện ABCD có AB , AC, AD đôi một vuông góc

 Thể tích khối tứ diện ABCD là:

( )

3

11

. . . .4.5.3 10 .

66

V AB AC AD cm= = =

Câu 20: Đáp án D

Trang 137

Ta có:

2

2 7 5 2

1

2 1 2 7 5 0

5

2

xx

x

xx

x

−+

=





=  − + = 



=



Vậy phương trình đã cho có 2 nghiệm là:

5

1;

2

xx==

Câu 21: Đáp án D

Dựa vào đồ thị hàm số ta thấy trong

 

2;3−

thì

( ) ( )

max 3 3

min 2 2

M f x f

m f x f

= = =







= = − = −





3 2 1.S M m = + = − =

Câu 22: Đáp án C

Hàm số

sinyx=

xác định trên .

Hàm số

2sinyx=

xác định trên nên tập xác định

.D =

Câu 23: Đáp án C

Sử dụng lý thuyết khối đa diện.

Hình lăng trụ tam giác đều có 4 mặt phẳng đối xứng như hình vẽ bên dưới, trong đó:

• 3 mặt phẳng tạo bởi 1 cạnh bên và trung điểm của các cạnh đối diện.

• 1 mặt phẳng tạo bởi trung điểm của 3 cạnh bên.

Câu 24: Đáp án C

Vì đường kính mặt cầu bằng a nên bán kính mặt cầu là

.

2

a

r =

Diện tích mặt cầu là

2

4.

2

a

Sa





==





Câu 25: Đáp án A

Ta có

2

' 3 3yx=−

1

0.

1

x

y

x

=





=



=−



Suy ra hàm số đạt giá trị cực đại tại

1, 1xx= = −

6.yx



=

Ta có

( ) ( )

3

1 6.1 6 0 1 3.1 5 31y và y



= =  = − + =

Do đó điểm cực tiểu của đồ thị là

( )

1;3M

Câu 26: Đáp án D

Trang 138

Sử dụng công thức từng phần:

bb

b

a

aa

udv uv vdu=−



( ) ( )

( )

( ) ( )

( )

2 2 2

2 ln 1 l ln 1 ln 1n1xx xdx x d x x x d x= − − −− = −



( ) ( )

2 2 2

1

ln 1 l

1

.1n

1

xd

x

x x x dx

x

x xx=



− + +



=



−−

−



−−



( )

2 2 2 2

11

ln 1 ln 1 1 ln 1

22

x x x x x C x x x x C= − − − − − + = − − − − +

Câu 27: Đáp án A

Đặt

2

x

t =

ta có

2

10t mt− + =

có nghiệm khi:

2

0

4 0 2

m

mm









 = −   



Khi đó

1 2 1 2

1 . 2 .2 2 0

x x x x

t t x x

+

= = =  + =

(luôn thỏa mãn).

Vậy

2.m 

Câu 28: Đáp án D

Giải phương trình lượng giác tìm nghiệm

xk



=+

sau đó cho nghiệm đó thuộc (0;2019) tìm số các giá

trị

k 

rồi suy ra số nghiệm của phương trinh đã cho.

2

cos2 2cos 3 0 2cos 2cos 4 0x x x x+ − =  + − =

( )

cos 1

2

cos 2

x

x k k

x ktm



=



  = 



=−



Phương trình có nghiệm thuộc

( )

0;2019

 

0 2 2019 0 321,33

1;2;...;321

kk

k



     



Câu 29: Đáp án A

( )

( ) ( ) ( )

: 2 2 0.

3

10

77

0;0;5 ,( )

17

3 3 3

Q x y z c

c

M P d M P

c

+ + + =

=−

+



  =  = 



=−



( )

: 2 2 3 0.Q x y z+ + − =

hoặc

( )

: 2 2 17 0.Q x y z+ + − =

Câu 30: Đáp án

Số điểm cực trị của đồ thị hàm số

( )

y f x=

là số nghiệm bội lẻ của phương trình

( )

0.fx



=

Ta có:

( ) ( )( )( )

4

3

1

0 2 1 3 5 0

2

5

x

f x x x x x

x

=







=  + − + =  = −



=−



Trong đó

1

3,

2

xx= = −

là các nghiệm bội lẻ và

5x =−

là nghiệm bội chẵn nên hàm số có hai điểm cực

trị.

Câu 31: Đáp án A

Trang 139

Đặt

2

1 1 2x t x t dx tdt+ =  = −  =

Đổi cận:

0 1; 3 2x t x t=  = =  =

32

2

01

1

.2

42

4 2 1

xt

dx tdt

t

x

−

=

+

++



2

22

3

2 3 2

11

1

1 6 1

2 3 3 6ln 2

2 2 3

t

dt t t dt t t t t

tt

−

   

= = − + − = − + − +

   

++

   



14 7 7

12ln2 6ln3 12ln2 6ln3

3 3 3

7; 12; 6 1a b c T a b c

   

= − − − = − +

   

   

 = = − =  = + + =

Câu 32: Đáp án A

Gọi M là trung điểm của SC. Chứng minh

( ) ( )

( )

;;SBC SCD BM DM=

Tính các cạnh BM, DM ,BD và sử dụng định lí cosin trong tam giác BDM.

Gọi M là trung điểm của SC .

Tam giác SBC cân tại B

.BM SC⊥

Xét tam giác SBD có SO là trung tuyến đồng thời là đường cao

SBC

cân tại

S SB SD a = =

SCD có SD CD a SCD = =  

cân tại D

.DM SC⊥

Ta có:

( ) ( )

( )

( ) ( )

( )

;;

SBC SCD SC

SBC BM SC SBC SCD BM DM

SCD DM SC

=





 ⊥  =





⊥



Xét hình chóp B.SAC ta có

BC BS BA a= = = 

Hình chiếu của B lên (SAC) trùng với tâm đường tròn

ngoại tiếp

.SAC

Ta có:

( )

BO AC gt

BO SAC O

BO SO SO ABCD

⊥





 ⊥ 



⊥⊥





là tâm đường tròn ngoại tiếp

.SAC



SAC

vuông cân tại S

2 6 2 3

2

33

2

a AC a

AC SO SA SC = =  = = =

Xét tam giác vuông OAB có:

2

2 2 2

3

2

3

3 2 3

2

3

a a a

OaABB OA BD OB=−− = = = =

Xét tam giác vuông BCM có:

22

2

6

3 3

aa

BM BC MC a DM= − = =− =

Áp dụng định lí cos trong tam giác BDM ta có:

Trang 140

2 2 2

2

2 2 4

3 3 3

cos 0 90

2

2.

3

a a a

BM DM BD

BMD BMD

a

BM DM

−

−+

+

= = =  =

Vậy

(( );( )) 90SBC SCD =

Câu 33: Đáp án C

Ta có:

11

2

22

1 2 1 2 3

2 3 0

1 2 1 2 3

z i z

zz

z i z



= +  = + =



− + = 



= −  = + =



( ) ( ) ( )

3 4 7

34

1 2 1 2

. 3 . 3 3 27 3.z z z z = = = =

Câu 34: Đáp án A

Hàm số

( )

y f x=

đồng biến trên

( ) ( ) ( )

;;0a b a bf x x



   

và bằng 0 tại hữu hạn điểm.

Ta có:

( )

2 1 2y f x



= − −

Với

( ) ( )

1 1 2 1 0x y f



=  = − −  

Loại đáp án B, C, D.

Câu 35: Đáp án A

( ) ( )

1;1;1 .I d P I=  

Tìm

?A



AH qua A có

( )

1;1;1 : 1

2

AH p

xt

u n AH y t

zt

=





= =  = − +





=+



Suy ra

( )

; 1; 2 .H t t t−+

Mà

( )

2 1 8

; ; .

3 3 3

H P H

−









Ta có:

4 1 10 1 2 7 1 1 1

; ; ; ; : .

3 3 3 3 3 3 1 2 7

x y z

A IA d

− − − −

   

  

 =  = =

   

−

   

Câu 36: Đáp án B

Lập số tự nhiên có 5 chữ số khác nhau từ tập

 

0;1;2;3;4;5;6 .A=

( )

54

76

2160.n A A  = − =

Gọi A là biến cố: “Số lập được chia hết cho 5 và các chữ số 1, 2, 3 luôn có mặt cạnh nhau”

Giả sử số có 5 chữ số cần tìm là

( )

0abcde a 

Do số cần tìm chia hết cho 5 nên

 

0;5e

TH1:

0e =

Buộc 3 số 1,2, 3, coi là 1 phần tử. Sắp xếp 3 số này trong buộc có 3! = 6 cách.

Chọn vị trí cho buộc (123) có 2 cách chọn.

Số cách chọn 1 số còn lại (khác 0, 1,2, 3) là 3 cách.

1.6.2.3 36Có=

số.

Trang 141

TH2:

5.e =

Buộc 3 số 1, 2, 3 coi là 1 phần tử. Sắp xếp 3 số này trong buộc có 3! = 6 cách.

Nếu buộc (123) đứng ở vị trí (abc), khi đó có 3 cách chọn

 

( )

0;4;6 .dd

Nếu buộc (123) đứng ở vị trí (bcd), khi đó có 2 cách chọn

 

( )

4;6 .aa

( )

Có1.6. 3 2 30 + =

( )

36 30 66.nA = + =

Vậy

( )

66 11

2160 360

nA

PA

n

= = =



Câu 37: Đáp án C

Gọi A', B' lần lượt các điểm đối xứng A, B qua CD. H là trung điểm của BB’, ta dễ dàng chứng minh

được C là trung điểm của

AA



.

Gọi V1 là thể tích khối nón có chiều cao CD, bán kính đáy AC.

V2 là thể tích khối nón cụt có chiều cao CH, bán kính đáy nhỏ BH, bán kính đáy lớn AC .

V3 là thể tích khối nón có chiều cao CH , bán kính đáy BH .

Kẻ

CK AD⊥

suy ra ABCK là hình vuông

.CK KD a = =

Áp dụng định lí Pytago trong tam giác vuông CKD ta có:

2 2 2 2

2.CD CK KD a a a= + = + =

Áp dụng định lí Pytago trong tam giác vuông ABC ta có:

2 2 2 2

2.AC AB BC a a a= + = + =

Tam giác vuông CKD vuông cân tại K:

45 45KDC BCH BCH=   =   

vuông cân tại H.

22

BC a

BH CH = = =

( )

3

2

1

1 1 2 2

. 2 2

3 3 3

a

V AC CD a a





 = = =

( )

22

2 2 2

2

1 1 7 2

. . 2 . 2

3 3 2 12

22

a a a a

V CH BH AC BH AC a a







= + + = + + =





23

2

3

1 1 2

. . .

3 3 2 12

2

a a a

V BH CH





= = =

Vậy thể tích khối tròn xoay sinh ra khi quay hình thang ABCD quanh trục CD là:

3 2 2 3

1 2 3

2 2 7 2 2 7 2

3 12 12 6

a a a a

V V V V

   

= + − = + − =

Câu 38: Đáp án D

Giải phương trình

( )

0fu



=

để tìm số cực trị của hàm số

( )

.fu

Trang 142

Hoặc lập luận để có số điểm cực trị của hàm số

( )

1y f x=−

bằng với số điểm cực trị của hàm số

( )

.y f x=

Từ hình vẽ ta thấy đồ thị

( )

fx



cắt trục Ox tại ba điểm phân biệt hay

( )

2

' 0 0

2

x

f x x

x

=−





=  =



=



nhưng chỉ có

2 nghiệm

( )

0, 2 làx x f x



==

đổi dấu từ dương sang âm hoặc từ âm sang dương, như vậy hàm số

( )

fx

có hai điểm cực trị.

Nhận thấy

( )

1 2 3

1 1 0 1 0 1

1 2 1

xx

f x f x x x

xx

− = − =







− = − − =  − =  =



− = = −



nhưng chỉ có hai nghiệm

( )

1; 1x x là f x



= = −

đổi dấu, như vậy hàm số

( )

fx

chỉ có hai điểm cực trị.

Câu 39: Đáp án D

Sau tháng thứ nhất, số tiền còn lại là

( )

1

200 1 4Ar=+−

Sau tháng thứ hai số tiền còn lại là:

( ) ( ) ( )

2

21

1 4 200 1 4 1 4A A r r r= + − = + − + −

….

Sau 12 tháng số tiền còn lại là

( ) ( ) ( )

( )

12 11

12

1 1 ..00 .2 1 4 1A r r r+ + += + − + +

( )

( ) ( )

12

12 12 12

1

20 0

1

4

1

0111 2 1

1

0

r

rr

−



− = − −



++

+−

+

=+

165,269=

triệu đồng)

Câu 40: Đáp án D

Sử dụng tính chất

( ) ( )

33

11

2I xf x dx tf t dt= = = −



Áp dụng phương pháp đổi biến, đặt

4tx=−

Sử dụng công thức

( ) ( ) ( ) ( )

b b b

a a a

f x dx g x dx f x g x dx+ = +





  

Ta có:

( ) ( )

33

11

2I xf x dx tf t dt= = = −



Đặt

4.t x dt dx= −  = −

Đổi cận

13

31

xt

=  =





=  =



( ) ( ) ( ) ( )

13

31

4 4 4 2I x f x dx x f x dx = − − − = − = −



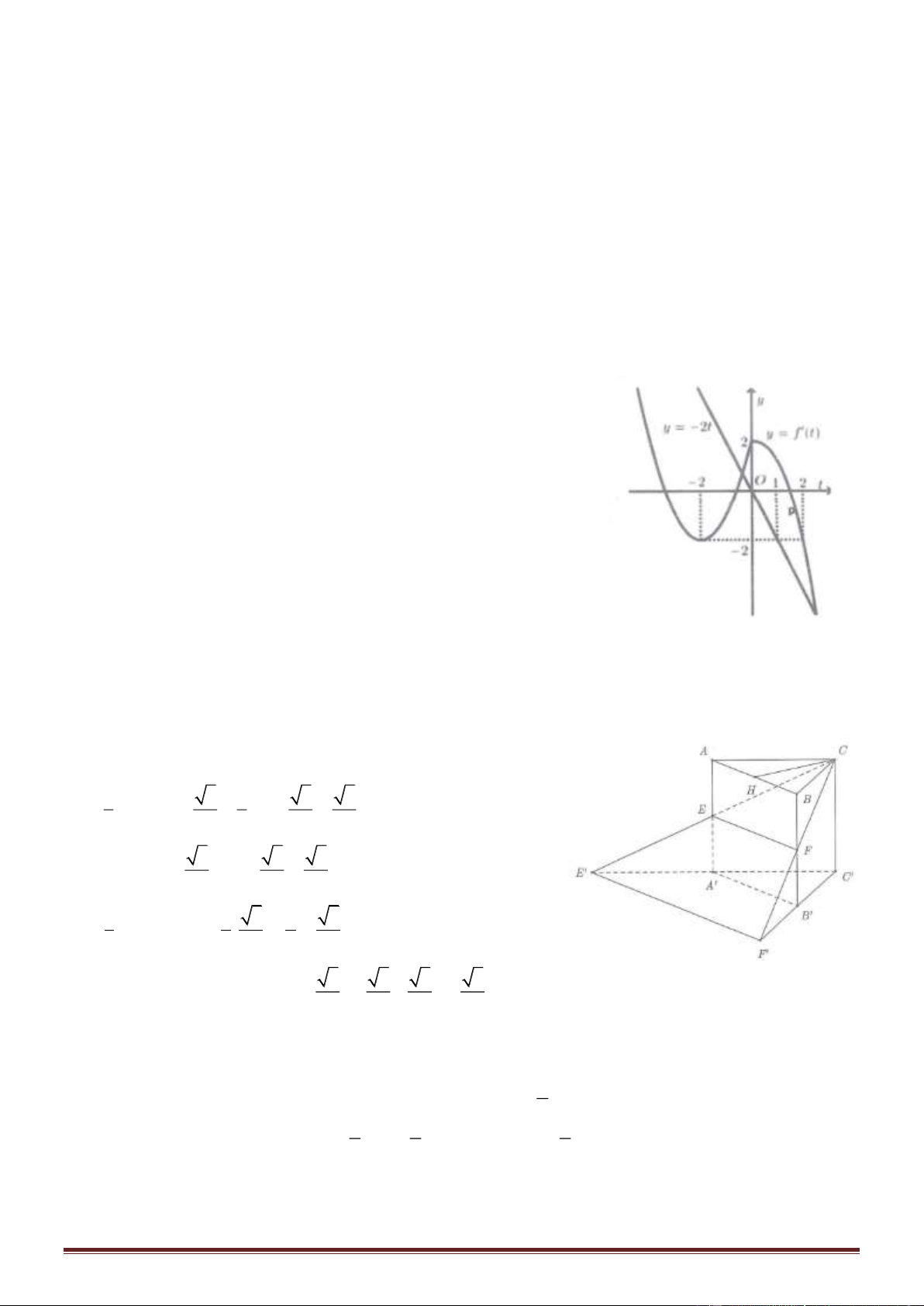
Trang 143

( ) ( ) ( )

33

11

2 4 4I xf x dx x f x dx = + − = −



( ) ( ) ( ) ( )

3 3 3

1 1 1

4 4 4 4 1x x f x dx f x dx f x dx

−

 − + = −  = −  = −

  

Câu 41: Đáp án A

Hàm số

( )

y f x=

đồng biến trên

( ) ( ) ( )

0;;,abfxbax



   

và bằng 0 tại hữu hạn điểm.

Ta có:

( ) ( ) ( )

1 2 2 0 1 2 1 0y f x x f x x

  

= − + − =  − + − =

Đặt

1tx=−

ta có

( ) ( ) ( )

2 0 2 0y f t t f t t

  

= + =  − − =

Vẽ đồ thị hàm số

( )

2y f t và y t



= = −

trên cùng mặt phẳng tọa độ ta

có:

Xét

( )

02y f t t



   − 

Đồ thị hàm số

( )

y f t



=

nằm trên đường

thẳng

2.yt=−

Xét

( ) ( )

1;2 0;1xt   

thỏa mãn.

Xét

( ) ( )

1;0 2; 1xt −   − − 

không thỏa mãn.

Xét

( ) ( )

0;1 1;0xt   − 

không thỏa mãn.

Xét

( ) ( )

2; 1 3; 2xt − −   − − 

không thỏa mãn.

Câu 42: Đáp án D

Gọi V1,V2,V3,V4 lần lượt là thể tích các khối

. , . , . , .ABC ABC C ABEF CCEF CC EFAB

        

V là thể tích khối đa diện EFA'B'E'F'.

Ta có:

22

3

1 3 1 3 3

. .1.2 .

3 4 3 4 3

V CC E F

  

= = =

( )

2

1

3 3 3

. 1.1 .

4 4 4

V AA AB



= = =

2

1 1 3 1 3

. . . .1.

3 3 2 2 12

V CH AB AE= = =

Vậy

( )

3 4 3 1 2

3 3 3 3

.

3 4 12 6

V V V V V V



= − = − − = − − =





Câu 43: Đáp án A

Tính số phần tử của không gian mẫu

Gọi A là biến cố “Mỗi hàng, mỗi cột đều có ít nhất 1 số lẻ”

:A

“Tồn tại hàng hoặc cột không có số lẻ”.

Tính số kết quả thuận lợi của biến cố

( )

1A P A P A P A  = −

Điền 9 số vào 9 ô vuông

( )

9!n  =

Trang 144

Gọi A là biến cố “Mỗi hàng, mỗi cột đều có ít nhất 1 số lẻ”

:A

“Tồn tại hàng hoặc cột không có số lẻ”

Do chỉ có 4 số chẵn nên chỉ có thể xảy ra trường hợp có 1 hàng hoặc 1 cột không có số lẻ.

Trường hợp 1: Hàng thứ nhất không có số lẻ

Chọn 3 số chẵn trong 4 số chẵn điền vào hàng đầu tiên có

4

3

24A =

cách

6 số còn lại điền vào 6 ô còn lại có 6! Cách

 có 24.6! cách

Tương tự cho 2 hàng còn lại và 3 cột còn lại

( )

6.24.6!nA=

Vậy

( )

6.24.6! 2 5

9! 7 7

P A P A= =  =

Câu 44: Đáp án D

Ta có:

3.SA SB AB a= = =

Gọi H là trung điểm của AB.

Do

( ) ( )

SAB ABCD⊥

nên

( )

.SH ABCD⊥

Khi đó:

3

.

2

a

SH =

Diện tích đáy

2

.3

ABCD

Sa=

Vậy thể tích khối chóp

3

.

13

. . .

32

S ABCD ABCD

a

V SH S==

Note 96: Phương pháp chung

Hệ quả: Cho hai mặt phẳng vuông góc theo giao tuyến b, nếu đường thẳng a nằm trong mặt phẳng này

vuông góc với giao tuyến b thì đường thẳng a cũng vuông góc với mặt phẳng kia.

( ) ( )

( )

,

P Q b

aP

a Q a b

=





⊥



⊥





Thể tích khối chóp có diện thích đáy là B, chiều cao là h là

1

. . .

3

V B h=

Diện tích hình vuông có cạnh a là

2

.Sa=

Câu 45: Đáp án A

Do



)

3

; cos 1;0

22

xx





   −





Ta có:

( ) ( )

cos2 2 1 cos 1 0 1 .x m x m− + + + =

2

2cos (2 1 cos 0

2cos cos cos ) 0

)

( ) (

x m x m

x x m x m

 − + + =

 − − − =



)

1

cos 1;0

( ( ) 0

2

cos

2cos 1) cosx

x

xm



=  −



 = 

=

−



−



Trang 145

Để phương trình (1) có nghiệm thì

1 0.m−  

Note: Phương pháp chung

Công thức lượng giác cơ bản:

2

cos2 2cos 1.



=−

Điều kiện có nghiệm của phương trình lượng giác cơ bản dạng

 

cos 1;1 .x m là m=  −

Câu 46: Đáp án D

Số phần tử của không gian mẫu là

4.4.4.4 256 = =

Gọi A là biến cố “Một toa có 3 người, một toa có 1 người, hai toa còn lại không có ai ”

Có

3

4

C

cách chọn 3 người trong 4 người và 4 cách chọn một toa cho nhóm 3 người đó lên.

Có 3 cách chọn toa cho người còn lại lên.

Số kết quả thuận lợi của biến cố A là

3

4

.4.3 48.

A

C = =

Vậy xác suất cần tính là

( )

48 3

.

256 16

PA==

Note 98: Phương pháp chung

Công thức xác suất của biến cố:

( )

.

nA

PA

n

=



Chọn ngẫu nhiên k phần tử trong n phần tử ta có số cách chọn được là

.

k

n

C

Câu 47: Đáp án B

(

)

(

)

3 2 3 2

2

0 0 0

3 2 3 2

1 1 1 1 1 1

lim lim lim

2

1 1 1 1

x x x

x x x x x

x

x x x x

→ → →

+ + − + + − +

===

+ + + + + +

Note 99: Phương pháp chung

Bài toán tìm giới hạn dạng vô định

0

.

0

Dùng phương pháp nhân liên hợp để khử vô định.

Một số biểu thức liên hợp của nhau:

( )( )

( )

22

2 2 3 3

•

• .

a b a b a b

a b a ab b a b

− + = −

= −− + +

Câu 48: Đáp án C

Ta có:

( ) ( )

322

)2 1 2 2 2( ) ( (3 2 1 2)f x x m m x f x x m x mx



= − + − +  −− = − + −

Để hàm số

( )

y f x=

có 5 cực trị thì đồ thị hàm số

( )

y f x=

phải có hai điểm cực trị nằm về phía bên

phải trục tung khi và chỉ khi

( )

0fx



=

có hai nghiệm phân biệt dương.

Trang 146

( ) ( )

( )

2

30

5

1

2 1 3 2 0

4

15

2 2 1

2

0

24

3

2

0

3

a

mm

m

mm

S

m

P

=



 −  





 = − − − 



−

     



=







−



=



Note 100: Phương pháp chung

Dạng đồ thị (C) của hàm

( )

y f x=

: Giữ nguyên phần đồ thị của (C) nằm bên phải trục tung, lấy đối

xứng qua trục tung phần đồ thị (C) nằm bên phải trục tung.

Hàm số chỉ có thể đạt cực trị tại điểm làm cho đạo hàm bằng 0 hoặc không xác định.

Câu 49: Đáp án A

Gọi

max .Ay=

Ta đặt

( )

2

2 1 1t x x t x= −  = − −

do đó

01t

Khi đó hàm số được viết lại là

34y t m= − +

với

 

0;1t 

ta suy ra

 

 

0;1

3 4 5 3

max 3 4 max 3 4 , 5 3

2

mm

A t m m m

− + + −

= − + = − + − 

Áp dụng BĐT trị tuyệt đối ta có:

3 4 5 3 3 4 5 3 3 4 5 3 1m m m m m m− + + − = − + −  − + − 

Do đó

1

.

2

A 

Đăng thức xảy ra

( )( )

3 4 5 3

3

.

2

3 4 5 3 0

mm

m

mm

 − + = −



=



− + − 





Note101: Phương pháp chung

A

có nghĩa khi

0.A 

Bất đẳng thức giá trị tuyệt đối

.a b a b+  +

Phương trình chưa giá trị tuyệt đối:

22

,.A B A B A B A B=  = =  = 

Nếu

( )

fx

có hai nghiệm phân biệt

12

x và x

. Dùng quy tắc “Trong trái ngoài cùng”. Trong khoảng 2

nghiệm thì

( )

fx

trái dấu với hệ số a; ngoài khoảng 2 nghiệm thì

( )

fx

cùng dấu với a.

Câu 50: Đáp án A

Kẻ

( )

.HE BD BD SHE⊥  ⊥

Kẻ

( ) ( )

( )

,.HF SE HF SBD d H SBD HF⊥  ⊥  =

Theo giả thiết

( )

/ / / /HK BD HK SBD

( ) ( )

( )

, , , .d HK SD d HK SBD d H SBD HF = = =

Trang 147

Có

2

2 2 2

5

42

aa

HD AH AD a= + = + =

22

17 5

3

44

aa

SH SD HD a = − = − =

HEB

vuông cân tại E (vì

45 ) .

2 2 2

o

HB a

HBE HE=  = =

SHE

vuông cân tại H nên có

2 2 2 2 2 2

1 1 1 8 1 25 3

.

3 3 5

a

HF

HF HE SH a a a

= + = + =  =

( )

3

,.

5

a

d HK SD=

Note 102: Phương pháp chung

Phương pháp tính khoảng cách giữa hai đường thẳng chéo nhau: Chọn mặt phẳng () chứa đường thẳng 

và song song với





. Khi đó:

( ) ( )

( )

,,dd





  = 

Định lí: đường thẳng vuông góc với mặt phẳng khi nó vuông góc với hai đường thẳng cắt nhau nằm trong

mặt phẳng:

( )

,

b c P

a b a c a P

bc







⊥ ⊥  ⊥









Định lý Pytago trong tam giác

ABC

vuông tại A có cạnh huyền BC:

2 2 2

.AB AC BC+=

Hệ thức lượng giác trong tam giác

ABC

vuông tại A, chiều cao AH:

2 2 2

1 1 1

.

AH AB AC

=+

TOP 10 đề thi thử QG môn Toán 2020 -Tập 6 (có đáp án)

Đề thi THPTQG môn Toán năm 2020 22 tài liệu

Toán 1.8 K tài liệu

Bình luận

TOP 10 đề thi thử QG môn Toán 2020 -Tập 6 (có đáp án)