Trang 1
ĐỀ 21
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1(NB): Cho hàm số
()y f x=
có bảng xét dấu đạo hàm như sau
Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên khoảng
( )
1;3 .−
B. Hàm số đồng biến trên khoảng
( ;0)−
.
C. Hàm số nghịch biến trên khoảng
( )
1;0
. D. Hàm số nghịch biến trên khoảng
( )
.1;−−
Câu 2(NB): Phương trình tiếp tuyến của đồ thị
23
3:)( xxyC −=
tại điểm có hoành độ bằng 1 là
A.
.13 += xy
B.
.53 +−= xy
C.
.13 +−= xy
D.
.53 −= xy
Câu 3(NB): Cho hàm số
y f(x)=
có đồ thị là hình bên.
Mệnh đề nào dưới đây sai?
A. Hàm số
y f(x)=
có ba cực trị. B. Hàm số
y f(x)=
đạt cực đại tại
x 2.=
C. Hàm số
y f(x)=
đạt cực tiểu tại
x 3.=−
D. Hàm số
y f(x)=
có hai cực đại.
Câu 4(NB): Đồ thị hàm số
32
32y x x= − − +
có dạng nào dưới đây ?
Hình 1
Hình 2
Hình 3
Hình 4
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Câu 5(NB) Với
a
là số thực dương tùy ý,
2
4
log
a
bằng:
3

Trang 2
A.
2
2 log a+
. B.
2
1
log a.
2
+
C.
2
2 log a.−
D.
2
1
log a.
2
−
Câu 6(NB):
Tập nghiệm của phương trình
x1
4 1 0
−
−=
là
A.
1.−
B.
1.
C.
0.
D.
2.
Câu 7(NB): Cho số
a,b,x
là các số thực dương thỏa mãn
logx 2loga 3logb.=+
Mệnh đề nào
dưới đây đúng ?
A.
23
x a b .=
B.
23
x a b .=+
C.
x 6ab.=
D.
x 6loga.logb.=
Câu 8(NB): Họ nguyên hàm của hàm số
x
f(x) 3 cosx=−
là
A.
x
3
sinx C.
ln3
−+
B.
x
3 ln3 sinx C.−+
C.
x
3
sinx C.
ln3
++
D.
x
3 ln3 sinx C.++
Câu 9(NB): Cho hàm số liên tục trên đoạn Diện tích của hình phẳng giới hạn bởi
đồ thị trục hoành, hai đường thẳng (Hình vẽ bên dưới) được xác định
bởi công thức nào dưới đây?
A.
0b
a0
S f(x)dx f(x)dx.=−
B.
0b
a0
S f(x)dx f (x)dx.=+
C.
0b
a0
S f(x)dx f (x)dx.= − −
D.
0b
a0
S f(x)dx f(x)dx.= − +
Câu 10(NB):
Cho số phức
z 3i.=−
Điểm M biểu diễn cho số phức z trên mặt phẳng Oxy có tọa
độ là
A.
( )
0; 3 .−
B.
( )
0;3 .
C.
( )
3;0 .−
D.
( )
3;0 .
Câu 11(NB): Thể tích của khối lăng trụ có chiều cao bằng
h
có thể tích bằng
B
là
A.
.Bh
B.
.
3
1
Bh
C.
.3Bh
D.
.
6
1
Bh
Câu 12(NB): Cho hình nón tròn xoay có chiều cao bằng 3, bán kính đáy bằng 4. Diện tích xung
quanh của hình nón đã cho bằng
A.
12π.
B.
20π.
C.
15π.
D.
36π.
Câu 13(NB): Trong không gian
0xyz
, cho
a (2; 3;1)=−
r
và
b (1;0;2)=
r
. Khi đó tích vô hướng
a.b
rr
bằng
A.
4.
B.
0.
C.
3.
D.
4.−
Câu 14(NB): Trong không gian
Oxyz
, cho mặt phẳng
( )
α
:
2x z 4 0− + =
. Véctơ nào dưới đây là
một véctơ pháp tuyến của mặt phẳng
(α)?
A.
a(2; 1;0).−
r
B.
b(2; 1;4).−
r
C.
c(2;1;4).
r
D.
d(2;0; 1).−
r
Câu 15(NB): Số tập hợp con có 3 phần tử của một tập hợp có 7 phần tử là
( )
y f x=
a;b .
( ) ( )
C :y f x ,=
x a,=
xb=
O
x
b
a
y
( )
y f x=

Trang 3
A.
3
7
C.
B.
3
7
A.
C.
3!.
D.
7!.
Câu 16(NB): Cho cấp số cộng có số hạng đầu công sai . Viết 5 số hạng đầu của
cấp số cộng đó.
A. B.
C. D.
Câu 17(TH): Cho hàm số
y f(x)=
có bảng biến thiên như sau
Số nghiệm của phương trình
f(x) 5 0− + =
là
A.
1.
B.
2.
C.
3.
D.
4.
Câu 18(TH): Giá trị nhỏ nhất của hàm số
54
24
+−= xxy
trên đoạn
2;1−
là
A.
1.
B.
2.
C.
3.
D.
5.
Câu 19(TH):Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số
2
31
1
−+
=
+
x
y
x
là
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 20(TH): Tập nghiệm của bất phương trình
2
3
log (x 2x) 1−
là
A.
) (
1;0 2;3 .−
B.
1;3 .−
C.
( )
0;2 .
D.
( )
1;3 .−
Câu 21(TH): Giá trị nhỏ nhất của hàm số
3x
y e x=−
trên đoạn
1;1−
là
A.
1
(ln3 1).
3
+
B.
3
e 1.−
C.
3
1
1.
e
+
D.
1
(1 ln3).
3
−
Câu 22(TH): Tập xác định của hàm số
23
y (x x 6)= − −
là
A.
( ) ( )
; 2 3; .− − +
B.
R \ 2;3 .−
C.
( )
0; .+
D.
(
)
; 2 3; .− − +
Câu 23(TH): Cho
2
1
3f(x) 2g(x) dx 1+=
và
2
1
2f(x) g(x) dx 3,− = −
khi đó
2
1
f(x)dx
bằng
A.
5.−
B.
11
.
7
C.
5.
D.
5
.
7
−
Câu 24(TH):
Tích phân
2
1
2dx 2 a
ln
3 5x 5 b
=
−
với
a
b
là phân số tối giản,
a,b
là các số nguyên dương.
Giá trị
ab−
bằng
A.
5.−
B.
5.
C.
3.
D.
3.−
Câu 25(TH): Tìm số thực
a
và b thỏa mãn
( )
ai b i 3 1 4i+ − = +
với
i
là đơn vị ảo.
A.
a 4;b 4.= − =
B.
a 4;b 4.==
C.
a 4;b 4.= = −
D.
a 1;b 1.==
,2
1
−=u
3=d
.10;7;4;1;2−
.6;4;1;1;3 −−−
.162;54;18;6;2 −−−−−
.48;24;12;6;3 −−−−

Trang 4
Câu 26(TH): Kí hiệu
12
z ,z
là hai nghiệm phức của phương trình
2
z 4z 5 0− + =
. Phần thực
a
của
số phức
22
12
w z z=+
bằng
A.
0.
B.
8.
C.
16.
D.
6.
Câu 27(TH): Cho hình chóp đều
S.ABCD
có cạnh đáy bằng
a 2,
góc giữa cạnh bên và mặt đáy
bằng
0
60 .
Thể tích khối chóp đã cho bằng
A.
3
a3
.
3
B.
3
2a 3
.
3
C.
3
4a 3.
D.
3
4a 3
.
3
Câu 28(TH): Cho hình nón tròn xoay có độ dài đường sinh là
2a
, góc ở đỉnh của hình nón bằng
60
. Thể tích của khối nón đã cho là
A.
3
3
a
. B.
3
3a
. C.
3
a
. D.
3
3
3
a
.
Câu 29(TH): Trong không gian
Oxy
, mặt cầu
(S)
có tâm
I(2;1; 1)−
tiếp xúc với mặt phẳng tọa
độ
(Oyz)
. Phương trình mặt
(S)
là
A.
( )
2
22
x 2 (y 1) (z 1) 4.+ + + + − =
B.
( )
2
22
x 2 (y 1) (z 1) 1.− + − + + =
C.
( )
2
22
x 2 (y 1) (z 1) 4.− + − + + =
D.
( )
2
22
x 2 (y 1) (z 1) 2.+ + − + + =
Câu 30(TH): Cho hình lập phương
ABCD.A'B'C'D'
, góc giữa đường thẳng
AC
và
A'D
bằng
A.
0
60 .
B.
0
45 .
C.
0
30 .
D.
0
90 .
Câu 31(VD):Giá trị lớn nhất của tham số thực
m
để hàm số
1)1(6)12(32
23
++++−= xmmxmxy
đồng biến trên khoảng
( )
2;+¥
bằng:
A. 2. B. 0. C. 1. D. 3.
Câu 32(VDT): Tập hợp tất cả các giá trị thực của tham số
m
để đường thẳng
y 2x m=+
cắt đồ
thị hàm số
x1
y
x1
+
=
−
tại hai điểm phân biệt là
A.
( )
0;3 .
B.
5
;1 .
2
−
C.
( )
4;9 .
D.
R.
Câu 33(VDT): Hằng tháng ông A gửi vào ngân hàng một số tiền cố định với lãi suất 0,5%/1
tháng. Sau đúng 5 năm kể từ ngày gửi đầu tiên ông rút được số tiền là 1 tỷ đồng bao gồm cả gốc
lẫn lãi. Biết rằng lãi suất không đổi và số tiền lãi sinh ra hằng tháng được nhập vào vốn. Hỏi số
tiền cố định hằng tháng ông A phải gửi gần với số tiền nào dưới đây?
A.
14.261.000
đồng. B.
14.260.000
đồng .
C.
14.261.500
đồng. D.
14.260.500
đồng.
Câu 34(VDT): Biết tích phân
2ln5ln
11
22
3
22
c
b
a
dx
xx
x
I −=
++−
=
, với a, b, c là các số
nguyên dương. Tính
.cbaS ++=
A.
.4=S
B.
.5=S
C.
.6=S
D.
.7=S

Trang 5
Câu 35(VDT): Cho số phức
z
thỏa mãn
( )
z 1 (z i)−+
là số thuần ảo. Biết rằng tập hợp các điểm
biểu diễn của số phức
z
là một đường tròn, tâm của đường tròn đó có tọa độ là
A.
11
;.
22
−
B.
11
;.
22
−−
C.
11
;.
22
−
D.
11
;.
22
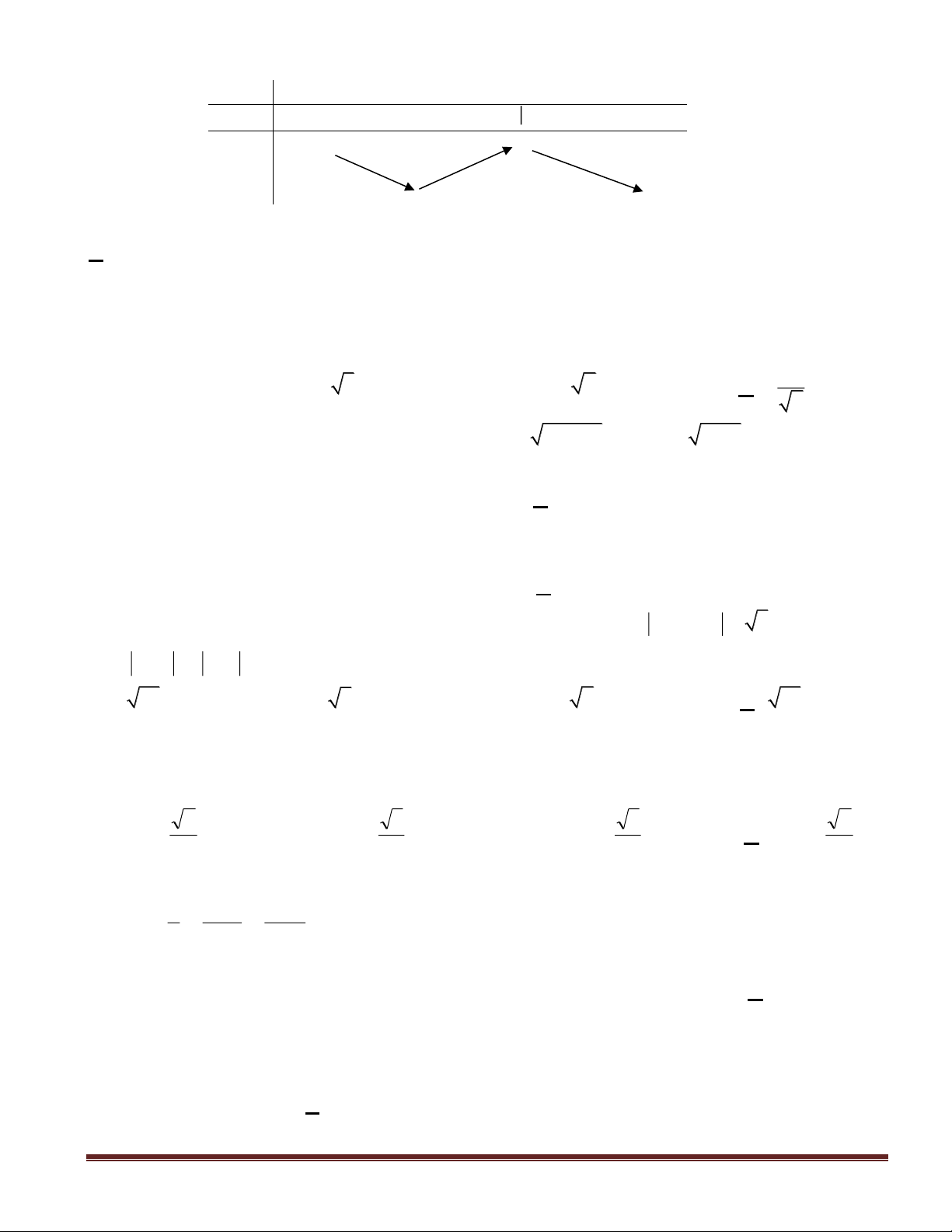
Câu 36(VDT): Một khối gỗ hình trụ tròn xoay có bán kính đáy bằng a, chiều cao bằng 2a. Người
ta khoét từ hai đầu khối gỗ hai nửa khối cầu mà đường tròn đáy của khối gỗ là đường tròn lớn của
mỗi nửa khối cầu. Tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ ban đầu là
A.
2
3
. B.
1
4
. C.
1
3
. D.
1
2
.
Câu 37(VDT): Trong không gian Oxyz cho điểm
A(1;1;1)
biết rằng hai điểm
M Ox,
N Oy
sao cho tam giác AMN vuông cân tại A. Khi đó độ dài MN bằng:
A.
3.
B.
3
.
2
C.
5
.
2
D.
3
.
2
Câu 38(VDT): Trong không gian
Oxyz
cho hai đường thẳng
12
x 1 t
x 2 y 2 z 3
d : , d : y 1 2t
2 1 1
z 1 t
=−
− + −
= = = +
−
= − +
và điểm
A(1;2;3).
Đường thẳng
qua
A
vuông góc với
1
d
và cắt
2
d
có phương trình là:
A.
x 1 y 2 z 3
.
1 3 5
− − −
==
−−
B.
x 1 y 2 z 3
.
1 3 5
− − −
==
− − −
C.
x 1 y 2 z 3
.
1 3 5
− − −
==
D.
x 1 y 2 z 3
.
1 3 5
− − −
==
−
Câu 39(VDT): Cho hình hộp chữ nhật
ABCD.A'B'C'D'
có đáy
ABCD
là hình vuông cạnh
a 2,
AA' 2a=
. Khoảng cách giữa
BD
và
CD'
bằng
A.
a 2.
B.
2a.
C.
2a
.
5
D.
a
.
5
Câu 40(VDT): Tập hợp tất cả các giá trị thực của tham số
m
để phương trình
cos2x (2m 1)cosx m 1 0− + + + =
có nghiệm trên khoảng
π 3π
;
22
là
A.
1;0 .−
B.
)
1;0 .−
C.
( )
1;0 .−
D.
1
1; .
2
−
r = a
h = 2a
Trang 6
Câu 41(VDC): Cho hàm số
y f(x)=
liên tục trên
R
và có bảng biến thiên như sau:
x
−
0 5
+
y’
- 0 + -
y
+
3
1
−
Khi đó hàm số
2
y g(x) f(x 4x)= = −
đồng biến trên khoảng
A.
( )
4;5 .
B.
( )
1;2 .−
C.
( )
5; .+
D.
( )
2;4 .
Câu 42(VDC): Tập hợp tất cả các giá trị thực của tham số
m
để đồ thị hàm số
42
y x 2mx 3= − −
có ba điểm cực trị sao cho bán kính đường tròn ngoại tiếp tam giác tạo bởi các điểm cực trị đạt giá
trị nhỏ nhất là
A.
1
. B.
3
. C.
3
2
. D.
3
1
2
.
Câu 43(VDC): Cho các số thực dương
a,b
thỏa mãn
2 2ab 3 ab a b (a 1)(b 1)− + − = + + + +
.
Tính tổng
T (2a 1)(2b 1).= + +
A.
T 1.=
B.
T 3.=
C.
T 5.=
D.
T 0.=
Câu 44(VDC): Tập hợp tất cả các giá trị thực của tham số m để bất phương trình
2
log x m.logx m 3 0+ + +
có nghiệm lớn hơn hoặc bằng 1.
A.
)
2; .+
B.
(
; 1 .− −
C.
(
; 2 .− −
D.
( )
; 3 .− −
Câu 45(VDC): Biết số phức
z
thỏa mãn đồng thời hai điều kiện
z 3 4i 5− − =
và biểu thức
22
M z 2 z i= + − −
đạt giá trị lớn nhất. Môđun của số phức
zi+
bằng
A.
2 41.
B.
3 5.
C.
5 2.
D.
41.
Câu 46(VDC): Cho hình chóp
SABC
có đáy
ABC
là tam giác vuông tại
.C
.2== ABSA
Canh
SA
vuông góc với mặt phẳng đáy
)(ABC
. Gọi
KH,
lần lượt là hình chiếu vuông góc của
A
lên
SB
và
SC
. Tính thể tích lớn nhất
max
V
của
SAHK
.
A.
.
3
2
max
=V
B.
.
6
3
max
=V
C.
.
3
3
max
=V
D.
.
6
2
max
=V
Câu 47(VDC): Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
)1;1;0(A
,
)1;2;1(B
và đường
thẳng
.
2
2
1
1
1
:
−
−
=
−
+
=
zyx
d
Tìm tọa độ điểm
M
thuộc
d
sao cho diện tích tam giác MAB có giá
trị nhỏ nhất.
A.
).2;3;2( −−M
B.
).2;1;0(M
C.
).0;2;1( −M
D.
).2;1;0( −M
Câu 48(VDC): Với các chữ số
0,1,2,3,4
có thể lập được bao nhiêu số tự nhiên gồm 9 chữ số,
trong đó chữ số 2 có mặt đúng ba lần, chữ số 1 có đúng hai lần, các chữ số còn lại có mặt đúng
một lần.
A.
62880.
B.
6720.
C.
32240.
D.
3360.
Trang 7
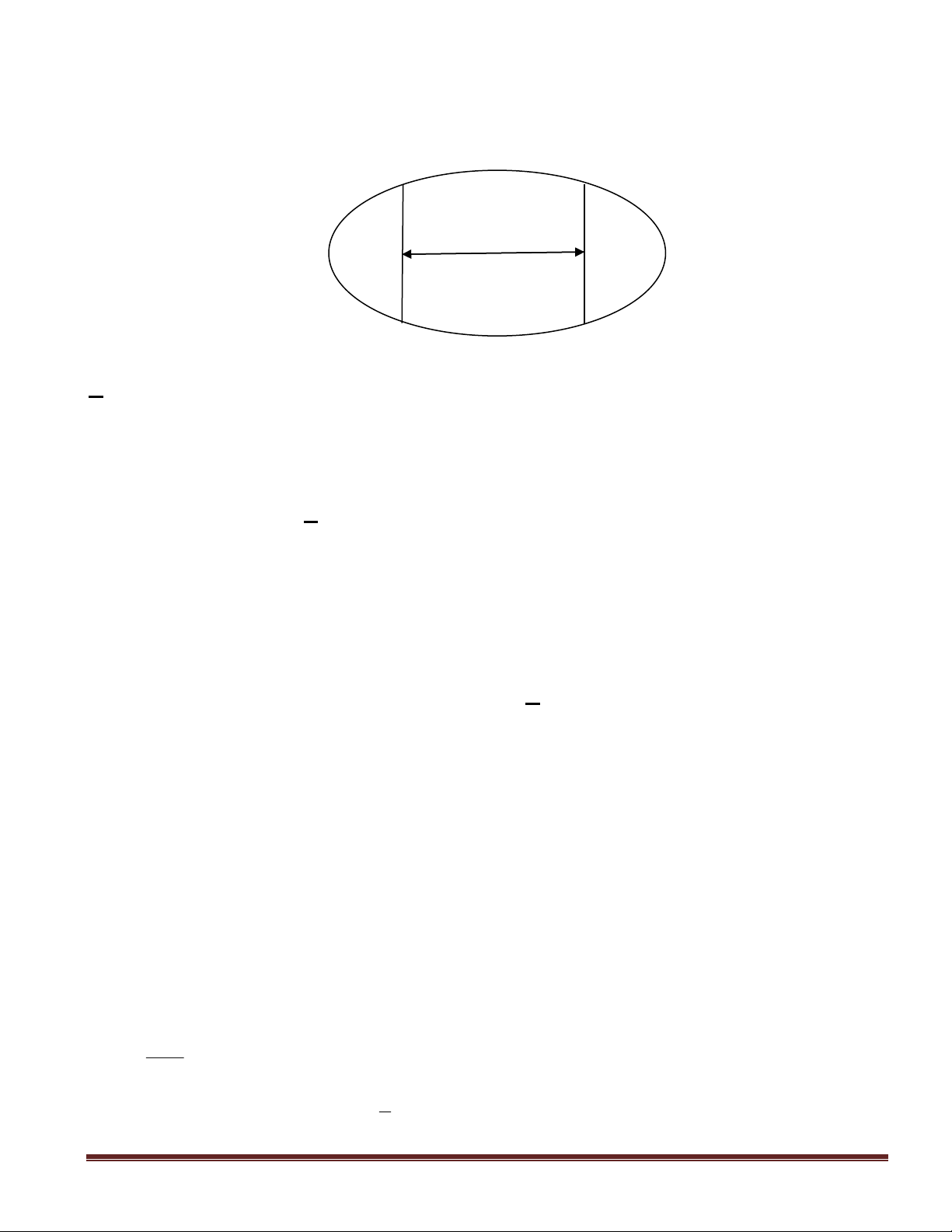
Câu 49(VDC): Một mảnh vườn hình elip có độ dài trục lớn bằng
20m
và độ dài trục bé bằng
12m
. Người ta muốn trồng hoa trên dãi đất rộng
10m
và nhận trục bé của elip làm trục đối
xứng(hình vẽ). Biết kinh phí để trồng hoa là
150.000
đồng /
2
1m .
Hỏi phải tốn bao nhiêu tiền để
trồng hoa trên dải đất đó(Số tiền được làm tròn đến hàng nghìn).
A. 17.219.000 đồng. B. 17.220.000 đồng. C. 8.610.000 đồng. D. 17.826.000 đồng.
Câu 50(VDC): Gọi S là tập tất cả các giá trị thực của tham số
m
để bất phương trình
( ) ( )
( )
3 2 2
2x 6x x 3 m 1 x 9 0+ + + − +
nghiệm đúng với mọi
xR
. Tích giá trị các phần tử thuộc
S bằng
A.
0.
B.
4.−
C.
4.
D.
2.
GIẢI CÁC CÂU VẬN DỤNG
Câu 31: Tìm giá trị lớn nhất của tham số thực
m
để hàm số
1)1(6)12(32
23
++++−= xmmxmxy
đồng biến trên khoảng
( )
.;2 +
A. 2. B. 0. C. 1. D. 3.
Giải: Ta có
22
y' 6x 6(2m 1)x 6m(m 1) 6[x (2m 1)x m(m 1)]= − + + + = − + + +
y' 0=
có
( )
2
2m 1 4m(m 1) 1 0 = + − + =
y' 0=
luôn có hai nghiệm
12
x x , m
Hàm số đồng biến trên khoảng
( )
2; y' 0+ =
có hai nghiệm
12
x x 2
1 2 1 2
1 2 1 2 1 2
(x 2)(x 2) 0 x x 4
x 2 x 2 0 x x 2(x x ) 4 0
− − +
− + − − + +
2m 1 4
m 1.
m(m 1) 2(2m 1) 4 0
+
+ − + +
Vậy giá trị lớn nhất là 1. Chon C.
Câu 32 : Tập hợp tất cả các giá trị thực của tham số
m
để đường thẳng
y 2x m=+
cắt đồ thị hàm
số
x1
y
x1
+
=
−
tại hai điểm phân biệt là
A.
( )
0;3 .
B.
5
;1 .
2
−
C.
( )
4;9 .
D.
R.
10m

Trang 8
Giải: Phương trình hoành độ giao điểm
x1
2x m
x1
+
=+
−
(với
x1
)
2
2x (m 3)x (m 1) 0 + − − + =
(1).
Đường thẳng
y 2x m=+
cắt đồ thị hàm số
x1
y
x1
+
=
−
tại hai điểm phân biệt
(1) có hai
nghiệm phân biệt khác 1.
Ta có
2
(1)
m 2m 17 0, m R = + +
và
2
2.1 (m 3).1 (m 1) 2+ − − + = −
(1) luôn có hai
nghiệm phân biệt . Chọn D.
Câu 33(VDT): Hằng tháng ông A gửi vào ngân hàng một số tiền cố định với lãi suất 0,5%/1
tháng. Sau đúng 5 năm kể từ ngày gửi đầu tiên ông rút được số tiền là 1 tỷ đồng bao gồm cả gốc
lẫn lãi. Biết rằng lãi suất không đổi và số tiền lãi sinh ra hằng tháng được nhập vào vốn. Hỏi số
tiền hằng tháng ông A phải gửi gần nhất với số tiền nào dưới đây?
A.
14.261.000
đồng. B.
14.260.000
đồng .
C.
14.261.500
đồng. D.
14.260.500
đồng.
Giải:
Gọi
r
lần lượt là lãi suất hằng tháng;
T
là số tiền nhận được sau 5 năm;
X
là số tiền gửi hằng
tháng.
Sau đúng 5 năm tổng số tiền ông A rút được là
60
X
T (1 r) 1 (1 r)
r
= + − +
( )
60 60
T.r 1000.000.000x0,5%
X 14.261.494,06.
(1 r) 1 (1 r) 1 0,5% (1 0,5%) 1
= =
+ − + + + −
Chọn C.
Câu 34(VDT): Biết tích phân
22
22
3
xa
I dx ln5 cln2
b
x 1 x 1
= = −
− + +
, với a, b, c là các số
nguyên dương và
a
b
là phân số tối giản. Tính
.cbaS ++=
A.
.4=S
B.
.5=S
C.
.6=S
D.
S 4.=−
Đặt
2 2 2
t x 1 t x 1 tdt xdx= + = + =
.
Đổi cận:
x 3 t 2
x 2 2 t 3
= =
= =
3 3 3
2 2 2
2 2 2
t 1 2t 1 1 dt
I dx dt
t t 2 2 t t 2 2 t t 2
+
= = −
+ − + − + −
2
3 3 3
1 1 1
ln t t 2 ln t 1 ln t 2
2 2 2
2 6 6
= + − − − + +
=
2
ln5 ln2
3
−
. Chon C.
Câu 35(VDT): Cho số phức
z
thỏa mãn
( )
z 1 (z i)−+
là số thuần ảo. Biết rằng tập hợp các điểm
biểu diễn của số phức
z
là một đường tròn, tâm của đường tròn đó có tọa độ là

Trang 9
A.
11
;.
22
B.
11
;.
22
−−
C.
11
;.
22
−
D.
11
;.
22
−
Giải:
( )
2
22
z 1 (z i) z zi z i a b a b (a b 1)i− + = + − − = + − − + + −
( )
z 1 (z i)−+
là số thuần ảo
22
22
1 1 1
a b a b 0 a b
2 2 2
+ − − = − + − =
Do đó tập hợp các điểm biểu diễn của
z
là một đường tròn tâm
1 1 1
I( ; ),r .
22
2
=
chọn A.
Câu 36(VDT): Một khối gỗ hình trụ tròn xoay có bán kính đáy bằng a, chiều cao bằng 2a. Người
ta khoét từ hai đầu khối gỗ hai nửa khối cầu mà đường tròn đáy của khối gỗ là đường tròn lớn của
mỗi nửa khối cầu. Tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ ban đầu là
A.
2
3
. B.
1
4
. C.
1
3
. D.
1
2
.
Giải : Hai nửa khối cầu ghép lại được khối cầu có thể tích là :
3
1
4
V πa .
3
=
Thể tích khối trụ tròn xoay ban đầu :
23
V π.a .2a 2a π.==
Tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ ban đầu là :
33
1
3
4
2a π πa
V V 1
3
.
V 2a π3
−
−
==
Câu 37(VDT): Trong không gian Oxyz cho điểm
A(1;1;1)
biết rằng hai điểm
M Ox,
N Oy
sao cho tam giác AMN vuông cân tại A. Khi đó độ dài MN bằng:
A.
3.
B.
3
.
2
C.
5
.
2
D.
3
.
2
Giải: Do
M Ox M(m;0;0)
,
N Oy N(0;n;0)
( )
AM m 1; 1; 1 = − − −
,
( )
AN 1;n 1; 1= − − −
Tam giác AMN vuông cân tại A nên
( ) ( )
22
22
(m 1) (n 1) 1 0
AM.AN 0
m 1 2 2 n 1
AM AN
− − − − + =
=
− + = + −
=
uuur uuur
( )
m 1 1 (n 1)
3
mn
m 1 n 1
2
− = − −
= =
− = −
Khi đó
3
MN .
2
=
Câu 38(VDT): Trong không gian
Oxyz
cho hai đường thẳng
Trang 10
12
x 1 t
x 2 y 2 z 3
d : , d : y 1 2t
2 1 1
z 1 t
=−
− + −
= = = +
−
= − +
và điểm
A(1;2;3).
Đường thẳng
qua
A
vuông góc với
1
d
và cắt
2
d
có phương trình là:
A.
x 1 y 2 z 3
.
1 3 5
− − −
==
−−
B.
x 1 y 2 z 3
.
1 3 5
− − −
==
− − −
C.
x 1 y 2 z 3
.
1 3 5
− − −
==
D.
x 1 y 2 z 3
.
1 3 5
− − −
==
−
Giải: Gọi
( )
α
là mặt phẳng qua A và vuông góc với đường thẳng
1
d
nhận
n (2; 1;1)=−
r
làm vectơ
pháp tuyến
phương trình
( )
α
:
2x y z 3 0− + − =
.
Gọi
( )
2
B αd=
B(2; 1;3)−
.
Đường thẳng
cần tìm là đường thẳng qua hai điểm A, B với
AB (1; 3; 5)= − −
uuur
Do đó
x 1 y 2 z 1
:.
1 3 5
− − −
= =
−−
chọn A.
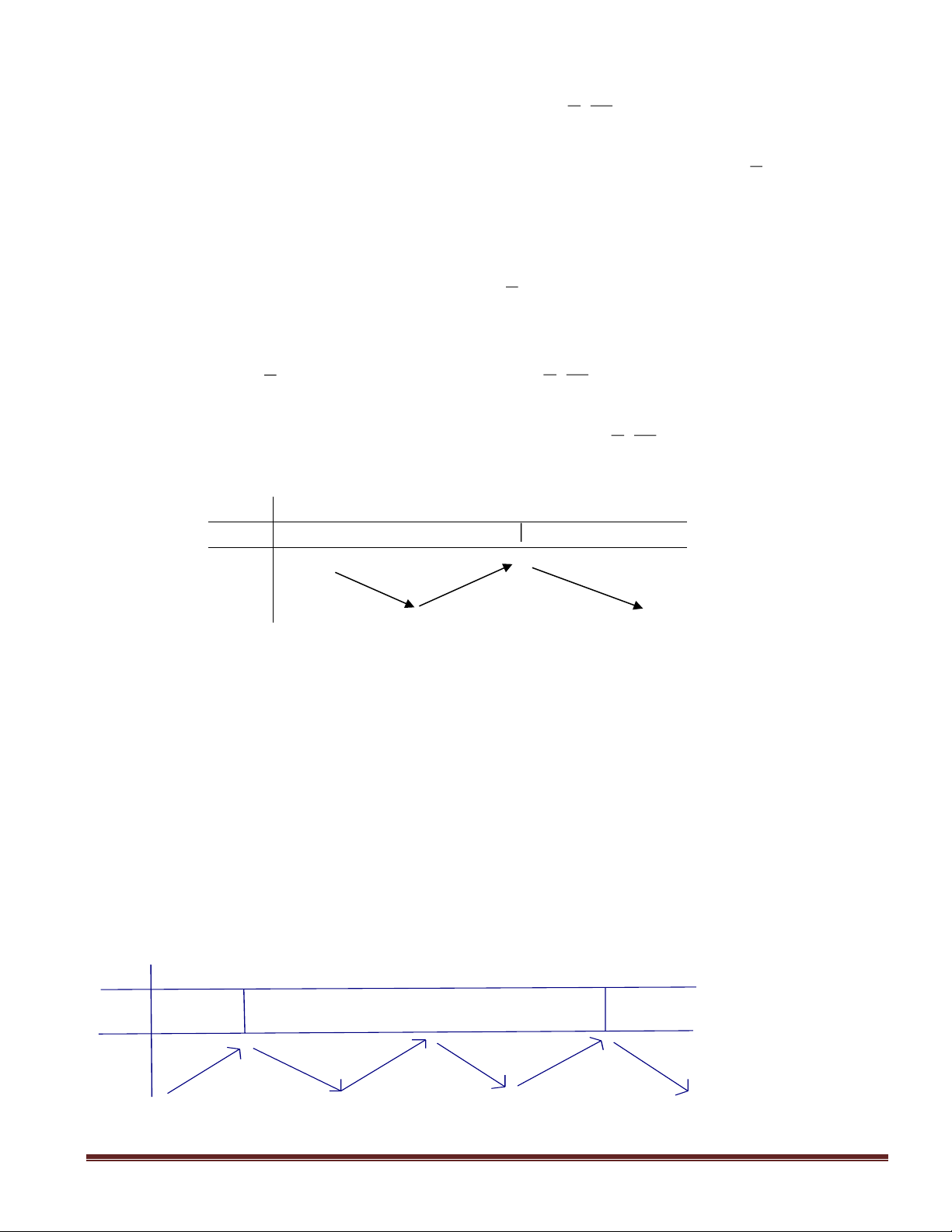
Câu 39(VDT): Cho hình hộp chữ nhật
ABCD.A'B'C'D'
có đáy
ABCD
là hình vuông cạnh
a 2,
AA' 2a=
. Khoảng cách giữa
BD
và
CD'
bằng
A.
a 2.
B.
2a.
C.
2a
.
5
D.
a
.
5
Giải: Mặt phẳng
( )
A'BD
chứa đường thẳng BD và
( )
A'BD / /CD'
nên
( ) ( ) ( )
d CD',BD d CD',(A'BD) d D',(A'BD)==
.
Lấy điểm M đối xứng với C’ qua D’, gọi N là trung điểm A’M
D'N A'M⊥
và
DN A'M⊥
Nên
(DND') A'M⊥
(DND') (A'BD)⊥
theo giao tuyến DN, kẻ
D'H DN(H DN)⊥
D'H (A'BD)⊥
do đó
( )
2a
d D',(A'BD) D'H .
5
==
Chọn C.
H
N
A
M
D'
C'
B'
A'
D
C
B
A
Trang 11
Câu 40(VDT): Tập hợp tất cả các giá trị thực của tham số
m
để phương trình
cos2x (2m 1)cosx m 1 0− + + + =
có nghiệm trên khoảng
π 3π
;
22
là
A.
1;0 .−
B.
)
1;0 .−
C.
( )
1;0 .−
D.
1
1; .
2
−
Giải:
2
cos2x (2m 1)cosx m 1 0 2cos x (2m 1)cosx m 0− + + + = − + + =
1
cosx
2
cosx m
=
=
Phương trình
1
cosx
2
=
không có nghiệm trên khoảng
π 3π
;
22
.
Do đó yêu cầu bài toán
cosx m=
có nghiệm thuộc khoảng
π 3π
;
22
)
m 1;0 . −
Chọn B.
Câu 41(VDC): Cho hàm số
y f(x)=
liên tục trên
R
và có bảng biến thiên như sau:
x
−
0 5
+
y’
- 0 + -
y
+
3
1
−
Khi đó hàm số
2
y g(x) f(x 4x)= = −
đồng biến trên khoảng
A.
( )
4;5 .
B.
( )
1;2 .−
C.
( )
5; .+
D.
( )
2;4 .
Từ bảng biến thiên ta thấy
f '(x) 0 x 0= =
và không có đạo hàm tại
x 5.=
f '(x) 0 0 x 5
và
x0
f '(x) 0 .
x5
Do đó
2
g'(x) (2x 4)f '(x 4x)= − −
;
x0
g'(x) 0 x 4
x2
=
= =
=
.
Hàm số
g(x)
không có đạo hàm tại
2
x1
x 4x 5 .
x5
=−
− =
=
BBT:
Dựa vào bảng biến thiên ta chọn A.
-
+
-
+
-
+
-
∞
+
∞
0
0
0
5
4
2
0
-1
g'(x)
x
g(x)

Trang 12
Câu 42(VDC): Tập hợp tất cả các giá trị thực của tham số
m
để đồ thị hàm số
42
y x 2mx 3= − −
có ba điểm cực trị sao cho bán kính đường tròn ngoại tiếp tam giác tạo bởi các điểm cực trị đạt giá
trị nhỏ nhất là
A.
1
. B.
3
. C.
3
2
. D.
3
1
2
.
Giải:
Ta có
2
2
x0
y' 4x(x m),y' 0
xm
=
= − =
=
Hàm số có ba cực trị khi
m 0.
Khi đó tọa độ ba điểm cực trị của đồ thị hàm số là
A(0; 3),−
2
B( m; m 3),−−
2
C( m; m 3)− − −
Ta có tam giác ABC cân tại A. Gọi H là trung điểm của BC
( )
2
AH
AH m ,sin ABC
AB
= =
Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC.
Ta có
24
2
AC AB.AC AB m m
2R
sin(ABC) AH AH m
+
= = = =
Mà
4
2
2
3
m m 1 1 3
m
m 2m 2m
4
+
= + +
33
33
2R R .
4 2 4
Đẳng thức xảy ra khi
2
3
11
mm
2m
2.
= =
Chọn D.
Câu 43(VDC): Cho các số thực dương
a,b
thỏa mãn
2 2ab 3 ab a b (a 1)(b 1)− + − = + + + +
.
Tính tổng
T (2a 1)(2b 1).= + +
A.
T 1.=
B.
T 3.=
C.
T 5.=
D.
T 0.=
Giải:
Ta có
2 2ab 3 ab a b (a 1)(b 1)− + − = + + + +
2 2ab 3 ab a b ab a b 1− + − = + + + + +
2 2ab 2 2ab a b a b − + − = + + +
f( 2 2ab) f( a b) − = +
(1)
Đặt
2
f(t) t t ;t 0.= +
Ta có
f '(t) 1 2t 0 t 0,= +
do đó
Phương trình (1)
2 2ab a b 2 2ab a b − = + − = +
4ab 2a 2b 4 + + =
( )( )
2a 1 2b 1 5+ + =
. Chọn C.
Câu 44(VDC): Tập hợp tất cả các giá trị thực của tham số m để bất phương trình
2
log x m.logx m 3 0+ + +
có nghiệm lớn hơn hoặc bằng 1.
A.
)
2; .+
B.
(
; 1 .− −
C.
(
; 2 .− −
D.
( )
; 3 .− −
Bất phương trình
2
log x m.logx m 3 0+ + +
2
log x 3
m
logx 1
+
−
+
.
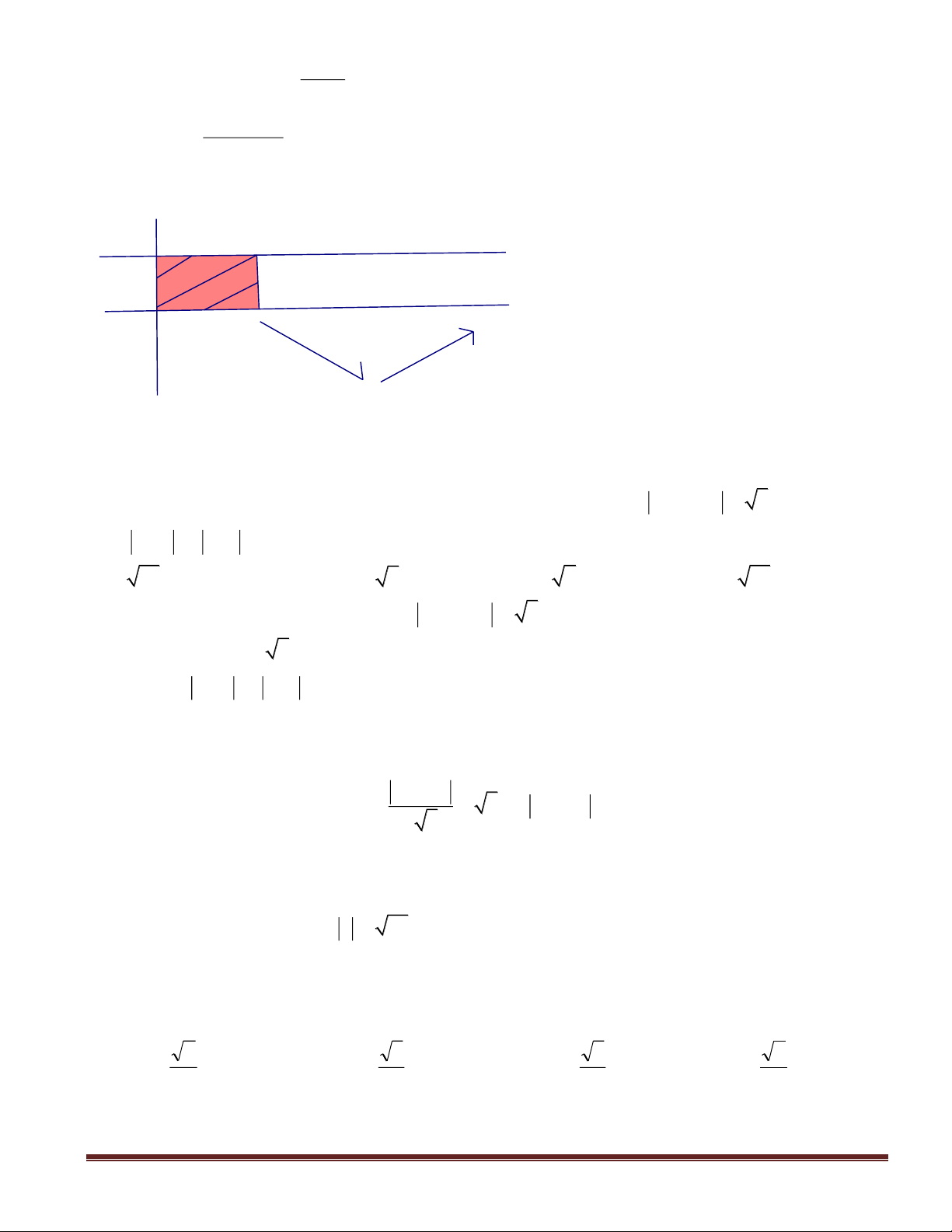
Trang 13
Xét hàm số
2
t3
f(t)
t1
+
=
+
với
t logx 0=
do
x 0.
( )
2
2
t 2t 3
f '(t)
t1
+−
=
+
;
f '(t) 0 t 1.= =
BBT:
Dựa vào BBT , YCBT
m 2 m 2. − −
Ta chọn C.
Câu 45(VDC): Biết số phức
z
thỏa mãn đồng thời hai điều kiện
z 3 4i 5− − =
và biểu thức
22
M z 2 z i= + − −
đạt giá trị lớn nhất. Môđun của số phức
zi+
bằng
A.
2 41.
B.
3 5.
C.
5 2.
D.
41.
Giải: Gọi
z x yi=+
(x,y R)
. Ta có
( ) ( )
22
z 3 4i 5 x 3 y 4 5− − = − + − =
đường tròn tâm
I(3;4)
, bán kính
R 5.=
( )
( )
22
2
2 2 2
M z 2 z i x 2 y x (y 1) 4x 2y 3= + − − = + + − + − = + +
d:4x 2y 3 M 0. + + − =
Do số phức
z
thỏa mãn đồng thời hai điều kiện nên đường tròn
( )
C
và đường thẳng
d
có
điểm chung
23 M
d(I,d) R 5 23 M 10
25
−
−
13 M 33.
( ) ( )
22
4x 2y 30 0
maxM 33
x 3 y 4 5
+ − =
=
− + − =
x5
z i 5 4i
y5
=
+ = −
=−
Vậy
z 41.=
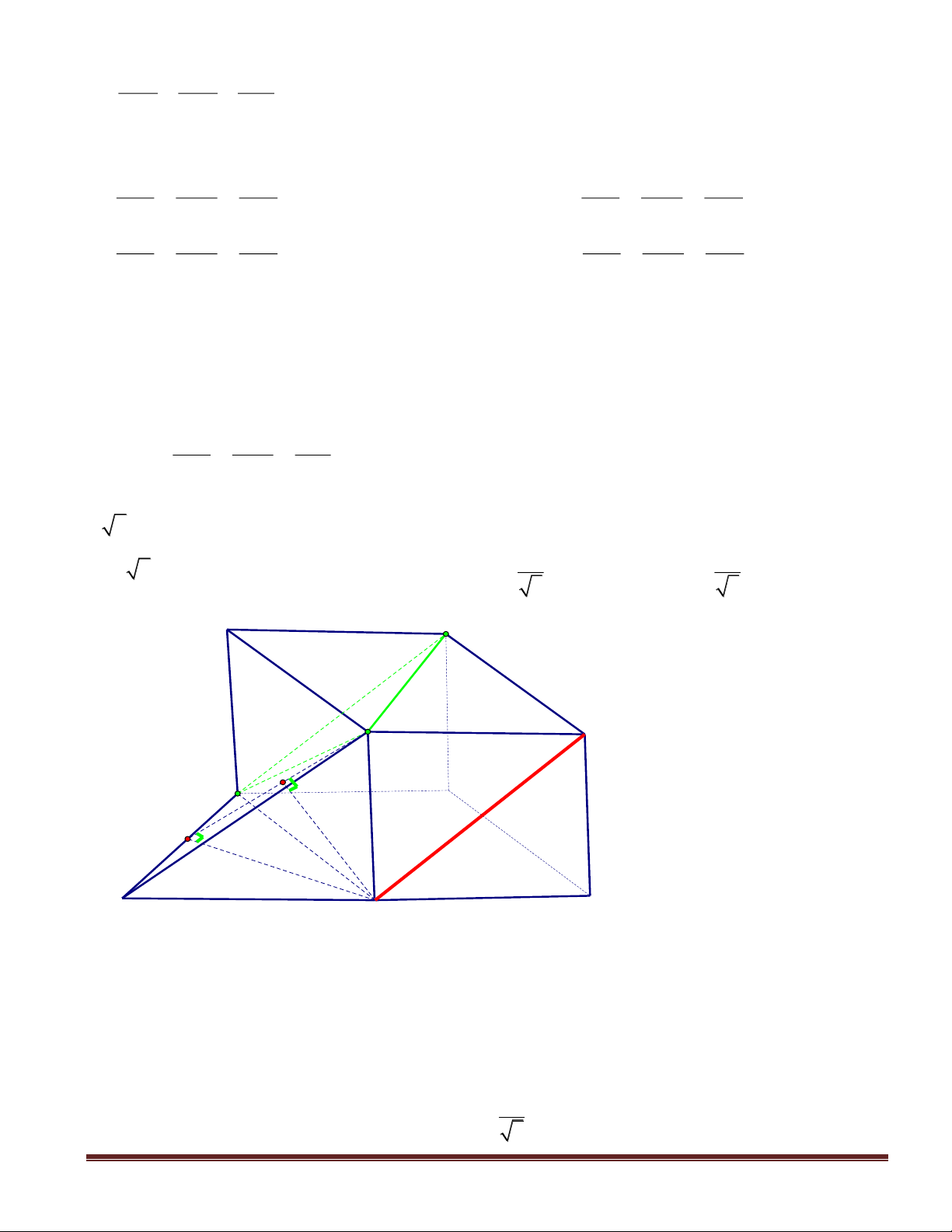
Câu 46(VDC):Cho hình chóp
SABC
có đáy
ABC
là tam giác vuông tại
.C
.2== ABSA
Canh
SA
vuông góc với mặt phẳng đáy
)(ABC
. Gọi
KH,
lần lượt là hình chiếu vuông góc của
A
lên
SB
và
SC
. Tính thể tích lớn nhất
max
V
của
SAHK
.
A.
.
3
2
max
=V
B.
.
6
3
max
=V
C.
.
3
3
max
=V
D.
.
6
2
max
=V
Đặt
AC x(0 x 2)=
.
+
∞
2
3
f'(t)
+
f(t)
-
+
∞
0
1
0
x

Trang 14
Tam giác vuông
ABC
có
2 2 2
BC AB AC 4 x .= − = −
Tam giác
SAB
cân tại
A,
có đường cao
AH
suy ra
H
là trung điểm của
SB
nên
SH 1
.
SB 2
=
Tam giác vuông
SAC
có
2
2
22
SK SA 4
SA SK.SC .
SC SC 4 x
= = =
+
Ta có
S.AHK
22
S.ABC
V
SH SK 1 4 2
. . .
V SB SC 2 x 4 x 4
= = =
++
S.AHK SABC ABC
22
2 2 1
V .V .S .SA
x 4 x 4 3
= =
++
2
2
2 x 4 x
.
3 x 4
−
=
+
.
Xét hàm số
2
2
2 x 4 x
f(x) .
3 x 4
−
=
+
trên khoảng
( )
0;2
, ta được
( )
0;2
22
maxf(x) f .
6
3
==
Câu 47(VDC): Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
)1;1;0(A
,
)1;2;1(B
và đường
thẳng
.
2
2
1
1
1
:
−
−
=
−
+
=
zyx
d
Tìm tọa độ điểm
M
thuộc
d
sao cho diện tích tam giác MAB có giá
trị nhỏ nhất.
A.
).2;3;2( −−M
B.
).2;1;0(M
C.
).0;2;1( −M
D.
).2;1;0( −M
Giải: Điểm
Md
nên
( )
M t; 1 t;2 2t− − −
( ) ( )
AM t; 2 t;1 2t ,AB 1;1;0= − − − =
uuur uuur
Đường thẳng
AB
qua A và nhận
AB
uuur
làm vectơ chỉ phương nên có phương trình:
x t'
y 1 t'
z1
=
=+
=
. Gọi H là hình chiếu vuông góc của M lên AB,
( )
H AB H t';1 t';1 +
MH (t' t;t' t 2;2t 1)= − + + −
uuur
Ta có
AB.MH 0=
uuur uuur
t' t t' t 2 0 t' 1.− + + − = =
( )
2
22
MH 1 t (t 3) (2t 1)= − + + + −
Diện tích tam giác MAB nhỏ nhất khi MH ngắn nhất.
( )
2
22
MH 1 t (t 3) (2t 1)= − + + + −
=
2
6t 11 11+
dấu “=” xảy ra khi
t0=
Vậy
).0;2;1( −M
Chọn C.
Câu 48(VDC): Với các chữ số
0,1,2,3,4
có thể lập được bao nhiêu số tự nhiên gồm 9 chữ số,
trong đó chữ số 2 có mặt đúng bốn lần, chữ số 1 có đúng hai lần, các chữ số còn lại có mặt đúng
một lần.
A.
362880.
B.
26880.
C.
302240.
D.
3360.
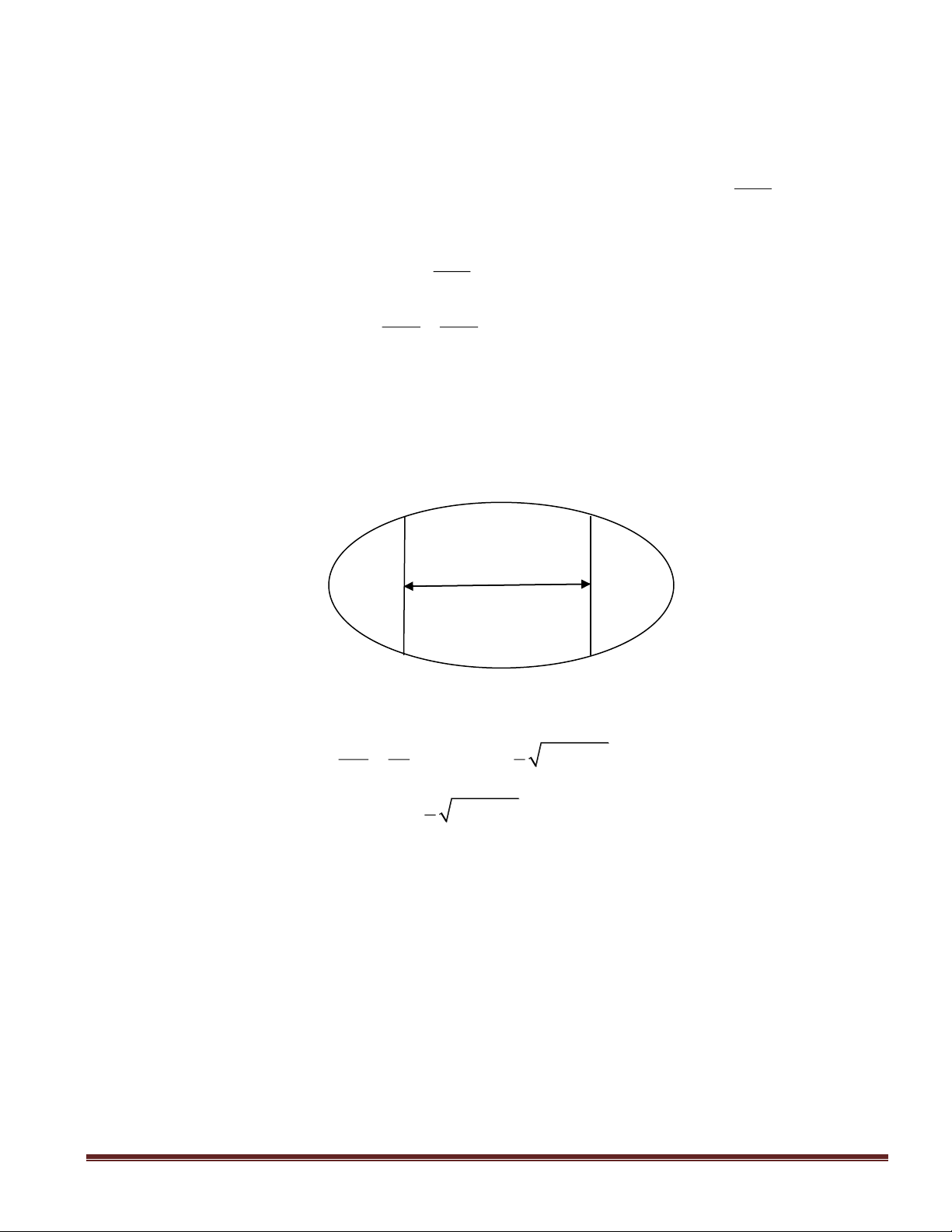
Giải: Giả sử các số tự nhiên gồm 9 chữ số tương ứng với 9 ô.
Trang 15
Do chữ số 2 có mặt đúng bốn lần, chữ số 1 có mặt đúng hai lần nên ta sẽ coi như tìm các số thỏa
mãn đề bài được tạo nên từ 9 số 0, 1, 2, 3, 4, 1, 2, 2, 2.
Số các hoán vị của 9 số 0, 1, 2, 3, 4, 1, 2, 2, 2 là
9!
.
Mặt khác chữ số 1 lặp lại hai lần, chữ số 2 lặp lại bốn lần nên số cách xếp là
9!
4!.2!
kể cả trường
hợp số 0 đứng đầu.
Trường hợp ô thứ nhất có chữ số 0 thì có
8!
4!.2!
Vậy số cần tìm thỏa mãn YCBT là:
9! 8!
6720
4!.2! 4!.2!
−=
Câu 49(VDC): Một mảnh vườn hình elip có độ dài trục lớn bằng
20m
và độ dài trục bé bằng
12m
. Người ta muốn trồng hoa trên dãi đất rộng
10m
và nhận trục bé của elip làm trục đối
xứng(hình vẽ). Biết kinh phí để trồng hoa là
150.000
đồng /
2
1m .
Hỏi phải tốn bao nhiêu tiền để
trồng hoa trên dải đất đó(Số tiền được làm tròn đến hàng nghìn).
A. 17.219.000 đồng. B. 17.220.000 đồng. C. 8.610.000 đồng. D. 17.826.000 đồng.
Giải: Gắn hệ trục Oxy sao cho gốc tọa độ O là tâm của elip và trục lớn nằm trên Ox, trục bé nằm
trên Oy. Phương trình Elip là:
22
2
x y 3
1 y 100 x
100 36 5
+ = = −
Diện tích dãi đất muốn trồng hoa:
5
2
5
3
S 2 100 x dx
5
−
=−
Số tiền để trồng hoa trên dãi đất đó:
150.000xS 17219000
. Chọn A.
Câu 50(VDC): Gọi S là tập tất cả các giá trị thực của tham số
m
để bất phương trình
( ) ( )
( )
3 2 2
2x 6x x 3 m 1 x 9 0+ + + − +
nghiệm đúng với mọi
xR
. Tích giá trị các phần tử thuộc
S bằng
A.
0.
B.
4.−
C.
4.
B.
2.
Ta có
( ) ( )
( )
3 2 2 2 2
f(x) 2x 6x x 3 m 1 x 9 (x 3)(2x 1)((m 1)x 9)= + + + − + = + + − +
Nếu
x3=−
không phải là nghiệm của phương trình
2
(m 1)x 9 0− + =
thì
f(x)
sẽ đổi dấu khi đi
qua
3−
. Do đó điều kiện cần để
f(x) 0, x R
là
x3=−
phải là nghiệm của
2
(m 1)x 9 0− + =
10m

Trang 16
2
m2
3m 12 0
m2
=−
− + =
=
Với
m2=
thì
22
f(x) 3(x 3) (2x 1) 0, x R= + +
do đó
m2=
thỏa mãn.
Với
m2=−
thì
22
f(x) 3(x 3) (2x 1) 0, x R= + +
do đó
m2=−
thỏa mãn.
Vậy
S 2;2 .=−
Chọn B.
ĐỀ 22
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1: Trong không gian Oxyz cho
(1;2;3)M
. Khoảng cách từ M đến mặt phẳng
()Oxz
bằng?
A. 2. B. 1. C. 3. D.
14
.
Câu 2: Cho lập phương MNPQ.M’N’P’Q’ có thể tích bằng 2. Nếu tăng độ dài mỗi cạnh lên 2 lần
thì thể tích của khối lập phương đó là:
A. 16. B. 8. C. 4. D. 32.
Câu 3: Cho hàm số
( )
y f x=
liên tục tại
0
x
và có bảng biến thiên sau:
Mệnh đề nào sau đây là đúng?
A. Hàm số có một điểm cực đại, một điểm cực tiểu.
B. Hàm số có một điểm cực đại, không có điểm cực tiểu.
C. Hàm số có một điểm cực đại, hai điểm cực tiểu.
D. Hàm số có hai điểm cực đại, một điểm cực tiểu.
Câu 4: Số hạng tổng quát trong khai triển của
( )
12
12− x
với
k N,k 12Σ
là.
A.
12
12−()
k k k k
Cx
. B.
12
12
2
−k k k
Cx
. C.
12
12−()
k k k
Cx
. D.
12
2−
k k k
Cx
.
Câu 5: Cho hai số phức
1
zi=
và
2
34zi=−
. Phần ảo của số phức
12
zz+
là:
A. -3. B. 3. C. -3i. D. 3i.
Câu 6: Xét các mệnh đề sau:
I.
2 .2 2
a b ab
=
. II.
17
35
16
x x x x x=
.
III.
( )
22
2 2 2 2
log 2 4log 4 0 log 4log 3 0x x x x− − = − − =
.
Số mệnh đề đúng là:
A. 1. B. 0. C. 2. D. 3.
Câu 7: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Trang 17
A.
3
3 1.y x x= - +
B.
2
1.y x x= - + -
C.
42
1.y x x= - +
D.
3
3 1.y x x= - + +
Câu 8: Công thức tính diện tích xung quanh của hình nón có đường sinh
l
và bán kính đường tròn
đáy
r
là:
A.
xq
S rl
=
. B.
2
2
xq
S r l
=
. C.
2
xq
S r l
=
. D.
2
xq
S rl
=
.
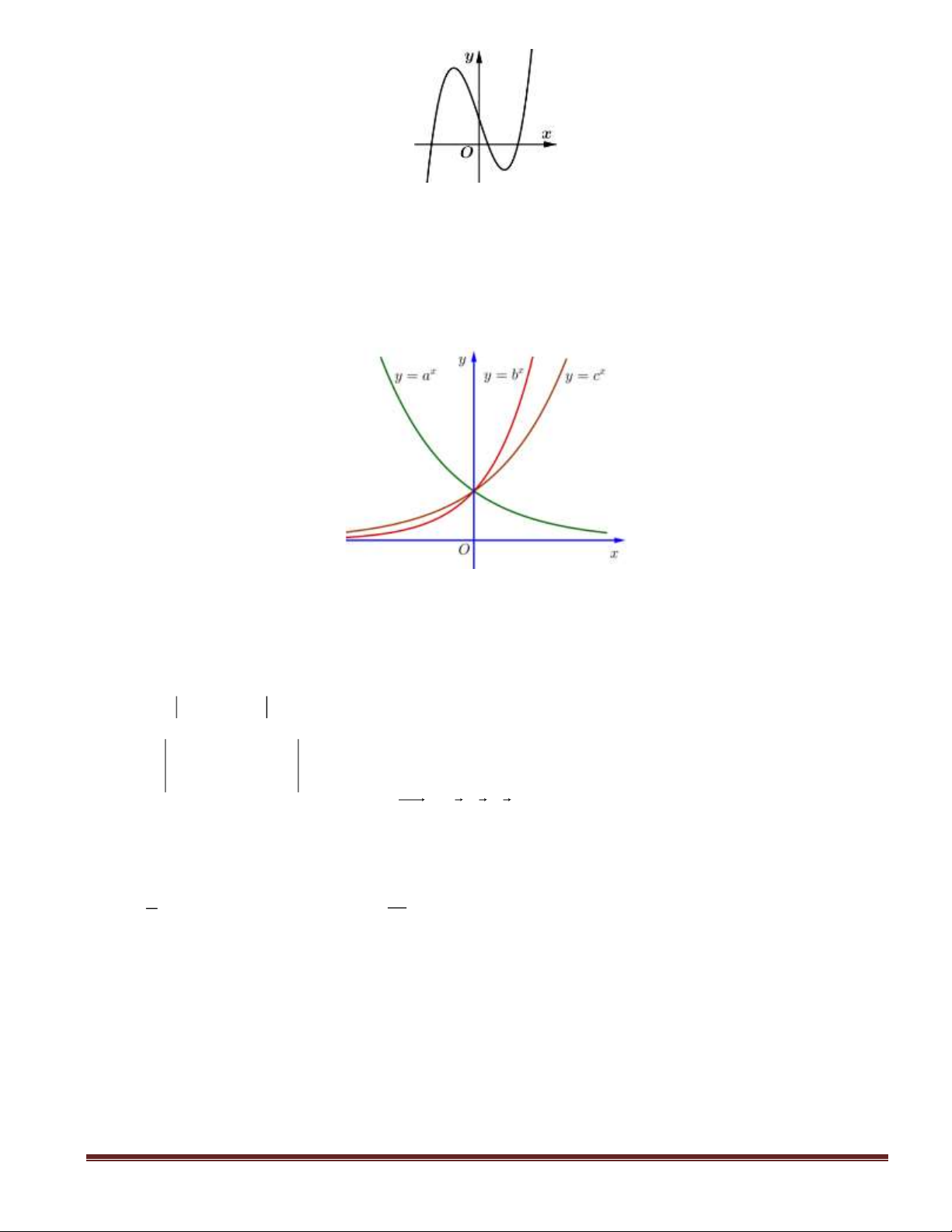
Câu 9: Cho ba số thực dương
a
,
b
,
c
và
1a
,
1b
,
1c
. Đồ thị các hàm số
x
ya=
,
x
yb=
,
x
yc=
được cho trong dưới hình vẽ dưới. Mệnh đề nào sau đây đúng?
A.
a c b
. B.
b c a
. C.
abc
. D.
c a b
.
Câu 10: Cho hàm số
( )
y f x=
và
( )
y g x=
liên tục trên đoạn [a;b]. Diện tích của hình phẳng giới
hạn bởi đồ thị hàm số
( ) ( )
, y f x y g x==
và hai đường thẳng
( )
, x a x b a b= =
được tính theo
công thức.
A.
( ) ( ) .
b
a
S f x g x dx=−
B.
( ) ( ) .
b
a
S f x g x dx
=−
C.
( ) ( ) .
b
a
S f x g x dx=−
D.
( ) ( ) .
b
a
S f x g x dx=−
Câu 11: Trong không gian Oxyz cho
2AO k i j= − +
. Tọa độ điểm A là?
A.
( )
1; 1; 2A −−
. B.
(2; 1;1)A −
. C.
( 2;1; 1)A −−
. D.
( 1;1;2)A −
.
Câu 12: Khẳng định nào sau đây sai?
A.
1
d lnx x C
x
=+
. B.
5
4
d
5
x
x x C=+
. C.
0dxC=
. D.
e d e
xx
xC=+
.
Câu 13: Cho cấp số nhân
( )
n
u
có
1
2u =−
và công bội
3q =
. Giá trị của
11
u
là.
A.
11
118098u =−
. B.
11
3072u =
. C.
11
354294u =−
. D.
2
354294u =
.
Câu 14: Trong không gian Oxyz cho ba mặt phẳng
2 6 0x y z+ − − =
;
2 3 13 0x y z− + + =
;
3 2 3 16 0x y z− + + =
cắt nhau tại điểm A. Tọa độ của A là?
A.
( 1;2; 3).A −−
B.
(1; 2;3).A −
C.
( 1; 2; 3).A − − −
D.
(1;2;3).A
Câu 15: Tập xác định của hàm số
( )
2
4
e
yx
−
=−
là.
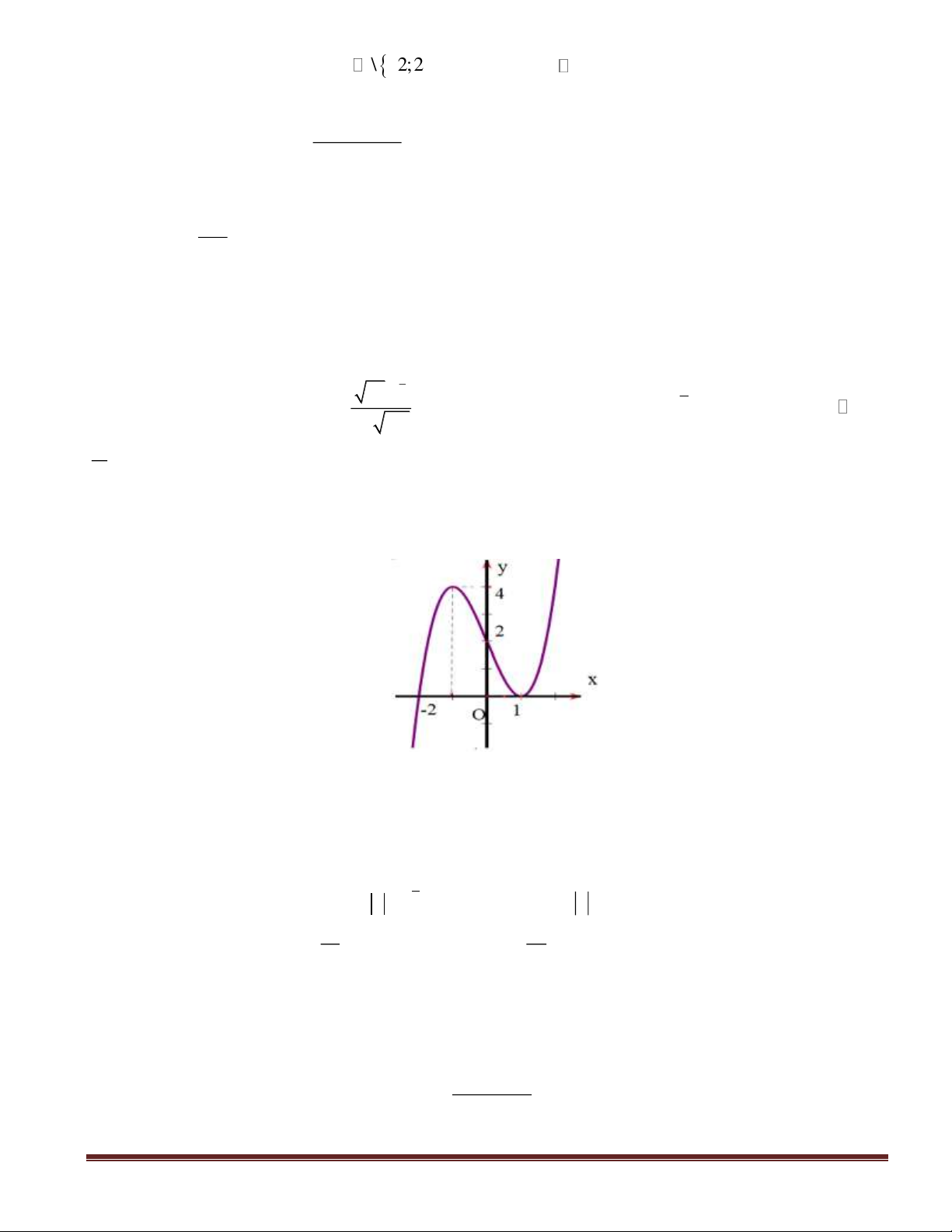
Trang 18
A.
( )
2;2D =−
. B.
\ 2;2D =−
. C.
D =
. D.
( ) ( )
; 2 2; .D = − − +
Câu 16: Đồ thị hàm số
2
2
6 5 1
2 9 5
xx
y
xx
−+
=
+−
có bao nhiêu đường tiệm cận đứng?
A. 1. B. 3. C. 4. D. 2.
Câu 17: Cho ba số thực dương a, b, c và a khác 1. Khẳng định nào sau đây là sai?
A.
ln
log
ln
a
a
b
b
=
. B.
( )
log log log .
a a a
bc b c=+
C.
log log
aa
bb
=
. D.
log
a
b
ab=
.
Câu 18: Trong không gian Oxyz, cho hai điểm
(1; 1;2)A −
và
(3;3;0)B
. Điểm nào sau đây thuộc
mặt phẳng trung trực của đoạn thẳng AB?
A.
(1;2;2)M
. B.
(1;1; 1)M −
. C.
(1;1;1)M
. D.
(1; 2;2)M −
.
Câu 19: Rút gọn biểu thức
7
3
5
3
7
42
.
.
aa
A
aa
−
=
với
0a
ta được kết quả
m
n
Aa=
, trong đó
m
,
*
n
và
m
n
là phân số tối giản. Khẳng định nào sau đây đúng?
A.
2
2 15mn+=
. B.
22
43mn+=
. C.
2
3 2 2mn−=
. D.
22
25mn+=
.
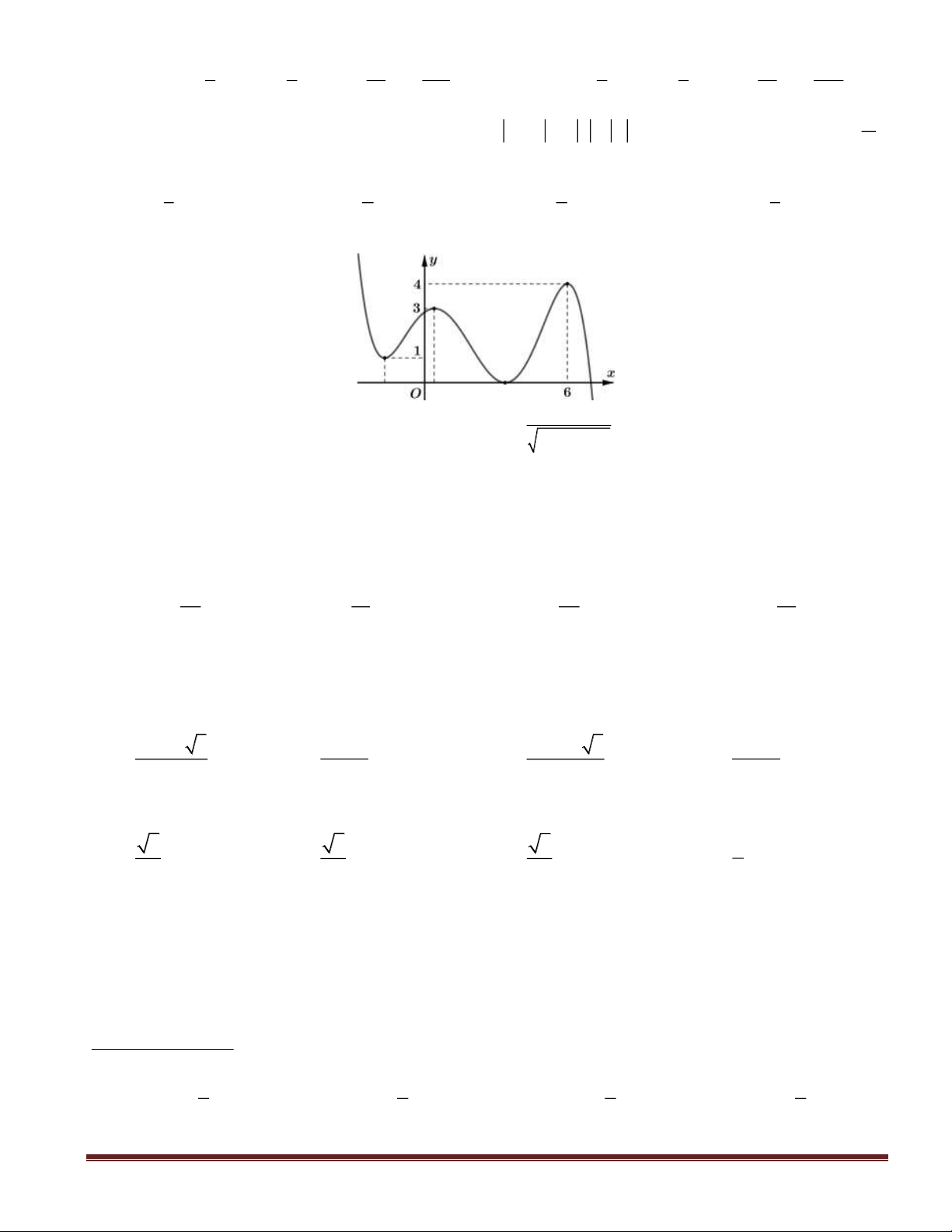
Câu 20: Cho hàm số
()y f x=
có đạo hàm liên tục trên R và đồ thị hàm số
()y f x
=
như hình vẽ.
Khẳng định sau đây là sai?
A. Hàm số
( )
y f x=
nghịch biến trên khoảng
( 1;1)−
.
B. Hàm số
( )
y f x=
đồng biến trên khoảng
( 2; 1)−−
.
C. Hàm số
( )
y f x=
đồng biến trên khoảng
(1; )+
.
D. Hàm số
( )
y f x=
nghịch biến trên khoảng
( ; 2)− −
.
Câu 21: Cho số phức
z
thỏa mãn
2 7 3z z i z− = − + +
. Tính
z
?
A. 5. B.
13
4
. C.
25
4
. D. 3.
Câu 22: Cho mặt phẳng
( ):3 4 5 2 0P x y z+ + + =
và đường thẳng
d
là giao tuyến của hai mặt
phẳng
( ): 2 1 0xy
− + =
và
( ): 2 3 0xz
− − =
. Gọi
là góc giữa đường thẳng
d
và mặt phẳng
()P
. Khi đó
bằng.
A. 60°. B. 45°. C. 30°. D. 90°.
Câu 23: Họ nguyên hàm của hàm số
( )
2
43
32
x
fx
xx
−
=
−+
là.

Trang 19
A.
( )
1
4ln 2 ln
2
x
F x x C
x
−
= − − +
−
. B.
( )
1
4ln 2 ln
2
x
F x x C
x
−
= − + +
−
.
C.
( )
2
4ln 2 ln
1
x
F x x C
x
−
= − − − +
−
. D.
( )
2
4ln 2 ln
1
x
F x x C
x
−
= − − +
−
.
Câu 24: Cho hàm số
2
2
mx
y
xm
+
=
+
,
m
là tham số thực. Gọi
S
là tập hợp tất cả các giá trị nguyên của
tham số
m
để hàm số nghịch biến trên khoảng
( )
0;1
. Tìm số phần tử của
S
?
A.
2
. B.
5
. C.
1
. D.
3
.
Câu 25: Một hình nón có đường kính đáy là
23a
, góc ở đỉnh là
0
120
. Tính thể tích của khối nón
đó theo
a
là.
A.
3
a
. B.
3
3 a
. C.
3
3a
. D.
3
23a
.
Câu 26: Cho
( )
2
1
2f x dx
−
=
và
4
2
2
2
x
g dx
−
=−
. Tính
( ) ( )
2
1
23I x f x g x dx
−
= + −
?
A.
17
2
I =
. B.
11
2
I =
. C.
23
2
I =
. D.
5
2
I =
.
Câu 27: Ông An có tất cả 20 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 2 triệu
đồng một tháng thì mọi căn hộ đều có người thuê. Nhưng cứ mỗi lần tăng giá cho thuê mỗi căn hộ
thêm chẵn 200 nghìn đồng thì có thêm 1 căn hộ bị bỏ trống. Hỏi khi tăng giá lên mức mỗi căn bao
nhiêu tiền một tháng thì ông An thu được tổng số tiền nhiều nhất trên một tháng là.
A. 3 triệu đồng. B. 2,4 triệu đồng. C. 2 triệu đồng. D. 3,4 triệu đồng.
Câu 28: Trong mặt phẳng phức, gọi A, B, C, D lần lượt là các điểm biểu diễn các số phức
1 2 3 4
1, 1 , 2 5 , 2.z z i z i z= − = − + = + =
Gọi S là diện tích tứ giác ABCD. Tính S?
A. S =
9
. B. S =
6
. C. S =
12
. D. S =
18
.
Câu 29: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều,
()SA ABC⊥
. Gọi
()P
là mặt phẳng
qua
B
và vuông góc với
SC
. Thiết diện của
()P
và hình chóp
.S ABC
là.
A. Tam giác vuông. B. Tam giác đều. C. Tam giác cân. D. Hình thang vuông.
Câu 30: Tập nghiệm của bất phương trình
( )
2
2
log 3 1 0xx− +
là.
A.
3 5 3 5
0; ;3
22
S
−+
=
. B.
3 5 3 5
0; ;3
22
S
−+
=
.
C.
3 5 3 5
;
22
S
−+
=
. D.
S =
.
Câu 31: Có bao nhiêu phương trình tiếp tuyến của đồ thị hàm số
42
43y x x= − −
biết tiếp tuyến
vuông góc với đường thẳng
4 3 0xy+ + =
.
A. 3. B. 1. C. 2. D. 0.
Câu 32: Trong không gian
Oxyz
, cho đường thẳng
1 1 1
:
2 2 1
x y z
d
− − +
==
−
và điểm
(1;2;3)I
. Gọi
K
là điểm đối xứng với
I
qua
d
. Lập phương trình mặt cầu
()S
tâm
K
cắt
d
tại hai điểm
A
và
B
biết đoạn
4AB =
là.
A.
2 2 2
1 8 41 185
( ): .
9 9 9 9
S x y z
− + + + + =
B.
2 2 2
1 8 41 293
( ): .
9 9 9 9
S x y z
+ + − + − =
Trang 20
C.
2 2 2
1 8 41 149
( ): .
9 9 9 9
S x y z
− + + + + =
D.
2 2 2
1 8 41 230
( ): .
9 9 9 9
S x y z
+ + − + − =
Câu 33: Cho các số phức z, w khác 0 và thõa mãn
2z w z w− = =
. Phần thực của số phức
z
u
w
=
là.
A.
1
8
a =
. B.
1
4
a =−
. C.
1
4
a =
. D.
1
8
a =−
.
Câu 34: Cho hàm số
( )
y f x=
liên tục trên
¡
, có đồ thị như hình vẽ.
Có bao nhiêu giá trị của tham số
m
để phương trình
( )
( )
3
2
2
4
3
25
mm
fx
fx
+
=+
+
có 3 nghiệm phân biệt
?
A. 1. B. 5. C. 2. D. 0.
Câu 35: Trong không gian với hệ tọa độ
Oxyz
cho mặt phẳng
( ): 2 2 7 0P x y z+ + + =
và ba điểm
(1;2; 1), (3;1; 2), (1; 2;1)ABC− − −
. Điểm
( ; ; ) ( )M a b c P
sao cho
2 2 2
MA MB MC−−
đạt giá trị lớn
nhất. Khi đó tổng
A a b c= + +
là.
A.
20
9
A =−
. B.
14
9
A =
. C.
20
9
A =
. D.
14
9
A =−
.
Câu 36: Bạn A muốn làm một chiếc thùng hình trụ không đáy từ nguyên liệu là mảnh tôn hình
tam giác đều
ABC
có cạnh bằng 90 (cm). Bạn muốn cắt mảnh tôn hình chữ nhật
MNPQ
từ mảnh
tôn nguyên liệu để tạo thành hình trụ có chiều cao bằng
MQ
. Thể tích lớn nhất của chiếc thùng
mà bạn A có thể làm được là.
A.
( )
3
13500. 3
cm
. B.
( )
3
91125
cm
2
. C.
( )
3
108000 3
cm
. D.
( )
3
91125
cm
4
.
Câu 37: Cho tứ diện đều
ABCD
cạnh
a
. Gọi
M
là trung điểm của
BC
. Tính cô-sin góc giữa hai
đường thẳng
AB
và
DM
là.
A.
3
6
. B.
3
2
. C.
3
3
. D.
1
2
.
Câu 38: Cho tập hợp
1;2;3;4;5;6 .S =
Gọi M là tập hợp các số tự nhiên có 6 chữ số đôi một
khác nhau lấy từ S sao cho tổng chữ số các hàng đơn vị, hàng chục và hàng trăm lớn hơn tổng chữ
số các hàng còn lại là 3. Tổng T của các phần tử của tập hợp M là.
A. T = 36011952. B. T = 11003984. C. T = 12003984. D. T = 18005967.
Câu 39: Cho hàm số f(x) có đạo hàm liên tục và nhận giá trị không âm trên đoạn
0;1
thỏa mãn
( ) ( )
( )
22
2
2
.'
1
x
f x f x
fx
e
=+
, với mọi
0;1x
. Biết f(0) = 1. Mệnh đề nào dưới đây đúng?
A.
( )
5
1 ;3
2
f
. B.
( )
7
1 3;
2
f
. C.
( )
5
1 2;
2
f
. D.
( )
3
1 ;2
2
f
.

Trang 21
Câu 40: Cho hình chóp S.ABC. Một mặt phẳng song song với mặt đáy (ABC) cắt các cạnh bên
SA, SB, SC lần lượt tại M, N, P. Kí hiệu M’, N’, P’ lần lượt là hình chiếu vuông góc của M, N, P
lên mặt phẳng đáy (ABC). Tìm tỉ số
SM
SA
để thể tích khối đa diện MNP.M’N’P’ lớn nhất ?
A.
SM
SA
=
2
3
. B.
SM
SA
=
1
4
. C.
SM
SA
=
3
4
. D.
SM
SA
=
1
3
.
Câu 41: Một bồn hoa hình elip tâm O có độ dài trục lớn bằng 6m, độ dài trục nhỏ bằng 4m. Người
ta chia bồn hoa thành 4 phần
1 2 3 4
, , ,S S S S
bởi hai Parabol có cùng đỉnh O đối xứng qua O như hình
vẽ bên dưới:
Hai đường Parabol này cắt đường elip tại bốn điểm A, B, C, D tạo thành một hình chữ nhật có
3 3 , 2 .AB m AD m==
Biết kinh phí để trồng hoa trên các phần
1
S
và
2
S
là 100.000 đồng/1m
2
,
kinh phí để trồng hoa trên các phần
34
,SS
là 120.000 đồng/1m
2
. Hỏi số tiền để trồng bồn hoa gần
nhất với số tiền nào sau đây.
A. 1.980.000 đồng. B. 1.900.000 đồng. C. 2.050.000 đồng D. 2.100.000 đồng.
Câu 42: Cho hình chóp S.ABC có đáy là tam giác vuông tại A,
2 , 2 3AB a AC a==
. Tam giác
SAB đều và nằm trong mặt phẳng vuông góc với đáy. Điểm M thuộc cạnh BC sao cho
1
4
BM BC=
. Hỏi cosin góc giữa hai mặt phẳng (SAM) và (SAC) bằng.
A.
2 13
13
. B.
3
5
. C.
4
5
. D.
3 13
13
.
Câu 43: Có bao nhiêu số nguyên
2019;2m−
để phương trình:
( ) ( )
35
( 1) log 4 1 log 2 1 2x x x x m− + + + = −
có đúng hai nghiệm thực?
A. 2022. B. 2021. C. 2. D. 1.
Câu 44: Giả sử
12
,zz
là hai trong số các số phức
z
thỏa mãn
21iz i+ − =
và
12
2zz−=
. Giá trị
lớn nhất của
12
zz+
bằng?
A. 4. B.
23
. C.
32
. D. 3.
Câu 45: Cho hàm số bậc ba
( )
fx
và
( )
( )
( )
2
,,g x f mx nx p m n p= + +
có đồ thị như hình dưới
(đường nét đứt là đồ thị của hàm
( )
,gx
đường thẳng
1
2
x =−
là trục đối xứng của đồ thị hàm số
( )
g x ).
Giá trị của biểu thức
( )( )( )
2 4 3P n m m p p n= + − +
bằng bao nhiêu?

Trang 22
A.
36.P =−
B.
24.P =−
C.
26.P =
D.
24.P =
Câu 46: Trong không gian
Oxyz
, cho điểm
(1;1;4)A
và đường thẳng
2 3 3
:
2 2 1
x y z
d
− + −
==
−
.
Điểm
M
chạy trên đường thẳng
d
và điểm
N
nằm trên tia đối của tia
MA
sao cho
. 12AM AN =
. Quỹ tích điểm
N
là đường cong có độ dài bằng bao nhiêu?
A.
4
3
. B.
2
3
. C.
. D.
3
.
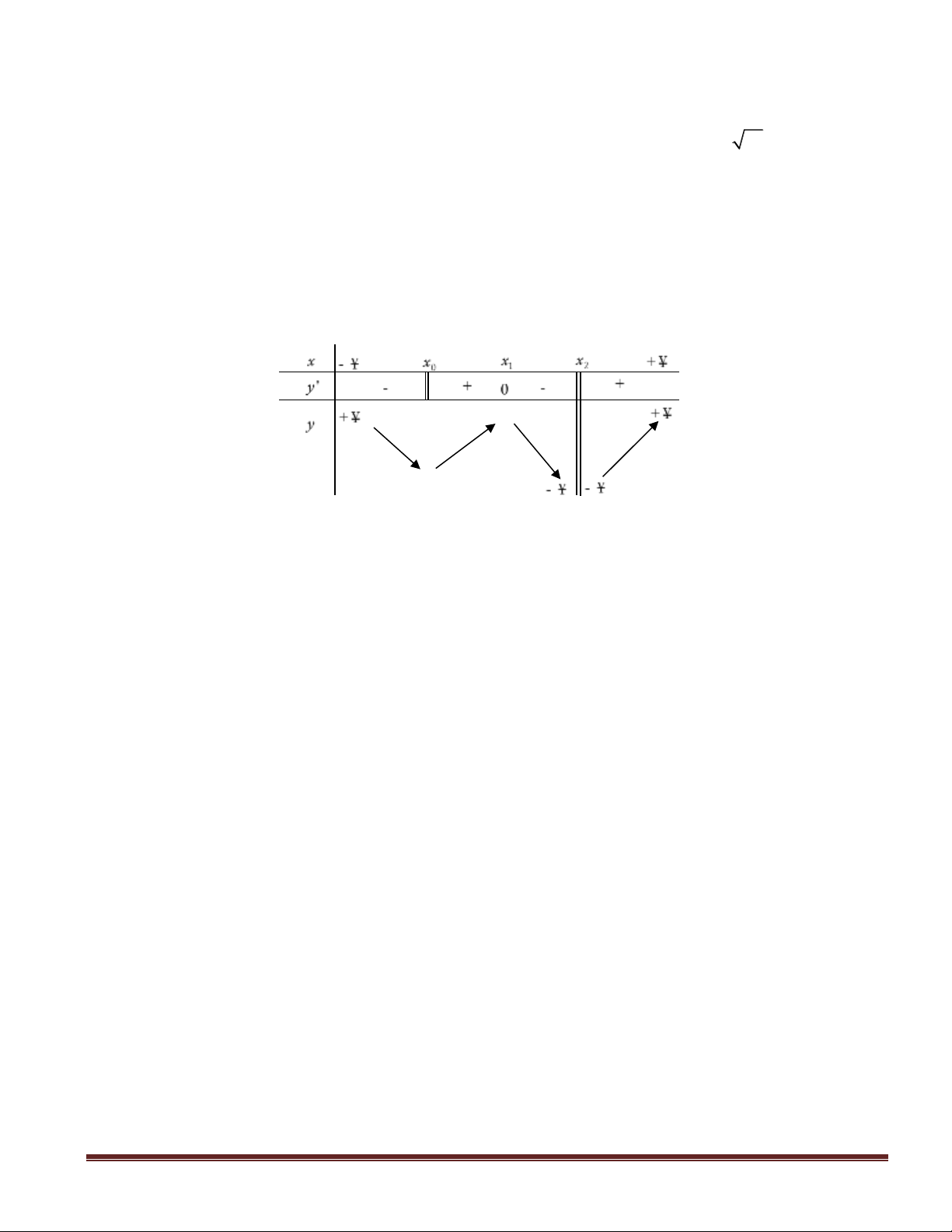
Câu 47: Cho hàm số
( )
fx
liên tục trên R và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên
của tham số m để phương trình
( )
2
3sin cos 1
44
2cosx sinx 4
xx
f f m m
− −
= + +
−+
có nghiệm?
A. 4. B. 5. C. Vô số. D. 3.
Câu 48: Cho hai số thực x, y thỏa mãn
( )
22
2
22
1
3 .log ( ) 1 log 1
2
xy
x y xy
+−
− = + −
. Giá trị lớn nhất của
biểu thức
( )
33
23P x y xy= + −
bằng.
A.
13
2
P =
. B.
17
2
P =
. C.
3P =
. D.
7P =
.
Câu 49: Cho hàm số
32
y x x ax b= + + +
cắt trục hoành tại ba điểm phân biệt có hoành độ
3 2 1
x x x
thỏa mãn
( )
2
1 2 3 1 2 2 3 3 1
6 6 3 96 64 48x x x x x x x x x+ + = + +
. Giá trị của biểu thức
11
a
S
b
=
là.
A.
1.S =−
B.
2.S =−
C.
2.S =
D.
0.S =
Câu 50: Cho hàm số
( )
2
2 4 3y x a x b= + + + +
. Gọi M là giá trị lớn nhất của hàm số trên đoạn
2;3−
. Khi M đạt giá trị nhỏ nhất, giá trị của biểu thức
4P a b=−
là.
A.
29.P =
B.
41.P =−
C.
40.P =
D.
41.P =
------------------ HẾT ------------------
Trang 23
PHẦN HƯỚNG DẪN GIẢI
Câu 1: Trong không gian Oxyz cho
(1;2;3)M
. Khoảng cách từ M đến mặt phẳng
()Oxz
bằng?
A. 2. B. 1. C. 3. D.
14
.
Lời giải
Chọn A.
Câu 2: Cho lập phương MNPQ.M’N’P’Q’ có thể tích bằng 2. Nếu tăng độ dài mỗi cạnh lên 2 lần
thì thể tích của khối lập phương đó là:
A. 16 B. 8 C. 4 D. 32
Lời giải
Chọn A.
Câu 3: Cho hàm số
( )
y f x=
liên tục tại
0
x
và có bảng biến thiên sau
Mệnh đề nào sau đây là đúng?
A. Hàm số có một điểm cực đại, một điểm cực tiểu.
B. Hàm số có một điểm cực đại, không có điểm cực tiểu.
C. Hàm số có một điểm cực đại, hai điểm cực tiểu.
D. Hàm số có hai điểm cực đại, một điểm cực tiểu.
Lời giải
Chọn A.
● Tại
2
xx=
hàm số
( )
y f x=
không xác định nên không đạt cực trị tại điểm này.
● Tại
1
xx=
thì dễ thấy hàm số đạt cực đại tại điểm này.
● Tại
0
xx=
, hàm số không có đạo hàm tại
0
x
nhưng liên tục tại
0
x
thì hàm số vẫn đạt cực trị tại
0
x
và theo như bảng biến thiên thì đó là cực tiểu.
Vậy hàm số có một điểm cực đại, một điểm cực tiểu.
Câu 4: Số hạng tổng quát trong khai triển của
( )
12
12− x
là
A.
12
12−()
k k k k
Cx
. B.
12
12
2
−k k k
Cx
. C.
12
12−()
k k k
Cx
. D.
12
2−
k k k
Cx
.
Lời giải
Chọn A. Ta có số hạng tổng quát trong khai triển là
( ) ( )
12 12
2 1 2− = −
kk
k k k k
C x C x
Câu 5: Cho 2 số phức
1
zi=
và
2
34zi=−
. Phần ảo của số phức
12
zz+
là?
A. -3. B. 3. C. -3i. D. 3i.
Lời giải
Chọn A.
12
(3 4 ) 3 3z z i i i+ = + − = −
Phần ảo -3.
Câu 6: Xét các mệnh đề sau
I.
( ) ( ) ( ) ( )
2
2 2 2 2
log 1 2log 1 6 2log 1 2log 1 6x x x x− + + = − + + =
.

Trang 24
II.
17
35
16
x x x x x=
.
III.
( )
22
2 2 2 2
log 2 4log 4 0 log 4log 3 0x x x x− − = − − =
.
Số mệnh đề đúng là
A. 1
.
B. 0
.
C.2. D.3.
Lời giải
Chọn A. Ý đúng là ý III.
Câu 7: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
3
3 1.y x x= - +
B.
2
1.y x x= - + -
C.
42
1.y x x= - +
D.
3
3 1.y x x= - + +
Lời giải
Chọn A.
Câu 8: Viết công thức tính diện tích xung quanh của hình nón có đường sinh
l
và bán kính đường
tròn đáy
r
.
A.
xq
S rl
=
. B.
2
2
xq
S r l
=
. C.
2
xq
S r l
=
. D.
2
xq
S rl
=
.
Lời giải
Chọn A.
Câu 9: Cho ba số dương
a
,
b
,
c
,
1a
,
1b
,
1c
. Đồ thị các hàm số
x
ya=
,
x
yb=
,
x
yc=
được
cho trong dưới hình vẽ dưới. Mệnh đề nào sau đây đúng?
A.
a c b
. B.
b c a
. C.
abc
. D.
c a b
.
Lời giải
Chọn A.
Dựa vào hình vẽ ta thấy hàm số
x
ya=
nghịch biến nên
1a
.
Hàm số
x
yb=
và
x
yc=
đồng biến nên
1b
,
1c
.
Xét
0
0xx=
ta thấy
00
xx
bc
bc
. Vậy
a c b
.
Câu 10: Cho hàm số y = f(x) và y = g(x)liên tục trên đoạn [a;b]. Diện tích của hình phẳng giới
hạn bởi đồ thị các hàm số y= f(x), y = g(x) và hai đường thẳng x = a, x = b (a < b) được tính theo
công thức:
A.
( ) ( ) .
b
a
S f x g x dx=−
B.
( ) ( ) .
b
a
S f x g x dx
=−

Trang 25
C.
( ) ( ) .
b
a
S f x g x dx=−
D.
( ) ( ) .
b
a
S f x g x dx=−
Lời giải
Chọn A.
Câu 11: Trong không gian Oxyz cho
2AO k i j= − +
. Tọa độ điểm A là?
A.
( )
1; 1; 2A −−
. B.
(2; 1;1)A −
. C.
( 2;1; 1)A −−
. D.
( 1;1;2)A −
.
Lời giải
Chọn A.
2 2 2 (1; 1; 2)AO k i j i j k OA i j k A= − + = − + + = − − − −
.
Câu 12: Khẳng định nào sau đây sai?
A.
1
d lnx x C
x
=+
. B.
5
4
d
5
x
x x C=+
. C.
0dxC=
. D.
e d e
xx
xC=+
.
Lời giải
Chọn A.
Câu 13: Cho cấp số nhân
( )
n
u
có
1
2u =−
và công bội
3q =
. Giá trị của
11
u
là:
A.
11
118098u =−
. B.
11
3072u =
. C.
11
354294u =−
. D.
2
354294u =
.
Lời giải
Chọn A.
Số hạng
2
u
là
( )
10 10
21
. 2 3 118098u u q= = − = −
Câu 14: Trong không gian Oxyz cho ba mặt phẳng
2 6 0x y z+ − − =
;
2 3 13 0x y z− + + =
;
3 2 3 16 0x y z− + + =
cắt nhau tại điểm A. Tọa độ của A là?
A.
( 1;2; 3).A −−
B.
(1; 2;3).A −
C.
( 1; 2; 3).A − − −
D.
(1;2;3).A
Lời giải
Chọn A.
Tọa độ điểm A là nghiệm của hệ phương trình:
2 6 0 1
2 3 13 0 2 ( 1;2; 3)
3 2 3 16 0 3
x y z x
x y z y A
x y z z
+ − − = = −
− + + = = − −
− + + = = −
.
Câu 15: Tập xác định của hàm số
( )
2
4
e
yx
−
=−
là:
A.
( )
2;2D =−
. B.
\ 2;2D =−
.
C.
D =
. D.
( ) ( )
; 2 2; .D = − − +
Lời giải
Chọn A.
Câu 16: Đồ thị hàm số
2
2
6 5 1
2 9 5
xx
y
xx
−+
=
+−
có bao nhiêu đường tiệm cận đứng?
A. 1. B. 3. C. 4. D. 2.
Lời giải
Chọn A.
Câu 17: Cho ba số dương a, b, c và a khác 1. Khẳng định nào sau đây là sai?
A.
ln
log
ln
a
a
b
b
=
. B.
( )
log log log .
a a a
bc b c=+
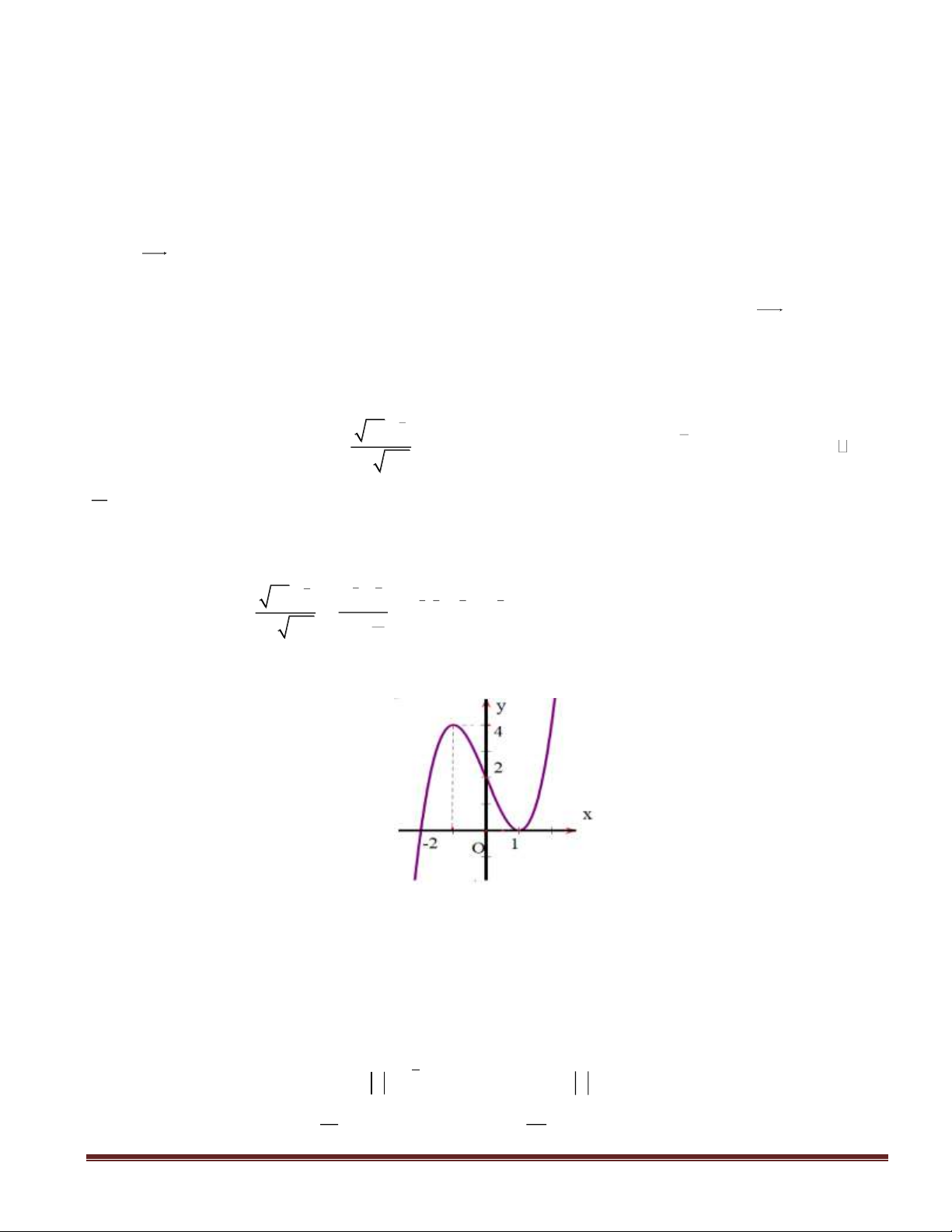
Trang 26
C.
log log
aa
bb
=
. D.
log
a
b
ab=
.
Lời giải
Chọn A.
Câu 18: Trong không gian Oxyz, cho hai điểm
(1; 1;2)A −
và
(3;3;0)B
. Điểm nào sau đây thuộc
mặt phẳng trung trực của đoạn thẳng AB?
A.
(1;2;2)M
. B.
(1;1; 1)M −
. C.
(1;1;1)M
. D.
(1; 2;2)M −
.
Lời giải
Chọn A.
Ta có
(2;4; 2)AB =−
.
Gọi M là trung điểm AB. Khi đó
(2;1;1)M
.
Mặt phẳng trung trực của đoạn thẳng AB là mặt phẳng đi qua điểm M và nhận
AB
làm VTPT
nên có phương trình là:
2( 2) 4( 1) 2( 1) 0 2 3 0x y z x y z− + − − − = + − − =
.
(1;2;2)M
thuộc mặt phẳng trung trực của đoạn thẳng AB.
Câu 19: Rút gọn biểu thức
7
3
5
3
7
42
.
.
aa
A
aa
−
=
với
0a
ta được kết quả
m
n
Aa=
, trong đó
m
,
*
n
và
m
n
là phân số tối giản. Khẳng định nào sau đây đúng?
A.
2
2 15mn+=
. B.
22
43mn+=
. C.
2
3 2 2mn−=
. D.
22
25mn+=
.
Lời giải
Chọn A. Ta có:
7
3
5
3
7
42
.
.
aa
A
aa
−
=
57
33
2
4
7
.
.
aa
aa
−
=
5 7 2
4
3 3 7
a
+ − +
=
2
7
a=
2
7
m
n
=
=
2
2 15mn + =
.
Câu 20: Cho hàm số
()y f x=
có đạo hàm liên tục trên R và đồ thị hàm số
()y f x
=
như hình vẽ.
Khẳng định sau đây là sai?
A. Hàm số
( )
y f x=
nghịch biến trên khoảng
( 1;1)−
B. Hàm số
( )
y f x=
đồng biến trên khoảng
( 2; 1)−−
C. Hàm số
( )
y f x=
đồng biến trên khoảng
(1; )+
D. Hàm số
( )
y f x=
nghịch biến trên khoảng
( ; 2)− −
Lời giải
Chọn A.
Câu 21: Cho số phức
z
thỏa mãn
2 7 3z z i z− = − + +
. Tính
z
?
A. 5. B.
13
4
. C.
25
4
. D. 3.

Trang 27
Lời giải
Chọn A.
Giả sử
( , )z x yi x y R= +
. Ta có:
22
2 7 3 2 2 7 ( 3)z z i z x y x yi x y i− = − + + = + − + = − + + +
22
4
27
3
23
x
x y x x
y
yy
=
+ − = − +
=
=+
. Vậy
5z =
.
Câu 22: Cho mặt phẳng
( ):3 4 5 2 0P x y z+ + + =
và đường thẳng
d
là giao tuyến của hai mặt
phẳng
( ): 2 1 0xy
− + =
;
( ): 2 3 0xz
− − =
. Gọi
là góc giữa đường thẳng
d
và mặt phẳng
()P
.
Khi đó
=
?
A. 60°. B. 45°. C. 30°. D. 90°.
Lời giải
Chọn A.
Đường thẳng d có phương trình:
2
1
,( )
2
3
2
xt
y t t R
zt
=
=
= − +
. Suy ra VTCP của
d
là
(2;1;1)
d
u =
Ta có:
2 2 2 2 2 2
.
2.3 1.4 1.5
3
sin( ,( )) cos( , )
2
.
2 1 1 . 3 4 5
d
d
d
un
d P u n
un
++
= = = =
+ + + +
( ,( )) 60dP=
.
Câu 23: Họ nguyên hàm của hàm số
( )
2
43
32
x
fx
xx
−
=
−+
là:
A.
( )
1
4ln 2 ln
2
x
F x x C
x
−
= − − +
−
. B.
( )
1
4ln 2 ln
2
x
F x x C
x
−
= − + +
−
.
C.
( )
2
4ln 2 ln
1
x
F x x C
x
−
= − − − +
−
. D.
( )
2
4ln 2 ln
1
x
F x x C
x
−
= − − +
−
.
Lời giải
Chọn A.
Câu 24: Cho hàm số
2
2
mx
y
xm
+
=
+
,
m
là tham số thực. Gọi
S
là tập hợp tất cả các giá trị nguyên
của tham số
m
để hàm số nghịch biến trên khoảng
( )
0;1
. Tìm số phần tử của
S
.
A.
2
. B.
5
. C.
1
. D.
3
.
Lời giải
Chọn A.
Tập xác định
\
2
m
D
=−
( )
2
2
4
2
m
y
xm
−
=
+
.

Trang 28
Yêu cầu bài toán
( )
2
40
0;1
2
m
m
−
−
22
0
2
1
2
m
m
m
−
−
−
22
0
2
m
m
m
−
−
02m
.
Câu 25: Một hình nón có đường kính đáy là
23a
, góc ở đỉnh là
0
120
. Tính thể tích của khối nón
đó theo
a
.
A.
3
a
. B.
3
3 a
. C.
3
3a
. D.
3
23a
.
Lời giải
Chọn A.
Gọi
S
là đỉnh hình nón,
O
là tâm đáy,
A
là một điểm thuộc đường tròn đáy.
Theo giả thiết dễ suy ra đường tròn đáy có bán kính
3(cm)R OA a==
và góc
0
0
120
60
2
ASO ==
. Xét tam giác
SOA
vuông tại
O
, ta có
0
3
tan60
3
OA a
SO a= = =
. Do đó
chiều cao hình nón là
ha=
.
Vậy thể tích khối nón là
2 2 3
11
.3 .
33
V R h a a a
= = =
.
Câu 26: Cho
( )
2
1
2f x dx
−
=
và
4
2
2
2
x
g dx
−
=−
. Tính
( ) ( )
2
1
23I x f x g x dx
−
= + −
?
A.
17
2
I =
. B.
11
2
I =
. C.
23
2
I =
. D.
5
2
I =
.
Lời giải
Chọn A.
Câu 27: Ông An có tất cả 20 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 2 triệu
đồng một tháng thì mọi căn hộ đều có người thuê. Nhưng cứ mỗi lần tăng giá cho thuê mỗi căn hộ
thêm chẵn 200 nghìn đồng thì có thêm 1 căn hộ bị bỏ trống. Hỏi khi tăng giá lên mức mỗi căn bao
nhiêu tiền một tháng thì ông An thu được tổng số tiền nhiều nhất trên một tháng?
A. 3 triệu đồng. B. 2,4 triệu đồng. C. 2 triệu đồng. D. 3,4 triệu đồng.
Lời giải
Chọn A.
Gọi x là số lần tăng
200
nghìn đồng
( )
0x >
để ông An thu được tổng số tiền nhiều nhất trên một
tháng.
Khi đó ông An cho thuê được số phòng là:
( )
20 x-
phòng.
Tổng số tiền ông An thu được trên một tháng là:
( )( )
( )
2
20 2.000.000 200.000 200.000 10 200x x x x- + = - + +
( )
2
200.000 5 225 45.000.000x
éù
= - - + £
êú
ëû
Dấu
'' ''=
xảy ra khi và khi
5.x =
Vậy ông An thu được tổng số tiền nhiều nhất trên một tháng khi ông tăng giá lên mức mỗi căn
3
triệu đồng một tháng.
Câu 28: Trong mặt phẳng phức, gọi A, B, C, D lần lượt là các điểm biểu diễn các số phức
1 2 3 4
1, 1 , 2 5 , 2.z z i z i z= − = − + = + =
Gọi S là diện tích tứ giác ABCD. Tính S?
A. S =
9
. B. S =
6
. C. S =
12
. D. S =
18
.
Lời giải
Chọn A.
Trang 29
Ta có
( 1;0); ( 1;1); (2;5); (2;0)A B C D− − →
ABCD là hình thang vuông tại A và D.
( ) ( )
. 1 5 .3
9
22
ABCD
AB CD AD
S
++
= = =
.
Câu 29: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều,
()SA ABC⊥
. Gọi
()P
là mặt
phẳng qua
B
và vuông góc với
SC
. Thiết diện của
()P
và hình chóp
.S ABC
là:
A. Tam giác vuông B. Tam giác đều C. Tam giác cân D. Hình thang vuông
Lời giải
Chọn A.
Gọi
I
là trung điểm cảu
AC
, kẻ
IH SC⊥
.
Ta có
BI AC⊥
,
.BI SA BI SC⊥⊥
Do đó
()SC BIH⊥
hay thiết diện là tam giác
BIH
.
Mà
BI SAC⊥
nên
BI IH⊥
hay thiết diện là tam giác vuông.
Câu 30: Tập nghiệm của bất phương trình
( )
2
2
log 3 1 0xx− +
là
A.
3 5 3 5
0; ;3
22
S
−+
=
. B.
3 5 3 5
0; ;3
22
S
−+
=
.
C.
3 5 3 5
;
22
S
−+
=
. D.
S =
.
Lời giải
Chọn A.
Điều kiện:
2
3 1 0xx− +
35
2
x
−
hoặc
35
2
x
+
.
Bất phương trình tương đương
2
3 1 1xx− +
2
30xx −
03x
Kết hợp với điều kiện ta được
3 5 3 5
0; ;3
22
x
−+
.
Câu 31: Có bao nhiêu phương trình tiếp tuyến của đồ thị hàm số
42
43y x x= − −
biết tiếp tuyến
vuông góc với đường thẳng
4 3 0xy+ + =
.
A. 3. B. 1. C. 2. D. 0.
Lời giải
Chọn A.
( ) ( )
4 2 3
4 3 ' 4 8y f x x x f x x x= = − − = −
Trang 30
Gọi
( )
,
MM
M x y
là tiếp điểm thì
( )
1
1
'1
15
4
2
M
M
M
x
fx
x
=−
− = −
=
.
Câu 32: Trong không gian
Oxyz
, cho đường thẳng
1 1 1
:
2 2 1
x y z
d
− − +
==
−
và điểm
(1;2;3)I
. Gọi
K
là điểm đối xứng với
I
qua
d
. Lập phương trình mặt cầu
()S
tâm
K
cắt
d
tại hai điểm
A
và
B
biết đoạn
4AB =
là:
A.
2 2 2
1 8 41 185
( ): .
9 9 9 9
S x y z
− + + + + =
B.
2 2 2
1 8 41 293
( ): .
9 9 9 9
S x y z
+ + − + − =
C.
2 2 2
1 8 41 149
( ): .
9 9 9 9
S x y z
− + + + + =
D.
2 2 2
1 8 41 230
( ): .
9 9 9 9
S x y z
+ + − + − =
Lời giải
Chọn A.
Gọi
(1 2 ;1 2 ; 1 )H t t t+ + − −
là hình chiếu vuông góc của
I
trên
d
.
( )
2 ; 1 2 ; 4 tIH t t= − + − −
;
(2;2; 1);
d
u =−
2
9
d
IH u t
−
⊥ =
.
Vậy:
5 5 7
( ; ; )
9 9 9
H
−
. Vì
K
đối xứng với
I
qua
d
nên
1 8 41
; ; .
9 9 9
K
−−
Khoảng cách từ
K
đến
d
là
149
3
HK =
, bán kính mặt cầu
185
3
R =
.
Vậy: mặt cầu
()S
có phương trình là:
2 2 2
1 8 41 185
9 9 9 9
x y z
− + + + + =
.
Câu 33: Cho các số phức
,wz
khác 0 và thõa mãn
2z w z w− = =
. Phần thực của số phức
z
u
w
=
là:
A.
1
8
a =
. B.
1
4
a =−
. C.
1
4
a =
. D.
1
8
a =−
.
Lời giải
Chọn A.
Ta có:
1
1
2
2
2 (*)
11
1
z
u
w
z w z w
zw
u
w
=
=
− = =
−
−=
=
Giả sử
,( , )u a bi a b R= +
. Khi đó
22
22
1
(*) (**)
4
( 1) 1
ab
ab
+=
− + =
.
Từ
11
(**) 2a 1 1
48
a − + = − =
.
Câu 34: Cho hàm số
( )
y f x=
liên tục trên
¡
, có đồ thị như hình vẽ.

Trang 31
Các bao nhiêu giá trị của tham số
m
để phương trình
( )
( )
3
2
2
4
3
25
mm
fx
fx
+
=+
+
có
3
nghiệm phân biệt
là?
A. 1. B. 5. C. 2. D. 0.
Lời giải
Chọn A.
Ta có
( )
( ) ( ) ( )
( )
( )
3
3
3
2 2 2
2
4
3 2 2 2 5 2 5.
25
mm
f x m m f x f x
fx
+
= + Û + = + + +
+
Xét hàm
( )
3
g t t t=+
và đi đến kết quả
( )
( )
2
2
2
25
2 5 2 .
45
2
m
f x m
m
fx
ì
ï
³
ï
ï
ï
+ = Û
í
-
ï
=
ï
ï
ï
î
Ta có
( )
( ) ( )
( ) ( )
2
2
2
2
45
1
45
2
.
2
45
2
2
m
fx
m
fx
m
fx
é
-
ê
=
ê
-
ê
=Û
ê
ê
-
=-
ê
ê
ë
Với điều kiện
5
2
m ³
thì phương trình
( )
2
luôn có
một nghiệm duy nhất, để phương trình đã cho có
3
nghiệm phân biệt
Û
( )
1
có
2
nghiệm phân
biệt khác nghiệm của phương trình
( )
2
¾ ¾ ¾®
ñoà thò
22
2
4 5 4 5 37 37
4 16 .
2 2 4 2
mm
mm
--
= Û = Û = Þ =
Vậy
có 1 giá trị m thỏa mãn.
Câu 35: Trong không gian với hệ tọa độ
Oxyz
cho mặt phẳng
( ): 2 2 7 0P x y z+ + + =
và ba điểm
(1;2; 1), (3;1; 2), (1; 2;1)ABC− − −
. Điểm
( ; ; ) ( )M a b c P
sao cho
2 2 2
MA MB MC−−
đạt giá trị lớn
nhất. Khi đó tổng
A a b c= + +
bằng bao nhiêu?
A.
20
9
A =−
. B.
14
9
A =
. C.
20
9
A =
. D.
14
9
A =−
.
Lời giải
Chọn A.
Ta có:
2 2 2 2
2 2 2 2
2 2 2 2
( 1) ( 2) ( 1)
( 3) ( 1) ( 2)
( 1) ( 2) ( 1)
MA a b c
MB a b c
MC a b c
= − + − + +
= − + − + +
= − + + + −
( )
2
2 2 2 2 2 2 2 2
6 6 14 4 3 ( 3)MA MB MC a a b b c a b c
− − = − + − − − − = − − + + +
Vậy
2 2 2 2 2 2
max min
min
( ) ( 3) ( 3)MA MB MC a b c MI
− − − + + +
với
(3; 3;0)I −
.
Mà
(3; 3;0)I −
cố định nên
min
MI M
là hình chiếu của
I
trên mặt phẳng
()P
.
Gọi
()d
là đường thẳng qua
(3; 3;0)I −
và vuông góc với mặt phẳng
()P
, ta có:
Trang 32
3
( ): 3 2
2
xt
d y t
zt
=+
= − +
=
Vì
( ) (3 ; 3 2 ;2 ).M d M t t t + − +
4 23 35 8
( ) (3 ) 2( 3 2 ) 2(2 ) 7 0 ( ; ; )
9 9 9 9
M P t t t t M
− − −
+ + − + + + = =
20
9
abc + + = −
.
Câu 36: Bạn
A
muốn làm một chiếc thùng hình trụ không đáy từ nguyên liệu là mảnh tôn hình
tam giác đều
ABC
có cạnh bằng
( )
90 cm
. Bạn muốn cắt mảnh tôn hình chữ nhật
MNPQ
từ mảnh
tôn nguyên liệu để tạo thành hình trụ có chiều cao bằng
MQ
. Thể tích lớn nhất của chiếc thùng
mà bạn A có thể làm được là
A.
( )
3
13500. 3
cm
. B.
( )
3
91125
cm
2
. C.
( )
3
108000 3
cm
. D.
( )
3
91125
cm
4
.
Lời giải
Chọn A.
Gọi
I
là trung điểm
BC
. Suy ra
I
là trung điểm
MN
. Đặt
MN x=
,
( )
0 90x
.
Ta có:
MQ BM
AI BI
=
( )
3
90
2
MQ x = −
; gọi
R
là bán kính của trụ
2
x
R
=
.
Thể tích của khối trụ là:
( )
( )
2
32
33
90 90
2 2 8
T
x
V x x x
= − = − +
Xét
( )
( )
32
3
90
8
f x x x
= − +
với
0 90x
.
( )
( )
2
3
3 180
8
f x x x
= − +
,
( )
0
0
60
x
fx
x
=
=
=
.
Khi đó suy ra
( ) ( )
(0;90)
13500. 3
max 60
x
f x f
==
.
Câu 37: Cho tứ diện đều
ABCD
cạnh
a
. Gọi
M
là trung điểm của
BC
. Tính cô-sin góc giữa hai
đường thẳng
AB
và
DM
?
A.
3
6
. B.
3
2
. C.
3
3
. D.
1
2
.
Lời giải
Chọn A.
N
P
Q
I
B
C
A
M
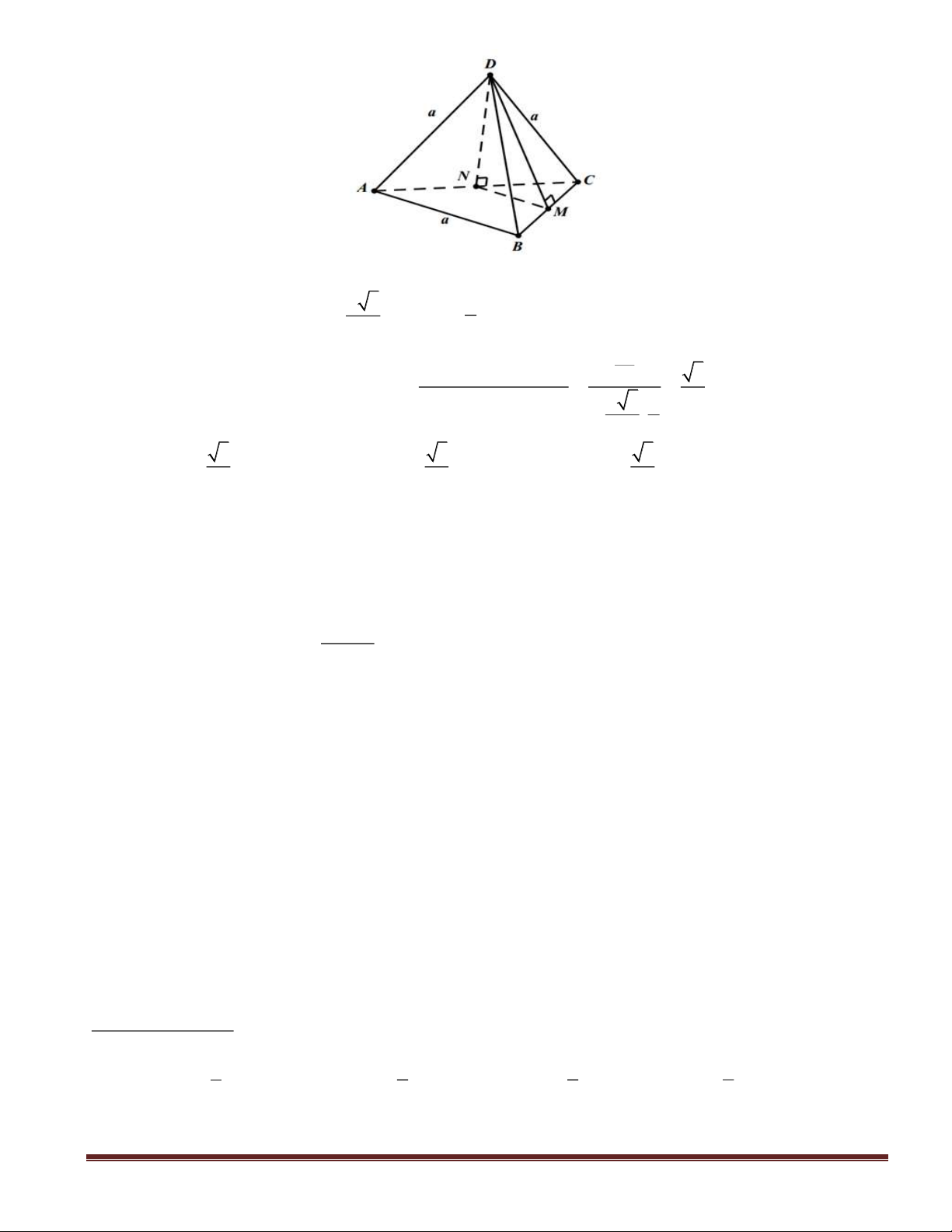
Trang 33
Gọi
N
là trung điểm của
AC
. Khi đó,
//AB MN
nên
( , ) ( , )DM AB DM MN=
.
Dễ dàng tính được
3
2
a
DM DN==
và
2
a
MN =
.
Trong tam giác
DMN
, ta có
2
2 2 2
3
4
cos
2 . 6
3
2. .
22
a
DM MN DN
DMN
DM MN
aa
+−
= = =
.
Vì
3
cos 0
6
DMN =
nên
3
cos(DM,MN)
6
=
. Vậy
3
cos( , )
6
DM AB =
.
Câu 38: Cho tập hợp
1;2;3;4;5;6 .S =
Gọi M là tập hợp các số tự nhiên có 6 chữ số đôi một khác
nhau lấy từ S sao cho tổng chữ số các hàng đơn vị, hàng chục và hàng trăm lớn hơn tổng chữ số
các hàng còn lại là 3. Tính tổng T của các phần tử của tập hợp M.
A. T = 36011952 B. T = 11003984 C. T = 12003984 D. T = 18005967
Lời giải
Chọn A.
Gọi số tự nhiên thỏa mãn là
abcdef
với
, , , , , 1;2;3;4;5;6 .a b c d e f
Do yêu cầu bài toán nên
12, 9d e f a b c+ + = + + =
hay
( )
; ; (1;2;6),(1;3;5),(2;3;4)abc
và
( )
; ; (3;4;5),(2;4;6),(1;5;6)d e f
tương ứng.
Xét hai bộ
(1;2;6)
và (3;4;5) thì ta lập được 3!.3!= 36 số, trong đó các chữ số 1,2,6 có mặt ở hàng
trăm
Nghìn 36 : 3 =12 lần, hàng chục nghìn 12 lần, hàng nghìn 12 lần và các chữ số 3,4,5 cũng có mặt
ở hàng trăm, chục, đơn vị 12 lần.
Tổng các số trong trường hợp này là:
( ) ( ) ( )
( ) ( )
5 4 3
2
12. 1 2 6 .10 12. 1 2 6 .10 12. 1 2 6 .10
12.(3 4 5).10 12. 3 4 5 .10 12. 3 4 5 .1 12003984
+ + + + + + + +
+ + + + + + + + + =
Tương tự ở hai cặp còn lại ta cũng có tổng các số bằng 12003984.
Khi đó tổng các phần tử của M là 12003984.3 = 36011952
Câu 39:Cho hàm số f(x) có đạo hàm liên tục và nhận giá trị không âm trên đoạn
0;1
thỏa mãn
( ) ( )
( )
22
2
2
.'
1
x
f x f x
fx
e
=+
, với mọi
0;1x
. Biết f(0) = 1. Mệnh đề nào dưới đây đúng?
A.
( )
5
1 ;3
2
f
B.
( )
7
1 3;
2
f
C.
( )
5
1 2;
2
f
D.
( )
3
1 ;2
2
f
Lời giải:
Chọn A.

Trang 34
Theo giả thiết có
( )
'fx
0, 0;1x
và
( ) (0) 1f x f=
( )
0;1x
.
Lấy căn hai vế đẳng thức đã cho có
( )
( )
2
2
. '( ) ( ). '
1 ( )
1 ( )
x
x
f x f x f x f x
f x e
e
fx
= + =
+
.
Do đó lấy tích phân hai vế trên đoạn
0;1
có:
( )
11
1
2
2
0
00
22
22
2
( ). '( )
1 ( ) 1
1 ( )
1 (1) 1 (0) 1 (1) ( 1 2) 1
5
1 ( 1 2) 1 ;3 .
2
x
f x f x
dx e dx f x e
fx
f f e f e
fe
= + = −
+
+ − + = − = − + −
= − + −
Câu 40: Cho hình chóp S.ABC. Một mặt phẳng song song với mặt đáy (ABC) cắt các cạnh bên
SA, SB, SC lần lượt tại M, N, P. Kí hiệu M’, N’, P’ lần lượt là hình chiếu vuông góc của M, N, P
lên mặt phẳng đáy (ABC). Tìm tỉ số
SM
SA
để thể tích khối đa diện MNP.M’N’P’ lớn nhất.
A.
SM
SA
=
2
3
B.
SM
SA
=
1
4
C.
SM
SA
=
3
4
D.
SM
SA
=
1
3
Lời giải:
Chọn A.
Kí hiệu
SM
SA
= x ( 0< x< 1), Theo Ta-lét ta có
MN NP MP SM
x
AB BC CA SA
= = = =
và
(M,(ABC))
1
( ,(ABC))
d AM
x
d S AS
= = −
vì vậy
2
.
MNP ABC
S x S=
và
( ,(ABC)) (1 ). ( ,( ))d M x d S ABC=−
Do đó
22
. ' ' ' .
. ( ,( )) (1 ). . ( ,( )) 3 (1 ).
MNP M N P MNP ABC S ABC
V S d M ABC x x S d S ABC x x V= = − = −
Sử dụng bất đẳng thức AM – GM ta có :
23
1 1 2 2 4
(1 ) . .(2 2 ) ( )
2 2 3 27
x x x
x x x x x
+ + −
− = − =
Vì vậy
. ' ' ' .
4
9
MNP M N P S ABC
VV
Dấu bằng xảy ra
2
22
3
x x x = − =
Câu 41: Một bồn hoa hình elip tâm O có độ dài trục lớn bằng 6m, độ dài trục nhỏ bằng 4m. Người
ta chia bồn hoa thành 4 phần
1 2 3 4
, , ,S S S S
bởi hai Parabol có cùng đỉnh O đối xứng qua O như hình
vẽ bên dưới:
Hai đường Parabol này cắt đường elip tại bốn điểm A, B, C, D tạo thành một hình chữ nhật có
3 3 , 2 .AB m AD m==
Biết kinh phí để trồng hoa trên các phần
1
S
và
2
S
là 100.000 đồng/1m
2
,

Trang 35
kinh phí để trồng hoa trên các phần
34
,SS
là 120.000 đồng/1m
2
. Hỏi số tiền để trồng bồn hoa gần
nhất với số tiền nào sau đây?
A. 1.980.000 đồng. B. 1.900.000 đồng. C. 2.050.000 đồng D. 2.100.000 đồng.
Lời giải
Chọn A. Phương trình elip với độ dài trục lớn 6m và độ dài trục nhỏ 4m là
22
1
94
xy
+=
Phương trình elip phía trên trục hoành là
2
21
9
x
y =−
; phần phía dưới trục hoành là
2
21
9
x
y = − −
Diện tích của hình elip là:
2
3
2 2 2
3
21
9
: 2 1 2 1 2 1 6 .
9 9 9
3; 3
oo
x
y
x x x
S y S dx
xx
−
=−
= − − = − − − − =
= − =
Vì
2
3 3 3 3
4
33
;
22
27
2
1
AB
AB
AB
xx
yx
AD
yy
−
=
==
=
=
==
là parabol qua các điểm O, A, B.
Diện tích hình phẳng
2
33
2
2
22
1 1 2
33
2
21
9
4 4 4 3
: 2 1 .
27 27 9 2
3 3 3 3
;
22
x
y
x
S y x S S x dx
xx
−
=−
+
= = = − − =
−
==
Vì vậy
3 4 0 1
2 2 3.S S S S
+ = − = −
Kinh phí trồng hoa
( ) ( )
1 2 3 4
.100.000 .120.000 1.975.978S S S S+ + +
đồng.
Câu 42: Cho hình chóp S.ABC có đáy là tam giác vuông tại A,
2 , 2 3AB a AC a==
. Tam giác
SAB đều và nằm trong mặt phẳng vuông góc cới đáy. Điểm M thuộc cạnh BC sao cho
1
4
BM BC=
Cosin góc giữa hai mặt phẳng (SAM) và (SAC) bằng :
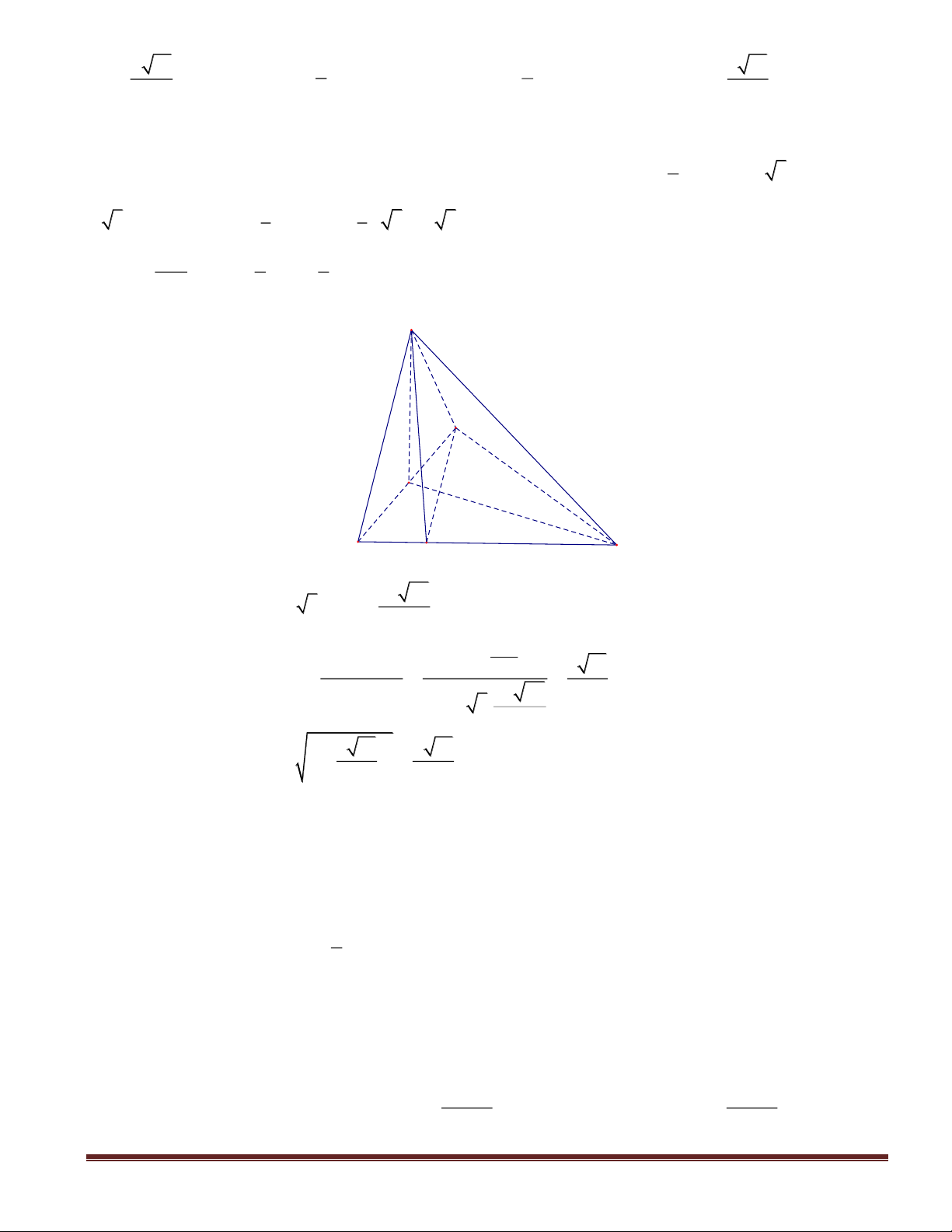
Trang 36
A.
2 13
13
B.
3
5
C.
4
5
D.
3 13
13
Lời giải:
Chọn A.
Gọi H là trung điểm cạnh AB
SH
⊥
AB
SH
⊥
(ABC) và
1
. 2 3
2
ABC
S AB AC==
2
a
và SH =
3a
. Vì vậy
23
.
11
.S 3.2 3 2
33
S ABC ABC
V SH a a a= = =
và
33
..
33
. .2 .
42
S AMC S ABC
CM
V V a a
CB
= = =
Ta có SA = 2a,
2
2
39
2 3,
4
SAC SAM
a
S a S==
Do đó sin((SAM),(SAC)) =
3
.
2
2
3
3.2 .
3.
3 13
2
2 . 13
39
2.2 3.
4
S AMC
SAC SAM
a
a
SAV
SS
a
a
==
Vậy cos
2
3 13 2 13
(( ),(SAC)) 1 ( )
13 13
SAM = − =
Câu 43: Có bao nhiêu số nguyên m
2019;2−
để phương trình:
35
( 1) log (4 1) log (2 1) 2x x x x m− + + + = −
có đúng hai nghiệm thực?
A. 2022 B. 2021 C. 2 D. 1
Lời giải:
Chọn A.
Điều kiện :
4 1 0
1
2 1 0
4
x
x
x
+
−
+
Nếu
12xm= =
phương trình trở thành:
35
35
1
( 1) log (4 1) log (2 1) 2( 1)
log (4 1) log (2 1) 2
x
x x x x
xx
=
− + + + = −
+ + + =
(phương trình có hai nghiệm nên m = 2 thỏa mãn)
Nếu
3 5 3 5
22
1; 2 log (4 1) log (2 1) log (4 1) log (2 1) 0
11
x m x m
x m x x x x
xx
−−
+ + + = + + + − =
−−
(1)
S
B
C
A
H
M
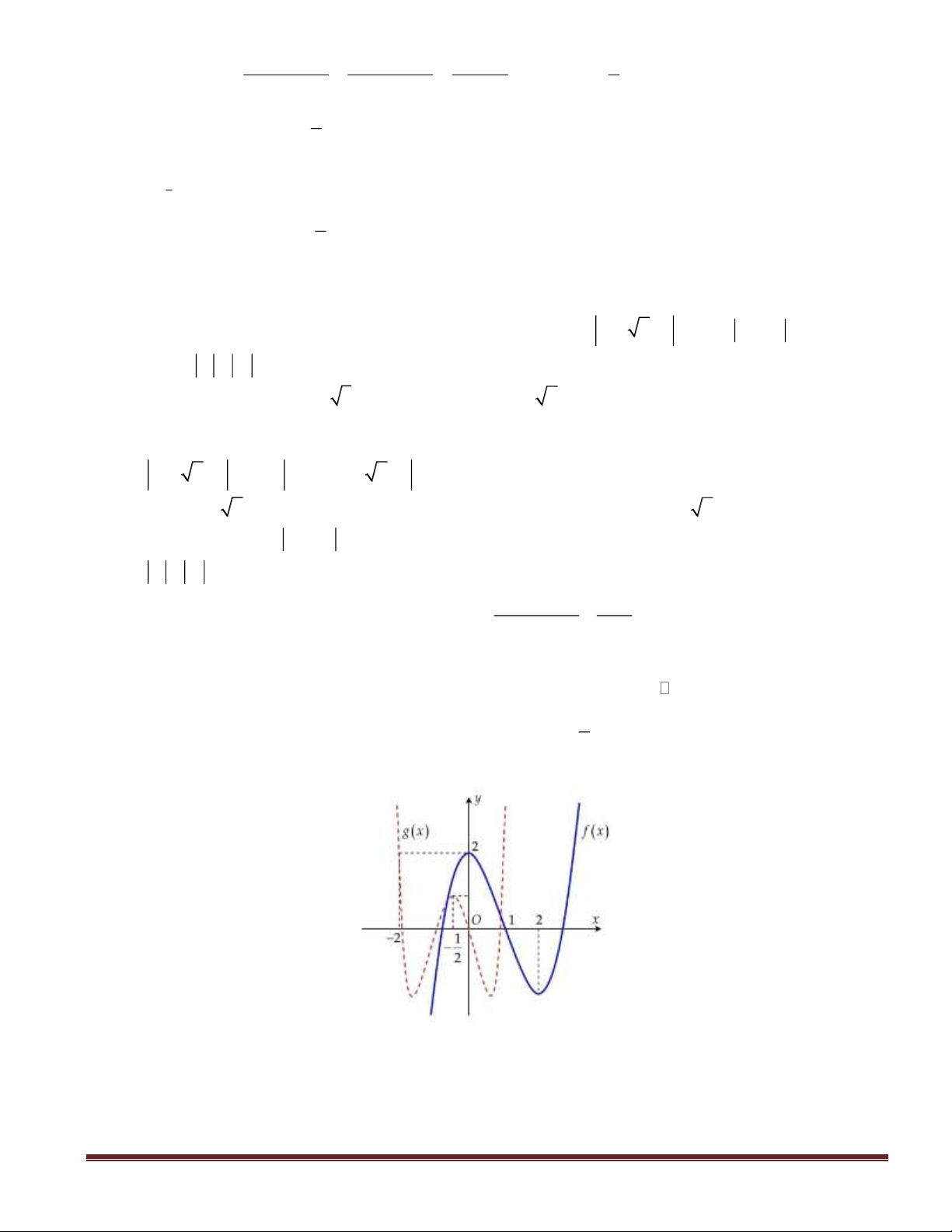
Trang 37
Xét hàm số
2
4 2 2 1
(x) 0, x ( ; ) \ 1 ; 2
(4 1)ln3 (2 1)ln5 4
( 1)
m
fm
xx
x
−
= + + − +
++
−
Do đó trên mỗi khoảng
( )
1
;1 ; 1;
4
− +
phương trình có tối đa một nghiệm
Ta có
( ) ( ) ( )
11
1
4
lim ;lim ;lim ;lim
x
xx
x
f x f x f x
+ − +
→
→→
→−
= − = + = − = +
Do đó trên mỗi khoảng
( )
1
;1 ; 1;
4
− +
phương trình (1) có một nghiệm thực duy nhất, vậy với
mọi
2m
phương trình (1) có hai nghiệm thực.
Vậy
2019;2m−
có tất cả 2022 số nguyên thỏa mãn.
Câu 44: Giả sử
12
,zz
là hai trong số các số phức
z
thỏa mãn
21iz i+ − =
và
12
2zz−=
. Giá trị
lớn nhất của
12
zz+
bằng?
A. 4. B.
23
. C.
32
. D. 3.
Lời giải
Chọn A.
Ta có:
2 1 ( ) 2 1iz i i x yi i+ − = + + − =
(với
( ; )z x yi x y R= +
)
22
( 1) ( 2) 1 ( ; )x y M x y − + − =
biểu diễn
z
thuộc đường tròn tâm
(1; 2)I
bán kính
1R =
.
Giả sử
12
( ); ( )A z B z
. Do
12
2 2 2z z AB R− = = =
nên
AB
là đường kính của đường tròn
( )
;IR
.
Lại có
12
z z OA OB+ = +
.
Mặt khác theo công thức trung tuyến ta có:
2 2 2
2 2 2
8
24
OA OB AB
OI OA OB
+
= − + =
.
Theo BĐT Bunhiascopky ta có
( )
2 2 2
2 ( ) 4OA OB OA OB OA OB+ + +
.
Câu 45: Cho hàm số bậc ba
( )
fx
và
( )
( )
( )
2
,,g x f mx nx p m n p= + +
có đồ thị như hình dưới
(đường nét đứt là đồ thị của hàm
( )
,gx
đường thẳng
1
2
x =−
là trục đối xứng của đồ thị hàm số
( )
g x ).
Giá trị của biểu thức
( )( )( )
2 4 3P n m m p p n= + − +
bằng bao nhiêu?
A.
36.P =−
B.
24.P =−
C.
26.P =
D.
24.P =
Lời giải
Chọn A.
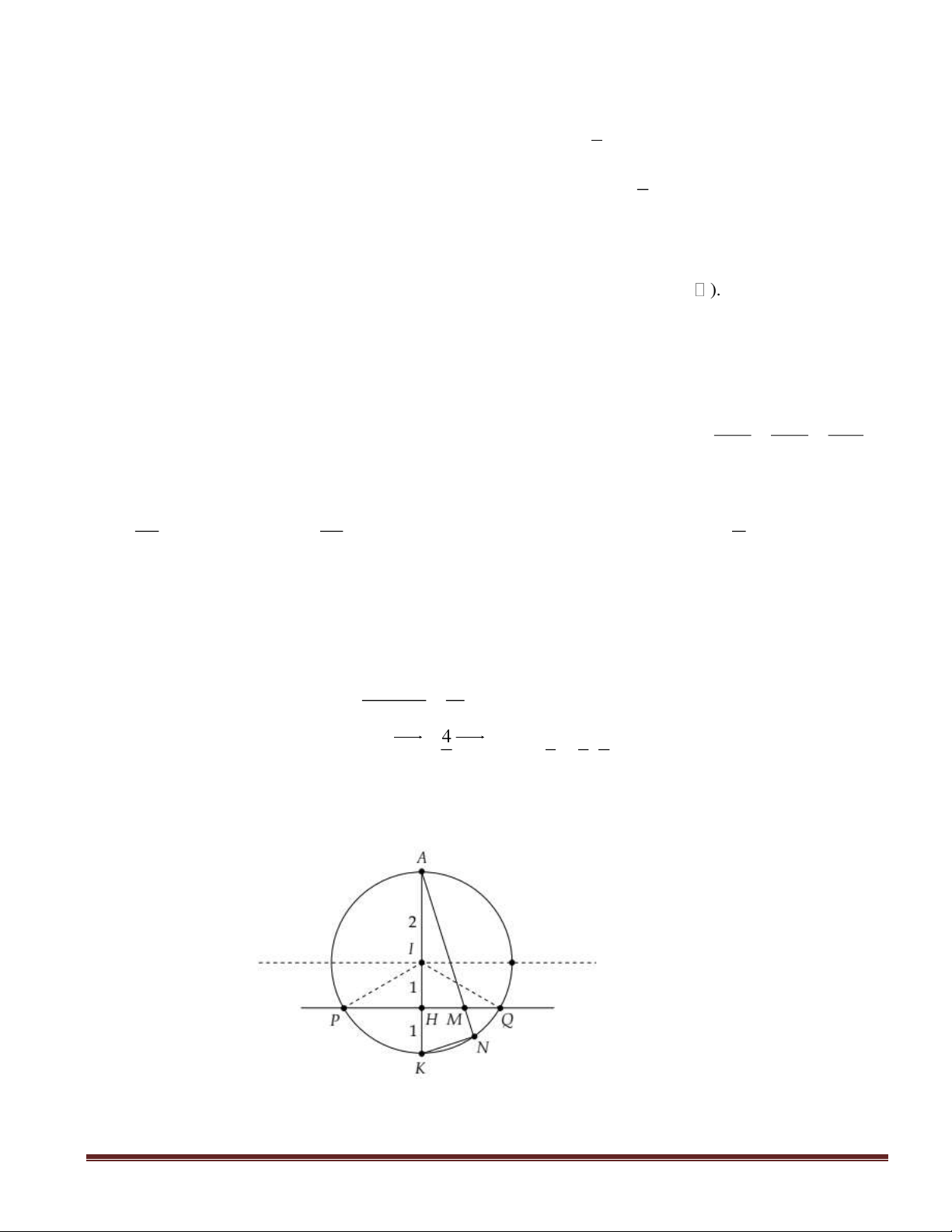
Trang 38
- Đầu tiên thấy rằng đồ thị hàm bậc ba
( )
fx
có hai điểm cực trị
( ) ( )
0;2 , 2; 2−
nên ta dễ dàng tìm
được
( )
32
f x x 3x 2= − +
(không làm được điều này bạn nên học lại kĩ phần cơ bản).
- Ta thấy đồ thị
( )
gx
có một điểm cực trị cho dữ liệu là
1
x
2
=−
nên ta nghĩ đến việc phải tính đạo
hàm
( ) ( )
( )
2
f ' mxg' x 2 x p ,mx n n++=+
tinh ý ta nhận ra rằng
1
x
2
=−
là nghiệm của phương trình
2mx n 0+=
(tại sao), điều này dẫn đến
m n.=
- Lúc này
( )
( ) ( ) ( )
32
2 2 2
g x f mx mx p mx mx p 3 mx mx p 2= + + = + + − + + +
có hệ số tự do là
32
p 3p 2,−+
lại thấy khi
x0=
thì
( )
32
g 0 0 p 3p 2 0 p 1= − + = =
(do
p ).
Tóm lại tới đây ta được
( )
( ) ( )
32
22
g x mx mx p 3 mx mx p 2= + + − + + +
- Thay
x2=−
ta có phương trình
( ) ( )
32
2 4m 2m 1 3 4m 2m 1 2 m 1.= − + − − + + =
Vậy
m n 1==
và
p1=
do đó
( )( )( )
2 4 3 36.P n m m p p n= + − + = −
Câu 46: Trong không gian
Oxyz
, cho điểm
(1;1;4)A
và đường thẳng
2 3 3
:
2 2 1
x y z
d
− + −
==
−
.
Điểm
M
chạy trên đường thẳng
d
và điểm
N
nằm trên tia đối của tia
MA
sao cho
. 12AM AN =
. Quỹ tích điểm
N
là đường cong có độ dài bằng bao nhiêu?
A.
4
3
. B.
2
3
. C.
. D.
3
.
Lời giải
Chọn A.
Gọi
H
là hình chiếu vuông góc của
A
lên đường thẳng
d
, dễ dàng tìm được
(0; 1;2)H −
Dựng một đường thẳng vuông góc với
AN
tại
N
cắt
AH
tại
K
. Khi đó hai tam giác vuông
AHM
và
ANK
đồng dạng với nhau.
. 12
. . 12 4
3
AM AN
AH AK AM AN AK
AH
= = = = =
Suy ra điểm
K
cố định và thỏa mãn:
4 1 5 4
( ; ; )
3 3 3 3
AK AH K= − −
Nhận thấy rằng
( , )N mp A d
;
90 ;ANK AN AM=
quỹ tích điểm
N
là cung tròn giới hạn
bởi đường thẳng
d
và đường tròn đường kính
AK
(nằm trong mặt phẳng chứa
A
và
d
)
Độ dài đường cong chứa
N
chính là độ dài cung tròn PQ như hình vẽ.
Ta có:
1IH =
,
2IP IQ==
.Suy ra:
60 120HIP HIQ PIQ= = =
.
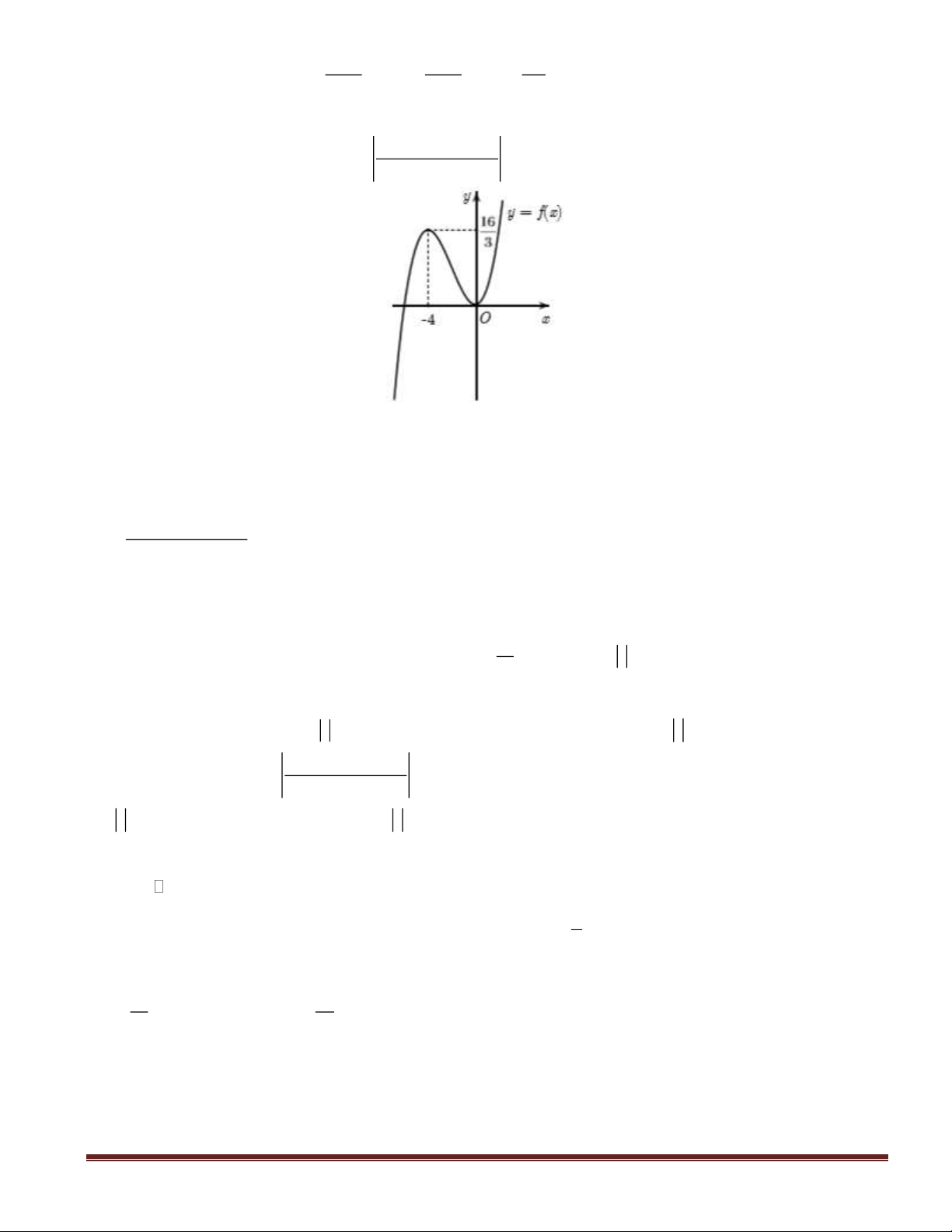
Trang 39
Độ dài cung
PQ
là
120 120 4
.2 . .2 .2
360 360 3
PQ R
= = =
.
Câu 47: Cho hàm số
( )
fx
liên tục trên R và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên
của tham số m để phương trình
( )
2
3sin cos 1
44
2cosx sinx 4
xx
f f m m
− −
= + +
−+
có nghiệm?
A. 4 B. 5 C. Vô số D. 3
Lời giải
Chọn A.
Vì
1 sinx 1; 1 cosx 1− −
nên
2cos sinx 3 2cosx sinx 4 0x− − − +
Đặt
( )
3sin cos 1
3sin cos 1 2cosx sinx 4
2cosx sinx 4
xx
t x x t
−−
= − − = − +
−+
( ) ( )
cos 2 1 sinx 3 4 1x t t t + − + = − −
Phương trình trên có nghiệm khi
( ) ( ) ( )
2 2 2
2 1 3 4 1t t t+ + + − −
2 2 2
9
5 10 10 16 8 1 11 2 9 0 1 0 1
11
t t t t t t t t + + + + − − −
Từ đồ thị hàm số ta thấy hàm số
( )
fx
đồng biến trên (0;1)
Nên phương trình
( )
( )
f x f t=
với
[0;1]t
có nghiệm duy nhất khi
0x t x=
Do đó phương trình
( )
2
3sin cos 1
4
2cosx sinx 4
xx
f f m m
− −
= + +
−+
có nghiệm
2
44t m m = + +
có nghiệm với
01t
( )
2
2
0 4 4 1 2 1 3 1m m m m + + + − −
Mà
m
nên
3; 2; 1 .m − − −
Vậy có 3 giá trị của m thỏa mãn yêu cầu.
Câu 50: Cho hai số thực x,y thỏa mãn
22
2
22
1
3 .log ( ) 1 log (1 )
2
xy
x y xy
+−
− = + −
. Giá trị lớn nhất của
biểu thức P=
( )
33
23x y xy+−
bằng :
A.
13
2
B.
17
2
C.3 D.7
Lời giải:
Chọn A.
Theo điều kiện ta có
0,1 0x y xy− −
và có biến đổi
22
22
22
3 .log ( ) log (2 2 )
xy
x y xy
+−
− = −

Trang 40
( )
22
2 2 2 2 2
22
3 .log 2 2 2 log (2 2 ) 2
xy
x y xy xy x y
+−
+ − + − = − + =
Vì nếu
2 2 0
2
2 3 .log (2 2 )x y VT xy VP+ − =
và
22
2xy+
thì
0
3 .log(2 2xy) VPVT − =
Vậy có
2
2
( ) 2
( ) 2 2 1 2 2
2
xy
x y xy xy x y
+−
+ − = = − +
và
3
2( ) 6 ( ) 3P x y xy x y xy= + − + −
Đặt
( )
2;2t x y= + −
thì
( )
( )
( ) ( )
2
32
2;2
3( 2) 13
2 3 ( 2) max 1
22
t
P f t t t t f t f
−
−
= = − − − = =
Dấu bằng đạt tại
1
1 1 3 1 3
1;
2 2 2
0,1 0
xy
x y xy x y
x y xy
+=
+−
+ = = − = =
− −
Câu 49: Cho hàm số
32
y x x ax b= + + +
cắt trục hoành tại ba điểm phân biệt có hoành độ
3 2 1
x x x
thỏa mãn
( )
2
1 2 3 1 2 2 3 3 1
6 6 3 96 64 48x x x x x x x x x+ + = + +
. Giá trị của biểu thức
11
a
S
b
=
là
A.
1.S =−
B.
2.S =−
C.
2.S =
D.
0.S =
Lời giải
Chọn A.
Ta có:
( )
2
1 2 3 1 2 2 3 3 1
6 6 3 96 64 48x x x x x x x x x+ + = + +
( ) ( )
12
22
2
1 2 3 1 3 2 3 1
32
32
2(3 2 ) 2 3 7 2 0 3
2
xx
x x x x x x x x
xx
=
− + − + − = =
=
Áp dụng viet bậc 3:
1 2 3
1 2 3
1 2 2 3 3 1
2
1 2 3
3
2 3 6
,,
11 11 11
1
36
1
11
36
11
x x x
x x x
x x x x x x a a S
x x x b
b
= − = − = −
+ + = −
+ + = = = −
=−
=−
Câu 50: Cho hàm số
( )
2
2 4 3y x a x b= + + + +
. Gọi M là giá trị lớn nhất của hàm số trên đoạn
2;3−
. Khi M đạt giá trị nhỏ nhất, giá trị của biểu thức
4P a b=−
là:
A.
29.P =
B.
41.P =−
C.
40.P =
D.
41.P =
Lời giải
Chọn A.
Xét
( )
2
2 4 3u x a x b= + + + +
trên đoạn
2;3−
có
4
' 0 4 4 0 .
4
a
u x a x
+
= + + = = −
Trường hợp 1: Nếu
( ) ( )
4
2;3 16 4
4
a
aa
+
− − −
ta có:
( ) ( )
max 2 , 3 max 2 3 , 3 33M u u a b a b= − = − − + +
2 3 3 33 (2 3) (3 33) 5 6
25.
2 2 2
a b a b a b a b a− − + + + − − + + + +
=
Trường hợp 2: Nếu
4
2;3 16 4
4
a
a
+
− − −
ta có:
Trang 41
( ) ( )
2
4
max 2 , 3 , max 2 3 , 3 33 , 1
48
aa
M u u u a b a b a b
+
= − − = − + + + + + − −
( ) ( )
2
2
2 3 3 33 2 1
2 3 3 33 2 1
8
8
44
a
a
a b a b a b
a b a b a b
− + + + + + + + − −
− + + + + + + + − −
( )
2
1 25 25
6
16 4 4
a= + +
So sánh hai trường hợp ta có:
min
25
.
4
M =
Dấu bằng xảy ra
2
6
25
2 3 3 33 1 29.
35
84
4
a
a
a b a b a b P
b
=−
− + + = + + = + − − = =
−
=
ĐỀ 23
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1. Cho hàm số
2
21
x
y
x
−
=
+
. Tìm mệnh đề đúng.
A. Hàm số luôn đồng biến trên tập xác định
1
\
2
DR
=−
.
B. Hàm số luôn nghịch biến trên tập xác định
1
\
2
DR
=−
.
C. Hàm số đồng biến trên khoảng
1
;
2
− −
.
D. Hàm số nghịch biến trên khoảng
1
;
2
− +
.
Câu 2. Tìm họ các nguyên hàm của hàm số
( )
3
2f x x=+
.
A.
4
1
2
4
x x C++
. B.
4
32x x C++
. C.
4
2x x C++
. D.
4
42x x C++
.
Câu 3. Cho hàm số
42
23y x x= − +
. Tìm số điểm cực trị của đồ thị hàm số đã cho.
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 4. Tính môđun của số phức
( )
= + , , .z a bi a b
A.
=+
22
.z a b
B.
=+.z a b
C.
=+
22
.z a b
D.
=−
22
.z a b
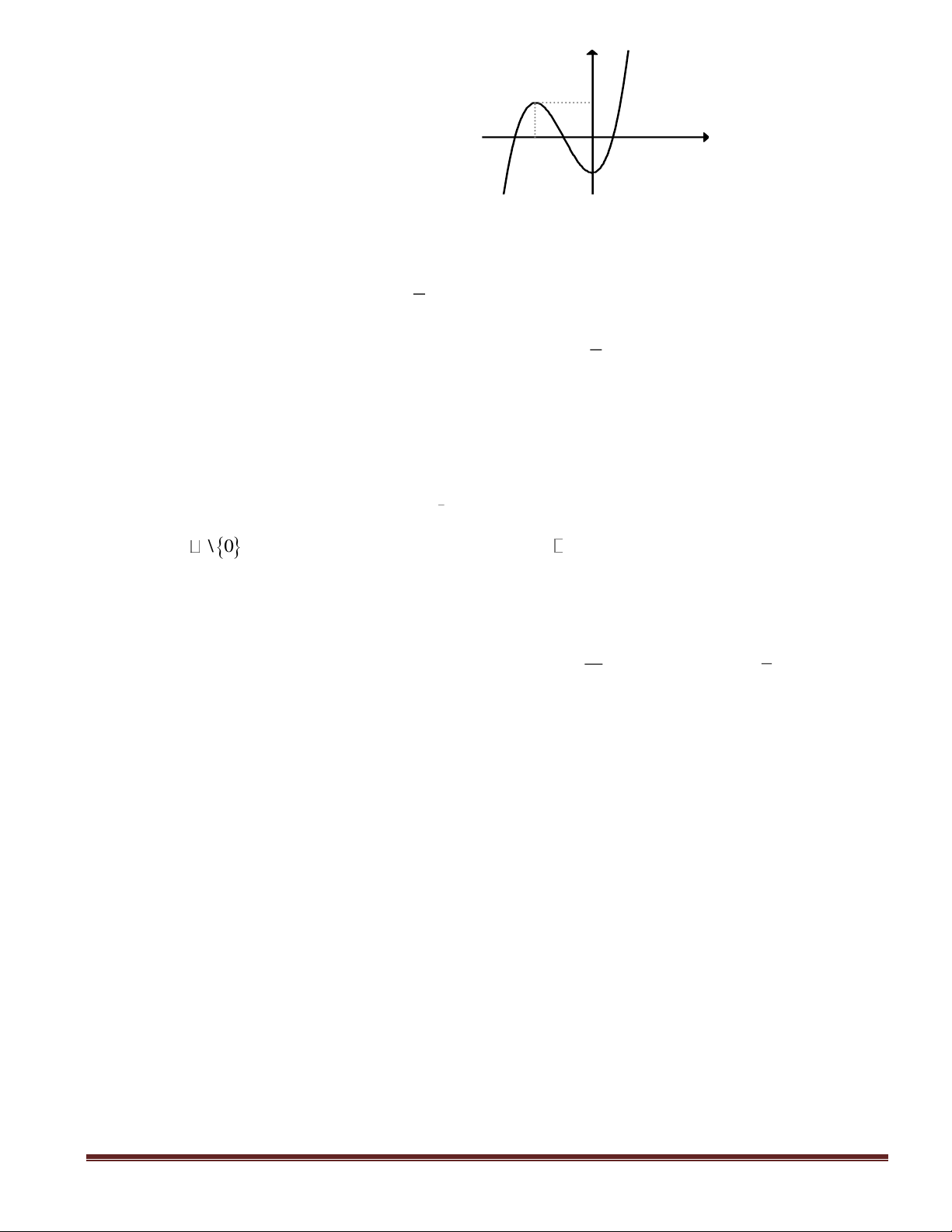
Trang 42
Câu 5. Đồ thị hình bên là của hàm số
nào trong các hàm số sau:
A.
32
32y x x= - - -
.
B.
32
32y x x= + -
.
C.
32
32y x x= - -
.
D.
32
32y x x= - + -
.
x
y
-2
-2
-1 O
2
Câu 6. Cho các số thực dương
,ab
bất kì. Khẳng định nào sau đây là khẳng định đúng?
A.
( ) ( )
log logab a b=+
.B.
( )
log log
b
a
a
b
=
.
C.
( )
log log logab a b=+
. D.
( )
log log
a
ab
b
=−
.
Câu 7. Một hình trụ có bán kính đáy bằng 3 và đường cao bằng 4. Tính diện tích xung quanh
xq
S
của
hình trụ.
A.
24
xq
S
=
.
B.
12
xq
S
=
.
C.
30
xq
S
=
.
D.
15
xq
S
=
.
Câu 8. Tìm tập xác định của hàm số
3
5
yx=−
.
A.
\0
B.
( )
;0−
C. D.
( )
0;+
Câu 9. Trong không gian Oxyz, cho điểm
( )
1; 2; 2A
và mặt phẳng
()
:
2 2 4 0x y z+ − − =
. Tính
khoảng cách
d
từ điểm
A
đến mặt phẳng
()
.
A.
3.d =
B.
1.d =
C.
13
.
3
d =
D.
1
.
3
d =
Câu 10. Trong không gian với hệ tọa độ
Oxyz
, viết phương trình mặt cầu tâm
( )
1;2;3I −
và có bán kính
bằng
2
.
A.
( ) ( ) ( )
2 2 2
21 3 4zyx − + + − =−
. B.
( ) ( ) ( )
2 2 2
21 3 2zyx + + + − =−
.
C.
( ) ( ) ( )
2 2 2
21 3 4zyx + + + + =+
. D.
( ) ( ) ( )
2 2 2
21 3 4zyx + + + − =−
.
Câu 11. Gọi
M
,
m
lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số
=−
32
3y x x
trên đoạn
−
2;1
.
Tính giá trị của
=+T M m
.
A.
=−20T
. B.
=−4T
. C.
= 2T
. D.
=−24T
.
Câu 12. Trong không gian Oxyz, cho hai điểm
( ) ( )
2;0;3 , 1;2;1AB
. Viết phương trình tham số của
đường thẳng d đi qua hai điểm A và B.
A.
12
2
23
xt
y
zt
= − +
=
= − +
. B.
2
2
34
xt
yt
zt
=+
=
= − +
. C.
2
2
32
xt
yt
zt
=+
=−
= − −
. D.
2
2
32
xt
yt
zt
=−
=
=−
.

Trang 43
Câu 13. Trong không gian với hệ trục tọa độ Oxyz, cho 2 mặt phẳng
( )
P :2x my 3z 5 0+ + − =
và
( )
Q :nx 8y 6z 2 0− − + =
với
( )
m,n R
. Xác định
n,m
để
mp(P)
song song với
mp(Q)
.
A.
n m 4==
. B.
n m 4= = −
. C.
n 4;m 4= = −
. D.
n 4;m 4= − =
.
Câu 14. Tìm xác định
D
của hàm số y =
3
cos x
.
A.
\ 2 ,
2
D R k k Z
= +
. B.
\,D R k k Z
=
.
C.
\,
2
D R k k Z
= +
. D.
\ 2 ,D R k k Z
=
.
Câu 15. Tìm tập nghiệm của bất phương trình
( )
2
1
2
log 3 2 1xx− + −
.
A.
( )
;1−
. B.
[0;2)
. C.
[0;1) (2;3]
. D.
[0;2) (3;7]
.
Câu 16. Tính thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi
,0y x y==
,
0, 2xx==
quanh trục hoành.
A.
2V =
(đvtt) B.
4V =
(đvtt) C.
4V p=
(đvtt) D.
2V p=
(đvtt)
Câu 17. Đồ thị hàm số
2
3
9
x
y
x
+
=
-
có bao nhiêu đường tiệm cận?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 18. Cho nhị thức
1
n
x
x
−
trong đó tổng 3 hệ số đầu tiên của khai triển nhị thức đó là
36
. Tìm số
hạng không chứa
x
trong khai triển nhị thức đã cho.
A.
525
. B.
252
. C.
252−
. D.
525−
.
Câu 19. Tìm tập nghiệm T của bất phương trình:
1
4 2 3
xx+
+
.
A.
( )
1; 3T =
. B.
( )
2; 4T =
. C.
( )
2
log 3; 5T =
. D.
( )
2
;log 3T = −
.
Câu 20. Biết
25
log 5, log 3ab==
. Tính giá trị của
24
log 15
được tính theo
a
.
A.
( )
1
3
ab
ab
+
+
. B.
1
1
ab
a
+
+
. C.
1
1
b
a
+
+
. D.
1ab
b
+
.
Câu 21. Anh Nam gửi 100 triệu đồng vào ngân hàng Vietcombank. Lãi suất hàng năm không thay đổi là
7,5%/năm. Nếu anh Nam hàng năm không rút lãi thì sau 5 năm số tiền anh Nam nhận được cả
vốn lẫn tiền lãi (kết quả làm tròn đến hàng ngàn) là bao nhiêu?.
A. 143.563.000đồng. B. 2.373.047.000đồng. C. 137.500.000đồng. D. 133.547.000đồng.
Câu 22. Tìm tập nghiệm
S
của bất phương trình
( )
1 1 0xx− +
.
A.
)
1;S = − +
. B.
( )
1 1;S = − +
. C.
)
1 1;S = − +
. D.
( )
1;S = +
.
Câu 23. Tính đạo hàm của hàm số
2
( ) sin 2 cos3f x x x=−
.
A.
'( ) sin4 3sin3f x x x=+
B.
'( ) 2sin 2 3sin3f x x x=+

Trang 44
C.
'( ) 2sin 4 3sin3f x x x=−
D.
'( ) 2sin 4 3sin3f x x x=+
.
Câu 24. Tứ diện
SABC
có
SA
vuông góc với mặt phẳng
( )
ABC
, tam giác
ABC
vuông tại
A
. Gọi
AH
là đường cao của tam giác
SAB
. Mệnh đề nào sau đây đúng?
A.
HA CS⊥
. B.
AB BC⊥
. C.
AH BC⊥
. D.
SA BC⊥
.
Câu 25. Cho cấp số cộng
( )
n
u
có
4
3u =−
và tổng của
9
số hạng đầu tiên là
9
45S =
. Tính
20
S
.
A.
20
1960S =
. B.
20
980S =
. C.
20
98S =
. D.
20
196S =
.
Câu 26. Cho hàm số
43mx m
y
xm
+−
=
+
,
m
là tham số. Gọi
S
là tập tất cả giá trị nguyên của
m
để hàm số
giảm trên từng khoảng xác định. Tìm số phần tử của
S
.
A.
4
. B.
3
. C.
6
. D.
0
.
Câu 27. Cho hình chóp tam giác
.S ABC
có SA vuông góc với mặt phẳng (ABC),
4SA =
, tam giác
ABC
vuông tại
A
,
5BC =
. Tính diện tích mặt cầu ngoại tiếp hình chóp
.S ABC
.
A.
25
. B.
41
. C.
10
. D.
2 41
.
Câu 28. Cho số phức
z
thỏa mãn điều kiện
3 4 2.zi− +
Trong mặt phẳng
Oxy
tập hợp điểm biểu
diễn số phức
21w z i= + −
là hình tròn có diện tích bằng bao nhiêu?
A.
9S
=
. B.
12S
=
. C.
16S
=
. D.
25S
=
.
Câu 29. Cho số phức thỏa mãn điều kiện . Tính môđun của số phức
+zz
.
A.
+=3.zz
B.
+=8.zz
C.
+=4.zz
.
D.
+=6.zz
Câu 30. Trong mặt phẳng với hệ tọa độ
Ox ,y
giả sử điểm
( ; )A a b
thuộc đường thẳng
: 3 0d x y- - =
và cách
: 2 1 0xy- + =
một khoảng bằng
5.
Tính
P ab=
biết
0.a >
A.
4
. B.
2-
. C.
2.
D.
4.-
Câu 31. Cho hình chóp
.DS ABC
có đáy là hình vuông cạnh
2a
,
3SA a=
và
( D)SA mp ABC⊥
. Tính
thể tích
V
của khối chop
.DS ABC
.
A.
3
43Va=
. B.
3
3
3
a
V =
.
C.
3
23
3
a
V =
. D.
3
43
3
a
V =
.
Câu 32. Tìm tất cả các giá trị của tham số
m
để
1x =
là hoành độ trung điểm của đoạn thẳng nối hai
điểm cực đại, cực tiểu của đồ thị hàm số
( ) ( )
32
1
2 2 3 2017
3
y x m x m x= - + + + +
.
A.
1m =-
. B.
1m ¹-
. C.
3
2
m =-
. D. Không có giá trị
m
.
Câu 33. Cho hình chóp
.DS ABC
có đáy là hình chữ nhật, SA vuông góc với (ABCD),
; D 2a; 3AB a A SA a= = =
. M là điểm trên SA sao cho
3
SA
AM =
. Tính thể tích
V
của khối
chóp
.S BCM
.
z
2 2 5z iz i− = +

Trang 45
A.
3
3
3
a
V =
. B.
3
23
9
a
V =
.
C.
3
23
3
a
V =
. D.
3
3
9
a
V =
.
Câu 34. Cho khối lăng trụ tam giác
. ' ' 'ABC A B C
có thể tích là
V
. Gọi
,MN
lần lượt là trung điểm hai
cạnh
AA'
và
'BB
. Tính thể tích của khối đa diện
.'ABC MNC
theo
V
.
A.
3
5
V
. B.
4
.
5
V
C.
2
.
3
V
D.
3
.
4
V
Câu 35. Cho hình nón có đường cao
20h cm=
, bán kính đáy
25r cm=
, O là tâm đáy. Thiết diện qua
đỉnh của hình nón cách tâm O của đáy một khoảng bằng 12cm. Tính diện tích
S
của thiết diện
này.
A.
( )
2
80 34 cm
. B.
( )
2
250 cm
. C.
( )
2
500 cm
. D.
( )
2
40 34 cm
.
Câu 36. Trong không gian với hệ tọa độ Oxyz, cho điểm
( )
M 1;2;0
và mặt phẳng
( )
:x y z 3 0 + + − =
.
Đường thẳng
nằm trong mặt
( )
, đi qua điểm
M
đồng thời cắt đường thẳng
x 2 y 2 z 3
d:
2 1 1
− − −
==
. Tìm một vecto chỉ phương
u
của đường thẳng
.
A.
u (1; 1; 2)= − −
. B.
u (1;0; 1)=−
. C.
u (1;1; 2)=−
. D.
u (1; 2;1)=−
.
Câu 37. Trong không gian hệ tọa độ Oxyz, mặt phẳng
( )
:P x y z 0+ + =
cắt mặt cầu
( ) ( ) ( ) ( )
:
2 2 2
S x 1 y 2 z 2 4+ + − + − =
theo một đường tròn (C) tâm I. Tìm tọa độ điểm I.
A.
( )
;;1 1 2−
. B.
( )
;;1 2 1−
. C.
( )
;;2 1 1−
. D.
( )
;1 23−−
.
Câu 38. Cho hàm số
( )
y f x=
có đạo hàm cấp một, đạo hàm cấp hai liên tục trên
0;1
và thỏa mãn
( ) ( )
11
00
dd
xx
e f x x e f x x
=
( )
1
0
0d
x
e f x x
=
. Tính giá trị của biểu thức
( ) ( )
( ) ( )
10
10
ef f
ef f
−
−
.
A.
1
B.
1−
C.
2
D.
2−
Câu 39. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt
đáy và
2SA a=
. Tìm số đo của góc giữa đường thẳng SC và mặt phẳng (SAB).
A.
0
30
B.
0
60
C.
0
90
D.
0
45
Câu 40. Hình lăng trụ
.ABC A B C
có đáy
ABC
là tam giác vuông tại
12; ; .A AB AC==
Hình chiếu
vuông góc của
A
trên
( )
ABC
nằm trên đường thẳng
BC
. Tính khoảng cách từ điểm
A
đến
mặt phẳng
( )
A BC
.
A.
3
2
B.
1
3
C.
25
5
D.
2
3
Câu 41. Cho tập
0;1;2;3;4;5;7;9A =
. Hỏi có bao nhiêu số tự nhiên có
8
chữ số khác nhau lập từ tập
A
, biết các chữ số chẵn không đứng cạnh nhau?
A.
7200
. B.
15000
. C.
10200
. D.
12000
.

Trang 46
Câu 42. Cho hàm số
( )
y f x=
liên tục trên có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của
n
để phương trình
( )
( )
( )
2
16cos 6sin2 8 1f x x f n n+ − = +
có nghiệm
x
?
A.
10
. B.
4
. C.
8
. D.
6
.
Câu 43. Cho hàm số
()y f x=
có đồ thị như hình vẽ
Hàm số
2
( 2 1) 2018y f x x= - + +
giảm trên khoảng nào dưới đây?
A.
( )
;1-¥
. B.
( )
2;+¥
. C.
( )
0;1
. D.
( )
1;2
.
Câu 44. Trên hệ trục tọa độ Oxy, cho hình vuông ABCD. Điểm M thuộc cạnh CD sao cho
2MC DM=
,
(0;2019)N
là trung điểm của BC, K là giao điểm hai đường thẳng
, AM BD
. Biết đường
thẳng
AM
có phương trình:
10 2018 0xy− + =
. Tính khoảng cách từ gốc tọa độ
O
đến đường
thẳng
NK
.
A.
2019
. B.
2019 101
. C.
2018
11
. D.
2019 101
101
.
Câu 45. Biết
32
3
63
3
sin 3
d3
1
x
x c d
ab
xx
−
= + + +
++
với
, , ,a b c d
là các số nguyên. Tính
a b c d+ + +
.
A.
28a b c d+ + + =
. B.
16a b c d+ + + =
. C.
14a b c d+ + + =
. D.
22a b c d+ + + =
.
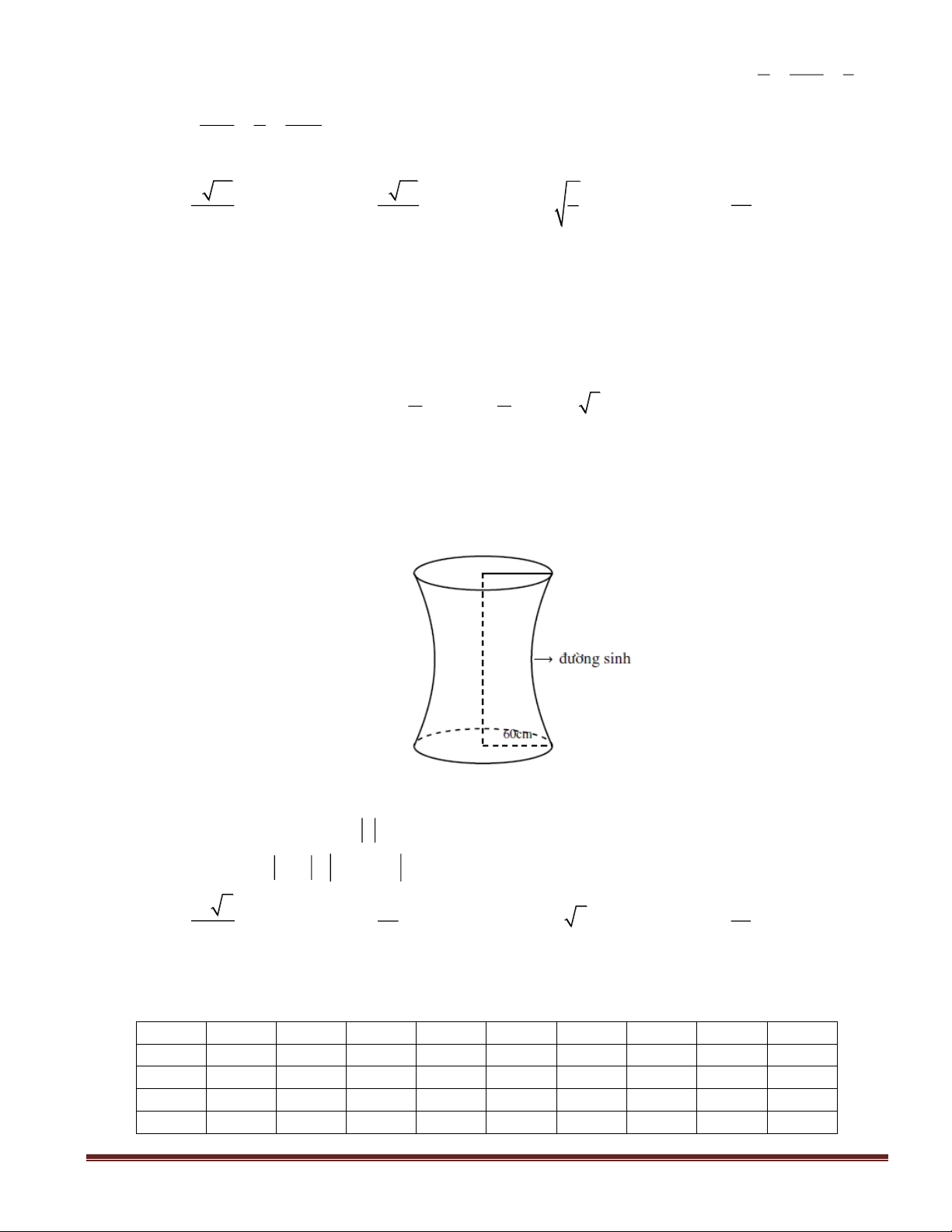
Trang 47
Câu 46. Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
1
x y 1 z
:
2 1 1
−
= =
−
và
2
x 1 y z 2
:
1 2 1
−+
= =
. Một mặt phẳng
( )
P
vuông góc với
1
, cắt trục
Oz
tại A và cắt
2
tại
B
. Tìm giá trị nhỏ nhất của đoạn
AB
.
A.
2 30
5
. B.
2 31
5
. C.
6
5
. D.
24
5
.
Câu 47. Số giá trị nguyên của tham số
m
thuộc đoạn
2019;2−
để phương trình
( ) ( ) ( )
35
1 log 4 1 log 2 1 2x x x x m− + + + = −
có đúng hai nghiệm thực là :
A.
2022
. B.
2021
. C.
2
. D.
1
.
Câu 48. Có bao nhiêu giá trị nguyên
m
để phương trình dưới đây có nghiệm?
2
4sin cos 3sin2 cos2
36
x x m x x
+ − = + −
.
A.
7
. B.
1
. C.
3
. D.
5
.
Câu 49. Cho chiếc trống như hình vẽ, có đường sinh là nửa elip được cắt bởi trục lớn với độ dài trục lớn
bằng 80 cm, độ dài trục bé bằng 60 cm và đáy trống là hình tròn có bán kính bằng 60 cm. Tính
thể tích của chiếc trống (kết quả làm tròn đến hàng đơn vị).
A. . B. . C. . D. .
Câu 50. Cho số phức
z
thỏa mãn
1.z =
Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
biểu thức
2
1 1 .P z z z= + + − +
Tính giá trị của
.Mm
.
A.
13 3
.
4
B.
39
.
4
C.
3 3.
D.
13
.
4
ĐÁP ÁN
1.C
2.A
3.B
4.A
5.B
6.C
7.A
8.D
9.B
10.D
11.A
12.D
13.D
14.C
15.C
16.D
17.B
18.C
19.D
20.A
21.A
22.C
23.D
24.D
25.B
26.A
27.B
28.C
29.D
30.B
31.D
32.D
33.B
34.C
35.C
36.C
37.C
38.A
39.A
40.C
41.D
42.D
43.D
44.D
45.A
46.A
47.A
48.D
49.B
50.A
V
3
344963cmV =
3
344964cmV =
3
208347cmV =
3
208346cmV =
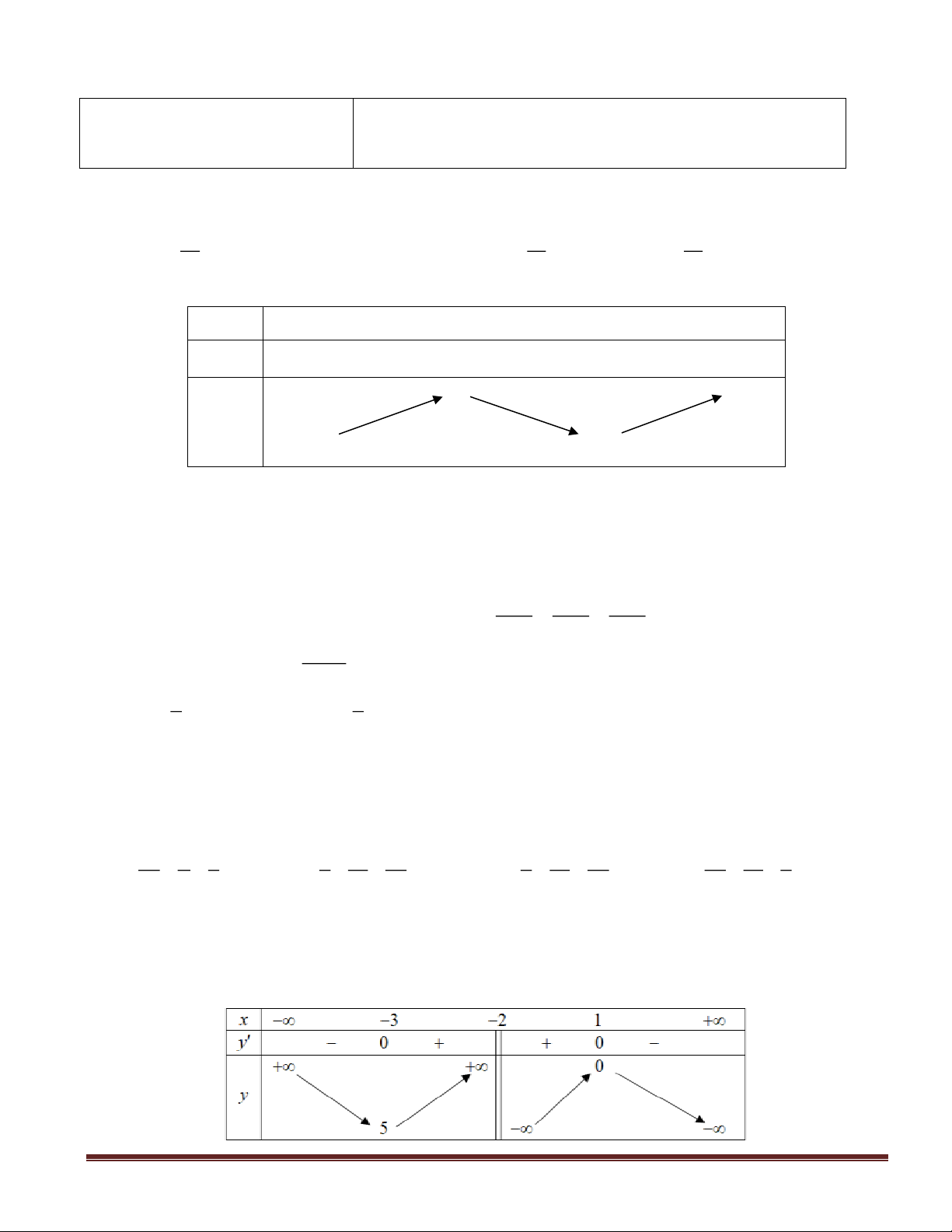
Trang 48
ĐỀ 24
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1. Nguyên hàm của hàm số
( )
2
f x x=
là :
A.
2
2
d
2
x
x x C=+
. B.
2
d2x x x C=+
. C.
3
2
d
3
x
x x C=+
. D.
3
2
d
3
x
xx=
.
Câu 2. Cho hàm số
( )
y f x=
có bảng biến thiên như sau
x
−
2
4
+
y'
+
0
−
+
y
3
+
−
2−
Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực đại tại
x4=
B. Hàm số đạt cực đại tại
x2=−
C. Hàm số đạt cực đại tại
x2=
D. Hàm số đạt cực đại tại
x3=
Câu 3. Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
( ) ( )
A 1;3;2 , B 3;5; 4 .−
Phương trình
mặt phẳng trung trực của AB là:
A.
x y 3z 9 0+ − + =
B.
x y 3z 2 0+ − + =
C.
x 3 y 5 z 4
1 1 3
− − +
==
−
D.
x y 3z 9 0+ − − =
Câu 4. Đồ thị hàm số
1
41
x
y
x
+
=
−
có đường tiệm cận ngang là đường thẳng nào dưới đây?
A.
1
4
x =
. B.
1
4
y =
. C.
1x =−
. D.
1y =−
.
Câu 5 . Cho
2
2
1
( 1) d 2.f x x x+=
Khi đó
5
2
( )dI f x x=
bằng
A.
1
. B.
2
. C.
4
. D.
1−
.
Câu 6. Trong không gian Oxyz, viết PT mp đi qua ba điểm
( ) ( )
,4;0;0 0; 1;0AB−
,
( )
0;0; 2C −
.
A.
1
4 1 2
x y z
+ + =
−
. B.
0
4 1 2
x y z
+ + =
−−
. C.
1
4 1 2
x y z
+ + =
−−
. D.
0
4 1 2
x y z
+ + =
−−
.
Câu 7 . Tìm tập hợp tất cả các giá trị của tham số m để phương trình
42
x 2x 3 m 0− − + =
có đúng
2 nghiệm thực.
A.
( )
;3−
B.
( )
;3 4−
C.
( )
3;− +
D.
( )
4 3;− − +
Câu 8. Cho hàm số
( )
y f x=
có bảng biến thiên sau:
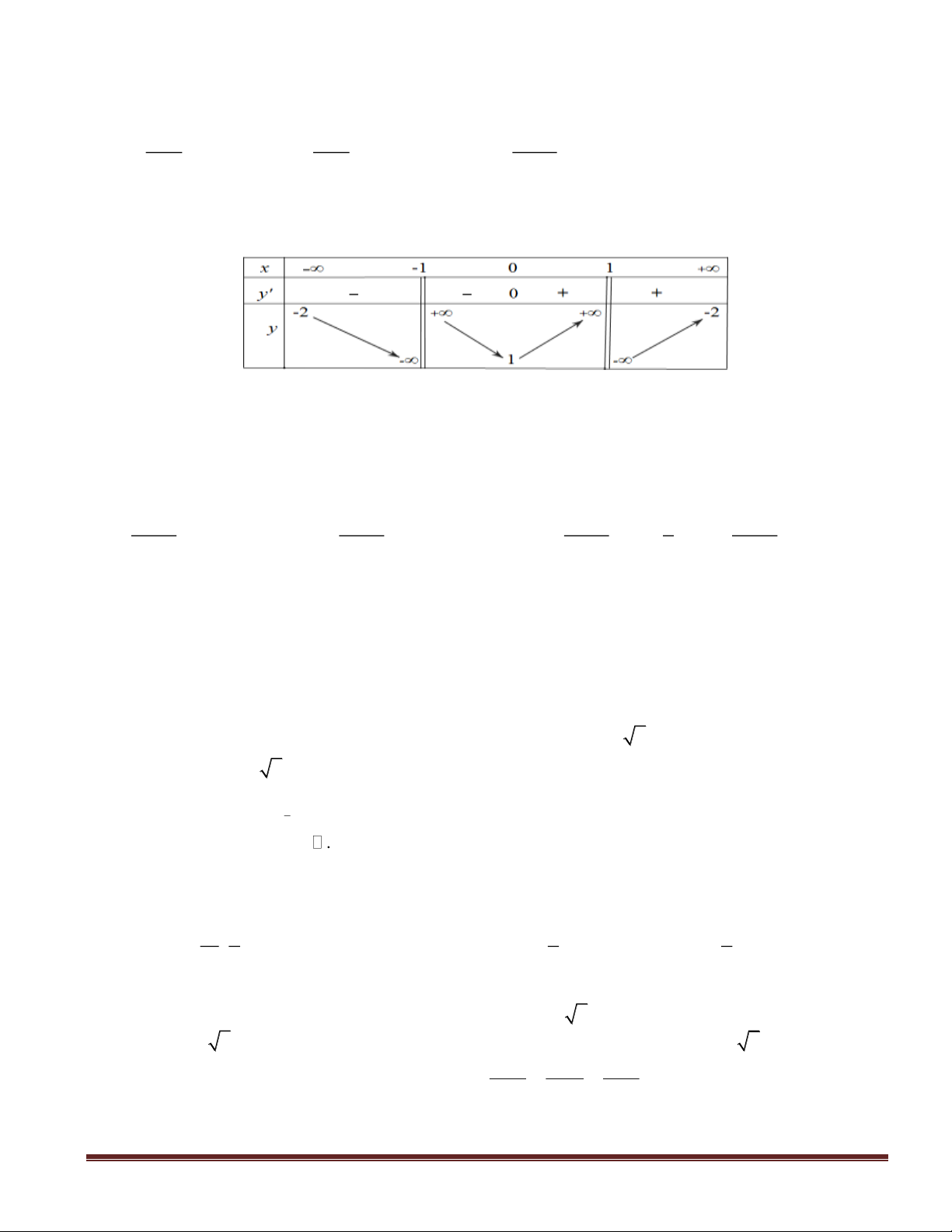
Trang 49
Tìm cực đại của hàm số
( )
y f x=
.
A.
3−
. B.
1
. C.
5
. D.
0
.
Câu 9. Hàm số nào sau đây đồng biến trên từng khoảng xác định của TXĐ ?
A.
5
1
x
y
x
+
=
−
B.
3
1
x
y
x
+
=
−
C.
35
1
x
y
x
−
=
−
D.
2
3 4 5y x x= − +
Câu 10. Cho hàm số
( )
y f x=
xác định trên
\ 1 ,R
liên tục trên mỗi khoảng xác định và có bảng
biến thiên như hình vẽ sau. Tìm tập hợp tất cả các giá trị của tham số
m
để phương trình
( )
f x m=
vô nghiệm.
A.
2; 1−
. B.
(
;2− −
. C.
)
1; +
. D.
)
2; 1−
.
Câu 11. Cho hàm số
32
3 6 1y x x x= + − +
có đồ thị
( )
C
.Viết phương trình tiếp tuyến của đồ thị
( )
C
biết hoành độ tiếp điểm bằng 1.
A.
36yx=−
. B.
37yx=−
. C.
34yx=−
. D.
35yx=−
.
Câu 12. Cho
a
là số thực dương và khác 1, mệnh đề nào sau đây là đúng?
A.
3
log
log
log 3
a
a
b
b=
. B.
( )
log
log 3
log 3
a
a
a
b
b=−
. C.
log
log
log 3 3
a
a
a
b
b
=
. D.
log
log 3
log 3
a
b
a
b
=
.
Câu 13. Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
(1;0; 2),A −
(1;1;1),B
(0; 1;2)C −
.
Biết rằng mặt phẳng đi qua ba điểm
,,A B C
có phương trình
7 0.x ay cz d+ + + =
Tính giá
trị biểu thức
2 2 2
.S a b c= + +
A.
29.
. B.
59.
C.
26.
D.
35.
Câu 14. Trong KG với hệ tọa độ Oxyz, cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
S : x 3 y 1 z 2 8.− + + + + =
Khi đó
tâm I và bán kính R của mặt cầu là
A.
( )
I 3; 1; 2 ,R 4− − =
B.
( )
I 3; 1; 2 ,R 2 2− − =
C.
( )
I 3;1;2 ,R 2 2−=
D.
( )
I 3;1;2 ,R 4−=
Câu 15. Hàm số
2
1
2
log ( 1)yx=+
có tập giá trị là
A.
( ;0].−
B.
.
C.
[0; ).+
D.
[1; ).+
Câu 16 . Các giá trị của tham số m để phương trình
( )
xx
12 4 m .3 m 0+ − − =
có nghiệm thực
khoảng
( )
1;0−
là:
A.
17 5
m;
16 2
B.
m 2;4
C.
5
m ;6
2
D.
5
m 1;
2
Câu 17. Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số
4 2 2
y x 2mx m 5m= − + −
có ba
điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn
4 2.
A.
0 m 2 2
B.
m0
C.
0 m 2
D.
2 m 2 2
Câu 18.Trong không gian Oxyz, đường thẳng
x 3 y 2 z 4
d:
1 1 2
−+−
==
−
cắt mặt phẳng
( )
Oxy
tại điểm
có tọa độ là:
Trang 50
A.
( )
3;2;0−
B.
( )
3; 2;0−
C.
( )
1;0;0−
D.
( )
1;0;0
Câu 19.Giá trị nhỏ nhất của hàm số
x
y xe=
trên đoạn
2;0−
là:
A.
0
B.
2
2
e
−
C.
e−
D.
1
e
−
Câu 20. Tìm giá trị thực của tham số
m
để phương trình
2
55
log log 1 0x m x m− + + =
có hai nghiệm
thực
12
,xx
thỏa mãn
12
625xx =
.
A. Không có giá trị
m
. B.
4m =
. C.
44m =
. D.
4m =−
.
Câu 21. Cho
( )
Fx
là một nguyên hàm của hàm số
( )
1
23
x
fx
e
=
+
thỏa mãn
( )
0 10F =
. Tìm
( )
Fx
.
A.
( )
( )
( )
1
10 ln 2 3
3
x
F x x e= + − +
. B.
( )
13
ln 10 ln5 ln2
32
x
F x x e
= − + + + −
.
C.
( )
( )
( )
1 ln5
ln 2 3 10
33
x
F x x e= − + + +
. D.
( )
1 3 ln5 ln2
ln 10
3 2 3
x
F x x e
−
= − + + −
.
Câu 22. Biết hệ số của
2
x
trong khai triển của
( )
13
n
x−
là
90
. Tìm
n
.
A.
5n =
. B.
8n =
. C.
6n =
. D.
7n =
.
Câu 23. Trong không gian
Oxyz
, cho hai vectơ
u
và
v
tạo với nhau một góc
o
120
và
2u =
,
5v =
. Tính
uv+
.
A.
39
. B.
5−
. C.
19
. D.
7
.
Câu 24. Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác cân, với
AB AC a==
và
góc
120BAC =
, cạnh bên
AA a
=
. Gọi
I
là trung điểm
CC
. Cosin của góc tạo bởi hai mặt phẳng
( )
ABC
và
( )
AB I
bằng
A.
33
11
. B.
11
11
. C.
10
10
. D.
30
10
.
Câu 25. Tìm
a
để các hàm số
2
2
3 1 2
khi 1
1
()
( 2)
khi 1
3
x
x
x
fx
ax
x
x
+−
−
=
−
−
liên tục tại
1.x =
A.
3
.
4
a
−
=
B.
3
.
4
a =
C.
1
.
2
a =
D.
1
.
2
a =−
Câu 26. Trong không gian Oxyz, cho hai điểm
( ) ( )
A 1;3; 2 ;B 3;7; 18− − − −
và mặt phẳng
( )
P :2x y z 1 0.− + + =
Điểm
( )
M a;b;c
thuộc
( )
P
sao cho mặt phẳng (ABM) vuông góc với (P) và
22
MA MB 246.+=
. Tính
S a b c.= + +
A .
0
B.
1−
C.
10
D.
13
Câu 27. Cho hình trụ có bán kính đáy là
Ra=
, mặt phẳng qua trục cắt hình trụ theo một thiết
diện có diện tích bằng
2
8a
. Diện tích xung quanh của hình trụ và thể tích khối trụ là:
A.
23
16 a ,16 a
B.
23
6 a ,3 a
C.
23
8 a ,4 a
D.
23
6 a ,6 a
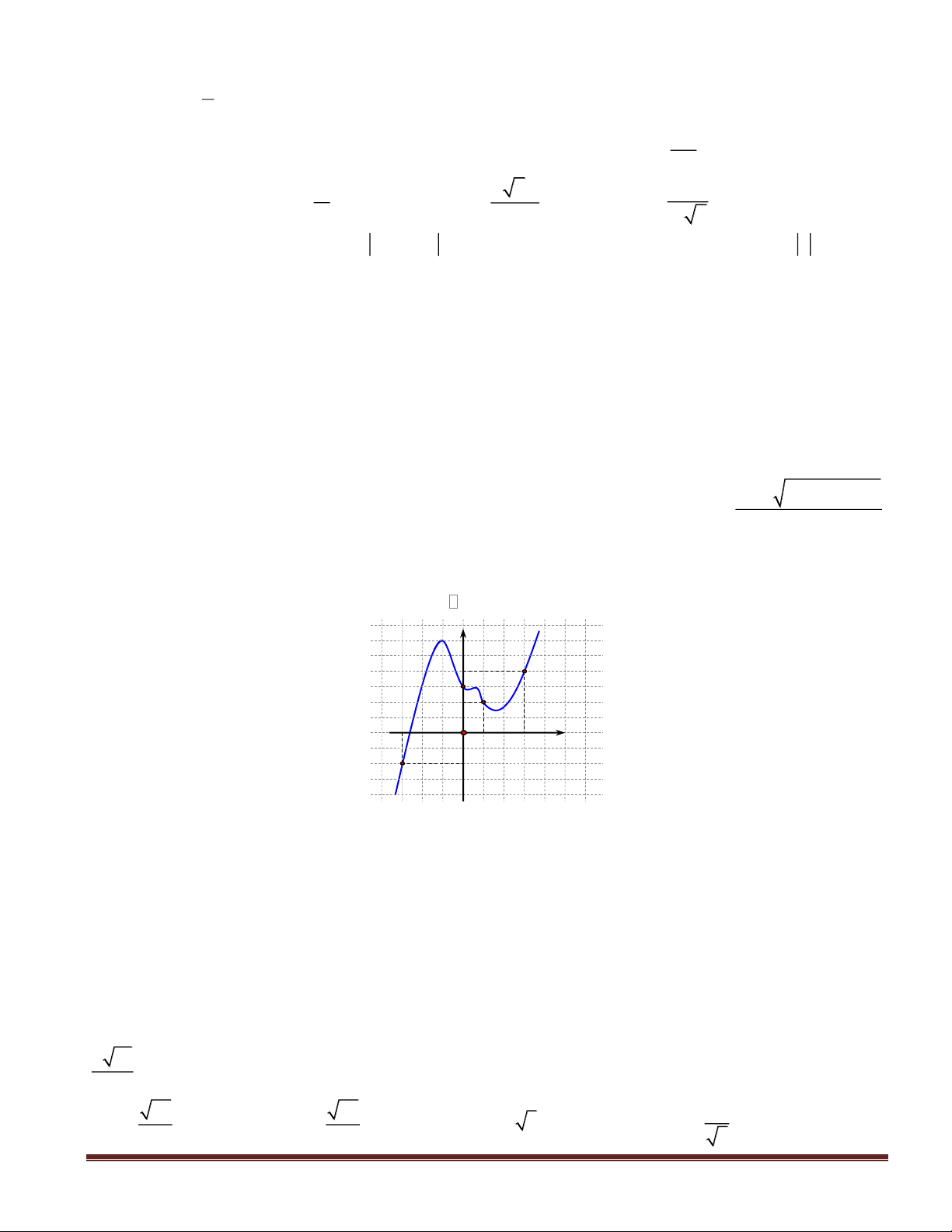
Trang 51
Câu 28. Dòng điện xoay chiều hình sin chạy qua mạch dao động LC lí tưởng có phương trình
0
i I sin wt
2
=+
. Ngoài ra
( )
i q' t=
với q là điện tích tức thời trong tụ. Tính từ lúc
t0=
, điện
lượng chuyển qua tiết diện thẳng của dây dẫn của mạch trong thời gian
2w
là:
A.
0
B.
0
I
w
C.
0
2I
w
D.
0
I
w2
Câu 29. Cho số phức
z
thỏa mãn
3 4 4.zi− + =
Giá trị nhỏ nhất và giá trị lớn nhất của
z
là
A.
0
và
3.
B.
0
và
4.
C.
1
và
9.
D.
1
và
81.
Câu 30 . Một cửa hàng bán lẻ mũ bảo hiểm Honda với giá
20 USD
. Với giá bán này cửa hàng chỉ
bán được khoảng
25
chiếc. Cửa hàng dự định sẽ giảm giá bán, ước tính cứ mỗi lần giảm giá bán đi
2 USD
thì số mũ bán được tăng thêm
40
chiếc. Xác định giá bán để cửa hàng thu được lợi nhuận
lớn nhất, biết rằng giá mua về của một chiếc mũ bảo hiểm Honda là
10 USD.
A.
16,625USD
B.
15,625USD
C.
16,575USD
D.
15,575USD
Câu 31. Có bao nhiêu số tự nhiên có sáu chữ số khác nhau từng đôi một, trong đó chữ số
5
đứng
liền giữa hai chữ số
1 và 4?
A.
249
B.
1500
C.
3204
D.
2942
Câu 32 . Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số
( )
2
2x m 1 x 1
y
x1
− − +
=
−
có đúng hai tiệm cận ngang?
A.
m1=
B.
( ) ( )
m 1;4 4; +
C.
m1
D.
m1
Câu 33. Cho hàm số
( )
y f x=
liên tục trên . Đồ thị hàm số
( )
'y f x=
như hình vẽ dưới.
Đặt
( ) ( ) ( )
2
21g x f x x= − +
. Mệnh đề nào dưới đây đúng ?
A.
( ) ( )
3;3
1Min g x g
−
=
. B.
( ) ( )
3;3
1Max g x g
−
=
. C.
( ) ( )
3;3
3Max g x g
−
=
.
D. Không tồn tại giá trị nhỏ nhất của
( )
gx
trên
3;3−
.
Câu 34. Tìm hệ số của
7
x
trong khai triển thành đa thức của
2
(2 3 )
n
x−
, biết
n
là số nguyên
dương thỏa mãn:
1 3 5 2 1
2 1 2 1 2 1 2 1
... 1024
n
n n n n
C C C C
+
+ + + +
+ + + + =
.
A.
2099529
. B.
2099520−
. C.
2099529−
. D.
2099520
.
Câu 35. Cho hình chóp
.S ABC
có
( )
SAB
và
( )
SBC
cùng vuông góc với mặt phẳng đáy,
góc giữa
SC
và đáy là
60
. Biết rằng tam giác
ABC
đều, khoảng cách giữa
AB
và
SC
là
2 15
5
. Tính
tan
, với
là góc giữa đường thẳng
SC
và mặt phẳng
( )
SAB
.
A.
39
13
. B.
39
3
. C.
3
. D.
1
3
.
O
1
3
x
2
4
2−
3−
y

Trang 52
Câu 36.Trong tất cả các số phức
z
thỏa mãn
-2 2 8zz+ + =
, gọi
,Mm
lần lượt là giá trị lớn
nhất, nhỏ nhất của
z
. Tính giá trị biểu thức
2
P M m=+
.
A.
16.
B.
10.−
C.
8.
D.
20.
Câu 37. Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
,,=B AB a
3,=BC a
biết
=SA a
và
vuông góc với mặt phẳng đáy. Một mặt phẳng
( )
đi qua A , vuông góc với SC tại H , cắt SB tại K
. Tính thể tích khối chóp
.S AHK
theo
.a
A.
3
3
.
30
a
B.
3
53
.
60
a
C.
3
3
.
60
a
D.
3
3
.
10
a
Câu 38. Xét các số phức
z a bi=+
( )
,ab
thỏa mãn
4 3 2z i z i− − = − +
. Tính
22
P a b=+
khi
1 3 1z i z i+ − + − +
đạt giá trị nhỏ nhất.
A.
137
9
P =
. B.
293
9
P =
. C.
449
32
P =
. D.
481
32
P =
.
Câu 39. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D,
AB AD 2a,CD a.= = =
Gọi I là trung điểm của cạnh AD, biết hai mặt phẳng
( ) ( )
SBI ; SCI
cùng
vuông góc với đáy và thể tích khối chóp S. ABCD bằng
3
3 15a
.
5
Tính góc giữa hai mặt phẳng
( ) ( )
SBC ; ABCD
.
A.
0
60
B.
0
30
C.
0
36
D.
0
45
Câu 40. Giá trị của m thuộc tập hợp nào dưới đât để
2
4 1 4 1
lim ?
22
→−
+ + +
=
−
x
xx
mx
A.
3;0−
. B.
6; 3−−
. C.
1;3
. D.
3;6
Câu 41. Biết
2
2
1
x
dx a b 2 c 35
3x 9x 1
= + +
+−
với a, b, c là các số hữu tỉ, tính
P a 2b c 7.= + + −
A.
86
27
B.
1
9
−
C.
67
27
D.
2−
Câu 42. Bình có bốn đôi giày khác nhau gồm bốn màu: đen, trắng, xanh và đỏ. Một buổi sáng đi
học, vì vội vàng, Bình đã lấy ngẫu nhiên hai chiếc giày từ bốn đôi giày đó. Tính xác suất để Bình
lấy được hai chiếc giày cùng màu.
A.
1
7
. B.
2
7
. C.
1
14
. D.
1
4
.
Câu 43. Cho hàm số
( )
fx
có đạo hàm liên tục trên
0;
2
thỏa mãn
( )
f 0 0,=
( )
2
2
0
f ' x dx ,
4
=
( )
2
0
sin x.f x dx .
4
=
Tính tích phân
( )
2
0
f x dx
A. 1 B.
2
C. 2 D.
4
Câu 44. Trong không gian với hệ tọa độ Oxyz, cho ba điểm
( ) ( )
8 4 8
M 2;2;1 ,N ; ; ,E 2;1; 1 .
333
−−
Đường thẳng
đi qua tâm đường tròn nội tiếp của tam giác OMN và vuông góc với mặt phẳng
(OMN). Khoảng cách từ điểm E đến đường thẳng
là:

Trang 53
A.
2 17
3
B.
3 17
5
C.
3 17
2
D.
5 17
3
Câu 45. Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng
( )
P :3x y z 5 0+ + − =
và
( )
Q :x 2y z 4 0.+ + − =
Khi đó, giao tuyến của (P) và (Q) có phương trình là
A.
xt
d : y 1 2t
z 6 t
=
= − +
=+
B.
xt
d : y 1 2t
z 6 5t
=
=−
=−
C.
x 3t
d: y 1 t
z 6 t
=
= − +
=+
D.
xt
d : y 1 2t
z 6 5t
=
= − +
=−
Câu 46. Trong kg Oxyz, cho hai điểm
và đường thẳng .
Tìm vecto chỉ phương
của đường thẳng
đi qua
và vuông góc với
đồng thời cách B một
khoảng lớn nhất.
A.
(4; 3;2)u =−
. B.
(2;0; 4)u =−
. C.
(2;2; 1)u =−
. D.
(1;0;2)D =
.
Câu 47. Trong không gian Oxyz, cho điểm
( )
1;0; 1A −
, mặt phẳng
( )
: 3 0P x y z+ − − =
. Mặt cầu
(S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA
bằng
62+
. Phương trình mặt cầu (S) là
A.
( ) ( ) ( )
2 2 2
2 2 1 9x y z+ + − + + =
và
( ) ( ) ( )
2 2 2
1 2 2 9x y z+ + − + + =
.
B.
( ) ( ) ( )
2 2 2
3 3 3 9x y z− + − + − =
và
( ) ( ) ( )
2 2 2
1 1 1 9x y z− + − + + =
.
C.
( ) ( ) ( )
2 2 2
2 2 1 9x y z− + − + − =
và
( )
2
22
39x y z+ + + =
.
D.
( ) ( ) ( )
2 2 2
1 2 2 9x y z+ + − + + =
và
( ) ( ) ( )
2 2 2
2 2 1 9x y z− + − + − =
.
Câu48. Tính giá trị của biểu thức
22
1P x y xy= + − +
, biết rằng
( )
2
2
1
1
2
4 log 14 2 1
x
x
yy
+−
= − − +
,
với
13
0; 1
2
xy −
.
A.
3P =
. B.
2P =
. C.
4P =
. D.
1P =
.
Câu 49. Cho hình lăng trụ tam giác đều ABC.A’B’C’, góc giữa hai mặt phẳng (A’BC) và (ABC)
bằng 60
0
. Gọi M là trung điểm cạnh BC, N là trung điểm cạnh CC’, biết khoảng cách từ M đến
mặt phẳng (AB’N) bằng
9
4 13
a
. Tính theo a thể tích
V
của khối chóp A.BB’C’C.
A.
3
3
.
4
a
V =
B.
3
.
3
a
V =
C.
3
2
.
3
a
V =
D.
3
.
2
a
V =
Câu 50.
Cho hình thang
ABCD
vuông tại
A
và
B
như hình vẽ
ở bên biết
3 ; 2 ; 5 .AD a AB a BC a= = =
Gọi
,EF
là hai
điểm lần lượt thuộc các đoạn thẳng
AD
và
BC
thoả
mãn
EF
song song với
AB
và
AE ED
. Cho hình
thang quay quanh
EF
ta được một khối tròn xoay.
Tính tỉ số
ED
EA
biết rằng khối tròn xoay thu được có
thể tích bằng
3
31
.
3
a
( ) ( )
1;2;1 , 1;2; 3AB−−
15
:
2 2 1
x y z
d
+−
==
−
u
A
d

Trang 54
A.
1
.
2
ED
EA
=
B.
3
.
4
ED
EA
=
C.
1
.
3
ED
EA
=
D.
2
.
3
ED
EA
=
……………………HẾT……………………
ĐÁP ÁN CHI TIẾT
Câu 1. Đáp án C
Câu 2 . Đáp án C
Câu 3. Đáp án D
Câu 4. Đáp án B
Câu 5 . Đáp án C
Đặt
2
1 d 2 dt x t x x= + =
.
Đổi cận :
12xt= =
25xt= =
.
Suy ra
25
2
12
1
( 1)xd ( )d
2
I f x x f t t= + =
.
Theo giả thiết
2I =
nên ta có
5
2
( )d 4f t t =
.
Vì tích phân không phụ thuộc vào biến nên chọn C.
Câu 6 . Đáp án C
Câu 7 . Đáp án B
Ta có:
42
PT x 2x 3 m − − = −
Xét hàm số
4 2 3
x0
y x 2x 3 y' 4x 4x 0
x 1;x 1
=
= − − = − =
= − =
Khi đó
( ) ( )
y 0 3;y 4= − = −
Phương trình có 3 nghiệm phân biệt
m 4 m 4
.
m 3 m 3
− = − =
− −
Câu 8. Đáp án D
Câu 9. Đáp án A
Câu 10. Đáp án D
Câu 11. Đáp án C
Gọi
( )
00
;M x y
là tiếp điểm.
Ta có:
2
3 6 6y x x
= + −
, do
00
1 1, (1) 3x y y
= = − =
.
Phương trình tiếp tuyến là:
0 0 0
'( )( ) 3( 1) 1 3 4y y x x x y y x y x= − + = − − = −
.
Câu 12. Đáp án A
Câu 13. Đáp án D
Câu 14. Đáp án B
Câu 15. Đáp án A
Câu 16 . Đáp án A
Câu 17. Đáp án C
Câu 18. Đáp án D
Phương pháp:
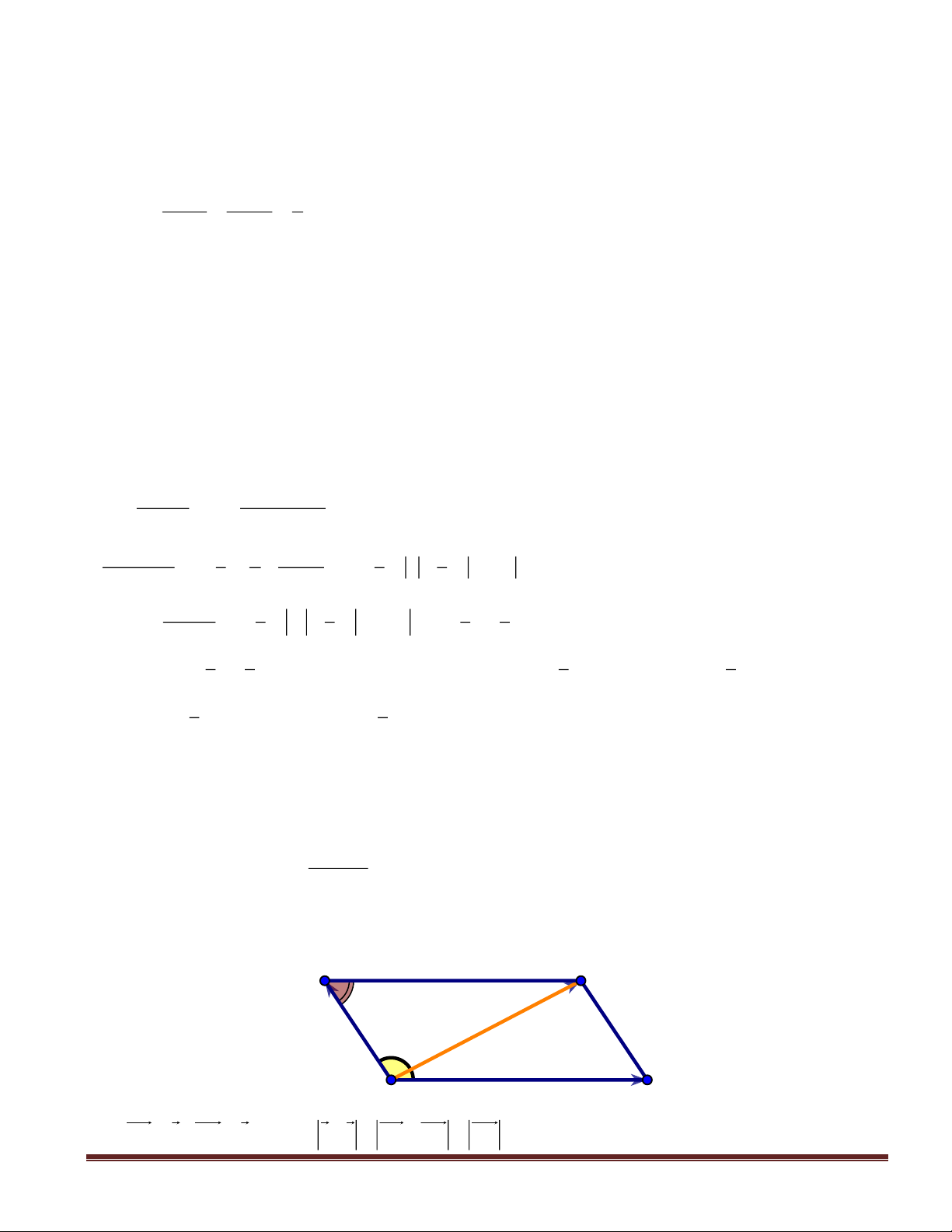
Trang 55
+) Gọi M là giao điểm của đường thẳng d và mặt phẳng (Oxy). Khi đó tọa độ điểm M thỏa mãn
phương trình đường thẳng d và mặt phẳng (Oxy).
+) Phương trình mặt phẳng
( )
Oxy :z 0=
Cách giải:
Gọi
( )
0 0 0
M x ;y ;z
là giao điểm của đường thẳng d và mặt phẳng
( )
0
Oxy z 0=
( )
0
00
0
x1
x 3 y 2
4
M d M 1;0;0
y0
1 1 2
=
−+
= =
=
−
Câu 19. Đáp án D
Câu 20. Đáp án A
ĐKXĐ:
0x
. Đặt
5
logtx=
, phương trình có dạng:
2
10t mt m− + + =
.
Khi đó phương trình có hai nghiệm
1 5 1
logtx=
,
2 5 2
logtx=
( )
1 2 5 1 5 2 5 1 2
log log log 4t t x x x x + = + = =
.
Do đó ta cần:
( )
2
2
4 1 0
4 4 0
4
4
mm
mm
m
m
− +
− −
=
=
(vô nghiệm).
Vậy không tồn tại giá trị
m
thỏa mãn.
Câu 21. Đáp án C
Xét
( )
1
dd
23
23
x
x
xx
e
xx
e
ee
=
+
+
. Đặt
xx
u e du e dx= =
. Khi đó nguyên hàm có dạng
( )
1 1 1 2 1 1
d d ln ln 2 3
2 3 3 2 3 3 3
u u u u C
u u u u
= − = − + +
++
.
Do đó:
( )
1 1 1 1 1
d ln ln 2 3 ln 2 3
2 3 3 3 3 3
x x x
x
x e e C x e C
e
= − + + = − + +
+
.
Do đó
( )
( )
11
ln 2 3
33
x
F x x e C= − + +
mà
( )
0 10F =
nên
11
ln5 10 10 ln5
33
CC− = = +
.
Vậy
( )
( )
11
ln 2 3 10 ln5
33
x
F x x e
= − + + +
.
Câu 22. Đáp án A
Ta có:
( ) ( ) ( )
11
1 3 3 3 .
nn
n k k
k k k
nn
kk
x C x C x
==
− = − = −
.
Xét hệ số của
2
x
, ta có
2k =
. Do đó hệ số
2
x
là
( )
( )
2
2 2 2
4(l)
1
. 3 90 10 10 20 0
5
2
nn
n
nn
C C n n
n
=−
−
− = = = − − =
=
.
Vậy
5n =
.
Câu 23. Đáp án C
Gọi
AB v=
,
AC u=
khi đó
u v AB AC AD AD+ = + = =
.
D
A
B
C
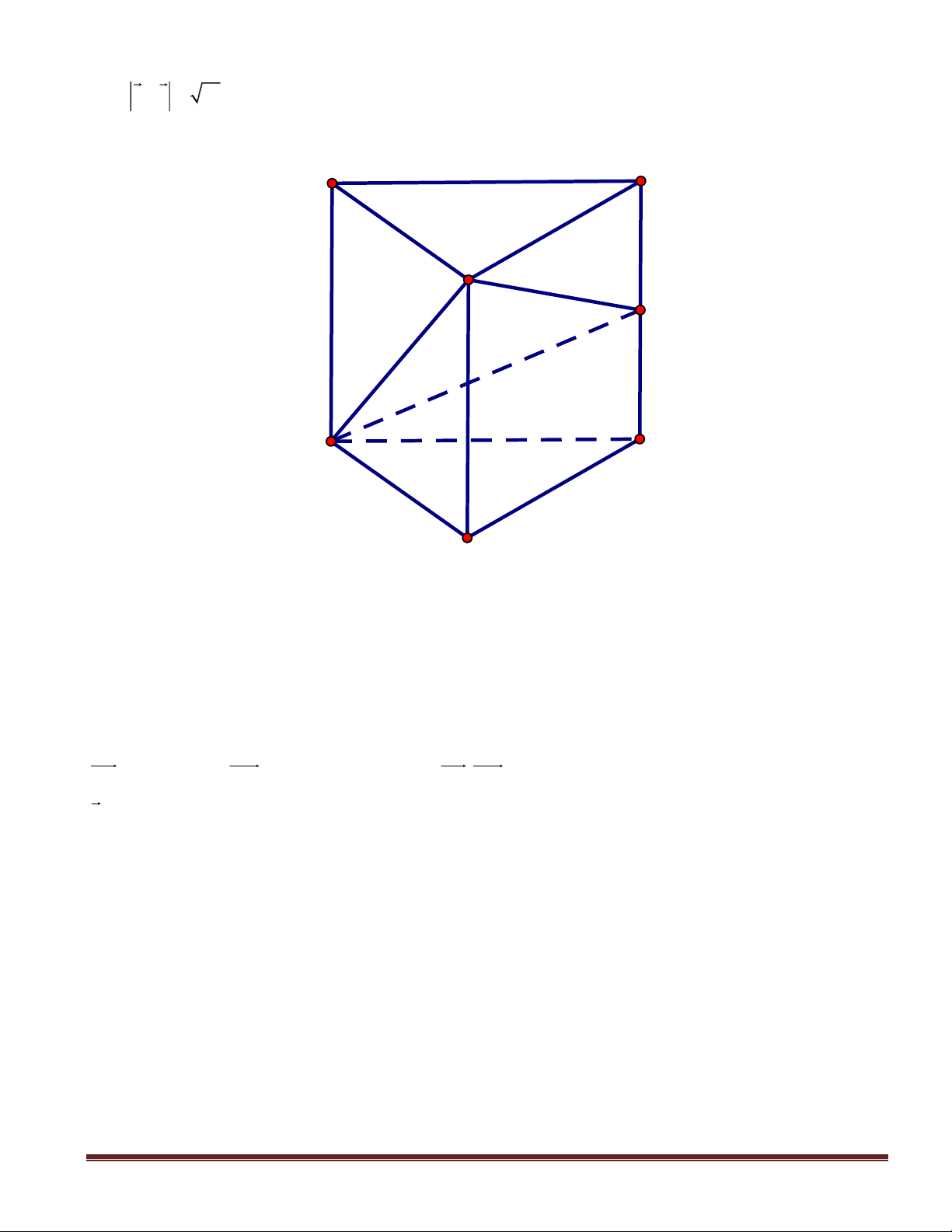
Trang 56
Xét tam giác
ACD
có
2 2 2
2 . .cosAD AC CD AC CD ACD= + −
2 2 o
5 2 2.5.2.cos60 19= + − =
.
Vậy
19uv+=
.
Câu 24. Đáp án D
Câu 25. Đáp án A
Câu 26. Đáp án B
Phương pháp:
Từ các giả thiết đã cho, lập hệ 3 phương trình ba ẩn a, b, c. Giải hệ phương trình tìm a, b, c và tính
tổng S.
Cách giải:
( )
( ) ( ) ( )
( )
( )
( ) ( ) ( )
P
M P 2a b c 1 0
AB 2;4; 16 ;AM a 1;b 3;c 2 AB;AM 16b 4c 40; 16a 2c 12; 4a 2b 2
n 2; 1;1
2 16b 4c 40 16a 2c 12 4a 2b 2 0
− + + =
= − − = + − + = + − − + − − − +
=−
+ − − − + − + − − + =
Ta
có
12a 30b 6c 66 2a 5b c 11 + + = + + =
( ) ( ) ( ) ( ) ( ) ( )
22
2 2 2 2 2 2
2 2 2
MA MB 246
a 1 b 3 c 2 a 3 b 7 c 18 246
a b c 4a 10b 20c 75 0
+=
+ + − + + + + + − + + =
+ + + − + + =
Khi đó ta có hệ phương trình
( )
( )
( )
2 2 2
2a b c 1 1
2a 5b c 11 2
a b C 4a 10b 20c 75 0 3
− + = −
+ + =
+ + + − + + =
( ) ( )
1 ; 2 b 2 2a 2 c 1 2a c 1 c 1 2a = − + = − + = = −
Thay vào (3) ta có
I
C'
B'
A
B
C
A'

Trang 57
( ) ( )
2
2 2 2
a 4 1 2a 4a 10.2 20 1 2a 75 0 5a 40a 80 0 a 8a 16 0
a 4 c 7
+ + − + − + − + = − + = − + =
= = −
Vậy
S a b c 4 2 7 1= + + = + − = −
Câu 27. Đáp án C
Phương pháp:
Diện tích xung quanh của hình trụ
xq
S 2 Rh=
và thể tích khối trụ
2
V r h=
Cách giải: Mặt phẳng qua trục cắt hình trụ theo thiết diện là hình chữ nhật có một cạnh là đường
kính đáy và một cạnh là chiều cao của hình lăng trụ.
Gọi h là chiều cao của hình trụ ta có
2
8a
h 4a
2a
==
Vậy diện tích xung quanh của hình trụ
2
xq
X 2 Rh 2 .a.4a 8 a= = =
và thể tích khối trụ
2 2 3
V R h .a .4a 4 a= = =
.
Câu 28. Đáp án C
Phương pháp: Điện lượng chuyển qua tiết diện thẳng của dây dẫn của mạch trong thời gian t là:
( )
t
0
Q i t dt=
Cách giải:
Điện lượng chuyển qua tiết diện thẳng của dây dẫn của mạch trong thời gian
2w
là:
2w
2w
0 0 0
0
0
0
I I I
Q I sin wt dt cos wt cos cos
2 w 2 w 2 w
= + = − + = − − =
Câu 29. Đáp án C
Câu 30 . Đáp án B
Ta gọi giá bán là
( )
20xx
khi đó giá bán giảm
20 x−
, khi đó số lượng chiếc mũ bán được là
20
25 .40 425 20
2
x
x
−
+ = −
chiếc.
Khi đó lợi nhuận là
( ) ( )
2
425 20 10 425 20 20 625 4250x x x x x− − − = − + −
. Đây là biểu thức bậc 2 đạt
giá trị lớn nhất khi
15,625.
2
b
x
a
= − =
Câu 31. Đáp án B
Gọi số cần tìm có dạng
abcdef
.
• Số cần tìm có dạng
154def
. Khi đó d có 7 cách chọn, e có 6 cách chọn, f có 5 cách chọn.
có 210 cách chọn.
• Số cần tìm có dạng
a154ef
. Khi đó a có 6 cách chọn, e có 6 cách chọn, f có 5 cách chọn.
có 180 cách chọn.
Hai khả năng
ab154f
và
abc154
cũng có số cách chọn như
a154ef
.
Suy ra có tổng số cách chọn là:
( )
210 180.3 .2 750+=
Câu 32 . Đáp án D
Câu 33. Đáp án B
Ta có:
( ) ( ) ( )
' 2 ' 2 1g x f x x= − +
;
( ) ( ) ( )
' 0 ' 1 1g x f x x= = +
.
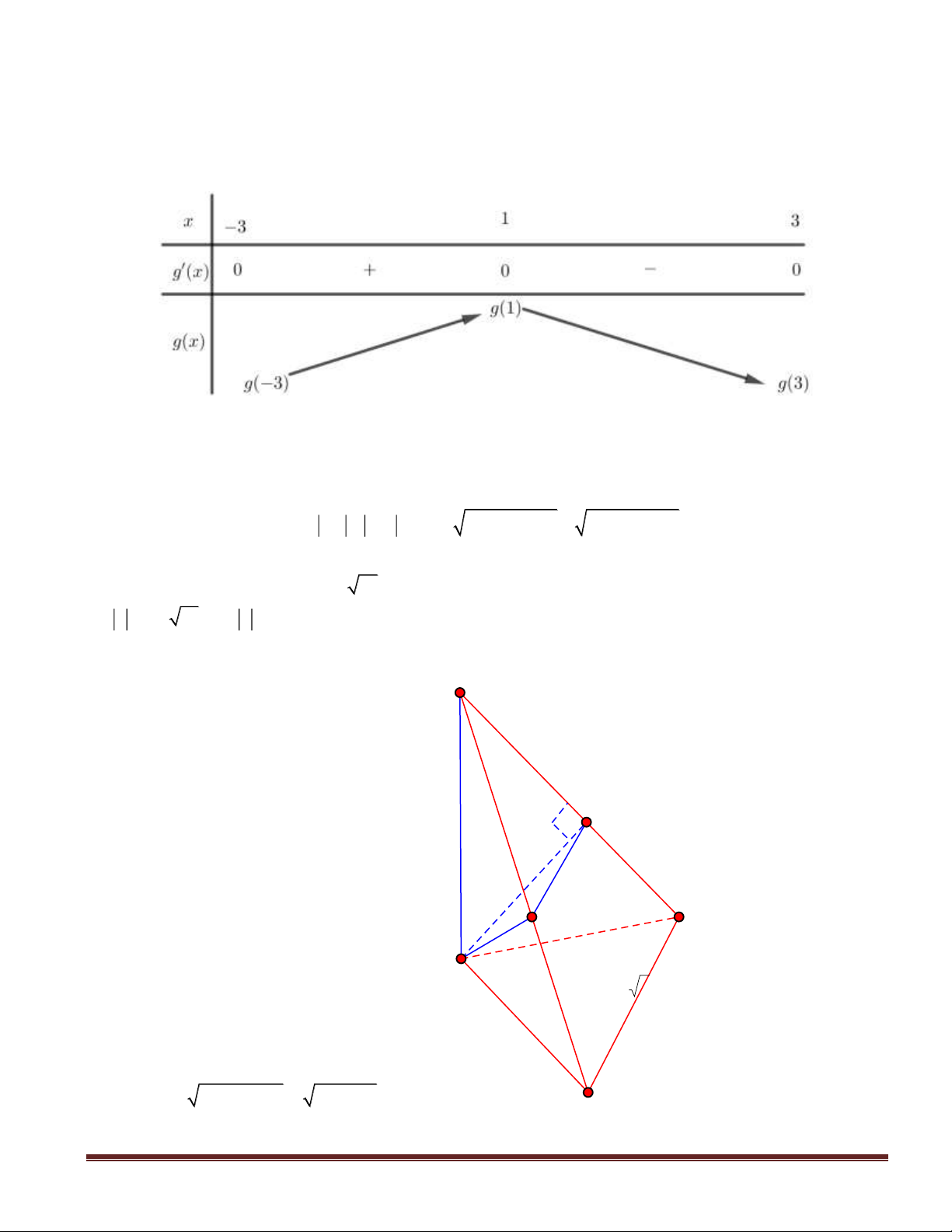
Trang 58
Quan sát đồ thị ta thấy đường thẳng
1yx=+
cắt đồ thị hàm số
( )
'y f x=
tại ba điểm
phân biệt có hoành độ lần lượt là
3;1;3−
. Do đó
( )
3
11
3
x
x
x
=−
=
=
.
Bảng biến thiên
Vậy
( ) ( )
3;3
1Max g x g
−
=
.
Câu 34. Đáp án B
Câu 35. Đáp án A
Câu 36. Đáp án A
2 2 2 2
12
8 ( 2) ( 2) 8 2.4
12
-Gäi z = a+bi (a,b R). Ta cã z-2 z+2
tËp hî p ®iÓm M(a;b) biÓu diÔn h×nh häc cña lµ ®- êng elip (E) hai tiªu ®iÓm F (2;0) vµ F (-2;0),
®é dµi trôc thùc lµ 8 a = 4,
+ = − + + + + = + =
a b a b MF MF
z
min max
12 , 4 .
16
b = 12
= = = =
=
z m z M
P
Câu 37. Đáp án C
Ta có
2 2 2 2
32AC AB BC a a a= + = + =
a
a
3
a
K
H
C
B
A
S

Trang 59
2 2 2 2
45SC SA AC a a a= + = + =
;
22
55
SA a a
SH
SC
a
= = =
;
2 2 2 2
2SB SA AB a a a= + = + =
. . 5
5. 2 2
SH SK SH SC a a a
SHK SBC SK
SB SC SB
a
= = = =
3
.
..
.
1 1 1 1 1 1 3
. . . . 3
10 10 3 10 3 2 60
5 5 2 2
S AHK
S AHK S ABC ABC
S ABC
V
SH SK a a a
V V SAdt a a a
V SC SB
aa
= = = = = = =
Câu 38. Đáp án C
Ta có:
4 3 2z i z i− − = − +
( ) ( )
22
22
4 3 ( 2) (1 )a b a b − + − = − + −
5ba = −
Đặt
1 3 1A z i z i= + − + − +
ta có:
( ) ( ) ( ) ( ) ( ) ( )
2 2 2 2 2 2
22
1 3 1 1 1 2 ( 1) ( 6)A a b a b a a a a= + + − + − + + = + + − + − + −
22
22
1 9 7 25
2 2 5 2 14 37 2
2 4 2 4
a a a a a a
= − + + − + = − + + − +
Chọn
1 3 7 5
; , ; (3;4)
2 2 2 2
u a v a u v
= − = − + =
Suy ra
( ) ( )
2 2 5 2A u v u v= + + =
Đẳng thức xảy ra khi
,uv
cùng hướng
71
13
22
8
0
5/3
5/3
a k a
a
v ku
k
k
k
− = −
=
=
=
=
.
Suy ra
27
3
b =
nên
449
32
P =
Vậy
A
nhỏ nhất bằng
52
khi
449
32
P =
Câu 39. Đáp án A
Phương pháp: Xác định góc giữa hai mặt phẳng bằng cách xác định góc giữa hai đường thẳng lần
lượt vuông góc với giao tuyến.
Cách giải:
( ) ( )
( ) ( )
( ) ( )
( )
SBI ABCD
SCI ABCD SI ABCD
SBI SCI
⊥
⊥ ⊥
⊥
Kẻ
IH CD⊥
ta có:
( )
BC IH
BC SIH BC SH
BC SI
⊥
⊥ ⊥
⊥
( ) ( )
( )
( )
( ) ( )
( )
( )
SBC ABCD BC
SBC SH BC
ABCD IH BC
SBC ; ABCD SH;IH SHI
=
⊥
⊥
= =
Ta có:
( ) ( )
2
ABCD
11
S AB CD .AD 2a a .2a 3a
22
= + = + =

Trang 60
3
S.ABCD
2
ABCD
3 15a
3.
3V
3 15
5
SI a
S 3a 5
= = =
Gọi E là trung điểm của
AB EC AD 2a = =
22
BC 4a a a 5 = + =
22
IBC ABCD ABI CDI
IBC
IBC
0
1 1 3
S S S S 3a .a.2a .a.a a
2 2 2
2S
1 3a 5
S IH.BC IH
2 BC 5
SI
tanSHI 3 60
IH
= − − = − − =
= = =
= = =
Câu 40. Đáp án B
2 1 2 1 2 1
1
4 1 4 1 4 4 1 4 4 1
lim lim lim
2 2 2 2 2
2
x x x
x x x x x x x x
mx mx
mx
− − − − −
−
→− →− →−
+ + + − + + + − + + +
= = =
−−
−
21
4
2
m
m
−
= = −
Câu 41. Đáp án B
Phương pháp: Nhân liên hợp, tách thành 2 tích phân và sử dụng phương pháp đặt ẩn phụ.
Cách giải:
(
)
( )
2
22
22
2
11
x 3x 9x 1
x
dx dx
9x 9x 1
3x 9x 1
−−
=
−−
+−
Đặt
2 2 2
1
9x 1 t 9x 1 t 18xdx 2tdt xdx tdt
9
− = − = = =
Đổi cận:
x 1 t 2 2
x 2 t 35
= =
= =
35
35
3
2
2
22
22
1 t 35 35 16 2
I t dt
9 27 27 27
= = = −
a7
16 2 35 35 16
I 7 b
27 27 27
35
c
27
1
P a 2b c 7
9
=
= + − =
=−
= + + − = −
Câu 42. Đáp án A
Chọn ngẫu nhiên hai chiếc giày từ bốn đôi giày có
2
8
C
cách.
Số cách chọn hai chiếc giày cùng màu là
4
cách.
Vậy xác suất để Bình lấy được hai chiếc giày cùng màu là
2
8
41
7C
=
.
Câu 43. Đáp án A
Trang 61
Lời giải:
Đặt
( ) ( )
u f x du f ' x dx
,
dv sin xdx v cos x
==
==
khi đó
( ) ( ) ( )
22
2
0
00
sin x.f x dx cosx.f ' x cosx.f ' x dx
= − +
( ) ( )
2
0
cos .f ' cos0.f 0 cosx.f ' x dx
4 2 2 4
= − + + =
Xét
( ) ( ) ( ) ( )
2 2 2 2 2
22
22
0 0 0 0 0
f ' x k.cosx dx 0 f ' x dx sin x.f x dx 2k cosx.f ' x dx k cos xdx 0
+ = + + + =
2
2k. k . 0 k 1.
4 4 4
+ + = = −
Khi đó
( ) ( )
2
2
0
f ' x cosx dx 0 f ' x cosx
− = =
Suy ra
( ) ( )
f x f ' x cosxdx sin x C= = = +
mà
( )
f 0 0 C 0= =
Vậy
( )
f x sin x= ⎯⎯→
2
0
sin xdx 1
=
Câu 44. Đáp án A
Lời giải:
Ta có
( )
OM;ON =k 1; 2;2
−
Vectơ chỉ phương của
( )
OM 2;2;1 OM 3= =
8 4 8
ON ; ; ON 4
333
= − =
Kẻ phân giác
( )
OF F MN
ta có:
OM MF 3 3 12 12
MF FN F 0; ;
ON NF 4 4 7 7
= = =
Gọi I là tâm đường tròn nội tiếp
( )
OMN I OF OI kOF, =
với
k0
Tam giác OMN vuông tại O, có bán kính đường tròn nội tiếp
r=1 IO 2.=
Mà
15 3 12 2
ME= ;OM=3;cosOMN= OF
7 5 7
⎯⎯→ =
suy ra
( )
12
OF OI I 0;1;1
7
=
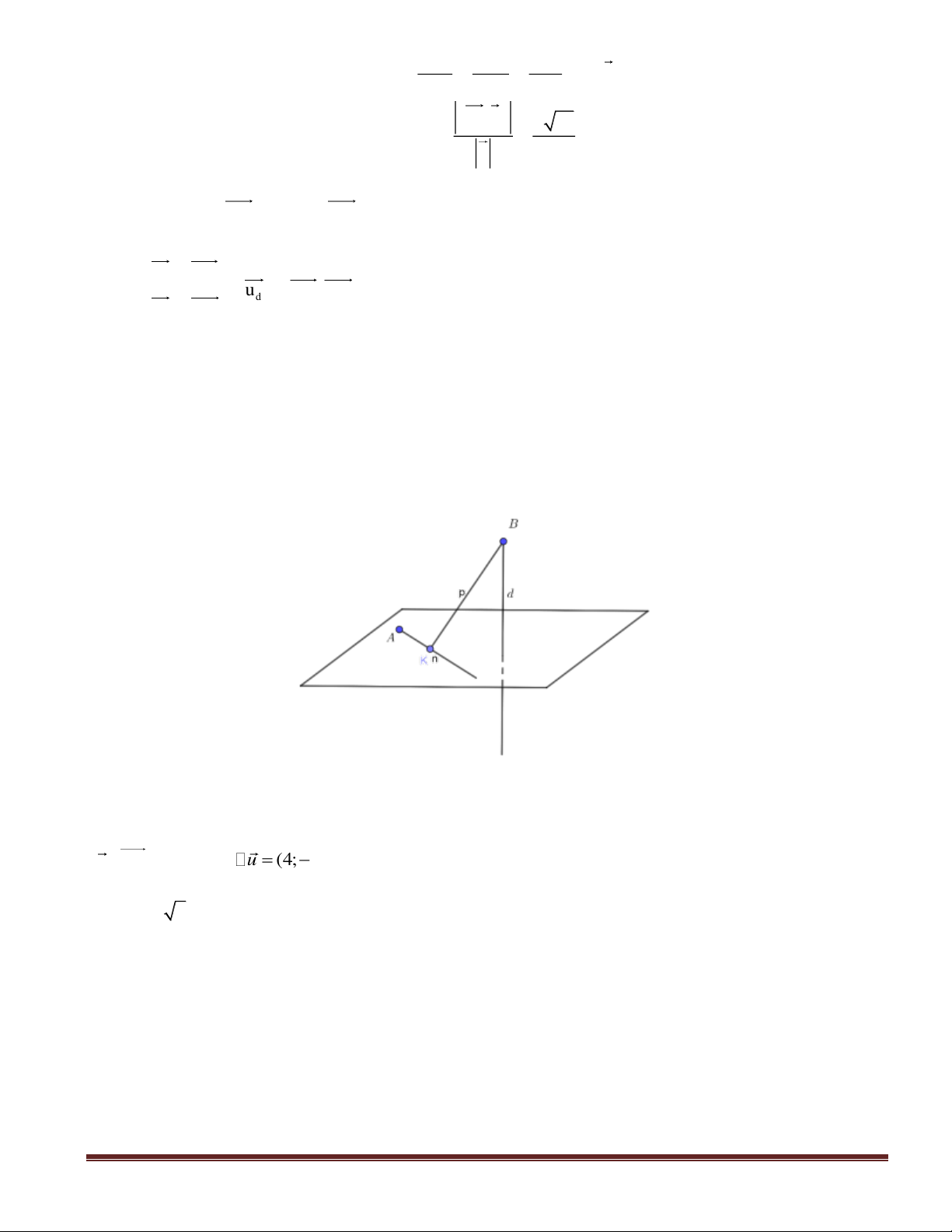
Trang 62
Phương trình đường thẳng
là
( )
x 1 y 3 z 1
:,
1 2 2
+ − +
= =
−
có
( )
u 1; 2;2 ,=−
đi qua
( )
I 0;1;1
Khoảng cách từ E đến đường thẳng
là
EI;u
2 17
d
3
u
==
Câu 45. Đáp án D
Lời giải: Ta có:
( )
( )
( )
( )
PQ
n 3;1;1 ,n 1; 2;1= = −
Gọi d là giao tuyến của (P) và (Q).
Ta có
( )
( )
( ) ( )
( )
d
P
d
PQ
d
Q
un
u n ;n 1; 2;5
un
⊥
=
=
−−
⊥
Xét hệ
3x y z 5 0
,
x 2y z 4 0
+ + − =
+ + − =
chọn
( )
y z 5 0 y 1
x 0 M 0; 1;6 d
2y z 4 0 z 6
+ − = = −
= −
+ − = =
Vậy phương trình đường thẳng cần tìm là
xt
d : y 1 2t
z 6 5t
=
= − +
=−
Câu 46. Đáp án A
Gọi K là hình chiếu của B lên đường thẳng
. Dễ thấy
.BK BA
Dấu bằng xảy ra khi và chỉ khi
vuông góc với AB. Vậy khoảng cách từ B đến
lớn nhất khi
vuông góc với AB.
Kết hợp với giả thiết
vuông góc với d, ta có vectơ chỉ phương của
là
; ] (8; 6;4) (4; 3;2).[
d
u AB u= − = −
Câu 47. Đáp án D
Do
2AB =
nên
3.IA IB==
Kết hợp với điểm I thuộc mặt phẳng (P), ta có hệ phương trình:
2 2 2 2 2 2
2 2 2 2 2 2 2 2 2
30
31
( 1) ( 1) 1 2
9 9 2 ( 1) 9
x y z
x y z z x
x y z x y z x z y
x y z x y z x x
+ − − =
+ − = = −
+ + = − + + + − = =
+ + = + + = + + − =
2
1 1 2
2 2 2
21
2 2 4 0
z x x x
y y y
zz
xx
= − = − =
= = =
= − =
− − =
.
Phương trình của các mặt cầu thỏa mãn yêu cầu đề bài là
Trang 63
( ) ( ) ( )
2 2 2
1 2 2 9x y z+ + − + + =
( ) ( ) ( )
2 2 2
2 2 1 9x y z− + − + − =
Câu 48. Đáp án B
Ta có
2
2
1
1
21
4 4 4
x
x
+−
−
=
(1).
Đặt
1ty=+
, do
13
1
2
y−
nên
30
0
2
t
.
Xét hàm số
( )
3
14 3f t t t= − +
liên tục trên đoạn
30
0;
2
có
( )
2
33f t t
= − +
( )
01f t t
= =
.
Bảng biến thiên
Suy ra
( ) ( )
1 16f t f=
( )
22
log 14 2 1 log 16 4yy
− − + =
(2).
Từ (1) và (2), ta có
( )
2
2
1
1
2
4 log 14 2 1
x
x
yy
+−
= − − +
2
2
2
1
1
0
11
x
x
x
y
ty
=
=
=
= + =
.
Khi đó
22
12P x y xy= + − + =
.
Câu 49. Đáp án A
+) Đặt
AB x=
Tam giác ABC đều cạnh a và M là trung điểm BC nên: AM ⊥ BC và
3
2
x
AM =
E
D
N
M
C'
B'
A
C
B
A'
H
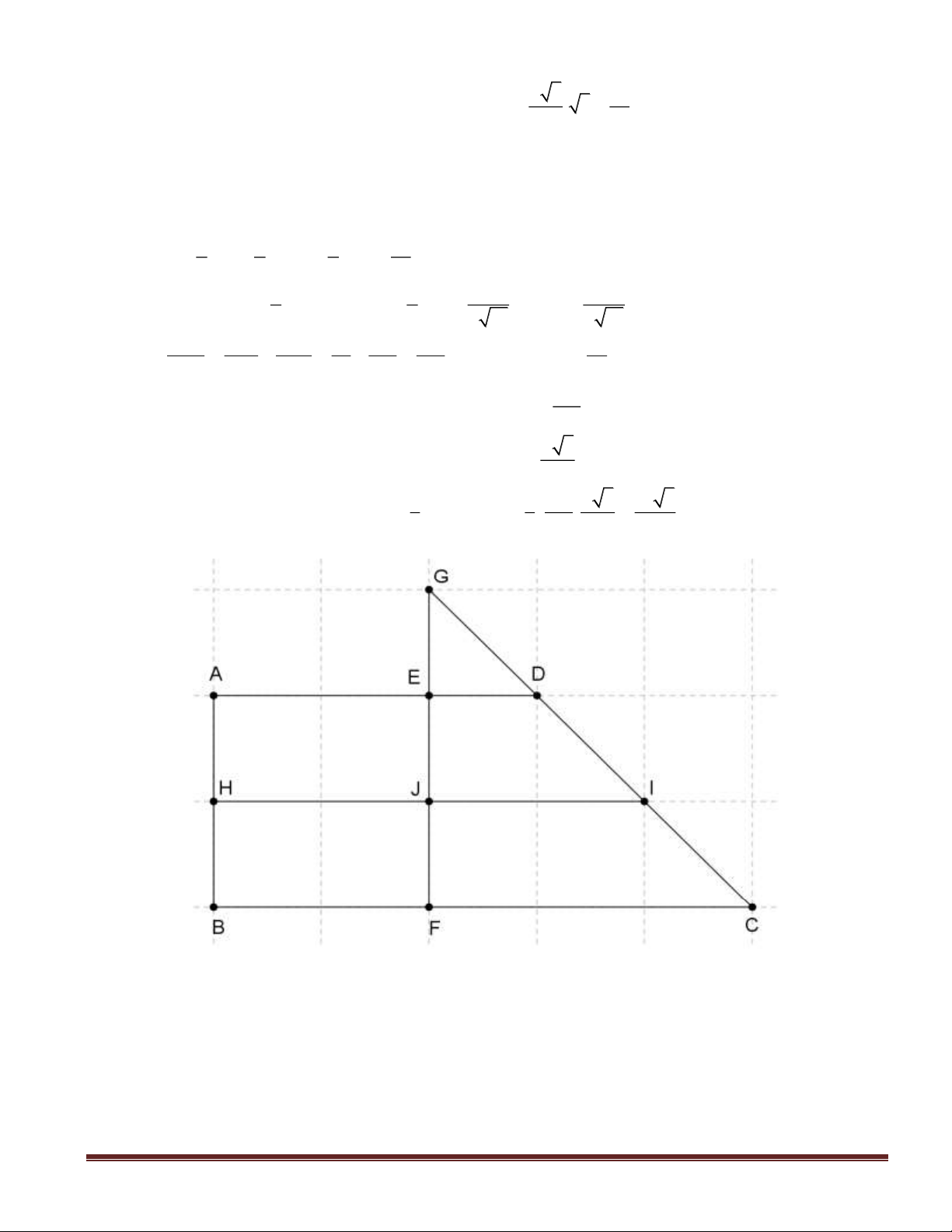
Trang 64
AM ⊥ BC và AA’⊥ BCA’M ⊥ BC Góc giữa hai mặt phẳng (A’BC) và (ABC) là
0
' 60A MA =
.
Tam giác A’AM vuông tại A nên:
0
33
AA' .tan60 . 3
22
xx
AM= = =
+) Trong mặt phẳng (BB’C’C), B’N cắt BC tại D. Khi đó C là trung điểm BD và
0
90BAD =
Gọi E là trung điểm AD, ta có: CE ⊥ AD. Dựng CH ⊥ NE (H NE).
AD ⊥ CE và AD ⊥ CN AD ⊥ (CNE) AD ⊥ CH
CH ⊥ NE và CH ⊥ AD CH ⊥ (AB’N).
Ta có:
1
22
x
CE AB==
,
13
CN '
24
x
CC==
Ta có
3 3 9 3
( ,( ' )) ( ,( ' ))
22
4 13 2 13
aa
d M AB N d C AB N CH CH= = = =
Ta lại có
2 2 2 2 2 2
1 1 1 4 16 52 3
AA'
9 9 2
a
xa
CH CE CN a x a
= + = + = = =
+) Diện tích hình chữ nhật BB’C’C là:
2
''
3
'.
2
BB C C
a
S BB BC==
AM ⊥ BC và AM ⊥ BB’ AM ⊥ (BB’C’C) và
3
.
2
a
AM =
Thể tích khối chóp S.ABCD là:
23
''
1 1 3 3 3
..
3 3 2 2 4
BB C C
a a a
V S AM = = =
Câu 50. Đáp án A
Đặt
3ED x AE a x= = −
, gọi
,,H J I
lần lượt là trung điểm của
,EFAB
và
DC
.
Ta có
AH HB EJ JF a= = = =
;
3BF AE a x= = −
;
GE ED x==
(vì
GED
là tam giác cân);
GJ JI a x= = +
(vì
GJI
là tam giác cân);
2GF FC a x= = +
(vì
GFC
là tam giác cân);
Khối tròn xoay sinh ra có thể tích là
.V
Ta có
1 2 3
.V V V V= + −
+) Trong đó
1
V
là thể tích khối trụ sinh ra bởi hình chữ nhật
AEJH
khi quay quanh
EJ
, ta có
( )
2
1
3.V a x a
=−
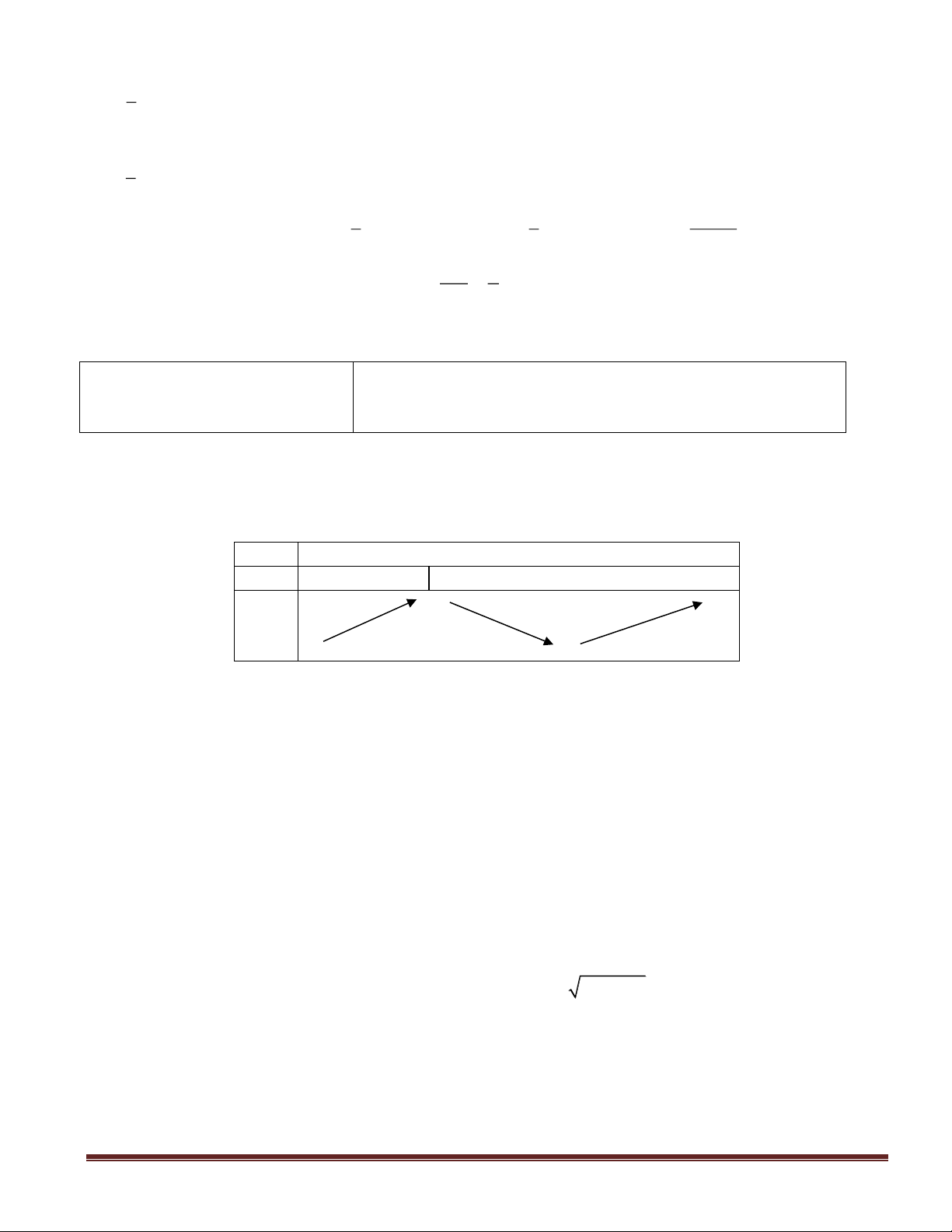
Trang 65
+) Trong đó
2
V
là thể tích khối nón sinh ra bởi tam giác vuông
GFC
khi quay quanh
GF
, ta có
( ) ( )
2
2
1
2 . 2
3
V a x a x
= + +
+) Trong đó
3
V
là thể tích khối nón sinh ra bởi tam giác vuông
IJG
khi quay quanh
GJ
, ta có
( ) ( )
2
3
1
.
3
V a x a x
= + +
Từ giả thiết ta có
( ) ( ) ( ) ( ) ( )
3
2 2 2
1 1 31
3 . 2 . 2 . .
3 3 3
a
a x a a x a x a x a x
− + + + − + + =
( )
22
2
3 2 0
x a kotm
a ax x
xa
=
− + =
=
Vậy
1
.
2
ED
EA
=
ĐỀ 25
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1. Hỏi hàm số
42
y x 2x 2019= − +
nghịch biến trên khoảng nào sau đây?
A.
( )
;1− −
B.
( )
1;1−
C.
( )
1;0−
D.
( )
;1−
Câu 2.Cho hàm số
y f(x)=
xác định, liên tục trên R và có bảng biến thiên :
x
−
0 1
+
y’
+
– 0 +
y
2
+
−
-3
Khẳng định nào sau đây là đúng ?
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng 2.
C. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -3.
D. Hàm số đạt cực đại tại x=0 và đạt cực tiểu tại x=1
Câu 3 .Cho hàm số
y f(x)=
có
x
limf(x) 3
→+
=
và
x
limf(x) 3
→−
=−
. Khẳng định nào sau đây là đúng ?
A. Đồ thị hàm số đã cho không có tiệm cận ngang.
B. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
y3=
và
y3=−
.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
x3=
và
x3=−
.
Câu 4.Biết
a=2log
,
b=3log
thì
45log
tính theo a và b bằng:
A.
12 +− ab
B.
12 ++ ab
C.
b15
D.
12 +− ba
Câu 5. Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số
x
y e 4x= − +
, trục hoành và hai đường
thẳng
x 1;x 2==
. Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh
trục hoành.
A.
2
V 6 e e= − +
B.
2
V 6 e e= − −
C.
( )
2
V 6 e e= − −
D.
( )
2
V 6 e e= − +
Câu 6. Cho số phức z thỏa mãn:
( )
4 3 4i z i− = −
. Điểm biểu diễn của z là:

Trang 66
A.
16 11
;
15 15
M
−
B.
16 13
;
17 17
M
−
C.
94
;
55
M
−
D.
9 23
;
25 25
M
−
Câu 7. Một hình trụ có bán kính
2r cm=
và chiều cao
23h cm=
. Khi đó diện tích xung quanh của
hình trụ là:
A.
( )
2
43 cm
B.
( )
2
83 cm
C.
( )
2
16 3 cm
D.
( )
2
23 cm
Câu 8. Trong không gian hệ tọa độ Oxyz, cho đường thẳng d có phương trình:
21
2
2
1 zyx
=
−
+
=
−
Véctơ nào sau đây là véctơ chỉ phương của đường thẳng:
A.
( )
0;2;1−=a
B.
( )
1;2;1−=a
C.
( )
2;1;1−=a
D.
( )
2;1;2 −=a
Câu 9. Trong không gian Oxyz, cho mặt phẳng (P) có phương trình 4x – 6y – 10z + 5 = 0. Tìm
khẳng định sai trong các khẳng định sau:
A. Một vectơ pháp tuyến của (P) là
( )
;;n = − −2 3 5
B. Mặt phẳng này cắt cả ba trục tọa độ.
C. Điểm
1
A 3; 2; (P)
2
D. Mặt phẳng (P) song song trục Ox
Câu 10 .Số hạng tổng quát của CSC được xác định bởi công thức nào sau đây .Với n
N
*
A. u
n
=u
1
+(n+1)d B.u
n
=u
1
+nd-d C.u
n
=u
2
+(n-1)d C.u
n
=u
1−n
+d
Câu 11. Đồ thị hàm số nào sau đây luôn nằm dưới trục hoành
A.
42
y x 3x 1= + −
B.
32
y x 2x x 1= − − + −
C.
42
y x 2x 2= − + −
D.
42
y x 4x 1= − − +
Câu 12. Nếu đường thẳng y = x là tiếp tuyến của parabol
( )
2
f x x bx c= + +
tại điểm
( )
1;1
thì cặp
( )
b;c
là cặp :
A.
( )
1;1
B.
( )
1; 1−
C.
( )
1;1−
D.
( )
1; 1−−
Câu 13.Số điểm chung của đồ thị hàm số
42
y x 7x 6= − −
và đồ thị hàm số
3
y x 13x=−
là:
A. 1 B. 2 C. 3 D. 4
Câu 14. Tìm số nghiệm nguyên âm của bất phương trình
13
9
1
3
1
−
xx
là :
A. 1
B. 2
C. 3
D. 0
Câu 15.Tìm tập xác định của hàm số
( )
2
ln 2 7 3y x x= − + −
A.
( )
1
D= ; 3;
2
− +
B.
1
;3
2
D
=
C.
)
1
D= ; 3;
2
− +
D.
1
;3
2
D
=
Câu 16: Cho
3
0
d ln 2 ln3
3
4 2 1
xa
x b c
x
= + +
++
với
a
,
b
,
c
là các số nguyên. Giá trị của
abc++
bằng
A.
1
. B.
2
. C.
7
. D.
9
.
Câu 17:Biết
( )
fx
là hàm liên tục trên và
( )
9
0
d9f x x =
. Khi đó giá trị của
( )
4
1
3 3 df x x−
là
Trang 67
A.
27
. B.
3
. C.
24
. D.
0
.
Câu 18:Cho hai số phức
1
12= − +zi
,
2
12= − −zi
. Giá trị của biểu thức
22
12
+zz
bằng
A.
10
. B.
10
. C.
6−
. D.
4
.
Câu 19: Một hình hộp đứng có đáy là hình thoi (không phải hình vuông) có bao nhiêu mặt phẳng
đối xứng?
A. 1. B. 3. C. 4. D. 2.
Câu 20: Cho khối lăng trụ
.ABCD A B C D
có thể tích bằng
12
, đáy
ABCD
là hình vuông tâm
O
.
Thể tích của khối chóp
.A BCO
bằng
A.
1
. B.
4
. C.
3
. D.
2
.
Câu 21:Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
( )
1; 0; 2I −
và mặt phẳng
( )
P
có
phương trình:
2 2 4 0x y z+ − + =
. Phương trình mặt cầu
( )
S
có tâm
I
và tiếp xúc với mặt phẳng
( )
P
là
A.
( ) ( )
22
2
1 2 9x y z− + + + =
. B.
( ) ( )
22
2
1 2 3x y z− + + + =
.
C.
( ) ( )
22
2
1 2 3x y z+ + + − =
. D.
( ) ( )
22
2
1 2 9x y z+ + + − =
.
Câu 22:Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
( )
0;0; 6A −
,
( )
8;0;0B
. Độ dài đoạn
thẳng
AB
bằng
A.
2
. B.
10
. C.
14
. D.
100
.
Câu 23:Tìm điều kiện cần và đủ của a, b, c để phương trình
sin cosa x b x c+=
có nghiệm?
A.
2 2 2
a b c+
B.
2 2 2
a b c+
C.
2 2 2
a b c+=
D.
2 2 2
a b c+
Câu 24:Cho hàm số
( )
2
2
42
0
.
5
2 khi x = 0
4
x
khix
x
fx
a
+−
=
−
Tìm giá trị thực của tham số a để hàm số
( )
fx
liên tục tại
0.x =
A.
3
4
a =−
B.
4
3
a =
C.
4
3
a =−
D.
3
4
a =
Câu 25 : Cho hình chóp tứ giác đều
.S ABCD
có tất cả các cạnh bằng
.a
Gọi
M
là điểm trên đoạn
SD
sao cho
2=SM MD
.
D
S
C
B
A
M
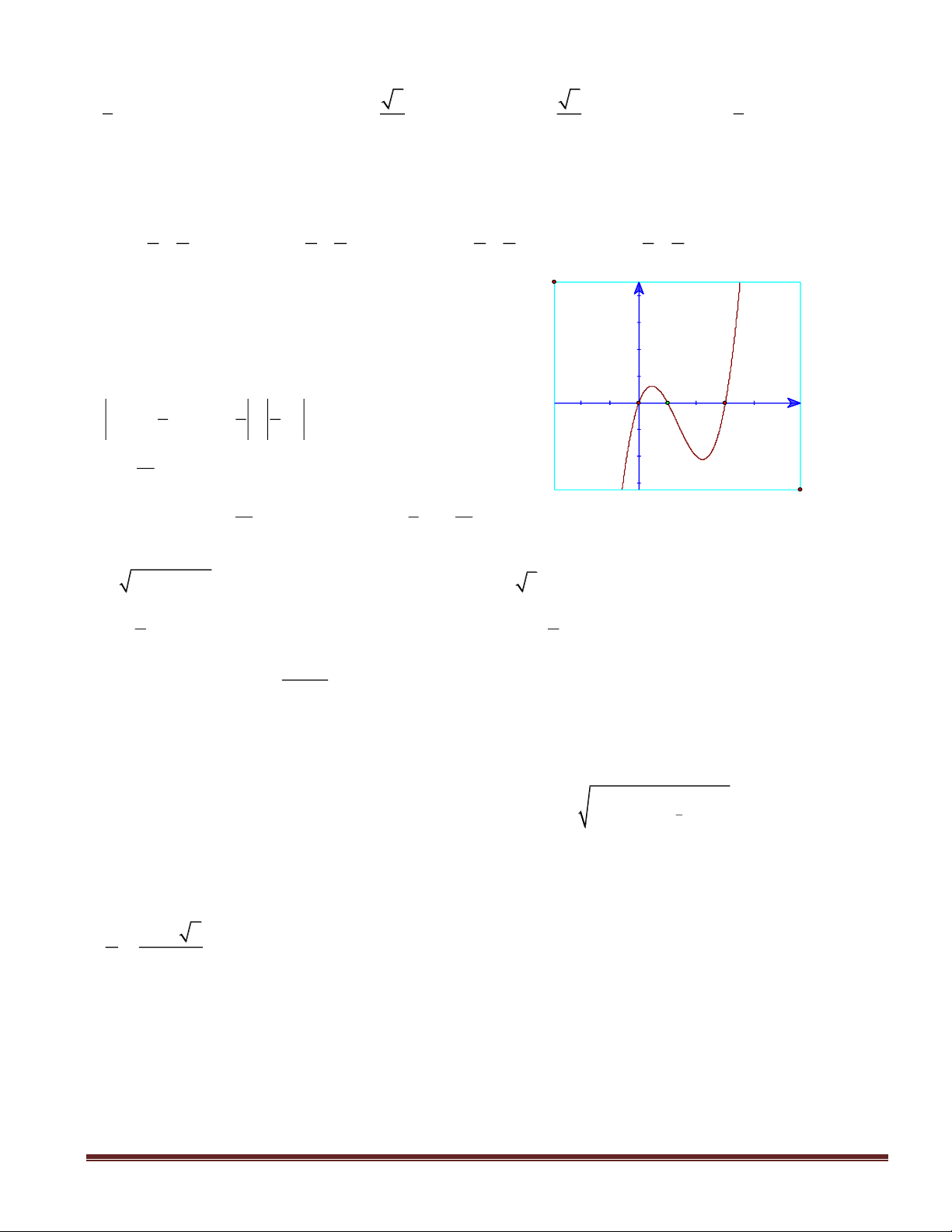
Trang 68
Tan góc giữa đường thẳng
BM
và mặt phẳng
( )
ABCD
là
A.
1
3
. B.
5
5
. C.
3
3
. D.
1
5
.
Câu 26:Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường thẳng d cắt hai trục Ox và Oy lần lượt
tại 2 điểm A(a;0) và
( )( )
0; 0, 0 .B b a b
Viết phương trình đường thẳng d.
A.
:0
xy
d
ab
+=
B.
:1
xy
d
ab
−=
C.
:1
xy
d
ab
+=
D.
:0
xy
d
ba
+=
Câu 27: Cho hàm số
()fx
liên tục trên R có đồ thị của đạo
hàm
( )
'fx
như hình bên. .Hàm số
2
()y f x=
có bao nhiêu
điểm cực trị.
A. 2 B. 3 C. 4 D. 5
Câu 28. Tìm tất cả các giá trị thực
k
để phương trình
32
31
2 3 1
2 2 2
k
x x x− − + + = −
có đúng
4
nghiệm phân biệt
A.
19
;5 .
4
k
B.
.k
C.
( )
19
2; 1 1; .
4
k
− −
D.
3 19
2; ;6 .
44
k
− −
Câu 29 Tìm tất cả các giá trị thực của tham số
m
sao cho bất phương trình
22
2 2 2 0m x x m x x− + + + −
có nghiệm
0;1 3x
+
.
A.
2
3
m
. B.
1m −
. C.
2
3
m
. D.
0m
.
Câu 30: Cho hàm số
2
23
x
y
x
+
=
+
có đồ thị (C). Đường thẳng d có phương trình
y ax b=+
là tiếp
tuyến của (C), biết d cắt trục hoành tại A và cắt trục tung tại B sao cho tam giác OAB cân tại O,
với O là gốc tọa độ. Tính
ab+
A. -1 B. -2 C. 0 D. -3
Câu 31. Có bao nhiêu giá trị
m
nguyên để phương trình
( )
2 2 2
2 1 4
2
log log 3 log 3x x m x+ − = −
có
nghiệm thuộc khoảng
( )
32;+
.
A. 3. B. 2. C. 1. D. 0.
Câu 32 Gọi
x
,
y
là các số thực dương thỏa mãn điều kiện
( )
9 12 16
log log logx y x y= = +
và
2
x a b
y
−+
=
, với
a
,
b
là hai số nguyên dương. Tính
.P a b=
.
A.
6P =
. B.
5P =
. C.
8P =
. D.
4P =
.
Câu 33: Một công ty dự kiến chi 1 tỷ đồng để làm các hộp hình trụ có thể tích là 5dm
3
để đựng sơn.
Biết chi phí để làm mặt xung quanh là 100.000 đồng/1m
2
và chi phí làm mặt đáy là 120.000
đồng/1m
2
. Số thùng sơn tối đa mà công ty này làm được là bao nhiêu thùng, biết rằng chi phí
các mối nối không đáng kể?
A. 58135 thùng. B. 48209 thùng. C. 67582 thùng. D. 61525 thùng.
x
y
O
1
3
Trang 69
Câu 34: Cho hàm số
( ) 0fx
và có đạo hàm trên R thỏa điều kiện
( )
( ) e 2 '( ) 0.
xx
f x f x e+ − =
Biết
(0) 3,f =
tính
( )
ln3 .f
A. 2. B. 4. C.
5.
D. 6.
Câu 35: Cho 2 số phức
12
,zz
thỏa phương trình
22z i iz− = +
và
12
1.zz−=
Tính
12
.P z z=+
A.
3.
B.
3
.
2
C.
2
.
2
D.
2.
Câu 36 Cho số phức
z
thỏa mãn
2z
. Giá trị nhỏ nhất của biểu thức
2 1 2 1 4P z z z z i= + + − + − −
bằng:
A
4 2 3+
. B.
23+
. C.
14
4
15
+
. D.
7
2
15
+
.
Câu 37: Cho tứ diện ABCD có
0 0 0
; 60 ; 60 ; 90AB AC AD a BAC CAD DAB= = = = = =
. Khoảng cách
giữa hai đường thẳng AC và BD là
A.
30
10
a
B.
2
a
C.
3
2
a
D.
2
2
a
Câu 38: Cho khối chóp tam giác S.ABC có đỉnh S và đáy là tam giác ABC. Gọi V là thể tích của
khối chóp. Mặt phẳng đi qua trọng tâm của ba mặt bên của khối chóp chia khối chóp thành hai
phần. Tính theo V thể tích của phần chứa đáy của khối chóp.
A.
37
64
V
B.
27
64
V
C.
19
27
V
D.
8
27
V
Câu 39: Cho hình trụ có đáy là hai đường tròn
( )
;OR
và
( )
';OR
, chiều cao bằng đường kính đáy.
Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn đáy tâm
'O
lấy điểm B. Thể tích của
khối tứ diện
'OO AB
có giá trị lớn nhất bằng:
A.
3
2
R
B.
3
3
3
R
C.
3
6
R
D.
3
3
R
Câu 40: Cho hình trụ có hai đáy là hai hình tròn
( )
;OR
và
( )
';OR
. AB là một dây cung của đường
tròn
( )
;OR
sao cho tam giác
'O AB
là tam giác đều và mặt phẳng
( )
'O AB
tạo với mặt phẳng chứa
đường tròn
( )
;OR
một góc 60
0
. Tính theo R thể tích V của khối trụ đã cho.
A.
3
7
7
R
V
=
B.
3
35
5
R
V
=
C.
3
5
5
R
V
=
D.
3
37
7
R
V
=
Câu 41: Chiều cao của khối trụ có thể tích lớn nhất nội tiếp trong hình cầu có bán kính R là
A.
43
.
3
R
B.
3.R
C.
3
.
3
R
D.
23
.
3
R
Câu 42: Cần sản xuất một vỏ hộp sữa hình trụ có thể tích V cho trước. Để tiết kiệm vật liệu
nhất thì bán kính đáy phải bằng.
Trang 70
A.
3
2
V
B.
3
2
V
C.
3
V
D.
3
3
V
Câu 43: Cho hình lăng trụ đứng ABC. A 'B 'C ' có đáy ABC là tam giác vuông tại A. Gọi E là trung
điểm của AB. Cho biết AB = 2a, BC =
13
, CC’ = 4a. Khoảng cách giữa hai đường thẳng A 'B
và CE bằng
A.
4
7
a
B.
12
7
a
C.
6
7
a
D.
3
7
a
Câu 44: Trong không gian với hệ tọa độ Oxyz cho hai mặt phẳng
( )
: 2 2 1 0P x y z+ − + =
,
( ) ( )
: 1 2019 0Q x my m z+ + − + =
. Khi hai mặt phẳng
( ) ( )
,PQ
tạo với nhau một góc nhỏ nhất thì
mặt phẳng
( )
Q
đi qua điểm M nào sau đây?
A.
( )
2019; 1;1M −
B.
( )
0; 2019;0M −
C.
( )
2019;1;1M −
D.
( )
0;0; 2019M −
Câu 45: Số hạng không chứa x trong khai triển
9
2
1
1 xx
x
+ + +
bằng
A.13051 B.13050 C.13049 D.13048
Câu 46: Cho hình chóp tam giác S.ABC có đáy ABC là một tam giác vuông cân tại B với trọng tâm
G, cạnh bên SA tạo với đáy
( )
ABC
một góc
0
30
. Biết hai mặt phẳng
( )
SBG
và
( )
SCG
cùng
vuông góc với mặt phẳng
( )
ABC
. Tính cosin của góc giữa hai đường thẳng SA và BC.
A.
15
5
B.
3 15
20
C.
15
10
D.
30
20
Câu 47: hệ phương trình:
có nghiệm (x
0
; y
0
) trong đó x
0
; y
0
là các số thực . Tổng
22
00
32P x y=+
bằng
A. 5 B. 3 C. 2 D. 0
Câu 48. Cho hàm số
( )
fx
liên tục và có đạo hàm trên
0; ,
2
p
æö
÷
ç
÷
ç
÷
ç
èø
thỏa mãn hệ thức
( ) ( )
3
tan .
cos
x
f x xf x
x
¢
+=
Biết rằng
3 3 ln 3
36
f f a b
pp
p
æ ö æ ö
÷÷
çç
- = +
÷÷
çç
÷÷
çç
è ø è ø
trong đó
, .abÎ ¤
Tính giá trị của
biểu thức
.P a b=+
A.
4
.
9
P =-
B.
2
.
9
P =-
C.
7
.
9
P =
D.
14
.
9
P =
Câu 49 Cho số phức
z a bi=+
thỏa mãn
3 2 12ab−=
. Gọi
12
,zz
là hai số phức thỏa mãn
1
3 4 1zi− − =
và
2
2 6 8 1zi− − =
. Giá trị nhỏ nhất của biểu thức
12
22P z z z z= − + − +
bằng
A.
9 3 2.−
B.
9945
.
13
C.
9 3 2.+
D.
9945
.
31
3
4
11
( 1)
x y x
xy
− − = −
−=

Trang 71
Câu 50: Cho 10 cái thẻ, mỗi thẻ được viết một số nguyên dương thuộc đoạn
1;10
sao cho hai thẻ
khác nhau được viết hai số khác nhau. Chọn ngẫu nhiên 3 thẻ và tính tích của ba số được ghi
trên 3 thẻ. Tính xác suất để tích của ba số trên 3 thẻ được chọn là một số chia hết cho 3.
A.
17
24
. B.
7
24
. C.
13
20
. D.
7
20
.
--------HẾT----
ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
D
C
A
D
B
B
D
D
B
C
C
C
A
D
A
B
B
B
A
A
B
D
D
D
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
C
D
D
A
D
D
B
A
C
A
A
B
C
D
D
D
A
C
C
A
C
B
C
B
A
Câu 1: Đáp án A
Ta có:
4 2 3
y x 2x 2019 y' 4x 4x= − + = −
. Khi đó
x0
y' 0
x1
=
=
=
Bảng biến thiên
X
−
1−
0 1
+
y'
−
0 + 0
−
0 +
Y
Dựa vào bảng biến thiên suy ra hàm số nghịch biến trên các khoảng
( ) ( )
; 1 , 0;1− −
. Suy ra đáp án A
đúng.
Câu 2.Cho hàm số
y f(x)=
xác định, liên tục trên R và có bảng biến thiên :
x
−
0 1
+
y’
+
– 0 +
y
2
+
−
-3
Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng 2.
C. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -3.
D. Hàm số đạt cực đại tại x=0 và đạt cực tiểu tại x=1
Chọn D
Câu 3.Cho hàm số
y f(x)=
có
x
limf(x) 3
→+
=
và
x
limf(x) 3
→−
=−
. Khẳng định nào sau đây là khẳng định
đúng ?

Trang 72
A. Đồ thị hàm số đã cho không có tiệm cận ngang.
B. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
y3=
và
y3=−
.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
x3=
và
x3=−
.
HD: Định lí
00
x
limf(x) y y y
→
= =
là tiệm cận ngang
0
0
xx
limf(x) x x
→
= =
là tiệm cận đứng
Chọn C
Câu 4 .HD :
10
log45 2log3 log 2log3 1 log2 2 1
2
ba= + = + − = − +
(BẤM MÁY TÍNH)
Chọn A.
12 +− ab
Câu 5: Đáp án D
( ) ( ) ( )
2
2
x 2 x 2
1
1
V 4x e dx 2x e 6 e e= − = − = − +
(BẤM MÁY TÍNH)
Câu 6 .HD:
3 4 16 13
4 17 17
i
zi
i
−
= = −
−
(BẤM MÁY TÍNH)
Chọn B.
16 13
;
17 17
M
−
Câu 7 . HD :Ta có
2r cm=
và
2 3 2 2 2.2 3 8 3
xq
l h cm S rl
= = = = =
.:(BẤM MÁY TÍNH)
Chọn B.
( )
2
83 cm
Câu 8.HD: Dễ thấy đáp án D.
( )
2;1;2 −=a
Câu 9.HD: Mặt phẳng (P) song song trục Ox. Chọn D
Câu 10.HD .Dễ thấy đáp án B .u
n
=u
1
+nd-d
Câu 11. HD:
( )
2
4 2 2
y x 2x 2 x 1 1 0= − + − = − − −
.Chọn C
Câu 12:
HD:Thấy rằng
( )
M 1;1
là điểm thuộc đường thẳng
yx=
không phụ thuộc vào a, b. Bởi vậy, đường
thẳng
yx=
là tiếp tuyến của parbol
( ) ( )
2
P :f x x bx c= + +
tại điểm
( )
M 1;1
khi và chỉ khi
( )
( ) ( )
MP
1 b c 1 b 1
2.1 b.1 1 c 1
f ' 1 g' 1
+ + = = −
+ = =
=
. Vậy cặp
( ) ( )
b;c 1;1=−
.Chọn C
Câu 13. Số giao điểm của đồ thị hàm số
42
y x 7x 6= − −
và
3
y x 13x=−
là : (BẤM MÁY TÍNH)
A. 1 B. 2 C. 3 D. 4
HD: Bấm máy tính ta được 3 giao điểm
Câu 14. Tìm nghiệm nguyên âm của bất phương trình
13
9
1
3
1
−
xx
là :
HD:Bất pt
223
3
1
3
1
−
xx
223 − xx
2− x
Chọn A.

Trang 73
Câu 15 .Tìm tập xác định của hàm số
( )
2
ln 2 7 3y x x= − + −
HD :
2
1
2 7 3 0 3
2
x x x− + −
. Chọn D
Câu 16 : Cho
3
0
d ln 2 ln3
3
4 2 1
xa
x b c
x
= + +
++
với
a
,
b
,
c
là các số nguyên. Giá trị của
abc++
bằng
A.
1
. B.
2
. C.
7
. D.
9
.
Lời giải
Chọn A.
Đặt
1tx=+
2
1tx = +
2
1xt = −
d 2 dx t t=
.
Đổi cận:
02xt= =
;
34xt= =
.
Khi đó:
2
2 2 2
2 3 3
22
1 1 1
1
1 6 7
.2 d d 2 3 d 3 6ln 2 12ln2 6ln3
4 2 2 2 3 3
t t t t
t t t t t t t t t
t t t
−−
= = − + − = − + − + = − +
+ + +
Suy ra
7
12
6
a
b
c
=
=−
=
1abc + + =
.
Câu 17: Biết
( )
fx
là hàm liên tục trên và
( )
9
0
d9f x x =
. Khi đó giá trị của
( )
4
1
3 3 df x x−
là
A.
27
. B.
3
. C.
24
. D.
0
.
Lời giải
Chọn B
Gọi
( )
4
1
3 3 dI f x x=−
.
Đặt
33tx=−
d 3dtx=
1
dd
3
xt=
. Đổi cận:
1 0;xt= =
49xt= =
.
Khi đó:
( )
9
0
1
d
3
I f t t=
1
.9
3
=
3=
.
Câu 18: Cho hai số phức
1
12= − +zi
,
2
12= − −zi
. Giá trị của biểu thức
22
12
+zz
bằng
A.
10
. B.
10
. C.
6−
. D.
4
.
Lời giải
Chọn B.
Ta có
( )
( )
( ) ( )
( )
22
22
2 2 2
2
12
1 2 1 2 10+ = − + + − + − =zz
.
.Câu 19: Chọn B.
Phương pháp:
Sử dụng lý thuyết khối đa diện để là bài toán.
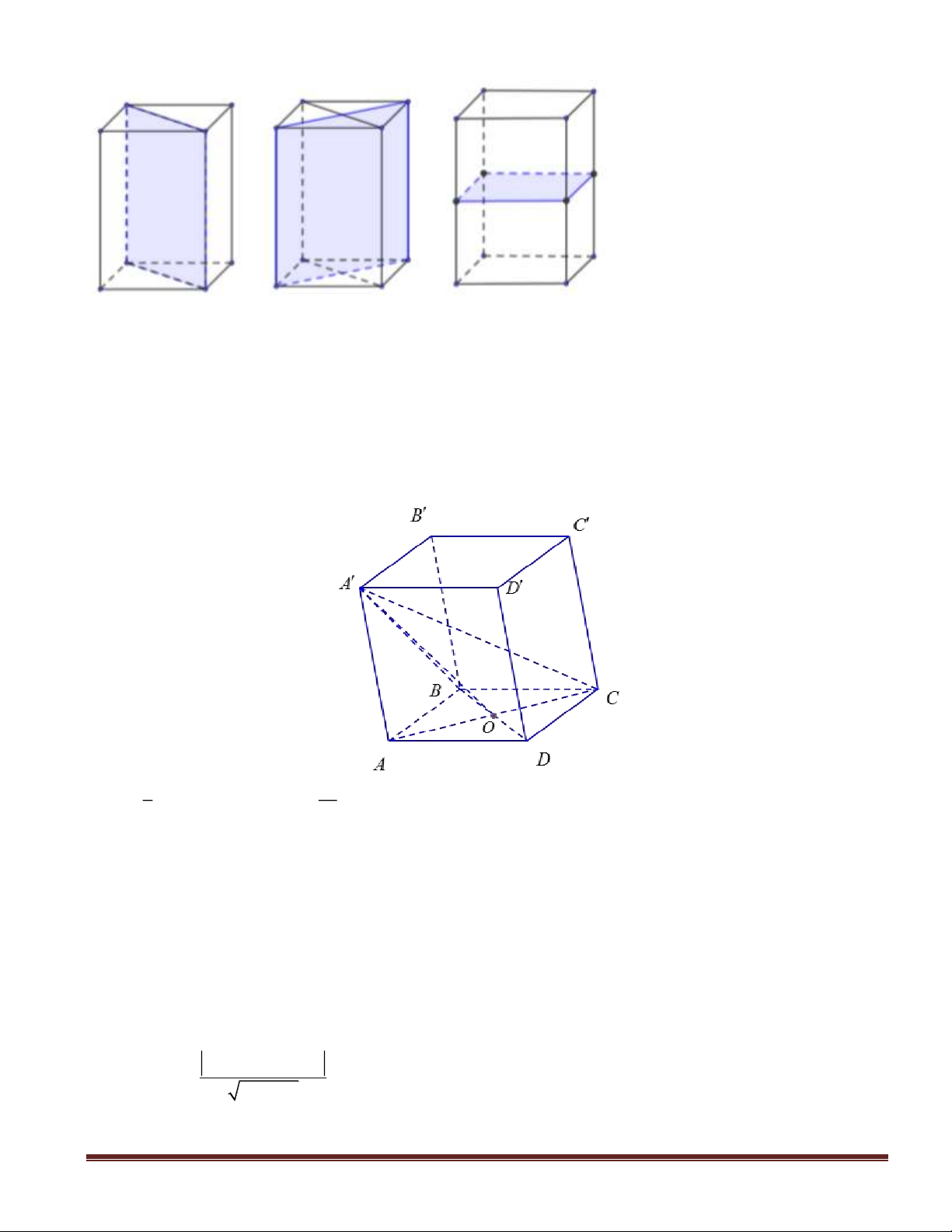
Trang 74
Cách giải:
Hình đã cho có 3 mặt phẳng đối xứng.
Câu 20:Cho khối lăng trụ
.ABCD A B C D
có thể tích bằng
12
, đáy
ABCD
là hình vuông tâm
O
. Thể tích
của khối chóp
.A BCO
bằng
A.
1
. B.
4
. C.
3
. D.
2
.
Lời giải
Chọn A.
( )
( )
..
11
, . 1
3 12
A BCO BCO ABCD A B C D
V d A BCO S V
= = =
.
Câu 21:Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
( )
1; 0; 2I −
và mặt phẳng
( )
P
có phương
trình:
2 2 4 0x y z+ − + =
. Phương trình mặt cầu
( )
S
có tâm
I
và tiếp xúc với mặt phẳng
( )
P
là
A.
( ) ( )
22
2
1 2 9x y z− + + + =
. B.
( ) ( )
22
2
1 2 3x y z− + + + =
.
C.
( ) ( )
22
2
1 2 3x y z+ + + − =
. D.
( ) ( )
22
2
1 2 9x y z+ + + − =
.
Lời giải
Chọn A.
Mặt cầu
( )
S
có tâm
I
và tiếp xúc với mặt phẳng
( )
P
nên bán kính mặt cầu là
( )
( )
,R d I P=
( )
1 0 2 2 4
1 4 4
+ − − +
=
++
3=
.
Vậy phương trình mặt cầu là
( ) ( )
22
2
1 2 9x y z− + + + =
.

Trang 75
Câu 22:Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
( )
0;0; 6A −
,
( )
8;0;0B
. Độ dài đoạn thẳng
AB
bằng
A.
2
. B.
10
. C.
14
. D.
100
.
Lời giải
Chọn B.
Áp dụng công thức ta có
10AB =
.
Câu 23: Chọn D.
Phương pháp:
Phương trình thuần nhất đối với sin và cos, dạng
sin cosa x b x c+=
có nghiệm
2 2 2
.a b c +
Cách giải:
Phương trình thuần nhất đối với sin và cos, dạng
sin cosa x b x c+=
có nghiệm
2 2 2
.a b c +
Câu 24: Chọn D.
Phương pháp:
Hàm số
( )
y f x=
liên tục tại
( ) ( ) ( )
00
00
lim lim .
x x x x
x x f x f x f x
+−
→→
= = =
Cách giải:
Ta có:
( )
5
0 2 .
4
fa=−
( )
(
)
(
)
(
)
22
2
2
0 0 0
22
4 2 4 2
42
lim lim lim
42
x x x
xx
x
fx
x
xx
→ → →
+ − + +
+−
==
++
(
)
2
2
00
22
4 4 1 1
lim lim .
4
42
42
xx
x
x
xx
→→
+−
= = =
++
++
Hàm số liên tục tại
( ) ( )
0
5 1 3
0 0 lim 2 .
4 4 4
x
x f f x x a
→
= = − = =
Câu 25:Cho hình chóp tứ giác đều
.S ABCD
có tất cả các cạnh bằng
.a
Gọi
M
là điểm trên đoạn
SD
sao
cho
2=SM MD
.
Tan góc giữa đường thẳng
BM
và mặt phẳng
( )
ABCD
là
A.
1
3
. B.
5
5
. C.
3
3
. D.
1
5
.
Lời giải
Chọn D.
D
S
C
B
A
M

Trang 76
Ta có
2=BD a
2
2
=
a
OD
.
Xét tam giác
SOD
vuông tại
O
có:
2
2 2 2
22
22
= − = − =
aa
SO SD OD a
.
Kẻ
⊥MH BD
tại
H
nên
( )
( )
; =BM ABCD MBH
Do
⊥MH BD
// MH SO
. Ta có
1
3
= = =
MH MD HD
SO SD OD
.
2
36
= =
SO a
MH
và
12
36
==
a
HD OD
2 5 2
2
66
= − = − =
aa
BH BD HD a
.
Xét tam giác
BHM
vuông tại
H
có:
( )
( )
tan ; ==
MH
BM ABCD MBH
BH
( )
( )
1
tan ;
5
=BM ABCD
.
Câu 26: Chọn C.
Phương pháp:
Viết phương trình đường thẳng dưới dạng phương trình đoạn chắn.
Cách giải:
Phương trình đường thẳng
( )
: 1.
xy
d
ab
+=
Câu 27: Cho hàm số
()fx
liên tục trên R có đồ thị của đạo
hàm
( )
'fx
như hình bên. .Hàm số
2
()y f x=
có bao
nhiêu
điểm cực trị.
A. 2 B. 3 C. 4 D. 5
HD: Dựa vào đồ thị ta thấy
0
'( ) 0 1.
3
x
f x x
x
=
= =
=
Đặt
2
( ) ( ).g x f x=
Ta có
2
2
22
2
0
0
00
'( ) 2 '( ) 0 1 .
'( ) 0 1
3
3
x
x
xx
g x xf x x
f x x
x
x
=
=
==
= = =
==
=
=
H
O
D
S
C
B
A
M
x
y
O
1
3

Trang 77
Dựa vào đồ thị
'( )y f x=
ta xét dấu
2
'( ) 2 '( )g x xf x=
và có bảng biến thiên như sau:
x
−
3−
1−
0
1
3
+
2
'( ) 2 '( )g x xf x=
– 0 + 0 – 0 + 0 – 0 +
2
( ) ( )g x f x=
Dựa vào bảng biến thiên ta dễ dàng chọn đáp án D.
Câu 28. Tìm tất cả các giá trị thực
k
để phương trình
32
31
2 3 1
2 2 2
k
x x x− − + + = −
có đúng
4
nghiệm
phân biệt
A.
19
;5 .
4
k
B.
.k
C.
( )
19
2; 1 1; .
4
k
− −
D.
3 19
2; ;6 .
44
k
− −
HD:Xét hàm số
32
31
23
22
y x x x= − − + +
. Ta có :
2
1
6 3 3. 0
1
2
x
y x x y
x
=−
= − − + =
=
Bảng biến thiên đồ thị hàm số
32
31
23
22
y x x x= − − + +
. Với :
32
1
31
2 3 0
7 33
22
8
x
x x x
x
=
− − + + =
−
=
Từ bảng biến thiên, nhận thấy: ycbt
19
6
11
4
12
3
82
2
4
k
k
k
−
− −
.
Câu 29 Tìm tất cả các giá trị thực của tham số
m
sao cho bất phương trình
22
2 2 2 0m x x m x x− + + + −
có nghiệm
0;1 3x
+
.
A.
2
3
m
. B.
1m −
. C.
2
3
m
. D.
0m
.
HD: Ta có
22
2 2 2 0m x x m x x− + + + −
(
)
22
2 2 1 2 0m x x x x− + + + −
2
2
2
2 2 1
xx
m
xx
−
− + +
(1)
Đặt:
2
22t x x= − +
22
22x x t− = −
.
Ta đi tìm điều kiện ràng buộc của
t
.
Xét hàm số
2
22t x x= − +
, với
0;1 3x
+
.
Ta có:
2
1
'
22
x
t
xx
−
=
−+
;
' 0 1tx= =
.
Tính:
( )
02t =
;
( )
11t =
;
( )
1 3 2t +=
.
Do đó, với
0;1 3x
+
suy ra
1;2t
.
Khi đó từ (1) suy ra:
2
2
1
t
m
t
−
+
, với
1;2t
.
Xét hàm số
( )
2
2
1
t
ft
t
−
=
+
, với
1;2t
.

Trang 78
Ta có
( )
( )
2
2
22
' 0, 1;2
1
tt
f t t
t
++
=
+
. Do đó hàm số
( )
ft
đồng biến trên đoạn
1;2
.
Suy ra
( ) ( )
1;2
2
max 2
3
m f t f = =
.
Câu 30: Cho hàm số
2
23
x
y
x
+
=
+
có đồ thị (C). Đường thẳng d có phương trình
y ax b=+
là tiếp
tuyến của (C), biết d cắt trục hoành tại A và cắt trục tung tại B sao cho tam giác OAB cân tại O,
với O là gốc tọa độ. Tính
ab+
A. -1 B. -2 C. 0 D. -3
Ta có:
( )
2
2 1 3
' 0,
2 3 2
23
x
y y x
x
x
+−
= = −
+
+
Hệ số góc của đường thẳng d chỉ có thể là
11a− = −
Gọi
( )
00
;M x y
là tiếp điểm
( )
( )
2
0
0
2
0
0
1
1
1 2 3 1
2
23
x
x
x
x
=−
−
= = − + =
=−
+
+)
( ) ( )
00
1 1 : 1 1 1x y d y x y x= − = = − + + = −
: Loại, do
yx=−
cắt 2 trục tọa độ tại điểm duy
nhất là O (0;0)
+)
( ) ( )
00
2 0 : 1 2 0 2 2 1 2 3x y d y x y x b a b= − = = − + + = − − = − + = − − = −
Câu 31. Có bao nhiêu giá trị
m
nguyên để phương trình
( )
2 2 2
2 1 4
2
log log 3 log 3x x m x+ − = −
có
nghiệm thuộc khoảng
( )
32;+
.
A. 3. B. 2. C. 1. D. 0.
Lời giải:
( )
2 2 2
2 1 4
2
log log 3 log 3x x m x+ − = −
.
Điều kiện
0x
. Phương trình trở thành
( )
2
2 2 2
log 2log 3 log 3x x m x− − = −
.
Đặt
2
logtx=
, ta có
32 5xt
, ta được
( )
2
2 3 3t t m t− − = −
( )( )
3
1
3
31
3
32
2
−
+
=
−
−+
=
−
−−
=
t
t
t
tt
t
tt
m
2
1
3
t
m
t
+
=
−
.
Xét
( )
1
3
t
gt
t
+
=
−
(
5t
)
( )
2
4
'( ) 0 5
3
g t t
t
−
=
−
. Suy ra hàm số
()gt
nghịch biến trên
( )
5;+
.
t
5
+
( )
'gt
−
( )
gt
3
1
Do đó
2
13m
. Giá trị
m
dương nên thỏa
13m
. Không có giá trị
m
nguyên dương
thỏa yêu cầu đề bài.
Câu 32 Gọi
x
,
y
là các số thực dương thỏa mãn điều kiện
( )
9 12 16
log log logx y x y= = +
và
2
x a b
y
−+
=
, với
a
,
b
là hai số nguyên dương. Tính
.P a b=
.
A.
6P =
. B.
5P =
. C.
8P =
. D.
4P =
.

Trang 79
HD:
Câu 33: Một công ty dự kiến chi 1 tỷ đồng để làm các hộp hình trụ có thể tích là 5dm
3
để đựng
sơn. Biết chi phí để làm mặt xung quanh là 100.000 đồng/1m
2
và chi phí làm mặt đáy là 120.000
đồng/1m
2
. Số thùng sơn tối đa mà công ty này làm được là bao nhiêu thùng, biết rằng chi phí
các mối nối không đáng kể?
A. 58135 thùng. B. 48209 thùng. C. 67582 thùng. D. 61525 thùng.
HD:
Gọi R, h là bán kính đáy và chiều cao của hộp
ta có: R > 0 & h > 0;
2
22
V5
V R h h
RR
= = =
100.000 đồng/1m
2
=1000 đồng/1dm
2
120.000 đồng/1m
2
=1200 đồng/1dm
2
Chi phí làm mặt xung quanh của hộp là:
1
2
10 10000
T 2 Rh.1000 R .1000
R
R
= = =
Chi phí làm mặt đáy của hộp là:
22
2
T 2 R .1200 2400 R= =
Tổng chi phí làm một hộp là:
22
12
10000 25
T T T 2400 R 400 6 R
RR
= + = + = +
/
2
25
T 400 12 R
R
−
= +
/
3
25
T 0 R
12
= =
2
3
3
25 25
minT 400 6
12
25
12
= +
3
3
1875
400 7500
2
= +
Số hộp tối đa là:
3
3
1000000000
maxS 58135.
1875
400 7500
2
=
+
Câu 34: Cho hàm số
( ) 0fx
và có đạo hàm trên R thỏa điều kiện
( )
( ) e 2 '( ) 0.
xx
f x f x e+ − =
Biết
(0) 3,f =
tính
( )
ln3 .f
A. 2. B. 4. C.
5.
D. 6.
HD: Ta có:
( )
'( )
( ) e 2 '( ) 0 .
( ) e 2
x
xx
x
f x e
f x f x e
fx
+ − = =
+
Lấy nguyên hàm 2 vế ta được
( )
ln ( ) ln 2
x
f x e C= + +
1
( ) 2
x
f x e C = + +
. Vì
(0) 3f =
nên
1
0C =
( ) 2
x
f x e = +
( )
ln3 5.f=
Câu 35: Cho 2 số phức
12
,zz
thỏa phương trình
22z i iz− = +
và
12
1.zz−=
Tính
12
.P z z=+
A.
3.
B.
3
.
2
C.
2
.
2
D.
2.
Giải: Gọi
.z x yi=+
Ta có
22
2 2 1.z i iz x y− = + + =
Gọi
,AB
lần lượt là điểm biểu diễn 2 số phức
12
,zz
.
Suy ra
,AB
thuộc đường tròn tâm
(0;0)O
, bán kính là
1. Suy ra
1, 1.OA OB==
Mặt khác
12
11z z OA OB BA AB OAB− = − = = =
đều
có cạnh là 1.
Khi đó
12
3
2 2 3.
2
P z z OA OB OM= + = + = = =
x
y
M
O
1
A
B
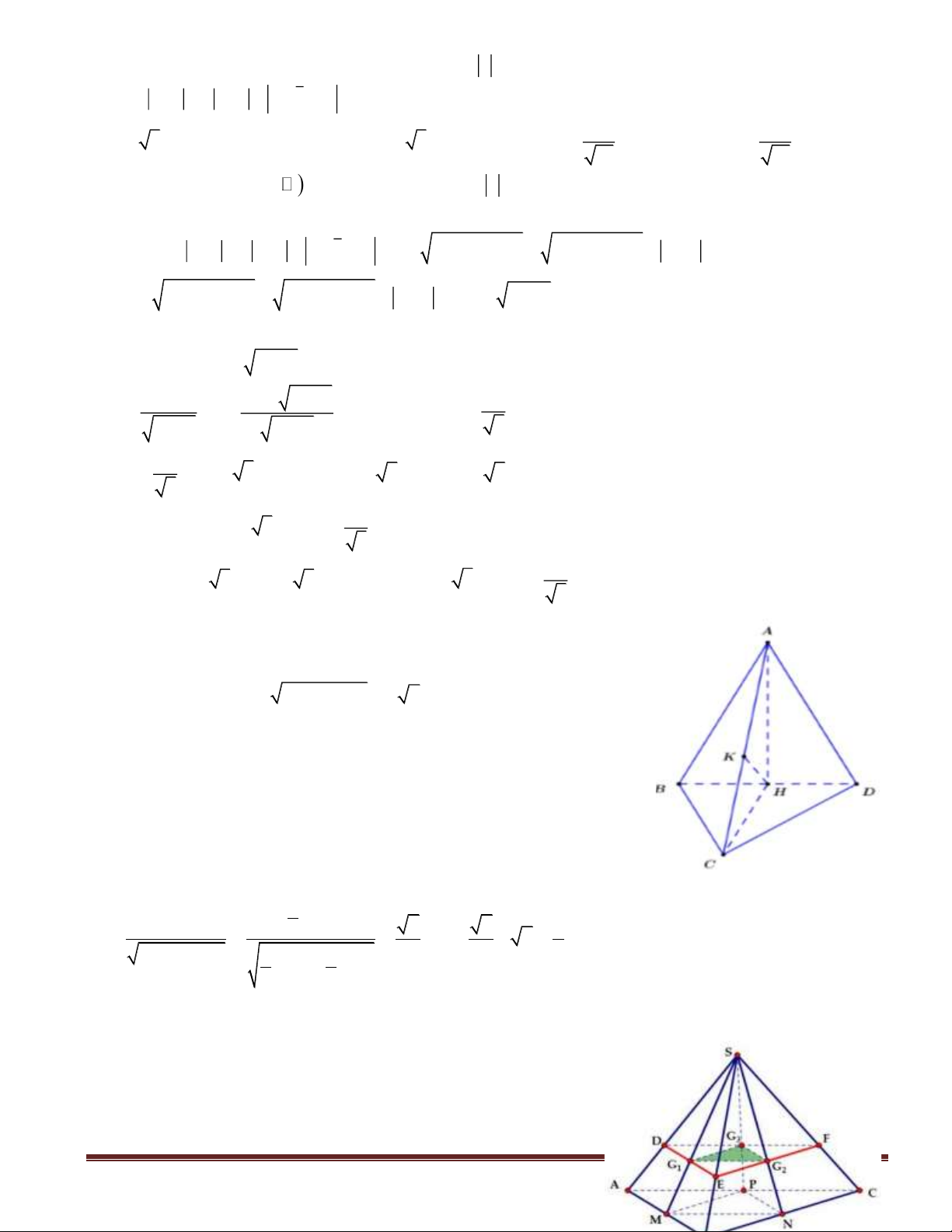
Trang 80
Câu 36 Cho số phức
z
thỏa mãn
2z
. Giá trị nhỏ nhất của biểu thức
2 1 2 1 4P z z z z i= + + − + − −
bằng:
A.
4 2 3+
. B.
23+
. C.
14
4
15
+
. D.
7
2
15
+
.
HD Gọi
( )
i, ,z x y x y= +
. Theo giả thiết, ta có
22
24z x y +
.
Suy ra
2 , 2xy−
.
Khi đó,
2 1 2 1 4P z z z z i= + + − + − −
( ) ( )
( )
22
22
2 1 1 2x y x y y= + + + − + + −
( ) ( )
( )
22
22
2 1 1 2P x y x y y = + + + − + + −
(
)
2
2 2 1 2yy + + −
.
Dấu “
=
” xảy ra khi
0x =
.
Xét hàm số
( )
2
2 1 2f y y y= + + −
trên đoạn
2; 2−
, ta có:
( )
2
2
1
1
y
fy
y
=−
+
2
2
21
1
yy
y
−+
=
+
;
( )
1
0
3
f y y
= =
.
Ta có
1
23
3
f
=+
;
( )
2 4 2 5f − = +
;
( )
2 2 5f =
.
Suy ra
( )
2; 2
min 2 3fy
−
=+
khi
1
3
y =
.
Do đó
( )
2 2 3 4 2 3P + = +
. Vậy
min
4 2 3P =+
khi
1
i
3
z =
.
Câu 37:Ta có:
00
; 60 ; 60AB AC AD a BAC CAD= = = = =
,ABC ACD
đều
BC CD a = =
.
Có
0 2 2
90 2BAD BD AB AD a = = + =
.
BCD
vuông cân tại C.
Gọi H là trung điểm của BD. Kẻ
KH AC⊥
.
( )
( )
,
CH BD
BD CAH BD KH
AH BD
d AC BD KH
⊥
⊥ ⊥
⊥
=
Xét
AHC
vuông tại H có đường cao KH ta có:
2
22
22
1
. 2 2
4
.2
4 4 2
11
44
BD
HC AH a
KH BD a
HC HA
BD BD
= = = = =
+
+
Chọn B.
Câu 38: Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC,
AC và
1 2 3
,,G G G
lần lượt là trọng tâm các tam giác
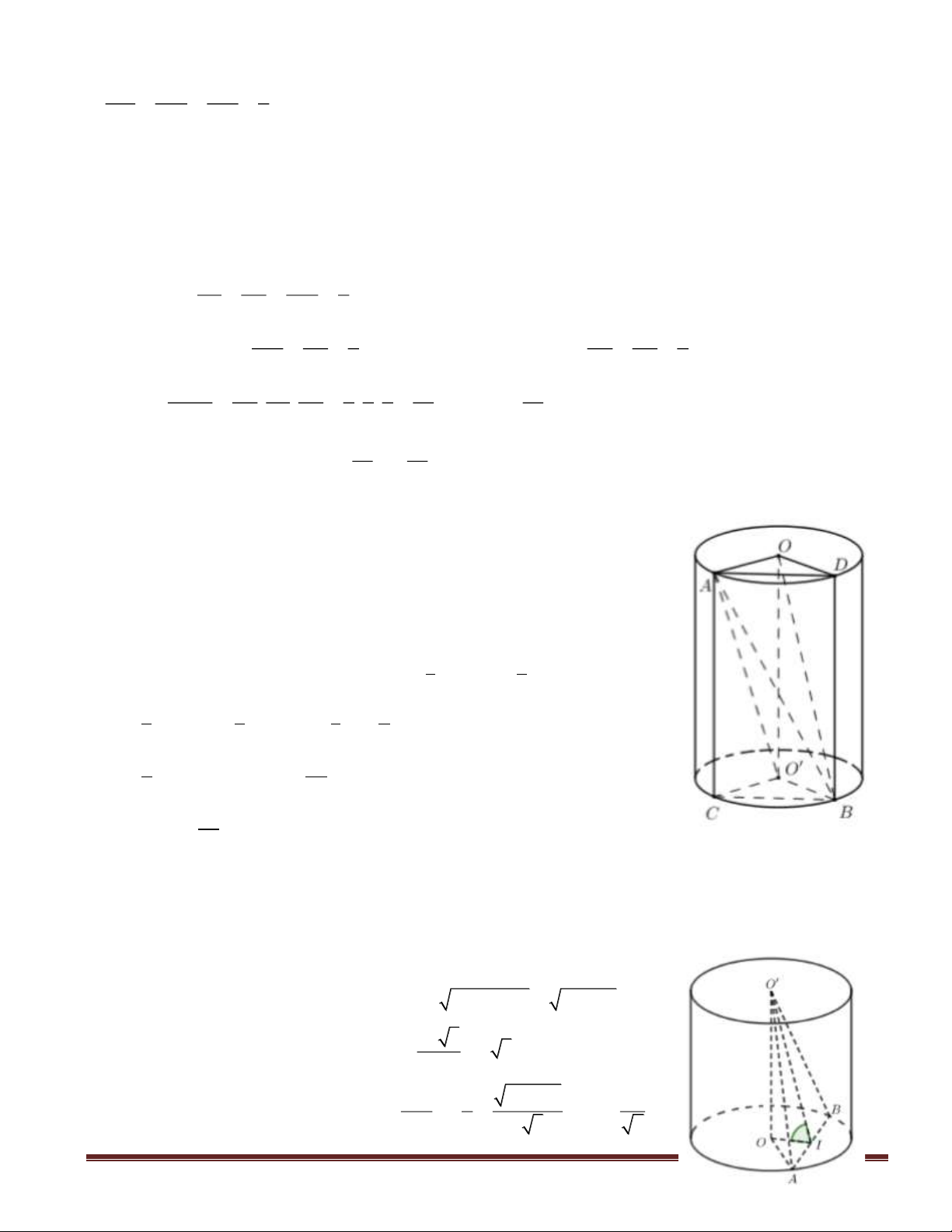
Trang 81
,,SAB SBC SAC
. Theo tính chất trọng tâm ta có
3
12
2
3
SG
SG SG
SM SN SP
= = =
Trong
( )
SBC
, qua
2
G
kẻ đường thẳng song song với BC cắt SB,
SC lần lượt tại E và F.
Trong
( )
SAC
, đường thẳng
3
FG
cắt SA tại D.
Lúc này
( ) ( )
1 2 3
GG G DEF
Vì
2
2
//
3
SG
SE SF
EF BC
SB SC SN
= = =
(theo định lý Ta-lét)
Lại có trong
SPC
có
3
3
22
/ / / /
33
SG
SF SD SF
FG PC DF BC
SP SC SA SC
= = = =
Từ đó ta có
.
.
.
2 2 2 8 8
. . . .
3 3 3 27 27
S DEF
S DEF
S ABC
V
SD SE SF
VV
V SA SB SC
= = = =
Nên phần chứa đáy hình chóp là
8 19
27 27
V V V−=
Chọn C.
Câu 39:Gọi C là hình chiếu của A lên mặt đáy chứa đường tròn
( )
';OR
và D là
hình chiếu của B lên mặt đáy chứa đường tròn
( )
;OR
.
Khi đó ta có lăng trụ đứng
.'OADO CB
.
Ta có
' . ' . ' '. . ' . ' . '
.'
3
2
3
'
11
33
1 1 1 1
. . . . .sin
3 3 3 2
1
.2 . .sin sin
63
max sin 1 '
3
OO AB OAD O CB A O BC O OAD OAD O CB OAD O CB OAD O CB
OAD O CB OAD
OO AB
V V V V V V V
V AC S AC OAOD AOD
R
R R AOD AOD
R
V AOD OA OD OA O B
= − − = − −
= = =
= =
= = ⊥ ⊥
Chọn: D
Câu 40: Gọi I là trung điểm của AB thì
' , .O I AB OI AB⊥⊥
Suy ra góc giữa
( )
'O AB
và
( )
;OR
là góc giữa
'OI
và OI hay
0
' 60 .O IO =
Đặt
2.AI x AB x= =
Tam giác vuông OIA có
2 2 2 2
,.OA R AI x OI OA AI R x= = = − = −
Tam giác
'O AB
đều cạnh
23
2 ' 3.
2
x
AB x O I x= = =
Tam giác
'O OI
vuông tại O nên
22
0
12
cos60 .
'2
37
OI R x R
x
OI
x
−
= = =
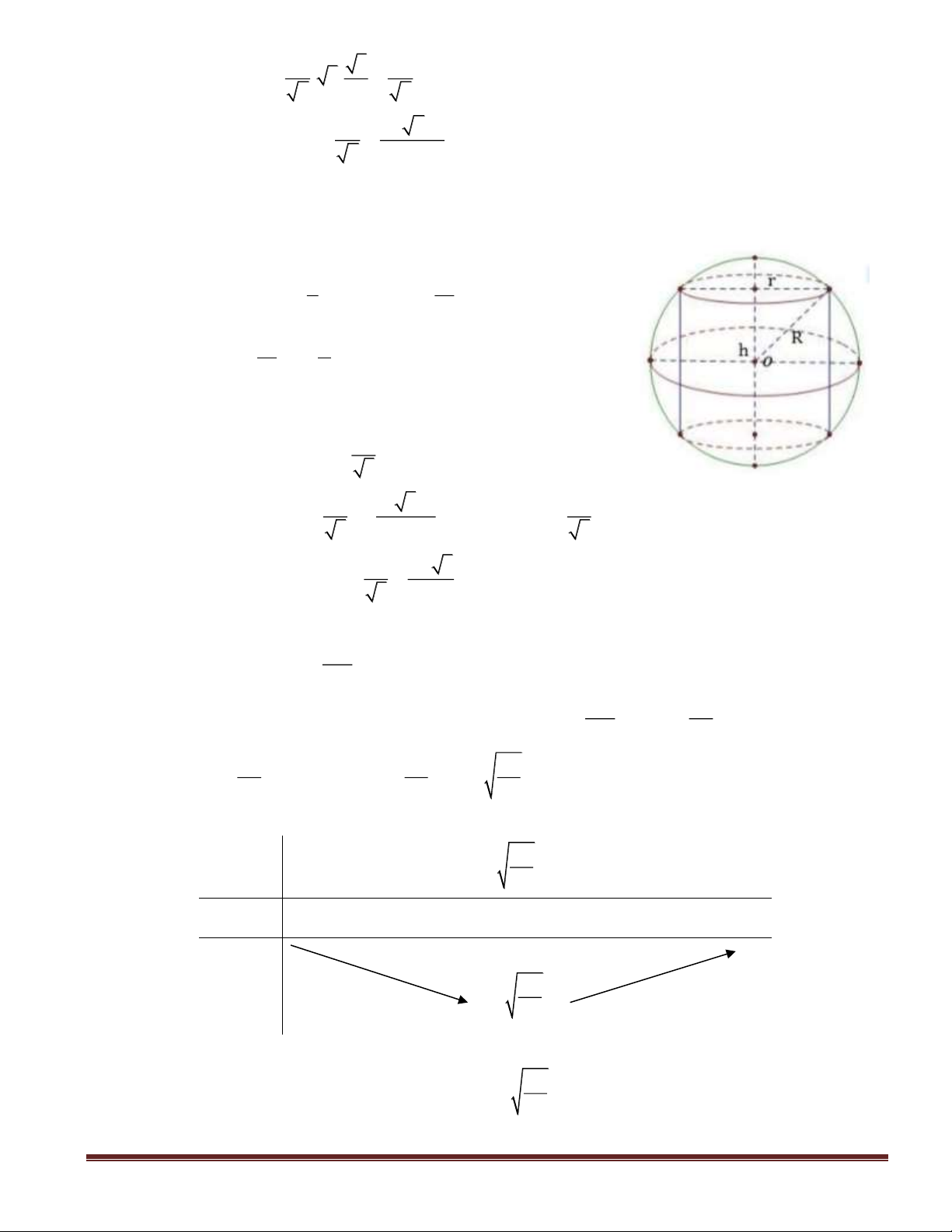
Trang 82
Suy ra
0
2 3 3
' ' .sin60 . 3. .
2
77
RR
OO O I= = =
Thể tích khối trụ
3
22
3 3 7
..
7
7
RR
V R h R
= = =
Chọn D.
Câu 41:Gọi d là khoảng cách từ tâm O đến mặt đáy của hình trụ, r là bán kính đáy.
Thể tích khối trụ:
2
tru
V r h
=
Mà
2
2
2 2 2 2 2 2 2
24
hh
R r d R r r R
= + = + = −
( )
2
2 2 2 3
4
44
tru
h
V r h R h R h h
= = − = −
Xét hàm số
( ) ( )
23
4 , 0f h R h h h R= −
có:
( ) ( )
22
2
' 4 3 , ' 0
3
R
f h R h f h h= − = =
Ta có:
( ) ( ) ( )
3
3
max
2 16 3 2
0 0, 3 ,
9
33
R R R
f f R R f f h f
= = = =
Vậy, thể tích khối trụ lớn nhất khi
2 2 3
3
3
RR
h ==
.
Chọn: D
Câu 42:Ta có:
2
2
V
V r h h
r
= =
Diện tích vật liệu để làm vỏ hộp là:
( )
2 2 2
2
2
2 2 2 2 . 2 , 0
tp
VV
S r rh r r r f r r
rr
= + = + = + =
Ta có:
( ) ( )
3
3
2
2
' 4 , ' 0
22
V V V
f r r f r r r
r
= − = = =
Bảng biến thiên:
r
0
3
2
V
+
( )
'fr
−
0
+
( )
fr
3
2
V
f
Vậy, để tiết kiệm vật liệu nhất thì bán kính đáy phải bằng
3
2
V
.
Chọn A.
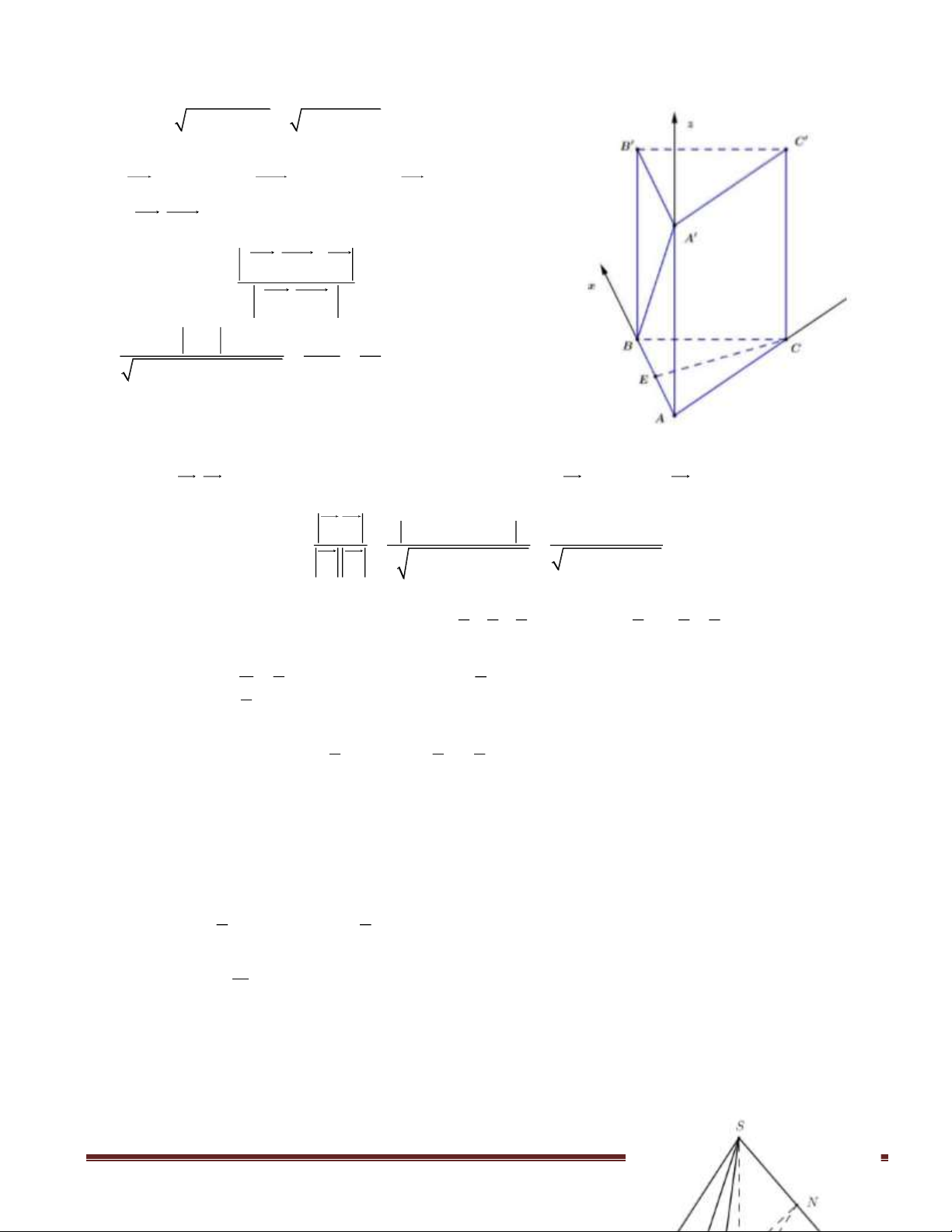
Trang 83
Câu 43:Chọn hệ trục như hình vẽ.
Ta có:
2 2 2 2
13 4 3AC BC AB a a a= − = − =
( ) ( ) ( ) ( ) ( )
( ) ( ) ( )
( )
( )
2 2 2
3
3
4 4 4
0;0;0 , ;0;0 , 2 ;0;0 ,C 0;3 ;0 , ' 0;0;4
; 3 ;0 , ' 2 ;0; 4 , ;0;0
, ' 12 ;4 ;6
, ' .
,'
,'
12
12
14
144 16 36
A E a B a a A a
CE a a A B a a EB a
CE A B a a a
CE A B EB
d CE A B
CE A B
a
a
a
a a a
= − = − =
=
=
==
++
2
6
7
a
=
Chọn C.
Câu 44:Gọi
,
PQ
nn
lần lượt là các VTPT của
( )
P
và
( )
Q
ta có
( ) ( )
1;2; 2 ; 1;m;m 1
PQ
nn= − = −
.
Khi đó ta có
( ) ( )
( )
( )
22
2
.
1 2 2 2
1
cos ;
2 2 2
3 1 1
PQ
PQ
nn
mm
PQ
nn
mm
mm
+ − +
= = =
−+
+ + −
Ta có
( )
2
2 2 2
1 1 1 1 3 3
2 2 2 2 2 2 2.m. 2 2
2 4 4 2 2 2
m m m m m m
− + = − + = − + − + = − +
( ) ( )
( )
12
cos ;
3
3
2
PQ =
. Dấu “=” xảy ra
1
2
m=
.
( ) ( )
( )
;PQ
nhỏ nhất
( )
1 1 1
: 2019 0
2 2 2
m Q x y z = + − + =
Khi đó
( )
Q
đi qua điểm
( )
2019;1;1M −
Chọn C.
Câu 45:
Ta có
( )
99
9
22
11
1 1 1x x x
xx
+ + + = + +
9 9 9 9
22
9 9 9 9
0 0 0 0
1
k k i k i k i
i
k i k i
C x C C C x
x
−
= = = =
==
.
Từ đây ta cho 2k – i = 0 thì tìm được 5 cặp (i, k) thỏa mãn là (0,0), (2,1), (4,2), (6,3), (8,4). Vậy số hạng
không chứa x là
1 2 2 4 3 6 4 8
9 9 9 9 9 9 9 9
1 13051.C C C C C C C C+ + + + =
Chọn A.
Câu 46:
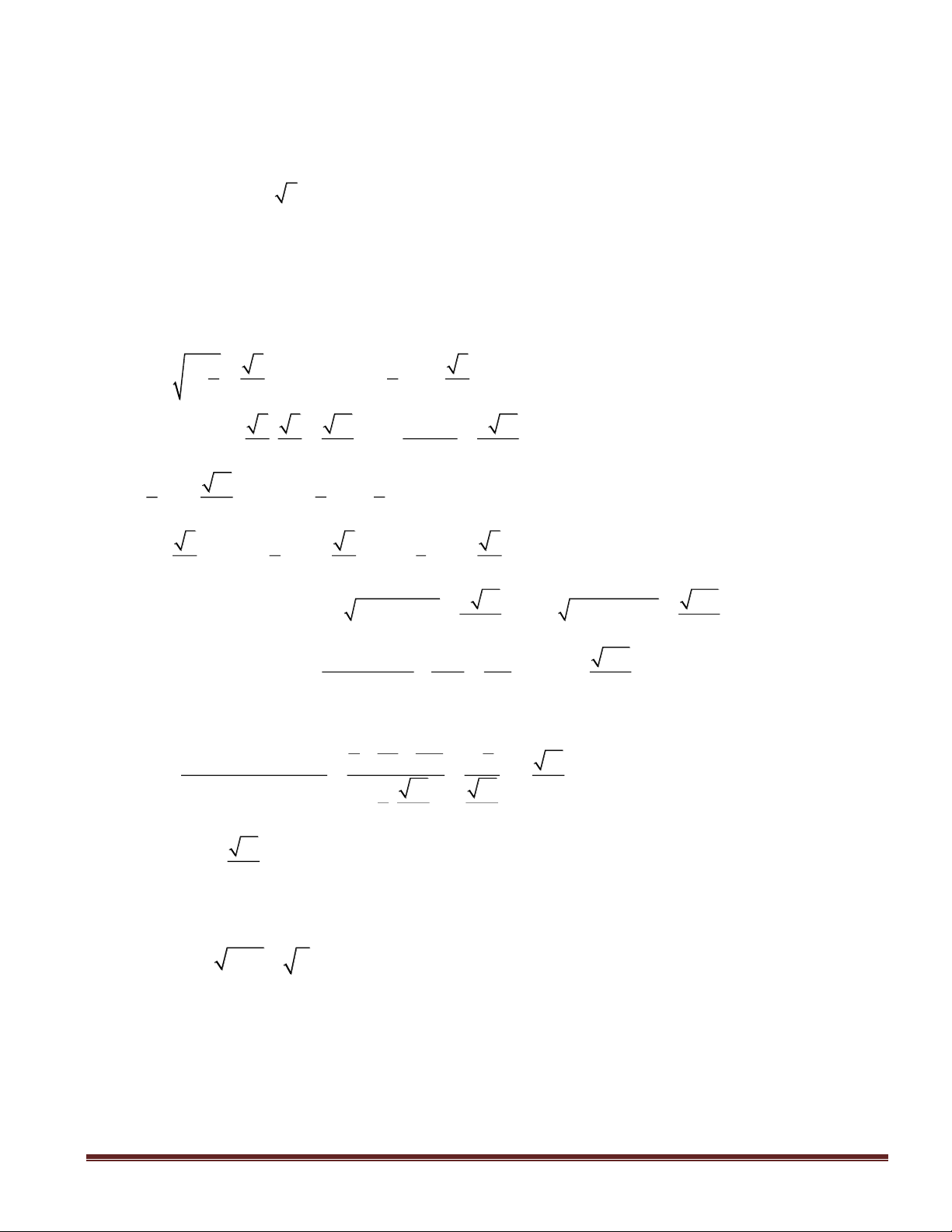
Trang 84
Ta có:
( ) ( )
( ) ( )
( ) ( )
( )
SBG ABG
SCG ABC SG ABC
SBG SCG SG
⊥
⊥ ⊥
⊥=
Gọi M, N, P, Q lần lượt là trung điểm của AB, SC, BC, AC.
Đặt
12AB BC AC= = =
Ta có:
( )
( )
( )
0
; ; 30SA ABC SA GA SAG = = =
Ta có NQ là đường trung bình của tam giác
//SAC NQ SA
MQ là đường trung bình của tam giác
//ABC MQ BC
( ) ( )
;;SA BC NQ MQ =
Ta có:
1 5 2 5
1
4 2 3 3
AP CM AG AP= + = = = =
0
0
5 3 15 2 15
.tan30 . ;
3 3 9 cos30 9
AG
SG AG SA = = = = =
1 15
29
NQ SA = =
và
11
22
MQ BC==
Ta có
5 2 5 1 5
;
2 3 3 3 6
MC GC MC GM MC= = = = =
Áp dụng định lí Pytago ta có:
2 2 2 2
2 15 105
;
9 18
SC SG GC SM SG GM= + = = + =
Xét tam giác SMC ta có:
2 2 2
2
65 195
2 4 108 18
SM MC SC
MN MN
+
= − = =
Áp dụng định lý cosin trong tam giác MNQ:
2 2 2
1 5 65 1
15
4 27 108 6
cos 0
2. . 10
1 15 15
2. .
2 9 9
MQ NQ MN
MQN
MQ NQ
+ − −
+−
= = = = −
Vậy
15
cos( ; )
10
SA BC =
.
Chọn: C
Câu 46: hệ phương trình:
có nghiệm (x
0
; y
0
) trong đó x
0
; y
0
là các số nguyên . Tổng
22
00
32P x y=+
bằng
A. 5 B. 1 C. 2 D. 0
3
4
11
( 1)
x y x
xy
− − = −
−=

Trang 85
Hướng dẫn giải
Điều kiện:
Biến đổi về hệ có dạng
(1)
Xét hàm số , là hàm số đồng biến trên
Xét hàm số
Miền xác định
Đạo hàm:
hàm số đồng biến trên D
Do đó phương trình (1):
Nếu có nghiệm thì nghiệm đó là duy nhất.
x=1 thoả mãn phương trình
x=1. y = 0 là nghiệm hệ chọn B
Câu 48. Cho hàm số
( )
fx
liên tục và có đạo hàm trên
0; ,
2
p
æö
÷
ç
÷
ç
÷
ç
èø
thỏa mãn hệ thức
( ) ( )
3
tan .
cos
x
f x xf x
x
¢
+=
Biết rằng
3 3 ln 3
36
f f a b
pp
p
æ ö æ ö
÷÷
çç
- = +
÷÷
çç
÷÷
çç
è ø è ø
trong đó
, .abÎ ¤
Tính giá trị của biểu thức
.P a b=+
A.
4
.
9
P =-
B.
2
.
9
P =-
C.
7
.
9
P =
D.
14
.
9
P =
Lời giải
Từ giả thiết, ta có
( ) ( ) ( )
22
cos sin sin .
cos cos
xx
xf x xf x xf x
xx
¢
éù
¢
+ = Û =
ëû
Suy ra
( )
2
sin d tan ln cos .
cos
x
xf x x x x x C
x
= = + +
ò
Với
32
. 3 ln 2 3 . 3 2 ln 2 2 .
3 2 3 3 3 3
x f f C
p p p p
p
æ ö æ ö
÷÷
çç
= ¾ ¾® = - ¾ ¾® = - +
÷÷
çç
÷÷
çç
è ø è ø
Với
1 3 1 1
. ln3 ln2 . 3 ln 3 2 ln 2 2 .
6 2 6 6 3 2 6 9
x f C f C
p p p p
p
æ ö æ ö
÷÷
çç
= ¾ ¾® = + - + ¾ ¾® = + - +
÷÷
çç
÷÷
çç
è ø è ø
Suy ra
5
54
3 3 ln 3 .
9
3 6 9 9
1
a
f f P a b
b
pp
p
ì
ï
ï
æ ö æ ö
=
ï
÷÷
çç
- = - ¾ ¾® ¾ ¾® = + = -
÷÷
í
çç
÷÷
çç
ï
è ø è ø
ï
=-
ï
î
Đáp án A
Câu 49:Cách giải:
+M(a,b) biểu diễn z, vì 3a-2b=12
:3 2 12M d x y= − =
Ta có:
Gọi
1 1 1 2 2 2
,z x y i z x y i= + = +
=>
22
1 1 1
| 3 4 | 1 ( 3) ( 4) 1z i x y− − = = − + − =
1 0 1
00
xx
yy
−
3
23
2
11
1 ( 1) 1
( 1)
x y x
x x x
xy
− − = −
− − − = −
−=
32
11x x x x − = − + − +
( ) 1f x x=+
)
1,D = +
32
( ) 1g x x x x= − + − +
)
1,D = +
2
'( ) 3 2 1 0,g x x x x D= − + −
( ) ( )f t g t=
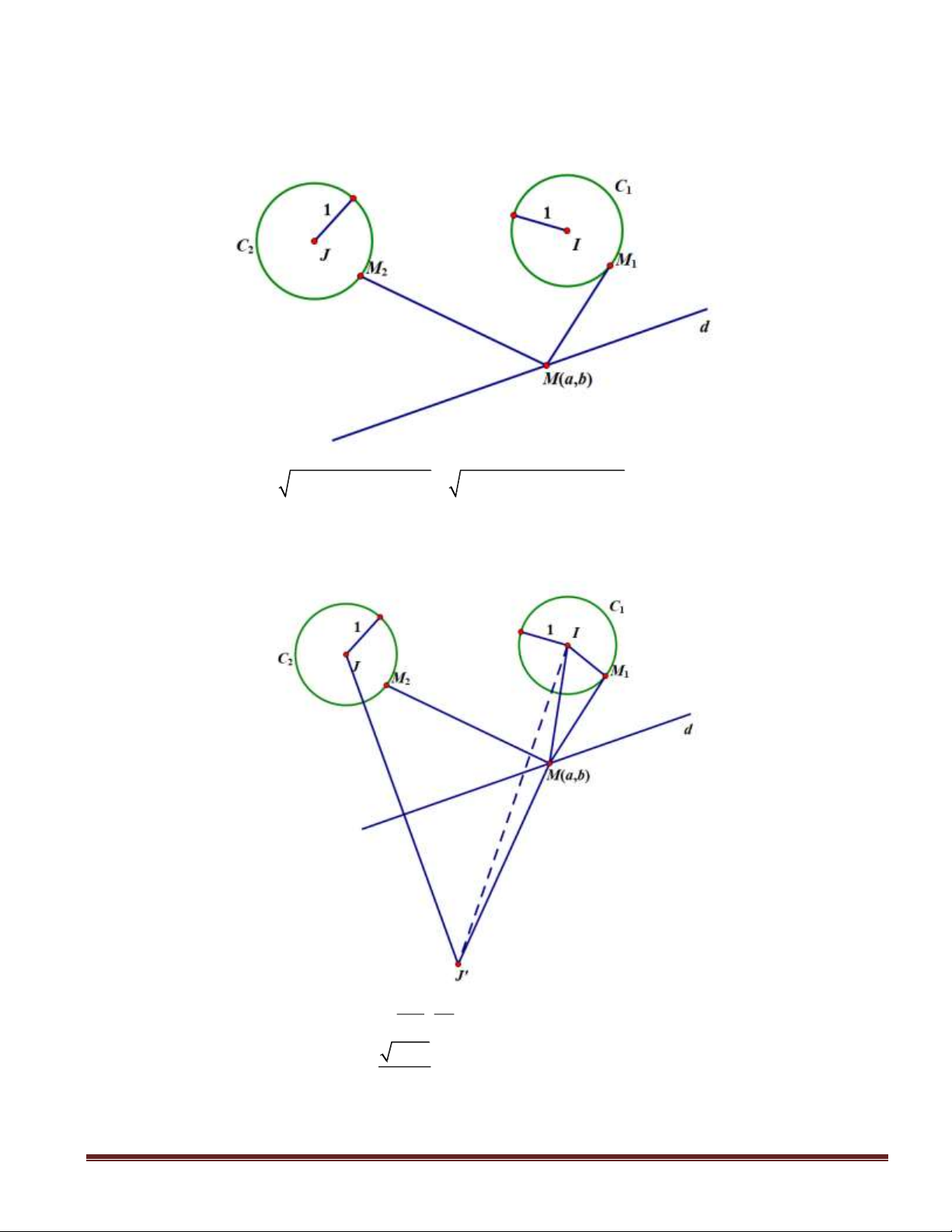
Trang 86
=>
1 1 1
( ; )M x y
biểu diễn
1
z
thuộc đường tròn
1
C
tâm
(3,4),R 1I =
22
2 2 2
| 2 6 8 | 1 (2 6) (2 8) 1z i x y− − = = − + − =
=>
2 2 2
( ; )M x y
biểu diễn 2
2
z
thuộc đường tròn
2
C
tâm
J(6,8),R 1=
2 2 2 2
1 2 1 1 2 2
12
1 1 2 2
| z z | | 2 | 2 ( ) ( ) ( 2 ) ( 2 ) 2
2
P z z a x b y a x b y
MM MM
MM M I MM M J
MI MJ
= − + − + = − + − + − + − +
= + +
= + + +
+
Gọi J’ là điểm đối xứng của J qua d =>
138 64
'( , )
13 13
J
Ta có:
9945
' IJ'
13
P MI MJ MI MJ + = + =
Vậy đáp án là B
Câu 50: A
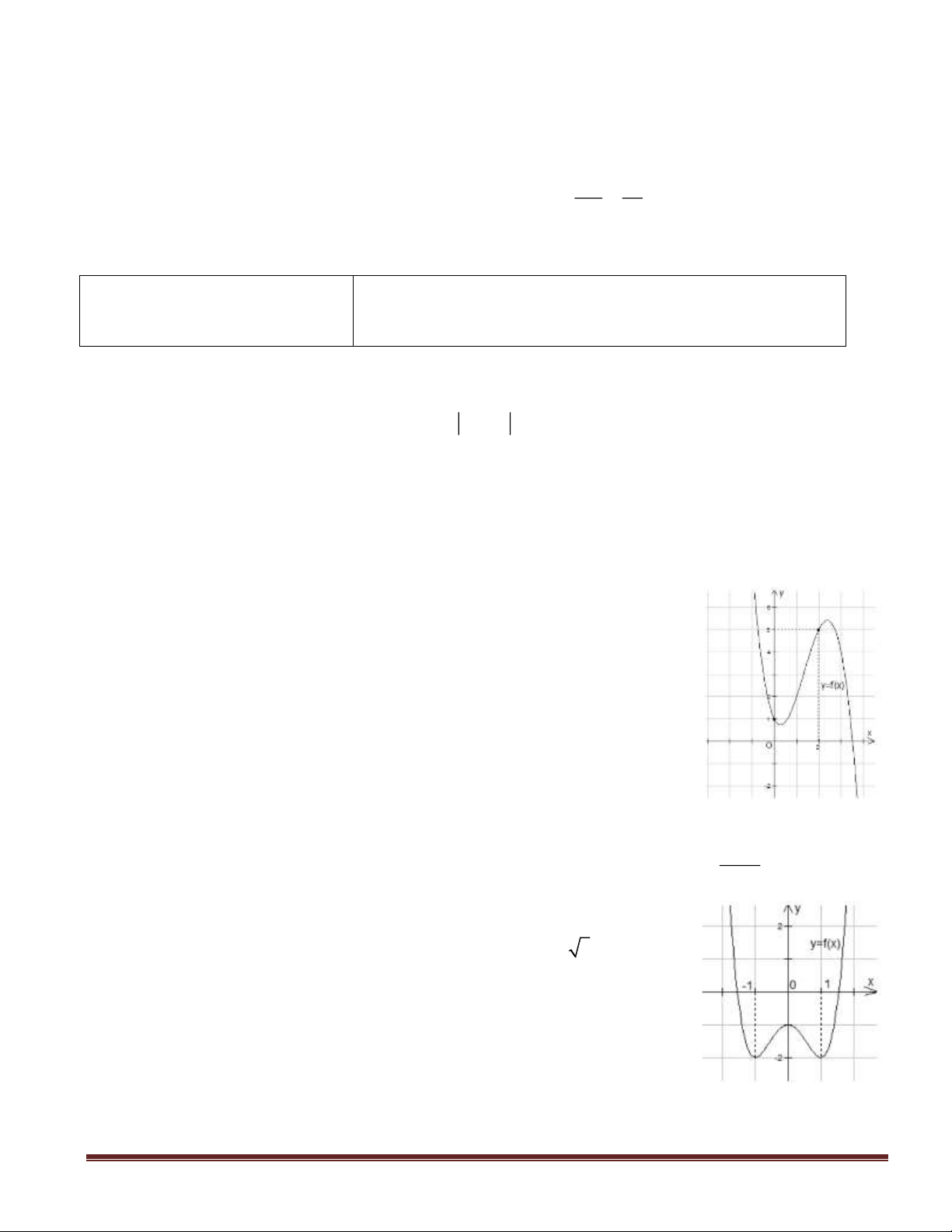
Trang 87
Số phần tử của không gian mẫu là
( )
3
10
120nC = =
.
Tích ba số không chia hết cho 3 khi và chỉ khi cả ba số đó đều không chia hết cho 3. Các thẻ được viết số
không chia hết cho 3 bao gồm 7 thẻ mang số 1; 2; 4; 5; 7; 8; 10. Số cách lấy được 3 thẻ mà tích ba số
viết trên ba thẻ không chia hết cho 3 là
3
7
35C =
. Suy ra, số cách lấy được 3 thẻ mà tích ba số viết trên ba
thẻ chia hết cho 3 là
33
10 7
85CC−=
. Do đó, xác suất cần tính là
85 17
120 24
=
.
ĐỀ 26
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1. Giả sử phương trình
( )
2
22
log 2 log 2 0x m x m− + + =
có hai nghiệm thực phân biệt
12
,xx
thỏa mãn
12
6xx+=
. Giá trị của biểu thức
12
xx−
là
A. 3. B. 8. C. 2. D. 4.
Câu 2. Một lớp học gồm có 20 học sinh nam và 15 học sinh nữ. Cần chọn ra 2 học sinh,
1 nam và 1 nữ để phân công trực nhật. Số cách chọn là
A. 300. B.
2
35
C
. C. 35. D.
2
35
A
.
Câu 3. Cho hàm số
( )
y f x=
có đồ thị đạo hàm
( )
'y f x=
như hình
bên. Khẳng định nào sau đây là đúng?
A. Hàm số
( )
2
y f x x x= − −
đạt cực đại tại
0x =
.
B. Hàm số
( )
2
y f x x x= − −
đạt cực tiểu tại
0x =
.
C. Hàm số
( )
2
y f x x x= − −
không đạt cực trị tại
0x =
.
D. Hàm số
( )
2
y f x x x= − −
không có cực trị.
Câu 4. Diện tích của mặt cầu bán kính 2a là
A.
2
4 a
. B.
2
16 a
. C.
2
16a
. D.
2
4
3
a
.
Câu 5. Cho hàm số
( )
y f x=
liên tục trên R và có đồ thị ở hình bên.
Số nghiệm dương phân biệt của phương trình
( )
3fx=−
là
A. 1. B. 3.
C. 2. D. 4.
Câu 6. Tập hợp các giá trị x thỏa mãn
;2 ; 3x x x+
theo thứ tự lập
thành một cấp số nhân là
A.
0;1
. B.
. C.
1
. D.
0
.
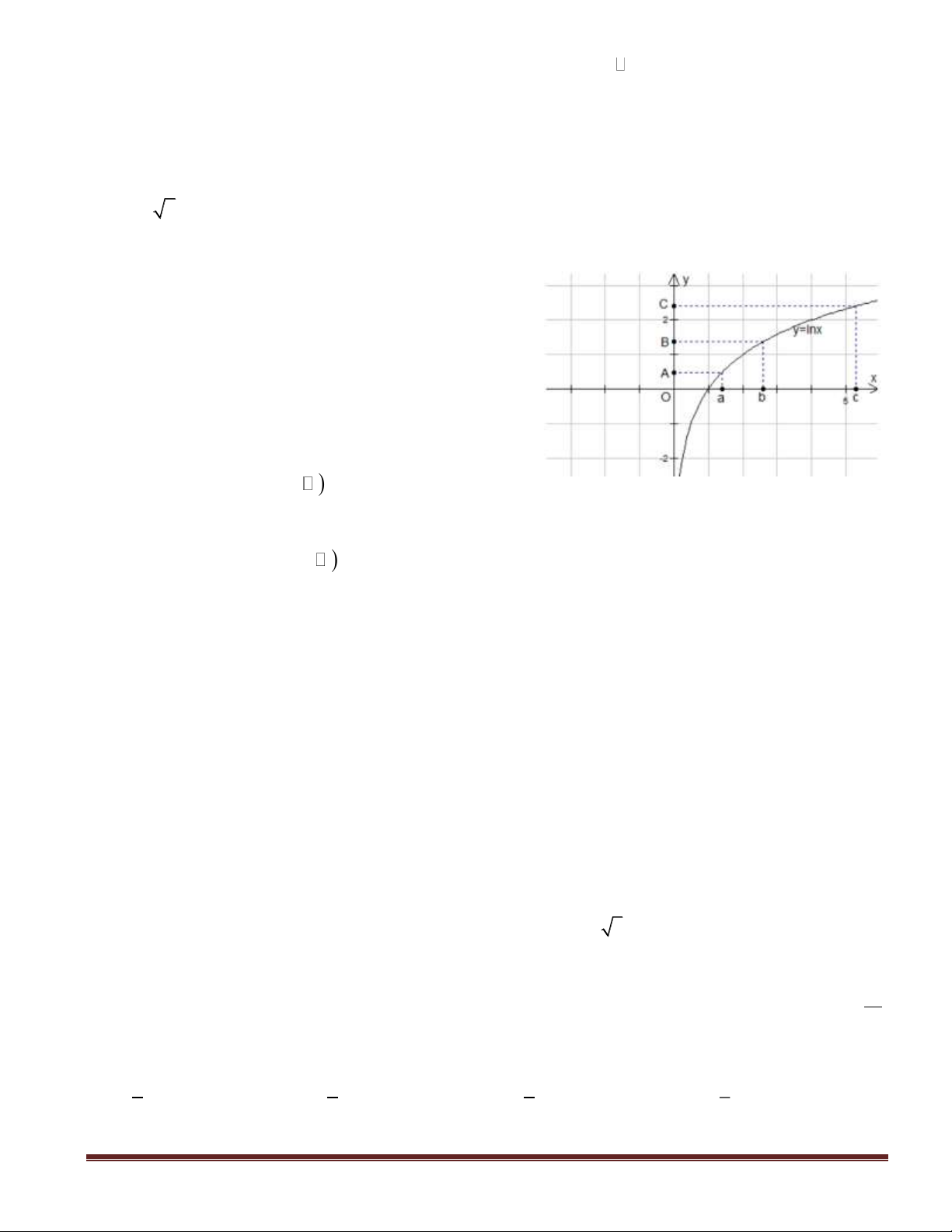
Trang 88
Câu 7. Cho hàm số
( )
y f x=
thỏa mãn
( )
2
'2f x x= − −
x
. Bất phương trình
( )
f x m
có nghiệm thuộc khoảng
( )
0;1
khi và chỉ khi
A.
( )
1mf
. B.
( )
0mf
. C.
( )
0mf
. D.
( )
1mf
.
Câu 8. Cho hình lập phương
. ' ' ' 'ABCD A B C D
cạnh a. Điểm M thuộc tia
'DD
thỏa mãn
6DM a=
. Góc giữa đường thẳng BM và mặt phẳng
( )
ABCD
là
A. 30°. B. 45°. C. 75°. D. 60°.
Câu 9. Trong hình dưới đây, điểm B là trung
điểm của đoạn thẳng AC. Khẳng định nào sau
đây là đúng?
A.
2a c b+=
. B.
2
ac b=
.
C.
2
2ac b=
. D.
ac b=
.
Câu 10.
( )
sin xdx f x C=+
khi và chỉ khi
A.
( ) ( )
cos f x x m m= +
.
B.
( )
cosf x x=
.
C.
( ) ( )
cos f x x m m= − +
.
D.
( )
cosf x x=−
.
Câu 11. Cho khối hộp chữ nhật
. ' ' ' 'ABCD A B C D
có
' , 3 , 5AA a AB a AC a= = =
. Thể tích của
khối hộp đã cho là
A.
3
5a
. B.
3
4a
. C.
3
12a
. D.
3
15a
.
Câu 12. Một người nhận hợp đồng dài hạn làm việc cho một công ty với mức lương khởi
điểm của mỗi tháng trong 3 năm đầu tiên là 6 triệu đồng/tháng. Tính từ ngày đầu tiên làm
việc, cứ sau đúng 3 năm liên tiếp thì tăng lương 10% so với mức lương một tháng người
đó đang hưởng. Nếu tính theo hợp đồng thì tháng đầu tiên của năm thứ 16 người đó nhận
được mức lương là bao nhiêu?
A.
4
6.1,1
(triệu đồng). B.
6
6.1,1
(triệu đồng). C.
5
6.1,1
(triệu đồng). D.
16
6.1,1
(triệu đồng).
Câu 13. Số nghiệm thực phân biệt của phương trình
2
23
x
=
là
A. 0. B. 2. C. 1. D. 3.
Câu 14. Gọi
n
S
là tổng n số hạng đầu tiên trong cấp số cộng
( )
n
a
. Biết
69
SS=
, tỉ số
3
5
a
a
bằng
A.
9
5
. B.
5
9
. C.
5
3
. D.
3
5
.
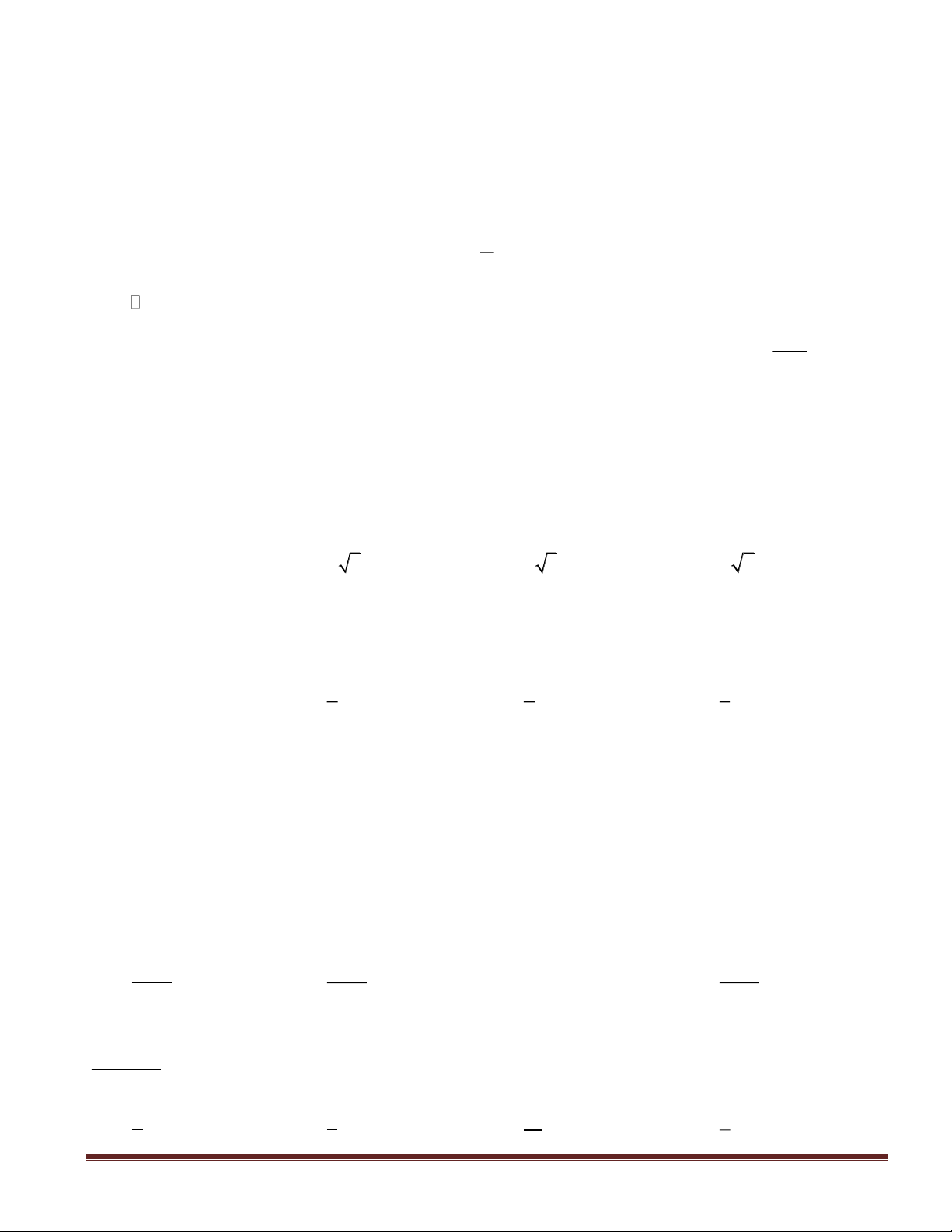
Trang 89
Câu 15. Cho hình lăng trụ
. ' ' ' 'ABCD A B C D
có đáy là hình chữ nhật và
40CAD =
. Số đo
góc giữa hai đường thẳng AC và
''BD
là
A. 40°. B. 20°. C. 50°. D. 80°.
Câu 16. Tập hợp các số thực m thỏa mãn hàm số
42
1y mx x= − +
có đúng 1 điểm cực trị là
A.
( )
;0−
. B.
(
;0−
. C.
( )
0;+
. D.
)
0;+
.
Câu 17. Tập nghiệm của bất phương trình
1
x
e
là
A. . B.
( )
;0−
. C.
( )
0;+
. D.
)
0;+
.
Câu 18. Các đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
1
1
x
y
x
−
=
+
lần lượt
là
A.
1, 1yx==
. B.
1, 1yx= − =
. C.
1, 1yx= − = −
. D.
1, 1yx= = −
.
Câu 19. Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a. Tam giác SAB đều và
nằm trong mặt phẳng vuông góc với mặt phẳng
( )
ABCD
. Khoảng cách giữa hai đường
thẳng BC và SD là
A. a. B.
3
2
a
. C.
3
3
a
. D.
2
2
a
.
Câu 20. Ba số
2 4 8
log 3; log 3; log 3aaa+++
theo thứ tự lập thành một cấp số nhân. Công bội
của cấp số nhân này bằng
A. 1. B.
1
4
. C.
1
2
. D.
1
3
.
Câu 21. Một bình đựng nước dạng hình nón (không có đáy), đừng đầy nước. Người ta
thả vào đó một khối cầu có đường kính bằng chiều cao của bình nước và đo được thể tích
nước tràn ra ngoài là
3
18 dm
. Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của
hình nón và đúng một nửa của khối cầu chìm trong nước (hình bên). Thể tích V của nước
còn lại trong bình bằng
A. 3. B. 8. C. 2. D. 4.
Câu 22. Hàm số nào trong các hàm số sau đây không là nguyên hàm của hàm số
2019
yx=
?
A.
2020
1
2020
x
+
. B.
2020
2020
x
. C.
2018
2019yx=
. D.
2020
1
2020
x
−
.
Câu 23. Cho hình lăng trụ đứng
. ' ' 'ABC A B C
có M là trung điểm của
'AA
. Tỉ số thể tích
.
. ' ' '
M ABC
ABC A B C
V
V
bằng
A.
1
6
. B.
1
3
. C.
1
12
. D.
1
2
.

Trang 90
Câu 24. Gọi A là tập hợp tất cả các số có dạng
abc
với
, , 1;2;3;4abc
. Số phần tử của
tập hợp A là
A.
3
4
C
. B.
4
3
. C.
3
4
A
. D.
3
4
.
Câu 25. Cho hàm số
3
yx=
có một nguyên hàm là
( )
Fx
. Khẳng định nào sau đây là
đúng?
A.
( ) ( )
2 0 16FF−=
. B.
( ) ( )
2 0 1FF−=
. C.
( ) ( )
2 0 8FF−=
. D.
( ) ( )
2 0 4FF−=
.
Câu 26. Cho hình lập phương
. ' ' ' 'ABCD A B C D
cạnh a. Các điểm M, N, P lần lượt thuộc
các đường thẳng
', ', 'AA BB CC
thỏa mãn diện tích của tam giác MNP bằng
2
a
. Góc giữa
hai mặt phẳng
( )
MNP
và
( )
ABCD
là
A. 60°. B. 30°. C. 45°. D. 120°.
Câu 27. Đạo hàm của hàm số
( )
log 1yx=−
bằng
A.
( )
1
1 ln10x −
. B.
1
1x −
. C.
1
1 x−
. D.
( )
1
1 ln10x−
.
Câu 28. Hàm số nào trong các hàm số sau đây là một nguyên hàm của hàm số
2x
ye
−
=
?
A.
2
2
x
e
y
−
=−
. B.
( )
2
2
x
y e C C
−
= − +
.
C.
( )
2
2
x
y e C C
−
= +
. D.
2
2
x
e
y
−
=
.
Câu 29. Hàm số
3
2
1
3
x
y x mx= − + − +
nghịch biến trên khoảng
( )
0;+
khi và chỉ khi
A.
)
1;m +
. B.
( )
1;m +
. C.
)
0;m +
. D.
( )
0;m +
.
Câu 30. Trong khai triển Newton của biểu thức
( )
2019
21x −
, số hạng chứa
18
x
là
A.
18 18
2019
2.C−
. B.
18 18 18
2019
2 Cx−
. C.
18 18 18
2019
2 Cx
. D.
18 18
2019
2.C
.
Câu 31. Hàm số
( )
y F x=
là một nguyên hàm của hàm số
1
y
x
=
trên
( )
;0−
thỏa mãn
( )
20F −=
. Khẳng định nào sau đây là đúng?
A.
( ) ( )
ln ;0
2
x
F x x
−
= −
.
B.
( ) ( )
ln ;0 F x x C x= + −
với C là một số thực bất kì.
C.
( ) ( )
ln ln2 ;0 F x x x= + −
.
D.
( ) ( ) ( )
ln ;0 F x x C x= − + −
với C là một số thực bất kì.
Câu 32. Nếu
3
log 5 a=
thì biểu thức
45
log 75
bằng
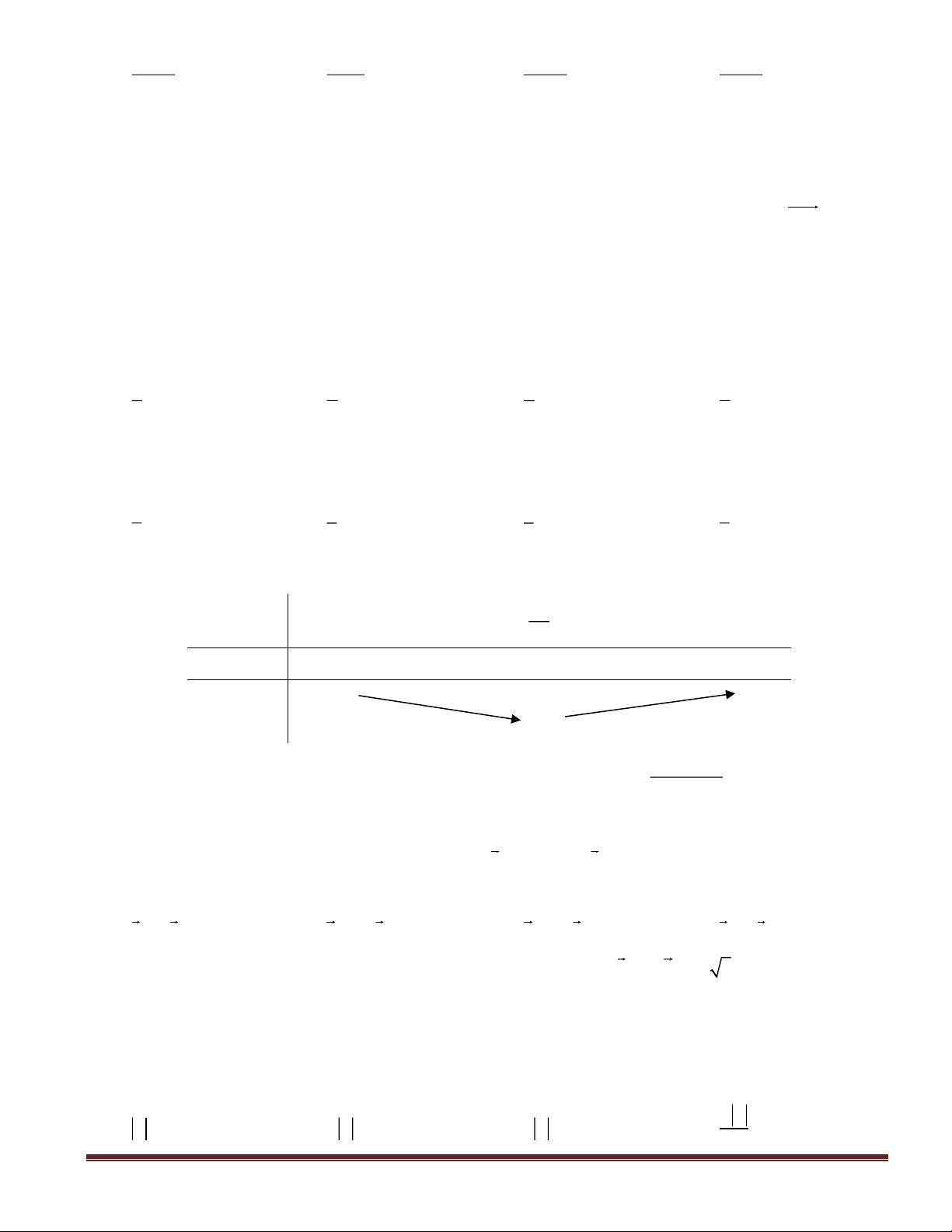
Trang 91
A.
2
12
a
a
+
+
. B.
1
2
a
a
+
+
. C.
12
2
a
a
+
+
. D.
12
1
a
a
+
+
.
Câu 33. Nếu một hình nón có diện tích xung quanh gấp đôi diện tích của hình tròn đáy
thì góc ở đỉnh của hình nón bằng
A. 15°. B. 60°. C. 30°. D. 120°.
Câu 34. Trong không gian tọa độ Oxyz, cho điểm
( )
;;M a b c
. Tọa độ của vectơ
MO
là
A.
( )
;;abc
. B.
( )
;;abc−
. C.
( )
;;abc− − −
. D.
( )
;;a b c−−
.
Câu 35. Xếp ngẫu nhiên 5 bạn An, Bình, Cường, Dũng, Đông ngồi vào một dãy 5 ghế
thẳng hàng (mỗi bạn ngồi 1 ghế). Xác suất các biến cố ‘hai bạn An và Bình không ngồi
cạnh nhau’ là
A.
3
5
. B.
2
5
. C.
1
5
. D.
4
5
.
Câu 36. Cho tam giác ABC vuông tại A.
,AB c AC b==
. Quay tam giác ABC xung quanh
đường thẳng chứa cạnh AB được một hình nón có thể tích bằng
A.
2
1
3
bc
. B.
2
1
3
bc
. C.
2
1
3
bc
. D.
2
1
3
bc
.
Câu 37. Cho hàm số
( )
y f x=
có bảng biến thiên như hình dưới đây.
x
−
1
2
−
+
'y
−
0
+
y
1
1
3−
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
( )
1
21
y
fx
=
−
là
A. 0. B. 1. C. 2. D. 3.
Câu 38. Trong không gian tọa độ Oxyz, cho
( ) ( )
1;2; 3 , 2; 4;6ab= − = − −
. Khẳng định nào sau
đây là đúng?
A.
2ab=
. B.
2ba=−
. C.
2ab=−
. D.
2ba=
.
Câu 39. Trong không gian tọa độ Oxyz, góc giữa hai vectơ
i
và
( )
3;0;1u =−
là
A. 120°. B. 30°. C. 60°. D. 150°.
Câu 40. Trong không gian tọa độ Oxyz, cho hình hộp
. ' ' ' 'ABCD A B C D
có
( ) ( )
0;0;0 , ;0;0A B a
,
( )
0;2 ;0Da
,
( )
' 0;0;2Aa
với
0a
. Độ dài đoạn thẳng
'AC
là
A.
a
. B.
2 a
. C.
3 a
. D.
3
2
a
.

Trang 92
Câu 41. Cho hình chóp S.ABC với ABC không là tam giác cân. Góc giữa các đường
thẳng SA, SB, SC và mặt phẳng
( )
ABC
bằng nhau. Hình chiếu vuông góc của điểm S lên
mặt phẳng
( )
ABC
là
A. Tâm đường tròn ngoại tiếp của tam giác ABC.
B. Trực tâm của tam giác ABC.
C. Trọng tâm của tam giác ABC.
D. Tâm đường tròn nội tiếp của tam giác ABC.
Câu 42. Cho hình chóp O.ABC có
OA OB OC a= = =
,
60 , 90AOB BOC = =
,
120COA =
.
Gọi S là trung điểm của OB. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là
A.
4
a
. B.
7
4
a
. C.
7
2
a
. D.
2
a
.
Câu 43. Cho hàm số
( )
y f x=
liên tục trên thỏa mãn
( )
2018x
f x dx e C
−
=+
. Khẳng định
nào sau đây là đúng?
A.
( )
2018
2018
x
f x e
−
=
. B.
( )
2018
2018
x
e
fx
−
=
. C.
( )
2018
2018
x
e
fx
−
=
−
. D.
( )
2018
2018
x
f x e
−
=−
.
Câu 44. Biểu thức
2
sin
lim
x
x
x
→
bằng:
A. 0. B.
2
. C.
2
. D. 1.
Câu 45. Tập nghiệm của bất phương trình
( )
0,5
log 1 1x −
là
A.
3
;
2
−
. B.
3
1;
2
.
C.
3
;
2
+
. D.
3
1;
2
.
Câu 46. Cho hàm số
( )
y f x=
liên tục trên R và có đồ thị như hình bên.
Phương trình
( )
2sinf x m=
có đúng ba nghiệm phân biệt thuộc đoạn
;
−
khi và chỉ khi
A.
3;1m−
. B.
( )
3;1m−
. C.
)
3;1m−
. D.
(
3;1m−
.
Câu 47. Trong không gian tọa độ Oxyz, cho
( ) ( ) ( )
2;0;0 , 0;2;0 , 0;0;2A B C
. Có tất cả bao
nhiêu điểm M trong không gian thỏa mãn M không trùng với các điểm A, B, C và
90AMB BMC CMA= = =
?
A. 0. B. 1. C. 2. D. 3.

Trang 93
Câu 48. Tập hợp các số thực m để phương trình
2
log xm=
có nghiệm thực là
A.
( )
0;+
. B.
)
0;+
. C.
( )
;0−
. D. .
Câu 49. Cho hàm số
( )
( )
2019
2
1f x x=−
. Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên . B. Hàm số đồng biến trên
( )
;0−
.
C. Hàm số nghịch biến trên
( )
;0−
. D. Hàm số nghịch biến trên .
Câu 50. Hàm số nào trong các hàm số sau đây có một nguyên hàm bằng
2
cos x
?
A.
3
cos
3
x
y =
. B.
( )
3
cos
3
x
y C C
−
= +
.
C.
sin2yx=−
. D.
( )
sin2 y x C C= +
.
ĐÁP ÁN
1. C
2. A
3. A
4. B
5. C
6. C
7. D
8. D
9. B
10. C
11. C
12. C
13. B
14. C
15. D
16. B
17. B
18. D
19. B
20. D
21. B
22. C
23. A
24. D
25. D
26. A
27. A
28. A
29. A
30. B
31. A
32. C
33. B
34. C
35. A
36. D
37. D
38. B
39. D
40. C
41. A
42. C
43. D
44. B
45. B
46. A
47. C
48. D
49. B
50. C
LỜI GIẢI CHI TIẾT
Câu 1. Chọn đáp án C
Phương pháp
+) Đặt điều kiện để phương trình có nghĩa.
+) Đặt ẩn phụ để giải phương trình:
2
log xt=
. Tìm điều kiện để phương trình có nghiệm.
+) Dựa vào dữ kiện
12
6xx+=
tìm m. Từ đó tính
12
xx−
.
Cách giải
Điều kiện:
0x
.
Đặt
2
log xt=
. Khi đó ta có phương trình:
( )
2
2 2 0t m t m− + + =
2
2 2 0t mt t m − − + =
(*)
( ) ( )
20t t m t m − − − =

Trang 94
( )( )
2
1
2
2
log
2
20
2 log 2
4
m
xm
tm
x
t m t
tx
x
=
=
=
− − =
==
=
Phương trình đã cho có hai nghiệm phân biệt:
( )
12
;*x x pt
có hai nghiệm phân biệt
2m
.
Ta có:
12
6 2 4 6 2 2 1
mm
x x m+ = + = = =
(tm).
12
2 4 2 4 2
m
xx − = − = − =
.
Câu 2. Chọn đáp án A
Phương pháp
Áp dụng quy tắc nhân.
Cách giải
Có 20 cách chọn 1 bạn nam
Có 15 cách chọn 1 bạn nữ
Số cách chọn 2 học sinh 1 nam và 1 nữ là:
20.15 300=
(cách
chọn)
Câu 3. Chọn đáp án A
Phương pháp
+) Quan sát đồ thị hàm số đã cho, và các đáp án trong đề bài,
chọn ra câu đúng.
+)
0
xx=
là điểm cực trị của hàm số
( ) ( )
0
'0y f x f x= =
.
+) Số điểm cực trị của đồ thị hàm số
( )
y f x=
là số nghiệm
bội lẻ của phương trình
( )
'0fx=
.
Cách giải
Ta có:
( ) ( )
2
' ' 2 1y f x x x y f x x= − − = − −
.
( ) ( )
' 0 ' 2 1 0 ' 2 1y f x x f x x = − − = = +
.
Số nghiệm của phương trình
( )
' 2 1f x x=+
là số giao điểm của đồ thị hàm số
( )
'y f x=
và
21yx=+
.
Dựa vào đồ thị hàm số ta thấy phương trình
( )
' 2 1f x x=+
có 2 nghiệm
0x =
và
2x =
, tuy
nhiên chỉ qua nghiệm
0x =
thì
'y
đổi dấu, do đó hàm số có 1 cực trị
0x =
.
Câu 4. Chọn đáp án B
Phương pháp
Công thức tính diện tích mặt cầu bán kính R là:
2
4SR
=
Cách giải

Trang 95
Diện tích của mặt cầu bán kính 2a là:
( )
2
2
4 2 16S a a
==
Câu 5. Chọn đáp án C
Phương pháp
Số nghiệm của phương trình
( )
f x m=
là số giao điểm của đồ thị hàm số
( )
y f x=
và đường
thẳng
ym=
.
Cách giải
Số nghiệm của phương trình
( )
3fx=−
là số giao điểm của đồ thị hàm số
( )
y f x=
và
đường thẳng
3y =−
.
Dựa vào đồ thị hàm số ta thấy đường thẳng
3y =−
cắt đồ thị hàm số
( )
y f x=
tại 4 điểm
phân biệt trong đó có 2 nghiệm dương và 2 nghiệm âm.
Câu 6. Chọn đáp án C
Phương pháp
Cho ba số a, b, c theo thứ tự lập thành CSN thì ta có:
2
b ac=
.
Cách giải
Ta có:
;2 ; 3x x x+
theo thứ tự lập thành CSN
( ) ( )
2
23x x x = +
( )
22
0
4 3 3 1 0
1
x
x x x x x
x
=
= + − =
=
+) Với
0x =
ta có CSN:
0;0;3
vô lý.
+) Với
1x =
ta có CSN:
1;2;4
có công bội là 2.
Chú ý: Sau khi tìm được x phải thử lại.
Câu 7. Chọn đáp án D
Phương pháp
Tìm hàm
( )
fx
bằng công thức nguyên hàm cơ bản:
( ) ( )
'f x f x dx=
Xét hàm số để giải bất phương trình: Ta có:
( ) ( )
( )
0;1
0;1 f x m x Min f x m
.
Cách giải
Ta có:
( ) ( ) ( )
3
2
' 2, ' 2
3
x
f x x x f x f x dx x C= − − = = − − +
Xét hàm số:
( )
3
2
3
x
f x x C= − − +
trên
( )
0;1
ta có:
( )
2
' 2 0,f x x x= − −
Hàm số luôn nghịch biến trên
Hàm số
( )
fx
nghịch biến trên
( )
( ) ( )
0;1
0;1 1Min f x f=
.
Vậy
( )
1mf
.
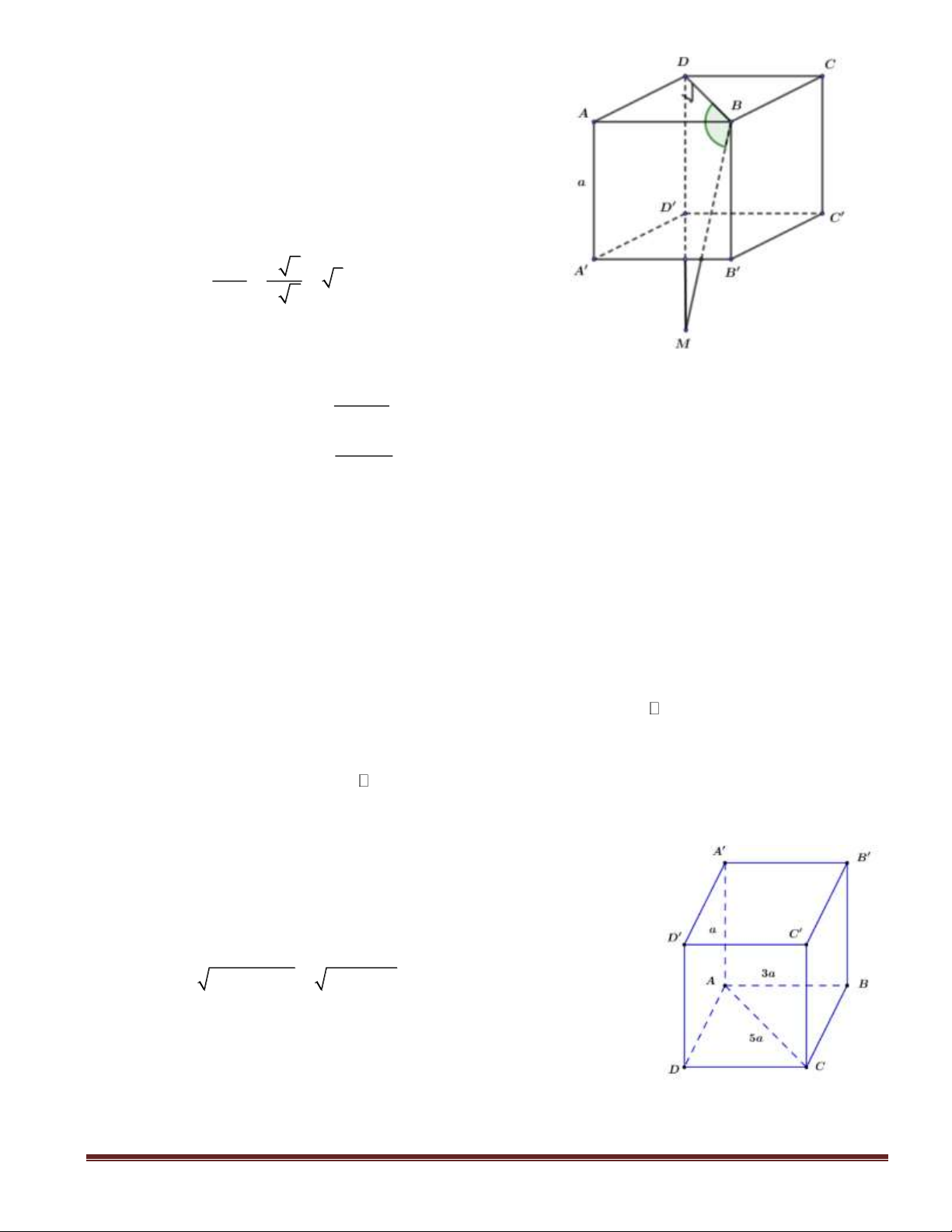
Trang 96
Câu 8. Chọn đáp án D
Phương pháp
Nhận thấy,
( )
( )
,BM ABCD MBD =
,
Áp dụng hệ thức lượng trong tam giác để tính.
Cách giải
Ta có:
( )
( )
;BM ABCD MBD =
Mà
6
tan 3 60
2
DM a
MBD MBD
DB
a
= = = =
Câu 9. Chọn đáp án B
Phương pháp
B là trung điểm AC
2
2
AC
B
AC
B
xx
x
yy
y
+
=
+
=
Cách giải
Dựa vào đồ thị hàm số ta thấy: A, B, C
lnyx=
.
( ) ( ) ( )
0;ln , 0;ln , 0;lnA a B b C c
.
Lại có B là trung điểm của AC
( )
22
ln ln 2ln ln lna c b ac b ac b + + = =
Câu 10. Chọn đáp án C
Phương pháp
Sử dụng công thức nguyên hàm cơ bản:
( )
sin cos xdx x C C= − +
Cách giải
Ta có:
( )
sin cos xdx x m m= − +
Câu 11. Chọn đáp án C
Phương pháp
Áp dụng định lý Py-ta-go tính độ dài đoạn thẳng AD.
Thể tích hình hộp chữ nhật có các kích thước a, b, c:
V abc=
.
Cách giải
Ta có:
2 2 2 2
25 9 4AD AC CD a a= − = − =
. (định lý Pytago)
3
. ' ' ' '
'. . .3 .4 12
ABCD A B C D
V AA AB AD a a a a= = =
.
Câu 12. Chọn đáp án C
Phương pháp
Sử dụng công thức:
( )
1
n
n
S A r=+
với:

Trang 97
A là số tiền lương tháng đầu tiên người đó nhận được.
r là số % lương người đó được tăng.
n là kì hạn người đó được tăng lương.
Cách giải
Đến năm thứ 16 thì người đó được tăng lương số lần là:
16
5
3
=
lần.
Áp dụng công thức:
( )
1
n
n
S A r=+
ta có số tiền người đó nhận được ở tháng đầu tiên của
năm thứ 16 là:
( )
5
5
6 1 10% 6.1,1+=
triệu đồng.
Câu 13. Chọn đáp án B
Phương pháp
Giải phương trình mũ:
( )
( )
log
fx
a
a b f x b= =
(
0 1, 0ab
)
Cách giải
Ta có:
2
2
2
2
2
log 3
2 3 log 3
log 3
x
x
x
x
=
= =
=−
Câu 14. Chọn đáp án C
Phương pháp
Công thức tổng quát của CSC có số hạng đầu
1
u
và công sai d là:
( )
1
1
n
u u n d= + −
.
Tổng của n số hạng đầu của CSC có số hạng đầu
1
u
và công sai d là:
( )
1
21
2
n
n u n d
S
+−
=
.
Cách giải
Gọi CSC có số hạng đầu
1
a
và công sai d.
Theo đề bài ta có:
( ) ( )
11
69
6 2 5 9 2 8
22
a d a d
SS
++
= =
11
11
4 10 6 24
2 14 7
a d a d
a d a d
+ = +
= − = −
3
1
51
2
7 2 5 5
4 7 4 3 3
a
ad
d d d
a a d a d d
+
− + −
= = = =
+ − + −
.
Câu 15. Chọn đáp án D
Phương pháp
Góc giữa hai đường thẳng a, b là góc giữa hai đường thẳng
', 'ab
với
/ / ', / / 'a a b b
.
Cách giải

Trang 98
Ta có
( ) ( )
/ / ' ' ; ' ' ' '; ' 'AC A C AC B D A C B D =
Gọi
; ' ' ' ' 'AC BD O A C B D O = =
.
Ta có
OAD
cân tại O
40 100 ' ' 'OAD ODA AOD A O D = = = =
( )
' '; ' ' 180 100 80A C B D = − =
.
Vậy
( )
; ' ' 80AC B D =
.
Câu 16. Chọn đáp án B
Phương pháp
Xét hàm số:
( )
42
0 y ax bx c a= + +
có:
3
' 4 2y ax bx=+
( )
( )
32
2
0
' 0 4 2 0 2 2 0
*
2
x
y ax bx x ax b
b
x
a
=
= + = + =
−
=
Hàm số có 1 cực trị
(*)
có
0 0 0 . 0
2
b b b
ab
a a a
−−
Cách giải
Ta có:
42
1y mx x= − +
Hàm số có 1 điểm cực trị
( )
10
00
0
00
0
m
ab m
m
am
m
−
.
+) Xét
2
0 1 ' 2 0 0m y x y x x= = − + = − = =
hàm số có 1 điểm cực trị.
Vậy
0m
thỏa mãn bài toán.
Câu 17. Chọn đáp án B
Phương pháp
Giải bất phương trình mũ:
01
1
0 0 1
khi
khi
x
xa
a
xa
.
Cách giải
Ta có:
1 0 1
x
ee
x do
.
Câu 18. Chọn đáp án D
Phương pháp
+) Đường thẳng
xa=
được gọi là TCĐ của đồ thị hàm số
( ) ( )
lim
xa
y f x f x
→
= =
.
+) Đường thẳng
yb=
được gọi là TCN của đồ thị hàm số
( ) ( )
lim
x
y f x f x b
→
= =
.
Cách giải
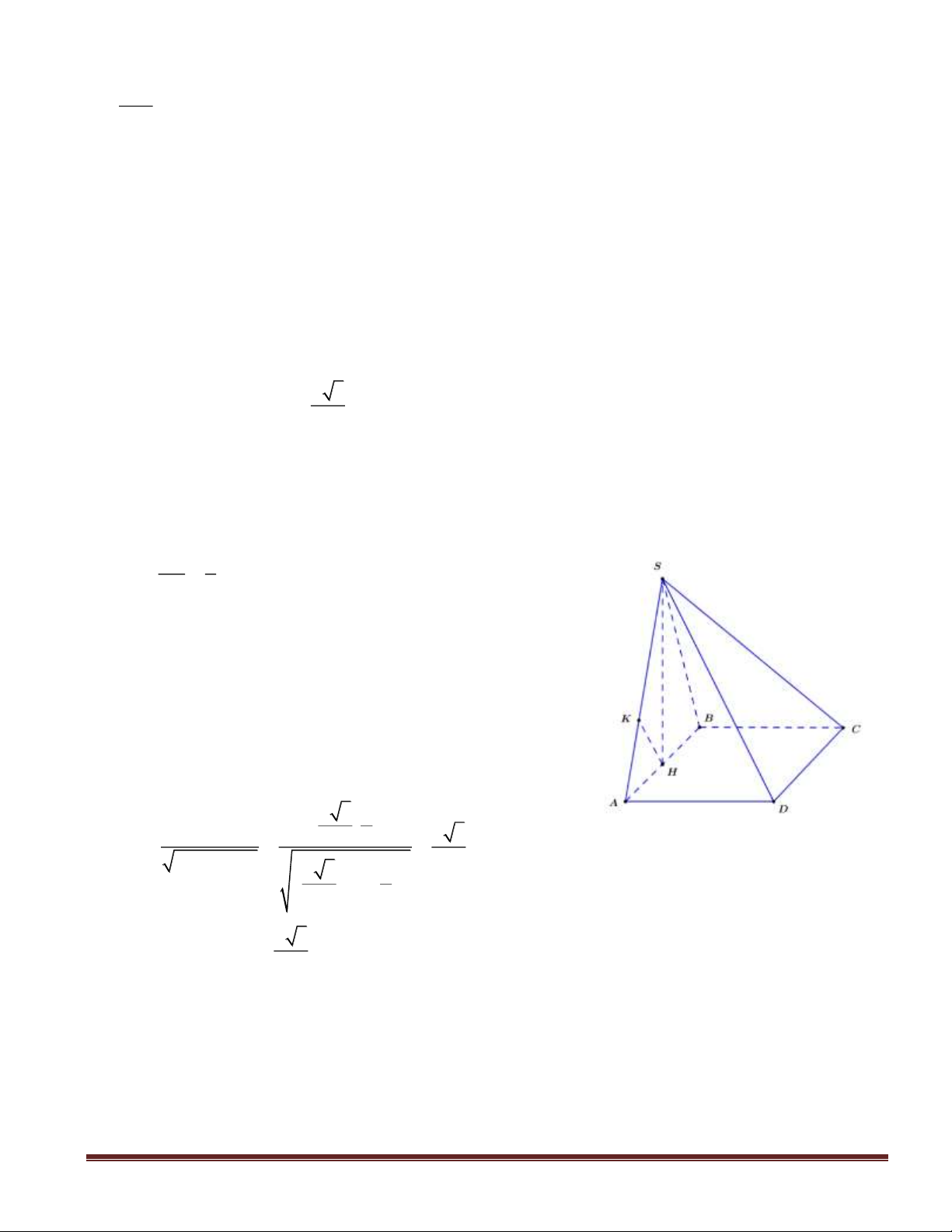
Trang 99
Ta có:
1 0 1 1x x x+ = = − = −
là TCĐ của đồ thị hàm số.
1
lim 1 1
1
x
x
y
x
→
−
= =
+
là TCN của đồ thị hàm số.
Câu 19. Chọn đáp án B
Phương pháp
Ta có:
( ) ( )
( )
( )
( )
( )
( )
, , , 2 ;d BC SD d BC SAD d B SAD d H SAD= = =
với H là trung điểm của AB.
Từ đó ta quy về tính
( )
( )
,d H SAD
.
Cách giải
Gọi H là trung điểm của AB
SH AB⊥
.
Ta có:
SAB
đều và
( ) ( ) ( )
SAB ABCD SH ABCD⊥ ⊥
SAB
đều cạnh
3
2
a
a SH=
.
Có:
( )
/ / / /BC AD BC SAD
( ) ( )
( )
( )
( )
; ; ;d BC SD d BC SAD d B SAD = =
( ) ( )
( )
( )
( )
; ; ;d BC SD d BC SAD d B SAD = =
Lại có:
( )
( )
( )
( )
1
; 2 ;
2
BA
d B SAD d H SAD
HA
= =
Kẻ
HK SA⊥
ta có:
( )
AD AB
SD SBA SD HK
AD SH
⊥
⊥ ⊥
⊥
( ) ( )
( )
;HK SAD d H SAD HK ⊥ =
.
Áp dụng hệ thức lượng cho
SHA
vuông tại H, có đường
cao HK:
2 2 2
2
3
.
.3
22
4
3
22
aa
SH HA a
HK
SA AH
aa
= = =
+
+
.
( )
3
;2
2
a
d BC SD HK = =
.
Câu 20. Chọn đáp án D
Phương pháp
Cho ba số a, b, c lập thành CSN thì ta có:
2
ac b=
Cách giải
Ta có:
2 4 8
log 3; log 3; log 3aaa+++
theo thứ tự lập thành cấp số nhân nên:
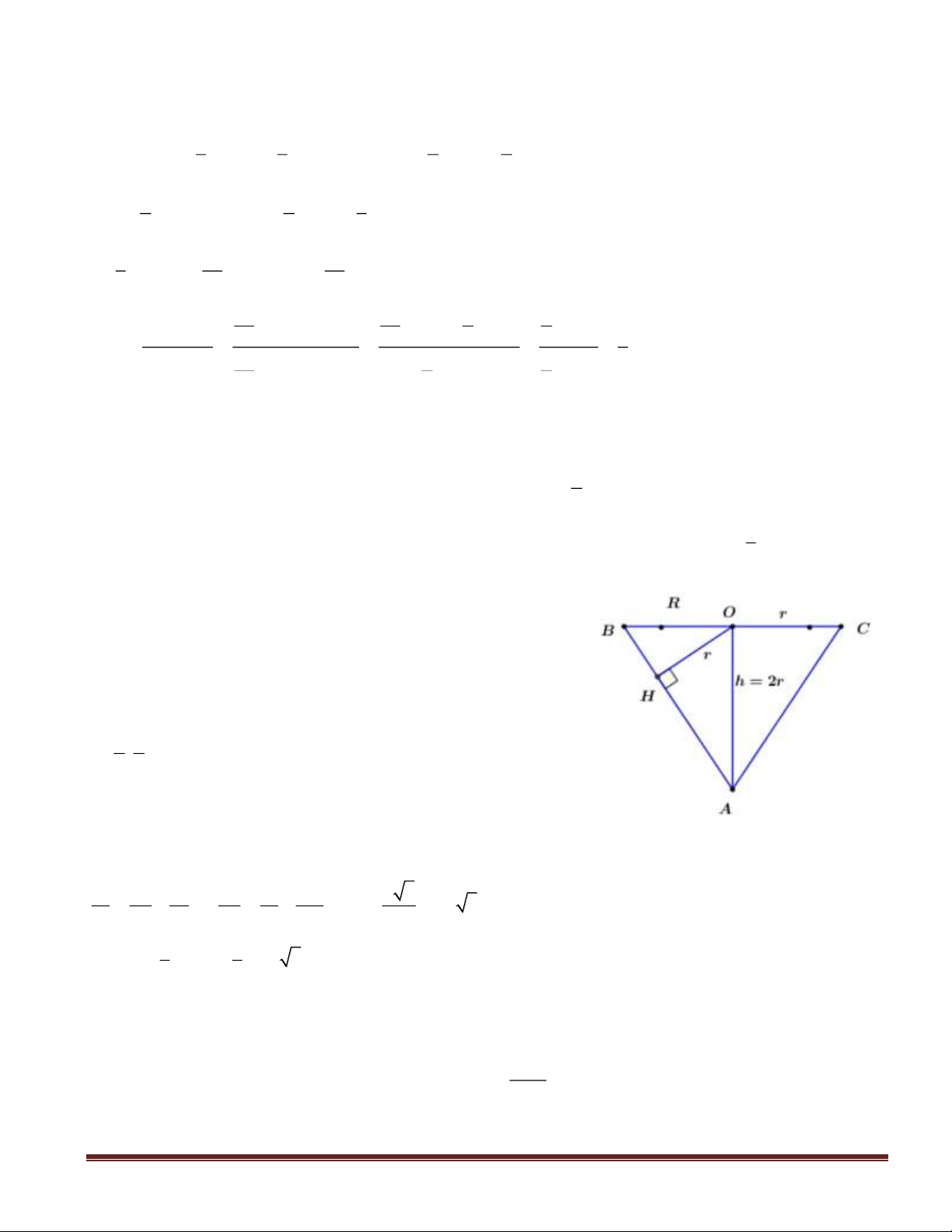
Trang 100
( )( ) ( )
2
2 8 4
log 3 log 3 log 3a a a+ + = +
( )
2 2 2
2 8 2 8 4 4
log 3 log 3 log 3.log 3 2 log 3 log 3a a a a + + + = + +
2
2 2 2 2 2 2
1 1 1 1
log 3 log 3 .log 3.log 3 2 log 3 log 3
3 3 2 4
aa
+ + = +
22
2 2 2 2
4 1 1
. log 3 log 3 log 3 log 3
3 4 3
a
− = −
2
2 2 2
1 1 1
log 3 log 3 log 3
3 12 4
aa
−−
= =
2 4 2 2 2
4
2
2 2 2 2
1 1 1 1
log 3 log 3 log 3 log 3 log 3
log 3
1
4 4 2 4
1 3 3
log 3 3
log 3 log 3 log 3 log 3
4 4 4
a
q
a
−−
++
+
= = = = =
−
+
+
Câu 21. Chọn đáp án B
Phương pháp
Công thức tính thể tích của khối cầu có bán kính r:
3
4
3
Vr
=
.
Công thức tính thể tích của khối nón có bán kính đáy R và chiều cao h:
2
1
3
V R h
=
Cách giải
Gọi r là bán kính của khối cầu, R là bán kính của khối
nón và h là chiều cao của khối nón.
Khi đó ta có:
2hr=
.
Theo đề bài ta có: thể tích của nửa khối cầu là:
3
18 dm
3
14
. 18 3
23
r r dm
= =
.
26h r dm = =
.
Áp dụng hệ thức lượng cho tam giác OAB vuông tại O,
có đường cao OH ta có:
2 2 2 2 2 2
1 1 1 1 1 1 2 3
23
43
R r dm
r R h R r r
= + = − = =
.
( )
2
23
11
. 2 3 .6 24
33
non
V R h dm
= = =
.
Câu 22. Chọn đáp án C
Phương pháp
Sử dụng công thức nguyên hàm cơ bản:
1
1
x
x dx C
+
=+
+
.
Cách giải

Trang 101
Ta có:
2020
2019
2020
x
x dx C= +
đáp án C sai.
Câu 23. Chọn đáp án A
Phương pháp
Sử dụng công thức tính tỉ lệ thể tích: Cho các điểm
,,M SA N SB P SC
ta có
..
SMNP
SABC
V
SM SN SP
V SA SB SC
=
.
Cách giải
Ta có:
. ' ' ' '
3
ABC A B C A ABC
VV=
.
Lại có:
' . ' ' '
'
1 1 1
' 2 2 6
MABC
MABC A ABC ABC A B C
A ABC
V
AM
V V V
V AA
= = = =
Câu 24. Chọn đáp án D
Phương pháp
Sử dụng quy tắc nhân để làm bài toán.
Cách giải
Ta có:
, , , 1;2;3;4abc a b c
ta chọn 3 chữ số trong tập hợp gồm 4 chữ số, trong đó các số a, b, c có thể bằng nhau
có
3
4
cách chọn.
Câu 25. Chọn đáp án D
Phương pháp
Sử dụng công thức tính tích phân, có
( )
Fx
là nguyên hàm của hàm số
( )
fx
thì ta có:
( ) ( ) ( ) ( )
b
b
a
a
f x dx F x F b F a= = −
.
Cách giải
Ta có:
4
3
4
x
x dx C=+
.
Ta có
( ) ( )
4
2
2 0 0 4
4
FF− = − =
.
Câu 26. Chọn đáp án A
Phương pháp
Sử dụng công thức
cos
ABC MNB
SS
=
với
( ) ( )
( )
,MNP ABCD
=
.
Cách giải
Trang 102
Ta có hình chiếu của tam giác MNP lên
( )
ABCD
chính là tam giác ABC
Gọi
( ) ( )
( )
;MNP ABCD
=
2
2
1
.cos cos cos 60
22
ABC MNB
a
S S a
= = = =
Câu 27. Chọn đáp án A
Phương pháp
Sử dụng công thức tính đạo hàm cơ bản:
( )
( )
( )
'
log '
ln10
fx
fx
fx
=
.
Cách giải
Ta có:
( )
( ) ( )
11
log 1 '
1 ln10 1 ln10
x
xx
−
− = =
−−
.
Câu 28. Chọn đáp án A
Phương pháp
Sử dụng công thức tính nguyên hàm cơ bản:
1
ax ax
e dx e C
a
=+
.
Cách giải
Ta có:
22
1
2
xx
e dx e C
−−
= − +
Câu 29. Chọn đáp án A
Phương pháp
Hàm số
( )
y f x=
nghịch biến trên
( ) ( ) ( )
; ' 0 ; a b f x x a b
và bằng 0 tại hữu hạn điểm.
Cách giải
Ta có:
2
'2y x x m= − + −
Hàm số đã cho nghịch biến trên
( ) ( )
0; ' 0 0; yx+ +
.
( ) ( )
22
2 0 0; 2 0; x x m x x x m x − + − + − − +
(*)
Xét hàm số
( )
( )
( )
2
0;
2 (*)g x x x m Min g x
+
= − −
Ta có:
( )
' 2 2 0 1g x x x= − = =
. Khi đó ta có BBT:
x
0
1
+
( )
'gx
−
0
+
( )
gx
+
+
1−
( )
( )
0;
11m Min g x m m
+
− − −
.
Câu 30. Chọn đáp án B

Trang 103
Phương pháp
Sử dụng công thức khai triển của nhị thức:
( )
0
n
n
k n k k
n
k
a b C a b
−
=
+=
.
Cách giải
Ta có:
( ) ( ) ( ) ( )
2019 2019
2019 2019 2019
2019 2019
00
2 1 2 . 1 2 . 1 .
k k k
k k k k
kk
x C x C x
−−
==
− = − = −
.
Để có số hạng chứa
18
18xk=
.
Vậy số hạng chứa
18
x
trong khai triển là:
( )
2001
18 18 18 18 18 18
2019 2019
.2 . 1 . 2C x C x− = −
.
Chú ý khi giải: Đề bài hỏi số hạng chứa
x
trong khai triển nên khi chọn mình chọn đáp
án cần có cả phần biến
x
, còn khi đề bài hỏi hệ số thì không cần kết luận phần biến.
Câu 31. Chọn đáp án A
Phương pháp
+) Tính nguyên hàm
( )
Fx
. Lưu ý điều kiện của x để phá trị tuyệt đối.
+) Dựa vào giả thiết
( )
20F −=
tìm C.
Cách giải
( ) ( ) ( )
1
ln ln 0 F x dx x C x C x
x
= = + = − +
( )
2 0 ln2 0 ln2F C C− = + = = −
( ) ( ) ( )
ln ln2 ln 0;
2
x
F x x x
= − − = − +
Câu 32. Chọn đáp án C
Phương pháp
Sử dụng các công thức
( )
log log log
log log
m
a a a
n
a
a
x y xy
n
bb
m
+=
=
(giả sử các biểu thức là có nghĩa).
Cách giải
( )
( ) ( )
2
45 45 45 45
22
35
12
log 75 log 3.5 log 3 2log 5
log 3 .5 log 3 .5
= = + = +
35
1 2 1 2
2
2 log 5 2log 3 1 2
1
a
a
= + = +
+ + +
+
1 2 1 2
2 2 2
aa
a a a
+
= + =
+ + +
Câu 33. Chọn đáp án B
Phương pháp

Trang 104
+) Sử dụng công thức tính diện tích xung quanh mặt nón có bán kính đáy r và đường sinh l
là
xq
S rl
=
tính l theo r.
+) Gọi góc ở đỉnh bằng
2 sin
r
l
=
.
Cách giải
2
2 2 2
xq day
S S rl r l r
= = =
Gọi góc ở đỉnh bằng
1
2 sin 30 2 60
22
rr
lr
= = = = =
.
Câu 34. Chọn đáp án C
Phương pháp
( )
;;
B A B A B A
AB x x y y z z= − − −
Cách giải
( )
;;MO a b c= − − −
Câu 35. Chọn đáp án A
Phương pháp
Sử dụng nguyên lí vách ngăn.
Cách giải
( )
5! 120n = =
Xếp Cường, Dũng, Đông vào 3 ghế bất kì có 3! cách, khi đó tạo ra 4 khoảng trống. Xếp An
và Bình vào hai trong 4 khoảng trống đó có 4.3 = 12 cách.
Gọi A là biến cố: “An và Bình không ngồi cạnh nhau
( )
3!.12 72nA = =
.
Vậy
( )
72 3
120 5
PA==
.
Câu 36. Chọn đáp án D
Phương pháp
Sử dụng công thức tính thể tích khối nón có bán kính đáy r và đương cao h là
2
1
3
V r h
=
.
Cách giải
Quay tam giác ABC quanh đường thẳng AB ta được khối nón có bán kính đáy
r AC b==
và
đường cao
h AB c==
. Khi đó thể tích của khối nón bằng
22
11
33
AC AB b c
=
.
Câu 37. Chọn đáp án D
Phương pháp
Cho hàm số
( )
y f x=
:

Trang 105
Nếu
00
lim
x
y y y y
→
= =
là TCN của đồ thị hàm số.
Nếu
0
0
lim
xx
y x x
→
= =
là TCĐ của đồ thị hàm số.
Cách giải
Ta có
( )
11
lim lim 1
2 1 2.1 1
xx
y
fx
→ →
= = =
−−
Đồ thị hàm số có TCN
1y =
.
Xét phương trình
( ) ( )
1
2 1 0
2
f x f x− = =
. Dựa vào BBT ta thấy phương trình
( )
1
2
fx=
có
2 nghiệm phân biệt, do đó đồ thị hàm số có 2 TCĐ.
Câu 38. Chọn đáp án B
Phương pháp
( ) ( ) ( )
12
1 1 1 2 2 2 1 2
12
; ; ; ; ; ; 0
a ka
u a b c v a b c u kv b kb k
c kc
=
= = =
=
Cách giải
Dễ thấy
2ab=−
Câu 39. Chọn đáp án D
Phương pháp
Sử dụng công thức:
( )
.
cos ,
.
iu
iu
iu
=
Cách giải
( )
( )
1;0;0 ; 3;0; 1iu= = − −
( ) ( )
. 3 3
cos ; ; 150
1.2 2
.
iu
i u i u
iu
−−
= = = =
.
Câu 40. Chọn đáp án C
Phương pháp
+) ABCD là hình bình hành
AB DC =
Tìm tọa độ điểm C.
+)
. ' ' ' 'ABCD A B C D
là hình hộp
''AA CC =
Tìm tọa độ điểm
'C
.
+) Tính
''AC AC=
.
Cách giải
Do ABCD là hình bình hành
( )
0
2 0 ;2 ;0
00
C
C
C
xa
AB DC y a C a a
z
−=
= − =
−=

Trang 106
. ' ' ' 'ABCD A B C D
là hình hộp
( )
'
'
'
0
' ' 2 0 ' ;2 ;2
02
C
C
C
xa
AA CC y a C a a a
za
−=
= − =
−=
( )
222
' ;2 ;2 ' ' 4 4 3AC a a a AC AC a a a a = = = + + =
.
Câu 41. Chọn đáp án A
Phương pháp
+) Gọi H là hình chiếu của S trên
( )
ABC
. Xác định các góc giữa các cạnh bên và đáy.
+) Chứng minh các tam giác SAH, SBH, SCH bằng nhau.
Cách giải
Gọi H là hình chiếu của S trên
( )
ABC
ta có
( )
,,SH ABC SH HA SH HB SH HC⊥ ⊥ ⊥ ⊥
.
( )
( )
( )
,;SA ABC SA AH SAH = =
( )
( )
( )
;;SB ABC SB BH SBH = =
( )
( )
( )
;;SC ABC SC CH SCH = =
SAH SBH SCH = =
Xét
v
SAH
,
v
SBH
,
v
SCH
có:
SH chung;
SAH SBH SCH = =
;
vvv
SAH SBH SCH = =
(cạnh góc vuông – góc
nhọn)
HA HB HC = =
H là tâm đường tròn ngoại tiếp tam giác ABC.
Câu 42. Chọn đáp án C
Phương pháp
Cách giải
OAB
đều
AB OA OB a = = =
Áp dụng định lí Pytago trong tam giác vuông OBC ta có:
22
2BC a a a= + =
.
Áp dụng định lý Cosin trong tam giác OAC ta có
2 2 2 2 2
1
2 . .cos120 2 . 3
2
AC OA OC OAOC a a a a
−
= + − = + − =

Trang 107
Xét tam giác ABC ta có:
2 2 2
AB BC AC ABC+ =
vuông tại B. Gọi H là trung điểm của AC
H là tâm đường tròn ngoại tiếp tam giác ABC.
Mà
( )
OA OB OC OH ABC OH= = ⊥
là trục của tam giác ABC. Gọi M là trung điểm của
SB, trong
( )
SBH
kẻ đường thẳng vuông góc với SB cắt OH tại I.
Ta có
I OH IA IB IC = =
.
Lại có
IS IB IA IB IC IS I= = = =
là tâm mặt cầu ngoại tiếp chóp S.ABC.
Ta có:
2
2 2 2
3
42
aa
OH OA AH a= − = − =
.
13
22
a
BH AC==
22
22
31
4 4 4
aa
OB OH BH a BM OB = + = + = =
;
3
4
a
OM =
~OBH OIM
(g.g)
33
.
33
24
4
2
aa
BH OH a
IM
a
IM OM
= = =
22
22
27 7
16 16 2
a a a
IB IM BM = + = + =
Câu 43. Chọn đáp án D
Phương pháp
( ) ( )
( )
'f x f x dx=
Cách giải
( ) ( ) ( )
( )
2018 2018
' 2018
xx
f x dx e C f x f x dx e
−−
= + = = −
Câu 44. Chọn đáp án B
Phương pháp
Vì hàm số
sin x
x
liên tục tại
2
x
=
nên
2
sin
lim
2
x
x
f
x
→
=
Cách giải
Vì hàm số
sin x
x
liên tục tại
2
x
=
nên
2
sin
sin 2
2
lim
2
2
x
x
f
x
→
= = =
.
Câu 45. Chọn đáp án B
Phương pháp
( ) ( ) ( )
log 0 1 0
b
a
f x b a f x a

Trang 108
Cách giải
( )
0,5
log 1 1 0 1 0,5 1 1,5x x x− −
Câu 46. Chọn đáp án A
Phương pháp
+) Đặt
2sintx=
, xác định điều kiện của t.
+) Khi đó phương trình trở thành
( )
f t m=
. Số nghiệm của phương trình là số giao điểm
của đồ thị hàm số
( )
y f t=
và đường thẳng
ym=
song song với trục hoành.
Cách giải
Đặt
2sintx=
, với
, 2;2xt
− −
.
Khi đó phương trình trở thành
( )
f t m=
. Số nghiệm của phương trình là số giao điểm của
đồ thị hàm số
( )
y f t=
và đường thẳng
ym=
song song với trục hoành.
Với mỗi
( )
2;2t −
sẽ cho ta 2 nghiệm
;x
−
, khi
2t =
cho ta 1 nghiệm x.
Khi đó phương trình ban đầu có 3 nghiệm
;x
−
Phương trình
( )
f t m=
có 1 nghiệm
2t =
và một nghiệm
( )
2;2t −
hoặc phương trình
( )
f t m=
có 1 nghiệm
2t =−
và một
nghiệm
( )
2;2t −
.
1m=
hoặc
3 1; 3mm= − −
.
Câu 47. Chọn đáp án C
Phương pháp
+) Gọi
( )
;;M a b c
.
+)
.0
90 . 0
.0
AM BM
AMB BMC CMA BM CM
CM AM
=
= = = =
=
Cách giải
Gọi
( ) ( ) ( ) ( )
; ; 2; ; , ; 2; , ; ; 2M a b c AM a b c BM a b c CM a b c = − = − = −
90AMB BMC CMA = = =
( ) ( )
( ) ( )
( ) ( )
2
2
2
2 2 0
.0
. 0 2 2 0
.0
2 2 0
a a b b c
AM BM
BM CM a b b c c
CM AM
a a b c c
− + − + =
=
= + − + − =
=
− + + − =
( )
2 2 2
2 2 2
2 2 2
2 2 0 *
2 2 0
2 2 0
a b c a b
a b c b c
a b c a c
+ + − − =
+ + − − =
+ + − − =
Trang 109
2 2 2 2 2 2a b b c c a a b c + = + = + = =
Thay vào (*) ta có:
( )
2
0;0;0
0
3 4 0
4
444
;;
3
333
M
a
aa
a
M
=
− =
=
(tm)
Vậy có 2 điểm M thỏa mãn yêu cầu bài toán.
Câu 48. Chọn đáp án D
Phương pháp
Hàm số
( )
2
log 0y x x=
có tập giá trị là .
Cách giải
Hàm số
( )
2
log 0y x x=
có tập giá trị là nên phương trình
2
log xm=
có nghiệm thực với
mọi giá trị của m.
Câu 49. Chọn đáp án B
Phương pháp
+) Sử dụng công thức tính đạo hàm hàm hợp tính
( )
'fx
.
+) Lập bảng xét dấu
( )
'fx
và kết luận các khoảng đơn điệu của hàm số.
Cách giải
Ta có:
( )
( )
( )
2018
2
1
' 2019 1 2 0
0
x
f x x x
x
=
= − − =
=
Bảng xét dấu:
x
−
1−
0
1
+
( )
'fx
+
0
+
0
−
0
−
Từ bảng xét dấu
( )
'fx
ta có hàm số đồng biến trên
( )
;0−
và nghịch biến trên
( )
0;+
Chú ý: Do các nghiệm
1x =
là các nghiệm bội chẵn nên qua đó
( )
'fx
không đổi dấu.
Câu 50. Chọn đáp án C
Phương pháp
Hàm số
( )
Fx
là một nguyên hàm của hàm số
( )
fx
thì
( ) ( )
'F x f x=
.
Cách giải
Ta có
( )
( )
2
cos ' 2cos sin 2sin cos sin2x x x x x x= − = − = −
Do đó hàm số
sin2yx=−
có một nguyên hàm bằng
2
cos x
.
ĐỀ 27
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút

Trang 110
Câu 1: Trong hệ trục tọa độ Oxy, một elip có độ dài trục lớn là 8, độ dài trục bé là 6 thì có phương trình
chính tắc là:
A.
22
1.
9 16
xy
+=
B.
22
1.
64 36
xy
+=
C.
22
1.
16 9
xy
+=
D.
22
1.
16 7
xy
+=
Câu 2: Trong không gian Oxyz, một vecto chỉ phương của đường thẳng
2
:1
1
xt
yt
z
=
= − +
=
là:
A.
( )
2; 1;1 .m=−
B.
( )
2; 1;0 .m=−
C.
( )
2;1;1 .m=
D.
( )
2; 1;0 .m= − −
Câu 3: Cho hai hàm
1
()
2
fx
x
=
và
2
()
2
x
gx=
. Tính góc giữa hai tiếp tuyến của đồ thị mỗi hàm số đã cho tại
giao điểm của chúng. A. 90
o
B. 60
o
C. 45
o
D. 30
o
Câu 4: Cho hình nón đỉnh S có bán kính
2,Ra=
góc ở đỉnh bằng
0
60 .
Diện tích xung quanh của hình
nón bằng A.
2
.a
B.
2
4.a
C.
2
6.a
D.
2
2.a
Câu 5: Cho hình phẳng (D) được giới hạn bởi các đường
0, 1, 0x x y= = =
và
21yx=+
. Thể tích V
của khối chóp tròn xoay tạo thành khi quay (D) quanh trục Ox được tính theo công thức
A.
1
0
21V x dx= +
B.
( )
1
0
21V x dx= +
C.
1
0
21V x dx=+
D.
1
0
(2 1)V x dx=+
Câu 6: Tìm các giá trị của tham số
m
để đồ thị hàm số y= x
4
-2mx
2
+ m có ba điểm cực trị . Đồng thời ba
điểm cực trị đó là ba đỉnh của một tam giác có bán kính đường tròn nội tiếp lớn hơn 1.
A.
1.m −
B.
2.m
C.
( ) ( )
; 1 2; .m − − +
D. Không tồn tại m.
Câu 7: Giá trị cực tiểu của hàm số
2
lny x x=
là
A.
1
.
2
CT
y
e
=−
B.
1
.
2
CT
y
e
=
C.
1
.
CT
y
e
=
D.
1
.
CT
y
e
=−
Câu 8: Một hình lăng trụ có 2018 mặt. Hỏi hình lăng trụ có tất cả bao nhiêu cạnh?
A. 6057. B. 6051. C. 6045. D. 6048.
Câu 9: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông, tam giác
SAB
cân tại
S
. Góc giữa mặt
bên
( )
SAB
và mặt đáy bằng
0
60
, góc giữa
SA
và mặt đáy bằng
0
45
. Biết thể tích khối chóp
.S ABCD
bằng
3
83
3
a
. Chiều cao của hình chóp
.S ABCD
bằng
A.
3a
. B.
6a
. C.
3
3
a
. D.
2
3
a
.
Câu 10: Cho hình hộp đứng
.ABCD ABCD
có cạnh bên
AA h
=
và diện tích tam giác ABC bằng S.
Thể tích của khối hộp
.ABCD ABCD
bằng

Trang 111
A.
1
.
3
V Sh=
B.
2
.
3
V Sh=
C.
.V Sh=
D.
2.V Sh=
Câu 11: Phương trình
( ) ( )
22
ln 1 ln 2018 0xx+ − =
có bao nhiêu nghiệm?
A. 1. B. 4. C. 3. D. 2.
Câu 12: Cho hàm số
2
2cos cos 1
.
cos 1
xx
y
x
++
=
+
Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số
đã cho. Khi đó M+m bằng
A.– 4. B.– 5 . C.– 6 . D. 3.
Câu 13: Cho hình trụ có bán kính R, chiều cao bằng h. Biết rằng hình trụ đó có diện tích toàn phần gấp
đôi diện tích xung quanh. Mệnh đề nào sau đây đúng?
A.
2.hR=
B. h = 2R. C. R = h. D. R = 2h.
Câu 14: Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác ABC được gọi là tam
giác trung bình của tam giác ABC.Ta xây dựng dãy các tam giác
1 1 1
,ABC
2 2 2 3 3 3
,,A B C A B C
,...sao
cho
1 1 1
A BC
là tam giác đều cạnh bằng 3 và mỗi số nguyên dương n 2 , tam giác
n n n
A B C
là tam
giác trung bình của tamgiác
1 1 1n n n
A B C
− − −
.Với mỗi số nguyên dương n kí hiệu S
n
tương ứng là diện
tích hình tròn ngoại tiếp tam giác
n n n
A B C
. Tính tổng
12
..... ....
n
S S S S= + + + +
A.
15
4
S
=
B. S = 4 . C.
9
2
S
=
D. S =
5 .
Câu 15: Cho hình chóp S.ABCD có
( )
2
3
. , 2,
2
ABCD
a
SA ABCD AC a S==
và góc giữa đường thẳng SC
và mặt phẳng (ABCD) bằng
0
60 .
Gọi H là hình chiếu vuông góc của A trên SC. Tính theo a thể tích khối
chóp H.ABCD .
A.
3
6
.
2
a
B.
3
6
.
4
a
C.
3
6
.
8
a
D.
3
36
.
4
a
Câu 16: Gieo một con súc sắc cân đói và đồng chất. Giả sử súc sắc xuất hiện mặt b chấm. Xác suất để
phương trình
2
20x bx+ + =
có hai nghiệm phân biệt là?
A.
1
.
2
B.
1
.
3
C.
5
.
6
D.
2
.
3
Câu 17: Cho hai số thực
0, 0xy
thay đổi và thỏa mãn điều kiện
22
()x y xy x y xy+ = + −
. Giá trị lớn
nhất
M
của biểu thức
33
11
A
xy
=+
là:
A.
0.M =
B.
0.M =
C.
1.M =
D.
16.M =
Câu 18: Khi đặt
3
logtx=
thì bất phương trình
( )
2
5
5
log 5 3log 5 0xx− −
trở thành bất phương trình
nào dưới đây?
A.
2
6 4 0.tt− −
B.
2
6 5 0.tt− −
C.
2
4 4 0.tt− −
D.
2
3 5 0.tt− −
Câu 19: Giải bất phương trình
2
4
3
1
4
x −
ta được tập nghiệm là T. Tìm T.
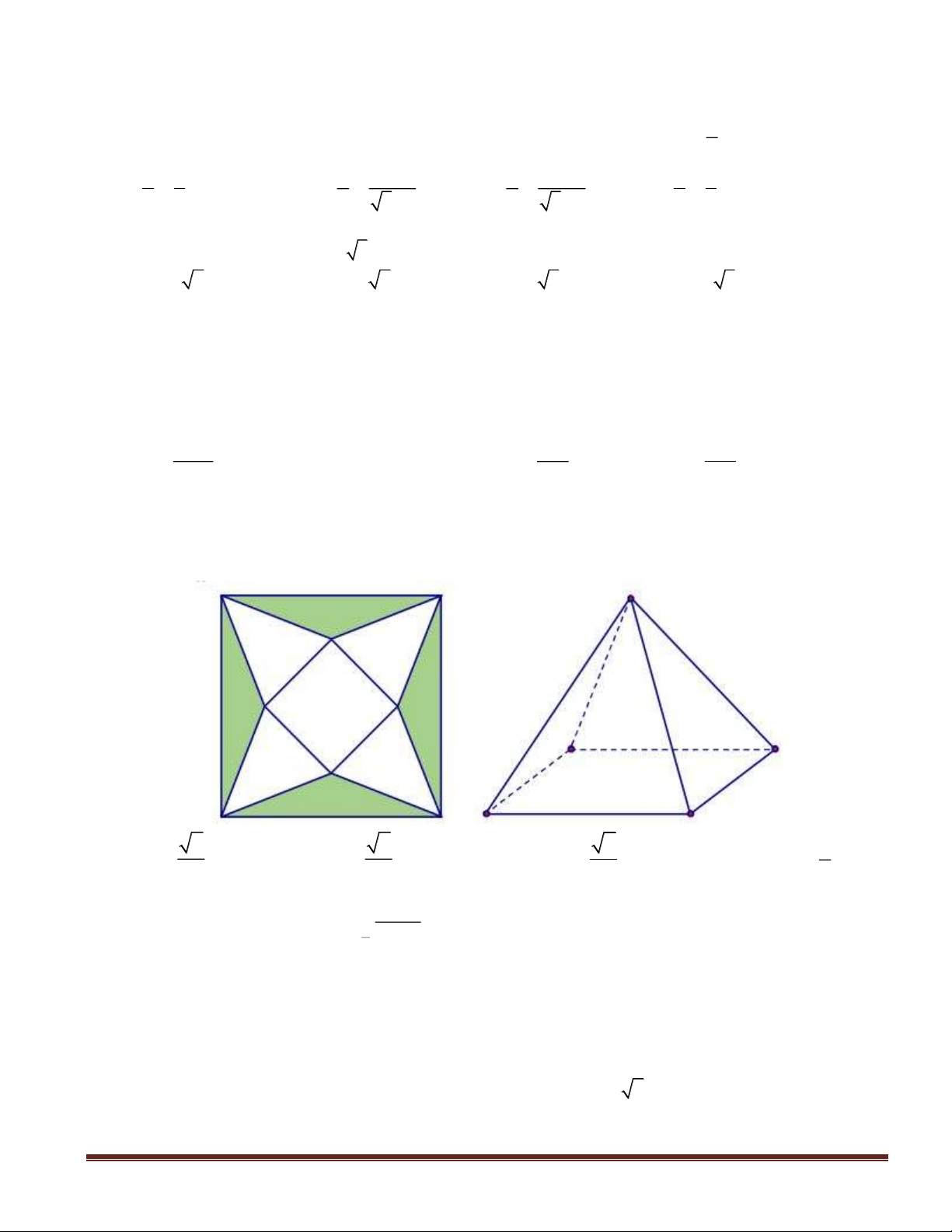
Trang 112
A.
2;2 .T =−
B.
)
2; .T = +
C.
(
; 2 .T = − −
D.
(
)
; 2 2; .T = − − +
Câu 20: Cho số dương
,xy
thỏa mãn
( )
6 9 4
log log log 2 2 .x y x y= = +
Tính tỉ số
?
x
y
A.
2
.
3
x
y
=
B.
2
.
31
x
y
=
−
C.
2
.
31
x
y
=
+
D.
3
.
2
x
y
=
Câu 21: Khi cắt khối nón (N) bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác
vuông cân có cạnh huyền bằng
2 3.a
Tính thể tích V của khối nón (N).
A.
3
3 6 .Va=
B.
3
6.Va=
C.
3
3.Va=
D.
3
3 3 .Va=
Câu 22: Biết tiếp tuyến của đồ thị hàm số
42
2y ax bx= + +
tại điểm A(-1;1) vuông góc với đường thẳng
2 3 0.xy− + =
Tính
22
?ab−
A.
22
10.ab−=
B.
22
13.ab−=
C.
22
2.ab− = −
D.
22
5.ab− = −
Câu 23: Một hình trụ có trục
OO
chứa tâm của một mặt cầu bán kính R, các đường tròn đáy của hình trụ
đều thuộc mặt cầu trên, đường cao của hình trụ đứng bằng R. Tính thể tích V của khối trụ.
A.
3
3
.
4
R
V
=
B.
3
.VR=
C.
3
.
4
R
V
=
D.
3
.
3
R
V
=
Câu 24: Cho một tấm nhôm hình vuông cạnh 1(m) như hình vẽ dưới đây. Người ta cắt phần tô
đậm của tấm nhôm rồi gập thành một hình chóp tứ giác đều có cạnh đáy bằng x(m), sao cho bốn
đỉnh của hình vuông gập lại thành đỉnh của hình chóp. Tìm giá trị của x để khối chóp nhận được
có thể tích lớn nhất.
A.
2
4
x =
B.
2
3
x =
C.
2
5
x =
D.
1
2
x =
Câu 25: Bất phương trình
21
3
37
log log 0
3
x
x
−
+
có tập nghiệm là
(
;.ab
Tính giá trị của
3P a b=−
là:
A. 5. B. 4. C. 10. D. 7.
Câu 26: Trong không gian với hệ trục tọa độ Oxyz cho hai điểm
( ) ( )
A l;0; 3 , B 3; 2; 5 .− − − −
Biết rằng tập
hợp các điểm M trong không gian thỏa mãn đẳng thức
22
AM BM 30+=
là một mặt cầu
( )
S
. Tọa độ tâm I
và bán kính R của mặt cầu
( )
S
là:
A.
( )
I 2; 2; 8 ;R 3− − − =
B.
( )
I 1; 1; 4 ;R 6− − − =
Trang 113
C.
( )
I 1; 1; 4 ;R 3− − − =
D.
( )
30
I 1; 1; 4 ;R
2
− − − =
Câu 27: Cho
,ab
là các số dương thỏa mãn
4 25
4
log log log .
2
ba
ab
−
==
Tính giá trị của
a
b
?
A.
6 2 5.
a
b
=−
B.
35
.
8
a
b
+
=
C.
6 2 5.
a
b
=+
D.
35
.
8
a
b
−
=
Câu 28: Trong không gian Oxyz, cho điểm M(1;0;-1). Mặt phẳng
( )
đi qua M và chứa trục Ox có
phương trình là?
A.
0.xz+=
B.
1 0.yz+ + =
C. y = 0. D.
0.x y z+ + =
Câu 29: Cho hàm số
( )
y f x=
có đạo hàm
( )
2
2 , .f x x x x
= −
Hàm số
( )
2y f x=−
đồng biến trên
khoảng?
A. (0;2). B. (-2;0). C.
( )
2; .+
D.
( )
; 2 .− −
Câu 30: Cho hàm số y
( )
fx=
có đồ thị
( )
'fx
như hình vẽ
Hàm
( )
2
1
2
x
y f x x= − + −
nghịch biến trên khoảng
A. (−3; 1). B. (−2; 0) . C. (1; 3). D.
3
1;
2
−
Câu 31: Cho hình lập phương
.ABCD ABCD
cạnh
a. Gọi M, N lần lượt là trung điểm của AC và
BC
(tham khảo hình vẽ bên). Khoảng cách giữa hai đường
thẳng MN và
BD
bằng
A.
5.a
B.
5
.
5
a
C.
3.a
D.
.
3
a
Câu 32: Cho hình lăng trụ đứng
.ABC ABC
có đáy ABC
là tam giác vuông,
.AB BC a==
Biết rằng góc giữa hai
mặt phẳng
( )
ACC
và
( )
ABC
bằng
0
60
(tham khảo
hình vẽ bên). Thể tích của khối chóp
..B ACCA
A.
3
.
3
a
B.
3
.
6
a

Trang 114
C.
3
.
2
a
D.
3
3
.
3
a
Câu 33: Tìm tất cả các giá trị của tham số thực m để hàm số
3 2 2
39y x mx m x= − −
nghịch biến trên
(0;1).
A.
1
.
3
m
B.
1.m−
C.
1
3
m
hoặc m < -1 D.
1
1.
3
m−
Câu 34: Tìm tất cả các giá trị của tham số thực m để phương trình
2
33
log 3log 2 7 0x x m− + − =
có hai
nghiệm thực
12
,xx
thỏa mãn
( )( )
12
3 3 72.xx+ + =
A.
61
.
2
m=
B.
3.m=
C. Không tồn tại. D.
9
.
2
m=
Câu 35: Sau khi khai triển và rút gọn biểu thức
( )
21
12
23
2
31
2f x x x
x
x
= + + +
thì
( )
fx
có bao nhiêu
số hạng?
A. 30. B. 32. C. 29. D. 35.
Câu 36: Cho đồ thị
( )
32
: 3 .C y x x=−
Có bao nhiêu số nguyên
( )
10;10b−
để có đúng một tiếp tuyến
của (C) đi qua điểm B(0;b)?
A. 17. B. 9. C. 2. D. 16.
Câu 37: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( )
( )
2
2
1 2 ,f x x x x
= − −
với mọi
.x
Có bao nhiêu giá
trị nguyên dương của tham số m để hàm số
( )
2
8y f x x m= − +
có 5 điểm cực trị?
A. 16. B. 17. C. 15. D. 18.
Câu 38: Trong không gian Oxyz cho các mặt phẳng
( ) ( )
: 2 1 0, :2 1 0P x y z Q x y z− + + = + + − =
. Gọi (S)
là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có
bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định
r sao cho chỉ đúng một mặt cầu (S) thỏa yêu cầu.
A.
3.r =
B.
2.r =
C.
3
.
2
r =
D.
32
.
2
r =
Câu 39: Có bao nhiêu giá trị nguyên âm của a để đồ thị hàm số
( )
32
10 1y x a x x= + + − +
cắt trục hoành
tại đúng một điểm?
A. 9. B. 8. C. 11. D. 10.
Câu 40: Giả sử
,ab
là các số thực sao cho
3 3 3 2
.10 .10
xx
x y a b+ = +
đúng với mọi số thực dương
,,x y z
thỏa mãn
( )
log x y z+=
và
( )
22
log 1.x y z+ = +
Giá trị của
ab+
bằng:
A.
31
.
2
−
B.
25
.
2
−
C.
31
.
2
D.
29
.
2
Câu 41: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2 , SA = 2 và SA vuông
góc với mặt phẳng đáy ( ABCD) . Gọi M , N là hai điểm thay đổi trên hai cạnh AB ,AD sao cho
mặt phẳng (SMC) vuông góc với mặt phẳng ( SNC) . Tính tổng
22
11
T
AN AM
=+
khi thể tích
khối chóp S.AMCN đạt giá trị lớn nhất.
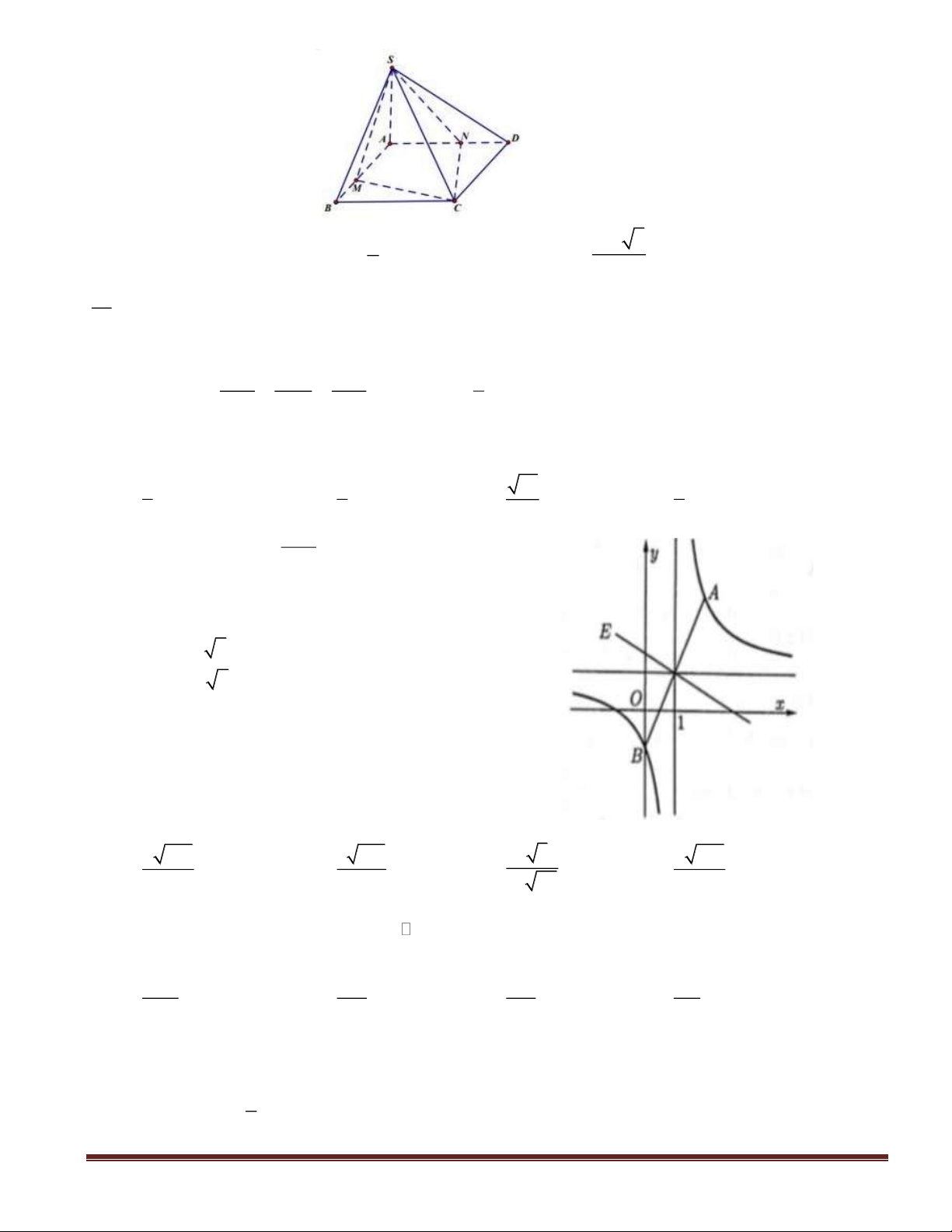
Trang 115
A. T = 2 . B. T =
5
4
. C. T =
23
4
+
. D. T =
13
9
.
Câu 42: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
( )
:2 2 2 0x y z + − − =
và đường thẳng có
phương trình
1 2 3
:
1 2 2
x y z
d
+ + +
==
và điểm
1
;1;1 .
2
A
Gọi
là đường thẳng nằm trong mặt phẳng
( )
, song song với d, đồng thời cách d một khoảng bằng 3. Đường thẳng
cắt mặt phẳng (Oxy) tại
điểm B. Độ dài đoạn thẳng AB bằng:
A.
7
.
3
B.
7
.
2
C.
21
.
2
D.
3
.
2
Câu 43: Cho hàm số
1
1
x
y
x
+
=
−
có đồ thị (C). Giả sử A,
B là hai điểm thuộc (C) và đối xứng nhau qua giao điểm
của hai đường tiệm cận. Dựng hình vuông AEBF. Tìm
diện tích nhỏ nhất của hình vuông AEBF.
A.
min
8 2.S =
B.
min
4 2.S =
C.
min
8.S =
D.
min
16.S =
Câu 44: Cho hình lăng trụ đứng
.ABC ABC
có
1, 2,AA 3AB AC
= = =
và
0
120 .BAC =
Gọi M, N lần
lượt là các điểm trên cạnh
,BB CC
sao cho
3 ; 2 .BM BM CN CN
==
Tính khoảng cách từ điểm M đến
mặt phẳng
( )
.ABN
A.
9 138
.
184
B.
3 138
.
46
C.
93
.
16 46
D.
9 138
.
46
Câu 45: Trong mặt phẳng Oxy, cho hình chữ nhật OMNP với M(0;10), N(100;10) và P(100;0). Gọi S là
tập hợp tất cả các điểm A(x;y) với
,xy
nằm bên trong (kể cả trên cạnh) của OMNP. Lấy ngẫu nhiên
một điểm
( )
;.A x y S
Xác suất để
90xy+
bằng:
A.
845
.
1111
B.
473
.
500
C.
169
.
200
D.
86
.
101
Câu 46: Trong không gian Oxyz, cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 8S x y z− + + + + =
và điểm
( )
1;1;2 .M −
Hai đường thẳng
12
,dd
qua điểm M và tiếp xúc với mặt cầu (S) lần lượt tại A, B. Biết góc giữa
1
d
và
2
d
bằng
,
với
3
cos .
4
=
Tính độ dài đoạn AB.
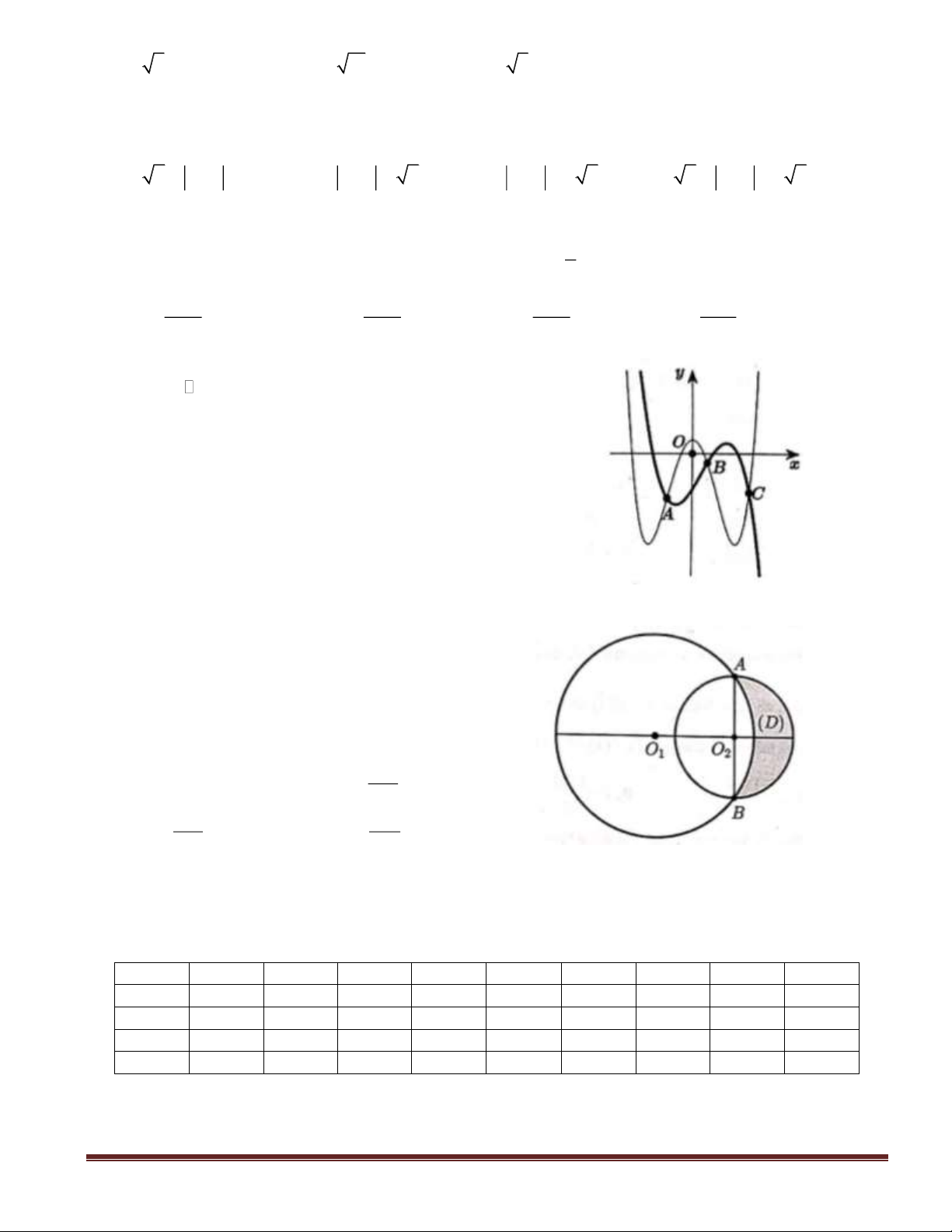
Trang 116
A.
7.
B.
11.
C.
5.
D. 7.
Câu 47: Cho hàm số
( )
y f x=
có đạo hàm
1.x =
Gọi
12
,dd
lần lươt là tiếp tuyến của đồ thị hàm số
( )
y f x=
và
( ) ( )
. 2 1y g x x f x= = −
tại điểm có hoành độ
1.x =
Biết rằng hai đường thẳng
12
,dd
vuông
góc nhau. Khẳng định nào sau đây đúng?
A.
( )
2 1 2.f
B.
( )
1 2.f
C.
( )
1 2 2.f
D.
( )
2 1 2 2.f
Câu 48: Cho hàm số
( )
y f x=
có đạo hàm liên tục trên đoạn [1;4], đồng biến trên đoạn [1;4] và thỏa mãn
đẳng thức
( ) ( )
2
2 . , 1;4 .x x f x f x x
+ =
Biết rằng
( )
3
1,
2
f =
tính
( )
4
1
?I f x dx=
A.
1186
.
45
I =
B.
1174
.
45
I =
C.
1222
.
45
I =
D.
1201
.
45
I =
Câu 49: Cho hai hàm số
( )
y f x=
và
( )
y g x=
là hai hàm số
liên tục trên có đồ thị hàm số
( )
y f x
=
là đường cong nét
đậm, đồ thị hàm số
( )
y g x
=
là đường cong nét mảnh như hình
vẽ. Gọi ba giao điểm A, B, C của
( )
y f x
=
và
( )
y g x
=
trên
hình vẽ lần lượt có hoành độ là a, b, c. Tìm giá trị nhỏ nhất của
hàm số
( ) ( ) ( )
h x f x g x=−
trên đoạn
;?ac
A.
( ) ( )
;
min 0 .
ac
h x h=
B.
( ) ( )
;
min .
ac
h x h a=
C.
( ) ( )
;
min .
ac
h x h b=
D.
( ) ( )
;
min .
ac
h x h c=
Câu 50: Cho hai đường tròn
( )
1
;5O
và
( )
2
;3O
cắt nhau
tại hai điểm A, B sao cho AB là 1 đường kính của đường
tròn
( )
2
.O
Gọi (D) là hình phẳng giới hạn bởi 2 đường
tròn (ở ngoài đường tròn lớn, phần tô màu như hình vẽ).
Quay (D) quanh trục O
1
O
2
ta được một khối tròn xoay.
Tính thể tích khối tròn xoay được tạo thành.
A.
36 .V =
B.
68
.
3
V
=
C.
14
.
3
V
=
D.
40
.
3
V
=
............................................ Hết ......................................................
ĐÁP ÁN THAM KHẢO
1-C
2-D
3-B
4-B
5-B
6-C
7-A
8-D
9-A
10-D
11-D
12-A
13-C
14-B
15-C
16-D
17-D
18-C
19-A
20-B
21-C
22-D
23-A
24-A
25-C
26-B
27-A
28-C
29-A
30-C
31-D
32-A
33-C
34-D
35-B
36-A
37-C
38-D
39-D
40-D
41-A
42-B
43-C
44-D
45-D
46-A
47-C
48-A
49-C
50-D

Trang 117
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: C
Elip có độ dài trục lớn là 8, độ dài trục bé là 6 nên
2 8 4
.
2 6 3
aa
bb
==
==
Phương trình elip là:
22
1.
16 9
xy
+=
Câu 2: D
Vecto chỉ phương của đường thẳng là
( )
2; 1;0 .m= − −
Câu 3: B
Vì
+ =
Các đẳng thức A, C và D đúng; đẳng thức B sai.
Câu 4: B
Đường kính đáy
2 2 2.d R a==
Do góc ở đỉnh bằng
0
60
nên thiết diện qua trục là tam giác đều.
Độ dài đường sinh là:
2 2.da==
Diện tích xung quanh của hình nón là:
2
. 2.2 2 4 .
xq
S R a a a= = =
Câu 5: B
Ta có:
( )
( )
11
2
00
2 1 2 1 .V x dx x dx= + = +
Câu 6:
Hàm số có 3 điểm cực trị khi
0m
Ba điểm cực trị là
( )
( ) ( )
22
0; , ; , ;A m B m m m C m m m− − −
Gọi
I
là trung điểm của
( )
2
0;BC I m m−
2
1
.
2
ABC
S AI BC m m
==
Chu vi của
ABC
là:
(
)
4
22p AB BC AC m m m= + + = + +
Bán kính đường tròn nội tiếp
ABC
là:
2
4
ABC
S
mm
r
p
m m m
==
++
Theo bài ra:
(
)
24
2
4
4
1 1 1
m m m m m
mm
r
m
m m m
+−
++
(vì
0m
)
(
)
4 2 2 5 2 2
1
20
2
m
m m m m m m m m m m m
m
−
+ − + + − −
So sánh điều kiện suy ra
2m
thỏa mãn.
Câu 7: A
Ta có: TXĐ:
( )
0; .D= +
Đạo hàm
2
0( )
1
2 ln . 2 ln 0
2ln 1 0
x loai
y x x x x x x
xx
=
= + = + =
+=
1
.x
e
=
Do
1
2ln 3 0y x y
e
= +
nên hàm số đạt cực tiểu tại
1
x
e
=
Khi đó
11
.
2
CT
yy
e
e
= = −
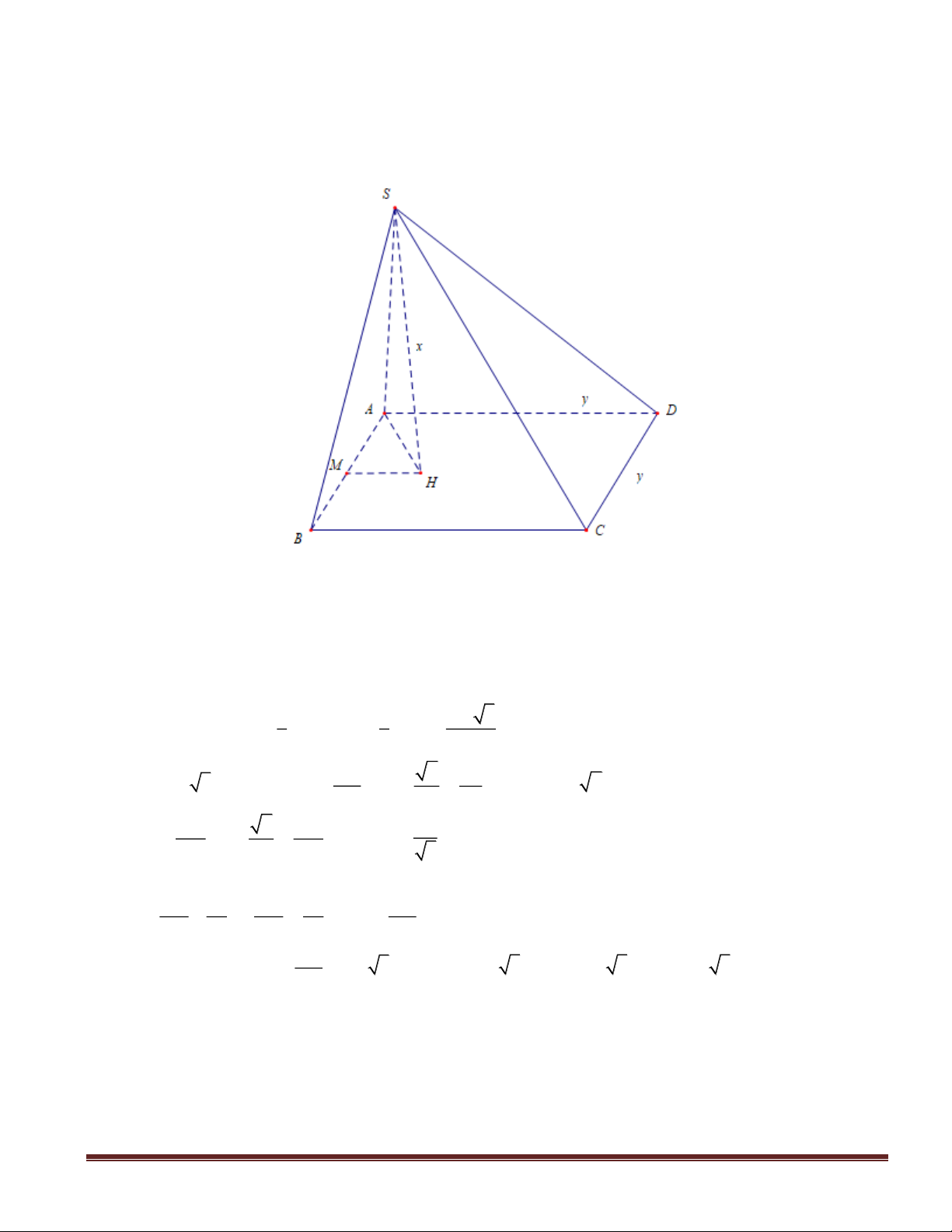
Trang 118
Câu 8: D
Hình lăng trụ đã cho có 2 mặt đáy và 2016 mặt bên.
Do đó có 2016 cạnh bên và 2 mặt đáy, mỗi mặt đáy có 2016 cạnh.
Do đó hình lăng trụ đã cho có: 2016.3 = 6048 cạnh.
Câu 9: C
Đáp án A
Giả sử
( )
⊥SH ABCD
tại
H
( ) ( )
0
, 46==SA ABCD SAH
Gọi
M
là trung điểm của
AB
SAB
cân
( )
(
)
⊥
⊥ = =
⊥
0
, 60
SM AB
SMH AB SAB ABCD SMH
maøSH AB
Đặt
3
2
1 1 8 3
. . .
3 3 3
=
= = =
=
SABCD ABCD
SH x
a
V S SH y x
AB y
23
. 8 3=x y a
(1)
sin =
SH
SAH
SA
2
2
=
x
SA
2=SA x
sin =
SH
SMH
SM
2
3
=
x
SM
2
3
=
x
SM
Xét
SAM
vuông tại
M
ta có:
2 2 2
=+SA SM MA
2 2 2 2 2
22
4 2 8
2
3 4 3 4 3
= + = =
x y x y x
xy
(2)
Thế (2) vào (1) ta được:
2
3
8
. 8 3
3
=
x
xa
33
33=xa
33 = =x a SH a
.
Câu 10: D
Ta có
.
2 2 2 .
ABCD ABC ABCD A BCD
S S S V Sh
= = =
Câu 11: D
Điều kiện:
2
2018 0.x −
Ta có
( ) ( )
( )
( )
2
22
2
ln 1 0
ln 1 ln 2018 0
ln 2018 0
x
xx
x
+=
+ − =
−=

Trang 119
( )
2
2
2
2
0
1 1 2019
2019
2018 1
2019
xl
xx
x
x
x
=
+ = =
=−
−=
=
nên phương trình có 2 nghiệm.
Câu 12:
Tập xác định:
D =
. Đặt
cos , 0 1t x t=
2
21
( ) , 0 1
1
tt
y f t t
t
++
= =
+
2
2
24
()
( 1)
tt
ft
t
+
=
+
;
0
( ) 0
2 0;1
t
ft
t
=
=
= −
(0) 1, (1) 2ff = =
Vậy
min 1, max 2yy==
Câu 13: C
Ta có
2
2 2 2 4 .
tp xq
S S Rh R Rh R h= + = =
Câu 14: Chọn B.
Tam giác A
1
B
1
C
1
đều cạnh bằng 3 có bán kính đường tròn ngoại tiếp là
1
3R =
và
2
11
SR
=
Tam giác A
2
B
2
C
2
đồng dạng với tam giác A
1
B
1
C
1
theo tỉ số
1
2
k =
nên có bán kính đường tròn
ngoại tiếp là
1
2
2
R
R =
và
2
2
11
2
2
22
RR
S
==
.
Tam giác A
3
B
3
C
3
đồng dạng với tam giác A
2
B
2
C
2
theo tỉ số
1
2
k =
nên có bán kính đường tròn
ngoại tiếp là
1
3
2
R
R =
và
2
2
21
3
4
22
RR
S
==
Câu 15: C
Do
( )
( )
00
; 60 60 6SC ABC SCA SA a= = =
SAC
vuông tại A có đường cao AH.
Khi đó
22
2
2 2 2
63
.
4
62
SA SH a
SA SH SC
SC
SC a a
= = = =
+
1
.
4
HC
SC
=
Do đó
( )
( )
( )
( )
1
;;
4
d H ABCD d C ABCD=

Trang 120
23
.ABCD .
3 1 1 3 6
. . 6. .
4 4 3 2 8
H SABCD
aa
V V a = = =
Câu 16: D
Phương trình
2
20x bx+ + =
có hai nghiệm phân biệt
2
8 0.b = −
Mà
*
1 6, 3;4;5;6 .b b b
Xác suất cần tìm là
42
.
63
=
Câu 17: D
22
3 3 2 2
3 3 3 3 3 3
1 1 ( )( ) 1 1x y x y x xy y x y
A
x y x y x y xy x y
+ + − + +
= + = = = = +
.
Đặt
x ty=
. Từ giả thiết ta có:
2 2 3 2 2
( ) ( 1) ( 1)x y xy x y xy t ty t t y+ = + − + = − +
Do đó
22
2
11
;
1
t t t t
y x ty
t t t
− + − +
= = =
++
. Từ đó
2
2
2
2
1 1 2 1
1
tt
A
x y t t
++
= + =
−+
.
Xét hàm số
( )
22
2
2
2
2 1 3 3
( ) ( )
1
1
t t t
f t f t
tt
tt
+ + − +
= =
−+
−+
.
Lập bảng biến thiên ta tìm giá trị lớn nhất của A là: 16 đạt được khi
1
2
xy==
.
Câu 18: C
Ta có:
( ) ( )
2
2
5 5 5
5
log 5 3log 5 0 log 5 6log 5 0x x x x
− − − −
2
2
5 5 5 5
1 log 6log 5 0 log 4log 4 0.x x x x + − − − −
Đặt
5
logtx=
thì bất phương trình trở thành
2
4 4 0.tt− −
Câu 19: A
Ta có:
22
4 4 0
2
3 3 3
1 4 0 2 2.
4 4 4
xx
xx
−−
− −
Câu 20: B
Đặt
( )
( )
694
6
log log log 2 2 9 2 6 9 4
2 2 4
t
t t t t
t
x
x x x y t y
xy
=
= = + = = + =
==
2
6 4 2 2
2 1 2 1 .
9 9 3 3
t t t t
+ = + =
Đặt
2
0
3
t
x
u
y
= =
ta có:
( )
2
2
2 1 1 3 .
31
u u u+ = = + =
−
Câu 21: C
Bán kính đáy của hình nón là
23
3,
2
a
ra==
chiều cao hình nón là
1
2
h =
cạnh huyền
3.a=
Thể tích
V của khối nón (N) là
23
1
3.
3
V r h a= =
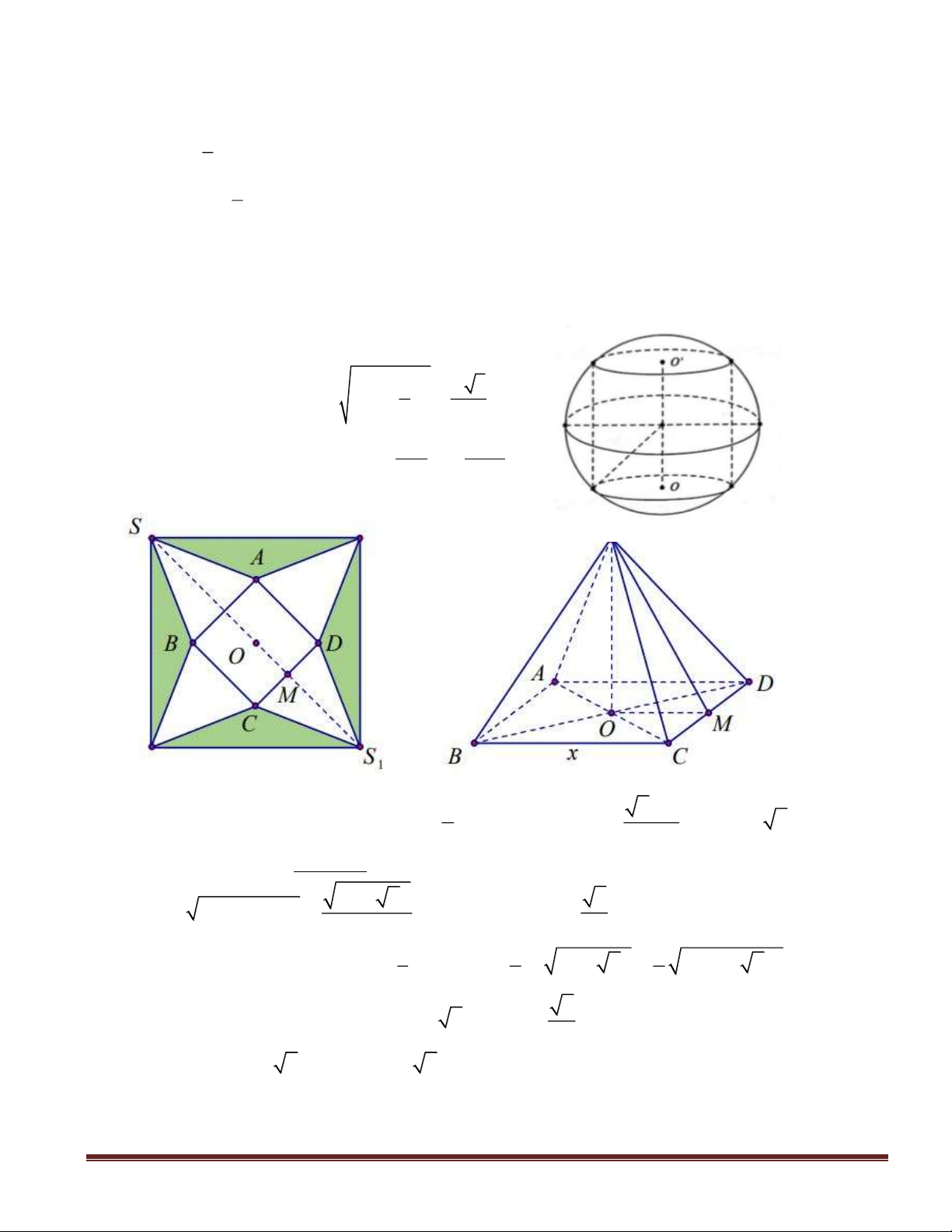
Trang 121
Câu 22: D
Do A(-1;1) thuộc đồ thị hàm số nên:
1 2 1(1).a b a b= + + + = −
Tiếp tuyến tại điểm A(-1;1) vuông góc với đường thẳng
( )
: 2 3 0 1 . 1.
d
d x y y k
− + = − = −
Trong đó
( )
3
1
; 4 2 1 4 2
2
d
k y ax bx y a b
= = + − = − −
Suy ra
( ) ( )
1
4 2 . 1 2 1 2 .
2
a b a b− − = − + =
Từ (1) và (2) suy ra
22
2; 3 5.a b a b= = − − = −
Câu 23: A
Ta có chiều cao hình trụ là h = R.
Bán kính đáy của hình trụ là:
2
2
3
.
22
hR
rR
= − =
Thể tích V của khối trụ là:
23
2
33
. . .
44
RR
V r h R
= = =
Câu 24: Chọn C.
Từ hình vuông ban đầu ta tính được
( )
11
2
, . 0 2
22
xx
OM S M S O OM x
−
= = − =
Khi gấp thành hình chóp S.ABCD . thì S
1
S nên ta có
1
SM S M=
Từ đó
22
2 2 2
2
x
SO SM OM
−
= − =
. (Điều kiện
2
0
2
x
)
Thể tích khối chóp S.ABCD:
2 4 5
.
1 1 1
. . 2 2 2 2 2 2
3 6 6
S ABCD ABCD
V S SO x x x x= = − = −
Ta thấy
.S ABCD
V
lớn nhất khi
( )
45
2
2 2 2 ,0
2
f x x x x= −
đạt giá trị lớn nhất
Ta có
( )
( )
3 4 3
' 8 10 2 2 4 5 2f x x x x x= − = −
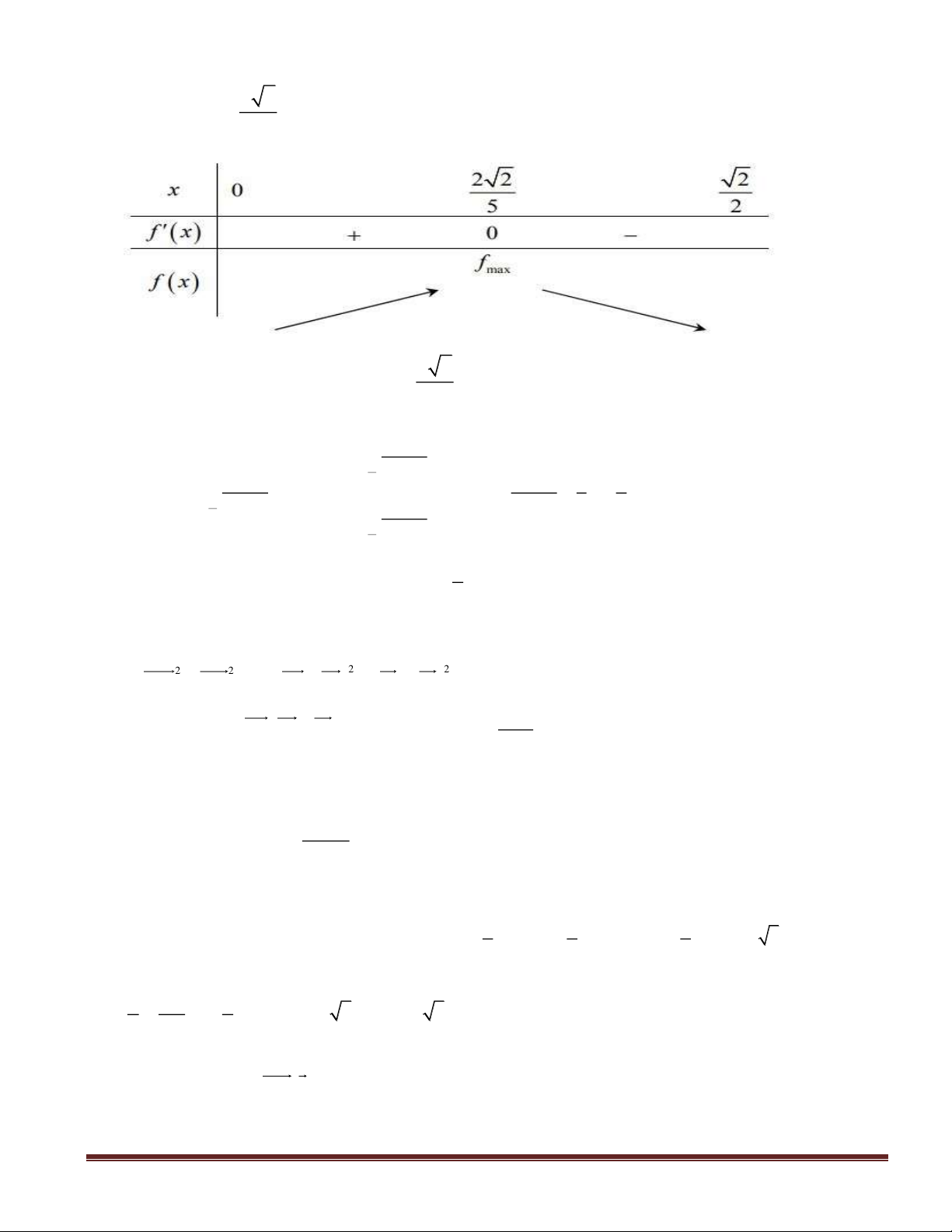
Trang 122
( )
0
'0
22
5
x
fx
x
=
=
=
Bảng biến thiên
Vậy:
.S ABCD
V
. lớn nhất khi và chỉ khi
22
5
x =
Câu 25: C
Ta có
1
3
21
3
1
3
37
log 0
3
3 7 3 7 1 7
log log 0 0 3.
3 3 7 3 3 3
log 1
3
x
x
xx
x
x x x
x
−
+
−−
+ − +
+
Do đó, tập nghiệm của bất phương trình là
(
7
;3 ; 3 4.
3
T a b P a b
= = = − =
Câu 26: B
Gọi
( )
2
I 1; 1; 4 ;AB 24− − − =
là trung điểm của AB khi đó
22
AM BM 30+=
Suy ra
( ) ( )
22
22
MA MB 30 MI IA MI IB 30+ = + + + =
( )
2
2 2 2 2
AB
2MI IA IB 2MI IA IB 30 2MI 30 MI 3.
2
+ + + + = = − =
Do đó mặt cầu
( )
S
tâm
( )
I 1; 1; 4 ;R 3− − − =
.
(Dethithpt.com)
Câu 27: A
Ta có
4 25
4 ; 25
4
log log log .
2
4 2.10
tt
t
ab
ba
a b t
ba
==
−
= = =
−=
Khi đó:
( ) ( )
2
22
2 2 2
4.25 4 2.10 2 2.2 .5 4. 5 0 2. 4 0 1 5
5 5 5
t t t
t t t t t t t
− = + − = + − = = − +
Vậy
( )
2
2
42
1 5 6 2 5.
5
25
t
t
t
a
b
= = = − + = −
Câu 28: C
Mặt phẳng
( )
nhận
;
Ox
OM u
là một VTPT.

Trang 123
Mà
( )
( )
( )
1;0; 1
; 0; 1;0 .
1;0;0
Ox
Ox
OM
OM u
u
=−
= −
=
Kết hợp với
( )
đi qua
( ) ( ) ( )
1;0; 1 : 0 0 0.M y y− − − = =
Câu 29: A
Ta có:
( ) ( )
2
2 0 0 2 0 0 2.y f x f x x x x
= − −
Câu 30: C
Xét hàm số
( )
2
1
2
x
Y f x x= − + −
có
( )
' ' 1 1y f x x= − − + −
.
y = 0
( ) ( ) ( )
1 3 4
' 1 1 0 ' 1 1 1 1 0
1 3 2
xx
f x x f x x x x
xx
− = − =
− − + − = − = − − − = =
− = = −
.
Ta có bảng biến thiên:
Do đó Hàm số
( )
2
1
2
x
y f x x= − + −
nghịch biến trên khoảng (1;3).
Câu 31: D
Giới thiệu các em 2 cách giải nhé:
Cách 1: hệ trục tọa độ với
( )
0;0;0A
( ) ( ) ( )
1;0;0 ; 0;1;0 ; 0;0;1B D A
Ta có:
1 1 1
; ;1 ; 1; ;0
2 2 2
MN
Khi đó
( )
1
1;1;0 ; ;0; 1
2
BD MN
= − = −
Suy ra
( )
1
; 2;2;1
2
BD MN
=−
Phương trình mặt phẳng chứa
BD
và song song
với MN là:
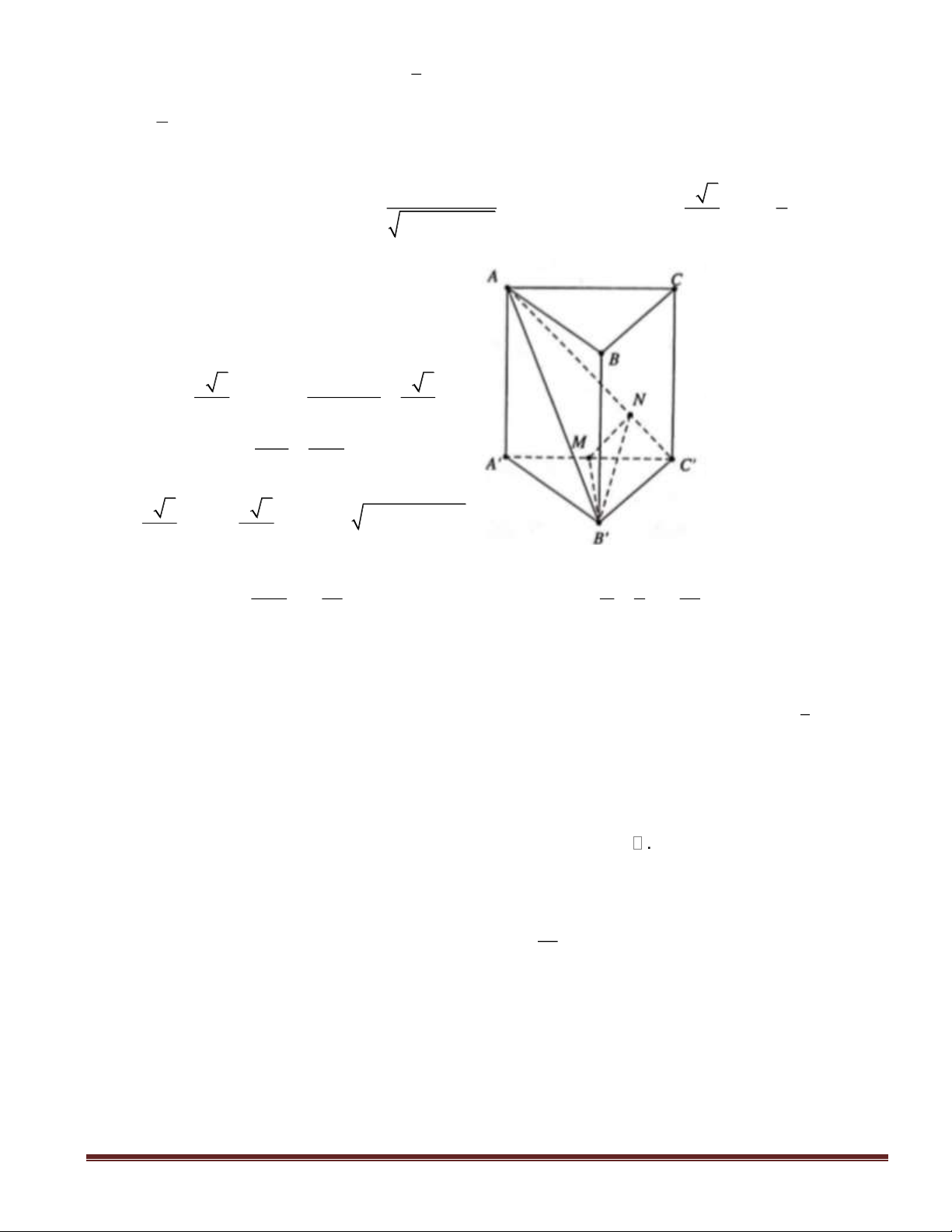
Trang 124
( ) ( )
( )
1
:2 2 2 0 ; .
3
P x y z d d N P+ + − = = =
Vậy
.
3
a
d =
Cách 2: Gọi P là trung điểm của
CD
suy ra
( )
( )
;d d O MNP=
Dựng
22
.
;OF ME d
MONE
OE NP OF
MO NE
⊥ ⊥ = =
+
trong đó
2
;.
43
aa
MO a NE d= = =
Câu 32: A
Dựng
( )
BM AC BM ACCA
⊥ ⊥
Dựng
( )
MN AC AC MNB
⊥ ⊥
Khi đó
( ) ( )
(
)
0
; 60ABC ACA MNB
==
Ta có:
26
26
tan
a BM a
BM MN
MNB
= = =
Mặt khác
tan
MN AA
ACA
CN AC
==
Trong đó
22
6 2 3
;
6 2 3
a a a
MN MC CN CM MN
= = = − =
Suy ra
AA a
=
Thể tích lăng trụ
2 3 3
..
2
..
2 2 3 3 3
B ACCA B BAC
AB a V a
V h V V V V V
= = = − = − = =
Câu 33: C
Ta có:
( )
( )( )
2 2 2 2
3 6 9 3 2 3 3 3y x mx m x mx m x m x m
= − − = − − = + −
TH1: Nếu
0 0 3m y m x m
−
nên hàm số nghịch biến trên
( )
31
1
0;1 .
03
m
m
m
−
TH2: Nếu
0 0 3m y m x m
−
nên hàm số nghịch biến trên
( )
1
0;1 1.
30
m
m
m
−
−
TH3: Nếu
( )
( )
2
0 3 0 0;1m y x x
= =
nên hàm số đồng biến trên
.
Câu 34: D
Đặt
2
3
log 3 2 7 0t x t t m= − + − =
PT có 2 nghiệm khi
( )
37
9 4 2 7 37 8 0
8
m m m = − − = −
Khi đó PT có 2 nghiệm
1
2
3 1 1 1
12
3 2 2
2
log 3
;
log
3
t
t
x t x
tt
xt
x
==
=
=
Khi đó theo định lý Vi-et ta có:
12
12
3
27
tt
t t m
+=
=−
Do
( )( ) ( )
(
)
1 2 1 2
1 2 1 2 1 2
3 3 72 3 62 3 .3 3 3 3 63
t t t t
x x x x x x+ = = + + = + + =

Trang 125
(
)
1 2 1 2 1 2 2 2
3
3 3 3 3 63 3 3 12 3 3 12
t t t t t t t t+−
+ + = + = + =
Đặt
( )
2
21
12
21
12
3
27 9
3 12 2 / .
9 2 1 2
t
tt
u
u u t t m t m
u u t t
= =
=
= + = = =
= = =
Câu 35: B
Số hạng tổng quát của khai triển
12
2
3
x
x
+
là
( )
12
12 2 12
12 12
3
. .3 . 0 12
k
k k k k k
C x C x k
x
−
−−
=
Khai triển có 12 + 1 = 13 số hạng.
Số hạng tổng quát của khai triển
21
3
2
1
2x
x
+
là
( )
( )
21
3 5 42
21 12
2
1
2 2 . 0 21
i
i
i k i i
C x C x i
x
−
−
=
Khai triển có 21 + 1 = 22 số hạng.
Cho
2 12 5 42 5 2 30k i i k− = − − =
PT này có 3 nghiệm nguyên (k;i) là
( ) ( ) ( )
0;6 ; 5;8 ; 10;5
Do đó
( )
fx
có 13 + 22 – 3 = 32 số hạng.
Câu 36: A
Phương trình tiếp tuyến của (C) tại
( )
32
0 0 0
;3M x x x−
có dạng:
( )
( )
2 3 2
0 0 0 0 0
3 6 3y x x x x x x= − − + −
Do tiếp tuyến đi qua điểm
( )
( )
( )
2 3 2 3 2
0 0 0 0 0 0 0
0; 3 6 3 2 3b b x x x x x x x = − − + − = − +
Để có đúng một tiếp tuyến của (C) đi qua B(0;b) thì phương trình
32
00
23b x x= − +
có duy nhất một
nghiệm. Xét hàm số
3 2 2
00
2 3 6 6 0
11
xy
y x x y x x
xy
= =
= − + = − + =
= =
Dựa vào đồ thị hàm số suy ra PT có 1 nghiệm khi
1
0
b
b
Với
( )
10;10b−
có 17 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Câu 37: C
Ta có:
( ) ( )
( )
( )
2
2
4
2 8 8 0
80
x
g x x f x x m
f x x m
=
= − − + =
− + =
(*).
Mà
( ) ( )
( )
( ) ( )
2
22
1 2 1 . 2 ; .f x x x x x x x x
= − − = − −
Suy ra
( )
( ) ( )( )
2
2
2 2 2 2
2
8 1 0 (1)
* 8 1 8 8 2 0 8 0 (2)
8 2 0 (3)
x x m
x x m x x m x x m x x m
x x m
− + − =
− + − − + − + − = − + =
− + − =
Để hàm số đã cho có 5 điểm cực trị khi và chỉ khi:
TH1. (1) có nghiệm kép x = 4, (2), (3) có 2 nghiệm phân biệt.
TH2. (1) không có nghiệm x = 4, (2), (3) có 2 nghiệm phân biệt.
Khi đó m < 16 là các giá trị thỏa mãn . Kết hợp
m
+
có 15 giá trị m cần tìm.
Câu 38: D
Gọi
( )
;0;0Ia
là tâm của mặt cầu (S) có bán kính R.
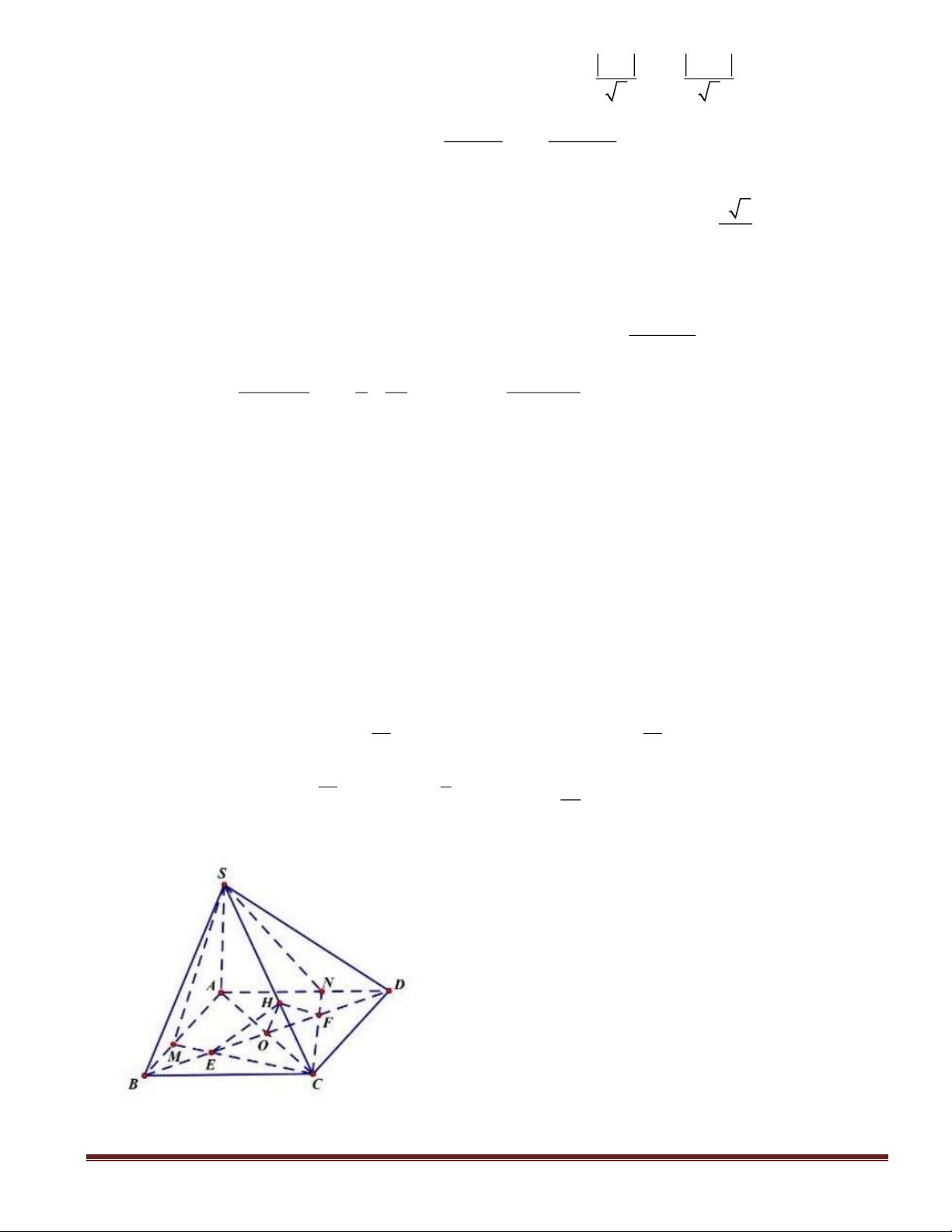
Trang 126
Khoảng cách từ tâm I đến hai mặt phẳng (P) và (Q) lần lượt là
12
1 2 1
;d .
66
aa
d
+−
==
Theo giả thiết, ta có
( ) ( )
22
2 2 2 2 2 2
12
1 2 1
24
66
aa
R d d r r
+−
= + = + + = +
2 2 2 2 2
2 25 4 4 1 6 3 6 6 24 0a a a a r a a r + + = − = + − + − =
(*).
Yêu cầu bài toán
(*) có nghiệm duy nhất
( )
( )
22
32
3 3 6 24 0 .
2
rr
= − − − = =
Câu 39: D
Phương trình hoành độ giao điểm của (C) và Ox là
( )
32
10 1 0x a x x+ + − + =
(*).
Dễ thấy x = 0 không là nghiệm phương trình (*). Khi đó
( )
3
2
1
* 10 .
xx
a
x
−+
− =
Xét hàm số
( )
3
22
1 1 1
,
xx
f x x
x
xx
−+
= = − +
có
( )
3
3
2
0 1.
xx
f x x
x
+−
= = =
Tính
( ) ( ) ( ) ( ) ( )
00
lim ; lim ; lim ; lim ; 1 1.
xx
xx
f x f x f x f x f
−+
→− →+
→→
= − = + = + = − =
Dựa vào bảng biến thiên ta thấy
( )
10f x a= − −
có nghiệm suy nhất
11.a −
Kết hợp với a là số nguyên âm
có 10 giá trị cần tìm.
Câu 40: D
Ta có
( )
( )
( )
22
22
2 2 1
log
10
10
log 1
10 10.10
z
zz
x y z
xy
x y x y
x y z
xy
+
+=
+=
+ = +
+ = +
+ = =
Khi đó
( )
( ) ( ) ( )
32
3 3 3 2 2 2
.10 .10 10 . 10
z z z z
x y a b x y x xy y a b+ = + + − + = +
( )
( )
( ) ( ) ( ) ( )
3 2 2
2 2 2 2
. . . .x y x xy y a x y b x y x xy y a x y b x y + − + = + + + − + = + + +
( ) ( ) ( )
2 2 2 2 2 2 2 2 2 2
. 2 . 2 .
10 10
bb
x xy y a x xy y x y x y xy a x y a xy
− + = + + + + + − = + + +
Đồng nhất hệ số, ta được
1
1
.
10 2
2 1 15
b
aa
ab
+ = = −
= − =
Vậy
29
.
2
ab+=
Câu 41: B
Cách 1: Chọn hệ trục tọa độ Oxyz sao cho A(0;0;0) , B(2;0;0) , D(0;2;0), S (0;0;2) . Suy ra
C(2;2;0). Đặt AM = x, AN = y, x y, 0;2 , suy ra M ( x;0;0), N (0; y;0) .
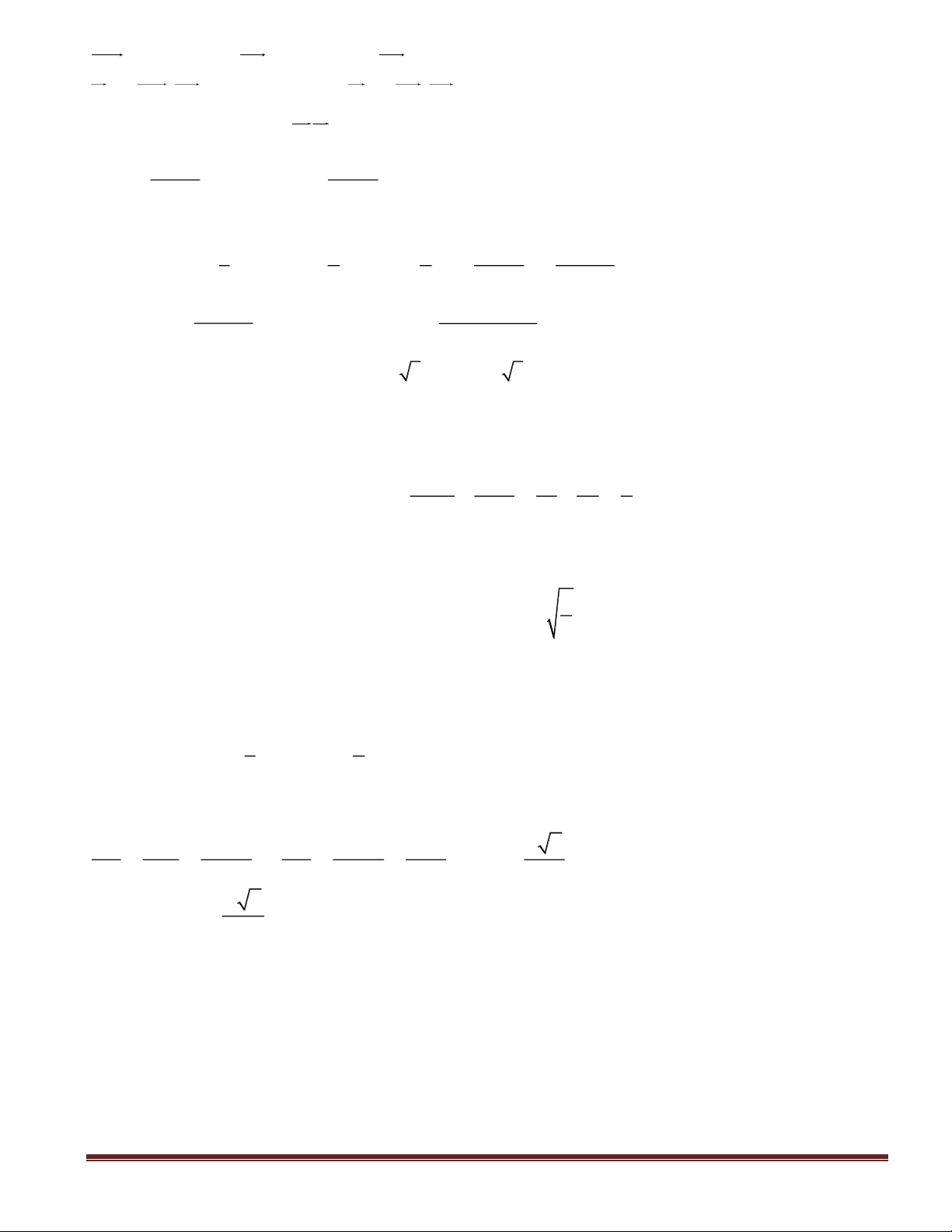
Trang 127
SM
= ( x;0;−2) ,
SC
=(2;2; − 2) ,
SN
= (0; y ; − 2) .
( ) ( )
12
; 4;2 4;2 , ; 4 2 ; 4; 2n SM SC x x n SN SC y y
= = − = = − − −
.
Do ( SMC) ⊥ (SNC) nên
( ) ( ) ( )
12
. 0 4 4 4 4 2 4 4 0 2 8n n y x xy xy x y= − − − − = + + =
82
2
x
y
x
−
=
+
, do y 2 nên
82
2
x
x
−
+
2 x 1
( ) ( )
4 2 2
AMCN ABCD BMC DNC
S S S S x y x y= − − = − − − − = +
.
Do đó
( )
2
.
1 2 2 8 2 2 8
.
3 3 3 2 3 2
S AMCD AMCN
xx
V SAS x y x
xx
−+
= = + = + =
++
.
Xét
( )
2
28
32
x
fx
x
+
=
+
với x
1;2
,
( )
( )
2
2
2 4 8
'
2
xx
fx
x
+−
=
+
( )
2
' 0 4 8 0 2 2 3; 2 2 3f x x x x x= + − = = − + = − −
(loại).
Lập BBT ta suy ra
( ) ( ) ( )
0;2
max 1 2 2f x f f= = =
.
Vậy
.
2 2 2 2
1
2
1 1 1 1 5
max 2
4
2
1
S AMCN
x
y
VT
AM AN x y
x
y
=
=
= = + = + =
=
=
.
Cách 2: Đặt AM = x, AN = y. Gọi O =AC DB ; E = BD CM ; F = BD CN .
H là hình chiếu vuông góc của O trên SC , khi đó: HO =
2
3
.
Ta có:
( )
SC OH SC HE
SC HBD
SC BD SC HF
⊥⊥
⊥
⊥⊥
.
Do đó góc giữa ( SCM ) và (SCN ) bằng góc giữa HE và HF . Suy ra HE ⊥HF .
Mặt khác
( )
.
12
.
33
S AMCN AMCN
V SAS x y= = +
.
Tính OE , OF :
Ta có: x 0 , y 0 và nếu x 2 , y 2 thì gọi K là trung điểm của AM , khi đó:
2
4 2 4 2 4 4
OE KM x OE EB OB x
OE
EB MB x x x x x
= = = = =
− − − −
Tương tự:
2
4
y
OF
y
=
−
. Mà
( )( )
2
. 2 2 12OE OF OH x y= + + =
.
Nếu x = 2 hoặc y = 2 thì ta cũng có
( )( )
2
. 2 2 12OE OF OH x y= + + =
.
Tóm lại:
( )( )
2 2 12xy+ + =
.

Trang 128
Suy ra:
( ) ( ) ( ) ( )
.
1 2 2 2 12
. 2 2 4 2 4
3 3 3 3 2
S AMCN AMCN
V SAS x y x y x
x
= = + = + + + − = + + −
+
. Do
đó .
.
2 2 2 2
1
2
1 1 1 1 5
max 2
4
2
1
S AMCN
x
y
VT
AM AN x y
x
y
=
=
= = + = + =
=
=
Câu 42: B
Dễ thấy
( )
d ⊥
và
( ) ( ) ( )
1; 2; 3 .d− − −
Ta có
( ) ( )
; ;0B Oxy B a b=
mà
( )
2 2 0B a b + − =
(1).
Lại có
( ) ( )
( )
( )
( )
/ / ; ; 3.d d d d B d = =
Đường thẳng d đi qua M(0;0;-1), có
( )
1;2;2 .
d
u =
Do đó
( )
( )
( ) ( ) ( )
2 2 2
;
2 2 1 2 2
;3
3
d
d
BM u
b a a b
d B d
u
− + − + −
= = =
(2).
Từ (1), (2) suy ra
( ) ( ) ( )
( ) ( ) ( )
; 1;4 1;4;0
.
; 2; 2 2; 2;0
a b B
a b B
= − ⎯⎯→ −
= − ⎯⎯→ −
Vậy
7
.
2
AB =
Câu 43: C
Gọi
( )
1
;,
1
a
A a C
a
+
−
vì I(1;1) là trung điểm của
3
2;
1
a
AB B a
a
−
−
−
Khi đó
( )
( )
( )
( )
22
22
4 16 4
2 2 ; 4 1 2 1 .
1
1
1
AB a AB a a
a
a
a
= − − = − + = − +
−
−
−
Áp dụng bất đẳng thức AM – GM, ta có
( )
( )
( )
( )
22
22
44
1 2 1 . 4.
11
aa
aa
− + − + =
−−
Suy ra
2 2 2
11
.4 8.
22
AEBF
S AE AB= = =
Vậy
min
8.S =
Câu 44: D
Tam giác ABC có
0
13
120 . . .sin
22
ABC
BAC S ABAC BAC
= = =
và
7.BC =
Ta có
.
.
33
44
ABM N ABM
ABB N A BB
SV
BM
S BB V
= = =
mà
. . . .
11
23
N ABB C A BB C ABBA ABC ABC
V V V V
= = =
Suy ra
. . .
3 1 1 3 3
.AA .S .
4 4 4 8
N ABM N ABB ABC A BC ABC
V V V
= = = =
Tam giác
ABN
có
10, 11AB BN
==
và
46
5.
2
ABN
AN S
= ⎯⎯→ =
Khi đó
( )
( )
( )
( )
.
1 9 3 46 9 138
. ; . ; : .
3 8 2 46
N ABM ABN
V d M ABN S d M ABN
= = =
Câu 45: D
Số phần tử của không gian mẫu tập hợp các điểm có tọa độ nguyên nằm trên hình chữ nhật OMNP là
( )
101 11.n =

Trang 129
Vì
0;100 ; 0;10xy
và
0 0;1;2;...;90
1 0;1;2;...;89
90
...
10 0;1;2;...;80
yx
yx
xy
yx
= ⎯⎯→ =
= ⎯⎯→ =
+
= ⎯⎯→ =
Khi đó có 91 + 90 + … + 81 = 946 cặp (x;y) thỏa mãn.
Vậy xác suất cần tính là
( )
( )
946 86
.
101 11 101
nX
P
n
= = =
Câu 46: A
Xét
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 8S x y z− + + + + =
có tâm I(1;-2;-1). Bán kính
2 2.R=
Tam giác MAI vuông tại A, có
2 2 2 2
14.MA MI IA MI R= − = − =
Tam giác MAB có
22
3
cos 2. . .cos 7.
4
AMB AB MA MB MAMB AMB= = + − =
Câu 47: C
Ta có
( ) ( ) ( ) ( ) ( )
. 2 1 2 1 2 . 2 1g x x f x g x f x x f x
= − = − + −
Suy ra
( ) ( ) ( )
1 1 2 1g f f
=+
mà d
1
vuông góc với d
2
( ) ( )
1 . 1 1fg
= −
( )
( ) ( )
( )
2
1 1 2 1 1 2. 1 1 . 1 1 0f f f f f f
+ = − + + =
(*).
Phương trình (*) có nghiệm khi và chỉ khi
( ) ( )
2
1 4.2 0 1 2 2.ff
= −
Câu 48: A
Vì
( )
y f x=
có hàm số đồng biến trên
( ) ( )
3
1;4 1 .
2
f x f =
Khi đó
( ) ( ) ( ) ( )
( )
( )
2
2 . 2 1
21
fx
x x f x f x x f x f x x
fx
+ = + = =
+
(*).
Lấy nguyên hàm 2 vế của (*), ta được
( )
( )
2
3
21
fx
dx xdx x x C
fx
= = +
+
(1).
Đặt
( )
( )
( )
( )
( )
21
2 1 2 1
f x f x
t f x dt dx dx dt t
f x f x
= + = = =
++
(2).
Từ (1), (2) suy ra
( )
2
21
3
f x x x C+ = +
mà
( )
3 3 2 4
1 2. 1 .
2 2 3 3
f C C= + = + =
Do đó
( ) ( )
2
2 4 1 2 4
2 1 1 .
3 3 2 3 3
f x x x f x x x
+ = + = + −
Vậy
( )
4
1
1186
.
45
f x dx =
Câu 49: C
Ta có
( ) ( ) ( )
0.
xa
h x f x g x x b
xc
=
= − = =
=

Trang 130
Với
;x a b
thì đồ thị
( )
gx
nằm trên
( )
fx
nên
( ) ( ) ( )
0g x f x h x
hàm số nghịch biến trên
đoạn
;.ab
Tương tự với
;x b c
thì
( )
hx
đồng biến.
Do đó
( ) ( )
;
.
ac
Minh x h b=
Câu 50: D
Gắn hệ trục tọa độ Oxy sao cho
1
OO
(gốc tọa độ).
Phương trình đường tròn
( )
1
;5O
là
2 2 2 2
5 25 .x y y x+ = −
Tam giác O
1
O
2
A vuông tại O
2
, có
2 2 2 2
1 2 1 2
5 3 4.OO O A O A= − = − =
Phương trình đường tròn (O
2
;3) là
( ) ( )
22
2
4 9 9 4 .x y y x− + = = − −
Gọi V
1
là thể tích khối tròn xoay sinh ra khi quay hình phẳng D
1
được giới hạn bởi các đường
( )
2
9 4 . 0, 4, 7y x y x x= − − = = =
quanh trục tung
( )
7
2
1
4
9 4 .V x dx
= − −
Gọi V
2
là thể tích khối tròn xoay sinh ra khi quay hình phẳng D
2
được giới hạn bởi các đường
2
25 , 0, 4, 5y x y x x= − = = =
quanh trục tung
( )
5
2
2
4
25 .V x dx = −
Khi đó, thể tích cần tính là
( )
( )
75
2
2
12
44
40
9 4 25 .
3
V V V x dx x dx
= − = − − − − =
ĐỀ 28
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1: Trong mặt phẳng cho 6 điểm phân biệt A, B, C, D, E, F. Hỏi có bao nhiêu vectơ khác vectơ –
không có điểm đầu và điểm cuối là một trong 6 điểm đã cho?
A. 6. B. 12. C. 15. D. 30.
Câu 2: Một cấp số cộng có số hạng đầu bằng 1, số hạng thứ tư bằng –11. Số hạng thứ 8 của cấp cộng đã
cho là
A. 27. B. 23. C. –27. D. –23.
Câu 3: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Hàm số nghịch biến trong khoảng nào dưới đây?
A.
( )
;0−
. B.
( )
1;− +
.
C.
( )
0;1
. D.
( )
1; +
.

Trang 131
Câu 4: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ bên. Giá trị cực tiểu của hàm số đã cho bằng
A. 2. B.
3−
.
C.
2y =−
. D. 1.
Câu 5: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
42
1
21
4
y x x= − + +
. B.
42
81y x x= − +
.
C.
42
1
2
4
y x x=−
. D.
42
1
21
4
y x x= − +
.
Câu 6: Cho
,x
y
là hai số thực dương và
,m
n
là hai số thực tùy ý. Mệnh đề nào dưới đây sai?
A.
( )
..
n
nn
x y x y=
. B.
.
m n m n
x x x
+
=
. C.
( )
n
n
mm
xx=
. D.
( )
.
n
m m n
xx=
.
Câu 7: Tìm cơ số x để
10
log 3 0,1
x
=−
.
A.
1
3
x =
. B.
3x =
. C.
1
3
x =−
. D.
3x =−
.
Câu 8: Mệnh đề nào dưới đây sai?
A.
( )
0, 1
ln
x
x
a
a dx C a a
a
= +
. B.
tan
cos
dx
xC
x
=+
.
C.
( )
1
1
1
x
xC
+
= +
+
. D.
ln
dx
xC
x
=+
.
Câu 9: Cho
( )
ln2
0
5f x dx =
. Tính
( )
ln2
0
2
x
I f x e dx
=+
.
A. I = 7. B. I = 9. C. I = 3. D. I = 6.
Câu 10: Trên mặt phẳng tọa độ Oxy, số phức nào dưới đây có điểm biểu diễn là
( )
1; 2M −
?
A.
12zi=+
. B.
12zi= − +
. C.
12zi=−
. D.
12zi= − −
.
Câu 11: Cho khối chóp có thể tích là V và diện tích đáy bằng S. Chiều cao h của khối chóp đã cho là
A.
3V
h
S
=
. B.
.h V S=
. C.
V
h
S
=
. D.
1
.
3
h V S=
.
Câu 12: Cho khối nón có bán kính đáy bằng a và chiều cao bằng 2a. Tính thể tích V của khối nón đã cho.
A.
3
2Va
=
. B.
3
4
3
a
V
=
. C.
3
3
a
V
=
. D.
3
2
3
a
V
=
.
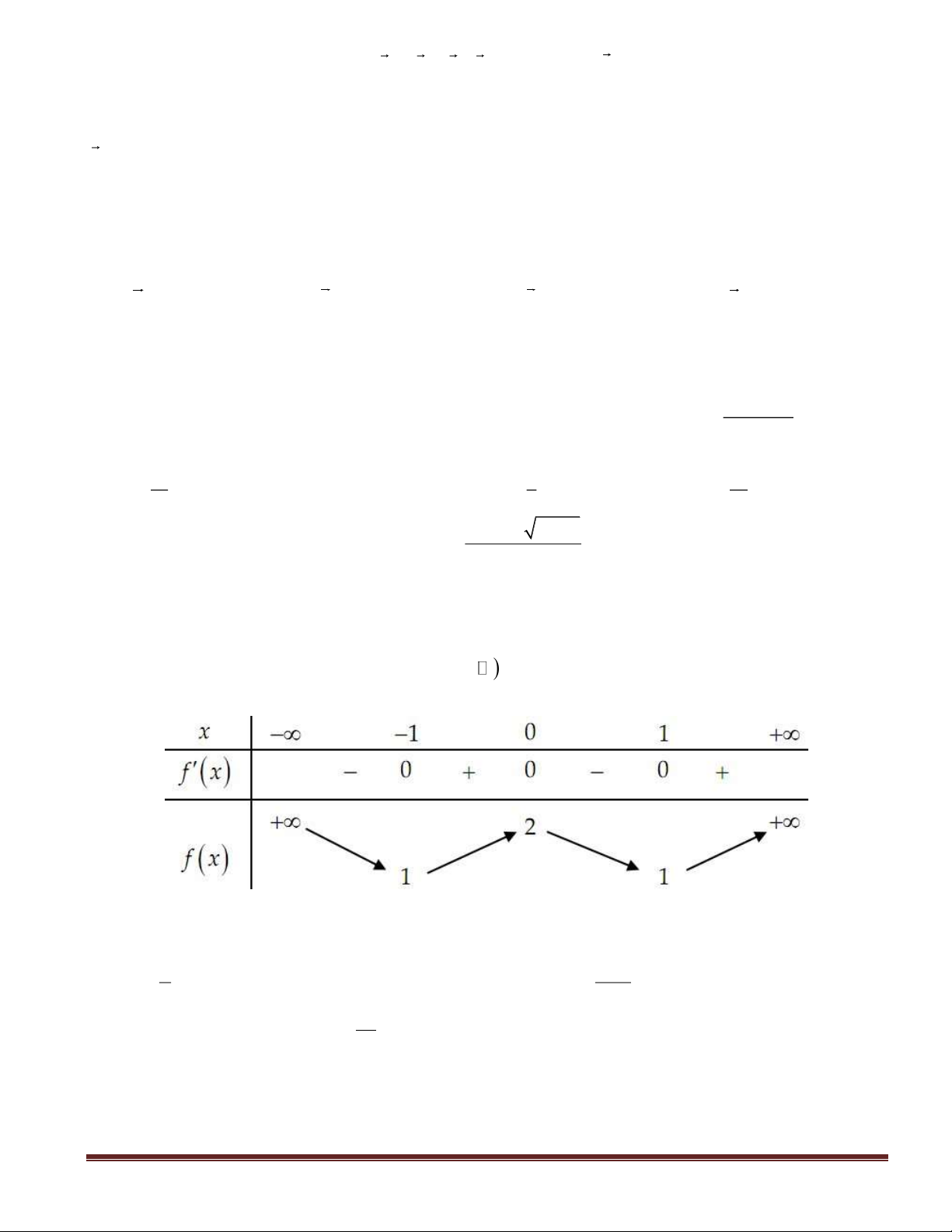
Trang 132
Câu 13: Trong không gian Oxyz, cho
23u i j k= − +
. Tọa độ vectơ
u
là
A.
( )
2;3; 1−−
. B.
( )
2;3;1
. C.
( )
2;1; 3−
. D.
( )
2; 3;1−
.
Câu 14: Phương trình tham số của đường thẳng d đi qua điểm
( )
1; 1;2A −
và có vectơ chỉ phương
(1;2; 3)u =−
là
A.
1
: 1 3
25
x
d y t
zt
=
= − +
=−
. B.
1
:2
32
xt
d y t
zt
=+
=−
= − +
. C.
1
: 1 2
23
xt
d y t
zt
=+
= − +
=−
. D.
1
:1
22
xt
d y t
zt
=+
= − −
=+
.
Câu 15: Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (P)
3 1 0x y z+ − + =
?
A.
(2; 6; 2)y = − −
. B.
( 1; 3;1)v = − −
. C.
( 1; 3; 1)x = − − −
. D.
(1;3;1)u =
.
Câu 16: Cho hàm số
32
4 6 10y x x= + −
. Mệnh đề nào dưới đây đúng?
A. Cực tiểu của hàm số bằng 0. B. Cực đại của hàm số bằng –1 .
C. Cực tiểu của hàm số bằng –10. D. Cực đại của hàm số bằng 8.
Câu 17: Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
2
1
1
xx
y
xx
−+
=
++
. Giá trị của
tổng M và m bằng
A.
11
3
−
. B. 3. C.
1
3
. D.
10
3
.
Câu 18: Số tiệm cận đứng của đồ thị hàm số
2
2
2 1 5
56
xx
y
xx
− − +
=
−+
là
A. 3. B. 1. C. 2. D. 0.
Câu 19: Cho hàm số
( ) ( )
42
,,f x ax bx c a b c= + +
và có bảng biến thiên như hình vẽ bên. Số nghiệm
thực dương của phương trình
( )
2 3 0fx−=
là
A. 3. B. 1 . C. 4. D. 2.
Câu 20: Cho a, b, c là các số thực dương thỏa mãn
log 1, log 2.b a c b= + = +
Mệnh đề nào dưới đây
đúng?
A.
log 1
a
bc
b
= + +
. B.
log( ) ( 1)( 2)ab b c= − −
. C.
1
log( )
2
b
ab
c
−
=
−
. D.
log( ) 3ab b c= + −
.
Câu 21: Đạo hàm của hàm số
x
x
y
2
=
là:
A.
' 2 ( ln2 1).
x
yx
−
=−
. B.
' 2 (1 ln2).
x
yx
−
=−
. C.
' 2 log 2.
x
e
y
−
=
. D.
' 2 (1 ln2).
x
yx=−
.
Câu 22: Tập nghiệm của bất phương trình
( )
log 2 1x
là
A.
(
;5−
. B.
( )
0;5
. C.
(
0;10
. D.
(
0;5
.
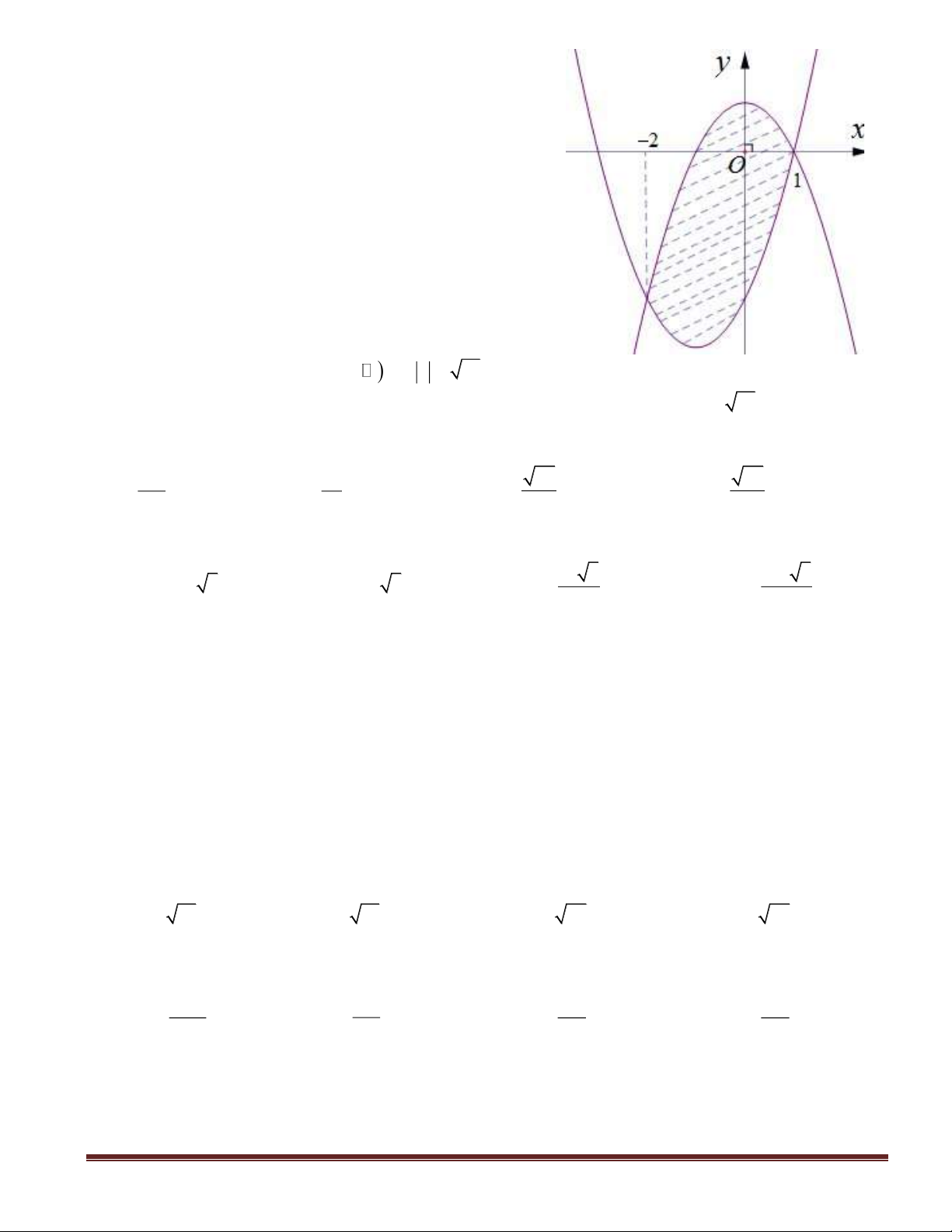
Trang 133
Câu 23: Cho hình (H) là hình phẳng giới hạn bởi parabol
2
23y x x= + −
, đường cong
2
1yx= − +
và trục hoành (phần
gạch chéo). Diện tích S của hình (H) được tính theo công
thức nào dưới đây?
A.
( )
1
2
22S x dx
−
=−
. B.
( )
1
2
2
2 2 4S x x
−
= + −
.
C.
( )
1
2
2
2 2 4S x x dx
−
= − − +
. D.
( )
1
2
22S x dx
−
= − +
.
Câu 24: Cho số phức
( )
1z bi b= +
và
10z =
.Giá trị của b bằng
A. 3. B.
3
. C. –3. D.
10
.
Câu 25: Một số phức z có phần thực và phần ảo lần lượt là các nghiệm thực dương và âm của phương
trình bậc hai
2
12 5 3 0xx+ − =
. Môđun của số phức z bằng
A.
97
144
. B.
97
12
. C.
97
144
. D.
97
12
.
Câu 26: Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân tại A,
2AB a=
. Mặt bên (SAB) là tam
giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích V của khối chóp S.ABC đã cho.
A.
3
43Va=
. B.
3
23Va=
. C.
3
3
3
a
V =
. D.
3
23
3
a
V =
.
Câu 27: Cho hình trụ có bán kính đáy a và chiều cao 3a. Tính diện tích toàn phần
tp
S
của hình trụ đã
cho.
A.
2
5
tp
Sa
=
. B.
2
6
tp
Sa
=
. C.
2
4
tp
Sa
=
. D.
2
8
tp
Sa
=
.
Câu 28: Trong không gian Oxyz, cho hai điểm
( )
1;2; 3M −
và
( )
3;0;1N
. Phương trình mặt cầu có đường
kính MN là
A.
( ) ( ) ( )
2 2 2
2 1 1 24x y z− + − + + =
. B.
( ) ( ) ( )
2 2 2
2 1 1 6x y z− + − + + =
.
C.
( ) ( ) ( )
2 2 2
2 1 1 12x y z− + − + + =
. D.
( ) ( ) ( )
2 2 2
2 1 1 24x y z+ + + + − =
.
Câu 29: Trong không gian Oxyz, khoảng cách h từ điểm
( )
0;1; 6A −
đến đường thẳng d
1
22
1
x
yt
zt
=
=+
=−
là
A.
17h =
. B.
10h =
. C.
46h =
. D.
66h =
.
Câu 30: Đội văn nghệ xung khích của nhà trường gồm 6 nam, 5 nữ. Chọn ngẫu nhiên 5 bạn để đảm
nhiệm 5 vai diễn khác nhau trong v kịch. Tính xác suất P để 5 bạn được chọn ra có đúng 3 nam, biết khả
năng của các bạn trong đội văn nghệ như nhau.
A.
5
1386
P =
. B.
100
321
P =
. C.
10
231
P =
. D.
100
231
P =
.
Câu 31: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông, AB = BC = a,
'AA a=
.
Góc giữa hai mặt (AB’C’) và (ABC) bằng
A. 60
0
. B. 45
0
. C. 30
0
. D. 90
0
.
Câu 32: Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O,
SO a=
.
Khoảng cách từ O đến mặt phẳng (SCD bằng
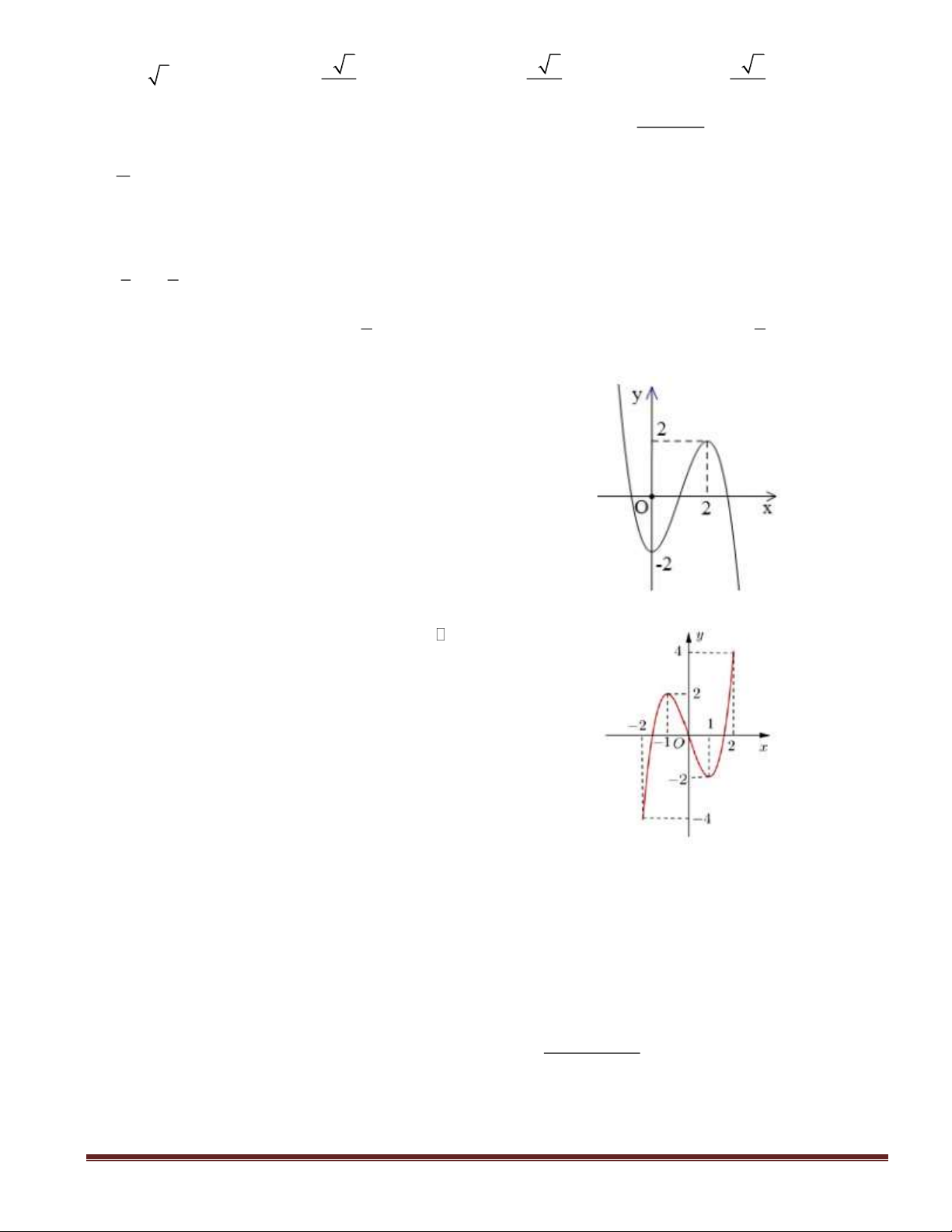
Trang 134
A.
3a
. B.
5
5
a
. C.
6
3
a
. D.
2
2
a
.
Câu 33: Tập hợp tất cả các giá trị thực của tham số m để hàm số
tan 2
tan
x
y
xm
−
=
−
đồng biến trên khoảng
0;
4
là
A.
)
2;+
. B.
)
1;2
. C.
(
)
;0 1;2−
. D.
(
;0−
.
Câu 34: Tập hợp tất cả các giá trị thực của tham số m để điểm cực tiểu của đồ thị hàm số
32
11
5
32
y x x mx= + + −
nằm bên phải trục tung là
A.
( )
;0−
. B.
1
;
4
−
. C.
(
;0−
. D.
1
0;
4
.
Câu 35: Cho hàm số
( )
y f x=
. Đồ thị hàm số
( )
'y f x=
có đồ thị như hình vẽ bên.
Bất phương trình
( )
lnf x m x−
đúng với mọi
( )
1;2x
khi và chỉ khi
A.
( )
1mf
. B.
( )
1mf
.
C.
( )
2 ln2mf−
. D.
( )
2 ln2mf−
.
Câu 36: Cho hàm số
( )
y f x=
liên tục trên và
có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị
thực của tham số m để phương trình
( )
x
f e m=
có
nghiệm thuộc khoảng
( )
0;ln2
là
A.
( )
4;4−
. B.
( )
2;4−
.
C.
(
2;4−
. D.
(
4;4−
.
Câu 37: Với giá trị nào của a thì phương trình
log log
4 3.2 2 0
aa
xx
− + =
có hai nghiệm và tổng bình phương
các nghiệm bằng 5?
A.
2a =
. B.
2a =
. C.
2a =−
. D.
1a =
.
Câu 38: Để mua nhà, ông A vay ngân hàng 300 triệu đồng theo phương thức trả góp. Cuối mỗi tháng bắt
đầu từ tháng thứ nhất ông A trả 5,5 triệu đồng và chịu lãi số tiền chưa trả là 0,5% mỗi tháng. Hỏi sau bao
lâu thì ông A trả hết số tiền đã vay?
A. 64 tháng. B. 65 tháng. C. 62 tháng. D. 63 tháng.
Câu 39: Cho hàm số f(x) thỏa mãn
( )
1fe=
và
( )
( )
2
2.
'
x
e x f x
fx
x
−
=
với mọi x dương. Tìm nguyên
hàm của hàm số
( )
3
.'x f x
.
A.
( ) ( )
3
. ' 3
x
x f x dx x e C= − +
. B.
( ) ( )
3
. ' 3
x
x f x dx x e C= − +
.

Trang 135
C.
( ) ( )
3
. ' 1
x
x f x dx x e C= − +
. D.
( )
2
3
. ' 2
2
x
x
x f x dx x e C
= − +
.
Câu 40: Biết
1 2 2
0 0 0
( ) 5; [ ( ) ( )] 5 à [ ( ) ( )] 7f x dx f x g x dx v f x g x dx= − = + =
. Tính
2
1
()f x dx
.
A. –3. B. 1. C. 7. D. –1.
Câu 41: Cho số phức z thỏa mãn
3 2 2zi− + =
. Giá trị nhỏ nhất của biểu thức
1P z i= + −
bằng
A. 5. B. 2. C. 3. D. 7.
Câu 42: Cho số phức z thỏa mãn
1 3 2 5z i z i− − + − − =
. Gọi M, m lần lượt là giá trị lớn nhất, giá trị
nhỏ nhất của môđun z. Giá trị của biểu thức M – m bằng
A.
5 13 5−
. B.
2 13 2−
. C.
5 13 5
5
−
. D.
13 2−
.
Câu 43: Một cơ sở sản xuất đồ gia dụng được đặt hàng làm các chiếc cốc hình nón không nắp bằng nhôm
có thể tích là . Để tiết kiệm sản xuất và mang lại lợi nhuận cao nhất thì cơ sở sẽ sản suất những
chiếc cốc hình nón có bán kính miệng cốc là sao cho ít tốn nguyên liệu nhất. Giá trị của R bằng
A.
6
3
2
a
. B.
3
9a
. C. 3a. D.
3
3
2
a
.
Câu 44: Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng ,
và mặt phẳng (P): . Phương trình nào dưới đây là phương trình mặt
phẳng đi qua giao điểm của d
1
và (P), đồng thời vuông góc với d
2
?
A. . B. . C. . D. .
Câu 45: Trong không gian Oxyz, cho hai điểm A(0;1;3), B(1;–2;1) và đường thẳng .
Tìm trên đường thẳng d một điểm M để đạt giá trị nhỏ nhất.
A. . B. . C. . D. .
Câu 46: Cho hàm số
3 2 2 2 2
3( 3 3) 3( 1) 2y x m m x m x m= − + + + + + +
. Gọi S là tập các giá trị của tham số
m
sao cho hàm số đồng biến trên
)
1; +
. Hỏi S là tập hợp con của tập hợp nào dưới đây?
A.
( ; 2)− −
. B.
( ;0)−
. C.
( 1; )− +
. D.
( 3;2)−
.
Câu 47: Cho ba hàm số
( )
y f x=
,
( ) ( )
y g x f x
==
,
( ) ( )
y h x g x
==
có đồ thị là
3
đường cong như hình vẽ
bên. Mệnh đề nào dưới đây đúng ?
A.
( ) ( ) ( )
1 1 1h g f− − −
.
B.
( ) ( ) ( )
1 1 1f g h− − −
.
C.
( ) ( ) ( )
1 1 1h f g− − −
.
D.
( ) ( ) ( )
1 1 1g h f− − −
.
3
9=Va
R
1
13
:2
2
xt
d y t
z
=+
= − +
=
2
12
:
2 1 2
x y z
d
−+
==
−
2 2 3 0x y z+ − =
2 2 13 0x y z− + − =
2 2 22 0x y z− + + =
2 2 13 0x y z− + + =
2 2 22 0x y z+ + − =
12
:
2 1 1
x y z
d
−+
==
−
22
2MA MB+
( )
5;2; 4M −
( )
1; 1; 1M −−−
( )
3;1; 3M −
( )
1;0; 2M −

Trang 136
Câu 48: Cho hàm số Số nghiệm thực của phương trình là
A. 4. B. 6. C. 9. D. 5.
Câu 49: Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB = 2BC. Góc giữa hai mặt
phẳng (AA’B) và (AA’C) bằng 30
0
. Hình chiếu vuông góc của A’ trên mặt phẳng (ABC) là trung điểm H
của AB. Gọi K là trung điểm AC. Biết khoảng cách giữa AA’ và HK bằng
3a
. Tính thể tích V của khối
lăng trụ đã cho.
A.
3
43
3
Va=
. B.
3
43Va=
. C.
3
83Va=
. D.
3
83
3
Va=
.
Câu 50: Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có điểm A trùng với gốc tọa độ,
( ) ( )
;0;0 , 0; ;0B a D a
,
( )
' 0;0;Ab
với
0, 0ab
. Gọi M là trung điểm cạnh CC’. Xét
4ab+=
, giá trị lớn
nhất của thể tích khối tứ diện A’BDM bằng
A.
27
64
. B.
27
128
. C.
4
27
. D.
9
128
.
---HẾT---
( )
32
3
3.
2
f x x x x= − + +
( )
( )
( )
1
21
f f x
fx
=
−
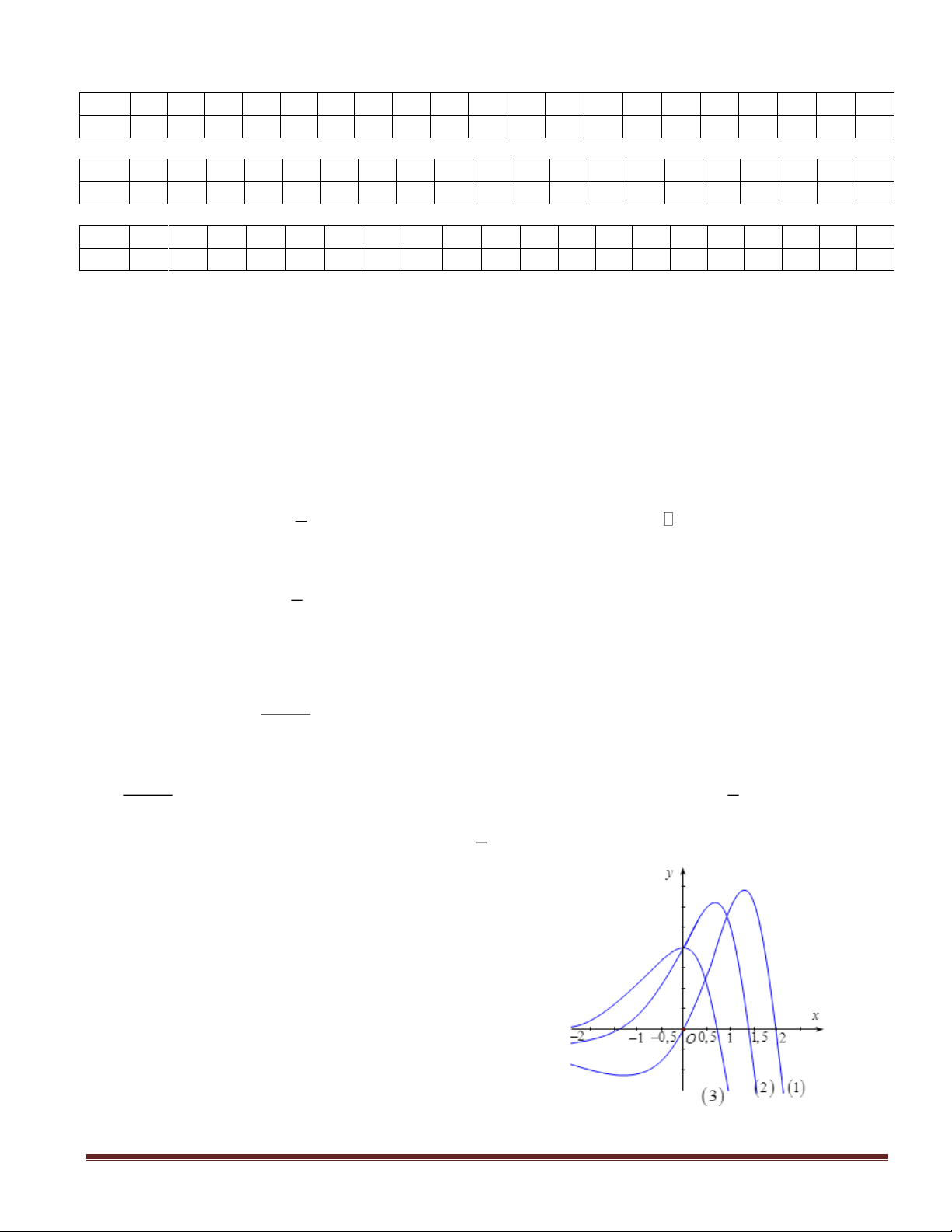
Trang 137
3. ĐÁP ÁN
Câu
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Đ.A
D
C
C
D
D
C
A
B
A
C
A
D
D
C
B
C
A
B
D
D
Câu
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
Đ.A
B
D
C
B
D
D
D
B
C
D
B
B
C
A
A
B
A
A
C
B
Câu
41
42
43
44
45
46
47
48
49
50
Đ.A
C
D
A
A
B
B
A
D
C
A
4. HƯỚNG DẪN
Câu 46: Cho hàm số
3 2 2 2 2
3( 3 3) 3( 1) 2y x m m x m x m= − + + + + + +
. Gọi S là tập các giá trị của tham số
m
sao cho hàm số đồng biến trên
)
1; +
. Hỏi S là tập hợp con của tập hợp nào dưới đây?
A.
( ; 2)− −
. B.
( ;0)−
. C.
( 1; )− +
. D.
( 3;2)−
.
Ta có :
( ) ( )
2
2 2 2
y=3 3 3 3 .2 3 1x m m x m
− + + + +
.
Khi đó :
( ) ( )
22
22
9 3 3 9. 1m m m
= + + − +
( )
( )
2
9 3 2 . 2 3 4m m m= + + +
.
TH1 : Nếu
0
2
3
m −
. Khi đó ta có
30a =
nên
0y
với mọi
x
. Do đó hàm số đã cho
đồng biến trên
)
1; +
.
TH2: Nếu
0
2
3
m −
. Khi đó
0y
=
có hai nghiệm phân biệt
1
x
và
2
x
.
Ta có
( ) ( )
12
0 ; ;y x x x
− +
và
( )
12
0;y x x x
. Do đó để hàm số đã cho đồng biến trên
)
1; +
thì
) ( )
2
1; ;x+ +
.
Ta có :
12
1xx
( ) ( )
12
12
1
2
1 . 1 0
xx
xx
+
− −
.
Xét
12
1
2
xx+
2
3 3 1mm + +
2
3 2 0mm + +
21m − −
( vô lý vì
2
3
m −
).
Vậy hàm số đã cho đồng biến trên
)
1; +
thì
2
3
m −
.
Câu 47: Cho ba hàm số
( )
y f x=
,
( ) ( )
y g x f x
==
,
( ) ( )
y h x g x
==
có đồ thị là
3
đường cong như hình vẽ
bên. Mệnh đề nào dưới đây đúng ?
A.
( ) ( ) ( )
1 1 1h g f− − −
.
B.
( ) ( ) ( )
1 1 1f g h− − −
.
C.
( ) ( ) ( )
1 1 1h f g− − −
.
D.
( ) ( ) ( )
1 1 1g h f− − −
.
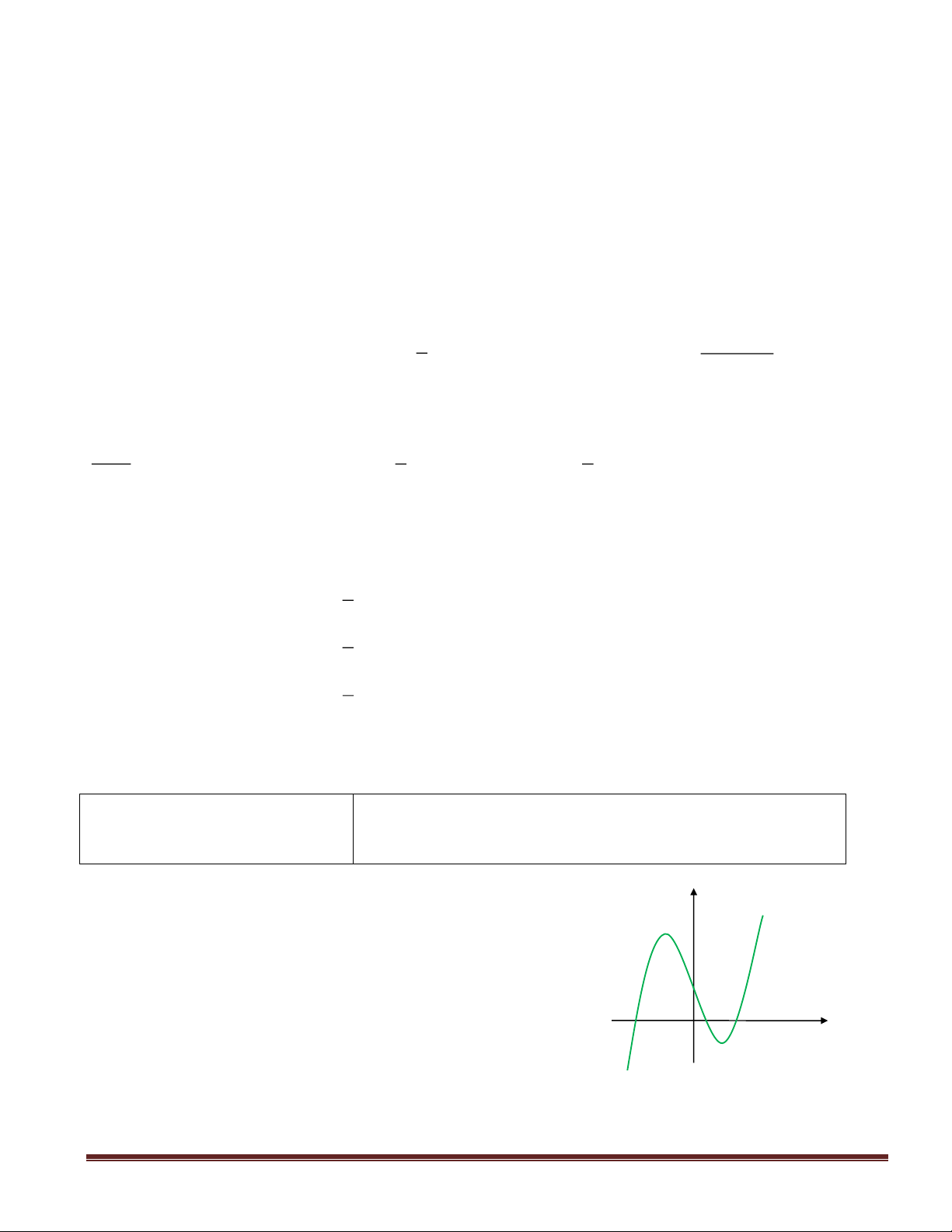
Trang 138
Nếu
( )
1
là đồ thị hàm số
( ) ( )
y h x g x
==
thì
( ) ( ) ( )
0 0;2g x x g x
đồng biến trên
( )
0;2
, trong
hai đồ thị còn lại không có đồ thị nào thoả mãn là đồ thị hàm số
( ) ( )
y g x f x
==
.
Nếu
( )
2
là đồ thị hàm số
( ) ( )
y h x g x
==
thì
( ) ( ) ( )
0 1,5;1,5g x x g x
−
đồng biến trên
( )
1,5;1,5−
,
( )
1
là đồ thị hàm số
( ) ( )
y g x f x
==
thì
( ) ( ) ( )
0 0;2f x x f x
đồng biến trên
( )
0;2
, nhưng
( )
3
không thoả mãn là đồ thị hàm số
( )
y f x=
.
Nếu
( )
3
là đồ thị hàm số
( ) ( )
y h x g x
==
thì
( ) ( ) ( )
0 ;1g x x g x
−
đồng biến trên
( )
;1−
, vậy
( )
2
là đồ thị hàm số
( ) ( )
y g x f x
==
và
( )
1
là đồ thị hàm số
( )
y f x=
.
Dựa vào đồ thị ta có
( ) ( ) ( )
1 1 1h g f− − −
.
Câu 48: Cho hàm số Số nghiệm thực của phương trình là
A. 4. B. 6. C. 9. D. 5.
Đặt
( )
t f x=
. Khi đó phương trình trở thành.
( )
( ) ( )
3 2 3 2
35
1 2 1 3 2 1 3 0 *
2 1 2 2
ft
f t t t t t t t t t
t
= = − − + + = − − − + =
−
.
1
2
3
3,05979197
0,8745059057
0,9342978758
t
t
t
−
.
+ Xét phương trình
32
1
3
3 3.05979197
2
x x x t− + + =
. Bấm máy tính ta được
1
nghiệm.
+ Xét phương trình
32
2
3
3 0,8745059057
2
x x x t− + + =
. Bấm máy tính ta được
3
nghiệm.
+ Xét phương trình
32
3
3
3 0,9342978758
2
x x x t− + + = −
. Bấm máy tính ta được
1
nghiệm.
Vậy phương trình đã cho có
5
nghiệm thực.
ĐỀ 29
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu 1 (NB): Hàm số nào dưới đây có đồ thị như hình vẽ?
A.
42
y x 2x 1= − + +
B.
42
y x 2x 1= − +
C.
32
y x 3x 1= − +
D.
32
y x 3x 1= − + +
Câu 2 (NB): Cho hàm số
f(x)
có bảng biến thiên
( )
32
3
3.
2
f x x x x= − + +
( )
( )
( )
1
21
f f x
fx
=
−
y
y
x
y
O
y
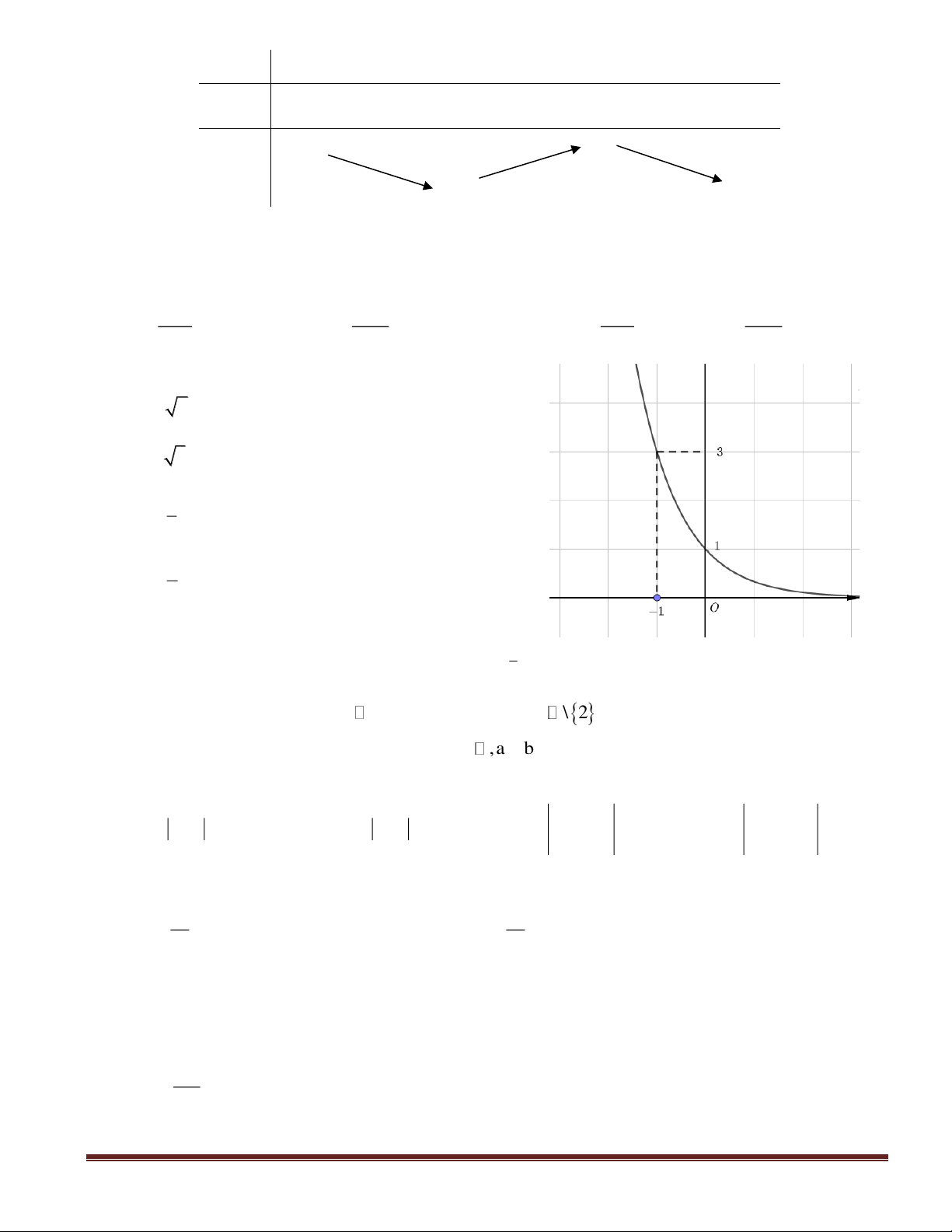
Trang 139
x
−
1
3
+
( )
'fx
−
0
+
0
−
( )
fx
+
2
1−
−
Hàm số đã cho đồng biến trên khoảng nào sau đây?
A.
( ;1)−
B.
( 1;2)−
C.
(3; )+
D.
(1;3)
Câu 3 (NB): Hàm số nào có đồ thị nhận đường thẳng x = 2 làm đường tiệm cận?
A.
1
1
y
x
=
+
B.
5
2
x
y
x
=
−
C.
1
2
1
yx
x
= − +
+
D.
2
2
y
x
=
+
Câu 4 (NB): Đồ thị hình bên là của hàm số nào?
A.
( )
2
x
y =
B.
( )
3
x
y =
C.
1
3
x
y
=
D.
1
2
x
y
=
Câu 5 (NB): Tìm tập xác định của hàm số
( )
3
2
27yx
=−
.
A.
( )
3;D = +
B.
D =
C.
\2D =
D.
[3; )D = +
Câu 6 (NB): Với hàm số
f(x)
tùy ý liên tục trên
,a b
, công thức tính diện tích của hình phẳng giới
hạn bởi đồ thị của hàm số
y f(x)=
, trục hoành và các đường thẳng
x a,x b==
.
A.
b
a
S f(x)dx=
B.
b
a
S f (x)dx=
C.
b
a
S f (x)dx=
D.
b
a
S f(x)dx=
Câu 7(NB): Tìm họ nguyên hàm của hàm số
( )
2
3f x x=+
.
A.
3
3
3
x
xC++
B.
3
3x x C++
C.
3
3
2
x
xC++
D.
2
3xC++
Câu 8 (NB): Số đỉnh của một hình bát diện đều .
A. 21 B. 14 C. 8 D. 6
Câu 9(NB): Một hình trụ có chu vi đáy bằng 10 cm và có chiều cao là 5cm. Tính thể tích V của hình
trụ?
A.
3
125
3
V cm=
B. V=50 cm
3
. C. V=500 cm
3
. D. V=125 cm
3
.

Trang 140
Câu 10(NB): Cho số phức
3zi=+
. Tính
z
.
A.
4z =
. B.
10z =
. C.
22z =
. D.
2z =
.
Câu 11 (NB): Trong các dãy số sau đây dãy số nào là cấp số nhân?
A. Dãy số
( )
n
u
, xác định bởi hệ :
( )
1
1
1
2 *: 2
nn
u
u u n n
−
=
= +
B. Dãy số các số tự nhiên
1;2;3;...
C. Dãy số
( )
n
u
, xác định bởi công thức
31
n
n
u =+
với
*n
D. Dãy số
2;2; 2;2;...; 2;2; 2;2;...− − − −
Câu 12(NB): Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng:
5 2 3 7 0x y z− − + =
. Tìm tọa độ
vectơ pháp tuyến
n
của mặt phẳng.
A.
( )
5;2; 3 .n = − −
B.
( )
5; 2; 3 .n = − − −
C.
( )
5;2;3 .n =−
D.
( )
5;2;3 .n =
Câu 13(NB): Trong không gian Oxyz, cho mặt cầu
( )
2 2 2
:( 4) ( 5) ( 3) 4S x y z− + + + − =
. Tìm tọa độ tâm
I và bán kính R của mặt cầu.
A.
( )
4;5; 3I −−
và
2R =
B.
( )
4; 5;3I −
và
2R =
C.
( )
4;5; 3I −−
và
4R =
D.
( )
4; 5;3I −
và
4R =
Câu 14(NB): Trong không gian Oxyz, cho đường thẳng
85
:
4 2 1
x y z
d
+ − −
==
−
. Tìm vectơ chỉ phương
của đường thẳng d.
A.
( )
4; 2; 1−−
B.
( )
4;2; 1−
C.
( )
4;2;1
D.
( )
4; 2;1−
Câu 15(NB): Cho tập hợp
M
có
10
phần tử. Tìm số tập con gồm
2
phần tử của
M
.
A.
2
10
A
. B.
2
10
C
. C.
2
10
. D.
8
10
A
.
Câu 16 (TH): Trong không gian Oxyz, cho hai điểm
A(1; 1;2)−
và
B(3;3;0)
. Viết phương trình mặt
phẳng trung trực của đường thẳng AB.
A.
x y z 2 0+ − − =
B.
x y z 2 0+ − + =
C.
x 2y z 3 0+ − − =
D.
x 2y z 3 0+ − + =
Câu 17 (TH): Trong không gian Oxyz, điểm nào dưới đây thuộc đường thẳng
x 1 y 1 z 2
2 1 3
− + −
==
−
?
A.
Q( 2;1; 3)−−
B.
P(2; 1;3)−
C.
M( 1;1;2)−
D.
N(1; 1;2)−
Câu 18(TH): Cho khối nón có chiều cao bằng 2a và bán kính đáy bằng a. Tính thể tích của khối nón đã
cho.
A.
3
4a
3
B.
3
2a
C.
3
2a
3
D.
3
4a
Câu 19 (TH): Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3. Tính thể tích khối lăng trụ đã cho .
A.
27 3
2
B.
27 3
4
C.
93
4
D.
93
2
Câu 20 (TH): Cho hình chóp SABCD, có đáy ABCD là hình vuông tâm O, cạnh bên vuông góc với mặt
đáy. Gọi M là trung điểm của SA, N là hình chiếu vuông góc của A lên SO. Mệnh đề nào sau đây đúng?

Trang 141
A.
AC (SBD)⊥
B.
DN (SAB)⊥
C.
AN (SOD)⊥
D.
AM (SBC)⊥
Câu 21(TH): Hàm số
32
1
35
3
y x x x= − − +
nghịch biến trên khoảng nào ?
A. (3;+∞). B. (-∞;+∞). C. (-∞;-1). D. (-1;3).
Câu 22 (TH): Đồ thị hàm số
2
6
1
x
y
x
−
=
−
có mấy đường tiệm cận?
A. 1. B. 3. C. 2. D. 0.
Câu 23 (TH): Cho số phức z thỏa mãn
(2 3i)z 4 3i 13 4i+ + − = +
. Tính mô đun của z.
A.
20 B. 4 C.
22
D.
10
Câu 24(TH): Giải phương trình
3
log (2x 1) 2−=
.
A.
x4=
B.
7
x
2
=
C.
9
x
2
=
D.
x5=
Câu 25(TH): Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ. Hỏi hàm số có bao nhiêu điểm cực
trị?
x
−
1−
0
1
+
'y
+
0
−
+
0
−
y
2
3
−
1−
1−
2
A. Có một điểm B. Có ba điểm C. Có hai điểm D. Có bốn điểm
Câu 26(TH): Với a là số thực dương bất kì, mệnh đề nào dưới đây đúng?
A.
( )
log 2018 2018logaa=
B.
2018
1
log log
2018
aa=
C.
( )
1
log 2018 log
2018
aa=
D.
2018
loga 2018loga=
Câu 27 (TH): Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập số thức R ?
A.
3
x
y
=
B.
1
3
logyx=
C.
( )
2
4
log 1yx
=+
D.
2
x
y
e
=
Câu 28 (TH): Đồ thị của hàm số
32
3 2 1y x x x= − + + −
và đồ thị hàm số
2
3 2 1y x x= − −
có tất cả bao
nhiêu điểm chung?
A. 0 B. 2 C. 3 D. 1
Câu 29 (TH): Tìm nguyên hàm của hàm số
( )
2
1
f(x)
x lnx 2
=
+
.
A.
1
f(x)dx C
lnx 2
=+
+
B.
1
f(x)dx C
lnx 2
−
=+
+
C.
x
f(x)dx C
lnx 2
=+
+
D.
f(x)dx ln x 2 C= + +
Câu 30(TH): Tập hợp tất cả các điểm biểu diễn các số phức
z
thỏa mãn:
24zi+ − =
là đường tròn. Tìm
tâm
I
và bán kính
R
của đường tròn đó.

Trang 142
A.
( )
2; 1I −
;
4R =
. B.
( )
2; 1I −
;
( )
2; 1I −
.
C.
( )
2; 1I −−
;
4R =
. D.
( )
2; 1I −−
;
2R =
.
Câu 31 (VD): Xét số phức z thỏa mãn
z2
z 2i
+
−
là số thuần ảo. Biết rằng tập hợp các điểm biểu diễn các số
phức z luôn thuộc một đường tròn cố định. Tìm bán kính của đường tròn đó.
A.
1 B.
2
C.
22
D. 2
Câu 32 (VD): Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số
3
y x 3x m= − +
có 5 điểm
cực trị?
A.
5 B. 3 C. 1 D. vô số
Câu 33 (VD): Cho hình lăng trụ đứng
. ' ' 'ABC A B C
có cạnh bên
' a 2AA =
. Biết đáy ABC là tam giác
vuông có
BA BC a==
, gọi M là trung điểm của BC. Tính khoảng cách giữa hai đường thẳng AM và B’C.
A.
( )
5
,'
5
a
d AM B C =
B.
( )
3
,'
3
a
d AM B C =
C.
( )
2
,'
2
a
d AM B C =
D.
( )
7
,'
7
a
d AM B C =
Câu 34 (VD): Một hình trụ có trục OO’ chứa tâm của một mặt cầu bán kính R, các đường tròn đáy của
hình trụ đều thuộc mặt cầu trên, đường cao của hình trụ bằng R. Tính thể tích V của khối trụ.
A.
3
3
4
R
V
=
B.
3
VR
=
C.
3
4
R
V
=
D.
3
3
R
V
=
Câu 35 (VD): Cho hàm số
()fx
thoả mãn
'( ) ( 1)
x
f x x e=+
và
(0) 1f =
. Tính
(2)f
A.
2
(2) 4 1fe=+
B.
2
(2) 2 1fe=+
C.
2
(2) 3 1fe=+
D.
2
(2) 1fe=+
Câu 36 (VD): Trong không gian với hệ tọa độ Oxyz, cho
( ) ( ) ( )
A 3;0;0 ;B 0;0;3 ;C 0; 3;0−−
và mặt phẳng
(P):
x y z 3 0+ + − =
. Tìm trên (P) điểm M sao cho
MA MB MC+−
nhỏ nhất.
A.
( )
M 3;3; 3−
B.
( )
M 3; 3;3−
C.
( )
M 3;3;3−
D.
( )
M 3; 3;3−−
Câu 37 (VD): Biết rằng tồn tại duy nhất bộ các số nguyên a, b, c sao cho
3
2
(4x 2)lnxdx a bln2 cln3+ = + +
. Giá trị của a + b + c bằng:
A.
19 B. -19 C. 5 D. -5
Câu 38 (VD): Tính tổng tất cả các giá trị của m biết đồ thị hàm số
32
2 ( 3) 4y x mx m x= − + + +
và đường
thẳng
4yx=+
cắt nhau tại 3 điểm phân biệt A(0;4), B, C sao cho diện tích tam giác IBC bằng
82
với
( )
1;3 .I
A.3 B. 8 C. 1 D. 5

Trang 143
Câu 39(VD): Kết quả thống kê cho biết ở thời điểm năm
2013
dân số Việt Nam là
90
triệu người, tốc độ
tăng dân số là
1,1%/
năm. Nếu mức tăng dân số ổn định như vậy thì dân số Việt Nam sẽ gấp đôi vào năm
nào?
A.
2050
. B.
2077
. C.
2070
. D.
2093
.
Câu 40 (VD): Tìm tất cả các giá trị của tham số
m
để phương trình
1
4 .2 2 0
xx
mm
+
− + =
có hai nghiệm
1
x
,
2
x
thoả mãn
12
3xx+=
.
A.
2m =
. B.
3m =
. C.
4m =
. D.
1m =
.
Câu 41 (VDC): Cho hàm số
y f(x)=
. Hàm số
y f '(x)=
có bảng xét dấu như sau:
x
−
2−
1
3
+
( )
'fx
−
0
+
1
+
0
−
Hàm số
( )
2
y f x 2x=+
nghịch biến trên khoảng nào dưới đây?
A.
(0;1)
B.
( 2; 1)−−
C.
( 2;1)−
D.
( 4; 3)−−
Câu 42(VDC): Người ta muốn xây dựng một bể bơi ( hình vẽ bên dưới) có thể tích là
( )
3
968
4 2 2
Vm=
+
.
Khi đó giá trị thực của x để diện tích xung quanh của bể bơi là nhỏ nhất thuộc khoảng nào sau đây?
A.
(0;3)
B.
(3;5)
C.
(5;6)
D.
(2;4)
Câu 43(VDC): Biết hai điểm B(a; b), C(c; d) thuộc hai nhánh của đồ thị hàm số
2
1
x
y
x
=
−
sao cho tam
giác ABC vuông cân tại đỉnh A(2; 0), tính giá trị biểu thức
T ab cd=+
.
A. 6 B. 0 C. -9 D. 8
Câu 44(VDC): Cho hàm số y = f(x) liên tục trên R thoả mãn
2
'( ) 2 . ( )
x
f x x f x e x R
−
+ =
và
(0) 0f =
.
Tính
(1)f
.
A.
2
(1)fe=
B.
1
(1)f
e
−
=
C.
2
1
(1)f
e
=
D.
1
(1)f
e
=
Câu 45(VDC): Cho các số phức
1 2 3
z ,z ,z
thỏa mãn
1 2 3
z z z 1= = =
và
3 3 3
1 2 3 1 2 3
z z z z z z 0+ + + =
. Đặt
1 2 3
z z z z= + +
, tính giá trị của
32
z 3 z−
.
A.
-2 B. -4 C. 4 D. 2

Trang 144
Câu 46(VDC): Cho khối chóp SABCD có đáy là hình bình hành,
0
3, 4, 120AB AD BAD= = =
. Cạnh
bên
23SA =
vuông góc với đáy. Gọi M, N, P lần lượt là trung điểm các cạnh SA, AD và BC,
là góc
giữa hai mặt phẳng
( )
SAC
và
( )
MNP
. Chọn khẳng định đúng trong các khẳng định sau đây.
A.
( )
00
60 ;90
B.
( )
00
0 ;30
C.
( )
00
30 ;45
D.
( )
00
45 ;60
Câu 47(VDC): Trong không gian Oxyz, cho hai điểm
A(3;1; 3),B(0; 2;3)−−
và mặt cầu (S):
( ) ( )
22
2
x 1 y z 3 1+ + + − =
. Xét điểm M thay đổi luôn thuộc mặt cầu (S), tính giá trị lớn nhất của
22
MA 2MB+
.
A.48 B.82 C. 84 D. 52
Câu 48(VDC): Trong không gian Oxyz, cho hai điểm
( ) ( )
1; 1;2 , 3; 4; 2AB− − −
và đường thẳng
24
:6
18
xt
d y t
zt
=+
=−
= − −
. Điểm
( )
,,I a b c
thuộc d là điểm thỏa mãn
IA IB+
đạt giá trị nhỏ nhất. Tính
T a b c= + +
.
A.
23
58
B.
43
58
−
C.
65
29
D.
21
58
−
Câu 49(VDC): Trong truyện cổ tích Cây tre trăm đốt (các đốt được tính từ 1 đến 100), khi không vác được
cây tre dài tận 100 đốt như vậy về nhà, anh Khoai ngồi khóc, Bụt liền hiện lên, bày cho anh ta : “Con hãy hô
câu thần chú Khc xuất, khc xuất thì cây tre sẽ rời ra, con sẽ mang được về nhà”. Biết rằng cây tre 100 đốt
được tách ra một cách ngẫu nhiên thành các đoạn ngắn có chiều dài là 2 đốt và 5 đốt (có thể chỉ có một loại).
Xác suất để có số đoạn 2 đốt nhiều hơn số đoạn 5 đốt đúng 1 đoạn gần với giá trị nào trong các giá trị dưới đây
?
A.0,142. B. 0,152. C. 0,132. D. 0,122.
Câu 50(VDC):Cho các số thực x, y dương và thỏa mãn
( )
22
2
22
log 2 1
22
2
log 2 log 8 .
3
xy
xy
xy
xy x
++
+
+
+
Tìm
giá trị nhỏ nhất của biểu thức
22
2
22
.
2
x xy y
P
xy y
−+
=
−
A.
3
.
2
B.
15
.
2
+
C.
5
.
2
D.
1
.
2
………………………..HẾT………………………..
ĐÁP ÁN - HƯỚNG DẪN GIẢI CHI TIẾT

Trang 145
1.C
2.D
3.B
4.C
5.A
6.A
7.A
8.D
9.D
10.B
11.D
12.C
13.B
14.D
15.B
16.C
17.D
18.C
19.B
20.C
21.D
22.B
23.D
24.D
25.C
26.D
27.D
28.C
29.B
30.C
31.B
32.B
33.D
34.A
35.B
36.C
37.C
38.C
39.B
40.C
41.B
42.A
43.D
44.D
45.A
46.A
47.C
48.D
49.D
50.C
Câu 31: Xét số phức z thỏa mãn
z2
z 2i
+
−
là số thuần ảo. Biết rằng tập hợp các điểm biểu diễn các số phức z
luôn thuộc một đường tròn cố định. Tính bán kính của đường tròn đó.
A.
1 B.
2
C.
22
D. 2
Giải : Gọi
z a bi=+
ta có:
( )
( )
( )( )
( )
2
2
22
22
22
(a 2) bi a (b 2)i
z 2 (a 2) bi
z 2i a (b 2i)i a (b 2)i a (b 2)i
(a 2)a (a 2)(b 2)i abi b(b 2)
a b 2
a 2 b 2 ab
a 2a b 2b
i
a b 2 a b 2
+ + − −
+ + +
==
− + − + − − −
+ − + − + + −
=
+−
+ − −
+ + −
=−
+ − + −
Để số trên là số thuần ảo
có phần thực bằng 0
22
a 2a b 2b 0 + + − =
Vậy tập hợp các điểm biểu diễn số phức z là đường tròn tâm
I( 1;1)−
, bán kính
( )
2
2
R 1 1 0 2= − + − =
Chọn B.
Câu 32: Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số
3
y x 3x m= − +
có 5 điểm cực trị?
A.
5 B. 3 C. 1 D. vô số
Giải:
Hàm số
3
y x 3x m= − +
có 5 điểm cực trị khi và chỉ khi hàm số
3
y x 3x m=−+
có 2 cực trị nằm về hai
phía của trục Ox.
Ta có:
3
x 1 y 2 m
y' x 3x m
x 1 y 2 m
= = − +
= − +
= − = +
Hai điểm cực trị nằm về 2 phía trục Ox
( )
2
2 m (2 m) 0 m 4 0 2 m 2 − + + − −
Kết hợp điều kiện
m m 1;0;1 −
. Vậy có 3 giá trị của m thỏa mãn ycbt.
Chọn B.
Câu 33: Cho hình lăng trụ đứng
. ' ' 'ABC A B C
có cạnh bên
' a 2AA =
. Biết đáy ABC là tam giác vuông
có
BA BC a==
, gọi M là trung điểm của BC. Tính khoảng cách giữa hai đường thẳng AM và B’C.
A.
( )
5
,'
5
a
d AM B C =
B.
( )
3
,'
3
a
d AM B C =
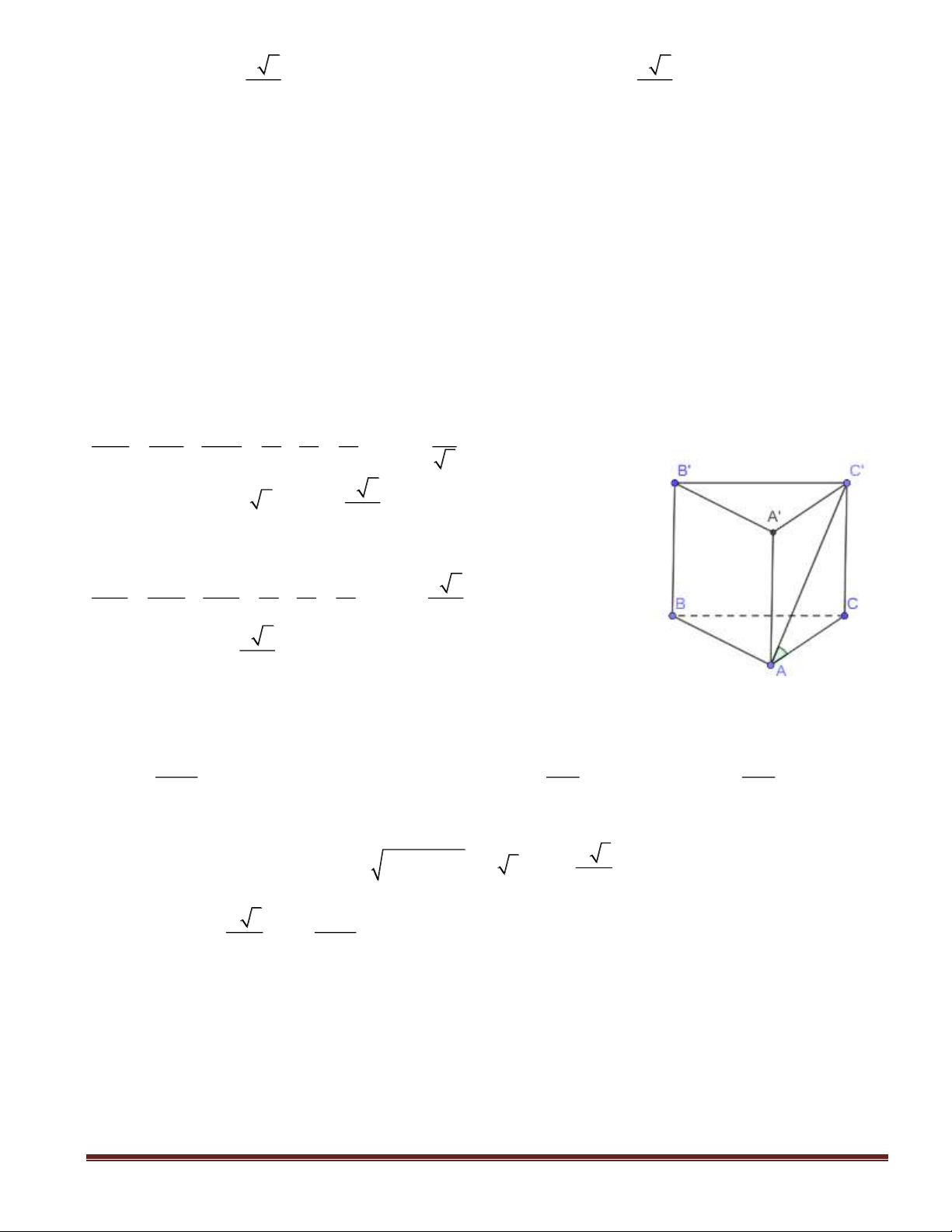
Trang 146
C.
( )
2
,'
2
a
d AM B C =
D.
( )
7
,'
7
a
d AM B C =
Giải:
Lấy N là trung điểm của
' / / 'BB MN B C
( do MN là đường trung bình tam giác BB’C)
Mà
( )
MN AMN
suy ra
( )
' / /B C AMN
Từ đó
( ) ( )
( )
( )
( )
( )
( )
; ' ' ; '; ;d AM B C d B C AMN d B AMN d B AMN= = =
Trong
( )
ABC
kẻ
BH AM⊥
tại H
Lại có
AM BN⊥
( do
( )
BN ABC⊥
) nên
( )
AM BHN⊥
suy ra
( ) ( )
AMN BHN⊥
Ta kẻ
BK HN⊥
tại K, khi đó
( ) ( )
( ) ( ) ( )
AMN BHN
AMN BHN HN BK AMN
BK HN
⊥
= ⊥
⊥
tại K.
Hay
( ) ( )
( )
; ' ;d AM B C d B AMN BK==
+ Tam giác ABM vuông tại B có BH là đường cao nên
2 2 2 2 2 2
1 1 1 1 4 5
5
a
BH
BH AB BM a a a
= + = + = → =
+ Ta có
2
' AA'=a 2
2
a
BB BN= =
+ Tam giác BHN vuông tại B có BK là đường cao nên
2 2 2 2 2 2
1 1 1 5 2 7 7
7
a
BK
BK BH BN a a a
= + = + = =
Vậy
( )
7
;'
7
a
d AM B C =
Chọn D.
Câu 34 : Một hình trụ có trục OO’ chứa tâm của một mặt cầu bán kính R, các đường tròn đáy của hình trụ
đều thuộc mặt cầu trên, đường cao của hình trụ bằng R. Tính thể tích V của khối trụ.
A.
3
3
4
R
V
=
B.
3
VR
=
C.
3
4
R
V
=
D.
3
3
R
V
=
Giải:
Đường kính đáy của khối trụ là:
( )
2
2
3
2 2 3
2
R
r R R R r= − = = =
2
3
2
33
24
RR
V r h R
= = = =
.
Chọn A.
Câu 35 : Cho hàm số
()fx
thoả mãn
'( ) ( 1)
x
f x x e=+
và
(0) 1f =
. Tính
(2)f
A.
2
(2) 4 1fe=+
B.
2
(2) 2 1fe=+
C.
2
(2) 3 1fe=+
D.
2
(2) 1fe=+
Giải:
Ta có
x x x x x
( ) ( 1)e e e e ef x x dx x dx dx x dx= + = + = +

Trang 147
Tính
x
eI dx=
Đặt
xx
ee
u x du dx
dv dx v
==
==
x x x x x
x x x x
xe e e e e
( ) e e e e
I dx x dx x C
f x x C x C
= = − = − +
= + − + = +
Lại có
0
(0) 1 0. 1 1f e C C= + = =
x 2 2
( ) e 1 (2) 2. 1 2 1f x x f e e= + = + = +
.
Chọn B.
Câu 36: Trong không gian với hệ tọa độ Oxyz, cho
( ) ( ) ( )
A 3;0;0 ;B 0;0;3 ;C 0; 3;0−−
và mặt phẳng (P):
x y z 3 0+ + − =
. Tìm trên (P) điểm M sao cho
MA MB MC+−
nhỏ nhất.
A.
( )
M 3;3; 3−
B.
( )
M 3; 3;3−
C.
( )
M 3;3;3−
D.
( )
M 3; 3;3−−
Giải:
Gọi điểm
I(a;b;c)
thỏa mãn
IA IB IC 0+ − =
Ta có:
IA ( 3 a; b; c)
3 a 0 a 3
IB ( a; b;3 c) IA IB IC ( 3 a;3 b;3 c) 0 3 b 0 b 3 I( 3;3;3)
3 c 0 c 3
IC ( a; 3 b; c)
= − − − −
− − = = −
= − − − + − = − − − − = − = = −
− = =
= − − − −
Ta có
( )
MA MB MC MI IA MI IB MI IC MI IA IB IC MI MI+ − = + + + − − = + + − = =
Do đó
MA MB MC+−
nhỏ nhất khi và chỉ khi MI nhỏ nhất
M là hình chiếu của I trên (P)
Ta thấy
3 3 3 3 0 I (P)− + + − =
Hình chiếu của I trên (P) là chính nó. Do đó
M I M( 3;3;3) −
Chọn C.
Câu 37: Biết rằng tồn tại duy nhất bộ các số nguyên a, b, c sao cho
3
2
(4x 2)lnxdx a bln2 cln3+ = + +
.
Tính giá trị của a + b + c.
A.
19 B. -19 C. 5 D. -5
Giải:
Đặt
( )
3
2
I 4x 2 lnxdx=+
Đặt
2
dx
du
u ln x
x
dv (4x 2)dx
v 2x 2x 2x(x 1)
=
=
=+
= + = +
3
3
2
2
2x(x 1)dx
I 2x(x 1)ln x |
x
+
= + −

Trang 148
3
2
2
3
2
I 24ln3 12ln2 2 (x 1)dx
x
I 24ln3 12ln2 2 x
2
15
I 24ln3 12ln2 2 4
2
I 24ln3 12ln2 7 a bln2 cln3
= − − +
= − − +
= − − −
= − − = + +
a7
b 12 a b c 7 12 24 5
c 24
=−
= − + + = − − + =
=
Chọn C.
Câu 38 : Tính tổng tất cả các giá trị của m biết đồ thị hàm số
32
2 ( 3) 4y x mx m x= − + + +
và đường thẳng
4yx=+
cắt nhau tại 3 điểm phân biệt A(0;4), B, C sao cho diện tích tam giác IBC bằng
82
với
( )
1;3 .I
A.3 B. 8 C. 1 D. 5
Giải:
Xét phương trình hoành độ giao điểm
3 2 3 2
x 2mx (m 3)x 4 x 4 x 2mx (m 2)x 0+ + + + = + + + + =
( )
2
2
x 0 y 4 A(0;4)
x x 2mx m 2 0
x 2mx m 2 0(1)
= =
+ + + =
+ + + =
Để
32
y x 2mx (m 3)x 4= + + + +
và đường thẳng
y x 4=+
cắt nhau tại 3 điểm phân biệt thì phương trình
(1) phải có 2 nghiệm phân biệt khác 0
2
m2
m m 2 0
m1
m0
2
'
2
m
= − −
−
+
−
Khi đó:
BC
x ;x
là 2 nghiệm của phương trình (1), áp dụng định lí Vi-ét ta có
BC
BC
x x 2m
x x m 2
+ = −
=+
Ta có
IBC
11
S d(I;BC).BC d(I;d).BC
22
==
IBC
2S
BC
d(I;d)
=
Mà
1 3 4
2.8 2
d(I;d) 2 BC 16
22
−+
= = = =
Ta có
( ) ( ) ( ) ( ) ( )
( ) ( )
2 2 2 2 2
2
B C B C B C B C B C
22
B C B C B C
2 2 2
BC x x y y x x x 4 x 4 2 x x
x x 128 x x 4x x 128
4m 4(m 2) 128 m m 2 32 m m 34 0
= − + − = − + + − − = −
− = + − =
− + = − − = − − =
Phương trình bậc hai ẩn m có 2 nghiệm phân biệt
12
m ,m
và
12
m m 1+=
.
Chọn C.

Trang 149
Câu 39: Kết quả thống kê cho biết ở thời điểm năm
2013
dân số Việt Nam là
90
triệu người, tốc độ tăng
dân số là
1,1%/
năm. Nếu mức tăng dân số ổn định như vậy thì dân số Việt Nam sẽ gấp đôi vào năm nào?
A.
2050
. B.
2077
. C.
2070
. D.
2093
.
Giải :
Dân số thế giới được ước tính theo công thức
.
ni
S Ae=
, trong đó
A
là dân số của năm lấy làm mốc tính,
S
là dân số sau
n
năm,
i
là tỉ lệ tăng dân số hàng năm.
Theo đề bài ta có:
1,1%.
. 180 90 63.01338005
ni n
S Ae e n= = =
.
Vậy sau khoảng hơn 63 năm thì dân số Việt Nam đạt ngưng
180
triệu hay vào khoảng năm
2077
.
Chọn B.
Câu 40: Tìm tất cả các giá trị của tham số
m
để phương trình
1
4 .2 2 0
xx
mm
+
− + =
có hai nghiệm
1
x
,
2
x
thoả mãn
12
3xx+=
.
A.
2m =
. B.
3m =
. C.
4m =
. D.
1m =
.
Giải:
Đặt
2
x
t =
,
0t
. Phương trình trở thành:
2
2 2 0t mt m− + =
( )
1
.
Phương trình đã cho có hai nghiệm
1
x
,
2
x
thỏa mãn
12
3xx+=
khi và chỉ khi phương trình
( )
1
có hai
nghiệm dương phân biệt thỏa mãn
1 2 1 2
3
12
. 2 .2 2 2 8
x x x x
tt
+
= = = =
.
Khi đó phương trình
( )
1
có:
2
20
20
4
20
28
mm
Sm
m
Pm
Pm
= −
=
=
=
==
.
Chọn C.
Câu 41 : Cho hàm số
y f(x)=
. Hàm số
y f '(x)=
có bảng xét dấu như sau:
x
−
2−
1
3
+
( )
'fx
−
0
+
0
+
0
−
Hàm số
( )
2
y f x 2x=+
nghịch biến trên khoảng nào dưới đây?
A.
(0;1)
B.
( 2; 1)−−
C.
( 2;1)−
D.
( 4; 3)−−
Giải:
Đặt
2
g(x) f(x 2x)=+
ta có
22
g'(x) (2x 2)f '(x 2x) 2(x 1)f '(x 2x)= + + = + +
Hàm số
y g(x)=
nghịch biến trên
(a;b) g'(x) 0 x (a;b)
và bằng 0 tại hữu hạn điểm.
Xét đáp án A ta có:
15
g' 3f ' 0
24
=
Loại đáp án A.
Xét đáp án C ta có:
( )
3
g' 2f ' 0 0
2
−
=
Loại đáp án C.
Xét đáp án D ta có:
7 21
g' 5f ' 0
24
− = −
Loại đáp án D.
Chọn B.
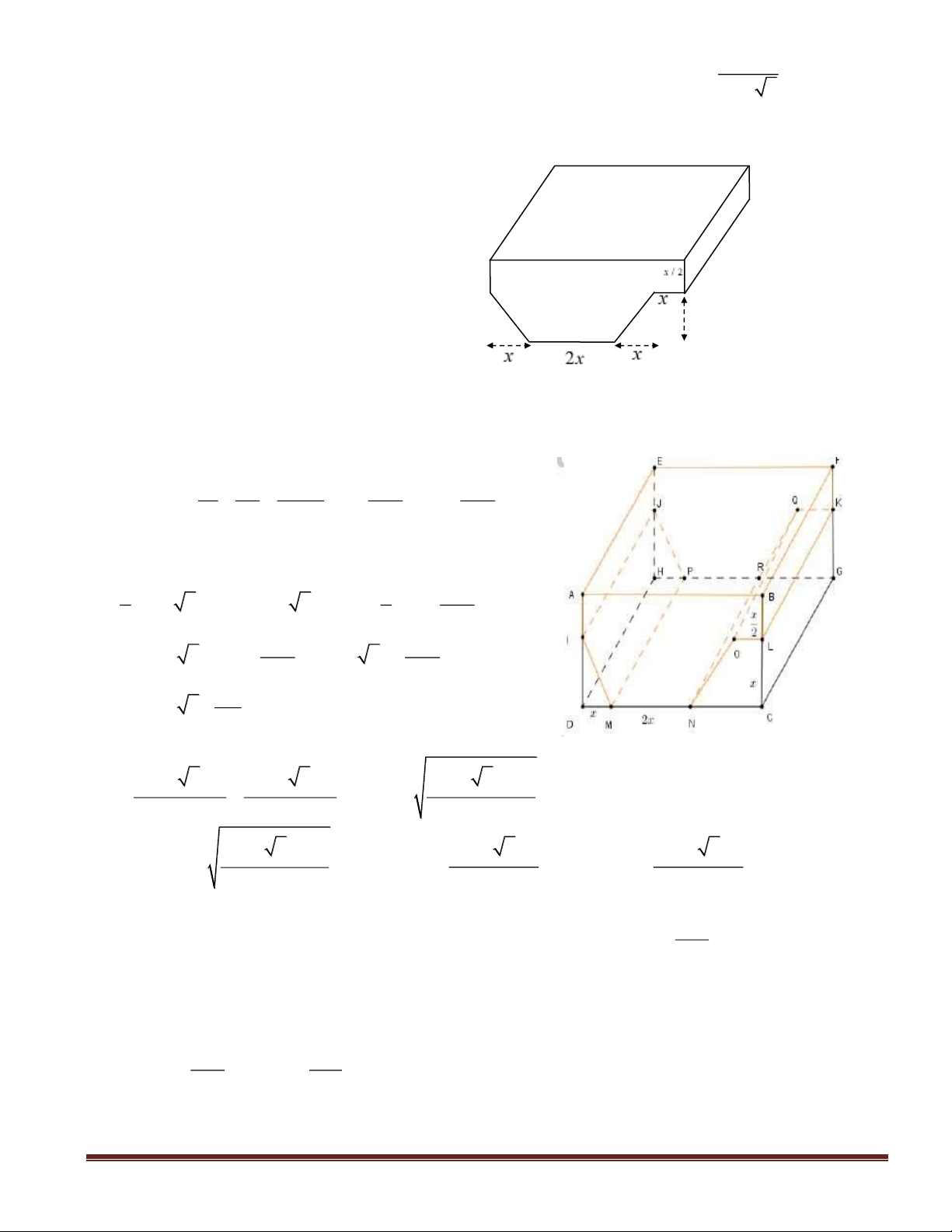
Trang 150
Câu 42: Người ta muốn xây dựng một bể bơi ( hình vẽ bên dưới) có thể tích là
( )
3
968
4 2 2
Vm=
+
. Khi đó
giá trị thực của x để diện tích xung quanh của bể bơi là nhỏ nhất thuộc khoảng nào sau đây?
A.
(0;3)
B.
(3;5)
C.
(5;6)
D.
(2;4)
Giải:
Gọi chiều cao của khối lăng trụ bể bơi là h ( h > 0) ta có
2
2
3 . 2 11 2
. 5 . .
2 2 2 2 11
x x x x x x V
V S h x h h
x
+
= = − − = =
Diện tích xung quanh của bể bơi là
2.
xq AIJE IMPJ MNPR NOQR OLKQ BLKF MNIABLON
S S S S S S S S= + + + + + +
( ) ( )
( )
2
2
2
2
2
11
. 2. 2. . 2. . . 2.
2 2 2
11 2
4 2 2 . 2 4 2 2 . 11
2 11
2
4 2 2 . 11
11
x x x
h x h x h x h x h h
xV
x h x x
x
V
x
x
+ + + + + +
= + + = + +
= + +
Áp dụng bất đẳng thức Cô-si cho ba số ta có
( ) ( ) ( )
2
2
3
2
4 2 2 . 4 2 2 . 4 2 2 .
11 3
11 11 11
xq
V V V
Sx
x
+ + +
= + +
Vậy
( )
2
2
3
4 2 2 .
3
11
xq
V
MinS
+
=
khi và chỉ khi
( ) ( )
23
4 2 2 4 2 2
11 8 2
11 121
VV
x x x
x
++
= = = =
Chọn A.
Câu 43: Biết hai điểm B(a; b), C(c; d) thuộc hai nhánh của đồ thị hàm số
2
1
x
y
x
=
−
sao cho tam giác ABC
vuông cân tại đỉnh A(2; 0), tính giá trị biểu thức
T ab cd=+
.
A. 6 B. 0 C. -9 D. 8
Giải:
Gọi
( )
22
;2 , ;2 1
11
B a C c a c
ac
+ +
−−
Gọi H, K lần lượt là hình chiếu của B, C trên trục
( )
,0 , ( ;0)Ox H a K c
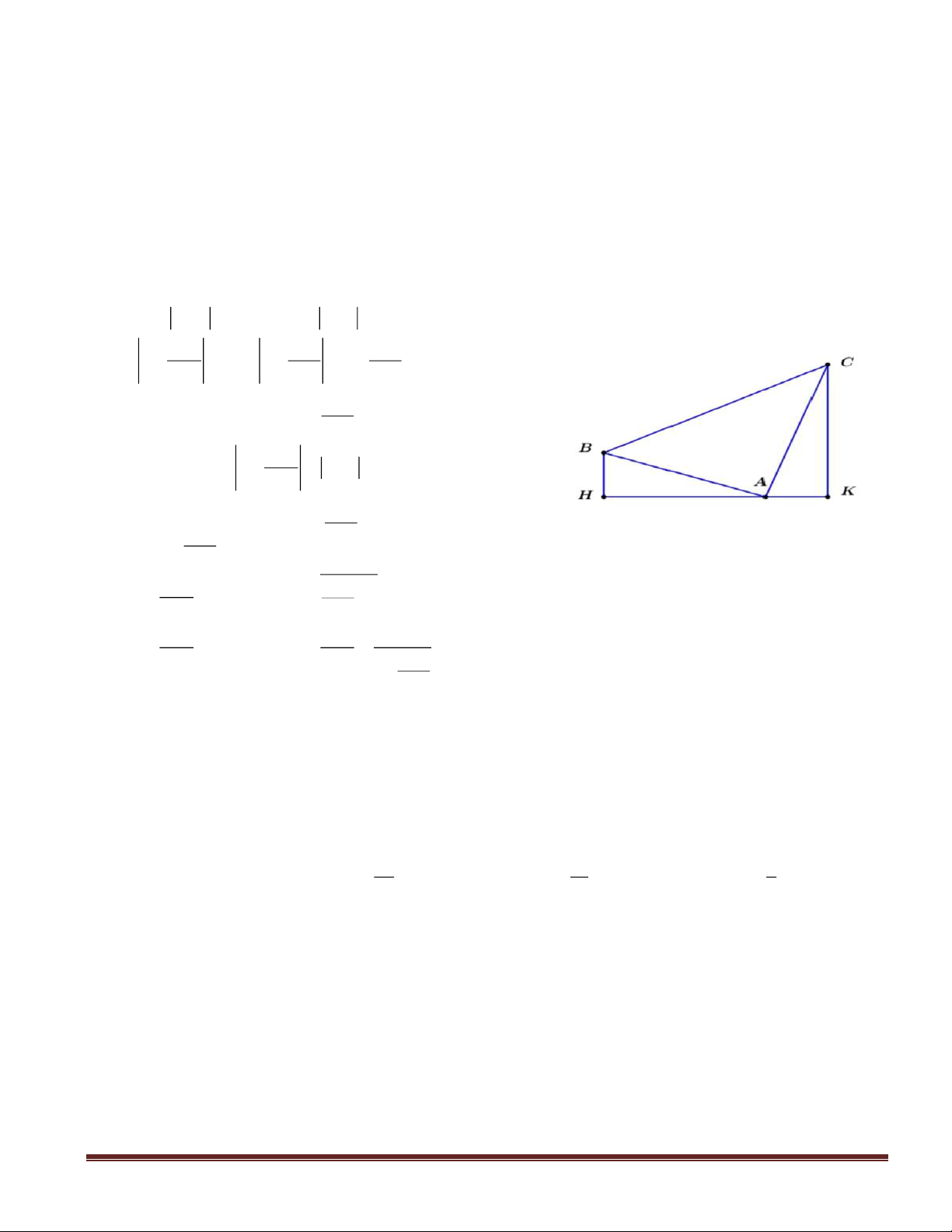
Trang 151
ABC
vuông cân
0
90
AB AC
BAC
=
=
=
Ta có:
BCA CAK ACK BAH ABH = + = +
Mà:
0
90BAH CAK + =
BAH ACK =
Xét
ABH
và
CAK
ta có:
()
()
()
BAH ACK CMT
AC AB gt
ABH CAK ch gn
=
=
= = −
,AH CK HB AK= = =
(các cạnh tương ứng bằng nhau)
Ta có:
( )
2 2 ; 2 ; 1AH a a AK c a− = − = −
2 2 2
2 ; 2 2 ( 1)
1 1 1
2
22
1
2
22
1
BH CK c
a c c
a
AH CK
c
HB AK
c
a
= + = + = +
+ − −
− = +
=
−
=
+ = −
−
2
2
1
1
2
42
1 ( )
2
2
22
1
3 (tm)
11
2 2 2
22
2
11
1
1
a
c
a
c
c
b tm
c
c
ac
cc
aa
c
=
−
=
−
+ = −
=−
+ = −
−
=
−−
+ = − = =
−−
−
−
( )
( )
( )
1;1
1 .1 3.3 8
3;3
B
T
C
−
= = − + =
Chọn D.
Câu 44 : Cho hàm số y = f(x) liên tục trên R thoả mãn
2
'( ) 2 . ( )
x
f x x f x e x R
−
+ =
và
(0) 0f =
. Tính
(1)f
.
A.
2
(1)fe=
B.
1
(1)f
e
−
=
C.
2
1
(1)f
e
=
D.
1
(1)f
e
=
Giải :
( )
2
2
22
2
22
x
x
xx
x
xx
f (x) 2x.f(x) e x R
e f '(x) 2x.f(x) 1
e f '(x) 2x.f(x)e 1
f(x) e ' 1
f(x)e x C f(x) (x C)e
−
−
+ =
+ =
+ =
=
= + = +
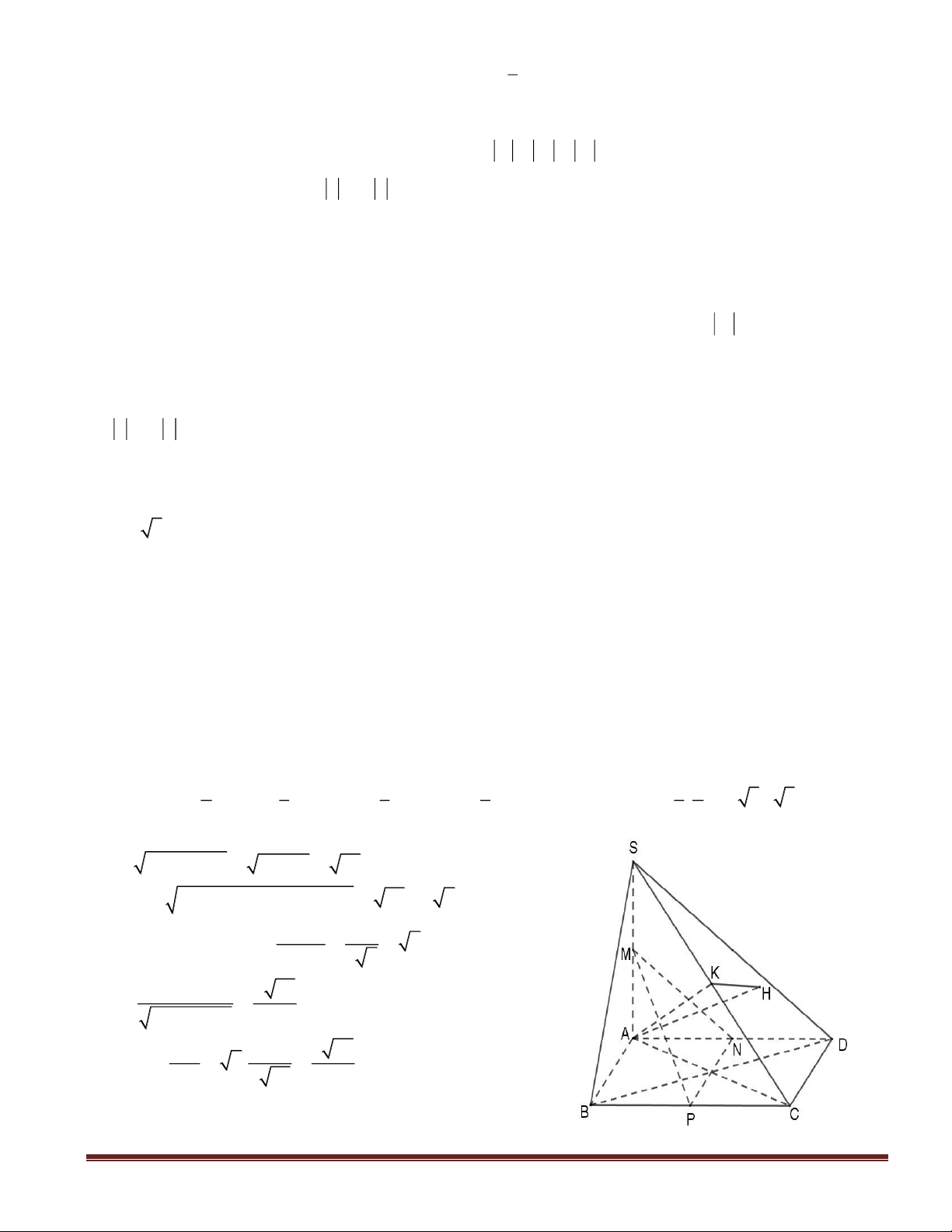
Trang 152
Ta có
2
x1
1
f(0) 0 C 0 f(x) xe f(1) 1.e
e
−−
= = = = =
Chọn D.
Câu 45 : Cho các số phức
1 2 3
z ,z ,z
thỏa mãn
1 2 3
z z z 1= = =
và
3 3 3
1 2 3 1 2 3
z z z z z z 0+ + + =
. Đặt
1 2 3
z z z z= + +
, tính giá trị của
32
z 3 z−
.
A.
-2 B. -4 C. 4 D. 2
Giải :
Do các giả thiết đã cho đúng với mọi cặp số phức
1 2 3
z ,z ,z
nên ta chọn
12
zz1==
, kết hợp giả thiết ta có:
3 3 3 3 3
1 2 2 1 2 3 3 3 3 3 3
z z z z z z 0 1 1 z z 0 z z 2 0 z 1+ + + = + + + = + + = = −
, thỏa mãn
3
z1=
Khi đó ta có 1 cặp
1 2 2
(z ,z ,z ) (1;1; 1)=−
thỏa mãn yêu cầu của bài toán. Khi đó
1 2 3
z z z z 1 1 1 1= + + = + − =
.
32
z 3 z 1 3.1 2 − = − = −
Chọn A.
Câu 46: Cho khối chóp SABCD có đáy là hình bình hành,
0
3, 4, 120AB AD BAD= = =
. Cạnh bên
23SA =
vuông góc với đáy. Gọi M, N, P lần lượt là trung điểm các cạnh SA, AD và BC,
là góc giữa
hai mặt phẳng
( )
SAC
và
( )
MNP
. Chọn khẳng định đúng trong các khẳng định sau đây.
A.
( )
00
60 ;90
B.
( )
00
0 ;30
C.
( )
00
30 ;45
D.
( )
00
45 ;60
Giải:
Ta có:
( ) ( )
//
//
//
MN SD
MNP SCD
NP CD
=
( ) ( )
( )
( ) ( )
( )
,,SAC MNP SAC SCD
= =
Gọi H là hình chiếu vuông góc của A xuống (SCD), K là hình chiếu của H xuống SC
AKH
=
Ta có:
1 1 1 1 1 1
. . .2 . . . .sin . .3.4. 3.2 3 6
2 3 3 3 3 2
SACD SABCD ABCD ABD
V V SAS SA S SA AB AD BAD= = = = = =
Có:
2 2 2 2
13 25AC SC SA AC= = + =
( )( )( )
( )
( )
( )
22
22
00
12 16 28
54 3 6
3
3.6
;6
36
. 2 39
5
5 5 26
sin 6. 60 ;90
26
2 39
SCD
SACD
SCD
SD SA AD
S p p a p b p c
V
AH d A CSD
S
SA AC
AK
SA AC
AH
AK
= + = + =
= − − − = =
= = = =
==
+
= = =
Chọn A.

Trang 153
Câu 47: Trong không gian Oxyz, cho hai điểm
A(3;1; 3),B(0; 2;3)−−
và mặt cầu (S):
( ) ( )
22
2
x 1 y z 3 1+ + + − =
. Xét điểm M thay đổi luôn thuộc mặt cầu (S), tính giá trị lớn nhất của
22
MA 2MB+
.
A.48 B.82 C. 84 D. 52
Giải:
Mặt cầu (S) có tâm
I( 1;0;3)−
, bán kính
R1=
Gọi
J(a;b;c)
là điểm thỏa mãn
JA 2.JB 0+=
Ta có:
JA (3 a,1 b, 3 c);JB ( a;2 b;3 c)= − − − − = − − −
a1
JA 2.JB (3 3a; 3 3b;3 3c) 0 b 1 J(1; 1;1)
c1
=
+ = − − − − = = − −
=
Khi đó ta có:
( ) ( )
22
22
2 2 2 2
2 2 2
const
0
T MA 2MB MJ JA 2 MJ JB
T MJ 2.MJ.JA JA 2MJ 4MJ.JB 2JB
T 3MJ 2MJ(JA 2JB) JA 2JB
= + = + + +
= + + + + +
= + + + +
Do đó
max max
T MJ
Ta có:
2 2 2
IJ (2; 1; 2) IJ 2 1 2 3 R 1 J= − − = + + = =
nằm ở phía ngoài mặt cầu (S). Khi đó
max
MJ IJ R 3 1 4= + = + =
Vậy
2 2 2 2 2 2 2
max
T 3.4 (2 2 4 ) 2.(1 1 2 ) 3.16 24 2.6 84= + + + + + + = + + =
Chọn C.
Câu 48: Trong không gian Oxyz, cho hai điểm
( ) ( )
1; 1;2 , 3; 4; 2AB− − −
và đường thẳng
24
:6
18
xt
d y t
zt
=+
=−
= − −
.
Điểm
( )
,,I a b c
thuộc d là điểm thỏa mãn
IA IB+
đạt giá trị nhỏ nhất. Tính
T a b c= + +
.
A.
23
58
B.
43
58
−
C.
65
29
D.
21
58
−
Giải:
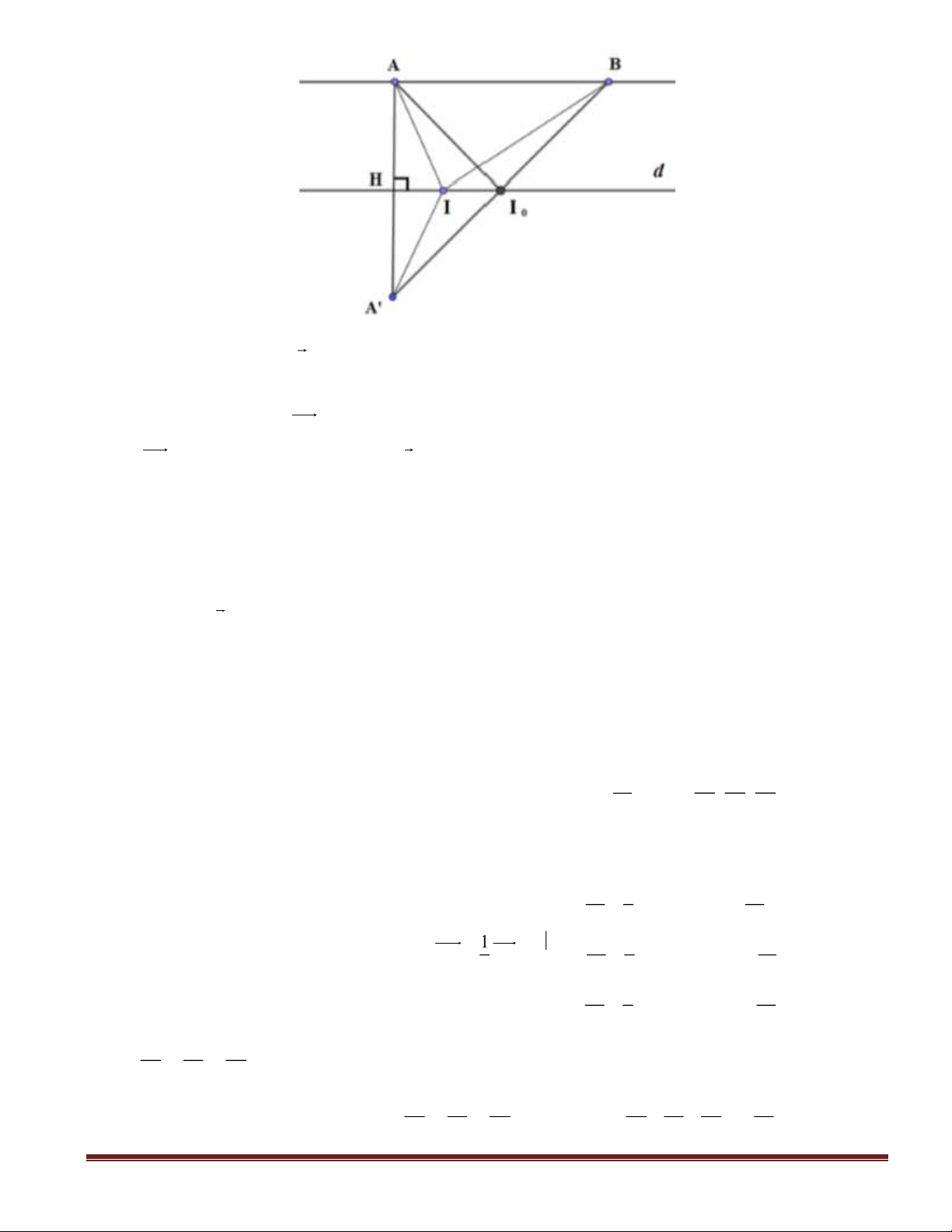
Trang 154
24
:6
18
xt
d y t
zt
=+
=−
= − −
có 1 VTCP
( )
4; 6; 8u = − −
( ) ( ) ( )
1; 1;2 , 3; 4; 2 2; 3; 4A B AB− − − = − −
Ta có:
( )
2; 3; 4AB = − −
cùng phương với
( )
4; 6; 8u = − −
Mà
( )
1; 1;2 / / , ,A d AB d A B d−
đồng phẳng
* Xét mặt phẳng chứa AB và d : Gọi A’ là điểm đối xứng của A qua
( )
;
là mặt phẳng qua A, vuông
góc với d
Khi đó, giao điểm H của
với
( )
là trung điểm của AA’
( )
có 1 VTPT
( )
2; 3; 4n −−
đi qua
( )
1; 1;2A −
có phương trình:
( ) ( ) ( )
2 1 3 1 4 2 0 2 3 4 3 0x y z x y z− − + − − = − − + =
24
:6
18
xt
H d y t
zt
=+
= −
= − −
Giả sử
( )
2 4 ; 6 ; 1 8H t t t+ − − −
( ) ( ) ( ) ( )
11
2 2 4 3 6 4 1 8 3 0 58 11 0
58
H t t t t t
+ − − − − − + = + = = −
36 33 15
;;
29 29 29
H
Ta có:
( )
min
IA IB IA IB A B IA IB A B
+ = + + =
khi và chỉ khi I trùng với I
0
là giao điểm của A’B và
HI
0
là đường trung bình của tam giác
( )
( )
00
00
00
0
36 1 65
.2
29 2 29
1 33 1 21
.3
2 29 2 58
15 1 43
.4
29 2 29
II
II
II
xx
A AB HI AB y y
zz
− = =
= − = − = −
− = − = −
0
65 21 43
;;
29 58 29
I
− −
Vậy để
IA IB+
đạt giá trị nhỏ nhất thì
65 21 43 65 21 43 21
;;
29 58 29 29 58 29 58
I a b c
− − + + = − − = −

Trang 155
Chọn D.
Câu 49: Trong truyện cổ tích Cây tre trăm đốt (các đốt được tính từ 1 đến 100), khi không vác được cây tre dài
tận 100 đốt như vậy về nhà, anh Khoai ngồi khóc, Bụt liền hiện lên, bày cho anh ta : “Con hãy hô câu thần chú
Khc xuất, khc xuất thì cây tre sẽ rời ra, con sẽ mang được về nhà”. Biết rằng cây tre 100 đốt được tách ra
một cách ngẫu nhiên thành các đoạn ngắn có chiều dài là 2 đốt và 5 đốt (có thể chỉ có một loại). Xác suất để có
số đoạn 2 đốt nhiều hơn số đoạn 5 đốt đúng 1 đoạn gần với giá trị nào trong các giá trị dưới đây ?
A.0,142. B. 0,152. C. 0,132. D. 0,122.
Giải :
Gọi số đoạn có chiều dài 2 đốt là x và số đoạn có chiều dài 5 đốt là y, ta có hệ phương trình
Gọi A là biến cố số đoạn 2 đốt nhiều hơn số đoạn 5 đốt đúng 1 đoạn” .
Xét các bộ số (x,y) thoả mãn (x,y
N) ta có bảng sau:
X
0
5
10
15
20
25
30
35
40
45
50
Y
20
18
16
14
12
10
8
6
4
2
0
Vậy
Chọn D.
Câu 50: Cho các số thực x, y dương và thỏa mãn
( )
22
2
22
log 2 1
22
2
log 2 log 8 .
3
xy
xy
xy
xy x
++
+
+
+
Tìm giá trị
nhỏ nhất của biểu thức
22
2
22
.
2
x xy y
P
xy y
−+
=
−
A.
3
.
2
B.
15
.
2
+
C.
5
.
2
D.
1
.
2
Giải:
Giả thiết
( ) ( )
2 2 2 2 2
2
2
log log 3 2 1 3x y xy x x y xy + − + + + +
( ) ( )
2 2 2 2 2 2
22
log 2 2 2 2 log 3 3x y x y xy x xy x + + + + + +
(*)
Vì hàm số
( )
2
logf t t t=+
đồng biến trên khoảng
( )
( ) ( )
2 2 2
0; (*) 2 2 3f x y f xy x+ + +
2
2 2 2 2 2
2 2 3 3 2 0 3. 2 0 1 2.
x x x
x y xy x x xy y
y y y
+ + − + − +
Khi đó
( )
2
2 2 2
2
22
2 2 2 2
,
21
2
2. 1
xx
yy
x xy y a a
P g a
x
a
xy y
y
−+
− + − +
= = = =
−
−
−
với
1;2 .
x
a
y
=
2 5 100 15
1 14
x y x
x y y
+ = =
− = =
( ) 1nA=
2 5 100xy+=
( ) 11n =
1
( ) 0,09
11
PA=
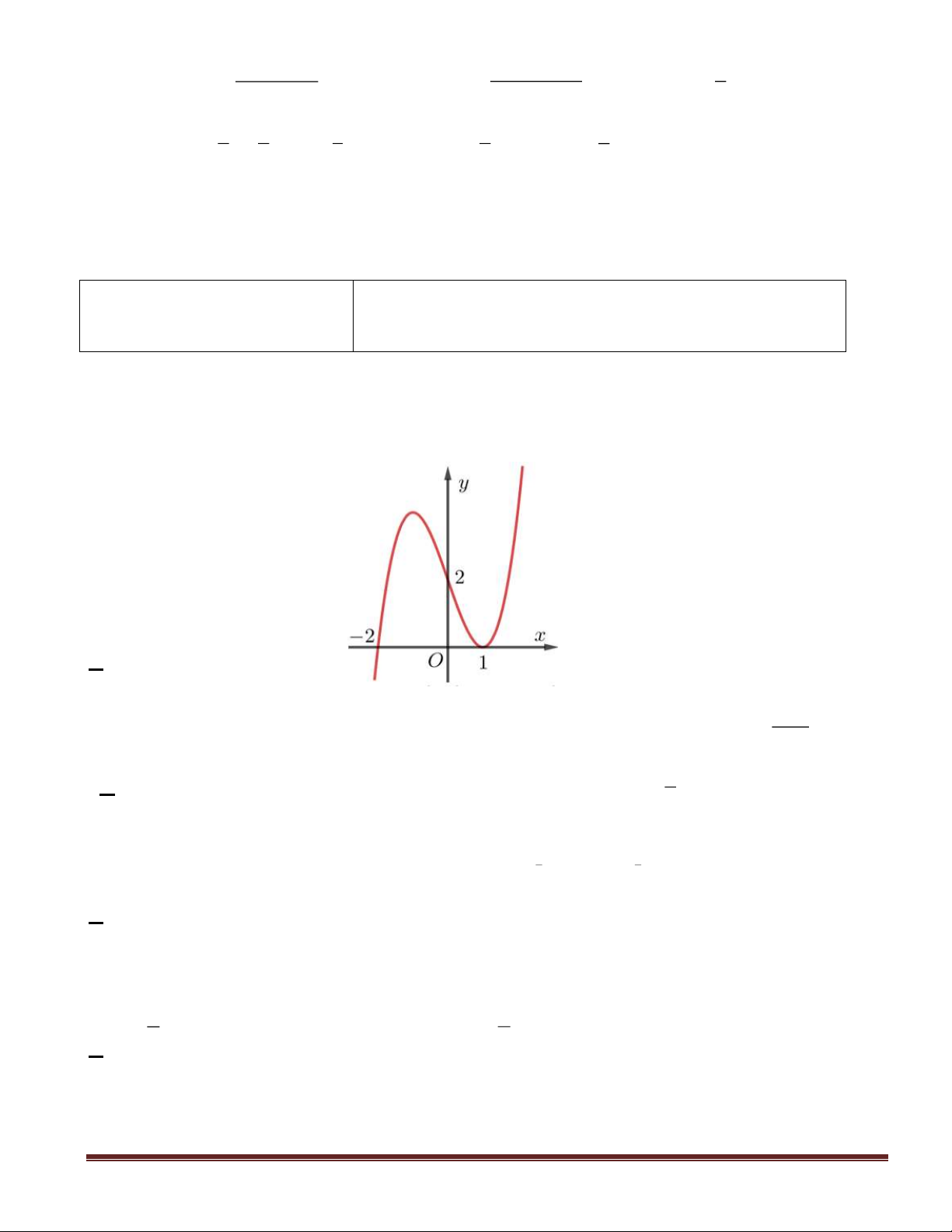
Trang 156
Xét hàm số
( )
2
22
21
aa
ga
a
−+
=
−
trên [1;2], có
( )
( )
( )
2
2
4 4 3 3
; 0 .
2
21
aa
g a g a a
a
−−
= = =
−
Tính
( ) ( ) ( )
[1;2]
3 5 8 5
1 3; ; 2 min .
2 2 3 2
g g g g a
= = = ⎯⎯→ =
Vậy
min
5
.
2
P =
Chọn C.
www.thuvienhoclieu.com
ĐỀ 30
ĐỀ THI THỬ THPT QUỐC GIA 2020
MÔN TOÁN
Thời gian: 90 phút
Câu1. Cho hàm số đa thức
32
y f(x) ax bx cx d= = + + +
có đồ thị như hình vẽ bên dưới. Hàm
số
y f(x)=
đồng biến trên khoảng nào sau đây?
A.
( )
1; +
. B.
( )
;0−
. C.
( )
2;0−
. D.
( )
0;2
.
Câu 2.Tìm các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
1
2
x
y
x
+
=
−
.
A.
2; 1xy==
. B.
2; 1xy= − =
. C.
1
2;
2
xy= = −
. D.
1; 2xy==
.
Câu 3:Kết luận nào đúng về số thực
a
nếu
41
34
( 1) ( 1)aa
--
- < -
.
A.
2a >
.
B.
0a >
.
C.
1a >
.
D.
12a<<
.
Câu 4.Cho a là số thực dương khác 1 và
,0xy
. Khẳng định nào sau đây là khẳng định
đúng?
A.
log log log
a a a
x
xy
y
=−
.
B.
log log ( )
aa
x
xy
y
=−
.
C.
( )
log log log
a a a
x y x y− = −
.
D.
( )
log log log
a a a
x y x y+ = +
Câu 5. Tìm
( )
sinx 3
x
dx+
.
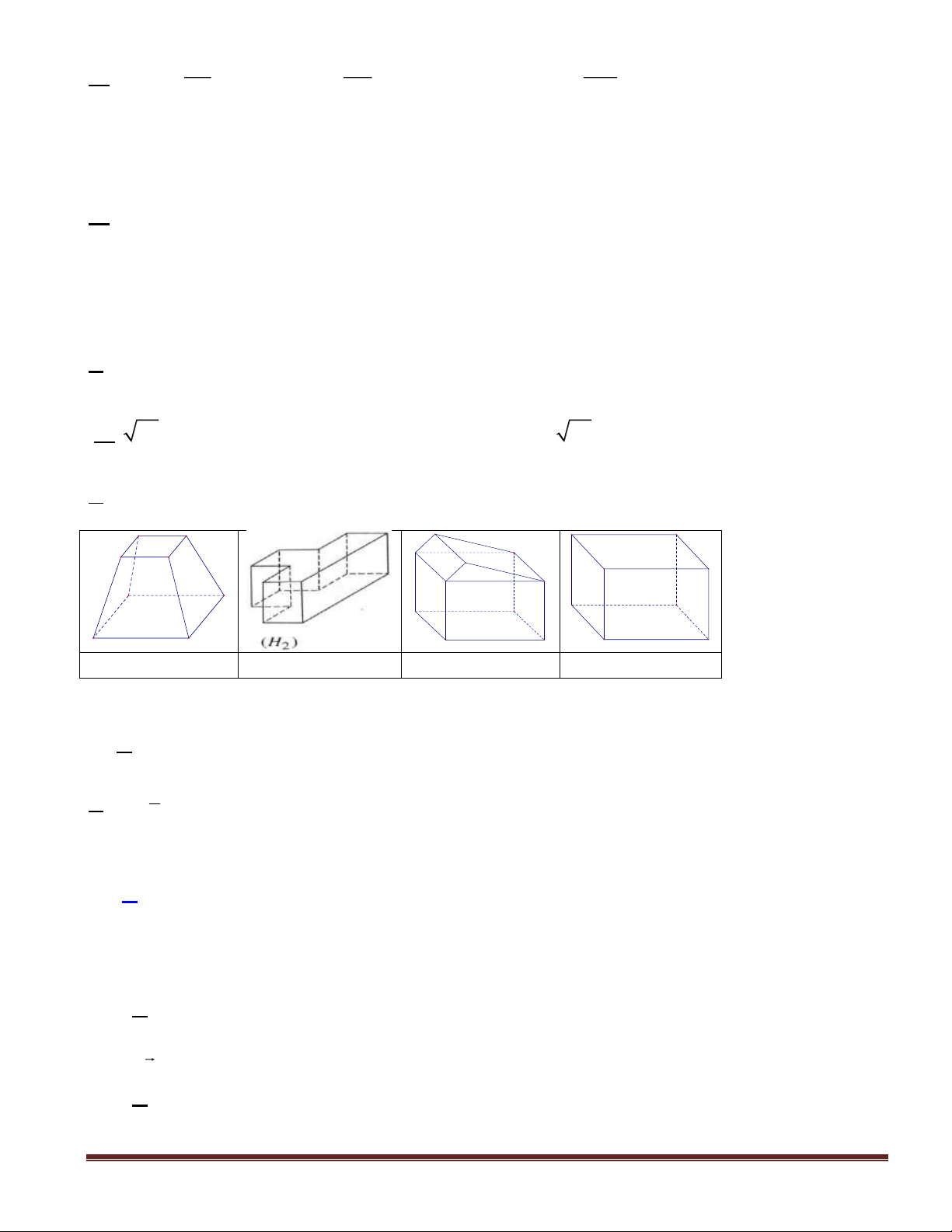
Trang 157
A.
3
cosx .
ln3
x
C− + +
B.
3
cosx .
ln
x
C
x
− + +
C.
1
3
cosx .
1
x
C
x
+
++
+
D.
cosx 3 .ln3 .
x
C++
Câu 6. Cho f(x) là hàm số liên tục trên đoạn
R
và
,,abc
l à ba số thực tùy ý. Khẳng định
nào sau đây là khẳng định sai ?
A.
( ) ( ) ( )
c b b
a a c
f x dx f x dx f x dx=+
. B.
( ) ( ) ( )
c b c
a a b
f x dx f x dx f x dx=+
.
C.
( ) ( ) ( )
c a a
b b c
f x dx f x dx f x dx=−
. D.
. ( ) ( )
cc
bb
a f x dx a f x dx=
.
Câu 7.Xác định phần thực của số phức
( ) ( )
2 3 1 2z i i= + − − +
.
A.3 B.
2−
C. - 3 D. 1
Câu 8. Tính mô đun của số phức:
2
(2 ) 1 3z i i= + + +
.
A.
65
B.
65
C.
34
D.
34
Câu 9.Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất:
A. Ba mặt. B. Hai mặt. C. Bốn mặt. D. Năm mặt
Câu 10. Cho các hình khối sau:
Hình 1
Hình 2
Hình 3
Hình 4
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình
không phải đa diện lồi là
A. Hình 2. B. Hình 4. C. Hình 3. D. Hình 1.
Câu 11. Cho mặt cầu có bán kính R . Thể tích V của khối cầu là :
A.
3
4
3
VR
=
B.
2
4VR
=
C.
2
2VR
=
D.
2
.VR
=
Câu 12. Cho khối nón tròn xoay có chiều cao
h
, đường sinh
l
và bán kính đường tròn đáy
bằng
R
. Diện tích toàn phần của khối nón là:
A.
()
tp
S R l R
=+
B.
( 2 )
tp
S R l R
=+
C.
2 ( )
tp
S R l R
=+
D.
(2 )
tp
S R l R
=+
Câu 13.Trong không gian với hệ tọa độ
,Oxyz
cho mặt phẳng
( )
:5 3 2 0P x z- + =
. Vectơ nào
dưới đây là một vectơ pháp tuyến của
( )
P
?
A.
( )
5;0; 3n =-
r
. B.
( )
5; 3;0n =-
r
. C.
( )
5; 3;2n =-
r
. D.
( )
3;0;5n =-
r
.
Câu 14.Trong không gian với hệ tọa độ
Oxyz
, cho vectơ
25a i k=-
r r r
. Khi đó, tìm tọa độ của
vectơ
a
.
A.
( )
2;0; 5a =-
r
. B.
( )
0;2; 5a =-
r
. C.
( )
2; 5;0a =-
r
. D.
( )
2; 5a =-
r
.
Câu 15. Công thức nào sau đây dùng để tính xác suất của biến cố
A
:

Trang 158
()
. ( )
()
nA
A P A
n
=
W
B.
()
()
()
n
PA
nA
W
=
C.
()
()
()
nA
PA
nB
=
D.
()
( ) 1
()
nA
PA
n
=-
W
Câu 16. Hệ số góc
k
của đường thẳng
12
:
3
xt
yt
ì
ï
=-
ï
D
í
ï
=+
ï
î
là
A.
1
2
k =-
. B.
3k =
C.
1
3
k =
. D.
2k =-
.
Câu 17.Tìm tập hợp tất cả các giá trị của tham số thực
m
để hàm số
32
1
4
3
y x mx x m= + + -
đồng biến trên khoảng
( )
;- ¥ + ¥
.
Câu 12. A.
2;2−
B.
( )
;2− −
C.
( )
2;+
D.
( )
;2−
Câu18. Tất cả các giá trị thực của tham số
m
để hàm số
42
( 1) 3y x m x= + − +
đạt cực tiểu tại
0x =
là:
A.m
1
B.m
1
C. m >1 D.m <1
Câu 19. Bà Hà gửi tiết kiệm ngân hàng với số tiền 50 triệu đồng với lãi suất 0,79% một
tháng, theo phương thức lãi kép. Tính số tiền cả vốn lân lãi bà Hà nhận được sau 2 năm.
(làm tròn đến hàng nghìn).
A.60.393.000. B. 50.793.000 . C.50.790. 000.
D.59.480.000
Câu 20.Tìm tập xác định D của hàm số
3
2
5
(4 ) .yx=-
A.D= (-2; 2). B.D= (-: 2) (2; +). C.D= R. D.D=R\{-2; 2}.
Câu 21. Biết tích phân
9
2
1
12
.
x
bc
x
xe
I dx a e e
x
xe
+
= + = + −
. Tính tổng
P a b c= + +
.
A.
6.P =−
B.
3.P =
C.
5.P =−
D.
8.P =−
Câu 22.Cho hàm số f(x) =
2
15 9 1
21
xx
x
+−
−
; F(x) =
2
(ax ) 2 1bx c x+ + −
,(Với x >
1
2
và a,b,c là
các số thực). Để hàm số F(x) là một nguyên hàm của f(x) thì giá trị của biểu thức T = a +
b + c là:
A.T = 12 B. T = 13 C. T = 11 D. T = 14
Câu 23.Cho số phức z :
7z =
, biết rằng tập hợp số phức w =
14zi+−
là một đường tròn
.Tìm toạ độ tâm I và bán kính R của đường tròng đó?
A. I(1;-4) và R = 7 B.I(1;4) và R = 7 C.I(-1;4) và R = 7 D.I(-1;- 4) và
R = 7
Câu 24. Gọi
1 2 3 4
, , ,z z z z
là 4 nghiệm của pt :
42
( 4) 4 0z m z m+ + + =
(1) .Có bao nhiêu giá trị
nguyên của m để
1 2 3 4
6z z z z+ + + =
.
Trang 159
A. 2 B. 3 C. 4 D. 5
Câu 25.
Cho hình chóp tam giác S.ABC. Gọi M,N, lần lượt là trung điểm của SB, SC .
Khi đó, tỉ số thể tích
SAMN
SABC
V
V
bằng bao nhiêu?
A.
B.
1
8
C.
1
2
D.
Câu26.Thiết diện qua trục của một hình nón là một tam giác vuông cân có diện tích
50
2
cm
.Thể tích của khối nón là:
A.
250 2
3
2
cm
B.
250 2
3
2
cm
C.
250 2
2
cm
D.
125 2
3
2
cm
Câu 27.Trong không gian với hệ toạ độ
Oxyz
, viết phương trình mặt cầu
( )
S
có tâm
( )
1;2;1I −
và tiếp xúc với mặt phẳng
( )
: 2 2 2 0P x y z− − − =
.
A.
( ) ( ) ( )
2 2 2
( ): 1 2 1 9S x y z+ + − + − =
. B.
( ) ( ) ( )
2 2 2
( ): 1 2 1 9S x y z− + + + + =
.
C.
( ) ( ) ( )
2 2 2
( ): 1 2 1 3S x y z− + + + + =
. D.
( ) ( ) ( )
2 2 2
( ): 1 2 1 3S x y z+ + − + − =
.
Câu 28.Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
(3;0; 1), (1; 1;3), (0;1;3)A B C−−
. Viết
phương trình mặt phẳng đi qua ba điểm
,,A B C
.
A.
8 4 5 19 0x y z+ + − =
. B.
2 3 0x y z− + − =
. C.
10 3 19 0x y z+ + − =
. D.
10 3 21 0x y z− − − =
.
Câu 29. Một lọ thuỷ tinh có dung tích 1000(ml) chứa đầy một dung dịch chất độc nồng độ
10% đã được chuyển sang bình khác,nhưng dung dịch chất độc sau khi đổ sang bình chứa
khác thì vẫn còn dính lại bình cũ là 0,1%. Để chất độc trong lọ
9
10
−
gam thì người ta
dùng 1000ml nước cất để rửa lọ bao nhiêu lần?
A. 3 lần B. 2 lần C. 4 lần D. 1 lần
Câu 30. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, cạnh bên SA vuông
góc với đáy, BH vuông góc với AC tại H. Khẳng định nào sau đây đúng ?
A.
BH SC⊥
.
B.
BH SB⊥
.
C.
()BH SAB⊥
.
D.
()BH SBC⊥
.
Câu 31: Cho hàm số y = f(x).Biết f(x) có đạo hàm là f ’(x)
và hàm số y = f ’(x) có đồ thị như hình vẽ bên.
Khi đó hàm số y = f( 3-2x) đồng biến trên khoảng nào sau đây ?
A.(-
;2) B.(1;3) C.(3;+
) D.(-
;3)
Câu 32. Tập hợp tất cả các giá trị của m để đồ thị hàm số
2
2018 x
y
x 2mx 4
+
=
−+
có hai đường tiệm cận đứng là:
1
4
3
4
-2
-4
1
O
3
-1
2
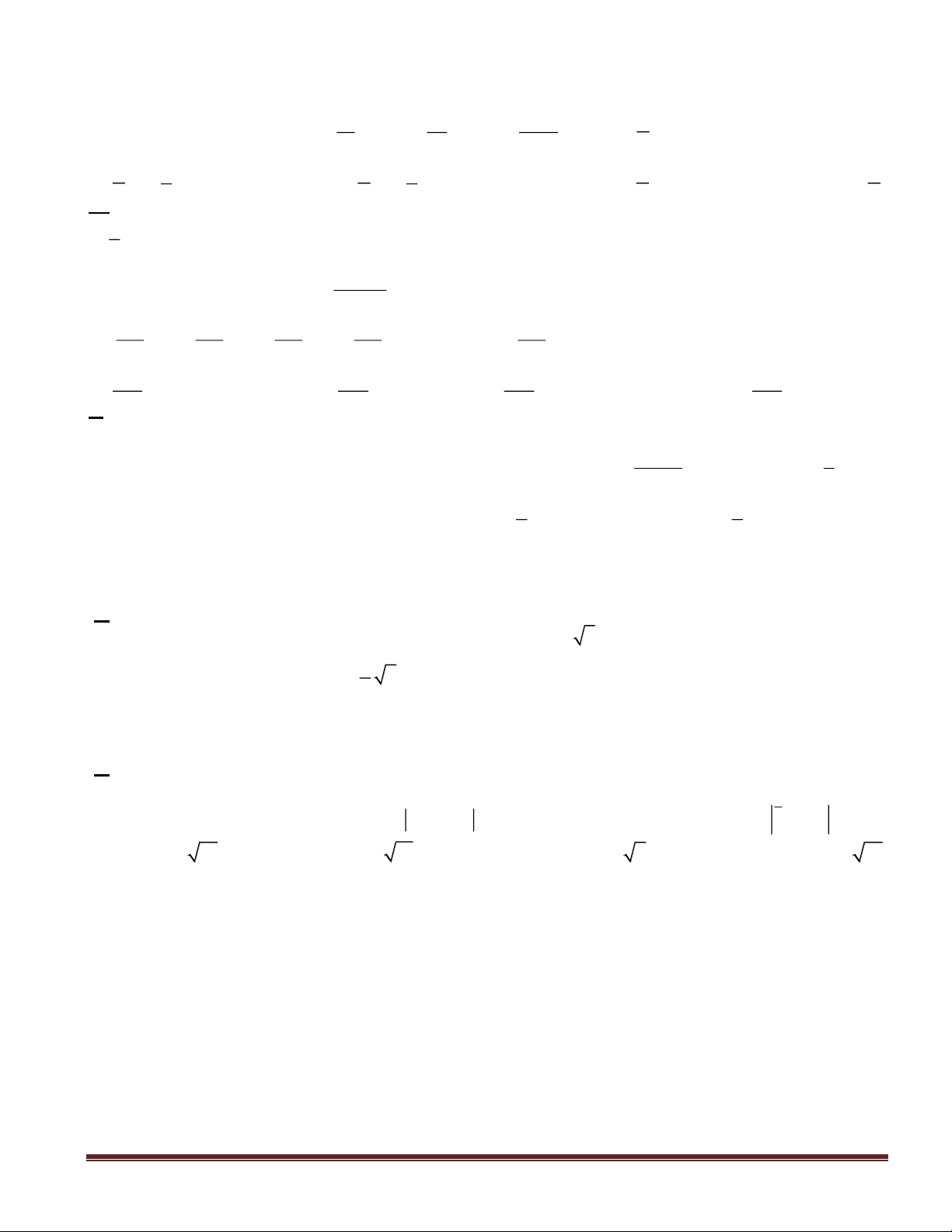
Trang 160
A.
( )
2;+
B.
( ; 2)− −
C.
( )
0;2
D.
( ) ( )
; 2 2;− − +
Câu 33.Cho x , y > 0 :
9 6 4
log log log
81 45 36
x y x y+
==
. Tính
x
y
A.
x
y
=
4
5
.
B.
x
y
=
5
4
.
C.
x
y
=
2
.
D.
x
y
=
1
2
.
Câu 34.Cho hàm số f(x) =
16
16 4
x
x
+
. Tính giá trị của biểu thức P =
1 2 3 4 100
............... .
100 100 100 100 100
f f f f f
+ + + + +
A.
503
10
. B.
253
5
C.
532
5
. D.
305
5
Câu 35.Diện tích hình phẳng giới hạn bởi các đường: y =
2
1
x
x
−+
+
,y =
2x−
x
=
1
2
Câu 13. được viết dưới dạng : S = aln2 -
b
c
( với a,b,c
*N
và
b
c
là phân số tối
giản). K hi đó tổng
Câu 14. P = a + b + c bằng:
A. P = 14 B .P= 16 C. P = 24 D . P = 15
Câu 36. Một mảnh vườn hình Elip có một tiêu cự F
2
(
7
; 0) và ngoại tiếp hình chữ nhật
có chiều dài 6m và chiều rộng
3
7
2
m
và (P) : y = x
2
chia mảnh vườn thành 2 phần , phần
có diện tích lớn để trồng hoa hồng ,biết chi phí trồng hoa hồng 100.000đồng /m
2
. Tính số
tiền để trồng hoa hồng hết phần diện tích đó (làm tròn đến hàng nghìn).
A. 3.108.000 đồng B. 3.100.000 đồng C. 3.112.000 đồng D.3.106.000
đồng
Câu 37. Cho số phức z thoả mãn:
2 3 2zi− − =
.Tìm giá trị lớn nhất của P =
1zi++
.
A. P = 2 +
13
B. P = 2+
11
C. P = 2
7+
D. P = 2 +
15
Câu 38.
Người ta muốn xây một bể chứa nước dạng khối hộp chữ nhật trong một phòng tắm. Biết
chiều dài, chiều rộng, chiều cao của khối hộp đó lần lượt là
3m
;
1,3m
;
1,8m
(người ta chỉ
xây hai mặt thành bể như hình vẽ bên). Biết mỗi viên gạch có chiều dài
20cm
, chiều rộng
10cm
, chiều cao
5cm
. Hỏi người ta sử dụng ít nhất bao nhiêu viên gạch để xây bể đó và thể
tích thực của bể chứa bao nhiêu lít nước? (Giả sử lượng xi măng và cát không đáng kể).
Trang 161
A.756 viên,
6264
lít. B. 756 viên,7020 lít.
C.774 viên, 6246 lít. D.774viên, 6264 lít.
Câu 39.Trong không gian với hệ toạ độ Oxyz
cho mặt cầu (S):
2 2 2
4 2 2 3 0x y z x y z+ + − + + − =
. Mặt phẳng (P)
chứa trục Oy và phương trình mp (P) có
dạng: ax + bz = 0 đồng thời mp (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có
bán kính bằng 3. Khi đó tổng T =
a
b
là:
( với a,b
*
N
và
a
b
là phân số tối giản)
A.
1
2
B.
2
3
C.
1
3
D.
3
4
Câu 40. Gọi
S
là tập hợp các nghiệm thuộc khoảng
( )
0;100
của phương trình
2
sin cos 3cos 3
22
xx
x
+ + =
. Tổng các phần tử của
S
là
A.
7375
3
. B.
7525
3
. C.
7400
3
. D.
7550
3
.
Câu 41. Gọi
X
là tập hợp các số tự nhiên có ba chữ số. Chọn ngẫu nhiên một số trong tập
hợp
X
. Tính xác suất
P
để số được chọn chia hết cho
3
.
A.
1
.
3
P =
B.
3
.
10
P =
C.
25
.
54
P =
D.
149
.
450
P =
Câu 42. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với
,2AB a AD a==
; cạnh
bên
SA a=
và vuông góc với đáy. Khoảng cách từ điểm A đến mặt phẳng
( )
SBD
bằng:
A.
2
3
a
. B.
23
3
a
. C.
25
5
a
. D.
3
2
a
.
Câu 15.Câu 43. Cho hàm số y =
3 2 3
3x mx m−+
(1) ( m là tham số) . Tìm m thuộc
khoảng nào sau đây sao cho đồ thị của hàm số (1) có hai điểm cực trị A,B đồng thời
diện tích của tam giác OAB bằng 16 (đvdt).( với O là gốc toạ độ)
A.m
4
( 3; )
3
−
B.m
1
( ;2)
4
C.m
(2;3)
D.m
( 4; 2) − −
Câu 44.Tìm tất cả các giá trị nguyên của tham số m
20;20−
để phương trình:
11
2 . 3 5 0
16 4
xx
mm
− + − =
có hai nghiệm âm phân biệt.
A.16. B.17. C.41. D. 40.
1,8m
1dm
1dm
3m
1,3m

Trang 162
Câu 45. Cho hàm số
()fx
có đạo hàm dương, liên tục trên
1
;
2
+
và thỏa mãn điều
kiện
1
( ) 0,
2
f x x
. Biết
1
(1)
4
f =
,
()
'( )
21
fx
fx
x
=
−
và tổng
2
(1) (2) (3) ... (2019)
a
P f f f f
b
= + + + + =
với
,a b N
và
a
b
là phân số tối giản. Tính
tổng
ab+
.
A.
2021.ab+=
B.
2020.ab+=
C.
2019.ab+=
D.
2022.ab+=
Câu 46.Giá trị của tích phân I =
1
2
0
ln(1 )
ln
1
xa
dx c
xb
+
=
+
,
( với b ,c là hai số nguyên dương nhỏ nhất
và a
R
). Khi đó tích
P = a .b.c thuộc khoảng nào sau đây? A.
( )
50;51
B.
( )
51;52
C.
( )
49;50
D.
( )
43;44
Câu 47. Cho hình chóp S.ABC có tất cả các cạnh bằng nhau và khoảng cách giữa hai cạnh
SA và
BC bằng
2
2
a
. Tính theo a thể tích của khối chóp S.ABC .
A.
3
.2
12
a
B.
3
2 . 2
3
a
C.
3
9 . 2
4
a
D.
3
.2
6
a
Câu 48.Cho một mặt cầu bán kính bằng
1
. Xét các hình chóp tam giác đều ngoại tiếp mặt
cầu trên. Hỏi thể tích nhỏ nhất của chúng là bao nhiêu?
A.
min 8 3V =
. B.
min 4 3V =
.
C.
min 9 3V =
. D.
min 16 3V =
.
Câu 49.Trong không gian với hệ toạ độ Oxyz cho ba điểm A(1;1;-2), B(-1;3;1),C(0;2;3)
và mặt phẳng (P) : 2x - y + 3z + 2 = 0. Một điểm M( x;y;z) thuộc (P) thoả mãn MA = MB
= MC. Tính tổng T = x + y +z.A.
89
14
−
. B.
83
14
−
. C.
87
14
−
. D.
79
14
−
.
Câu 50.Trong không gian với hệ toạ độ Oxyz cho phương trình mặt phẳng (Q): x +2y + 2z
– 1 = 0 , mặt phẳng (P) chứa trục Oz mp(P) có dạng: Ax + By = 0,
22
0AB+
và mp (P)
tạo với (Q) một góc nhỏ nhất.Tinh tích A = 2A.B (A và B là 2 số nguyên dương nhỏ
nhất)
A. 4. B. 8. C. -4. D. -8.
Giải: (VDC)

Trang 163
Câu 16.Câu 43: Cho hàm số y =
3 2 3
3x mx m−+
(1) ( m là tham số) . Tìm m thuộc
khoảng nào sau đây sao cho đồ thị của hàm số (1) có hai điểm cực trị A,B đồng thời
diện tích của tam giác OAB bằng 16 (đvdt).( với O là gốc toạ độ)
A.m
4
( 3; )
3
−
B.m
1
( ;2)
4
C.m
(2;3)
D.m
( 4; 2) − −
HD: y’ = 3
2
6x mx−
, y’ = 0
0
2
A
B
x
xm
=
=
( m
0
)
3
3
3
A
B
ym
ym
=
=−
Câu 17.
1
.d
2
OAB
S OA
=
( d = d(B,OA) =
2m
vì O,A
)Oy
3
1
.2
2
OAB
S m m
=
3
1
.2
2
mm
= 16
2
2
m
m
=
=−
Chọn đáp án A.
Câu 44:Tìm tất cả các giá trị nguyên của tham số m
20;20−
để phương trình:
11
2 . 3 5 0
16 4
xx
mm
− + − =
có hai nghiệm âm phân biệt.
A.16. B.17. C.41. D. 40.
HD: Đặt t =
1
4
x
. ( t > 0) .Suy ra x =
1
4
log t
Ta có phương trình:
2
2 3 5 0t mt m− + − =
.(*) Theo YCBT tìm m để (*) có 2 nghiệm phân
biệt
12
,tt
thoả: 1<
12
tt
Câu 18.
=
2
35mm−+
> 0,
m
. Suy ra
2
1
3 5 1t m m m= − − +
4m
Vì m là số nguyên
thuộc
20;20−
Và m > 4 . Suy ra có 16 giá trị nguyên của m thoả mãn theo yêu cầu của bài toán
Chọn đáp án A.
Câu 45. Cho hàm số
()fx
có đạo hàm dương, liên tục trên
1
;
2
+
và thỏa mãn điều
kiện
1
( ) 0,
2
f x x
. Biết
1
(1)
4
f =
,
()
'( )
21
fx
fx
x
=
−
và tổng
2
(1) (2) (3) ... (2019)
a
P f f f f
b
= + + + + =
với
,a b N
và
a
b
là phân số tối giản. Tính
tổng
ab+
.
A.
2021.ab+=
B.
2020.ab+=
C.
2019.ab+=
D.
2022.ab+=
HD: Giải: Xét trên khoảng
1
;
2
+
()
'( )
21
fx
fx
x
=
−
'( ) 1
( ) 2 1
fx
f x x
=
−
. Lấy nguyên hàm hai vế, ta có:
Trang 164
'( ) 1
( ) 2 1
fx
dx dx
f x x
=
−
( Có công thức
11
.2 ax+b
ax+b
dx C
a
=+
)
( ( ))
21
()
d f x
xC
fx
= − +
(với
C
là hằng số). (Có công thức
2
du
uC
u
=+
)
2 ( ) 2 1f x x C = − +
1
( ) 2 1
2
f x x C = − +
Vì
1
(1)
4
f =
nên
0C =
. Do đó
( )
11
( ) 2 1 ( ) 2 1
24
f x x f x x= − = −
f(1) =
1
4
; f(2) =
3
4
; f(3)=
5
4
;…………….f(2019) =
4037
4
Suy ra
(1) (2) (3) ... (2019)P f f f f= + + + +
=
( )
1
1 3 5 ...... 4037
4
+ + + +
( Cấp số cộng
1
1, 2ud==
)
=
( )
2
1 2019 2019
. 1 4037
4 2 2
+=
, suy ra a= 2019, b=2. Chọn đáp án A.
Hay sử dụng máy tính:
2019 2019
11
1
( ) (2 1) 1019090,25
4
xx
f x x
==
= − =
. Bấm shift, Sto, A. Ta có:
2019
2
A =
.
Chọn Đáp án : A.
Câu 46.Giá trị của tích phân I =
1
2
0
ln(1 )
ln
1
xa
dx c
xb
+
=
+
( với b ,c là hai số nguyên dương nhỏ nhất
và a
R
). Khi đó tích
P = a .b.c thuộc khoảng nào sau đây?
A.
( )
50;51
B.
( )
51;52
C.
( )
49;50
D.
( )
43;44
HD:
Đặt : x = tant (t
;
22
−
. Suy ra dx = 1 + tan
2
t dt. Đổi cận: x = 0
0t=
; x= 1
4
t
=
I =
2
4
2
0
ln(1 tan )(1 tan )
1 tan
tt
dt
t
++
+
=
4
0
ln(1 anx)dxt
+
Đặt t =
4
x
−
dt dx = −
. Đổi cận: x =0
4
t
=
;
x
=
4
0t=
.
I =
4
0
2
ln( )
1 tan
dt
t
+
=
4
0
2
ln( )
1 tanx
dx
+
= ln2
4
0
dx
- I = ln2.
4
0
x
- I =
4
ln2 - I
Suy ra I =
ln2
8
,suy ra a =
,b=8,c=2 .
Chọn Đáp án A.

Trang 165
M
J
H
I
C
B
A
S
Câu 47: Cho hình chóp S.ABCD có tất cả các cạnh bằng nhau và khoảng cách giữa hai cạnh
SA và
BC bằng
2
2
a
. Tính theo a thể tích của khối chóp S.ABC .
A.
3
.6
16
a
B.
3
.6
8
a
C.
3
.6
12
a
D.
3
.6
6
a
HD:
Gọi độ dài cạnh của hình chóp là 2x (x>0).M là trung điểm của cạnh AD, suy ra OM = x
Tam giác SOD vuông tại O, OD =
2x
, SD = 2x . Suy ra SO =
2x
Trong tam giác SOM ( tam giác này vuông tại O)dựng OH
SM⊥
, Chứng minh OH
⊥
(SAD)
Suy ra d( O; (SAD) = OH và
2 2 2
1 1 1
OH OM OS
=+
=
22
11
2xx
+
6
3
x
OH=
BC //AD
BC// (SAD)
d(BC;SA) = 2d(O;(SAD)) = 2OH
2
2
a
=
2
6
3
x
3
4
a
x=
Câu 19.Suy ra :
.
1
.
3
S ABCD ABCD
V SO S==
3
.6
16
a
Câu 20.Chọn Đáp Án: A.
Câu 48.Cho một mặt cầu bán kính bằng
1
. Xét các hình chóp tam giác đều ngoại tiếp mặt
cầu trên. Hỏi thể tích nhỏ nhất của chúng là bao nhiêu?
A.
min 8 3V =
. B.
min 4 3V =
.
C.
min 9 3V =
. D.
min 16 3V =
.
Hướng dẫn giải
Gọi cạnh đáy của hình chóp là
a
Ta có
SIJ SMH~
( )
( )
( )
( )
22
2
2 2 2
2 2 2 2
2 2 2
2
2
2
1
( 2 1)
12 2 0
2
12
12
SI IJ
MH SH IH IJ SH HM
SM MH
MH SH SH HM
MH SH SH SH HM
a SH a SH
a
SH a
a
= − = +
− = +
− + = +
− − =
=
−
4
2
24
1 3 2 3 1
.
1 12
3 12 12 6
ABC
a
V S SH
a
aa
= = =
−
−
Ta có
24
1 12 1
48aa
−
83S
Chọn đáp án: A

Trang 166
Câu 49.Trong không gian với hệ toạ độ Oxyz cho ba điểm A(1;1;-2), B(-1;3;1),C(0;2;3)
và mặt phẳng (P) : 2x - y + 3z + 2 = 0. Một điểm M( x;y;z) thuộc (P) thoả mãn MA = MB
= MC. Tính tổng T = x + y +z.
A.
89
14
−
. B.
83
14
−
. C.
87
14
−
. D.
79
14
−
.
HD: Theo YCBT:
22
22
()MP
MA MB
MA MC
=
=
( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( )
2 2 2 2 2 2
2 2 2 2 2
2
2 3 2
1 1 2 1 3 1
1 1 2 2 3
x y z
x y z x y z
x y z x y z
− + = −
− + − + + = + + − + −
− + − + + = + − + −
2 3 2
4 4 6 5
2 2 10 7
x y z
x y z
x y z
− + = −
− − = −
− − = −
54
14
47
14
9
14
x
y
z
−
=
−
=
=
Suy ra T = x + y + z =
89
14
−
Chọn Đáp án: A.
Câu 50.Trong không gian với hệ toạ độ Oxyz cho phương trình mặt phẳng (Q): x +2y + 2z
– 1 = 0 , mặt phẳng (P) chứa trục Oz mp(P) có dạng: Ax + By = 0,
22
0AB+
Và mp (P) tạo với (Q) một góc nhỏ nhất.Tinh tích A = 2A.B
(A và B là 2 số nguyên dương nhỏ nhất)
A. 4. B. 8. C. -4. D. -8.
HD: (P) chứa Oz .suy ra pt mp(P): Ax+By =0 (
22
0AB+
)
VTPT của mp(P) là
1
( ; ;0)n A B=
, VTPT của mp(Q) là
2
(1;2;2)n =
Ta có: cos((P),(Q)) =
12
11
.
.
nn
nn
=
( )
2
2
2
22
22
2
2
2
11
33
3.
1
A
AB
AB
B
AB
A
AB
B
+
+
+
==
+
+
+
(B
0
)
Đặt: t =
A
B
. Theo YCBT ta tìm t sao cho hàm số : y =
( )
2
2
2
1
t
t
+
+
đạt giá trị lớn nhất.
Bấm máy tính suy ra giá trị của t =
1
2
Suy ra
A
B
=
1
2
suy ra a =1; b =2
Chọn đáp án: A.
Bấm Tải xuống để xem toàn bộ.




