TOP 10 đề tự luận ôn tập kiểm tra cuối học kì 1 Toán 10 có lời giải chi tiết

iới thiệu đến quý thầy, cô giáo và các em học sinh tuyển tập 10 đề tự luận ôn tập kiểm tra cuối học kì 1 Toán 10 có lời giải chi tiết. Tài liệu gồm 95 trang, được biên soạn bởi thầy giáo Hoàng Xuân Nhàn, mời bạn đọc đón xem

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 10

Môn: Toán 10

Thông tin:

95 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
Năm học 2022 - 2023
10 đề tự luận
100 câu trắc nghiệm
Hoàng Xuân Nhàn
Đề số 01: ........................................................................................................... 01
Hướng dẫn giải Đề số 01: ............................................................................... 02
Đề số 02: ........................................................................................................... 07
Hướng dẫn giải Đề số 02: ............................................................................... 08
Đề số 03: ........................................................................................................... 12
Hướng dẫn giải Đề số 03: ............................................................................... 13
Đề số 04: ........................................................................................................... 17
Hướng dẫn giải Đề số 04: ............................................................................... 18
Đề số 05: ........................................................................................................... 22
Hướng dẫn giải Đề số 05: ............................................................................... 23
Đề số 06: ........................................................................................................... 28
Hướng dẫn giải Đề số 06: ............................................................................... 29
Đề số 07: ........................................................................................................... 33
Hướng dẫn giải Đề số 07: ............................................................................... 34
Đề số 08: ........................................................................................................... 38
Hướng dẫn giải Đề số 08: ............................................................................... 39
Đề số 09: ........................................................................................................... 42
Hướng dẫn giải Đề số 09: ............................................................................... 43
Đề số 10: ........................................................................................................... 47
Hướng dẫn giải Đề số 10: ............................................................................... 48
100 Câu trắc nghiệm Toán 10 ôn tập học kì 1: ............................................ 52
Hướng dẫn giải 100 câu trắc nghiệm toán 10: ............................................. 65
MỤC LỤC
1
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
ÑEÀ REØN LUYEÄN SOÁ 01
Time: 90 phuùt
Câu 1. Cho đoạn
( )
5;1 , 3;2= − = −AB
. Tìm
,A B A B
,
\,AB
( )
,C A C A B
.
Câu 2. Tìm tập xác định của các hàm số sau:
a)
1yx=+
; b)
( )
3 1 1
2
x
y
xx
−+
=
+
.
Câu 3. Xác định hàm số bậc hai có đồ thị là parabol
( )
P
biết:
a)
( )
2
:4P y ax x c= − +
có đnh l
( )
2; 1I −−
.
b)
( )
2
:P y ax bx c= + +
đi qua điểm
( )
0;5A
v có đnh
( )
3; 4I −
.
Câu 4. Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau:
20
5 4.
25
xy
xy
xy
−
− −
+
Câu 5.
a) Cho
2
cos
3
=−
và
( )
00
90 ;180
. Tính
sin , tan

và
cot
.
b) Cho
tan 2
=
. Tính
33
sin cos
sin 3cos 2sin
C

−
=
++
.
Câu 6. Trên nóc một tòa nhà có một cột ăng-ten cao 5 m. Từ
vị trí quan sát A cao 7 m so với mặt đất, có thể nhìn
thấy đnh B và chân C của cột ăng-ten dưới góc 50
o
và
40
o
so với phương nằm ngang. Tính chiều cao của tòa
nh đó.
Câu 7. Cho tam giác ABC. Xác định các vectơ:
a)
44u AB AC=−
;
b)
24v AB AC BC= + −
.
Câu 8. Cho năm điểm O, A, B, C, D . Chứng minh ba điểm A,
B, C thẳng hàng biết rằng:
a)
2 3 0OA OB OC+ − =
; b)
2 4 3 0OA BD OC DO AD+ − + − =
.
Câu 9. Một nhóm 11 học sinh tham gia một kì thi. Số điểm thi của 11 học sinh đó được sắp xếp từ thấp
đến cao theo thang điểm 100 như sau: 0; 0; 63; 65; 69; 70; 72; 78; 81; 85; 89.
a) Tìm điểm số trung bình của nhóm 11 học sinh này.
b) Tìm trung vị và mốt của mẫu số liệu đã cho.
Câu 10. Một xưởng sản xuất hai loại sản phẩm là sản phẩm loại I và sản phẩm loại II:
• Mỗi kg sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, thu lời được 40 nghìn.
• Mỗi kg sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ, thu lời được 30 nghìn.
Xưởng có 200 kg nguyên liệu và 1200 giờ làm việc tối đa. Nên sản xuất mỗi loại sản phẩm bao nhiêu để
có mức lời cao nhất?
================HẾT===============
2
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Höôùng daãn giaûi ñeà soá 01
Câu 1. Cho đoạn
( )
5;1 , 3;2= − = −AB
. Tìm
,A B A B
,
\,AB
( )
,C A C A B
.
Hướng dẫn giải:
Ta có:
) (
5;2 , 3;1 = − = −A B A B
,
\ 5; 3 .= − −AB
( ) ( ) ( ) ( ) ( )
)
\ ; 5 1; , \ ; 5 2; .= = − − + = = − − +C A A C A B A B
Câu 2. Tìm tập xác định của các hàm số sau:
a)
1yx=+
; b)
( )
3 1 1
2
x
y
xx
−+
=
+
.
Hướng dẫn giải:
a) Hm số xác định khi v ch khi
1 0 1xx+ −
.
Tập xác định hm số:
)
1;= − + D
.
d) Hm số xác định khi v ch khi
2 0 2
0
00
xx
x
xx
+ −




.
Tập xác định hm số:
( )
0;D = +
.
Câu 3. Xác định hàm số bậc hai có đồ thị là parabol
( )
P
biết:
a)
( )
2
:4P y ax x c= − +
có đnh l
( )
2; 1I −−
.
b)
( )
2
:P y ax bx c= + +
đi qua điểm
( )
0;5A
v có đnh
( )
3; 4I −
.
Hướng dẫn giải:
a)
( )
P
có đnh
( )
2; 1I −−
nên
( ) ( )
2
4
2
1
22
5
. 2 4 2 1
I
I
b
x
a
aa
c
y a c
= − = = −
=−

=−
= − − − + = −
.
Vậy hàm số bậc hai được xác định là
2
45y x x= − − −
.
b)
( )
P
qua
( )
0;5A
nên
5c =
; honh độ đnh
3 6 0
2
I
b
x a b
a
= − = + =
(1).
Mặt khác điểm
( )
3; 4I −
thuộc (P) nên
2
4 .3 .3a b c− = + +
5
9 3 9 3 3
c
a b a b
=
+ = − + = −
(2).
Giải hệ phương trình (1), (2) ta có:
1, 6ab= = −
. Vậy hàm số được xác định:
2
65y x x= − +
.
Câu 4. Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau:
20
5 4.
25
xy
xy
xy
−
− −
+
3
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Hướng dẫn giải:
Vẽ các đường thẳng
12
: 2 0, :5 4,d x y d x y− = − = −
3
: 2 5.d x y+=
Ta thấy
( )
1;1M
thỏa mãn miền nghiệm
của hệ bất phương trình vì khi thay
1, 1xy==
vào hệ,
ta có:
1 2.1 0
5.1 1 4
1 2.1 5
−
− −
+
(đúng).
Gạch bỏ các phần không thuộc miền nghiệm của mỗi bất
phương trình (nửa mặt phẳng có bờ l các đường
1 2 3
,,d d d
và không chứa điểm M) . Khi đó, miền nghiệm của bất phương trình chính l miền
của tam giác ABC (kể cả ba cạnh của nó) , trong đó
3 29
;
11 11
A

−


,
55
;
24
B



,
84
;
99
C

−−


.
Câu 5.
a) Cho
2
cos
3
=−
và
( )
00
90 ;180
. Tính
sin
và
cot
.
b) Cho
tan 2
=
. Tính
33
sin cos
sin 3cos 2sin
C

−
=
++
.
Hướng dẫn giải:
a) Vì
( )
00
90 ;180
nên
sin 0
.
Ta có:
2 2 2 2
45
sin cos 1 sin 1 cos 1
99
+ = = − = − =
mà
sin 0
, nên
5
sin
3
=
;
2
cos 2
3
cot
sin
55
3
−
= = = −
.
b) Do
sin
tan 2 cos 0
cos

= =
.
Chia cả tử và mẫu của T cho
3
cos x
, ta có:
3 3 2 2
33
3
2
3 3 3
sin cos sin 1 1
.
cos cos cos cos cos
sin 1
sin 3cos 2sin
tan 3 2 .
cos cos
cos cos cos
−−
==
++
++
C

( ) ( )
( )
22
32
tan tan 1 tan 1
tan 3 2tan tan 1
+ − +
=
+ + +
.
4
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Suy ra
( ) ( )
( )
( )
3 2 1
2 2 1 2 1
2 2 3 2 2 2 1 3 8 2
C
−
+ − +
==
+ + + +
.
Câu 6. Trên nóc một tòa nhà có một cột ăng-ten cao 5 m. Từ vị trí quan sát A cao 7 m so với mặt đất, có
thể nhìn thấy đnh B và chân C của cột ăng-ten dưới góc 50
o
và 40
o
so với phương nằm ngang. Tính
chiều cao của tòa nh đó.
Hướng dẫn giải:
Xét tam giác ABC có
0 0 0
50 40 10A = − =
,
0 0 0
90 50 40B =−=
.
Áp dụng định lí Sin cho tam giác ABC ta có;
0
0
sin 5sin 40
18,5 m
sin sin10
aB
AC b
A
= = =
.
Xét tam giác ACD vuông tại D:
00
sin40 .sin40 11,89 m
CD
CD AC
AC
= =
.
Suy ra:
18,89 mCH CD DH= +
. Vậy chiều cao tòa nhà xấp x
18,89 m
.
Câu 7. Cho tam giác ABC. Xác định các vectơ:
a)
44u AB AC=−
; b)
24v AB AC BC= + −
.
Hướng dẫn giải:
a) Ta có:
( )
4 4 4 4u AB AC AB AC CB= − = − =
.
b) Ta có:
24v AB AC BC= + −
( )
23AB AC AC BC= + + −
23AB AC AB= + +
( )
3 AB AC=+
3.2 6AI AI==
(với I l trung điểm đoạn BC).
Câu 8. Cho năm điểm O, A, B, C, D . Chứng minh ba điểm A, B, C thẳng hàng biết rằng:
a)
2 3 0OA OB OC+ − =
; b)
2 4 3 0OA BD OC DO AD+ − + − =
.
Định hướng:
a) Biến đổi hệ thức và khử (làm mất) điểm O để hệ thức sau cùng chỉ còn chứa ba điểm A, B, C.
5
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
b) Biến đổi và khử (làm mất) hai điểm O, D để hệ thức sau cùng chỉ còn chứa ba điểm A, B, C.
Hướng dẫn giải:
a) Ta có:
2 3 0 2 2 3 3 0
3
2 3 0 .
2
+ − = + + − − =
− = =
OA OB OC OA OA AB OA AC
AB AC AB AC
Vậy hai vectơ
,AB AC
cùng phương nên ba điểm A, B, C thẳng hàng.
b) Ta có:
2 4 3 0+ − + − =OA BD OC DO AD
( ) ( )
4 3 0 − + − + − =OA OC OA OD BD AD
( )
4 3 0 3 0CA DA BD AD CA DA BD BD AD + + − = + + + − =
30CA BA BA + + =
1
4
4
BA AC AB AC = = −
.
Vậy hai vectơ
,AB AC
cùng phương nên ba điểm A, B, C thẳng hàng.
Câu 9. Một nhóm 11 học sinh tham gia một kì thi. Số điểm thi của 11 học sinh đó được sắp xếp từ thấp
đến cao theo thang điểm 100 như sau: 0; 0; 63; 65; 69; 70; 72; 78; 81; 85; 89.
a) Tìm điểm số trung bình của nhóm 11 học sinh này.
b) Tìm trung vị và mốt của mẫu số liệu đã cho.
Hướng dẫn giải:
a) Điểm trung bình là:
x
=
0 0 63 ... 85 89 672
11 11
+ + + + +
=
61,09.
b) Vì
11n =
(lẻ) nên trung vị là số chính giữa của mẫu số liệu này (vị trí thứ 6). Vậy trung vị là 70.
Vì giá trị 0 xuất hiện 2 lần (nhiều nhất) trong mẫu số liệu nên 0 là mốt của mẫu số liệu này.
Câu 10. Một xưởng sản xuất hai loại sản phẩm là sản phẩm loại I và sản phẩm loại II:
• Mỗi kg sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, thu lời được 40 nghìn.
• Mỗi kg sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ, thu lời được 30 nghìn.
Xưởng có 200 kg nguyên liệu và 1200 giờ làm việc tối đa. Nên sản xuất mỗi loại sản phẩm bao nhiêu để
có mức lời cao nhất?
Hướng dẫn giải:
Gọi
,xy
lần lượt là số kg sản phẩm loại I và loại II m xưởng
sản xuất được.
Tổng nguyên liệu được dùng là 2x + 4y (kg); tổng thời gian sản
xuất là 30x + 15y (giờ); x , y
0.
Ta có hệbất phương trình:
2 4 200
30 15 1200
0
0
xy
xy
x
y
+
+
2 100
2 80
0
0
xy
xy
x
y
+
+
.
Vẽ trên cùng hệ trục các đường thẳng
1
: 2 100d x y+=
,
2
:2 80d x y+=
,
3
:0dy=
,
4
:0dx=
.
6
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Ta có điểm
( )
1;1M
thuộc miền nghiệm của hệ bất phương trình vì khi thay tọa độ điểm này vào hệ:
1 2.1 100
2.1 1 80
10
10
+
+
(đúng).
Gạch bỏ các phần không thuộc miền nghiệm của mỗi bất phương trình trong hệ (nửa mặt phẳng có
bờ l các đường thẳng
1 2 3 4
, , ,d d d d
và không chứa điểm M). Khi đó miền nghiệm của hệ bất phương
trình chính là miền của tứ giác OABC (kể cả các cạnh của tứ giác đó) với
( ) ( )
0;0 , 0;50 ,OA
( ) ( )
20;40 , 40;0BC
.
Lãi thu về từ việc sản xuất hai sản phẩm:
( )
; 40 30F x y x y=+
(nghìn đồng).
Tại
( )
0;0O
, ta có
( )
0;0 0F =
; tại
( )
0;50A
, ta có
( )
0 ; 50 1500F =
; tại
( )
20;40B
, ta có
( )
20 ; 40 2000F =
; tại
( )
40;0C
, ta có
( )
40 ; 0 1600F =
.
Vậy lãi suất cao nhất thu được bằng 2 000 000 đồng, khi đó
20, 40xy==
(tức l xưởng cần sản
xuất ra 20 sản phẩm loại I và 40 sản phẩm loại II).
7
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
ÑEÀ REØN LUYEÄN SOÁ 2
Time: 90 phuùt
Câu 1. Viết các tập hợp sau bằng cách liệt kê các phần tử của nó:
a)
22
0( )( 2 2)2 3 –A x x x x x= − − =
; b)
*2
3 30B x n=
.
Câu 2. Cho các tập hợp
( )
;Am= −
và
3 1;3 3B m m= − +
. Tìm
m
để
A C B
.
Câu 3. Tìm tập xác định của các hàm số sau:
a)
2 3 1y x x= − + +
; b)
2
1
23
x
y
xx
−
=
−+
;
Câu 4. Xét sự biến thiên của các hàm số sau trên khoảng
( )
1; +
:
a)
( )
3
1
fx
x
=
−
; b)
( )
1
f x x
x
=+
.
Câu 5. Biểu diễn miền nghiệm của hệ bất phương trình sau:
4
22
8
6; 6
xy
xy
xy
xy
− −
− + −
+
−
.
Câu 6. Lập bảng biến thiên và cho biến sự đồng biến, nghịch biến của hàm số. Tìm giá trị lớn nhất, nhỏ
nhất (nếu có) của hàm số trên tập xác định của nó.
a)
2
25y x x= − + −
; b)
2
3yx= − +
;
Câu 7. Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ
nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ. Biết chiều
cao cổng parabol là 4 m, cửa chính (ở giữa parabol) cao 3 m và
rộng 4 m. Tính khoảng cách giữa hai chân cổng parabol ấy
(đoạn AB trên hình vẽ).
Câu 8. Khoảng cách từ
A
đến
B
không thể đo trực tiếp được vì phải
qua một đầm lầy. Người ta xác định được một điểm
C
mà từ đó
có thể nhìn được
A
và
B
dưới một góc
60
. Biết
200 mCA =
,
180 mCB =
. Khoảng cách
AB
bằng bao nhiêu?
Câu 9. Cho hình bình hành ABCD có tâm O, M là một điểm bất kỳ.
Chứng minh rằng:
a)
56AB AC AD AC+ + =
;
b)
4MA MB MC MD MO+ + + =
.
Câu 10. Cho tam giác
ABC
và một điểm M tùy ý, G là trọng tâm tam giác ABC. Điểm N thỏa mãn
4MN MA MB MC= + +
. Chứng minh rằng đường thẳng MN luôn qua một điểm cố định.
================HẾT===============
8
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Höôùng daãn giaûi ñeà soá 02
Câu 1. Viết các tập hợp sau bằng cách liệt kê các phần tử của nó:
a)
22
0( )( 2 2)2 3 –A x x x x x= − − =
; b)
*2
3 30B x n=
.
Hướng dẫn giải:
a)
1
;0;2
2
A

=−


vì
2
22
2
.(
2
)
0
20
22( 3 – 2 0 2
2 3 2
1
)
0
x
xx
x x x x x
xx
x
=
−=
− − = =
− − =
=−
b)
2;3;4;5B =
.
Câu 2. Cho các tập hợp
( )
;Am= −
và
3 1;3 3B m m= − +
. Tìm
m
để
A C B
.
Hướng dẫn giải:
Ta có:
( ) ( )
;3 1 3 3;C B m m= − − + +
. Vì vậy:
A C B
31mm −
1
2
m
.
Câu 3. Tìm tập xác định của các hàm số sau:
a)
2 3 1y x x= − + +
; b)
2
1
23
x
y
xx
−
=
−+
;
Hướng dẫn giải:
a) Hàm số xác định khi và chỉ khi
3 0 3
13
1 0 1
xx
x
xx
−

−

+ −

.
Tập xác định hàm số:
1;3D =−
.
b) Hàm số xác định khi và chỉ khi
( )
2
2
2 3 0 1 2 0x x x x− + − +
. Tập xác định
hàm số:
D =
.
Câu 4. Xét sự biến thiên của các hàm số sau trên khoảng
( )
1; +
:
a)
( )
3
1
fx
x
=
−
; b)
( )
1
f x x
x
=+
.
Hướng dẫn giải:
a) Xét
( )
12
, 1;xx +
và
12
xx
.
Khi đó:
( ) ( )
( ) ( )
( )( )
( )
( )( )
2 1 2 1
12
1 2 1 2 1 2
3 1 3 1 3
33
1 1 1 1 1 1
x x x x
f x f x
x x x x x x
− − − −
− = − = =
− − − − − −
.
Vì
( ) ( ) ( )( )
1 2 2 1 1 2 1 2
3 0; , 1; 1 1 0x x x x x x x x − + − −
.
Suy ra
( )
( )( )
( ) ( ) ( ) ( )
21
1 2 1 2
12
3
00
11
xx
f x f x f x f x
xx
−
−
−−
Vậy hàm số đã cho nghịch biến trên khoảng
( )
1; +
.
9
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
b) Xét
( )
12
, 1;xx +
và
12
xx
. Khi đó:
( ) ( ) ( )
21
1 2 1 2 1 2
1 2 1 2
11
xx
f x f x x x x x
x x x x

−
− = + − + = − +


( ) ( )
12
1 2 1 2
1 2 1 2
1
1
1
xx
x x x x
x x x x
−
= − − = −
.
Vì
( )
12
1 2 1 2 1 2
12
1
0; , 1; 0
xx
x x x x x x
xx
−
− +
.
Suy ra
( ) ( ) ( ) ( ) ( )
12
1 2 1 2 1 2
12
1
00
xx
x x f x f x f x f x
xx

−
− −


.
Vậy hàm số đã cho đồng biến trên khoảng
( )
1; +
.
Câu 5. Biểu diễn miền nghiệm của hệ bất phương trình sau:
4
22
8
6; 6
xy
xy
xy
xy
− −
− + −
+
−
.
Hướng dẫn giải:
Vẽ các đường thẳng
12
: 4, : 2 2,d x y d x y− − = − + = −
3 4 5
: 8, : 6, : 6d x y d x d y+ = = − =
.
Ta có điểm
( )
0;0O
thuộc miền nghiệm của hệ bất phương trình
vì khi thay
0, 0xy==
vào hệ, ta được:
0 4, 0 2, 0 8, 0 6, 0 6 − −
(đúng).
Gạch bỏ các phần không thuộc miền nghiệm của mỗi bất phương
trình trong hệ (nửa mặt phẳng có bờ là các đường thẳng
1 2 3 4 5
, , , ,d d d d d
và không chứa điểm O). Khi đó miền nghiệm của
hệ bất phương trình chính là miền của ngũ giác ABCDE (không kể
các cạnh BC, CD, DE) với
( ) ( ) ( ) ( ) ( )
6;6 , 6;2 , 2; 2 , 6;2 , 2;6 .A B C D E− − − −
Câu 6. Lập bảng biến thiên và cho biến sự đồng biến, nghịch biến của hàm số. Tìm giá trị lớn nhất, nhỏ
nhất (nếu có) của hàm số trên tập xác định của nó.
a)
2
25y x x= − + −
; b)
2
3yx= − +
;
Hướng dẫn giải:
a)
2
25y x x= − + −
; (
1, 2, 5a b c= − = = −
).
Tọa độ đỉnh I của parabol:
( )
2
1, 1 2.1 5 4 hay 1; 4
2
II
b
x y I
a
= − = = − + − = − −
.
Định hướng cho bảng biến thiên: Do
10a = −
nên bề lõm parabol hướng xuống.
Bảng biến thiên:
Kết luận:
10
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
• Hàm số đã cho đồng biến trên khoảng
( )
;1−
và
nghịch biến trên khoảng
( )
1;+
.
• Giá trị lớn nhất của hàm số là
max
4y =−
, khi đó
1x =
.
(Hàm số không có giá trị nhỏ nhất).
b)
2
3yx= − +
; (
1, 0, 3a b c= − = =
).
b) Tọa độ đỉnh I của parabol:
( )
2
0, 0 3 3 hay 0;3
2
II
b
x y I
a
= − = = − + =
.
Định hướng cho bảng biến thiên: Do
10a = −
nên bề lõm parabol hướng xuống.
Bảng biến thiên:
Kết luận:
• Hàm số đã cho đồng biến trên khoảng
( )
;0−
và nghịch biến trên khoảng
( )
0;+
.
• Giá trị lớn nhất của hàm số là
max
3y =
, khi
đó
0x =
. (Hàm số không có giá trị nhỏ nhất).
Câu 7. Một chiếc cổng hình parabol bao gồm một cửa chính hình
chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ.
Biết chiều cao cổng parabol là 4 m, cửa chính (ở giữa
parabol) cao 3 m và rộng 4 m. Tính khoảng cách giữa hai
chân cổng parabol ấy (đoạn AB trên hình vẽ).
Hướng dẫn giải:
Dựng trục Oxy như hình vẽ. Gọi
( ) ( )
2
:0P y ax bx c a= + +
.
Vì
( )
P
qua các điểm
( ) ( ) ( )
0;4 , 2;3 , 2;3I E F −
nên
1
4
4
4 2 3 0
4 2 3 4
a
c
a b c b
a b c c
=−
=
+ + = =


− + = =
.
Ta có
( )
2
1
:4
4
P y x= − +
.
Hai điểm A, B là giao điểm của (P) với Ox nên hoành độ thỏa mãn
2
1
4 0 4
4
xx− + = =
.
Do vậy
( ) ( )
4;0 , 4;0 8A B AB− =
.
11
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Câu 8. Khoảng cách từ
A
đến
B
không thể đo trực tiếp được vì phải qua
một đầm lầy. Người ta xác định được một điểm
C
mà từ đó có
thể nhìn được
A
và
B
dưới một góc
60
. Biết
200 mCA =
,
180 mCB =
. Khoảng cách
AB
bằng bao nhiêu?
Hướng dẫn giải:
Ta có:
2 2 2
2 . .cos60 36 400AB CA CB CACB= + − =
20 91 190,79mAB =
.
Câu 9. Cho hình bình hành ABCD có tâm O, M là một điểm bất kỳ. Chứng minh rằng:
a)
56AB AC AD AC+ + =
; b)
4MA MB MC MD MO+ + + =
.
Hướng dẫn giải:
a) Ta có:
( )
5 5 5 6AB AC AD AB AD AC AC AC AC+ + = + + = + =
.
b) Ta có:
MA MB MC MD+ + +
MO OA MO OB MO OC MO OD= + + + + + + +
00
44MO OA OC OB OD MO
= + + + + =
.
Câu 10. Cho tam giác
ABC
và một điểm M tùy ý, G là trọng tâm tam giác ABC. Điểm N thỏa mãn
4MN MA MB MC= + +
. Chứng minh rằng đường thẳng MN luôn qua một điểm cố định.
Hướng dẫn giải:
Ta có:
( )
43= + + = + + +MN MA MB MC MN MA MA MB MC
33 = +MN MA MG
( )
36MN MA MG MN MI = + =
(với I là trung điểm AG).
Vậy hai vectơ
,MN MI
cùng phương nên ba điểm
,,M N I
thẳng hàng.
Do đó đường thẳng MN luôn qua điểm I cố định.
12
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
ÑEÀ REØN LUYEÄN SOÁ 03
Time: 90 phuùt
Câu 1. Giả sử
2;4;6 , 2;6 , 4;6 , 4;6;8A B C D= = = =
. Hãy xác định xem tập nào là tập con của
tập nào?
Câu 2. Một lớp có
45
học sinh, đăng kí chơi ít nhất một trong hai môn thể thao là bóng đá và cầu lông. Có
30
em đăng kí môn bóng đá,
25
em đăng kí môn cầu lông. Hỏi có bao nhiêu em đăng kí cả hai
môn thể thao?
Câu 3. Tìm tập xác định mỗi hàm số sau:
a)
3
1y x x= − − +
; b)
1
2
y
x
=
−
.
Câu 4. Tìm parabol
( )
2
:2P y ax bx= + +
trong các trưng hp sau:
a) Parabol
( )
P
đi qua
( )
3;4A
và có trc đối xng là
3
2
x =−
.
b) Parabol
( )
P
đi qua
( )
1;6B −
và có tung độ đnh là
1
4
−
.
Câu 5.
a) Cho
tan cot m

+=
. Tìm
m
để
22
tan cot 7

+=
.
b) Tính
0 0 0 0
tan1 tan2 tan3 ...tan89B =
.
Câu 6. Một hộ nông dân định trồng da và củ đậu trên diện tích
8ha
. Trên diện tích mỗi
ha
, nếu trồng da thì
cần 20 công và thu 3 triệu đồng, nếu trồng củ đậu thì cần 30 công và thu 4 triệu đồng. Hỏi cần trồng mỗi
loại cây trên với diện tích là bao nhiêu
ha
để thu đưc nhiều tiền nhất, biết rằng tổng số công không
quá 180?
Câu 7. Cho tam giác ABC biết cạnh a = 137,5 cm,
00
83 , 57BC==
. Tính góc A, bán kính R của đưng
tròn ngoại tiếp, cạnh b và c của tam giác.
Câu 8. Cho hình vuông ABCD có cạnh bằng 10, M là trung điểm canh AB. Tìm độ dài vectơ tổng:
a)
AB AD+
; b)
AM AD+
.
Câu 9. Cho tam giác ABC. Hai điểm M, N đưc xác định bởi các hệ thc:
0BC MA+=
,
30AB NA AC− − =
. Chng minh hai đưng thẳng MN và AC song song.
Câu 10. Khi quả bóng đưc đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của quả
bóng là một cung parabol trong mặt phẳng Oth trong đó t là thi gian (tính bằng giây) kể từ khi quả
bóng đưc đá lên, h là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng đưc đá lên từ
độ cao ban đầu 1,2m so với mặt đất; sau đó 1 giây nó đạt độ cao 8,5m; sau 2 giây nó đạt độ cao 6m.
Hãy tìm hàm số bậc hai biểu thị độ cao h theo thi gian t và có phần đồ thị trùng với quỹ đạo quả
bóng trong tình huống này.
================HẾT===============
13
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Höôùng daãn giaûi ñeà soá 03
Câu 1. Giả sử
2;4;6 , 2;6 , 4;6 , 4;6;8A B C D= = = =
. Hãy xác định xem tập nào là tập con của
tập nào?
Hướng dẫn giải:
Vì 2 ∈ A, 6 ∈ A ⇒ B ⊂ A. Vì 4 ∈ A, 6 ∈ A ⇒ C ⊂ A. Vì 4 ∈ D, 6 ∈ D ⇒ C ⊂ D.
Ngoài ra không còn tập nào là con của tập nào nữa.
Câu 2. Một lớp có
45
học sinh, đăng kí chơi ít nhất một trong hai môn thể thao là bóng đá và cầu lông. Có
30
em đăng kí môn bóng đá,
25
em đăng kí môn cầu lông. Hỏi có bao nhiêu em đăng kí cả hai
môn thể thao?
Hướng dẫn giải:
☺ Cách giải 1: Gọi x là số học sinh tham gia cả hai môn thể
thao bóng đá và cầu lông. Dựa vào biểu đồ Ven, ta có:
Số học sinh ch tham gia bóng đá là
30 x−
(em), số học sinh ch
tham gia cầu lông là
25 x−
(em).
Ta có:
( ) ( )
30 25 45 10x x x x− + + − = =
.
Vậy có 10 học sinh của lớp đăng ký cả hai môn bóng đá và cầu lông.
☺ Cách giải 2: Dựa vào công thc
A B A B A B = + −
trong đó ký hiệu
AB
là số phần
tử của tập
AB
, ký hiệu
,,A B A B
lần lưt là số phần tử của các tập
,,A B A B
.
Gọi
A
là tập hp các em học sinh đăng ký môn bóng đá,
B
là tập hp các em đăng kí cầu lông.
Số học sinh của lớp đăng ký cả hai môn thể thao trên là:
AB
.
Ta có:
A B A B A B = + −
30 25 45 10A B A B A B = + − = + − =
(em).
Vậy có
10
bạn đăng ký cả hai môn.
Câu 3. Tìm tập xác định mỗi hàm số sau:
a)
3
1y x x= − − +
; b)
1
2
y
x
=
−
.
Hướng dẫn giải:
a) Hàm số xác định với mọi x thuộc . Tập xác định hàm số:
D =
.
b) Hàm số xác định
2 0 2 2 2x x x − −
. Tập xác định hàm số:
( )
2;2D =−
.
Câu 4. Tìm parabol
( )
2
:2P y ax bx= + +
trong các trưng hp sau:
a) Parabol
( )
P
đi qua
( )
3;4A
và có trc đối xng là
3
2
x =−
.
b) Parabol
( )
P
đi qua
( )
1;6B −
và có tung độ đnh là
1
4
−
.
Hướng dẫn giải:
14
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
a)
( )
P
có trc đối xng
3
30
22
b
x a b
a
= − = − − =
(1);
( )
P
qua
( )
3;4A
nên
9 3 2 4ab+ + =
(2).
Giải hệ (1) và (2) suy ra
11
,
93
ab==
. Vậy
( )
2
11
:2
93
P y x x= + +
.
b)
( )
P
đi qua
( )
1;6 2 6 4 (1).B a b a b− − + = = +
Tung độ đnh I của parabol:
2
22
1
4 9 (2)
44
c
a b ac a b a
a
=
− = − = − = =
.
Thay (1) vào (2):
( )
22
12
9 4 9 36 0
3
b
b b b b
b
=
= + − − =
=−
.
Với
12b =
thì
16a =
, khi đó:
( )
2
: 16 12 2P y x x= + +
.
Với
3b =−
thì
1a =
, khi đó:
( )
2
: 3 2P y x x= − +
.
Câu 5.
a) Cho
tan cot m

+=
. Tìm
m
để
22
tan cot 7

+=
.
b) Tính
0 0 0 0
tan1 tan2 tan3 ...tan89B =
.
Hướng dẫn giải:
a) Ta có:
( )
2
2 2 2
7 tan cot tan cot 2 2m
= + = + − = −
2
9m=
3m =
.
b)
0 0 0 0
tan1 tan2 tan3 ...tan89B =
( ) ( ) ( )
0 0 0 0 0 0 0
tan1 tan89 . tan2 tan88 ...... tan 44 tan46 .tan45=
( ) ( ) ( )
0 0 0 0 0 0 0
tan1 .cot1 . tan2 cot 2 ...... tan 44 cot 44 .tan45 1.1......1 1= = =
.
Câu 6. Một hộ nông dân định trồng da và củ đậu trên diện tích
8ha
. Trên diện tích mỗi
ha
, nếu trồng da thì
cần 20 công và thu 3 triệu đồng, nếu trồng củ đậu thì cần 30 công và thu 4 triệu đồng. Hỏi cần trồng mỗi
loại cây trên với diện tích là bao nhiêu
ha
để thu đưc nhiều tiền nhất, biết rằng tổng số công không
quá 180.
Hướng dẫn giải:
Gọi
,xy
lần lưt là số
ha
trồng da và củ đậu. Điều kiện:
0 8, 0 8xy
.
Tổng diện tích trồng là
xy+
(ha); tổng số công cần thiết là 20x + 30y (công).
Số tiền thu đưc là
( )
, 3 4T x y x y=+
. Ta có hệ bất phương
trình
0 8 0 8
0 8 0 8
88
20 30 180 2 3 18
xx
yy
x y x y
x y x y




+ +


+ +

(*).
Miền nghiệm của hệ (*) là miền t giác
OABC
(kề cả
biên) với
( ) ( ) ( ) ( )
0;0 0;6 , 6;2 , 0;8O A B C
Khi đó
( )
,T x y
đạt cực đại tại một trong các đnh của t giác
OABC
.
Ta có:
( ) ( ) ( )
0,0 0; 0;6 24; 6;2 26;T T T= = =
( )
8;0 24T =
.
15
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Vậy giá trị lớn nhất của
( )
,T x y
bằng 26 (triệu đồng), khi đó
6, 2xy==
(tc là hộ nông dân cần trồng
6
ha
da và 2
ha
củ đậu để có thể thu lại số tiền nhiều nhất).
Câu 7. Cho tam giác ABC biết cạnh a = 137,5 cm,
00
83 , 57BC==
. Tính góc A, bán kính R của đưng
tròn ngoại tiếp, cạnh b và c của tam giác.
Hướng dẫn giải:
Ta có:
( )
( )
0 0 0 0 0
180 180 83 57 40A B C= − + = − + =
.
Theo định lí Sin:
2
sin sin sinC
a b c
R
AB
= = =
.
Suy ra
0
137,5
106,96 cm
2sin 2sin40
a
R
A
= =
;
0
0
sin 137,5.sin83
212,32 cm
sin sin 40
aB
b
A
= =
;
0
0
sin 137,5.sin57
179,4 cm
sin sin40
aC
c
A
= =
.
Câu 8. Cho hình vuông ABCD có cạnh bằng 10, M là trung điểm canh AB. Tìm độ dài vectơ tổng:
a)
AB AD+
; b)
AM AD+
.
Hướng dẫn giải:
a) Theo quy tắc hình bình hành, ta có:
AB AD AC+=
.
Theo định lí Pytago:
2 2 2 2 2
10 10 200 10 2AC AB BC AC= + = + = =
.
Vậy
10 2.AB AD AC AC+ = = =
b) Ta có:
,AM MB AD BC==
.
Khi đó:
AM AD MB BC MC+ = + =
(quy tắc ba điểm).
Áp dng định lí Pytago cho tam giác MBC:
2 2 2 2 2
5 10 125 5 5MC MB BC MC= + = + = =
.
Vậy
55AM AD MC MC+ = = =
.
Câu 9. Cho tam giác ABC. Hai điểm M, N đưc xác định bởi các hệ thc:
0BC MA+=
,
30AB NA AC− − =
. Chng minh hai đưng thẳng MN và AC song song.
Hướng dẫn giải:
Ta có:
( ) ( )
3 0 3 0BC MA AB NA AC AB BC AC MA AN+ + − − = + − + + =
3 0 2AC AC MN MN AC − + = =
.
Suy ra hai vectơ
,MN AC
cùng phương (1).
Xét:
0BC MA AM BC+ = =
. Do đó M là một đnh của hình bình hành ABCM hay M không
thuộc đưng thẳng AC (2)
Từ (1) và (2) suy ra hai đưng thẳng MN và AC song song.
16
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Câu 10. Khi quả bóng đưc đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của quả
bóng là một cung parabol trong mặt phẳng Oth trong đó t là thi gian (tính bằng giây) kể từ khi quả
bóng đưc đá lên, h là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng đưc đá lên từ
độ cao ban đầu 1,2m so với mặt đất; sau đó 1 giây nó đạt độ cao 8,5m; sau 2 giây nó đạt độ cao 6m.
Hãy tìm hàm số bậc hai biểu thị độ cao h theo thi gian t và có phần đồ thị trùng với quỹ đạo quả
bóng trong tình huống này.
Hướng dẫn giải:
Chọn hệ trc Oth như hình vẽ, gọi parabo (P):
2
h at bt c= + +
.
(P) qua ba điểm
( ) ( ) ( )
0;1,2 , 1;8,5 , 2;6A B C
nên thỏa mãn
1,2 4,9
8,5 12,2
4 2 6 1,2
ca
a b c b
a b c c
= = −


+ + = =


+ + = =

.
Vậy hàm số đưc xác định là
2
4,9 12,2 1,2y t t= − + +
.
17
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
ÑEÀ REØN LUYEÄN SOÁ 04
Time: 90 phuùt
Câu 1. Xác định các tập hợp sau:
a)
( ) ( )
3;7 0;10−
; b)
( ) ( )
;5 2;− +
.
Câu 2. Tìm tập xác định mỗi hàm số sau:
a)
3
2
2
x
y
xx
+
=
+
; b)
( )( )
22
32
1
x
y
x x x x
−
=
− + −
.
Câu 3. Tìm ta đ giao đim ca các đưng sau:
a)
( )
2
: 1, : 4 3d y x P y x x= − + = − +
;
b)
( ) ( )
22
12
: 2 1, : 2 2 2.P y x x P y x x= + − = − +
Câu 4. Đơn giản các biu thức sau (giả sử mỗi biu thức sau luôn có nghĩa):
a)
sin
cot
1 cos
x
Ax
x
=+
+
; b)
( ) ( )
2
1 sin tan 1 sinB x x x= − +
.
Câu 5. Chứng minh biu thức sau không phụ thuc vào biến x:
( )
( ) ( )
4 4 6 6
3 sin cos 2 sin cosf x x x x x= + − +
.
Câu 6. Cho bốn đim A, B, C, D. Chứng minh rằng:
a)
AB CD AD CB+ = +
; b)
AB CD AC DB− = +
.
Câu 7. Cho các tập hợp
( )
;Am= −
và
3 1;3 3B m m= − +
. Tìm
m
đ
A C B
.
Câu 8. Cho tam giác
ABC
thỏa mãn điều kiện
a b c b c a
b c a a b c
h h h h h h
h h h h h h
+ + = + +
. Chứng minh tam giác
ABC
là
tam giác cân.
Câu 9. Tìm a đ hàm số
1
3 2 2
y
x a a x
=
+ − + + −
xác định với mi
1;1x−
.
Câu 10. Cho tam giác
ABC
có trng tâm G. Tìm tập hợp đim
M
thỏa mãn mỗi hệ thức sau:
2MA MB MC AM AB+ − = −
.
Câu 11. Mt gia đình cần ít nhất 900 g chất protein và 400 g chất lipit trong thức ăn mỗi ngày. Biết rằng thịt
bò chứa 80% protein và 20% lipit. Thịt lợn chứa 60% protein và 40% lipit. Biết rằng gia đình này
chỉ mua nhiều nhất là 1 600 g thịt bò, 1 100 g thịt lợn, giá tiền 1 kg thịt bò là 45 000 đồng, 1 kg thịt
lợn là 35 000 đồng. Giả sử gia đình mua x kg thịt bò và y kg thịt lợn.
a) Lập hệ bất phương trình biu thị các điều kiện ca bài toán rồi biu diễn hình hc miền nghiệm
(S) ca hệ đó.
b) Gi T (nghìn đồng) là số tiền phải trả cho x (kilogam) thịt bò và y (kilogam) thịt lợn. Hãy biu diễn
T theo x, y.
c) Hỏi gia đình đó phải mua bao nhiêu kilogam thịt mỗi loại đ chi phí là ít nhất?
================HẾT===============
18
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Höôùng daãn giaûi ñeà soá 04
Câu 1. Xác định các tập hợp sau:
a)
( ) ( )
3;7 0;10−
; b)
( ) ( )
;5 2;− +
;
Hướng dẫn giải:
a)
( ) ( ) ( )
3;7 0;10 0;7− =
.
b)
( ) ( ) ( )
;5 2; 2;5− + =
.
Câu 2. Tìm tập xác định mỗi hàm số sau:
a)
3
2
2
x
y
xx
+
=
+
; b)
( )( )
22
32
1
x
y
x x x x
−
=
− + −
.
Hướng dẫn giải:
a) Hàm số xác định
00
2 0 2
xx
xx




+ −

.
Tập xác định hàm số:
( )
2; \ 0D = − +
.
b) Hàm số xác định
( )( )
( )
2
2
22
2
13
0
10
10
24
0
10
x
xx
x x x x
xx
xx

− +
− +

− + −


−
−
01
01
x
xx
xx
. Tập xác định hàm số:
\ 0;1D =
.
Câu 3. Tìm ta đ giao đim ca các đưng sau:
a)
( )
2
: 1, : 4 3d y x P y x x= − + = − +
;
b)
( ) ( )
22
12
: 2 1, : 2 2 2.P y x x P y x x= + − = − +
Hướng dẫn giải:
a) Phương trình hoành đ giao đim ca d và (P):
22
1
4 3 1 3 2 0
2
x
x x x x x
x
=
− + = − + − + =
=
.
Với
1x =
thì
0y =
; với
2x =
thì
1y =−
. Vậy d và (P) có hai giao đim là
( ) ( )
1;0 , 2; 1−
.
b) Phương trình hoành đ giao đim ca
( )
1
P
và
( )
2
:P
22
2 2 2 2 1x x x x− + = + −
2
4 3 0xx − + =
1
3
x
x
=
=
. Với
1x =
thì
2y =
; với
3x =
thì
14y =
.
Vậy hai parabol đã cho cắt nhau tại hai đim:
( ) ( )
1;2 , 3;14
.
Câu 4. Đơn giản các biu thức sau (giả sử mỗi biu thức sau luôn có nghĩa):
19
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
a)
sin
cot
1 cos
x
Ax
x
=+
+
; b)
( ) ( )
2
1 sin tan 1 sinB x x x= − +
.
Hướng dẫn giải:
a)
( )
( )
cos 1 cos sin .sin
sin cos sin
cot
1 cos sin 1 cos sin 1 cos
x x x x
x x x
Ax
x x x x x
++
= + = + =
+ + +
( ) ( )
22
1
sin 1 cos sin 1 cos s
cc
in
os cos sin os 1
x x x x x
x x x x
= = =
+
+
+
+
+
.
b)
( ) ( )
( )
2
2 2 2 2 2
2
sin
1 sin tan 1 sin 1 sin tan cos . sin
cos
x
B x x x x x x x
x
= − + = − = =
.
Câu 5. Chứng minh biu thức sau không phụ thuc vào biến x:
( )
( ) ( )
4 4 6 6
3 sin cos 2 sin cosf x x x x x= + − +
.
Hướng dẫn giải:
Ta có:
4 4 2 2
sin cos 1 2sin cosx x x x+ = −
,
6 6 2 2
sin cos 1 3sin cosx x x x+ = −
.
Suy ra:
( )
( ) ( )
2 2 2 2
3 1 2sin cos 2 1 3sin cos 1f x x x x x= − − − =
.
Vậy biu thức không phụ thuc vào x.
Câu 6. Cho bốn đim A, B, C, D. Chứng minh rằng:
a)
AB CD AD CB+ = +
; b)
AB CD AC DB− = +
.
Hướng dẫn giải:
a) Ta có:
AB CD AD CB+ = +
0AB CD AD CB + − − =
0AB CD DA BC + + + =
( ) ( )
0AB BC CD DA + + + =
0AC CA + =
(luôn đúng).
b) Ta có:
0AB CD AC DB AB CD AC DB− = + − − − =
0AB DC CA BD + + + =
( ) ( )
00AB BD DC CA AD DA + + + = + =
(luôn đúng).
Câu 7. Cho các tập hợp
( )
;Am= −
và
3 1;3 3B m m= − +
. Tìm
m
đ
A C B
.
Hướng dẫn giải:
Ta có:
( ) ( )
;3 1 3 3;C B m m= − − + +
.
Vì vậy:
A C B
31mm −
1
2
m
.
Câu 8. Cho tam giác
ABC
thỏa mãn điều kiện
a b c b c a
b c a a b c
h h h h h h
h h h h h h
+ + = + +
. Chứng minh tam giác
ABC
là
tam giác cân.
Hướng dẫn giải:
20
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Ta có:
2 2 2
1 1 1
,,
2 2 2
ABC ABC ABC
ABC a b c a b c
S S S
S h a h b h c h h h
a b c
= = = = = =
.
Ta có:
a b c b c a
b c a a b c
h h h h h h
b c a a b c
h h h h h h a b c b c a
+ + = + + + + = + +
2 2 2 2 2 2
b c c a a b a c b a c b + + = + +
2
( )( ) 0a b ab c ac bc − + − − =
( )( )( ) 0
ab
a b b c a c b c
ac
=
− − − = =
=
. Vậy tam giác
ABC
cân.
Câu 9. Tìm a đ hàm số
1
3 2 2
y
x a a x
=
+ − + + −
xác định với mi
1;1x−
.
Hướng dẫn giải:
Hàm số xác định
3 2 0 2 3
2 0 2
x a x a
a x x a
+ − −



+ − +

.
Trường hợp 1:
2 3 2 0a a a− +
.
Khi đó tập xác định hàm số
D =
không th chứa đoạn
1;1−
.
Trường hợp 2:
2 3 2 0a a a− +
(*). Khi đó tập xác định hàm số
2 3 ; 2D a a= − +
.
Hàm số xác định
1;1 1;1 2 3 ; 2x a a − − − +
2 3 1 1
1
1 2 1
aa
a
aa
− −


+ −

(thỏa (*)).
Vậy với
1a
thì hàm số đã cho xác định với mi
1;1x−
.
Câu 10. Cho tam giác
ABC
có trng tâm G. Tìm tập hợp đim
M
thỏa mãn hệ thức sau:
2MA MB MC AM AB+ − = −
.
Hướng dẫn giải:
Ta có:
23MA MB MC AM AB MA MB MC MC BM+ − = − + + − =
33MG MC BM − =
( )
3 3 3MG MC BM CG BM BM CG − = = =
.
Nhận xét: Ba đim B, C, G cố định. Vậy tập hợp đim M là đưng tròn tâm B, bán kính
3R CG=
.
Câu 11. Mt gia đình cần ít nhất 900 g chất protein và 400 g chất lipit trong thức ăn mỗi ngày. Biết rằng thịt
bò chứa 80% protein và 20% lipit. Thịt lợn chứa 60% protein và 40% lipit. Biết rằng gia đình này
chỉ mua nhiều nhất là 1 600 g thịt bò, 1 100 g thịt lợn, giá tiền 1 kg thịt bò là 45 000 đồng, 1 kg thịt
lợn là 35 000 đồng. Giả sử gia đình mua x kg thịt bò và y kg thịt lợn.
a) Lập hệ bất phương trình biu thị các điều kiện ca bài toán rồi biu diễn hình hc miền nghiệm
(S) ca hệ đó.
b) Gi T (nghìn đồng) là số tiền phải trả cho x (kilogam) thịt bò và y (kilogam) thịt lợn. Hãy biu diễn
T theo x, y.
c) Hỏi gia đình đó phải mua bao nhiêu kilogam thịt mỗi loại đ chi phí là ít nhất?
Hướng dẫn giải:
21
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
a) Giả sử gia đình đó mua x (kg) thịt bò và y (kg) thịt lợn.
Điều kiện: 0 ≤ x ≤ 1,6; 0 ≤ y ≤ 1,1.
Khi đó lượng protein có được là 80%x + 60% y và
lượng lipit có được là 20%x + 40% y.
Vì gia đình đó cần ít nhất 0,9 kg protein và 0,4 kg
lipit trong thức ăn mỗi ngày nên điều kiện tương ứng
là : 80%x + 60%y ≥ 0,9 và 20%x + 40%y ≥ 0,4.
Ta có hệ bất phương trình:
0 1,6
0 1,1
4 3 4,5
22
x
y
xy
xy


+
+
.
Miền nghiệm ca hệ trên là miền ca tứ giác lồi
ABCD (k cả biên) được mô tả ở hình bên.
b) Chi phí đ mua x (kg) thịt bò và y (kg) thịt lợn là: T = 45x + 35y (nghìn đồng).
c) Ta đã biết T đạt giá trị nhỏ nhất tại mt trong các đỉnh tứ giác ABCD trong đó
( )
0,3;1,1A
,
( ) ( ) ( )
1,6;1,1 , 1,6;0,2 , 0,6;0,7B C D
.
Xét
( )
0,3;1,1A
, ta có
45.0,3 35.1,1 52T = + =
; xét
( )
1,6;1,1B
, ta có
45.1,6 35.1,1 110,5T = + =
;
xét
( )
1,6;0,2C
, ta có
45.1,6 35.0,2 79T = + =
; xét
( )
0,6;0,7D
, ta có
45.0,6 35.0,7 51,5T =+=
.
So sánh các giá trị trên, ta thấy được T đạt giá trị nhỏ nhất bằng 51,5 (nghìn đồng), khi đó
0,6
0,7
x
y
=
=
(tức là gia đình đó mua 0,6kg thịt bò và 0,7 kg thịt lợn thì chi phí là ít nhất).
22
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
ÑEÀ REØN LUYEÄN SOÁ 05
Time: 90 phuùt
ơ
Câu 1. Cho
)
3;A = +
,
( )
0; 4B =
. Tìm
, , \ , \A B A B A B B A
,
,C A C B
.
Câu 2. Cho tập hợp
; ; ; ; ;X a b c d e g=
.
a) Xác định tập Y sao cho
YX
và
\ ; ;X Y b c e=
.
b) Xác định hai tập A, B sao cho
, \ ; , \ ; ;A B X B A d e A B a b c = = =
.
Câu 3. Tìm tập xác định mỗi hàm số sau:
a)
2
32x
y
xx
−
=
−
; b)
21y x x= + + −
;
Câu 4. Vẽ đồ thị hàm số
2
41y x x= − +
.
Câu 5. Cho hình vuông
ABCD
có cạnh bằng
a
.
Tính
AD AB+
và
AD AC+
.
Câu 6. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
( )
2
31f x x x= − +
biết
0;4x
.
Câu 7. Một dòng sông chảy từ phía bắc xuống phía nam với vận
tốc 10 km/h, có một chiếc ca nô chuyển động từ phía đông
sang phía tây với vận tốc 35 km/h so với dòng nước. Tìm
vận tốc của ca nô so với bờ.
Câu 8. Có ba nhóm máy X, Y, Z dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị sản
phẩm mỗi loại lần lượt phải dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và số
máy của từng nhóm cần thiết
để sản xuất ra một đơn vị sản
phẩm thuộc mỗi loại được
dùng cho trong bảng bên.
Một đơn vị sản phẩm loại I lãi 3
nghìn đồng, một đơn vị sản
phẩm loại II lãi 5 nghìn đồng.
Hãy lập kế hoạch sản xuất để
cho tổng số tiền lãi thu được là
cao nhất.
Câu 9. Cho tam giác
ABC
thỏa mãn điều kiện
2 2 2
4
a
m b c=+
, trong đó
a
m
là độ dài trung tuyến tam giác
kẻ từ A; a, b, c là các cạnh của tam giác. Chứng minh tam giác
ABC
là tam giác vuông.
Câu 10. Một cái cây dạng thẳng đứng bị gió mạnh làm gãy
không hoàn toàn (hai đoạn thân bị gãy vẫn dính liền
nhau như hình vẽ). Một người muốn đo chiều cao của
cây trước khi gãy, người ấy đó được đoạn thẳng nối
từ gốc cây đến ngọn cây (đã ngã) là
6mAB =
, hai
góc
00
76 , 35CAB CBA==
. Tính chiều dài của cây
trước khi bị gãy (giả sử sự biến dạng lúc gãy không
ảnh hưởng đến tổng độ dài của cây).
================HẾT===============
23
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Höôùng daãn giaûi ñeà soá 05
Câu 1. Cho
)
3;A = +
,
( )
0; 4B =
. Tìm
, , \ , \A B A B A B B A
,
,C A C B
.
Hướng dẫn giải:
Ta có:
)
3;4AB=
,
( )
0;AB = +
,
)
\ 4;AB= +
,
( )
\ 0; 3BA=
,
( )
\ ;3C A A= = −
,
(
)
\ ;0 4;C B B= = − +
.
Câu 2. Cho tập hợp
; ; ; ; ;X a b c d e g=
.
a) Xác định tập Y sao cho
YX
và
\ ; ;X Y b c e=
.
b) Xác định hai tập A, B sao cho
, \ ; , \ ; ;A B X B A d e A B a b c = = =
.
Hướng dẫn giải:
a) Ta có:
\ ; ;X Y b c e=
nên a, d, g thuộc Y và b, c, e không thuộc Y. Mặt khác do
YX
nên Y không chứa
phần tử nào ngoài
, , , , ,a b c d e g
. Vậy
;;Y a d g=
.
b) Do
\;B A d e=
nên B có chứa d, e và A không chứa d, e. Vì
\ ; ;A B a b c=
nên A có chứa a, b,
c và B không chứa a, b, c. Ta lại có
A B X=
nên g thuộc A hoặc g thuộc B. Mặt khác
\ , \g B A g A B
nên g thuộc A và g thuộc B. Vậy
; ; ; , ; ;A a b c g B d e g==
.
Câu 3. Tìm tập xác định mỗi hàm số sau:
a)
2
32x
y
xx
−
=
−
; b)
21y x x= + + −
;
Hướng dẫn giải:
a) Hàm số xác định
2
0
0
1
x
xx
x
−
. Tập xác định hàm số:
\ 0;1D =
.
b) Hàm số xác định
2 0 2
1
1 0 1
xx
x
xx
+ −


−

. Tập xác định hàm số:
)
1;D = +
.
Câu 4. Vẽ các đồ thị hàm số
2
41y x x= − +
.
Hướng dẫn giải:
Xét
( )
2
4 1; 1, 4, 1y x x a b c= − + = = − =
.
Tọa độ đỉnh I của parabol:
( )
2
4
2, 2 4.2 1 3
2 2.1
II
b
xy
a
−
= − = − = = − + = −
hay
( )
2; 3I −
.
Phương trình trục đối xứng parabol:
2x =
. Vì
10a =
nên bề lõm parabol hướng lên.
24
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Để ý: Nếu ta tìm giao điểm giữa parabol với Ox, tức là giải phương trình
2
4 1 0− + =xx
trước, tuy nhiên phương trình này cho ta hai nghiệm vô tỉ (không
đẹp). Chính vì thế nên ta chọn giải pháp lập bảng giá trị để tìm ra năm cặp (x ; y)
thỏa hàm số với đỉnh I làm tâm của bảng giá trị đó.
Bảng giá trị:
Đồ thị hàm số:
Câu 5. Cho hình vuông
ABCD
có cạnh bằng
a
. Tính
AD AB+
và
AD AC+
.
Hướng dẫn giải:
Tính
AD AB+
:
Theo quy tắc hình bình hành, ta có
AD AB AC+=
.
Theo định lí Pytago:
2 2 2
AC AB BC=+
2 2 2
22a a a AC a= + = =
Vậy
AD AB+
AC=
AC=
2a=
.
Tính
AD AC+
:
Gọi E là điểm đối xứng với B qua C. Do
, //CE AD a CE AD==
nên ADEC là hình bình hành.
Ta có:
AD AC AE+=
. Áp dụng định lí Pytago cho tam giác ABE:
( )
2
2 2 2 2 2
2 5 5AE AB BE a a a AE a= + = + = =
.
Vậy
5AD AC AE a+ = =
.
Câu 6. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
( )
2
31f x x x= − +
biết
0;4x
;
Hướng dẫn giải:
25
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
( )
2
31f x x x= − +
. Ta có:
3
1, 3, 1
22
b
a b c
a
= = − = − =
và
35
24
f

=−


. Vì
10a =
nên bề lõm đồ thị hướng lên.
Bảng biến thiên hàm số khi
0;4x
là:
Ta có thể kết luận: Với
0;4x
, hàm số đạt giá trị lớn nhất bằng 5, khi đó
4x =
; hàm số đạt giá
trị nhỏ nhất bằng
5
4
−
, khi đó
3
2
x =
.
Câu 7. Một dòng sông chảy từ phía bắc xuống phía nam
với vận tốc 10 km/h, có một chiếc ca nô chuyển
động từ phía đông sang phía tây với vận tốc 35
km/h so với dòng nước. Tìm vận tốc của ca nô
so với bờ.
Hướng dẫn giải:
Gọi
12
,vv
lần lượt là vectơ vận tốc của dòng
nước đối với bờ và ca nô đối với dòng nước.
Khi đó vận tốc của ca nô đối với bờ chính là
tổng
12
vv+
.
Đặt
12
,v AD v AB==
với
A
là vị trí của ca nô.
Vẽ hình bình hành ABCD, ta có:
12
v v AB AD AC+ = + =
.
Theo định lí Pytago:
22
10 35 5 53 36,4AC = + =
km/h.
Vậy vận tốc của ca nô đối với bờ là xấp xỉ
36,4
km/h.
Câu 8. Có ba nhóm máy X, Y, Z dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị sản
phẩm mỗi loại lần lượt phải dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và
số máy của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được dùng cho
trong bảng sau:
Nhóm
Số máy trong
mỗi nhóm
Số máy trong từng nhóm để sản xuất ra một đơn vị
sản phẩm
Loại I
Loại II
X
10
2
2
Y
4
0
2
Z
12
2
4
26
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Một đơn vị sản phẩm loại I lãi 3 nghìn đồng, một đơn vị sản phẩm loại II lãi 5 nghìn đồng. Hãy lập kế
hoạch sản xuất để cho tổng số tiền lãi thu được là cao nhất.
Hướng dẫn giải:
Gọi x là số đơn vị sản phẩm loại I, y là số đơn vị sản phẩm loại II sản xuất ra.
Như vậy tiền lãi có được là
( )
; 3 5F x y x y=+
(nghìn đồng).
Theo giả thiết, số máy cần dùng nhóm X: 2x + 2y
(máy); số máy cần dùng ở nhóm Y là 0x + 2y (máy);
số máy cần dùng ở nhóm Z là 2x + 4y (máy).
Ta có hệ bất phương trình (*):
2 2 10
24
2 4 12
0, 0
xy
y
xy
xy
+
+

.
Miền nghiệm của hệ (*) được biểu diễn là miền của ngũ giác OABCD với
( ) ( ) ( ) ( ) ( )
0;0 , 0;2 , 2;2 , 4;1 , 5;0O A B C D
.
Xét
( )
0;0O
, ta có
( )
0;0 3.0 5.0 0F = + =
; xét
( )
0;2A
, ta có
( )
0;2 3.0 5.2 10F = + =
; xét
( )
2;2B
,
ta có
( )
2;2 3.2 5.2 16F = + =
; xét
( )
4;1C
, ta có
( )
4;1 3.4 5.1 17F = + =
; xét
( )
5;0D
, ta có
( )
5;0 3.5 5.0 15F = + =
.
Từ các kết quả trên, ta thấy khoản lãi lớn nhất (
( )
;F x y
lớn nhất) bằng 17 (ngàn đồng), khi đó người
ta cần làm ra 4 sản phẩm loại I và 1 sản phẩm loại II (tức là
4, 1xy==
).
Câu 9. Cho tam giác
ABC
thỏa mãn điều kiện
2 2 2
4
a
m b c=+
, trong đó
a
m
là độ dài trung tuyến tam giác
kẻ từ A; a, b, c là các cạnh của tam giác. Chứng minh tam giác
ABC
là tam giác vuông.
Hướng dẫn giải:
Ta có :
2 2 2
2 2 2 2 2
2( )
4 2( )
4
aa
b c a
m m b c a
+−
= = + −
.
Kết hợp giả thiết:
2 2 2 2 2 2 2 2 2 2 2
4 2( )
a
m b c b c a b c b c a= + + − = + + =
.
Vậy tam giác
ABC
vuông tại A.
Câu 10. Một cái cây dạng thẳng đứng bị gió mạnh làm gãy không hoàn toàn (hai đoạn thân bị gãy vẫn dính
liền nhau như hình vẽ). Một người muốn đo chiều cao của cây trước khi gãy, người ấy đó được
đoạn thẳng nối từ gốc cây đến ngọn cây (đã ngã) là
6mAB =
, hai góc
00
76 , 35CAB CBA==
.
Tính chiều dài của cây trước khi bị gãy (giả sử sự biến dạng lúc gãy không ảnh hưởng đến tổng độ
dài của cây).
27
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Hướng dẫn giải:
Ta có:
( )
0
180C A B= − +
( )
0 0 0 0
180 76 35 69= − + =
.
Theo định lí Sin:
sin sin sin
AB AC BC
C B A
==
0
0
.sin 6.sin35
3,69 m;
sin sin69
AB B
AC
C
= =
0
0
.sin 6.sin76
6,24 m
sin sin69
AB A
BC
C
= =
9,93 mAC BC +
.
Vậy chiều cao ban đầu của cây xấp xỉ bằng
9,93 m
.
28
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
ÑEÀ REØN LUYEÄN SOÁ 06
Time: 90 phuùt
ơ
Câu 1. Cho
1; 2; 3; 4; 5=A
. Viết tất cả các tập con của
A
có ít nhất ba phần tử.
Câu 2. Xét xem các cặp số (x ; y) sau đây có là nghiệm của hệ bất phương trình
20
2 3 2 0
xy
xy
+ −
− +
?
a)
( )
0;0
; b)
( )
1;1
; c)
( )
2;1−
.
Câu 3. Tìm tập xác định của các hàm số sau:
a)
3
3
1
2
x
yx
x
−
= + −
+
; b)
12
4 2 1 3
x
y
xx
−
=
+−
.
Câu 4. Xác định hàm số bậc hai có đồ thị là parabol
( )
P
biết:
a)
( )
2
:P y ax bx c= + +
có giá trị lớn nhất bằng 1 khi x = 2, đồng thời
( )
P
qua
( )
4; 3M −
.
b)
( )
2
:P y ax bx c= + +
có giá trị nhỏ nhất bằng
1−
; biết
( )
P
đi qua đim
( )
1;7A −
và
( )
P
cắt Oy
tại đim có tung độ bằng 1.
Câu 5. Cho mẫu số liệu thống kê về sản lượng chè thu được trong 1 năm (kg/sào) của 10 hộ gia đình:
112
111
112
113
114
116
115
114
115
114
a) Tìm giá trị trung bình của mẫu số liệu trên.
b) Viết mẫu số liệu trên theo thứ tự không giảm và tìm trung vị, mốt của nó.
Câu 6. Cho tam giác
ABC
có
00
20 , 31BC==
, cạnh
210 cmb AC==
. Tính góc A, độ dài các cạnh còn
lại và bán kính R của đường tròn ngoại tiếp tam giác ABC.
Câu 7. Cho hai đim phân biệt
,AB
. Xác định các đim
,MN
sao cho:
a)
20AB BM+=
; b)
2 3 0NA NB−=
.
Câu 8. Một người cần đặt một tiệc cưới ước tính khoảng 30 đến 35 bàn. Nhà hàng thứ nhất đề nghị anh nay đóng
tiền cố định 20 triệu đồng, sau khi tiệc cưới diễn ra sẽ đóng khoản còn lại với số tiền 2 triệu đồng/1 bàn.
Nhà hàng thứ hai đề nghị anh đóng tiền cố định 10 triệu đồng, sau khi tiệc cưới diễn ra sẽ đóng khoản còn
lại với số tiền 2,5 triệu/1 bàn. Hỏi anh này nên lựa chọn nhà hàng nào đ tiết kiệm được chi phí cho tiệc
cưới (giả sử rằng chất lượng phục vụ hai nhà hàng trên là ngang nhau)?
Câu 9. Biết hai lực cùng tác động vào một vật tạo với nhau góc 40
o
. Cường độ của hai lực đó là 3N và 4N.
Tính cường độ của lực tổng hợp.
Câu 10. Cho hình vuông
ABCD
cạnh
a
và số thực
k
. Tìm tập hợp đim
M
sao cho
..MAMC MB MD k+=
.
================HẾT===============
29
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Höôùng daãn giaûi ñeà soá 06
Câu 1. Cho
1; 2; 3; 4; 5=A
. Viết tất cả các tập con của
A
có ít nhất ba phần tử.
Hướng dẫn giải:
Các tập con có ít nhất ba phầu tử của
A
là:
1; 2; 3 , 1; 2; 4 ,
1; 2;5 ,
1; 3; 4 ,
1; 3; 5 , 1; 4; 5 ,
2; 3; 4 ,
2; 3; 5 , 2; 4; 5 , 3; 4; 5 , 1; 2; 3;4 ,
1; 2; 3;5 , 1; 2; 4;5 , 1; 3; 4;5 , 2; 3;4; 5 , 1; 2; 3;4;5
(gồm
16
tập).
Câu 2. Xét xem các cặp số (x ; y) sau đây có là nghiệm của hệ bất phương trình
20
2 3 2 0
xy
xy
+ −
− +
?
a)
( )
0;0
; b)
( )
1;1
; c)
( )
2;1−
.
Hướng dẫn giải:
a) Thay
0, 0xy==
vào hệ bất phương trình, ta được :
0 0 2 0
2.0 3.0 2 0
+ −
− +
(đúng), do đó cặp số
( )
0;0
là một nghiệm của hệ đã cho.
b) Thay
1, 1xy==
vào hệ bất phương trình, ta được :
1 1 2 0
2.1 3.1 2 0
+ −
− +
(đúng), do đó cặp số
( )
1;1
là một nghiệm của hệ đã cho.
c) Thay
2, 1xy= − =
vào hệ bất phương trình, ta được :
( )
( )
2 1 2 0
2 2 3.1 2 0
− + −
− − +
(sai), do đó cặp số
( )
2;1−
không là một nghiệm của hệ đã cho.
Câu 3. Tìm tập xác định của các hàm số sau:
a)
3
3
1
2
x
yx
x
−
= + −
+
; b)
12
4 2 1 3
x
y
xx
−
=
+−
.
Hướng dẫn giải:
a) Hàm số xác định khi và chỉ khi
3 0 3 0
3
0
2 0 2 0
2
xx
x
xx
x
− −

−

+ +
+

33
23
22
xx
x
xx


−

− −

. Tập xác định hàm số:
(
2;3D =−
.
b) Hàm số xác định khi và chỉ khi
2 1 0
(*)
4 2 1 3 0
x
xx
+
+ −
.
Xét
( )
2
30
4 2 1 3 0 4 2 1 3
16 2 1 9
x
x x x x
xx
+ − = + =
+=
0
4
4
4
9
x
x
xx
=
= = −
.
30
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Do vậy
1
(*)
2
4
x
x
−
. Tập xác định hàm số:
1
; \ 4
2
D

= − +

.
Câu 4. Xác định hàm số bậc hai có đồ thị là parabol
( )
P
biết:
a)
( )
2
:P y ax bx c= + +
có giá trị lớn nhất bằng 1 khi x = 2, đồng thời
( )
P
qua
( )
4; 3M −
.
b)
( )
2
:P y ax bx c= + +
có giá trị nhỏ nhất bằng
1−
; biết
( )
P
đi qua đim
( )
1;7A −
và
( )
P
cắt Oy
tại đim có tung độ bằng 1.
Hướng dẫn giải:
a) Theo giá thiết thì
2 4 0 (1)
2
b
ab
a
− = + =
; (P) qua hai đim
( ) ( )
2;1 , 4; 3IM−
nên
4 2 1 (2)
16 4 3 (3)
a b c
a b c
+ + =
+ + = −
. Giải hệ (1), (2), (3):
1
4
3
a
b
c
=−
=
=−
. Vậy hàm số được xác định:
2
43y x x= − + −
.
b)
( )
P
đi qua hai đim
( )
1;7A −
và
( )
0;1B
nên
7 6 6 (1)
1 1 1
a b c a b a b
c c c
− + = − = = +

= = =
.
Mặt khác
22
1
min
44
1
4 4 4
c
b ac a b
y
a a a
=
− −
= − = − = = −
22
4 4 8 0 (2)a b a b a − = − − =
.
Thay (1) vào (2):
( )
2
12
8 6 0
4
b
bb
b
=
− + =
=−
.
Với
12b =
thì
18 0a =
(nhận). Hàm số được xác định:
2
18 12 1y x x= + +
.
Với
4b =−
thì
20a =
(nhận). Hàm số được xác định:
2
2 4 1y x x= − +
.
Câu 5. Cho mẫu số liệu thống kê về sản lượng chè thu được trong 1 năm (kg/sào) của 10 hộ gia đình:
112
111
112
113
114
116
115
114
115
114
a) Tìm giá trị trung bình của mẫu số liệu trên.
b) Viết mẫu số liệu trên theo thứ tự không giảm và tìm trung vị, mốt của nó.
Hướng dẫn giải:
a) Sản lượng chè trung bình thu được trong một năm của mỗi gia đình là
112 111 112 113 114 116 115 114 115 114
113,6
10
x
+ + + + + + + + +
=
(kg/sào).
b) Ta viết lại mẫu số liệu trên theo thứ tự không giảm:
111
112
112
113
114
114
114
115
115
116
Vì số giá trị của mẫu
10n =
(chẵn) nên trung bình cộng hai số chính giữa mẫu chính là trung vị,
vậy trung vị là:
114 114
114
2
+
=
.
Trong mẫu trên, giá trị 114 xuất hiện nhiều nhất (3 lần) nên 114 là mốt của mẫu số liệu đã cho.
31
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Câu 6. Cho tam giác
ABC
có
00
20 , 31BC==
, cạnh
210 cmb AC==
. Tính góc A, độ dài các cạnh còn
lại và bán kính R của đường tròn ngoại tiếp tam giác ABC.
Hướng dẫn giải:
Ta có:
( )
( )
0 0 0 0
180 180 20 31 129A B C= − + = − + =
.
Theo định lí Sin:
2
sin sin sin
a b c
R
A B C
= = =
.
Suy ra:
sin
sin
bA
a
B
=
0
0
210.sin129
477,2 cm
sin20
=
;
0
0
sin 210.sin31
316,2 cm
sin sin 20
bC
c
B
= =
;
0
477,2
307,02 cm
2sin 2sin129
a
R
A
=
.
Câu 7. Cho hai đim phân biệt
,AB
. Xác định các đim
,MN
sao cho:
a)
20AB BM+=
; b)
2 3 0NA NB−=
.
Hướng dẫn giải:
a) Ta có:
( )
2 0 0 0AB BM AB BM BM AM BM+ = + + = + =
.
Vậy M là trung đim của đoạn AB.
b) Ta có:
2 3 0 2 3( ) 0 3 0 3NA NB NA NA AB NA AB AN AB− = − + = − − = =
.
Do vậy hai vectơ
,AN AB
cùng hướng và
3AN AB=
.
Câu 8. Một người cần đặt một tiệc cưới ước tính khoảng 30 đến 35 bàn. Nhà hàng thứ nhất đề nghị anh nay đóng
tiền cố định 20 triệu đồng, sau khi tiệc cưới diễn ra sẽ đóng khoản còn lại với số tiền 2 triệu đồng/1 bàn.
Nhà hàng thứ hai đề nghị anh đóng tiền cố định 10 triệu đồng, sau khi tiệc cưới diễn ra sẽ đóng khoản còn
lại với số tiền 2,5 triệu/1 bàn. Hỏi anh này nên lựa chọn nhà hàng nào đ tiết kiệm được chi phí cho tiệc
cưới (giả sử rằng chất lượng phục vụ hai nhà hàng trên là ngang nhau)?
Hướng dẫn giải:
Gọi x là số bàn tiệc thực tế trong đám cưới (x nguyên dương và
30;35x
) và y (triệu đồng) là số
tiền mà người đó phải trả cho nhà hàng.
Nếu đăng ký tại nhà hàng thứ nhất, người đó sẽ trả tiền theo công thức:
2 20yx=+
.
Với
30;35x
thì
80;90y
, tức là người đó phải trả khoản tiền khoảng 80 triệu đến 90 triệu
cho nhà hàng thứ nhất.
Nếu đăng ký tại nhà hàng thứ hai, người đó sẽ trả tiền theo công thức:
2,5 10yx=+
.
Với
30;35x
thì
85;97,5y
, tức là người đó phải trả khoản tiền khoảng 85 triệu đến 97,5
triệu cho nhà hàng thứ hai.
Vậy, nếu chất lượng phục vụ hai nhà hàng là tương đương, người đó nên chọn nhà hàng thứ nhất đ
tiết kiệm một khoản chi phí tiệc cưới.
32
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Câu 9. Biết hai lực cùng tác động vào một vật tạo với nhau góc 40
o
. Cường độ của hai lực đó là 3N và 4N.
Tính cường độ của lực tổng hợp.
Hướng dẫn giải:
Giả sử vật được đặt ở vị trí A, hai lực tác động vào A
lần lượt là các vectơ
,AB AD
có độ lớn là 3N, 4N.
Vẽ hình bình hành ABCD, ta có hợp lực tác động vào
A là:
AB AD AC+=
.
Do ABCD là hình bình hành nên
4AD BC==
.
Ta có:
0 0 0
180 40 140ABC = − =
. Xét tam giác ABC,
theo định lí Cô-sin ta có:
2 2 2 2 2 0
2 . .cos 3 4 2.3.4.cos140 43,39= + − = + − AC AB BC AB BC ABC
6,59AC
.
Vậy độ lớn của lực tổng hợp tác động vào vật A là xấp xỉ
6,59
N.
Câu 10. Cho hình vuông
ABCD
cạnh
a
và số thực
k
. Tìm tập hợp đim
M
sao cho
..MAMC MB MD k+=
.
Hướng dẫn giải:
Gọi
I
là tâm của hình vuông
ABCD
.
Ta có :
( )( )
.MAMC MI IA MI IC= + +
( )( )
MI IA MI IA= + −
22
22
MI IA MI IA= − = −
.
Hoàn toàn tương tự, ta có:
22
.MB MD MI IB=−
.
Khi đó:
..MAMC MB MD k+=
2 2 2 2 2
2 2 2MI IA IB k MI IA k − − = − =
2
2 2 2
2 2 2
k k a
MI IA MI = + = +
2
2
ka
MI
+
=
(trong đó
2
2
2
2
2
2 2 2
AC a a
IA


= = =





).
Nếu
2
ka−
: Tập hợp đim
M
là tập rỗng.
Nếu
2
ka=−
thì
0MI M I=
(đim
M
trùng với đim
I
).
Nếu
2
ka−
thì
2
2
ka
MI
+
=
.
Khi đó tập hợp đim
M
là đường tròn tâm
I
, bán kính
2
2
ka
R
+
=
.
33
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
ÑEÀ REØN LUYEÄN SOÁ 07
Time: 90 phuùt
ơ
Câu 1. Cho
2
2 3 1 0 , 2 1 1A x x x B x x= − + = = − =
. Tìm
,AB
, \ , \A B A B B A
.
Câu 2. Biểu diễn miền nghiệm của hệ sau trên mặt phẳng tọa độ:
3
0
0
xy
x
y
+
.
Câu 3. Xét sự biến thiên của hàm số
( )
2
21f x x=−
trên
( )
;0−
.
Câu 4. Cho
1
sin
3
=
với
00
90 180

. Tính
cos
và
tan
.
Câu 5. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
( )
2
31f x x x= − +
với
0;4x
.
Câu 6. Bảng số liệu sau thống kê nhiệt độ tại Thành phố Hồ Chí Minh trong một lần đo vào một ngày của
năm 2021 :
Giờ đo
1h
4h
7h
10h
13h
16h
19h
22h
Nhiệt độ (độ C)
27
26
28
32
34
35
30
28
Tìm số trung bình, phương sai và độ lệch chuẩn của mẫu số liệu đã cho (làm tròn kết quả đến hàng
phần trăm).
Câu 7. Chứng minh rằng trong một hình bình hành, tổng bình phương các cạnh bằng tổng bình phương hai
đường chéo của hình bình hành đó.
Câu 8. Cho
ABC
vuông tại
B
có
0
30A =
,
AB a=
. Gọi
I
là trung điểm của
AC
. Hãy tnh:
a)
BA BC+
; b)
AB AC+
.
Câu 9. Cho tam giác ABC có trọng tâm G. Tìm vị trí của M để tổng
2 2 2
P MA MB MC=++
đạt giá trị nhỏ
nhất
min
P
. Tính
min
P
theo GA, GB, GC.
Câu 10. Cổng Arch tại thành phố St Louis của Mỹ có hình dạng của một parabol. Biết khoảng cách giữa hai
chân cổng là 162 m . Trên thành cổng, tại vị tr có độ cao 43 m so với mặt đất, người ta thả một sợi
dây chạm đất và vị trí chạm đất này cách chân cổng (điểm A) một khoảng 10 m. Hãy tính gần đúng
độ cao của cổng Arch (tnh chnh xác đến hàng phần chục).
================HẾT===============
34
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Höôùng daãn giaûi ñeà soá 07
Câu 1. Cho
2
2 3 1 0 , 2 1 1A x x x B x x= − + = = − =
. Tìm
,AB
, \ , \A B A B B A
.
Hướng dẫn giải:
Ta có:
2
1
1
2 3 1 0 1;
1
2
2
x
x x A
x
=

− + = =

=

;
2 1 1 1
2 1 1 0;1
2 1 1 0
xx
xB
xx
− = =

− = =

− = − =

.
Vậy
1AB=
,
1
0; ;1
2
AB

=


,
1
\
2
AB

=


,
\0BA=
.
Câu 2. Biểu diễn miền nghiệm của hệ sau trên mặt phẳng tọa độ:
3
0
0
xy
x
y
+
.
Hướng dẫn giải:
Vẽ các đường thẳng
:3d x y+=
,
: 0, : 0Ox y Oy x==
.
Chọn điểm
( )
1;1M
, thay tọa độ M vào (1):
1 1 3+
(đúng), do
vậy
( )
1;1
là nghiệm của (1), ta gạch bỏ nửa mặt phẳng bờ là
đường thẳng d không chứa điểm M.
Tương tự như thế, thay tọa độ M vào (2) và (3) ta thấy đều thỏa
mãn, do vậy
( )
1;1
cũng là nghiệm của (2) và (3). Ta gạch bỏ
nửa mặt phẳng có bờ là đường thẳng Ox, Oy mà không chứa M.
Miền nghiệm của hệ bất phương trình là miền tam giác ABC
(gồm tam giác ABC và miền trong của nó). (Xem hình bên).
Câu 3. Xét sự biến thiên của hàm số
( )
2
21f x x=−
trên
( )
;0−
.
Hướng dẫn giải:
Lấy
1, 2
xx
tùy ý thuộc
( )
;0−
,
12
xx
.
Xét
( ) ( )
( ) ( )
( )( )
22
1 2 1 2 1 2 1 2
2 1 2 1 2f x f x x x x x x x− = − − − = − +
.
Vì
1 2 1 2
0x x x x −
;
( )
1 2 1 2
, ;0 0x x x x − +
. Do vậy
( )( )
1 2 1 2
20x x x x− +
.
Suy ra
( ) ( ) ( ) ( )
1 2 1 2
0f x f x f x f x−
.
Vậy hàm số đã cho nghịch biến trên
( )
;0−
.
Câu 4. Cho
1
sin
3
=
với
00
90 180

. Tính
cos
và
tan
.
Hướng dẫn giải:
Vì
00
90 180

nên
cos 0
.
35
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Ta có:
2
2 2 2 2
1 8 2 2
sin cos 1 cos 1 sin 1 cos
3 9 3

+ = = − = − = = −


.
Do đó:
1
sin 1
3
tan
cos
2 2 2 2
3
= = = −
−
.
Câu 5. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
( )
2
31f x x x= − +
với
0;4x
.
Hướng dẫn giải:
Ta có:
3
1, 3, 1
22
b
a b c
a
= = − = − =
và
35
24
f

=−


. Vì
10a =
nên bề lõm đồ thị hướng lên.
Bảng biến thiên hàm số khi
0;4x
là:
Ta có thể kết luận: Với
0;4x
, hàm số đạt giá trị lớn nhất bằng 5, khi đó
4x =
; hàm số đạt giá
trị nhỏ nhất bằng
5
4
−
, khi đó
3
2
x =
.
Câu 6. Bảng số liệu sau thống kê nhiệt độ tại Thành phố Hồ Chí Minh trong một lần đo vào một ngày của
năm 2021 :
Giờ đo
1h
4h
7h
10h
13h
16h
19h
22h
Nhiệt độ (độ C)
27
26
28
32
34
35
30
28
Tìm số trung bình, phương sai và độ lệch chuẩn của mẫu số liệu đã cho (làm tròn kết quả đến hàng
phần trăm).
Hướng dẫn giải:
Số trung bình là :
27 26 ... 30 28
30
8
x
+ + + +
==
(
0
C
).
Phương sai :
2 2 2 2
1 2 8
1
( ) ( ) ... ( )
8
s x x x x x x

= − + − + + −

( ) ( ) ( )
2 2 2
1
27 30 26 30 ... 28 30 9,75
8

= − + − + + − =

.
Độ lệch chuẩn :
2
3,12ss=
(
0
C
).
Câu 7. Chứng minh rằng trong một hình bình hành, tổng bình phương các cạnh bằng tổng bình phương hai
đường chéo của hình bình hành đó.
Hướng dẫn giải:
Gọi O là giao điểm hai đường chéo của hình bình hành ABCD nên O là trung điểm của AC và BD.
Áp dụng công thức đường trung tuyến trong tam giác ABD ta có:
36
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
2 2 2
2
24
AB AD BD
OA
+
=−
2 2 2 2
4 2 4
AC AB AD BD+
= −
( )
2 2 2 2
2AC AB AD BD = + −
( )
2 2 2 2
2AC BD AB AD + = +
2 2 2 2 2 2
AC BD AB AB AD AD + = + + +
2 2 2 2 2 2
AC BD AB CD BC AD + = + + +
(điều phải chứn minh).
Câu 8. Cho
ABC
vuông tại
B
có
0
30A =
,
AB a=
. Gọi
I
là trung điểm của
AC
. Hãy tnh:
a)
BA BC+
; b)
AB AC+
.
Hướng dẫn giải:
Xét
ABC
vuông tại B:
0
3
tan .tan tan30
3
BC a
A BC AB A a
AB
= = = =
,
2
2 2 2
3 2 3
33
aa
AC AB BC a

= + = + =



.
a) Ta có:
23
2 2 2 2.
23
AC a
BA BC BI BI BI AC+ = = = = = =
.
b) Gọi M là trung điểm của BC, ta có:
22
2 2 2 2AB AC AM AM AM AB BM+ = = = = +
2
2
3 39
2
63
aa
a

= + =



.
Câu 9. Cho tam giác ABC có trọng tâm G. Tìm vị trí của M để tổng
2 2 2
P MA MB MC=++
đạt giá trị nhỏ
nhất
min
P
. Tính
min
P
theo GA, GB, GC.
Hướng dẫn giải:
Ta có:
2 2 2
2 2 2
+ + = + +MA MB MC MA MB MC
( ) ( ) ( )
2 2 2
= + + + + +MG GA MG GB MG GC
2 2 2 2 2 2
2 . 2 . 2 .MG MGGA GA MG MGGB GB MG MGGC GC= + + + + + + + +
2 2 2 2
0
32

= + + + + + +

MG GA GB GC MG GA GB GC
2 2 2 2
3= + + +MG GA GB GC
.
Nhận xét: Các điểm A, B, C, G cố định, do đó
2 2 2
GA GB GC++
không đổi.
P nhỏ nhất khi và chỉ khi MG nhỏ nhất
0MG =
M trùng với G.
Khi đó:
2 2 2
min
P GA GB GC=++
.
Câu 10. Cổng Arch tại thành phố St Louis của Mỹ có hình dạng của một parabol. Biết khoảng cách giữa hai
chân cổng là 162 m . Trên thành cổng, tại vị tr có độ cao 43 m so với mặt đất, người ta thả một sợi
dây chạm đất và vị trí chạm đất này cách chân cổng (điểm A) một khoảng 10 m. Hãy tính gần đúng
độ cao của cổng Arch (tnh chnh xác đến hàng phần chục).
37
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Hướng dẫn giải:
Dựng hệ trục Oxy như hình vẽ và gọi hàm số tương ứng cổng Arch là:
( )
2
0y ax bx c a= + +
.
Vì parabol qua ba điểm
( ) ( ) ( )
0;0 , 162;0 , 10;43A B M
nên:
2
2
43
0
1520
162 162 0
3483
10 10 43
760
c
a
a b c
b
a b c
=
=−
+ + =


=
+ + =
.
Do vậy ta xác định được hàm số là
2
43 3483
1520 760
y x x= − +
.
Đỉnh I của parabol có tọa độ:
81
2
I
b
x
a
= − =
,
185,6
I
y
.
Vậy, chiều cao của cổng gần bằng
185,6m
.
38
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
ÑEÀ REØN LUYEÄN SOÁ 08
Time: 90 phuùt
ơ
Câu 1.
a) Cho
4;4 , 1;7AB= − =
. Tìm
, , \ , \A B A B A B B A
.
b) Cho hai tập hợp
( )
4;3A =−
và
( )
7;B m m=−
. Tìm
m
để
BA
.
Câu 2. Xét sự đồng biến, nghịch biến hàm số
( )
1
x
fx
x
−
=
+
trên
( )
1;− +
.
Câu 3. Cho
1
cos
2
x =
. Tính giá trị biểu thức
22
3sin 4cosx xP =+
.
Câu 4. Cho tam giác cân
ABC
có
0
120A =
và
AB AC a==
. Lấy điểm
M
trên cạnh
BC
sao cho
2
5
BC
BM =
. Tính độ dài
AM
.
Câu 5. Xác định hàm số bậc hai có đồ thị là parabol
( )
2
:4P y ax x c= − +
có trc đối xứng l l đưng
thng
2x =
v ct trc honh tại điểm
( )
3;0M
.
Câu 6. Mẫu số liệu sau ghi rõ số tiền thưởng tết Nguyên Đán của 13 nhân viên của một công ty (đơn vị :
triệu đồng) : 10 10 11 12 12 13 14,5 15 18 20 20 21 28.
a) Tìm tứ phân vị của mẫu số liệu.
b) Tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu.
Câu 7. Trong một cuộc thi pha chế, mỗi đội chơi được sử dng tối đa 24 g hương liệu, 9 lít nước và 210 g
đưng để pha chế nước cam v nước táo. Để pha chế 1 lít nước cam cần 30 g đưng, 1 lít nước và 1
g hương liệu; pha chế 1 lít nước táo cần 10 g đưng, 1 lít nước v 4 g hương liệu. Mỗi lít nước cam
nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điển thưởng. Hỏi cần pha chế bao nhiêu
lít nước trái cây mỗi loại để được số điểm thưởng là lớn nhất?
Câu 8. Cho tam giác
ABC
có hai đưng trung tuyến
,BN CP
. Hãy biểu thị mỗi vectơ
,AB BC
theo cặp
vectơ
,BN CP
.
Câu 9. Một ngưi dùng một lực
F
có độ lớn 90 N làm một vật dịch chuyển một đoạn 100 m. Biết lực
F
hợp với hướng dịch chuyển một góc
0
60
. Tính công sinh ra bởi lực
F
.
================HẾT===============
39
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Höôùng daãn giaûi ñeà soá 08
Câu 1.
a) Cho
4;4 , 1;7AB= − =
. Tìm
, , \ , \A B A B A B B A
.
b) Cho hai tập hợp
( )
4;3A =−
và
( )
7;B m m=−
. Tìm
m
để
BA
.
Hướng dẫn giải:
a) Ta có:
1; 4AB=
,
4; 7AB = −
,
)
\ 4; 1AB=−
,
(
\ 4; 7BA=
.
b) Ta có:
BA
khi và chỉ khi
7 4 3
3
33
mm
m
mm
− −

=



.
Câu 2. Xét sự đồng biến, nghịch biến hàm số
( )
1
x
fx
x
−
=
+
trên
( )
1;− +
.
Hướng dẫn giải:
Xét tùy ý
( )
12
, 1;xx − +
và
12
xx
.
Khi đó:
( ) ( )
( )( ) ( )( )
1 2 1 2 1 1 2 2 2 1
12
1 2 1 2 1 2
1 1 1 1 1 1
x x x x x x x x x x
f x f x
x x x x x x
− − − − + + −
− = − = =
+ + + + + +
.
Do
( ) ( )( )
1 2 1 2
, 1; 1 1 0x x x x − + + +
;
1 2 2 1
0x x x x −
.
Vì vậy
( )( )
( ) ( ) ( ) ( )
21
1 2 1 2
12
00
11
xx
f x f x f x f x
xx
−
−
++
.
Vậy hàm số đã cho nghịch biến trên
( )
1;− +
.
Câu 3. Cho
1
cos
2
x =
. Tính giá trị biểu thức
22
3sin 4cosx xP =+
.
Hướng dẫn giải:
Ta có:
( )
2 2 2 2 2
1 13
3sin 4cos 3 1 cos 4cos 3 cos 3
44
P x x x xx= + = − + = + = + =
.
Câu 4. Cho tam giác cân
ABC
có
0
120A =
và
AB AC a==
. Lấy điểm
M
trên cạnh
BC
sao cho
2
5
BC
BM =
. Tính độ dài
AM
.
Hướng dẫn giải:
40
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Ta có:
2 2 0
2 cos120BC AB AC ABAC= + −
22
1
2 . . 3
2
a a a a a

= + − − =


23
5
a
BM=
;
2 2 0
2 . .cos30AM AB BM AB BM= + −
2
2
2 3 2 3 3 7
2 . .
5 5 2 5
a a a
aa

= + − =



.
Câu 5. Xác định hàm số bậc hai có đồ thị là parabol
( )
2
:4P y ax x c= − +
có trc đối xứng l l đưng
thng
2x =
v ct trc honh tại điểm
( )
3;0M
.
Hướng dẫn giải:
( )
P
có trc đối xứng
4
21
22
b
xa
aa
= − = = =
; (P) lại qua
( )
3;0M
1
2
0 .3 4.3 3
a
a c c
=
= − + =
.
Vậy hàm số bậc hai được xác định:
2
43y x x= − +
.
Câu 6. Mẫu số liệu sau ghi rõ số tiền thưởng tết Nguyên Đán của 13 nhân viên của một công ty (đơn vị :
triệu đồng) : 10 10 11 12 12 13 14,5 15 18 20 20 21 28.
a) Tìm tứ phân vị của mẫu số liệu.
b) Tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu.
Hướng dẫn giải:
a) Mẫu gồm 13 giá trị theo thứ tự không giảm: 10 10 11 12 12 13 14,5 15 18 20 20 21 28 ;
trung vị là 14,5; nên tứ phân vị thứ hai :
2
14,5Q =
.
Xét nửa mẫu bên trái: 10 10 11 12 12 13; tứ phân vị thứ nhất:
1
11,5Q =
.
Xét nửa mẫu bên phải: 15 18 20 20 21 28; tứ phân vị thứ nhất:
3
20Q =
.
Vậy tứ phân vị của mẫu là
1 2 3
11,5; 14,5; 20Q Q Q= = =
.
b) Giá trị lớn nhất và nhỏ nhất của số liệu lần lượt là
max min
28, 10xx==
.
Khoảng biến thiên là :
max min
18R x x= − =
.
Khoảng tứ phân vị là :
31
8,5Q Q Q = − =
.
Câu 7. Trong một cuộc thi pha chế, mỗi đội chơi được sử dng tối đa 24 g hương liệu, 9 lít nước và 210 g
đưng để pha chế nước cam v nước táo. Để pha chế 1 lít nước cam cần 30 g đưng, 1 lít nước và 1
g hương liệu; pha chế 1 lít nước táo cần 10 g đưng, 1 lít nước v 4 g hương liệu. Mỗi lít nước cam
nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điển thưởng. Hỏi cần pha chế bao nhiêu
lít nước trái cây mỗi loại để được số điểm thưởng là lớn nhất?
Hướng dẫn giải:
Gọi x, y lần lượt là số lít nước cam và táo do một đội pha chế thực hiện được
( )
,0xy
.
Số điểm thưởng của đội là:
( )
; 60 80F x y x y=+
.
Số gam đưng cần dùng là:
30 10xy+
.
Số lít nước cần dùng là:
xy+
.
Số gam hương liệu cần dùng là:
4xy+
.
41
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Vì trong cuộc thi pha chế, mỗi đội chơi sử dng tối đa 24 g hương liệu, 9 lít nước v 210 g đưng
nên ta có hệ bất phương trình:
4 24
9
30 10 210
0
0
xy
xy
xy
x
y
+
+
+
(*).
Biểu diễn miền nghiệm của hệ (*) như hình bên, ta thấy
rằng miền nghiệm của hệ chính là miền của ngũ giác
OABCD với 5 đỉnh là:
( ) ( ) ( ) ( ) ( )
0;0 , 0;6 , 4;5 , 6;3 , 7;0O A B C D
.
Ta biết rằng biểu thức hai biến
( )
; 60 80F x y x y=+
sẽ
đạt giá trị lớn nhất (và nhỏ nhất) khi cặp
( )
;xy
nhận một
trong các tọa độ đỉnh của ngũ giác OABCD.
Ta có:
( )
0;0 60.0 80.0 0F = + =
,
( )
0;6 60.0 80.6 480F = + =
,
( )
4;5 60.4 80.5 640F = + =
,
( )
6;3 60.6 80.3 600F = + =
,
( )
7;0 60.7 80.0 420F = + =
.
Vậy
( )
;F x y
đạt giá trị lớn nhất bằng 640, khi đó
( ) ( )
; 4;5xy=
.
Như vậy để được số điểm thưởng là lớn nhất thì ngưi chơi cần pha chế 4 lít nước cam v 5 lít nước
táo.
Câu 8. Cho tam giác
ABC
có hai đưng trung tuyến
,BN CP
. Hãy biểu thị mỗi vectơ
,AB BC
theo cặp
vectơ
,BN CP
.
Hướng dẫn giải:
Gọi G là trọng tâm của tam giác
ABC
, ta có :
0GA GB GC GB GC GA+ + = + = −
.
Khi đó:
( )
AB GB GA GB GB GC= − = + +
2GB GC=+
22
2. .
33
BN CP= − −
42
33
BN CP= − −
;
22
33
BC GC GB CP BN= − = − +
.
Câu 9. Một ngưi dùng một lực
F
có độ lớn 90 N làm một
vật dịch chuyển một đoạn 100 m. Biết lực
F
hợp
với hướng dịch chuyển một góc
0
60
. Tính công sinh
ra bởi lực
F
.
Hướng dẫn giải:
Đặt
OM s=
l đoạn đưng mà vật di chuyển được với O l điểm đặt vật ban đầu.
Công sinh ra bởi lực
F
là:
( )
. . .cos ,A F OM F OM F OM==
0
90.100.cos60 4500J==
.
42
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
ÑEÀ REØN LUYEÄN SOÁ 09
Time: 90 phuùt
ơ
Câu 1.
a) Xác định hai tập hợp A, B biết rằng:
\ 1;5;7;8 ,AB=
\ 2;10 ,BA=
3;6;9AB=
.
b) Trong một trường THPT, khối
10
có
160
em học sinh tham gia câu lạc bộ Toán,
140
em học
sinh tham gia câu lạc bộ Tin,
10
em học sinh tham gia cả hai câu lạc bộ. Biết rằng tất cả học sinh
khối 10 đều tham gia ít nhất một trong hai câu lạc bộ trên. Hỏi khối
10
có bao nhiêu học sinh?
Câu 2. Tìm tập xác định của các hàm số sau:
a)
2
1
x
y
xx
+
=
+
; b)
( )
2
2
1 khi 1
1 khi 1
x x x
fx
xx
+ −
=
−
.
Câu 3. Vẽ đồ thị hàm số
2
28y x x= − −
.
Câu 4. Tìm giá trị m biết parabol
2
y x x m= + +
có đỉnh nằm trên đường thẳng
3
4
y =
.
Câu 5. Hàm lượng Natri (đơn vị miligam, 1 mg = 0,001 g) trong 100 g một số loại ngũ cốc được cho như
sau :
0
340
70
140
200
180
210
150
100
130
140
180
190
160
290
50
220
180
200
210
Hãy tìm tứ phân vị của mẫu trên. Các tứ phân vị này cho ta thông tin gì?
Câu 6. Chứng minh rằng :
1 cot tan 1
1 cot tan 1
xx
xx
++
=
−−
(các biểu thức đều có nghĩa).
Câu 7. Cho hàm số
2 3 4
1
x
y x m
xm
= − + +
+−
với
m
là tham số. Tìm
m
để hàm số có tập xác định là
)
0;+
.
Câu 8. Cho tam giác
ABC
có
2b c a+=
. Chứng minh rằng:
6Rr bc=
, trong đó
,Rr
lần lượt là bán kính
đường tròn ngoại tiếp và nội tiếp tam giác
.ABC
Câu 9. Cho hình thang ABCD vuông tại A và B , biết
,3AD a BC a==
và cạnh
2.AB a=
a) Tính
. , .AB BD BC BD
và
..AC BD
b) Gọi I, J lần lượt là trung điểm của AB, CD. Tính
.AC IJ
.
Câu 10. Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm
I
và
II
. Mỗi
sản phẩm
I
bán lãi
500
nghìn đồng, mỗi sản phẩm
II
bán lãi
400
nghìn đồng. Để sản xuất được
một sản phẩm
I
thì Chiến phải làm việc trong
3
giờ, Bình phải làm việc trong 1 giờ. Để sản xuất
được một sản phẩm
II
thì Chiến phải làm việc trong 2 giờ, Bình phải làm việc trong
6
giờ. Một
người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm
việc quá
180
giờ và Bình không thể làm việc quá
220
giờ. Hỏi số tiền lãi lớn nhất trong một tháng
của xưởng là bao nhiêu?
================HẾT===============
43
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Höôùng daãn giaûi ñeà soá 09
Câu 1.
a) Xác định hai tập hợp A, B biết rằng:
\ 1;5;7;8 ,AB=
\ 2;10 ,BA=
3;6;9AB=
.
b) Trong một trường THPT, khối
10
có
160
em học sinh tham gia câu lạc bộ Toán,
140
em học
sinh tham gia câu lạc bộ Tin,
10
em học sinh tham gia cả hai câu lạc bộ. Biết rằng tất cả học sinh
khối 10 đều tham gia ít nhất một trong hai câu lạc bộ trên. Hỏi khối
10
có bao nhiêu học sinh?
Hướng dẫn giải:
a) Ta thực hiện biểu đồ Ven như hình bên.
Vì vậy:
1;5;7;8 3;6;9 1;3;5;6;7;8;9A = =
,
2;10 3;6;9 2;3;6;9;10B = =
.
b)
☺ Cách giải 1: Dựa vào biểu đồ Ven, ta có:
Số học sinh khối 10 chỉ tham gia câu lạc bộ Toán:
160 10 150−=
(em).
Số học sinh khối 10 chỉ tham gia câu lạc bộ Tin:
140 10 130−=
(em).
Tổng số học sinh khối 10 là:
150 10 130 290+ + =
(em).
☺ Cách giải 2: Dựa vào công thức
A B A B A B = + −
trong đó ký hiệu
AB
là số phần tử của tập
AB
, ký hiệu
,,A B A B
lần lượt là số phần tử của các tập
,,A B A B
.
Gọi A là tập hợp các học sinh khối 10 tham giác câu lạc bộ Toán,
B là tập hợp các học sinh khối 10 tham gia câu lạc bộ Tin.
Ta có:
160 140 10 290A B A B A B = + − = + − =
(em).
Câu 2. Tìm tập xác định của các hàm số sau:
a)
2
1
x
y
xx
+
=
+
; b)
( )
2
2
1 khi 1
1 khi 1
x x x
fx
xx
+ −
=
−
.
Hướng dẫn giải:
a) Hàm số xác định khi và chỉ khi
00
1 0 1
xx
xx



+ −

.
Vậy tập xác định hàm số là:
( )
1; \ 0D = − +
.
b) Khi
1x
thì
( )
2
1f x x x= + −
luôn xác định; khi
1x
thì
( )
2
1f x x=−
luôn xác định.
Vậy tập xác định hàm số:
( )
)
;1 1;D = − + =
.
Câu 3. Vẽ đồ thị hàm số
2
28y x x= − −
.
Hướng dẫn giải:
Đỉnh I có tọa độ:
( )
1, 9 hay 1; 9
2
II
b
x y I
a
= − = = − −
.
Trục đối xứng parabol:
1x =
.
44
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Vì
10a =
nên bề lõm parabol hướng lên.
Ta có bảng giá trị:
Đồ thị hàm số:
Câu 4. Tìm giá trị m biết parabol
2
y x x m= + +
có đỉnh nằm trên đường thẳng
3
4
y =
.
Hướng dẫn giải:
Tọa độ đỉnh I của parabol:
1
22
I
b
x
a
−
= − =
2
1 1 1 1 1
hay ;
2 2 4 2 4
I
y m m I m
− − −
= + + = − −
.
Vì
3
( ):
4
I d y=
nên
13
1
44
mm− = =
.
Câu 5. Hàm lượng Natri (đơn vị miligam, 1 mg = 0,001 g) trong 100 g một số loại ngũ cốc được cho như
sau :
0
340
70
140
200
180
210
150
100
130
140
180
190
160
290
50
220
180
200
210
Hãy tìm tứ phân vị của mẫu trên. Các tứ phân vị này cho ta thông tin gì?
Hướng dẫn giải:
Sắp xếp các giá trị của mẫu theo thứ tự không giảm :
0 50 70 100 130 140 140 150 160 180 180 180 190 200 200 210 210 220 290 340 ;
( )
20n =
.
Tứ phân vị thứ hai chính là trung vị của mẫu :
2
180 180
180
2
Q
+
==
.
Xét nửa mẫu bên trái : 0 50 70 100 130 140 140 150 160 180 .
Tứ phân vị thứ nhất chính là trung vị nửa mẫu này :
1
130 140
135
2
Q
+
==
.
Xét nửa mẫu bên phải : 180 180 190 200 200 210 210 220 290 340.
Tứ phân vị thứ ba chính là trung vị nửa mẫu này :
3
200 210
205
2
Q
+
==
.
Biểu diễn tứ phân vị trên trục số :
Các tứ phân vị cho ta hình ảnh phân bố của mẫu số liệu. Khoảng cách từ
1
Q
đến
2
Q
là 45 trong khi
khoảng cách từ
2
Q
đến
3
Q
là 25. Điều này cho thấy mẫu số liệu tập trung với mật độ cao ở bên
phải
2
Q
và mật độ thấp ở bên trái
2
Q
.
45
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Câu 6. Chứng minh rằng :
1 cot tan 1
1 cot tan 1
xx
xx
++
=
−−
(các biểu thức đều có nghĩa).
Hướng dẫn giải:
Ta có:
1 tan 1
1
1 cot tan 1
t an t an
1 tan 1
1 cot tan 1
1
tan tan
x
xx
xx
x
xx
xx
+
+
++
= = =
−
−−
−
(điều phải chứng minh).
Câu 7. Cho hàm số
2 3 4
1
x
y x m
xm
= − + +
+−
với
m
là tham số. Tìm
m
để hàm số có tập xác định là
)
0;+
.
Hướng dẫn giải:
Hàm số xác định
34
2 3 4 0
2
10
1
m
xm
x
xm
xm
−
− +


+ −
−
.
Trường hợp 1:
3 4 6
1
25
m
mm
−
−
, tập xác định hàm số
34
; \ 1
2
m
Dm
−

= + −

.
Tập xác định này không thể bằng
)
0;+
theo đề bài. Do đó
6
5
m
không thỏa mãn.
Trường hợp 2:
3 4 6
1
25
m
mm
−
−
, tập xác định của hàm số là
34
;
2
m
D
−

= +

.
Do đó, hàm số có tập xác định là
)
3 4 4
0; 0
23
m
m
−
+ = =
(thỏa mãn).
Vậy
4
3
m =
là giá trị cần tìm.
Câu 8. Cho tam giác
ABC
có
2b c a+=
. Chứng minh rằng:
6Rr bc=
, trong đó
,Rr
lần lượt là bán kính
đường tròn ngoại tiếp và nội tiếp tam giác
.ABC
Hướng dẫn giải:
Ta có:
3
;
4 2 2
ABC ABC
abc a b c a
S S pr r r
R

++
= = = =
(vì
2b c a+=
).
Do đó:
3
2 12 6
42
abc a
r abc aRr bc Rr
R
= = =
(điều phải chứn minh).
Câu 9. Cho hình thang ABCD vuông tại A và B , biết
,3AD a BC a==
và cạnh
2.AB a=
a) Tính
. , .AB BD BC BD
và
..AC BD
b) Gọi I, J lần lượt là trung điểm của AB, CD. Tính
.AC IJ
.
Hướng dẫn giải:
a) Tính
.AB BD
. Ta có:
( )
0
. . .AB BD AB BA AD AB BA AB AD= + = +
2
22
. 4 .AB BA AB AB a= = − = − = −
46
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Tính
.BC BD
. Ta có:
( )
. . .cos ,BC BD BC BD BC BD=
. .cosBC BD DBC=
. .cosBC BD BDA=
3
. . . 3 .
AD
BC BD BC AD a
BD
= = =
(trong đó
DBC
BDA=
vì là hai góc so le trong).
Tính
.AC BD
.
Ta có:
( )( )
. . . . .AC BD AB BC BA AD AB BA AB AD BC BA BC AD= + + = + + +
( )
2
2
0 2 2 2
0 0 . .cos0 3 . .1 2 3AB BC AD AB a a a a a= − + + + = − + = − + = −
.
b) Tính
.AC IJ
. Ta có:
( )
02
0
. . . . . .cos0 3 .2 .1 6AC IJ AB BC IJ AB IJ BC IJ BC IJ a a a= + = + = = =
.
Câu 10. Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm
I
và
II
. Mỗi
sản phẩm
I
bán lãi
500
nghìn đồng, mỗi sản phẩm
II
bán lãi
400
nghìn đồng. Để sản xuất được
một sản phẩm
I
thì Chiến phải làm việc trong
3
giờ, Bình phải làm việc trong 1 giờ. Để sản xuất
được một sản phẩm
II
thì Chiến phải làm việc trong 2 giờ, Bình phải làm việc trong
6
giờ. Một
người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm
việc quá
180
giờ và Bình không thể làm việc quá
220
giờ. Hỏi số tiền lãi lớn nhất trong một tháng
của xưởng là bao nhiêu?
Hướng dẫn giải:
Gọi
x
,
y
lần lượt là số sản phẩm loại
I
và loại
II
được sản xuất ra. Điều kiện
x
,
y
nguyên
dương.
Ta có hệ bất phương trình:
3 2 180
6 220
0
0
xy
xy
x
y
+
+
(
*
,xy
).
Miền nghiệm của hệ chính là miền của tứ giác OABC (bỏ đi
điểm O), trong đó
( )
60;0A
,
( )
40;30B
,
110
0;
3
C



(vì
*
,xy
nên ta loại điểm C).
Tiền lãi trong một tháng của xưởng là
0,5 0,4T x y=+
(triệu đồng).
Ta thấy
T
chỉ đạt giá trị lớn nhất chỉ có thể tại các điểm
A
,
B
.
Tại
( )
60;0A
thì
0,5.60 0,4.0 30T = + =
. Tại
( )
40;30B
thì
0,5.40 0,4.30 32T = + =
.
Vậy tiền lãi lớn nhất trong một tháng của xưởng là
32
triệu đồng, khi đó số sản phẩm loại I là 40,
số sản phẩm loại II là 30.
Lưu ý: Dù đã bỏ qua hai điểm O, C do chúng không thỏa điều kiện cho miền nghiệm hệ bất
phương trình, ta vẫn phải tính giá trị
T
tại hai điểm O, C; khi đó ta thấy hai giá trị này nhỏ hơn
32, điều này đồng nghĩa với việc giá trị lớn nhất của T tồn tại, và
max
32=T
.
47
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
ÑEÀ REØN LUYEÄN SOÁ 10
Time: 90 phuùt
ơ
Câu 1.
a) Cho
A
= {1; 3; 5}. Liệt kê các tập con của tập
A
.
b) Tìm tập hợp X sao cho
; ; ; ;a b X a b c d
.
Câu 2. Cho hàm số
2
2
khi 0
1
( ) 1 khi 0 2
1 khi 2
x
x
f x x x
xx
−
= +
−
Tnh:
( 2), (0), (1), (3)f f f f−
.
Câu 3. Cho hàm số:
21
mx
y
xm
=
− + −
với
m
là tham số.
a) Tìm tập xác định của hàm số theo tham số
m
.
b) Tìm
m
để hàm số xác định trên
( )
0;1
.
Câu 4. Tìm các hệ số a, b, c của hàm số bậc hai
2
y ax bx c= + +
biết rằng đồ thị hàm số đi qua gốc tọa độ
O, đồng thời có đỉnh
( )
1; 3I −−
.
Câu 5. Người ta tiến hành phỏng vấn một số người về chất lượng của một loại sản phẩm mới. Người điều
tra yêu cầu cho điểm sản phẩm (thang điểm 100) và thu được kết quả như sau:
80 65 51 48 45 61 30 35 84 83 60 58 75 72 68
39 41 54 61 72 75 72 61 58 65
Tìm phương sai và độ lệch chuẩn. Em có nhận xét gì về các kết quả nhận được?
Câu 6. Xét hệ phương trình
21
0
xy
xy
−
+
(*).
a) Hệ (*) có phải là hệ phương trình bậc nhất hai ẩn x, y hay không?
b) Cặp số
( )
1;2
có phải là một nghiệm của (*) không?
Câu 7. Cho
1
tan
3
=
. Tính giá trị của biểu thức
3sin 4cos
2sin 5cos
A


+
=
−
.
Câu 8. Cho
ABC
nội tiếp đường tròn tâm O, H là trực tâm tam giác, D là điểm đối xứng của A qua O.
Chứng minh rằng:
a)
2HA HB HC HO+ + =
; b)
OA OB OC OH+ + =
.
Câu 9. Cho tam giác
ABC
. Tìm tập hợp điểm
M
sao cho
( )
2 3 0MA MB CB BC+ + =
.
Câu 10. Muốn đo chiều cao của Tháp Chàm Por Klong Garai ở Ninh
Thuận, người ta lấy hai điểm A và B trên mặt đất có khoảng
cách AB = 12 m cùng thẳng hàng với chân C của tháp để đặt
hai giác kế (hình bên). Chân của giác kế có chiều cao h =
1,3m. Gọi D là đỉnh tháp và hai điểm A
1
, B
1
cùng thẳng hàng
với C
1
thuộc chiều cao CD của tháp. Người ta đo được
0
11
49DAC =
,
0
11
35DB C =
. Chiều cao CD của tháp đó gần
nhất với kết quả nào sau đây?
================HẾT===============
48
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Höôùng daãn giaûi ñeà soá 10
Câu 1.
a) Cho
A
= {1; 3; 5}. Liệt kê các tập con của tập
A
.
b) Tìm tập hợp X sao cho
; ; ; ;a b X a b c d
.
Hướng dẫn giải:
a) Các tập con của
A
gồm:
, {1}, {3}, {5}, {1; 3}, {1; 5}, {3; 5}, {1; 3; 5}.
b) Theo đề bài, ta có tập hợp X phải chứa 2 phần tử là a và b, nhưng không được chứa phần tử nào
khác 4 phần tử a, b, c, d. Do đó các tập hợp X có thể là :
; , ; ; , ; ; , ; ; ;X a b X a b c X a b d X a b c d= = = =
.
Câu 2. Cho hàm số
2
2
khi 0
1
( ) 1 khi 0 2
1 khi 2
x
x
f x x x
xx
−
= +
−
Tnh:
( 2), (0), (1), (3)f f f f−
.
Hướng dẫn giải:
Với
20x = −
, ta có:
( )
22
2
2 1 3
f − = = −
−−
. Với
0 0;2x =
, ta có:
( )
0 0 1 1f = + =
.
Với
1 0;2x =
, ta có:
( )
1 1 1 2f = + =
. Với
32x =
, ta có:
( )
3 3 1 2f = + =
.
Câu 3. Cho hàm số:
21
mx
y
xm
=
− + −
với
m
là tham số.
a) Tìm tập xác định của hàm số theo tham số
m
.
b) Tìm
m
để hàm số xác định trên
( )
0;1
.
Hướng dẫn giải:
a) Hàm số xác định
2 0 2
2
1
2 1 0 2 1
x m x m
xm
xm
x m x m
− + −

−

−
− + − − +


.
Tập xác định của hàm số là
)
2; \ 1D m m= − + −
.
b) Hàm số xác định trên
( ) ( )
) ( )
0;1 0;1 2; 1 1;m m m − − − +
( )
)
( ) ( )
20
0;1 2; 1
2
11
0;1 1;
1
10
m
mm
m
m
m
m
m
−
− −
=
−
− +
−
.
Vậy
(
;1 2m −
thỏa mãn đề bài.
Câu 4. Tìm các hệ số a, b, c của hàm số bậc hai
2
y ax bx c= + +
biết rằng đồ thị hàm số đi qua gốc tọa độ
O, đồng thời có đỉnh
( )
1; 3I −−
.
Hướng dẫn giải:
Parabol qua gốc tọa độ O
( )
0;0 0c=
.
49
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Parabol có đỉnh
( )
1; 3I −−
nên
2 0 3
1
2
36
3
b
a b a
a
a b b
ab
− = =
− = −



− = − =

− = −
. Vậy
3, 6, 0a b c= = =
.
Câu 5. Người ta tiến hành phỏng vấn một số người về chất lượng của một loại sản phẩm mới. Người điều
tra yêu cầu cho điểm sản phẩm (thang điểm 100) và thu được kết quả như sau:
80 65 51 48 45 61 30 35 84 83 60 58 75 72 68
39 41 54 61 72 75 72 61 58 65
Tìm phương sai và độ lệch chuẩn. Em có nhận xét gì về các kết quả nhận được?
Hướng dẫn giải:
Ta có:
80 65 ... 65
60,52
25
x
+ + +
==
(điểm).
Phương sai:
2 2 2 2
1 2 25
1
( ) ( ) ... ( ) 212,73
25
s x x x x x x

= − + − + + −

.
Độ lệch chuẩn
2
14,59ss=
(điểm).
Nhận xét: Mức độ chênh lệch điểm giữa các giá trị là khá lớn.
Câu 6. Xét hệ phương trình
21
0
xy
xy
−
+
(*).
a) Hệ (*) có phải là hệ phương trình bậc nhất hai ẩn x, y hay không?
b) Cặp số
( )
1;2
có phải là một nghiệm của (*) không?
Hướng dẫn giải:
a) Hai bất phương trình
2 1, 0x y x y− +
đều có dạng bậc nhất hai ẩn x, y nên hệ đã cho chnh là hệ bất
phương trình bậc nhất hai ẩn x, y.
b) Thay cặp số
( )
1;2
vào mỗi bất phương trình của hệ (*), ta có:
31
30
−
(đúng), vì vậy
( )
1;2
là một
nghiệm của hệ (*).
Câu 7. Cho
1
tan
3
=
. Tính giá trị của biểu thức
3sin 4cos
2sin 5cos
A


+
=
−
.
Hướng dẫn giải:
Vì
sin 1
tan
cos 3
==
nên
cos 0
. Chia cả tử và mẫu của P cho
cos
, ta được:
sin 1
3 4 3. 4
3tan 4 15
cos 3
sin 1
2tan 5 13
2 5 2. 5
cos 3
A
++
+
= = = = −
−
−−
.
Câu 8. Cho
ABC
nội tiếp đường tròn tâm O, H là trực tâm tam giác, D là điểm đối xứng của A qua O.
Chứng minh rằng:
a)
2HA HB HC HO+ + =
; b)
OA OB OC OH+ + =
.
Hướng dẫn giải:
50
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
a) Xét tam giác ABD nội tiếp đường tròn đường kính AD nên
AB BD⊥
.
Mặt khác
AB CH⊥
nên
// (1).BD CH
Tương tự, tam giác ACD nội tiếp đường tròn đường kính AD nên
AC CD⊥
; mặt khác
AC BH⊥
nên
// (2).CD BH
Từ (1) và (2) suy ra
BDCH
là hình bình hành.
Ta có:
2HA HB HC HA HD HO+ + = + =
(vì O là trung điểm AD).
b) Ta có:
OA OB OC OH HA OH HB OH HC+ + = + + + + +
( )
3 3 2OH HA HB HC OH HO OH= + + + = + =
.
Câu 9. Cho tam giác
ABC
. Tìm tập hợp điểm
M
sao cho
( )
2 3 0MA MB CB BC+ + =
.
Hướng dẫn giải:
Gọi
I
là điểm thỏa mãn
( )
2 0 2 0IA IB IA IA AB+ = + + =
2
3 2 0
3
IA AB AI AB + = =
.
Do đó điểm I cố định (thuộc đoạn AB và
2
3
AI AB=
). Ta có:
( )
2 3 0MA MB CB BC+ + =
( ) ( )
2 3 . 0MI IA MI IB CB BC

+ + + + =

( )
0
3 2 3 . 0
+ + + =



MI IA IB CB BC
2
2
3 . 3 0 .MI BC BC MI BC BC − = =
.
Gọi
,MI

lần lượt là hình chiếu của
,MI
trên đường thẳng
BC
.
Ta có:
( )
00
. . . . . .MI BC MM M I I I BC MM BC M I BC I I BC M I BC
= + + = + + =
.
Do vậy
22
..MI BC BC M I BC BC

= =
.
Vì
2
0BC
nên
,M I BC

cùng hướng, khi đó:
22
..M I BC BC M I BC BC M I BC
= = =
.
Do
I
cố định nên
I
cố định, suy ra
M
cố định.
Vậy tập hợp điểm
M
là đường thẳng đi qua
M
và vuông góc với
BC
.
Câu 10. Muốn đo chiều cao của Tháp Chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm A và B
trên mặt đất có khoảng cách AB = 12 m cùng thẳng hàng với chân C của tháp để đặt hai giác kế
(hình bên). Chân của giác kế có chiều cao h = 1,3m. Gọi D là đỉnh tháp và hai điểm A
1
, B
1
cùng
thẳng hàng với C
1
thuộc chiều cao CD của tháp. Người ta đo được
0
11
49DAC =
,
0
11
35DB C =
.
Chiều cao CD của tháp đó gần nhất với kết quả nào sau đây?
51
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Hướng dẫn giải:
Ta có:
11
12mA B AB==
.
Xét hai tam giác
11
DC A
và
11
DC B
có:
0
1 1 1
.cot 49C A C D=
,
0
1 1 1
.cot35C B C D=
.
Ta có:
( )
00
1 1 1 1 1 1 1
cot35 cot 49A B C B C A C D= − = −
11
1
00
cot35 cot49
AB
CD=
−
00
12
21,47 m
cot35 cot 49
=
−
.
Suy ra:
11
22,77 mCD CC C D= +
. Vậy chiều cao của tháp xấp xỉ
22,77 m
.
52
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
100 CAÂU TRAÉC NGHIEÄM TOAÙN 10
OÂN TAÄP KIEÅM TRA HOÏC KÌ I NAÊM HOÏC 2022 - 2023
Câu 1. Câu nào trong các câu sau không phải là mệnh đề?
A.
2
x
. B.
2 2 5+=
. C.
2
là một số hữu tỷ. D.
4
2
2
=
.
Câu 2. Mệnh đề nào sau là mệnh đề sai?
A.
n
:
2nn
. B.
2
:n n n =
. C.
2
:0xx
. D.
2
:x x x
.
Câu 3. Trong các mệnh đề sau, mệnh đề nào đúng ?
A.
2
,1nn +
không chia hết cho
3
. B.
, 3 3x x x
.
C.
( )
2
, 1 1x x x − −
. D.
n
,
2
1n +
chia hết cho
4
.
Câu 4. Cho mệnh đề A: “
2
, 7 0x x x − +
”. Mệnh đề phủ định của A là:
A.
2
, 7 0x x x − +
. B.
2
, 7 0x x x − +
.
C. Không tồn tại
x
để
2
70xx− +
. D.
2
, 7 0x x x − +
.
Câu 5. Phủ định của mệnh đề “
2
, 5 3 1x x x − =
” là :
A. “
2
, 5 3 1x x x −
”. B. “
2
, 5 3 1x x x − =
”.
C. “
2
, 5 3 1x x x −
”. D. “
2
, 5 3 1x x x −
”.
Câu 6. Cho mệnh đề: “Nếu 2 góc ở vị trí so le trong thì hai góc đó bằng nhau”. Trong các mệnh đề sau đây, đâu
là mệnh đề đảo của mệnh đề trên?
A. Nếu 2 góc bằng nhau thì hai góc đó ở vị trí so le trong.
B. Nếu 2 góc không ở vị trí so le trong thì hai góc đó không bằng nhau.
C. Nếu 2 góc không bằng nhau thì hai góc đó không ở vị trí so le trong.
D. Nếu 2 góc ở vị trí so le trong thì hai góc đó không bằng nhau.
Câu 7. Tìm số phần tử của tập hợp
,3= A x x
?
A.
3
. B.
4
. C.
5
. D.
6
.
Câu 8. Liệt kê các phần tử của tập hợp
2 1 , 3 5= − − A k k k
ta được
A.
3; 2; 1;0;1;2;3;4;5= − − −A
. B.
7; 5; 3; 1;1;3;5;7;9= − − − −A
.
C.
6; 4; 2;0;2;4;6;8;10= − − −A
. D.
5; 3; 1;1;3;5;7= − − −A
.
Câu 9. Cho hai tập hợp
1;2;3;4;5=A
và
0;2;4;6;8=B
. Tìm tập hợp
=C A B
là
A.
=C
. B.
2;4=C
.
C.
0;1;2;3;4;5;6;8=C
. D.
1;3;5=C
.
Câu 10. Cho hai tập hợp
0;2;4;6;8=A
và
1;2;3;4;5=B
. Tìm tập hợp
=C A B
.
A.
=C
. B.
2;4=C
.
C.
0;1;2;3;4;5;6;8=C
. D.
1;3;5=C
.
53
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Câu 11. Cho
1;2;3;4;5=A
,
0;2;4;6;8=B
. Tìm tập hợp
( ) ( )
\C A B A B=
?
A.
=C
. B.
2;4=C
.
C.
0;1;3;5;6;8=C
. D.
1;3;5=C
.
Câu 12. Cho
3;4;5;6;7=A
và
0;2;4;6;8=B
. Tìm
( ) ( )
\\C A B B A=
.
A.
=C
. B.
4;6=C
. C.
0;2;3;5;7;8=C
. D.
3;5;7=C
.
Câu 13. Tập
X
có bao nhiêu tập hợp con, biết
X
có
3
phần tử?
A.
2
. B.
4
. C.
6
. D.
8
.
Câu 14. Tập hợp
1 1 1 1 1
; ; ; ;
3 8 15 24 35

=


A
bằng tập hợp nào dưới đây?
A.
( )
1
,1 5
1



+


nn
nn
. B.
1
,1 5
21


+

nn
n
.
C.
( )
1
,1 5
2



+


nn
nn
. D.
2
1
,1 5
2


+

nn
n
.
Câu 15. Tập hợp
2
60A x x x= − −
bằng tập hợp nào dưới đây?
A.
. B.
0;1;2;3
. C.
1;0;1;2−
. D.
2; 1;0;1;2;3−−
.
Câu 16. Cho tập hợp
(
2
;1Am
= − −
,
)
1;= +B
. Tìm tất cả giá trị của
m
để
= AB
.
A.
2m
. B.
02m
. C.
2m
. D.
22m−
.
Câu 17. Cho hai nửa khoảng
4
;
1
A
m

= −
+

và
)
1;B = +
. Số giá trị nguyên m để
AB
là
A.
3
. B.
4
. C.
5
. D. Vô số.
Câu 18. Cho hai tập hợp khác rỗng
(
( )
2;7 , 1;A m B m= − = − +
. Tìm tất cả giá trị m để
( )
1;AB = +
.
A.
3.m
B.
2m =
. C.
0m
. D.
1m
.
Câu 19. Bất phương trình nào sau đây không phải là bất phương trình bậc nhất hai ẩn?
A.
2 3 0.xy+
B.
2.xy+
C.
2
0.xy+
D.
1
23
xy
−
.
Câu 20. Cặp số
( )
1; 1−
là nghiệm của bất phương trình
A.
41xy+
. B.
20xy+ −
. C.
0xy− −
. D.
3 1 0xy− − −
.
Câu 21. Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình
21xy+
?
A.
( )
0;0
. B.
( )
3; 7−
. C.
( )
2;1−
. D.
( )
0;1
.
Câu 22. Miền nghiệm của bất phương trình
( ) ( )
2 2 2 2 1x y x− + + − −
là nửa mặt phẳng chứa điểm
A.
( )
2;2
. B.
( )
1;3−
. C.
( )
4;3−
. D.
( )
5;0
.
Câu 23. Miền nghiệm (miền không bị gạch trong hình) của bất phương trình
34xy−
là
54
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
A.
B.
C.
D.
Câu 24. Phần không được gạch chéo trong hình (kể cả biên), là miền nghiệm của bất phương trình nào bên
dưới?
A.
3xy−
.
B.
23xy−
.
C.
23xy−
.
D.
3xy−
.
Câu 25. Miền nghiệm của hệ bất phương trình
0
3 3 0
50
xy
xy
xy
−
− +
+ −
là phần mặt phẳng chứa điểm
A.
( )
5;3
. B.
( )
0;0
. C.
( )
1; 1−
. D.
( )
2;2−
.
Câu 26. Cho hệ bất phương trình
0
2 5 0
xy
xy
+
+
có tập nghiệm là
S
. Khẳng định nào sau đây là khẳng định
đúng?
A.
( )
1;1 S
. B.
( )
1; 1 S− −
. C.
1
1;
2
S

−


. D.
12
;
25
S

−


.
55
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Câu 27. Miền biểu diễn nghiệm của hệ
3 2 5
2
xy
xy
+
− −
là phần không gạch chéo (không kể biên) của hình nào
trong các phương án bên dưới?
A.
B.
C.
D.
Câu 28. Cho biết miền nghiệm của một hệ bất phương trình bậc nhất hai ẩn
x, y chính là miền của tam giác ABC như hình bên. Tìm tổng của giá
trị lớn nhất, giá trị nhỏ nhất biểu thức
( )
; 5 2 2025F x y x y= − +
.
A.
3075
.
B.
5000
.
C.
4035
.
D.
4050
.
Câu 29. Cho các giá trị
,xy
thỏa điều kiện
20
2 1 0
3 2 0
xy
xy
xy
− +
− −
− −
. Tìm giá trị lớn nhất của biểu thức
32T x y=+
.
A.
19
. B.
25
. C.
14
. D. 20.
Câu 30. Bạn An kinh doanh hai mặt hàng handmade là vòng tay và vòng đeo cổ. Mỗi vòng tay làm trong 4
giờ, bán được 40 ngàn đồng. Mỗi vòng đeo cổ làm trong 6 giờ, bán được 80 ngàn đồng. Mỗi tuần bạn
An bán được không quá 15 vòng tay và 4 vòng đeo cổ. Tính số giờ tối thiểu trong tuần An cần dùng
để làm ra sản phẩm và bán được ít nhất 400 ngàn đồng?
56
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
A.
40
. B.
25
. C.
32
. D. 20.
Câu 31. Tìm tập xác định
D
của hàm số
( )( )
21
.
2 1 3
x
y
xx
−
=
+−
A.
( )
3; .D = +
B.
1
\ ;3 .
2
D

=−

C.
1
;
2
D

= − +


. D.
.D =
Câu 32. Tìm tập xác định
D
của hàm số
6 3 1.y x x= − − −
A.
( )
1;2 .D =
B.
1;2 .D =
C.
1;3 .D =
D.
1;2 .D =−
Câu 33. Tìm tập xác định
D
của hàm số
22
.
xx
y
x
− + +
=
A.
2;2 .D =−
B.
( )
2;2 \ 0 .D =−
C.
2;2 \ 0 .D =−
D.
.D =
Câu 34. Tìm tập xác định
D
của hàm số
2
1
.
6
x
y
xx
+
=
−−
A.
3.D =
B.
)
1; \ 3 .D = − +
C.
.D =
D.
)
1; .D = − +
Câu 35. Hàm số
1
2
y
x
=
−
nghịch biến trên khoảng nào dưới đây?
A.
( )
;2 .−
B.
( )
2; .+
C.
( )
2; .− +
D.
( )
2;2 .−
Câu 36. Cho hàm số
( )
30y ax a= +
. Tìm điều kiện của
a
để hàm số đồng biến trên ?
A.
0.a
B.
0.a
C.
.a
D.
1.a =
Câu 37. Điểm nào sau đây thuộc đồ thị hàm số
2 –1 3 2y x x= + −
?
A.
( )
2; 6
. B.
( )
1; 1−
. C.
( )
2; 10−−
. D.
( )
0; 4−
.
Câu 38. Cho hàm số
( )
(
2
2
, ;0
1
1 , 0;2
1 , 2;5
x
x
y x x
xx
−
−
= +
−
. Tính
( )
4f
, ta được kết quả:
A.
2
3
. B.
15
. C.
5
. D.
7
.
Câu 39. Hàm số
1
21
x
x
y
m
+
−
=
+
xác định trên
)
0;1
khi:
A.
1
2
m
. B.
1m
. C.
1
2
m
hoặc
1m
. D.
2m
hoặc
1m
.
57
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Câu 40. Cho hàm số
( )
y f x=
xác định trên đoạn
1;5−
có đồ thị như hình vẽ sau. Hãy chọn khẳng định
đúng về sự biến thiên của hàm số
( )
y f x=
trên đoạn
1;5−
.
A. Hàm số đồng biến trên các đoạn
1;1 , 1;2−
và nghịch biến trên các đoạn
2;3 , 3;5 .
B. Hàm số nghịch biến trên các đoạn
1;1 , 2;3−
và đồng biến trên các đoạn
1;2 , 3;5 .
C. Hàm số đồng biến trên các đoạn
1;1 , 2;3−
và nghịch biến trên các đoạn
1;2 , 3;5 .
D. Hàm số nghịch biến trên các đoạn
1;1 , 1;2−
và đồng biến trên các đoạn
2;3 , 3;5 .
Câu 41. Cho hàm số bậc hai
( )
2
0y ax bx c a= + +
. Chọn mệnh đề sai trong các khẳng định sau:
A. Nếu
0a
thì đồ thị hàm số có bề lõm hướng lên trên.
B. Nếu
0a
thì đồ thị hàm số có bề lõm hướng xuống dưới.
C. Đồ thị hàm số có đỉnh
;
24
b
I
aa

−−


.
D. Đồ thị hàm số luôn nhận trục
Oy
làm trục đối xứng.
Câu 42. Cho hàm số
( )
2
0y ax bx c a= + +
có đồ thị (P) như hình bên. Khẳng định nào sau đây là khẳng
định sai?
A. Hàm số đồng biến trên khoảng
( )
;3−
.
B. Hàm số nghịch biến trên khoảng
( )
3;+
.
C. Hàm số nghịch biến trên khoảng
( )
1;+
.
D. Hàm số đồng biến trên khoảng
( )
;1−
.
Câu 43. Parabol
( )
2
: 6 1P y x x= − + +
. Khi đó
A. Có trục đối xứng
6x =
và đi qua điểm
( )
0;1A
.
B. Có trục đối xứng
6x =−
và đi qua điểm
( )
1;6A
.
C. Có trục đối xứng
3x =
và đi qua điểm
( )
2;9A
.
D. Có trục đối xứng
3x =
và đi qua điểm
( )
3;9A
.
Câu 44. Xác định hàm số
2
2y x bx c= + +
biết đồ thị hàm số này đi qua hai điểm
( ) ( )
0;1 , 2;7AB−
.
A.
2
9 53
2
55
y x x= + −
. B.
2
21y x x= + +
. C.
2
21y x x= − +
. D.
2
21y x x= + −
.
Câu 45. Xác định parabol
( )
2
:4P y ax x c= − +
biết
( )
P
có đỉnh là
1
;2
2
I

−


là:
58
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
A.
2
4 4 1y x x= − − +
. B.
2
1
24
2
y x x= − − +
. C.
2
1
24
2
y x x= − −
. D.
2
4 4 1y x x= − −
.
Câu 46. Tọa độ đỉnh
I
của parabol
( )
2
:4P y x x= − +
là
A.
( )
2; 12I −−
. B.
( )
2; 4I
. C.
( )
1; 5I −−
. D.
( )
1; 3I
.
Câu 47. Hàm số
2
1yx= − +
nghịch biến trên khoảng nào sau đây?
A.
( )
0;+
. B.
( )
;0−
.
C.
( )
;0−
và
( )
0;+
. D.
( )
;1− −
và
( )
1;+
.
Câu 48. Giao điểm của parabol
( )
P
:
2
54y x x= + +
với trục hoành:
A.
( )
1;0−
,
( )
4;0−
. B.
( )
0; 1 ,−
( )
0; 4−
. C.
( )
1;0−
,
( )
0; 4−
. D.
( )
0; 1 ,−
( )
4;0−
.
Câu 49. Tìm tất cả giá trị của
m
để đỉnh của parabol
2
y x x m= + +
nằm trên đường thẳng
3
4
y =
.
A.
2m =
. B.
0m =
. C.
1m =
. D.
2m =−
.
Câu 50. Parabol
2
y x x c= + +
cắt đường phân giác của góc phần tư thứ nhất tại điểm có hoành độ
1x =
. Khi
đó
c
bằng:
A.
1
2
. B.
2−
. C.
2
. D.
1−
.
Câu 51. Biểu thức
2 0 2 0 2 0 2 0
cos 10 cos 20 cos 30 ... cos 180A = + + + +
có giá trị bằng:
A.
9A=
. B.
3A=
. C.
12A =
. D.
6A =
.
Câu 52. Giá trị của
oo
tan30 cot30+
bằng bao nhiêu?
A.
4
3
. B.
13
3
+
. C.
2
3
. D.
2
.
Câu 53. Cho góc
thỏa mãn
oo
0 90

. Khẳng định nào sau đây đúng?
A.
( )
2 2 o
sin sin 90 0

+ − =
. B.
( )
2 2 o
sin sin 90 2

+ − =
.
C.
( )
2 2 o
sin sin 90 1

+ − =
. D.
( )
2 2 o
sin sin 90 3
+ − =
.
Câu 54. Mệnh đề nào sau đây về tam giác
ABC
là sai?
A. Góc
B
nhọn khi và chỉ khi
2 2 2
b a c+
.
B. Góc
A
vuông khi và chỉ khi
2 2 2
a b c=+
.
C. Góc
C
tù khi và chỉ khi
2 2 2
c a b+
.
D. Góc
A
tù khi và chỉ khi
2 2 2
b a c+
.
Câu 55. Rút gọn biểu thức
2
1 sin
2sin .cos
x
P
xx
−
=
ta được
A.
1
tan
2
Px=
. B.
1
cot
2
Px=
. C.
2cotPx=
. D.
2tanPx=
.
Câu 56. Biểu thức
( )
2
cot tanaa+
bằng
A.
22
11
sin cos

−
. B.
22
cot tan 2aa+
. C.
22
11
sin cos

+
. D.
22
cot tan 2aa+
.
Câu 57. Cho
là góc tù và
5
sin
13
=
. Giá trị của biểu thức
3sin 2cos+

là
59
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
A.
3
. B.
9
13
−
. C.
3−
. D.
9
13
.
Câu 58. Cho góc
thỏa mãn
5
sin cos
2
+=

. Giá trị của
sin .cos

là:
A.
1
8
. B.
1
4
. C.
1
2
. D.
1
8
−
.
Câu 59. Cho
ABC
vuông tại
A
có
5=AC
cm,
13=BC
cm. Gọi góc
=ABC
và
=ACB
. Hãy chọn
khẳng định đúng khi so sánh độ lớn của hai góc
và
.
A.

. B.

. C.
=

. D.

.
Câu 60. Cho tam giác
ABC
có diện tích bằng
26
cm
2
và
8=AB
cm,
13=AC
cm. Giá trị
sin A
bằng bao
nhiêu?
A.
1
4
. B.
30
. C.
1
2
. D.
150
.
Câu 61. Cho giác
ABC
có
5=a
,
26=b
,
135=C
.Tính diện tích của
ABC
.
A.
5 13
2
−
. B.
5 13
. C.
5 13
2
. D.
5 26
.
Câu 62. Tam giác
ABC
có
=BC a
và
30=A
. Tính bán kính đường tròn ngoại tiếp
ABC
.
A.
a
. B.
3
3
a
. C.
2a
. D.
2
a
.
Câu 63. Cho
ABC
biết
6=a
,
2=b
,
13=+c
. Độ dài đường cao ứng với góc nhỏ nhất của
ABC
bằng?
A.
13
2
+
. B.
( )
6 1 3
4
+
. C.
13
6
+
. D.
33
2
+
.
Câu 64. Cho
ABC
có ba cạnh lần lượt là
5=a
,
8=b
,
11=c
. Độ dài đường trung tuyến vẽ từ đỉnh
C
bằng:
A.
57
4
. B.
57
2
. C.
57
. D.
57
.
Câu 65. Cho góc
60xOy =
. Gọi
A
và
B
là hai điểm di động lần lượt trên tia
Ox
và tia
Oy
sao cho
23AB =
. Độ dài lớn nhất của đoạn
OA
bằng:
A.
43
. B.
2
. C.
4
. D.
1
.
Câu 66. Hai chiếc ca nô cùng xuất phát từ cảng
A
, đi thẳng theo hai
hướng tạo với nhau góc
60
. Ca nô
B
chạy với vận tốc
20
hải
lí một giờ. Ca nô
C
chạy với tốc độ
25
hải lí một giờ. Hỏi sau
2
giờ, hai ca nô cách nhau một khoảng xấp xỉ bao nhiêu hải lí
(kết quả làm tròn đến hàng đơn vị)? (1 hải lí
1,852
km).
A.
46
.
B.
23
.
C.
25
.
D.
56
.
60
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Câu 67. Từ đỉnh C một tháp có chiều cao
40CD =
m,
người ta nhìn hai điểm
A
và
B
trên mặt đất
dưới các góc nhìn là
34 26
và
72 12
so với
phương thẳng đứng của tháp. Ba điểm
, , A B D
thẳng hàng. Khoảng cách
AB
gần nhất với kết
quả nào sau đây?
A.
97m.
B.
100m.
C.
120m.
D.
83m.
Câu 68. Khi khai quật tại một ngôi làng cổ, người ta tìm được mảnh
của một chiếc đĩa phẳng hình tròn bị vỡ. Các nhà khảo cổ đo
được kích thước ba cạnh tam giác ABC (nội tiếp vành tròn
đĩa) là
3,7
cm;
4,3
cm và
7,5
cm. Họ muốn làm một chiếc
đĩa mới mô phỏng theo chiếc đĩa này. Hỏi chiếc đĩa cần làm
có bán kính bằng bao nhiêu? (Kết quả làm tròn đến hàng đơn
vị).
A.
6,1
cm.
B.
5,7
cm.
C.
6,8
cm.
D.
5,3
cm.
Câu 69. Cho tam giác
ABC
có độ dài ba đường trung tuyến lần lượt bằng 15, 18, 27. Tính diện tích
S
của
tam giác
ABC
.
A.
105 2
. B.
125
. C.
105
. D.
120 2
.
Câu 70. Cho
ABC
có
8AB =
,
5AC =
,
60A =
. Tính bán kính đường tròn cắt cả ba cạnh của
ABC
và
chắn trên mỗi cạnh một dây có độ dài bằng 4:
A.
7
. B.
3
. C.
23+
. D.
7
.
Câu 71. Hãy tìm khẳng định sai. Nếu hai véc tơ bằng nhau thì chúng luôn có đặc điểm sau
A. Cùng điểm gốc. B. Cùng phương.
C. Có độ dài bằng nhau. D. cùng hướng.
Câu 72. Mệnh đề nào sau đây đúng?
A. Có duy nhất một vectơ cùng phương với mọi vectơ.
B. Có ít nhất hai vectơ có cùng phương với mọi vectơ.
C. Có vô số vectơ cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ.
Câu 73. Cho hình bình hành
ABCD
tâm
O
. Khi đó
OA OB−
bằng
A.
OC OB+
. B.
AB
. C.
OC OD−
. D.
CD
.
Câu 74. Cho
5
điểm
, , , ,M N P Q R
. Vectơ tổng
MN PQ RN NP QR+ + + +
bằng:
A.
MP
. B.
PR
. C.
MR
. D.
MN
.
Câu 75. Cho hình bình hành
ABCD
. Có bao nhiêu vectơ có điểm đầu và điểm cuối là các đỉnh của hình bình
hành, bằng véc tơ
AD
(không kể véc tơ
AD
) ?
A.
1
. B.
2
. C.
3
. D.
4
.
61
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Câu 76. Cho tam giác đều
ABC
cạnh
a
. Mệnh đề nào sau đây là đúng?
A.
AB AC=
. B.
AC a=
. C.
AC BC=
. D.
AB a=
.
Câu 77. Hình bình hành
ABCD
là một hình chữ nhật nếu nó thỏa mãn điều kiện nào trong các điều kiện sau
đây?
A.
AC BC=
. B.
AC BD=
. C.
AC AD=
. D.
AC BD=
.
Câu 78. Cho tứ giác
ABCD
. Nếu
AB DC=
và
AC BD=
thì
ABCD
A. Không là hình bình hành. B. Là hình vuông.
C. Là hình chữ nhật. D. Là hình thoi.
Câu 79. Cho hình bình hành
ABCD
. Tổng các véc tơ
AB AC AD++
là
A.
2AC
. B.
AC
. C.
1
3
AC
. D.
2
3
AC
.
Câu 80. Cho 4 điểm bất kì
, , ,A B C O
. Đẳng thức nào sau đây là đúng?
A.
OA CA CO=−
. B.
AB AC BC=+
. C.
AB OB OA=+
. D.
OA OB BA=−
.
Câu 81. Cho tam giác đều
ABC
cạnh
2a
có
G
là trọng tâm. Khi đó giá trị
AB GC−
là:
A.
3
3
a
. B.
23
3
a
. C.
2
3
a
. D.
43
3
a
.
Câu 82. Cho tứ giác
ABCD
. Gọi
,MN
lần lượt là trung điểm của các cạnh
,AB CD
.
K
là điểm đối xứng
với
M
qua
N
. Khi đó khẳng định nào sau đây là đúng?
A.
MK AD BC=−
. B.
MK AD BC=+
. C.
MK AB CD=+
. D.
MK AC BD=−
.
Câu 83. Cho tam giác
ABC
. Điểm
M
thỏa mãn
0MA MB MC− + =
thì
A.
M
là điểm sao cho tứ giác
ABMC
là hình bình hành.
B.
M
là trọng tâm tam giác
ABC
.
C.
M
là điểm sao cho tứ giác
BAMC
là hình bình hành.
D.
M
thuộc đường trung trực của
AB
.
Câu 84. Cho nửa đường tròn tâm
O
, đường kính
2PQ =
. Trên nửa đường tròn đó ta lấy các điểm
,,A B C
khác
,PQ
sao cho theo thứ tự đó, chúng chia nửa đường tròn thành bốn phần bằng nhau. Khi đó
OA OC OB++
bằng:
A.
3
. B.
12+
. C.
22+
. D.
2
.
Câu 85. Cho
ABC
. Gọi
M
là điểm thỏa mãn
3MB MA=
. Khi đó biểu diễn
AM
theo
AB
và
AC
là
A.
1
3
4
AM AB AC=+
. B.
1
0.
2
AM AB AC= − +
.
C.
11
46
AM AB AC=+
. D.
11
26
AM AB AC=+
.
Câu 86. Cho tam giác
ABC
. Gọi
M
là trung điểm của
AB
,
D
là trung điểm của
BC
,
N
là điểm thuộc
AC
sao cho
2CN NA=
,
K
là trung điểm của
MN
. Khi đó khẳng định nào sau đây là đúng?
A.
11
46
AK AB AC=+
. B.
11
23
AK AB AC=+
.
62
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
C.
1
2
AK AD=
. D.
2
5
AK AD=
.
Câu 87. Cho tam giác
ABC
với phân giác trong
AD
. Biết
5AB =
,
6BC =
,
7CA =
. Khi đó
AD
bằng:
A.
57
12 12
AB AC+
. B.
75
12 12
AB AC−
. C.
75
12 12
AB AC+
. D.
57
12 12
AB AC−
.
Câu 88. Cho tam giác
ABC
. Gọi
I
là trung điểm của
BC
,
H
là điểm đối xứng của
I
qua
C
. Khi đó khẳng
định nào sau đây là đúng?
A.
AH AC AI=+
. B.
2AH AC AI=−
.
C.
2AH AC AB=−
. D.
AH AB AC AI= + +
.
Câu 89. Cho hai điểm cố định
,AB
. Tập hợp các điểm
M
thỏa mãn
MA MB MA MB+ = −
là:
A. Đường tròn đường kính
AB
. B. Đường trung trực của
AB
.
C. Đường tròn bán kính
AB
. D. Nửa đường tròn đường kính
AB
.
Câu 90. Cho tam giác
ABC
có trọng tâm
G
. Tập hợp các điểm
M
sao cho
MA MB MC AB AC+ + = −
là:
A. Đường tròn tâm
G
đường kính
BC
. B. Đường tròn tâm
G
đường kính
1
3
BC
.
C. Đường tròn tâm
G
bán kính
1
3
BC
. D. Đường tròn tâm
G
đường kính
3MG
.
Câu 91. Cho tứ giác
ABCD
. Gọi
,MN
lần lượt là trung điểm của
,AB CD
. Đẳng thức nào sau đây là đúng?.
A. . B. .
C. . D. .
Câu 92. Cho hình thang , hai đường chéo và cắt nhau tại O. Qua O kẻ MN song song với
( là đáy của hình thang, ). Đặt , . Khi đó khẳng định nào
sau đây là đúng?
A. . B. .
C. . D. .
Câu 93. Cho tam giác đều
ABC
cạnh
.a
Biết rằng tập hợp các điểm
M
thỏa mãn đẳng thức
2 3 4MA MB MC MB MA+ + = −
là đường tròn cố định có bán kính
.R
Tính bán kính
R
theo
.a
A.
3
a
r =
. B.
9
a
r =
. C.
2
a
r =
. D.
6
a
r =
.
Câu 94. Cho ba vectơ
a
,
b
,
c
thỏa:
4a =
,
1b =
,
5c =
và
( )
5 3 0b a c− + =
. Khi đó biểu thức
. . .M a b b c c a= + +
có giá trị bằng
A.
29
. B.
67
2
. C.
18,25
. D.
18,25−
.
2
BC AD
MN
+
=
MN BC AD=+
MN AC BD=+
( )
1
2
MN BC AD=+
ABCD
AC
BD
AB
AB
,M AD N BC
AB a=
DC b=
aAB bDC
MN
ab
+
=
+
bAB aDC
MN
ab
+
=
+
aAB bDC
MN
ab
−
=
+
bAB aDC
MN
ab
−
=
+
63
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Câu 95. Cho tam giác ABC vuông tại A với
3, 4AB AC==
. Các điểm
,MN
lần lượt thuộc các cạnh
,AB AC
thỏa mãn
1AM AN==
. Tích vô hướng
.BN CM
bằng
A. 1. B. −1. C. −7. D. 7.
Câu 96. Gọi
S
là diện tích tam giác
ABC
. Mệnh đề nào sau đây đúng?
A.
( )
2
22
1
..
2
S AB AC AB AC=−
. B.
( )
2
22
..S AB AC AB AC=−
.
C.
( )
2
22
1
..
2
S AB AC AB AC=−
. D.
( )
2
22
..S AB AC AB AC=−
.
Câu 97. Đoạn thẳng
AB
có độ dài
2a
,
I
là trung điểm
AB
. Khi
2
.3MAMB a=
. Độ dài
MI
là
A.
2a
. B.
a
. C.
3a
. D.
7a
.
Câu 98. Cho đoạn thẳng
4AB =
. Tập hợp các điểm
M
thỏa mãn
22
8MA MB−=
là
A. Một đường thẳng. B. Một đoạn thẳng. C. Một đường tròn. D. Một điểm.
Câu 99. Một máy bay đang bay từ hướng đông sang hướng tây với tốc độ 700 km/h thì gặp luồng gió thổi từ
hướng đông bắc sang hướng tây nam với tốc độ 40 km/h. Máy bay bị thay đổi vận tốc sau khi gặp
gió thổi. Tìm tốc độ mới của máy bay (làm tròn kết quả đến hàng phần trăm).
A.
911,12 km/h
. B.
724,32 km/h
. C.
728,83 km/h
. D.
813,13 km/h
.
Câu 100. Một chiếc thuyền cố gắng đi thẳng qua một con sông với tốc độ 0,75 m/s. Tuy nhiên dòng nước trên
con sông đó chảy với tốc độ 1,2 m/s về hướng bên trái (hình vẽ). Tính tốc độ dịch chuyển của thuyền
so với bờ (kết quả làm tròn đến hàng phần nghìn).
A.
1,215
m/s. B.
1,112
m/s. C.
1,312
m/s. D.
1,415
m/s.
64
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Höôùng daãn giaûi 100 caâu traéc nghieäm TOAÙN 10
OÂN TAÄP KIEÅM TRA HOÏC KÌ I NAÊM HOÏC 2022 - 2023
Câu 1. Câu nào trong các câu sau không phải là mệnh đề?
A.
2
x
. B.
2 2 5+=
. C.
2
là một số hữu tỷ. D.
4
2
2
=
.
Hướng dẫn giải:
Chọn A.
Phát biểu A không là một mệnh đề, nó là mệnh đề chứa biến.
Câu 2. Mệnh đề nào sau là mệnh đề sai?
A.
n
:
2nn
. B.
2
:n n n =
. C.
2
:0xx
. D.
2
:x x x
.
Hướng dẫn giải:
Chọn C.
Với
0x =
thì
2
00x =
là khẳng định sai.
Câu 3. Trong các mệnh đề sau, mệnh đề nào đúng ?
A.
2
,1nn +
không chia hết cho
3
. B.
, 3 3x x x
.
C.
( )
2
, 1 1x x x − −
. D.
n
,
2
1n +
chia hết cho
4
.
Hướng dẫn giải:
Chọn A.
“
2
,1nn +
không chia hết cho
3
” là mệnh đề đúng. Ta chứng minh bằng ba trường hợp sau:
Xét
( )
3n k k=
thì
22
1 9 1nk+ = +
không chia hết cho 3.
Xét
( )
31n k k= +
thì
( )
2
22
1 3 1 1 9 6 2n k k k+ = + + = + +
không chia hết cho 3.
Xét
( )
32n k k= +
thì
( )
2
22
1 3 2 1 9 12 5n k k k+ = + + = + +
không chia hết cho 3.
Câu 4. Cho mệnh đề A: “
2
, 7 0x x x − +
”. Mệnh đề phủ định của A là:
A.
2
, 7 0x x x − +
. B.
2
, 7 0x x x − +
.
C. Không tồn tại
x
để
2
70xx− +
. D.
2
, 7 0x x x − +
.
Hướng dẫn giải:
Chọn D.
Câu 5. Phủ định của mệnh đề “
2
, 5 3 1x x x − =
” là :
A. “
2
, 5 3 1x x x −
”. B. “
2
, 5 3 1x x x − =
”.
C. “
2
, 5 3 1x x x −
”. D. “
2
, 5 3 1x x x −
”.
Hướng dẫn giải:
Chọn C.
Câu 6. Cho mệnh đề: “Nếu 2 góc ở vị trí so le trong thì hai góc đó bằng nhau”. Trong các mệnh đề sau đây, đâu
là mệnh đề đảo của mệnh đề trên?
A. Nếu 2 góc bằng nhau thì hai góc đó ở vị trí so le trong.
B. Nếu 2 góc không ở vị trí so le trong thì hai góc đó không bằng nhau.
65
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
C. Nếu 2 góc không bằng nhau thì hai góc đó không ở vị trí so le trong.
D. Nếu 2 góc ở vị trí so le trong thì hai góc đó không bằng nhau.
Hướng dẫn giải:
Chọn A.
Câu 7. Tìm số phần tử của tập hợp
,3= A x x
?
A.
3
. B.
4
. C.
5
. D.
6
.
Hướng dẫn giải:
Chọn C.
Ta có:
2, 1,0,1,2= − −A
nên A có 5 phần tử.
Câu 8. Liệt kê các phần tử của tập hợp
2 1 , 3 5= − − A k k k
ta được
A.
3; 2; 1;0;1;2;3;4;5= − − −A
. B.
7; 5; 3; 1;1;3;5;7;9= − − − −A
.
C.
6; 4; 2;0;2;4;6;8;10= − − −A
. D.
5; 3; 1;1;3;5;7= − − −A
.
Hướng dẫn giải:
Chọn B.
Vì
k
,
35− k
nên
k
chỉ nhận giá trị thuộc tập hợp
3; 2; 1;0;1;2;3;4;5− − −
.
Vậy
2 1 , 3 5 7; 5; 3; 1;1;3;5;7;9= − − = − − − −A k k k
.
Câu 9. Cho hai tập hợp
1;2;3;4;5=A
và
0;2;4;6;8=B
. Tìm tập hợp
=C A B
là
A.
=C
. B.
2;4=C
.
C.
0;1;2;3;4;5;6;8=C
. D.
1;3;5=C
.
Hướng dẫn giải:
Chọn B.
Câu 10. Cho hai tập hợp
0;2;4;6;8=A
và
1;2;3;4;5=B
. Tìm tập hợp
=C A B
.
A.
=C
. B.
2;4=C
.
C.
0;1;2;3;4;5;6;8=C
. D.
1;3;5=C
.
Hướng dẫn giải:
Chọn C.
Câu 11. Cho
1;2;3;4;5=A
,
0;2;4;6;8=B
. Tìm tập hợp
( ) ( )
\C A B A B=
?
A.
=C
. B.
2;4=C
.
C.
0;1;3;5;6;8=C
. D.
1;3;5=C
.
Hướng dẫn giải:
Chọn C.
0;1;2;3;4;5;6;8=AB
và
2;4=AB
nên
( ) ( )
\ 0;1;3;5;6;8C A B A B= =
.
Câu 12. Cho
3;4;5;6;7=A
và
0;2;4;6;8=B
. Tìm
( ) ( )
\\C A B B A=
.
A.
=C
. B.
4;6=C
. C.
0;2;3;5;7;8=C
. D.
3;5;7=C
.
Hướng dẫn giải:
Chọn C.
\ 3;5;7=AB
và
\ 0;2;8=BA
nên
( ) ( )
\ \ 0;2;3;5;7;8= =C A B B A
.
66
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Câu 13. Tập
X
có bao nhiêu tập hợp con, biết
X
có
3
phần tử?
A.
2
. B.
4
. C.
6
. D.
8
.
Hướng dẫn giải:
Chọn D.
Số phần tử của X là:
3
28=
.
Câu 14. Tập hợp
1 1 1 1 1
; ; ; ;
3 8 15 24 35

=


A
bằng tập hợp nào dưới đây?
A.
( )
1
,1 5
1



+


nn
nn
. B.
1
,1 5
21


+

nn
n
.
C.
( )
1
,1 5
2



+


nn
nn
. D.
2
1
,1 5
2


+

nn
n
.
Hướng dẫn giải:
Chọn C.
Xét tập hợp của phương án C, ta có thể liệt kê bảng giá trị sau :
n
1
2
3
4
5
( )
1
2+nn
1
3
1
8
1
15
1
24
1
35
Vậy tập hợp
( )
1 1 1 1 1 1
; ; ; ; ,1 5
3 8 15 24 35 2



= =
+



A n n
nn
.
Câu 15. Tập hợp
2
60A x x x= − −
bằng tập hợp nào dưới đây?
A.
. B.
0;1;2;3
. C.
1;0;1;2−
. D.
2; 1;0;1;2;3−−
.
Hướng dẫn giải:
Chọn D.
Xét
( )( )
2
2 0 2 0
6 0 2 3 0
3 0 3 0
xx
x x x x
xx
+ +

− − + −

− −

22
23
32
xx
x
xx
− −

−



.
Vậy
2; 1;0;1;2;3A = − −
.
Câu 16. Cho tập hợp
(
2
;1Am
= − −
,
)
1;= +B
. Tìm tất cả giá trị của
m
để
= AB
.
A.
2m
. B.
02m
. C.
2m
. D.
22m−
.
Hướng dẫn giải:
Chọn D.
Ta có:
= AB
22
1 1 2 2 2 2m m m m − −
.
Câu 17. Cho hai nửa khoảng
4
;
1
A
m

= −
+

và
)
1;B = +
. Số giá trị nguyên m để
AB
là
A.
3
. B.
4
. C.
5
. D. Vô số.
Hướng dẫn giải:
Chọn B.
67
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Ta có:
4 4 3
1 1 0 0
1 1 1
m
AB
m m m
−
−
+ + +
3 0 3
1 0 1
13
3 0 3
1 0 1
mm
mm
m
mm
mm
−



+ −


−

−



+ −



.
Vậy
0;1;2;3m
nên có 4 giá trị nguyên m thỏa mãn.
Câu 18. Cho hai tập hợp khác rỗng
(
( )
2;7 , 1;A m B m= − = − +
. Tìm tất cả giá trị m để
( )
1;AB = +
.
A.
3.m
B.
2m =
. C.
0m
. D.
1m
.
Hướng dẫn giải:
Chọn B.
Điều kiện:
2 7 5mm −
(1).
Nhận thấy
( )
1;A +
, vì vậy:
( )
1;AB = +
1 1 2mm − = =
(thỏa (1)).
Câu 19. Bất phương trình nào sau đây không phải là bất phương trình bậc nhất hai ẩn?
A.
2 3 0.xy+
B.
2.xy+
C.
2
0.xy+
D.
1
23
xy
−
.
Hướng dẫn giải:
Chọn C
Câu 20. Cặp số
( )
1; 1−
là nghiệm của bất phương trình
A.
41xy+
. B.
20xy+ −
. C.
0xy− −
. D.
3 1 0xy− − −
.
Hướng dẫn giải:
Chọn A
Thay
1, 1xy= = −
vào phương án A, ta có :
( )
1 4 1 1 3 1+ − −
(đúng).
Câu 21. Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình
21xy+
?
A.
( )
0;0
. B.
( )
3; 7−
. C.
( )
2;1−
. D.
( )
0;1
.
Hướng dẫn giải:
Chọn D
Thay
0, 1xy==
vào bất phương trình:
2.0 1 1+
(sai).
Câu 22. Miền nghiệm của bất phương trình
( ) ( )
2 2 2 2 1x y x− + + − −
là nửa mặt phẳng chứa điểm
A.
( )
2;2
. B.
( )
1;3−
. C.
( )
4;3−
. D.
( )
5;0
.
Hướng dẫn giải:
Chọn C
Ta có:
( ) ( )
2 2 2 2 1x y x− + + − −
2 2 4 2 2x y x − + + − −
2 4 (*)xy +
.
Thay cặp số
( )
4;3−
vào (*), ta có:
4 2.3 4− +
(đúng).
Câu 23. Miền nghiệm (miền không bị gạch trong hình) của bất phương trình
34xy−
là
68
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
A.
B.
C.
D.
Hướng dẫn giải:
Chọn A
Xét đường thẳng biên là
:3 4d x y−=
luôn đi qua hai điểm
( )
4
0; 4 , ;0
3

−


nên ta loại C, D.
Thay tọa độ điểm
( )
2;0M
vào bất phương trình thì thỏa mãn, suy ra điểm M thuộc miền nghiệm của
bất phương trình (là miền không bị gạch) nên loại B.
Câu 24. Phần không được gạch chéo trong hình (kể cả biên), là miền nghiệm của bất phương trình nào bên
dưới?
A.
3xy−
.
B.
23xy−
.
C.
23xy−
.
D.
3xy−
.
Hướng dẫn giải:
Chọn B
Ta thấy miền nghiệm bất phương trình có biên là đường thẳng đi qua hai điểm
( )
3
0; 3 , ;0
2

−


nên
loại A, D.
69
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Theo hình thì điểm
( )
2; 2M −
thuộc miền nghiệm, thay
2, 2xy= = −
vào mỗi bất phương trình
trong hai phương án B, C, ta thấy B thỏa mãn vì
( )
2.2 2 3− −
(đúng).
Câu 25. Miền nghiệm của hệ bất phương trình
0
3 3 0
50
xy
xy
xy
−
− +
+ −
là phần mặt phẳng chứa điểm
A.
( )
5;3
. B.
( )
0;0
. C.
( )
1; 1−
. D.
( )
2;2−
.
Hướng dẫn giải:
Chọn A
Thay
5, 3xx==
vào hệ bất phương trình:
5 3 0
5 3.3 3 0
5 3 5 0
−
− +
+ −
(đúng).
Câu 26. Cho hệ bất phương trình
0
2 5 0
xy
xy
+
+
có tập nghiệm là
S
. Khẳng định nào sau đây là khẳng định
đúng?
A.
( )
1;1 S
. B.
( )
1; 1 S− −
. C.
1
1;
2
S

−


. D.
12
;
25
S

−


.
Hướng dẫn giải:
Chọn C
Thay
1
1,
2
xy= = −
vào hệ bất phương trình:
1
10
2
1
2.1 5 0
2

+ −


+ −


(đúng).
Câu 27. Miền biểu diễn nghiệm của hệ
3 2 5
2
xy
xy
+
− −
là phần không gạch chéo (không kể biên) của hình nào
trong các phương án bên dưới?
A.
B.
70
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
C.
D.
Hướng dẫn giải:
Chọn B
Xét cặp số
( )
0;3
, thay
0, 3xy==
vào hệ ta thấy thỏa mãn. Vì vậy điểm
( )
0;3
thuộc miền nghiệm
của hệ đã cho. Trong 4 phương án, chỉ có phương án B thỏa mãn.
Câu 28. Cho biết miền nghiệm của một hệ bất phương trình bậc nhất hai ẩn
x, y chính là miền của tam giác ABC như hình bên. Tìm tổng của giá
trị lớn nhất, giá trị nhỏ nhất biểu thức
( )
; 5 2 2025F x y x y= − +
.
A.
3075
.
B.
5000
.
C.
4035
.
D.
4050
.
Hướng dẫn giải:
Chọn D
Miền nghiệm được cho là miền của tam giác ABC với
( ) ( ) ( )
2;0 , 2;0 , 2;4A B C−
.
Ta biết rằng biểu thức
( )
;F x y
đạt giá trị lớn nhất, giá trị nhỏ nhất tại các đỉnh của tam giác ABC.
Xét
( )
2;0A −
,
( ) ( )
2;0 5 2 2.0 2025 2015F − = − − + =
.
Xét
( )
2;0B
,
( )
2;0 5.2 2.0 2025 2035F = − + =
.
Xét
( )
2;4C
,
( )
2;4 5.2 2.4 2025 2027F = − + =
.
Do vậy
( ) ( ) ( ) ( )
max min max min
; 2035, ; 2015 ; ; 4050.= = + =F x y F x y F x y F x y
Câu 29. Cho các giá trị
,xy
thỏa điều kiện
20
2 1 0
3 2 0
xy
xy
xy
− +
− −
− −
. Tìm giá trị lớn nhất của biểu thức
32T x y=+
.
A.
19
. B.
25
. C.
14
. D. 20.
Hướng dẫn giải:
Chọn A
Miền nghiệm của hệ đã cho là miền của tam giác
ABC
, trong
đó
( )
1;1A
,
( )
2;4B
,
( )
3;5C
.
Giá trị lớn nhất của
32T x y=+
đạt được tại các đỉnh của tam
giác
ABC
.
71
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Xét
( )
1;1A
,
( )
1;1 3.1 2.1 5
A
TT= = + =
.
Xét
( )
2;4B
,
( )
2;4 3.2 2.4 14
B
TT= = + =
.
Xét
( )
3;5C
,
( )
3;5 3.3 2.5 19
C
TT= = + =
.
Vậy giá trị lớn nhất của
32T x y=+
là
19
, khi đó:
3x =
và
5y =
.
Câu 30. Bạn An kinh doanh hai mặt hàng handmade là vòng tay và vòng đeo cổ. Mỗi vòng tay làm trong 4
giờ, bán được 40 ngàn đồng. Mỗi vòng đeo cổ làm trong 6 giờ, bán được 80 ngàn đồng. Mỗi tuần bạn
An bán được không quá 15 vòng tay và 4 vòng đeo cổ. Tính số giờ tối thiểu trong tuần An cần dùng
để làm ra sản phẩm và bán được ít nhất 400 ngàn đồng?
A.
40
. B.
25
. C.
32
. D. 20.
Hướng dẫn giải:
Chọn C
Gọi
,xy
là số vòng tay và vòng đeo cổ trong tuần An làm
được. Điều kiện:
,xy
.
Tổng thời gian để làm ra hai sản phẩm trên là:
( )
; 4 6T x y x y=+
.
Theo giả thiết, ta có:
40 80 400 2 10
0 15 0 15
0 4 0 4
x y x y
xx
yy
+ +





(*).
Hệ (*) có miền nghiệm chính là miền tứ giác ABCD, trong
đó
( )
10;0 ,A
( )
15;0 ,B
( )
15;4C
,
( )
2;4D
, được biểu diễn như hình bên.
Ta biết rằng
( )
; 4 6T x y x y=+
đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác ABCD.
Tại
( )
10;0 ,A
( )
10;0 4.10 6.0 40T = + =
.
Tại
( )
15;0 ,B
( )
15;0 4.15 6.0 60T = + =
.
Tại
( )
15;4C
,
( )
15;4 4.15 6.4 84T = + =
.
Tại
( )
2;4D
,
( )
2;4 4.2 6.4 32T =+=
.
Vậy
( )
;T x y
đạt giá trị nhỏ nhất bằng 32, khi đó
2, 4xy==
. Nói cách khác, mỗi tuần An cần làm
ra 2 vòng tay và 4 vòng đeo cổ để khoảng thời gian bỏ ra là ít nhất (32 giờ), đáp ứng thu nhập tối
thiểu 400 ngàn đồng.
Câu 31. Tìm tập xác định
D
của hàm số
( )( )
21
.
2 1 3
x
y
xx
−
=
+−
A.
( )
3; .D = +
B.
1
\ ;3 .
2
D

=−

C.
1
;
2
D

= − +


. D.
.D =
72
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Hướng dẫn giải:
Chọn B.
Hàm số xác định khi
1
2 1 0
2
30
3
x
x
x
x
+
−

−
.
Vậy tập xác định của hàm số là
1
\ ;3
2
D

=−

.
Câu 32. Tìm tập xác định
D
của hàm số
6 3 1.y x x= − − −
A.
( )
1;2 .D =
B.
1;2 .D =
C.
1;3 .D =
D.
1;2 .D =−
Hướng dẫn giải:
Chọn B.
Hàm số xác định khi và chỉ khi
6 3 0 2
1 2.
1 0 1
xx
x
xx
−


−

Vậy tập xác định của hàm số là
1;2 .D =
Câu 33. Tìm tập xác định
D
của hàm số
22
.
xx
y
x
− + +
=
A.
2;2 .D =−
B.
( )
2;2 \ 0 .D =−
C.
2;2 \ 0 .D =−
D.
.D =
Hướng dẫn giải:
Chọn C.
Hàm số xác định khi và chỉ khi
2 0 2
2 0 2
00
xx
xx
xx
−


+ −




.
Vậy tập xác định của hàm số là
2;2 \ 0 .D =−
Câu 34. Tìm tập xác định
D
của hàm số
2
1
.
6
x
y
xx
+
=
−−
A.
3.D =
B.
)
1; \ 3 .D = − +
C.
.D =
D.
)
1; .D = − +
Hướng dẫn giải:
Chọn B.
Hàm số xác định khi và chỉ khi
2
1
10
1
3.
3
60
2
x
x
x
x
x
xx
x
−
+
−
− −
−
Vậy tập xác định của hàm số là
)
1; \ 3D = − +
.
Câu 35. Hàm số
1
2
y
x
=
−
nghịch biến trên khoảng nào dưới đây?
A.
( )
;2 .−
B.
( )
2; .+
C.
( )
2; .− +
D.
( )
2;2 .−
73
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Hướng dẫn giải:
Chọn B.
Tập xác định
\2D =
. Xét
( ) ( )
21
21
f x f x
T
xx
−
=
−
với mọi
1 2 1 2
,,x x D x x
.
Ta có :
( )( )
12
21
21
2 1 2 1
22
11
22
22
− − +
−
−−
−−
==
−−
xx
xx
xx
T
x x x x
( )( )( ) ( )( )
12
2 1 2 1 2 1
1
2 2 2 2
−
= = −
− − − − −
xx
x x x x x x
Vì
( )
( )( )
11
12
22
21
2 2 0
2
, 2; 0
2 2 0
22
xx
xx
xx
xx
−

−
+

−
−−

.
Vậy
0T
nên hàm số đã cho nghịch biến trên
( )
2;+
.
Câu 36. Cho hàm số
( )
30y ax a= +
. Tìm điều kiện của
a
để hàm số đồng biến trên ?
A.
0.a
B.
0.a
C.
.a
D.
1.a =
Hướng dẫn giải:
Chọn A.
Tập xác định
D =
. Xét
( ) ( )
21
21
f x f x
A
xx
−
=
−
với mọi
1 2 1 2
,;x x x x
.
Ta có:
( ) ( ) ( )
2 1 2 1
2 1 2 1
33
.
ax ax a x x
Aa
x x x x
+ − + −
= = =
−−
Vậy với
0a
thì hàm số đã cho đồng biến trên .
Câu 37. Điểm nào sau đây thuộc đồ thị hàm số
2 –1 3 2y x x= + −
?
A.
( )
2; 6
. B.
( )
1; 1−
. C.
( )
2; 10−−
. D.
( )
0; 4−
.
Hướng dẫn giải:
Chọn A.
Câu 38. Cho hàm số
( )
(
2
2
, ;0
1
1 , 0;2
1 , 2;5
x
x
y x x
xx
−
−
= +
−
. Tính
( )
4f
, ta được kết quả:
A.
2
3
. B.
15
. C.
5
. D.
7
.
Hướng dẫn giải:
Chọn B.
Với
(
4 2;5x =
thì
( ) ( )
22
1 4 4 1 15.f x fx = − = − =
Câu 39. Hàm số
1
21
x
x
y
m
+
−
=
+
xác định trên
)
0;1
khi:
74
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
A.
1
2
m
. B.
1m
. C.
1
2
m
hoặc
1m
. D.
2m
hoặc
1m
.
Hướng dẫn giải:
Chọn C.
Hàm số xác định
)
0;1x
khi và chỉ khi
)
12 1 0 0, ;x m x− +
)
1
2 1 0
2 1 ,
2
21
1
0;1
1
m
m
m x x
m
m
−
−
−
.
Câu 40. Cho hàm số
( )
y f x=
xác định trên đoạn
1;5−
có đồ thị như hình vẽ sau. Hãy chọn khẳng định
đúng về sự biến thiên của hàm số
( )
y f x=
trên đoạn
1;5−
.
A. Hàm số đồng biến trên các đoạn
1;1 , 1;2−
và nghịch biến trên các đoạn
2;3 , 3;5 .
B. Hàm số nghịch biến trên các đoạn
1;1 , 2;3−
và đồng biến trên các đoạn
1;2 , 3;5 .
C. Hàm số đồng biến trên các đoạn
1;1 , 2;3−
và nghịch biến trên các đoạn
1;2 , 3;5 .
D. Hàm số nghịch biến trên các đoạn
1;1 , 1;2−
và đồng biến trên các đoạn
2;3 , 3;5 .
Hướng dẫn giải:
Chọn C.
Câu 41. Cho hàm số bậc hai
( )
2
0y ax bx c a= + +
. Chọn mệnh đề sai trong các khẳng định sau:
A. Nếu
0a
thì đồ thị hàm số có bề lõm hướng lên trên.
B. Nếu
0a
thì đồ thị hàm số có bề lõm hướng xuống dưới.
C. Đồ thị hàm số có đỉnh
;
24
b
I
aa

−−


.
D. Đồ thị hàm số luôn nhận trục
Oy
làm trục đối xứng.
Hướng dẫn giải:
Chọn D.
Đồ thị hàm số bậc hai
( )
2
0y ax bx c a= + +
nhận trục đối xứng là
2
b
x
a
=−
.
Chỉ có đồ thị hàm số
( )
2
0y ax a=
mới luôn nhận trục
Oy
làm trục đối xứng.
Câu 42. Cho hàm số
( )
2
0y ax bx c a= + +
có đồ thị (P) như hình bên. Khẳng định nào sau đây là khẳng
định sai?
A. Hàm số đồng biến trên khoảng
( )
;3−
.
B. Hàm số nghịch biến trên khoảng
( )
3;+
.
75
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
C. Hàm số nghịch biến trên khoảng
( )
1;+
.
D. Hàm số đồng biến trên khoảng
( )
;1−
.
Hướng dẫn giải:
Chọn C.
Câu 43. Parabol
( )
2
: 6 1P y x x= − + +
. Khi đó
A. Có trục đối xứng
6x =
và đi qua điểm
( )
0;1A
.
B. Có trục đối xứng
6x =−
và đi qua điểm
( )
1;6A
.
C. Có trục đối xứng
3x =
và đi qua điểm
( )
2;9A
.
D. Có trục đối xứng
3x =
và đi qua điểm
( )
3;9A
.
Hướng dẫn giải:
Chọn C.
Trục đối xứng của (P) là
6
hay 3.
22
b
xx
a
−
= − = =
−
Ta có:
2
2 6.2 1 9− + + =
( ) ( )
2;9AP
.
Câu 44. Xác định hàm số
2
2y x bx c= + +
biết đồ thị hàm số này đi qua hai điểm
( ) ( )
0;1 , 2;7AB−
.
A.
2
9 53
2
55
y x x= + −
. B.
2
21y x x= + +
.
C.
2
21y x x= − +
. D.
2
21y x x= + −
.
Hướng dẫn giải:
Chọn B.
Parabol qua hai điểm
( ) ( )
0;1 , 2;7AB−
nên
11
8 2 7 1
cc
b c b
==


− + = =

.
Câu 45. Xác định parabol
( )
2
:4P y ax x c= − +
biết
( )
P
có đỉnh là
1
;2
2
I

−


là:
A.
2
4 4 1y x x= − − +
. B.
2
1
24
2
y x x= − − +
.
C.
2
1
24
2
y x x= − −
. D.
2
4 4 1y x x= − −
.
Hướng dẫn giải:
Chọn D.
Vì parabol có đỉnh là
1
;2
2
I

−


nên ta có hệ phương trình
41
4
22
a
a
= =
.
76
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Mặt khác
1
;2
2
I

−


thuộc
( )
P
nên
4
1
4. 2 1
42
a
a
cc
=
− + = − = −
.
Câu 46. Tọa độ đỉnh
I
của parabol
( )
2
:4P y x x= − +
là
A.
( )
2; 12I −−
. B.
( )
2; 4I
. C.
( )
1; 5I −−
. D.
( )
1; 3I
.
Hướng dẫn giải:
Chọn B.
Tọa độ đỉnh
I
:
2
2
2
2 4.2 4
I
I
b
x
a
y
= − =
= − + =
( )
2; 4I
.
Câu 47. Hàm số
2
1yx= − +
nghịch biến trên khoảng nào sau đây?
A.
( )
0;+
. B.
( )
;0−
.
C.
( )
;0−
và
( )
0;+
. D.
( )
;1− −
và
( )
1;+
.
Hướng dẫn giải:
Chọn A.
Hàm số
2
1yx= − +
có:
10a = −
và
0
2
b
a
−=
Hàm số nghịch biến trên khoảng
( )
0;+
.
Câu 48. Giao điểm của parabol
( )
P
:
2
54y x x= + +
với trục hoành:
A.
( )
1;0−
,
( )
4;0−
. B.
( )
0; 1 ,−
( )
0; 4−
.
C.
( )
1;0−
,
( )
0; 4−
. D.
( )
0; 1 ,−
( )
4;0−
.
Hướng dẫn giải:
Chọn A.
Phương trình hoành độ giao điểm của (P) với Ox:
2
1
5 4 0
4
x
xx
x
=−
+ + =
=−
.
Vậy hai giao điểm tìm được là
( )
1;0−
và
( )
4;0−
.
Câu 49. Tìm tất cả giá trị của
m
để đỉnh của parabol
2
y x x m= + +
nằm trên đường thẳng
3
4
y =
.
A.
2m =
. B.
0m =
. C.
1m =
. D.
2m =−
.
Hướng dẫn giải:
Chọn C.
Parabol có đỉnh
11
;
24
Im

−−


. Do
3
:
4
I d y=
13
1
44
mm − = =
.
Câu 50. Parabol
2
y x x c= + +
cắt đường phân giác của góc phần tư thứ nhất tại điểm có hoành độ
1x =
. Khi
đó
c
bằng:
A.
1
2
. B.
2−
. C.
2
. D.
1−
.
Hướng dẫn giải:
Chọn D.
Đường phân giác góc phần tư thứ nhất có phương trình
:d y x=
.
Với
1x =
thì
1y =
nên giao điểm của parabol với d là
( )
1;1A
.
77
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Thay tọa độ điểm A vào hàm số bậc hai, ta được:
2
1 1 1 1cc= + + = −
.
Câu 51. Biểu thức
2 0 2 0 2 0 2 0
cos 10 cos 20 cos 30 ... cos 180A = + + + +
có giá trị bằng:
A.
9A=
. B.
3A=
. C.
12A =
. D.
6A =
.
Hướng dẫn giải:
Chọn A.
Ta có:
( ) ( )
2 0 2 0 2 0 2 0 2 0 2 0
cos 10 cos 170 ... cos 80 cos 100 cos 90 cos 180A = + + + + + +
( )
2 0 2 0 2 0
2 cos 10 cos 20 ... cos 80 1= + + + +
( ) ( ) ( )
2 0 2 0 2 0 2 0 2 0 2 0
2 cos 10 cos 80 cos 20 cos 70 ... cos 40 cos 50 1

= + + + + + + +

= 9.
Câu 52. Giá trị của
oo
tan30 cot30+
bằng bao nhiêu?
A.
4
3
. B.
13
3
+
. C.
2
3
. D.
2
.
Hướng dẫn giải:
Chọn A.
Ta có:
oo
3 4 3
tan30 cot30 3
33
+ = + =
.
Câu 53. Cho góc
thỏa mãn
oo
0 90

. Khẳng định nào sau đây đúng?
A.
( )
2 2 o
sin sin 90 0

+ − =
. B.
( )
2 2 o
sin sin 90 2

+ − =
.
C.
( )
2 2 o
sin sin 90 1

+ − =
. D.
( )
2 2 o
sin sin 90 3
+ − =
.
Hướng dẫn giải:
Chọn C.
Ta có:
( )
2 2 o 2 2
sin sin 90 sin cos 1
+ − = + =
.
Câu 54. Mệnh đề nào sau đây về tam giác
ABC
là sai?
A. Góc
B
nhọn khi và chỉ khi
2 2 2
b a c+
.
B. Góc
A
vuông khi và chỉ khi
2 2 2
a b c=+
.
C. Góc
C
tù khi và chỉ khi
2 2 2
c a b+
.
D. Góc
A
tù khi và chỉ khi
2 2 2
b a c+
.
Hướng dẫn giải:
Chọn D.
Trong
ABC
, ta có:
A
tù khi và chỉ khi
2 2 2
cos 0 0
2
b c a
A
bc
+−
2 2 2 2 2 2
0b c a a b c + − +
. Do đó khẳng định trong D sai.
Câu 55. Rút gọn biểu thức
2
1 sin
2sin .cos
x
P
xx
−
=
ta được
A.
1
tan
2
Px=
. B.
1
cot
2
Px=
. C.
2cotPx=
. D.
2tanPx=
.
Hướng dẫn giải:
Chọn B.
78
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Ta có:
22
1 sin cos cos 1
cot
2sin .cos 2sin .cos 2sin 2
x x x
Px
x x x x x
−
= = = =
.
Câu 56. Biểu thức
( )
2
cot tanaa+
bằng
A.
22
11
sin cos

−
. B.
22
cot tan 2aa+
.
C.
22
11
sin cos

+
. D.
22
cot tan 2aa+
.
Hướng dẫn giải:
Chọn C.
Ta có:
( )
( ) ( )
2
22
22
22
cot tan cot 2cot .tan tan
11
cot 1 tan 1 .
sin cos
+ = + +
= + + + = +
a a a a a a
aa
aa
Câu 57. Cho
là góc tù và
5
sin
13
=
. Giá trị của biểu thức
3sin 2cos+

là
A.
3
. B.
9
13
−
. C.
3−
. D.
9
13
.
Hướng dẫn giải:
Chọn B.
Vì
là góc tù nên
cos 0
. Ta có:
22
144 12
cos 1 sin cos
169 13
= − = = −
.
Khi đó:
5 12 9
3sin 2cos 3 2
13 13 13


+ = + − = −


.
Câu 58. Cho góc
thỏa mãn
5
sin cos
2
+=

. Giá trị của
sin .cos

là:
A.
1
8
. B.
1
4
. C.
1
2
. D.
1
8
−
.
Hướng dẫn giải:
Chọn A.
Ta có:
( )
2
22
55
sin cos sin cos sin cos 2sin cos
24
+ = + = + + =
51
1 2sin cos sin cos
48
+ = =
.
Câu 59. Cho
ABC
vuông tại
A
có
5=AC
cm,
13=BC
cm. Gọi góc
=ABC
và
=ACB
. Hãy chọn
khẳng định đúng khi so sánh độ lớn của hai góc
và
.
A.

. B.

. C.
=

. D.

.
Hướng dẫn giải:
Chọn A.
79
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Do
ABC
vuông tại
A
nên
2 2 2 2 2 2
13 5 12 12AB BC AC AB= − = − = =
cm.
Ta biết rằng, trong một tam giác góc nào đối diện với cạnh lớn hơn
thì góc đó lớn hơn góc được so sánh, ta có:
5 12AC AB

= =
.
Câu 60. Cho tam giác
ABC
có diện tích bằng
26
cm
2
và
8=AB
cm,
13=AC
cm. Giá trị
sin A
bằng bao
nhiêu?
A.
1
4
. B.
30
. C.
1
2
. D.
150
.
Hướng dẫn giải:
Chọn C.
Diện tích tam giác ABC là :
1 2 2.26 1
. .sin sin
2 . 8.13 2
S
S AB AC A A
AB AC
= = = =
.
Câu 61. Cho giác
ABC
có
5=a
,
26=b
,
135=C
.Tính diện tích của
ABC
.
A.
5 13
2
−
. B.
5 13
. C.
5 13
2
. D.
5 26
.
Hướng dẫn giải:
Chọn C.
Diện tích tam giác ABC là:
1 1 5 13
.sin .5. 26.sin135
2 2 2
S ab C= = =
.
Câu 62. Tam giác
ABC
có
=BC a
và
30=A
. Tính bán kính đường tròn ngoại tiếp
ABC
.
A.
a
. B.
3
3
a
. C.
2a
. D.
2
a
.
Hướng dẫn giải:
Chọn A.
Theo định lí sin ta có:
22
sin sin30
BC a
R a R a
A
= = = =
.
Câu 63. Cho
ABC
biết
6=a
,
2=b
,
13=+c
. Độ dài đường cao ứng với góc nhỏ nhất của
ABC
bằng?
A.
13
2
+
. B.
( )
6 1 3
4
+
. C.
13
6
+
. D.
33
2
+
.
Hướng dẫn giải:
Chọn D.
Trong một tam giác, đối diện với cạnh bé hơn là góc bé hơn nên góc
B
là góc nhỏ nhất (và là góc
nhọn) của
ABC
.
Diện tích
ABC
:
1 1 sin
sin
22
bb
ac B
S ac B bh h
b
= = =
(
b
h
là đường cao tam giác ứng với góc B).
Áp dụng định lí côsin cho tam giác ABC, có:
80
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
( )
( )
2
2 2 2 2
6 1 3 2 2
cos sin 45
22
2. 6. 1 3
a c b
B B B
ac
+ − + + −
= = = = =
+
.
Vậy
( )
6 1 3 sin45 3 3
22
b
h
+ +
==
.
Câu 64. Cho
ABC
có ba cạnh lần lượt là
5=a
,
8=b
,
11=c
. Độ dài đường trung tuyến vẽ từ đỉnh
C
bằng:
A.
57
4
. B.
57
2
. C.
57
. D.
57
.
Hướng dẫn giải:
Chọn B.
Ta có:
2 2 2 2 2 2
2
5 8 11 57 57
2 4 2 4 4 2
cc
a b c
mm
++
= − = − = =
.
Câu 65. Cho góc
60xOy =
. Gọi
A
và
B
là hai điểm di động lần lượt trên tia
Ox
và tia
Oy
sao cho
23AB =
. Độ dài lớn nhất của đoạn
OA
bằng:
A.
43
. B.
2
. C.
4
. D.
1
.
Hướng dẫn giải:
Chọn C.
Áp dụng định lí sin cho
OAB
ta có:
23
4
sin sin60
3
2
OA AB
B
= = =
4sinOA B=
.
Vì
sin 1B
nên
4sin 4OA B=
.
Khi
4OA =
(lớn nhất) thì
0
90B =
.
Câu 66. Hai chiếc ca nô cùng xuất phát từ cảng
A
, đi thẳng theo hai
hướng tạo với nhau góc
60
. Ca nô
B
chạy với vận tốc
20
hải
lí một giờ. Ca nô
C
chạy với tốc độ
25
hải lí một giờ. Hỏi sau
2
giờ, hai ca nô cách nhau một khoảng xấp xỉ bao nhiêu hải lí
(kết quả làm tròn đến hàng đơn vị)? (1 hải lí
1,852
km).
A.
46
.
B.
23
.
C.
25
.
D.
56
.
Hướng dẫn giải:
Chọn A.
Sau 2 giờ, ca nô
B
đi được
40
hải lí, canô
C
đi được
50
hải lí.
Xét
ABC
có
40AB =
,
50AC =
và
A 60=
.
Áp dụng định lí côsin cho
ABC
ta có:
2 2 2
2 . .cosBC AB AC AB AC A= + −
81
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
22
40 50 2.40.50.cos60 2100 10 21 46BC= + − = =
.
Vậy sau 2 giờ, hai ca nô cách nhau một khoảng xấp xỉ 46 hải lí.
Câu 67. Từ đỉnh C một tháp có chiều cao
40CD =
m,
người ta nhìn hai điểm
A
và
B
trên mặt đất
dưới các góc nhìn là
34 26
và
72 12
so với
phương thẳng đứng của tháp. Ba điểm
, , A B D
thẳng hàng. Khoảng cách
AB
gần nhất với kết
quả nào sau đây?
A.
97m.
B.
100m.
C.
120m.
D.
83m.
Hướng dẫn giải:
Chọn A.
Xét
ACD
vuông tại
D
, ta có:
tan34 26 40.tan34 26
AD
AD
CD

= =
.
Xét
BCD
vuông tại
D
, ta có:
tan72 12 40tan72 12
BD
BD
CD

= =
.
Suy ra:
( )
40 tan72 12 tan34 26 97AB BD AD

= − = −
m.
Câu 68. Khi khai quật tại một ngôi làng cổ, người ta tìm được mảnh
của một chiếc đĩa phẳng hình tròn bị vỡ. Các nhà khảo cổ đo
được kích thước ba cạnh tam giác ABC (nội tiếp vành tròn
đĩa) là
3,7
cm;
4,3
cm và
7,5
cm. Họ muốn làm một chiếc
đĩa mới mô phỏng theo chiếc đĩa này. Hỏi chiếc đĩa cần làm
có bán kính bằng bao nhiêu? (Kết quả làm tròn đến hàng đơn
vị).
A.
6,1
cm.
B.
5,7
cm.
C.
6,8
cm.
D.
5,3
cm.
Hướng dẫn giải:
82
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Chọn B.
Nửa chu vi tam giác là
7,75
2
abc
p
++
==
cm.
Gọi S, R lần lượt là diện tích và bán kính đường tròn ngoại tiếp
tam giác ABC.
Theo công thức Hê-rông ta có:
( )( )( )
5,2S p p a p b p c= − − −
cm
2
.
Ta lại có:
4,3.3,7.7,5
5,7
4 4 4.5,2
abc abc
SR
RS
= = =
cm.
Câu 69. Cho tam giác
ABC
có độ dài ba đường trung tuyến lần lượt bằng 15, 18, 27. Tính diện tích
S
của
tam giác
ABC
.
A.
105 2
. B.
125
. C.
105
. D.
120 2
.
Hướng dẫn giải:
Chọn D.
Gọi
I
là trung điểm
BC
,
G
là trọng tâm tam giác
ABC
, ta có:
33
ABC
ABC GBC
GBC
S
AI
SS
S GI

= = =
.
Lấy
D
là điểm đối xứng với
G
qua
I
, ta có
BGCD
là hình bình hành (do có hai đường chéo cắt
nhau tại trung điểm của mỗi đường).
Suy ra:
1
2
GBC BGD BGCD
S S S

==
. Do vậy:
3
ABC BGD
SS

=
.
Tam giác
BDG
có độ dài 3 cạnh bằng
2
3
độ dài ba đường
trung tuyến tương ứng của
ABC
, độ dài ba cạnh đó là
10, 12, 18.
Nửa chu vi tam giác BDG là:
10 12 18
20
2
p
++
==
.
Diện tích tam giác BDG:
( )( )( )
20 20 10 20 12 20 18 40 2
BGD
S
= − − − =
.
Diện tích tam giác ABC:
3.40 2 120 2
ABC
S
==
.
Câu 70. Cho
ABC
có
8AB =
,
5AC =
,
60A =
. Tính bán kính đường tròn cắt cả ba cạnh của
ABC
và
chắn trên mỗi cạnh một dây có độ dài bằng 4:
A.
7
. B.
3
. C.
23+
. D.
7
.
Hướng dẫn giải:
Chọn D.
83
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Gọi
O
là tâm đường tròn bán kính
R
cần tìm và
,,I J K
theo
thứ tự là hình chiếu vuông góc của
O
trên
,,BC AC AB
.
Theo giả thiết :
1 1 2 2 1 2
4BC C A A B= = =
OI OJ OK = =
O
là tâm đường tròn nội tiếp tam giác
ABC
.
Suy ra
2 2 2 2 2 2
1 1 1
R OB OI IB r IB= = + = +
(*)
(r là bán kính đường tròn nội tiếp tam giác ABC).
Ta có:
22
2 . cosBC AB AC AB AC A= + −
0
64 25 2.8.5.cos60 7= + − =
.
Nửa chu vi tam giác ABC:
8 5 7
10
2
p
++
==
; diện tích tam
giác ABC:
0
10
1
. .sin60 10 3
2
ABC
ABC
S pr r
S AB AC
==
==
10 10 3 3rr = =
.
Ta lại có:
11
1
2
2
BC
IB ==
. Thay vào (*):
2
22
3 2 7 7RR= + = =
.
Câu 71. Hãy tìm khẳng định sai. Nếu hai véc tơ bằng nhau thì chúng luôn có đặc điểm sau
A. Cùng điểm gốc. B. Cùng phương.
C. Có độ dài bằng nhau. D. cùng hướng.
Hướng dẫn giải:
Chọn A.
Câu 72. Mệnh đề nào sau đây đúng?
A. Có duy nhất một vectơ cùng phương với mọi vectơ.
B. Có ít nhất hai vectơ có cùng phương với mọi vectơ.
C. Có vô số vectơ cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ.
Hướng dẫn giải:
Chọn A.
Theo quy ước thì vectơ không luôn cùng phương với mọi vectơ.
Câu 73. Cho hình bình hành
ABCD
tâm
O
. Khi đó
OA OB−
bằng
A.
OC OB+
. B.
AB
. C.
OC OD−
. D.
CD
.
Hướng dẫn giải:
Chọn D.
Ta có:
OA OB BA CD− = =
.
Câu 74. Cho
5
điểm
, , , ,M N P Q R
. Vectơ tổng
MN PQ RN NP QR+ + + +
bằng:
A.
MP
. B.
PR
. C.
MR
. D.
MN
.
Hướng dẫn giải:
Chọn D.
Ta có:
( ) ( )
MN PQ RN NP QR MN NP PQ QR RN+ + + + = + + + +
MP PR RN MR RN MN= + + = + =
.
84
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Câu 75. Cho hình bình hành
ABCD
. Có bao nhiêu vectơ có điểm đầu và điểm cuối là các đỉnh của hình bình
hành, bằng véc tơ
AD
(không kể véc tơ
AD
) ?
A.
1
. B.
2
. C.
3
. D.
4
.
Hướng dẫn giải:
Chọn A.
Ta có:
BC AD=
và
BC
là duy nhất.
Câu 76. Cho tam giác đều
ABC
cạnh
a
. Mệnh đề nào sau đây là đúng?
A.
AB AC=
. B.
AC a=
. C.
AC BC=
. D.
AB a=
.
Hướng dẫn giải:
Chọn D.
Câu 77. Hình bình hành
ABCD
là một hình chữ nhật nếu nó thỏa mãn điều kiện nào trong các điều kiện sau
đây?
A.
AC BC=
. B.
AC BD=
. C.
AC AD=
. D.
AC BD=
.
Hướng dẫn giải:
Chọn B.
Một hình bình hành có hai đường chéo bằng nhau thì nó là hình chữ nhật.
Câu 78. Cho tứ giác
ABCD
. Nếu
AB DC=
và
AC BD=
thì
ABCD
A. Không là hình bình hành. B. Là hình vuông.
C. Là hình chữ nhật. D. Là hình thoi.
Hướng dẫn giải:
Chọn C.
Vì
AB DC=
nên ABCD là hình bình hành, mặt khác
AC BD=
(hai đường chéo bằng nhau); vì
vậy ABCD là hình chữ nhật.
Câu 79. Cho hình bình hành
ABCD
. Tổng các véc tơ
AB AC AD++
là
A.
2AC
. B.
AC
. C.
1
3
AC
. D.
2
3
AC
.
Hướng dẫn giải:
Chọn A.
Ta có:
( )
2AB AC AD AB AD AC AC AC AC+ + = + + = + =
.
Câu 80. Cho 4 điểm bất kì
, , ,A B C O
. Đẳng thức nào sau đây là đúng?
A.
OA CA CO=−
. B.
AB AC BC=+
.
C.
AB OB OA=+
. D.
OA OB BA=−
.
Hướng dẫn giải:
Chọn A.
Câu 81. Cho tam giác đều
ABC
cạnh
2a
có
G
là trọng tâm. Khi đó giá trị
AB GC−
là:
A.
3
3
a
. B.
23
3
a
. C.
2
3
a
. D.
43
3
a
.
Hướng dẫn giải:
Chọn D.
85
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Vẽ hình bình hành ABKG, ta có:
AB GK=
.
Khi đó:
22
AB GC GK GC CK CK BK BC− = − = = = +
;
2 2 2 3 2 3
.
3 3 2 3
aa
BK AG AM= = = =
.
Do vậy:
( )
2
2
2 3 4 3
2
33
aa
AB GC a
− = + =



.
Câu 82. Cho tứ giác
ABCD
. Gọi
,MN
lần lượt là trung điểm của các cạnh
,AB CD
.
K
là điểm đối xứng
với
M
qua
N
. Khi đó khẳng định nào sau đây là đúng?
A.
MK AD BC=−
. B.
MK AD BC=+
. C.
MK AB CD=+
. D.
MK AC BD=−
.
Hướng dẫn giải:
Chọn B.
Xét tứ giác MCKD có N là trung điểm của mỗi đường chéo MK, CD nên MCKD là hình bình hành.
Ta có:
MK MC MD MB BC MA AD= + = + + +
0
MA MB BC AD BC AD
= + + + = +

.
Câu 83. Cho tam giác
ABC
. Điểm
M
thỏa mãn
0MA MB MC− + =
thì
A.
M
là điểm sao cho tứ giác
ABMC
là hình bình hành.
B.
M
là trọng tâm tam giác
ABC
.
C.
M
là điểm sao cho tứ giác
BAMC
là hình bình hành.
D.
M
thuộc đường trung trực của
AB
.
Hướng dẫn giải:
Chọn C.
Ta có:
00MA MB MC BA MC BA CM− + = + = =
.
Do đó BAMC là hình bình hành.
86
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Câu 84. Cho nửa đường tròn tâm
O
, đường kính
2PQ =
. Trên nửa đường tròn đó ta lấy các điểm
,,A B C
khác
,PQ
sao cho theo thứ tự đó, chúng chia nửa đường tròn thành bốn phần bằng nhau. Khi đó
OA OC OB++
bằng:
A.
3
. B.
12+
. C.
22+
. D.
2
.
Hướng dẫn giải:
Chọn B.
Gọi I là trung điểm AC. Ta có:
2OA OC OI+=
.
Tam giác
AOC
vuông cân tại O, cạnh góc vuông bằng
1
(bằng bán kính nửa đường tròn) nên
2
2
OI =
.
Khi đó:
2
2 2 1 2 1
2
OA OC OB OI OB+ + = + = + = +
.
Câu 85. Cho
ABC
. Gọi
M
là điểm thỏa mãn
3MB MA=
. Khi đó biểu diễn
AM
theo
AB
và
AC
là
A.
1
3
4
AM AB AC=+
. B.
1
0.
2
AM AB AC= − +
.
C.
11
46
AM AB AC=+
. D.
11
26
AM AB AC=+
.
Hướng dẫn giải:
Chọn B.
Ta có:
11
0.
22
AM AB AB AC= − = − +
.
Câu 86. Cho tam giác
ABC
. Gọi
M
là trung điểm của
AB
,
D
là trung điểm của
BC
,
N
là điểm thuộc
AC
sao cho
2CN NA=
,
K
là trung điểm của
MN
. Khi đó khẳng định nào sau đây là đúng?
A.
11
46
AK AB AC=+
. B.
11
23
AK AB AC=+
.
C.
1
2
AK AD=
. D.
2
5
AK AD=
.
Hướng dẫn giải:
Chọn A.
87
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Ta có:
( )
1 1 1 1 1
..
2 2 2 2 3
AK AM AN AB AC= + = +
11
46
AB AC=+
.
Câu 87. Cho tam giác
ABC
với phân giác trong
AD
. Biết
5AB =
,
6BC =
,
7CA =
. Khi đó
AD
bằng:
A.
57
12 12
AB AC+
. B.
75
12 12
AB AC−
. C.
75
12 12
AB AC+
. D.
57
12 12
AB AC−
.
Hướng dẫn giải:
Chọn C.
Vì
AD
là phân giác trong của tam giác
ABC
nên:
5
7
BD AB
DC AC
==
mà
,BD DC
cùng hướng nên
( )
55
77
BD DC AD AB AC AD= − = −
12 5 7 5
7 7 12 12
AD AB AC AD AB AC = + = +
.
Câu 88. Cho tam giác
ABC
. Gọi
I
là trung điểm của
BC
,
H
là điểm đối xứng của
I
qua
C
. Khi đó khẳng
định nào sau đây là đúng?
A.
AH AC AI=+
. B.
2AH AC AI=−
.
C.
2AH AC AB=−
. D.
AH AB AC AI= + +
.
Hướng dẫn giải:
Chọn B.
Ta có:
AH AC CH AC IC= + = +
( )
2AC AC AI AC AI= + − = −
.
Câu 89. Cho hai điểm cố định
,AB
. Tập hợp các điểm
M
thỏa mãn
MA MB MA MB+ = −
là:
A. Đường tròn đường kính
AB
. B. Đường trung trực của
AB
.
C. Đường tròn bán kính
AB
. D. Nửa đường tròn đường kính
AB
.
88
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
N
M
B
A
D
C
Hướng dẫn giải:
Chọn A.
Gọi I là trung điểm đoạn thẳng AB, ta có:
2MA MB MA MB MI BA+ = − =
2
2
AB
MI AB IM = =
.
Vậy tập hợp điểm M là đường tròn tâm I, bán kính
2
AB
R =
(đường kính AB).
Câu 90. Cho tam giác
ABC
có trọng tâm
G
. Tập hợp các điểm
M
sao cho
MA MB MC AB AC+ + = −
là:
A. Đường tròn tâm
G
đường kính
BC
. B. Đường tròn tâm
G
đường kính
1
3
BC
.
C. Đường tròn tâm
G
bán kính
1
3
BC
. D. Đường tròn tâm
G
đường kính
3MG
.
Hướng dẫn giải:
Chọn C.
Ta có:
33
3
BC
MA MB MC AB AC MG CB GM BC GM+ + = − = = =
.
Vậy tập hợp điểm M là đường tròn tâm G, bán kính
3
BC
.
Câu 91. Cho tứ giác
ABCD
. Gọi
,MN
lần lượt là trung điểm của
,AB CD
. Đẳng thức nào sau đây là đúng?.
A. . B. .
C. . D. .
Hướng dẫn giải:
Chọn D.
Ta có:
( )
1
2
MN MC MD=+
( ) ( )
11
22
MB BC MA AD BC AD= + + + = +
.
Câu 92. Cho hình thang , hai đường chéo và cắt nhau tại O. Qua O kẻ MN song song với
( là đáy của hình thang, ). Đặt , . Khi đó khẳng định nào
sau đây là đúng?
A. . B. .
C. . D. .
Hướng dẫn giải:
Chọn B.
2
BC AD
MN
+
=
MN BC AD=+
MN AC BD=+
( )
1
2
MN BC AD=+
ABCD
AC
BD
AB
AB
,M AD N BC
AB a=
DC b=
aAB bDC
MN
ab
+
=
+
bAB aDC
MN
ab
+
=
+
aAB bDC
MN
ab
−
=
+
bAB aDC
MN
ab
−
=
+
89
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Áp dụng định lí Ta-lét trong tam giác ta có:
;
MO DO ON BO
AB DB DC BD
==
.
Từ đó suy ra
;
DO BO
MO AB ON DC
DB BD
==
DO BO
MN MO ON AB DC
DB BD
= + = +
(1).
Mặt khác, ta có:
1
MO DM
MO MO ab
AB DA
MO
MO AM
a b a b
DC AD
=
+ = =
+
=
.
Suy ra
( )
2
ab
DO MO b
ab
DB AB a a b
+
= = =
+
. Tương tự ta có
( )
3
BO a
BD a b
=
+
.
Từ (1), (2) và (3) ta có
bAB aDC
MN
ab
+
=
+
.
Câu 93. Cho tam giác đều
ABC
cạnh
.a
Biết rằng tập hợp các điểm
M
thỏa mãn đẳng thức
2 3 4MA MB MC MB MA+ + = −
là đường tròn cố định có bán kính
.R
Tính bán kính
R
theo
.a
A.
3
a
r =
. B.
9
a
r =
. C.
2
a
r =
. D.
6
a
r =
.
Hướng dẫn giải:
Chọn B.
Gọi
G
là trọng tâm của tam giác
.ABC
Chọn điểm
I
sao cho
2 3 4 0IA IB IC+ + =
( )
1
3 0 9
9
IA IB IC IC IA IG CA IG CA + + + − = = =
hay điểm I cố định.
Ta có:
( ) ( ) ( )
2 3 4 2 3 4MA MB MC MI IA MI IB MI IC+ + = + + + + +
0
9 2 3 4 9MI IA IB IC MI= + + + =
.
Do vậy
2 3 4 9 9
9
AB
MA MB MC MB MA MI AB MI AB MI+ + = − = = =
.
Vậy tập hợp các điểm
M
cần tìm là đường tròn tâm
,I
bán kính
.
99
AB a
r ==
Câu 94. Cho ba vectơ
a
,
b
,
c
thỏa:
4a =
,
1b =
,
5c =
và
( )
5 3 0b a c− + =
. Khi đó biểu thức
. . .M a b b c c a= + +
có giá trị bằng
A.
29
. B.
67
2
. C.
18,25
. D.
18,25−
.
90
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Hướng dẫn giải:
Chọn A.
Ta có:
( )
5 3 0b a c− + =
( )
53a b c − =
( )
2
2
25 9a b c − =
(
)
2 2 2
25 2 9a ab b c − + =
( )
2 2 2
25 4 2 1 9.5ab − + =
.4ab=
(1).
Tương tự:
( )
5 3 0b a c− + =
2 2 2
5 5 3 25 25 9 30a b c a b c bc = + = + +
2 2 2
25.4 25.1 9.5 30 5bc bc = + + =
.5bc=
(2).
( )
5 3 0b a c− + =
2 2 2
5 5 3 25 25 9 30 .b a c b a c a c = − = + −
2 2 2
25.1 25.4 9.5 30 . . 20ac a c = + − =
(3).
Từ (1), (2), (3) suy ra :
4 5 20 29M = + + =
.
Câu 95. Cho tam giác ABC vuông tại A với
3, 4AB AC==
. Các điểm
,MN
lần lượt thuộc các cạnh
,AB AC
thỏa mãn
1AM AN==
. Tích vô hướng
.BN CM
bằng
A. 1. B. −1. C. −7. D. 7.
Hướng dẫn giải:
Chọn C.
Ta có:
( )( )
00
. . . . .BN CM BA AN CA AM BACA BA AM AN CA AN AM= + + = + + +
11
..
34
AB AB AC AC= − −
2 2 2 2
1 1 1 1
.3 .4 7
3 4 3 4
AB AC= − − = − − = −
.
Câu 96. Gọi
S
là diện tích tam giác
ABC
. Mệnh đề nào sau đây đúng?
A.
( )
2
22
1
..
2
S AB AC AB AC=−
. B.
( )
2
22
..S AB AC AB AC=−
.
C.
( )
2
22
1
..
2
S AB AC AB AC=−
. D.
( )
2
22
..S AB AC AB AC=−
.
Hướng dẫn giải:
Chọn A.
Ta có :
1
. sin
2
S AB AC A=
2
1
. 1 cos
2
AB AC A=−
2
1.
.1
2.
AB AC
AB AC
AB AC

=−


( )
( )
2
22
2
22
22
..
11
. . .
2 . 2
AB AC AB AC
AB AC AB AC AB AC
AB AC
−
= = −
.
91
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
Câu 97. Đoạn thẳng
AB
có độ dài
2a
,
I
là trung điểm
AB
. Khi
2
.3MAMB a=
. Độ dài
MI
là
A.
2a
. B.
a
. C.
3a
. D.
7a
.
Hướng dẫn giải:
Chọn A.
Ta có :
( )( ) ( )( )
2 2 2
. 3 3 3MA MB a MI IA MI IB a MI IA MI IA a= + + = + − =
22
2
3MI IA a − =
2
2 2 2 2 2
3 3 2
2
AB
MI a MI a a MI a

− = − = =


.
Câu 98. Cho đoạn thẳng
4AB =
. Tập hợp các điểm
M
thỏa mãn
22
8MA MB−=
là
A. Một đường thẳng. B. Một đoạn thẳng. C. Một đường tròn. D. Một điểm.
Hướng dẫn giải:
Chọn A.
Gọi
I
là trung điểm của
AB
.
Ta có:
22
22
88MA MB MA MB− = − =
( )( )
8MA MB MA MB − + =
.2. 8 . 4BA MI BAMI = =
.
Gọi H là hình chiếu của M trên AB, ta có:
( )
. 4 . 4BA MI BA MH HI= + =
0
. . 4 . 4BA MH BA HI BA HI + = =
(*).
Từ (*) ta có:
.0BA HI
nên
,BA HI
cùng hướng; đồng thời
44
. 4 1
4
AB HI HI
AB
= = = =
.
Vậy H là trung điểm đoạn BI và tập hợp điểm M là đường thẳng qua H, vuông góc với AB.
Câu 99. Một máy bay đang bay từ hướng đông sang hướng tây với tốc độ 700 km/h thì gặp luồng gió thổi từ
hướng đông bắc sang hướng tây nam với tốc độ 40 km/h. Máy bay bị thay đổi vận tốc sau khi gặp
gió thổi. Tìm tốc độ mới của máy bay (làm tròn kết quả đến hàng phần trăm).
A.
911,12 km/h
. B.
724,32 km/h
. C.
728,83 km/h
. D.
813,13 km/h
.
Hướng dẫn giải:
Chọn C.
Đặt
12
,v OA v OB==
lần lượt là vectơ vận tốc ban đầu của máy bay và của gió;
v OC=
là vận tốc
của máy bay sau khi gặp luồng gió thổi. Ta có
12
v v v=+
và OACB là hình bình hành.
Xét tam giác OAC có
0
135 , 700, 40OAC OA AC= = =
2 2 2
2 . .cosOC AO AC AO AC OAC = + −
2 2 0
700 40 2.700.40.cos135= + −
92
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom
Zalo: 0969 343 344
531197,98 728,83OC
km/h.
Vậy tốc độ mới của máy bay sau khi gặp gió xấp xỉ bằng
728,83
km/h.
Câu 100. Một chiếc thuyền cố gắng đi thẳng qua một con sông với tốc độ 0,75 m/s. Tuy nhiên dòng nước trên
con sông đó chảy với tốc độ 1,2 m/s về hướng bên trái (hình vẽ). Tính tốc độ dịch chuyển của thuyền
so với bờ (kết quả làm tròn đến hàng phần nghìn).
A.
1,215
m/s. B.
1,112
m/s. C.
1,312
m/s. D.
1,415
m/s.
Hướng dẫn giải:
Chọn D.
Gọi
1
v OA=
là vectơ vận tốc của thuyền đối với nước,
2
v OB=
là vectơ vận tốc của nước đối với bờ
và
v OC=
là vận tốc của thuyền đối với bờ. Ta có:
12
v v v=+
hay OACB là hình bình hành.
Xét tam giác vuông OAC ta có:
2 2 2 2
3 89
0,75 1,2 1,415
20
OC OA AC= + = + =
m/s.
Vậy tốc độ dịch chuyển của thuyền so với bờ xấp xỉ bằng
1,415
m/s.
Chuùc caùc em hoïc sinh oân taäp
thaät toát vaø gaët haùi nhieàu thaønh coâng!
Hoàng Xuân Nhàn
| 1/95
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Năm học 2022 - 2023  10 đề tự luận  100 câu trắc nghiệm Hoàng Xuân Nhàn MỤC LỤC
Đề số 01: ........................................................................................................... 01
Hướng dẫn giải Đề số 01: ............................................................................... 02
Đề số 02: ........................................................................................................... 07
Hướng dẫn giải Đề số 02: ............................................................................... 08
Đề số 03: ........................................................................................................... 12
Hướng dẫn giải Đề số 03: ............................................................................... 13
Đề số 04: ........................................................................................................... 17
Hướng dẫn giải Đề số 04: ............................................................................... 18
Đề số 05: ........................................................................................................... 22
Hướng dẫn giải Đề số 05: ............................................................................... 23
Đề số 06: ........................................................................................................... 28
Hướng dẫn giải Đề số 06: ............................................................................... 29
Đề số 07: ........................................................................................................... 33
Hướng dẫn giải Đề số 07: ............................................................................... 34
Đề số 08: ........................................................................................................... 38
Hướng dẫn giải Đề số 08: ............................................................................... 39
Đề số 09: ........................................................................................................... 42
Hướng dẫn giải Đề số 09: ............................................................................... 43
Đề số 10: ........................................................................................................... 47
Hướng dẫn giải Đề số 10: ............................................................................... 48
100 Câu trắc nghiệm Toán 10 ôn tập học kì 1: ............................................ 52
Hướng dẫn giải 100 câu trắc nghiệm toán 10: ............................................. 65
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
ÑEÀ REØN LUYEÄN SOÁ 01 Time: 90 phuùt
Câu 1. Cho đoạn A = −5; 
1 , B = (−3; 2) . Tìm A ,
B AB , A \ , B C ,
A C ( A B) .
Câu 2. Tìm tập xác định của các hàm số sau: 3 x −1 +1 a) y = x +1 ; b) y = ( . x + 2) x
Câu 3. Xác định hàm số bậc hai có đồ thị là parabol ( P) biết: a) ( P) 2
: y = ax − 4x + c có đỉnh là I ( 2 − ;− ) 1 . b) ( P) 2
: y = ax + bx + c đi qua điểm A(0;5) và có đỉnh I (3; −4) .
x − 2y  0 
Câu 4. Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau: 5
x − y  −4. x + 2y  5  Câu 5. 2 a) Cho cos = − và   ( 0 0
90 ;180 ) . Tính sin, tan và cot . 3 sin − cos
b) Cho tan = 2 . Tính C = 3 3 sin  + 3cos  + . 2sin
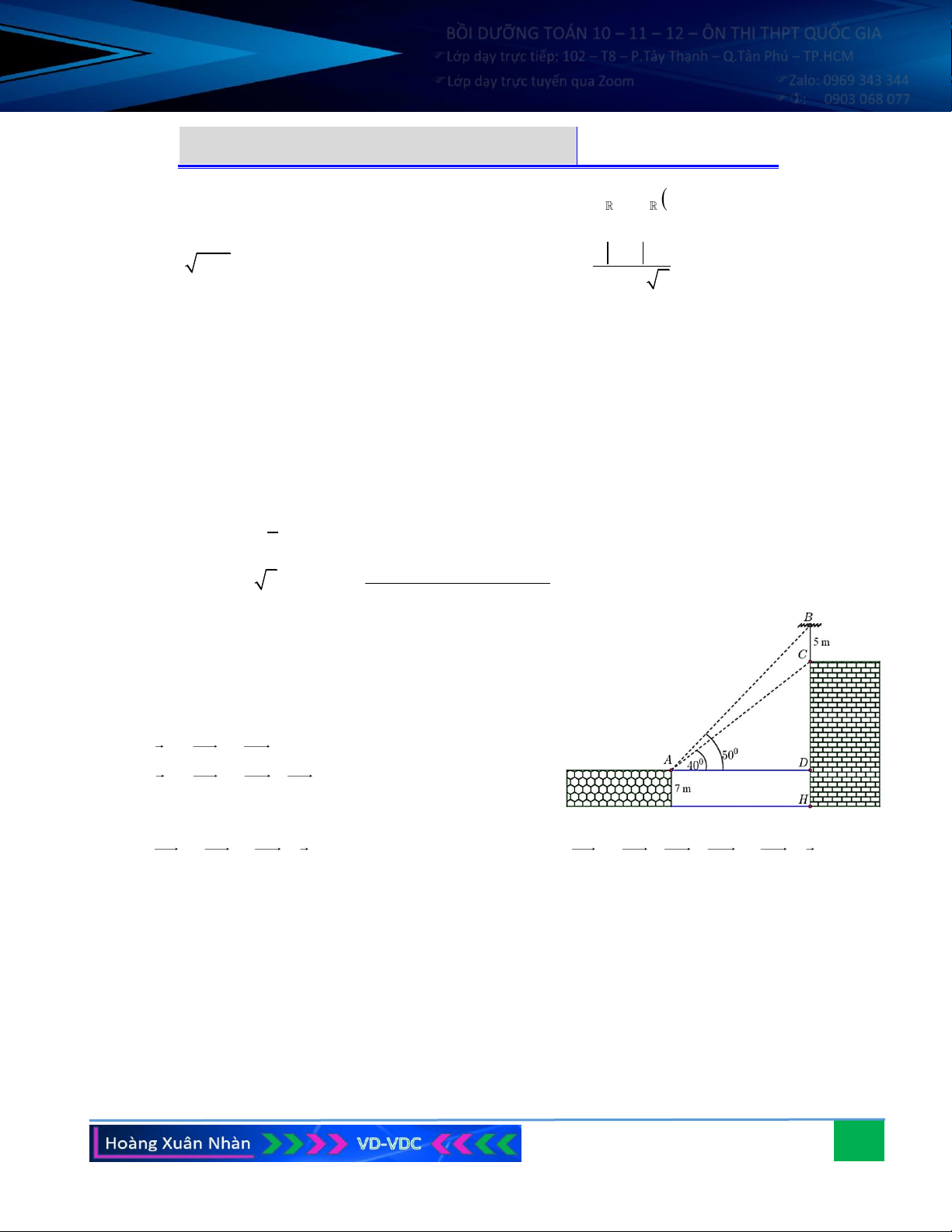
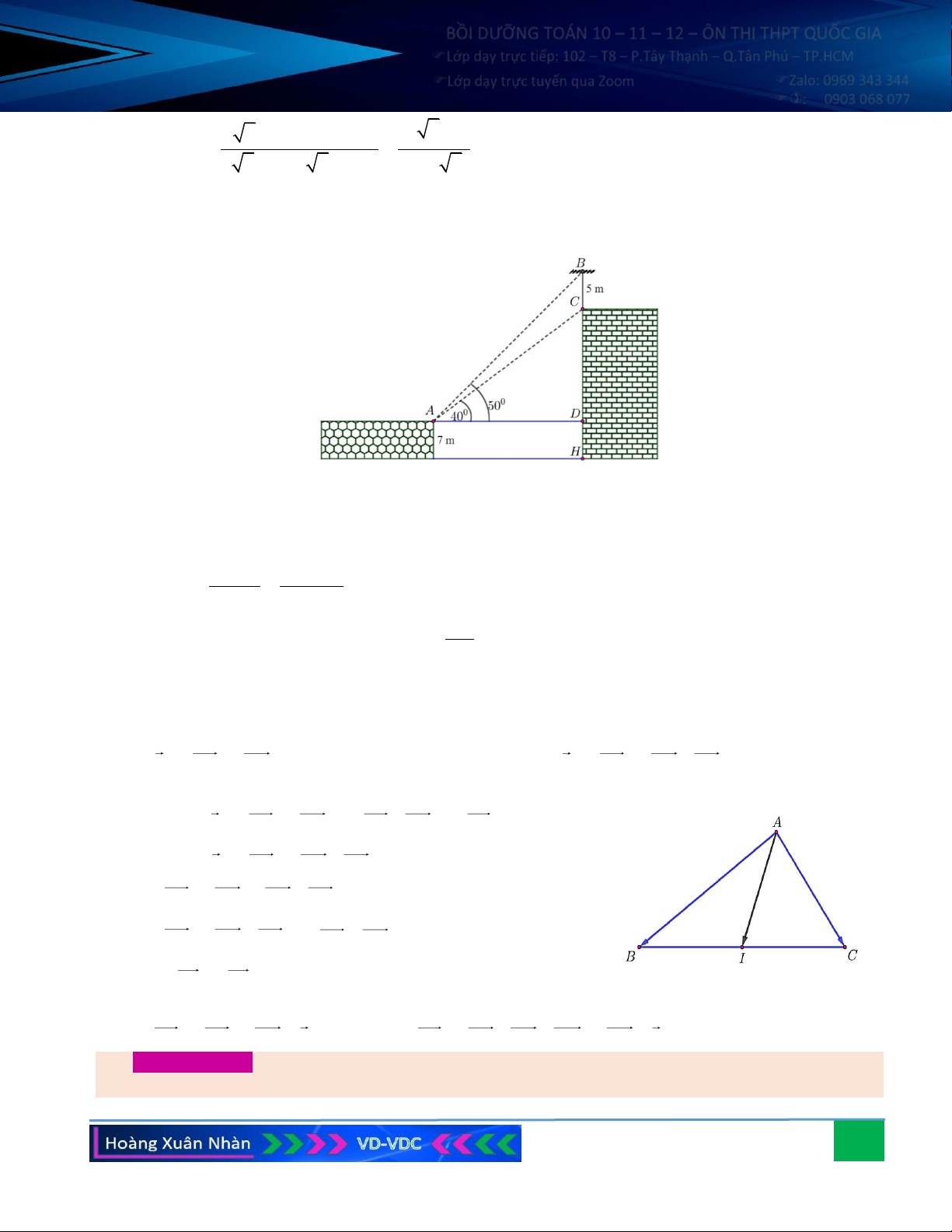
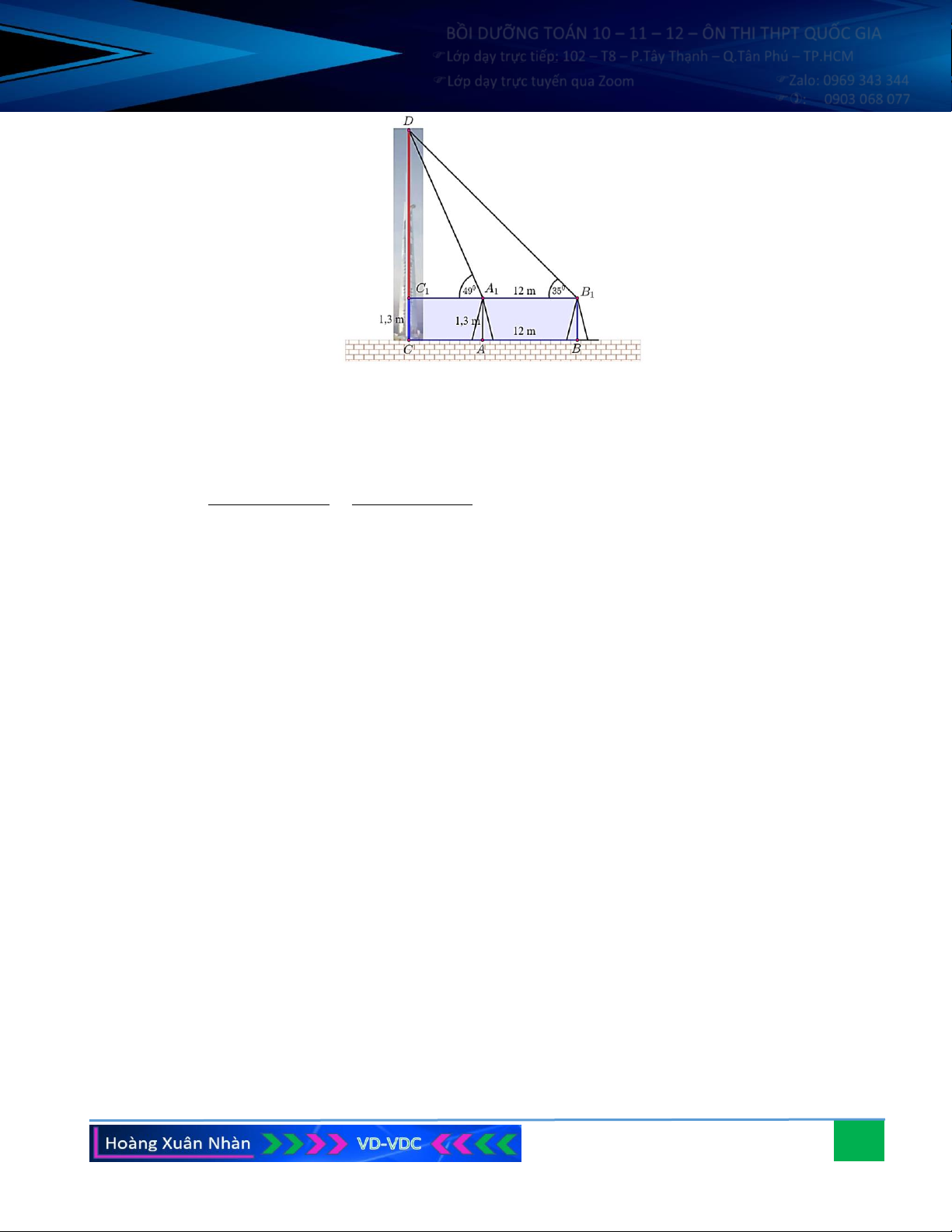
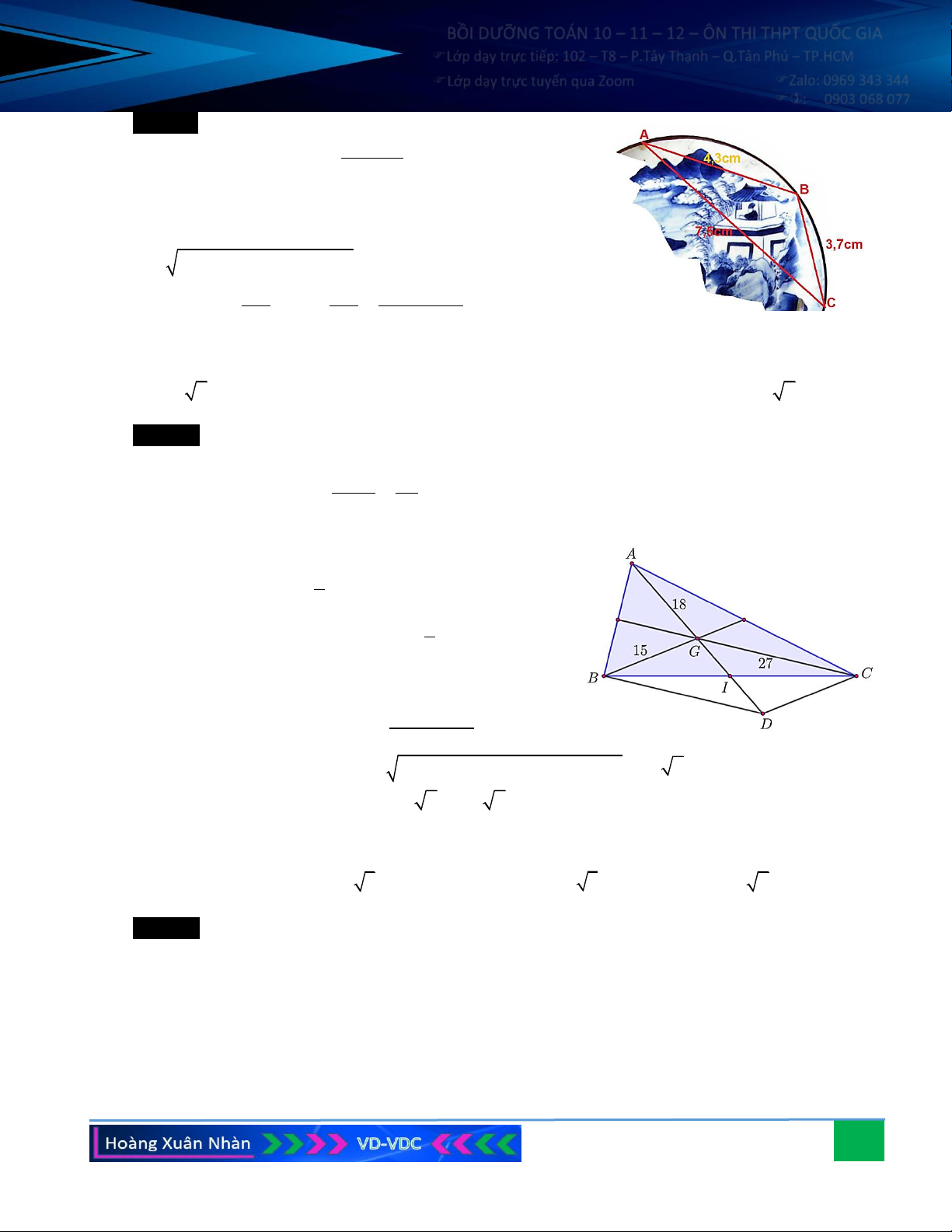
Câu 6. Trên nóc một tòa nhà có một cột ăng-ten cao 5 m. Từ
vị trí quan sát A cao 7 m so với mặt đất, có thể nhìn
thấy đỉnh B và chân C của cột ăng-ten dưới góc 50o và
40o so với phương nằm ngang. Tính chiều cao của tòa nhà đó.
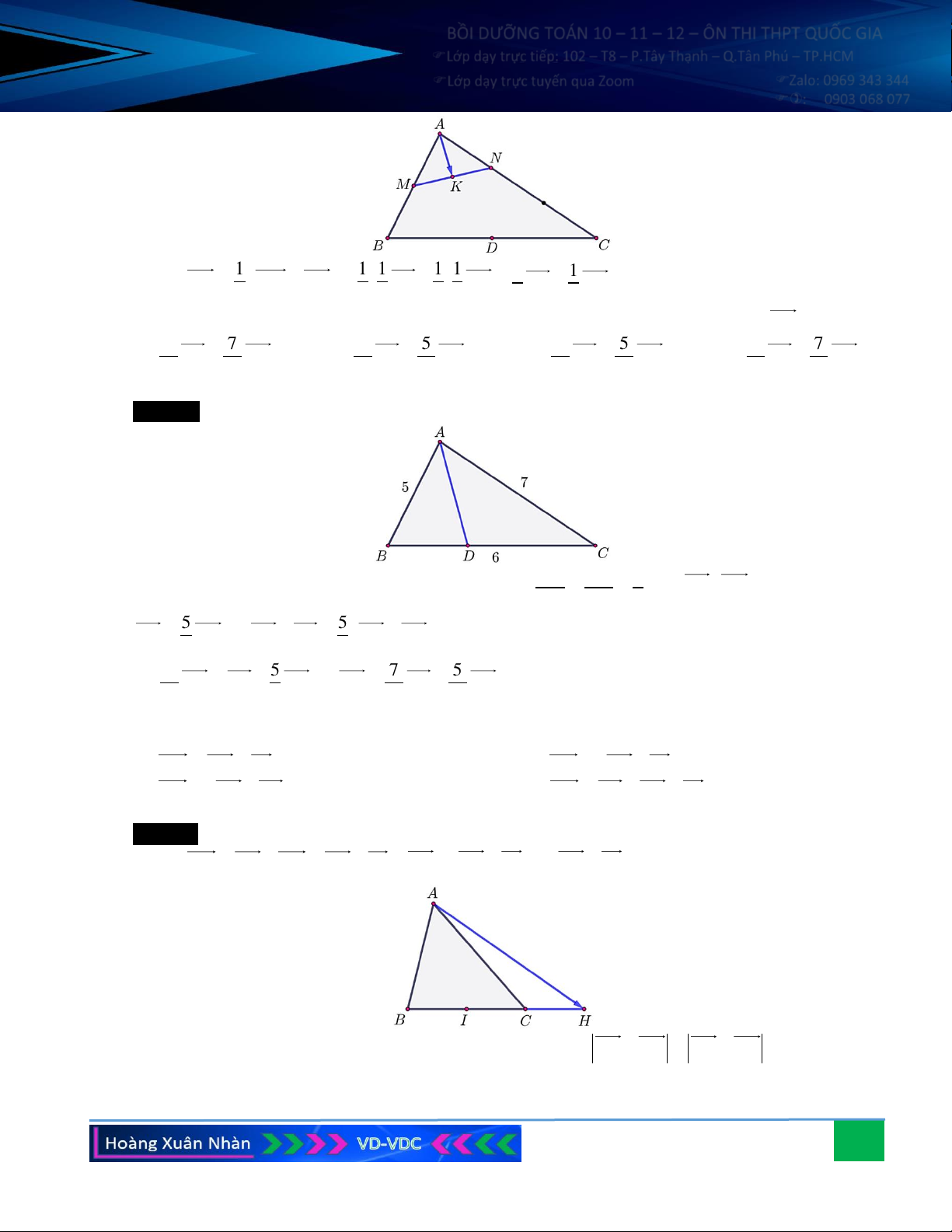
Câu 7. Cho tam giác ABC. Xác định các vectơ:
a) u = 4AB − 4AC ;
b) v = 2AB + 4AC − BC .
Câu 8. Cho năm điểm O, A, B, C, D . Chứng minh ba điểm A,
B, C thẳng hàng biết rằng:
a) OA + 2OB − 3OC = 0 ;
b) 2OA + 4BD − OC + DO − 3AD = 0 .
Câu 9. Một nhóm 11 học sinh tham gia một kì thi. Số điểm thi của 11 học sinh đó được sắp xếp từ thấp
đến cao theo thang điểm 100 như sau: 0; 0; 63; 65; 69; 70; 72; 78; 81; 85; 89.
a) Tìm điểm số trung bình của nhóm 11 học sinh này.
b) Tìm trung vị và mốt của mẫu số liệu đã cho.
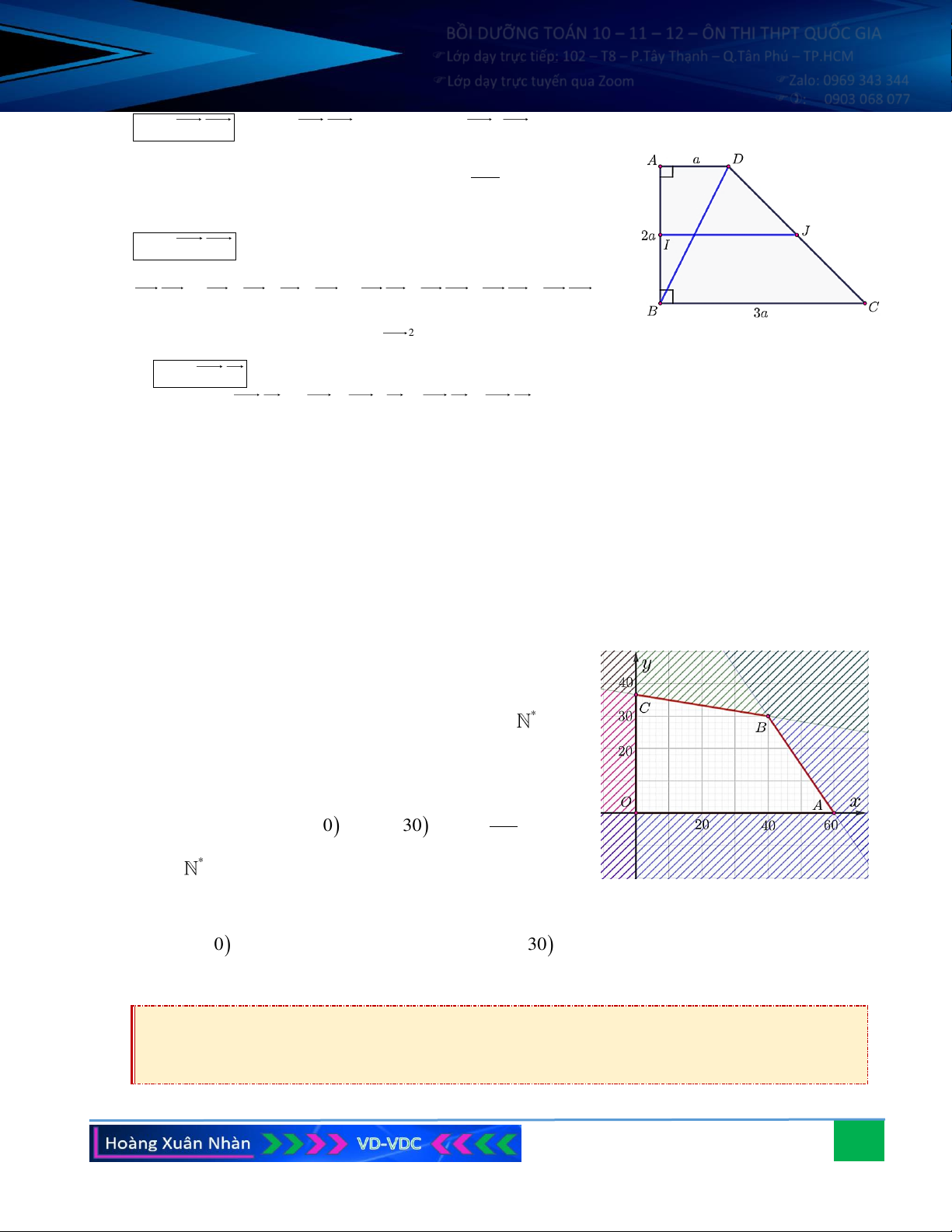
Câu 10. Một xưởng sản xuất hai loại sản phẩm là sản phẩm loại I và sản phẩm loại II:
• Mỗi kg sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, thu lời được 40 nghìn.
• Mỗi kg sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ, thu lời được 30 nghìn.
Xưởng có 200 kg nguyên liệu và 1200 giờ làm việc tối đa. Nên sản xuất mỗi loại sản phẩm bao nhiêu để có mức lời cao nhất?
================HẾT=============== 1
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Höôùng daãn giaûi ñeà soá 01
Câu 1. Cho đoạn A = −5; 
1 , B = (−3; 2) . Tìm A ,
B AB , A \ , B C ,
A C ( A B) . Hướng dẫn giải:
Ta có: A B =  5
− ;2), AB = ( 3 − ; 
1 , A \ B =  5 − ;−  3 . C A = \ A = ( ; − 5
− ) (1;+), C ( AB) = \ ( AB) = ( ; − −5)2;+).
Câu 2. Tìm tập xác định của các hàm số sau: 3 x −1 +1 a) y = x +1 ; b) y = ( . x + 2) x Hướng dẫn giải:
a) Hàm số xác định khi và chỉ khi x +1 0  x  1 − .
Tập xác định hàm số: D = −1;+ ) . x + 2  0 x  2 −
d) Hàm số xác định khi và chỉ khi     x  0 . x  0 x  0
Tập xác định hàm số: D = (0;+ ) .
Câu 3. Xác định hàm số bậc hai có đồ thị là parabol ( P) biết: a) ( P) 2
: y = ax − 4x + c có đỉnh là I ( 2 − ;− ) 1 . b) ( P) 2
: y = ax + bx + c đi qua điểm A(0;5) và có đỉnh I (3; −4) . Hướng dẫn giải: b 4 x = − = = 2 −   = − I a 1
a) ( P) có đỉnh I ( 2 − ;− ) 1 nên 2a 2a    .  c = − y = a − − − + c = −  I ( )2 ( ) 5 . 2 4 2 1
Vậy hàm số bậc hai được xác định là 2
y = −x − 4x − 5 . b
b) ( P) qua A(0;5) nên c = 5 ; hoành độ đỉnh x = −
= 3  6a + b = 0 (1). I 2a c=5
Mặt khác điểm I (3; −4) thuộc (P) nên 2 4 − = . a 3 + .
b 3 + c  9a + 3b = 9
−  3a + b = 3 − (2).
Giải hệ phương trình (1), (2) ta có: a = 1, b = 6
− . Vậy hàm số được xác định: 2
y = x − 6x + 5 .
x − 2y  0 
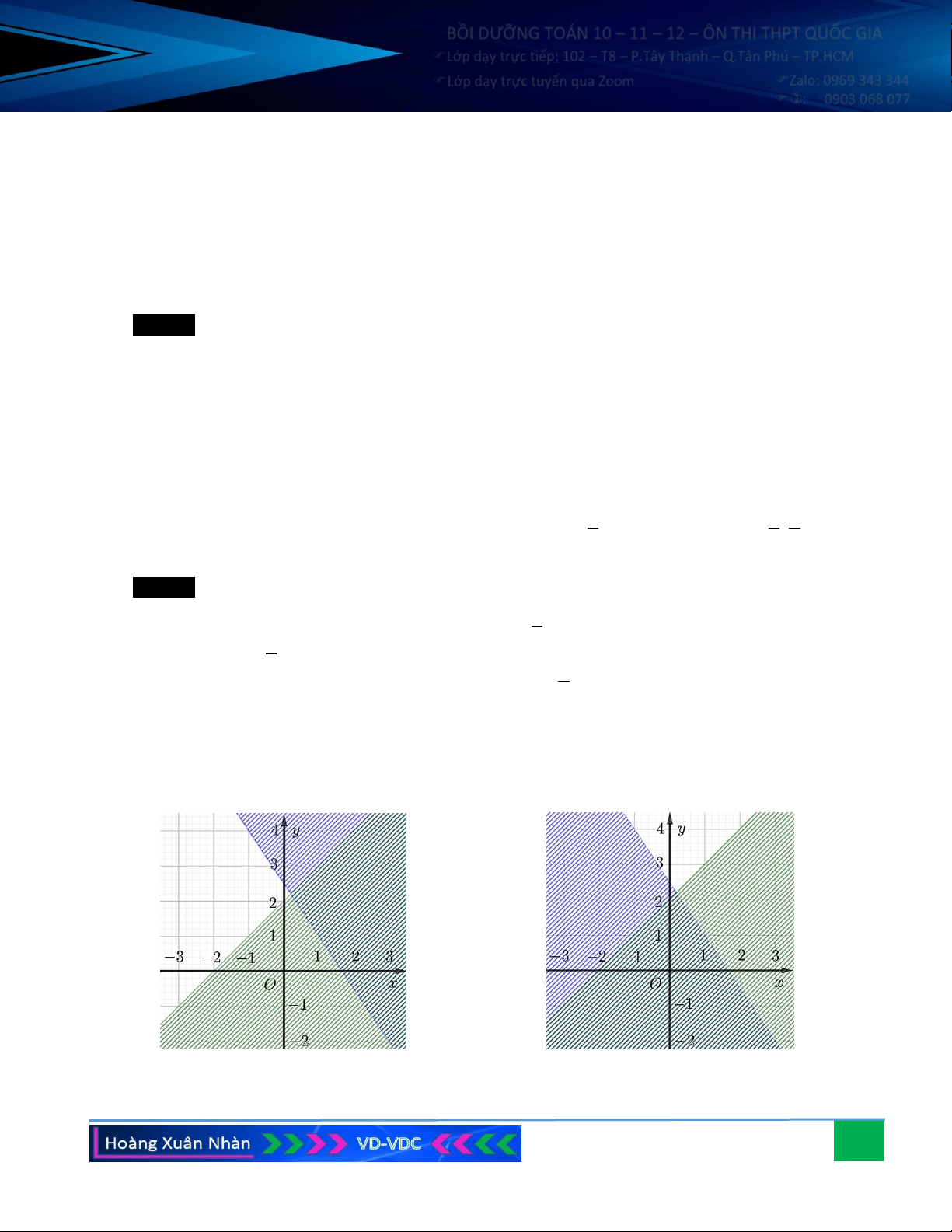
Câu 4. Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau: 5
x − y  −4. x + 2y  5  2
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 Hướng dẫn giải:
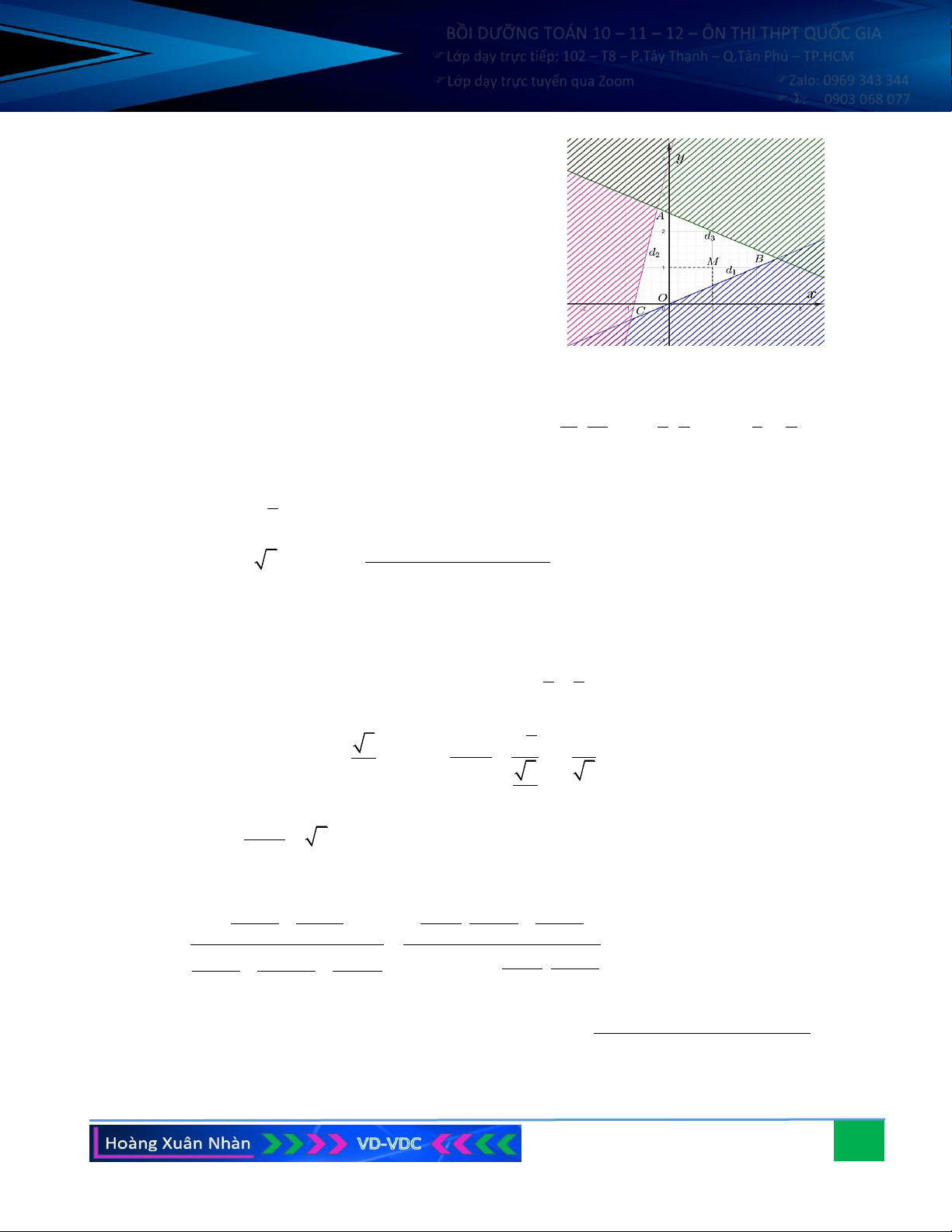
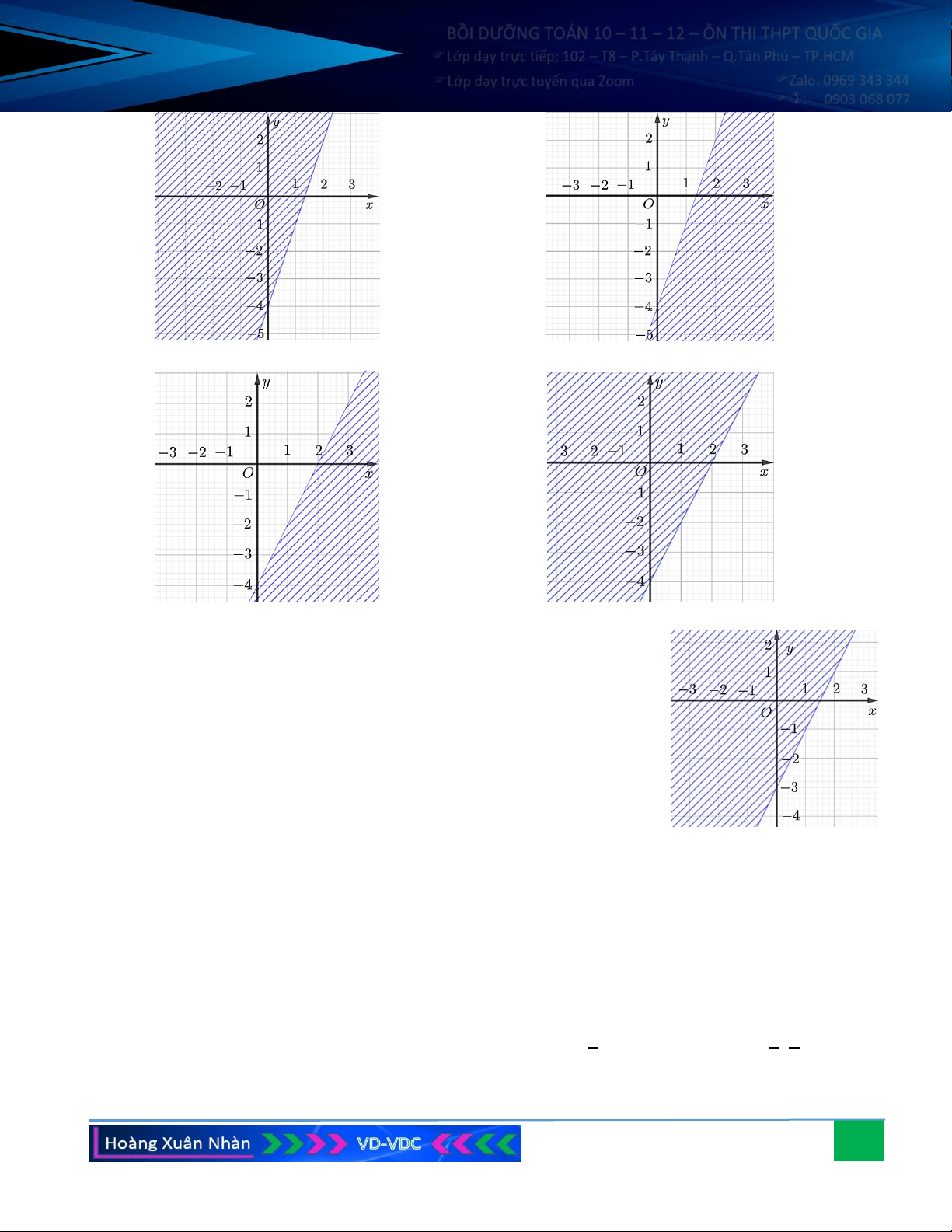
Vẽ các đường thẳng d : x − 2y = 0, d : 5x − y = 4 − , 1 2
d : x + 2y = 5. Ta thấy M (1; ) 1 thỏa mãn miền nghiệm 3
của hệ bất phương trình vì khi thay x =1, y =1 vào hệ, 1  − 2.1 0  ta có: 5  .1−1 4 − (đúng). 1+ 2.1 5 
Gạch bỏ các phần không thuộc miền nghiệm của mỗi bất
phương trình (nửa mặt phẳng có bờ là các đường
d , d , d và không chứa điểm M) . Khi đó, miền nghiệm của bất phương trình chính là miền 1 2 3       của tam giác 5 5 8 4
ABC (kể cả ba cạnh của nó) , trong đó 3 29 A − ;   , B ;  , C − ;−   .  11 11   2 4   9 9  Câu 5. 2 a) Cho cos = − và   ( 0 0
90 ;180 ) . Tính sin và cot . 3 sin − cos
b) Cho tan = 2 . Tính C = 3 3 sin  + 3cos  + . 2sin Hướng dẫn giải: a) Vì   ( 0 0 90 ;180 ) nên sin  0. 4 5 Ta có: 2 2 2 2
sin  + cos  = 1  sin  = 1− cos  = 1− = 9 9 2 − 5 cos 2
mà sin  0, nên sin = ; 3 cot  = = = − . 3 sin  5 5 3 sin b) Do tan = = 2  cos  0 . cos
Chia cả tử và mẫu của T cho 3 cos x , ta có: sin  cos sin  1 1 − . − 3 3 2 2      cos cos cos cos cos C = = 3 3 sin  3cos  2sin  sin  1 3 + + tan  + 3 + 2 . 2 3 3 3 cos  cos  cos  cos cos  tan ( 2 tan  + ) 1 − ( 2 tan  + ) 1 = . 3 tan  + 3 + 2 tan ( 2 tan  + ) 1 3
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 ( + )−( + ) 3( 2 − ) 1 2 2 1 2 1 Suy ra C = = . 2 2 + 3 + 2 2 (2 + ) 1 3 + 8 2
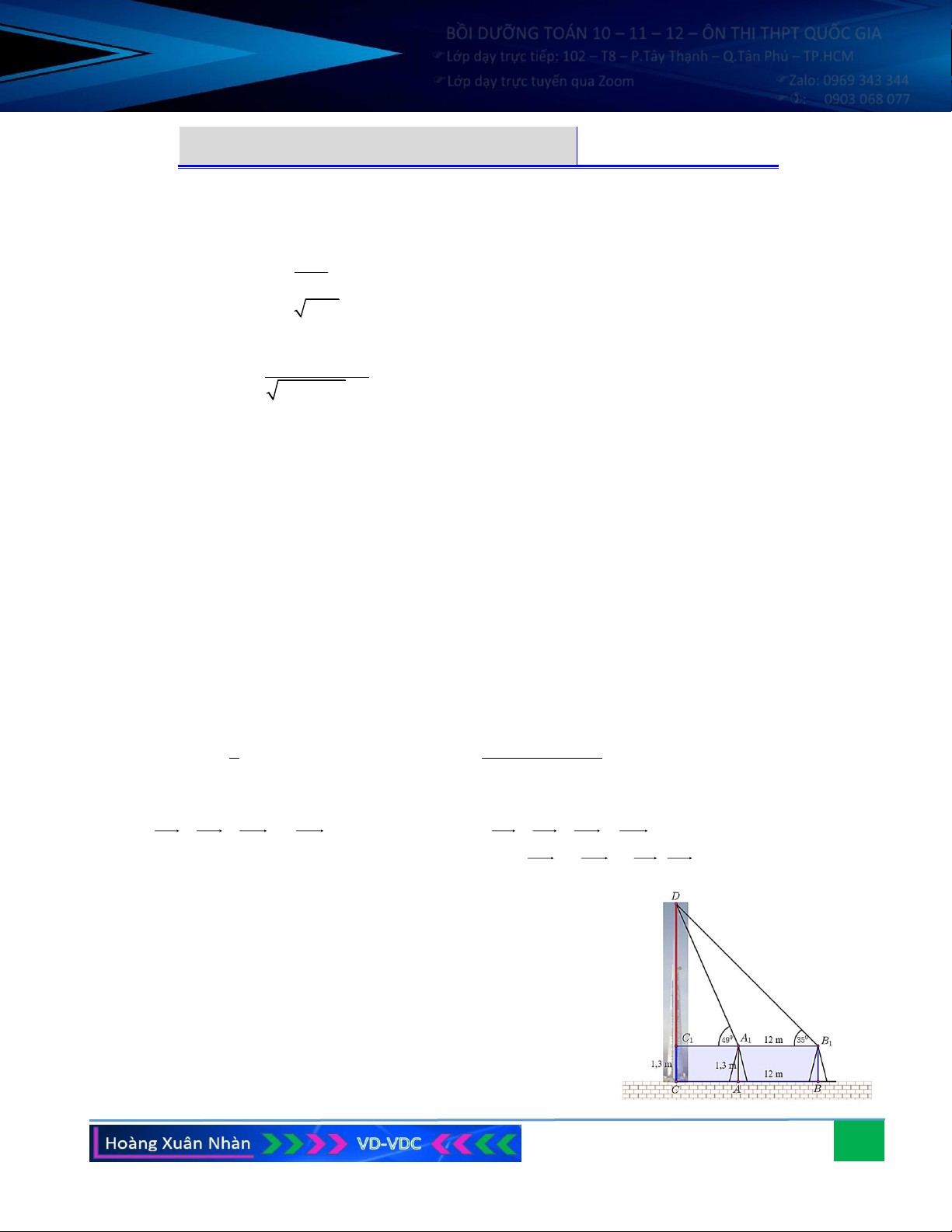
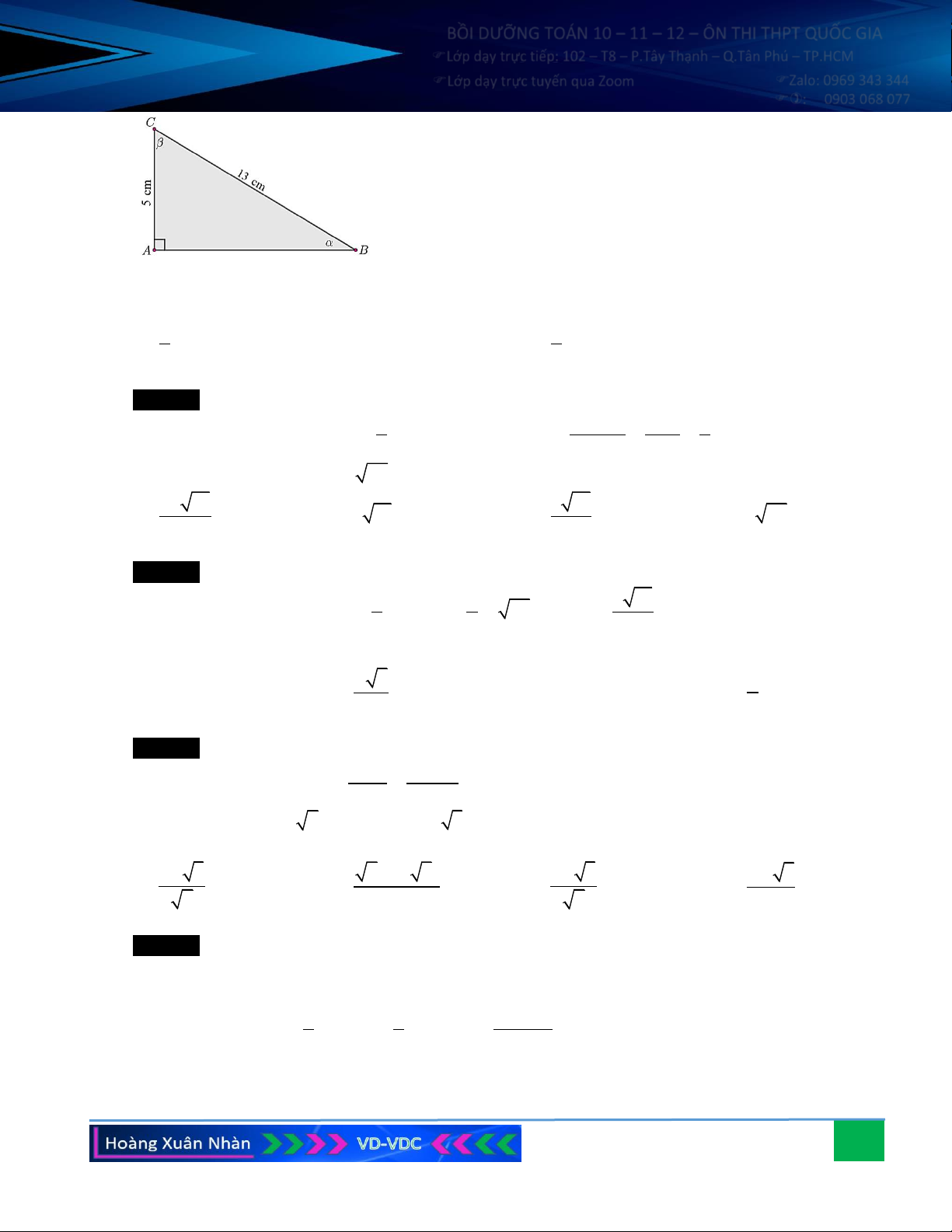
Câu 6. Trên nóc một tòa nhà có một cột ăng-ten cao 5 m. Từ vị trí quan sát A cao 7 m so với mặt đất, có
thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 50o và 40o so với phương nằm ngang. Tính
chiều cao của tòa nhà đó. Hướng dẫn giải: Xét tam giác ABC có 0 0 0 A = 50 − 40 = 10 , 0 0 0 B = 90 − 50 = 40 .
Áp dụng định lí Sin cho tam giác ABC ta có; 0 a sin B 5sin 40 AC = b = = 18,5 m . 0 sin A sin10 CD
Xét tam giác ACD vuông tại D: 0 0 sin 40 =
CD = AC.sin 40 11,89 m . AC
Suy ra: CH = CD + DH  18,89 m . Vậy chiều cao tòa nhà xấp xỉ 18,89 m .
Câu 7. Cho tam giác ABC. Xác định các vectơ:
a) u = 4AB − 4AC ;
b) v = 2AB + 4AC − BC . Hướng dẫn giải:
a) Ta có: u = 4AB − 4 AC = 4 ( AB − AC) = 4CB .
b) Ta có: v = 2AB + 4AC − BC
= 2 AB + 3AC + ( AC − BC)
= 2AB + 3AC + AB = 3( AB + AC )
= 3.2AI = 6AI (với I là trung điểm đoạn BC).
Câu 8. Cho năm điểm O, A, B, C, D . Chứng minh ba điểm A, B, C thẳng hàng biết rằng:
a) OA + 2OB − 3OC = 0 ;
b) 2OA + 4BD − OC + DO − 3AD = 0 . Định hướng:
a) Biến đổi hệ thức và khử (làm mất) điểm O để hệ thức sau cùng chỉ còn chứa ba điểm A, B, C. 4
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
b) Biến đổi và khử (làm mất) hai điểm O, D để hệ thức sau cùng chỉ còn chứa ba điểm A, B, C. Hướng dẫn giải:
a) Ta có: OA + 2OB − 3OC = 0  OA + 2OA + 2AB − 3OA − 3AC = 0 3
 2AB − 3AC = 0  AB = AC. 2
Vậy hai vectơ AB, AC cùng phương nên ba điểm A, B, C thẳng hàng. 
b) Ta có: 2OA + 4BD − OC + DO − 3AD = 0
 (OA−OC)+(OA−OD)+ 4BD −3AD = 0
CA + DA + 4BD − 3AD = 0  CA + DA + BD + 3(BD − AD) = 0
CA+ BA+3BA = 1
0  4BA = AC AB = − AC . 4
Vậy hai vectơ AB, AC cùng phương nên ba điểm A, B, C thẳng hàng. 
Câu 9. Một nhóm 11 học sinh tham gia một kì thi. Số điểm thi của 11 học sinh đó được sắp xếp từ thấp
đến cao theo thang điểm 100 như sau: 0; 0; 63; 65; 69; 70; 72; 78; 81; 85; 89.
a) Tìm điểm số trung bình của nhóm 11 học sinh này.
b) Tìm trung vị và mốt của mẫu số liệu đã cho. Hướng dẫn giải: 0 + 0 + 63 + ... + 85 + 89 672
a) Điểm trung bình là: x = =  61,09. 11 11
b) Vì n = 11 (lẻ) nên trung vị là số chính giữa của mẫu số liệu này (vị trí thứ 6). Vậy trung vị là 70.
Vì giá trị 0 xuất hiện 2 lần (nhiều nhất) trong mẫu số liệu nên 0 là mốt của mẫu số liệu này.
Câu 10. Một xưởng sản xuất hai loại sản phẩm là sản phẩm loại I và sản phẩm loại II:
• Mỗi kg sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, thu lời được 40 nghìn.
• Mỗi kg sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ, thu lời được 30 nghìn.
Xưởng có 200 kg nguyên liệu và 1200 giờ làm việc tối đa. Nên sản xuất mỗi loại sản phẩm bao nhiêu để có mức lời cao nhất? Hướng dẫn giải: Gọi ,
x y lần lượt là số kg sản phẩm loại I và loại II mà xưởng sản xuất được.
Tổng nguyên liệu được dùng là 2x + 4y (kg); tổng thời gian sản
xuất là 30x + 15y (giờ); x , y  0.
2x + 4y  200 x + 2y 100   30
x +15y 1200 2x + y  80
Ta có hệbất phương trình:    . x  0  x  0  y  0 y  0
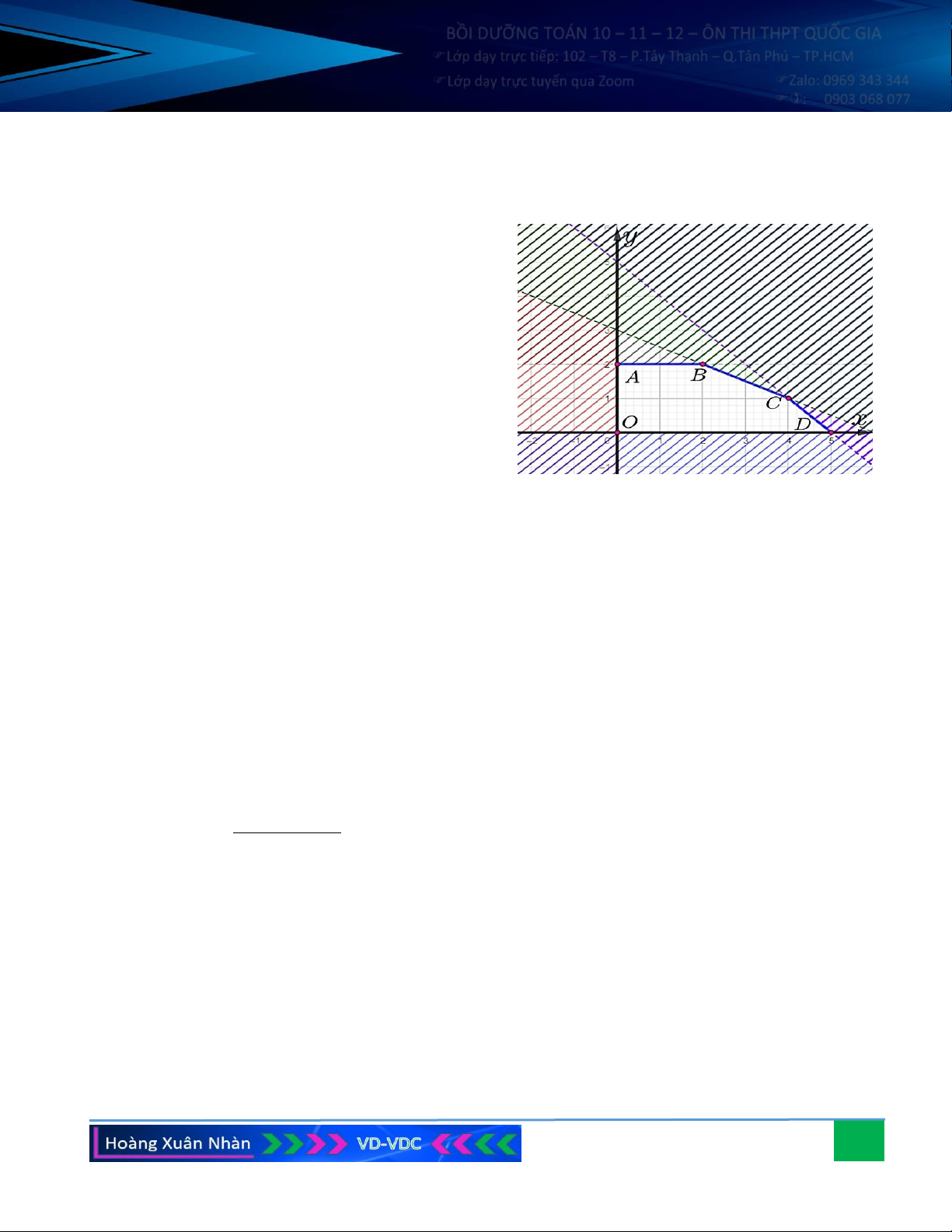
Vẽ trên cùng hệ trục các đường thẳng d : x + 2 y = 100 , d : 2x + y = 80 , d : y = 0 , d : x = 0 . 1 2 3 4 5
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 Ta có điểm M (1; )
1 thuộc miền nghiệm của hệ bất phương trình vì khi thay tọa độ điểm này vào hệ: 1  + 2.1 100  2.1+1 80   (đúng). 1  0  1   0
Gạch bỏ các phần không thuộc miền nghiệm của mỗi bất phương trình trong hệ (nửa mặt phẳng có
bờ là các đường thẳng d , d , d , d và không chứa điểm M). Khi đó miền nghiệm của hệ bất phương 1 2 3 4
trình chính là miền của tứ giác OABC (kể cả các cạnh của tứ giác đó) với O (0;0), A(0;50),
B (20; 40), C (40;0) .
Lãi thu về từ việc sản xuất hai sản phẩm: F ( x ; y) = 40x + 30 y (nghìn đồng).
Tại O (0;0) , ta có F (0;0) = 0 ; tại A(0;50) , ta có F (0 ; 50) = 1500 ; tại B (20; 40) , ta có
F (20 ; 40) = 2000 ; tại C (40;0) , ta có F (40 ; 0) = 1600 .
Vậy lãi suất cao nhất thu được bằng 2 000 000 đồng, khi đó x = 20, y = 40 (tức là xưởng cần sản
xuất ra 20 sản phẩm loại I và 40 sản phẩm loại II). 6
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
ÑEÀ REØN LUYEÄN SOÁ 2 Time: 90 phuùt
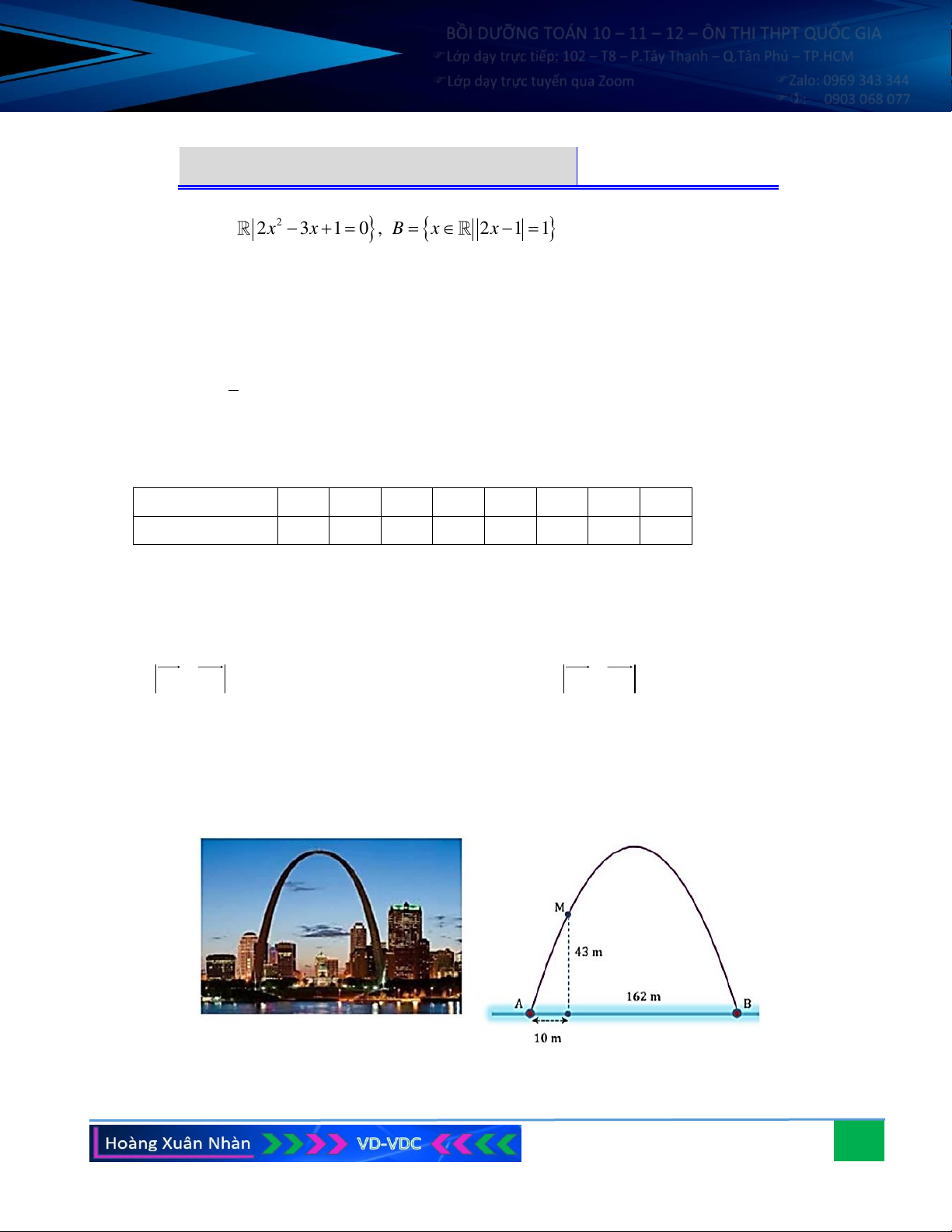
Câu 1. Viết các tập hợp sau bằng cách liệt kê các phần tử của nó: a) A =  2 2 x
(2x − x )(2x − 3x – 2) =  0 ; b) B =  * 2 x  3  n   30 .
Câu 2. Cho các tập hợp A = ( ;
− m) và B = 3m −1;3m + 
3 . Tìm m để A C B .
Câu 3. Tìm tập xác định của các hàm số sau: x −1
a) y = 2 3 − x + x +1 ; b) y = ; 2 x − 2x + 3
Câu 4. Xét sự biến thiên của các hàm số sau trên khoảng (1; +) : a) f ( x) 3 = = + . x − ; b) ( ) 1 f x x 1 x
−x − y  4 
−x + 2y  −2
Câu 5. Biểu diễn miền nghiệm của hệ bất phương trình sau:  . x + y  8  x  6 − ; y  6
Câu 6. Lập bảng biến thiên và cho biến sự đồng biến, nghịch biến của hàm số. Tìm giá trị lớn nhất, nhỏ
nhất (nếu có) của hàm số trên tập xác định của nó. a) 2
y = −x + 2x − 5 ; b) 2 y = −x + 3 ;
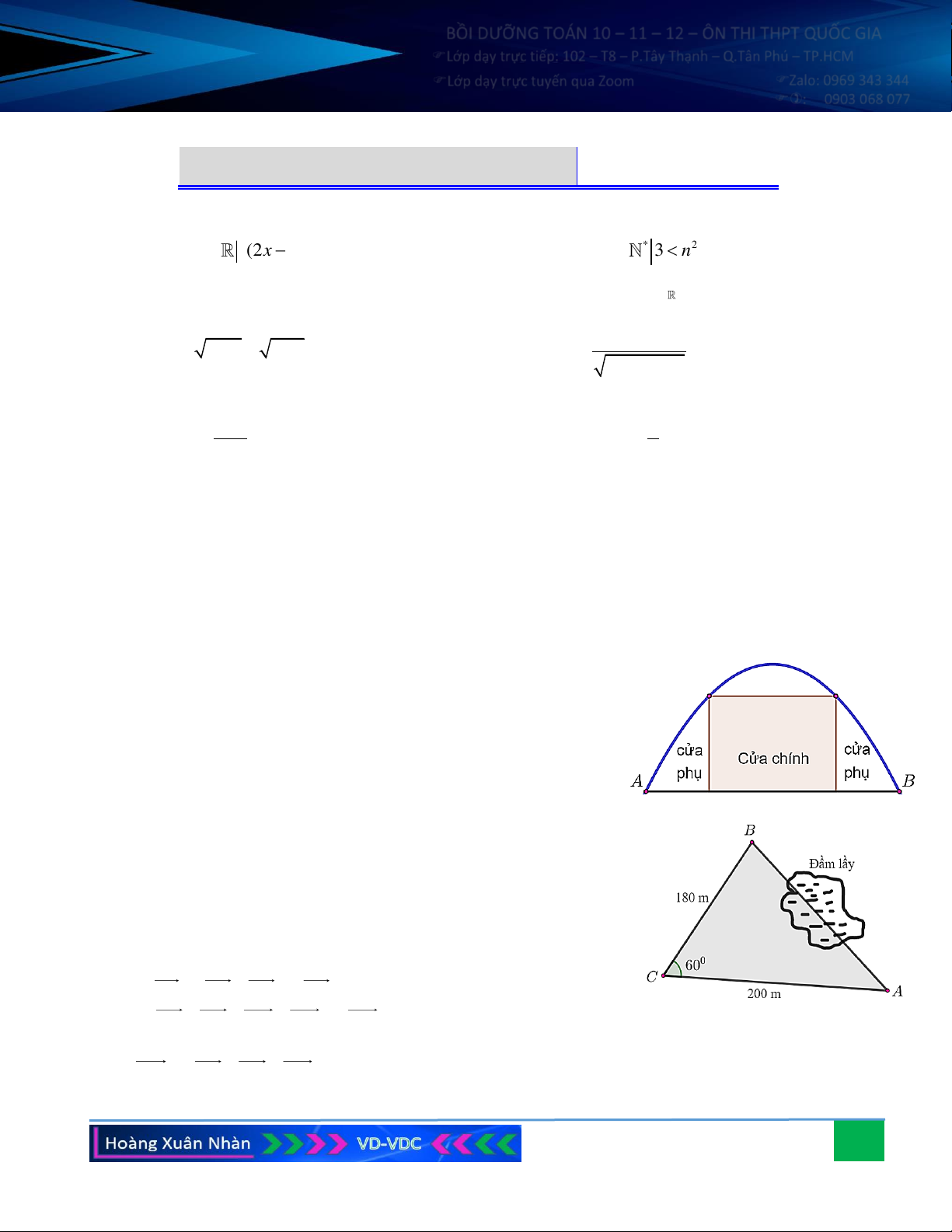
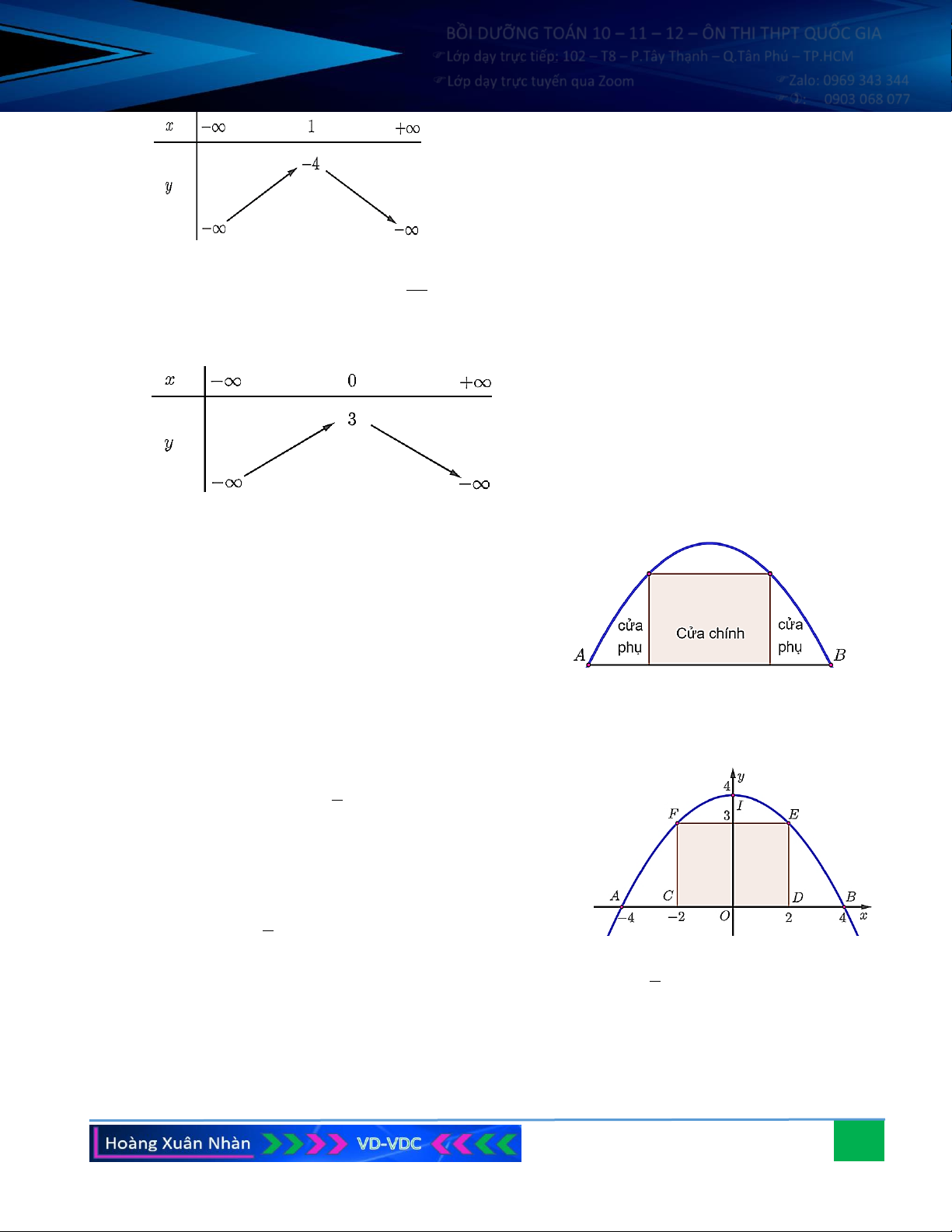
Câu 7. Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ
nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ. Biết chiều
cao cổng parabol là 4 m, cửa chính (ở giữa parabol) cao 3 m và
rộng 4 m. Tính khoảng cách giữa hai chân cổng parabol ấy
(đoạn AB trên hình vẽ).
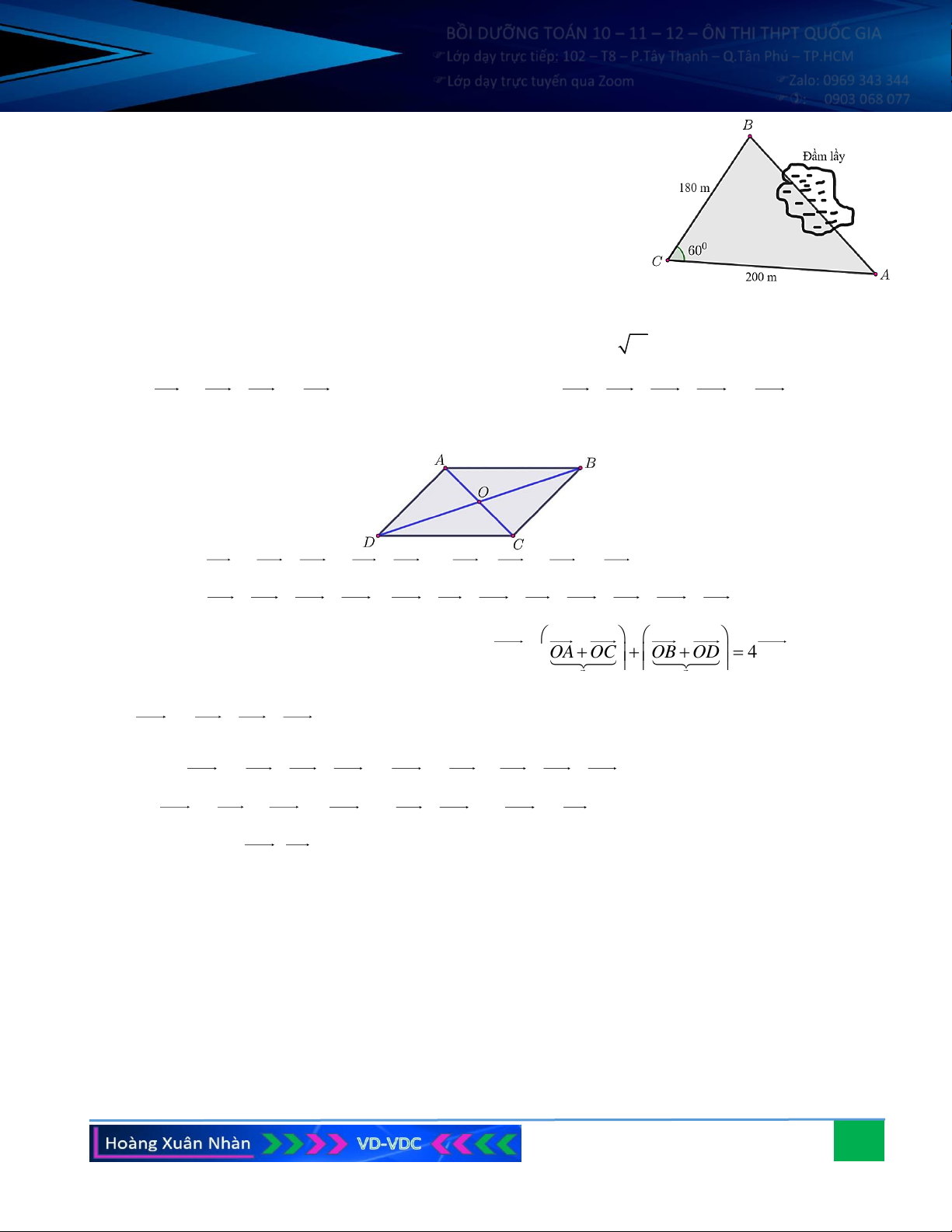
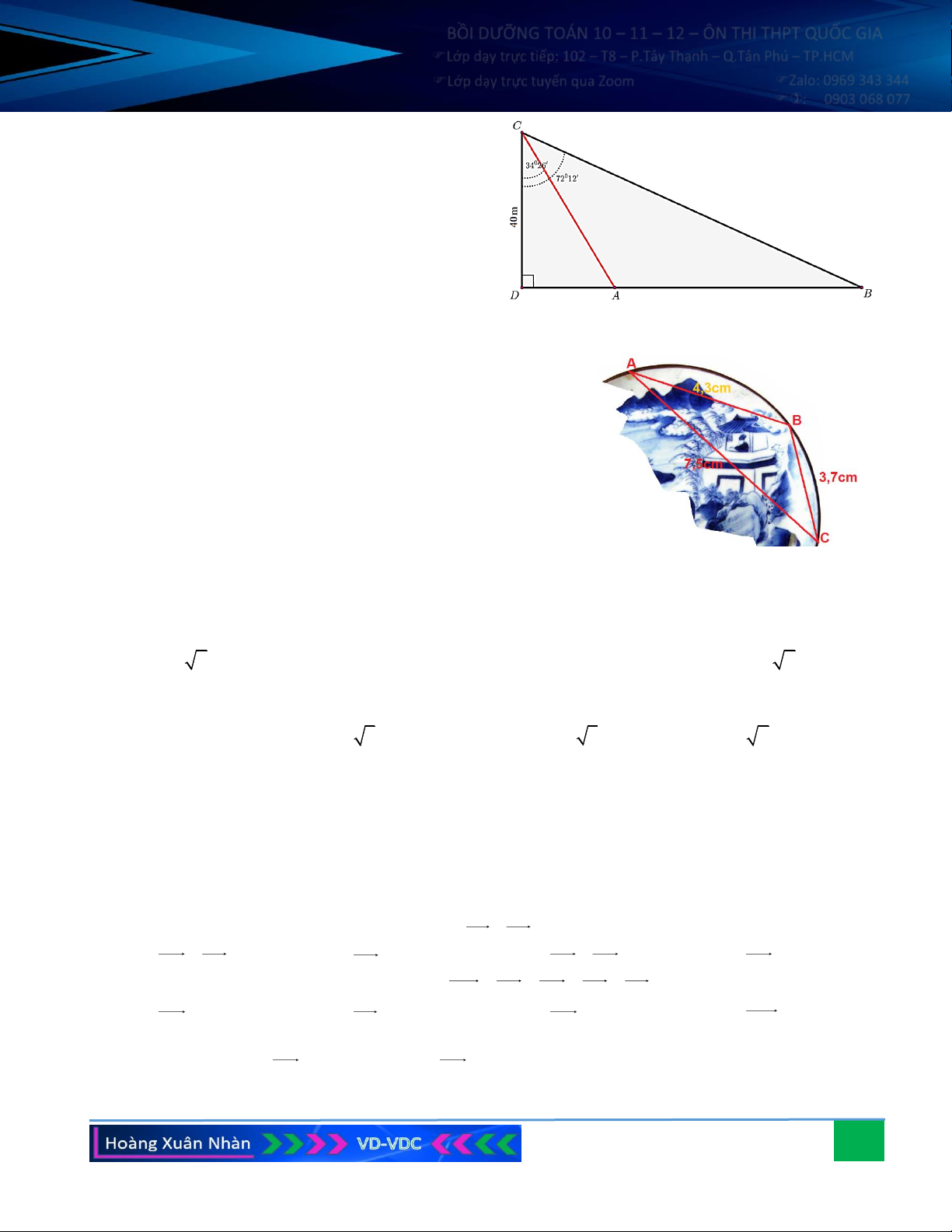
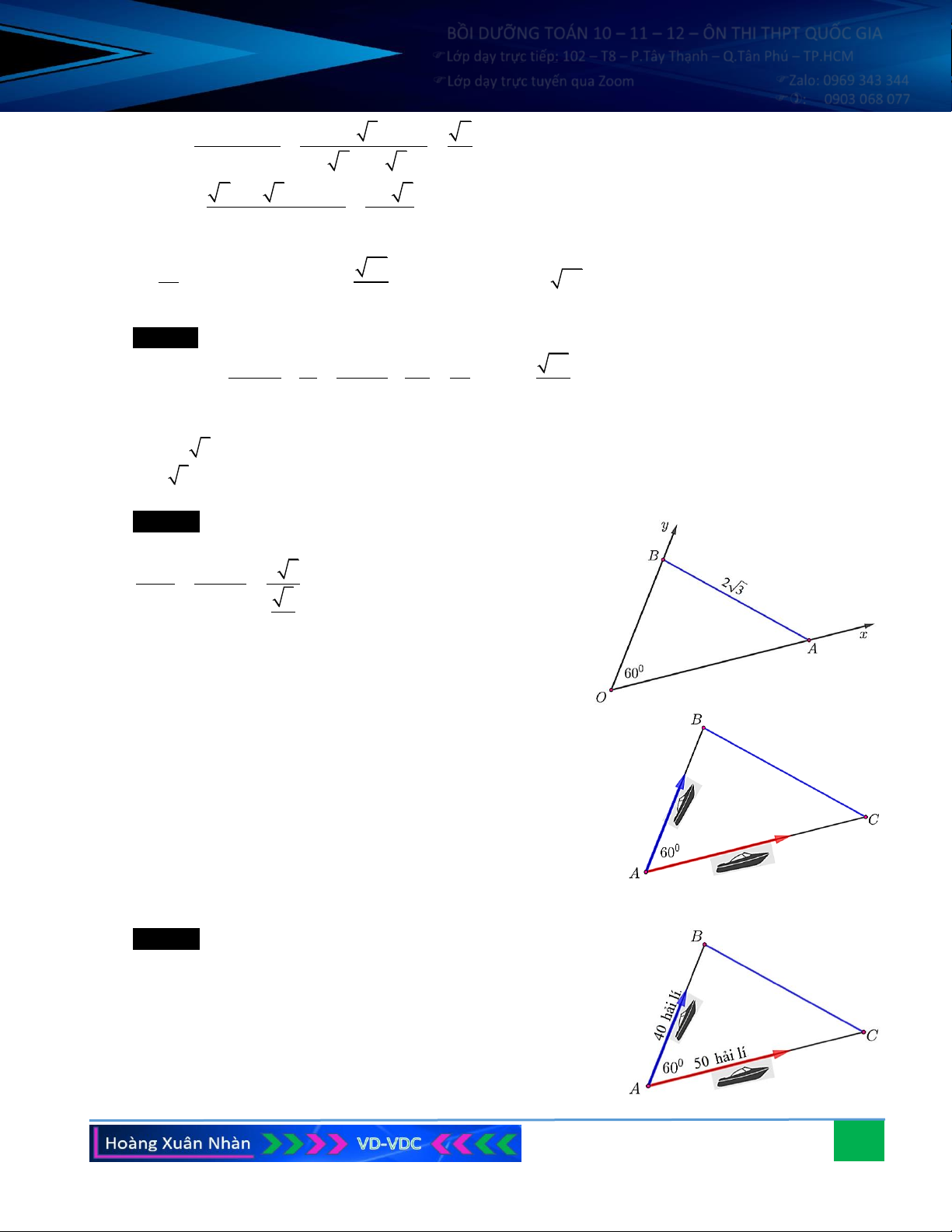
Câu 8. Khoảng cách từ A đến B không thể đo trực tiếp được vì phải
qua một đầm lầy. Người ta xác định được một điểm C mà từ đó
có thể nhìn được A và B dưới một góc 60 . Biết CA = 200 m ,
CB =180 m . Khoảng cách AB bằng bao nhiêu?
Câu 9. Cho hình bình hành ABCD có tâm O, M là một điểm bất kỳ. Chứng minh rằng:
a) AB + 5AC + AD = 6AC ;
b) MA + MB + MC + MD = 4MO .
Câu 10. Cho tam giác ABC và một điểm M tùy ý, G là trọng tâm tam giác ABC. Điểm N thỏa mãn
MN = 4MA + MB + MC . Chứng minh rằng đường thẳng MN luôn qua một điểm cố định.
================HẾT=============== 7
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Höôùng daãn giaûi ñeà soá 02
Câu 1. Viết các tập hợp sau bằng cách liệt kê các phần tử của nó: a) A =  2 2 x
(2x − x )(2x − 3x – 2) =  0 ; b) B =  * 2 x  3  n   30 . Hướng dẫn giải:  x = 0  2 1  2x − x = 0 
a) A = − ;0; 2 vì 2 2
(2x − x )(2x − 3x – 2) = 0    x = 2 .   2  2
2x − 3x − 2 = 0  1 x = −  2 b) B = 2;3; 4;  5 .
Câu 2. Cho các tập hợp A = ( ;
− m) và B = 3m −1;3m + 
3 . Tìm m để A C B . Hướng dẫn giải: Ta có: C B = ( ; − 3m − )
1  (3m + 3; +) . Vì vậy: A C B m  3m − 1 1  m  . 2
Câu 3. Tìm tập xác định của các hàm số sau: x −1
a) y = 2 3 − x + x +1 ; b) y = ; 2 x − 2x + 3 Hướng dẫn giải: 3  − x  0 x  3
a) Hàm số xác định khi và chỉ khi     1 −  x  3. x +1 0 x  1 −
Tập xác định hàm số: D =  1; − 3.
b) Hàm số xác định khi và chỉ khi x − x +   (x − )2 2 2 3 0 1 + 2  0  x  . Tập xác định hàm số: D = .
Câu 4. Xét sự biến thiên của các hàm số sau trên khoảng (1; +) : a) f ( x) 3 = = + . x − ; b) ( ) 1 f x x 1 x Hướng dẫn giải:
a) Xét x , x  1; + và x x . 1 2 ( ) 1 2 3 3
3 x −1 − 3 x −1 3 x − x 2 1 ( 2 1)
Khi đó: f ( x − f x = − = = 1 ) ( 2) ( ) ( ) x −1 x −1 x −1 x −1 x −1 x − . 1 1 2 ( 1 )( 2 ) ( 1 )( 2 )
Vì x x  3 x − x  0; x , x  1; +  x −1 x −1  0 . 1 2 ( 2 1) 1 2 ( ) ( 1 )( 2 ) 3( x − x 2 1 ) Suy ra (
 0  f x − f x  0  f x f x x −1 x − 1 1 )( 2 ) ( 1) ( 2) ( 1) ( 2)
Vậy hàm số đã cho nghịch biến trên khoảng (1; +) . 8
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 1  1  x − x
b) Xét x , x  1; + và x x . Khi đó: f ( x − f x = x +
−  x +  = x − x + 1 ) ( 2) 1 2 ( 1 2) 2 1 1 2 ( ) 1 2 x x x x 1  2  1 2 = ( − ) 1   x x −  x x 1−
 = ( x − x ) 1 1 2  . 1 2 1 2 x x x x  1 2   1 2  x x −1
Vì x x x − x  0; x , x  (1; +) 1 2   0 . 1 2 1 2 1 2 x x 1 2  x x −1
Suy ra ( x − x ) 1 2 
  0  f x − f x  0  f x f x . 1 2 ( 1) ( 2) ( 1) ( 2) x x  1 2 
Vậy hàm số đã cho đồng biến trên khoảng (1; +) .
−x − y  4 
−x + 2y  −2
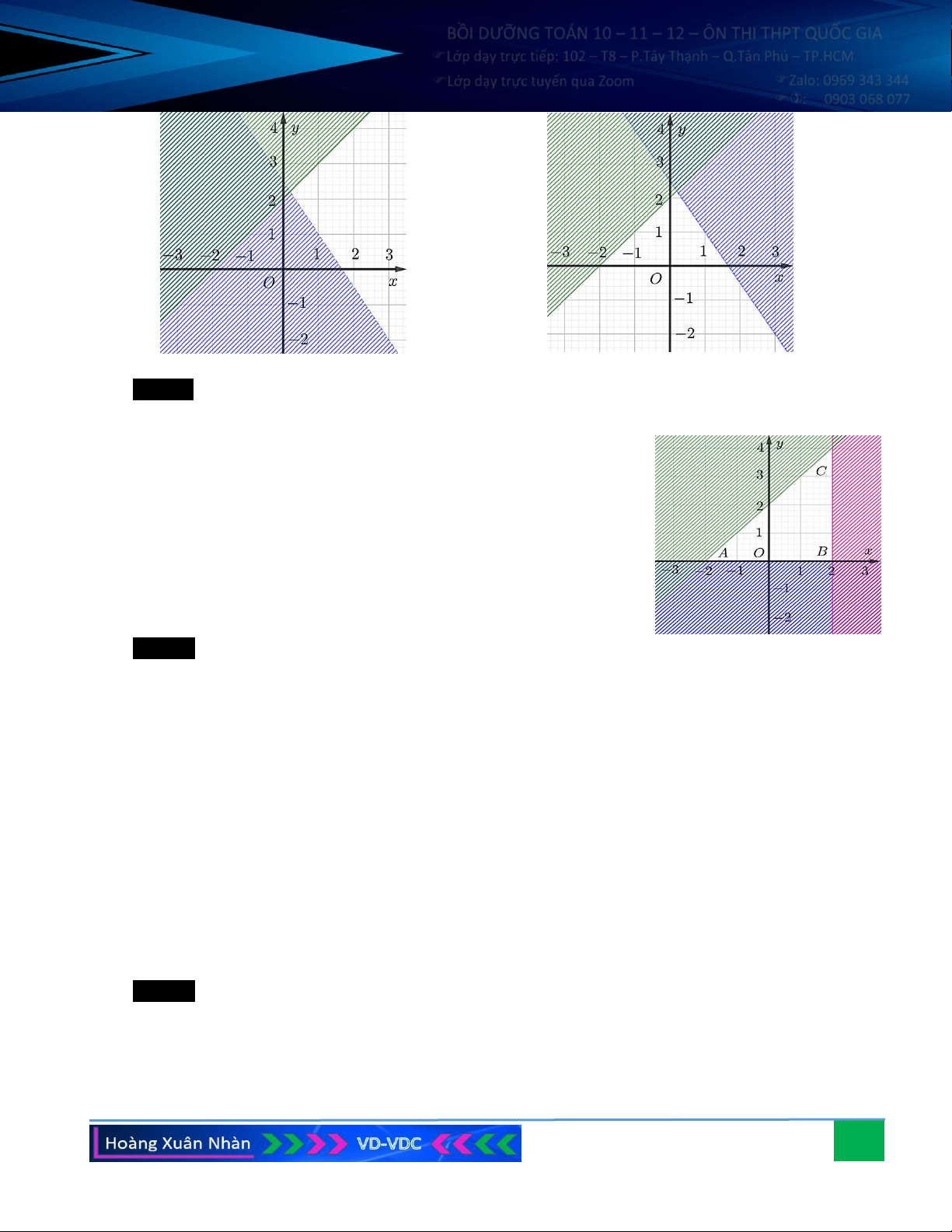
Câu 5. Biểu diễn miền nghiệm của hệ bất phương trình sau:  . x + y  8  x  6 − ; y  6 Hướng dẫn giải:
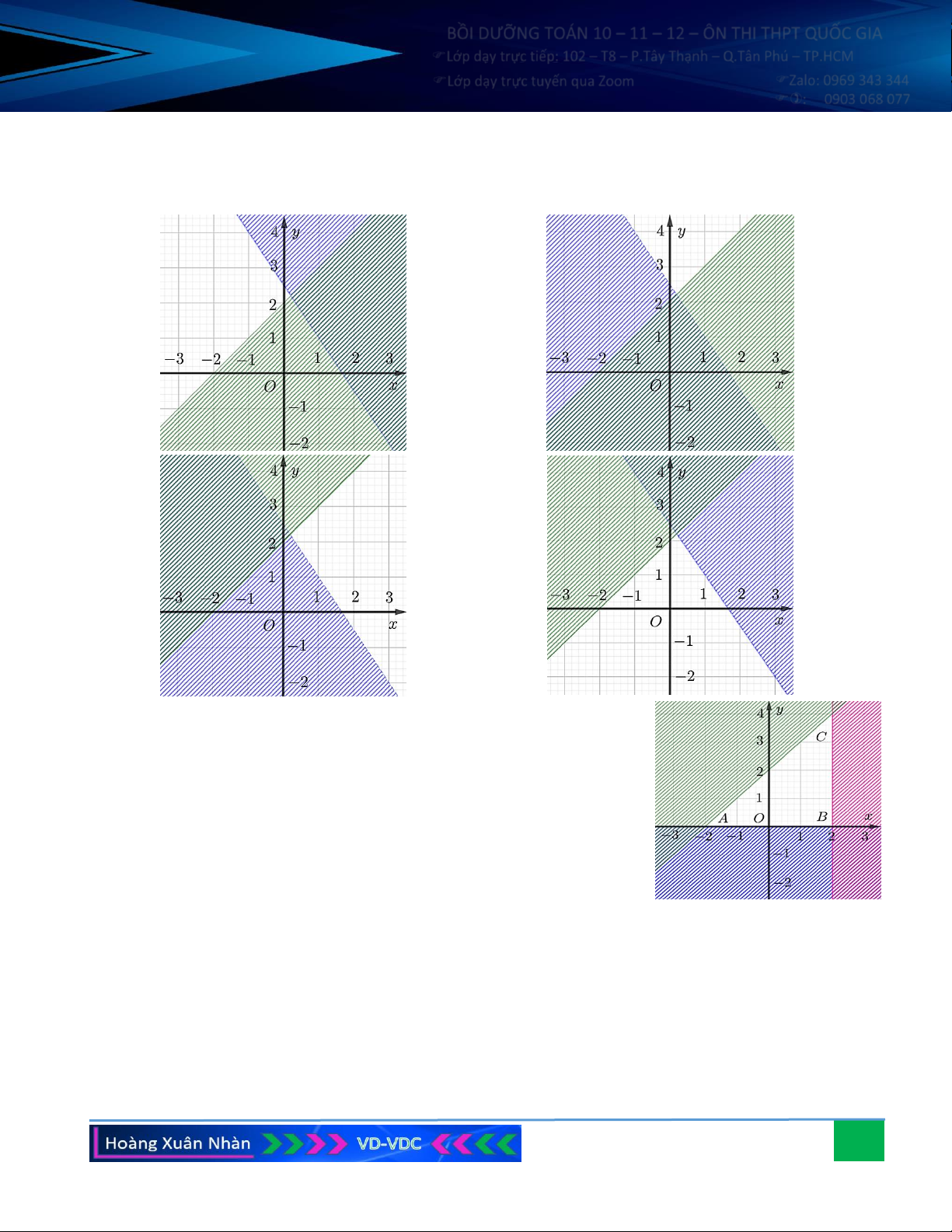
Vẽ các đường thẳng d : −x − y = 4, d : −x + 2y = 2
− , d : x + y = 8, d : x = 6
− , d : y = 6 . 1 2 3 4 5
Ta có điểm O (0;0) thuộc miền nghiệm của hệ bất phương trình vì khi thay x = 0, y = 0 vào hệ, ta được: 0  4, 0  2 − , 0  8, 0  6 − , 0  6 (đúng).
Gạch bỏ các phần không thuộc miền nghiệm của mỗi bất phương
trình trong hệ (nửa mặt phẳng có bờ là các đường thẳng
d , d , d , d , d và không chứa điểm O). Khi đó miền nghiệm của 1 2 3 4 5
hệ bất phương trình chính là miền của ngũ giác ABCDE (không kể
các cạnh BC, CD, DE) với A( 6 − ;6), B( 6 − ;2), C ( 2
− ;− 2), D(6;2), E (2;6).
Câu 6. Lập bảng biến thiên và cho biến sự đồng biến, nghịch biến của hàm số. Tìm giá trị lớn nhất, nhỏ
nhất (nếu có) của hàm số trên tập xác định của nó. a) 2
y = −x + 2x − 5 ; b) 2 y = −x + 3 ; Hướng dẫn giải: a) 2
y = −x + 2x − 5 ; ( a = 1
− , b = 2, c = 5 − ). b
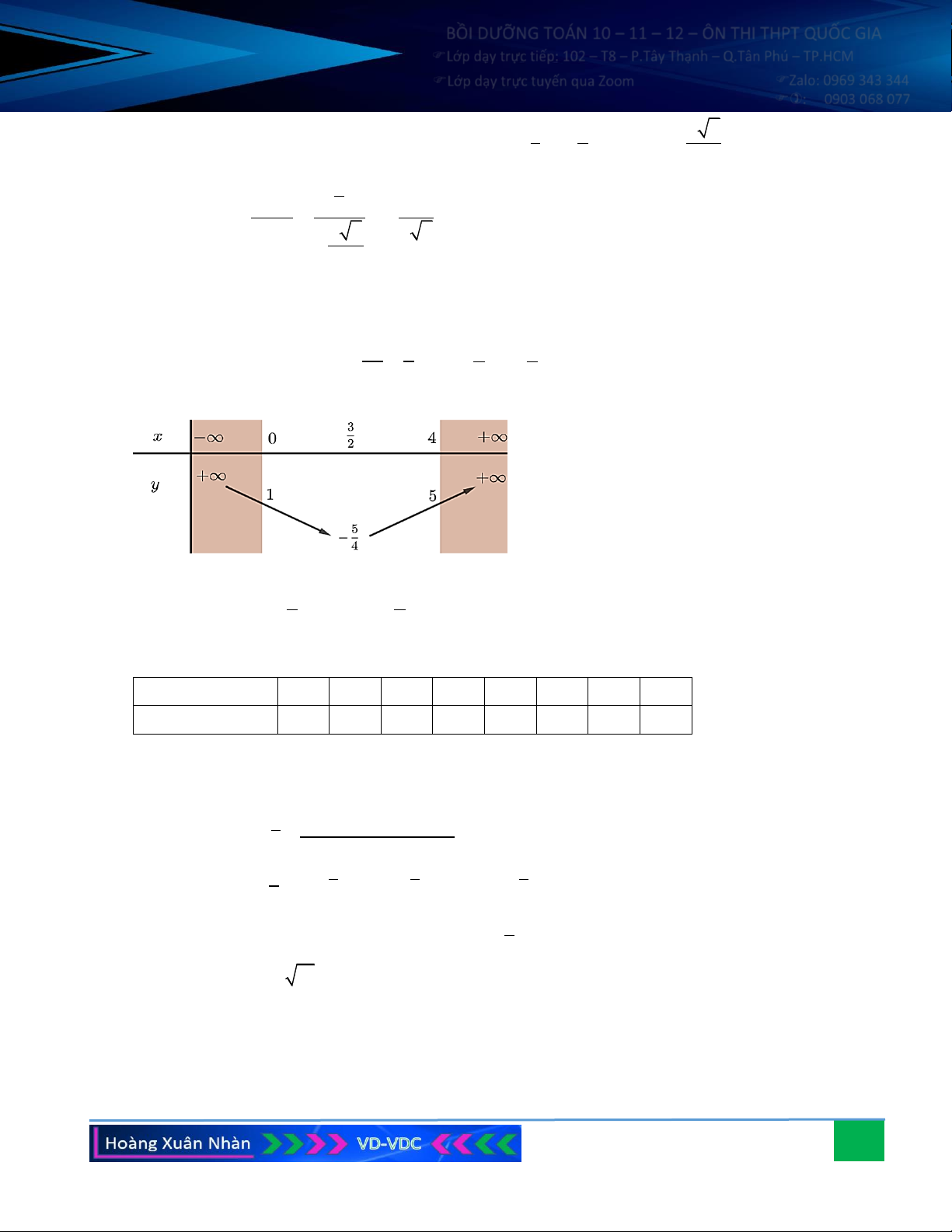
Tọa độ đỉnh I của parabol: 2 x = − =1, y = 1 − + 2.1− 5 = 4 − hay I − . I I (1; 4) 2a
Định hướng cho bảng biến thiên: Do a = 1
−  0 nên bề lõm parabol hướng xuống. Bảng biến thiên: Kết luận: 9
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
• Hàm số đã cho đồng biến trên khoảng (− ) ;1 và
nghịch biến trên khoảng (1; + ) .
• Giá trị lớn nhất của hàm số là y = 4 − , khi đó x =1. max
(Hàm số không có giá trị nhỏ nhất). b) 2
y = −x + 3 ; ( a = 1
− , b = 0, c = 3). b
b) Tọa độ đỉnh I của parabol: 2 x = − = 0, y = 0 − + 3 = 3 hay I . I I (0;3) 2a
Định hướng cho bảng biến thiên: Do a = 1
−  0 nên bề lõm parabol hướng xuống. Bảng biến thiên: Kết luận:
• Hàm số đã cho đồng biến trên khoảng
(−;0) và nghịch biến trên khoảng (0;+ ) .
• Giá trị lớn nhất của hàm số là y = 3, khi max
đó x = 0 . (Hàm số không có giá trị nhỏ nhất).
Câu 7. Một chiếc cổng hình parabol bao gồm một cửa chính hình
chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ.
Biết chiều cao cổng parabol là 4 m, cửa chính (ở giữa
parabol) cao 3 m và rộng 4 m. Tính khoảng cách giữa hai
chân cổng parabol ấy (đoạn AB trên hình vẽ). Hướng dẫn giải:
Dựng trục Oxy như hình vẽ. Gọi ( P) 2
: y = ax + bx + c (a  0) .
Vì ( P) qua các điểm I (0; 4), E (2;3), F ( 2 − ;3) nên  1 a = − c = 4  4  
4a + 2b + c = 3  b  = 0 .  
4a − 2b + c = 3 c = 4    1 Ta có ( P) 2 : y = − x + 4 . 4 Hai điể 1
m A, B là giao điểm của (P) với Ox nên hoành độ thỏa mãn 2
− x + 4 = 0  x = 4  . 4
Do vậy A(−4;0), B (4;0)  AB = 8 . 10
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Câu 8. Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua
một đầm lầy. Người ta xác định được một điểm C mà từ đó có
thể nhìn được A và B dưới một góc 60 . Biết CA = 200 m ,
CB =180 m . Khoảng cách AB bằng bao nhiêu? Hướng dẫn giải: Ta có: 2 2 2
AB = CA + CB − 2C . AC .
B cos 60 = 36 400  AB = 20 91  190, 79 m .
Câu 9. Cho hình bình hành ABCD có tâm O, M là một điểm bất kỳ. Chứng minh rằng:
a) AB + 5AC + AD = 6AC ;
b) MA + MB + MC + MD = 4MO . Hướng dẫn giải:
a) Ta có: AB + 5AC + AD = ( AB + AD) + 5AC = AC + 5AC = 6AC . 
b) Ta có: MA + MB + MC + MD = MO + OA + MO + OB + MO + OC + MO + OD    
= 4MO +  OA + OC  + OB + OD  = 4MO     .   0   0 
Câu 10. Cho tam giác ABC và một điểm M tùy ý, G là trọng tâm tam giác ABC. Điểm N thỏa mãn
MN = 4MA + MB + MC . Chứng minh rằng đường thẳng MN luôn qua một điểm cố định. Hướng dẫn giải:
Ta có: MN = 4MA + MB + MC MN = 3MA + (MA + MB + MC )
MN = 3MA+3MG MN = 3(MA+ MG)  MN = 6MI (với I là trung điểm AG).
Vậy hai vectơ MN , MI cùng phương nên ba điểm M , N, I thẳng hàng.
Do đó đường thẳng MN luôn qua điểm I cố định. 11
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
ÑEÀ REØN LUYEÄN SOÁ 03 Time: 90 phuùt
Câu 1. Giả sử A = 2; 4;  6 , B = 2;  6 , C = 4;  6 , D = 4;6; 
8 . Hãy xác định xem tập nào là tập con của tập nào?
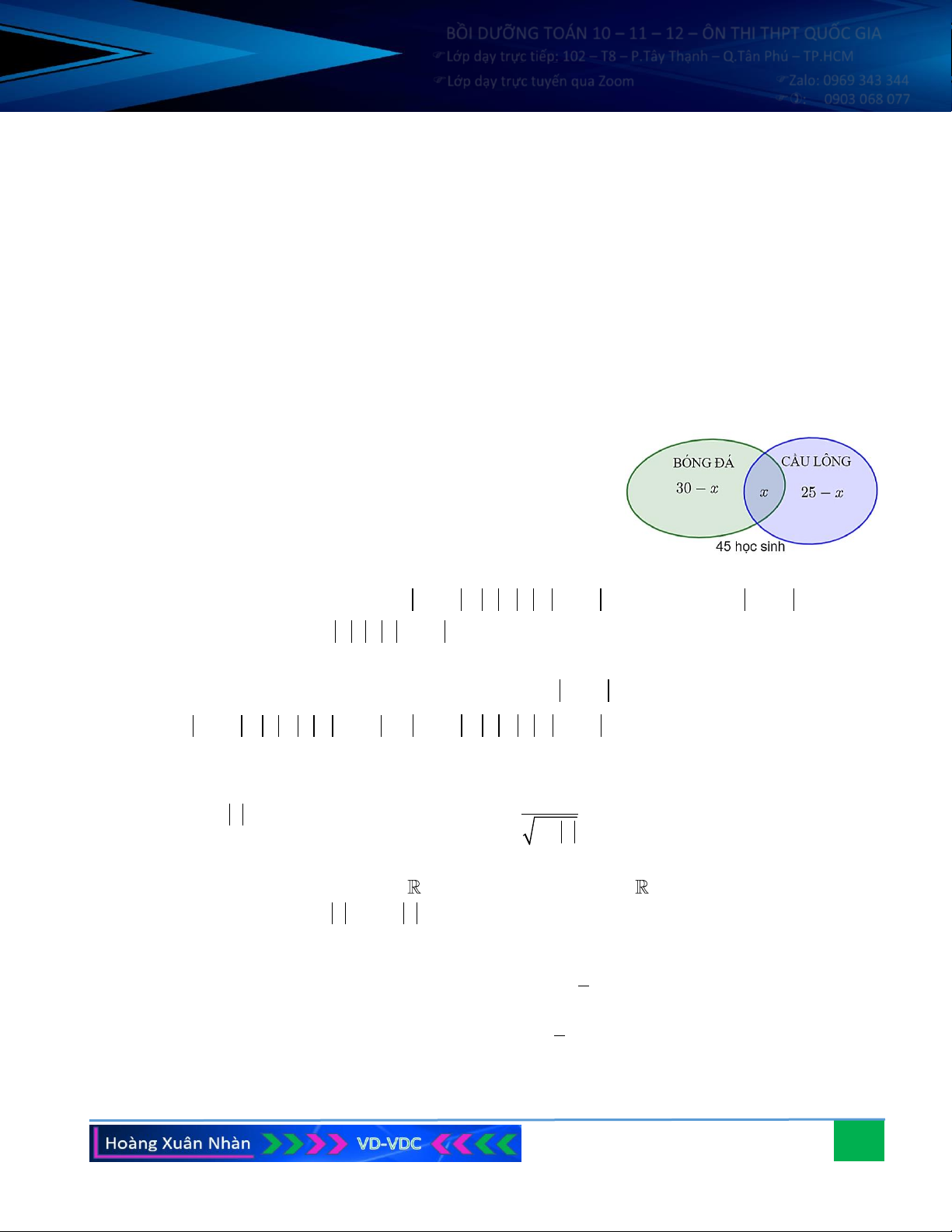
Câu 2. Một lớp có 45 học sinh, đăng kí chơi ít nhất một trong hai môn thể thao là bóng đá và cầu lông. Có
30 em đăng kí môn bóng đá, 25 em đăng kí môn cầu lông. Hỏi có bao nhiêu em đăng kí cả hai môn thể thao?
Câu 3. Tìm tập xác định mỗi hàm số sau: 1 a) 3
y = −x − x +1; b) y = . 2 − x
Câu 4. Tìm parabol ( P) 2
: y = ax + bx + 2 trong các trường hợp sau: 3
a) Parabol ( P) đi qua A(3; 4) và có trục đối xứng là x = − . 2 1
b) Parabol ( P) đi qua B (−1;6) và có tung độ đỉnh là − . 4 Câu 5.
a) Cho tan + cot = m . Tìm m để 2 2 tan  + cot  = 7 . b) Tính 0 0 0 0
B = tan1 tan 2 tan 3 ...tan 89 .
Câu 6. Một hộ nông dân định trồng dứa và củ đậu trên diện tích 8ha . Trên diện tích mỗi ha , nếu trồng dứa thì
cần 20 công và thu 3 triệu đồng, nếu trồng củ đậu thì cần 30 công và thu 4 triệu đồng. Hỏi cần trồng mỗi
loại cây trên với diện tích là bao nhiêu ha để thu được nhiều tiền nhất, biết rằng tổng số công không quá 180?
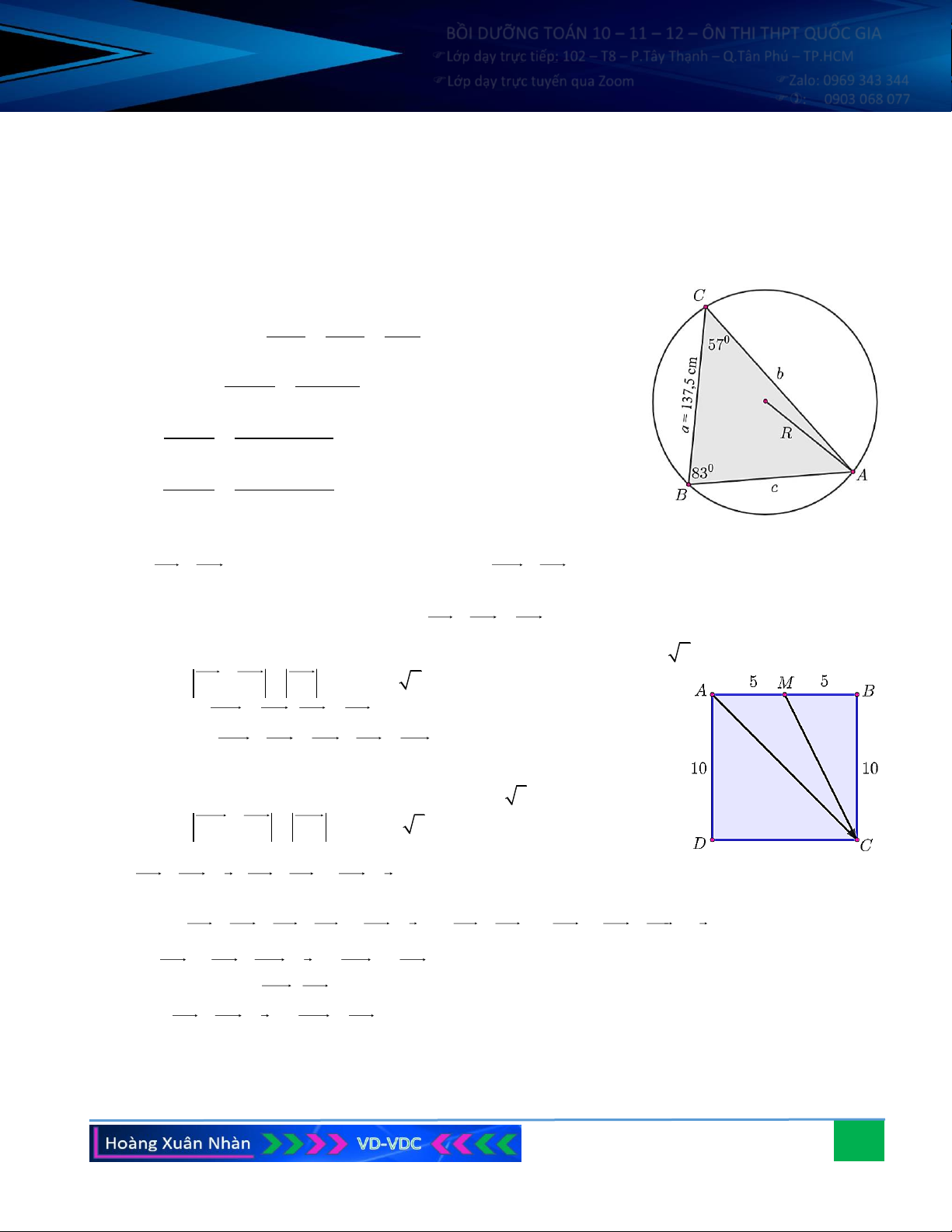
Câu 7. Cho tam giác ABC biết cạnh a = 137,5 cm, 0 0
B = 83 , C = 57 . Tính góc A, bán kính R của đường
tròn ngoại tiếp, cạnh b và c của tam giác.
Câu 8. Cho hình vuông ABCD có cạnh bằng 10, M là trung điểm canh AB. Tìm độ dài vectơ tổng: a) AB + AD ; b) AM + AD .
Câu 9. Cho tam giác ABC. Hai điểm M, N được xác định bởi các hệ thức: BC + MA = 0 ,
AB − NA − 3AC = 0 . Chứng minh hai đường thẳng MN và AC song song.
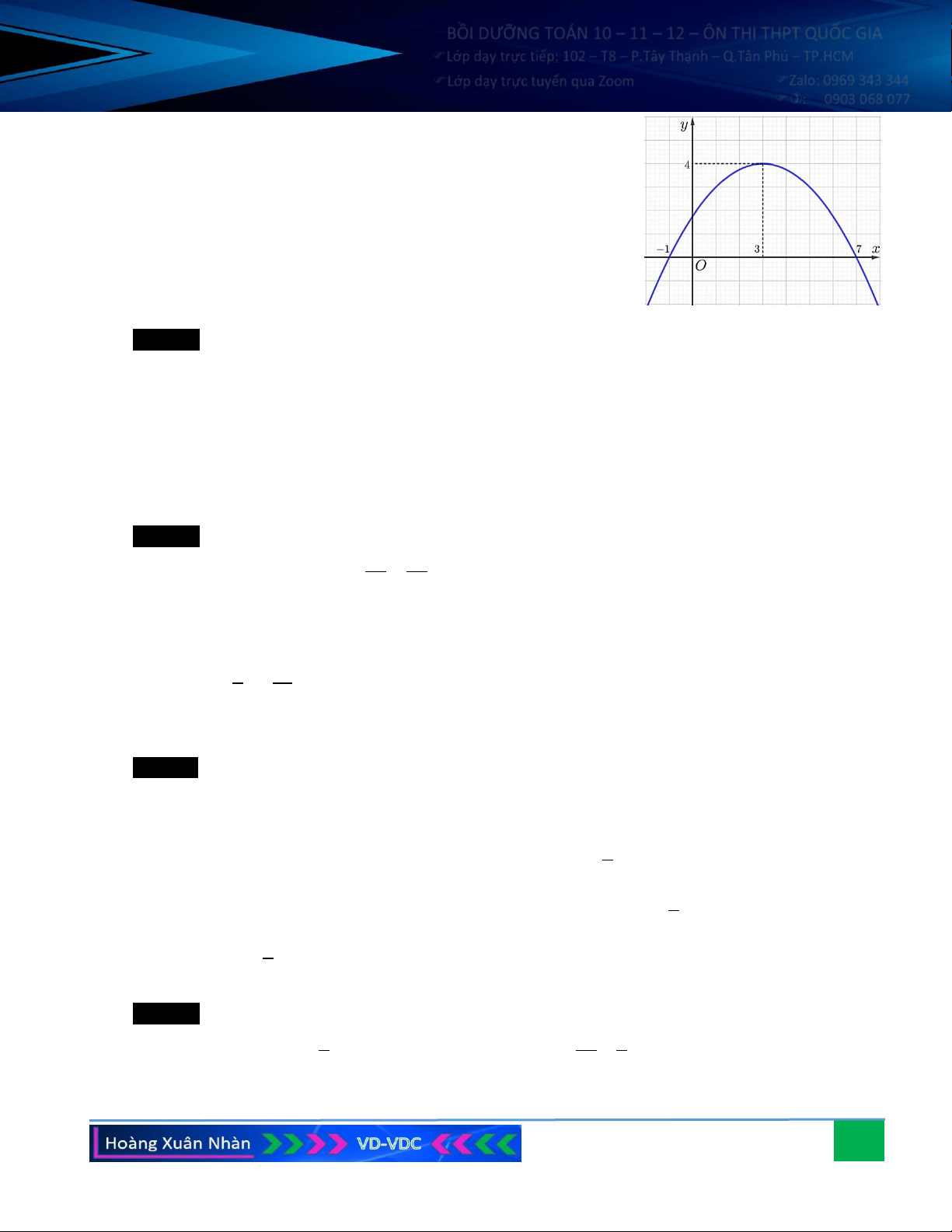
Câu 10. Khi quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của quả
bóng là một cung parabol trong mặt phẳng Oth trong đó t là thời gian (tính bằng giây) kể từ khi quả
bóng được đá lên, h là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá lên từ
độ cao ban đầu 1,2m so với mặt đất; sau đó 1 giây nó đạt độ cao 8,5m; sau 2 giây nó đạt độ cao 6m.
Hãy tìm hàm số bậc hai biểu thị độ cao h theo thời gian t và có phần đồ thị trùng với quỹ đạo quả
bóng trong tình huống này.
================HẾT=============== 12
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Höôùng daãn giaûi ñeà soá 03
Câu 1. Giả sử A = 2; 4;  6 , B = 2;  6 , C = 4;  6 , D = 4;6; 
8 . Hãy xác định xem tập nào là tập con của tập nào? Hướng dẫn giải:
Vì 2 ∈ A, 6 ∈ A ⇒ B ⊂ A. Vì 4 ∈ A, 6 ∈ A ⇒ C ⊂ A. Vì 4 ∈ D, 6 ∈ D ⇒ C ⊂ D.
Ngoài ra không còn tập nào là con của tập nào nữa.
Câu 2. Một lớp có 45 học sinh, đăng kí chơi ít nhất một trong hai môn thể thao là bóng đá và cầu lông. Có
30 em đăng kí môn bóng đá, 25 em đăng kí môn cầu lông. Hỏi có bao nhiêu em đăng kí cả hai môn thể thao? Hướng dẫn giải:
☺ Cách giải 1: Gọi x là số học sinh tham gia cả hai môn thể
thao bóng đá và cầu lông. Dựa vào biểu đồ Ven, ta có:
Số học sinh chỉ tham gia bóng đá là 30 − x (em), số học sinh chỉ
tham gia cầu lông là 25 − x (em).
Ta có: (30 − x) + x + (25 − x) = 45  x = 10 .
Vậy có 10 học sinh của lớp đăng ký cả hai môn bóng đá và cầu lông.
☺ Cách giải 2: Dựa vào công thức A B = A + B − A B trong đó ký hiệu A B là số phần
tử của tập AB , ký hiệu A , B , A B lần lượt là số phần tử của các tập , A , B AB .
Gọi A là tập hợp các em học sinh đăng ký môn bóng đá, B là tập hợp các em đăng kí cầu lông.
Số học sinh của lớp đăng ký cả hai môn thể thao trên là: A B .
Ta có: A B = A + B − A B A B = A + B − A B = 30 + 25 − 45 = 10 (em).
Vậy có 10 bạn đăng ký cả hai môn.
Câu 3. Tìm tập xác định mỗi hàm số sau: 1 a) 3
y = −x − x +1; b) y = . 2 − x Hướng dẫn giải:
a) Hàm số xác định với mọi x thuộc . Tập xác định hàm số: D = .
b) Hàm số xác định  2 − x  0  x  2  −2  x  2 . Tập xác định hàm số: D = ( 2 − ;2).
Câu 4. Tìm parabol ( P) 2
: y = ax + bx + 2 trong các trường hợp sau: 3
a) Parabol ( P) đi qua A(3; 4) và có trục đối xứng là x = − . 2 1
b) Parabol ( P) đi qua B (−1;6) và có tung độ đỉnh là − . 4 Hướng dẫn giải: 13
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 b
a) ( P) có trục đối xứng 3 x = −
= −  3a − b = 0 (1); (P) qua A(3;4) nên 9a +3b + 2 = 4 (2). 2a 2
Giải hệ (1) và (2) suy ra 1 1 1 1 a = , b = . Vậy (P) 2 : y = x + x + 2 . 9 3 9 3
b) ( P) đi qua B ( 1
− ;6)  a − b + 2 = 6  a = b + 4 (1). c=2  Tung độ đỉnh 1 I của parabol: 2 2 −
= −   = a b − 4ac = ab = 9a (2) . 4a 4 b =12 Thay (1) vào (2): 2 b = 9(b + 4) 2
b − 9b − 36 = 0   . b = 3 −
Với b =12 thì a =16 , khi đó: (P) 2
: y = 16x +12x + 2 . Với b = 3
− thì a =1, khi đó: (P) 2
: y = x − 3x + 2 . Câu 5.
a) Cho tan + cot = m . Tìm m để 2 2 tan  + cot  = 7 . b) Tính 0 0 0 0
B = tan1 tan 2 tan 3 ...tan 89 . Hướng dẫn giải: a) Ta có: =  +  = (  +  )2 2 2 2 7 tan cot tan cot − 2 = m − 2 2
m = 9  m = 3  . b) 0 0 0 0
B = tan1 tan 2 tan 3 ...tan 89 = ( 0 0 ) ( 0 0 ) ( 0 0 ) 0
tan1 tan 89 . tan 2 tan 88 ...... tan 44 tan 46 . tan 45 = ( 0 0 ) ( 0 0 ) ( 0 0 ) 0
tan1 .cot1 . tan 2 cot 2 ...... tan 44 cot 44 . tan 45 = 1.1......1 = 1 .
Câu 6. Một hộ nông dân định trồng dứa và củ đậu trên diện tích 8ha . Trên diện tích mỗi ha , nếu trồng dứa thì
cần 20 công và thu 3 triệu đồng, nếu trồng củ đậu thì cần 30 công và thu 4 triệu đồng. Hỏi cần trồng mỗi
loại cây trên với diện tích là bao nhiêu ha để thu được nhiều tiền nhất, biết rằng tổng số công không quá 180. Hướng dẫn giải: Gọi ,
x y lần lượt là số ha trồng dứa và củ đậu. Điều kiện: 0  x  8, 0  y  8 .
Tổng diện tích trồng là x + y (ha); tổng số công cần thiết là 20x + 30y (công).
Số tiền thu được là T ( x, y) = 3x + 4 y . Ta có hệ bất phương 0  x  8 0  x  8   0  y  8 0  y  8 trình    (*). x + y  8 x + y  8  
20x +30y 180 2x +3y 18
Miền nghiệm của hệ (*) là miền tứ giác OABC (kề cả
biên) với O (0;0) A(0;6), B (6; 2),C (0;8) Khi đó T ( x, y)
đạt cực đại tại một trong các đỉnh của tứ giác OABC .
Ta có: T (0, 0) = 0; T (0;6) = 24; T (6; 2) = 26; T (8;0) = 24 . 14
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Vậy giá trị lớn nhất của T ( x, y) bằng 26 (triệu đồng), khi đó x = 6, y = 2 (tức là hộ nông dân cần trồng
6 ha dứa và 2 ha củ đậu để có thể thu lại số tiền nhiều nhất).
Câu 7. Cho tam giác ABC biết cạnh a = 137,5 cm, 0 0
B = 83 , C = 57 . Tính góc A, bán kính R của đường
tròn ngoại tiếp, cạnh b và c của tam giác. Hướng dẫn giải: Ta có: 0 A = − (B +C) 0 = − ( 0 0 + ) 0 180 180 83 57 = 40 . a b c Theo định lí Sin: = = = 2R . sin A sin B sinC a 137, 5 Suy ra R = = 106,96 cm ; 0 2sin A 2sin 40 0 a sin B 137,5.sin 83 b = =  212,32 cm ; 0 sin A sin 40 0 a sin C 137,5.sin 57 c = = 179,4 cm . 0 sin A sin 40
Câu 8. Cho hình vuông ABCD có cạnh bằng 10, M là trung điểm canh AB. Tìm độ dài vectơ tổng: a) AB + AD ; b) AM + AD . Hướng dẫn giải:
a) Theo quy tắc hình bình hành, ta có: AB + AD = AC . Theo định lí Pytago: 2 2 2 2 2
AC = AB + BC = 10 +10 = 200  AC =10 2 .
Vậy AB + AD = AC = AC = 10 2.
b) Ta có: AM = MB, AD = BC .
Khi đó: AM + AD = MB + BC = MC (quy tắc ba điểm).
Áp dụng định lí Pytago cho tam giác MBC: 2 2 2 2 2
MC = MB + BC = 5 +10 = 125  MC = 5 5 .
Vậy AM + AD = MC = MC = 5 5 .
Câu 9. Cho tam giác ABC. Hai điểm M, N được xác định bởi các hệ thức:
BC + MA = 0 , AB − NA − 3AC = 0 . Chứng minh hai đường thẳng MN và AC song song. Hướng dẫn giải:
Ta có: BC + MA + AB − NA − 3AC = 0  ( AB + BC ) − 3AC + (MA + AN ) = 0
AC −3AC + MN = 0  MN = 2AC .
Suy ra hai vectơ MN , AC cùng phương (1).
Xét: BC + MA = 0  AM = BC . Do đó M là một đỉnh của hình bình hành ABCM hay M không
thuộc đường thẳng AC (2)
Từ (1) và (2) suy ra hai đường thẳng MN và AC song song.  15
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Câu 10. Khi quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của quả
bóng là một cung parabol trong mặt phẳng Oth trong đó t là thời gian (tính bằng giây) kể từ khi quả
bóng được đá lên, h là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá lên từ
độ cao ban đầu 1,2m so với mặt đất; sau đó 1 giây nó đạt độ cao 8,5m; sau 2 giây nó đạt độ cao 6m.
Hãy tìm hàm số bậc hai biểu thị độ cao h theo thời gian t và có phần đồ thị trùng với quỹ đạo quả
bóng trong tình huống này. Hướng dẫn giải:
Chọn hệ trục Oth như hình vẽ, gọi parabo (P): 2
h = at + bt + c . c =1,2 a = 4 − ,9  
(P) qua ba điểm A(0;1, 2), B (1;8,5), C (2;6) nên thỏa mãn a + b + c = 8,5  b  =12,2 .  
4a + 2b + c = 6 c = 1, 2  
Vậy hàm số được xác định là 2 y = 4
− ,9t +12,2t +1,2 . 16
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
ÑEÀ REØN LUYEÄN SOÁ 04 Time: 90 phuùt
Câu 1. Xác định các tập hợp sau: a) ( 3
− ;7) (0;10) ; b) ( ; − 5) (2;+) .
Câu 2. Tìm tập xác định mỗi hàm số sau: 3 x + 2 3x − 2 a) y = ; b) y = . x x + 2 ( 2x − x+ )1( 2 x − x )
Câu 3. Tìm tọa độ giao điểm của các đường sau: a) d y = −x + (P) 2 : 1,
: y = x − 4x + 3 ; b) ( P ) 2
: y = x + 2x −1, ( P ) 2
: y = 2x − 2x + 2. 1 2
Câu 4. Đơn giản các biểu thức sau (giả sử mỗi biểu thức sau luôn có nghĩa): sin x a) A = cot x + 2
B = 1− sin x tan x 1+ sin x . 1+ ; b) ( ) ( ) cos x
Câu 5. Chứng minh biểu thức sau không phụ thuộc vào biến x: f ( x) = ( 4 4 x + x) − ( 6 6 3 sin cos
2 sin x + cos x) .
Câu 6. Cho bốn điểm A, B, C, D. Chứng minh rằng:
a) AB + CD = AD + CB ;
b) AB − CD = AC + DB .
Câu 7. Cho các tập hợp A = ( ;
− m) và B = 3m −1;3m + 
3 . Tìm m để A C B . h h h h h h
Câu 8. Cho tam giác ABC thỏa mãn điều kiện a b c b c a + + = + +
. Chứng minh tam giác ABC là h h h h h h b c a a b c tam giác cân. 1
Câu 9. Tìm a để hàm số y =
xác định với mọi x −  1;1 .
x + 3a − 2 + a + 2 − x
Câu 10. Cho tam giác ABC có trọng tâm G. Tìm tập hợp điểm M thỏa mãn mỗi hệ thức sau:
MA + MB − 2MC = AM − AB .
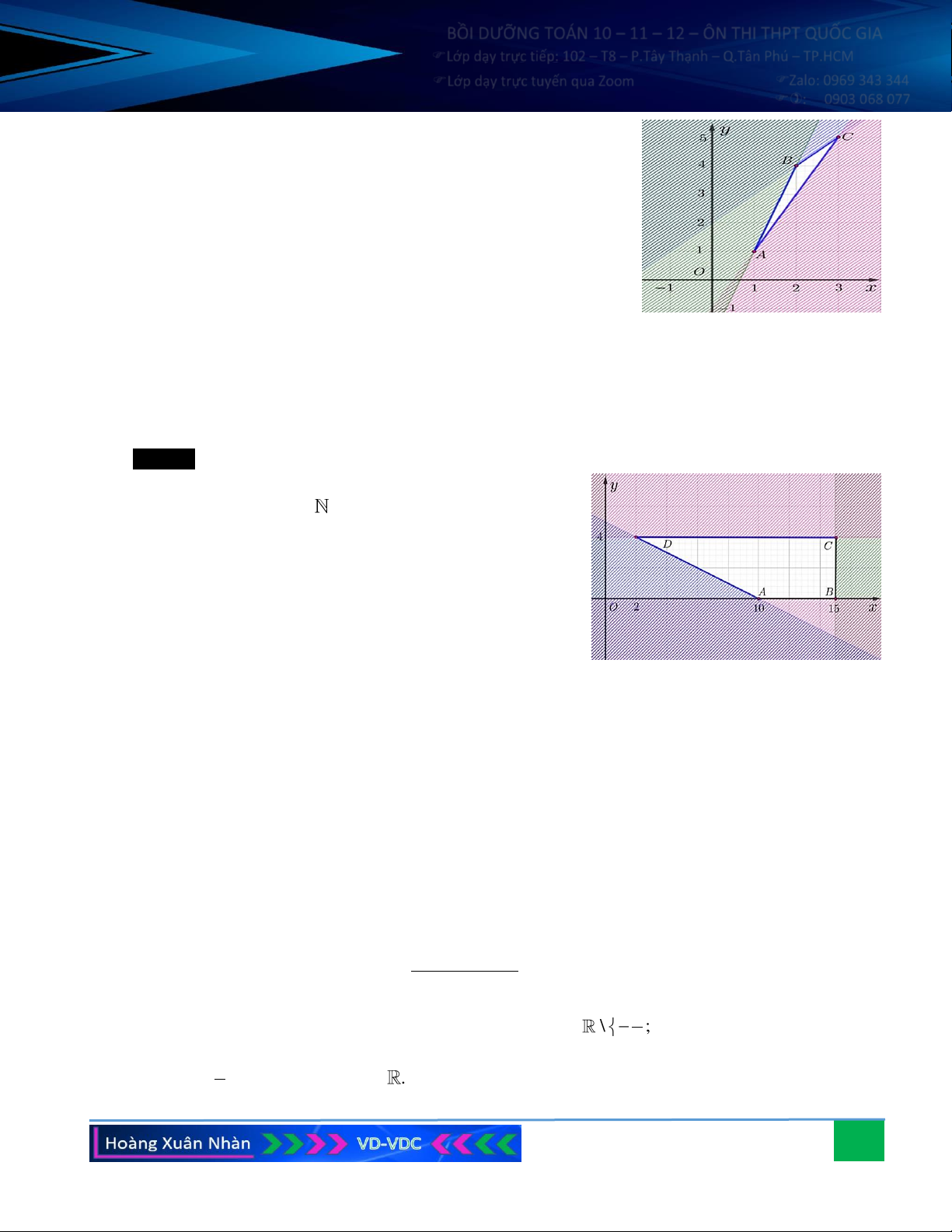
Câu 11. Một gia đình cần ít nhất 900 g chất protein và 400 g chất lipit trong thức ăn mỗi ngày. Biết rằng thịt
bò chứa 80% protein và 20% lipit. Thịt lợn chứa 60% protein và 40% lipit. Biết rằng gia đình này
chỉ mua nhiều nhất là 1 600 g thịt bò, 1 100 g thịt lợn, giá tiền 1 kg thịt bò là 45 000 đồng, 1 kg thịt
lợn là 35 000 đồng. Giả sử gia đình mua x kg thịt bò và y kg thịt lợn.
a) Lập hệ bất phương trình biểu thị các điều kiện của bài toán rồi biểu diễn hình học miền nghiệm (S) của hệ đó.
b) Gọi T (nghìn đồng) là số tiền phải trả cho x (kilogam) thịt bò và y (kilogam) thịt lợn. Hãy biểu diễn
T theo x, y.
c) Hỏi gia đình đó phải mua bao nhiêu kilogam thịt mỗi loại để chi phí là ít nhất?
================HẾT=============== 17
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Höôùng daãn giaûi ñeà soá 04
Câu 1. Xác định các tập hợp sau: a) ( 3
− ;7)(0;10) ; b) ( ; − 5)(2;+) ; Hướng dẫn giải: a) ( 3
− ;7)(0;10) = (0;7). b) ( ;
− 5)(2;+) = (2;5) .
Câu 2. Tìm tập xác định mỗi hàm số sau: 3 x + 2 3x − 2 a) y = ; b) y = . x x + 2 ( 2x − x+ )1( 2 x − x ) Hướng dẫn giải: x  0 x  0
a) Hàm số xác định     . x + 2  0 x  2 −
Tập xác định hàm số: D = ( 2 − ;+ ) \  0 . 2  1  3 2
x − x +1 0  x − +  0 b) Hàm số xác định (   2 x − x + ) 1 ( 2
x − x )  0      2  4 2
x − x  0 x  (1− x)  0 x   
x  0  x  1. Tập xác định hàm số: D = \0;  1 .
x  0  x  1
Câu 3. Tìm tọa độ giao điểm của các đường sau: a) d y = −x + (P) 2 : 1,
: y = x − 4x + 3 ; b) ( P ) 2
: y = x + 2x −1, ( P ) 2
: y = 2x − 2x + 2. 1 2 Hướng dẫn giải: x =1
a) Phương trình hoành độ giao điểm của d và (P): 2 2
x − 4x + 3 = −x +1  x − 3x + 2 = 0   . x = 2
Với x =1 thì y = 0; với x = 2 thì y = 1
− . Vậy d và (P) có hai giao điểm là (1;0),(2;− ) 1 .
b) Phương trình hoành độ giao điểm của (P và (P : 2 2
2x − 2x + 2 = x + 2x −1 2 ) 1 ) x = 2
x − 4x +3 = 1 0  
. Với x =1 thì y = 2 ; với x = 3 thì y =14. x = 3
Vậy hai parabol đã cho cắt nhau tại hai điểm: (1;2), (3;14) .
Câu 4. Đơn giản các biểu thức sau (giả sử mỗi biểu thức sau luôn có nghĩa): 18
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 sin x a) A = cot x + 2
B = 1− sin x tan x 1+ sin x . 1+ ; b) ( ) ( ) cos x Hướng dẫn giải: sin x cos x sin x
cos x (1+ cos x) + sin . x sin x a) A = cot x + = + = 1+ cos x sin x 1+ cos x sin x (1+ cos x) 2 2
cos x + cos x + sin x cos x +1 1 = = = . sin x (1+ cos x) sin x (1+ cos x) sin x sin x
b) B = (1− sin x) tan x (1+ sin x) = (1− sin x) 2 2 2 2 2 2 tan x = cos . x = sin x . 2 cos x
Câu 5. Chứng minh biểu thức sau không phụ thuộc vào biến x: f ( x) = ( 4 4 x + x) − ( 6 6 3 sin cos
2 sin x + cos x) . Hướng dẫn giải: Ta có: 4 4 2 2
sin x + cos x =1− 2sin x cos x , 6 6 2 2
sin x + cos x = 1− 3sin x cos x .
Suy ra: f ( x) = ( 2 2 − x x) − ( 2 2 3 1 2 sin cos
2 1− 3sin x cos x) = 1.
Vậy biểu thức không phụ thuộc vào x. 
Câu 6. Cho bốn điểm A, B, C, D. Chứng minh rằng:
a) AB + CD = AD + CB ;
b) AB − CD = AC + DB . Hướng dẫn giải:
a) Ta có: AB + CD = AD + CB AB + CD − AD − CB = 0
AB + CD + DA+ BC = 0  ( AB + BC)+(CD + DA) = 0
AC +CA = 0 (luôn đúng). 
b) Ta có: AB − CD = AC + DB AB − CD − AC − DB = 0
AB + DC + CA+ BD = 0
 ( AB + BD)+(DC +CA) = 0  AD + DA = 0 (luôn đúng). 
Câu 7. Cho các tập hợp A = ( ;
− m) và B = 3m −1;3m + 
3 . Tìm m để A C B . Hướng dẫn giải: Ta có: C B = ( ; − 3m − ) 1  (3m + 3; +) .
Vì vậy: A C B m  3m − 1 1  m  . 2 h h h h h h
Câu 8. Cho tam giác ABC thỏa mãn điều kiện a b c b c a + + = + +
. Chứng minh tam giác ABC là h h h h h h b c a a b c tam giác cân. Hướng dẫn giải: 19
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 1 1 1 2S 2S 2S Ta có: ABC S
= h a = h b = h c h = , ABC h = , ABC h = . ABC 2 a 2 b 2 c a b c a b c h h h h h h b c a a b c Ta có: a b c b c a + + = + +  + + = + + h h h h h h a b c b c a b c a a b c 2 2 2 2 2 2
b c + c a + a b = a c +b a + c b 2  (a − )
b (ab + c − ac − b ) c = 0 a = b
 (a − b)(b − c)(a − c) = 0  b = c
. Vậy tam giác ABC cân.  a = c  1
Câu 9. Tìm a để hàm số y =
xác định với mọi x −  1;1 .
x + 3a − 2 + a + 2 − x Hướng dẫn giải:
x + 3a − 2  0
x  2 − 3a Hàm số xác định     .
a + 2 − x  0 x a + 2
Trường hợp 1: 2 −3a a + 2  a  0 .
Khi đó tập xác định hàm số D =  không thể chứa đoạn −1;  1 .
Trường hợp 2: 2 −3a a + 2  a  0 (*). Khi đó tập xác định hàm số D = 2 − 3a;a + 2 .  − a  − a
Hàm số xác định x  −  1;1  − 
1;1  2 − 3a ; a + 2 3 1 1 2    
a 1 (thỏa (*)). 1   a + 2 a  1 −
Vậy với a 1 thì hàm số đã cho xác định với mọi x −  1;1 .
Câu 10. Cho tam giác ABC có trọng tâm G. Tìm tập hợp điểm M thỏa mãn hệ thức sau:
MA + MB − 2MC = AM − AB . Hướng dẫn giải:
Ta có: MA + MB − 2MC = AM − AB MA + MB + MC − 3MC = BM
 3MG − 3MC = BM  3(MG − MC) = BM  3 CG = BM BM = 3CG .
Nhận xét: Ba điểm B, C, G cố định. Vậy tập hợp điểm M là đường tròn tâm B, bán kính R = 3CG .
Câu 11. Một gia đình cần ít nhất 900 g chất protein và 400 g chất lipit trong thức ăn mỗi ngày. Biết rằng thịt
bò chứa 80% protein và 20% lipit. Thịt lợn chứa 60% protein và 40% lipit. Biết rằng gia đình này
chỉ mua nhiều nhất là 1 600 g thịt bò, 1 100 g thịt lợn, giá tiền 1 kg thịt bò là 45 000 đồng, 1 kg thịt
lợn là 35 000 đồng. Giả sử gia đình mua x kg thịt bò và y kg thịt lợn.
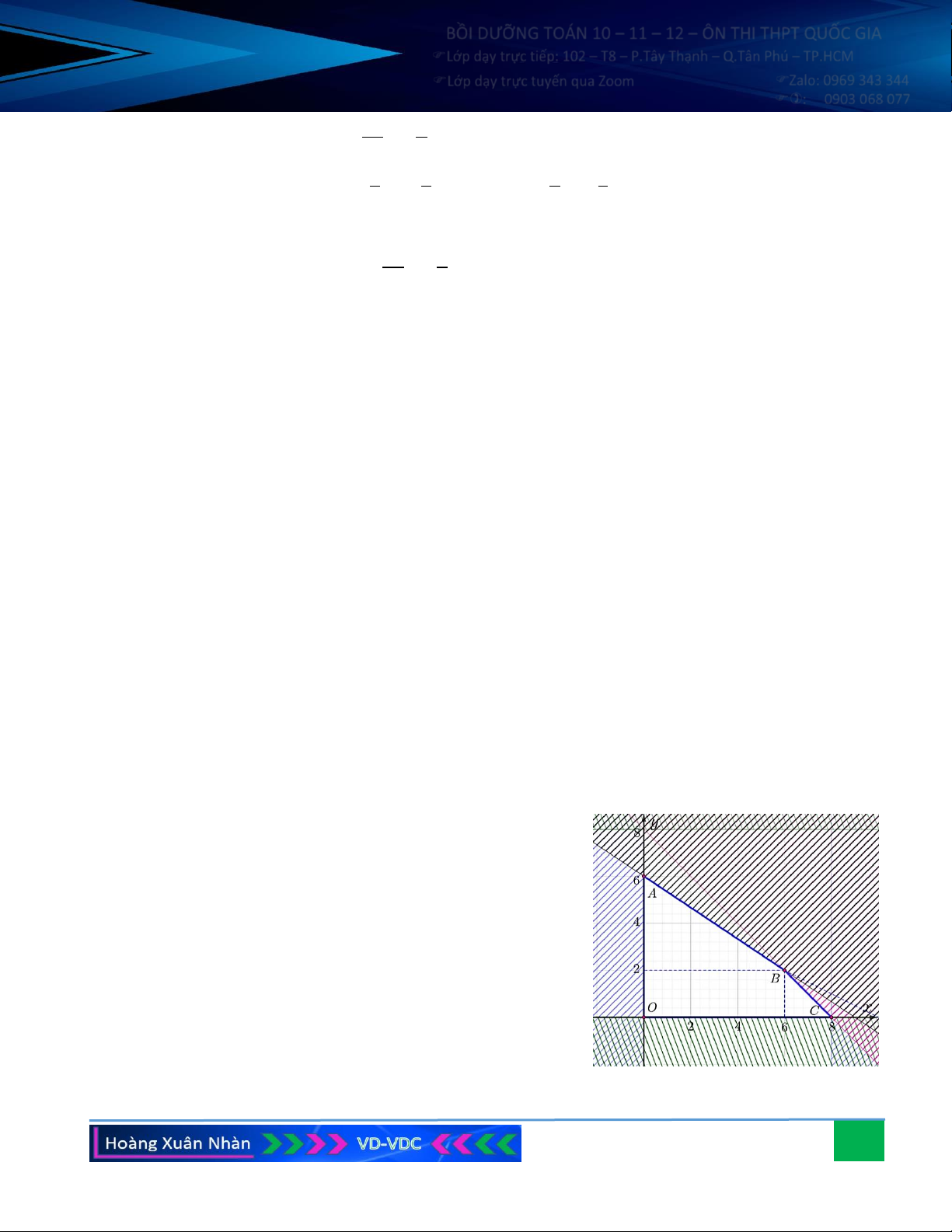
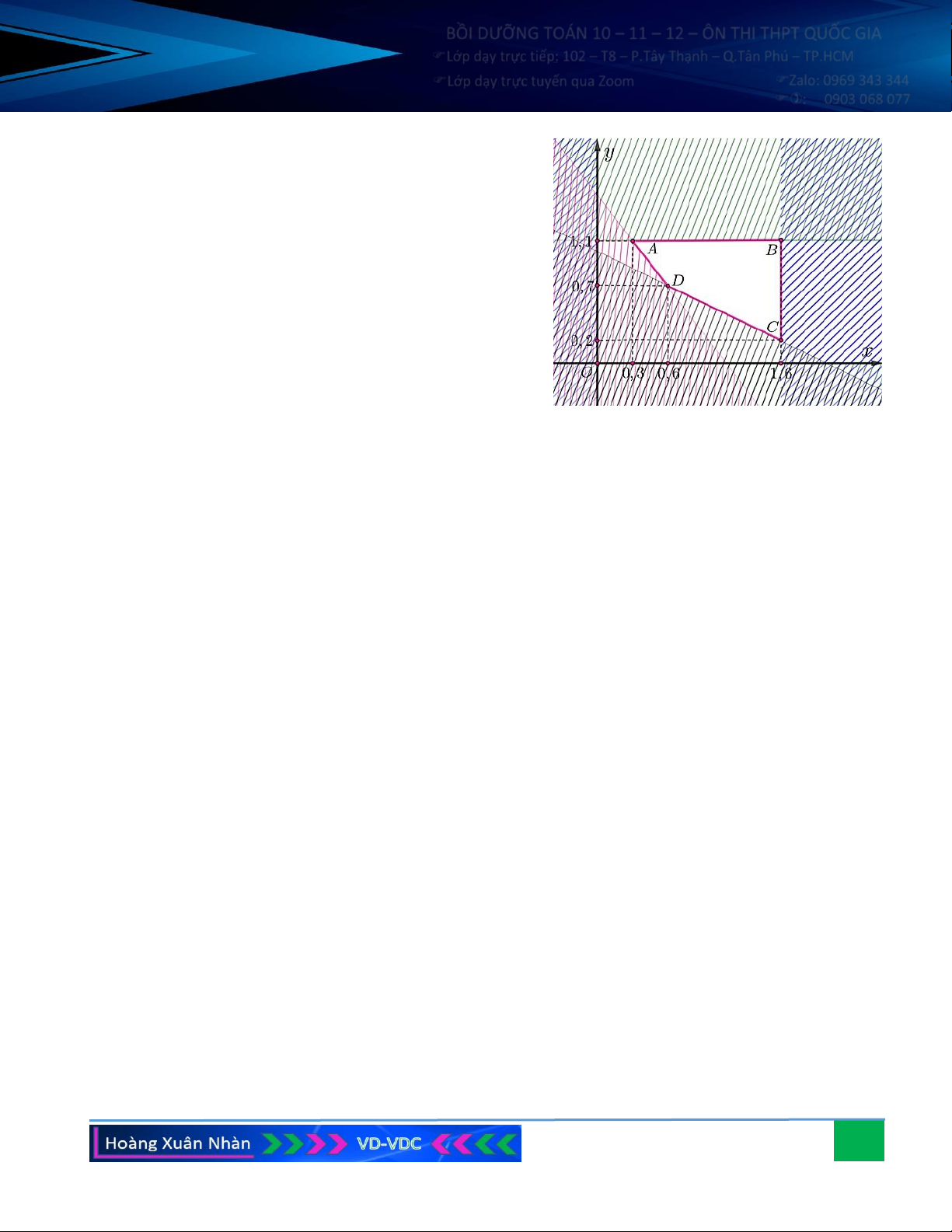
a) Lập hệ bất phương trình biểu thị các điều kiện của bài toán rồi biểu diễn hình học miền nghiệm (S) của hệ đó.
b) Gọi T (nghìn đồng) là số tiền phải trả cho x (kilogam) thịt bò và y (kilogam) thịt lợn. Hãy biểu diễn
T theo x, y.
c) Hỏi gia đình đó phải mua bao nhiêu kilogam thịt mỗi loại để chi phí là ít nhất? Hướng dẫn giải: 20
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
a) Giả sử gia đình đó mua x (kg) thịt bò và y (kg) thịt lợn.
Điều kiện: 0 ≤ x ≤ 1,6; 0 ≤ y ≤ 1,1.
Khi đó lượng protein có được là 80%x + 60% y và
lượng lipit có được là 20%x + 40% y.
Vì gia đình đó cần ít nhất 0,9 kg protein và 0,4 kg
lipit trong thức ăn mỗi ngày nên điều kiện tương ứng
là : 80%x + 60%y ≥ 0,9 và 20%x + 40%y ≥ 0,4. 0  x  1,6  0  y  1,1
Ta có hệ bất phương trình:  . 4x + 3y  4, 5 
x + 2y  2
Miền nghiệm của hệ trên là miền của tứ giác lồi
ABCD (kể cả biên) được mô tả ở hình bên.
b) Chi phí để mua x (kg) thịt bò và y (kg) thịt lợn là: T = 45x + 35y (nghìn đồng).
c) Ta đã biết T đạt giá trị nhỏ nhất tại một trong các đỉnh tứ giác ABCD trong đó A(0,3;1, ) 1 , B (1, 6;1, )
1 , C (1, 6;0, 2), D (0, 6;0, 7) . Xét A(0,3;1, )
1 , ta có T = 45.0,3 + 35.1,1 = 52 ; xét B (1, 6;1, )
1 , ta có T = 45.1, 6 + 35.1,1 =110,5 ;
xét C (1, 6;0, 2) , ta có T = 45.1,6 + 35.0, 2 = 79 ; xét D (0, 6;0, 7) , ta có T = 45.0,6 + 35.0,7 = 51,5 . x = 0,6
So sánh các giá trị trên, ta thấy được T đạt giá trị nhỏ nhất bằng 51,5 (nghìn đồng), khi đó   y = 0,7
(tức là gia đình đó mua 0,6kg thịt bò và 0,7 kg thịt lợn thì chi phí là ít nhất). 21
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
ÑEÀ REØN LUYEÄN SOÁ 05 Time: 90 phuùt ơ
Câu 1. Cho A = 3; + ) , B = (0; 4) . Tìm A , B A , B A \ ,
B B \ A , C , A C B .
Câu 2. Cho tập hợp X = a; ; b ; c d; ; e g .
a) Xác định tập Y sao cho Y X và X \ Y =  ; b ; c e .
b) Xác định hai tập A, B sao cho A B = X , B \ A = d; 
e , A \ B = a; ; b c .
Câu 3. Tìm tập xác định mỗi hàm số sau: 3x − 2 a) y = y = x + + x − ; 2 x − ; b) 2 1 x
Câu 4. Vẽ đồ thị hàm số 2
y = x − 4x +1.
Câu 5. Cho hình vuông ABCD có cạnh bằng a .
Tính AD + AB và AD + AC .
Câu 6. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số f ( x) 2
= x − 3x +1 biết x 0;4.
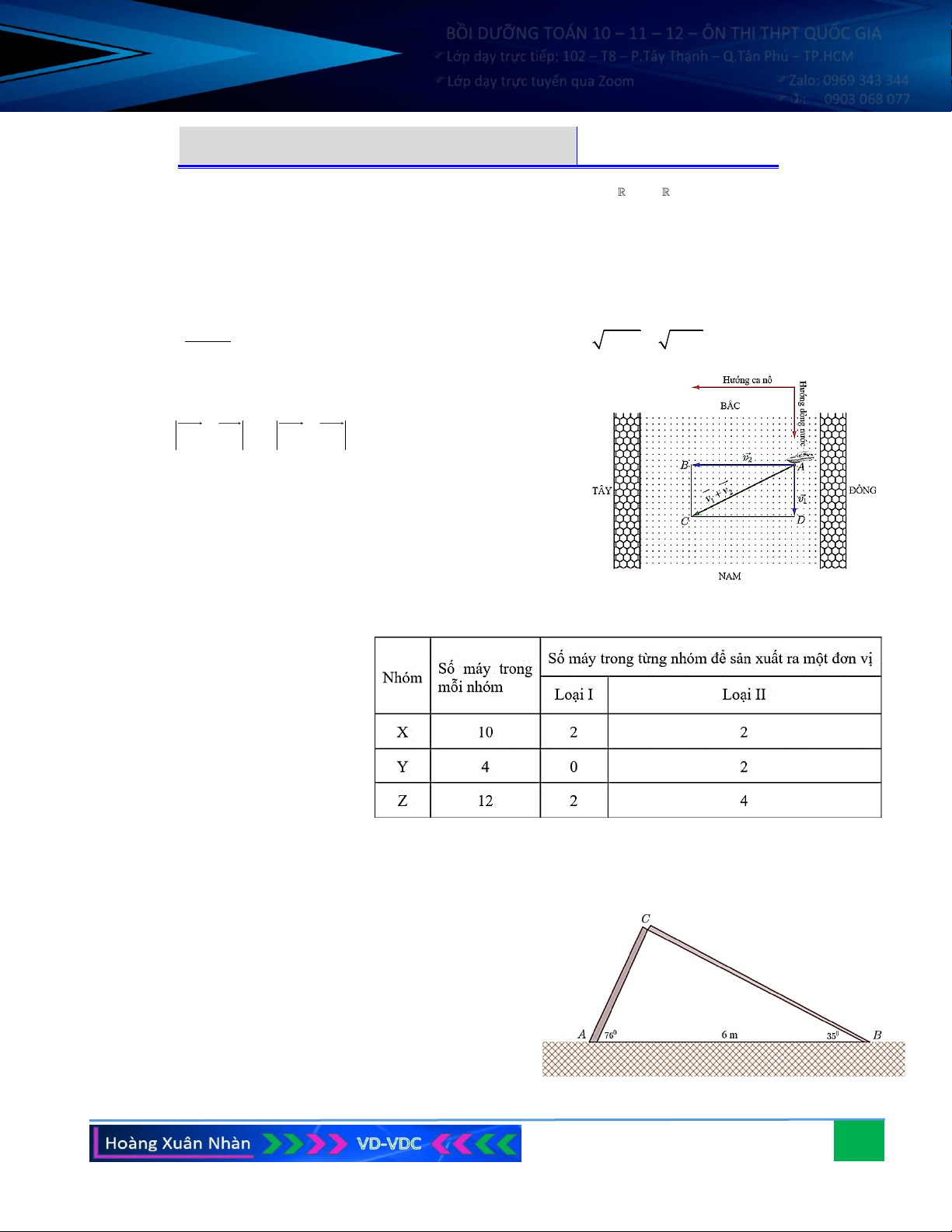
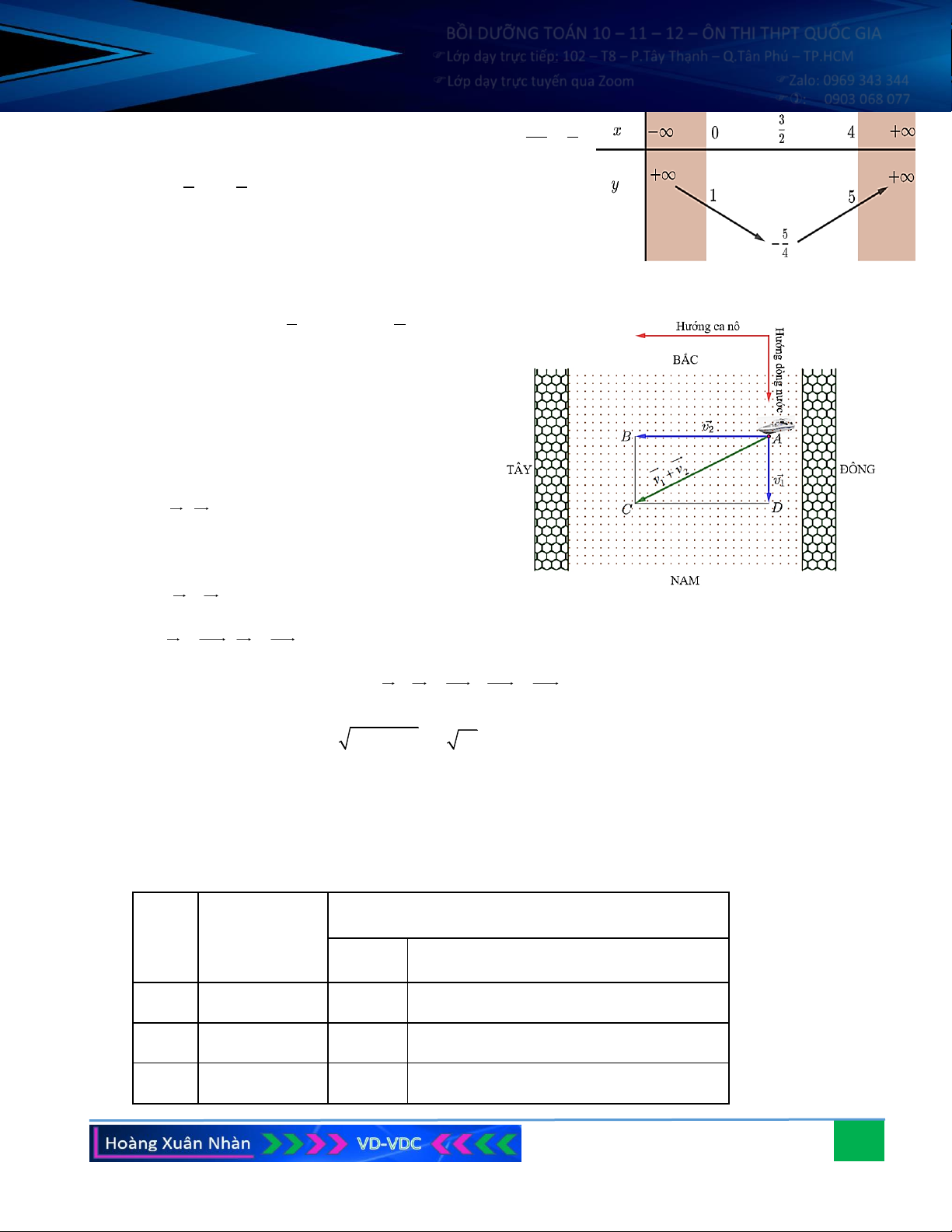
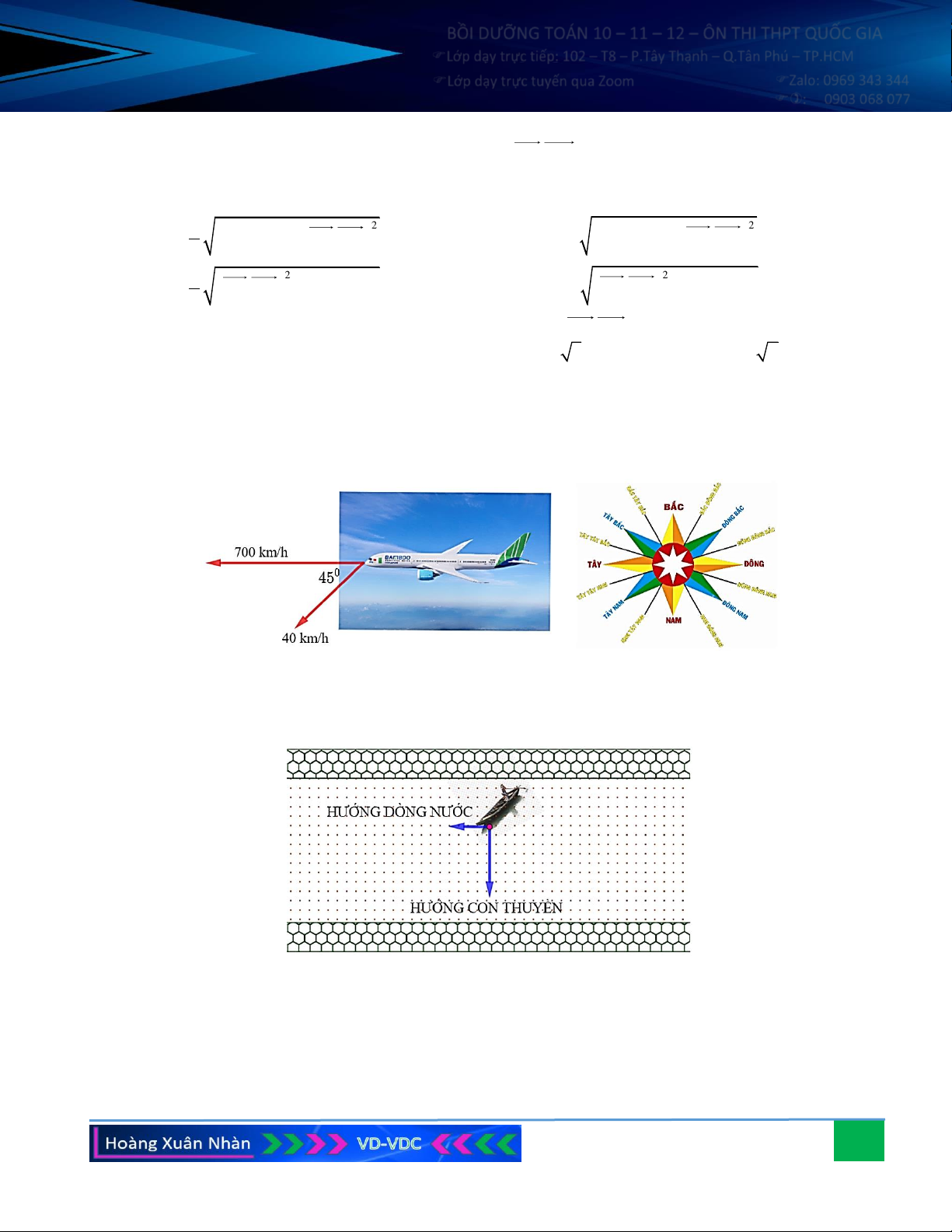
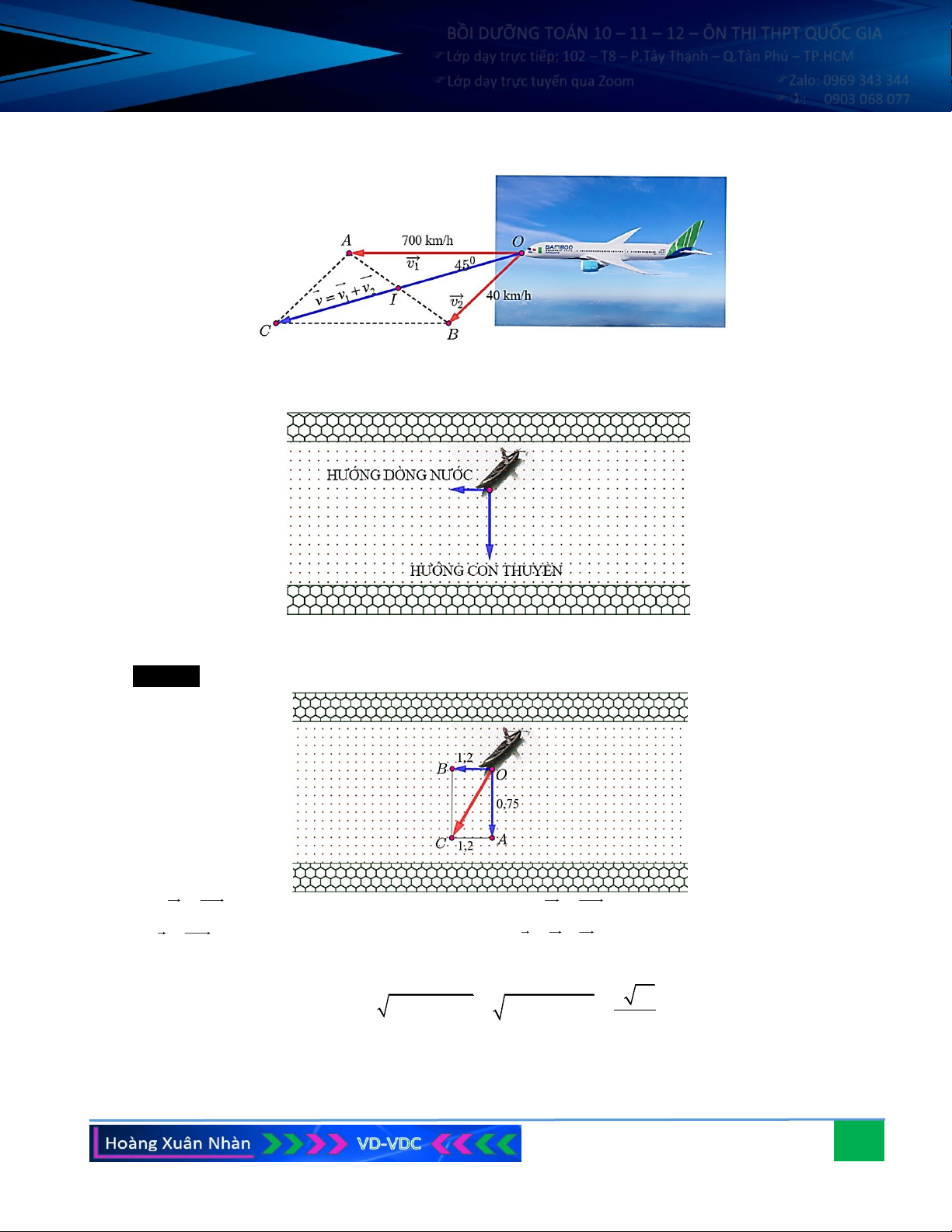
Câu 7. Một dòng sông chảy từ phía bắc xuống phía nam với vận
tốc 10 km/h, có một chiếc ca nô chuyển động từ phía đông
sang phía tây với vận tốc 35 km/h so với dòng nước. Tìm
vận tốc của ca nô so với bờ.
Câu 8. Có ba nhóm máy X, Y, Z dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị sản
phẩm mỗi loại lần lượt phải dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và số
máy của từng nhóm cần thiết
để sản xuất ra một đơn vị sản
phẩm thuộc mỗi loại được dùng cho trong bảng bên.
Một đơn vị sản phẩm loại I lãi 3
nghìn đồng, một đơn vị sản
phẩm loại II lãi 5 nghìn đồng.
Hãy lập kế hoạch sản xuất để
cho tổng số tiền lãi thu được là cao nhất.
Câu 9. Cho tam giác ABC thỏa mãn điều kiện 2 2 2
4m = b + c , trong đó m là độ dài trung tuyến tam giác a a
kẻ từ A; a, b, c là các cạnh của tam giác. Chứng minh tam giác ABC là tam giác vuông.
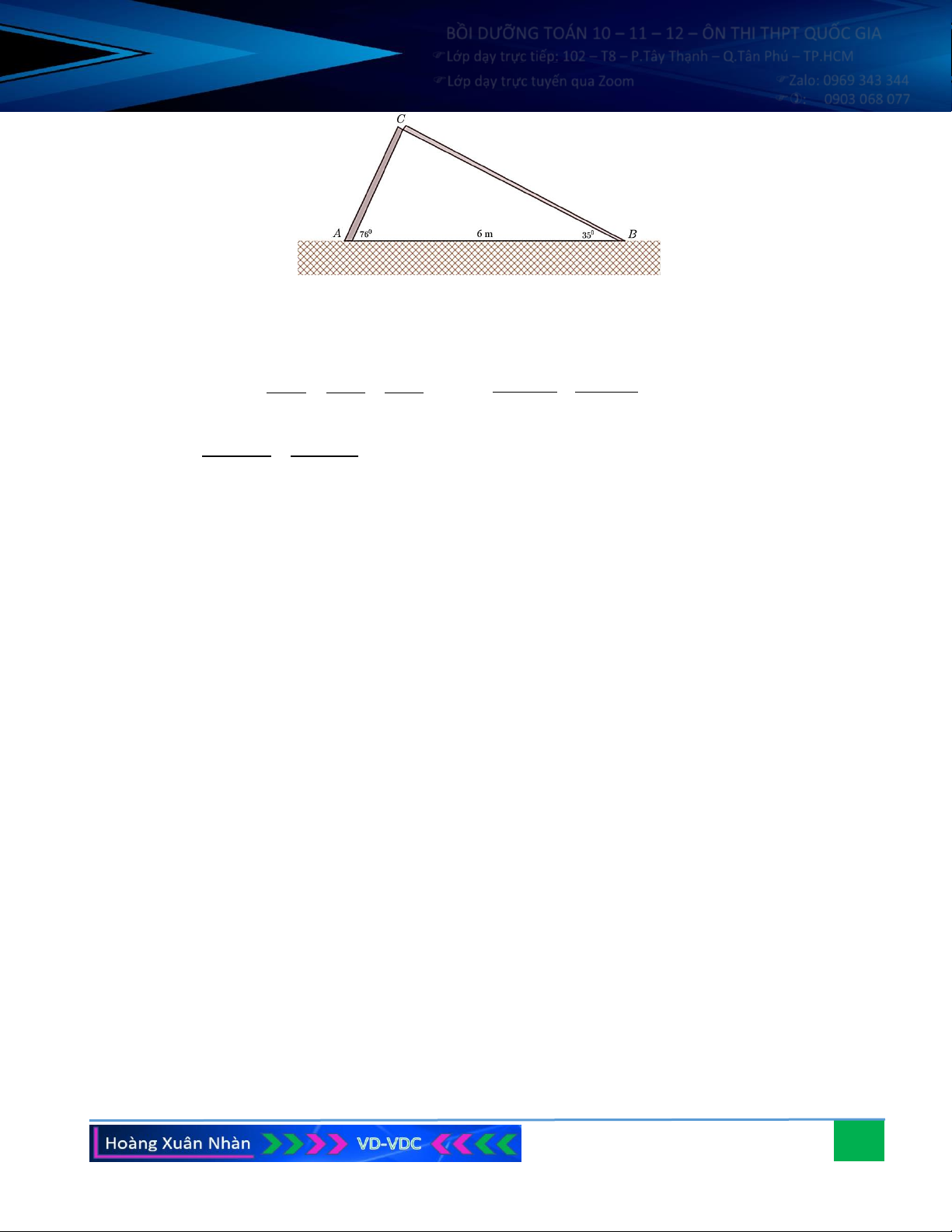
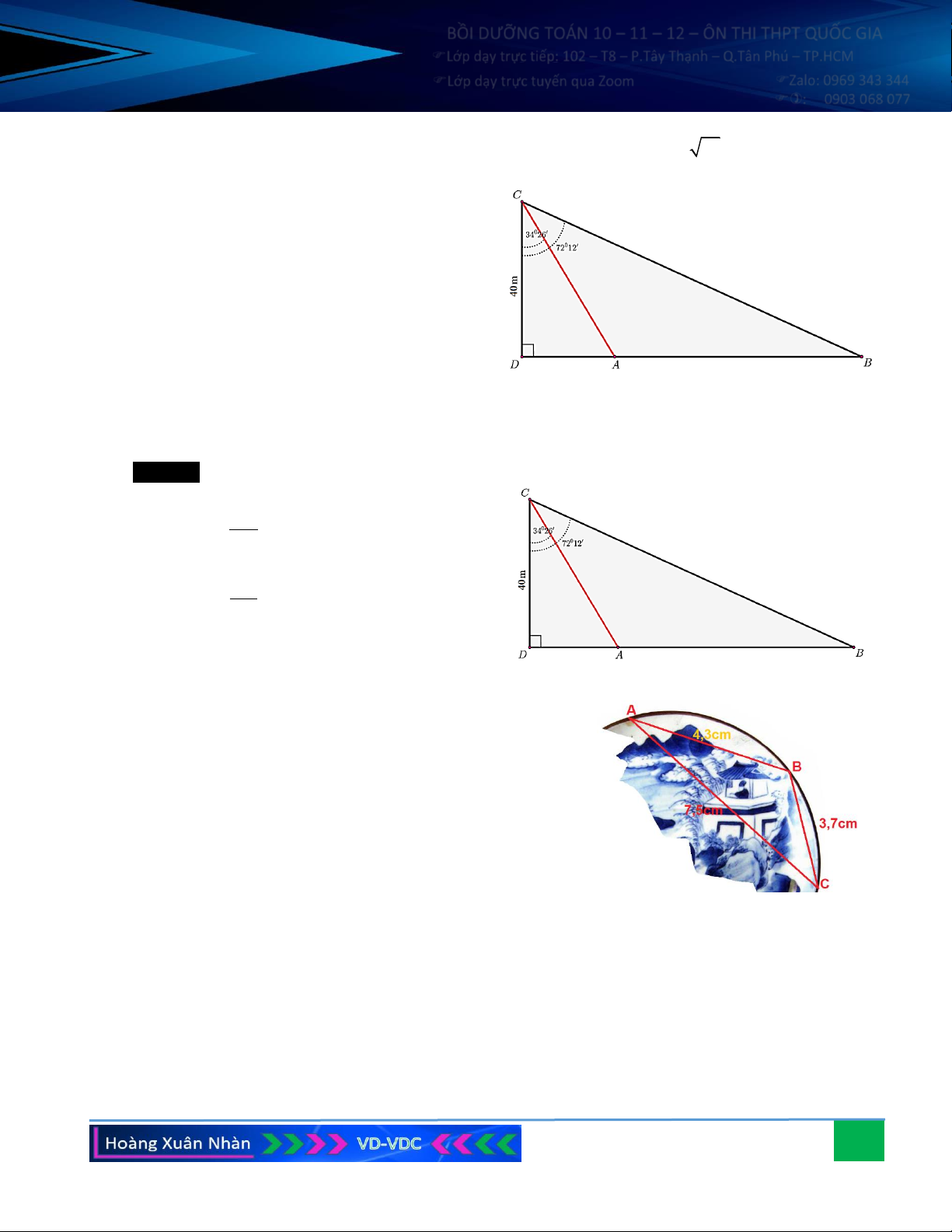
Câu 10. Một cái cây dạng thẳng đứng bị gió mạnh làm gãy
không hoàn toàn (hai đoạn thân bị gãy vẫn dính liền
nhau như hình vẽ). Một người muốn đo chiều cao của
cây trước khi gãy, người ấy đó được đoạn thẳng nối
từ gốc cây đến ngọn cây (đã ngã) là AB = 6 m , hai góc 0 0
CAB = 76 , CBA = 35 . Tính chiều dài của cây
trước khi bị gãy (giả sử sự biến dạng lúc gãy không
ảnh hưởng đến tổng độ dài của cây).
================HẾT=============== 22
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Höôùng daãn giaûi ñeà soá 05
Câu 1. Cho A = 3; + ) , B = (0; 4) . Tìm A , B A , B A \ ,
B B \ A , C , A C B . Hướng dẫn giải:
Ta có: A B = 3; 4) , A B = (0; + ) , A \ B = 4; + ) , B \ A = (0; 3) , C A = \ A = ( ; − 3) , C B = \ B = ( ; − 04;+) .
Câu 2. Cho tập hợp X = a; ; b ; c d; ; e g .
a) Xác định tập Y sao cho Y X và X \ Y =  ; b ; c e .
b) Xác định hai tập A, B sao cho A B = X , B \ A = d; 
e , A \ B = a; ; b c . Hướng dẫn giải:
a) Ta có: X \ Y =  ; b ; c
e nên a, d, g thuộc Y và b, c, e không thuộc Y. Mặt khác do Y X nên Y không chứa phần tử nào ngoài , a , b , c d, ,
e g . Vậy Y = a; d; g .
b) Do B \ A = d; 
e nên B có chứa d, e và A không chứa d, e. Vì A \ B = a; ; b
c nên A có chứa a, b,
c và B không chứa a, b, c. Ta lại có AB = X nên g thuộc A hoặc g thuộc B. Mặt khác g B \ ,
A g A \ B nên g thuộc A và g thuộc B. Vậy A = a; ; b ;
c g, B = d; ; e g .
Câu 3. Tìm tập xác định mỗi hàm số sau: 3x − 2 a) y = y = x + + x − ; 2 x − ; b) 2 1 x Hướng dẫn giải: x  0 a) Hàm số xác định 2
x − x  0  
. Tập xác định hàm số: D = \ 0;  1 . x  1 x + 2  0 x  2 −
b) Hàm số xác định    
x 1. Tập xác định hàm số: D = 1;+ ) . x −1 0 x 1
Câu 4. Vẽ các đồ thị hàm số 2
y = x − 4x +1. Hướng dẫn giải: Xét 2
y = x − 4x +1; (a = 1, b = 4 − , c = ) 1 . b 4 −
Tọa độ đỉnh I của parabol: x = − = − = 2, y = −
+ = − hay I (2;− 3) . I I (2)2 4.2 1 3 2a 2.1
Phương trình trục đối xứng parabol: x = 2 . Vì a =1  0 nên bề lõm parabol hướng lên. 23
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Để ý: Nếu ta tìm giao điểm giữa parabol với Ox, tức là giải phương trình 2
x − 4x +1 = 0 trước, tuy nhiên phương trình này cho ta hai nghiệm vô tỉ (không
đẹp). Chính vì thế nên ta chọn giải pháp lập bảng giá trị để tìm ra năm cặp (x ; y)
thỏa hàm số với đỉnh I làm tâm của bảng giá trị đó. Bảng giá trị: Đồ thị hàm số:
Câu 5. Cho hình vuông ABCD có cạnh bằng a . Tính AD + AB và AD + AC . Hướng dẫn giải:
Tính AD + AB :
Theo quy tắc hình bình hành, ta có AD + AB = AC . Theo định lí Pytago: 2 2 2
AC = AB + BC 2 2 2
= a + a = 2a AC = a 2
Vậy AD + AB = AC = AC = a 2 .
Tính AD + AC :
Gọi E là điểm đối xứng với B qua C. Do CE = AD = ,
a CE//AD nên ADEC là hình bình hành.
Ta có: AD + AC = AE . Áp dụng định lí Pytago cho tam giác ABE:
AE = AB + BE = a + ( a)2 2 2 2 2 2 2
= 5a AE = a 5 .
Vậy AD + AC = AE = a 5 .
Câu 6. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số f ( x) 2
= x − 3x +1 biết x 0;4; Hướng dẫn giải: 24
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 b 3 f ( x) 2
= x − 3x +1. Ta có: a =1, b = 3 − , c =1 − = 2a 2  3  5 và f = −  
. Vì a = 1  0 nên bề lõm đồ thị hướng lên.  2  4
Bảng biến thiên hàm số khi x 0; 4 là:
Ta có thể kết luận: Với x 0; 4, hàm số đạt giá trị lớn nhất bằng 5, khi đó x = 4 ; hàm số đạt giá 5
trị nhỏ nhất bằng − , khi đó 3 x = . 4 2
Câu 7. Một dòng sông chảy từ phía bắc xuống phía nam
với vận tốc 10 km/h, có một chiếc ca nô chuyển
động từ phía đông sang phía tây với vận tốc 35
km/h so với dòng nước. Tìm vận tốc của ca nô so với bờ. Hướng dẫn giải:
Gọi v , v lần lượt là vectơ vận tốc của dòng 1 2
nước đối với bờ và ca nô đối với dòng nước.
Khi đó vận tốc của ca nô đối với bờ chính là tổng v + v . 1 2
Đặt v = AD, v = AB với A là vị trí của ca nô. 1 2
Vẽ hình bình hành ABCD, ta có: v + v = AB + AD = AC . 1 2 Theo định lí Pytago: 2 2
AC = 10 + 35 = 5 53  36, 4 km/h.
Vậy vận tốc của ca nô đối với bờ là xấp xỉ 36, 4 km/h.
Câu 8. Có ba nhóm máy X, Y, Z dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị sản
phẩm mỗi loại lần lượt phải dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và
số máy của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được dùng cho trong bảng sau: Số máy
Số máy trong từng nhóm để sản xuất ra một đơn vị trong Nhóm mỗi nhóm sản phẩm Loại I Loại II X 10 2 2 Y 4 0 2 Z 12 2 4 25
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Một đơn vị sản phẩm loại I lãi 3 nghìn đồng, một đơn vị sản phẩm loại II lãi 5 nghìn đồng. Hãy lập kế
hoạch sản xuất để cho tổng số tiền lãi thu được là cao nhất. Hướng dẫn giải:
Gọi x là số đơn vị sản phẩm loại I, y là số đơn vị sản phẩm loại II sản xuất ra.
Như vậy tiền lãi có được là F ( x; y) = 3x + 5y (nghìn đồng).
Theo giả thiết, số máy cần dùng nhóm X: 2x + 2y
(máy); số máy cần dùng ở nhóm Y là 0x + 2y (máy);
số máy cần dùng ở nhóm Z là 2x + 4y (máy).
2x + 2y  10  2y  4
Ta có hệ bất phương trình (*):  . 2x + 4 y  12 
x  0, y  0
Miền nghiệm của hệ (*) được biểu diễn là miền của ngũ giác OABCD với
O (0;0), A(0; 2), B (2; 2), C (4; ) 1 , D (5;0) .
Xét O (0; 0) , ta có F (0;0) = 3.0 + 5.0 = 0 ; xét A(0; 2) , ta có F (0; 2) = 3.0 + 5.2 = 10 ; xét B (2; 2) ,
ta có F (2; 2) = 3.2 + 5.2 = 16 ; xét C (4; ) 1 , ta có F (4; )
1 = 3.4 + 5.1 = 17 ; xét D (5;0) , ta có
F (5;0) = 3.5 + 5.0 = 15 .
Từ các kết quả trên, ta thấy khoản lãi lớn nhất ( F ( x ; y ) lớn nhất) bằng 17 (ngàn đồng), khi đó người
ta cần làm ra 4 sản phẩm loại I và 1 sản phẩm loại II (tức là x = 4, y = 1).
Câu 9. Cho tam giác ABC thỏa mãn điều kiện 2 2 2
4m = b + c , trong đó m là độ dài trung tuyến tam giác a a
kẻ từ A; a, b, c là các cạnh của tam giác. Chứng minh tam giác ABC là tam giác vuông. Hướng dẫn giải: 2 2 2
2(b + c ) − a Ta có : 2 2 2 2 2 m =
 4m = 2(b + c ) − a . a 4 a Kết hợp giả thiết: 2 2 2 2 2 2 2 2 2 2 2
4m = b + c  2(b + c ) − a = b + c b + c = a . a
Vậy tam giác ABC vuông tại A. 
Câu 10. Một cái cây dạng thẳng đứng bị gió mạnh làm gãy không hoàn toàn (hai đoạn thân bị gãy vẫn dính
liền nhau như hình vẽ). Một người muốn đo chiều cao của cây trước khi gãy, người ấy đó được
đoạn thẳng nối từ gốc cây đến ngọn cây (đã ngã) là AB = 6 m , hai góc 0 0
CAB = 76 , CBA = 35 .
Tính chiều dài của cây trước khi bị gãy (giả sử sự biến dạng lúc gãy không ảnh hưởng đến tổng độ dài của cây). 26
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 Hướng dẫn giải: Ta có: 0
C = 180 − ( A + B) 0 = − ( 0 0 + ) 0 180 76 35 = 69 . 0 Theo đị AB AC BC A . B sin B 6.sin 35 nh lí Sin: = =  AC = =  3,69 m; sin C sin B sin A 0 sin C sin 69 0 A . B sin A 6.sin 76  BC = =
 6,24 m  AC + BC  9,93 m . 0 sin C sin 69
Vậy chiều cao ban đầu của cây xấp xỉ bằng 9,93 m . 27
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
ÑEÀ REØN LUYEÄN SOÁ 06 Time: 90 phuùt ơ
Câu 1. Cho A = 1; 2; 3; 4; 
5 . Viết tất cả các tập con của A có ít nhất ba phần tử.
x + y − 2  0
Câu 2. Xét xem các cặp số (x ; y) sau đây có là nghiệm của hệ bất phương trình  ?
2x − 3y + 2  0 a) (0;0) ; b) (1; ) 1 ; c) (−2; ) 1 .
Câu 3. Tìm tập xác định của các hàm số sau: 3 − x 1− 2x a) 3 y = + x −1 ; b) y = . x + 2 4 2x +1 − 3x
Câu 4. Xác định hàm số bậc hai có đồ thị là parabol ( P) biết: a) ( P) 2
: y = ax + bx + c có giá trị lớn nhất bằng 1 khi x = 2, đồng thời ( P) qua M (4; − 3) . b) ( P) 2
: y = ax + bx + c có giá trị nhỏ nhất bằng 1
− ; biết (P) đi qua điểm A(−1;7) và (P) cắt Oy
tại điểm có tung độ bằng 1.
Câu 5. Cho mẫu số liệu thống kê về sản lượng chè thu được trong 1 năm (kg/sào) của 10 hộ gia đình: 112 111 112 113 114 116 115 114 115 114
a) Tìm giá trị trung bình của mẫu số liệu trên.
b) Viết mẫu số liệu trên theo thứ tự không giảm và tìm trung vị, mốt của nó.
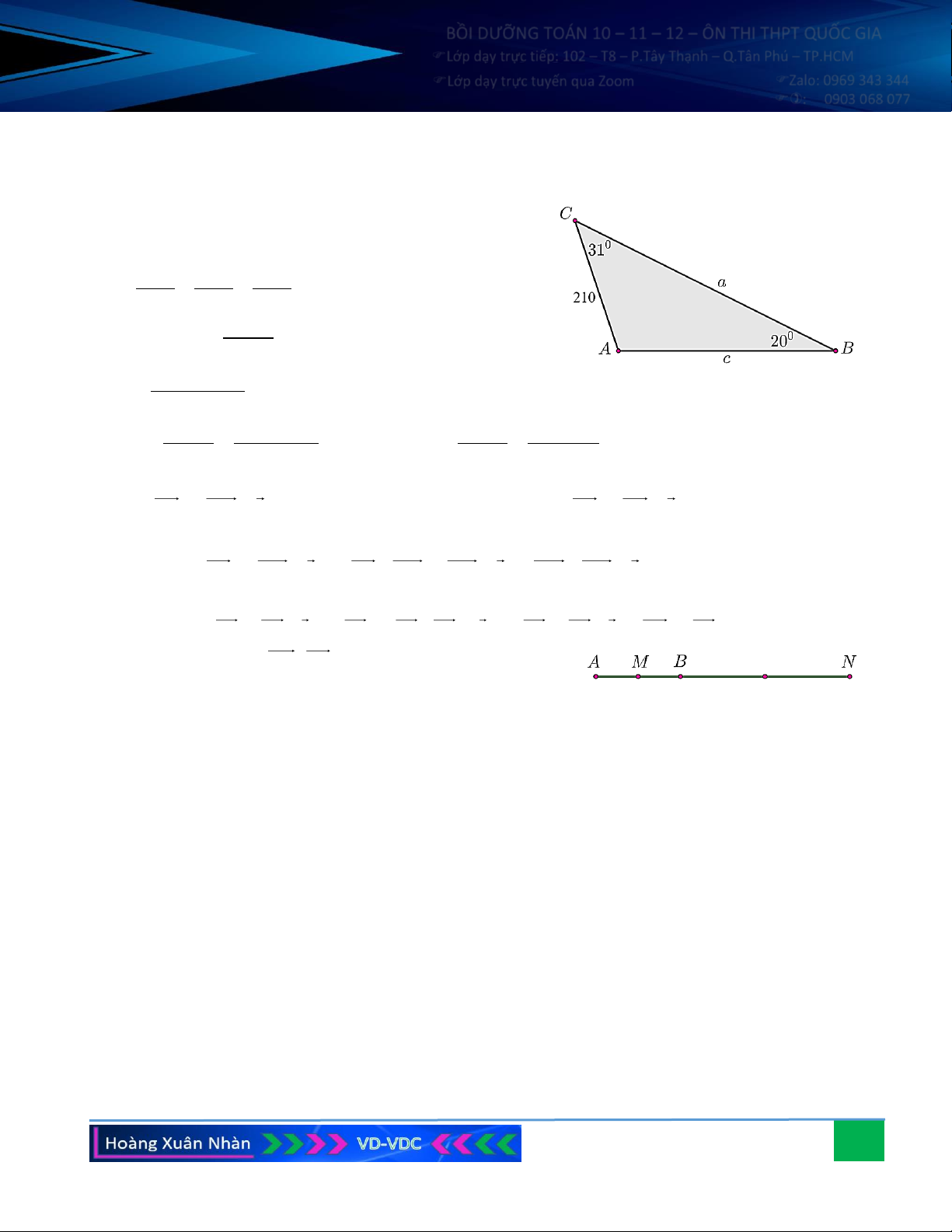
Câu 6. Cho tam giác ABC có 0 0
B = 20 , C = 31 , cạnh b = AC = 210 cm . Tính góc A, độ dài các cạnh còn
lại và bán kính R của đường tròn ngoại tiếp tam giác ABC.
Câu 7. Cho hai điểm phân biệt ,
A B . Xác định các điểm M , N sao cho:
a) AB + 2BM = 0 ;
b) 2NA − 3NB = 0 .
Câu 8. Một người cần đặt một tiệc cưới ước tính khoảng 30 đến 35 bàn. Nhà hàng thứ nhất đề nghị anh nay đóng
tiền cố định 20 triệu đồng, sau khi tiệc cưới diễn ra sẽ đóng khoản còn lại với số tiền 2 triệu đồng/1 bàn.
Nhà hàng thứ hai đề nghị anh đóng tiền cố định 10 triệu đồng, sau khi tiệc cưới diễn ra sẽ đóng khoản còn
lại với số tiền 2,5 triệu/1 bàn. Hỏi anh này nên lựa chọn nhà hàng nào để tiết kiệm được chi phí cho tiệc
cưới (giả sử rằng chất lượng phục vụ hai nhà hàng trên là ngang nhau)?
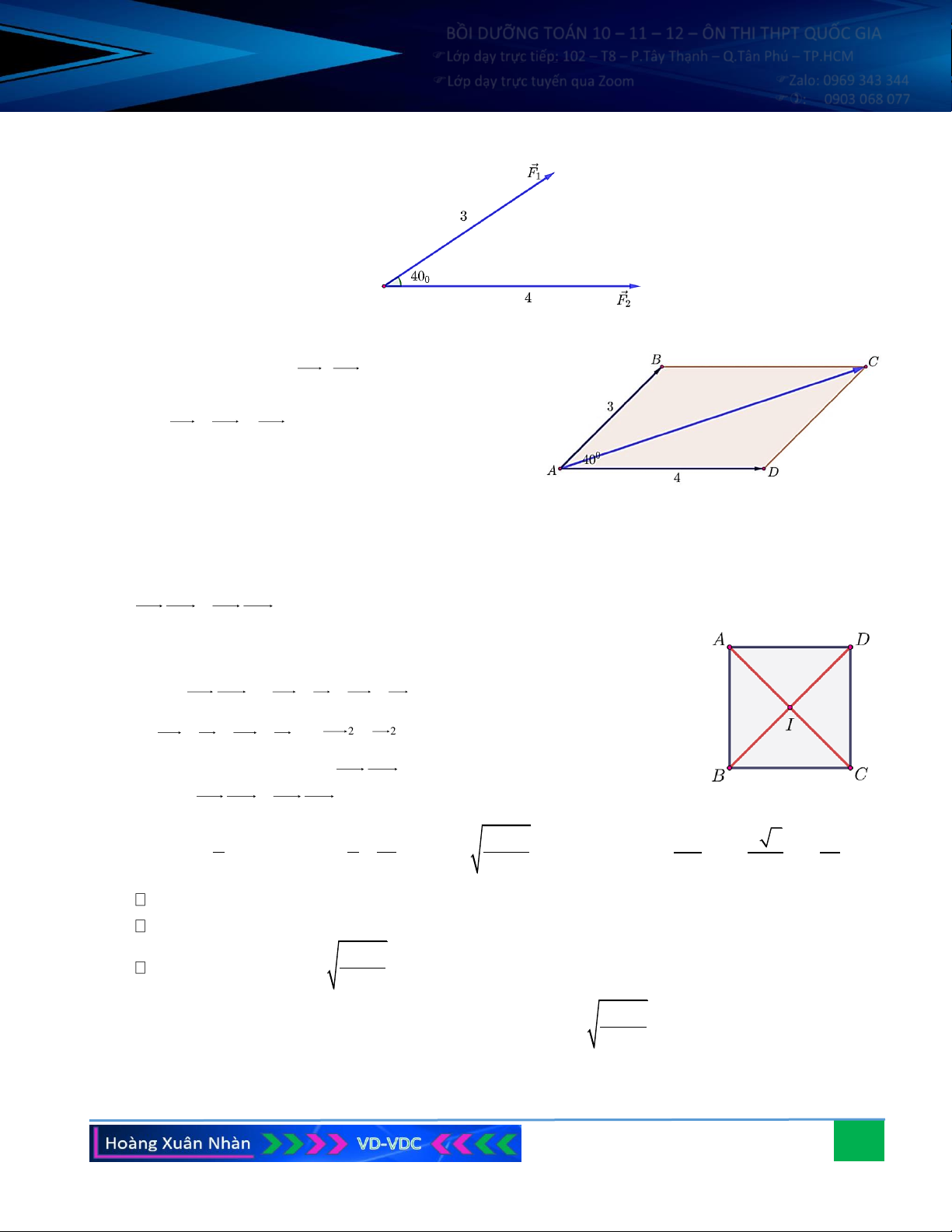
Câu 9. Biết hai lực cùng tác động vào một vật tạo với nhau góc 40o . Cường độ của hai lực đó là 3N và 4N.
Tính cường độ của lực tổng hợp.
Câu 10. Cho hình vuông ABCD cạnh a và số thực k . Tìm tập hợp điểm M sao cho M . A MC + M . B MD = k .
================HẾT=============== 28
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Höôùng daãn giaûi ñeà soá 06
Câu 1. Cho A = 1; 2; 3; 4; 
5 . Viết tất cả các tập con của A có ít nhất ba phần tử. Hướng dẫn giải:
Các tập con có ít nhất ba phầu tử của A là: 1; 2;  3 , 1; 2;  4 , 1; 2;  5 , 1; 3;  4 , 1; 3;  5 , 1; 4;  5 , 2; 3;  4 , 2; 3;  5 , 2; 4;  5 , 3; 4;  5 , 1; 2; 3;  4 , 1; 2; 3;  5 , 1; 2; 4;  5 , 1; 3; 4;  5 , 2; 3; 4;  5 ,1; 2; 3; 4;  5 (gồm 16 tập).
x + y − 2  0
Câu 2. Xét xem các cặp số (x ; y) sau đây có là nghiệm của hệ bất phương trình  ?
2x − 3y + 2  0 a) (0;0) ; b) (1; ) 1 ; c) (−2; ) 1 . Hướng dẫn giải:  0 + 0 − 2  0
a) Thay x = 0, y = 0 vào hệ bất phương trình, ta được :  (đúng), do đó cặp số 2.0 − 3.0 + 2  0
(0;0) là một nghiệm của hệ đã cho.  1+1− 2  0
b) Thay x = 1, y =1 vào hệ bất phương trình, ta được : 
(đúng), do đó cặp số (1; ) 1 2.1− 3.1+ 2  0
là một nghiệm của hệ đã cho.  ( 2 − ) +1− 2  0 c) Thay x = 2
− , y =1 vào hệ bất phương trình, ta được :  (sai), do đó cặp số 2  ( 2 − ) −3.1+ 2  0 (−2; )
1 không là một nghiệm của hệ đã cho.
Câu 3. Tìm tập xác định của các hàm số sau: 3 − x 1− 2x a) 3 y = + x −1 ; b) y = . x + 2 4 2x +1 − 3x Hướng dẫn giải: 3 − x 3  − x  0 3  − x  0
a) Hàm số xác định khi và chỉ khi  0     x + 2
x + 2  0 x + 2  0 x  3 x  3      2
−  x  3. Tập xác định hàm số: D = ( 2 − ;  3 . x  2 − x  2 − 2x +1  0 
b) Hàm số xác định khi và chỉ khi  (*) .
4 2x +1 −3x  0 x  0 3  x  0  
Xét 4 2x +1 − 3x = 0  4 2x +1 = 3x     4  x = 4 . 1  6  (2x + ) 2 1 = 9x
x = 4  x = −  9 29
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077  1 x  −   Do vậy 1 (*)  
2 . Tập xác định hàm số: D = − ; +  \     4 .   2  x  4
Câu 4. Xác định hàm số bậc hai có đồ thị là parabol ( P) biết: a) ( P) 2
: y = ax + bx + c có giá trị lớn nhất bằng 1 khi x = 2, đồng thời ( P) qua M (4; − 3) . b) ( P) 2
: y = ax + bx + c có giá trị nhỏ nhất bằng 1
− ; biết (P) đi qua điểm A(−1;7) và (P) cắt Oy
tại điểm có tung độ bằng 1. Hướng dẫn giải: b a) Theo giá thiết thì −
= 2  4a + b = 0 (1) ; (P) qua hai điểm I (2; ) 1 , M (4; − 3) nên 2aa = 1 −
4a + 2b + c =1 (2)  
. Giải hệ (1), (2), (3): b
 = 4 . Vậy hàm số được xác định: 2
y = −x + 4x − 3 . 1
 6a + 4b + c = 3 − (3) c = 3 − 
a − b + c = 7 a − b = 6 a = b + 6 (1)
b) ( P) đi qua hai điểm A(−1;7) và B (0; ) 1 nên      . c =1 c =1 c =1 2 2 c 1 b 4ac =  − 4a − b Mặt khác y = − = − = = 1 − min 4a 4a 4a 2 2  4a −b = 4
− a b −8a = 0 (2) . b =12 Thay (1) vào (2): 2
b − 8(b + 6) = 0   . b = 4 −
Với b = 12 thì a =18  0 (nhận). Hàm số được xác định: 2
y = 18x +12x +1. Với b = 4
− thì a = 2  0 (nhận). Hàm số được xác định: 2
y = 2x − 4x +1.
Câu 5. Cho mẫu số liệu thống kê về sản lượng chè thu được trong 1 năm (kg/sào) của 10 hộ gia đình: 112 111 112 113 114 116 115 114 115 114
a) Tìm giá trị trung bình của mẫu số liệu trên.
b) Viết mẫu số liệu trên theo thứ tự không giảm và tìm trung vị, mốt của nó. Hướng dẫn giải:
a) Sản lượng chè trung bình thu được trong một năm của mỗi gia đình là
112 +111+112 +113 +114 +116 +115 +114 +115 +114 x = 113,6 (kg/sào). 10
b) Ta viết lại mẫu số liệu trên theo thứ tự không giảm: 111 112 112 113 114 114 114 115 115 116
Vì số giá trị của mẫu n = 10 (chẵn) nên trung bình cộng hai số chính giữa mẫu chính là trung vị, 114 +114 vậy trung vị là: =114 . 2
Trong mẫu trên, giá trị 114 xuất hiện nhiều nhất (3 lần) nên 114 là mốt của mẫu số liệu đã cho. 30
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Câu 6. Cho tam giác ABC có 0 0
B = 20 , C = 31 , cạnh b = AC = 210 cm . Tính góc A, độ dài các cạnh còn
lại và bán kính R của đường tròn ngoại tiếp tam giác ABC. Hướng dẫn giải: Ta có: 0 A = − (B +C) = − ( 0 0 + ) 0 180 180 20 31 =129 . Theo định lí Sin: a b c = = = 2R . sin A sin B sin C b sin A Suy ra: a = sin B 0 210.sin129 =  477,2 cm ; 0 sin 20 0 b sin C 210.sin 31 a 477, 2 c = =  316,2 cm ; R =   307,02 cm . 0 sin B sin 20 0 2sin A 2sin129
Câu 7. Cho hai điểm phân biệt ,
A B . Xác định các điểm M , N sao cho:
a) AB + 2BM = 0 ;
b) 2NA − 3NB = 0 . Hướng dẫn giải:
a) Ta có: AB + 2BM = 0  ( AB + BM ) + BM = 0  AM + BM = 0 .
Vậy M là trung điểm của đoạn AB.
b) Ta có: 2NA − 3NB = 0  2NA − 3(NA + AB) = 0  −NA − 3AB = 0  AN = 3AB .
Do vậy hai vectơ AN , AB cùng hướng và AN = 3AB .
Câu 8. Một người cần đặt một tiệc cưới ước tính khoảng 30 đến 35 bàn. Nhà hàng thứ nhất đề nghị anh nay đóng
tiền cố định 20 triệu đồng, sau khi tiệc cưới diễn ra sẽ đóng khoản còn lại với số tiền 2 triệu đồng/1 bàn.
Nhà hàng thứ hai đề nghị anh đóng tiền cố định 10 triệu đồng, sau khi tiệc cưới diễn ra sẽ đóng khoản còn
lại với số tiền 2,5 triệu/1 bàn. Hỏi anh này nên lựa chọn nhà hàng nào để tiết kiệm được chi phí cho tiệc
cưới (giả sử rằng chất lượng phục vụ hai nhà hàng trên là ngang nhau)? Hướng dẫn giải:
Gọi x là số bàn tiệc thực tế trong đám cưới (x nguyên dương và x 30;35 ) và y (triệu đồng) là số
tiền mà người đó phải trả cho nhà hàng.
Nếu đăng ký tại nhà hàng thứ nhất, người đó sẽ trả tiền theo công thức: y = 2x + 20 .
Với x 30;35 thì y 80;90, tức là người đó phải trả khoản tiền khoảng 80 triệu đến 90 triệu cho nhà hàng thứ nhất.
Nếu đăng ký tại nhà hàng thứ hai, người đó sẽ trả tiền theo công thức: y = 2,5x +10 .
Với x 30;35 thì y 85;97,5, tức là người đó phải trả khoản tiền khoảng 85 triệu đến 97,5
triệu cho nhà hàng thứ hai.
Vậy, nếu chất lượng phục vụ hai nhà hàng là tương đương, người đó nên chọn nhà hàng thứ nhất để
tiết kiệm một khoản chi phí tiệc cưới. 31
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Câu 9. Biết hai lực cùng tác động vào một vật tạo với nhau góc 40o . Cường độ của hai lực đó là 3N và 4N.
Tính cường độ của lực tổng hợp. Hướng dẫn giải:
Giả sử vật được đặt ở vị trí A, hai lực tác động vào A
lần lượt là các vectơ AB, AD có độ lớn là 3N, 4N.
Vẽ hình bình hành ABCD, ta có hợp lực tác động vào
A là: AB + AD = AC .
Do ABCD là hình bình hành nên AD = BC = 4. Ta có: 0 0 0
ABC = 180 − 40 = 140 . Xét tam giác ABC,
theo định lí Cô-sin ta có: 2 2 2 2 2 0
AC = AB + BC − 2 .
AB BC.cos ABC = 3 + 4 − 2.3.4.cos140  43, 39  AC  6,59 .
Vậy độ lớn của lực tổng hợp tác động vào vật A là xấp xỉ 6,59 N.
Câu 10. Cho hình vuông ABCD cạnh a và số thực k . Tìm tập hợp điểm M sao cho M . A MC + M . B MD = k . Hướng dẫn giải:
Gọi I là tâm của hình vuông ABCD . Ta có : M .
A MC = (MI + IA)(MI + IC) = ( 2 2
MI + IA)(MI − IA) 2 2
= MI − IA = MI − IA .
Hoàn toàn tương tự, ta có: 2 2 M .
B MD = MI − IB . Khi đó: M . A MC + M . B MD = k 2 2 2 2 2
 2MI − IA − IB = k  2MI − 2IA = k 2 2 2 k k a 2 k + a 2  AC   a 2  a 2 2 2
MI = + IA MI = +  MI = (trong đó 2 IA = =     = ). 2 2 2 2    2  2 2   Nếu 2
k  −a : Tập hợp điểm M là tập rỗng. Nếu 2
k = −a thì MI = 0  M I (điểm M trùng với điểm I ). 2 k + a Nếu 2
k  −a thì MI = . 2 2 + Khi đó tậ k a
p hợp điểm M là đường tròn tâm I , bán kính R = . 2 32
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
ÑEÀ REØN LUYEÄN SOÁ 07 Time: 90 phuùt ơ
Câu 1. Cho A =  2 x
2x − 3x +1 =  0 , B = x  2x −1 =  1 . Tìm A  , B A , B A \ , B B \ A. x + y  3 
Câu 2. Biểu diễn miền nghiệm của hệ sau trên mặt phẳng tọa độ: x  0 . y  0 
Câu 3. Xét sự biến thiên của hàm số f ( x) 2
= 2x −1 trên (−;0) . 1 Câu 4. Cho sin  = với 0 0
90    180 . Tính cos và tan . 3
Câu 5. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số f ( x) 2
= x − 3x +1 với x 0;4.
Câu 6. Bảng số liệu sau thống kê nhiệt độ tại Thành phố Hồ Chí Minh trong một lần đo vào một ngày của năm 2021 : Giờ đo 1h 4h 7h 10h 13h 16h 19h 22h Nhiệt độ (độ C) 27 26 28 32 34 35 30 28
Tìm số trung bình, phương sai và độ lệch chuẩn của mẫu số liệu đã cho (làm tròn kết quả đến hàng phần trăm).
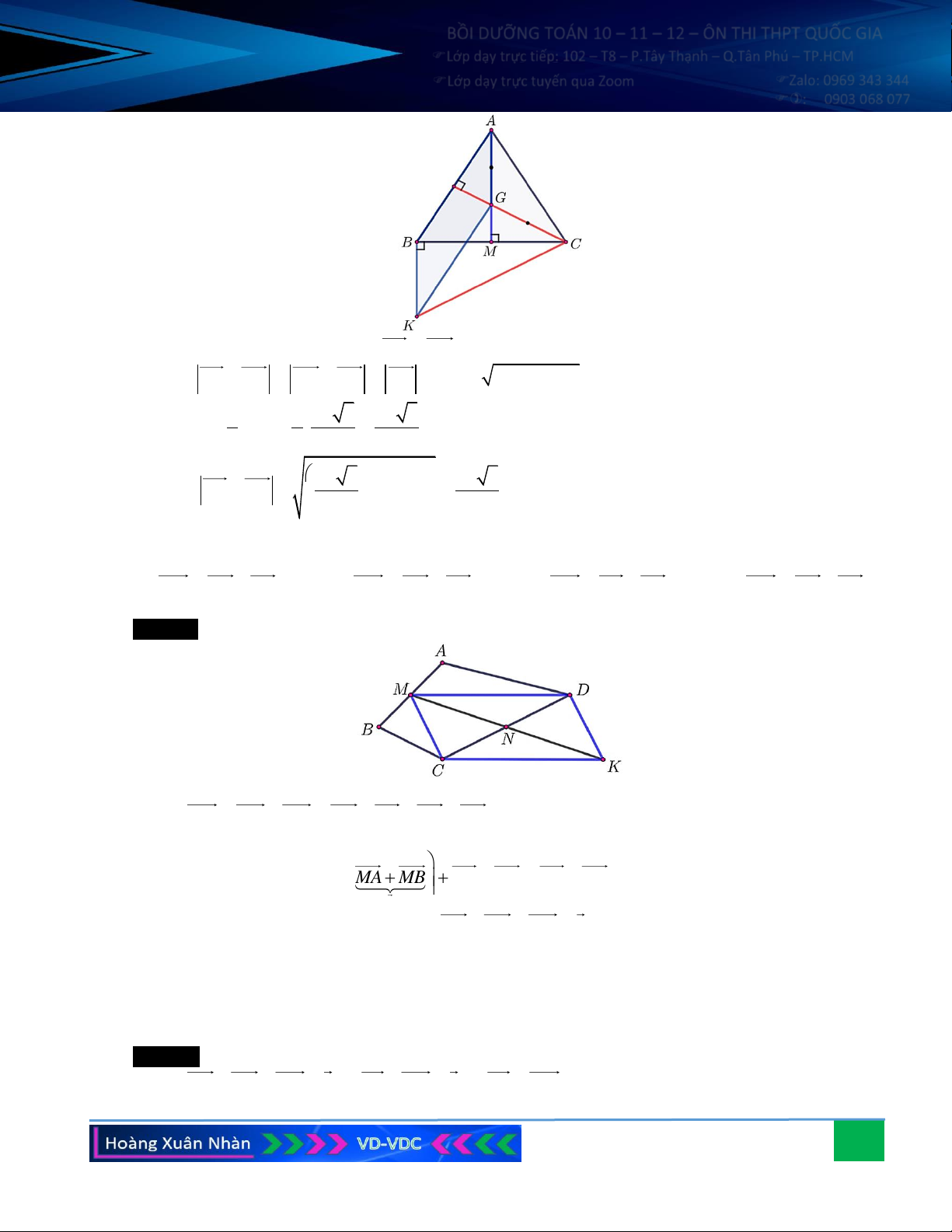
Câu 7. Chứng minh rằng trong một hình bình hành, tổng bình phương các cạnh bằng tổng bình phương hai
đường chéo của hình bình hành đó. Câu 8. Cho ABC  vuông tại B có 0
A = 30 , AB = a . Gọi I là trung điểm của AC . Hãy tính: a) BA + BC ; b) AB + AC .
Câu 9. Cho tam giác ABC có trọng tâm G. Tìm vị trí của M để tổng 2 2 2
P = MA + MB + MC đạt giá trị nhỏ nhất P . Tính P theo GA, GB, GC. min min
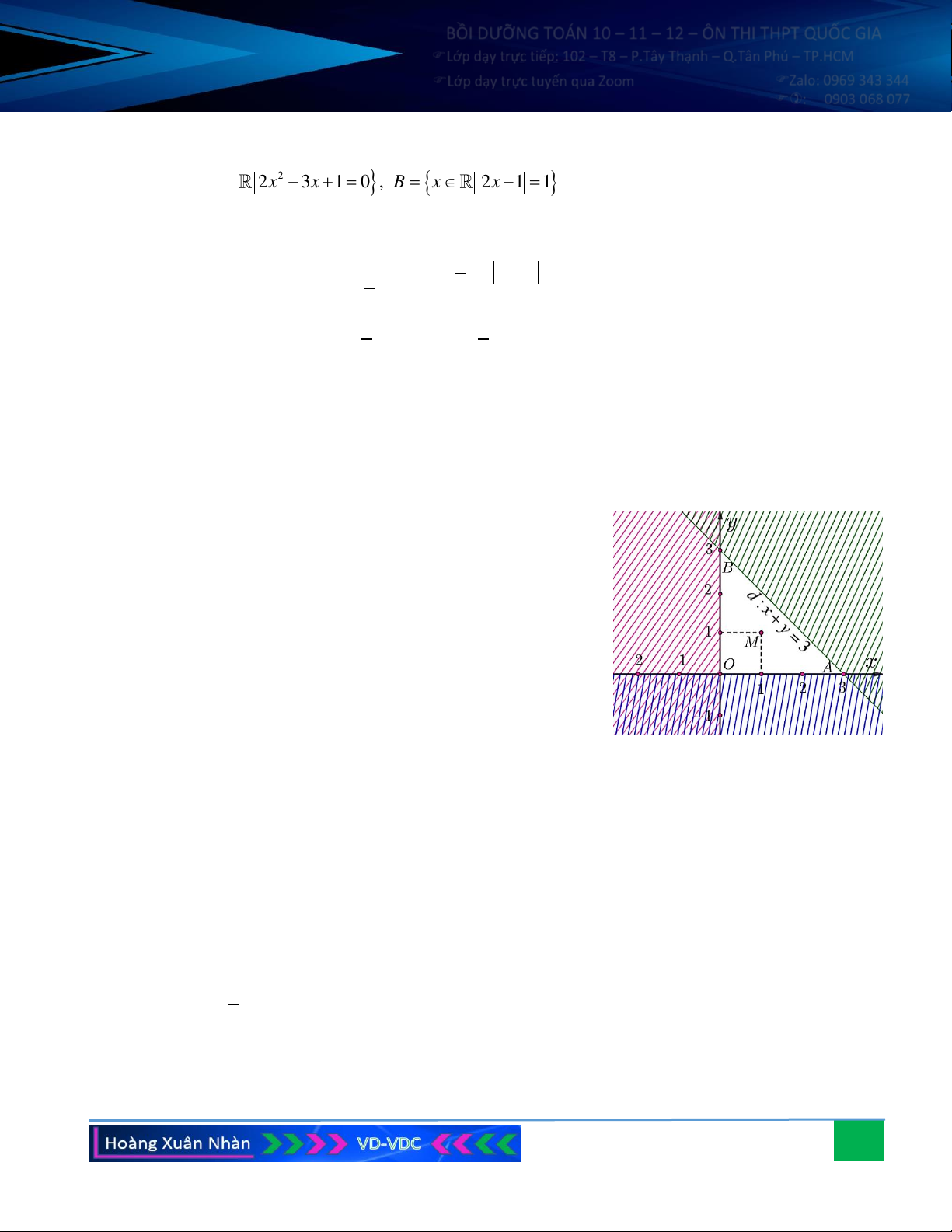
Câu 10. Cổng Arch tại thành phố St Louis của Mỹ có hình dạng của một parabol. Biết khoảng cách giữa hai
chân cổng là 162 m . Trên thành cổng, tại vị trí có độ cao 43 m so với mặt đất, người ta thả một sợi
dây chạm đất và vị trí chạm đất này cách chân cổng (điểm A) một khoảng 10 m. Hãy tính gần đúng
độ cao của cổng Arch (tính chính xác đến hàng phần chục).
================HẾT=============== 33
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Höôùng daãn giaûi ñeà soá 07
Câu 1. Cho A =  2 x
2x − 3x +1 =  0 , B = x  2x −1 =  1 . Tìm A  , B A , B A \ , B B \ A. Hướng dẫn giải: x =1  1  2x −1 =1 x =1 Ta có: 2 2x 3x 1 0  − + =  1  A = 1  ;  − =    =  ; 2x 1 1 B   0  ;1 . x =  2 2x −1 = 1 − x = 0  2  1  1 
Vậy A B =  
1 , A B = 0; ;1 , A \ B =   , B \ A =   0 .  2  2 x + y  3 
Câu 2. Biểu diễn miền nghiệm của hệ sau trên mặt phẳng tọa độ: x  0 . y  0  Hướng dẫn giải:
Vẽ các đường thẳng d : x + y = 3 , Ox : y = 0, Oy : x = 0 . Chọn điểm M (1; )
1 , thay tọa độ M vào (1): 1+1  3 (đúng), do vậy (1; )
1 là nghiệm của (1), ta gạch bỏ nửa mặt phẳng bờ là
đường thẳng d không chứa điểm M.
Tương tự như thế, thay tọa độ M vào (2) và (3) ta thấy đều thỏa mãn, do vậy (1; )
1 cũng là nghiệm của (2) và (3). Ta gạch bỏ
nửa mặt phẳng có bờ là đường thẳng Ox, Oy mà không chứa M.
Miền nghiệm của hệ bất phương trình là miền tam giác ABC
(gồm tam giác ABC và miền trong của nó). (Xem hình bên).
Câu 3. Xét sự biến thiên của hàm số f ( x) 2
= 2x −1 trên (−;0) . Hướng dẫn giải:
Lấy x x tùy ý thuộc (− ; 0) , x x . 1, 2 1 2
Xét f ( x ) − f ( x ) = ( 2 2x − ) 1 − ( 2
2x −1 = 2 x − x x + x . 1 2 1 2 ) ( 1 2)( 1 2)
Vì x x x − x  0 ; x , x  − ; 0  x + x  0 . Do vậy 2( x − x x + x  0 . 1 2 ) ( 1 2 ) 1 2 ( ) 1 2 1 2 1 2
Suy ra f ( x − f x  0  f x f x . 1 ) ( 2 ) ( 1) ( 2 )
Vậy hàm số đã cho nghịch biến trên (− ; 0) . 1 Câu 4. Cho sin  = với 0 0
90    180 . Tính cos và tan . 3
Hướng dẫn giải: Vì 0 0
90    180 nên cos  0 . 34
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 2  1  8 2 2 Ta có: 2 2 2 2
sin  + cos  = 1  cos  = 1− sin  = 1− =  cos = −   .  3  9 3 1 sin  1 Do đó: 3 tan  = = = − . cos 2 2 2 2 − 3
Câu 5. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số f ( x) 2
= x − 3x +1 với x 0;4.
Hướng dẫn giải: b 3  3  5
Ta có: a = 1, b = 3 − , c =1 − = và f = −  
. Vì a = 1  0 nên bề lõm đồ thị hướng lên. 2a 2  2  4
Bảng biến thiên hàm số khi x 0; 4 là:
Ta có thể kết luận: Với x 0; 4, hàm số đạt giá trị lớn nhất bằng 5, khi đó x = 4 ; hàm số đạt giá 5
trị nhỏ nhất bằng − , khi đó 3 x = . 4 2
Câu 6. Bảng số liệu sau thống kê nhiệt độ tại Thành phố Hồ Chí Minh trong một lần đo vào một ngày của năm 2021 : Giờ đo 1h 4h 7h 10h 13h 16h 19h 22h Nhiệt độ (độ C) 27 26 28 32 34 35 30 28
Tìm số trung bình, phương sai và độ lệch chuẩn của mẫu số liệu đã cho (làm tròn kết quả đến hàng phần trăm).
Hướng dẫn giải: 27 + 26 + ... + 30 + 28
Số trung bình là : x = = 30 ( 0C ). 8 Phương sai 1 : 2 2 2 2 s =
(x − x) + (x − x) +...+ (x − x)   1 2 8  8 1
= (27 −30)2 + (26 −30)2 +...+ (28−30)2  = 9,75 8   . Độ lệch chuẩn : 2 s =
s  3,12 ( 0C ).
Câu 7. Chứng minh rằng trong một hình bình hành, tổng bình phương các cạnh bằng tổng bình phương hai
đường chéo của hình bình hành đó. Hướng dẫn giải:
Gọi O là giao điểm hai đường chéo của hình bình hành ABCD nên O là trung điểm của AC và BD.
Áp dụng công thức đường trung tuyến trong tam giác ABD ta có: 35
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 2 2 2 AB + AD BD 2 OA = − 2 4 2 2 2 2 AC AB + AD BD  = − 4 2 4 2  AC = ( 2 2 AB + AD ) 2 2 − BD 2 2
AC + BD = ( 2 2 2 AB + AD ) 2 2 2 2 2 2
AC + BD = AB + AB + AD + AD 2 2 2 2 2 2
AC + BD = AB + CD + BC + AD (điều phải chứn minh). Câu 8. Cho ABC  vuông tại B có 0
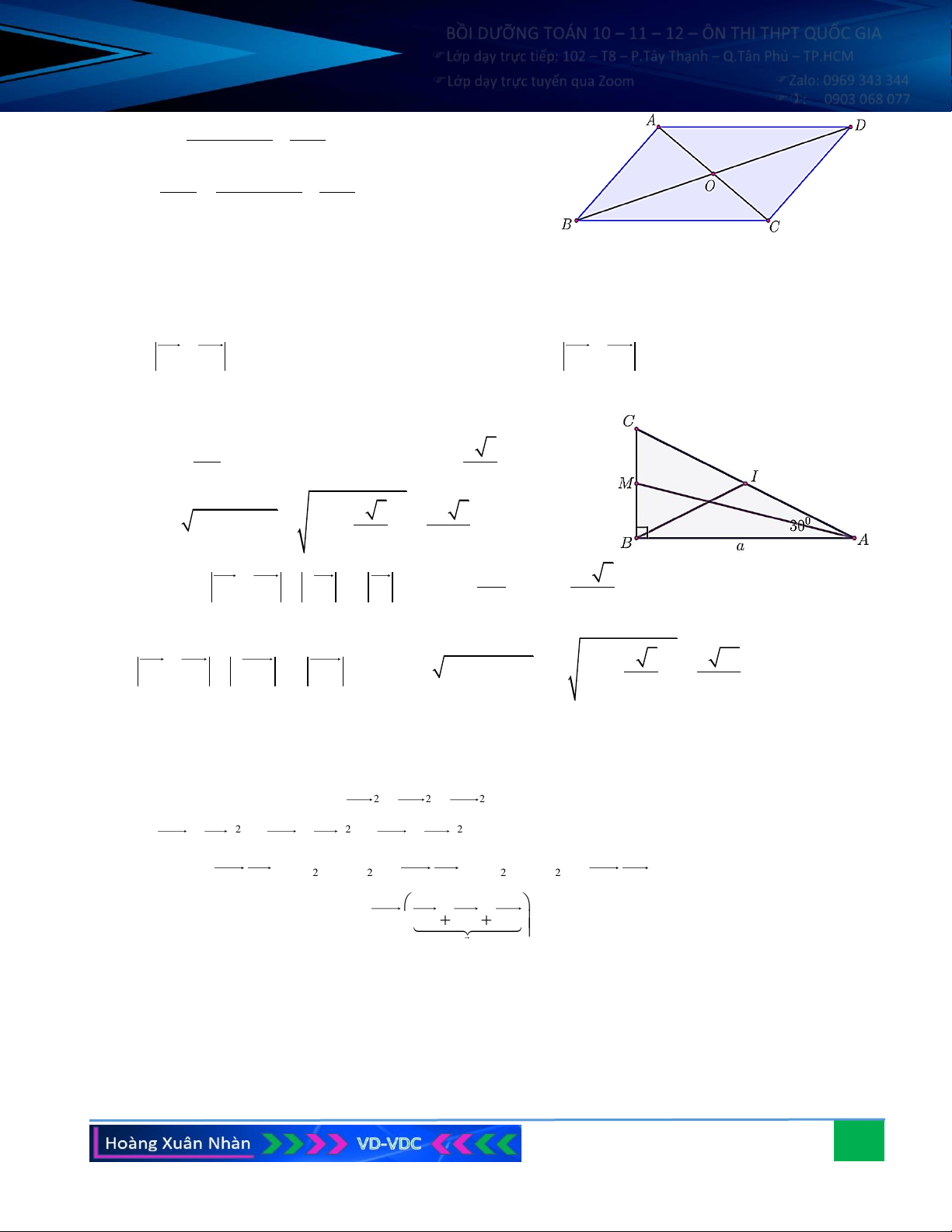
A = 30 , AB = a . Gọi I là trung điểm của AC . Hãy tính: a) BA + BC ; b) AB + AC . Hướng dẫn giải: Xét ABC  vuông tại B: BC a 3 0 tan A =  BC = A .
B tan A = a tan 30 = , AB 3 2  a 3  2a 3 2 2 2 AC = AB + BC = a +   =   . 3 3   AC 2a 3
a) Ta có: BA + BC = 2BI = 2 BI = 2BI = 2. = AC = . 2 3
b) Gọi M là trung điểm của BC, ta có: 2  a 3  a 39 2 2
AB + AC = 2AM = 2 AM = 2AM = 2 AB + BM 2 = 2 a +   =   . 6 3  
Câu 9. Cho tam giác ABC có trọng tâm G. Tìm vị trí của M để tổng 2 2 2
P = MA + MB + MC đạt giá trị nhỏ nhất P . Tính P theo GA, GB, GC. min min Hướng dẫn giải: 2 2 2 Ta có: 2 2 2
MA + MB + MC = MA + MB + MC
(MG GA)2 (MG GB)2 (MG GC)2 = + + + + + 2 2 2 2 2 2 = MG + 2M .
G GA + GA + MG + 2M .
G GB + GB + MG + 2M . G GC + GC   2 2 2 2
= 3MG + GA + GB + GC + 2MG GA + GB + GC  2 2 2 2 
 = 3MG + GA + GB + GC .  0 
Nhận xét: Các điểm A, B, C, G cố định, do đó 2 2 2
GA + GB + GC không đổi.
P nhỏ nhất khi và chỉ khi MG nhỏ nhất  MG = 0  M trùng với G. Khi đó: 2 2 2 P
= GA + GB + GC . min
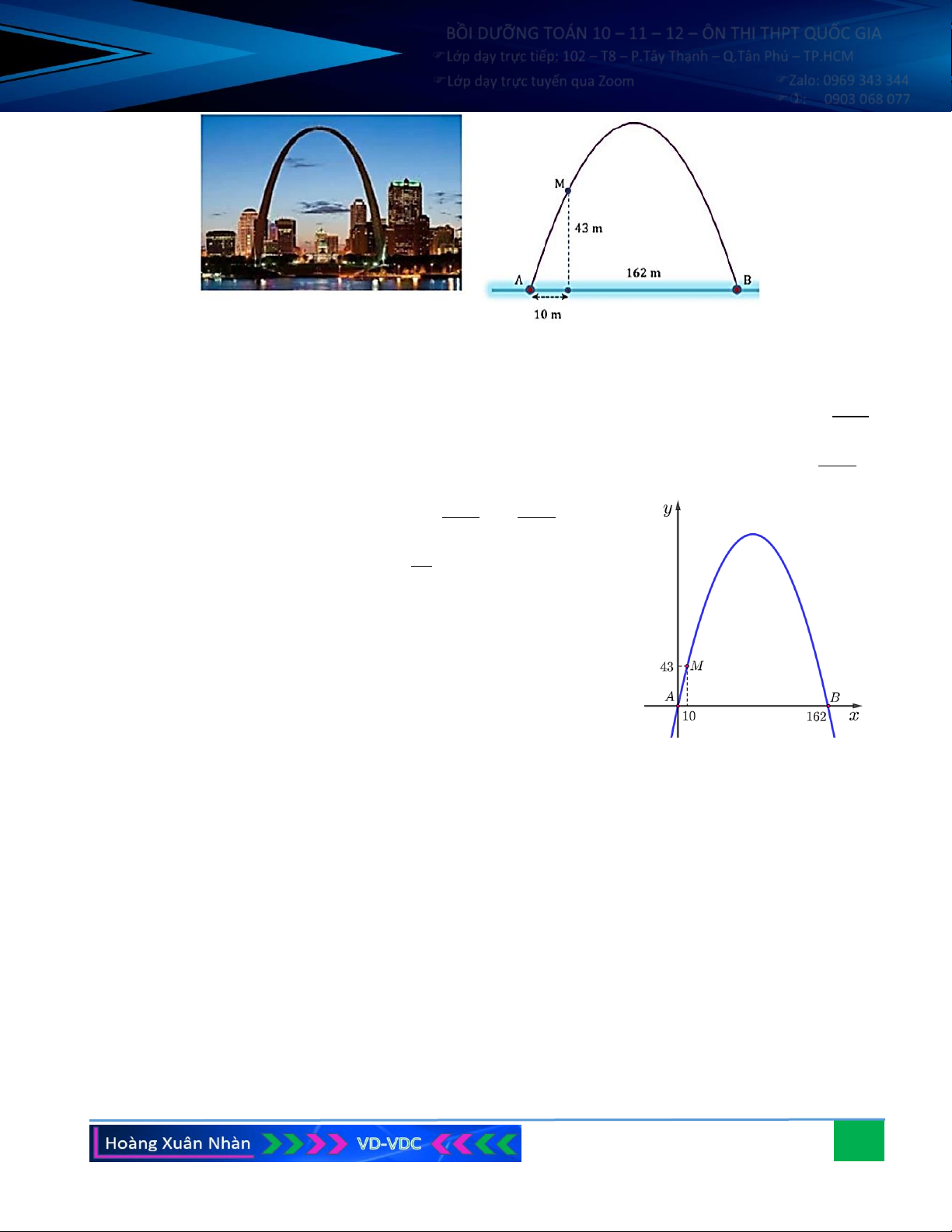
Câu 10. Cổng Arch tại thành phố St Louis của Mỹ có hình dạng của một parabol. Biết khoảng cách giữa hai
chân cổng là 162 m . Trên thành cổng, tại vị trí có độ cao 43 m so với mặt đất, người ta thả một sợi
dây chạm đất và vị trí chạm đất này cách chân cổng (điểm A) một khoảng 10 m. Hãy tính gần đúng
độ cao của cổng Arch (tính chính xác đến hàng phần chục). 36
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 Hướng dẫn giải:
Dựng hệ trục Oxy như hình vẽ và gọi hàm số tương ứng cổng Arch là: 2
y = ax + bx + c (a  0) .  =  43 c 0 a = −    Vì parabol qua ba điể 1520
m A(0;0), B (162;0), M (10; 43) nên: 2 1
 62 a +162b + c = 0   . 3483   2 10 +10 + = 43 b a b c =   760 43 3483
Do vậy ta xác định được hàm số là 2 y = − x + x . 1520 760 Đỉ b
nh I của parabol có tọa độ: x = − = 81, y 185,6 . I 2a I
Vậy, chiều cao của cổng gần bằng 185, 6 m . 37
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
ÑEÀ REØN LUYEÄN SOÁ 08 Time: 90 phuùt ơ Câu 1.
a) Cho A = −4; 4, B = 1;7 . Tìm A , B A , B A \ , B B \ A .
b) Cho hai tập hợp A = ( 4
− ;3) và B = (m − 7;m). Tìm m để B A. −x
Câu 2. Xét sự đồng biến, nghịch biến hàm số f ( x) = 1; − +  . x + trên ( ) 1 1
Câu 3. Cho cos x =
. Tính giá trị biểu thức 2 2
P = 3sin x + 4cos x . 2
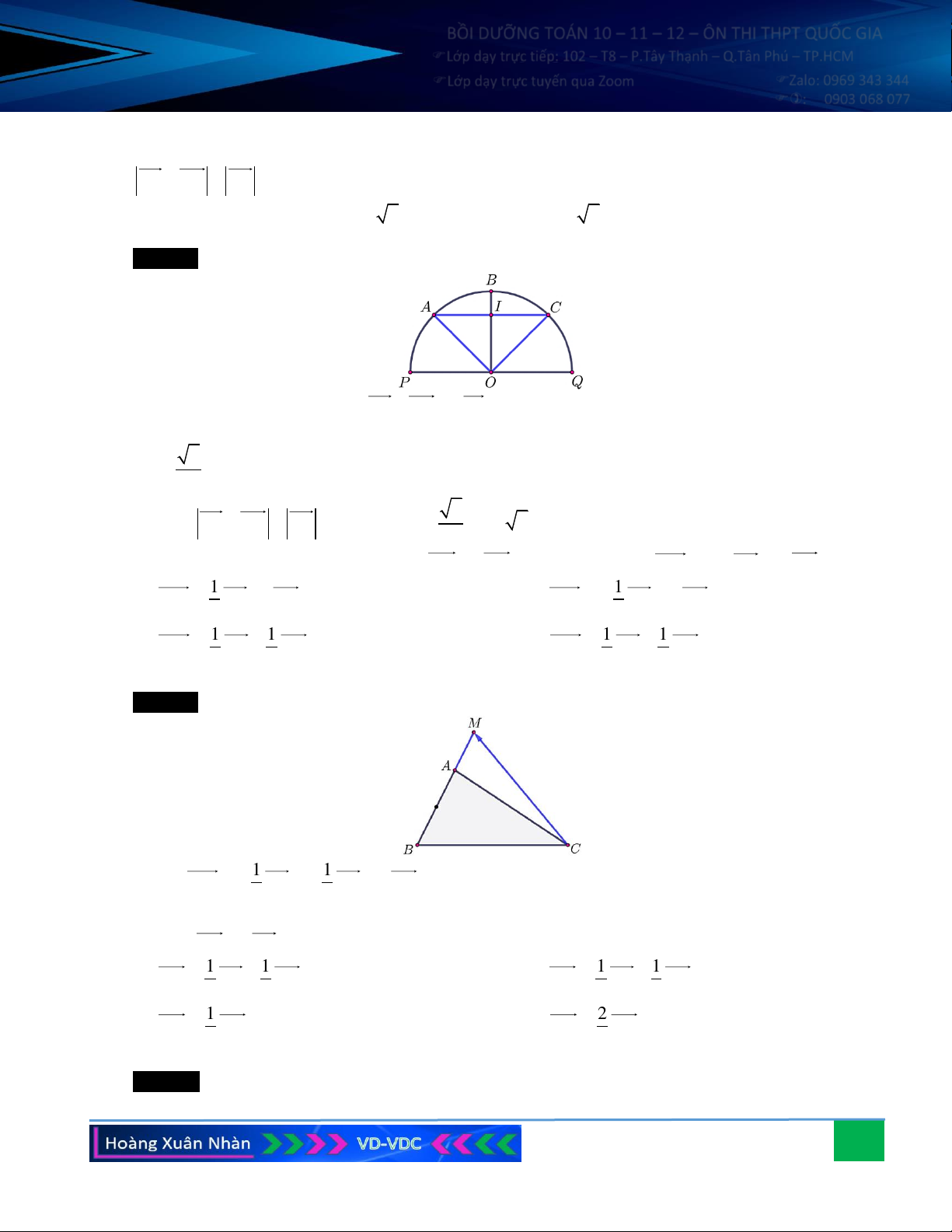
Câu 4. Cho tam giác cân ABC có 0
A = 120 và AB = AC = a . Lấy điểm M trên cạnh BC sao cho 2BC BM =
. Tính độ dài AM . 5
Câu 5. Xác định hàm số bậc hai có đồ thị là parabol ( P) 2
: y = ax − 4x + c có trục đối xứng là là đường
thẳng x = 2 và cắt trục hoành tại điểm M (3;0) .
Câu 6. Mẫu số liệu sau ghi rõ số tiền thưởng tết Nguyên Đán của 13 nhân viên của một công ty (đơn vị :
triệu đồng) : 10 10 11 12 12 13 14,5 15 18 20 20 21 28.
a) Tìm tứ phân vị của mẫu số liệu.
b) Tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu.
Câu 7. Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 g hương liệu, 9 lít nước và 210 g
đường để pha chế nước cam và nước táo. Để pha chế 1 lít nước cam cần 30 g đường, 1 lít nước và 1
g hương liệu; pha chế 1 lít nước táo cần 10 g đường, 1 lít nước và 4 g hương liệu. Mỗi lít nước cam
nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điển thưởng. Hỏi cần pha chế bao nhiêu
lít nước trái cây mỗi loại để được số điểm thưởng là lớn nhất?
Câu 8. Cho tam giác ABC có hai đường trung tuyến BN, CP . Hãy biểu thị mỗi vectơ AB, BC theo cặp vectơ BN, CP .
Câu 9. Một người dùng một lực F có độ lớn 90 N làm một vật dịch chuyển một đoạn 100 m. Biết lực F
hợp với hướng dịch chuyển một góc 0
60 . Tính công sinh ra bởi lực F .
================HẾT=============== 38
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Höôùng daãn giaûi ñeà soá 08 Câu 1.
a) Cho A = −4; 4, B = 1;7 . Tìm A , B A , B A \ , B B \ A .
b) Cho hai tập hợp A = ( 4
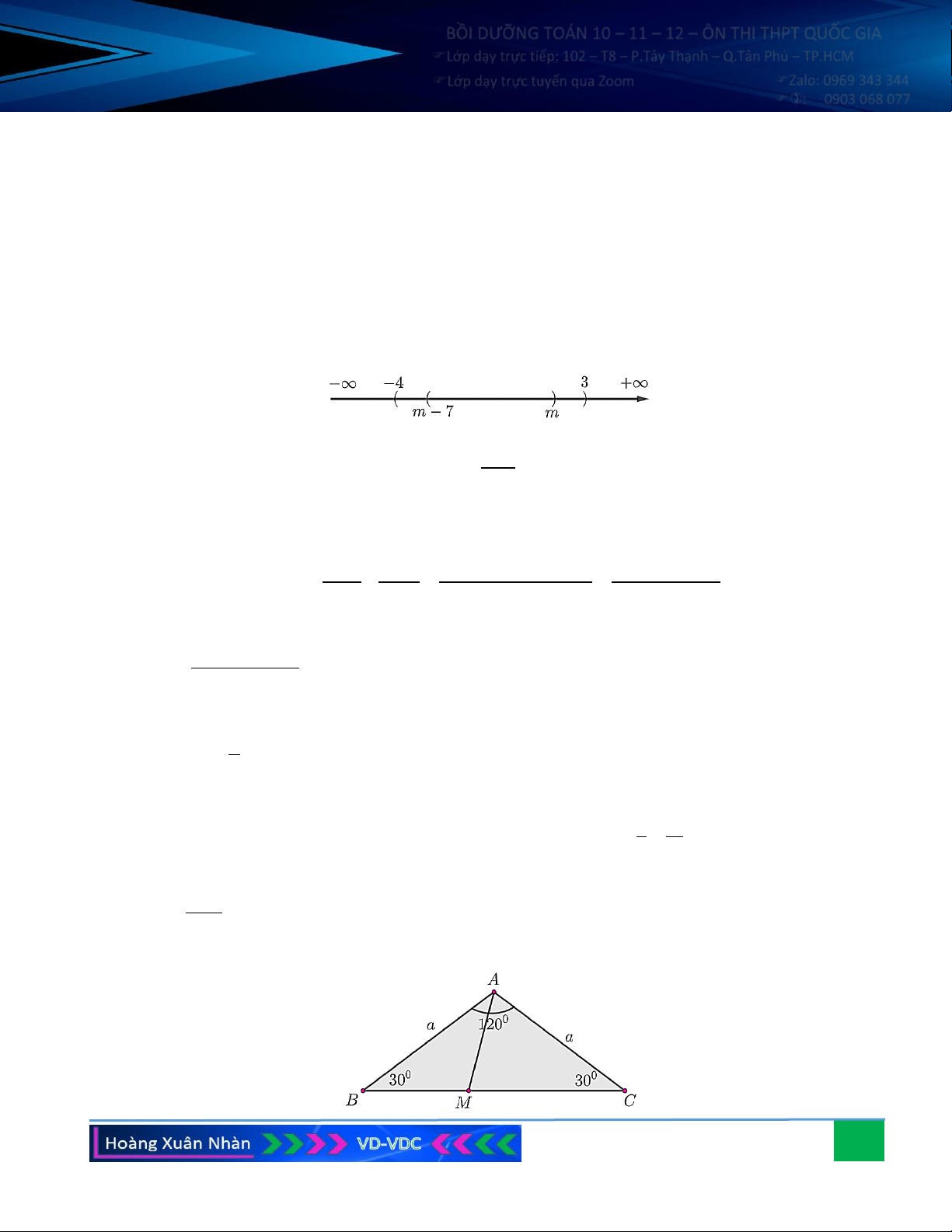
− ;3) và B = (m − 7;m). Tìm m để B A. Hướng dẫn giải:
a) Ta có: A B = 1; 4 , A B = −4; 7, A \ B =  4 − ; )
1 , B \ A = (4; 7 . m − 7  4 − m  3
b) Ta có: B A khi và chỉ khi     m = 3. m  3 m  3 −x
Câu 2. Xét sự đồng biến, nghịch biến hàm số f ( x) = 1; − +  . x + trên ( ) 1 Hướng dẫn giải:
Xét tùy ý x , x  1;
− +  và x x . 1 2 ( ) 1 2 −x −x
−x x − x + x x + x x − x
Khi đó: f ( x ) − f ( x ) 1 2 1 2 1 1 2 2 2 1 = − = = 1 2 x +1 x +1 x +1 x +1 x +1 x + . 1 1 2 ( 1 )( 2 ) ( 1 )( 2 ) Do x , x  1;
− +   x +1 x +1  0 ; x x x − x  0 . 1 2 ( ) ( 1 )( 2 ) 1 2 2 1 x − x Vì vậy 2 1 (
 0  f x − f x  0  f x f x x +1 x + . 1 1 )( 2 ) ( 1) ( 2) ( 1) ( 2)
Vậy hàm số đã cho nghịch biến trên ( 1; − + ) . 1
Câu 3. Cho cos x =
. Tính giá trị biểu thức 2 2
P = 3sin x + 4cos x . 2 Hướng dẫn giải: 1 13 Ta có: 2 2
P = 3sin x + 4 cos x = 3( 2 1− cos x) 2 2
+ 4cos x = 3+ cos x = 3+ = . 4 4
Câu 4. Cho tam giác cân ABC có 0
A = 120 và AB = AC = a . Lấy điểm M trên cạnh BC sao cho 2BC BM =
. Tính độ dài AM . 5 Hướng dẫn giải: 39
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077  1  2a 3 Ta có: 2 2 0 BC =
AB + AC − 2 ABAC cos120 2 2 = a + a − 2 . a . a − = a 3    BM = ;  2  5 2  2a 3  2a 3 3 a 7 2 2 0 AM = AB + BM − 2 . AB BM .cos 30 2 = a +   − 2 . a . =   . 5 5 2 5  
Câu 5. Xác định hàm số bậc hai có đồ thị là parabol ( P) 2
: y = ax − 4x + c có trục đối xứng là là đường
thẳng x = 2 và cắt trục hoành tại điểm M (3;0) . Hướng dẫn giải: ( b 4 a 1 =
P) có trục đối xứng x = − =
= 2  a =1; (P) lại qua M (3;0) 2  0 = .3 a
− 4.3+ cc = 3 . 2a 2a
Vậy hàm số bậc hai được xác định: 2
y = x − 4x + 3 .
Câu 6. Mẫu số liệu sau ghi rõ số tiền thưởng tết Nguyên Đán của 13 nhân viên của một công ty (đơn vị :
triệu đồng) : 10 10 11 12 12 13 14,5 15 18 20 20 21 28.
a) Tìm tứ phân vị của mẫu số liệu.
b) Tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu. Hướng dẫn giải:
a) Mẫu gồm 13 giá trị theo thứ tự không giảm: 10 10 11 12 12 13 14,5 15 18 20 20 21 28 ;
trung vị là 14,5; nên tứ phân vị thứ hai : Q = 14, 5 . 2
Xét nửa mẫu bên trái: 10 10 11 12 12 13; tứ phân vị thứ nhất: Q = 11,5 . 1
Xét nửa mẫu bên phải: 15 18 20 20 21 28; tứ phân vị thứ nhất: Q = 20 . 3
Vậy tứ phân vị của mẫu là Q = 11,5; Q = 14,5; Q = 20 . 1 2 3
b) Giá trị lớn nhất và nhỏ nhất của số liệu lần lượt là x = 28, x =10. max min
Khoảng biến thiên là : R = x − x =18. max min
Khoảng tứ phân vị là : Q
 = Q −Q = 8,5. 3 1
Câu 7. Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 g hương liệu, 9 lít nước và 210 g
đường để pha chế nước cam và nước táo. Để pha chế 1 lít nước cam cần 30 g đường, 1 lít nước và 1
g hương liệu; pha chế 1 lít nước táo cần 10 g đường, 1 lít nước và 4 g hương liệu. Mỗi lít nước cam
nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điển thưởng. Hỏi cần pha chế bao nhiêu
lít nước trái cây mỗi loại để được số điểm thưởng là lớn nhất? Hướng dẫn giải:
Gọi x, y lần lượt là số lít nước cam và táo do một đội pha chế thực hiện được ( x, y  0) .
Số điểm thưởng của đội là: F ( x ; y) = 60x + 80 y .
Số gam đường cần dùng là: 30x +10y .
Số lít nước cần dùng là: x + y .
Số gam hương liệu cần dùng là: x + 4y . 40
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Vì trong cuộc thi pha chế, mỗi đội chơi sử dụng tối đa 24 g hương liệu, 9 lít nước và 210 g đường x + 4y  24 x+ y  9 
nên ta có hệ bất phương trình: 3
 0x +10y  210 (*). x  0  y  0 
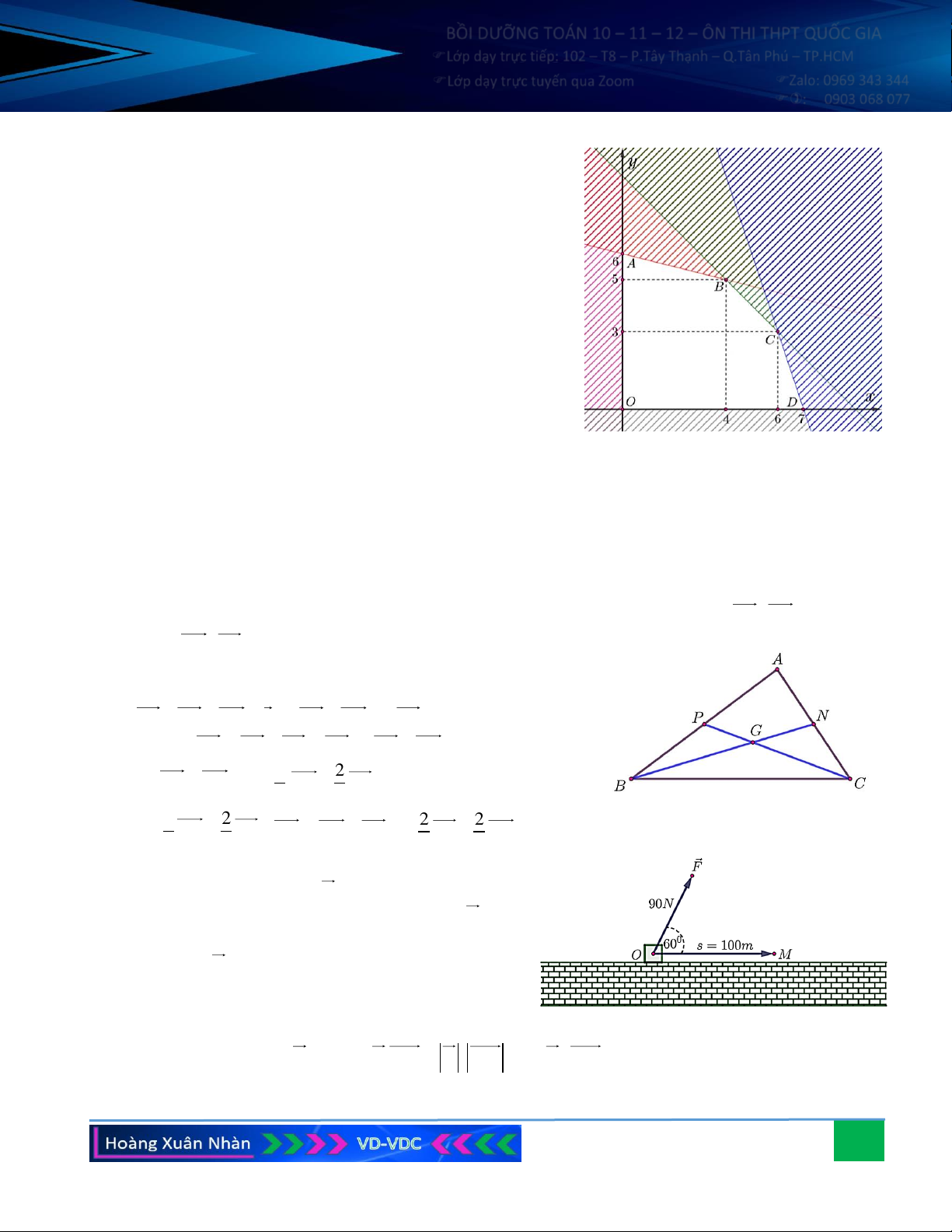
Biểu diễn miền nghiệm của hệ (*) như hình bên, ta thấy
rằng miền nghiệm của hệ chính là miền của ngũ giác
OABCD với 5 đỉnh là:
O (0;0), A(0;6), B (4;5), C (6;3), D (7;0) .
Ta biết rằng biểu thức hai biến F ( x ; y) = 60x + 80 y sẽ
đạt giá trị lớn nhất (và nhỏ nhất) khi cặp ( x; y) nhận một
trong các tọa độ đỉnh của ngũ giác OABCD.
Ta có: F (0;0) = 60.0 + 80.0 = 0 , F (0;6) = 60.0 + 80.6 = 480 , F (4;5) = 60.4 + 80.5 = 640 ,
F (6;3) = 60.6 + 80.3 = 600 , F (7;0) = 60.7 + 80.0 = 420 .
Vậy F ( x ; y ) đạt giá trị lớn nhất bằng 640, khi đó ( x ; y) = (4;5) .
Như vậy để được số điểm thưởng là lớn nhất thì người chơi cần pha chế 4 lít nước cam và 5 lít nước táo.
Câu 8. Cho tam giác ABC có hai đường trung tuyến BN, CP . Hãy biểu thị mỗi vectơ AB, BC theo cặp vectơ BN, CP . Hướng dẫn giải:
Gọi G là trọng tâm của tam giác ABC , ta có :
GA + GB + GC = 0  GB + GC = G − A.
Khi đó: AB = GB − GA = GB + (GB + GC ) = 2GB + 2 2 GC = 2
− . .BN − CP 3 3 4 2 = − 2 2 BN −
CP ; BC = GC − GB = − CP + BN 3 3 3 3 .
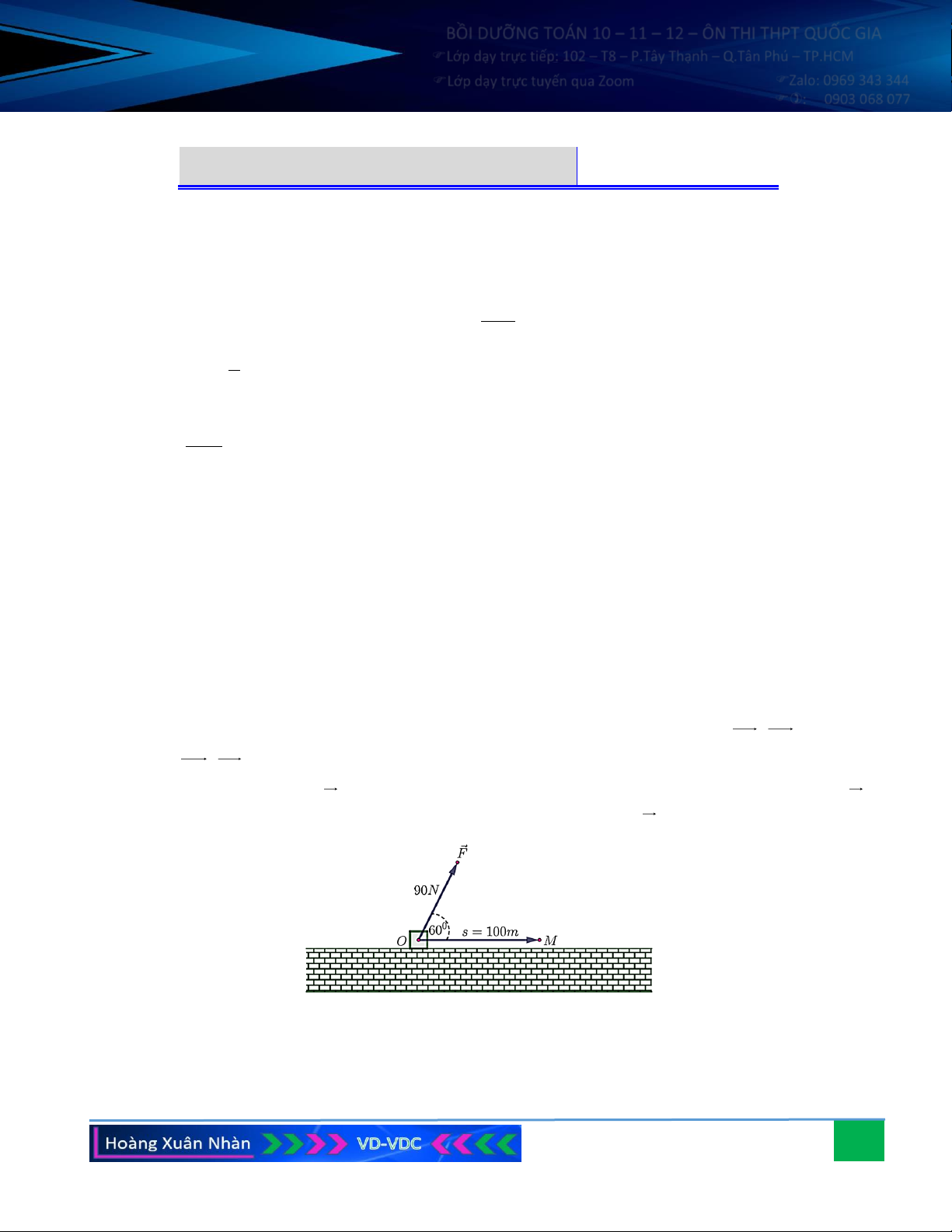
Câu 9. Một người dùng một lực F có độ lớn 90 N làm một
vật dịch chuyển một đoạn 100 m. Biết lực F hợp
với hướng dịch chuyển một góc 0 60 . Tính công sinh ra bởi lực F . Hướng dẫn giải:
Đặt OM = s là đoạn đường mà vật di chuyển được với O là điểm đặt vật ban đầu.
Công sinh ra bởi lực F là: A = F.OM = F . OM .cos (F, OM ) 0 = 90.100.cos60 = 4500J . 41
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
ÑEÀ REØN LUYEÄN SOÁ 09 Time: 90 phuùt ơ Câu 1.
a) Xác định hai tập hợp A, B biết rằng: A \ B = 1;5;7; 
8 , B \ A = 2;1 
0 , A B = 3;6;  9 .
b) Trong một trường THPT, khối 10 có 160 em học sinh tham gia câu lạc bộ Toán, 140 em học
sinh tham gia câu lạc bộ Tin, 10 em học sinh tham gia cả hai câu lạc bộ. Biết rằng tất cả học sinh
khối 10 đều tham gia ít nhất một trong hai câu lạc bộ trên. Hỏi khối 10 có bao nhiêu học sinh?
Câu 2. Tìm tập xác định của các hàm số sau: 2 x + 2
x + x −1 khi x 1  a) y = ; b) f ( x) =  . x x +1 2  x −1 khi x  1
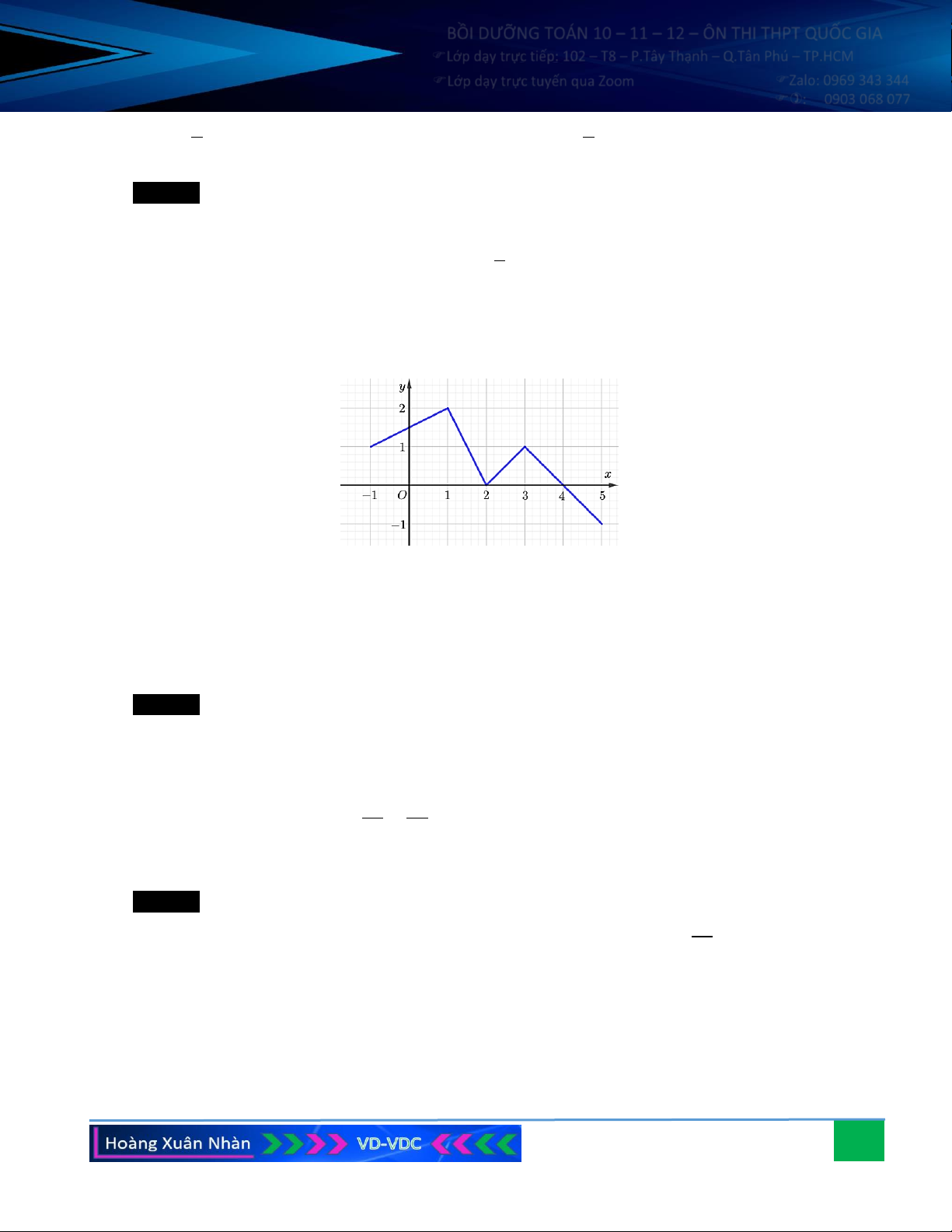
Câu 3. Vẽ đồ thị hàm số 2
y = x − 2x − 8 . 3
Câu 4. Tìm giá trị m biết parabol 2
y = x + x + m có đỉnh nằm trên đường thẳng y = . 4
Câu 5. Hàm lượng Natri (đơn vị miligam, 1 mg = 0,001 g) trong 100 g một số loại ngũ cốc được cho như sau : 0 340 70 140 200 180 210 150 100 130 140 180 190 160 290 50 220 180 200 210
Hãy tìm tứ phân vị của mẫu trên. Các tứ phân vị này cho ta thông tin gì? 1 + cot x tan x + 1
Câu 6. Chứng minh rằng : = 1 − cot x
tan x − (các biểu thức đều có nghĩa). 1 x
Câu 7. Cho hàm số y =
2x − 3m + 4 + x + m− với m là tham số. Tìm m để hàm số có tập xác định là 1 0;+) .
Câu 8. Cho tam giác ABC có b + c = 2a . Chứng minh rằng: 6Rr = bc , trong đó ,
R r lần lượt là bán kính
đường tròn ngoại tiếp và nội tiếp tam giác . ABC
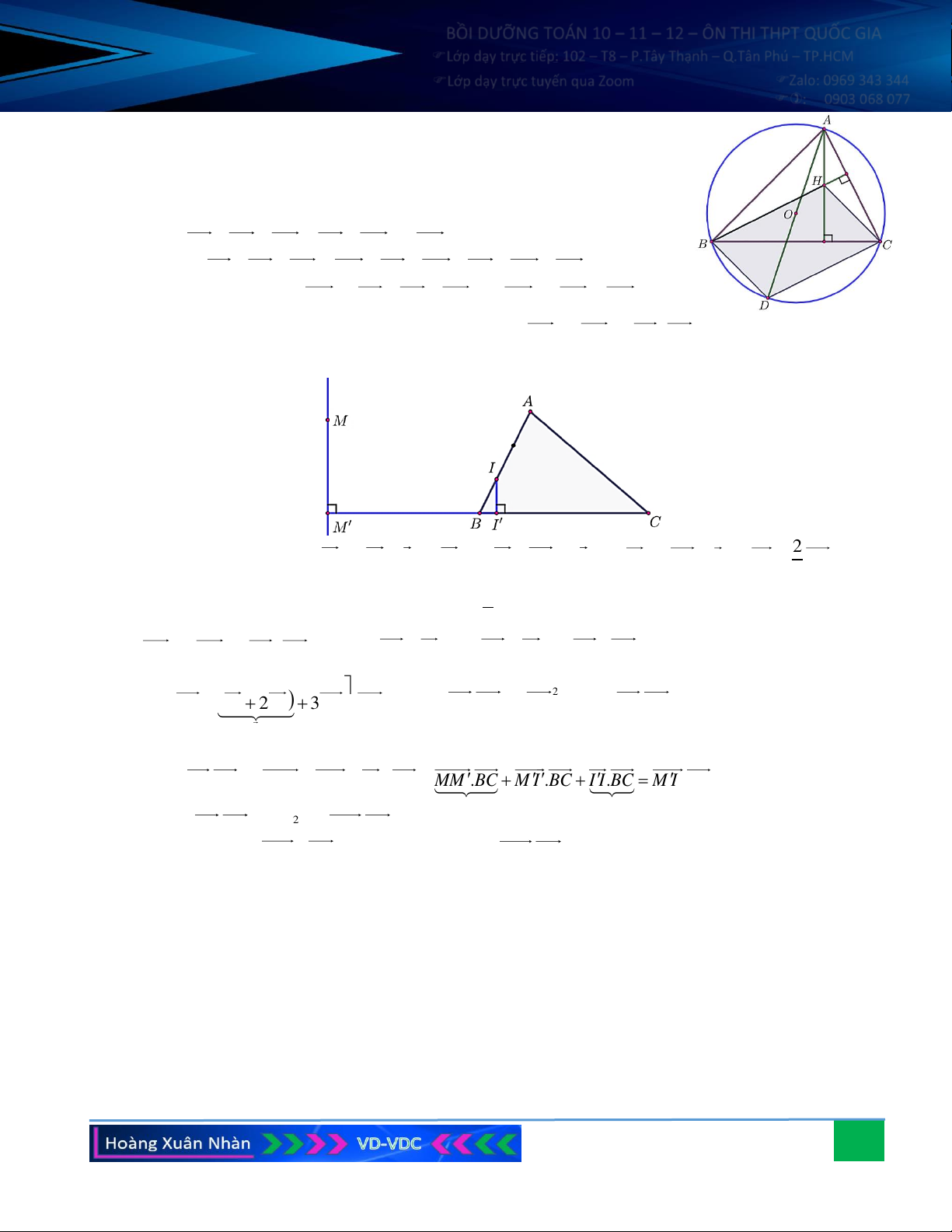
Câu 9. Cho hình thang ABCD vuông tại A và B , biết AD = ,
a BC = 3a và cạnh AB = 2 . a a) Tính A .
B BD, BC.BD và A . C B . D
b) Gọi I, J lần lượt là trung điểm của AB, CD. Tính A . C IJ .
Câu 10. Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm I và II . Mỗi
sản phẩm I bán lãi 500 nghìn đồng, mỗi sản phẩm II bán lãi 400 nghìn đồng. Để sản xuất được
một sản phẩm I thì Chiến phải làm việc trong 3 giờ, Bình phải làm việc trong 1 giờ. Để sản xuất
được một sản phẩm II thì Chiến phải làm việc trong 2 giờ, Bình phải làm việc trong 6 giờ. Một
người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm
việc quá 180 giờ và Bình không thể làm việc quá 220 giờ. Hỏi số tiền lãi lớn nhất trong một tháng
của xưởng là bao nhiêu?
================HẾT=============== 42
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Höôùng daãn giaûi ñeà soá 09 Câu 1.
a) Xác định hai tập hợp A, B biết rằng: A \ B = 1;5;7; 
8 , B \ A = 2;1 
0 , A B = 3;6;  9 .
b) Trong một trường THPT, khối 10 có 160 em học sinh tham gia câu lạc bộ Toán, 140 em học
sinh tham gia câu lạc bộ Tin, 10 em học sinh tham gia cả hai câu lạc bộ. Biết rằng tất cả học sinh
khối 10 đều tham gia ít nhất một trong hai câu lạc bộ trên. Hỏi khối 10 có bao nhiêu học sinh? Hướng dẫn giải:
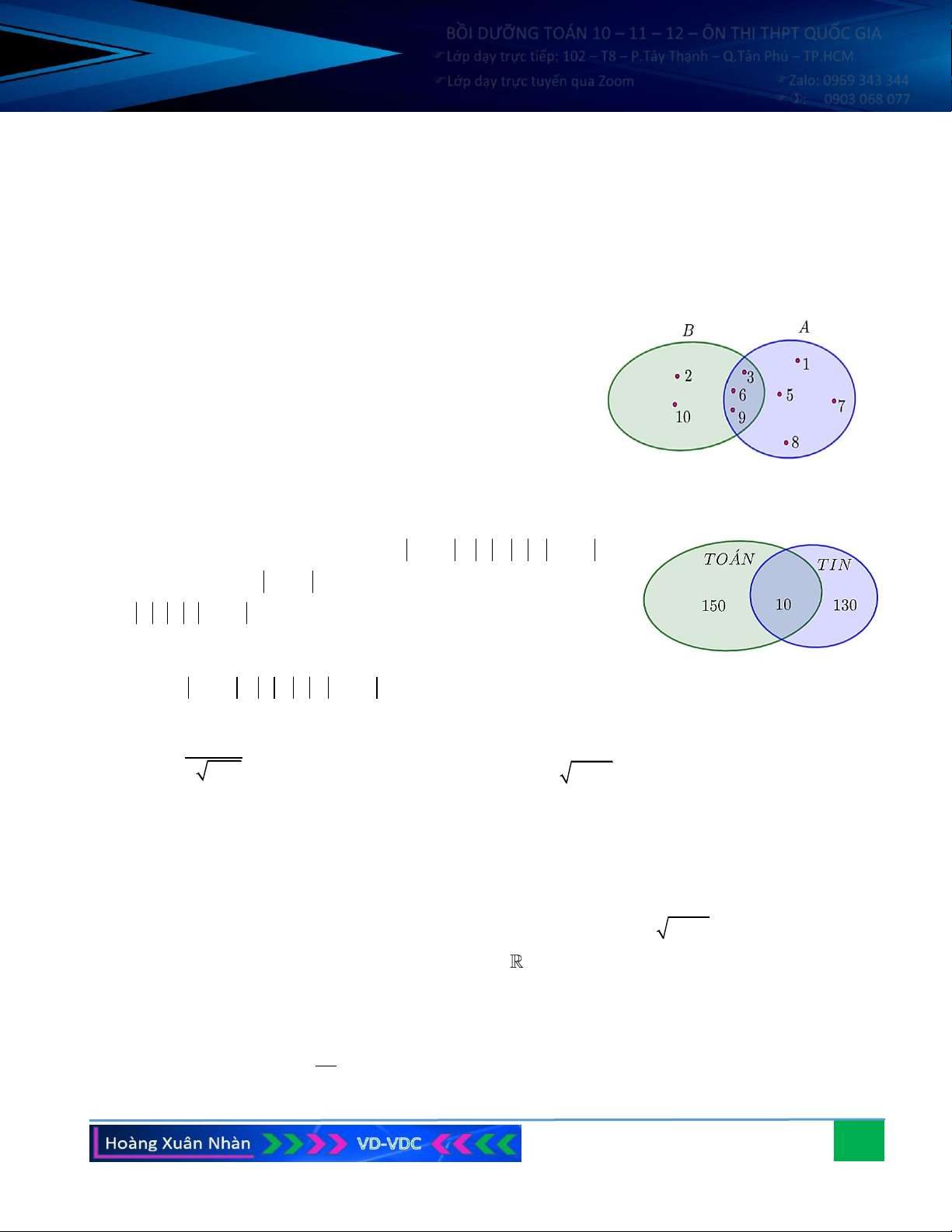
a) Ta thực hiện biểu đồ Ven như hình bên.
Vì vậy: A = 1;5;7;  8 3;6;  9 = 1;3;5;6;7;8;  9 , B = 2;  10 3;6;  9 = 2;3;6;9;  10 . b)
☺ Cách giải 1: Dựa vào biểu đồ Ven, ta có:
Số học sinh khối 10 chỉ tham gia câu lạc bộ Toán: 160 −10 = 150 (em).
Số học sinh khối 10 chỉ tham gia câu lạc bộ Tin: 140 −10 = 130 (em).
Tổng số học sinh khối 10 là: 150 +10 +130 = 290 (em).
☺ Cách giải 2: Dựa vào công thức A B = A + B − A B
trong đó ký hiệu A B là số phần tử của tập AB , ký hiệu
A , B , A B lần lượt là số phần tử của các tập , A , B AB .
Gọi A là tập hợp các học sinh khối 10 tham giác câu lạc bộ Toán,
B là tập hợp các học sinh khối 10 tham gia câu lạc bộ Tin.
Ta có: A B = A + B − A B = 160 +140 −10 = 290 (em).
Câu 2. Tìm tập xác định của các hàm số sau: 2 x + 2
x + x −1 khi x 1  a) y = ; b) f ( x) =  . x x +1 2  x −1 khi x  1 Hướng dẫn giải: x  0 x  0
a) Hàm số xác định khi và chỉ khi    . x +1  0 x  1 −
Vậy tập xác định hàm số là: D = ( 1; − + ) \  0 .
b) Khi x  1 thì f ( x) 2
= x + x −1 luôn xác định; khi x 1 thì f (x) 2
= x −1 luôn xác định.
Vậy tập xác định hàm số: D = (−; ) 1  1; + ) = .
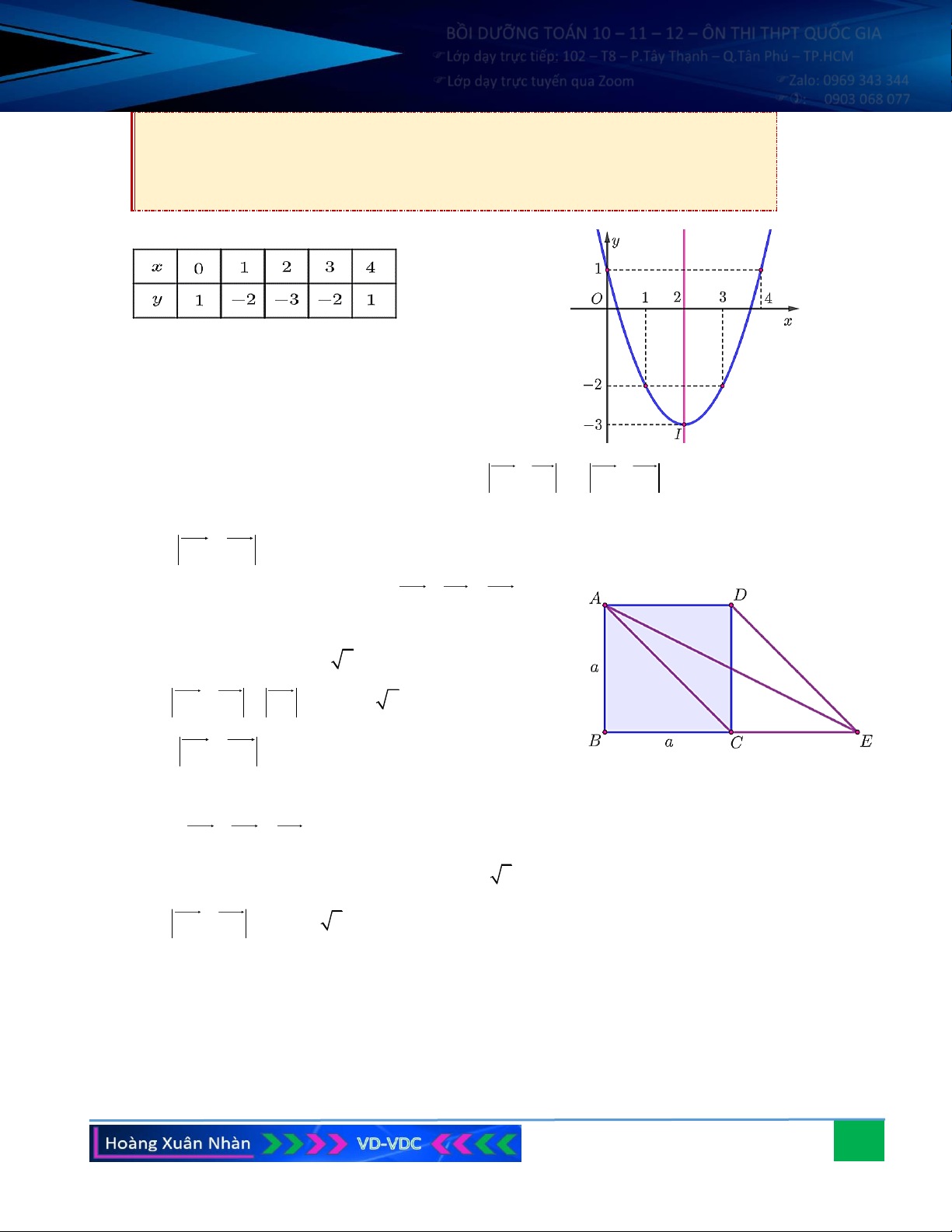
Câu 3. Vẽ đồ thị hàm số 2
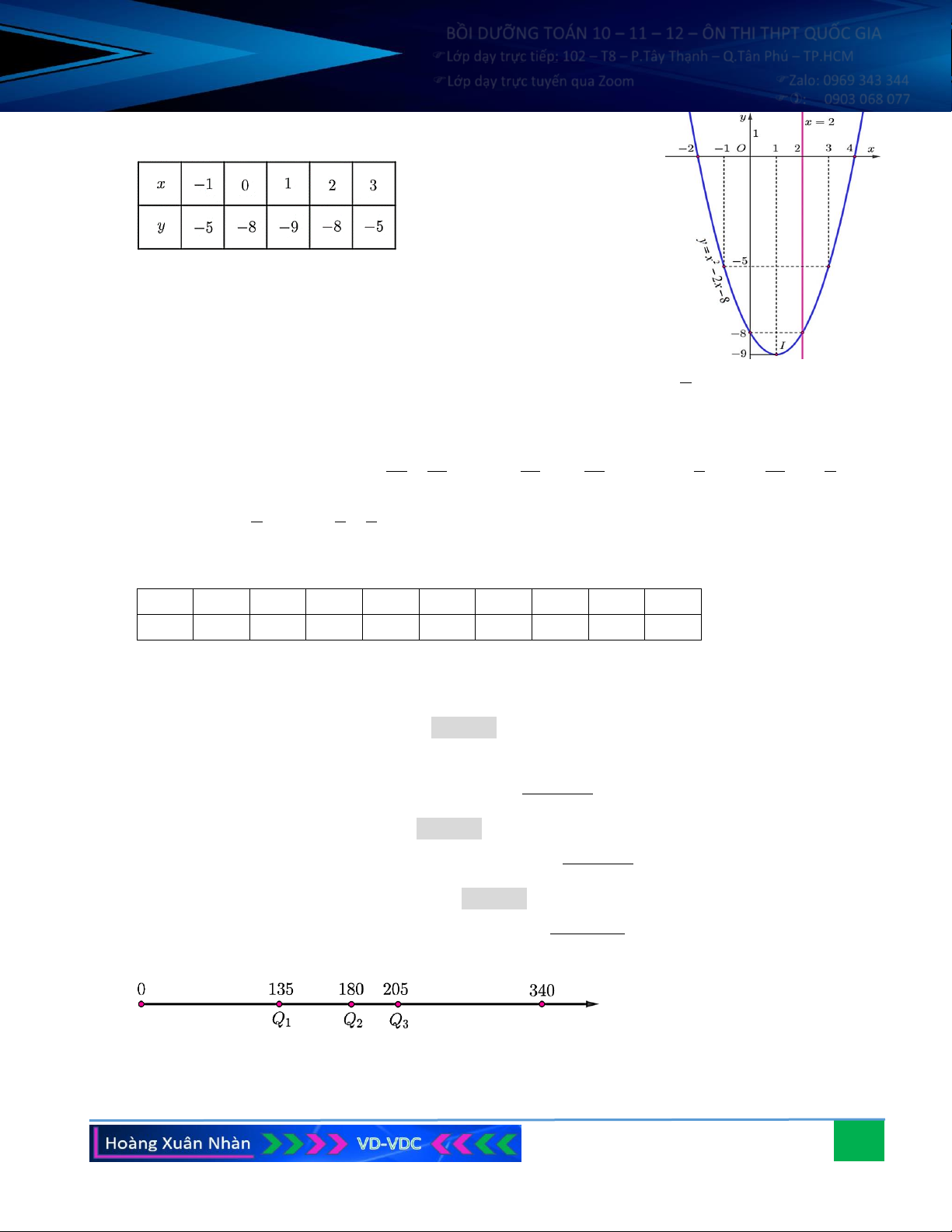
y = x − 2x − 8 . Hướng dẫn giải: Đỉ b
nh I có tọa độ: x = − =1, y = 9 − hay I − . I I (1; 9) 2a
Trục đối xứng parabol: x = 1. 43
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Vì a = 1  0 nên bề lõm parabol hướng lên. Ta có bảng giá trị: Đồ thị hàm số: 3
Câu 4. Tìm giá trị m biết parabol 2
y = x + x + m có đỉnh nằm trên đường thẳng y = . 4 Hướng dẫn giải: 2 b 1 −  1 −   1 −  1  1 − 1 
Tọa độ đỉnh I của parabol: x = − =  y = +
+ m = m − hay I ; m − . I       2a 2 I  2   2  4  2 4  3 1 3
Vì I  (d ) : y = nên m − =  m =1. 4 4 4
Câu 5. Hàm lượng Natri (đơn vị miligam, 1 mg = 0,001 g) trong 100 g một số loại ngũ cốc được cho như sau : 0 340 70 140 200 180 210 150 100 130 140 180 190 160 290 50 220 180 200 210
Hãy tìm tứ phân vị của mẫu trên. Các tứ phân vị này cho ta thông tin gì? Hướng dẫn giải:
Sắp xếp các giá trị của mẫu theo thứ tự không giảm :
0 50 70 100 130 140 140 150 160 180 180 180 190 200 200 210 210 220 290 340 ; (n = 20). 180 +180
Tứ phân vị thứ hai chính là trung vị của mẫu : Q = =180 . 2 2
Xét nửa mẫu bên trái : 0 50 70 100 130 140 140 150 160 180 . 130 +140
Tứ phân vị thứ nhất chính là trung vị nửa mẫu này : Q = =135 . 1 2
Xét nửa mẫu bên phải : 180 180 190 200 200 210 210 220 290 340. 200 + 210
Tứ phân vị thứ ba chính là trung vị nửa mẫu này : Q = = 205. 3 2
Biểu diễn tứ phân vị trên trục số :
Các tứ phân vị cho ta hình ảnh phân bố của mẫu số liệu. Khoảng cách từ Q đến Q là 45 trong khi 1 2
khoảng cách từ Q đến Q là 25. Điều này cho thấy mẫu số liệu tập trung với mật độ cao ở bên 2 3
phải Q và mật độ thấp ở bên trái Q . 2 2 44
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 1 + cot x tan x + 1
Câu 6. Chứng minh rằng : = 1 − cot x
tan x − (các biểu thức đều có nghĩa). 1 Hướng dẫn giải: 1 tan x + 1 1 + 1 + cot x tan x + 1 Ta có: t anx t anx = = =
(điều phải chứng minh). 1 − cot x 1 tan x − 1 tan x − 1 1 − tan x tan x x
Câu 7. Cho hàm số y =
2x − 3m + 4 + x + m− với m là tham số. Tìm m để hàm số có tập xác định là 1 0;+) . Hướng dẫn giải:  3m − 4
2x − 3m + 4  0 x  Hàm số xác định     2 .
x + m −1  0
 x 1−m 3m − 4 6  −  Trườ 3m 4
ng hợp 1: 1− m
m  , tập xác định hàm số D = ; + \ 1−    m . 2 5  2  6
Tập xác định này không thể bằng 0; +) theo đề bài. Do đó m  không thỏa mãn. 5 3m − 4 6  −  Trườ 3m 4
ng hợp 2: 1− m
m  , tập xác định của hàm số là D = ; +   . 2 5  2  m −
Do đó, hàm số có tập xác định là  +) 3 4 4 0; 
= 0  m = (thỏa mãn). 2 3 4 Vậy m = là giá trị cần tìm. 3
Câu 8. Cho tam giác ABC có b + c = 2a . Chứng minh rằng: 6Rr = bc , trong đó ,
R r lần lượt là bán kính
đường tròn ngoại tiếp và nội tiếp tam giác . ABC Hướng dẫn giải: abc a + b + c 3a Ta có: S = ; S = pr = r =
r (vì b + c = 2a ). ABC  4 ABC R 2 2 Do đó: abc 3a =
r  2abc = 12aRr bc = 6Rr (điều phải chứn minh). 4R 2
Câu 9. Cho hình thang ABCD vuông tại A và B , biết AD = ,
a BC = 3a và cạnh AB = 2 . a a) Tính A .
B BD, BC.BD và A . C B . D
b) Gọi I, J lần lượt là trung điểm của AB, CD. Tính A . C IJ . Hướng dẫn giải: a) Tính A .
B BD . Ta có: A .
B BD = AB (BA + AD) = A . B BA + A . B AD 0 2 2 2 = .
AB BA = − AB = − AB = −4a . 45
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 Tính B .
C BD . Ta có: BC.BD = BC.B .
D cos (BC, BD) = B . C B . D cos DBC AD = B . C B . D cos BDA 3 = BC.B . D
= BC.AD = 3a . BD
(trong đó DBC = BDA vì là hai góc so le trong). Tính A . C BD . Ta có:
AC.BD = ( AB + BC)(BA + AD) = A . B BA + A .
B AD + BC.BA + BC.AD 2 2 0 2
= −AB + + + BC AD
= −AB + a a = −( a) 2 2 0 0 . .cos 0 3 . .1 2 + 3a = −a . b) Tính A . C IJ . Ta có:
AC.IJ = ( AB + BC) 0 2 .IJ = A .
B IJ + BC.IJ = BC.IJ .cos 0 = 3 .2 a .1 a = 6a . 0
Câu 10. Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm I và II . Mỗi
sản phẩm I bán lãi 500 nghìn đồng, mỗi sản phẩm II bán lãi 400 nghìn đồng. Để sản xuất được
một sản phẩm I thì Chiến phải làm việc trong 3 giờ, Bình phải làm việc trong 1 giờ. Để sản xuất
được một sản phẩm II thì Chiến phải làm việc trong 2 giờ, Bình phải làm việc trong 6 giờ. Một
người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm
việc quá 180 giờ và Bình không thể làm việc quá 220 giờ. Hỏi số tiền lãi lớn nhất trong một tháng
của xưởng là bao nhiêu? Hướng dẫn giải:
Gọi x , y lần lượt là số sản phẩm loại I và loại II được sản xuất ra. Điều kiện x , y nguyên dương. 3
x + 2y 180 
x + 6y  220
Ta có hệ bất phương trình:  ( * , x y  ). x  0  y  0
Miền nghiệm của hệ chính là miền của tứ giác OABC (bỏ đi   điể 110
m O), trong đó A(60; 0) , B (40; 30) , C 0;   (vì  3  * , x y
nên ta loại điểm C).
Tiền lãi trong một tháng của xưởng là T = 0,5x + 0, 4y (triệu đồng).
Ta thấy T chỉ đạt giá trị lớn nhất chỉ có thể tại các điểm A , B .
Tại A(60; 0) thì T = 0,5.60 + 0, 4.0 = 30 . Tại B (40; 30) thì T = 0,5.40 + 0, 4.30 = 32 .
Vậy tiền lãi lớn nhất trong một tháng của xưởng là 32 triệu đồng, khi đó số sản phẩm loại I là 40,
số sản phẩm loại II là 30.
Lưu ý: Dù đã bỏ qua hai điểm O, C do chúng không thỏa điều kiện cho miền nghiệm hệ bất
phương trình, ta vẫn phải tính giá trị T tại hai điểm O, C; khi đó ta thấy hai giá trị này nhỏ hơn
32, điều này đồng nghĩa với việc giá trị lớn nhất của T tồn tại, và T = 32 . max 46
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
ÑEÀ REØN LUYEÄN SOÁ 10 Time: 90 phuùt ơ Câu 1.
a) Cho A = {1; 3; 5}. Liệt kê các tập con của tập A .
b) Tìm tập hợp X sao cho  ; a
b X   ; a ; b ; c d .  2 khi x  0  x −1  Câu 2. Cho hàm số  f (x) =
x +1 khi 0  x  2  − 
Tính: f ( 2), f (0), f (1), f (3) . 2
x −1 khi x  2 mx
Câu 3. Cho hàm số: y =
với m là tham số. x − m + 2 −1
a) Tìm tập xác định của hàm số theo tham số m .
b) Tìm m để hàm số xác định trên (0; ) 1 .
Câu 4. Tìm các hệ số a, b, c của hàm số bậc hai 2
y = ax + bx + c biết rằng đồ thị hàm số đi qua gốc tọa độ
O, đồng thời có đỉnh I ( 1; − − 3) .
Câu 5. Người ta tiến hành phỏng vấn một số người về chất lượng của một loại sản phẩm mới. Người điều
tra yêu cầu cho điểm sản phẩm (thang điểm 100) và thu được kết quả như sau:
80 65 51 48 45 61 30 35 84 83 60 58 75 72 68 39 41 54 61 72 75 72 61 58 65
Tìm phương sai và độ lệch chuẩn. Em có nhận xét gì về các kết quả nhận được? x − 2y 1
Câu 6. Xét hệ phương trình  (*). x + y  0
a) Hệ (*) có phải là hệ phương trình bậc nhất hai ẩn x, y hay không?
b) Cặp số (1; 2) có phải là một nghiệm của (*) không? 1 3sin  + 4 cos Câu 7. Cho tan =
. Tính giá trị của biểu thức A = 3 2 sin  − . 5 cos Câu 8. Cho ABC
nội tiếp đường tròn tâm O, H là trực tâm tam giác, D là điểm đối xứng của A qua O. Chứng minh rằng:
a) HA + HB + HC = 2HO ;
b) OA + OB + OC = OH .
Câu 9. Cho tam giác ABC . Tìm tập hợp điểm M sao cho (MA + 2MB + 3CB) BC = 0 .
Câu 10. Muốn đo chiều cao của Tháp Chàm Por Klong Garai ở Ninh
Thuận, người ta lấy hai điểm A và B trên mặt đất có khoảng
cách AB = 12 m cùng thẳng hàng với chân C của tháp để đặt
hai giác kế (hình bên). Chân của giác kế có chiều cao h =
1,3m. Gọi D là đỉnh tháp và hai điểm A1, B1 cùng thẳng hàng
với C1 thuộc chiều cao CD của tháp. Người ta đo được 0 DA C = 49 , 0
DB C = 35 . Chiều cao CD của tháp đó gần 1 1 1 1
nhất với kết quả nào sau đây?
================HẾT=============== 47
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Höôùng daãn giaûi ñeà soá 10 Câu 1.
a) Cho A = {1; 3; 5}. Liệt kê các tập con của tập A .
b) Tìm tập hợp X sao cho  ; a
b X   ; a ; b ; c d . Hướng dẫn giải:
a) Các tập con của A gồm:  , {1}, {3}, {5}, {1; 3}, {1; 5}, {3; 5}, {1; 3; 5}.
b) Theo đề bài, ta có tập hợp X phải chứa 2 phần tử là a và b, nhưng không được chứa phần tử nào
khác 4 phần tử a, b, c, d. Do đó các tập hợp X có thể là : X = a; 
b , X = a; ; b
c , X = a; ;
b d, X =a; ; b c; d.  2 khi x  0  x −1  
Câu 2. Cho hàm số f (x) =
x +1 khi 0  x  2   Tính: f ( 2
− ), f (0), f (1), f (3) . 2
x −1 khi x  2 Hướng dẫn giải: Với x = 2
−  0 , ta có: f (− ) 2 2 2 = = −
x = 0  0; 2 , ta có: f (0) = 0 +1 = 1 . 2 − − . Với   1 3
Với x = 10;2, ta có: f ( ) 1 = 1+1 =
2 . Với x = 3  2 , ta có: f (3) = 3 +1 = 2 . mx
Câu 3. Cho hàm số: y =
với m là tham số. x − m + 2 −1
a) Tìm tập xác định của hàm số theo tham số m .
b) Tìm m để hàm số xác định trên (0; ) 1 . Hướng dẫn giải:
x − m + 2  0 
x m − 2  x m − 2
a) Hàm số xác định       .
 x − m + 2 −1 0
 x − m + 2 1  x m −1
Tập xác định của hàm số là D = m − 2; + ) \ m −  1 .
b) Hàm số xác định trên (0; ) 1  (0; )
1  m − 2; m − ) 1  (m −1; +) ( )    −  m − m − ) m 2 0 0;1 2; 1  m = 2   .  ( )  (   −    m − +) m 1 1 0;1 1;  m 1  m−1 0 Vậy m  ( ; −  1   2 thỏa mãn đề bài.
Câu 4. Tìm các hệ số a, b, c của hàm số bậc hai 2
y = ax + bx + c biết rằng đồ thị hàm số đi qua gốc tọa độ
O, đồng thời có đỉnh I ( 1; − − 3) . Hướng dẫn giải:
Parabol qua gốc tọa độ O (0;0)  c = 0 . 48
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077  b − = 1 − 2a − b = 0 a = 3
Parabol có đỉnh I ( 1; − − 3) nên  2a    
. Vậy a = 3, b = 6, c = 0 .  a − b = 3 − b  = 6 a − b = 3 −
Câu 5. Người ta tiến hành phỏng vấn một số người về chất lượng của một loại sản phẩm mới. Người điều
tra yêu cầu cho điểm sản phẩm (thang điểm 100) và thu được kết quả như sau:
80 65 51 48 45 61 30 35 84 83 60 58 75 72 68 39 41 54 61 72 75 72 61 58 65
Tìm phương sai và độ lệch chuẩn. Em có nhận xét gì về các kết quả nhận được? Hướng dẫn giải: 80 + 65 + ... + 65 Ta có: x = = 60,52 (điểm). 25 Phương sai: 1 2 2 2 2 s =
(x − x) + (x − x) +...+ (x − x)   212,73  1 2 25  . 25 Độ lệch chuẩn 2 s =
s  14, 59 (điểm).
Nhận xét: Mức độ chênh lệch điểm giữa các giá trị là khá lớn. x − 2y 1
Câu 6. Xét hệ phương trình  (*). x + y  0
a) Hệ (*) có phải là hệ phương trình bậc nhất hai ẩn x, y hay không?
b) Cặp số (1; 2) có phải là một nghiệm của (*) không? Hướng dẫn giải:
a) Hai bất phương trình x − 2y 1, x + y  0 đều có dạng bậc nhất hai ẩn x, y nên hệ đã cho chính là hệ bất
phương trình bậc nhất hai ẩn x, y.  3 − 1
b) Thay cặp số (1; 2) vào mỗi bất phương trình của hệ (*), ta có: 
(đúng), vì vậy (1; 2) là một 3   0 nghiệm của hệ (*). 1 3sin  + 4 cos Câu 7. Cho tan =
. Tính giá trị của biểu thức A = 3 2 sin  − . 5 cos Hướng dẫn giải: sin 1 Vì tan =
= nên cos  0. Chia cả tử và mẫu của P cho cos , ta được: cos 3 sin  1 3 + 4 3. + 4  3 tan  + 4 15 cos 3 A = = = = − . sin  2 tan  − 5 1 13 2 − 5 2. − 5 cos 3 Câu 8. Cho ABC
nội tiếp đường tròn tâm O, H là trực tâm tam giác, D là điểm đối xứng của A qua O. Chứng minh rằng:
a) HA + HB + HC = 2HO ;
b) OA + OB + OC = OH . Hướng dẫn giải: 49
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
a) Xét tam giác ABD nội tiếp đường tròn đường kính AD nên AB ⊥ BD .
Mặt khác AB ⊥ CH nên BD//CH (1).
Tương tự, tam giác ACD nội tiếp đường tròn đường kính AD nên
AC ⊥ CD ; mặt khác AC ⊥ BH nên CD//BH (2).
Từ (1) và (2) suy ra BDCH là hình bình hành.
Ta có: HA + HB + HC = HA + HD = 2HO (vì O là trung điểm AD). 
b) Ta có: OA + OB + OC = OH + HA + OH + HB + OH + HC
= 3OH + (HA+ HB + HC) = 3OH + 2HO = OH . 
Câu 9. Cho tam giác ABC . Tìm tập hợp điểm M sao cho (MA + 2MB + 3CB) BC = 0 . Hướng dẫn giải:
Gọi I là điểm thỏa mãn IA + 2IB = 0  IA + 2 (IA + AB) = 2
0  3IA + 2AB = 0  AI = AB . 3 Do đó điể 2
m I cố định (thuộc đoạn AB và AI = AB ). Ta có: 3
(MA+2MB+3CB)BC = 0  (MI +IA)+2(MI +IB)+3CB.BC =0      2
3MI + ( IA + 2IB) + 3CB.BC = 0 2
 3MI.BC − 3BC = 0  MI.BC = BC .   0  Gọi M ,
I lần lượt là hình chiếu của M, I trên đường thẳng BC .
Ta có: MI.BC = (MM  + M I + I I ).BC = MM .BC + M I .BC + I I.BC = M I .BC . 0 0 Do vậy 2 2
MI.BC = BC M I .BC = BC . Vì 2
BC  0 nên M I ,
BC cùng hướng, khi đó: 2 2
M I .BC = BC M I .BC = BC M I  = BC .
Do I cố định nên I  cố định, suy ra M  cố định.
Vậy tập hợp điểm M là đường thẳng đi qua M  và vuông góc với BC .
Câu 10. Muốn đo chiều cao của Tháp Chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm A và B
trên mặt đất có khoảng cách AB = 12 m cùng thẳng hàng với chân C của tháp để đặt hai giác kế
(hình bên). Chân của giác kế có chiều cao h = 1,3m. Gọi D là đỉnh tháp và hai điểm A1, B1 cùng
thẳng hàng với C1 thuộc chiều cao CD của tháp. Người ta đo được 0 DA C = 49 , 0 DB C = 35 . 1 1 1 1
Chiều cao CD của tháp đó gần nhất với kết quả nào sau đây? 50
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 Hướng dẫn giải:
Ta có: A B = AB = 12 m . 1 1
Xét hai tam giác DC A và DC B có: 0 C A = C . D cot 49 , 0 C B = C . D cot 35 . 1 1 1 1 1 1 1 1 1 1
Ta có: A B = C B − C A = C D ( 0 0 cot 35 − cot 49 1 1 1 1 1 1 1 ) A B 12 1 1  C D = =  21,47 m . 1 0 0 cot 35 − cot 49 0 0 cot 35 − cot 49
Suy ra: CD = CC + C D  22, 77 m. Vậy chiều cao của tháp xấp xỉ 22, 77 m . 1 1 51
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
100 CAÂU TRAÉC NGHIEÄM TOAÙN 10
OÂN TAÄP KIEÅM TRA HOÏC KÌ I NAÊM HOÏC 2022 - 2023
Câu 1. Câu nào trong các câu sau không phải là mệnh đề? 4 A. 2   x . B. 2 + 2 = 5 .
C. 2 là một số hữu tỷ. D. = 2 . 2
Câu 2. Mệnh đề nào sau là mệnh đề sai? A. n
  : n  2n . B. 2 n
  : n = n . C. 2 x   : x  0 . D. 2 x
  : x x .
Câu 3. Trong các mệnh đề sau, mệnh đề nào đúng ? A. 2 n
  , n +1 không chia hết cho 3 . B. x
  , x  3  x  3 . C. x   (x − )2 , 1  x −1. D. n   , 2
n +1 chia hết cho 4 .
Câu 4. Cho mệnh đề A: “ 2 x
  , x − x + 7  0 ”. Mệnh đề phủ định của A là: A. 2 x
  , x − x + 7  0 . B. 2 x
  , x − x + 7  0.
C. Không tồn tại x để 2
x − x + 7  0 . D. 2 x
  , x − x + 7  0.
Câu 5. Phủ định của mệnh đề “ 2 x
  , 5x −3x =1” là : A. “ 2 x
  , 5x −3x 1”. B. “ 2 x
  , 5x −3x =1”. C. “ 2 x
  , 5x −3x 1”. D. “ 2
x  , 5x − 3x  1”.
Câu 6. Cho mệnh đề: “Nếu 2 góc ở vị trí so le trong thì hai góc đó bằng nhau”. Trong các mệnh đề sau đây, đâu
là mệnh đề đảo của mệnh đề trên?
A. Nếu 2 góc bằng nhau thì hai góc đó ở vị trí so le trong.
B. Nếu 2 góc không ở vị trí so le trong thì hai góc đó không bằng nhau.
C. Nếu 2 góc không bằng nhau thì hai góc đó không ở vị trí so le trong.
D. Nếu 2 góc ở vị trí so le trong thì hai góc đó không bằng nhau.
Câu 7. Tìm số phần tử của tập hợp A = x  , x   3 ? A. 3 . B. 4 . C. 5 . D. 6 .
Câu 8. Liệt kê các phần tử của tập hợp A = 2k −1 k  , 3 −  k   5 ta được A. A =  3 − ; 2 − ; 1 − ;0;1;2;3;4;  5 . B. A =  7 − ; 5 − ; 3 − ; 1 − ;1;3;5;7;  9 . C. A =  6 − ; 4 − ; 2 − ;0;2;4;6;8;  10 . D. A =  5 − ; 3 − ; 1 − ;1;3;5;  7 .
Câu 9. Cho hai tập hợp A = 1; 2;3; 4; 
5 và B = 0; 2; 4;6; 
8 . Tìm tập hợp C = AB là A. C =  . B. C = 2;  4 .
C. C = 0;1; 2;3; 4;5;6;  8 .
D. C = 1;3;  5 .
Câu 10. Cho hai tập hợp A = 0; 2; 4;6; 
8 và B = 1; 2;3; 4; 
5 . Tìm tập hợp C = AB . A. C =  . B. C = 2;  4 .
C. C = 0;1; 2;3; 4;5;6;  8 .
D. C = 1;3;  5 . 52
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Câu 11. Cho A = 1; 2;3; 4; 
5 , B = 0; 2; 4;6; 
8 . Tìm tập hợp C = ( A B) \ ( A B) ? A. C =  . B. C = 2;  4 .
C. C = 0;1;3;5;6;  8 .
D. C = 1;3;  5 .
Câu 12. Cho A = 3; 4;5;6; 
7 và B = 0; 2; 4;6; 
8 . Tìm C = ( A \ B)  ( B \ A) . A. C =  . B. C = 4;  6 .
C. C = 0; 2;3;5;7; 
8 . D. C = 3;5;  7 .
Câu 13. Tập X có bao nhiêu tập hợp con, biết X có 3 phần tử? A. 2 . B. 4 . C. 6 . D. 8 . 1 1 1 1 1 
Câu 14. Tập hợp A =  ; ; ; ;
 bằng tập hợp nào dưới đây? 3 8 15 24 35  1   1  A. n n . B.
n  ,1  n  5 .
n(n )  ,1  5 +1  2n +1   1   1  C. n n . D.
n  ,1  n  5 . n(n )  ,1  5 + 2  2 n + 2 
Câu 15. Tập hợp A =  2 x
x − x − 6  
0 bằng tập hợp nào dưới đây? A.  . B. 0;1; 2;  3 . C.  1 − ;0;1;  2 . D.  2 − ; 1 − ;0;1;2;  3 .
Câu 16. Cho tập hợp A = ( 2 − ;
m −1 , B = 1;+) . Tìm tất cả giá trị của m để AB =. A. m  2 .
B. 0  m  2 . C. m  2 .
D. − 2  m  2 .  4 
Câu 17. Cho hai nửa khoảng A = ; − 
 và B = 1;+) . Số giá trị nguyên m để AB   là  m +1 A. 3 . B. 4 . C. 5 . D. Vô số.
Câu 18. Cho hai tập hợp khác rỗng A = (2;7 − m, B = (m −1; +) . Tìm tất cả giá trị m để A B = (1; +) . A. m  3. B. m = 2 .
C. m  0 . D. m  1.
Câu 19. Bất phương trình nào sau đây không phải là bất phương trình bậc nhất hai ẩn? x y
A. 2x + 3y  0.
B. x + y  2. C. 2 x + y  0. D. − 1 . 2 3
Câu 20. Cặp số ( 1; − )
1 là nghiệm của bất phương trình
A. x + 4y 1.
B. x + y − 2  0 .
C. −x − y  0 .
D. −x − 3y −1  0 .
Câu 21. Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình 2x + y 1? A. (0; 0) . B. (3; − 7) . C. (−2; ) 1 . D. (0; ) 1 .
Câu 22. Miền nghiệm của bất phương trình −x + 2 + 2 ( y − 2)  2(1− x) là nửa mặt phẳng chứa điểm A. (2; 2) . B. (−1;3) . C. (−4;3) . D. (5;0) .
Câu 23. Miền nghiệm (miền không bị gạch trong hình) của bất phương trình 3x − y  4 là 53
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 A. B. C. D.
Câu 24. Phần không được gạch chéo trong hình (kể cả biên), là miền nghiệm của bất phương trình nào bên dưới?
A. x − y  3.
B. 2x − y  3 .
C. 2x − y  3 .
D. x − y  3.
x − y  0 
Câu 25. Miền nghiệm của hệ bất phương trình x − 3y + 3  0 là phần mặt phẳng chứa điểm
x + y −5  0  A. (5;3) . B. (0; 0) . C. (1; − ) 1 . D. (−2; 2) . x + y  0
Câu 26. Cho hệ bất phương trình 
có tập nghiệm là S . Khẳng định nào sau đây là khẳng định 2x + 5y  0 đúng?  1   1 2  A. (1; ) 1  S . B. ( 1; − − ) 1  S . C. 1; −  S   . D. − ;  S   .  2   2 5  54
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 3  x + 2y  5
Câu 27. Miền biểu diễn nghiệm của hệ 
là phần không gạch chéo (không kể biên) của hình nào x − y  2 −
trong các phương án bên dưới? A. B. C. D.
Câu 28. Cho biết miền nghiệm của một hệ bất phương trình bậc nhất hai ẩn
x, y chính là miền của tam giác ABC như hình bên. Tìm tổng của giá
trị lớn nhất, giá trị nhỏ nhất biểu thức F ( x ; y) = 5x − 2 y + 2025 . A. 3075 . B. 5000 . C. 4035 . D. 4050 .
x − y + 2  0 
Câu 29. Cho các giá trị ,
x y thỏa điều kiện 2x − y −1  0 . Tìm giá trị lớn nhất của biểu thức T = 3x + 2y .
3x − y − 2  0  A. 19 . B. 25 . C. 14 . D. 20.
Câu 30. Bạn An kinh doanh hai mặt hàng handmade là vòng tay và vòng đeo cổ. Mỗi vòng tay làm trong 4
giờ, bán được 40 ngàn đồng. Mỗi vòng đeo cổ làm trong 6 giờ, bán được 80 ngàn đồng. Mỗi tuần bạn
An bán được không quá 15 vòng tay và 4 vòng đeo cổ. Tính số giờ tối thiểu trong tuần An cần dùng
để làm ra sản phẩm và bán được ít nhất 400 ngàn đồng? 55
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 A. 40 . B. 25 . C. 32 . D. 20. 2x −1
Câu 31. Tìm tập xác định D của hàm số y = ( x + )( x − ) . 2 1 3  1 
A. D = (3; + ). B. D = \ − ;3.  2   1 
C. D = − ; +    .
D. D = .  2 
Câu 32. Tìm tập xác định D của hàm số y = 6 − 3x − x −1.
A. D = (1; 2).
B. D = 1; 2. C. D = 1;  3 . D. D =  1; − 2. 2 − x + x + 2
Câu 33. Tìm tập xác định D của hàm số y = . x
A. D = −2; 2. B. D = ( 2 − ;2) \  0 . C. D =  2 − ;2\  0 .
D. D = . x +1
Câu 34. Tìm tập xác định D của hàm số y = . 2 x − x − 6 A. D =   3 . B. D =  1; − + ) \  3 .
C. D = .
D. D = −1; + ). 1
Câu 35. Hàm số y =
nghịch biến trên khoảng nào dưới đây? x − 2
A. (− ; 2). B. (2; + ). C. ( 2 − ;+ ). D. (−2; 2).
Câu 36. Cho hàm số y = ax + 3 (a  0) . Tìm điều kiện của a để hàm số đồng biến trên ?
A. a  0.
B. a  0.
C. a  .
D. a = 1.
Câu 37. Điểm nào sau đây thuộc đồ thị hàm số y = 2 x – 1 + 3 x − 2 ? A. (2; 6) . B. (1; − ) 1 . C. ( 2 − ;−10) . D. (0; − 4) .  2 , x(− ;  0)  x −1 
Câu 38. Cho hàm số y =  x +1 , x 0; 2 . Tính f (4) , ta được kết quả:  2 x −1 , x   (2;5  2 A. . B.15 . C. 5 . D. 7 . 3 x +1
Câu 39. Hàm số y = 0;1 khi:
x − 2m + xác định trên  ) 1 1 1 A. m  . B. m  1. C. m  hoặc m  1.
D. m  2 hoặc m  1. 2 2 56
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Câu 40. Cho hàm số y = f ( x) xác định trên đoạn −1;5 có đồ thị như hình vẽ sau. Hãy chọn khẳng định
đúng về sự biến thiên của hàm số y = f ( x) trên đoạn −1;5.
A. Hàm số đồng biến trên các đoạn  1; − 
1 , 1; 2 và nghịch biến trên các đoạn 2;  3 , 3;5.
B. Hàm số nghịch biến trên các đoạn  1; −  1 , 2; 
3 và đồng biến trên các đoạn 1; 2, 3;5.
C. Hàm số đồng biến trên các đoạn  1; −  1 , 2; 
3 và nghịch biến trên các đoạn 1; 2, 3;5.
D. Hàm số nghịch biến trên các đoạn  1; − 
1 , 1; 2 và đồng biến trên các đoạn 2;  3 , 3;5.
Câu 41. Cho hàm số bậc hai 2
y = ax + bx + c (a  0) . Chọn mệnh đề sai trong các khẳng định sau:
A. Nếu a  0 thì đồ thị hàm số có bề lõm hướng lên trên.
B. Nếu a  0 thì đồ thị hàm số có bề lõm hướng xuống dưới.  b  
C. Đồ thị hàm số có đỉnh I − ; −   .  2a 4a
D. Đồ thị hàm số luôn nhận trục Oy làm trục đối xứng. Câu 42. Cho hàm số 2
y = ax + bx + c (a  0) có đồ thị (P) như hình bên. Khẳng định nào sau đây là khẳng định sai?
A. Hàm số đồng biến trên khoảng (− ;3) .
B. Hàm số nghịch biến trên khoảng (3; + ) .
C. Hàm số nghịch biến trên khoảng (1; + ) .
D. Hàm số đồng biến trên khoảng (− ) ;1 .
Câu 43. Parabol ( P) 2
: y = −x + 6x +1. Khi đó
A. Có trục đối xứng x = 6 và đi qua điểm A(0; ) 1 .
B. Có trục đối xứng x = 6
− và đi qua điểm A(1;6) .
C. Có trục đối xứng x = 3 và đi qua điểm A(2;9) .
D. Có trục đối xứng x = 3 và đi qua điểm A(3;9) .
Câu 44. Xác định hàm số 2
y = 2x + bx + c biết đồ thị hàm số này đi qua hai điểm A(0; ) 1 , B ( 2 − ;7) . 9 53 A. 2 y = 2x + x − . B. 2
y = 2x + x +1. C. 2
y = 2x − x +1. D. 2
y = 2x + x −1. 5 5  1 
Câu 45. Xác định parabol ( P) 2
: y = ax − 4x + c biết ( P) có đỉnh là I ; 2 −   là:  2  57
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 1 1 A. 2 y = 4
− x − 4x +1. B. 2 y = 2
− x − 4x + . C. 2
y = 2x − 4x − . D. 2
y = 4x − 4x −1. 2 2
Câu 46. Tọa độ đỉnh I của parabol ( P) 2
: y = −x + 4x là A. I ( 2 − ; −12) . B. I (2; 4) . C. I ( 1; − − 5) . D. I (1; 3) . Câu 47. Hàm số 2
y = −x +1 nghịch biến trên khoảng nào sau đây? A. (0; +) . B. (− ; 0) .
C. (− ; 0) và (0; +) . D. (− ; − ) 1 và (1; +) .
Câu 48. Giao điểm của parabol ( P) : 2
y = x + 5x + 4 với trục hoành:
A. (−1;0) , (−4;0) . B. (0; − ) 1 , (0; − 4) .
C. (−1;0) , (0; −4) . D. (0; − ) 1 , (−4; 0) . 3
Câu 49. Tìm tất cả giá trị của m để đỉnh của parabol 2
y = x + x + m nằm trên đường thẳng y = . 4 A. m = 2 . B. m = 0 . C. m = 1. D. m = 2 − . Câu 50. Parabol 2
y = x + x + c cắt đường phân giác của góc phần tư thứ nhất tại điểm có hoành độ x = 1 . Khi đó c bằng: 1 A. . B. 2 − . C. 2 . D. 1 − . 2 Câu 51. Biểu thức 2 0 2 0 2 0 2 0
A = cos 10 + cos 20 + cos 30 + ... + cos 180 có giá trị bằng: A. A = 9 . B. A = 3 . C. A = 12 . D. A = 6 .
Câu 52. Giá trị của o o
tan 30 + cot 30 bằng bao nhiêu? 4 1+ 3 2 A. . B. . C. . D. 2 . 3 3 3
Câu 53. Cho góc  thỏa mãn o o
0    90 . Khẳng định nào sau đây đúng? A. 2 2  + ( o sin sin 90 −  ) = 0 . B. 2 2  + ( o sin sin 90 −  ) = 2 . C. 2 2  + ( o sin sin 90 −  ) = 1. D. 2 2 + ( o sin sin 90 −  ) = 3 .
Câu 54. Mệnh đề nào sau đây về tam giác ABC là sai?
A. Góc B nhọn khi và chỉ khi 2 2 2
b a + c .
B. Góc A vuông khi và chỉ khi 2 2 2
a = b + c .
C. Góc C tù khi và chỉ khi 2 2 2
c a + b .
D. Góc A tù khi và chỉ khi 2 2 2
b a + c . 2 1− sin x
Câu 55. Rút gọn biểu thức P = ta được 2sin . x cos x 1 1 A. P = tan x . B. P = cot x .
C. P = 2cot x .
D. P = 2 tan x . 2 2
Câu 56. Biểu thức ( a + a)2 cot tan bằng 1 1 1 1 A. − . B. 2 2
cot a + tan a2 . C. + . D. 2 2
cot a tan a + 2 . 2 2 sin  cos  2 2 sin  cos  5
Câu 57. Cho  là góc tù và sin =
. Giá trị của biểu thức 3sin + 2cos là 13 58
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 9 9 A. 3 . B. − . C. 3 − . D. . 13 13 5
Câu 58. Cho góc  thỏa mãn sin + cos =
. Giá trị của sin.cos là: 2 1 1 1 1 A. . B. . C. . D. − . 8 4 2 8
Câu 59. Cho ABC vuông tại A có AC = 5 cm, BC = 13 cm. Gọi góc ABC =  và ACB =  . Hãy chọn
khẳng định đúng khi so sánh độ lớn của hai góc  và  . A.    . B.    . C.  =  . D.    .
Câu 60. Cho tam giác ABC có diện tích bằng 26 cm2 và AB = 8 cm, AC = 13cm. Giá trị sin A bằng bao nhiêu? 1 1 A. . B. 30 . C. . D. 150 . 4 2
Câu 61. Cho giác ABC có a = 5 , b =
26 , C = 135 .Tính diện tích của ABC . −5 13 5 13 A. . B. 5 13 . C. . D. 5 26 . 2 2
Câu 62. Tam giác ABC có BC = a và A = 30 . Tính bán kính đường tròn ngoại tiếp ABC . a 3 a A. a . B. . C. 2a . D. . 3 2
Câu 63. Cho ABC biết a = 6 , b = 2 , c = 1+ 3 . Độ dài đường cao ứng với góc nhỏ nhất của ABC bằng? 1+ 3 6 (1+ 3 ) 1+ 3 3 + 3 A. . B. . C. . D. . 2 4 6 2
Câu 64. Cho ABC có ba cạnh lần lượt là a = 5 , b = 8 , c = 11. Độ dài đường trung tuyến vẽ từ đỉnh C bằng: 57 57 A. . B. . C. 57 . D. 57 . 4 2
Câu 65. Cho góc xOy = 60 . Gọi A và B là hai điểm di động lần lượt trên tia Ox và tia Oy sao cho
AB = 2 3 . Độ dài lớn nhất của đoạn OA bằng: A. 4 3 . B. 2 . C. 4 . D. 1.
Câu 66. Hai chiếc ca nô cùng xuất phát từ cảng A , đi thẳng theo hai
hướng tạo với nhau góc 60 . Ca nô B chạy với vận tốc 20 hải
lí một giờ. Ca nô C chạy với tốc độ 25 hải lí một giờ. Hỏi sau
2 giờ, hai ca nô cách nhau một khoảng xấp xỉ bao nhiêu hải lí
(kết quả làm tròn đến hàng đơn vị)? (1 hải lí  1,852 km). A. 46 . B. 23. C. 25 . D. 56 . 59
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Câu 67. Từ đỉnh C một tháp có chiều cao CD = 40m,
người ta nhìn hai điểm A và B trên mặt đất
dưới các góc nhìn là 34 2  6 và 72 1  2 so với
phương thẳng đứng của tháp. Ba điểm , A , B D
thẳng hàng. Khoảng cách AB gần nhất với kết quả nào sau đây? A. 97 m. B.100 m. C. 120 m. D. 83m.
Câu 68. Khi khai quật tại một ngôi làng cổ, người ta tìm được mảnh
của một chiếc đĩa phẳng hình tròn bị vỡ. Các nhà khảo cổ đo
được kích thước ba cạnh tam giác ABC (nội tiếp vành tròn
đĩa) là 3,7 cm; 4,3cm và 7,5 cm. Họ muốn làm một chiếc
đĩa mới mô phỏng theo chiếc đĩa này. Hỏi chiếc đĩa cần làm
có bán kính bằng bao nhiêu? (Kết quả làm tròn đến hàng đơn vị). A. 6,1 cm. B. 5, 7 cm. C. 6,8 cm. D. 5,3 cm.
Câu 69. Cho tam giác ABC có độ dài ba đường trung tuyến lần lượt bằng 15, 18, 27. Tính diện tích S của tam giác ABC . A. 105 2 . B. 125 . C. 105 . D. 120 2 . Câu 70. Cho ABC
có AB = 8 , AC = 5, A = 60 . Tính bán kính đường tròn cắt cả ba cạnh của ABC  và
chắn trên mỗi cạnh một dây có độ dài bằng 4: A. 7 . B. 3 . C. 2 + 3 . D. 7 .
Câu 71. Hãy tìm khẳng định sai. Nếu hai véc tơ bằng nhau thì chúng luôn có đặc điểm sau
A. Cùng điểm gốc. B. Cùng phương.
C. Có độ dài bằng nhau. D. cùng hướng.
Câu 72. Mệnh đề nào sau đây đúng?
A. Có duy nhất một vectơ cùng phương với mọi vectơ.
B. Có ít nhất hai vectơ có cùng phương với mọi vectơ.
C. Có vô số vectơ cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ.
Câu 73. Cho hình bình hành ABCD tâm O . Khi đó OA − OB bằng
A. OC + OB . B. AB .
C. OC − OD . D. CD .
Câu 74. Cho 5 điểm M , N, , P ,
Q R . Vectơ tổng MN + PQ + RN + NP + QR bằng: A. MP . B. PR . C. MR . D. MN .
Câu 75. Cho hình bình hành ABCD . Có bao nhiêu vectơ có điểm đầu và điểm cuối là các đỉnh của hình bình
hành, bằng véc tơ AD (không kể véc tơ AD ) ? A. 1. B. 2 . C. 3 . D. 4 . 60
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Câu 76. Cho tam giác đều ABC cạnh a . Mệnh đề nào sau đây là đúng?
A. AB = AC .
B. AC = a .
C. AC = BC .
D. AB = a .
Câu 77. Hình bình hành ABCD là một hình chữ nhật nếu nó thỏa mãn điều kiện nào trong các điều kiện sau đây?
A. AC = BC .
B. AC = BD .
C. AC = AD .
D. AC = BD .
Câu 78. Cho tứ giác ABCD . Nếu AB = DC và AC = BD thì ABCD
A. Không là hình bình hành. B. Là hình vuông.
C. Là hình chữ nhật. D. Là hình thoi.
Câu 79. Cho hình bình hành ABCD . Tổng các véc tơ AB + AC + AD là 1 2 A. 2AC . B. AC . C. AC . D. AC . 3 3
Câu 80. Cho 4 điểm bất kì , A ,
B C, O . Đẳng thức nào sau đây là đúng?
A. OA = CA − CO .
B. AB = AC + BC .
C. AB = OB + OA .
D. OA = OB − BA.
Câu 81. Cho tam giác đều ABC cạnh 2a có G là trọng tâm. Khi đó giá trị AB − GC là: a 3 2a 3 2a 4a 3 A. . B. . C. . D. . 3 3 3 3
Câu 82. Cho tứ giác ABCD . Gọi M , N lần lượt là trung điểm của các cạnh A ,
B CD . K là điểm đối xứng
với M qua N . Khi đó khẳng định nào sau đây là đúng?
A. MK = AD − BC .
B. MK = AD + BC .
C. MK = AB + CD .
D. MK = AC − BD .
Câu 83. Cho tam giác ABC . Điểm M thỏa mãn MA − MB + MC = 0 thì
A. M là điểm sao cho tứ giác ABMC là hình bình hành.
B. M là trọng tâm tam giác ABC .
C. M là điểm sao cho tứ giác BAMC là hình bình hành.
D. M thuộc đường trung trực của AB .
Câu 84. Cho nửa đường tròn tâm O , đường kính PQ = 2. Trên nửa đường tròn đó ta lấy các điểm , A , B C khác ,
P Q sao cho theo thứ tự đó, chúng chia nửa đường tròn thành bốn phần bằng nhau. Khi đó
OA + OC + OB bằng: A. 3 . B. 1+ 2 . C. 2 + 2 . D. 2 . Câu 85. Cho ABC
. Gọi M là điểm thỏa mãn MB = 3MA . Khi đó biểu diễn AM theo AB và AC là 1 1 A. AM = AB + 3AC . B. AM = − AB + 0.AC . 4 2 1 1 1 1 C. AM = AB + AC . D. AM = AB + AC . 4 6 2 6
Câu 86. Cho tam giác ABC . Gọi M là trung điểm của AB , D là trung điểm của BC , N là điểm thuộc AC
sao cho CN = 2NA , K là trung điểm của MN . Khi đó khẳng định nào sau đây là đúng? 1 1 1 1 A. AK = AB + AC . B. AK = AB + AC . 4 6 2 3 61
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 1 2 C. AK = AD . D. AK = AD . 2 5
Câu 87. Cho tam giác ABC với phân giác trong AD . Biết AB = 5 , BC = 6 , CA = 7 . Khi đó AD bằng: 5 7 7 5 7 5 5 7 A. AB + AC . B. AB − AC . C. AB + AC . D. AB − AC . 12 12 12 12 12 12 12 12
Câu 88. Cho tam giác ABC . Gọi I là trung điểm của BC , H là điểm đối xứng của I qua C . Khi đó khẳng
định nào sau đây là đúng?
A. AH = AC + AI .
B. AH = 2AC − AI .
C. AH = 2AC − AB .
D. AH = AB + AC + AI .
Câu 89. Cho hai điểm cố định ,
A B . Tập hợp các điểm M thỏa mãn MA + MB = MA − MB là:
A. Đường tròn đường kính AB .
B. Đường trung trực của AB .
C. Đường tròn bán kính AB .
D. Nửa đường tròn đường kính AB .
Câu 90. Cho tam giác ABC có trọng tâm G . Tập hợp các điểm M sao cho MA + MB + MC = AB − AC là: 1
A. Đường tròn tâm G đường kính BC .
B. Đường tròn tâm G đường kính BC . 3 1
C. Đường tròn tâm G bán kính BC .
D. Đường tròn tâm G đường kính 3MG . 3
Câu 91. Cho tứ giác ABCD . Gọi M , N lần lượt là trung điểm của A ,
B CD . Đẳng thức nào sau đây là đúng?. BC + AD A. MN = .
B. MN = BC + AD . 2 1
C. MN = AC + BD . D. MN = (BC + AD). 2
Câu 92. Cho hình thang ABCD , hai đường chéo AC và BD cắt nhau tại O. Qua O kẻ MN song song với
AB ( AB là đáy của hình thang, M A ,
D N BC ). Đặt AB = a , DC = b . Khi đó khẳng định nào sau đây là đúng? a AB + bDC b AB + aDC A. MN = . B. MN = . a + b a + b a AB − bDC b AB − aDC C. MN = . D. MN = . a + b a + b
Câu 93. Cho tam giác đều ABC cạnh .
a Biết rằng tập hợp các điểm M thỏa mãn đẳng thức
2MA + 3MB + 4MC = MB − MA là đường tròn cố định có bán kính .
R Tính bán kính R theo . a a a a a A. r = . B. r = . C. r = . D. r = . 3 9 2 6
Câu 94. Cho ba vectơ a , b , c thỏa: a = 4 , b = 1, c = 5 và 5(b − a) + 3c = 0 . Khi đó biểu thức
M = a .b + b .c + c .a có giá trị bằng 67 A. 29 . B. . C. 18, 25 . D. 1 − 8,25. 2 62
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Câu 95. Cho tam giác ABC vuông tại A với AB = 3, AC = 4 . Các điểm M , N lần lượt thuộc các cạnh A ,
B AC thỏa mãn AM = AN = 1. Tích vô hướng BN.CM bằng A. 1. B. −1. C. −7. D. 7.
Câu 96. Gọi S là diện tích tam giác ABC . Mệnh đề nào sau đây đúng? 1 A. S =
AB .AC − ( A . B AC )2 2 2 . B. S =
AB AC − ( AB AC)2 2 2 . . . 2 1 C. S = (A .BAC)2 2 2 − AB .AC .
D. S = ( AB AC)2 2 2 . − AB .AC . 2
Câu 97. Đoạn thẳng AB có độ dài 2a , I là trung điểm AB . Khi 2 M .
A MB = 3a . Độ dài MI là A. 2a . B. a . C. a 3 . D. a 7 .
Câu 98. Cho đoạn thẳng AB = 4 . Tập hợp các điểm M thỏa mãn 2 2
MA − MB = 8 là
A. Một đường thẳng.
B. Một đoạn thẳng.
C. Một đường tròn. D. Một điểm.
Câu 99. Một máy bay đang bay từ hướng đông sang hướng tây với tốc độ 700 km/h thì gặp luồng gió thổi từ
hướng đông bắc sang hướng tây nam với tốc độ 40 km/h. Máy bay bị thay đổi vận tốc sau khi gặp
gió thổi. Tìm tốc độ mới của máy bay (làm tròn kết quả đến hàng phần trăm). A. 911,12 km/h . B. 724,32 km/h . C. 728,83 km/h . D. 813,13 km/h .
Câu 100. Một chiếc thuyền cố gắng đi thẳng qua một con sông với tốc độ 0,75 m/s. Tuy nhiên dòng nước trên
con sông đó chảy với tốc độ 1,2 m/s về hướng bên trái (hình vẽ). Tính tốc độ dịch chuyển của thuyền
so với bờ (kết quả làm tròn đến hàng phần nghìn). A. 1, 215 m/s. B. 1,112 m/s. C. 1,312 m/s. D. 1, 415 m/s. 63
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Höôùng daãn giaûi 100 caâu traéc nghieäm TOAÙN 10
OÂN TAÄP KIEÅM TRA HOÏC KÌ I NAÊM HOÏC 2022 - 2023
Câu 1. Câu nào trong các câu sau không phải là mệnh đề? 4 A. 2   x . B. 2 + 2 = 5 .
C. 2 là một số hữu tỷ. D. = 2 . 2 Hướng dẫn giải: Chọn A.
Phát biểu A không là một mệnh đề, nó là mệnh đề chứa biến.
Câu 2. Mệnh đề nào sau là mệnh đề sai? A. n
  : n  2n . B. 2 n
  : n = n . C. 2 x   : x  0 . D. 2 x
  : x x . Hướng dẫn giải: Chọn C. Với x = 0 thì 2
x = 0  0 là khẳng định sai.
Câu 3. Trong các mệnh đề sau, mệnh đề nào đúng ? A. 2 n
  , n +1 không chia hết cho 3 . B. x
  , x  3  x  3 . C. x   (x − )2 , 1  x −1. D. n   , 2
n +1 chia hết cho 4 . Hướng dẫn giải: Chọn A. “ 2 n
  , n +1 không chia hết cho 3 ” là mệnh đề đúng. Ta chứng minh bằng ba trường hợp sau:
Xét n = 3k (k  ) thì 2 2
n +1 = 9k +1 không chia hết cho 3.
Xét n = 3k +1 (k  ) thì n + = ( k + )2 2 2 1 3 1
+1 = 9k + 6k + 2 không chia hết cho 3.
Xét n = 3k + 2 (k  ) thì n + = ( k + )2 2 2 1 3 2
+1 = 9k +12k + 5 không chia hết cho 3.
Câu 4. Cho mệnh đề A: “ 2 x
  , x − x + 7  0 ”. Mệnh đề phủ định của A là: A. 2 x
  , x − x + 7  0 . B. 2 x
  , x − x + 7  0.
C. Không tồn tại x để 2
x − x + 7  0 . D. 2 x
  , x − x + 7  0. Hướng dẫn giải: Chọn D.
Câu 5. Phủ định của mệnh đề “ 2 x
  , 5x −3x =1” là : A. “ 2 x
  , 5x −3x 1”. B. “ 2 x
  , 5x −3x =1”. C. “ 2 x
  , 5x −3x 1”. D. “ 2
x  , 5x − 3x  1”. Hướng dẫn giải: Chọn C.
Câu 6. Cho mệnh đề: “Nếu 2 góc ở vị trí so le trong thì hai góc đó bằng nhau”. Trong các mệnh đề sau đây, đâu
là mệnh đề đảo của mệnh đề trên?
A. Nếu 2 góc bằng nhau thì hai góc đó ở vị trí so le trong.
B. Nếu 2 góc không ở vị trí so le trong thì hai góc đó không bằng nhau. 64
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
C. Nếu 2 góc không bằng nhau thì hai góc đó không ở vị trí so le trong.
D. Nếu 2 góc ở vị trí so le trong thì hai góc đó không bằng nhau. Hướng dẫn giải: Chọn A.
Câu 7. Tìm số phần tử của tập hợp A = x  , x   3 ? A. 3 . B. 4 . C. 5 . D. 6 . Hướng dẫn giải: Chọn C. Ta có: A =  2 − , 1 − ,0,1, 
2 nên A có 5 phần tử.
Câu 8. Liệt kê các phần tử của tập hợp A = 2k −1 k  , 3 −  k   5 ta được A. A =  3 − ; 2 − ; 1 − ;0;1;2;3;4;  5 . B. A =  7 − ; 5 − ; 3 − ; 1 − ;1;3;5;7;  9 . C. A =  6 − ; 4 − ; 2 − ;0;2;4;6;8;  10 . D. A =  5 − ; 3 − ; 1 − ;1;3;5;  7 . Hướng dẫn giải: Chọn B. Vì k  , 3
−  k  5 nên k chỉ nhận giá trị thuộc tập hợp  3 − ; 2 − ; 1 − ;0;1;2;3;4;  5 .
Vậy A = 2k −1 k  , 3 −  k   5 =  7 − ; 5 − ;−3;−1;1;3;5;7;  9 .
Câu 9. Cho hai tập hợp A = 1; 2;3; 4; 
5 và B = 0; 2; 4;6; 
8 . Tìm tập hợp C = AB là A. C =  . B. C = 2;  4 .
C. C = 0;1; 2;3; 4;5;6;  8 .
D. C = 1;3;  5 . Hướng dẫn giải: Chọn B.
Câu 10. Cho hai tập hợp A = 0; 2; 4;6; 
8 và B = 1; 2;3; 4; 
5 . Tìm tập hợp C = AB . A. C =  . B. C = 2;  4 .
C. C = 0;1; 2;3; 4;5;6;  8 .
D. C = 1;3;  5 . Hướng dẫn giải: Chọn C.
Câu 11. Cho A = 1; 2;3; 4; 
5 , B = 0; 2; 4;6; 
8 . Tìm tập hợp C = ( A B) \ ( A B) ? A. C =  . B. C = 2;  4 .
C. C = 0;1;3;5;6;  8 .
D. C = 1;3;  5 . Hướng dẫn giải: Chọn C.
A B = 0;1; 2;3; 4;5;6; 
8 và A B = 2; 
4 nên C = ( A B) \ ( A B) = 0;1;3;5;6;  8 .
Câu 12. Cho A = 3; 4;5;6; 
7 và B = 0; 2; 4;6; 
8 . Tìm C = ( A \ B)  ( B \ A) . A. C =  . B. C = 4;  6 .
C. C = 0; 2;3;5;7; 
8 . D. C = 3;5;  7 . Hướng dẫn giải: Chọn C.
A \ B = 3;5; 
7 và B \ A = 0; 2; 
8 nên C = ( A \ B)  ( B \ A) = 0; 2;3;5;7;  8 . 65
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Câu 13. Tập X có bao nhiêu tập hợp con, biết X có 3 phần tử? A. 2 . B. 4 . C. 6 . D. 8 . Hướng dẫn giải: Chọn D.
Số phần tử của X là: 3 2 = 8 . 1 1 1 1 1 
Câu 14. Tập hợp A =  ; ; ; ;
 bằng tập hợp nào dưới đây? 3 8 15 24 35  1   1  A. n n . B.
n  ,1  n  5 .
n(n )  ,1  5 +1  2n +1   1   1  C. n n . D.
n  ,1  n  5 . n(n )  ,1  5 + 2  2 n + 2  Hướng dẫn giải: Chọn C.
Xét tập hợp của phương án C, ta có thể liệt kê bảng giá trị sau : n 1 2 3 4 5 1 1 1 1 1 1 n (n + 2) 3 8 15 24 35 1 1 1 1 1   1 
Vậy tập hợp A =  ; ; ; ;  =  n n . 
 n(n + )  ,1  5 3 8 15 24 35 2 
Câu 15. Tập hợp A =  2 x
x − x − 6  
0 bằng tập hợp nào dưới đây? A.  . B. 0;1; 2;  3 . C.  1 − ;0;1;  2 . D.  2 − ; 1 − ;0;1;2;  3 . Hướng dẫn giải: Chọn D.
x + 2  0 x + 2  0 x  2 − x  2 − Xét 2
x − x − 6  0  ( x + 2)( x − 3)  0          2 −  x  3.
x − 3  0 x − 3  0 x  3 x  2
Vậy A = −2; −1;0;1; 2;  3 .
Câu 16. Cho tập hợp A = ( 2 − ;
m −1 , B = 1;+) . Tìm tất cả giá trị của m để AB =. A. m  2 .
B. 0  m  2 . C. m  2 .
D. − 2  m  2 . Hướng dẫn giải: Chọn D.
Ta có: AB =  2 2
m −1 1  m  2  m  2  − 2  m  2 .  4 
Câu 17. Cho hai nửa khoảng A = ; − 
 và B = 1;+) . Số giá trị nguyên m để AB   là  m +1 A. 3 . B. 4 . C. 5 . D. Vô số. Hướng dẫn giải: Chọn B. 66
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 4 4 3 − m
Ta có: A B    1  −1 0   0 m +1 m +1 m +1  3  − m  0 m  3   m +1  0 m  1 −    1 −  m  3  . 3  m 0  −  m  3   m +1 0 m  1 −
Vậy m 0;1;2; 
3 nên có 4 giá trị nguyên m thỏa mãn.
Câu 18. Cho hai tập hợp khác rỗng A = (2;7 − m, B = (m −1; +) . Tìm tất cả giá trị m để A B = (1; +) . A. m  3. B. m = 2 .
C. m  0 . D. m  1. Hướng dẫn giải: Chọn B.
Điều kiện: 2  7 − m m  5 (1).
Nhận thấy A  (1; +) , vì vậy: A B = (1; +)  m −1 =1  m = 2 (thỏa (1)).
Câu 19. Bất phương trình nào sau đây không phải là bất phương trình bậc nhất hai ẩn? x y
A. 2x + 3y  0.
B. x + y  2. C. 2 x + y  0. D. − 1 . 2 3 Hướng dẫn giải: Chọn C
Câu 20. Cặp số ( 1; − )
1 là nghiệm của bất phương trình
A. x + 4y 1.
B. x + y − 2  0 .
C. −x − y  0 .
D. −x − 3y −1  0 . Hướng dẫn giải: Chọn A
Thay x = 1, y = 1
− vào phương án A, ta có : 1+ 4(− )
1  1  −3  1 (đúng).
Câu 21. Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình 2x + y 1? A. (0; 0) . B. (3; − 7) . C. (−2; ) 1 . D. (0; ) 1 . Hướng dẫn giải: Chọn D
Thay x = 0, y = 1 vào bất phương trình: 2.0 +1 1 (sai).
Câu 22. Miền nghiệm của bất phương trình −x + 2 + 2 ( y − 2)  2(1− x) là nửa mặt phẳng chứa điểm A. (2; 2) . B. (−1;3) . C. (−4;3) . D. (5;0) . Hướng dẫn giải: Chọn C
Ta có: −x + 2 + 2 ( y − 2)  2(1− x)  −x + 2 + 2y − 4  2 − 2x x + 2y  4 (*) .
Thay cặp số (−4;3) vào (*), ta có: 4 − + 2.3  4 (đúng).
Câu 23. Miền nghiệm (miền không bị gạch trong hình) của bất phương trình 3x − y  4 là 67
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 A. B. C. D. Hướng dẫn giải: Chọn A  
Xét đường thẳng biên là d :3x − y = 4 luôn đi qua hai điểm ( − ) 4 0; 4 , ; 0 
 nên ta loại C, D.  3 
Thay tọa độ điểm M (2; 0) vào bất phương trình thì thỏa mãn, suy ra điểm M thuộc miền nghiệm của
bất phương trình (là miền không bị gạch) nên loại B.
Câu 24. Phần không được gạch chéo trong hình (kể cả biên), là miền nghiệm của bất phương trình nào bên dưới?
A. x − y  3.
B. 2x − y  3 .
C. 2x − y  3 .
D. x − y  3. Hướng dẫn giải: Chọn B  
Ta thấy miền nghiệm bất phương trình có biên là đường thẳng đi qua hai điểm ( − ) 3 0; 3 , ; 0   nên  2  loại A, D. 68
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Theo hình thì điểm M (2;− 2) thuộc miền nghiệm, thay x = 2, y = 2
− vào mỗi bất phương trình
trong hai phương án B, C, ta thấy B thỏa mãn vì 2.2 − (−2)  3 (đúng).
x − y  0 
Câu 25. Miền nghiệm của hệ bất phương trình x − 3y + 3  0 là phần mặt phẳng chứa điểm
x + y −5  0  A. (5;3) . B. (0;0) . C. (1; − ) 1 . D. (−2; 2) . Hướng dẫn giải: Chọn A  5 − 3  0 
Thay x = 5, x = 3 vào hệ bất phương trình: 5 − 3.3 + 3  0 (đúng).  5+ 3−5  0  x + y  0
Câu 26. Cho hệ bất phương trình 
có tập nghiệm là S . Khẳng định nào sau đây là khẳng định 2x + 5y  0 đúng?  1   1 2  A. (1; ) 1  S . B. ( 1; − − ) 1  S . C. 1; −  S   . D. − ;  S   .  2   2 5  Hướng dẫn giải: Chọn C   1  1+ −  0    1   2 
Thay x = 1, y = −
vào hệ bất phương trình:  (đúng). 2   1  2.1+ 5 −  0     2  3  x + 2y  5
Câu 27. Miền biểu diễn nghiệm của hệ 
là phần không gạch chéo (không kể biên) của hình nào x − y  2 −
trong các phương án bên dưới? A. B. 69
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 C. D. Hướng dẫn giải: Chọn B
Xét cặp số (0;3) , thay x = 0, y = 3 vào hệ ta thấy thỏa mãn. Vì vậy điểm (0;3) thuộc miền nghiệm
của hệ đã cho. Trong 4 phương án, chỉ có phương án B thỏa mãn.
Câu 28. Cho biết miền nghiệm của một hệ bất phương trình bậc nhất hai ẩn
x, y chính là miền của tam giác ABC như hình bên. Tìm tổng của giá
trị lớn nhất, giá trị nhỏ nhất biểu thức F ( x ; y) = 5x − 2 y + 2025 . A. 3075 . B. 5000 . C. 4035 . D. 4050 . Hướng dẫn giải: Chọn D
Miền nghiệm được cho là miền của tam giác ABC với A( 2
− ;0), B(2;0), C (2;4) .
Ta biết rằng biểu thức F ( x ; y ) đạt giá trị lớn nhất, giá trị nhỏ nhất tại các đỉnh của tam giác ABC.
Xét A(−2; 0) , F ( 2 − ;0) = 5( 2 − ) − 2.0 + 2025 = 2015 .
Xét B (2; 0) , F (2;0) = 5.2 − 2.0 + 2025 = 2035 .
Xét C (2; 4) , F (2; 4) = 5.2 − 2.4 + 2025 = 2027 .
Do vậy F ( x; y)
= 2035, F (x; y) = 2015  F (x; y) + F (x; y) = 4050. max min max min
x − y + 2  0 
Câu 29. Cho các giá trị ,
x y thỏa điều kiện 2x − y −1  0 . Tìm giá trị lớn nhất của biểu thức T = 3x + 2y .
3x − y − 2  0  A. 19 . B. 25 . C. 14 . D. 20. Hướng dẫn giải: Chọn A
Miền nghiệm của hệ đã cho là miền của tam giác ABC , trong đó A(1; )
1 , B (2; 4) , C (3;5) .
Giá trị lớn nhất của T = 3x + 2y đạt được tại các đỉnh của tam giác ABC . 70
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 Xét A(1; ) 1 , T = T (1; ) 1 = 3.1+ 2.1 = 5 . A
Xét B (2; 4) , T = T (2; 4) = 3.2 + 2.4 = 14 . B
Xét C (3;5) , T = T (3;5) = 3.3 + 2.5 = 19 . C
Vậy giá trị lớn nhất của T = 3x + 2y là 19 , khi đó: x = 3 và y = 5 .
Câu 30. Bạn An kinh doanh hai mặt hàng handmade là vòng tay và vòng đeo cổ. Mỗi vòng tay làm trong 4
giờ, bán được 40 ngàn đồng. Mỗi vòng đeo cổ làm trong 6 giờ, bán được 80 ngàn đồng. Mỗi tuần bạn
An bán được không quá 15 vòng tay và 4 vòng đeo cổ. Tính số giờ tối thiểu trong tuần An cần dùng
để làm ra sản phẩm và bán được ít nhất 400 ngàn đồng? A. 40 . B. 25 . C. 32 . D. 20. Hướng dẫn giải: Chọn C Gọi ,
x y là số vòng tay và vòng đeo cổ trong tuần An làm được. Điều kiện: , x y  .
Tổng thời gian để làm ra hai sản phẩm trên là:
T ( x; y) = 4x + 6 y .
40x + 80y  400 x + 2y 10  
Theo giả thiết, ta có: 0  x  15
 0  x 15 (*).   0  y  4 0  y  4  
Hệ (*) có miền nghiệm chính là miền tứ giác ABCD, trong
đó A(10;0), B(15;0), C (15;4) , D (2;4), được biểu diễn như hình bên.
Ta biết rằng T ( x ; y) = 4x + 6 y đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác ABCD.
Tại A(10;0), T (10;0) = 4.10 + 6.0 = 40 .
Tại B (15;0), T (15;0) = 4.15 + 6.0 = 60 .
Tại C (15; 4) , T (15; 4) = 4.15 + 6.4 = 84 .
Tại D (2; 4) , T (2; 4) = 4.2 + 6.4 = 32 .
Vậy T ( x ; y) đạt giá trị nhỏ nhất bằng 32, khi đó x = 2, y = 4 . Nói cách khác, mỗi tuần An cần làm
ra 2 vòng tay và 4 vòng đeo cổ để khoảng thời gian bỏ ra là ít nhất (32 giờ), đáp ứng thu nhập tối thiểu 400 ngàn đồng. 2x −1
Câu 31. Tìm tập xác định D của hàm số y = ( x + )( x − ) . 2 1 3  1 
A. D = (3; + ). B. D = \ − ;3.  2   1 
C. D = − ; +    .
D. D = .  2  71
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 Hướng dẫn giải: Chọn B.  1 2x +1  0 x  − Hàm số xác định khi    2 . x − 3  0 x  3  1 
Vậy tập xác định của hàm số là D = \ − ;3 .  2 
Câu 32. Tìm tập xác định D của hàm số y = 6 − 3x − x −1.
A. D = (1; 2).
B. D = 1; 2. C. D = 1;  3 . D. D =  1; − 2. Hướng dẫn giải: Chọn B. 6 − 3x  0 x  2
Hàm số xác định khi và chỉ khi   
 1 x  2. x −1 0 x 1
Vậy tập xác định của hàm số là D = 1; 2. 2 − x + x + 2
Câu 33. Tìm tập xác định D của hàm số y = . x
A. D = −2; 2. B. D = ( 2 − ;2) \  0 . C. D =  2 − ;2\  0 .
D. D = . Hướng dẫn giải: Chọn C. 2 − x  0 x  2  
Hàm số xác định khi và chỉ khi x + 2  0  x  2 − .   x  0 x  0  
Vậy tập xác định của hàm số là D =  2 − ;2\  0 . x +1
Câu 34. Tìm tập xác định D của hàm số y = . 2 x − x − 6 A. D =   3 . B. D =  1; − + ) \  3 .
C. D = .
D. D = −1; + ). Hướng dẫn giải: Chọn B. x  1 − x +1 0  x  1 −
Hàm số xác định khi và chỉ khi   x  3   . 2
x − x − 6  0  x  3 x  2 − 
Vậy tập xác định của hàm số là D =  1; − + ) \  3 . 1
Câu 35. Hàm số y =
nghịch biến trên khoảng nào dưới đây? x − 2
A. (− ; 2). B. (2; + ). C. ( 2 − ;+ ). D. (−2; 2). 72
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 Hướng dẫn giải: Chọn B.
f ( x − f x 2 ) ( 1) Tập xác định D = \   2 . Xét T =
với mọi x , x  , D x x . x − x 1 2 1 2 2 1 1 1
x − 2 − x + 2 1 2 − x − 2 x − 2 (x −2 x −2 2 1 2 )( 1 ) Ta có : T = = x − x x − x 2 1 2 1 x − x 1 1 2 = ( = − x − 2 x − 2 x − x x − 2 x − 2 2 )( 1 )( 2 1) ( 2 )( 1 ) x  2 x − 2  0 2 −
Vì x , x (2; +) 1 1       0 . 1 2 x  2 x − 2  0   x − 2 x − 2 2 2 ( 2 )( 1 )
Vậy T  0 nên hàm số đã cho nghịch biến trên (2; + ) .
Câu 36. Cho hàm số y = ax + 3 (a  0) . Tìm điều kiện của a để hàm số đồng biến trên ?
A. a  0.
B. a  0.
C. a  .
D. a = 1. Hướng dẫn giải: Chọn A.
f ( x − f x 2 ) ( 1) Tập xác định D = . Xét A =
với mọi x , x  ; x x . x − x 1 2 1 2 2 1
(ax +3 − ax +3 a x − x 2 ) ( 1 ) ( 2 1) Ta có: A = = = . a x − x x − x 2 1 2 1
Vậy với a  0 thì hàm số đã cho đồng biến trên .
Câu 37. Điểm nào sau đây thuộc đồ thị hàm số y = 2 x – 1 + 3 x − 2 ? A. (2; 6) . B. (1; − ) 1 . C. ( 2 − ;−10) . D. (0; − 4) . Hướng dẫn giải: Chọn A.  2 , x(− ;  0)  x −1 
Câu 38. Cho hàm số y =  x +1 , x 0; 2 . Tính f (4) , ta được kết quả:  2 x −1 , x   (2;5  2 A. . B.15 . C. 5 . D. 7 . 3 Hướng dẫn giải: Chọn B.
Với x = 4  (2;5 thì f ( x) 2
= x −  f ( ) 2 1 4 = 4 −1 = 15. x +1
Câu 39. Hàm số y = 0;1 khi:
x − 2m + xác định trên  ) 1 73
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 1 1 A. m  . B. m  1. C. m  hoặc m  1.
D. m  2 hoặc m  1. 2 2 Hướng dẫn giải: Chọn C. Hàm số xác định x  0; ) 1 khi và chỉ khi
x − 2m +1  0, x  0; ) 1  1   m −  m m x x 0 ) 2 1 0 2 1 , ;1   −       2 . 2m −11  m 1
Câu 40. Cho hàm số y = f ( x) xác định trên đoạn −1;5 có đồ thị như hình vẽ sau. Hãy chọn khẳng định
đúng về sự biến thiên của hàm số y = f ( x) trên đoạn −1;5.
A. Hàm số đồng biến trên các đoạn  1; − 
1 , 1; 2 và nghịch biến trên các đoạn 2;  3 , 3;5.
B. Hàm số nghịch biến trên các đoạn  1; −  1 , 2; 
3 và đồng biến trên các đoạn 1; 2, 3;5.
C. Hàm số đồng biến trên các đoạn  1; −  1 , 2; 
3 và nghịch biến trên các đoạn 1; 2, 3;5.
D. Hàm số nghịch biến trên các đoạn  1; − 
1 , 1; 2 và đồng biến trên các đoạn 2;  3 , 3;5. Hướng dẫn giải: Chọn C.
Câu 41. Cho hàm số bậc hai 2
y = ax + bx + c (a  0) . Chọn mệnh đề sai trong các khẳng định sau:
A. Nếu a  0 thì đồ thị hàm số có bề lõm hướng lên trên.
B. Nếu a  0 thì đồ thị hàm số có bề lõm hướng xuống dưới.  b  
C. Đồ thị hàm số có đỉnh I − ; −   .  2a 4a
D. Đồ thị hàm số luôn nhận trục Oy làm trục đối xứng. Hướng dẫn giải: Chọn D. Đồ b thị hàm số bậc hai 2
y = ax + bx + c (a  0) nhận trục đối xứng là x = − . 2a
Chỉ có đồ thị hàm số 2
y = ax (a  0) mới luôn nhận trục Oy làm trục đối xứng. Câu 42. Cho hàm số 2
y = ax + bx + c (a  0) có đồ thị (P) như hình bên. Khẳng định nào sau đây là khẳng định sai?
A. Hàm số đồng biến trên khoảng (− ;3) .
B. Hàm số nghịch biến trên khoảng (3; + ) . 74
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
C. Hàm số nghịch biến trên khoảng (1; + ) .
D. Hàm số đồng biến trên khoảng (− ) ;1 . Hướng dẫn giải: Chọn C.
Câu 43. Parabol ( P) 2
: y = −x + 6x +1. Khi đó
A. Có trục đối xứng x = 6 và đi qua điểm A(0; ) 1 .
B. Có trục đối xứng x = 6
− và đi qua điểm A(1;6) .
C. Có trục đối xứng x = 3 và đi qua điểm A(2;9) .
D. Có trục đối xứng x = 3 và đi qua điểm A(3;9) . Hướng dẫn giải: Chọn C. b 6 −
Trục đối xứng của (P) là x = − = hay x = 3. 2a 2 − Ta có: 2 2
− + 6.2+1= 9  A(2;9)(P).
Câu 44. Xác định hàm số 2
y = 2x + bx + c biết đồ thị hàm số này đi qua hai điểm A(0; ) 1 , B ( 2 − ;7) . 9 53 A. 2 y = 2x + x − . B. 2
y = 2x + x +1. 5 5 C. 2
y = 2x − x +1. D. 2
y = 2x + x −1. Hướng dẫn giải: Chọn B. c =1 c =1
Parabol qua hai điểm A(0; ) 1 , B ( 2 − ;7) nên    . 8
 − 2b + c = 7 b  =1  1 
Câu 45. Xác định parabol ( P) 2
: y = ax − 4x + c biết ( P) có đỉnh là I ; 2 −   là:  2  1 A. 2 y = 4
− x − 4x +1. B. 2 y = 2
− x − 4x + . 2 1 C. 2
y = 2x − 4x − . D. 2
y = 4x − 4x −1. 2 Hướng dẫn giải: Chọn D.   Vì parabol có đỉ 1 nh là I ; 2 − 
 nên ta có hệ phương trình 4 1 =  a = 4 .  2  2a 2 75
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077  1  a=4 a 1 Mặt khác I ; 2 − 
 thuộc (P) nên − 4. + c = 2 −  c = 1 − .  2  4 2
Câu 46. Tọa độ đỉnh I của parabol ( P) 2
: y = −x + 4x là A. I ( 2 − ; −12) . B. I (2; 4) . C. I ( 1; − − 5) . D. I (1; 3) . Hướng dẫn giải: Chọn B. bx = − = 2
Tọa độ đỉnh I : I  2aI (2; 4) . 2 y = 2 − + 4.2 = 4  I Câu 47. Hàm số 2
y = −x +1 nghịch biến trên khoảng nào sau đây? A. (0; +) . B. (− ; 0) .
C. (− ; 0) và (0; +) . D. (− ; − ) 1 và (1; +) . Hướng dẫn giải: Chọn A. b Hàm số 2
y = −x +1 có: a = 1 −  0 và −
= 0 Hàm số nghịch biến trên khoảng (0;+) . 2a
Câu 48. Giao điểm của parabol ( P) : 2
y = x + 5x + 4 với trục hoành:
A. (−1;0) , (−4; 0) . B. (0; − ) 1 , (0; − 4) .
C. (−1;0) , (0; −4) . D. (0; − ) 1 , (−4; 0) . Hướng dẫn giải: Chọn A.x = 1 −
Phương trình hoành độ giao điểm của (P) với Ox: 2
x + 5x + 4 = 0   . x = 4 −
Vậy hai giao điểm tìm được là (−1;0) và (−4; 0) . 3
Câu 49. Tìm tất cả giá trị của m để đỉnh của parabol 2
y = x + x + m nằm trên đường thẳng y = . 4 A. m = 2 . B. m = 0 . C. m = 1. D. m = 2 − . Hướng dẫn giải: Chọn C.   Parabol có đỉ 1 1 3 1 3 nh I − ; m − 
 . Do I d : y =  m − =  m = 1.  2 4  4 4 4 Câu 50. Parabol 2
y = x + x + c cắt đường phân giác của góc phần tư thứ nhất tại điểm có hoành độ x = 1 . Khi đó c bằng: 1 A. . B. 2 − . C. 2 . D. 1 − . 2 Hướng dẫn giải: Chọn D.
Đường phân giác góc phần tư thứ nhất có phương trình d : y = x .
Với x = 1 thì y = 1 nên giao điểm của parabol với d là A(1; ) 1 . 76
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Thay tọa độ điểm A vào hàm số bậc hai, ta được: 2
1 = 1 +1+ c c = 1 − . Câu 51. Biểu thức 2 0 2 0 2 0 2 0
A = cos 10 + cos 20 + cos 30 + ... + cos 180 có giá trị bằng: A. A = 9 . B. A = 3 . C. A = 12 . D. A = 6 . Hướng dẫn giải: Chọn A. Ta có: A = ( 2 0 2 0 + )+ +( 2 0 2 0 + ) 2 0 2 0 cos 10 cos 170 ... cos 80 cos 100 + cos 90 + cos 180 = ( 2 0 2 0 2 0
2 cos 10 + cos 20 + ... + cos 80 ) +1 = ( 2 0 2 0 + )+( 2 0 2 0 + )+ +( 2 0 2 0 2 cos 10 cos 80 cos 20 cos 70 ... cos 40 + cos 50 ) +1  = 9.
Câu 52. Giá trị của o o
tan 30 + cot 30 bằng bao nhiêu? 4 1+ 3 2 A. . B. . C. . D. 2 . 3 3 3 Hướng dẫn giải: Chọn A. 3 4 3 Ta có: o o tan 30 + cot 30 = + 3 = . 3 3
Câu 53. Cho góc  thỏa mãn o o
0    90 . Khẳng định nào sau đây đúng? A. 2 2  + ( o sin sin 90 −  ) = 0 . B. 2 2  + ( o sin sin 90 −  ) = 2 . C. 2 2  + ( o sin sin 90 −  ) = 1. D. 2 2 + ( o sin sin 90 −  ) = 3 . Hướng dẫn giải: Chọn C. Ta có: 2 2  + ( o −) 2 2 sin sin 90 = sin  + cos  =1.
Câu 54. Mệnh đề nào sau đây về tam giác ABC là sai?
A. Góc B nhọn khi và chỉ khi 2 2 2
b a + c .
B. Góc A vuông khi và chỉ khi 2 2 2
a = b + c .
C. Góc C tù khi và chỉ khi 2 2 2
c a + b .
D. Góc A tù khi và chỉ khi 2 2 2
b a + c . Hướng dẫn giải: Chọn D. 2 2 2
b + c − a Trong ABC
, ta có: A tù khi và chỉ khi cos A  0   0 2bc 2 2 2 2 2 2
b + c − a  0  a b + c . Do đó khẳng định trong D sai. 2 1− sin x
Câu 55. Rút gọn biểu thức P = ta được 2sin . x cos x 1 1 A. P = tan x . B. P = cot x .
C. P = 2cot x .
D. P = 2 tan x . 2 2 Hướng dẫn giải: Chọn B. 77
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 2 2 1− sin x cos x cos x 1 Ta có: P = = = = cot x . 2sin . x cos x 2sin . x cos x 2sin x 2
Câu 56. Biểu thức ( a + a)2 cot tan bằng 1 1 A. − . B. 2 2
cot a + tan a2 . 2 2 sin  cos  1 1 C. + . D. 2 2
cot a tan a + 2 . 2 2 sin  cos  Hướng dẫn giải: Chọn C.
Ta có: (cot a + tan a)2 2 2 = cot a + 2cot .
a tan a + tan a = ( 1 1 2 cot a + ) 1 + ( 2 tan a + ) 1 = + . 2 2 sin a cos a 5
Câu 57. Cho  là góc tù và sin =
. Giá trị của biểu thức 3sin + 2cos là 13 9 9 A. 3 . B. − . C. 3 − . D. . 13 13 Hướng dẫn giải: Chọn B. 144 12
Vì  là góc tù nên cos  0 . Ta có: 2 2 cos  = 1− sin  =  cos = − . 169 13 Khi đó: 5 12 9 3sin 2 cos   + = 3 + 2 − = −   . 13  13  13 5
Câu 58. Cho góc  thỏa mãn sin + cos =
. Giá trị của sin.cos là: 2 1 1 1 1 A. . B. . C. . D. − . 8 4 2 8 Hướng dẫn giải: Chọn A. Ta có: 5 sin + cos =  (sin + cos )2 5 2 2
= sin  + cos  + 2sin cos = 2 4 5 1
1+ 2sin cos =  sin cos = . 4 8
Câu 59. Cho ABC vuông tại A có AC = 5 cm, BC = 13 cm. Gọi góc ABC =  và ACB =  . Hãy chọn
khẳng định đúng khi so sánh độ lớn của hai góc  và  . A.    . B.    . C.  =  . D.    . Hướng dẫn giải: Chọn A. 78
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 Do ABC  vuông tại A nên 2 2 2 2 2 2
AB = BC − AC = 13 − 5 = 12  AB = 12 cm.
Ta biết rằng, trong một tam giác góc nào đối diện với cạnh lớn hơn
thì góc đó lớn hơn góc được so sánh, ta có:
AC = 5  12 = AB     .
Câu 60. Cho tam giác ABC có diện tích bằng 26 cm2 và AB = 8 cm, AC = 13cm. Giá trị sin A bằng bao nhiêu? 1 1 A. . B. 30 . C. . D. 150 . 4 2 Hướng dẫn giải: Chọn C. 1 2S 2.26 1
Diện tích tam giác ABC là : S = A .
B AC.sin A  sin A = = = . 2 A . B AC 8.13 2
Câu 61. Cho giác ABC có a = 5 , b =
26 , C = 135 .Tính diện tích của ABC . −5 13 5 13 A. . B. 5 13 . C. . D. 5 26 . 2 2 Hướng dẫn giải: Chọn C. 1 1 5 13
Diện tích tam giác ABC là: S = a . b sin C = .5. 26.sin135 = . 2 2 2
Câu 62. Tam giác ABC có BC = a và A = 30 . Tính bán kính đường tròn ngoại tiếp ABC . a 3 a A. a . B. . C. 2a . D. . 3 2 Hướng dẫn giải: Chọn A. BC a
Theo định lí sin ta có: 2R = =
= 2a R = a . sin A sin 30
Câu 63. Cho ABC biết a = 6 , b = 2 , c = 1+ 3 . Độ dài đường cao ứng với góc nhỏ nhất của ABC bằng? 1+ 3 6 (1+ 3 ) 1+ 3 3 + 3 A. . B. . C. . D. . 2 4 6 2 Hướng dẫn giải: Chọn D.
Trong một tam giác, đối diện với cạnh bé hơn là góc bé hơn nên góc B là góc nhỏ nhất (và là góc nhọn) của ABC  . 1 1 ac sin B Diện tích ABC  : S = ac sin B = bh h =
( h là đường cao tam giác ứng với góc B). 2 2 b b b b
Áp dụng định lí côsin cho tam giác ABC, có: 79
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
a + c − b + ( + )2 2 2 2 2 6 1 3 − 2 2 cos B = = = = B B =  . ac 2. 6.(1+ 3 ) sin 45 2 2 6 (1+ 3 )sin 45 3 + 3 Vậy h = = . b 2 2
Câu 64. Cho ABC có ba cạnh lần lượt là a = 5 , b = 8 , c = 11. Độ dài đường trung tuyến vẽ từ đỉnh C bằng: 57 57 A. . B. . C. 57 . D. 57 . 4 2 Hướng dẫn giải: Chọn B. 2 2 2 2 2 2 a + b c 5 + 8 11 57 57 Ta có: 2 m = − = − =  m = . c 2 4 2 4 4 c 2
Câu 65. Cho góc xOy = 60 . Gọi A và B là hai điểm di động lần lượt trên tia Ox và tia Oy sao cho
AB = 2 3 . Độ dài lớn nhất của đoạn OA bằng: A. 4 3 . B. 2 . C. 4 . D. 1. Hướng dẫn giải: Chọn C.
Áp dụng định lí sin cho OAB ta có: OA AB 2 3 = = = 4 sin B sin 60 3 2
OA = 4sin B .
Vì sin B  1 nên OA = 4sin B  4 .
Khi OA = 4 (lớn nhất) thì 0 B = 90 .
Câu 66. Hai chiếc ca nô cùng xuất phát từ cảng A , đi thẳng theo hai
hướng tạo với nhau góc 60 . Ca nô B chạy với vận tốc 20 hải
lí một giờ. Ca nô C chạy với tốc độ 25 hải lí một giờ. Hỏi sau
2 giờ, hai ca nô cách nhau một khoảng xấp xỉ bao nhiêu hải lí
(kết quả làm tròn đến hàng đơn vị)? (1 hải lí  1,852 km). A. 46 . B. 23. C. 25 . D. 56 . Hướng dẫn giải: Chọn A.
Sau 2 giờ, ca nô B đi được 40 hải lí, canô C đi được 50 hải lí. Xét ABC
có AB = 40 , AC = 50 và A = 60 .
Áp dụng định lí côsin cho ABC  ta có: 2 2 2
BC = AB + AC − 2 A . B A . C cos A 80
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 2 2
= 40 +50 − 2.40.50.cos60 = 2100  BC =10 21  46 .
Vậy sau 2 giờ, hai ca nô cách nhau một khoảng xấp xỉ 46 hải lí.
Câu 67. Từ đỉnh C một tháp có chiều cao CD = 40m,
người ta nhìn hai điểm A và B trên mặt đất
dưới các góc nhìn là 34 2  6 và 72 1  2 so với
phương thẳng đứng của tháp. Ba điểm , A , B D
thẳng hàng. Khoảng cách AB gần nhất với kết quả nào sau đây? A. 97 m. B.100 m. C. 120 m. D. 83m. Hướng dẫn giải: Chọn A. Xét ACD vuông tại D , ta có: AD tan 34 2  6 =  AD = 40.tan 34 2  6 . CD Xét BCD vuông tại D , ta có: BD tan 72 1  2 =  BD = 40 tan 72 1  2. CD Suy ra:
AB = BD − AD = 40(tan 72 12   − tan 34 26  )  97 m.
Câu 68. Khi khai quật tại một ngôi làng cổ, người ta tìm được mảnh
của một chiếc đĩa phẳng hình tròn bị vỡ. Các nhà khảo cổ đo
được kích thước ba cạnh tam giác ABC (nội tiếp vành tròn
đĩa) là 3,7 cm; 4,3cm và 7,5 cm. Họ muốn làm một chiếc
đĩa mới mô phỏng theo chiếc đĩa này. Hỏi chiếc đĩa cần làm
có bán kính bằng bao nhiêu? (Kết quả làm tròn đến hàng đơn vị). A. 6,1 cm. B. 5, 7 cm. C. 6,8 cm. D. 5,3 cm. Hướng dẫn giải: 81
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 Chọn B. a + b + c
Nửa chu vi tam giác là p = = 7,75 cm. 2
Gọi S, R lần lượt là diện tích và bán kính đường tròn ngoại tiếp tam giác ABC. Theo công thức Hê-rông ta có: S =
p ( p − a)( p − b)( p − c)  5, 2 cm2. abc abc 4, 3.3, 7.7, 5 Ta lại có: S =  R = =  5,7 cm. 4R 4S 4.5, 2
Câu 69. Cho tam giác ABC có độ dài ba đường trung tuyến lần lượt bằng 15, 18, 27. Tính diện tích S của tam giác ABC . A. 105 2 . B. 125 . C. 105 . D. 120 2 . Hướng dẫn giải: Chọn D.
Gọi I là trung điểm BC , G là trọng tâm tam giác ABC , ta có: S AI ABC  = = 3  S = 3S . ABC GBC S GI GBC
Lấy D là điểm đối xứng với G qua I , ta có BGCD là hình bình hành (do có hai đường chéo cắt
nhau tại trung điểm của mỗi đường). 1 Suy ra: S = S = S . Do vậy: S = 3S . GBC BGD   2 BGCD ABC BGD 2
Tam giác BDG có độ dài 3 cạnh bằng độ dài ba đường 3
trung tuyến tương ứng của ABC
, độ dài ba cạnh đó là 10, 12, 18. 10 +12 +18
Nửa chu vi tam giác BDG là: p = = 20 . 2
Diện tích tam giác BDG: S = 20 − − − =  (20 10)(20 12)(20 18) 40 2 . BGD
Diện tích tam giác ABC: S = 3.40 2 =120 2 . ABCCâu 70. Cho ABC
có AB = 8 , AC = 5, A = 60 . Tính bán kính đường tròn cắt cả ba cạnh của ABC  và
chắn trên mỗi cạnh một dây có độ dài bằng 4: A. 7 . B. 3 . C. 2 + 3 . D. 7 . Hướng dẫn giải: Chọn D. 82
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Gọi O là tâm đường tròn bán kính R cần tìm và I, J , K theo
thứ tự là hình chiếu vuông góc của O trên BC, AC, AB .
Theo giả thiết : B C = C A = A B = 4  OI = OJ = OK 1 1 2 2 1 2
O là tâm đường tròn nội tiếp tam giác ABC  . Suy ra 2 2 2 2 2 2
R = OB = OI + IB = r + IB (*) 1 1 1
(r là bán kính đường tròn nội tiếp tam giác ABC). Ta có: 2 2 BC = AB + AC − 2 . AB AC cos A 0
= 64 + 25 − 2.8.5.cos60 = 7 . 8 + 5 + 7
Nửa chu vi tam giác ABC: p = =10 ; diện tích tam 2 giác ABC: S = pr =10r ABC    1
10r =10 3  r = 3 . 0 S = A . B AC.sin 60 = 10 3  ABC   2 B C 2 Ta lại có: 1 1 IB = = 2 . Thay vào (*): 2 2
R = 3 + 2 = 7  R = 7 . 1 2
Câu 71. Hãy tìm khẳng định sai. Nếu hai véc tơ bằng nhau thì chúng luôn có đặc điểm sau
A. Cùng điểm gốc. B. Cùng phương.
C. Có độ dài bằng nhau. D. cùng hướng. Hướng dẫn giải: Chọn A.
Câu 72. Mệnh đề nào sau đây đúng?
A. Có duy nhất một vectơ cùng phương với mọi vectơ.
B. Có ít nhất hai vectơ có cùng phương với mọi vectơ.
C. Có vô số vectơ cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ. Hướng dẫn giải: Chọn A.
Theo quy ước thì vectơ không luôn cùng phương với mọi vectơ.
Câu 73. Cho hình bình hành ABCD tâm O . Khi đó OA − OB bằng
A. OC + OB . B. AB .
C. OC − OD . D. CD . Hướng dẫn giải: Chọn D.
Ta có: OA − OB = BA = CD .
Câu 74. Cho 5 điểm M , N, , P ,
Q R . Vectơ tổng MN + PQ + RN + NP + QR bằng: A. MP . B. PR . C. MR . D. MN . Hướng dẫn giải: Chọn D.
Ta có: MN + PQ + RN + NP + QR = (MN + NP) + (PQ + QR) + RN
= MP + PR + RN = MR + RN = MN . 83
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Câu 75. Cho hình bình hành ABCD . Có bao nhiêu vectơ có điểm đầu và điểm cuối là các đỉnh của hình bình
hành, bằng véc tơ AD (không kể véc tơ AD ) ? A. 1. B. 2 . C. 3 . D. 4 . Hướng dẫn giải: Chọn A.
Ta có: BC = AD và BC là duy nhất.
Câu 76. Cho tam giác đều ABC cạnh a . Mệnh đề nào sau đây là đúng?
A. AB = AC .
B. AC = a .
C. AC = BC .
D. AB = a . Hướng dẫn giải: Chọn D.
Câu 77. Hình bình hành ABCD là một hình chữ nhật nếu nó thỏa mãn điều kiện nào trong các điều kiện sau đây?
A. AC = BC .
B. AC = BD .
C. AC = AD .
D. AC = BD . Hướng dẫn giải: Chọn B.
Một hình bình hành có hai đường chéo bằng nhau thì nó là hình chữ nhật.
Câu 78. Cho tứ giác ABCD . Nếu AB = DC và AC = BD thì ABCD
A. Không là hình bình hành. B. Là hình vuông.
C. Là hình chữ nhật. D. Là hình thoi. Hướng dẫn giải: Chọn C.
Vì AB = DC nên ABCD là hình bình hành, mặt khác AC = BD (hai đường chéo bằng nhau); vì
vậy ABCD là hình chữ nhật.
Câu 79. Cho hình bình hành ABCD . Tổng các véc tơ AB + AC + AD là 1 2 A. 2AC . B. AC . C. AC . D. AC . 3 3 Hướng dẫn giải: Chọn A.
Ta có: AB + AC + AD = ( AB + AD) + AC = AC + AC = 2AC .
Câu 80. Cho 4 điểm bất kì , A ,
B C, O . Đẳng thức nào sau đây là đúng?
A. OA = CA − CO .
B. AB = AC + BC .
C. AB = OB + OA .
D. OA = OB − BA. Hướng dẫn giải: Chọn A.
Câu 81. Cho tam giác đều ABC cạnh 2a có G là trọng tâm. Khi đó giá trị AB − GC là: a 3 2a 3 2a 4a 3 A. . B. . C. . D. . 3 3 3 3 Hướng dẫn giải: Chọn D. 84
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Vẽ hình bình hành ABKG, ta có: AB = GK . Khi đó: 2 2
AB − GC = GK − GC = CK = CK = BK + BC ; 2 2 2a 3 2a 3 BK = AG = AM = . = . 3 3 2 3 2  2a 3  2 4a 3
Do vậy: AB − GC =   + (2a) =   . 3 3  
Câu 82. Cho tứ giác ABCD . Gọi M , N lần lượt là trung điểm của các cạnh A ,
B CD . K là điểm đối xứng
với M qua N . Khi đó khẳng định nào sau đây là đúng?
A. MK = AD − BC .
B. MK = AD + BC .
C. MK = AB + CD .
D. MK = AC − BD . Hướng dẫn giải: Chọn B.
Xét tứ giác MCKD có N là trung điểm của mỗi đường chéo MK, CD nên MCKD là hình bình hành.
Ta có: MK = MC + MD = MB + BC + MA + AD  
=  MA+ MB + BC + AD = BC + AD   .  0 
Câu 83. Cho tam giác ABC . Điểm M thỏa mãn MA − MB + MC = 0 thì
A. M là điểm sao cho tứ giác ABMC là hình bình hành.
B. M là trọng tâm tam giác ABC .
C. M là điểm sao cho tứ giác BAMC là hình bình hành.
D. M thuộc đường trung trực của AB . Hướng dẫn giải: Chọn C.
Ta có: MA − MB + MC = 0  BA + MC = 0  BA = CM .
Do đó BAMC là hình bình hành. 85
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Câu 84. Cho nửa đường tròn tâm O , đường kính PQ = 2. Trên nửa đường tròn đó ta lấy các điểm , A , B C khác ,
P Q sao cho theo thứ tự đó, chúng chia nửa đường tròn thành bốn phần bằng nhau. Khi đó
OA + OC + OB bằng: A. 3 . B. 1+ 2 . C. 2 + 2 . D. 2 . Hướng dẫn giải: Chọn B.
Gọi I là trung điểm AC. Ta có: OA + OC = 2OI .
Tam giác AOC vuông cân tại O, cạnh góc vuông bằng 1 (bằng bán kính nửa đường tròn) nên 2 OI = . 2 2
Khi đó: OA + OC + OB = 2OI + OB = 2 +1 = 2 +1. 2 Câu 85. Cho ABC
. Gọi M là điểm thỏa mãn MB = 3MA . Khi đó biểu diễn AM theo AB và AC là 1 1 A. AM = AB + 3AC . B. AM = − AB + 0.AC . 4 2 1 1 1 1 C. AM = AB + AC . D. AM = AB + AC . 4 6 2 6 Hướng dẫn giải: Chọn B. 1 1 Ta có: AM = − AB = − AB + 0.AC . 2 2
Câu 86. Cho tam giác ABC . Gọi M là trung điểm của AB , D là trung điểm của BC , N là điểm thuộc AC
sao cho CN = 2NA , K là trung điểm của MN . Khi đó khẳng định nào sau đây là đúng? 1 1 1 1 A. AK = AB + AC . B. AK = AB + AC . 4 6 2 3 1 2 C. AK = AD . D. AK = AD . 2 5 Hướng dẫn giải: Chọn A. 86
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 1 1 1 1 1 Ta có: AK =
(AM + AN)= . AB+ 1 1 . AC = AB + AC . 2 2 2 2 3 4 6
Câu 87. Cho tam giác ABC với phân giác trong AD . Biết AB = 5 , BC = 6 , CA = 7 . Khi đó AD bằng: 5 7 7 5 7 5 5 7 A. AB + AC . B. AB − AC . C. AB + AC . D. AB − AC . 12 12 12 12 12 12 12 12 Hướng dẫn giải: Chọn C. BD AB 5
Vì AD là phân giác trong của tam giác ABC nên: =
= mà BD, DC cùng hướng nên DC AC 7 5 5 BD =
DC AD − AB = (AC − AD) 7 7 12 5 7 5  AD = AB + AC AD = AB + AC . 7 7 12 12
Câu 88. Cho tam giác ABC . Gọi I là trung điểm của BC , H là điểm đối xứng của I qua C . Khi đó khẳng
định nào sau đây là đúng?
A. AH = AC + AI .
B. AH = 2AC − AI .
C. AH = 2AC − AB .
D. AH = AB + AC + AI . Hướng dẫn giải: Chọn B.
Ta có: AH = AC + CH = AC + IC = AC + ( AC − AI ) = 2AC − AI .
Câu 89. Cho hai điểm cố định ,
A B . Tập hợp các điểm M thỏa mãn MA + MB = MA − MB là:
A. Đường tròn đường kính AB .
B. Đường trung trực của AB .
C. Đường tròn bán kính AB .
D. Nửa đường tròn đường kính AB . 87
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 Hướng dẫn giải: Chọn A.
Gọi I là trung điểm đoạn thẳng AB, ta có: AB
MA + MB = MA − MB  2MI = BA  2MI = AB IM = . 2 AB
Vậy tập hợp điểm M là đường tròn tâm I, bán kính R = (đường kính AB). 2
Câu 90. Cho tam giác ABC có trọng tâm G . Tập hợp các điểm M sao cho MA + MB + MC = AB − AC là: 1
A. Đường tròn tâm G đường kính BC .
B. Đường tròn tâm G đường kính BC . 3 1
C. Đường tròn tâm G bán kính BC .
D. Đường tròn tâm G đường kính 3MG . 3 Hướng dẫn giải: Chọn C. BC
Ta có: MA + MB + MC = AB − AC  3MG = CB  3GM = BC GM = . 3 BC
Vậy tập hợp điểm M là đường tròn tâm G, bán kính . 3
Câu 91. Cho tứ giác ABCD . Gọi M , N lần lượt là trung điểm của A ,
B CD . Đẳng thức nào sau đây là đúng?. BC + AD A. MN = .
B. MN = BC + AD . 2 1
C. MN = AC + BD . D. MN = (BC + AD). 2 B Hướng dẫn giải: C Chọn D. M 1 Ta có: MN = (MC +MD) N 2 1
= (MB + BC + MA+ AD) 1 = (BC + AD). A D 2 2
Câu 92. Cho hình thang ABCD , hai đường chéo AC và BD cắt nhau tại O. Qua O kẻ MN song song với
AB ( AB là đáy của hình thang, M A ,
D N BC ). Đặt AB = a , DC = b . Khi đó khẳng định nào sau đây là đúng? a AB + bDC b AB + aDC A. MN = . B. MN = . a + b a + b a AB − bDC b AB − aDC C. MN = . D. MN = . a + b a + b Hướng dẫn giải: Chọn B. 88
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 MO DO ON BO
Áp dụng định lí Ta-lét trong tam giác ta có: = ; = . AB DB DC BD DO BO DO BO Từ đó suy ra MO = A ; B ON =
DC MN = MO + ON = AB + DC (1). DB BD DB BDMO DM =  AB DA MO MO ab Mặt khác, ta có:   + = 1 MO = . MO AM a b a + b  =  DC AD ab DO MO + b BO a Suy ra a b = = = (2). Tương tự ta có = (3) . DB AB a a + b BD a + b b AB + aDC
Từ (1), (2) và (3) ta có MN = a + . b
Câu 93. Cho tam giác đều ABC cạnh .
a Biết rằng tập hợp các điểm M thỏa mãn đẳng thức
2MA + 3MB + 4MC = MB − MA là đường tròn cố định có bán kính .
R Tính bán kính R theo . a a a a a A. r = . B. r = . C. r = . D. r = . 3 9 2 6 Hướng dẫn giải: Chọn B.
Gọi G là trọng tâm của tam giác . ABC
Chọn điểm I sao cho 2IA + 3IB + 4IC = 0
 (IA+ IB + IC) 1 3
+ IC − IA = 0  9 IG = CA IG = CA hay điểm I cố định. 9
Ta có: 2MA + 3MB + 4MC = 2 (MI + IA) + 3(MI + IB) + 4(MI + IC )
= 9MI + 2IA + 3IB + 4IC = 9MI . 0 AB
Do vậy 2MA + 3MB + 4MC = MB − MA  9MI = AB  9MI = AB MI = . 9 AB a
Vậy tập hợp các điểm M cần tìm là đường tròn tâm I , bán kính r = = . 9 9
Câu 94. Cho ba vectơ a , b , c thỏa: a = 4 , b = 1, c = 5 và 5(b − a) + 3c = 0 . Khi đó biểu thức
M = a .b + b .c + c .a có giá trị bằng 67 A. 29 . B. . C. 18, 25 . D. 1 − 8,25. 2 89
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077 Hướng dẫn giải: Chọn A.
Ta có: 5(b − a) + 3c = 0  5(a − b) = 3c  (a−b)2 2 25 = 9c  ( 2 2
a − ab + b ) 2 25 2 = 9c  ( 2 2 − ab + ) 2 25 4 2 1 = 9.5  . a b = 4 (1).
Tương tự: 5(b − a) + 3c = 2 2 2
0  5a = 5b + 3c  25a = 25b + 9c + 30bc 2 2 2
 25.4 = 25.1 +9.5 +30bc bc = 5  . b c = 5 (2).
5(b − a) + 3c = 2 2 2
0  5b = 5a − 3c  25b = 25a + 9c − 30 . a c 2 2 2  25.1 = 25.4 + 9.5 −30 . a c  . a c = 20 (3).
Từ (1), (2), (3) suy ra : M = 4 + 5+ 20 = 29 .
Câu 95. Cho tam giác ABC vuông tại A với AB = 3, AC = 4 . Các điểm M , N lần lượt thuộc các cạnh A ,
B AC thỏa mãn AM = AN = 1. Tích vô hướng BN.CM bằng A. 1. B. −1. C. −7. D. 7. Hướng dẫn giải: Chọn C.
Ta có: BN.CM = (BA + AN )(CA + AM ) = B . A CA + B .
A AM + AN.CA + AN.AM 0 0 1 1 = − 1 1 1 1 A . B AB − AC. AC 2 2 2 2
= − AB − AC = − .3 − .4 = 7 − . 3 4 3 4 3 4
Câu 96. Gọi S là diện tích tam giác ABC . Mệnh đề nào sau đây đúng? 1 A. S =
AB .AC − ( A . B AC )2 2 2 . B. S =
AB AC − ( AB AC)2 2 2 . . . 2 1 C. S = (A .BAC)2 2 2 − AB .AC .
D. S = ( AB AC)2 2 2 . − AB .AC . 2 Hướng dẫn giải: Chọn A. 2 1 1 1  A . B AC  Ta có : S = A . B AC sin A 2 = A .
B AC 1− cos A = A . B AC 1−   2 2 2 A . B AC  
AB .AC − ( A . 1 B AC )2 2 2 1 = A . B AC =
AB .AC − ( A . B AC )2 2 2 . 2 2 2 AB .AC 2 90
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
Câu 97. Đoạn thẳng AB có độ dài 2a , I là trung điểm AB . Khi 2 M .
A MB = 3a . Độ dài MI là A. 2a . B. a . C. a 3 . D. a 7 . Hướng dẫn giải: Chọn A. Ta có : 2
MA MB = a  (MI + IA)(MI + IB) 2
= a  (MI + IA)(MI − IA) 2 . 3 3 = 3a 2 2 2   2  AB
MI − IA = 3a 2 2 2 2 2  MI −
= 3a MI − a = 3a MI = 2a   .  2 
Câu 98. Cho đoạn thẳng AB = 4 . Tập hợp các điểm M thỏa mãn 2 2
MA − MB = 8 là
A. Một đường thẳng.
B. Một đoạn thẳng.
C. Một đường tròn. D. Một điểm. Hướng dẫn giải: Chọn A.
Gọi I là trung điểm của AB . 2 2 Ta có: 2 2
MA − MB = 8  MA − MB = 8
 (MA− MB)(MA+ MB) = 8  B .
A 2.MI = 8  B . A MI = 4 .
Gọi H là hình chiếu của M trên AB, ta có: B . A MI = 4  B .
A (MH + HI ) = 4  B . A MH + B . A HI = 4  B . A HI = 4 (*). 0 Từ (*) ta có: B .
A HI  0 nên B ,
A HI cùng hướng; đồng thời 4 4 A .
B HI = 4  HI = = =1. AB 4
Vậy H là trung điểm đoạn BI và tập hợp điểm M là đường thẳng qua H, vuông góc với AB.
Câu 99. Một máy bay đang bay từ hướng đông sang hướng tây với tốc độ 700 km/h thì gặp luồng gió thổi từ
hướng đông bắc sang hướng tây nam với tốc độ 40 km/h. Máy bay bị thay đổi vận tốc sau khi gặp
gió thổi. Tìm tốc độ mới của máy bay (làm tròn kết quả đến hàng phần trăm). A. 911,12 km/h . B. 724,32 km/h . C. 728,83 km/h . D. 813,13 km/h . Hướng dẫn giải: Chọn C.
Đặt v = O ,
A v = OB lần lượt là vectơ vận tốc ban đầu của máy bay và của gió; v = OC là vận tốc 1 2
của máy bay sau khi gặp luồng gió thổi. Ta có v = v + v và OACB là hình bình hành. 1 2 Xét tam giác OAC có 0
OAC = 135 , OA = 700, AC = 40 2 2 2
OC = AO + AC − 2A . O A . C cos OAC 2 2 0
= 700 + 40 − 2.700.40.cos135 91
BỒI DƯỠNG TOÁN 10 – 11 – 12 – ÔN THI THPT QUỐC GIA
Lớp dạy trực tiếp: 102 – T8 – P.Tây Thạnh – Q.Tân Phú – TP.HCM
Lớp dạy trực tuyến qua Zoom Zalo: 0969 343 344 : 0903 068 077
 531197,98  OC  728,83 km/h.
Vậy tốc độ mới của máy bay sau khi gặp gió xấp xỉ bằng 728,83 km/h.
Câu 100. Một chiếc thuyền cố gắng đi thẳng qua một con sông với tốc độ 0,75 m/s. Tuy nhiên dòng nước trên
con sông đó chảy với tốc độ 1,2 m/s về hướng bên trái (hình vẽ). Tính tốc độ dịch chuyển của thuyền
so với bờ (kết quả làm tròn đến hàng phần nghìn). A. 1, 215 m/s. B. 1,112 m/s. C. 1,312 m/s. D. 1, 415 m/s. Hướng dẫn giải: Chọn D.
Gọi v = OA là vectơ vận tốc của thuyền đối với nước, v = OB là vectơ vận tốc của nước đối với bờ 1 2
và v = OC là vận tốc của thuyền đối với bờ. Ta có: v = v + v hay OACB là hình bình hành. 1 2
Xét tam giác vuông OAC ta có: 3 89 2 2 2 2
OC = OA + AC = 0, 75 +1, 2 = 1,415 m/s. 20
Vậy tốc độ dịch chuyển của thuyền so với bờ xấp xỉ bằng 1, 415 m/s. 92
Chuùc caùc em hoïc sinh oân taäp
thaät toát vaø gaët haùi nhieàu thaønh coâng! Hoàng Xuân Nhàn