































Preview text:
ĐỀ 1
ĐỀ KIỂM TRA 1 TIẾT
CHƯƠNG 1 TOÁN GIẢI TÍCH 11 Thời gian: 45 phút
I. PHẦN 1: TRẮC NGHIỆM (6 điểm).
Câu 1: Goi S là tập hợp tất cả các giá trị nguyên của m để phương trình 3sin x - 4cos x = m có nghiệm.
Tìm số phần tử của S. A. Vô số. B. 0. C. 10. D. 11.
Câu 2: Tìm nghiệm của phương trình tan x = 3 . A. 0 0 x = 60 + k360 . B. 0 0 x = -60 + 180 k . C. 0 0 x = 60 + 180 k . D. 0 0 x = 30 + 180 k .
Câu 3: Tìm nghiệm của phương trình 3 sinx + o c sx = -1. é p é p ì p é p x = + k2p x = - + k2p ïx = - + k2p x = - + k2p A. ê 3 . B. ê 3 . C. í 3 . D. ê 3 . ê ê ê ëx = p + k2p ëx = p + k2p ïîx = p + k2p ëx = p + kp
Câu 4: Tìm tất cả các giá trị của m để phương trình sin 2x = m +1 có nghiệm. A. 2 - £ m £ 0.
B. 0 £ m £ 2 . C. 1 - £ m £ 1 . D. 3 - £ m £ 1. 2sinx- 2 é 7p 9p ù
Câu 5: Gọi S là tổng tất cả các nghiệm của phương trình = 0 thuộc đoạn - ; . æ p ö ê ú sin x + ë 4 4 û ç ÷ è 4 ø Tìm S. 3p p p p A. S = 5 . B. S = . C. S = . D. S = - . 4 4 4 4
Câu 6: Mệnh đề nào sau đây sai ? A. cos x = 1
- Û x = p + k2p (k ÎZ).
B. tan x = 0 Û x = kp (k Î Z). p p C. sin x = 1
- Û x = - + k2p (k Î Z).
D. sin x = 1 Û x =
+ kp (k Î Z). 2 2
Câu 7: Tìm nghiệm của phương trình cos2x=-1. p p p
A. x = p + k2p B. x = + kp . C. x = + kp . D. x = + k2p . 2 4 2
Câu 8: Tìm nghiệm của phương trình 2
sin x + 5sin x + 4 = 0. p p p
A. x = k2p . B. x = + k2p . C. x = - + k2p . D. x = + k2p . 4 2 2
Câu 9: Phương trình nào sau đây vô nghiệm? A. tan x = 10 . B. sinx = 1 5. C. cos2x = 1
. D. cot x = - . 3 2 x
Câu 10: Tìm tập giá trị T của hàm số y = os c . 2 é ù A. T = [ 2; - 2] B. T = [ 1 - 1 1 ; ] 1 C. T = - ;
D. T = R ê 2 2ú ë û
Câu 11: Cho hàm số y = osx c
. Khẳng định nào sau đây là đúng?
A. y là hàm số vừa chẵn vừa lẻ.
B. y là hàm số không chẵn, không lẻ.
C. y là hàm số lẻ.
D. y là hàm số chẵn.
Câu 12: Tìm chu kì T của hàm số y = sinx . A. T = p . B. T = 4p . C. T = 2p . D. T = 3p . Trang 1 1
Câu 13: Tìm tập xác định D của hàm số y = . 1- sin x ì p ü
A. D = R \ í- + k2p ,k Î Z ý.
B. D = R \ {p + k2p,k ÎZ}. î 2 þ ìp ü
C. D = R \ {k2p,k ÎZ}.
D. D = R \ í + k2p ,k Î Z ý . î 2 þ p
Câu 14: x = - là một nghiệm của phương trình nào sau đây?. 6
A. 2sin x -1 = 0
B. 2cos x + 3 = 0.
C. 2sin x +1 = 0.
D. 2cos x +1 = 0 .
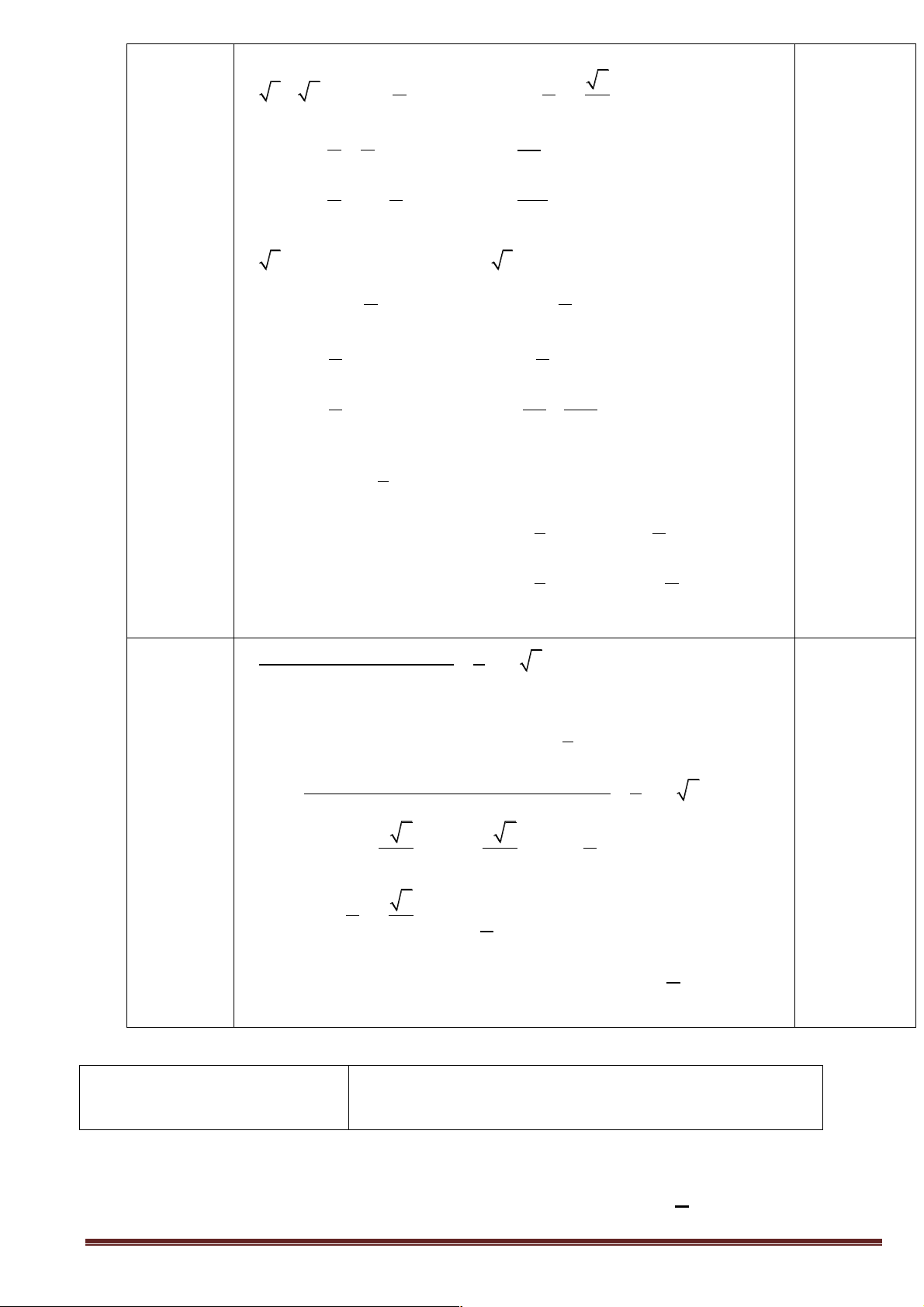
Câu 15: Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây.
Hàm số đó là hàm số nào?
A. y = sin x.
B. y = cos x .
C. y = cot x.
D. y = tan x.
II. PHẦN 2: TỰ LUẬN (4 điểm). æ p ö
Câu 1. (1,0 đ) Tìm tập xác định của hàm số y = cot x - . ç ÷ è 7 ø
Câu 2. (3,0 đ) Giải các phương trình sau
1. 2cos x -1 = 0 .
2. 2cos 2x - 2sin 2x = 2 .
3. 3cos2x + 8sin3xcos x +16cos x = 4sin 4x + 22sin x + 23. ĐÁP ÁN
I. PHẦN 1: TRẮC NGHIỆM Câu 1 2 3 4 5 6 7 8 9 10 ĐA D C B A A D B C B B Câu 11 12 13 14 15 16 17 18 19 20 ĐA D C D C A A II. PHẦN 2: TỰ LUẬN Câu NỘI DUNG BIỂU ĐIỂM Câu 1 æ p ö (1,0 điểm)
Tìm tập xác định của hàm số y = cot x - . ç ÷ è 7 ø æ p ö p 0,5
Hàm số xác định Û sin x -
¹ 0 Û x - ¹ kp ç ÷ è 7 ø 7 Trang 2 p ìp ü
Û x ¹ + kp Suy ra, tập xác định D = R \ í + kp,k Î Z ý 0,5 7 î 7 þ Câu 2.1
Giải phương trình sau 2cos x -1 = 0 .
(1,0 điểm) 1 p 0,5 pt Û os c x= Û os c x=cos 2 3 é p x = + k2p 0,5 ê 3 Û ê p êx = - + k2p êë 3 Câu 2.2
Giải phương trình sau 2cos 2x - 2sin 2x = 2
(1,0 điểm) 1 1 1 p p 0,5 pt Û cos2x - sin 2x = 1
Û sin cos2x - cos sin 2x = 2 2 2 4 4 2 é p x = - kp p p ê æ ö 24 Û sin - 2x = sin Û ç ÷ ê 0,5 è 4 ø 6 7p êx = - - kp êë 24 Câu 2.3 Giải phương trình sau
(1,0 điểm)
3cos2x +8sin3xcos x +16cos x = 4sin 4x + 22sin x + 23
pt Û 3cos 2x + 4sin 2x +16cos x - 22sin x - 23 = 0 0,25 2 Û 6s
- in x - 22sin x - 20 + 4sin 2x +16cos x = 0 æ 5 ö 6 - sin x + ç
÷(sin x + 2) + 8cos x(sin x + 2) = 0 è 3 ø Û (sin x + 2)( 6 - sin-10 +8cos x) = 0 0,25 ésin x = 2 - (VN) ê 0,25 ësin(x -a) = 1 - p
Û x = a - + k2p 0,25 2 ĐỀ 2
ĐỀ KIỂM TRA 1 TIẾT
CHƯƠNG 1 TOÁN GIẢI TÍCH 11 Thời gian: 45 phút
Câu 1: [3] Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 3 sin 2x +1 là:
A. max y = 2 + 3 ; min y = - 1
B. max y = 2 + 3 ; min y = 2 - 3
C. max y = 3 +1;min y = - 3 +1
D. max y = 3 ; min y = 2 - 3 p
Câu 2: [1] Cho hàm số f (x) = sinx, giá trị hàm số tại x = là: 3 1 -1 3 - 3 A. . B. . C. . D. . 2 2 2 2
Câu 3: [1] Nghiệm của phương trình cos x = 1là: Trang 3 p p
A. x = k2p
B. x = kp C. x = + k2p D. x = + kp 2 2
Câu 4: [3] Với giá trị nào của m thì phương trình 2 2 o
c s x - sin x + 1 - m = 0 có nghiệm: 25 21 25 25 A. 2 - < m < B. 0 < m < C. 0 £ m £ D. 2 £ m £ 8 8 8 8 3
Câu 5: [2] Nghiệm dương nhỏ nhất của phương trình sin 2x = là 2 p p p A. 0 B. C. D. 3 4 6
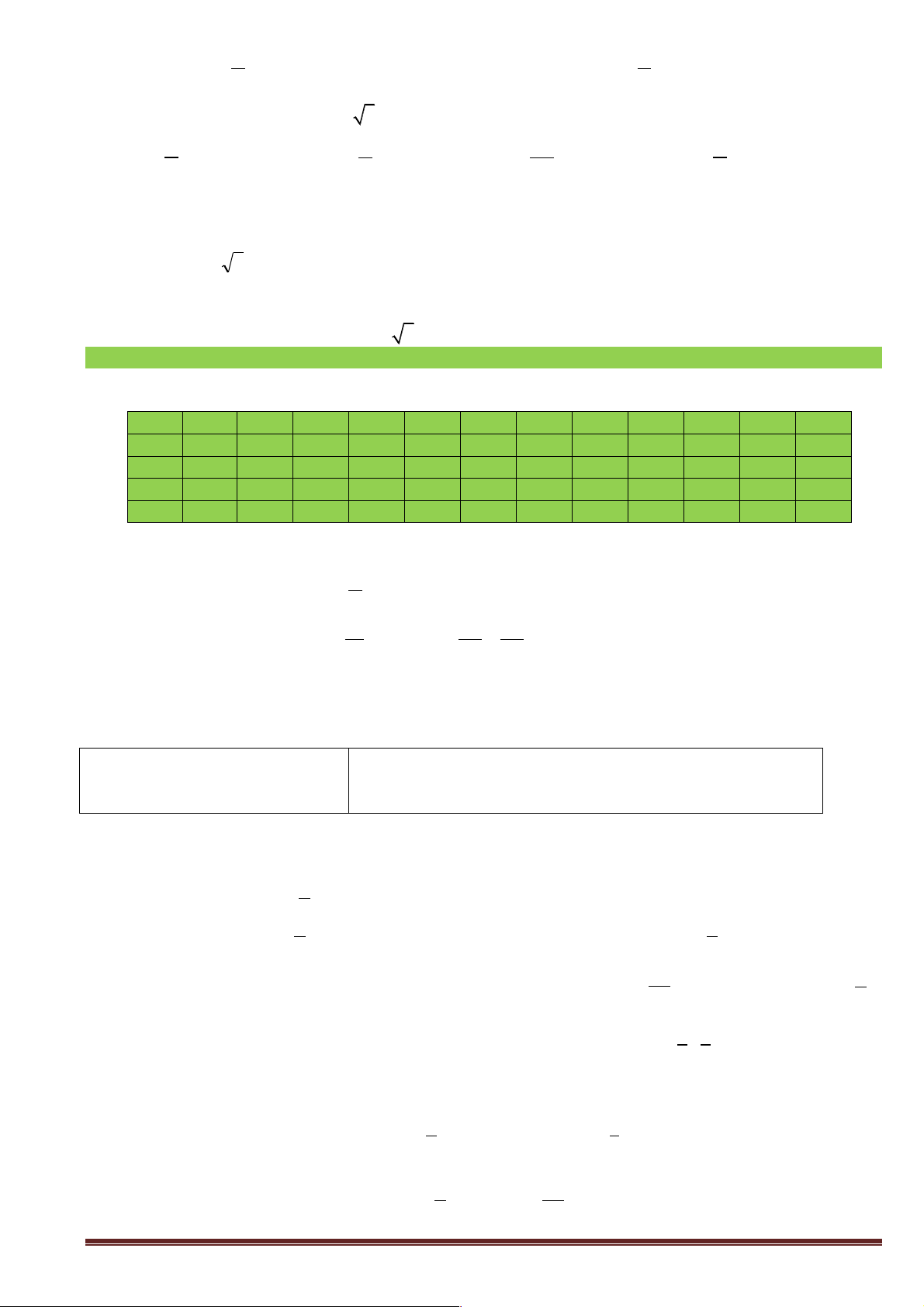
Câu 6: [3] Nghiệm của phương trình 2sin x +1 = 0 được biểu diễn trên đường tròn lượng giác ở hình bên là những điểm nào ? y B D C A¢ O x A E F B¢
A. Điểm C , điểm F . B. Điểm D , điểm C .
C. Điểm E , điểm D . D. Điểm E , điểm F .
2sin x + cos x + 3
Câu 7: [4] Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số y =
lần lượt là M , m.
-sin x + 2cos x + 4
Khi đó tổng M + m bằng: 2 24 4 A. . B. 5 . C. . D. . 11 11 11
Câu 8: [1] Nghiệm phương trình: 1+ tan x = 0 là p p p p x = + kp . x = + k2p . x = - + k2p . x = - + kp . A. 4 B. 4 C. 4 D. 4
Câu 9: [2] Tập xác định của hàm số y = tan x là: ìp ü
D = ! \ í + k2p ,k Î"ý. B. D = ! . î 2 A. þ ìp ü
D = ! \{kp,k Î } " .
D = ! \ í + kp,k Î"ý. C. î 2 D. þ
Câu 10: [2] Hàm số nào có đồ thị trên ( p
- ;p ) được thể hiện như hình dưới đây? Trang 4 y π 1 - 2 O x -π π 1 π -1 2 A. y = cot . x B. y = tan . x C. y = cos . x D. y = sin . x
Câu 11: [3] Phương trình 2cos x - 3 = 0 có bao nhiêu nghiệm thuộc đoạn [0;2p .] A. 2 . B. 4 . C. 1. D. 3 . æ p ö
Câu 12: [4] Phương trình ( x + x)2 sin 3 cos = 5 + cos 4x +
có mấy nghiệm dương bé hơn 10? ç ÷ è 3 ø A. 3 . B. 7 . C. 4 . D. 0 .
Câu 13: [3] Tìm số điểm phân biệt biểu diễn các nghiệm của phương trình 2
sin 2x - cos 2x +1 = 0 trên
đường tròn lượng giác. A. 3 . B. 2 . C. 1. D. 4 .
Câu 14: [2] Trong các phương trình sau phương trình nào vô nghiệm: ( - I ) 1 cos x = ; (II ) 3 sin x =
; (III ) sin x + cos x = 2. 3 2 A. (II). B. (I). C. (III). D. (I), (II), (III).
Câu 15: [1] Nghiệm của phương trình 2
cos x - cos x = 0thỏa điều kiện: 0 < x < p p p p p A. x = - B. x = C. x = D. x = 2 2 6 4
Câu 16: [1] Nghiệm âm lớn nhất của phương trình 3 sin x + cos x = 0 là: p - p - p - p - A. x = . B. x = . C. x = . D. x = . 12 4 3 6
Câu 17: [2] Hàm số nào dưới đây có tập xác định là T = R . sinx
A. y = cot x .
B. y = cos x . C. y = .
D. y = tan x . 2cos x -1
Câu 18: [3] Điều kiện của tham số m để phương trình msin 2x + 3 cos 2x = m + 1 vô nghiệm là:
A. m £ 1.
B. m > 1.
C. m ³ 1.
D. m < 1.
Câu 19: [2] Tổng tất cả các nghiệm thuộc [0;2p ] của phương trình 2sin x - 3 = 0là: p 2p p A. p 5 B. C. D. 3 3 3
Câu 20: [3] Hàm số y = sin 2x là hàm tuần hoàn với chu kì: p p A. T = . B. T = . C. T = p . D. T = 2p . 2 4
Câu 21: [2] Nghiệm của phương trình sin x – 3 cos x = 0 là: p p p p
A. x = + kp , k Î!. B. x =
+ kp ,k Î !. C. x = + k2p,k Î!. D. x = + k2p,k Î !. 3 4 6 2
Câu 22: [1] Điều kiện có nghiệm của phương trình a X + b X = c ( 2 2 cos sin
a + b ¹ 0) là: Trang 5 A. 2 2 2
a + b ³ c . B. 2 2 2
a + b < c . C. 2 2
a + b ³ c . D. 2 2 2
a + b > c .
Câu 23: [1] Giá trị lớn nhất của hàm số y = cos 2x trên R là: A. 1 - B. 1 C. 2 - D. 2
Câu 24: [1] Nghiệm của phương trình sin x = 1 - là: p p p
A. x = - + k2p B. x = + kp
C. x = - + kp
D. x = kp 2 6 2 é p p ù
Câu 25: [2] Phương trình sin 3x = sinx có nghiệm trên - ; là: ê 2 2 ú ë û p p 2p A. B. 0 C. D. 6 3 3 ----------- HẾT ---------- ĐÁP ÁN Câu 1 2 3 4 5 6 7 8 9 10 ĐA C C A C D D C D D D Câu 11 12 13 14 15 16 17 18 19 20 ĐA A C B B B D B B A C Câu 21 22 23 24 25 26 27 28 29 30 ĐA A A B A B ĐỀ 3
ĐỀ KIỂM TRA 1 TIẾT
CHƯƠNG 1 TOÁN GIẢI TÍCH 11 Thời gian: 45 phút
I. TRẮC NGHIỆM(4 điểm) 1- sin 2x
Câu 1: Tập xác định của hàm số y = là: cos 3x -1 ì p 2 ü ì ü
A. D = ! \ík , k p p Î"ý
B. D = ! \í + k , k Î"ý î 3 þ î 2 3 þ ìp p 2 ü ì ü
C. D = ! \í + k , k p Î"ý
D. D = ! \ík , k Î"ý î 2 3 þ î 3 þ 3tan 2x - 3
Câu 2: Tập xác định của hàm số y = là: 3 sin2x -cos2x ì p p p p ü
A. D = ! \í + k , + k ; k Î"ý B. î12 2 6 2 þ ìp p p p ü
D = ! \í + k , + k ; kÎ"ý î 4 2 12 2 þ ìp p p ü ì ü C. D = ! \í + p k , + k ; k p p p p Î"ý
D. D = ! \í + k ; + k k Î"ý î 4 12 2 þ î 6 2 4 2 þ
Câu 3: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 3sinx+4cosx+1là: Trang 6
A. max y = 6, min y = -2
B. maxy = 4, min y = -4
C. max y = 6, min y = -4
D. max y = 6, min y = -1 p
Câu 4: Nghiệm của phương trình tan(4x - ) = - 3 là: 3 p p k A. x = + ,k p Î ! B. x = - + p k ,k Î! 2 4 3 p p k k C. x = + ,k p Î ! D. x = ,k Î! 3 4 4 æ 1 ö 1
Câu 5: Nghiệm của phương trình sin 4x + = là: ç ÷ è 2 ø 3 é 1 p é 1 1 1 p x = - + ê k x = - - arcsin + ê k A. ê 8 2 , kÎ 8 4 3 2 ! B. ê , ê p p ê p 1 1 1 p x = + ê k
x = - - arcsin + k ë 4 2 êë 4 8 4 3 2 k Î! é 1 1 1 p x é 1 1 1 p = - arcsin + ê k x = - - arcsin + ê k C. ê 8 4 3 2 , k Î 8 4 3 2 ! D. ê , k Î! ê p 1 1 1 p x ê p 1 1 p = - - arcsin + ê k x = - arcsin + k ë 4 8 4 3 2 êë 4 4 3 2 p
Câu 6: Nghiệm của phương trình cos7x + sin(2x - ) = 0 là: 5 é p k p 2 x é p 3 k p 2 = + ê x = - + ê A. ê 50 5 (kÎ!) B. ê 50 5 (kÎ!) ê p 17 p k x ê p 17 p k = + ê x = + ë 90 9 êë 30 9 é p k p 2 x é p 3 k p 2 = + ê x = + ê C. ê 50 5 (kÎ!) D. ê 50 5 (kÎ!) ê p k p 2 x ê p 17 k p 2 = + ê x = + ë 30 9 êë 90 9
Câu 7: Khẳng định nào sau đây đúng về phương trình 2 sin 2x = 3 + cos 2x
A. Có 1 họ nghiệm B. Có 2 họ nghiệm C. Vô nghiệm
D. Có 1 nghiệm duy nhất
Câu 8: Phương trình 3 sin 2x - cos 2x + 1 = 0 có nghiệm là: éx = p k éx = p k A. ê p (kÎ!) B. ê p 2 (kÎ!) êx = + p êx = + 2 p k ê k ë 3 êë 3 éx = 2 p k éx = p k C. ê p 2 (kÎ!) D. ê p 2 (kÎ!) êx = + 2 p êx = + p ê k k ë 3 êë 3
Câu 9: Cho phương trình 2 2
sin x - ( 3 +1)sin x cos x + 3 cos x = 0. Nghiệm của phương trình là: p p
A. x = - + kp , k Î Z
B. x = ± + kp , k Î Z 4 3 é p x = + kp 3p ê C. x =
+ kp ,k Î Z D. 4 ê
, k Î Z 4 p êx = + kp êë 3
Câu 10: Với giá trị nào của m thì phương trình 2 2 o
c s x - sin x +1- m = 0 có nghiệm Trang 7 25 A. 0 £ m £ 25 B. 0 < m < 25 C. 2 £ m £ 25 D. 2 < m < 8 8 8 8
II. TỰ LUẬN (6 điểm) sin x
Câu 1: Tìm tập xác định của hàm số y = tan 3x -1 x
Câu 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 3 cos + 3 - 2 2
Câu 3: Giải phương trình: æ p ö a) 3 - 6 sin 2x - = 0 ç ÷ è 3 ø b)
3 sin 2x = cos 2x + 2sin 3x x c) 2 2 4 - sin x +16sin -1 = 0 2
1+ cos x + cos 2x + cos 3x 2
Câu 4: Giải phương trình = (3 - 3 sin x) 2
2cos x + cos x -1 3
...................................................... HẾT ......................................................
Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm. ĐÁP ÁN I. TRẮC NGHIỆM
1.A 2.B 3.C 4.D 5.B 6.D 7.C 8.D. 9.D 10.A II. TỰ LUẬN CÂU/ BÀI NỘI DUNG BIỂU ĐIỂM Câu 1 ĐK: (1,0 điểm) ì p ì p kp 0,25đx3 3x ¹ + kp x ¹ + ì ¹ ï ï cos3x 0 ï 2 ï 6 3 í Û í Û í (k ÎZ) 0,25đ îtan 3x -1 ¹ 0 p p kp 3 ï x kp ï ¹ + x ¹ + ïî 4 ïî 12 3 ìp kp p kp ü
TXĐ: D = R \ í + ; + ;k Î Z ý î 6 3 12 3 þ Câu 2 Ta có: (1,0 điểm) x 0,25đ 1 - £ cos £1 0,25đx2 2 x x
Û 2 £ cos + 3 £ 4 Û 3 2 £ 3 cos + 3 £ 6 0,25đ 2 2 x
Û 3 2 - 2 £ 3 cos + 3 - 2 £ 4 2
Vậy max y = 4;min y = 3 2 - 2 Trang 8 Câu 3 a) (3,0 điểm) 0,25đ æ p ö æ p ö 2 3 - 6 sin 2x - = 0 Û sin 2x - = ç ÷ ç ÷ è 3 ø è 3 ø 2 0,5đ+0,25đ é p p é 7p 2x - = + k2p x = + kp ê 3 4 ê 24 Û ê Û ê (k ÎZ ) p p 13p 0,25đ ê2x p k2p ê - = - + x = + kp 0,25đ êë 3 4 êë 24 b) 0,25đ+0,25đ
3 sin 2x = cos 2x + 2sin 3x Û 3 sin 2x - cos 2x = 2sin 3x æ p ö æ p ö Û 2sin 2x -
= 2sin 3x Û sin 2x - = sin 3x ç ÷ ç ÷ è 6 ø è 6 ø 0,25đ+0,25đ ì p ì p 2x - = 3x + k2p x = - - k2p ï 6 ï ï ï 6 0,25đ+0,25đ Û í Û í (k ÎZ ) p 7p k2p ï2x p 3x k2p ï - = - + x = + ïî 6 ïî 30 5 c) x 2 2 4 - sin x +16sin -1 = 0 Û 4 - ( 2
1- cos x) +8(1- cos x) -1 = 0 2 é 1 é p cos x = x = + k2p ê ê 2 2 3
Û 4cos x -8cos x + 3 = 0 Û ê Û ê (k ÎZ ) 3 p
êcos x = (VN) êx = - + k2p êë 2 êë 3 Câu 4
1+ cos x + cos 2x + cos 3x 2 (1,0 điểm) = (3 - 3 sin x) 2
2cos x + cos x -1 3 0,25đ ìcos x ¹ 1 - ï 2
ĐK: 2cos x + cos x -1 ¹ 0 Û í 1 0,25đ cos x ¹ - ïî 2 1+ cos x + 2 2cos x -1+ 3
4cos x - 3cos x 2 pt Û = (3 - 3 sin x) 2 0,25đ
2cos x + cos x -1 3 2 3 4 3 æ p ö Û 2cos x = 2 - sin x Û sin x + = 2 ç ÷ 3 3 è 3 ø 0,25đ éx = k p 2 æ p ö 3 ê Û sin x + = Û p (kÎ ç ÷ Z) 3 2 ê è ø x = + k p ê 2 ë 3 p
So với ĐK nghiệm của phương trình là: x = k p 2 và x = + k p 2 3 ĐỀ 4
ĐỀ KIỂM TRA 1 TIẾT
CHƯƠNG 1 TOÁN GIẢI TÍCH 11 Thời gian: 45 phút
Câu 1: Giá trị lớn nhất và nhỏ nhất của hàm số y = 4sin 2x - 5 là: A. 1 và -9 B. 1 - và -5 C. 9 và -1 D. -1 và -9 Trang 9
Câu 2: Phương trình 2 tan x - 2cot x - 3 = 0 có số nghiệm thuộc khoảng ( p - ;0) là: A. 1 B. 2 C. 3 D. 4
Câu 3: Nghiệm dương bé nhất của phương trình 2
2 tan x - 5tan x + 3 = 0 là: 3 3p p p A. arctan B. C. D. - 2 4 4 3
Câu 4: . Phương trình 2√3 sin '𝑥 − !* cos '𝑥 − !* + 2𝑐𝑜𝑠# '𝑥 − !* = √3 + 1 có nghiệm là: " " " 𝑥 = $! + 𝑘𝜋 𝑥 = '! + 𝑘𝜋 𝑥 = $! + 𝑘𝜋 𝑥 = '! + 𝑘𝜋 A. 3 " 𝑘𝜖ℤ B. 3 & , 𝑘𝜖ℤ C. 3 & , 𝑘𝜖ℤ D. 3 " , 𝑘𝜖ℤ 𝑥 = %! + 𝑘𝜋 𝑥 = $! + 𝑘𝜋 𝑥 = $! + 𝑘𝜋 𝑥 = $! + 𝑘𝜋 #& (# () #&
Câu 5: Phương trình lượng giác: 2
cos x - 3sin x - 4 = 0 có nghiệm là: p p A. x = p - + k2p B. x = - + k2p C. x = + kp D. Vô nghiệm 2 6
Câu 6: Các họ nghiệm của phương trình: sin 2x + 3cosx = 0 là: é p x = + k2p ê p A. 2 ê
B. x = ± + k2p p ê 6 x = ± + kp êë 6 é p x = + kp ê éx = k2p C. 2 ê D. ê p p 7p ê êx = ± + k2p
x = - + k2p ; x = + k2p êë ë 3 6 6
Câu 7: Tất cả các nghiệm của phương trình 3 sinx - cosx = 0 là: p p p p x = - + kp x = - + kp x = + kp x = + kp A. 6 B. 3 C. 3 D. 6
Câu 8: Với giá trị nào của m thì phương trình sin x + m = 1 có nghiệm A. 2 - £ m £ 0 B. m £ 0 C. 0 £ m £ 2 D. m ³ 1
Câu 9: Số nghiệm thuộc é0;p ù của phương trình 2 2
sin 3x cos x là: ë û = A. 4. B. 6. C. 2 D. 8.
Câu 10: Phương trình lượng giác: 2sinx + 2 = 0 có tất cả họ nghiệm là: é 5p é 3p é p é p x = + k2p ê x = + k2p ê x = + k2p ê x = + k2p ê A. 4 ê B. 4 ê C. 4 ê D. 4 ê p - ê 3 - p 3p p - x = + k2p ê = + p ê = + p ê = + p ê x k2 x k2 x k2 ë 4 êë 4 êë 4 êë 4 æ p ö
Câu 11: Số nghiệm của phương trình sin x + cos x = 1 trên khoảng 0; là ç ÷ è 2 ø A. 0 B. 1 C. 2 D. 3
Câu 12: Tất cả các nghiệm của phương trình sin2x – sinx cosx = 0 là: p p p x =
+ kp; x = + kp x = + kp A. 4 2 B. 4 p p x = + kp
x = kp ; x = + kp C. 2 D. 4 cot x
Câu 13: Điều kiện xác định của hàm số y = là: sinx -1 Trang 10 p p p x ¹ + k2p
x ¹ k2p; x ¹
+ kp C. x ¹ k2p
x ¹ kp; x ¹ + k2p A. 2 2 2 B. D.
Câu 14: Tất cả các nghiệm của phương trình: sin2x + sin2x – 3cos2x = -3 là 1 - A.
B. x=kp; x = arctan( ) + kp 2 C. x = D. x =
Câu 15: Trong các phương trình sau phương trình nào vô nghiệm: (I) cosx = 5 + 3 (II) sinx = 1– 2 (III) sinx + cosx = 2 A. (I) B. (I) và (III) C. (II) D. (III) tan x
Câu 16: Điều kiện xác định của hàm số y = là: sin x p p A. x ¹ kp B. x ¹ + kp C. x ¹ k2p D. x ¹ k 2 2
Câu 17: Phương trình cos x + sin x = 0 có số nghiệm thuộc đoạn [0;p ] là: A. 4 B. 1 C. 3 D. 2 p
Câu 18: Nghiệm của phương trình : 2 2 o c s x - 3 o
c sx +1 = 0 thõa điều kiện 0 < x £ là: 2 p p p p A. x = B. x = C. x = 5 D. x = 3 2 6 6 p
Câu 19. Điều kiện xác định của hàm số y = cot(2x + ): 3 p - p p p A. x ¹
+ k B. x ¹ + k 6 2 6 2 p - p - p C. x ¹
+ kp D. x ¹ + k 6 12 2
Câu 20: . phương trình co 3
s x + cos2x=2cosx.cos2x-1 tương đương với phương trình: 1 - 1 A. cosx=0; cosx= B. cosx= ; cosx 0 = 2 2 1 - C. cosx=0; cosx= 1 D . cosx=1; cosx= 2 ĐÁP ÁN Câu 1 2 3 4 5 6 7 8 9 10 ĐA D B C D D C D C B A Câu 11 12 13 14 15 16 17 18 19 20 ĐA A D D B B D B A A B ĐỀ 5
ĐỀ KIỂM TRA 1 TIẾT
CHƯƠNG 1 TOÁN GIẢI TÍCH 11 Thời gian: 45 phút
PHẦN 1: TRẮC NGHIỆM (15 câu – 6đ)
Câu 1: Nghiệm dương bé nhất của phương trình: 2
2sin x + 5sin x - 3 = 0 là: Trang 11 p p p p A. x = B. x = 3 C. x = 5 D. x = 6 2 2 6
Câu 2: Điều kiện để phương trình .
m sin x - 3cos x = 5 có nghiệm là: ém £ 4 - A. m ³ 4 B. 4 - £ m £ 4 C. m ³ 34 D. ê ëm ³ 4 tan x
Câu 3 Tập xác định của hàm số y = là: cos x -1 ì p ì p p x ¹ + kp ïx ¹ + kp ïï A. x ¹ k2p B. x = + k2p C. í 2 2 D. í 3 ï p îx ¹ k2p ïx ¹ + kp ïî 3
Câu 4: Nghiệm của phương trình lượng giác: 2
cos x - cos x = 0 thỏa điều kiện 0 < x < p là: p p - A. x = B. x = 0 C. x = p D. x = 2 2 1
Câu 5: Tập xác định của hàm số y = là sin x - cos x p p A. x ¹ kp B. x ¹ k2p C. x ¹ + kp D. x ¹ + kp 2 4
Câu 6: Tập giá trị của hàm số 2
y = cos 2x + 4sin x - 2 là: A. [-2 ; 3] B. [-1 ; 3] C. [-2 ; 2] D. [-1 ; 1]
Câu 7: Giá trị nhỏ nhất và giái trị lớn nhất của hàm số 2
y = 3cos x +1 lần lượt là: a. 1 và 4 b. -1 và 4 c. 0 và 3 d. 0 và 4
Câu 8: Hàm số nào sau đây là hàm số chẵn
a. y = sin 2x b. y = cos3x c. y = tan x d. y = cot 4x
Câu 9: Giải phương trình sinx +1.5cot x = 0 ta có nghiệm là: 2p 2p p p a. x = + k2p à v x = - + k2p, k Î 2 2 Z b. x = + kp à v x = -
+ kp, k Î Z 3 3 3 3 2p p p c. x =
+ kp , k Î Z d. x = + k2p à
v x = - + k2p , k Î Z 3 3 3
Câu 10: Nghiệm của phương trình 2sin x +1 = 0 là: p p p p a. x = - + kp à v x =
+ kp , k Î Z
b. x = - + k2p à v x =
+ k2p, k Î Z 6 6 6 6 p 7p p p
c. x = - + k2p à v x = + k2p 5 , k Î Z d. x = + k2p à v x =
+ k2p, k Î Z 6 6 6 6
Câu 11: Các giá trị của xÎ[0; 3p ] để cos x =1 là: a. 0 à v 2p b. 0, p à v 2p c. 0 à v p d. 0, 2p à v 3p
Câu 12: Giải phương trình sin 2x - 3 cos 2x =1 ta có nghiệm là: p 7p p p a. x = + kp à v x =
+ kp, k Î Z b. x = + kp à v x =
+ kp, k Î Z 4 12 4 12 7p p p p c. x = + kp à v x = + kp 7 7
, k Î Z d. x = + kp à v x =
+ kp, k Î Z 4 12 4 12
Câu 13: Giải phương trình 3 t anx - 6cot+ 2 3 -3 = 0 ta có nghiệm là: p p a. x = + kp à v x = tan( 2
- ) + kp, k Î Z b. x = + kp à v x = arctan( 2
- ) + kp, k Î Z 3 3 p c. x =
+ kp , k Î Z d. x = 3 + kp à v x = 2
- + kp , k Î Z 3
Câu 14: Giải phương trình 3 t an(x+15 )
° - 3 = 0 ta có nghiệm là:
a. x = 60° + kp , k Î Z b. x = 45 ± ° + 180 k °, k Î Z Trang 12 c. x = 45° + 180 k °, k Î Z d. x = 60° + 180 k °, k Î Z æ p ö
Câu 15: Giải phương trình 1+ t anx = 2 2 sin x + ta có nghiệm là: ç ÷ è 4 ø p p
a. x = - + kp , k Î Z
b. x = ± + k2p , k Î Z 4 3 p p p p -
c. x = ± + kp à
v x = ± + kp , k Î Z
d. x = ± + k2p à v x =
+ kp, k Î Z 3 4 3 4 PHẦN 2: TỰ LUẬN
Câu 1: (3đ) Giải các phương trình sau: 1 a. cot(x -p ) =
3 sin 2x - 2 = cos 2x b. 3
Câu 2: (1đ) Tìm ba nghiệm âm lớn nhất của phương trình: 2
sin x + sin 2x = cos x + 2cos x ĐÁP ÁN PHẦN 1: TRẮC NGHIỆM 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 A D A A C D A B A C A A B C D PHẦN 2: TỰ LUẬN Câu 1 a. p 4p 1.0+0.5 x -p = + kp Û x = + kp ,k Î! 3 3 Câu 1b p 0.5
3 sin 2x - cos 2x = 2 Û sin(2x - ) = 1 6 p 0.5 x = + kp;k Î! 3 ìp ü 0.5
S = í + kp;k Î!ý î 3 þ
Câu 2: Giải phương trình: 2
sin x + sin 2x = cos x + 2cos x
Û (sin x - cos x)(1+ 2cos x) = 0 0.25 é p 0.25 x = + kp ê 4 Û ê ;k Î ! 2p êx = ± + k2p êë 3 ìp 2p ü S = í + kp;± + k2p;k Î !ý î 4 3 þ 2p 4p p , , .
Ba nghiệm dương nhỏ nhất là 3 3 4 p - 2 - p 3 - p 0.5 , , .
Ba nghiệm âm lớn nhất là 3 3 4 ĐỀ 6
ĐỀ KIỂM TRA 1 TIẾT Trang 13
CHƯƠNG 1 TOÁN GIẢI TÍCH 11 Thời gian: 45 phút p
Câu 1: Cho phương trình: sin(2x - ) +1 = 0, nghiệm của pt là: 6 p p A. x =
+ kp ,k Î Z B. x = - + kp ,k Î Z 4 2 p p C. x =
+ kp ,k Î Z D. x = - + kp ,k Î Z 6 6
Câu 2: Cho phương trình: 2cos2x + 2 = 0, nghiệm của pt là: p 3p
A. x = ± + kp , k Î Z B. x = + k2p ,k Î Z 4 8 3p p C. x = ±
+ kp ,k Î Z D. x = - + kp ,k Î Z 8 6
Câu 3: Cho phương trình: sin 2x - 2cos x = 0 , nghiệm của pt là: p 3p A. x =
+ kp ,k Î Z B. x = + k2p ,k Î Z 8 4 p p C. x =
+ kp ,k Î Z D. x = - + kp ,k Î Z 2 6
Câu 4: Nghiệm của phương trình 2cosx-1 = 0 (với k Î! ) là p p p p
A. x = ± + kp
B. x = ± + k2p
C. x = ± + k2p
D. x = ± + kp 6 6 3 3
Câu 5: Cho phương trình: 2sin 3x - 3 = 0, nghiệm của pt thuộc khoảng ( ; o p )là: ìp 2p ü ìp 2p 7p 8p ü A. í ; ý B. í ; ; ; ý î 3 3 þ î 9 9 9 9 þ ìp 2p 3p 5p ü C. Đáp số khác D. í ; ; ; ý î 6 6 6 6 þ p
Câu 6: Cho phương trình: tan(2x - ) + 3 = 0, nghiệm của pt là: 4 p 3p p p A. x = ±
+ kp,k Î Z B. x =
+ k2p ,k Î Z C. x = -
+ k ,k Î Z D. Đáp số khác 14 4 24 2
Câu 7: Cho phương trình: tan x + cot 2x = 0 , nghiệm của pt là: p p
A. x = ± + kp , k Î Z B. x =
+ k2p ,k Î Z C. Vô nghiệm D. Đáp số khác 2 4
Câu 8: Cho phương trình: 2sin 2 3x = , nghi 1 ệm của pt là: p p p p p
A. x = k , k Î Z B. x = k , k Î Z C. x = k , k Î Z D. x = + k 2 3 4 12 6
Câu 9: Phương trình : 3.sin 3x + cos3x = -
1 tương đương với phương trình nào sau đây : æ p ö 1 æ p ö p A. sin 3x- = - B. sin 3x + = - ç ÷ ç ÷ è 6 ø 2 è 6 ø 6 æ p ö 1 æ p ö 1 C. sin 3x - = D. sin 3x + = - ç ÷ ç ÷ è 6 ø 2 è 6 ø 2
Câu 10: Cho phương trình: cos 2x = 2cos x -1, nghiệm của pt là: p p p A. x =
+ kp; x = k2p ,k Î Z B. x = k ,k Î Z C. x = ± + kp ,k Î Z D. Vô ngiệm 2 2 2
Câu 11: Cho phương trình: cos 2x + sin x -1 = 0, nghiệm của pt là: p p A. x =
+ kp; x = k2p ,k Î Z B. x = p + k ,k Î Z 2 3 Trang 14 p p 5p
C. x = ± + kp , k Î Z D. x =
+ k2p; x = kp; x = + k2p ,k Î Z 6 6 6
Câu 12: Phương trình 3 sin 2x - o
c s2x = 2 (với k Î! ) có nghiệm là: π A. + 2π π k B. + π π k C. - + π π k D. + π k 6 3 3 3
Câu 13: Nghiệm của phương trình 0 tan(2x -15 ) = 1 , với 0 0 90 - < x < 90 là A. 0 x = 60 - , 0 x = 30 B. 0 x = 30 - C. 0 x = 60 - D. 0 x = 30 æ 2x p ö
Câu 14: Phương trình: sin -
= 0 (với k Î! ) có nghiệm là : ç ÷ è 3 3 ø p k3p p k p p A. x = + 2 3 B. x = + C. x =
+ kp D. x = kp 2 2 3 2 3 x
Câu 15: Nghiệm của phương trình 0
cot( +10 ) = - 3 (với k Î ! ) là 4 A. 0 0 x = 200 - + k720 B. 0 0 x = 20 - + k360 C. 0 0 x = 160 - + k720 D. 0 0 x = 200 - + k360
Câu 16: Nghiệm của phương trình 3 tan 3x-3 = 0 (với k Î! ) là p kp p kp p kp p kp A. x = + B. x = + C. x = + D. x = + 9 9 9 3 3 3 3 9 x
Câu 17: Nghiệm của phương trình cos = cos 2 (với k Î! ) là 3
A. x = ± 2 + kp
B. x = 3 2 + k6p C. x = 3 ± 2 + k6p
D. x = ± 2 + k4p
Câu 18: Nghiệm của phương trình 2
2cos x + sin x +1 = 0 (với k Î! ) là p p
A. x = - + k2p B. x = + k2p
C. x = kp
D. x = k2p 2 2
Câu 19: Phương trình sin x + cos x = 2 sin5x (với k Î! ) có nghiệm là: p p p p π π π π p p p p p p p p A.
+ k , + k B. + k , + k C. + k , + k D. + k , + k 16 2 8 3 4 2 6 3 12 2 24 3 18 2 9 3
Câu 20: Nghiệm của phương trình 2
2cos x - 3cos x +1 = 0 (với k Î! ) là p p p
A. x = k2p B. x = k2p , x = ± + k2p C. x = - + k2p D. x = + k2p 3 3 3 1
Câu 21: Nghiệm của phương trình cos x cos5x = cos 6x (với k Î ! ) là 2 p kp kp p kp A. x = + kp B. x = C. x = D. x = + 8 2 4 8 4 2 2 2 3
Câu 22: Cho phương trình: sin x + sin 2x + sin 3x = , nghiệm của pt là: 2 p p p
A. x = ±p + k , k Î Z B. x = k , k Î Z C. x = ± + kp , k Î Z D. Vô ngiệm 2 3 3
Câu 23: Phương trình 2 2
2sin x + sin x cos x - cos x = 0 (với k Î! ) có nghiệm là: π π 1 A. + π k B. + π k ,arctan( ) + π k 4 4 2 π 1 C. - + π, k arctan( ) + π 1 π k
D. - + k2π,arctan( ) + k2π 4 2 4 2
Câu 24: Cho phương trình: sin x - sin 2x + sin 3x = 0 , nghiệm của pt là: p p p A. x = k
+ kp ,k Î Z B. x = ± + k2p; x = k ,k Î Z 2 3 2 Trang 15 p
C. x = ± + kp , k Î Z D. Đáp số khác 6
Câu 25: Phương trình tan x + 3cot x = 4 (với k Î ! ) có nghiệm là: π
A. + k2π,arctan 3 + π k2π B. + π k C. arctan 4 + π π k D. + π k ,arctan 3 + π k 4 4 4 ĐÁP ÁN Câu 1 2 3 4 5 6 7 8 9 10 ĐA D C C C B C C D D A Câu 11 12 13 14 15 16 17 18 19 20 ĐA D D A A C B C A A B Câu 21 22 23 24 25 26 27 28 29 30 ĐA D C C B D ĐỀ 7
ĐỀ KIỂM TRA 1 TIẾT
CHƯƠNG 1 TOÁN GIẢI TÍCH 11 Thời gian: 45 phút
Câu 1: Mệnh đề nào sau đây sai?
A. Hàm số y = sin x có chu kỳ 2p .
B. Hàm số y = cos x có chu kỳ 2p .
C. Hàm số y = cot x có chu kỳ 2p .
D. Hàm số y = tan x có chu kỳ p .
Câu 2: Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = 3sin 2x - 5 lần lượt là: A. 8 - à v - 2. B. 2 à v 8. C. 5 - à v 2. D. 5 - à v 3.
Câu 3: Điều kiện xác định của hàm số y = cotx là: p p p p x ¹ + kp x ¹ + k x ¹ + kp A. 2
B. x ¹ kp C. 8 2 D. 4
Câu 4: Hàm số y = sin x có đồ thị đối xứng qua đâu:
A. Qua gốc tọa độ.
B. Qua đường thẳng y = x . C. Qua trục tung. D. Qua trục hoành.
Câu 5: Tất cả các nghiệm của pt 2cos2x = –2 là: p p x = + kp x = + k2p A. 2
B. x = k2p
C. x = p + k2p D. 2
Câu 6: Tất cả các nghiệm của phương trình sinx + 3 cos x = 2 là: p 5p p p
x = - + k2p; x = + 2 k2p x = + k2p; x = + k2p A. 4 4 B. 3 3 p 3p p p
x = - + k2p; x = + 5 k2p x = - + k2p; x = + k2p C. 4 4 D. 12 12 æ p ö 2sin 4x - -1 = 0 ç ÷
Câu 7: Tất cả các nghiệm của phương trình è 3 ø là: p p 7p p A. x = + k ; x = + k
B. x = kp; x = p + k2p 8 2 24 2 p p
x = k2p ; x = + k2p
x = p + k2p; x = k C. 2 D. 2 Trang 16
Câu 8: Tất cả các nghiệm của pt 3 sinx + cos x = 0 là: p p p p - x = + kp x = - + kp x = + kp x = + kp A. 6 B. 3 C. 3 D. 6
Câu 9: Tất cả các nghiệm của pt cos2x – sinx cosx = 0 là: p p x = + kp x = + kp A. 4 B. 2 5p 7p p p x = + kp; x = + kp x =
+ kp; x = + kp C. 6 6 D. 4 2
Câu 10: Tất cả các nghiệm của phương trình tanx + cotx = –2 là: p p p p x = + kp x = - + kp x = + k2p x = - + k2p A. 4 B. 4 C. 4 D. 4 1
Câu 11: Nghiệm của phương trình sinx = , ( với k Î Z ) 2 p p k p p 5 A. x = + B. x = + k p 2 ; x = + k p 2 4 2 6 6 p p 2 C. x = + p k D. x = ± + k p 2 4 3
Câu 12 : Giải phương trình tan2x = 3 , ( với k Î Z ) p 1 k p 2p p k A. x = ± + p k B. x = + C. x = ± + p k D. x = ± + 6 10 5 3 9 3
II. Phần tự luận : (4 điểm)
Câu 1 : (2điểm) Giải phương trình : 3 cos5x + sin5x = 2cos3x
Câu 2 : (2 điểm) Giải phương trình : tan(3x - 300) = 1/ 3 ĐÁP ÁN
I/ Phần trắc nghiệm : ( 6 điểm ) Câu 1 2 3 4 5 6 7 8 9 10 11 12 A x x x x B x x x C x x D x x x
II/ Phần tự luận : ( 4 điểm) p
Câu 1 : Biến đổi đưa về : cos (5x - ) = cos3x 6 p p p k
Nghiệm của phương trình là : x = + p k ; x = + với k nguyên. 12 48 4
Câu 2 : Điều kiện : x ¹ 400 + k600
Biến đổi đưa về : tan(3x - 300) = tan300
Nghiệm của phương trình là : x = 200 + k600 ĐỀ 8
ĐỀ KIỂM TRA 1 TIẾT
CHƯƠNG 1 TOÁN GIẢI TÍCH 11 Trang 17 Thời gian: 45 phút
Câu 1 : Giải phương trình tan2x = 3 , ( với k Î Z ) p p 1 k 2p p k A. x = ± + p k B. x = ± + p k C. x = + D. x = ± + 6 3 10 5 9 3 p
Câu 2 : Hàm số nào sau đây có tập xác định là : D = R\{
+ kp,k Î Z } 2 A. y = sinx B. y = cotx C. y = cosx D. y = tanx p
Câu 3 : Giá trị lớn nhất của hàm số y = 5 sin(x + ) – 1 là : 6 A. 2 B. 4 C. 3 D.5 1
Câu 4 : Giải phương trình sinx = , ( với k Î Z ), có nghiệm là : 2 p p 5 p p k A. x = + k p 2 ; x = + k p 2 C. x = + 6 6 4 2 p p 2 B. x = + p k D. x = ± + k p 2 4 3
Câu 5 : cho các hàm số sau : y = sinx; y = cosx; y = tanx; y = cotx
Trong các hàm số trên có bao nhiêu hàm số lẻ và bao nhiêu hàm số chẳn ? A. 2 lẻ, 2 chẳn B. 1 lẻ,3 chẳn C. 4 lẻ D .3 lẻ, 1 chẳn
Câu 6 : Một nghiệm của phương trình 4tan2x – 5tanx + 1 = 0 là : ( với k Î Z ) p p 5p p A. + kp B. + kp C. + kp D. + kp 12 4 8 6
Câu 7 : Hàm số nào sau đây có tập xác định là : D = R\{ kp , kÎZ } A. y = cotx B. y = tanx C. y = cosx D. y = sinx
Câu 8: Tất cả các nghiệm của pt sin2x – sinx cosx = 0 là: p p x = + kp x = + kp A. 4 B. 2 p p p x =
+ kp; x = + kp C. x =
+ kp; x = kp D. 4 2 4
Câu 9: Tất cả các nghiệm của pt 2sin2x = –2 là: p p x = + kp p p x = + k2p A. 2 B. x = + kp
C. x = - + kp D. 2 4 4
Câu 10: Tất cả các nghiệm của phương trình sinx + 3 cos x = 2 là: p 5p p p
x = - + k2p; x = + 2 k2p x = + k2p; x = + k2p A. 4 4 B. 3 3 p 3p p p
x = - + k2p; x = + 5 k2p x = - + k2p; x = + k2p C. 4 4 D. 12 12 æ p ö 2sin 4x - -1 = 0 ç ÷
Câu 11: Tất cả các nghiệm của phương trình è 3 ø là: p p 7p p A. x = + k ; x = + k
B. x = kp; x = p + k2p 8 2 24 2 Trang 18 p p
x = k2p ; x = + k2p
x = p + k2p; x = k C. 2 D. 2
Câu 12: Tất cả các nghiệm của pt 3 sinx + cos x = 0 là: p p p - p x = + kp x = - + kp x = + kp x = + kp A. 6 B. 3 C. 6 D. 3
II/ Phần tự luận : (4 điểm)
Câu 1 : (2điểm) Giải phương trình : 3 sin5x - cos5x = 2sin3x
Câu 2 : (3 điểm) Giải phương trình : cot(3x - 300) = 1/ 3 ĐÁP ÁN
I/ Phần trắc nghiệm : ( 6 điểm ) Câu 1 2 3 4 5 6 7 8 9 10 11 12 A x x x B x x x C x x x D x x x
II/ Phần tự luận : ( 4 điểm) p
Câu 1 : Biến đổi đưa về : sin(5x - ) = sin3x 6 p 7p kp
Nghiệm của phương trình là : x = + p k ; x = + với k nguyên. 12 48 4
Câu 2 : Điều kiện : x ¹ 100 + k600
Biến đổi đưa về : cot(3x - 300) = cot600
Nghiệm của phương trình là : x = 300 + k600 ĐỀ 9
ĐỀ KIỂM TRA 1 TIẾT
CHƯƠNG 1 TOÁN GIẢI TÍCH 11 Thời gian: 45 phút
C©u 1 : Nghiệm của phương trình 2𝑐𝑜𝑠!𝑥 − 3𝑠𝑖𝑛𝑥 + 3 = 0 là : A. 𝜋
𝑥 = + 𝑘𝜋, 𝑣ớ𝑖 𝑘 ∈ 𝑍 B.
𝑥 = 𝑘2𝜋, 𝑣ớ𝑖 𝑘 ∈ 𝑍 2 C. 𝜋 𝜋
𝑥 = + 𝑘2𝜋, 𝑣ớ𝑖 𝑘 ∈ 𝑍 D.
𝑥 = − + 𝑘2𝜋, 𝑣ớ𝑖 𝑘 ∈ 𝑍 2 2
C©u 2 : Chu kỳ tuần hoàn của hàm số 𝑦 = 𝑠𝑖𝑛!𝑥 + 1 là: A. 𝜋 B. 2𝜋 C. √2𝜋 D. √𝜋
C©u 3 : Các giá trị của m để phương trình !
3𝑠𝑖𝑛!𝑥 − 2𝑠𝑖𝑛2𝑥 − (𝑚 − 4)𝑐𝑜𝑠!𝑥 = 2 có đúng 2 nghiệm thuộc [ ; ! ) là : " # A. −2 ≤ 𝑚 ≤ 5
B. 𝑚 ≤ −2; 𝑚 ≥ 5 C. −2 < 𝑚 < 5 D. −2 < 𝑚 ≤ 5
C©u 4 : Tập xác định của hàm số 𝑦 = 𝑡𝑎𝑛𝑥 + 𝑐𝑜𝑡𝑥 là : A. R
B. R\"𝑘 ! , 𝑘 ∈ 𝑍'
C. R\C" + 𝑘𝜋, 𝑘 ∈ 𝑍D
D. R\{𝑘𝜋, 𝑘 ∈ 𝑍} # !
C©u 5 : Nghiệm của phương trình 𝑠𝑖𝑛2𝑥 − 𝑐𝑜𝑠𝑥 = 0 là : A. 𝜋 5𝜋 𝑥 = + 𝑘2𝜋; 𝑥 =
+ 𝑘2𝜋 , 𝑣ớ𝑖 𝑘 ∈ 𝑍 6 6 Trang 19 B. 𝜋 𝜋 5𝜋
𝑥 = + 𝑘𝜋; 𝑥 = + 𝑘2𝜋; 𝑥 =
+ 𝑘2𝜋 , 𝑣ớ𝑖 𝑘 ∈ 𝑍 2 6 6 C. 𝜋 𝜋 2𝜋
𝑥 = + 𝑘𝜋; 𝑥 = + 𝑘2𝜋; 𝑥 =
+ 𝑘2𝜋 , 𝑣ớ𝑖 𝑘 ∈ 𝑍 2 3 3 D. 𝜋 𝜋
𝑥 = + 𝑘𝜋; 𝑥 = + 𝑘2𝜋, 𝑣ớ𝑖 𝑘 ∈ 𝑍 2 6
C©u 6 : Khẳng định nào sau đây là đúng ?
A. Hàm số 𝑦 = 𝑡𝑎𝑛𝑥 tuần hoàn với chu kỳ 𝜋
B. Hàm số 𝑦 = 𝑡𝑎𝑛𝑥 là hàm số chẵn
C. Hàm số 𝑦 = 𝑡𝑎𝑛𝑥 nghịch biến trên mỗi khoảng xác định
D. Hàm số 𝑦 = 𝑐𝑜𝑡𝑥 đồng biến trên mỗi khoảng xác định C©u 7 : $%&'
Tam giác ABC có tính chất gì nếu các góc của nó thỏa mãn hệ thức : = )*&*' $%&( )*&*( A. Vuông B. Cân C. Vuông cân D. Vuông hoặc cân
C©u 8 : Phương trình 𝑠𝑖𝑛𝑥 = − + có các nghiệm thuộc đoạn [0; 2𝜋] là : # 𝜋 7𝜋 ,! 𝜋 5𝜋 7𝜋 5𝜋 A. ; B. ; ++! C. ; D. ; 6 6 - - 6 6 6 6
C©u 9 : Phương trình 𝑐𝑜𝑠 K2𝑥 + "L = − √# có bao nhiêu nghiệm thuộc K− " ; "L ? # ! ! ! A. 0 B. 2 C. 3 D. 1
C©u 10 : Cho phương trình √3𝑡𝑎𝑛𝑥 − 𝑐𝑜𝑡𝑥 − √3 + 1 = 0, đặt M là tổng các nghiệm thuộc (0; 2𝜋) của +#.
phương trình. Biểu thức có giá trị là : "+! A. 4 B. 2 C. 1 D. 3
C©u 11 : Nghiệm dương nhỏ nhất của phương trình √3𝑠𝑖𝑛2𝑥 + 2𝑐𝑜𝑠!𝑥 = −√2 + 1 là : 5𝜋 𝜋 𝜋 11𝜋 A. B. C. D. 24 4 12 24
C©u 12 : Phương trình 2𝑐𝑜𝑠# / = 𝑚# − 𝑚 + 1 có 2 nghiệm thuộc 5− ! ; !6 khi : # # # A. 1 − √5 1 + √5 B. 1 − √5 1 + √5 ≤ 𝑚 ≤
< 𝑚 ≤ 0; 1 ≤ 𝑚 < 2 2 2 2 C. 1 + √5 D. 1 − √5 1 ≤ 𝑚 ≤ ≤ 𝑚 ≤ 0 2 2
C©u 13 : Giá trị lớn nhất của hàm số 𝑦 = 2𝑐𝑜𝑡𝑥 + 1 trên [− " ; 0) là: % A. - 1 B. Không tồn tại C. 1 D. 3
C©u 14 : Đồ thị sau là đồ thị của hàm y số nào ? 2 y - 𝜋 − " 0 " 𝜋 x ! ! -2 A. 𝑦 = 2𝑠𝑖𝑛𝑥 B. 𝑦 = 𝑠𝑖𝑛2𝑥 C. 𝑦 = −2𝑠𝑖𝑛𝑥 D. 𝑦 = 𝑠𝑖𝑛𝑥 + 1
C©u 15 : Biết phương trình 3𝑐𝑜𝑠𝑥 + 2√3𝑠𝑖𝑛𝑥 = & , có các nghiệm là : !
𝑥 = 𝛼 ± 𝛽 + 𝑘2𝜋, 𝑘 ∈ 𝑍. Hãy chọn khẳng định đúng trong các khẳng định sau : A. 3 9
𝛼 = 𝑎𝑟𝑐𝑠𝑖𝑛
𝑣à 𝛽 = 𝑎𝑟𝑐𝑐𝑜𝑠 √21 2√21 B. 2 9 𝑠𝑖𝑛𝛼 = 𝑣à 𝑠𝑖𝑛𝛽 = √7 2√21 C. 3 9
𝛼 = 𝑎𝑟𝑐𝑐𝑜𝑠
𝑣à 𝛽 = 𝑎𝑟𝑐𝑠𝑖𝑛 √21 2√21 D. 3 9 𝑐𝑜𝑠𝛼 = 𝑣à 𝑐𝑜𝑠𝛽 = √21 2√21 Trang 20
C©u 16 : Phương trình 3𝑠𝑖𝑛!𝑥 − (𝑚 − 2)𝑠𝑖𝑛2𝑥 + (𝑚 + 6)𝑐𝑜𝑠!𝑥 = 2 có nghiệm khi : A. 𝑚 ≥ 0 B. 0 < 𝑚 < 5 C. 𝑚 ≤ 0; 𝑚 ≥ 5 D. 𝑚 ≤ 5
C©u 17 : Chọn khẳng định sai.
A. Hàm số 𝑦 = 𝑡𝑎𝑛𝑥 có tập xác dịnh là R\{𝑘𝜋, 𝑘 ∈ 𝑍} B.
Hàm số 𝑦 = 𝑐𝑜𝑠𝑥 có tập giá trị là [−1; 1]
C. Hàm số 𝑦 = 𝑠𝑖𝑛𝑥 có tập xác dịnh là R
D. Hàm số 𝑦 = 𝑐𝑜𝑡𝑥 có tập giá trị là R
C©u 18 : Số nghiệm của phương trình : 𝑠𝑖𝑛𝑥 − √3𝑐𝑜𝑠𝑥 = 2𝑠𝑖𝑛5𝑥 trong khoảng (0; 𝜋) là : A. 4 B. 3 C. 6 D. 5
C©u 19 : Giá trị lớn nhất và nhỏ nhất của hàm số 𝑦 = (𝑠𝑖𝑛𝑥 − 𝑐𝑜𝑠𝑥)! + 2𝑐𝑜𝑠2𝑥 + 3𝑠𝑖𝑛𝑥. 𝑐𝑜𝑠𝑥 là A. B. 17 17 2 2 T 𝑣à − T 1 + T 𝑣à 1 − T 2 2 17 17 C. 17 17 D. 𝑣à − √17 √17 2 2 1 + 𝑣à 1 − 2 2
C©u 20 : Cho hàm số 𝑦 = 3𝑐𝑜𝑠(1 − 3𝑥) hãy chọn khẳng định đúng trong các khẳng định sau : A. #!
Hàm số là hàm số tuần hoàn với chu kỳ
B. Tập giá trị của hàm số là [−1; 1] 0
C. Hàm số là hàm số tuần hoàn với chu kỳ 2𝜋
D. Hàm số là hàm số chẵn
C©u 21 : Trong khoảng 70; !9, phương trình 𝑠𝑖𝑛!4𝑥 + 3𝑠𝑖𝑛4𝑥.𝑐𝑜𝑠4𝑥 − 4𝑐𝑜𝑠!4𝑥 = 0 có bao nhiêu # nghiệm ? A. 3 B. 1 C. 4 D. 2
C©u 22 : Phương trình 𝑐𝑜𝑠4𝑥 = 𝑐𝑜𝑠!3𝑥 + 𝑚𝑠𝑖𝑛!𝑥 có nghiệm thuộc 70; ! 9 khi : +# A. −2 < 𝑚 < 1 B. 𝑚 > −2 C. 0 < 𝑚 < 1 D. 𝑚 > 0
C©u 23 : Trên [−𝜋; 𝜋] đồ thị hàm số 𝑦 = 𝑠𝑖𝑛𝑥 + 1 và đường thẳng 𝑦 = 0 cắt nhau tại bao nhiêu điểm? # A. 2 B. 1 C. 3 D. 0
C©u 24 : Phương trình √9 − 𝑥!𝑡𝑎𝑛(𝑥 − 2) = 0 có mấy nghiệm ? A. 1 B. 4 C. 3 D. 2
C©u 25 : Hàm số 𝑦 = )*&/1023)/ có tập xác định là : 23)#/423)/1# A.
𝑅\{(2𝑘 + 1)𝜋, 𝑘 ∈ 𝑍} B.
𝑅\{𝑘𝜋, 𝑘 ∈ 𝑍} C.
𝑅\{𝑘2𝜋, 𝑘 ∈ 𝑍} D. 𝜋
𝑅\ C + 𝑘2𝜋, 𝑘 ∈ 𝑍D 2 ĐÁP ÁN 1 2 3 4 5 6 7 8 9 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5
C A D B B A D B B C D B A A D C A D D A C C A B C ĐỀ 10
ĐỀ KIỂM TRA 1 TIẾT
CHƯƠNG 1 TOÁN GIẢI TÍCH 11 Thời gian: 45 phút
Câu 1: Tất cả các nghiệm của phương trình 3 sinx + cosx = 0 là: p p p p x = - + kp x = - + kp x = + kp x = + kp A. 6 B. 3 C. 3 D. 6
Câu 2: Với giá trị nào của m thì phương trình sin x - m =1 có nghiệm A. 2 - £ m £ 0 B. m £ 0 C. 0 £ m £ 1 D. m ³ 1
Câu 3: Hàng ngày mực nước của con kênh lên, xuống theo thủy triều. Độ sâu h(m) của mực nước trong
kênh được tính tại thời điểm t(giờ, 0
) trong một ngày được tính bởi công thức Trang 21 h = 3.cos
. Hỏi trong một ngày có mấy thời điểm mực nước của con kênh đạt độ sâu lớn nhất ? A. 2. B. 1. C. 4 D. 3.
Câu 4: Tìm tất cả các giá trị của m để phương trình: m.sinx +cosx = có nghiệm? A. m B. C. m D. m
Câu 5: Số nghiệm của phương trình sin x + cos x = 1 trên khoảng (0;p ) là A. 0 B. 1 C. 2 D. 3
Câu 6: Tất cả các nghiệm của phương trình cos2x – sinx cosx = 0 là: p p p x =
+ kp; x = + kp x = + kp A. 4 2 B. 4 p p p x = + 5 7 kp x = + kp; x = + kp C. 2 D. 6 6
Câu 7: Tất cả các nghiệm của phương trình: sin2x + sin2x – 3cos2x = 1 là A. x = , B. C. x = D. x =
Câu 8: Hàm số y =sin2x là hàm số tuần hoàn với chu kỳ? A. T = 2 B. T = C. T = 4 D. T = cot x
Câu 9: Điều kiện xác định của hàm số y = là: cos x p p A. x ¹ kp B. x ¹ + kp C. x ¹ k2p D. x ¹ k 2 2
Câu 10: Phương trình cos x = sin x có số nghiệm thuộc đoạn [ p - ;p ] là: A. 4 B. 5 C. 6 D. 2 p
Câu 11: Nghiệm của phương trình lượng giác: 2
2sin x - 3sin x +1 = 0 thõa điều kiện 0 £ x < là: 2 p p p p A. x = B. x = C. x = 5 D. x = 3 2 6 6
Câu 12: Điều kiện xác định của hàm số y = cotx là: p p p p x ¹ + k x ¹ + kp
C. x ¹ kp x ¹ + kp A. 8 2 B. 2 D. 4 tan x
Câu 13: Điều kiện xác định của hàm số y = là: cos x -1 ì p ì p p ¹ + p ïx ¹ + kp x k ïï x ¹ + k2p í 2 2 C. x ¹ k2p í A. 3 ï p ï
B. îx ¹ k2p x ¹ + kp D. ïî 3
Câu 14: Giá trị lớn nhất của hàm số 2
y =1- 2cos x - cos x là: A. 2 B. 0 C. 3 D. 5
Câu 15: Giá trị lớn nhất của hàm số y = 2sin 3x - 3 là: A. 1 B. 1 - C. 5 D. 3 æ p ö
Câu 16: Phương trình 2 tan x - 2cot x - 3 = 0 có số nghiệm thuộc khoảng - ;p là: ç ÷ è 2 ø A. 1 B. 2 C. 3 D. 4
Câu 17: Nghiệm âm lớn nhất của phương trình 2
2 tan x + 5tan x + 3 = 0 là: Trang 22 5p p p p A. - B. - C. - D. - 6 4 6 3 p
Câu 18: Tất cả các nghiệm của phương trình 2sin(4x – ) – 1 = 0 là: 3 p p 7p p p x = + k ; x = + k
x = p + k2p; x = k A. 8 2 24 2 B. 2 p
C. x = kp ; x = p + k2p
x = k2p ; x = + k2p D. 2
Câu 19: Phương trình lượng giác: 2
sin x - 3cos x - 4 = 0 có nghiệm là: p p A. x = p - + k2p B. x = - + k2p C. x = + kp D. Vô nghiệm 2 6
Câu 20: Phương trình lượng giác: 3.tan x + 3 = 0 có nghiệm là: p p p p A. x = - + kp B. x = + kp C. x = - + k2p D. x = + kp 3 3 3 6
----------------------------------------------- ----------- HẾT ---------- ĐỀ 11
ĐỀ KIỂM TRA 1 TIẾT
CHƯƠNG 1 TOÁN GIẢI TÍCH 11 Thời gian: 45 phút
A. TRẮC NGHIỆM ( 4 điểm ) 1
Câu 1: Tập xác định của hàm số y = là : sin 2x p p A. ! \{k ,k Î" . } B. {k ,k Î } ! C. ! \{k , p k Î } " . D. ! \{2k , p k Î } " . 2 2
Câu 2: Tập xác định của hàm số o y = cot(2x + 30 ) là : A. o o ! \{15 + k90 ,k Î } " . B. o o ! \{ 1 - 5 + k180 ,k Î } " o o o o C. ! \{ 3 - 0 + k90 ,k Î" . } D. ! \{ 1 - 5 + k90 ,k Î } " . Câu 3:
Giải phương trình lượng giác cos x = cos1 : A. { 1 ± + k , p kÎ } ! B. {1+ k 2 , p k Î } ! . C. { 1 - + k 2 , p k Î! . } D. { 1 ± + k 2 , p k Î! . } p
Câu 4: Giải phương trình lượng giác tan(x + ) = - 3 : 6 p p p p A. {- + k , p k Î! . } B. { + k , p k Î } ! C. {- + k , p k Î! . } D. { + k , p k Î } ! . 2 2 6 6
Câu 5: Giải phương trình lượng giác 3 tan x -1 = 0 : A. o o {60 + k360 ,k Î! . } B. o o {30 + k90 ,k Î } ! o o o o C. {30 - k180 ,k Î }
! . D. {60 - k180 ,k Î! . } Câu 6: Cho phương trình 2 2
cos 2x + (m - m -1)sin 2x +1 = 0 .Định m để phương trình có một p nghiệm x = . 4 Trang 23 A. m Î{ 1 - ;0 } B. mÎ{0;1}. C. m = 1 - . D. m = 0.
Câu 7: Giải phương trình lượng giác sin 4x + 3 cos 4x - 2 = 0 : p p 5p p p p A. {- + k ; + k ,k Î! . } B. {- + k ,k Î } ! 48 2 48 2 48 2 5p p p p 5p p C. { + k ,k Î } ! . D. { + k ;- + k ,k Î! . } 48 2 48 2 48 2
Câu 8: Giải phương trình lượng giác 3(sin x + cos x) -sin 2x -3 = 0: p p D. {- + k 2 ; p m2 ; p k,mÎ! . } B. { + k 2 ; p k Î } ! 2 2 p C. {m2 ; p mÎ } ! . A. { + k 2 ; p m2 ; p k,mÎ } ! . 2
B. TỰ LUẬN ( 6 điểm ) Câu 1: ( 2 điểm) x
a) Giải phương trình lượng giác tan = 2 . ( 1 điểm) 3 p
b) Giải phương trình lượng giác sin 4x = sin(x + ) . ( 1 điểm) 3 Câu 2: ( 2 điểm)
a) Giải phương trình lượng giác sin 2x = cos3x . ( 1 điểm)
b) Giải phương trình lượng giác 2
sin x - 2cosx + 2 = 0 . ( 1 điểm)
Câu 3: ( 1 điểm) Giải phương trình lượng giác cosx - 3 sin x = 2 .
Câu 4: ( 1 điểm) Giải phương trình lượng giác sin x + sin 2x = cosx + cos2x . . . . . . . HẾT . . . . ĐÁP ÁN
A. TRẮC NGHIỆM ( 4 điểm ) 1 2 3 4 5 6 7 8 A D D A C B A A
B. TỰ LUẬN ( 6 điểm ) x x
Câu 1. ( 1 điểm) a) tan = 2 Û = arctan 2 + kp 0,5đ 3 3 Û x = 2arctan 2 + k3 , p k Î! 0,5đ é p 4x = x + + k2p p ê ( 1 điểm) b) 3 sin 4x = sin(x + ) Û 0,25đ x 2 ê 3 p ê4x = p - (x + ) + k2p ë 3 p k2p 2p k2p Þ x = + ;x = + ,k Î ! 0,25đ x 2 9 3 15 5 Trang 24 é p 3x = - 2x + k2p p ê
Câu 2. ( 1 điểm) a) 2
sin 2x = cos3x Û cos3x = cos( - 2x) Û 0,25đ x 2 ê 2 p ê3x = -( - 2x) + k2p ë 2 p k2p p Þ x = + ;x = - + k2 , p k Î! 0,25đ x 2 10 5 2 ( 1 điểm) b) 2 2
sin x - 2cosx + 2 = 0 Û cos x + 2cosx - 3 = 0 0,25đ écos x = 3 - (loai) Û 0,25đ x 2 ê ëcos x =1 (n) Ta có : cos x =1 Û x = k2 , p kÎ! 0,25đ 1 3 2
Câu 3. ( 1 điểm) cosx - 3 sin x = 2 Û cosx - sin x = 0,25đ 2 2 2 p p Û cos(x + ) = cos 0,25đ 3 4 p 7p Þ x = - + k2 ; p x = - + k2 , p k Î ! 0,25đ x 2 12 12
Câu 4. ( 1 điểm) sin x + sin 2x = cosx + cos2x Û sin x - cosx = cos2x -sin 2x 0,25đ p p p p
Û 2 sin(x - ) = - 2 sin(2x - ) Û sin(x - ) = sin( - 2x) 0,25đ 4 4 4 4 p 2p Þ x = + k ;x = -p - k2 , p k Î ! 0,25đ x 2 6 3 ĐỀ 12
ĐỀ KIỂM TRA 1 TIẾT
CHƯƠNG 1 TOÁN GIẢI TÍCH 11 Thời gian: 45 phút
I. TRẮC NGHIỆM KHÁCH QUAN: (6 điểm)
Câu 1: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. y = sin x B. y = os c x C. y = tan x
D. y = cot x
Câu 2: Tìm chu kỳ tuần hoàn T của hàm số y = tan x A. T = 0 B. T = 4p C. T = 2p D. T = p
Câu 3: Đường cong trong hình là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào ?
A. y = sin x B. y = os c x C. y = tan x
D. y = cot x
Câu 4: Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = 4sin x + 5
A. m = 1 và M = 9
B. m = 0và M = 5
C. m = 1 và M = 5 D. m = 5 và M = 9 1
Câu 5: Giải phương trình cos x = 2 p p p
A. x = ± + kp
B. x = ± + kp
C. x = ± + k2p D. 6 3 6 p x = ± + k2p 3
Câu 6: Phương trình nào sau đây vô nghiệm?
A. 2sin x +1 = 0
B. 2cos x - 3 = 0 C. tan x -1 = 0 D. 3 cot x +1 = 0 Trang 25
Câu 7: Hàm số y = os
c x đồng biến trên khoảng nào sau đây? æ p ö æ p ö æ p ö A. ;p B. (0;p ) C. 0; D. - ;0 ç ÷ ç ÷ ç ÷ è 2 ø è 2 ø è 2 ø
Câu 8: Khẳng định nào sau đây là sai? p
A. sinx = 1 Û x = + kp
tan x = 0 Û x = kp
cos x = 1 Û x = k2p D. 2 B. C. p cot x = 0 Û x = + kp 2 æ p ö
Câu 9: Tìm tập xác định của hàm số y = tan x - ç ÷ è 3 ø ì5p ü ìp ü A. D = ! \ í + kp ,k Î"ý
B. D = ! \ í + kp ,k Î"ý î 6 þ î 3 þ ì5p ü D = ! \ í + k2p ,k Î"ý
D. D = ! \{kp,k Î" } C. î 6 þ
Câu 10: Giải phương trình 2
tan x - 2 tan x +1 = 0 p p p A. x = + kp
B. x = + k2p x = - + kp D. 4 4 C. 4 p x = - + k2p 4
Câu 11: Tìm phương trình tương đương với phương trình 3 cos x - sinx =1. æ p ö 1 æ p ö 1 æ p ö 1
A. cosç x - ÷ = B. cos x - = C. cos x + = D. ç ÷ ç ÷ è 6 ø 2 è 3 ø 2 è 6 ø 2 æ p ö 1 cos x + = ç ÷ è 3 ø 2
Câu 12: Gọi x nghiệm dương nhỏ nhất và x nghiệm âm lớn nhất của phương trình 1 2
sin2x + 3 cos 2x = 2. Tính giá trị của biểu thức P = x - x . 1 2 p p p A. 5 P = - B. P = C. P = p D. P = 6 3 6
Câu 13: Tìm số điểm biểu diễn các nghiệm của phương trình os
c x = sin 2x trên đường tròn lượng giác. A. 4 B. 3 C. 5 D. 6
Câu 14: Tìm tất cả các giá trị của tham số m để phương trình 2 2
sin x + (m -1)sin 2x - (m +1)cos x = m có nghiệm. A. m ³ 2 - B. m < 2 - C. 2 - £ m £ 1 D. m > 1 sin 3x - sinx
Câu 15: Tính tổng các nghiệm trong khoảng (0;3p )của phương trình = o c s2x + sin 2 x 2sinx p p A. 15 B. 5p 9 C. D. 4p 2 2
II. TỰ LUẬN(4 điểm). cosx
Câu 1 (1.0 điểm). Tìm tập xác định của hàm số y = 2sin x -1
Câu 2 (3.0 điểm). Giải các phương trình sau: a) tan x - 3 = 0 b) 2
2cos x - cos x - 3 = 0 x - x
c) sin 3x - 4sin x cos 2x = cos 3 sin 0. d) = 0 2sin x -1 Trang 26 ĐÁP ÁN I. TRẮC NGHIỆM Câu 1 2 3 4 5 6 7 8 9 10 ĐA B D A A D B D A A A Câu 11 12 13 14 15 16 17 18 19 20 ĐA C C A C C II. TỰ LUẬN cosx
Câu 1 (1.0 điểm). Tìm tập xác định của hàm số y = 2sin x -1 ì p x ¹ + k2p 1 p ïï Hàm số xác định 6
Û 2sin x -1 ¹ 0 Û sin x ¹ Û sin x ¹ sin Û í 2 6 5p ïx ¹ + l2p ïî 6 ìp 5p ü
Vậy D = R \ í + k2p;
+ l2p | k,l Î Z ý î 6 6 þ
Câu 2 (3.0 điểm). Giải các phương trình sau: p p
a) tan x - 3 = 0 Û tan x = 3 Û tan x = tan Û x = + kp 3 3 écos x = 1 - b) 2 2cos x cos x 3 0 ê - - = Û 3 Û x = p + k2p êcos x = (VN) ë 2
c) sin 3x - 4sin x cos 2x = 0.
Phương trình Û sin3x - 2(sin3x -sin x) = 0
Û -sin 3x + 2sin x = 0 Û x( 2 sin 4sin x - ) 1 = 0 éx = kp
Û sin x(1- 2cos2x) = 0 ê Û p êx = ± + kp ë 6 cos x - 3 sin x d) = 0 2sin x -1 ì p x ¹ + k2p 1 ïï Điều kiện 6 sin x ¹ Û í , k Î . ! 2 5p ïx ¹ + k2p ïî 6
Với điều kiện trên ta có 1 3
cos x - 3 sin x = 0 Û cos x - sin x = 0 2 2 æ p ö p p p Û os c x +
= 0 Û x + = + lp Û x = + lp ,l Î . ç ÷ ! è 3 ø 3 2 6 5p
Đối chiếu với điều kiện ta có nghiệm của phương trình là x = - + k2p ,k Î . ! 6 ĐỀ 13
ĐỀ KIỂM TRA 1 TIẾT
CHƯƠNG 1 TOÁN GIẢI TÍCH 11 Trang 27 Thời gian: 45 phút p
Câu 1: Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = 7 - 2cos(x + ) lần lượt là: 4 A. 2 - à v 7 B. 2 - à v 2 C. 5 à v 9 D. 4 à v 7
Câu 2: Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = 4 sin x + 3 -1 lần lượt là: A. 2 à v 2 B. 2 à v 4 C. 4 2 à v 8 D. 4 2 -1 à v 7
Câu 3: Giá trị nhỏ nhất của hàm số 2
y = sin x - 4sin x -5 là: A. 20 - B. 9 - C. 0 D. 9
Câu 4: Giá trị lớn nhất của hàm số 2
y =1- 2cos x - cos x là: A. 2 B. 5 C. 0 D. 3
Câu 5: Với giá trị nào của m thì phương trình sin x - m = 1 có nghiệm là: A. 0 £ m £ 1 B. m £ 0 C. m ³ 1 D. 2 - £ m £ 0
Câu 6: Phương trình lượng giác: 3cot x - 3 = 0 có họ nghiệm là: p p p A. x = + kp B. x = + kp C. x = + k2p D. Vô nghiệm 6 3 3
Câu 7: Phương trình lượng giác: 2
cos x + 2cos x -3 = 0 có họ nghiệm là: p A. x = k2p B. x = 0 C. x = + k2p D. Vô nghiệm 2
Câu 8: Phương trình lượng giác: 2cos x + 2 = 0 có tất cả họ nghiệm là: é p é 3p é 5p é p x = + k2p ê x = + k2p ê x = + k2p ê x = + k2p ê A. 4 ê B. 4 ê C. 4 ê D. 4 ê 3p ê 3 - p 5 - p p - x = + k2p ê = + p ê = + p ê = + p ê x k2 x k2 x k2 ë 4 êë 4 êë 4 êë 4 cot x
Câu 9: Điều kiện xác định của hàm số y = là: cos x p p A. x = + kp B. x = k2p C. x = kp D. x ¹ k 2 2 1
Câu 10: Điều kiện xác định của hàm số y = là sin x - cos x p p
A. x ¹ kp
B. x ¹ k2p C. x ¹ + kp D. x ¹ + kp 2 4
Câu 11: Phương trình: cos x - m = 0 vô nghiệm khi m là: ém < 1 - A. B. m > 1 C. 1 - £ m £ 1 D. m < 1 - ê ëm >1
Câu 12: Điều kiện xác định của hàm số y = cos x là A. x > 0 B. x ³ 0 C. R D. x ¹ 0 1 -
Câu 13: Phương trình: sin 2x =
có bao nhiêu nghiệm thỏa: 0 < x < p 2 A. 1 B. 3 C. 2 D. 4 1 p - p
Câu 14: Phương trình: sin x = có nghiệm thỏa £ x £ là: 2 2 2 5p p p p A. x = + k2p B. x = C. x = + k2p D. x = 6 6 3 3 Trang 28
Câu 15: Số nghiệm của phương trình sin x + cos x = 1 trên khoảng (0;p ) là A. 0 B. 1 C. 2 D. 3 2sin x +1
Câu 16: Điều kiện xác định của hàm số y = là 1- cos x p p
A. x ¹ k2p
B. x ¹ kp C. x ¹ + kp D. x ¹ + k2p 2 2
Câu 17: Khảng định nào sau đây là đúng p p
A. cos x ¹ 1 Û x ¹ + kp
B. cos x ¹ 0 Û x ¹ + kp 2 2 p p C. cos x ¹ 1
- Û x ¹ - + k2p
D. cos x ¹ 0 Û x ¹ + k2p 2 2
Câu 18: Điều kiện để phương trình 3sin x + m cos x = 5 vô nghiệm là ém £ 4 - A. B. m > 4 C. m < 4 - D. 4 - < m < 4 ê ëm ³ 4
Câu 19: Các họ nghiệm của phương trình: sin x + cos x = 1 là: é p éx = k2p p x = + k2p ê
A. x = k2p B. ê p C. x = + k2p D. 4 ê êx = + k2p 4 p ë ê 2 x = - + k2p êë 4 æ p ö
Câu 20: Điều kiện xác định của hàm số y = tan 2x - là ç ÷ è 3 ø p kp p p p p A. x ¹ + 5 B. x ¹ + kp C. x ¹ + 5 kp D. x ¹ + k 6 2 12 2 12 2 x
Câu 21: Phương trình lượng giác: 2cos + 3 = 0 có tất cả họ nghiệm là: 2 5p p p p A. x = ± + 5 k2p B. x = ± + 5 k2p C. x = ± + 5 k4p D. x = ± + k4p 3 6 6 3
Câu 22: Phương trình lượng giác: cos x - 3 sin x = 0 có họ nghiệm là: p p p A. x = + k2p B. Vô nghiệm
C. x = - + k2p D. x = + kp 6 6 2
Câu 23: Phương trình lượng giác: 3.tan x + 3 = 0 có họ nghiệm là: p p p p A. x = + kp B. x = - + k2p C. x = + kp D. x = - + kp 3 3 6 3
Câu 24: Điều kiện để phương trình .
m sin x - 3cos x = 5 có nghiệm là: ém £ 4 - A. m ³ 4 B. 4 - £ m £ 4 C. m ³ 34 D. ê ëm ³ 4
Câu 25: Điều kiện xác định của hàm số y = tan 2x là p - kp p p kp p A. x ¹ + B. x ¹ + kp C. x ¹ + D. x ¹ + kp 4 2 2 4 2 4 ĐÁP ÁN Câu 1 2 3 4 5 6 7 8 9 10 ĐA C D B A D B A B D D Câu 11 12 13 14 15 16 17 18 19 20 Trang 29 ĐA A B C B B A B D B D Câu 21 22 23 24 25 26 27 28 29 30 ĐA D C D D C ĐỀ 14
ĐỀ KIỂM TRA 1 TIẾT
CHƯƠNG 1 TOÁN GIẢI TÍCH 11 Thời gian: 45 phút
I. Phần Trắc Nghiệm: tan x
Câu 1: Điều kiện xác định của hàm số y = là: cos x -1 ì p ì p p x ¹ + kp ïx ¹ + kp ïï A. x ¹ k2p B. x = + k2p C. í 2 2 D. í 3 ï p îx ¹ k2p ïx ¹ + kp ïî 3
Câu 2: Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = 3sin 2x - 5 lần lượt là: A. 8 - à v - 2 B. 2 à v 8 C. 5 - à v 2 D. -5 à v 3
Câu 3: Tìm m để phương trình 5cos x - msin x = m +1 có nghiệm. A. m £ 13 - B. m £ 12 C. m £ 24 D. m ³ 24
Câu 4: Phương trình lượng giác: 2
sin x - 3cos x - 4 = 0 có họ nghiệm là: p p A. x = - + k2p B. x = p - + k2p C. x = + kp D. Vô nghiệm 2 6
Câu 5: Phương trình lượng giác: 2cot x - 3 = 0 có tất cả họ nghiệm là: é p x = + k2p ê 3 p p A. 6 ê B. x = arc cot
+ kp C. x = + kp D. x = + kp p - ê 2 6 3 x = + k2p êë 6
Câu 6: Phương trình lượng giác: 3.tan x - 3 = 0 có tất cả họ nghiệm là: p p p p A. x = + kp B. x = - + k2p C. x = + kp D. x = - + kp 3 3 6 3 3
Câu 7: Phương trình: 2
cos 2x + cos 2x - = 0 có tất cả họ nghiệm là: 4 2p p p p A. x = ± + kp
B. x = ± + kp
C. x = ± + kp
D. x = ± + k2p 3 3 6 6
Câu 8: Nghiệm của phương trình lượng giác: 2
sin x - 2sin x = 0 có họ nghiệm là: p p
A. x = k2p
B. x = kp C. x = + kp D. x = + k2p 2 2 1- sin x
Câu 9: Điều kiện xác định của hàm số y = là cos x p p p A. x ¹ + k2p B. x ¹ + kp
C. x ¹ - + k2p
D. x ¹ kp 2 2 2
Câu 10: Phương trình nào sau đây vô nghiệm:
A. sin x + 3 = 0 B. 2
2cos x - cos x -1 = 0
C. tan x + 3 = 0 D. 3sin x – 2 = 0
Câu 11: Phương trình lượng giác: 0
cos3x = cos12 có tất cả họ nghiệm là: Trang 30 p p k p p - k p p k p A. x = ± + 2 k2p B. x = ± + 2 C. x = + 2 D. x = + 15 45 3 45 3 45 3
Câu 12: Nghiệm dương bé nhất của phương trình: 2
2sin x + 5sin x - 3 = 0 là: 5p p p p A. x = B. x = 3 C. x = D. x = 6 2 2 6 æ p ö
Câu 13: Số nghiệm của phương trình: sin x + =
1 với p £ x £ 5p là: ç ÷ è 4 ø A. 1 B. 0 C. 2 D. 3 æ 2x ö
Câu 14: Phương trình: 0 sin
- 60 = 0 có tất cả họ nghiệm là: ç ÷ è 3 ø 5p k3p p p k p A. x = ± +
B. x = kp C. x = + 3 kp D. x = + 2 2 3 2 2
Câu 15: Trong các phương trình sau phương trình nào có nghiệm: A. 3 sin x = 1 1 2 B. cos 4x = 4 2
C. 2sin x + 3cos x = 1 D. 2
cot x - cot x + 5 = 0
II. Phần Tự Luận: Câu 1. 2 tan x
a) Tìm tập xác định của hàm số y = 2sin x - 3 æ p ö
b) Tìm GTLN, GTNN của hàm số : y = 2sin x + - 5 ç ÷ è 3 ø
Câu 2. Giải các phương trình : 1 a) sin ( 0 x + 45 ) + = 0 2
b) cos2x + 3sin x = 2 Câu 3.
a) Giải các phương trình : 3sin 2x - cos2x = 3 æ p ö
b) Tìm nghiệm thuộc (0;2p )của phương trình : 1+ tan x = 2 2 sin x + ç ÷ è 4 ø 1 Câu 4. Cho 4 4
3sin x - cos x = . Tính giá trị biểu thức: 4 4
A = sin x + 3cos x 2 ĐÁP ÁN
I. Phần Trắc Nghiệm: Câu 1 2 3 4 5 6 7 8 9 10 ĐA C A B D B A C B B A Câu 11 12 13 14 15 16 17 18 19 20 Trang 31 ĐA B D D D C
II. Phần Tự Luận: Câu 1 ( 3,0 điểm) ì p x ¹ + kp ï 2 ï ìcos x ¹ 0 ï ï p a) Điều kiện í Û íx ¹ + k2p ïî2sin x - 3 ¹ 0 3 ï ï 2p x ¹ + k2p ïî 3 ìp p p 2 ü
Tập xác định : D = R \ í + kp ; + k2p; + k2p ý î 2 3 3 þ p -1 £ sin(x + ) £ 1 Û b) 3 p
-7 £ 2sin(x + ) - 5 £ -3 3 5 - p GTNN bằng -7 khi x = + k2p . 6 p GTLN bằng 3 - khi x = + k2p 6 Câu 2 ( 3,0 điểm) - o 1 o 1 a) sin(x+ 45 ) + = 0 Û sin(x+ 45 ) = 2 2
sin(x 45o ) sin( 30o Û + = - ) o o éx = 75 - + k360 Û ê ,k Î!
ëx =165o + k360o 2
cos 2x + 3sin x = 2 Û 1- 2sin x + 3sin x = 2 b) 2
Û 2sin x - 3sin x +1 = 0 é = sinx 1 ê Û 1 êsinx = ë 2 é p x = + k2p ê 2 ê p ê
Û x = + k2p ,k Î ! ê 6 ê 5p êx = + k2p êë 6 Câu 3 ( 3,0 điểm) Trang 32 3 1 3 a) pt Û
sin 2x - cos 2x = 2 2 2 p p 3 Û sin 2 . x cos - cos 2 . x sin = 6 6 2 p p Û sin(2x - ) = sin 6 3 é p p é p 2x - = + k2p x = + kp ê 6 3 ê 4 Û ê Û ê ;k Î Z ê p 2p 5p 2x k2p ê - = + x = + kp êë 6 3 êë 12 p
b) Điều kiện : cos x ¹ 0 Û x ¹ + kp 2 sinx Û 1+ = 2(sinx + cos x) cos x
Û (sinx + cos x)(2cosx-1) = 0 p - TH1: sinx + cosx = 0 Û x = + kp 4 p
TH2: 2cos x -1 = 0 Û x = ± + k2p 3 p p p p Từ ĐK và x Î 3 7 5
(0;2p )nên ta có nghiệm là : x = ; ; ; 4 4 3 3 Câu 4 ( 1,0 điểm)
ĐÆt t = sin2 x Þ cos2 x = 1- t(0 £ t £ ) 1 é 1 t = (tm) ê 2 Theo gt tacã: 2
4t + 4t - 3 = 0 Û ê 3 êt = - (L) êë 2 ì 1 2 sin x = ïï 2 Þ í 1 2 ïcos x = ïî 2 Þ A = 1 ĐỀ 15
ĐỀ KIỂM TRA 1 TIẾT
CHƯƠNG 1 TOÁN GIẢI TÍCH 11 Thời gian: 45 phút
I. Phần Trắc Nghiệm: 1- sin x
Câu 1: Điều kiện xác định của hàm số y = là sin x +1 p p A. x ¹ + k2p B. x ¹ 3 k2p C. x ¹ + k2p
D. x ¹ p + k2p 2 2 Trang 33 1- 3cos x
Câu 2: Tập xác định của hàm số y = là sin x p kp A. x ¹ + kp
B. x ¹ k2p C. x ¹
D. x ¹ kp 2 2 æ p ö
Câu 3: Số nghiệm của phương trình: 2 cos x +
=1 với 0 £ x £ 2p là: ç ÷ è 3 ø A. 0 B. 2 C. 1 D. 3 p
Câu 4: Nghiệm của phương trình lượng giác: 2
2sin x - 3sin x +1 = 0 thõa điều kiện 0 £ x < là: 2 p p p p A. x = B. x = C. x = 5 D. x = 3 2 6 6
Câu 5: Giải phương trình: 2
tan x = 3 có tất cả họ nghiệm là: p p p A. x = - + kp B. x = ± + kp C. vô nghiệm D. x = + kp 3 3 3
Câu 6: Các họ nghiệm của phương trình: sin .
x (2cos x - 3) = 0 là: éx = kp éx = kp éx = k2p p A. ê p B. ê p C. ê p
D. x = ± + k2p êx = ± + k2p êx = ± + kp êx = ± + k2p 6 ë 6 ë 6 ë 3
Câu 7: Phương trình nào sau đây vô nghiệm:
A. 3 sin 2x - cos 2x = 2
B. 3sin x - 4cos x = 5 p C. sin x = cos
D. 3 sin x - cos x = 3 - 4
Câu 8: Phương trình: 3.sin 3x + cos3x = -
1 tương đương với phương trình nào sau đây: æ p ö 1 æ p ö p æ p ö 1 æ p ö 1 A. sin 3x - = - B. sin 3x + = - C. sin 3x + = - D. sin 3x + = ç ÷ ç ÷ ç ÷ ç ÷ è 6 ø 2 è 6 ø 6 è 6 ø 2 è 6 ø 2
Câu 39: Khảng định nào sau đây là sai p A. sin x = 1
- Û x = - + k2p
B. sin x = 0 Û x = kp 2 p
C. sin x = 0 Û x = k2p
D. sin x =1 Û x = + k2p 2
Câu 10: Nghiệm của phương trình lượng giác: 2
cos x - cos x = 0 thỏa điều kiện 0 £ x £ p là: p p A. x = B. x = 0 C. x = p D. x = 4 2
II. Phần Tự Luận:
Câu 1. Tìm tập xác định của hàm số y = tan 2x .
Câu 2: Giải phương trình a) 2
sin x - 4sin x + 3 = 0. b) cos3x + sin 2x -sin 4x = 0. æ p ö
Câu 3: Tính tổng T các nghiệm của phương trình 2 2
cos x - sin 2x = 2 + cos + x trên khoảng ç ÷ è 2 ø (0;2p ).
Câu 4: Cho phương trình: ( x + )( x - m x) 2 cos 1 cos 2 cos
= msin x. Tìm m để phương trình có đúng hai é 2p ù nghiệm thuộc đoạn 0; . ê 3 ú ë û Trang 34 ĐÁP ÁN
I. Phần Trắc Nghiệm: Câu 1 2 3 4 5 6 7 8 9 10 ĐA C D B C B A D C C D
II. Phần Tự Luận:
Câu 1. Tìm tập xác định của hàm số y = tan 2x . Giải p p p
Điều kiện: cos 2x ¹ 0 Û 2x ¹
+ kp Û x ¹ + k ,k Î!. 2 4 2 ìp p ü
Vậy tập xác định là D = ! \ í + k ,k Î"ý. î 4 2 þ
Câu 2: Giải phương trình a) 2
sin x - 4sin x + 3 = 0. ésin x =1 Ta có 2
sin x - 4sin x + 3 = 0 Û . ê ësin x = 3 p
Với sin x = 1 Û x = + k2p , k Î!. 2
Với sin x = 3 phương trình vô nghiệm.
b) cos3x + sin 2x -sin 4x = 0.
Ta có: cos3x + sin 2x -sin 4x = 0 Û cos3x - 2cos3 .
x sin x = 0 Û cos3x(1- 2sin x) = 0 é p p x = + k ê 6 3 écos3x = 0 ê écos3x = 0 p ê ê p p Û Û ê
1 Û x = + k2p , k Î! Û x = + k , k Î!. 1 ë - 2sin x = 0 êsin x = ê 6 6 3 ë 2 ê 5p êx = + k2p êë 6 æ p ö
Câu 3: Tính tổng T các nghiệm của phương trình 2 2
cos x - sin 2x = 2 + cos + x trên khoảng ç ÷ è 2 ø (0;2p ). æ p ö
Tính tổng T các nghiệm của phương trình 2 2
cos x - sin 2x = 2 + cos
+ x trên khoảng (0;2p ). ç ÷ è 2 ø Giải æ p ö Ta có 2 2
cos x - sin 2x = 2 + cos + x Û 2 2
cos x -sin 2x = 2 +sin x ç ÷ è 2 ø æ p p Û ö
cos2x -sin 2x = 2 Û cos 2x +
= 1Û 2x + = k2p , k Î! ç ÷ è 4 ø 4 p
Û x = - + kp , k Î! 8 Trang 35 p
Vì 0 < x < 2p Û 0 < - + kp < 2p Û 1 17 < k < 8 8 8 7p 15p
Vì k Î ! nên k Î{1; } 2 Þ x = ; x = 1 2 8 8 11p Vậy x + x = . 1 2 4
Câu 4: Cho phương trình: ( x + )( x - m x) 2 cos 1 cos 2 cos
= msin x. Tìm m để phương trình có đúng hai é 2p ù nghiệm thuộc đoạn 0; . ê 3 ú ë û Giải Ta có ( x + )( x - m x) 2 cos 1 cos 2 cos
= msin x Û (cos x + ) 1 co
é s2x - mcos x + m ë (cos x- )1ù = 0 û écos 2x = m ( ) 1 Û (cos x + )
1 [cos2x - m] = 0 Û êcos x = 1 - ë (2) é 2p ù
Phương trình (2) Û x = p + k2p , k Î! . Vì x Î 0;
nên không tồn tại k thỏa mãn. ê 3 ú ë û é 2p ù
Theo đề phương trình có đúng hai nghiệm thuộc đoạn 0; nên phương trình ( ) 1 có đúng ê 3 ú ë û é 2p ù
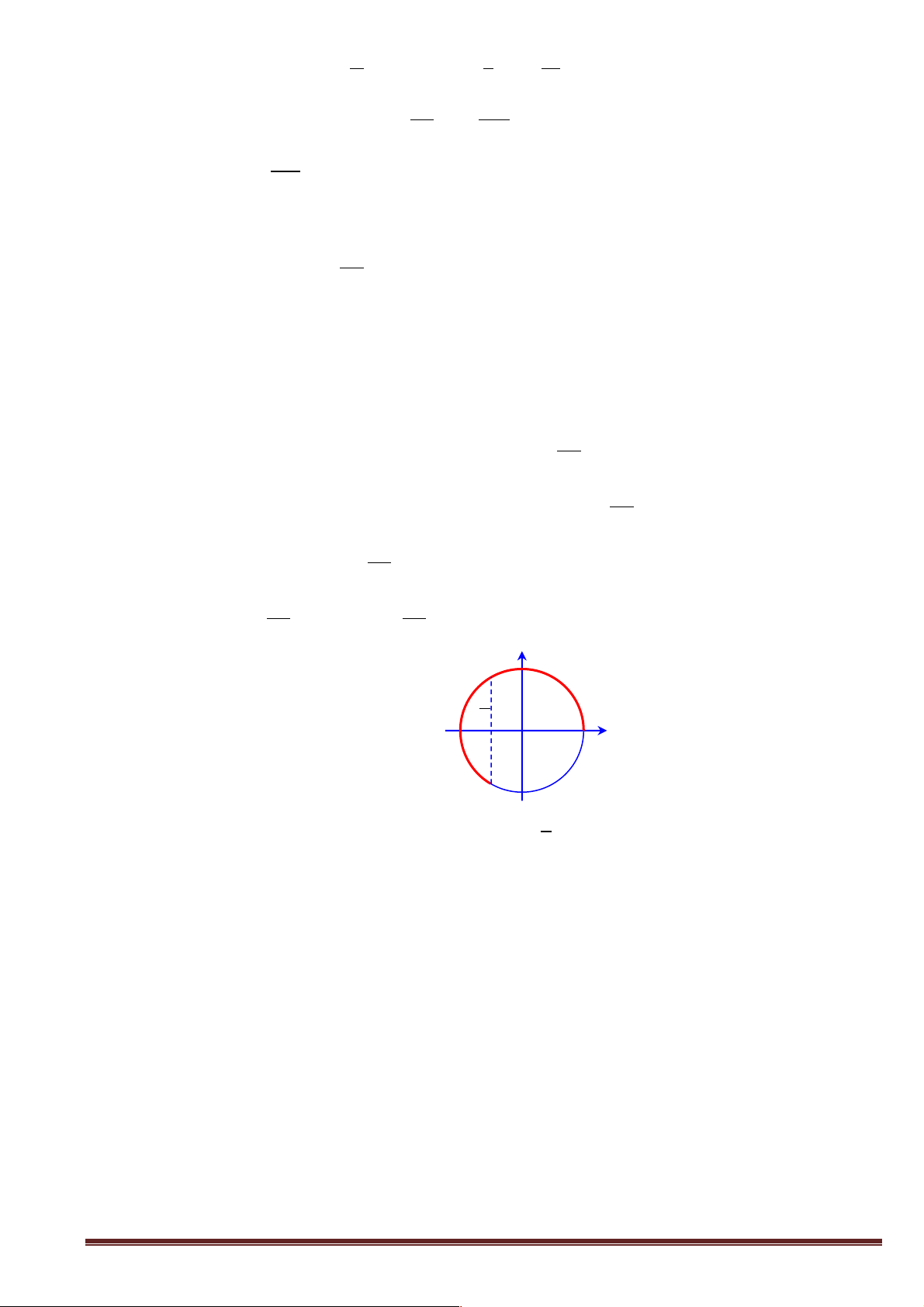
hai nghiệm thuộc đoạn 0; . ê 3 ú ë û é 2p ù é 4p ù Ta có x Î 0; nên 2x Î 0; . ê 3 ú ë û ê 3 ú ë û y 1 - 1 - 2 O x æ 1 ù Do đó ( )
1 có hai nghiệm phân biệt khi m Î 1; - - . ç 2 ú è û Trang 36



