Top 15 đề thi HSG cấp huyện Toán 7 có lời giải chi tiết

Nhằm cung cấp tư liệu để các em học sinh lớp 7 ôn luyện chuẩn bị cho kỳ thi học sinh giỏi Toán lớp 7 cấp huyện, THCS.TOANMATH.com giới thiệu đến các em tài liệu tuyển chọn 15 đề thi HSG cấp huyện

31 16 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 7

Môn: Toán 7

Thông tin:

74 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
1
Trang 1
MỤC LỤC
ĐỀ SỐ 1. HUYỆN ĐỨC PHỔ - NĂM 15 – 16 ................................................................... 2
ĐỀ SỐ 2. ĐỀ HSG CẤP HUYỆN ........................................................................................ 8
ĐỀ SỐ 3. ĐỀ HSG CẤP HUYỆN ...................................................................................... 13
ĐỀ SỐ 4. ĐỀ HSG CẤP HUYỆN ...................................................................................... 17
ĐỀ SỐ 5. ĐỀ HSG CẤP HUYỆN ...................................................................................... 21
ĐỀ SỐ 6. ĐỀ HSG CẤP HUYỆN ...................................................................................... 25
ĐỀ SỐ 7. ĐỀ HSG CẤP HUYỆN ...................................................................................... 30
ĐỀ SỐ 8. ĐỀ HSG CẤP HUYỆN ...................................................................................... 33
ĐỀ SỐ 9. ĐỀ HSG CẤP HUYỆN ...................................................................................... 37
ĐỀ SỐ 10. ĐỀ HSG CẤP HUYỆN .................................................................................... 44
ĐỀ SỐ 11. ĐỀ HSG CẤP HUYỆN .................................................................................... 50
ĐỀ SỐ 12. ĐỀ HSG CẤP HUYỆN .................................................................................... 55
ĐỀ SỐ 13. ĐỀ HSG CẤP HUYỆN .................................................................................... 59
ĐỀ SỐ 14. ĐỀ HSG CẤP HUYỆN .................................................................................... 64
ĐỀ SỐ 15. ĐỀ HSG CẤP HUYỆN .................................................................................... 69
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
2
Trang 2
ĐỀ SỐ 1. HUYỆN ĐỨC PHỔ - NĂM 15 – 16
Câu 1: (5 điểm)
a) Tính giá trị biểu thức
1 1
2014 2016
a aP
, với
1
2015
a .
b) Tìm số nguyên x để tích hai phân số
6
1x
và
1
3
x
là một số nguyên.
Câu 2: (5 điểm)
a) Cho
2; 2a b
. Chứng minh
ab a b
b) Cho ba hình chữ nhật, biết diện tích của hình thứ nhất và diện tích của hình thứ hai tỉ lệ
với 4 và 5, diện tích hình thứ hai và diện tích hình thứ ba tỉ lệ với 7 và 8, hình thứ nhất và
hình thứ hai có cùng chiều dài và tổng các chiều rộng của chúng là 27 cm, hình thứ hai và
hình thứ ba có cùng chiều rộng, chiều dài của hình thứ ba là 24 cm. Tính diện tích của mỗi
hình chữ nhật đó.
Câu 3: (3 điểm)
Cho ∆DEF vuông tại D và
, kẻ DH vuông góc với EF (H thuộc cạnh EF). Gọi M
là trung điểm của EF.
a) Chứng minh
MDH E F
b) Chứng minh
EF DE DF DH
Câu 4: (2 điểm)
Cho các số
1 2 3 15
0 ....a a a a
. Chứng minh rằng
1 2 3 15
5 10 15
...
5
a a a a
a a a
Câu 5: (5 điểm)
Cho ∆ABC có
120A
. Các tia phân giác BE, CF của
ABC
và
ACB
cắt nhau tại I (E, F lần
lượt thuộc các cạnh AC, AB). Trên cạnh BC lấy hai điểm M, N sao cho
0
30BIM CIN
.
a) Tính số đo của
MIN
.
b) Chứng minh CE + BF < BC
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
3
Trang 3
HƯỚNG DẪN CHẤM
Câu
NỘI DUNG ĐÁP ÁN
Điểm
1
2.5 đ
a) Tính giá trị biểu thức
1 1
2014 2016
a aP
, với
1
2015
a .
Thay
1
2015
a vào biểu thức
1 1 1 1
2015 2014 2015 2016
P
Ta có
1 1 1 1
2014 2015 2015 2016
P
1 1
2014 2016
P
2016 2014 2
2014.2016 2014.2016
P
1 1
1007.2016 203
0112
P
0.25
0.5
0.5
0.5
0.75
2.5 đ
b) Tìm số nguyên x để tích hai phân số
6
1x
và
1
3
x
là một số nguyên.
Đặt
6 1
A
1 3
x
x
2 1
1 1
x
x
2( 1)
1
x
x
2 2
1
x
x
2( 1) 4
1
x
x
4
2
1x
Để A nhận giá trị nguyên thì
1x
là Ư(4) =
1; 2; 4
Suy ra
0; 2;1; 3;3; 5
x
0.25
0.25
0.25
0.25
0.5
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
4
Trang 4
2
2đ
2. a) Cho
2; 2a b
. Chứng minh
ab a b
Từ
1 1
2
2
a
a
1 1
2
2
b
b
Suy ra
1 1
1
a b
1
a b
ab
Vậy
ab a b
0.5
0.5
0.5
0.5
3đ
b)
Gọi diện tích ba hình chữ nhật lần lượt là
1 2 3
, ,S S S
, chiều dài, chiều rộng
tương ứng là
1 1 2 2 3 3
, ; , ; ,d r d r d r
theo đề bài ta có:
1 2
2 3
4 7
;
5 8
S S
S S
và
1 2 1 2 2 3 3
; 27; , 24d d r r r r d
Vì hình thứ nhất và hình thứ hai cùng chiều dài
1 1 1 2 1 2
2 2
4 27
3
5 4 5 9 9
S r r r r r
S r
Suy ra chiều rộng
1 2
12 , 15r cm r cm
Vì hình thứ hai và hình thứ ba cùng chiều rộng
2 2 3
2
3 3
7
7 7.24
21
8 8 8
S d d
d cm
S d
Vậy diện tích hình thứ hai
2
2 2 2
21.15 315
S d r cm
Diện tích hình thứ nhất
2
1 2
4 4
.315 252
5 5
S S cm
Diện tích hình thứ ba
2
3 2
8 8
.315 360
7 7
S S cm
0.5
0.5
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
5
Trang 5
3đ
a) Chứng minh
MDH E F
Vì M là trung điểm của EF suy ra
MD ME MF
MDE
cân tại M
E MDE
Mà
HDE F
cùng phụ với
E
Ta có
MDH MDE HDE
Vậy
MDH E F
b) Chứng minh
EF DE DF DH
Trên cạnh EF lấy K sao cho
EK ED
, trên cạnh DF lấy I sao cho
DI DH
Ta có
EF DE EF EK KF
DF DH DF DI IF
Ta cần chứng minh
KF IF
-
EK ED
DEK
cân
EDK EKD
-
0
90EDK KDI EKD HDK
KDI HDK
0.5
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
I
K
M
H
D
E
F
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
6
Trang 6
-
DHK DIK
(c-g-c)
0
90KID DHK
Trong ∆KIF vuông tại I
KF FI
điều phải chứng minh
0.25
0.25
4
(2đ)
Ta có
1 2 3 4 5 5
5a a a a a a
6 7 8 9 10 10
5a a a a a a
11 12 13 14 15 15
5a a a a a a
Suy ra
1 2 15 5 10 15
........ 5( )a a a a a a
Vậy
1 2 3 15
5 10 15
...
5
a a a a
a a a
0.5
0.5
0.5
0.5
5
(5đ)
- Vẽ hình đúng, đủ, chính xác.
a) Tính số đo của
MIN
.
Ta có
180 60ABC ACB A
0
1 1
30
2 2
B C
0
150BIC
Mà
0
30BIM CIN
0
90MIN
b) Chứng minh
CE BF BC
-
0
150BIC
0
30FIB EIC
0.5
0.5
0.5
0.5
0.5
0.25
0.25
120°
N
M
I
F
E
A
C
B
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
7
Trang 7
Suy ra
BFI BMI
(g-c-g)
BF BM
-
CNI CEI
( g-c-g)
CN CE
Do đó
CE BF BM CN BM MN NC BC
Vậy
CE BF BC
0.5
0.5
0.5
0.25
0.25
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám
khảo cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
8
Trang 8
ĐỀ SỐ 2. ĐỀ HSG CẤP HUYỆN
Câu 1.
a. Thực hiện phép tính:
3 3
0,375 0,3
1,5 1 0,75
11 12
5 5 5
0,265 0, 5 2,5 1,25
11 12 3
b. So sánh:
50 26 1
và
168
.
Câu 2.
a. Tìm
x
biết:
2 3 2 2 1
x x x
b. Tìm
;x y Z
biết:
2 5xy x y
c. Tìm x; y; z biết:
2 3x y
;
4 5y z
và
4 3 5 7x y z
Câu 3.
a. Tìm đa thức bậc hai biết
1 .f x f x x
Từ đó áp dụng tính tổng
1 2 3 ....S n
.
b. Cho
2 3 3 2
2 3
bz cy cx az ay bx
a b c
Chứng minh:
2 3
x y z
a b c
.
Câu 4.
Cho tam giác ABC (
90
o
BAC
), đường cao AH. Gọi E; F lần lượt là điểm đối xứng của H
qua AB; AC, đường thẳng EF cắt AB; AC lần lượt tại M và N. Chứng minh rằng:
a.
AE AF
;
b. HA là phân giác của
MHN
;
c.
// ;CM EH
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
9
Trang 9
HƯỚNG DẪN CHẤM
Câu
Ý
Nội dung
Điểm
Câu 1
1,5
điểm
a. 0,5
điểm
A =
3 3 3 3 3 3 3
8 10 11 12 2 3 4
53 5 5 5 5 5 5
100 10 11 12 2 3 4
1 1 1 1 1 1 1
3 3
8 10 11 12 2 3 4
53 1 1 1 1 1 1
5 5
100 10 11 12 2 3 4
A
165 132 120 110
3
1320
3
5
53 66 60 55
5
100 660
263
3.
3
1320
53 49 5
5.
100 660
263
3.
3 3945 3 1881
1320
1749 1225 5 5948 5 29740
3300
0.25
0.25
b. 1
điểm
Ta có:
50 49 7
;
26 25 5
Vậy:
50 26 1 7 5 1 13 169 168
0.5
0,5
Câu 2
4
điểm
a. 1
điểm
Nếu
2x
ta có:
2 2 3 2 1 6x x x x
Nếu
3
2
2
x
ta có:
2 2 3 2 1 2x x x x
(loại)
Nếu
3
2
x
ta có:
4
2 3 2 2 1
5
x x x x
Vậy:
6x
;
4
5
x
0.25
0.25
0.25
0.25
b. 1.5
Ta có:
2 5 ( 2) ( 2) 3xy x y x y y
0. 5
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
10
Trang 10
điểm
(y 2)(x 1) 3.1 1.3 ( 1).( 3) ( 3).( 1)
2y
3 1
1
3
1x
1 3
3
1
x
2 4
2
0
y
1
1
3
5
0. 5
0.5
c. 1.5
điểm
Từ:
2 3 ;4 5 8 12 15x y y z x y z
4 3 5
1 1 1 1 1 1
8 12 15 2 4 3
x y z x y z
4 3 5 7
12
1 1 1 7
2 4 3 12
x y z
1 3
12
8 2
x
;
1
y 12. 1
12
;
1 4
12
15 5
z
0. 5
0.5
0. 5
Câu 3
1.5
điểm
a. 0.5
điểm
Đa thức bậc hai cần tìm có dạng:
2
f x ax bx c
( 0)a
Ta có :
2
1 1 1
f x a x b x c
.
1 2
f x f x ax a b x
2 1
0
a
b a
1
2
1
2
a
b
Vậy đa thức cần tìm là:
2
1 1
2 2
f x x x c
(
c
là hằng số tùy ý).
Áp dụng:
+ Với
1x
ta có :
1 1 0 .
f f
+ Với
2x
ta có :
1 2 1 .
f f
………………………………….
+ Với
x n
ta có :
1 .
n f n f n
1 2 3S n
0f n f
2
1
2 2 2
n n
n n
c c
0.25
0.25
b. 1
điểm
2 3 3 2
2 3
bz cy cx az ay bx
a b c
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
11
Trang 11
2 2 2
2 2 2
2 3 6 2 3 6
4 9
2 3 6 2 3 6
0
4 9
abz acy bcx abz acy bcx
a b c
abz acy bcx abz acy bcx
a b c
2 3 0bz cy
3 2
z y
c b
(1)
3 0cx az
3
x z
a c
(2); Từ (1) và (2) suy ra:
2 3
x y z
a b c
0.5
0.25
0.25
Câu 4
3
điểm
Hình
vẽ
0. 5 đ
0.25
a. 1
điểm
Vì AB là trung trực của EH nên ta có:
AE AH
(1)
Vì AC là trung trực của HF nên ta có:
AH AF
(2)
Từ (1) và (2) suy ra:
AE AF
0.25
0.25
0. 5
b. 1
điểm
Vì
M AB
nên MB là phân giác
EMH
MB là phân giác ngoài
góc M của tam giác
MNH
Vì
N AC
nên NC là phân giác
FNH
NC là phân giác ngoài góc
N của tam giác
MNH
Do MB; NC cắt nhau tại A nên HA là phân giác trong góc H của tam
giác
MNH
hay HA là phân giác của
MHN
.
0.25
0.25
0.5
c. 1
điểm
Ta có
AH BC
(gt) mà HM là phân giác
MHN
HB là phân giác
ngoài góc H của tam giác
HMN
MB là phân giác ngoài góc M của tam giác
HMN
(cmt)
NB là
0.25
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
12
Trang 12
phân giác trong góc N của tam giác
HMN
BN AC
( Hai đường phân giác của hai góc kề bù thì vuông góc
với nhau).
// BN HF
( cùng vuông góc với AC)
Chứng minh tương tự ta có:
0.25
0.25
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
13
Trang 13
ĐỀ SỐ 3. ĐỀ HSG CẤP HUYỆN
Bài 1 ( 2,0 điểm). Tính hợp lý các biểu thức sau:
a)
1 5 1 5
27 13
4 8 4 8
b)
1 3 4
2
2 4 9
c)
2 3
2 4
2 .10 2 .6
2 .15 2
Bài 2 ( 2,5 điểm). Tìm x biết:
a)
2
3( 2) 4
5
x
b)
1
5 7
3
x
c)
7 5
(2 1) (2 1)x x
Bài 3 (1,5 điểm):
Ba đội cùng chuyển một khối lượng gạch như nhau. Thời gian để đội thứ nhất, đội
thứ hai và đội thứ ba làm xong công việc lần lượt là 2 giờ, 3 giờ, 4 giờ. Tính số người tham
gia làm việc của mỗi đội, biết rằng số người của đội thứ ba ít hơn số người của đội thứ hai
là 5 người.
Bài 4 (3,5điểm):
Cho tam giác ABC vuông tại A với
3
4
AB
AC
và
15BC cm
. Tia phân giác góc C cắt
AB tại D. Kẻ
DE BC
(E BC)
a) Chứng minh
.AC CE
b) Tính độ dài AB; AC.
c) Trên tia AB lấy điểm F sao cho
AF AC
. Kẻ tia
Fx FA
cắt tia DE tại M. Tính
DCM
.
Bài 5 (0,5điểm):
Tìm giá trị lớn nhất của biêu thức: A =
2
x x
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
14
Trang 14
HƯỚNG DẪN CHẤM
Câu
Nội dung
Điểm
1
2,0đ
1 5 1 5 5 1 1 5 35
) 27 13 (27 13 ) 14.
4 8 4 8 8 4 4 8 4
a
0,75
1 3 4 1 2 1 2 7
)2 2
2 4 9 4 3 2 3 6
b
0,75
2 3 3 3 3
2 4 2 4 2 2
2 .10 2 .6 2 .5 2 .6 2 (5 6) 2.11
) 2
11
2 .15 2 2 .15 2 2 (15 2 )
c
0,5
1
2,5đ
a)
2
3( 2) 4
5
x
2
3( 2) 4
5
x
18
3( 2)
5
x
6
2
5
x
16
5
x
0,25
0,25
0,25
0,25
1
5 7
3
x
1
12
3
x
1
12
3
x hoặc
1
12
3
x
5
3
3
x hoặc
37
3
x
0,25
0,25
0,5
7 5
(2 1) (2 1)x x
5 2
(2 1) (2 1) 1 0
x x
0,25
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
15
Trang 15
1
2 1 0
2
2 1 1
1
2 1 1
0
x
x
x
x
x
x
0,25
3
1,5đ
Gọi số người tham gia làm việc của đội thứ nhất, đội thứ hai, đội thứ ba
lần lượt là x; y; z (giờ).
ĐK: ; ; 0x y z
Cùng một khối lượng công việc, số người tham gia và thời gian làm việc
tỷ lệ lệ nghịch.
Theo bài ra ta có:
2 3 4x y z
và – 5y z
5
60
1 1 1 1 1
3 4 3 4 12
y z y z
20, 15, 30y z x
(thoả mãn điều kiện bài toán)
Vậy số người tham gia làm việc của đội thứ nhất, đội thứ hai, đội thứ ba
lần lượt là 30 người, 20người, 15 người
0,25
0,5
0,25
0,25
0,25
4
3,5đ
Vẽ hình, ghi GT, KL đúng :
0,5đ
a) Chứng minh được
ACD ECD
( cạnh huyền- góc nhọn)
AC CE
(hai cạnh tương ứng)
1
0,5
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
16
Trang 16
b)
3
( )
4 3 4
AB AB AC
gt
AC
2 2 2 2 2 2
15
9
9 16 9 16 25 25
AB AC AB AC BC
2
9.9 81 9AB AB cm
2
9.16 144 12AC AC cm
0,25
0,5
0,25
c) Kẻ
Cy Fx
cắt nhau tại K
Ta thấy
AC AF FK CK CE
và
0
90ACK
Chứng minh được
CEM CKM
( cạnh huyền- cạnh góc vuông)
ECM KCM
(hai góc tương ứng)
Mà
1 1
90 45
2 2
DCM DCE ECM ACK
0,25
0,25
5
0,5đ
Xét các trường hợp:
+ TH1 :
2 ( 2) 2x A x x
+TH2 :
0 2 2 2 2 2x A x x x
+ TH3 :
0 2 2 2x A x x
Với mọi giá trị của x thì
2A
Vậy giá trị lớn nhất của A bằng 2 khi
2x
0,25
0,25
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
17
Trang 17
ĐỀ SỐ 4. ĐỀ HSG CẤP HUYỆN
Câu 1(5 điểm):
a) Cho biểu thức:
4P x xy y
. Tính giá trị của P với
1,5;
x
0,75y
b) Rút gọn biểu thức:
12 5 6
6
2 4 5
2 .3 4 .81
A
2 .3 8 .3
Câu 2 (4điểm):
a) Tìm x, y, z, biết:
2 3 ; 4 5 x y y z
và
11x y z
b) Tìm x, biết:
1 2 3 4x x x x
Câu 3(3 điểm). Cho hàm số:
3
4
y f x x x
a) Tính
0 ,
f
0,5
f
b) Chứng minh:
.f a f a
Câu 4: (1,0 điểm): Tìm cặp số nguyên
;x y
biết:
. x y x y
Câu 5: (6 điểm):Cho
ABC
có góc
90A
. Vẽ ra ngoài tam giác
ABC
các tam giác vuông
cân tại A là
ABM
và
ACN
a) Chứng minh rằng:
AMC ABN
b) Chứng minh:
BN CM;
c) Kẻ
(H BC)
. Chứng minh AH đi qua trung điểm của MN.
Câu 6 : (1 điểm):Cho ba số a, b, c thõa mãn:
0 1 2a b c
và
1a b c
. Tìm giá
trị nhỏ nhất của
c
.
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
18
Trang 18
HƯỚNG DẪN CHẤM
Câu
Nội dung
Điểm
Câu 1
(5điểm)
a) Ta có:
1,5 1,5
x x
hoặc
1,5x
+) Với
1,5x
và
0,75y
thì
1,5 4.1, 5 0, 75 0, 75 1,5 1 3 6 0, 75 5,25
P
+) Với
1,5x
và
0,75y
thì
1,5 4 1,5 . 0,75 0, 75 1,5 1 3 0,75 6, 75
P
1,5
1,5
b)
12 5 6
6
2 4 5
2 .3 4 .81
A
2 .3 8 .3
=
12 5 12 4 12 4
12 6 12 5 12 5
2 .3 2 .3 2 .3 (3 1) 1
3
2 .3 2 .3 2 .3 (3 1)
2
Câu 2
(4 điểm)
a)
2 3 ; 4 5 x y y z
; ;
3 2 5 4 15 10 10 8
x y y z x y y z
11 1
15 10 8 15 10 8 33 3
x y z x y z
10 8
5; ;
3 3
x y z
1
1
b)
1 2 3 4x x x x
(1)
Vì
VT 0
4 0x
hay
0x
, do đó:
1 1; 2 2; 3 3
x x x x x x
(1) 1 2 3 4 6x x x x x
1
1
Câu 3
(3điểm)
a)
0 0
f
3
1 1 1 1
( 0,5) 4 0
2 2 2 2
f
1
1
b)
3
3
4 4
f a a a a a
0,5
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
19
Trang 19
3 3
( ) 4 4f a a a a a
f a f a
0,5
Câu 4
(1 điểm)
.x y x y
( 1) y
1
y
xy x y x y x
y
vì
1 1 1 1 1 1x z y y y y y
,
do đó
1 1y
2y
hoặc 0y
Nếu
2y
thì
2x
Nếu 0y thì 0x
Vậy các cặp số nguyên (x;y) là: (0,0) và (2;2)
0,5
0,5
Câu 5
(6 điểm)
a) Xét
AMC
và
ABN
, có:
AM AB
(
AMB
vuông
cân)
AC AN
(
ACN
vuông
cân)
MAC NAC
(
90 BAC
)
Suy ra
AMC ABN
(c - g - c)
Hình vẽ 0,5 đ
1,0
0,5
0,5
b) Gọi I là giao điểm của BN với AC, K là giao điểm của BN với MC.
Xét
KIC
và
AIN
, có:
ANI KCI
( AMC ABN)
AIN KIC
(đối đỉnh)
IKC NAI 90
, do đó:
MC BN
1
1
0,5
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
20
Trang 20
c) Kẻ
ME AH
tại E,
NF AH
tại F. Gọi D là giao điểm của MN và
AH.
- Ta có:
BAH MAE 90
(vì
90MAB
)
Lại có
MAE AME 90
, nên
AME BAH
Xét
MAE
và
ABH
, vuông tại E và H, có:
AME BAH
(chứng minh trên)
MA AB
Suy ra
MAE ABH
(cạnh huyền-góc nhọn)
ME AH
- Chứng minh tương tự ta có
AFN CHA
FN AH
Xét
MED
và
NFD
, vuông tại E và F, có:
ME NF( AH)
EMD FND
(phụ với
MDE
và
FDN
, mà
MDE FDN
)
MED NFD BD ND
Vậy AH đi qua trung điểm của MN.
0,25
0,25
0,25
0,25
Câu 6
(1 điểm)
Vì:
0 1 2a b c
nên
1 2 2 2 20 a b c c c c
0 4 3 6c
(vì
1a b c
)
Hay
3 2c
2
3
c
.
Vậy giá trị nhỏ nhất của c là:
2
3
khi đó
5
3
a b
0,5
0,5
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
21
Trang 21
ĐỀ SỐ 5. ĐỀ HSG CẤP HUYỆN
Bài 1: (4 điểm)
Chứng minh rằng với mọi n nguyên dương thì:
2 2
3 2 3 2
n n n n
chia hết cho 10.
Bài 2: (3điểm)
Cho 2 đa thức :
2 3 4 2009 2010
1 ...
P x x x x x x x
và
2 3 4 2009 2010
1 ...
Q x x x x x x x
. Giá trị của biểu thức
1 1
2 2
P Q
có dạng
biểu diễn hữu tỉ là
;
a
b
a,b
; a,b là 2 số nguyên tố cùng nhau. Chứng minh
5a
Bài 3: (3 điểm)
Cho dãy tỉ số bằng nhau:
2 2 2 2a b c d a b c d a b c d a b c d
a b c d
Hãy tìm giá trị của biểu thức:
a b b c c d d a
M
c d d a a b b c
Bài 4: (4điểm)
Cho
a b c
M
a b b c c a
với a, b, c > 0.
a) Chứng minh
1.M
b) Chứng tỏ rằng
M
không phải là số nguyên.
Bài 5: (3,5 điểm)
Cho tam giác ABC cân tại A, trên cạnh AB lấy điểm D, trên tia đối của tia CA lấy
điểm E sao cho
CE BD
. Gọi I là trung điểm của DE. chứng minh ba điểm B, I, C thẳng
hàng.
Bài 6: (2,5 điểm)
Cho
ABC
cân tại A, có
100A
, tia phân giác của góc ABC cắt AC tại D. Chứng minh:
AD BD BC
.
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
22
Trang 22
HƯỚNG DẪN CHẤM
Bài
Đáp án
Điểm
1(4điểm)
2 2 2 2
3 2 3 2 3 3 2 2
n n n n n n n n
1,0đ
10.3 5.2
n n
1,5đ
Vì n nguyên dương nên
2 2 5.2 10
n n
và
10.3 10
n
1,0đ
Vậy:
2 2
3 2 3 2 10
n n n n
0,5đ
2 (3điểm)
Đặt
3 5 2009
1 1 1 1 1 1
2 ...
2 2 2 2 2 2
A P Q
( 1)
suy ra
3 2007
1 1 1
4 10 ...
2 2 2
A
(2)
Từ ( 1) và ( 2) suy ra
2009
2012
2009
2009
1
8
1 2 1
2
3 8
2 3
3.2
a
A A
b
( 2 điểm)
Ta thấy:
2012 1006
2 1 4 1 3
;
2012
2 – 1
và
2009
2
là 2 số nguyên tố cùng nhau
nên
2012
2 – 1 3 .a
2012 503
3 2 1 16 1a
. Vì
503
16
có chữ số tận cùng là 6 nên 3a có chữ số
tận cùng là 5 suy ra số này chia hết cho 5. 3,5 là 2 số nguyên tố cùng nhau
nên
5a
.
3,0đ
3 (3điểm)
Từ
2 2 2 2a b c d a b c d a b c d a b c d
a b c d
=>
2 2
1 1
a b c d a b c d
a b
=
2 2
1 1
a b c d a b c d
c d
1,0đ
=>
a b c d a b c d a b c d a b c d
a b c d
0,5đ
Nếu
0a b c d
thì
a b c d
, khi đó:
1 1 1 1 4M
0,5đ
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
23
Trang 23
Nếu
0a b c d
thì
;a b c d
;b c d a
; .c d a b d a b c
Khi đó:
1 1 1 1 4.
M
1,0đ
4 (4điểm)
a) Vì
, , 0a b c
nên:
; ;
a a b b c c
a b a b c b c a b c c a a b c
1,0đ
=>
a b c
M
a b b c c a
1
a b c
a b c
Vậy:
1 M
(1)
1,0đ
b) Mà:
a b c
a b b c c a
+
b c a
a b b c a c
=
a b b c c a
a b a b b c b c c a c a
= 3
1,0đ
Vì
b c a
a b b c a c
> 1 (tương tự câu a)
Suy ra: M =
2
a b c
a b b c c a
. (2)
0,5đ
Từ (1) và (2) suy ra:
1 2M
nên M không phải là số nguyên.
0,5đ
5 (3,5 điểm)
Học sinh vẽ hình đúng
0,5đ
I
A
B
C
E
D
F
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
24
Trang 24
Kẻ
//DF AC
(F thuộc BC)
DFB ACB
(2 góc đồng vị)
Mà
ABC ACB
(tam giác ABC cân)
DFB ABC
cân tại D
1,5đ
, mà
DF CE
(gt)
DF CE
0,5đ
IDF IEC
(c-g-c)
DIF EIC
0,5đ
Vậy: 3 điểm B, I, C thẳng hàng (vì 3 điểm D, I, E thẳng hàng)
0,5đ
6 (2,5 điểm)
HS vẽ hình đúng
0,5đ
Trên cạnh BC lấy 2 điểm E,F sao cho:
BE BA
và
.
HS chứng minh được:
AD DE
0,5đ
HS chứng minh được:
DFE
cân tại D
Suy ra:
DE DF
0,5đ
HS chứng minh được:
DFC
cân tại F
Suy ra:
.
Suy ra:
DE FC
Suy ra:
.AD BD BC
1,0đ
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
A
B
C
D
F
E
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
25
Trang 25
ĐỀ SỐ 6. ĐỀ HSG CẤP HUYỆN
Bài 1 (4 điểm):
a) So sánh hai số:
39
– 5
và
91
– 2
b) Chứng minh rằng: Số
2 2 1
11 12
n n
A
chia hết cho
133
, với mọi n
N
Bài 2 (4 điểm):
a) Tìm tất cả các cặp số
; x y
thỏa mãn:
2012 2013
2 7 3 0
x y x
b) Tìm số tự nhiên n và chữ số a biết rằng:
1 2 3 . . .
n aaa
Bài 3 (4 điểm): Ba lớp 7 ở trường K có tất cả 147 học sinh. Nếu đưa
1
3
số học sinh của lớp
1
7A
,
1
4
số học sinh của lớp
2
7A
và
1
5
số học sinh của lớp
3
7A
đi thi học sinh giỏi cấp huyện
thì số học sinh còn lại của ba lớp bằng nhau. Tính tổng số học sinh của mỗi lớp 7 ở trường
K.
Bài 4 (4 điểm): Cho tam giác ABC có
3 6A B C
.
a) Tính số đo các góc của tam giác ABC.
b) Kẻ AD vuông góc với BC (D thuộc BC). Chứng minh:
.AD BD CD
Bài 5 (4 điểm): Cho tam giác ABC cân ở A. Trên cạnh AB lấy điểm M, trên tia đối của tia
CA lấy điểm N sao cho
2 .AM AN AB
a) Chứng minh rằng:
BM CN
b) Chứng minh rằng: BC đi qua trung điểm của đoạn thẳng MN.
c) Đường trung trực của MN và tia phân giác của góc BAC cắt nhau tại K. Chứng minh
rằng:
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
26
Trang 26
HƯỚNG DẪN CHẤM
Bài
Đáp án
Điểm
1
4
điểm
a) So sánh hai số:
–
39
5
và
–
91
2
2,0đ
Ta có:
13
39 39 3 13
( 5) 5 5 125
0,75đ
13
91 91 7 13
( 2) 2 2 128
0,75đ
Ta thấy:
13 13 13 13 39 91
125 128 125 128 ( 5) ( 2)
0,5đ
b) Chứng minh: Số
n 2 2n 1
A 11 12
chia hết cho 133, với mọi
n
2,0đ
Ta có:
2 2 1 2 2
11 12 11 11 12 12 121.11 12.144
n
n n n n n
A
(133 12) 11 12.144 133.11 12.11 12.144
n n n n n
133.11 12. 144 11
n n n
1,0đ
Ta thấy:
133.11 133
n
144 11 (144 11) 133 12. 144 11 133
n n n n
0,5đ
Do đó suy ra:
133.11 12. 144 11
n n n
chia hết cho 133
Vậy: số
n 2 2n 1
A 11 12
chia hết cho 133, với mọi
n
0,5đ
2
4
điểm
a) Tìm tất cả các cặp số (x; y): 2,0đ
Ta có: 2012 là số tự nhiên chẵn
2012
(2x y 7) 0
và
2013
3 0 3 0
x x
0,5đ
Do đó, từ
2012 2013
2 7 3 0
x y x
suy ra:
2012
2 – 7 0
x y
và
2013
3 0
x
0,5đ
2 – 7 0x y
(1) và
– 3 0x
(2)
0,5đ
Từ (2)
3x
0,5đ
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
27
Trang 27
Từ (1)
2 7 2.3 7 13y x
Vậy cặp số
; x y
cần tìm là
3; 13
b) Tìm số tự nhiên n và chữ số a
2,0đ
Ta có:
1
1 2 3 . . .
2
n n
n
và
.111 .3.37aaa a a
0,5đ
Do đó, từ
1 2 3 . . . 1 2.3.37.n aaa n n a
1
n n
chia hết cho số nguyên tố 37
n
hoặc
1n
chia hết cho 37 (1)
0,5đ
Mặt khác:
( 1)
999 ( 1) 1998 45
2
n n
aaa n n n
(2)
Từ (1) và (2) suy ra hoặc
37n
, hoặc
1 37n
0,5đ
- Với
37n
thì
37.38
703
2
aaa (không thỏa mãn)
- Với
1 37n
thì
36.37
666
2
aaa (thỏa mãn)
Vậy
36n
và
6.a
0,5đ
3
4
điểm
Tính tổng số học sinh của mỗi lớp 7 ở trường K.
4,0đ
Gọi tổng số học sinh của
1 2 3
7 , 7 , 7A A A
lần lượt là a, b, c (a,b,c
N*)
Theo bài ra ta có :
1 1 1
3 4 5
a a b b c c
(*) và
147a b c
1,0đ
Từ (*)
2 3 4
3 4 5
a b c
12 12 12
18 16 15
a b c
18 16 15
a b c
1,0đ
Áp dụng tính chất dãy tỷ số bằng nhau ta có :
18 16 15
a b c
=
147
3
18 16 15 49
a b c
.
1,0đ
Suy ra :
54, 48, 45a b c
1,0đ
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
28
Trang 28
Vậy tổng số học sinh của 7A
1
, 7A
2
, 7A
3
lần lượt là 54, 48 và 45.
4
4
điểm
a) Tính số đo các góc của
:ABC
2,0đ
Từ
3 6A B C
ˆ ˆ
ˆ ˆ ˆ ˆ
180
20
6 2 1 6 2 1 9
A B C A B C
1,0đ
ˆ
6.20 120
ˆ
2.20 40
ˆ
1.20 20
A
B
C
Vậy:
ˆ
ˆ ˆ
120 ; 40 ; 20A B C
1,0đ
b) Chứng minh AD < BD < CD.
2,0đ
- Trong
ACD
có
2 1
90 ; 20 70 50ADC C A A
- Xét
ADB có
1
ˆ
ˆ
40 50 (1)B A AD BD
1,0đ
- Xét
ABC có
0 0 2 2
ˆ ˆ
40 20B C AB AC AB AC
(*)
- Áp dụng định lý Pytago cho hai tam giác vuông ADB và ADC có:
2 2 2
AB AD BD
và
2 2 2
AC AD CD
Do đó, từ (*)
2 2 2 2
AD BD AD CD
2 2
BD CD BD CD
(2)
Từ (1) và (2)
AD BD CD
1,0đ
5
4
điểm
a) Chứng minh rằng:
BM CN
1,0đ
Theo giả thiết, ta có:
2AB AB AB AB AM BM
AM AN AM AC CN
ABC
cân ở A
AB AC
Do đó, từ
A 2AM N AB
BM CN
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
29
Trang 29
b) Chứng minh rằng: BC đi qua trung điểm của đoạn thẳng MN.
1,5đ
Qua M kẻ
// ME AC
(E
BC)
ABC cân ở A
BME
cân ở M
EM BM CN
0,75đ
MEI NCI
(g-c-g)
IM IN
Vậy: BC đi qua trung điểm của MN.
0,75đ
c) Chứng minh rằng:
KC AN
1,5đ
+ K thuộc đường trung trực của MN
KM KN
(1)
+
ABK ACK
(c-g-c)
KB KC
(2);
ABK ACK
(*)
+ Kết quả câu c/m câu a)
BM CN
(3)
0,5đ
+ Từ (1), (2) và (3)
BMK CNK
(c-c-c)
ABK NCK
(**)
0,5đ
+ Từ (*) và (**)
180
90
2
ACK NCK
KC AN
0,5đ
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
30
Trang 30
ĐỀ SỐ 7. ĐỀ HSG CẤP HUYỆN
Bài 1: (6 điểm)
a) Tìm x, biết
2
1
3
x
;
b) Tính giá trị của biểu thức sau:
2
2 3 1
3 2
x x
A
x
với
2
1
3
x
Bài 2: (3 điểm)
a) Tìm chữ số tận cùng của A biết
2 2
3 – 2 3 – 2
n n n n
A
biết
*
n
b) Tìm các giá trị nguyên của x để
3
2
x
x
nhận giá trị nguyên.
Bài 3: (4 điểm)
Cho đa thức
f x
xác định với mọi x thỏa mãn:
2
. 2 – 9 . .x f x x f x
a) Tính
5 .
f
b) Chứng minh rằng f(x) có ít nhất 3 nghiệm.
Bài 4: (6 điểm)
Cho tam giác ABC, trung tuyến AM. Trên nửa mặt phẳng chứa đỉnh C bờ là đường thẳng
AB dựng đoạn AE vuông góc với AB và
.AE AB
Trên nửa mặt phẳng chứa đỉnh B bờ là
đường thẳng AC dựng đoạn AF vuông góc với AC và
AF AC
. Chứng minh rằng:
a)
b)
2EF AM
c)
.AM EF
Bài 5: (1 điểm)
Cho
, , , a b c d
là các số dương. Tìm giá trị nhỏ nhất của biểu thức:
A x a x b x c x d
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
31
Trang 31
HƯỚNG DẪN CHẤM
Bài Hướng dẫn chấm Điểm
1
(6đ)
a) Ta có
2 5
1
2
3 3
1
2 1
3
1
3 3
x x
x
x x
4.0đ
b) Từ câu a) Với
5
3
x
thay vào A ta được
14
27
A
Với
1
3
x
thay vào A ta được
2
9
A
2.0đ
2
(3đ)
a)
2 2
3 – 2 3 – 2
n n n n
A
9. 9 1 .3 3 – 4.2 – 2 3 – 4 1 .2 31 .
– 5 2
0
.
n n n n n n n n
10.3 10
n
và
5.2 10
n
(do
*
n
hay
1n
)
10A
Chứng minh A chia hết cho 10 suy ra chữ số tận cùng của A là 0
1.5đ
b) Ta có:
3 2 5 5
1 2 (5) 1; 5
2 2 2
x x
Z x U
x x x
1;3; 3;7x
1.5đ
3
(4đ)
a) Ta có với
3 5 0
x f
b)
0 0 0 0
x f x
là một nghiệm
3 5 0 5
x f x
là một nghiệm
3 1 0 1
x f x
là một nghiệm
Vậy f(x) có ít nhất là 3 nghiệm.
2.0đ
2.0đ
4
(6đ)
a) Chứng minh
( )ABF AEC cgc FB EC
b) Trên tia đối của tia MA lấy K sao cho
2AK AM
. Ta có
ABM KCM
//CK AB
0
180ACK CAB EAF CAB
ACK EAF
EAF và KCA có
;AE AB CK
AF AC
(gt);
ACK EAF
EAF KCA
(cgc)
2 .EF AK AM
c) Từ
EAF KCA
CAK AFE
0
90AFE FAK CAK FAK
AK EF
3.0đ
1.5đ
1.5đ
M
I
A
B
C
E
K
F
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
32
Trang 32
5
(1đ)
Không mất tính tổng quát, giả sử
a b c d
Áp dụng BĐT
a b a b
, dấu bằng xảy ra
0ab
ta có:
x a x d x a d x x a d x d a
(1)
x b x c x b c x x b c x c b
(2)
Suy ra
A c d a b
Dấu “=” xảy ra khi và chỉ khi dấu “=” ở (1) và (2)
xảy ra
– – 0
x a d x
và
( )( ) 0x b c x
a x d
và
b x c
Do đó
minA c d a b b x c
1.0đ
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
33
Trang 33
ĐỀ SỐ 8. ĐỀ HSG CẤP HUYỆN
Bài 1: ( 2,0 điểm)
a. Tìm x, y biết:
4 4
7 7
x
y
và
22x y
b. Cho
3 4
x y
và
5 6
y z
. Tính
2 3 4
3 4 5
x y z
M
x y z
Bài 2: ( 2,0 điểm)
Thực hiện tính:
a.
2010 2009 2008
2 2 2 ... 2 1S
b.
1 1 1 1
1 1 2 1 2 3 1 2 3 4 ... 1 2 3 ... 16
2 3 4 16
P
Bài 3: ( 2,0 điểm)
Tìm x biết:
a.
1 2 3 4 5 30 31
. . . . ... . 2
4 6 8 10 12 62 64
x
b.
5 5 5 5 5 5 5 5 5 5
5 5 5 5 5
4 4 4 4 6 6 6 6 6 6
. 2
3 3 3 2 2
x
Bài 4: ( 4,0 điểm)
Cho tam giác ABC có
90B
và
2B C
. Kẻ đường cao AH. Trên tia đối của tia BA lấy
điểm E sao cho
BE BH
. Đường thẳng HE cắt AC tại D.
a. Chứng minh
.BEH ACB
b. Chứng minh
.DH DC DA
c. Lấy B’ sao cho H là trung điểm của
'BB
. Chứng minh
'AB C
cân.
d. Chứng minh
AE HC
.
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
34
Trang 34
HƯỚNG DẪN CHẤM
Bài 1: (2,0 điểm)
28 7 28 4x y
0,25
4 7 4 7
x y x y
0,25
22
2
4 7 11
x y
8; 14x y
0,25
3 4 15 20
x y x y
;
5 6 20 24
y z y z
15 20 24
x y z
(1)
0,25
(1)
2 3 4 2 3 4
30 60 96 30 60 96
x y z x y z
0,25
(1)
3 4 5 3 4 5
45 80 120 45 80 120
x y z x y z
0,25
2 3 4 3 4 5 2 3
: :
30 60 96 45 80 120 30 45
x y z x y z x x
0,25
2 3 4 245 2 3 4 186
. 1
186 3 4 5 3 4 5 245
x y z x y z
M
x y z x y z
0,25
Bài 2: ( 2,0 điểm)
Thực hiện tính:
2011 2010 2009 2
2 2 22 ... 2 2S
0,25
2011 2010 2010 2009 2009 2 2
2 2 2 2 2 ... 2 2 2 2 12S S
0,25
2011 2010
2 2.2 1S
0,25
2011 2011
2 2 1 1S
0,25
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
35
Trang 35
1 2.3 1 3.4 1 4.5 1 16.17
1 . . ...
2 2 3 2 4 2 16 2
P
0,25
2 3 4 5 17
. ...
2 2 2 2 2
0,25
1
1 2 3 ... 17 1
2
0,25
1 17.18
1 76
2 2
0,25
Bài 3: ( 2,0 điểm)
6
1 2 3 4 5 30 31
. . . . ... . 2
2.2 2.3 2.4 2.5 2.6 2.31
2
x
0,25
30 6
1.2.3.4...30.31
2
1.2.3.4...30.31.2 .2
x
0,25
36
1
2
2
x
0,25
36x
0,25
5 5
5 5
4.4 6.6
. 2
3.3 2.2
x
0,25
6 6
6 6
4 6
. 2
3 2
x
0,25
6 6
6 4
. 2
3 2
x
0,25
12
2 2 12
x
x
0,25
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
36
Trang 36
Bài 4: ( 4,0 điểm)
Câu a: 0,75 điểm
Hình vẽ:
BEH
cân tại B nên
1
E H
0,25
1
2ABC E H E
0,25
2 ABC C BEH ACB
0,25
Câu b: 1,25 điểm
Chứng tỏ được
DHC
cân tại D
nên
DC DH
.
0,50
DAH
có:
90DAH C
0,25
2
90 90
DHA H C
0,25
DAH
cân tại D nên
.DA DH
0,25
Câu c: 1,0 điểm
Câu d: 1,0 điểm
'ABB
cân tại A nên
' 2B B C
0,25
' 'AB AB CB
0,25
1
' B A C
nên
1
2
C A C
0,50
'BE BH B H
0,25
1
C A
'AB C
cân tại B’
0,25
Có:
AE AB BE
' 'HC CB B H
AE HC
0,50
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
1
2
1
A
E
C
B
B'
H
D
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
37
Trang 37
ĐỀ SỐ 9. ĐỀ HSG CẤP HUYỆN
I. Phần trắc nghiệm khách quan: (6 điểm)
Câu 1: Giá trị của x trong biểu thức
2
( 1) 0,25x
là:
A.
9 1
;
4 4
. B.
1 9
;
4 4
. C.
9 1
;
4 4
. D.
9 1
;
4 4
.
Câu 2: Cho
50xOy
, điểm A nằm trên Oy. Qua A vẽ tia
Am
. Để
Am
song song với Ox
thì số đo của
OAm
là:
A.
50
. B.
130
. C.
50
và
130
D.
80
.
Câu 3: Cho hàm số
y f x
xác định với mọi
1x
. Biết
1 . – 1
f n n f n
và
1 1
f
. Giá trị của f(4) là:
A. 3. B. 5. C. 6. D. 1.
Câu 4: Cho tam giác ABC vuông tại B,
6AB
,
A 30
. Phân giác góc C cắt AB tại D.
Khi đó độ dài đoạn thẳng BD và AD lần lượt là:
A. 2; 4 . B. 3; 3. C. 4; 2. D. 1; 5.
Câu 5: Cho
2
4
m
a
. Kết quả của
6
2 5
m
a
là:
A.
123
. B.
133
. C. 123 D.
128
.
Câu 6: Cho tam giác DEF có
= .E F
Tia phân giác của góc D cắt EF tại I . Ta có:
A.
DIE DIF
. B.
DE DF, IDE IDF
.
C.
; IE IF DI EF
D Cả A, B,C đều đúng
Câu 7: Biết
9a b
. Kết quả của phép tính
0, ( ) 0, ( )a b b a
là:
A. 2. B. 1. C. 0,5. D. 1,5 .
Câu 8: Cho
2
6 . 36
a b a b
. Giá trị lớn nhất của
.x a b
là:
A. 6 B.
6
C. 7. D. 5.
Câu 9: Cho tam giác ABC, hai đường trung tuyến BM, CN. Biết
AC AB
. Khi đó độ dài
hai đoạn thẳng BM và CN là:
A.
BM CN
B.
BM CN
C.
BM CN
D.
BM CN
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
38
Trang 38
Câu 10: Điểm thuộc đồ thị hàm số
2y x
là :
A.
1; 2
M
. B.
1;2
N
. C.
0 ; 2
P
. D.
1; 2
Q
Câu 11: Biết rằng lãi suất hàng năm của tiền gửi tiết kiệm theo mức 5% năm là một hàm số
theo số tiền gửi:
0, 005i p
. Nếu tiền gửi là 175000 thì tiền lãi sẽ là:
A. 8850 đ B. 8750 đ C. 7850 đ D.7750 đ
Câu 12: Cho tam giác ABC cân tại A
20A
. Trên cạnh AB lấy điểm D sao cho
AD BC
.
Số đo của góc BDC là:
A.
50
B.
70
C.
30
D.
80
II. Phần tự luận (14 điểm)
Câu 1.(3 điểm)
a, Chứng tỏ rằng:
2017 2016 2
75. 4 4 ... 4 4 1 25
M chia hết cho
2
10
b, Cho tích
.a b
là số chính phương và
, 1
a b
. Chứng minh rằng a và b đều là số chính
phương.
Câu 2.(4 điểm)
2.1 Cho đa thức
2 .( 3) ( 7) 5( 403)A x x x x x
Tính giá trị của A khi
4x
. Tìm x để
2015A
2.2 Học sinh khối 7 của một trường gồm 3 lớp tham gia trồng cây. Lớp 7A trồng toàn bộ
32,5%
số cây. Biết số cây lớp 7B và 7C trồng được theo tỉ lệ 1,5 và 1,2. Hỏi số cây cả 3 lớp
trồng được là bao nhiêu, biết số cây của lớp 7A trồng được ít hơn số cây của lớp 7B trồng
được là 120 cây.
Câu 3.(5 điểm)
1. Cho đoạn thẳng AB. Trên cùng một nửa mặt phẳng có bờ là đường thẳng AB vẽ hai tia
Ax và By lần lượt vuông góc với AB tại A và B. Gọi O là trung điểm của đoạn thẳng AB. Trên
tia Ax lấy điểm C và trên tia By lấy điểm D sao cho
90COD
.
a) Chứng minh rằng:
.AC BD CD
b) Chứng minh rằng:
2
.
4
AB
AC BD
2. Cho tam giác nhọn ABC, trực tâm H. Chứng minh rằng:
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
39
Trang 39
2
( )
3
AB AC BHA HB H
C
C
Câu 4.(2 điểm)
Tìm giá trị nhỏ nhất của A, biết :
7 5 2 3 2000
A x y z x xy yz zx
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
40
Trang 40
HƯỚNG DẪN CHẤM
I. Phần trắc nghiệm khách quan: (6 điểm)
Câu 1 2 3 4 5 6 7 8 9 10 11 12
Đ. án A C C A B D B A C D B C
II. Phần tự luận (14 điểm)
Câu Nội dung chính Điểm
1(4
điểm)
2017 2016 2
M 75. 4 4 4 4 1 25
2017 2016 2
25.(4 1) 4 4 4 4 1 25
2017 2016 2 2017 2016 2
25 4 4 4 4 4 1 4 4 4 4 1 25
2018 2017 2 2017 2016 2
25. 4 4 4 4 25 4 4 4 4 1 25
2018
25.4 25 25
2018 2017 2017
25.4 25.4.4 100.4 100
Vậy
2
M 10
b, Đặt
2
. a b c
(1)
Gọi
,
a c d
nên
a d, c d
Hay
.a m d
và
.c n d
với
, 1
m n
Thay vào (1) ta được
2 2
. . .m d b n d
2 2
.m b n d b n
vì
, 1 ,a b b d
Và
2 2
n b b n
Thay vào (1) ta có
2
a d
đpcm
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,5
0,5
2(4
điểm)
1. Ta có
2 2
2 6 7 5 2015A x x x x x
2
4 2015x x
a, Với
4x
ta được
2015A
1
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
41
Trang 41
b,
2
0
2015 4 0 ( 4) 0
4
x
A x x x x
x
2. Gọi số cây ba lớp trồng lần lượt là a, b, c ( cây, a,b,c
N*)
Theo đề bài ta có
: 1,5 : 1,2b c
và
– 120b a
32,5%
a a b c
Vậy cả 3 lớp trồng được số cây là 2400 cây
1
1
1
3(5
điểm)
A, Vẽ tia CO cắt tia đối của tia By tại điểm E.
Chứng minh
;
AOC BOE g c g AC BE CO EO
Chứng minh
DOC DOE c g c CD ED
Mà
ED EB BD AC BD
.
Từ đó :
CD AC BD
(đpcm)
b, Áp dụng định lí Pytago vào các tam giác vuông BOE và BOD ta có:
2 2 2
2 2 2 2 2
2 2 2
2
OE OB EB
OE OD OB EB DB
OD OB DB
0,25
0,25
0,25
0,25
0,25
0,5
y
x
D
E
O
A
B
C
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
42
Trang 42
Mà
2 2 2
;OE OD DE
Nên
2 2 2 2
2DE OB EB DB
2
2 . .( )OB EB DE BD DB DE BE
2
2 . . . .OB EB DE EB BD DB DE DB BE
2
2 . . 2 .OB EB DE DB DE BD BE
2 2 2
2 . 2 . 2 2 .OB DE EB DB BD BE OB DE BD BE
Suy ra
2 2
2 2 . 0 .OB BD BE BD BE OB
Mà ;
2
AB
BE AC OB .
Vậy
2
2
.
2 4
AB AB
AC BD
(đpcm)
2.
Qua H kẻ đường thẳng song song với AB cắt AC tại D, kẻ đường thẳng
song song với AC cắt AB tại E
Ta có
AHD HAE
(g –c-g)
;AD HE AE HD
AHD
có
HA HD AD
nên
HA AE AD
(1)
Từ đó
HBE
vuông nên
HB BE
(2)
Tương tự ta có
HC DC
(3)
Từ 1,2,3 ta có
HA HB HC AB AC
(4)
Tương tự
HA HB HC AB BC
(5)
HA HB HC BC AC
(6)
Từ đó suy ra
2
3
HA AB AC
C
H CB H B đpcm
0,25
0,25
0,25
0,25
0,25
0,25
0,25
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
43
Trang 43
4
(2
điểm)
Ta có
7 5 0
x y
;
2 3 0
z x
và
2000 0
xy yz zx
Nên
7 5 2 3 2000 0
A x y z x xy yz zx
Mà A = 0 khi và chỉ khi
7 5 2 3 2000 0
x y z x xy yz zx
Có: 7 5 0 7 5
5 7
x y
x y x y
2 3 0
2 3
x z
z x
2000 0 2000
xy yz zx xy yz zx
Từ đó tìm được
20; 28; 30
20; 28; 30
x y z
x y z
A 0
, mà
0 ( , , ) (20;28;30)A x y z
hoặc
( , , ) ( 20; 28; 30)x y z
Vậy min
0 ( , , ) (20;28;30)A x y z
hoặc
( , , ) ( 20; 28; 30)x y z
1
1
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
44
Trang 44
ĐỀ SỐ 10. ĐỀ HSG CẤP HUYỆN
Bài 1: Thực hiện phép tính (6 điểm).
a)
3 2 5 9
: .
4 3 9 4
; b)
1
1
1
45 1 1 1
19 2 3 4
; c)
15 9 20 9
10 19 29 6
5.4 .9 4.3 .8
5.2 .6 7.2 .27
.
Bài 2: (6 điểm)
a) Tìm x, biết:
2 1 – 3 2 2 – 4 2 3 16
x x x
;
b) Tìm x, biết:
1 21
3 : 2 1
2 22
x
c) Tìm x, y, z biết:
2 3 2
5 15
x y y z
và
2 .x z y
Bài 3: (1,5 điểm) Cho tỉ lệ thức
a c
b d
.
Chứng minh rằng :
2 2 .a c b d a c b d
Bài 4: (4,5 điểm) Cho tam giác ABC vuông tại A; K là trung điểm của BC. Trên tia đối của
tia KA lấy D , sao cho
.KD KA
a. Chứng minh:
// .CD AB
b. Gọi H là trung điểm của AC; BH cắt AD tại M; DH cắt BC tại N .
Chứng minh rằng:
ABH CDH
c. Chứng minh:
HMN
cân.
Bài 5: (2 điểm): Chứng minh rằng số có dạng
abcabc
luôn chia hết cho 11.
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
45
Trang 45
HƯỚNG DẪN CHẤM
Bài 1: Thực hiện phép tính (6 điểm).
Giải:
a)
3 2 5 9
: .
4 3 9 4
3 2 5 9 3 1 9
: :
4 3 9 4 4 9 4
0,75đ
=
3 9 9 36
. 9
4 1 4 4
0,75đ
b)
1
1
1
4
1
3
1
2
1
19
45
1
1
1
45 1 1 1 45 1
19 2 3 4 19 1 1
2 1
4
3
1,0đ
=
45 26 19
1
19 19 19
1,0đ
c)
15 9 20 9
10 19 29 6
5.4 .9 4.3 .8
5.2 .6 7.2 .27
15 9 20 9
10 19 29 6
5.4 .9 4.3 .8
5.2 .6 7.2 .27
=
2.15 2.9 2 20 3.9
10 19 19 29 3.6
5.2 .3 2 .3 .2
5.2 .2 .3 7.2 .3
01đ
29 18 2
29 18
2 .3 5.2 3
2 .3 5.3 7
01đ
=
10 9 1
15 7 8
0,5đ
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
46
Trang 46
Bài 2: (6 điểm)
Giải:
a. Tìm x, biết:
2(x-1)-3(2 x+2)-4(2 x+3)=16
2 2 6 6 8 12 16x x x
0,25đ
12 – 20 16x
0,25đ
12 36x
0,50đ
3x
0,50đ
b. Tìm x, biết:
1 21
3 : 2 1
2 22
x
Nếu
1
2
x
. Ta có: (vì nếu
1
2
x
thì
)
0,25đ
1 21
3 : 2 1
2 22
x
7 21
: (2 1)
2 22
x
0,25đ
7 21 7 22 11
2x 1 :
2 22 2 21 3
0,25đ
11 14
2x 1
3 3
0,25đ
14 7 1
x : 2
3 3 2
(thỏa mãn)
0,25đ
Nếu
1
2
x
. Ta có:
0,25đ
1 21
3 : 2 1
2 22
x
7 21
: (1 2 )
2 22
x
0,25đ
11 8
2 1
3 3
x
0,25đ
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
47
Trang 47
8 4 1
x : ( 2)
3 3 2
0,25đ
Vậy
7
3
x
hoặc
4
3
x
0,25đ
c. Tìm x, y, z biết :
2 3 2
5 15
x y y z
và
2x z y
Từ
2x z y
ta có:
– 2 0x y z
hay
2 – 4 2 0x y z
hay
2 – – 3 2 0x y y z
0,25đ
hay
2 – 3 – 2x y y z
0,25đ
Vậy nếu:
2 3 2
5 15
x y y z
thì:
2 – 3 – 2 0x y y z
(vì
5 15
).
0,25đ
Từ
2 – 0x y
suy ra:
1
2
x
y
0,25đ
Từ
3 – 2 0y z
và
2 2 0x z y x z y z
hay
1
2
– 0
yy z
0,25đ
hay
3
2
0
y z
hay
2
3
y z
suy ra:
1
3
x z
0,25đ
Vậy các giá trị x, y, z cần tìm là:
1 2
; ;
3 3
x z y z z
hoặc
1 3
; ;
2 2
x y y z y
hoặc
{ ; 2 ; 3 } |x y x z x
0,5đ
Bài 3: (1,5 điểm) Cho tỉ lệ thức
a c
b d
.
Chứng minh rằng :
2 2a c b d a c b d
Ta có:
2 2a c b d a c b d
2 2 2 2ab ad cb cd ab ad cb cd
0,75đ
cb ad
suy ra:
a c
b d
0,75đ
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
48
Trang 48
Bài 4: (4,5 điểm) Cho tam giác ABC vuông tại A; K là trung điểm của BC. Trên tia đối của
tia KA lấy D , sao cho
.KD KA
a. Chứng minh:
// .CD AB
b. Gọi H là trung điểm của AC; BH cắt AD tại M; DH cắt BC tại N .
Chứng minh rằng:
ABH CDH
c. Chứng minh:
HMN
cân.
Giải:
a/ Chứng minh CD song song với AB.
Xét 2 tam giác
ABK
và
DCK
có:
0,25đ
BK CK
(gt)
BKA CKD
(đối đỉnh)
0,25đ
AK DK
(gt) 0,25đ
ABK DCK
(c-g-c) 0,25đ
DCK DBK
; mà
90ABC ACB
90ACD ACB BCD
0,25đ
90ACD BAC
//AB CD
(
và
).
0,25đ
b. Chứng minh rằng:
ABH CDH
Xét 2 tam giác vuông:
ABH
và
CDH
có:
0,25đ
BA CD
(do
ABK DCK
)
AH CH
(gt) 0,25đ
N
M
H
D
K
A
C
B
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
49
Trang 49
ABH CDH
(c-g-c) 0,50đ
c. Chứng minh:
HMN
cân.
Xét 2 tam giác vuông:
ABC
và
CDA
có:
0,25đ
;
90ACD BAC
; AC cạnh chung:
ABC CDA
(c-g-c)
ACB CAD
0,25đ
mà:
AH CH
(gt) và
MHA NHC
(vì
ABH CDH
)
0,50đ
AMH CNH
(g-c-g) 0,50đ
MH NH
. Vậy
HMN
cân tại H 0,50đ
Bài 5: (2 điểm): Chứng minh rằng số có dạng
abcabc
luôn chia hết cho 11.
Giải:
Ta có:
5 4 3 2
.10 .10 .10 .10 .10abcabc a b c a b c
0,25đ
2 3 3 3
.10 10 1 .10 10 1 . 10 1
a b c
0,50đ
3 2
10 1 a.10 b.10 c
0,50đ
2 2
(1000 1) a 10 b.10 c 1001 a.10 b.10 c
0,25đ
2
11.91 a.10 b.10 c 11
0,25đ
Vậy
11abcabc
0,25đ
Hết
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
50
Trang 50
ĐỀ SỐ 11. ĐỀ HSG CẤP HUYỆN
Câu 1 (2,5 điểm).
Tính:
a)
7,3.10,5+7,3.15+2,7.10,5+15.2,7
b)
9 10 10 19 3 9 4
6 2 12 : 2 27 15.4 .9
Câu 2 (5 điểm).
So sánh A và B trong mỗi trường hợp sau:
a)
2012
4025
A
;
1999
3997
B
b)
21
A 3
;
31
B 2
c)
2011 2011 2011 2011
.....
1.2 3.4 5.6 1999.2000
A ;
2012 2012 2012 2012
.....
1001 1002 1003 2000
B
Câu 3 (5 điểm).
a) Chứng minh rằng:
1 2 3 100
3 3 3 3
x x x x
chia hết cho 120 (với x
N)
b) Cho
3 2 2 4 4 3
4 3 2
x y z x y z
. Chứng minh rằng:
2 3 4
x y z
c) Cho f(x) là hàm số xác định với mọi x thỏa mãn điều kiện
1 2 1 2
. .
f x x f x f x
và
2 10
f
. Tính
32 .
f
Câu 4 (5 điểm). Cho tam giác ABC có
AB AC
. Trên tia đối của tia CA lấy điểm D sao
cho
. Gọi I là giao điểm các đường trung trực của BC và AD.
a) Chứng minh
AIB DIC
b) Chứng minh AI là tia phân giác của góc BAC.
c) Kẻ IE vuông góc với AB, chứng minh
1
AE AD
2
.
Câu 5 (2,5 điểm). Cho 100 số hữu tỉ trong đó tích của bất kì ba số nào cũng là một số âm.
Chứng minh rằng tất cả 100 số đó đều là số âm.
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
51
Trang 51
HƯỚNG DẪN CHẤM
CÂU
ý
ĐÁP ÁN
ĐIỂM
Câu
1
(2,5đ
)
a
1,5đ
7,3.10,5+7,3.15+2,7.10,5+15.2,7
10,5 (7, 3 2, 7) 15.(7, 3 2,7)
=10,5.10+15.10
=105+150=255
0,5
0,5
0,5
b
1đ
10 10 19 3 9 4
69.2 12 : 2 27 15.4.
.9
9 9 10 20 10 19 9 18 8
3 2 2 2 3 : 2 3 3.5 2 3
19 9 18 9
2 3 (1 2.3) : 2 3 (2 5)
=(2.7) : 7=2
0,5
0,25
0,25
Câu
2
(5đ)
a
2đ
2012 2012 1 1 1999 1999 2012 1999
;
4025 4024 2 2 3998 3997 4025 3997
2012 1999
4025 3997
. Vậy
A B
1,5
0,5
b
1,5đ
10
21 2 10
3 3. 3 3.9
A
10
31 3 10
2 2. 2 2.8
B
Suy ra
A B
0,5
0,5
0,5
c
1,5đ
2011 2011 2011 2011
.....
1.2 3.4 5.6 1999.2000
A
1 1 1 1 1 1 1
2011. 1 ....
2 3 4 5 6 1999 2000
1 1 1 1 1 1 1
2011. 1 .... ....
3 5 1999 2 4 6 2000
1 1 1 1 1 1 1 1 1 1 1
2011. 1 .... 2. ....
2 3 4 5 6 1999 2000 2 4 6 2000
0,25
0,25
0,25
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
52
Trang 52
1 1 1 1 1 1 1 1 1
2011. 1 .... 1 ....
2 3 4 1999 2000 2 3 999 1000
1 1 1 1 1
2011. ....
1001 1002 1003 1999 2000
1 1 1 1
2012. .....
1001 1002 1003 2000
B
Suy ra
A B
0,25
0,25
0,25
Câu
3
(5đ)
a
2,5đ
1 2 3 100
3 3 3 3
x x x x
1 2 3 4 5 6 7 8
3 3 3 3 3 3 3 3
x x x x x x x x
97 98 99 100
3 3 3 3
x x x x
2 3 4 4 2 3 4 96 2 3 4
3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
x x x
4 96
3 .120 3 .12 .0 3 120
x x x
4 96
120 3 3 3 120
x x x
(đpcm)
0,75
0,75
0,5
0,5
b
1,5đ
3 2 2 4 4 3
4 3 2
x y z x y z
. Suy ra:
4(3 2 ) 3(2 4 ) 2(4 3 )
12 8 6 12 8 6
0
16 9 4 29
x y z x y z
x y z x y z
Vậy
3 2
0 3 2 (1)
4 2 3
x y x y
x y
2 4
0 2 4 (2)
3 2 4
z x x z
z x
Từ (1) và (2) ta được
2 3 4
x y z
0,75
0,25
0,25
0,25
c
1đ
Vì
1 2 1 2
. .
f x x f x f x
nên
4 2.2 2 . 2 10. 10 100
f f f f
(16) (4.4) (4) . (4) 100.100 10000f f f f
(32) (16.2) (16). (2) 10000.10 100000f f f f
0,5
0,25
0,25
Hình vẽ 0,5
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
53
Trang 53
Câu
4
(5đ)
a
1,5đ
Vì I là giao điểm các đường trung trực của BC và AD
nên
,IB IC
IA ID
Lại có
AB CD
(gt)
Do đó
AIB DIC
(c.c.c)
0,25
0,5
0,25
0,5
b
1,5đ
AID
cân ở I, suy ra
DAI D
AIB DIC
(câu a), suy ra
BAI D
Do đó
.DAI BAI
Vậy AI là tia phân giác của góc BAC
0,5
0,250
,5
0,25
c
1,5đ
Kẻ
IP AD
, ta có
AIE AIP
( cạnh huyền-góc nhọn)
AE AP
Mà
2
AD
AP (vì P là trung điểm AD)
Suy ra
1
AE AD
2
0,5
0,25
0,5
0,25
Câu
5
a
1đ
Trong 100 số đã cho, phải có ít nhất một số âm (vì nếu cả 100 số đều
dương thì tích của ba số bất kì không thể là một số âm).
Ta tách riêng số âm đó ra. Chia 99 số còn lại thành 33 nhóm, mỗi nhóm
3 thừa số.
Theo đề bài, mỗi nhóm đều có tích là một số âm nên tích của 33 nhóm
0,25
0,25
0,25
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
54
Trang 54
(2,5đ
)
tức là của 99 số là một số âm.
Nhân số âm này với số âm đã tách riêng từ đầu ta được tích của 100 số
là một số dương
0,25
b
1,5đ
Sắp xếp 100 số đã cho theo thứ tự tăng dần, chẳng hạn
1 2 3 100
a a a a
Các
số này đều khác 0 (vì nếu có 1 thừa số bằng 0 thì tích của nó với
hai thừa số khác cũng bằng 0, trái với đề bài).
Xét tích
98 99 100
. . 0a a a
98
0a
(vì nếu
98
0 a
thì
99
0a
,
100
0a
,
tích của ba số này không thể là một số âm).
Vậy
1 2 3 98
, , , ..., a a a a
là các số âm.
Xét tích
1 2 99
. . 0a a a
mà
1 2
0a a
nên
99
0a
Xét tích
1 2 100
. . 0a a a
mà
1 2
0a a
nên
100
0a
Vậy tất cả 100 số đã cho đều là số âm.
0,25
0,25
0,25
0,25
0,25
0,25
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
55
Trang 55
ĐỀ SỐ 12. ĐỀ HSG CẤP HUYỆN
Bài 1 (5 điểm)
a) Thực hiện phép tính:
12 5 6 2 10 3 5 2
6 3
9 3
2 4 5
2 .3 4 .9 5 .7 25 .49
125.7 5 .14
2 .3 8 .3
A
b) Tính giá trị biểu thức:
1.2.3 2.3.4 3.4.5 4.5.6 17.18.19B
c) Tìm một số tự nhiên có 3 chữ số, biết rằng nếu tăng chữ số hàng trăm thêm
n
đơn vị
đồng thời giảm chữ số hàng chục và giảm chữ số hàng đơn vị đi
n
đơn vị thì được một
số có 3 chữ số gấp
n
lần số có 3 chữ số ban đầu.
Bài 2 (3 điểm)
a) Tìm các số x, y, z biết rằng:
3 4 , 5 6x y y z
và
30xyz
.
b) Tìm x biết:
1 3 3
1,6
2 4 5
x
Bài 3 (3 điểm)
1) Cho hàm số
– 1y f x m x
a) Tìm m biết:
2 – –1 7
f f
b) Cho
5m
. Tìm x biết
3 – 2 20
f x
2) Cho các đơn thức
2 2
1
A x yz
2
,
2 2
3
4
B xy z
,
3
C x y
Chứng minh rằng các đơn thức A, B, C không thể cùng nhận giá trị âm.
Bài 4 (7 điểm). Cho
ABC
nhọn có góc
60A
. Phân giác
ABC
cắt AC tại D, phân giác
ACB
cắt AB tại E. BD cắt CE tại I.
a) Tính số đo góc BIC.
b) Trên cạnh BC lấy điểm F sao cho
. Chứng minh
.CID CIF
c) Trên tia IF lấy điểm M sao cho
IM IB IC
. Chứng minh
BCM
là tam giác đều.
Bài 5 (2 điểm)
Tìm số tự nhiên n thỏa mãn điều kiện:
2 3 4 n n 11
2.2 3.2 4.2 n 2 2
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
56
Trang 56
HƯỚNG DẪN CHẤM
BÀI
Ý NỘI DUNG ĐIỂM
1
(5đ)
a
12 5 6 2 10 3 5 2 12 5 12 4 10 3 10 4
6 3 12 6 12 5 9 3 9 3 3
9 3
2 4 5
2 .3 4 .9 5 .7 25 .49 2 .3 2 .3 5 .7 5 .7
2 .3 2 .3 5 .7 5 .2 .7
125.7 5 .14
2 .3 8 .3
A
0.5
12 4 10 3
12 5
9 3 3
2 .3 3 1 5 .7 1 7
2 .3 3 1
5 .7 1 2
A
0.5
2 5.( 6)
3.4 9
A
0.5
1 10 7
6 3 2
A
0.5
b
4 1.2.3.4 2.3.4. 5 – 1 3.4.5. 6 – 2 17.18.19. 20 – 16
B
0.5
4 1.2.3.4 2.3.4.5 – 1.2.3.4 3.4.5.6 – 2.3.4.5 17.18.19.20 – 16.17.18.19B
0.5
4 17.18.19.20B
0.5
17.18.19.5 29070B
0.5
c
Gọi số có 3 chữ số cầìm tìm là
abc
(a, b, c là STN có 1 chữ số,
0a
)
Theo bài ra ta có:
( )( )( ) .a n b n c n n abc
0.25
100 10 – – 100 10
a n b n c n n a b c
100 100 10 – 10 – 100 10a n b n c n an bn cn
100 1 10 – 1 – 1 89n a n b n c n
1 100 10 89n a b c n
0.25
89 – 1 n n
mà
89; – 1 1
n
nên
– 1n n
0.25
Tìm được
2n
Số có 3 chữ số cần tìm là 178
0.25
2
(3đ)
a
;
4 3 6 5 8 6 5
x y y z x y z
k
0.25
8 , 6 , 5x k y k z k
0.25
3
1
30 8 .6 .5 30 240 30
2
xyz k k k k k
0.5
5
4, 3,
2
x y z
0.5
b
1 3 3 1 3 8 3
1,6
2 4 5 2 4 5 5
x x
0.25
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
57
Trang 57
1 3
1
2 4
x
0.25
1 1
2 4
x
0.5
3
;
4
x
1
4
x
0.5
3
(3đ)
1.a
Vì
(2) ( 1) 7 ( 2) 2 ( 1) ( 1) 7f f m m
0.25
2m 4 m 1 7
0.25
3 5 7 4m m
0.5
1.b
Với
5m
ta có hàm số
4y f x x
0.25
Vì
(3 2 ) 20 4(3 2 ) 20f x x
0.25
12 8x 20 x 1
0.5
2
Giả sử cả 3 đơn thức A, B, C cùng có giá trị âm
. .A B C
có giá trị âm (1)
0.25
Mặt khác:
6 4 4
3
.B.
8
A C x y z
0.25
Vì
6 4 4
0
3
8
x y z
,x y
. .A B C
0
;x y
(2) 0.25
Ta thấy (1) mâu thuẫn với (2)
điều giả sử sai.
Vậy ba đơn thức A, B, C không thể cùng có giá trị âm.
0.25
4
(7đ)
Vẽ hình đúng, ghi đúng giả thiết, kết luận
0.5
4
3
2
12
1
N
M
C
F
E
D
I
B
A
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
58
Trang 58
a
BD là phân giác của góc ABC nên
1 2
2
ABC
B B
CE là phân giác của góc ACB nên
1 2
2
ACB
C C
0.5
Mà tam giác ABC có
0
180A B C
suy ra
60 180ABC ACB
0.5
2 1
ABC ACB 120 B C 60
0.5
120BIC
0.5
b
BIE BIF
(cgc)
BIE BIF
0.5
BIC 120 BIE 60 BIE BIF 60
0.5
Mà
BIE BIF CIF 180 CIF 60
0.5
0
CID BIE 60
(đ.đ)
CIF CID 60
0.5
CID CIF
(gcg) 0.5
c
Trên đoạn IM lấy điểm N sao cho
IB IN
NM IC
0.5
BIN
đều
BN BI
và
120BNM
0.5
BNM BIC
(cgc) 0.5
BM BC
và
2 4
B B
BCM
đều
0.5
5
(2đ)
Đặt
2 3 4 n
S 2.2 3.2 4.2 n.2
3 4 5 n 1 2 3 4 n
S 2S S 2.2 3.2 4.2 n 2 2.2 3.2 4.2 n.2
0.5
1 3 3 4 1
2 2 2 2 2 2
n n n
S n
0.5
Đặt
3 4 n 1 n
T 2 2 2 2
. Tính được
n 1 3
T 2T T 2 2
0.5
n 1 3 n 1 3 n 1
S n.2 2 2 2 (n 1).2
n 1 n 11 10 10
(n 1) 2 2 n 1 2 n 2 1 1025
0.5
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
59
Trang 59
ĐỀ SỐ 13. ĐỀ HSG CẤP HUYỆN
Câu 1. (1,5 điểm)
a)
2 2 1 1
0, 4 0,25
2014
9 11 3 5
:
7 7 1 2015
1,4 1 0, 875 0, 7
9 11 6
M
b) Tìm x, biết:
2 2
1 2
x x x
.
Câu 2. (2,5 điểm)
a) Cho a, b, c là ba số thực khác 0, thoả mãn điều kiện:
a b c b c a c a b
c a b
.
Hãy tính giá trị của biểu thức
1 1 1
b a c
B
a c b
.
b) Ba lớp 7A, 7B, 7C cùng mua một số gói tăm từ thiện, lúc đầu số gói tăm dự định chia
cho ba lớp tỉ lệ với
5 : 6 : 7
nhưng sau đó chia theo tỉ lệ
4 : 5 : 6
nên có một lớp nhận nhiều
hơn dự định 4 gói. Tính tổng số gói tăm mà ba lớp đã mua.
Câu 3. (2,0 điểm)
a) Tìm giá trị nhỏ nhất của biểu thức
A 2 2 2 2013
x x
với x là số nguyên.
b) Tìm nghiệm nguyên dương của phương trình
x y z xyz
.
Câu 4. (3,0 điểm) Cho
xAy 60
có tia phân giác
Az
. Từ điểm B trên
Ax
kẻ
BH
vuông
góc với
Ay
tại H, kẻ
BK
vuông góc với
Az
và
Bt
song song với
Ay
,
Bt
cắt
Az
tại C. Từ
C kẻ
CM
vuông góc với
Ay
tại M . Chứng minh :
a ) K là trung điểm của AC.
b )
KMC
là tam giác đều.
c) Cho BK = 2cm. Tính các cạnh
AKM
Câu 5. (1,0 điểm). Cho ba số dương
0 1a b c
chứng minh rằng:
2
1 1 1
a b c
bc ac ab
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
60
Trang 60
HƯỚNG DẪN CHẤM
Câu
Nội dung
Điểm
Câu 1
(1,5 điểm)
1) Ta có:
2 2 1 1
0, 4 0,25
2014
9 11 3 5
:
7 7 1 2015
1,4 1 0, 875 0, 7
9 11 6
M
2 2 2 1 1 1
2014
5 9 11 3 4 5
:
7 7 7 7 7 7 2015
5 9 11 6 8 10
1 1 1 1 1 1
2
5 9 11 3 4 5
2014
:
2015
1 1 1 7 1 1 1
7
5 9 11 2 3 4 5
2 2 2014
: 0
7 7 2015
0.25đ
0.25đ
0.25đ
2) vì
2
| 1 | 0x x
nên (1)
2 2
| 1 | 2x x x
hay
- 1 2
x
+)
3x
+)
0.25đ
0.25đ
0.25đ
Câu 2
(2,5 điểm)
1)
+Nếu
a b c 0
Theo tính chất dãy tỉ số bằng nhau ,ta có:
1
a b c b c a c a b a b c b c a c a b
c a b a b c
mà
1 1 1 2
a b c b c a c a b
c a b
2
a b b c c a
c a b
Vậy
B 1 1 1 8
b a c b a c a b c
a c b a c b
0.25đ
0.25đ
0.25đ
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
61
Trang 61
+Nếu
0a b c
Theo tính chất dãy tỉ số bằng nhau ,ta có:
0
a b c b c a c a b a b c b c a c a b
c a b a b c
mà
1 1 1 1
a b c b c a c a b
c a b
1
a b b c c a
c a b
Vậy
B 1 1 1 1
b a c b a c a b c
a c b a c b
0.25đ
0.25đ
0.25đ
2) Gọi tổng số gói tăm 3 lớp cùng mua là x ( x là số tự nhiên khác 0)
Số gói tăm dự định chia chia cho 3 lớp 7A, 7B, 7C lúc đầu lần lượt là:
a, b, c
Ta có:
5 6 7
; ;
5 6 7 18 18 18 18 3 18
a b c a b c x x x x x
a b c
(1)
Số gói tăm sau đó chia cho 3 lớp lần lượt là a’, b’, c’, ta có:
' ' ' ' ' 4 5 6
; ;
4 5 6 15 15 15 15 3
'
'
1
'
5
'
a b c a b c x x x x x
a b c
(2)
So sánh (1) và (2) ta có:
a a ;b b ; c c
nên lớp 7C nhận nhiều
hơn lúc đầu.
Vây:
'– 4c c
hay
6 7
4 4 360
15 18 90
x x x
x
Vậy số gói tăm 3 lớp đã mua là 360 gói.
0,25đ
0,25đ
0,25đ
0,25đ
Câu 3
(2,0 điểm)
1) Ta có:
2 2 2 2013 | 2 2 | | 2013 2 |A x x x x
2 2 2013 2 2015
x x
Dấu “=” xảy ra khi
2013
(2 2)(2013 2 ) 0 1
2
x x x
Vậy
2015Min A
khi
2013
1
2
x ,
x
0,25đ
0,25đ
0,25đ
0,25đ
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
62
Trang 62
2) Vì x,y,z nguyên dương nên ta giả sử
1 x y z
Theo bài ra
2 2 2 2
1 1 1 1 1 1 3
1
yz yx zx
x x x x
2
3 1x x
Thay vào đầu bài ta có
1 1 0y z yz y yz z
(1 ) (1 ) 2 0y z z
(y 1)(z 1) 2
TH1:
1 1 2y y
và
z 1 2 z 3
TH2:
1 2 3y y
và
1 1 2z z
Vậy có hai cặp nghiệp nguyên thỏa mãn
(1,2,3);(1,3,2)
0,25đ
0,25đ
0,25đ
0,25đ
Câu 4
(3,0 điểm)
Vẽ hình , GT _ KL
a,
ABC
cân tại B do
CAB ACB
MAC
và BK là đường cao
BK là đường trung tuyến
K là trung điểm của AC
0,25đ
0,5đ
0,25đ
b,
ABH BAK
( cạnh huyền + góc nhọn )
BH AK
( hai cạnh t. ý ) mà
1
AK AC
2
1
BH AC
2
Ta có :
BH CM
( t/c cặp đoạn chắn )
mà
1
CK BH AC CM CK
2
MKC
là tam giác cân ( 1 )
0,25đ
0,25đ
0,25đ
y
z
x
M
C
K
H
A
B
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
63
Trang 63
Mặt khác
90MCB
và
30ACB
60MCK
(2)
Từ (1) và (2)
MKC
là tam giác đều
0,25đ
c) Vì
ABK
vuông tại K mà
KAB 30
AB 2BK 2.2 4 cm
Vì
ABK
vuông tại K nên theo Pitago ta có:
2 2
AK 16 4 12AB BK
Mà
1
KC AC KC AK 12
2
KCM
đều
KC KM 12
Theo phần b)
AB BC 4
AH BK 2
HM BC
(
HBCM
là hình chữ nhật)
AM AH HM 6
0,25đ
0,25đ
0,25đ
0,25đ
Câu 5
(1 điểm)
Vì
0 1a b c
nên:
1 1
( 1)( 1) 0 1
1 1
c c
a b ab a b
ab a b ab a b
(1)
Tương tự:
1
a a
bc b c
(2) ;
1
b b
ac a c
(3)
Do đó:
1 1 1
a b c a b c
bc ac ab b c a c a b
(4)
Mà
2( )
2 2 2
2
a b c
a b c a b c
b c a c a b a b c a b c a b c a b c
(5)
Từ (4) và (5) suy ra:
2
1 1 1
a b c
bc ac ab
(đpcm)
0,25đ
0,25đ
0,25đ
0,25đ
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
64
Trang 64
ĐỀ SỐ 14. ĐỀ HSG CẤP HUYỆN
Câu 1: (4,0 điểm)
1. Thực hiện phép tính:
7 3 3
7
7 2
2 9 3
.5 :
5 4 16
.
2 .5 512
A
2. Cho
16 25 9
9 16 25
x y z
và
3
2 1 15x
. Tính
.B x y z
Câu 2: (4,0 điểm)
1. Tìm x, y biết:
3
10
x x y và
3
50
y x y .
2. Tìm x biết:
1
3 0.
2
x x
Câu 3: (5,0 điểm)
1. Tìm số tự nhiên n để phân số
7 8
2 3
n
n
có giá trị lớn nhất.
2. Cho đa thức p(x) = ax
3
+ bx
2
+ cx + d với a, b, c, d là các hệ số nguyên. Biết rằng,
5
p x
với mọi x nguyên. Chứng minh rằng a, b, c, d đều chia hết cho 5.
3. Gọi a, b,c là độ dài các cạnh của một tam giác. Chứng minh rằng:
The linked image cannot be display ed. The file may have been moved, renamed, or d eleted. Verify that the link points to the correct file and location.
Câu 4: (5,0 điểm). Cho tam giác ABC cân tại A. Trên cạnh BC lấy điểm D (D khác B, C).
Trên tia đối của tia CB, lấy điểm E sao cho CE = BD. Đường vuông góc với BC kẻ từ D cắt
AB tại M. Đường vuông góc với BC kẻ từ E cắt đường thẳng AC tại N, MN cắt BC tại I.
1. Chứng minh DM = EN.
2. Chứng minh IM = IN, BC < MN.
3. Gọi O là giao của đường phân giác góc A và đường thẳng vuông góc với MN tại I.
Chứng minh rằng
BMO CNO
. Từ đó suy ra điểm O cố định.
Câu 5: (2,0 đ) Cho các số thực dương a và b thỏa mãn
100 100 101 101 102 102
a b a b a b
Hãy tính giá trị của biểu thức:
2014 2015
.P a b
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
65
Trang 65
HƯỚNG DẪN CHẤM
Câu
Nội dung
Điểm
1
(4,0đ)
1.
7 3 3 7 3
7
6 3
7 3
7 2 7 2 7 2 7 2 7 2
7 2 2
2 9 3 2 9 3
.5 : .5 :
2 2 3
5 4 16 5 4 16
2 12 1
.
2
2 .5 512 2 .5 2 .2 2 .5 2 .2
2 5 2
A
2,0
2. Ta có:
3 3 3 3 3
2 1 15 2 16 8 2 2.x x x x x
Suy ra:
18 25 9
9 16 25
y z
Do đó, ta có:
18 25
25 32 57.
9 16
y
y y
18 9
9 50 41.
9 25
z
z z
Vậy
2 57 41 100.B x y z
0,5
0,25
0,5
0,5
0,25
2
(4,0đ)
1. Trừ từng vế hai đẳng thức đã cho ta được:
2
2
3 3 9 3
10 50 25 5
x x y y x y x y x y x y
Suy ra:
3
.
5
x y
Thay
3
5
x y
vào hai đẳng thức đã cho ta được
1 1
; .
2 10
x y
Thay
3
5
x y
vào hai đẳng thức đã cho ta được
1 1
; .
2 10
x y
0,75
0,25
0,5
0,5
2. Từ
1
3 0
2
x x
suy ra
– 3x
và
1
2
x
cùng dấu.
Dễ thấy
1
3
2
x x
nên ta có:
– 3x
và
1
2
x
cùng dương
3 0 3x x
– 3x
và
1
2
x
cùng âm
1 1
0
2 2
x x
0,25
0,5
0,5
0,5
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
66
Trang 66
Vậy
3x
hoặc
1
2
x
0,25
3
(5,0đ)
1. Ta có:
2 7 8 7 2 3 5
7 8 7 5
.
2 3 2
2 2 3 2 2 3 2 2 3
n n
n
n
n n n
Phân số đã cho có giá trị lớn nhất khi và chỉ khi
5
2 2 3
n
lớn nhất.
Từ đó suy ra:
2.n
Vậy giá trị lớn nhất của phân số đã cho bằng 6 khi
2.n
0,75
0,25
0,75
0,25
2. Vì
5
p x
với mọi x nguyên nên
0 5p d
p(1) a b c d 5
(1)
( 1) 5p a b c d
(2)
Từ (1) và (2) suy ra
2( ) 5b d
và
2( ) 5a c
Vì
2 5
b d
, mà
2;5 1
nên
5 5b d b
2 8 4 2 5 p a b c d
mà
d 5;b 5
nên
8 2 5.a c
Kết hợp với
2( ) 5 6 5 5a c a a
vì
6;5 1
. Từ đó suy ra
5c
Vậy a, b, c, d đều chia hết cho 5.
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
3. Vì
a b c
nên
1 .
a a a a
b c b c b c a
(1)
Tương tự, ta có:
1 .
b b b b
c a c a c a b
(2)
1 .
c c c c
a b a b a b c
(3)
Từ (1), (2) và (3) suy ra:
2 2 2
2.
a b c a b c
b c c a a b a b c
0,25
0,25
0,25
0,25
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
67
Trang 67
4
(5,0đ)
1.
Tam giác ABC cân tại A nên
; ;ABC ACB NCE ACB
(đối đỉnh)
Do đó:
( . . )MDB NEC g c g DM EN
.
0,75
0,75
2. Ta có
( . . )MDI NEI g c g MI NI
Vì
BD CE
nên
BC DE
.
Lại có
,DI MI
IE IN
nên
DE DI IE MI IN MN
Suy ra
.BC MN
0,5
0,75
0,25
3) Ta chứng minh được:
( . . ) , .ABO ACO c g c OC OB ABO ACO
( . . ) .MIO NIO c g c OM ON
Ta lại có:
.BM CN
Do đó
( . . )BMO CNO c c c
MBO NCO
, Mà:
MBO ACO
suy ra
NCO ACO
, mà đây là hai góc
kề bù nên CO
AN.
Vì tam giác ABC cho trước, O là giao của phân giác góc A và đường vuông góc
với AC tại C nên O cố dịnh.
0,75
0,5
0,5
0,25
5
(2,0đ)
Ta có đẳng thức:
102 102 101 101 100 100
a b a b a b ab a b
với mọi a, b.
Kết hợp với:
100 100 101 101 102 102
a b a b a b
0,5
0,5
C
I
B
E
M
N
A
O
D
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
68
Trang 68
Suy ra:
1 1 1 0.
a b ab a b
100 101 102
100 101 102
1 1 1 1 1
1 1 1 1 1
a b b b b
b a a a a
Do đó
2014 2015 2014 2015
1 1 2.P a b
0,5
0,5
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
69
Trang 69
ĐỀ SỐ 15. ĐỀ HSG CẤP HUYỆN
Bài 1: (4,0 điểm).
a) Tính giá trị biểu thức A =
1
2 3, 5
3
1 1
: 4 3
6 7
+7,5
b) Rút gọn biểu thức: B =
4 2 9
7 7 7 4
2.8 .27 4.6
2 .6 2 .40.9
c) Tìm đa thức M biết rằng:
2 2 2
5 2 6 9
M x xy x xy y
.
Tính giá trị của M khi x, y thỏa mãn
2012 2014
2 5 3 4 0
x y
.
Bài 2: (4,0 điểm).
a) Tìm x :
1 1 1
x
2 5 3
b) Tìm x, y, z biết:
2 3 ;x y
4 5y z
và
11x y z
c) Tìm x, biết :
1 11
2 2
n n
x x
(Với n là số tự nhiên)
Bài 3: (4,0 điểm).
a) Tìm độ dài 3 cạnh của tam giác có chu vi bằng 13cm. Biết độ dài 3 đường cao tương ứng
lần lượt là 2cm, 3cm, 4cm.
b) Tìm x, y nguyên biết :
2 2xy x y
Bài 4: (6,0 điểm). Cho tam giác
ABC
(
AB AC
,
60B
). Hai phân giác AD và CE của
ABC
cắt nhau ở I, từ trung điểm M của BC kẻ đường vuông góc với đường phân giác AI
tại H, cắt AB ở P, cắt AC ở K.
a) Tính
AIC
b) Tính độ dài cạnh AK biết PK = 6cm, AH = 4 cm.
c) Chứng minh
IDE
cân.
Bài 5: (2.0 điểm) Chứng minh rằng
10
là số vô tỉ.
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
70
Trang 70
HƯỚNG DẪN CHẤM
Nội dung Điểm
Bài 1
(4,0đ)
.
Câu a: (1 điểm)
1 1 1
2 3, 5 : 4 3 7,5
3 6 7
A
7 7 25 22 15
:
3 2 6 7 2
35 43 15
:
6 42 2
245 15 490 645 155
43 2 86 86 86
Câu b: ( 1 điểm)
B=
4 2 9
7 7 7 4
2.8 .27 4.6
2 .6 2 .40.9
=
13 6 11 9
14 7 10 8
2 .3 2 .3
2 .3 2 .3 .5
=
11 6 2 3
10 7 4
2 .3 . 2 3
2 .3 . 2 3.5
=
2
3
Câu c: (2 điểm)
2 2 2
5 2 6 9
M x xy x xy y
2 2 2
6 9 5 2
M x xy y x xy
2 2 2 2 2
6 9 5 2 11M x xy y x xy x xy y
Ta có
2012 2014
2 5 3 4 0
x y
Ta có :
2012
2012 2014
2014
2 5 0
2 5 3 4 0
3 4 0
x
x y
y
Mà
2012 2014
2 5 3 4 0
x y
2012 2014
2 5 3 4 0
x y
0.5 đ
0,5đ
0,5đ
0.5
0.5
0,5
0.25
0.5
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
71
Trang 71
=>
2012
2014
1
2
2 5 0
2
1
3 4 0
1
3
x
x
y
y
. Vậy
2
x
y
Vậy
2 2
5 5 4 4 25 110 16 1159
M 11
2 2 3 3 4 3 9 36
0.25
2.
(1,0đ)
1 1 1
x
2 5 3
1 1 1
5 2 3
x
1 1
5 6
x
TH1:
1 1
5 6
x
1
30
x
TH2:
1 1
5 6
x
1 1 11
6 5 30
x
Vậy
1 11
;
30 30
x x
0,25đ
0,25đ
0,25đ
0,25đ
b.
(1,5đ)
Ta có :
2 3 x y
suy ra
3 2
x y
hay
15 10
x y
4 5 y z
suy ra
5 4
y z
hay
10 8
y z
Vậy
15 10 8
x y z
Theo tính chất dãy tỉ số bằng nhau
15 10 8
x y z
=
15 10 8
x y z
=
11 1
33 3
Suy ra
10 8
5, ,
3 3
x y z
0.25đ
0.5đ
0.5đ
0.25
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
72
Trang 72
c
1,5
điểm
1 11
( 2) ( 2)
n n
x x
1 11
( 2) ( 2) 0
n n
x x
1 10
( 2) 1 ( 2) 0
n
x x
TH 1:
n 1
(x 2) 0
suy ra
2x
TH2:
10
1 ( 2) 0x
10
( 2) 1x
2 1x
suy ra
1x
2 1x
suy ra
3x
Vậy
2; 1; 3x x x
0.25
0.5
0.25
0.5
Bài 3
(4.0đ)
a
(2.0đ)
Gọi độ dài ba cạnh của tam giác là x, y,z ( cm) ( x,y,z > 0)
Theo bài ra ta có :
13x y z
và
2 3 4 2
ABC
x y z S
Suy ra
6 4 3
x y z
Áp dụng tính chất dãy tỷ số bằng nhau
6 4 3
x y z
=
13
1
6 4 3 13
x y z
suy ra
6; 4 ; 3x y z
KL:
0,25 đ
0,75 đ
0,75
0.25
b.
(2,0đ)
2 – – 2xy x y
4 2 2 4xy x y
2 2 1 2 1 5
x y y
2 1 2 1 5
y x
HS xét 4 trường hợp tìm ra
1; 3 ; 3;1 ; 2;0 ; 0; 2
,x y
( Mỗi trường hợp đúng cho 0.25 đ)
Vậy
1; 3 ; 3;1 ; 2;0 ; 0; 2
,x y
0,5 đ
0,5 đ
1 đ
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
73
Trang 73
Bài 4
(6.0đ)
1
(2.0đ)
a/ Ta có
60ABC
suy ra
120BAC BCA
AD là phân giác của
BAC
suy ra
1
IAC BAC
2
CE là phân giác của
ACB
suy ra
1
ICA BCA
2
Suy ra
1
IAC ICA 120 60
2
Vây
120AIC
0.5đ
0.5đ
0.5đ
0.25đ
0.25đ
2
(2đ)
b/ Xét
AHP
và
AHK
có
PAH KAH
( AH là phân giác của
BAC
)
AH chung
PHA KHA 90
Suy ra
AHP AHK
(g-c-g) suy ra
PH KH
( 2 cạnh tương
ứng). Vậy
3HK cm
Vì
AHK
vuông ở H theo định lý Pitago ta có
2 2 2 2 2
4 3 25AK AH HK
Suy ra
5 AK cm
0.5 đ
0,5 đ
0.5
0.25
0.25
c
(2.0đ)
Vì
120AIC
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 !
[Document title]
Toán Họa tổng hợp
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
74
Trang 74
Do đó
AIE DIC 60
Trên cạnh AC lấy điểm F sao cho
AF AE
Xét
EAI
và
FAI
có
AE AF
EAI FAI
AI chung
Vậy
EAI FAI
(c-g-c)
suy ra
IE IF
(hai cạnh tương ứng) (1)
AIE AIF 60
suy ra
FIC AIC AIF 60
Xét
DIC
và
FIC
có
DIC FIC 60
; Cạnh IC chung;
DIC FCI
Suy ra
DIC FIC
( g-c-g)
Suy ra
ID IF
(hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra
IDE
cân tại I
0,25 đ
0,5 đ
0.25
0.5
0.25
0.25
Bài 5
(2,0đ)
Giả sử
10
là số hữu tỷ
10
a
b
( a,b là số tự nhiên , b khác 0 ;
; 1
a b
)
2
2
10
a
b
Suy ra
2 2
10a b
2 2 2
a 2 a 4 10b 4 b 2 b 2
Vậy
(a;b) 1
trái giả sử.
Nên
10
là số vô tỷ
0.25đ
0.5đ
0.25đ
0.25đ
0.5đ
0.25đ
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
| 1/74
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Toán Họa tổng hợp Trang 1 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 MỤC LỤC
ĐỀ SỐ 1. HUYỆN ĐỨC PHỔ - NĂM 15 – 16 ................................................................... 2
ĐỀ SỐ 2. ĐỀ HSG CẤP HUYỆN ........................................................................................ 8
ĐỀ SỐ 3. ĐỀ HSG CẤP HUYỆN ...................................................................................... 13
ĐỀ SỐ 4. ĐỀ HSG CẤP HUYỆN ...................................................................................... 17
ĐỀ SỐ 5. ĐỀ HSG CẤP HUYỆN ...................................................................................... 21
ĐỀ SỐ 6. ĐỀ HSG CẤP HUYỆN ...................................................................................... 25
ĐỀ SỐ 7. ĐỀ HSG CẤP HUYỆN ...................................................................................... 30
ĐỀ SỐ 8. ĐỀ HSG CẤP HUYỆN ...................................................................................... 33
ĐỀ SỐ 9. ĐỀ HSG CẤP HUYỆN ...................................................................................... 37
ĐỀ SỐ 10. ĐỀ HSG CẤP HUYỆN .................................................................................... 44
ĐỀ SỐ 11. ĐỀ HSG CẤP HUYỆN .................................................................................... 50
ĐỀ SỐ 12. ĐỀ HSG CẤP HUYỆN .................................................................................... 55
ĐỀ SỐ 13. ĐỀ HSG CẤP HUYỆN .................................................................................... 59
ĐỀ SỐ 14. ĐỀ HSG CẤP HUYỆN .................................................................................... 64
ĐỀ SỐ 15. ĐỀ HSG CẤP HUYỆN .................................................................................... 69
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 1
Toán Họa tổng hợp Trang 2 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
ĐỀ SỐ 1. HUYỆN ĐỨC PHỔ - NĂM 15 – 16
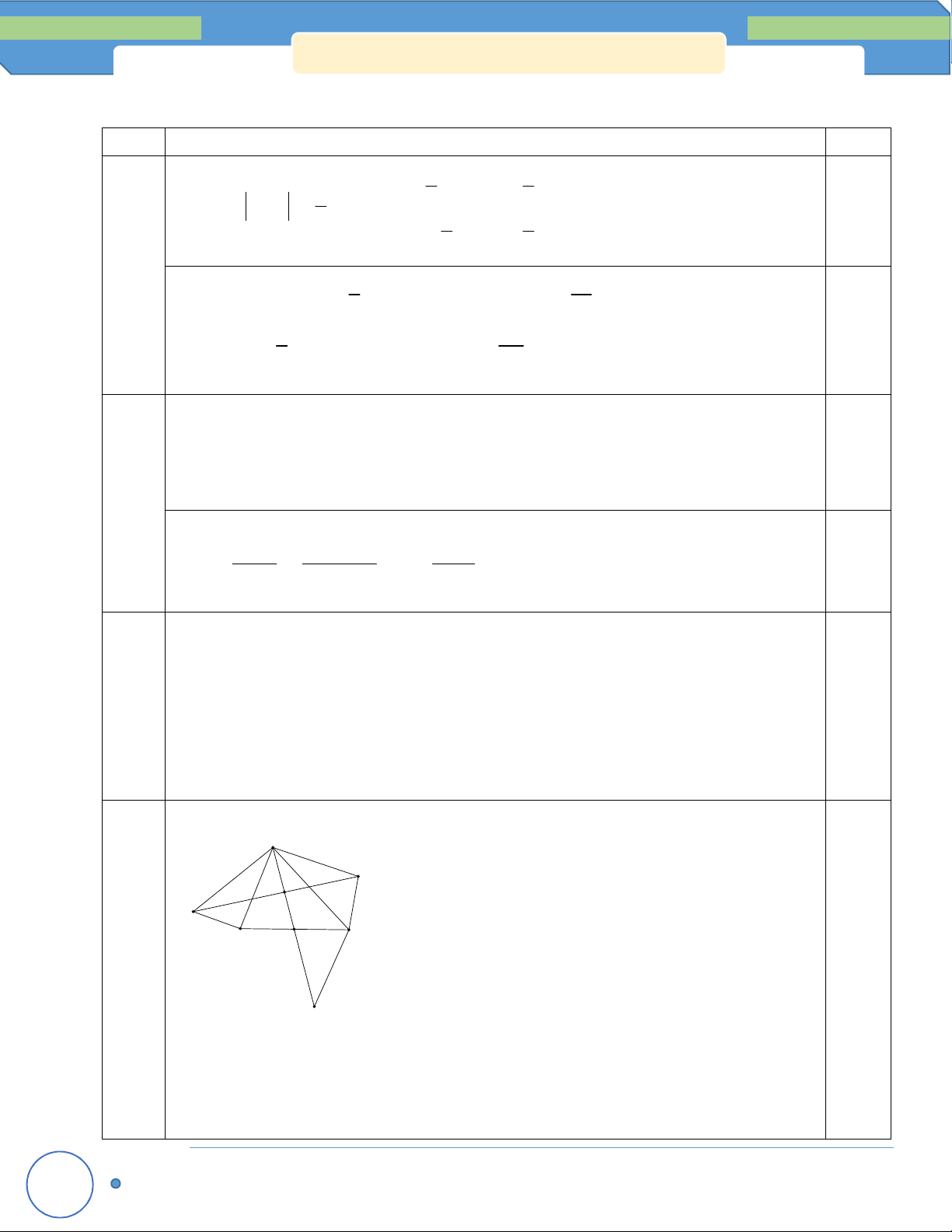
Câu 1: (5 điểm) 1 1 1
a) Tính giá trị biểu thức P a   a  , với a  . 2014 2016 2015 6 x  1
b) Tìm số nguyên x để tích hai phân số và là một số nguyên. x  1 3
Câu 2: (5 điểm)
a) Choa  2; b  2 . Chứng minh ab a b
b) Cho ba hình chữ nhật, biết diện tích của hình thứ nhất và diện tích của hình thứ hai tỉ lệ
với 4 và 5, diện tích hình thứ hai và diện tích hình thứ ba tỉ lệ với 7 và 8, hình thứ nhất và
hình thứ hai có cùng chiều dài và tổng các chiều rộng của chúng là 27 cm, hình thứ hai và
hình thứ ba có cùng chiều rộng, chiều dài của hình thứ ba là 24 cm. Tính diện tích của mỗi hình chữ nhật đó.
Câu 3: (3 điểm)
Cho ∆DEF vuông tại D và DF DE , kẻ DH vuông góc với EF (H thuộc cạnh EF). Gọi M là trung điểm của EF.   
a) Chứng minh MDH E F
b) Chứng minh EF DE DF DH
Câu 4: (2 điểm)
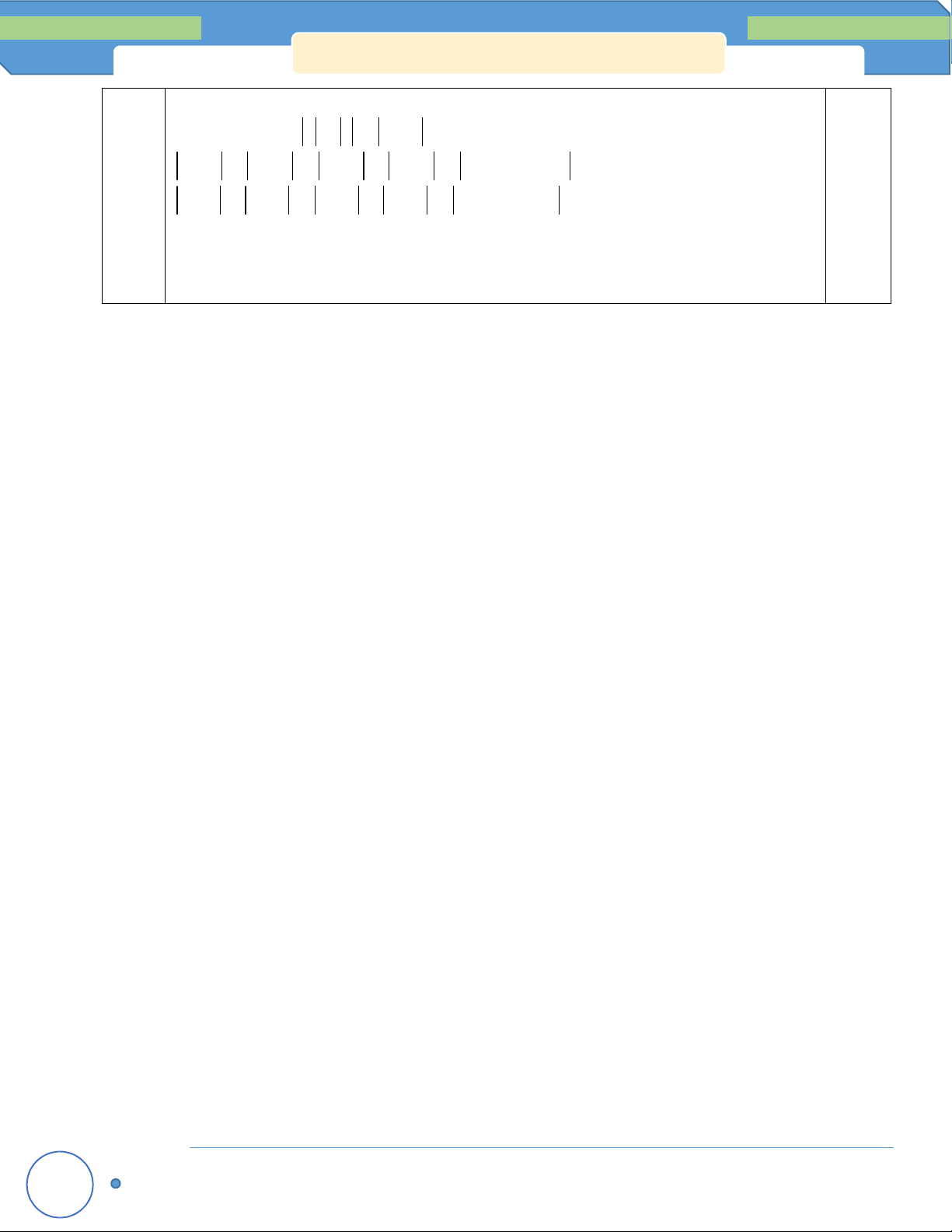
a a a  ...  a
Cho các số 0  a a a  ....  a . Chứng minh rằng 1 2 3 15  5 1 2 3 15
a a a 5 10 15
Câu 5: (5 điểm)   
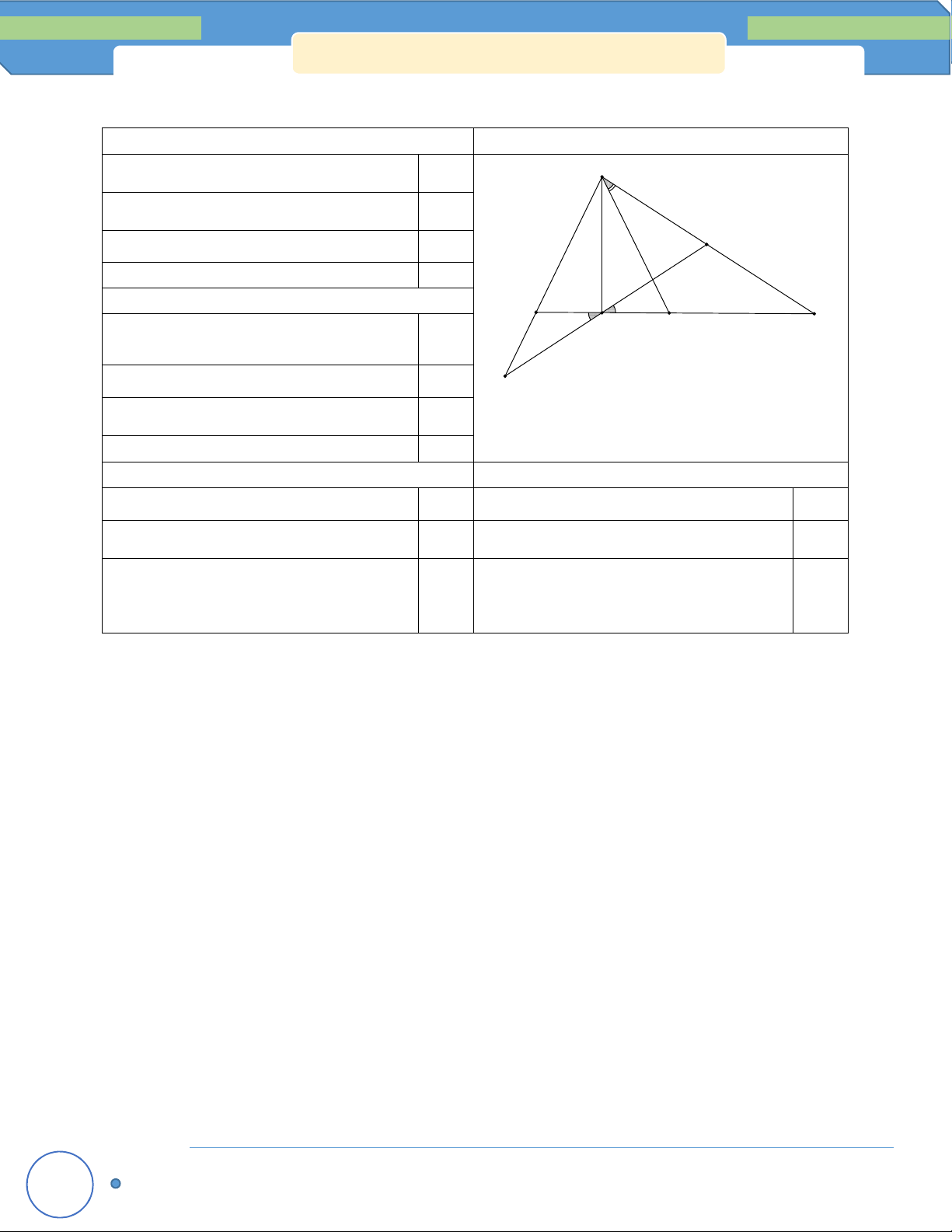
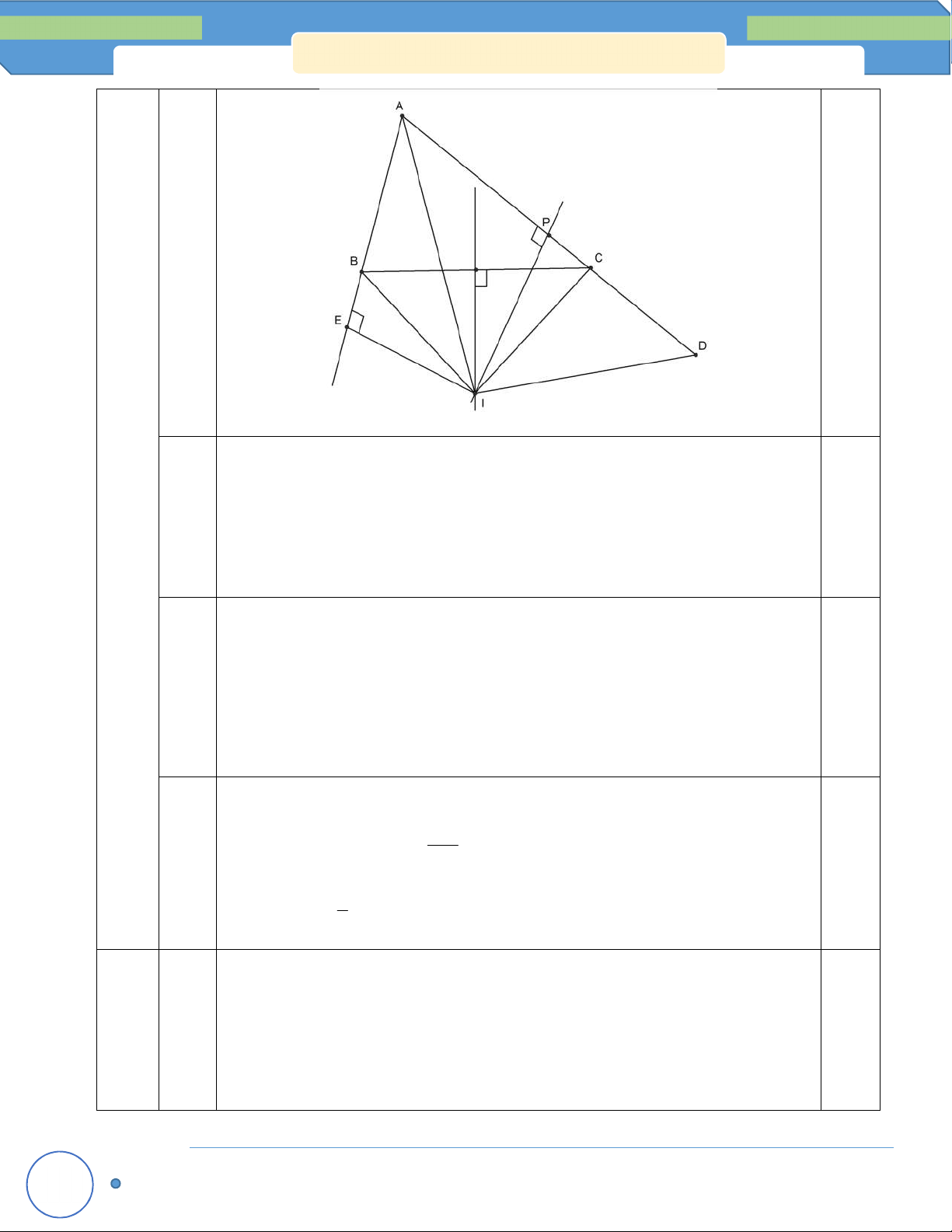
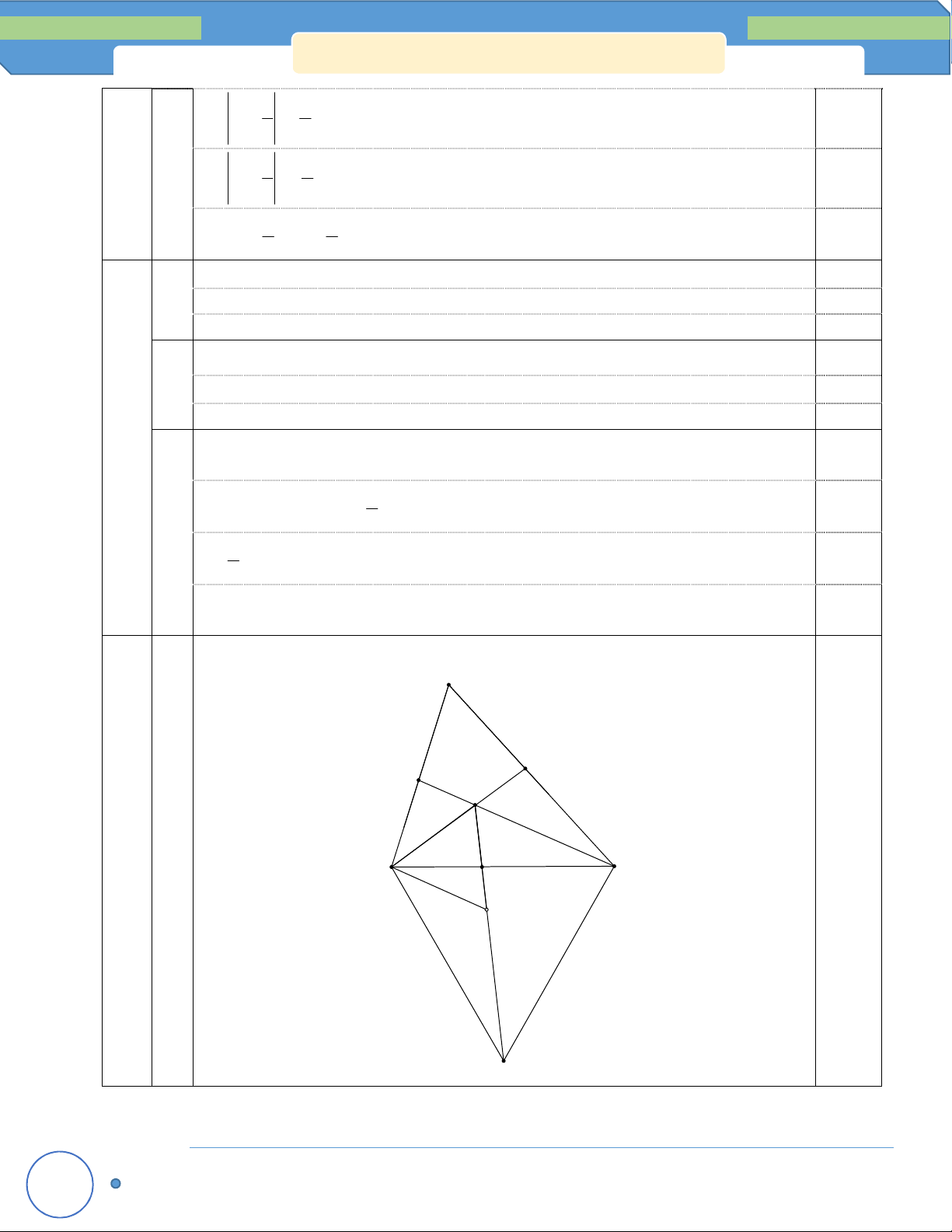
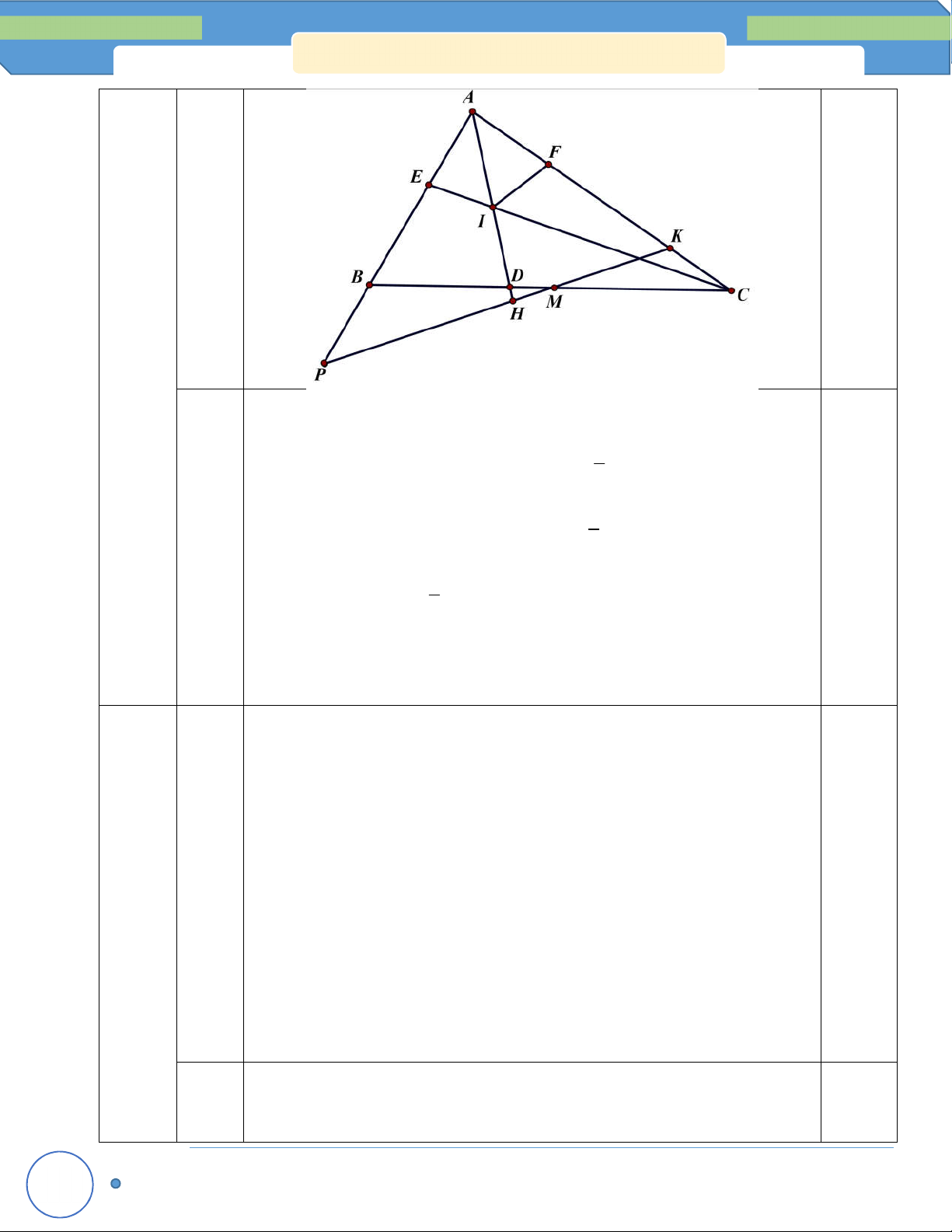
Cho ∆ABC có A  120 . Các tia phân giác BE, CF của ABC và ACB cắt nhau tại I (E, F lần  
lượt thuộc các cạnh AC, AB). Trên cạnh BC lấy hai điểm M, N sao cho 0
BIM CIN  30 . 
a) Tính số đo của MIN .
b) Chứng minh CE + BF < BC
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 2
Toán Họa tổng hợp Trang 3 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 HƯỚNG DẪN CHẤM Câu NỘI DUNG ĐÁP ÁN Điểm 1 1 1 1
a) Tính giá trị biểu thức P a   a  , với a  . 2014 2016 2015 1 1 1 1 1 Thay a
vào biểu thức P     0.25 2015 2015 2014 2015 2016 1 1 1 1 Ta có P     0.5 2014 2015 2015 2016 2.5 đ 1 1 P   2014 2016 0.5 2016  2014 2 P   2014.2016 2014.2016 0.5 1 1 P   0.75 1007.2016 2030112 6 x  1
b) Tìm số nguyên x để tích hai phân số và là một số nguyên. x  1 3 6 x  1 2.5 đ Đặt A   0.25 x  1 3 2 x  1   x  1 1 0.25 2(x  1) x  1 0.25 2x  2  x  1 2(x  1)  4 4   2  x  1 x  1 0.25
Để A nhận giá trị nguyên thì x  1 là Ư(4) = 1;2;4 0.5
Suy ra x  0;2;1;3;3;  5
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 3
Toán Họa tổng hợp Trang 4 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 2
2. a) Choa  2; b  2 . Chứng minh ab a b 1 1 0.5 Từ a  2   a 2 1 1 b  2   0.5 b 2 2đ 1 1 a b Suy ra   1   1 a b ab 0.5
Vậy ab a b 0.5 b)
Gọi diện tích ba hình chữ nhật lần lượt là S ,S ,S , chiều dài, chiều rộng 0.5 1 2 3 3đ
tương ứng là d ,r ;d ,r ;d ,r theo đề bài ta có: 1 1 2 2 3 3 0.5 S 4 S 7 0.25 1 2  ;
 và d d ;r r  27;r r ,d  24 S 5 S 8 1 2 1 2 2 3 3 2 3
Vì hình thứ nhất và hình thứ hai cùng chiều dài S 4 r r r r r 27 1 1 1 2 1 2        3 0.25 S 5 r 4 5 9 9 2 2 0.25
Suy ra chiều rộng r  12c , m r  15cm 1 2
Vì hình thứ hai và hình thứ ba cùng chiều rộng 0.25 S 7 d 7d 7.24 2 2 3    d    21cm 0.25 2 S 8 d 8 8 3 3
Vậy diện tích hình thứ hai 2
S d r  21.15  315 cm 2 2 2 0.25 4 4 0.25
Diện tích hình thứ nhất 2
S S  .315  252 cm 1 2 5 5 8 8 Diện tích hình thứ ba 2
S S  .315  360 cm 3 2 0.25 7 7
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 4
Toán Họa tổng hợp Trang 5 [Document title]
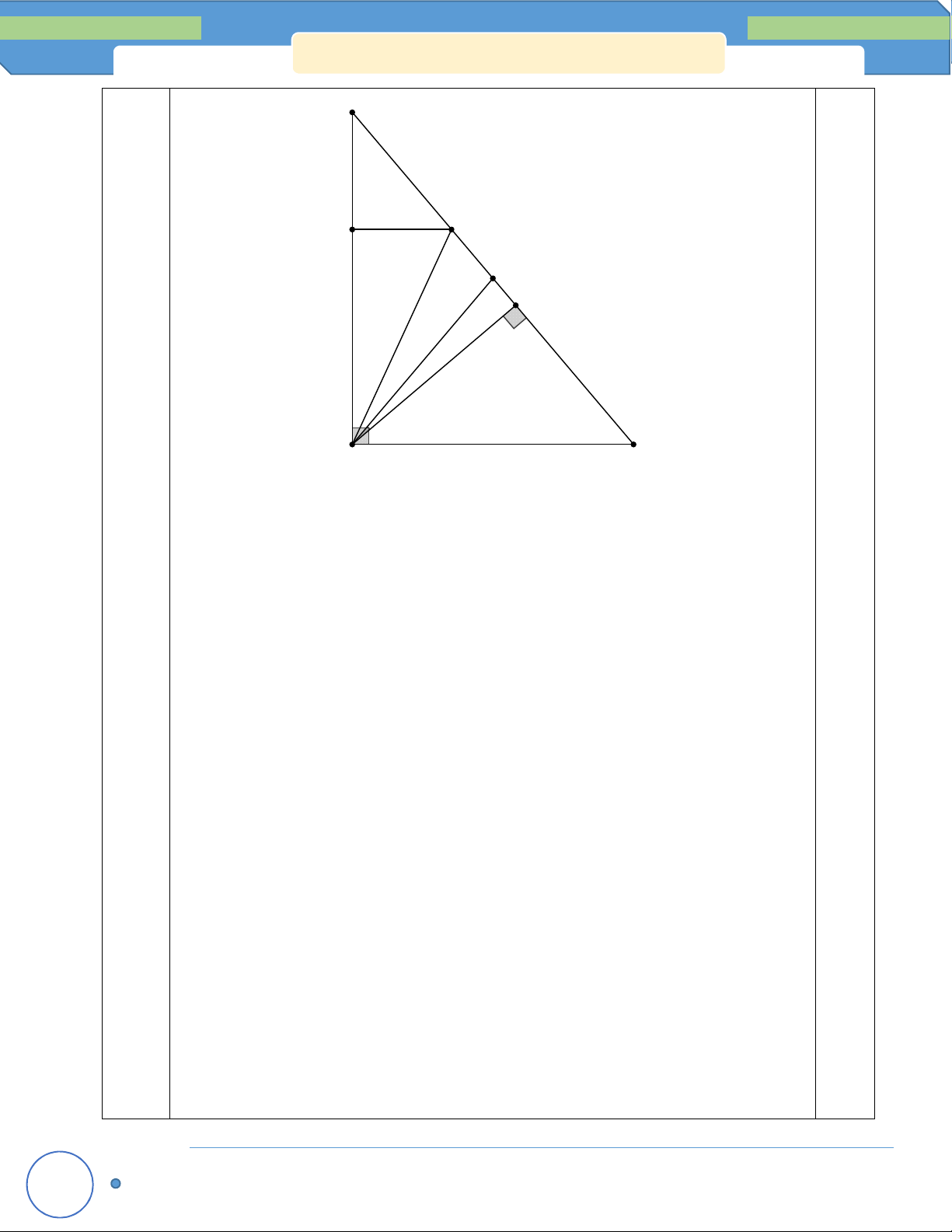
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 3đ F K I M H D E    0.5
a) Chứng minh MDH E F
Vì M là trung điểm của EF suy ra MD ME MF 0.25    M
DE cân tại M  E MDE 0.25   
Mà HDE F cùng phụ với E   
Ta có MDH MDE HDE 0.25   
Vậy MDH E F 0.25
b) Chứng minh EF DE DF DH
Trên cạnh EF lấy K sao choEK ED , trên cạnh DF lấy I sao choDI DH
Ta có EF DE EF EK KF 0.25
DF DH DF DI IF
Ta cần chứng minh KF IF 0.25  
- EK ED DE
K cân  EDK EKD     0.25 - 0
EDK KDI EKD HDK  90   
KDI HDK 0.25
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 5
Toán Họa tổng hợp Trang 6 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 - DHK   DIK  (c-g-c)    0
KID DHK  90 0.25
Trong ∆KIF vuông tại I  KF FI điều phải chứng minh 0.25 4
Ta có a a a a a  5a 1 2 3 4 5 5 (2đ)
a a a a a  5a 0.5 6 7 8 9 10 10 0.5
a a a a a  5a 11 12 13 14 15 15 0.5
Suy ra a a  ........  a  5(a a a ) 1 2 15 5 10 15
a a a  ...  a Vậy 1 2 3 15  5 0.5
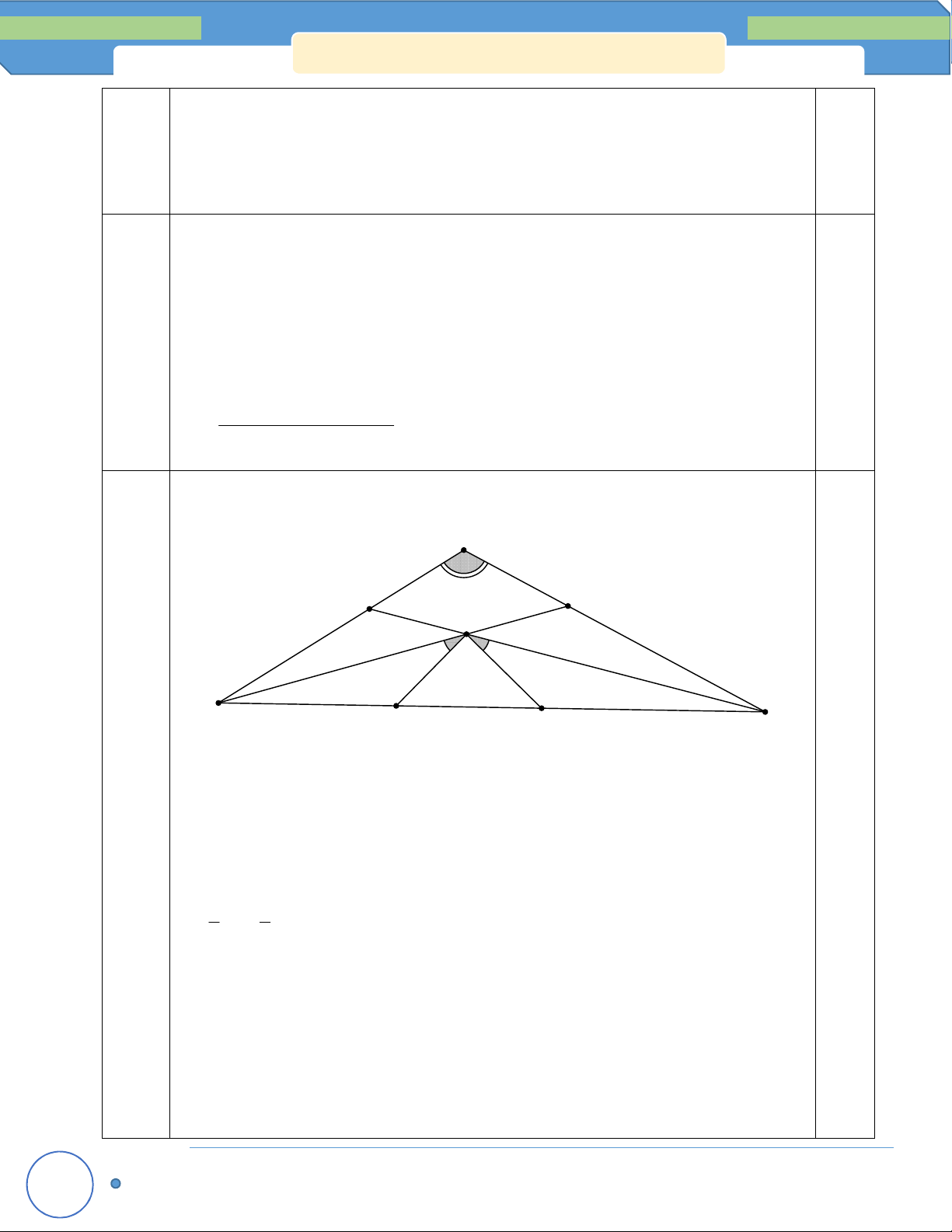
a a a 5 10 15 5 A (5đ) 120° F E I B M C N 0.5
- Vẽ hình đúng, đủ, chính xác.  0.5
a) Tính số đo của MIN . 0.5   
Ta có ABC ACB  180  A  60 0.5 1 1    0 B C  30 0.5 2 2 0.25   0 BIC  150   Mà 0
BIM CIN  30   0 MIN  90 0.25
b) Chứng minh CE BF BC    - 0 BIC  150  0
FIB EIC  30
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 6
Toán Họa tổng hợp Trang 7 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 Suy ra B  FI  BM 
I (g-c-g)  BF BM 0.5 - CNI   CE 
I ( g-c-g)  CN CE 0.5
Do đó CE  BF  BM  CN  BM  MN  NC  BC 0.5
Vậy CE BF BC 0.25 0.25
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám
khảo cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 7
Toán Họa tổng hợp Trang 8 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
ĐỀ SỐ 2. ĐỀ HSG CẤP HUYỆN Câu 1. 3 3 0, 375  0, 3   1, 5  1  0, 75 a. Thực hiện phép tính: 11 12  5 5 5 0,265  0, 5   2, 5   1,25 11 12 3
b. So sánh: 50  26  1 và 168 . Câu 2.
a. Tìm x biết: x  2  3  2x  2x  1
b. Tìm x;y Z biết: xy  2x y  5
c. Tìm x; y; z biết: 2x  3y ; 4y  5z và 4x  3y  5z  7 Câu 3.
a. Tìm đa thức bậc hai biết f x   f x   1  x.
Từ đó áp dụng tính tổngS  1  2  3  ....  n . 2bz  3cy 3cx az ay  2bx x y z b. Cho   Chứng minh:   . a 2b 3c a 2b 3c Câu 4.  Cho tam giác ABC ( 90o BAC
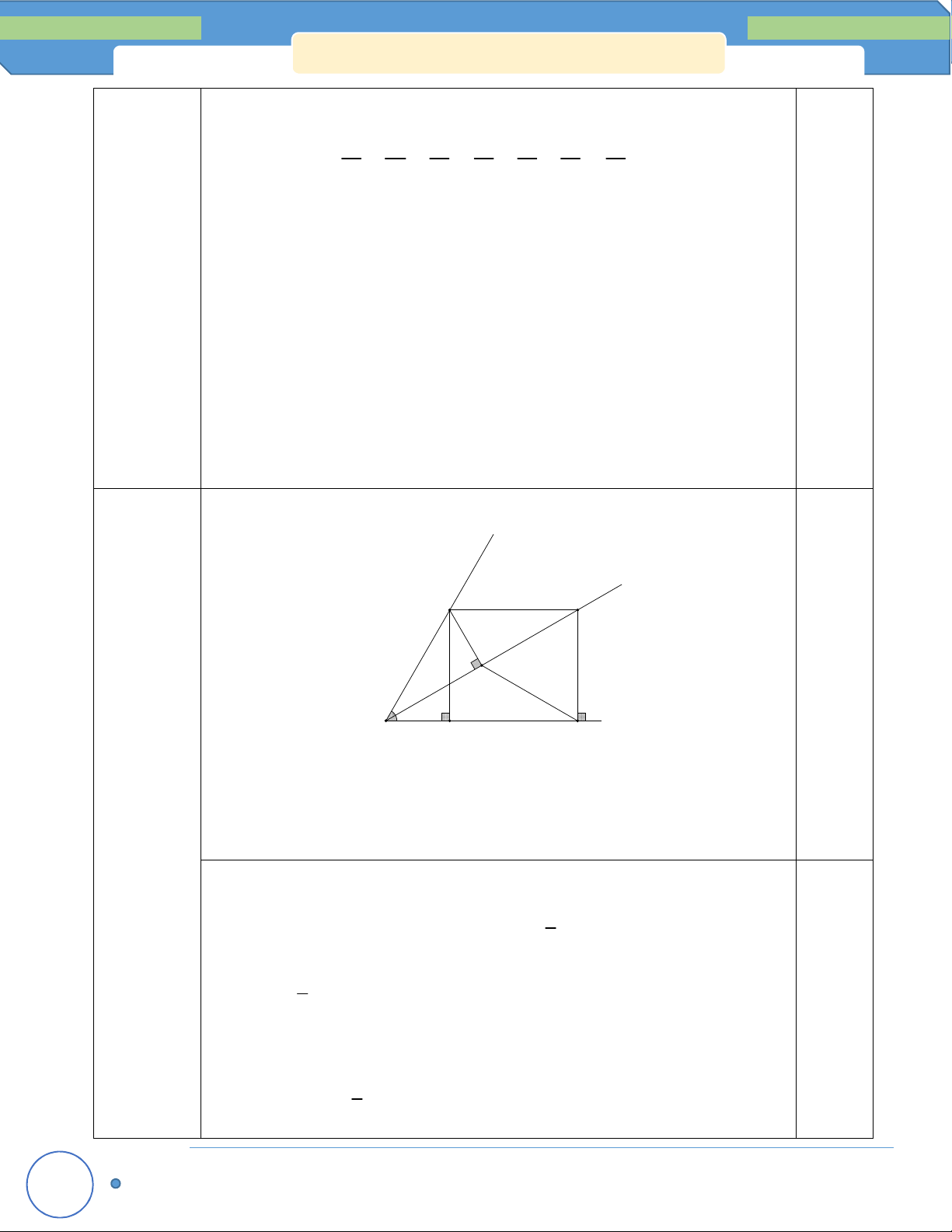
), đường cao AH. Gọi E; F lần lượt là điểm đối xứng của H
qua AB; AC, đường thẳng EF cắt AB; AC lần lượt tại M và N. Chứng minh rằng: a. AE AF ; 
b. HA là phân giác của MHN ;
c. CM //EH; BN //FH.
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 8
Toán Họa tổng hợp Trang 9 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 HƯỚNG DẪN CHẤM Câu Ý Nội dung Điểm a. 0,5 3 3 3 3 3 3 3      điểm A = 8 10 11 12 2 3 4  53 5 5 5 5 5 5       100 10 11 12 2 3 4 1 1 1 1     1 1 1 3     3      8 10 11 12   2 3 4 A   0.25 53  1 1 1     1 1 1   5      5      100  10 11 12   2 3 4 165 132 120 110    3     1320  3 Câu 1   53  66 60 55     5  5        1,5 100  660  điểm 263 3. 3 1320   53 49 5  5. 100 660 0.25 263 3. 3 3945 3 1881 1320      1749  1225 5 5948 5 29740 3300 b. 1
Ta có: 50  49  7 ; 26  25  5 0.5 điểm 0,5
Vậy: 50  26  1  7  5  1  13  169  168 a. 1
Nếu x  2 ta có: x  2  2x  3  2x  1  x  6 0.25 điểm 3 0.25 Nếu
x  2 ta có: 2  x  2x  3  2x  1  x  2 (loại) 2 Câu 2 3 4 x
2  x  3  2x  2x  1  x 4 Nếu ta có: 0.25 2 5 điểm 4
Vậy: x  6 ; x  5 0.25
b. 1.5 Ta có: xy  2x y  5  x(y  2)  (y  2)  3 0. 5
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 9
Toán Họa tổng hợp Trang 10 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 điểm
 (y  2)(x  1)  3.1  1.3  (1).(3)  (3).(1) 0. 5 y  2 3 1 1 3 x  1 1 3 3 1 0.5 x 2 4 2 0 y 1 1 3 5 
c. 1.5 Từ: 2x  3y; 4y  5z  8x  12y  15z 0. 5 điểm x y z 4x 3y 5z
4x  3y  5z 7         12 1 1 1 1 1 1 1 1 1 7   8 12 15 2 4 3 2 4 3 12 0.5 1 3 1 1 4 x  12   y  12.  1 ; z  12   8 2 ; 12 15 5 0. 5
a. 0.5 Đa thức bậc hai cần tìm có dạng:   2
f x ax bx c (a  0) điểm 2
Ta có : f x  
1  a x  
1  b x   1  c .  1  2  a  1 a   0.25
f x f x  
1  2ax a b x     2   b  a  0    1 b    2 1 1
Vậy đa thức cần tìm là: f x 2
x x c (c là hằng số tùy ý). 2 2 Câu 3 Áp dụng: 1.5 điểm
+ Với x  1 ta có : 1  f   1  f 0.
+ Với x  2 ta có : 1  f 2  f   1 . 0.25
………………………………….
+ Với x n ta có : n f n  f n   1 . 2 n n n n   1
S  1  2  3   n f n f 0    c c  2 2 2 b. 1 2bz  3cy 3cx az ay  2bx    điểm a 2b 3c
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 10
Toán Họa tổng hợp Trang 11 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 2abz  3acy 6bcx  2abz 3acy  6bcx   2 2 2 a 4b 9c
2abz  3acy  6bcx  2abz  3acy  6bcx 0.5   0 2 2 2
a  4b  9c 0.25 z y
 2bz  3cy  0   (1) 3c 2b 0.25 x z x y z
 3cx az  0  
(2); Từ (1) và (2) suy ra:   a 3c a 2b 3c Câu 4 Hình 0.25 3 vẽ điểm 0. 5 đ a. 1
Vì AB là trung trực của EH nên ta có: AE AH (1) 0.25
điểm Vì AC là trung trực của HF nên ta có: AH AF (2) 0.25
Từ (1) và (2) suy ra: AE AF 0. 5 b. 1 
Vì M AB nên MB là phân giác EMH  MB là phân giác ngoài 0.25
điểm góc M của tam giác MNH
Vì N AC nên NC là phân giác FNH  NC là phân giác ngoài góc 0.25
N của tam giác MNH
Do MB; NC cắt nhau tại A nên HA là phân giác trong góc H của tam 0.5
giác MNH hay HA là phân giác của MHN . c. 1 
Ta có AH  BC (gt) mà HM là phân giác MHN  HB là phân giác 0.25
điểm ngoài góc H của tam giác HMN
MB là phân giác ngoài góc M của tam giác HMN (cmt)  NB là
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 11
Toán Họa tổng hợp Trang 12 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
phân giác trong góc N của tam giác HMN 0.25
 BN  AC ( Hai đường phân giác của hai góc kề bù thì vuông góc
với nhau).  BN // HF ( cùng vuông góc với AC) 0.25
Chứng minh tương tự ta có: EH //CM
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 12
Toán Họa tổng hợp Trang 13 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
ĐỀ SỐ 3. ĐỀ HSG CẤP HUYỆN
Bài 1 ( 2,0 điểm). Tính hợp lý các biểu thức sau: 1 5 1 5 a) 27   13  4 8 4 8 1 3 4 b) 2   2 4 9 2 3 2 .10  2 .6 c) 2 4 2 .15  2
Bài 2 ( 2,5 điểm). Tìm x biết: 2 a) 3(x  2)   4 5 1 b) x   5  7 3 c) 7 5
(2x  1)  (2x  1)
Bài 3 (1,5 điểm):
Ba đội cùng chuyển một khối lượng gạch như nhau. Thời gian để đội thứ nhất, đội
thứ hai và đội thứ ba làm xong công việc lần lượt là 2 giờ, 3 giờ, 4 giờ. Tính số người tham
gia làm việc của mỗi đội, biết rằng số người của đội thứ ba ít hơn số người của đội thứ hai là 5 người.
Bài 4 (3,5điểm): AB 3
Cho tam giác ABC vuông tại A với 
vàBC  15cm . Tia phân giác góc C cắt AC 4
AB tại D. Kẻ DE  BC (E  BC)
a) Chứng minh AC CE. b) Tính độ dài AB; AC. 
c) Trên tia AB lấy điểm F sao cho AF AC . Kẻ tia Fx  FA cắt tia DE tại M. Tính DCM .
Bài 5 (0,5điểm):
Tìm giá trị lớn nhất của biêu thức: A = x x  2
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 13
Toán Họa tổng hợp Trang 14 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 HƯỚNG DẪN CHẤM Câu Nội dung Điểm 1 1 5 1 5 5 1 1 5 35 a) 27   13   (27  13 )  14.  4 8 4 8 8 4 4 8 4 2,0đ 0,75 1 3 4 1 2 1 2 7 b)2    2     2 4 9 4 3 2 3 6 0,75 2 3 3 3 3 2 .10  2 .6 2 .5  2 .6 2 (5  6) 2.11 c)     2 2 4 2 4 2 2 2 .15  2 2 .15  2 2 (15  2 ) 11 0,5 1 2 a) 3(x  2)   4 5 2,5đ 2 3(x  2)  4  0,25 5 18 3(x  2)  5 0,25 6 x  2  5 0,25 16 x 0,25 5 1 x   5  7 3 1 x   12 0,25 3 1 1 x
 12 hoặc x   12 0,25 3 3 5 3 37
x  hoặc x   3 3 0,5 7 5
(2x  1)  (2x  1) 5 x   2 (2 1) (2x  1)   1  0 0,25
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 14
Toán Họa tổng hợp Trang 15 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7   1 2x  1  0  x     2 2
x 1  1       x  1 0,25    2  x 1 1        x  0  3
Gọi số người tham gia làm việc của đội thứ nhất, đội thứ hai, đội thứ ba
lần lượt là x; y; z (giờ). 1,5đ 0,25
ĐK: x; y; z  0
Cùng một khối lượng công việc, số người tham gia và thời gian làm việc tỷ lệ lệ nghịch. 0,5
Theo bài ra ta có: 2x  3y  4z và y – z  5 y z y z 5     60 1 1 1 1 1 0,25  3 4 3 4 12
y  20,z  15,x  30 (thoả mãn điều kiện bài toán) 0,25
Vậy số người tham gia làm việc của đội thứ nhất, đội thứ hai, đội thứ ba 0,25
lần lượt là 30 người, 20người, 15 người 4
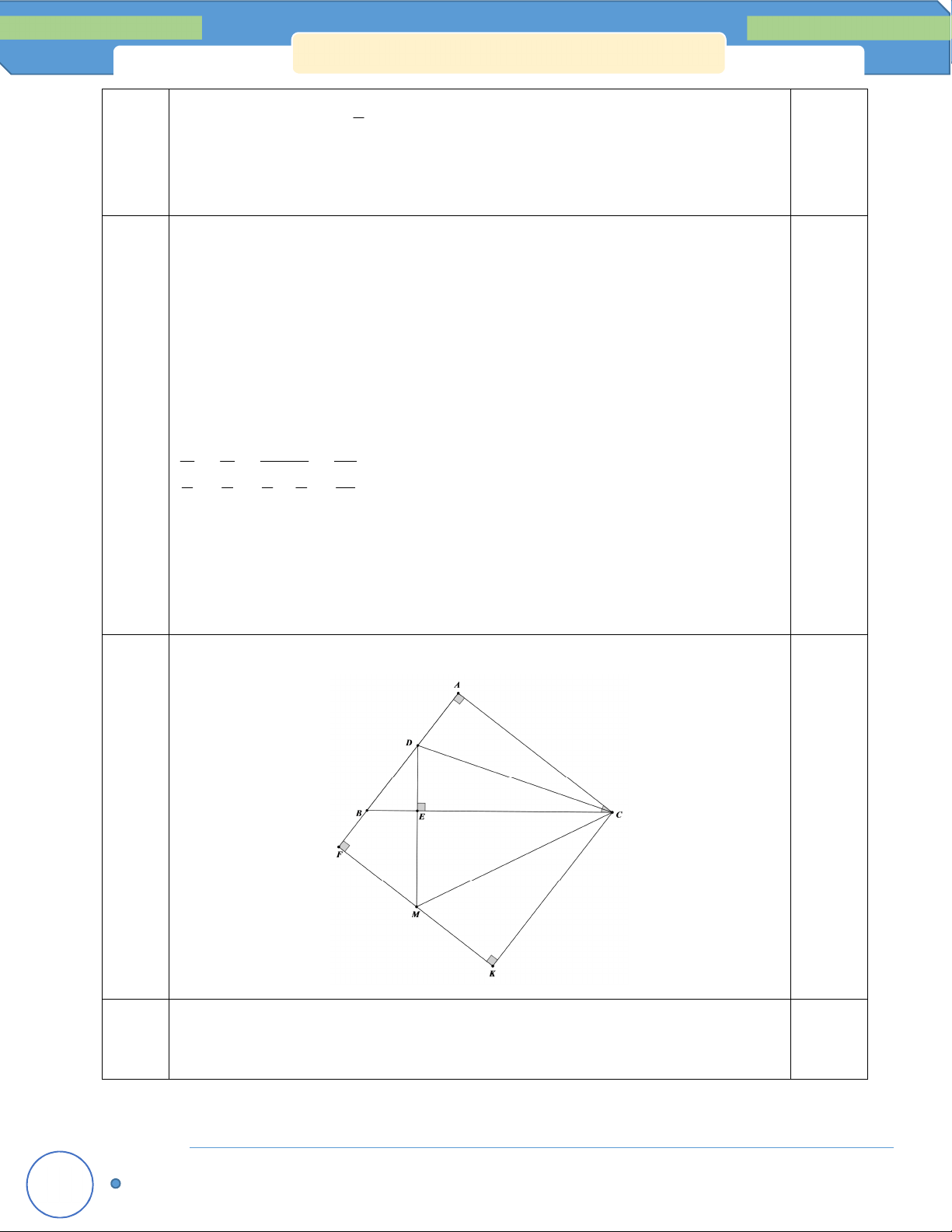
Vẽ hình, ghi GT, KL đúng : 0,5đ 3,5đ
a) Chứng minh được ACD EC
D ( cạnh huyền- góc nhọn) 1
AC CE (hai cạnh tương ứng) 0,5
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 15
Toán Họa tổng hợp Trang 16 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 AB 3 AB AC 0,25 b)  (gt)   AC 4 3 4 2 2 2 2 2 2 AB AC AB AC BC 15       9 0,5 9 16 9  16 25 25 2
AB  9.9  81  AB  9cm 0,25 2
AC  9.16  144  AC  12cm
c) Kẻ Cy Fx cắt nhau tại K
Ta thấy AC  AF  FK  CK  CE và 0 ACK  90 0,25 Chứng minh được CEM C
KM ( cạnh huyền- cạnh góc vuông)   0,25
ECM KCM (hai góc tương ứng)    1  1
Mà DCM DCE ECM
ACK   90  45 2 2 5 Xét các trường hợp: 0,5đ
+ TH1 : x  2  A x  (x  2)  2
+TH2 : 0  x  2  A x x  2  2x  2  2 0,25
+ TH3 : x  0  A x
  x  2  2  2
 Với mọi giá trị của x thì A  2
Vậy giá trị lớn nhất của A bằng 2 khi x  2 0,25
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 16
Toán Họa tổng hợp Trang 17 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
ĐỀ SỐ 4. ĐỀ HSG CẤP HUYỆN
Câu 1(5 điểm):
a) Cho biểu thức: P x  4xy y . Tính giá trị của P với x  1, 5; y  0, 75 12 5 6 2 .3  4 .81
b) Rút gọn biểu thức: A  2 6 2 4 5 .3  8 .3
Câu 2 (4điểm):
a) Tìm x, y, z, biết: 2x  3y; 4y  5z và x y z  11
b) Tìm x, biết: x  1  x  2  x  3  4x
Câu 3(3 điểm). Cho hàm số: y f x  3
 4x x a) Tính f   0 , f 0,  5
b) Chứng minh: f a
   f a.
Câu 4: (1,0 điểm): Tìm cặp số nguyên x;y biết: x y x.y
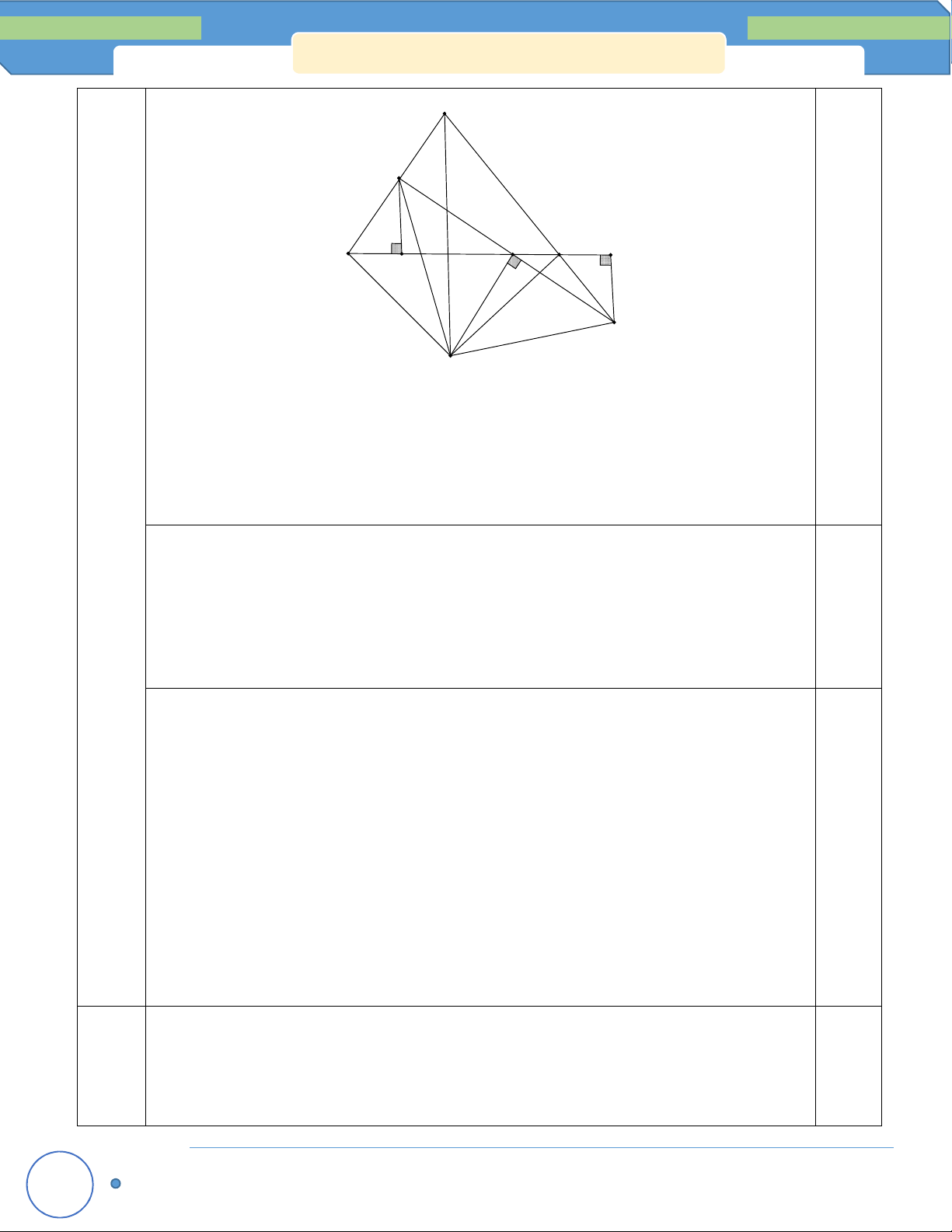
Câu 5: (6 điểm):Cho A
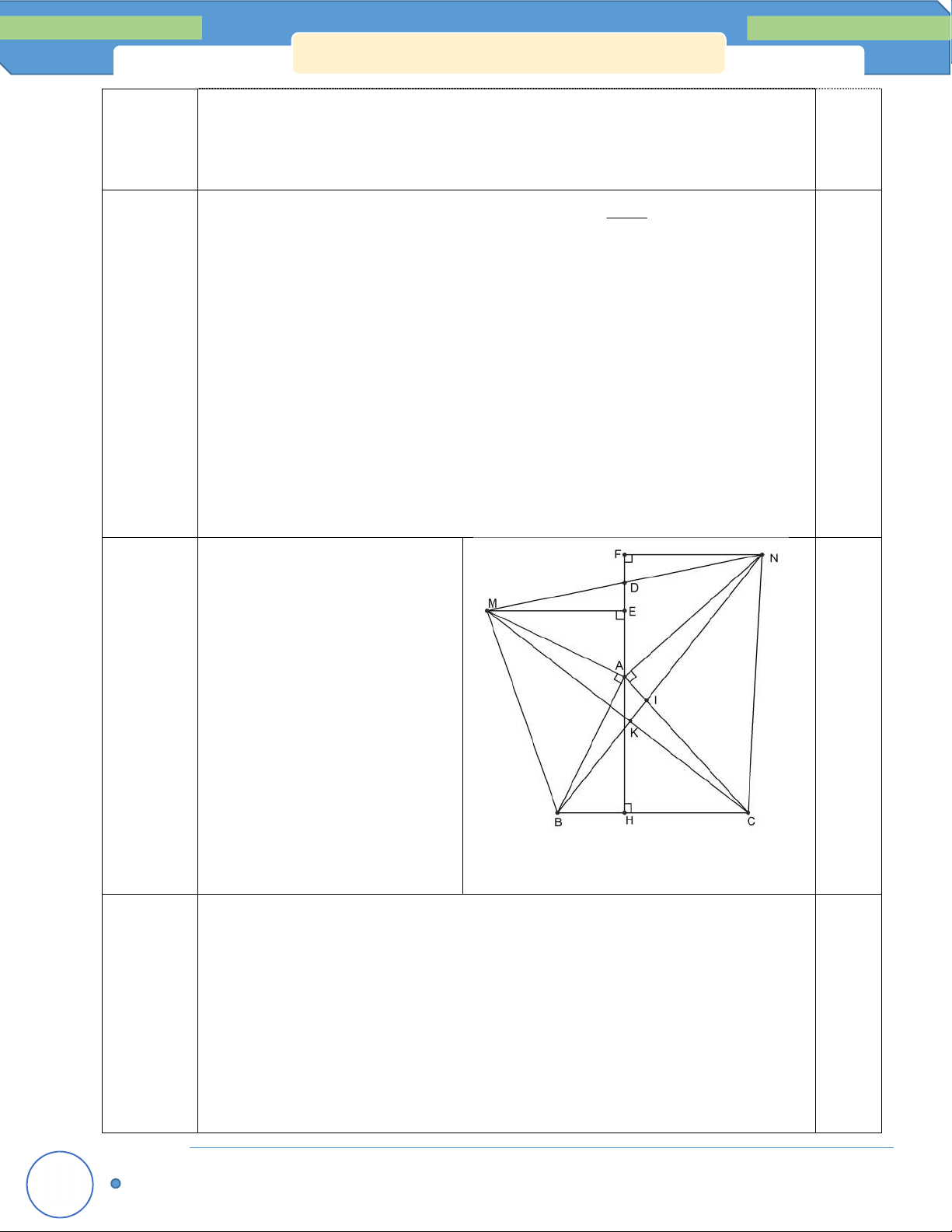
BC có gócA  90 . Vẽ ra ngoài tam giác ABC các tam giác vuông cân tại A là A  BM và AC  N a) Chứng minh rằng: AMC   AB  N b) Chứng minh: BN  CM;
c) Kẻ AH  BC (H  BC). Chứng minh AH đi qua trung điểm của MN.
Câu 6 : (1 điểm):Cho ba số a, b, c thõa mãn: 0  a b  1  c  2 và a b c  1 . Tìm giá
trị nhỏ nhất của c .
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 17
Toán Họa tổng hợp Trang 18 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 HƯỚNG DẪN CHẤM Câu Nội dung Điểm
a) Ta có: x  1, 5  x  1, 5 hoặc x  1, 5
+) Với x  1, 5 và y  0, 75 thì 1,5
P  1, 5  4.1, 50, 
75  0, 75  1, 51  3 Câu 1  6  0, 75  5,25 1,5 (5điểm)
+) Với x  1, 5 và y  0, 75 thì
P  1, 5  41, 
5 .0,75 0,75  1,51  3  0,75  6,75 12 5 6 2 .3  4 .81 12 5 12 4 12 4 2 .3  2 .3 2 .3 (3  1) 1 b) A  =    12 6 12 5 12 5 2 6 2 4 5 .3  8 .3 2 .3  2 .3 2 .3 (3  1) 3 2 x y y z x y y z 1
a) 2x  3y; 4y  5z   ;    ;  3 2 5 4 15 10 10 8 x y z
x y z 11 1       15 10 8 15  10  8 33 3 10 8
x  5;y  ;z  3 3 1 Câu 2 (4 điểm)
b) x  1  x  2  x  3  4x (1)
Vì VT  0  4x  0 hay x  0 , do đó: 1
x  1  x  1; x  2  x  2; x  3  x  3 1
(1)  x  1  x  2  x  3  4x x  6 a) f   0  0 1 Câu 3 3  1 1   1 1 1 f ( 0  ,5)  4         0   (3điểm)  2 2 2 2 b) f a      a  3 3 4
a  4a a 0,5
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 18
Toán Họa tổng hợp Trang 19 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7  3  3 f
 (a)   4a a  4a a    0,5  f a
   f aCâu 4 y
x y x.y xy x y x(y  1)  y  x y  1 (1 điểm)
vì x z y y  1  y  1  1y  1  1y  1 , 0,5
do đó y  1  1  y  2 hoặc y  0
Nếu y  2 thì x  2
Nếu y  0 thì x  0 0,5
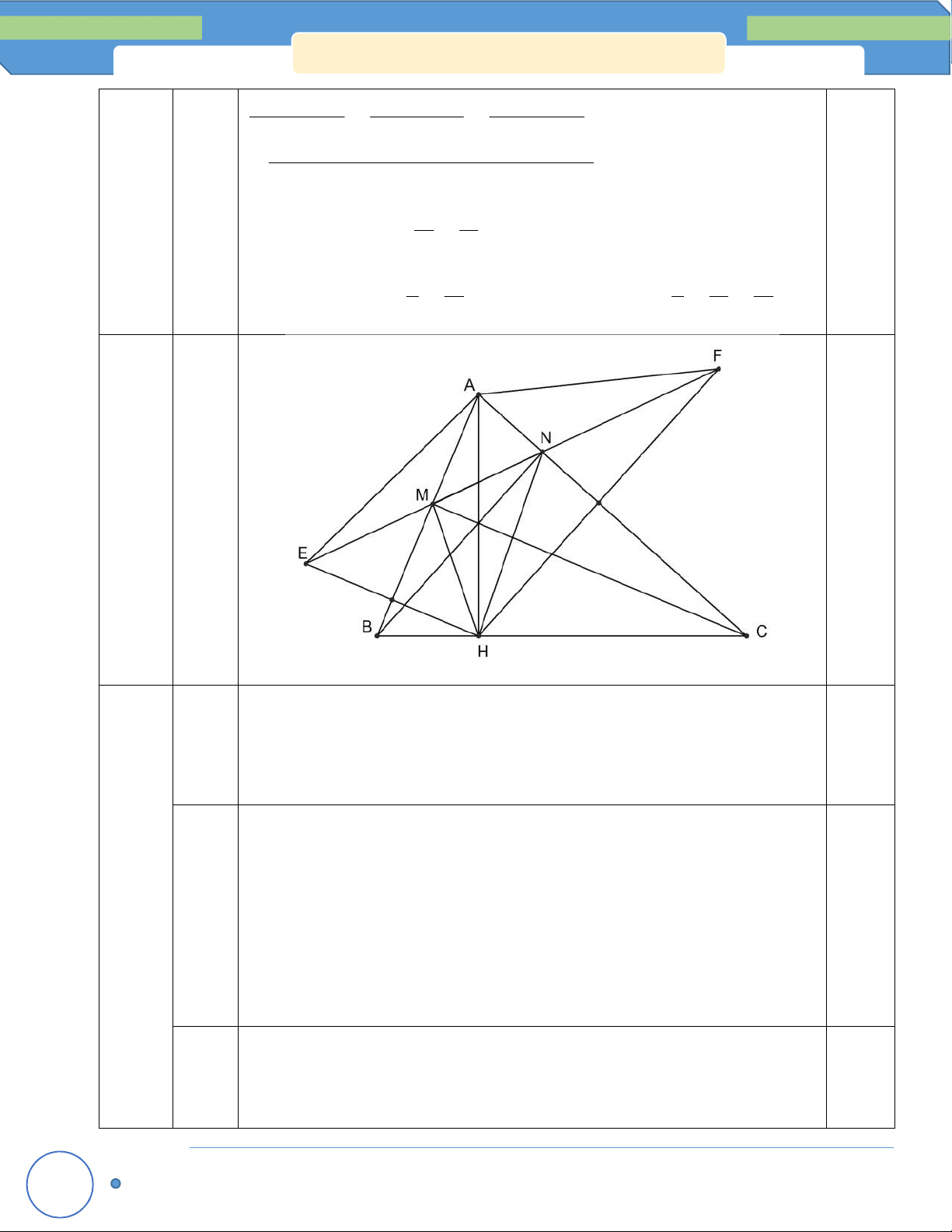
Vậy các cặp số nguyên (x;y) là: (0,0) và (2;2) Câu 5 a) Xét AMC và ABN , có: (6 điểm)
AM AB ( AMB vuông cân) 1,0
AC AN ( ACN vuông cân)   0,5 MAC NAC  ( 90  BAC ) 0,5 Suy ra AMC ABN (c - g - c) Hình vẽ 0,5 đ
b) Gọi I là giao điểm của BN với AC, K là giao điểm của BN với MC. Xét KIC  và AIN  , có:   ANI  KCI ( AMC   AB  N)   1 AIN  KIC (đối đỉnh) 1  
 IKC  NAI  90 , do đó: MC  BN 0,5
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 19
Toán Họa tổng hợp Trang 20 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
c) Kẻ ME  AH tại E, NF AH tại F. Gọi D là giao điểm của MN và AH.   
- Ta có: BAH  MAE  90 (vìMAB  90 )    
Lại có MAE  AME  90 , nên AME  BAH Xét MAE  và A
BH , vuông tại E và H, có:   AME  BAH (chứng minh trên) MAAB Suy ra MAE   AB  H (cạnh huyền-góc nhọn)  ME AH 0,25
- Chứng minh tương tự ta có AF  N  CHA   FN AH 0,25 Xét MED và N
FD , vuông tại E và F, có: ME  NF( AH)       0,25
EMD FND (phụ vớiMDE và FDN , màMDE FDN )
 MED  NFD  BD  ND 0,25
Vậy AH đi qua trung điểm của MN. Câu 6
Vì: 0  a b  1  c  2 nên (1 điểm)
0  a b  1  c  2  c  2  c  2  c  2
 0  4  3c  6 (vì a b c  1 ) 0,5 2 Hay 3c  2   c   . 3 2 5
Vậy giá trị nhỏ nhất của c là:  khi đó a b  0,5 3 3
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 20
Toán Họa tổng hợp Trang 21 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
ĐỀ SỐ 5. ĐỀ HSG CẤP HUYỆN Bài 1: (4 điểm)
Chứng minh rằng với mọi n nguyên dương thì: n 2  n 2 3 2  
 3n  2n chia hết cho 10. Bài 2: (3điểm)
Cho 2 đa thức :P x  2 3 4 2009 2010
 1  x x x x  ...  xx và 1    1 Q x 2 3 4 2009 2010
 1  x x x x  ...  xx  
. Giá trị của biểu thức P   Q    có dạng 2   2 a
biểu diễn hữu tỉ là ; a,b   ; a,b là 2 số nguyên tố cùng nhau. Chứng minh a 5 b Bài 3: (3 điểm)
Cho dãy tỉ số bằng nhau:
2a b c d
a  2b c d
a b  2c d
a b c  2d    a b c d a b b c c d d a
Hãy tìm giá trị của biểu thức: M     c d d a a b b c Bài 4: (4điểm) a b c Cho M    với a, b, c > 0. a b b c c a
a) Chứng minh M  1.
b) Chứng tỏ rằng M không phải là số nguyên. Bài 5: (3,5 điểm)
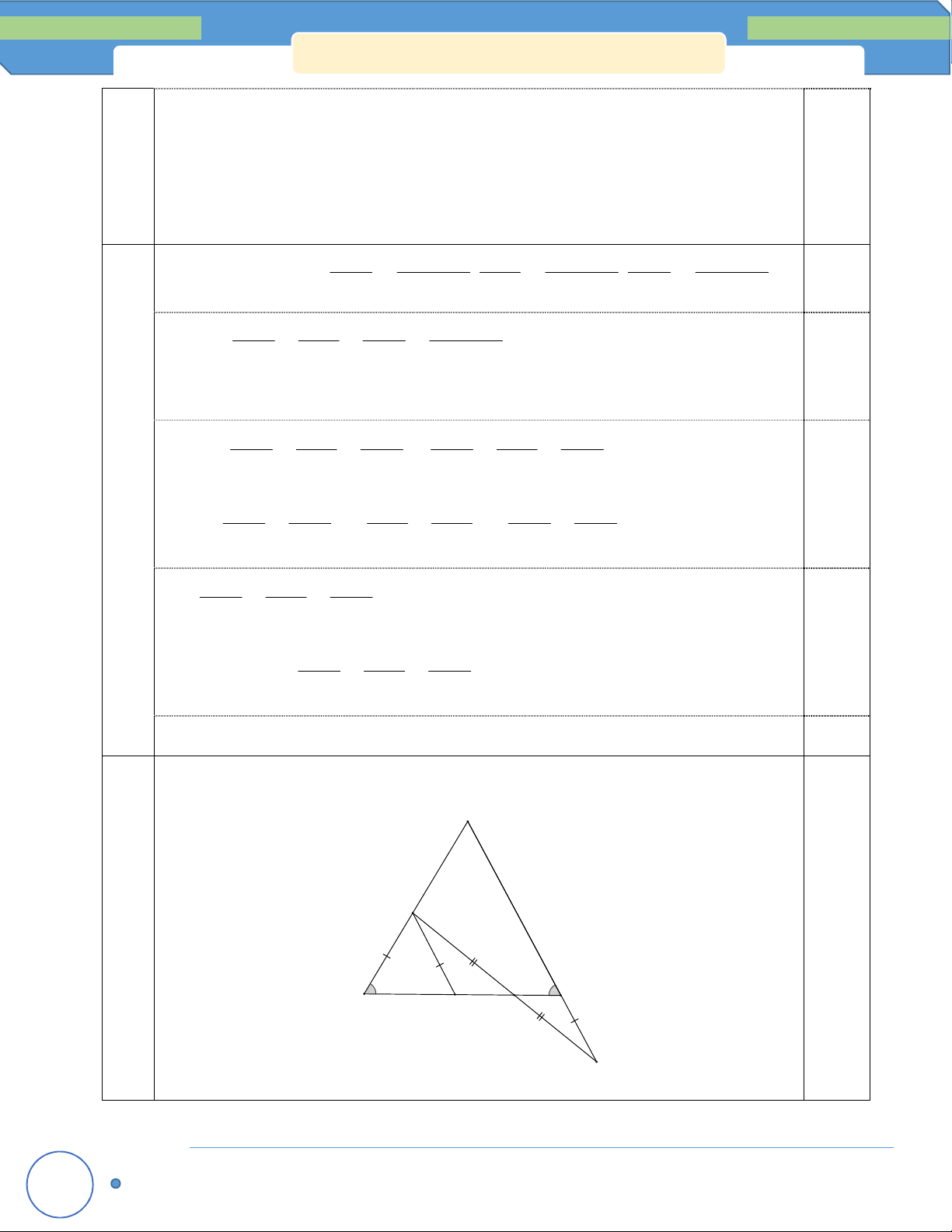
Cho tam giác ABC cân tại A, trên cạnh AB lấy điểm D, trên tia đối của tia CA lấy
điểm E sao cho CE BD . Gọi I là trung điểm của DE. chứng minh ba điểm B, I, C thẳng hàng. Bài 6: (2,5 điểm)  Cho A
BC cân tại A, có A  100 , tia phân giác của góc ABC cắt AC tại D. Chứng minh:
AD BD BC .
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 21
Toán Họa tổng hợp Trang 22 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 HƯỚNG DẪN CHẤM Bài Đáp án Điểm n 2  n 2  n n
n 2 n  n 2 3 2 3 2 3 3 2         2n 1,0đ n n   ểm) 10.3 5.2 1,5đ
Vì n nguyên dương nên 2n 2 5.2n  10 và 10.3n 10 1,0đ 1(4đi Vậy: n 2  n 2 3 2  
 3n  2n 10 0,5đ 3 5 2009 1 1 1 1 1 1            
Đặt A P   Q    2           ...     ( 1) 2   2   2   2   2   2 3 2007 1 1 1      
suy ra 4A  10        ...     (2) 2   2   2 1 2009 8  2012   2009 1   2  1 a Từ ( 1) và ( 2) suy ra 2 3A  8     A      2009 2 3 3.2 b ểm) 3,0đ ( 2 điểm) 2 (3đi Ta thấy: 2012 1006 2  1  4  13 ; 2012 2 – 1 và 2009 2
là 2 số nguyên tố cùng nhau nên 2012 2 – 1  3a. 2012 503 3a  2  1  16  1 . Vì 503
16 có chữ số tận cùng là 6 nên 3a có chữ số
tận cùng là 5 suy ra số này chia hết cho 5. 3,5 là 2 số nguyên tố cùng nhau nên a 5 .
2a b c d
a  2b c d
a b  2c d
a b c  2d Từ    a b c d
2a b c d
a  2b c d =>  1   1= 1,0đ a b ểm)
a b  2c d
a b c  2d  1   1 c d 3 (3đi
a b c d
a b c d
a b c d
a b c d =>    0,5đ a b c d
Nếu a b c d  0 thì a b c d , khi đó: M  1  1  1  1  4 0,5đ
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 22
Toán Họa tổng hợp Trang 23 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
Nếu a b c d  0 thì a b  c d; b c  d a;
c d  a b;d a  b c. 1,0đ
Khi đó: M    1    1   1    1   4. a a b b c c a) Vì , a , b c  0 nên:  ;  ;  1,0đ a b
a b c b c
a b c c a
a b c a b c
a b c => M      1 a b b c c a
a b c 1,0đ
Vậy: M  1 (1) a b c     b c a            b) Mà:  + a b b c
c a  a b b c
a c  ểm) 1,0đ a b   b c   c a        =            = 3 4 (4đi
a b a b b
 c b c   c a
c a   b c a    Vì      > 1 (tương tự câu a) a b b c
a c  0,5đ a b c    Suy ra: M =      2  . (2) a b b c
c a 
Từ (1) và (2) suy ra: 1  M  2 nên M không phải là số nguyên. 0,5đ Học sinh vẽ hình đúng A ểm) D 0,5đ 5 (3,5 đi B C F I E
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 23
Toán Họa tổng hợp Trang 24 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
Kẻ DF//AC (F thuộc BC)  
DFB ACB (2 góc đồng vị) 1,5đ  
Mà ABC ACB (tam giác ABC cân)  
DFB ABC  DBF cân tại D
DB DF , mà DF CE (gt) 0,5đ DF CE
 IDF  IEC (c-g-c) 0,5đ   DIF EIC
Vậy: 3 điểm B, I, C thẳng hàng (vì 3 điểm D, I, E thẳng hàng) 0,5đ HS vẽ hình đúng A D 0,5đ B C E F
Trên cạnh BC lấy 2 điểm E,F sao cho: ểm)
BE BA và BF BD . 0,5đ 6 (2,5 đi
HS chứng minh được: AD DE
HS chứng minh được: DFE cân tại D 0,5đ
Suy ra: DE DF
HS chứng minh được: DFC  cân tại F
Suy ra:DF FC . 1,0đ
Suy ra: DE FC
Suy ra: AD BD BC.
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 24
Toán Họa tổng hợp Trang 25 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
ĐỀ SỐ 6. ĐỀ HSG CẤP HUYỆN Bài 1 (4 điểm): a) So sánh hai số:  39 – 5 và  91 – 2 b) Chứng minh rằng: Số n 2  2n 1 A 11 12   
chia hết cho133 , với mọi n N Bài 2 (4 điểm):
a) Tìm tất cả các cặp số x; y thỏa mãn:  x y  2012 2013 2 7  x  3  0
b) Tìm số tự nhiên n và chữ số a biết rằng: 1  2  3  . . .  n aaa 1
Bài 3 (4 điểm): Ba lớp 7 ở trường K có tất cả 147 học sinh. Nếu đưa số học sinh của lớp 3 1 1
7A , số học sinh của lớp 7A và số học sinh của lớp 7A đi thi học sinh giỏi cấp huyện 1 4 2 5 3
thì số học sinh còn lại của ba lớp bằng nhau. Tính tổng số học sinh của mỗi lớp 7 ở trường K.   
Bài 4 (4 điểm): Cho tam giác ABC có A  3B  6C .
a) Tính số đo các góc của tam giác ABC.
b) Kẻ AD vuông góc với BC (D thuộc BC). Chứng minh: AD BD CD.
Bài 5 (4 điểm): Cho tam giác ABC cân ở A. Trên cạnh AB lấy điểm M, trên tia đối của tia
CA lấy điểm N sao cho AM AN  2AB.
a) Chứng minh rằng: BM CN
b) Chứng minh rằng: BC đi qua trung điểm của đoạn thẳng MN.
c) Đường trung trực của MN và tia phân giác của góc BAC cắt nhau tại K. Chứng minh rằng: KC  AC
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 25
Toán Họa tổng hợp Trang 26 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 HƯỚNG DẪN CHẤM Bài Đáp án Điểm 39 91
a) So sánh hai số:  – 5 và –  2 2,0đ 0,75đ Ta có:      13 39 39 3 13 ( 5) 5 5  125 0,75đ      13 91 91 7 13 ( 2) 2 2  128 Ta thấy: 13 13 13 13 39 91
125  128  125  128  (5)  (2) 0,5đ b) Chứng minh: Số n2 2n   1 A 11 12
chia hết cho 133, với mọi n   2,0đ 1 n Ta có: n 2 2n 1 2 n  2 11 12 11 11 12 12  121.11n 12.144n A           4 điểm (133 12) 11n 12.144n 133.11n 12.11n 12.144n        1,0đ 133.11n 12.144n 11n    
Ta thấy: 133.11n 133 0,5đ 144n 11n (144 11) 133 12.144n 11n      133
Do đó suy ra: 133.11n 12.144n 11n    chia hết cho 133 0,5đ Vậy: số n 2  2n 1 A 11 12   
chia hết cho 133, với mọi n  
a) Tìm tất cả các cặp số (x; y): 2,0đ
Ta có: 2012 là số tự nhiên chẵn 2012  (2x  y  7)  0 0,5đ 2013
và x  3  0  x  3  0 2 4
Do đó, từ  x y  2012 2013 2 7  x  3  0 điểm 0,5đ 2013
suy ra:  x y  2012 2 – 7  0 và x  3  0
 2x – y  7  0 (1) và x – 3  0 (2) 0,5đ Từ (2)  x  3 0,5đ
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 26
Toán Họa tổng hợp Trang 27 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
Từ (1)  y  2x  7  2.3  7  13
Vậy cặp số x; y cần tìm là 3; 13
b) Tìm số tự nhiên n và chữ số a 2,0đ n n   1
Ta có: 1  2  3  . . .  n
và aaa a.111  a.3.37 0,5đ 2
Do đó, từ 1  2  3  . . .  n aaa n n   1  2.3.37.a
n n  
1 chia hết cho số nguyên tố 37 0,5đ
n hoặc n  1 chia hết cho 37 (1) n(n  1) Mặt khác:
aaa  999  n(n  1)  1998  n  45 (2) 2 0,5đ
Từ (1) và (2) suy ra hoặc n  37 , hoặc n  1  37 37.38
- Với n  37 thì aaa
 703 (không thỏa mãn) 2 36.37
- Với n  1  37 thì aaa   666 (thỏa mãn) 2 0,5đ
Vậy n  36 và a  6.
Tính tổng số học sinh của mỗi lớp 7 ở trường K. 4,0đ
Gọi tổng số học sinh của 7A , 7A , 7A lần lượt là a, b, c (a,b,cN*) 1 2 3 1 1 1 1,0đ
Theo bài ra ta có : a a b b c c (*) và a b c  147 3 4 5 3 2a 3b 4c 12a 12b 12c a b c 4 Từ (*)          1,0đ 3 4 5 18 16 15 18 16 15 điểm
Áp dụng tính chất dãy tỷ số bằng nhau ta có : a b c
a b c 147 1,0đ   =   3 . 18 16 15 18  16  15 49
Suy ra : a  54,b  48,c  45 1,0đ
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 27
Toán Họa tổng hợp Trang 28 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
Vậy tổng số học sinh của 7A1, 7A2, 7A3 lần lượt là 54, 48 và 45.
a) Tính số đo các góc của ABC : 2,0đ    ˆ ˆ ˆ ˆ ˆ ˆ A B C
A B C 180
Từ A  3B  6C       20 1,0đ 6 2 1 6  2  1 9 ˆ
A  6.20  120 ˆ
B  2.20  40 ˆ C  1.20  20 1,0đ Vậy: ˆ ˆ ˆ A  120 ;  B  40 ;  C  20
b) Chứng minh AD < BD < CD. 2,0đ 4 - Trong ACD có 4     ADC  90 ;
C  20  A  70 A  50 điểm 2 1 1,0đ - Xét  ADB có ˆ ˆ
B  40 A  50  AD BD (1) 1 - Xét  ABC có 0 0 2 2 ˆ ˆ B  40 C   20
AB AC AB AC (*)
- Áp dụng định lý Pytago cho hai tam giác vuông ADB và ADC có: 2 2 2 AB  AD  BD và 2 2 2 AC  AD  CD 1,0đ Do đó, từ (*) 2 2 2 2  AD  BD  AD  CD 2 2
 BD  CD  BD  CD (2)
Từ (1) và (2)  AD  BD  CD
a) Chứng minh rằng: BM CN 1,0đ Theo giả thiết, ta có: 5
2AB  AB  AB  AB  AM  BM 4
AM  AN  AM  AC  CN điểm A
BC cân ở A  AB AC
Do đó, từ AM  AN  2AB BM CN
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 28
Toán Họa tổng hợp Trang 29 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
b) Chứng minh rằng: BC đi qua trung điểm của đoạn thẳng MN. 1,5đ
Qua M kẻ ME // AC (E  BC) 0,75đ
 ABC cân ở A  BM
E cân ở M  EM  BM  CN  ME  I  NCI 
(g-c-g)  IM IN 0,75đ
Vậy: BC đi qua trung điểm của MN.
c) Chứng minh rằng: KC  AN 1,5đ
+ K thuộc đường trung trực của MN  KM KN (1)   + AB  K  ACK 
(c-g-c)  KB KC (2); ABK ACK (*) 0,5đ
+ Kết quả câu c/m câu a) BM CN (3)   + Từ (1), (2) và (3)  B  MK  CNK 
(c-c-c)  ABK NCK (**) 0,5đ  + Từ (*) và (**)   180 ACK NCK   90  KC  AN 0,5đ 2
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 29
Toán Họa tổng hợp Trang 30 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
ĐỀ SỐ 7. ĐỀ HSG CẤP HUYỆN
Bài 1: (6 điểm) 2
a) Tìm x, biết x  1  ; 3 2 2x  3x  1 2
b) Tính giá trị của biểu thức sau: A  với x  1  3x  2 3
Bài 2: (3 điểm)
a) Tìm chữ số tận cùng của A biết n 2 n 2 3 – 2 3n – 2n A     biết * n   x  3
b) Tìm các giá trị nguyên của x để nhận giá trị nguyên. x  2
Bài 3: (4 điểm)
Cho đa thức f x  xác định với mọi x thỏa mãn: x f x     2 . 2 x –  9 .f x. a) Tính f 5.
b) Chứng minh rằng f(x) có ít nhất 3 nghiệm.
Bài 4: (6 điểm)
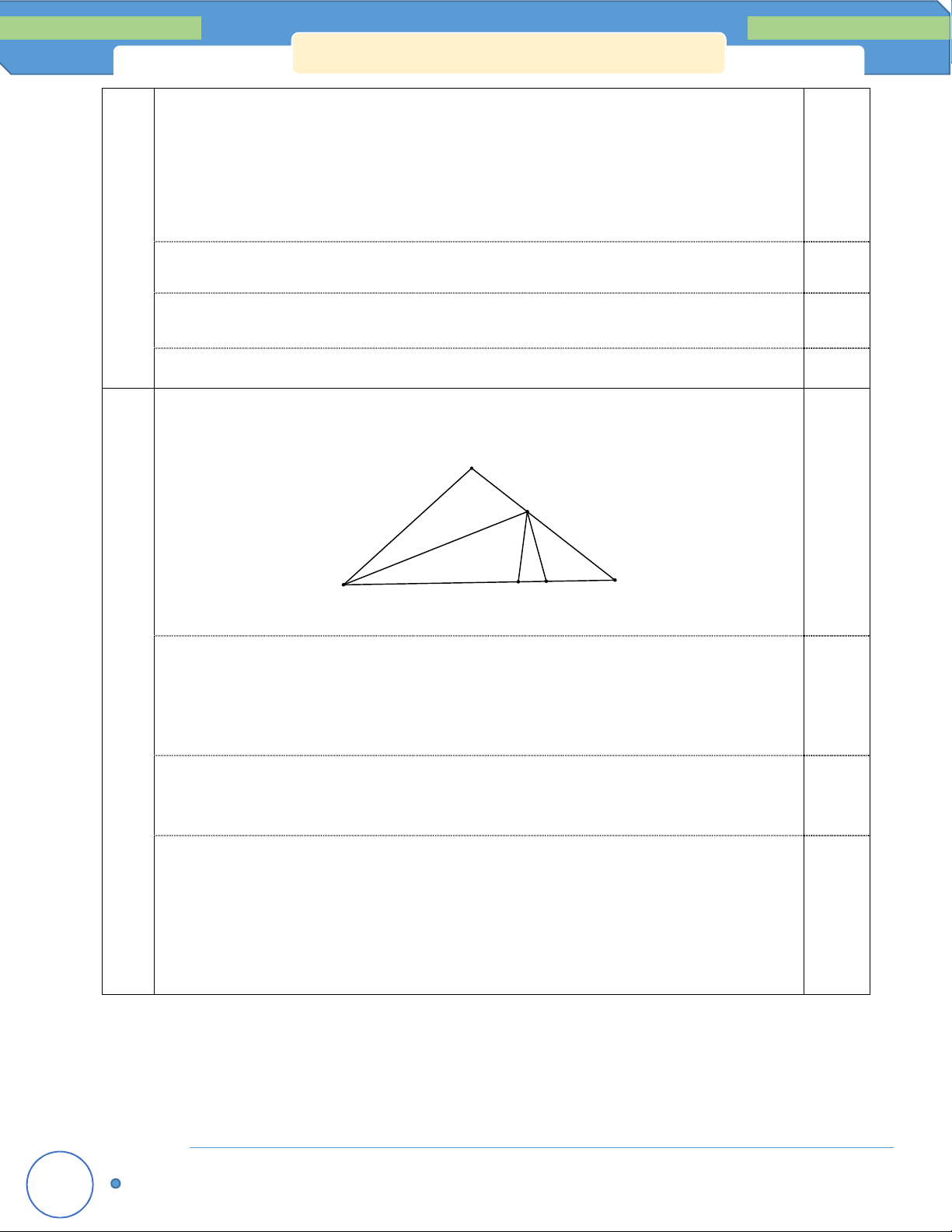
Cho tam giác ABC, trung tuyến AM. Trên nửa mặt phẳng chứa đỉnh C bờ là đường thẳng
AB dựng đoạn AE vuông góc với AB và AE AB. Trên nửa mặt phẳng chứa đỉnh B bờ là
đường thẳng AC dựng đoạn AF vuông góc với AC vàAF AC . Chứng minh rằng: a) FB EC b) EF  2AM c) AM EF.
Bài 5: (1 điểm) Cho , a , b ,
c d là các số dương. Tìm giá trị nhỏ nhất của biểu thức:
A x a x b x c x d
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 30
Toán Họa tổng hợp Trang 31 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 HƯỚNG DẪN CHẤM Bài Hướng dẫn chấm Điểm  2  5 x  1   2 x    a) Ta có 3 3 x  1      3  2  1 4.0đ x  1   x     3  3 1 5 14
(6đ) b) Từ câu a) Với x  thay vào A ta được A  3 27 1 2 2.0đ Với x
thay vào A ta được A  3 9 a) n 2 n 2 3 – 2 3n – 2n A     9.3n
3n – 4.2n – 2n
9 1.3n – 4  1.2n 1 .03n – 5.2n      1.5đ
10.3n 10 và 5.2n 10 (do *
n   hay n  1 ) A10 2
Chứng minh A chia hết cho 10 suy ra chữ số tận cùng của A là 0 (3đ) b) Ta có: x  3 x  2  5 5   1 
Z x  2 U(5)   1  ;  5 1.5đ x  2 x  2 x  2  x  1;3;3;7
a) Ta có với x  3  f 5  0 2.0đ
b) x  0  f 0  0  x  0 là một nghiệm 2.0đ 3
x  3  f 5  0  x  5 là một nghiệm (4đ)
x  3  f  
1  0  x  1 là một nghiệm
Vậy f(x) có ít nhất là 3 nghiệm. a) Chứng minh ABF A
EC(cgc)  FB EC 3.0đ A
b) Trên tia đối của tia MA lấy K sao cho E
AK  2AM . Ta có ABM KCM CK//AB I F     0
ACK CAB EAF CAB  180 C B M   4
ACK EAF 1.5đ (6đ)
EAF và KCA có AE AB CK; K AF AC   ACK EAF (gt);
 EAF KC
A (cgc)  EF AK  2AM.   c) Từ EAF KC
A CAK AFE     0
AFE FAK CAK FAK  90 AK EF 1.5đ
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 31
Toán Họa tổng hợp Trang 32 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
Không mất tính tổng quát, giả sửa b c d
Áp dụng BĐT a b a b , dấu bằng xảy ra  ab  0 ta có:
x a x d x a d x x a d x d a (1) 5 1.0đ
x b x c x b c x x b c x c b (2) (1đ)
Suy ra A  c  d  a  b Dấu “=” xảy ra khi và chỉ khi dấu “=” ở (1) và (2)
xảy ra  x – ad – x   0 và (x b)(c x)  0  a x d và b  x  c
Do đó min A c d a b b x c
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 32
Toán Họa tổng hợp Trang 33 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
ĐỀ SỐ 8. ĐỀ HSG CẤP HUYỆN
Bài 1: ( 2,0 điểm) 4  x 4 a. Tìm x, y biết:
 và x y  22 7  y 7 x y y z
2x  3y  4z b. Cho
 và  . Tính M  3 4 5 6
3x  4y  5z
Bài 2: ( 2,0 điểm) Thực hiện tính: a. 2010 2009 2008 S  2  2  2 ...  2  1 1 1 1 1
b. P  1  1  2  1  2  3  1  2  3  4  ... 
1 2  3 ... 16 2 3 4 16
Bài 3: ( 2,0 điểm) Tìm x biết: 1 2 3 4 5 30 31 a. . . . . ... . 2x  4 6 8 10 12 62 64 5 5 5 5 5 5 5 5 5 5
4  4  4  4 6  6  6  6  6  6 b. .  2x 5 5 5 5 5 3  3  3 2  2
Bài 4: ( 4,0 điểm)   
Cho tam giác ABC có B  90 và B  2C . Kẻ đường cao AH. Trên tia đối của tia BA lấy
điểm E sao cho BE BH . Đường thẳng HE cắt AC tại D.  
a. Chứng minh BEH ACB.
b. Chứng minh DH DC  . DA
c. Lấy B’ sao cho H là trung điểm của BB ' . Chứng minh AB 'C cân.
d. Chứng minh AE HC .
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 33
Toán Họa tổng hợp Trang 34 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 HƯỚNG DẪN CHẤM
Bài 1: (2,0 điểm)
 28  7x  28  4y 0,25 x y x y    0,25 4 7 4  7 x y 22   
 2  x  8;y  14 0,25 4 7 11 x y x y y z y z x y z    ;       (1) 0,25 3 4 15 20 5 6 20 24 15 20 24 2x 3y 4z
2x  3y  4z (1)     0,25 30 60 96 30  60  96 3x 4y 5z
3x  4y  5z (1)     0,25 45 80 120 45  80  120
2x  3y  4z
3x  4y  5z 2x 3x  :  : 0,25
30  60  96 45  80  120 30 45
2x  3y  4z 245
2x  3y  4z 186  .  1  M   0,25 186
3x  4y  5z
3x  4y  5z 245
Bài 2: ( 2,0 điểm) Thực hiện tính: 2011 2010 2009 2 2S  2  2  2 ...  2  2 0,25 2011 2010 2010 2009 2009 2 2 2S S  2  2  2  2  2
 ...  2  2  2  2  1 0,25 2011 2010 S  2  2.2  1 0,25 2011 2011 S  2  2  1  1 0,25
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 34
Toán Họa tổng hợp Trang 35 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 1 2.3 1 3.4 1 4.5 1 16.17 P  1  .  .   ...  0,25 2 2 3 2 4 2 16 2 2 3 4 5 17   .    ...  0,25 2 2 2 2 2 1
 1  2  3  ...  17   1 0,25 2 1 17.18       1  76 2  0,25  2 
Bài 3: ( 2,0 điểm) 1 2 3 4 5 30 31 . . . . ... . 2x  0,25 6 2.2 2.3 2.4 2.5 2.6 2.31 2 1.2.3.4...30.31 2x  0,25 30 6 1.2.3.4...30.31.2 .2 1 2x  0,25 36 2 x  36 0,25 5 5 4.4 6.6 . 2x  0,25 5 5 3.3 2.2 6 6 4 6 . 2x  0,25 6 6 3 2 6 6 6 4     .     2x  0,25 3   2 12
2  2x x  12 0,25
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 35
Toán Họa tổng hợp Trang 36 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
Bài 4: ( 4,0 điểm)
Câu a: 0,75 điểm Hình vẽ: BEH   
cân tại B nên E H A 1 0,25    
ABC E H  2E 0,25 1 1     D
ABC  2C BEH ACB 0,25
Câu b: 1,25 điểm 2 B C
Chứng tỏ được DHC  cân tại D 1 H B' 0,50
nênDC DH . DAH   
có: DAH  90 C 0,25 E   
DHA  90  H  90 C 0,25 2  DAH
cân tại D nên DA DH. 0,25
Câu c: 1,0 điểm
Câu d: 1,0 điểm ABB '   
cân tại A nên B '  B  2C 0,25 AB AB '  CB ' 0,25    B '    
BE BH B H 1
A C nên 2C A C 0,50 ' 0,25 1    C A    A
B 'C cân tại B’ Có: AE AB BE 1
0,25 HC CB ' B ' H 0,50  AE HC
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 36
Toán Họa tổng hợp Trang 37 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
ĐỀ SỐ 9. ĐỀ HSG CẤP HUYỆN
I. Phần trắc nghiệm khách quan: (6 điểm)
Câu 1: Giá trị của x trong biểu thức 2
( x  1)  0,25 là: 9 1 1 9 9 1 9 1 A. ; . B.  ; . C. ; . D.  ; . 4 4 4 4 4 4 4 4 
Câu 2: Cho xOy  50 , điểm A nằm trên Oy. Qua A vẽ tia Am . Để Am song song với Ox 
thì số đo của OAm là: A. 50 . B.130 . C. 50 và 130 D. 80 .
Câu 3: Cho hàm số y f x  xác định với mọix  1 . Biết f n  n  
1 .f n –  1 và f  
1  1 . Giá trị của f(4) là: A. 3. B. 5. C. 6. D. 1. 
Câu 4: Cho tam giác ABC vuông tại B, AB  6 , A  30 . Phân giác góc C cắt AB tại D.
Khi đó độ dài đoạn thẳng BD và AD lần lượt là: A. 2; 4 . B. 3; 3. C. 4; 2. D. 1; 5. Câu 5: Cho 2m a   4 . Kết quả của 6 2 m a  5 là: A.123 . B.133 . C. 123 D. 128 .  
Câu 6: Cho tam giác DEF có E=F. Tia phân giác của góc D cắt EF tại I . Ta có:   A. DIE   D  IF . B. DE  DF, IDE  IDF .
C.IE IF; DI EF D Cả A, B,C đều đúng
Câu 7: Biết a b  9 . Kết quả của phép tính 0,a(b)  0, ( b a) là: A. 2. B. 1. C. 0,5. D. 1,5 .
Câu 8: Choa b2 6
a.b  36 . Giá trị lớn nhất của x a.b là: A. 6 B.  6 C. 7. D. 5.
Câu 9: Cho tam giác ABC, hai đường trung tuyến BM, CN. Biết AC AB . Khi đó độ dài
hai đoạn thẳng BM và CN là: A. BM  CN B. BM  CN C. BM  CN D. BM CN
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 37
Toán Họa tổng hợp Trang 38 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
Câu 10: Điểm thuộc đồ thị hàm số y   2x là : A.M 1;2 . B.N 1;2  . C.P 0 ;2 . D. Q 1; 2
Câu 11: Biết rằng lãi suất hàng năm của tiền gửi tiết kiệm theo mức 5% năm là một hàm số
theo số tiền gửi:i  0, 005p . Nếu tiền gửi là 175000 thì tiền lãi sẽ là: A. 8850 đ B. 8750 đ C. 7850 đ D.7750 đ 
Câu 12: Cho tam giác ABC cân tại A A  20 . Trên cạnh AB lấy điểm D sao choAD BC . Số đo của góc BDC là: A. 50 B. 70 C. 30 D. 80
II. Phần tự luận (14 điểm) Câu 1.(3 điểm)
a, Chứng tỏ rằng: M   2017 2016 2 75. 4  4  ...  4  4   1  25 chia hết cho 2 10
b, Cho tích a.b là số chính phương vàa,b  1 . Chứng minh rằng a và b đều là số chính phương. Câu 2.(4 điểm)
2.1 Cho đa thức A  2x.(x  3)  x(x  7)  5(x  403)
Tính giá trị của A khix  4 . Tìm x để A  2015
2.2 Học sinh khối 7 của một trường gồm 3 lớp tham gia trồng cây. Lớp 7A trồng toàn bộ
32, 5% số cây. Biết số cây lớp 7B và 7C trồng được theo tỉ lệ 1,5 và 1,2. Hỏi số cây cả 3 lớp
trồng được là bao nhiêu, biết số cây của lớp 7A trồng được ít hơn số cây của lớp 7B trồng được là 120 cây. Câu 3.(5 điểm)
1. Cho đoạn thẳng AB. Trên cùng một nửa mặt phẳng có bờ là đường thẳng AB vẽ hai tia
Ax và By lần lượt vuông góc với AB tại A và B. Gọi O là trung điểm của đoạn thẳng AB. Trên 
tia Ax lấy điểm C và trên tia By lấy điểm D sao choCOD  90 .
a) Chứng minh rằng: AC BD CD. 2 AB
b) Chứng minh rằng: AC.BD  4
2. Cho tam giác nhọn ABC, trực tâm H. Chứng minh rằng:
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 38
Toán Họa tổng hợp Trang 39 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 2
HA HB HC  (AB AC BC ) 3 Câu 4.(2 điểm)
Tìm giá trị nhỏ nhất của A, biết : A  7x  5y  2z  3x xy yz zx  2000
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 39
Toán Họa tổng hợp Trang 40 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 HƯỚNG DẪN CHẤM
I. Phần trắc nghiệm khách quan: (6 điểm) Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đ. án A C C A B D B A C D B C
II. Phần tự luận (14 điểm) Câu Nội dung chính Điểm 1(4   2017 2016 2 M 75. 4  4    4  4   1  25 điểm) 0,25    2017 2016 2 25.(4 1) 4  4  4  4   1  25 0,25    2017 2016 2   2017 2016 2 25 4 4 4 4 4 1 4 4 4 4 1               25      2018 2017 2        2017 2016 2 25. 4 4 4 4 25 4  4   4  4   1  25 0,25 0,25 2018  25.4  25  25 0,25 2018 2017 2017  25.4  25.4.4  100.4 100 0,25 Vậy 2 M10 b, Đặt 2
a.b c (1) 0,25
Gọi a,c  d nên ad, cd
Hay a m.d và c n.d với m,n  1 0,25 Thay vào (1) ta được 2 2
m.d.b n .d 0,5 2 2
m b n .d bn vì a,b  1   , b d 0,5 Và 2 2 n b
  b n Thay vào (1) ta có 2
a d  đpcm 2(4 1. Ta có 2 2
A  2x  6x x  7x  5x  2015 2
x  4x  2015 điểm)
a, Với x  4 ta được A  2015 1
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 40
Toán Họa tổng hợp Trang 41 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 x  0 b, 2 A 2015 x 4x 0 x(x 4) 0           x  4  1
2. Gọi số cây ba lớp trồng lần lượt là a, b, c ( cây, a,b,c N*)
Theo đề bài ta có b : c  1, 5 : 1, 2 và b – a  120 1
a  32, 5%a b c
Vậy cả 3 lớp trồng được số cây là 2400 cây 1 3(5 x điểm) y C D A B O 0,25 E 0,25
A, Vẽ tia CO cắt tia đối của tia By tại điểm E. 0,25 Chứng minh AOC BOE
g c g  AC BE;CO EO 0,25 Chứng minh D
OC DOE c g c  CD ED
Mà ED EB BD AC BD . 0,25
Từ đó : CD AC BD (đpcm)
b, Áp dụng định lí Pytago vào các tam giác vuông BOE và BOD ta có:  2 2 2 OE   OB EB  2 2 2 2 2 0,5 
OE OD  2OB EB DB 2 2 2 OD   OB DB 
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 41
Toán Họa tổng hợp Trang 42 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 Mà 2 2 2
OE OD DE ; Nên 2 2 2 2
DE  2OB EB DB 2
 2OB EB.DE BD  DB.(DE BE) 0,25 2
 2OB EB.DE EB.BD DB.DE DB.BE 2
 2OB  EB.DE DB.DE 2BD.BE 2
OB DE EB DB 2 2 2 .
 2BD.BE  2OB DE  2BD.BE 0,25 Suy ra 2 2
2OB  2BD.BE  0  BD.BE OB AB
Mà BE AC ;OB  . 2 2 2 AB    AB
Vậy AC .BD       (đpcm)  2  4 2.
Qua H kẻ đường thẳng song song với AB cắt AC tại D, kẻ đường thẳng
song song với AC cắt AB tại E 0,25 Ta có AHD   HAE  (g –c-g)
AD HE;AE HD 0,25 AHD 
có HA  HD  AD nên HA  AE  AD (1) 0,25 Từ đó HE  BH H
BE vuông nên HB BE (2) 0,25
Tương tự ta có HC DC (3)
Từ 1,2,3 ta có HA  HB  HC  AB  AC (4) 0,25
Tương tự HA  HB  HC  AB  BC (5)
HA  HB  HC  BC  AC (6) 2
Từ đó suy ra HA HB HC  AB AC BC  đpcm 3
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 42
Toán Họa tổng hợp Trang 43 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 4
Ta có 7x  5y  0 ; 2z  3x  0 và xy yz zx  2000  0 (2
Nên A  7x  5y  2z  3x xy yz zx  2000  0 điểm) 1 Mà A = 0 khi và chỉ khi
7x  5y  2z  3x xy yz zx  2000  0 x y
Có: 7x  5y  0  7x  5y   5 7 x z
2z  3x  0   2 3
xy yz zx  2000  0  xy yz zx  2000 x
  20;y  28;z  30 Từ đó tìm được  x   20;y  28  ;z  30   1
A  0 , mà A  0  (x, ,
y z)  (20;28; 30) hoặc (x, ,
y z)  (20;28;30)
Vậy min A  0  (x, ,
y z)  (20;28; 30) hoặc (x, ,
y z)  (20;28;30)
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 43
Toán Họa tổng hợp Trang 44 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
ĐỀ SỐ 10. ĐỀ HSG CẤP HUYỆN
Bài 1: Thực hiện phép tính (6 điểm). 1   1   1     3 2 5    9 45 1 1 1   15 9 20 9       5.4 .9  4.3 .8 a) :     . ; b)
         ; c) . 4 3 9 4 19 2 3   4       10 19 29 6     5.2 .6  7.2 .27   Bài 2: (6 điểm)
a) Tìm x, biết: 2x   1 – 32x  
2 – 42x  3  16 ; 1 21
b) Tìm x, biết: 3 : 2x  1  2 22 2x y 3y  2z c) Tìm x, y, z biết: 
và x z  2y. 5 15 a c
Bài 3: (1,5 điểm) Cho tỉ lệ thức  . b d
Chứng minh rằng : a  2cb d  a cb  2d.
Bài 4: (4,5 điểm) Cho tam giác ABC vuông tại A; K là trung điểm của BC. Trên tia đối của
tia KA lấy D , sao cho KD  . KA
a. Chứng minh: CD//AB.
b. Gọi H là trung điểm của AC; BH cắt AD tại M; DH cắt BC tại N . Chứng minh rằng: AB  H  CDH  c. Chứng minh: HMN cân.
Bài 5: (2 điểm): Chứng minh rằng số có dạng abcabc luôn chia hết cho 11.
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 44
Toán Họa tổng hợp Trang 45 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 HƯỚNG DẪN CHẤM
Bài 1: Thực hiện phép tính (6 điểm). Giải: 3 2 5   9 a) :     . 4 3 9 4 3 2 5   9 3 1 9 0,75đ :      :  4 3 9 4 4 9 4 3 9 9 36 0,75đ = .    9 4 1 4 4 1  1  1    45  1  1  1   b)         19  2  3  4        1   1     1   45 1 1 1           45 1
                 19 2 3   4    19 1 1     1,0đ    2 1  4 3 45 26 19 =    1 1,0đ 19 19 19 15 9 20 9 5.4 .9  4.3 .8 c) 10 19 29 6 5.2 .6  7.2 .27 15 9 20 9 5.4 .9  4.3 .8 2.15 2.9 2 20 3.9 5.2 .3  2 .3 .2 = 01đ 10 19 29 6 5.2 .6  7.2 .27 10 19 19 29 3.6 5.2 .2 .3  7.2 .3 29 18 2 .3  2 5.2  3   01đ 29 18 2 .3 5.3  7 10  9 1 =   0,5đ 15  7 8
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 45
Toán Họa tổng hợp Trang 46 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 Bài 2: (6 điểm) Giải:
a. Tìm x, biết: 2(x-1)-3(2 x+2)-4(2 x+3)=16
2x  2  6x  6  8x  12  16 0,25đ 12x – 20  16 0,25đ 12x  36 0,50đ x  3 0,50đ 1 21
b. Tìm x, biết: 3 : 2x  1  2 22 1 1 Nếu x
. Ta có: (vì nếu x  thì2x – 1  0 ) 0,25đ 2 2 1 21 3 : 2x  1  2 22 7 21 : (2x  1)  0,25đ 2 22 7 21 7 22 11 2x  1  :    0,25đ 2 22 2 21 3 11 14 2x   1  0,25đ 3 3 14 7 1 x  : 2   (thỏa mãn) 0,25đ 3 3 2 1 Nếu x  . Ta có: 0,25đ 2 1 21 3 : 2x  1  2 22 7 21 : (1  2x)  0,25đ 2 22 11 8 2  x   1  0,25đ 3 3
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 46
Toán Họa tổng hợp Trang 47 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 8 4 1 x  : ( 2  )    0,25đ 3 3 2 7 4 Vậy x  hoặc x   0,25đ 3 3 2x y 3y  2z c. Tìm x, y, z biết : 
và x z  2y 5 15
Từ x z  2y ta có:
x – 2y z  0 hay 2x – 4y  2z  0 hay 2x – y – 3y  2z  0 0,25đ
hay 2x – y  3y – 2z 0,25đ 2x y 3y  2z Vậy nếu: 
thì: 2x – y  3y – 2z  0 (vì 5  15 ). 0,25đ 5 15 1
Từ 2x – y  0 suy ra: x y 0,25đ 2 1
Từ 3y – 2z  0 và x z  2y x z y  2z  0 hay y y – z  0 0,25đ 2 3 2 1
hay y z  0 hay y
z suy ra: x z 0,25đ 2 3 3  1 2   
Vậy các giá trị x, y, z cần tìm là: x
  z; y z; z     3 3    0,5đ  1 3    hoặc x
  y;y  ;  z y
x   y x z x  hoặc { ; 2 ; 3 } | 2 2    a c
Bài 3: (1,5 điểm) Cho tỉ lệ thức  . b d
Chứng minh rằng : a  2cb d  a cb  2d Ta có:
a  2cb d  a cb  2d
ab ad  2cb  2cd ab  2ad cb  2cd 0,75đ a c
cb ad suy ra:  0,75đ b d
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 47
Toán Họa tổng hợp Trang 48 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
Bài 4: (4,5 điểm) Cho tam giác ABC vuông tại A; K là trung điểm của BC. Trên tia đối của
tia KA lấy D , sao cho KD  . KA
a. Chứng minh: CD//AB.
b. Gọi H là trung điểm của AC; BH cắt AD tại M; DH cắt BC tại N . Chứng minh rằng: AB  H  CDH  c. Chứng minh: HMN cân. Giải: B D K M N A H C
a/ Chứng minh CD song song với AB. Xét 2 tam giác ABK và DCK  có: 0,25đ BK CK (gt)  
BKA CKD (đối đỉnh) 0,25đ AK DK (gt) 0,25đ  ABK   D  CK (c-g-c) 0,25đ       
DCK DBK ; mà ABC ACB  90  ACD ACB BCD  90 0,25đ  
ACD  90  BAC AB//CD ( AB  AC và CD  AC ). 0,25đ
b. Chứng minh rằng: ABH CDH
Xét 2 tam giác vuông: ABH và CDH có: 0,25đ
BA CD (do ABK DCK  ) AH CH (gt) 0,25đ
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 48
Toán Họa tổng hợp Trang 49 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 ABH CDH (c-g-c) 0,50đ
c. Chứng minh: HMN cân.
Xét 2 tam giác vuông: ABC và C
DA có: 0,25đ AB CD  
; ACD  90  BAC ; AC cạnh chung:  ABC CDA  (c-g-c)  
ACB CAD 0,25đ  
mà: AH CH (gt) và MHA NHC (vì AB  H  CDH  ) 0,50đ  AM  H  CNH  (g-c-g) 0,50đ
MH NH . Vậy HMN cân tại H 0,50đ
Bài 5: (2 điểm): Chứng minh rằng số có dạng abcabc luôn chia hết cho 11. Giải: Ta có: 5 4 3 2
abcabc a.10  .10 b  .10 ca.10  .10 bc 0,25đ 2 3 3 3  a.10 10   1  .10 b
10  1 .c10  1 0,50đ 3 2  10   1 a.10  b.10   c 0,50đ 2 2
 (1000  1)a 10  b.10  
c  1001a.10  b.10   c 0,25đ 2
 11.91a.10  b.10   c 11 0,25đ Vậy abcabc11 0,25đ Hết
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 49
Toán Họa tổng hợp Trang 50 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
ĐỀ SỐ 11. ĐỀ HSG CẤP HUYỆN
Câu 1 (2,5 điểm). Tính:
a) 7,3.10,5+7,3.15+2,7.10,5+15.2,7 b)  9 10 10     19 3 9 4 6 2 12 : 2  27  15.4 .9 
Câu 2 (5 điểm).
So sánh A và B trong mỗi trường hợp sau: 2012 1999 a) A  ; B  4025 3997 b) 21 A  3 ; 31 B  2 2011 2011 2011 2011 2012 2012 2012 2012 c) A     .....  ; B     .....  1.2 3.4 5.6 1999.2000 1001 1002 1003 2000
Câu 3 (5 điểm).
a) Chứng minh rằng: x 1  x 2  x 3 x 100 3 3 3 3     
chia hết cho 120 (với x N) 3x  2y 2z  4x 4y  3z x y z b) Cho   . Chứng minh rằng:   4 3 2 2 3 4
c) Cho f(x) là hàm số xác định với mọi x thỏa mãn điều kiện f x .x f x .f x và 1 2   1  2
f 2  10 . Tính f   32 .
Câu 4 (5 điểm). Cho tam giác ABC có AB AC . Trên tia đối của tia CA lấy điểm D sao
cho CD AB . Gọi I là giao điểm các đường trung trực của BC và AD. a) Chứng minh AIB DIC
b) Chứng minh AI là tia phân giác của góc BAC. 1
c) Kẻ IE vuông góc với AB, chứng minh AE  AD . 2
Câu 5 (2,5 điểm). Cho 100 số hữu tỉ trong đó tích của bất kì ba số nào cũng là một số âm.
Chứng minh rằng tất cả 100 số đó đều là số âm.
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 50
Toán Họa tổng hợp Trang 51 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 HƯỚNG DẪN CHẤM CÂU ý ĐÁP ÁN ĐIỂM Câu a
7,3.10,5+7,3.15+2,7.10,5+15.2,7 1
1,5đ  10, 5  (7, 3  2, 7)  15.(7, 3  2, 7) 0,5 =10,5.10+15.10 0,5 (2,5đ =105+150=255 0,5 ) b  10 10    19 3 9 4 69.2 12 : 2 .27  15.4 .9  1đ 0,5   9 9 10 20 10       19 9 18 8 3 2 2 2 3
: 2  3  3.5  2  3  0,25 19 9 18 9 2  3 (1 2.3) : 2 3 (2 5)          0,25 =(2.7) : 7=2 Câu a 2012 2012 1 1 1999 1999 2012 1999 1,5   ;     2 4025 4024 2 2 3998 3997 4025 3997 2đ 2012  1999  
. Vậy A B 0,5 4025 3997 (5đ) b 0,5 A    10 21 2 10 3 3. 3  3.9 1,5đ 0,5 B    10 31 3 10 2 2. 2  2.8 0,5 Suy ra A B c 2011 2011 2011 2011 A     .....  1.2 3.4 5.6 1999.2000 1,5đ  1 1 1 1 1 1 1   2011. 1
      ....      0,25  2 3 4 5 6 1999 2000 0,25  1 1 1     1 1 1 1   2011. 1     ....         ....      3 5 1999    2 4 6 2000    1 1 1 1 1 1 1     1 1 1 1   2011. 1
       ....     2.       ....         2 3 4 5 6 1999 2000 2 4 6 2000    0,25
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 51
Toán Họa tổng hợp Trang 52 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7  1 1 1 1 1     1 1 1 1   2011. 1      ....     1        ....          2 3 4 1999 2000  2 3 999 1000     0,25 1 1 1 1 1   2011.    ....      1001 1002 1003 1999 2000 0,25  1 1 1 1    B  2012.    .....    1001 1002 1003 2000 Suy ra A B 0,25 a x 1  x 2  x 3 x 100 3 3 3 3      Câu
2,5đ   x 1  x 2  x 3 x 4     x 5 x 6  x 7  x 8 3 3 3 3 3  3  3  3  0,75 3 x 97  x 98  x 99  x 10  0 3  3  3  3  0,75 x   2 3 4     x 4   2 3 4     x 96    2 3 4 3 3 3 3 3 3 3 3 3 3 3 3  3  3  3  (5đ) 0,5 x x 4 x 96 
 3 .120  3 .120   3 .120 0,5 x x 4 x 96   1203  3   3 120 (đpcm) b 3x  2y 2z  4x 4y  3z   . Suy ra: 4 3 2 1,5đ 4(3x  2y) 3(2z  4x) 2(4y  3z)
12x  8y  6z 12x  8y  6z     0 16 9 4 29 0,75 3x  2y x y Vậy
 0  3x  2y   (1) 4 2 3 0,25 2z  4x x z
 0  2z  4x   (2) 0,25 3 2 4 x y z Từ (1) và (2) ta được   2 3 4 0,25 c
Vì f x .x f x .f x nên 1 2   1  2 1đ
f 4  f 2.2  f 2. f 2  10. 10  100 0,5
f (16)  f (4.4)  f (4) . f (4)  100.100  10000 0,25
f (32)  f (16.2)  f (16).f (2)  10000.10  100000 0,25 Hình vẽ 0,5
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 52
Toán Họa tổng hợp Trang 53 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 Câu 4 (5đ) a
Vì I là giao điểm các đường trung trực của BC và AD 0,25
1,5đ nên IB IC, IA ID 0,5
Lại có AB CD (gt) 0,25 Do đó AIB   D  IC (c.c.c) 0,5 b AID  
cân ở I, suy ra DAI D 0,5 1,5đ 0,250 AIB   D  IC   (câu a), suy ra BAI  D ,5  
Do đó DAI BAI. 0,25
Vậy AI là tia phân giác của góc BAC c
Kẻ IP  AD , ta có AIE A
IP ( cạnh huyền-góc nhọn) 0,5 1,5đ AD  0,25
AE AP Mà AP  (vì P là trung điểm AD) 2 0,5 1 Suy ra AE  AD 0,25 2 a
Trong 100 số đã cho, phải có ít nhất một số âm (vì nếu cả 100 số đều 0,25
dương thì tích của ba số bất kì không thể là một số âm). Câu 1đ 0,25
Ta tách riêng số âm đó ra. Chia 99 số còn lại thành 33 nhóm, mỗi nhóm 5 3 thừa số. 0,25
Theo đề bài, mỗi nhóm đều có tích là một số âm nên tích của 33 nhóm
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 53
Toán Họa tổng hợp Trang 54 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 (2,5đ
tức là của 99 số là một số âm. )
Nhân số âm này với số âm đã tách riêng từ đầu ta được tích của 100 số 0,25 là một số dương b
Sắp xếp 100 số đã cho theo thứ tự tăng dần, chẳng hạn 1,5đ a  a  a    a 0,25 1 2 3 100 Các
số này đều khác 0 (vì nếu có 1 thừa số bằng 0 thì tích của nó với
hai thừa số khác cũng bằng 0, trái với đề bài). 0,25
Xét tích a .a .a
 0  a  0 (vì nếu a  0 thìa  0 , a  0 , 98 99 100 98 98 99 100
tích của ba số này không thể là một số âm). 0,25
Vậy a , a , a , ..., a là các số âm. 1 2 3 98
Xét tích a .a .a  0 mà a a  0 nên a  0 1 2 99 1 2 99 0,25
Xét tích a .a .a
 0 mà a a  0 nên a  0 0,25 1 2 100 1 2 100
Vậy tất cả 100 số đã cho đều là số âm. 0,25
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 54
Toán Họa tổng hợp Trang 55 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
ĐỀ SỐ 12. ĐỀ HSG CẤP HUYỆN
Bài 1 (5 điểm) 12 5 6 2 10 3 5 2 2 .3  4 .9 5 .7  25 .49 a) Thực hiện phép tính: A    22 6 4 5 .3  8 .3 125.73 9 3  5 .14
b) Tính giá trị biểu thức:
B  1.2.3  2.3.4  3.4.5  4.5.6    17.18.19
c) Tìm một số tự nhiên có 3 chữ số, biết rằng nếu tăng chữ số hàng trăm thêm n đơn vị
đồng thời giảm chữ số hàng chục và giảm chữ số hàng đơn vị đi n đơn vị thì được một
số có 3 chữ số gấp n lần số có 3 chữ số ban đầu.
Bài 2 (3 điểm)
a) Tìm các số x, y, z biết rằng: 3x  4 ,
y 5y  6z vàxyz  30 . 1 3 3 b) Tìm x biết: x    1  ,6  2 4 5
Bài 3 (3 điểm)
1) Cho hàm số y f x   m –  1 x
a) Tìm m biết: f 2 – f   –1  7
b) Chom  5 . Tìm x biết f 3 – 2x   20 1 3 2) Cho các đơn thức 2 2 A   x yz , 2 2
B   xy z , 3 C  x y 2 4
Chứng minh rằng các đơn thức A, B, C không thể cùng nhận giá trị âm.  
Bài 4 (7 điểm). Cho A
BC nhọn có gócA  60 . Phân giác ABC cắt AC tại D, phân giác 
ACB cắt AB tại E. BD cắt CE tại I. a) Tính số đo góc BIC.
b) Trên cạnh BC lấy điểm F sao cho BF BE . Chứng minh CID CIF.
c) Trên tia IF lấy điểm M sao choIM IB IC . Chứng minh BCM  là tam giác đều.
Bài 5 (2 điểm)
Tìm số tự nhiên n thỏa mãn điều kiện: 2 3 4 n n 11 2.2 3.2 4.2 n 2 2       
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 55
Toán Họa tổng hợp Trang 56 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 HƯỚNG DẪN CHẤM BÀI Ý NỘI DUNG ĐIỂM 12 5 6 2 10 3 5 2 12 5 12 4 10 3 10 4 2 .3  4 .9 5 .7  25 .49 2 .3  2 .3 5 .7  5 .7 A      0.5 2 2 6 4 5 .3  8 .3  3 12 6 12 5 9 3 9 3 3 9 3 2 .3  2 .3 5 .7  5 .2 .7 125.7  5 .14 12 4 2 .3 3   10 3 1 5 .7 1  7 A   12 5 0.5 a 2 .3 3   9 3 1 5 .7  3 1  2  2 5.( 6  ) A   0.5 3.4 9 1 10  7 A    0.5 6 3 2
4B  1.2.3.4  2.3.4.5 – 
1  3.4.5.6 – 2   17.18.19.20 – 16 0.5
4B  1.2.3.4  2.3.4.5 – 1.2.3.4  3.4.5.6 – 2.3.4.5  17.18.19.20 – 16.17.18.19 b 0.5 1 4B  17.18.19.20 0.5 (5đ)
B  17.18.19.5  29070 0.5
Gọi số có 3 chữ số cầìm tìm là abc (a, b, c là STN có 1 chữ số,a  0 ) 0.25
Theo bài ra ta có: (a n)(b n)(c n)  n.abc
 100a n  10b – n  c – n  n 100a  10b c
 100a  100n  10b – 10n c – n  100an  10bn cn 0.25 c  100n  
1 a  10n – 
1 b  n –  1 c  89n  n  
1 100a  10b c  89n  89n n
 – 1 mà 89; n – 
1  1 nên n n – 1 0.25 Tìm được n  2
Số có 3 chữ số cần tìm là 178 0.25 x y y z x y z   ;      k 0.25 4 3 6 5 8 6 5
x  8k, y  6k, z  5k 0.25 2 a 1 3
xyz  30  8k.6k.5k  30  240k  30  k  0.5 (3đ) 2 5
x  4,y  3,z  2 0.5 1 3 3 1 3 8 3 b x    1  ,6   x      2 4 5 2 4 5 5 0.25
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 56
Toán Họa tổng hợp Trang 57 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 1 3  x    1 2 4 0.25 1 1  x   2 4 0.5 3 1  x  ; x  0.5 4 4
Vì f (2)  f (1)  7  (m  2)  2  (m  1)  (1)  7 0.25
1.a  2m  4  m  1  7 0.25
 3m  5  7  m  4 0.5
Với m  5 ta có hàm số y f x   4x 0.25
1.b Vì f (3  2x)  20  4(3  2x)  20 0.25
 12  8x  20  x  1 0.5 3
Giả sử cả 3 đơn thức A, B, C cùng có giá trị âm (3đ)  0.25 .
A B.C có giá trị âm (1) 3 Mặt khác: 6 4 4 .
A B.C x y z 0.25 8 2 3 Vì 6 4 4
x y z  0  x, y  .
A B.C  0  x; y (2) 0.25 8
Ta thấy (1) mâu thuẫn với (2)  điều giả sử sai. 0.25
Vậy ba đơn thức A, B, C không thể cùng có giá trị âm.
Vẽ hình đúng, ghi đúng giả thiết, kết luận A D E I 4 2 1 2 1 0.5 (7đ) B 3 F C 4 N M
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 57
Toán Họa tổng hợp Trang 58 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7    ABC
BD là phân giác của góc ABC nên B B  1 2 2  0.5   ACB
CE là phân giác của góc ACB nên C C  1 2 2 a    Mà tam giác ABC có 0
A B C  180 suy ra   0.5
60  ABC ACB  180    
 ABC  ACB  120  B  C  60 2 1 0.5   BIC  120 0.5 B  IE  BIF   
(cgc)  BIE BIF 0.5    
BIC  120  BIE  60  BIE  BIF  60 0.5 b    
Mà BIE  BIF  CIF  180  CIF  60 0.5   0 CID  BIE  60  
(đ.đ)  CIF  CID  60 0.5  CID   CIF  (gcg) 0.5
Trên đoạn IM lấy điểm N sao cho IB  IN  NM  IC 0.5   BIN
đều  BN  BI và BNM  120 0.5 c  B  NM  B  IC (cgc) 0.5   
BM BC và B B BCM  đều 0.5 2 4 Đặt 2 3 4 n
S  2.2  3.2  4.2   n.2  3 4 5 n 1           2 3 4 n 0.5 S 2S S 2.2 3.2 4.2 n 2
2.2  3.2  4.2   n.2  n 1  3 3 4 n 1  n 5 S n  2
 2  2  2  2  2  0.5 (2đ) Đặt 3 4 n 1  n T  2  2   2  2 . Tính được n 1  3 T  2T  T  2  2 0.5  n 1  3 n 1  3 n 1 S n.2 2 2 2 (n 1).2        0.5 n 1  n 1  1 10 10 (n  1)  2  2
 n  1  2  n  2  1  1025
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 58
Toán Họa tổng hợp Trang 59 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
ĐỀ SỐ 13. ĐỀ HSG CẤP HUYỆN
Câu 1. (1,5 điểm)  2 2 1 1  0,4    0,25        2014 a) 9 11 3 5 M     : 7 7 1      2015 1, 4   1  0, 875  0, 7  9 11 6  b) Tìm x, biết: 2 2
x x  1  x  2 .
Câu 2. (2,5 điểm)
a b c
b c a
c a b
a) Cho a, b, c là ba số thực khác 0, thoả mãn điều kiện:   . c a bb  a  c     
Hãy tính giá trị của biểu thức B  1    1    1     .  a   c   b 
b) Ba lớp 7A, 7B, 7C cùng mua một số gói tăm từ thiện, lúc đầu số gói tăm dự định chia
cho ba lớp tỉ lệ với 5 : 6 : 7 nhưng sau đó chia theo tỉ lệ 4 : 5 : 6 nên có một lớp nhận nhiều
hơn dự định 4 gói. Tính tổng số gói tăm mà ba lớp đã mua.
Câu 3. (2,0 điểm)
a) Tìm giá trị nhỏ nhất của biểu thức A  2x  2  2x  2013 với x là số nguyên.
b) Tìm nghiệm nguyên dương của phương trình x y z xyz . 
Câu 4. (3,0 điểm) Cho xAy  60 có tia phân giác Az . Từ điểm B trên Ax kẻ BH vuông
góc với Ay tại H, kẻ BK vuông góc với Az và Bt song song vớiAy , Bt cắt Az tại C. Từ
C kẻ CM vuông góc với Ay tại M . Chứng minh :
a ) K là trung điểm của AC. b ) KM  C là tam giác đều.
c) Cho BK = 2cm. Tính các cạnh AKM 
Câu 5. (1,0 điểm). Cho ba số dương 0  a b c  1 chứng minh rằng: a b c    2 bc  1 ac  1 ab  1
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 59
Toán Họa tổng hợp Trang 60 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 HƯỚNG DẪN CHẤM Câu Nội dung Điểm  2 2 1 1   0, 4    0,25        2014 1) Ta có: 9 11 3 5 M     : 7 7 1      2015 1, 4   1  0, 875  0, 7  9 11 6   2 2 2 1 1 1              2014 5 9 11 3 4 5     : 7 7 7 7 7 7    0.25đ   2015        5 9 11 6 8 10       Câu 1  1 1 1   1 1 1  0.25đ 2                5 9 11   3 4 5      2014      (1,5 điểm)  :    1 1 1    7 1 1 1   2015 7                 5 9 11 2 3 4 5   0.25đ 2 2   2014     :  0  7 7 2015 2) vì 2
x  | x  1 | 0 nên (1) 2 2
x  | x  1 | x  2 hay x - 1  2 0.25đ +)  x  3 0.25đ +)  x  1 0.25đ 1) +Nếu a  b  c  0
Theo tính chất dãy tỉ số bằng nhau ,ta có:
a b c
b c a
c a b
a b c b c a c a b     1 c a b
a b c Câu 2 0.25đ
a b c
b c a
c a b       (2,5 điểm) mà 1 1 1 2 c a b a b b c c a 0.25đ     2 c a bb    a    c    ba    ca    bc       Vậy B  1    1    1          8 0.25đ   a   c   b     a   c   b 
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 60
Toán Họa tổng hợp Trang 61 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
+Nếu a b c  0
Theo tính chất dãy tỉ số bằng nhau ,ta có:
a b c
b c a
c a b
a b c b c a c a b     0 0.25đ c a b
a b c
a b c
b c a
c a b mà  1   1   1  1 c a b a b b c c a 0.25đ     1 c a bb    a    c    ba    ca    bc       Vậy B  1    1    1          1 0.25đ   a   c   b     a   c   b 
2) Gọi tổng số gói tăm 3 lớp cùng mua là x ( x là số tự nhiên khác 0)
Số gói tăm dự định chia chia cho 3 lớp 7A, 7B, 7C lúc đầu lần lượt là: a, b, c 0,25đ a b c
a b c x 5x 6x x 7x Ta có:      a  ;b   ;c  (1) 5 6 7 18 18 18 18 3 18 0,25đ
Số gói tăm sau đó chia cho 3 lớp lần lượt là a’, b’, c’, ta có: a ' b ' c '
a ' b ' c ' x 4x 5x x 6x      a '  ;b '   ;c '  (2) 4 5 6 15 15 15 15 3 15 So sánh (1) và (2) ta có: a a; b b; c c  
 nên lớp 7C nhận nhiều 0,25đ hơn lúc đầu. 6x 7x x
Vây: c '– c  4 hay   4   4  x  360 15 18 90 0,25đ
Vậy số gói tăm 3 lớp đã mua là 360 gói.
1) Ta có: A  2x  2  2x  2013 | 2x  2 |  | 2013  2x | 0,25đ 0,25đ
 2x  2  2013  2x  2015 Câu 3 2013
(2,0 điểm) Dấu “=” xảy ra khi (2x  2)(2013  2x)  0  1  x  2 0,25đ 2013 0,25đ
Vậy Min A  2015 khi 1   x  , x   2
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 61
Toán Họa tổng hợp Trang 62 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
2) Vì x,y,z nguyên dương nên ta giả sử 1  x y z 1 1 1 1 1 1 3 Theo bài ra 1        2 2 2 2 yz yx zx x x x x 0,25đ 2
x  3  x  1
Thay vào đầu bài ta có 1  y z yz y yz  1  z  0
y(1  z)  (1  z)  2  0 0,25đ  (y  1)(z  1)  2
TH1: y  1  1  y  2 và z  1  2  z  3 0,25đ
TH2: y  1  2  y  3 và z  1  1  z  2
Vậy có hai cặp nghiệp nguyên thỏa mãn (1, 2, 3);(1, 3,2) 0,25đ Vẽ hình , GT _ KL x z C B 0,25đ K A H M y     MACCâu 4 a, AB 
C cân tại B do CAB ACB và BK là đường cao 0,5đ (3,0 điểm) 0,25đ
 BK là đường trung tuyến K là trung điểm của AC b, AB  H  B
 AK ( cạnh huyền + góc nhọn ) 1 0,25đ
 BH  AK ( hai cạnh t. ý ) mà AK  AC 2 1  BH  AC 2 0,25đ
Ta có : BH CM ( t/c cặp đoạn chắn ) 1 mà CK  BH 
AC  CM  CK  MKC là tam giác cân ( 1 ) 2 0,25đ
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 62
Toán Họa tổng hợp Trang 63 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7  
Mặt khác MCB  90 và ACB  30  0,25đ  MCK  60 (2) Từ (1) và (2)  M  KC là tam giác đều  c) Vì AB 
K vuông tại K mà KAB  30  AB  2BK  2.2  4 cm 0,25đ Vì AB 
K vuông tại K nên theo Pitago ta có: 2 2
AK  AB BK  16  4  12 0,25đ 1 Mà KC  AC  KC  AK  12 2 KCM  đều  KC  KM  12 0,25đ
Theo phần b) AB  BC  4 AH  BK  2
HM BC (HBCM là hình chữ nhật) 0,25đ  AM  AH  HM  6 Câu 5
Vì 0  a b c  1 nên: (1 điểm) 1 1 c c
(a 1)(b 1)  0  ab  1  a b     (1) ab  1 a b ab  1 a b 0,25đ a a b b Tương tự:  (2) ;  (3) bc  1 b c ac  1 a c a b c a b c 0,25đ Do đó:      (4) bc  1 ac  1 ab  1 b c a c a b a b c 2a 2b 2c
2(a b c) Mà        2 (5) 0,25đ b c a c a b
a b c
a b c
a b c
a b c a b c Từ (4) và (5) suy ra:    2 (đpcm) bc  1 ac  1 ab  1 0,25đ
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 63
Toán Họa tổng hợp Trang 64 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
ĐỀ SỐ 14. ĐỀ HSG CẤP HUYỆN Câu 1: (4,0 điểm) 7 3 3 2 9     3   7
  .5    :     5   4   16
1. Thực hiện phép tính: A  . 7 2 2 .5  512 x  16 y  25 z  9 2. Cho   và 3
2x  1  15 . Tính B x y z. 9 16 25 Câu 2: (4,0 điểm)
1. Tìm x, y biết: x x y 3 
và y x y 3   . 10 50    
2. Tìm x biết: x   1 3 x     0.   2 Câu 3: (5,0 điểm) 7n  8
1. Tìm số tự nhiên n để phân số có giá trị lớn nhất. 2n  3
2. Cho đa thức p(x) = ax3 + bx2 + cx + d với a, b, c, d là các hệ số nguyên. Biết rằng, p x5
với mọi x nguyên. Chứng minh rằng a, b, c, d đều chia hết cho 5.
The link ed image cannot be displayed. The file may hav e been mov ed, renamed, or deleted. Verify that the link points to the correct file and location.
3. Gọi a, b,c là độ dài các cạnh của một tam giác. Chứng minh rằng:
Câu 4: (5,0 điểm). Cho tam giác ABC cân tại A. Trên cạnh BC lấy điểm D (D khác B, C).
Trên tia đối của tia CB, lấy điểm E sao cho CE = BD. Đường vuông góc với BC kẻ từ D cắt
AB tại M. Đường vuông góc với BC kẻ từ E cắt đường thẳng AC tại N, MN cắt BC tại I.
1. Chứng minh DM = EN.
2. Chứng minh IM = IN, BC < MN.
3. Gọi O là giao của đường phân giác góc A và đường thẳng vuông góc với MN tại I. Chứng minh rằng BMO C
NO . Từ đó suy ra điểm O cố định.
Câu 5: (2,0 đ) Cho các số thực dương a và b thỏa mãn 100 100 101 101 102 102 ababab
Hãy tính giá trị của biểu thức: 2014 2015 P ab .
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 64
Toán Họa tổng hợp Trang 65 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 HƯỚNG DẪN CHẤM Câu Nội dung Điểm 7 3 3 7 3 2 9     3     2     9 3   2,0 7  .5     :             .5              :  6           2     3 7 3 2  3 5 4 16 5 4 16 2 12  1 1. A      . 7 2 7 2 7 2 7 2 7 2 7 2 .5  512 2 .5  2 .2 2 .5  2 .2 2  2 2 5  2  2 2. Ta có: 3 3 3 3 3
2x  1  15  2x  16  x  8  x  2  x  2. 0,5 18 y  25 z  9 1 Suy ra:   9 16 25 0,25 (4,0đ) 18 y  25 Do đó, ta có: 
y  25  32  y  57. 9 16 0,5 18 z  9 
z  9  50  z  41. 9 25 0,5
Vậy B x y z  2  57  41  100. 0,25
1. Trừ từng vế hai đẳng thức đã cho ta được: 2     0,75
x x y  y x y 3 3          
x yx y 9 
 x y2 3       10  50 25  5 3
Suy ra: x y   . 0,25 5 3 1 1 Thay x y
vào hai đẳng thức đã cho ta được x  ;y   . 5 2 10 0,5 2 3 1 1
Thay x y   vào hai đẳng thức đã cho ta được x   ;y  . 5 2 10 (4,0đ) 0,5     1 0,25 2. Từ x   1 3 x     0  x x   suy ra – 3 và cùng dấu.  2 2 1
Dễ thấy x  3  x  nên ta có: 0,5 2 0,5 1
x – 3 và x
cùng dương  x  3  0  x  3 2 0,5 1 1 1
x – 3 và x  cùng âm  x   0  x   2 2 2
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 65
Toán Họa tổng hợp Trang 66 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 1 0,25
Vậy x  3 hoặc x   2 2 
7n  8 72n n   3  5 7 8 7 5 1. Ta có:     n  22n  3 22n  3 22n  . 2 3 2 3 0,75 5
Phân số đã cho có giá trị lớn nhất khi và chỉ khi lớn nhất. 22n   3 0,25
Từ đó suy ra: n  2. 0,75
Vậy giá trị lớn nhất của phân số đã cho bằng 6 khi n  2. 0,25
2. Vì p x 5 với mọi x nguyên nên p   0  d 5 0,25
p(1)  a  b  c  d5 (1) 0,25 ( p 1)  a
  b c d 5 0,25 (2) 0,25
Từ (1) và (2) suy ra 2(b d)5 và 2(a c)5 0,25 3
Vì2b d5 , mà 2; 
5  1 nên b d 5  b5 0,25
(5,0đ) p 2  8a  4b  2c d5 mà d5;b5 nên 8a  2c5. 0,25
Kết hợp với 2(a c)5  6a 5  a 5 vì6;5  1 . Từ đó suy ra c5
Vậy a, b, c, d đều chia hết cho 5. 0,25 a a a a
3. Vì a b c nên  1   . (1) b c b c
b c a 0,25 b b b b Tương tự, ta có:  1   . (2) c a c a
c a b 0,25 c c c c  1   . (3) a b a b
a b c a b c
2a  2b  2c 0,25 Từ (1), (2) và (3) suy ra:     2. b c c a a b
a b c 0,25
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 66
Toán Họa tổng hợp Trang 67 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 A M I C E B D N O 1.    
Tam giác ABC cân tại A nên ABC ACB; NCE ACB; (đối đỉnh) 0,75 Do đó: MDB NEC(g. .
c g)  DM EN . 0,75 4 2. Ta có MDI NEI(g. .
c g)  MI NI 0,5 (5,0đ)
Vì BD CE nên BC DE .
Lại có DI MI, IE IN nên DE  DI  IE  MI  IN  MN 0,75
Suy ra BC MN. 0,25 3) Ta chứng minh được:   ABO ACO( .
c g.c)  OC O , B ABO ACO. 0,75 MIO NIO( .
c g.c)  OM ON.
Ta lại có: BM CN. Do đó BMO CNO( . c . c c) 0,5    MBO NCO    
, Mà: MBO ACO suy ra NCO ACO , mà đây là hai góc kề bù nên CO  AN. 0,5
Vì tam giác ABC cho trước, O là giao của phân giác góc A và đường vuông góc
với AC tại C nên O cố dịnh. 0,25 Ta có đẳng thức: 102 102    101 101      100 100 a b a b a b ab a
b  với mọi a, b. 0,5 5
(2,0đ) Kết hợp với: 100 100 101 101 102 102 ababab 0,5
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 67
Toán Họa tổng hợp Trang 68 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
Suy ra: 1  a b ab  a   1 b   1  0.  100 101 102 0,5
a  1  1  b  1  b  1  bb  1    100 101 102
b  1  1  a  1  a  1  aa  1  0,5  Do đó 2014 2015 2014 2015 P ab  1  1  2.
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 68
Toán Họa tổng hợp Trang 69 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7
ĐỀ SỐ 15. ĐỀ HSG CẤP HUYỆN Bài 1: (4,0 điểm).  1     1 1  
a) Tính giá trị biểu thức A = 2   3,5  :  4   3   +7,5  3   6 7 4 2 9 2.8 .27  4.6
b) Rút gọn biểu thức: B = 7 7 7 4 2 .6  2 .40.9
c) Tìm đa thức M biết rằng: M   2 x xy 2 2 5 2
 6x  9xy y . 2012 2014
Tính giá trị của M khi x, y thỏa mãn 2x  5  3y  4  0 .
Bài 2: (4,0 điểm). 1 1 1 a) Tìm x :  x   2 5 3
b) Tìm x, y, z biết: 2x  3y; 4y  5z và x y z  11 n 1  n 11 
c) Tìm x, biết : x  2  x   2
(Với n là số tự nhiên) Bài 3: (4,0 điểm).
a) Tìm độ dài 3 cạnh của tam giác có chu vi bằng 13cm. Biết độ dài 3 đường cao tương ứng
lần lượt là 2cm, 3cm, 4cm.
b) Tìm x, y nguyên biết : 2xy x y  2 
Bài 4: (6,0 điểm). Cho tam giác ABC ( AB AC , B  60 ). Hai phân giác AD và CE của A
BC cắt nhau ở I, từ trung điểm M của BC kẻ đường vuông góc với đường phân giác AI
tại H, cắt AB ở P, cắt AC ở K.  a) Tính AIC
b) Tính độ dài cạnh AK biết PK = 6cm, AH = 4 cm. c) Chứng minh IDE cân.
Bài 5: (2.0 điểm) Chứng minh rằng 10 là số vô tỉ.
------------------------------------------Hết---------------------------------------------
Cán bộ coi thi không giải thích gì thêm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 69
Toán Họa tổng hợp Trang 70 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 HƯỚNG DẪN CHẤM Nội dung Điểm Câu a: (1 điểm)  1     1 1 A  2   3,5 :    4   3   7,5   3     6 7 0.5 đ 7 7    25 22    15     :      3 2    6 7  2 35 43 15  :  0,5đ 6 42 2 245  15 490 645 155      43 2 86 86 86 Câu b: ( 1 điểm) 4 2 9 2.8 .27  4.6 0,5đ B= 7 7 7 4 2 .6  2 .40.9 13 6 11 9 2 .3  2 .3 = Bài 1 14 7 10 8 2 .3  2 .3 .5 . (4,0đ) 0.5 11 6 2 .3 . 2 3 2  3  2 = = 10 7 2 .3 . 4 2   3.5 3 Câu c: (2 điểm) M   2 x xy 2 2 5 2
 6x  9xy y 0.5 2 2
M x xy y   2 6 9 5x  2xy 0,5  2 2 2 2 2
M  6x  9xy y  5x  2xy x  11xy y 2012 2014 Ta có 2x  5  3y  4  0 0.25 2x   2012 5  0 2012 2014 Ta có :   2x  5  3y  4  0 2014    
3y  4  0  0.5 2012 2014 2012 2014 Mà2x  5  3y  4
 0  2x  5  3y  4  0
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 70
Toán Họa tổng hợp Trang 71 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7     1 0.25   x x   2  2012 1 x    2 2 5 0   => 2    2   . Vậy  y  2014  1 3 4  0  1  y     1 y   1  3  3 2 2 5   5  4    4    25 110 16 115  9
Vậy M     11            2 2  3    3  4 3 9 36 1 1 1  x   2 5 3 1 1 1 x    5 2 3 0,25đ 1 1 x   2. 5 6 (1,0đ) 1 1 1 TH1: x    x   5 6 30 0,25đ 1 1 1 1 11 TH2: x
   x      5 6 6 5 30 0,25đ 1 11 Vậy x   ;x   0,25đ 30 30 x y x y 0.25đ
Ta có : 2x  3y suy ra  hay  3 2 15 10 y z y z
4y  5z suy ra  hay  5 4 10 8 x y z b. Vậy   15 10 8 0.5đ
(1,5đ) Theo tính chất dãy tỉ số bằng nhau x y z
x y z 11 1   0.5đ = =  15 10 8 15  10  8 33 3 10 8
Suy ra x  5,y  ,z  0.25 3 3
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 71
Toán Họa tổng hợp Trang 72 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 n 1  n 11 (x 2) (x 2)     n 1  n 11 (x 2) (x 2)      0 0.25 n 1  10 (x 2) 1  (x 2)      0    c TH 1: n 1 (x  2)
 0 suy ra x  2 0.5 1,5 TH2: 10 1  (x  2)  0 điểm 10 (x  2)  1 0.25
x  2  1 suy ra x  1
x  2  1 suy ra x  3
Vậy x  2;x  1;x  3 0.5
Gọi độ dài ba cạnh của tam giác là x, y,z ( cm) ( x,y,z > 0) 0,25 đ
Theo bài ra ta có : x y z  13
và 2x  3y  4z  2S ABC x y z 0,75 đ a Suy ra   6 4 3
(2.0đ) Áp dụng tính chất dãy tỷ số bằng nhau x y
z x y z 13 0,75   =   1 6 4 3 6  4  3 13 0.25 Bài 3
suy ra x  6; y  4 ; z  3 KL: (4.0đ)
2xy – x – y  2
4xy  2x  2y  4 0,5 đ 2x 2y   1  2y  1  5 b. 2y   1 2x   1  5 0,5 đ
(2,0đ) HS xét 4 trường hợp tìm ra  x,y    1; 3;3; 1; 2  ;  0 ;0; 2  
( Mỗi trường hợp đúng cho 0.25 đ) 1 đ
Vậy x,y    1; 3;3; 1; 2  ;  0 ;0; 2  
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 72
Toán Họa tổng hợp Trang 73 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7 Bài 4 (6.0đ)   
a/ Ta có ABC  60 suy ra BAC BCA  120 0.5đ   1 
AD là phân giác của BAC suy ra IAC  BAC 2 0.5đ 1   1 
CE là phân giác của ACB suy ra ICA  BCA 2 (2.0đ) 0.5đ   1 Suy ra IAC  ICA   120  60 2 0.25đ  0.25đ Vây AIC  120 b/ Xét AHP và AHK có   PAH  KAH 
( AH là phân giác của BAC ) 0.5 đ AH chung   2 PHA  KHA  90    0,5 đ (2đ) Suy ra AHP
AHK (g-c-g) suy ra PH KH ( 2 cạnh tương
ứng). Vậy HK  3cm Vì A
HK vuông ở H theo định lý Pitago ta có 0.5 2 2 2 2 2
AK AH HK  4  3  25 0.25
Suy ra AK  5 cm 0.25 c  Vì AIC  120 (2.0đ)
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 73
Toán Họa tổng hợp Trang 74 [Document title]
ĐỀ KIỂM TRA HSG MÔN TOÁN 7   Do đó AIE  DIC  60 0,25 đ
Trên cạnh AC lấy điểm F sao cho AF AE 0,5 đ Xét EAI và FAI có AE AF   EAI  FAI AI chung Vậy EAI   FAI  (c-g-c) 0.25
suy ra IE IF (hai cạnh tương ứng) (1)   AIE  AIF  60   
suy ra FIC  AIC  AIF  60 0.5 Xét DIC  và FIC có   DIC  FIC  60  
; Cạnh IC chung; DIC  FCI 0.25 Suy ra DIC   F  IC ( g-c-g)
Suy ra ID IF (hai cạnh tương ứng) (2) 0.25
Từ (1) và (2) suy ra IDE cân tại I Bài 5
Giả sử 10 là số hữu tỷ 0.25đ (2,0đ) a 0.5đ 10 
( a,b là số tự nhiên , b khác 0 ;a;b  1 ) b 0.25đ 2 a  10 Suy ra 2 2 a  10b 2 b 0.25đ 2 2 2
a2  a 4  10b 4  b 2  b2 0.5đ
Vậy (a; b)  1 trái giả sử. Nên 10 là số vô tỷ 0.25đ
- Một bài toán có thể có nhiều cách giải khác nếu đúng và phù hợp đều đạt điểm tối đa. Giám khảo
cần thảo lụân, thống nhất đáp án và biểu điểm trước khi chấm.
Sản phẩm dành tặng Tập thể thầy cô giáo tham gia soạn giáo án Dạy thêm Toán 7 ! 74