Top 200 bài toán phương trình lượng giác – Cao Văn Tú

Tài liệu được soạn theo nhu cầu của các bạn học sinh khối trường THPT (đặc biệt là khối 12).

– Biên soạn theo cấu trúc câu hỏi trong đề thi tuyển sinh Đại học – Cao đẳng của Bộ GD&ĐT.

32 16 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Hàm số lượng giác và phương trình lượng giác (KNTT)

Môn: Toán 11

Thông tin:

85 trang 9 tháng trước

Tác giả:

Profile Kim Oanh
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
1
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
TUYỂN TẬP 200 BÀI TẬP LƯỢNG GIÁC
CÓ LỜI GIẢI CHI TIẾT NĂM 2015
- Tài liệu được soạn theo nhu cầu của các bạn học sinh khối trường THPT (đặc
biệt là khối 12).
- Biên soạn theo cấu trúc câu hỏi trong đề thi tuyển sinh Đại học – Cao đẳng của
Bộ GD&ĐT.
- Tài liệu do tập thể tác giả biên soạn:
1. Cao Văn Tú – CN.Mảng Toán – Khoa CNTT – Trường ĐH CNTT&TT Thái
Nguyên (Chủ biên)
2. Cô Trần Thị Ngọc Loan – CLB Gia Sư Thái Nguyên(Đồng chủ biên).
3. Thầy Vũ Khắc Mạnh – CLB Gia sư Bắc Giang (Tư vấn).
4. Nguyễn Thị Kiều Trang – SV Khoa Toán – Trường ĐHSP Thái Nguyên.
5. Nguyễn Trường Giang – Khoa CNTT – Trường ĐH CNTT&TT Thái
Nguyên.
6. Lý Thị Thanh Nga – SVNC – Khoa Toán – Trường ĐH SP Thái Nguyên.
7. Ngô Thị Lý – Khoa CNTT – Trường ĐH CNTT&TT Thái Nguyên.
- Tài liệu được lưu hành nội bộ - Nghiêm cấm sao chép dưới mọi hình thức.
- Nếu chưa được sự đồng ý của ban Biên soạn mà tự động post tài liệu thì đều
được coi là vi phạm nội quy của nhóm.
- Tài liệu đã được bổ sung và chỉnh lý lần thứ 2.
Tuy nhóm Biên soạn đã cố gắng hết sức nhưng cũng không thể tránh khỏi sự
sai xót nhất định.
Rất mong các bạn có thể phản hồi những chỗ sai xót về địa chỉ email:
caotua5lg3@gmail.com !
Xin chân thành cám ơn!!!
Chúc các bạn học tập và ôn thi thật tốt!!!
Thái Nguyên, tháng 07 năm 2014
Trưởng nhóm Biên soạn
Cao Văn Tú
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
2
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Giải
22
sin sin2 2cos 2x x x
sinx ( 2 cosx – sinx ) = 0
sin 0
tan 2 arctan2
x x k
x x k





cos2 3sin 2 0xx
Giải
22
1 2sin 3sin 2 0 2sin 3sin 1 0x x x x
2
2
sin 1
2,
1
6
sin
2
5
2
6
xk
x
x k k
x
xk


3sin cos 2xx
Giải
3sin cos 2xx
3 1 2
sin cos
2 2 2
xx
2
sin cos cos sin
6 6 2
xx

sin( ) sin
64
x

2
2
64
12
,
37
22
6 4 12
xk
xk
k
x k x k




3sin cos 2xx
Giải
22
sin sin2 2cos 2x x x
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
3
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
3 1 2
sin cos
2 2 2
xx
2
sin cos cos sin
6 6 2
xx

sin( ) sin
64
x

5
2
2
64
12
,
3 11
22
6 4 12
xk
xk
k
x k x k




Bài 5: Giải phương trình :
22
2sin 3sin cos 5cos 0x x x x
Giải
2
2 n 3 n 5 0ta x ta x
tan 1
4
,
5
5
tan
arctan( )
2
2
x
xk
k
x
xk


3(sin5 cos ) 4(sin cos5 )x x x x
Giải
3sin5 4cos5 4sin 3cosx x x x
3 4 4 3
sin5 cos5 sin cos
5 5 5 5
x x x x
sin5 cos cos5 sin sin sin cos cosx x x x
,
34
( cos , sin )
55


sin(5 ) cos( )xx

sin(5 ) sin( )
2
xx

52
12 3 3
2
52
2 8 2
xk
x x k
x x k x k

Bài 7: Giải phương trình :
3
3sin3 3cos9 1 4sin 3x x x
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
4
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Giải
3
(3sin3 4sin 3 ) 3cos9 1x x x
sin9 3cos9 1xx
sin(9 ) sin
36
x

2
18 9
72
54 9
xk
xk




Bài 8: Giải phương trình :
1
tan sin2 cos2 2(2cos ) 0
cos
x x x x
x
Giải
Điều kiện:
cos 0
2
x x k
sin 2
(1) sin2 cos2 4cos 0
cos cos
x
x x x
xx
22
sin 2sin cos cos2 cos 2(2cos 1) 0x x x x x x
2
sin (1 2cos ) cos2 cos 2cos2 0x x x x x
sin cos2 cos2 cos 2cos2 0x x x x x
cos2 (sin cos 2) 0x x x
cos2 0
sin cos 2( )
42
x
xk
x x vn


31
8sin
cos sin
x
xx

Giải
Điều kiện:
sin2 0
2
x x k
2
(*) 8sin cos 3sin cosx x x x
4(1 cos2 )cos 3sin cosx x x x
4cos2 cos 3sin 3cosx x x x
2(cos3 cos ) 3sin 3cosx x x x
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
5
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
13
cos3 cos sin
22
x x x
cos3 cos( )
3
xx
6
12 2
xk
xk


C2
2
(*) 8sin cos 3sin cosx x x x
2
8(1 cos )cos 3sin cosx x x x
3
8cos 8cos 3sin 3cosx x x x
3
6cos 8cos 3sin cosx x x x
3
13
4cos 3cos cos sin
22
x x x x
cos3 cos( )
3
xx
6
12 2
xk
xk


.
Bài 10: Giải phương trình :
9sin 6cos 3sin2 cos2 8x x x x
Giải
2
6sin cos 6cos 2sin 9sin 7 0x x x x x
6cos (sin 1) (sin 1)(2sin 7) 0x x x x
(sin 1)(6cos 2sin 7) 0x x x
sin 1
6cos 2sin 7
x
xx

2
2
xk
Bài 11: Giải phương trình :
sin2 2cos2 1 sin 4cosx x x x
Giải
2
2sin cos 2(2cos 1) 1 sin 4cos 0x x x x x
2
sin (2cos 1) 4cos 4cos 3 0x x x x
Bài 12: Giải phương trình :
2sin2 cos2 7sin 2cos 4x x x x
Giải
2
4sin cos (1 2sin ) 7sin 2cos 4 0x x x x x
2
2cos (2sin 1) (2sin 7sin 3) 0x x x x
2cos (2sin 1) (2sin 1)(sin 3) 0x x x x
(2sin 1)(2cos sin 3) 0x x x
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
6
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
2sin 1 0
2cos sin 3,( )
x
x x vn


2
6
5
2
6
xk
xk


Bài 13: Giải phương trình :
sin2 cos2 3sin cos 2x x x x
Giải
2
2sin cos (1 2sin ) 3sin cos 2 0x x x x x
2
(2sin cos cos ) (2sin 3sin 1) 0x x x x x
cos (2sin 1) (2sin 1)(sin 1) 0x x x x
(2sin 1)(cos sin 1) 0x x x
2sin 1
cos sin 1
x
xx

2
6
2sin 1
5
2
6
xk
x
xk


2
2
cos sin 1 cos( )
42
2
2
xk
x x x
xk

Bài 14: Giải phương trình :
2
(sin2 3cos2 ) 5 cos(2 )
6
x x x
Giải
Ta có:
13
sin2 3cos2 2( sin2 cos2 ) 2cos(2 )
2 2 6
x x x x x
Đặt:
sin2 3cos2 , 2 2t x x t
Phương trình trở thành:
2
5
2
t
t 
2
2 10 0tt
2
5
2
t
t

5
:
2
t
loại
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
7
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
7
2:2cos(2 ) 2
6 12
t x x k

Bài 15: Giải phương trình :
3
2cos cos2 sin 0x x x
Giải
2
2cos (cos 1) (1 sin ) 0x x x
2
2(1 sin )(cos 1) (1 sin ) 0x x x
2(1 sin )(1 sin )(cos 1) (1 sin ) 0x x x x
(1 sin )[2(1 sin )(cos 1) 1] 0x x x
(1 sin )[1 2sin cos 2(sin cos )] 0x x x x x
sin 1
1 2sin cos 2(sin cos ) 0
x
x x x x
sin 1 2
2
x x k
1 2sin cos 2(sin cos ) 0x x x x
2
(sin cos ) 2(sin cos ) 0x x x x
(sin cos )(sin cos 2) 0x x x x
sin cos 0xx
tan 1
4
x x k
Bài 16: Giải phương trình :
2
1 cos2
1 cot2
sin 2
x
x
x

.
Giải
Điều kiện:
sin2 0
2
x x k
2
1 cos2
(*) 1 cot2
1 cos 2
x
x
x
1
1 cot2
1 cos2
x
x
cos2 1
1
sin2 1 cos2
x
xx
sin2 (1 cos2 ) cos2 (1 cos2 ) sin2x x x x x
sin2 cos2 cos2 (1 cos2 ) 0x x x x
cos2 (sin2 cos2 1) 0x x x
cos2 0
sin2 cos2 1
x
xx
cos2 0
42
x x k

sin2 cos2 1xx
sin(2 ) sin( )
44
x

4
2
xk
xk

Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
8
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Vậy,phương trình có nghiệm:
42
xk


Bài 17: Giải phương trình :
44
4(sin cos ) 3sin4 2x x x
Giải
2 2 2 2 2
4[(sin cos ) 2sin cos ] 3sin4 2x x x x x
2
1
4(1 sin 2 ) 3sin4 2
2
xx
cos4 3sin4 2xx
42
12 2
xk
xk



Bài 18: Giải phương trình :
33
1
1 sin 2 cos 2 sin4
2
x x x
.
Giải
2 sin4 2(sin2 cos2 )(1 sin2 cos2 ) 0x x x x x
(2 sin4 ) (sin2 cos2 )(2 sin4 ) 0x x x x
(2 sin4 )(sin2 cos2 1) 0x x x
sin2 cos2 1xx
2
sin(2 )
42
x
4
2
xk
xk

Bài 19: Giải phương trình :
tan 3cot 4(sin 3cos )x x x x
Giải
Điều kiện:
sin2 0
2
x x k
sin cos
(*) 3 4(sin 3cos )
cos sin
xx
xx
xx
22
sin 3cos 4sin cos (sin 3cos ) 0x x x x x x
(sin 3cos )(sin 3cos ) 4sin cos (sin 3cos ) 0x x x x x x x x
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
9
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
(sin 3cos )(sin 3cos 4sin cos ) 0x x x x x x
sin 3cos 0
sin 3cos 4sin cos 0
xx
x x x x

sin 3cos 0 tan 3
3
x x x x k
sin 3cos 4sin cos 0x x x x
2sin2 sin 3cosx x x
13
sin2 sin cos
22
x x x
sin2 sin( )
3
xx
2
3
42
93
xk
xk


Vậy,phương trình có nghiệm là:
;
3
xk
42
93
xk


Bài 20: Giải phương trình :
33
sin cos sin cosx x x x
Giải
23
sin (sin 1) cos cos 0x x x x
23
sin cos cos cos 0x x x x
2
cos ( sin cos cos 1) 0x x x x
2
cos 0
sin cos cos 1
x
x x x
cos 0
2
x x k
2
sin cos cos 1x x x
1 1 cos2
sin2 1
22
x
x
sin2 cos2 3,( )x x vn
Vậy,phương trình có nghiệm là:
,
2
x k k
Bài 21: Giải phương trình :
44
1
cos sin ( )
44
xx
Giải
22
1 1 1
(1 cos2 ) [1 cos(2 )]
4 4 2 4
xx
22
(1 cos2 ) (1 sin2 ) 1xx
sin2 cos2 1xx
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
10
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
3
cos(2 ) cos
44
x

2
2
4
xk
xk

Bài 22: Giải phương trình :
33
4sin cos3 4cos sin3 3 3cos4 3x x x x x
Giải
3 3 3 3
4sin (4cos 3cos ) 4cos (3sin 4sin ) 3 3cos4 3x x x x x x x
33
12sin cos 12cos sin 3 3cos4 3x x x x x
22
4sin cos (cos sin ) 3cos4 1x x x x x
2sin2 cos2 3cos4 1x x x
sin4 3cos4 1xx
1 3 1
sin4 cos4
2 2 2
xx
sin(4 ) sin
36
x

24 2
,
82
xk
k
xk




Bài 23: Cho phương trình:
22
2sin sin cos cosx x x x m
(*)
a.Tìm m sao cho phương trình có nghiệm.
b.Giải phương trình khi m = -1.
Giải
11
(*) (1 cos2 ) sin2 (1 cos2 )
22
x x x m
sin2 3cos2 2 1x x m
a. (*)có nghiệm khi:
2 2 2
c a b
2
(1 2 ) 1 9m
2
4 4 9 0mm
1 10 1 10
22
m

b.Khi m = -1 phương trình trở thành:
sin2 3cos2 3xx
1 3 3
sin2 cos2
10 10 10
xx
sin2 cos cos2 sin sin ,xx
13
( cos , sin )
10 10


sin(2 ) sinx

22
22
xk
xk
2
xk
xk

Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
11
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Bài 24: Cho phương trình:
2
3
5 4sin( )
6tan
2
sin 1 tan
x
x

(*)
a.Giải phương trình khi
4

b.Tìm để phương trình (*) có nghiệm
Giải
Ta có:
3
sin( ) sin( ) cos
22
x x x

2
2
6tan
6tan cos 3sin2 ,cos 0
1 tan
5 4cos
(*) 3sin2
sin
x
x

3sin2 sin 4cos 5xx
(**)
a. khi
4

phương trình trở thành:
3sin 4cos 5xx
34
sin cos 1
55
xx
34
sin cos cos sin 1,( cos , sin )
55
xx
sin( ) 1x
2
2
xk

b.Phương trình có nghiệm khi:
2
cos 0
(3sin2 ) 16 25

2
cos 0
sin 2 1
2
cos 0
sin 2 1
cos2 0
42
k


Bài 25: Giải phương trình :
cos3 sin3
5(sin ) 3 cos2
1 2sin2
xx
xx
x
Giải
Điều kiện:
1
12
sin2 ,
7
2
12
xk
xk
xk

Ta có:
cos3 sin3 sin 2sin2 sin cos3 sin3
5(sin ) 5
1 2sin2 1 2sin2
x x x x x x x
x
xx


Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
12
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
sin cos cos3 cos3 sin3
5
1 2sin2
x x x x x
x
(sin3 sin ) cos
5
1 2sin2
x x x
x

2sin2 cos cos
5
1 2sin2
x x x
x
(2sin 1)cos
5
1 2sin2
xx
x
5cosx
(1) 5cos cos2 3xx
2
2cos 5cos 2 0xx
1
cos
2
x
2
3
xk
Bài 26: Giải phương trình :
22
cos 3 cos2 cos 0x x x
Giải
11
(1 cos6 )cos2 (1 cos2 ) 0
22
x x x
cos6 cos2 1 0xx
(*)
Cách 1:
3
(*) (4cos 2 3cos2 )cos2 1 0x x x
42
4cos 2 2cos 2 1 0xx
2
cos 2 1x
sin2 0x
2
xk

Cách 2:
1
(*) (cos8 cos4 ) 1 0
2
xx
cos8 cos4 2 0xx
2
2cos 4 cos4 3 0xx
cos4 1x
2
xk

Cách 3:
cos6 cos2 1
(*)
cos6 cos2 1
xx
xx

Cách 4:
1
(*) (cos8 cos4 ) 1 0
2
xx
cos8 cos4 2xx
cos8 cos4 1xx
Bài 26: Giải phương trình :
44
3
cos sin cos( )sin(3 ) 0
4 4 2
x x x x

Giải
2 2 2 2 2
13
(sin cos ) 2sin cos [sin(4 ) sin2 ] 0
2 2 2
x x x x x x
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
13
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
2
1 1 3
1 sin 2 ( cos4 sin2 ) 0
2 2 2
x x x
22
1 1 1 1
sin 2 (1 2sin 2 ) sin2 0
2 2 2 2
x x x
2
sin 2 sin2 2 0xx
sin2 1x
4
xk
Bài 27: Giải phương trình :
2
5sin 2 3(1 sin )tanx x x
Giải
Điều kiện:
cos 0
2
x x k
2
2
sin
(1) 5sin 2 3(1 sin )
cos
x
xx
x
2
2
sin
5sin 2 3(1 sin )
1 sin
x
xx
x
2
3sin
5sin 2
1 sin
x
x
x
2
2sin 3sin 2 0xx
1
sin
2
x
2
6
5
2
6
xk
xk


Bài 28: Giải phương trình :
11
2sin3 2cos3
sin cos
xx
xx
.
Giải
Điều kiện:
sin2 0
2
x x k
11
(*) 2(sin3 cos3 )
sin cos
xx
xx
33
11
2[3(sin cos ) 4(sin cos ]
sin cos
x x x x
xx
22
sin cos
2(sin cos )[3 4(sin sin cos cos )]
sin cos
xx
x x x x x x
xx
sin cos
2(sin cos )( 1 4sin cos ) 0
sin cos
xx
x x x x
xx
1
(sin cos )( 2 8sin cos ) 0
sin cos
x x x x
xx
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
14
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
2
(sin cos )(4sin2 2) 0
sin2
x x x
x
2
(sin cos )(4sin 2 2sin2 2) 0x x x x
2
sin cos 0
4sin 2 2sin2 2 0
xx
xx

tan 1
sin2 1
sin2 1/ 2
x
x
x



4
12
7
12
xk
xk
xk

Bài 29: Giải phương trình :
2
cos (2sin 3 2) 2cos 1
1
1 sin2
x x x
x
(*)
Giải
Điều kiện:
sin2 1
4
x x k
2
(*) 2sin cos 3 2cos 2cos 1 1 sin2x x x x x
2
2cos 3 2cos 2 0xx
2
cos
2
x
4
xk
Đối chiếu điều kiện phương trình có nghiệm:
,
4
x k k
Bài 30: Giải phương trình :
3 3 1
cos cos cos sin sin sin
2 2 2 2 2
x x x x
xx
Giải
1 1 1
cos (cos2 cos ) sin (cos2 cos )
2 2 2
x x x x x x
2
cos cos2 cos sin cos2 sin cos 1x x x x x x x
2
cos2 (sin cos ) 1 sin sin cos 1 0x x x x x x
cos2 (sin cos ) sin (sin cos ) 0x x x x x x
(sin cos )(cos2 sin ) 0x x x x
2
(sin cos )( 2sin sin 1) 0x x x x
2
sin cos 0
2sin sin 1 0
xx
xx

Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
15
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
tan 1
sin 1
sin 1/ 2
x
x
x

4
2
2
5
22
66
xk
xk
x k x k


Bài 31: Giải phương trình :
3
4cos 3 2sin2 8cosx x x
Giải
3
4cos 6 2sin cos 8cos 0x x x x
2
2cos (2cos 3 2sin 4) 0x x x
2
2cos (2sin 3 2sin 2) 0x x x
cos 0
2
sin
2
x
x
2
2
4
3
2
4
xk
xk
xk


Bài 32: Giải phương trình :
cos(2 ) cos(2 ) 4sin 2 2(1 sin )
44
x x x x

Giải
2cos2 cos 4sin 2 2 2sin 0
4
x x x
2
2(1 2sin ) 4sin 2 2 2sin 0x x x
2
2 2sin (4 2)sin 2 0xx
1
sin
2
x
2
6
5
2
6
xk
xk


Bài 33: Giải phương trình :
22
3cot 2 2sin (2 3 2)cosx x x
(1)
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
16
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Giải
Điều kiện:
sin 0x x k
2
42
cos cos
(1) 3 2 2 (2 3 2)
sin sin
xx
xx
Đặt:
2
cos
sin
x
t
x
phương trình trở thành:
2
2
3 (2 3 2) 2 2 0
2
3
t
tt
t
2
2 cos 2
:
3 sin 3
x
t
x
2
3cos 2(1 cos )xx
2
2cos 3cos 2 0xx
1
cos
2
x
2
3
xk
2
cos
2 : 2
sin
x
t
x
2
cos 2(1 cos )xx
2
2cos cos 2 0xx
2
cos
2
x
2
4
xk
Vậy,phương trình có nghiệm:
2 , 2
34
x k x k


Bài 34: Giải phương trình :
22
4sin 2 6sin 9 3cos2
0
cos
x x x
x
(*)
Giải
Điều kiện:
cos 0
2
x x k
2
(*) 4(1 cos 2 ) 3(1 cos2 ) 9 3cos 0x x x
2
4cos 2 6cos 2 0xx
cos2 1
1
cos2
2
x
x


2
3
xk
xk

Vậy,phương trình có nghiệm:
3
xk
Bài 35: Giải phương trình :
cos cos3 2cos5 0x x x
Giải
(cos5 cos ) (cos5 cos3 ) 0x x x x
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
17
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Giải
8 8 4 4 2 4 4
sin cos (sin cos ) 2sin cosx x x x x x
2 2 2 2 2 2 4
1
[(sin cos ) 2sin cos )] sin 2
8
x x x x x
2 2 4
11
(1 sin 2 ) sin 2
28
xx
24
1
1 sin 2 sin 2
8
xx
2 4 2
1
(*) 16(1 sin 2 sin 2 ) 17(1 sin 2 )
8
x x x
42
2sin 2 sin 2 1 0xx
2
1
sin 2
2
x
2
1 2sin 2 0x
cos4 0x
84
xk

Bài 37: Giải phương trình :
5
3
sin 5cos sin
22
xx
x
(*)
Giải
Ta thấy:
cos 0 2 cos 1
2
x
x k x

Thay vào phương trình (*) ta được:
5
sin( 5 ) sin( )
22
kk


không thỏa mãn với mọi k
2cos3 cos2 2cos4 cos 0x x x x
32
(4cos 3cos )cos2 (2cos 2 1)cos 0x x x x x
22
cos [(4cos 3)cos2 2cos 2 1] 0x x x x
2
cos {[2(1 cos2 ) 3]cos2 2cos 2 1} 0x x x x
2
cos (4cos 2 cos2 1) 0x x x
cos 0
1 17
cos
8
1 17
cos
8
x
x
x

2
1 17
arccos 2
8
1 17
arccos 2
8
xk
xk
xk

Bài 36: Giải phương trình :
8 8 2
17
sin cos cos 2
16
x x x
(*)
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
18
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Do đó
cos
2
x
không là nghiệm của phương trình nên:
5
3
(*) sin cos 5cos sin cos
2 2 2 2
x x x x
x
15
3
(sin3 sin2 ) cos sin
22
x x x x
33
3sin 4sin 2sin cos 5cos sin 0x x x x x x
23
sin (3 4sin 2cos 5cos ) 0x x x x
32
sin (5cos 4cos 2cos 1) 0x x x x
sin 0
cos 1
1 21
cos
10
1 21
cos
10
x
x
x
x


2
1 21
arccos 2
10
1 21
arccos 2
10
xk
xk
xk
xk


Vậy,phương trình có nghiệm:
2xk
,
1 21
arccos 2
10
xk

1 21
arccos 2
10
xk

Bài 38: Giải phương trình :
2
sin2 (cot tan2 ) 4cosx x x x
(1)
Giải
Điều kiện:
sin 0
cos2 0
42
xk
x
x
xk





Ta có:
cos sin2
cot tan2
sin cos2
xx
xx
xx
cos2 cos sin2 sin
sin cos2
x x x x
xx
cos
sin cos2
x
xx
cos
2
(1) 2sin cos 4cos
sin cos2
x
x x x
xx

2
cos
2
2cos
cos2
x
x
x

2
cos (1 2cos2 ) 0xx
cos 0
cos2 1/ 2
x
x
2
6
xk
xk

Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
19
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Vậy,phương trình có nghiệm:
2
xk

,
6
xk
Bài 39: Giải phương trình :
68
2
2cos 1 3cos
55
xx

Giải
12 4
2
(1 cos ) 1 2(2cos 1)
55
xx
4 4 4
32
2 4cos 3cos 2(2cos 1)
5 5 5
x x x
Đặt:
4
cos , 1 1
5
x
tt
phương trình trở thành:
32
4 6 3 5 0t t t
1
1 21
4
t
t
45
cos 1
52
x
xk
4 1 21 5 1 21 5
cos arccos
5 4 4 4 2
x
xk

Vậy,phương trình có nghiệm:
5
2
xk
,
5 1 21 5
arccos
4 4 2
xk
Bài 40: Giải phương trình :
3
tan ( ) tan 1
4
xx
(1)
Giải
Điều kiện:
cos 0
2
3
cos( ) 0
4
4
x
xk
x
xk






3
(tan 1)
(1) tan 1
3
(1 tan )
x
x
x
33
(tan 1) (tan 1)(1 tan )x x x
32
(tan 1)[(1 tan ) (tan 1) ] 0x x x
32
(tan 1)(tan 2tan 5tan ) 0x x x x
2
tan (tan 1)(tan 2tan 5) 0x x x x
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
20
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
tan 0
tan 1
x
x
4
xk
xk

C2: Đặt:
4
tx

Bài 41: Giải phương trình :
44
sin 2 cos 2
4
cos 4
tan( )tan( )
44
xx
x
xx


(1)
Giải
Điều kiện:
sin( )cos( ) 0
44
sin( )cos( ) 0
44
xx
xx


sin( 2 ) 0
4
cos2 0
sin( 2 ) 0
4
x
x
x


1 tan 1 tan
tan( )tan( ) . 1
4 4 1 tan 1 tan
xx
xx
xx



4 4 4
(1) sin 2 cos 2 cos 4x x x
2 2 4
1 2sin 2 cos 2 cos 4x x x
1
24
1 sin 4 cos 4
2
xx
1
24
1 (1 cos 4 ) cos 4
2
xx
42
2cos 4 cos 4 1 0xx
2
cos 4 1x
2
1 cos 4 0x
sin4 0x
4
xk

Vậy,phương trình có nghiệm:
2
xk
Bài 42: Giải phương trình :
12
48 (1 cot2 cot ) 0
42
cos sin
xx
xx
(*)
Giải
Điều kiện:
sin2 0
2
x x k
Ta có:
cos2 cos
1 cot2 cot 1
sin2 sin
xx
xx
xx
cos2 sin sin2 sin
sin2 cos
x x x x
xx
cos
2
2sin cos
x
xx
1
2
2sin x
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
21
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
11
(*) 48 0
44
cos sinxx
11
48
44
cos sinxx
4 4 4 4
48sin cos sin cosx x x x
1
42
3sin 2 1 sin 2
2
xx
42
6sin 2 sin 2 2 0xx
1
2
sin 2
2
x
2
1 2sin 2 0x
cos4 0x
84
xk

Vậy,phương trình có nghiệm:
84
xk


Bài 43: Giải phương trình :
5
8 8 10 10
sin cos 2(sin cos ) cos2
4
x x x x x
Giải
5
8 2 8 2
sin (1 2sin ) cos (2cos 1) cos2
4
x x x x x
5
88
sin cos2 cos cos2 cos2
4
x x x x x
88
4cos2 (cos sin ) 5cos2 0x x x x
4 4 4 4
4cos2 (cos sin )(cos sin ) 5cos2 0x x x x x x
2 2 2 2 4 4
4cos2 (cos sin )(cos sin )(cos sin ) 5cos2 0x x x x x x x x
1
2 2 2
4cos2 (cos sin )(1 sin 2 ) 5cos2 0
2
x x x x x
1
22
4cos 2 (1 sin 2 ) 5cos2 0
2
x x x
2
4cos2 (4cos2 2cos2 sin 2 5) 0x x x x
2
4cos2 [4cos2 2cos2 (1 cos 2 ) 5] 0x x x x
3
4cos2 (2cos 2 2cos2 5) 0x x x
cos2 0x
42
xk

Bài 44: (Đề thi tuyển sinh ĐH – CĐ 2010, khối A)
Giải phương trình :
1 sin os2 sin
1
4
cos
1 tanx
2
x c x x
x



Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
22
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Giải
Điều kiện:
cos 0 sin 1
tanx 1 tanx 1
xx



Khi đó
1 sin os2 sin
1
4
cos
1 tanx
2
x c x x
x



cos 1 sinx cos2 2.sin cos sin cos
4
x x x x x x



1 sinx cos2 2.sin sin cos
4
x x x x



(do
cos 0x
)
2
2
sin cos sin os2 0 sin cos sin 1 2sin 0
tan 1
sin cos
sin cos 0
sin 1 sin 1
2sin sin 1 0
1
1
sin
sin /
2
2
.2
1
6
sin
7
2
.2
6
x x x c x x x x x
xL
xx
xx
x x L
xx
x
x t m
xk
x k Z
xk






Bài 45: Cho hàm số: y= -x
3
+3x
2
+3(m-1)x-3m
2
+1.
1, Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m=1.
2. Tìm m để đồ thị hàm số có cực đại , cực tiểu và hai điểm cực đại cực tiểu ấy cách đều
đường thẳng x-y-2=0.
Giải
2. Điều kiên để hàm số có cực trị : m >0
Chia y cho y’ ta có phương trình đường thẳng đi qua hai điểm cực tri la:
y= 2mx-3m
2
+m.
Thỏa mãn yêu cầu bài ra
TH 1: BA song song với d
TH2: d đi qua trung điểm của AB
Đáp số: m=
2
1
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
23
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
m=
6
213
Bài 46: (Đề thi tuyển sinh ĐH – CĐ 2006, khối B)
Giải phương trình
cot sin 1 tan .tan 4
2
x
x x x



Giải
Lời giải: Điều kiện
cos 0
sinx 0 sin2x 0
os 0
2
x
x
c
Ta có
sin
cos sinx
2
cot sin 1 tan .tan 4 sinx 1 . 4
2 sinx cos
os
2
x
xx
x x x
x
x
c








cos . os sinx.sin
cos cos sinx
22
sinx 4 4
sinx sinx cos
cos . os
2
xx
xc
xx
x
x
xc





21
4 sin2 /
sin2 2
2 .2
.
6
12
55
2 .2 .
6 12
x t m
x
xk
xk
kZ
x k x k




Bài 47: Giải phương trình :
1 1 2
cos sin2 sin4x x x

.
Giải
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
24
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Điều kiện
2
cos 0 sin 1 sin 1 sin 1
sin2x 0 sinx 0 sinx 0 sinx 0
sin4 0 os2 0
1 2sin 0
2
sin
2
x x x x
x c x
x
x





Khi đó
1 1 2
cos sin2 sin4x x x

2
sin 1
4sinx. os2 2 os2 2 sinx 2sin sinx-1 0 sin 0
1
sin
2
x
c x c x x x
x

Đối chiếu với điều kiện ta được
.2
1
6
sin
5
2
.2
6
xk
x k Z
xk


Vậy phương trình có nghiệm là
.2
6
5
.2
6
xk
kZ
xk


Bài 48: Giải phương trình :
44
4
sin 2 os 2
os 4
tan tan
44
x c x
cx
xx


Giải
Điều kiện
sin 0
4
os 0 sin 2 0
42
os2 0 sin2 1
sin 0 sin 2 0
42
os 0
4
x
c x x
c x x
xx
cx













Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
25
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Nhận thấy
tan .tan 1
44
xx

, do đó phương trình đã cho trở thành
4 4 4 2 4 4 2
2
1
sin 2 os 2 os 4 1 sin 4 os 4 2 os 4 os 4 1 0
2
sin2 0
os 4 1 sin4 0
os2 0
x c x c x x c x c x c x
x
c x x
cx
Đối chiếu điều kiện ta được
sin2 0
2
x x k k Z
Bài 49: Giải phương trình :
24
sin 2 os 2 1
0
sin .cos
x c x
xx

.
Giải
Điều kiện
sin2 0x
Khi đó phương trình đã cho trở thành
2
2 4 4 2
2
os 2 0 sin2 1
sin 2 os 2 1 0 os 2 os 2 0
sin2 0
os 2 1
c x x
x c x c x c x
x
cx
Đối chiếu điều kiện ta được
sin2 1 2 .2 .
24
x x k x k k Z


Bài 50: Giải phương trình :
os3 .tan5 sin7c x x x
Giải
Điều kiện
os5 0cx
Khi đó phương trình đã cho trở thành
2
2sin5 . os3 2sin7 . os5 sin8 sin12
20 10
k
x
xc x xc x x x k Z
k
x


Với
2
k
x
thì
5
os5 os os 2 os 0 2
2 2 2
k k k
c x c c k c k m m Z
Với
20 10
k
x


thì
os5 os 0
42
k
c x c




Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
26
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Vậy phương trình đã cho có nghiệm là
;,
20 10
k
x m x m k Z

Bài 51: (Đề thi tuyển sinh ĐH – CĐ, 2011, khối A)
Giải phương trình
2
1 sin2x+cos2
2sinxsin2
1 cot x
x
x
Giải
Điều kiện
sin 0 cos 1xx
Khi đó phương trình đã cho trở thành
2 2 2
sin 1 sin2 os2 2 2sin .cos 1 2sin .cos 2 os 1 2 2cos
cos 0 /
2cos sinx cos 2 0
sinx cos 2 *
x x c x x x x x c x x
x t m
xx
x

Giả sử
sin 0 cos 1xx
, khi đó
* 0 1 2
(vô lí)
Do đó phương trình tương đương với
cos 0
2
cos 1
2
4
4
x
xk
x
xk






Vậy phương trình có nghiệm là
2
2
4
xk
kZ
xk


Bài 52: Giải phương trình :
1
3sinx 2cos 3 1 tanx
cos
x
x
Giải
Điều kiện
os 0 sin 1c x x
Khi đó
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
27
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
1
3sinx 2cos 3 1 tanx cos 3sinx 2cos 3 cos sinx 1
cos
cos 3sinx 2cos cos 3sinx 2cos 1
cos 3sinx 2cos 1 3sinx 2cos 1 0
cos 1 0 1
3sinx 2cos 1 cos 1 0
3sinx 2cos 1 0 2
x x x x
x
x x x x
x x x
x
xx
x

1 cos 1x
thoả mãn điều kiện, do đó ta được
2,x k k Z

Tiếp theo giả sử
os 0 sin 1c x x
, thay vào (2) ta được
3 1 0
(vô lí)
Tức là các nghiệm của (2) đều thoả mãn điều kiện.
Giải (2) ta được
1
ar os 2
13
x cc k k Z

,
(với
23
os ; sin
13 13
c


)
Vậy phương trình có nghiệm
2
1
ar os 2
13
xk
kZ
x cc k

.
Bài 53: Giải phương trình :
2
2
tan tanx 2
sin
tan 1 2 4
x
x
x




Giải
Điều kiện
os 0 sin 1c x x
Khi đó
2
22
2
2
tan tanx 2 2 2 2
sin os tan tanx sinx cos
tan 1 2 4 2 2 2
1
sin cos .sinx sinx cos 2sinx sinx cos sinx cos 0
2
sinx cos 2sinx 1 0 *
x
x c x x x
x
x x x x x
x







Giả sử
os 0 sin 1c x x
, thay vào (*) ta được
1 2 1 0
(vô lí)
Tức là các nghiệm của (*) đều thoả mãn điều kiện.
Giải (*) ta được
35
; 2 ; 2
4 6 6
x k x k x k k Z
Bài 54: Giải phương trình :
tan5 .tan2 1xx
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
28
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Giải
Điều kiện
1
os5 0
10 5
,
os2 0
2
42
xm
cx
m n Z
cx
xn






phương trình tương đương với
1
tan5 tan5 cot2
tan2 14 7
x x x x k k Z
x

+ Đối chiếu điều kiện (1)
Giả sử
12
14 7 10 5 5
m
k m k m
Do
,k m Z
nên
1 2 1
:2
52
mt
t Z t m t

Lại do
,t m Z
nên
1
: 2 1
2
t
s Z s t s
Từ đó
73ks
. Suy ra
14 7
xk


với
73ks
thoả mãn phương trình
+ Đối chiếu điều kiện (2)
Giả sử
4 14 5 3
14 7 4 2
k n k n
Ta thấy vế trái của (3) chẵn, vế phải của (3) lẻ nên không tồn tại
,k n Z
thoả mãn (3).
Từ đó suy ra điều kiên (2) luôn được thoả mãn.
Vậy phương trình đã cho có nghiệm là
14 7
x k k Z

Bài 55: (Đề thi tuyển sinh ĐH – CĐ 2011, khối D)
Giải phương trình
sin2x+2cos sinx 1
0
tanx+ 3
x
Giải
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
29
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Điều kiện
tanx 3
3
,
cos 0
2
xm
m n Z
x
xn





Khi đó phươngtrình đã cho trở thành
sin2x+2cos sinx 1 0 2cos sinx 1 sinx 1 0
sinx 1
x2
2
sinx 1 2cos 1 0
1
cos
2
2
3
xx
k
x
x
xk

Kết hợp với điều kiện trên đường tròn lượng giác (như hình bên)
ta được nghiệm của phương trình là
2
3
x k k Z
Bài 56: (Đề thi tuyển sinh ĐH – CĐ 2006, khối A)
Giải phương trình
66
2 cos sin sin .cos
0
2 2sin
x x x x
x

Giải
Điều kiện
2
2
4
sinx ,
3
2
2
4
xm
m n Z
xn


Khi đó phương trình đã cho trở thành
66
2
2
2 cos sin sin .cos 0
31
2 1 sin 2 sin2 0
42
3sin 2 sin2 4 0 sin2 1
4
x x x x
xx
x x x
x k k Z



Kết hợp với điều kiện trên đường tròn lượng giác (như hình bên) ta được nghiệm của
phương trình là
5
2
4
x k k Z
3
2
2
2
3
3
O
y
x
o
y
x
4
3
4
5
4
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
30
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Bài 57: Giải phương trình :
sin sin2
1
sin3
xx
x

Giải
Điều kiện
sin3 0 3
3
x x k x k
Khi đó
sin sin2
1 sin sin2 sin3 0
sin3
2sin2 .cos sin2 0
xx
x x x
x
x x x
sin2 0
sin2 2cos 1 0
1
cos
2
x
xx
x

2
2
2
3
xk
xk
Kết hợp với điều kiện trên đường tròn lượng giác
Ta được nghiệm của phương trình là
2
xk

.
Bài 58: [ĐH A02] Tìm
x 0;2
:
cos3x sin3x
5 sinx cos2x 3
1 2sin2x



Giải
Điều kiện :
1
sin2
2
x 
cos3x sin3x sinx 2sinxsin2x cos3x sin3x
5 sinx 5
1 2sin2x 1 sin2x


sin cos cos3 cos3 sin3
5
1 2sin2
x x x x x
x



sin3 sin cos 2sin2 cos cos
55
1 2sin2 1 2sin2
x x x x x x
xx


cos (1 2sin2 )
5 5cos
1 2sin2
xx
x
x




(1)
2
5cos cos2 3 2cos 5cos 3 0x x x x
cos 2 (L)
1
cos cos
23
x
x

O
x
2
y
2
3
3
2
3
4
3
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
31
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
cos cos
3
x
2
3
2
3
xk
k
xk

Vì
0;2x
Nên nghiệm của phương trình :
5
;
33
xx


Bài 59: [ĐH B02]
2 2 2 2
sin 3x cos 4x sin 5x cos 6x
Giải
2 2 2 2
sin 3x cos 4x sin 5x cos 6x
1 cos6 1 cos8 1 cos10 1 cos12
2 2 2 2
x x x x
cos12 cos10 cos8 cos6x x x x
2cos (cos11 cos7 ) 0 4cos .sin9 .sin2 0x x x x x x
9
2
k
x
k
k
x
Bài 60: [ĐH D02] Tìm
x 0;14
:
cos3x 4cos2x 3cosx 4 0
Giải
Tìm
x 0;14
:
cos3x 4cos2x 3cosx 4 0
(1)
Ta có :
3
cos3 4cos 3cosx x x
(1)
cos3 3cos 4(1 cos2 ) 0x x x
32
4cos 8cos 0xx
2
4cos cos 2 0 cos 0x x x
;
2
x k k
Vì
(0;14)x
3 5 7
; ; ;
2 3 2 2
x



Bài 61: [Dự bị 1 ĐH02] Xác định m để phương trình sau có ít nhất 1 nghiệm thuộc
0;
2



44
2 sin x cos x cos4x sin2x m 0
Giải
Xác định m để phương trình sau có ít nhất 1 nghiệm thuộc
0;
2



:
44
2 sin x cos x cos4x sin2x m 0
(1)
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
32
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
(1)
2 2 2
2 1 2sin cos 1 sin 2 2sin2 0x x x x m
2
3 3sin 2 2sin2 0m x x
2
3 2 ( 3) 0t t m
(2) với
sin2tx
Ta có :
0; 2 0; 0;1
2
x x t



Bài toán thành : Xác định m để phương trình sau có ít nhất 1 nghiệm thuộc đoạn
0;1
(2)
2
3 2 3t t m
Đặt
2
3 2 (P)
3 d
y t t
ym


Số nghiệm của (2) là số giao điểm của d và (P)
Khảo sát hàm số :
2
32y t t
0;1t
' 6 2yt
1
' 0 6 2 0
3
y t t
BBT
Phương trình (2) có ít nhất một nghiện trên đoạn
0;1
1
31
3
10
2
3
m
m
Bài 62: [Dự bị 2 ĐH02]
44
sin x cos x 1 1
cot2x
5sin2x 2 8sin2x

Giải
44
sin x cos x 1 1
cot2x
5sin2x 2 8sin2x

(1)
Điều kiện :
sin2 0x
(1)
22
1 2sin cos 1 1
cos2
5 2 8
xx
x
2
2
sin 2 5 5 5
1 cos2 2 (1 cos 2 ) 5cos2
2 2 8 4
x
x x x
1
3
x
'y
y


0
0
1
3
0
1
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
33
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
2
9
cos2 ( )
9
2
cos 2 5cos2 0
1
4
cos2
2
xL
xx
x
22
36
cos2 cos
3
2
36
x k x k
xk
x k x k










Bài 63: [Dự bị 3 ĐH02]
2
4
4
2 sin 2x sin3x
tan x 1
cos x

Giải
Điều kiện :
cos 0x
(1)
4 4 2
sin cos (2 sin 2 )sin3x x x x
2
2
22
sin 2
1 (2 sin 2 )sin3
2
2 sin 2 (2 sin 2 )2sin3
x
xx
x x x
2
(2 sin 2 )(1 2sin3 ) 0
1
1 2sin3 0 sin3
2
xx
xx
;
sin3 sin
6
x
32
6
5
32
6
2
18 3
52
18 3
xk
xk
k
x
k
x






k
Bài 64: [Dự bị 4 ĐH02]
2
x
tanx cosx cos x sinx 1 tanx.tan
2



Giải
2
x
tanx cosx cos x sinx 1 tanx.tan
2



(1)
Điều kiện :
cos 0
cos 0
2
x
x
Ta có :
sin sin cos cos sin sin
2 2 2
1 tan .tan 1
2
cos cos cos cos
22
x x x
x x x
x
x
xx
xx
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
34
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
cos
1
2
cos
cos cos
2
x
x
x
x
x




(1)
2
sin
tan cos cos
cos
x
x x x
x
cos 0 (L)
cos (1 cos ) 0
cos 1
x
xx
x
2;x k k
Bài 65: [Dự bị 5 ĐH02] Cho phương trình :
2sinx cosx 1
a
sinx 2cosx 3


a) Giải phương trình với
1
a=
3
b) Tìm a để phương trình trên có nghiệm.
Giải
a)Với
1
3
a
, phương trình thành :
2sinx cosx 1 1
sinx 2cosx 3 3


(1)
vì :
sin 2cos 3 0 x x x
(1)
6sin 3cos 3 sin 2cos 3
5sin 5cos 0 sin cos 0
2sin 0 sin 0
44
x x x x
x x x x
xx

sin 0
4 4 4
x x k x k




k
b)
2sinx cosx 1
a sinx cosx 1 a sinx 2cosx 3
sinx 2cosx 3


(2 )sin (2 1)cos 3 1a x a x a
(2)
Điều kiện để phương trình (2) có nghiệm :
2 2 2
2
2 2 1 3 1 4 6 4 0a a a a a
1
2
2
a
Bài 66: [Dự bị 6 ĐH02]
2
1
sinx
8cos x
Giải
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
35
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
2
1
sinx
8cos x
(1)
Điều kiện :
cos 0
sin 0
x
x
(1)
2 2 2
2
1
sin 1 8sin cos
8cos
x x x
x
2
2sin 2 1 0 cos4 0 4
2 8 4
k
x x x k x
Vì :
sin 0x
2
8
xm

;
3
2
8
xm

;
m
;
5
2
8
xm

;
7
2
8
xm

Bài 67: [ĐH A03]
2
cos2x 1
cotx 1 sin x sin2x
1 tanx 2
Giải
2
cos2x 1
cotx 1 sin x sin2x
1 tanx 2
(1)
Điều kiện :
sin2 0
tan 1
x
x

(1)
22
cos cos sin
1 sin (sin cos )
sin
sin
1
cos
x x x
x x x
x
x
x
22
2
cos sin cos (cos sin )
sin (sin cos )
sin sin cos
cos sin
cos (cos sin ) sin (sin cos )
sin
(cos sin ) sin sin cos 1 0
x x x x x
x x x
x x x
xx
x x x x x x
x
x x x x x

2
cos sin 0
sin sin cos 1 0
xx
x x x

*
cos sin 0 2 cos 0
4
x x x



cos 0 ;
4 4 2 4
x x k x k k




*
2
1 cos2 sin2
sin sin cos 1 0 1 0
22
xx
x x x
sin2 cos2 3 0xx
( vô nghiệm )
Bài 68: [ĐH B03]
2
cotx tanx 4sin2x
sin2x
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
36
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Giải
Điều kiện :
sin2 0x
(1)
cos sin 2
4sin2
sin cos sin2
xx
x
x x x
22
22
cos sin 2
4sin2
sin cos sin2
2cos2 4sin 2 2 2cos2 4 1 cos 2 2
xx
x
x x x
x x x x
2
cos2 1
2cos cos2 1 0
1
cos2
2
x
xx
x

3
xk
k
xk
Bài 69: [ĐH D03]
2 2 2
xx
sin tan x cos 0
2 4 2



Giải
Điều kiện :
cos 0x
(1)
2
2
1 sin 1
1 cos 1 cos
2 2 cos 2
x
xx
x






22
22
1 sin sin 1 cos cos
1 sin 1 cos 1 cos 1 sin
x x x x
x x x x
1 sin 1 cos sin cos 0x x x x
sin 1 sin 1
2
cos 1 cos 1 2
sin cos 0
sin 0
4
4
xk
xx
x x x k
xx
xk
x








So với điều kiện :
cos 0x
Nghiệm của (1) :
2
4
xk
k
xk


Bài 70: [Dự bị 1 ĐH A03]
3 tanx tanx 2sinx 6cosx 0
Giải
3 tanx tanx 2sinx 6cosx 0
Điều kiện :
cos 0x
sin sin 2sin cos
3 6cos 0
cos cos
x x x x
x
xx



Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
37
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
2 2 2
22
22
3cos sin 1 2cos 6cos 0
3cos 1 2cos sin 1 2cos 0
1 2cos 3cos sin 0
x x x x
x x x x
x x x
2
2
2
1
cos
1 2cos 0
1
2
cos
1
4
4cos 1 0
cos
4
x
x
x
x
x



1 1 2
1 cos cos2 cos
2 2 3
xx
>
2
22
2
3
cos2 cos
2
3
22
3
xk
x
xk


3
3
xk
k
xk


Bài 71: [Dự bị 2 ĐH A03]
2
cos2x cosx 2tan x 1 2
Giải
Điều kiện :
cos 0x
2
2sin
cos2 cos 2
cos
x
xx
x
2
2
2
2sin
cos 2 cos2 1 2sin
cos
1
2sin 1 1 cos
cos
x
x x x
x
xx
x



2
2(1 cos )(1 cos ) (1 cos )cosx x x x
2
1 cos 2(1 cos ) cos 0x x x


2
cos 1
cos 1
1
cos
2cos 5cos 2 0
2
x
x
x
xx



->
2
3
xk
xk


Bài 72: [Dự bị 1 ĐH B03]
62
3cos4x 8cos x 2cos x 3 0
Giải
62
3cos4x 8cos x 2cos x 3 0
24
3(1 cos4 ) 2cos (4cos 1) 0x x x
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
38
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
2 2 2 2
2 2 2
22
42
42
6cos 2 2cos (2cos 1)(2cos 1) 0
6cos 2 cos (2cos 1)cos2 0
cos2 3cos2 cos (2cos 1) 0
cos2 2cos 5cos 3 0
cos2 0
2cos 5cos 3 0
x x x x
x x x x
x x x x
x x x
x
xx


*
cos2 0 2
2 4 2
k
x x k x
;
k
*
2
4 2 2
2
cos 1
2cos 5cos 3 0 sin 0
3
cos ( )
2
x
x x x
xL
>
42
k
x
k
xk


Bài 73: [Dự bị 2 ĐH B03]
2
x
2 3 cosx 2sin
24
1
2cosx 1



Giải
Điều kiện :
1
cos
2
x
(1)
(2 3)cos 1 cos 2cos 1
2
2cos 3cos 1 sin 2cos 1
3cos sin 0
31
cos sin 0 cos cos sin sin 0
2 2 6 6
cos 0 ;
6 6 2 3
x x x
x x x x
xx
x x x x
x x k x k k











Vì :
1
cos
2
x
Nên nghiệm của phương trình :
4
2;
3
x k k
Bài 74: [Dự bị 1 ĐH D03]
2
cos x cosx 1
2 1 sinx
sinx cosx

Giải
Điều kiện :
sin cos 2sin 0
4
x x x



(1)
2
(1 sin )(cos 1) 2(1 sin )(sin cos )x x x x x
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
39
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
2
1 sin (1 sin )(cos 1) 2(sin cos ) 0
1 sin cos 1 sin cos sin 2sin 2cos 0
1 sin sin 1 sin cos cos 0
1 sin (1 sin ) cos (1 sin ) 0
sin 1
1 sin 1 cos 0
cos 1
x x x x x
x x x x x x x
x x x x x
x x x x
x
xx
x


Bài 75: [Dự bị 2 ĐH D03]
2cos4x
cotx tanx
sin2x

Giải
22
2
cos sin cos4
sin cos sin cos
cos sin cos4
cos2 cos4 2cos 2 cos2 1 0
cos2 1( )
12
cos2 cos
23
x x x
x x x x
x x x
x x x x
xL
x
;
3
x k k
Bài 76: [ĐH B04]
2
5sinx 2 3(1 sinx)tan x
Giải
2
2
(5sin 2)(1 sin ) 3sin
1
sin sin
2sin 3sin 2 0
26
sin 2
x x x
x
xx
x


2
6
5
2
6
xk
k
xk


Bài 77: [ĐH D04]
2cosx 1 2sinx cosx sin2x sinx
Giải
Điều kiện :
sin2 0 cos2 1xx
(1)
2cos4
cot tan
sin2
x
xx
x
2
5sinx 2 3(1 sinx)tan x
Điều kiện :
cos 0x
2
2
3sin
5sin 2 (1 sin )
1 sin
x
xx
x
2cosx 1 2sinx cosx sin2x sinx
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
40
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
(2cos 1)(2sin cos ) sin (2cos 1)
2cos 1 sin cos 0
1
cos cos
cos
2cos 1
3
2
sin cos 0
2sin 0
sin 0
4
4
x x x x x
x x x
x
x
x
xx
x
x









Bài 78: [Dự bị 1 ĐH A04]
sinx sin2x 3 cosx cox2x
Giải
Bài 79: [Dự bị 2 ĐH A04]
1 sinx 1 cosx 1
Giải
sinx sin2x 3 cosx cox2x
sin sin2 3cos 3cos2
sin 3cos 3cos2 sin2
1 3 3 1
sin cos cos2 sin2
2 2 2 2
x x x x
x x x x
x x x x
sin cos 2
36
sin cos 2 sin 2
3 2 3 3
sin 2 sin 0
33
3
sin 0
3
23
2sin cos 0
2 3 2
cos 0
2
xx
x x x
xx
x
xx
x









3
23
22
22
93
2
x
k
x
k
k
x
xk
k






Chú ý :
1 sin 0x
;
1 cos 0x
(1)
2 (sin cos ) 2 (1 sin )(1 cos ) 1x x x x
2 (sin cos ) 2 1 (sin cos ) sin cos 1x x x x x x
(2)
Đặt :
sin cost x x
;
2t
,khi đó :
2
1
sin cos
2
t
xx
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
41
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
2
2
21
(2) 1 2 0
2
1 2 ( 1) 0 1 2 1 0
tt
t
t t t t

(3)
1 sin cos 1 cos cos
44
t x x x




2
44
2
44
xk
xk


2
2
2
k
k
xk

Bài 80: [Dự bị 1 ĐH B04]
33
4 sin x cos x cosx 3sinx
Giải
33
32
32
2
2
2
4sin 4cos cos 3sin 0
4sin 4cos (1 sin ) cos 3sin 0
4sin 3cos 4sin cos 3sin 0
3(cos sin ) 4sin (cos sin ) 0
(cos sin ) 3 4sin 0
2 cos 0
4
cos sin 0
3
sin
3
2
sin
4
sin
x x x x
x x x x x
x x x x x
x x x x x
x x x
x
xx
x
x





3
2
x

4
3
xk
k
xk

Bài 81: [Dự bị 2 ĐH B04]
11
2 2cos x
cosx sinx 4



Giải
2 1 1tt
(3) ( nhận xét và suy ra :
1t
)
33
4 sin x cos x cosx 3sinx
11
2 2cos x
cosx sinx 4



Điều kiện :
sin2 0x
(1)
sin cos 2 2 cos
4
x x x



Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
42
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Bài 82: [Dự bị 1 ĐH D04]
sin4xsin7x cos3xcos6x
Giải
.
11
cos11 cos( 3 ) cos9 cos3
22
cos11 cos3 cos9 cos3
cos11 cos9 0
10
10
cos10 0
20
2
2cos10 cos 0
cos 0
2
2
x x x x
x x x x
xx
xk
xk
x
x x k
x
xk
xk




Bài 83: [Dự bị 2 ĐH D04]
sin2x 2 2 sinx cosx 5 0
Giải
cos 1 2
44
x x k k





Bài 84: [ĐH A05]
22
cos 3xcos2x cos x 0
Giải
1
2cos 2 2cos . sin2
4 4 2
cos 1 sin2 0
4
cos 0
42
4
22
sin2 1
2
x x x
xx
xk
x
k
xk
x










>
4
4
xk
k
xk

42
k
x

sin2x 2 2 sinx cosx 5 0
(1)
Đặt
sin cost x x
với
22t
2
sin2 1xt
(1)
2
32
2 2 6 0
2
t
tt
t

Với
2 sin cos 2t x x
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
43
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
2
2
(1 cos6 )cos2 1 cos2
0
22
cos2 cos6 cos2 1 cos2 0
cos6 cos2 1 0 cos8 cos4 2 0
2cos 4 1 cos4 2 0
cos4 1
2cos 4 cos4 3 0
3
cos4
2
x x x
x x x x
x x x x
xx
x
xx
x


Bài 85: [ĐH B05]
1 sin cosx sin2x cos2x 0
Giải
2
sin cos 2sin cos 2cos 0
(sin cos ) 2cos (sin cos ) 0
sin cos 0
(sin cos ) 1 2cos 0
12
cos cos
23
x x x x x
x x x x x
xx
x x x
x

Bài 86: [ĐH D05]
44
3
cos x sin x cos x sin 3x 0
4 4 2

Giải
22
2
13
1 2sin cos sin 4 sin2 0
2 2 2
2 sin 2 cos4 sin2 3 0
x x x x
x x x






22
2
sin 2 (1 2sin 2 ) sin2 1 0
sin2 1
sin 2 sin2 2 0
sin2 2
x x x
x
xx
x

Bài 87: [Dự bị 1 ĐH A05] Tìm
x 0;
22
x3
4sin 3cos2x 1 2cos x
24



Giải
Tìm
x 0;
của :
22
x3
4sin 3cos2x 1 2cos x
24



3
2(1 cos ) 3cos2 1 1 cos 2
2
x x x



2 2cos 3cos2 2 sin2x x x
2cos 3cos2 sin2x x x
(chia 2 vế cho 2)
22
cos 3xcos2x cos x 0
1 sin cosx sin2x cos2x 0
44
3
cos x sin x cos x sin 3x 0
4 4 2

Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
44
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
31
cos cos2 sin2 cos( ) cos 2
2 2 6
x x x x x



22
6
cos 2 cos( )
6
22
6
x x k
xx
x x k





1
12
2
2
5
18 3
;
7
2
6
k
x
kk
xk


Vì
1
1
1
5 17
0;1 ;
(0; )
18 18
k
k x x
k

Vì
2
2
2
5
1
(0; )
6
k
kx
k
5
18
3 17
cos 2 sin2
2 18
5
6
x
x x x
x




Bài 88: [Dự bị 2 ĐH A05]
3
2 2cos x 3cosx sinx 0
4



Giải
3
2 2cos x 3cosx sinx 0
4



3
3
3 3 2 2
2cos 3cos sin 0
4
(cos sin ) 3cos sin 0
cos sin 3cos sin 3cos sin 3cos sin 0
x x x
x x x x
x x x x x x x x






3
3 2 2 2
cos 0
sin sin 0
cos 0
1 tan 3tan 3tan 3(1 tan ) tan (1 tan ) 0
x
xx
x
x x x x x x

22
sin 1 cos 0
tan 1 tan 1
xx
xx






Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
45
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Bài 89: [Dự bị 1 ĐH B05]
3
2 2cos x 3cosx sinx 0
4



Giải
3
2 2cos x 3cosx sinx 0
4



3
3
3 3 2 2
2cos 3cos sin 0
4
(cos sin ) 3cos sin 0
cos sin 3cos sin 3cos sin 3cos sin 0
x x x
x x x x
x x x x x x x x






3
3 2 2 2
cos 0
sin sin 0
cos 0
1 tan 3tan 3tan 3(1 tan ) tan (1 tan ) 0
x
xx
x
x x x x x x

22
sin 1 cos 0
tan 1 tan 1
xx
xx






Bài 90: [Dự bị 2 ĐH B05]
2
2
cos2x 1
tan x 3tan x
2
cos x




Giải
2
2
cos2x 1
tan x 3tan x
2
cos x




(1)
Điều kiện :
sin2 0x
(1)
2
2
2
2sin
cot 3tan
cos
x
xx
x
23
1
tan 0 tan 1 tan 1
tan
x x x
x
->
;
4
x k k
Bài 91: [Dự bị 1 ĐH D05]
3 sinx
tan x 2
2 1 cosx



Giải
3 sinx
tan x 2
2 1 cosx



(1) Điều kiện :
sin 0x
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
46
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
(1)
2
22
sin cos sin
cot 2 2
1 cos sin 1 cos
cos (1 cos ) sin 2sin (1 cos )
cos cos sin 2sin (1 cos )
cos 1( )
(1 cos ) 1 2sin 0
1
sin sin
26
x x x
x
x x x
x x x x x
x x x x x
xL
xx
x



Bài 92: [Dự bị 2 ĐH D05]
sin2x cos2x 3sinx cosx 2 0
Giải
sin2x cos2x 3sinx cosx 2 0
2
2
2sin cos 1 2sin 3sin cos 2 0
2sin (2cos 3)sin cos 1 0 (1)
x x x x x
x x x x
Chú ý : (1) là phương trình bậc 2 với biến
sinx
Ta có :
22
(2cos 3) 8(cos 1) (2cos 1)x x x
Nghiệm của (1) :
2cos 3 2cos 1
sin cos 1
4
2cos 3 2cos 1 1
sin
42
xx
xx
xx
x

2
1
6
sin sin
5
26
2
6
xk
xk
xk


1
sin cos 1 sin cos 1 sin sin
44
2
x x x x x




Bài 93: [ĐH A06]
66
2 cos x sin x sin xcosx
0
2 2sin x

Giải
66
2 cos x sin x sin xcosx
0
2 2sin x

(1) điều kiện :
2
sin
2
x
(1)
66
2 sin cos sin cos 0x x x
2
2
3sin 2 1
2 1 sin2 0
42
sin2 1
3sin 2 sin2 4 0
4
sin2
3
x
x
x
xx
x



Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
47
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
sin2 1 2 2 ;
24
x x k x k k


vì :
2
sin
2
x
2
4
3
2
4
xk
xk


Nghiệm của (1):
5
2;
4
x k k
Bài 94: [ĐH B06]
x
cotx sinx 1 tanxtan 4
2



Giải
x
cotx sinx 1 tanxtan 4
2



(1)
Điều kiện :
sin2 0
cos 0
2
x
x
Ta có :
1
1 tan .tan
2 cos
x
x
x

(1)
cos sin 1
44
sin cos sin cos
xx
x x x x
22
1
6
2sin2 1 sin2 sin
5
26
22
6
xk
xx
xk


Bài 95: [ĐH D06]
cos3x cos2x cosx 1 0
Giải
cos3x cos2x cosx 1 0
2
2
cos3 cos cos2 1 0
2sin2 sin 2sin 0
2sin sin2 sin 0 2sin (2sin cos sin ) 0
sin 0
2sin 2cos 1 0
1
cos cos
23
x x x
x x x
x x x x x x x
x
xx
x

Bài 96: [Dự bị 1 ĐH A06]
33
2 3 2
cos3xcos x sin3xsin x
8

Giải
33
2 3 2
cos3xcos x sin3xsin x
8

(1)
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
48
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Ta có
33
33
1
cos3 4cos 3cos cos cos3 3cos
4
1
sin3 3sin 4sin sin 3sin sin3
4
x x x x x x
x x x x x x
(1)
1 2 3 2
cos3 cos3 3cos sin3 3sin sin3
48
x x x x x x


22
2 3 2
cos3 cos3 3cos sin3 3sin sin3
2
32
cos 3cos3 cos 3sin3 sin sin 3 1
2
32
1 3 cos3 cos sin3 sin 1
2
2
cos4 sin 4 2 ;
2 4 4
x x x x x x
x x x x x x
x x x x
x x k k

Bài 97: [Dự bị 2 ĐH A06]
2sin 2x 4sinx 1 0
6



Giải
2sin 2x 4sinx 1 0
6



2
2 sin2 cos cos2 sin 4sin 1 0
66
3sin2 cos2 4sin 1 0
2 3sin cos 4sin 2sin 0
2sin 3cos sin 2 0
sin 0
cos 1
3cos sin 2 0
6
x x x
x x x
x x x x
x x x
xk
x
x
xx








Bài 98: [Dự bị 1 ĐH B06]
2 2 2
2sin x 1 tan 2x 3 2cos x 1 0
Giải
2 2 2
2sin x 1 tan 2x 3 2cos x 1 0
(1)
điều kiện :
cos2 0x
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
49
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
(1)
2
22
cos2 .tan 2 3cos2 0
cos2 tan 2 3 0 tan 2 3
tan2 tan
tan2 3
3
tan2 3
tan2 tan
3
x x x
x x x
x
x
x
x






Bài 99: [Dự bị 2 ĐH B06]
cos2x 1 2cosx sinx cosx 0
Giải
cos2x 1 2cosx sinx cosx 0
22
(cos sin ) (1 2cos )(sin cos ) 0
(cos sin ) cos sin 2cos 1 0
cos 0
cos sin 0
4
sin cos 1
1
sin sin
44
2
x x x x x
x x x x x
x
xx
xx
x











4 2 4
2 2
4 4 2
32
2
44
x k x k
x k x k k
xk
xk












Bài 100: [Dự bị 1 ĐH D06]
3 3 2
cos x sin x 2sin x 1
Giải
3 3 2
cos x sin x 2sin x 1
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
50
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
22
sin cos 1 sin cos cos2
sin cos 1 sin cos cos sin
sin cos sin cos sin cos 1 0
sin cos 1 sin cos (1 sin ) 0
sin cos 1 sin 1 cos 0
sin 0
4
sin cos 0
sin 1
2
cos 1
x x x x x
x x x x x x
x x x x x x
x x x x x
x x x x
x
xx
xx
x







2
2
k
xk
Bài 101: [Dự bị 2 ĐH D06]
32
4sin x 4sin x 3sin2x 6cosx 0
Giải
32
4sin x 4sin x 3sin2x 6cosx 0
2
2
2
2
4sin (sin 1) 6cos (sin 1) 0
(sin 1)(4sin 6cos ) 0
(sin 1) 4(1 cos ) 6cos 0
sin 1
sin 1
cos 2
2cos 3cos 2 0
1
cos
2
x x x x
x x x
x x x
x
x
x
xx
x





Bài 102: [ĐH A07]
22
1 sin x cosx 1 cos x sinx 1 sin2x
Giải
22
1 sin x cosx 1 cos x sinx 1 sin2x
2 2 2
2
cos sin cos sin cos sin (sin cos )
(sin cos ) sin cos (sin cos ) (sin cos ) 0
(sin cos ) 1 sin cos sin cos 0
sin cos 0
(sin cos )(1 sin )(1 cos ) 0 1 sin 0
1 cos 0
x x x x x x x x
x x x x x x x x
x x x x x x
xx
x x x x x
x


Bài 103: [ĐH B07]
2
2sin 2x sin7x 1 sinx
Giải
2
2sin 2x sin7x 1 sinx
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
51
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
2
sin7 sin 2sin 2 1 0
2cos4 .sin3 cos4 0
cos4 0
cos4 2sin3 1 0
1
sin3 sin
26
x x x
x x x
x
xx
x

Bài 104: [ĐH D07]
2
xx
sin cos 3cosx 2
22



Giải
2
xx
sin cos 3cosx 2
22



1 sin 3cos 2
sin 3cos 1
2
1
36
sin sin
5
3 2 6
2
36
xx
xx
xk
x
xk






Bài 105: [Dự bị 1 ĐH A07]
11
sin2 sin 2cot2
2sin sin2
x x x
xx
Giải
11
sin2 sin 2cot2
2sin sin2
x x x
xx
(1) điều kiện :
sin2 0x
(1)
2
sin 2 sin2 sin cos 1 2cos2x x x x x
22
2
2
2
sin 2 1 cos (2sin 1) 2cos2
cos 2 cos2 .cos 2cos2 0
cos2 (cos2 cos 2) 0
cos2 0
cos2 (2cos cos 1) 0
2cos cos 1 0 ( )
x x x x
x x x x
x x x
x
x x x
x x VN
Bài 106: [Dự bị 2 ĐH A07]
2
2cos 2 3sin cos 1 3(sin 3cos )x x x x x
Giải
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
52
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
2
2
2cos 2 3sin cos 1 3(sin 3cos )
2cos 1 3sin2 2 3(sin 3cos )
cos2 3sin2 2 3(sin 3cos )
1 3 1 3
2 2 cos2 sin2 6 sin cos
2 2 2 2
2 2cos 2 6cos
36
1 cos2 3cos
6
x x x x x
x x x x
x x x x
x x x x
xx
xx




2
6
2cos 3cos 0
66
cos 0
6
cos 2cos 3 0
66
3
cos
62
xx
x
xx
x
















Bài 107: [Dự bị 1 ĐH B07]
53
sin cos 2cos
2 4 2 4 2
x x x

Giải
53
sin cos 2cos
2 4 2 4 2
x x x

53
sin sin 2cos
2 4 2 4 2 2
x x x



33
2cos sin 2cos
4 2 2 2
33
2cos cos 2cos
4 2 2
3
cos 0
2
3
cos 2 2cos 0
2
24
cos
42
xx
x
xx
x
x
x
x
x













2
33
2;
2
2
k
x
x k k
xk




Bài 108: [Dự bị 2 ĐH B07]
sin2 cos
tan cot
cos sin
xx
xx
xx
Giải
sin2 cos2
tan cot
cos sin
xx
xx
xx
(1) điều kiện :
sin2 0x
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
53
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
(1)
cos2 .cos sin2 .sin sin cos
sin cos cos sin
x x x x x x
x x x x
22
2
cos sin cos
sin cos sin cos
cos cos2 0
cos 1 ( )
2cos cos 1 0
1
cos
2
x x x
x x x x
xx
xL
xx
x


Bài 109: [Dự bị 1 ĐH D07]
2 2sin cos 1
12
xx




Giải
2 2sin cos 1
12
xx




2 sin 2 sin 1
12 12
1
sin 2 sin
12 12
2
sin sin sin 2sin cos
12 4 12 6 12
55
sin cos cos sin
12 12 2 12 12
x
x
x
x














5
22
12 12
7
22
12 12
xk
xk


Bài 110: [Dự bị 2 ĐH D07]
(1 tan )(1 sin2 ) 1 tanx x x
Giải
(1 tan )(1 sin2 ) 1 tanx x x
(1) điều kiện :
cos 0x
(1)
2
cos sin sin cos
.(sin cos )
cos cos
x x x x
xx
xx

2
22
(cos sin )(sin cos ) cos sin
(cos sin ) (cos sin )(cos sin ) 1 0
(cos sin )(cos sin 1) 0
cos sin 0
(cos sin )(cos2 1) 0
cos2 1
x x x x x x
x x x x x x
x x x x
xx
x x x
x

Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
54
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
cos 0
4
42
2
cos2 1
x
xk
xk
x







Bài 111: [ĐH A08]
1 1 7
4sin x
3
sinx 4
sin x
2






Giải
1 1 7
4sin x
3
sinx 4
sin x
2






(1)
Điều kiện :
sin 0x
và
3
sin 0
2
x




(1)
11
2 2(sin cos )
sin cos
xx
xx
Chú ý :
3
sin cos
2
xx




71
sin sin sin cos
44
2
x x x x

(1)
11
2 2(sin cos )
sin cos
xx
xx
sin cos
2 2(sin cos )
sin cos
1
(sin cos ) 2 2 0
sin cos
sin cos 0
1 2sin2
2 sin cos 0
2
sin2
sin2 sin
24
xx
xx
xx
xx
xx
xx
x
xx
x
x











Bài 112: [ĐH B08]
3 3 2 2
sin x 3cos x sinxcos x 3sin xcosx
Giải
3 3 2 2
sin x 3cos x sinxcos x 3sin xcosx
2 2 2 2
sin (cos sin ) 3cos (cos sin ) 0
cos2 (sin 3cos ) 0
cos2 0
cos2 0
sin 0
sin 3cos 0
3
x x x x x x
x x x
x
x
x
xx






Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
55
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
2sinx 1 cos2x sin2x 1 2cosx
2
4sin cos sin2 1 2cos
sin2 (2cos 1) (1 2cos ) 0
(2cos 1)(sin2 1) 0
1
2cos 1
cos
2
sin2 1
sin2 1
x x x x
x x x
xx
x
x
x
x



Bài 113[ĐH D08]
2sinx 1 cos2x sin2x 1 2cosx
Giải
2sinx 1 cos2x sin2x 1 2cosx
2
4sin cos sin2 1 2cos
sin2 (2cos 1) (1 2cos ) 0
(2cos 1)(sin2 1) 0
1
2cos 1
cos
2
sin2 1
sin2 1
x x x x
x x x
xx
x
x
x
x



Bài 114: [CĐ 08]
sin3x 3cos3x 2sin2x
Giải
sin3x 3cos3x 2sin2x
13
sin3 cos3 sin2
22
3 2 2
3
sin 3 sin2
3
3 2 2
3
x x x
x x k
x x k
x x k




Bài 115: [Dự bị 1 ĐH A08]
2
tan cot 4cos 2x x x
Giải
2
tan cot 4cos 2x x x
(1) điều kiện :
sin2 0x
(1)
2
cos sin
4cos 2 0
sin cos
xx
x
xx
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
56
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
2
cos2 2cos 2 sin2 0
cos2 sin4 .cos2 0
2
cos2 0
2
cos2 (1 sin4 ) 0
sin4 1
42
4
x x x
x x x
xk
x
xx
x
xk


Bài 116: [Dự bị 2 ĐH A08]
2
sin 2 sin
4 4 2
xx

Giải
2
sin 2 sin
4 4 2
xx

2
11
sin2 cos2 sin cos 1
22
sin2 sin (1 cos2 ) cos 0
sin (2cos 1) 2cos cos 0
sin (2cos 1) cos (2cos 1) 0
(2cos 1)(sin cos ) 0
1
cos
2cos 1 0
2
sin cos 0
sin 0
4
x x x x
x x x x
x x x x
x x x x
x x x
x
x
xx
x







Bài 117: [Dự bị 1 ĐH B08]
1
2sin sin 2
3 6 2
xx

Giải
1
2sin sin 2
3 6 2
xx

Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
57
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
2
3 1 1
sin 3cos sin2 cos2
2 2 2
1 2sin 1
sin 3cos 3sin cos
22
3cos 1 sin sin 1 sin 0
(1 sin )( 3cos sin ) 0
2
sin 1
2
3cos sin 0
sin 0
3
x x x x
x
x x x x
x x x x
x x x
xk
x
xx
x











Bài 118: [Dự bị 2 ĐH B08]
2
3sin cos2 sin2 4sin cos
2
x
x x x x
Giải
2
3sin cos2 sin2 4sin cos
2
x
x x x x
2
1 cos
3sin cos2 sin2 4sin
2
3sin cos2 sin2 2sin sin2
cos2 sin 0 2sin sin 1 0
sin 1
1
sin sin
26
x
x x x x
x x x x x
x x x x
x
x






Bài 119: [Dự bị 1 ĐH D08]
44
4 sin cos cos4 sin2 0x x x x
Giải
44
4 sin cos cos4 sin2 0x x x x
2
2
2
sin 2
4 1 1 2sin 2 sin2 0
2
sin2 1
4sin 2 sin2 5 0
5
sin2 ( )
4
x
xx
x
xx
xL




Bài 120: [Dự bị 2 ĐH D08]
2
2
tan tan 2
sin
tan 1 2 4
xx
x
x




Giải
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
58
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
2
2
tan tan 2
sin
tan 1 2 4
xx
x
x




(1) điều kiện :
cos 0x
(1)
2
2
tan tan 1
sin cos
tan 1 2
xx
xx
x
22
2
2
2
2cos tan tan sin cos
sin sin cos
2cos sin cos
cos
2sin sin cos sin cos 0
sin cos 2sin 1 0
sin 0
sin cos 0
4
2sin 1
1
sin cos
26
x x x x x
x x x
x x x
x
x x x x x
x x x
x
xx
x
x










Bài 121: [ĐH A09]
Giải
(1) điều kiện :
sin 1
1
sin
2
x
x

(1)
1 2sin cos 3(1 sin2 )(1 sin )x x x x
2
cos sin2 3 1 sin 2sin
cos sin2 3 cos2 sin
cos 3sin sin2 3cos2
1 3 1 3
cos sin sin2 cos2
2 2 2 2
22
63
cos cos 2
36
22
63
2
2
2
18 3
x x x x
x x x x
x x x x
x x x x
x x k
xx
x x k
xk
k
k
x






Bài 122: [ĐH B09]
3
sinx cosxsin2x 3cos3x 2 cos4x sin x
(1 2sinx)cosx
3
(1 2sinx)(1 sinx)

(1 2sinx)cosx
3
(1 2sinx)(1 sinx)

Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
59
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Giải
3
sinx cosxsin2x 3cos3x 2 cos4x sin x
2
sin 1 2sin cos sin2 3cos3 2cos4
sin cos2 cos sin2 3cos3 2cos4
sin3 3cos3 2cos4
13
sin3 cos3 cos4
22
x x x x x x
x x x x x x
x x x
x x x
4 3 2
6
cos 3 cos4
6
4 3 2
6
x x k
xx
x x k



Bài 123: [ĐH D09]
3cos5x 2sin3xcos2x sinx 0
Giải
3cos5x 2sin3xcos2x sinx 0
3cos5 sin5 sin sin 0
31
3cos5 sin5 2sin cos5 sin5 sin
22
5 2 6 2
33
sin 5 sin
22
3
5 2 4 2
33
x x x x
x x x x x x
x x k x k
xx
x x k x k













Bài 124: [CĐ 09]
2
(1 2sinx) cosx 1 sinx cosx
Giải
2
(1 2sinx) cosx 1 sinx cosx
2
2
(1 4sin 4sin )cos 1 sin cos
cos 2sin2 4sin cos 1 sin cos 0
1
sin2 sin
2sin2 1 sin 2sin2 1 0
26
sin 1
x x x x x
x x x x x x
x
x x x
x


Bài 125: [ĐH A10]
1 sinx os2 sin
1
4
cos
1 tanx
2
c x x
x



Giải
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
60
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com



1 sinx cos2x sin x
4
1
cosx
1 tanx
2
. Điều kiện:

cosx 0
tanx 1
pt

1 sinx cos2x sinx cosx
cosx
sinx
1
cosx

cosx 1 sinx cos2x sinx cosx
cosx
cosx sinx
1 sinx cos2x 0
2
2cos x sinx 0
2
2 1 sin x sinx 0
2
2 sin x sinx 2 0
1 17
sinx >1 (loaïi)
4
1 17
sinx (thoûa ñk)
4









1 17
x arcsin k2
4
kZ
1 17
x arcsin k2
4
Bài 126: [ĐH B10]
sin2x+cos2 cos 2cos2 sinx 0x x x
Giải
(sin2x + cos2x)cosx + 2cos2x – sinx = 0
cos2x (cosx + 2) + sinx (2cos
2
x – 1) = 0
cos2x (cosx + 2) + sinx.cos2x = 0
cos2x (cosx + sinx + 2 = 0) cos2x = 0
2x =
2
k
x =
42
k

(k Z)
Bài 127: [ĐH D10]
sin2 os2 3sin cos 1 0x c x x x
Giải
Các anh (chị) tự giải.
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
61
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Bài 128: [ĐH A11]
2
1 sin2 os2
2sinxsin2
1 cot
x c x
x
x

Giải
2
1 sin2 cos2
2.sin .sin2
1 cot
xx
xx
x

22
sin (1 sin2 cos2 ) 2 2sin cosx x x x x
(ĐK : sinx ≠ 0)
1 sin2 cos2 2 2cosx x x
2
2cos 2sin cos 2 2cos 0x x x x
2cos (cos sin 2) 0x x x
cosx = 0 hay cosx + sinx =
2
cosx = 0 hay
sin 1
4
x




x =
2
k
hay x =
2
4
k
(k Z)
Bài 129: [DB A11]
9sin 6cos 3sin2 cos2 8x x x x
Giải
Tham khảo thêm
Bài 130: [ĐH B11]
sin2 cos sinxcos os2 sinx cosx x x c x x
Giải
Phương trình đã cho tương đương :
2sinxcos
2
x + sinxcosx = 2cos
2
x – 1 + sinx + cosx
sinxcosx (2cosx + 1) = cosx (2cosx + 1) – 1 + sinx
cosx(2cosx + 1)(sinx – 1) – sinx + 1 = 0
sinx = 1 hay cosx(2cosx + 1) – 1 = 0
x =
2
2
k
hay 2cos
2
x + cosx – 1 = 0
x =
2
2
k
hay cosx = – 1 hay cosx =
1
2
x =
2
2
k
hay x = + k2 hay x =
2
3
k

(k Z)
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
62
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Bài 131: [ĐH D11]
sin2 2cos sinx 1
0
tanx 3
xx
Giải
sin2 2cos sin 1
0
tan 3
x x x
x
đk : tg
3x 
; cosx 0
Pt sin2x + 2cosx sinx 1 = 0 2sinxcosx + 2cosx (sinx + 1) = 0
2cosx (sinx + 1) (sinx + 1)= 0 (2cosx 1)(sinx + 1) = 0
1
2
cos
3
2
sin 1
2
2
xk
x
x
xk


so đk ta có nghiệm của pt :
2 ( )
3
x k k
Bài 132: [ĐH A12]
3sin2 cos2 2cos 1x x x
Giải
2
3sin2 cos2 2cos 1 2 3sin cos 2cos 1 2cos 1
cos 0
cos 3sin cos 1 0
3 1 1
sin cos
2 2 2
2
2
2
2 2 , ,
1
66
sin
2
5
62
2
2
3
66
x x x x x x x
x
x x x
xx
xk
xk
xk
x m x m k n m
x
xn
xn













Bài 133: [ĐH B12]
2(cos 3sin )cos cos 3sin 1.x x x x x
Giải
2(cos 3sin )cos cos 3sin 1x x x x x
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
63
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
(2cos 1)(cos 1) 3sin (2cos 1) 0
1
cos
2
2cos 1 0
2
2
3
1
cos 3sin 1
cos
2
32
x x x x
x
x
xk
xx
x
xk







Bài 134: [ĐH D12] sin3x + cos3x – sinx + cosx =
2
cos2x
Giải
sin3x + cos3x – sinx + cosx =
2
cos2x sin3x – sinx + cos3x + cosx =
2
cos2x
2sinxcos2x + 2cos2xcosx =
2
cos2x cos2x = 0 hay 2sinx + 2cosx =
2
cos2x = 0 hay
1
sin( )
42
x

x =
42
k

hay x =
2
12
k

hay x =
7
2
12
k
(với k Z).
Bài 135: [ĐH A13]
1 tanx 2 2sin x
4



Giải
1+tanx=2(sinx+cosx)
cosx+sinx = 2(sinx+cosx)cosx (hiển nhiên cosx=0 không là nghiệm)
sinx+cosx=0 hay cosx =
1
2
tanx=-1 hay cosx =
1
2
2,
43
x k hay x k k


Bài 136: [ĐH B13]
2
sin5 2cos 1xx
Giải
2
sin5 2cos 1xx
sin5x = 1 – 2 cos
2
x = -cos2x = sin(2x - /2)
5x = 2x -
2
+ k2 hay 5x = - 2x +
2
+ k2, k Z
x =
2
63
k


hay x =
32
14 7
k

, k Z
Bài 137: [ĐH D13]
sin3 cos2 sinx 0xx
Giải
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
64
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
2cos2 sin cos2 0 cos2 2sin 1 0 x x x x x
cos2 0
,
42
1
7
sin
2 2 ,
2
66
x
x k k Z
x
x k hay x k k Z





Bài 138: Giải phương trình :
)
2
sin(2
cossin
2sin
cot
2
1
x
xx
x
x
Giải
PT
0cos2
cossin
cossin2
sin2
cos
x
xx
xx
x
x
2
cos 2 cos
0
sin cos
2 sin
xx
xx
x
cos sin( ) sin2 0
4
x x x



+)
.,
2
0cos kkxx
+)
nm
n
x
mx
nxx
mxx
xx ,
3
2
4
2
4
2
4
2
2
4
2
)
4
sin(2sin
.,
3
2
4
t
t
x
Đối chiếu điều kiện ta có nghiệm của pt là
kx
2
;
.,,
3
2
4
tk
t
x
Bài 139: Giải phương trình
2
4
2
1 tan
8 os ( ) sin4 2.
4 1 tan
x
c x x
x
Giải
Đk:
0
2
cos x x k
,ta có
2
2 inx 1 2 n
4
cos( x ) cosx s , sin x cos x si
4
22
3
4
os 1 2
os inx
cos x sinx c x sin x sin x
cos x sinx c x sin x s cos x
sin3 cos2 sin 0 x x x
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
65
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
3
0sinx cosx sinx
0
00
4
xk
sinx x k
cos x sinx tan x
xk





Vậy pt có 2 nghiệm:
4
xk
xk

Bài 140: Giải phương trình
2cot)cos1(3
2
5
sin5
2
xxx
Giải
ĐKXĐ
Zkkx ,
Pt(1)
2
cos1
cos
)cos1(3cos5
2
2
x
x
xx
2
cos1
cos3
cos5
2
x
x
x
02cos3cos2
2
xx
2
1
cos
2cos
x
x
2cos x
vô nghiệm
Zllxx ,2
32
1
cos
, thỏa mãn điều kiện.
Bài 141: Gi¶i ph-¬ng tr×nh:
1 2(cos sin )
tan cot 2 cot 1
xx
x x x

Giải
§iÒu kiÖn:sinx.cosx
0 vµ cotx
1
Ph¬ng tr×nh t¬ng ®¬ng
1 2(cos sin )
sin cos2 cos
1
cos sin2 sin
xx
x x x
x x x

cosx =
2
2
x =
2
4
k

§èi chiÕu ®iÒu kiÖn pt cã 1 hä nghiÖm x =
2
4
k

Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
66
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Bài 142: Giải phương trình sin2x + cosx-
2
sin
x
4



-1= 0.
Giải
Pt đã cho tương đương:
01sin)1(sincos201)cos(sincos2sin xxxxxxx
01cos21sin xx
1sin x
hoặc
2
1
cos x
sin 1 2 .
2
x x k
1
os 2
23
c x x k
.
Vậy, nghiệm của phương trình đã cho là:
2
2
xk
;
2
3
xk
(
kZ
).
Bài 143: Giải phương trình :
2
2 os3x.cosx+ 3(1 sin2x)=2 3 os (2 )
4
c c x

Giải
Bài 144: Giải phương trình:
2
sin .sin4 2 2.cos 4 3.cos .sin .cos2
6
x x x x x x



Giải
os4x+cos2x+ 3(1 sin2 ) 3 1 os(4x+ )
2
os4x+ 3sin4 os2x+ 3sin2 0
PT c x c
c x c x



sin(4 ) sin(2 ) 0
66
18 3
2sin(3 ). osx=0
6
x=
2
xx
xk
xc
k


Vậy PT có hai nghiệm
2
xk

và
18 3
xk

.
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
67
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Bài 145: Giải phương trình
3 os2x+sin2x- (4+ 3) osx-sinx+2+ 3=0cc
Giải
2
2
3(2 os x-1)+2sinx. os x - (4+ 3) osx-sinx+2+ 3=0
(2sinx. os x-sinx)+2 3 os x- (4+ 3) osx+2=0
sinx ( 2cosx-1)+( 2cosx-1)( 3cosx-2)=0
( 2cosx-1) sinx+ 3cosx-2 0
pt c c c
c c c

1
osx= (1)
2
sinx+ 3cosx-2=0 (2)
(1) 2 ( )
3
c
pt
x k k Z
13
(2) sinx+ cosx=1 sin( ) 1 2 ( )
2 2 3 6
x x k k Z

Bài 146: Giải phương trình
(1 cos )cot cos2 sin sin2x x x x x
.
Giải
Điều kiện:
cos .sin2 .sin . tan cot2 0
cot 1
x x x x x
x

ĐK: Ta có:
sin .sin4 2 2cos 3.cos .sin4
6
x x x x x



sin4 sin 3cos 2 2cos
6
x x x x



sin4 2
sin4 2 cos 0
6
cos 0
6
x vn
xx
x







Với :
cos 0
63
x x k k Z




Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
68
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Từ (1) ta có:
2 cos sin
1 cos .sin2
2sin
sin cos2 cos
cos
1
cos sin2 sin
xx
xx
x
x x x
x
x x x

2sin .cos 2sinx x x
2
2
4
cos
2
2
4
xk
xk
xk

Giao với điều kiện, ta được họ nghiệm của phương trình đã cho là
2
4
x k k
Bài 147: Giải phương trình
(1 cos )cot cos2 sin sin2x x x x x
.
Giải
Phương trình
(1 cos )cot cos2 sin sin2x x x x x
(1)
Điều kiện:
sin 0 ( )x x k k
Khi đó: (1)
cos
(1 cos ) cos2 sin sin2
sin
x
x x x x
x
2 2 2
2 2 2
cos cos cos2 sin sin 2sin cos
cos (1 2sin ) cos2 sin (cos sin ) 0
x x x x x x x
x x x x x x
cos cos2 cos2 sin cos2 0 cos2 (cos sin 1) 0
cos2 0 cos sin 1 0
x x x x x x x x
x x x
+
cos2 0 ( )
42
x x k k

.
+
1
cos sin 1 0 cos 2
4 4 4
2
x x x x l



2
2
2
xl
xl

Kết hợp điều kiện phương trình đã cho có các nghiệm là:
42
xk


,
2
2
xl

( , )kl
.
Bài 148: Gi¶i ph-¬ng tr×nh sau:
2
2017
2.sin sin 2 1 tan
42
x x x

Giải
§iÒu kiÖn:
cos 0 ( )
2
x x k k Z
+Víi ®k trªn pt ®· cho t-¬ng ®-¬ng:
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
69
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
1 cos 2 sin(2 1008 ) 1 tan
22
x x x




1 sin2 cos2 1 tanx x x
sin2 cos2 tan 0x x x
2
sin
2sin .cos 2cos (1 ) 0
cos
x
x x x
x
sin cos
2cos .(sin cos ) 0
cos
xx
x x x
x
1
(sin cos ).(2cos ) 0
cos
x x x
x
2sin .cos2 0
4
xx
4
sin 0
4
cos2 0
4
2
xk
x
k
x
x



(tm®k)
VËy pt ®· cho cã 1 hä nghiÖm:
42
k
x


(hä
42
k

chøa
4
k

)
Bài 149: Giải phương trình sau:
23
2
2
cos cos 1
cos2 tan
cos
xx
xx
x


Giải
ĐK cosx ≠ 0, pt được đưa về
2 2 2
cos2 tan 1 cos (1 tan ) 2cos cos -1 0x x x x x x
Giải tiếp được cosx = 1 và cosx = 0,5 rồi đối chiếu đk để đưa ra ĐS:
22
2 , 2 ; hay
33
x k x k x k


.
Bài 150: Giải phương trình:
(1 cos )cos 1
(1 cos )(1 2cos ) tan
xx
x x x

()x
Giải
1 cos cos
1
1 cos 1 2cos tan
xx
x x x

1
ĐK:
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
70
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
cos 1
1 sin2x 0
cos
2
1
cosx
cos 0
2
sin 0
x
x
x
x




PT
1
2
sin sin .cos 1 cos 2cosx x x x x
sin cos 1 sin .cos 2 1 sin 1 sin 0x x x x x x
1 sin 2sin cos 1 0x x x
sin 1
2sin cos 1 0
x Loai
xx
2sin cos 1xx
2
2 2 /
x k loai
x k T m



Vậy PT
1
có các nghiệm
2 2 ,xk

k
Với
thỏa mãn:
2
cos
5
1
sin
5
Bài 151: Giải phương trình:
33
sin cos cos2 .cot .cot
44
x x x x x

Giải
* Giải phương trình:
33
sin cos cos2 .cot .cot
44
x x x x x

(1)
33
(1) cos sin cos2 .cot( ).cot( )
44
PT x x x x x

(2)
* ĐK:
sin( ).sin( ) 0 sin( ).cos( ) 0 sin( 2 ) 0
4 4 4 4 2
cos2 0 2
2 4 2
x x x x x
x x k x k
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
71
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
33
(2) cos sin cos2 (cos sin )(1 sin .cos ) (cos sin )(cos sin )
tan 1
cos sin 0 tan 1
sin 1
1 sin .cos cos sin (1 cos )(1 sin ) 0
cos 1
, 2 , 2
42
PT x x x x x x x x x x x
x
x x x
x
x x x x x x
x
x k x k x k




- Kết hợp với điều kiện ta được 2 họ nghiệm :
2 , 2
2
x k x k

,
k
Bài 152: Giải phương trình:
x x x x
3
2 2 cos2 sin2 cos 4sin 0
44

.
Giải
x x x x x(sin cos ) 4(cos sin ) sin2 4 0


xk
4
;
x k x k
3
2 ; 2
2

Bài 153: Giải phương trình:
x x x x
2 2 2 2
sin 3 cos 4 sin 5 cos 6
Giải
x x x x
2 2 2 2
si n 3 cos 4 sin 5 c os 6
x x xcos (cos7 cos11 ) 0
k
x
k
x
2
9
Bài 154: Tìm nghiệm trên khoảng
0;
2



của phương trình:
x
xx
22
3
4sin 3sin 2 1 2cos
2 2 4

Giải
(2)
xxsin 2 sin
32





x k k Z a
x l l Z b
52
( ) ( )
18 3
5
2 ( ) ( )
6

Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
72
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Bài 155: Giải phương trình:
x x x
xx
11
sin2 sin 2cot2
2sin sin2
Giải
(1)
2
2 2 2 2
20
x x x x
x
cos cos cos cos
sin
cos2x = 0
xk
42


Bài 156: Giải phương trình:
x x
xx
3sin2 2sin
2
sin2 .cos
(1)
Giải
(1)
2(1 cos )sin (2cos 1) 0
sin 0, cos 0

x x x
xx
2cosx – 1 = 0
2
3
xk
Bài 157: Giải phương trình:
cos2 5 2(2 cos )(sin cos ) x x x x
(1)
Giải
(1)
x x x x
2
(cos –sin ) 4(cos –sin )–5 0
x k x k22
2
Bài 158: Tìm các nghiệm thực của phương trình sau thoả mãn
1
3
1 log 0x
:
sin .tan2 3(sin 3tan2 ) 3 3 x x x x
Giải
(2)
(sin 3)(tan2 3) 0 xx
;
62

x k k Z
Kết hợp với điều kiện ta được k = 1; 2 nên
5
;
36

xx
Bài 159: Giải phương trình:
33
2 3 2
cos3 cos sin3 sin
8
x x x x
Giải
(1) cos4x =
2
2
16 2

xk
Bài 160: Giải phương trình: 9sinx + 6cosx – 3sin2x + cos2x = 8
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
73
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Giải
PT (1– sinx)(6cosx + 2sinx – 7) = 0 1– sinx = 0
2
2
xk
Bài 161: Tìm nghiệm của phương trình:
23
cos sin 2 x cos x x
thoả mãn :
13x
Giải
PT
(cos 1)(cos sin sin .cos 2) 0 x x x x x
2
xk
. Vì
1 3 2 4 xx
nên nghiệm là: x = 0
Bài 162: Giải phương trình:
(sin2 sin 4)cos 2
0
2sin 3
x x x
x
Giải
Bài 163: Giải phương trình:
sin cos 4sin2 1 x x x
.
Giải
PT
(2cos 1)(sin cos 2) 0
2sin 3 0

x x x
x
2
3
xk
Bài 164: Giải phương trình: cos
2
3x.cos2x – cos
2
x = 0.
Giải
Đặt
sin cos , 0 t x x t
. PT
2
4 3 0tt
xk
2
.
Bài 165: Giải phương trình.
3sin2 2sin
2
sin2 .cos
x x
xx
Giải
Dùng công thức hạ bậc. ĐS:
()
2
x k k Z
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
74
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Bài 166: Giải phương trình: 4cos
4
x – cos2x
13
cos4 cos
24

x
x
=
7
2
Giải
PT
2 1 2 0
00
x x x
xx
( cos )(sin sin )
sin , cos

2
3
xk
Bài 167 : Giải phương trình:
2
cos . cos 1
2 1 sin
sin cos

xx
x
xx
Giải
PT cos2x +
3
cos
4
x
= 2
cos2 1
3
cos 1
4
x
x
( ; )
8
3
xk
km
m
x
x = 8n
Bài 168: Giải phương trình:
22
1 sin sin cos sin 2cos
2 2 4 2



x x x
xx
Giải
PT
2
sin sin 1 2sin 2sin 1 0
2 2 2
x x x
x
4



xk
xk
xk
Bài 169: Giải phương trình:
33
sin .sin3 cos cos3 1
8
tan tan
63



x x x x
xx
Giải
Điều kiện:
sin sin cos cos 0
6 3 6 3
x x x x
Ta có
tan tan tan cot 1
6 3 6 6
x x x x
PT
33
1
sin .sin3 cos cos3
8
x x x x
1 cos2 cos2 cos4 1 cos2 cos2 cos4 1
2 2 2 2 8
x x x x x x
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
75
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
3
1 1 1
2(cos2 cos2 cos4 ) cos 2 cos2
2 8 2
x x x x x
6
6

x k (loaïi)
xk
Vậy phương trình có nghiệm
6
xk
,
()k
Bài 170: Giải phương trình:
33
sin .(1 cot ) cos (1 tan ) 2sin2 x x x x x
.
Giải
ĐKXĐ:
2
k
x
sao cho
sin2 0x
.
Khi đó, VT =
3 3 2 2
sin cos sin cos cos sin x x x x x x
=
22
(sin cos )(sin sin cos cos ) sin cos (sin cos ) x x x x x x x x x x
=
sin cosxx
PT
2
sin cos 0
sin cos 2sin2
(sin cos ) 2sin2 (1)


xx
x x x
x x x
(1)
1 sin2 2sin2 sin2 1( 0) x x x
22
24


x k x k
Để thoả mãn điều kiện
sin cos 0xx
, các nghiệm chỉ có thể là:
2
4
xk
Bài 171: Tìm giá trị nhỏ nhất của hàm số: y =
2
cos
sin (2cos sin )
x
x x x
với 0 < x
3
.
Giải
Với
0
3
x
thì
0 tan 3x
và
sin 0,cos 0, 2cos sin 0 x x x x
22
3
2
2 2 3
2
cos
1 tan 1 tan
cos
sin 2cos sin
tan (2 tan ) 2tan tan
.
cos cos


x
xx
x
y
x x x
x x x x
xx
Đặt:
tan ; 0 3 t x t
2
23
1
( ) ; 0 3
2
t
y f t t
tt
4 2 3 2
2 3 2 2 3 2 2 3 2
3 4 ( 3 4) ( 1)( 4)
( ) ( ) 0 ( 0 1).
(2 ) (2 ) (2 )

t t t t t t t t t t
f t f t t t
t t t t t t
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
76
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Từ BBT ta có:
min ( ) 2 1
4
f t t x
. Vậy:
0;
3
2
4


miny khi x
.
Bài 172: Giải phương trình:
sin 3 sin2 sin
44

x x x
.
Giải
PT
sin3 cos3 sin2 (sin cos ) x x x x x
(sinx + cosx)(sin2x 1) = 0
sin cos 0 tan 1
sin2 1 0 sin2 1




x x x
xx
4
4
4

xk
xk
xk
Bài 173: Giải phương trình: cos
2
x + cosx + sin
3
x = 0
Giải
PT cosx(1 + cosx) + 8
33
sin cos
22
xx
= 0
2
2cos cos (1 cos )sin 0
2
x
x x x
cos 0
2
sin cos sin .cos 0
x
x x x x
Bài 174: Giải phương trình:
1
cos3 cos2 cos
2
x x x
Giải
Nếu
cos 0 2 ,
2

x
x k k Z
, phương trình vô nghiệm.
Nếu
cos 0 2 ,
2

x
x k k Z
, nhân hai vế phương trình cho
2
2
x
cos
ta được:
2cos cos3 2cos cos2 2cos cos cos
2 2 2 2
x x x x
x x x

tích thành tông
7
0
2
x
cos
2
,
77

x k k
, đối chiếu điều kiện: k ≠ 3 + 7m, mZ .
Bài 175: Tìm tổng tất cả các nghiệm x thuộc [ 2; 40] của phương trình: sinx – cos2x = 0.
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
77
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Giải
Ta có: sinx – cos2x = 0 2sin
2
x + sinx –1 = 0
2
,
63

x k k
.
Vì x [ 2; 40] nên
2 3 3
2 40 2 40
6 3 2 6 2 6

kk
0,7 k 18,8 k
1,2,3,...,18
.
Gọi S là tổng các nghiệm thoả YCBT: S =
2
18. (1 2 3 ... 18) 117
63

.
2) Điều kiện:
13x
. PT
2 2 2
log 1 log (3 ) log ( 1) 0
13

x x x
x
2
1 17
1 3 1 4 0
2
x x x x x x
(tmđk)
Bài 176: Giải phương trình:
tan tan .sin3 sin sin2
63

x x x x x
Giải
Điều kiện:
cos .cos 0
63

xx
PT
sin sin
63
sin3 sin sin2
cos cos
63




xx
x x x
xx
– sin3x = sinx + sin2x
sin2x(2cosx + 1) = 0
sin2 0
2
1
2
cos
2
2
3


k
x
x
x
xk
Kết hợp điều kiện, nghiệm của phương trình là:
2
2
2
3
k
x
xk
Bài 177 : Giải phương trình :
22
1 8 21 1
2cos os 3 sin2( ) 3cos sin x
3 3 2 3




x c x x x
.
Giải
PT
1 sin 0
(1 sin )(6cos sin 8) 0 1 sin 0
6cos sin 8 0

x
x x x x
xx
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
78
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Bài 178: Giải phương trình:
11
sin2 sin 2cot2
2sin sin2
x x x
xx
Giải
PT cos
2
2x cosxcos2x = 2cos2x và sin2x 0
2
cos2 0 2cos cos 1 0( ) x x x VN
cos2x = 0
2
2 4 2
x k x k
Bài 179: Giải phương trình:
2sin
4
(1 sin2 ) 1 tan
cos



x
xx
x
Giải
Điều kiện
cos 0 ,
2
x x k k
.
Ta có PT
2
cos sin cos sin
cos sin
cos cos

x x x x
xx
xx
(cos sin )(cos2 1) 0 x x x
cos sin 0
,
4
cos2 1 0


xx
xm
m
x
xm
.
Bài 180: Giải phương trình:
2 2 3 3
tan tan .sin cos 1 0 x x x x
Giải
ĐK:
2
xk
. PT
2 3 3
tan (1 sin ) (1 cos ) 0 x x x
(1 cos )(1 sin )(sin cos )(sin cos sin cos ) 0 x x x x x x x x
2 ; ; 2 ; 2
4 4 4
x k x k x k x k
Bài 181: Giải phương trình: 2cos3x +
3
sinx + cosx = 0
Giải
PT cos
cos3
3



xx
cos
cos( 3 )
3



xx
32


k
x
Bài 182: Giải phương trình:
66
22
sin cos 1
tan2
cos sin 4
xx
x
xx
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
79
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Giải
Điều kiện: cos2x ≠ 0
()
42

k
xk
PT
2
31
1 sin 2 sin2
44
xx
3sin
2
2x + sin2x – 4 = 0
sin2x = 1
4
xk
( không thoả). Vậy phương trình vô nghiệm.
Bài 183: Giải phương trình: cos3xcos
3
x – sin3xsin
3
x =
2 3 2
8
Giải
PT
2
cos4 ,
2 16 2

x x k k Z
Bài 184: Giải phương trình :
3 3
2
cos cos3 sin sin3
4
x x x x
Giải
PT
cos 2x=
1
2
x=
()
8

kk
Bài 185: Giải phương trình:
cot 3 tan 2cot2 3 x x x
.
Giải
Điều kiện:
sin cos 0
2
x x x k
.
Ta có:
22
cos2 cos sin
2cot2 2 2 cot tan
sin2 2sin cos
x x x
x x x
x x x
.
PT
2
cot 3
3 cot 3 cot cot 1 ,
4
cot 7cot 6 0
x
x x x x k k
xx
Bài 186: Giải phương trình:
x x x
2
2cos 3 4cos4 15sin2 21
4



Giải
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
80
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
PT
x x x
32
sin 2 2sin 2 3sin2 6 0
xsin2 1
xk
4
Bài 187: Giải phương trình:
xx
2
1
(1 4sin )sin3
2

Giải
Nhận xét: cosx = 0 không phải là nghiệm của PT. Nhân 2 vế của PT với cosx, ta được:
PT
x x x x
3
2sin3 (4cos 3cos ) cos
x x x2sin3 .cos3 cos
xxsin6 sin
2




kk
xx
22
14 7 10 5
Bài 188: Giải phương trình:
x x x x
2
1
sin sin2 1 cos cos
2
Giải
PT
x x x(sin 1)(sin cos 2) 0
xsin 1
xk2
2

.
Bài 189: Giải phương trình:
xx
x
xx
3sin 3tan
2cos 2
tan sin

Giải
Điều kiện:
x
x
cos 0
sin 0
. PT
x
1
cos
2

xk
2
2
3
.
Bài 190: Giải phương trình:
xx
x x x
1 2(cos sin )
tan cot2 cot 1

Giải
Điều kiện:
x
x
x
sin 0
cos 0
cot 1
. PT
x
2
cos
2
xk2
4
.
Bài 191: Giải phương trình:
sin3 3sin2 cos2 3sin 3cos 2 0x x x x x
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
81
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Giải
sin3 3sin2 cos2 3sin 3cos 2 0x x x x x
(sin3 sin ) 2sin 3sin2 (cos2 2 3cos ) 0x x x x x x
2
2sin2 .cos 2sin 6.sin .cos (2cos 3cos 1) 0x x x x x x x
22
2sin cos 2sin 6sin cos (2cos 3cos 1) 0x x x x x x x
2
11
(2sin 1)(2cos 3cos 1) 0 sin ,cos 1,cos
22
x x x x x x
+)
15
sin 2 , 2
2 6 6
x x k x k


+)
1
cos 2
23
x x k
+)
cos 1 2x x k
KL:Vậy phương trình có 5 họ nghiệm như trên.
Bài 192: Giải phương trình:
2
(2sin 1)(3cos4 2sin ) 4cos 1
8
1 sin
x x x x
x
()x
Giải
2
2sin 1 3cos4 2sin 4cos 1
8
1 sin
x x x x
x
1
Đk:
1 sin 0 2 ,
2
x x l l
*
PT
1
2
2sin 1 3cos4 2sin 4cos 1 8 8sinx x x x x
2
2sin 1 3cos4 2sin 4sin 8sin 3x x x x x
2sin 1 3cos4 2sin 2sin 1 2sin 3x x x x x
2sin 1 0
cos4 1
x
x

Với
2sin 1 0x
2
6
7
2
6
xk
xk

Với
cos4 1
2
k
xx
Kết hợp với điều kiện
*
PT
1
có các nghiệm
2
63
xk

xk
,
k
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
82
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Bài 193: Giải phương trình sau:
2
5
4sin os(3x + 2013 ) - 2sin 2 2 sin
2 2 2
x c x x
Giải
Bài 194: Giải phương trình:
sin3 cos3
cos2 sin (1 tan )
2sin2 1
xx
x x x
x
.
Giải
Đk
1
sin2
(*)
2
cos 0
x
x
. Với đk (*) phương trình đã cho tương đương:
33
22
3sin 4sin 4cos 3cos
cos2 sin(1 tan )
2sin2 1
(sin cos )(2sin2 1) sin (sin cos )
cos sin
2sin2 1 cos
x x x x
xx
x
x x x x x x
xx
xx
sin cos 0 (1)
sin
cos sin 1 (2)
cos
xx
x
xx
x

(1) tan 1 ,
4
x x k k
cos sin 0 tan 1
(2) (cos sin )(1 cos ) 0 ( )
4
1 cos 0 cos 1
2
x x x
xk
x x x k
xx
xk






So với đk (*) suy ra các họ nghiệm của pt là:
, 2 ,
4
x k x k k
Bài 195: Giải phương trình
tan( ).tan( ) 2 os2 1
66
x x c x

.
Giải
PT
2
4 os os3 2 os2x 2 osc x c x c c x
os3 osc x c x
32
32
x x k
x x k
2
xk

.
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
83
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
ĐK:
cos( ) 0 ( )
6 6 2 3
2
cos( ) 0 ( )
6 6 2 3
x x k x k
x x k x k



Ta có:
11
sin( ).sin( )
cos2
1 2cos2
66
42
11
2cos2 1
cos( ).cos( ) cos2
6 6 2 4
xx
x
x
VT
x
x x x



Vậy
1
22
cos2
6
(1 2 os2 )(2cos2 2) 0
3
2
cos2x=-1
2x= 2
x=
2
xk
xk
x
PT c x x
k
k

Đối chiếu đk ta có:
;x=
62
x k k


là các họ nghiệm của phương trình
Bài 196: Giải phương trình
2
2cos 2 3sin cos 1 3(sin 3cos )x x x x x
.
Giải
2
2cos 2 3sin cos 1 3(sin 3cos )x x x x x
2
(sin 3cos ) 3(sin 3cos ) 0x x x x
sin 3cos 0 sin 3cos 3x x x x
(1)
Phương trình
sin 3cos 3xx
vô nghiệm vì
222
3)3(1
Nên (1)
tan 3
3
x x k
(
k
). Vậy, PT có nghiệm là:
3
xk
(
k
).
Bài 197: Giải phương trình
3
sinx - 3cosx - 2 =
cos2x
-
3
sin2x
Giải
3
sinx - 3cosx - 2 =
cos2x
-
3
sin2x (1) (1)
3
sinx(2cosx + 1) = 2cos
2
x + 3cosx + 1
(2cosx + 1)(cosx -
3
sinx + 1) = 0
cosx = -
1
2
hoặc cosx -
3
sinx + 1 = 0 (1’)
* cosx = -
1
2
x =
2
3
+ k2
(1’)
cos(x +
3
) = -
1
2
x =
3
+ k2 hoặc x = - + k2
Bài 198: Giải phương trình :
44
sin cos 1
tan cot
sin2 2
xx
xx
x

Giải
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
84
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
44
sin cos 1
tan cot
sin2 2
xx
xx
x

(1)
Điều kiện:
sin2 0x
2
1
1 sin 2
1 sin cos
2
(1)
sin2 2 cos sin
x
xx
x x x



2
1
1 sin 2
1
2
sin2 sin2
x
xx

2
1
1 sin 2 1 sin2 0
2
xx
Vậy phương trình đã cho vô nghiệm.
Bài 199: Giải phương trình:
2 os6x+2cos4x- 3 os2x = sin2x+ 3cc
Giải
2 os6x+2cos4x- 3 os2x=sin2x+ 3cc
4cos5xcosx = 2sinxcosx + 2
3
cos
2
x
os x=0
2cos5x =sinx+ 3cos
c
x
cos 0
os5x=cos(x- )
6
x
c
2
24 2
36 3
xk
k
x
k
x




Bài 200: Giải phương trình :
2
sin4
3
cos
3
cos
22
x
xx
Giải
Ta có:
2
sin4
2
2
3
2
cos1
2
2
3
2
cos1
2
sin4
3
cos
3
cos
22
x
xx
x
xx
02cos
3
2
cos22sin02
3
2
cos2
3
2
cos2sin
xxxxx
03sinsin202cos2sin
2
xxxx
)(
2
3
sin
1sin
VNx
x
2
2
kx
(k Z)
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
85
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
- Tài liệu do tập thể tác giả biên soạn:
8. Cao Văn Tú – CN.Mảng Toán – Khoa CNTT – Trường ĐH CNTT&TT Thái
Nguyên (Chủ biên)
9. Cô Trần Thị Ngọc Loan – CLB Gia Sư Thái Nguyên(Đồng chủ biên).
10. Thầy Vũ Khắc Mạnh – CLB Gia sư Bắc Giang (Tư vấn).
11. Nguyễn Thị Kiều Trang – SV Khoa Toán – Trường ĐHSP Thái Nguyên.
12. Nguyễn Trường Giang – Khoa CNTT – Trường ĐH CNTT&TT Thái
Nguyên.
13. Lý Thị Thanh Nga – SVNC – Khoa Toán – Trường ĐH SP Thái Nguyên.
14. Ngô Thị Lý – Khoa CNTT – Trường ĐH CNTT&TT Thái Nguyên.
- Tài liệu được lưu hành nội bộ - Nghiêm cấm sao chép dưới mọi hình thức.
- Nếu chưa được sự đồng ý của ban Biên soạn mà tự động post tài liệu thì đều
được coi là vi phạm nội quy của nhóm.
- Tài liệu đã được bổ sung và chỉnh lý lần thứ 2.
Tuy nhóm Biên soạn đã cố gắng hết sức nhưng cũng không thể tránh khỏi sự
sai xót nhất định.
Rất mong các bạn có thể phản hồi những chỗ sai xót về địa chỉ email:
caotua5lg3@gmail.com !
Xin chân thành cám ơn!!!
Chúc các bạn học tập và ôn thi thật tốt!!!
Thái Nguyên, tháng 07năm 2014
Trưởng nhóm Biên soạn
Cao Văn Tú
| 1/85
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
TUYỂN TẬP 200 BÀI TẬP LƯỢNG GIÁC
CÓ LỜI GIẢI CHI TIẾT NĂM 2015
- Tài liệu được soạn theo nhu cầu của các bạn học sinh khối trường THPT (đặc
biệt là khối 12).
- Biên soạn theo cấu trúc câu hỏi trong đề thi tuyển sinh Đại học – Cao đẳng của
Bộ GD&ĐT.
- Tài liệu do tập thể tác giả biên soạn:
1. Cao Văn Tú – CN.Mảng Toán – Khoa CNTT – Trường ĐH CNTT&TT Thái
Nguyên (Chủ biên)
2. Cô Trần Thị Ngọc Loan – CLB Gia Sư Thái Nguyên(Đồng chủ biên).
3. Thầy Vũ Khắc Mạnh – CLB Gia sư Bắc Giang (Tư vấn).
4. Nguyễn Thị Kiều Trang – SV Khoa Toán – Trường ĐHSP Thái Nguyên.
5. Nguyễn Trường Giang – Khoa CNTT – Trường ĐH CNTT&TT Thái Nguyên.
6. Lý Thị Thanh Nga – SVNC – Khoa Toán – Trường ĐH SP Thái Nguyên.
7. Ngô Thị Lý – Khoa CNTT – Trường ĐH CNTT&TT Thái Nguyên.
- Tài liệu được lưu hành nội bộ - Nghiêm cấm sao chép dưới mọi hình thức.
- Nếu chưa được sự đồng ý của ban Biên soạn mà tự động post tài liệu thì đều
được coi là vi phạm nội quy của nhóm.
- Tài liệu đã được bổ sung và chỉnh lý lần thứ 2.
Tuy nhóm Biên soạn đã cố gắng hết sức nhưng cũng không thể tránh khỏi sự sai xót nhất định.
Rất mong các bạn có thể phản hồi những chỗ sai xót về địa chỉ email: caotua5lg3@gmail.com ! Xin chân thành cám ơn!!!
Chúc các bạn học tập và ôn thi thật tốt!!!
Thái Nguyên, tháng 07 năm 2014
Trưởng nhóm Biên soạn Cao Văn Tú 1
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
Bài 1: Giải phương trình : 2 2
sin x sin 2x  2cos x  2 Giải 2 2
sin x sin 2x  2cos x  2 sin x  0  x k
 sinx ( 2 cosx – sinx ) = 0     tan x  2 
x  arctan 2  k
Bài 2: Giải phương trình : cos2x  3sin x  2  0 Giải 2 2
1 2sin x 3sin x  2  0  2sin x 3sin x 1 0   x   k2  2  sin x 1      1  x
k2 ,k  s  in x   6  2  5 x   k2  6
Bài 3: Giải phương trình : 3sin x  cos x  2 Giải
3sin x  cos x  3 1 2 2 
sin x  cos x  2 2 2   2  
 sin xcos  cos xsin 
 sin(x  )  sin 6 6 2 6 4      x    k2 x   k2   6 4  12    ,k   3 7   x    k2 x   k2  6 4  12
Bài 4: Giải phương trình : 3sin x  cos x  2 Giải 2
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 3 1 2 
sin x  cos x  2 2 2   2  
 sin xcos  cos xsin 
 sin(x  )  sin 6 6 2 6 4     5 x    k2 x   k2   6 4 12     ,k   3 11   x    k2 x   k2  6 4  12
Bài 5: Giải phương trình : 2 2
2sin x  3sin xcos x  5cos x  0 Giải 2
 2tan x 3tan x 5  0    tan x 1 x   k   4  5   ,k   tan x   5   x  arctan( ) 2  k  2
Bài 6: Giải phương trình : 3(sin5x  cos )
x  4(sin x  cos5 ) x Giải
 3sin5x  4cos5x  4sin x  3cos x 3 4 4 3
 sin5x  cos5x  sin x  cos x 5 5 5 5 3 4
 sin5xcos  cos5xsin  sin xsin  cos xcos , (  cos,  sin) 5 5 
 sin(5x )  cos(x )  sin(5x )  sin(  x  ) 2       5x  
x   k2 x    k   2 12 3 3          5x    
x   k2 x   k  2  8 2
Bài 7: Giải phương trình : 3
3sin3x  3cos9x 1 4sin 3x 3
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! Giải 3 (3sin3x  4sin 3 )
x  3cos9x 1   2   x   k  18 9
 sin9x  3cos9x 1  sin(9x  )  sin   3 6 7 2 x   k  54 9 Bài 8: 1
Giải phương trình : tan x  sin 2x  cos 2x  2(2cos x  )  0 cos x Giải
Điều kiện: cos x  0  x   k 2 sin x 2 (1) 
 sin 2x  cos2x  4cos x   0 cos x cos x 2 2
 sin x  2sin xcos x  cos2xcos x  2(2cos x 1)  0 2  sin x(1 2cos )
x  cos 2xcos x  2cos 2x  0
 sin xcos2x  cos2xcos x  2cos2x  0  cos2x  0  
 cos2x(sin x  cos x  2)  0  x   k  s
 in x  cos x  2(v ) n 4 2 Bài 9: 3 1
Giải phương trình : 8sin x   cos x sin x Giải
Điều kiện: sin 2x  0  x k 2 2
(*)  8sin xcos x  3sin x  cos x  4(1 cos2 )
x cos x  3sin x  cos x  4
 cos2xcos x  3sin x 3cos x  2  (cos3x  cos )
x  3sin x  3cos x 4
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!   x   k 1 3   6
 cos3x  cos x
sin x  cos3x  cos(x  )   2 2 3  
x    k  12 2 C2 2
(*)  8sin xcos x  3sin x  cos x 2 8(1cos )
x cos x  3sin x  cos x 3
8cos x 8cos x  3sin x 3cos x 3
 6cos x 8cos x  3sin x  cos x 1 3  3
 4cos x  3cos x  cos x
sin x  cos3x  cos(x  ) 2 2 3   x   k  6     .
x    k  12 2
Bài 10: Giải phương trình : 9sin x  6cos x  3sin 2x  cos2x  8 Giải 2
 6sin xcos x  6cos x  2sin x 9sin x  7  0  6cos (
x sin x 1)  (sin x 1)(2sin x  7)  0
 (sin x 1)(6cos x  2sin x  7)  0  sin x 1     x   k2
6cos x  2sin x  7 2
Bài 11: Giải phương trình : sin 2x  2cos2x 1 sin x  4cos x Giải 2
 2sin xcos x  2(2cos x 1) 1 sin x  4cos x  0 2
 sin x(2cos x 1)  4cos x  4cos x 3  0
Bài 12: Giải phương trình : 2sin 2x  cos2x  7sin x  2cos x  4 Giải 2
 4sin xcos x  (1 2sin x)  7sin x  2cos x  4  0 2
 2cos x(2sin x 1)  (2sin x  7sin x  3)  0  2cos (
x 2sin x 1)  (2sin x 1)(sin x  3)  0
 (2sin x 1)(2cos x  sin x  3)  0 5
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!       x k2 2sin x 1  0  6    
2cos x  sin x  3,(v ) n 5 x   k2  6
Bài 13: Giải phương trình : sin 2x  cos2x  3sin x  cos x  2 Giải 2
 2sin xcos x  (1 2sin )
x  3sin x  cos x  2  0 2
 (2sin xcos x  cos )
x  (2sin x  3sin x 1)  0  cos (
x 2sin x 1)  (2sin x 1)(sin x 1)  0  x
 (2sin x 1)(cos x  sin x 1)  2sin 1 0  
cos x  sin x 1   x   k2  6 2  sin x 1  5 x   k2  6  x k2  2 cos x sin x 1 cos(x )          4 2
x   k2  2 
Bài 14: Giải phương trình : 2
(sin 2x  3 cos 2x)  5  cos(2x  ) 6 Giải  Ta có: 1 3
sin 2x  3 cos 2x  2( sin 2x
cos 2x)  2cos(2x  ) 2 2 6
Đặt: t  sin 2x  3cos2x, 2   t  2 t  2  Phương trình trở t  thành: 2 t  5  2
 2t t 10  0  5 2  t   2 5 t   :loại 2 6
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!  7 t   2
 : 2cos(2x  )  2   x   k 6 12
Bài 15: Giải phương trình : 3
2cos x  cos2x  sin x  0 Giải 2
 2cos x(cos x 1)  (1 sin ) x  0 2  2(1 sin )
x (cos x 1)  (1 sin ) x  0  2(1 sin ) x (1 sin )
x (cos x 1)  (1 sin ) x  0  (1 sin ) x [2(1 sin )
x (cos x 1) 1]  0
 (1 sin x)[1 2sin xcos x  2(sin x  cos x)]  0  sin x 1   1
  2sin xcos x  2(sin x  cos ) x  0 
sin x 1 x   k2 2 1
  2sin xcos x  2(sin x  cos ) x  0 2
 (sin x  cos x)  2(sin x  cos x)  0
 (sin x  cos x)(sin x  cos x  2)  0  sin x  cos x  0   tan x  1
  x    k 4  Bài 16: 1 cos 2x
Giải phương trình : 1 cot 2x  . 2 sin 2x Giải
Điều kiện: sin 2x  0  x k 2 1 cos 2x 1 cos 2x 1 (*)  1 cot 2x  1 cot 2x  1  2 1 cos 2x 1 cos 2x sin 2x 1 cos 2x  sin2 ( x 1 cos2 ) x  cos2 ( x 1 cos2 ) x  sin 2x
 sin2xcos2x  cos2x(1 cos2x)  0  cos2 (
x sin 2x  cos2x 1)  0  cos2x  0   s
 in2x  cos2x  1   
cos2x  0  x   k 4 2     x    k   4
sin 2x  cos2x  1
  sin(2x  )  sin( )   4 4 
x   k  2 7
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!  
Vậy,phương trình có nghiệm: x   k 4 2
Bài 17: Giải phương trình : 4 4 4(sin x  cos )
x  3sin 4x  2 Giải 2 2 2 2 2  4[(sin x  cos ) x  2sin xcos ]
x  3sin 4x  2    x   k 1  2
 4(1 sin 2x)  3sin4x  2  cos4x  3sin4x  2  4 2   2  
x    k  12 2 Bài 18: 1
Giải phương trình : 3 3
1 sin 2x  cos 2x  sin 4x . 2 Giải
 2  sin4x  2(sin2x  cos2 )
x (1 sin 2xcos 2 ) x  0  (2  sin4 )
x  (sin 2x  cos 2 ) x (2  sin 4 ) x  0  (2  sin4 )
x (sin 2x  cos2x 1)  0  sin 2x  cos2x  1     x    k 2 
 sin(2x  )   4   4 2 
x   k  2
Bài 19: Giải phương trình : tan x 3cot x  4(sin x  3cos ) x Giải
Điều kiện: sin 2x  0  x k 2 sin x cos x (*)   3
 4(sin x  3cos x) cos x sin x 2 2
sin x 3cos x  4sin xcos (
x sin x  3cos ) x  0 (sin x  3cos )
x (sin x  3cos )
x  4sin xcos (
x sin x  3cos ) x  0 8
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! (sin x  3cos )
x (sin x  3cos x  4sin xcos ) x  0 
sin x  3 cos x  0   s
 in x  3cos x  4sin xcos x  0 
sin x  3cos x  0  tan x   3  x    k 3
sin x  3cos x  4sin xcos x  0  2sin2x  sin x  3cos x   x    k2 1 3   3
 sin2x  sin x
cos x  sin 2x  sin(x  )   2 2 3 4 2 x   k  9 3   
Vậy,phương trình có nghiệm là: x    4 2 k ; x   k 3 9 3
Bài 20: Giải phương trình : 3 3
sin x  cos x  sin x  cos x Giải 2 3
 sin x(sin x 1)  cos x  cos x  0 2 3
 sin xcos x  cos x  cos x  0 2
 cos x(sin xcos x  cos x 1)  0  cos x  0   2
sin xcos x  cos x  1  
cos x  0  x   k 2  x 2
  sin xcos x  cos x  1  1 1 cos 2   sin2x   1
  sin2x  cos2x  3,(v ) n 2 2 
Vậy,phương trình có nghiệm là: x   k,k  2  Bài 21: 1
Giải phương trình : 4 4
cos x  sin (x  )  4 4 Giải 1 1  1 2 2  (1 cos2 )
x  [1 cos(2x  )]  4 4 2 4 2 2  (1 cos2 ) x  (1 sin2 ) x
1  sin2x  cos2x  1  9
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!    x   k2 3   2 cos(2x  )  cos   4 4 
x    k  4
Bài 22: Giải phương trình : 3 3
4sin xcos3x  4cos xsin3x  3 3cos4x  3 Giải 3 3 3 3  4sin (
x 4cos x  3cos ) x  4cos (
x 3sin x  4sin )
x  3 3cos4x  3 3 3  1
 2sin xcos x 12cos xsin x 3 3cos4x  3 2 2  4sin xcos ( x cos x  sin )
x  3cos4x 1
 2sin2xcos2x  3cos4x 1 sin4x  3cos4x 1    x    k 1 3 1     sin4x  cos 4x
 sin(4x  )  sin 24 2   ,k  2 2 2 3 6    x   k  8 2
Bài 23: Cho phương trình: 2 2
2sin x  sin xcos x  cos x m (*)
a.Tìm m sao cho phương trình có nghiệm.
b.Giải phương trình khi m = -1. Giải 1 1 (*)  (1 cos 2 )
x  sin 2x  (1 cos 2 )
x m  sin 2x  3cos2x  2  m 1 2 2 a. (*)có nghiệm khi: 2 2 2
c a b 2  (1 2 ) m 1 9 2
 4m  4m  9  0 1 10 1 10   m  2 2
b.Khi m = -1 phương trình trở thành:
sin 2x  3cos2x  1 3 3 3  sin 2x  cos 2x  10 10 10
sin2xcos  cos2xsin  1 3 sin, (  cos,  sin) 10 10     x k
x      k    sin(2x )  2 2 sin    
2x      k2
x    k  2 10
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 3 5  4sin(  ) x
Bài 24: Cho phương trình: 6tan 2  2 sin x 1 (*) tan  
a.Giải phương trình khi    4
b.Tìm để phương trình (*) có nghiệm Giải   Ta có: 3 sin(
x)  sin(  x)  cos x 2 2 6 tan 2
 6tan cos   3sin 2,cos  0 2 1 tan  5  4cos x (*) 
 3sin 2  3sin2 sin x  4cos x  5 (**) sin x  a. khi   
phương trình trở thành: 4 3 4
3sin x  4cos x  5
  sin x  cos x  1  5 5 3 4
 sin xcos  cos xsin  1
 ,(  cos,  sin) 5 5   sin(x )  1
  x    k2 2
b.Phương trình có nghiệm khi:  cos  0  cos  0  cos  0       
 cos 2  0     k 2 (  3sin2) 16  25 2 s  in 2 1 2 s  in 2 1 4 2  Bài 25 cos3x sin 3x
: Giải phương trình : 5(sin x  )  3  cos 2x 1 2sin 2x Giải   x    k  Điề 1 12
u kiện: sin 2x     ,k  2 7  x   k  12     Ta có: cos3x sin 3x sin x 2sin 2xsin x cos3x sin 3x 5(sin x  )  5 1 2sin 2x 1 2sin 2x 11
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
sin x  cos x  cos3x  cos3x  sin 3x  5 1 2sin 2x
(sin 3x  sin x)  cos x
2sin 2xcos x  cos x  5  5 1 2sin 2x 1 2sin 2x
(2sin x 1)cos x  5  1 5cos x 2sin 2x
(1)  5cos x  cos2x  3 2
 2cos x  5cos x  2  0 1   cos x   x    k2 2 3
Bài 26: Giải phương trình : 2 2
cos 3xcos 2x  cos x  0 Giải 1 1 
(1 cos6x)cos 2x  (1 cos 2 ) x  0 2 2
 cos6xcos2x 1 0 (*) Cách 1: 3
(*)  (4cos 2x  3cos 2 )
x cos 2x 1  0 4 2
 4cos 2x  2cos 2x 1 0  2
 cos 2x 1  sin2x  0  x k 2 Cách 2: 1 (*)  (cos8x  cos 4 )
x 1  0  cos8x  cos4x  2  0 2  2
 2cos 4x  cos4x  3  0  cos4x 1  x k 2
 cos6x  cos2x 1
Cách 3: (*)  
cos6x  cos2x  1  Cách 4: 1 (*)  (cos8x  cos 4 )
x 1  0  cos8x  cos4x  2 2
 cos8x  cos4x 1   Bài 26 3
: Giải phương trình : 4 4
cos x  sin x  cos(x  )sin(3x  )   0 4 4 2 Giải 1  3 2 2 2 2 2
 (sin x  cos x)  2sin xcos x  [sin(4x  )  sin2 ] x   0 2 2 2 12
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 1 1 3 2
1 sin 2x  (cos4x  sin2 ) x   0 2 2 2 1 1 1 1 2 2
  sin 2x  (1 2sin 2x)  sin2x   0 2 2 2 2  2
 sin 2x  sin2x  2  0  sin2x 1  x   k 4
Bài 27: Giải phương trình : 2
5sin x  2  3(1 sin ) x tan x Giải
Điều kiện: cos x  0  x   k 2 2 sin x 2 sin x
(1)  5sin x  2  3(1 sin ) x
 5sin x  2  3(1 sin ) x 2 cos x 2 1 sin x 2 3sin x  1 5sin x  2   x
x    sin x  1 2 2sin 3sin 2 0 sin x 2   x   k2  6   5 x   k2  6 Bài 28: 1 1
Giải phương trình : 2sin 3x   2cos3x  . sin x cos x Giải
Điều kiện: sin 2x  0  x k 2 1 1
(*)  2(sin 3x  cos3x)   sin x cos x 1 1 3 3
 2[3(sin x  cos x)  4(sin x  cos x]   sin x cos x sin x  cos x 2 2
 2(sin x  cos x)[3  4(sin x  sin xcos x  cos x)]  sin x cos x sin x  cos x
 2(sin x  cos x)( 1
  4sin xcos x)   0 sin x cos x 1
 (sin x  cos x)( 2
  8sin xcos x  )  0 sin xcos x 13
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 2
 (sin x  cos x)(4sin 2x   2)  0 sin 2x 2
 (sin x  cos x)(4sin 2x  2sin2x  2)  0   x    k   tan x  1  4  
sin x  cos x  0       sin 2x 1  x    k 2
4sin 2x  2sin2x  2  0   12 s  in2x  1  / 2   7  x   k  12 2    Bài 2
cos x(2sin x 3 2) 2cos x 1
9: Giải phương trình : 1 1 (*) sin 2x Giải
Điều kiện: sin 2x  1
  x    k 4 2
(*)  2sin xcos x  3 2 cos x  2cos x 11 sin 2x 2  2
 2cos x 3 2cos x  2  0  cos x   x    k 2 4 
Đối chiếu điều kiện phương trình có nghiệm: x   k,k  4 Bài 30 x 3x x 3x 1
: Giải phương trình : cos xcos cos  sin xsin sin  2 2 2 2 2 Giải 1 1 1
 cos x(cos2x  cos x)  sin x(cos2x  cos x)  2 2 2 2
 cos xcos2x  cos x  sin xcos2x  sin xcos x 1 2  cos2 (
x sin x  cos x) 1 sin x  sin xcos x 1  0  cos2 (
x sin x  cos x)  sin x(sin x  cos x)  0
 (sin x  cos x)(cos2x  sin x)  0 2
 (sin x  cos x)( 2
 sin x  sin x 1)  0
 sin x  cos x  0   2
2sin x  sin x 1 0 14
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!   x    k   tan x  1  4      sin x  1    x    k2  2 s  in x 1/ 2    5
x   k2  x   k2  6 6
Bài 31: Giải phương trình : 3
4cos x  3 2 sin 2x  8cos x Giải 3
 4cos x  6 2sin xcos x 8cos x  0 2  2cos (
x 2cos x  3 2 sin x  4)  0 2  2cos (
x 2sin x  3 2 sin x  2)  0   x   k   2 cos x  0          2  x k2 sin x    4  2  3 x   k2  4  
Bài 32: Giải phương trình : cos(2x  )  cos(2x  )  4sin x  2  2(1 sin ) x 4 4 Giải
 2cos2xcos  4sin x  2  2  2sin x  0 4 2  2(1 2sin )
x  4sin x  2  2  2 sin x  0 2
 2 2sin x (4  2)sin x  2  0   x   k2 1  6  sin x    2 5 x   k2  6
Bài 33: Giải phương trình : 2 2
3cot x  2 2 sin x  (2  3 2)cos x (1) 15
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! Giải
Điều kiện: sin x  0  x k 2 cos x cos x (1)  3  2 2  (2  3 2) 4 2 sin x sin x t   2 cos x  Đặt: t
phương trình trở thành: 2
3t  (2  3 2)t  2 2  0  2 2 sin xt   3 2 cos x 2 t   :  2
 3cos x  2(1 cos ) x 2
 2cos x  3cos x  2  0 2 3 sin x 3 1 
 cos x   x    k2 2 3 cos x t   2 :  2 2
 cos x  2(1cos ) x 2
 2cos x  cos x  2  0 2 sin x 2   cos x   x    k2 2 4  
Vậy,phương trình có nghiệm: x  
k2, x    k2 3 4 2 2    Bài 34:
4sin 2x 6sin x 9 3cos 2x Giải phương trình :  0 (*) cos x Giải
Điều kiện: cos x  0  x   k 2 2
(*)  4(1 cos 2x)  3(1 cos 2x)  9  3cos x  0 2
 4cos 2x  6cos x  2  0    cos2x  1  x   k   2  1    cos 2x      2 x    k  3 
Vậy,phương trình có nghiệm: x    k 3
Bài 35: Giải phương trình : cos x  cos3x  2cos5x  0 Giải
 (cos5x  cos x)  (cos5x  cos3x)  0 16
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
 2cos3xcos2x  2cos4xcos x  0 3 2
 (4cos x  3cos x)cos2x  (2cos 2x 1)cos x  0 2 2  cos [
x (4cos x  3)cos 2x  2cos 2x 1]  0 2  cos { x [2(1 cos 2 )
x  3]cos 2x  2cos 2x 1}  0 2
 cos x(4cos 2x  cos2x 1)  0     x   k cos x  0   2   1 17  1 17  cos x    x  arccos  k2  8  8   1 17  1 17 cos x        x arccos k2  8  8 Bài 36 17
: Giải phương trình : 8 8 2
sin x  cos x  cos 2x (*) 16 Giải 8 8 4 4 2 4 4
sin x  cos x  (sin x  cos ) x  2sin xcos x 1 2 2 2 2 2 2 4
[(sin x  cos x)  2sin xcos x)]  sin 2x 8 1 1 1 2 2 4
 (1 sin 2x)  sin 2x 2 4
1 sin 2x  sin 2x 2 8 8 1 2 4 2
(*) 16(1 sin 2x  sin 2x) 17(1 sin 2x) 4 2
 2sin 2x  sin 2x 1 0 8 1   2  sin 2x  2
1 2sin 2x  0  cos4x  0  x   k 2 8 4 Bài 37: 5x 3 x
Giải phương trình : sin  5cos xsin (*) 2 2 Giải x Ta thấy: cos
 0  x    k2  cos x  1  2
Thay vào phương trình (*) ta được: 5  sin(
 5k)  sin(  k)không thỏa mãn với mọi k 2 2 17
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! Do đó x
cos không là nghiệm của phương trình nên: 2 5x x 3 x x 3 (*)  sin cos  1 5 5cos xsin cos  (sin3x  sin2 )
x  cos xsin x 2 2 2 2 2 2 3 3
3sin x  4sin x  2sin xcos x 5cos xsin x  0 2 3 sin (
x 3  4sin x  2cos x  5cos ) x  0 3 2 sin (
x 5cos x  4cos x  2cos x 1)  0  sin x  0  x k   cos x 1  x k2        1 21   1 21 cos x   x  arccos  k2 10  10   1   21     1 21 cos x        x arccos k2 10  10 1   21
Vậy,phương trình có nghiệm: x k2 , x   arccos  k2 10 1   21 x   arccos  k2 10
Bài 38: Giải phương trình : 2 sin 2 (
x cot x  tan 2 ) x  4cos x (1) Giải   x k  sin x  0  Điều kiện:      cos 2x  0 x   k     4 2 x x x x x x x Ta có: cos sin 2
cot x  tan 2x   cos 2 cos sin 2 sin  cos  sin x cos 2x sin x cos 2x sin xcos 2x cos x 2
(1)  2sin xcos x  4cos x sin xcos 2x 2 cos x 2   2cos x 2  cos ( x 1 2cos2 ) x  0 cos 2x       x k cos x  0  2     cos2x 1/ 2 
x    k  6 18
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!  
Vậy,phương trình có nghiệm: x
k , x    k 2 6 Bài 39 2 6x 8x
: Giải phương trình : 2cos 1 3cos 5 5 Giải 12x 2 4x  3 4x 4x 2 4x (1 cos ) 1  2(2cos 1)  2  4cos  3cos  2(2cos 1) 5 5 5 5 5 Đặ 4x t: t  cos , 1
  t 1phương trình trở thành: 5  t 1  3 2
4t  6t  3t  5  0  1 21  t   4 4x 5  cos 1 x k 5 2 4x 1 21 5 1 21 5  cos   x   arccos  k 5 4 4 4 2 5 5 1 21 5
Vậy,phương trình có nghiệm: x k , x   arccos  k 2 4 4 2  Bài 40: 3
Giải phương trình : tan (x  )  tan x 1 (1) 4 Giải    cos x  0 x   k    Điề 2 u kiện:     cos(x  )  0 3    4 x   k  4 3 (tan x 1) (1)   tan x 1 3 3
 (tan x 1)  (tan x 1)(1 tan ) x 3 (1 tan x) 3 2
 (tan x 1)[(1 tan ) x
 (tan x 1) ]  0 3 2
 (tan x 1)(tan x  2tan x  5tan ) x  0 2  tan (
x tan x 1)(tan x  2tan x  5)  0 19
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!     x k tan x  0      tan x 1
x   k  4 
C2: Đặt: t x  4 4 4  Bài 41: sin 2x cos 2x Giải phương trình : 4  cos 4x   (1) tan(  x)tan(  ) x 4 4 Giải      sin(  x)cos(  ) x  0     sin( 2x) 0  Điề 4 4 4 u kiện:        cos 2x 0  s
 in(  x)cos(  ) x  0      sin( 2x) 0 4 4  4  
1 tan x 1 tan x tan(
x)tan(  x)  . 1 4 4 1 tan x 1 tan x 4 4 4
(1)  sin 2x  cos 2x  cos 4x 2 2 4
1 2sin 2xcos 2x  cos 4x 1 2 4 1 2 4
1 sin 4x  cos 4x 1 (1 cos 4 ) x  cos 4x 2 2 4 2
 2cos 4x cos 4x 1 0 2  cos 4x 1  2
1 cos 4x  0  sin4x  0  x k 4 
Vậy,phương trình có nghiệm: x k 2 Bài 42: 1 2
Giải phương trình : 48   (1 cot 2xcot ) x  0 (*) 4 2 cos x sin x Giải
Điều kiện: sin 2x  0  x k 2 x x
cos 2xsin x  sin 2xsin x Ta có: cos 2 cos
1 cot 2xcot x 1  sin 2xsin x sin 2xcos x cos x 1   2 2sin xcos x 2 2sin x 20
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 1 1 1 1 (*)  48    0  48   4 4 cos x sin x 4 4 cos x sin x 4 1 2 4 4 4 4
 48sin xcos x  sin x  cos x  3sin 2x 1 sin 2x 2 2 1 4 2
 6sin 2x sin 2x  2  0  sin 2x  2 1 2sin 2x  0 2  
 cos4x  0  x   k 8 4  
Vậy,phương trình có nghiệm: x   k 8 4 Bài 43: 8 8 10 10 5
Giải phương trình : sin x  cos x  2(sin x  cos ) x  cos 2x 4 Giải 8 2 8 2 5  sin x(1 2sin ) x  cos (
x 2cos x 1)  cos 2x 4 8 8 5
 sin xcos2x  cos xcos2x  cos2x 4 8 8  4cos2 ( x cos x  sin )
x  5cos2x  0 4 4 4 4  4cos2 ( x cos x  sin ) x (cos x  sin )
x  5cos2x  0 2 2 2 2 4 4  4cos2 ( x cos x  sin ) x (cos x  sin ) x (cos x  sin )
x  5cos2x  0 2 2 1 2  4cos2 (
x cos x  sin x)(1 sin 2 )
x  5cos 2x  0 2 2 1 2  4cos 2 ( x 1 sin 2 )
x  5cos 2x  0 2 2  4cos2 (4
x cos2x  2cos2xsin 2x  5)  0 2  4cos2 [4
x cos2x  2cos2 ( x 1 cos 2 ) x  5]  0   3  4cos2 (2
x cos 2x  2cos2x  5)  0  cos 2x  0  x   k 4 2
Bài 44: (Đề thi tuyển sinh ĐH – CĐ 2010, khối A)     1 sin x  o
c s2xsin x     4  1 Giải phương trình  : cos x 1 t anx 2 21
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! Giải c  os x  0 s  in x  1 Điều kiện:    tan x  1  t anx  1      1 sin x  o
c s2xsin x     4  1 Khi đó  cos x 1 t anx 2   
 cos x1sinx cos2x 2.sin x   cos x  
sin xcosx  4      
1 sinx  cos 2x 2.sin x   
 sin x  cos x (do cos x  0)  4 
 sin x  cos xsin x  o
c s2x  0  sin x  cos x 2
sin x 1 2sin x  0      tan x  1 sin cos  L x x  s
 in x  cos x  0      sin x 1  s   in x 1 L 2
2sin x sin x 1 0   1 1 s  in x   s  in x   t / m  2  2   x    k.2 1  6
 sin x     k Z 2 7   x   k.2  6
Bài 45: Cho hàm số: y= -x3+3x2+3(m-1)x-3m2+1.
1, Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m=1.
2. Tìm m để đồ thị hàm số có cực đại , cực tiểu và hai điểm cực đại cực tiểu ấy cách đều đường thẳng x-y-2=0. Giải
2. Điều kiên để hàm số có cực trị : m >0
Chia y cho y’ ta có phương trình đường thẳng đi qua hai điểm cực tri la: y= 2mx-3m2 +m.
Thỏa mãn yêu cầu bài ra  TH 1: BA song song với d
TH2: d đi qua trung điểm của AB 1 Đáp số: m= 2 22
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 3  21 m= 6
Bài 46: (Đề thi tuyển sinh ĐH – CĐ 2006, khối B) x
Giải phương trình cot x  sin x 1 tan . x tan  4    2  Giải  c  os x  0  Lời giải:     Điều kiện sinx 0 s in2x 0  x  o c s  0  2  x  sin  x  cos x  s inx  2 Ta có           
cot x sin x 1 tan . x tan 4 s inx 1 . 4  2  s inx cos x x  os c   2   x x  cos . x o c s  sinx.sin cos x   cos x s inx 2 2   sinx   4    4 s inx x s inx cos x  cos . x o c s   2  2 1   4  sin 2x  t / m sin 2x 2     2x   k.2 x   k.   6 12     k Z 5   5  2x   k.2 x   k.  6  12 1 1 2
Bài 47: Giải phương trình :   . cos x sin 2x sin 4x Giải 23
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!   c  os x  0 s  in x  1 s  in x  1 sin x   1      Điều kiện            s in2x 0 s inx 0 s inx 0 s inx 0     2 sin 4x  0 o c s2x  0   1   2sin x  0 2 s  in x    2 1 1 2 Khi đó   cos x sin 2x sin 4x  s  in x  1    4sinx. o c s2x  2 o
c s2x  2  s inx  2 2sin x  s inx-  1  0  sin x  0   1 s  in x   2   x   k.2 1  6 Đối chiếu với sin x    k Z điều kiện ta được 2 5   x   k.2  6   x   k.2  6
Vậy phương trình có nghiệm là  k Z 5   x   k.2  6 4 4 sin 2x  o c s 2x 4 Bài 48:  Giải phương trình : o c s 4x       tan  x tan  x      4   4  Giải     sin  x  0     4            o c s  x  0 sin  2x  0        4    2  Điều kiện         o c s2x 0 sin 2x 1         sin  x  0 sin  2x  0      4      2       o c s  x  0      4  24
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!       Nhận thấy tan  x .tan  x 1    
, do đó phương trình đã cho trở thành  4   4  1 4 4 4 2 4 4 2 sin 2x  o c s 2x  o
c s 4x  1 sin 4x  o c s 4x  2 o c s 4x  o
c s 4x 1  0 2 s  in 2x  0 2  o
c s 4x  1  sin 4x  0   ocs2x  0 
Đối chiếu điều kiện ta được sin 2x  0  x kk Z 2 2 4 sin 2x  o c s 2x 1
Bài 49: Giải phương trình :  0 . sin . x cos x Giải
Điều kiện sin 2x  0
Khi đó phương trình đã cho trở thành 2  o c s 2x  0 s  in 2x  1 2 4 4 2 sin 2x  o
c s 2x 1  0  o c s 2x  o
c s 2x  0     2  o c s 2x 1 s  in 2x  0  
Đối chiếu điều kiện ta được sin 2x 1 2x
k.2  x   k. kZ 2 4
Bài 50: Giải phương trình : o c s3 .
x tan5x  sin 7x Giải Điều kiện o c s5x  0
Khi đó phương trình đã cho trở thành  kx   2 2sin 5 . x o
c s3x  2sin 7 . x o
c s5x  sin 8x  sin12x   k Z  k x    20 10       k 5k k k  Với x  thì o c s5x  o c s  o c s  k2  o c s
 0  k  2m     mZ 2 2  2   2   k   k  Với x   thì o c s5x  o c s   0   20 10  4 2  25
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! k
Vậy phương trình đã cho có nghiệm là x m; x    , m k Z  20 10
Bài 51: (Đề thi tuyển sinh ĐH – CĐ, 2011, khối A) 1 sin2x+cos 2x Giải phương trình  2 sinxsin 2x 2 1 cot x Giải
Điều kiện sin x  0 cos x  1
Khi đó phương trình đã cho trở thành 2 x  x c x 2 2 sin 1 sin 2 os2  2 2 sin .
x cos x 1 2sin . x cos x  2 o
c s x 1  2 2 cos xx t m
 2cos xsinx cos x 2 cos 0  / 
 0  sinxcosx 2    *
Giả sử sin x  0  cos x  1, khi đó   *  0 1  2 (vô lí)   cos x  0 x   k 
Do đó phương trình tương đương vớ  i 2       cos x  1       4 x   k2    4   x   k  2
Vậy phương trình có nghiệm là  k Z 
x  k2  4
Bài 52: Giải phương trình :  x     1 3sinx 2cos 3 1 t anx  cos x Giải Điều kiện o
c sx  0  sin x  1 Khi đó 26
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! x     1 3s inx 2cos 3 1 t anx 
 cos x3sinx  2cos x  3cos x sinx1 cos x
 cos x3sinx  2cos xcos x  3sinx  2cos x 1
 cos x3sinx  2cos x  
1  3sinx  2cos x   1  0 cos x 1 0      x   x   1 3s inx 2cos 1 cos 1  0  3
 sinx  2cos x 1  0  2
 1 cosx 1 thoả mãn điều kiện, do đó ta được x k2, k Z Tiếp theo giả sử o
c sx  0 sin x  1, thay vào (2) ta được 3  1 0 (vô lí)
Tức là các nghiệm của (2) đều thoả mãn điều kiện. Giải (2) ta được 1
x    arc o c s
k2 k Z , 13 (với 2 3 o c s  ; sin  ) 13 13 x k2
Vậy phương trình có nghiệm  1 k Z  .
x    arc o c s  k2  13 2 tan x  t anx 2   
Bài 53: Giải phương trình :  sin x    2 tan x 1 2  4  Giải Điều kiện o
c sx  0  sin x  1 Khi đó 2 tan x  t anx 2    2  2 2  2  sin x   o c s x    2 tan x  t anx   sinx  cos x  2  tan x 1 2 4 2  2 2       1 2  sin x  cos . x sinx 
sinx cos x  2sinxsinx cos xsinx cos x  0 2
 sinx  cos x2sinx   1  0   * Giả sử o
c sx  0 sin x  1, thay vào (*) ta được   1 2    1  0 (vô lí)
Tức là các nghiệm của (*) đều thoả mãn điều kiện. 3  5
Giải (*) ta được x
k; x   k2; x   k2 kZ 4 6 6
Bài 54: Giải phương trình : tan5 . x tan 2x 1 27
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! Giải    x   m  1    Điều kiện o c s5x 0  10 5     , m n Z   o c s2x  0   x   n 2  4 2
phương trình tương đương với 1   tan 5x
 tan5x  cot 2x x   kkZ tan 2x 14 7
+ Đối chiếu điều kiện (1)     1 2m Giả sử  k
m k m 14 7 10 5 5  m t
Do k, m Z nên 1 2 1 t  Z : t   m  2t  5 2 t
Lại do t,mZ nên 1 s  Z : s
t  2s 1 2  
Từ đó k  7s  3. Suy ra x
k với k  7s 3 thoả mãn phương trình 14 7
+ Đối chiếu điều kiện (2)     Giả sử
k   n  4k 14n  5   3 14 7 4 2
Ta thấy vế trái của (3) chẵn, vế phải của (3) lẻ nên không tồn tại k, nZ thoả mãn (3).
Từ đó suy ra điều kiên (2) luôn được thoả mãn.  
Vậy phương trình đã cho có nghiệm là x   kk Z 14 7
Bài 55: (Đề thi tuyển sinh ĐH – CĐ 2011, khối D)
sin2x +2cos x  sinx 1 Giải phương trình  0 tanx + 3 Giải 28
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!   y x    m       Điề t anx 3 3 u kiện     , m n Z  c  os x  0    x   n   2  2 2  3
Khi đó phươngtrình đã cho trở 3 thành
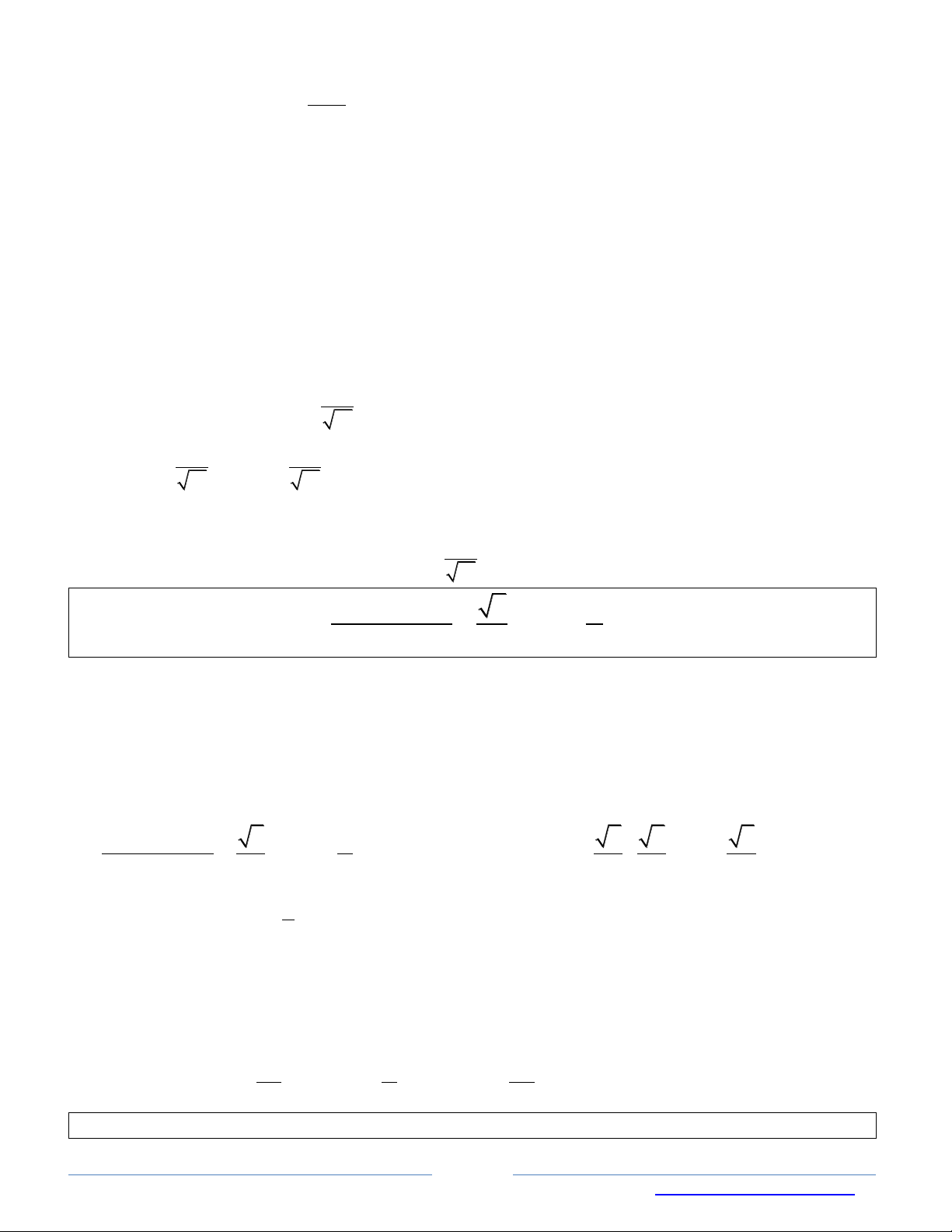
sin2x +2cos x  sinx 1  0  2cos x sinx   1  sinx   1  0   s  inx  1  x    k2 O      x x    2 sinx 1 2cos 1  0  1   cos x     x    k2 2   3   
Kết hợp với điều kiện trên đường tròn lượng giác (như hình bên)  3 2 
ta được nghiệm của phương trình là x   k2 kZ 3
Bài 56: (Đề thi tuyển sinh ĐH – CĐ 2006, khối A)  6 6
2 cos x  sin x sin . x cos x Giải phương trình  0 2  2sin x Giải y   3  x   2 m   Điều kiện 2 4 4 4 sinx     , m n Z  2 3 x   n2  4 o x
Khi đó phương trình đã cho trở thành 2 6 6
cos x  sin x sin . x cos x  0 5  4 3  1 2
 2 1 sin 2x  sin 2x  0    4  2 2
 3sin 2x  sin 2x  4  0  sin 2x 1 
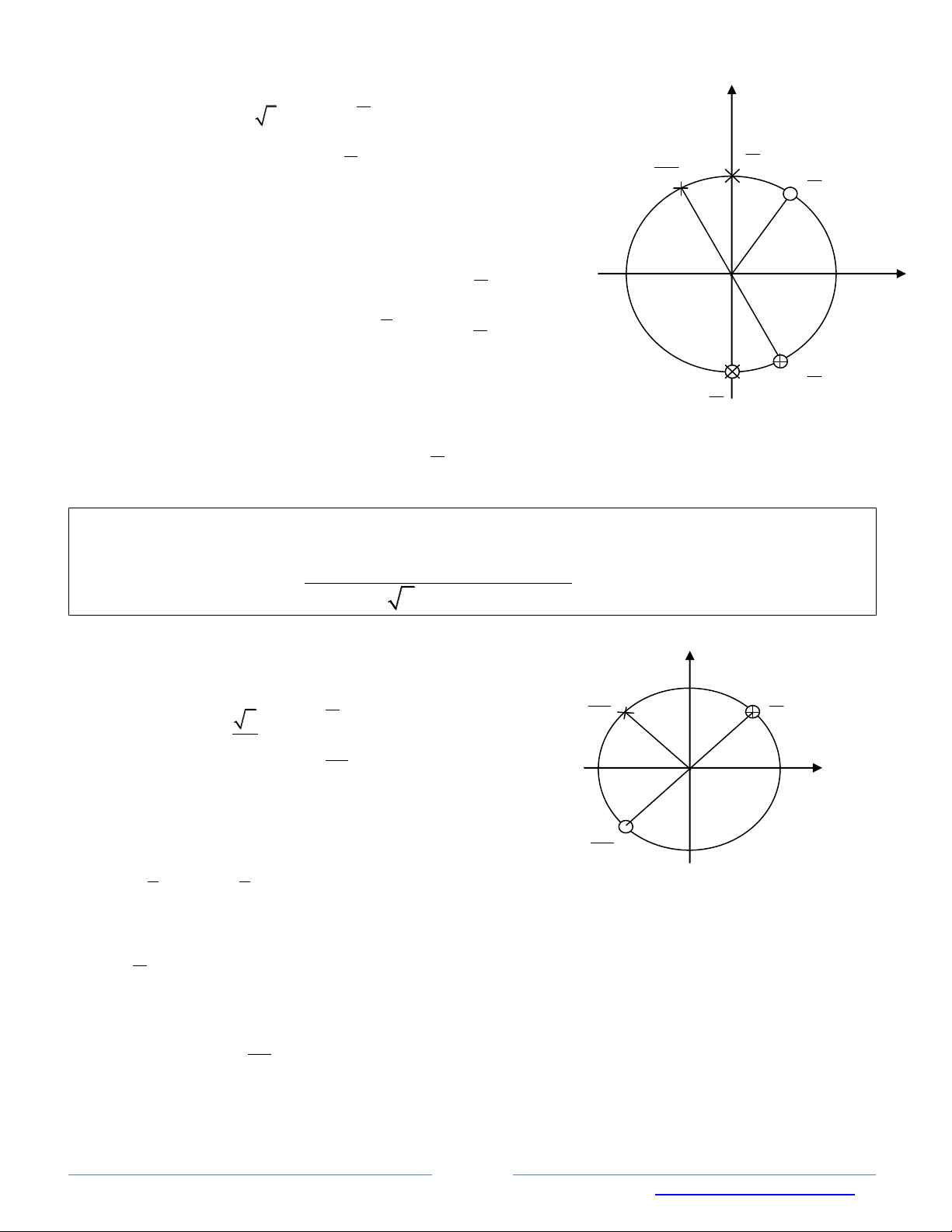
x   k k Z  4
Kết hợp với điều kiện trên đường tròn lượng giác (như hình bên) ta được nghiệm của 5 x   k2 kZ phương trình là 4 29
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! sin x  sin 2x
Bài 57: Giải phương trình :  1  sin 3x y  Giải 2 2   Điều kiện 3
sin 3x  0  3x k  x k 3 3
sin x  sin 2x        Khi đó 1
sin x sin 2x sin 3x 0 sin 3x O x  2sin 2 .
x cos x  sin 2x  0   s  in 2x  0 x k  4  2  sin 2x 2cos x 1 0      1    3  3 cos x   2    2 x    k2  2 3
Kết hợp với điều kiện trên đường tròn lượng giác
Ta được nghiệm của phương trình là  x   k. 2 Bài 58  cos3x  sin 3x 
: [ĐH A02] Tìm x 0;2 : 5 sin x   cos2x  3    1 2sin 2x  Giải Điề 1
u kiện : sin 2x   2  cos3x  sin 3x 
 sin x  2sin xsin 2x  cos3x sin3x  5 sin x   5      1 2sin 2x   1 sin 2x 
 sin x  cos x cos3x cos3x sin3x   5   1 2sin 2x
 sin3x sin x  cos x
 2sin 2xcos x  cos x   5  5      1 2sin 2x   1 2sin 2x   cos ( x 1 2sin 2 ) x   5  5cos x    1 2sin 2x  (1) 2
5cos x  cos2x32cos x5cos x3 0 cos x  2 (L)   1   cos x   cos  2 3 30
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!       x k2  3 cos x  cos   k  3   x    k2  3  
Vì x0;2  Nên nghiệm của phương trình : 5 x  ; x  3 3 Bài 59: [ĐH B02] 2 2 2 2
sin 3x  cos 4x  sin 5x  cos 6x Giải 2 2 2 2
sin 3x  cos 4x  sin 5x  cos 6x
1 cos 6x 1 cos8x
1 cos10x 1 cos12x     2 2 2 2
cos12x cos10x  cos8x cos6xkx   2cos (
x cos11x cos7 ) x  0  4  cos . x sin9 . x sin 2x  9 0  k k   x   2
Bài 60: [ĐH D02] Tìm x 0;1 
4 : cos3x  4cos 2x  3cos x  4  0 Giải Tìm x 0;1 
4 : cos3x  4cos 2x  3cos x  4  0 (1) Ta có : 3
cos3x  4cos x 3cos x
(1)  cos3x 3cos x  4(1 cos2 ) x  0 3 2
 4cos x8cos x  0       2
 4cos xcos x 2  0  cos x  0 x   k;k Vì x 3 5 7 (0;14) x  ; ; ;  2  2 3 2 2  Bài 61:  
[Dự bị 1 ĐH02] Xác định m để phương trình sau có ít nhất 1 nghiệm thuộc 0;    2  4 4
2 sin x  cos x  cos4x  sin 2x  m  0 Giải   Xác định m để 
phương trình sau có ít nhất 1 nghiệm thuộc 0;   :  2  4 4
2 sin x  cos x  cos4x  sin 2x  m  0 (1) 31
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! (1)   2 2  x x 2 2 1 2sin cos
1sin 2x  2sin2x m  0 2
3m3sin 2x 2sin2x  0 2
 3t  2t  (m  3)  0 (2) với t  sin2x   Ta có :  x  0;
 2x0;t    0; 1  2 
Bài toán thành : Xác định m để phương trình sau có ít nhất 1 nghiệm thuộc đoạn 0;  1 (2) 2
3t 2t m3 2    Đặ y 3t 2t (P) t 
y m 3 d
Số nghiệm của (2) là số giao điểm của d và (P) Khảo sát hàm số : 2
y  3t  2t t 0;  1
y '  6t  2 1
y '  0  6t  2  0  t  3 BBT 1 x  0 1  3 y '  0  y 0 1  3 1
   m  3 1
Phương trình (2) có ít nhấ 3
t một nghiện trên đoạn 0;  1 10    m  2  3 4 4 sin x  cos x 1 1 Bài 62:   [Dự bị 2 ĐH02] cot 2x 5sin 2x 2 8sin 2x Giải 4 4 sin x  cos x 1 1  cot 2x  (1) 5sin 2x 2 8sin 2x
Điều kiện : sin 2x  0 2 2
1 2sin x cos x 1 1 (1)   cos 2x  5 2 8 2 sin 2x 5 5 5 2 1
 cos 2x   2  (1 cos 2x)  5cos 2x  2 2 8 4 32
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!  9     cos 2x  ( ) L 2x   k2 x   k 9     2 2  3 6
cos 2x  5cos 2x   0   cos 2x  cos     k  4 1  3     cos 2x            x k2 x k 2  3  6  2 2  sin 2x sin 3x 4 
Bài 63: [Dự bị 3 ĐH02] tan x 1  4 cos x Giải
Điều kiện : cos x  0 (1) 4 4 2
 sin x  cos x  (2 sin 2x)sin3x 2 sin 2x 2 1  (2 sin 2 ) x sin 3x 2 2 2
 2 sin 2x  (2 sin 2 ) x 2sin 3x   3x   k2  6  5   2
 (2 sin 2x)(1 2sin3x)  0     3x k2  6 1 ; sin 3x  sin
1 2sin3x  0  sin3x  6   k2 2 x    18 3  5   k2 x    18 3 k   x 
Bài 64: [Dự bị 4 ĐH02] 2
tan x  cos x  cos x  sin x 1 tan x.tan    2  Giải  x  2
tan x  cos x  cos x  sin x 1 tan x.tan   (1)  2  c  os x  0  Điều kiện :  x cos  0  2 x x x sin x sin cos x cos  sin xsin Ta có : x 2 2 2 1 tan . x tan 1  2 x x cos x cos cos x cos 2 2 33
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! x  cos x     2  1   x cos x cos x cos 2 sin x (1) 2
 tan x  cos x cos x  cos x cos x  0 (L)
 cos x(1 cos x)  0  
x k2;k cos x 1 2sin x  cos x 1
Bài 65: [Dự bị 5 ĐH02] Cho phương trình :  a sin x  2cos x  3 1
a) Giải phương trình với a= 3
b) Tìm a để phương trình trên có nghiệm. Giải 1  
a)Với a  , phương trình thành : 2sin x cos x 1 1  (1) 3 sin x  2cos x  3 3
vì : sin x 2cos x 3  0 x  
 6sin x  3cos x  3  sin x  2cos x  3
(1)  5sin x  5cos x  0  sin x  cos x  0        2 sin x   0  sin x   0      4   4       sin x
 0  x   k  x    k    4  4 4 k 2sin x  cos x 1 b)
 a  sin x cos x 1 a sin x 2cosx 3 sin x  2cos x  3 (2 )
a sin x  (2a 1)cos x  3a 1  (2)
Điều kiện để phương trình (2) có nghiệm :
  a2  a  2   a  2 2 2 2 1 3
1  4a  6a  4  0 1
   a  2 2 Bài 66: 1 [Dự bị 6 ĐH02]  sin x 2 8cos x Giải 34
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 1  sin x (1) 2 8cos x cos x  0 Điều kiện :  sin  x  0 1 (1) 2 2 2 
 sin x 1 8sin xcos x 2 8cos x   k 2
 2sin 2x 1 0  cos4x  0  4x   k  x   2 8 4 Vì : sin x  0  3 5 7 x   2 m  ; x   2
m  ; m ; x   2 m  ; x   2 m  8 8 8 8 Bài 67: [ĐH A03] cos 2x 1 2 cot x 1   sin x  sin 2x 1 tan x 2 Giải cos 2x 1 2 cot x 1   sin x  sin 2x (1) 1 tan x 2 s  in 2x  0 Điều kiện :  tan x  1  2 2 cos x cos x  sin x (1)  1 sin (
x sin x  cos ) x sin x sin x 1 cosx 2 2 cos x  sin x cos ( x cos x  sin ) x  
 sin x(sin x  cos ) x sin x sin x  cos x cos x  sin x
 cos x(cos x sin ) x  sin (
x sin x  cos ) x sin x
 (cos x sin x) 2
sin x  sin x cos x   1  0
cos x sin x  0   2 s
 in x sin xcos x 1 0   
* cos x  sin x  0  2 cos x   0    4         cos x
 0  x    k  x   k;k     4  4 2 4 1 cos 2x sin 2x * 2
sin x  sin x cos x 1  0   1 0 2 2
sin2x cos2x3  0 ( vô nghiệm ) Bài 68: [ĐH B03] 2
cot x  tan x  4sin 2x  sin 2x 35
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! Giải
Điều kiện : sin 2x  0 cos x sin x 2 (1)    4sin 2x  sin x cos x sin 2x 2 2 cos x  sin x 2   4sin 2x  sin x cos x sin 2x 2
 2cos 2x  4sin 2x  2  2cos 2x  4 2 1 cos 2x  2 cos2x 1 x k 2 
2cos x cos 2x 1 0       1     k cos 2x         x k 2  3 Bài 69:   [ĐH D03] x  x 2 2 2 sin  tan x  cos  0    2 4  2 Giải
Điều kiện : cos x  0 2 1     sin x 1 (1)  1 cos x   1 cos x    2   2   2  cos x 2  1sin x 2
sin x  1 cos x 2 cos x  1sin x 2
1 cos x  1 cos x 2 1 sin x
 1sin x1cos xsin x cos x  0     x   k s  in x 1 sin x  1  2     cos x  1   cos x  1 
x    k2    s
 in x  cos x  0       s  in x   0
x    k     4   4
So với điều kiện : cos x  0
x    k2 Nghiệm của (1) :   k   x    k  4
Bài 70: [Dự bị 1 ĐH A03] 3 tan xtan x  2sin x  6cosx  0 Giải
3  tan x tan x  2sin x  6cos x  0 Điều kiện : cos x  0
sin x  sin x  2sin x cos x   3  6cos x  0   cos x  cos x 36
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 2 2
 3cos x sin x1 2cos x 2  6cos x  0 2
 3cos x1 2cos x 2
sin x1 2cos x  0
 1 2cos x 2 2
3cos x  sin x  0  1 cos x   1   2cos x  0  2 1 2      cos x  2 4cos x 1 0 1  2 4 cos x   4  2 2x   k2 1 1 2    2 3 1 cos x
 cos2x    cos > cos 2x  cos   2 2 3 3 2   2x    k2  3   x   k  3   k    x    k  3
Bài 71: [Dự bị 2 ĐH A03]   2 cos 2x cos x 2tan x   1  2 Giải
Điều kiện : cos x  0 2 2sin x  cos2x   cos x  2 cos x 2 2sin x 2 
 cos x  2  cos 2x 1 2sin x cos x 2  2(1 cos ) x (1 cos ) x  (1 cos ) x cos x  1  2  2sin x 1 1 cos x    cos x    x 2 1 cos 2(1cos )
x  cos x  0   cos x  1  
x    k cos x  1       1 ->  2
2cos x 5cos x  2  0 cos x        x k2 2  3
Bài 72: [Dự bị 1 ĐH B03] 6 2
3cos4x 8cos x  2cos x  3  0 Giải 6 2
3cos4x 8cos x  2cos x  3  0 2 4  3(1 cos4 ) x  2cos (
x 4cos x 1)  0 37
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 2 2 2 2  6cos 2x  2cos (
x 2cos x 1)(2cos x 1)  0 2 2 2
 6cos 2x  cos x(2cos x 1)cos2x  0 2 2  cos2x 3  cos2x cos (
x 2cos x 1)  0    cos2x 4 2
2cos x  5cos x  3  0 cos2x  0   4 2
2cos x 5cos x  3  0   k
* cos 2x  0  2x
k  x   ; k  2 4 2 2 cos x 1   k  x   * 4 2 2
2cos x  5cos x  3  0   sin x  0  3 > 4 2 k 2 cos x  ( ) L      2 x k     2  3 x 2 cos x  2sin    Bài 73:  2 4  [Dự bị 2 ĐH B03]  1 2cos x 1 Giải Điề 1 u kiện : cos x  2    
 (2  3)cos x  1 cos x   2cos x 1      2 
 2cos x  3 cos x 1 sin x  2cos x 1
(1)  3 cos x  sin x  0 3 1   
cos x  sin x  0  cos x cos  sin xsin  0 2 2 6 6        cos x
 0  x    k  x   k;k     6  6 2 3  Vì : 1 cos x
Nên nghiệm của phương trình : 4 x   k2;k  2 3 2 cos x cos x   Bài 74: 1 [Dự bị 1 ĐH D03]  21 sin x sin x  cos x Giải   Điề 
u kiện : sin x  cos x  2 sin x   0    4  (1) 2  (1sin )
x (cos x 1)  2(1 sin )
x (sin x  cos x) 38
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
 1sin x(1sin x)(cos x 1)  2(sin x  cos x)  0
 1sin xcos x 1sin xcos x sin x  2sin x 2cos x  0
 1sin xsin x 1sin xcos x  cos x  0
 1sin x(1sin x)  cos x(1sin x)  0       x2   x sin x 1 1 sin 1 cos
 0  cosx 1
Bài 75: [Dự bị 2 ĐH D03] 2cos 4x cot x  tan x  sin 2x Giải
Điều kiện : sin 2x  0  cos2x  1  2cos 4x
(1)  cot x  tan x  sin 2x cos x sin x cos 4x    sin x cos x sin x cos x 2 2
 cos x sin x  cos4x  2
 cos2x  cos4x  2cos 2x cos2x 1  0  x    k;k  3 cos2x 1( ) L   1 2
cos2x    cos  2 3 Bài 76: [ĐH B04] 2
5sin x  2  3(1 sin x) tan x Giải 2
5sin x  2  3(1 sin x) tan x Điều kiện : cos x  0 2 3sin x  5sin x  2  (1 sin x) 2 1 sin x 2
 (5sin x  2)(1 sin ) x  3sin x   x   k2   1  6 sin x   sin   k 2 
 2sin x  3sin x  2  0  2 6    5 x   k2 s  in x  2   6
Bài 77: [ĐH D04] 2cosx  
1 2sin x  cos x  sin 2x  sin x Giải
2cosx  12sinx cosx  sin2x sinx 39
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
 (2cos x 1)(2sin x  cos x)  sin ( x 2cos x 1)  2cos x  
1 sin x  cos x  0  1   cos x  cos x  cos 2cos x 1   2 3     
sin xcosx 0         2 sin x   0 sin x   0         4    4 
Bài 78: [Dự bị 1 ĐH A04] sin x  sin 2x  3cosx  cox2x Giải
sin x  sin 2x  3 cos x  cox2x
 sin x  sin 2x  3 cos x  3 cos2x
 sin x  3 cos x  3 cos2x sin 2x 1 3 3 1  sin x  cos x
cos 2x  sin 2x 2 2 2 2       3x      sin x   cos 2x      k   3   6  2 3  x                 k sin x   cos  2x   sin 2x         2 2  3   2  3   3   2 k2       x     sin 2x   sin x   0      9 3   3   3 
x    k2   3x   sin   0 k       3x   x   2 3   2sin  cos  0        2 3   2   x cos  0  2
Bài 79: [Dự bị 2 ĐH A04] 1 sin x  1 cos x 1 Giải
Chú ý : 1sin x  0 ; 1cos x  0
(1)  2  (sin x  cos ) x  2 (1sin ) x (1 cos ) x 1
 2(sin x  cos )
x  2 1 (sin x  cos )
x sin x cos x 1 (2) 2  Đặ t 1
t : t  sin x  cos x ; t  2 ,khi đó : sin x cos x  2 40
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 2 t  2t 1 (2)  1 t  2  0 2 2
1t  2 (t 1)  0 1t  2 t 1  0
 2 t 1  t 1 (3) ( nhận xét và suy ra : ) (3) t 1    
t 1 sin x  cos x 1 cos x   cos    4  4    x    k2   4 4     k2      2 k   x     k2     x k2  4 4
Bài 80: [Dự bị 1 ĐH B04]  3 3
4 sin x  cos x  cos x  3sin x Giải 3 3 3 3
4sin x  cos x  cos x  3sin x
 4sin x  4cos x  cos x 3sin x  0 3 2
 4sin x  4cos x(1sin x)  cos x 3sin x  0 3 2
 4sin x  3cos x  4sin xcos x 3sin x  0 2
 3(cos x sin x)  4sin x(cos x sin x)  0
 (cos x sin x) 2 3  4sin x  0      2 cos x   0     4   
cos x  sin x  0  3   3  sin x  2 s  in x  2   4  3 sin x    2    x   k  4  k  
x    k  3 Bài 81:    [Dự bị 2 ĐH B04] 1 1   2 2 cos x    cos x sin x  4  Giải 1 1      2 2 cos x  
 Điều kiện : sin2x  0 cos x sin x  4    
(1)  sin x  cos x  2 2 cos x     4  41
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!       1   2 cos x   2 2 cos x  . sin 2x      4   4  2         x k   k  cos x  
1 sin 2x  0 > 4  k   x    4    4 2 x    k        4 x    k cos x   0     4 2   4    k    s  in2x  1  2x    k2  2
Bài 82: [Dự bị 1 ĐH D04] sin4xsin7x  cos3xcos6x Giải 1    x   x  1 cos11 cos( 3 ) 
cos9xcos3x 2 2
 cos11x  cos3x  cos9x  cos3x
 cos11x  cos9x  0 .     10x   kx   10 k  cos10x  0   2 20
 2cos10xcos x  0       k  cos x  0     x   kx   k  2  2
Bài 83: [Dự bị 2 ĐH D04] sin 2x  2 2 sin x  cosx 5  0 Giải
sin 2x  2 2 sin x  cos x  5  0 (1)
Đặt t  sin x cos x với  2  t  2 2 sin2x t 1  t   3 2 (1) 2
t  2 2t  6  0   t    2
Với t   2  sin x  cos x   2      cos x   1
  x     k2 k     4  4 Bài 84: [ĐH A05] 2 2
cos 3xcos2x  cos x  0 Giải 42
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 2 2 cos 3xcos2x  cos x  0
(1 cos 6x) cos 2x 1 cos 2x    0 2 2
 cos2x  cos6xcos2x 1 cos2x  0
 cos6xcos2x 1 0  cos8x  cos4x  2  0 2
 2cos 4x 1 cos4x  2  0 cos4x 1 2 2cos 4x cos 4x 3 0       3 cos4x    2
Bài 85: [ĐH B05] 1sin cosx sin2x  cos2x  0 Giải 2
1 sin cos x  sin 2x  cos2x  0  sin x  cos x  2sin x cos x  2cos x  0
 (sin x  cos x)  2cos (
x sin x  cos ) x  0 s
 in x  cos x  0 
 (sin x  cos x)1 2cos x  0  1 2
cos x    cos  2 3 Bài 86:      [ĐH D05]  3 4 4 cos x  sin x  cos x  sin 3x    0      4   4  2 Giải       3 4 4 1      3 2 2 cos x  sin x  cos x  sin 3x    0    
1 2sin xcos x  sin 4x  sin 2x   0      4   4  2 2   2   2 2
 2 sin 2x cos4x sin 2x 3  0 2 2
 sin 2x  (1 2sin 2x)  sin 2x 1  0 s  in 2x 1 2
 sin 2x  sin 2x  2  0  sin2x  2 Bài 87: x  3 
[Dự bị 1 ĐH A05] Tìm x 0; 2 2 4sin  3cos2x 1 2cos x    2  4  Giải x  3 
Tìm x 0; của : 2 2 4sin  3cos2x 1 2cos x    2  4   3   2(1cos )
x  3 cos 2x 11 cos 2x     2 
 2  2cos x  3 cos2x  2 sin 2x  2
 cos x  3 cos2x sin 2x (chia 2 vế cho 2) 43
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 3 1  cos x cos 2x sin 2x cos(         ) x  cos 2x    2 2  6    2x
   x k2     6  cos 2x   cos(  x)      6    2x   
  x k2  6  5 k 2 1 x    18 3   k ; k  1 2  7 x    k 2 2  6 k    Vì 1 5 17 
k  0;1  x  ; x  1   k (0;  ) 18 18 1 k   Vì 2 5 
k 1 x  2 k (0;  ) 6 2  5 x   18   3  17   cos 2x
 sin 2x x    2    18  5 x   6 Bài 88   
: [Dự bị 2 ĐH A05] 3 2 2 cos x   3cos x  sin x  0    4  Giải    3 2 2 cos x   3cos x  sin x  0    4  3      2 cos x
3cos x sin x  0      4  3
 (cos x  sin x) 3cos x sin x  0 3 3 2 2
 cos x  sin x  3cos xsin x  3cos xsin x 3cos x sin x  0  c  os x  0  3 s
 in x sin x  0 2 2      sin x 1 cos x 0      c  os x  0  tan x 1 tan x 1  3 2 2 2  1
  tan x  3tan x  3tan x 3(1 tan x)  tan x(1 tan x)  0 44
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! Bài 89:    [Dự bị 1 ĐH B05] 3 2 2 cos x   3cos x  sin x  0    4  Giải    3 2 2 cos x   3cos x  sin x  0    4  3      2 cos x
3cos x sin x  0      4  3
 (cos x  sin x) 3cos x sin x  0 3 3 2 2
 cos x  sin x  3cos xsin x  3cos xsin x 3cos x sin x  0  c  os x  0  3 s
 in x sin x  0 2 2      sin x 1 cos x 0      c  os x  0  tan x 1 tan x 1  3 2 2 2  1
  tan x  3tan x  3tan x 3(1 tan x)  tan x(1 tan x)  0 Bài 90:    cos 2x 1 [Dự bị 2 ĐH B05] 2 tan  x  3tan x    2  2  cos x Giải    cos 2x 1 2 tan  x  3tan x    (1) 2  2  cos x
Điều kiện : sin 2x  0 2 2sin x (1) 2
 cot x 3tan x   2 cos x 1  2 3 
 tan x  0  tan x  1   tan x  1
 -> x    k ; k tan x 4 Bài 91:    [Dự bị 1 ĐH D05] 3 sin x tan  x   2    2  1 cos x Giải  3  sin x tan  x   2  
(1) Điều kiện : sin x  0  2  1 cos x 45
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! sin x cos x sin x  cot x   2    2 1 cos x sin x 1 cos x 2
 cos x(1 cos x)  sin x  2sin x(1 cos x) (1) 2 2
 cos x  cos x  sin x  2sin x(1 cos x) cos x  1  ( ) L
 (1 cos x)1 2sin x  0  1  s  in x   sin  2 6
Bài 92: [Dự bị 2 ĐH D05] sin2x  cos2x 3sin x cosx  2  0 Giải
sin 2x  cos2x  3sin x  cos x  2  0 2
 2sin xcos x 1 2sin x 3sin x cos x  2  0 2
 2sin x (2cos x 3)sin x  cos x 1 0 (1)
Chú ý : (1) là phương trình bậc 2 với biến sin x Ta có : 2 2
  (2cos x  3) 8(cos x 1)  (2cos x 1) 
2cos x  3  2cos x 1 sin x   cos x 1  Nghiệm của (1) : 4 
2cos x  3  2cos x 1 1 sin x    4 2   x   k2    1 6 sin x   sin   k  2 6 5   x   k2  6    1 
sin x  cos x 1  sin x  cos x 1  sin x    sin    4  2 4  6 6
2 cos x  sin x  sin x cos x Bài 93: [ĐH A06]  0 2  2sin x Giải  6 6
2 cos x  sin x  sin x cos x  2
0 (1) điều kiện : sin x  2  2sin x 2 (1)   6 6
2 sin  cos x sin xcos x  0 2  3sin 2x  1  21   sin 2x  0  4  2 s  in 2x 1 2 3sin 2x sin 2x 4 0       4 s  in 2x   3 46
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!  
sin 2x 1  2x
k2  x   k ;k  2 4   x   k2   vì : 2 5 4 sin x   
Nghiệm của (1): x   k2;k  2 3  4 x   k2  4 Bài 94: [ĐH B06]  x  cot x  sin x 1 tan x tan  4    2  Giải  x  cot x  sin x 1 tan x tan  4   (1)  2  s  in 2x  0  Điề x u kiện :  x Ta có : 1 1 tan . x tan  cos  0  2 cos x  2 cos x sin x 1 (1)    4   4 sin x cos x sin x cos x   2x   k2 1   6
 2sin 2x 1 sin 2x   sin   2 6 5   2x   k2  6
Bài 95: [ĐH D06] cos3x  cos2x cosx 1 0 Giải
cos3x  cos2x  cos x 1  0
 cos3x  cos x  cos 2x 1 0 2
 2sin 2xsin x  2sin x  0
 2sin xsin 2x sin x  0  2sin x(2sin xcos x sin x)  0 s  in x  0 2 
 2sin x2cos x   1  0  1  cos x   cos  2 3 Bài 96: 2  3 2 [Dự bị 1 ĐH A06] 3 3
cos3x cos x  sin 3x sin x  8 Giải 2  3 2 3 3
cos3x cos x  sin 3x sin x  (1) 8 47
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 1 3 3
cos 3x  4cos x  3cos x  cos x
cos3x 3cos x Ta có 4 1 3 3
sin 3x  3sin x  4sin x  sin x
3sin xsin3x 4 1 2  3 2 (1) 
cos3xcos3x 3cos xsin3x3sin x sin3x    4 8   x x x  x x x 2 3 2 cos 3 cos 3 3cos sin 3 3sin sin 3  2 3 2 2 2
 cos x  3cos3xcos x 3sin3xsin x  sin 3x 1 2    x x x x 3 2 1 3 cos 3 cos sin 3 sin 1 2 2    cos4x
 sin  4x    k2;k  2 4 4 Bài 97   
: [Dự bị 2 ĐH A06] 2sin 2x   4sin x 1  0    6  Giải    2sin 2x   4sin x 1  0    6     
 2 sin 2xcos  cos 2xsin  4sin x 1  0    6 6 
 3 sin 2x  cos 2x  4sin x 1  0 2
 2 3 sin xcos x  4sin x  2sin x  0
 2sin x 3cos x sin x 2  0 x k s  in x  0        
 3 cos x  sin x  2  0 cos x   1      6 
Bài 98: [Dự bị 1 ĐH B06]  2   2   2
2sin x 1 tan 2x 3 2cos x   1  0 Giải  2   2   2
2sin x 1 tan 2x 3 2cos x   1  0 (1)
điều kiện : cos 2x  0 48
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 2  cos 2 .
x tan 2x  3cos 2x  0 (1)  cos 2x  2 tan 2x  3 2  0  tan 2x  3   tan 2x  tan tan 2x  3  3     tan 2x   3     tan 2x  tan       3 
Bài 99: [Dự bị 2 ĐH B06] cos2x  1 2cosxsin x cosx  0 Giải
cos 2x  1 2cos xsin x  cos x  0 2 2
 (cos x sin x)  (1 2cos x)(sin x  cos x)  0
 (cos x sin x)cos x sin x  2cos x   1  0     cos x   0   
cos x sin x  0  4    
sin xcosx 1     1  s  in x    sin     4  2 4      x    kx   k   4 2 4       
x    k2  x   k2 k   4 4  2    3
x    k2 x    k2   4 4 
Bài 100: [Dự bị 1 ĐH D06] 3 3 2
cos x  sin x  2sin x 1 Giải 3 3 2
cos x  sin x  2sin x 1 49
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
 sin x  cos x1sin xcos x  cos2x
 sin x  cos x1sin xcos x 2 2
 cos x sin x
 sin x  cos xsin x cos x sin xcos x   1  0
 sin x  cos x   1sin x
cos (x1sin )x  0 
 sin x  cos x1sin x1cos x  0     sin x   0     4  s
 in x  cos x  0      sin x  1   x     k2  2 cos x 1   x k2  
Bài 101: [Dự bị 2 ĐH D06] 3 2
4sin x  4sin x 3sin 2x  6cos x  0 Giải 3 2
4sin x  4sin x 3sin 2x  6cos x  0 2
 4sin x(sin x 1)  6cos x(sin x 1)  0 2
 (sin x 1)(4sin x  6cos ) x  0 2
 (sin x 1) 4(1 cos x)  6cos x  0    s  in x  1  s  in x  1      cos x  2  2
2cos x 3cos x  2  0  1 cos x    2
Bài 102: [ĐH A07]  2     2 1 sin x cos x
1 cos xsin x 1 sin 2x Giải  2     2 1 sin x cos x
1 cos xsin x 1 sin 2x 2 2 2
 cos x  sin xcos x  sin x  cos xsin x  (sin x  cos x) 2
 (sin x  cos x)  sin xcos x(sin x  cos x)  (sin x  cos x)  0
 (sin x  cos x)1sin xcos x sin x cos x  0 s
 in x  cos x  0 
 (sin x  cos x)(1sin x)(1 cos x)  0  1sin x  0  1   cos x  0 
Bài 103: [ĐH B07] 2
2sin 2x  sin 7x 1  sin x Giải 2
2sin 2x  sin 7x 1  sin x 50
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 2
 sin 7x sin x  2sin 2x 1 0  2cos4 .
x sin 3x  cos 4x  0 cos4x  0 
 cos4x2sin3x   1  0  1  s  in3x   sin  2 6 2 Bài 104:  x x  [ĐH D07] sin  cos  3 cos x  2    2 2  Giải 2  x x  sin  cos  3 cos x  2    2 2 
1 sin x  3 cos x  2
 sin x  3 cos x 1    x    k2  1     3 6  sin x    sin      3  2 6   5 x    k2  3 6
Bài 105: [Dự bị 1 ĐH A07] 1 1
sin 2x  sin x    2cot 2x 2sin x sin 2x Giải 1 1
sin 2x  sin x  
 2cot 2x (1) điều kiện : sin2x  0 2sin x sin 2x (1) 2
sin 2xsin2xsin xcos x 1   2cos2x 2 2
 sin 2x 1 cos x(2sin x 1)  2cos 2x 2
 cos 2x  cos 2 .
x cos x  2cos 2x  0
 cos 2x(cos 2x  cos x  2)  0 cos 2x  0 2
 cos 2x(2cos x  cos x 1)  0   2
2cos x  cos x 1 0 (VN)
Bài 106: [Dự bị 2 ĐH A07] 2
2cos x  2 3sin xcos x 1 3(sin x  3 cos ) x Giải 51
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 2
2cos x  2 3 sin x cos x 1  3(sin x  3 cos ) x 2
 2cos x 1 3 sin 2x  2  3(sin x  3 cos ) x
 cos 2x  3 sin 2x  2  3(sin x  3 cos ) x  1 3   1 3 
 2  2 cos2x
sin 2x   6 sin x  cos x   2 2   2 2             2  2cos 2x   6cos x       3   6         1 cos 2 x   3cos x       6   6        2  2cos x  3cos x   0      6   6      cos x   0            6   cos x  2cos x  3  0          6    6       3 cos x       6  2 Bài 107: x    x   x [Dự bị 1 ĐH B07] 5 3 sin  cos   2 cos      2 4   2 4  2 Giải  5x    x   3x sin  cos   2 cos      2 4   2 4  2  5x      x  3x  sin  sin    2 cos       2 4   2  4 2  2     3x   3x     2cos x  sin   2 cos     k2  x   4   2 2  2  3 3     3x 3x    2  cos x  cos  2 cos  
x   k2 ;k   4  2 2  2   3x
x    k2  cos  0   3x     2   cos 2  2cos x   0      2   4      2 cos x         4  2 Bài 108: x x
[Dự bị 2 ĐH B07] sin 2 cos 
 tan x cot x cos x sin x Giải sin 2x cos 2x
 tan x cot x (1) điều kiện : sin2x  0 cos x sin x 52
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! cos 2 .
x cos x  sin 2 . x sin x sin x cos x (1)    sin x cos x cos x sin x 2 2 cos x sin x  cos x   sin x cos x sin x cos x
 cos x  cos2x  0 cos x  1  ( ) L 2 2cos x cos x 1 0       1 cos x   2 Bài 109:   
[Dự bị 1 ĐH D07] 2 2 sin x  cos x 1    12  Giải    2 2 sin x  cos x 1    12         2 sin 2x  sin 1       12  12      1  sin 2x  sin     12  12 2         sin x   sin  sin  2sin cos    12  4 12 6 12       5  5  sin x   cos  cos   sin      12  12  2 12  12   5 2x    k2  12 12    7 2x   k2  12 12
Bài 110: [Dự bị 2 ĐH D07] (1tan ) x (1sin 2 )
x 1 tan x Giải (1 tan ) x (1sin 2 )
x 1 tan x (1) điều kiện : cos x  0 cos x  sin x sin x  cos x (1) 2  .(sin x  cos ) x  cos x cos x 2
 (cos x sin x)(sin x  cos x)  cos x  sin x
 (cos x  sin x)(cos x sin x)(cos x sin x)   1  0 2 2
 (cos x  sin x)(cos x sin x 1)  0
cos x  sin x  0
 (cos x  sin x)(cos 2x 1)  0  cos2x 1 53
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!        cos x   0    x    k    4   4 2   cos2x 1 2x kBài 111:    [ĐH A08] 1 1 7   4sin  x   sin x  3   4  sin x     2  Giải 1 1  7    4sin  x   (1) sin x  3   4  sin x     2    Điề 
u kiện : sin x  0 và 3 sin x   0    2  1 1 (1)    2  2(sin x  cos ) x sin x cos x   Chú ý 3  : sin x   cos x    2   7     1 sin
x  sin x       
sin xcosx  4   4  2 1 1 (1)    2  2(sin x  cos ) x sin x cos x sin x  cos x   2
 2(sin x  cos x) sin x cos x  1 
 (sin x  cos x)  2 2  0    sin xcos x  s
 in x  cos x  0       x x 1 2 sin 2x 2 sin cos    0  2       sin 2x sin 2x    sin       2  4 
Bài 112: [ĐH B08] 3 3 2 2
sin x  3 cos x  sin x cos x  3 sin x cos x Giải 3 3 2 2
sin x  3 cos x  sin x cos x  3 sin x cos x 2 2 2 2
 sin x(cos x sin x)  3 cos x(cos x sin x)  0
 cos 2x(sin x  3 cos x)  0 cos 2x  0 cos 2x  0         s
 in x  3 cos x  0 sin x   0     3  54
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
2sin x 1 cos 2x  sin 2x 1 2cos x 2
 4sin xcos x sin 2x 1 2cos x
 sin 2x(2cos x 1) (1 2cos ) x  0
 (2cos x 1)(sin 2x 1)  0  1 2cos x  1  cos x       2 s  in 2x 1 sin2x 1
Bài 113[ĐH D08] 2sin x1 cos2x  sin2x 1 2cosx Giải
2sin x1 cos2x  sin 2x 1 2cos x 2
 4sin xcos x sin 2x 1 2cos x
 sin 2x(2cos x 1) (1 2cos ) x  0
 (2cos x 1)(sin 2x 1)  0  1 2cos x  1  cos x       2 s  in 2x 1 sin2x 1
Bài 114: [CĐ 08] sin3x  3 cos3x  2sin 2x Giải
sin 3x  3 cos3x  2sin 2x 1 3  sin3x  cos3x  sin 2x 2 2   3x   2x k2     3  sin 3x   sin 2x     k   3    3x
   2x k2  3
Bài 115: [Dự bị 1 ĐH A08] 2
tan x  cot x  4cos 2x Giải 2
tan x  cot x  4cos 2x (1) điều kiện : sin 2x  0 cos x sin x (1) 2    4cos 2x  0 sin x cos x 55
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 2
 cos2x  2cos 2xsin 2x  0  cos2x sin 4 . x cos 2x  0   2x   k cos2x  0  2  cos2 ( x 1 sin 4 ) x  0     s  in 4x  1  
4x   k2  4      Bài 116: [Dự bị 2 ĐH A08] 2 sin 2x   sin x        4   4  2 Giải       2 sin 2x   sin x        4   4  2 1   x x 1 sin 2 cos 2 
sin xcos x 1 2 2
 sin 2x sin x  (1 cos2x)  cos x  0 2
 sin x(2cos x 1)  2cos x  cos x  0
 sin x(2cos x 1)  cos x(2cos x 1)  0
 (2cos x 1)(sin x  cos x)  0  1 cos x  2cos x 1 0    2   
sin xcosx 0     sin x   0      4  Bài 117:       [Dự bị 1 ĐH B08] 1 2sin x  sin 2x        3   6  2 Giải       1 2sin x  sin 2x        3   6  2 56
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!  3 1  1
 sin x  3 cos x 
sin 2x  cos 2x    2 2  2   2 1 2sin x 1
 sin x  3 cos x  3 sin xcos x   2 2
 3 cos x1sin x sin x1sin x  0
 (1sin x)( 3 cos x  sin x)  0   x   k2 s  in x 1  2    
 3 cos x  sin x  0     sin x   0      3  Bài 118: x [Dự bị 2 ĐH B08] 2
3sin x  cos 2x  sin 2x  4sin x cos 2 Giải x 2
3sin x  cos 2x  sin 2x  4sin x cos 2 1 cos x
 3sin x  cos 2x  sin 2x  4sin x   2 
 3sin x  cos 2x  sin 2x  2sin x  sin 2x 2
 cos 2x  sin x  0  2sin x sin x 1 0 s  in x 1   1    s
 in x    sin     2  6 
Bài 119: [Dự bị 1 ĐH D08]  4 4
4 sin x  cos x cos4x sin 2x  0 Giải  4 4
4 sin x  cos x cos4x sin 2x  0 2  sin 2x  2  41
 1 2sin 2x  sin 2x  0  2  s  in 2x  1  2 4sin 2x sin 2x 5 0       5 s  in 2x  ( ) L  4 2    Bài 120: tan x tan x 2  [Dự bị 2 ĐH D08]  sin x    2 tan x 1 2  4  Giải 57
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 2 tan x  tan x 2     sin x  
 (1) điều kiện : cos x  0 2 tan x 1 2  4  2 tan x  tan x 1 (1)   sin x  cos x 2   tan x  1 2 2  2cos x 2
tan x  tan x  sin x  cos x 2
 sin x  sin xcos x  2  2cos x
  sin x  cos x 2  cos x
 2sin xsin x  cos x sin x  cos x  0
 sin x  cos x2sin x   1  0     sin x   0    s
 in x  cos x  0  4      2sin x 1  1  sin x   cos  2 6 Bài 121: (1 2sin x) cos x [ĐH A09]  3 (1 2sin x)(1  sin x) Giải s  in x 1 (1 2sin x)cos x   3 (1) điều kiện :  1 (1 2sin x)(1 sin x) sin x    2
(1)  1 2sin xcos x  3(1 sin 2x)(1 sin x)  x x   2 cos sin 2
3 1 sin x  2sin x
 cos x sin 2x  3 cos2x sin x
 cos x  3sin x  sin 2x  3 cos2x 1 3 1 3  cos x  sin x  sin 2x  cos 2x 2 2 2 2    2x
x   k2        6 3  cos x   cos 2x         3   6     2x
 x   k2  6 3   x   k2  2   k   k2 x     18 3
Bài 122: [ĐH B09]     3 sin x cos x sin 2x 3 cos3x 2 cos 4x  sin x 58
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! Giải     3 sin x cos x sin 2x 3 cos3x 2 cos 4x  sin x  x  2 sin
1 2sin x  cos xsin 2x  3 cos3x  2cos 4x
 sin xcos2x  cos xsin 2x  3 cos3x  2cos4x
sin 3x  3 cos3x  2cos 4x 1 3  sin3x  cos3x  cos 4x 2 2   4x  3x   k2     6  cos 3x   cos4x      6    4x  3
x   k2  6
Bài 123: [ĐH D09] 3 cos5x  2sin3xcos2x  sin x  0 Giải
3 cos5x  2sin 3x cos 2x  sin x  0
 3 cos5x sin5x sin xsin x  0 3 1
 3 cos5x sin5x  2sin x
cos 5x  sin 5x  sin x 2 2     x  5x k2 6x   k2      3 3  sin
5x  sin x        3  2   2   x   5x k2 4  x   k2  3  3
Bài 124: [CĐ 09] 2
(1 2sin x) cos x 1 sin x  cos x Giải 2
(1 2sin x) cos x 1 sin x  cos x 2
 (1 4sin x  4sin x)cos x 1 sin x  cos x 2
 cos x  2sin 2x  4sin xcos x 1sin x  cos x  0  1       x    x x   sin 2x sin 2sin 2 1 sin 2sin 2 1  0  2 6  sin x  1      1 s inx  o
c s2xsin x     4  1
Bài 125: [ĐH A10]  cos x 1 t anx 2 Giải 59
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
1sinxcos2x   sin x     4  1 cosx  0  cosx 1 tanx . Điều kiện:  2 tanx  1
1sinxcos2xsinxcosx pt   cosx sinx 1 cosx
cosx1sinx  cos2xsinx cosx   cosx cosx sinx
1 sinx  cos2x  0  2
2cos x sinx  0    2 2 1 sin xsinx  0  1 17 sinx  >1 (loaïi)  2
2sin xsinx2  0   4  1 17 sinx  (thoûa ñk)  4  1 17  x  arcsin   k2  4       kZ   1 17  x    arcsin   k2   4    
Bài 126: [ĐH B10] sin2x+cos2xcos x  2cos2x sinx  0 Giải
(sin2x + cos2x)cosx + 2cos2x – sinx = 0
 cos2x (cosx + 2) + sinx (2cos2x – 1) = 0
 cos2x (cosx + 2) + sinx.cos2x = 0
 cos2x (cosx + sinx + 2 = 0)  cos2x = 0     2x =
k  x =  k (k  Z) 2 4 2
Bài 127: [ĐH D10] sin2x  o
c s2x  3sin x  cos x 1 0 Giải
Các anh (chị) tự giải. 60
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! Bài 128: 1 sin 2x  o c s2x [ĐH A11]
 2 sin xsin 2x 2 1 cot x Giải
1 sin2x  cos 2x  2.sin . x sin2x 2 1 cot x  2 2 sin (
x 1sin2x  cos 2 )
x  2 2 sin xcos x (ĐK : sinx ≠ 0)
1sin2x cos2x  2 2 cos x 2
 2cos x  2sin xcos x 2 2 cos x  0  2cos (
x cos x sin x  2)  0
 cosx = 0 hay cosx + sinx = 2     cosx = 0 hay sin x  1    4   
 x =  k hay x =  k2 (k  Z) 2 4
Bài 129: [DB A11] 9sin x 6cos x 3sin2x cos2x 8 Giải Tham khảo thêm
Bài 130: [ĐH B11] sin2xcos x sin xcos x  o
c s2x  sinx  cos x Giải
Phương trình đã cho tương đương :
2sinxcos2x + sinxcosx = 2cos2x – 1 + sinx + cosx
 sinxcosx (2cosx + 1) = cosx (2cosx + 1) – 1 + sinx
 cosx(2cosx + 1)(sinx – 1) – sinx + 1 = 0
 sinx = 1 hay cosx(2cosx + 1) – 1 = 0 
 x =  k2 hay 2cos2x + cosx – 1 = 0 2   1 x =
k2 hay cosx = – 1 hay cosx = 2 2    x =
k2 hay x =  + k2 hay x =   k2 (k  Z) 2 3 61
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! Bài 131: x x   [ĐH D11] sin 2 2cos s inx 1  0 t anx  3 Giải
sin 2x  2cos x  sin x 1
 0 đk : tg x   3 ; cosx  0 tan x  3
Pt  sin2x + 2cosx  sinx  1 = 0  2sinxcosx + 2cosx  (sinx + 1) = 0
 2cosx (sinx + 1)  (sinx + 1)= 0  (2cosx  1)(sinx + 1) = 0    1 x    k2 cos x    3   2       
so đk ta có nghiệm của pt : x k2 (k )   3 s  in x  1  x    k2  2
Bài 132: [ĐH A12] 3sin 2x  cos2x  2cos x 1 Giải 2
3sin2xcos2x  2cos x 1
 2 3sin xcosx2cos x 1  2cos x 1       x xx  cos x 0 cos 3 sin cos 1 0   3 1 1 
sin x cos x  2 2 2   x k      2 x kx k   2  2     x   2 m   x 2 m   k, ,nm      1  6 6 sin x    2   6  2  5 x  2 n  x   2 n   3  6 6
Bài 133: [ĐH B12] 2(cos x  3sin )
x cos x  cos x  3sin x 1. Giải 2(cos x  3sin )
x cos x  cos x  3sin x 1 62
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
 (2cos x 1)(cos x 1)  3sin x(2cos x 1)  0  1 cos x        2 2 cos x 1 0 2 x    k2       3
cos x  3sin x 1     1  cos x     x k2   3  2
Bài 134: [ĐH D12] sin3x + cos3x – sinx + cosx = 2 cos2x Giải
sin3x + cos3x – sinx + cosx = 2 cos2x  sin3x – sinx + cos3x + cosx = 2 cos2x
 2sinxcos2x + 2cos2xcosx = 2 cos2x  cos2x = 0 hay 2sinx + 2cosx = 2  1
 cos2x = 0 hay sin(x  )  4 2    7
 x =  k hay x =   k2 hay x =
k2 (với k  Z). 4 2 12 12   
Bài 135: [ĐH A13] 1 tan x  2 2 sin x     4  Giải 1+tanx=2(sinx+cosx)
 cosx+sinx = 2(sinx+cosx)cosx (hiển nhiên cosx=0 không là nghiệm) 1 1  sinx+cosx=0 hay cosx =  tanx=-1 hay cosx = 2 2  
x    khay x    k2 ,k  4 3
Bài 136: [ĐH B13] 2
sin5x  2cos x  1 Giải 2
sin5x  2cos x 1  sin5x = 1 – 2 cos2x = -cos2x = sin(2x - /2)  
 5x = 2x - + k2 hay 5x =  - 2x + + k2, k  Z 2 2  k2 3 k2  x =   hay x =  , k  Z 6 3 14 7
Bài 137: [ĐH D13] sin3x cos2x sinx 0 Giải 63
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
sin3x  cos 2x sin x  0
 2cos2xsin x cos2x  0  cos2x2sin x   1  0    cos2x  0 x
k ,k Z   4 2  1   s  in x    7   x  
k2 hay x   k2, 2 k Z  6 6 xBài 138: 1 sin 2 Giải phương trình : cot x   2sin( x  ) 2 sin x  cos x 2 Giải cos x 2sin x cos x 2 cos x 2 cos x PT    2cos x  0    0 2 sin x sin x  cos x 2 sin x sin x  cos x   
 cos x sin(x  )  sin 2x  0    4  
+) cos x  0  x
k, k  .  2     
2x x   m2
x   m2 +) 4 4
sin 2x  sin( x  )     m, n  4     n2
2x    x     n2 4 x    4 3  t2  x   , t  .  4 3 Đố   t2
i chiếu điều kiện ta có nghiệm của pt là x    k ; x   , k, t  .  2 4 3 2 Bài 139  1 tan x
: Giải phương trình 4 8 o c s (x  )  sin 4x  2. 2 4 1 tan x Giải Đk:  
cos x  0  x   k ,ta có cos( x
) cos x s
, sin x  cos x si 2 2 inx 1 2 n 2 4
 cos x sin x4   2 2 o
c s x sin x1 sin2x
 cos x sin x   o
c s x sin x3 4
sinx cos x 64
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
sin xcos x sinx3  0 x k sin x  0 x k       
cos x sin x  0 tan x  0
x   k  4 x k Vậy pt có 2 nghiệm:    x   k  4 Bài 140:  5 
Giải phương trình 5sin  x  1 ( 3  cos ) x cot2 x  2  2  Giải
ĐKXĐ x k,k Z cos2 x Pt(1)  5cos x  1 ( 3  cos x)  2 1 cos2 x 3cos2  x 5cos x   2  2cos2 x  c 3 osx  2  0 1 cos x cos x  2    cos x  1  2  cosx  2  vô nghiệm 1  cos x
x    l2,l Z , thỏa mãn điều kiện. 2 3 Bài 141: 1 2(cos x  sin ) x Gi¶i ph-¬ng tr×nh:  tan x  cot 2x cot x 1 Giải
§iÒu kiÖn:sinx.cosx  0 vµ cotx  1 Ph¬ng tr×nh t¬ng ®¬ng 1 2(cos x  sin ) x  sin x cos 2x cos x  1 cos x sin 2x sin x  2  cosx = x =   k2 2 4 
§èi chiÕu ®iÒu kiÖn pt cã 1 hä nghiÖm x =   k2 4 65
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! Bài 142:   
Giải phương trình sin2x + cosx- 2 sin x    -1= 0.  4  Giải
Pt đã cho tương đương: sin2x cosx (sinx cos ) x 1  0  2cos ( x sinx  ) 1 sinx 1  0   1 sin x   1 2cos x   1  0  sin x  1  hoặc cos x  2   sin x  1
  x    k2. 2  1  o c sx
x    2k . 2 3  
Vậy, nghiệm của phương trình đã cho là: x    k2 ; x  
 2k ( k Z ). 2 3 Bài 143:  Giải phương trình : 2 2 o
c s3x.cosx+ 3(1 sin2x)=2 3 o c s (2x  ) 4 Giải    PT  o
c s4x+cos2x+ 3(1 sin 2 ) x  3 1 o c s(4x+ )    2   o
c s4x+ 3 sin 4x  o
c s2x+ 3 sin 2x  0  
 sin(4x  ) sin(2x  )  0 6 6    x    k   18 3  2sin(3x  ). o c sx=0   6   x=  k  2   
Vậy PT có hai nghiệm x
k và x    k . 2 18 3 Bài 144:   Giải phương trình: 2 sin .
x sin 4x  2 2.cos  x  4 3.cos . x sin . x cos 2x    6  Giải 66
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! ĐK: Ta có:    sin .
x sin 4x  2 2 cos  x  3.cos . x sin 4x    6     
sin 4x sin x  3 cos x  2 2 cos  x      6  s
 in 4x  2 vn       sin 4x  2 cos  x  0         6  cos  x  0      6  Với :      cos
x  0  x   k   k Z  6  3
Bài 145: Giải phương trình 3 o c s2x +sin2x - (4+ 3) o
c sx -sinx+2+ 3=0 Giải 2 pt  3(2 o c s x-1) + 2sinx. o c s x - (4+ 3) o c sx -sinx+2+ 3=0 2  (2sinx. o c s x-sinx)+2 3 o c s x- (4+ 3) o c sx+2=0
 sinx ( 2cosx-1)+( 2cosx-1)( 3cosx-2)=0
 ( 2cosx-1)sinx+ 3cosx-2  0  1 o c sx= (1)  pt  2 sinx+ 3cosx-2=0 (2)  (1)  x  
k2 (k Z) 3 1 3   (2)  sinx+
cosx=1  sin(x  ) 1
x   k2 (k Z) 2 2 3 6
Bài 146: Giải phương trình (1cos )
x cot x  cos2x sin x  sin 2x . Giải c
 os .xsin2 .xsin .xtan x cot 2x  Điề 0 u kiện:  c  ot x 1 67
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 1
2 cos x  sin x cos . x sin 2x Từ (1) ta có:    2 sin x sin x cos 2x cos x cos x  1 cos x sin 2x sin x  2sin .
x cos x  2 sin x   x   k2 2  4  cos x    k   2 
x   k2  4 
Giao với điều kiện, ta được họ nghiệm của phương trình đã cho là x  
k2 k   4
Bài 147: Giải phương trình (1cos )
x cot x  cos2x sin x  sin 2x . Giải Phương trình (1cos )
x cot x  cos2x sin x  sin 2x (1)
Điều kiện: sin x  0  x k (k  ) Khi đó: x (1)  cos (1 cos ) x
cos2x sin x  sin 2x sin x 2 2 2
 cos x  cos x  cos2xsin x sin x  2sin xcos x 2 2 2  cos ( x 1 2sin )
x  cos 2xsin x  (cos x sin ) x  0
 cos xcos2x  cos2xsin x  cos2x  0  cos2 (
x cos x  sin x 1)  0
 cos2x  0  cos x  sin x 1  0  
+ cos 2x  0  x
k (k  ) . 4 2      1   x   l2
+ cos x  sin x 1  0  cos x  
x    l2     2  4  2 4 4  x l2
Kết hợp điều kiện phương trình đã cho có các nghiệm là:    x
k , x  l2 (k,l  ) . 4 2 2 Bài 148:     2017  Gi¶i ph-¬ng tr×nh sau: 2 2.sin x  sin 2x  1 tan x      4   2  Giải
§iÒu kiÖn: cos x  0  x
k (k Z) 2
+Víi ®k trªn pt ®· cho t-¬ng ®-¬ng: 68
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!     1 cos 2x
sin(2x  1008) 1 tan x    2  2
1sin 2x cos2x 1 tan x
 sin 2x  cos2x  tan x  0 sin x 2  2sin .
x cos x  2cos x  (1 )  0 cos x sin x  cos x  2cos .
x (sin x  cos ) x   0 cos x 1  (sin x  cos ) x .(2cos x  )  0 cos x 2 sin x    .cos2x0 4 x     k s  inx     4 0 4   (tm®k) k     cos 2x 0 x   4  2  k  k
VËy pt ®· cho cã 1 hä nghiÖm:  x   (hä  chøa   k ) 4 2 4 2 4 2 3   Bài 149: cos x cos x 1 Giải phương trình sau: 2
cos 2x  tan x  2 cos x Giải
ĐK cosx ≠ 0, pt được đưa về 2 2 2
cos2x  tan x 1 cos x  (1 tan )
x  2cos x  cos x -1  0
Giải tiếp được cosx = 1 và cosx = 0,5 rồi đối chiếu đk để đưa ra ĐS: 2 2
x k2 , x  
k2; hay x k . 3 3  Bài 150: x x Giải phương trình: (1 cos ) cos 1  (x  )
(1 cos x)(1 2cos x) tan x Giải
1cos xcosx 1     1
1 cos x1 2cos x tan x ĐK: 69
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! c  os x  1   1 s  in 2x  0  cos x    2   1 cos x   cos x  0  2   sin x  0 PT   1 2 sin xsin .
x cos x 1cos x  2cos x
 sin x  cos x 1sin .
x cos x  21sin x1 sin x  0
 1sin x2sin x  cos x   1  0 s  in x 1 Loai  
2sin x  cos x 1 0
 2sin x  cos x  1 
x    k2 loai   x  2    k2  T / m Vậy PT  
1 có các nghiệm x  2
  k2, k  Với  thỏa mãn:  2 cos   5  1 s  in   5 Bài      
151: Giải phương trình: 3 3
sin x  cos x  cos 2 . x cot x  .cot x       4   4  Giải      
* Giải phương trình: 3 3
sin x  cos x  cos 2 . x cot x  .cot x      (1)  4   4    3 3
PT(1)  cos x  sin x  cos 2 . x cot(  ) x .cot(  ) x (2) 4 4 * ĐK:      sin(
x).sin(  x)  0  sin(  x).cos(  x)  0  sin(  2 ) x  0 4 4 4 4 2   
 cos 2x  0  2x   k  x   k 2 4 2 70
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 3 3
PT (2)  cos x  sin x  cos 2x  (cos x  sin x)(1 sin .
x cos x)  (cos x  sin x)(cos x  sin x) tan x 1
cos x sin x  0 tan x 1     sin x 1   1  sin . x cos x cos x sin x
(1 cos x)(1 sin x) 0        cos x 1   
x   k, x   k2, x k2 4 2 
- Kết hợp với điều kiện ta được 2 họ nghiệm : x
k2, x k2 , k  2  3    
Bài 152: Giải phương trình: 2 2 cos2x  sin2x cos x
  4sin x    0  4   4  . Giải
 (sin x  cos x)4(cos x sin x) sin2x  4  0    3
x    k  2;   2 4 ; x k x k 2 Bài 2 2 2 2
153: Giải phương trình: sin 3x  cos 4x  sin 5x  cos 6x Giải k x    2 2 2 2 2
sin 3x  cos 4x  sin 5x  cos 6x  cos x(cos7x  cos1 x 1 )  0   kx    9 Bài   
154: Tìm nghiệm trên khoảng 0; của phương trình: 2    2  x      3 
4sin     3sin 2x 2
 1 2cos  x  2 2 4        Giải  5 2       x   k
(k Z) (a) 
(2) sin2x    sin  x 18 3   3   2  x 5   l2 l ( Z) b ( )  6 71
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! Bài 1 1
155: Giải phương trình: sin2x  sin x    2cot 2x 2sin x sin2x Giải  2
cos x  cos x cos x  cos x   (1) 2 2 2 2   s 
 cos2x = 0  x k  in2x  0 4 2 Bài 3sin2  2sin
156: Giải phương trình: x x 2 sin2x.cos x (1) Giải 2  (1 cos ) x sin (
x 2cos x 1)  0 
(1)
 2cosx – 1 = 0 x    k2 s
 in x  0, cos x  0 3
Bài 157: Giải phương trình: cos2x  5  2(2  cos )
x (sin x  cos ) x (1) Giải (1) x x 2
(cos –sin )  4(cosx –sin x) –5  0 x   k2  x    k2 2
Bài 158: Tìm các nghiệm thực của phương trình sau thoả mãn 1 log x  0 1 : 3 sin .
x tan 2x  3(sin x  3 tan 2x)  3 3 Giải  
(2)  (sin x  3)(tan 2x  3)  0  x    k ;k Z 6 2  
Kết hợp với điều kiện ta được k = 1; 2 nên 5 x  ; x  3 6  Bài 159: 2 3 2 Giải phương trình: 3 3
cos3xcos x  sin3xsin x  8 Giải  
(1)  cos4x = 2  x  k 2 16 2
Bài 160: Giải phương trình: 9sinx + 6cosx – 3sin2x + cos2x = 8 72
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! Giải
PT  (1– sinx)(6cosx + 2sinx – 7) = 0  1– sinx = 0  x   k2 2
Bài 161: Tìm nghiệm của phương trình: 2 3
cos x cos x  sin x  2 thoả mãn : x 1  3 Giải
PT  (cos x 1)(cos x  sin x  sin .
x cos x  2)  0  x k 2 . Vì x 1  3  2   x  4 nên nghiệm là: x = 0
(sin 2x  sin x  4)cos x  2
Bài 162: Giải phương trình:  0 2sin x  3 Giải
Bài 163: Giải phương trình: sin x  cos x  4sin 2x 1. Giải (
 2cos x 1)(sin xcos x  2)  0   x   k  PT     2 2sin x  3  0 3
Bài 164: Giải phương trình: cos23x.cos2x – cos2x = 0. Giải Đặ 
t t  sin x  cos x , t  0 . PT  2
4t t 3  0  x k 2 . Bài 165:
3sin 2x  2sin x
Giải phương trình.  2 sin 2 . x cos x Giải
Dùng công thức hạ bậc. ĐS: x k (k Z ) 2 73
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 1 3 7
Bài 166: Giải phương trình: 4cos4x – cos2x  cos4  x x cos = 2 4 2 Giải
 (  cos x)(sin x sin x)   PT  2 1 2 0 x    k  s   2
 in x  0, cos x  0 3 2 cos .
x cos x   1
Bài 167 : Giải phương trình:  21sin x sin x  cos x Giải c  os2x  1 x   k 3x   PT  cos2x + cos = 2   3x   8
m  (k;m )  x = 8n 4 cos 1  x    4  3 x x   x
Bài 168: Giải phương trình: 2 2
1 sin sin x  cos sin x  2cos    2 2  4 2  Giải x  x x  x   k PT 2  sin x sin 1 2sin  2sin 1  0      x   k   2  2 2 
x   k4 3 3 sin .
x sin 3x  cos x cos3x 1 Bài 169:   Giải phương trình:       8 tan x  tan x       6   3  Giải            
Điều kiện: sin x  sin x  cos x  cos x   0          6   3   6   3              Ta có tan x  tan x   tan x  cot  x  1           6   3   6   6  1 PT 3 3  sin .
x sin 3x  cos xcos3x  8
1 cos 2x cos 2x  cos 4x
1 cos 2x cos 2x  cos 4x 1      2 2 2 2 8 74
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!   x    k (loaïi) 1 1 1  3
 2(cos2x  cos2xcos4x)   cos 2x   cos2x  6   2 8 2   x      k  6 
Vậy phương trình có nghiệm x    
k , (k  ) 6
Bài 170: Giải phương trình: 3 3 sin .
x (1 cot x)  cos x(1 tan x)  2sin 2x . Giải ĐKXĐ:   k x
sao cho sin 2x  0 . 2 Khi đó, VT = 3 3 2 2
sin x  cos x  sin xcos x  cos xsin x = 2 2 (sin x  cos )
x (sin x  sin xcos x  cos ) x  sin xcos (
x sin x  cos )
x = sin x  cos x s
 in x  cos x  0
PT  sin x  cos x  2sin 2x   2 (
 sin x  cos x)  2sin 2x (1)  
(1)  1 sin 2x  2sin 2x  sin 2x 1( 0)  2x   2  k x    k 2 4 
Để thoả mãn điều kiện sin x  cos x  0 , các nghiệm chỉ có thể là: x   2  k 4 cos x Bài 171:
Tìm giá trị nhỏ nhất của hàm số: y = 2 với 0 < x  .
sin x(2cos x  sin x) 3 Giải
Với 0  x  thì 0  tan x  3 và sin x  0,cos x  0, 2cos x  sin x  0 3 cos x 2 2 3  x   1 tan 1 tan cos    x x y 2 2 2 3
sin x 2cos x  sin x tan ( x 2  tan ) x 2tan x  tan x . 2 cos x cos x 2 1 t
 Đặt: t  tan ;x 0  t  3  y f (t)  ; 0  t  3 2 3 2t t 4 2 3 2
t  3t  4t
t(t  3t  4)
t(t 1)(t t  4) f (t)   
f (t)  0  (t  0  t 1). 2 3 2 2 3 2 2 3 2 (2t t ) (2t t ) (2t t ) 75
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!  
 Từ BBT ta có: min f (t)  2  t 1  x  . Vậy: miny  2 khi x  . 4    4 0;    3  Bài 172:       Giải phương trình: sin 3x
 sin 2xsin x      .  4   4  Giải
PT  sin3x  cos3x  sin 2 (
x sin x  cos ) x s
 in x  cos x  0 tan x  1 
 (sinx + cosx)(sin2x  1) = 0     s  in2x 1 0 s  in2x 1   x      k  4    x     k   4 x     k 4
Bài 173: Giải phương trình: cos2x + cosx + sin3x = 0 Giải x x x PT  cosx(1 + cosx) + 8 3 3 sin cos = 0  2 2cos
cosx (1cos )xsin x0 2 2 2  x cos  0   2  s
 in x cos x  sin . x cos x  0 1
Bài 174: Giải phương trình: cos3x  cos2x  cos x 2 Giải x
 Nếu cos  0  x    k2,k Z , phương trình vô nghiệm. 2 x x
 Nếu cos  0  x   k2,k Z , nhân hai vế phương trình cho 2cos ta được: 2 2 x x x x 7x
2cos cos3x  2cos cos 2x  2cos cos x  cos  tích thà  nh tông cos  0 2 2 2 2 2  2  x   k , k
, đối chiếu điều kiện: k ≠ 3 + 7m, mZ . 7 7
Bài 175: Tìm tổng tất cả các nghiệm x thuộc [ 2; 40] của phương trình: sinx – cos2x = 0. 76
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! Giải  2
Ta có: sinx – cos2x = 0  2sin2x + sinx –1 = 0  x   k ,k  . 6 3         Vì x [ 2; 40] nên 2 3 3 2   k  40  2   k  40      6 3 2  6  2  6 
 0,7  k  18,8  k 1,2,3,...,1  8 .  2
Gọi S là tổng các nghiệm thoả YCBT: S = 18. 
(1 2  3  ... 18) 117 . 6 3 l
 og x 1  log (3 x)  log (x 1)  0 2  
2) Điều kiện: 1 x  3. PT  2 2  1   x  3 
 x  13 x 1 17 2
x 1 x x  4  0  x  (tmđk) 2      
Bài 176: Giải phương trình: tan x  tan x
.sin 3x  sin x sin 2     x  6   3  Giải      
Điều kiện: cos x .cos x   0      6   3        sin x  sin x      PT  6   3  
sin 3x  sin x  sin 2x  – sin3x = sinx + sin2x       cos x  cos x       6   3    k s  in 2x  0 x    sin2x(2cosx + 1) = 0  2  1    cos x    2  x    k2 2   3   x k
Kết hợp điều kiện, nghiệm của phương trình là: 2   2 x    2   k  3
Bài 177 : Giải phương trình : 1 8 21 1 2 2cos x o
c s  x 3  2 sin 2(x         )  3cos x    sin x . 3 3  2  3 Giải 1  sin x  0
PT  (1 sin x)(6cos x  sin x 8)  0  1sin x  0 
6cos x  sin x 8  0 77
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 1 1
Bài 178: Giải phương trình: sin 2x  sin x    2cot 2x 2sin x sin 2x Giải
PT   cos22x  cosxcos2x = 2cos2x và sin2x  0     2 cos2x  0 
2cos x  cos x 1 0(VN)  cos2x = 0  2x    k x   k 2 4 2    2 sin   x   Bài 179: 4 Giải phương trình: (1 sin 2 )
x 1 tan x cos x Giải
Điều kiện cos x  0  x    k ,k  . 2 cos x  sin x cos x  sin x Ta có PT 
cosx sin x2   (cos x  sin )
x (cos 2x 1)  0 cos x cos x  
cos x  sin x  0 x      m   4 , m   . cos 2x 1  0  x   m
Bài 180: Giải phương trình: 2 2 3 3 tan x  tan .
x sin x  cos x 1  0 Giải  ĐK: x    k . PT  2 3 3 tan ( x 1 sin ) x  (1 cos ) x  0  2  (1 cos ) x (1 sin )
x (sin x  cos )
x (sin x  cos x  sin xcos ) x  0   
x k2; x    k ; x
  k2; x    k2 4 4 4
Bài 181: Giải phương trình: 2cos3x + 3 sinx + cosx = 0 Giải         PT  cos x   cos3   x  cos x  cos(  3 ) x    k x    3   3  3 2 6 6 sin x  cos x 1
Bài 182: Giải phương trình:  tan 2x 2 2 cos x  sin x 4 78
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! Giải   k
Điều kiện: cos2x ≠ 0  x   (k  ) 4 2 3 1 PT 2
1 sin 2x  sin2x  3sin22x + sin2x – 4 = 0 4 4 
 sin2x = 1  x   
k ( không thoả). Vậy phương trình vô nghiệm. 4 Bài 183:
Giải phương trình: cos3xcos3x – sin3xsin3x = 2 3 2 8 Giải   PT  2 cos 4x   x  
k ,k Z 2 16 2
Bài 184: Giải phương trình : 3 3 2
cos xcos3x  sin xsin3x 4 Giải
PT  cos 2x= 1  x=    k (k   ) 2 8
Bài 185: Giải phương trình: cot x  3 tan x  2cot 2x  3 . Giải
Điều kiện: sin xcos x  0  x k . 2 2 2 cos 2x cos x  sin x Ta có: 2cot 2x  2  2
 cot x  tan x . sin 2x 2sin x cos x c  ot x  3 
PT  3  cot x  3  cot x  
 cot x 1 x   k,k 2 c
 ot x  7cot x  6  0 4    Bài 186: 2 Giải phương trình:
2cos  3x  4cos4x 15sin2x  21  4  Giải 79
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 3 2 
PT  sin 2x  2sin 2x 3sin2x  6  0  sin2x  1
  x    k 4 2 1
Bài 187: Giải phương trình:
(1 4sin x)sin3x  2 Giải
Nhận xét: cosx = 0 không phải là nghiệm của PT. Nhân 2 vế của PT với cosx, ta được: PT  x 3
2sin3 (4cos x 3cos x)  cos x  2sin x 3 .cos x 3  cosx   
 sin6x  sin  x 2     k2  k2  x    x   14 7 10 5 1
Bài 188: Giải phương trình:
sin x  sin2x 1 cos x 2  cos x 2 Giải
PT  (sin x 1)(sin x  cos x 2)  0  sin x 1  x   k2 2 .
3sin x  3tan x
Bài 189: Giải phương trình:  2cos x  2 tan x sin x Giải cos x  0 2 Điều kiện:      2 s  . PT  x 1 cos  x k .  in x  0 2 3 1
2(cos x sin x)
Bài 190: Giải phương trình:  tan x  cot 2x cot x 1 Giải s  in x  0  
Điều kiện: cos x  0 . PT  x 2 cos   x    k2 .  2 4 cot x  1
Bài 191: Giải phương trình: sin3x 3sin2x cos2x 3sin x 3cos x 2  0 80
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! Giải
sin3x 3sin 2x cos2x 3sin x 3cos x 2  0  (sin3x sin )
x  2sin x 3sin 2x (cos2x  23cos ) x  0 2  2sin 2 .
x cos x  2sin x  6.sin .
x cos x  (2cos x  3cos x 1)  0 2 2
 2sin xcos x  2sin x 6sin xcos x (2cos x 3cos x 1)  0 1 1 2
 (2sin x 1)(2cos x 3cos x 1)  0  sin x  ,cos x 1,cos x 2 2 1  5 +) sin x
x   k2, x   k2 2 6 6 1  +) cos x
x    k2 2 3
+) cos x 1 x k2
KL:Vậy phương trình có 5 họ nghiệm như trên. 2     Bài 192:
(2sin x 1)(3cos 4x 2sin ) x 4cos x 1
Giải phương trình:  8 (x  ) 1 sin x Giải x   x x 2 2sin 1 3cos 4 2sin
 4cos x 1 8  1 1 sin x Đk:  
1 sin x  0  x
l2,l    * 2 PT   1   x   x x 2 2sin 1 3cos 4 2sin
 4cos x 1 88sin x   x   x x 2 2sin 1 3cos 4 2sin
 4sin x 8sin x 3  2sin x  
1 3cos 4x  2sin x  2sin x   1 2sin x   3 2sin x 1  0     cos 4x 1   x    k2   Với 6
2sin x 1 0   7   x   k2  6  k
Với cos 4x 1 x  2  2
Kết hợp với điều kiện   * PT  
1 có các nghiệm x    k 6 3
x k , k 81
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
Bài 193: Giải phương trình sau:          2 5 4sin x   o
c s(3x + 2013 ) - 2sin
 2x  2  sin x         2   2   2  Giải PT 2  4 o c s x  o c s3x  2 o c s2x  2  o c sx  o c s3x  o c sx
3x x k2  
3x  x k2   x k . 2 Bài 194 sin 3x  cos3x
: Giải phương trình: cos 2x   sin ( x 1 tan ) x 2sin 2x  . 1 Giải  1 s  in 2x Đk  2
(*) . Với đk (*) phương trình đã cho tương đương: c  os x  0 3 3
3sin x  4sin x  4cos x  3cos x cos 2x   sin(1 tan x) s
 in x  cos x  0 (1) 2sin 2x 1   sin x
(sin x  cos x)(2sin 2x 1) sin (
x sin x  cos ) x
cos x sin x 1 (2) 2 2
 cos x sin x    cos x 2sin 2x 1 cos x  (1)  tan x  1
  x    k,k  4  
cos x sin x  0 tan x 1 x   k (2)
(cos x sin x)(1 cos x) 0           4 (k  ) 1   cos x  0 cos x  1  
x    k2 
So với đk (*) suy ra các họ nghiệm của pt là: x  
k, x    k2,k  4
Bài 195: Giải phương trình   tan(x  ).tan(x  )  2 o c s2x 1. 6 6 Giải 82
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!        cos(x  )  0 (x  )   kx   k    ĐK:  6  6 2  3         2 c  os(x ) 0 (  x ) k       x   k  6  6 2  3 Ta có:   1 1 sin(x  ).sin(x  )  cos2x 1 2cos2 6 6 4 2 x VT      1 1 2cos 2x  1 cos(x  ).cos(x  ) cos 2x  6 6 2 4    1   x    k       Vậy cos 2x 2x k2   6 PT  (1  2 o
c s2x)(2cos 2x  2)  0  2  3      cos2x=-1 2x= k2   x=  k  2  
Đối chiếu đk ta có: x    k;x=  k là các họ nghiệm của phương trình 6 2
Bài 196: Giải phương trình 2
2cos x  2 3sin xcos x 1 3(sin x  3 cos ) x . Giải 2
2cos x  2 3sin xcos x 1 3(sin x  3 cos ) x 2  (sin x  3cos )
x 3(sin x  3 cos ) x  0
 sin x  3 cos x  0 sin x  3 cos x  3 (1)
Phương trình sin x  3 cos x  3vô nghiệm vì 2 2 2 1  ( 3)  3 Nên (1)  
 tan x   3  x    k ( k  ). Vậy, PT có nghiệm là: x    k ( k  ). 3 3
Bài 197: Giải phương trình 3 sinx - 3cosx - 2 = cos2x - 3 sin2x Giải
3 sinx - 3cosx - 2 = cos 2x - 3 sin2x (1) (1)  3 sinx(2cosx + 1) = 2cos2x + 3cosx + 1  1
(2cosx + 1)(cosx - 3 sinx + 1) = 0  cosx = - hoặc cosx - 3 sinx + 1 = 0 (1’) 2 1 2 * cosx = -  x = + k2 2 3 (1’)   1  cos(x + ) = -  x = + k2 hoặc x = - + k2 3 2 3 4 4 sin x  cos x 1
Bài 198: Giải phương trình :
 tan x  cot x sin 2x 2 Giải 83
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ! 4 4 sin x  cos x 1
 tan x  cot x (1) sin 2x 2
Điều kiện: sin2x  0 1 2 1 1 sin 2x 2 1 sin 2x 1  sin x cos 2 x  1 1 (1)      2   2
1 sin 2x 1  sin 2x  0 sin 2x 2  cos x sin x  sin 2x sin 2x 2
Vậy phương trình đã cho vô nghiệm.
Bài 199: Giải phương trình: 2 o c s6x +2cos4x - 3 o c s2x = sin2x + 3 Giải 2 o c s6x+2cos4x- 3 o
c s2x =sin2x+ 3 4cos5xcosx = 2sinxcosx + 2 3 cos2x   x   k  2  cos x  0  o c s x=0    k       x   
2cos5x =sinx+ 3 cos x  o c s5x=cos(x- )  24 2  6   k x    36 3      x 2 2 4 sin
Bài 200: Giải phương trình : cos   x  cos   x   3   3  2 Giải  2   2  1 cos  2x 1 cos  2x   Ta có:      x      x 2 2 4 sin 3 3 4 sin cos 
x  cos   x      3   3  2 2 2 2  2   2  2
 sin x  2  cos  2x  cos
 2x  0  sin x  2  2cos cos2x  0  3   3  3 sinx  2co 2
s x  0  2sin2 x  sinx  3  0 sin x  1   
x   k   2 (k  Z) sin x   3 2  (VN) 2 84
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com
Tuyển tập 200 bài tập về Lượng giác có lời giải chi tiết năm 2015 Lưu hành nội bộ!
- Tài liệu do tập thể tác giả biên soạn:
8. Cao Văn Tú – CN.Mảng Toán – Khoa CNTT – Trường ĐH CNTT&TT Thái
Nguyên (Chủ biên)
9. Cô Trần Thị Ngọc Loan – CLB Gia Sư Thái Nguyên(Đồng chủ biên).
10. Thầy Vũ Khắc Mạnh – CLB Gia sư Bắc Giang (Tư vấn).
11. Nguyễn Thị Kiều Trang – SV Khoa Toán – Trường ĐHSP Thái Nguyên.
12. Nguyễn Trường Giang – Khoa CNTT – Trường ĐH CNTT&TT Thái Nguyên.
13. Lý Thị Thanh Nga – SVNC – Khoa Toán – Trường ĐH SP Thái Nguyên.
14. Ngô Thị Lý – Khoa CNTT – Trường ĐH CNTT&TT Thái Nguyên.
- Tài liệu được lưu hành nội bộ - Nghiêm cấm sao chép dưới mọi hình thức.
- Nếu chưa được sự đồng ý của ban Biên soạn mà tự động post tài liệu thì đều
được coi là vi phạm nội quy của nhóm.
- Tài liệu đã được bổ sung và chỉnh lý lần thứ 2.
Tuy nhóm Biên soạn đã cố gắng hết sức nhưng cũng không thể tránh khỏi sự sai xót nhất định.
Rất mong các bạn có thể phản hồi những chỗ sai xót về địa chỉ email:
caotua5lg3@gmail.com ! Xin chân thành cám ơn!!!
Chúc các bạn học tập và ôn thi thật tốt!!!
Thái Nguyên, tháng 07năm 2014
Trưởng nhóm Biên soạn Cao Văn Tú 85
Chủ biên: Cao Văn Tú
Email: caotua5lg3@gmail.com