














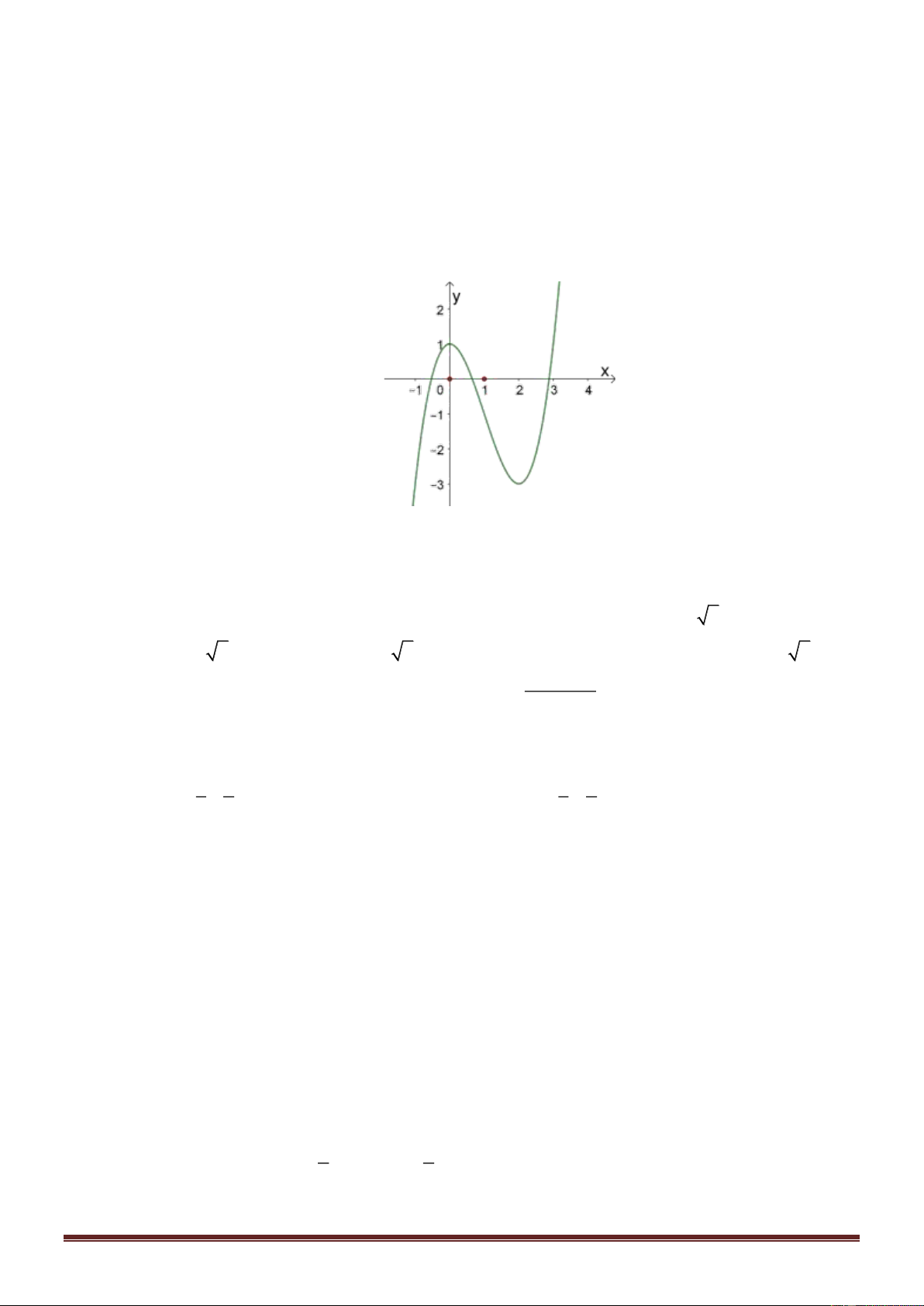




























































Preview text:
ĐỀ THI THỬ THPT QUỐC GIA 2020 ĐỀ 41 MÔN TOÁN Thời gian: 90 phút − x
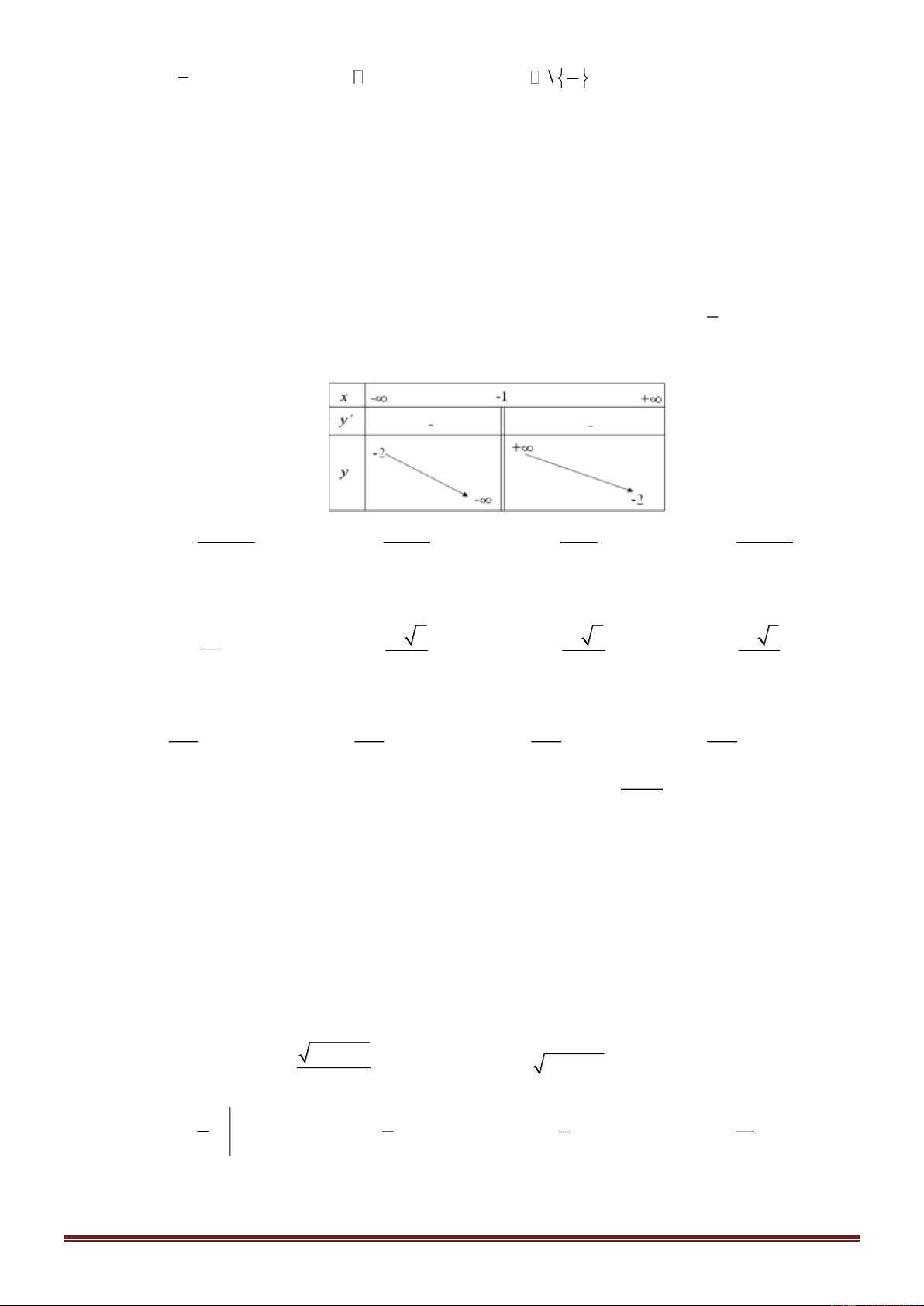
Câu 1: Tìm tiệm cận đứng của đồ thị hàm số 2 y = . x + 2 A. y = 2. B. y = 1. − C. x = 2. − D. x = 1. −
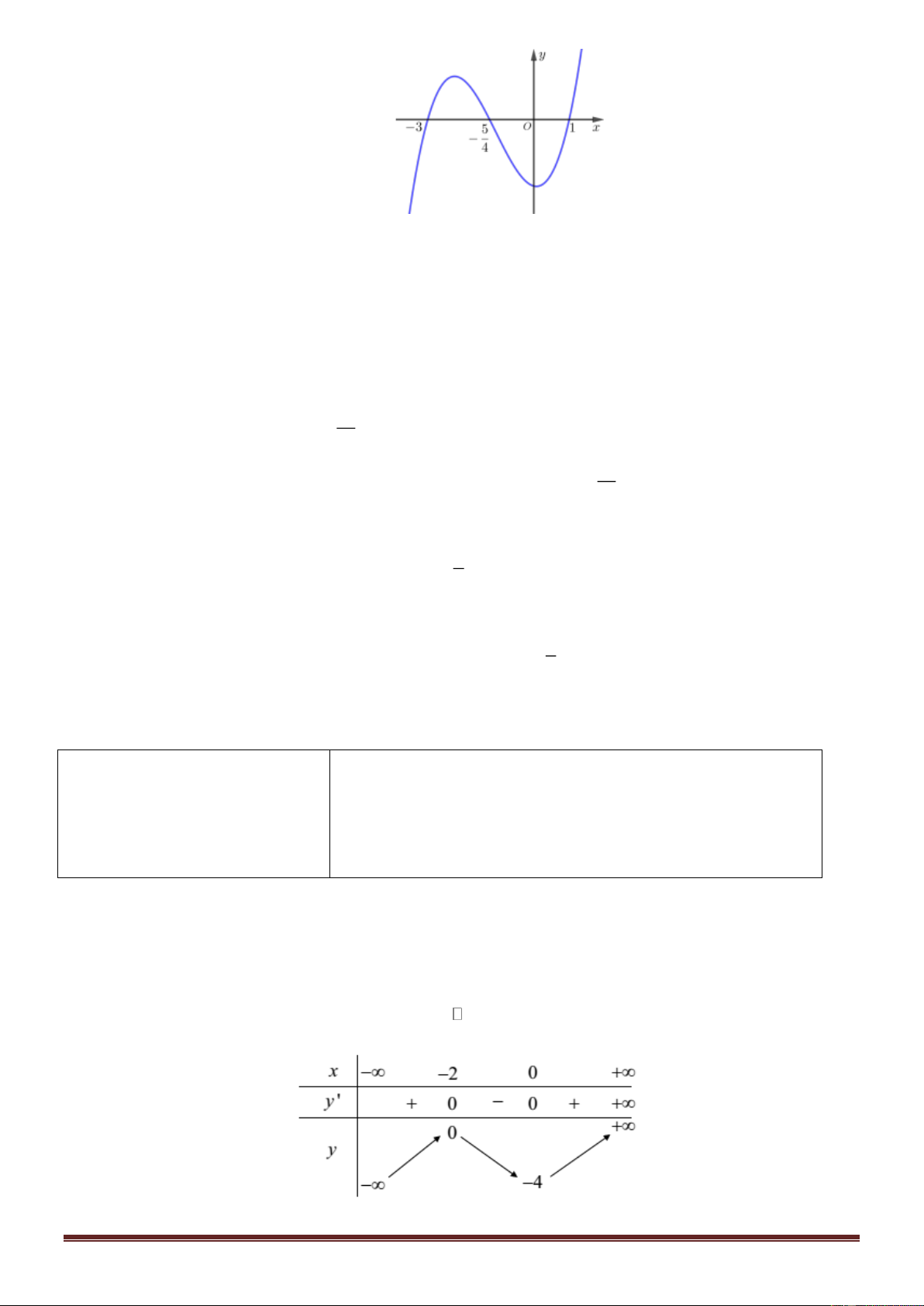
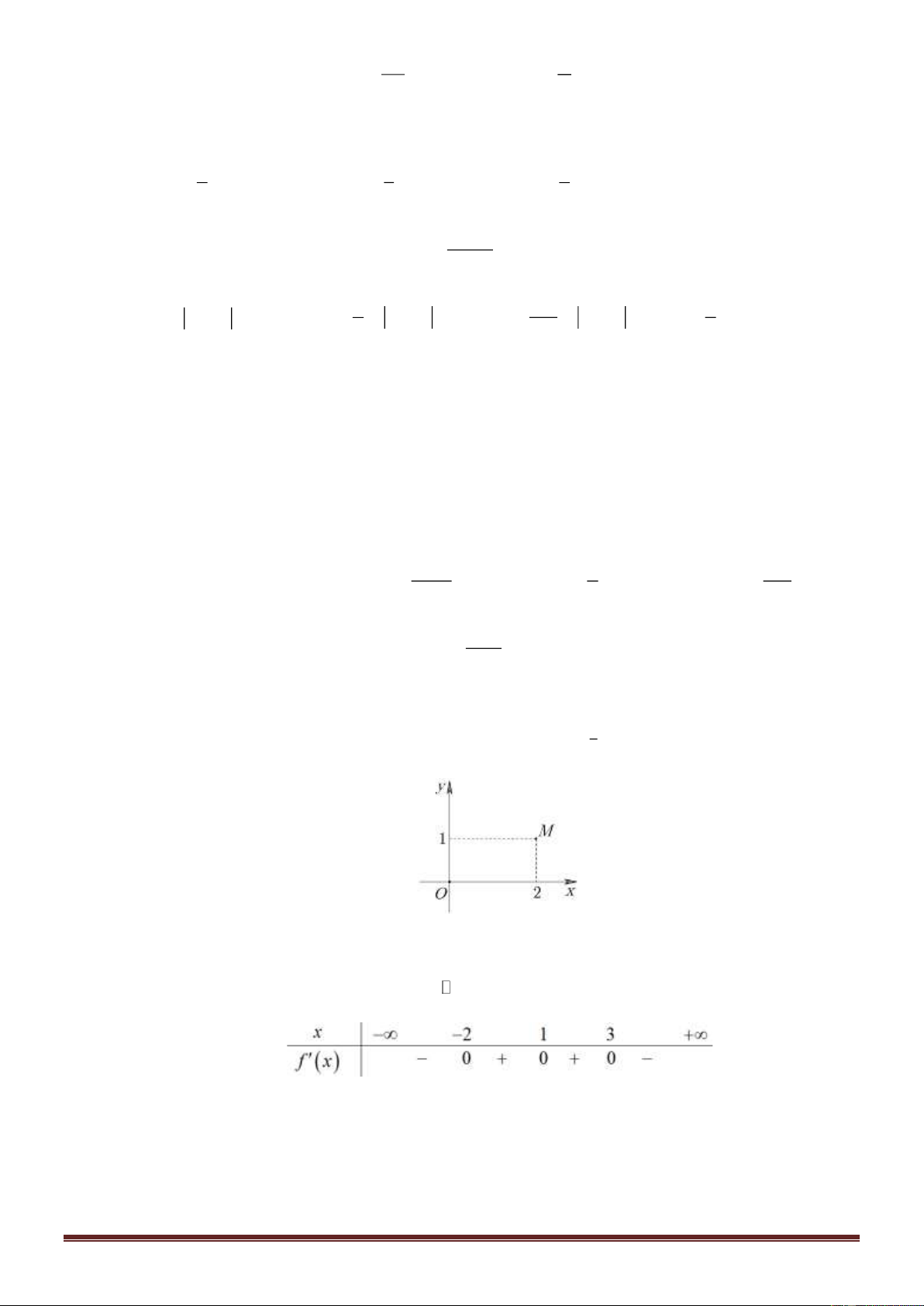
Câu 2. Cho hàm số y = f ( )
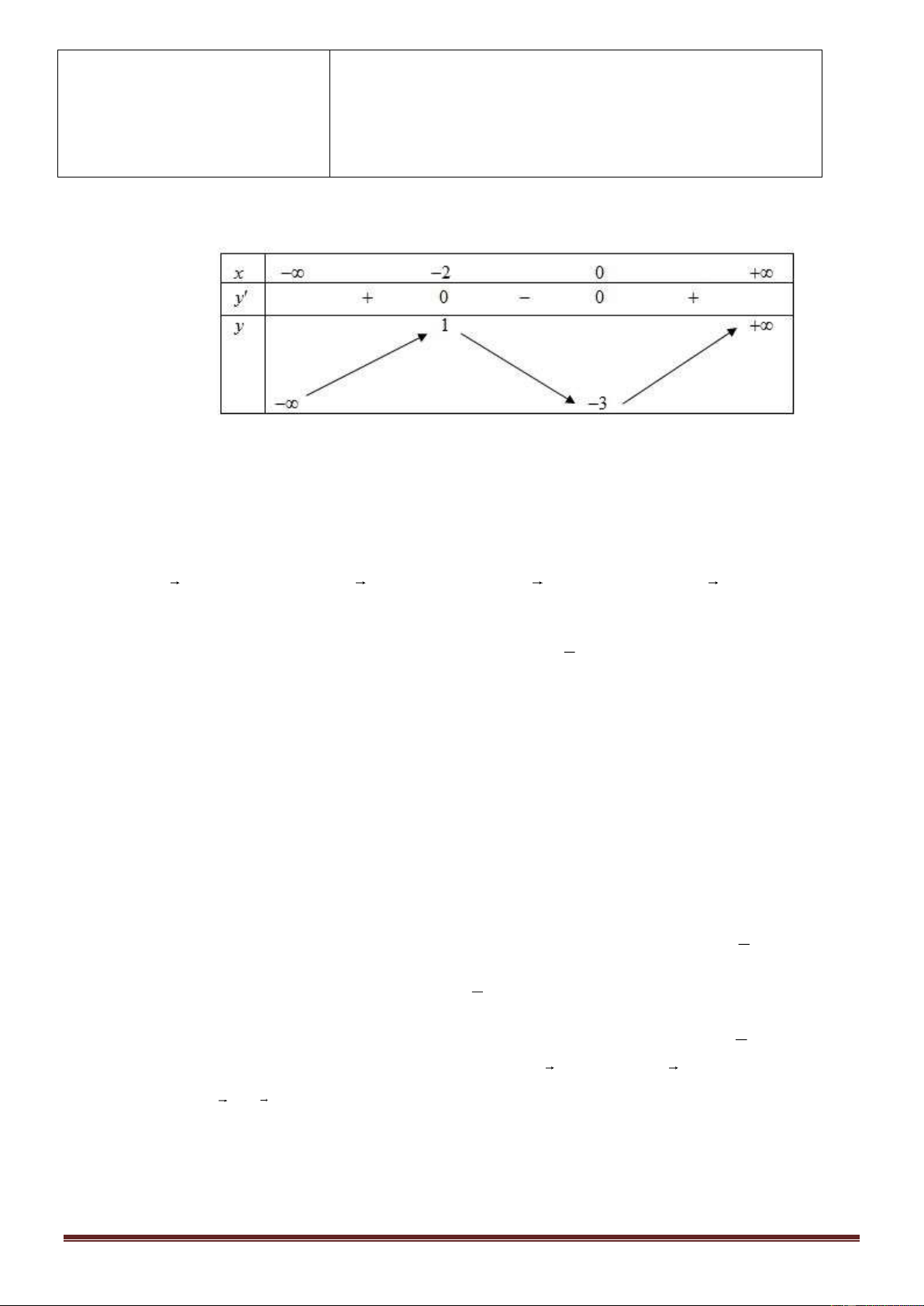
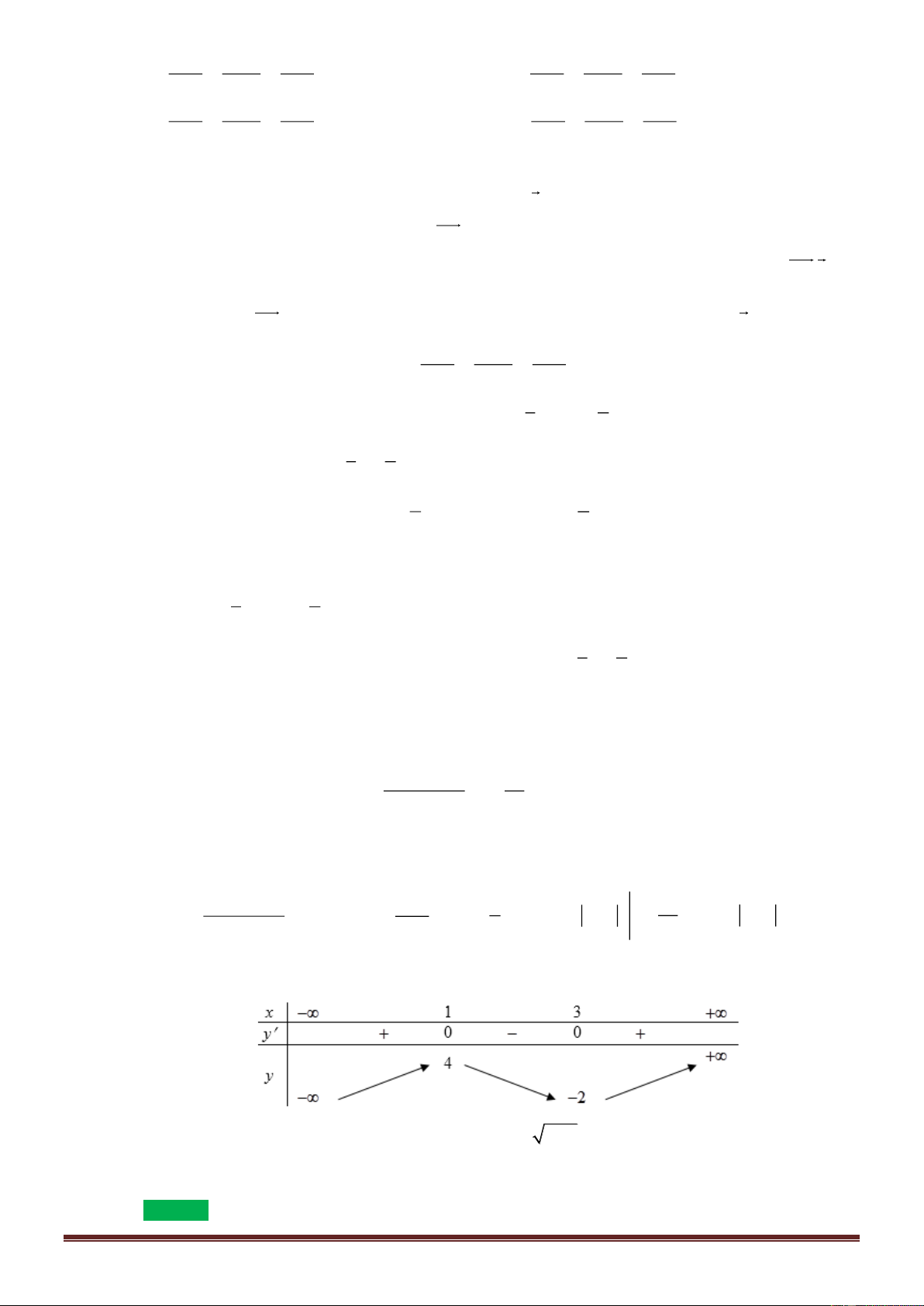
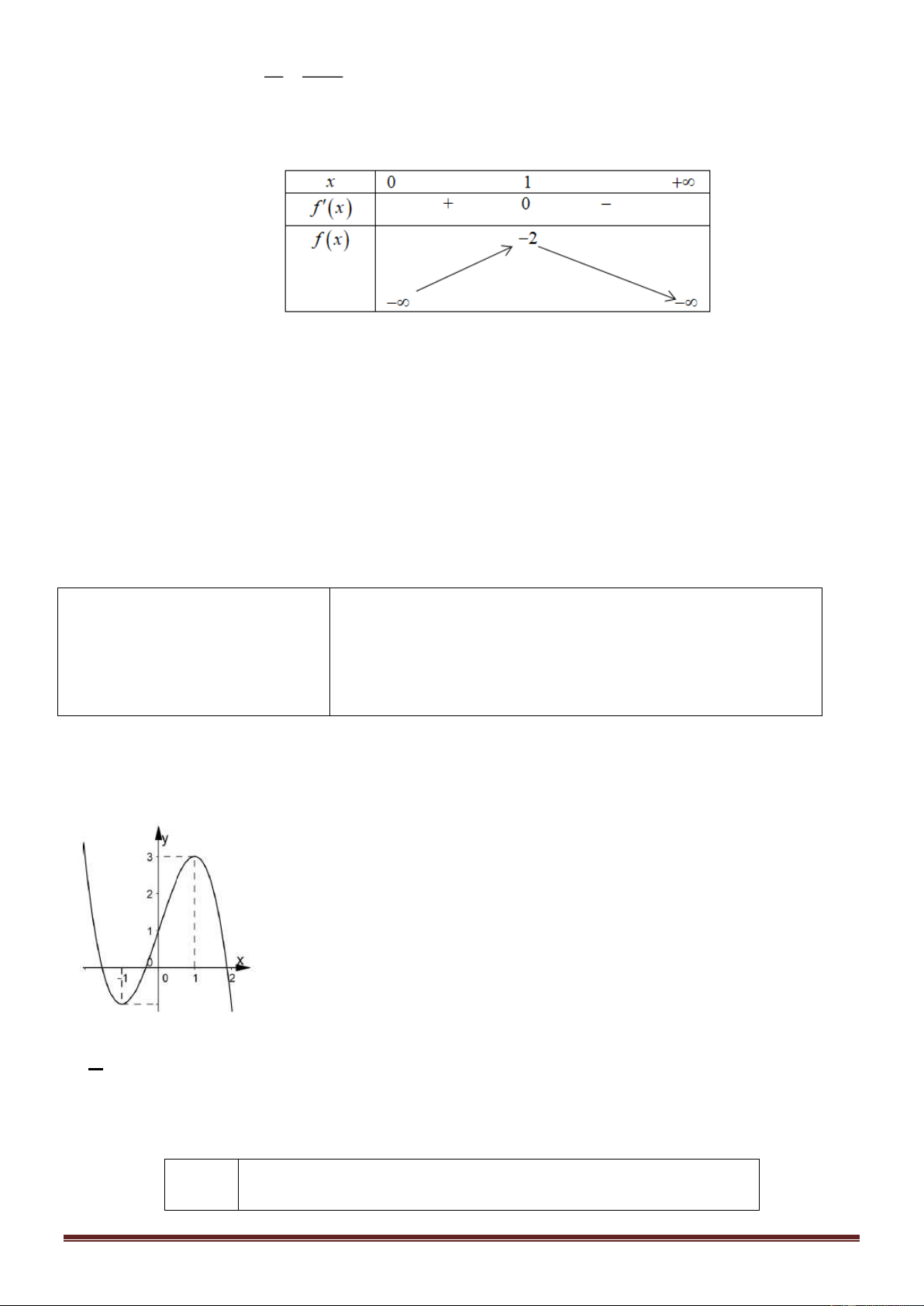
x có bảng biến thiên như sau. x − 0 2 + y’ + 0 – 0 + y – 1 + − –5
Hỏi hàm số y = f ( )
x nghịch biến trên khoảng nào dưới đây? A. (0;2) . B. ( ;0 − ). C. ( 5; − +) . D. (2;+) . y
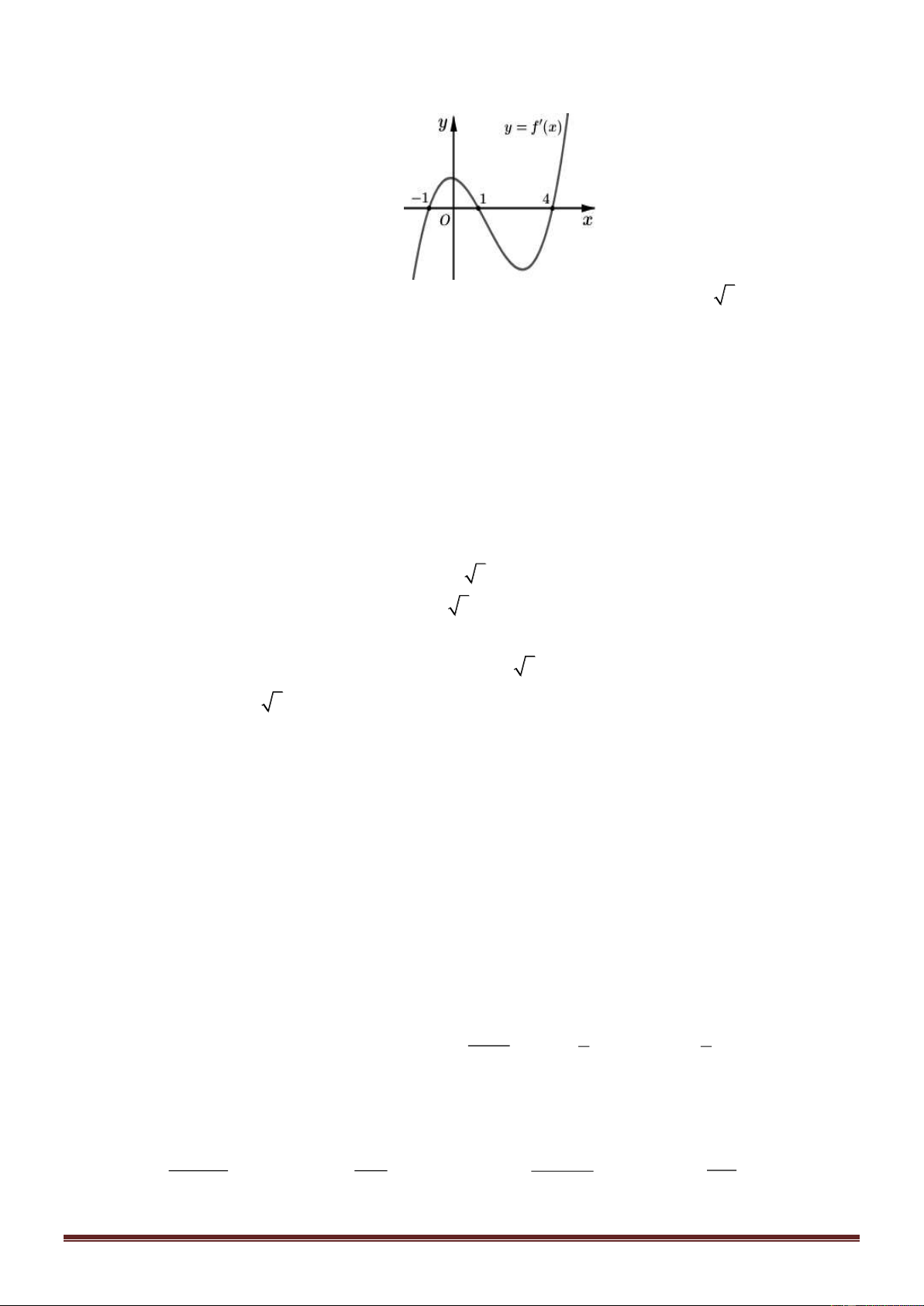
Câu 3: Cho hàm số y = f (x ) xác định, liên tục trên đoạn é 2;3ù - ê 3 ë
úû và có đồ thị là đường cong trong hình vẽ bên. Tìm 2 − O x
số điểm cực đại của hàm số y = f (x) trên đoạn é 2;3ù - êë úû
A. 1. B. 0 . C. 2. D. 3 .
Câu 4: Cho hàm số y = f (x) có lim f (x) = 0 và lim f (x) = + . Mệnh đề nào sau đây là đúng? x→+ x→−
A. Đồ thị hàm số y = f (x) không có tiệm cận ngang.
B. Đồ thị hàm số y = f (x) có một tiệm cận đứng là đường thẳng x = 0.
C. Đồ thị hàm số y = f (x) có một tiệm cận ngang là trục hoành.
D. Đồ thị hàm số y = f (x) có một tiệm cận đứng là đường thẳng y = 0.
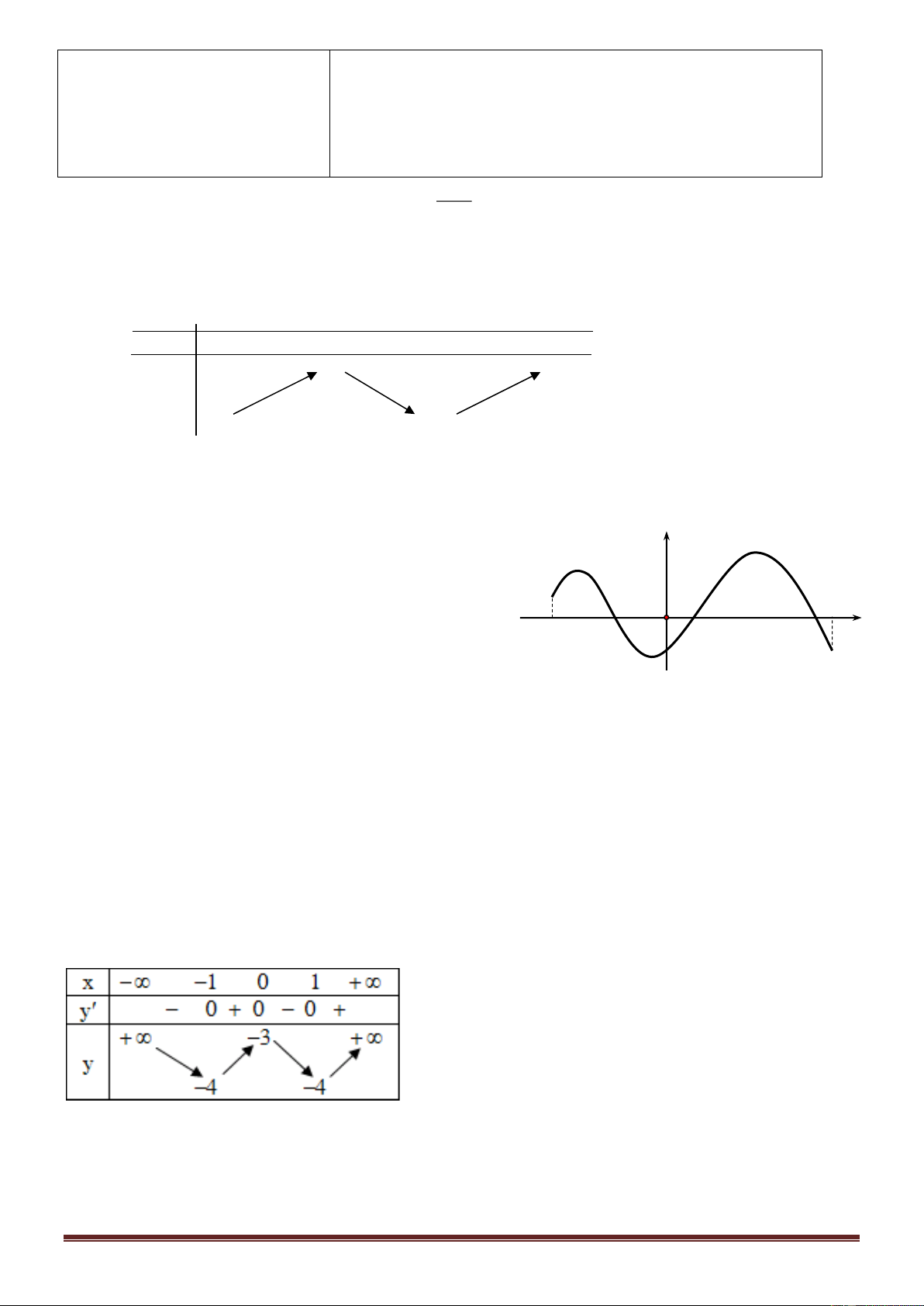
Câu 5: Cho hàm số có bảng biến thiên như sau
Tìm số nghiệm của phương trình f ( ) x + 3 = 0 . A. 3. B. 4. C. 1. D. 2. Trang 1
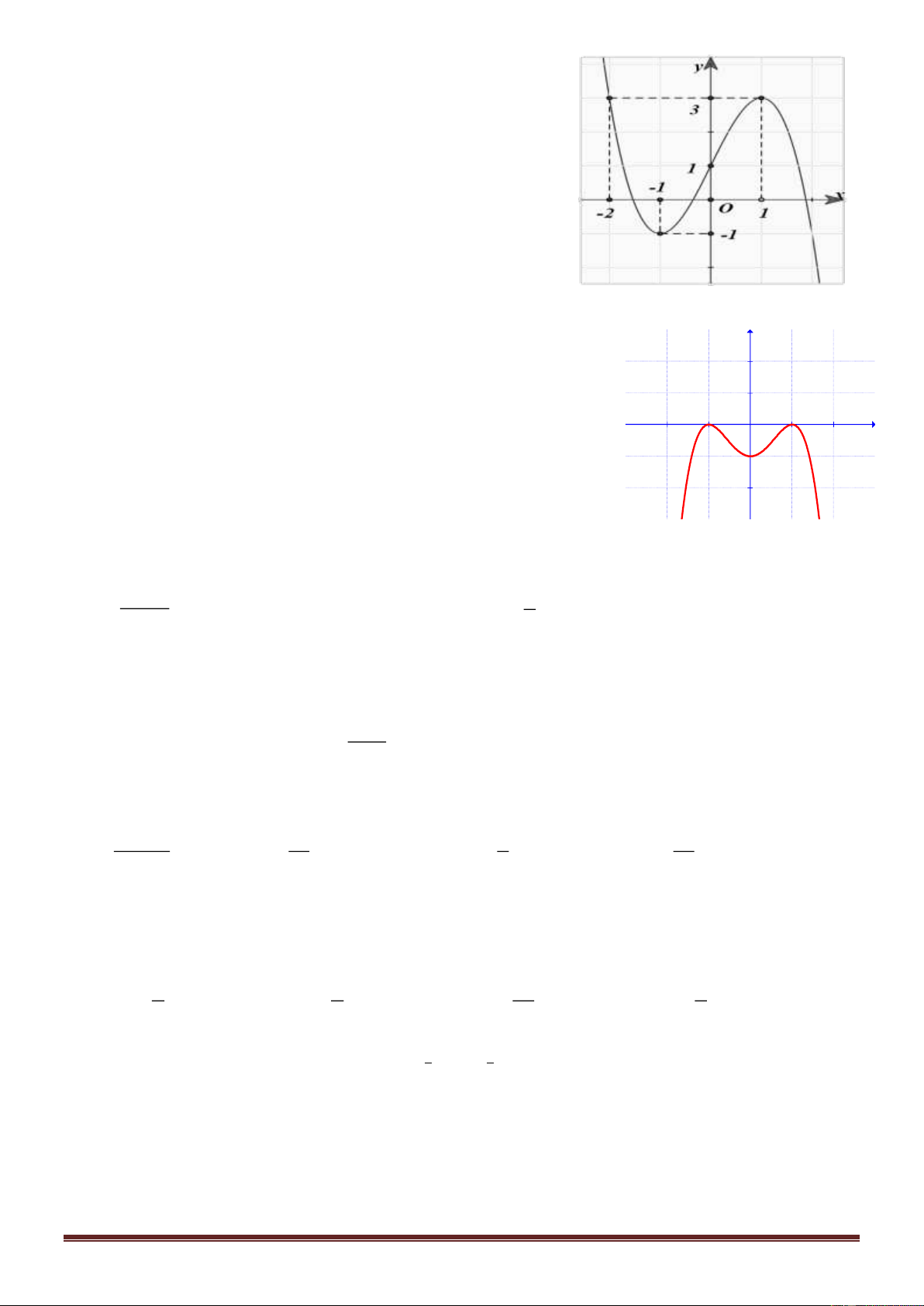
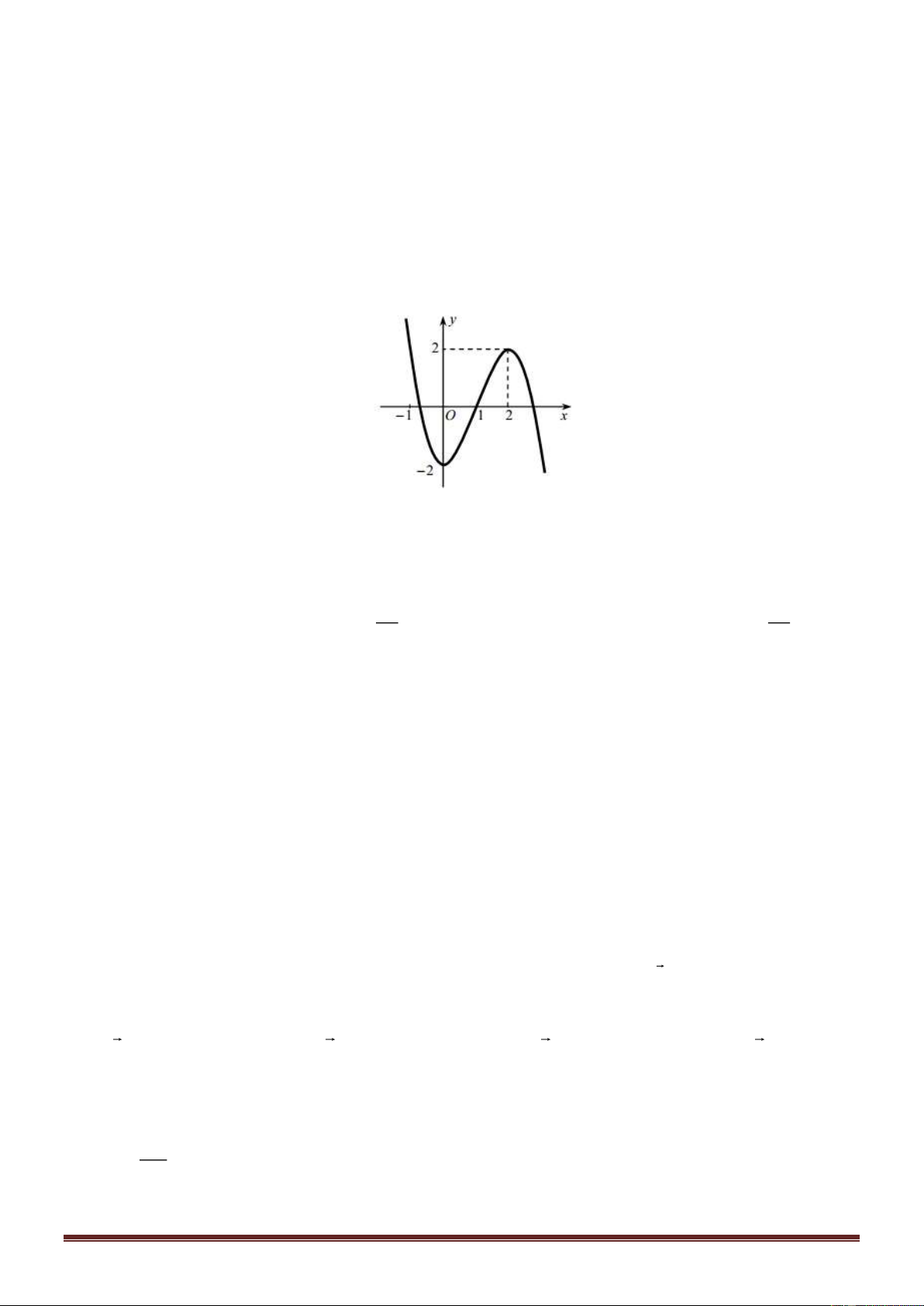
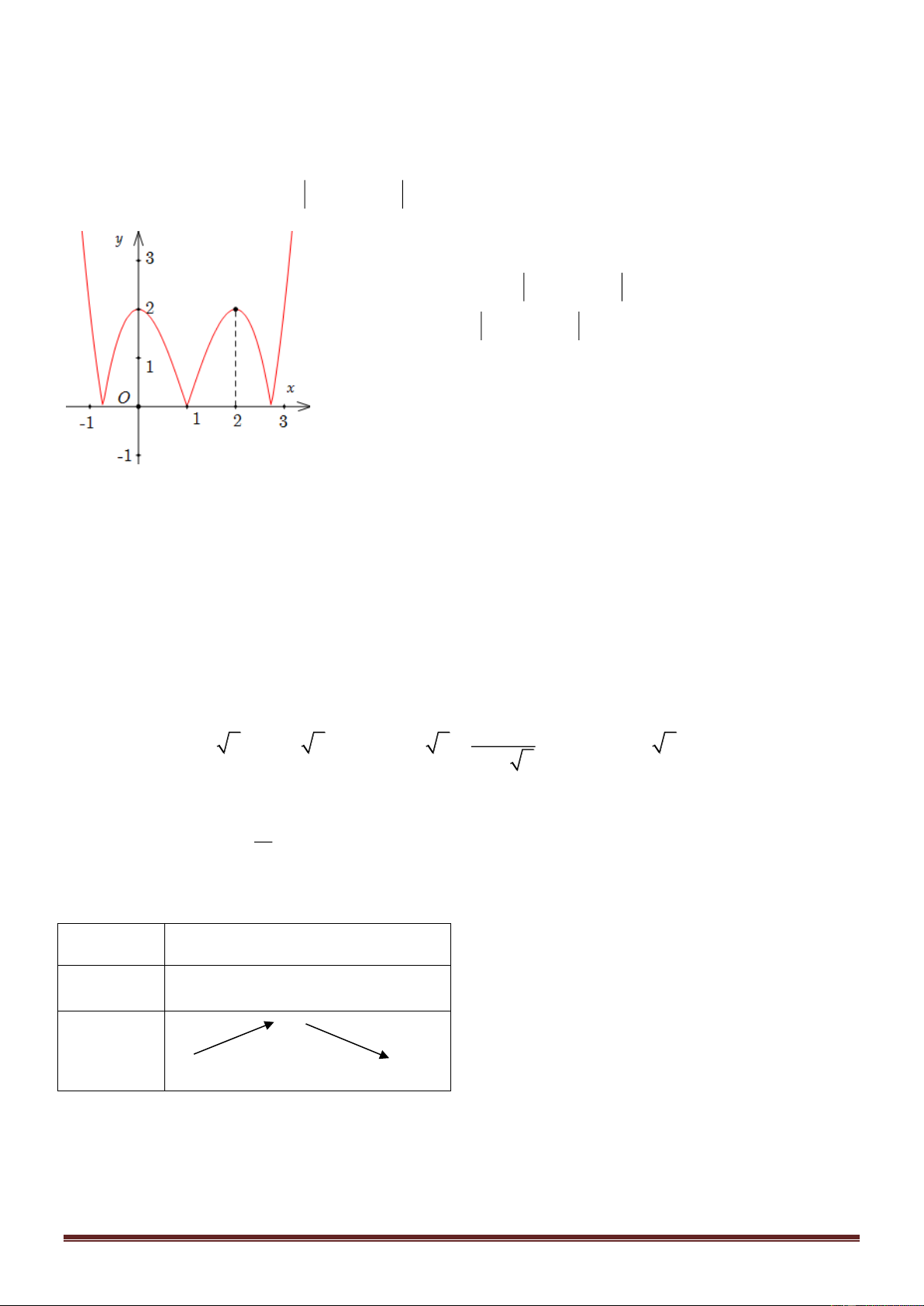
Câu 6: Cho hàm số y = f ( )
x liên tục trên đoạn 2 − ;0và có đồ
thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ
nhất của hàm số đã cho trên 2
− ;0. Tìm giá trị P = M + m. A. P = 3. B. P = 4. C. P = 1. D. P = 2.
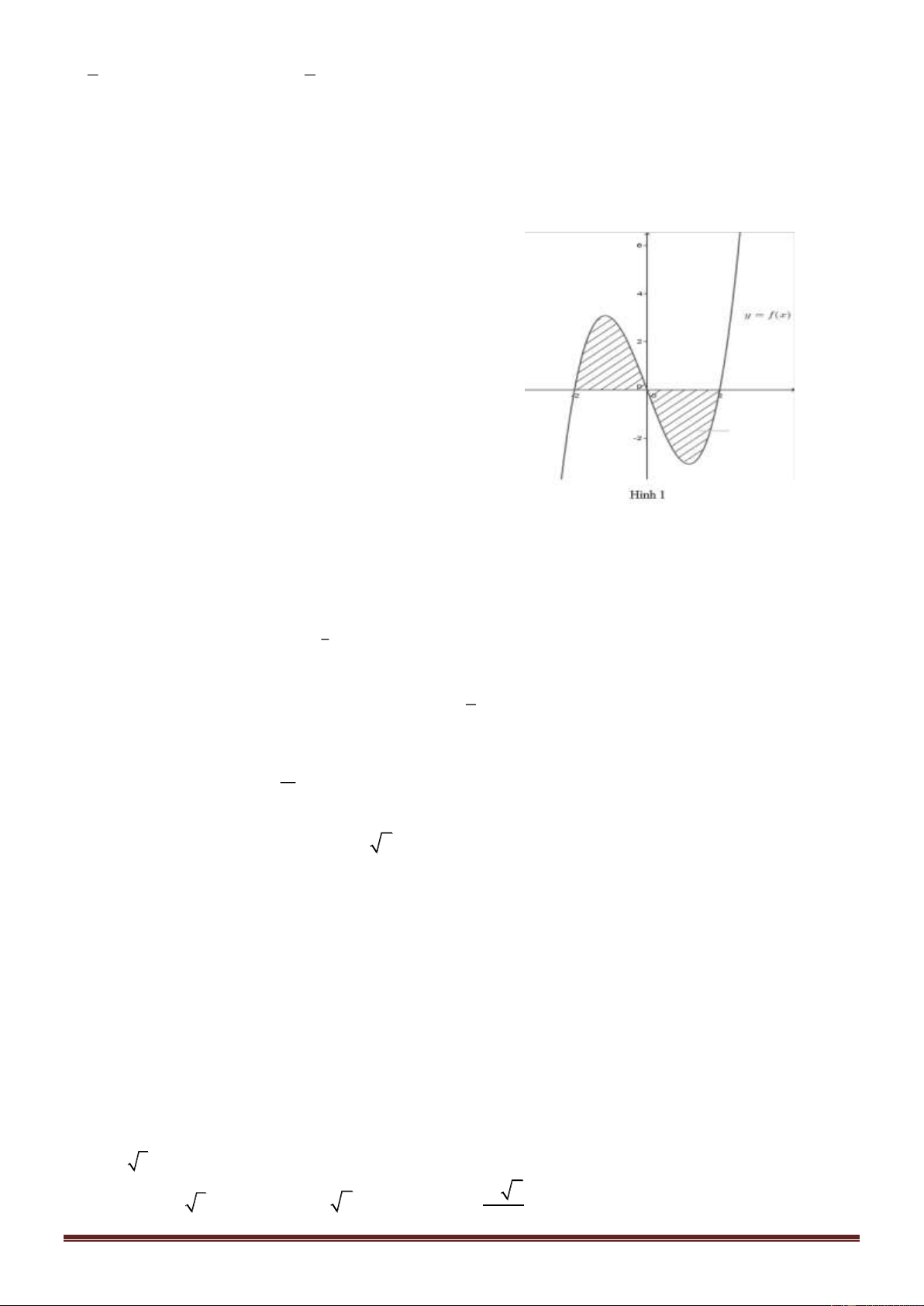
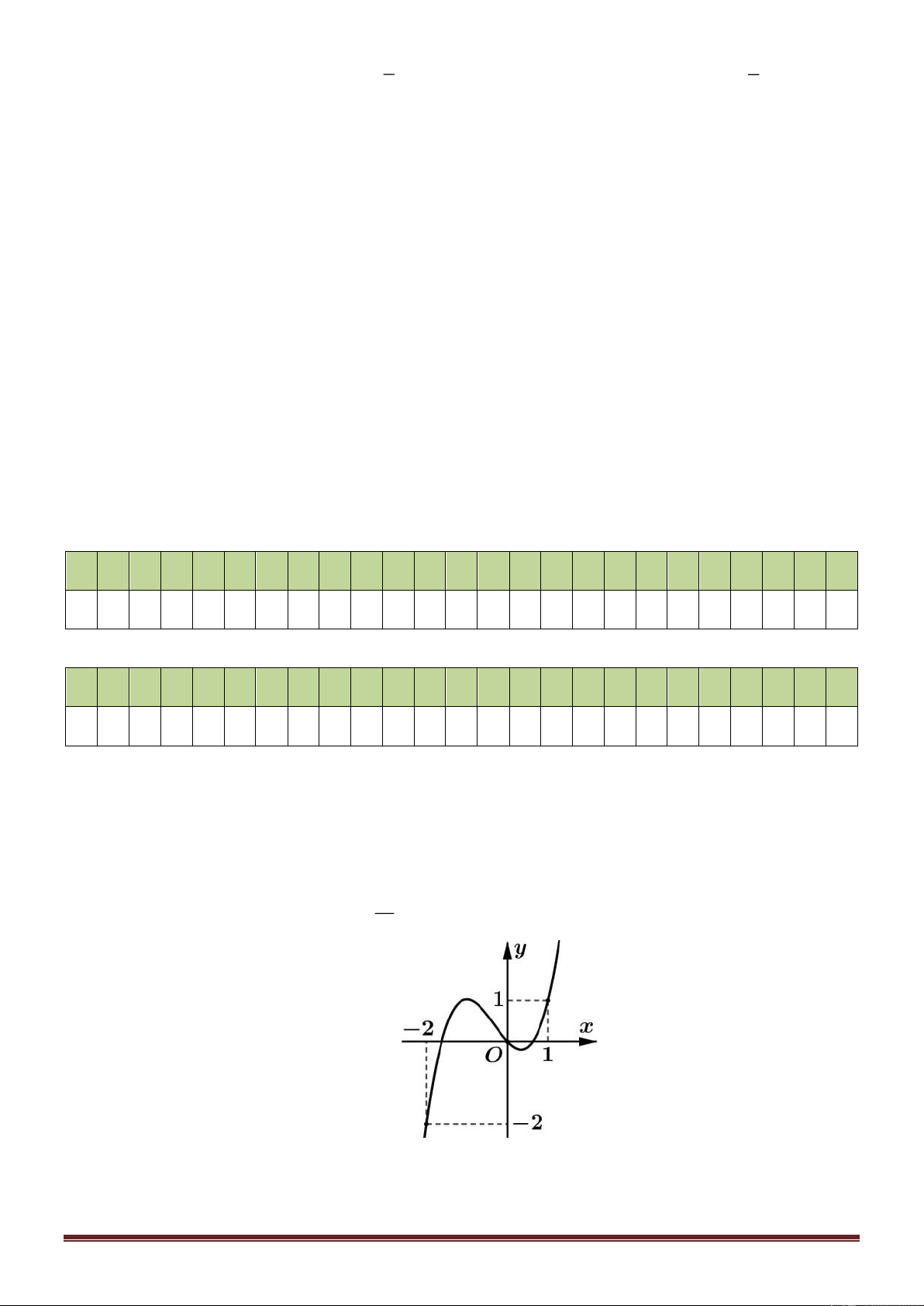
Câu 7: Đường cong trong hình bên là đồ thị của hàm số nào dưới y đây ? 2 1 A. 4 2
y = x − 2x + 3. . x -2 -1 1 2 B. 4 2
y = −x − 2x −1. -1 C. 4 2
y = x + 2x −1. -2 D. 4 2
y = −x + 2x −1.
Câu 8: Cho x và y là hai số dương bất kì. Tìm mệnh đề sai trong các mệnh đề sau: log x 1 A. 5
= log (x − y). B. log = −log . x 5 log y 5 5 x 5 3 C. log x = 3log . x D. log .
x y = log x + log . y 5 ( ) 5 5 5 5
Câu 9: Tính đạo hàm của hàm số 2019 x 3 y e − = . 1 A. 2019 3 ' 2019. x y e − = . B. 2019 x 3 y ' .e − = . C. 2018 3 ' 2019. x y e − = D. 2019 3 ' x y e − = . 2019
Câu 10: Cho a = log 5 và b = log 3 . Tính giá trị của biểu thức P = log 675 theo a,b. 2 2 3 2a + 3b 2a a 2a A. . B. . C. P = + 3. D. P = +1. b b b b 2
Câu 11: Gọi x ; x các nghiệm của phương trình log x + 6log x - 4 = 0 . Tính giá trị của biểu thức 1 2 2 4 P = x .x 1 2 . 1 1 1 1 A. P = . B. P = . C. P = . D. P = . 8 4 16 2 1 2𝑥 1 𝑥+2
Câu 12: Tìm tập nghiệm của bất phương trình ( ) > ( ) . 3 3 A. ( ;2 − ) .
B. (0;9) . C. (2;+) . D. (0;2) .
Câu 13: Tìm họ nguyên hàm của hàm số f ( ) x = x + sin . x Trang 2 1 1 A. 2
x − cos x + C. B. 2
x + cos x + C.
C. 1− cos x + . C D. 1+ cos x + . C 2 2 3 3 2
Câu 14: Biết rằng f (x)dx = 5; f (x)dx = 3 . Tính f (x)dx . 1 2 1 A. 2 B. 2 − C. 1 D. 5
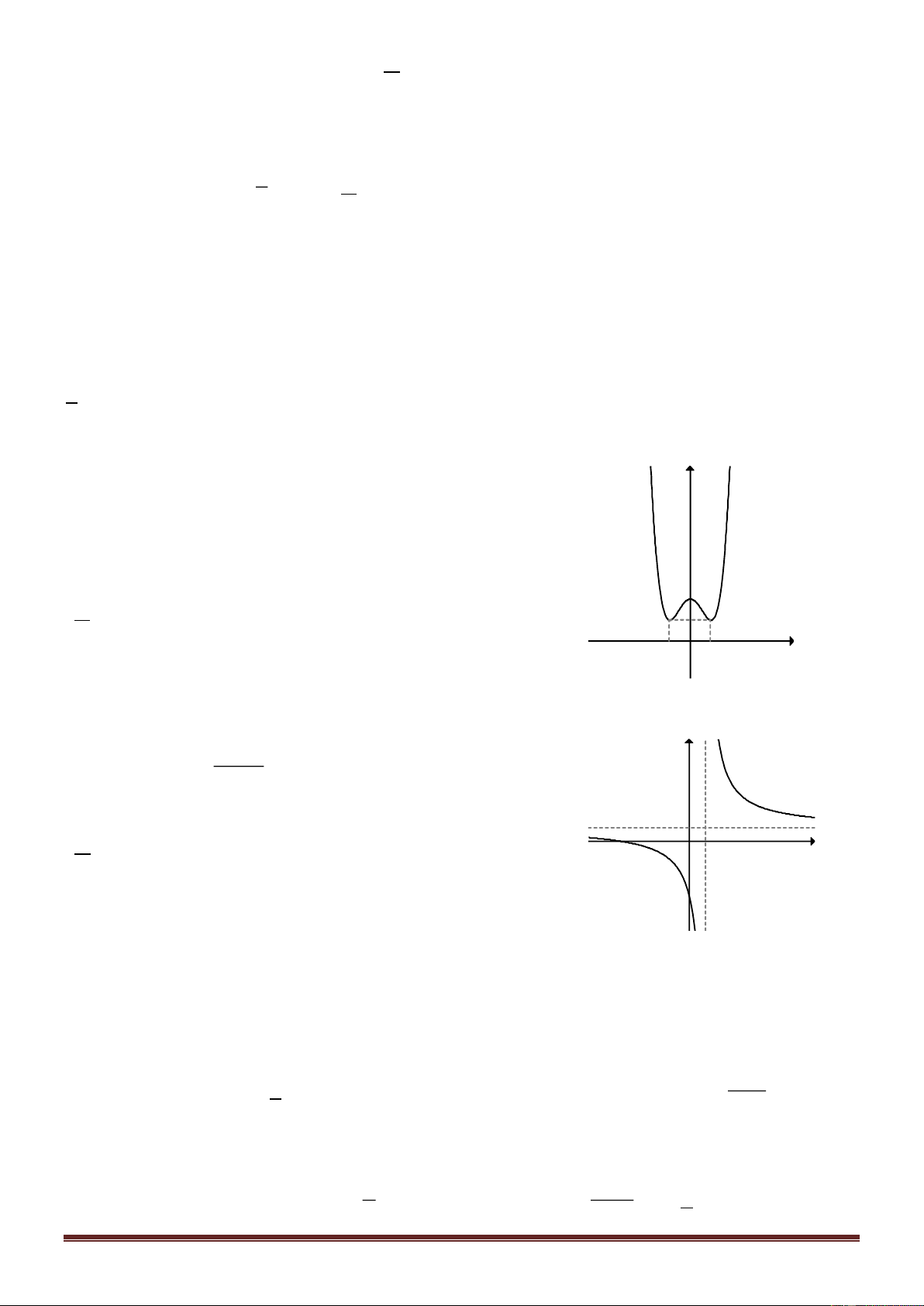
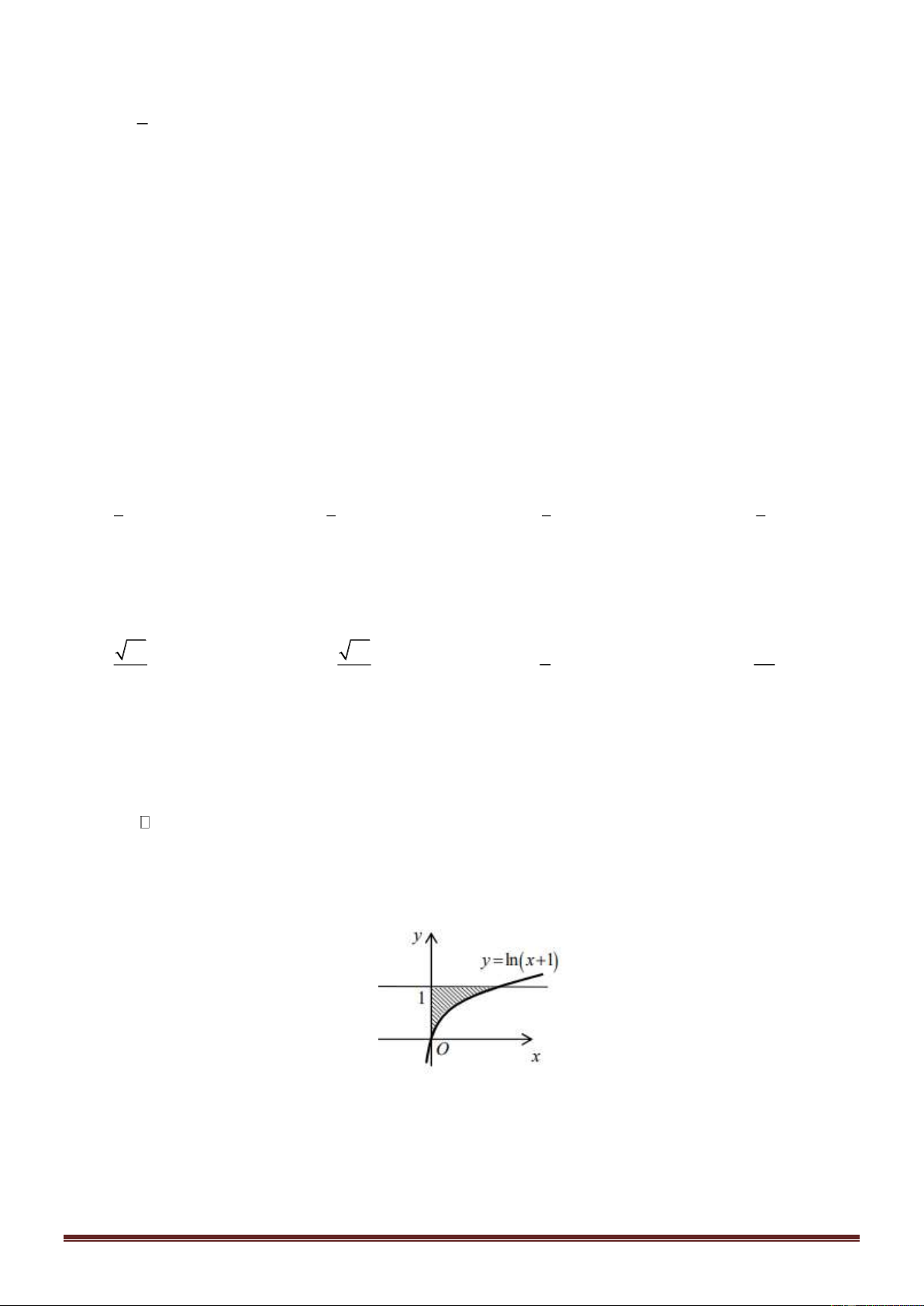
Câu 15: Cho đồ thị hàm số y = f (x) . Diện tích hình
phẳng (phần gạch chéo trong Hình 1) là: 2 A. f (x)dx . 2 − 2 − 2 B. f (x)dx + f (x)dx. 0 0 0 0 C. f (x)dx + f (x)dx. 2 2 − 1 2 D. f
(x)dx + f (x)dx. 2 − 1
Câu 16: Cho số phức z = 2 − 3i . Tìm điểm biểu diễn M của số phức z trong mặt phẳng tọa độ oxy. A. M (2; 3 − ) . B. M (2;3) . C. M ( 3 − ;2) . D. M (3; 2) .
Câu 17: Cho số phức z thỏa mãn z − i = 3 − 2z . Tìm số phức z. 1
A. z =1+ i . B. z =1−i . C. z = 1+ i . D. z = 1 − +i . 3
Câu 18: Gọi z , z là hai nghiệm phương trình 2
z + 2z + 8 = 0; trong đó z có phần ảo dương. số phức 1 2 1
Tìm số phức: w = (2z + z z . 1 2 ) 1
A. z = 12 + 6i .
B. z = 10 + 2 7i .
C. z = 9 − 6i . D. z = 1 − 2 + 6i .
Câu 19. Tính thể tích của khối hộp chữ nhật có 3 kích thức lần lượt là 5,6,7. A. 210 . B. 70 . C. 105 . D. 125.
Câu 20. Một hình trụ có bán kính đáy bằng r = 5cm và có chiều cao h = 30cm . Tính thể tích của hình trụ. A. 750 (cm3) B. 4500 (cm3) C. 250 (cm3) D. 750 (cm3).
Câu 21: Cho hình chóp S.ABCD, ABCD là hình vuông có cạnh bằng a, cạnh bên SA vuông góc với mặt
phẳng (ABCD), SA = a . Tính góc giữa đường thẳng SC và mặt phẳng (ABCD). A. 0 45 . B. 0 60 . C. 0 30 . D. 0 90 .
Câu 22. Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đáy bằng a. Biết đường chéo của mặt
bên là a 3. Tính thể tích khối lăng trụ đã cho. 3 a 2 3 A. 3 a 3 . B. 3 a 2 . C. . D. 2a . 3 Trang 3
Câu 23 : Mặt nón tròn xoay có đỉnh S. Gọi I là tâm của đường tròn đáy. Biết đường sinh bằng a 2 , góc
giữa đường sinh và mặt phẳng đáy bằng 0
60 . Tính diện tích toàn phần của hình nón. 2 2 a 2 3πa A. 2 a .
B. 3 a . C. . . 2 D. 2
Câu 24 : Trong không gian Oxyz cho hai vecto a = (1;3; 5 − ), b = ( 5
− ;4;2) . Tìm tích vô hướng của hai vecto . a b . A. −3 . B. 3 . C. 27 . D. −9 .
Câu 25: Trong không gian Oxyz, viết phương trình mặt phẳng (Oyz) . A. x = 0 . B. y = 0 . C. z = 0 . D. y + z = 0. x = t
Câu 26: Trong không gian cho đường thẳng d: y = 7 + 3t . Tìm một vecto chỉ phương u của đường z = −2t thẳng d. A. u = (1;3; 2 − ).
B. u = (1;3; 2) . C. u = (1;7; 2 − ) .
D. u = (1;7; 2) .
Câu 27: Viết phương trình mặt cầu tâm I (3; 2
− ;4) và tiếp xúc với (P):2x − y+2z +4 = 0 . 2 2 2 400 2 2 2 400
A. (x − 3) + ( y + 2) + (z − 4) = .
B. (x + 3) + ( y − 2) + (z + 4) = . 9 9 2 2 2 20 2 2 2 20
C. (x − 3) + (y + 2) + (z − 4) = .
D. (x + 3) + (y − 2) + (z + 4) = . 3 3 − +
Câu 28: Mặt phẳng (P) đi qua 2 điểm A(2;1;0), B(3;0; )
1 và song song với () x 1 y 1 z : = = . Tính 1 1 − 2
khoảng cách giữa đường thẳng () và mặt phẳng (P): 3 3 2 3 A. . B. . C. . D. . 2 2 2 2
Câu 29: Một hộp có chứa 8 bóng đèn màu đỏ và 5 bóng đèn màu xanh. Hỏi có bao nhiêu cách chọn được
một bóng đèn trong hộp. A. 13. B. 5. C. 8 . D. 40. 1
Câu 30: Cho cấp số nhân (u với u = − ; u = 3 − 2 . Tìm công bội q. n ) 1 7 2 1 A. q = . B. q = 2 . C. q = 4 . D. q = 1 . 2
Câu 31: Tìm m để các điểm cực đại và cực tiểu của đồ thị hàm số y = (m + ) 3 2
2 x + 3x + mx − 5 có hoành độ dương . A. 3 − m 2 − .
B. 2 m 3 . C. 1 − m 1. D. 2 − m 2 . Trang 4 2x +1
Câu 32: Cho hàm số y =
có đồ thị là (C) . Tìm tất cả các giá trị của m để đường thẳng (d ) đi qua x − 2
A(0;2) có hệ số góc m cắt đồ thị (C) tại 2 điểm thuộc 2 nhánh của đồ thị. A. m 0 . B. m 0. C. m 5 − .
D. m 0 hoặc m 5 − .
Câu 33: Phương trình log x log x log 27 9 9 3 4 −6.2 + 2 = 0 có hai nghiệm là x − 1, x2 . Khi đó tính x x . 1 2 A. 72. B. 27. C. 77. D. 90.
Câu 34: Anh A làm việc tại một công ty lương khởi điểm 700000đ/ 1 tháng. Cứ sau 3 năm anh A tăng
thêm 7%. Hỏi sau 37 năm anh A nhận được tổng số tiền là bao nhiêu? A. 450807890. B. 450788972. C. 440788972. D. 45087980. x
Câu 35: Gọi F(x) là nguyên hàm của hàm số f (x) =
thỏa mãn F(2) = 0. Tìm nghiệm phương 2 8 − x trình F(x) = x. A. x = 0. B. x = 1. C. x = 2. D. x = 1− 3 . 1 2x + 3
Câu 36: Biết tích phân dx
= aln2 +b. Tìm giá trị của a. 2 − x 0 A. 7. B. 2. C. 3. D. 1.
Câu 37: Trong mặt phẳng phức tập hợp các điểm biểu diễn số phức z = x + yi thỏa mãn z − i = z − 3i + 2 là:
A. Đường tròn (C) tâm I(0; )
1 , bán kinh R = 3 . B. Đường thẳng d: x + 2y + 3 = 0 .
C. Đường tròn (C) tâm I( 2 − ; 3
− ) , bán kinh R = 3. D. Đường thẳng d: y = 0.
Câu 38: Cho lăng trụ tam giác ABC.A B C có tất cả các cạnh bằng a, góc tạo bởi cạnh bên và mặt phẳng 1 1 1
đáy bằng 300. Hình chiếu H của điểm A lên mặt phẳng ( A B C 1 1
1 ) thuộc đường thẳng B1C1. Tính khoảng
cách giữa hai đường thẳng AA1 và BC1 theo a. a 3 a 3 2a 4a A. . B. . C. . D. . 2 4 3 3
Câu 39: Một bình đựng nước có dạng hình nón (không có đáy),
đựng đầy nước. Người ta thả vào đó một khối cầu có đường kính
bằng chiều cao của bình nước và đo được thể tích nước tràn ra
ngoài là 18 (dm3). Biết rằng khối cầu tiếp xúc với tất cả các
đường sinh của hình nón và đúng một nửa của khối cầu đã chìm
trong nước (hình dưới). Tính thể tích nước còn lại trong bình. A. 24 (dm3). B. 54 (dm3). C. 6 (dm3). D. 12 (dm3).
Câu 40: Trong không gian Oxyz, cho điểm M(8, - 2, 4). Gọi A, B, C lần lượt là hình chiếu của M trên
các trục Ox, Oy, Oz. Tìm phương trình mặt phẳng đi qua ba điểm A, B và C .
A. x + 4y + 2z −8 = 0 .
B. x − 4y + 2z −8 = 0 .
C. −x − 4y + 2z −8 = 0 . D. x + 4y − 2z −8 = 0 . Trang 5 Câu 41: Cho hàm số 3 2
y = −x + 4x +1 có đồ thị là (C ) và điểm M (m )
;1 . Gọi S là tập hợp tất cả các
giá trị thực của m để qua M kẻ được đúng 2 tiếp tuyến đến đồ thị (C) . Tính tổng giá trị tất cả các phần tử của S . 40 16 20 A. 5 . B. . C. . D. . 9 9 3 Câu 42: Cho hàm số ( ) 3 2
f x = ax + bx + cx + d , ( , a , b , c d
) thỏa mãn a 0 , d 2018 ,
a + b + c + d − 2018 0 . Tìm số điểm cực trị của hàm số y = f ( x) − 2018 . A. 2. B. 1. C. 3. D. 5. Câu 43: Cho hàm số 2
y = x + m ( 2 2018 − x + )
1 − 2021 với m là tham số thực. Gọi S là tổng tất cả
các giá trị nguyên của tham số m để đồ thị của hàm số đã cho cắt trục hoành tại đúng hai điểm phân biệt. Tính S . A. 960 . B. 986 . C. 984 . D. 990 . 2 2 x y
Câu 44: Trong mặt phẳng tọa độ Oxy cho ( E) có phương trình +
=1,(a,b 0) và đường tròn 2 2 a b (C) 2 2
: x + y = 7. Tính tích a.b để diện tích elip ( E) gấp 7 lần diện tích hình tròn (C ) .
A. ab = 7 .
B. ab = 7 7 . C. ab = 7 . D. ab = 49 .
Câu 45: Cho số phức z thỏa mãn z − 2 − 3i = 1. Tìm giá trị lớn nhất của z +1+ i . A. 13 + 2 . B. 4 . C. 6 . D. 13 +1 .
Câu 46: Cho hình chóp đều S.ABCD, đáy là hình vuông cạnh a, cạnh bên tạo với đáy một góc 600. Gọi
M là trung điểm của SC. Mặt phẳng qua AM song song với BD cắt SB tại E và SD tại F. Tính thể tích của khối chóp S. AEMF. 3 3 3 3 a 6 a 6 a 6 a 6 A. . B. . C. . D. . 18 36 24 12
Câu 47: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) : x + y + z −1 = 0 và hai điểm A(1; 3 − ;0); B(5; 1 − ; 2 − ) . Điểm M ( ; a ;
b c) trên mặt phẳng (P) sao cho MA − MB đạt giá trị lớn nhất.
Tính tổng a + b + c : A. 1. B. 11. C. 5. D. 6.
Câu 48: Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1;1; ) 1 và đường thẳng x −1 y z +1 d : = =
. Viết phương trình đường thẳng đi qua A và cắt d sao cho khoảng cách từ gốc tọa 2 2 − 1 −
độ đến là nhỏ nhất. x −1 y − 2 z −1 x −1 y − 2 z −1 A. = = . B. = = . 1 − 3 9 1 3 9 x −1 y − 2 z −1 x −1 y − 2 z −1 C. = = . D. = = . 1 3 − 9 1 3 9 − Trang 6
Câu 49: Cho tập A 1;2;3;4;5;6;7;8;
9 . Lập ngẫu nhiên một số có 3 chữ số khác nhau với các chữ số
chọn từ tập A. Tính xác suất để số lập được chia hết cho 6. 78 75 57 75 A. . B. . C. . D. . 504 504 540 540 2 3 x − x − 2 2x +1
Câu 50: Giải bất phương trình x +1 trên tập số thực. 3 2x +1 − 3 + + A. = − 1 5 S 1; 0 ;13 . B. = 1 5 S 0;1 ;13 . 2 2 + + B. C. = 1 5 S 0;1 − ;13 . D. = (− ) 1 5 S 1; 0 − ;13 . 2 2
………………………. HẾT………………………. ĐÁP ÁN Câu 1: C Câu 11:A Câu 21: A Câu 31:A Câu 41:B Câu 2: A Câu 12: A Câu 22: B Câu 32:B Câu 42:D Câu3: C Câu 13:A Câu 23:D Câu 33:A Câu 43:C Câu 4: C Câu 14:A Câu 24:A Câu 34:A Câu 44:D Câu 5: A Câu 15:C Câu 25:A Câu 35:B Câu 45:D Câu 6: D Câu 16: A Câu 26:A Câu 36:A Câu 46:A Câu 7: D Câu 17:A Câu 27:A Câu 37: B Câu 47: A Câu 8: A Câu 18: B Câu 28: D Câu 38:B Câu 48:B Câu 9: B Câu 19: A Câu 29:A Câu 39:C Câu 49:A Câu 10: Câu 20:A Câu 30:B Câu 40: B Câu 50: B A GIẢI CHI TIẾT Câu 41:
Phương trình tiếp tuyến của đồ thị (C) đi qua M (m )
;1 và có hệ số góc k là: y = k ( x − m) +1.
Để qua M kẻ được đúng 2 tiếp tuyến đến đồ thị (C) điều kiện là hệ phương trình sau có đúng hai
nghiệm x phân biệt 3 2
−x + 4x +1 = k (x − m) +1 3 2 (
−x + 4x +1 = k (x − m)+1 ( ) 1 I ) ( 3 2 − 2 x + 4x + 3
− x + 8x = k (2) )1 = k Thay (2) vào ( ) 1 ta được 3 2 −x + x + = ( 2 4 1 3
− x + 8x)(x − m) +1 2
x 2x − (3m + 4) x +8m = 0 x = 0 2 2x −
(3m + 4) x +8m = 0 (3)
Như vậy, hệ (I ) có đúng hai nghiêm khi và chỉ khi phương trình (3) có một nghiệm bằng 0 và một
nghiệm khác 0 ; hoặc phương trình (3) có nghiệm duy nhất khác 0 .
Phương trình (3) có nghiệm x = 0 khi và chỉ khi m = 0 . Khi đó, phương trình (3) trở thành Trang 7 x = 0 2
2x − 4x = 0 ; x = 2
Do đó m = 0 thỏa mãn.
Phương trình (3) có nghiệm duy nhất khác 0 điều kiện là = ( m + )2 3 4 − 4.2.8m = 0 3m + 4 0 4
= (3m + 4)2 − 4.2.8m = 0 m = 4 + 4 3m 4 . 0 m = 9 4 Như vậy 4 S = 0; ; 4. 9
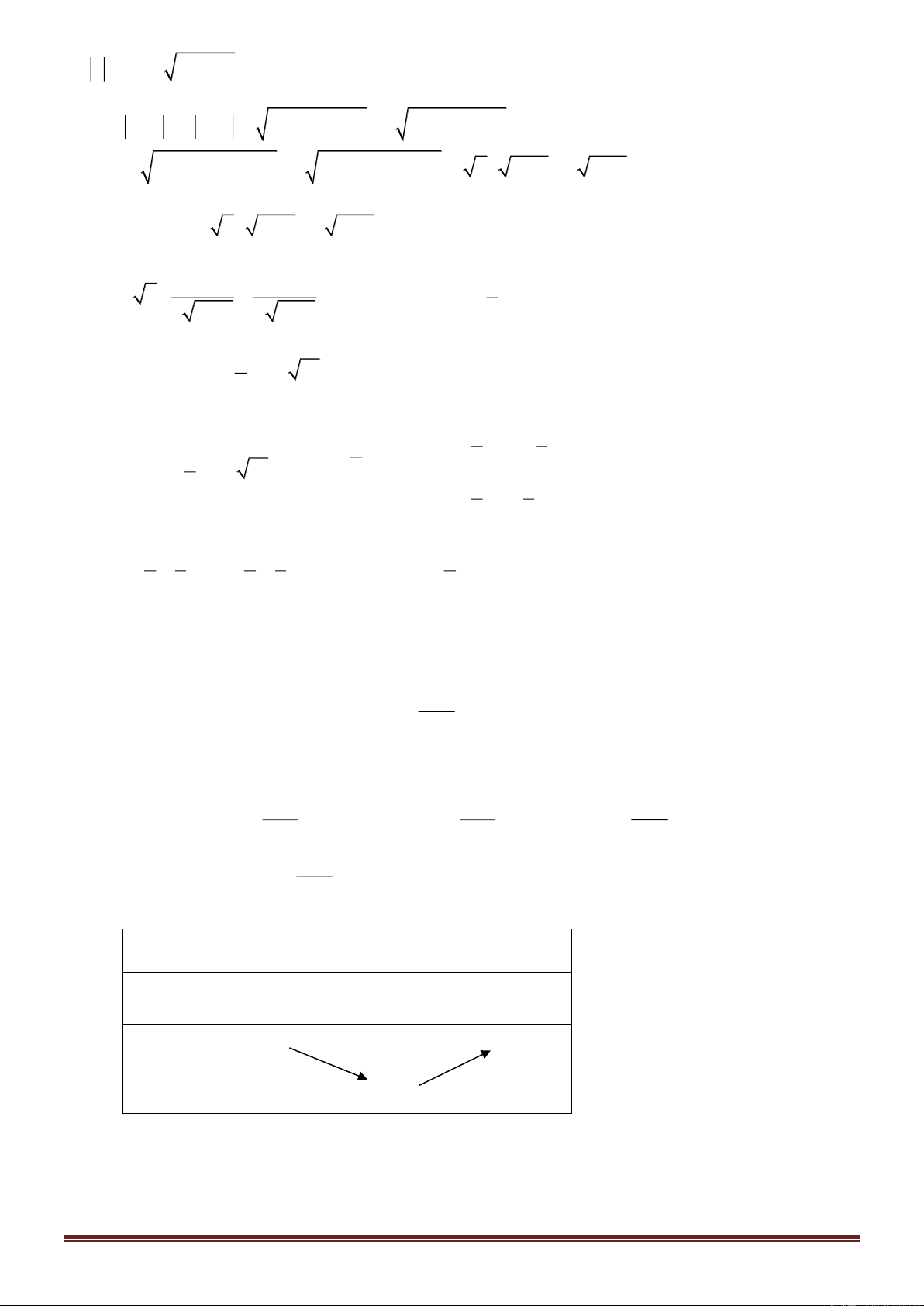
Tổng giá trị tất cả các phần tử của 4 40 S là 0 + + 4 = . 9 9 Câu 42: Chọn D
- Xét hàm số g ( x) = f ( x) − 2018 3 2
= ax +bx + cx + d − 2018. g (0) = d − 2018 Ta có: . g ( )
1 = a + b + c + d − 2018 g (0) 0
Theo giả thiết, ta được . g ( ) 1 0
lim g (x) = + x→+
- Lại do: a 0 nên
1: g ( ) 0 và
0: g () 0 .
lim g ( x) = − x→−
g ( ).g (0) 0
Do đó: g (0).g ( )
1 0 g ( x) = 0 có 3 nghiệm phân biệt thuộc khoảng (; ) . g ( ) 1 .g ( ) 0
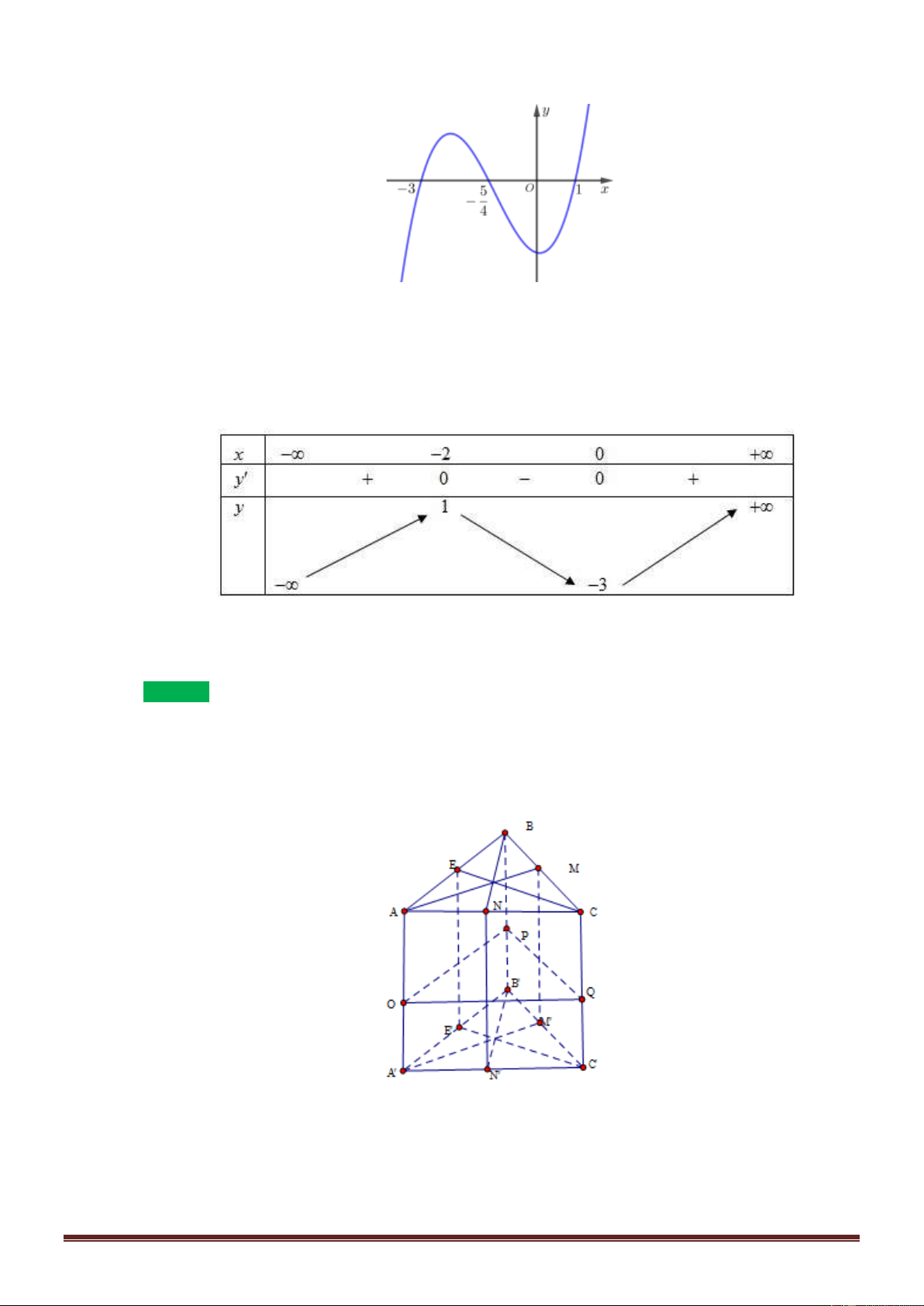
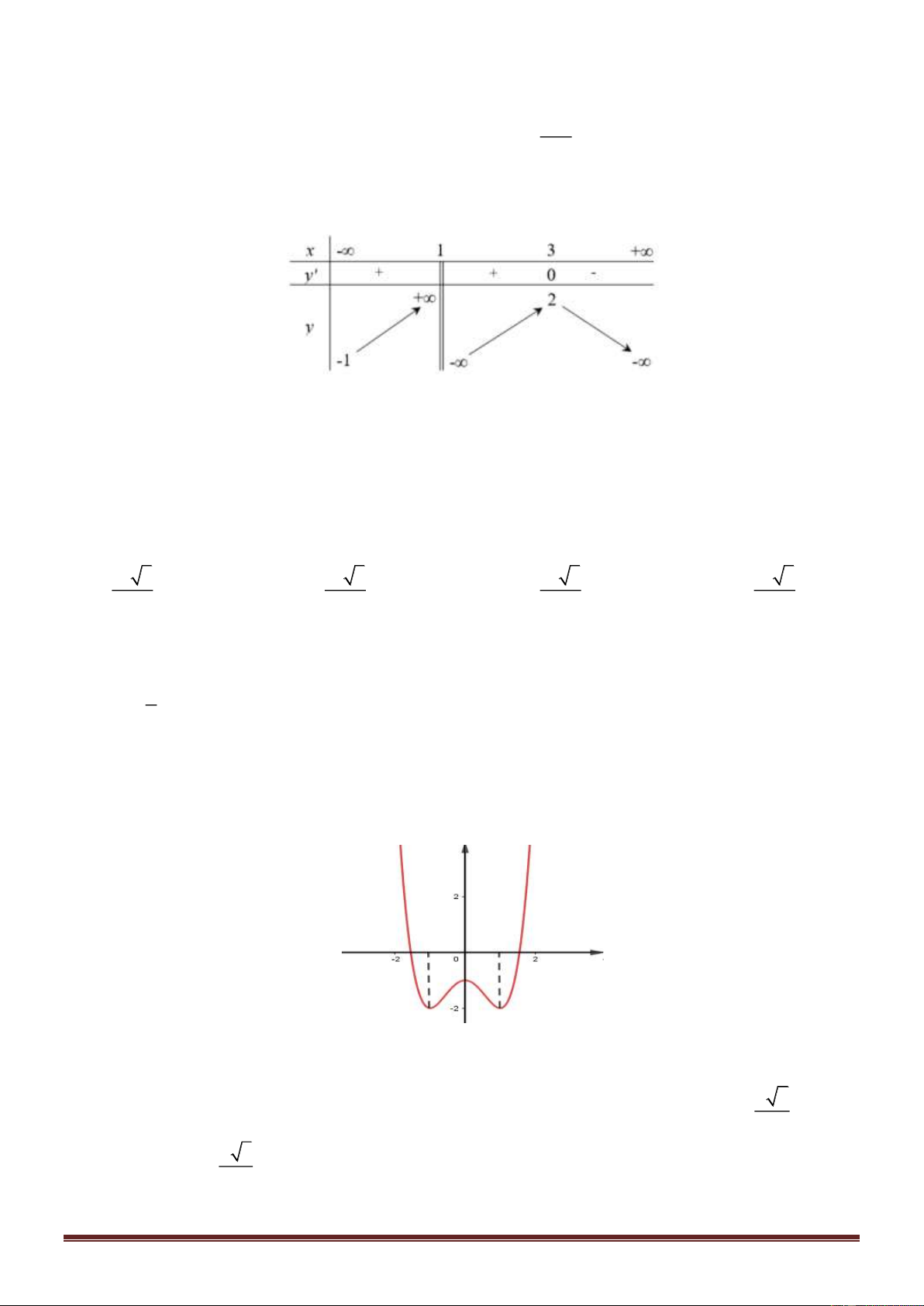
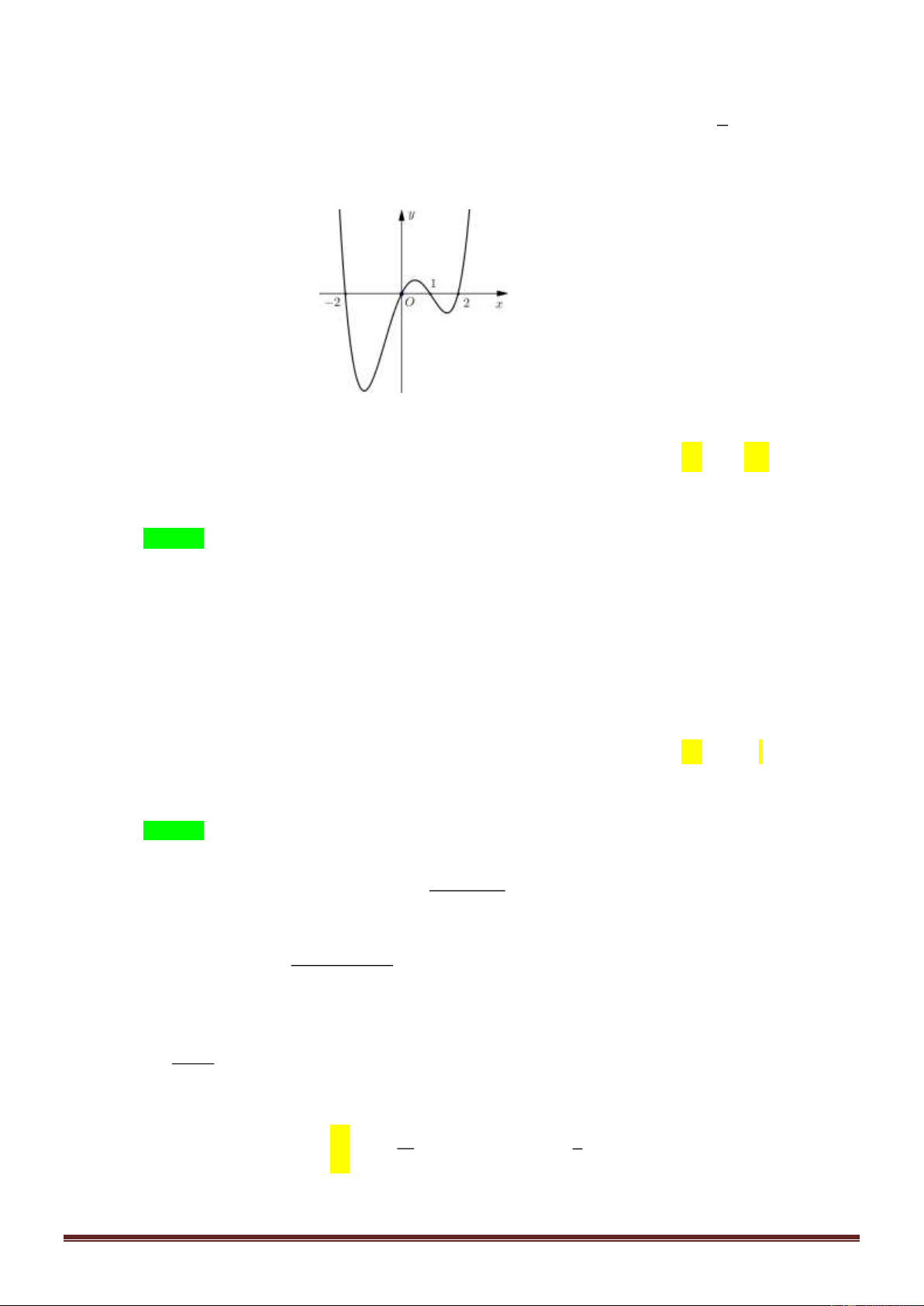
Hay hàm số y = g ( x) có đồ thị dạng y f(x)=(1/3)*(x+1)*(2x-1)*(x-2) x -2 -1 O 1 2
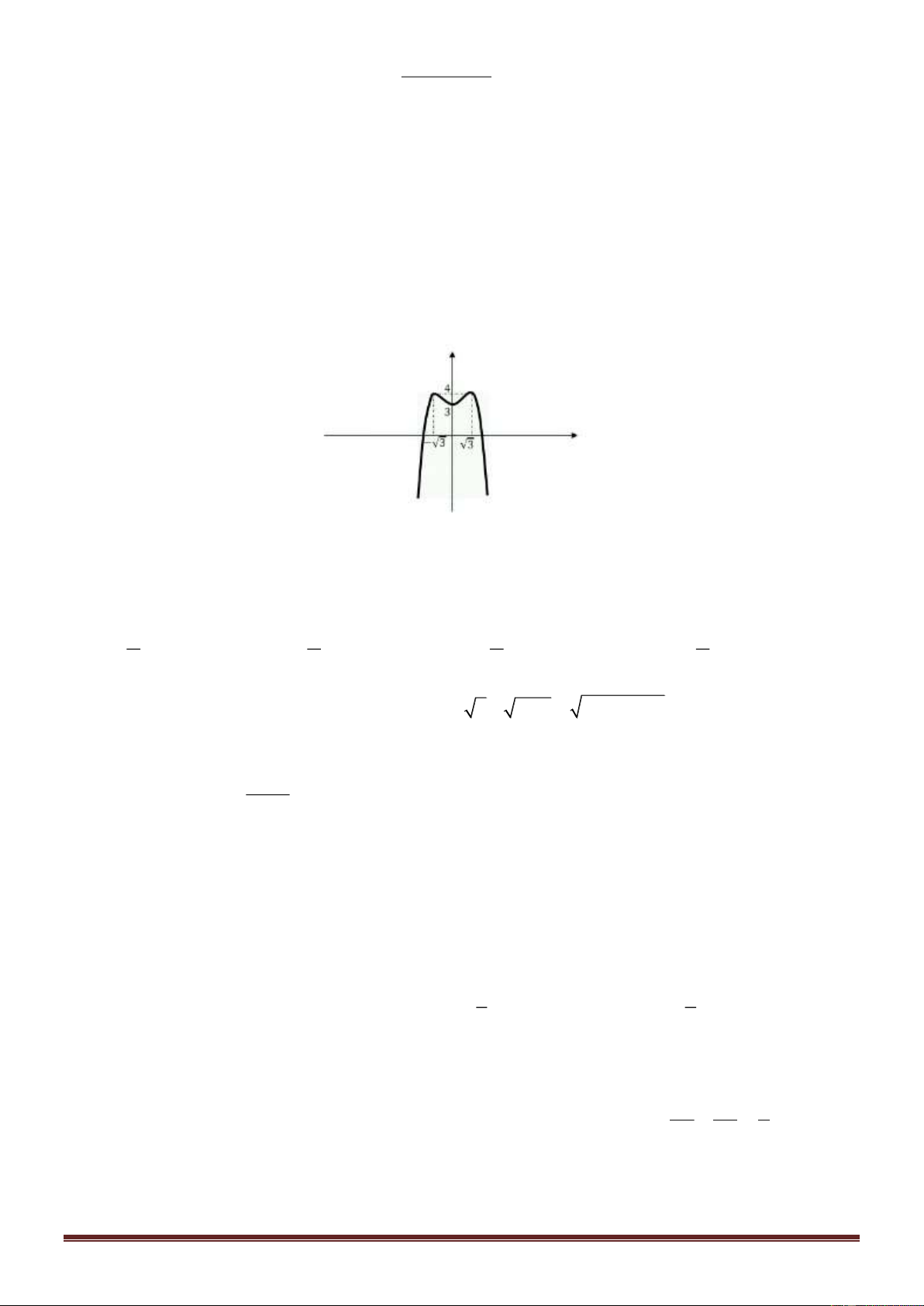
Khi đó đồ thị hàm số y = g ( x) có dạng Trang 8
f(x)=abs((1/3)*(x+1)*(2x-1)*(x-2)) y x -2 -1 O 1 2
Vậy hàm số y = f ( x) − 2018 có 5 điểm cực trị. Câu 43: Chọn C Đặt 2
2018 − x = t;0 t 2018 Khi đó 2
y = x + m( 2 2018- x + ) 1 - 2021 2
= - t + m(t + ) 1 - 3 2
= - t + mt + m- ( 3 ) * ;
Theo đề bài, để đồ thị hàm số cắt trục hoành tại hai điểm phân biệt thì phương trình ( )
* cần có 1 nghiệm dương
thỏa mãn 0 t 2018 TH1: ( ) * có 1 nghiệm kép. 2
= m − 4m+12 = 0 (loại) TH2: ( )
* có 2 nghiệm trái dấu. −(m − ) 3 0 m 3 ( ) 1 ( )
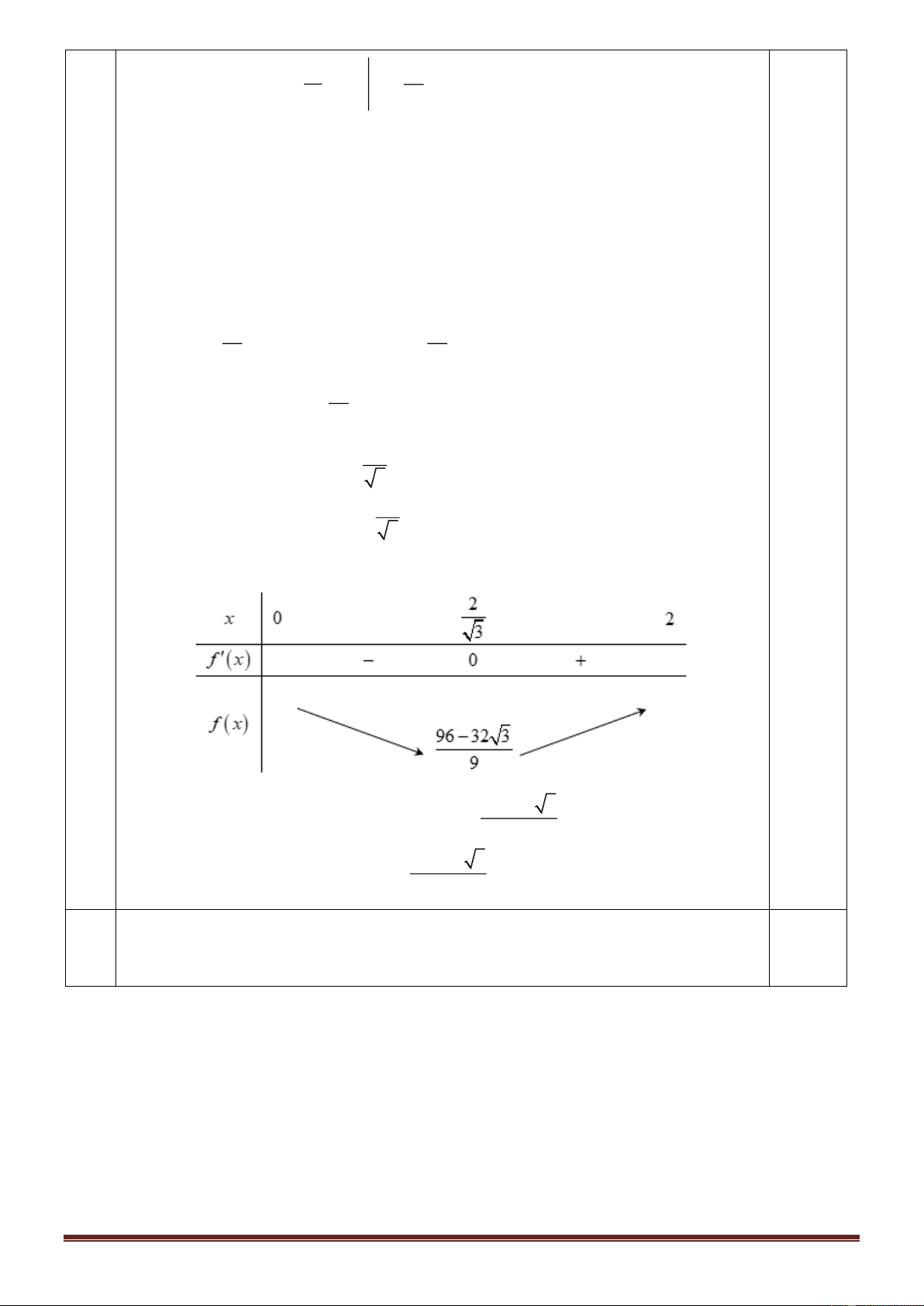
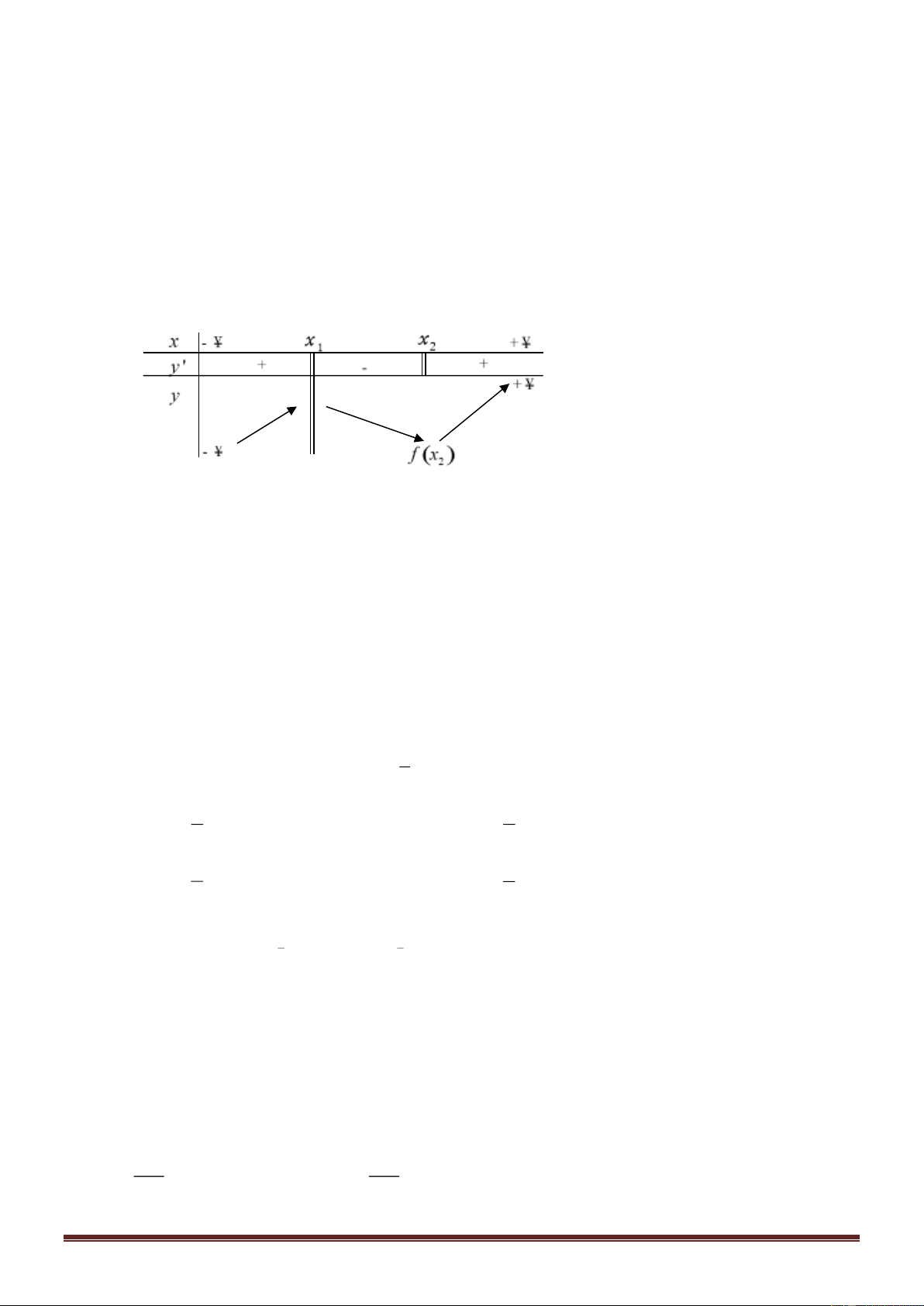
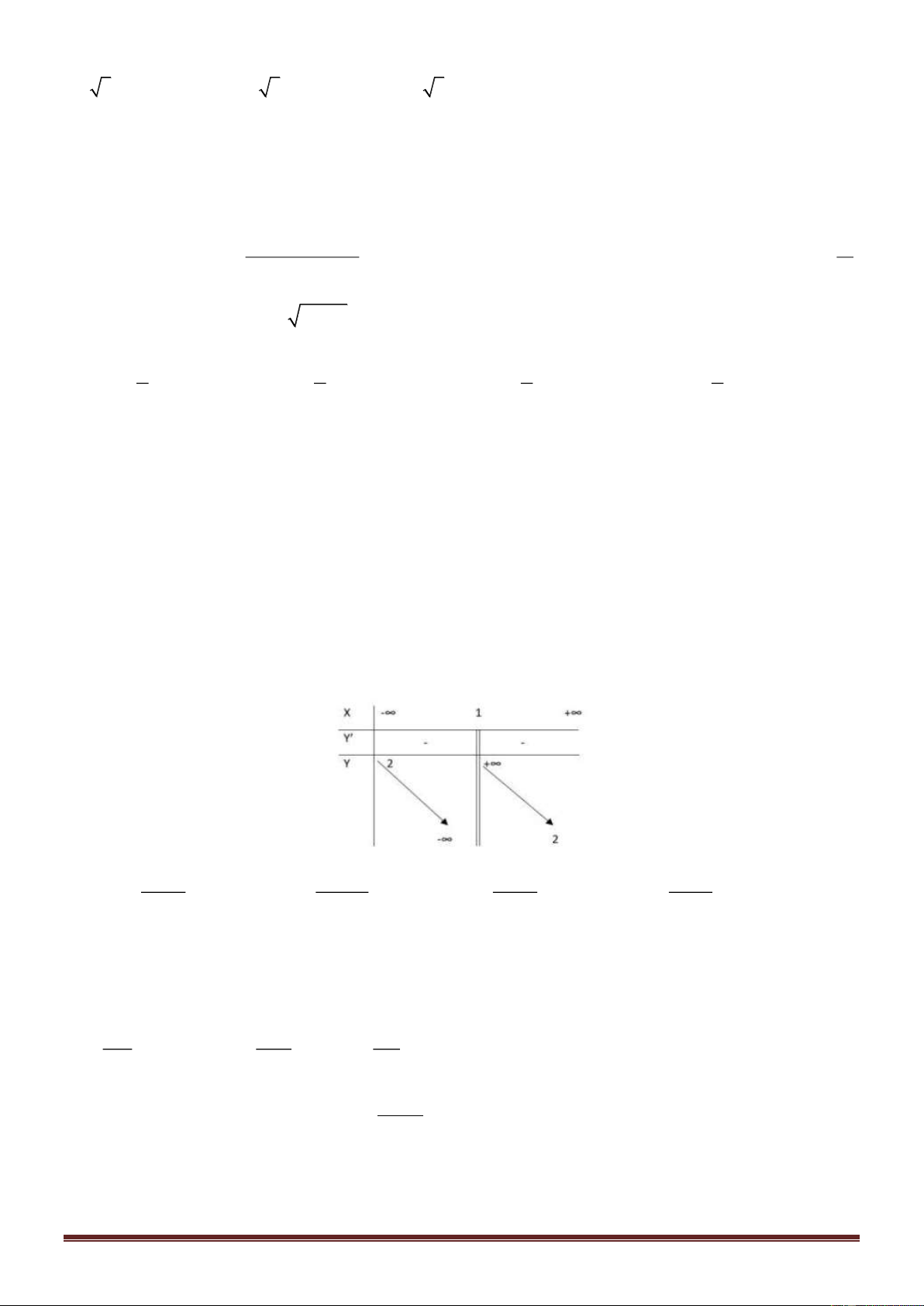
* có 1 nghiệm dương trên khoảng 0 t 2018 nên ta xét GTLN của m với 0 t 2018 2 t + 3 2 y = 0 t
− + mt + m − 3 = 0 m = t 0; 2018 ) t + 1 2 x + 3 2 x + 2x − 3 x = −3 Xét hàm y = x
0; 2018 , ta có y = = 0 x + , ) 1 (x + )2 1 x = 1 Lập BBT ta có 2021 44 3 m
44,009 S = i = 984 2018 +1 i=4 44/ Chọn D. 2 2 x y b + =1,(a,b 0) 2 2 y = a − x . 2 2 a b a a 2 b a − 2 x d a x b Diện tích (E) là 2 2 ( S a x x E) = 4 = 4 − d a a 0 0 Trang 9
Đặt x = a sin t, t − ; dx = a cos tdt . 2 2
Đổi cận: x = 0 t = 0; x = a t = 2 a a = b S 4 a2.cos2tdt = 2ab ab E (1+cos2t) ( ) dt = a 0 0 Mà ta có 2 ( S ) = . π R = 7 . π C
Theo giả thiết ta có (S ) = 7. (S ) ab = 4 9 ab = 49. E C 45/ Chọn D
Gọi z = x + yi ta có z − 2 − 3i = x + yi − 2 − 3i = x − 2 + ( y − ) 3 i .
Theo giả thiết ( x − )2 + ( y − )2 2 3
= 1 nên điểm M biểu diễn cho số phức z nằm trên đường tròn tâm I (2;3) bán kính R =1. M2 2 2
Ta có z +1+ i = x − yi +1+ i = x +1+ (1− y)i = ( x + ) 1 + ( y − ) 1 . M1 I Gọi M ( ; x y) và H ( 1 − ; )
1 thì HM = ( x + ) + ( y − )2 2 1 1 . H
Do M chạy trên đường tròn, H cố định nên MH lớn nhất khi M là giao của HI với đường tròn. x = 2 + 3t 1
Phương trình HI :
, giao của HI và đường tròn ứng với t thỏa mãn: 2 2
9t + 4t = 1 t = nên y = 3 + 2t 13 3 2 3 2 M 2 + ;3 + , M 2 − ;3 − . 13 13 13 13
Tính độ dài MH ta lấy kết quả HM = 13 +1 . Câu 47:
Kiểm tra thấy A và B nằm khác phía so với mặt phẳng (P)
Ta tìm được điểm đối xứng với B qua (P) là B'( 1 − ; 3 − ;4)
Lại có MA − MB = MA − MB ' AB ' = const .
Vậy MA − MB đạt giá trị lớn nhất khi M, A, B’ thẳng hàng hay M là giao điểm của đường thẳng AB’ với mặt phẳng (P). x = 1+ t
Đường thẳng AB’ có phương trình tham số là y = 3 − (t ) . z = 2 − t
Tọa độ điểm M ứng với tham số t là nghiệm của phương trình (1+t) +(− ) 3 + ( 2
− t) −1= 0 t = 3 − M ( 2 − ; 3 − ;6) Suy ra a = 2 − ,b = 3 − ,c = 6
Vậy a + b + c = 1.
Câu 48: Đáp án B Trang 10
Đường thẳng nằm trong mặt phẳng (P) qua A và chứa d. Khi đó
(P):3x+2y− z −4 = 0.
Gọi H là hình chiếu vuông góc của O lên (P) . Tọa độ điểm H là nghiệm của hệ x = 3t y = 2t 6 4 2 H ; ; − . z = t − 7 7 7 3
x + 2y − z −4 = 0
Gọi K là hình chiếu vuông góc của O lên , khi ấy d ( ;
O ) = OK OH . d ( ;
O ) nhỏ nhất K H H .
Đường thẳng qua hai điểm A và H nên có phương trình là x −1 y − 2 z −1 = =
. (Rõ ràng cắt d). 1 3 9 Câu 49:
Số chia hết cho 6 là số chia hết cho 3 và số đó là số chẵn.
- Số chia hết cho 3 là số a a a có tổng ba chữ số (a + a + a ) chia hết cho 3. 1 2 3 1 2 3
- Số chẵn là số chó chữ số tận cùng chia hết cho 2.
Để lập được số có 3 chữ số khác nhau từ tập A sao cho số đó chia hết cho 6 ta chia làm hai giai đoạn.
1/ chọn bộ ba chữ số khác nhau từ tạp A sao cho tổng 3 chữ số cộng lại chia hết cho 3 và trong ba chữ số đó có ít nhất 1 chữ số chẵn.
2/ Xếp mỗi bộ chọn được thành số có 3 chữ số sao cho số tận cùng phảit là số chẵn.
Để chọn và xếp khoa học ta nên chia ra ba trường hợp nhỏ như sau:
TH1: trong 3 chữ số chỉ có một chữ số chẵn, gồm có các bộ số sau: 1;2; 3 , 1;2; 9 , 1;3; 8 , 1;4; 7 , 1;5; 6 , 2;3; 7 , 2;7; 9 , 3;4; 5 , 3;6; 9 , 3;7; 8 , 4;5; 9 , 5;6; 7 , 7;8; 9 .
Với trường hợp này: số cách chọn và xếp là: 1 N = C *1* 2 *1 = 26 TH 1 13
TH2: trong 3 chữ số chỉ có hai chữ số chẵn, gồm có các bộ số sau: 1;2; 6 , 1;6; 8 , 2;3; 4 , 2;4; 9 , 2;5; 8 , 2;6; 7 , 3;4; 8 , 4;5; 6 , 4;8; 9 6;7; 8 Trang 11
Với trường hợp này số cách chọn và xếp là: 1 N = C * 2 * 2 *1 = 40 TH 2 10
TH3: trong 3 chữ số chọn được đề là chữ số chẵn, gồm có các bộ số sau: 2;4; 6 , 4;6; 8
Với trường hợp này số ccáh chọn và xếp là: 1 N = C *3! = 12 TH 3 2
Số cách chọn số có 3 chữ số khác nhau sao cho số đó chia hết cho 6 là: N + N + N = 78 TH1 TH 2 TH 3
Phép thử: lập số có 3 chữ số khác nhau từ A n() 3 = A = 504 9
A: là biến cố lập được số có ba chữ số khác nhau sao cho số đó chia hết cho 6. N ( ) A = N + N + N TH1 TH 2 TH 3 N ( ) A 78
Xác suất của biến cố A: P( ) A = = 0.155 N ( ) 504
***********HẾT*********** ĐỀ 42
ĐỀ THI THỬ THPT QUỐC GIA 2020 MÔN TOÁN Thời gian: 90 phút 3 x Câu 1.Cho hàm số 2 y =
− x + x . Mệnh đề nào sau đây là đúng? 3
A. Hàm số đã cho đồng biến trên .
B.Hàm số đã cho nghịch biến trên ( ) ;1 − .
C.Hàm số đã cho đồng biến trên (1;+) và nghịch biến trên ( ) ;1 − .
D.Hàm số đã cho đồng biến trên ( ) ;1
− và nghịch biến (1;+).
Câu 2.Nếu hàm số y = f (x) đồng biến trên khoảng (0;2) thì hàm số y = f (2x) đồng biến trên khoảng nào? Trang 12 A. (0; 2) . B. (0; 4) . C. (0; ) 1 . D. ( 2 − ;0). Câu 3. Cho hàm số ( ) = ( − )2 2 f x x
3 . Tìm giá trị cực đại của hàm số f '(x) A. − 1 8 . B. . C. 8. D. 9 . 2
Câu 4. Cho hàm số y = f (x) có lim f (x) = 0 và lim f (x) = + . Khẳng định nào sau đây là khẳng định x→+ x→− đúng?
A. Đồ thị hàm số không có tiệm cận ngang.
B. Đồ thị hàm số có hai tiệm cận ngang.
C. Đồ thị hàm số có một tiệm cận ngang là trục hoành.
D. Đồ thị hàm số có một tiệm cận đứng là đường thẳng y = 0.
Câu 5. Đường cong trong hình bên là đồ thị của một hàm số trong bốn y
hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ? 4 2 A. y = −x + 2x + 2 . y 2 4 2 B. y = x − 2x + 2 . 1 x 4 2 -1 O 1 C. y = x − 4x + 2 . 4 2 D. y = x − 2x + 3 . ax + b y Câu 6. Hàm số y =
với a 0 có đồ thị như hình vẽ bên. Mệnh cx + d
đề nào sau đây là đúng? A. b 0, c 0, d 0. O x B. b 0, c 0, d 0. C. b 0, c 0, d 0. D. b 0, c 0, d 0.
Câu .7.Tính đạo hàm của hàm số x y = 12 . x 12 / x 1 − / x / x / A. y = x.12
B. y = 12 .ln12 C. y = 12 D. y = ln13
Câu 8.Kết quả tính đạo hàm nào sau đây sai ? 1 A. ( )/ x x 3 = 3 .ln 3 B. ( )/ 1 ln x = C. (log x = ( )/ 2x 2x e = e 3 )/ D. x x ln 3 Trang 13 0 1 Câu 9.Tính
dx kết quả nào sau đây đúng? x−2 1 − 4 2 5 3 A. ln . B. ln . C. ln . D. 2 ln . 3 3 7 7
Câu 10. Tìm nguyên hàm của hàm số f (x) = 2sin x A. 2sin xdx = 2 cos x + C. B. = + 2 2sin xdx sin x C. C. 2 sin xdx = sin 2x + C. D. = − + 2sin xdx 2 cos x C.
Câu 11. Cho hai số phức z = 1+ 3i, z = 2
− − 5i. Phần ảo của số phức z + z bằng 1 2 1 2 A. −1. B. -2i. C. −2. D. 3.
Câu 12.Cho số phức z = 3− 2i . Tìm môđun của số phức w = iz − z A. –1. B.1. C. 2. D. 2 .
Câu 13.Thể tích của khối hộp đứng có diện tích đáy bằng S, độ dài cạnh bên bằng h. Sh Sh Sh A. Sh. B. . C. . D. . 3 6 2
Câu 14.Cho hình chóp S.ABCD có đáy ABCD là hình thoi, O là giao điểm của AC và BD, cạnh đáy bằng a, góc 0 3a
ABC = 60 , SO ⊥ (ABCD) và SO =
. Khi đó tìm thể tích của khối chóp. 4 3 a 3 3 a 2 3 a 2 3 a 3 A. . B. . C. . D. . 4 8 4 8
Câu 15.Cho tam giác đều ABC cạnh a quay xung quanh đường cao AH tạo nên một hình nón.
Tính diện tích xung quanh của hình nón đã cho. 2 2 a 3 1 2 1 A. a . B. . C. a 3 . D. a . 4 2 12
Câu16.Trong không gian với hệ trục tọa độ Oxyz, cho a = i
− + 2j−3k . Tính tọa độ của vectơ a A. (2; 1 − ; 3 − ). B. (-2;1;3) C. (2; 3 − ;− ) 1 . D. ( 1 − ;2; 3 − ).
Câu 17.Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d vuông góc với mặt phẳng
(P):4x −z +3= 0. Vectơ nào dưới đây là một vec-tơ chỉ phương của đường thẳng d ? A. u = (4;1; − )
1 . B. u = (4; −1; 3) . C. u = (4; 0; − ) 1 . D. u = (4;1; 3) .
Câu18.Trong mặt phẳng tọa độ Oxyz , cho ba điểm M (2;0;0) , N(0; − 5
1;0) và ln . Tìm phương trình mặt 3 phẳng (MNP) Trang 14 x y z x y z x y z A. + + = 0 . B. + + = 1 − . C. + + = x y z . 1 D. + + =1. 2 1 − 2 2 1 − 2 2 1 2 2 1 − 2
Câu19.Tìm tập xác định của hàm số y = tan 2x .
A. D = R \ + k , k . B. D = R \ + k , k . 4 2 2
C. D = R \ k , k . D. D = R \ k2 , k . 2
Câu 20.Trong các dãy số sau, dãy số nào là một cấp số nhân ?
A. 1,-3,9,-27,81. B. 1,-3,-6,-9,-12. C. 1,-2,-4,-8,-16. D. 0,3,9,27,81.
Câu 21. Biết rằng đồ thị hàm số 3 2 y = x − 3x + 2x −1 2
cắt đồ thị hàm số y = x − 3x + 1 tại hai điểm phân biệt
A và B. Tính độ dài đoạn thẳng AB . A. AB = 3. B. AB = 2 2. C. AB = 2. D. AB = 1.
Câu 22. Tập giá trị của hàm số ( ) 9 f x = x +
với x 2; 4 là đoạn a; b . Tính P = b − a . x A. P = 13 6. B. P = 25 . C. P = 1 . D. P = . 2 4 2 a b Câu 23. Cho ( 2 − ) 1 ( 2 − )
1 . Kết luận nào sau đây đúng ?
A. a b B. a b C. a = b D. a b
Câu 24 .Tìm hàm số tương ứng có đồ thị là đường cong ở hình bên x −x A. y = 2 B. y = 2 C. y = log x D. y = − log x 2 2
Câu 25.Tìm tập xác định D của hàm số A. D = R \ 2; 3 B. D = (2; ) 3 C. D = (− ;
2)(3;+) D. D = 2; 3
Câu 26. Tìm tập nghiệm S của bất phương trình log 3x − 2 log 6 − 5x 2 ( ) 2 ( ) Trang 15 6 2 2 6 A. S = 1; B.S = ;1 C.S = (1; +) D.S = ; 5 3 3 5 x
Câu 27. Tìm nguyên hàm của hàm số f ( x ) 3 = . 4 x + 1 3x 4 A. f (x) 4 dx = + C. B. f (x)dx = ln(x + )1+C. 4 2x + 6 3 4 1 4 C. f (x)dx = x ln(x + )1+C. D. f (x)dx = ln(x + )1+C. 4 2 2 Câu 28. Nếu f (x)dx = 2 thì I = 3f
(x)−2dx bằng bao nhiêu? 1 1 A. I = 2 . B. I = 3 . C. I = 4 . D. I =1. Câu 29.Gọi z 2 + + =
1 và z2 là 2 nghiệm phức của phương trình: z 2z 10
0 . Tính giá trị của biểu thức 2 2 A = z + z 1 2 A. 10 B. 30 C. 20 D. 40
Câu 30. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Hình chiếu vuông góc của S lên (ABC)
trùng với trung điểm H của cạnh BC . Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC). A. 60 .
B. 75 . C. 45 D. 30 .
Câu 31. Cho hình lập phương cạnh a. Diện tích mặt cầu ngoại tiếp hình lập phương đó bằng 2 3 a 2 A. . B. 2 a 2 . C. a 2 . D. 3 a . 4
Câu 32.Trong không gian Oxyz , phương trình của mặt phẳng (P) đi qua điểm B(2;1; − ) 3 , đồng thời vuông
góc với hai mặt phẳng (Q): x + y + 3z = 0 , (R): 2x − y + z = 0 là
A. 4x + 5y − 3z + 22 = 0. B. 4x − 5y − 3z −12 = 0 .
C. 2x + y − 3z −14 = 0 D. 4x + 5y − 3z − 22 = 0 . x −1 y + 2 z
Câu 33. Tìm phương trình đường thẳng song song với đường thẳng d : = = và cắt hai đường 1 1 1 − x +1 y +1 z − 2 x −1 y − 2 z − 3 thẳng d : = = ; d : = = 1 2 1 1 − 2 1 − 1 3 x +1 y +1 z − 2 x −1 y z −1 A. = = . B. = = . 1 − 1 − 1 1 1 1 − Trang 16 x −1 y − 2 z − 3 x −1 y z −1 C. = = . D. = = . 1 1 1 − 1 1 − 1
Câu 34 .Một tổ có 10 học sinh gồm 6 nam và 4 nữ. Giáo viên cần chọn ngẫu nhiên hai bạn hát song ca. Tính xác
suất P để hai học sinh được chọn là một cặp song ca nam nữ. 4 A. P = 8 . B. P = 12 . C. P = 2 . D. P = . 15 15 19 9
Câu 35.Một tổ gồm 12học sinh trong đó có bạn An. Hỏi có bao nhiêu cách chọn 4 em đi trực giao
thông trong đó phải có An? A. 990 . B. 495 . C. 220 . D. 165 .
Câu 36. Có bao nhiêu giá trị nguyên của tham số thực m thuộc khoảng ( 1 − 000;1000) để hàm số 3 = − ( + ) 2 y 2x 3 2m 1 x + 6m (m + )
1 x +1 đồng biến trên khoảng (2; +) ? A. 999. B.1001. C.998. D.1998.
Câu 37. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn 2
− 017;2019 để hàm số 1 3 2 y =
x − mx + (m + 2) x có hai điểm cực trị nằm trong khoảng (0; +). 3 A. 2016. B. 2017. C. 2018. D. 4035.
Câu 38.Tìm tất cả các giá trị thực của tham số m để phương trình sau có hai nghiệm thực phân biệt log ( 2 1 − x + log x + m − 4 = 0 3 ) 1 ( ) 3 1 A. − m 21 0 B. 5 m 21 C. 5 m 1 D. − m 2 4 4 4 4 b
Câu 39. Cho hai số thực a và b thỏa mãn a b và x sin xdx = đồng thời = và a cos a 0 b cos b = − . a b
Tính tích phân I = cos xdx . a A. I = − . B. I = 145 . C. I = . D. I = 0 . 12 2
Câu 40.Có bao nhiêu số phức z thỏa mãn biết 2 z = z + z (1) A. 1 B. 5 C. 2 D. 3
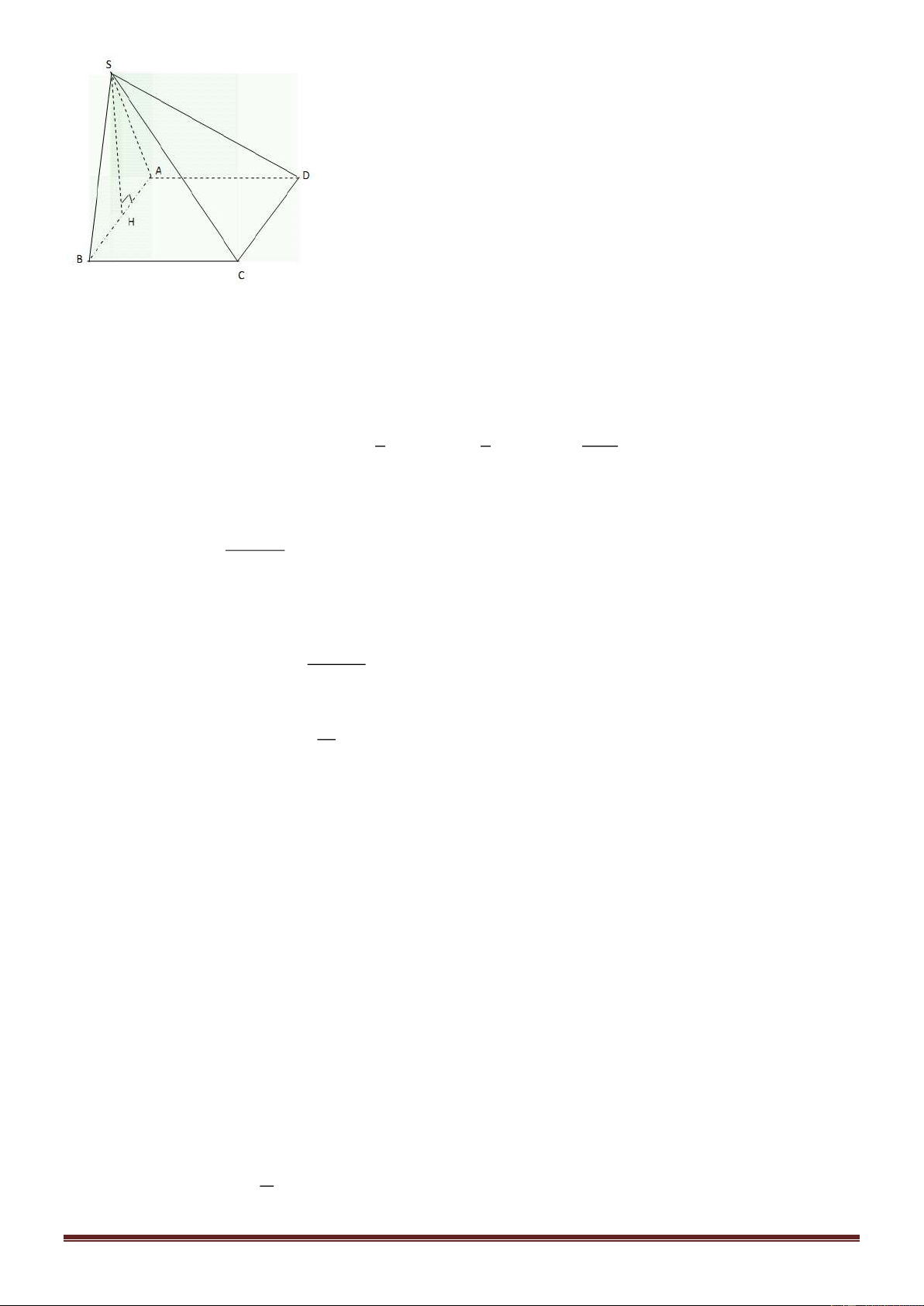
Câu 41.Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA = a vuông góc với mặt phẳng đáy ( SM
ABCD). Điểm M thuộc cạnh SA sao cho
= k. Xác định k sao cho mặt phẳng (MBC) chia khối SA
chóp đã cho thành hai phần có thể tích bằng nhau. Trang 17 1 − + 3 − + − + + A. k = 1 5 . B. k = 1 2 . C.k = 1 5 . D.k = . 2 2 2 4
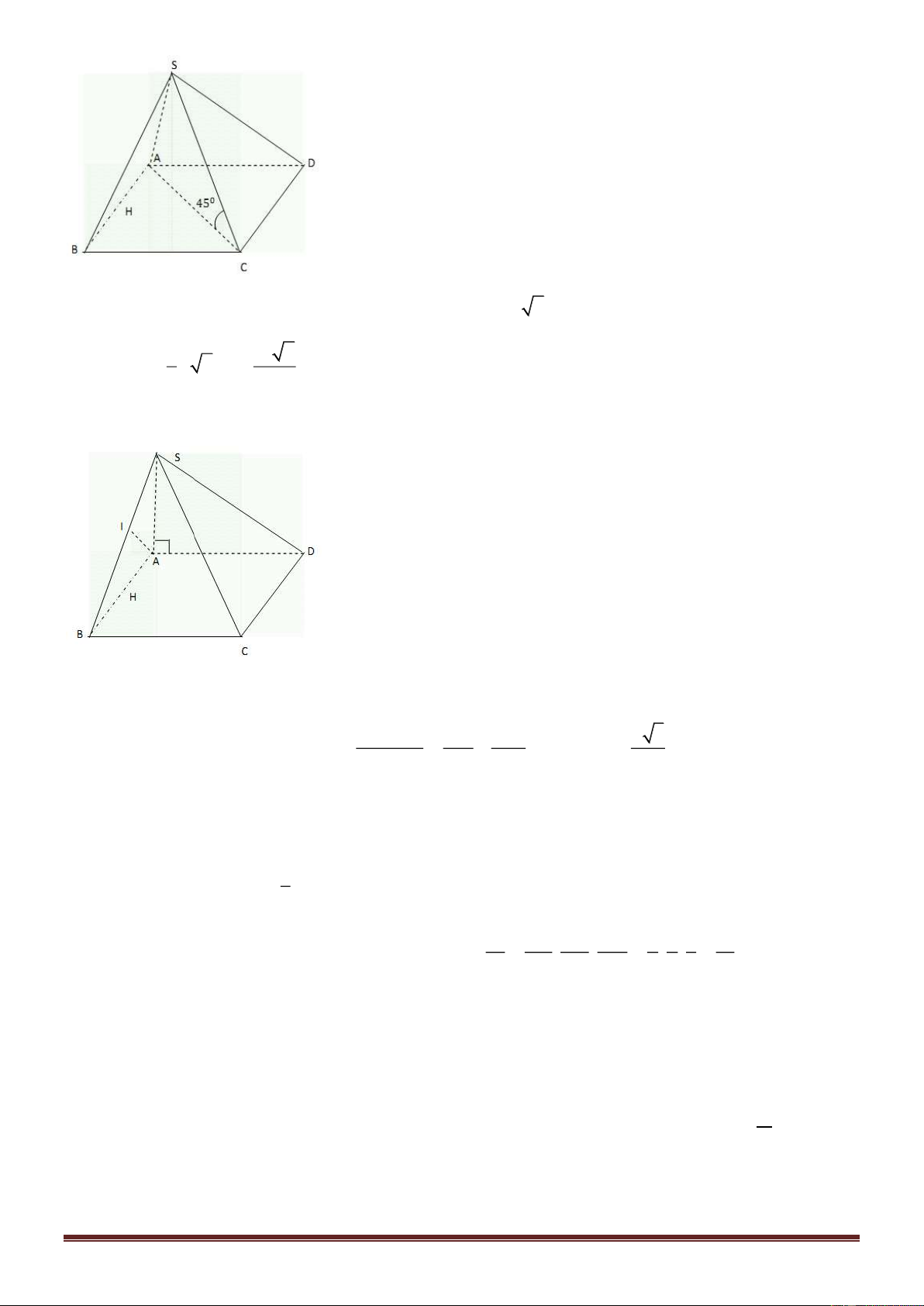
Câu 42.Cho hình chóp S.ABCD có SA ⊥ ( ABCD) đáy ABCD là hình thoi cạnh bằng a 0 và B = 60 . Biết
SA = 2a . Tính khoảng cách từ A đến SC 3a 2 2a 5 5a 6 4a 3 A. . B. . C. . D. . 2 5 2 3
Câu 43Trong không gian với hệ trục tọa độ Oxyz , cho điểm M(1;1; )
1 . Mặt phẳng (P) đi qua M và cắt chiều
dương của các trục Ox , Oy , Oz lần lượt tại các điểm A , B, C thỏa mãn OA = 2OB. Tính giá trị nhỏ nhất
của thể tích khối tứ diện OABC . 64 10 9 81 A. . B. . C. . D. . 27 3 2 16 x =1 x = 4 + t
Câu 44.Trong không gian Oxyz cho hai đường thẳng : y = 2 + t , : y = 3 − 2t . Gọi (S) là 1 2 z = −t z = 1 − t
mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng và . Bán kính mặt cầu (S) . 1 2 10 11 3 A. . B. . C. . D. 2 . 2 2 2 = +
Câu 45.Cho đường thẳng x 1 2t có PTTS:
. Tìm toạ độ điểm M nằm trên và cách điểm A (1 ) ;1 một y = 3 + t khoảng bằng 13 . 13 6 A. M (3; 4) hoặc M − ; . B. M (3; 4). 5 5 13 6 18 1 C. M − ; . D. M (2;3). hoặc M − ; . 5 5 5 5
Câu 46 .Cho hàm số bậc ba ( ) 3 2
f x = ax + bx + cx + d có đồ thị như hình vẽ bên. ( 2x −3x +2) x −1
Hỏi đồ thị hàm số g (x) =
có bao nhiêu đường tiệm cận đứng? 2 x f (x) − f (x) A. 5 B.3 C. 6 D. 4
Câu 47.Cho hai hàm số y = f (x) và y = g(x) là hai hàm số liên tục trên có đồ thị
hàm số y = f '(x) là đường cong nét đậm, đồ thị hàm số y = g '(x) là đường cong nét
mảnh như hình vẽ. Gọi ba giao điểm A, B, C của y = f '(x) và y = g '(x) trên hình vẽ Trang 18
lần lượt có hoành độ là a,b,c. Tìm giá trị nhỏ nhất của hàm số h (x) = f (x) − g(x) trên đoạn a;c? A. min h ( x ) = h (0). B. min h ( x ) = h (a ). a;c a;c C. min h ( x ) = h (b). D. min h ( x ) = h (c). a;c a;c
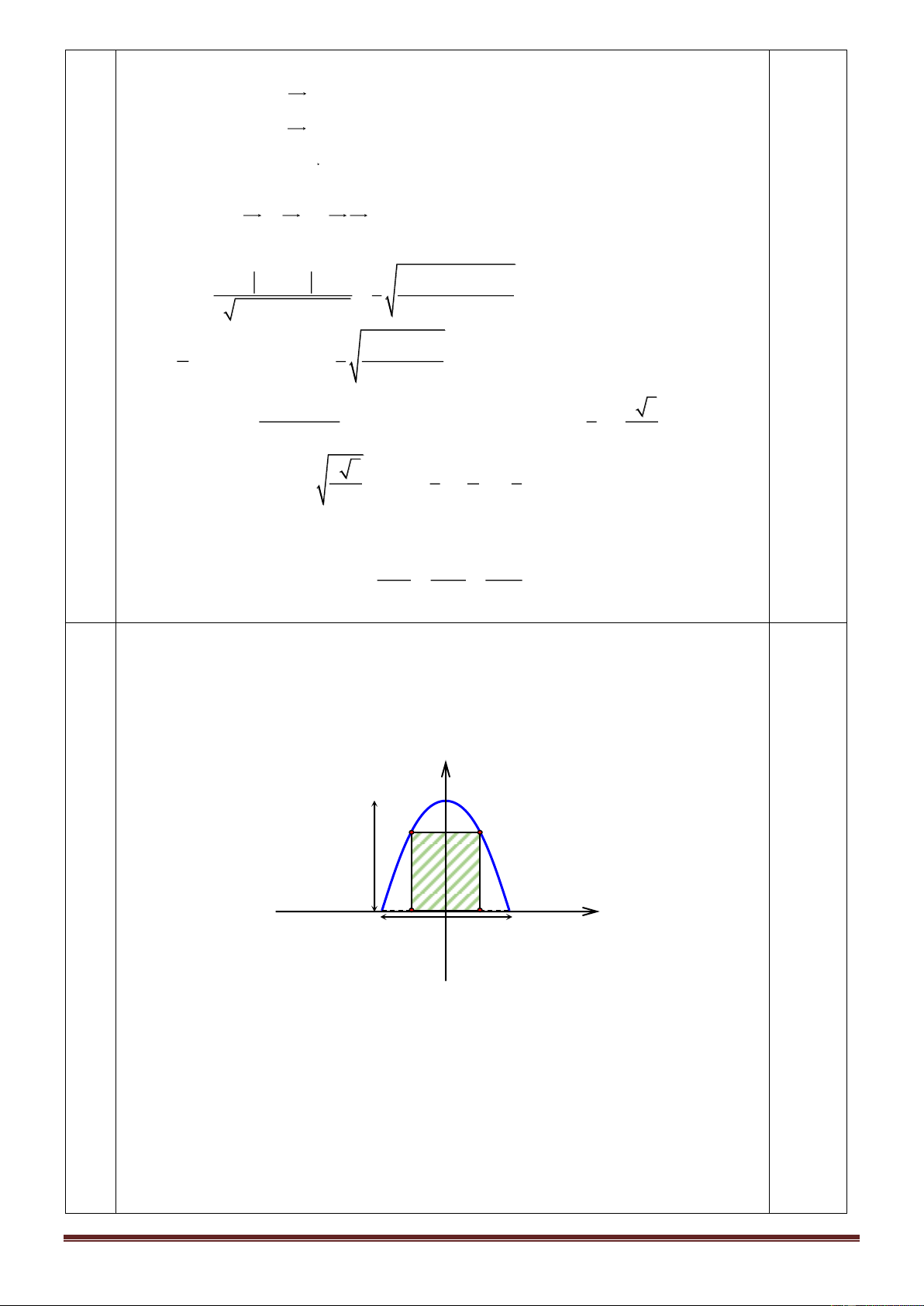
Câu 48. Một khuôn viên dạng nửa hình tròn có đường kính bằng 4 5 (m). Trên đó người thiết kế hai phần để
trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm nửa hình tròn và hai đầu mút của cánh hoa
nằm trên nửa đường tròn (phần tô màu), cách nhau một khoảng bằng 4 (m),phần còn lại của khuôn viên (phần
không tô màu) dành để trồng cỏ Nhật Bản.
Biết các kích thước cho như hình vẽ và kinh phí để trồng cỏ Nhật Bản là 100.000 đồng/m2. Hỏi cần bao nhiêu
tiền để trồng cỏ Nhật Bản trên phần đất đó? (Số tiền được làm tròn đến hàng nghìn)
A. 3.895.000 (đồng). B. 1.948.000 (đồng). C. 2.388.000 (đồng). D. 1.194.000 (đồng).
Câu 49. Cho số phức z = a + bi thỏa mãn 3a − 2b = 12. Gọi z , z là hai số phức thỏa mãn z − 3 − 4i =1 1 2 1
và 2z − 6 − 8i = 1. Giá trị nhỏ nhất của biểu thức P = z − z + z − 2z + 2 bằng 2 1 2 A. 9 − 9945 3 2. B. . C. 9 + 9945 3 2. D. . 13 31
Câu 50. Trong không gian Oxyz, cho hai điểm A (10;6; 2 − ), B(5;10; 9 − ) và mặt phẳng
():2x + 2y+ z −12 = 0. Điểm M di động trên () sao cho MAvà MB luôn tạo với () các
góc bằng nhau. Biết rằng M luôn thuộc một đường tròn ( )
cố định. Tính hoành độ của tâm đường tròn ( ) A. 4 − 9 . B. . C. 2 D. 10. 2 ĐÁP ÁN 1A 2C 3C 4C 5B 6A 7B 8D 9B 10D 11C 12D 13A 14D 15C 16D 17C 18D 19A 20A 21D 22D 23B 24A 25B 26A 27D 28C 29C 30C 31D 32D 33B 34B 35D 36B 37B 38C 39D 40D 41B 42B 43D 44B 45A 46B 47C 48B 49B 50C
LỜI GIẢI CÁC CÂU VẬN DỤNG CAO Trang 19 Câu 46.
Lời giải. Đáp án B
Dễ thấy x = 0 không là tiệm cận đứng của đồ thị hàm số vì TXĐ x 1. f (x) = 0 ( ) 1 Ta xét phương trình: 2 f (x) − f (x) = 0 . f (x) =1 (2)
Dựa vào đồ thị hàm số, ta thấy rằng
Phương trình (1), có hai nghiệm phân biệt là x 1; x = 2 (nghiệm kép). 1 2
Phương trình (2), có ba nghiệm phân biệt là x =1; x 1; 2 ; x 2. 3 4 ( ) 5 x −1 Do đó 2 f (x) − f (x) = (x − )
1 (x − 2).h (x) suy ra g (x) = . x.h (x)
Mà h (x) = 0 có 3 nghiệm lớn hơn 1 (2; x ; x y = g (x) 4 5 ) ĐTHS có 3 đường TCĐ. Câu 47.
Lời giải. Đáp án C. x = a
Ta có h '( x ) = f '(x ) − g '(x ) = 0 x = b. x = c
Với x a; b thì đồ thị g '(x) nằm trên f '(x)
nên g '(x) f '(x) h '(x) 0
hàm số nghịch biến trên đoạn a;b.
Tương tự với x b;c thì h (x) đồng biến. Do đó Min h (x) = h (b). a;c Câu 48 Chọn B Trang 20
Đặt hệ trục tọa độ như hình vẽ. Khi đó phương trình nửa đường tròn là = − x = ( )2 2 2 2 2 y R 2 5 − x = 20 − x .
Phương trình parabol (P) có đỉnh là gốc O 2
sẽ có dạng y = ax . Mặt khác (P) qua điểm M (2; 4) do đó: = (− )2 4 a 2 a =1.
Phần diện tích của hình phẳng giới hạn bởi (P) và nửa đường tròn.( phần tô màu) 2 Ta có công thức 2 2 S = 20 − x − x dx 11,94m . 1 ( ) 2 2 − 1
Vậy phần diện tích trồng cỏ là S = S −S 19,47592654 trongco hinhtron 1 2
Vậy số tiền cần có là S
100000 1.948.000 (đồng).đồng. trongxo Câu 49. Chọn B Cách giải
+M(a,b) biểu diễn z, vì 3a-2b=12 = Md :3x − 2y =12 Ta có: 2 2
Gọi z = x + y i, z = x + y i =>| z − 3 − 4i |=1 = (x − 3) + (y − 4) =1 1 1 1 2 2 2 1 1 1
=> M (x ; y ) biểu diễn z thuộc đường tròn C tâm I(3, 4), R = 1 1 1 1 1 1 2 2
| 2z − 6 − 8i |=1= (2x − 6) + (2y − 8) =1 2 2 2
=> M (x ; y ) biểu diễn 2 z thuộc đường tròn C tâm J(6,8), R = 1 2 2 2 2 2 Trang 21 2 2 2 2 P | = z− z | + | z − 2z | 2
+ = (a − x ) + (b − y ) + (a − 2x ) + (b − 2y ) + 2 1 2 1 1 2 2 = MM + MM + 2 1 2 = MM + M I + MM + M J 1 1 2 2 MI + MJ 138 64
Gọi J’ là điểm đối xứng của J qua d => J '( , ) 13 13 9945
Ta có: P MI + MJ = MI + MJ ' IJ ' = 13 Vậy đáp án là B Câu 50. Chọn C A B H M K Trang 22
Gọi H, K lần lượt là hình chiếu vuông góc của A, B trên mặt phẳng () , khi đó: = ( ()) 2.10 + 2.6 + ( 2 − ) −12 AH d A; = = 6; 2 2 2 2 + 2 +1 = ( ()) 2.5 + 2.10 + ( 9 − ) −12 BK d B; = = 3 . 2 2 2 2 + 2 +1
Vì MA , MB với () các góc bằng nhau nên AMH = BMK . Từ AH = 2BK suy ra MA = 2M . B Gọi M(x; y;z), ta có: MA = 2MB 2 2 MA = 4MB
( − )2 + ( − )2 + ( + )2 = ( − )2 + ( − )2 + ( + )2 x 10 y 6 z 2 4 x 5 y 10 z 9 2 2 2 20 68 68 x + y + z − x − y + z + 228 = 0 . 3 3 3 10 34 34
Như vậy, điểm M nằm trên mặt cầu (S) có tâm I ; ; −
và bán kính R = 2 10 . Do đó, đường tròn 3 3 3 ( )
là giao của mặt cầu (S) và mặt phẳng () , nên tâm J của đường tròn D là hình chiếu vuông góc của I trên mặt phẳng () . 10 x = + 2t 3 34
Phương trình đường thẳng d đi qua I và vuông góc với mặt phẳng () là y = + 2t . 3 34 z = − + t 3 10 x = + 2t x = 2 3 y =10 34 y = + 2t Tọa độ điểm J 38
là nghiệm (x; y; z) của hệ phương trình: 3 = − . z 34 3 z = − + t 2 3 t = − 2x + 2y + z −12 = 0 3 38 Vậy J = 2;10; − . 3 Trang 23
ĐỀ THI THỬ THPT QUỐC GIA 2020 ĐỀ 43 MÔN TOÁN Thời gian: 90 phút Câu 1.
Cho hàm số y = f (x) liên tục và có bảng biến thiên như sau:
Hàm số y = f (x) nghịch biến trên khoảng nào dưới đây? A. (0; + ) . B. (− ; − 2). C. (−2; 0) . D. (−3; ) 1 . Câu 2.
Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng? A. 4 mặt phẳng. B. 1 mặt phẳng. C. 2 mặt phẳng. D. 3 mặt phẳng. Câu 3.
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( )
P : 2x − 4y + 6z −1 = 0 . Mặt phẳng ( P)
có một vectơ pháp tuyến là A. n = (1; 2 − ;3) .
B. n = (2; 4;6) .
C. n = (1; 2;3) . D. n = ( 1 − ;2;3) . Câu 4.
Cho a , b , c là các số thực dương, a khác 1. Tìm mệnh đề sai trong các mệnh đề sau: b A. log bc = b + c log
= log b − log c a ( ) log log . B. . a a a a a c C. log bc = b c log ( c b = c b a ) .log a ( ) log .log . D. . a a a Câu 5.
Tìm số giao điểm của đồ thị hàm số 3 2
y = x + 2x − 4x +1 và đường thẳng y = 2 . A. 1. B. 0 . C. 3 . D. 2 . 2 Câu 6.
Cho y = f ( x) , y = g ( x) là các hàm số có đạo hàm liên tục trên 0;2 và g
(x).f (x)dx = 2, 0 2 2 g
(x).f (x)dx =3. Tính tích phân I = f
(x).g(x) dx. 0 0 A. I = 1 − . B. I = 6 . C. I = 5 . D. I =1. Câu 7.
Tính thể tích V của
khối chóp có đáy là hình vuông cạnh 2a và chiều cao là 3a 4 A. 3 V = 4a . B. 3 V = 2a . C. 3 V =12a . D. 3 V = a 3 1 Câu 8.
Tìm nghiệm của phương trình log ( x + ) 1 = . 9 2 A. x = 4 − . B. x = 2 . C. x = 7 4 . D. x = . 2 Câu 9.
Trong không gian với hệ tọa độ Oxyz , cho hai véctơ u = (1;1;− 2) và v = ( 1 − ;0; ) 1 . Góc tạo bởi
hai véctơ u và v là A. o 30 . B. o 120 . C. o 60 . D. o 150 .
Câu 10. Hàm số nào sau đây là một nguyên hàm của hàm số 2 3x + sin x ?
A. 6x + cos x . B. 3 x + cos x . C. 3 x − cos x .
D. 6x − cos x . Trang 24
Câu 11. Trong không gian với hệ tọa độ Oxyz cho điểm A(1; 1
− ;2)và mặt phẳng (P): 2x − y + z +1= 0.
Mặt phẳng (Q) đi qua điểm Avà song song với (P) . Phương trình mặt phẳng (Q)là:
A. 2x − y + z − 5 = 0 .
B. 2x − y + z = 0 .
C. x + y + z − 2 = 0.
D. 2x + y − z +1 = 0 .
Câu 12. Cho cấp số cộng (u u = −15 u = 60 n ) có ;
. Tổng 20 số hạng đầu tiên của cấp số cộng là: 5 20 A. S = 250 . B. S = 200 . C. S = 200 − . D. S = 25 − . 20 20 20 20
Câu 13. Cho số phức z = 4
− + 5i . Biểu diễn hình học của z là điểm có tọa độ A. ( 4 − ;5) . B. ( 4 − ; 5 − ) . C. (4; 5 − ) . D. (4;5) .
Câu 14. Cho hàm số y = f ( x) như hình vẽ dưới đây
Hỏi f (x) là hàm số nào trong các hàm số dưới đây? A. f ( x) 3 2 = x +3x − 4 . B. f ( x) 3 2 = x −3x +1. C. f ( x) 3 = x −3x +1. D. f ( x) 3 2 = −x + 3x +1.
Câu 15. Tổng giá trị nhỏ nhất và lớn nhất của hàm số 5
y = x − 5x + 1 trên đoạn 0; 2 là A. 2 − − 2 . B. 4 − + 2 . C. 2 − . D. 2 − 2 . 2 x + x − 2
Câu 16. Phương trình tiệm cận đứng của đồ thị hàm số y = là x − 2 A. y = 2 − . B. x = 2 − . C. y = 2 . D. x = 2 .
Câu 17. Tìm tất cả các số phức z thỏa mãn 2z − 3(1+ i) = iz + 7 − 3i . 8 4 A. z = − i . B. z = 4 − 8 4 2i . C. z = + i .
D. z = 4 + 2i . 5 5 5 5
Câu 18. Trong không gian với hệ tọa độ Oxyz , cho hình bình hành ABCE có A(3;1;2) , B (1;0; ) 1 và
C (2;3;0) . Tọa độ đỉnh E là A. E (4;4; ) 1 . B. E (0;2;− ) 1 . C. E (1;1;2) . D. E (1;3;− ) 1 .
Câu 19. Hệ số của 10
x trong biểu thức P = ( x − x )5 2 2 3 bằng A. 357 . B. 243. C. 628 . D. 243 − .
Câu 20. Gọi z , z là các nghiệm phức của phương trình 2
z − 2z + 5 = 0 . Giá trị của biểu thức 4 4 z + z 1 2 1 2 bằng. A. 14 . B. −7 . C. −14 . D. 7 .
Câu 21. Trong không gian với hệ tọa độ Oxyz
cho hai mặt phẳng (P) + − + = : 2x my z 1 0 và
(Q): x+3y +(2m+ )
3 z − 2 = 0 . Giá trị của m để ( P) ⊥ (Q) là: A. m = 1 − . B. m = 1. C. m = 0 . D. m = 2 . 2 4 x 1 − 5x 1 + 3 4 3 − x 1 1
Câu 22. Cho bất phương trình:
. Tập nghiệm của bất phương trình là: 2 2 Trang 25 3 3 A. ; + . B. . C. \ . D. . 2 2
Câu 23. Một chất điểm chuyển động có phương trình 4 2
S = 2t + 6t − 3t +1 với t tính bằng giây (s) và S
tính bằng mét (m). Hỏi gia tốc của chuyển động tại thời điểm t = 3(s) bằng bao nhiêu? A. 88 ( 2 m/s ) . B. 228 ( 2 m/s ) . C. 64 ( 2 m/s ) . D. 76 ( 2 m/s ) .
Câu 24. Tính đạo hàm của hàm số ( ) 2 3 e x f x − = . A. ( ) 2 3 2.e x f x − = . B. ( ) 2 3 2.e x f x − = − . C. ( ) 3 2.ex f x − = . D. ( ) 2 3 e x f x − = .
Câu 25. Thiết diện qua trục của một hình trụ là một hình vuông có cạnh bằng 2a . Thể tích khối trụ bằng: 2 A. 3 a . B. 3 2 a . C. 3 4 a . D. 3 a . 3
Câu 26. Cho biết bảng biến thiên ở hình dưới là của một trong bốn hàm số được liệt kê dưới đây. Hãy tìm hàm số đó. 2 − x − 4 x − 4 2 − x 2 − x + 3 A. y = . B. y = . C. y = . D. y = . x +1 2x + 2 x +1 x +1
Câu 27. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Hai mặt phẳng (SAC), (SAB) cùng
vuông góc với đáy và SC tạo với đáy góc o
60 . Thể tích của khối chóp S.ABCD là 3 a 3 a 2 3 a 6 3 a 3 A. V = . B. V = . C. V = . D. V = . 3 3 3 3
Câu 28. Một lớp có 12 học sinh nữ và 18 học sinh nam. Cô giáo chủ nhiệm chọn ngẫu nhiên 4 học
sinh trong lớp. Xác suất để cô giáo chủ nhiệm chọn được nhóm có cả học sinh nam và nữ là 530 503 503 530 A. . B. . C. . D. . 906 609 906 609 x −1
Câu 29. Tập hợp tất cả các giá trị thực của tham số m để hàm số y =
nghịch biến trên khoảng x + m (0;2) là
A. S = 0;+) . B. S = (− ) ;1 . C. S = (− ; − 2 . D. S = ( 1 − ;+) .
Câu 30. Cho hình lập phương ABC .
D A' B 'C ' D ' . Tính góc giữa hai đường thẳng AC và A' B A. 60 . B. 45 . C. 75 . D. 90 .
Câu 31. Số nghiệm của phương trình: log x + 3log 2 = 4 là 2 x A. 0 . B. 1. C. 4 . D. 2 .
Câu 32. Một khối nón có thể tích bằng 30 . Nếu tăng chiều cao lên 3 lần và tăng bán kính mặt đáy lên
2 lần thì thể tích khối nón mới bằng A. 360 . B. 180 . C. 240 . D. 720 . e 1+ 3ln x
Câu 33. Tính tích phân I =
dx bằng cách đặt t = +
x , mệnh đề nào dưới đây sai? 1 3ln x 1 2 2 2 2 2 2 A. 3 I = t . B. I = tdt . C. 2 I = t dt . D. I = . 14 9 1 3 3 9 1 1
Câu 34. Cho tứ diện đều cạnh bằng a . Khoảng cách từ trọng tâm của mặt này đến một mặt khác bằng Trang 26 a 6 a 3 a 3 a 6 A. . B. . C. . D. . 3 9 6 9
Câu 35. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x + y − z + 9 = 0 , đường thẳng x − 3 y − 3 z d : =
= và điểm A(1;2;− )
1 . Viết phương trình đường thẳng đi qua điểm A cắt 1 3 2
d và song song với mặt phẳng ( P) . x −1 y − 2 z +1 x −1 y − 2 z +1 A. = = . B. = = . 1 − 2 1 − 1 2 1 − x −1 y − 2 z +1 x − y − z + C. = = 1 2 1 . D. = = . 1 2 1 1 − 2 1 1 2
Câu 36. Tìm điểm M có hoành độ âm trên đồ thị (C) 3 : y = x − x +
sao cho tiếp tuyến tại M vuông 3 3 1 2
góc với đường thẳng y = − x + . 3 3 A. M ( 2 − ; 4 − ). B. M 1 − ; . C. M 2; . D. M ( 2 − ;0). 3 3 a 2 2 x + 2x + 2 a
Câu 37. Xác định số a dương sao cho dx =
+ a + ln 3. Giá trị của là a x +1 2 0 A. a = 1 . B. a = 2 . C. a = 3. D. a = 4 − .
Câu 38. Cho hàm số y = f ( x) có bảng biến thiên:
Tìm tất cả các giá trị của m để bất phương trình f ( x −1+ ) 1 m có nghiệm? A. m 1. B. m 2 − . C. m 4. D. m 0 .
Câu 39. Cho số phức z thỏa mãn điều kiện z −1+ 2i 2 . Trong hệ tọa độ Oxy , tập hợp điểm biểu
diễn số phức w = 3z − 2 + i , là hình tròn có diện tích bằng A. 25 . B. 16 . C. 36 . D. 9 .
Câu 40. Trong không gian với hệ tọa độ Oxyz , cho các điểm A(1;1;2) ; B( 3 − ;3;− ) 1 . Điểm
M ( x ; y ; z (Oxy) 2 2 MA + MB x 0 0 0 ) thuộc mặt phẳng sao cho
nhỏ nhất. Giá trị của là 0 A. 1. B. 1. − C. 2. D. 0.
Câu 41. Giả sử z , z là hai nghiệm phức của phương trình (2 + i) z z − (1− 2i) z = 1+ 3i và z − z = 1 1 2 1 2
. Tính M = 2z + 3z . 1 2 A. M = 19 . B. M = 25 . C. M = 5. D. M = 19 .
Câu 42. Cho hàm số y = f (x) liên tục trên đoạn 1 − ;
4 và có đồ thị hàm số y = f ( x) như hình bên.
Hỏi hàm số g ( x) = f ( 2 x + )
1 nghịch biến trên khoảng nào trong các khoảng sau? Trang 27 A. ( 1 − ; ) 1 . B. (0; ) 1 . C. (1; 4) . D. ( 3;4).
Câu 43. Một người vay ngân hàng 500 triệu đồng với lãi suất 1, 2% tháng để mua xe ô tô. Nếu mỗi
tháng người đó trả ngân hàng 10 triệu đồng và thời điểm bắt đầu trả cách thời điểm vay là đúng
một tháng. Hỏi sau ít nhất bao nhiêu tháng thì người đó trả hết nợ? Biết rằng lãi suất không thay đổi. A. 70 tháng. B. 80 tháng. C. 85 tháng. D. 77 tháng.
Câu 44. Cho tập X = 1;2;3;.......;
8 . Lập từ X số tự nhiên có 8 chữ số đôi một khác nhau. Xác suất để
lập được số chia hết cho 1111 là 2 2 2 A A A 4!4! 2 2 2 C C C 384 A. 8 6 4 . B. . C. 8 6 4 . D. . 8! 8! 8! 8!
Câu 45. Cho tứ diện ABCD có thể tích bằng 1. Gọi N, P lần lượt là trung điểm của BC,CD ; M là
điểm thuộc cạnh AB sao cho BM = 2AM . Mặt phẳng (MNP) cắt cạnh AD tại Q. Thể tích
của khối đa diện lồi MAQNCP là 7 5 7 5 A. . B. . C. . D. . 9 16 18 8
Câu 46. Trong không gian Oxyz , cho điểm E (2;1;3), mặt phẳng (P ): 2x + 2y - z - 3 = 0 và mặt 2 2 2
cầu (S ): (x - 3) + (y - 2) + (z - 5) = 36 . Gọi D là đường thẳng đi qua E , nằm trong
(P ) và cắt (S ) tại hai điểm có khoảng cách nhỏ nhất. Biết D có một vec-tơ chỉ phương r
u = (2018;y ;z
T = z - y . 0 0 ). Tính 0 0 A. T = 0 . B. T = - 2018 . C. T = 2018 . D. T = 1009.
Câu 47. Một mặt bàn hình elip có chiều dài là 120cm , chiều rộng là là 60cm . Anh Phượng muốn gắn
đá hoa cương và dán gạch tranh trên mặt bàn theo hình (phần đá hoa cương bên ngoài và điểm
nhấn bên trong là bộ tranh gồm 2 miếng gạch với kích thước mỗi miếng là 25cm 40cm). Biết
rằng đá hoa cương có giá 600.000 vnđ/ 2
m và bộ tranh gạch có giá 300.000 vnđ/bộ. Hỏi số
tiền để gắn đá hoa cương và dán gạch tranh theo cách trên gần nhất với số tiền nào dưới đây?
A. 519.000 đồng.
B. 610.000 đồng.
C. 639.000 đồng.
D. 279.000 đồng.
Câu 48. Cho hàm số f (x ) có bảng xét dấu của đạo hàm như sau:
Hàm số y = f (- x + ) 3 2 3
2 + x + 3x - 9x nghịch biến trên khoảng nào dưới đây? A. (- ¥ ;- 2). B. (2;+ ¥ ). C. (0;2). D. (- 2; ) 1 .
Câu 49. Có bao nhiêu giá trị của tham số m để hàm số 9 y = x + ( 2 m - m ) 5 x + ( 3 2 m - m + m ) 4 3 7 4
x + 2019 đồng biến trên ¡ ? A. 3 . B. 2 . C. 4 . D. 1 . Trang 28
Câu 50. Cho hàm số ( ) 4 3 2
f x = ax + bx + cx + dx + m , (với , a , b , c ,
d m Î R ). Hàm số y = f ( ¢ x ) có
đồ thị như hình vẽ bên dưới:
Tập nghiệm của phương trình f (x ) = m có số phần tử là: A. 1. B. 2 . C. 3 . D. 4 . HƯỚNG DẪN GIẢI Câu 1.
Cho hàm số y = f (x) liên tục và có bảng biến thiên như sau:
Hàm số y = f (x) nghịch biến trên khoảng nào dưới đây? A. (0; + ) . B. (− ; − 2). C. (−2; 0) . D. (−3; ) 1 . Lời giải Chọn C.
Dựa vào BBT nhận thấy y 0 trên khoảng ( 2 − ;0) . Câu 2.
Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng? A. 4 mặt phẳng. B. 1 mặt phẳng. C. 2 mặt phẳng. D. 3 mặt phẳng. Lời giải Chọn A.
Xét hình lăng trụ tam giác đều AB .
C A' B 'C '. Gọi là E , M , N , E ', M ', N ', O, P, Q lần
lượt là trung điểm của AB , BC , CA , A' B' , B 'C ', C ' A', AA', BB', CC '; ta có 4 mặt phẳng
đối xứng của lăng trụ đều AB .
C A' B 'C ' là ( AMM ' A') , (BNN ' B') , (CEE 'C '), (OPQ). Câu 3.
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( )
P : 2x − 4y + 6z −1 = 0 . Mặt phẳng ( P)
có một vectơ pháp tuyến là Trang 29 A. n = (1; 2 − ;3) .
B. n = (2; 4;6) .
C. n = (1; 2;3) . D. n = ( 1 − ;2;3) . Lời giải Chọn A. Mặt phẳng ( 1
P) có một vectơ pháp tuyến là n = (2; 4 − ;6) n = (1; 2
− ;3) cũng là một vectơ 2
pháp tuyến của (P) . Câu 4.
Cho a , b , c là các số thực dương, a khác 1. Tìm mệnh đề sai trong các mệnh đề sau: b A. log bc = b + c log
= log b − log c a ( ) log log . B. . a a a a a c C. log bc = b c log ( c b = c b a ) .log a ( ) log .log . D. . a a a Lời giải Chọn C. Ta có log bc = b + c log bc = b c a ( ) log .log a ( ) log log nên sai. a a a a 3 2 Câu 5.
Tìm số giao điểm của đồ thị hàm số y = x + 2x − 4x +1 và đường thẳng y = 2 . A. 1. B. 0 . C. 3 . D. 2 . Lời giải Chọn C.
Phương trình hoành độ giao điểm: 3 2
x + 2x − 4x +1 = 2 3 2
x + 2x −4x −1= 0 . x = 2 −
Xét hàm số f (x) 3 2
= x + 2x − 4x −1
ta có: f ( x) 2
= 3x + 4x − 4 , f (x) = 0 2 . x = 3 Mà f (− ) 2 67 2 . f = 7. −
0 suy ra đồ thị f (x) cắt trục hoành tại 3 điểm phân biệt. 3 27
Cách khác: Dùng Casio giải phương trình bậc ba, máy cho ra kết quả 3 nghiệm phân biệt . 2 Câu 6.
Cho y = f ( x) , y = g ( x) là các hàm số có đạo hàm liên tục trên 0;2 và g
(x).f (x)dx = 2, 0 2 2 g
(x).f (x)dx =3. Tính tích phân I = f
(x).g(x) dx. 0 0 A. I = 1 − . B. I = 6 . C. I = 5 . D. I =1. Lời giải Chọn C. 2 2
Xét tích phân I = f
(x).g(x) dx = f
(x).g(x)+ f (x).g(x)dx 0 0 2 2 = g
(x).f (x)dx+ g
(x).f (x)dx = 5. 0 0 Câu 7.
Tính thể tích V của
khối chóp có đáy là hình vuông cạnh 2a và chiều cao là 3a 4 A. 3 V = 4a . B. 3 V = 2a . C. 3 V =12a . D. 3 V = a 3 Lời giải Chọn A. Thể tích 1 V = (2a)2 3 .3a = 4a . 3 1 Câu 8.
Tìm nghiệm của phương trình log ( x + ) 1 = . 9 2 A. x = 4 − . B. x = 2 . C. x = 7 4 . D. x = . 2 Trang 30 Lời giải Chọn B. 1 log ( x + ) 1 2 1 =
x +1 = 9 x = 2 . 9 2 Câu 9.
Trong không gian với hệ tọa độ Oxyz , cho hai véctơ u = (1;1; − 2) và v = ( 1 − ;0; ) 1 . Góc tạo bởi
hai véctơ u và v là A. o 30 . B. o 120 . C. o 60 . D. o 150 . Lời giải Chọn D. u v 1.(− ) 1 +1.0 +1.( 2 − ) 3 Ta có (u v) . cos ; = = = − . u . v 1 +1 + ( 2 − )2. (− )2 2 2 2 2 1 + 0 +1 2
Suy ra, góc giữa hai véctơ này bằng o 150 .
Câu 10. Hàm số nào sau đây là một nguyên hàm của hàm số 2 3x + sin x ?
A. 6x + cos x . B. 3 x + cos x . C. 3 x − cos x .
D. 6x − cos x . Lời giải Chọn C. Ta có ( 2 x + x) 3 3 sin
dx = x − cos x + C .
Câu 11. Trong không gian với hệ tọa độ Oxyz cho điểm A(1; 1
− ;2)và mặt phẳng (P): 2x − y + z +1= 0.
Mặt phẳng (Q) đi qua điểm Avà song song với (P) . Phương trình mặt phẳng (Q)là:
A. 2x − y + z − 5 = 0 .
B. 2x − y + z = 0 .
C. x + y + z − 2 = 0.
D. 2x + y − z +1= 0 . Lời giải Chọn A.
Mặt phẳng (Q) đi qua A(1;−1;2) và song song với mặt phẳng (P) nên có phương trình là: 2( x − ) 1 − ( y + ) 1 + (
1 z − 2) = 0 hay 2x − y + z −5 = 0
Câu 12. Cho cấp số cộng (u u = −15 u = 60 n ) có ;
. Tổng 20 số hạng đầu tiên của cấp số cộng là: 5 20 A. S = 250 . B. S = 200 . C. S = 200 − . D. S = 25 − . 20 20 20 20 Lời giải Chọn A. Cấp số cộng (u u d
n ) có số hạng đầu , công sai . 1 u = 15 − u + 4d = 1 − 5 u = 35 − 5 Ta có 1 1 . u = 60 u +19d = 60 d = 5 20 1 (u +u .20 35 − + 60 .20 1 20 ) ( )
Tổng 20 số hạng đầu tiên của cấp số cộng là S = = = 250 . 20 2 2
Câu 13. Cho số phức z = 4
− + 5i . Biểu diễn hình học của z là điểm có tọa độ A. ( 4 − ;5) . B. ( 4 − ; 5 − ) . C. (4; 5 − ) . D. (4;5) . Lời giải Chọn A Số phức z = 4
− + 5i có phần thực a = 4
− ; phần ảo b = 5 nên điểm biểu diễn hình học của số phức z l à ( 4 − ;5).
Câu 14. Cho hàm số y = f ( x) như hình vẽ dưới đây Trang 31
Hỏi f (x) là hàm số nào trong các hàm số dưới đây? A. f ( x) 3 2 = x +3x − 4 . B. f ( x) 3 2 = x −3x +1. C. f ( x) 3 = x −3x +1. D. f ( x) 3 2 = −x + 3x +1. Lời giải Chọn C.
Dựa vào hình dạng đồ thị hàm số có hai điểm cực trị tại x = 0 và x = 2 , cắt trục tung tại điểm
có tung độ y =1 và có hệ số a 0 .
Như vậy chỉ có hàm số ở phương án C thỏa mãn.
Câu 15. Tổng giá trị nhỏ nhất và lớn nhất của hàm số 5
y = x − 5x + 1 trên đoạn 0; 2 là A. 2 − − 2 . B. 4 − + 2 . C. 2 − . D. 2 − 2 . Lời giải Chọn C. 2 x = 1 4
y = 5x − 5 . y = 0 4 x =1 . 2 x = 1 − x = 1 0; 2 2 x = 1 . x = 1 − 0; 2
Ta có: f (0) = 1; f ( 2) = − 2 +1; f ( ) 1 = 3 − . Vậy:1-3=-2 2 x + x − 2
Câu 16. Phương trình tiệm cận đứng của đồ thị hàm số y = là x − 2 A. y = 2 − . B. x = 2 − . C. y = 2 . D. x = 2 . Lời giải Chọn D.
□ Tập xác định D = \ 2 .
□ lim y = + , lim y = − đồ thị hàm số có một tiệm cận đứng x = 2 . + − x→2 x→2
Câu 17. Tìm tất cả các số phức z thỏa mãn 2z − 3(1+ i) = iz + 7 − 3i . 8 4 A. z = − i . B. z = 4 − 8 4 2i . C. z = + i .
D. z = 4 + 2i . 5 5 5 5 Lời giải Chọn D
Ta có: 2z − 3(1+ i) = iz + 7 − 3i (2 − i) z = 10 10 z = z = 4+ 2i. 2 − i
Câu 18. Trong không gian với hệ tọa độ Oxyz , cho hình bình hành ABCE có A(3;1;2) , B (1;0; ) 1 và
C (2;3;0) . Tọa độ đỉnh E là Trang 32 A. E (4;4; ) 1 . B. E (0;2;− ) 1 . C. E (1;1;2) . D. E (1;3;− ) 1 . Lời giải Chọn A.
x + x = x + x x = 4 A C B E E
ABCE là hình bình hành nên y + y = y + y y = 4 E (4;4; ) 1 . A C B E E
z + z = z + z z = 1 A C B E E
Câu 19. Hệ số của 10
x trong biểu thức P = ( x − x )5 2 2 3 bằng A. 357 . B. 243. C. 628 . D. 243 − . Lời giải Chọn D. −
Số hạng tổng quát trong khai triển biểu thức trên là k k k T = C 2x 3 − x k 1 + 5 ( ) ( )5 2 −k −k k = 2k C 3 − x 5 ( )5 ( )10 . Số hạng chứa 10
x ứng với thỏa mãn 10 − k =10 k = 0 .
Với k = 0 thì hệ số của 10 x là C 2 3 − = 243 − 5 ( )5 0 0 .
Câu 20. Gọi z , z là các nghiệm phức của phương trình 2
z − 2z + 5 = 0 . Giá trị của biểu thức 4 4 z + z 1 2 1 2 bằng. A. 14 . B. −7 . C. −14 . D. 7 . Lời giải Chọn C z =1+ 2i Ta có 2 z − 2z + 5 = 0 1 . z =1−2i 2 4 4 Nên 4 4
z + z = (1+ 2i) + (1− 2i) = 1 − 4 . 1 2
Câu 21. Trong không gian với hệ tọa độ Oxyz cho hai mặt phẳng (P) + − + = : 2x my z 1 0 và
(Q): x+3y +(2m+ )
3 z − 2 = 0 . Giá trị của m để ( P) ⊥ (Q) là: A. m = 1 − . B. m = 1. C. m = 0 . D. m = 2 . Lời giải Chọn B.
Ta có một vectơ pháp tuyến của mặt phẳng (P) là n = (2; ; m − ) 1 .
Một vectơ pháp tuyến của mặt phẳng (Q) là n = (1;3;2m + 3) .
Mặt phẳng (P) vuông góc với mặt phẳng (Q) khi và chỉ khi . n n = 0 2.1+ . m 3−1.(2m + ) 3 = 0 m = 1. 2 4 x 1 − 5x 1 + 3 4 3 − x 1 1
Câu 22. Cho bất phương trình:
. Tập nghiệm của bất phương trình là: 2 2 3 3 A. ; + . B. . C. \ . D. . 2 2 Lời giải Chọn C. 2 4 x 1 − 5x 1 + 3 4−3x 1 1 2 2 2
4x −15x +13 4−3x 2
4x −12x +9 0 ( x − )2 3 2 3 0 x . 2 Trang 33 3
Vậy tập nghiệm của bất phương trình là \ . 2
Câu 23. Một chất điểm chuyển động có phương trình 4 2
S = 2t + 6t − 3t +1 với t tính bằng giây (s) và
S tính bằng mét (m). Hỏi gia tốc của chuyển động tại thời điểm t = 3(s) bằng bao nhiêu? A. 88 ( 2 m/s ) . B. 228 ( 2 m/s ) . C. 64 ( 2 m/s ) . D. 76 ( 2 m/s ) . Lời giải Chọn B.
Ta có: v(t) = S(t) 3
= 8t +12t −3 , suy ra a(t) = v(t) 2 = 24t +12. Suy ra a ( ) 2 3 = 24.3 +12 = 228 ( 2 m/s ) .
Câu 24. Tính đạo hàm của hàm số ( ) 2 3 e x f x − = . A. ( ) 2 3 2.e x f x − = . B. ( ) 2 3 2.e x f x − = − . C. ( ) 3 2.ex f x − = . D. ( ) 2 3 e x f x − = . Lời giải Chọn A.
Ta có f ( x) = ( x − ) 2x−3 2 x−3 2 3 .e = 2.e .
Câu 25. Thiết diện qua trục của một hình trụ là một hình vuông có cạnh bằng 2a . Thể tích khối trụ bằng: 2 A. 3 a . B. 3 2 a . C. 3 4 a . D. 3 a . 3 Lời giải Chọn B.
bán kính đáy r = a ; chiều cao h = 2a Thể tích khối trụ là 2 3
V = r .h = 2a .
Câu 26. Cho biết bảng biến thiên ở hình dưới là của một trong bốn hàm số được liệt kê dưới đây. Hãy tìm hàm số đó. 2 − x − 4 x − 4 2 − x 2 − x + 3 A. y = . B. y = . C. y = . D. y = . x +1 2x + 2 x +1 x +1 Lời giải Chọn D. Ta có lim y = 2 − và lim y = 2
− nên đồ thị hàm số có đường tiệm cận ngang y = 2 − . x→− x→+
lim y = + và lim y = − nên đồ thị hàm số có đường tiệm cận đứng x = 1 − . + − x ( → − ) 1 x ( → − ) 1 − +
Hàm số luôn nghịch biến trên từng khoảng xác định nên 2x 3 y = là hàm số cần tìm. x +1
Câu 27. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Hai mặt phẳng (SAC) , (SAB) cùng
vuông góc với đáy và SC tạo với đáy góc o
60 . Thể tích của khối chóp S.ABCD là 3 a 3 a 2 3 a 6 A. V = . B. V = . C. V = . D. . 3 3 3 Lời giải Chọn C.
Do ABCD là hình vuông cạnh a nên AC = a 2 và 2 S = a . ABCD
(SAC), (SAB) cùng vuông góc với đáy nên suy ra SA ⊥ (ABCD). Trang 34
(SC,(ABCD)) = SCA o = 60 .
Trong tam giác vuông SAC , ta có SA = AC.tan SCA = a 2. 3 = a 6 . 2 3 Vậy 1 a 6.a a 6 V = SA S = = . S.ABCD 3 ABCD 3 3
Câu 28. Một lớp có 12 học sinh nữ và 18 học sinh nam. Cô giáo chủ nhiệm chọn ngẫu nhiên 4 học
sinh trong lớp. Xác suất để cô giáo chủ nhiệm chọn được nhóm có cả học sinh nam và nữ là 530 503 503 530 A. . B. . C. . D. . 906 609 906 609 Lời giải Chọn D.
Xét phép thử: “Chọn ngẫu nhiên 4 học sinh trong lớp có 12 học sinh nữ và 18 học sinh nam”
Số phần tử của không gian mẫu n() 4 = C . 30
Xét biến cố A: “Cô chọn được nhóm có cả học sinh nam và nữ”
A là biến cố chọn được 4 học sinh nam hoặc 4 học sinh nữ
n( A) = n() − n(A) 4 4 4
= C −C −C . 30 18 12 n A Vậy P( A) ( ) 530 = = . n () 609 x −1
Câu 29. Tập hợp tất cả các giá trị thực của tham số m để hàm số y =
nghịch biến trên khoảng x + m (0;2) là
A. S = 0;+) . B. S = (− ) ;1 . C. S = (− ; − 2 . D. S = ( 1 − ;+) . Lời giải Chọn C. m 1 − m 1 − − m +1 0 Hàm số x 1 y =
nghịch biến trên khoảng (0;2) khi
−m 0 m 0 x + m −m (0;2) −m 2 m 2 − Vậy S = (− ; − 2 .
Câu 30. Cho hình lập phương ABC .
D A' B 'C ' D ' . Tính góc giữa hai đường thẳng AC và A' B A. 60 . B. 45 . C. 75 . D. 90 . Lời giải Chọn A. Ta có A B//D C ; AC D đều Góc ( AC, A B
) = ( AC, D C ) = AD C = 60 .
Câu 31. Số nghiệm của phương trình: log x + 3log 2 = 4 là 2 x A. 0 . B. 1. C. 4 . D. 2 . Lời giải Chọn D.
Điều kiện: 0 x 1. Trang 35 x = 2 log x =1
log x + 3log 2 = 4 log x + 3log 2 − 4 = 0 2 1 . 2 x 2 x = − log x 4 x = 2 16
Vậy phương trình đã cho có 2 nghiệm.
Câu 32. Một khối nón có thể tích bằng 30 . Nếu tăng chiều cao lên 3 lần và tăng bán kính mặt đáy
lên 2 lần thì thể tích khối nón mới bằng A. 360 . B. 180 . C. 240 . D. 720 . Lời giải Chọn A.
Thể tích ban đầu của hình nón là 1 2 V = R h . 3
Sau khi tăng chiều cao 3 lần và bán kính đáy tăng 2 lần thì thể tích của hình nón là 1 1
V = (2R)2 (3h) 2
=12. R h =12.30 = 360 . 3 3 e 1+ 3ln x
Câu 33. Tính tích phân I =
dx bằng cách đặt t = +
x , mệnh đề nào dưới đây sai? 1 3ln x 1 2 2 2 2 2 2 A. 3 I = t . B. I = tdt . C. 2 I = t dt . D. I = . 14 9 1 3 3 9 1 1 Lời giải Chọn B. e 1+ 3ln x 2t dx I = dx , đặt t = + x 2 t =1+ 3 3ln x 2 d t t = dx dt = . 1 3ln x x 3 x 1
Đổi cận: x =1 t = ;
1 x = e t = 2 . 2 2 2 = 2 2 14 dt 3 = t = . t I 3 9 1 9 1
Câu 34. Cho tứ diện đều cạnh bằng a . Khoảng cách từ trọng tâm của mặt này đến một mặt khác bằng a 6 a 3 a 3 a 6 A. . B. . C. . D. . 3 9 6 9 Lời giải Chọn D.
Không mất tính tổng quát, gọi tứ diện là ABCD , ta tính khoảng cách
từ trọng tâm G của tam giác ADC đến mặt phẳng BCD.
Gọi H là trọng tâm các tam giác BCD , M là trung điểm CD . .
A BCD là hình chóp đều nên AH ⊥ (BCD) . GK MG 1
Kẻ GK / / AH , K BM thì GK ⊥ (BCD), = = AH MA 3 1 GK = AH . 3 2 a 3 a 6 1 6 Mà 2 2 AH = AB − BH 2 = a − = .Vậy d ( ,
G (BCD)) = GK = = a AH . 3 3 3 9
Câu 35. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x + y − z + 9 = 0 , đường thẳng x − 3 y − 3 z d : =
= và điểm A(1;2;− )
1 . Viết phương trình đường thẳng đi qua điểm A cắt 1 3 2
d và song song với mặt phẳng ( P) . Trang 36 x −1 y − 2 z +1 x −1 y − 2 z +1 A. = = . B. = = . 1 − 2 1 − 1 2 1 − x −1 y − 2 z +1 x − y − z + C. = = 1 2 1 . D. = = . 1 2 1 1 − 2 1 Lời giải Chọn A
Ta có một véc tơ pháp tuyến của mặt phẳng (P) là n = (1;1;− ) 1 .
Gọi B = d thì B(3+t;3+3t;2t) AB = (2 + t;3t +1;2t + ) 1 .
Do đường thẳng song song với mặt phẳng (P) nên ta có A . B n = 0
2 + t + 3t +1− 2t −1= 0 t = 1 − . Với t = 1 − thì AB = (1; 2 − ;− )
1 một véc tơ chỉ phương của đường thẳng là u = ( 1 − ;2 ) ;1 . − − +
Vậy phương trình đường thẳng x 1 y 2 z 1 là = = . 1 − 2 1 1 2
Câu 36. Tìm điểm M có hoành độ âm trên đồ thị (C) 3 : y = x − x +
sao cho tiếp tuyến tại M vuông 3 3 1 2
góc với đường thẳng y = − x + . 3 3 A. M ( 2 − ; 4 − ). B. M 1 − ; . C. M 2; . D. M ( 2 − ;0). 3 3 Lời giải Chọn D. Gọi 1 2 3
M x ; x − x + . 0 0 0 3 3 1 2
Do tiếp tuyến tại M vuông góc với đường thẳng y = − x + nên ta có hệ số góc của tiếp 3 3
tuyến tại M là k = 3. Ta có 2
y = x −1. Theo đề bài ta có phương trình 2 x −1 = 3 2
x = 4 x = 2 .
Theo đề bài điểm M có hoành độ âm nên M ( 2 − ;0). a 2 2 x + 2x + 2 a
Câu 37. Xác định số a dương sao cho dx =
+ a + ln 3. Giá trị của là a x +1 2 0 A. a = 1 . B. a = 2 . C. a = 3. D. a = 4 − . Lời giải Chọn B a 2 a x + 2x + 2 a 1 1 2 a Ta có dx = x +1+ dx 2 =
x + x + ln x +1 = + a + ln a +1 . x +1 x +1 2 2 0 0 0
Do a là số dương nên a = 2 .
Câu 38. Cho hàm số y = f ( x) có bảng biến thiên:
Tìm tất cả các giá trị của m để bất phương trình f ( x −1+ ) 1 m có nghiệm? A. m 1. B. m 2 − . C. m 4. D. m 0 . Lời giải Chọn B. Trang 37
Đặt x −1 +1 = t . Với x
1 thì x −1 +1 1 t . 1
Do đó bất phương trình f ( x −1+ )
1 m có nghiệm khi và chỉ khi bất phương trình f (t) m có nghiệm t 1.
Dựa vào bảng biến thiên ta có m 2 − .
Câu 39. Cho số phức z thỏa mãn điều kiện z −1+ 2i 2 . Trong hệ tọa độ Oxy , tập hợp điểm biểu
diễn số phức w = 3z − 2 + i , là hình tròn có diện tích bằng A. 25 . B. 16 . C. 36 . D. 9 . Lời giải Chọn C
Giả sử w = a + bi ( 2
a, b , i = − ) 1 .
w = 3( z −1+ 2i) +1− 5i w−1+ 5i = 3( z −1+ 2i) w −1+ 5i = 3 ( z −1+ 2i) w−1+ 5i 6 (a − )
1 + (b + 5)i 6 .
Vậy tập hợp số phức w = 3z − 2 + i là đường tròn có bán kính bằng 6 . Diện tích hình tròn là 2 6 = 36 .
Câu 40. Trong không gian với hệ tọa độ Oxyz , cho các điểm A(1;1;2) ; B( 3 − ;3;− ) 1 . Điểm
M ( x ; y ; z (Oxy) 2 2 MA + MB x 0 0 0 ) thuộc mặt phẳng sao cho
nhỏ nhất. Giá trị của là 0 A. 1. B. 1. − C. 2. D. 0. Lời giải Chọn B. Gọi điểm 1 I ( ; x ;
y z) thỏa mãn IA + IB = 0 I 1 − ;2;
là trung điểm AB . 2 2 2 Ta có 2 2
MA + MB = (MI + IA) + (MI + IB) 2 2 2
= 2MI + IA + IB + 2MI (IA+ IB) 2 2 2
= 2MI + IA + IB . Vì 2 2
IA + IB không đổi, suy ra 2 2
MA + MB nhỏ nhất khi và chỉ khi MI nhỏ nhất.
Khi đó M là hình chiếu vuông góc của I lên (Oxy) M ( 1 − ;2;0) x = 1 − . 0
Câu 41. Giả sử z , z là hai nghiệm phức của phương trình (2 + i) z z − (1− 2i) z = 1+ 3i và z − z = 1 1 2 1 2
. Tính M = 2z + 3z . 1 2 A. M = 19 . B. M = 25 . C. M = 5. D. M = 19 . Lời giải Chọn D
Từ giả thiết, ta có ( 2 2 2 2 z − )
1 + ( z + 2)i . z = 10
(2 z )1 ( z 2) − + + . z = 10 4 2
5 z + 5 z −10 = 0 z =1 (vì z 0).
Gọi z = x + y i và z = x + y i . Ta có z = z = 1 nên 2 2 2 2
x + y = x + y = 1. 1 1 1 2 2 2 1 2 1 1 2 2 Mặt khác, 2 2 1
z − z = 1 nên ( x − x + y − y =1 x x + y y = 1 2 ) ( 1 2) . Suy ra . 1 2 1 2 1 2 2 Khi đó 2 2
M = 2z + 3z = (2x + 3x + 2y + 3y 1 2 ) ( 1 2 ) 1 2 = 4( 2 2 x + y ) + 9( 2 2 y + y +12 x x + y y 1 1 1 2 ) ( 1 2 1 2 ) Vậy M = 19 . Trang 38
Câu 42. Cho hàm số y = f (x) liên tục trên đoạn 1 − ;
4 và có đồ thị hàm số y = f ( x) như hình bên.
Hỏi hàm số g ( x) = f ( 2 x + )
1 nghịch biến trên khoảng nào trong các khoảng sau? A. ( 1 − ; ) 1 . B. (0; ) 1 . C. (1; 4) . D. ( 3;4). Lời giải Chọn B.
Xét hàm số g ( x) = f ( 2 x + )
1 ta có g( x) = xf ( 2 2 x + ) 1 . x 0 f ( 2 x + ) 1 0
Hàm số g ( x) = f ( 2 x + )
1 nghịch biến g( x) 0 xf ( 2 x + ) 1 0 x 0 f ( 2 x + ) 1 0 x 0 x 0 2 1 x +1 4 2 x 3 0 x 3 . x 0 x 0 x − 3 2 x +1 4 2 x 3 Xét trên đoạn 1 − ;
4 ta có g( x) 0 0 x 3 hàm số g ( x) = f ( 2 x + ) 1 nghịch biến
trên khoảng (0; 3) hàm số g (x) = f ( 2 x + )
1 nghịch biến trên khoảng (0; ) 1
Câu 43. Một người vay ngân hàng 500 triệu đồng với lãi suất 1, 2% tháng để mua xe ô tô. Nếu mỗi
tháng người đó trả ngân hàng 10 triệu đồng và thời điểm bắt đầu trả cách thời điểm vay là đúng
một tháng. Hỏi sau ít nhất bao nhiêu tháng thì người đó trả hết nợ? Biết rằng lãi suất không thay đổi. A. 70 tháng. B. 80 tháng. C. 85 tháng. D. 77 tháng. Lời giải Chọn D
Đặt P = 500 triệu đồng và a =1,012 .
Tháng 1 người đó nợ aP , đã trả 10 triệu đồng nên còn nợ aP −10 . Tháng 2 người đó nợ 2
a P −10a , đã trả 10 triệu đồng nên còn nợ 2
a P −10a −10. …
Sau tháng n người đó còn nợ n n 1 a P 10a − − −...−10a −10.
Giả sử người đó trả hết nợ sau n tháng. Khi đó: n a − 5 n 5 n n 1 a P 10a − − −...−10a −10 = n 1 0 a P = 10.
a = n = log . a −1 2 1,012 2
Do đó cần ít nhất 77 tháng người đó trả hết nợ.
Câu 44. Cho tập X = 1;2;3;.......;
8 . Lập từ X số tự nhiên có 8 chữ số đôi một khác nhau. Xác suất để
lập được số chia hết cho 1111 là 2 2 2 A A A 4!4! 2 2 2 C C C 384 A. 8 6 4 . B. . C. 8 6 4 . D. . 8! 8! 8! 8! Lời giải Trang 39 Chọn D. Ta có:
Số các số tự nhiên có 8 chữ số đôi một khác nhau được lập từ X là: n() = 8!= 40320 .
Gọi A là biến cố lập từ X số tự nhiên có 8 chữ số đôi một khác nhau chia hết cho 1111
Gọi số tự nhiên có 8 chữ số cần tìm chia hết cho 1111có dạng: m = a a a a a a a a 1 2 3 4 5 6 7 8
Ta có: các số a khác nhau và a
a + a +...+ a =1+ 2 +...+ 8 = 36 i 1;2;3;4;5;6;7; 8 i 1 2 8
m là số chia hết cho 9
Do 1111 và 9 nguyên tố cùng nhau nên suy ra m 9999
Đặt x = a a a a và y = a a a a 1 2 3 4 5 6 7 8 4
m =10 x + y =10000x + y = 9999x +(x + y) chia hết cho 9999
(x + y)chia hết cho 9999
mà 0 x + y 9999 + 9999 = 2.9999
x + y = 9999
Do đó: a + a = a + a = a + a = a + a = 9 1 5 2 6 3 7 4 5 Vì a (1;8) (2;7) (3;6) (4;5) i 1;2;3;4;5;6;7;
8 nên ta có 4 cặp số thỏa điều kiện là: , , ,
Với mỗi cách chọn a luôn có b thỏa a + b = 9 i i i i
Vậy: a có 8 cách chọn. 1 a có 6 cách chọn. 2 a có 4 cách chọn. 3 a có 2 cách chọn. 4
Vậy các số thỏa yêu cầu là: 8.6.4.2 = 384 . n( A) = 384
Vậy xác suất biến cố A là: p ( A) 384 1 = = . 8! 105
Câu 45. Cho tứ diện ABCD có thể tích bằng 1. Gọi N, P lần lượt là trung điểm của BC,CD ; M là
điểm thuộc cạnh AB sao cho BM = 2AM . Mặt phẳng (MNP) cắt cạnh AD tại Q. Thể tích
của khối đa diện lồi MAQNCP là 7 5 7 5 A. . B. . C. . D. . 9 16 18 8 Lời giải Chọn C.
Gọi I = MN Ç AC , kẻ AK song song với BC . Trang 40 AK AM 1 AK 1
Tam giác MAK đồng dạng với tam giác MBN nên = = Þ = hay Alà trung NB BM 2 NC 2
điểm của IC . Suy ra M , Q lần lượt là trọng tâm các tam giác ICB , ICD. Khi đó 1 S = S d Q MAI = d D ABC MAI ABC ( ( )) 1 , , ( ,( )) 3 3 1 1 1 1 1 Ta có V = .d , Q MAI .S = . d , D ABC S = V = Q. AMI ( ( )) MAI ( ( )) . 3 9 3 ABC 9 ABCD 9 VI.QAM IQ IA IM 2 9 1 = . . = Þ V = V = I .PCN I . V IP IC IN 9 2 QAM 2 I .PCN Vậy 7 V = V - V = . MAQNCP I .PCN I .QAM 18
Câu 46. Trong không gian Oxyz , cho điểm E (2;1;3), mặt phẳng (P ): 2x + 2y - z - 3 = 0 và mặt 2 2 2
cầu (S ): (x - 3) + (y - 2) + (z - 5) = 36 . Gọi D là đường thẳng đi qua E , nằm trong
(P ) và cắt (S ) tại hai điểm có khoảng cách nhỏ nhất. Biết D có một vec-tơ chỉ phương r
u = (2018;y ;z
T = z - y . 0 0 ). Tính 0 0 A. T = 0 . B. T = - 2018 . C. T = 2018 . D. T = 1009. Lời giải Chọn C (S) I A H E B (P)
Mặt cầu (S ) có tâm I (3;2;5
) và bán kính R = 6. 2 2 2 IE = 1 + 1 + 2 =
6 < R Þ điểm E nằm trong mặt cầu (S . )
Gọi H là hình chiếu của I trên mặt phẳng (P ), A và B là hai giao điểm của D với (S .)
Khi đó, AB nhỏ nhất Û AB ^ HE , mà AB ^ IH nên A B ^ (HIE ) Þ AB ^ IE . uur éuur uur ù Suy ra: u = n ê ;EI = ú - = - D P (5; 5; ) 0 5(1; 1; ) 0 . ë û r
Suy ra u = (2018;- 2018;0), do đó T = z - y = 2018. 0 0
Câu 47. Một mặt bàn hình elip có chiều dài là 120cm , chiều rộng là là 60cm . Anh Phượng muốn gắn
đá hoa cương và dán gạch tranh trên mặt bàn theo hình (phần đá hoa cương bên ngoài và điểm
nhấn bên trong là bộ tranh gồm 2 miếng gạch với kích thước mỗi miếng là 25cm 40cm). Biết
rằng đá hoa cương có giá và bộ tranh gạch có giá 300.000 vnđ/bộ. Hỏi số tiền để gắn đá hoa
cương và dán gạch tranh theo cách trên gần nhất với số tiền nào dưới đây? Trang 41
A. 519.000 đồng.
B. 610.000 đồng.
C. 639.000 đồng.
D. 279.000 đồng. Lời giải Chọn A 2 2 x y
Gọi phương trình chính tắc của elip (E ) có dạng: + = 1 2 2 a b
ìï A A = 1,2 = 2a ìïa = 0,6 2 2 Với ï x y 1 1 2 ï í Û í Þ (E ) 2 : + = 1 Û y = ± 0, 36 - x .
ï B B = 0, 6 = 2b ïb = 0, 3 ï 0, 36 0, 09 2 1 2 î ïî
Suy ra diên tích của hình elip là: 0,6 0,6 1 2 2 S = 4 0, 36 - x dx = 2
0, 36 - x dx = 0,18p m ò ò E ( 2). ( ) 2 0 0
Gọi S ;S lần lượt là diện tích phần đá hoa cương và bộ tranh 1 2
Ta có: S = 2´ 0, 25 ´ 0, 4 = 0, ( 2 2 m S = S
- S = 0, 18p - 0, m E ( 2 2 1 2 ) 2 )Suy ra: . ( )
Gọi T là tổng chi phí. Khi đó ta cóT = (0,18p - 0,2).600000 + 300000 ; 519.000 (đồng).
Câu 48. Cho hàm số f (x ) có bảng xét dấu của đạo hàm như sau:
Hàm số y = f (- x + ) 3 2 3
2 + x + 3x - 9x nghịch biến trên khoảng nào dưới đây? A. (- ¥ ;- 2). B. (2;+ ¥ ). C. (0;2). D. (- 2; ) 1 . Lời giải Chọn D é ù Ta có y ¢= - f ( ¢ - x + ) 2 + x + x - = - f ( ¢ - x + )+ ( 2 3 2 3 6 9 3 2 x + 2x - ê ) 3 . Xét dấu của ú ë û
f (−x + 2) và 2
x + 2x - 3 ta có bảng: Trang 42
Suy ra hàm số nghịch biến trên khoảng (- 3; )
1 . Do đó ta chọn D
Câu 49. Có bao nhiêu giá trị của tham số m để hàm số 9 y = x + ( 2 m - m ) 5 x + ( 3 2 m - m + m ) 4 3 7 4
x + 2019 đồng biến trên ¡ ? A. 3 . B. 2 . C. 4 . D. 1 . Lời giải Chọn A Ta có 8 y ¢= x + ( 2 m - m ) 4 x + m ( 2 m - m + ) 3 9 5 4 3 7 4 x 3 é 5 ù = x x + m ê
(m - )x + m ( 2 9 5 1 4 3m - 7m + 4) 3 = x .g x ú ë û ( ) với g(x) 5 =
x + m (m - )x + m ( 2 9 5 1 4 3m - 7m + ) 4 . ìï m ¹ 0 ïïï Nếu ï 4 ï g ( ) 0 ¹ 0 Û í m ¹ . Thì y
¢ sẽ đổi dấu khi đi qua điểm x = 0 , do đó hàm số sẽ không ï 3 ïïïm ¹ 1 ïïî đồng biến trên ¡ .
Do đó để hàm số đồng biến trên ¡ một điều kiện cần là g ( ) 0 = 0 m é = 0 ê ê m ( 4 2 m 7m 4) 0 m ê Û - + = Û = . ê 3 êm ê = 1 êë Điều kiện đủ : Với m = 0 có 8
y ¢= 9x ³ 0, " x Î ¡ nên hàm số đã cho đồng biến trên ¡ . Với m = 1 có 8
y ¢= 9x ³ 0, " x Î ¡ nên hàm số đã cho đồng biến trên ¡ . 4 æ 20ö Với ç ÷ m = có 4 4 y ¢= x 9 ç x +
÷³ 0, " x Î ¡ nên hàm số đã cho đồng biến trên ¡ . ç ÷ 3 çè 9 ÷ ø m é = 0 ê ê Vậy với 4 m ê =
thì hàm số đã cho đồng biến trên ¡ . ê 3 êm ê = 1 êë
Câu 50. Cho hàm số ( ) 4 3 2
f x = ax + bx + cx + dx + m , (với , a , b , c ,
d m Î R ). Hàm số y = f ( ¢ x ) có
đồ thị như hình vẽ bên dưới: Trang 43
Tập nghiệm của phương trình f (x ) = m có số phần tử là: A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn C Ta có f ( ¢ x ) 3 2
= 4ax + 3bx + 2cx + d ( ) 1 .
Dựa vào đồ thị ta có f (
¢ x )= a (x - ) 1 (4x + ) 5 (x + ) 3 3 2
= 4ax + 13ax - 2ax - 15a (2) và a ¹ 0 . Từ ( 13 ) 1 và (2 ) suy ra b =
a , c = - a và d = - 15a . 3 æ 13 ö Khi đó: ç ÷
f (x ) = m Û 4 3 2
ax + bx + cx + dx = 0 Û 4 3 2 a x ç +
x - x - 15x ÷= 0 ç ÷ çè 3 ÷ø x é = 0 ê ê 5 4 3 2
Û 3x + 13x - 3x - 45x = 0 x ê Û = . ê 3 êxê = - 3 êë ìï 5 üï
Vậy tập nghiệm của phương trình ï ï
f (x ) = m là S = í ;0;- 3ý. ï 3 ï ïî ïþ -----HẾT----- ĐỀ 44
ĐỀ THI THỬ THPT QUỐC GIA 2020 MÔN TOÁN Thời gian: 90 phút
Câu 1. Thể tích của hình lập phương có cạnh bằng 2 là bao nhiêu? A. V = 6 . B. V = 8 . C. V = 4 . D. V = 16 .
Câu 2. Cho hàm số y = f ( x) xác định và liên tục trên
và có bảng biến thiên như sau. .
Mệnh đề nào sau đây ĐÚNG? Trang 44
A. Hàm số có cực đại tại x = 2 − .
B. Hàm số có cực tiểu tại x = 4 − .
C. Hàm số có giá trị cực tiểu bằng 0 .
D. Hàm số có giá trị cực đại bằng 2 − .
Câu 3. Trong không gian với hệ tọa độ Oxyz , cho hai điểm M (3;0;0) , N (0;0; 4) . Tính độ dài đoạn thẳng MN . A. MN = 1. B. MN = 7 . C. MN = 5 . D. MN = 10 .
Câu 4. Cho đồ thị hàm số y = f ( x) có đồ thị như hình vẽ. Hàm số y = f ( x) đồng biến trên khoảng nào dưới đây? A. ( 2 − ; 2) . B. ( ; − 0). C. (0; 2) . D. (2; + ) .
Câu 5. Cho các số thực a , m , n và a dương. Mệnh đề nào sau đây đúng? m m − − a − − a A. m n m a = a −n . B. m n a = . C. m n m n a = a −a . D. m n a = . n a n 9 9 9 Câu 6. Giả sử f
(x)dx =37 và g (x)dx = 1
− 6. Khi đó, I = 2 f
(x)+3g(x)dx bằng 0 0 0 A. I = 26 . B. I = 58 . C. I = 143 . D. I = 122 .
Câu 7. Một hình trụ có bán kính đáy r = a , độ dài đường sinh l = 2a . Tính diện tích xung quanh của hình trụ. A. 2 4 a . B. 2 2 a . C. 2 5 a . D. 2 6 a . x+
Câu 8. Tìm tập nghiệm S của phương trình 1 2 = 8 A. S = 1 .
B. S = − 1 . C. S = 4 . D. S = 2 .
Câu 9. Trong không gian Oxyz , cho hai điểm A(0; 1 − ; 2
− ) và B(2;2;2). Vectơ a nào dưới đây là một vectơ
chỉ phương của đường thẳng AB ?
A. a = (2;1;0) .
B. a = (2;3;4) . C. a = ( 2 − ;1;0).
D. a = (2;3;0) .
Câu 10. Tính = 3x I dx . 3x A. I = + C . B. = 3x I ln 3+ C . ln 3 C. = 3x I + C . D. = 3x I + ln3+C . Trang 45
Câu 11. Trong không gian Oxyz , cho mặt phẳng (P) : 2x − z + 5 = 0 . Một véc tơ pháp tuyến của ( P) là A. n 2; 0;1 n 2;1;5 n 2;0; 1 − n 2; 1 − ;5 3 ( ) 2 ( ) 1 ( ) 4 ( ). B. . C. . D. .
Câu 12. Trong khai triển ( + )n a b
, số hạng tổng quát của khai triển? − + − + − + − + + − − A. k 1 n 1 n k 1 C a b . B. k n k k C a b . C. k 1 n k 1 k 1 C a b . D. k n k n k C a b . n n n n
Câu 13. Công thức nào sau đây là đúng với cấp số cộng có số hạng đầu u , công sai d , n 2. ? 1
A. u = u + d .
B. u = u + n +1 d n 1 ( ) . n 1
C. u = u − n −1 d
u = u + n −1 d n 1 ( ) n 1 ( ) . D. .
Câu 14. Trong hình vẽ bên, điểm M biểu diễn số phức z . Số phức z là A. 2 − i . B. 1+ 2i . C. 1− 2i . D. 2 + i .
Câu 15. Đường cong bên là điểm biểu diễn của đồ thị hàm số nào sau đây 4 2 4 2
A. y = −x + 4x + 3 .
B. y = x − 2x + 3 . 3 4 2
C. y = −x + 3x + 3 .
D. y = −x + 2x + 3 . x +
Câu 16. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f ( x) 1 = trên đoạn 3; 5 . Khi x −1
đó M − m bằng 7 1 3 A. . B. . C. 2 . D. . 2 2 8 2 4
Câu 17. Cho hàm số f ( x) có đạo hàm là f ( x) = x ( x + ) 1 ( x − 2) x
. Số điểm cực tiểu của hàm số
y = f ( x) là A. 3 . B. 2 . C. 0 . D. 1. Trang 46
Câu 18. Cho số phức z thỏa mãn z (3+ 4i) −18 + i = 0 . Khi đó số phức z bằng 1 A. 6 − i . B. 2 − 3i . C. 2 + 3i . D. 2 − 1− 3i . 4
Câu 19. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A( 2 − ;1; ) 1 và B(0;−1; )
1 . Viết phương trình mặt
cầu đường kính AB . 2 2 2 2 A. ( x − ) 2 1 + y + (z + ) 1 = 2 . B. ( x + ) 2 1 + y + (z − ) 1 = 8 . 2 2 2 2 C. ( x + ) 2 1 + y + (z − ) 1 = 2 . D. ( x − ) 2 1 + y + (z + ) 1 = 8 .
Câu 20. Cho log 5 = a . Tính log 25000 theo a . A. 2a + 3. B. 2 5a . C. 2 2a +1. D. 5a .
Câu 21. Gọi z là nghiệm phức có phần ảo âm của phương trình 2
z + 2z + 2 = 0 . Tìm số phức liên hợp của 1
w = (1+ 2i) z . 1 A. w = 3 − −i .
B. w = 1− 3i .
C. w = 1+ 3i . D. w = 3 − + i .
Câu 22. Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng (P) : x + 2y − 2z + 3 = 0 , mặt phẳng
(Q): x−3y +5z −2 = 0. Cosin của góc giữa hai mặt phẳng (P), (Q) là 35 35 5 − A. . B. − 5 . C. . D. . 7 7 7 7
Câu 23. Tập nghiệm của bất phương trình log ( 2 x + 2 3 3 ) là: A. S = (− ; − 5 5;+ ) . B. S = . C. S = . D. P = 5 − ; 5 .
Câu 24. Cho ( H ) là hình phẳng giới hạn bởi đồ thị hàm số y = ln ( x + )
1 , đường thẳng y =1 và trục tung (phần tô đậm trong hình vẽ).
Diện tích của (H ) bằng A. e − 2 B. e −1 C. 1 D. ln 2 Trang 47
Câu 25. Cho tam giác SOA vuông tại O có OA = 3 cm , SA = 5 cm , quay tam giác SOA xung quanh cạnh SO
được hình nón. Thể tích của khối nón tương ứng là: 80 A. ( 3 12 cm ) . B. ( 3 15 cm ) . C. ( 3 cm ) . D. ( 3 36 cm ) . 3
Câu 26. Cho hàm số y = f ( x) có bảng biến thiên như sau
Đồ thị hàm số y = f ( x) có tổng số bao nhiêu tiệm cận (chỉ xét các tiệm cận đứng và ngang)? A. 2 . B. 0 . C. 1. D. 3 .
Câu 27. Cho hình lăng trụ tam giác đều AB . C A B C
có cạnh đáy bằng a . Góc giữa đường thẳng A B và mặt
phẳng ( ABC) bằng 45. Tính thể tích của khối lăng trụ AB . C A B C . 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 24 4 6 12
Câu 28. Đạo hàm hàm số 2
y = x (ln x − ) 1 là: 1 A. y = −1.
B. y = ln x −1. x C. y =1.
D. y = x (2ln x − ) 1 .
Câu 29. Cho hàm số y = f ( x) có đồ thị như hình vẽ bên. Số nghiệm của phương trình f ( x) +1 = 0 là A. 1. B. 3 . C. 4 . D. 2 . 6
Câu 30. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại đỉnh A , cạnh BC = a , = a AC các cạnh 3 a 3
bên SA = SB = SC =
. Tính góc tạo bởi mặt bên (SAB) và mặt phẳng đáy ( ABC). 2 Trang 48 A. . B. . C. . D. arctan 3 . 6 3 4
Câu 31. Tổng tất cả các nghiệm của phương trình log
3.2x −1 = 2x +1 2 ( ) bằng 3 1 A. . B. . C. 1 − . D. 0 . 2 2
Câu 32. Người ta cho vào một chiếc hộp hình trụ 3 quả bóng tennis hình cầu. Biết đáy hình trụ bằng hình tròn lớn
trên quả bóng và chiều cao hình trụ bằng ba lần đường kính quả bóng. Gọi S là tổng diện tích 3 quả bóng và S 1 2 S
là diện tích xung quanh của hình trụ. Tỉ số diện tích 1 là: S2 A. 5 . B. 1. C. 3 . D. 2 . x + x +
Câu 33. Cho F ( x) là nguyên hàm của hàm số f ( x) 2 1 =
và F (0) = 2018. Tính F ( 2 − ). x +1 A. F ( 2 − ) không xác định. B. F ( 2 − ) = 2 . C. F ( 2 − ) = 2018. D. F ( 2 − ) = 2020 .
Câu 34. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Tam giác SAB đều và nằm trong mặt phẳng
vuông góc với đáy. Gọi M , N lần lượt là trung điểm của AB , AD . Tính khoảng cách từ điểm D đến mặt
phẳng (SCN ) theo a . a 3 a 3 a 2 4a 3 A. . B. . C. . D. . 3 4 4 3 x = 1+ t
Câu 35. Trong không gian Oxyz , đường vuông góc chung của hai đường thẳng d : y = 0 và z = −5+t x = 0
d : y = 4 − 2t có phương trình là z = 5+3t x − 4 y z + 2 x − 4 y z − 2 A. = = . B. = = . 1 − 3 1 2 3 − 2 − x + 4 y z − 2 x − 4 y z + 2 C. = = . D. = = . 2 − 3 2 2 − 3 2 2 x
Câu 36. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y =
− mx + ln (x − ) 1 đồng biến trên 2 khoảng (1;+) ? A. 3 . B. 4 . C. 2 . D. 1. Trang 49
Câu 37. Cho số phức z thỏa mãn ( z − 2 + i)( z − 2 − i) = 25 . Biết tập hợp các điểm M biểu diễn số phức
w = 2z − 2 + 3i là đường tròn tâm I ( ;
a b) và bán kính c . Giá trị của a + b + c bằng A. 17 . B. 20 . C. 10 . D. 18 . e 3 + ln x a − b c Câu 38. Biết dx =
, trong đó , , là các số nguyên dương và c . Tính giá trị a b c 4 x 3 1
S = a + b + c . A. S = 13 B. S = 28 C. S = 25 D. S = 16
Câu 39. Tất cả các giá trị của m để bất phương trình (3
+1)12x + (2 − )6x + 3x m m
0 có nghiệm đúng x 0 là: 1 1 A. ( 2; − +). B. − ; − . C. 2; − − . D. (− ; 2 − ]. 3 3
Câu 40. Cho một đa giác đều gồm 2n đỉnh (n 2, n ) . Chọn ngẫu nhiên ba đỉnh trong số 2n đỉnh của đa 1
giác, xác suất ba đỉnh được chọn tạo thành một tam giác vuông là . Tìm n 5 A. n = 5 . B. n = 4 . C. n = 10 . D. n = 8 .
Câu 41. Trong không gian với hệ tọa độ Oxyz , cho ( A −1; 2; 1) , (
B 2; −1; 3) , C( 3; 5; −1) . Điểm M( ; a ; b ) c
trên mặt phẳng (Oyz) sao cho MA + 2MB − CM đạt giá trị nhỏ nhất. Khi đó ta có 2b + c bằng A. 1 − . B. 4 . C. 1. D. 4 − .
Câu 42. Cho số phức z có z = 2018. Diện tích của đa giác có các đỉnh là các điểm biểu diễn của z và các 0 0 0 1 1 1
nghiệm của phương trình = +
được viết dạng n 3 , n
. Chữ số hàng đơn vị của n là z + z z z 0 0 A. 9 B. 8 C. 3 D. 4
Câu 43. Cho hàm số f ( x) có đồ thị (C ) như hình vẽ. 5
Tìm số nghiệm thuộc − ;
của phương trình f (2sin x + 2) =1? 6 6 A. 2 . B. 3 . C. 1. D. 0 . Trang 50
Câu 44. Ông Trung vay ngân hàng 800 triệu đồng theo hình thức trả góp hàng tháng trong 60 tháng. Lãi suất
ngân hàng cố định 0,5 /tháng. Mỗi tháng ông Trung phải trả (lần đầu tiên phải trả là 1 tháng sau khi vay) số tiền
gốc là số tiền vay ban đầu chia cho 60 và số tiền lãi sinh ra từ số tiền gốc còn nợ ngân hàng. Tổng số tiền lãi mà
ông Trung phải trả trong toàn bộ quá trình trả nợ là bao nhiêu?
A. 118.000.000 đồng.
B. 126.066.666 đồng.
C. 122.000.000 đồng.
D. 135.500.000 đồng.
Câu 45. Trong không gian với hệ tọa độ Oxyz, gọi d đi qua điểm A(1; 1 − ;2), song song với ( x + y − z
P) : 2x − y − z + 3 = 1 1
0 , đồng thời tạo với đường thẳng : =
= một góc lớn nhất. Phương trình 1 2 − 2
đường thẳng d là x −1 y +1 z − 2 x −1 y +1 z + 2 A. = = . B. = = . 1 5 − 7 4 5 − 7 x −1 y +1 z − 2 x − y + z − C. = = 1 1 2 . D. = = . 4 5 7 1 5 − 7 −
Câu 46. Trong đợt hội trại “Khi tôi 18 ” được tổ chức tại trường THPT X, Đoàn trường có thực hiện một dự án ảnh
trưng bày trên một pano có dạng parabol như hình vẽ. Biết rằng Đoàn trường sẽ yêu cầu các lớp gửi hình dự thi và
dán lên khu vực hình chữ nhật ABCD , phần còn lại sẽ được trang trí hoa văn cho phù hợp. Chi phí dán hoa văn là 200.000 đồng cho một 2
m bảng. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên pano sẽ là bao nhiêu (làm
tròn đến hàng nghìn)? A B 4 m D C 4 m A. 900.000 đồng. B. 1.232.000 đồng. C. 902.000 đồng. D. 1.230.000 đồng.
Câu 47. Cho tứ diện ABCD và các điểm M , N , P lần lượt thuộc các cạnh BC , BD , AC sao cho
BC = 4BM , AC = 3AP , BD = 2BN . Tính tỉ số thể tích hai phần của khối tứ diện ABCD được phân chia bởi mp(MNP) . 7 7 8 8 A. . B. . C. . D. . 13 15 15 13
Câu 48. Cho hàm số y = f ( x) có đồ thị của hàm số y = f ( x) được cho như hình bên. Hàm số
y = − f ( − x) 2 2 2
+ x nghịch biến trên khoảng Trang 51 y 3 1 O 2 3 −1 4 5 x −2 A. ( 3 − ; − 2). B. ( 2 − ; − ) 1 . C. ( 1 − ; 0). D. (0; 2) .
Câu 49. Tìm m để bất phương trình x + 2 (2 − x)(2x + 2) m + 4( 2 − x + 2x + 2) có nghiệm? A. m 8 − . B. m 1 − − 4 3 . C. m 7 − . D. 8 − m 7 − . Câu 50. Cho hàm số = ( ) 4 2 y
f x = ax + bx + c biết a 0 , c 2017 và a + b + c 2017 . Số cực trị của hàm số
y = f ( x) − 2017 là A. 1. B. 7 . C. 5 . D. 3 . HẾT Trang 52
ĐÁP ÁN VÀ LỜI GIẢI Câu Lời giải Đáp án 1 B 2 A 3 C 4 C 5 A 6 A 7 D 8 B 9 A 10 A 11 C 12 B 13 D 14 A 15 D Lời giải Chọn B 2 −
Ta có f ( x) = 0, x 3;5 2 do đó: (x − ) 16 1 B 3
M = max f ( x) = f (3) = 2 ; m = min f ( x) = f (5) = 3; 5 3; 5 2 3 1
Suy ra M − m = 2 − = . 2 2 Lời giải Chọn D
f ( x) = 0 x ( x + )2 1 ( x − 2)4 17 Ta có
= 0 . Do x = 0 là nghiệm đơn, còn các nghiệm D x = 1
− và x = 2 là các nghiệm bội chẵn nên chỉ có x = 0 là nghiệm mà f (x) đổi dấu từ
“âm” sang “dương” theo chiều từ trái sang phải. Do đó x = 0 là điểm cực tiểu duy nhất của hàm số đã cho. 18 Lời giải B Trang 53 Chọn B −i Ta có z ( + i) 18
3 4 −18 + i = 0 z = = 2 −3i . 3 + 4i Lời giải Chọn C
Theo đề ta có mặt cầu đường kính AB có tâm là trung điểm I ( 1 − ;0; ) 1 của AB và bán 19 C AB kính R = = 2 . 2 Nên phương trì 2 2
nh mặt cầu là: ( x + ) 2
1 + y + ( z − ) 1 = 2. Lời giải Chọn 20 A A Ta có: log 25000 = ( 2 3
log 5 .10 ) = 2log5+3log10 = 2a + 3. Lời giải Chọn C 21 C z = 1 − + i 2
Ta có z + 2z + 2 = 0 z = 1 − − i . 1 z = 1 − − i
Do đó, w = (1+ 2i) z = 1+ 2i 1 − −i = 1 − + 2 + 1
− − 2 i =1−3i w =1+3i 1 ( )( ) ( ) ( ) . Lời giải Chọn A
Ta có véc tơ pháp tuyến của mặt phẳng (P) là n = (1;2; 2 − P
) , véc tơ pháp tuyến của
mặt phẳng (Q) là n = (1; 3 − ;5 Q ) . 22 A
Gọi là góc giữa hai mặt phẳng (P) , (Q) ta có n .n 1.1+ 2.( 3 − ) − P Q 2.5 15 cos = = = 35 = . n n 1 + 2 + ( 2 − )2 1 + ( 3 − )2 2 2 2 2 + 3 35 7 P Q 5 Lời giải 23 Chọn D D Ta có: log ( 2 x + 2 3 2 x + 2 27 2 x 25 5 − x 5 3 ) . Lời giải Chọn C 24 C
Phương trình hoành độ giao điểm của hàm số y = ln (x + )
1 và đường thẳng y =1 là ln ( x + ) 1 = 1 x = e −1. Trang 54 e 1 −
Diện tích của (H ) là S = ln ( x + ) 1 dx . 0 u = (x + ) 1 ln 1 du = dx Đặt x +1 . Khi đó dv = dx v = x +1 e 1 − − S = ( x + ) 1 ln ( x + ) e 1 1 − dx = e − (e− ) 1 = 1. 0 0 Lời giải Chọn A S 25 A O A 2 2 1 1
SO = SA − OA = 4 ; 2 V = r h 2 = .3 .4 =12 ( 3 cm ). 3 3 Lời giải Chọn A
Dựa vào BBT ta thấy lim y = − ; lim y = + nên đồ thị hàm số có 1 tiệm cận đứng là + − x 1 → x 1 → 26 x = 1 . A lim y = 1
− nên đồ thị hàm số có 1 tiệm cận ngang là y = 1 − . x→−
Vậy đồ thị hàm số có 2 tiệm cận. Lời giải Chọn B 27 B
Theo giả thiết, ta có AA ⊥ ( ABC) BA là hình chiếu vuông góc của A B trên ( ABC) Trang 55
Góc giữa đường thẳng A B
và mặt phẳng ( ABC) là ABA = 45 Do ABA
vuông cân tại A AA = AB = a 3 a 3
Vậy thể tích của khối lăng trụ AB . C A B C .là V = . 4 Lời giải Chọn D 28 D 1 Ta có 2
y = x (ln x − )
1 y = 2x (ln x − ) 2 1 + x . = x(2ln x − ) 1 . x Lời giải Chọn B 29 B
Giả sử hàm số y = f ( x) có đồ thị (C ) .
Ta có: f ( x) +1 = 0 f ( x) = 1
− là phương trình hoành độ giao điểm của (C) và đường
thẳng d : y = 1
− . Do đó số nghiệm của phương trình chính là số giao điểm của (C) và (d ) .
Dựa vào đồ thị hai hàm số ta có (C ) và (d ) có 3 điểm chung nên phương trình có 3 nghiệm. Lời giải Chọn B a 3
Vì SA = SB = SC =
nên hình chiếu của S trùng với H là tâm đường tròn ngoại tiếp 2
đáy ABC . Nhận xét H là trung điểm BC . S 30 B C A M H B
Gọi M là trung điểm AB , nhận xét AB ⊥ (SMH ) nên góc tạo bởi mặt bên (SAB) và mặt Trang 56
phẳng đáy ( ABC) là góc SMH . a 2
Xét tam giác SBH có 2 2 SH = SB − BH = . 2 a 2 SH
Xét tam giác SMH có 2 tan M = = = 3 o M = 60 . MH a 6 6 Lời giải Chọn C
Điều kiện 3.2x . 1 31 + Ta có log
3.2x −1 = 2x +1 x x x − = − = ( x )2 2 1 3.2 1 2 3.2 1 2. 2 2 ( ) C 2x =1 x = 0 S = 1 − . x 1 2 = x = 1 − 2 Chọn B
Giả sử bán kính quả bóng tennis là r khi đó bán kính hình trụ là r và đường cao của hình trụ là 6r .
Tổng diện tích ba quả bóng là: 2 2
S = 3.4 r = 12 r . 32 1 B
Diện tích xung quanh của hình trụ là: 2
S = 2 r.6r = 12 r . 2 S Suy ra: 1 = 1 . S2 Lời giải Chọn D x + x + x 33 Ta có F ( x) 2 2 1 1 = dx = x + dx = + ln x +1 + C . D x +1 x +1 2 2 x
Theo bài ra F (0) = C = 2018, nên F ( x) =
+ ln x +1 + 2018 F (−2) = 2020 . 2 34 Lời giải C Chọn C Trang 57 a 3
M là trung điểm của AB thì SM ⊥ ( ABCD) . Ta có SM = . 2 ID
Gọi I là giao điểm của NC và MD . Ta có d ( ; D (SCN )) =
d (M ;(SCN )). IM
Vì ABCD là hình vuông nên NC ⊥ DM tại I . I .
D CN = DN.DC a .a DN.DC a 5 2 a a a ID = = = 5 5 3 5
IM = DM − ID = − = CN a 5 5 2 5 10 2 ID 2 = . IM 3 IM ⊥ CN Do
CN ⊥ (SMI ) . Kẻ MH ⊥ SI , vì CN ⊥ MH nên MH ⊥ (SCN ) C N ⊥ SM
MH = d (M;(SCN)). 1 1 1 4 20 32
Trong tam giác SMI có = + = + = . 2 2 2 MH SM MI 2 2 2 3a 9a 9a 3a 2 a Vậy MH =
d (D (SCN )) 2 ; = . 8 4 Lời giải Chọn D
Giả sử AB là đường vuông góc chung của d và d với A d , B d . Ta có u = u = − (0; 2;3 d ) d (1;0 ) ;1 , , A
(a +1;0;a − 5)
BA = (a +1;2b − 4;a −3b −10) . B (0;4 − 2 ; b 3b + 5) 35 D d ⊥ AB u .BA = 0 ( a + )
1 + (a − 3b −10) = 0 a = 3 Khi đó d d ⊥ AB u = − − + − − = = − .BA 0
2(2b 4) 3(a 3b 10) 0 b 1 d A(4;0; 2 − ) BA = (4; 6 − ; 4 − ) u = ( 2
− ;3;2) là một VTCP của AB . B (0;6;2) x − 4 y z + 2
Kết hợp với AB qua A(4;0; 2 − ) AB : = = . 2 − 3 2 Lời giải 36 A Chọn A Trang 58 1
Ta có y = x − m + . x −1 2 Để hàm số x y =
− mx + ln (x − )
1 đồng biến trên khoảng (1;+) thì y 0 với 2 x (1;+) 1 x + m với x
(1;+) m min f (x) . x −1 (1;+)
Xét hàm số f ( x) 1 = x +
trên khoảng (1;+) ta có x −1 f ( x) 1 = x − + + (x − ) 1 1 1 2 1
+1 3 min f (x) = 3. Do m + nên x −1 (x − ) 1 (1;+) m1;2; 3 . Lời giải Chọn D
Giả sử z = a + bi ( ;
a b ) và w = x + yi ( ; x y ).
(z −2+i)(z −2−i) = 25 a−2+ (b+ )
1 i a − 2 − (b+ ) 1 i = 25
(a − )2 + (b + )2 2 1 = 25 ( ) 1 Theo giả thiết:
w = 2z − 2 + 3i x + yi = 2(a − bi) − 2 + 3i x + yi = 2a − 2 + (3− 2b)i . 37 D x + 2 a = x = 2a − 2 2 (2) . y = 3− 2b 3 − y b = 2 2 2 x + 2 3− y 2 2 Thay (2) vào ( ) 1 ta được: − 2 + +1 = 25
(x −2) +( y −5) =100. 2 2
Suy ra, tập hợp điểm biểu diễn của số phức w là đường tròn tâm I (2;5) và bán kính R = 10 .
Vậy a + b + c =17 . Lời giải Chọn C 38 x C Đặt t = 3 + d ln x 2 d t t = . x
Đổi : Với x = 1 t = 3 ; x = e t = 2 . Trang 59 e 3 + ln x 2 − 2 I = dx 2 = 2 t dt = 16 6 3 t = . 2 3 x 3 3 3 1 3
a =16 , b = 6, c = 3 S = a + b + c = 25. Lời giải Chọn D
Đặt 2x = t . Do x 0 t 1. Khi đó ta có : 2
(3m+1) t + (2 − m) t+1 0, t 1 . 2 t − − 2t −1 2 2
(3t − t) m − t − 2t −1 t 1 m t 1. 2 3t − t 2 t − − 2t −1 2 7t + 6t −1
Xét hàm số f (t) =
trên 1; + f '(t) = 0 t (1;+) 2 ( ) . 2 2 39 3t − t (3 t − t) D BBT. .
Do đó m lim f (t) = 2
− thỏa mãn yêu cầu bài toán. + t 1 → Lời giải Chọn D
Ta có một đa giác đều 2n cạnh có n đường chéo đi qua tâm. Ta lấy hai đường chéo thì tạo
thành một hình chữ nhật. Mỗi một hình chữ nhật sẽ có bốn tam giác vuông. Vậy số tam giác 4.n!
vuông tạo thành từ đa giác đều 2n đỉnh là 2 4.C = = 2n n −1 , n 2 ( ! n − 2) ( ) ! 40 D 2n ! 2 .
n 2n −1 2n − 2 3 ( ) ( )( )
Không gian mẫu là: C = = , 2n 3 ( ! 2n − 3)! 6 12n (n − ) 1 3 Xác suất là: P = = , 2n (2n − ) 1 (2n − 2) (2n− ) 1 1 3 1 Theo bài ra thì P =
= 15 = 2n −1 n = 8 . 5 2n −1 5 Lời giải 41 B Chọn B Trang 60
Gọi G là trọng tâm tam giác ABC .
MA + 2MB − CM = MA + MB + MC + MB = 3MG + MB
Nên MA + 2MB − CM = 3MG + MB = 3MN + MN + 3NG + NB
Gọi N là điểm thỏa 3NG + NB = 0 nên 3MG + MB = 4MN .
Để MA + 2MB − CM đạt giá trị nhỏ nhất thì 4MN đạt giá trị nhỏ nhất hay M là hình
chiếu của N lên mặt phẳng (Oyz) . 4
Tọa độ trọng tâm của tam giác ABC là: G ; 2; 1 . 3 1 x = x + x N (3 G B ) 3
(x − x + x − x = 4 G N ) ( B N ) 0 1
3NG + NB = 0 3
( y − y + y − y = y = y + y N (3 G B ) G N ) ( B N ) 0 4 3( z − z + z − z = G N ) ( B N ) 0 1 z = z + z N (3 G B ) 4 1 4 3 x = 3. + 2 = N x 4 3 N 2 1 5 3 5 3 5 3 y = − y = N ; ; M 0; ; N (3.2 ) 1 nên . Vậy tọa độ điểm N 4 4 2 4 2 4 2 1 3 z = + z = N (3.1 3) 4 N 2
hay 2b + c = 4 . Lời giải Chọn C z 0 Điều kiện: z 0 0 1 1 1 Ta có: = + .z z
= z + z z + z + z z 2 2
z + z.z + z = 0 0 ( 0 ) 0 ( 0 ) 0 0 z + z z z 0 0 0 42 C 2 z z z 1 3 1 3 + +1 = 0 = −
i z = −
i z = z z z 0 1,2 z 2 2 2 2 0 0 0 1 3
Ta có: z = z = −
i z = z = 2018 và z + z + z = 0. 1 2 0 2 2 0 0 1 2
Do đó z , z , z được biểu diễn bởi ba điểm M , M , M tạo thành một tam giác đều nằm 0 1 2 0 1 2
trên đường tròn tâm O bán kính R = 2018. Trang 61 3
Tam giác đều này có chiều cao: h = 2
R và độ dài cạnh: a = 2 3 .h = . R = 3.R 2 3 3 2 1 2 3R 2 3.2018
Diện tích tam giác: S = . a h = . 3 = . 3 = 3054243. 3 . 2 4 4
Vậy n = 3054243 có chữ số hàng đơn vị là 3. Lời giải Chọn D 1
Đặt t = 2sin x + 5 2 , x − ; t − ;1 . 6 6 2 43
Phương trình f (2sin x + 2) =1 f (t) =1. D
Từ đồ thị hàm số f ( x) ta suy ra phương trình f (t) = 1
1 không có nghiệm t − ;1 . 2 5
Vậy số nghiệm thuộc − ;
của phương trình f (2sin x + 2) =1 là 0 . 6 6 Lời giải Chọn C
Gọi số tiền gốc ban đầu là N và phần trăm lãi là r .
Tháng thứ nhất ông Trung phải trả số tiền lãi là: N.r . 59
Tháng thứ hai ông Trung phải trả số tiền lãi là: N.r . 60 58
Tháng thứ ba ông Trung phải trả số tiền lãi là: N.r . 60 ... 44 1 C
Tháng thứ sáu mươi ông Trung phải trả số tiền lãi là: N.r . 60
Tổng số tiền lãi mà ông Trung phải trả trong suốt quá trình lãi là: 59 58 1 N.r + .N.r + .N.r + ... + 59 58 1 .N.r = 1+ + +...+ N.r 60 60 60 60 60 60 60.(60 + ) 1 = 1+ N.r 2.60 61 = .800.0,5% = 122.000.000 . 2
Vậy tổng số tiền lãi mà ông Trung phải trả trong toàn bộ quá trình trả nợ là 122.000.000 đồng. 45 Lời giải A Trang 62 Chọn A
có vectơ chỉ phương a = − (1; 2;2)
d có vectơ chỉ phương a = ( ; a ; b c d )
(P) có vectơ pháp tuyến n = − − P (2; 1; ) 1
Vì d / / ( P) nên a ⊥ n a .n = 0 2a − b − c = 0 c = 2a − b d P d P a − b a − b cos ( , d ) 5 4 1 (5 4 )2 = = 2 2 2 2 − + 3 5a − 4ab + 2 3 5 4 2 b a ab b a 1 5t − 4 Đặt t = , ta có: cos (, d ) ( )2 = b 2 3 5t − 4t + 2 5t − 4
Xét hàm số f (t ) ( )2 = , ta suy ra được: f (t ) 1 5 3 max = f − = 2 5t − 4t + 2 5 3 a Do đó: ( d) 5 3 1 1 max cos , = t = − = − 27 5 b 5
Chọn a =1 b = 5 − ,c = 7 x −1 y +1 z − 2
Vậy phương trình đường thẳng d là = = . 1 5 − 7
Hướng dẫn giải Chọn C
Đặt hệ trục tọa độ như hình vẽ, khi đó phương trình đường parabol có dạng: 2
y = ax + b . y 4 A B 4 m x O 46 D C C 2 − 4 m 2
Parabol cắt trục tung tại điểm (0;4) và cắt trục hoành tại (2;0) nên: b = 4 a = −1 . 2 . a 2 + b = 0 b = 4
Do đó, phương trình parabol là 2 y = −x + 4 .
Diện tích hình phẳng giới hạn bởi đường parabol và trục hoành là: Trang 63 2 2 3 x 32 S = ( 2
−x + 4 d x = − + 4x = 1 ) . 3 3 2 − 2 −
Gọi C (t;0) B ( 2
t; 4 − t ) với 0 t 2 .
Ta có CD = 2t và 2
BC = 4 − t . Diện tích hình chữ nhật ABCD là S = . CD BC = t ( 2 2 . 4 − t ) 3 = 2 − t +8t . 2
Diện tích phần trang trí hoa văn là: 32 32
S = S − S = − ( 3 2 − t + 8t) 3 = 2t −8t + . 1 2 3 3 32
Xét hàm số f (t) 3 = 2t −8t + với 0 t 2 . 3 2 t = (0;2) 3 Ta có f (t ) 2 = 6t −8 = 0 . 2 t = − (0;2) 3 Bảng biến thiên: 96 − 32 3
Như vậy, diện tích phần trang trí nhỏ nhất là bằng 2
m , khi đó chi phí thấp nhất 9 96 − 32 3
cho việc hoàn tất hoa văn trên pano sẽ là: .200000 902000 đồng. 9 Lời giải 47 A Chọn A Trang 64 A P Q K E B N D C
Gọi E = MN CD , Q = EQ AD , do đó mặt phẳng (MNP) cắt tứ diện ABCDtheo
thiết diện là tứ giác MNQP . 1
Gọi I là trung điểm CD thì NI CB và NI = BC , do BC = 4BM nên suy ra 2 2 EN EI NI NI = 2 MC . Bởi vậy = = = . 3 EM EC MC 3 EI 2 ED
Từ I là trung điểm CD và = 1 suy ra = . EC 3 EC 3 EK KD ED
Kẻ DK AC với K 1 EP , ta có = =
= . Mặt khác AC = 3AP nên suy ra EP AC EC 3 KD 2 = QD QK KD 2 . Do đó = = = . AP 3 QA QP AP 3 QK 2 EK EQ Từ = 1 và = 3 suy ra = . QP 3 EP 3 EP 5
Gọi V là thể tích khối tứ diện ABCD , V là thể tích khối đa diện ABMNQP , V là thể 1 2
tích khối đa diện CDMNQP . S CM CP 3 2 1 1 Ta có CMP = . = . = S = S . S CB CA 4 3 2 CMP 2 CAB C AB ED 1 3 Vì
= nên d (E;( ABC)) = d ( ;
D ( ABC)) . Do đó : EC 3 2 1 1 1 3 3 1 3 V = S .d E; ABC = . S . .d ; D ABC = . S .d ; D ABC = V E.CMP C MP ( ( )) C AB ( ( )) C AB ( ( )) 3 3 2 2 4 3 4 . VE.DNQ ED EN EQ 1 2 3 2 = 2 2 3 1 . . = . . = , nên suy ra V = V = . V = V . V EC EM EP 3 3 5 15 E.DNQ E. 15 CMP 15 4 10 E.CMP 3 1 13
Từ đó ta có V = V −V = V − V = V . 2 E.CMP E.DNQ 4 10 20 Trang 65 13 7
Và V = V −V = V − V = V . 1 2 20 20 V 7 Như vậy : 1 = V 13 2 Lời giải Chọn C y = 2 − f (2− x) 2 +
y = −(2 − x) 2 f (2 − x) + 48 Ta có x 2x C
y = 2 f (2 − x) + 2x y 0 f (2 − x) + x 0 f (2 − x) (2 − x) − 2 .
Dựa vào đồ thị ta thấy đường thẳng y = x − 2 cắt đồ thị y = f (x) tại hai điểm có hoành độ 1 x 2 nguyên liên tiếp là 1
và cũng từ đồ thị ta thấy f (x) x − 2 trên miền 2 x 3 x = 3 2
nên f (2 − x) (2 − x) − 2 trên miền 2 2 − x 3 1 − x 0 .
Vậy hàm số nghịch biến trên khoảng (−1; 0) . Lời giải. Chọn C •
Điều kiện: x 1 − ;2.
Xét hàm số g ( x) = 2 − x + 2x + 2 trên đoạn 1 − ; 2 . Có g( x) 1 1 = − +
, g( x) = 0 x =1. 2 2 − x 2x + 2 49 C g (− ) 1 = 3 , g ( ) 1 = 3 , g (2) = 6 .
Suy ra max g ( x) = 3 , min g ( x) = 3 . 1 − ;2 1 − ;2 •
Đặt t = 2 − x + 2x + 2 , t 3;3 2
t = x + 4+ 2 2− x 2x + 2 . ( )( )
Bất phương trình đã cho trở thành: 2
t − 4 m + 4t 2
t −4t −4 m .
Xét hàm số f (t) 2
= t − 4t − 4 trên đoạn 3;3 . Trang 66
Có f (t ) = 2t − 4 , f (t ) = 0 t = 2 . f ( 3) = 4 − 3 −1, f (2) = 8 − , f ( ) 3 = 7 − .
Suy ra max f (t ) = 7 − . 3;3
Để bất phương trình đã cho có nghiệm thì m max f (t ) hay m 7 − . 3;3 Vậy m 7 − . Lời giải Chọn B Hàm số = ( ) 4 2 y
f x = ax + bx + c xác định và liên tục trên D = .
Ta có f (0) = c 2017 0 . f (− ) 1 = f ( )
1 = a + b + c 2017 Do đó f (− ) 1 − 2017 . f
(0) − 2017 0 và f 1 − 2017. f 0 − 2017 0 ( ) ( )
Mặt khác lim f (x) = + nên
0, 0 sao cho f () 2017, f ( ) 2017 x→ f
( ) − 2017. f (− )
1 − 2017 0 và f − 2017 . f 1 − 2017 0 ( ) ( ) 50 B
Suy ra đồ thị hàm số y = f (x) − 2017 cắt trục hoành tại bốn điểm phân biệt
Đồ thị hàm số y = f ( x) − 2017 có dạng
Vậy số cực trị của hàm số y = f ( x) − 2017 là 7 . ĐỀ 45
ĐỀ THI THỬ THPT QUỐC GIA 2020 Trang 67 MÔN TOÁN Thời gian: 90 phút 3 2
Câu 1: Hàm số y = x − 3x + 7 có tất cả bao nhiêu cực trị? A. 2. B. 3. C. 1. D. 0. 5
Câu 2: Tiệm cận ngang của đồ thị hàm số y =
là đường thẳng có phương trình nào? x −1 A. y = 5. B. x = 0. C. x = 1. D. y = 0.
Câu 3: Điểm cực tiểu của đồ thị hàm số y = −x3 + x2 + 5x − 5 là 5 æ 40ö A. (−1; −8). B. (0; −5). C.ç ; ÷ ç ÷. D. (1; 0). çè3 27÷ø
Câu 4: Cho hàm số y = f(x) có bảng biến thiên như sau: x -∞ 0 2 +∞ y' - 0 + 0 - +∞ 0 y -4 -∞
Bảng biến thiên trên là của hàm số nào sau đây? 3 3 2 3 2 3 2
A. y = - x - 4 . B. y = x - 3x - 4 . C. y = - x + 3x - 4 . D. y = - x + 3x - 2 . 4 6 4 Câu 5: Biến đổi 3 P = x
x với x > 0 thành dạng lũy thừa với số mũ hữu tỉ, ta được 4 4 2 A. 9 P = x . B. 3 P = x . C. P = x. D. P = x . 3x 1 −
Câu 6: Tính số nghiệm của phương trình 2. 5 =10. A. 0. B. 2. C. 1. D. 3.
Câu 7: Tìm họ nguyên hàm của hàm số f(x) = sin 5x. A. f(x)dx = 5 − cos5x + C. B. = + f(x)dx 5cos5x C. 1 C. f(x)dx = − cos5x + C. D. 1 f(x)dx = − cos5x + C. 5 5 4
Câu 8: Trong các hàm số dưới đây, hàm số nào là nguyên hàm của f(x) = − 5? 1− 3x 4 − A. ln |1− 3x | 5 − x. B. 4ln |1− 3x | 5 − x. 3 4 − C. ln |1− 3x | .
D. 4ln |1− 3x|. 3
Câu 9: Điểm nào sau đây biểu diễn cho số phức z = 2i −1 trên mặt phẳng Oxy? Trang 68 A. M(1; -2). B. M(2; -1). C. M(1; 2). D. M(-1; 2).
Câu 10: Tính thể tích V của khối lăng trụ có chiều cao bằng 4 và diện tích đáy bằng 3. A. V = 6. B. V = 4. C. V = 12. D. V = 2.
Câu 11: Số mặt phẳng đối xứng của hình chóp tứ giác đều S.ABCD là A. 2. B. 6. C. 7. D. 4.
Câu 12: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): −x + 2y − 3z +17 = 0 . Vectơ nào dưới đây là
một vectơ pháp tuyến của mặt phẳng (P)? A. n = (3; 2 − ;1). B. n = (1; 2;3) . C. n = (1; 2 − ;3). D. n = ( 1 − ;2; 3 − ) .
Câu 13: Cho hai vectơ a = (1; −1; 2) và b = (0; 2; ) 1 . Tính v = a + 2b . A. v = (1;3; 4) . B. v = (1;1;3) . C. v = (1; 3 − ;1) . D. v = (2;3;5) . x = 2 + 3t
Câu 14: Trong không gian với hệ tọa độ vuông góc Oxyz, cho đường thẳng d : y = 5 − 4t , t và điểm z = 6 − + 7t
A(1;2;3). Tìm phương trình mặt phẳng đi qua A và vuông góc với đường thẳng d.
A. x + y + z – 3 = 0.
B. 3x – 4y + 7z –16 = 0.
C. 2x – 5y − 6z – 3 = 0.
D. x + y + 3z – 20 = 0.
Câu 15: Có tất cả bao nhiêu số tự nhiên có 3 chữ số? A. 901. B. 900. C. 899. D. 1000.
Câu 16. Cho tập hợp A gồm 12 phần tử. Tính số tập con gồm 4 phần tử của tập hợp A. 4 A. C 8 . B. C 8 . C. A 4 . D. A . 12 12 12 12
Câu 17: Cho một cấp số cộng có 20 số hạng. Đẳng thức nào sau đây là sai? A. u + u = u + u . B. u + u = u + u . 1 20 8 13 1 20 2 19 C. u + u = u + u . D. u + u = u + u 1 20 9 11 1 20 5 16
Câu 18: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với đáy ABC. Khẳng định nào dưới đây là sai? A. SB ⊥ BC . B. SA ⊥ AB. C. SA ⊥ BC . D. SB ⊥ AC . 2 2
Câu 19: Tìm phương trình tiếp tuyến của đồ thị hàm số y = f (x) = (x −1) tại điểm M(2;9) . A. y = 6x − 3. B. y = 8x − 7. C. y = 24x − 39. D. y = 6x + 21.
Câu 20: Cho hàm số y = f (x) có bảng biến thiên như sau: x 0 1 y' 2 y Trang 69
Tìm tất cả các giá trị thực của tham số m sao cho phương trình f (x) = m có đúng hai nghiệm. A. m 1 − , m = 2. B. m 1 − , m = 2. C. m 2. D. m 2.
Câu 21: Cho hàm số y = f (x) có bảng biến thiên như sau:
Mệnh đề nào sau đây đúng? A.
Hàm số đã cho có một điểm cực đại và một điểm cực tiểu. B.
Hàm số đã cho không có cực trị. C.
Hàm số đã cho có một điểm cực đại và không có điểm cực tiểu. D.
Hàm số đã cho có một điểm cực tiểu và không có điểm cực đại.
Câu 22: Tìm tập xác định của hàm số = (− − − )5e 2 y x 3x 2 . A. (− ; − 2). B. ( 1 − ;+ ) . C. ( 2 − ;− ) 1 . D. 2 − ;− 1 . 2 2 x +5x 1
Câu 23: Tìm tập nghiệm của bất phương trình 27 . 3 3 3 A. − ; − ( ; − + ). B. − ; −1 . 2 2 3 3 C. − ; − 1 − ;+ ) . D. − ; −1 . 2 2
Câu 24: Bất phương trình log (3x + )
1 log ( x + 7) có bao nhiêu nghiệm nguyên ? 1 1 2 2 A. 1. B. 2. C. 3. D. 4. Câu 25: Gọi x , x x x
là hai nghiệm của phương trình 9 − 3.3 + 2 = 0 . Tính giá trị của biểu thức S = x .x . 1 2 1 2 A. S = 0 . B. S = 5 . C. S = 9 . D. S = 2 .
Câu 26: Diện tích hình phẳng giới hạn bởi các đường y = x3 – 4x, trục Ox, x = -3, x = 4 bằng 119 201 A. . B. 44. C. . D. 36. 4 4 Trang 70 4 4 4 Câu 27: Cho f (x)dx =10 và g (x)dx = 5. Tính I = 3 f (x)−5g(x)dx. 2 2 2 A. I = 5. B. I = 15 . C. I = 5 − . D. I = 10 .
Câu 28: Cho số phức z = 3 − 4i . Tính mô đun của số phức 2z. A. 4. B. 10. C. 5. D. 25
Câu 29: Biết z = a + bi (a,b ) là số phức thỏa mãn (3 − 2i)z −10i −8 =15 −8i . Tính a + b. A. a + b = 5 . B. a + b = - 1 . C. a + b = 9 . D. a + b = 1.
Câu 30: Cho hình chóp S.ABC có SA vuông góc với đáy, SA = a, tam giác ABC vuông cân tại A, AB = a. Tính
thể tích V của khối chóp S.ABC. 3 a 3 a 3 a 3 2a A. V = . B. V = . C. V = . D. V = . 6 2 3 3
Câu 31: Cho hình vuông ABCD có cạnh bằng 4. Quay đường tròn ngoại tiếp hình vuông đã cho quanh 1 đường
chéo ta được một mặt cầu. Tính diện tích S của mặt cầu đó. A. 32 . B. 16 . C. 8 . D. 64 .
Câu 32: Trong không gian cho tam giác OIM vuông tại I. Khi quay tam giác OIM quanh cạnh góc vuông OI thì
đường gấp khúc OMI tạo thành một khối tròn xoay. Gọi Sxq là diện tích xung quanh của khối tạo thành. Phát biểu nào sau đây đúng? A. S
= .IM.OM B. S = 2.IM.OM C. S = .IM.IO D. S = 2.IM.IO xq xq xq xq
Câu 33: Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A(1;0;0), B(0;2;0), C(0;0;4). Tìm phương trình của mặt phẳng (ABC).
A. 4x + 2y + z + 4 = 0.
B. x + 2y + 4z − 4 = 0.
C. 4x + 2y + z −1 = 0.
D. 4x + 2y + z − 4 = 0. x −1 y z +1
Câu 34: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng : = = và mặt phẳng 1 − 2 3
(P): x+2y −3z +2 = 0. Tìm tọa độ giao điểm I của và (P). 5 4 2 2
A. I(1;0;1) . B. I − ; ; 1 . C. I(0;2;2) . D. I ; ;0 . 3 3 3 3
Câu 35: Trong mặt phẳng tọa độ Oxy cho tam giác ABC có A(1;-1), B(5;-3) và C thuộc trục Oy, trọng tâm G của
tam giác ABC thuộc trục Ox. Tìm tọa độ điểm C. A. C(0;-4). B. C(0;4). C. C(0;2). D. C(2;4).
Câu 36 (VDT): Cho hàm số y = −x3 − mx2 + (−3m + 6)x + 5 với m là tham số. Có bao nhiêu giá trị nguyên
của m để hàm số nghịch biến trên khoảng (−∞; +∞)? A. 2. B. 3. C. 4. D. 5. 2 x x
Câu 37 (VDT): Cho hàm số f (x) = 4 .9 . Mệnh đề nào dưới đây sai? 2 2
A. f (x) 1 x + x log 9 0. B. f (x) 1 2 − x + x log 9 0. 4 0,5 2 x
C. f (x) 1 x + x log 4 0.
D. f (x) 1 x (lg 4 + lg9 ) 0. 9 Trang 71 1 e
Câu 38 (VDT): Cho F(x) = f (x)
là một nguyên hàm của hàm số . Tính I = f ( x)ln xdx . 2 2x x 1 2 e − 3 2 2 − e 2 e − 2 2 3 − e A. I = . B. I = . C. I = . D. I = . 2 2e 2 e 2 e 2 2e 2 − iz z + 2i
Câu 39 (VDT): Cho số phức z = a + bi (a, b ) thỏa mãn −
= 2z và z 1. Tính giá trị biểu 2 + i 1− 2i thức 2 2 P = a + b − ab . A. P = 0 . B. P = 29 . 1 C. P = . D. P = 5 . 100
Câu 40 (VDT): Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(4;2;2), B(0;0;7) và đường thẳng x − 3 y − 6 z −1 d : = =
. Tìm điểm C thuộc đường thẳng d sao cho tam giác ABC cân tại A. 2 − 2 1 A. C( 1 − ;8;2) hoặc C(9;0; 2 − ) . B. C(1; 8 − ;2) hoặc C(9;0; 2 − ) .
C. C(1;8;2) hoặc C(9;0; 2 − ) . D. C(1;8; 2 − ) hoặc C(9;0; 2 − ) .
Câu 41 (VDT): Trong không gian với hệ tọa độ Oxyz, cho điểm I(3; 4; -2). Tìm phương trình mặt cầu tâm I tiếp xúc với trục Oz. 2 2 2 2 2 2
A. (x − 3) + (y − 4) + (z + 2) = 25.
B. (x − 3) + (y − 4) + (z + 2) = 4. 2 2 2 2 2 2
C. (x + 3) + (y + 4) + (z − 2) = 20.
D. (x − 3) + (y − 4) + (z + 2) = 5.
Câu 42 (VDT): Trong một cuộc thi “Rung chuông Vàng”, có 20 bạn lọt vào vòng chung kết. Để sắp xếp vị trí
chơi, ban tổ chức đã chia các bạn vào 4 nhóm A, B, C, D, mỗi nhóm có 5 bạn. Việc sắp xếp được thực hiện bằng
cách bốc thăm ngẫu nhiên. Tính sác xuất để cả 5 bạn nữ vào cùng 1 nhóm. 4 2 4 2 A. . B. . C. . D. . 5 C 5 C 5 C 5 C 20 20 15 15
Câu 43 (VDT): Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt phẳng đáy. Biết
SA = 2 2a, AB = a, BC = 2a. Tính khoảng cách giữa 2 đường thẳng BD và SC. 6a 7a 2 7a A. B. 7a C. D. 5 7 7 3 2
Câu 44 (VDC): Tìm tất cả giá trị thực của tham số m để phương trình x − 3x + 2 − m = 1 có 6 nghiệm phân biệt. A. 1 m 3. B. 2 − m 0. C. 1 − m 1. D. 0 m 2.
Câu 45 (VDC): Cho hàm số y = f (x) có đạo hàm liên tục trên R.
Đồ thị hàm số y = f (x) như hình vẽ sau. Số điểm cực trị của hàm số
y = f (x) − 2018x + 2019 là: Trang 72 A. 3 . B. 1 . C. 4 . D. 2 .
Câu 46 (VDC): Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình ( + )x + ( − )x 3 2 2 m 3 2 2 = 8 có đúng 2 nghiệm? A. 15. B. 16. C. 0. D. 17.
Câu 47 (VDC): Cho số phức z thỏa mãn z = 1, tìm phần thực của số phức z biết rằng biểu thức P =
1+ z + 3 1− z đạt giá trị lớn nhất. 4 3 A. − 3 . B. − 4 . C. . D. . 5 5 5 5 3
Câu 48 (VDC): Để thiết kế một chiếc bể cá hình hộp chữ nhật có chiều cao là 60cm , thể tích 96000cm , người
thợ dùng loại kính để sử dụng làm mặt bên có giá thành 2
70.000 VNĐ / m và loại kính để làm mặt đáy có giá 2
thành 100.000 VNĐ / m . Tính chi phí thấp nhất để hoàn thành bể cá. A. 32.000 VNĐ . B. 83.200 VNĐ . C. 99.200 VNĐ .
D. 832.000 VNĐ .
Câu 49 (VDC): Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (2;0;0) và M(1;1;1). Mặt phẳng (P) thay đổi
qua AM và cắt các tia Oy, Oz lần lượt tại B(0;b;0), C(0;0;c). Tính giá trị nhỏ nhất của diện tích tam giác ABC. A. 4 6. B. 96. C. 16. D. 4.
Câu 50 (VDC): Có bao nhiêu giá trị nguyên của tham số m để phương trình dưới đây có nghiệm? 2 4sin x + .cos x −
= m + 3sin 2x − cos2x 3 6 A. 5. B. 1. C. 3. D. 7. --- HẾT --- ĐÁP ÁN 1A 2D 3A 4C 5C 6C 7D 8A 9D 10C 11D 12C 13A 14B 15B 16A 17C 18D 19C 20B 21D 22C 23D 24C 25A 26C 27A 28B 29C 30A 31A 32A 33D 34B 35B 36C 37C 38A 39B 40C 41A 42A 43D 44C 45B 46A 47A 48B 49A 50A
LỜI GIẢI CÁC CÂU Ở MỨC ĐỘ VDT VÀ VDC
Câu 36: Chọn C. 2 y ' = 3x − − 2mx + ( 3 − m + 6)
Để hàm số nghịch biến trên R y' 0, x R Trang 73 2 2 m + 3( 3
− m + 6) 0 m − 9m +18 0 3 m 6
Các giá trị cần tìm là : 3, 4, 5, 6. 2 2 Câu 37. Ta có: x x x x 2
f (x) 1 4 .9 1 log 4 .9 0 x + x log 9 0. 4 4 2 2 x x x x 2 f (x) 1 4 .9 1 log 4 .9 0 2 − x + x log 9 0. 0,5 ( ) 0,5 2 2 x x x x 2
f (x) 1 4 .9 1 log 4 .9 0 x + x log 4 0. 9 9 2 2 x x x x 2 x f (x) 1 4 .9
1 lg4 .9 0 xlg4 + x lg9 0 x(lg4+lg9 ) 0.
Vậy chọn C. Câu 38. Chọn A. 1 f (x) 1 Do F(x) = f (x)
là một nguyên hàm của hàm số nên = 2 2x x 2 x 2x ( ) 1 f x = − . 2 x 1 e u = ln x du = dx Tính I = f ( x)ln xdx . Đặt x . dv = f (x)dx 1 v = f (x) e f x e e 2 − Khi đó 1 1 e 3 I = f (x).ln (x) e ( ) − dx = − .ln x − = . 2 ( ) 1 x 2 x 2x 2 2e 1 1 1 Câu 39. Chọn B. 2 − iz z + 2i − − + − − − = 2i z z 2i 2z 4i 2z − = 2z = 2z 2 + i 1− 2i 1− 2i 1− 2i 1− 2i
−z − 2i = (1− 2i)z a
− − bi − 2i = (1− 2i)(a − bi) − = − = a
− −(b + 2)i = (a − 2b) −(2a + a a 2b a 1 b)i P = 1. b + 2 = 2a + b b = 1 Câu 40. Chọn C x = 3 − 2t
Pt tham số của đt d là: y = 6 + 2t . z =1+ t
Vì C d nên C(3 − 2t;6 + 2t;1+ t ). AB = ( 4 − ; 2 − ;5) AB = 3 5 = (− − + − ) = ( + )2 + ( + )2 + ( − )2 AC 1 2t; 4 2t; t 1 AC 2t 1 2t 4 t 1 Trang 74
Vì tam giác ABC cân tại điểm A nên AB = AC 2 2 2 (2t + ) 1 + (2t + 4) + (t − ) 1 = 3 5 t =1 C(1;8;2) t = 3 − C(9;0; 2 − ) Câu 41. Đáp án A |[𝑂𝐼 ⃗⃗ ,𝑢 ⃗⃗⃗⃗ ]| 𝑢 ⃗ 𝑜𝑧 𝑜𝑧
⃗⃗ = (0; 0; 1) và 𝑂𝐼
⃗⃗ = (3; 4; −2) , R= d(I,Oz) = = 5 |𝑢 ⃗ 𝑂𝑍 ⃗⃗⃗ | 2 2 2 Vậy ( ) S : (x − )
3 + (y − 4) + (z − 2) = 25 Câu 42. Chọn A Ta có: KG Mẫu: có 5 5 5 5 n( )
= C C C C cách chia 20 bạn vào 4 nhóm, mỗi nhóm 5 bạn 20 15 10 5
Gọi A là biến cố: “cả 5 bạn nữ vào cùng 1 nhóm”
Nếu 5 bạn nữ cùng thuộc nhóm A thì có 5 5 5
C C C cách xếp các bạn nam vào các nhóm còn lại. 15 10 5
Vì vai trò các nhóm như nhau nên: 5 5 5 n(A) = 4C C C 15 10 5 5 5 5 4C C C 4 Suy ra: 15 10 5 P(A) = = . 5 5 5 5 5 C C C C C 20 15 10 5 20 Câu 43. Đáp án D
Gọi O là tâm hình chữ nhật ABCD. Dựng Cx / /BD ( ) = ( ( )) = ( ( )) 1 d BD;SC d BD; SCx d O; SCx = d(A;(SCx)) 2
Dựng AE ⊥ Cx, AF ⊥ SE d (A;(SCx)) = AF AB.AD 4a
Do BD / /Cx AE = 2d (A;BD) = 2. = 2 2 AB + AD 5 AE.SA 4a 7 2a 7 Suy ra d = AF = = d = A 2 2 AE + SA 7 7 Câu 44: Chọn C. 3 2 3 2
Ta có: x − 3x + 2 − m = 1 x − 3x + 2 = m +1. Xét hàm số 3 2 y = x − 3x + 2 Trang 75 x = 0 2 y = 3x − 6x; y = 0 . x = 2 Đồ thị hàm số 3 2 y = x − 3x + 2 .
Từ đó ta suy ra đồ thị hàm số 3 2 y = x − 3x + 2 .
Số nghiệm của phương trình 3 2
x − 3x + 2 − m = 1 là hoành độ giao điểm của đồ thi hàm số 3 2
y = x − 3x + 2 và đường thẳng y = m +1.
Nhìn vào đồ thị ta thấy để phương trình có 6 nghiệm cần: 0 m +1 2 1 − m 1.
Câu 45: Chọn B Ta có f
(x) − 2018x + 2019 = f (x)−2018 .
Đồ thị hàm số y = f (x) − 2018 được suy ra từ đồ thị hàm số y = f (x) bằng cách tịnh tiến sang xuống dưới
2018 đơn vị. Do đó đồ thị hàm số y = f (x) − 2018 chỉ cắt trục hoành tại 1 điểm và đổi dấu qua điểm đó nên
hàm số y = f (x) − 2018x + 2019 có một điểm cực trị. (3+2 2).(3−2 2) 1 t = (3 + 2 2 )x Câu 46. Ta có =1 3 − 2 2 = . Đặt (t 0), do tính chất 3 + 2 2
hàm số mũ, ứng với mỗi giá trị t>0 tìm được 1 giá trị x. m Phương trình trở thành 2 t +
= 8 m = −t + 8t . Đặt 2
f (t) = −t + 8t f '(t) = 2 − t + 8 = 0 t = 4. t Bảng biến thiên: t 0 4 + f '(t) + 0 – m = f (t) 16 0 −
Dựa vào bảng biên thiên ta thấy để phương trình có đúng 2 nghiệm thì m (0;16). Trên khoảng này có 15 giá trị nguyên. Chọn A. Câu 47. Đáp án: A
Giả sử z = x + yi,(x, yR) Trang 76 2 2 2 2 Vì z = 1 x + y = 1 x + y = 1 1+ z + 3 1− z = (x + )2 1 + y + 3 (x − )2 2 2 1 + y Khi đó: = (x + )2 1 +1− x + 3 (x + )2 2 2 1 +1− x = 2 ( 1+ x + 3 1− x )
Xét hàm số f (x) = 2 ( 1+ x + 3 1− x ) trên đoạn 1 − ; 1 ta có: ( ) 1 3 = − ( ) 4 f ' x 2 ;f ' x = 0 x = − 2 1+ x 2 1− x 5 Ta có: (− ) 4 f 1 = 6;f − = 2 10 5 4 3 4 x = − ; y = − 4 x = − Vậy 5 5 f = f − = 2 10 5 max 5 4 3 2 2 y =1− x x = − ; y = 5 5 4 3 4 3 Vậy z = − − i, z = − + 4 i. nên phần thực là: − 5 5 5 5 5 Câu 48. Chọn B
Gọi x, y(m) (x 0,y 0) là chiều dài và chiều rộng của đáy bể, khi đó theo đề bài ta suy ra ( ) 0,16 V x = 0,6xy = 0,096 y = x
Giá thành của bể cá được xác định bởi hàm số sau:
f (x) = (2.0,6.x + 2.0,6.y).70000 +100000.xy 0,16 0,16 0,16 = 2.0,6 x + .70000 +100000.x. = 84000 x + +16000 x x x 0,16 ' f (x) ' = 84000 1− , f x = 0 x = 0, 4 2 ( ) x Bảng biến thiên x 0 0, 4 + ' f (x) - 0 + + + f (x) f (0, 4)
Dựa vào bảng biến thiên suy ra chi phí thấp nhất để hoàn thành bể cá là f (0,4) = 83.200 VNĐ Câu 49. Đáp án A Trang 77 x y z
PT mặt phẳng (P) có dạng: + + =1. Vì M 1 1 1 (P) nên + + =1 bc = 2(b + c) 2 b c 2 b c 1
Diện tích tam giác ABC là S = 2 2 2
AB,AC = b + c + (b + c) . 2
Vì b2 + c2 ≥ 2bc và (b + c)2 ≥ 4bc nên S
6bc. Mà bc = 2(b + c) ≥ 4 bc nên bc ≥ 16.
Do đó: S 96 = 4 6. Dấu bằng xảy ra khi b = c = 4. Vậy mín = 4 6. Câu 50. Chọn A
Phương trình ban đầu tương đương với 2 2 sin 2x + + sin
= m + 3sin 2x − cos 2x 6 2 2 − 2 2 3sin 2 + cos2 + 2 =
+ 3sin 2 − cos2 cos2 = m x x m x x x 2
Phương trình ban đầu có nghiệm khi và chỉ khi 2 m − 2 1 − m(− ; 2 +) 2 − m 2 2 m − 2 2 − m 2 1 2
Với là m số nguyên ta sẽ được m = −2; m = −1; m = 0;m = 1;m = 2.
ĐỀ THI THỬ THPT QUỐC GIA 2020 ĐỀ 46 MÔN TOÁN Thời gian: 90 phút x −1
Câu 1: Cho hàm số y =
. Tìm tất cả các giá trị của m để đồ thị hàm số có ba đường tiệm cận. 2 mx − 2x + 3 m 0 m 0 1 m 0 m A. m 1 − B. 5 C. m 1 − D. 1 m 1 m 0 1 3 m m 3 5 −x +1
Câu 2: Cho hàm số y =
. Trong các khoảng sau khoảng nào hàm số không nghịch biến 3x +1 1 1 A. − ; + B. (5;7) C. − ; − D. ( 1 − ;2) 3 3 Câu 3: Cho hàm số 3
y = sin x − 3sinx+1 xét trên (0; ) . GTLN của hàm số bằng Trang 78 A. 2 B. 1 C. 0 D. -1
Câu 4: Cho hình chóp S.ABC có SA ⊥ ( ABC); SA = a . Diện tích tam giác ABC bằng 2
3a . Khi đó thế tích của khối chóp là: 3 a A. 3 3a B. 3 a C. 3 3a D. 3
Câu 5: Gọi M, N lần lượt là GTLN, GTNN của hàm số: 4 2
y = 2x − 4x +1 trên 1 − ;
3 . Khi đó tổng M+N bằng: A. 128 B. 0 C. 127 D. 126
Câu 6: Cho một hình lăng trụ đứng có đáy là tam giác đều .Thể tích của hình lăng trụ là V. Để diện tích toàn phần
của hình lăng trụ nhỏ nhất thì cạnh đáy của lăng trụ là: A. 3 4V B. 3 V C. 3 2V D. 3 6V Câu 7: Cho hàm số 4
y = mx + (m − ) 2
1 x +1− 2m . Tìm tất cả các giá trị của m để hàm số có 3 điểm cực trị.
A. 1 m 2 B. 1 − m 0 C. m 1
D. 0 m 1
Câu 8: Cho hàm số y = f ( x) có đạo hàm f ( x) = x ( x + )( x − )3 2 ' 1 2
1 . Số điểm cực trị của hàm số A. 4 B. 3 C. 1 D. 2 (m + ) 1 x + 2
Câu 9: Cho hàm số y =
. Đồ thị hàm số nhận trục hoành và trục tung làm tiệm cận ngang và tiệm cận x − n +1
đứng. Khi đó tổng m+n bằng: A. 1 B. 0 C. -1 D. 2 Câu 10: Cho hàm số 4 2 2
y = x − 2m x + 2m +1. Xác định m để tiếp tuyến của đồ thị hàm số tại giao điểm của đồ
thị với đường thẳng (d ) : x =1 song song với đường thẳng () : y = 1 − 2x + 4 A. m = 1 B. m = 3 C. m = 2 D. m = 0 Câu 11: Cho hàm số 3 2
y = 2x − 6x + x −1 . Tìm điểm nằm trên đồ thị hàm số sao cho tiếp tuyến tại điểm đó có hệ số góc nhỏ nhất. A. (1;8) B. (8; ) 1 C. (1; 4 − ) D. ( 4 − ; ) 1 Câu 12: Cho hàm số 4 2 y = 2
− x + 3x + 5. Mệnh đề nào sau đây sai
A. Đồ thị hàm số luôn nhận trục tung làm trục đối xứng. B. Đồ thị hàm số luôn có 3 điểm cực trị.
C. Đồ thị hàm số không cắt trục hoành. D. Đồ thị hàm số luôn đi qua điểm A(1;6)
(m − )1sin x − 2
Câu 13: Cho hàm số y =
. Tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên sin x − m m m −1 m 0 khoảng 0; A. 1 − m 1 2 B. C. D. 2 m 2 m 2 m 1 Trang 79
Câu 14: Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng a. Khi đó diện tích toàn phần của hình chóp là: A. 2 3a B. ( − ) 2 3 1 a C. ( + ) 2 3 1 a D. 2 a Câu 15: Cho hàm số 3 2 2
y = x − 3x + m − 2m . Tìm tất cả các giá trị của tham số m để giá trị cực đại của hàm số m = −1 m = 1 m = 0 bằng 3 A. B. C.
D. Không tồn tại m m = 3 m = −3 m = 2 1− cos x 2
Câu 16: Cho hàm số y =
. GTNN của hàm số bằng: A. 0 B. -1 C. 1 D.
sin x + cos x − 2 11
Câu 17: Cho hàm số f (x) = 2 2x − 1 − x . Tìm nghiệm bất phương trình f (x) 0 . 5 3 1 5 A. T = ; 4 B. T = ; + C. T = ; + D. T = ; + 2 2 2 2
Câu 18: Một công ty bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 2.000.000
đồng một tháng thì mọi căn hộ đều có người thuê và cứ tăng thêm giá cho thuê mỗi căn hộ 100.000 đồng một tháng
thì sẽ có 2 căn hộ bị bỏ trống. Hỏi muốn có thu nhập cao nhất thì công ty đó phải cho thuê mỗi căn hộ với giá bao
nhiêu một tháng. A. 2.225.000. B. 2.100.000
C. 2.200.000 D. 2.250.000 Câu 19: Cho hàm số 3 2
y = 2x − 3x + 5 . Điểm cực đại của đồ thị hàm số đã cho là: A. (1; 4) B. (4 ) ;1 C. (5;0) D. (0;5)
Câu 20: Bảng biến thiên sau là của hàm số nào: 2x 2 − x −1 2x −1 2x −1 A. y = B. y = C. y = D. y = −x +1 x +1 −x +1 x +1
Câu 21: Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB = 4 ;
a AD = 2a . Tam giác SAB là tam giác cân
tại S và nằm trong mặt phẳng vuông góc với mặt đáy. Góc giữa mặt phẳng (SBC) và (ABCD) bằng 450. Khi đó thể
tích khối chóp S.ABCD là: 3 4a 3 16a 3 8a A. B. C. D. 3 16a 3 3 3 3x + 2
Câu 22: Những điểm trên đồ thị hàm số y =
mà tại đó tiếp tuyến có hệ số góc bằng 4 là: x + 2 A. (1; ) 1 ;(3;7) B. (1;− ) 1 ;(3; 7 − ) C. ( 1 − ;− ) 1 ;( 3 − ;7) D. ( 1 − ; ) 1 ;( 3 − ; 7 − ) Trang 80 2 2x + mx −1
Câu 23: Tìm m để tiếp tuyến của đồ thị (C): y =
tại điểm có hoành độ bằng 4 vuông góc với đường x − 3
thẳng d: x −12y +1= 0.
A. m=3 B. m=2 C. m=1 D. m= -1 Câu 24: Cho hàm số 3 2
y = x − 6x + mx +1 . Tìm tất cả các giá trị của m để hàm số đồng biến trên khoảng (− ; +) A. m 0
B. m 0 C. m 12 D. m 12
Câu 25: Đây là đồ thị của hàm số nào: A. 4 2
y = −x + 2x + 3 B. 4 2
y = x + 2x + 3 C. 4 2
y = x − 2x − 3 D. 4 2
y = x − 2x + 3 Câu 26: Cho hàm số 2
f (x) = 2x +16 cos x − cos 2x . Giải phương trình f '( ) x = 0 A. x =
+ k2 B. x = − + k C. x = + k D. x = + k 2 2 2 3
Câu 27: Tìm tất cả các giá trị của m để bất phương trình: 2
x + 4 − x 4x − x + m có nghiệm x 0; 4 A. m 5 B. m 5 C. m 4 D. m 4 x + 2
Câu 28: Cho hàm số y =
. Xác định m để đường thẳng y = mx + m − luôn cắt đồ thị hàm số tại hai điểm 2x + 1 1
phân biệt thuộc cùng một nhánh của đồ thị. m 3 − m − A. B. m = 0 C. m 3 0 D. m 0 m 1 Câu 29: Cho hàm số 4
y = mx + ( m + ) 2 2
1 x +1 . Tìm tất cả các giá trị của m để hàm số có một điểm cực tiểu. A. m 1 0
B. Không tồn tại m C. − m 1 0 D. m − 2 2 2 n
Câu 30: Khai triển và rút gọn biểu thức 1 − x + 1 (
2 − x) +...+ n 1
( − x) thu được đa thức 1 7 1 n
P(x) = a + a x + ...+ a x . Tính hệ số a biết rằng n là số nguyên dương thoả mãn + = . 0 1 n 8 C 2 C 3 n n n A. 78 B. 87 C. 98 D. 89 Trang 81 Câu 31: Cho hàm số 3
y = x − x + 2 . Phương trình tiếp tuyến của đồ thị hàm số tại điểm M (0;2) là
A. y = −x + 2
B. y = x + 2
C. y = −x − 2
D. y = x − 2
Câu 32: Một hộp đựng 11 viên bi gồm 4 viên bi xanh và 7 viên bi đỏ. Lấy ngẫu nhiên 2 viên bi. Tính xác suất để
lấy được 2 viên bi cùng màu? 26 A. p(A) = 27 B. p(A) = 28 C. p(A) = 29 D. p(A) = 55 55 55 55 1
Câu 33: Đồ thị hàm số 3 2 y =
x − 4x + 5 có bao nhiêu tiếp tuyến song song với trục hoành: 3 A. 0 B. 1 C. 2 D. 3
Câu 34 Cho cấp số cộng (u ) , biết u = 3
− ;u =1.Tính tổng 20 số hạng đầu S n 2 4 20 A. S
=181 B. S = 281 C. S = 280 D. S =180 20 20 20 20
Câu 35: Trong mặt phẳng Oxy cho điểm M(-2;5) tìm tọa độ điểm M’ ảnh của điểm M qua phép tịnh tiến theo véc tơ v = ( 2 − ;3). A. M ( 4;−8) B. M ( 4 − ; 8 − ) C. M (4;8) D. M ( −4;8)
Câu 36: Cho hàm số S.ABCD có đáy là hình vuông cạnh a. Các mặt bên (SAB), (SAD) cùng vuông góc với mặt
đáy (ABCD); Góc giữa SC và mặt (ABCD) bằng 450. Thể tích của khối chóp S.ABCD. 3 3a 3 2a 3 3a 3 2a A. B. C. D. 3 2 2 3
Câu 37: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Các mặt bên (SAB), (SAD) cùng vuông góc với mặt
đáy (ABCD); SA = a 3 . Khi đó khoảng cách từ A đến mặt (SBC) là: a 2 a 3 a a A. B. C. D. 2 2 2 3
Câu 38: Mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất A. Năm cạnh B. Bốn cạnh C. Ba cạnh D. Hai cạnh
Câu 39: Một kim tự tháp ở Ai Cập được xây dựng vào khoảng 2500 trước công nguyên. Kim tự tháp này là một
khối chóp tứ giác đều có chiều cao 154m; độ dài cạnh đáy là 270m. Khi đó thể tích của khối kim tự tháp là: A. 3.742.200 B. 3.640.000
C. 3.500.000 D. 3.545.000 1
Câu 40: Cho hàm số S.ABC. Trên 3 cạnh SA, SB, SC lần lượt lấy 3 điểm A', B', C' sao cho SA ' = SA ; 2 1 1 SB ' = S ; B SC ' =
SC . Gọi V và V' lần lượt là thể tích của các khối chóp S.ABCD và S'.A'B'C'. Khi đó tỷ số 2 2 V ' 1 1 1 1 là: A. B. C. D. V 8 12 6 16 Câu 41: Cho hàm số 3 2
y = x + 3x + mx + m − 2 . Tìm tất cả các giá trị của tham số m để đồ thị hàm số có hai điểm
cực trị nằm về hai phía của trục tung. A. m 0 B. m 3 C. m 0 D. m 0 Trang 82
Câu 42: Người ta gọt một khối lập phương bằng gỗ để lấy khối tám mặt đều nội tiếp nó ( tức là khối cố các đỉnh là
các tâm của các mặt khối lập phương). Biết cạnh của khối lập phương bằng a. Hãy tính thể tích của khối tám mặt 3 a 3 a 3 a 3 a đều đó: A. B. C. D. 6 12 4 8
Câu 43: Đồ thị hàm số 3 2
y = x − x cắt trục hoành tại mấy điểm A. 1 B. 3 C. 2 D. 0
Câu 44: Cho lăng trụ tam giác ABC.A'B'C' có góc giữa hai mặt phẳng (A’BC) và (ABC) bằng 0
60 , AB = a . Khi
đó thể tích của khối ABCC’B’ bằng 3 3a 3 a 3 3 3 A. 3 a 3 B. C. D. 3 a 4 4 4 1 sin 2x
Câu 45: Tính tổng các nghiệm của phương trình : cot x +
= 2sin( x + ) với x0; 2 sin x + cos x 2 4 5 5 4 A. B. C. D. 3 3 4 5
Câu 46: Trong hộp có 5 quả cầu trắng , 3 quả cầu xanh và 2 quả cầu đỏ. Lấy ngẫu nhiên trong hộp 3 quả cầu . Tính
xác suất để 3 quả cầu lấy ra cùng màu. A. P ( A) 11 = B. P ( A) 11 = C. P ( A) 11 = D. P ( A) 11 = 120 12 102 121
Câu 47: Cho khối lăng trụ đều ABC.A'B'C' và M là trng điểm của cạnh AB. Mặt phẳng (B’C’M) chia khối lăng trụ
thành hai phần. Tính tỷ số thể tích của hai phần đó: 7 6 1 3 A. B. C. D. 5 5 4 8 −x + 6
Câu 48: Số đường tiệm cận của đồ thị hàm số y = là: 2 2x + 3 A. 0 B. 2 C. 3 D. 1 1
Câu 49: Cho hàm số y =
sin 3x + msin x . Tìm tất cả các giá trị của m để hàm số đạt cực tiểu tại điểm x = 3 3 A. m 0 B. m = 0
C. Không tồn tại m D. m = 2 Câu 50: Cho hàm số 3 2
y = x − 3x + mx +1 và (d ) : y = x +1. Tìm tất cả các giá trị của tham số m để đồ thị hàm
số cắt (d) tại ba điểm phân biệt có hoành độ x , x , x thỏa mãn 2 2 2
x + x + x 1 1 2 3 1 2 3 13 m A. 4 B. m 5
C. 0 m 5
D. 5 m 10 m 1 ĐÁP ÁN Trang 83 1. A 2. D 3. B 4. B 5. D 6. A 7. D 8. D 9. B 10. C 11. C 12. C 13. B 14. C 15. B 16. A 17. A 18. D 19. D 20. D 21. B 22. C 23. D 24. C 25. A 26. C 27. D 28. A 29. D 30. D 31. D 32. B 33. C 34. C 35. D 36. D 37. B 38. C 39. A 40. B 41. D 42. A 43. C 44. C 45. B 46. A 47. A 48. B 49. C 50. A HƯỚNG DẪN GIẢI x −1
Câu 1: Chọn A.Nhận thấy đồ thị hàm số y =
có 3 đường tiệm cận khi hàm số đã cho có 0 dạng 2 mx − 2x + 3 x −
bậc nhất trên bậc 2 hay m 0 (khi m = 1 0 thì hàm số y =
có 2 tiệm cận đứng và tiệm cận ngang) 2 − x + 3 x −1
Điều kiện để đồ thị hàm số y = có 3 tiệm cận là 2
mx − 2x + 3 = 0 có 2 nghiệm phân biệt khác 1 tức 2 mx − 2x + 3 m 1 − là 2
= b − 4ac = 4−12m 0 và m +1 1
0 hay m và m − .
1 Vậy m 0 thỏa mãn yêu cầu bài ra. 3 1 m 3 1 − 4 − 1
Câu 2: Chọn D D = \ y ' = 0 x
D nên hàm số luôn nghịch biến trên − ; − và 3 (3x + )2 1 3 1
− ;+ . Vậy hàm số không nghịch biến trên ( 1 − ;2). 3
Câu 3: Chọn B Với x 0; → sin x0;
1 Đặt sin x = t (t 0 ;1 ) Theo bài ra ta có 3
y = t − 3t + 1 2
y ' = 3t − 3; y ' = 0 t = 1;t = 1 −
Vẽ nhanh bảng biến thiên của hàm số 3
y = t − 3t +1 với t 0;
1 ta thấy giá trị lớn nhất của hàm số là y (0) =1. 1 1
Câu 4: Chọn B Vì SA ⊥ ( ABC) nên 2 3 V = .S . A S = . .
a 3a = a . Chọn B. SABC 3 ABC 3 Câu 5: Chọn D 4 2
y = 2x − 4x +1 ta có 3 y ' = 8x − 8 ,
x y ' = 0 x = 1
− ; x = 0; x =1
Vì hàm số liên tục và xác định trên đoạn nên ta có GTNN y = y (− ) 1 = 1 − → N = 1 − x 1 − ; 3
GTLN y = y (3) = 127 → M = 127 .Vậy M + N =127 −1 =126. x 1 − ; 3
Câu 6: Chọn A Gọi cạnh đáy của lăng trụ là a, chiều cao lăng trụ là h. .Theo bài ra ta có 2 a 3 4V 2 a 3 4V V = .h → h =
. Diện tích toàn phần của lăng trụ là S = S + S = + 3 . a 2 4 toan phan 2 day xung quanh a 3 2 2 a 3 Trang 84
Áp dụng bất đẳng thức AM - GM ta có 2 a 3 4 3V 2 2 a 3 2 3V 2 3V a 2 2 3V 2 3V S = + 3 = + + 3 . . toan phan 2 a 2 a a 2 a a 2 a 3 2 3V 2 3V Dấu bằng xảy ra khi = = hay 3 a = 4V . 2 a a
Câu 7: Chọn D Ta có 4
y = mx + (m − ) 2
1 x +1− 2m x = 0 3
y ' = 4mx + 2(m − ) 1 x y = x( 2 ' 0
4mx + 2m − 2) = 0 2
4mx + 2m − 2 = 0 (I )
Hàm số c 3 điểm cực trị khi và chỉ khi phương trình y ' = 0 có 3 nghiệm phân biệt. Vậy (I) có 2 nghiệm phân biệt
khác 0 hay 0 m 1. 1
Câu 8: Chọn D. Lập bảng xét dấu của f '(x) các em sẽ thấy được các điểm cực trị là 1
− ; , khi đi qua điểm 0 thì 2 b −
không đổi dấu Nhận xét:Các em chú ý tới ( + )n ax
b thì n chẵn không đổi dấu qua
, còn n lẻ thì đổi dấu a b − a ax + b d
Câu 9: Chọn B. Đồ thị hàm số bậc nhất trên bậc nhất y =
có đường tiệm cận đứng x = − và tiệm cận cx + d c a (m + ) 1 x + 2 ngang y =
. Đồ thị hàm số y =
có tiệm cận đứng và tiệm cận ngang lần lượt là trục tung và trục c x − n +1
hoành hay n −1+ m +1 = 0 n + m = 0 .
Câu 10: Chọn C. Phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm x = y = ( 2 − m )(x − ) 2 1; 4 4 1 − 2m + 4 4 − 4m = 1 − 2
Điều kiện để đường thẳng trên song song với đường thẳng () : y = 1 − 2x + 4 là → m = 2 2 2m 4
Câu 11. Chọn C. Gọi x0 là hoành độ của tiếp điểm theo bài ra ta có
y '( x = 6x −12x +1 = 6 x − 2x +1 −5 = 6 x −1 − 5 0 ) ( ) ( )2 2 2
Dấu bằng xảy ra khi x = 1.Vậy điểm cần tìm là (1; 4 − ) 0
Câu 12: Chọn C A. Đúng vì đồ thị hàm trùng phương luôn nhận trục tung là trục đối xứng
B. Đúng vì phương trình 3
y ' = 8x + 6x = 0 luôn có 3 nghiệm phân biệt nên đồ thị hàm số có 3 điểm cực trị.
C. Sai D. Đúng Trang 85
(2−m)(m+ )10 m 1 −
Câu 13: Chọn B Để hàm số nghịch biến trên 0; thì → m 2 2 sin x m x 0; 2 m (0; ) 1
Câu 14: Chọn C. Diện tích toàn phần của hình chóp đều đó là S = S + S = + a toan phan ABCD SAB ( ) 2 4. 3 1 2 y ' = 3x − 6 ,
x y ' = 0 x = 0; x = 2 y"(0) = 6
− ; y"(2) = 6 . Áp dụng quy tắc 2 anh đã nêu ở trên ta thấy hàm số đạt cực đại tại x = 0 . Từ đề bài ta có m = − Câu 15. y ( ) 2
0 = 3 m − 2m = 1 3 hay . Chọn A m = 3 1− cos x
Câu 16: Chọn B. y =
y sin x + ( y + )
1 cos x = 2 y +1 . Điều kiện để phương trình
sin x + cos x − 2
a sin x + b cos x = c có nghiệm là 2 2 2
a + b c .
Vậy ta có y + ( y + )2 ( y + )2 2 1 2 1 hay 1
− y 0 suy ra GTNN của hàm số y là -1 2
Câu 17. Chọn D. f (x) = 2 2x −1 − x f '(x) = −1 ; ĐK 1 x 2x −1 2 2 f '(x) 0
−1 0 2x −1 2 − 5 2x 1 4 x 2x −1 2 5
So với điều kiện, suy ra tập nghiệm bất phương trình là T = ; + 2
Câu 18: Chọn D .Gọi số căn hộ bị bỏ trống là x ( x 0;50)
Số tiền 1 tháng thu được khi cho thuê nhà là (2000000 + 50000x)(50 − x)
Khảo sát hàm số trên với x 0;50 ta được số tiền lớn nhất công ty thu được khi x = 5 hay số tiền cho thuê mỗi tháng là 2.250.000 . Câu 19: Chọn D 3 2 2
y = 2x − 3x + 5, y ' = 6x − 6 ,
x y ' = 0 x = 0, x = 1 . y"(0) = 6 − ; y"( ) 1 = 6
Áp dụng quy tắc 2 anh đã nêu ở trên ta có điểm cực đại của đồ thị hàm số là (0;5)
Câu 20: Chọn D .Nhìn vào đồ thị hàm số ta thấy hàm số có tiệm cận ngang y = 2 và tiệm cận đứng x =1
Quan sát đáp án ta thấy đáp án D thỏa mãn các điều trên. ax + b a −
Nhắc lại, đối với đồ thị hàm số y =
ta có tiệm cận ngang y = d
và tiệm cận đứng x = . cx + d c c Câu 21: Chọn B Trang 86 (
SAB) ⊥ ( ABCD)
Kẻ SH ⊥ AB .Ta có AB = (SAB) ( ABCD) → SH ⊥ ( ABCD).Suy ra góc giữa (SBC) và (ABCD) là SBH SH ⊥ AB 3 1 1 16a Nên 0
SBH = 45 hay SH = 2a V = .SH.S = .2 .2 a .4 a a = dvtt SABCD ABCD ( ) 3 3 3
Câu 22: Chọn C Với những bài toán có tính trắc nghiệm ta chỉ cần giải phương trình y '(x) = 4 là tìm được yêu 4 x = 1 −
cầu đề bài. Ta có y ' = , y ' = 4 ( x + 2)2 x = 3 −
Sau khi tính được hoành độ sẽ ra được tung độ nên chọn C. 3m +17
Câu 23: Chọn D. Ta có : y ' = 2 −
.Khi x = 4 thì hệ số góc của tiếp tuyến là k = y '(4) = 3 − m−15 (x −3)2 1
Đường thẳng d có hệ số góc là k = . d 12
Để tiếp tuyến và đường thẳng d vuông góc nhau thì k.k = 1 − m = 1 − .Vậy m = 1 − . d Câu 24: Chọn C 2
y ' = 3 x −12x + m , hàm số đã cho đồng biến trên (− ;
+) khi y' 0 hay
(x − x+ )+m− (x− )2 2 3 4 4 12 0 3
2 + m −12 0 m 12
Câu 25: Chọn A Dựa vào đồ thị hàm số đã cho ta có các nhận xét sau:
- Đồ thị hàm số quay xuống nên ta loại đáp án B,C - Các điểm ( 1
− ;4),(1;4),(0;3) lần lượt là các điểm cực trị của hàm số. Các điểm đó là nghiệm của phương trình
y ' = 0 nên ta chọn A.
Câu 26: Chọn C Ta có : f '( )
x = 4x −16sin x + 2sin 2x ; f '( )
x = 4 −16cos x + 4cos 2x Theo đề : f '( ) x = 0 2
4−16cos x + 4cos2x = 0 2cos x −4cos x = 0 cos x = 0 x = + k cos x = 2(VN) 2 Trang 87
Vậy nghiệm của phương trình là x = + k 2
Câu 27: Chọn D . Ý tưởng bài toán này sẽ là chuyển hết m sang một bên, x sang một bên . Sau đó khảo sát hàm số
f(x). Dựa vào đó ta đánh giá m theo giá trị lớn nhất và giá trị nhỏ nhất trên khoảng đoạn theo yêu cầu bài toán. 2
x + 4 − x 4x − x + m 2 2
4 + 2 4x − x 4x − x + m
+ a a + m(a ) −(a − )2 2 4 2 0; 2 5 1 m
Suy ra m 4 nên chọn D x + 2
Câu 28: Chọn A. Phương trình hoành độ giao điểm của y =
và y = mx + m − là 2x + 1 1 x + 2 2
= mx + m −1 2mx + (3m −3) x + m −3 = 0 . 2x +1 3 − 3m x + x = 1 2 Gọi 2m
x ; x lần lượt là nghiệm của phương trình. Theo hệ thức Vi-et ta có 1 2 m − 3 x x = 1 2 2m −1
Điều kiện để phương trình bậc 2 trên có 2 nghiệm phân biệt và khác là 2 m 0 ( m − )2 − m (m − ) m 0 3 3 4.2 . 3 0 →
Điều kiện để 2 giao điểm cùng thuộc 1 nhánh là m 3 − 1 1 2 . m
− .(3m −3) + m −3 0 4 2 1 1 x + x + 0 1 2 2 2 1 1 Hay x x + x + x + 0 → m 0 1 2 ( 1 2) 2 4 m 0
Vậy điều kiện m thỏa mãn yêu cầu bài toán là nên chọn A. m 3 −
Câu 29. Chọn D. Ta có 3
y ' = 4mx + 2(2m + ) 1 x
Xét trường hợp 1 : m = 0 hiển nhiên đúng
Xét trường hợp 2: m 0 ta có 4
y = mx + ( m + ) 2 2
1 x +1 là hàm trùng phương. Để hàm số có 1 cực tiểu thì
m 0 và phương trình y ' = 0 có nghiệm duy nhất. x = 0 Xét y ' = 0 2
2mx + 2m +1 = 0 ( ) 1 Trang 88
Để phương trình y ' = 0 có nghiệm duy nhất thì phương trình (1) có nghiệm nghiệm bằng 0, hoặc vô nghiệm. Suy
ra m 0 thì phương trình (1) vô nghiệm. Tuy nhiên nếu làm đến đây các em chọn A sẽ là sai lầm, vì lời giải trên
mới chỉ xét trường hợp có hàm có duy nhất 1 cực tiểu. 1 cực tiểu cũng còn trường hợp nữa là 1 cực tiểu và 2 cực 2 − m −1 1 −
đại hay phương trình (1) có 2 phân biệt khác 0 hay 0 m 0 2m 2 1
Kết hợp cả 2 trường hợp ta có m − nên chọn D. 2 n 3 1 7 1 n 3
Câu 30: Chọn D . Ta có + = n = . 9 2 3 2 ! 3 . 7 1 C C n 2
n − 5n − 36 = 0 n n + = n(n − ) 1 n(n − )( 1 n − ) 2 n
Suy ra a là hệ số của 8
x trong biểu thức 1 ( 8 − x)8 + 9 1 ( − x)9. Đó là . 8 8 C + . 9 8 C = . 89 8 8 9
Câu 31: Chọn D.Phương trình tiếp tuyến của đồ thị hàm số tại điểm M (0;2) là
y = y '(0)( x − 0) + y (2) = −x + 2 nên chọn D.
Câu 32: Chọn B Số phần tử không gian mẫu là: 2 n( ) = C = 55 11
Gọi A là biến cố lấy được 2 viên cùng màu=> 2 2 n(A) = C + C = n(A) 27 27 . p(A) = = 4 7 n( ) 55
Câu 33: Chọn C .Phương trình trục hoành là y = 0
Tiếp tuyến song song với trục hoành nên có hệ số góc bằng 0 hay y ' = 0 Ta có 2
y ' = x − 8x = 0 → x = 0; x = 8 vậy có 2 tiếp tuyến song song với trục hoành nên chọn C.
Câu 34: Chọn C Sử dụng công thức u = u + (n −1)d , theo đầu bài ta có hệ: n 1 u = u + d = 3 − 2d = 4 d = 2 2 1
u = u + 3d = 1 u = 3 − − d u = 5 − 4 1 1 1 .( n n −1)d 20.19.2
Áp dụng công thức S = . n u + S = 20.( 5 − ) + = 280 n 1 2 20 2 x = x + a x = 4 −
Câu 35: Chọn D Gọi M(x,y); M’(x’,y’); T (M) = M M ( 4 − ;8) V y = y + b y = 8
Đây là câu dễ, các em nhìn vào đồ thị đã cho sẽ thấy A,B,C sai . (
SAB) ⊥ ( ABCD) Câu 36: Chọn D Vì (
SAD) ⊥ ( ABCD)
→ SA ⊥ ( ABCD).Suy ra góc giữa SC và mặt đáy là góc SCA SA = (SAB) (SAD) Trang 89
Theo bài ra góc đó bằng 450 nên 0
SCA = 45 suy ra SA = AC = a 2 3 1 a 2 Vậy 2 S = a 2.a = nên Chọn D. SABCD 3 3 Câu 37. Chọn B
Tương tự câu trên ta có SA ⊥ ( ABCD) .Kẻ AI ⊥ SB dễ dàng chứng minh được d
= AI (tham khảo) Áp (A,(SBC)) 1 1 1 a 3
dụng hệ thức lượng trong tam giác vuông = + → d = . Chọn B 2 2 2 (A,(SBC)) d( SA AB 2 A,(SBC))
Câu 38: Chọn C. Đúng theo lý thuyết SGK. Các em có thể xem thêm các dạng toán về khối đa diện đều trong sách
hình học lớp 12 (các bài tập 1,2,3,4 trang 25 bài 5,6 trang 26). 1 Câu 39: Chọn A 2 V = .154.270 = 3742200 m kim tu thap ( 3) chọn A 3 V '
SA' SB ' SC ' 1 1 1 1
Câu 40: Chọn B . Áp dụng công thức tính tỉ số thể tích ta có = . . = . . = nên chọn B V SA SB SC 2 2 3 12
Chú ý: Công thức trên chỉ áp dụng cho tứ diện thôi nhé các em.
Câu 41: Chọn D Với hàm số bậc 3 ta có nhận xét sau: điều kiện để hai cực trị nằm ở hai phía của trục tung là x .x 0 . 2
y ' = 3x + 6x + m CD CT m
Hoành độ của 2 điểm cực trị là nghiệm của phương trình y ' = 0 . Theo định lí Vi-et ta có x .x = . CD CT 3
Theo điều kiện nói trên ta có m 0 nên chọn D. Trang 90 a a
Câu 42. Chọn A Tính tính được cạnh của hình bát diện đều bằng
. Thể tích hình bát diện đều có cạnh là 2 2 3 a 2 3 2 a V = = nên chọn A. 3 6 3 x 2
Nhận xét: Ta có công thức tính thể tích của hình bát diện đều cạnh x là V = 3
Câu 43. Chọn C.. Xét phương trình hoành độ giao điểm ta có phương trình 3 2
x − x = 0 có 2 nghiệm nên đồ thị
hàm số cắt trục hoành tại 2 điểm
Câu 44: Chọn C. Kẻ AH ⊥ BC khi đó ta có góc giữa 2 mặt phẳng (A'BC) và (ABC) là góc A'HA theo bài ra góc a 2 đó bằng 600 nên ta có 0 A' HA = 3
60 → A' A = AH.tan 60 = V =V −V = V . 2 ABCC ' B'
ABCC ' B' A' A' ABC '
ABCC ' B' A' 3 Chọn C. 1 sin 2x
Câu 45: Chọn B Giải phương trình: cot x + = 2sin( x + ) 2 sin x + cos x 2
Điều kiện: sin x ,
0 sin x + cos x . 0 cos x 2 sin x cos x Pt đã cho trở thành + − 2cos x = 0 2 sin x sin x + cos x 2 cos x 2 cos x −
= 0 cos x sin(x + ) − sin 2x = 0 2 sin x sin x + cos x 4
+) cos x = 0 x =
+ k , k . 2 2x = x + + m2 x = + m2 4 4 t2
+) sin 2x = sin(x + ) ,
m n Z x = + , t . 4 n2 4 3
2x = − x − + n2 x = + 4 4 3 11 5
Đối chiếu điều kiện ta có nghiệm của pt là x = ; x = ; x =
x + x + x = 1 2 3 1 2 3 2 4 12 3
Câu 46: Chọn A n() 3 = C =120 10 Trang 91 n A 11
Gọi A là biến cố: “Ba quả lấy ra cùng màu” n ( A) 3 3
= C + C =11 P( A) ( ) = = 0,09 5 3 n() 120
Câu 47: Chọn A Gọi N là trung điểm AC, khi đó ta có thấy mặt phẳng (B'C'NM) chia hình lăng trụ thành 2 phần 1 1 1 5
AMN.C'A'B'C' và BB'MNC'C. V = V +V = A' . A S + A' . A S = V
AMNC ' A' B '
MB ' A'C ' C ' AMN A' B 'C ' A' B 'C ' 3 3 4 . ' ' ' 12 ABC A B C 5 1− 7
Hay tỉ số 2 khối đó là 12 = nên chọn A. 5 5 12 1
Câu 48: Chọn B lim y =
nên đồ thị hàm số có 2 tiệm cận ngang x→ 2
Câu 49: Chọn C Áp dụng quy tắc 2 ta có hàm số đạt cực tiểu tại điểm x = tương đương 3 y ' = 0 cos ( )+ mcos = 0 3 3 y " 0 3 − sin ( )− msin 0 3 3
Hệ này vô nghiệm nên chọn C
Câu 50: Chọn A Phương trình hoành độ giao điểm là 3 2 3 2
x − 3x + mx +1 = x +1 x − 3x + (m − ) 1 x = 0( ) 1 . Để đồ thị hàm số 3 2
y = x − 3x + mx +1 cắt đường thẳng (d) tại ba điểm phân biệt thì phương trình (1) có 3 nghiệm phân biệt hay x ( 2
x − 3x + m − )
1 = 0 có 3 nghiệm phân biệt ( x = 0 2
x −3x + m −1 = 0 1 ) . Suy ra có 2 nghiệm 13
phân biệt khác 0 hay m 1, m 4
Theo hệ thức Vi-ét ta có: x + x = 3, x .x = m −1 2 2 2 3 Từ đề bài ta có: 2 2 2 2
x + x + x 1 3 − 2 m −1 1→ m 5 1 2 3 ( ) 13
Vậy m 1, m nên chọn A 4 ĐỀ 47
ĐỀ THI THỬ THPT QUỐC GIA 2020 MÔN TOÁN Thời gian: 90 phút 1− 3cos x Câu 1:
Tìm điều kiện xác định của hàm số y = sin x Trang 92 k
A. x k2 . B. x . C. x + k .
D. x k . 2 2 Câu 2:
Thể tích V của khối lăng trụ có chiều cao bằng h và diện tích đáy bằng B là 1 A. V = 1 Bh . B. V = 1 Bh . C. V = Bh .
D. V = Bh . 2 3 6 Câu 3:
Tìm họ nguyên hàm của hàm số f ( x) 1 = 2x + 3 1 A. ln 2x + 3 + 1 C . B. ln 2x + 3 + 1 C . C.
ln 2x + 3 + C . D. lg (2x + 3) + C . 2 ln 2 2 Câu 4: Cho hàm số 4 2
y = x − 2x . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng ( 1 − ; ) 1 .
B. Hàm số nghịch biến trên khoảng (− ; 2 − ).
C. Hàm số đồng biến trên khoảng (− ; 2 − ).
D. Hàm số nghịch biến trên khoảng ( 1 − ; ) 1 . Câu 5:
Cho hàm số f ( x) = log ( 2 x +1 f ( ) 1 2 ), tính . A. f ( ) 1 = 1. B. f ( ) 1 1 = . C. f ( ) 1 1 = . D. f ( ) 1 1 = . 2 ln 2 2 ln 2 x +1 Câu 6:
Đường tiệm cận đứng của đồ thị hàm số y = là x − 2 A. y = 2 . B. x = 1 . C. y =1 D. x = 2 . Câu 7:
Trong hình vẽ bên, điểm M biểu diễn số phức z . Số phức z là A. 1 − 2i . B. 2 + i . C. 1 + 2i . D. 2 − i . Câu 8:
Cho hàm số y = f (x) có đạo hàm trên và bảng xét dấu của đạo hàm như sau:
Hỏi hàm số y = f ( x) có bao nhiêu điểm cực trị? A. 2 . B. 1. C. 3 . D. 0 . Câu 9:
Phương trình tiếp tuyến của đường cong 3 2
y = x + 3x − 2 tại điểm có hoành độ x = 1 là 0 Trang 93
A. y = 9x + 7 . B. y = 9 − x − 7 . C. y = 9 − x + 7 .
D. y = 9x − 7 .
Câu 10: Trong không gian với hệ trục tọa độ Oxyz , cho hai mặt phẳng ( ) : x + 2y − z −1 = 0 và
():2x+4y −mz −2 = 0. Tìm m để () và ( ) song song với nhau. A. m = 1. B. m = 2. − C. m = 2. D. Không tồn tại . m
Câu 11: Cho số phức z thỏa mãn z −1+ i = z + 2 . Trong mặt phẳng phức, quỹ tích điểm biểu diễn các số phức z
A. là đường thẳng 3x + y +1 = 0 .
B. là đường thẳng 3x − y +1 = 0 .
C. là đường thẳng 3x − y −1 = 0 .
D. là đường thẳng 3x − y −1 = 0 .
Câu 12: Tìm hệ số của số hạng chứa 3
x trong khai triển nhị thức Niutơn của ( x − )6 2 1 . A. 160 . B. 960 − . C. 960 . D. 160 − .
Câu 13: Quay hình vuông ABCD cạnh a xung quanh một cạnh. Thể tích của khối trụ được tạo thành là 1 A. 3 a . B. 3 2 a . C. 3 3 a . D. 3 a . 3
Câu 14: Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm A( 1
− ;2;−3) , B(1;0;2) , C( ; x ; y − 2)
thẳng hàng. Khi đó tính tổng x + y ?
A. x + y =1.
B. x + y = 11 17 .
C. x + y = − 11 .
D. x + y = . 5 5 1
Câu 15: Tìm họ nguyên hàm của hàm số 2 = − 3x y x + . x 3 3x x 1 3 x x 1 A. − − + C,C . B. − 3 + + C,C . 2 3 ln 3 x 2 3 x 3 3x x 3 3x x C. −
+ ln x + C,C . D. −
− ln x + C,C . 3 ln 3 3 ln 3 3 x
Câu 16: Tìm tất cả các giá trị thực của tham số m để hàm số 2 y = −
+ mx − 2mx +1 có hai điểm cực 3 trị. m 0
A. 0 m 2 . B. m 2 . C. m 0 . D. . m 2
Câu 17: Trong các dãy số sau, dãy số nào là một cấp số cộng? A. 1, 3 − , 6 − , 9 − , 12 − . B. 1, 2 − , 4 − , 6 − , 8 − . C. 1, 3 − , 5 − , 7 − , 9 − . D. 1, 3 − , 7 − , , 11 − 15 − .
Câu 18: Một tổ có 7 nam sinh và 3 nữ sinh. Chọn ngẫu nhiên 2 học sinh. Xác suất để 2 học sinh được chọn đều là nữ bằng 1 1 3 7 A. . B. . C. . D. . 2 15 8 8 Trang 94
Câu 19: Tìm họ nguyên hàm của hàm số f ( x) = sin 3x A. 3 − cos3x + C . B. 3cos 3x + 1 C . C. cos 3x + 1 C .
D. − cos 3x + C . 3 3
Câu 20: Trong không gian với hệ trục tọa độ Oxyz , điểm M (3;4; 2
− ) thuộc mặt phẳng nào trong các mặt phẳng sau?
A. (S ) : x + y + z + 5 = 0.
B. (P) : z − 2 = 0 .
C. (Q) : x −1 = 0 .
D. (R) : x + y − 7 = 0 .
Câu 21: Cho số phức z = 3 − 2i . Tìm phần thực và phần ảo của số phức z .
A. Phần thực bằng 3 và phần ảo bằng 2i .
B. Phần thực bằng –3 và phần ảo bằng 2 − .
C. Phần thực bằng –3 và phần ảo bằng −2i .
D. Phần thực bằng 3 và phần ảo bằng 2 .
Câu 22: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng a 2 . Tính khoảng
cách d từ tâm O của đáy ABCD đến một mặt bên theo a . 2a 5 a a a A. d = 3 . B. d = 5 . C. d = 2 . D. d = . 3 2 2 3
Câu 23: Trong không gian với hệ trục tọa độ Oxyz , cho a = i
− + 2 j − 3k . Tọa độ của vectơ a là A. ( 1 − ;2;− ) 3 . B. (2;− 3;− ) 1 . C. (2;−1;− ) 3 . D. ( 3 − ;2;− ) 1 .
Câu 24: Trong các hàm số sau, hàm số nào nghịch biến trên tập số thực ? x x 2 A. y = .
B. log x . C. y = log ( 2 + π = π 2x )1. D. y . e 2 3 3 4
Câu 25: Cho đồ thị hàm số y = f ( x) như hình bên. Khẳng định nào sau đây là đúng? y 1 1 − O x
A. Đồ thị hàm số có tiệm cận đứng x = 0 , tiệm cận ngang y =1.
B. Hàm số có hai cực trị.
C. Đồ thị hàm số chỉ có một đường tiệm cận. Trang 95
D. Hàm số đồng biến trong khoảng (−;0) và (0; + ) . 3 dx
Câu 26: Tính tích phân I = . x+2 0 21 A. I = − 5 . B. I = 5 ln . C. I = 4581 log . D. I = . 100 2 2 5000
Câu 27: Trong không gian với hệ trục tọa độ Oxyz , cho điểm M (1;2; )
3 . Hình chiếu của M lên trục Oy là điểm A. Q (0;2;0) . B. R (1;0;0) . C. P (1;0; ) 3 . D. S (0;0; ) 3 .
Câu 28: Cho khối nón có bán kính đáy r = 3, chiều cao h = 2. Tính thể tích V của khối nón.
A. V = 3 2 .
B. V = 9 2 .
C. V = 2 .
D. V = 3 11. 2 ln x b b
Câu 29: Cho tích phân I = dx =
+ a ln 2 với là số thực, và là các số dương, đồng thời a b c 2 x c c 1
là phân số tối giản. Tính giá trị của biểu thức P = 2a + 3b + c .
A. P = 6 .
B. P = 5 . C. P = 6 − . D. P = 4 .
Câu 30: Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng đáy ( ABC ). Biết SA = a ,
tam giác ABC là tam giác vuông cân tại A , AB = 2a . Tính theo a thể tích V của khối chóp S.ABC . 3 a 3 a 3 2a A. V = . B. V = . 3 C. V = .
D. V = 2a . 6 2 3
Câu 31: Trong không gian với hệ trục tọa độ Oxyz , phương trình nào dưới đây là phương trình mặt + − phẳng đi qua x y z M (1; 1 − 1 2
; 2) và vuông góc với đường thẳng : = = . 2 1 − 3
A. 2x − y + 3z + 9 = 0 .
B. 2x + y + 3z − 9 = 0 . C. 2x − y + 3z − 9 = 0 . D. 2x − y + 3z − 6 = 0 .
Câu 32: Cho hàm số y = f ( x) có bảng biến thiên như bên dưới. Trang 96
Mệnh đề nào dưới đây sai?
A. Hàm số nghịch biến trên khoảng ( 1 − ;0) .
B. Hàm số đồng biến trên khoảng ( ;3 − ) .
C. Hàm số nghịch biến trên khoảng (0 ) ;1 .
D. Hàm số đồng biến trên khoảng (2; +) . x = t
Câu 33: Trong không gian với hệ trục tọa độ Oxyz . Đường thẳng d : y = 1− t đi qua điểm nào sau z = 2 +t đây? A. K (1; 1 − ; ) 1 . B. E (1;1; 2) . C. H (1;2;0) . D. F (0;1; 2) . −
Câu 34: Tìm tập xác định D của hàm số y = ( x − ) 4 2 1 . A. D = . B. D = \ 1 − ; 1 . C. D = (− ; − ) 1 (1;+) . D. D = ( 1 − ; ) 1 . x 1
Câu 35: Tập nghiệm của bất phương trình 9
trên tập số thực là 3 A. (2;+) . B. (− ; 2 − ). C. ( ; − 2) . D. ( 2; − +).
Câu 36: Giá trị của m để hàm số 3
y = x + 2(m – ) 2
1 x + m –1 x + 5 ( ) đồng biến trên là 7 A. m (− ; 1) ( ;+ ) 7 . B. m 1; . 4 4 7 C. m (− ; 1][ ;+ ) 7 . D. m 1; . 4 4
Câu 37: Cho hình chóp S.ABCD , có đáy là hình chữ nhật, AB = a, AD = 2a, SA = a 3 và SA vuông
góc với đáy. Gọi E, F, K lần lượt là trung điểm của BC, SB và .
SA Tính khoảng cách từ F
đến mặt phẳng (KED) . 66 33 a 66 33 A. a . B. a . C. . D. a . 44 44 11 11
Câu 38: Cho hình hộp chữ nhật ABC . D A B C D
, có AB = a, AD = a 2, góc giữa AC và mặt phẳng
(ABCD) bằng 30. Gọi H là hình chiếu vuông góc của Atrên A B
và K là hình chiếu vuông
góc của A trên A . D
Tính góc giữa hai mặt phẳng ( AHK ) và ( ABB A ). A. 60 . B. 45 . C. 90 . D. 30 . Trang 97
Câu 39: Cho hàm số y = f ( x) có đạo hàm f ( x) liên tục trên 2 − ;
1 . Hình bên là đồ thị của hàm số x
y = f ( x). Đặt g ( x) = f ( x) 2 − . 2
Khẳng định nào sau đây đúng? A. g ( ) 1 g ( 2
− ) g (0). B. g (0) g ( ) 1 g ( 2 − ). C. g ( 2 − ) g ( )
1 g (0). D. g (0) g ( 2 − ) g ( ) 1 .
Câu 40: Cho tam giác ABC đều cạnh a , đường thẳng d đi qua A và vuông góc với mặt phẳng
(ABC). Gọi S là điểm thay đổi trên đường thẳng d , H là trực tâm tam giác SBC . Biết rằng
khi điểm S thay đổi trên đường thẳng d thì điểm H nằm trên đường tròn (C). Trong số các
mặt cầu chứa đường tròn (C) , bán kính mặt cầu nhỏ nhất là a 3 a 2 a 3 A. . B. a . C. . D. . 6 2 12
Câu 41: Cho 2 số phức z ; z thoả mãn z + 5 = 5; z +1− 3i = z − 3− 6i . Giá trị nhỏ nhất của biểu 1 2 1 2 2
thức P = z − z là 1 2 3 5 A. P = 3. B. P = . C. P = . D. P = 5. min min 2 min 2 min
Câu 42: Tìm tất cả các giá trị của tham số m để phương trình 4(log x
− log x + m = 0 2 )2 có nghiệm 1 2 thuộc khoảng (0 ) ;1 1 1 1 A. m 0; .
B. m(− ;0 . C. ; + . D. m − ; . 4 4 4
Câu 43: Cho hàm số y = f ( x) , biết rằng hàm số y = f '( x) có đồ thị như hình bên. Trang 98
Hàm số y = f (2 − x) + 2019 đồng biến trên các khoảng A. ( 2 − ;0) và (1;2). B. ( 2 − ;0) và (2;4). C. (0 ) ;1 và (1; 2) . D. (0 ) ;1 và (2;4).
Câu 44: Một người gửi tiết kiệm ngân hàng với lãi suất 0,6% /tháng theo cách sau: mỗi tháng (vào đầu
tháng) người đó gửi vào ngân hàng 5 triệu đồng và ngân hàng tính lãi suất (lãi suất không đổi)
dựa trên số tiền tiết kiệm thực tế có trong ngân hàng. Hỏi sau 10 năm, số tiền của người đó có
được gần nhất với số tiền nào dưới đây (cả gốc và lãi, đơn vị triệu đồng)? A. 880, 29. B. 880,16 . C. 880 . D. 880, 26. x +
Câu 45: Tìm giá trị thực của tham số m để đường thẳng d : y = − 3x + 2 1
m cắt đồ thị hàm số y = x−1
(C) tại hai điểm phân biệt A và B sao cho trọng tâm tam giác OAB thuộc đường thẳng
:x−2y −2=0, với O là gốc tọa độ. A. m = 11 0. B. m = − 1 .
C. m = − . D. m = 2 − . 5 5
Câu 46: Trong không gian với hệ trục tọa độ $Oxyz$, cho tam giác ABC có A(2;3;3) , phương trình − − −
đường trung tuyến kẻ từ x 3 y 3 z 2 B là = =
, phương trình đường phân giác trong của 1 − 2 1 − x − 2 y − 4 z − 2 góc C là = =
. Đường thẳng AB có một véc-tơ chỉ phương là 2 1 − 1 −
A. u = (2;1; − ) 1 . B. u = (1; 2; ) 1 .
C. u = (0;1; − ) 1 . D. u = (1; 1 − ;0) . 1 f x
Câu 47: Cho F (x) = − ( )
là một nguyên hàm của hàm số
. Tìm nguyên hàm của hàm số 3 3x x f ( ) x ln x . ln x 1 ln x 1 A. f ( x)ln d x x = + + C . B. f ( x)ln d x x = − + + C . 3 5 x 5x 3 3 x 3x ln x 1 ln x 1 C. f ( x)ln d x x = + + C . D. f ( x)ln d x x = − + C . 3 3 x 3x 3 5 x 5x
Câu 48: Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(0; 2 − ;− ) 1 , B( 2 − ; 4 − ; ) 3 , C (1;3;− ) 1 và
mặt phẳng (P) : x + y − 2z −3 = 0 . Biết điểm M ( ; a ;
b c)(P) thỏa mãn MA + MB + 2MC đạt
giá trị nhỏ nhất. Tính T = a + b + c . Trang 99 A. T = 1 − 1 . B. T = . C. T = 1 0 . D. T = − . 2 2
Câu 49: Đội văn nghệ của trường THPT Hùng Vương có 9 học sinh, trong đó có 4 học sinh lớp 12 , 3
học sinh lớp 11 và 2 học sinh lớp 10 . Hỏi có bao nhiêu cách chọn ra một nhóm có ít nhất ba
học sinh để biểu diễn dịp 26 tháng 3 sao cho mỗi khối phải có ít nhất một học sinh, biết rằng
năng khiếu văn nghệ của các em là như nhau. A. 24 . B. 315 . C. 420 . D. 25 .
Câu 50: Số giá trị nguyên của m 10 để hàm số y = ( 2 ln x + mx + )
1 đồng biến trên (0;+) là A. 8 . B. 10 . C. 9 . D. 11.
----------HẾT---------- ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 D D B B D D D A D D A D D A C D D B D D D D A A A
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 B A A D C C B D B B D A B C D C D D D B C C C B B
HƯỚNG DẪN GIẢI CÁC CÂU VD - VDC
Câu 39: [VD] Cho hàm số y = f ( x) có đạo hàm f ( x) liên tục trên 2 − ;
1 . Hình bên là đồ thị của hàm số x
y = f ( x). Đặt g ( x) = f ( x) 2 − . 2
Khẳng định nào sau đây đúng? A. g ( ) 1 g ( 2
− ) g (0). B. g (0) g ( ) 1 g ( 2 − ). Trang 100 C. g ( 2 − ) g ( )
1 g (0). D. g (0) g ( 2 − ) g ( ) 1 . Lời giải Chọn C.
Ta có g '( x) = f '( x) − x = 0 f '( x) = x .Qua đồ thị ta được f '( x) = x x = 0; x = 2 − ; x =1. Ta
được bảng biến thiên: 0
Lại có, qua đồ thị thì g(0) − g( 2)
− = ( f '(x)− x)dx = S ; 1 2 − 1 g (0) − g ( )
1 = ( f '(x) − x)dx = S mà S S g( 2
− ) g(1) g(0) . 2 2 1 0 Câu 40:
[VD] Cho tam giác ABC đều cạnh a , đường thẳng d đi qua A và vuông góc với mặt phẳng ( ABC ) .
Gọi S là điểm thay đổi trên đường thẳng d , H là trực tâm tam giác SBC . Biết rằng khi điểm S thay
đổi trên đường thẳng d thì điểm H nằm trên đường tròn (C) . Trong số các mặt cầu chứa đường tròn
(C), bán kính mặt cầu nhỏ nhất là a 3 a 2 a 3 A. . B. a . C. . D. . 6 2 12 Lời giải Chọn D. Trang 101 S F E H A C K D B
Gọi K là trọng tâm tam giác ABC . Vì tam giác ABC đều nên K cũng là trực tâm tam giác ABC .
Gọi D , E lần lượt là trung điểm BC , AC . BC ⊥ AD Ta có
BC ⊥ (SAD) BC ⊥ SD . BC ⊥ SA
Kẻ BF ⊥ SC với F SC . Gọi H = SD BF suy ra H là trực tâm của tam giác SBC .
Từ BC ⊥ (SAD) và HK (SAD) suy ra BC ⊥ HK . ( ) 1 AC ⊥ BE Ta có
AC ⊥ (BEF ) AC ⊥ HK . (2) AC ⊥ BF Từ ( )
1 và (2) ta có HK ⊥ (SBC) HK ⊥ SD .
Rõ ràng mặt phẳng (d, D) cố định nên khi S thay đổi trên d thì H luôn nằm trên mặt phẳng cố định ( 1 a 3
d, D) . Mặt khác DHK = 90 nên H thuộc đường tròn (C) đường kính DK = AD = . 3 6
Trong số các mặt cầu chứa đường tròn (C) , mặt cầu nhận (C) là đường tròn lớn là mặt cầu có bán a 3
kính nhỏ nhất. Bán kính của mặt cầu này là R = . 12
Câu 41: [VD] Cho 2 số phức z ; z thoả mãn z + 5 = 5; z +1− 3i = z − 3 − 6i . Giá trị nhỏ nhất của biểu 1 2 1 2 2
thức P = z − z là 1 2 3 5 A. P = 3. B. P = . C. P = . D. P = 5. min min 2 min 2 min Lời giải Chọn C. Trang 102 N M I C D
Gọi M, N lần lượt là các điểm biểu diễn số phức z ; z . Khi đó M nằm trên đường tròn tâm 1 2 I ( 5
− ;0) , bán kính R = 5; N nằm trên đường thẳng trung trực của đoạn thẳng AB với A( 1 − ;3) , B (3;6) .
Phương trình đường thẳng là 8x + 6y −35 = 0 . 8. 5 − + 6.0 −35 15
Khoảng cách từ điểm I đến là d (I;) ( ) = = 5 = R . 2 2 + 2 8 6 15 5 5
Ta có P = z − z = MN d I; − R = − 5 = P = 1 2 ( ) . Vậy . min 2 2 2
Câu 42: [VD] Tìm tất cả các giá trị của tham số m để phương trình 4(log x
− log x + m = 0 2 )2 có nghiệm 1 2 thuộc khoảng (0 ) ;1 1 1 1 A. m 0; .
B. m(− ;0 . C. ; + . D. m − ; . 4 4 4 Lời giải Chọn D. 2 2 Ta có 4 (log x
− log x + m = 0 log x + log x + m = 0 ( ) 1 2 ) 1 ( 2 ) 2 2
Đặt t = log x . Khi x (0; ) 1 thì t 0 . 2 Phưng trình trở thành 2
t + t + m = 0 (2)
Phương trình đã cho có nghiệm thuộc khoảng (0 )
;1 khi và chỉ khi phương trình (2) có nghiệm t 0 . Ta có các khả năng sau :
Phương trình (2) có nghiệm t 0 t m 0 . 1 2 =1− 4m 0 1
Phương trình (2) có nghiệm t t 0 S = 1 − 0 0 m . 1 2 4 P = m 0 Trang 103
Phương trình (2) có nghiệm t t = 0 m = 0 . 1 2 1
Vậy, điều kiện để phương trình đã cho có nghiệm thuộc khoảng (0 ) ;1 là m − ; . 4
Câu 43: [VD] Cho hàm số y = f ( x) , biết rằng hàm số y = f '( x) có đồ thị như hình bên.
Hàm số y = f (2 − x) + 2019 đồng biến trên các khoảng A. ( 2 − ;0) và (1;2). B. ( 2 − ;0) và (2;4). C. (0 ) ;1 và (1; 2) . D. (0 ) ;1 và (2;4). Lời giải Chọn D. 2 − 2 − x 0 2 x 4
Ta có y = − f (2 − x) 0 f (2 − x) 0 1 2 − x 2 0 x 1 .
Câu 44: [VD] Một người gửi tiết kiệm ngân hàng với lãi suất 0,6% /tháng theo cách sau: mỗi tháng (vào
đầu tháng) người đó gửi vào ngân hàng 5 triệu đồng và ngân hàng tính lãi suất (lãi suất không
đổi) dựa trên số tiền tiết kiệm thực tế có trong ngân hàng. Hỏi sau 10 năm, số tiền của người đó
có được gần nhất với số tiền nào dưới đây (cả gốc và lãi, đơn vị triệu đồng)? A. 880, 29. B. 880,16 . C. 880. D. 880, 26. Lời giải Chọn D. n 1+ r −1
Ta có công thức tính số tiền T = . A (1+ r ) ( ) . r + − T = ( + ) ( )120 1 0, 6 1 5. 1 0, 6% 880,26 . 0, 6%
Câu 45: [VD] Tìm giá trị thực của tham số m để đường thẳng d : y = − 3x + m cắt đồ thị hàm số 2x +1 y =
(C) tại hai điểm phân biệt A và B sao cho trọng tâm tam giác OAB thuộc đường x −1
thẳng :x −2y −2=0, với O là gốc tọa độ. A. m = 11 0. B. m = − 1 .
C. m = − . D. m = 2 − . 5 5 Lời giải Trang 104 Chọn B. 2x +1
Hoành độ giao điểm là nghiệm phương trình 3 − x + m =
, điều kiện x 1. x −1 (x − ) 1 ( 3
− x + m) = 2x +1 2 3x −(m+ ) 1 x + m +1 = 0 f ( ) 1 0
Để phương trình có hai nghiệm phân biệt khác 1 thì m(− ) ;1 (11; +) 0
Khi đó gọi A(x ;−3x + m , B x ;−3x + m 1 1 ) ( 2 2 ). x + x 3
− x −3x + 2m
Vì G là trọng tâm tam giác OAB nên 1 2 1 2 G ; 3 3 m +1 x + x = 1 2 3
m +1 m −1 Theo viet ta có: G ; m +1 9 3 x .x = 1 2 3 m + m − − Vì G thuộc 1 1 11 nên − 2. − 2 = 0 m = . 9 3 5
Câu 46: [VD] Trong không gian với hệ trục tọa độ Oxyz , cho tam giác ABC có A(2;3;3) , phương trình x − 3 y − 3 z − 2
đường trung tuyến kẻ từ B là = =
, phương trình đường phân giác trong của góc C là 1 − 2 1 − x − 2 y − 4 z − 2 = = . Đường thẳng
có một véc-tơ chỉ phương là 2 1 − 1 − AB
A. u = (2;1; − ) 1 . B. u = (1; 2; ) 1 .
C. u = (0;1; − ) 1 . D. u = (1; 1 − ;0) . Lời giải Chọn C. x − 3 y − 3 z − 2
Gọi M là trung điểm của AC BM : = = . 1 − 2 1 −
Gọi E là chân đường phân giác trong góc C của tam giác ABC Trang 105 x − 2 y − 4 z − 2 CE : = = . 2 1 − 1 −
Ta có: M BM M (3− t;3+ 2t;2 − t ) .
Vì M là trung điểm AC C (4 − 2t;3+ 4t;1− 2t ) .
Mà C CE t = 0 C (4;3; ) 1 .
Gọi (P) là mặt phẳng qua A(2;3;3) và vuông góc với CE (P) : 2x − y − z + 2 = 0 .
Gọi I là giao điểm của CE và (P) I (2;4;2) .
Gọi J là điểm đối xứng của A lên qua CE J BC .
I là trung điểm của AJ J (2;5; ) 1 .
Phương trình cạnh BC qua C (4;3; ) 1 và có VTCP CJ = ( 2 − ;2;0) là x = 4 − 2t
BC : y = 3 + 2t . z =1
Vì B là giao điểm của BC và BM B (2;5; ) 1 .
Vậy đường thẳng AB có một VTCP là AB = (0;2;− 2) hay u = − AB (0;1; ) 1 . 1 f x
Câu 47: [VD] Cho F (x) = − ( )
là một nguyên hàm của hàm số
. Tìm nguyên hàm của hàm số 3 3x x f '( ) x ln x . ln x 1 ln x 1 A. f '(x) ln d x x = + + C . B. f '(x) ln d x x = − + + C . 3 5 x 5x 3 3 x 3x ln x 1 ln x 1 C. f '(x) ln d x x = + + C . D. f '(x) ln d x x = − + C . 3 3 x 3x 3 5 x 5x Lời giải Chọn C. 1 f x
Ta có F (x) = − ( )
là một nguyên hàm của hàm số nên 3 3x x F( x) f ( x) 1 f ( x) = − = 3 x 3x x ( ) 1 3 f x =
f (x) = − . 3 x 4 x Trang 106 3 ln x Khi đó f (x)ln d x x = − ln d x x = 3 − dx . 4 4 x x dx u = ln x du = Đặt x − . 3 dv = dx 1 4 v x = 3 x f (x) ln x dx ln x 1 ln d x x = − = + + C . 3 4 3 3 x x x 3x
Câu 48: [VD] Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(0; 2 − ;− ) 1 , B( 2 − ; 4 − ; ) 3 , C (1;3;− ) 1 và
mặt phẳng (P) : x + y − 2z −3 = 0 . Biết điểm M ( ; a ;
b c)(P) thỏa mãn MA + MB + 2MC đạt giá
trị nhỏ nhất. Tính T = a + b + c . A. T = 1 − 1 . B. T = . C. T = 1 0 . D. T = − . 2 2 Lời giải Chọn C.
Gọi I là trung điểm của AB I ( 1 − ;−3; ) 1 .
Gọi J là trung điểm của IC J (0;0;0) .
Khi đó MA + MB + 2MC = 2MI + 2MC = 4MJ = 4MJ .
MA + MB + 2MC đạt giá trị nhỏ nhất MJ ngắn nhất M là hình chiếu vuông góc của J lên (P).
Gọi là đường thẳng qua J (0;0;0) và vuông góc với (P) x = t
Ta có : y = t . z = 2 − t 1 1
Khi đó M là giao điểm của và (P) M ; ; −1 . 2 2 1 1 Suy ra a = ,b = , c = 1 − . 2 2
Vậy T = a + b + c = 0 .
Câu 49: [VDC] Đội văn nghệ của trường THPT Hùng Vương có 9 học sinh, trong đó có 4 học sinh
lớp 12 , 3 học sinh lớp 11 và 2 học sinh lớp 10. Hỏi có bao nhiêu cách chọn ra một nhóm có ít
nhất ba học sinh để biểu diễn dịp 26 tháng 3 sao cho mỗi khối phải có ít nhất một học sinh,
biết rằng năng khiếu văn nghệ của các em là như nhau. Trang 107 A. 24 . B. 315 . C. 420 . D. 25 . Lời giải Chọn B. Chọn k k
học sinh bất kì trong 9 học sinh, có C cách chọn. 9 9
Số cách chọn được một nhóm có ít nhất 3 học sinh để biểu diễn văn nghệ là k C = 466 cách. 9 k =3
Xét trường hợp chọn được k học sinh trong đó không có đủ học sinh ba khối trong đội văn nghệ, điều kiện k 3 .
Trường hợp 1: Học sinh chỉ ở 1 khối lớp, suy ra k 4 k 3; 4 .
Số cách chọn thỏa mãn là 3 3 4
C + C + C = 6 cách. 3 4 4
Trường hợp 2: k học sinh thuộc 2 khối lớp: 7
+ Có ở khối 11 và 12 , khi đó 3 k 7 : Số cách chọn là k C −( 3 3 4 C + C + C = 93 7 3 4 4 ) cách. k =3 6 + Có ở 2 khối 10 và 12 k C −( 3 4 C + C = 37 6 4 4 )
, khi đó 3 k 6 : Số cách chọn là cách. k =3 5 + Có ở 2 khối 10 và k 3 ,
11 khi đó 3 k 5: Số cách chọn là C −C =15 cách. 5 3 k =3
Vậy số cách chọn được nhóm ít nhất 3 học sinh sao cho mỗi khối phải có ít nhất một học sinh là
466 − 6 − 93 − 37 −15 = 315 cách.
Câu 50: [VDC] Số giá trị nguyên của m 10 để hàm số y = ( 2 ln x + mx + )
1 đồng biến trên (0;+) là A. 8 . B. 10 . C. 9 . D. 11. Lời giải Chọn B. 2
x + mx +1 0 Hàm số y = ( 2 ln x + mx + ) 1 + x (0;+) 2x m y = 0 2 x + mx +1 m 2 − x x (0;+) ( ) 1 2
x + mx +1 0 x (0;+) 2 . + x 1 2x + m 0 m − x (0;+) (2) x Xét bất phương trình ( ) 1 : Có ( ) 1 m 0 ( ) * x +
Xét bất phương trình (2) : Xét hàm số f ( x) 2 1 = − trên (0; +). x Trang 108 1 1− x Có f ( x) 2 = −1+ =
, f ( x) = 0 x =1 (do x 0 ). 2 2 x x
BBT của hàm f (x) trên (0;+)
Từ bảng suy ra (2) m 2 − ( ) ** . Kết hợp ( ) * và ( )
** ta được m 0 thỏa mãn yêu cầu bài toán.
Do m nguyên và m 10 nên m0;1;2;...;
9 , có 10 giá trị thỏa mãn. ĐỀ 48
ĐỀ THI THỬ THPT QUỐC GIA 2020 MÔN TOÁN Thời gian: 90 phút
Câu 1. Đường cong hình bên là đồ thị của hàm số nào sau đây? A. 3 y = −x + 3x +1 B. 3 y = −x + 3x −1 C. 3 y = x − 3x +1 D. 3 2 y = −x + 3x +1
Câu 2: Cho hàm số y = f (x) có bảng biến thiên như hình bên. Chọn khẳng định đúng? x − -2 0 2 + Trang 109 y ' - 0 + - 0 + y + + -1 -2 -2
A. Đồ thị hàm số có ba điểm cực trị
B. Hàm số có hai điểm cực trị
C. Giá trị nhỏ nhất của hàm số là –2
D. Đồ thị hàm số đối xứng qua trục tung
Câu 3: Đồ thị hàm số nào có đường tiệm cận ngang? 2 x + 2 x −10 A. 2 y = x − x + 3 B. y = C. 3 2 y = x − 2x + 3 D. y = x −10 2 x + 2
Câu 5. Trong các mệnh đề sau mệnh đề sai. 1 1 1
A. lim = 0. B. limC = C (C R ). C. lim = (k *
N ). D. limqn = + với q > 1. n k n k
Câu 5. Cho tam giác ABC là tam giác đều cạnh a, gọi H là trung điểm cạnh BC. Hình nón nhận
được khi quay tam giác ABC xung quanh trục AH có diện tích đáy bằng bao nhiêu? 2 a 2 a A. . B. 2 2 a . C. . D. 2 a . 2 4 Câu 6: Hàm số 3
y = −x + 3x có cực đại là: A. 1 B. 2 C. –1 D. –2
Câu 7. Cho a > 0 khi đó 4 3
a được viết dưới dạng lũy thừa với số mũ hửu tỷ là: 4 3 3 A. 3 a B. 4 a C. 12 a D. 2 a 4
Câu 8: Tìm đạo hàm của hàm số 3 y = x 1 4 1 3 7 4 7 3 A. 3 y ' = x . B. 3 y ' = x . C. 3 y ' = x . D. 3 y ' = x . 3 4 3 4 V
Câu 9: Cho hình chóp SABC. Gọi M, N lần lượt là trung điểm SA, SB. Khi đó tỷ số SMNC bằng: VSABC Trang 110 1 1 1 A. 4 B. C. D. 2 4 8 2 1 1
Câu 10. Tìm họ nguyên hàm của hàm số y = 3x − − ? 2 x x 1 1 A. 3
y = x − ln x + + c B. 3
y = x − ln x + + c x x 1 1 2 C. 3
y = x − ln x +
D. y = 3x + + + c x 2 3 x x
Câu 11. Cho hai số phức 2019 x 3 y e − = và 2019 3 ' 2019. x y e − =
. Phần ảo của số phức 1 2019 x 3 y ' .e − = là 2019 A. 12. B. 11. C. 1. D. 2018 3 ' 2019. x y e − = .
Câu 12. Mặt cầu tâm I ( 1 − ;2; 3
− ) và đi qua điểm A(2;0;0) có phương trình: 2 2 2 2 2 2 A. ( x + )
1 + ( y − 2) + ( z + 3) = 22. B. ( x + )
1 + ( y − 2) + ( z + 3) = 11. 2 2 2 2 2 2 C. ( x − )
1 + ( y + 2) + ( z − 3) = 22. D. ( x − )
1 + ( y − 2) + ( z − 3) = 22.
Câu 13. Cho vectơ a = (1;3;4) , tìm vectơ b cùng phương với vectơ a A. b = ( 2 − ; 6 − ; 8
− ). B. b = ( 2 − ; 6 − ;8). C. b = ( 2 − ;6;8). D. b = (2; 6 − ; 8 − ).
Câu 14. Cho tập hợp M có 10 phần tử. Số cách chọn ra hai phần tử của M và sắp xếp hai phần tử đó là A. 2 C . B. 2 A . C. 2 C + 2!. D. 2 A + 2!. 10 10 10 10
Câu 15 . Nếu tăng chiều cao của một khối trụ lên gấp 2 lần và tăng bán kính đáy của nó lên gấp 3
lần thì thể tích của khối trụ mới sẽ tăng bao nhiêu lần so với so với thể tích của khối trụ ban đầu. A. 18 lần. B. 36 lần. C. 12 lần. D. 6 lần.
Câu 16: Cho hàm số . Chọn phát biểu đúng ?
A. Hàm số nghịch biến các khoảng (− ; −1) vµ ( −1; + )
B. Hàm số luôn đồng biến trên R.
C. Hàm số đồng biến trên các khoảng (− ; 1) vµ (1; + ) .
D. Hàm số đồng biến trên các khoảng (− ; −1) vµ ( −1; + ) .
Câu 17 Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số: 3 2
y = x − 3x +1 trên 1;
2 . Khi đó tổng M+m bằng bao nhiêu ? A. 2. B. -4. C. 0. D. -2. Trang 111
Câu 18. Rút gọn biểu thức P=(x > 0) . A. P= . B. P= . C. P= . D. P= .
Câu 19. Cho các số thực dương a, b với a khác 1. Khẳng định nào sau đây đúng? 1 A. log (ab) log b log (ab) 2 2log b 2 = + 2 = . B. . a a 2 a a 1 1 1 C. log (ab) log b log (ab) log b 2 = + 2 = . D. . a a 4 a a 2 2 13 15 Câu 20. Nếu 7 8 a
a ;log ( 2 + 5) log (2 + 3) b b thì: A. 0 < a < 1, b > 1
B . 0 < a < 1, 0 < b < 1 C a > 1, b > 1
D. a > 1 , 0 < b < 1
Câu 21. Trong không gian Oxyz , cho mặt phẳng (P) : 2x − 2y − z −3 = 0 và điểm I(1;0;2).
Phương trình mặt cầu tâm I và tiếp xúc với mặt phẳng (P) là: 2 2 2 2 A. ( x − ) 2
1 + y + ( z − 2) = 1. B. ( x + ) 2 1
+ y + (z + 2) =1. 2 2 2 2 C. ( x + ) 2
1 + y + ( z + 2) = 3 . D. ( x − ) 2
1 + y + ( z − 2) = 3 .
Câu 21. Tìm họ nguyên hàm của hàm số ? z =1−i 1 A. z = 1 + i . B. . z = 1 − +i 3 C. . D. + + = . z , z 2 z 2z 8 0; 1 2 x = 1+ t
Câu 22. Tính khoảng cách giữa mặt phẳng ( ) : 2x − y − 2z − 4 = 0 và đường thẳng d: y = 2 + 4t . z = t − 1 4 A. . B. . C. 0. D. 2. 3 3
Câu 23.Số phức z= 1−2+6i thỏa mãn: z − (2 + 3i) z =1− 9i là A. 70 . B. 105 .
C. r = 5cm .
D. h =30cm
Câu 24. Tìm số phức 750 thỏa mãn hệ thức z − (2 + i) = 10 và 250 .
A. SA = a . B. 0 45 . C. 0 60 . D. 0 30 . Trang 112
Câu 25. Trong không gian với hệ trục tọa độ Oxyz , mặt phẳng ( ) đi qua M (0; 2 − ;3) , song song − + với đường thẳng x 2 y 1 d : =
= z và vuông góc với mặt phẳng ( ): x + y − z = 0 có phương 2 3 − trình:
A. 2x −3y −5z −9 = 0 .
B. 2x −3y + 5z −9 = 0 .
C. 2x + 3y + 5z + 9 = 0 .
D. 2x + 3y + 5z −9 = 0 . 4 a b
Câu 26. Biết I = x ln (2x + ) 1 dx =
ln 3 − c , trong đó a, b, c là các số nguyên dương và là 0 b c
phân số tối giản. Tính S = a + b + c . A. S = 60 B. S = 70 C. S = 72 D. S = 68
Câu 27. Trong không gian với hệ trục tọa độ Oxyz . Tọa độ giao điểm M của mặt phẳng
(P):2x+3y + z −4 = 0 với trục Ox là ? 4 A. M (0,0, 4) . B. M 0, , 0 . C. M (3,0,0) . D. M (2,0,0) . 3
Câu 28. Với điều kiện nào của m thì phương trình x x
9 − 2m3 + m + 2 = 0 có 2 nghiệm phân biệt? A. m>2. B. m<2. C. m>3. D.2 m 3
Câu 29. Cho hình chóp S.ABC đáy là tam giác vuông tại B và có cạnh AB bằng 2. SA vuông góc
với đáy và SA bằng 2 2 . Tính khoảng cách từ A đến mặt phẳng (SBC). 2 2 2 3 2 6 A. . B. . C. 2 6 . D. . 3 3 3 1 2 f (x)
Câu 30. Hàm số f ( x) liên tục trên R và f (x) + 2 f
= 3x . Tính I = dx . x x 1 2 3 2 − 2 2 − A. . B. . C. . D. . 2 3 3 3
Câu 31. Trong mặt phẳng phức () , các số phức 3
z + 2i −1 = z + i 2 2 thỏa . Tìm số phức 2 biết
rằng z −1− 3i nhỏ nhất. A.(u 1 1 u = − ; u = 3 − 2 q = q = 2 n ) . B. 1 7 2 . C. 2 . D. .
Câu 32. Trong mặt phẳng phức () , trong tất cả các số phức z = x + yi thỏa z −1+ 2i =1. Biết rằng z + 3− a
1 đạt giá trị nhỏ nhất. Tính P = ? b −1 −9 7 7 − A. .. B. . . C. . D. . 7 13 9 13 Trang 113 x = 2
Câu 33. Trong không gian Oxyz , cho d : y = t và mặt cầu 2 2 2
(S) : x + y + z − 2x − 4 y + 2z + 5 = 0. z =1− t
Tọa độ điểm M trên (S ) sao cho d (M,d ) đạt GTLN là: A. (1;2; ) 1 − . B.. (2; 2; 1 − ). C. (0;2; 1 − ) . .D. ( 3 − ; 2 − ; ) 1 . 1
Câu 34. Một vật chuyển động theo quy luật 3 2 s = −
t +9t , với t (giây) là khoảng thời gian 2
tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong thời gian đó. Hỏi
trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu ?
A. 216 (m/s). B. 30 (m/s). C. 400 (m/s). D. 54 (m/s). 4 3
Câu 35. Cho khối cầu (S) có bán kính R. Một khối trụ có thể tích bằng 3
R và nội tiếp khối 9
cầu (S). Chiều cao khối trụ bằng: 2 3 2 3 A. R . B. R . C. R . D. R 2 . 3 2 3
Câu 36. Cho hàm số y = f ( ) x có đạo hàm 2 2
y = f '(x) = x (x − 9)(x − 4) . Xét hàm số 2
y = g(x) = f (x ) trên R. Hàm số đồng biến trên khoảng nào trong các khoảng sau? A. (3; ) + . B. (2; ) + . C. (2;3) . D.( 2 − ;3) .
Câu 37. Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Gọi M là trung
điểm SA. Tính góc giữa hai mặt phẳng (MBD) và (ABCD). A. . 0 45 B.. 0 30 C. 0 60 . D. 0 90 .
Câu 38. Cho hàm số f (x) nhận giá trị dương, có đạo hàm liên tục trên (0; ) + thỏa mãn 1 f (2) = và 2
f '(x) + (2x + 4) f (x) = 0 tính f (1) + f (2) + f (3) 15 7 11 11 7 A. . B. . C. . D. . 15 15 30 30
Câu 39:Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Trên các cạnh AD 2
và BC lần lượt lấy các điểm P, Q sao cho AP = 2 AD và BQ =
BC . Hãy biểu thị MN theo 3 3 MP , MQ . Trang 114 3 3 A. MN = MP + 2 2 MQ B. MN = MP + MQ 4 4 3 3 1 1 C. MN = MP + 1 1 MQ D. MN = MP + MQ 3 3 2 2
Câu 40. Cho tập A = 1,2,...,10
0 . Gọi S là tập hợp tất cả các tập con của A, mỗi tập con gồm 2
phần tử có tổng bằng 100. Chọn ngẫu nhiên một phần tử thuộc S. Xác suất để chọn được phần tử
có tích hai số là một số chính phương bằng 6 4 4 2 A. . B. . C. . D. . 49 99 49 33 2 2
Câu 41. Số đường tiệm cận của đồ thị hàm số 4x −1 + 3x + 2 y = 2 x − x A. 2. B. 3. C. 4. D. 1.
Câu 42 : Cho hàm số y = f ( x) thỏa mãn điều kiện f ' ( x) 2 = x (x + )( 2
1 x + 2mx + 4) . Có bao
nhiêu giá trị nguyên âm của m để hàm số = ( 2 y
f x ) có đúng 1 điểm cực trị? A. 1. B. 2. C. 3. D. 4.
Câu 43. Cho hàm số y = f ( x) 4 2
= ax + bx + c(a 0) có min f (x) = f (− ) 1 . Giá trị nhỏ nhất x ( − 0 ; ) của hàm số y = 1
f ( x) trên đoạn ;2 bằng : 2 a a A. c + 7 8a . B. c − 9 . C. c + . D. c - a 16 16
Câu 44. Cho tam giác ABC vuông có độ dài cạnh huyền bằng 5(đơn vị độ dài). Người ta quay
tam giác ABC quanh trục là một cạnh góc vuông để sinh ra hình nón có thể tích lớn nhất. Xác
định kích thước của tam giác vuông đó 2 5 A. 5 và . B. 3 và 4. C. 10 và 15 . .D. 13 và 2 3 . 3 3
Câu 45. Tìm tất cả các giá trị nguyên của tham số m để hàm số 4 y = x − ( 2 m + ) 2 2 1 x + 2 y có 3
điểm cực trị sao cho giá trị cực tiểu đạt giá trị lớn nhất. A. m = 2 . B. m = 0 . C. m = 1. D. m = 2 − .
Câu 46: Cho hàm số y = f ( x) thỏa mãn điều kiện 2 f ( + x) 3 1 2
= x − f (1− x). Lập phương trình
tiếp tuyến với đồ thị hàm số y = f (x) tại điểm có hoành độ x = 1? Trang 115 1 6 A. y = − x − 1 6 . B. y = − x + 1 6 . C. y = x − 1 6 D. y = x + 7 7 7 7 7 7 7 7
Câu 47. Cho x,y là các số thực lớn hơn 1 và thỏa mãn x2 + 9y2 = 6xy. Tính giá trị của biểu thức 1+ log x + log y 12 12 M = . 2 log (x + 3y) 12 1 1 1 A.M = B. M = 1 C. D. 4 2 3
Câu 48. Cho khối lăng trụ tứ giác đều ABCD.A’B’C’D’ có thể tích V và khối lăng trụ tam giác
đều PQR.P’Q’R’ có thể tích W. Hai khối lăng trụ có chu vi đáy bằng nhau và có diện tích xung
quanh bằng nhau. Tỉ số k = V bằng: W 3 3 3 2 3 A. k = B. k = 3 C. k = D. k = 2 4 3
Câu 49. Trong không gian với hệ tọa độ Oxyz, gọi d đi qua điểm A(1; 1 − ;2) , song song với ( x + y − z
P) : 2x − y − z + 3 = 1 1
0 , đồng thời tạo với đường thẳng : =
= một góc lớn nhất. Phương trình 1 2 − 2
đường thẳng d là. x −1 y +1 z − 2 x −1 y +1 z + 2 A. = = . B. = = . 1 5 − 7 4 5 − 7 x −1 y +1 z − 2 x − y + z − C. = = 1 1 2 . D. = = . 4 5 7 1 5 − 7 −
Câu 50. Trong không gian với hệ trục toạ độ Oxyz ,cho tứ diện ABCD có điểm A(1;1; ) 1 , B(2;0;2) , C ( 1 − ; 1
− ;0), D(0;3;4). Trên các cạnh A ,
B AC, AD lần lượt lấy các điểm B ',C ', D ' thỏa : AB AC AD + +
= 4 . Viết phương trình mặt phẳng (B'C 'D') biết tứ diện AB'C 'D' có thể tích AB ' AC ' AD ' nhỏ nhất ?
A.16x + 40y − 44z + 39 = 0.
B.16x + 40y + 44z −39 = 0 .
C.16x − 40y − 44z + 39 = 0 .
D.16x − 40y − 44z −39 = 0 .
GIẢI CÂU VẬN DỤNG CAO 1 1 3
Câu 30: thay x bởi ta được f
+ 2 f (x) = x x x 1 3 f + 2 f (x) = x x Ta có hệ ta được 2 f (x) = − x 1
f (x) + 2 f = 3x x x Trang 116 2 Khi đó f (x) 3 I = dx = x 2 1 2 Gọi + = 1+ 5 S 0;1 −
;13 là điểm biểu diễn số phức = (− ) 1 5 S 1; 0 − ;13 2 2
Gọi (C ) là điểm biểu diễn số phức k
Gọi y =k(x−m)+1 là điểm biểu diễn số phức M Ta có : x 3 2
−x +4x +1=k(x−m)+1 3 2
−x+4x+1=k (x−m)+1 () ( 1 I) ( 3 2 − 2 x +4x +
3−x +8x=k (2)
)1 =k Tập hợp điểm biểu diễn số phức là đường trung trục ( 2) . (
A 1;3) là điểm biểu diễn số phức 1+ 3i Để 2 x = 0
x2x −(3m+4)x+8m=0 nhỏ nhất khi (I ) ( 3) 2 2x −
(3m + 4) x +8m = 0 (3) tại
Câu 32 : Gọi = 1+ 5 S 0;1 −
;13 là điểm biểu diễn số phức 0 2 Gọi ( A 3
− ;1) là điểm biểu diễn số phức 3 − + i Ta có : 2 2
z −1+ 2i =1 (x −1) + ( y + 2) =1. Vậy tập hợp điểm biểu diễn số phức là đường tròn tâm I (1, 2 − ), R =1
đường thẳng AI : 3x + 4y + 5 = 0 9 1 − 3 x = ; y = 2 2 − + + = xét hệ pt (x 1) ( y 2) 1 5 5 3
x + 4y + 5 = 0 1 7 − x = ; y = 5 5 thử lại ta được 1 7 z = − i 5 5 x −1 P = = y 7
Câu 33. Ta có: d(I, d) =1 = R suy ra (S) tiếp xúc với d và tiếp điểm là H(2;2; 1 − )
Gọi H là hình chiếu vuông góc của I trên d H(2; 2; -1). x =1+ t Đường thẳng
IH có pt: y = 2 ,t . z = 1 −
Tọa độ giao điểm của IH và (S) là: ( A 0;2; 1
− ), B H(2;2; 1 − ). Trang 117 Ta có: d( ,
A (d)) = AH = 2 d( , B ( ) P ) = BH = 0. d( ,
A (d)) = 2 d(M,(d)) d( , B (d)) = 0. Vậy M(0;2; 1 − ).
Câu 36. Ta có: 2 5 2 2 2
g '(x) = 2xf '(x ) = 2x (x − 9)(x − 4) = 0 x = 0 x = 3 x = 3 − x = 2 x = 2 −
Bảng biến thiên của hàm số y = g( ) x
Câu 37. Ta có góc giữa hai mặt phẳng (MBD) và (ABCD) là góc 0 MOC = 45 Câu 38. : vì 2
f '(x) + (2x + 4) f (x) = 0 và f (x) nhận giá trị dương, có đạo hàm liên tục trên − f '(x) 1 (0; ) + nên = 2x + 4suy ra 2 = x + 4x + 1 c vì f (2) = nên c=3 2 f (x) f (x) 15 Do đó 1 1 2
= x + 4x + 3 f (x) = 2 f (x) x + 4x + 3 Do đó 1 1 1 7
f (1) + f (2) + f (3) = + + = 8 15 24 30
Câu 39. Ta có MN = MA + AD + DN
MN = MB + BC + CN
Do đó 2MN = AD + 1 BC hay MN = ( AD + BC) 2 1 3 3 MN = ( AP + 3 BQ) =
( AM + MP + BM + MQ) 2 2 2 4 Trang 118 3 = (MP + MQ) 4
Câu 40. Ta tìm số cặp số (a;b) thoả mãn 1 a b 100, a + b = 100 a 1,2,...,4 9 ,b = 100 − 49
Có 49 cặp (a;b) thỏa mãn. Do đó S gồm 49 phần tử:
Ta tìm số cặp (a;b) thoả mãn
1 a b 100 2 2 2 2 2 2 2 2 a + b = 100
(100 − a) = c c + (50 − a) = 50 = 30 + 40 = 14 + 48 . 2
ab = c , 2 c 49 51 50 − a = 30 − = Do đó 50 a 40
a {2,10,20,36}. Vậy có 4 cặp số (a;b)có tổng bằng 100 và tích của chúng là một 50 − a = 14 50 − a = 48
số chính phương. Xác suất cần tính bằng 4 . 49 1 1
Câu 41. TXD D = −;− 1 ; (1;+ ) lim y = + ;
lim y = − ; lim y = 3; 2 2 + − x 1 → x 1 → x→ x = 0
Câu 42 y' = 2x. f ' ( 2 x ) 5 = 2x ( 2 x + ) 1 ( 4 2
x + 2mx + 4), y' = 0 2 . Lập BBT suy ra 2
m = −x − 2 x m.
Câu 43. Ta có x = 0 là một cực trị, min f ( x) = f (− ) 1 nên x = 1
là cực tiểu.. GTNN là f(1). x ( − 0 ; ) 1 1 1
Câu 44. Gọi x y là độ dài hai cạnh góc vuông, 2 V = r h = ( 2 25 − y ) y = f ( y) . Lập BBT 3 3 3 x = 0 Câu 45. 3 0 = y = 4x − 4 ( 2 m + ) 1 x
Hàm số đã cho luôn có 3 điểm cực trị với mọi 2
x = m +1
m. Do hệ số a =1 0 , nên x
= m + y = − m + + (m + )2 2 1 1 y 1. CT CT ( )2 2 2 1 1 2. Vì Vậy giá CT
trị cực tiểu đạt giá trị lớn nhất bằng 1 khi m = 0. Câu 46 2 x = 0, f ( ) 3 1 = − f ( ) 1 f ( ) 1 = 0 f ( ) 1 = 1
− ; 4(1+ 2x) f ' (1+ 2x) 2
=1− 3 f (1− x) f ' (1− x) 4 f ( ) 1 f ' ( ) 2 1 = 1− 3 f ( ) 1 f ' ( ) 1 ( ) 1 + f ( ) 1 = 0, ( ) 1 0 = 1
+ f ( ) = − f ' ( ) 1 1 1 1 1 = −
→ y = − (x − ) 1 −1 7 7 Trang 119
Câu 47: Từ x2 + 9y2 = 6xy chia hai vế cho xy ta được: x y + 9 = 6 y x x Đặt t =
suy ra t = 3 => x = 3y thay vào biểu thức M => kết quả B y
Câu 48: Từ giả thuyết => Hai khối lăng trụ đó có cùng chiều cao
Gọi a là chu vi đáy tính được canh của hình vuông và tam giác đều theo a => Kết quả C
Câu 49. có vectơ chỉ phương a = − (1; 2;2)
d có vectơ chỉ phương a = (a; ; b c d )
(P) có vectơ pháp tuyến n = − − P (2; 1; ) 1
Vì d / / (P) nên a ⊥ n a .n = 0 2a − b − c = 0 c = 2a − b d P d P a − b a − b cos (,d ) 5 4 1 (5 4 )2 = = 2 2 2 2 − +
3 5a − 4ab + 2b 3 5a 4ab 2b − Đặt a 1 5t 4 t = , ta có: cos (,d ) ( )2 = b 2 3 5t − 4t + 2 5t − 4 Xét hàm số f (t) ( )2 = , ta suy ra được: f (t) 1 5 3 max = f − = 2 5t − 4t + 2 5 3 Do đó: ( d) 5 3 1 a 1 max cos , = t = − = − 27 5 b 5
Chọn a = 1 b = 5 − ,c = 7 − + −
Vậy phương trình đường thẳng x 1 y 1 z 2 d là = = 1 5 − 7
Câu 50. Áp dụng bất đẳng thức AM −GM ta có : AB AC AD A . B AC.AD 3 4 = + + 3 AB ' AC ' AD '
AB '.AC '.AD '
AB '.AC '.AD ' 27 V
AB '.AC '.AD ' 27 27
AB'C ' D' = V V A . B AC.AD 64 V A . B A . C AD 64
AB 'C ' D' 64 ABCD ABCD Để AB ' AC ' AD ' 3 V = = = 3 7 1 7
AB' = AB B' ; ;
AB 'C ' D ' nhỏ nhất khi và chỉ khi AB AC AD 4 4 4 4 4 Lúc đó mặt phẳng ( 7 1 7
B 'C ' D ') song song với mặt phẳng (BCD) và đi qua B ' ; ; 4 4 4
(B'C 'D'):16x + 40y −44z +39 = 0. Trang 120




