







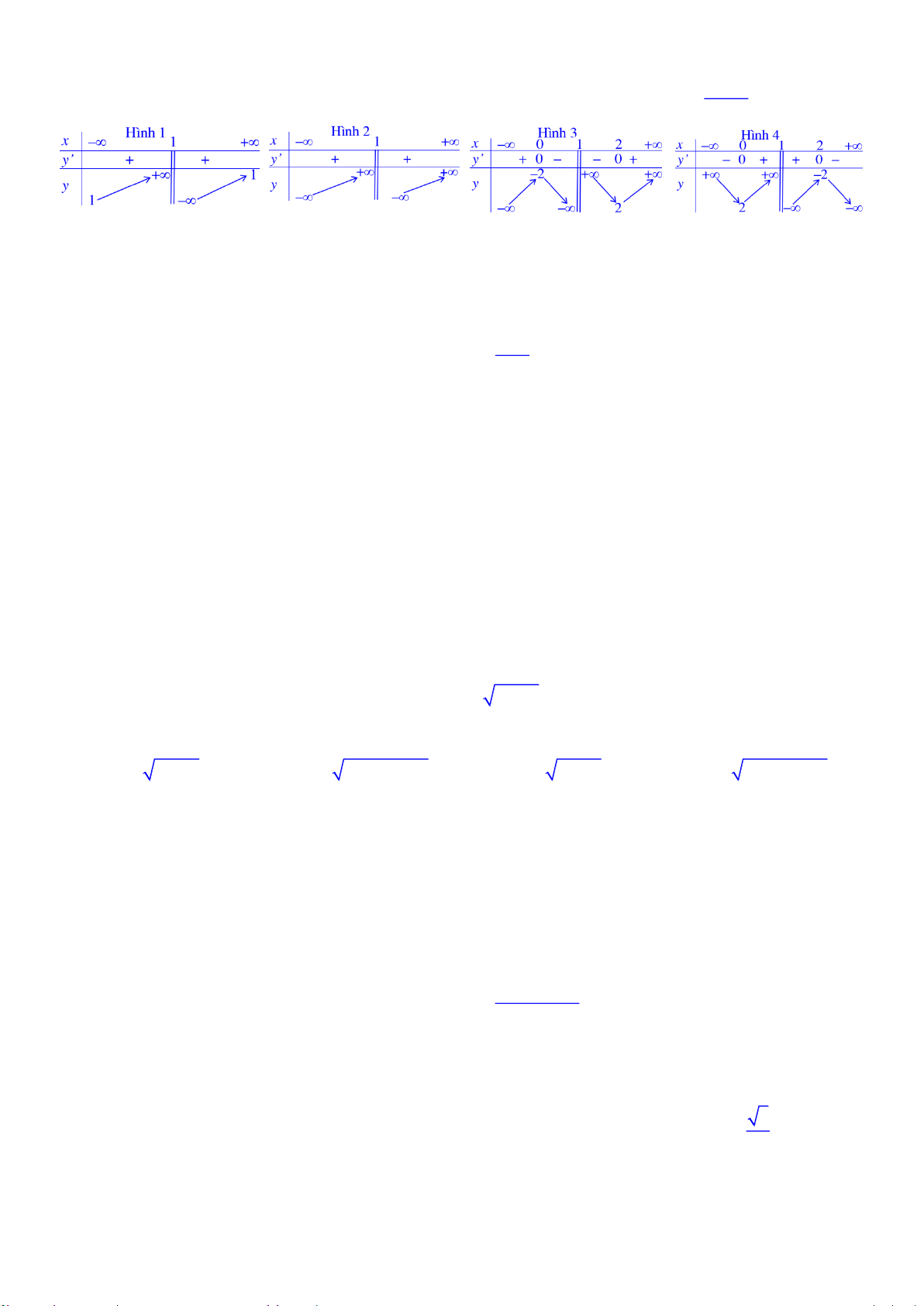

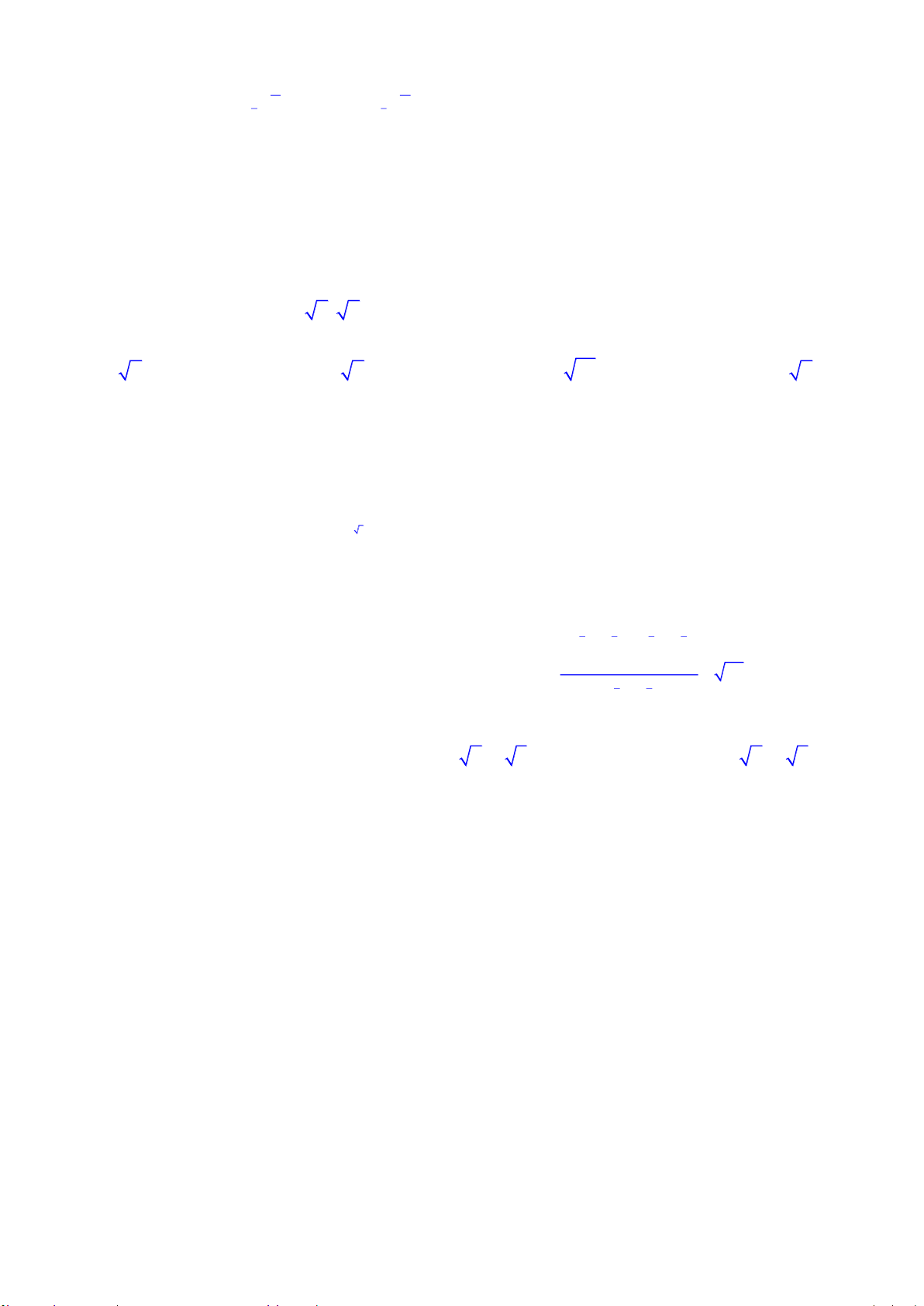








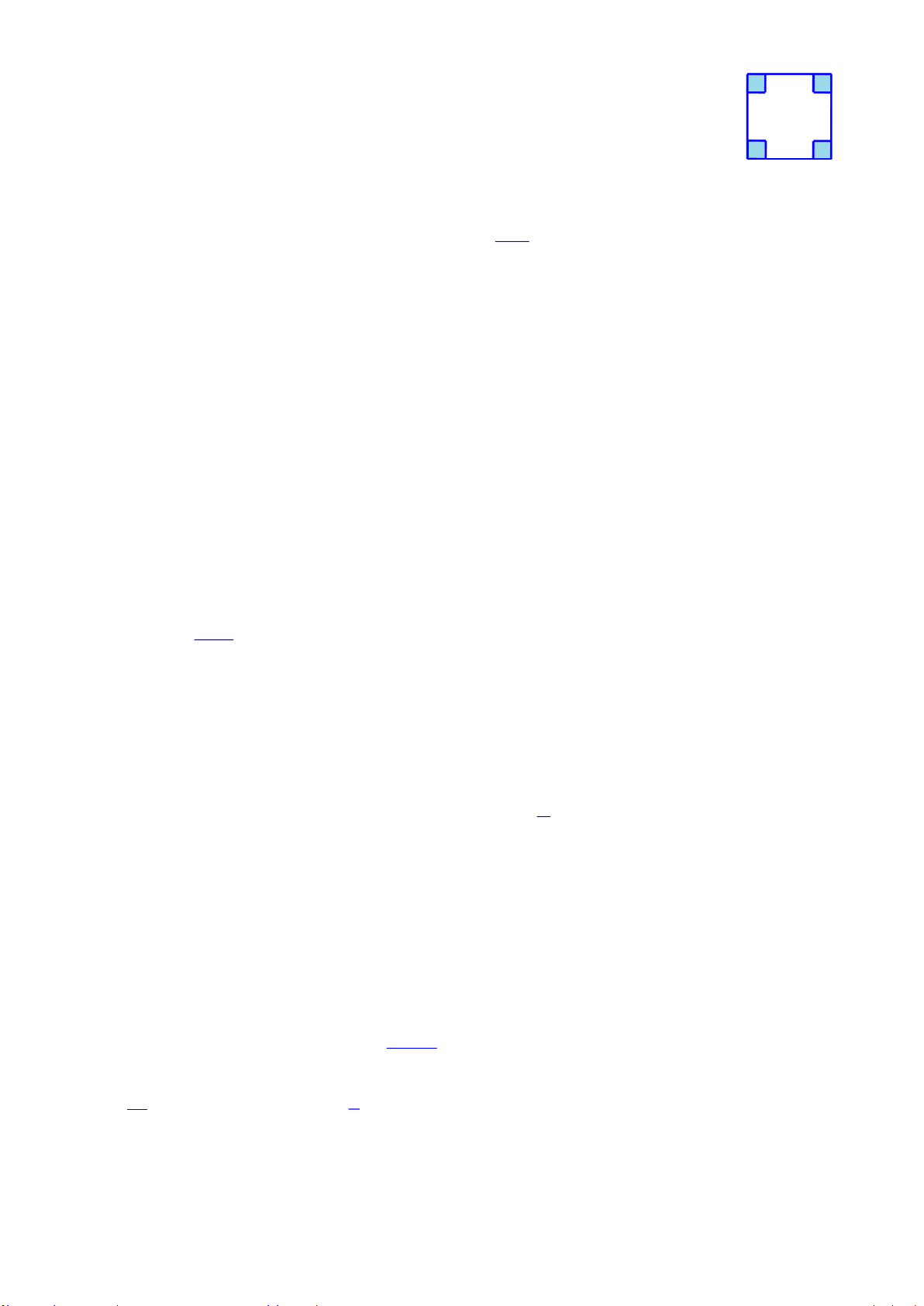












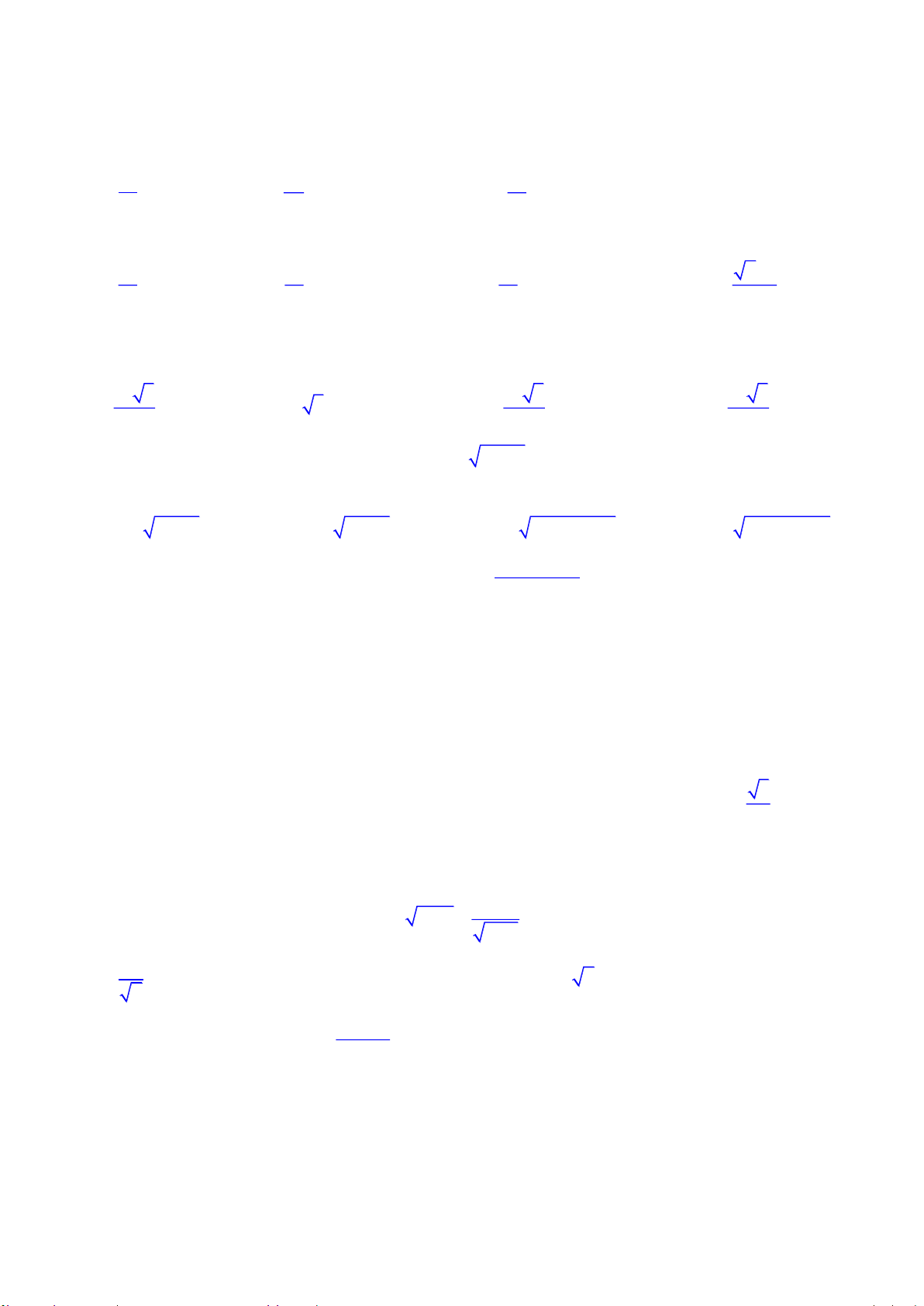






Preview text:
Đáp án Mã đề 912 Toán 12 KTCL giữa HK1 2016 – 2017
Đáp án Mã đề 508 Toán 12 KTCL giữa HK1 2016 – 2017 1A 2C 3C 4B 5C 6D 7A 8A 9D 10A 1B 2B 3C 4A 5B 6D 7D 8B 9C 10B 11C 12B 13B 14A 15B 16A 17D 18C 19D 20D 11A 12B 13D 14A 15B 16C 17A 18A 19C 20D 21B 22A 23C 24A 25B 26C 27A 28C 29B 30C 21B 22B 23B 24D 25D 26D 27A 28A 29C 30A 31B 32A 33C 34D 35B 36D 37D 38D 39A 40D 31C 32C 33B 34C 35C 36D 37D 38C 39A 40B 41B 42B 43D 44B 45D 46A 47C 48C 49A 50B 41C 42D 43B 44C 45D 46A 47D 48A 49A 50A
Đáp án Mã đề 911 Toán 12 KTCL giữa HK1 2016 – 2017
Đáp án Mã đề 507 Toán 12 KTCL giữa HK1 2016 – 2017 1A 2B 3C 4A 5C 6D 7B 8B 9A 10D 1C 2B 3A 4C 5B 6C 7D 8A 9B 10B 11C 12C 13C 14D 15B 16D 17A 18C 19B 20A 11D 12A 13A 14B 15D 16C 17C 18A 19C 20B 21D 22B 23A 24D 25C 26B 27A 28B 29B 30A 21D 22A 23C 24D 25C 26D 27C 28C 29B 30A 31D 32A 33C 34D 35B 36A 37C 38A 39D 40C 31C 32A 33D 34B 35A 36C 37D 38B 39D 40A 41B 42A 43B 44D 45B 46C 47A 48D 49C 50D 41D 42B 43C 44B 45D 46A 47A 48B 49B 50D
Đáp án Mã đề 910 Toán 12 KTCL giữa HK1 2016 – 2017
Đáp án Mã đề 506 Toán 12 KTCL giữa HK1 2016 – 2017 1A 2D 3D 4A 5C 6D 7B 8A 9C 10A 1C 2A 3B 4D 5D 6A 7C 8C 9B 10A 11D 12B 13A 14A 15B 16C 17D 18D 19B 20C 11A 12C 13D 14C 15D 16D 17C 18D 19C 20A 21B 22A 23B 24D 25C 26D 27B 28A 29B 30C 21B 22C 23B 24B 25B 26D 27D 28C 29A 30A 31B 32A 33A 34C 35D 36B 37C 38A 39D 40C 31C 32C 33B 34A 35D 36A 37B 38C 39D 40C 41C 42D 43A 44C 45D 46C 47B 48A 49B 50B 41B 42B 43D 44B 45B 46B 47A 48A 49A 50D
Đáp án Mã đề 909 Toán 12 KTCL giữa HK1 2016 – 2017
Đáp án Mã đề 505 Toán 12 KTCL giữa HK1 2016 – 2017 1C 2A 3A 4D 5B 6A 7C 8B 9C 10A 1D 2A 3A 4D 5C 6D 7A 8B 9A 10B 11B 12D 13B 14A 15A 16D 17C 18B 19A 20C 11C 12A 13D 14D 15B 16B 17A 18B 19A 20C 21D 22B 23D 24B 25B 26C 27D 28C 29D 30B 21B 22C 23A 24B 25D 26B 27A 28D 29B 30C 31C 32C 33A 34B 35D 36C 37A 38B 39C 40A 31B 32D 33C 34A 35C 36B 37A 38C 39D 40B 41D 42C 43D 44A 45B 46B 47C 48A 49D 50D 41D 42C 43C 44D 45C 46D 47C 48B 49C 50A
Đáp án Mã đề 104 Toán 12 KTCL giữa HK1 2016 – 2017
Đáp án Mã đề 102 Toán 12 KTCL giữa HK1 2016 – 2017 1C 2B 3C 4C 5A 6B 7A 8A 9B 10D 1A 2D 3B 4B 5D 6C 7D 8A 9B 10D 11C 12C 13B 14A 15C 16A 17B 18A 19A 20C 11C 12C 13A 14B 15D 16B 17D 18A 19B 20C 21C 22C 23B 24D 25C 26A 27D 28A 29C 30B 21C 22D 23A 24D 25C 26B 27D 28B 29C 30A 31D 32D 33D 34A 35A 36D 37B 38B 39A 40D 31D 32A 33D 34A 35A 36A 37C 38A 39D 40C 41D 42B 43C 44C 45D 46B 47D 48B 49B 50D 41C 42B 43A 44C 45B 46B 47B 48B 49C 50A
Đáp án Mã đề 103 Toán 12 KTCL giữa HK1 2016 – 2017
Đáp án Mã đề 101 Toán 12 KTCL giữa HK1 2016 – 2017 1B 2C 3D 4D 5A 6B 7C 8D 9D 10B 1C 2B 3B 4D 5A 6D 7C 8D 9C 10C 11A 12C 13A 14B 15C 16D 17C 18A 19D 20B 11D 12B 13A 14C 15C 16C 17A 18B 19D 20C 21C 22B 23C 24D 25D 26A 27B 28A 29A 30C 21B 22A 23C 24A 25A 26B 27D 28B 29B 30A 31B 32B 33D 34A 35C 36B 37D 38C 39B 40A 31C 32B 33D 34D 35B 36A 37A 38D 39C 40A 41D 42B 43C 44A 45D 46C 47A 48B 49A 50A 41C 42D 43D 44A 45B 46B 47A 48C 49B 50D
TRƯỜNG THPT NGUYỄN GIA THIỀU ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA HỌC KỲ 1
BỘ MÔN TOÁN Môn toán lớp 12, năm học 2016 – 2017
Đề chính thức gồm 06 trang Thời gian làm bài 90 phút Mã đề 101
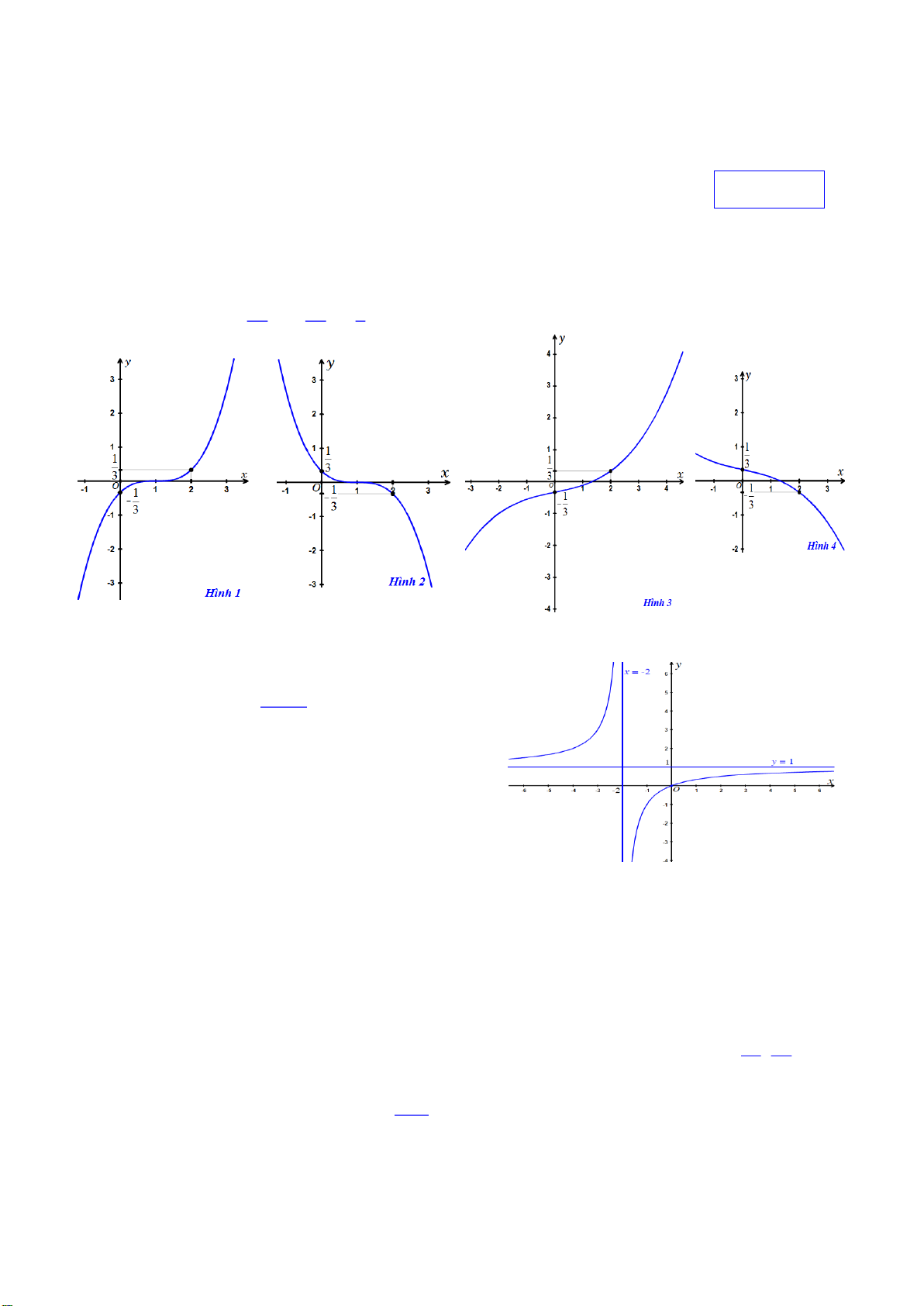
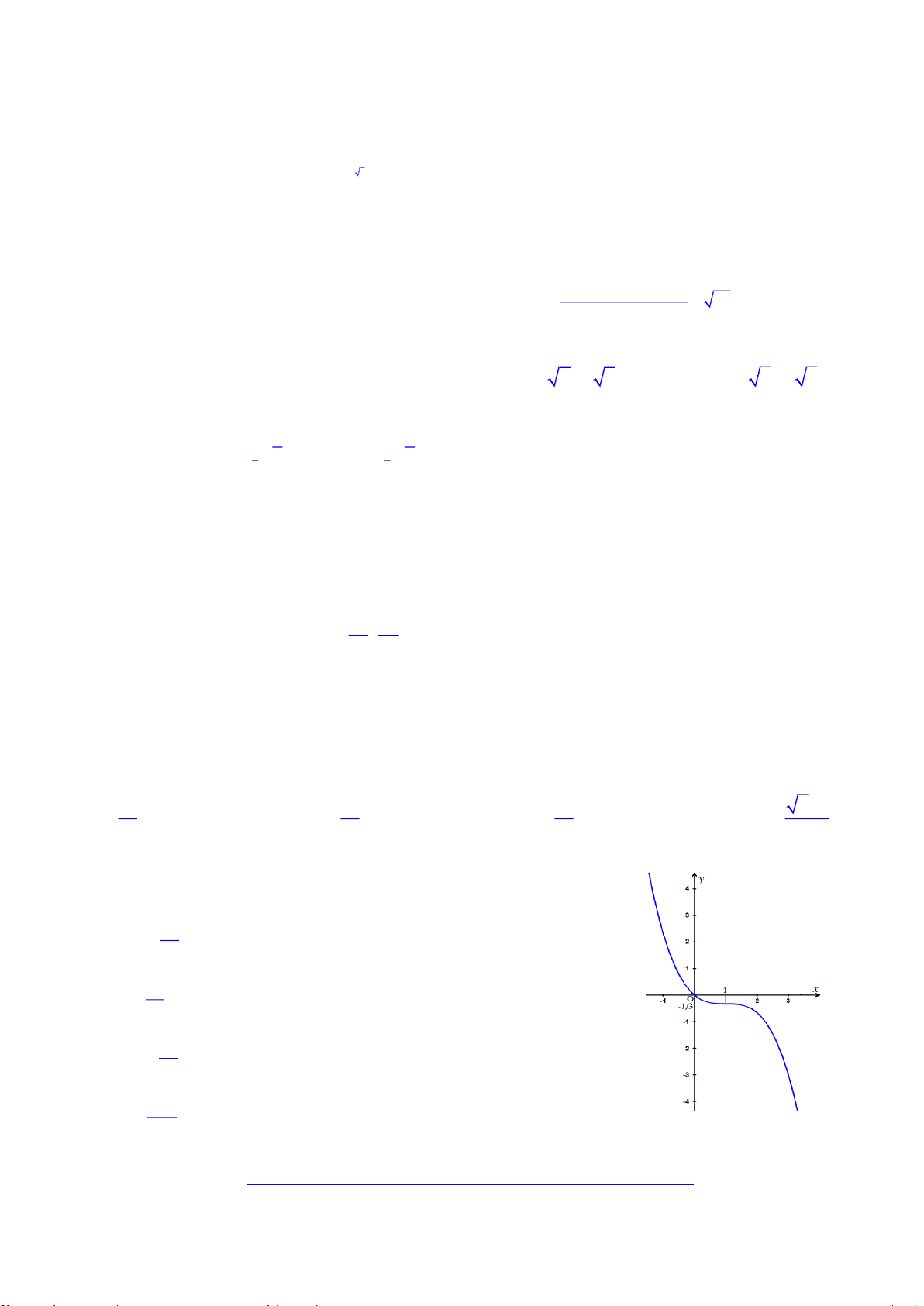
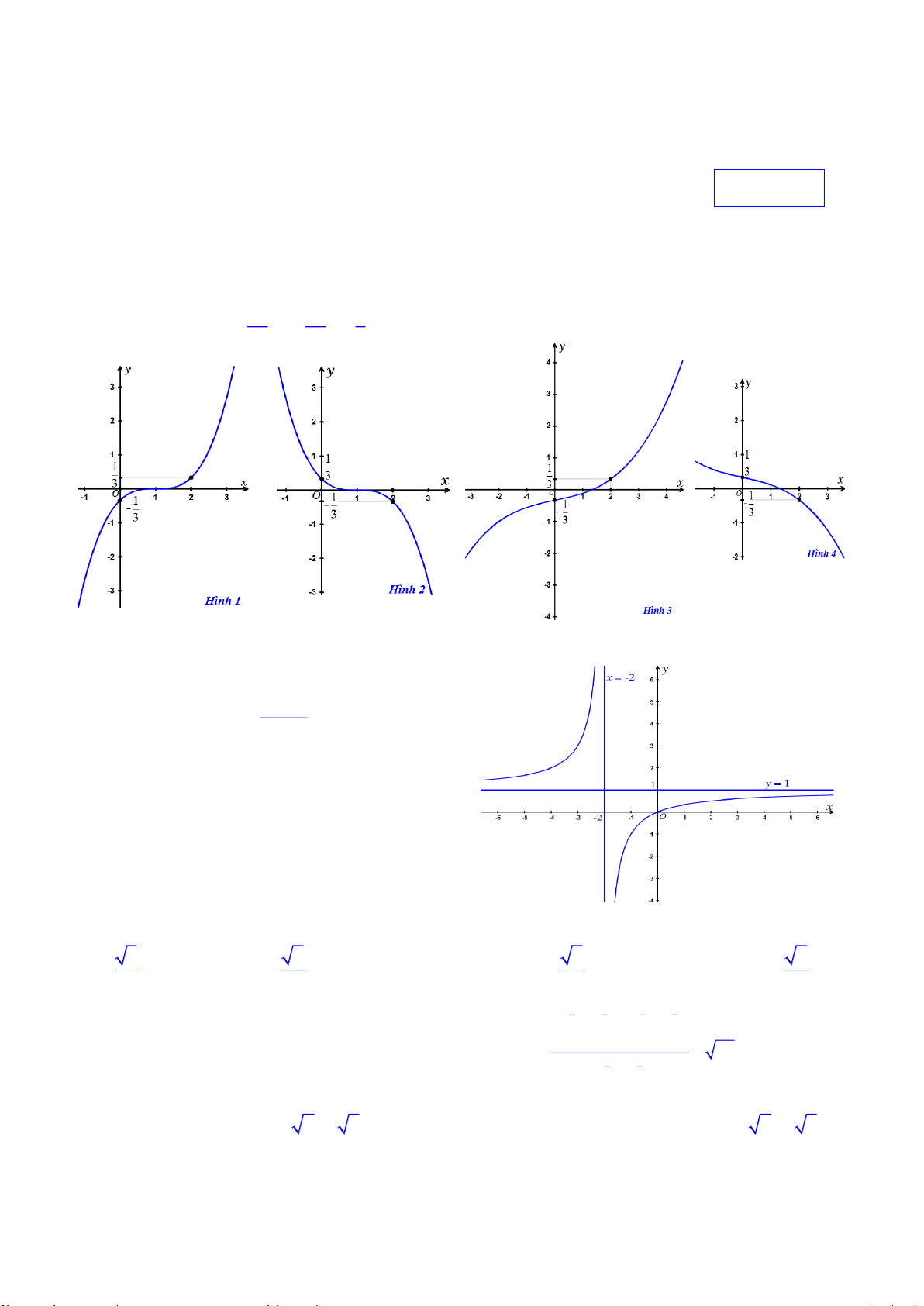
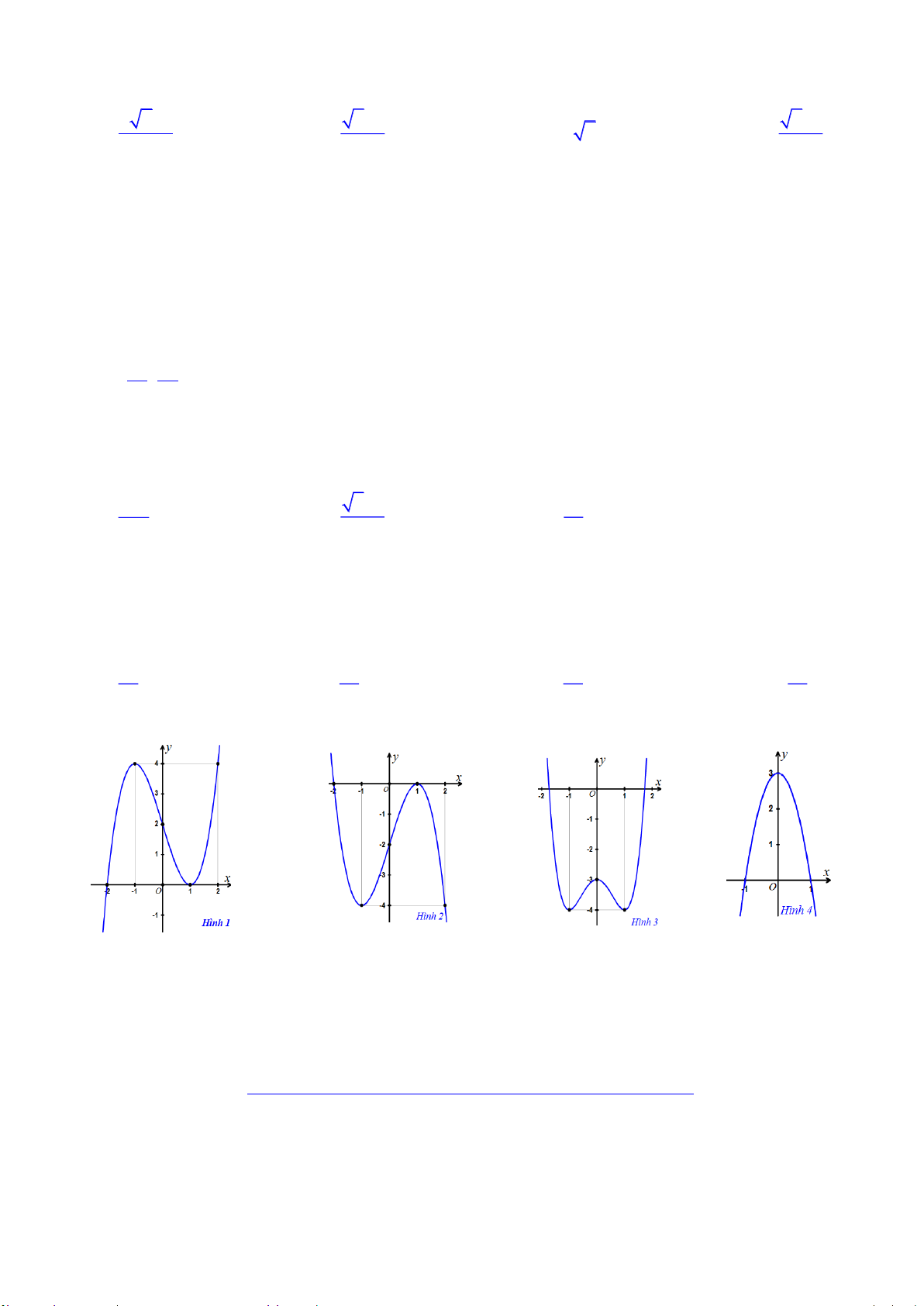
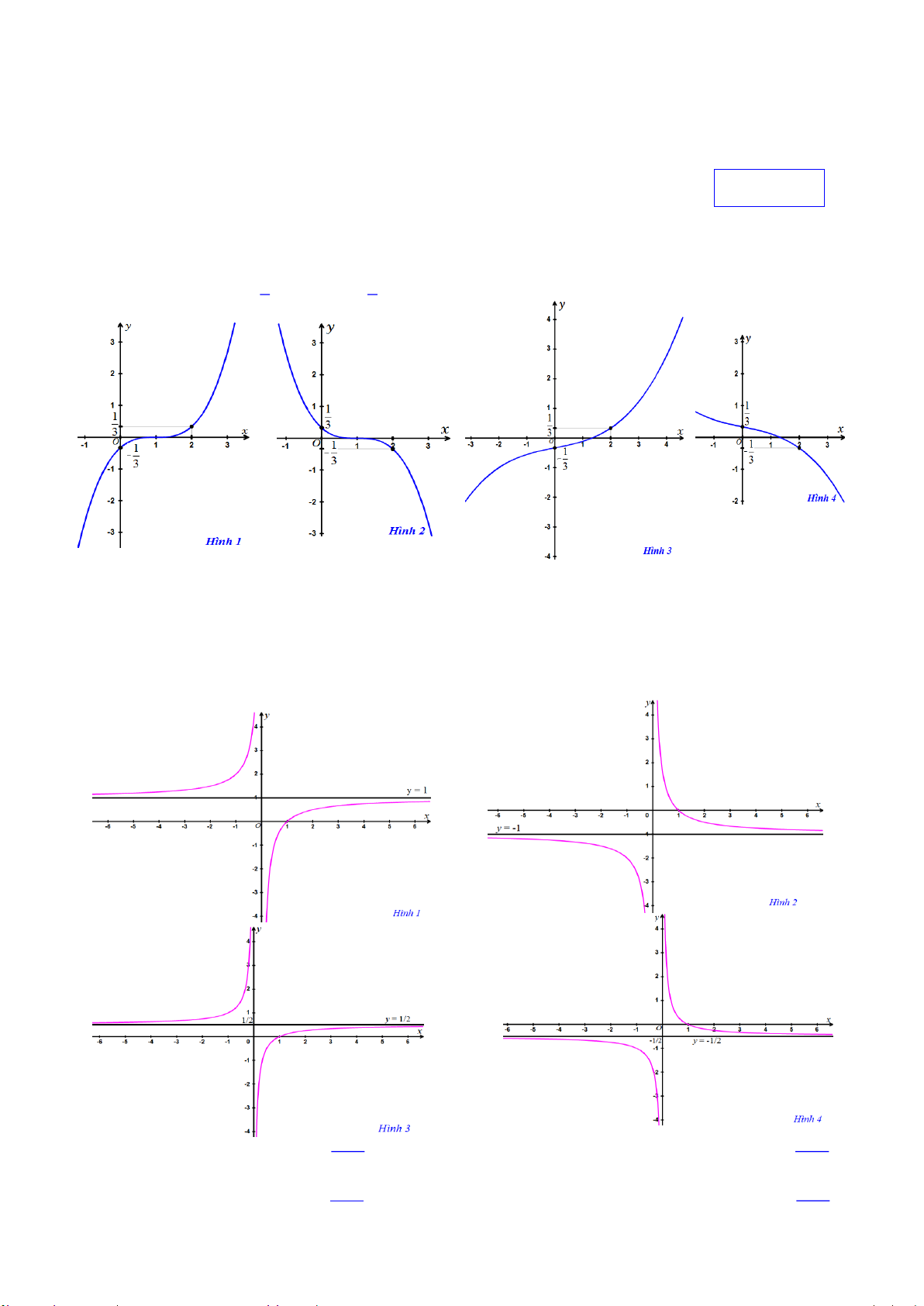
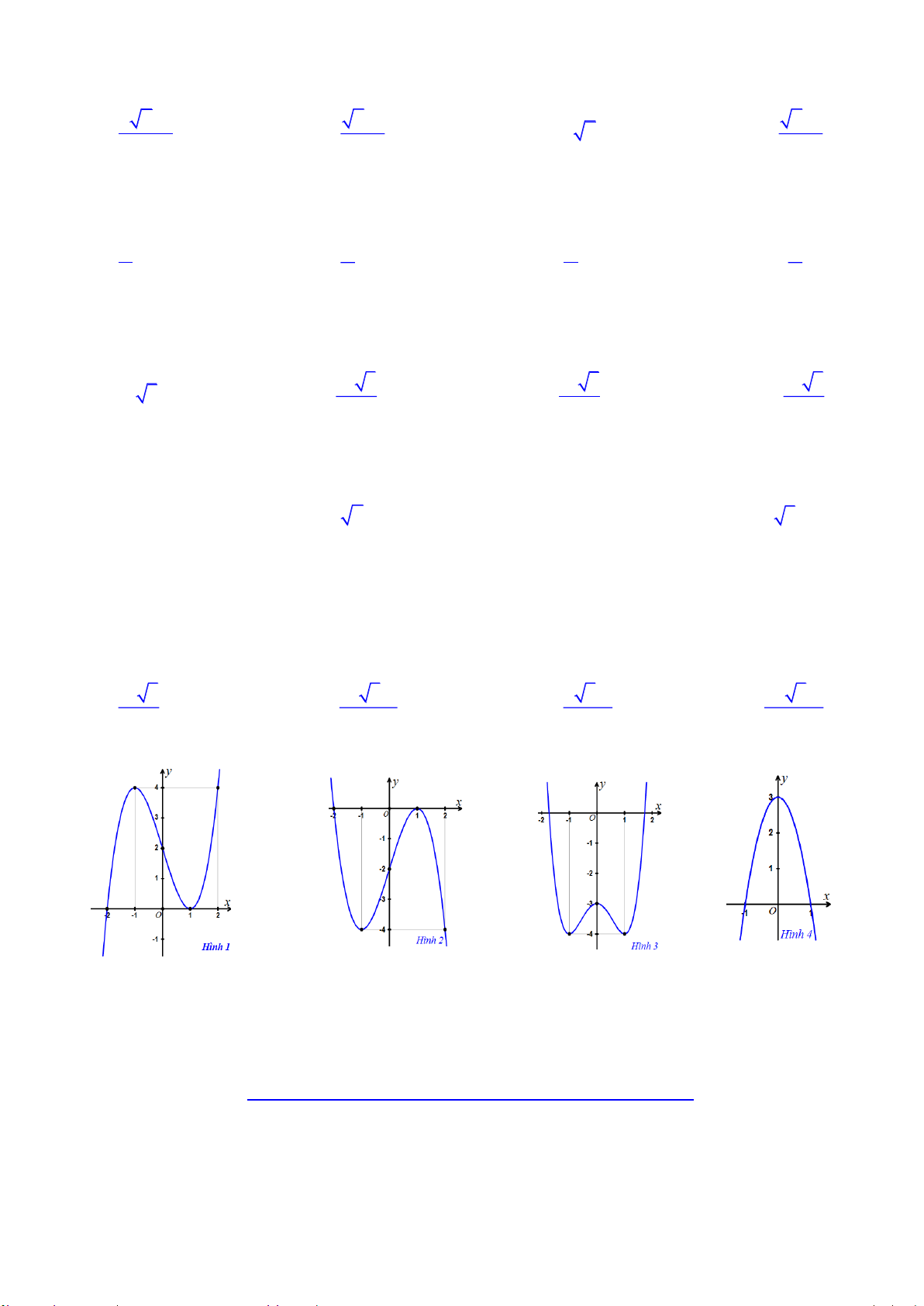
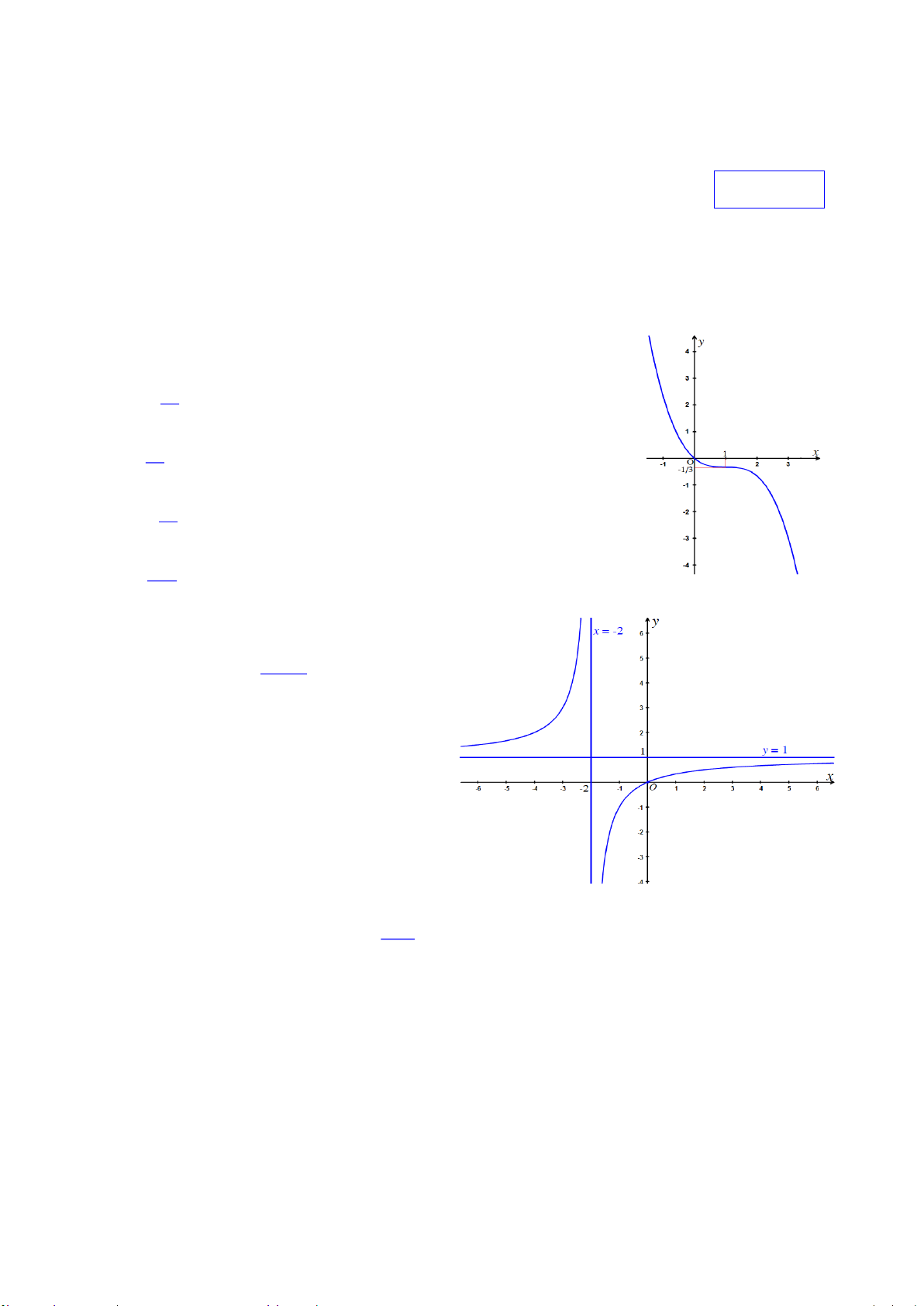
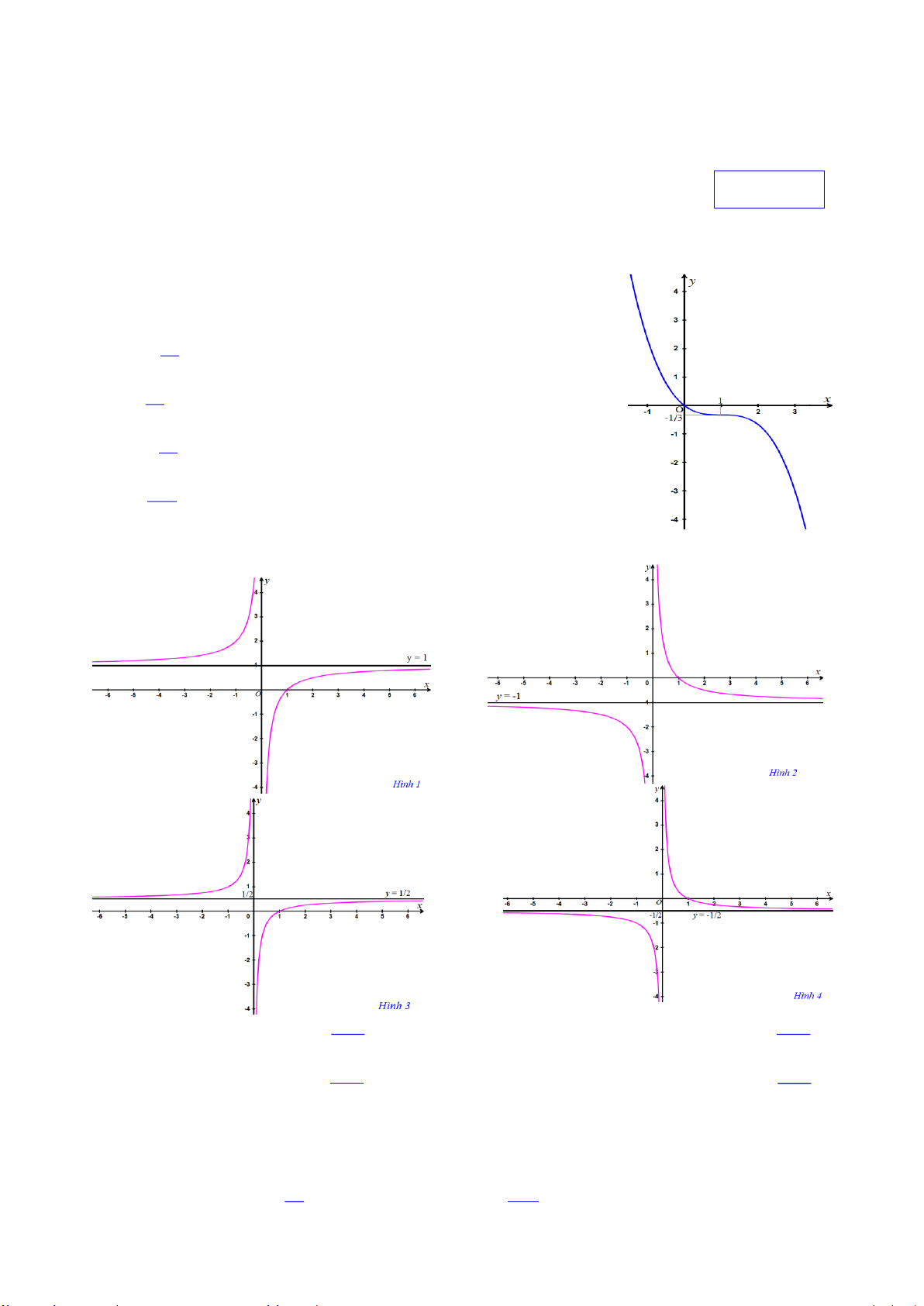
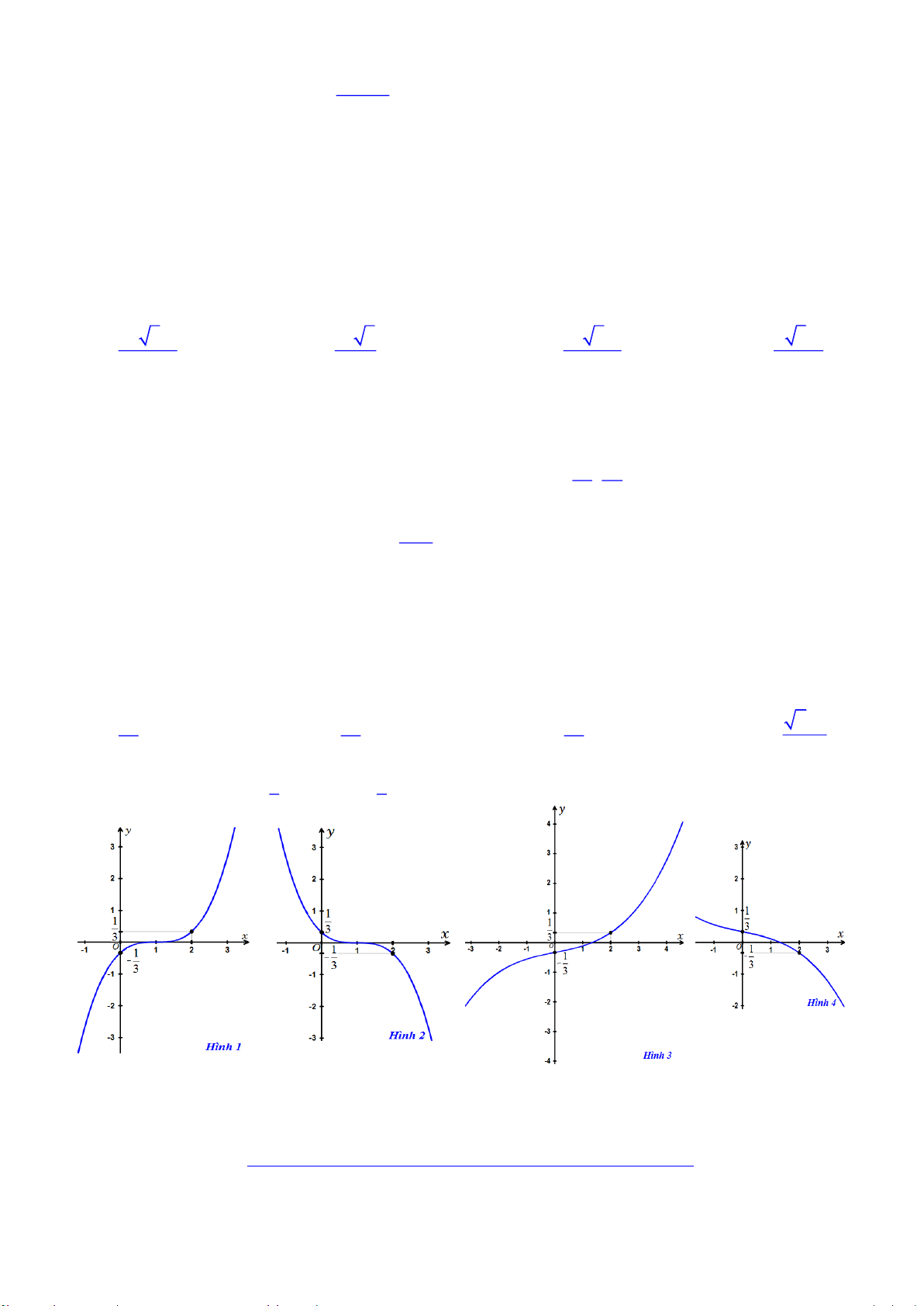
Hä vµ tªn häc sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Líp: . . . . . . . . . 1 5 1 Câu 1. Hàm số 3 y x x có đồ thị là 27 27 3
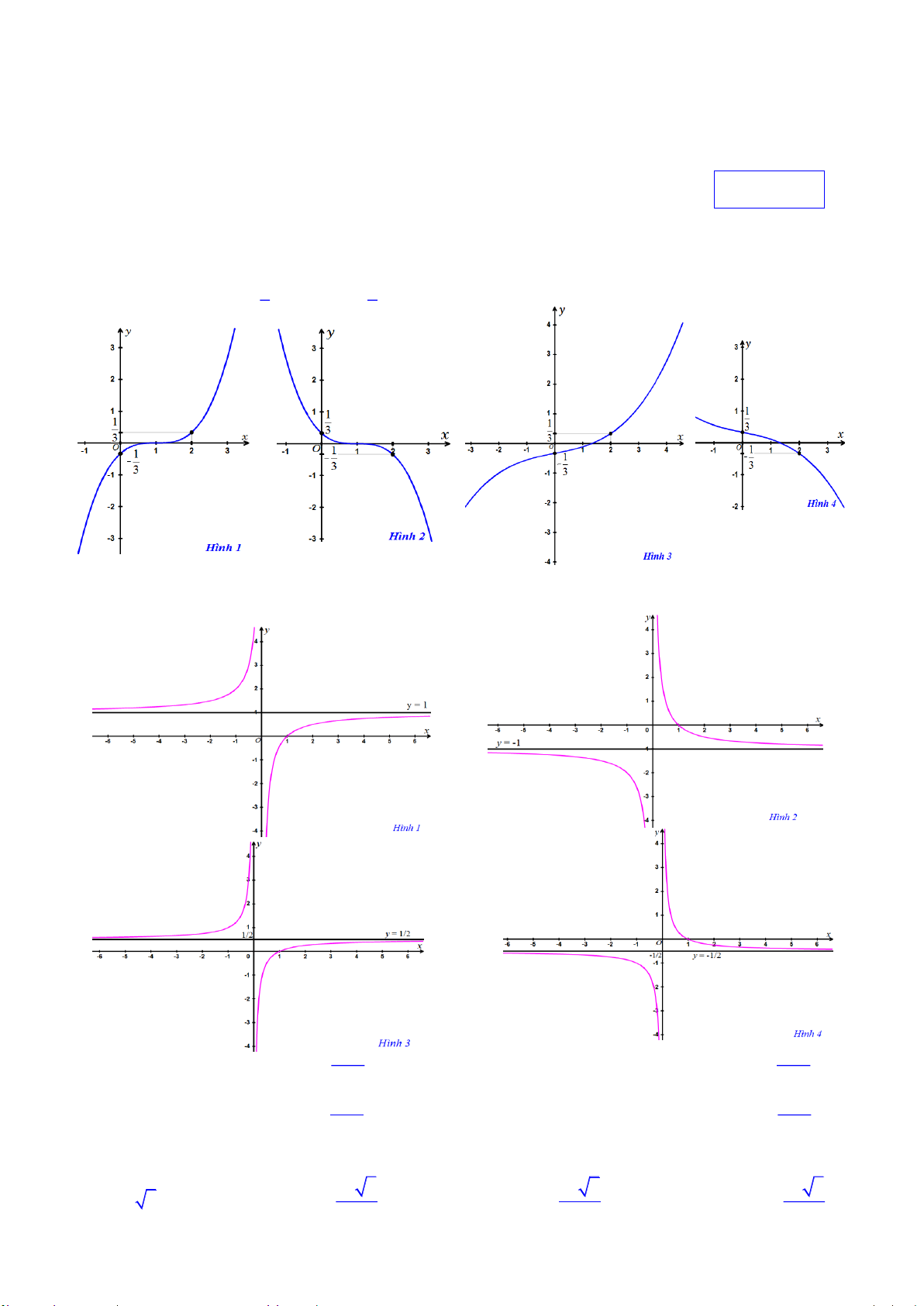
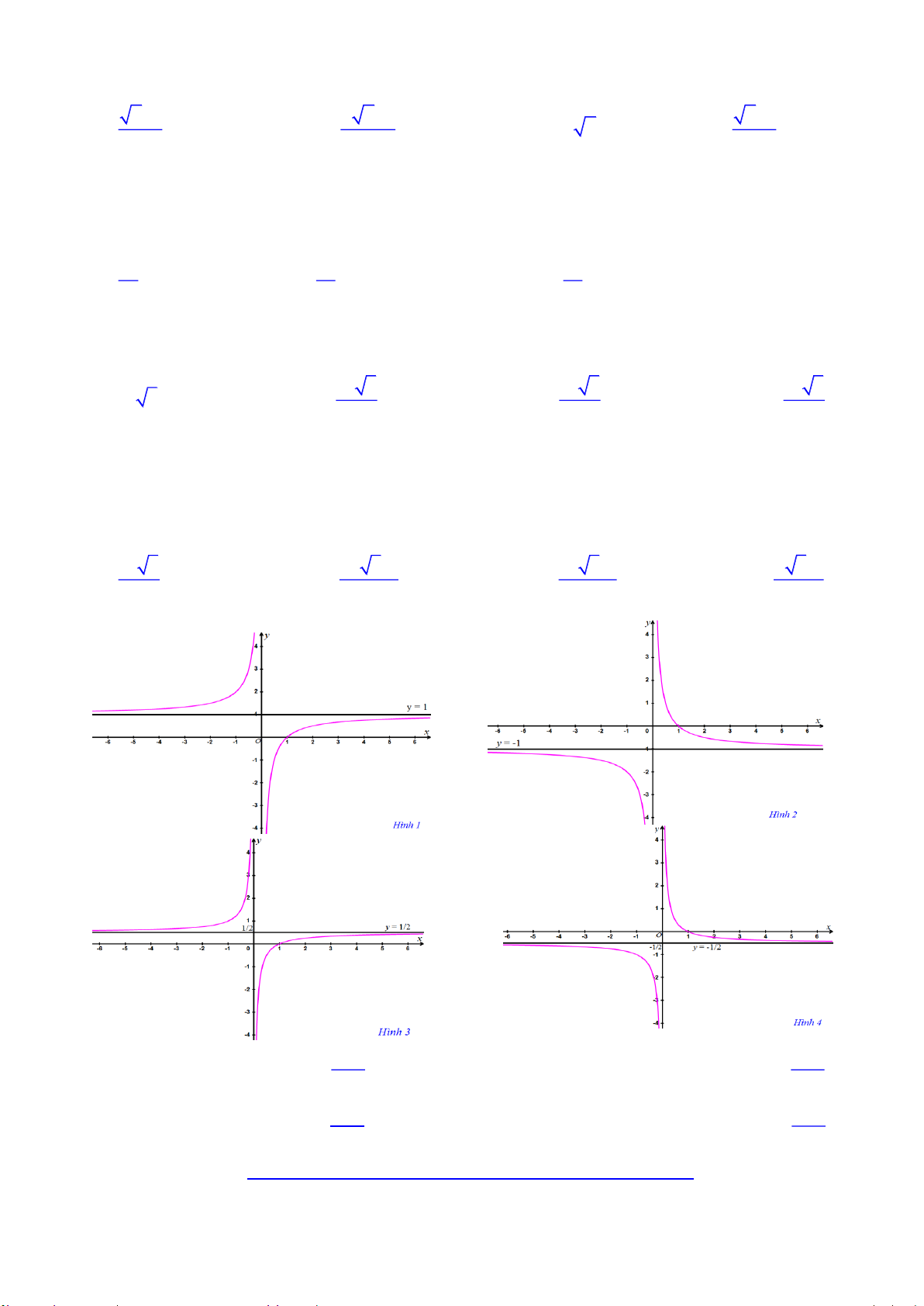
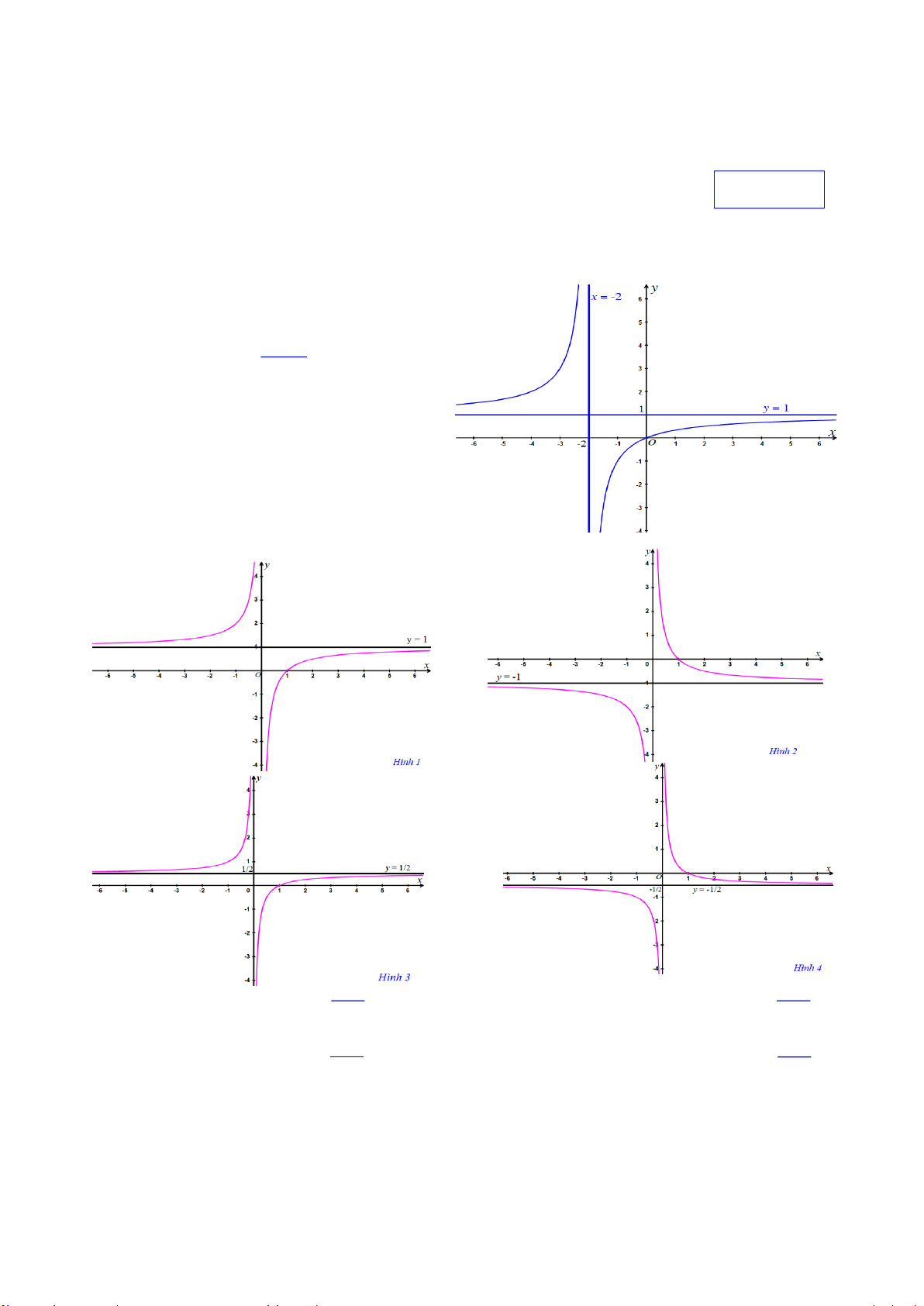
A. Đồ thị trên hình 1 B. Đồ thị trên hình 2
C. Đồ thị trên hình 3 D. Đồ thị trên hình 4
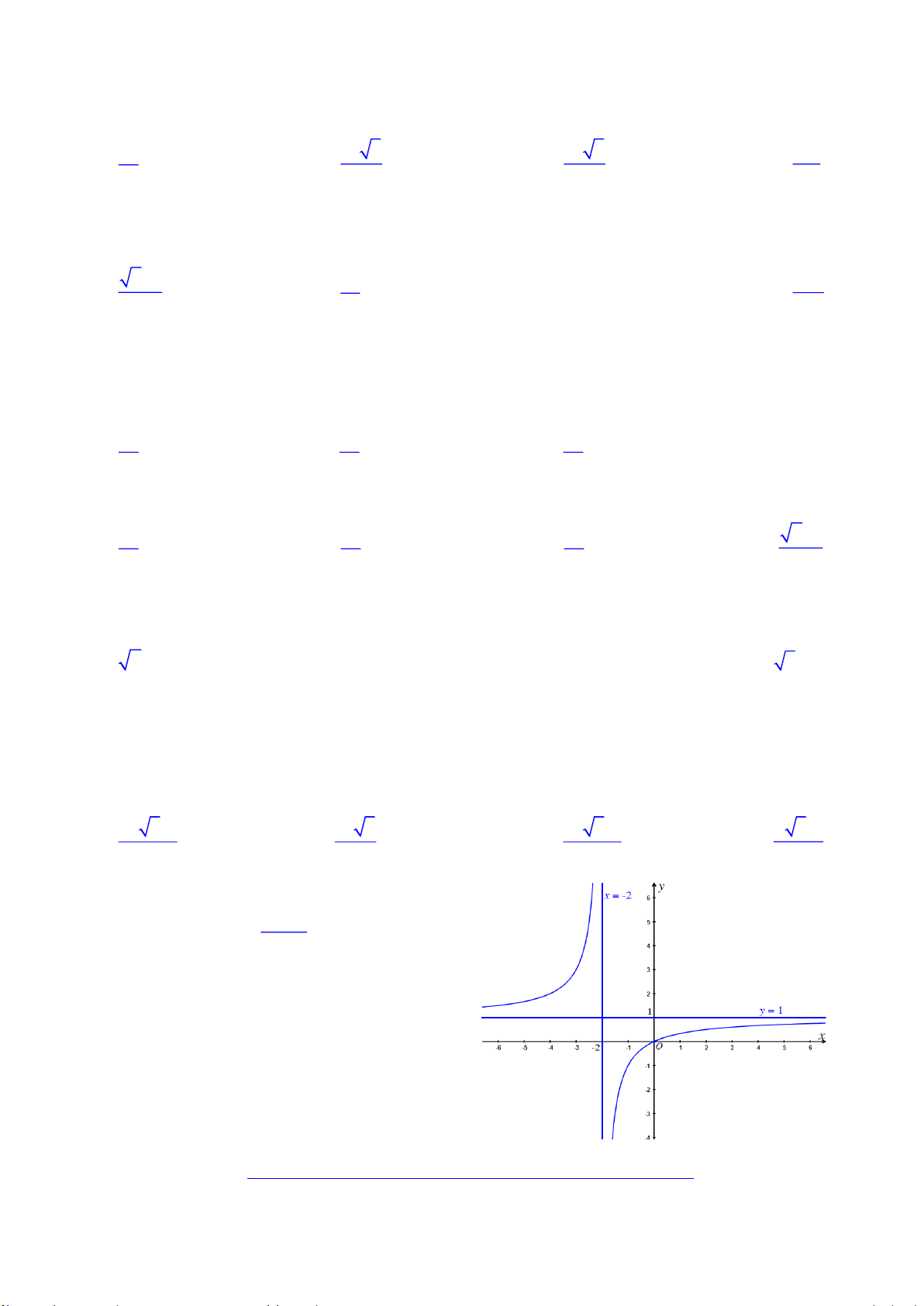
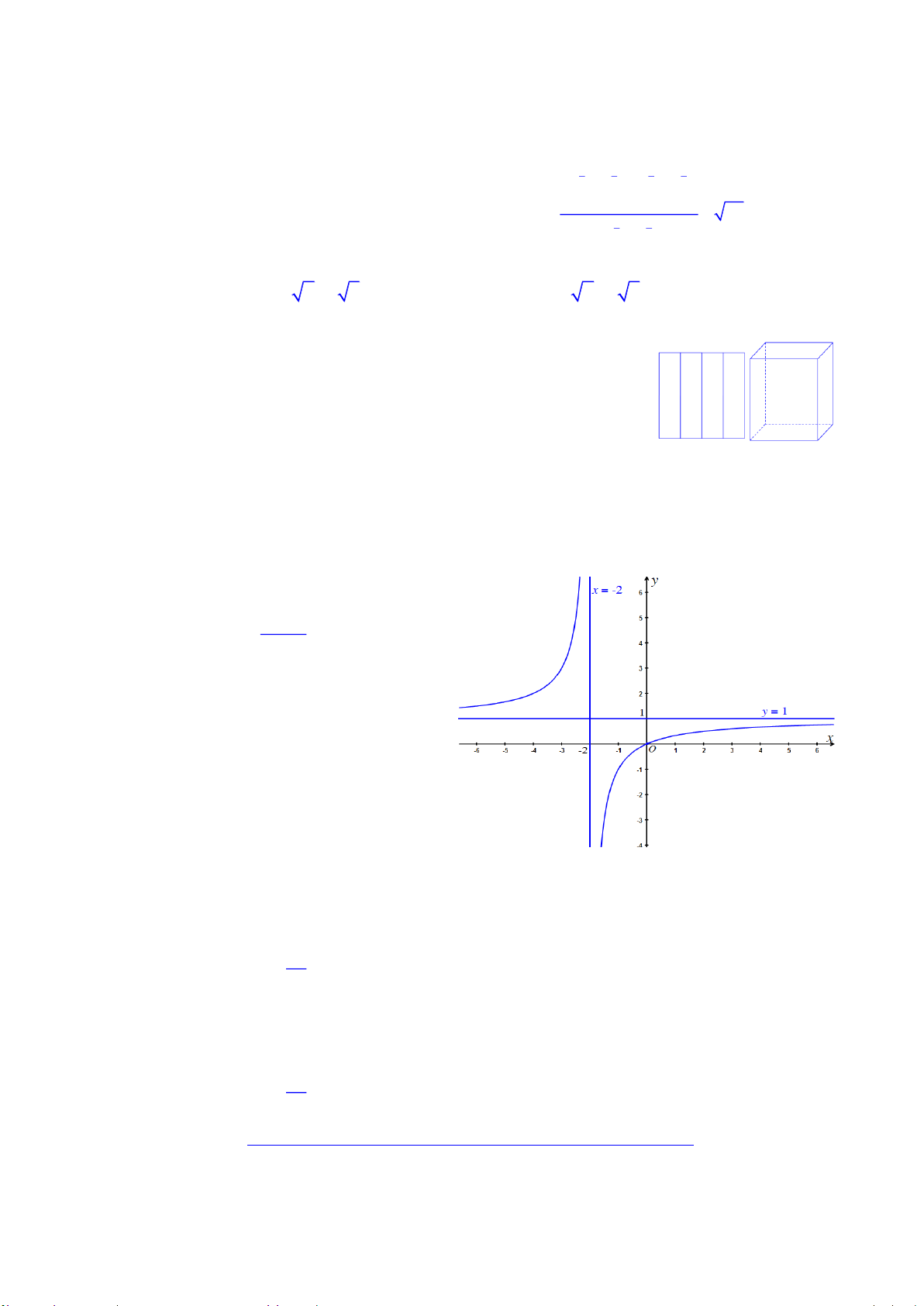
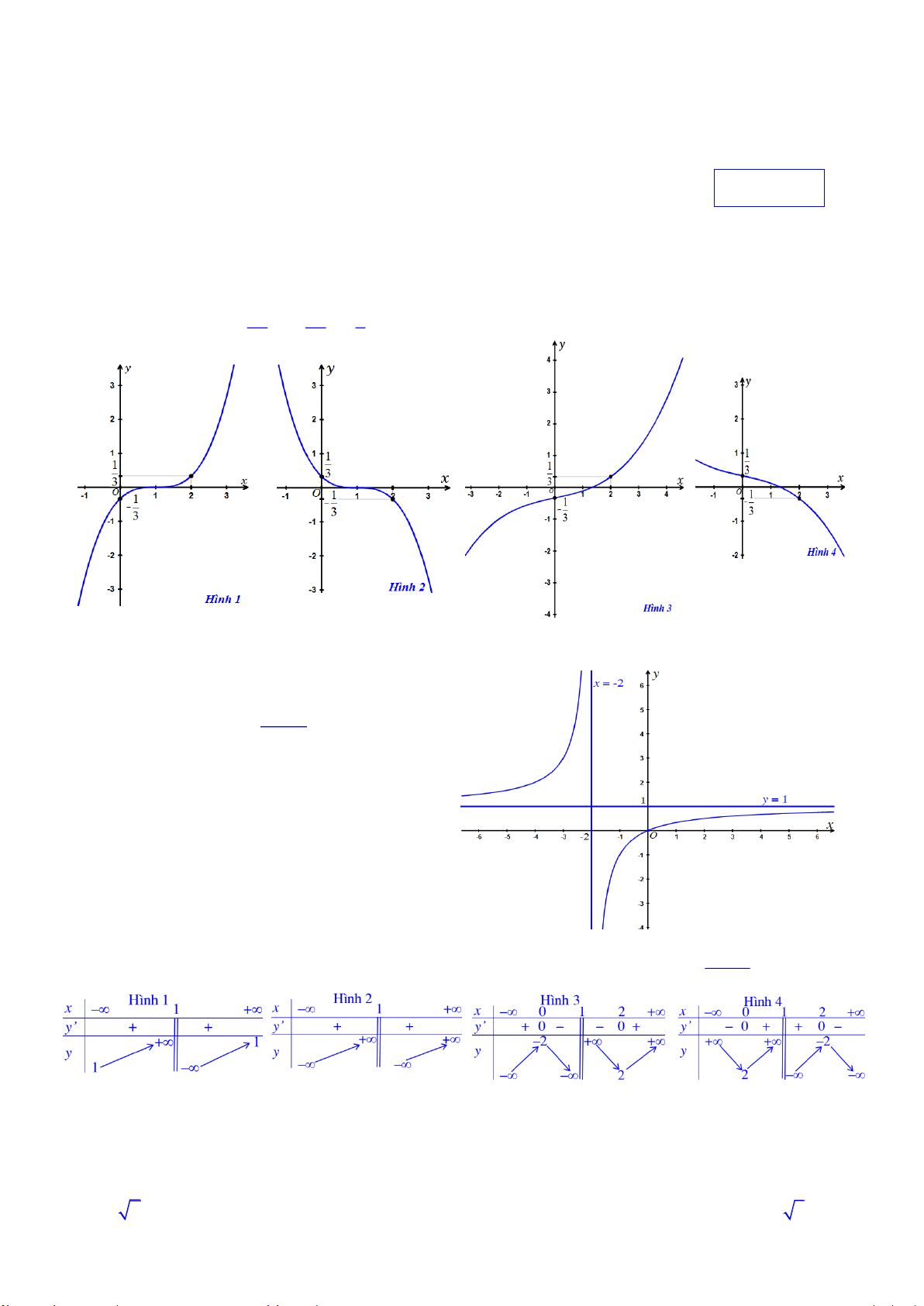
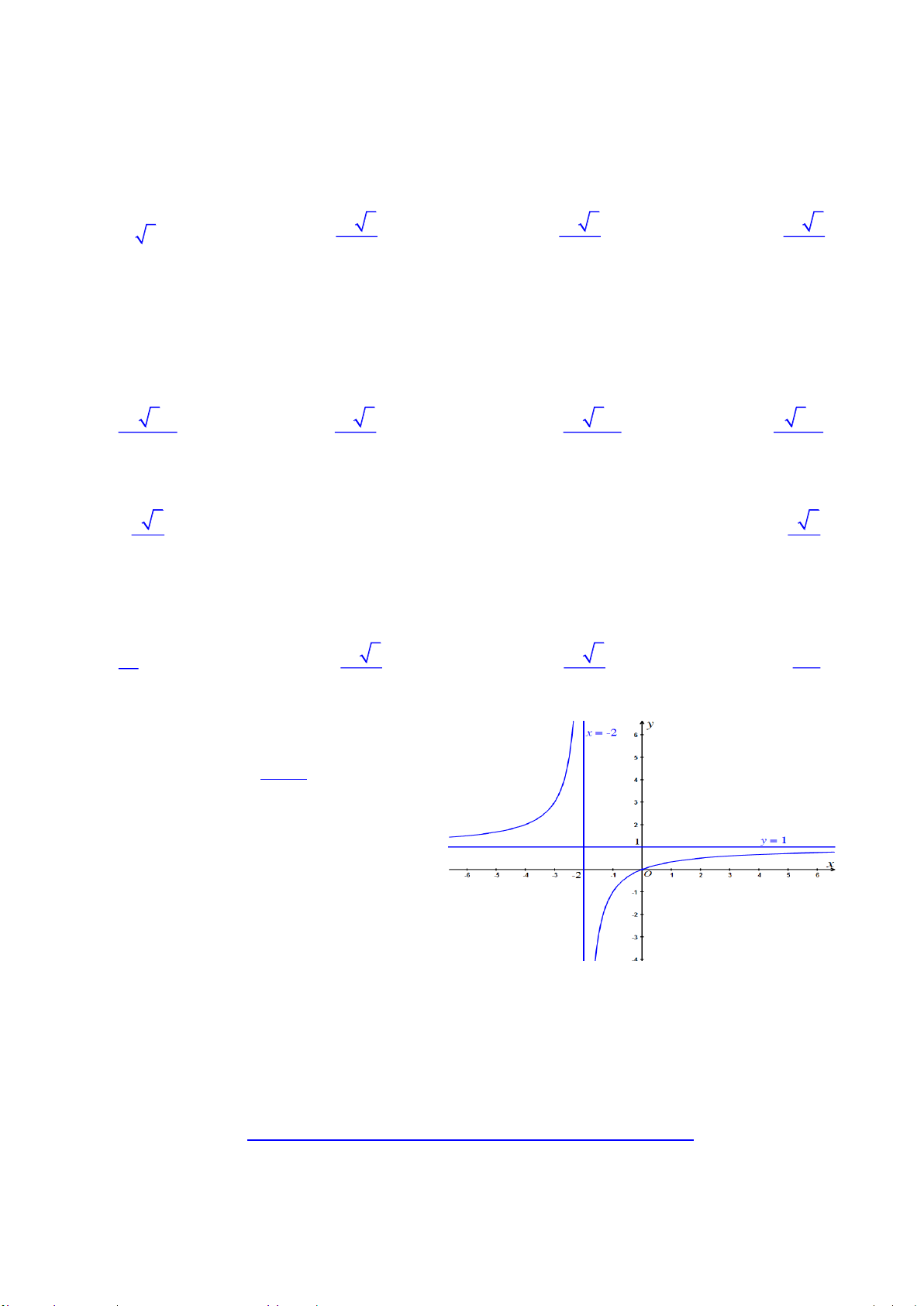
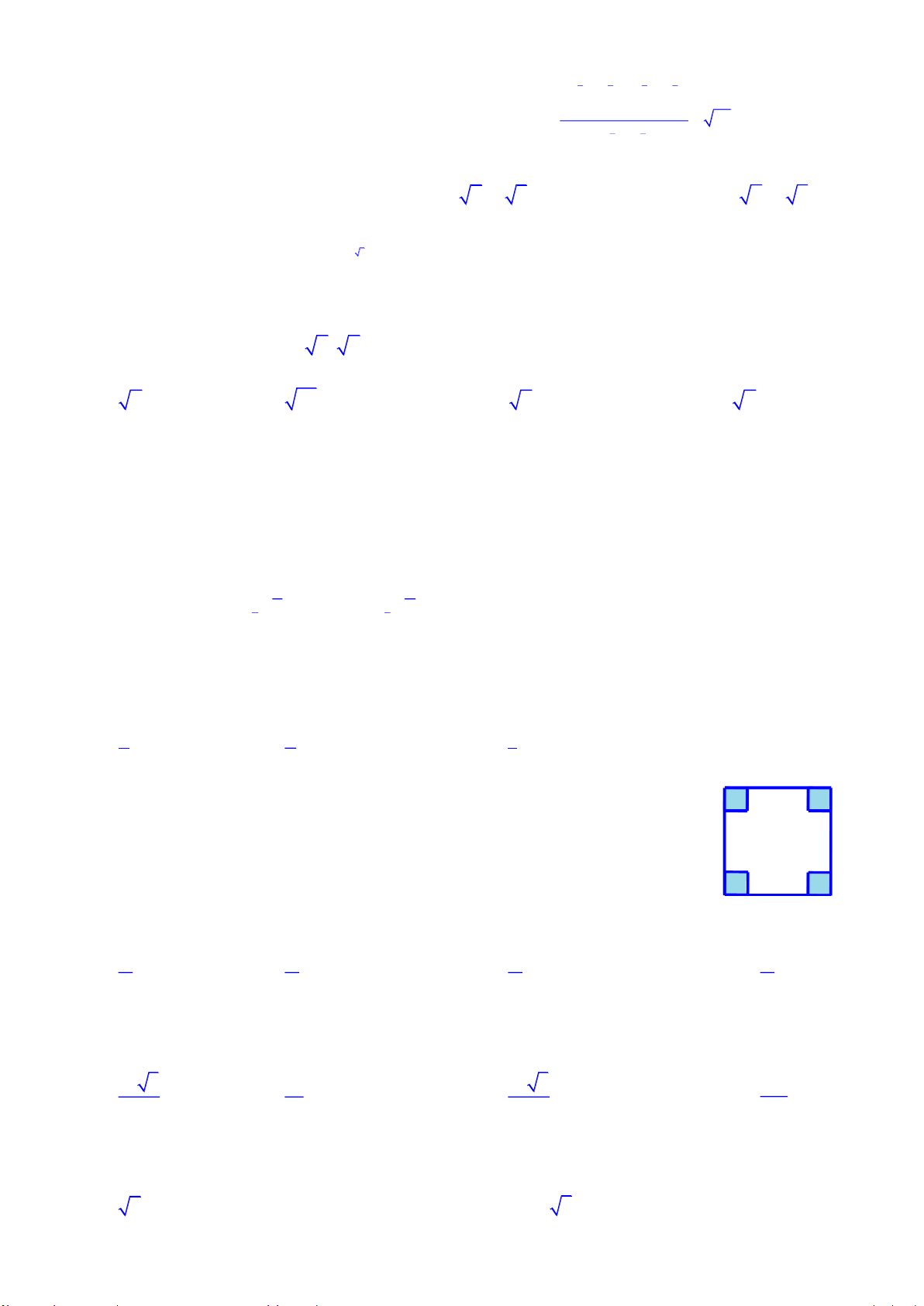
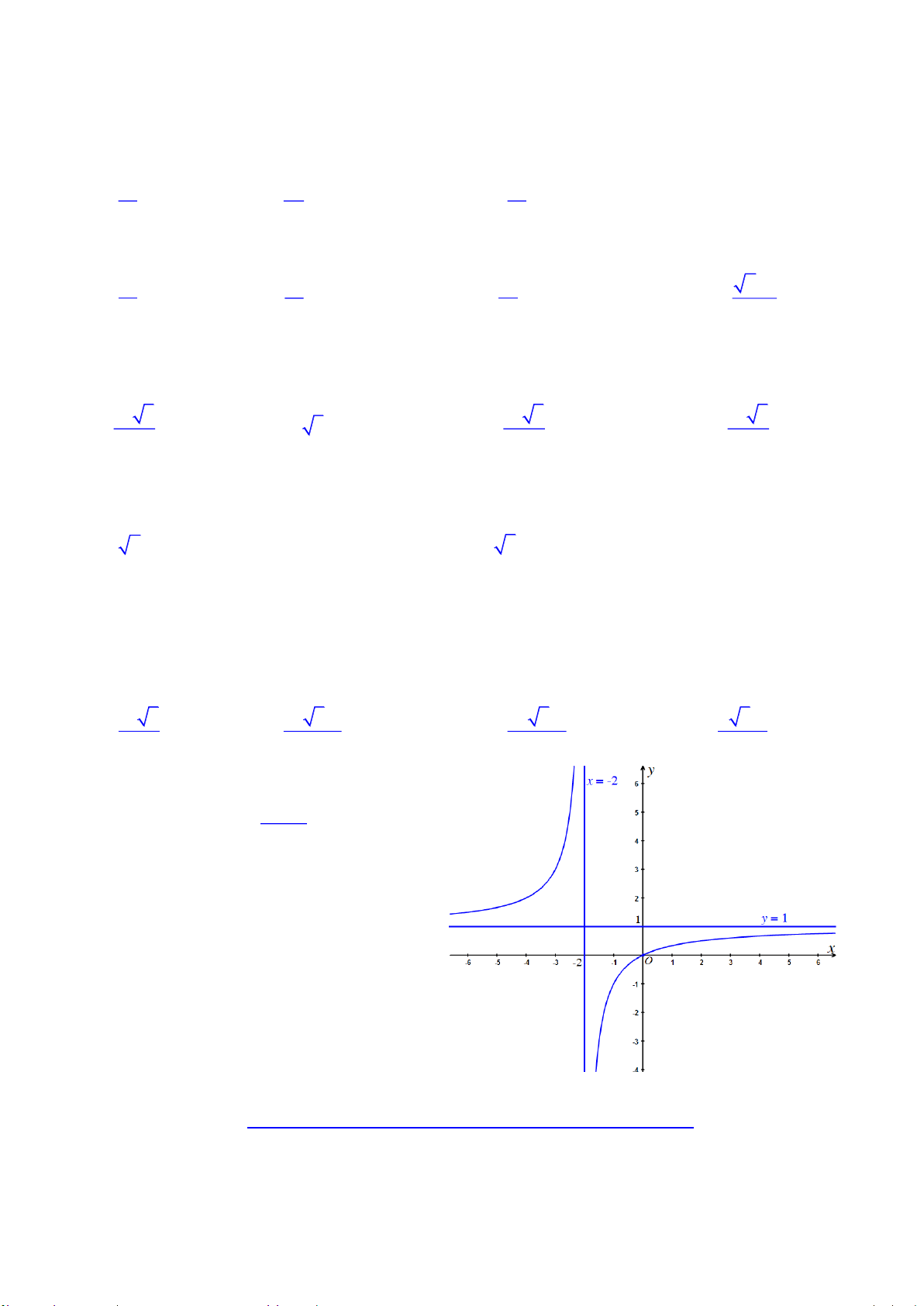
Câu 2. Chän ph-¬ng ¸n tr¶ lêi ®óng: x b
§å thÞ cña hµm sè y cx nh- h×nh d-íi ®©y. d
Khi ®ã gi¸ trÞ b, c, d lÇn l-ît lµ A. 1, 1, 2 B. 0, 1, 2 C. 2, 1, 1 D. 0, 1, 1 Câu 3. Hàm số 4 3 2
y x 4x x 6x 10 có
A. Một cực đại và hai cực tiểu
B. Một cực tiểu và không có cực đại
C. Hai cực đại và một cực tiểu
D. Một cực đại và không có cực tiểu Câu 4. Cho hµm sè 3
y x 3x 1 cã ®å thÞ (C), mét ®-êng th¼ng qua M(1; 3) vµ tiÕp xóc víi (C)
c¾t (C) t¹i ®iÓm thø hai N (N kh«ng trïng M). Khi ®ã täa ®é ®iÓm N lµ 1 3 A. (2; –1) B. (–1; –1) C. (0; 1) D. ; 2 8 x
Câu 5. Cho ®å thÞ (C) cña hàm số y y x . MÖnh ®Ò nµo d-íi ®©y
x vµ ®-êng th¼ng d: 4 1 ®óng A. d vµ (C) tiÕp xóc
B. d vµ (C) c¾t nhau t¹i hai ®iÓm ph©n biÖt C. d vµ (C) kh«ng c¾t nhau
D. d lµ tiÖm cËn xiªn cña (C) H 1/6 Mã đề 101
Câu 6. Hình lập phương có bao nhiêu mặt phẳng đối xứng A. 3 B. 4 C. 6 D. 9
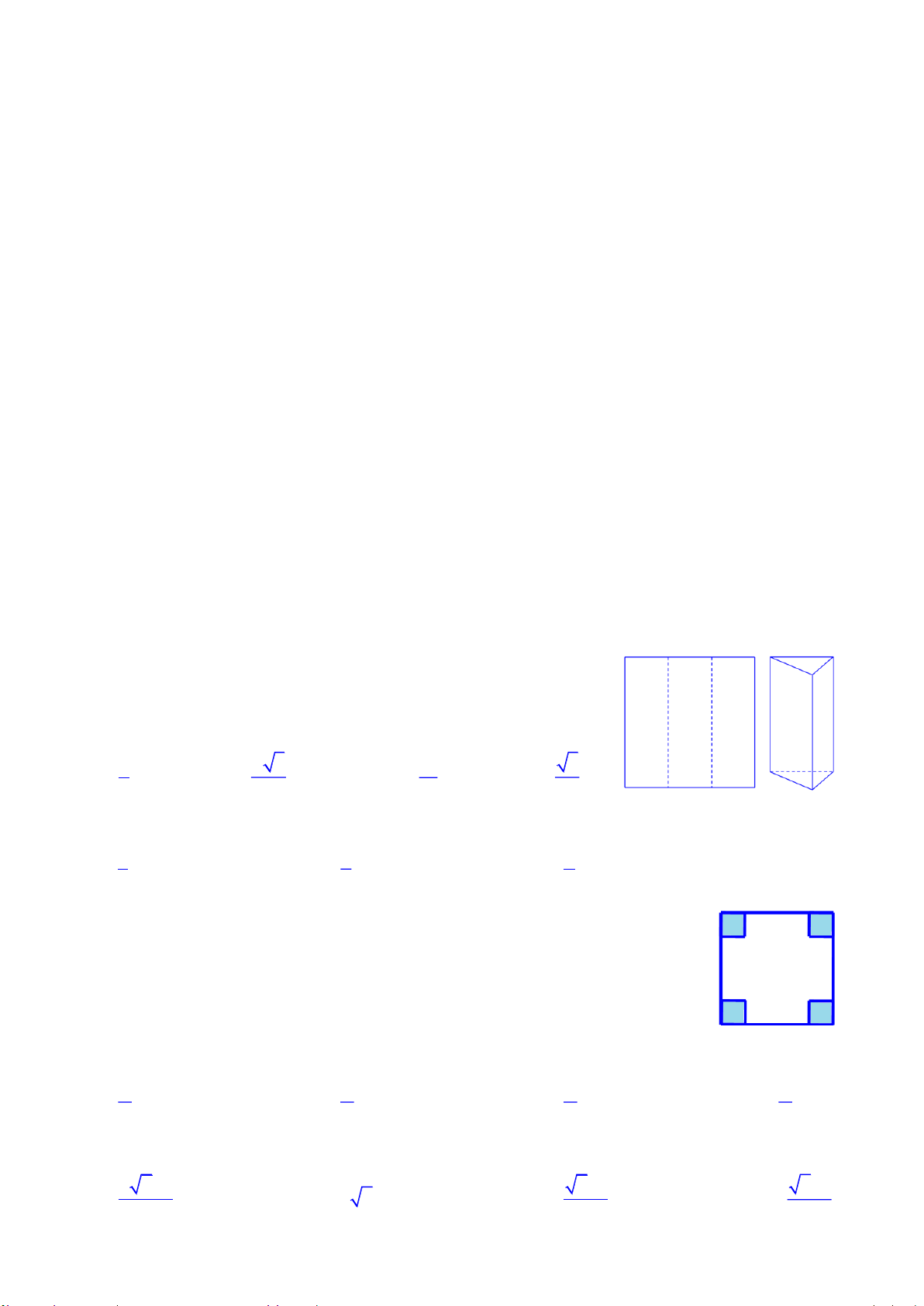
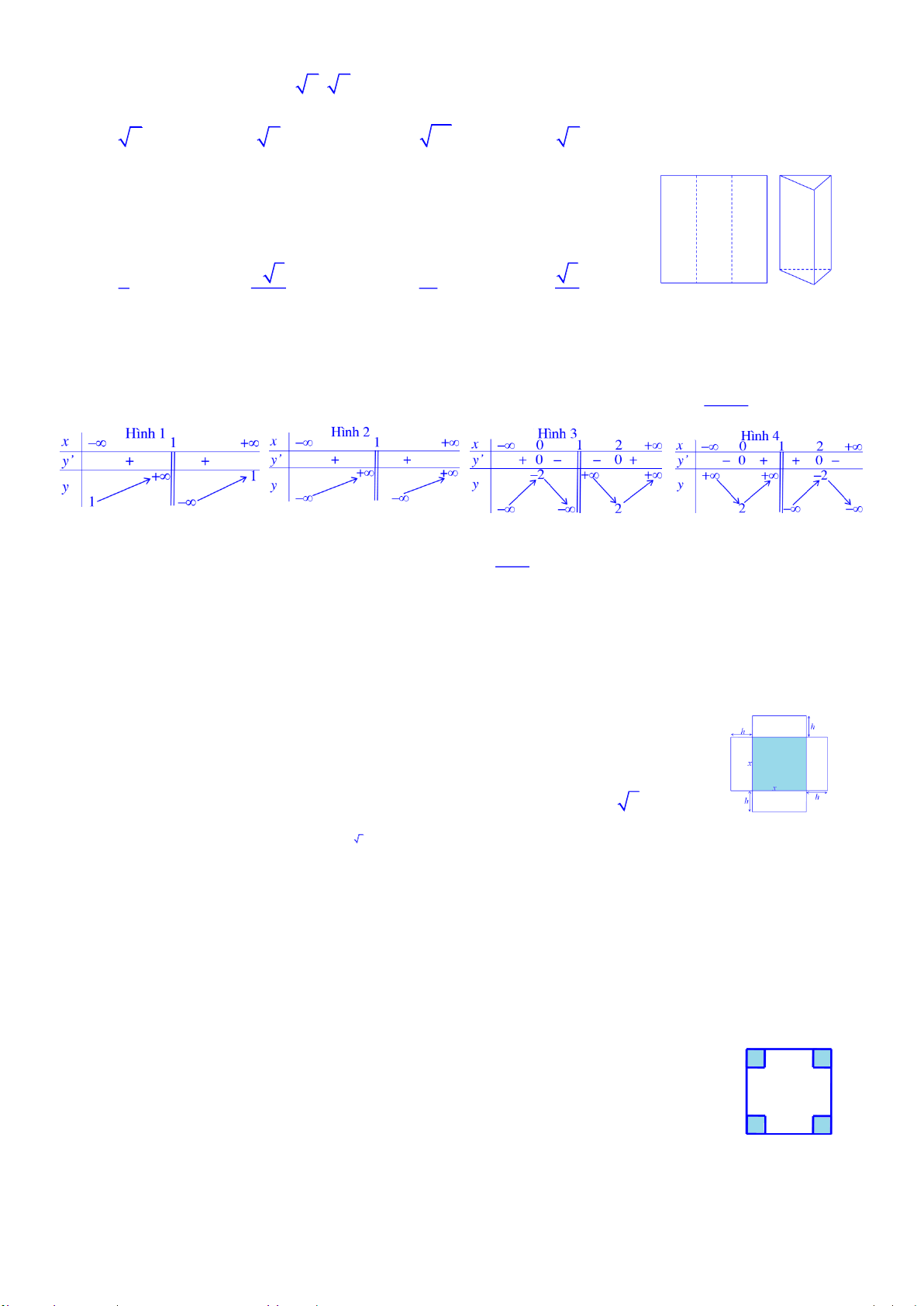
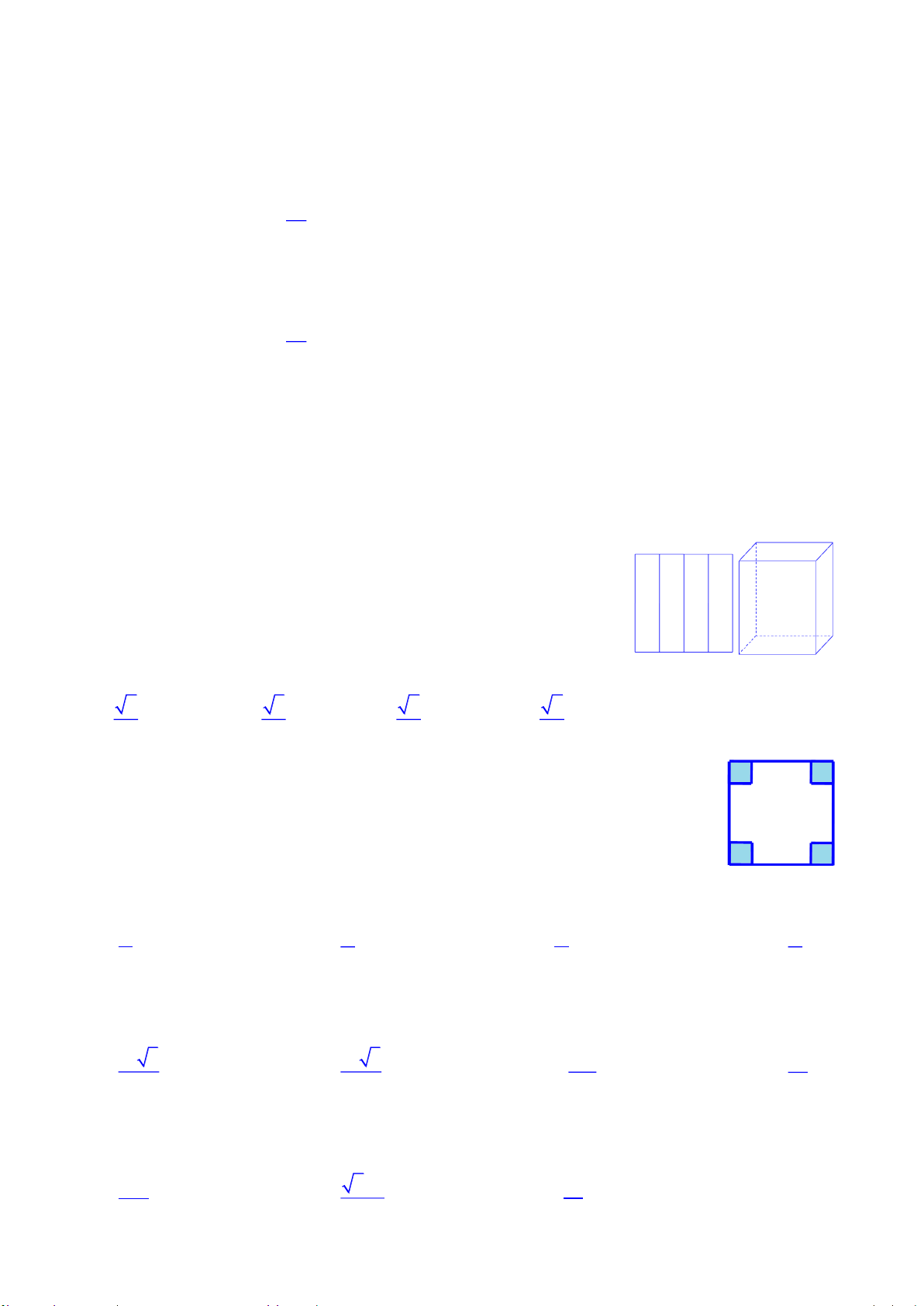
Câu 7. Một hộp không nắp được làm từ mảnh các tông theo mẫu hình bên.
Hộp có đáy là hình vuông cạnh x (cm), chiều cao h (cm) và có thể tích là 4cm3.
Tìm giá trị của x sao cho diện tích của mảnh các tông nhỏ nhất A. 8 cm B. 4 cm C. 2 cm D. 3 2 2 cm 500 50 Câu 8. Tỉ số bằng 250 25 A. 250 10 B. 250 2 C. 500 2 D. 500 10
Câu 9. Cho M = 32000 và N = 41500. Khi đó A. M = N B. M < N C. M > N D. M ≤ N
Câu 10. Nếu a 0 thì tích 6 3 a . a bằng A. 9 a B. 9 2 a C. a D. 18 a
Câu 11. Nếu log b log c thì a a
A. 0 b c B. b c 0 và a 0 C. c b 0 và a 1 D. 0 b c và 0 a 1
Câu 12. Cho 0 a 1 , khi đó 3log 2 a a bằng A. 16 B. 8 C. 6 D. 2
Câu 13. Cho E = log45 và F = log54. Khi đó A. E > F B. E = F C. E < F D. E ≥ F
Câu 14. Biết log 2 ;
a log 3 b . Tính log 5 5 305 theo a, b 1 1 A. a b B. a b 1 C. a b D. 1 a b 3 3 3 3 4 4 4 4
a b a b
Câu 15. Cho hai số dương khác nhau a, b . Rút gọn biểu thức ab bằng 1 1 2 2 a b A. a b B. 2 a b C. a b D. 2 a b
Câu 16. Thể tích khối tứ diện đều có cạnh bằng 1 là 3 2 2 2 A. B. C. D. 4 4 12 6 H 2/6 Mã đề 101
Câu 17. Một người gửi 6 triệu đồng vào ngân hàng theo thể thức lãi kép, kì hạn 1 năm với lãi suất
7,56% một năm. Hỏi sau bao nhiêu năm người gửi sẽ có ít nhất 12 triệu đồng từ số tiền gửi ban đầu
(giả sử lãi suất không thay đổi) ? A. 10 năm B. 1 năm C. 8 năm D. 15 năm
Câu 18. Với một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc tấm bìa một
hình vuông cạnh 12cm rồi gấp lại thành một hình hộp chữ nhật không có nắp.
Nếu dung tích của cái hộp đó là 4800cm3 thì cạnh tấm bìa có độ dài là A. 36cm B. 44cm C. 38cm D. 42cm
Câu 19. Cho hình hộp ABCD.A’B’C’D’ có thể tích V. Thể tích khối tứ diện ACB’D’ là V V V V A. B. C. D. 8 6 4 3
Câu 20. Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = a , AC = 2a và SA vuông
góc với đáy. Góc giữa (SBC) và (ABC) bằng 600. Thể tích khối chóp S.ABC bằng 3 a 3 3 a 3 3 a 3 3a A. B. C. D. 3 2 2 2
Câu 21. Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với đáy và AB = a ,
AD = 2a , góc giữa SB và đáy bằng 450. Thể tích khối chóp S.ABCD là 3 2 a 3 a A. 3 2a B. C. D. Đáp án khác 3 3
Câu 22. Thể tích của khối tám mặt đều có cạnh bằng a là 3 2 a 3 2 2 a 3 2 a A. B. C. 3 2 2 a D. 3 3 9
Câu 23. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 1cm, SA 2cm và SA vuông góc với
đáy. Khoảng cách giữa hai đường thẳng BC và SD là A. 2 cm B. 2 cm C. 1 cm D. 5 cm
Câu 24. Khi viết 22008 trong hệ thập phân ta được một số có bao nhiêu chữ số (lấy giá trị gần đúng của log2 là 0,3010) A. 605 chữ số B. 606 chữ số C. 2008 chữ số D. 2007 chữ số
Câu 25. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a .
SA (ABC) và SA = a . Gọi (α) là mặt phẳng qua A và vuông góc với SB đồng thời cắt SB, SC tại
M, N. Khi đó thể tích khối chóp S.AMN bằng 3 a 3 a 3 a A. B. C. D. Đáp án khác 24 6 12
Câu 26. Cho hàm số 4 2
y ax bx c trong đó a 0 và b 0. Khi đó hàm số có
A. Hai cực tiểu và một cực đại B. Hai cực đại và một cực tiểu C. Một cực đại D. Một cực tiểu H 3/6 Mã đề 101
Câu 27. Cho tứ diện AEFG có thể tích là V và AE, AF, AG vuông góc với nhau từng đôi một. Gọi
B, C, D lần lượt là trung điểm của các đoạn thẳng GE, EF, FG. Thể tích khối tứ diện ABCD bằng V V V V A. B. C. D. 2 3 6 4
Câu 28. Cho hình lăng trụ đứng MNP.M' N'P' có tất cả các cạnh bằng a . Thể tích của khối lăng trụ bằng 3 a 3 3 a 3 3 a 3 A. 3 a 3 B. C. D. 4 2 3
Câu 29. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AC = 2a , tam
giác SAC đều và nằm trên mặt phẳng vuông góc với đáy. Trên cạnh SA lấy điểm M sao cho
MA = 2MS. Mặt phẳng (α) qua M và song song với (ABC) cắt SB, SC tại N, P. Khi đó thể tích khối
chóp cụt ABC.MNP bằng 3 a 3 3 26 3a 3 80 3a 3 2 3a A. B. C. D. 3 81 81 9 2 x 2
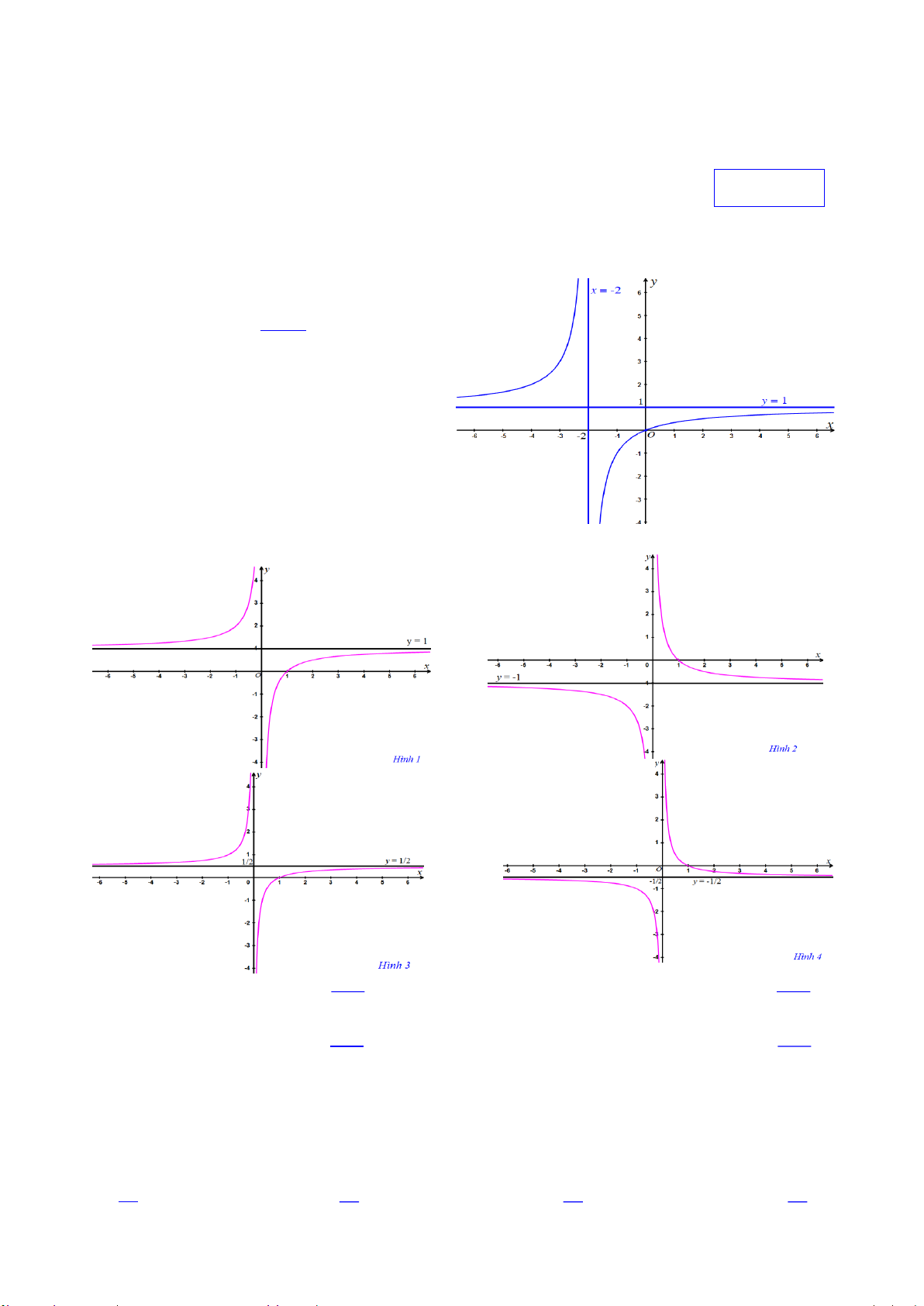
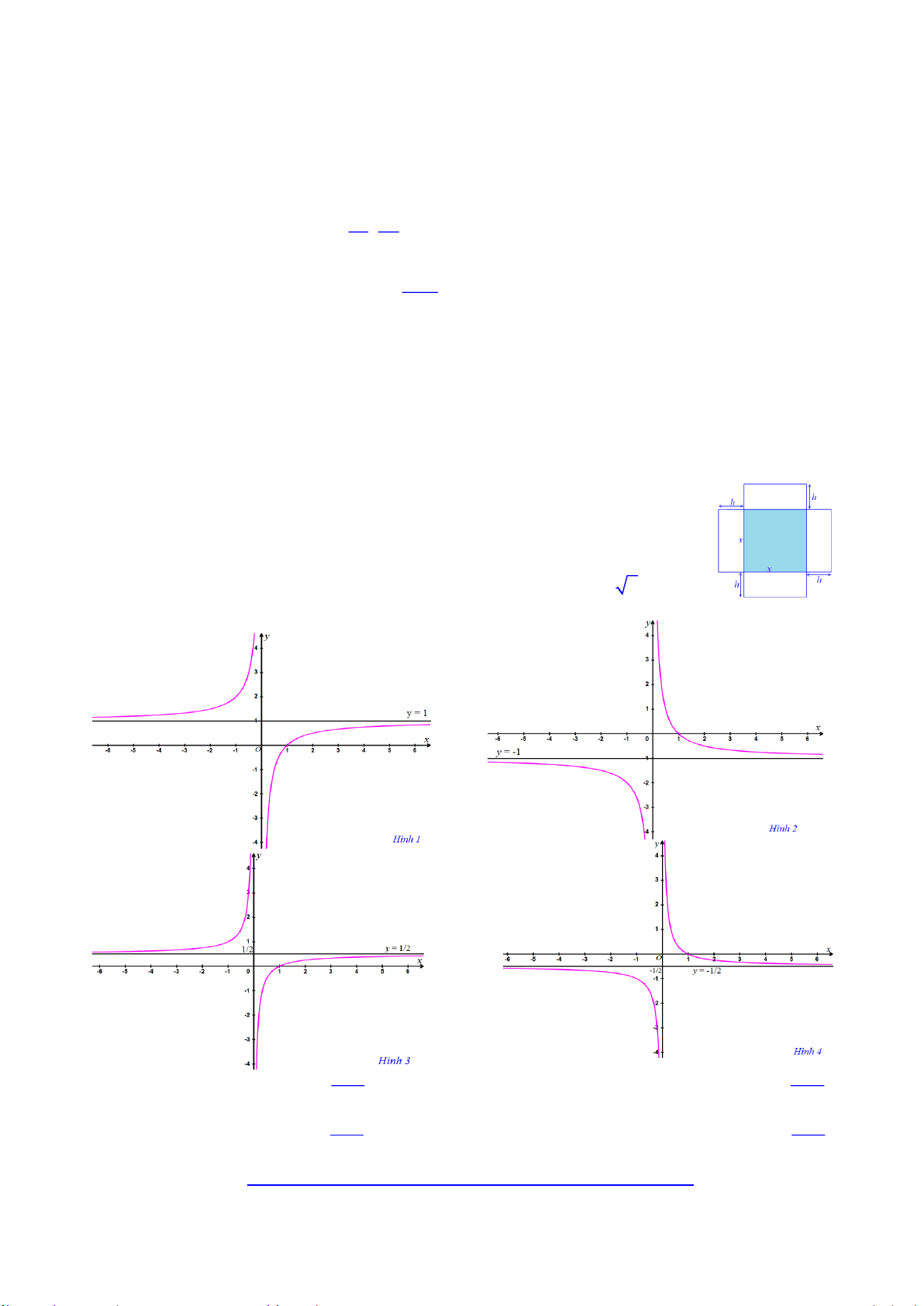
Câu 30. Mét trong c¸c h×nh d-íi ®©y, h×nh nµo cã b¶ng biÕn thiªn cña hµm sè y x 1 A. H×nh 2 B. H×nh 1 C. H×nh 4 D. H×nh 3 1
Câu 31. Một khoảng đồng biến của hàm số y x 2 x là 1 A. 2 ; B. ; C. 1
; D. ; 1
Câu 32. Cho ®-êng cong (C) cã ph-¬ng tr×nh 2 y
x 2 , tÞnh tiÕn (C) theo phương trục hoành
sang phải 3 ®¬n vÞ ta ®-îc ®-êng cong cã ph-¬ng tr×nh lµ A. 2 y x 2 3 B. 2 y x 6x 11 C. 2 y x 2 3 D. 2 y x 6x 11 Câu 33. Cho hµm sè 3 2
y x 6x 3(m 2)x m 6 ®¹t cùc ®¹i, cùc tiÓu t¹i x , x sao cho 1 2
x 1 x th× gi¸ trÞ cña m lµ 1 2 A. m 1 B. m 1 C. m 1 D. m 1 Câu 34. Hàm số 3 2
y x 6x mx 1 đồng biến trên kho¶ng (0; +∞) khi giá trị của m là A. m 0 B. m 12 C. m 12 D. m 0 Câu 35. Hµm sè 4 2
y mx (m 1)x 1 2m chØ cã mét cùc trÞ khi A. m 1
B. m 0 hoÆc m 1 C. m 0 D. 0 m 1 H 4/6 Mã đề 101 Câu 36. Hàm số 3
y x 12x 1 có
A. Cực đại bằng 17 và cực tiểu bằng 15
B. Cực đại bằng 17 và cực tiểu bằng 0
C. Cực đại bằng 0 và cực tiểu bằng 15 D. Cực đại bằng 15
và cực tiểu bằng 17
Câu 37. Hàm số f cã ®¹o hµm 2
f '(x) x(2x 3) (3x 2) . Sè ®iÓm cùc trÞ cña hàm số f lµ A. 2 B. 4 C. 3 D. 1
Câu 38. Đồ thị cña hàm số 2
y x 1 x có
A. Tiệm cận đứng và có tiệm cận xiên
B. Tiệm cận đứng và có tiệm cận ngang
C. Tiệm cận xiên và không có tiệm cận ngang
D. Tiệm cận ngang và có tiệm cận xiên Câu 39. Hµm sè 4 3
y x mx 11m 4 ®¹t cùc tiÓu t¹i x 3 khi A. m 6 B. m 4 C. m 4 D. m 6
Câu 40. Sè ®-êng th¼ng ®i qua ®iÓm M(–1
; 3 ) vµ tiÕp xóc víi ®å thÞ cña hµm sè 3 y x 3x lµ A. 2 B. 0 C. 3 D. 1 x 3
Câu 41. Cho đồ thị (C) cña hàm số y
d y mx m . Ph-¬ng ¸n nµo
x vµ ®-êng th¼ng : 2 1 1 d-íi ®©y ®óng
A. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt
B. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt khi m 0
C. d lu«n ®i qua mét ®iÓm cè ®Þnh cña (C) khi m biÕn thiªn
D. (C) vµ d tiÕp xóc víi nhau khi m 2
Câu 42. Cho điểm O và số thực k 0 . Mệnh đề nào dưới đây sai
A. Phép vị tự tâm O tỉ số k là một phép đồng dạng khi k 0
B. Phép vị tự tâm O tỉ số k 1
là một phép đối xứng tâm
C. Phép vị tự tâm O tỉ số k 1 là một phép đồng nhất
D. Phép vị tự tâm O tỉ số k luôn là một phép đồng dạng
Câu 43. Trong các mệnh đề sau đây, mệnh đề nào đúng
A. Phép vị tự biến mặt phẳng thành mặt phẳng song song với nó
B. Không có phép vị tự nào biến hai điểm phân biệt A và B lần lượt thành A và B
C. Phép vị tự biến đường thẳng thành đường thẳng song song với nó
D. Phép vị tự biến mặt phẳng qua tâm vị tự thành chính nó
Câu 44. Từ một tấm bìa hình vuông cạnh bằng 4cm, ta gấp nó thành
4 phần đều nhau rồi gấp thành một hình hộp chữ nhật (không nắp)
như hình bên. Hỏi thể tích khối hộp này bằng bao nhiêu A. 4cm3 B. 1cm3 C. 16cm3 D. 8cm3
Câu 45. Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất A. Hai mặt B. Ba mặt C. Bốn mặt D. Năm mặt H 5/6 Mã đề 101
Câu 46. Gi¸ trÞ nhá nhÊt cña hµm sè 2 2 y
x 2x 5
x 4x 8 trªn ®o¹n [–1 ; 1] lµ A. 2 2 5 B. 5 C. 2 13 D. §¸p sè kh¸c mx m
Câu 47. §å thÞ cña hµm sè y
c¾t ®-êng th¼ng d: y x 6 t¹i hai ®iÓm ph©n biÖt thuéc x hai nh¸nh cña nã khi: A. m 0 B. m 0 C. m 6 D. m 0
Câu 48. Khối hai mươi mặt đều thuộc loại A. {3 ; 4} B. {4 ; 3} C. {3 ; 5} D. {5 ; 3}
Câu 49. Cho tứ diện ABCD có trọng tâm G. Gọi A’, B’, C’, D’ lần lượt là trọng tâm các tam giác
BCD, CDA, ABD, ABC. Mệnh đề nào dưới đây đúng
A. A’, B’, C’, D’ đồng phẳng 1
B. Phép vị tự tâm G tỉ số
biến ABCD thành A’B’C’D’ 3
C. A’B’C’D’ và ABCD là hai hình bằng nhau 1
D. Phép vị tự tâm G tỉ số
biến A’B’C’D’ thành ABCD 3
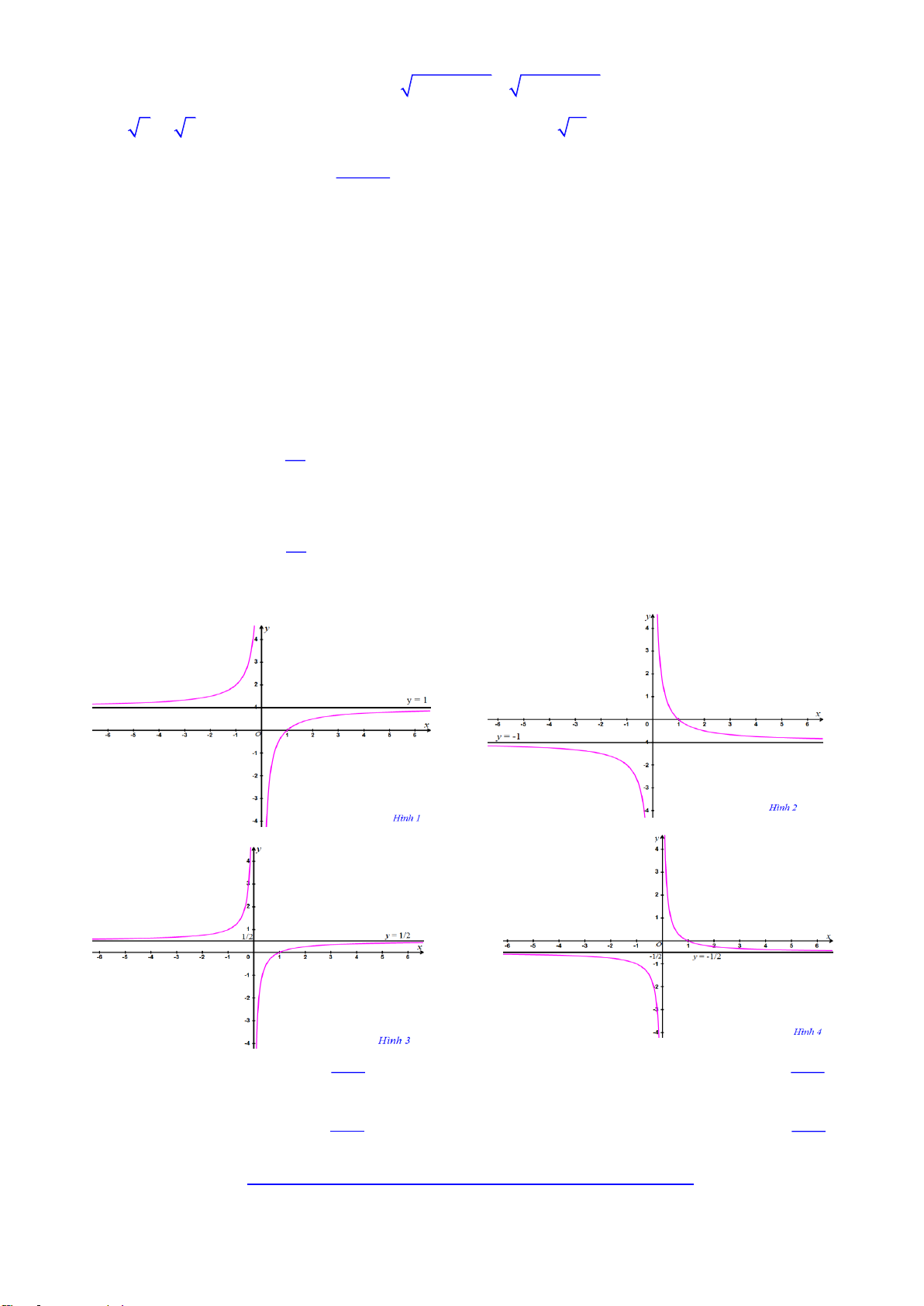
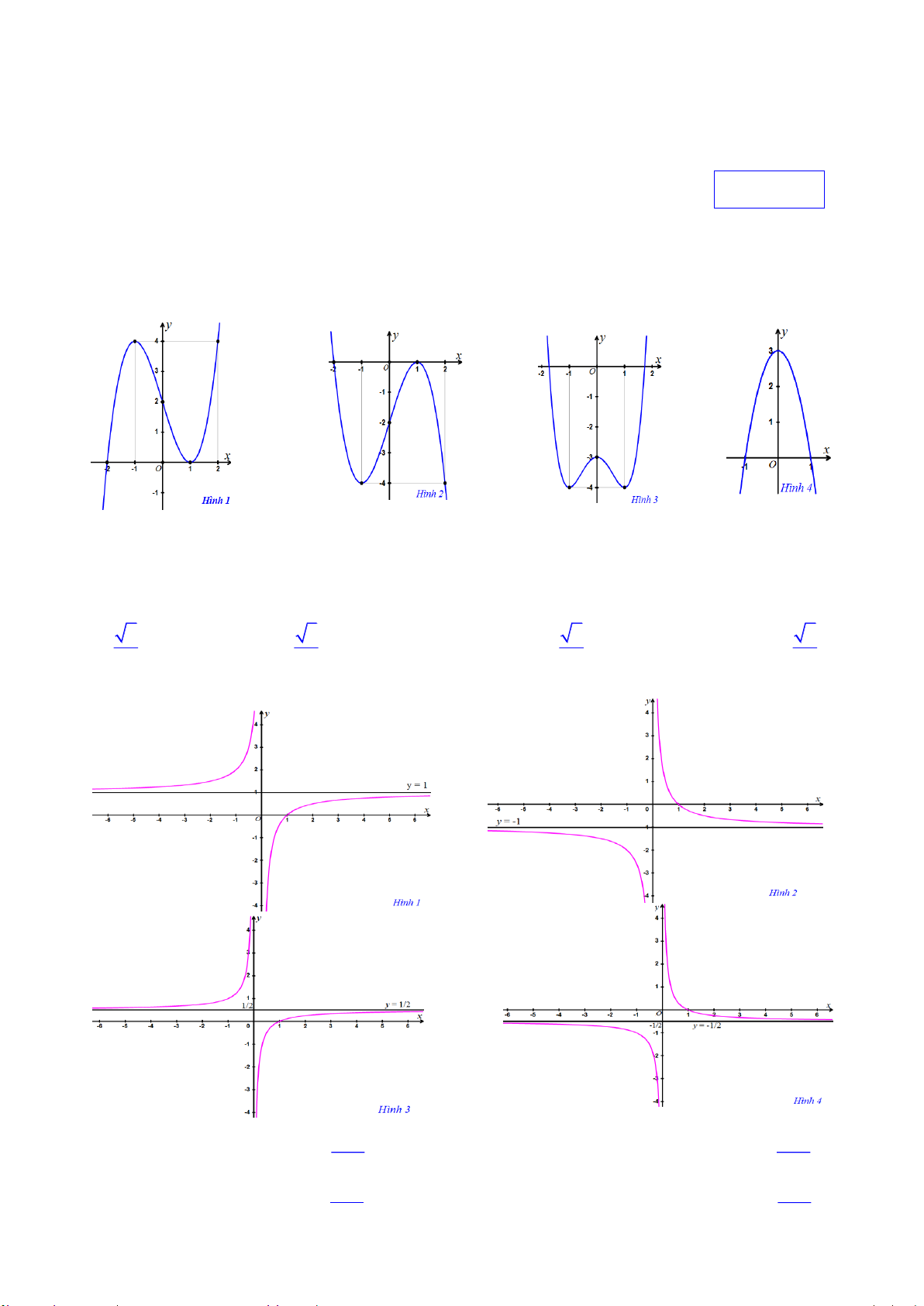
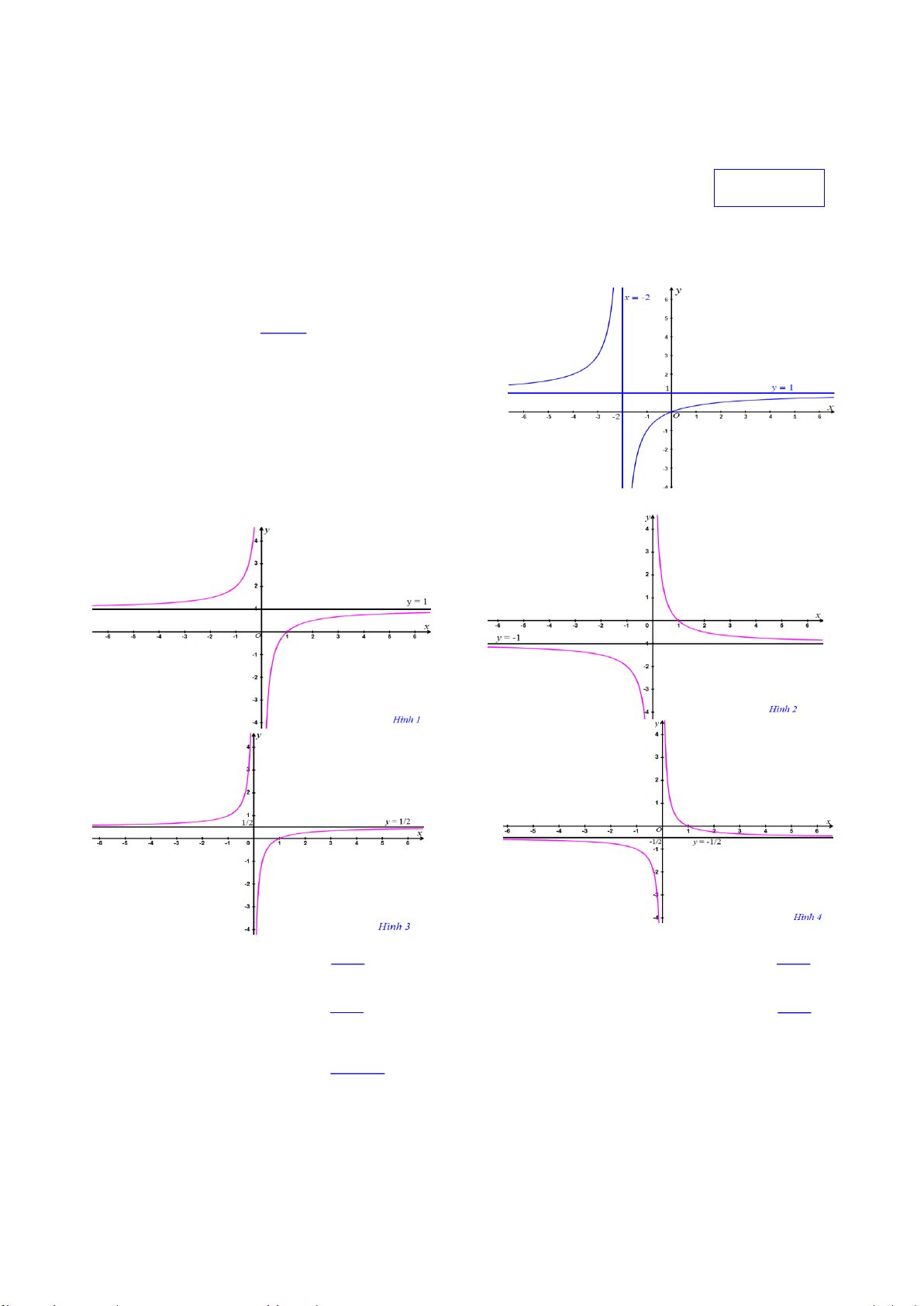
Câu 50. Cho các đồ thị trên các hình sau. Chỉ ra câu trả lời đúng x 1 1 x
A. Hình 2 có đồ thị hàm số y
B. Hình 1 có đồ thị hàm số y x x x 1 1 x
C. Hình 3 có đồ thị hàm số y y
D. Hình 4 có đồ thị hàm số . 2x 2x
Cán bộ coi kiểm tra không giải thích gì thêm H 6/6 Mã đề 101
TRƯỜNG THPT NGUYỄN GIA THIỀU ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA HỌC KỲ 1
BỘ MÔN TOÁN Môn toán lớp 12, năm học 2016 – 2017
Đề chính thức gồm 06 trang Thời gian làm bài 90 phút Mã đề 102
Hä vµ tªn häc sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Líp: . . . . . . . . .
Câu 1. Khi viết 22008 trong hệ thập phân ta được một số có bao nhiêu chữ số (lấy giá trị gần đúng của log2 là 0,3010) A. 605 chữ số B. 606 chữ số C. 2008 chữ số D. 2007 chữ số
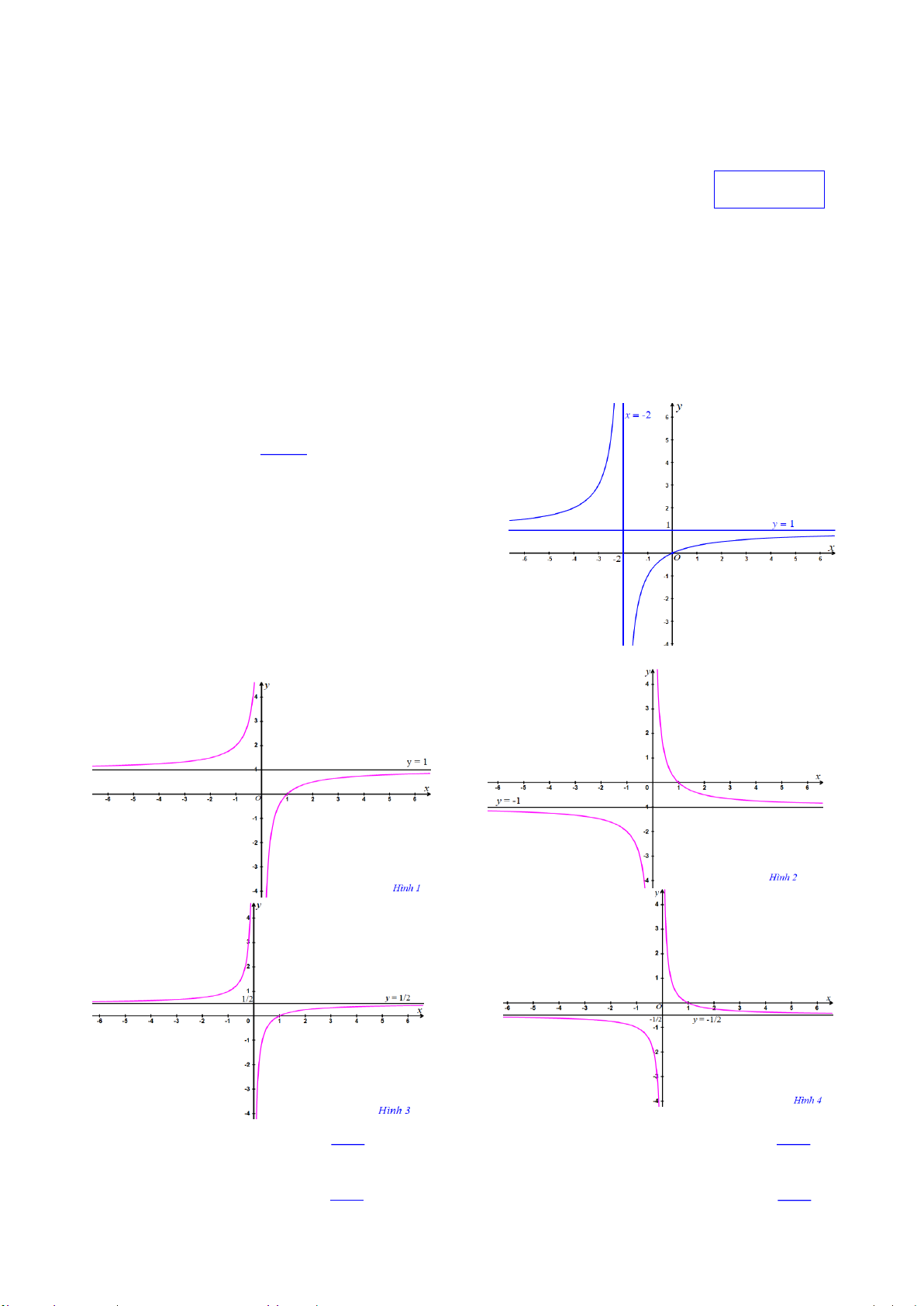
Câu 2. Chän ph-¬ng ¸n tr¶ lêi ®óng: x b
§å thÞ cña hµm sè y cx nh- h×nh d-íi ®©y. d
Khi ®ã gi¸ trÞ b, c, d lÇn l-ît lµ A. 1, 1, 2 B. 0, 1, 1 C. –2, 1, 1 D. 0, 1, 2
Câu 3. Cho các đồ thị trên các hình sau. Chỉ ra câu trả lời đúng x 1 1 x
A. Hình 2 có đồ thị hàm số y
B. Hình 4 có đồ thị hàm số y x 2x 1 x x 1
C. Hình 1 có đồ thị hàm số y
D. Hình 3 có đồ thị hàm số y x 2x H 1/6 Mã đề 102 1
Câu 4. T×m a , b ®Ó ®å thÞ cña hàm số 4 2 y
x bx a cã ®iÓm cùc tiÓu M(2 ; 4) 4
A. a 2, b 0 B. Kh«ng tån t¹i C. a 2
, b 0 D. a 0, b 2
Câu 5. Từ một tấm bìa hình vuông cạnh bằng 3cm, ta gấp nó thành
3 phần đều nhau rồi gấp thành một hình lăng trụ đứng (không đáy)
như hình bên. Hỏi thể tích khối lăng trụ này bằng bao nhiêu 1 1 3 3 3 A. cm3 B. cm3 C. cm3 D. cm3 4 12 4 4 2 x 2
Câu 6. Mét trong c¸c h×nh d-íi ®©y, h×nh nµo cã b¶ng biÕn thiªn cña hµm sè y x 1 A. H×nh 4 B. H×nh 3 C. H×nh 2 D. H×nh 1 x
Câu 7. Cho ®å thÞ (C) cña hàm số y
y x . Hỏi mÖnh ®Ò nµo ®óng
x vµ ®-êng th¼ng d: 4 1
A. d lµ tiÖm cËn xiªn cña (C)
B. d vµ (C) c¾t nhau t¹i hai ®iÓm ph©n biÖt C. d vµ (C) kh«ng c¾t nhau D. d vµ (C) tiÕp xóc
Câu 8. Mệnh đề nào dưới đây đúng
A. Phép biến hình biến mỗi điểm M trong không gian thành chính nó có là phép dời hình
B. Phép đối xứng qua mặt phẳng biến một tứ diện thành chính nó
C. Phép tịnh tiến biến một đường thẳng thành đường thẳng song song với nó
D. Tứ diện đều có đúng một mặt phẳng đối xứng
Câu 9. Một hộp không nắp được làm từ mảnh các tông theo mẫu hình bên.
Hộp có đáy là hình vuông cạnh x (cm), chiều cao h (cm) và có thể tích là 4cm3.
Tìm giá trị của x sao cho diện tích của mảnh các tông nhỏ nhất A. 8 cm B. 2 cm C. 4 cm D. 3 2 2 cm
Câu 10. Một người gửi 15 triệu đồng vào ngân hàng theo thể thức lãi kép kỳ hạn 1 năm với lãi suất
7,56% một năm. Giả sử lãi suất không thay đổi, hỏi số tiền người đó thu được (cả vốn lẫn lãi) sau 5
năm là bao nhiêu triệu đồng (làm tròn đến chữ số thập phân thứ hai) ?
A. 22,59 triệu đồng B. 20,59 triệu đồng C. 19,19 triệu đồng D. 21,59 triệu đồng
Câu 11. Cho hình lập phương ABCD.A'B'C'D' cạnh 1. Thể tích của khối chóp A'.ABCD bằng 1 1 1 A. B. C. D. 1 6 2 3
Câu 12. Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất A. Hai mặt B. Bốn mặt C. Ba mặt D. Năm mặt H 2/6 Mã đề 102 1
Câu 13. Gi¸ trÞ nhá nhÊt cña hµm sè y x 7 trªn kho¶ng ( 1 ;) lµ x 1 5 A. B. 0 C. 5 2 D. 2 2 Câu 14. Hàm số 3 2
y x 3x mx 2 nghÞch biÕn trªn kho¶ng (0 ; 2) khi m nhËn gi¸ trÞ A. m 3 B. m 3 C. m 3 D. m 0 1
Câu 15. Một khoảng đồng biến của hàm số y x 2 x là 1 A. 2 ; B. ; C. ; 1 D. 1 ;
Câu 16. Cho khối tứ diện ABCD. Lấy một điểm M nằm giữa A và B, một điểm N nằm giữa C và
D. Bằng hai mặt phẳng (MCD) và (NAB) ta chia khối tứ diện đã cho thành bốn khối tứ diện A. AMNC, AMND, AMCD, BMNC B. AMNC, AMND, BMNC, BMND C. AMCD, AMND, BMNC, BMND D. BMCD, BMND, AMNC, AMND
Câu 17. Thể tích của khối tám mặt đều có cạnh bằng a là 3 2 2 a 3 2 a 3 2 a A. B. 3 2 2 a C. D. 3 9 3 500 50 Câu 18. Tỉ số bằng 250 25 A. 250 100 B. 250 10 C. 250 2 D. 500 2
Câu 19. Với một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc tấm bìa một
hình vuông cạnh 12cm rồi gấp lại thành một hình hộp chữ nhật không có nắp.
Nếu dung tích của cái hộp đó là 4800cm3 thì cạnh tấm bìa có độ dài là A. 36cm B. 44cm C. 38cm D. 42cm
Câu 20. Hàm số f cã ®¹o hµm 2 2 2
f '(x) x (2x 3) (3x 2) . Sè ®iÓm cùc trÞ cña hàm số f lµ A. 1 B. 3 C. 0 D. 2
Câu 21. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AC = 2a , tam
giác SAC đều và nằm trên mặt phẳng vuông góc với đáy. Trên cạnh SA lấy điểm M sao cho
MA = 2MS. Mặt phẳng (α) qua M và song song với (ABC) cắt SB, SC tại N, P. Khi đó thể tích khối
chóp cụt ABC.MNP bằng 3 a 3 3 80 3a 3 26 3a 3 2 3a A. B. C. D. 3 81 81 9 3 Câu 22. Cho hµm sè 4 2
y x 2x 1 cã ®å thÞ (C). §iÓm M trªn (C) cã hoµnh ®é x lµ ®iÓm 3 g× cña (C) A. §iÓm cùc tiÓu B. §iÓm cùc ®¹i C. §iÓm th-êng D. §iÓm uèn H 3/6 Mã đề 102
Câu 23. Cho hàm số 4 2
y ax bx c trong đó a 0 và b 0 . Khi đó hàm số có
A. Một cực đại B. Một cực tiểu C. Hai cực tiểu và một cực đại D. Hai cực đại và một cực tiểu
Câu 24. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 1cm, SA 2cm và SA vuông góc với
đáy. Khoảng cách giữa hai đường thẳng BC và SD là A. 2 cm B. 2 cm C. 5 cm D. 1 cm
Câu 25. Cho tứ diện ABCD có trọng tâm G. Gọi A’, B’, C’, D’ lần lượt là trọng tâm các tam giác
BCD, CDA, ABD, ABC. Mệnh đề nào dưới đây đúng
A. A’, B’, C’, D’ đồng phẳng
B. A’B’C’D’ và ABCD là hai hình bằng nhau 1
C. Phép vị tự tâm G tỉ số
biến ABCD thành A’B’C’D’ 3 1
D. Phép vị tự tâm G tỉ số
biến A’B’C’D’ thành ABCD 3 Câu 26. Hàm số 3
y x 12x 1 có
A. Cực đại bằng 17 và cực tiểu bằng 0
B. Cực đại bằng 17 và cực tiểu bằng 15
C. Cực đại bằng 0 và cực tiểu bằng 15 D. Cực đại bằng 15
và cực tiểu bằng 17
Câu 27. Nếu a 0 thì tích 6 3 a . a bằng A. 9 a B. 9 2 a C. 18 a D. a
Câu 28. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a .
SA (ABC) và SA = a . Gọi (α) là mặt phẳng qua A và vuông góc với SB đồng thời cắt SB, SC tại
M, N. Khi đó thể tích khối chóp S.AMN bằng 3 a 3 a 3 a A. B. C. D. Đáp án khác 6 24 12 x 2
Câu 29. Víi gi¸ trÞ nµo cña m th× ®å thÞ hµm sè y 2 x 4x
chØ cã mét tiÖm cËn ®øng vµ mét m tiÖm cËn ngang A. 0 B. 2 C. 4 D. 1
Câu 30. Cho hình hộp ABCD.A’B’C’D’ có thể tích V. Thể tích khối tứ diện ACB’D’ là V V V V A. B. C. D. 3 8 6 4 Câu 31. Hàm số 4 3 2
y x 4x x 6x 10 có
A. Một cực đại và hai cực tiểu
B. Một cực đại và không có cực tiểu
C. Hai cực đại và một cực tiểu
D. Một cực tiểu và không có cực đại
Câu 32. Số mặt phẳng đối xứng của hình bát diện đều là A. 9 B. 3 C. 6 D. 12 H 4/6 Mã đề 102
Câu 33. Cho ®-êng cong (C) cã ph-¬ng tr×nh 2 y
x 2 , tÞnh tiÕn (C) theo phương trục hoành
sang tr¸i 3 ®¬n vÞ ta ®-îc ®-êng cong cã ph-¬ng tr×nh lµ A. 2 y x 2 3 B. 2 y x 2 3 C. 2 y x 6x 11 D. 2 y x 6x 11
Câu 34. Nếu log b log c thì a a
A. b c 0 và a 1 B. b c 0 và 0 a 1 C. b c 0 và a 0 D. c b 0 và a 1
Câu 35. Cho hình lăng trụ đứng MNP.M' N'P' có tất cả các cạnh bằng a . Thể tích của khối lăng trụ bằng 3 a 3 3 a 3 3 a 3 A. B. 3 a 3 C. D. 4 2 3 Câu 36. Hµm sè 4 2
y mx (m 1)x 1 2m chØ cã mét cùc trÞ khi
A. m 0 hoÆc m 1 B. m 1 C. m 0 D. 0 m 1
Câu 37. Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với đáy và AB = a ,
AD = 2a , góc giữa SB và đáy bằng 450. Thể tích khối chóp S.ABCD là 3 a 3 2 a A. 3 2a B. C. D. Đáp án khác 3 3 x 3
Câu 38. Cho đồ thị (C) cña hàm số y
d y mx m . Ph-¬ng ¸n nµo
x vµ ®-êng th¼ng : 2 1 1 d-íi ®©y ®óng
A. d lu«n ®i qua mét ®iÓm cè ®Þnh cña (C) khi m biÕn thiªn
B. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt
C. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt khi m 0
D. (C) vµ d tiÕp xóc víi nhau khi m 2
Câu 39. Khối tám mặt đều thuộc loại A. {4 ; 3} B. {3 ; 3} C {3 ; 5} D. {3 ; 4} Câu 40. Cho hµm sè 3 2
y x 6x 3(m 2)x m 6 ®¹t cùc ®¹i, cùc tiÓu t¹i x , x sao cho 1 2
x 1 x th× gi¸ trÞ cña m lµ 1 2 A. m 1 B. m 1 C. m 1 D. m 1 mx m
Câu 41. §å thÞ cña hµm sè y
c¾t ®-êng th¼ng d: y x 6 t¹i hai ®iÓm ph©n biÖt thuéc x hai nh¸nh cña nã khi: A. m 0 B. m 6 C. m 0 D. m 0
Câu 42. Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = a , AC = 2a và SA vuông
góc với đáy. Góc giữa (SBC) và (ABC) bằng 600. Thể tích khối chóp S.ABC bằng 3 a 3 3 a 3 a 3 3 3a A. B. C. D. 3 2 2 2 H 5/6 Mã đề 102
Câu 43. Cho log1218 = a , log2454 = b . Khi đó A. ab + 5(a – b) = 1 B. ab = 5(a – b) C. ab – 5(a – b) = 1 D. ab = 5(b – a)
Câu 44. Cho 0 a 1 , khi đó log 4 a a bằng A. 4 B. 2 C. 16 D. 1 3 3 3 3 4 4 4 4
a b a b
Câu 45. Cho hai số dương khác nhau a, b . Rút gọn biểu thức ab bằng 1 1 2 2 a b A. a b B. a b C. 2 a b D. 2 a b 5 3 Câu 46. Cho E = log và F = log . Khi đó 2 3 5 2 3 3 A. E = F B. E < F C. E > F D. E ≥ F Câu 47. Cho hµm sè 3
y x 3x 1 cã ®å thÞ (C), mét ®-êng th¼ng qua M(1; 3) vµ tiÕp xóc víi
(C) c¾t (C) t¹i ®iÓm thø hai N (N kh«ng trïng M). Khi ®ã täa ®é ®iÓm N lµ 1 3 A. (2; –1) B. ; C. (–1; –1) D. (0; 1) 2 8
Câu 48. Cho M = 32000 và N = 41500. Khi đó A. M = N B. M > N C. M < N D. M ≤ N
Câu 49. Cho hình lập phương ABCD.A’B’C’D’ cạnh a , tâm O. Thể tích khối tứ diện AA’B’O là 3 a 3 a 3 a 3 2 a A. B. C. D. 8 9 12 3
Câu 50. Chän ph-¬ng ¸n tr¶ lêi ®óng:
H×nh d-íi ®©y lµ ®å thÞ cña hµm sè nµo 3 x A. 2 y x x 3 3 x B. 2 y x x 3 3 x C. 2 y x x 3 3 x D. y . 3
Cán bộ coi kiểm tra không giải thích gì thêm H 6/6 Mã đề 102
TRƯỜNG THPT NGUYỄN GIA THIỀU ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA HỌC KỲ 1
BỘ MÔN TOÁN Môn toán lớp 12, năm học 2016 – 2017
Đề chính thức gồm 06 trang Thời gian làm bài 90 phút Mã đề 103
Hä vµ tªn häc sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Líp: . . . . . . . . . 1 1 Câu 1. Hàm số 3 2 y
x x x có đồ thị là 3 3
A. Đồ thị trên hình 1 B. Đồ thị trên hình 2
C. Đồ thị trên hình 3 D. Đồ thị trên hình 4
Câu 2. Cho các đồ thị trên các hình sau. Chỉ ra câu trả lời đúng x 1 1 x
A. Hình 2 có đồ thị hàm số y
B. Hình 1 có đồ thị hàm số y x x 1 x x 1
C. Hình 4 có đồ thị hàm số y
D. Hình 3 có đồ thị hàm số y 2x 2x
Câu 3. Cho hình lăng trụ đứng ABC.MNP có tất cả các cạnh bằng a . Thể tích của khối lăng trụ là 3 a 3 3 a 3 3 a 3 A. 3 a 3 B. C. D. 2 3 4 H 1/6 Mã đề 103 2 x 2
Câu 4. Mét trong c¸c h×nh d-íi ®©y, h×nh nµo cã b¶ng biÕn thiªn cña hµm sè y x 1 A. H×nh 4 B. H×nh 1 C. H×nh 3 D. H×nh 2 Câu 5. Cho hàm số 4 2
y ax bx c trong đó a 0 và b 0 . Khi đó hàm số có
A. Hai cực tiểu và một cực đại B. Hai cực đại và một cực tiểu C. Một cực đại D. Một cực tiểu 1
Câu 6. Một khoảng đồng biến của hàm số y x 2 x là 1 A. 2 ; B. 1 ; C. ; D. ; 1 Câu 7. Hàm số 3 2
y x 3x mx 2 nghÞch biÕn trªn kho¶ng (0 ; 2) khi m nhËn gi¸ trÞ A. m 3 B. m 3 C. m 3 D. m 0 Câu 8. Hàm số 3
y x 12x 1 có A. Cực đại bằng 15
và cực tiểu bằng 17 B. Cực đại bằng 17 và cực tiểu bằng 0
C. Cực đại bằng 0 và cực tiểu bằng 15
D. Cực đại bằng 17 và cực tiểu bằng 15 Câu 9. Hµm sè 4 2
y mx (m 1)x 1 2m chØ cã mét cùc trÞ khi A. m 1 B. m 0 C. 0 m 1
D. m 0 hoÆc m 1
Câu 10. Cho ®-êng cong (C) cã ph-¬ng tr×nh 2 y
x 2 , tÞnh tiÕn (C) theo phương trục hoành
sang tr¸i 3 ®¬n vÞ ta ®-îc ®-êng cong cã ph-¬ng tr×nh lµ A. 2 y x 2 3 B. 2 y
x 6x 11 C. 2 y x 2 3 D. 2 y x 6x 11 Câu 11. Cho hµm sè 3 2
y x 6x 3(m 2)x m 6 ®¹t cùc ®¹i, cùc tiÓu t¹i x , x sao cho 1 2
x 1 x th× gi¸ trÞ cña m lµ 1 2 A. m 1 B. m 1 C. m 1 D. m 1
Câu 12. Hàm số f cã ®¹o hµm 2 2
f '(x) x (2x 3) (3x 2) . Sè ®iÓm cùc trÞ cña hàm số f lµ A. 0 B. 3 C. 1 D. 2 x 2
Câu 13. Víi gi¸ trÞ nµo cña m th× ®å thÞ hµm sè y 2 x 4x
chØ cã mét tiÖm cËn ®øng vµ mét m tiÖm cËn ngang A. 4 B. 3 C. 2 D. 1 3 Câu 14. Cho hµm sè 4 2
y x 2x 1 cã ®å thÞ (C). §iÓm M trªn (C) cã hoµnh ®é x lµ ®iÓm 3 g× cña (C) A. §iÓm th-êng B. §iÓm uèn C. §iÓm cùc tiÓu D. §iÓm cùc ®¹i H 2/6 Mã đề 103
Câu 15. Số ®-êng th¼ng đi qua điểm M 0; 7
vµ tiÕp xóc víi đồ thị hàm số 4 2
y x 5x 7 là A. 1 B. 2 C. 3 D. 4 mx m
Câu 16. §å thÞ cña hµm sè y
c¾t ®-êng th¼ng d: y x 6 t¹i hai ®iÓm ph©n biÖt thuéc x hai nh¸nh cña nã khi: A. m 6 B. m 0 C. m 0 D. m 0 Câu 17. Cho hµm sè 3
y x 3x 1 cã ®å thÞ (C), mét ®-êng th¼ng qua M(1; 3) vµ tiÕp xóc víi
(C) c¾t (C) t¹i ®iÓm thø hai N (N kh«ng trïng M). Khi ®ã täa ®é ®iÓm N lµ 1 3 A. (2; –1) B. (–1; –1) C. ; D. (0; 1) 2 8 Câu 18. Hàm số 4 3 2
y x 4x x 6x 10 có
A. Một cực tiểu và không có cực đại
B. Một cực đại và hai cực tiểu
C. Hai cực đại và một cực tiểu
D. Một cực đại và không có cực tiểu
Câu 19. Hµm sè y sin 2x 2 cos x cã gi¸ trÞ lín nhÊt trªn ®o¹n [– ; ] lµ 3 3 3 3 A. B. 3 C. 3 D. 2 2 x 3
Câu 20. Cho đồ thị (C) cña hàm số y
d y mx m . Ph-¬ng ¸n nµo
x vµ ®-êng th¼ng : 2 1 1 d-íi ®©y ®óng
A. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt
B. d lu«n ®i qua mét ®iÓm cè ®Þnh cña (C) khi m biÕn thiªn
C. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt khi m 0
D. (C) vµ d tiÕp xóc víi nhau khi m 2 x
Câu 21. Cho ®å thÞ (C) cña hàm số y y x . MÖnh ®Ò nµo d-íi ®©y
x vµ ®-êng th¼ng d: 4 1 ®óng A. d vµ (C) kh«ng c¾t nhau
B. d vµ (C) c¾t nhau t¹i hai ®iÓm ph©n biÖt C. d vµ (C) tiÕp xóc
D. d lµ tiÖm cËn xiªn cña (C)
Câu 22. Một hộp không nắp được làm từ mảnh các tông theo mẫu hình bên.
Hộp có đáy là hình vuông cạnh x (cm), chiều cao h (cm) và có thể tích là 4cm3.
Tìm giá trị của x sao cho diện tích của mảnh các tông nhỏ nhất A. 8 cm B. 2 cm C. 4 cm D. 3 2 2 cm 500 50 Câu 23. Tỉ số bằng 250 25 A. 250 10 B. 250 2 C. 250 100 D. 260 2 H 3/6 Mã đề 103 5 3 Câu 24. Cho E = log và F = log . Khi đó 2 3 5 2 3 3 A. E = F B. E > F C. E ≥ F D. E < F
Câu 25. Cho M = 32000 và N = 41500. Khi đó A. M = N B. M < N C. M ≤ N D. M > N
Câu 26. Nếu a 0 thì tích 6 3 a . a bằng A. a B. 9 a C. 9 2 a D. 18 a
Câu 27. Nếu log b log c thì a a
A. b c 0 và 0 a 1 B. b c 0 và a 1 C. b c 0 và a 0 D. c b 0 và a 1
Câu 28. Cho 0 a 1 , khi đó log 4 a a bằng A. 16 B. 4 C. 2 D. 1 3 3 3 3 4 4 4 4
a b a b
Câu 29. Cho hai số dương khác nhau a, b . Rút gọn biểu thức ab bằng 1 1 2 2 a b A. a b B. a b C. 2 a b D. 2 a b
Câu 30. Cho log1218 = a , log2454 = b . Khi đó A. ab = 5(a – b) B. ab – 5(a – b) = 1 C. ab + 5(a – b) = 1 D. ab = 5(b – a)
Câu 31. Một người gửi 15 triệu đồng vào ngân hàng theo thể thức lãi kép kỳ hạn 1 năm với lãi suất
7,56% một năm. Giả sử lãi suất không thay đổi, hỏi số tiền người đó thu được (cả vốn lẫn lãi) sau 5
năm là bao nhiêu triệu đồng (làm tròn đến chữ số thập phân thứ hai) ?
A. 22,59 triệu đồng B. 21,59 triệu đồng C. 20,59 triệu đồng D. 19,19 triệu đồng
Câu 32. Cho điểm O và số thực k 0 . Mệnh đề nào dưới đây sai
A. Phép vị tự tâm O tỉ số k là một phép đồng dạng khi k 0
B. Phép vị tự tâm O tỉ số k luôn là một phép đồng dạng
C. Phép vị tự tâm O tỉ số k 1
là một phép đối xứng tâm
D. Phép vị tự tâm O tỉ số k 1 là một phép đồng nhất H 4/6 Mã đề 103
Câu 33. Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất A. Năm mặt B. Hai mặt C. Bốn mặt D. Ba mặt
Câu 34. Khối tám mặt đều thuộc loại A. {3 ; 4} B. {4 ; 3} C. {3 ; 3} D. {3 ; 5}
Câu 35. Cho khối tứ diện ABCD. Lấy một điểm M nằm giữa A và B, một điểm N nằm giữa C và
D. Bằng hai mặt phẳng (MCD) và (NAB) ta chia khối tứ diện đã cho thành bốn khối tứ diện A. AMNC, AMND, AMCD, BMNC B. AMCD, AMND, BMNC, BMND C. AMNC, AMND, BMNC, BMND D. BMCD, BMND, AMNC, AMND
Câu 36. Số mặt phẳng đối xứng của hình bát diện đều là A. 3 B. 9 C. 6 D. 12
Câu 37. Khi viết 22008 trong hệ thập phân ta được một số có bao nhiêu chữ số (lấy giá trị gần đúng của log2 là 0,3010) A. 606 chữ số B. 2008 chữ số C. 2007 chữ số D. 605 chữ số
Câu 38. Mệnh đề nào dưới đây đúng
A. Phép đối xứng qua mặt phẳng biến một tứ diện thành chính nó
B. Phép tịnh tiến biến một đường thẳng thành đường thẳng song song với nó
C. Phép biến hình biến mỗi điểm M trong không gian thành chính nó có là phép dời hình
D. Tứ diện đều có đúng một mặt phẳng đối xứng
Câu 39. Từ một tấm bìa hình vuông cạnh bằng 3cm, ta gấp nó thành
3 phần đều nhau rồi gấp thành một hình lăng trụ đứng (không đáy)
như hình bên. Hỏi thể tích khối lăng trụ này bằng bao nhiêu 1 3 3 1 3 A. cm3 B. cm3 C. cm3 D. cm3 4 4 12 4
Câu 40. Cho hình lập phương ABCD.A'B'C'D' cạnh 1. Thể tích của khối chóp A'.ABCD bằng 1 1 1 A. B. C. D. 1 3 6 2
Câu 41. Với một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc tấm bìa một
hình vuông cạnh 12cm rồi gấp lại thành một hình hộp chữ nhật không có nắp.
Nếu dung tích của cái hộp đó là 4800cm3 thì cạnh tấm bìa có độ dài là A. 36cm B. 38cm C. 42cm D. 44cm
Câu 42. Cho hình hộp ABCD.A’B’C’D’ có thể tích V. Thể tích khối tứ diện ACB’D’ là V V V V A. B. C. D. 8 3 6 4
Câu 43. Thể tích của khối tám mặt đều có cạnh bằng a là 3 2 2 a 3 2 a 3 2 a A. B. 3 2 2 a C. D. 3 3 9 H 5/6 Mã đề 103
Câu 44. Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = a , AC = 2a và SA vuông
góc với đáy. Góc giữa (SBC) và (ABC) bằng 600. Thể tích khối chóp S.ABC bằng 3 a 3 a 3 3 a 3 3 3a A. B. C. D. 2 3 2 2
Câu 45. Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với đáy và AB = a ,
AD = 2a , góc giữa SB và đáy bằng 450. Thể tích khối chóp S.ABCD là 3 6 a 3 a 3 2 a A. B. C. 3 2a D. 18 3 3
Câu 46. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a .
SA (ABC) và SA = a . Gọi (α) là mặt phẳng qua A và vuông góc với SB đồng thời cắt SB, SC tại
M, N. Khi đó thể tích khối chóp S.AMN bằng 3 a 3 a 3 a A. B. C. D. Đáp án khác 6 12 24
Câu 47. Cho hình lập phương ABCD.A’B’C’D’ cạnh a , tâm O. Thể tích khối tứ diện AA’B’O là 3 a 3 a 3 a 3 2 a A. B. C. D. 12 8 9 3
Câu 48. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 1cm, SA 2cm và SA vuông góc với
đáy. Khoảng cách giữa hai đường thẳng BC và SD là A. 2 cm B. 1 cm C. 2 cm D. 5 cm
Câu 49. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AC = 2a , tam
giác SAC đều và nằm trên mặt phẳng vuông góc với đáy. Trên cạnh SA lấy điểm M sao cho
MA = 2MS. Mặt phẳng (α) qua M và song song với (ABC) cắt SB, SC tại N, P. Khi đó thể tích khối
chóp cụt ABC.MNP bằng 3 26 3a 3 a 3 3 80 3a 3 2 3a A. B. C. D. 81 3 81 9
Câu 50. Chän ph-¬ng ¸n tr¶ lêi ®óng: x b
§å thÞ cña hµm sè y cx nh- h×nh d-íi ®©y. d
Khi ®ã gi¸ trÞ b, c, d lÇn l-ît lµ A. 0, 1, 2 B. 1, 1, 2 C. 0, 1, 1 D. –2, 1, 1.
Cán bộ coi kiểm tra không giải thích gì thêm H 6/6 Mã đề 103
TRƯỜNG THPT NGUYỄN GIA THIỀU ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA HỌC KỲ 1
BỘ MÔN TOÁN Môn toán lớp 12, năm học 2016 – 2017
Đề chính thức gồm 06 trang Thời gian làm bài 90 phút Mã đề 104
Hä vµ tªn häc sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Líp: . . . . . . . . . 1 5 1 Câu 1. Hàm số 3 y x x có đồ thị là 27 27 3
A. Đồ thị trên hình 1 B. Đồ thị trên hình 2
C. Đồ thị trên hình 3 D. Đồ thị trên hình 4
Câu 2. Chän ph-¬ng ¸n tr¶ lêi ®óng: x b
§å thÞ cña hµm sè y cx nh- h×nh d-íi ®©y. d
Khi ®ã gi¸ trÞ b, c, d lÇn l-ît lµ A. 1, 1, 2 B. 0, 1, 2 C. 2, 1, 1 D. 0, 1, 1
Câu 3. Thể tích khối tứ diện đều có cạnh bằng 1 là 3 2 2 2 A. B. C. D. 4 4 12 6 3 3 3 3 4 4 4 4
a b a b
Câu 4. Cho hai số dương khác nhau a, b . Rút gọn biểu thức ab bằng 1 1 2 2 a b A. a b B. 2 a b C. a b D. 2 a b
Câu 5. Cho E = log45 và F = log54. Khi đó A. E > F B. E = F C. E < F D. E ≥ F H 1/6 Mã đề 104
Câu 6. Với một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc tấm bìa một
hình vuông cạnh 12cm rồi gấp lại thành một hình hộp chữ nhật không có nắp.
Nếu dung tích của cái hộp đó là 4800cm3 thì cạnh tấm bìa có độ dài là A. 36cm B. 44cm C. 38cm D. 42cm
Câu 7. Hàm số f cã ®¹o hµm 2
f '(x) x(2x 3) (3x 2) . Sè ®iÓm cùc trÞ cña hàm số f lµ A. 2 B. 4 C. 3 D. 1
Câu 8. Từ một tấm bìa hình vuông cạnh bằng 4cm, ta gấp nó thành
4 phần đều nhau rồi gấp thành một hình hộp chữ nhật (không nắp)
như hình bên. Hỏi thể tích khối hộp này bằng bao nhiêu A. 4cm3
B. 1cm3 C. 16cm3 D. 8cm3 Câu 9. Cho hàm số 4 2
y ax bx c trong đó a 0 và b 0. Khi đó hàm số có
A. Hai cực tiểu và một cực đại B. Hai cực đại và một cực tiểu C. Một cực đại D. Một cực tiểu
Câu 10. Nếu log b log c thì a a
A. 0 b c B. b c 0 và a 0 C. c b 0 và a 1 D. 0 b c và 0 a 1
Câu 11. Một hộp không nắp được làm từ mảnh các tông theo mẫu hình bên.
Hộp có đáy là hình vuông cạnh x (cm), chiều cao h (cm) và có thể tích là 4cm3.
Tìm giá trị của x sao cho diện tích của mảnh các tông nhỏ nhất A. 8 cm B. 4 cm C. 2 cm D. 3 2 2 cm Câu 12. Hµm sè 4 3
y x mx 11m 4 ®¹t cùc tiÓu t¹i x 3 khi A. m 6 B. m 4 C. m 4 D. m 6
Câu 13. Cho ®-êng cong (C) cã ph-¬ng tr×nh 2 y
x 2 , tÞnh tiÕn (C) theo phương trục hoành
sang phải 3 ®¬n vÞ ta ®-îc ®-êng cong cã ph-¬ng tr×nh lµ A. 2 y x 2 3 B. 2 y x 6x 11 C. 2 y x 2 3 D. 2 y x 6x 11
Câu 14. Một người gửi 6 triệu đồng vào ngân hàng theo thể thức lãi kép, kì hạn 1 năm với lãi suất
7,56% một năm. Hỏi sau bao nhiêu năm người gửi sẽ có ít nhất 12 triệu đồng từ số tiền gửi ban đầu
(giả sử lãi suất không thay đổi) ? A. 10 năm B. 1 năm C. 8 năm D. 15 năm
Câu 15. Khối hai mươi mặt đều thuộc loại A. {3 ; 4} B. {4 ; 3} C. {3 ; 5} D. {5 ; 3}
Câu 16. Thể tích của khối tám mặt đều có cạnh bằng a là 3 2 a 3 2 2 a 3 2 a A. B. C. 3 2 2 a D. 3 3 9
Câu 17. Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất A. Hai mặt B. Ba mặt C. Bốn mặt D. Năm mặt H 2/6 Mã đề 104 2 x 2
Câu 18. Mét trong c¸c h×nh d-íi ®©y, h×nh nµo cã b¶ng biÕn thiªn cña hµm sè y x 1 A. H×nh 2 B. H×nh 1 C. H×nh 4 D. H×nh 3 Câu 19. Hàm số 3
y x 12x 1 có
A. Cực đại bằng 17 và cực tiểu bằng 15
B. Cực đại bằng 17 và cực tiểu bằng 0
C. Cực đại bằng 0 và cực tiểu bằng 15 D. Cực đại bằng 15
và cực tiểu bằng 17 1
Câu 20. Một khoảng đồng biến của hàm số y x 2 x là 1 A. 2 ; B. ; C. 1
; D. ; 1
Câu 21. Nếu a 0 thì tích 6 3 a . a bằng A. 9 a B. 9 2 a C. a D. 18 a
Câu 22. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 1cm, SA 2cm và SA vuông góc với
đáy. Khoảng cách giữa hai đường thẳng BC và SD là A. 2 cm B. 2 cm C. 1 cm D. 5 cm Câu 23. Hµm sè 4 2
y mx (m 1)x 1 2m chØ cã mét cùc trÞ khi A. m 1
B. m 0 hoÆc m 1 C. m 0 D. 0 m 1
Câu 24. Cho điểm O và số thực k 0 . Mệnh đề nào dưới đây sai
A. Phép vị tự tâm O tỉ số k là một phép đồng dạng khi k 0
B. Phép vị tự tâm O tỉ số k 1
là một phép đối xứng tâm
C. Phép vị tự tâm O tỉ số k 1 là một phép đồng nhất
D. Phép vị tự tâm O tỉ số k luôn là một phép đồng dạng
Câu 25. Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = a , AC = 2a và SA vuông
góc với đáy. Góc giữa (SBC) và (ABC) bằng 600. Thể tích khối chóp S.ABC bằng 3 a 3 3 a 3 3 a 3 3a A. B. C. D. 3 2 2 2
Câu 26. Sè ®-êng th¼ng ®i qua ®iÓm M(–1
; 3 ) vµ tiÕp xóc víi ®å thÞ cña hµm sè 3 y x 3x lµ A. 2 B. 0 C. 3 D. 1
Câu 27. Đồ thị cña hàm số 2
y x 1 x có
A. Tiệm cận đứng và có tiệm cận xiên
B. Tiệm cận đứng và có tiệm cận ngang
C. Tiệm cận xiên và không có tiệm cận ngang
D. Tiệm cận ngang và có tiệm cận xiên H 3/6 Mã đề 104
Câu 28. Cho khối tứ diện ABCD. Lấy một điểm M nằm giữa A và B, một điểm N nằm giữa C và
D. Bằng hai mặt phẳng (MCD) và (NAB) ta chia khối tứ diện đã cho thành bốn khối tứ diện A. AMNC, AMND, BMNC, BMND B. AMNC, AMND, AMCD, BMNC C. AMCD, AMND, BMNC, BMND D. BMCD, BMND, AMNC, AMND
Câu 29. Biết log 2 ;
a log 3 b . Tính log 5 5 305 theo a, b 1 1 A. a b B. a b 1 C. D. a b 1 a b
Câu 30. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AC = 2a , tam
giác SAC đều và nằm trên mặt phẳng vuông góc với đáy. Trên cạnh SA lấy điểm M sao cho
MA = 2MS. Mặt phẳng (α) qua M và song song với (ABC) cắt SB, SC tại N, P. Khi đó thể tích khối
chóp cụt ABC.MNP bằng 3 a 3 3 26 3a 3 80 3a 3 2 3a A. B. C. D. 3 81 81 9 Câu 31. Cho hµm sè 3 2
y x 6x 3(m 2)x m 6 ®¹t cùc ®¹i, cùc tiÓu t¹i x , x sao cho 1 2
x 1 x th× gi¸ trÞ cña m lµ 1 2 A. m 1 B. m 1 C. m 1 D. m 1 500 50 Câu 32. Tỉ số bằng 250 25 A. 250 10 B. 250 2 C. 500 2 D. 500 10
Câu 33. Cho tứ diện AEFG có thể tích là V và AE, AF, AG vuông góc với nhau từng đôi một. Gọi
B, C, D lần lượt là trung điểm của các đoạn thẳng GE, EF, FG. Thể tích khối tứ diện ABCD bằng V V V V A. B. C. D. 2 3 6 4 mx m
Câu 34. §å thÞ cña hµm sè y
c¾t ®-êng th¼ng d: y x 6 t¹i hai ®iÓm ph©n biÖt thuéc x hai nh¸nh cña nã khi: A. m 0 B. m 0 C. m 6 D. m 0 x
Câu 35. Cho ®å thÞ (C) cña hàm số y y x . MÖnh ®Ò nµo d-íi ®©y
x vµ ®-êng th¼ng d: 4 1 ®óng A. d vµ (C) tiÕp xóc
B. d vµ (C) c¾t nhau t¹i hai ®iÓm ph©n biÖt C. d vµ (C) kh«ng c¾t nhau
D. d lµ tiÖm cËn xiªn cña (C) Câu 36. Hàm số 3 2
y x 6x mx 1 đồng biến trên kho¶ng (0; +∞) khi giá trị của m là A. m 0 B. m 12 C. m 12 D. m 0 H 4/6 Mã đề 104
Câu 37. Cho tứ diện ABCD có trọng tâm G. Gọi A’, B’, C’, D’ lần lượt là trọng tâm các tam giác
BCD, CDA, ABD, ABC. Mệnh đề nào dưới đây đúng
A. A’, B’, C’, D’ đồng phẳng 1
B. Phép vị tự tâm G tỉ số
biến ABCD thành A’B’C’D’ 3
C. A’B’C’D’ và ABCD là hai hình bằng nhau 1
D. Phép vị tự tâm G tỉ số
biến A’B’C’D’ thành ABCD 3
Câu 38. Cho hình lăng trụ đứng MNP.M' N'P' có tất cả các cạnh bằng a . Thể tích của khối lăng trụ bằng 3 a 3 3 a 3 3 a 3 A. 3 a 3 B. C. D. 4 2 3
Câu 39. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a .
SA (ABC) và SA = a . Gọi (α) là mặt phẳng qua A và vuông góc với SB đồng thời cắt SB, SC tại
M, N. Khi đó thể tích khối chóp S.AMN bằng 3 a 3 a 3 a A. B. C. D. Đáp án khác 24 6 12
Câu 40. Cho hình hộp ABCD.A’B’C’D’ có thể tích V. Thể tích khối tứ diện ACB’D’ là V V V V A. B. C. D. 8 6 4 3
Câu 41. Khi viết 22008 trong hệ thập phân ta được một số có bao nhiêu chữ số (lấy giá trị gần đúng của log2 là 0,3010) A. 606 chữ số B. 2008 chữ số C. 2007 chữ số D. 605 chữ số
Câu 42. Cho 0 a 1 , khi đó 3log 2 a a bằng A. 16 B. 8 C. 6 D. 2 x 3
Câu 43. Cho đồ thị (C) cña hàm số y
d y mx m . Ph-¬ng ¸n nµo
x vµ ®-êng th¼ng : 2 1 1 d-íi ®©y ®óng
A. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt
B. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt khi m 0
C. d lu«n ®i qua mét ®iÓm cè ®Þnh cña (C) khi m biÕn thiªn
D. (C) vµ d tiÕp xóc víi nhau khi m 2
Câu 44. Cho M = 32000 và N = 41500. Khi đó A. M = N B. M < N C. M > N D. M ≤ N H 5/6 Mã đề 104
Câu 45. Hình lập phương có bao nhiêu mặt phẳng đối xứng A. 3 B. 4 C. 6 D. 9 Câu 46. Hàm số 4 3 2
y x 4x x 6x 10 có
A. Một cực đại và hai cực tiểu
B. Một cực tiểu và không có cực đại
C. Hai cực đại và một cực tiểu
D. Một cực đại và không có cực tiểu Câu 47. Cho hµm sè 3
y x 3x 1 cã ®å thÞ (C), mét ®-êng th¼ng qua M(1; 3) vµ tiÕp xóc víi
(C) c¾t (C) t¹i ®iÓm thø hai N (N kh«ng trïng M). Khi ®ã täa ®é ®iÓm N lµ 1 3 A. (2; –1) B. (–1; –1) C. (0; 1) D. ; 2 8
Câu 48. Gi¸ trÞ nhá nhÊt cña hµm sè 2 2 y
x 2x 5
x 4x 8 trªn ®o¹n [–1 ; 1] lµ A. 2 2 5 B. 5 C. 2 13 D. §¸p sè kh¸c
Câu 49. Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với đáy và AB = a ,
AD = 2a , góc giữa SB và đáy bằng 450. Thể tích khối chóp S.ABCD là 3 2 a 3 a A. 3 2a B. C. D. Đáp án khác 3 3
Câu 50. Cho các đồ thị trên các hình sau. Chỉ ra câu trả lời đúng x 1 1 x
A. Hình 2 có đồ thị hàm số y
B. Hình 1 có đồ thị hàm số y x x x 1 1 x
C. Hình 3 có đồ thị hàm số y y
D. Hình 4 có đồ thị hàm số . 2x 2x
Cán bộ coi kiểm tra không giải thích gì thêm H 6/6 Mã đề 104
TRƯỜNG THPT NGUYỄN GIA THIỀU ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA HỌC KỲ 1
BỘ MÔN TOÁN Môn toán lớp 12, năm học 2016 – 2017
Đề chính thức gồm 06 trang Thời gian làm bài 90 phút Mã đề 505
Hä vµ tªn häc sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Líp: . . . . . . . . .
Câu 1. Cho các đồ thị trên các hình sau. Chỉ ra câu trả lời đúng
A. Hình 4 có đồ thị hàm số 4 2
y x 2x 3
B. Hình 3 có đồ thị hàm số 3
y x 3x 2
C. Hình 2 có đồ thị hàm số 4 2
y x 2x 3
D. Hình 1 có đồ thị hàm số 3
y x 3x 2
Câu 2. Thể tích khối tứ diện đều có cạnh bằng 1 là 2 3 2 2 A. B. C. D. 12 4 4 6
Câu 3. Cho các đồ thị trên các hình sau. Chỉ ra câu trả lời đúng 1 x x 1
A. Hình 4 có đồ thị hàm số y
B. Hình 2 có đồ thị hàm số y 2x x 1 x x 1
C. Hình 1 có đồ thị hàm số y
D. Hình 3 có đồ thị hàm số y x 2x H 1/6 Mã đề 505
Câu 4. Với một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc tấm bìa một
hình vuông cạnh 12cm rồi gấp lại thành một hình hộp chữ nhật không có nắp.
Nếu dung tích của cái hộp đó là 4800cm3 thì cạnh tấm bìa có độ dài là A. 36cm B. 38cm C. 42cm D. 44cm
Câu 5. Cho hình hộp ABCD.A’B’C’D’ có thể tích V. Thể tích khối tứ diện ACB’D’ là V V V V A. B. C. D. 8 6 3 4
Câu 6. Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = a , AC = 2a và SA vuông góc
với đáy. Góc giữa (SBC) và (ABC) bằng 600. Thể tích khối chóp S.ABC bằng 3 a 3 3 a 3 3 3a 3 a A. B. C. D. 3 2 2 2
Câu 7. Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với đáy và AB = a ,
AD = 2a , góc giữa SB và đáy bằng 450. Thể tích khối chóp S.ABCD là 3 2 a 3 6 a 3 a A. B. C. D. 3 2a 3 18 3
Câu 8. Thể tích của khối tám mặt đều có cạnh bằng a là 3 2 2 a 3 2 a 3 2 a A. B. C. 3 2 2 a D. 3 3 9
Câu 9. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a .
SA (ABC) và SA = a . Gọi (α) là mặt phẳng qua A và vuông góc với SB đồng thời cắt SB, SC tại
M, N. Khi đó thể tích khối chóp S.AMN bằng 3 a 3 a 3 a 3 a A. B. C. D. 24 6 12 18
Câu 10. Cho tứ diện AEFG có thể tích là V và AE, AF, AG vuông góc với nhau từng đôi một. Gọi
B, C, D lần lượt là trung điểm của các đoạn thẳng GE, EF, FG. Thể tích khối tứ diện ABCD bằng V V V V A. B. C. D. 2 4 3 6
Câu 11. Cho hình lăng trụ đứng MNP.M' N'P' có tất cả các cạnh bằng a . Thể tích của khối lăng trụ bằng 3 a 3 3 a 3 3 a 3 A. 3 a 3 B. C. D. 2 4 3
Câu 12. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 1cm, SA 2cm và SA vuông góc với
đáy. Khoảng cách giữa hai đường thẳng BC và SD là A. 1 cm B. 2 cm C. 2 cm D. 5 cm
Câu 13. Cho hàm số 4 2
y ax bx c trong đó a 0 và b 0. Khi đó hàm số có
A. Hai cực tiểu và một cực đại B. Hai cực đại và một cực tiểu C. Một cực đại D. Một cực tiểu H 2/6 Mã đề 505
Câu 14. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AC = 2a , tam
giác SAC đều và nằm trên mặt phẳng vuông góc với đáy. Trên cạnh SA lấy điểm M sao cho
MA = 2MS. Mặt phẳng (α) qua M và song song với (ABC) cắt SB, SC tại N, P. Khi đó thể tích khối
chóp cụt ABC.MNP bằng 3 a 3 3 80 3a 3 2 3a 3 26 3a A. B. C. D. 3 81 9 81
Câu 15. Biết log 2 ;
a log 3 b . Tính log 5 5 305 theo a, b 1 1 A. a b B. C. a b 1 D. a b 1 a b 500 50 Câu 16. Tỉ số bằng 250 25 A. 250 10 B. 500 10 C. 250 2 D. 260 2
Câu 17. Cho M = 32000 và N = 41500. Khi đó A. M > N B. M = N C. M < N D. M ≤ N 2 x 2
Câu 18. Mét trong c¸c h×nh d-íi ®©y, h×nh nµo cã b¶ng biÕn thiªn cña hµm sè y x 1 A. H×nh 1 B. H×nh 2 C. H×nh 3 D. H×nh 4 1
Câu 19. Một khoảng đồng biến của hàm số y x 2 là x 1 A. ; 1 B. 2 ;
C. ; D. ; 1 Câu 20. Hàm số 3 2
y x 6x mx 1 đồng biến trên kho¶ng (0; +∞) khi giá trị của m là A. m 0 B. m 12 C. m 0 D. m 12 Câu 21. Hàm số 3
y x 12x 1 có
A. Cực đại bằng 17 và cực tiểu bằng 0
B. Cực đại bằng 17 và cực tiểu bằng 15
C. Cực đại bằng 0 và cực tiểu bằng 15 D. Cực đại bằng 15
và cực tiểu bằng 17 Câu 22. Hµm sè 4 2
y mx (m 1)x 1 2m chØ cã mét cùc trÞ khi A. m 1 B. m 0
C. m 0 hoÆc m 1 D. 0 m 1
Câu 23. Cho ®-êng cong (C) cã ph-¬ng tr×nh 2 y
x 2 , tÞnh tiÕn (C) theo phương trục hoành
sang phải 3 ®¬n vÞ ta ®-îc ®-êng cong cã ph-¬ng tr×nh lµ A. 2 y
x 6x 11 B. 2 y x 2 3 C. 2 y x 2 3 D. 2 y x 6x 11 H 3/6 Mã đề 505 Câu 24. Cho hµm sè 3 2
y x 6x 3(m 2)x m 6 ®¹t cùc ®¹i, cùc tiÓu t¹i x , x sao cho 1 2
x 1 x th× gi¸ trÞ cña m lµ 1 2 A. m 1 B. m 1 C. m 1 D. m 1
Câu 25. Hàm số f cã ®¹o hµm 3
f '(x) x (2x 3)(3x 2) . Sè ®iÓm cùc trÞ cña hàm số f lµ A. 0 B. 1 C. 2 D. 3
Câu 26. Đồ thị cña hàm số 2
y x 1 x có
A. Tiệm cận đứng và có tiệm cận xiên
B. Tiệm cận ngang và có tiệm cận xiên
C. Tiệm cận xiên và không có tiệm cận ngang
D. Tiệm cận đứng và có tiệm cận ngang
Câu 27. Hµm sè y cos 3x m sin x 9 ®¹t cùc ®¹i t¹i x khi 3
A. Không tồn tại m B. m 18 C. m 1 D. m 0 2 2x 1
Câu 28. C¸c ®å thÞ cña hai hàm số y vµ 2
y 2x x tiÕp xóc víi nhau t¹i ®iÓm cã täa ®é x 1 1 A. ;1 B. ; 0 C. (–1 ; 3) D. (1 ; 1) 2 2
Câu 29. Nếu a 0 thì tích 6 3 a . a bằng A. 9 a B. a C. 9 2 a D. 18 a Câu 30. Cho hµm sè 4 2
y x 2x 4 cã ®å thÞ (C) vµ hai ®iÓm A(0 ; –16), B(–1 ; –8). T×m täa ®é
®iÓm M trªn (C) sao cho tam gi¸c MAB cã diÖn tÝch nhá nhÊt A. (1 ; –1) B. (1 ; 2) C. (–1 ; –1) D. (2 ; 20) mx m
Câu 31. §å thÞ cña hµm sè y
c¾t ®-êng th¼ng d: y x 6 t¹i hai ®iÓm ph©n biÖt thuéc x hai nh¸nh cña nã khi: A. m 0 B. m 0 C. m 6 D. m 0
Câu 32. Một hộp không nắp được làm từ mảnh các tông theo mẫu hình bên.
Hộp có đáy là hình vuông cạnh x (cm), chiều cao h (cm) và có thể tích là 4cm3.
Tìm giá trị của x sao cho diện tích của mảnh các tông nhỏ nhất A. 8 cm B. 4 cm C. 3 2 2 cm D. 2 cm
Câu 33. Một người gửi 6 triệu đồng vào ngân hàng theo thể thức lãi kép, kì hạn 1 năm với lãi suất
7,56% một năm. Hỏi sau bao nhiêu năm người gửi sẽ có ít nhất 12 triệu đồng từ số tiền gửi ban đầu
(giả sử lãi suất không thay đổi) ? A. 1 năm B. 8 năm C. 10 năm D. 15 năm
Câu 34. Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất A. Ba mặt B. Hai mặt C. Năm mặt D. Bốn mặt H 4/6 Mã đề 505
Câu 35. Cho điểm O và số thực k 0 . Mệnh đề nào dưới đây sai
A. Phép vị tự tâm O tỉ số k là một phép đồng dạng khi k 0
B. Phép vị tự tâm O tỉ số k 1
là một phép đối xứng tâm
C. Phép vị tự tâm O tỉ số k luôn là một phép đồng dạng
D. Phép vị tự tâm O tỉ số k 1 là một phép đồng nhất
Câu 36. Khối hai mươi mặt đều thuộc loại A. {3 ; 4} B. {3 ; 5} C. {4 ; 3} D. {5 ; 3} Câu 37. Cho hµm sè 3
y x 3x 1 cã ®å thÞ (C), mét ®-êng th¼ng qua M(1; 3) vµ tiÕp xóc víi
(C) c¾t (C) t¹i ®iÓm thø hai N (N kh«ng trïng M). Khi ®ã täa ®é ®iÓm N lµ 1 3 A. ; B. (2; –1) C. (–1; –1) D. (0; 1) 2 8 Câu 38. Hàm số 4 3 2
y x 4x x 6x 10 có
A. Một cực đại và hai cực tiểu
B. Một cực đại và không có cực tiểu
C. Một cực tiểu và không có cực đại
D. Hai cực đại và một cực tiểu x 3
Câu 39. Cho đồ thị (C) cña hàm số y
vµ ®-êng th¼ng d : y mx 2m 1. Ph-¬ng ¸n nµo x 1 d-íi ®©y ®óng
A. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt
B. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt khi m 0
C. (C) vµ d tiÕp xóc víi nhau khi m 2
D. d lu«n ®i qua mét ®iÓm cè ®Þnh cña (C) khi m biÕn thiªn x
Câu 40. Cho ®å thÞ (C) cña hàm số y
vµ ®-êng th¼ng d: y x 4 . MÖnh ®Ò nµo d-íi ®©y x 1 ®óng
A. d lµ tiÖm cËn xiªn cña (C) B. d vµ (C) tiÕp xóc
C. d vµ (C) c¾t nhau t¹i hai ®iÓm ph©n biÖt
D. d vµ (C) kh«ng c¾t nhau
Câu 41. Cho khối tứ diện ABCD. Lấy một điểm M nằm giữa A và B, một điểm N nằm giữa C và
D. Bằng hai mặt phẳng (MCD) và (NAB) ta chia khối tứ diện đã cho thành bốn khối tứ diện A. AMNC, AMND, AMCD, BMNC B. AMCD, AMND, BMNC, BMND C. BMCD, BMND, AMNC, AMND D. AMNC, AMND, BMNC, BMND
Câu 42. Số mặt phẳng đối xứng của hình tứ diện đều là A. 4 B. 8 C. 6 D. 10
Câu 43. Nếu log b log c thì a a
A. c b 0 và a 1 B. và và và b c 0 a 0 C. 0 b c 0 a 1 D. c b 0 a 1
Câu 44. Cho 0 a 1 , khi đó 3log 2 a a bằng A. 16 B. 6 C. 2 D. 8 H 5/6 Mã đề 505
Câu 45. Cho E = log45 và F = log54. Khi đó A. E = F B. E < F C. E > F D. E ≥ F 3 3 3 3 4 4 4 4
a b a b
Câu 46. Cho hai số dương khác nhau a, b . Rút gọn biểu thức ab bằng 1 1 2 2 a b A. a b B. 2 a b C. 2 a b D. a b
Câu 47. Từ một tấm bìa hình vuông cạnh bằng 4cm, ta gấp nó thành
4 phần đều nhau rồi gấp thành một hình hộp chữ nhật (không nắp)
như hình bên. Hỏi thể tích khối hộp này bằng bao nhiêu A. 1cm3 B. 16cm3 C. 4cm3 D. 8cm3
Câu 48. Khi viết 22008 trong hệ thập phân ta được một số có bao nhiêu chữ số (lấy giá trị gần đúng của log2 là 0,3010) A. 606 chữ số B. 605 chữ số
C. 2008 chữ số D. 2007 chữ số
Câu 49. Chän ph-¬ng ¸n tr¶ lêi ®óng: x b
§å thÞ cña hµm sè y nh- h×nh d-íi ®©y. cx d
Khi ®ã gi¸ trÞ b, c, d lÇn l-ît lµ A. 1, 1, 2 B. 2, 1, 1 C. 0, 1, 2 D. 0, 1, 1
Câu 50. Cho tứ diện ABCD có trọng tâm G. Gọi A’, B’, C’, D’ lần lượt là trọng tâm các tam giác
BCD, CDA, ABD, ABC. Mệnh đề nào dưới đây đúng 1
A. Phép vị tự tâm G tỉ số
biến ABCD thành A’B’C’D’ 3
B. A’, B’, C’, D’ đồng phẳng
C. A’B’C’D’ và ABCD là hai hình bằng nhau 1
D. Phép vị tự tâm G tỉ số
biến A’B’C’D’ thành ABCD. 3
Cán bộ coi kiểm tra không giải thích gì thêm H 6/6 Mã đề 505
TRƯỜNG THPT NGUYỄN GIA THIỀU ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA HỌC KỲ 1
BỘ MÔN TOÁN Môn toán lớp 12, năm học 2016 – 2017
Đề chính thức gồm 06 trang Thời gian làm bài 90 phút Mã đề 506
Hä vµ tªn häc sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Líp: . . . . . . . . .
Câu 1. Chän ph-¬ng ¸n tr¶ lêi ®óng: x b
§å thÞ cña hµm sè y nh- h×nh d-íi ®©y. cx d
Khi ®ã gi¸ trÞ b, c, d lÇn l-ît lµ A. 1, 1, 2 B. 2, 1, 1 C. 0, 1, 2 D. 0, 1, 1
Câu 2. Cho các đồ thị trên các hình sau. Chỉ ra câu trả lời đúng 1 x x 1
A. Hình 4 có đồ thị hàm số y
B. Hình 2 có đồ thị hàm số y 2x x 1 x x 1
C. Hình 1 có đồ thị hàm số y
D. Hình 3 có đồ thị hàm số y x 2x mx m
Câu 3. §å thÞ cña hµm sè y
c¾t ®-êng th¼ng d: y x 6 t¹i hai ®iÓm ph©n biÖt thuéc x hai nh¸nh cña nã khi: A. m 0 B. m 0 C. m 6 D. m 0
Câu 4. Hàm số f cã ®¹o hµm 3
f '(x) x (2x 3)(3x 2) . Sè ®iÓm cùc trÞ cña hàm số f lµ A. 0 B. 1 C. 2 D. 3 H 1 /6 Mã đề 506
Câu 5. Với một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc tấm bìa một
hình vuông cạnh 12cm rồi gấp lại thành một hình hộp chữ nhật không có nắp.
Nếu dung tích của cái hộp đó là 4800cm3 thì cạnh tấm bìa có độ dài là A. 36cm B. 38cm C. 42cm D. 44cm 1
Câu 6. Một khoảng đồng biến của hàm số y x 2 là x 1 A. ; 1 B. 2 ;
C. ; D. ; 1 Câu 7. Hàm số 4 3 2
y x 4x x 6x 10 có
A. Một cực đại và hai cực tiểu
B. Một cực đại và không có cực tiểu
C. Một cực tiểu và không có cực đại
D. Hai cực đại và một cực tiểu
Câu 8. Cho điểm O và số thực k 0 . Mệnh đề nào dưới đây sai
A. Phép vị tự tâm O tỉ số k là một phép đồng dạng khi k 0
B. Phép vị tự tâm O tỉ số k 1
là một phép đối xứng tâm
C. Phép vị tự tâm O tỉ số k luôn là một phép đồng dạng
D. Phép vị tự tâm O tỉ số k 1 là một phép đồng nhất 500 50 Câu 9. Tỉ số bằng 250 25 A. 250 10 B. 500 10 C. 250 2 D. 260 2
Câu 10. Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất A. Ba mặt B. Hai mặt C. Năm mặt D. Bốn mặt
Câu 11. Hµm sè y cos 3x m sin x 9 ®¹t cùc ®¹i t¹i x khi 3
A. Không tồn tại m B. m 18 C. m 1 D. m 0
Câu 12. Một người gửi 6 triệu đồng vào ngân hàng theo thể thức lãi kép, kì hạn 1 năm với lãi suất
7,56% một năm. Hỏi sau bao nhiêu năm người gửi sẽ có ít nhất 12 triệu đồng từ số tiền gửi ban đầu
(giả sử lãi suất không thay đổi) ? A. 1 năm B. 8 năm C. 10 năm D. 15 năm 2 2x 1
Câu 13. C¸c ®å thÞ cña hai hàm số y vµ 2
y 2x x tiÕp xóc víi nhau t¹i ®iÓm cã täa ®é x 1 1 A. ;1 B. ; 0 C. (–1 ; 3) D. (1 ; 1) 2 2
Câu 14. Nếu log b log c thì a a
A. c b 0 và a 1 B. và và và b c 0 a 0 C. 0 b c 0 a 1 D. c b 0 a 1 H 2 /6 Mã đề 506
Câu 15. Cho khối tứ diện ABCD. Lấy một điểm M nằm giữa A và B, một điểm N nằm giữa C và
D. Bằng hai mặt phẳng (MCD) và (NAB) ta chia khối tứ diện đã cho thành bốn khối tứ diện A. AMNC, AMND, AMCD, BMNC B. AMCD, AMND, BMNC, BMND C. BMCD, BMND, AMNC, AMND
D. AMNC, AMND, BMNC, BMND x 3
Câu 16. Cho đồ thị (C) cña hàm số y
vµ ®-êng th¼ng d : y mx 2m 1. Ph-¬ng ¸n nµo x 1 d-íi ®©y ®óng
A. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt
B. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt khi m 0
C. (C) vµ d tiÕp xóc víi nhau khi m 2
D. d lu«n ®i qua mét ®iÓm cè ®Þnh cña (C) khi m biÕn thiªn Câu 17. Cho hµm sè 4 2
y x 2x 4 cã ®å thÞ (C) vµ hai ®iÓm A(0 ; –16), B(–1 ; –8). T×m täa ®é
®iÓm M trªn (C) sao cho tam gi¸c MAB cã diÖn tÝch nhá nhÊt A. (1 ; –1) B. (1 ; 2) C. (–1 ; –1) D. (2 ; 20)
Câu 18. Một hộp không nắp được làm từ mảnh các tông theo mẫu hình bên.
Hộp có đáy là hình vuông cạnh x (cm), chiều cao h (cm) và có thể tích là 4cm3.
Tìm giá trị của x sao cho diện tích của mảnh các tông nhỏ nhất A. 8 cm B. 4 cm C. 3 2 2 cm D. 2 cm Câu 19. Hµm sè 4 2
y mx (m 1)x 1 2m chØ cã mét cùc trÞ khi A. m 1 B. m 0
C. m 0 hoÆc m 1 D. 0 m 1
Câu 20. Cho tứ diện ABCD có trọng tâm G. Gọi A’, B’, C’, D’ lần lượt là trọng tâm các tam giác
BCD, CDA, ABD, ABC. Mệnh đề nào dưới đây đúng 1
A. Phép vị tự tâm G tỉ số
biến ABCD thành A’B’C’D’ 3
B. A’, B’, C’, D’ đồng phẳng
C. A’B’C’D’ và ABCD là hai hình bằng nhau 1
D. Phép vị tự tâm G tỉ số
biến A’B’C’D’ thành ABCD 3 x
Câu 21. Cho ®å thÞ (C) cña hàm số y y x . MÖnh ®Ò nµo d-íi ®©y
x vµ ®-êng th¼ng d: 4 1 ®óng
A. d lµ tiÖm cËn xiªn cña (C) B. d vµ (C) tiÕp xóc
C. d vµ (C) c¾t nhau t¹i hai ®iÓm ph©n biÖt
D. d vµ (C) kh«ng c¾t nhau
Câu 22. Từ một tấm bìa hình vuông cạnh bằng 4cm, ta gấp nó thành
4 phần đều nhau rồi gấp thành một hình hộp chữ nhật (không nắp)
như hình bên. Hỏi thể tích khối hộp này bằng bao nhiêu A. 1cm3 B. 16cm3 C. 4cm3 D. 8cm3 H 3 /6 Mã đề 506 Câu 23. Hàm số 3
y x 12x 1 có
A. Cực đại bằng 17 và cực tiểu bằng 0
B. Cực đại bằng 17 và cực tiểu bằng 15
C. Cực đại bằng 0 và cực tiểu bằng 15 D. Cực đại bằng 15
và cực tiểu bằng 17
Câu 24. Khi viết 22008 trong hệ thập phân ta được một số có bao nhiêu chữ số (lấy giá trị gần đúng của log2 là 0,3010) A. 606 chữ số B. 605 chữ số
C. 2008 chữ số D. 2007 chữ số
Câu 25. Nếu a 0 thì tích 6 3 a . a bằng A. 9 a B. a C. 9 2 a D. 18 a 3 3 3 3 4 4 4 4
a b a b
Câu 26. Cho hai số dương khác nhau a, b . Rút gọn biểu thức ab bằng 1 1 2 2 a b A. a b B. 2 a b C. 2 a b D. a b
Câu 27. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AC = 2a , tam
giác SAC đều và nằm trên mặt phẳng vuông góc với đáy. Trên cạnh SA lấy điểm M sao cho
MA = 2MS. Mặt phẳng (α) qua M và song song với (ABC) cắt SB, SC tại N, P. Khi đó thể tích khối
chóp cụt ABC.MNP bằng 3 a 3 3 80 3a 3 2 3a 3 26 3a A. B. C. D. 3 81 9 81
Câu 28. Số mặt phẳng đối xứng của hình tứ diện đều là A. 4 B. 8 C. 6 D. 10
Câu 29. Thể tích khối tứ diện đều có cạnh bằng 1 là 2 3 2 2 A. B. C. D. 12 4 4 6
Câu 30. Cho M = 32000 và N = 41500. Khi đó A. M > N B. M = N C. M < N D. M ≤ N Câu 31. Hàm số 3 2
y x 6x mx 1 đồng biến trên kho¶ng (0; +∞) khi giá trị của m là A. m 0 B. m 12 C. m 0 D. m 12
Câu 32. Cho hình hộp ABCD.A’B’C’D’ có thể tích V. Thể tích khối tứ diện ACB’D’ là V V V V A. B. C. D. 8 6 3 4
Câu 33. Biết log 2 ;
a log 3 b . Tính log 5 5 305 theo a, b 1 1 A. a b B. a b D. a b C. 1 1 a b H 4 /6 Mã đề 506
Câu 34. Cho ®-êng cong (C) cã ph-¬ng tr×nh 2 y
x 2 , tÞnh tiÕn (C) theo phương trục hoành
sang phải 3 ®¬n vÞ ta ®-îc ®-êng cong cã ph-¬ng tr×nh lµ A. 2 y
x 6x 11 B. 2 y x 2 3 C. 2 y x 2 3 D. 2 y x 6x 11
Câu 35. Cho 0 a 1 , khi đó 3log 2 a a bằng A. 16 B. 6 C. 2 D. 8
Câu 36. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 1cm, SA 2cm và SA vuông góc với
đáy. Khoảng cách giữa hai đường thẳng BC và SD là A. 1 cm B. 2 cm C. 2 cm D. 5 cm
Câu 37. Đồ thị cña hàm số 2
y x 1 x có
A. Tiệm cận đứng và có tiệm cận xiên
B. Tiệm cận ngang và có tiệm cận xiên
C. Tiệm cận xiên và không có tiệm cận ngang
D. Tiệm cận đứng và có tiệm cận ngang
Câu 38. Cho hình lăng trụ đứng ABC.MNP có tất cả các cạnh bằng a . Thể tích của khối lăng trụ là 3 a 3 3 a 3 3 a 3 A. 3 a 3 B. C. D. 2 4 3
Câu 39. Cho hàm số 4 2
y ax bx c trong đó a 0 và b 0. Khi đó hàm số có
A. Hai cực tiểu và một cực đại B. Hai cực đại và một cực tiểu C. Một cực đại D. Một cực tiểu
Câu 40. Cho E = log45 và F = log54. Khi đó A. E = F B. E < F C. E > F D. E ≥ F
Câu 41. Khối hai mươi mặt đều thuộc loại A. {3 ; 4} B. {3 ; 5} C. {4 ; 3} D. {5 ; 3}
Câu 42. Cho tứ diện AEFG có thể tích là V và AE, AF, AG vuông góc với nhau từng đôi một. Gọi
B, C, D lần lượt là trung điểm của các đoạn thẳng GE, EF, FG. Thể tích khối tứ diện ABCD bằng V V V V A. B. C. D. 2 4 3 6
Câu 43. Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = a , AC = 2a và SA vuông
góc với đáy. Góc giữa (SBC) và (ABC) bằng 600. Thể tích khối chóp S.ABC bằng 3 a 3 3 a 3 3 3a 3 a A. B. C. D. 3 2 2 2 2 x 2
Câu 44. Mét trong c¸c h×nh d-íi ®©y, h×nh nµo cã b¶ng biÕn thiªn cña hµm sè y x 1 A. H×nh 1 B. H×nh 2 C. H×nh 3 D. H×nh 4 H 5 /6 Mã đề 506
Câu 45. Thể tích của khối tám mặt đều có cạnh bằng a là 3 2 2 a 3 2 a 3 2 a A. B. C. 3 2 2 a D. 3 3 9 Câu 46. Cho hµm sè 3 2
y x 6x 3(m 2)x m 6 ®¹t cùc ®¹i, cùc tiÓu t¹i x , x sao cho 1 2
x 1 x th× gi¸ trÞ cña m lµ 1 2 A. m 1 B. m 1 C. m 1 D. m 1 Câu 47. Cho hµm sè 3
y x 3x 1 cã ®å thÞ (C), mét ®-êng th¼ng qua M(1; 3) vµ tiÕp xóc víi
(C) c¾t (C) t¹i ®iÓm thø hai N (N kh«ng trïng M). Khi ®ã täa ®é ®iÓm N lµ 1 3 A. ; B. (2; –1) C. (–1; –1) D. (0; 1) 2 8
Câu 48. Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với đáy và AB = a ,
AD = 2a , góc giữa SB và đáy bằng 450. Thể tích khối chóp S.ABCD là 3 2 a 3 6 a 3 a A. B. C. D. 3 2a 3 18 3
Câu 49. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a .
SA (ABC) và SA = a . Gọi (α) là mặt phẳng qua A và vuông góc với SB đồng thời cắt SB, SC tại
M, N. Khi đó thể tích khối chóp S.AMN bằng 3 a 3 a 3 a 3 a A. B. C. D. 24 6 12 18
Câu 50. Cho các đồ thị trên các hình sau. Chỉ ra câu trả lời đúng
A. Hình 4 có đồ thị hàm số 4 2
y x 2x 3
B. Hình 3 có đồ thị hàm số 3
y x 3x 2
C. Hình 2 có đồ thị hàm số 4 2
y x 2x 3
D. Hình 1 có đồ thị hàm số 3
y x 3x 2 .
Cán bộ coi kiểm tra không giải thích gì thêm H 6 /6 Mã đề 506
TRƯỜNG THPT NGUYỄN GIA THIỀU ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA HỌC KỲ 1
BỘ MÔN TOÁN Môn toán lớp 12, năm học 2016 – 2017
Đề chính thức gồm 06 trang Thời gian làm bài 90 phút Mã đề 507
Hä vµ tªn häc sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Líp: . . . . . . . . . 1 5 1 Câu 1. Hàm số 3 y x x có đồ thị là 27 27 3
A. Đồ thị trên hình 1 B. Đồ thị trên hình 2
C. Đồ thị trên hình 3 D. Đồ thị trên hình 4
Câu 2. Chän ph-¬ng ¸n tr¶ lêi ®óng: x b
§å thÞ cña hµm sè y cx nh- h×nh d-íi ®©y. d
Khi ®ã gi¸ trÞ b, c, d lÇn l-ît lµ A. 1, 1, 2 B. 0, 1, 2 C. 2, 1, 1 D. 0, 1, 1 2 x 2
Câu 3. Mét trong c¸c h×nh d-íi ®©y, h×nh nµo cã b¶ng biÕn thiªn cña hµm sè y x 1 A. H×nh 2 B. H×nh 1 C. H×nh 4 D. H×nh 3
Câu 4. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 1cm, SA 2cm và SA vuông góc với
đáy. Khoảng cách giữa hai đường thẳng BC và SD là A. 2 cm B. 2 cm C. 1 cm D. 5 cm H 1/6 Mã đề 507 Câu 5. Cho hàm số 4 2
y ax bx c trong đó a 0 và b 0. Khi đó hàm số có
A. Hai cực tiểu và một cực đại B. Hai cực đại và một cực tiểu C. Một cực đại D. Một cực tiểu 1
Câu 6. Một khoảng đồng biến của hàm số y x 2 là x 1 A. 2 ; B. ; C. 1
; D. ; 1 Câu 7. Hàm số 3 2
y x 6x mx 1 đồng biến trên kho¶ng (0; +∞) khi giá trị của m là A. m 0 B. m 12 C. m 12 D. m 0 Câu 8. Hàm số 3
y x 12x 1 có
A. Cực đại bằng 17 và cực tiểu bằng 15
B. Cực đại bằng 17 và cực tiểu bằng 0
C. Cực đại bằng 0 và cực tiểu bằng 15 D. Cực đại bằng 15
và cực tiểu bằng 17 Câu 9. Hµm sè 4 2
y mx (m 1)x 1 2m chØ cã mét cùc trÞ khi A. m 1
B. m 0 hoÆc m 1 C. m 0 D. 0 m 1
Câu 10. Cho ®-êng cong (C) cã ph-¬ng tr×nh 2 y
x 2 , tÞnh tiÕn (C) theo phương trục hoành
sang phải 3 ®¬n vÞ ta ®-îc ®-êng cong cã ph-¬ng tr×nh lµ A. 2 y x 2 3 B. 2 y x 6x 11 C. 2 y x 2 3 D. 2 y x 6x 11 Câu 11. Cho hµm sè 3 2
y x 6x 3(m 2)x m 6 ®¹t cùc ®¹i, cùc tiÓu t¹i x , x sao cho 1 2
x 1 x th× gi¸ trÞ cña m lµ 1 2 A. m 1 B. m 1 C. m 1 D. m 1
Câu 12. Hàm số f cã ®¹o hµm 2
f '(x) x(2x 3) (3x 2) . Sè ®iÓm cùc trÞ cña hàm số f lµ A. 2 B. 4 C. 3 D. 1
Câu 13. Sè ®-êng th¼ng ®i qua ®iÓm M(–1
; 3 ) vµ tiÕp xóc víi ®å thÞ cña hµm sè 3 y x 3x lµ A. 2 B. 0 C. 3 D. 1
Câu 14. Gi¸ trÞ nhá nhÊt cña hµm sè 2 2 y
x 2x 5
x 4x 8 trªn ®o¹n [–1 ; 1] lµ A. 2 2 5 B. 5 C. 2 13 D. §¸p sè kh¸c
Câu 15. Đồ thị cña hàm số 2
y x 1 x có
A. Tiệm cận đứng và có tiệm cận xiên
B. Tiệm cận đứng và có tiệm cận ngang
C. Tiệm cận xiên và không có tiệm cận ngang
D. Tiệm cận ngang và có tiệm cận xiên Câu 16. Hµm sè 4 3
y x mx 11m 4 ®¹t cùc tiÓu t¹i x 3 khi A. m 6 B. m 4 C. m 4 D. m 6
Câu 17. Cho M = 32000 và N = 41500. Khi đó A. M = N B. M < N C. M > N D. M ≤ N H 2/6 Mã đề 507 mx m
Câu 18. §å thÞ cña hµm sè y
c¾t ®-êng th¼ng d: y x 6 t¹i hai ®iÓm ph©n biÖt thuéc x hai nh¸nh cña nã khi: A. m 0 B. m 0 C. m 6 D. m 0 x 3
Câu 19. Cho đồ thị (C) cña hàm số y
vµ ®-êng th¼ng d : y mx 2m 1. Ph-¬ng ¸n nµo x 1 d-íi ®©y ®óng
A. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt
B. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt khi m 0
C. d lu«n ®i qua mét ®iÓm cè ®Þnh cña (C) khi m biÕn thiªn
D. (C) vµ d tiÕp xóc víi nhau khi m 2 Câu 20. Hàm số 4 3 2
y x 4x x 6x 10 có
A. Một cực đại và hai cực tiểu
B. Một cực tiểu và không có cực đại
C. Hai cực đại và một cực tiểu
D. Một cực đại và không có cực tiểu Câu 21. Cho hµm sè 3
y x 3x 1 cã ®å thÞ (C), mét ®-êng th¼ng qua M(1; 3) vµ tiÕp xóc víi
(C) c¾t (C) t¹i ®iÓm thø hai N (N kh«ng trïng M). Khi ®ã täa ®é ®iÓm N lµ 1 3 A. (2; –1) B. (–1; –1) C. (0; 1) D. ; 2 8 x
Câu 22. Cho ®å thÞ (C) cña hàm số y y x . MÖnh ®Ò nµo d-íi ®©y
x vµ ®-êng th¼ng d: 4 1 ®óng A. d vµ (C) tiÕp xóc
B. d vµ (C) c¾t nhau t¹i hai ®iÓm ph©n biÖt C. d vµ (C) kh«ng c¾t nhau
D. d lµ tiÖm cËn xiªn cña (C)
Câu 23. Một hộp không nắp được làm từ mảnh các tông theo mẫu hình bên.
Hộp có đáy là hình vuông cạnh x (cm), chiều cao h (cm) và có thể tích là 4cm3.
Tìm giá trị của x sao cho diện tích của mảnh các tông nhỏ nhất A. 8 cm B. 4 cm C. 2 cm D. 3 2 2 cm 500 50 Câu 24. Tỉ số bằng 250 25 A. 250 10 B. 250 2 C. 500 2 D. 500 10
Câu 25. Khối hai mươi mặt đều thuộc loại A. {3 ; 4} B. {4 ; 3} C. {3 ; 5} D. {5 ; 3}
Câu 26. Nếu log b log c thì a a
A. 0 b c B. b c 0 và a 0 C. c b 0 và a 1 D. 0 b c và 0 a 1 H 3/6 Mã đề 507 3 3 3 3 4 4 4 4
a b a b
Câu 27. Cho hai số dương khác nhau a, b . Rút gọn biểu thức ab bằng 1 1 2 2 a b A. a b B. 2 a b C. a b D. 2 a b
Câu 28. Nếu a 0 thì tích 6 3 a . a bằng A. 9 a B. 9 2 a C. a D. 18 a
Câu 29. Cho 0 a 1 , khi đó 3log 2 a a bằng A. 16 B. 8 C. 6 D. 2
Câu 30. Cho E = log45 và F = log54. Khi đó A. E > F B. E = F C. E < F D. E ≥ F
Câu 31. Biết log 2 ;
a log 3 b . Tính log 5 5 305 theo a, b 1 1 A. a b B. a b 1 C. a b D. 1 a b
Câu 32. Một người gửi 6 triệu đồng vào ngân hàng theo thể thức lãi kép, kì hạn 1 năm với lãi suất
7,56% một năm. Hỏi sau bao nhiêu năm người gửi sẽ có ít nhất 12 triệu đồng từ số tiền gửi ban đầu
(giả sử lãi suất không thay đổi) ? A. 10 năm B. 1 năm C. 8 năm D. 12 năm
Câu 33. Khi viết 22008 trong hệ thập phân ta được một số có bao nhiêu chữ số (lấy giá trị gần đúng của log2 là 0,3010) A. 606 chữ số B. 2008 chữ số C. 2007 chữ số D. 605 chữ số
Câu 34. Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất A. Hai mặt B. Ba mặt C. Bốn mặt D. Năm mặt
Câu 35. Cho khối tứ diện ABCD. Lấy một điểm M nằm giữa A và B, một điểm N nằm giữa C và
D. Bằng hai mặt phẳng (MCD) và (NAB) ta chia khối tứ diện đã cho thành bốn khối tứ diện A. AMNC, AMND, BMNC, BMND B. AMNC, AMND, AMCD, BMNC C. AMCD, AMND, BMNC, BMND D. BMCD, BMND, AMNC, AMND
Câu 36. Thể tích khối tứ diện đều có cạnh bằng 1 là 3 2 2 2 A. B. C. D. 4 4 12 6
Câu 37. Hình lập phương có bao nhiêu mặt phẳng đối xứng A. 3 B. 4 C. 6 D. 9 H 4/6 Mã đề 507
Câu 38. Cho tứ diện ABCD có trọng tâm G. Gọi A’, B’, C’, D’ lần lượt là trọng tâm các tam giác
BCD, CDA, ABD, ABC. Mệnh đề nào dưới đây đúng
A. A’, B’, C’, D’ đồng phẳng 1
B. Phép vị tự tâm G tỉ số
biến ABCD thành A’B’C’D’ 3
C. A’B’C’D’ và ABCD là hai hình bằng nhau 1
D. Phép vị tự tâm G tỉ số
biến A’B’C’D’ thành ABCD 3
Câu 39. Trong các mệnh đề sau đây, mệnh đề nào đúng
A. Phép vị tự biến mặt phẳng thành mặt phẳng song song với nó
B. Không có phép vị tự nào biến hai điểm phân biệt A và B lần lượt thành A và B
C. Phép vị tự biến đường thẳng thành đường thẳng song song với nó
D. Phép vị tự biến mặt phẳng qua tâm vị tự thành chính nó
Câu 40. Từ một tấm bìa hình vuông cạnh bằng 4cm, ta gấp nó thành
4 phần đều nhau rồi gấp thành một hình hộp chữ nhật (không nắp)
như hình bên. Hỏi thể tích khối hộp này bằng bao nhiêu A. 4cm3 B. 1cm3 C. 16cm3 D. 8cm3
Câu 41. Cho hình hộp ABCD.A’B’C’D’ có thể tích V. Thể tích khối tứ diện ACB’D’ là V V V V A. B. C. D. 8 6 4 3
Câu 42. Với một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc tấm bìa một
hình vuông cạnh 12cm rồi gấp lại thành một hình hộp chữ nhật không có nắp.
Nếu dung tích của cái hộp đó là 4800cm3 thì cạnh tấm bìa có độ dài là A. 36cm B. 44cm C. 38cm D. 42cm
Câu 43. Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = a , AC = 2a và SA vuông
góc với đáy. Góc giữa (SBC) và (ABC) bằng 600. Thể tích khối chóp S.ABC bằng 3 a 3 3 a 3 3 a 3 3a A. B. C. D. 3 2 2 2
Câu 44. Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với đáy và AB = a ,
AD = 2a , góc giữa SB và đáy bằng 450. Thể tích khối chóp S.ABCD là 3 2 a 3 a A. 3 2a B. C. D. Đáp án khác 3 3
Câu 45. Cho tứ diện AEFG có thể tích là V và AE, AF, AG vuông góc với nhau từng đôi một. Gọi
B, C, D lần lượt là trung điểm của các đoạn thẳng GE, EF, FG. Thể tích khối tứ diện ABCD bằng V V V V A. B. C. D. 2 3 6 4 H 5/6 Mã đề 507
Câu 46. Thể tích của khối tám mặt đều có cạnh bằng a là 3 2 a 3 2 2 a 3 2 a A. B. C. 3 2 2 a D. 3 3 9
Câu 47. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a .
SA (ABC) và SA = a . Gọi (α) là mặt phẳng qua A và vuông góc với SB đồng thời cắt SB, SC tại
M, N. Khi đó thể tích khối chóp S.AMN bằng 3 a 3 a 3 a A. B. C. D. Đáp án khác 24 6 12
Câu 48. Cho hình lăng trụ đứng MNP.M' N'P' có tất cả các cạnh bằng a . Thể tích của khối lăng trụ bằng 3 a 3 3 a 3 3 a 3 A. 3 a 3 B. C. D. 4 2 3
Câu 49. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AC = 2a , tam
giác SAC đều và nằm trên mặt phẳng vuông góc với đáy. Trên cạnh SA lấy điểm M sao cho
MA = 2MS. Mặt phẳng (α) qua M và song song với (ABC) cắt SB, SC tại N, P. Khi đó thể tích khối
chóp cụt ABC.MNP bằng 3 a 3 3 26 3a 3 80 3a 3 2 3a A. B. C. D. 3 81 81 9
Câu 50. Cho các đồ thị trên các hình sau. Chỉ ra câu trả lời đúng x 1 1 x
A. Hình 2 có đồ thị hàm số y
B. Hình 1 có đồ thị hàm số y x x x 1 1 x
C. Hình 3 có đồ thị hàm số y y
D. Hình 4 có đồ thị hàm số . 2x 2x
Cán bộ coi kiểm tra không giải thích gì thêm H 6/6 Mã đề 507
TRƯỜNG THPT NGUYỄN GIA THIỀU ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA HỌC KỲ 1
BỘ MÔN TOÁN Môn toán lớp 12, năm học 2016 – 2017
Đề chính thức gồm 06 trang Thời gian làm bài 90 phút Mã đề 508
Hä vµ tªn häc sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Líp: . . . . . . . . . 1 1 Câu 1. Hàm số 3 2 y
x x x có đồ thị là 3 3
A. Đồ thị trên hình 1 B. Đồ thị trên hình 2
C. Đồ thị trên hình 3 D. Đồ thị trên hình 4
Câu 2. Nếu log b log c thì a a
A. b c 0 và 0 a 1 B. b c 0 và a 1 C. b c 0 và a 0 D. c b 0 và a 1
Câu 3. Cho các đồ thị trên các hình sau. Chỉ ra câu trả lời đúng x 1 1 x
A. Hình 2 có đồ thị hàm số y
B. Hình 1 có đồ thị hàm số y x x 1 x x 1
C. Hình 4 có đồ thị hàm số y
D. Hình 3 có đồ thị hàm số y 2x 2x H 1/6 Mã đề 508
Câu 4. Nếu a 0 thì tích 6 3 a . a bằng A. a B. 9 a C. 9 2 a D. 18 a
Câu 5. Từ một tấm bìa hình vuông cạnh bằng 3cm, ta gấp nó thành
3 phần đều nhau rồi gấp thành một hình lăng trụ đứng (không đáy)
như hình bên. Hỏi thể tích khối lăng trụ này bằng bao nhiêu 1 3 3 1 3 A. cm3 B. cm3 C. cm3 D. cm3 4 4 12 4
Câu 6. Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất A. Năm mặt B. Hai mặt C. Bốn mặt D. Ba mặt 2 x 2
Câu 7. Mét trong c¸c h×nh d-íi ®©y, h×nh nµo cã b¶ng biÕn thiªn cña hµm sè y x 1 A. H×nh 4 B. H×nh 1 C. H×nh 3 D. H×nh 2 1
Câu 8. Một khoảng đồng biến của hàm số y x 2 x là 1 A. 2 ; B. 1 ; C. ; D. ; 1
Câu 9. Hàm số f cã ®¹o hµm 2 2
f '(x) x (2x 3) (3x 2) . Sè ®iÓm cùc trÞ cña hàm số f lµ A. 0 B. 3 C. 1 D. 2
Câu 10. Một hộp không nắp được làm từ mảnh các tông theo mẫu hình bên.
Hộp có đáy là hình vuông cạnh x (cm), chiều cao h (cm) và có thể tích là 4cm3.
Tìm giá trị của x sao cho diện tích của mảnh các tông nhỏ nhất A. 8 cm B. 2 cm C. 4 cm D. 3 2 2 cm
Câu 11. Cho 0 a 1 , khi đó log 4 a a bằng A. 16 B. 4 C. 2 D. 1
Câu 12. Một người gửi 15 triệu đồng vào ngân hàng theo thể thức lãi kép kỳ hạn 1 năm với lãi suất
7,56% một năm. Giả sử lãi suất không thay đổi, hỏi số tiền người đó thu được (cả vốn lẫn lãi) sau 5
năm là bao nhiêu triệu đồng (làm tròn đến chữ số thập phân thứ hai) ?
A. 22,59 triệu đồng B. 21,59 triệu đồng C. 20,59 triệu đồng D. 19,19 triệu đồng
Câu 13. Với một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc tấm bìa một
hình vuông cạnh 12cm rồi gấp lại thành một hình hộp chữ nhật không có nắp.
Nếu dung tích của cái hộp đó là 4800cm3 thì cạnh tấm bìa có độ dài là A. 36cm B. 38cm C. 42cm D. 44cm
Câu 14. Cho hàm số 4 2
y ax bx c trong đó a 0 và b 0 . Khi đó hàm số có
A. Hai cực tiểu và một cực đại B. Hai cực đại và một cực tiểu C. Một cực đại D. Một cực tiểu H 2/6 Mã đề 508 3 Câu 15. Cho hµm sè 4 2
y x 2x 1 cã ®å thÞ (C). §iÓm M trªn (C) cã hoµnh ®é x lµ ®iÓm 3 g× cña (C) A. §iÓm th-êng B. §iÓm uèn
C. §iÓm cùc tiÓu D. §iÓm cùc ®¹i
Câu 16. Cho khối tứ diện ABCD. Lấy một điểm M nằm giữa A và B, một điểm N nằm giữa C và
D. Bằng hai mặt phẳng (MCD) và (NAB) ta chia khối tứ diện đã cho thành bốn khối tứ diện A. AMNC, AMND, AMCD, BMNC B. AMCD, AMND, BMNC, BMND C. AMNC, AMND, BMNC, BMND D. BMCD, BMND, AMNC, AMND
Câu 17. Khối tám mặt đều thuộc loại A. {3 ; 4} B. {4 ; 3} C. {3 ; 3} D. {3 ; 5} Câu 18. Hàm số 4 3 2
y x 4x x 6x 10 có
A. Một cực tiểu và không có cực đại
B. Một cực đại và hai cực tiểu
C. Hai cực đại và một cực tiểu
D. Một cực đại và không có cực tiểu 500 50 Câu 19. Tỉ số bằng 250 25 A. 250 10 B. 250 2 C. 250 100 D. 260 2 mx m
Câu 20. §å thÞ cña hµm sè y
c¾t ®-êng th¼ng d: y x 6 t¹i hai ®iÓm ph©n biÖt thuéc x hai nh¸nh cña nã khi: A. m 6 B. m 0 C. m 0 D. m 0
Câu 21. Cho điểm O và số thực k 0 . Mệnh đề nào dưới đây sai
A. Phép vị tự tâm O tỉ số k là một phép đồng dạng khi k 0
B. Phép vị tự tâm O tỉ số k luôn là một phép đồng dạng
C. Phép vị tự tâm O tỉ số k 1
là một phép đối xứng tâm
D. Phép vị tự tâm O tỉ số k 1 là một phép đồng nhất
Câu 22. Cho ®-êng cong (C) cã ph-¬ng tr×nh 2 y
x 2 , tÞnh tiÕn (C) theo phương trục hoành
sang tr¸i 3 ®¬n vÞ ta ®-îc ®-êng cong cã ph-¬ng tr×nh lµ A. 2 y x 2 3 B. 2 y
x 6x 11 C. 2 y x 2 3 D. 2 y x 6x 11
Câu 23. Số mặt phẳng đối xứng của hình bát diện đều là A. 3 B. 9 C. 6 D. 12 Câu 24. Hàm số 3
y x 12x 1 có A. Cực đại bằng 15
và cực tiểu bằng 17 B. Cực đại bằng 17 và cực tiểu bằng 0
C. Cực đại bằng 0 và cực tiểu bằng 15
D. Cực đại bằng 17 và cực tiểu bằng 15 5 3 Câu 25. Cho E = log và F = log . Khi đó 2 3 5 2 3 3 A. E = F B. E > F C. E ≥ F D. E < F H 3/6 Mã đề 508
Câu 26. Cho tứ diện ABCD có trọng tâm G. Gọi A’, B’, C’, D’ lần lượt là trọng tâm các tam giác
BCD, CDA, ABD, ABC. Mệnh đề nào dưới đây đúng
A. A’, B’, C’, D’ đồng phẳng
B. A’B’C’D’ và ABCD là hai hình bằng nhau 1
C. Phép vị tự tâm G tỉ số
biến A’B’C’D’ thành ABCD 3 1
D. Phép vị tự tâm G tỉ số
biến ABCD thành A’B’C’D’ 3 x 2
Câu 27. Víi gi¸ trÞ nµo cña m th× ®å thÞ hµm sè y 2 x 4x
chØ cã mét tiÖm cËn ®øng vµ mét m tiÖm cËn ngang A. 4 B. 3 C. 2 D. 1
Câu 28. Cho hình lập phương ABCD.A'B'C'D' cạnh 1. Thể tích của khối chóp A'.ABCD bằng 1 1 1 A. B. C. D. 1 3 6 2
Câu 29. Số ®-êng th¼ng đi qua điểm M 0; 7
vµ tiÕp xóc víi đồ thị hàm số 4 2
y x 5x 7 là A. 1 B. 2 C. 3 D. 4 3 3 3 3 4 4 4 4
a b a b
Câu 30. Cho hai số dương khác nhau a, b . Rút gọn biểu thức ab bằng 1 1 2 2 a b A. a b
B. a b C. 2 a b D. 2 a b
Câu 31. Thể tích của khối tám mặt đều có cạnh bằng a là 3 2 2 a 3 2 a 3 2 a A. B. 3 2 2 a C. D. 3 3 9 x
Câu 32. Cho ®å thÞ (C) cña hàm số y y x . MÖnh ®Ò nµo d-íi ®©y
x vµ ®-êng th¼ng d: 4 1 ®óng A. d vµ (C) kh«ng c¾t nhau
B. d vµ (C) c¾t nhau t¹i hai ®iÓm ph©n biÖt C. d vµ (C) tiÕp xóc
D. d lµ tiÖm cËn xiªn cña (C)
Câu 33. Cho hình hộp ABCD.A’B’C’D’ có thể tích V. Thể tích khối tứ diện ACB’D’ là V V V V A. B. C. D. 8 3 6 4 Câu 34. Cho hµm sè 3
y x 3x 1 cã ®å thÞ (C), mét ®-êng th¼ng qua M(1; 3) vµ tiÕp xóc víi
(C) c¾t (C) t¹i ®iÓm thø hai N (N kh«ng trïng M). Khi ®ã täa ®é ®iÓm N lµ 1 3 A. (2; –1) B. (–1; –1) C. ; D. (0; 1) 2 8 H 4/6 Mã đề 508
Câu 35. Mệnh đề nào dưới đây đúng
A. Phép đối xứng qua mặt phẳng biến một tứ diện thành chính nó
B. Phép tịnh tiến biến một đường thẳng thành đường thẳng song song với nó
C. Phép biến hình biến mỗi điểm M trong không gian thành chính nó có là phép dời hình
D. Tứ diện đều có đúng một mặt phẳng đối xứng Câu 36. Hµm sè 4 2
y mx (m 1)x 1 2m chØ cã mét cùc trÞ khi A. m 1 B. m 0 C. 0 m 1
D. m 0 hoÆc m 1
Câu 37. Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với đáy và AB = a ,
AD = 2a , góc giữa SB và đáy bằng 450. Thể tích khối chóp S.ABCD là 3 6 a 3 a 3 2 a A. B. C. 3 2a D. 18 3 3
Câu 38. Cho log1218 = a , log2454 = b . Khi đó A. ab = 5(a – b) B. ab – 5(a – b) = 1 C. ab + 5(a – b) = 1 D. ab = 5(b – a)
Câu 39. Cho hình lập phương ABCD.A’B’C’D’ cạnh a , tâm O. Thể tích khối tứ diện AA’B’O là 3 a 3 a 3 a 3 2 a A. B. C. D. 12 8 9 3
Câu 40. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 1cm, SA 2cm và SA vuông góc với
đáy. Khoảng cách giữa hai đường thẳng BC và SD là A. 2 cm B. 1 cm C. 2 cm D. 5 cm
Câu 41. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a .
SA (ABC) và SA = a . Gọi (α) là mặt phẳng qua A và vuông góc với SB đồng thời cắt SB, SC tại
M, N. Khi đó thể tích khối chóp S.AMN bằng 3 a 3 a 3 a A. B. C. D. Đáp án khác 6 12 24
Câu 42. Cho M = 32000 và N = 41500. Khi đó A. M = N B. M < N C. M ≤ N D. M > N x 3
Câu 43. Cho đồ thị (C) cña hàm số y
d y mx m . Ph-¬ng ¸n nµo
x vµ ®-êng th¼ng : 2 1 1 d-íi ®©y ®óng
A. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt
B. d lu«n ®i qua mét ®iÓm cè ®Þnh cña (C) khi m biÕn thiªn
C. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt khi m 0
D. (C) vµ d tiÕp xóc víi nhau khi m 2 H 5/6 Mã đề 508 Câu 44. Hàm số 3 2
y x 3x mx 2 nghÞch biÕn trªn kho¶ng (0 ; 2) khi m nhËn gi¸ trÞ A. m 3 B. m 3 C. m 3 D. m 0
Câu 45. Cho hình lăng trụ đứng ABC.A’B’C’ có tất cả các cạnh bằng a . Thể tích của khối lăng trụ bằng 3 a 3 3 a 3 3 a 3 A. 3 a 3 B. C. D. 2 3 4
Câu 46. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AC = 2a , tam
giác SAC đều và nằm trên mặt phẳng vuông góc với đáy. Trên cạnh SA lấy điểm M sao cho
MA = 2MS. Mặt phẳng (α) qua M và song song với (ABC) cắt SB, SC tại N, P. Khi đó thể tích khối
chóp cụt ABC.MNP bằng 3 26 3a 3 a 3 3 80 3a 3 2 3a A. B. C. D. 81 3 81 9
Câu 47. Hµm sè y sin 2x 2 cos x cã gi¸ trÞ lín nhÊt trªn ®o¹n [– ; ] lµ 3 3 3 3 A. B. 3 C. 3 D. 2 2
Câu 48. Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = a , AC = 2a và SA vuông
góc với đáy. Góc giữa (SBC) và (ABC) bằng 600. Thể tích khối chóp S.ABC bằng 3 a 3 a 3 3 a 3 3 3a A. B. C. D. 2 3 2 2
Câu 49. Chän ph-¬ng ¸n tr¶ lêi ®óng: x b
§å thÞ cña hµm sè y cx nh- h×nh d-íi ®©y. d
Khi ®ã gi¸ trÞ b, c, d lÇn l-ît lµ A. 0, 1, 2 B. 1, 1, 2 C. 0, 1, 1 D. –2, 1, 1 Câu 50. Cho hµm sè 3 2
y x 6x 3(m 2)x m 6 ®¹t cùc ®¹i, cùc tiÓu t¹i x , x sao cho 1 2
x 1 x th× gi¸ trÞ cña m lµ 1 2 A. m 1 B. m 1 C. m 1 D. m 1 .
Cán bộ coi kiểm tra không giải thích gì thêm H 6/6 Mã đề 508
TRƯỜNG THPT NGUYỄN GIA THIỀU ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA HỌC KỲ 1
BỘ MÔN TOÁN Môn toán lớp 12, năm học 2016 – 2017
Đề chính thức gồm 06 trang Thời gian làm bài 90 phút Mã đề 909
Hä vµ tªn häc sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Líp: . . . . . . . . .
Câu 1. Chän ph-¬ng ¸n tr¶ lêi ®óng: x b
§å thÞ cña hµm sè y nh- h×nh d-íi ®©y. cx d
Khi ®ã gi¸ trÞ b, c, d lÇn l-ît lµ A. 1, 1, 2 B. 2, 1, 1 C. 0, 1, 2 D. 0, 1, 1
Câu 2. Cho các đồ thị trên các hình sau. Chỉ ra câu trả lời đúng 1 x x 1
A. Hình 4 có đồ thị hàm số y
B. Hình 2 có đồ thị hàm số y 2x x 1 x x 1
C. Hình 1 có đồ thị hàm số y
D. Hình 3 có đồ thị hàm số y x 2x
Câu 3. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a .
SA (ABC) và SA = a . Gọi (α) là mặt phẳng qua A và vuông góc với SB đồng thời cắt SB, SC tại
M, N. Khi đó thể tích khối chóp S.AMN bằng 3 a 3 a 3 a 3 a A. B. C. D. 24 6 12 18 H 1/6 Mã đề 909 Câu 4. Cho hàm số 4 2
y ax bx c trong đó a 0 và b 0. Khi đó hàm số có
A. Hai cực tiểu và một cực đại B. Hai cực đại và một cực tiểu C. Một cực đại D. Một cực tiểu 2 x 2
Câu 5. Mét trong c¸c h×nh d-íi ®©y, h×nh nµo cã b¶ng biÕn thiªn cña hµm sè y x 1 A. H×nh 1 B. H×nh 2 C. H×nh 3 D. H×nh 4 1
Câu 6. Một khoảng đồng biến của hàm số y x 2 là x 1 A. ; 1 B. 2 ;
C. ; D. ; 1 Câu 7. Hàm số 3 2
y x 6x mx 1 đồng biến trên kho¶ng (0; +∞) khi giá trị của m là A. m 0 B. m 12 C. m 0 D. m 12 Câu 8. Hàm số 3
y x 12x 1 có
A. Cực đại bằng 17 và cực tiểu bằng 0
B. Cực đại bằng 17 và cực tiểu bằng 15
C. Cực đại bằng 0 và cực tiểu bằng 15 D. Cực đại bằng 15
và cực tiểu bằng 17 Câu 9. Hµm sè 4 2
y mx (m 1)x 1 2m chØ cã mét cùc trÞ khi A. m 1 B. m 0
C. m 0 hoÆc m 1 D. 0 m 1
Câu 10. Cho ®-êng cong (C) cã ph-¬ng tr×nh 2 y
x 2 , tÞnh tiÕn (C) theo phương trục hoành
sang phải 3 ®¬n vÞ ta ®-îc ®-êng cong cã ph-¬ng tr×nh lµ A. 2 y
x 6x 11 B. 2 y x 2 3 C. 2 y x 2 3 D. 2 y x 6x 11 Câu 11. Cho hµm sè 3 2
y x 6x 3(m 2)x m 6 ®¹t cùc ®¹i, cùc tiÓu t¹i x , x sao cho 1 2
x 1 x th× gi¸ trÞ cña m lµ 1 2 A. m 1 B. m 1 C. m 1 D. m 1
Câu 12. Hàm số f cã ®¹o hµm 3
f '(x) x (2x 3)(3x 2) . Sè ®iÓm cùc trÞ cña hàm số f lµ A. 0 B. 1 C. 2 D. 3
Câu 13. Đồ thị cña hàm số 2
y x 1 x có
A. Tiệm cận đứng và có tiệm cận xiên
B. Tiệm cận ngang và có tiệm cận xiên
C. Tiệm cận xiên và không có tiệm cận ngang
D. Tiệm cận đứng và có tiệm cận ngang
Câu 14. Hµm sè y cos 3x m sin x 9 ®¹t cùc ®¹i t¹i x khi 3
A. Không tồn tại m B. m 18 C. m 1 D. m 0
Câu 15. Cho M = 32000 và N = 41500. Khi đó A. M > N B. M = N C. M < N D. M ≤ N H 2/6 Mã đề 909 2 2x 1
Câu 16. C¸c ®å thÞ cña hai hàm số y vµ 2
y 2x x tiÕp xóc víi nhau t¹i ®iÓm cã täa ®é x 1 1 A. ;1 B. ; 0 C. (–1 ; 3) D. (1 ; 1) 2 2 Câu 17. Cho hµm sè 4 2
y x 2x 4 cã ®å thÞ (C) vµ hai ®iÓm A(0 ; –16), B(–1 ; –8). T×m täa ®é
®iÓm M trªn (C) sao cho tam gi¸c MAB cã diÖn tÝch nhá nhÊt A. (1 ; –1) B. (1 ; 2) C. (–1 ; –1) D. (2 ; 20) mx m
Câu 18. §å thÞ cña hµm sè y
c¾t ®-êng th¼ng d: y x 6 t¹i hai ®iÓm ph©n biÖt thuéc x hai nh¸nh cña nã khi: A. m 0 B. m 0 C. m 6 D. m 0 Câu 19. Cho hµm sè 3
y x 3x 1 cã ®å thÞ (C), mét ®-êng th¼ng qua M(1; 3) vµ tiÕp xóc víi
(C) c¾t (C) t¹i ®iÓm thø hai N (N kh«ng trïng M). Khi ®ã täa ®é ®iÓm N lµ 1 3 A. ; B. (2; –1) C. (–1; –1) D. (0; 1) 2 8 Câu 20. Hàm số 4 3 2
y x 4x x 6x 10 có
A. Một cực đại và hai cực tiểu
B. Một cực đại và không có cực tiểu
C. Một cực tiểu và không có cực đại
D. Hai cực đại và một cực tiểu x 3
Câu 21. Cho đồ thị (C) cña hàm số y
vµ ®-êng th¼ng d : y mx 2m 1. Ph-¬ng ¸n nµo x 1 d-íi ®©y ®óng
A. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt
B. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt khi m 0
C. (C) vµ d tiÕp xóc víi nhau khi m 2
D. d lu«n ®i qua mét ®iÓm cè ®Þnh cña (C) khi m biÕn thiªn x
Câu 22. Cho ®å thÞ (C) cña hàm số y
vµ ®-êng th¼ng d: y x 4 . MÖnh ®Ò nµo d-íi ®©y x 1 ®óng
A. d lµ tiÖm cËn xiªn cña (C) B. d vµ (C) tiÕp xóc
C. d vµ (C) c¾t nhau t¹i hai ®iÓm ph©n biÖt
D. d vµ (C) kh«ng c¾t nhau
Câu 23. Một hộp không nắp được làm từ mảnh các tông theo mẫu hình bên.
Hộp có đáy là hình vuông cạnh x (cm), chiều cao h (cm) và có thể tích là 4cm3.
Tìm giá trị của x sao cho diện tích của mảnh các tông nhỏ nhất A. 8 cm B. 4 cm C. 3 2 2 cm D. 2 cm 500 50 Câu 24. Tỉ số bằng 250 25 A. 250 10 B. 500 10 C. 250 2 D. 260 2 H 3/6 Mã đề 909
Câu 25. Nếu a 0 thì tích 6 3 a . a bằng A. 9 a B. a C. 9 2 a D. 18 a
Câu 26. Nếu log b log c thì a a
A. c b 0 và a 1 B. và và và b c 0 a 0 C. 0 b c 0 a 1 D. c b 0 a 1
Câu 27. Cho 0 a 1 , khi đó 3log 2 a a bằng A. 16 B. 6 C. 2 D. 8
Câu 28. Cho E = log45 và F = log54. Khi đó A. E = F B. E < F C. E > F D. E ≥ F 3 3 3 3 4 4 4 4
a b a b
Câu 29. Cho hai số dương khác nhau a, b . Rút gọn biểu thức ab bằng 1 1 2 2 a b A. a b B. 2 a b C. 2 a b D. a b
Câu 30. Biết log 2 ;
a log 3 b . Tính log 5 5 305 theo a, b 1 1 A. a b B. C. a b 1 D. a b 1 a b
Câu 31. Một người gửi 6 triệu đồng vào ngân hàng theo thể thức lãi kép, kì hạn 1 năm với lãi suất
7,56% một năm. Hỏi sau bao nhiêu năm người gửi sẽ có ít nhất 12 triệu đồng từ số tiền gửi ban đầu
(giả sử lãi suất không thay đổi) ? A. 1 năm B. 8 năm C. 10 năm D. 15 năm
Câu 32. Cho điểm O và số thực k 0 . Mệnh đề nào dưới đây sai
A. Phép vị tự tâm O tỉ số k là một phép đồng dạng khi k 0
B. Phép vị tự tâm O tỉ số k 1
là một phép đối xứng tâm
C. Phép vị tự tâm O tỉ số k luôn là một phép đồng dạng
D. Phép vị tự tâm O tỉ số k 1 là một phép đồng nhất
Câu 33. Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất A. Ba mặt B. Hai mặt C. Năm mặt D. Bốn mặt
Câu 34. Khối hai mươi mặt đều thuộc loại A. {3 ; 4} B. {3 ; 5} C. {4 ; 3} D. {5 ; 3}
Câu 35. Cho khối tứ diện ABCD. Lấy một điểm M nằm giữa A và B, một điểm N nằm giữa C và
D. Bằng hai mặt phẳng (MCD) và (NAB) ta chia khối tứ diện đã cho thành bốn khối tứ diện A. AMNC, AMND, AMCD, BMNC B. AMCD, AMND, BMNC, BMND C. BMCD, BMND, AMNC, AMND D. AMNC, AMND, BMNC, BMND H 4/6 Mã đề 909
Câu 36. Số mặt phẳng đối xứng của hình tứ diện đều là A. 4 B. 8 C. 6 D. 10
Câu 37. Cho tứ diện ABCD có trọng tâm G. Gọi A’, B’, C’, D’ lần lượt là trọng tâm các tam giác
BCD, CDA, ABD, ABC. Mệnh đề nào dưới đây đúng 1
A. Phép vị tự tâm G tỉ số
biến ABCD thành A’B’C’D’ 3
B. A’, B’, C’, D’ đồng phẳng
C. A’B’C’D’ và ABCD là hai hình bằng nhau 1
D. Phép vị tự tâm G tỉ số
biến A’B’C’D’ thành ABCD 3
Câu 38. Trong các mệnh đề sau đây, mệnh đề nào đúng
A. Phép vị tự biến mặt phẳng thành mặt phẳng song song với nó
B. Phép vị tự biến mặt phẳng qua tâm vị tự thành chính nó
C. Không có phép vị tự nào biến hai điểm phân biệt A và B lần lượt thành A và B
D. Phép vị tự biến đường thẳng thành đường thẳng song song với nó
Câu 39. Từ một tấm bìa hình vuông cạnh bằng 4cm, ta gấp nó thành
4 phần đều nhau rồi gấp thành một hình hộp chữ nhật (không nắp)
như hình bên. Hỏi thể tích khối hộp này bằng bao nhiêu A. 1cm3 B. 16cm3 C. 4cm3 D. 8cm3
Câu 40. Thể tích khối tứ diện đều có cạnh bằng 1 là 2 3 2 2 A. B. C. D. 12 4 4 6
Câu 41. Với một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc tấm bìa một
hình vuông cạnh 12cm rồi gấp lại thành một hình hộp chữ nhật không có nắp.
Nếu dung tích của cái hộp đó là 4800cm3 thì cạnh tấm bìa có độ dài là A. 36cm B. 38cm C. 42cm D. 44cm
Câu 42. Cho hình hộp ABCD.A’B’C’D’ có thể tích V. Thể tích khối tứ diện ACB’D’ là V V V V A. B. C. D. 8 6 3 4
Câu 43. Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = a , AC = 2a và SA vuông
góc với đáy. Góc giữa (SBC) và (ABC) bằng 600. Thể tích khối chóp S.ABC bằng 3 a 3 3 a 3 3 3a 3 a A. B. C. D. 3 2 2 2
Câu 44. Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với đáy và AB = a ,
AD = 2a , góc giữa SB và đáy bằng 450. Thể tích khối chóp S.ABCD là 3 2 a 3 6 a 3 a A. B. C. D. 3 2a 3 18 3 H 5/6 Mã đề 909
Câu 45. Thể tích của khối tám mặt đều có cạnh bằng a là 3 2 2 a 3 2 a 3 2 a A. B. C. 3 2 2 a D. 3 3 9
Câu 46. Cho tứ diện AEFG có thể tích là V và AE, AF, AG vuông góc với nhau từng đôi một. Gọi
B, C, D lần lượt là trung điểm của các đoạn thẳng GE, EF, FG. Thể tích khối tứ diện ABCD bằng V V V V A. B. C. D. 2 4 3 6
Câu 47. Cho hình lăng trụ đứng MNP.M' N'P' có tất cả các cạnh bằng a . Thể tích của khối lăng trụ bằng 3 a 3 3 a 3 3 a 3 A. 3 a 3 B. C. D. 2 4 3
Câu 48. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 1cm, SA 2cm và SA vuông góc với
đáy. Khoảng cách giữa hai đường thẳng BC và SD là A. 1 cm B. 2 cm C. 2 cm D. 5 cm
Câu 49. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AC = 2a , tam
giác SAC đều và nằm trên mặt phẳng vuông góc với đáy. Trên cạnh SA lấy điểm M sao cho
MA = 2MS. Mặt phẳng (α) qua M và song song với (ABC) cắt SB, SC tại N, P. Khi đó thể tích khối
chóp cụt ABC.MNP bằng 3 a 3 3 80 3a 3 2 3a 3 26 3a A. B. C. D. 3 81 9 81
Câu 50. Cho các đồ thị trên các hình sau. Chỉ ra câu trả lời đúng
A. Hình 4 có đồ thị hàm số 4 2
y x 2x 3
B. Hình 3 có đồ thị hàm số 3
y x 3x 2
C. Hình 2 có đồ thị hàm số 4 2
y x 2x 3
D. Hình 1 có đồ thị hàm số 3
y x 3x 2 .
Cán bộ coi kiểm tra không giải thích gì thêm H 6/6 Mã đề 909
TRƯỜNG THPT NGUYỄN GIA THIỀU ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA HỌC KỲ 1
BỘ MÔN TOÁN Môn toán lớp 12, năm học 2016 – 2017
Đề chính thức gồm 06 trang Thời gian làm bài 90 phút Mã đề 910
Hä vµ tªn häc sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Líp: . . . . . . . . .
Câu 1. Chän ph-¬ng ¸n tr¶ lêi ®óng:
H×nh d-íi ®©y lµ ®å thÞ cña hµm sè nµo 3 x A. 2 y x x 3 3 x B. 2 y x x 3 3 x C. 2 y x x 3 3 x D. y 3
Câu 2. Chän ph-¬ng ¸n tr¶ lêi ®óng: x b
§å thÞ cña hµm sè y cx nh- h×nh d-íi ®©y. d
Khi ®ã gi¸ trÞ b, c, d lÇn l-ît lµ A. 1, 1, 2 B. 0, 1, 1 C. –2, 1, 1 D. 0, 1, 2 x
Câu 3. Cho ®å thÞ (C) cña hàm số y
y x . Hỏi mÖnh ®Ò nµo ®óng
x vµ ®-êng th¼ng d: 4 1
A. d lµ tiÖm cËn xiªn cña (C)
B. d vµ (C) c¾t nhau t¹i hai ®iÓm ph©n biÖt C. d vµ (C) kh«ng c¾t nhau
D. d vµ (C) tiÕp xóc
Câu 4. Cho điểm O và số thực k 0 . Mệnh đề nào dưới đây sai
A. Phép vị tự tâm O tỉ số k luôn là một phép đồng dạng
B. Phép vị tự tâm O tỉ số k là một phép đồng dạng khi k 0
C. Phép vị tự tâm O tỉ số k 1
là một phép đối xứng tâm
D. Phép vị tự tâm O tỉ số k 1 là một phép đồng nhất H 1/6 Mã đề 910
Câu 5. Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất A. Hai mặt B. Bốn mặt C. Ba mặt D. Năm mặt
Câu 6. Khối tám mặt đều thuộc loại A. {4 ; 3} B. {3 ; 3} C {3 ; 5} D. {3 ; 4}
Câu 7. Cho khối tứ diện ABCD. Lấy một điểm M nằm giữa A và B, một điểm N nằm giữa C và D.
Bằng hai mặt phẳng (MCD) và (NAB) ta chia khối tứ diện đã cho thành bốn khối tứ diện A. AMNC, AMND, AMCD, BMNC B. AMNC, AMND, BMNC, BMND C. AMCD, AMND, BMNC, BMND D. BMCD, BMND, AMNC, AMND
Câu 8. Số mặt phẳng đối xứng của hình bát diện đều là A. 9 B. 3 C. 6 D. 12
Câu 9. Cho tứ diện ABCD có trọng tâm G. Gọi A’, B’, C’, D’ lần lượt là trọng tâm các tam giác
BCD, CDA, ABD, ABC. Mệnh đề nào dưới đây đúng
A. A’, B’, C’, D’ đồng phẳng
B. A’B’C’D’ và ABCD là hai hình bằng nhau 1
C. Phép vị tự tâm G tỉ số
biến ABCD thành A’B’C’D’ 3 1
D. Phép vị tự tâm G tỉ số
biến A’B’C’D’ thành ABCD 3
Câu 10. Mệnh đề nào dưới đây đúng
A. Phép biến hình biến mỗi điểm M trong không gian thành chính nó có là phép dời hình
B. Phép đối xứng qua mặt phẳng biến một tứ diện thành chính nó
C. Phép tịnh tiến biến một đường thẳng thành đường thẳng song song với nó
D. Tứ diện đều có đúng một mặt phẳng đối xứng
Câu 11. Từ một tấm bìa hình vuông cạnh bằng 3cm, ta gấp nó thành
3 phần đều nhau rồi gấp thành một hình lăng trụ đứng (không đáy)
như hình bên. Hỏi thể tích khối lăng trụ này bằng bao nhiêu 1 1 3 3 3 A. cm3 B. cm3 C. cm3 D. cm3 4 12 4 4
Câu 12. Cho M = 32000 và N = 41500. Khi đó A. M = N B. M > N C. M < N D. M ≤ N
Câu 13. Nếu log b log c thì a a
A. b c 0 và a 1 B. b c 0 và 0 a 1 C. b c 0 và a 0 D. c b 0 và a 1 500 50 Câu 14. Tỉ số bằng 250 25 A. 250 100 B. 250 10 C. 250 2 D. 500 2 H 2/6 Mã đề 910 3 3 3 3 4 4 4 4
a b a b
Câu 15. Cho hai số dương khác nhau a, b . Rút gọn biểu thức ab bằng 1 1 2 2 a b A. a b B. a b C. 2 a b D. 2 a b
Câu 16. Cho 0 a 1 , khi đó log 4 a a bằng A. 4 B. 2 C. 16 D. 1
Câu 17. Nếu a 0 thì tích 6 3 a . a bằng A. 9 a B. 9 2 a C. 18 a D. a
Câu 18. Một người gửi 15 triệu đồng vào ngân hàng theo thể thức lãi kép kỳ hạn 1 năm với lãi suất
7,56% một năm. Giả sử lãi suất không thay đổi, hỏi số tiền người đó thu được (cả vốn lẫn lãi) sau 5
năm là bao nhiêu triệu đồng (làm tròn đến chữ số thập phân thứ hai) ?
A. 22,59 triệu đồng B. 20,59 triệu đồng C. 19,19 triệu đồng D. 21,59 triệu đồng 5 3 Câu 19. Cho E = log và F = log . Khi đó 2 3 5 2 3 3 A. E = F B. E < F C. E > F D. E ≥ F
Câu 20. Cho hình lập phương ABCD.A'B'C'D' cạnh 1. Thể tích của khối chóp A'.ABCD bằng 1 1 1 A. B. C. D. 1 6 2 3
Câu 21. Với một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc tấm bìa một
hình vuông cạnh 12cm rồi gấp lại thành một hình hộp chữ nhật không có nắp.
Nếu dung tích của cái hộp đó là 4800cm3 thì cạnh tấm bìa có độ dài là A. 36cm B. 44cm C. 38cm D. 42cm
Câu 22. Cho hình hộp ABCD.A’B’C’D’ có thể tích V. Thể tích khối tứ diện ACB’D’ là V V V V A. B. C. D. 3 8 6 4
Câu 23. Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = a , AC = 2a và SA vuông
góc với đáy. Góc giữa (SBC) và (ABC) bằng 600. Thể tích khối chóp S.ABC bằng 3 a 3 3 a 3 a 3 3 3a A. B. C. D. 3 2 2 2
Câu 24. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 1cm, SA 2cm và SA vuông góc với
đáy. Khoảng cách giữa hai đường thẳng BC và SD là A. 2 cm B. 2 cm C. 5 cm D. 1 cm H 3/6 Mã đề 910
Câu 25. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AC = 2a , tam
giác SAC đều và nằm trên mặt phẳng vuông góc với đáy. Trên cạnh SA lấy điểm M sao cho
MA = 2MS. Mặt phẳng (α) qua M và song song với (ABC) cắt SB, SC tại N, P. Khi đó thể tích khối
chóp cụt ABC.MNP bằng 3 a 3 3 80 3a 3 26 3a 3 2 3a A. B. C. D. 3 81 81 9 1
Câu 26. Một khoảng đồng biến của hàm số y x 2 x là 1 A. 2 ; B. ; C. ; 1 D. 1 ; Câu 27. Hàm số 3 2
y x 3x mx 2 nghÞch biÕn trªn kho¶ng (0 ; 2) khi m nhËn gi¸ trÞ A. m 3 B. m 3 C. m 3 D. m 0
Câu 28. Cho hàm số 4 2
y ax bx c trong đó a 0 và b 0 . Khi đó hàm số có
A. Một cực đại B. Một cực tiểu C. Hai cực tiểu và một cực đại D. Hai cực đại và một cực tiểu 1
Câu 29. T×m a , b ®Ó ®å thÞ cña hàm số 4 2 y
x bx a cã ®iÓm cùc tiÓu M(2 ; 4) 4
A. a 2, b 0 B. Kh«ng tån t¹i C. a 2
, b 0 D. a 0, b 2 2 x 2
Câu 30. Mét trong c¸c h×nh d-íi ®©y, h×nh nµo cã b¶ng biÕn thiªn cña hµm sè y x 1 A. H×nh 4 B. H×nh 3 C. H×nh 2 D. H×nh 1 Câu 31. Hàm số 3
y x 12x 1 có
A. Cực đại bằng 17 và cực tiểu bằng 0
B. Cực đại bằng 17 và cực tiểu bằng 15
C. Cực đại bằng 0 và cực tiểu bằng 15 D. Cực đại bằng 15
và cực tiểu bằng 17 Câu 32. Hµm sè 4 2
y mx (m 1)x 1 2m chØ cã mét cùc trÞ khi
A. m 0 hoÆc m 1 B. m 1 C. m 0 D. 0 m 1
Câu 33. Cho log1218 = a , log2454 = b . Khi đó A. ab + 5(a – b) = 1 B. ab = 5(a – b) C. ab – 5(a – b) = 1 D. ab = 5(b – a)
Câu 34. Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với đáy và AB = a ,
AD = 2a , góc giữa SB và đáy bằng 450. Thể tích khối chóp S.ABCD là 3 a 3 2 a A. 3 2a B. C. D. Đáp án khác 3 3
Câu 35. Thể tích của khối tám mặt đều có cạnh bằng a là 3 2 2 a 3 2 a 3 2 a A. B. 3 2 2 a C. D. 3 9 3 H 4/6 Mã đề 910
Câu 36. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a .
SA (ABC) và SA = a . Gọi (α) là mặt phẳng qua A và vuông góc với SB đồng thời cắt SB, SC tại
M, N. Khi đó thể tích khối chóp S.AMN bằng 3 a 3 a 3 a A. B. C. D. Đáp án khác 6 24 12
Câu 37. Cho hình lập phương ABCD.A’B’C’D’ cạnh a , tâm O. Thể tích khối tứ diện AA’B’O là 3 a 3 a 3 a 3 2 a A. B. C. D. 8 9 12 3
Câu 38. Cho hình lăng trụ đứng MNP.M' N'P' có tất cả các cạnh bằng a . Thể tích của khối lăng trụ bằng 3 a 3 3 a 3 3 a 3 A. B. 3 a 3 C. D. 4 2 3
Câu 39. Cho ®-êng cong (C) cã ph-¬ng tr×nh 2 y
x 2 , tÞnh tiÕn (C) theo phương trục hoành
sang tr¸i 3 ®¬n vÞ ta ®-îc ®-êng cong cã ph-¬ng tr×nh lµ A. 2 y x 2 3 B. 2 y x 2 3 C. 2 y x 6x 11 D. 2 y x 6x 11 x 2
Câu 40. Víi gi¸ trÞ nµo cña m th× ®å thÞ hµm sè y 2 x 4x
chØ cã mét tiÖm cËn ®øng vµ mét m tiÖm cËn ngang A. 0 B. 2 C. 4 D. 1 Câu 41. Cho hµm sè 3 2
y x 6x 3(m 2)x m 6 ®¹t cùc ®¹i, cùc tiÓu t¹i x , x sao cho 1 2
x 1 x th× gi¸ trÞ cña m lµ 1 2 A. m 1 B. m 1 C. m 1 D. m 1 3 Câu 42. Cho hµm sè 4 2
y x 2x 1 cã ®å thÞ (C). §iÓm M trªn (C) cã hoµnh ®é x lµ ®iÓm 3 g× cña (C) A. §iÓm cùc tiÓu B. §iÓm cùc ®¹i C. §iÓm th-êng D. §iÓm uèn 1
Câu 43. Gi¸ trÞ nhá nhÊt cña hµm sè y x 7 trªn kho¶ng ( 1 ;) lµ x 1 5 A. B. 0 C. 5 2 D. 2 2 mx m
Câu 44. §å thÞ cña hµm sè y
c¾t ®-êng th¼ng d: y x 6 t¹i hai ®iÓm ph©n biÖt thuéc x hai nh¸nh cña nã khi: A. m 0 B. m 6 C. m 0 D. m 0 Câu 45. Hàm số 4 3 2
y x 4x x 6x 10 có
A. Một cực đại và hai cực tiểu
B. Một cực đại và không có cực tiểu
C. Hai cực đại và một cực tiểu
D. Một cực tiểu và không có cực đại H 5/6 Mã đề 910
Câu 46. Hàm số f cã ®¹o hµm 2 2 2
f '(x) x (2x 3) (3x 2) . Sè ®iÓm cùc trÞ cña hàm số f lµ A. 1 B. 3 C. 0 D. 2 Câu 47. Cho hµm sè 3
y x 3x 1 cã ®å thÞ (C), mét ®-êng th¼ng qua M(1; 3) vµ tiÕp xóc víi
(C) c¾t (C) t¹i ®iÓm thø hai N (N kh«ng trïng M). Khi ®ã täa ®é ®iÓm N lµ 1 3 A. (2; –1) B. ; C. (–1; –1) D. (0; 1) 2 8 x 3
Câu 48. Cho đồ thị (C) cña hàm số y
d y mx m . Ph-¬ng ¸n nµo
x vµ ®-êng th¼ng : 2 1 1 d-íi ®©y ®óng
A. d lu«n ®i qua mét ®iÓm cè ®Þnh cña (C) khi m biÕn thiªn
B. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt
C. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt khi m 0
D. (C) vµ d tiÕp xóc víi nhau khi m 2
Câu 49. Một hộp không nắp được làm từ mảnh các tông theo mẫu hình bên.
Hộp có đáy là hình vuông cạnh x (cm), chiều cao h (cm) và có thể tích là 4cm3.
Tìm giá trị của x sao cho diện tích của mảnh các tông nhỏ nhất A. 8 cm B. 2 cm C. 4 cm D. 3 2 2 cm
Câu 50. Cho các đồ thị trên các hình sau. Chỉ ra câu trả lời đúng x 1 1 x
A. Hình 2 có đồ thị hàm số y
B. Hình 4 có đồ thị hàm số y x 2x 1 x x 1
C. Hình 1 có đồ thị hàm số y
D. Hình 3 có đồ thị hàm số y x . 2x
Cán bộ coi kiểm tra không giải thích gì thêm H 6/6 Mã đề 910
TRƯỜNG THPT NGUYỄN GIA THIỀU ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA HỌC KỲ 1
BỘ MÔN TOÁN Môn toán lớp 12, năm học 2016 – 2017
Đề chính thức gồm 06 trang Thời gian làm bài 90 phút Mã đề 911
Hä vµ tªn häc sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Líp: . . . . . . . . .
Câu 1. Chän ph-¬ng ¸n tr¶ lêi ®óng:
H×nh d-íi ®©y lµ ®å thÞ cña hµm sè nµo 3 x A. 2 y x x 3 3 x B. 2 y x x 3 3 x C. 2 y x x 3 3 x D. y 3
Câu 2. Cho các đồ thị trên các hình sau. Chỉ ra câu trả lời đúng x 1 1 x
A. Hình 2 có đồ thị hàm số y
B. Hình 4 có đồ thị hàm số y x 2x 1 x x 1
C. Hình 1 có đồ thị hàm số y
D. Hình 3 có đồ thị hàm số y x 2x
Câu 3. Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với đáy và AB = a ,
AD = 2a , góc giữa SB và đáy bằng 450. Thể tích khối chóp S.ABCD là 3 a 3 2 a A. 3 2a B. C. D. Đáp án khác 3 3 H 1/6 Mã đề 911 Câu 4. Cho hàm số 4 2
y ax bx c trong đó a 0 và b 0 . Khi đó hàm số có
A. Một cực đại B. Một cực tiểu C. Hai cực tiểu và một cực đại D. Hai cực đại và một cực tiểu 2 x 2
Câu 5. Mét trong c¸c h×nh d-íi ®©y, h×nh nµo cã b¶ng biÕn thiªn cña hµm sè y x 1 A. H×nh 4 B. H×nh 3 C. H×nh 2 D. H×nh 1 1
Câu 6. Một khoảng đồng biến của hàm số y x 2 x là 1 A. 2 ; B. ; C. ; 1 D. 1 ; Câu 7. Hàm số 3 2
y x 3x mx 2 nghÞch biÕn trªn kho¶ng (0 ; 2) khi m nhËn gi¸ trÞ A. m 3 B. m 3 C. m 3 D. m 0 Câu 8. Hàm số 3
y x 12x 1 có
A. Cực đại bằng 17 và cực tiểu bằng 0
B. Cực đại bằng 17 và cực tiểu bằng 15
C. Cực đại bằng 0 và cực tiểu bằng 15 D. Cực đại bằng 15
và cực tiểu bằng 17 Câu 9. Hµm sè 4 2
y mx (m 1)x 1 2m chØ cã mét cùc trÞ khi
A. m 0 hoÆc m 1 B. m 1 C. m 0 D. 0 m 1
Câu 10. Cho ®-êng cong (C) cã ph-¬ng tr×nh 2 y
x 2 , tÞnh tiÕn (C) theo phương trục hoành
sang tr¸i 3 ®¬n vÞ ta ®-îc ®-êng cong cã ph-¬ng tr×nh lµ A. 2 y x 2 3 B. 2 y x 2 3 C. 2 y x 6x 11 D. 2 y x 6x 11 Câu 11. Cho hµm sè 3 2
y x 6x 3(m 2)x m 6 ®¹t cùc ®¹i, cùc tiÓu t¹i x , x sao cho 1 2
x 1 x th× gi¸ trÞ cña m lµ 1 2 A. m 1 B. m 1 C. m 1 D. m 1
Câu 12. Hàm số f cã ®¹o hµm 2 2 2
f '(x) x (2x 3) (3x 2) . Sè ®iÓm cùc trÞ cña hàm số f lµ A. 1 B. 3 C. 0 D. 2 x 2
Câu 13. Víi gi¸ trÞ nµo cña m th× ®å thÞ hµm sè y 2 x 4x
chØ cã mét tiÖm cËn ®øng vµ mét m tiÖm cËn ngang A. 0 B. 2 C. 4 D. 1 Câu 14. Hàm số 4 3 2
y x 4x x 6x 10 có
A. Một cực đại và hai cực tiểu
B. Một cực đại và không có cực tiểu
C. Hai cực đại và một cực tiểu
D. Một cực tiểu và không có cực đại 1
Câu 15. T×m a , b ®Ó ®å thÞ cña hàm số 4 2 y
x bx a cã ®iÓm cùc tiÓu M(2 ; 4) 4
A. a 2, b 0 B. Kh«ng tån t¹i C. a 2
, b 0 D. a 0, b 2 H 2/6 Mã đề 911 3 Câu 16. Cho hµm sè 4 2
y x 2x 1 cã ®å thÞ (C). §iÓm M trªn (C) cã hoµnh ®é x lµ ®iÓm 3 g× cña (C) A. §iÓm cùc tiÓu B. §iÓm cùc ®¹i C. §iÓm th-êng D. §iÓm uèn 1
Câu 17. Gi¸ trÞ nhá nhÊt cña hµm sè y x 7 trªn kho¶ng ( 1 ;) lµ x 1 5 A. B. 0 C. 5 2 D. 2 2 mx m
Câu 18. §å thÞ cña hµm sè y
c¾t ®-êng th¼ng d: y x 6 t¹i hai ®iÓm ph©n biÖt thuéc x hai nh¸nh cña nã khi: A. m 0 B. m 6 C. m 0 D. m 0 Câu 19. Cho hµm sè 3
y x 3x 1 cã ®å thÞ (C), mét ®-êng th¼ng qua M(1; 3) vµ tiÕp xóc víi
(C) c¾t (C) t¹i ®iÓm thø hai N (N kh«ng trïng M). Khi ®ã täa ®é ®iÓm N lµ 1 3 A. (2; –1) B. ; C. (–1; –1) D. (0; 1) 2 8 x 3
Câu 20. Cho đồ thị (C) cña hàm số y
d y mx m . Ph-¬ng ¸n nµo
x vµ ®-êng th¼ng : 2 1 1 d-íi ®©y ®óng
A. d lu«n ®i qua mét ®iÓm cè ®Þnh cña (C) khi m biÕn thiªn
B. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt
C. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt khi m 0
D. (C) vµ d tiÕp xóc víi nhau khi m 2 x
Câu 21. Cho ®å thÞ (C) cña hàm số y
y x . Hỏi mÖnh ®Ò nµo ®óng
x vµ ®-êng th¼ng d: 4 1
A. d lµ tiÖm cËn xiªn cña (C)
B. d vµ (C) c¾t nhau t¹i hai ®iÓm ph©n biÖt C. d vµ (C) kh«ng c¾t nhau D. d vµ (C) tiÕp xóc
Câu 22. Một hộp không nắp được làm từ mảnh các tông theo mẫu hình bên.
Hộp có đáy là hình vuông cạnh x (cm), chiều cao h (cm) và có thể tích là 4cm3.
Tìm giá trị của x sao cho diện tích của mảnh các tông nhỏ nhất A. 8 cm B. 2 cm C. 4 cm D. 3 2 2 cm 500 50 Câu 23. Tỉ số bằng 250 25 A. 250 100 B. 250 10 C. 250 2 D. 500 2
Câu 24. Nếu a 0 thì tích 6 3 a . a bằng A. 9 a B. 9 2 a C. 18 a D. a H 3/6 Mã đề 911
Câu 25. Cho 0 a 1 , khi đó log 4 a a bằng A. 4 B. 2 C. 16 D. 1
Câu 26. Cho M = 32000 và N = 41500. Khi đó A. M = N B. M > N C. M < N D. M ≤ N
Câu 27. Nếu log b log c thì a a
A. b c 0 và a 1 B. b c 0 và 0 a 1 C. b c 0 và a 0 D. c b 0 và a 1 5 3 Câu 28. Cho E = log và F = log . Khi đó 2 3 5 2 3 3 A. E = F B. E < F C. E > F D. E ≥ F 3 3 3 3 4 4 4 4
a b a b
Câu 29. Cho hai số dương khác nhau a, b . Rút gọn biểu thức ab bằng 1 1 2 2 a b A. a b B. a b C. 2 a b D. 2 a b
Câu 30. Cho log1218 = a , log2454 = b . Khi đó A. ab + 5(a – b) = 1 B. ab = 5(a – b) C. ab – 5(a – b) = 1 D. ab = 5(b – a)
Câu 31. Một người gửi 15 triệu đồng vào ngân hàng theo thể thức lãi kép kỳ hạn 1 năm với lãi suất
7,56% một năm. Giả sử lãi suất không thay đổi, hỏi số tiền người đó thu được (cả vốn lẫn lãi) sau 5
năm là bao nhiêu triệu đồng (làm tròn đến chữ số thập phân thứ hai) ?
A. 22,59 triệu đồng B. 20,59 triệu đồng C. 19,19 triệu đồng D. 21,59 triệu đồng
Câu 32. Cho điểm O và số thực k 0 . Mệnh đề nào dưới đây sai
A. Phép vị tự tâm O tỉ số k luôn là một phép đồng dạng
B. Phép vị tự tâm O tỉ số k là một phép đồng dạng khi k 0
C. Phép vị tự tâm O tỉ số k 1
là một phép đối xứng tâm
D. Phép vị tự tâm O tỉ số k 1 là một phép đồng nhất
Câu 33. Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất A. Hai mặt B. Bốn mặt C. Ba mặt D. Năm mặt
Câu 34. Khối tám mặt đều thuộc loại A. {4 ; 3} B. {3 ; 3} C {3 ; 5} D. {3 ; 4}
Câu 35. Cho khối tứ diện ABCD. Lấy một điểm M nằm giữa A và B, một điểm N nằm giữa C và
D. Bằng hai mặt phẳng (MCD) và (NAB) ta chia khối tứ diện đã cho thành bốn khối tứ diện A. AMNC, AMND, AMCD, BMNC B. AMNC, AMND, BMNC, BMND C. AMCD, AMND, BMNC, BMND D. BMCD, BMND, AMNC, AMND H 4/6 Mã đề 911
Câu 36. Số mặt phẳng đối xứng của hình bát diện đều là A. 9 B. 3 C. 6 D. 12
Câu 37. Cho tứ diện ABCD có trọng tâm G. Gọi A’, B’, C’, D’ lần lượt là trọng tâm các tam giác
BCD, CDA, ABD, ABC. Mệnh đề nào dưới đây đúng
A. A’, B’, C’, D’ đồng phẳng
B. A’B’C’D’ và ABCD là hai hình bằng nhau 1
C. Phép vị tự tâm G tỉ số
biến ABCD thành A’B’C’D’ 3 1
D. Phép vị tự tâm G tỉ số
biến A’B’C’D’ thành ABCD 3
Câu 38. Mệnh đề nào dưới đây đúng
A. Phép biến hình biến mỗi điểm M trong không gian thành chính nó có là phép dời hình
B. Phép đối xứng qua mặt phẳng biến một tứ diện thành chính nó
C. Phép tịnh tiến biến một đường thẳng thành đường thẳng song song với nó
D. Tứ diện đều có đúng một mặt phẳng đối xứng
Câu 39. Từ một tấm bìa hình vuông cạnh bằng 3cm, ta gấp nó thành
3 phần đều nhau rồi gấp thành một hình lăng trụ đứng (không đáy)
như hình bên. Hỏi thể tích khối lăng trụ này bằng bao nhiêu 1 1 3 3 3 A. cm3 B. cm3 C. cm3 D. cm3 4 12 4 4
Câu 40. Cho hình lập phương ABCD.A'B'C'D' cạnh 1. Thể tích của khối chóp A'.ABCD bằng 1 1 1 A. B. C. D. 1 6 2 3
Câu 41. Với một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc tấm bìa một
hình vuông cạnh 12cm rồi gấp lại thành một hình hộp chữ nhật không có nắp.
Nếu dung tích của cái hộp đó là 4800cm3 thì cạnh tấm bìa có độ dài là A. 36cm B. 44cm C. 38cm D. 42cm
Câu 42. Cho hình hộp ABCD.A’B’C’D’ có thể tích V. Thể tích khối tứ diện ACB’D’ là V V V V A. B. C. D. 3 8 6 4
Câu 43. Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = a , AC = 2a và SA vuông
góc với đáy. Góc giữa (SBC) và (ABC) bằng 600. Thể tích khối chóp S.ABC bằng 3 a 3 3 a 3 a 3 3 3a A. B. C. D. 3 2 2 2
Câu 44. Thể tích của khối tám mặt đều có cạnh bằng a là 3 2 2 a 3 2 a 3 2 a A. B. 3 2 2 a C. D. 3 9 3 H 5/6 Mã đề 911
Câu 45. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a .
SA (ABC) và SA = a . Gọi (α) là mặt phẳng qua A và vuông góc với SB đồng thời cắt SB, SC tại
M, N. Khi đó thể tích khối chóp S.AMN bằng 3 a 3 a 3 a A. B. C. D. Đáp án khác 6 24 12
Câu 46. Cho hình lập phương ABCD.A’B’C’D’ cạnh a , tâm O. Thể tích khối tứ diện AA’B’O là 3 a 3 a 3 a 3 2 a A. B. C. D. 8 9 12 3
Câu 47. Cho hình lăng trụ đứng MNP.M' N'P' có tất cả các cạnh bằng a . Thể tích của khối lăng trụ bằng 3 a 3 3 a 3 3 a 3 A. B. 3 a 3 C. D. 4 2 3
Câu 48. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 1cm, SA 2cm và SA vuông góc với
đáy. Khoảng cách giữa hai đường thẳng BC và SD là A. 2 cm B. 2 cm C. 5 cm D. 1 cm
Câu 49. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AC = 2a , tam
giác SAC đều và nằm trên mặt phẳng vuông góc với đáy. Trên cạnh SA lấy điểm M sao cho
MA = 2MS. Mặt phẳng (α) qua M và song song với (ABC) cắt SB, SC tại N, P. Khi đó thể tích khối
chóp cụt ABC.MNP bằng 3 a 3 3 80 3a 3 26 3a 3 2 3a A. B. C. D. 3 81 81 9
Câu 50. Chän ph-¬ng ¸n tr¶ lêi ®óng: x b
§å thÞ cña hµm sè y cx nh- h×nh d-íi ®©y. d
Khi ®ã gi¸ trÞ b, c, d lÇn l-ît lµ A. 1, 1, 2 B. 0, 1, 1 C. –2, 1, 1 D. 0, 1, 2.
Cán bộ coi kiểm tra không giải thích gì thêm H 6/6 Mã đề 911
TRƯỜNG THPT NGUYỄN GIA THIỀU ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA HỌC KỲ 1
BỘ MÔN TOÁN Môn toán lớp 12, năm học 2016 – 2017
Đề chính thức gồm 06 trang Thời gian làm bài 90 phút Mã đề 912
Hä vµ tªn häc sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Líp: . . . . . . . . .
Câu 1. Chän ph-¬ng ¸n tr¶ lêi ®óng: x b
§å thÞ cña hµm sè y cx nh- h×nh d-íi ®©y. d
Khi ®ã gi¸ trÞ b, c, d lÇn l-ît lµ A. 0, 1, 2 B. 1, 1, 2 C. 0, 1, 1 D. –2, 1, 1
Câu 2. Cho các đồ thị trên các hình sau. Chỉ ra câu trả lời đúng x 1 1 x
A. Hình 2 có đồ thị hàm số y
B. Hình 1 có đồ thị hàm số y x x 1 x x 1
C. Hình 4 có đồ thị hàm số y
D. Hình 3 có đồ thị hàm số y 2x 2x
Câu 3. Mệnh đề nào dưới đây đúng
A. Phép đối xứng qua mặt phẳng biến một tứ diện thành chính nó
B. Phép tịnh tiến biến một đường thẳng thành đường thẳng song song với nó
C. Phép biến hình biến mỗi điểm M trong không gian thành chính nó có là phép dời hình
D. Tứ diện đều có đúng một mặt phẳng đối xứng H 1/6 Mã đề 912
Câu 4. Từ một tấm bìa hình vuông cạnh bằng 3cm, ta gấp nó thành
3 phần đều nhau rồi gấp thành một hình lăng trụ đứng (không đáy)
như hình bên. Hỏi thể tích khối lăng trụ này bằng bao nhiêu 1 3 3 1 3 A. cm3 B. cm3 C. cm3 D. cm3 4 4 12 4 500 50 Câu 5. Tỉ số bằng 250 25 A. 250 10 B. 250 2 C. 250 100 D. 260 2
Câu 6. Cho M = 32000 và N = 41500. Khi đó A. M = N B. M < N C. M ≤ N D. M > N
Câu 7. Nếu a 0 thì tích 6 3 a . a bằng A. a B. 9 a C. 9 2 a D. 18 a
Câu 8. Cho 0 a 1 , khi đó log 4 a a bằng A. 16 B. 4 C. 2 D. 1 5 3 Câu 9. Cho E = log và F = log . Khi đó 2 3 5 2 3 3 A. E = F B. E > F C. E ≥ F D. E < F 3 3 3 3 4 4 4 4
a b a b
Câu 10. Cho hai số dương khác nhau a, b . Rút gọn biểu thức ab bằng 1 1 2 2 a b A. a b B. a b C. 2 a b D. 2 a b
Câu 11. Cho log1218 = a , log2454 = b . Khi đó A. ab = 5(a – b) B. ab – 5(a – b) = 1 C. ab + 5(a – b) = 1 D. ab = 5(b – a)
Câu 12. Nếu log b log c thì a a
A. b c 0 và 0 a 1 B. b c 0 và a 1 C. b c 0 và a 0 D. c b 0 và a 1
Câu 13. Một người gửi 15 triệu đồng vào ngân hàng theo thể thức lãi kép kỳ hạn 1 năm với lãi suất
7,56% một năm. Giả sử lãi suất không thay đổi, hỏi số tiền người đó thu được (cả vốn lẫn lãi) sau 5
năm là bao nhiêu triệu đồng (làm tròn đến chữ số thập phân thứ hai) ?
A. 22,59 triệu đồng B. 21,59 triệu đồng C. 20,59 triệu đồng D. 19,19 triệu đồng H 2/6 Mã đề 912
Câu 14. Cho hàm số 4 2
y ax bx c trong đó a 0 và b 0 . Khi đó hàm số có
A. Hai cực tiểu và một cực đại B. Hai cực đại và một cực tiểu C. Một cực đại D. Một cực tiểu 1
Câu 15. Một khoảng đồng biến của hàm số y x 2 x là 1 A. 2 ; B. 1 ; C. ; D. ; 1
Câu 16. Cho hình lập phương ABCD.A'B'C'D' cạnh 1. Thể tích của khối chóp A'.ABCD bằng 1 1 1 A. B. C. D. 1 3 6 2
Câu 17. Với một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc tấm bìa một
hình vuông cạnh 12cm rồi gấp lại thành một hình hộp chữ nhật không có nắp.
Nếu dung tích của cái hộp đó là 4800cm3 thì cạnh tấm bìa có độ dài là A. 36cm B. 38cm C. 42cm D. 44cm Câu 18. Hàm số 3 2
y x 3x mx 2 nghÞch biÕn trªn kho¶ng (0 ; 2) khi m nhËn gi¸ trÞ A. m 3 B. m 3 C. m 3 D. m 0 Câu 19. Hàm số 3
y x 12x 1 có A. Cực đại bằng 15
và cực tiểu bằng 17 B. Cực đại bằng 17 và cực tiểu bằng 0
C. Cực đại bằng 0 và cực tiểu bằng 15
D. Cực đại bằng 17 và cực tiểu bằng 15 Câu 20. Hµm sè 4 2
y mx (m 1)x 1 2m chØ cã mét cùc trÞ khi A. m 1 B. m 0 C. 0 m 1
D. m 0 hoÆc m 1
Câu 21. Cho ®-êng cong (C) cã ph-¬ng tr×nh 2 y
x 2 , tÞnh tiÕn (C) theo phương trục hoành
sang tr¸i 3 ®¬n vÞ ta ®-îc ®-êng cong cã ph-¬ng tr×nh lµ A. 2 y x 2 3 B. 2 y
x 6x 11 C. 2 y x 2 3 D. 2 y x 6x 11 Câu 22. Cho hµm sè 3 2
y x 6x 3(m 2)x m 6 ®¹t cùc ®¹i, cùc tiÓu t¹i x , x sao cho 1 2
x 1 x th× gi¸ trÞ cña m lµ 1 2 A. m 1 B. m 1 C. m 1 D. m 1
Câu 23. Hàm số f cã ®¹o hµm 2 2
f '(x) x (2x 3) (3x 2) . Sè ®iÓm cùc trÞ cña hàm số f lµ A. 0 B. 3 C. 1 D. 2 x 2
Câu 24. Víi gi¸ trÞ nµo cña m th× ®å thÞ hµm sè y 2 x 4x
chØ cã mét tiÖm cËn ®øng vµ mét m tiÖm cËn ngang A. 4 B. 3 C. 2 D. 1 3 Câu 25. Cho hµm sè 4 2
y x 2x 1 cã ®å thÞ (C). §iÓm M trªn (C) cã hoµnh ®é x lµ ®iÓm 3 g× cña (C) A. §iÓm th-êng B. §iÓm uèn C. §iÓm cùc tiÓu D. §iÓm cùc ®¹i H 3/6 Mã đề 912
Câu 26. Số ®-êng th¼ng đi qua điểm M 0; 7
vµ tiÕp xóc víi đồ thị hàm số 4 2
y x 5x 7 là A. 1 B. 2 C. 3 D. 4
Câu 27. Khối tám mặt đều thuộc loại A. {3 ; 4} B. {4 ; 3} C. {3 ; 3} D. {3 ; 5}
Câu 28. Cho khối tứ diện ABCD. Lấy một điểm M nằm giữa A và B, một điểm N nằm giữa C và
D. Bằng hai mặt phẳng (MCD) và (NAB) ta chia khối tứ diện đã cho thành bốn khối tứ diện A. AMNC, AMND, AMCD, BMNC B. AMCD, AMND, BMNC, BMND C. AMNC, AMND, BMNC, BMND D. BMCD, BMND, AMNC, AMND
Câu 29. Số mặt phẳng đối xứng của hình bát diện đều là A. 3 B. 9 C. 6 D. 12
Câu 30. Thể tích của khối tám mặt đều có cạnh bằng a là 3 2 2 a 3 2 a 3 2 a A. B. 3 2 2 a C. D. 3 3 9
Câu 31. Cho hình hộp ABCD.A’B’C’D’ có thể tích V. Thể tích khối tứ diện ACB’D’ là V V V V A. B. C. D. 8 3 6 4
Câu 32. Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = a , AC = 2a và SA vuông
góc với đáy. Góc giữa (SBC) và (ABC) bằng 600. Thể tích khối chóp S.ABC bằng 3 a 3 a 3 3 a 3 3 3a A. B. C. D. 2 3 2 2
Câu 33. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a .
SA (ABC) và SA = a . Gọi (α) là mặt phẳng qua A và vuông góc với SB đồng thời cắt SB, SC tại
M, N. Khi đó thể tích khối chóp S.AMN bằng 3 a 3 a 3 a A. B. C. D. Đáp án khác 6 12 24 2 x 2
Câu 34. Mét trong c¸c h×nh d-íi ®©y, h×nh nµo cã b¶ng biÕn thiªn cña hµm sè y x 1 A. H×nh 4 B. H×nh 1 C. H×nh 3 D. H×nh 2
Câu 35. Cho điểm O và số thực k 0 . Mệnh đề nào dưới đây sai
A. Phép vị tự tâm O tỉ số k là một phép đồng dạng khi k 0
B. Phép vị tự tâm O tỉ số k luôn là một phép đồng dạng
C. Phép vị tự tâm O tỉ số k 1
là một phép đối xứng tâm
D. Phép vị tự tâm O tỉ số k 1 là một phép đồng nhất
Câu 36. Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất A. Năm mặt B. Hai mặt C. Bốn mặt D. Ba mặt H 4/6 Mã đề 912
Câu 37. Cho hình lăng trụ đứng MNP.M' N'P' có tất cả các cạnh bằng a . Thể tích của khối lăng trụ bằng 3 a 3 3 a 3 3 a 3 A. 3 a 3 B. C. D. 2 3 4
Câu 38. Cho tứ diện ABCD có trọng tâm G. Gọi A’, B’, C’, D’ lần lượt là trọng tâm các tam giác
BCD, CDA, ABD, ABC. Mệnh đề nào dưới đây đúng
A. A’, B’, C’, D’ đồng phẳng
B. A’B’C’D’ và ABCD là hai hình bằng nhau 1
C. Phép vị tự tâm G tỉ số
biến A’B’C’D’ thành ABCD 3 1
D. Phép vị tự tâm G tỉ số
biến ABCD thành A’B’C’D’ 3 Câu 39. Hàm số 4 3 2
y x 4x x 6x 10 có
A. Một cực tiểu và không có cực đại
B. Một cực đại và hai cực tiểu
C. Hai cực đại và một cực tiểu
D. Một cực đại và không có cực tiểu
Câu 40. Hµm sè y sin 2x 2 cos x cã gi¸ trÞ lín nhÊt trªn ®o¹n [– ; ] lµ 3 3 3 3 A. B. 3 C. 3 D. 2 2 x 3
Câu 41. Cho đồ thị (C) cña hàm số y
d y mx m . Ph-¬ng ¸n nµo
x vµ ®-êng th¼ng : 2 1 1 d-íi ®©y ®óng
A. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt
B. d lu«n ®i qua mét ®iÓm cè ®Þnh cña (C) khi m biÕn thiªn
C. (C) vµ d lu«n c¾t nhau t¹i hai ®iÓm ph©n biÖt khi m 0
D. (C) vµ d tiÕp xóc víi nhau khi m 2
Câu 42. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 1cm, SA 2cm và SA vuông góc với
đáy. Khoảng cách giữa hai đường thẳng BC và SD là A. 2 cm B. 1 cm C. 2 cm D. 5 cm
Câu 43. Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với đáy và AB = a ,
AD = 2a , góc giữa SB và đáy bằng 450. Thể tích khối chóp S.ABCD là 3 6 a 3 a 3 2 a A. B. C. 3 2a D. 18 3 3
Câu 44. Một hộp không nắp được làm từ mảnh các tông theo mẫu hình bên.
Hộp có đáy là hình vuông cạnh x (cm), chiều cao h (cm) và có thể tích là 4cm3.
Tìm giá trị của x sao cho diện tích của mảnh các tông nhỏ nhất A. 8 cm B. 2 cm C. 4 cm D. 3 2 2 cm H 5/6 Mã đề 912 mx m
Câu 45. §å thÞ cña hµm sè y
c¾t ®-êng th¼ng d: y x 6 t¹i hai ®iÓm ph©n biÖt thuéc x hai nh¸nh cña nã khi: A. m 6 B. m 0 C. m 0 D. m 0
Câu 46. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AC = 2a , tam
giác SAC đều và nằm trên mặt phẳng vuông góc với đáy. Trên cạnh SA lấy điểm M sao cho
MA = 2MS. Mặt phẳng (α) qua M và song song với (ABC) cắt SB, SC tại N, P. Khi đó thể tích khối
chóp cụt ABC.MNP bằng 3 26 3a 3 a 3 3 80 3a 3 2 3a A. B. C. D. . 81 3 81 9 Câu 47. Cho hµm sè 3
y x 3x 1 cã ®å thÞ (C), mét ®-êng th¼ng qua M(1; 3) vµ tiÕp xóc víi
(C) c¾t (C) t¹i ®iÓm thø hai N (N kh«ng trïng M). Khi ®ã täa ®é ®iÓm N lµ 1 3 A. (2; –1) B. (–1; –1) C. ; D. (0; 1) 2 8 x
Câu 48. Cho ®å thÞ (C) cña hàm số y y x . MÖnh ®Ò nµo d-íi ®©y
x vµ ®-êng th¼ng d: 4 1 ®óng A. d vµ (C) kh«ng c¾t nhau
B. d vµ (C) c¾t nhau t¹i hai ®iÓm ph©n biÖt C. d vµ (C) tiÕp xóc
D. d lµ tiÖm cËn xiªn cña (C)
Câu 49. Cho hình lập phương ABCD.A’B’C’D’ cạnh a , tâm O. Thể tích khối tứ diện AA’B’O là 3 a 3 a 3 a 3 2 a A. B. C. D. 12 8 9 3 1 1 Câu 50. Hàm số 3 2 y
x x x có đồ thị là 3 3
A. Đồ thị trên hình 1 B. Đồ thị trên hình 2
C. Đồ thị trên hình 3 D. Đồ thị trên hình 4.
Cán bộ coi kiểm tra không giải thích gì thêm H 6/6 Mã đề 912




