TOP15 đề ôn tập học kỳ 1 Toán 10 năm học 2020 – 2021 – Đặng Việt Đông

ĐẶNG VIỆT ĐÔNG

15 ĐỀ ÔN TẬP HỌC KỲ I

MÔN TOÁN – LỚP 10

NĂM HỌC 2020 - 2021

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 1 Môn Toán – Lớp 10

(Th

ời gian l

àm bài 90 phút)

Không k

ể thời gian phát đề

Câu 1. Cho tam giác

ABC

, trọng tâm

G

, gọi

I

là trung điểm

BC

,

M

là điểm thỏa mãn:

2 3

MA MB MC MB MC

   

    

. Khi đó tập hợp điểm

M

là:

A. Đường trung trực của

IG

. B. Đường tròn tâm

I

, bán kính

BC

.

C. Đường tròn tâm

G

, bán kính

BC

. D. Đường trung trực của

BC

.

Câu 2. Giá trị

2

x



là điều kiện của phương trình nào sau đây?

A.

1

2 0.

x x

x

   

B.

1

2

4

x x

x

  



.

C.

1

0

2

x

 



. D.

1

2 1

2

x x

x

  



.

Câu 3. Tìm tất cả các giá trị của

m

để hai đồ thị hàm số

2

2 3

y x x

   

và

2

y x m

 

có điểm

chung?

A.

7

2

m

 

. B.

7

2

m

 

. C.

7

2

m

 

. D.

7

2

m

 

.

Câu 4. Cho mệnh đề

2

" , 3 2 0"

x x x

    



. Mệnh đề phủ định của mệnh đề trên là:

A.

2

, 3 2 0

x x x

    



. B.

2

, 3 2 0

x x x

    



.

C.

2

, 3 2 0

x x x

    



. D.

2

, 3 2 0

x x x

    



.

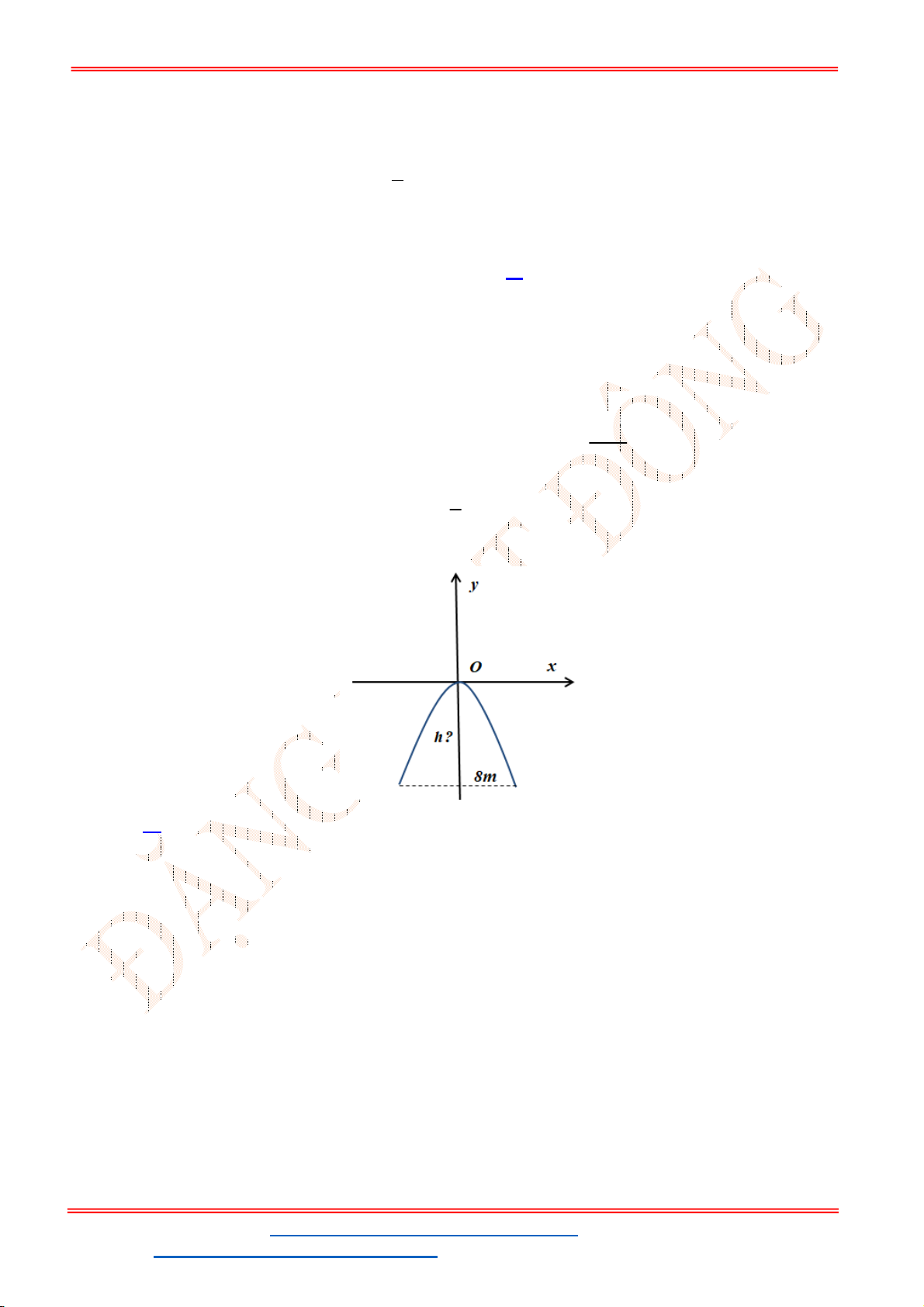
Câu 5. Một chiếc cổng hình parabol dạng

2

1

2

y x

  có chiều rộng

8

d m



. Hãy tính chiều cao

h

của

cổng? (Xem hình minh họa dưới đây).

A.

8

h m



. B.

9

h m



. C.

7

h m



. D.

5

h m



.

Câu 6. Xác định phương trình của parabol

2

y ax bx c

  

đi qua 3 điểm





0; 1

A



,





1; 1

B



,





1;1

C  ?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

2

1

y x x

  

. B.

2

1

y x x

  

. C.

2

1

y x x

  

. D.

2

1

y x x

  

.

Câu 7. Biết rằng đồ thị hàm số

y ax b

 

đi qua điểm





2; 1

E



và song song với đường thẳng

ON

với

O

là gốc tọa độ và





1;3

N . Tính giá trị biểu thức

2 2

S a b

 

.

A.

40

S

 

. B.

58

S



. C.

4

S

 

. D.

58

S

 

.

Câu 8. Cho tập hợp





1;5

A  và





; 1

B m m

 

. Có bao nhiêu giá trị nguyên của

m

để

A

giao

B

là

một khoảng?

A. 5. B. 3. C. 4. D. 2.

Câu 9. Cho hàm số

 

2

2 1 khi 0

3 khi 0

x x

y f x

x x

 



 







. Giá trị của biểu thức









1 1

P f f

   là:

A.

2



. B.

0

. C.

1

. D.

4

.

Câu 10. Cho





2

: 12 35 0

A xx x  



 ,

1

: 0

7

x

B x

x



 

  

 



 

 . Tập

\

B A

là:

A.





1; 5 {7}

 . B.





1; 5 {7}

 . C.





1; 5

. D.





1; 5

.

Câu 11. Véctơ có điểm đầu là

A

, điểm cuối là

B

được kí hiệu là:

A.

AB

. B.

AB



. C.

AB



. D.

BA



.

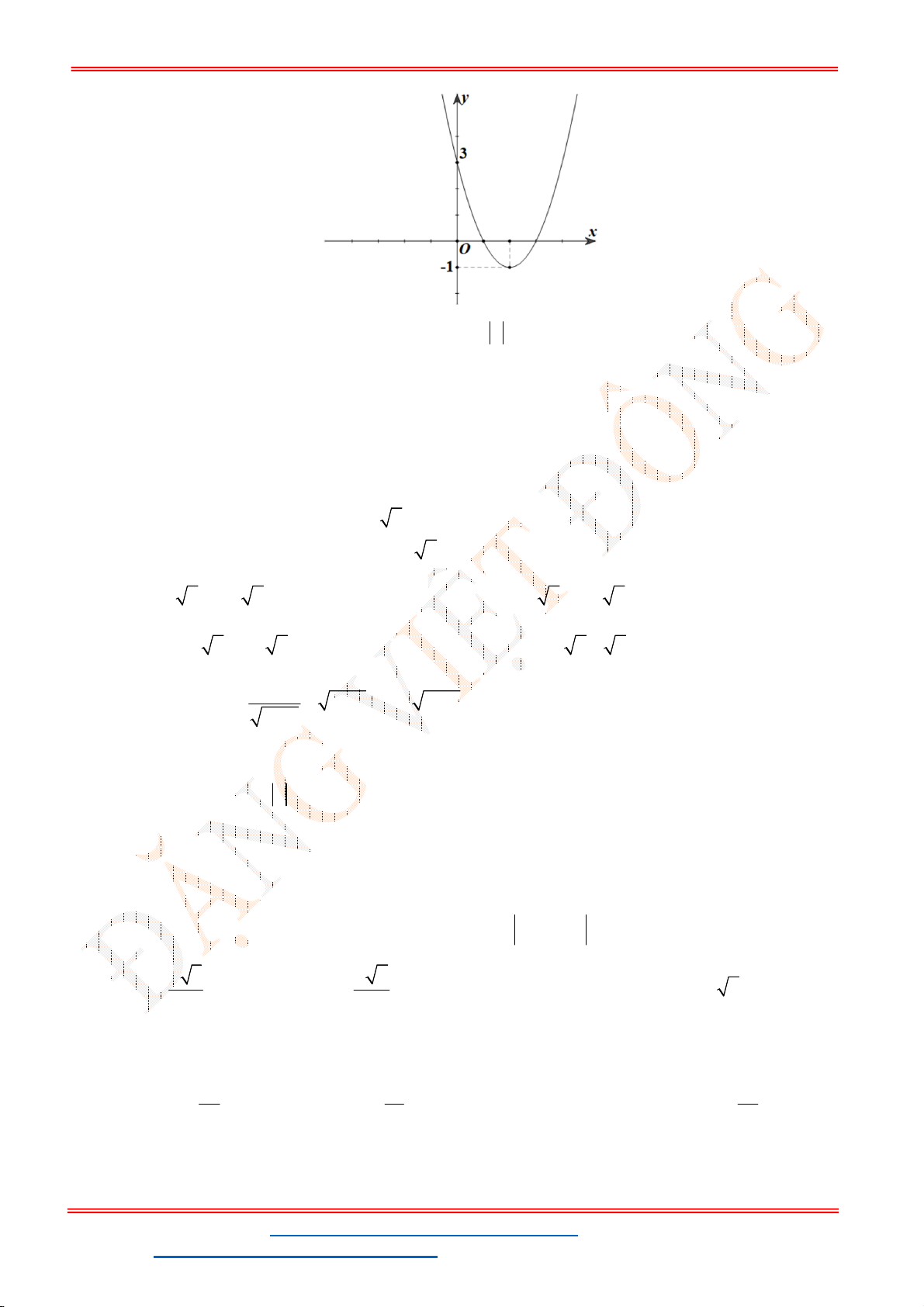
Câu 12. Cho đồ thị hàm số





2

2 1

y x x P

   (hình vẽ sau). Dựa vào đồ thị





P

xác định số giá trị

nguyên dương của

m

để phương trình

2

2 2 2 0

x x m

   

có nghiệm





1;2 ?

x 

A.

3

. B.

0

. C.

1

. D.

2

.

Câu 13. Biểu thức





4 2 2 2

cos cos sin sin

f x x x x x

   có giá trị bằng:

A.

1



. B.

2

. C.

2



. D.

1

.

Câu 14. Cho tập hợp





;3

A   ,





5

B x x

  

 ,





1;7

C  . Tập hợp





A B C

  là:

A.





1;5

. B.





5;7

. C.



. D.





1;3

.

Câu 15. Có bao nhiêu giá trị thực của

m

để phương trình





2 2

1 2

m x m m

   

vô nghiệm?

A. 2. B. 0. C. 1. D. 3.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 16. Cho tam giác

OAB

vuông cân tại

O

, cạnh

4

OA



. Tính

2

OA OB



 

.

A.

2 4 5

OA OB 

 

. B.

2 12 5

OA OB 

 

.

C.

2 4

OA OB

 

 

. D.

2 12

OA OB

 

 

.

Câu 17. Trong mặt phẳng tọa độ

Oxy

, cho tam giác

ABC

có













5;3 , 2; 1 , 1;5

A B C  . Gọi





;

H a b

là trực tâm của tam giác

ABC

. Tính tổng

a b



?

A.

1

. B.

5

. C.

5



. D.

1



.

Câu 18. Trong mặt phẳng tọa độ

Oxy

, cho tam giác

ABC

có













1; 2 , 1;1 , 5 ; 1

A B C

 

. Tính

cos

A

?

A.

1

5



. B.

1

5

. C.

2

5



. D.

2

5

.

Câu 19. Trong





1;10

có bao nhiêu giá trị nguyên của

m

để phương trình

2

1 2

m x x m

x

  





có hai

nghiệm phân biệt?

A.

7

. B.

9

. C.

10

. D.

8

.

Câu 20. Trong hệ toạ độ

Oxy

, cho tam giác

ABC

với









2;3 , 4; 1

A B

 

, trọng tâm của tam giác là





2; 1

G



. Toạ độ đỉnh

C

là:

A.





6; 4



. B.





2;1

. C.





4; 5



. D.





6; 3



.

Câu 21. Phương trình

1 3

x x

  

có một nghiệm nằm trong khoảng nào sau đây?

A.





5;9

. B.





1;3

. C.





4;7

. D.





0;2

.

Câu 22. Tập tất cả các giá trị của

m

để phương trình





2

2 2 1 0

m x mx

   

có hai nghiệm trái dấu là:

A.





1;2

m  . B.





\ 2





.

C.





; 2

m

  

. D.









; 1 2;m

    

.

Câu 23. Giả sử

1

x

và

2

x

là hai nghiệm của phương trình

2

3 10 0

x x

  

. Giá trị của tổng

1 2

1 1

x x



là:

A.

3

10

. B.

10

3

. C.

10

3



. D.

3

10



.

Câu 24. Phương trình

2 3 1

x

 

tương đương với phương trình nào dưới đây?

A.

3 2 3 1 3

x x x

     

. B. 2 3

x x x

 

.

C.





3 2 3 3

x x x

   

. D.





4 2 3 4

x x x

   

.

Câu 25. Tìm tất cả các giá trị của

m

để phương trình





2

1 1 0

m x m

   

có nghiệm duy nhất?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

1

m



. B.

1

m



hoặc

1

m

 

.

C.

1

m

 

. D.

1

m



và

1

m

 

.

Câu 26. Tính tổng tất cả các nghiệm của phương trình:

2 3 5

x x

  

?

A.

1

4

. B.

1

4



. C.

13

4



. D.

13

4

.

Câu 27. Cho tập





:1 2 7

S x x

    

 . Trong các tập sau đây, tập nào bằng tập

S

?

A.









;3 1;

  

. B.









6;1 3;10

  .

C.









;1 3;

  

. D.









5;1 3;9

  .

Câu 28. Trong mặt phẳng tọa độ

Oxy

, cho hai điểm





3;2

A  ,





4;3

B . Tìm điểm

M

thuộc trục

Ox

và

có hoành độ dương để tam giác

MAB

vuông tại

M

.

A.





7;0

M . B.





3;0

M . C.





9;0

M . D.





5;0

M .

Câu 29. Cho tam giác

ABC

có trọng tâm

G

. Khi đó:

A.

1 1

3 2

AG AB AC

 

  

. B.

1 1

2 2

AG AB AC

 

  

.

C.

1 1

3 3

AG AB AC

 

  

. D.

2 2

3 3

AG AB AC

 

  

.

Câu 30. Cho ba điểm

, ,

A B C

phân biệt. Tập hợp những điểm

M

mà

. .

CM CB CACB



   

là:

A. Đường thẳng đi qua

A

và vuông góc với

BC

.

B. Đường thẳng đi qua

B

và vuông góc với

AC

.

C. Đường thẳng đi qua

C

và vuông góc với

AB

.

D. Đường tròn đường kính

AB

.

Câu 31. Số nghiệm phương trình









4 2

2 5 5 7 1 2 0

x x

    

là:

A.

0

. B.

2

. C.

4

. D.

1

.

Câu 32. Trong hệ trục tọa độ

Oxy

, cho hai điểm





3;1

A  và





1; 3

B



. Tọa độ của vectơ

AB



là:

A.





1; 1

 

. B.





4;4

 . C.





4; 4



. D.





2; 2

 

.

Câu 33. Hình vẽ sau đây là biểu diễn trên trục số của tập hợp nào sau đây?

A.





\ 1;5



. B.





\ 1;5



. C.





\ 1;5



. D.





\ 1;5



.

Câu 34. Cho hàm số





2

y f x ax bx c

   

có đồ thị sau:

]

(

1

5

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Có bao nhiêu giá trị nguyên của

m

để

2

1

ax b x c m

   

có bốn nghiệm phân biệt?

A.

3

. B.

4

. C.

2

. D.

5

.

Câu 35. Cho tam giác

ABC

. Điểm

M

thỏa mãn

2

AB AC AM

 

  

. Chọn khẳng định đúng?

A.

M

trùng với

A

. B.

M

là trọng tâm của tam giác

ABC

.

C.

M

trùng với

B

hoặc

C

. D.

M

là trung điểm của

BC

.

Câu 36. Nghiệm của hệ phương trình:

2 1

3 2 2

x y



 





 





là:

A.





2 2;2 2 3

 

. B.





2 2;2 2 3

 

.

C.





2 2;3 2 2

 

. D.





2 2;2 2 3

 

.

Câu 37. Phương trình

4

2 2

2

x x x

x

    



có bao nhiêu nghiệm?

A.

1

. B.

2

. C. Vô số. D.

0

.

Câu 38. Cho





: 5

A x x

  

 . Phần bù của

A

trong tập số thực là:

A.





5;5

 . B.









; 5 5;

   

.

C.









; 5 5;

   

. D.





5;5

 .

Câu 39. Cho hình vuông

ABCD

có cạnh bằng

a

. Độ dài

AD AB



 

bằng:

A.

3

2

a

. B.

2

a

. C.

2

a

. D.

2

a

.

Câu 40. Trong hệ tọa độ

Oxy

, cho điểm





3; 2

A



,





4;5

B . Tìm tọa độ điểm

M

trên trục hoành sao

cho

A

,

B

,

M

thẳng hàng?

A.

24

;0

7

M

 

 

 

. B.

17

;0

7

M

 

 

 

. C.





1;0

M . D.

23

;0

7

M

 

 

 

.

Câu 41. Đồ thị hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án

A

,

B

,

C

,

D

dưới đây. Hỏi hàm số đó là hàm số nào?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

2

2 1

y x x

  

. B.

2

3 6 1

y x x

  

. C.

2

2 1

y x x

   

. D.

2

3 6

y x x

  

.

Câu 42. Cho 3 điểm

M

,

N

,

P

thẳng hàng trong đó

N

nằm giữa

M

và

P

. khi đó các cặp véc tơ nào

sau đây cùng hướng?

A.

MN



và

MP



. B.

MN



và

PN



. C.

NM



và

NP



. D.

MP



và

PN



.

Câu 43. Số nghiệm của phương trình :





2

4 3 2 0

x x x

   

là:

A.

2

. B.

3

. C.

1

. D.

4

.

Câu 44. Cho hàm số

2

( ) 2( 6) 2

y f x mx m x

    

. Có bao nhiêu giá trị nguyên của tham số

m

để

hàm số

( )

f x

nghịch biến trên khoảng





;2

 ?

A.

3

. B. vô số. C.

1

. D.

2

.

Câu 45. Tập xác định của hàm số

1

3

y x

x

  



là:

A.





\ 3

D 



. B.





3;D

 

. C.





3;D

 

. D.





;3

D   .

Câu 46. Cho góc



tù. Khẳng định nào sau đây là đúng?

A.

tan 0





. B.

cos 0





. C.

cot 0





. D.

sin 0





.

Câu 47. Trong mặt phẳng tọa độ

Oxy

, cho hai điểm





2; 5

A



và





4;1

B . Tọa độ trung điểm

I

của

đoạn thẳng

AB

là:

A.





3; 2

I



. B.





3;2

I . C.





1;3

I . D.





1; 3

I

 

.

Câu 48. Trong một lớp học có

100

học sinh,

35

học sinh chơi bóng đá và

45

học sinh chơi bóng

chuyền,

10

học sinh chơi cả hai môn thể thao. Hỏi có bao nhiêu học sinh không chơi môn thể

thao nào? (Biết rằng chỉ có hai môn thể thao là bóng đá và bóng chuyền).

A.

60

. B.

70

. C.

30

. D.

20

.

Câu 49. Trong mặt phẳng tọa độ

Oxy

, tìm tọa độ của điểm

N

trên cạnh

BC

của tam giác

ABC

biết:





2; 1

A



,





3;4

B ,





0; 1

C



và 3S

ABN ACN

S

 

 (Trong đó , S

ABN ACN

S

 

lần lượt là diện tích

các tam giác

ABN

và

ACN

) ?

A.

1 1

;

3 3

N

 



 

 

. B.

3 1

;

4 4

N

 

 

 

. C.

1 1

;

3 3

N

 



 

 

. D.

1 3

;

4 4

N

 

 

 

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 50. Cho tam giác

ABC

cân tại

A

có cạnh bên bằng

6

và góc



120

BAC

 

. Điểm

M

thuộc cạnh

AB

sao cho

1

3

AM AB

 và điểm

N

là trung điểm của cạnh

AC

. Tính tích vô hướng

.

BN CM

 

.

A.

51



. B.

9



. C.

9

. D.

51

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG HDG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 1 Môn Toán – Lớp 10

(Th

ời gian l

àm bài 90 phú

t)

Không k

ể thời gian phát đề

Câu 1. Cho tam giác

ABC

, trọng tâm

G

, gọi

I

là trung điểm

BC

,

M

là điểm thỏa mãn:

2 3

MA MB MC MB MC

   

    

. Khi đó tập hợp điểm

M

là:

A. Đường trung trực của

IG

. B. Đường tròn tâm

I

, bán kính

BC

.

C. Đường tròn tâm

G

, bán kính

BC

. D. Đường trung trực của

BC

.

Lời giải

Chọn A

Theo tính chất trọng tâm và trung điểm ta có:

3

MA MB MC MG

  

   

;

2

MB MC MI

 

  

.

Khi đó:

2 3

MA MB MC MB MC

   

    

2 3 3 2

MG MI

 

 

6 6

MG MI

 

MG MI

 

M



thuộc đường trung trực của đoạn

IG

.

Câu 2. Giá trị

2

x



là điều kiện của phương trình nào sau đây?

A.

1

2 0.

x x

x

   

B.

1

2

4

x x

x

  



.

C.

1

0

2

x

 



. D.

1

2 1

2

x x

x

  



.

Lời giải

Chọn A

Xét đáp án A. Phương trình

1

2 0

x x

x

   

có điều kiện xác định là

0 0

2

2 0 2

x x

x

x x

 

 

  

 

  

 

.

Câu 3. Tìm tất cả các giá trị của

m

để hai đồ thị hàm số

2

2 3

y x x

   

và

2

y x m

 

có điểm

chung?

A.

7

2

m

 

. B.

7

2

m

 

. C.

7

2

m

 

. D.

7

2

m

 

.

Lời giải

Chọn D

Phương trình hoành độ giao điểm của đồ thị hai hàm số đã cho là:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

2 2 2

2 3 2 2 3 0

x x x m x x m

         

(1)

Hai đồ thị của hai hàm số đã cho có điểm chung khi và chỉ khi





1

có nghiệm

7

' 0 7 2 0

2

m m

        

.

Câu 4. Cho mệnh đề

2

" , 3 2 0"

x x x

    



. Mệnh đề phủ định của mệnh đề trên là:

A.

2

, 3 2 0

x x x

    



. B.

2

, 3 2 0

x x x

    



.

C.

2

, 3 2 0

x x x

    



. D.

2

, 3 2 0

x x x

    



.

Lời giải

Chọn B

Phủ định của mệnh đề





" , "

x p x

 



là mệnh đề

 

" , "

x p x

   .

Câu 5. Một chiếc cổng hình parabol dạng

2

1

2

y x

  có chiều rộng

8

d m



. Hãy tính chiều cao

h

của

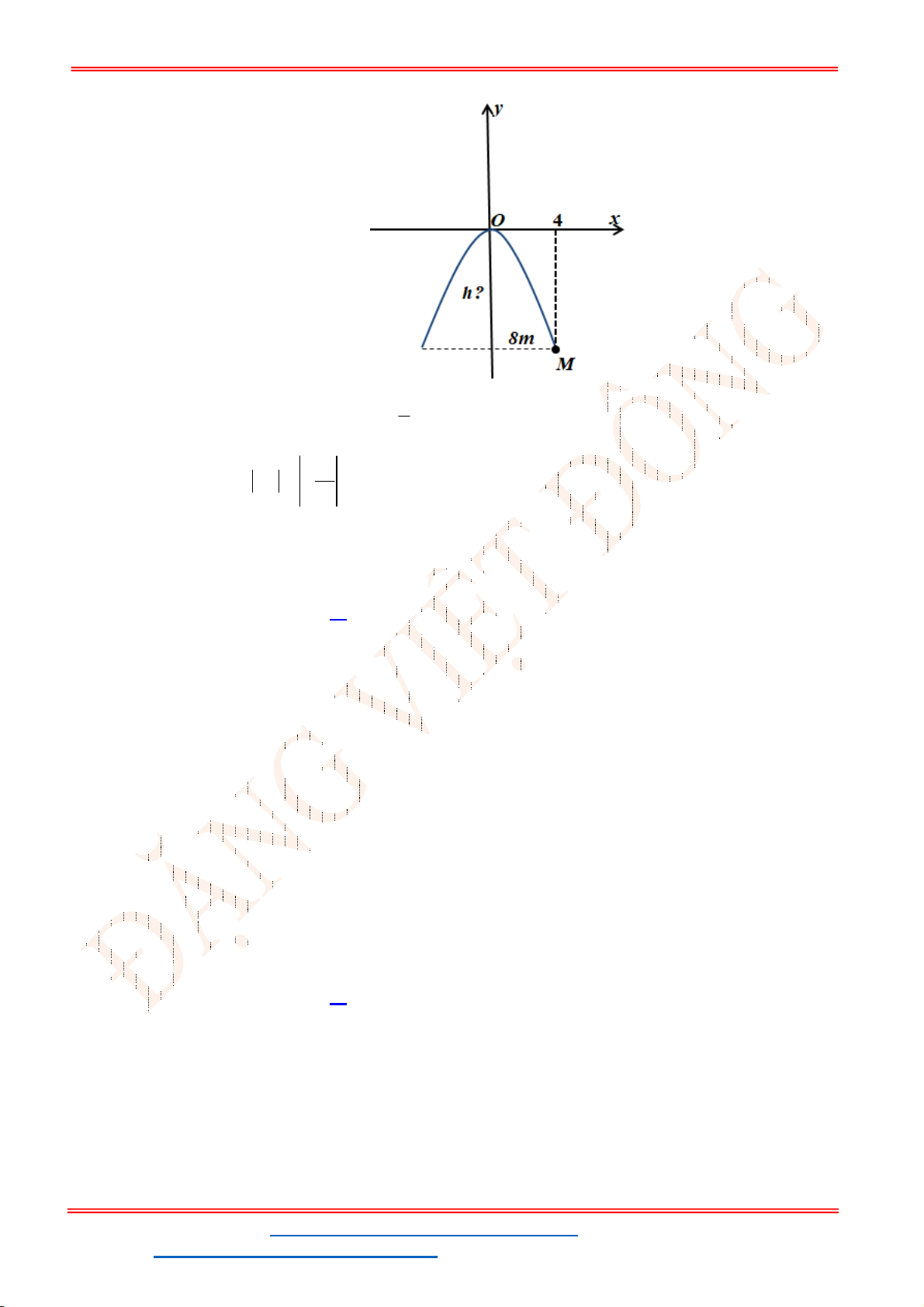
cổng? (Xem hình minh họa dưới đây).

A.

8

h m



. B.

9

h m



. C.

7

h m



. D.

5

h m



.

Lời giải

Chọn A

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Dựa vào đồ thị hàm parabol

2

1

2

y x

  ta có hoành độ điểm

M

là 4.

Chiều cao

2

4

8

2

M

h y

   

.

Câu 6. Xác định phương trình của parabol

2

y ax bx c

  

đi qua 3 điểm





0; 1

A



,





1; 1

B



,





1;1

C  ?

A.

2

1

y x x

  

. B.

2

1

y x x

  

. C.

2

1

y x x

  

. D.

2

1

y x x

  

.

Lời giải

Chọn B

Do parabol đi qua

3

điểm





0; 1

A



,





1; 1

B



,





1;1

C  nên ta có hệ phương trình

0. 0. 1 1

1 1

a b c a

a b c b

a b c c

    

 

 

      

 

 

    

 

Vậy phương trình của parabol cần tìm là

2

1

y x x

  

.

Câu 7. Biết rằng đồ thị hàm số

y ax b

 

đi qua điểm





2; 1

E



và song song với đường thẳng

ON

với

O

là gốc tọa độ và





1;3

N . Tính giá trị biểu thức

2 2

S a b

 

.

A.

40

S

 

. B.

58

S



. C.

4

S

 

. D.

58

S

 

.

Lời giải

Chọn B

Gọi :

d y ax b

 

Vì đường thẳng

ON

đi qua gốc tọa độ nên phương trình có dạng

'

y a x



.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay





1;3 3 .1 3

N ON a a

 

    

.

Vì

d

song song với

ON

nên

3, 0

a b

 

.





2; 1 1 3.2 7

E d b b

        

(nhận).

Vậy

2 2

58

S a b

  

.

Cách khác: vì

2 2

0

S a b

  

Câu 8. Cho tập hợp





1;5

A  và





; 1

B m m

 

. Có bao nhiêu giá trị nguyên của

m

để

A

giao

B

là

một khoảng?

A. 5. B. 3. C. 4. D. 2.

Lời giải

Chọn C

Để

A B



là một khoảng thì

1 1

0 5

5

m

 



  







.

Vậy





1;2;3;4

m . Chọn đáp án C.

Câu 9. Cho hàm số

 

2

2 1 khi 0

3 khi 0

x x

y f x

x x

 



 







. Giá trị của biểu thức









1 1

P f f

   là:

A.

2



. B.

0

. C.

1

. D.

4

.

Lời giải

Chọn D

   

2

1 3. 1 3

f

   

.





1 2.1 1 1

f

  

.

Vậy









1 1 3 1 4

P f f

     

.

Câu 10. Cho





2

: 12 35 0

A xx x  



 ,

1

: 0

7

x

B x

x



 

  

 



 

 . Tập

\

B A

là:

A.





1; 5 {7}

 . B.





1; 5 {7}

 . C.





1; 5

. D.





1; 5

.

Lời giải

Chọn D

Ta có:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

 

2

5 0

7 0

5

12 35 0 ( 5)( 7) 0 5; 7

7

5 0

7 0

x

x x x x

x

  







 









          







 









 







.





7

1 0

7

7 1

1

7 0

0 1 1; 7

( 1)( 7) 0 7

7

1 0

7 0

x

x x

x

x x

x x x

x







  







 

  





 

 

       

    



   



 

 





 













 









.

Dẫn đến









2

7

: 12 3

5;

5 0A x xx    .





1

: 0 1x

; 7

7

B

x



 

 



 









 .

Vậy









:1 5 1; 5 .

\B A xx   



Câu 11. Vectơ có điểm đầu là

A

, điểm cuối là

B

được kí hiệu là:

A.

AB

. B.

AB



. C.

AB



. D.

BA



.

Lời giải

Chọn B.

Câu 12. Cho đồ thị hàm số





2

2 1

y x x P

   (hình vẽ sau). Dựa vào đồ thị





P

xác định số giá trị

nguyên dương của

m

để phương trình

2

2 2 2 0

x x m

   

có nghiệm





1;2 ?

x 

A.

3

. B.

0

. C.

1

. D.

2

.

Lời giải

Chọn D

Ta có phương trình

2 2

2 2 2 0 2 1 1 2

x x m x x m

        





1

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Khi đó, nghiệm của phương trình





1

là số giao điểm của đồ thị





P

và đường thẳng

1 2 .

y m

 

Dựa vào đồ thị





P

, để phương trình

2

2 2 2 0

x x m

   

có nghiệm





1;2

x  thì

1 3

2 1 2 2 3 2 1 .

2 2

m m m



           

Vậy có

2

giá trị nguyên dương là

0, 1.

m m

 

Câu 13. Biểu thức





4 2 2 2

cos cos sin sin

f x x x x x

   có giá trị bằng:

A.

1



. B.

2

. C.

2



. D.

1

.

Lời giải

Chọn D

Ta có





4 2 2 2

cos cos sin sin

f x x x x x

  





2 2 2 2

2 2

cos cos sin sin

cos sin

1.

x x x x

x x

  

 



Câu 14. Cho tập hợp





;3

A   ,





5

B x x

  

 ,





1;7

C  . Tập hợp





A B C

  là

A.





1;5

. B.





5;7

. C.



. D.





1;3

.

Lời giải

Chọn D

Ta có:





5

B x x

  







5;B

  

.





1;B C

  

.

Suy ra:









1;3

A B C   .

Câu 15. Có bao nhiêu giá trị thực của

m

để phương trình





2 2

1 2

m x m m

   

vô nghiệm?

A. 2. B. 0. C. 1. D. 3.

Lời giải

Chọn C

Để phương trình

ax b



vô nghiệm thì

0

a

b











.

Do đó

2

1

1 0

1 1.

2 0

2

m

m m

m

 



 

 

    

 

  



 





ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Vậy chỉ có duy nhất một giá trị

m

thỏa mãn yêu cầu đề bài.

Câu 16. Cho tam giác

OAB

vuông cân tại

O

, cạnh

4

OA



. Tính

2

OA OB



 

.

A.

2 4 5

OA OB 

 

. B.

2 12 5

OA OB 

 

.

C.

2 4

OA OB

 

 

. D.

2 12

OA OB

 

 

.

Lời giải

Chọn A

Cách 1:

Theo giả thiết ta có:

4

. 0

OA OB

OAOB

 













 

Khi đó

2

2 2

2 4O 4 . 80

OA OB A OB OAOB

    

   

.

Vậy

2 4 5

OA OB 

 

.

Cách 2:

Trong mặt phẳng

Oxy

, chọn









, 0;4

0;4A B .

Suy ra tọa độ vectơ

2

u OA OB

 

  

là

(8; 4)

u

 



.

Vậy

2 4 5

u OA OB  

  

.

Câu 17. Trong mặt phẳng tọa độ

Oxy

, cho tam giác

ABC

có













5;3 , 2; 1 , 1;5

A B C  . Gọi





;

H a b

là trực tâm của tam giác

ABC

. Tính tổng

a b



?

A.

1

. B.

5

. C.

5



. D.

1



.

Lời giải

Chọn B

Ta có

   

5; 3 ; 3;6

2; 1 ; 6;2

AH a b BC

BH a b AC



    





    





 

Do





;

H a b

là trực tâm của tam giác

ABC

nên ta có:









   

3 5 6 3 0

. 0 3

5

2

6 2 2 1 0

. 0

a b

AH BC a

a b

b

a b

BH AC



    

 



 

    

  



    









 

.

Câu 18. Trong mặt phẳng tọa độ

Oxy

, cho tam giác

ABC

có













1; 2 , 1;1 , 5 ; 1

A B C

 

. Tính

cos

A

?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

1

5



. B.

1

5

. C.

2

5



. D.

2

5

.

Lời giải

Chọn A

Ta có









2; 1 , 4 ; 3

AB AC

  

 

.

 









     

2 2 2

2

2.4 1 . 3

. 1

cos cos ;

5

.

2 1 . 4 3

AB AC

A AB AC

AB AC

   



   

    

 

.

Câu 19. Trong





1;10

có bao nhiêu giá trị nguyên của

m

để phương trình

2

1 2

m x x m

x

  





có hai

nghiệm phân biệt?

A.

7

. B.

9

. C.

10

. D.

8

.

Lời giải

Chọn D

Điều kiện:

1

x



.

Với điều kiện đó

2

1 2

m x x m

x

  









1













   

2

2 2 1

4 2 2

3 4 0 2 .

m x x m x

m x x x mx m

x m x m

     

      

      

     

2 2

2

3 4.1 4 10 25 5

m m m m m

          

Để phương trình





1

có hai nghiệm phân biệt thì phương trình





2

có hai nghiệm phân biệt

khác

1



. Do đó

 

    

2

5 0

5 5

2 6 0 3

1 3 1 4 0

m

m m



 

 

 



 

  

  

 

       





.

Vì





1;10

m nên

m

nhận

8

giá trị nguyên là :

1;2;4;6;7;8;9;10.

Câu 20. Trong hệ toạ độ

Oxy

, cho tam giác

ABC

với









2;3 , 4; 1

A B

 

, trọng tâm của tam giác là





2; 1

G



. Toạ độ đỉnh

C

là:

A.





6; 4



. B.





2;1

. C.





4; 5



. D.





6; 3



.

Lời giải

Chọn C.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Vì

G

là trọng tâm tam giác

ABC

nên

 

2 4

2

4

3

3 1 5

1

3

C

A B C

G

C

A B C C C

G

x

x x x

x

y y y y y

y

  

  











 

 

  

      



 



 





.

Vậy toạ độ đỉnh

C

là





4; 5



.

Câu 21. Phương trình

1 3

x x

  

có một nghiệm nằm trong khoảng nào sau đây ?

A.





5;9

. B.





1;3

. C.





4;7

. D.





0;2

.

Lời giải

Chọn C

 

2

2 2

3

3 0

3 3

1 3 5

5

1 6 9 7 10 0

1 3

2

x

x x

x x x

x

x x x x x

x x

x





 



 

 

 

        





   

      

  



 











.

Vậy phương trình có nghiệm

5

x



.

Câu 22. Tập tất cả các giá trị của

m

để phương trình

2

( 2) 2 1 0

m x mx

   

có hai nghiệm trái dấu là:

A.





1;2

m  . B.





\ 2





.

C.





; 2

m

  

. D.









; 1 2;m

    

.

Lời giải

Chọn C

Phương trình có hai nghiệm trái dấu khi





2 .1 0 2

m m

    

.

Câu 23. Giả sử

1

x

và

2

x

là hai nghiệm của phương trình

2

3 10 0

x x

  

. Giá trị của tổng

1 2

1 1

x x



là:

A.

3

10

. B.

10

3

. C.

10

3



. D.

3

10



.

Lời giải

Chọn A

Theo hệ thức Vi-ét ta có:

1 2

3

b

x x

a



   

và

1 2

. 10

c

x x

a

  

.

1 2

1 2 1 2

1 1 3 3

. 10 10

x x

T

x x x x





    



.

Câu 24. Phương trình

2 3 1

x

 

tương đương với phương trình nào dưới đây?

A.

3 2 3 1 3

x x x

     

. B. 2 3

x x x

 

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

C.





3 2 3 3

x x x

   

. D.





4 2 3 4

x x x

   

.

Lời giải

Chọn B

+ Xét phương trình:

2 3 1

x

 

. Điều kiện:

3

2

x



.

Bình phương hai vế

2 3 1 2

x x

    

(TM).

+ Xét phương trình:

3 2 3 1 3

x x x

     





A

Điều kiện:

3

2

3

x







 









.





A

2 3 1 2 3 1 2

x x x

       





KTM

.

+ Xét phương trình: 2 3

x x x

 





B

Điều kiện:

3

2

x



. Vì

3

2

x



nên:





B

2 3 1 2 3 1 2

x x x

       





TM

+ Xét phương trình:





3 2 3 3

x x x

   





C

Điều kiện:

3

2

x



.





C

 

3

3 2 3 1 0

2

2 3 1

x

x x

x









      





 







TM

.

+ Xét phương trình:





4 2 3 4

x x x

   





D

Điều kiện:

3

2

x



.





D

 

4

4 2 3 1 0

2

2 3 1

x

x x

x









      





 







TM

.

Vì phương trình ban đầu và phương trình





B

có cùng tập nghiệm nên hai phương trình tương

đương.

Câu 25. Tìm tất cả các giá trị của m để phương trình





2

1 1 0

m x m

   

có nghiệm duy nhất?

A.

1

m



. B.

1

m



hoặc

1

m

 

.

C.

1

m

 

. D.

1

m



và

1

m

 

.

Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Chọn D

Để phương trình có nghiệm duy nhất thì

2

1 0 1

m m

    

.

Câu 26. Tính tổng tất cả các nghiệm của phương trình:

2 3 5

x x

  

?

A.

1

4

. B.

1

4



. C.

13

4



. D.

13

4

.

Lời giải

Chọn D

Ta có phương trình tương đương với

 

3

2 3 5

2 3

2

4 7 7

2 3 5

4

x

x x

x

x x

x







  





 





   













.

Vậy tổng các nghiệm của phương trình là

3 7 13

2 4 4

 

.

Câu 27. Cho tập





:1 2 7

S x x

    

 . Trong các tập sau đây, tập nào bằng tập

S

?

A.









;3 1;

  

. B.









6;1 3;10

  .

C.









;1 3;

  

. D.









5;1 3;9

  .

Lời giải

Chọn D

Ta có





:1 2 7

S x x

    

 .

Xét bất phương trình

2 1 3

2 1

5 1

1 2 7

2 1 1

3 9

2 7

7 2 7 5 9

x x

x

x x

x

x x

    

 

  

  



  

 

      

   

  

 



 

 





 



      

 

.

Vậy









5;1 3;9

S    .

Câu 28. Trong mặt phẳng tọa độ

Oxy

, cho hai điểm





3;2

A  ,





4;3

B . Tìm điểm

M

thuộc trục

Ox

và

có hoành độ dương để tam giác

MAB

vuông tại

M

.

A.





7;0

M . B.





3;0

M . C.





9;0

M . D.





5;0

M .

Lời giải

Chọn B

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Gọi

( ;0)

M x

là điểm cần tìm thuộc trục

Ox

và

0

x



. Khi đó

( 3 ;2)

MA x

  



và

(4 ;3)

MB x

 



.

Vì tam giác

MAB

vuông tại

M

nên hai véctơ

MA



và

MB



vuông góc với nhau nên tích vô

hướng của chúng bằng 0.

MA



.

MB



3

0 ( 3 )(4 ) 6 0

2

x

x x

x





       



 



Vậy điểm cần tìm là

(3;0)

M .

Câu 29. Cho tam giác

ABC

có trọng tâm

G

. Khi đó:

A.

1 1

3 2

AG AB AC

 

  

. B.

1 1

2 2

AG AB AC

 

  

.

C.

1 1

3 3

AG AB AC

 

  

. D.

2 2

3 3

AG AB AC

 

  

.

Lời giải

Chọn C

G

M

C

B

A

Gọi

M

là trung điểm của

BC

.

Vì

G

là trọng tâm của tam giác

ABC

nên

2

.

3

AG AM



 

Mà





1

2 .

2

AB AC AM AM AB AC

    

     

Do đó









2 1 1

. .

3 2 3

AG AB AC AB AC

   

    

Câu 30. Cho ba điểm

, ,

A B C

phân biệt. Tập hợp những điểm

M

mà

. .

CM CB CACB



   

là:

A. Đường thẳng đi qua

A

và vuông góc với

BC

.

B. Đường thẳng đi qua

B

và vuông góc với

AC

.

C. Đường thẳng đi qua

C

và vuông góc với

AB

.

D. Đường tròn đường kính

AB

.

Lời giải

Chọn A

Ta có:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 20

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay





. . . . 0

CM CB CACB CM CA CB AM CB

    

         

.

AM CB

 

Vậy tập hợp điểm

M

là đường thẳng đi qua

A

và vuông góc với

BC

.

Câu 31. Số nghiệm phương trình









4 2

2 5 5 7 1 2 0

x x

    

là:

A.

0

. B.

2

. C.

4

. D.

1

.

Lời giải

Chọn B

Đặt





2

0

t x t

 

, khi đó phương trình đã cho trở thành:









2

2 5 5 7 1 2 0

t t

    





*









2

5 4 2 5 .7 1 2 0

     







*

có 2 nghiệm phân biệt

1

2

t t











Tích 2 nghiệm:





7 1 2

0

2 5

P



 









*

có 2 nghiệm phân biệt

1 2

,

t t

trái dấu:

1 2

0

t t

 

.

Vì

0

t



nên ta chỉ nhận

2

t t



. Khi đó :

2

2 2 2

t t x t x t

     

Vậy phương trình đã cho có

2

nghiệm phân biệt.

Câu 32. Trong hệ trục tọa độ

Oxy

, cho hai điểm





3;1

A  và





1; 3

B



. Tọa độ của vectơ

AB



là:

A.





1; 1

 

. B.





4;4

 . C.





4; 4



. D.





2; 2

 

.

Lời giải

Chọn C

Áp dụng công thức





;

B A B A

AB x x y y

  



Với





3;1

A  và





1; 3

B



, ta có:













1 3 ; 3 1 4; 4

AB

      



.

Câu 33. Hình vẽ sau đây là biểu diễn trên trục số của tập hợp nào dưới đây?

A.





\ 1;5



. B.





\ 1;5



. C.





\ 1;5



. D.





\ 1;5



.

Lời giải

Chọn C

Ta có:













\ 1;5 ;1 5;

   



.

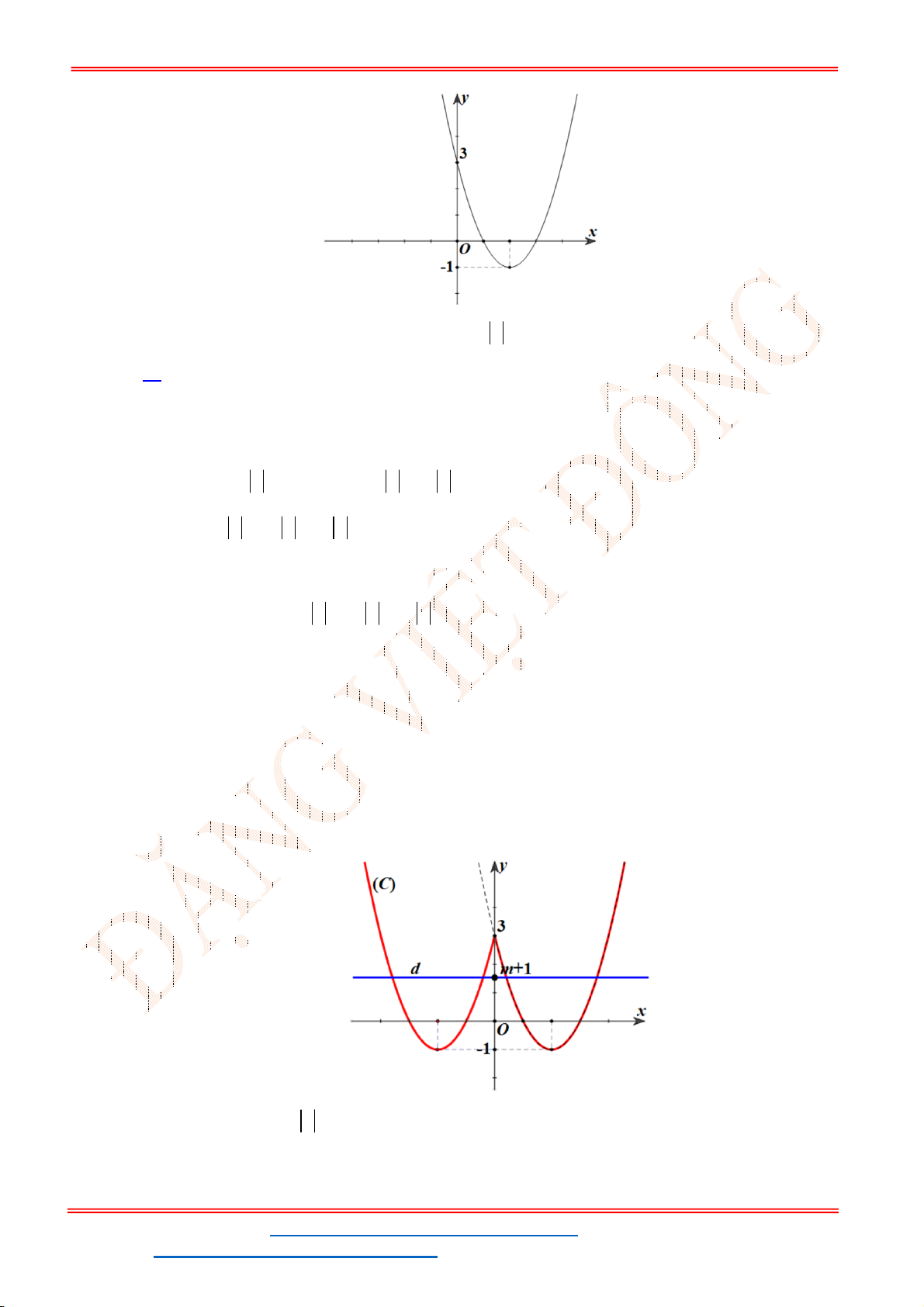
Câu 34. Cho hàm số





2

y f x ax bx c

   

có đồ thị sau

]

(

1

5

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 21

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Có bao nhiêu giá trị nguyên của

m

để

2

1

ax b x c m

   

có bốn nghiệm phân biệt?

A.

3

. B.

4

. C.

2

. D.

5

.

Lời giải

Chọn A.

Ta có:

2

1 1

ax b x c m a x b x c m

        

.

Gọi





2

y f x a x b x c

   

có đồ thị





.

P



1

y m

 

có đồ thị là đường thẳng

.

d

Vẽ đồ thị

 





2

: .

P y f x a x b x c



   

Từ hàm số





2

y f x ax bx c

   

có đồ thị





P

đã cho.

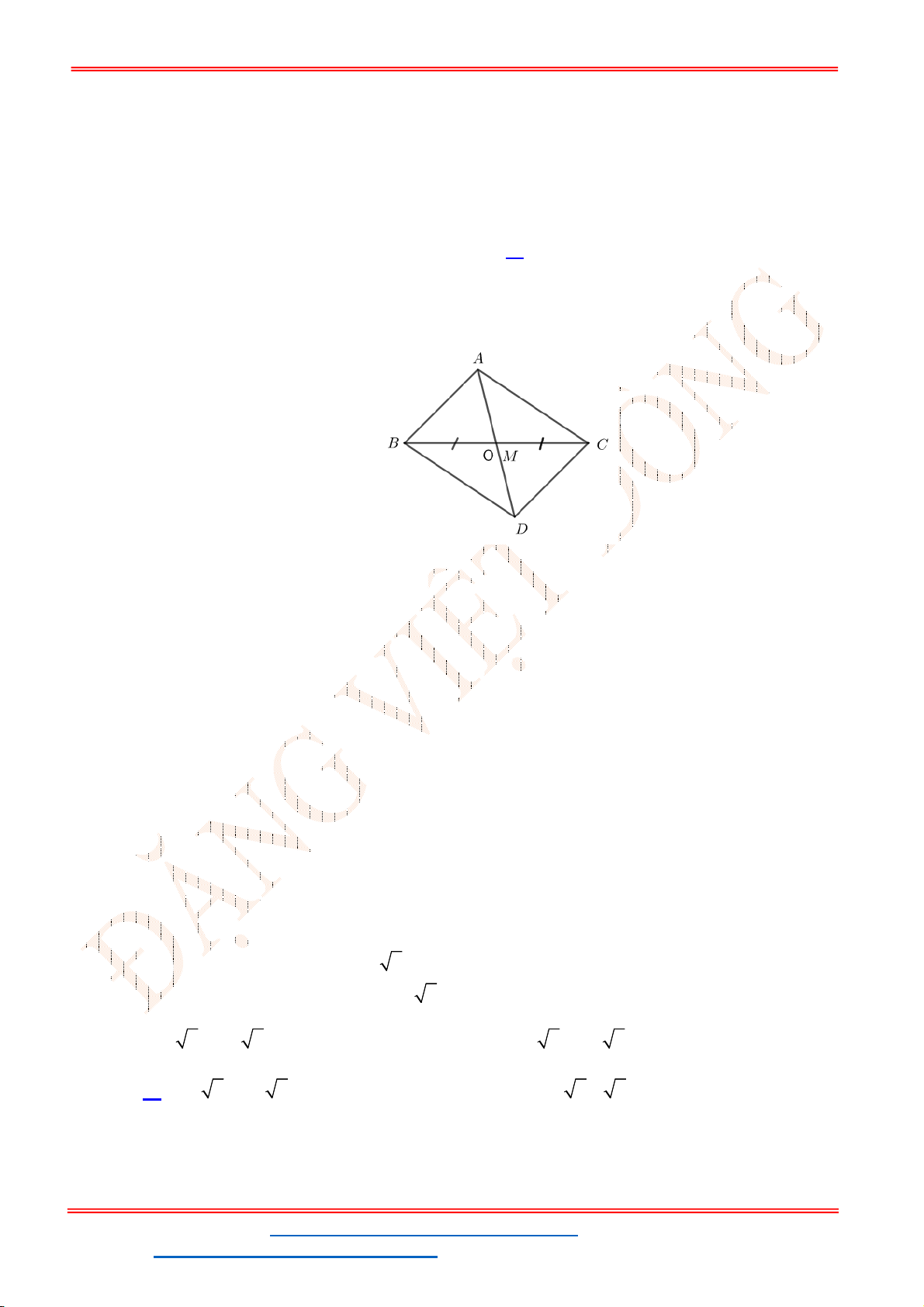
Đồ thị





P



gồm 2 phần:

Phần

1

: Giữ nguyên phần đồ thị





P

bên phải trục

Oy

và điểm





0;3

(Xóa phần đồ thị





P

bên trái trục

Oy

).

Phần

2

: Lấy đối xứng phần

1

qua trục

.

Oy

Phương trình

2

1

ax b x c m

   

có bốn nghiệm phân biệt





P



 và

d

có bốn điểm chung.

Dựa vào đồ thị





P



ta được

1 1 3 2 2.

m m

       

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 22

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Do

m

là số nguyên nên





1;0;1 .

m 

Vậy có

3

giá trị nguyên của

.

m

Câu 35. Cho tam giác

ABC

. Điểm

M

thỏa mãn

2

AB AC AM

 

  

. Chọn khẳng định đúng?

A.

M

trùng với

A

. B.

M

là trọng tâm của tam giác

ABC

.

C.

M

trùng với

B

hoặc

C

. D.

M

là trung điểm của

BC

.

Lời giải

Chọn D

Cách 1

Dựng hình bình hành

ABDC

,

O

là giao điểm hai đường chéo.

Khi đó

2

AB AC AD AO

  

   

.

M thỏa mãn

2

AB AC AM

 

  

0 0

AM AO AM AO OM M O

        

      

.

Vậy

M

là trung điểm của

BC

.

Cách 2

Ta có

2 2

0

AB AC AM AM MB AM MC AM

AM MB MC AM

MB MC

      

   

  

       

   

  

Vậy

M

là trung điểm của

BC

.

Câu 36. Nghiệm của hệ phương trình:

2 1

3 2 2

x y



 





 





là:

A.





2 2;2 2 3

 

. B.





2 2;2 2 3

 

.

C.





2 2;3 2 2

 

. D.





2 2;2 2 3

 

.

Lời giải

Chọn C

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 23

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

 

2 2

2 1 2 2 2 2 2

1 2. 2 2

3 2 2 3 2 2 3 2 2

x

x y x y x

y

x y x y y



 

  

     

   

  

   

  

     

  



  



.

Câu 37. Phương trình

4

2 2

2

x x x

x

    



có bao nhiêu nghiệm?

A.

1

. B.

2

. C. Vô số. D.

0

.

Lời giải

Chọn A

Điều kiện:

2 0 2

2 0 2 2

2 0 2

x x

x x x

x x

   

 

 

     

 

 

  

 

.

2

x



thỏa phương trình đã cho nên

2

x



là nghiệm.

Vậy phương trình đã cho có một nghiệm.

Câu 38. Cho





: 5

A x x

  

 . Phần bù của

A

trong tập số thực là:

A.





5;5

 . B.









; 5 5;

   

.

C.









; 5 5;

   

. D.





5;5

 .

Lời giải

Chọn B

Vì

5

x



5 5

x

   

nên

[ 5;5]

A

 













; 5 5;C A

     



.

Câu 39. Cho hình vuông

ABCD

có cạnh bằng

a

. Độ dài

AD AB



 

bằng:

A.

3

2

a

. B.

2

a

. C.

2

a

. D.

2

a

.

Lời giải

Chọn D

Ta có:

2

AD AB AC AC a

   

  

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 24

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 40. Trong hệ tọa độ

Oxy

, cho điểm





3; 2

A



,





4;5

B . Tìm tọa độ điểm

M

trên trục hoành sao

cho

A

,

B

,

M

thẳng hàng?

A.

24

;0

7

M

 

 

 

. B.

17

;0

7

M

 

 

 

. C.





1;0

M . D.

23

;0

7

M

 

 

 

.

Lời giải

Chọn D

Gọi





;0

M

M x Ox

 sao cho

A

,

B

,

M

thẳng hàng

AB



cùng phương với

AM



. Với





1;7

AB 



và





3;2

M

AM x 



3

2 23

1 7 7

M

x



    . Vậy

23

;0

7

M

 

 

 

.

Câu 41. Đồ thị hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án

A

,

B

,

C

,

D

dưới đây. Hỏi hàm số đó là hàm số nào?

A.

2

2 1

y x x

  

. B.

2

3 6 1

y x x

  

. C.

2

2 1

y x x

   

. D.

2

3 6

y x x

  

.

Lời giải

Chọn B

Đồ thị trên là đồ thị của hàm số bậc hai có dạng





2

0

y ax bx c a

   

.

Dựa trên hình dáng đồ thị thì

0

a



. Loại đáp án C và D.

Đồ thị hàm số đi qua điểm





0;1

nên

1

c



.

Đồ thị hàm số đi qua điểm





1 ; 2

 

. Thử đáp án A và B thì ta thấy hàm số đáp án B thoả mãn.

Câu 42. Cho 3 điểm

M

,

N

,

P

thẳng hàng trong đó

N

nằm giữa

M

và

P

. khi đó các cặp véc tơ nào

sau đây cùng hướng?

A.

MN



và

MP



. B.

MN



và

PN



. C.

NM



và

NP



. D.

MP



và

PN



.

Lời giải

Chọn A

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 25

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 43. Số nghiệm của phương trình





2

4 3 2 0

x x x

   

là:

A.

2

. B.

3

. C.

1

. D.

4

.

Lời giải

Chọn A

ĐK:

2

x



.

2

1 ( )

4 3 0

3 ( )

2 0

2 ( )

x l

x x

pt x tm

x

x tm





  



  



 









.

Câu 44. Cho hàm số

2

( ) 2( 6) 2

y f x mx m x

    

. Có bao nhiêu giá trị nguyên của tham số

m

để

hàm số

( )

f x

nghịch biến trên khoảng





;2

 ?

A.

3

. B. vô số. C.

1

. D.

2

.

Lời giải

Chọn A

+)

0

m



,

( ) 12 2

f x x

  

, hàm số này nghịch biến trên



nên nghịch biến trên khoảng





;2

 .

+)

0

m



không thỏa mãn vì khi đó hàm số sẽ nghịch biến trên

( 6)

;

m

 

 



 

 

.

+)

0

m



, yêu cầu trở thành

( 6)

2 2 6 2

m

m m m

m



       

. Ta được

0 2

m

 

Vậy

0 2

m

 

nên có 3 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.

Câu 45. Tập xác định của hàm số

1

3

y x

x

  



là:

A.





\ 3

D 



. B.





3;D

 

. C.





3;D

 

. D.





;3

D   .

Lời giải

Chọn C

Tập xác định của hàm số là những giá trị

x

thỏa mãn:

3 0

3

3 0

x

 



 



 



.

Câu 46. Cho góc



tù. Khẳng định nào sau đây là đúng?

A.

tan 0





. B.

cos 0





. C.

cot 0





. D.

sin 0





.

Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 26

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Chọn B

Khi

90 180



   

thì

sin 0,cos 0,tan 0,cot 0

   

   

.

Câu 47. Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai điểm





2; 5

A



và





4;1

B . Tọa độ trung điểm

I

của đoạn thẳng

AB

là:

A.





3; 2

I



. B.





3;2

I . C.





1;3

I . D.





1; 3

I

 

.

Lời giải

Chọn A

Tọa độ trung điểm

I

của đoạn thẳng

AB

là

 

3

2

3; 2

2

A B

I

A B I

I

x x

x

I

y y y

y















  

 

  











.

Câu 48. Trong một lớp học có

100

học sinh,

35

học sinh chơi bóng đá và

45

học sinh chơi bóng

chuyền,

10

học sinh chơi cả hai môn thể thao. Hỏi có bao nhiêu học sinh không chơi môn thể

thao nào? (Biết rằng chỉ có hai môn thể thao là bóng đá và bóng chuyền).

A.

60

. B.

70

. C.

30

. D.

20

.

Lời giải

Chọn C

Số học sinh chỉ chơi bóng đá là

35 10 25

 

(học sinh).

Số học sinh chỉ chơi bóng chuyền là

45 10 35

 

(học sinh).

Số học sinh không chơi môn thể thao nào là

100 25 35 10 30

   

(học sinh).

Câu 49. Trong mặt phẳng tọa độ

Oxy

, tìm tọa độ của điểm

N

trên cạnh

BC

của tam giác

ABC

biết:





2; 1

A



,





3;4

B ,





0; 1

C



và 3S

ABN ACN

S

 

 (Trong đó , S

ABN ACN

S

 

lần lượt là diện tích

các tam giác

ABN

và

ACN

) ?

A.

1 1

;

3 3

N

 



 

 

. B.

3 1

;

4 4

N

 

 

 

. C.

1 1

;

3 3

N

 



 

 

. D.

1 3

;

4 4

N

 

 

 

.

Lời giải

Chọn B

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 27

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

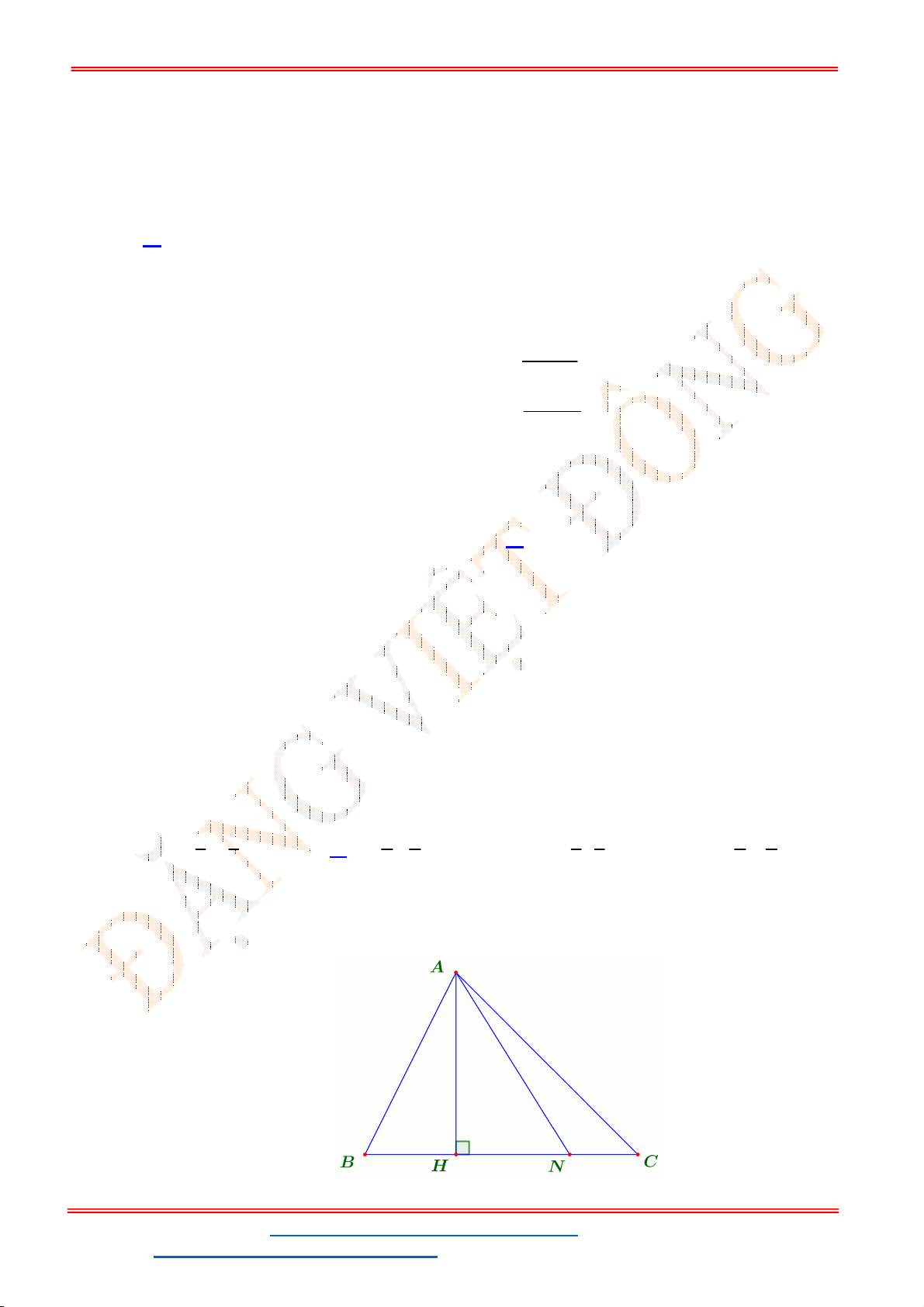
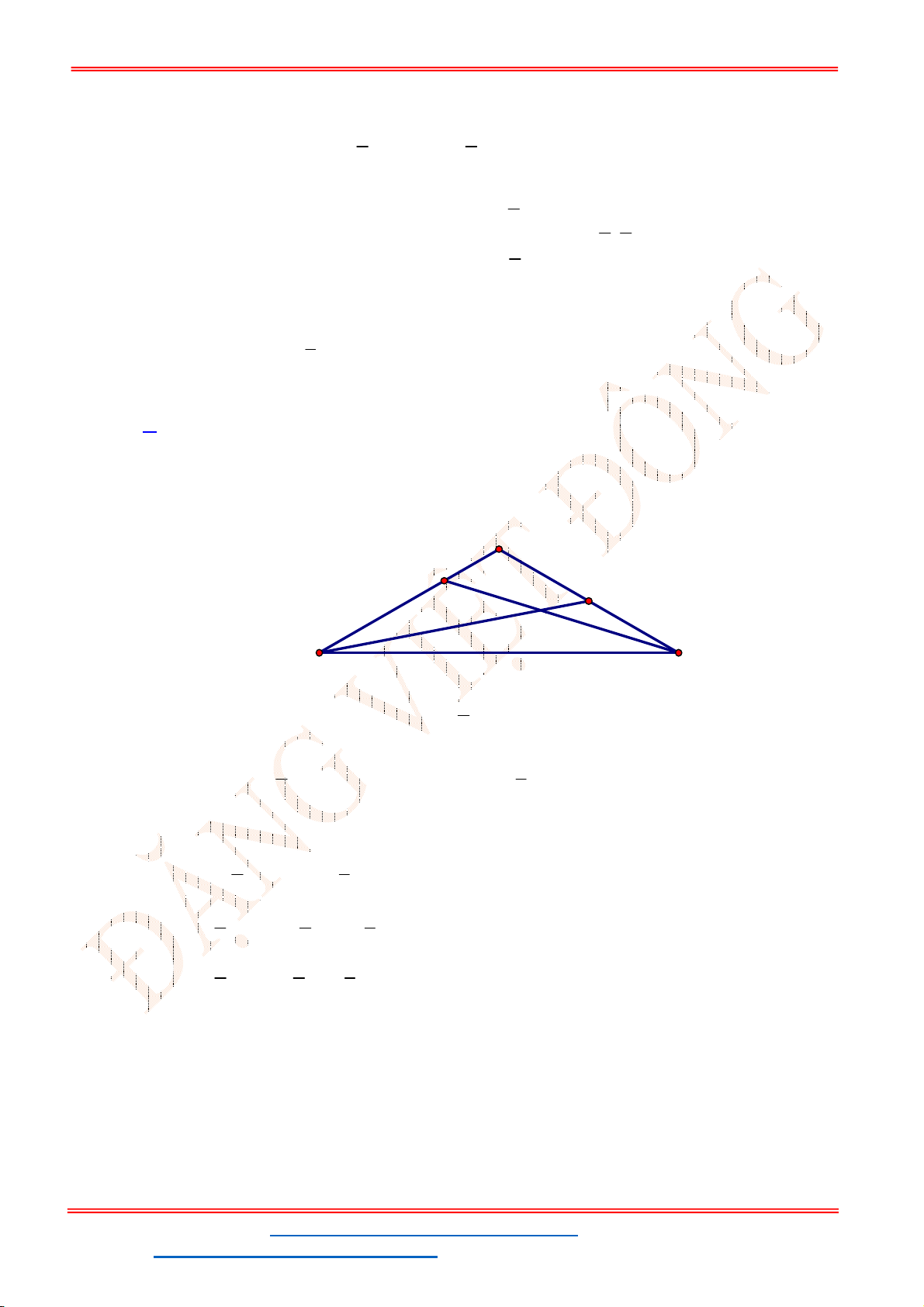
Gọi

H

là chân đường cao tam giác

ABC

vẽ từ

A

.

Theo đề 3S

ABN ACN

S

 

 nên

1 1

. 3 . 3 3

2 2

BN AH CN AH BN CN BN CN

      

 

.

Với





;

N x y

ta có hệ

3

3 3.

4

4 3.( 1) 1

4

x

x x

y y

y







  







 

   











. Vậy

3 1

;

4 4

N

 

 

 

.

Câu 50. Cho tam giác

ABC

cân tại

A

có cạnh bên bằng

6

và góc



120

BAC

 

. Điểm

M

thuộc cạnh

AB

sao cho

1

3

AM AB

 và điểm

N

là trung điểm của cạnh

AC

. Tính tích vô hướng

.

BN CM

 

.

A.

51



. B.

9



. C.

9

. D.

51

.

Lời giải

Chọn A

120

0 6

6

N

C

B

A

M

Ta có:

1

. . .cos120 6.6. 18

2

AB AC AB AC

 

     

 

 

 

.

1

2

BN AN AB AC AB

   

    

;

1

3

CM AM AC AB AC

   

    

.

Vậy

 

2 2

1 1

. .

2 3

1 1 1

. .

6 2 3

7 1 1

. 18 .6 .6

6 2 3

51.

BN CM AC AB AB AC

AC AB AC AB AB AC

   

  

   

   

   

   

 

     

     

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 2 Môn Toán – Lớp 10

(Th

ời gian l

àm bài 90 phút)

Không k

ể thời gian phát đề

Câu 1: Tọa độ đỉnh của parabol





2

: 2 3

P y x x

   

là

A.





2;3

 . B.





1; 2



. C.





1;2

 . D.





2; 3



.

Câu 2: Cho hai tập hợp





0;1;2;3;4

A  và





0;2;4;6;8

B  . Hỏi tập hợp









\ \

A B B A

 có bao

nhiêu phần tử?

A. 10. B. 3. C. 7. D. 4.

Câu 3: Cho đồ thị





2

: 4 2

P y x x

  

. Điểm nào dưới đây thuộc





P

?

A.





1; 3



. B.





2; 6

 

. C.





1; 4

 

. D.





3;18

.

Câu 4: Phát biểu nào sau đây sai?

A.

2020

chia hết cho

101

. B.

9

là số chính phương.

C.

91

là số nguyên tố. D.

5

là ước của

125

.

Câu 5: Đồ thị hàm sô

2

3 4 1

y x x

  

nhận đường thẳng nào dưới đây làm trục đối xứng?

A.

2

3

y



. B.

4

3

x



. C.

2

3

x

 

. D.

1

3

x

 

.

Câu 6: Trong mặt phẳng toạ độ

Oxy

, cho điểm





4;3

A ,





0; 1

B



,





1; 2

C



. Tìm toạ độ điểm

M

biết rằng véctơ

2 3 3

MA MB MC

  

  

có toạ độ là





1;7

.

A.





3; 1



. B.





6;5

. C.





2; 3

 

. D.





1; 2



.

Câu 7: Gọi

1 2

,

x x

là các nghiệm của phương trình

2

4 15 0

x x

  

. Tính

1 2

x x



A. 4. B. 8. C.

76

. D.

56

.

Câu 8: Cho tam giác

ABC

có

AM

là đường trung tuyến. Gọi

I

là trung điểm của

AM

. Trong các

mệnh đề sau, mệnh đề nào đúng?

A.

2 0

IA IB IC

  

   

. B.

2 2 0

IA IB IC

  

   

.

C.

0

IA IB IC

  

   

. D.

2 0

IA IB IC

  

   

.

Câu 9: Gọi





; ;z

x y

là nghiệm của hệ phương trình

5 5

3 2 11

2 3

x y z

  





  





    



Tính

2 2 2

.

x y z

 

A.

16.

B.

8.

C.

9.

D.

14.

Câu 10: Hàm số nào dưới đây đồng biến trên tập

?



A.

2 3 .

y x

  

B.

2.

y x

  

C.

2

.

y

x



D.

3.

y x

 

Câu 11: Cho phương trình

3 2 2 2

3 (4 12 11) (2 3) 0

x x m m x m

      

. Tập hợp các giá trị của tham số

m

để phương trình có 3 nghiệm phân biệt là

A.

( ;2)



B.

( 2; 1)

 

C.

(1;2)

D.

( 1;1)



Câu 12: Gọi

0

m

là giá trị của

m

để hệ phương trình

3

2

9

x y m

mx y m

 







  





có vô số nghiệm. Khi đó

A.

0

1

;2

2

m

 



 

 

B.

0

1

0;

2

m

 



 

 

C.

0

1

;0

2

m

 

 

 

 

D.

0

1

1;

2

m

 

  

 

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 13: Có bao nhiêu giá trị nguyên của tham số

m

để phương trình





 

2

6 10 10 3

x x m x    

có 4 nghiệm phân biệt?

A. 13. B. 14. C. 15. D. 16.

Câu 14: Gọi

S

là tập hợp tất cả các giá trị của tham số

m

để đồ thị hàm số

2

5 2

y x x m

   cắt trục

Ox

tại hai điểm phân biệt

A

,

B

thỏa mãn

4

OA OB



. Tổng các phần tử của

S

bằng

A.

32

9



. B.

41

9



. C.

43

9

. D.

68

9

.

Câu 15: Trong mặt phẳng

Oxy

, cho ba điểm

( 6;0); (0;2)

A B



và

C( 6;2)



. Tìm tọa độ tâm của đường

tròn ngoại tiếp tam giác

ABC

.

A.

( 2;0).



B.

( 2;1).



C.

(3; 1).



D.

( 3;1).



Câu 16: Xác định hàm số bậc hai

2

y ax x c

  

biết đồ thị hàm số đi qua

(1; 2)

A



và

(2;3).

B

A.

2

3 5.

y x x

  

B.

2

2 3.

y x x

  

C.

2

3 4.

y x x

  

D.

2

4 3.

y x x

   

Câu 17: Cho hệ phương trình

( 1) 2

2 ( 2) 4

x m y m

mx m y

   





  



. Biết rằng có hai giá trị của tham số

m

là

1

m

,

2

m

để hệ phương trình có nghiệm

0

( ;2)

x . Tính

1 2

m m



.

A.

1

3



. B.

7

3

. C.

4

3



. D.

2

3

.

Câu 18: Tìm số phần tử của tập hợp





| 3 4

A x x

    



.

A.

6

. B.

5

. C.

8

. D.

7

.

Câu 19: Tìm tập xác định của hàm số

2

3

y x

x

  



.

A.





2;

 

. B.





3;



. C.









2; \ 3

  . D.





\ 3



.

Câu 20: Tìm tập nghiệm của phương trình

2

3 4 4 3 2

x x x

   

.

A.





0

. B.

8

;0

3

 



 

 

. C.



. D.

8

3

 



 

 

.

Câu 21: Cho hình thoi

ABCD

có



60

BAD

 

và

BD a



. Gọi

,

M N

lần lượt là trung điểm của

,

AD DC

. Tích

.

BM BN

 

bằng

A.

2

3

8

a

. B.

2

3

4

a

. C.

2

3 3

8

a

. D.

2

3

4

a

.

Câu 22: Phương trình

3 2 5

x x

  

có hai nghiệm

1 2

,

x x

. Tính

1 2

x x



.

A.

14

3

. B.

28

3



. C.

7

3

. D.

14

3



.

Câu 23: Đường thẳng đi qua hai điểm





1;4

A  và

(2; 7)

B



có phương trình là

A.

11 3 1 0.

x y

  

B.

3 11 1 0.

x y

  

C.

11 3 1 0.

x y

  

D.

3 11 1 0.

x y

  

Câu 24: Hàm số

2

5 6

y x x

   

đồng biến trên khoảng nào dưới đây?

A.





1;4 .

B.





3;4

. C.





2;3

. D.





1;2

.

Câu 25: Trong mặt phẳng tọa độ

Oxy

, cho các véc tơ





3; 1

a

 



,





5; 4

b

 



;





1; 5

c

 



. Biết

c xa yb

 



 

. Tính

x y



.

A. 2. B.

5



. C.

1



. D.

4

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 26: Trong mặt phẳng với hệ trục tọa độ





; ;

O i j

 

cho điểm

M

thỏa mãn

2 3

OM i j

  



 

. Tọa độ

của điểm

M

là

A.





2;3

 . B.





2; 3



. C.





3; 2



. D.





3;2

 .`

Câu 27: Cho









1; 2 , 2;2

u v   

 

. Tọa độ của vectơ

2

u v



 

là

A.





1;3

 . B.





2;1

 . C.





2;4

. D.





0; 2



.

Câu 28: Cho hàm số

 

4 1

4

1

3 4

x

khi x

f x

x

x khi x



 







 



 



. Tính









5 5

f f

 

.

A.

5

2



. B.

15

2

. C.

17

2

. D.

3

2



.

Câu 29: Gọi

,

M N

lần lượt là trung điểm các cạnh

,

CD AB

của hình bình hành. Tìm mệnh đề đúng

trong các mệnh đề sau:

A.

2 2

1

.

2

AM DN AB AD

 

 

. B.

2 2

1

.

4

AM DN AB AD

 

 

.

C.

2 2

1

.

4

AM DN AB AD

 

 

. D.

2 2

1

.

4

AM DN AB AD

 

 

.

Câu 30: Trong mặt phẳng với hệ trục tọa độ





, ,

O i j

 

cho các vectơ

2 3j

u i

 

  

và

1

3

v ki j

 

  

. Biết

u v



 

, khi đó

k

bằng

A.

1

2



. B.

1

2

. C.

4



. D.

4

.

Câu 31: Tìm tập hợp các phần tử của tham số m để hàm số

2 2 2

y x m x m

   

có tập xác định là



.

A.

(0; )



. B.





\ 0



. C.





0;



. D.

( ;0].



Câu 32: Tìm tập nghiệm của phương trình:

4 1 5 0

x

  

.

A.





2

. B.



. C.

1

4

 



 

 

. D.





6

.

Câu 33: Cho tam giác

ABC

, lấy điểm

M

trên cạnh

BC

sao cho

3

BM MC



. Biểu diễn

AM



theo 2

véc tơ

AB



và

AC



ta được

A.

3 1

4 4

AM AB AC

 

  

. B.

1 4

3 3

AM AB AC

 

  

.

C.

1 3

4 4

AM AB AC

 

  

. D.

4 1

3 3

AM AB AC

 

  

.

Câu 34: Cho hàm số





2

5 5 1

y m x x

   

. Hàm số đã cho là hàm số bậc nhất khi

A.

5

m



. B.

5

m



. C.

5

m



. D.

5

m



.

Câu 35: Cho tam giác đều

ABC

có cạnh bằng

a

. Khi đó

AB CA



 

bằng

A.

2

a

. B.

a

. C.

3

2

a

. D.

3

a

.

Câu 36: Tìm tập nghiệm của phương trình

4 2

5 6 0

x x

  

.

A.





1; 6

. B.





6; 6



. C.





1; 6;1; 6

 

. D.





1;6

 .

Câu 37: Tìm điều kiện của tham số

m

để phương trình





2

5 4 2

m x m x

  

có nghiệm.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

5

2

m  

. B.

1

m

 

. C.

5

2

m  

. D.

1

m

 

.

Câu 38: Cho hình chữ nhật

ABCD

có

AB a



,

2

AC a



. Tính góc giữa hai vectơ

CA



và

DC



.

A.

60



. B.

45



. C.

150



. D.

120



.

Câu 39: Cho Parabol





2

:

P y ax bx c

  

với

0

a



và có tọa độ đỉnh là





2;5

. Tìm điều kiện của

tham số

m

để phương trình

2

ax bx c m

  

vô nghiệm.

A.





2;5

m . B.

5

m



. C.

2

m



. D.

2 5

m

 

.

Câu 40: Có tất cả bao nhiêu số nguyên

m

để phương trình

2 24

4 2 2 5 4

x m x x

    

có nghiệm?

A.

2

. B.

3

. C.

4

. D.

1

.

Câu 41: Hàm số nào dưới đây là hàm số chẵn trên tập xác định của nó?

A.

4

y

x



. B.

3

4 2

y x x

 

. C.

4 2

3 1

y x x

   

. D.

1

y x

 

.

Câu 42: Trong các phương trình dưới đây, phương trình nào tương tương với phương trình

2

4

x



?

A.

2

4

x x x

  

. B.

2

2 4 0

x x

  

.

C.

2

2 4 0

x x

  

. D.

2

x



.

Câu 43: Tìm giao điểm của Parabol

2

( ) : y 2 5

P x x

   

với trục

Oy

.

A.





0; 5



. B.





5;0

. C.





1;4

. D.





0;5

.

Câu 44: Gọi

A

,

B

là các giao điểm của đồ thị hàm số





2

3 2

f x x

 

và





2

2 4

g x x x

  

. Phương

trình đường thẳng

AB

là

A.

3 16

y x

  

. B.

4 11

y x

 

. C.

4 9

y x

  

. D.

3 12

y x

 

.

Câu 45: Cho tập hợp

A

gồm 3 phần tử. Hỏi tập

A

có tất cả bao nhiêu tập con?

A.

8

. B.

3

. C.

6

. D.

4

.

Câu 46: Cho hình vuông

ABCD

có cạnh bằng

.

a

. Tích

.

AB AC

 

bằng

A.

2

a

. B.

2

a

. C.

0

. D.

2

a

.

Câu 47: Cho phương trình

2 2

2 0

x x m

  

.Biết rằng có hai giá trị

1 2

,

m m

của tham số

m

để phương

trình có hai nghiệm

1 2

,

x x

thỏa mãn

3 3

1 2

10 0

x x

  

. Tính

1 2

m m

.

A.

1

3

. B.

1

3



. C.

3

4



. D.

3

4

.

Câu 48: Trong mặt phẳng tọa độ

Ox ,

y

cho các điểm

   

7

; 1 , 2;1 2 , 3 1;

3

A m B m C m

 

   

 

 

. Biết rằng

có 2 giá trị

1 2

,

m m

của tham số

m

để

, ,

A B C

thẳng hàng. Tính

1 2

m m

 .

A.

1

6

. B.

4

3



. C.

13

6

. D.

1

6



.

Câu 49: Cho tam giác ABC, lấy các điểm trên

,

M N

cạnh

BC

sao cho

BM MN NC

 

. Gọi

1 2

,

G G

lần lượt là trọng tâm các tam giác ,

ABN ACM

. Biết rằng

1 2

G G



được biểu diễn theo 2 vec tơ

,

AB AC

 

dưới dạng

1 2

G G x AB yAC

 

  

. Khi đó tổng

x y



bằng

A.

0

. B.

2

3

. C.

4

3

. D.

1

.

Câu 50: Trong mặt phẳng tọa độ

Oxy

, cho hình bình hành

ABCD

với













2; 2 , 3;4 , 1;5

A B C  . Khi

đó điểm

D

có tọa độ là

A.





5;6

. B.





0;11

. C.





0; 1



. D.





2; 1

 

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG HDG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 2 Môn Toán – Lớp 10

(Thời gian làm bài 90 phút)

Không k

ể thời gian phát đề

Câu 1. Tọa độ đỉnh của parabol





2

: 2 3

P y x x

   

là

A.





2;3

 . B.





1; 2



. C.





1;2

 . D.





2; 3



.

Lời giải

Chọn B

Gọi





0 0

;

I x y

là đỉnh của parabol





P

 

0

2

1

2 2 1

b

x

a

     



.

2 2

0 0 0

2 3 1 2.1 3 2

y x x

         

.





1; 2

I

 

.

Câu 2. Cho hai tập hợp





0;1;2;3;4

A  và





0;2;4;6;8

B  . Hỏi tập hợp









\ \

A B B A

 có bao nhiêu

phần tử?

A. 10. B. 3. C. 7. D. 4.

Lời giải

Chọn D

Ta có





\ 1;3

A B  ;





\ 6;8

B A 













\ \ 1;3;6;8

A B B A  









\ \

A B B A

  có 4 phần tử.

Câu 3. Cho đồ thị





2

: 4 2

P y x x

  

. Điểm nào dưới đây thuộc





P

?

A.





1; 3



. B.





2; 6

 

. C.





1; 4

 

. D.





3;18

.

Lời giải

Chọn B

Thay

2

6

x

y

 





 



vào





2

: 4 2

P y x x

  

, ta được:

   

2

6 2 4 2 2 6 6

         

(đúng)

Vậy









2; 6

P

   .

Câu 4. Phát biểu nào sau đây sai?

A.

2020

chia hết cho

101

. B.

9

là số chính phương.

C.

91

là số nguyên tố. D.

5

là ước của

125

.

Lời giải

Chọn A

Câu 5. Đồ thị hàm sô

2

3 4 1

y x x

  

nhận đường thẳng nào dưới đây làm trục đối xứng?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

2

3

y



. B.

4

3

x



. C.

2

3

x

 

. D.

1

3

x

 

.

Lời giải

Chọn C

Đồ thị hàm số

2

3 4 1

y x x

  

nhận đường thẳng

2

b

x

a

 

hay

2

3

x

 

làm trục đối xứng.

Câu 6. Trong mặt phẳng toạ độ

Oxy

, cho điểm





4;3

A ,





0; 1

B



,





1; 2

C



. Tìm toạ độ điểm

M

biết

rằng véctơ

2 3 3

MA MB MC

  

  

có toạ độ là





1;7

.

A.





3; 1



. B.





6;5

. C.





2; 3

 

. D.





1; 2



.

Lời giải

Chọn B

Gọi





0 0

;

M x y

. Khi đó





0 0

4 ;3

MA x y

  



,





0 0

; 1

MB x y

   



,





0 0

1 ; 2

MC x y

   



.

Do vậy

2 3 3

MA MB MC

  

  

có toạ độ là





1;7

.













     

0 0 0

2 4 3 3 1 1

2 3 3 1 3 2 7

x x x

y y y

      







        





2 12

2 10

x

y













6

5

x

y













.

Vậy





6;5

M .

Câu 7 . Gọi

1 2

,

x x

là các nghiệm của phương trình

2

4 15 0

x x

  

. Tính

1 2

x x



.

A. 4. B. 8.

C.

76

. D.

56

.

Lời giải

Chọn C.

Áp dụng định lý Vi-et:

1 2

4

. 15

x x

  





 



.

Xét





 

2

1 2 1 2 1 2

4 16 60 76

x x x x x x

      

1 2

76

x x   .

Câu 8. Cho tam giác

ABC

có

AM

là đường trung tuyến. Gọi

I

là trung điểm của

AM

. Trong các

mệnh đề sau, mệnh đề nào đúng?

A.

2 0

IA IB IC

  

   

.

B.

2 2 0

IA IB IC

  

   

.

C.

0

IA IB IC

  

   

.

D.

2 0

IA IB IC

  

   

.

Lời giải

Chọn D.

I

là trung điểm của

AM

nên

0

IA IM IA IM

    

    

.

Xét đáp án A sai vì:

2

IA IB IC IA IC IA IB CA BA

       

        

.

Xét đáp án B sai vì:

2 2 4 3

IA IB IC IA IM IM

    

     

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Xét đáp án C sai vì:

2

IA IB IC IA IM IM

    

     

.

Xét đáp án D đúng vì:

2 2 2 0

IA IB IC IA IM

    

     

.

Câu 9. Gọi





; ;z

x y

là nghiệm của hệ phương trình

5 5

3 2 11

2 3

x y z

  





  





    



Tính

2 2 2

.

x y z

 

A.

16.

B.

8.

C.

9.

D.

14.

Lời giải

Chọn C

Ta có

5 5 5 5 5 5 5 5

3 2 11 16 9 50 16 9 50 16 9 50

2 3 11 6 10 195 390 2

x y z x y z x y z x y z

x y z y z y z y z

x y z y z z z

           

   

   

              

   

   

         

   

5 5 5 5 1

16 9 50 2 2

2 2 2

x y z x y z x

y z y y

z z z

      

  

  

         

  

  

  

  

.

Vậy

2 2 2

9.

x y z

  

Câu 10. Hàm số nào dưới đây đồng biến trên tập

?



A.

2 3 .

y x

  

B.

2.

y x

  

C.

2

.

y

x



D.

3.

y x

 

Lời giải

Chọn A

Xét 4 đáp án ta loại được đáp án C và D vì không có tập xác định là

.



Xét đáp án B có tập xác định là



và có hệ số

1 0

a

  

nên hàm số nghịch biến trên tập

.



Xét đáp án A có tập xác định là



và có hệ số

3 0

a

 

nên hàm số đồng biến trên tập

.



Vậy hàm số

2 3

y x

  

đồng biến trên tập

.



Câu 11. Cho phương trình

3 2 2 2

3 (4 12 11) (2 3) 0

x x m m x m

      

. Tập hợp các giá trị của tham số

m

để phương trình có 3 nghiệm phân biệt là

A.

( ;2)



. B.

( 2; 1)

 

. C.

(1;2)

. D.

( 1;1)



.

Lời giải

Chọn C

 

3 2 2 2 3 2 2 2 2

2 2

3 (4 12 11) (2 3) 0 2 2 (2 3) (2 3) 0

( 1) 2 (2 3) 0 (1)

x x m m x m x x x x m x m

x x x m

               

     

Phương trình

(1)

có 3 nghiệm phân biệt khi và chỉ khi phương trình

2 2

2 (2 3) 0 (2)

x x m   

có 2 nghiệm phân biệt khác

1



.

+) Xét phương trình

(2)

có

2

4 4.(2 3)

m    .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Phương trình

(2)

có 2 nghiệm phân biệt khi và chỉ khi

2

0 (2 3) 1 1 2 3 1 1 2

m m m

            

Để

(2)

có nghiệm khác

1



khi

2 2 2

( 1) 2( 1) (2 3) 0 (2 3) 1

m m

        

luôn đúng với

1 2

m

 

Câu 12. Gọi

0

m

là giá trị của

m

để hệ phương trình

3

2

9

x y m

mx y m

 







  





có vô số nghiệm. Khi đó

A.

0

1

;2

2

m

 



 

 

. B.

0

1

0;

2

m

 



 

 

. C.

0

1

;0

2

m

 

 

 

 

. D.

0

1

1;

2

m

 

  

 

 

.

Lời giải

Chọn B

Xét với

0

m



:

Hệ phương trình có nghiệm duy nhất

Xét với

2

9

m



:

Hệ phương trình có nghiệm duy nhất

Xét với

2

0,

9

m m

 

:

Hệ phương trình vô số nghiệm khi và chỉ khi

1 3 1

2

1 3

9

m

   



Câu 13. Có bao nhiêu giá trị nguyên của tham số

m

để phương trình





 

2

6 10 10 3

x x m x     có

4 nghiệm phân biệt ?

A. 13. B. 14. C. 15. D. 16.

Lời giải

Chọn C

Đặt

 

2

3 , 0

t x t

  

. Khi đó phương trình trên có dạng:

 

2

1 10

t m t

  





2

8 1 0 *

t t m     .

Theo yêu cầu đề bài, để phương trình ban đầu có 4 nghiệm phân biệt khi và chỉ khi phương

trình





*

có hai nghiệm phân biệt cùng dương.

0 60 4 0

15

0 8 0 1 15

1

0 1 0

m

S m

m

P m

   

 





 

        

  

 



 

  

 

.

Vậy





0;1;2;3;4;5;6;...;13;14

m . Có 15 giá trị nguyên của

m

thõa mãn bài toán.

Câu 14. Gọi

S

là tập hợp tất cả các giá trị của tham số

m

để đồ thị hàm số

2

5 2

y x x m

   cắt trục

Ox

tại hai điểm phân biệt

A

,

B

thỏa mãn

4

OA OB



. Tổng các phần tử của

S

bằng

A.

32

9



. B.

41

9



. C.

43

9

. D.

68

9

.

Lời giải

Chọn A

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Để đồ thị hàm số

2

5 2

y x x m

   cắt trục

Ox

tại hai điểm phân biệt khi và chỉ khi phương

trình

2

5 2 0

x x m

  

có hai nghiệm phân biệt, tức

25

0 25 8 0

8

m m      

.

Gọi





1

,0

A x ,





2

,0

B x . Theo yêu cầu đề bài ta có:

1 2

4

4 4

4

x x

OA OB x x

x x





   



 



.

Với

1 2 1 2 2 2 1

4 5 5 1 4

x x x x x x x

           

.

Thay

1 2

4, 1

x x

   

vào

1 2

. 2 4 2

P x x m m

    

(TM).

Với

1 2 1 2 2 2 1

5 20

4 3 5

3 3

x x x x x x x            

.

Thay

1 2

20 5

,

3 3

x x

  

vào

1 2

100 50

. 2

9 9

P x x m m

      

(TM).

Vậy

50 32

2

9 9

S     

.

Câu 15 . Trong mặt phẳng

Oxy

, cho ba điểm

( 6;0); (0;2)

A B



và

C( 6;2)



. Tìm tọa độ tâm của đường

tròn ngoại tiếp tam giác

ABC

.

A.

( 2;0).



B.

( 2;1).



C.

(3; 1).



D.

( 3;1).



Lời giải

Chọn D

Ta có

(0;2); ( 6;0) . 0

AC BC AC BC

    

   

.



Tam giác

ABC

vuông tại

C

.



Tâm của đường tròn ngoại tiếp tam giác

ABC

là trung điểm của cạnh

AB

Vậy tọa độ tâm của đường tròn ngoại tiếp tam giác

ABC

là:

( 3;1).



Câu 16. Xác định hàm số bậc hai

2

y ax x c

  

biết đồ thị hàm số đi qua

(1; 2)

A



và

(2;3).

B

A.

2

3 5.

y x x

  

B.

2

2 3.

y x x

  

C.

2

3 4.

y x x

  

D.

2

4 3.

y x x

   

Lời giải

Chọn B

Đồ thị hàm số

2

y ax x c

  

đi qua

(1; 2)

A



và

(2;3)

B .

2 1 1 2

3 4 2 4 5 3

a c a c a

a c a c c

       

  

  

  

      

  

.

Vậy hàm số bậc hai là

2

2 3.

y x x

  

Câu 17. Cho hệ phương trình

( 1) 2

2 ( 2) 4

x m y m

mx m y

   





  



. Biết rằng có hai giá trị của tham số

m

là

1

m

,

2

m

để hệ phương trình có nghiệm

0

( ;2)

x . Tính

1 2

m m



.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

1

3



. B.

7

3

. C.

4

3



. D.

2

3

.

Lời giải

Chọn A

Vì hệ đã cho có nghiệm

0

( ;2)

x nên ta có:

0

0 0

2

0 0

3

( 1)2 2 3

1

2 ( 2)2 4 . 2 2

3 4 0

4

3

x m

x m m x m

m

mx m m x m

m m

m









    



 

 



  

   



     

  



 















.

Vậy có hai giá trị của

m

là

1

m



,

2

4

3

m

 

nên ta có

1 2

1

3

m m

  

.

Câu 18. Tìm số phần tử của tập hợp





| 3 4

A x x

    



.

A.

6

. B.

5

. C.

8

. D.

7

.

Lời giải

Chọn D

Ta có :









| 3 4 2; 1;0;1;2;3;4

A x x       



, suy ra

( ) 7

n A



.

Câu 19. Tìm tập xác định của hàm số

2

3

y x

x

  



.

A.





2;

 

. B.





3;



. C.









2; \ 3

  . D.





\ 3



.

Lời giải

Chọn C

Điều kiện xác định:



  

2 0 2

2; \ 3

3 0 3

x x

x

x x

   

 

    

 

  

 

.

Vậy tập xác định của hàm số là









2; \ 3

  .

Câu 20. Tìm tập nghiệm của phương trình

2

3 4 4 3 2

x x x

   

.

A.





0

. B.

8

;0

3

 



 

 

. C.



. D.

8

3

 



 

 

.

Lời giải

Chọn A

Ta có:

 

2

3 2 0

3 4 4 3 2 3

3 4 4 3 2

6 16 0

x

x x x

x x



 



 

 

     

 

   





 



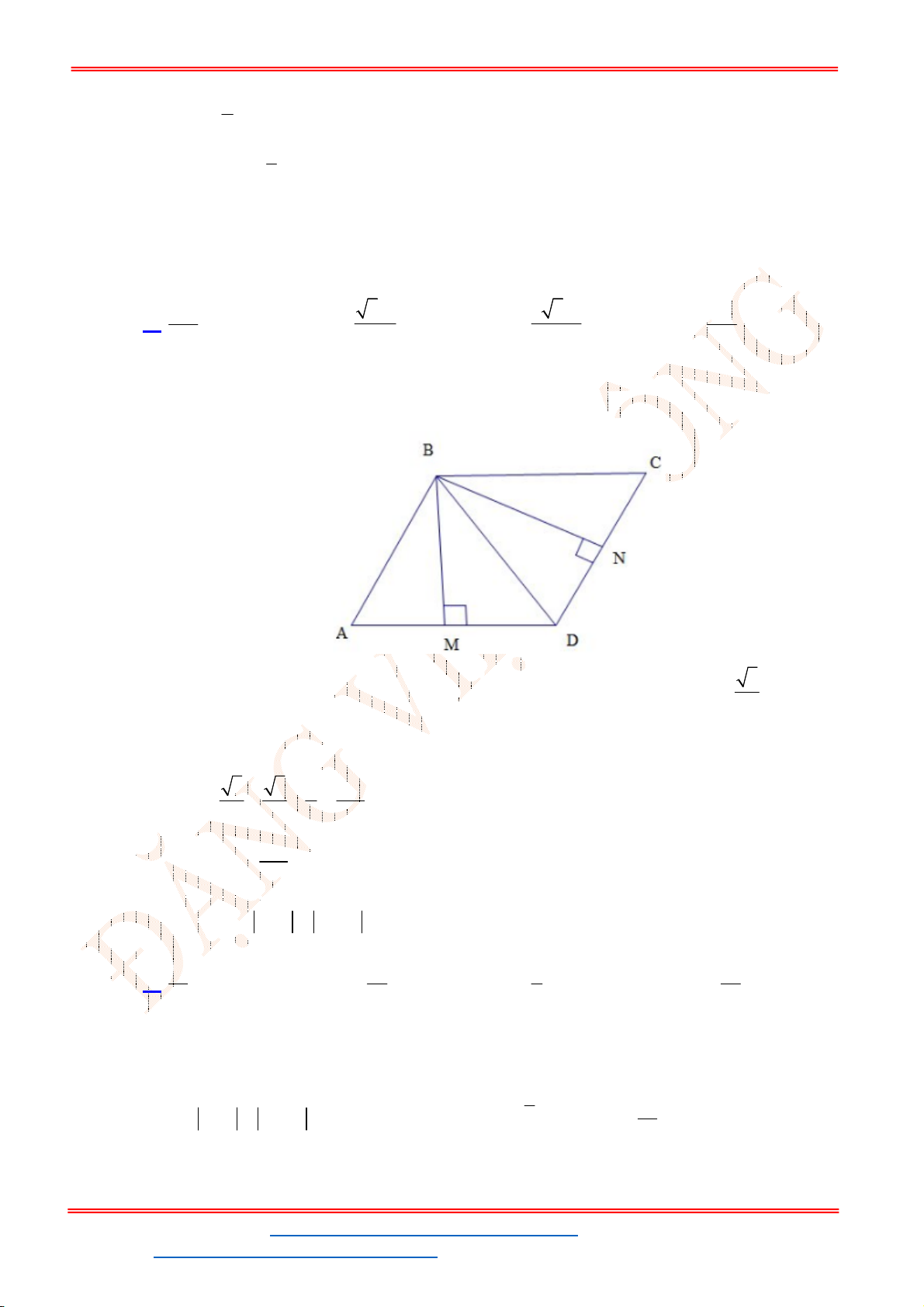
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

2

3

0

8

0,

3

x

x x



 



  





  





.

Vậy tập nghiệm của phương trình là





0

.

Câu 21. Cho hình thoi

ABCD

có



60

BAD

 

và

BD a



. Gọi

,

M N

lần lượt là trung điểm của ,

AD DC

. Tích

.

BM BN

 

bằng

A.

2

3

8

a

. B.

2

3

4

a

. C.

2

3 3

8

a

. D.

2

3

4

a

.

Lời giải

Chọn A

Ta có : Tam giác

ABD

,

BCD

là hai tam giác đều cạnh

a

. Suy ra

3

2

BM BN a

 

.

Khi đó :







. . .cos , . .cos . .cos60

BM BN BM BN BM BN BM BN MBN BM BN

   

   

2

3 3 1 3

. .

2 2 2 8

a

a a 

.

Vậy

2

3

.

8

a

BM BN 

 

.

Câu 22. Phương trình

3 2 5

x x

  

có hai nghiệm

1 2

,

x x

. Tính

1 2

x x



.

A.

14

3

. B.

28

3



. C.

7

3

. D.

14

3



.

Lời giải

Chọn A.

Ta có:

1

1 2

1

8

3 2 5

14

3 2 5

3

3 2 5

3

2

x x

x

x x x x

x x

x



  







       



   







.

Câu 23. Đường thẳng đi qua hai điểm





1;4

A  và

(2; 7)

B



có phương trình là :

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

11 3 1 0.

x y

  

B.

3 11 1 0.

x y

  

C.

11 3 1 0.

x y

  

D.

3 11 1 0.

x y

  

Lời giải

Chọn C

Ta có





1;4

A  ,

(2; 7)

B



vì đường thẳng qua

,

A B

nên nhận

AB



là vtcp.









3; 11 11;3 .

AB

v AB n   

  

Phương trình đường thẳng

AB

:









11 2 3 7 0 11 3 1 0

x y x y

       

.

Câu 24. Hàm số

2

5 6

y x x

   

đồng biến trên khoảng nào dưới đây?.

A.





1;4 .

B.





3;4

. C.





2;3

. D.





1;2

.

Lời giải

Chọn D

Ta có

2

5 6

y x x

   

đỉnh

5 49

; .

2 4

I

 



 

 

Do

1 0

a

  

nên.

Hàm số đồng biến trên khoảng

5

;

2

 



 

 

và nghịch biến trên khoảng

5

;

2

 



 

 

.

Nhận thấy chỉ có

 

5

1;2 ;

2

 

 

 

 

. Do đó chọn đáp án D.

Câu 25. Trong mặt phẳng tọa độ

Oxy

, cho các véc tơ





3; 1

a

 



,





5; 4

b

 



;





1; 5

c

 



. Biết

c xa yb

 



 

. Tính

x y



.

A. 2. B.

5



. C.

1



. D.

4

.

Lời giải

Chọn C

Vì

c xa yb

 



 

nên ta có

   

3 5 1

3 5 1 3

1 4 5

4 5 2

x y

x y x

x y

x y y

   

   



 

 

  

      

    

 



3 2 1

x y

      

.

Câu 26. Trong mặt phẳng với hệ trục tọa độ





; ;

O i j

 

cho điểm

M

thỏa mãn

2 3

OM i j

  



 

. Tọa độ

của điểm

M

là

A.





2;3

 . B.





2; 3



. C.





3; 2



. D.





3;2

 .`

Lời giải

Chọn A

2 3

OM i j

  



 

nên tọa độ điểm

M

là





2;3

 .

Câu 27 . Cho









1; 2 , 2;2

u v   

 

. Tọa độ của vectơ

2

u v



 

là

A.





1;3

 . B.





2;1

 . C.





2;4

. D.





0; 2



.

Lời giải

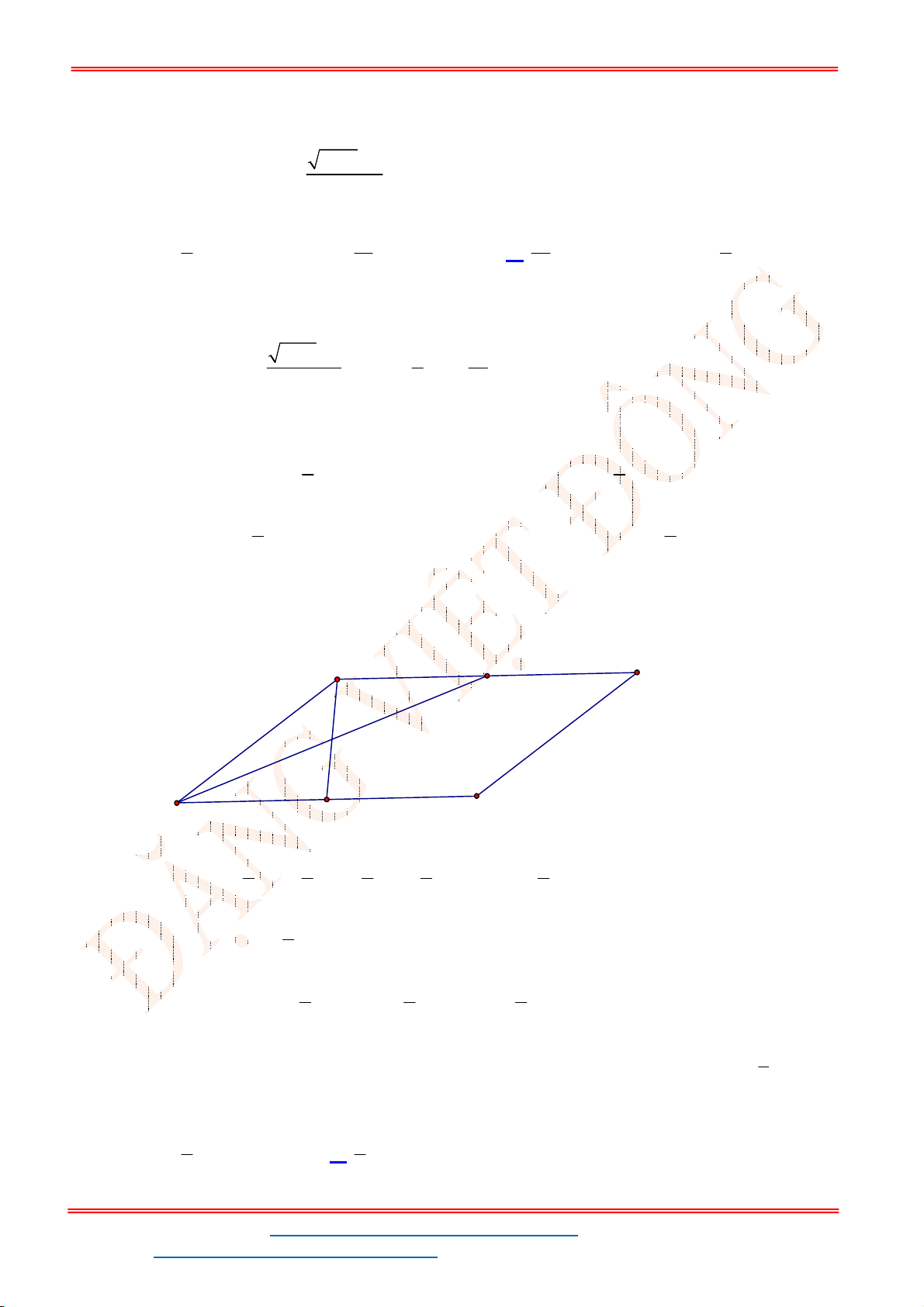
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Chọn D

















2 2. 1 2;2 2 2 0; 2

u v

       

 

.

Câu 28. Cho hàm số

 

4 1

4

1

3 4

x

khi x

f x

x

x khi x



 







 



 



. Tính









5 5

f f

 

.

A.

5

2



. B.

15

2

. C.

17

2

. D.

3

2



.

Lời giải

Chọn C

   

5 4 1 1 17

5 5 3 5 8

5 1 2 2

f f

 

       



.

Câu 29: Gọi

,

M N

lần lượt là trung điểm các cạnh

,

CD AB

của hình bình hành . Tìm mệnh đề đúng

trong các mệnh đề sau:

A.

2 2

1

.

2

AM DN AB AD

 

 

. B.

2 2

1

.

4

AM DN AB AD

 

 

.

C.

2 2

1

.

4

AM DN AB AD

 

 

. D.

2 2

1

.

4

AM DN AB AD

 

 

.

Lời giải

Chọn B

Ta có

 

1 1 1 1 1

2 2 2 2 2

AM AD AC AD AB AD AB AD

      

       

.

1

2

DN DA AN AB AD

   

    

.

Khi đó:

2 2

1 1 1

.

2 2 4

AM DN AB AD AB AD AB AD

  

    

  

  

     

.

Câu 30: Trong mặt phẳng với hệ trục tọa độ





, ,

O i j

 

cho các vectơ

2 3j

u i

 

  

và

1

3

v ki j

 

  

. Biết

u v



 

, khi đó

k

bằng

A.

1

2



. B.

1

2

. C.

4



. D.

4

.

N

M

D

A

B

C

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Lời giải

Chọn B

Ta có





2; 3

u

 



,

1

;

3

v k

 



 

 



. Vì

1 1

. 0 2 3. 0

3 2

u v u v k k

       

   

.

Câu 31. Tìm tập hợp các phần tử của tham số m để hàm số

2 2 2

y x m x m

   

có tập xác định là



.

A.

(0; )



. B.





\ 0



. C.





0;



. D.

( ;0].



Lời giải

Chọn D

Hàm số xác định

2

0, 0.

x m x m

      



Vậy: Tập hợp các phần tử của

m

là:

( ;0].



Câu 32. Tìm tập nghiệm của phương trình :

4 1 5 0

x

  

.

A.





2

. B.



. C.

1

4

 



 

 

. D.





6

.

Lời giải

Chọn B

Điều kiện xác định:

1

4

x





.

Ta thấy :

4 1 5 5.

1

, .

4

0

VT x

x

VP



   





 









nên phương trình đã cho vô nghiệm.

Vậy: Tập nghiệm của phương trình:

S

 

.

Câu 33. Cho tam giác

ABC

, lấy điểm

M

trên cạnh

BC

sao cho

3

BM MC



. Biểu diễn

AM



theo 2 véc

tơ

AB



và

AC



ta được

A.

3 1

4 4

AM AB AC

 

  

. B.

1 4

3 3

AM AB AC

 

  

.

C.

1 3

4 4

AM AB AC

 

  

. D.

4 1

3 3

AM AB AC

 

  

.

Lời giải

Chọn C

Vì

3

BM MC



nên

3 3 0

BM MC BM CM

   

    

.

Ta có:





 

1

3 3 3 2

AM AB BM

AM AC CM AM AC CM

 

    

  

     

Từ





1

và





2

suy ra:

4 3 3 3

AM AB AC BM CM AB AC

     

      

hay

1 3

4 4

AM AB AC

 

  

.

Vậy

1 3

4 4

AM AB AC

 

  

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 34. Cho hàm số





2

5 5 1

y m x x

   

. Hàm số đã cho là hàm số bậc nhất khi

A.

5

m



. B.

5

m



. C.

5

m



. D.

5

m



.

Lời giải

Chọn B

Hàm số đã cho là hàm số bậc nhất khi

5 0 5

m m

   

.

Câu 35. Cho tam giác đều

ABC

có cạnh bằng

a

. Khi đó

AB CA



 

bằng

A.

2

a

. B.

a

. C.

3

2

a

. D.

3

a

.

Lời giải

Chọn B

Ta có

AB CA CB CB a

   

  

.

Câu 36. Tìm tập nghiệm của phương trình

4 2

5 6 0

x x

  

.

A.





1; 6

. B.





6; 6



. C.





1; 6;1; 6

 

. D.





1;6

 .

Lời giải

Chọn B

Ta có

2

4 2

2

1 6

5 6 0

6

x x

x



  

    





 





.

Câu 37. Tìm điều kiện của tham số

m

để phương trình





2

5 4 2

m x m x

  

có nghiệm

A.

5

2

m  

. B.

1

m

 

. C.

5

2

m  

. D.

1

m

 

.

Lời giải

Chọn D

Ta có





2

5 4 2

m x m x

  





2

5 5 2

m x m

  

.

Phương trình có nghiệm

2

5 5 0

1

5 5 0

2 0

m



 



   



 













.

Câu 38. Cho hình chữ nhật

ABCD

có

AB a



,

2

AC a



. Tính góc giữa hai vectơ

CA



và

DC



.

A.

60



. B.

45



. C.

150



. D.

120



.

Lời giải

Chọn D

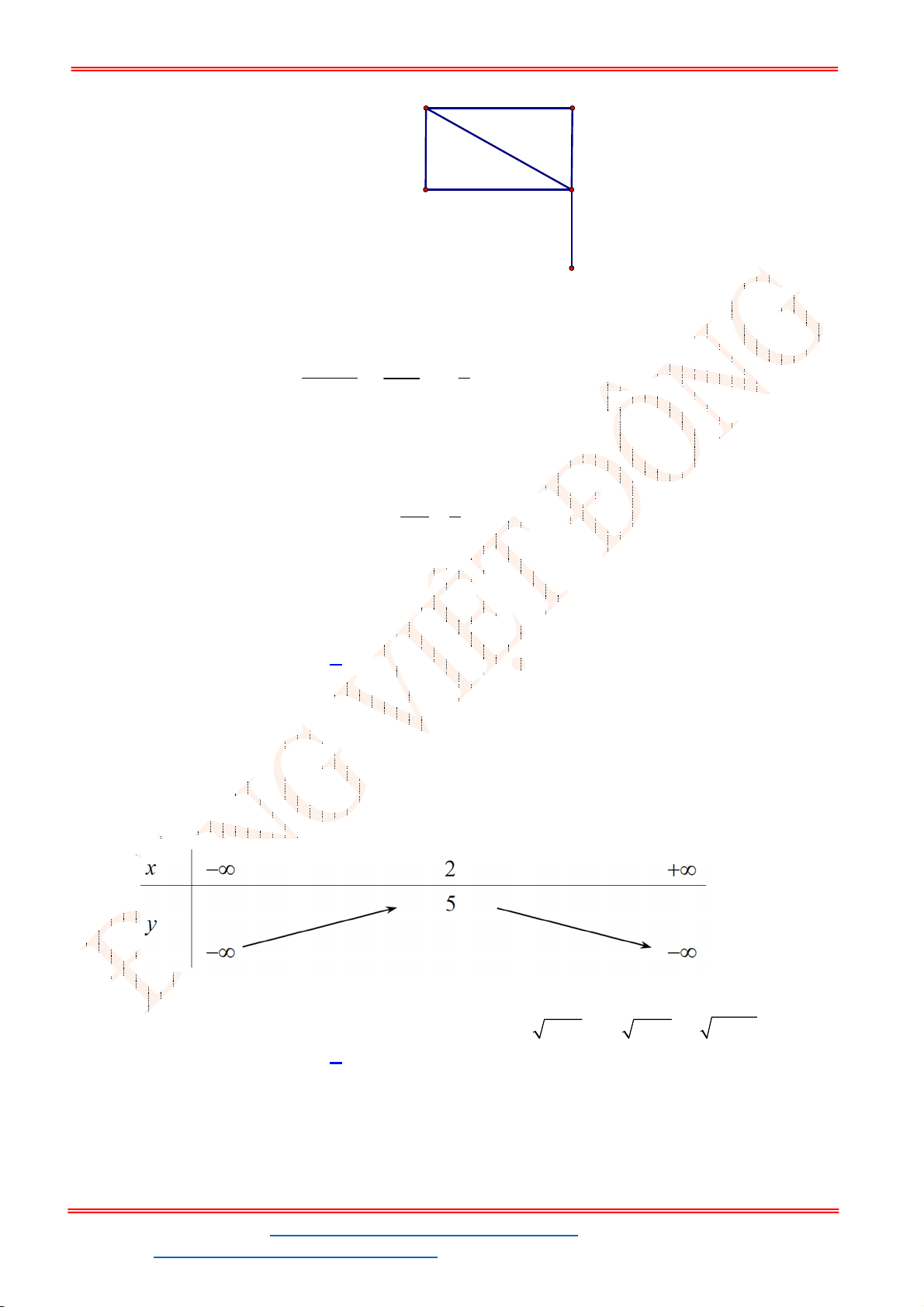
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Cách 1: Xét

.CA DC

 

 

.CD DA DC 

  

. .CD DC DA DC 

   

2

CD 

2

a 

.

Nên

 

cos ,CA DC

 

.

CA DC



 

2

2 .

a

a a





1

2

 

. Suy ra:

 

, 120CA DC  

 

.

Cách 2: Vẽ

CE DC

 

.

Khi đó:

 

,CA DC

 

 

,CA CE

 



ACE



180 ACD  

.

Xét tam giác

ACD

có



cos ACD

CD

AC



1

2





60ACD  

.

Do đó:

 

, 120CA DC  

 

.

Câu 39. Cho Parabol

 

2

:P y ax bx c   với

0a 

và có tọa độ đỉnh là

 

2;5 . Tìm điều kiện của tham

số

m

để phương trình

2

ax bx c m  

vô nghiệm.

A.

 

2;5m . B.

5m 

. C.

2m 

. D.

2 5m 

.

Lời giải

Chọn B

+ Số nghiệm của phương trình

2

ax bx c m  

 

1 là số giao điểm của

 

P với đường thẳng

:d y m .

+ Ta có BBT:

+ Dựa vào BBT, phương trình

 

1 vô nghiệm khi và chỉ khi

5m 

.

Câu 40. Có tất cả bao nhiêu số nguyên

m

để phương trình

2 24

4 2 2 5 4x m x x    

có nghiệm?

A. 2 . B.

3

. C. 4 . D. 1.

Lời giải

Chọn B

+) Đk:

2x 

.

A

D

B

C

E

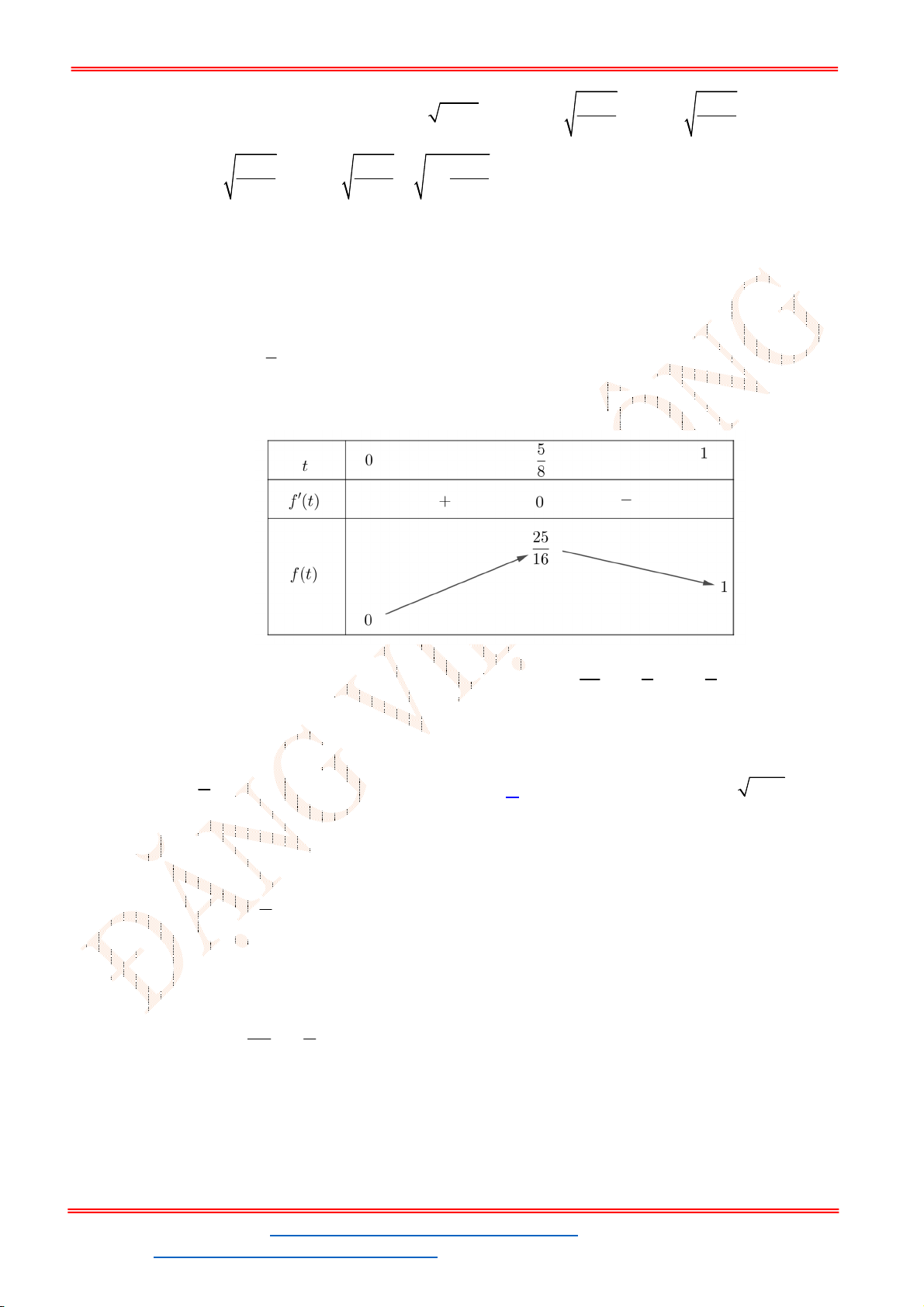
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

+) Chia cả 2 vế của phương trình cho

2x 

ta được:

2

4

2 2

4 5

2 2

x x

m

x x

 

 

 

 

1

+) Đặt

4

2

x

t

x







(do

4 4

2 4

1

2 2

x

t

x x



  

 

nên

0 1t 

).

Phương trình

 

1 trở thành

 

2 2

4 5 2t t m   ,





0;1t  .

+) Phương trình đã cho có nghiệm



 

2 có nghiệm trên





0;1 .

Xét hàm số

 

2

4 5f t t t   trên





0;1 ta có:

 

8 5f t t



  

 

5

0

8

f t t



  

.

Bảng biến thiên của hàm số

 

2

4 5f t t t   trên





0;1

Từ bảng trên ta thấy

 

2 có nghiệm trên





0;1

2

25 5 5

0

16 4 4

m m      

.

Mà

m

nên

 

1;0;1m  . Vậy có tất cả

3

giá trị nguyên của

m

thỏa mãn yêu cầu bài toán.

Câu 41. Hàm số nào dưới đây là hàm số chẵn trên tập xác định của nó?

A.

4

y

x



. B.

3

4 2y x x  . C.

4 2

3 1y x x   

.

D.

1y x 

.

Lời giải

Chọn C

+) Hàm số

 

4

y f x

x

 

.

Tập xác định

 

\ 0D   .

x D 

ta có

x D 

.

Xét

   

4 4

f x f x

x x

     



 

f x là hàm số lẻ



Loại

.A

+)

Hàm số

 

3

4 2y x x f x  

.

Tập xác định

D   .

x D 

ta có

x D 

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Xét

     





 

3

4 2 4 2

f x x x x x f x

         







f x

là hàm số lẻ



Loại

.

B

+) Hàm số





4 2

3 1

y x x f x

    

Tập xác định

D





.

x D

 

ta có

x D

 

.

Xét

   





 

4

2 4 2

3 1 3 1

f x x x x x f x

          







f x

là hàm số chẵn



Chọn

.

C

+) Hàm số





1

y x f x

  

.

Tập xác định





1:D

   

.

Vì

5

D



mà

5

D

 



hàm số





f x

không chẵn, không lẻ trên

D



Loại

.

D

Câu 42. Trong các phương trình dưới đây, phương trình nào tương tương với phương trình

2

4

x



?

A.

2

4

x x x

  

. B.

2

2 4 0

x x

  

. C.

2

2 4 0

x x

  

. D.

2

x



.

Lời giải

Chọn D

Hai phương trình tương đương khi chúng có cùng tập nghiệm

Ta có:

2

4 2

x x

   

.

+ pt thứ 1: Điều kiện

0

x



.

2 2

2

4 4

2

x

x x x x

x





     



 



.

Do

0

x



nên ta nhận nghiệm

2

x



.

Phương trình này không thỏa mãn.

+ pt thứ 2:

2

1 5

2 4 0

1 5

x

x x

x



 

   



 





. Phương trình này không thỏa mãn.

+ pt thứ 3:

2

2 4 0

x x

  

: phương trình vô nghiệm nên không thỏa mãn.

+ pt thứ 4:

2 2

x x

   

. Phương trình này thỏa mãn yêu cầu.

Câu 43. Tìm giao điểm của Parabol

2

( ) : y 2 5

P x x

   

với trục

Oy

.

A.





0; 5



. B.





5;0

. C.





1;4

. D.





0;5

.

Lời giải

Chọn D

Giao điểm của

2

( ) : y 2 5

P x x

   

với trục

Oy

0.

x

 

Thay

0 5.

x y

  

Câu 44. Gọi

A

,

B

là các giao điểm của đồ thị hàm số





2

3 2

f x x

 

và





2

2 4

g x x x

  

. Phương

trình đường thẳng

AB

là

A.

3 16

y x

  

. B.

4 11

y x

 

. C.

4 9

y x

  

. D.

3 12

y x

 

.

Lời giải

Chọn A

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Phương trình hoành độ giao điểm là

2 2 2

2

3 2 2 4 6 0

3

x

x x x x x

x





        



 



.

Với

2 10

x y

  

,

3 25

x y

   

. Suy ra









2;10 , 3;25

A B  .

Phương trình đường thẳng

AB

là

2 10

3 16

3 2 25 10

A A

B A B A

x x y y x y

y x

x x y y

   

      

    

.

Câu 45. Cho tập hợp

A

gồm 3 phần tử. Hỏi tập

A

có tất cả bao nhiêu tập con?

A.

8

. B.

3

. C.

6

. D.

4

.

Lời giải

Chọn A

Giả sử tập

{a;b;c}

A



. Các tập hợp con của

A

là:

,{ },{ },{ },{ ; },{ ; },{ ; },{ ; ; }

a b c a b a c b c a b c



.

Vậy

A

có 8 tập con.

Công thức tính nhanh: số tập con là

3

2 8



.

Câu 46. Cho hình vuông

ABCD

có cạnh bằng

.

a

. Tích

.

AB AC

 

bằng

A.

2

a

. B.

2

a

. C.

0

. D.

2

a

.

Lời giải

Chọn A

Có





2 2

. . . .

AB AC AB AB AD AB AB AB AD AB a

     

        

.

Câu 47. Cho phương trình

2 2

2 0

x x m

  

.Biết rằng có hai giá trị

1 2

,

m m

của tham số

m

để phương

trình có hai nghiệm

1 2

,

x x

thỏa mãn

3 3

1 2

10 0

x x

  

.Tính

1 2

m m

.

A.

1

3

. B.

1

3



. C.

3

4



. D.

3

4

.

Lời giải

Chọn A

2

' 1 0

m

   

với mọi

m

nên phương trình

2 2

2 0 (1)

x x m   luôn có hai nghiệm phân

biệt với mọi

m

.

Áp dụng định lí viet cho phương trình

(1)

ta được

1 2

2

1 2

2

(2)

x x

x x m

  





 



.

3 3

1 2

10 0

x x

  

   

3

1 2 1 2 1 2

3 10 0 (3)

x x x x x x     

.

Từ





2

và





3

ta có

2

1

2 6 0

3

m m     .

Vậy

1 2

1

3

m m



.

Câu 48. Trong mặt phẳng tọa độ

Ox ,

y

cho các điểm

   

7

; 1 , 2;1 2 , 3 1;

3

A m B m C m

 

   

 

 

. Biết rằng có

2 giá trị

1 2

,

m m

của tham số

m

để

, ,

A B C

thẳng hàng. Tính

1 2

m m

 .

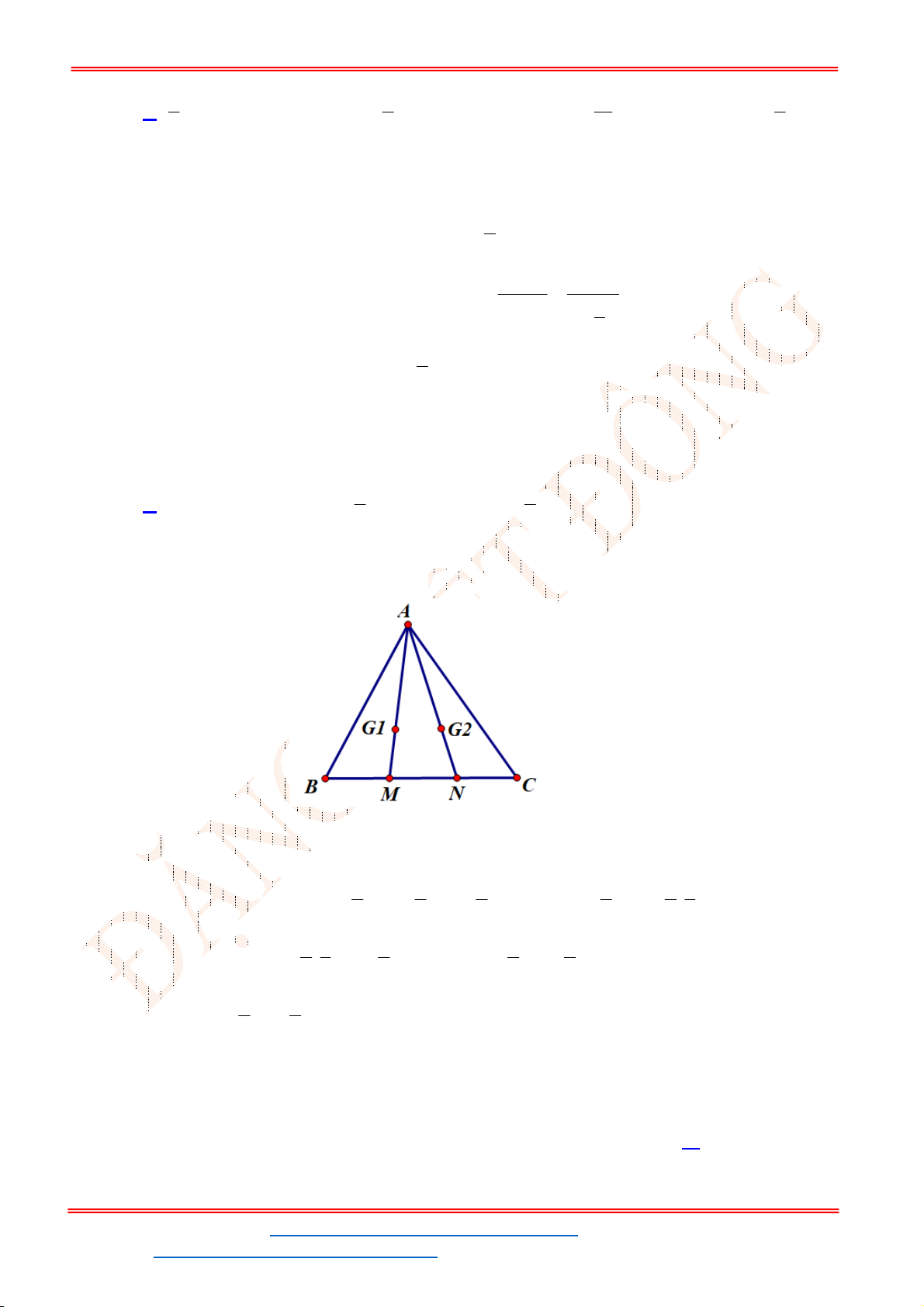
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 20

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

1

6

. B.

4

3



. C.

13

6

. D.

1

6



.

Lời giải

Chọn A

Ta có:

 

4

2 ;2 2 , 2 1;

3

AB m m AC m

 

     

 

 

 

.

, ,

A B C

thẳng hàng

,

AB AC



 

cùng phương

2

2 2 2

6 7 0

4

2 1

3

m m

m

 

     





có 2

nghiệm phân biệt. Do đó:

1 2

1

6

m m

 

.

Câu 49. Cho tam giác ABC, lấy các điểm trên

,

M N

cạnh

BC

sao cho

BM MN NC

 

. Gọi

1 2

,

G G

lần

lượt là trọng tâm các tam giác ,

ABN ACM

. Biết rằng

1 2

G G



được biểu diễn theo 2 vec tơ

,

AB AC

 

dưới dạng

1 2

G G x AB yAC

 

  

. Khi đó tổng

x y



bằng

A.

0

. B.

2

3

. C.

4

3

. D.

1

.

Lời giải

Chọn A

Do

1

G

là trọng tâm tam ABN giác với trung tuyến AM,

2

G

là trọng tâm tam giác

AMC

với

trung tuyến

AN

nên:

Ta có

 

1 2 2 1

2 2 2 2 2 1

.

3 3 3 3 3 3

G G AG AG AM AN AM AN MN BC

       

        



 

1 2

2 1 2 2 2

.

3 3 9 9 9

G G BC AC AB AB AC

     

     

Suy ra

2 2

;

9 9

x y

  

.

Vậy

0

x y

 

.

Câu 50. Trong mặt phẳng tọa độ

Oxy

, cho hình bình hành

ABCD

với













2; 2 , 3;4 , 1;5

A B C  . Khi

đó điểm

D

có tọa độ là

A.





5;6

. B.





0;11

. C.





0; 1



. D.





2; 1

 

.

Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 21

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Chọn D

ABCD

là hình bình hành

AB DC

 

 

trong đó





1;6

AB 



và





1 ;5

D D

DC x y

   



 

1 1 2

2; 1

6 5 1

D D

x x

D

y y

    

 

    

 

   

 

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 3 Môn Toán – Lớp 10

(Thời gian làm bài 90 phút)

Không k

ể thời gian phát đề

PHẦN I: TRẮC NGHIỆM

Câu 1: Cho hệ phương trình

2 2 2

4

.

x y

x y m

 





 



Khẳng định nào sau đây là đúng?

A. Hệ có nghiệm duy nhất khi và chỉ khi

2.

m



B. Hệ có nghiệm khi và chỉ khi

8.

m 

C. Hệ vô nghiệm khi và chỉ khi

0.

m



D. Hệ có nghiệm với mọi

.

m

Câu 2:

Các cạnh của tam giác

ABC

thỏa mãn

3 3 3

2

b c a

a

b c a

 



 

. Số đo góc

A

là:

A.

120



. B.

60



. C.

45



. D.

30



.

Câu 3: Cho





0 0

;

x y

là nghiệm của hệ phương trình

2 3

5 4 0

x y

 





  



. Tính giá trị của biểu thức

4 4

0 0

.

P x y

 

A.

0

P



. B.

2

P



. C.

4

P



. D.

8

P



.

Câu 4: Cho hình bình hành

ABCD

. Trong các khẳng định sau, khẳng định nào sai?

A.

AD CB



 

. B.

AD CB



 

. C.

AB DC



 

. D.

AB CD



 

.

Câu 5: Trong mặt phẳng tọa độ

Oxy

, cho hai vectơ





2;5

a 



,





6; 14

b  



. Góc tạo bởi hai vectơ

a



,

b



là:

A.

60



. B.

135



. C.

45



. D.

120



.

Câu 6: Cho





| 2 1 3

A x x

   



,





1; 3

B m m

  

. Gọi

S

là tập hợp tất cả các số nguyên

m

để

A B

  

. Tổng tất cả các phần tử của

S

bằng

A.

0

. B.

5

. C.

4

. D.

9

.

Câu 7: Gọi

G

là trọng tâm tam giác đều

ABC

có cạnh bằng

a

. Trong các mệnh đề sau, tìm mệnh đề

sai?

A.

2

.

2

a

AB GA

 

 

. B.

2

1

.

2

AB AC a



 

. C.

2

.

6

a

GAGB 

 

. D.

2

.

2

a

AB CB 

 

.

Câu 8: Cho

, ,

a b c

  

là ba vectơ khác

0



. Xét 3 mệnh đề sau:





I . .

a b a c b c

  

     

 









II . . . .

a b c a b c



     

 





2

2 2

III . .

a b a b



   

Trong ba mệnh đề trên mệnh đề nào sai?

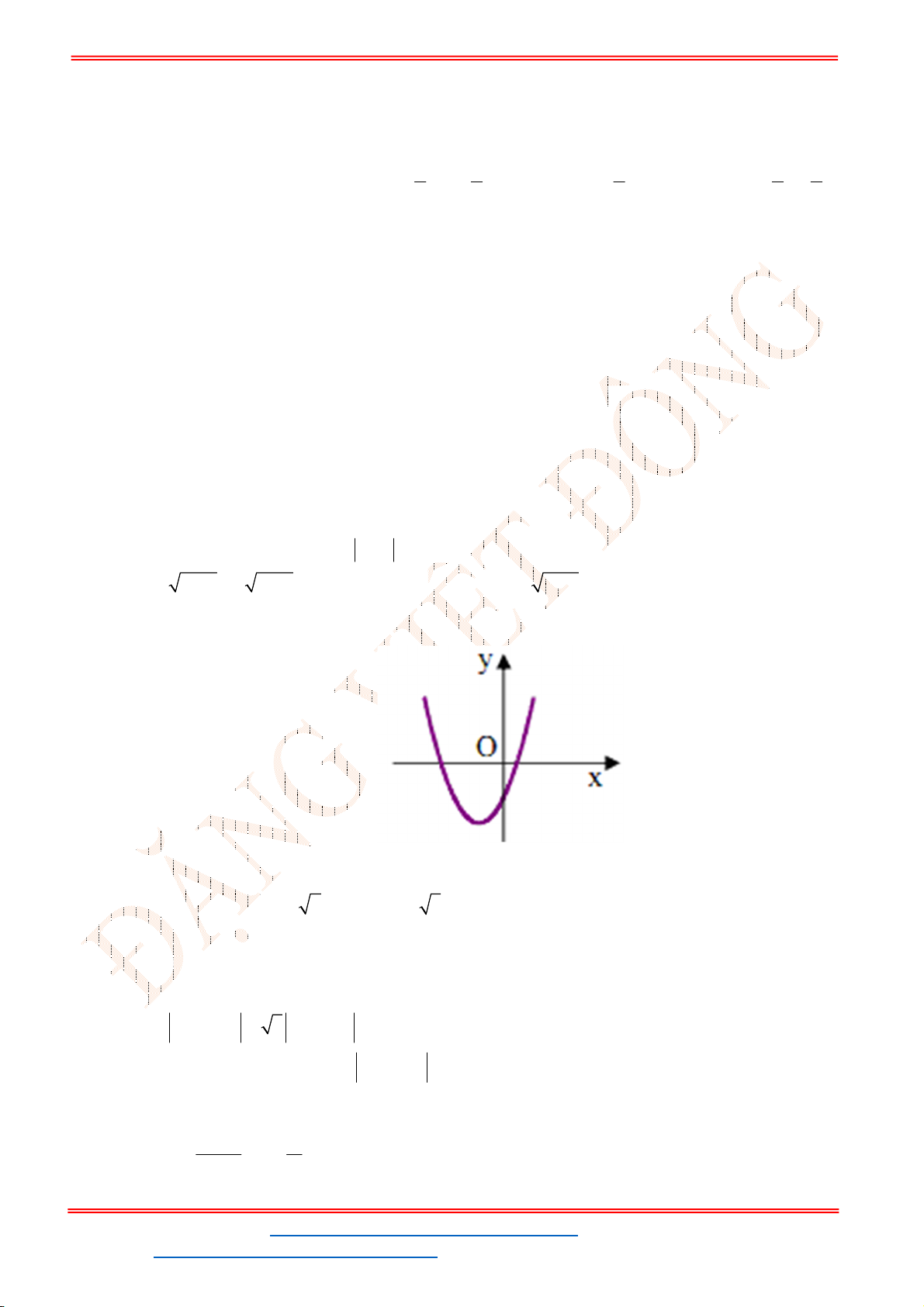
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A. I và II và III. B. I và III. C. I và II. D. II và III.

Câu 9: Cho tập

  

 

3 3 2

| 4 2 5 2 0M x x x x x x     

. Viết tập M bằng cách liệt kê các phần tử

A.

 

0;2M 

. B.

1 5

;0;2;

2 2

M

 

 

 

 

. C.

5

0;2;

2

M

 



 

 

. D.

1 5

0; ;2;

2 2

M

 



 

 

.

Câu 10: Cho

0 0

90 180a 

và các mệnh đề sau:

P: “

sin .cos 0a a 

”; Q: “

tan .cos 0a a 

”; R: “

cot .cos 0a a 

”. Hãy chọn khẳng định đúng?

A. P, Q, R đúng. B. P, Q đúng, R sai. C. P, R đúng, Q sai. D. Q, R đúng, P sai.

Câu 11: Trong các mệnh đề sau đây, mệnh đề nào sai?

A. Hai số tự nhiên chia hết cho

7

là điều kiện đủ để tổng hai số đó chia hết cho

7

.

B. Một số tự nhiên chia hết cho 2 là điều kiện cần để số đó chia hết cho 4 .

C. Một tam giác là tam giác vuông là điều kiện cần và đủ để nó có một góc bằng tổng hai góc

còn lại.

D. Hai tam giác là tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một góc bằng

nhau.

Câu 12: Chỉ ra khẳng định sai?

A.

2

1 1x x    . B.

2 2

2 2 1 ( 2) (2 1)x x x x      

.

C.

2 3 2 2 0x x x     

. D.

3 2 3 4x x    

.

Câu 13: Nếu hàm số

2

y ax bx c   có đồ thị như sau thì dấu các hệ số của nó là

A. 0; 0; 0.a b c   B. 0; 0; 0.a b c   C. 0; 0;c 0.a b   D. 0; 0; 0.a b c  

Câu 14: Phương trình

4 2

2( 2 1) 4 3 5 0x x    

 

1

có bao nhiêu nghiệm?

A.

0

. B.

4

. C.

2

. D. 3.

Câu 15: Cho tam giác đều

ABC

cạnh

a

, trọng tâm

G

. Phát biểu nào đúng?

A.

3 .AB AC AB CA  

   

B.

.GA GB GC 

  

C.

AB AC

 

. D.

2 .AB AC a 

 

Câu 16: Cho tam giác

ABC

. Mệnh đề nào sai?

A.

cos sin .

2 2

A B C



B.

 

cos cos 0.A B C  

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

C.





tan tan

A B C

 

. D.





sin sin

A B C

 

.

Câu 17: Có bao nhiêu giá trị nguyên của tham số





2020;2020

m 

để phương trình





2

2 1

x m x x m   

có hai nghiệm phân biệt?

A.

2022

. B.

2020

. C.

2019

. D.

2021

.

Câu 18: Cho các số thực

, , ,

a b c d

dương. Tìm mệnh đề sai?

A.

a b

c d c d





 







. B. 1

a a a c

b b b c



  



. C.

a b

ac bd

c d





 







. D.

a a a

  

.

Câu 19: Cho hình bình hành

ABCD

có

4 ; 5 ; 7

AB cm BC cm BD cm

  

. Độ dài đoạn

AC

bằng bao

nhiêu

cm

? (Tính chính xác đến hàng phần trăm)

A.





6,25

cm

. B.





5,74

cm

. C.





5,67

cm

. D.





5,93

cm

.

Câu 20: Đồ thị hàm số

y ax b

 

đi qua đỉnh của Parabol





2

: 2 3

P y x x

  

thì

a b



bằng

A.

2



. B.

1

. C.

2

. D.

1



.

Câu 21: Cho

,

u v

là các số thực thỏa mãn

2 2

2 3 2

u v

 

. Gọi

M

,

m

lần lượt là giá trị lớn nhất, giá trị

nhỏ nhất của biểu thức









2

3 6 1

P u u v

    . Khi đó

M m



bằng.

A.

83

4

. B.

59

4

. C.

14

. D.

65

4

.

Câu 22: Trong mặt phẳng tọa độ

Oxy

, cho tam giác

ABC

với













2;4 , 3;1 , 3; 1

A B C

 

. Gọi

H

là

chân đường cao kẻ từ đỉnh

A

của tam giác

ABC

. Tọa độ điểm

H

là

A.

3 2

;

5 5

 



 

 

. B.

3 1

;

5 5

 



 

 

. C.

4 2

;

5 5

 



 

 

. D.

5 3

;

8 8

 



 

 

.

Câu 23: Cho hai tập





0;6

A 

,





: 2

B x x

  

 . Hợp của hai tập

A

và

B

là

A.





0;2

. B.





2;6

 . C.





2;6

 . D.





0;2

.

Câu 24: Trong mặt phẳng

Oxy

, cho ba điểm

(3; 1)

A



;

( 4;2)

B



;

(4;3)

C . Tìm tọa độ điểm

D

để tứ

giác

ABCD

là hình bình hành.

A.

( 3;6)

D



. B.

(0;11)

D . C.

(11;0)

D . D.

(3; 6)

D



.

Câu 25: Gọi

S

là tập hợp tất cả các giá trị của

m

để đồ thị hàm số





2

2 3

y m m x

  

cắt trục hoành tại

điểm có hoành độ bằng

1

. Tính tổng các phần tử của

S

.

A.

3

. B.

2

. C.

2



. D.

0

.

Câu 26: Phương trình





3 2

a x b

  

vô nghiệm với giá trị

,

a b

là:

A.

a

tùy ý,

2

b



. B.

3

a



,

b

tùy ý. C.

3, 2

a b

 

. D.

3, 2

a b

 

.

Câu 27: Trong mặt phẳng tọa độ

Oxy

, cho





2 3 2

a j i

 

  

thì véctơ

a



có tọa độ là cặp số:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.







3; 2

.

B.







6; 4

. C.







2;3

. D.







4;6

.

Câu 28: Cho phương trình

2 2

2 2 9 0

x mx m

   

có hai nghiệm

1 2

;

x x

. Tìm giá trị lớn nhất của biểu

thức









1 2

1 1

A x x

  

.

A.

17

2



. B.

4

. C.

16

. D.

17

2

.

Câu 29: Cho tam giác

ABC

có trọng tâm

G

. Gọi

N

là điểm thỏa mãn

1

2

CN BC



 

. Đẳng thức nào sau

đây là đúng?

A.

3 1

4 2

AC AG AN

 

  

. B.

2 1

3 2

AC AG AN

 

  

.C.

4 1

3 2

AC AG AN

 

  

.D.

2 1

3 2

AC AG AN

 

  

.

Câu 30: Giải bóng đá SEA Games có

4

đội lọt vào vòng bán kết: Việt Nam, Thái Lan, Indonesia,

Singapo. Trước các trận đấu,

3

bạn dự đoán như sau: An: Singapo nhì, Thái lan ba; Bình: Việt

Nam nhì, Thái lan thứ

4

; Tuấn: Singapo nhất, Indonesia nhì. Kết quả mỗi bạn đoán đúng là

1

đội và sai

1

đội. Thứ tự đoạt giải: nhất, nhì, ba,bốn là:

A. Việt Nam, Singapo, Thái Lan, Indonesia.B. Singapo,Việt Nam, Indonesia, Thái Lan.

C. Singapo,Việt Nam, Thái Lan, Indonesia. D. Thái Lan,Việt Nam, Indonesia, Singapo.

Câu 31: Cho hai hàm số

 

1

f x

x



và





4 2

g 1

x x x

   

. Mệnh đề nào đúng?

A.





f x

và





g x

đều là hàm chẵn. B.





f x

lẻ,





g x

chẵn.

C.





f x

và





g x

đều là hàm lẻ. D.





f x

chẵn,





g x

lẻ.

Câu 32: Hai tàu thủy cùng xuất phát từ vị trí A, đi theo hai hướng và tạo với nhau một góc

0

60

. Tàu thứ

nhất chạy với vận tốc

30km/h

, tàu thứ hai chạy với vận tốc

40km/h

. Hỏi sau

2

giờ hai tàu

cách xa nhau bao nhiêu

km

?

A.

25 10

. B.

30 10

. C.

18 13

. D.

20 13

.

Câu 33: Cho hình bình hành

ABCD

. Gọi

,

M N

là hai điểm thỏa mãn: .

Cho

G

là trọng tâm của tam giác

BMN

. Gọi

E

là điểm thỏa mãn:





1

CE x BC

 

 

. Tìm

x

để

ba điểm

, ,

A G E

thẳng hàng.

A.

5

8

x



. B.

6

11

x



. C.

7

12

x



. D.

5

9

x



.

Câu 34: Trong các mệnh đề sau đây, mệnh đề nào đúng?

A. Tổng độ dài hai cạnh của một tam giác luôn luôn lớn hơn độ dài cạnh còn lại.

B. Hai tam giác có diện tích bằng nhau thì hai tam giác đó bằng nhau.

C. Số 9 là số nguyên tố.

D. Nếu một số tự nhiên chia hết cho 3 thì số đó chia hết cho 6.

Câu 35: Mệnh đề phủ định của mệnh đề “

2

: 3 4 1 0

x x x

    



” là mệnh đề

2. 0, 0

MA MB NC ND

   

     

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A. “

2

: 3 4 1 0

x x x

    



”. B. “

2

: 3 4 1 0

x x x

    



”.

C. “

2

: 3 4 1 0

x x x

    



”. D. “

2

: 3 4 1 0

x x x

    



”.

PHẦN II: TỰ LUẬN

Bài 1: (1 điểm) Trong mặt phẳng tọa độ

Oxy

, cho hai điểm





1; 2

A



,





4;3

B

.

a) Tính độ dài đoạn thẳng

AB

.

b) Tìm tọa độ điểm

M

trên trục tung sao cho tam giác

ABM

vuông tại

A

.

Bài 2a. (1 điểm) Tìm

m

để hệ phương trình

2

2 0

3 4 0

x xy

x xy x y m



 





    





có 3 nghiệm phân biệt.

Bài 2b. (1 điểm) Cho

x

,

y

là hai số thực thỏa mãn





2 2

2 1

x y xy

  

.Tìm giá trị lớn nhất và giá trị nhỏ

nhất của biểu thức:









2

4 4

2 1

P x y x y

    

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG HDG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 3 Môn Toán – Lớp 10

(Thời gian làm bài 90 phút)

Không k

ể thời gian phát đề

Câu 1: Cho hệ phương trình

2 2 2

4

.

x y

x y m

 





 



Khẳng định nào sau đây là đúng?

A. Hệ có nghiệm duy nhất khi và chỉ khi

2.

m



B. Hệ có nghiệm khi và chỉ khi

8.

m 

C. Hệ vô nghiệm khi và chỉ khi

0.

m



D. Hệ có nghiệm với mọi

.

m

Lời giải

Chọn B

Ta có

 





 

2

2 2 2

2 2

4

4 1

4

2 8 16 0 2

y x

x y

x y m

x x m

 

  



 



 

 

  

 

  

   



 



Hệ đã cho có nghiệm khi và chỉ khi phương trình





2

có nghiệm, tức là





2 2

4 2 16 0 8.

m m



      

Câu 2:

Các cạnh của tam giác

ABC

thỏa mãn

3 3 3

2

b c a

a

b c a

 



 

. Số đo góc

A

là:

A.

120



. B.

60



. C.

45



. D.

30



.

Lời giải

Chọn B

Ta có

 

3 3 3

2 3 3 3 2 3

b c a

a b c a a b c a

b c a

 

      

 













2 2 2

b c b bc c a b c

     

2 2 2

b c a bc

   

.

Do đó theo định lý cosin ta có

2 2 2

1

cos 60

2 2 2

b c a bc

A A

bc bc

 

     

.

Câu 3: Cho





0 0

;

x y

là nghiệm của hệ phương trình

2 3

5 4 0

x y

 





  



. Tính giá trị của biểu thức

4 4

0 0

.

P x y

 

A.

0

P



. B.

2

P



. C.

4

P



. D.

8

P



.

Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Chọn B

Ta có

 

2 3

2 3 11 11 0 1

5 2 3 4 0

5 4 0 2 3 1

y x

x y x x

x x

x y y x y

 

    

  



  

   

   

      



  



.

Vậy

0

1

x



,

0

1

y



nên

 

4

1 1 2

P

   

.

Câu 4: Cho hình bình hành

ABCD

. Trong các khẳng định sau, khẳng định nào sai?

A.

A D C B



 

. B.

AD CB



 

. C.

AB D C



 

. D.

AB CD



 

.

Lời giải

Chọn A

Ta có:

AD B C C B

  

  

. Suy ra phương án A sai.

AD BC AD CB

  

 

. Suy ra phương án B đúng.

AB D C



 

. Suy ra phương án C đúng.

AB CD AB CD

  

 

. Suy ra phương án D đúng.

Câu 5: Trong mặt phẳng tọa độ

O xy

, cho hai vectơ





2;5

a 



,





6; 14

b  



. Góc tạo bởi hai vectơ

a



,

b



là:

A.

60



. B.

135



. C.

45



. D.

120



.

Lời giải

Chọn B

Ta có:

2 2

2 5 29

a   



;

 

2

6 14 232

b    



.

 

. 2.6 5.( 14) 58 2

cos ;

2

29. 232 58. 2

.

a b

   

   

 

Vậy





; 135

a b

 

 

.

Câu 6: Cho





| 2 1 3

A x x

   



,





1; 3

B m m

  

. Gọi

S

là tập hợp tất cả các số nguyên

m

để

A B

  

. Tổng tất cả các phần tử của

S

bằng

A.

0

. B.

5

. C.

4

. D.

9

.

Lời giải

Chọn C

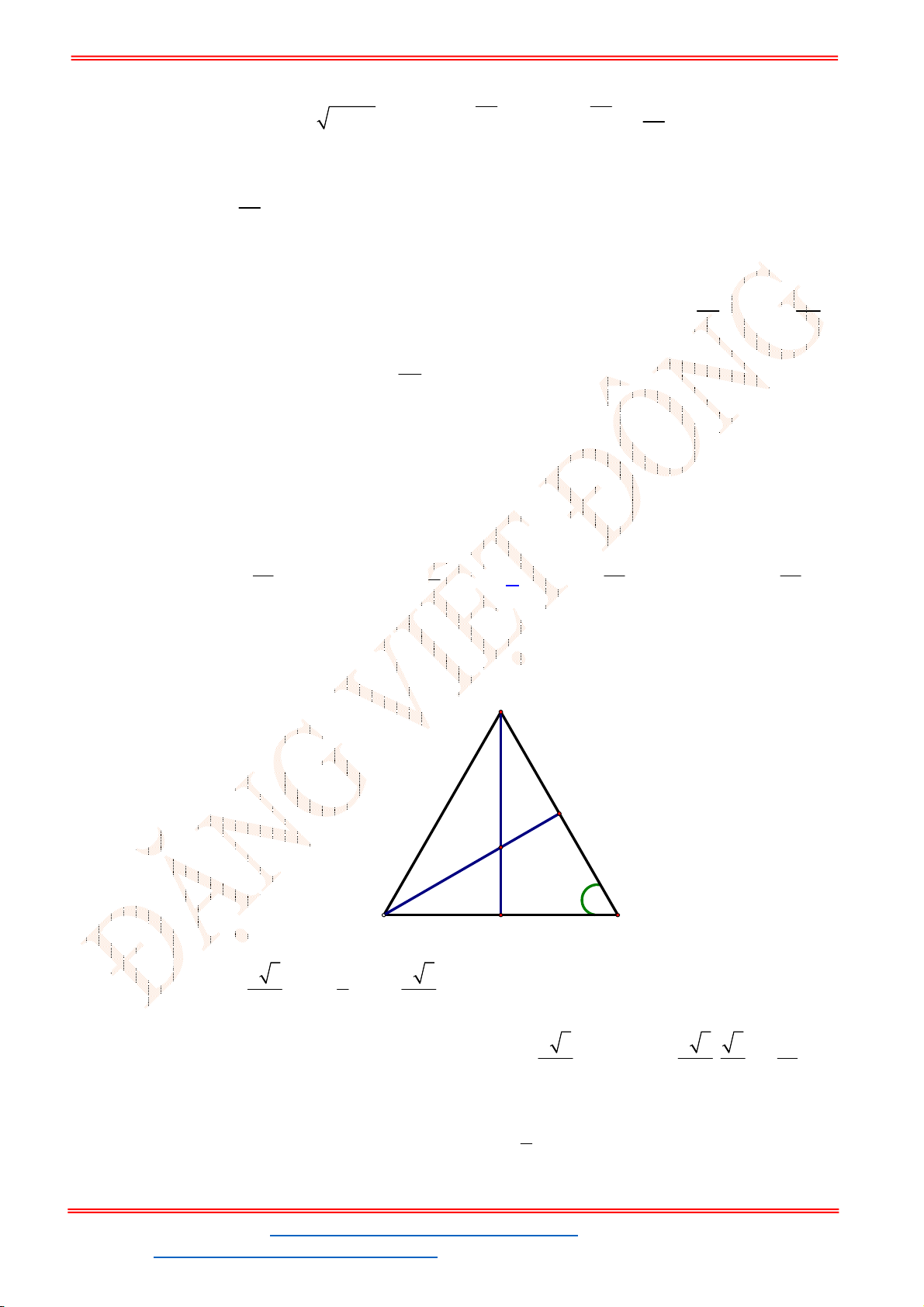
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Giải bất phương trình:

1 1

1

2 1 3 4

2 2

2

2 1 9 4

x x

 

 

 



 

      

 

 

  

 

.

Do đó

1

;4

2

A



 







 

.

Ta tìm điều kiện để

A B

  

. Điều này xảy ra khi và chỉ khi

4 1 5

1 7

3

2 2

m m

  

 

 



 

 

  

 

.

Do đó

A B

  

khi và chỉ khi

7

5

2

m



 

.

Mà

m





nên





3; 2; 1;0;1;2;3;4

S    

.

Vậy tổng tất cả các phần tử của

S

bằng 4.

Câu 7: Gọi

G

là trọng tâm tam giác đều

ABC

có cạnh bằng

a

. Trong các mệnh đề sau, tìm mệnh đề

sai?

A.

2

.

2

a

ABGA

 

 

. B.

2

1

.

2

AB AC a



 

. C.

2

.

6

a

GAGB 

 

. D.

2

.

2

a

ABCB 

 

.

Lời giải

Chọn C

Ta có:

3 2 3

;

2 3 3

a a

AM AG AM  

. Suy ra:

+)

 

2

3 3 3

. . . .cos , . .cos30 . .

3 3 2 2

a a a

ABGA AB AG AB AG AB AG a a

          

     

. Do đó

mệnh đề ở phương án A đúng.

+)

 

2

1

. . .cos , . .cos 60

2

AB AC AB AC AB AC a a a

   

   

. Do đó mệnh đề ở phương án B đúng.

60°

a

G

M

B

A

C

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

+)

 

2 2

3 3 1

. . .cos , . .cos120 .

3 3 3 2 6

a a a a

GAGB GAGB GA GB

 

      

 

 

   

. Do đó mệnh đề ở

phương án C sai.

+)

 

2

. . . .cos , . .cos60

2

a

ABCB BABC BABC BA BC aa   

     

. Do đó mệnh đề ở phương án D

đúng.

Câu 8: Cho

, ,

a b c

  

là ba vectơ khác

0



. Xét 3 mệnh đề sau:





I . .

ab ac b c

  

     

 









II . . . .

a b c a b c



     

 





2

2 2

III . .

ab a b



   

Trong ba mệnh đề trên mệnh đề nào sai?

A. I và II và III. B. I và III. C. I và II. D. II và III.

Lời giải

Chọn A

Cả 3 mệnh đề đều sai, chẳng hạn chọn













1;0 , 0;1 , 0;2

a b c  

  

. Khi đó ta kiểm tra

được:

+)

. . 0

a b a c

 

   

nhưng

b c



 

nên (I) sai.

+)





. . 0. 0

a b c c

 

    

và





. . 2 0

a b c a

 

    

nên (II) sai.

+)





2

. 0 0

ab

 

 

và

2 2

. 1.1 1 0

a b

  

 

nên (III) sai.

Câu 9: Cho tập













3 3 2

| 4 2 5 2 0

M x x x x x x

     



. Viết tập

M

bằng cách liệt kê các phần tử

A.





0;2

M 

. B.

1 5

;0;2;

2 2

M

 

 

 

 

. C.

5

0;2;

2

M

 



 

 

. D.

1 5

0; ;2;

2 2

M

 



 

 

.

Lời giải

Chọn A

Xét phương trình









3 3 2

4 2 5 2 0

x x x x x

   

3

3 2

4 0

2 5 2 0

x x

x x x



 





  



 

2

1

0;

4 1 0

2

1

2 5 2 0

0; 2;

2

x x

x x x



  



 



 



  



  







.

Mà

x





nên ta có





0;2

M 

.

Câu 10: Cho

0 0

90 180

a 

và các mệnh đề sau:

P: “

sin .cos 0

a a



”; Q: “

tan .cos 0

a a



”; R: “

cot .cos 0

a a



”. Hãy chọn khẳng định đúng?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A. P, Q, R đúng. B. P, Q đúng, R sai. C. P, R đúng, Q sai. D. Q, R đúng, P sai.

Lời giải

Chọn B

Vì

0 0

90 180

a 

nên

cos 0, sin 0, tan 0, cot 0

a a a a

   

. Do đó ta có

sin .cos 0

tan .cos 0

cot .cos 0

a a

















.

Vậy P, Q đúng, R sai.

Câu 11: Trong các mệnh đề sau đây, mệnh đề nào sai?

A. Hai số tự nhiên chia hết cho

7

là điều kiện đủ để tổng hai số đó chia hết cho

7

.

B. Một số tự nhiên chia hết cho

2

là điều kiện cần để số đó chia hết cho

4

.

C. Một tam giác là tam giác vuông là điều kiện cần và đủ để nó có một góc bằng tổng hai góc

còn lại.

D. Hai tam giác là tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một góc bằng

nhau.

Lời giải

Chọn D

Phương án D sai vì :

“Hai tam giác bằng nhau thì chúng đồng dạng và có một góc bằng nhau” là mệnh đề đúng;

nhưng mệnh đề: “Hai tam giác đồng dạng và có một góc bằng nhau thì hai tam giác đó bằng

nhau” là sai. Thật vậy xét

ABC



vuông tại

A

, có đường cao

AH

Khi đó





.

ABH CAH g g

 



nhưng hai tam giác này không bằng nhau.

Câu 12: Chỉ ra khẳng định sai?

A.

2

1 1

x x

   

. B.

2 2

2 2 1 ( 2) (2 1)

x x x x

      

.

C.

2 3 2 2 0

x x x

     

. D.

3 2 3 4

x x

    

.

Lời giải

Chọn B

Xét hai phương trình

2 2 1

x x

  

(1) và

2 2

( 2) (2 1)

x x

  

(2)

2 2

2

1

2 1 0

1

2 2 1

2

3

( 2) (2 1)

3 8 3 0

x

x x x

x x



 

 





      

 

  





  



2 2 2

3

( 2) (2 1) 3 8 3 0

1

3

x

x x x x

x

 





       







ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Hai phương trình (1) và (2) không có cùng tập nghiệm nên không tương đương.

Câu 13: Nếu hàm số

2

y ax bx c  

có đồ thị như sau thì dấu các hệ số của nó là

A.

0; 0; 0.a b c  

B.

0; 0; 0.a b c  

C.

0; 0; c 0.a b  

D.

0; 0; 0.a b c  

Lời giải

Chọn A

Parabol quay bề lõm lên trên ta suy ra:

0a 

;

Đỉnh của Parabol nằm bên trái trục tung, hoành độ đỉnh âm, ta có:

0

2

b

a





. Suy ra:

0;b 

Parabol cắt trục hoành tại hai điểm nằm về hai phía của trục tung nên:

Phương trình

2

0ax bx c  

có hai nghiệm trái dấu. Suy ra:

. 0a c 

hay

0;c 

Vậy:

0; 0; 0.a b c  

Câu 14: Phương trình

4 2

2( 2 1) 4 3 5 0x x    

 

1

có bao nhiêu nghiệm?

A.

0

. B.

4

. C.

2

. D.

3

.

Lời giải

Chọn C

Đặt

2

, 0t x t 

Phương trình

 

1

trở thành

2

2( 2 1)t 4 3 5 0 (2)t     

. Do

. 1.(4 3 5) 0ac   



Phương trình

 

2

có 2 nghiệm phân biệt

1

2

0

t t

 





 



.

Kết hợp với điều kiện

2

0t t t  

là nghiệm của

 

2

.

Với

2

2 2 2

t t x t x t     

nên phương trình

(1)

có

2

nghiệm phân biệt.

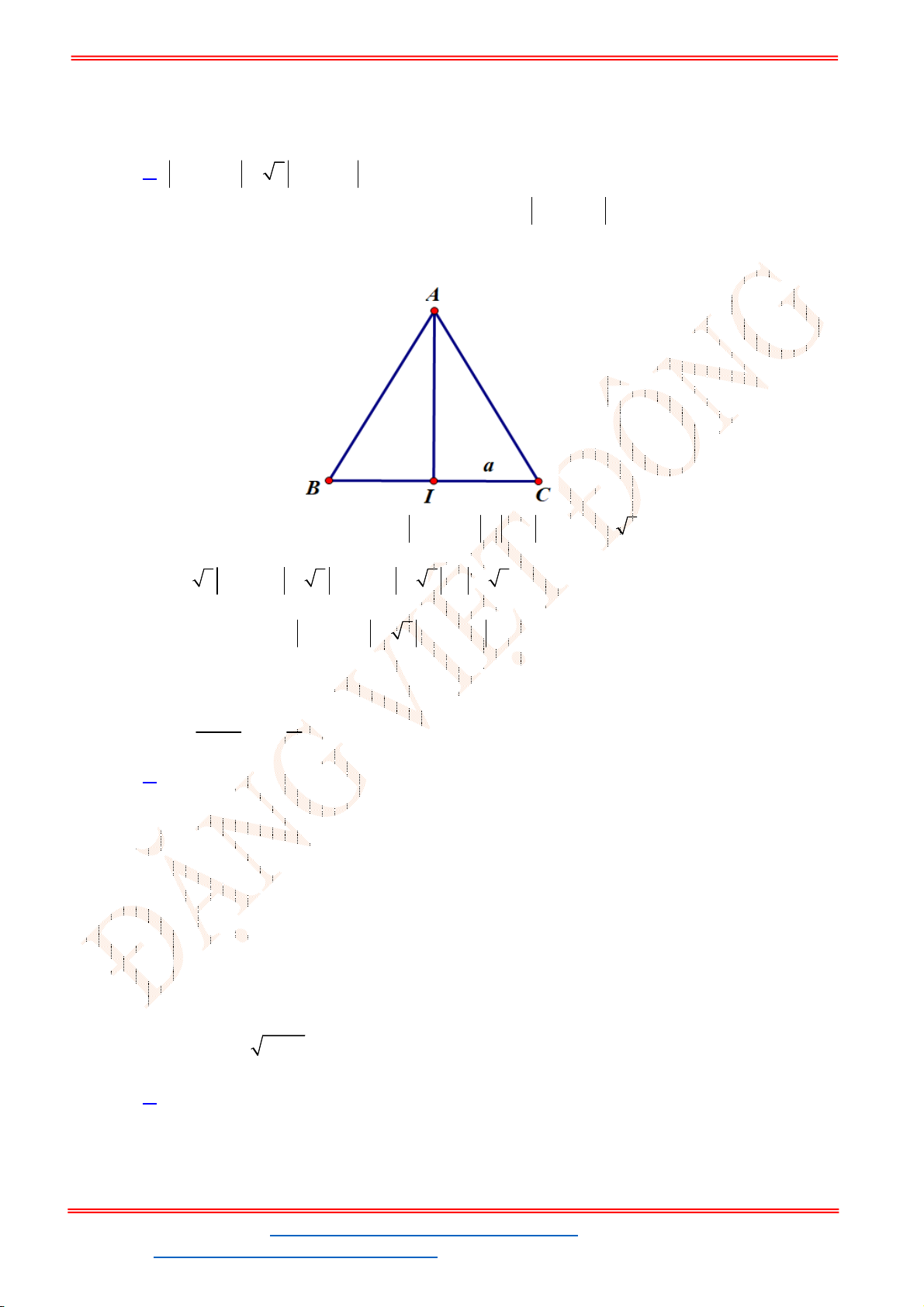
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Vậy chọn đáp án C.

Câu 15: Cho tam giác đều

ABC

cạnh

a

, trọng tâm

G

. Phát biểu nào đúng?

A.

3 .

AB AC AB CA

  

   

B.

.

G A G B G C

 

  

C.

A B A C



 

. D.

2 .

AB AC a

 

 

Lời giải

Chọn A

Gọi

I

là trung điểm của

AB

ta có

2 2 3

AB AC AI AI a

   

  

. (1)

Ta có

3 3 3 3 .

AB CA CA AB CB a

    

    

(2)

Từ (1) và (2) suy ra

3 .

AB AC AB CA

  

   

Câu 16: Cho tam giác

ABC

. Mệnh đề nào sai?

A.

cos sin .

2 2

A B C





B.





cos cos 0.

A B C

  

C.





tan tan

A B C

 

. D.





sin sin

A B C

 

.

Lời giải

Chọn C

Trong tam giác

ABC

ta luôn có:.









0 0 0

180 180 tan tan 180 tan

A B C A B C A B C C

            

.

Vậy ta chọn phương án C

Câu 17: Có bao nhiêu giá trị nguyên của tham số





2020;2020

m 

để phương trình





2

2 1

x m x x m   

có hai nghiệm phân biệt?

A.

2022

. B.

2020

. C.

2019

. D.

2021

.

Lời giải

Chọn A

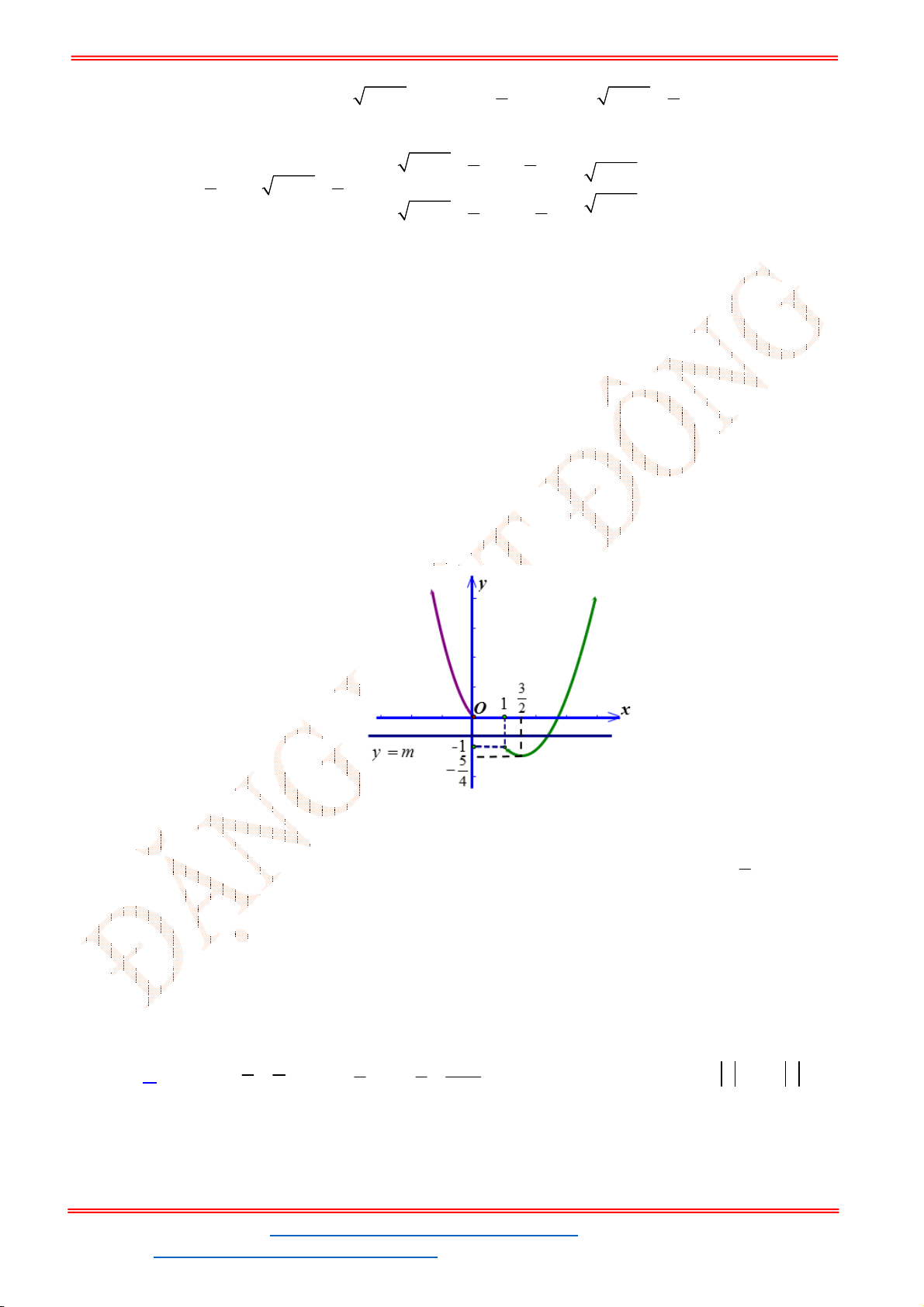
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

PT

 

2 2

1 1

1 ( ) ( )

4 4

x x x m x m x x x m x m

             

2 2

1 1

1

1 1

2 2

1 1

2 2

x m x

x x m

x m x



   

 

  

   

      

 

   

   

  

 



    





 

2

2 2

1

3 1

1 1

2

0

x m x

x x m

x x

x x m

x m x

x





  





  









 





 



 



 

 

  

























PT





1

có hai nghiệm phân biệt



Hệ pt





2

có hai nghiệm phân biệt.

Vẽ trên cùng một hệ trục tọa độ đồ thị hàm số

xxy 

2

( với

0



x

) và

đồ thị hàm số

13

2

 xxy

( với

1



x

).

Số nghiệm của hệ





2

chính là số giao điểm của đường thẳng

m

y



với hai nhánh đồ thị trên.

Dựa vào đồ thị trên, hệ





2

có hai nghiệm phân biệt khi và chỉ khi

0

m



hoặc

5

1

4

m

   

.

Kết hợp với điều kiện:





2020;2020 ,m m

  



suy ra:





1;0;1;2;...;2020

m 

.

Vậy có tất cả

2022

giá trị của

m

thỏa mãn yêu cầu bài toán.

Câu 18: Cho các số thực

, , ,

a b c d

dương. Tìm mệnh đề sai?

A.

a b

c d c d





 







. B.

1

a a a c

b b b c



  



. C.

a b

ac bd

c d





 







. D.

a a a

  

.

Lời giải

Chọn A

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Mệnh đề

a b

c d c d





 







sai

Vì với ví dụ cụ thể:

1 2

1 1

2 6 2 3

a b

c d c d

  



   



  



là mệnh đề sai.

Câu 19: Cho hình bình hành

ABCD

có

4 ; 5 ; 7

AB cm BC cm BD cm

  

. Độ dài đoạn

AC

bằng bao

nhiêu

cm

? (Tính chính xác đến hàng phần trăm)

A.





6,25

cm

. B.





5,74

cm

. C.





5,67

cm

. D.





5,93

cm

.

Lời giải

Chọn B

Gọi

I

là giao điểm của

AC

và

BD

.

Áp dụng công thức độ dài đường trung tuyến trong tam giác

ABD

ta có

2 2 2

2

2 4

AB AD BD

AI



 

2 2 2

2

4 5 7

2 4

AI



  

2

33

4

AI 

 

33

2

AI cm

 

 

33

2 2. 5,74

2

AC AI cm

   

.

Câu 20: Đồ thị hàm số

y ax b

 

đi qua đỉnh của Parabol





2

: 2 3

P y x x

  

thì

a b



bằng

A.

2



. B.

1

. C.

2

. D.

1



.

Lời giải

Chọn C

Toạ độ đỉnh của





2

: 2 3

P y x x

  

là

 

; 1;2

2 4

b

I I

a a



 

  

 

 

Đồ thị hàm số

y ax b

 

đi qua đỉnh của Parabol





2

P a b

  

.

Câu 21: Cho

,

u v

là các số thực thỏa mãn

2 2

2 3 2

u v

 

. Gọi

M

,

m

lần lượt là giá trị lớn nhất, giá trị

nhỏ nhất của biểu thức









2

3 6 1

P u u v

    . Khi đó

M m



bằng.

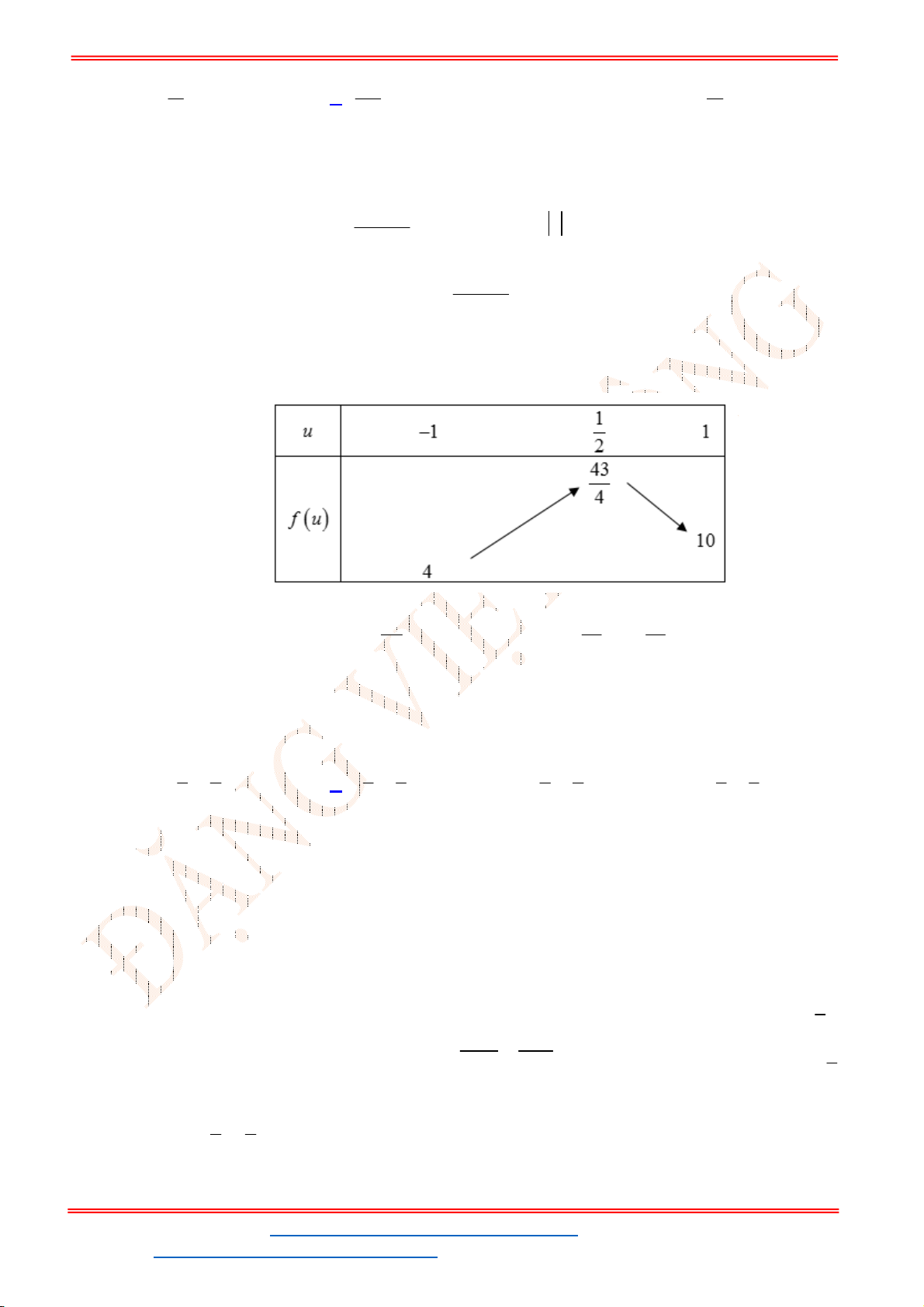
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

83

4

. B.

5 9

4

. C.

14

. D.

65

4

.

Lời giải

Chọn B

Ta có

2

2 2 2

2 2

2 3 2

3

u

u v v



   

, suy ra điều kiện

1

u



.

 

2

2 2

3 6 1 3 6 1

3

u

P u u v u u

 



       

 

 

2

3 3 10

u u

   

.

Xét hàm số





2

3 3 10

f u u u

   

trên đoạn





1;1



có bảng biến thiên như sau

Từ bảng biến thiên suy ra

43

4

M 

và

4

m



nên

43 59

4

4 4

M m   

.

Câu 22: Trong mặt phẳng tọa độ

Oxy

, cho tam giác

ABC

với













2;4 , 3;1 , 3; 1

A B C

 

. Gọi

H

là

chân đường cao kẻ từ đỉnh

A

của tam giác

ABC

. Tọa độ điểm

H

là

A.

3 2

;

5 5

 



 

 

. B.

3 1

;

5 5

 



 

 

. C.

4 2

;

5 5

 



 

 

. D.

5 3

;

8 8

 



 

 

.

Lời giải

Chọn B

Giả sử





;

H a b

, ta có:













2; 4 , 3; 1 , 6; 2

AH a b BH a b BC

       

  

.

Điểm

H

là chân đường cao kẻ từ đỉnh

A

của tam giác

ABC

nên ta có:

AH BC



 

và

,

BH BC

 

cùng phương









6 2 2 4 0

3 1

6 2

a b

   









 









3

3 2

5

3 0 1

5

a

a b

b







 





 

 

 





 





.

Vậy

3 1

;

5 5

H

 



 

 

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 23: Cho hai tập





0;6

A 

,





: 2

B x x

  

 . Hợp của hai tập

A

và

B

là

A.





0;2

. B.





2;6



. C.





2;6



. D.





0;2

.

Lời giải

Chọn C

Câu 24: Trong mặt phẳng

Oxy

, cho ba điểm

(3; 1)

A



;

( 4; 2)

B



;

(4;3)

C

. Tìm tọa độ điểm

D

để tứ

giác

ABCD

là hình bình hành.

A.

( 3;6)

D



. B.

(0;11)

D

. C.

(11; 0)

D

. D.

(3; 6)

D



.

Lời giải

Chọn C

Gọi điểm

( ; )

D x y

. Ta có

( 7;3)

AB  



;

(8;1)

BC 



;

(4 ;3 )

DC x y

  



.

Ta thấy

A B



và

B C



không cùng phương nên

; ;

A B C

không thẳng hàng.

Tứ giác

ABCD

là hình bình hành

4 7 11

3 3 0

x x

AB DC

y y

   

 

   

 

  

 

 

.

Vậy

(11; 0)

D

.

Câu 25: Gọi

S

là tập hợp tất cả các giá trị của

m

để đồ thị hàm số





2

2 3

y m m x

  

cắt trục hoành tại

điểm có hoành độ bằng

1

. Tính tổng các phần tử của

S

.

A.

3

. B.

2

. C.

2



. D.

0

.

Lời giải

Chọn B

Phương trình hoành độ giao điểm:





2

2 3 0

m m x

  

.

Vì hàm số đã cho cắt trục hoành tại điểm có hoành độ

1

 

2

1

2 3 0 1;3

3

m

m m S

m

 



       







. Do đó tổng các phần tử của

S

là

1 3 2

  

.

Câu 26: Phương trình





3 2

a x b

  

vô nghiệm với giá trị

,

a b

là:

A.

a

tùy ý,

2

b



. B.

3

a



,

b

tùy ý. C.

3, 2

a b

 

. D.

3, 2

a b

 

.

Lời giải

Chọn D









3 2 3 2

a x b a x b

      

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Phương trình đã cho vô nghiệm

3 0 3

2 0 2

a a

b b

  

 

 

 

  

 

.

Câu 27: Trong mặt phẳng tọa độ

Oxy

, cho





2 3 2

a j i

 

  

thì véctơ

a



có tọa độ là cặp số:

A.







3; 2

.

B.







6; 4

. C.







2;3

. D.







4;6

.

Lời giải

Chọn D

Ta có









2 3 2 4 6 4;6

a j i i j a       

     

.

Câu 28: Cho phương trình

2 2

2 2 9 0

x mx m

   

có hai nghiệm

1 2

;

x x

. Tìm giá trị lớn nhất của biểu

thức









1 2

1 1

A x x

  

.

A.

17

2



. B.

4

. C.

16

. D.

17

2

.

Lời giải

Chọn C

 Ta có

2 2 2

' 2 9 9

m m m

      

.

 Phương trình có hai nghiệm

1 2

;

x x

khi





2

' 0 9 0 3;3

m m        

.

 Theo định lý Viet:

1 2

2

1 2

2

. 2 9

x x m

 





 



. Ta được





2 2

1 2 1 2

1 2 9 2 1 2 2 8

A x x x x m m m m

          

 Xét hàm số





2

2 2 8

f m m m

  

,





3;3

m 

. Ta có BBT của hàm





f m

trên đoạn





3;3



như sau:

 Từ BBT suy ra giá trị lớn nhất của

A

là

16

đạt tại

3

m

 

.

Câu 29: Cho tam giác

ABC

có trọng tâm

G

. Gọi

N

là điểm thỏa mãn

1

2

CN BC



 

. Đẳng thức nào sau

đây là đúng?

m

f

m( )

4

16

-

17

2

+∞

-∞

1

2

3

-3

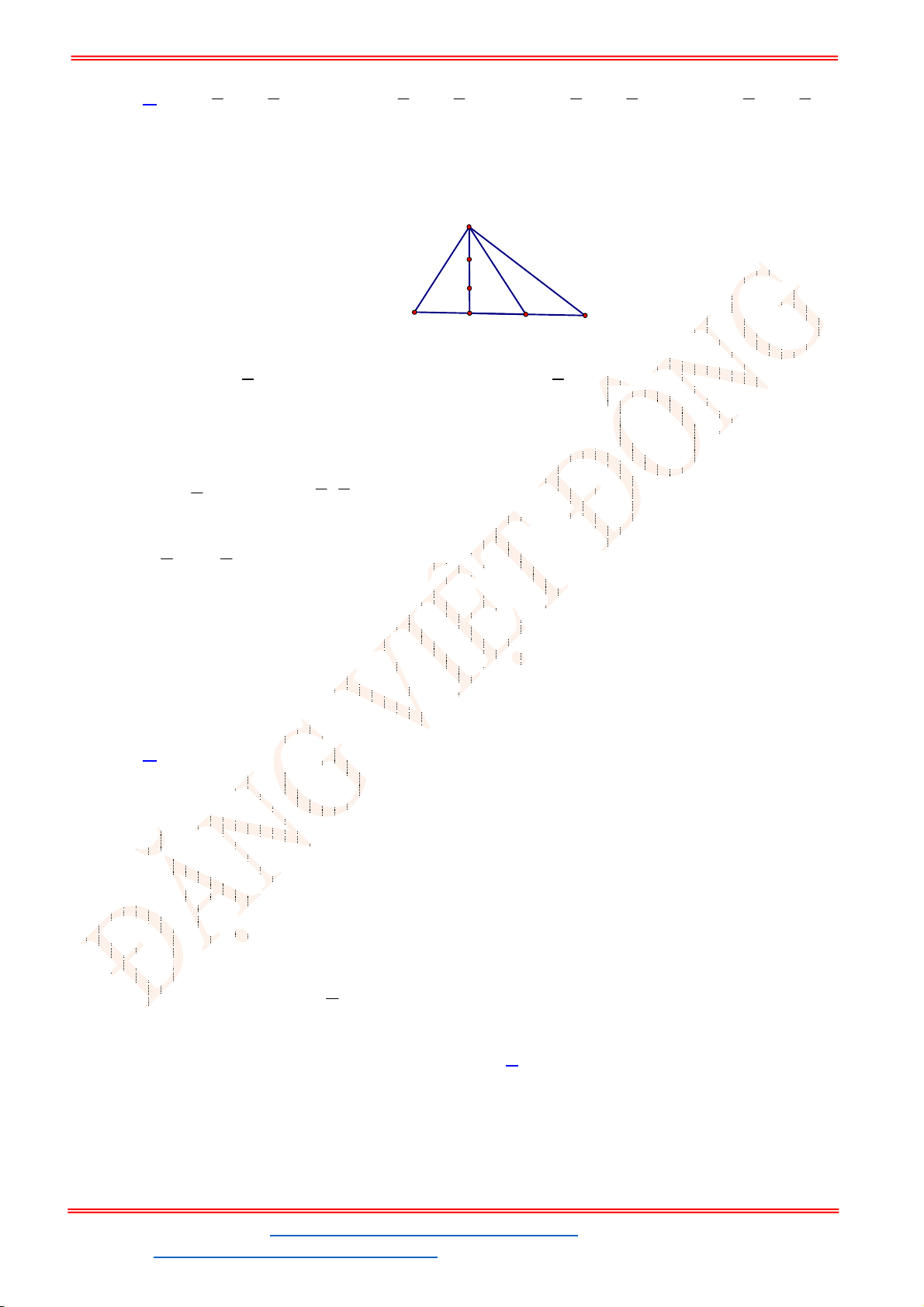
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

3 1

4 2

AC AG AN

 

  

. B.

2 1

3 2

AC AG AN

 

  

.C.

4 1

3 2

AC AG AN

 

  

.D.

2 1

3 2

AC AG AN

 

  

.

Lời giải

Chọn A

Ta có:

1

2

CN BC



 

C N





,

B C



cùng hướng và

1

2

CN BC



.

Gọi

M

là trung điểm

BC

. Khi đó, chứng minh được

C

là trung điểm

MN

. Suy ra

 

1

2

AC AM AN

 

  

1 3

2 2

AG AN

 

 

 

 

 

( vì

G

là trọng tâm tam giác

ABC

)

3 1

4 2

AG AN

 

 

.

Câu 30: Giải bóng đá SEA Games có

4

đội lọt vào vòng bán kết: Việt Nam, Thái Lan, Indonesia,

Singapo. Trước các trận đấu,

3

bạn dự đoán như sau: An: Singapo nhì, Thái lan ba; Bình: Việt

Nam nhì, Thái lan thứ

4

; Tuấn: Singapo nhất, Indonesia nhì. Kết quả mỗi bạn đoán đúng là

1

đội và sai

1

đội. Thứ tự đoạt giải: nhất, nhì, ba,bốn là:

A. Việt Nam, Singapo, Thái Lan, Indonesia.B. Singapo,Việt Nam, Indonesia, Thái Lan.

C. Singapo,Việt Nam, Thái Lan, Indonesia.D. Thái Lan,Việt Nam, Indonesia, Singapo.

Lời giải

Chọn C

Giả sử An đoán Singapo nhì đúng thì Tuấn đoán sai Singapo nhất là sai và Indonesia nhì đúng



mâu thuẫn vì hai đội cùng về nhì.Vậy An đoán Thái lan ba là đúng, Bình đoán Việt nam nhì

đúng, Tuấn đoán Singapo nhất đúng.

Kết quả là: Singapo,Việt Nam, Thái Lan, Indonesia.

Câu 31: Cho hai hàm số

 

1

f x

x



và





4 2

g 1

x x x

   

. Mệnh đề nào đúng?

A.





f x

và





g x

đều là hàm chẵn. B.





f x

lẻ,





g x

chẵn.

C.





f x

và





g x

đều là hàm lẻ. D.





f x

chẵn,





g x

lẻ.

Lời giải

Chọn B

A

B

N

M

C

G

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

*Xét hàm số

 

1

f x

x



Ta có: Tập xác định





\ 0

D



.

,

x D x D

   

   

1

f x f x

x

    

, suy ra hàm số lẻ

*Xét hàm số





4 2

1

g x x x

  

Ta có: Tập xác định

D





.

,

x D x D

   

















4 2

1 1

g x x x x x g x

           

, suy ra hàm số chẵn

Vậy





f x

lẻ,





g x

chẵn.

Câu 32: Hai tàu thủy cùng xuất phát từ vị trí A, đi theo hai hướng và tạo với nhau một góc

0

60

. Tàu

thứ nhất chạy với vận tốc

30 km /h

, tàu thứ hai chạy với vận tốc

40 km/h

. Hỏi sau

2

giờ hai

tàu cách xa nhau bao nhiêu

km

?

A.

25 10

. B.

30 10

. C.

18 13

. D.

20 13

.

Lời giải

Chọn D

Sau 2 giờ tàu thứ nhất cách vị trí A một khoảng cách





30 2 60

AB . km

 

Và tàu thứ hai cách vị trí A một khoảng cách





40 2 80

AC . km

 

Khi đó hai tàu cách nhau một khoảng cách

BC

.

Theo định lý Côsin, ta có:

A

C

B

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 20

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay





2 2 2

2 0

2

3600 6400 2 60 80 60

5200

20 13

BC AB AC AB.AC.cosA

BC . . .cos

BC km

  

   



 

Câu 33: Cho hình bình hành

ABCD

. Gọi

,

M N

là hai điểm thỏa mãn: .

Cho

G

là trọng tâm của tam giác

BMN

. Gọi

E

là điểm thỏa mãn:





1

CE x BC

 

 

. Tìm

x

để

ba điểm

, ,

A G E

thẳng hàng.

A.

5

8

x



. B.

6

11

x



. C.

7

12

x



. D.

5

9

x



.

Lời giải

Chọn B

Do









1 1

CE x BC BE BC x BC BE xBC

       

      

Gọi

I

là trung điểm

MB

. Ta có:

1 2 1

= =

2 3 6

NI ND DA AI AB BC AB AB BC

      

        

Ta có:

A E AB B E AB x BC

   

    





 

1

1 2

1

2 3

1 2

1

2 3

1 2 1

1

2 3 6

1 7

3 18

CE x BC

CN NG GE x BC

AB NI GE x BC

GE x BC AB NI

GE x BC AB AB BC

GE x BC AB

 

    

     

    

 

     

 

 

 

   

 

 

 

   

   

   

    

  

Để

, ,

A G E

thẳng hàng

, 0

GE kAE k

  

 

Khi đó:

 

1 7

3 18

1

6

3

11

7

18

x BC AB k AB xBC

x kx

x

k

 

   

 

 



 



 



 



 

 

 

 

 







   

.

2. 0, 0

MA MB NC ND

   

     

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 21

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Vậy

6

11

x



.

Câu 34: Trong các mệnh đề sau đây, mệnh đề nào đúng?

A. Tổng độ dài hai cạnh của một tam giác luôn luôn lớn hơn độ dài cạnh còn lại.

B. Hai tam giác có diện tích bằng nhau thì hai tam giác đó bằng nhau.

C. Số 9 là số nguyên tố.

D. Nếu một số tự nhiên chia hết cho 3 thì số đó chia hết cho 6.

Lời giải

Chọn A

A đúng, bất đẳng thức trong tam giác.

B sai, ví dụ: Trong 1 tam giác

ABC

bất kì và có trung tuyến





AM M BC



, diện tích

AMB



bằng diện tích

A M C



nhưng hai tam đó không bằng nhau.

C sai, vì 9 chia hết cho 1,3,9 nên không phải là số nguyên tố.

D sai, ví dụ: 9 chia hết cho 3 nhưng không chia hết cho 6.

Câu 35: Mệnh đề phủ định của mệnh đề “

2

: 3 4 1 0

x x x

    



” là mệnh đề

A. “

2

: 3 4 1 0

x x x

    



”. B. “

2

: 3 4 1 0

x x x

    



”.

C. “

2

: 3 4 1 0

x x x

    



”. D. “

2

: 3 4 1 0

x x x

    



”.

Lời giải

Chọn A

PHẦN II: PHẦN TỰ LUẬN

Bài 1: (1 điểm) Trong mặt phẳng tọa độ

Oxy

, cho hai điểm





1; 2

A



,





4;3

B

.

a) Tính độ dài đoạn thẳng

AB

.

b) Tìm tọa độ điểm

M

trên trục tung sao cho tam giác

ABM

vuông tại

A

.

Lời giải

a) Độ dài đoạn thẳng

   

2 2

4 1 3 2 34

AB     

.

b) Vì

M O y



, giả sử





0;

M m

.

Ta có





1; 2

AM m

  



;





3;5

AB 



.

Tam giác

ABC

vuông tại

A

nên

. 0

AM AB



 





1.3 2 .5 0

m

    

7

5 7 0

5

m m

     

.

Vậy

7

0;

5

M

 



 

 

là điểm cần tìm.

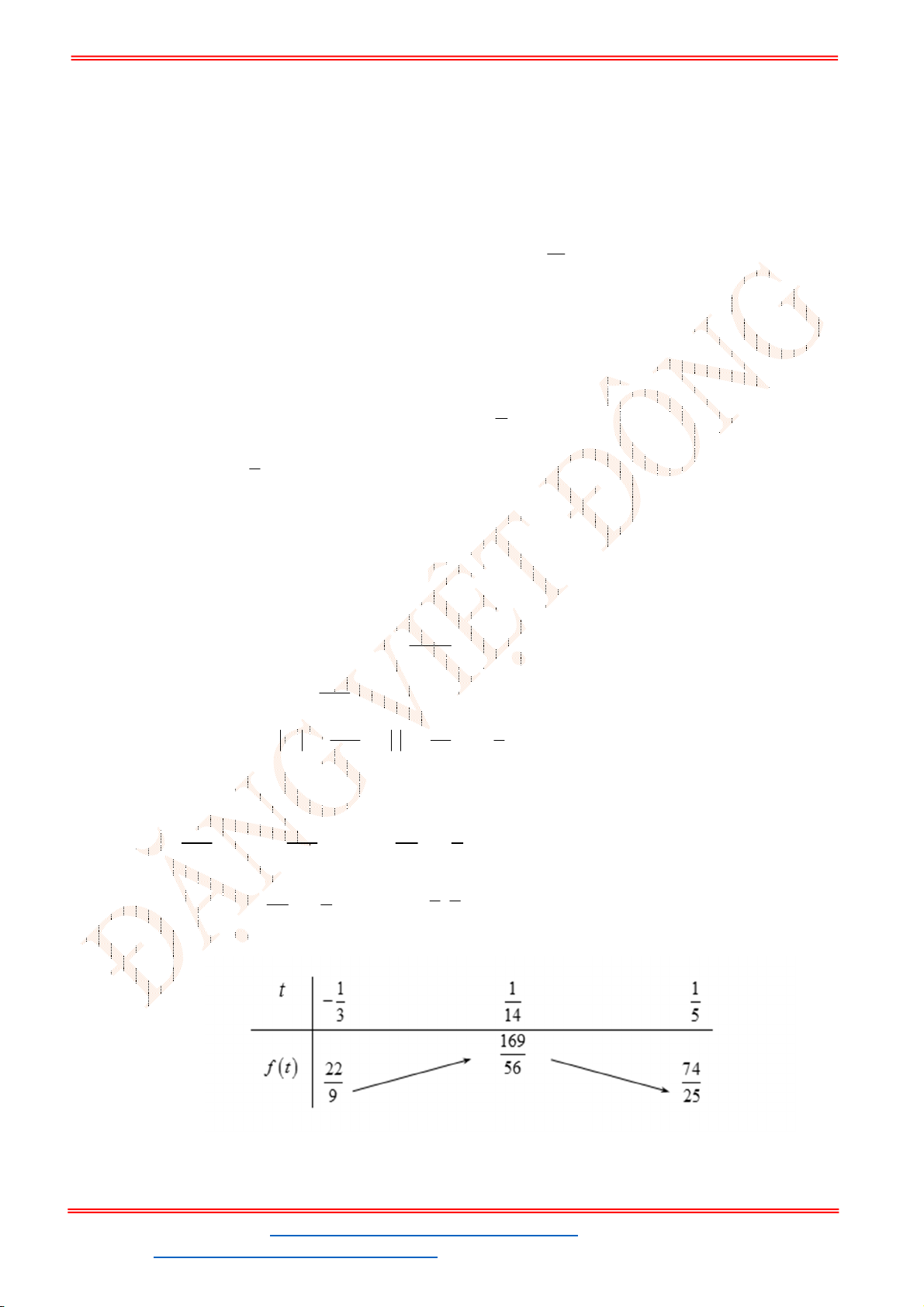
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 22

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Bài 2a. (1 điểm) Tìm

m

để hệ phương trình

2

2 0

3 4 0

x xy

x xy x y m



 





    





có 3 nghiệm phân biệt.

Lời giải

Ta có

2

0

2 0

2

x

x xy

y x





  







.

Với

0x 

thay vào phương trình thứ hai ta được

4

m

y 

.

Với

2y x

thay vào phương trình thứ hai ta được

2

7 7 0x x m  

(*)

.

Nếu

0m 

thì hệ có 2 nghiệm là

0

x

y











và

1

2

x

y











.

Nếu

0m 

thì hệ có 3 nghiệm phân biệt khi phương trình

(*)

có hai nghiệm phân biệt. Điều này

tương đương với

2

( 7) 28 0m   

7

4

m 

.

Vậy với

7

4

0

m















thì hệ có ba nghiệm phân biệt.

Bài 2b. (1 điểm) Cho

x

,

y

là hai số thực thỏa mãn

 

2 2

2 1x y xy   .Tìm giá trị lớn nhất và giá trị nhỏ

nhất của biểu thức:

 

2

4 4

2 1P x y x y    

.

Lời giải

Từ:

 

2 2 2 2

1

2 1

2

xy

x y xy x y



     

.

Đặt

2 2

1

2

t

t xy x y



   

.

Ta có:

2 2

1 1 1

2 2

2 3 5

t

x y xy t t

 

      

.

 





 

2

2 2

4 4 2 2 2 2

2 1 2 2 1 2P x y x y x y xy x y xy           

2

2 2

1 1 7 1

2 4 2 2 3

2 2 2 2

t t

t t t t

  

 

       

 

 

.

Xét hàm

 

2

7 1

3

2 2

f t t t



  

trên

1 1

;

3 5

 



 

 

.

Bảng biến thiên:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 23

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Khi

2 2

1

13 3 17

14

1

14

56

13

14

13 3 17

28

56

x

xy

t

x y

y















 

  

 

 

 













.

Khi

2 2

1 3

1

3 3

2

3

xy x

t

x y

y







  



 

   

 

 

 







.

Vậy:

169

56

MaxP 

khi

1 13 3 17

;

56

13 3 17

14

56

x y



 



.

22

9

MinP 

khi

3 3

;

3 3

x y



 

.

Đề nghị sửa:

2 2

1

119

1

14

13

14

1

28

14





  



 

  

 

 

 







xy

x y

t

x y

xy

119 3 7 119 3 7

28 28

119 3 7 119 3 7

28 28

 

 

 

 

 

 

 

 

 

 

 

x x

y y

119 3 7 119 3 7

28 28

119 3 7 119 3 7

28 28

 

   

 

 

 

 

   

 

 

 

 

x x

y y

2 2

1 3 3

1

3 3 3

2

3

3 3

3

3 3

 



    

 



  

    

  

  

 

  



 



 

xy x x

t

x y

y y

Vậy:

169 22

, .

56 9

 MaxP MinP

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 4 Môn Toán – Lớp 10

(Thời gian làm bài 90 phút)

Không k

ể thời gian phát đề

Câu 1: Số các giá trị nguyên của

m

để phương trình

2

3 0

x x m

  

có bốn nghiệm phân biệt là

A. vô số. B.

0

. C.

2

. D.

4

.

Câu 2: Cho parabol





2

: 4

P y ax bx

  

đi qua điểm





1;7

A và có trục đối xứng

1

x

 

. Tích

ab

nhận

giá trị bằng

A.

6



. B.

4

. C.

18



. D.

2

.

Câu 3: Nghiệm của hệ phương trình

2 2

2 3 10

x y

  





 



là

A.









; 2;2

x y  . B.









; 3;6

x y  . C.









; 2; 2

x y

  

. D.









; 1; 2

x y

 

.

Câu 4: Cho đoạn thẳng

6

AB



. Tập hợp các điểm

M

thỏa mãn

2 2

18

MA MB

 

là

A. một đoạn thẳng. B. một điểm. C. một đường tròn. D. một đường thẳng.

Câu 5: Trong mặt phẳng tọa độ

Oxy

,

cho tam giác

ABC

vuông tại





2;2

A . Biết





4; 2

C



và

B Oy



. Tìm

tọa độ điểm

B

.

A.





0;3

B

. B.





0; 3

B



. C.





0;1

B

. D.





0; 1 .

B



Câu 6: Lớp

10D

có

37

học sinh, trong đó có

17

học sinh thích môn Văn,

19

học sinh thích môn Toán,

9

em không thích môn nào. Số học sinh thích cả hai môn là

A.

2

học sinh. B.

6

học sinh. C.

13

học sinh. D.

8

học sinh.

Câu 7: Phương trình

4

2 2

x

x x





 

có tất cả bao nhiêu nghiệm nguyên?

A.

1

. B. Vô số. C.

2

. D.

0

.

Câu 8: Tìm tất cả các giá trị thực của tham số

m

để đường thẳng

2

y x

 

cắt parabol





2

: 2

P y x mx

  

tại đúng một điểm.

A.

3

5

m







 



. B.

3

m



. C.

5

m

 

. D.

m

 

.

Câu 9: Cho các vectơ

a



,

b



có độ dài bằng

1

và

3 4 13

a b 

 

. Tính





cos ,

a b

 

.

A.

1

2

. B.

1

. C.

1

4

. D.

3

2

.

Câu 10: Cho tam giác

ABC

nhọn có

3

BC a



và bán kính đường tròn ngoại tiếp tam giác

ABC

là

3

R a



.

Tính số đo góc

A

.

A.

120

 

A

. B.

45

 

A

. C.

30

 

A

. D.

60

 

A

.

Câu 11: Số nghiệm của hệ phương trình

2 2

5

xy x y

x y

  





 



là

A.

2

. B.

0

. C.

1

. D.

3

.

Câu 12: Cho tam giác

ABC

là tam giác đều,

O

là tâm đường tròn ngoại tiếp tam giác

ABC

. Tìm mệnh đề

đúng trong các mệnh đề sau.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

OA OB OC

 

  

. B.

2

OA OB OC

 

  

. C.

OA OB CO

 

  

. D.

2

OA OB CO

 

  

.

Câu 13: Cho Parabol





2

: 2

P y x bx c

   

có điểm





2;10

M là điểm có tung độ lớn nhất. Tính giá trị của

c

.

A.

22

. B.

6.

C.

12.

D.

10.

Câu 14: Trong các hàm số sau đâu là hàm số bậc nhất?

A.









2

1 1 2 .

y x x x x

    

B.





2

1

2 1 .

y x

x

  

C.

2

1 .

y x

 

D.

6 2

.

x

y

x





Câu 15: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?

A.

:3 3

n

n n

   



. B.

1 2 6 7

  

.

C.

6 4 10 7

  

. D.

 

2

: 2

x x x

   

 .

Câu 16: Số nghiệm của phương trình





2

3 9 20 0

x x x

   

là:

A.

0

. B.

1

. C.

2

. D.

3

.

Câu 17: Cho ba điểm bất kỳ

, ,

M N P

. Đẳng thức nào sau đây sai?

A.

PM NM NP

 

  

. B.

MN NP PM

  

  

. C.

MN MP PN

 

  

. D.

NP MP NM

 

  

.

Câu 18: Trong mặt phẳng tọa độ

Oxy

, cho









1;3 ; 1; 8

A B

 

. Tìm điều kiện của

a

để điểm





;0

M a

thỏa

mãn góc



AMB

là một góc tù.

A.





5;5

a 

. B.





5;a

 

. C.





; 5

a

  

. D.

 

5

5;5 \ .

11

a

 

 

 

 

Câu 19: Một học sinh giải phương trình





2

2 4 2

x x *

  như sau:

Bước 1: Điều kiện xác định là



.

Bước 2:





2 2

2 4 4

* x x

  

Bước 3:

2

x

 

. Vậy phương trình có nghiệm

2

x



và

2

x

 

Lời giải trên đúng hay sai, nếu sai thì sai bắt đầu từ bước nào?

A. Lời giải đúng. B. Lời giải sai từ bước 1.

C. Lời giải sai từ bước 2. D. Lời giải sai từ bước 3.

Câu 20: Đồ thị hàm số nào sau đây nhận trục tung làm trục đối xứng?

A.

3

y x x

 

. B.

3 3

y x x

   

. C.





2

1

y x

 

. D.

1

x

y

x





.

Câu 21: Phương trình

2 2

7 6 2 4

x x x x

    

có bao nhiêu nghiệm nguyên âm?

A. 2. B. 0. C. 1. D. 3.

Câu 22: Có bao nhiêu giá trị của tham số

m

để hai đường thẳng





1

: 1 3 2

d y m x m

   

và





2

: 1 2 1

d y m x m

   

song song với nhau?

A.

3

. B.

2

. C.

1

. D.

0

.

Câu 23: Cho tam giác

ABC

có

4cm



AB

;

12cm



AC

và góc



120



BAC

. Tính diện tích tam giác

ABC

.

A.

12 3

(

2

cm

). B.

24 3

(

2

cm

). C.

12

(

2

cm

). D.

24

(

2

cm

).

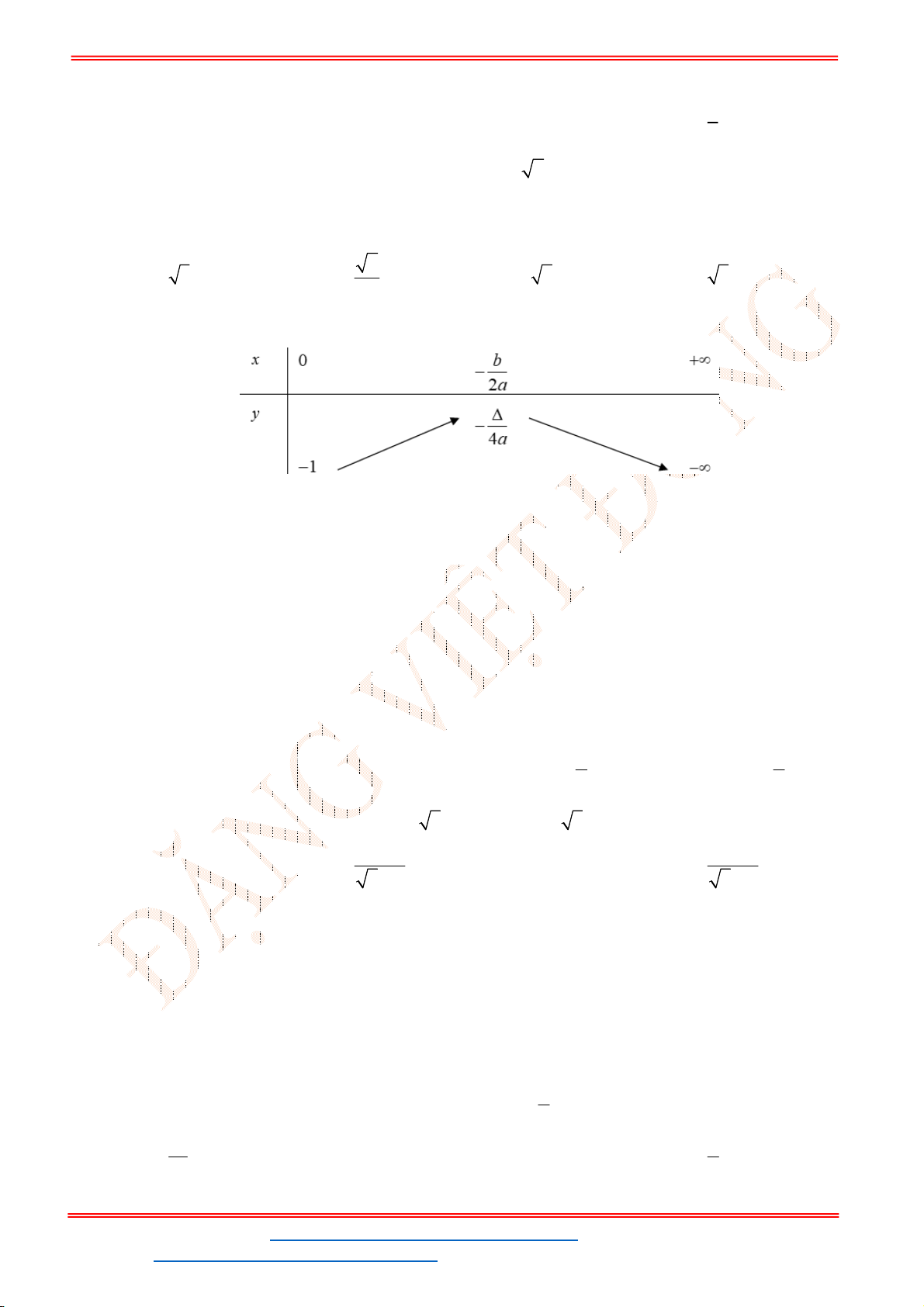
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 24: Trong các khẳng định sau, khẳng định nào đúng với mọi giá trị thực của a?

A.

3

a a



. B.

2 2

2

a a

  . C.

2 3

a a

  

. D.

1

3

a a

 

.

Câu 25: Cho tam giác

ABC

thỏa mãn

2 2 2

2 . 0

BC AC AB BC AC

   

. Khi đó, góc

C

có số đo là

A.



150

C

 

. B.



60

C

 

. C.



45

C

 

. D.



30

C

 

.

Câu 26: Cho hình bình hành

ABCD

có



1, 2, 60

AB AD DAB

   

. Tính độ dài cạnh

AC

.

A.

3

. B.

7

3

. C.

7

. D.

5

.

Câu 27: Cho hàm số

2

( 0)

y ax bx c a

   

có bảng biến thiên như hình vẽ dưới đây

Xác định dấu của

, ,

a b c

A.

0, 0, 0

a b c

  

. B.

0, 0, 0

a b c

  

. C.

0, 0, 0

a b c

  

D.

0, 0, 0

a b c

  

.

Câu 28: Cho hàm số

2

( ) 4 2

y f x x x

   

trong các mệnh đề dưới đây mệnh đề nào đúng?

A.









2019 2019

2 3f f   .

B.









2019 2019

2 3f f .

C. Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 2.

D. Đồ thị hàm số nhận đường thẳng

2

x

 

làm trục đối xứng.

Câu 29: Trong mặt phẳng tọa độ

Oxy

, cho tam giác

ABC

có













5;3 , 2; 1 , 1;5

A B C  . Tìm tọa độ điểm

H

là trực tâm tam giác

ABC

.

A.





3;2

H . B.





3; 2

H



. C.

7

2;

3

H

 

 

 

. D.

7

2;

3

H

 

 

 

 

.

Câu 30: Tổng các nghiệm của phương trình









4 2

3 2 4 3 2 0

x x

    

là

A.

1



. B.

4

3 2



. C.

0

. D.

2

3 2



.

Câu 31: Cho

,

a b

là hai số thực tùy ý. Mệnh đề nào sau đây đúng?

A. Nếu

2 2

a b



thì

a b



. B. Nếu

a b



thì

2 2

a b



.

C. Nếu

a b



và

0

a



thì

2 2

a b



. D. Nếu

a b



và

0

b



thì

2 2

a b



.

Câu 32: Trong mặt phẳng tọa độ

Oxy

, cho hình bình hành

ABCD

có





1;2

A ,





2;4

B  ,





0;3

C . Tìm tọa

độ điểm

D

.

A.





3;1

 . B.





3;1

. C.





3; 1



. D.





3; 1

 

.

Câu 33: Giá trị lớn nhất của hàm số

2

3 2 5

y x x

   

trên

2

;1

3

 



 

 

là

A.

16

3

. B.

5

. C.

1

. D.

7

3

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 34: Cho tam giác

ABC

có

. .

AB BC BC AC

 

   

. Tam giác

ABC

có tính chất gì?

A.

ABC



vuông tại

A

. B.

ABC



cân tại

B

.C.

ABC



vuông tại

B

. D.

ABC



cân tại

A

.

Câu 35: Cho tam giác

ABC

có

10

AB



,

17

AC



,

15

BC



. Tính

.

AB AC

 

.

A.

164

. B.

164



. C.

82



. D.

82

.

Câu 36: Tập xác định của hàm số

2

4 2

12

x x

y

x x

  



 

là

A.





2;4

 . B.









3; 2 2;4

    . C.





2;4

 . D.





2;4

 .

Câu 37: Tìm giá trị của tham số

m

để đỉnh

I

của đồ thị hàm số

2

6

y x x m

   

thuộc đường thẳng

2019

y x

 

.

A.

2020

m



. B.

2000

m



. C.

2036

m



. D.

2013

m



.

Câu 38: Cho tam giác

ABC

vuông cân tại

A

có

2

BC a



. Tính độ dài

BA BC



 

.

A.

2 5

a

. B.

5

a

. C.

3

a

. D.

2 3

a

.

Câu 39: Biết đường thẳng

: 4

d y x

  

cắt parabol





2

: 2

P y x x

 

tại hai điểm phân biệt

A

và

B

. Tìm

tọa độ trọng tâm

G

của tam giác

OAB

.

A.

1 7

;

3 3

G

 

 

 

. B.





1; 2

G



.

C.

1 17 9 17

;

3 3

G

 

 

 

 

. D.

1 7

;

2 2

G

 

 

 

.

Câu 40: Cho hệ phương trình

2 1

2 2 1

  





  



mx y m

x my m

với

m

là tham số thực. Tìm tất cả các giá trị của

m

để hệ

phương trình đã cho vô nghiệm.

A.

2.

m

 

B.

2.

m

 

C.

2.

m



D.

2.

m



Câu 41: Giá trị nhỏ nhất của hàm số

6

( )

2 2

x

f x

x

 



với

2

x



là số có dạng

3

a b



(

,

a b

là các số nguyên).

Tính

2 2

.

a b



A.

5.

B.

6.

C.

3.

D.

4.

Câu 42: Số các giá trị thực của tham số

m

để phương trình









2 1

0

1

x mx

x

 





có nghiệm duy nhất là

A.

3

. B.

2

. C.

0

. D.

1

.

Câu 43: Tìm tất cả các giá trị thực của tham số

m

để phương trình

4 2

2 1

x x m

  

có hai nghiệm phân biệt.

A.

0

m



. B.

0

m



. C.

1

m



hoặc

0

m



. D.

0 1

m

 

.

Câu 44: Tìm tất cả các giá trị thực của tham số

m

để phương trình

3 2

0

x mx x m

   

có ba nghiệm thực

phân biệt.

A.

1

m

 

. B.

1

m

 

. C.

1

m



hoặc

0

m



. D.

0 1

m

 

.

Câu 45: Cho phương trình

2

1 0

x mx m

    

với

m

là tham số thực. Tính tổng

S

tất cả các giá trị thực

của tham số

m

để phương trình có hai nghiệm phân biệt

1 2

,

x x

thỏa mãn

1 2

4

x x

 

.

A.

2

S



B.

2

S

 

. C.

4

S

 

D.

5

S



.

Câu 46: Cho phương trình

2

10 2

x x m x

   

. Tìm tất cả các giá trị thực của tham số

m

để phương trình

đã cho vô nghiệm.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

16 20m 

. B.

3 16m  

C.

m  

. D.

16m 

.

Câu 47: Tập tất cả các giá trị của tham số

m

để phương trình

2 2

1x x m  

có nghiệm là

 

;a b

. Tính

S a b  ?

A.

0.

B.

9

.

4

C.

1.

D.

1

.

4

Câu 48: Cho hàm số

2

2y x x  có đồ thị như hình vẽ. Gọi

S

là tập các giá trị nguyên của

m

đề phương

trình

2

2 1x x m   có hai nghiệm phân biệt. Tính tổng các phần tử của tập

S

.

A. 1 . B. 2 . C. 4 . D.

0

.

Câu 49: Trong hệ tọa độ Oxy cho ba điểm

 

1; 4A  ,

 

4;5B và

 

0; 9C  . Điểm

M

di chuyển trên trục

Ox

.

Đặt

2 2 3

Q MA MB MB MC

   

   

. Biết giá trị nhỏ nhất của Q có dạng

a b

trong đó

a

,

b

là các

số nguyên dương và

a

,

20b 

. Tính

a b

.

A.

15

. B.

17

. C.

14

. D.

11

.

Câu 50: Cho

,x y

thoả mãn

2 2

x y a  . Xác định

a

, biết rằng giá trị lớn nhất của 2 3P x y  với , 0x y 

là

117

.

A.

9a 

. B.

13a 

. C.

5a 

. D.

3 3a 

.

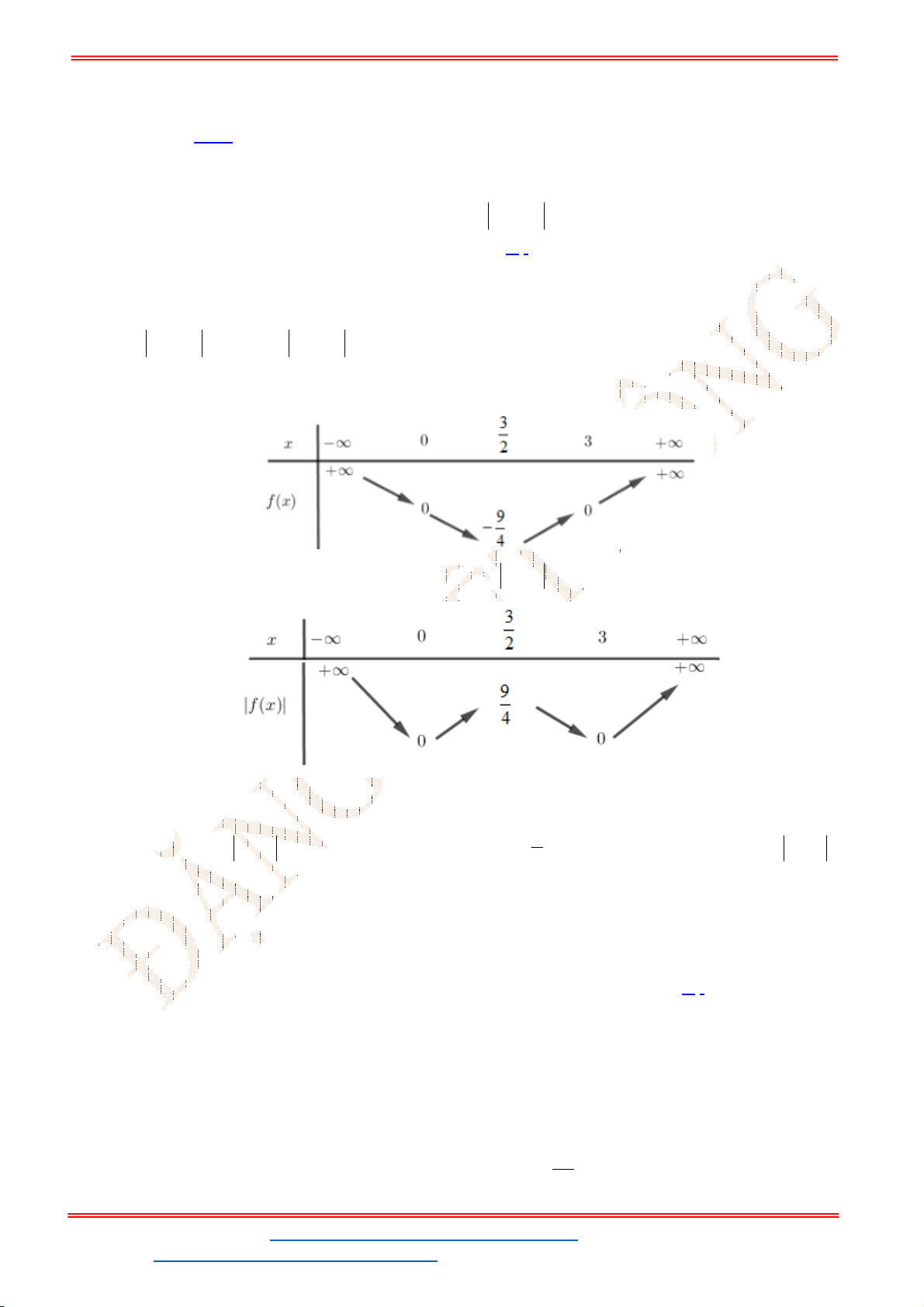
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG HDG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 4 Môn Toán – Lớp 10

(Th

ời gian l

àm bài 90 phút)

Không k

ể thời gian phát đề

Câu 1: Số các giá trị nguyên của

m

để phương trình

2

3 0

x x m

  

có bốn nghiệm phân biệt là

A. vô số. B.

0

. C.

2

. D.

4

.

Lời giải.

Chọn C

2 2

3 0 3

x x m x x m

     

(*)

Xét hàm số





2

3

f x x x

 

, ta có bảng biến thiên của hàm số





y f x

 như sau:

Từ đó ta suy ra bảng biến thiên của hàm số





y f x

 như sau:

Yêu cầu bài toán



phương trình (*) có 4 nghiệm phân biệt



đường thẳng

y m



cắt đồ thị

hàm số





y f x

 tại

4

điểm phân biệt

9

0

4

m

  

(dựa vào BBT của hàm số





y f x

 ).

Do

m





nên





1;2

m .

Câu 2: Cho parabol





2

: 4

P y ax bx

  

đi qua điểm





1;7

A và có trục đối xứng

1

x

 

. Tích

ab

nhận

giá trị bằng

A.

6



. B.

4

. C.

18



. D.

2

.

Lời giải

Chọn D

Đồ thị hàm số

2

4

y ax bx

  

là parabol nên

0

a



.

Parabol đi qua điểm





1;7

A nên ta có

2

7 .1 .1 4 3

a b a b

     

.

Trục đối xứng của parabol là đường thẳng

1

x

 

nên

1 2

2

b

b a

a



   

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Vậy ta có hệ:

3

2 0

a b

 





 



1

1.2 2

2

a

ab

b





   







.

Câu 3: Nghiệm của hệ phương trình

2 2

2 3 10

x y

  





 



là

A.









; 2;2

x y  . B.









; 3;6

x y  . C.









; 2; 2

x y

  

. D.









; 1; 2

x y

 

.

Lời giải.

Chọn A

Ta có:

 

2 2

2 2 2 2 2

2 2 2 3 10

2 3 10 7 14 2

x y

x y x y x

y y

x y y y

 



     

  



  

   

  

   



  



.

Vậy hệ phương trình đã cho có nghiệm là:









; 2;2

x y  .

Câu 4: Cho đoạn thẳng

6

AB



. Tập hợp các điểm

M

thỏa mãn

2 2

18

MA MB

 

là

A. một đoạn thẳng. B. một điểm. C. một đường tròn. D. một đường thẳng.

Lời giải

Chọn B

Gọi

I

là trung điểm của

AB

0

IA IB

  

  

và

3

IA IB

 

.

Giả sử

M

là điểm thỏa mãn bài toán.

Ta có:

2 2

18 18

MA MB MA MB

    

 









2 2

18

MI IA MI IB

    

   





2 2 2

2 2 . 18

MI MI IA IB IA IB

     

     

2 2 2 2

2 18 0

MI IA IB MI

     

.

Do đó:

M

trùng

I

. Vậy tập hợp các điểm

M

thỏa mãn bài toán là một điểm.

Câu 5: Trong mặt phẳng tọa độ

Oxy

,

cho tam giác

ABC

vuông tại





2;2

A . Biết





4; 2

C



và

B Oy



. Tìm

tọa độ điểm

B

.

A.





0;3

B

. B.





0; 3

B



. C.





0;1

B

. D.





0; 1 .

B



Lời giải

Chọn C

Do

B Oy



nên

B

có tọa độ





0;

y

, y





. Khi đó





2; 2

AB y

  



;





2; 4

AC

 



.

Tam giác

ABC

vuông tại

A

nên

. 0

AB AC



 













2 .2 2 . 4 0

y

     

1

y

 

.

Vậy





0;1

B .

Câu 6: Lớp

10D

có

37

học sinh, trong đó có

17

học sinh thích môn Văn,

19

học sinh thích môn Toán,

9

em không thích môn nào. Số học sinh thích cả hai môn là

A.

2

học sinh. B.

6

học sinh. C.

13

học sinh. D.

8

học sinh.

Lời giải

Chọn D

Gọi số học sinh thích cả hai môn là

x

(

0 17

x

 

). Khi đó số học sinh chỉ thích môn Văn là

17

x



,

số học sinh chỉ thích môn Toán là

19

x



.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Ta có:









9 17 19 37 8

x x x x

       

.

Câu 7: Phương trình

4

2 2

x

x x





 

có tất cả bao nhiêu nghiệm nguyên?

A.

1

. B. Vô số. C.

2

. D.

0

.

Lời giải

Chọn C

Điều kiện xác định:

2

x



.

Khi đó phương trình đã cho tương đương với

4 4 4 0 4

x x x x

       

.

Kết hợp với điều kiện xác định ta có nghiệm của phương trình là

2 4

x

 

.

Do

x





nên





3;4

x . Vậy phương trình có

2

nghiệm nguyên.

Câu 8: Tìm tất cả các giá trị thực của tham số

m

để đường thẳng

2

y x

 

cắt parabol





2

: 2

P y x mx

  

tại đúng một điểm.

A.

3

5

m







 



. B.

3

m



. C.

5

m

 

. D.

m

 

.

Lời giải

Chọn A

Phương trình hoành độ giao điểm của đường thẳng

d

:

2

y x

 

và pararabol





P

là:





2 2

2 2 1 4 0

x x mx x m x

        

(1)

Đường thẳng

d

cắt parabol





P

tại đúng một điểm khi và chỉ khi phương trình (1) có nghiệm kép.

Điều này tương đương với

 

2

3

1 4.4 2 15 0

5

m

m m m

m





        



 



.

Câu 9: Cho các vectơ

a



,

b



có độ dài bằng

1

và

3 4 13

a b 

 

. Tính





cos ,

a b

 

.

A.

1

2

. B.

1

. C.

1

4

. D.

3

2

.

Lời giải

Chọn A

Ta có:

3 4 13

a b 

 

2

3 4 13

a b

  

 





2

3 4 13

a b

  

 

2 2

9 24 . 16 13

a a b b

   

   

.





2 2

9 24 os , 16 13

a a b c a b b

   

     





9.1 24.1.1. os , 16.1 13

c a b

   

 

.





1

os ,

2

c a b

 

 

.

Câu 10: Cho tam giác

ABC

nhọn có

3

BC a



và bán kính đường tròn ngoại tiếp tam giác

ABC

là

3

R a



.

Tính số đo góc

A

.

A.

120

 

A

. B.

45

 

A

. C.

30

 

A

. D.

60

 

A

.

Lời giải

Chọn D

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Áp dụng định lý sin trong tam giác

ABC

, ta có

3 3

2 sin

sin 2 2

2 3

    

BC BC a

R A

A R

a

.

Suy ra

60

 

A

(do tam giác

ABC

nhọn).

Câu 11: Số nghiệm của hệ phương trình

2 2

5

xy x y

x y

  





 



là

A.

2

. B.

0

. C.

1

. D.

3

.

Lời giải

Chọn A

Đặt

 









S x y

P xy

( Điều kiện:

2

4



S P

)

Ta được hệ phương trình

2

5

2 5

 





 



S P

 

2

5

2 5 5

2 15 0

 





 

 

  

  





P S

S S

5

5 10

 







  



S

P S

hoặc

3

5 2







  



S

P S

.

Với

5; 10

  

S P thì

2

4 25 40 15 0

     

S P nên ta loại trường hợp này.

Với

3; 2

S P

 

thì

2

4 9 8 1 0

    

S P nên khi đó

,

x y

là nghiệm của phương trình

2

1

3 2 0

2

X

X X

X





   







Ta có nghiệm hệ phương trình là

( ; ) (1;2)

x y



hoặc

( ; ) (2;1)

x y



.

Câu 12: Cho tam giác

ABC

là tam giác đều,

O

là tâm đường tròn ngoại tiếp tam giác

ABC

. Tìm mệnh đề

đúng trong các mệnh đề sau.

A.

OA OB OC

 

  

. B.

2

OA OB OC

 

  

. C.

OA OB CO

 

  

. D.

2

OA OB CO

 

  

.

Lời giải

Chọn C

Do

ABC



đều nên

O

cũng là trọng tâm của

ABC



.

Khi đó

0

OA OB OC OA OB CO

     

      

.

Câu 13: Cho Parabol





2

: 2

P y x bx c

   

có điểm





2;10

M là điểm có tung độ lớn nhất. Tính giá trị của

c

.

A.

22

. B.

6.

C.

12.

D.

10.

Lời giải

Chọn B

Từ đề bài suy ra

1.

a

 

Ta có: điểm





2;10

M là điểm có tung độ lớn nhất nên đồ thị hàm số

2

y x bx c

   

là Parabol có

tọa độ đỉnh là





2;10

M .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

   

2

22

2

6

10 2 4

2;10

b

c

b c

M P















  

  



   









.

Câu 14: Trong các hàm số sau đâu là hàm số bậc nhất?

A.









2

1 1 2 .

y x x x x

    

B.





2

1

2 1 .

y x

x

  

C.

2

1 .

y x

 

D.

6 2

.

x

y

x





Lời giải

Chọn A

Ta có









2 2 2

1 1 2 1 2 2 1

y x x x x x x x x

          

là hàm số bậc nhất.

Câu 15: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?

A.

:3 3

n

n n

   



. B.

1 2 6 7

  

.

C.

6 4 10 7

  

. D.

 

2

: 2

x x x

   

 .

Lời giải

Chọn D

 Với

1

n



thì

3 3; 3 4

n

  

nên đáp án A là đúng.

 Ta có mệnh đề

:"1 2"

P



và mệnh đề

:"6 7"

Q



là mệnh đề sai nên mệnh đề

P Q



hay mệnh

đề

1 2 6 7

  

là mệnh đề đúng. Đáp án B đúng.

 Ta có mệnh đề

:"6 4"

P



là mệnh đề sai và mệnh đề

:"10 7"

Q



là mệnh đề đúng nên mệnh đề

P Q



hay mệnh đề

6 4 10 7

  

là mệnh đề đúng. Đáp án C đúng.

 Với

1x

  



thì

 

2

2 9

x

 

;

2

1

x



nên mệnh đề

 

2

: 2

x x x

   

 là mệnh đề sai.

Câu 16: Số nghiệm của phương trình





2

3 9 20 0

x x x

   

là

A.

0

. B.

1

. C.

2

. D.

3

.

Lời giải

Chọn B

Điều kiện xác định:

3.

x



Khi đó phương trình





 





  



  



  









2

3 tháa m·n

3 0

4 kh«ng tháa m·n

9 20 0

5 kh«ng tháa m·n

x

x x

x

.

Vậy phương trình đã cho có

1

nghiệm.

Câu 17: Cho ba điểm bất kỳ

, ,

M N P

. Đẳng thức nào sau đây sai?

A.

PM NM NP

 

  

. B.

MN NP PM

  

  

. C.

MN MP PN

 

  

. D.

NP MP NM

 

  

.

Lời giải

Chọn C

Đẳng thức

MN MP PN

 

  

sai. (Đẳng thức

MN MP PN

 

  

chỉ đúng trong trường hợp đặc

biệt

P N



).

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 18: Trong mặt phẳng tọa độ

Oxy

, cho









1;3 ; 1; 8

A B

 

. Tìm điều kiện của

a

để điểm





;0

M a

thỏa

mãn góc



AMB

là một góc tù.

A.





5;5

a 

. B.





5;a

 

. C.





; 5

a

  

. D.

 

5

5;5 \ .

11

a

 

 

 

 

Lời giải

Chọn D

Ta có:









1 ;3 ; 1 ; 8 ;

MA a MB a

   

 

 









   

2 2

1 1 24

cos ;

1 9 1 64

a a

MA MB

a a

   



    

 

.

Góc



AMB

là một góc tù





;

MA MB



 

là một góc tù







cos ; 0

MA MB



 

và

;

MA MB

 

không

ngược hướng.

+)

;

MA MB

 

cùng phương

 

8 5

1 1 8 8 3 3

3 11

a a a a a

             

Khi đó

6 16

;3 ; ; 8

11 11

MA MB



   



   

   

 

nên

;

MA MB

 

ngược hướng. Do đó

5

11

a



(1)

+)





cos ; 0

MA MB



 









   

2

2 2

1 1 24

0 25 0 5 5 (2)

1 9. 1 64

a a

   

        

    

Từ (1) và (2),

 

5

5;5 \

11

a

 

 

 

 

.

Câu này ở phương án D nguyên văn trong đề gốc là: D.





5;5

a 

.

Chúng tôi nghĩ đề ra sai và đã sửa lại thành D.

 

5

5;5 \ .

11

a

 

 

 

 

Câu 19: Một học sinh giải phương trình





2

2 4 2

x x *

  như sau:

Bước 1: Điều kiện xác định là



.

Bước 2:





2 2

2 4 4

* x x

  

Bước 3:

2

x

 

. Vậy phương trình có nghiệm

2

x



và

2

x

 

Lời giải trên đúng hay sai, nếu sai thì sai bắt đầu từ bước nào?

A. Lời giải đúng. B. Lời giải sai từ bước 1.

C. Lời giải sai từ bước 2. D. Lời giải sai từ bước 3.

Lời giải

Chọn C

2

2 2 2

0

2 0 0

2 4 2 2

2 4 4 2

2

x

x x

x x x

x



 



 



 

  

      

  

  

  

 

  

 



.

Câu 20: Đồ thị hàm số nào sau đây nhận trục tung làm trục đối xứng?

A.

3

y x x

 

. B.

3 3

y x x

   

. C.





2

1

y x

 

. D.

1

x

y

x





.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Lời giải

Chọn B

Đồ thị hàm số nhận trục tung làm trục đối xứng khi hàm số là hàm chẵn.

Xét hàm số





3 3

    

y f x x x , ta có: TXĐ:

D





và









3 3 3 3

f x x x x x f x

           

,

x

 



.

Suy ra hàm số trên là hàm số chẵn nên đồ thị nhận trục tung làm trục đối xứng.

Câu 21: Phương trình

2 2

7 6 2 4

x x x x

    

có bao nhiêu nghiệm nguyên âm?

A. 2. B. 0. C. 1. D. 3.

Lời giải

Chọn B

Ta có:

2 2

2

5

7 6 2 4

7 6 2 4 2

5

7 6 2 4

2 9 10 0

5

2

x

x x x x

x x x x x

x x x x

x x

x











    



        



     





  











.

Vậy phương trình không có nghiệm nguyên âm.

Câu 22: Có bao nhiêu giá trị của tham số

m

để hai đường thẳng





1

: 1 3 2

d y m x m

   

và





2

: 1 2 1

d y m x m

   

song song với nhau?

A.

3

. B.

2

. C.

1

. D.

0

.

Lời giải

Chọn C





1

: 1 3 2

d y m x m

   

có hệ số

1

a m

 

,

1

3 2

b m

 





2

: 1 2 1

d y m x m

   

có hệ số

2

1

a m

 

,

1

2 1

b m

 

1

d

và

2

d

song song

1 2

a a

b b













2

1 1

3 2 2 1

m m



  





  



0

1

m

 























0

m



.

Câu 23: Cho tam giác

ABC

có

4cm



AB

;

12cm



AC

và góc



120

BAC

 

. Tính diện tích tam giác

ABC

.

A.

12 3

(

2

cm

). B.

24 3

(

2

cm

). C.

12

(

2

cm

). D.

24

(

2

cm

).

Lời giải

Chọn A

Diện tích tam giác

ABC

là



1

. .sin

2

S AB AC BAC



1

.4.12.sin120

2

 

12 3



(

2

cm

)

Câu 24: Trong các khẳng định sau, khẳng định nào đúng với mọi giá trị thực của

a

?

A.

3

a a



. B.

2 2

2

a a

  . C.

2 3

a a

  

. D.

1

3

a a

 

.

Lời giải

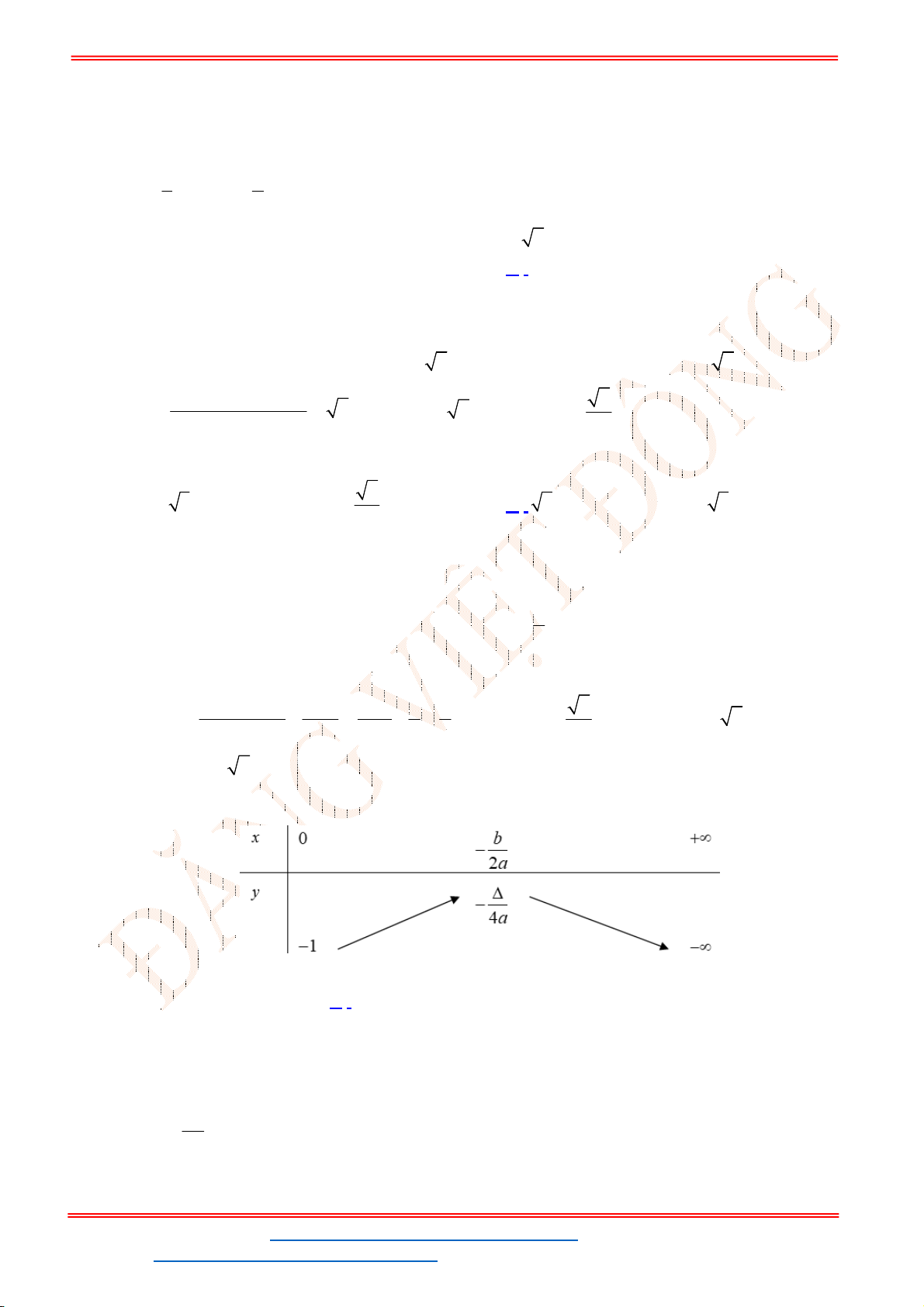
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Chọn C

A.

3 2 0 0

a a a a

    

B.

2 2 2

2 3 0 0

a a a a

     

C.

2 3 2 3

a a

    

(luôn đúng với mọi a).

D.

1 4

0 0

3 3

a a a a

     

Câu 25: Cho tam giác

ABC

thỏa mãn

2 2 2

2 . 0

BC AC AB BC AC

   

. Khi đó, góc

C

có số đo là

A.



150

C

 

. B.



60

C

 

. C.



45

C

 

. D.



30

C

 

.

Lời giải

Chọn C

Theo đề ra ta có:

2 2 2

2 . 0

BC AC AB BC AC

   

2 2 2

2 .

BC AC AB BC AC

   

2 2 2

2

.

BC AC AB

BC AC

 

 

2cos 2 0

C

  

2

cos

2

C 



45

C

  

.

Câu 26: Cho hình bình hành

ABCD

có



1, 2, 60

AB AD DAB

   

. Tính độ dài cạnh

AC

.

A.

3

. B.

7

3

. C.

7

. D.

5

.

Lời giải

Gọi

O

là tâm của hình bình hành

ABCD

. Xét tam giác

ABD

, áp dụng định lý cosin ta có,

2 2 2

1

2. . .cos60 1 4 2.1.2. 3

2

BD AB AD AB AD

       

.

Mặt khác, áp dụng công thức tính độ dài đường trung tuyến

AO

trong tam giác

ABD

, ta có

2 2 2

2

1 4 3 7

2 4 2 4 4

AB AD BD

AO

 

    

. Suy ra

7

2

AO 

2 7

AC AO  

.

Vậy

7

AC 

.

Câu 27: Cho hàm số

2

( 0)

y ax bx c a

   

có bảng biến thiên như hình vẽ dưới đây

Xác định dấu của

, ,

a b c

A.

0, 0, 0

a b c

  

. B.

0, 0, 0

a b c

  

. C.

0, 0, 0

a b c

  

D.

0, 0, 0

a b c

  

.

Lời giải

Chọn B

Từ bảng biến thiên ta thấy đồ thị hàm số có bề lõm quay xuống nên

0

a



.

Vì

0

2

b

a

 

nên

0

b



.

Giao điểm của đồ thị hàm số với trục

Oy

là điểm

(0; 1)



nên

1 0

c

  

.

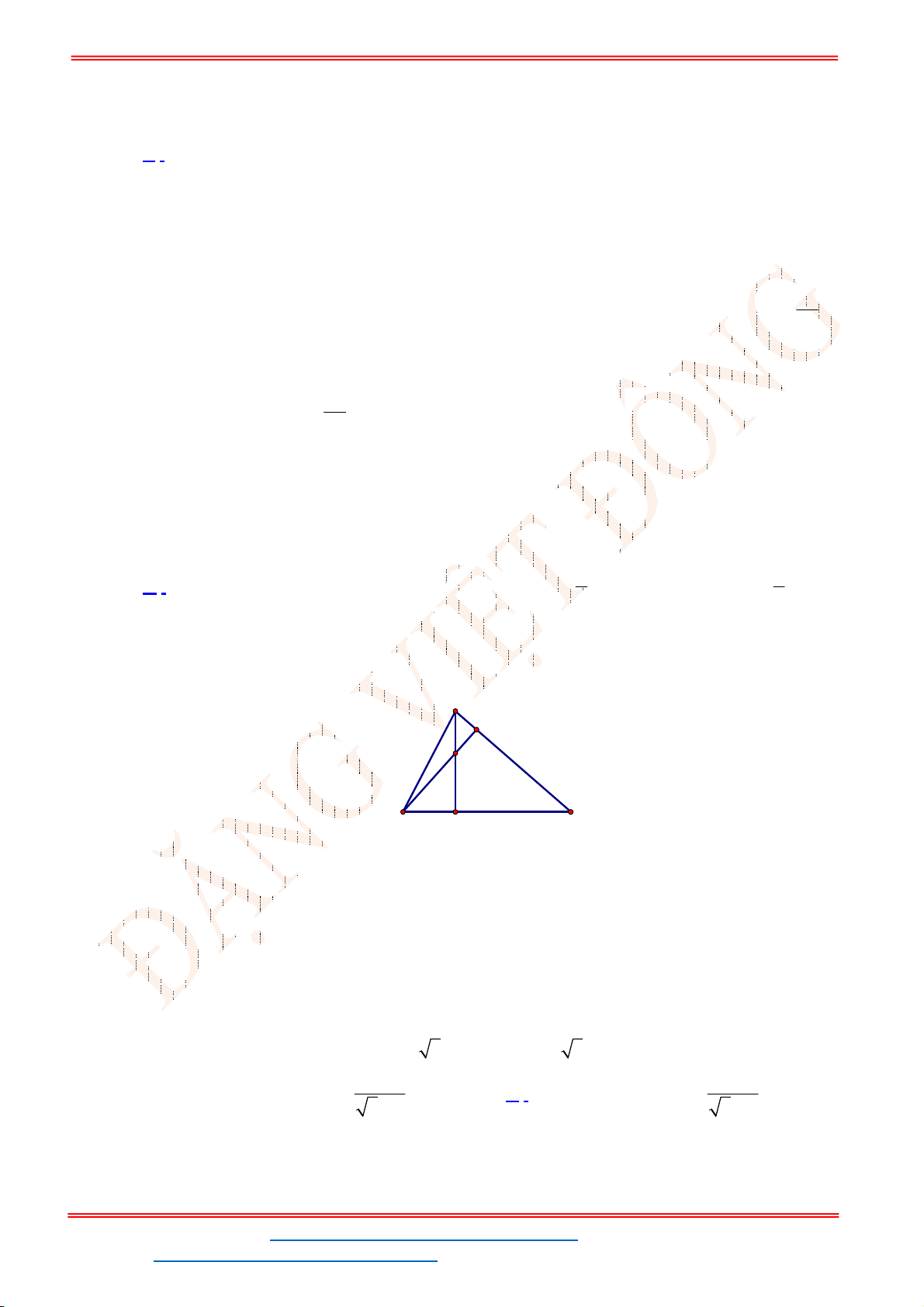
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 28: Cho hàm số

2

( ) 4 2

y f x x x

   

trong các mệnh đề dưới đây mệnh đề nào đúng?

A.









2019 2019

2 3f f   .

B.









2019 2019

2 3f f .

C. Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 2.

D. Đồ thị hàm số nhận đường thẳng

2

x

 

làm trục đối xứng.

Lời giải

Chọn B

+) Hàm số đã cho là hàm số bậc

2

chỉ có đúng một trục đối xứng là đường thẳng

2

b

x

a

  

làm

trục đối xứng



D sai.

+)





2 2 0

f

  



C sai.

+) Hệ số

1 0

a

 

và

2

b

a

 

nên hàm số đồng biến trên khoảng





2;



, nghịch biến trên

khoảng





;2

 . Từ đó, vì

2019 2019

2 2 3

    nên









2019 2019

2 3f f  



A sai.

Ta cũng có

2019 2019

3 2

2



nên

2019 2019

(2 ) (3 )

f f



B đúng.

Câu 29: Trong mặt phẳng tọa độ

Oxy

, cho tam giác

ABC

có













5;3 , 2; 1 , 1;5

A B C  . Tìm tọa độ điểm

H

là trực tâm tam giác

ABC

.

A.





3;2

H . B.





3; 2

H



. C.

7

2;

3

H

 

 

 

. D.

7

2;

3

H

 

 

 

 

.

Lời giải

Chọn A

Gọi





;

H x y

là trực tâm của tam giác

ABC

. Khi đó

. 0

AH BC

BH AC















 

(*).









5; 3 ; 3;6

AH x y BC    

 

;









2; 1 ; 6;2

BH x y AC    

 

.

(*)









   

3 5 6 3 0

6 2 2 1 0

x y

    









    





2 1 3

3 7 2

x y x

x y y

   

 

 

 

  

 

. Vậy :





3;2

H .

Câu 30: Tổng các nghiệm của phương trình









4 2

3 2 4 3 2 0

x x

    

là

A.

1



. B.

4

3 2



. C.

0

. D.

2

3 2



.

Lời giải

Chọn C

H

C

B

A

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Đặt

2

t x



, điều kiện:

0

t



.

Khi đó phương trình









4 2

3 2 4 3 2 0

x x

    





1

trở thành:









 

2

3 2 4 3 2 0 *

t t    

.

Nhận thấy phương trình





*

có





2

. 3 2 0

a c

   

nên phương trình





*

có hai nghiệm phân

biệt:

1

0

t



(loại)

2

, 0

t



(nhận). Suy ra phương trình





1

có 2 nghiệm là:

1 2 2 2

,

x t x t

   .

Vậy

1 2 2 2

0

x x t t

    

.

Câu 31: Cho

,

a b

là hai số thực tùy ý. Mệnh đề nào sau đây đúng?

A. Nếu

2 2

a b



thì

a b



. B. Nếu

a b



thì

2 2

a b



.

C. Nếu

a b



và

0

a



thì

2 2

a b



. D. Nếu

a b



và

0

b



thì

2 2

a b



.

Lời giải

Chọn C

Phương án A sai với

1, 2

a b

  

.

Phương án B sai với

1, 0

a b

  

.

Phương án C đúng vì

2 2

0

a b

a b a b

a





    







.

Phương án D sai với

1, 1

a b

  

.

Câu 32: Trong mặt phẳng tọa độ

Oxy

, cho hình bình hành

ABCD

có





1;2

A ,





2;4

B  ,





0;3

C . Tìm tọa

độ điểm

D

.

A.





3;1

 . B.





3;1

. C.





3; 1



. D.





3; 1

 

.

Lời giải

Chọn B

Giả sử điểm





;

D D

D x y

.

Ta có:





;3

D D

DC x y

  



;





3;2

AB  



;





1;1

AC  



AB





và

AC



không cùng phương, hay

, ,

A B C

không thẳng hàng.

Do đó

ABCD

là hình bình hành

3 3

3 2 1

   

 

   

 

  

 

 

D D

x x

AB DC

y y

. Vậy tọa độ điểm

D

là





3;1

.

Câu 33: Giá trị lớn nhất của hàm số

2

3 2 5

y x x

   

trên

2

;1

3

 



 

 

là

A.

16

3

. B.

5

. C.

1

. D.

7

3

.

Lời giải

Chọn A

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Cách 1: Hàm số

2

3 2 5

y x x

   

là hàm số bậc hai có hệ số

3 0

a

  

và đồ thị của nó là Parabol

có tọa độ đỉnh là

1 16

;

3 3

 

 

 

.

Bảng biến thiên của hàm số trên đoạn

2

;1

3

 



 

 

là:

Vậy giá trị lớn nhất của hàm số trên

2

;1

3

 



 

 

là

16

3

.

Câu 34: Cho tam giác

ABC

có

. .

AB BC BC AC

 

   

. Tam giác

ABC

có tính chất gì?

A.

ABC



vuông tại

A

. B.

ABC



cân tại

B

.

C.

ABC



vuông tại

B

. D.

ABC



cân tại

A

.

Lời giải

Chọn D

Cách 1:

Gọi

M

là trung điểm của

BC

2

AB AC AM

  

  

.

Ta có:





. . . 0

AB BC BC AC BC AB AC

    

      

.2 0

BC AM BC AM

   

 

.

Vậy

ABC



cân tại

A

.

Cách 2:

Ta có:

. . . .

AB BC BC AC BA BC CB CA

     

       

. .cos . .cos

BA BC B CB CA C

 

.cos .cos

AB B AC C

 

2 2 2 2 2 2

. .

2. . 2. .

BC BA AC CA CB AB

AB AC

BC BA CACB

   

 

2 2 2 2 2 2

BC BA AC CA CB AB

     

2 2

2A 2.

B AC

 

AB AC

 

Vậy

ABC



cân tại

A

.

Câu 35: Cho tam giác

ABC

có

10

AB



,

17

AC



,

15

BC



. Tính

.

AB AC

 

.

A.

164

. B.

164



. C.

82



. D.

82

.

Lời giải

Chọn D

Ta có:





2

BC BC AC AB

  

  

2 2

2 .

AB AB AC AC

  

   

2 2

2 .

AB AB AC AC

  

 

Vậy

2 2 2

.

2

AB AC BC

AB AC

 



 

2 2 2

10 17 15

. 82

2

AB AC

 

  

 

.

Câu 36: Tập xác định của hàm số

2

4 2

12

x x

y

x x

  



 

là

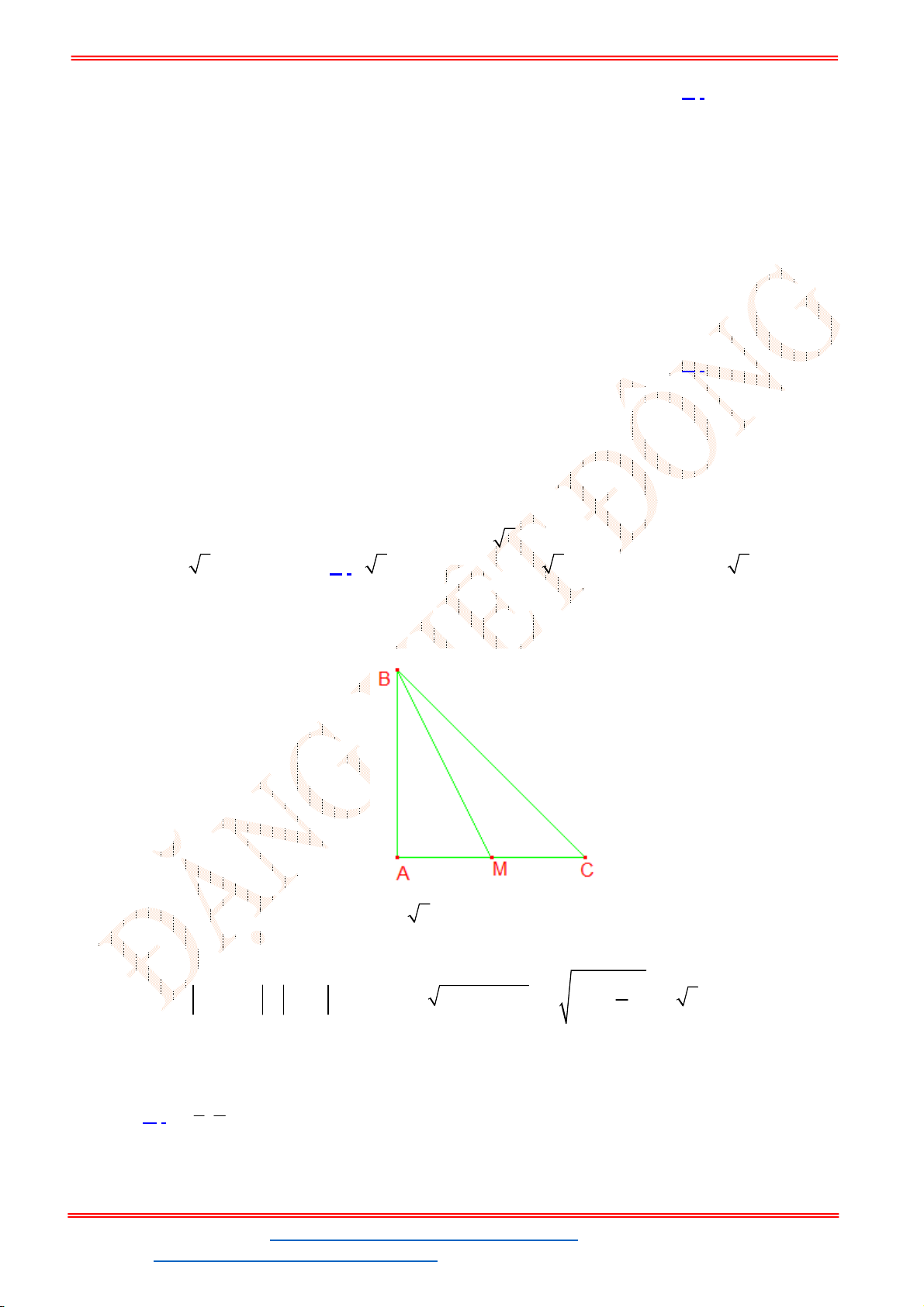
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.





2;4

 . B.









3; 2 2;4

    . C.





2;4

 . D.





2;4

 .

Lời giải

Chọn D

ĐKXĐ:

2

4

4 0

2

2 0 2 4

3

12 0

4

x

x x

x

x x

x





 



 

 

      

 

 

 

  









. Vậy, tập xác định của hàm số là





2;4

D   .

Câu 37: Tìm giá trị của tham số

m

để đỉnh

I

của đồ thị hàm số

2

6

y x x m

   

thuộc đường thẳng

2019

y x

 

.

A.

2020

m



. B.

2000

m



. C.

2036

m



. D.

2013

m



.

Lời giải

Chọn D

Đồ thị hàm số

2

6

y x x m

   

là parabol có đỉnh





3;9

I m

 .

Đỉnh





3;9

I m

 thuộc đường thẳng

2019 9 3 2019 2013

y x m m

       

.

Câu 38: Cho tam giác

ABC

vuông cân tại

A

có

2

BC a



. Tính độ dài

BA BC



 

.

A.

2 5

a

. B.

5

a

. C.

3

a

. D.

2 3

a

.

Lời giải

Chọn B

ABC



vuông cân tại

A

có

2

BC a



nên

AB AC a

 

Gọi

M

là trung điểm

AC

Ta có

2

BA BC BM

 

  

2

BM



2 2

2

AB AM

 

2

2 5

2

a

a a

 

  

 

 

Câu 39: Biết đường thẳng

: 4

d y x

  

cắt parabol





2

: 2

P y x x

 

tại hai điểm phân biệt

A

và

B

. Tìm

tọa độ trọng tâm

G

của tam giác

OAB

.

A.

1 7

;

3 3

G

 

 

 

. B.





1; 2

G



.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

C.

1 17 9 17

;

3 3

G

 

 

 

 

. D.

1 7

;

2 2

G

 

 

 

.

Lời giải

Chọn A

Xét phương trình hoành độ giao điểm của

d

và





P

:

2

2 4

x x x

   





2

4 0 *

x x   





*

có hai nghiệm phân biệt

1 2

;

x x

thỏa mãn:

1 2

1

x x

 

. Khi đó giao điểm của

d

và





P

lần lượt là









1 1 2 2

; 4 , ; 4

A x x B x x

   

Tọa độ trọng tâm

G

của tam giác

OAB

là

1 2 1 2

8

;

3 3

x x x x

G

   

 

 

 

hay

1 7

;

3 3

G

 

 

 

Câu 40: Cho hệ phương trình

2 1

2 2 1

  





  



mx y m

x my m

với

m

là tham số thực. Tìm tất cả các giá trị của

m

để hệ

phương trình đã cho vô nghiệm.

A.

2.

m

 

B.

2.

m

 

C.

2.

m



D.

2.

m



Lời giải

Chọn A

Cách 1:

Ta có các định thức

2 2 2

4; 3 2; 2 3 2

x y

D m D m m D m m

       

.

Hệ vô nghiệm thì

2

0

2

m

D

m





 



 



+ Khi

2 : 0; 0.

x y

m D D

  

( Hệ vô số nghiệm).

+ Khi

2 : 12; 12.

x y

m D D   

( Hệ vô nghiệm).

Cách 2:

Ta có

2 1

2 2 1

  





  



mx y m

x my m

 

   

1

1 1

2

1

2 1 1 2 1 *

2

y m x

x m m x m



   

 









     

 









*

2 2

3

2 1 0

2 2 2

m m m

x

 

     

 

 





**

.

Hệ phương trình đã cho vô nghiệm khi và chỉ khi





**

pt vô nghiệm

2

2 0

2

1 2

3

2

1 0

2 2

m

m m

m

 









 



 



 

     

 

 



  

 







.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 41: Giá trị nhỏ nhất của hàm số

6

( )

2 2

x

f x

x

 



với

2

x



là số có dạng

3

a b



(

,

a b

là các số nguyên).

Tính

2 2

.

a b



A.

5.

B.

6.

C.

3.

D.

4.

Lời giải

Chọn A

Với

2

x



thì

2 0

x

 

nên

6 2 6 2 6

( ) 1 2 . 1 2 3 1

2 2 2 2 2 2

x x x

f x

x x x

 

        

  

.

Dấu bằng xảy ra khi và chỉ khi

 

2 6

2 2 3 vì 2

2 2

x

x x

x



    



Vậy giá trị nhỏ nhất của hàm số

( )

f x

là

2 2

2 3 1 2; 1 5.

a b a b

      

Chú ý: Trong đề gốc thiếu giả thiết

,

a b

là các số nguyên, chúng tôi đã phải thêm điều kiện này

vào trong đề ra để bài toán có thể giải được.

Câu 42: Số các giá trị thực của tham số

m

để phương trình









2 1

0

1

x mx

x

 





có nghiệm duy nhất là

A.

3

. B.

2

. C.

0

. D.

1

.

Lời giải

Chọn A









 

2 1

0 1

1

 





x mx

x

; Điều kiện xác định:

1

x

 

.

Với điều kiện trên, phương trình





1

  

2 0

2 1 0

1 0

x

x mx

mx

 



    



 



 

2

1 2

x

mx









 



Phương trình





1

có nghiệm duy nhất







2

vô nghiệm hoặc





2

có nghiệm

2

x



hoặc





2

có

nghiệm

1

x

 

.

(2) vô nghiệm khi

0

m



; (2) có nghiệm

2

x



khi

1

2

m

 

; (2) có nghiệm

1

x

 

khi

1

m



.

Vậy có 3 giá trị của

m

thỏa mãn yêu cầu bài toán.

Câu 43: Tìm tất cả các giá trị thực của tham số

m

để phương trình

4 2

2 1

x x m

  

có hai nghiệm phân biệt.

A.

0

m



. B.

0

m



. C.

1

m



hoặc

0

m



. D.

0 1

m

 

.

Lời giải

Chọn C

4 2

2 1

x x m

  

(1); Đặt

2

t x



(

0

t



).

Khi đó phương trình (1) trở thành:

2

2 1

t t m

  

2

2 1 0

t t m

    

. (2)

Phương trình (1) có hai nghiệm phân biệt khi và chỉ khi phương trình (2) có hai nghiệm phân biệt

trái dấu hoặc có nghiệm kép dương

0

' 0

0

ac

S









 















1 0

0

2 0

m

 























1

0

m













.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 20

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 44: Tìm tất cả các giá trị thực của tham số

m

để phương trình

3 2

0

x mx x m

   

có ba nghiệm thực

phân biệt.

A.

1

m

 

. B.

1

m

 

. C.

1

m



hoặc

0

m



. D.

0 1

m

 

.

Lời giải

Chọn B

   

 

3 2 2 2 2

1

0 ( 1) 1 0 1 0

x

x mx x m x x m x x x m

x m

 



             







.

Yêu cầu bài toán

1

m

  

.

Câu 45: Cho phương trình

2

1 0

x mx m

    

với

m

là tham số thực. Tính tổng

S

tất cả các giá trị thực

của tham số

m

để phương trình có hai nghiệm phân biệt

1 2

,

x x

thỏa mãn

1 2

4

x x

 

.

A.

2

S



B.

2

S

 

. C.

4

S

 

D.

5

S



.

Lời giải

Chọn B

Phương trình có hai nghiệm phân biệt

1 2

; 0

x x

  

   

2

4 1 0 2 0 2

m m m m

         

.

Khi đó phương trình có hai nghiệm phân biệt:









1 2

2 2

1, 1

2 2

m m m m

x x m

     

     

 

.

Ta có

1 2

1 3 2

4 1 1 4 1 3 ( )

1 3 4

m m

x x m m tm

m m

   



          



    



.

Suy ra

2

S

 

.

Câu 46: Cho phương trình

2

10 2

x x m x

   

. Tìm tất cả các giá trị thực của tham số

m

để phương trình

đã cho vô nghiệm.

A.

16 20

m

 

. B.

3 16

m

  

C.

m





. D.

16

m



.

Lời giải

Chọn D

2

10 2

x x m x

   

 

2

2 0

10 2

x

x x m x

 









   





2 2

2

10 4 4

x

x x m x x









    



2

6 4

x

x m









 



2

4

6

x

m

x



















Để phương trình vô nghiệm thì

4

2 4 12 16

6

m

m m



     

.

Câu 47: Tập tất cả các giá trị của tham số

m

để phương trình

2 2

1

x x m

  

có nghiệm là





;

a b

. Tính

S a b

 

.

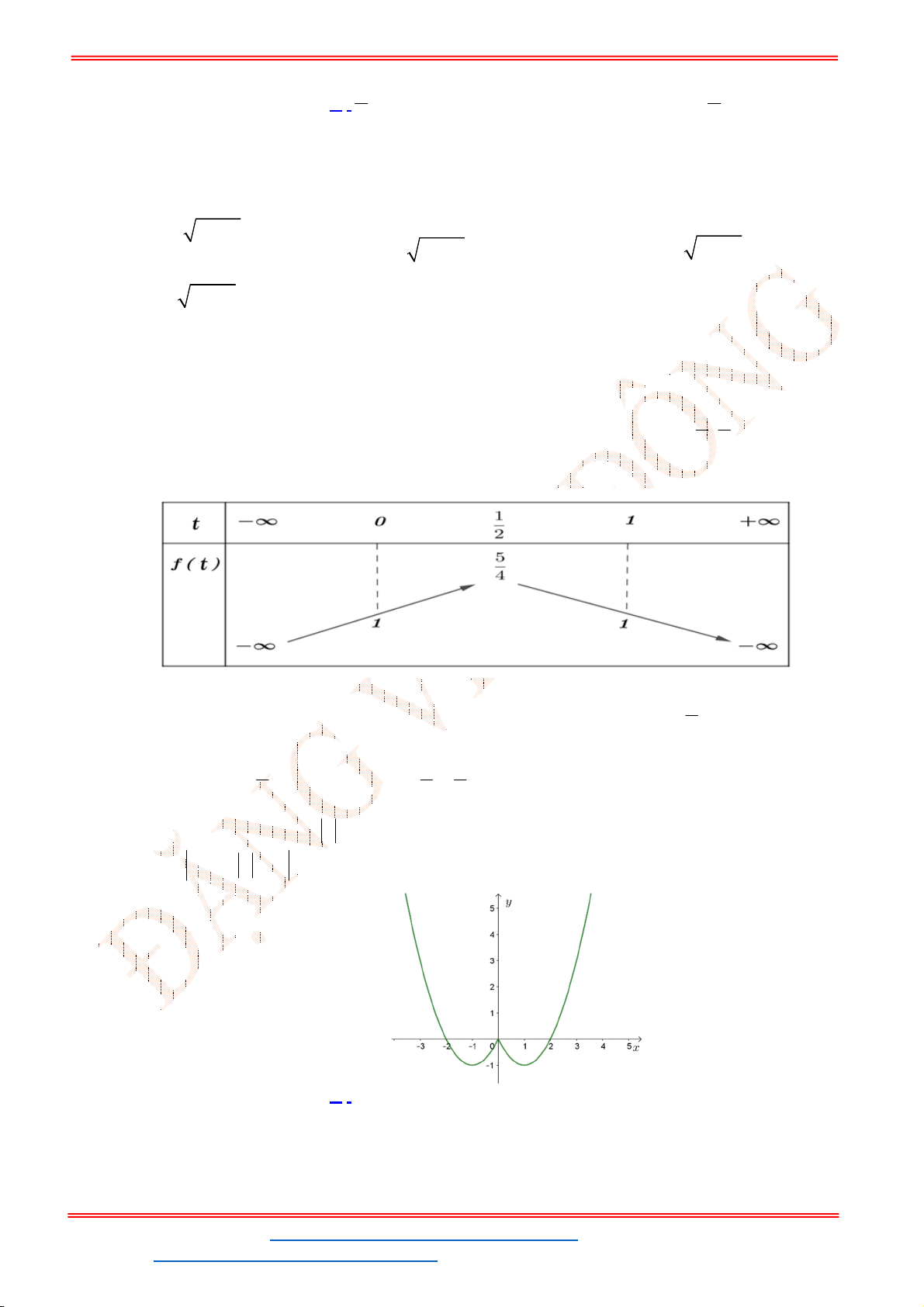
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 21

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

0.

B.

9

.

4

C.

1.

D.

1

.

4

Lời giải

Chọn B

2 2

1x x m  

2

2 2

1 0

(1 ) 1 1 0

x

x x m



 







      





 

2 2

1 1

(1 ) 1 1 0 *

  









      





x

x x m

Đặt

2

1 x t 

. Điều kiện

 

0;1t

. Phương trình

(*)

trở thành:

2

1t t m    (**)

Số nghiệm của phương trình (**) là số giao điểm của đồ thị hàm số

2

( ) 1f t t t   

trên

 

0;1

và đường thẳng

y m

vuông góc với trục Oy.

Xét đồ thị hàm số

2

( ) 1f t t t   

là đường parabol có đỉnh là điểm

1 5

;

2 4

I

 

 

 

, vì

1 0a   

nên

bề lõm quay xuống dưới. Ta có bảng biến thiên sau:

Dựa vào bảng biến thiên, ta có: Phương trình (**) có nghiệm 

5

1;

4

m

 



 

 

.

Vậy

5

1;

4

a b 

5 9

1

4 4

S a b     

.

Câu 48: Cho hàm số

2

2y x x  có đồ thị như hình vẽ. Gọi

S

là tập các giá trị nguyên của

m

đề phương

trình

2

2 1x x m   có hai nghiệm phân biệt. Tính tổng các phần tử của tập

S

.

A. 1 . B. 2 . C. 4 . D.

0

.

Lời giải

Chọn B

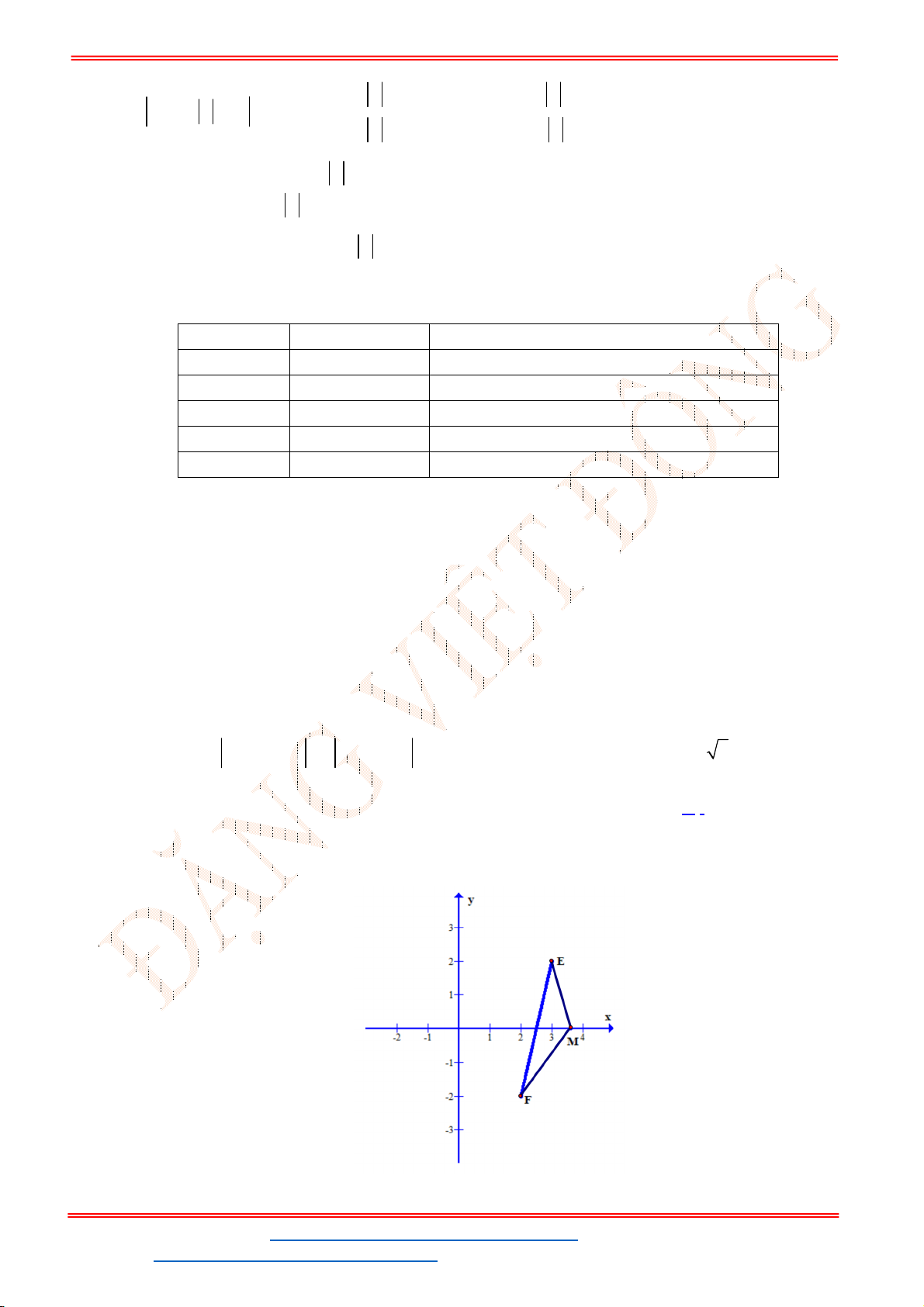
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 22

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

 

2 2

2

2 2

2 1 2 1 1

2 1

2 1 2 1 2

x x m x x m

x x m

x x m x x m

 

     

    

 

       

 

 

Xét phương trình

2

2x x k  (3). Số nghiệm của phương trình này là số giao điểm của đồ thị

hàm số

2

2y x x  và đường thẳng

y k

.

Từ đồ thị hàm số

2

2y x x  ta có kết luận sau:

k

Số giao điểm

Kết luận về số nghiệm của PT (3)

1

k

 

0 Phương trình vô nghiệm

1

k

 

2 Phương trình có 2 nghiệm phân biệt

1 0

k

  

4 Phương trình có 4 nghiệm phân biệt

0

k



3 Phương trình có 3 nghiệm phân biệt

0

k



2 Phương trình có 2 nghiệm phân biệt

Do

 

1 1m m m     

nên để phương trình đã cho có hai nghiệm phân biệt thì phương

trình

 

1

có hai nghiệm phân biệt và phương trình

 

2

vô nghiệm.

Điều đó tương đương với:

1 1 0

2

1 1 2

0 1

1 0 1

m m

m

m m

m

m m

    

 





 

 

   

 

 



 



 

 

  

 

 

.

Do

m

nên

2m 

. Vậy

 

2S 

. Tổng các phần tử của tập

S

là 2 .

Câu 49: Trong hệ tọa độ Oxy cho ba điểm

 

1; 4A  ,

 

4;5B và

 

0; 9C  . Điểm

M

di chuyển trên trục

Ox

.

Đặt

2 2 3

Q MA MB MB MC

   

   

. Biết giá trị nhỏ nhất của Q có dạng

a b

trong đó

a

,

b

là các

số nguyên dương và

a

,

20b 

. Tính

a b

.

A.

15

. B.

17

. C.

14

. D.

11

.

Lời giải

Chọn D

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 23

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Giả sử





;0

M x Ox

 . Ta có:





1 ; 4

MA x

  



,





4 ;5

MB x

 



,





; 9

MC x

  



.





2 9 3 ;6

MA MB x

   

 

,





4 2 ; 4

MB MC x

   

 

.

Do đó

     

2 2 2

2

2 9 3 6 3 4 2 4

Q x x      

   

2 2

6 3 2 6 2 ( 2)

x x      





6

ME MF

  . Trong đó





3;2

E ,





2; 2

F



.

Ta có

17

ME MF EF  



6 17

Q 

Dấu “ = “ xảy ra 

M

là giao điểm của đoạn

EF

và trục

Ox



5

( ;0)

2

M

.

Suy ra

Q

đạt giá trị nhỏ nhất là

6 17

. Do đó theo giả thiết ta có

6

17

a

b











.Vậy

11

a b

  

.

Câu 50: Cho

,

x y

thoả mãn

2 2

x y a

 

. Xác định

a

, biết rằng giá trị lớn nhất của

2 3

P x y

 

với

, 0

x y



là

117

.

A.

9

a



. B.

13

a 

. C.

5

a



. D.

3 3

a 

.

Lời giải

Chọn A

Ta có:

2 2

0

a x y

  

;

 









2

2 2 2 2 2 2

2 3 2 3 13

P x y x y P a

       .

2 2

2

13

13 ( 0, 0)

2 3

3

13

a

x

x y

P a do x y

a

x y a

y











 

    

 

 

 









Vậy

13

MaxP a



. Theo giả thiết, ta có:

13 117 9

a a

  

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 5 Môn Toán – Lớp 10

(Th

ời gian l

àm bài 90 phút)

Không kể thời gian phát đề

I. CÂU HỎI TRẮC NGHIỆM

Câu 1. Câu nào sau đây không phải là mệnh đề ?

A.

4

là một số nguyên tố. B.

6

là bội của

2

.

C. Nước là một loại chất lỏng. D. Trời hôm nay đẹp quá!

Câu 2. Mệnh đề phủ định của mệnh đề

:" x , x 1 0"

P

   



là

A.

:" x ,x 1 0"

P

   



. B.

:" x ,x 1 0"

P

   



.

C.

:" x ,x 1 0"

P

   



. D.

:" x ,x 1 0"

P

   



.

Câu 3. Số phần tử của tập hợp





3 2

| 2 13 6 0

A x x x x

     

 là

A.

0

. B.

1

. C.

2

. D.

3

.

Câu 4. Cho









3;2 , 1;A B

     

. Xác định

A B



.

A.





1;2



. B.





1;2



. C.





1;2



. D.





1;2



Câu 5. Tìm tập xác định

D

của hàm số 2 5

y x x

  

.

A.





0;D

  

. B.

5

;

2

D

 

  





 

. C.

5

;

2

D

 

 





 

. D.





;0

D  

.

Câu 6. Cho hàm số





2

4

f x x

 

. Khẳng định nào sau đây là đúng ?

A.





f x

là hàm số vừa chẵn, vừa lẻ. B.





f x

là hàm số không chẵn, không lẻ.

C.





f x

là hàm số lẻ. D.





f x

là hàm số chẵn.

Câu 7. Đồ thị hình bên biểu diễn hàm số nào sau đây?

A.

2

y x

 

. B.

2

y x

 

. C.

2

y x

  

. D.

2

y x

  

.

Câu 8. Trục đối xứng của parabol





2

: 2 6 2020

P y x x  

là

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

3

y

 

. B.

3

2

y

 

. C.

3

x

 

. D.

3

2

x

 

.

Câu 9. Cho hàm số bậc hai

2

3 4 5

y x x

   

. Hàm số đồng biến trên khoảng nào dưới đây ?

A.





1;



. B.

4

;

3

 



 

 

. C.





1;1



. D.





5;0



.

Câu 10. Cho phương trình

5 2 4 2 5

x x

  

. Tập nghiệm của phương trình là

A.

S

 

. B.

5

2

S

 



 

 

. C.

5

;

2

S

 

 

 

 

. D.

5

;0

2

S

 



 

 

.

Câu 11. [Mức độ 1] Hệ phương trình

2 4

4 2 5 0

x y

 





   



có tất cả bao nhiêu nghiệm?

A. Vô số. B.

1

. C.

2

. D.

0

.

Câu 12. Cho bốn điểm

, , ,

A B C D

phân biệt. Khi đó

AB DC BC AD

  

   

bằng vectơ nào sau đây?

A.

0



. B.

BD



. C.

AC



. D.

2

DC



.

Câu 13. Cho hai điểm phân biệt

A

và

B

. Gọi

I

là trung điểm đoạn thẳng

AB

. Đẳng thức nào sau đây

đúng?

A.

0

IA IB

 

  

. B.

IA IB AB

 

  

. C.

IA IB AB

 

  

. D.

0

IA IB

 

  

.

Câu 14. Trong mặt phẳng tọa độ

Oxy

, cho





1;2

a  



,





3;2

b 



. Tọa độ của vectơ

2 3

v a b

  

  

là

A.





8;2

v 



. B.





11;8

v 



. C.





11;2

v 



. D.





2;4

v 



.

Câu 15. Cho hai vectơ

a



và

b



khác

0



. Xác định góc



giữa hai vectơ

a



và

b



khi

. . .

a b a b

 

   

A.

o

180



 . B.

o

0





. C.

o

90



 . D.

o

45



 .

Câu 16. Trong các mệnh đề sau đây, có bao nhiêu mệnh đề đúng ?

(I): “17 là số nguyên tố”

(II): “Tam giác vuông có một đường trung tuyến bằng một nửa cạnh huyền”

(III): “Hình thang có hai cạnh bên bằng nhau là hình thang cân”

(IV): “Mọi hình chữ nhật đều nội tiếp được đường tròn”

A.

4

. B.

3

. C.

2

. D.

1

.

Câu 17. Cho





; ; ;

A a b m n



,





; ;

B b c m



và





; ;

C a m n



. Hãy chọn khẳng định đúng.

A.













\ ; ;

A B A C a m n

  

. B.













\ ; ; ;

A B A C a c m n

  

.

C.













\ ; ; ;

A B A C a b m n

  

. D.













\ ;

A B A C a n

  

.

Câu 18. Cho hàm số





2

.

f x x x

 

Khẳng định nào sau đây là đúng.

A.





f x

là hàm số lẻ.

B.





f x

là hàm số chẵn.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

C. Đồ thị của hàm số





f x

đối xứng qua gốc tọa độ.

D. Đồ thị của hàm số





f x

đối xứng qua trục hoành.

Câu 19. Tìm tất cả các giá trị của

m

để hàm số

2

y m x x

  

làm hàm số bậc nhất.

A.

0

m



. B.

0

m



. C.



. D.

m

 



.

Câu 20. Biết một viên đạn được bắn ra theo quỹ đạo là một parabol có phương trình









2

( 3) 9

s t t km

   

, với

t

là thời gian tính bằng giây. Hỏi khi nào viên đạn đạt độ cao

8

km

?

A.

4

t s



. B.

5

t s



. C.

3

t s



. D.

2

t s



.

Câu 21. Tìm tất cả các giá trị của tham số

m

để phương trình

2 1

0

3

x m

x

 





có nghiệm.

A.

5

m



. B.

5

m



. C.

7

m



. D.

7

m



.

Câu 22. Tìm tất cả các giá trị của tham số

m

để phương trình









2

1 4 0

x x x m

   

có

3

nghiệm phân

biệt.

A.

4

3

m











. B.

4

m



. C.

4

m



. D.

4

m



.

Câu 23. Cho hình chữ nhật

ABCD

biết

4

AB a



và

3

AD a



. Khi đó

AB AD



 

bằng

A.

6

a

. B.

7

a

. C.

25

a

. D.

5

a

.

Câu 24. Trong hệ tọa độ

Oxy

, cho tam giác

ABC

có trọng tâm là

G

. Biết





4;0

A ,





2; 3

B



,





5; 1

G .

Khi đó tọa độ điểm

C

là

A.





6; 9

. B.

11 2

;

3 3

 



 

 

. C.





11; 2



. D.





9; 6

.

Câu 25. Trong mặt phẳng tọa độ

Oxy

cho các điểm





1;3

A

,





4;0

B

,





2; 5

C



. Tọa độ điểm

M

thỏa

mãn

3 0

MA MB MC

  

   

là

A.





1;18

M

. B.





1;18

M 

. C.





18;1

M 

. D.





1; 18

M 

.

Câu 26. Cho tập





;

A m

  

và tập





2 5;23

B m 

. Gọi

S

là tập hợp các số thực

m

để

A B A

 

.

Hỏi

S

là tập con của tập hợp nào sau đây?

A.





; 23

 

. B.





;0



. C.





23;

 

. D.



.

Câu 27. Tất cả các giá trị của

m

để hàm số









2 2 2

2

2 2 2

1

x x m x

y

x m

  



 

là hàm số chẵn có tổng bằng

A.

1



. B.

1

. C.

2

. D.

0

.

Câu 28. Xác định hàm số

2

y ax bx c

  

, biết hàm số đạt giá trị nhỏ nhất bằng

4

tại

2

x

 

và đồ thị

hàm số đi qua điểm

(0;6)

A .

A.

2

1

2 6

2

y x x

  

. B.

2

2 6

y x x

  

. C.

2

6 6

y x x

  

. D.

2

4

y x x

  

.

Câu 29. Xác định tất cả các giá trị của tham số

m

để phương trình

2

4 3 0

x x m

   

có hai nghiệm phân

biệt

1

x

,

2

x

thoả mãn

1 2

0 3

x x

  

.

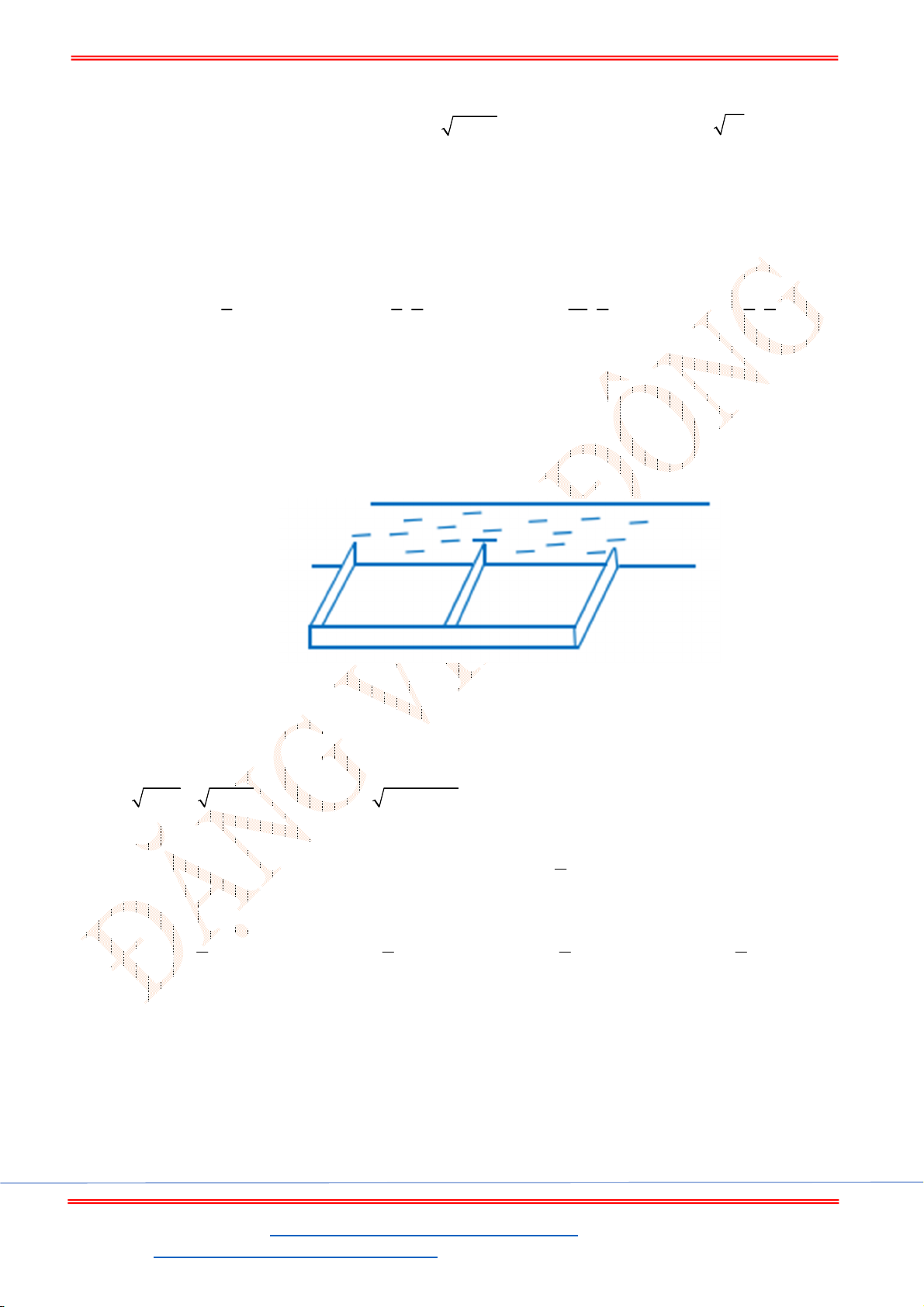
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

7 6m   

. B.

7 3m   

. C.

6m  

. D.

6 3m   

.

Câu 30. Biết phương trình

 

2

3 2 1 1 5 3x x x x    

có một nghiệm là

33x a b 

với ,a b là

các số hữu tỉ. Tính

5a b

.

A. 12. B.

6

. C. 1. D.

3

.

Câu 31. Cho tam giác

MNP

có

4MN 

;

8MP 

;



60PMN  . Điểm E trên tia MP sao cho

NE

vuông góc với trung tuyến MF của tam giác

MNP

. Đặt

ME kMP

 

. Phát biểu nào dưới đây

là đúng về số

k

?

A.

1

0;

5

k

 



 

 

. B.

1 2

;

5 5

k

 



 

 

. C.

1 1

;

10 2

k

 



 

 

. D.

1 3

;

2 4

k

 



 

 

.

Câu 32. Một người nông dân có 15.000.000 vnđ để làm một cái hàng rào hình chữ E dọc theo một con

sông (như hình vẽ) để làm một khu đất có hai phần chữ nhật để trồng rau. Đối với mặt hàng rào

song song với bờ sông thì chi phí nguyên vật liệu là 60.000 vnđ/m, còn đối với ba mặt hàng rào

song song nhau thì chi phí nguyên vật liệu là 50.000vnđ/m. Tìm diện tích lớn nhất của đất rào

thu được.

A. 50

2

m . B. 3125

2

m . C. 1250

2

m . D.

6250

2

m .

Câu 33. Cho phương trình:

 

2

2 2 2

9 2 1 – 6 9 5 15 06x x m x x m m      

.

Tìm

m

để phương trình có nghiệm.

A.

m  

. B. 1m   . C.

m  

. D.

2m 

.

Câu 34. Có bao nhiêu tham số nguyên

m

để phương trình

 

2

2 10 10 11 3 3 0x x x x x m       

có đúng 2 nghiệm phân biệt.

A. 4 . B.

16

. C.

15

. D.

17

.

Câu 35. Cho tam giác

ABC

. Gọi D là điểm xác định bởi

3

4

AD AC

 

, I là trung điểm của BD . Gọi E

là điểm thoả mãn

BE xBC

 

. Tìm

x

để ba điểm

, ,A I E

thẳng hàng.

A.

7

8

x  . B.

8

7

x  . C.

7

3

x  . D.

3

7

x  .

II. TỰ LUẬN

Bài 1. Cho hàm số

2

2 3y x x   có đồ thị là

 

P

.

a. Lập bảng biến thiên và vẽ đồ thị





P

.

b. Tìm các giá trị của tham số

m

sao cho phương trình

2

2 3 0x x m    có 2 nghiệm phân biệt.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Bài 2. Trong mặt phẳng với hệ tọa độ

Oxy

, cho các điểm





2;3

A 

,





2;1

B

,





0; 3

C



và





1; 2

D

 

.

Tìm điểm

M

có hoành độ dương thuộc đường thẳng

: 1 0

d x y

  

sao cho





3 . 6

MA MB MC MD

  

   

.

Bài 3. Giải phương trình





2

4 3 1 8 5 6 2

x x x x x

      

.

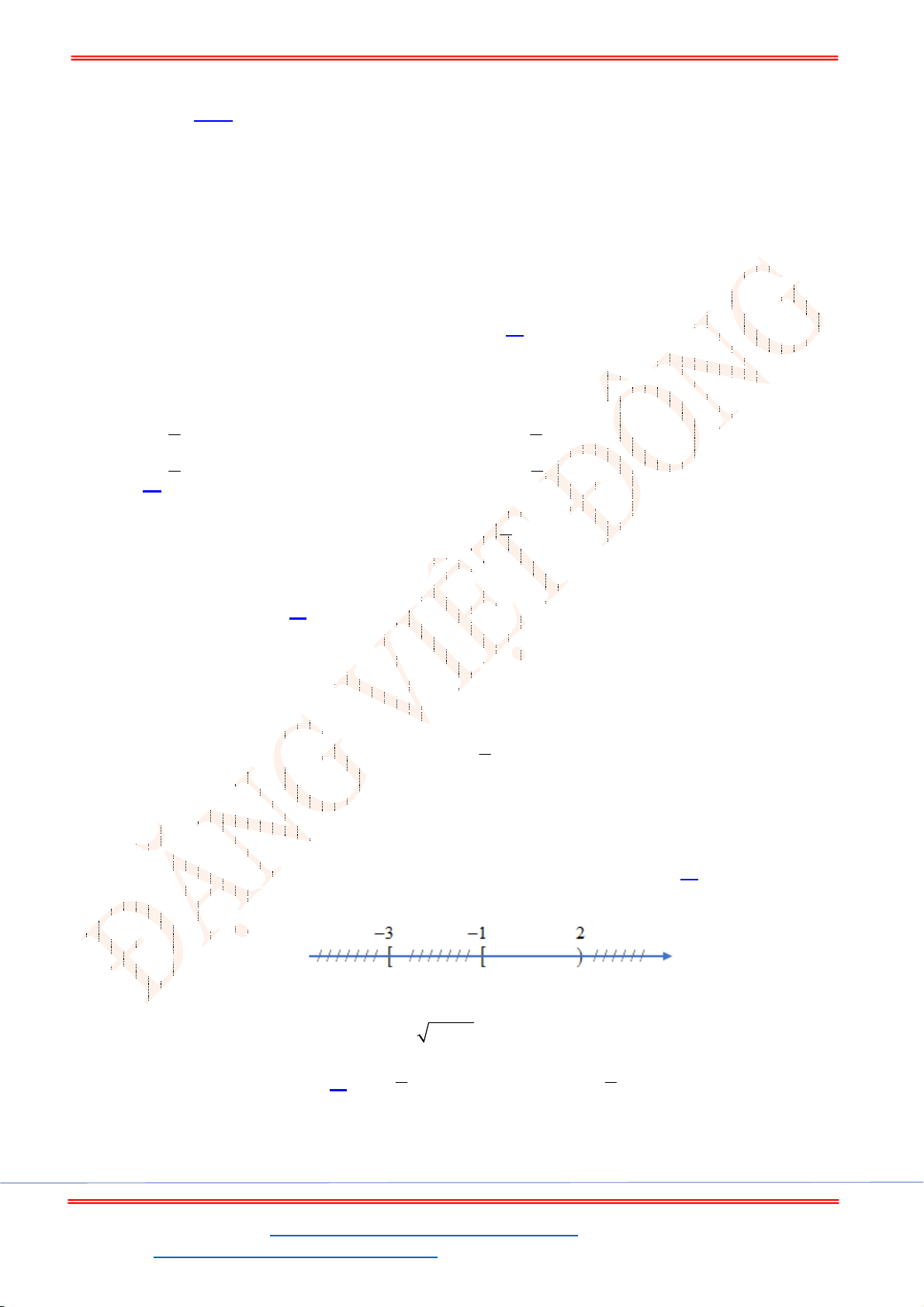
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG HDG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 5 Môn Toán – Lớp 10

(Th

ời gian l

àm bài 90

phút)

Không kể thời gian phát đề

I. CÂU HỎI TRẮC NGHIỆM

Câu 1. Câu nào sau đây không phải là mệnh đề?

A.

4

là một số nguyên tố. B.

6

là bội của

2

.

C. Nước là một loại chất lỏng. D. Trời hôm nay đẹp quá!

Lời giải

Câu cảm thán không là mệnh đề.

Câu 2. Mệnh đề phủ định của mệnh đề

:" x , x 1 0"

P

   



là:

A.

:" x ,x 1 0"

P

   



. B.

:" x ,x 1 0"

P

   



.

C.

:" x ,x 1 0"

P

   



. D.

:" x ,x 1 0"

P

   



.

Lời giải

Mệnh đề phủ định của

:" x , x 1 0"

P

   



là

:" x ,x 1 0"

P

   



.

Câu 3. Số phần tử của tập hợp





3 2

| 2 13 6 0

A x x x x

     

 là

A.

0

. B.

1

. C.

2

. D.

3

.

Lời giải

Xét phương trình

3 2

2

2 13 6 0 3

1

2

x

x x x x

x





 



       



 







.

Vậy





2

A 

.

Câu 4. Cho









3;2 , 1;A B

     

. Xác định

A B



A.





1;2



. B.





1;2



. C.





1;2



. D.





1;2



.

Lời giải

Biểu diễn lên trục số ta được





1;2

A B  

.

Câu 5. Tìm tập xác định

D

của hàm số 2 5

y x x

  

.

A.





0;D

  

. B.

5

;

2

D

 

  





 

. C.

5

;

2

D

 

 





 

. D.





;0

D  

.

Lời giải

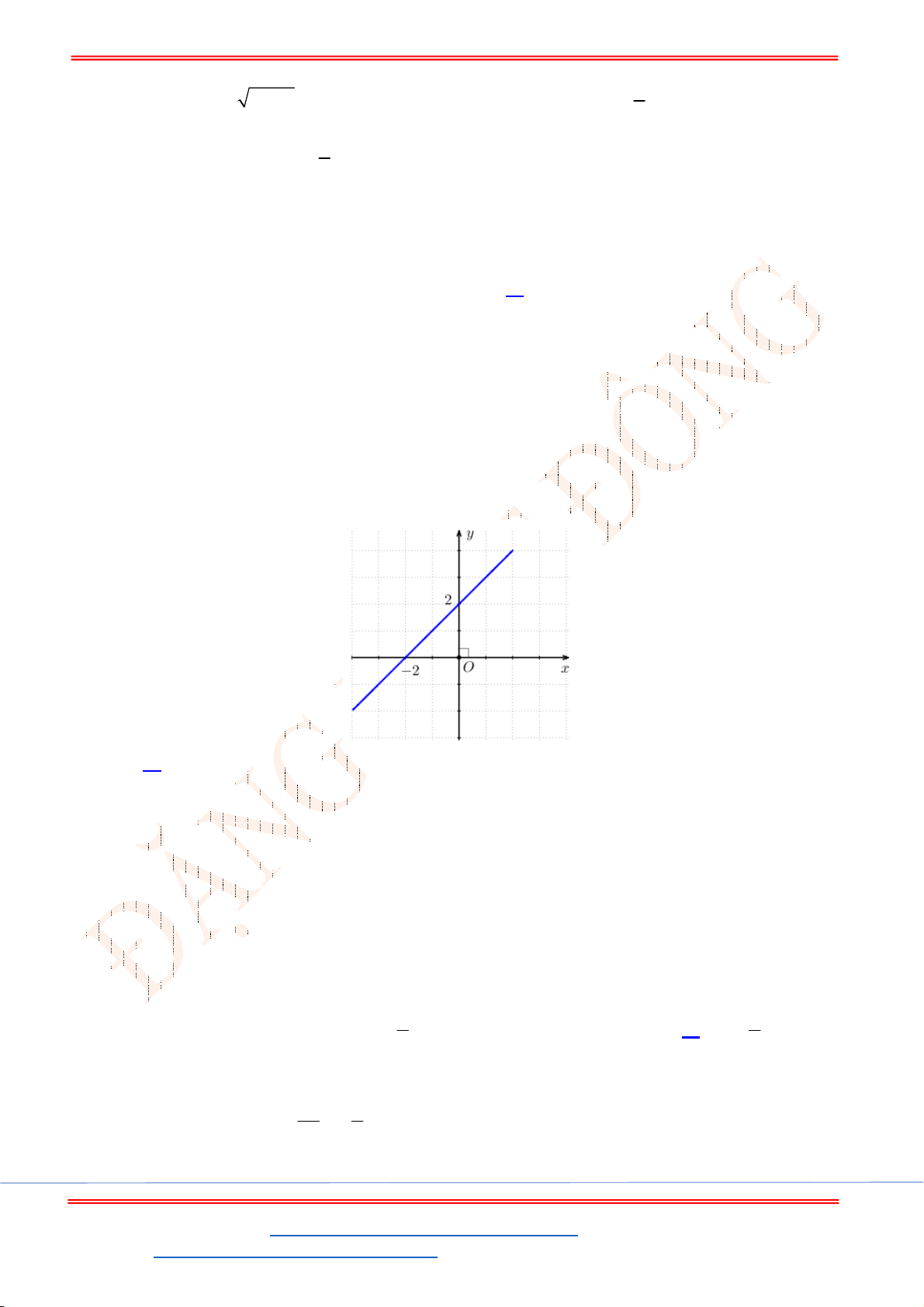
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Hàm số 2 5

y x x

  

xác định khi và chỉ khi

5

2 5 0

2

x x

   

.

Vậy tập xác định

5

;

2

D

 

  





 

.

Câu 6. Cho hàm số





2

4

f x x

 

. Khẳng định nào sau đây là đúng ?

A.





f x

là hàm số vừa chẵn, vừa lẻ. B.





f x

là hàm số không chẵn, không lẻ.

C.





f x

là hàm số lẻ. D.





f x

là hàm số chẵn.

Lời giải

Xét





2

4

f x x

 

có TXĐ

D





.

Ta có

x D x D

    

.

     

2

4 4

f x x x f x

      

.

Nên





f x

là hàm số chẵn.

Câu 7. Đồ thị hình bên biểu diễn hàm số nào sau đây?

A.

2

y x

 

. B.

2

y x

 

. C.

2

y x

  

. D.

2

y x

  

.

Lời giải

Giả sử hàm số cần tìm có dạng:





0

y ax b a

  

.

Đồ thị hàm số đi qua hai điểm









0;2 , 2;0



nên ta có:

2 1

0 2 2

b a

a b b

 

 



 

   

 

.

Vậy hàm số cần tìm là

2

y x

 

.

Câu 8. Trục đối xứng của parabol





2

: 2 6 2020

P y x x  

là

A.

3

y

 

. B.

3

2

y

 

. C.

3

x

 

. D.

3

2

x

 

.

Lời giải

Trục đối xứng

3

2 2

b

x

a

   

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 9. Cho hàm số bậc hai

2

3 4 5

y x x

   

. Hàm số đồng biến trên khoảng nào dưới đây ?

A.





1;



. B.

4

;

3

 



 

 

.

C.





1;1



. D.





5;0



.

Lời giải

Ta có

1 0

a

  

và

2

2 3

I

b

x

a

  

nên hàm số đồng biến trên

2

;

3

 



 

 

, nghịch biến trên

2

;

3

 



 

 

. Do đó đáp án D đúng.

Câu 10. Cho phương trình

5 2 4 2 5

x x

  

. Tập nghiệm của phương trình là

A.

S

 

. B.

5

2

S

 



 

 

. C.

5

;

2

S

 

 

 

 

. D.

5

;0

2

S

 



 

 

.

Lời giải

Điều kiện:

5 2 0

5

2 5 0

2

x

 



 



 



.

Thử lại thì

5

2

x



thỏa phương trình. Vậy

5

2

S

 



 

 

.

Câu 11. Hệ phương trình

2 4

4 2 5 0

x y

 





   



có tất cả bao nhiêu nghiệm?

A. Vô số. B.

1

. C.

2

. D.

0

.

Lời giải

Ta có:

2 4 4 2 8 2 4

4 2 5 4 2 5 0 13

x y x y x y

x y x y

     

  

 

  

      

  

(Vô lý).

Vậy hệ phương trình đã cho vô nghiệm.

Câu 12. Cho bốn điểm

, , ,

A B C D

phân biệt. Khi đó

AB DC BC AD

  

   

bằng vectơ nào sau đây?

A.

0



. B.

BD



. C.

AC



. D.

2

DC



.

Lời giải

Ta có:









0

AB DC BC AD AB BC AD DC AC AC

         

         



.

Câu 13. Cho hai điểm phân biệt

A

và

B

. Gọi

I

là trung điểm đoạn thẳng

AB

. Đẳng thức nào sau đây

đúng?

A.

0

IA IB

 

  

. B.

IA IB AB

 

  

. C.

IA IB AB

 

  

. D.

0

IA IB

 

  

.

Lời giải

Do

I

là trung điểm đoạn thẳng

AB

nên

IA



và

IB



là hai vectơ đối nhau. Suy ra

0

IA IB

 

  

.

Câu 14. Trong mặt phẳng tọa độ

Oxy

, cho





1;2

a  



,





3;2

b 



. Tọa độ của vectơ

2 3

v a b

  

  

là

A.





8;2

v 



. B.





11;8

v 



. C.





11;2

v 



. D.





2;4

v 



.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Lời giải

Giả sử





;

v x y





, suy ra





2. 1 3.3 11

2.2 3.2 2

x

y

    







   





. Vậy





11;2

v 



.

Câu 15. Cho hai vectơ

a



và

b



khác

0



. Xác định góc



giữa hai vectơ

a



và

b



khi

. . .

a b a b

 

   

A.

o

180



 . B.

o

0





. C.

o

90



 . D.

o

45



 .

Lời giải

Ta có





. . .cos ,

a b a b a b



     

.

Mà theo giả thiết

. .

a b a b

 

   

, suy ra









0

cos , 1 , 180

a b a b   

   

Câu 16. Trong các mệnh đề sau đây, có bao nhiêu mệnh đề đúng ?

(I): “17 là số nguyên tố”

(II): “Tam giác vuông có một đường trung tuyến bằng một nửa cạnh huyền”

(III): “Hình thang có hai cạnh bên bằng nhau là hình thang cân”

(IV): “Mọi hình chữ nhật đều nội tiếp được đường tròn”

A.

4

. B.

3

. C.

2

. D.

1

.

Lời giải

(I): 17 là số nguyên tố vì chỉ có 2 ước là 1 và 17 suy ra (I) là mệnh đề đúng.

(II): Tam giác

ABC

vuông tại

A

có đường trung tuyến

AM

bằng

1

2

BC

suy ra (II) là mệnh

đề đúng.

(III): Hình thang có hai cạnh bên bằng nhau có thể là hình bình hành suy ra (III) là mệnh đề sai.

(IV): Mọi hình chữ nhật có tổng hai góc đối diện bằng

0

180

nên nội tiếp được đường tròn.

Câu 17. Cho





; ; ;

A a b m n



,





; ;

B b c m



và





; ;

C a m n



. Hãy chọn khẳng định đúng.

A.













\ ; ;

A B A C a m n

  

. B.













\ ; ; ;

A B A C a c m n

  

.

C.













\ ; ; ;

A B A C a b m n

  

. D.













\ ;

A B A C a n

  

.

Lời giải

Ta có





\ ;

A B a n



,





; ;

A C a m n

 

suy ra













\ ; ;

A B A C a m n

  

.

Câu 18. Cho hàm số





2

.

f x x x

 

Khẳng định nào sau đây là đúng.

A.





f x

là hàm số lẻ.

B.





f x

là hàm số chẵn.

C. Đồ thị của hàm số





f x

đối xứng qua gốc tọa độ.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

D. Đồ thị của hàm số





f x

đối xứng qua trục hoành.

Lời giải

TXĐ:

D





là tập đối xứng (vì

D D

x x

    

)

Ta có













2

f x x x x x f x

       

Vậy





f x

là hàm số chẵn trên



.

Câu 19. Tìm tất cả các giá trị của

m

để hàm số

2

y m x x

  

làm hàm số bậc nhất.

A.

0

m



. B.

0

m



. C.



. D.

m

 



.

Lời giải

Xét





2 2

2 1 2

y m x x m x

     

. Vì

2

1 0,m m

   



nên hàm số đã cho luôn là hàm số

bậc nhất với mọi giá trị của

m

.

Câu 20. Biết một viên đạn được bắn ra theo quỹ đạo là một parabol có phương trình









2

( 3) 9

s t t km

   

, với

t

là thời gian tính bằng giây. Hỏi khi nào viên đạn đạt độ cao

8

km

?

A.

4

t s



. B.

5

t s



.

C.

3

t s



. D.

2

t s



.

Lời giải

Quả đạn đạt độ cao

8

km

khi

 





 

2 2

1

8 ( 3) 9 8 ( 3) 1

2

t KTM

s t t t

t TM

 

         









Câu 21. Tìm tất cả các giá trị của tham số

m

để phương trình

2 1

0

3

x m

x

 





có nghiệm.

A.

5

m



. B.

5

m



. C.

7

m



. D.

7

m



.

Lời giải

Điều kiện xác định:

3

x



.

2 1 1

0 2 1 0

2

3

x m m

x m x

x

  

      



.

Để phương trình có nghiệm thì

1

3 7.

2

m



  

Câu 22. Tìm tất cả các giá trị của tham số

m

để phương trình









2

1 4 0

x x x m

   

có

3

nghiệm phân

biệt.

A.

4

3

m











. B.

4

m



. C.

4

m



. D.

4

m



.

Lời giải

 

2

1

1 4 0

4 0

x

x x x m

x x m





    



  



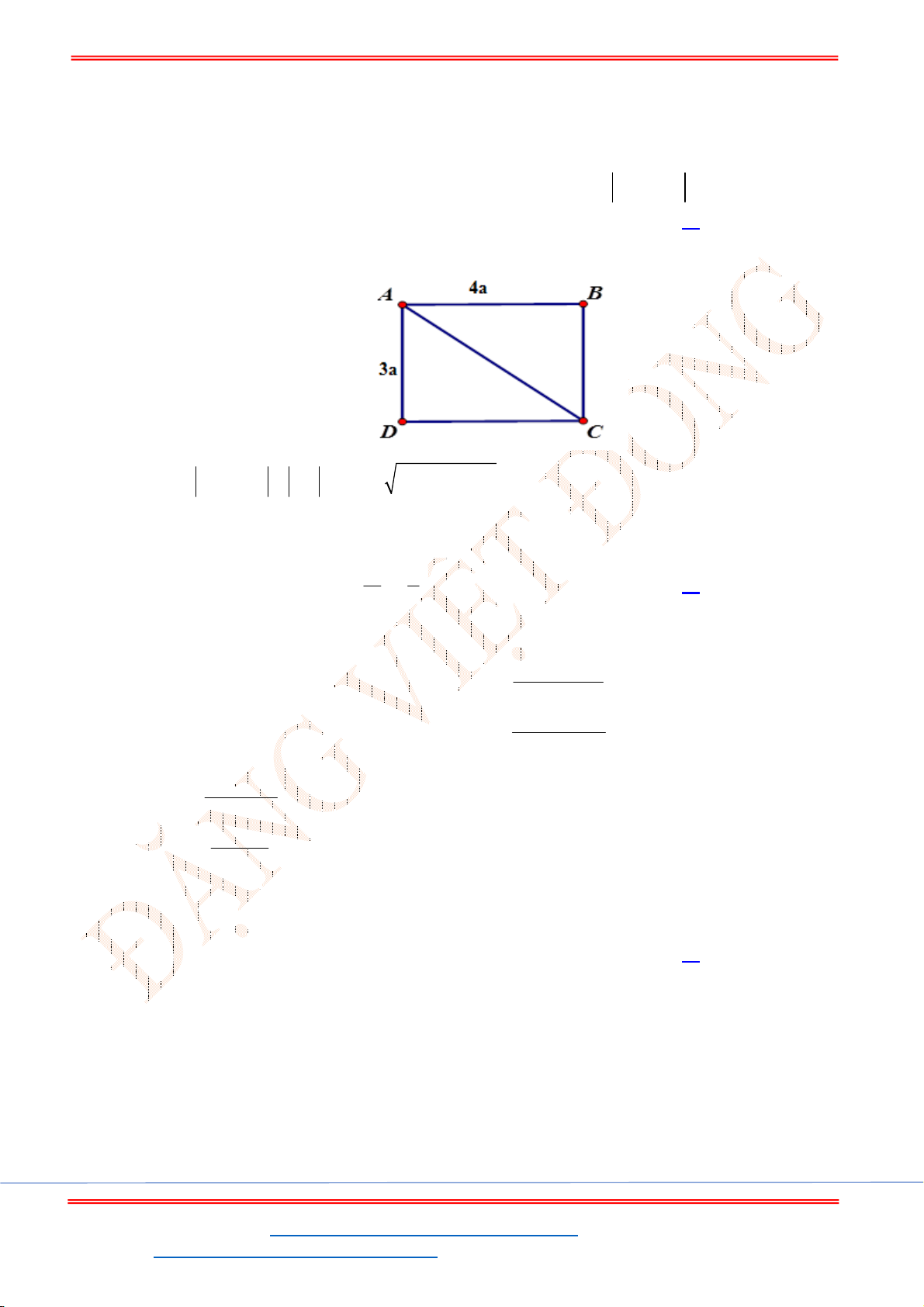
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Phương trình









2

1 4 0

x x x m

   

có

3

nghiệm phân biệt khi và chỉ khi phương trình

2

4 0

x x m

  

có

2

nghiệm phân biệt khác

1

2

4 0

4

3

1 4.1 0

m



   





 

 



  



Câu 23. Cho hình chữ nhật

ABCD

biết

4

AB a



và

3

AD a



. Khi đó

AB AD



 

bằng

A.

6

a

. B.

7

a

. C.

25

a

. D.

5

a

.

Lời giải

Ta có:

   

2 2

4 3 5

AB AD AC AC a a a

     

  

.

Câu 24. Trong hệ tọa độ

Oxy

, cho tam giác

ABC

có trọng tâm là

G

. Biết





4;0

A ,





2; 3

B



,





5; 1

G .

Khi đó tọa độ điểm

C

là

A.





6; 9

. B.

11 2

;

3 3

 



 

 

. C.





11; 2



. D.





9; 6

.

Lời giải

Điểm

G

trọng tâm của tam giác

ABC

3

A B C

G

A B C

G

x x x

x

y y y

y

 











 









 

4 2

5

9

3

9; 6

6

3

1

3

C

x

C

y

 













  

 



 











.

Câu 25. Trong mặt phẳng tọa độ

Oxy

cho các điểm





1;3

A

,





4;0

B

,





2; 5

C



. Tọa độ điểm

M

thỏa

mãn

3 0

MA MB MC

  

   

là

A.





1;18

M

. B.





1;18

M 

. C.





18;1

M 

. D.





1; 18

M 

.

Lời giải

Gọi điểm





;

M M

M x y

.

Theo bài ra













     

1 4 3 2 0

1

3 0

18

3 0 3 5 0

M M M

M

M M M

x x x

x

MA MB MC

y

y y y

     







    

 

 

      







   

.

Vậy





1; 18

M 

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 26. Cho tập





;

A m

  

và tập





2 5;23

B m 

. Gọi

S

là tập hợp các số thực

m

để

A B A

 

.

Hỏi

S

là tập con của tập hợp nào sau đây?

A.





; 23

 

. B.





;0



. C.





23;

 

. D.



.

Lời giải

2 5 23 14

23

23 23

m m

A B A B A m

m m

  

 

        

 

   

 

.

Suy ra









; 23 ;0

S     

.

Câu 27. Tất cả các giá trị của

m

để hàm số









2 2 2

2

2 2 2

1

x x m x

y

x m

  



 

là hàm số chẵn có tổng bằng

A.

1



. B.

1

. C.

2

. D.

0

.

Lời giải

Điều kiện cần:

Hàm số đã cho là hàm số chẵn cần

   

















2 2 2 2 2 2

2 2

2 2 2 2 2 2

1 1

x x m x x x m x

f x f x x D

x m x m

     

     

   





















2 2 2 2 2 2 2

2 2 2 2 2 2 2 2 0

x x m x x x m x m x x D

            

2

1 1

m m

    

.

Điều kiện đủ:

* Với

1

m



hàm số trở thành





2 2

2

1 1

x x

y

x





 

.

Điều kiện xác định

 

2 2

1 1 0 1 1 0 \ 0

x x x D           vậy

x D x D

    

.

x D

 

ta có

 





 

2 2

2

1 1

x x

f x f x

x



  

 

hàm số đã cho là hàm số chẵn, suy ra

1

m



thỏa

mãn.

*Với

1

m

 

hàm số trở thành





2 2

2

1 1

x x

y

x





 

.

Điều kiện xác định

2

1 1 0x D

    



vậy

x D x D

    

.

x D

 

ta có

 





 

2 2

2

1 1

x x

f x f x

x



  

 

hàm số đã cho là hàm số chẵn, vậy

1

m

 

thỏa

mãn.

Vậy có hai giá trị của

m

để hàm số đã cho là hàm chẵn là

1

m

 

và tổng của chúng bằng

0

.

Câu 28. Xác định hàm số

2

y ax bx c

  

, biết hàm số đạt giá trị nhỏ nhất bằng

4

tại

2

x

 

và đồ thị

hàm số đi qua điểm

(0;6)

A .

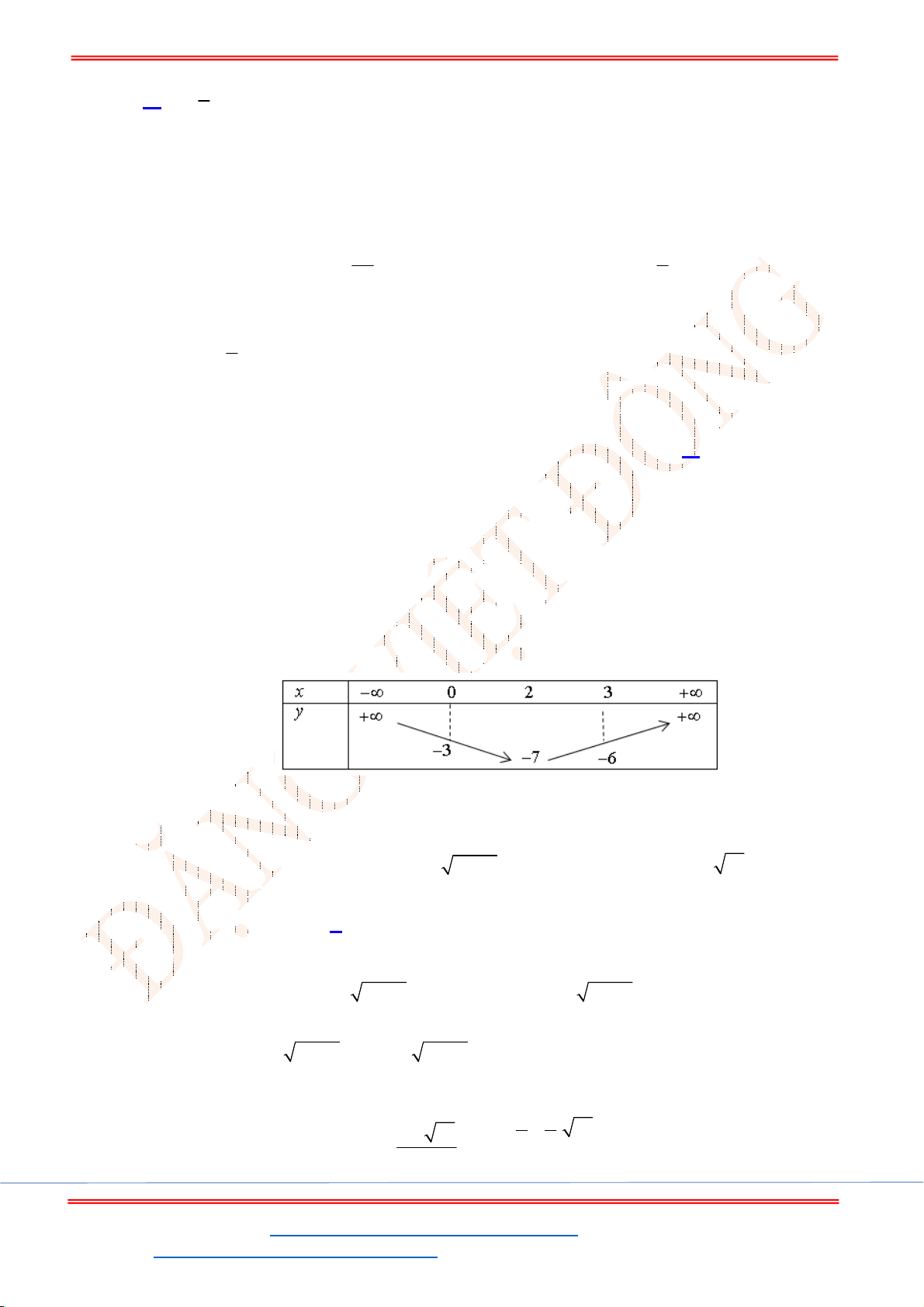
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

2

1

2 6

2

y x x

  

. B.

2

2 6

y x x

  

. C.

2

6 6

y x x

  

. D.

2

4

y x x

  

.

Lời giải

Đồ thị hàm số đi qua điểm





0;6

A , suy ra

6

c



.

Hàm số đạt giá trị nhỏ nhất bằng 4 tại

2

x

 

nên

1

4 0

2

4 2 6 4

2

4 2 4

b

a b

a

a b

b

a b c

 

 

  





 

 

  

  



 



  



Suy ra

2

1

2 6

2

y x x

  

là hàm số cần tìm.

Câu 29. Xác định tất cả các giá trị của tham số

m

để phương trình

2

4 3 0

x x m

   

có hai nghiệm phân

biệt

1

x

,

2

x

thoả mãn

1 2

0 3

x x

  

.

A.

7 6

m

   

. B.

7 3

m

   

. C.

6

m

 

. D.

6 3

m

   

.

Lời giải

Phương trình đã cho

2

4 3

x x m

   

.

Phương trình trên là phương trình hoành độ giao điểm của đường thẳng

y m



và parabol

2

4 3

y x x

  

.

Ta có: Parabol

2

4 3

y x x

  

có tọa độ đỉnh





2; 7

I



.

Bảng biến thiên

Dựa vào bảng biến thiên ta thấy: Phương trình

2

4 3 0

x x m

   

có hai nghiệm phân biệt

1

x

,

2

x

thoả mãn

1 2

0 3

x x

  



6 3

m

   

.

Câu 30. Biết phương trình

 





2

3 2 1 1 5 3

x x x x

    

có một nghiệm là

33

x a b 

với

,

a b



là

các số hữu tỉ. Tính

5

a b



.

A.

12

. B.

6

. C.

1

. D.

3

.

Lời giải

Ta có

 





     

2

3 2 1 1 5 3 1 2. 1 5 3 5 3 0

x x x x x x x x

            

 

2

1 0

1 5 3 0 5 3 1

5 3 1

x

x x x x

x x

 





         



  





2

1

7 33

7 4 0

2

x

x x

x











 

 



  









7 1

. 33

2 2

x  

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Vậy

7

2

1

2

a

b

















nên

5 6.

a b

 

Câu 31. Cho tam giác

MNP

có

4

MN



;

8

MP



;



60

PMN

 

. Điểm

E

trên tia

MP

sao cho

NE

vuông góc với trung tuyến

MF

của tam giác

MNP

. Đặt

ME kMP



 

. Phát biểu nào dưới đây

là đúng về số

k

?

A.

1

0;

5

k

 



 

 

. B.

1 2

;

5 5

k

 



 

 

. C.

1 1

;

10 2

k

 



 

 

. D.

1 3

;

2 4

k

 



 

 

.

Lời giải

Ta có:

NE ME MN

 

  

kMP MN

 

 

và

 

1

2

MF MN MP

 

  

.

NE

vuông góc với

MF

. 0

NE MF

 

 

   

1

. 0

2

kMP MN MN MP

   

   

2 2

. . . . 0

k MP MN k MP MN MN MP

    

   

 





1 . . .cos , 64 16 0

k MN MP MN MP k

    

 

 

1

1 .4.8. 64 16 0

2

k k

    

2

5

k

 

.

Vậy

2 1 1

;

5 10 2

k

 

 

 

 

.

Câu 32. Một người nông dân có

15.000.000

vnđ để làm một cái hàng rào hình chữ

E

dọc theo một con

sông (như hình vẽ) để làm một khu đất có hai phần chữ nhật để trồng rau. Đối với mặt hàng rào

song song với bờ sông thì chi phí nguyên vật liệu là

60.000

vnđ/m, còn đối với ba mặt hàng rào

song song nhau thì chi phí nguyên vật liệu là

50.000

vnđ/m. Tìm diện tích lớn nhất của đất rào

thu được.

A. 50

2

m

. B. 3125

2

m

. C. 1250

2

m

. D.

6250

2

m

.

E

F

M

N

P

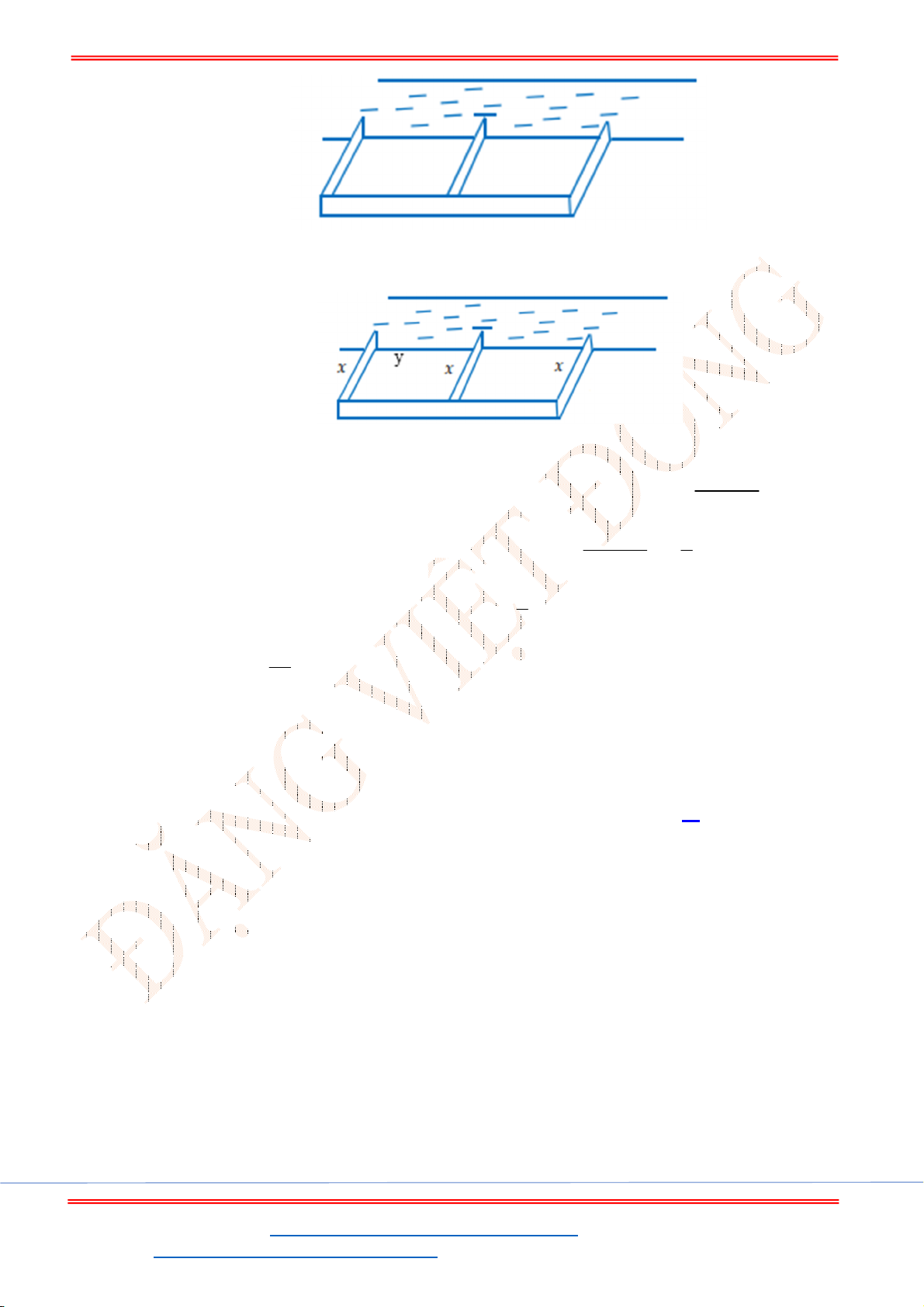
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Lời giải

Phân tích ta đặt các kích thước của hàng rào như hình vẽ

Giá thành làm rào là:

3 .50000 2 .60000 15000000x y 

 5 4 500x y  

500 5

4

x

y



 .

Diện tích khu vườn sau khi được rào là:

 

500 5

.2 .2.

4

x

S x x y x



 

2

5

250

2

x x   .

Diện tích khu vườn lớn nhất khi hàm số

 

2

5

250

2

S x x x   đạt giá trị lớn nhất.

Khi đó:

max

6250

4

S

a



  

2

m .

Vậy diện tích lớn nhất của đất rào thu được là

6250

2

m .

Câu 33. Cho phương trình:

 

2

2 2 2

9 2 1 – 6 9 5 15 06x x m x x m m      

.

Tìm

m

để phương trình có nghiệm.

A.

m  

. B. 1m   . C.

m  

. D.

2m 

.

Lời giải

Đặt

 

2

6 9 3 0t x x x t      

.

Phương trình trở thành:

 

2 2

2 1 5 15 0t m t m m      (2).

Phương trình ban đầu có nghiệm khi PT (2) có nghiệm

0t 

.

Xét

 

2

1 5 15 7 14m m m m



       

.

Nếu

0 2m



   

thì phương trình (2) có nghiệm kép là:

3 0t  

nên

2m 

thỏa mãn yêu

cầu bài toán.

Ngoài ra, phương trình (2) có nghiệm

0t 

trong các trường hợp sau:

Trường hợp 1: phương trình (2) có 2 nghiệm

1 2

,t t

thỏa mãn

1 2

0 t t 

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

 

2

0 2

1 0 1 2;

5 15 0

m

S m m m

m

P m m





  



 

         

 

 



   





.

Trường hợp 2: phương trình (2) có 2 nghiệm

1 2

,

t t

thỏa mãn

1 2

0

t t

 

.

2

5 15 0P m m m

       

.

Vậy tập hợp các giá trị

m

thỏa điều kiện bài toán là:





2;



.

Câu 34. Có bao nhiêu tham số nguyên

m

để phương trình









2

2 10 10 11 3 3 0

x x x x x m

       

có đúng

2

nghiệm phân biệt.

A.

4

. B.

16

. C.

15

. D.

17

.

Lời giải

Điều kiện





2;10

3

x

m

x

  













.

Phương trình









2

2 10 10 11 3 3 0

x x x x x m

       

 

2

2 10

1;4

10 11 0

3

3 3 0

3

x x

x

x x

m

x

x m



  

 



    











  









.

Yêu cầu bài toán tương đương





3

1 4 0;15

3

m



     .

Vậy có

15

giá trị nguyên.

Câu 35. Cho tam giác

ABC

. Gọi

D

là điểm xác định bởi

3

4

AD AC



 

,

I

là trung điểm của

BD

. Gọi

E

là điểm thoả mãn

BE xBC



 

. Tìm

x

để ba điểm

, ,

A I E

thẳng hàng.

A.

7

8

x



. B.

8

7

x



. C.

7

3

x



. D.

3

7

x



.

Lời giải

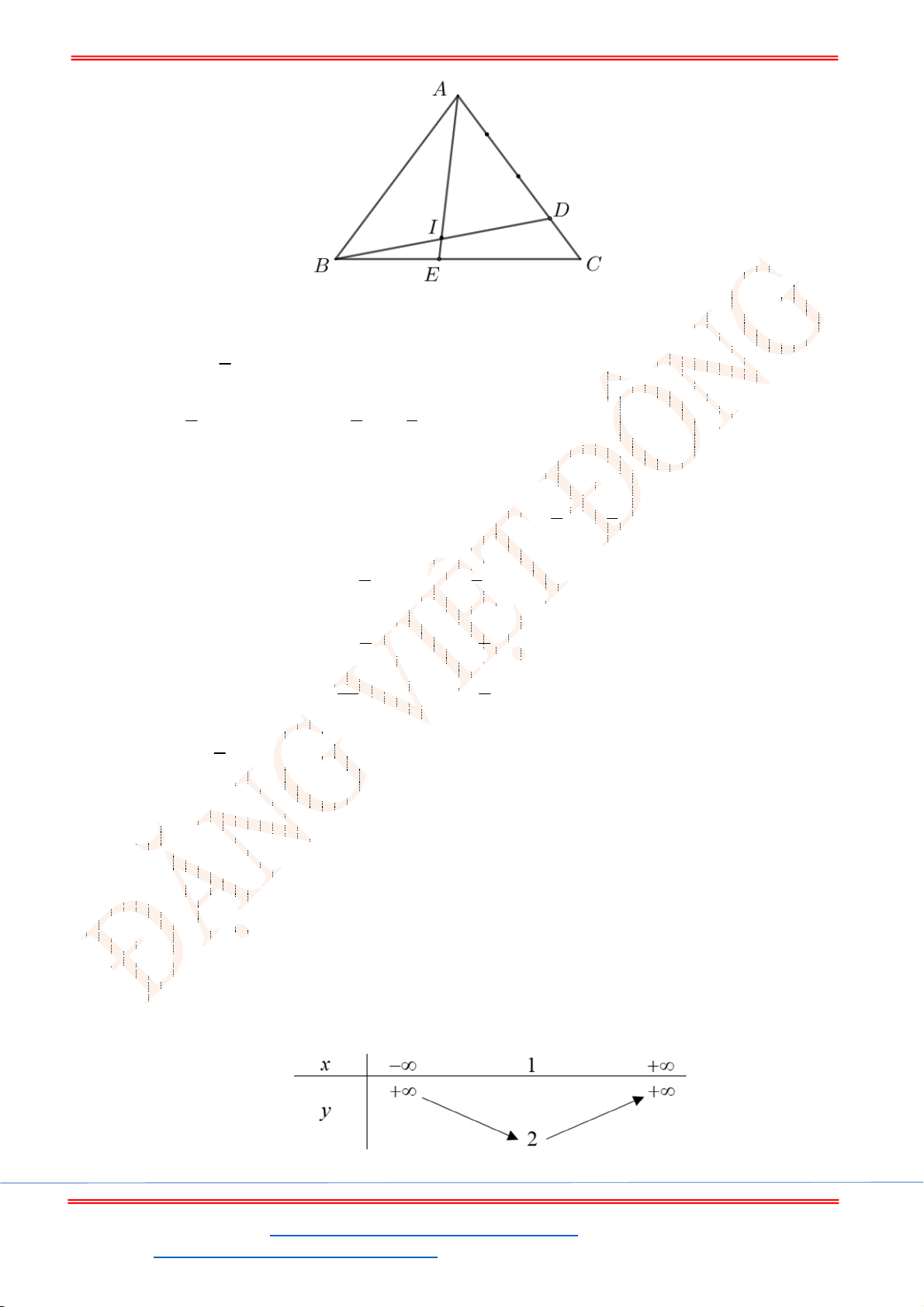
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Ta có:

 

1BE xBC AE x AB xAC    

    

Do

3

4

AD AC

 

và I là trung điểm của BD nên

 

1 1 3

2 2 8

AI AD AB AI AB AC    

     

.

, ,A E I

thẳng hàng khi và chỉ khi ,AI AE

 

cùng phương

 

1 3

: . 1

2 8

k AE k AI x AB xAC k AB AC

 

        

 

 

     



1 3

1 0

2 8

x k AB x k AC

   

     

   

   

  

31

1 0

72

3 8

0

8

7

x

x k

k

x

k





  



 

 

 

 

 



 



.

Vậy

3

7

x  .

II. TỰ LUẬN

Bài 1. Cho hàm số

2

2 3y x x   có đồ thị là

 

P

.

a. Lập bảng biến thiên và vẽ đồ thị

 

P

.

b. Tìm các giá trị của tham số

m

sao cho phương trình

2

2 3 0

x x m

   

có 2 nghiệm phân biệt.

Lời giải

a. Lập bảng biến thiên và vẽ đồ thị





P

.

Hàm số xác định trên  .

Đồ thị có đỉnh

 

1;2I

và có trục đối xứng là đường thẳng

1x 

.

Bảng biến thiên

Hàm số đồng biến trên

 

1;

, hàm số nghịch biến trên

 

;1

.

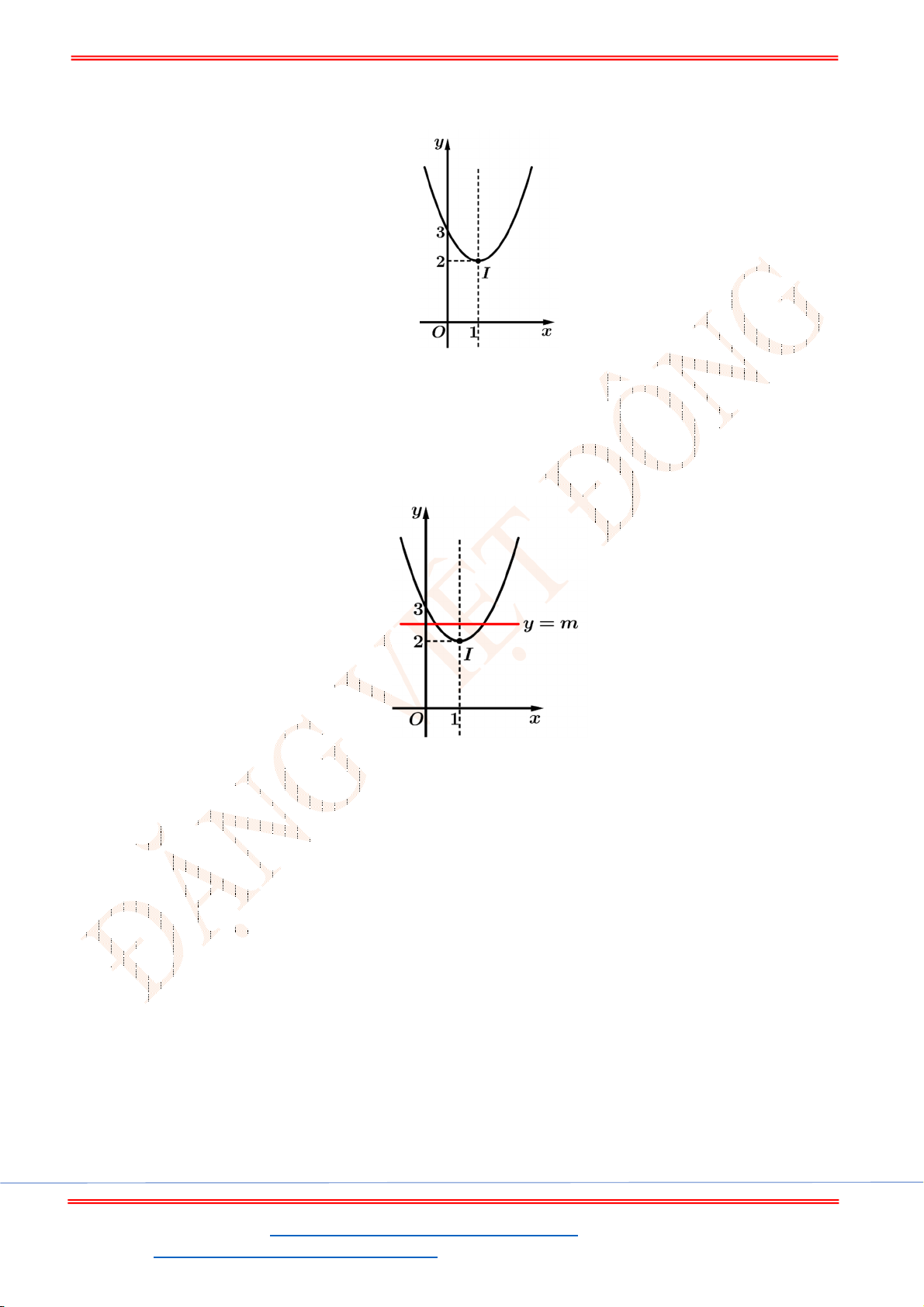
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Giao điểm với trục Oy là điểm





0;3

.

Đồ thị hàm số

b. Tìm các giá trị của tham số

m

sao cho phương trình

2

2 3 0x x m    có 2 nghiệm phân biệt.

Ta có

2 2

2 3 0 2 3x x m m x x        .

Vậy số nghiệm của phương trình đã cho là số giao điểm của đường thẳng

y m

với

 

2

: 2 3P y x x  

.

Dựa vào đồ thị ta thấy đường thẳng

y m

cắt

 

2

: 2 3P y x x  

tại 2 điểm khi

2m 

.

Vậy phương trình

2

2 3 0x x m    có 2 nghiệm phân biệt khi

2m 

.

Bài 2. Trong mặt phẳng với hệ tọa độ Oxy , cho các điểm

 

2;3A 

,

 

2;1B

,

 

0; 3C 

và

 

1; 2D  

. Tìm điểm M có hoành độ dương thuộc đường thẳng : 1 0d x y   sao cho

 

3 . 6MA MB MC MD  

   

.

Lời giải

Giả sử

 

; : 1 0 1M x y d x y y x      

.

Ta có

 

2 ;3MA x y   



,

 

2 ;1MB x y  



,

 

; 3MC x y   



,

 

1 ; 2MD x y    



.

Suy ra

 

3 8; 3MA MB MC x y    

  

.

Ta có

 

3 . 6MA MB MC MD  

   

     

8 1 3 2 6x x y y        

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

















8 1 2 3 6 0

x x x x

         

2

2 6 8 0

x x

    

1

4

x

 











.

Do

0

x



nên

4

x



, suy ra

5

y



.

Vậy





4;5

M

.

Bài 3. Giải phương trình





2

4 3 1 8 5 6 2

x x x x x

      

.

Lời giải





2

4 3 1 8 5 6 2

x x x x x

      

(điều kiện

1

3

x

 

)

     

1 8 5 2 6 2 1 0

x x x x x

   

         

   









2

1 4 1

4 1

0

8 5 2 6 2 1

x x x

x x

x x x x

   

  

  

     

 

2

1 1

4 1 0

8 5 2 6 2 1

x

x x

x x x x



 

     

 

     

 

 

2

4 1 0

2 5

1 1

0

2 5

8 5 2 6 2 1

x x

x

x x x x



   



 





 



 

 





     



Vo ânghieäm

(thỏa mãn điều kiện).

Vậy tập nghiệm của phương trình là





2 5 ;2 5

S   

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 6 Môn Toán – Lớp 10

(Th

ời gian l

àm bài 90 phút)

Không k

ể thời gian phát đề

Câu 1. Cho

4

điểm bất kì

A

,

B

,

C

,

O

. Đẳng thức nào sau đây là đúng?

A.

OA CA CO

 

  

. B.

OA OB BA

 

  

. C.

0

BC AC AB

  

   

. D.

0

OA BA OB

  

   

.

Câu 2.

Hệ phương trình

2

4

2 5 0

x y x

x y



 



  



có hai nghiệm là





1 1

;

x y

và





2 2

;

x y

. Biết





0;0

O ,





1 1

;

A x y

,





2 2

;

B x y

khi đó tích vô hướng

.

OA OB

 

bằng

A.

5

. B.

10

. C.

10



. D.

5



.

Câu 3. Tổng các nghiệm của phương trình

2

1 3 5 2 3

2 2 4

x x x

  

 

  

là

A.

15

4

. B.

15

4



. C.

5

. D.

5



.

Câu 4. Cho



và



là hai góc bù nhau. Chọn đẳng thức sai trong các đẳng thức sau:

A.

tan tan

 

 

. B.

sin sin

 



. C.

cot cot

 



. D.

cos cos

 

 

.

Câu 5. Giá trị nhỏ nhất của hàm số

 

2

2 1

x

f x

x

 



với

1

x



là

A.

2 2

. B.

5

2

. C.

3

. D.

2

.

Câu 6. Suy luận nào sau đây đúng?

A.

a b

c d





 







. B.

0

a b

ac bd

c d

 



 



 



.

C.

a b

a c b d

c d





   







. D.

a b

ac bd

c d





 







.

Câu 7. Cho hình vuông

ABCD

có độ dài cạnh bằng

2

. Lấy điểm

M

trên đoạn

BC

sao cho

3

MB MC



,

N

là trung điểm của cạnh

AB

. Tính tích vô hướng .

DC MN

 

ta được kết quả bằng

A.

2



. B.

4



. C.

4

. D.

2

.

Câu 8. Cho hình chữ nhật

ABCD

tâm

O

. Gọi

M

,

N

lần lượt là trung điểm của các cạnh

AB

,

AD

.

Chọn khẳng định đúng trong các khẳng định sau:

A.

AB CD



 

. B.

AN MO



 

. C.

OC OD



 

. D.

AM BM



 

.

Câu 9. Cho hàm số

2

y ax bx c

  

có đồ thị như hình vẽ dưới đây. Chọn khẳng định đúng trong các

khẳng định sau:

A.

0

a



,

0

b



,

0

c



. B.

0

a



,

0

b



,

0

c



.

C.

0

a



,

0

b



,

0

c



. D.

0

a



,

0

b



,

0

c



.

Câu 10. Số phần tử của tập hợp





2

1 , 2

k kA k  





bằng

A.

1

. B.

5

. C.

3

. D.

2

.

x

y

O

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 11. Trong hệ tọa độ

Oxy

, cho các vectơ





3;1

a 



,





2;6

b  



,





11; 3

c

 



. Nếu

c ma nb

 

  

thì

khẳng định nào sau đây đúng?

A.

2; 4

m n

  

. B.

3; 1

m n

  

. C.

2; 4

m n

  

. D.

3; 1

m n

  

.

Câu 12. Cho phương trình

2

0

x bx c

  

có hai nghiệm thực

1

x

,

2

x

thoả mãn:

1 2

1

x x

 

và

2

1

2 .

2

b c

 

Giá trị lớn nhất của biểu thức

3

2 3 1

P bc b b

   

bằng

A.

5

4



. B.

5

4

. C.

5

2

. D.

5

2



.

Câu 13. Hệ phương trình nào sau đây là hệ hai phương trình bậc nhất hai ẩn:

A.

2

1

0

x y z

x y

  





 



. B.

3 1

2 2

x y

 





 



. C.

2

5 1

0

x y



 





 





. D.

2

1 0

x x

x



  



 



.

Câu 14. Trong hệ tọa độ

Oxy

, nếu tam giác

ABC

có trọng tâm





1; 5

G



và các đỉnh





1; 3

A



,





2;5

C

thì đỉnh

B

có tọa độ là

A.





0; 17

 . B.





0; 23

 . C.





1; 23

 . D.





1; 13

 .

Câu 15. Cho hai tập hợp





0;1;2;3;4

A  ,





2;3;4;5;6

B  . Tập hợp









\ \

A B B A

 là

A.





0;1;5;6 .

B.





5;6 .

C.





2;3;4 .

D.





1;2 .

Câu 16. Điều kiện xác định của phương trình 1 2 3

x x x

    

là

A.

2 3

x

 

. B.

2

x



. C.

2 3

x

 

. D.

2

x



.

Câu 17. Tìm tập xác định

D

của hàm số

2 1

6

1 1

x

y x

x



  

 

.

A.

D





. B.





;6

D   . C.





1;D

 

. D.





1;6

D  .

Câu 18. Cho hình thang

ABCD

vuông tại

A

,

D

có

AB a



,

2

AD a



và

3

CD a



. Gọi

M

,

N

lần

lượt là trung điểm của các cạnh

AD

và

DC

. Khi đó

1

2

AM DC



 

bằng

A.

5

2

a

. B.

5

a

. C.

3

a

. D.

3

2

a

.

Câu 19. Tìm điều kiện của tham số

m

để hàm số









2 2 1

y m x x m

   

đồng biến trên



.

A.

1

2

m

 

. B.

1

2

m

 

. C.

2

m

 

. D.

1

m

 

.

Câu 20. Cho mệnh đề





2

:" , 1 0"

P x x x x

    



. Mệnh đề phủ định của mệnh đề





P x

là

A.

2

" , 1 0"

x x x

    



. B.

2

" , 1 0"

x x x

    



.

C. " 

2

, 1 0"

x x x

   



. D.

2

" , 1 0"

x x x

    



.

Câu 21. Cho lục giác đều

ABCDEF

tâm O. Chọn khẳng định sai trong các khẳng định sau:

A.

BO BA OD

 

  

. B.

1

2

AF AB AD

 

  

. C.

BE FC DA

 

  

. D.

2

BO ED BD

 

  

.

Câu 22. Cho

ABC



đều có cạnh bằng

a

, gọi

H

là trung điểm của cạnh

BC

. Độ dài của vectơ

HA HC



 

bằng

A.

a

. B.

2

a

. C.

3

2

a

. D.

3

a

.

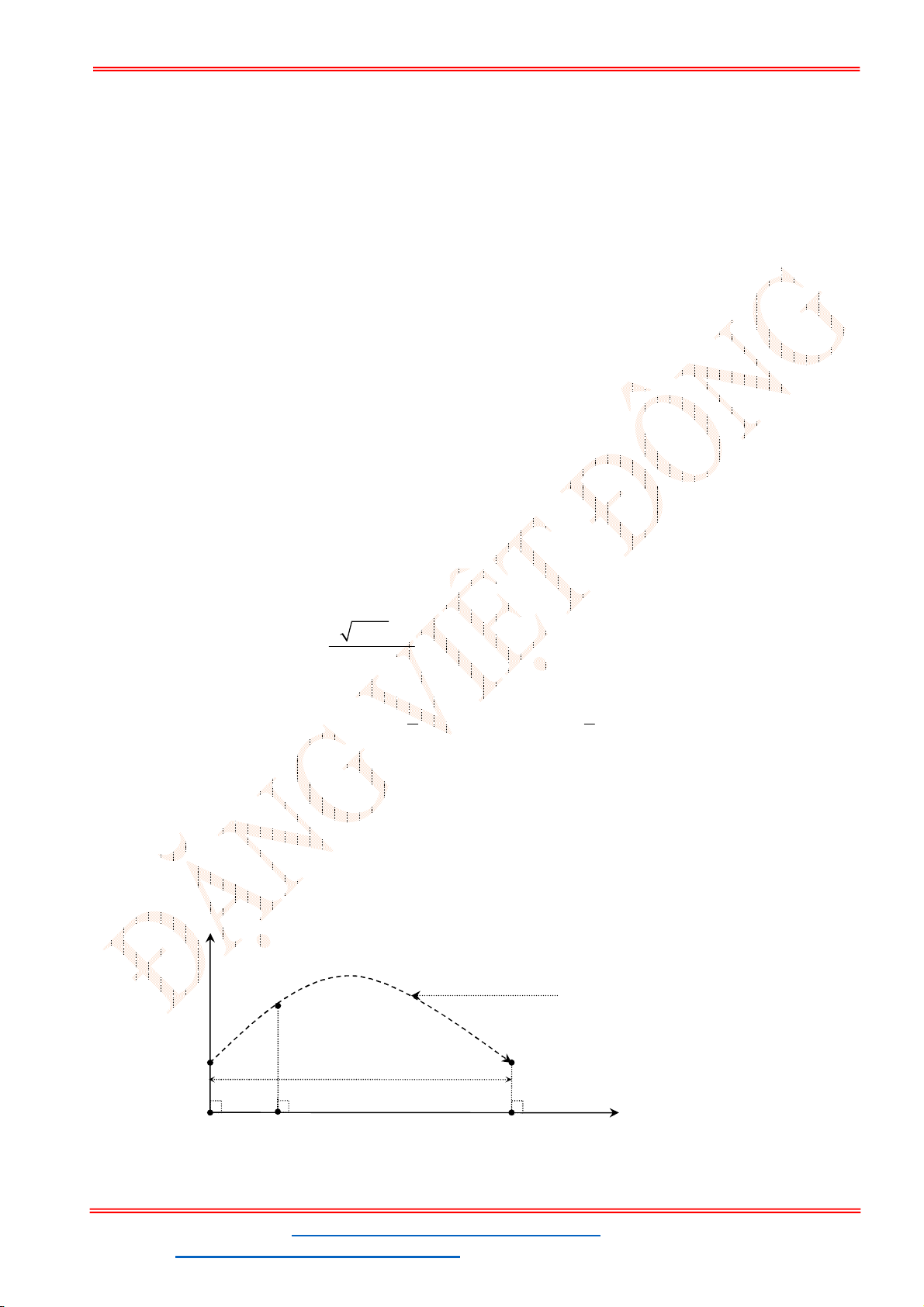
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 23. Nghiệm của hệ phương trình

2 7

2 5

4 3 11

x y z

  





  





  



là

A.





1; 3; 0

 . B.





1; 0;3

 . C.





3; 1;0

  . D.





3;0; 1



.

Câu 24. Với điều kiện nào của tham số m thì phương trình





2

3 4 1

m x m x

   

có nghiệm thực duy

nhất?

A.

0

m



. B.

1

m

 

. C.

1

m

 

. D.

1

m



.

Câu 25. Cho hình bình hành

ABCD

tâm

I

. Đẳng thức nào sau đây đúng?

A.

BC DB AB

 

  

. B.

AB IA BI

 

  

. C.

0

AB DC

 

  

. D.

AC AB AD

 

  

.

Câu 26. Phủ định của mệnh đề: “Có ít nhất một số vô tỷ là số thập phân vô hạn tuần hoàn” là mệnh đề

nào sau đây.

A. Mọi số vô tỷ đều là số thập phân vô hạn tuần hoàn.

B. Có ít nhất một số vô tỷ là số thập phân vô hạn không tuần hoàn.

C. Mọi số vô tỷ đều là số thập phân vô hạn không tuần hoàn.

D. Mọi số vô tỷ đều là số thập phân tuần hoàn.

Câu 27. Tập hợp









2018; 2018 2018;

   

bằng tập hợp nào sau đây:

A.





2018

. B.



. C.





; 2018

 . D.





2018;

 

.

Câu 28. Tam giác

ABC

vuông tại

A

,



50

ABC

 

. Kết luận nào sau đây sai?

A.





, 120

AC CB

 

 

. B.





, 40

CA CB

 

 

. C.





, 90

AB CA

 

 

. D.





, 50

BA BC

 

 

.

Câu 29. Cho hàm số

 

2

kh

2 2 3

2

1

+1 2

i

khi

x

x x

f x

 



















. Tính giá trị biểu thức









2 2 .

P f f

  

A.

4

P



. B.

5

3

P



. C.

8

3

P



. D.

6

P



.

Câu 30. An và Bình là hai học sinh của trường THPT Phúc Thọ tham gia câu lạc bộ bóng rổ của trường

để thư giãn và rèn luyện thân thể. Trong trận đấu kỷ niệm ngày thành lập Đoàn, An đứng tại vị

trí

O

thực hiện một đường chuyền bóng dài cho Bình đứng tại vị trí

H

, quả bóng di chuyển

theo một đường parabol (hình vẽ bên dưới). Quả bóng rời tay An ở vị trí

A

và tay Bình bắt

được quả bóng ở vị trí

B

, khi quả bóng di chuyển từ An đến Bình thì đi qua điểm

C

. Quy ước

trục

Ox

là trục đi qua hai điểm

O

và

H

, trục

Oy

đi qua hai điểm

O

và

A

như hình vẽ. Biết

rằng

1,7 m

OA BH

 

;

3,4625 m

CK



;

2,5 m

OK



;

10 m

OH



. Hãy xác định khoảng cách

lớn nhất của quả bóng so với mặt đất khi An chuyền bóng cho Bình.

A.





4,03 m

. B.





4,06 m

. C.





4,02 m

. D.





4,05 m

.

B

O

H

C

K

M

ặt đất

Quỹ đạo parabol

y

3,4625m

mmmm

OH =10m

=10

m

A

1,7m

x

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 31. Gọi

S

là tập hợp các giá trị thực của tham số

m

sao cho parabol





2

: 6

P y x x m

  

cắt

Ox

tại hai điểm phân biệt

,

A B

thỏa mãn

5.

OA OB



. Tính tổng

T

các phần tử của

S

.

A.

45

4

T

 

. B.

4

T



. C.

25

4

T

 

. D.

29

4

T

 

.

Câu 32. Cho hai tập hợp





4;1

A   ,





3;

B m

  . Tìm

m

để

A B A

 

.

A.

1

m



. B.

3 1

m

  

. C.

3 1

m

  

. D.

1

m



.

Câu 33. Một miếng đất hình chữ nhật có chiều rộng

43 0,5

x m m

 

và chiều dài

63 0,5

y m m

 

. Tính

chu vi

P

của miếng đất đã cho.

A.

212 1

P m m

 

. B.

212 4

P m m

 

. C.

212 0,5

P m m

 

. D.

212 2

P m m

 

.

Câu 34. Trong hệ tọa độ

Oxy

, cho hai vectơ









7; 2 , 3; 4

a b

   

 

. Tích vô hướng

.

a b

 

bằng

A.

26



. B.

13

. C.

29

. D.

12

.

Câu 35. Cho hình bình hành

ABCD

,

M

là điểm tùy ý. Chọn khẳng định đúng trong các khẳng định

sau:

A.

MA MB MC MD

  

   

. B.

MC MB MA MD

  

   

.

C.

MC CB MD DA

  

   

. D.

MA MC MB MD

  

   

.

Câu 36. Cho hàm số





2

y f x ax bx c

   

có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị thực

của tham số

m

để phương trình





2020 0

f x m

  

có duy nhất một nghiệm.

A.

2015.

m



B.

2019.

m



C.

2017.

m



D.

2018.

m



Câu 37. Hệ phương trình

1

2

mx y m

x my

  





 



có nghiệm duy nhất khi:

A.

2

m

 

. B.

2

m



. C.

1

m







 



. D.

2

m







 



.

Câu 38. Trong các câu sau có bao nhiêu câu là mệnh đề?

a) Cố lên, sắp đến nơi rồi!

b) Số 15 là số nguyên tố.

c) Tổng các góc của một tam giác là

180 .



d)

x

là số nguyên dương.

A.

3.

B.

4.

C.

1.

D.

2.

Câu 39. Lớp

1

10



có

6

học sinh giỏi Toán,

4

học sinh giỏi Lý,

5

học sinh giỏi Hóa,

2

học sinh giỏi

Toán và Lý,

3

học sinh giỏi Toán và Hóa,

2

học sinh giỏi Lý và Hóa,

1

học sinh giỏi cả

3

môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp

1

10



là

A.

15.

B.

23.

C.

7.

D.

9.

Câu 40. Cho tam giác ABC, đặt

CA a



 

,

CB b



 

. Lấy các điểm

A



,

B



sao cho

2 ,

CA a



 

 

2

CB b





 

.

Gọi I là giao điểm của

A B



và

B A



. Giả sử

CI ma nb

 

  

, khi đó tỉ số

m

n

bằng

x

y

O

1

2

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

1

4

. B.

1

3

. C.

2

3

. D.

2

5

.

Câu 41.

Phương trình

2 3 2

x x

  

có nghiệm thực duy nhất dạng

2

x a b

 

,





,a b



. Khi đó

2 3

a b



bằng

A.

12.

B.

10.

C.

8.

D.

6

.

Câu 42. Trong hệ tọa độ

Oxy

, cho hai điểm





6; 3

A



,





2; 5

B

 

. Trung điểm của đoạn thẳng

AB

là

A.





8;2

I  . B.





2; 4

I



. C.





2; 8

I



. D.





4;2

I  .

Câu 43. Với hai số thực

a

,

b

bất kì và khác

0

, bất đẳng thức nào sau đây luôn đúng?

A.

2 2

0

a ab b

  

. B.

0

a b

 

. C.

2 2

0

a ab b

  

. D.

0

a b

 

.

Câu 44. Biết rằng parabol





2

: 4

P y ax x c

  

có hoành độ đỉnh bằng

3



và đi qua điểm





2;1

M  .

Tính tổng

S a c

 

.

A.

5.

S

 

B.

5.

S



C.

1.

S



D.

4.

S



Câu 45. Cho hình bình hành

ABCD

. Gọi

M

,

N

lần lượt là trung điểm của các cạnh

BC

và

CD

. Đặt

a AM



 

,

b AN



 

. Hãy phân tích vectơ

AC



theo

2

vectơ

a



và

b



.

A.

2 2

3 3

AC a b

 

  

. B.

3

AC a b

 

  

. C.

1 2

3 3

AC a b

 

  

. D.

2

4

3

AC a b

 

  

.

Câu 46. Phát biểu nào sau đây là sai?

A. Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.

B. Vectơ là đoạn thẳng có hướng.

C. Hai vectơ cùng hướng thì cùng phương.

D. Hai vectơ cùng phương thì cùng hướng.

Câu 47. Nghiệm của phương trình

3 2 2 3

x x

  

là

1

x

,

2

x

. Tích

1 2

.

x x

bằng

A.

1

.

5



B.

1.

C.

1.



D.

5.

Câu 48. Trong hệ tọa độ

Oxy

, cho tam giác

ABC

có





2;2

A ,





5;3

B  ,





2;4

C  . Gọi





;

H x y

là hình

chiếu của đỉnh

A

lên đường thẳng

BC

. Tính giá trị của biểu thức

2 2

P x y

 

.

A.

13

P



. B.

26

P



. C.

25

P



. D.

17

P



.

Câu 49. Cặp số nào sau đây là nghiệm của hệ phương trình

2 2

3 3

30

35

x y xy

x y



 





 





?

A.





3;2

. B.





3; 2

 

. C.





3;2

 . D.





3; 2



.

Câu 50. Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?

A. Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.

B. Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.

C. Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.

D. Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.

----------HẾT----------

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG HDG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 6 Môn Toán – Lớp 10

(Th

ời

gian làm bài 90 phút)

Không kể thời gian phát đề

Câu 1. Cho

4

điểm bất kì

A

,

B

,

C

,

O

. Đẳng thức nào sau đây là đúng?

A.

OA CA CO

 

  

. B.

OA OB BA

 

  

. C.

0

BC AC AB

  

   

. D.

0

OA BA OB

  

   

.

Lời giải

Chọn C

Ta có

0

BC AC AB

  

   

0

BC AB AC

   

   

0

BC CB

  

  

0

BB

 

 

(luôn đúng).

Câu 2.

Hệ phương trình

2

4

2 5 0

x y x

x y



 



  



có hai nghiệm là





1 1

;

x y

và





2 2

;

x y

. Biết





0;0

O ,





1 1

;

A x y

,





2 2

;

B x y

khi đó tích vô hướng

.

OA OB

 

bằng

A.

5

. B.

10

. C.

10



. D.

5



.

Lời giải

Chọn C

2

4

2 5 0

x y x

x y



 



  



2

4

5 2

x y x

y x



 





 



2

5 2 4

5 2

x x x

y x



  





 



2

6 5 0

5 2

x x

y x



  





 



1

3

5

x

y

x

y

 

























 







.

Giả sử





1;3

A ,





5; 5

B



. Do đó





1;3

OA 



,





5; 5

OB

 



.

Vậy

. 5 15

OA OB

 

 

10

 

.

Câu 3. Tổng các nghiệm của phương trình

2

1 3 5 2 3

2 2 4

x x x

  

 

  

là

A.

15

4

. B.

15

4



. C.

5

. D.

5



.

Lời giải

Chọn A

Điều kiện

2

2 0

4 0

x



 



 





 



2

x

 











.

Phương trình

2

1 3 5 2 3

2 2 4

x x x

  

 

  

















  

2

1 2 3 5 2

2 3

2 2 4

x x x x

x

x x x

    



 

  





2 2

2

2 2

3 2 3 10

2 3

4 4

x x x x

x

x x

    

 

 

 

2 2 2

3 2 3 10 2 3

x x x x x

        

2 2

2 4 12 2 3

x x x

      

4 15

x

   

15

4

x

 

.

Câu 4. Cho



và



là hai góc bù nhau. Chọn đẳng thức sai trong các đẳng thức sau:

A.

tan tan

 

 

. B.

sin sin

 



. C.

cot cot

 



. D.

cos cos

 

 

.

Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Chọn C

Ta có



và



là hai góc bù nhau nên

  

 

. Do đó

cot cot

 

 

;

tan tan

 

 

và

cos cos

 

 

. Do đó phương án C sai.

Câu 5. Giá trị nhỏ nhất của hàm số

 

2

2 1

x

f x

x

 



với

1

x



là

A.

2 2

. B.

5

2

. C.

3

. D.

2

.

Lời giải

Chọn B

 

1 2 1

2 1 2

x

f x

x



  



.

Áp dụng bất đẳng thức Côsi cho hai số dương

1

2

x



và

2

1

x



ta có:

1 2 1 2

2 .

2 1 2 1

x x

 

 

 

1 2

2

2 1

x



  



1 2 1 5

2 1 2 2

x



   



.

Dấu bằng xảy ra khi và chỉ khi

1 2

2 1

x



 



 

2

1 4

x

  

1 2

x

  

(vì

1

x



)

3

x

 

.

Do đó giá trị nhỏ nhất của hàm số

 

2

2 1

x

f x

x

 



với

1

x



là

5

2

khi

3

x



.

Câu 6. Suy luận nào sau đây đúng?

A.

a b

c d





 







. B.

0

a b

ac bd

c d

 



 



 



.

C.

a b

a c b d

c d





   







. D.

a b

ac bd

c d





 







.

Lời giải

Chọn B

0

a b

ac bd

c d

 



 



 



(theo tính chất của bất đẳng thức).

Câu 7. Cho hình vuông

ABCD

có độ dài cạnh bằng

2

. Lấy điểm

M

trên đoạn

BC

sao cho

3

MB MC



,

N

là trung điểm của cạnh

AB

. Tính tích vô hướng .

DC MN

 

ta được kết quả bằng

A.

2



. B.

4



. C.

4

. D.

2

.

Lời giải

Chọn A

N

M

D

C

A

B

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

 

2

1 1 1

. . . 0 . 2 2

2 2 2

.DC MN DC MB BN DC MB DC BN DC DC DC

 

             

 

 

         

  

.

Câu 8. Cho hình chữ nhật

ABCD

tâm

O

. Gọi

M

,

N

lần lượt là trung điểm của các cạnh

AB

,

AD

.

Chọn khẳng định đúng trong các khẳng định sau:

A.

AB CD



 

. B.

AN MO



 

. C.

OC OD



 

. D.

AM BM



 

.

Lời giải

Chọn B

N

M

O

C

A

B

D

Dễ thấy tứ giác

ANOM

là hình chữ nhật nên

AN MO



 

.

Câu 9. Cho hàm số

2

y ax bx c

  

có đồ thị như hình vẽ dưới đây. Chọn khẳng định đúng trong các

khẳng định sau:

A.

0

a



,

0

b



,

0

c



. B.

0

a



,

0

b



,

0

c



.

C.

0

a



,

0

b



,

0

c



. D.

0

a



,

0

b



,

0

c



.

Lời giải

Chọn C

Dựa vào đồ thị hàm số ta nhận thấy

Parabol có bề lõm hướng lên trên nên

0

a



.

Parabol cắt trục

Oy

tại điểm có tung độ âm nên

0

c



.

Parabol có trục đối xứng

0

2

b

x

a

  

nên

0

b



(do

0

a



).

Vậy

0

a



,

0

b



,

0

c



.

Câu 10. Số phần tử của tập hợp





2

1 , 2

k kA k  





bằng

A.

1

. B.

5

. C.

3

. D.

2

.

Lời giải

Chọn C

Ta có:

 

2

1 1;2;5

2

k







  











nên tập

A

có

3

phần tử.

Câu 11. Trong hệ tọa độ

Oxy

, cho các vectơ





3;1

a 



,





2;6

b  



,





11; 3

c

 



. Nếu

c ma nb

 

  

thì

khẳng định nào sau đây đúng?

x

y

O

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

2; 4

m n

  

. B.

3; 1

m n

  

. C.

2; 4

m n

  

. D.

3; 1

m n

  

.

Lời giải

Chọn B

Ta có:

c ma nb

 

  

nên

3 2 11 3

6 3 1

m n m

m n n

  

 



 

    

 

.

Vậy

3; 1

m n

  

.

Câu 12. Cho phương trình

2

0

x bx c

  

có hai nghiệm thực

1

x

,

2

x

thoả mãn:

1 2

1

x x

 

và

2

1

2 .

2

b c

 

Giá trị lớn nhất của biểu thức

3

2 3 1

P bc b b

   

bằng

A.

5

4



. B.

5

4

. C.

5

2

. D.

5

2



.

Lời giải

Chọn D

Phương trình

2

0

x bx c

  

có hai nghiệm thực

1 2

,

x x

nên theo định lí Vi-et ta có:

1 2

1 1

x x b b

      

;

2 2 3

1 1 1 1

2 2

2 2 4 2

b c c b bc b b

       

3 3

1

3 1

2

7 5

1 .

2 2

P b b b b

P b P

     

      

Dấu “=” xảy ra khi và chỉ khi

1

1; .

4

b c

 

Câu 13. Hệ phương trình nào sau đây là hệ hai phương trình bậc nhất hai ẩn:

A.

2

1

0

x y z

x y

  





 



. B.

3 1

2 2

x y

 





 



. C.

2

5 1

0

x y



 





 





. D.

2

1 0

x x

x



  



 



.

Lời giải

Chọn B

Câu 14. Trong hệ tọa độ

Oxy

, nếu tam giác

ABC

có trọng tâm





1; 5

G



và các đỉnh





1; 3

A



,





2;5

C

thì đỉnh

B

có tọa độ là

A.





0; 17

 . B.





0; 23

 . C.





1; 23

 . D.





1; 13

 .

Lời giải

Chọn A

Vì





1; 5

G



là trọng tâm tam giác

ABC

nên:

3

A B C

G

B G A C

A B C B G A C

G

x x x

x

x x x x

y y y y y y y

y

 







  







 

    











 

3.1 1 2

3. 5 3 5

B

x

y

  









   





0

17

B

x

y









 



.

Vậy





0; 17

B  .

Câu 15. Cho hai tập hợp





0;1;2;3;4

A  ,





2;3;4;5;6

B  . Tập hợp









\ \

A B B A

 là

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.





0;1;5;6 .

B.





5;6 .

C.





2;3;4 .

D.





1;2 .

Lời giải

Chọn A





















\ \ 0;1 5;6 0;1;5;6

A B B A    .

Câu 16. Điều kiện xác định của phương trình 1 2 3

x x x

    

là

A.

2 3

x

 

. B.

2

x



. C.

2 3

x

 

. D.

2

x



.

Lời giải

Chọn A

Phương trình xác định khi

1 0

2 0

3 0

x

 





 





 



2

3

x







 









2 3

x

  

.

Câu 17. Tìm tập xác định

D

của hàm số

2 1

6

1 1

x

y x

x



  

 

.

A.

D





. B.





;6

D   . C.





1;D

 

. D.





1;6

D  .

Lời giải

Chọn D

Hàm số xác định khi

6 0

1 0

1 1 0

x



 



 





  



6

1

x













1 6

x

  

.

Vậy tập xác định của hàm số là





1;6

D  .

Câu 18. Cho hình thang

ABCD

vuông tại

A

,

D

có

AB a



,

2

AD a



và

3

CD a



. Gọi

M

,

N

lần

lượt là trung điểm của các cạnh

AD

và

DC

. Khi đó

1

2

AM DC



 

bằng

A.

5

2

a

. B.

5

a

. C.

3

a

. D.

3

2

a

.

Lời giải

Chọn A

N

C

D

M

A

B

Vì

M

là trung điểm của

AD

nên

2

AM AD



 

.

Vì

N

là trung điểm của

CD

nên

1

2

DC DN



 

.

Ta có

1

2

AM DC AD DN AN

   

    

1

2

AM DC AN

  

  

.

Xét tam giác vuông

ADN

có

2

AD a



,

3

2

a

DN  nên

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

2 2

AN AD DN

 

2

9

4

a

a 

5

2

a

 .

Vậy

1 5

2

2 2

a

AM DC 

 

.

Câu 19. Tìm điều kiện của tham số

m

để hàm số









2 2 1

y m x x m

   

đồng biến trên



.

A.

1

2

m

 

. B.

1

2

m

 

. C.

2

m

 

. D.

1

m

 

.

Lời giải

Chọn D

Ta có









2 2 1

y m x x m

   





1 2

y m x m

     .

Hàm số đồng biến trên



khi và chỉ khi





1 0

m

  

1

m

  

.

Câu 20. Cho mệnh đề





2

:" , 1 0"

P x x x x

    



. Mệnh đề phủ định của mệnh đề





P x

là

A.

2

" , 1 0"

x x x

    



. B.

2

" , 1 0"

x x x

    



.

C. " 

2

, 1 0"

x x x

   



. D.

2

" , 1 0"

x x x

    



.

Lời giải

Chọn B

Phủ định của mệnh đề

2

" , 1 0"

x x x

    



là mệnh đề

2

" , 1 0"

x x x

    



.

Câu 21. Cho lục giác đều

ABCDEF

tâm O. Chọn khẳng định sai trong các khẳng định sau:

A.

BO BA OD

 

  

. B.

1

2

AF AB AD

 

  

. C.

BE FC DA

 

  

. D.

2

BO ED BD

 

  

.

Lời giải

Chọn C

F

E

D

C

B

A

O

Ta có

2 2

BE FC OE OC

  

   

2

OD AD

 

 

suy ra đáp án C sai.

Các đáp còn lại đúng.

Câu 22. Cho

ABC



đều có cạnh bằng

a

, gọi

H

là trung điểm của cạnh

BC

. Độ dài của vectơ

HA HC



 

bằng

A.

a

. B.

2

a

. C.

3

2

a

. D.

3

a

.

Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Chọn A

Ta có

HA HC CA CA a

   

  

.

Câu 23. Nghiệm của hệ phương trình

2 7

2 5

4 3 11

x y z

  





  





  



là

A.





1; 3; 0

 . B.





1; 0;3

 . C.





3; 1;0

  . D.





3;0; 1



.

Lời giải

Chọn D

Giải hệ phương trình

Ta có

2 7 2 7

2 5 2 7 2 5

4 3 11 4 6 3 21 11

x y z y x z

x y z x x z z

      

 

 

        

 

 

       

 

2 7

3 3 12

2 4 10

y x z

x z

   





  





   



2 7 3

4 0

2 5 1

y x z x

x z y

x z z

    

 

 

    

 

 

     

 

.

Vậy hệ có nghiệm duy nhất









; ; 3;0; 1

x y z

 

.

Câu 24. Với điều kiện nào của tham số m thì phương trình





2

3 4 1

m x m x

   

có nghiệm thực duy

nhất?

A.

0

m



. B.

1

m

 

. C.

1

m

 

. D.

1

m



.

Lời giải

Chọn B

Ta có





2

3 4 1

m x m x

   





2

3 3 1

m x m

   

Để thỏa mãn yêu cầu bài toán thì

2

3 3 0

m

 

1

m

  

.

Câu 25. Cho hình bình hành

ABCD

tâm

I

. Đẳng thức nào sau đây đúng?

A.

BC DB AB

 

  

. B.

AB IA BI

 

  

. C.

0

AB DC

 

  

. D.

AC AB AD

 

  

.

Lời giải

Chọn B

I

D

C

B

A

Ta có

BC DB DC

 

  

suy ra A sai.

Lai có

AB IA BI AB BI IA BA

     

      

suy ra B sai.

Ta có

2

AB DC AB

 

  

suy ra C sai.

Mặt khác

AC AB AD

 

  

theo quy tắc hình bình hành suy ra D đúng.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 26. Phủ định của mệnh đề: “Có ít nhất một số vô tỷ là số thập phân vô hạn tuần hoàn” là mệnh đề

nào sau đây.

A. Mọi số vô tỷ đều là số thập phân vô hạn tuần hoàn.

B. Có ít nhất một số vô tỷ là số thập phân vô hạn không tuần hoàn.

C. Mọi số vô tỷ đều là số thập phân vô hạn không tuần hoàn.

D. Mọi số vô tỷ đều là số thập phân tuần hoàn.

Lời giải

Chọn C

Câu 27. Tập hợp









2018; 2018 2018;

   

bằng tập hợp nào sau đây:

A.





2018

. B.



. C.





; 2018

 . D.





2018;

 

.

Lời giải

Chọn A

Ta có:













2018; 2018 2018; 2018

     .

Câu 28. Tam giác

ABC

vuông tại

A

,



50

ABC

 

. Kết luận nào sau đây sai?

A.





, 120

AC CB

 

 

. B.





, 40

CA CB

 

 

. C.





, 90

AB CA

 

 

. D.





, 50

BA BC

 

 

.

Lời giải

50

o

AC

CB

50

o

D

A

B

C

Chọn A

+ Dựng hình bình hành

ABCD

, khi đó









, , 90 50 140

AC CB AC AD

      

   



A sai.

+







, 40

CA CB ABC

  

 



B đúng.

+ Vì





, 90

AB AC AB CA

   

 



C đúng.

+







, 50

BA BC ABC

  

 



D đúng.

Câu 29. Cho hàm số

 

2

kh

2 2 3

2

1

+1 2

i

khi

x

x x

f x

 



















. Tính giá trị biểu thức









2 2 .

P f f

  

A.

4

P



. B.

5

3

P



. C.

8

3

P



. D.

6

P



.

Lời giải

Chọn D

Ta có

     

2

2 2 2 3

2 2 2 1 6

2 1

P f f

 

       



.

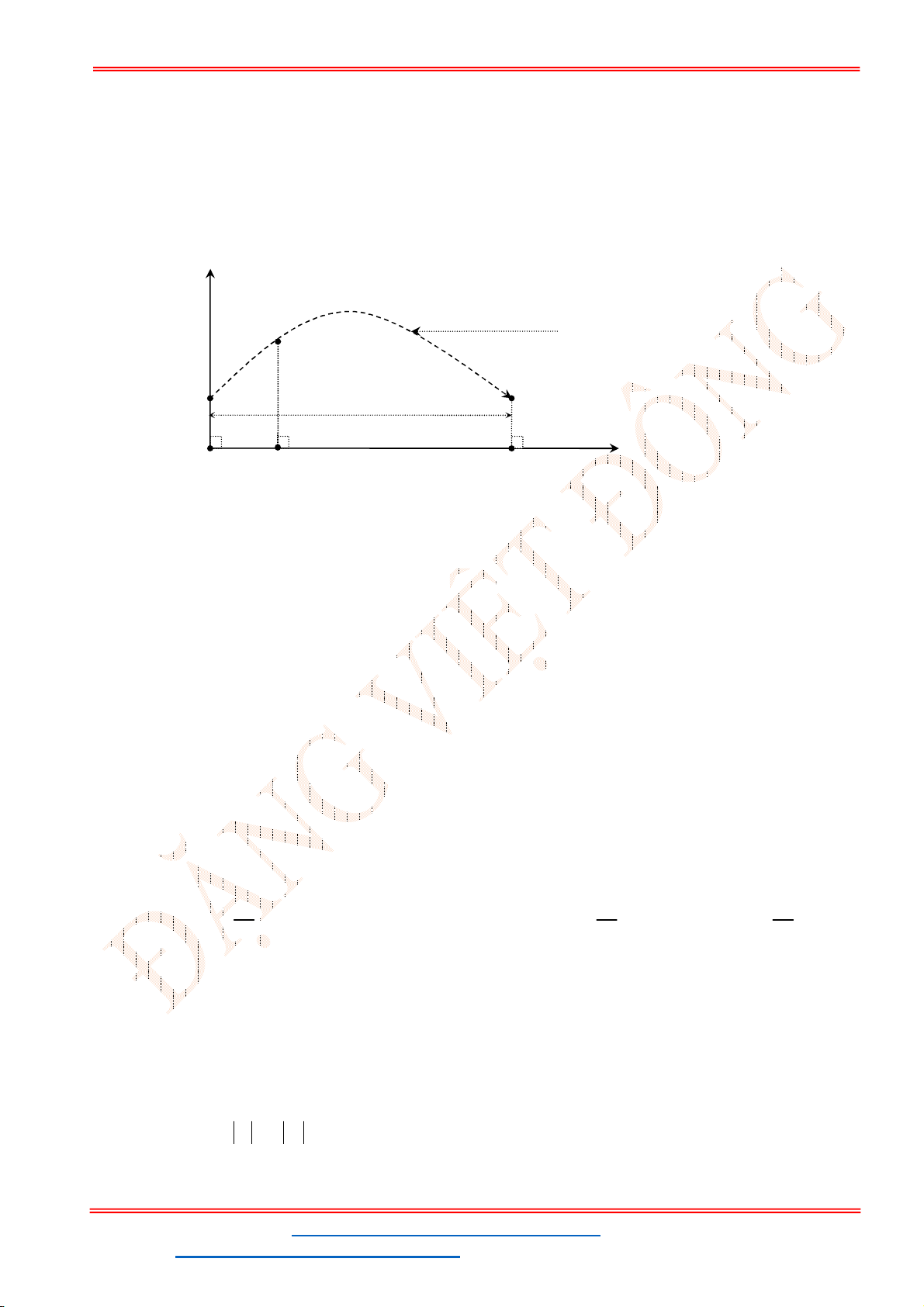
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 30. An và Bình là hai học sinh của trường THPT Phúc Thọ tham gia câu lạc bộ bóng rổ của trường

để thư giãn và rèn luyện thân thể. Trong trận đấu kỷ niệm ngày thành lập Đoàn, An đứng tại vị

trí

O

thực hiện một đường chuyền bóng dài cho Bình đứng tại vị trí

H

, quả bóng di chuyển

theo một đường parabol (hình vẽ bên dưới). Quả bóng rời tay An ở vị trí

A

và tay Bình bắt

được quả bóng ở vị trí

B

, khi quả bóng di chuyển từ An đến Bình thì đi qua điểm

C

. Quy ước

trục

Ox

là trục đi qua hai điểm

O

và

H

, trục

Oy

đi qua hai điểm

O

và

A

như hình vẽ. Biết

rằng

1,7 m

OA BH

 

;

3,4625 m

CK



;

2,5 m

OK



;

10 m

OH



. Hãy xác định khoảng cách

lớn nhất của quả bóng so với mặt đất khi An chuyền bóng cho Bình.

A.





4,03 m

. B.





4,06 m

. C.





4,02 m

. D.





4,05 m

.

Lời giải

Chọn D

Quỹ đạo của quả bóng có dạng Parabol





2

: .

P y a x bx c

  

.

Từ hình vẽ,





P

đi qua các điểm





0;1,7

A ,





10;1,7

B ,





2,5; 3,4625

C .

Thay tọa độ các điểm trên vào phương trình của





2

: .

P y a x bx c

  

, được

 

2 2

2

1,7

0,094

.10 .10 1,7 0,94 : 0,094 0,94 1,7

1,7

.2,5 .2,5 3,4625

c

a

a b c b P y x x

c

a b c





 





         

 

 



  



.





P

có tọa độ đỉnh





5;4,05

I .

Suy ra khoảng cách lớn nhất của quả bóng so với mặt đất là

4,05

m

.

Câu 31. Gọi

S

là tập hợp các giá trị thực của tham số

m

sao cho parabol





2

: 6

P y x x m

  

cắt

Ox

tại hai điểm phân biệt

,

A B

thỏa mãn

5.

OA OB



. Tính tổng

T

các phần tử của

S

.

A.

45

4

T

 

. B.

4

T



. C.

25

4

T

 

. D.

29

4

T

 

.

Lời giải

Chọn C

Phương trình

2

6 0

x x m

  

có hai nghiệm phân biệt

1 0

9 0

a

m

 









   



9

m

 

Gọi

1 2

,

x x

là 2 nghiệm của phương trình, có

1 2

6

x x m

x x







  



.

Theo đề

1 2

5

x x

 .

B

O

H

C

K

M

ặt đất

Quỹ đạo parabol

y

3,4625m

mmmm

OH =10m

=10

m

A

1,7m

x

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Trường hợp 1:

2

1 2 1

1

5 5

5

x

x x x

m

 





   









.

Trường hợp 2:

1 2

5

x x

 

2

1

3

2

15

2

45

4

x

m







  





 





Vậy

25

4

T

 

.

Câu 32. Cho hai tập hợp





4;1

A   ,





3;

B m

  . Tìm

m

để

A B A

 

.

A.

1

m



. B.

3 1

m

  

. C.

3 1

m

  

. D.

1

m



.

Lời giải

Chọn B

Điều kiện tồn tại tập hợp

B

là

3

m

 

.

Ta có:

A B A

 

B A

 

1

m

 

.

Do đó:

A B A

 

thì

3 1

m

  

.

Câu 33. Một miếng đất hình chữ nhật có chiều rộng

43 0,5

x m m

 

và chiều dài

63 0,5

y m m

 

. Tính

chu vi

P

của miếng đất đã cho.

A.

212 1

P m m

 

. B.

212 4

P m m

 

. C.

212 0,5

P m m

 

. D.

212 2

P m m

 

.

Lời giải

Chọn D

Chu vi hình chữ nhật:





43 63 .2 212

P m

   với cận trên





0,5 0,5 .2 2

m

  và cận dưới





0,5 0,5 .2 2

m

   

Vậy

212 2

P m m

 

.

Câu 34. Trong hệ tọa độ

Oxy

, cho hai vectơ









7; 2 , 3; 4

a b

   

 

. Tích vô hướng

.

a b

 

bằng

A.

26



. B.

13

. C.

29

. D.

12

.

Lời giải

Chọn C

. 29

a b



 

.

Câu 35. Cho hình bình hành

ABCD

,

M

là điểm tùy ý. Chọn khẳng định đúng trong các khẳng định

sau:

A.

MA MB MC MD

  

   

. B.

MC MB MA MD

  

   

.

C.

MC CB MD DA

  

   

. D.

MA MC MB MD

  

   

.

Lời giải

Chọn D

Gọi

E

là tâm hình bình hành thì

2.

MA MC MB MD ME

   

    

.

Câu 36. Cho hàm số





2

y f x ax bx c

   

có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị thực

của tham số

m

để phương trình





2020 0

f x m

  

có duy nhất một nghiệm.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

2015.

m



B.

2019.

m



C.

2017.

m



D.

2018.

m



Lời giải

Chọn D

Ta có





2020 0

f x m

  





2020

f x m

  

. Số nghiệm của phương trình là số giao điểm

của đồ thị hàm số





y f x

 và đường thẳng 2020

y m

 

. Dựa vào đồ thị suy ra

2020 2

m

 

2018

m

 

.

Câu 37. Hệ phương trình

1

2

mx y m

x my

  





 



có nghiệm duy nhất khi:

A.

2

m

 

. B.

2

m



. C.

1

m







 



. D.

2

m







 



.

Lời giải

Chọn C

Ta có

2

1

m

D m

m

  

.

Để hệ phương trình đã cho có nghiệm duy nhất thì

0

D



1

m









 



.

Câu 38. Trong các câu sau có bao nhiêu câu là mệnh đề?

a) Cố lên, sắp đến nơi rồi!

b) Số 15 là số nguyên tố.

c) Tổng các góc của một tam giác là

180 .



d)

x

là số nguyên dương.

A.

3.

B.

4.

C.

1.

D.

2.

Lời giải

Chọn D

a) không phải là mệnh đề.

b) là mệnh đề.

c) là mệnh đề.

d) không là mệnh đề.

Câu 39. Lớp

1

10



có

6

học sinh giỏi Toán,

4

học sinh giỏi Lý,

5

học sinh giỏi Hóa,

2

học sinh giỏi

Toán và Lý,

3

học sinh giỏi Toán và Hóa,

2

học sinh giỏi Lý và Hóa,

1

học sinh giỏi cả

3

môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp

1

10



là

A.

15.

B.

23.

C.

7.

D.

9.

Lời giải

Chọn D

x

y

O

1

2

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Cách 1: Số học sinh giỏi ít nhất một môn là

T L H T L H T L T H L H T L H

             





6 4 5 2 3 2 1 9

       

học sinh

Cách 2: Số học sinh chỉ giỏi Toán là

6 (2 3 1) 2

   

học sinh.

Số học sinh chỉ giỏi Lý là





4 2 2 1 1

   

học sinh.

Số học sinh chỉ giỏi Hóa là





5 3 2 1 1

   

học sinh.

Số học sinh chỉ giỏi một môn là

2 1 1 4

  

học sinh.

Số học sinh giỏi hai môn là

1 2 1 4

  

học sinh.

Số học sinh giỏi cả ba môn là 1 học sinh.

Vậy số học sinh giỏi ít nhất một môn là

4 4 1 9

  

học sinh.

Câu 40. Cho tam giác ABC, đặt

CA a



 

,

CB b



 

. Lấy các điểm

A



,

B



sao cho

2 ,

CA a



 

 

2

CB b





 

.

Gọi I là giao điểm của

A B



và

B A



. Giả sử

CI ma nb

 

  

, khi đó tỉ số

m

n

bằng

A.

1

4

. B.

1

3

. C.

2

3

. D.

2

5

.

Lời giải

Chọn B

Cách 1: Áp dụng định lí Menelauyt cho tam giác

B AC



ta có:

. . 1

IA BB A C

IB BC A A

 



 

2

.1. 1

3

IA

IB

 



3

2

IA

IB

 



.

Cách 2: (Cho học sinh không biết định lí Menelauyt)

Giả sử

.

IA k AB





. Ta có:

A B A C CB

 

 

  

2

CA CB

 

 

2

a b

 

 

.

A I A A AI

 

 

  

3 .

CA k AB



 

 





3 .

CA k AC CB



  

  





3 . 2

a k a b

   

  





3 2 .

k a k b

  

 

.

Do ;

A I A B

 

 

cùng phương nên

3 2

2 1

k k





3

5

k

 

.

Ta có

CI CA AI

 

  

3

5

CA AB



 

 





3

5

CA CB CA



  

  





3

2

5

CA CB CA

  

  

6 2

5 5

CB CA

 

 

2 6

5 5

a b

 

 

.

Do đó

2

5

6

5

m

n

















1

3

m

n

 

.

T

L

H

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

I

B'

A'

A

B

C

Câu 41.

Phương trình

2 3 2

x x

  

có nghiệm thực duy nhất dạng

2

x a b

 

,





,a b



. Khi đó

2 3

a b



bằng

A.

12.

B.

10.

C.

8.

D.

6

.

Lời giải

Chọn A

Ta có

2 3 2

x x

  

 

2

2 0

2 3 2

x

x x

 









  





2

6 1 0

x

x x









  



 

2

3 2 2 /

3 2 2

x

x t m

x l









 











 







Suy ra

3, 2

a b

 

. Vậy

2 3 12

a b

 

.

Câu 42. Trong hệ tọa độ

Oxy

, cho hai điểm





6; 3

A



,





2; 5

B

 

. Trung điểm của đoạn thẳng

AB

là

A.





8;2

I  . B.





2; 4

I



. C.





2; 8

I



. D.





4;2

I  .

Lời giải

Chọn B

Tọa độ trung điểm của đoạn thẳng

AB

là









6 2 3 5

;

2 2

I

    

 

 

 





2; 4

I

 

.

Câu 43. Với hai số thực

a

,

b

bất kì và khác

0

, bất đẳng thức nào sau đây luôn đúng?

A.

2 2

0

a ab b

  

. B.

0

a b

 

. C.

2 2

0

a ab b

  

. D.

0

a b

 

.

Lời giải

Chọn A

Ta có

2

2 2

3

0

2 4

b b

a ab b a

 

     

 

 

,

, 0

a b

 

.

Câu 44. Biết rằng parabol





2

: 4

P y ax x c

  

có hoành độ đỉnh bằng

3



và đi qua điểm





2;1

M  .

Tính tổng

S a c

 

.

A.

5.

S

 

B.

5.

S



C.

1.

S



D.

4.

S



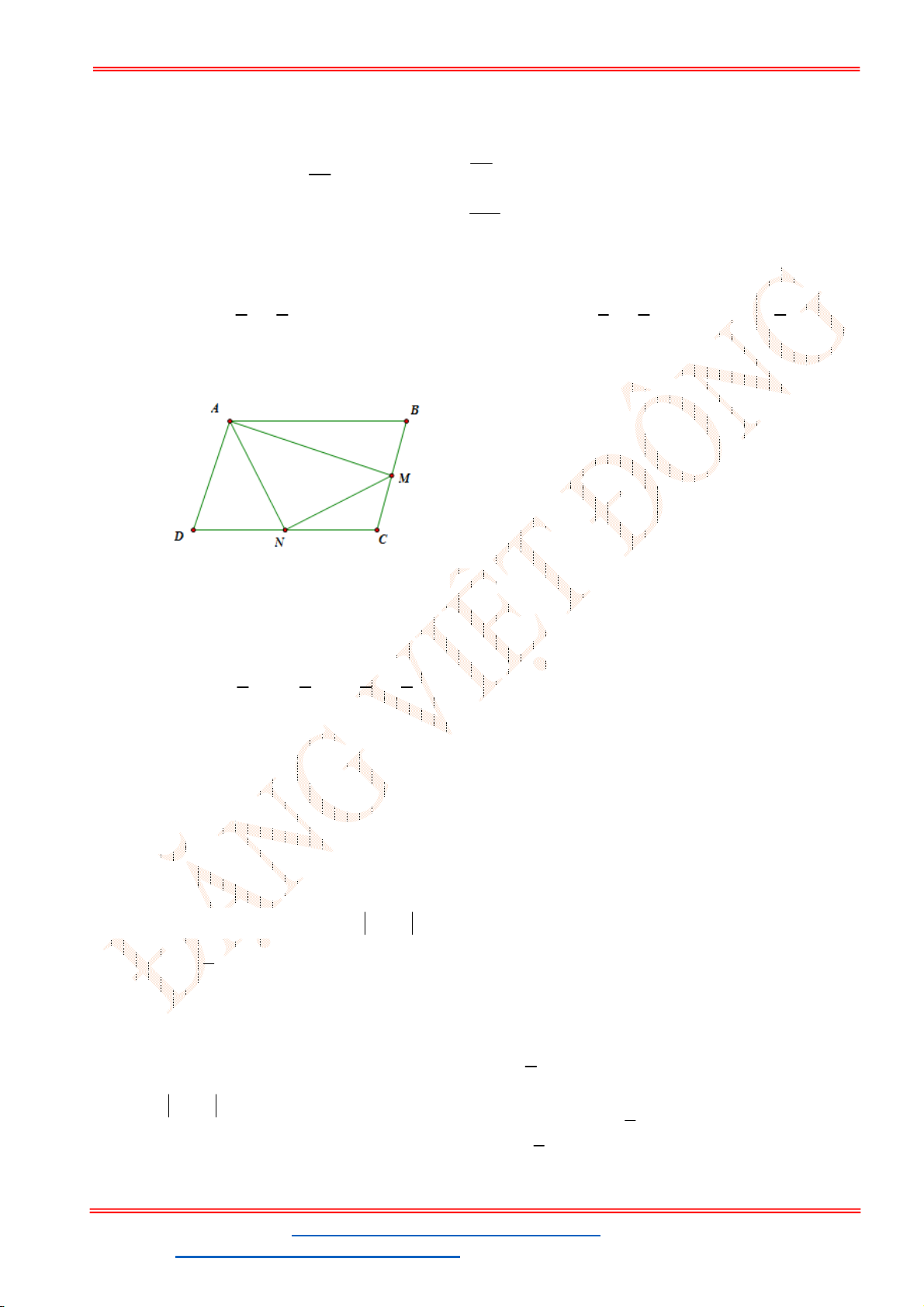
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Lời giải

Chọn A

Từ giả thiết ta có

4

3

2

4 8 1

a

a c



 







  



2

3

13

3

a

b























5

a b

   

.

Câu 45. Cho hình bình hành

ABCD

. Gọi

M

,

N

lần lượt là trung điểm của các cạnh

BC

và

CD

. Đặt

a AM



 

,

b AN



 

. Hãy phân tích vectơ

AC



theo

2

vectơ

a



và

b



.

A.

2 2

3 3

AC a b

 

  

. B.

3

AC a b

 

  

. C.

1 2

3 3

AC a b

 

  

. D.

2

4

3

AC a b

 

  

.

Lời giải

Chọn A

Ta có

AC AB AD

 

  









3

AC AB AC AD AC

    

    

3 2 2

AC AM AN

  

  

2 2 2 2

3 3 3 3

AC AM AN a b

    

    

.

Câu 46. Phát biểu nào sau đây là sai?

A. Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.

B. Vectơ là đoạn thẳng có hướng.

C. Hai vectơ cùng hướng thì cùng phương.

D. Hai vectơ cùng phương thì cùng hướng.

Lời giải

Chọn D

Hai véc tơ cùng phương thì có thể cùng hướng hoặc ngược hướng.

Câu 47. Nghiệm của phương trình

3 2 2 3

x x

  

là

1

x

,

2

x

. Tích

1 2

.

x x

bằng

A.

1

.

5



B.

1.

C.

1.



D.

5.

Lời giải

Chọn C

3 2 2 3

x x

  

2 3 0

3 2 2 3

x

x x

 







  









   





3

2

5

1

5

x



 



 













 





5

1

5

x











 



.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 20

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Khi đó

1 2

. 1

x x

 

.

Câu 48. Trong hệ tọa độ

Oxy

, cho tam giác

ABC

có





2;2

A ,





5;3

B  ,





2;4

C  . Gọi





;

H x y

là hình

chiếu của đỉnh

A

lên đường thẳng

BC

. Tính giá trị của biểu thức

2 2

P x y

 

.

A.

13

P



. B.

26

P



. C.

25

P



. D.

17

P



.

Lời giải

Chọn B

Gọi





;

H x y

là hình chiếu của

A

lên đường thẳng

BC

.

Ta có

. 0

AH BC

H BC















 

. 0

AH BC



 









2 .3 2 .1 0

x y

    





3 8 0 1

x y   

,

BH BC

 

cùng phương

5 3

3 1

x y

 

 





3 14 0 2

x y   

Giải hệ ta được

1

x



và

5

y



.

Câu 49. Cặp số nào sau đây là nghiệm của hệ phương trình

2 2

3 3

30

35

x y xy

x y



 





 





?

A.





3;2

. B.





3; 2

 

. C.





3;2

 . D.





3; 2



.

Lời giải

Chọn A

Ta có

2 2

3 3

30

35

x y xy

x y



 





 









   

2

30

3 35

xy x y

x y x y xy

 







 

   



 



Đặt

2

; ; 4

S x y P xy S P

   

Hệ trở thành

3

30

3 35

SP

S SP







 



3

30

125

SP

S













5

6

S

P













3

2

x

y













hoặc

2

3

x

y











.

Câu 50. Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?

A. Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.

B. Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.

C. Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.

D. Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.

Lời giải

Chọn B

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 7 Môn Toán – Lớp 10

(Th

ời gian l

àm bài 90 phút)

Không k

ể thời gian phát đề

I. PHẦN TRẮC NGHIỆM

Câu 1: Gọi

G

là trọng tâm tam giác

ABC

và

M

là điểm tùy ý. Chọn khẳng định sai trong các khẳng

định sau.

A.

0

AG BG CG

  

   

. B.

3

MA MB MC MG

  

   

.

C.

0

GA GB GC

  

   

. D.

MA MB MC MG

  

   

.

Câu 2: Cho hai tập hợp





3;10

A  và





5;12

B  . Tập

\

A B

bằng

A.





5;10

. B.





3;5

. C.





3;12

. D.





3;5

.

Câu 3: Cho





1; 2

M



và





3;4

N  . Khoảng cách giữa hai điểm

M

và

N

bằng

A.

2 13

. B.

6

. C.

3 6

. D.

4

.

Câu 4: Hãy liệt kê các phần tử của tập hợp





2

| 1 0

X x x x

    

 .

A.

X

 

. B.





X

 

. C.





0

X  . D.

0

X



.

Câu 5: Sử dụng các kí hiệu “khoảng” , “nữa khoảng” và “đoạn” để viết lại tập hợp





4 9

A x R x

   

.

A.





4;9

A  . B.





4;9

A  . C.





4;9

A  . D.





4;9

.

Câu 6: Nghiệm của hệ phương trình

3 5 2

4 2 7

x y

 





 



.

A.

1

;2

3

 



 

 

. B.

3 1

;

2 2

 

 

 

 

. C.

1 3

;

2 2

 

 

 

. D.

3 1

;

2 2

 

 

 

.

Câu 7: Tập nghiệm của phương trình

1

x x x

  

.

A.

S R



. B.

S

 

. C.





0

S  . D.





1

S

 

.

Câu 8: Nghiệm của phương trình

5 6 6

x x

  

bằng

A.

15

. B.

6

. C.

2

và

15

. D.

2

.

Câu 9: Cho tam giác

ABC

có



0 0

90 , 60

A B  và

AB a



. Khi đó

.

AC CB

 

bằng:

A.

2

a

 . B.

2

a

. C.

2

3

a

. D.

2

3

a

 .

Câu 10: Cho tam giác đều

ABC

cạnh bằng

2

a

. Khi đó

AB AC



 

bằng:

A.

a

. B.

2 3

a

. C.

3

2

a

. D.

2

a

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 11: Tập nghiệm của phương trình





2

2 4 3 0

x x x

   

là:

A.





2;3

S  . B.





2

S  . C.





1;3

S  . D.





1;2;3

S  .

Câu 12: Trong hệ trục tọa độ

Oxy

, cho





2;5

a 



và





3;1

b  



. Khi đó, giá trị của

.

a b

 

bằng

A.

5



. B.

1

. C.

13

. D.

1



.

Câu 13: Trong hệ trục tọa độ

Oxy

, cho













4;1 , 2;4 , 2; 2

A B C

 

. Tọa độ trọng tâm

G

của tam giác

ABC

là:

A.

3

0;

2

G

 

 

 

. B.





0;1

G . C.





0;3

G . D.

3

;0

2

G

 

 

 

.

Câu 14: Trong mặt phẳng

Oxy

, cho













2;0 , 5; 4 , 5;1

A B C   . Tọa độ điểm

D

để tứ giác

ABCD

là

hình bình hành là:

A.





12;5

 . B.





8; 5



. C.





12; 5

 

. D.





8;5

.

Câu 15: Cho mệnh đề

2

:" : 7 0"

A x x x

    



. Mệnh đề phủ định của

A

là:

A.

2

: 7 0

x x x

    



. B.

2

: 7 0

x x x

    



.

C.

2

: 7 0

x x x

    



. D.

2

: 7 0

x x x

    



.

Câu 16: Tập nghiệm của phương trình

3 2

x x

  

là:

A.

S

 

. B.

1

2;

2

S

 

 

 

 

. C.

1

2

S

 



 

 

. D.

1

2

S

 

 

 

 

.

Câu 17: Cho hình bình hành

ABCD

. Khi đó đẳng thức nào sau đây đúng?

A.

BA BD BC

 

  

. B.

AB AD BD

 

  

. C.

BA BC BD

 

  

. D.

AB AC AD

 

  

.

Câu 18: Trong hệ trục toạ độ

Oxy

, cho hai điểm





1;1

M ,





4; 1

N



. Tính độ dài của vectơ

MN



.

A.

13

MN 



. B.

5

MN





. C.

29

MN 



. D.

3

MN





.

Câu 19: Hoành độ đỉnh của parabol





2

: 2 4 3

P y x x

  

bằng

A.

2



. B.

2

. C.

1



. D.

1

.

Câu 20: Trong hệ trục toạ độ

Oxy

, cho hai điểm





2; 1

A



,





4;3

B . Toạ độ của vectơ

AB



bằng

A.





8; 3

AB

 



. B.





2; 4

AB

  



. C.





2;4

AB 



. D.





6;2

AB 



.

Câu 21: Trong hệ trục tọa độ

Ox

y

, tọa độ của vectơ

8 3

a j i

 

  

bằng

A.





3;8

a  



. B.





3; 8

a

 



. C.





8;3

a 



. D.





8; 3

a

 



.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 22: Trong các mệnh đề dưới đây, mệnh đề nào là mệnh đề đúng?

A.

2

: 1 0

x x

   



. B.

2

: 0

x x

  



. C.

2

:2 1 0

x x

   



. D.

2

: 2 0

x x

   



.

Câu 23: Phương trình

2

3 1 0

x x m

   

có nghiệm khi và chỉ khi

A.

5

4

m



. B.

5

4

m



. C.

5

4

m

 

. D.

4

5

m



.

Câu 24: Điều kiện xác định của phương trình

2 2

2 3

5

1 1

x

x x

 

 

là

A.





\ 1

D

 



. B.





\ 1

D

 



. C.





\ 1

D 



. D.

D





.

Câu 25: Trong các hàm dưới đây, hàm số nào là hàm số chẵn?

A.

3

2

y x x

 

. B.

4 2

3 5

y x x

  

. C.

1

y x

 

. D.

2

y x x

 

.

Câu 26: Cho hàm số





5

y f x x

  

. Khẳng định nào sau đây sai?

A.





1 5

f

 

. B.





2 10

f

 

. C.

1

5

f

 

 

 

 

. D.





2 10

f



.

Câu 27: Cho hai vectơ





4;3

a 



và





1;7

b 



. Số đo góc



giữa hai vectơ

a



và

b



bằng

A.

45



. B.

90



. C.

60



. D.

30



.

Câu 28: Cho parabol





2

: 3 6 1

P y x x

   

. Chọn khẳng định sai

A.





P

có đỉnh





1;2

I . B.





P

cắt trục tung tại điểm





0; 1

A



.

C.





P

hướng bề lõm lên trên. D.





P

có trục đối xứng

1

x



.

Câu 29: Tập xác định

D

của hàm số

3 1

2 2

x

y

x







là:

A.

D





. B.





1;D

 

. C.





1;D

 

. D.





\ 1

D 



.

Câu 30: Tìm

a

và

b

biết rằng đường thẳng

y ax b

 

đi qua





1; 1

M



và song song với đường

2 3

y x

 

A.

1

2

a

b

 









. B.

2

3

a

b







 



. C.

2

4

a

b











. D.

2

3

a

b











.

Câu 31: Mệnh đề nào sau đây là mệnh đề sai ?

A.

2

: 0

x x

  



. B.

2

:

n n n

  



. C.

: 2

n n n

  



. D.

2

:

x x x

  



.

Câu 32: Cho





1;5

A  ,





1;3;5

B  . Chọn kết quả đúng trong các kết quả sau:

A.





1;3

A B  . B.





1

A B  . C.





1;5

A B  . D.





3;5

A B  .

Câu 33: Cho hai vectơ

a



và

b



khác

0



. Xác định góc



giữa hai vectơ

a



và

b



biết rằng

. .

a b a b

 

   

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

90



 

. B.

0



 

. C.

45



 

. D.

180



 

.

Câu 34: Trong mặt phẳng tọa độ

Oxy

, cho hai vectơ





3; 4

u



và





8; 6

v 



. Khẳng định nào sau đây là

đúng?

A.

u v

 

 

. B.

u



vuông góc với

v



.

C.

u v



 

. . D.

u



và

v



cùng phương.

Câu 35: Cho hàm số









0

f x ax b a

  

. Mệnh đề nào sau đây là đúng?

A. Hàm số đồng biến trên ;

b

a

 

 

 

 

. B. Hàm số đồng biến trên



khi

0

a



.

C. Hàm số đồng biến trên ;

b

a

 

 

 

 

. D. Hàm số đồng biến trên



khi

0

a



.

II. PHẦN TỰ LUẬN

Câu 36: (1 điểm) Cho parabol





P

2

y x mx n

  

(

,

m n

là tham số). Xác định

,

m n

để





P

có đỉnh





2; 1

I



Câu 37: (1 điểm) Trong mặt phẳng Oxy, cho 2 điểm





1;3

B  và





3;1

C

a) Tính độ dài vectơ

BC



.

b) Tìm tọa độ điểm A sao cho tam giác ABC vuông cân tại A?

Câu 38: (1 điểm) Giải hệ phương trình

3 3 2 2

2 2

0

2 9 2 1 4

x y x y xy x y

x y y x x



     





      





.

---HẾT---

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG HDG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 7 Môn Toán – Lớp 10

(Thời gian làm bài 90 phút)

Không k

ể thời gian phát đề

I. PHẦN TRẮC NGHIỆM

Câu 1: Gọi

G

là trọng tâm tam giác

ABC

và

M

là điểm tùy ý. Chọn khẳng định sai trong các khẳng

định sau.

A.

0

AG BG CG

  

   

. B.

3

MA MB MC MG

  

   

.

C.

0

GA GB GC

  

   

. D.

MA MB MC MG

  

   

.

Lời giải

Chọn D

MA MB MC MG GA MG GB MG GC

       

        





3 3

MG GA GB GC MG

    

    

.

( Do

G

là trọng tâm tam giác

ABC

nên

0

GA GB GC

  

   

)

Vậy mệnh đề sai là

MA MB MC MG

  

   

.

Câu 2: Cho hai tập hợp





3;10

A  và





5;12

B  . Tập

\

A B

bằng

A.





5;10

. B.





3;5

. C.





3;12

. D.





3;5

.

Lời giải

Chọn D





\ 3;5

A B  .

Câu 3: Cho





1; 2

M



và





3;4

N  . Khoảng cách giữa hai điểm

M

và

N

bằng

A.

2 13

. B.

6

. C.

3 6

. D.

4

.

Lời giải

Chọn A

 

2

1 3 2 4 2 13

MN        .

Câu 4: Hãy liệt kê các phần tử của tập hợp





2

| 1 0

X x x x

    

 .

A.

X

 

. B.





X

 

. C.





0

X  . D.

0

X



.

Lời giải

Chọn A

2

1 0

x x

  

vô nghiệm nên





2

| 1 0X x x x

      

 .

Câu 5: Sử dụng các kí hiệu “khoảng” , “nữa khoảng” và “đoạn” để viết lại tập hợp





4 9

A x R x

   

.

A.





4;9

A  . B.





4;9

A  . C.





4;9

A  . D.





4;9

.

Lời giải

Chọn B

Câu 6: Nghiệm của hệ phương trình

3 5 2

4 2 7

x y

 





 



.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

1

;2

3

 



 

 

. B.

3 1

;

2 2

 

 

 

 

. C.

1 3

;

2 2

 

 

 

. D.

3 1

;

2 2

 

 

 

.

Lời giải

Chọn D

Câu 7: Tập nghiệm của phương trình

1

x x x

  

.

A.

S R



. B.

S

 

. C.





0

S  . D.





1

S

 

.

Lời giải

Chọn B

Điều kiện:

0

x



.

1

x x x

  

1

x

  

(không thỏa điều kiện)

Vậy

S

 

.

Câu 8: Nghiệm của phương trình

5 6 6

x x

  

bằng

A.

15

. B.

6

. C.

2

và

15

. D.

2

.

Lời giải

Chọn A

Ta có :

5 6 6

x x

  

 

2

6 0

5 6 6

x

x x

 









  





2

6

5 6 12 36

x

x x x









   



2

6

2( )

17 30 0

15

x

x l

x x

x











 





 

  











. Vậy





15

S  .

Câu 9: Cho tam giác

ABC

có



0 0

90 , 60

A B  và

AB a



. Khi đó

.

AC CB

 

bằng:

A.

2

a

 . B.

2

a

. C.

2

3

a

. D.

2

3

a

 .

Lời giải

Chọn D

Ta có:



2

3

. . .cos 3 .2 . 3

2

AC CB CACB C a a a

     

 

.

Câu 10: Cho tam giác đều

ABC

cạnh bằng

2

a

. Khi đó

AB AC



 

bằng:

A.

a

. B.

2 3

a

. C.

3

2

a

. D.

2

a

.

Lời giải

Chọn B

Ta có:

3

2 2. .2 2 3

2

AB AC AM a a

   

  

.

Câu 11: Tập nghiệm của phương trình





2

2 4 3 0

x x x

   

là:

A.





2;3

S  . B.





2

S  . C.





1;3

S  . D.





1;2;3

S  .

Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Chọn A

Điều kiện:

2

x



.

Phương trình trở thành:

2

2 0

4 3 0

x

x x

 





  





0 ( )

1 ( )

3 ( )

x n

x l

x n















.

Vậy





2;3

S  .

Câu 12: Trong hệ trục tọa độ

Oxy

, cho





2;5

a 



và





3;1

b  



. Khi đó, giá trị của

.

a b

 

bằng

A.

5



. B.

1

. C.

13

. D.

1



.

Lời giải

Chọn D

Ta có:





. 2. 3 5.1 1

a b

    

 

.

Câu 13: Trong hệ trục tọa độ

Oxy

, cho













4;1 , 2;4 , 2; 2

A B C

 

. Tọa độ trọng tâm

G

của tam giác

ABC

là:

A.

3

0;

2

G

 

 

 

. B.





0;1

G . C.





0;3

G . D.

3

;0

2

G

 

 

 

.

Lời giải

Chọn B

G

là trọng tâm của tam giác

ABC

nên ta có

4 2 2

0

3

1 4 2

1

3

G

x

y

  



 





 



 





. Vậy





0;1

G .

Câu 14: Trong mặt phẳng

Oxy

, cho













2;0 , 5; 4 , 5;1

A B C   . Tọa độ điểm

D

để tứ giác

ABCD

là

hình bình hành là:

A.





12;5

 . B.





8; 5



. C.





12; 5

 

. D.





8;5

.

Lời giải

Chọn A

Gọi





;

D x y

, ta có









7; 4 , 5 ;1

AB DC x y

     

 

ABCD

là hình bình hành

7 5 12

4 1 5

x x

AB DC

y y

    

 

   

 

   

 

 





12; 5

D  .

Câu 15: Cho mệnh đề

2

:" : 7 0"

A x x x

    



. Mệnh đề phủ định của

A

là:

A.

2

: 7 0

x x x

    



. B.

2

: 7 0

x x x

    



.

C.

2

: 7 0

x x x

    



. D.

2

: 7 0

x x x

    



.

Lời giải

Chọn A

Câu 16: Tập nghiệm của phương trình

3 2

x x

  

là:

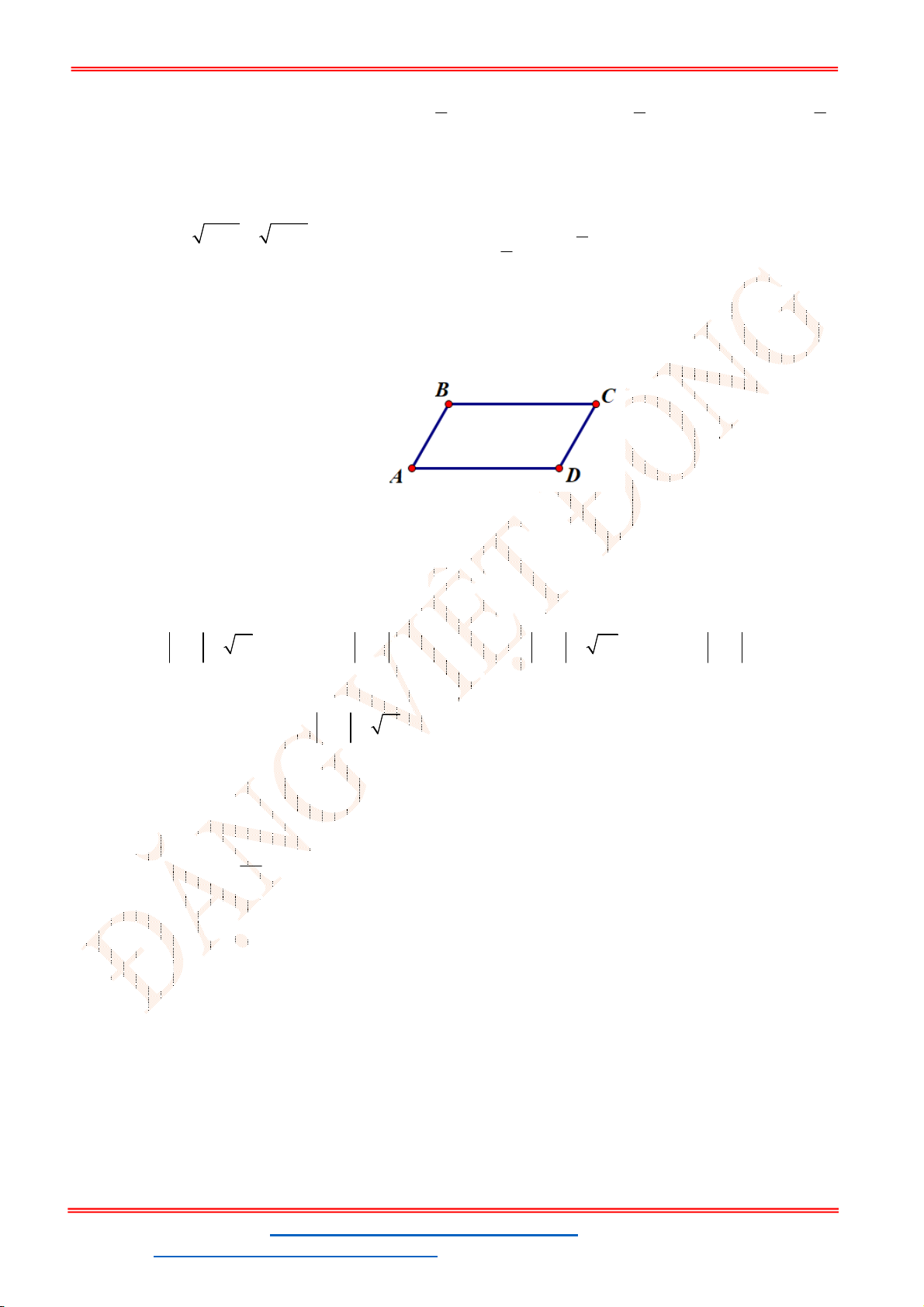
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

S

 

. B.

1

2;

2

S

 

 

 

 

. C.

1

2

S

 



 

 

. D.

1

2

S

 

 

 

 

.

Lời giải

Chọn C

Ta có

2

2 0

1

3 2

1

3 2

2

x

x x x

x x

x

 



 





      

 

  









.

Câu 17: Cho hình bình hành

ABCD

. Khi đó đẳng thức nào sau đây đúng?

A.

BA BD BC

 

  

. B.

AB AD BD

 

  

. C.

BA BC BD

 

  

. D.

AB AC AD

 

  

.

Lời giải

Chọn C

Phương án A sai, vì

2

BA BD BM

 

  

với

M

là trung điểm của đoạn

AD

.

Phương án B sai, vì

AB AD AC

 

  

(quy tắc hình bình hành).

Phương án C đúng, vì

BA BC BD

 

  

(quy tắc hình bình hành).

Phương án D sai, vì

2

AB AC AN

 

  

với

N

là trung điểm của đoạn

BC

.

Câu 18: Trong hệ trục toạ độ

Oxy

, cho hai điểm





1;1

M ,





4; 1

N



. Tính độ dài của vectơ

MN



.

A.

13

MN 



. B.

5

MN





. C.

29

MN 



. D.

3

MN





.

Lời giải

Chọn A

Ta có

 

3; 2 13

MN MN   

 

.

Câu 19: Hoành độ đỉnh của parabol





2

: 2 4 3

P y x x

  

bằng

A.

2



. B.

2

. C.

1



. D.

1

.

Lời giải

Chọn D

Ta có

1

2

I

b

x

a

  

. Vậy hoành độ đỉnh của





P

là

1

I

x



.

Câu 20: Trong hệ trục toạ độ

Oxy

, cho hai điểm





2; 1

A



,





4;3

B . Toạ độ của vectơ

AB



bằng

A.





8; 3

AB

 



. B.





2; 4

AB

  



. C.





2;4

AB 



. D.





6;2

AB 



.

Lời giải

Chọn C

Câu 21: Trong hệ trục tọa độ

Ox

y

, tọa độ của vectơ

8 3

a j i

 

  

bằng

A.





3;8

a  



. B.





3; 8

a

 



. C.





8;3

a 



. D.





8; 3

a

 



.

Lời giải

Chọn A

Theo định nghĩa vectơ





3;8

a  



.

Câu 22: Trong các mệnh đề dưới đây, mệnh đề nào là mệnh đề đúng?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

2

: 1 0

x x

   



. B.

2

: 0

x x

  



. C.

2

:2 1 0

x x

   



. D.

2

: 2 0

x x

   



.

Lời giải

Chọn C

 Ta có:

2 2

0 1 1

x x

   

với

x

 



. Vậy loại A.

 Ta có:

2

0

x



với

x

 



. Vậy loại B.



2 2

1 2 2

2 1 0

2 2 2

x x x        , mà

0

x x

  



. Vậy C đúng.







2

2 0 2 loai

x x     vì

x





. Vây loại D.

Câu 23: Phương trình

2

3 1 0

x x m

   

có nghiệm khi và chỉ khi

A.

5

4

m



. B.

5

4

m



. C.

5

4

m

 

. D.

4

5

m



.

Lời giải

Chọn B

Phương trình có nghiệm khi và chỉ khi

   

2

5

0 3 4.1. 1 0

4

m m

        

.

Câu 24: Điều kiện xác định của phương trình

2 2

2 3

5

1 1

x

x x

 

 

là

A.





\ 1

D

 



. B.





\ 1

D

 



. C.





\ 1

D 



. D.

D





.

Lời giải

Chọn D

Điều kiện xác định:

2

1 0

x

 

Mà





2

1 1x x   



.

Câu 25: Trong các hàm dưới đây, hàm số nào là hàm số chẵn?

A.

3

2

y x x

 

. B.

4 2

3 5

y x x

  

. C.

1

y x

 

. D.

2

y x x

 

.

Lời giải

Chọn B

Xét hàm số





4 2

3 5

y f x x x

   

Tập xác định

D





.

Với

x x

   

 

và

       

4 2

3 5 3 5f x x x x x f x x

           



.

Vậy

4 2

3 5

y x x

  

là hàm số chẵn.

Câu 26: Cho hàm số





5

y f x x

  

. Khẳng định nào sau đây sai?

A.





1 5

f

 

. B.





2 10

f

 

. C.

1

5

f

 

 

 

 

. D.





2 10

f



.

Lời giải

Chọn C

Có

1 1

5. 1

5 5

f

 

  

 

 

nên khẳng định

1

5

f

 

 

 

 

sai.

Câu 27: Cho hai vectơ





4;3

a 



và





1;7

b 



. Số đo góc



giữa hai vectơ

a



và

b



bằng

A.

45



. B.

90



. C.

60



. D.

30



.

Lời giải

Chọn A.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Có

 

2 2 2 2

. 4.1 3.7 1

cos ,

2

.

4 3 . 1 7

a b



  

 







, 45

a b

  



.

Câu 28: Cho parabol





2

: 3 6 1

P y x x

   

. Chọn khẳng định sai

A.





P

có đỉnh





1;2

I . B.





P

cắt trục tung tại điểm





0; 1

A



.

C.





P

hướng bề lõm lên trên. D.





P

có trục đối xứng

1

x



.

Lời giải

Chọn C

Do





P

có hệ số

3 0

a

  

nên





P

hướng bề lõm xuống dưới. Vậy chọn C.

Câu 29: Tập xác định

D

của hàm số

3 1

2 2

x

y

x







là:

A.

D





. B.





1;D

 

. C.





1;D

 

. D.





\ 1

D 



.

Lời giải

Chọn D

Điều kiện

2 2 0

x

 

1

x

 

.

Tập xác định





\ 1

D 



.

Câu 30: Tìm

a

và

b

biết rằng đường thẳng

y ax b

 

đi qua





1; 1

M



và song song với đường

2 3

y x

 

A.

1

2

a

b

 









. B.

2

3

a

b







 



. C.

2

4

a

b











. D.

2

3

a

b











.

Lời giải

Chọn B

Đường thẳng

y ax b

 

đi qua





1; 1

M



và song song với đường

2 3

y x

 

nên

1

2

3

a b

a

b

  















2

3

a

b









 



Câu 31: Mệnh đề nào sau đây là mệnh đề sai ?

A.

2

: 0

x x

  



. B.

2

:

n n n

  



. C.

: 2

n n n

  



. D.

2

:

x x x

  



.

Lời giải

Chọn A

Ta có

2

0

x



,

x

 





Đáp án A sai.

Câu 32: Cho





1;5

A  ,





1;3;5

B  . Chọn kết quả đúng trong các kết quả sau:

A.





1;3

A B  . B.





1

A B  . C.





1;5

A B  . D.





3;5

A B  .

Lời giải

Chọn C

Ta có





1;5

A B  .

Câu 33: Cho hai vectơ

a



và

b



khác

0



. Xác định góc



giữa hai vectơ

a



và

b



biết rằng

. .

a b a b

 

   

A.

90



 

. B.

0



 

. C.

45



 

. D.

180



 

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Lời giải

Chọn D

Ta có

. .

a b a b

 

   





cos ; .

a b a b a b

  

     









cos ; 1 ; 180

a b a b

     

   

Câu 34: Trong mặt phẳng tọa độ

Oxy

, cho hai vectơ





3; 4

u



và





8; 6

v 



. Khẳng định nào sau đây là

đúng?

A.

u v

 

 

. B.

u



vuông góc với

v



.

C.

u v



 

. . D.

u



và

v



cùng phương.

Lời giải

Chọn B

Ta có





. 3. 8 4.6 0

u v

   

 

u v

 

 

.

Câu 35: Cho hàm số









0

f x ax b a

  

. Mệnh đề nào sau đây là đúng?

A. Hàm số đồng biến trên ;

b

a

 

 

 

 

. B. Hàm số đồng biến trên



khi

0

a



.

C. Hàm số đồng biến trên ;

b

a

 

 

 

 

. D. Hàm số đồng biến trên



khi

0

a



.

Lời giải

Chọn D

Theo định nghĩa Sgk, hàm số









0

f x ax b a

  

đồng biến trên



khi

0

a



.

II. PHẦN TỰ LUẬN

Câu 36: Cho parabol





P

2

y x mx n

  

(

,

m n

là tham số). Xác định

,

m n

để





P

có đỉnh





2; 1

I



Lời giải

Ta có

2 4

2.1

I

m

x m

     

Thay

1

x

 

,

4

m

 

vào phương trình:

2

y x mx n

  

.

Ta có





2

1 2 2. 4

n

    

3

n

 

.

Vậy

1

m

 

,

3

n



.

Câu 37: (1 điểm) Trong mặt phẳng Oxy, cho 2 điểm





1;3

B  và





3;1

C

a) Tính độ dài vectơ

BC



.

b) Tìm tọa độ điểm A sao cho tam giác ABC vuông cân tại A?

Lời giải

a) Ta có:

   

2

4; 2 4 2 20 2 5

BC BC       

 

b) Gọi





;

A A

A x y

là điểm cần tìm

Gọi I là trung điểm BC





1;2

I .

 

1; 2

4; 2

A A

IA x y

BC



  





 









ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Tam giác ABC vuông cân tại

 





 

2

0;0

. 0

2;4

1 12

A A

A

y x

A

IA BC

A

xBC IA











 

  



 

 













 

.

Vậy có 2 điểm thỏa mãn là:





0;0

A hoặc





2;4

A .

Câu 38: (1 điểm) Giải hệ phương trình

3 3 2 2

2 2

0

2 9 2 1 4

x y x y xy x y

x y y x x



     





      





.

Lời giải









3 3 2 2 2 2

0 1 0

x y x y xy x y x y x y x y

            

Khi đó

2 2 2 2

2 9 2 1 4 2 9 2 1 4

x y y x x x x x x x

              

2 2

2 9 3 2 1 1 0

2 2

x x

x x x x

   

          

   

   

2 2

7 7

2 2

4 4

0

2 9 3 2 1 1

2 2

x x x x

x x

x x x x

 

  

   

       

   

   

2

2 2

0; 0

7 1 1

2 0

8 8

4

;

2 9 3 2 1 1

7 7

2 2

x y

x x

x y

x x x x

 

 



 

 



 

    

 



   

 

 

 

       

   



 

   

 

.

Thay vào hệ phương trình thấy thỏa mãn.

Vậy hệ có nghiệm là

0; 0

8 8

;

7 7

x y

 





 



.

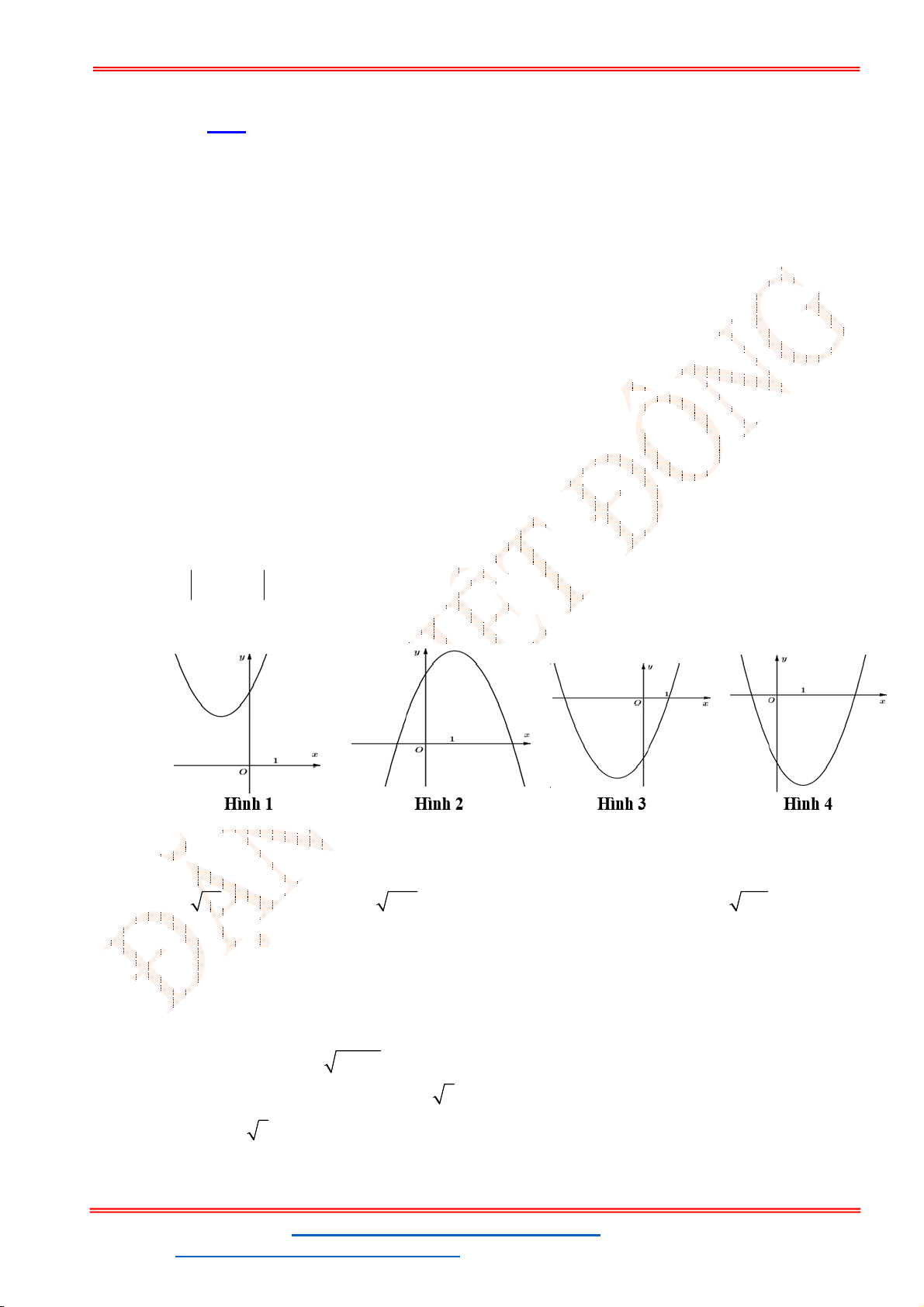
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 8 Môn Toán – Lớp 10

(Th

ời gian l

àm bài 90 phút)

Không k

ể thời gian phát đề

Câu 1. Gọi

1 2

,

m m

là hai giá trị khác nhau của

m

để phương trình

2 2

3 3 4 0

x x m m

    

có hai

nghiệm phân biệt

1 2

,

x x

sao cho

1 2

2



x x

. Tính

1 2 1 2

 

m m m m

A.

4

. B.

3

. C.

6

. D.

5

.

Câu 2. Trong các phát biểu sau, có bao nhiêu phát biểu là mệnh đề đúng?

a) Số

2

là số nguyên tố.

b) Số

2018

3 1



chia hết cho

2

.

c) Đường chéo của hình bình hành là đường phân giác của góc ở đỉnh nằm trên đường chéo của

hình bình hành đó.

d) Mọi hình chữ nhật đều có chiều dài lớn hơn chiều rộng.

e) Một số chia hết cho

28

thì chia hết cho

8

.

A.

2

. B.

4

. C.

1

. D.

3

.

Câu 3. Gọi

0

m

là giá trị của

m

để phương trình









2 1 0

m x x

   

vô nghiệm. Khẳng nào sau đây

đúng ?

A.

0

m



. B.





0

2;0 .

m   C.





0

0;1 .

m  . D.





0

1;1 .

m  

Câu 4. Cho hình vuông

ABCD

tâm

O

. Đẳng thức nào sau đây sai?

A.

 

 

BO DO AC

. B.  

  

DA OC OB

. C. 

 

AB DC

. D.  

  

AO DO CD

.

Câu 5. Đồ thị nào sau đây là đồ thị của hàm số

2

2 3

  

y x x

?

A. Hình 2. B. Hình 4. C. Hình 3. D. Hình 1.

Câu 6. Cho tam giác



ABC

có



0

9, 8, 60

  AB BC ABC . Tính độ dài đoạn

AC

A.

73

. B.

217

. C.

8

D.

113

.

Câu 7. Cho hàm số

2

4 1

y x x

  

.Chọn khẳng định đúng trong các khẳng định sau:

A. Hàm số nghịch biến trên khoảng





;3

 . B. Hàm số đồng biến trên khoảng





3;



.

C. Hàm số có giá trị nhỏ nhất là

3



. D. Đồ thị hàm số đi qua điểm





0;1

A .

Câu 8. Cho hàm số

 





2

3 2 khi 1 2

4 khi 2

x x

f x

x x



   







 





. Tính giá trị





3

f

.

A. không xác định. B.





3 5

f 

hoặc





3 3

f



.

C.





3 5

f 

. D.





3 3

f



.

Câu 9. Tính tổng bình phương các nghiệm của phương trình

2

2 13 0

x x

  

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

30

. B.

4

. C.

22



. D.

28

.

Câu 10. Gọi

0

m

là giá trị của

m

để hệ phương trình

3

2

9

x y m

mx y m

 







  





có vô số nghiệm. Khi đó :

A.

0

1

1;

2

m

 

  

 

 

. B.

0

1

0;

2

m

 



 

 

. C.

0

1

;2

2

m

 



 

 

. D.

0

1

;0

2

m

 

 

 

 

.

Câu 11. Hệ phương trình

3

2019

x y x

y x y



 





 





có số nghiệm là:

A.

4

. B.

6

. C.

1

. D.

3

.

Câu 12. Số nghiệm của phương trình

2

1 2

x x

  

là :

A.

0

. B.

2

. C.

3

. D.

1

.

Câu 13. Tập xác định của hàm số

1

4

y x

x

  



là

A.





1;4

. B.





1;4

. C.





1;4

. D.





1;4

.

Câu 14. Cho



ABC

có







1;2

A ,





0;3

B ,







5; 2

C . Tìm tọa độ chân đường cao hạ từ đỉnh

A

của



ABC

.

A.





0;3

. B.





0; 3



. C.





3;0

. D.





3;0



.

Câu 15. Cho các đường thẳng sau:

1

3

: 2

3

d y x

 

;

2

1

: 1

3

d y x

 

;

3

: 1 2

3

d y x

 

   

 

 

;

4

3

: 1

3

d y x

 

. Khẳng định nào đúng trong các khẳng định sau?

A.

2 3 4

, ,

d d d

song song với nhau. B.

2

d

và

4

d

song song với nhau.

C.

1

d

và

4

d

vuông góc với nhau. D.

2

d

và

3

d

song song với nhau.

Câu 16. Số nghiệm của phương trình





2

3 2 3

0

1

x x x

x

  





là

A.

2

. B.

1

. C.

3

. D.

0

.

Câu 17. Có bao nhiêu giá trị nguyên của

m

để đường thẳng

3

y mx

 

không có điểm chung với

Parabol

2

1

y x





?

A.

6

. B.

9

. C.

7

. D.

8

.

Câu 18. Tìm tất cả các giá trị của tham số

m

để phương trình





2

0

3

x m x m

x

  





có nghiệm.

A.





; 1

m





 

. B.





1;m



 



. C.





1;m

  

. D. m





.

Câu 19. Chọn khẳng định sai trong các khẳng định sau:

A. Hàm số

 

2

1

y x

 

là hàm số chẵn. B. Hàm số

3

y x



là hàm số lẻ.

C. Hàm số

2

2 2

y x x

  

xác định trên



. D. Hàm số

2

1

y x

 

là hàm số chẵn..

Câu 20. Phương trình

3 2 5

x x

  

có hai nghiệm

1 2

,

x x

. Tính

1 2

x x



.

A.

14

3



. B.

28

3



. C.

7

3

. D.

14

3

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 21. Cho





3;4

A ;





2;1

B  ;





0;5

C . Tính độ dài trung tuyến

AM

của

ABC



.

A.

13

. B.

5

. C.

4

D.

17

.

Câu 22. Số giá trị nguyên của

m

để phương trình

2

4 1

x m

  

có bốn nghiệm phân biệt là

A.

4

. B.

2

. C.

3

. D.

5

.

Câu 23. Cho tam giác

ABC

vuông cân tại

A

,

AB a



. Tính độ dài vectơ 4

AB AC



 

.

A.

20

a

. B.

5

a

. C.

17

a

. D.

17

a

.

Câu 24. Cho phương trình

  

1 5 3 1 5

x x x x m

      

. Có tất cả bao nhiêu giá trị nguyên của

m

để phương trình trên có nghiệm?

A.

6

. B.

8

. C.

7

. D. vô số

Câu 25. Biết phương trình

4 2 2

3 1 0

x mx m

   

có bốn nghiệm phân biệt

1 2 2 4

, , ,

x x x x

. Tính

1 2 3 4 1 2 3 4

M x x x x x x x x

     được kết quả là:

A.

2

1

M m

  

. B.

3

M m

 

. C.

3

M m



. D.

2

1

M m

 

.

Câu 26. Tìm

,

a b

để đồ thị hàm số

y ax b

 

đi qua hai điểm





1; 2

A



,





3;5

B  .

A.

7 1

;

4 4

a b

 

. B.

7 1

;

4 4

a b

   

.

C.

1 7

;

4 4

a b

   

. D.

1 4

;

7 7

a b

   

.

Câu 27. Tìm tất cả các giá trị của tham số

m

để phương trình





2

2 2

m m x mx x m

      nghiệm

đúng với x

 



.

A.

2

m



. B.

2

m

 

. C.

1

m



. D.

1

m

 

.

Câu 28. Biết phương trình

2

1 3 3 1

x x x

    

có hai nghiệm

1

x

,

2

x

. Tính giá trị biểu thức









1 2

1 1

x x

 

.

A.

0

. B.

1

. C.

2

. D.

3

.

Câu 29. Xác định hàm số

2

y ax bx c

  

biết đồ thị của hàm số cắt trục tung tại điểm có tung độ là

3



và giá trị nhỏ nhất của hàm số là

25

8

 tại

1

4

x



.

A.

2

2 3

y x x

   

. B.

2

1

. 3

2

y x x

  

. C.

2

2 3

y x x

  

. D.

2

2 3

y x x

  

.

Câu 30. Cho các tập hợp:

A



{cam, táo, mít, dừa},

B



{cam, táo },

C



{dừa, ổi, cam, táo, xoài}. Tìm

tập hợp





\

A B C



.

A. {cam, táo}. B. {mít}. C. {mít, dừa}. D. {dừa}.

Câu 31. Hệ phương trình

2

1

2 2 2 0

x y

x x y

 





   



có số nghiệm là

A.

1

. B.

2

. C.

4

. D.

0

.

Câu 32. Tìm tất cả các giá trị của tham số

m

để phương trình





2

2 2 4 0

x m x m

    

có hai nghiệm

phân biệt

A.

6

m



. B.

6

m



. C.

6

m



. D.

m



.

Câu 33. Hệ phương trình

2

2 2

2

2 9

x xy

x xy y



 





  





có nghiệm là





0 0

;

x y

thỏa

0

1

x



. Tính

0 0

x y



.

A.

5

. B.

3

. C.

1

. D.

4

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 34. Cho

4

a b

 

 

,

2

a





,

3

b





. Tính

a b



 

.

A.

3

. B.

10

. C.

12

. D.

2

.

Câu 35. Đầu năm học, thầy chủ nhiệm phát phiếu điều tra sở thích về ba môn Văn, Sử, Địa. Biết rằng

mỗi bạn đều thích ít nhất một trong ba môn đó. Kết quả là: có

4

bạn thích học ba môn, có

9

bạn thích Văn và Sử, có

5

bạn thích Sử và Địa, có

11

bạn thích văn và địa, có

24

bạn thích

môn Văn, có

19

bạn thích Sử và có

22

bạn thích Địa. Hỏi có bao nhiêu bạn không thích Địa?

A.

21

. B.

23

. C.

24

. D.

22

.

Câu 36. Cho





1;4

M ,





1;3

N  ,





0;6

P . Gọi





;

Q a b

là điểm thõa mãn

NPMQ

là hình bình hành.

Tổng

a b



bằng:

A.

1

. B.

0

. C.

2



. D.

1



.

Câu 37. Cho

ABC



có



5, 40 , 60

AB A B

   

. Độ dài

BC

gần nhất với kết quả nào?

A.

3,8.

B.

3,7

. C.

3,5

. D.

3,1

.

Câu 38. Cho

ABC



đều,

6

AB



và

M

là trung điểm của

.

BC

Tính tích vô hướng

.

AB MA

 

bằng

A.

27



. B.

27

. C.

18

. D.

18



.

Câu 39. Cho

(0;3), (4;0), ( 2; 5)

A B C

 

. Tính

. .

AB BC

 

A.

16

. B.

9

. C.

10



. D.

9



.

Câu 40. Cho hai véctơ

a



,

b



khác véctơ-không thỏa mãn

1

.

2

a b a b

 

   

. Góc giữa hai véctơ

a



,

b



là:

A.

60



. B.

120



. C.

150



. D.

30



.

Câu 41. Tìm tất cả các giá trị của tham số

m

để hàm số









1 2

y m x m

    đồng biến trên



.

A.

1

m



. B.

1

m



. C.

1

m



. D.

1

m



.

Câu 42. Cho tam giác đều

ABC

, gọi

D

là điểm thỏa mãn

2

DC BD



 

. Gọi

R

,

r

lần lượt là bán kính

đường tròn ngoại tiếp và nội tiếp tam giác

ADC

. Tính tỉ số

R

r

.

A.

7 5 7

9



. B.

5 7 7

9



. C.

7 5 5

9



. D.

5

2

.

Câu 43. Phương trình

2

2 1 2 1 2

x x x x x

       

có số nghiệm là

A.

1

. B.

3

. C.

2

. D.

0

.

Câu 44. Cho tam giác

ABC

có

2

AB



,

3

AC



,

ˆ

60

A

 

. Tính độ dài đường phân giác trong góc

A

của tam giác

ABC

.

A.

12

5

. B.

6 2

5

. C.

6 3

5

. D.

6

5

.

Câu 45. Tính diện tích tam giác

ABC

biết

3

AB



,

5

BC



,

6

CA



.

A.

8

. B.

48

. C.

6

. D.

56

.

Câu 46. Cho

ABC



có

3, 5

AB BC

 

và độ dài trung tuyến

13

BM  . Tính độ dài

AC

.

A.

9

2

. B.

11

. C.

4

. D.

10

.

Câu 47. Cho

ABC



vuông ở

A

, biết



30 , 3

C AB

  

. Tính độ dài đường trung tuyến

AM

.

A.

4

. B.

3

. C.

5

2

. D.

7

2

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 48. Tìm tất cả các giá trị của ham số

m

để phương trình









2 2

1 1 3 0

m x m x

    

có hai

nghiệm trái dấu

A.

1

m



. B.

0

m



. C.

0

m



. D.

1

m



.

Câu 49. Cho hàm số

2

2 8 khi 2

2 12 khi 2

x x x

y

x x



  





 



. Gọi

M

,

m

lần lượt là giá trị lớn nhất và giá trị nhỏ

nhất của hàm số khi





1;4

x  . Tính

M m



.

A.

14



. B.

13



. C.

4



. D.

9



.

Câu 50. Biết hệ phương trình

2 4

2 3

y x xy

 





 



có nghiệm





0 0

;

x y

với

0

x



. Tỉ số

0

y

x

bằng:

A.

2

. B.

1

2

. C.

1



. D.

1

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG HDG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 8 Môn Toán – Lớp 10

(Thời gian làm bài 90 phút)

Không k

ể thời gian phát đề

Câu 1. Gọi

1 2

,

m m

là hai giá trị khác nhau của

m

để phương trình

2 2

3 3 4 0

x x m m

    

có hai

nghiệm phân biệt

1 2

,

x x

sao cho

1 2

2



x x

. Tính

1 2 1 2

 

m m m m

A.

4

. B.

3

. C.

6

. D.

5

.

Lời giải

Chọn D

Tập xác định

D





.

Ta có

 





2

2 2

3 4 3 4 4 12 7

m m m m

         

Phương trình có hai nghiệm phân biệt

2

0 4 12 7 0

       

m m

Với điều kiện trên, phương trình có hai nghiệm phân biệt

1 2

,

x x

Theo hệ thức Vi-ét ta có





 

1 2

2

1 2

3 1

3 4 2

x x

x x m m

 





  





Khi đó

1 2

2

x x

 nên thay vào (1):

2 2 1

3 3 1 2

x x x

    

Thay

2 1

1 2

x x

  

vào (3):





 

2 2

1

2 3 4 3 2 0

2

m tm

m m m m

m tm



       









Vậy

1 2 1 2

1 2 1.2 5.

m m m m

     

Câu 2. Trong các phát biểu sau, có bao nhiêu phát biểu là mệnh đề đúng?

a) Số

2

là số nguyên tố.

b) Số

2018

3 1



chia hết cho

2

.

c) Đường chéo của hình bình hành là đường phân giác của góc ở đỉnh nằm trên đường chéo của

hình bình hành đó.

d) Mọi hình chữ nhật đều có chiều dài lớn hơn chiều rộng.

e) Một số chia hết cho

28

thì chia hết cho

8

.

A.

2

. B.

4

. C.

1

. D.

3

.

Lời giải

Chọn A

Ta có “Số

2

là số nguyên tố” là mệnh đề đúng.

“Số

2018

3 1



chia hết cho

2

” là mệnh đề đúng.

“Đường chéo của hình bình hành là đường phân giác của góc ở đỉnh nằm trên đường chéo của

hình bình hành đó” là mệnh đề sai.

“Mọi hình chữ nhật đều có chiều dài lớn hơn chiều rộng” là mệnh đề sai vì trường hợp đặc biệt

là hình vuông.

“Một số chia hết cho

28

thì chia hết cho

8

” là mệnh đề sai, vì

28 28;28



không chia hết cho

8

.

Vậy có hai phát biểu là mệnh đề đúng.

Câu 3. Gọi

0

m

là giá trị của

m

để phương trình









2 1 0

m x x

   

vô nghiệm. Khẳng nào sau đây

đúng ?

A.

0

m



. B.





0

2;0 .

m   C.





0

0;1 .

m  . D.





0

1;1 .

m  

Lời giải

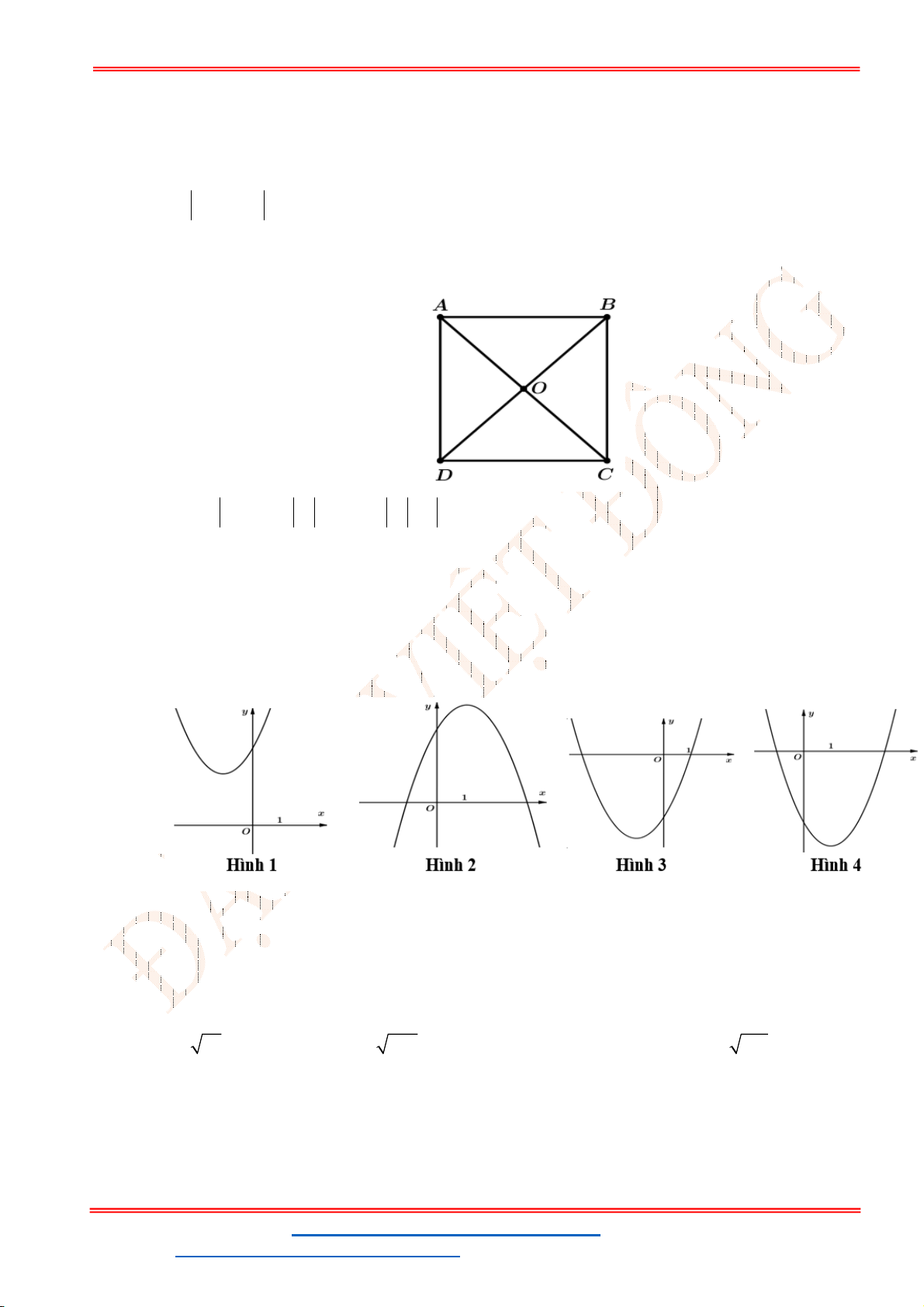
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Chọn B

Phương trình

















2 1 0 1 1 0 1

m x x m x       

Phương trình (1) vô nghiệm khi

1 0 1

m m

    

Câu 4. Cho hình vuông

ABCD

tâm

O

. Đẳng thức nào sau đây sai?

A.

 

 

BO DO AC

. B.  

  

DA OC OB

. C. 

 

AB DC

. D.  

  

AO DO CD

.

Lời giải

Chọn D

Ta có:

     

    

BO DO BO OD BD BD AC

suy ra đáp án A đúng.

    

     

DA OC DA AC DO OB

suy ra đáp án B đúng.







 









 

AB DC

suy ra đáp án C đúng.

    

     

AO DO AO OB AB DC

suy ra đáp án D sai.

Câu 5. Đồ thị nào sau đây là đồ thị của hàm số

2

2 3

  

y x x

?

A. Hình 2. B. Hình 4. C. Hình 3. D. Hình 1.

Lời giải

Chọn B

Hàm số

2

2 3

  

y x x

có hệ số

1 0

 

a

và có trục đối xứng

1



x

. Do đó chọn Hình 4.

Câu 6. Cho tam giác



ABC

có



0

9, 8, 60

  AB BC ABC . Tính độ dài đoạn

AC

A.

73

. B.

217

. C.

8

D.

113

.

Lời giải

Chọn A

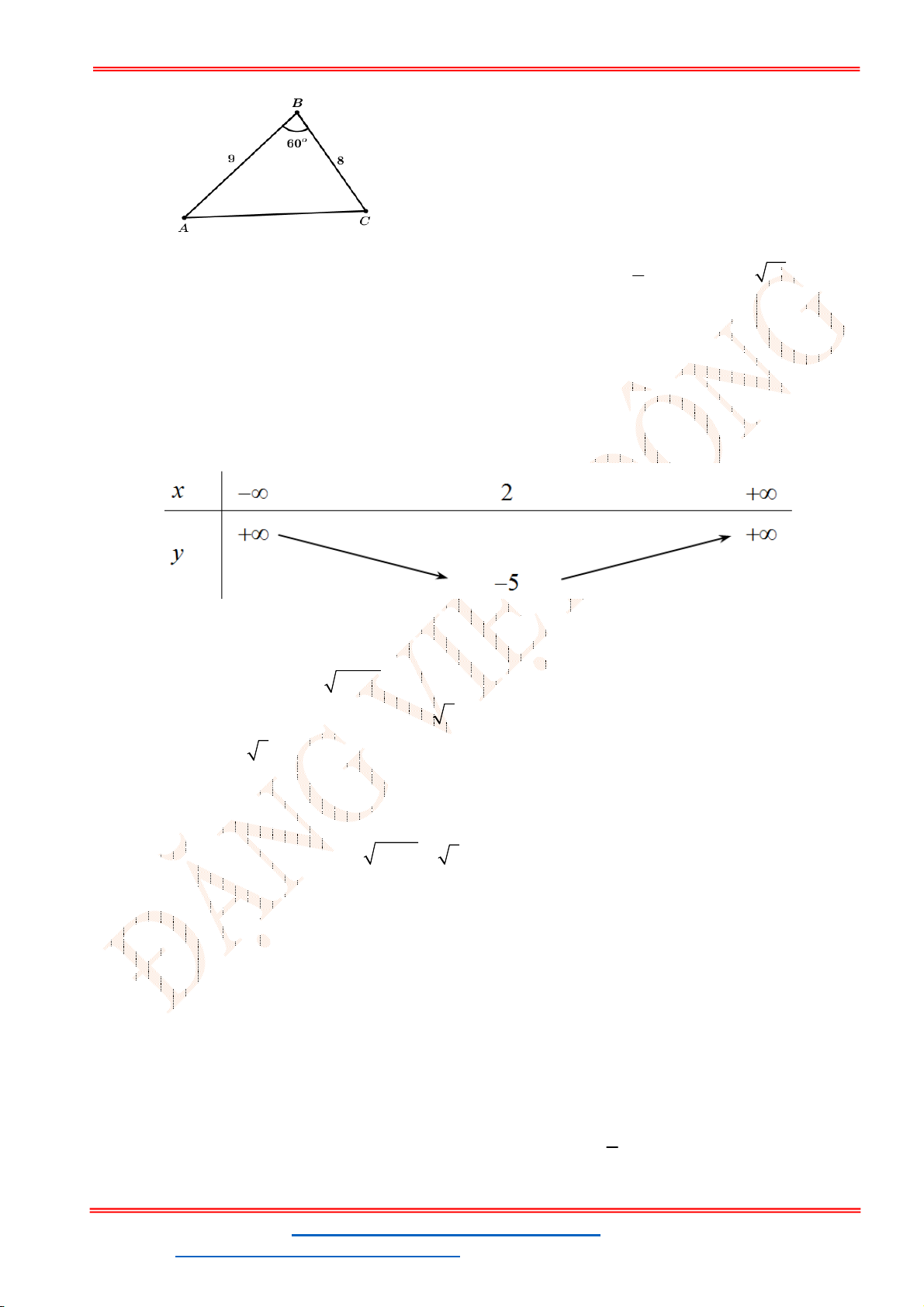
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Ta có:



2 2 2 2 2

1

2 . .cos 8 9 2.9.8. 73 73

2

        AC AB BC AB BC ABC AC

Câu 7. Cho hàm số

2

4 1

y x x

  

.Chọn khẳng định đúng trong các khẳng định sau:

A. Hàm số nghịch biến trên khoảng





;3

 . B. Hàm số đồng biến trên khoảng





3;



.

C. Hàm số có giá trị nhỏ nhất là

3



. D. Đồ thị hàm số đi qua điểm





0;1

A .

Lời giải

Chọn B

* Dựa vào BBT hàm số đồng biến trên khoảng





3;



.

Câu 8. Cho hàm số

 





2

3 2 khi 1 2

4 khi 2

x x

f x

x x



   







 





. Tính giá trị





3

f

.

A. không xác định. B.





3 5

f 

hoặc





3 3

f



.

C.





3 5

f 

. D.





3 3

f



.

Lời giải

Chọn C

Với

3 2

x

 

nên

 

2

3 3 4 5

f    .

Câu 9. Tính tổng bình phương các nghiệm của phương trình

2

2 13 0

x x

  

.

A.

30

. B.

4

. C.

22



. D.

28

.

Lời giải

Chọn A

Ta thấy

0

ac



nên phương trình luôn có hai nghiệm phân biệt. Theo Viette ta có

1 2

2

13

x x

 





 



.

   

2

2 2 2

1 2 1 2 1 2

2 2 2 13 30

x x x x x x

       

.

Câu 10. Gọi

0

m

là giá trị của

m

để hệ phương trình

3

2

9

x y m

mx y m

 







  





có vô số nghiệm. Khi đó :

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

0

1

1;

2

m

 

  

 

 

. B.

0

1

0;

2

m

 



 

 

. C.

0

1

;2

2

m

 



 

 

. D.

0

1

;0

2

m

 

 

 

 

.

Lời giải

Chọn B

Từ phương trình đầu, ta có

3

x m y

 

. Thay vào phương trình còn lại, ta được :

 

2

3

9

m m y y m

    

 

2

3 1 0

9

m y m m

     

.

Hệ có vô số nghiệm khi và chỉ khi

2

1

3

3 1 0

1

2

3

0

3

9

2

3

m

m m

m







  



 



  



 



  

 



















.

Câu 11. Hệ phương trình

3

2019

x y x

y x y



 





 





có số nghiệm là:

A.

4

. B.

6

. C.

1

. D.

3

.

Lời giải

Chọn D





 

3

2019 1

2019 2

x y x

y x y



 





 





Trừ vế theo vế, ta được:













3 3 2 2

2019 2020 0

x y x y x y x y x xy y

          

2 2

2020

x y

x xy y









  



.

Cộng vế theo vế, ta được :

















3 3 2 2

2019 2020 0

x y x y x y x y x xy y x y

           

2 2

0

2020

x y

x xy y

 







  



.

Với

0

x y





  



 



(nhận).

Với

2 2

2 505

2020

2 505

x

y

x xy y

x y

x

y

















 

 













  









 











(nhận).

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Với

2 2

2 505

2020

2 505

x

y

x xy y

x y

x

y















 

 

  









 



  



















(loại).

Với

2 2

2020 0

2 0

0

2020

x xy y x

xy

y

x xy y



   





  









 







.

Với

0 2 505

x y    (loại).

Với

0 2 505

y x    (loại).

Câu 12. Số nghiệm của phương trình

2

1 2

x x

  

là :

A.

0

. B.

2

. C.

3

. D.

1

.

Lời giải

Chọn A

Ta có

 

2

1 1

13

1 2 1 2

2 2

1 1

1 2

13

2 2

x

x l

x x x x

x x

x l















  





      

 



 

   









  







.

Vậy phương trình vô nghiệm.

Câu 13. Tập xác định của hàm số

1

4

y x

x

  



là

A.





1;4

. B.





1;4

. C.





1;4

. D.





1;4

.

Lời giải

Chọn D

Hàm số

1

4

y x

x

  



các định khi và chỉ khi

1 0 1

4 0 4

x x

  

 



 

  

 

.

Vậy tập xác định của hàm số là





1;4

D  .

Câu 14. Cho



ABC

có







1;2

A ,





0;3

B ,







5; 2

C . Tìm tọa độ chân đường cao hạ từ đỉnh

A

của



ABC

.

A.





0;3

. B.





0; 3



. C.





3;0

. D.





3;0



.

Lời giải

Chọn A

Gọi





;

H x y

là tọa độ chân đường cao hạ từ

A

.

Ta có:

AH BC











. 0 5. 1 5 2 0 3

AH BC x y x y

          

 

,





1

.

H BC



nên

BH



và

BC



cùng phương

3

5 5

x y



    







2

Từ





1

và





2

suy ra

0; 3

x y

 

. Vậy





0;3

H .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 15. Cho các đường thẳng sau:

1

3

: 2

3

d y x

 

;

2

1

: 1

3

d y x

 

;

3

: 1 2

3

d y x

 

   

 

 

;

4

3

: 1

3

d y x

 

. Khẳng định nào đúng trong các khẳng định sau?

A.

2 3 4

, ,

d d d

song song với nhau. B.

2

d

và

4

d

song song với nhau.

C.

1

d

và

4

d

vuông góc với nhau. D.

2

d

và

3

d

song song với nhau.

Lời giải

Chọn B

Ta có các đường thẳng được viết lại như sau:

1

: 3 2

d y x

 

;

2

1

: 1

3

d y x

 

;

3

1

: 1

3

d y x

 

;

4

3

: 1

3

d y x

 

. Từ đó suy ra

2

d

và

3

d

trùng nhau;

2

d

và

4

d

song song với nhau;

3

d

và

4

d

song song với nhau.

Câu 16. Số nghiệm của phương trình





2

3 2 3

0

1

x x x

x

  





là

A.

2

. B.

1

. C.

3

. D.

0

.

Lời giải

Chọn B





2

3 2 3

0

1

x x x

x

  









1

Đk:

3

x



Khi đó

 

2

1

3 2 0

2

3 0

3

1

x

x x

x









  



  



 









Kết hợp điều kiện ta có tập nghiệm của phương trình là:





3

S



.

Câu 17. Có bao nhiêu giá trị nguyên của

m

để đường thẳng

3

y mx

 

không có điểm chung với

Parabol

2

1

y x





?

A.

6

. B.

9

. C.

7

. D.

8

.

Lời giải

Chọn C

Phương trình hoành độ giao điểm:

2

1 3

xx m

  

2

4 0

x mx

   





1

Để đường thẳng và Parabol không có điểm chung thì phương trình





1

vô nghiệm

Hay

2

16 0 4 4

mm

     





3; 2; 1;0;1;2;3

m

    

.

Câu 18. Tìm tất cả các giá trị của tham số

m

để phương trình





2

0

3

x m x m

x

  





có nghiệm.

A.





; 1

m





 

. B.





1;m



 



. C.





1;m

  

. D. m





.

Lời giải

Chọn B





2

0

3

x m x m

x

  









1

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Đk:

3

x







1

3

x m

 

Để





1

có nghiệm thì 3 3

1

m m









.

Câu 19. Chọn khẳng định sai trong các khẳng định sau:

A. Hàm số

 

2

1

y x

 

là hàm số chẵn. B. Hàm số

3

y x



là hàm số lẻ.

C. Hàm số

2

2 2

y x x

  

xác định trên



. D. Hàm số

2

1

y x

 

là hàm số chẵn..

Lời giải

Chọn A

Xét hàm số

   

2

1

y f x x

  

TXĐ:

D





.

,

x D x D

   

.

Với

   









   

1 1

1, 1 0, 1 4

1 1

f f

x f f

f f

 



    



  





Do đó

 

2

1

y x

 

không phải hàm số chẵn, cũng không phải hàm số lẻ.

Câu 20. Phương trình

3 2 5

x x

  

có hai nghiệm

1 2

,

x x

. Tính

1 2

x x



.

A.

14

3



. B.

28

3



. C.

7

3

. D.

14

3

.

Lời giải

Chọn D

8

3 2 5

3

3 2 5

2

x x

x

x x

x



  







    



   







Tổng hai nghiệm

1 2

8 14

2

3 3

x x   

Câu 21. Cho





3;4

A ;





2;1

B  ;





0;5

C . Tính độ dài trung tuyến

AM

của

ABC



.

A.

13

. B.

5

. C.

4

D.

17

.

Lời giải

Chọn D

M

là trung điểm

BC

suy ra





1;3

M 

   

2 2

1 3 3 4 17

AM      

Câu 22. Số giá trị nguyên của

m

để phương trình

2

4 1

x m

  

có bốn nghiệm phân biệt là

A.

4

. B.

2

. C.

3

. D.

5

.

Lời giải

Chọn C

Ta có đồ thị hàm số

2

4

y x

 

như sau:

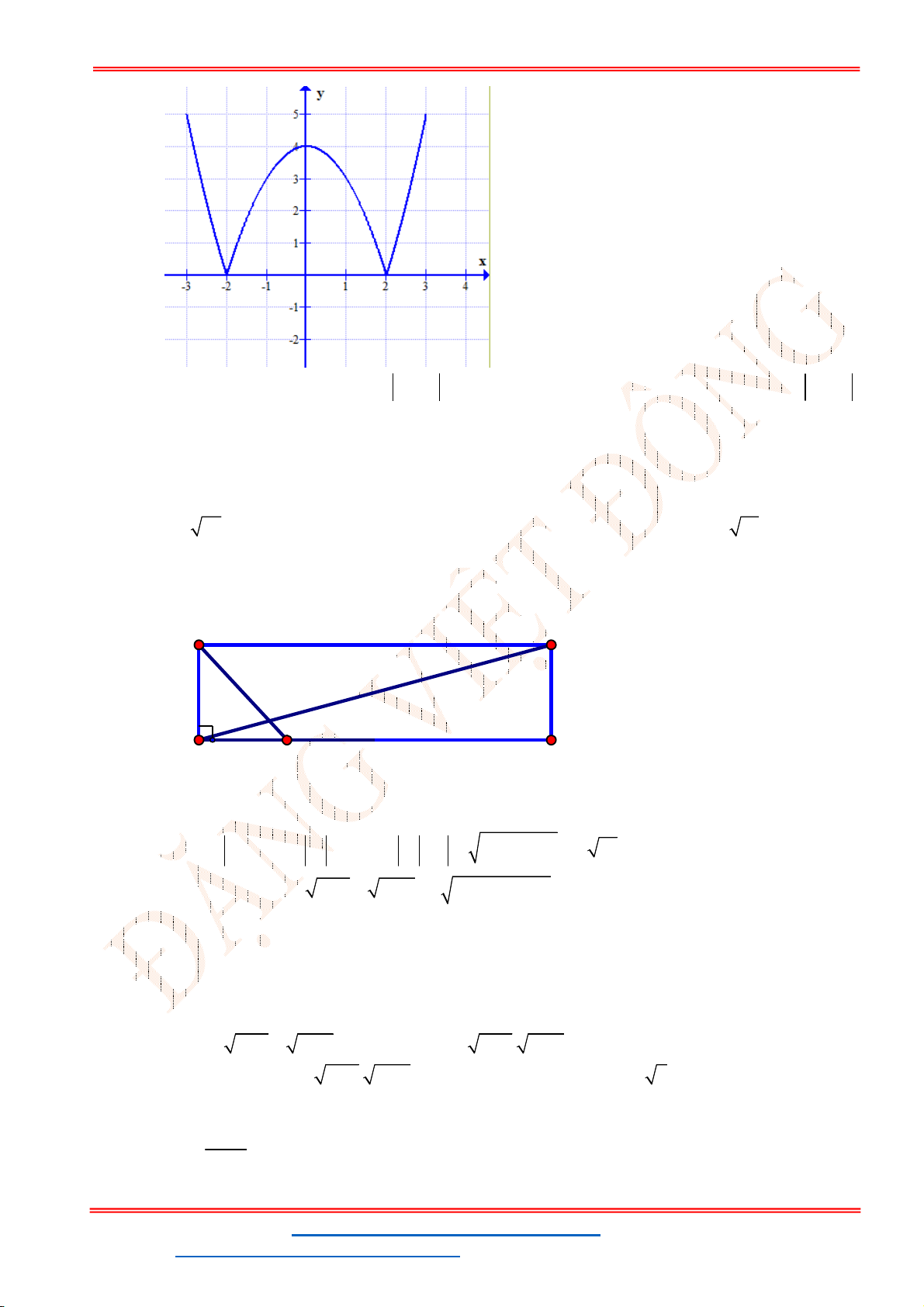
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Số nghiệm của phương trình

2

4 1

x m

  

là số giao điểm của đồ thị hàm số

2

4

y x

 

và

đường thẳng

1

y m

 

.

Từ đồ thị ta suy ra phương trình trên có bốn nghiệm phân biệt khi và chỉ khi

0 1 4 1 3

m m

      

. Vậy có

3

giá trị nguyên của

m

thỏa mãn.

Câu 23. Cho tam giác

ABC

vuông cân tại

A

,

AB a



. Tính độ dài vectơ 4

AB AC



 

.

A.

20

a

. B.

5

a

. C.

17

a

. D.

17

a

.

Lời giải

Chọn D

a

C

E

A

D

B

Dựng các điểm

,

D E

sao cho 4

AD AC



 

và tứ giác

ABED

là hình bình hành.

Khi đó

 

2

4 4 17

AB AC AB AD AE a a a      

    

.

Câu 24. Cho phương trình

  

1 5 3 1 5

x x x x m

      

. Có tất cả bao nhiêu giá trị nguyên của

m

để phương trình trên có nghiệm?

A.

6

. B.

8

. C.

7

. D. vô số

Lời giải

Chọn C

Đặt 1 5

t x x

   

. Ta có

2

4 2. 1. 5 4 2

t x x t

      

.

Mặt khác









2

4 2. 1. 5 2 1 5 6 6

t x x x x t            .

Phương trình đã cho trở thành:

2

4

3. 3 2 12 2

2

t

t m t t m



      .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Xét hàm số





2

3 2 12

f t t t

  

với

2; 6

t

 



 

.

Hàm số

f

đồng biến trên

2; 6

 

 

nên

   





 

2 6 4 6 2 6

f f t f f t     

.

Vậy phương trình đã cho có nghiệm khi và chỉ khi

4 6 2 6

m  

Do

m

nguyên nên





4;5;...;10

m .

Câu 25. Biết phương trình

4 2 2

3 1 0

x mx m

   

có bốn nghiệm phân biệt

1 2 2 4

, , ,

x x x x

. Tính

1 2 3 4 1 2 3 4

M x x x x x x x x

     được kết quả là:

A.

2

1

M m

  

. B.

3

M m

 

. C.

3

M m



. D.

2

1

M m

 

.

Lời giải

Chọn D

Đặt





2

, 0

t x t

 

Phương trình trở thành

3 2

3 1 0

t mt m

   

Phương trình

4 2 2

3 1 0

x mx m

   

có bốn nghiệm phân biệt

1 2 2 4

, , ,

x x x x

khi phương trình

3 2

3 1 0

t mt m

   

có hai nghiêm dương phân biệt

1 2

,

t t

2

0 5 4 0

2

0 3 0

5

0

1 0

m

S m m

P

m



   





     

 

 



 



.

Khi đó ta có

1 1 2 1 3 2 4 2

; ; ;

x t x t x t x t

      .

Do đó

2

1 2

0 . 1

M t t m

   

.

Câu 26. Tìm

,

a b

để đồ thị hàm số

y ax b

 

đi qua hai điểm





1; 2

A



,





3;5

B  .

A.

7 1

;

4 4

a b

 

. B.

7 1

;

4 4

a b

   

.

C.

1 7

;

4 4

a b

   

. D.

1 4

;

7 7

a b

   

.

Lời giải

Chọn B

Đồ thị hàm số

y ax b

 

đi qua hai điểm





1; 2

A



,





3;5

B  nên ta có hệ phương trình

7

2

4

3 5 1

4

a

a b

b



 



  







 

  





 





.

Câu 27. Tìm tất cả các giá trị của tham số

m

để phương trình





2

2 2

m m x mx x m

      nghiệm

đúng với x

 



.

A.

2

m



. B.

2

m

 

. C.

1

m



. D.

1

m

 

.

Lời giải

Chọn C









2 2

2 2 1 2 2 0

m m x mx x m m x m

          

Để phương trình nghiệm đúng với x

 



thì

2

1 0

1

2 2 0

m



 

 



 



.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 28. Biết phương trình

2

1 3 3 1

x x x

    

có hai nghiệm

1

x

,

2

x

. Tính giá trị biểu thức









1 2

1 1

x x

 

.

A.

0

. B.

1

. C.

2

. D.

3

.

Lời giải

Chọn A

Điều kiện xác định:

1

x



.

Phương trình tương đương với





1 1 3 1. 1

x x x

    

 

1 0

1 3 1

x



 







  



1

4 2 3 1

x









  



1

3 2 3

x









 



Vậy ta có









1 2

1 1 0

x x

  

.

Câu 29. Xác định hàm số

2

y ax bx c

  

biết đồ thị của hàm số cắt trục tung tại điểm có tung độ là

3



và giá trị nhỏ nhất của hàm số là

25

8

 tại

1

4

x



.

A.

2

2 3

y x x

   

. B.

2

1

. 3

2

y x x

  

. C.

2

2 3

y x x

  

. D.

2

2 3

y x x

  

.

Lời giải

Chọn C

+ Đồ thị cắt trục tung tại điểm





0;

A c

3

c

  

.

+ Giá trị nhỏ nhất của hàm số là

25

8

 tại

1

4

x



nên đỉnh của đồ thị hàm số là

1 25

;

4 8

I

 



 

 

Suy ra

1

2 4 0 2

2 4

1 1 25 4 2 1

. 3

16 4 8

b

a b a

a

a b b

a b









  

 



 

  

    

 



   





Vậy hàm số cần tìm là

2

2 3

y x x

  

.

Câu 30. Cho các tập hợp:

A



{cam, táo, mít, dừa},

B



{cam, táo },

C



{dừa, ổi, cam, táo, xoài}. Tìm

tập hợp





\

A B C



.

A. {cam, táo}. B. {mít}. C. {mít, dừa}. D. {dừa}.

Lời giải

Chọn D

Ta có





\

A B C

 

{dừa}.

Câu 31. Hệ phương trình

2

1

2 2 2 0

x y

x x y

 





   



có số nghiệm là

A.

1

. B.

2

. C.

4

. D.

0

.

Lời giải

Chọn A

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

2

1

2 2 2 0

x y

x x y

 





   



 

2

1

2

1

2 2 1 2 0

y x

x

y

x x x

 









 

 

 

    





.

Câu 32. Tìm tất cả các giá trị của tham số

m

để phương trình





2

2 2 4 0

x m x m

    

có hai nghiệm

phân biệt

A.

6

m



. B.

6

m



. C.

6

m



. D.

m



.

Lời giải

Chọn C

Phương trình





2

2 2 4 0

x m x m

    

có

     

2 2

2

2 8 4 12 36 6 0,

m m m m m m

           

Phương trình





2

2 2 4 0

x m x m

    

có hai nghiệm phân biệt

0 6

m

    

.

Câu 33. Hệ phương trình

2

2 2

2

2 9

x xy

x xy y



 





  





có nghiệm là





0 0

;

x y

thỏa

0

1

x



. Tính

0 0

x y



.

A.

5

. B.

3

. C.

1

. D.

4

Lời giải

Chọn B

2

2 2

2

2 9

x xy

x xy y



 





  













2 2 2

9 2 2

x xy x xy y

    

2 2

5 11 2 0

x xy y

   

2

1

5

x y















.

Với

2

x y



thay vào phương trình đầu trong hệ ta được

2 2

4 2 2

y y

 

1

y

  

. Vậy trong

trường hợp này ta được hai nghiệm









2;1 , 2; 1

 

.

Với

5

y x



thay vào phương trình đầu trong hệ ta được

2 2

5 2

x x

 

vô nghiệm. Vậy trong

trường hợp này ta không thu được nghiệm.

Với điều kiện

0

1

x



thì nghiệm cần tìm là





2;1

.

Câu 34. Cho

4

a b

 

 

,

2

a





,

3

b





. Tính

a b



 

.

A.

3

. B.

10

. C.

12

. D.

2

.

Lời giải

Chọn B





2

4 16

a b a b

    

   

2 2

2 16 4 2 9 16 2 3

a ab b ab ab

         

       

2

2 2

2 2 3 3 10

a b a ab b

       

     

10

a b  

 

.

Câu 35. Đầu năm học, thầy chủ nhiệm phát phiếu điều tra sở thích về ba môn Văn, Sử, Địa. Biết rằng

mỗi bạn đều thích ít nhất một trong ba môn đó. Kết quả là: có

4

bạn thích học ba môn, có

9

bạn thích Văn và Sử, có

5

bạn thích Sử và Địa, có

11

bạn thích văn và địa, có

24

bạn thích

môn Văn, có

19

bạn thích Sử và có

22

bạn thích Địa. Hỏi có bao nhiêu bạn không thích Địa?

A.

21

. B.

23

. C.

24

. D.

22

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Lời giải

Chọn D

Gọi

, ,

a b c

lần luợt là số học sinh chỉ thích học một môn Văn, hoặc Sử, hoặc Địa.

Gọi

, ,

x y z

lần lượt là số học sinh thích học đúng hai môn Văn và Sử, Sử và Địa, Văn và Địa.

Ta có:

4 24 5

4 19 1

4 22 7

4 9 8

4 5 9

4 11 10

a x z x

b x y y

c y z z

x a

y b

z c

    

 

 

    

 

    



 

  

 

  

 

  

 

Vậy số học sinh không thích học môn Địa là:

8 9 5 22

a b x

     

.

Câu 36. Cho





1;4

M ,





1;3

N  ,





0;6

P . Gọi





;

Q a b

là điểm thõa mãn

NPMQ

là hình bình hành.

Tổng

a b



bằng:

A.

1

. B.

0

. C.

2



. D.

1



.

Lời giải

Chọn A

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

NPMQ

là hình bình hành thì

PM NQ



 





1; 2

PM

 







1; 3

NQ a b

  



1 1 0

3 2 1

a a

b b

  

 

 

 

   

 

Vậy

0 1 1

a b

   

.

Câu 37. Cho

ABC



có



5, 40 , 60

AB A B

   

. Độ dài

BC

gần nhất với kết quả nào?

A.

3,8.

B.

3,7

. C.

3,5

. D.

3,1

.

Lời giải

Chọn D







180 40 60 80 .

C

       

Áp đụng định lý sin vào

ABC



:

5

.sin .sin40 3,26.

sin sin sin sin80

AB BC AB

BC A

C A C

     



Câu 38. Cho

ABC



đều,

6

AB



và

M

là trung điểm của

.

BC

Tính tích vô hướng

.

AB MA

 

bằng

A.

27



. B.

27

. C.

18

. D.

18



.

Lời giải

Chọn A

M

A

B

C

ABC



là tam giác đều nên

AM

là trung tuyến đồng thời là phân giác nên:



30 .

BAM

 

Ta có:

6 3

. . . .cos( , ) 6. .cos30 27.

2

AB MA AB AM AB AM AB AM

        

   

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 39. Cho

(0;3), (4;0), ( 2; 5)

A B C

 

. Tính

. .

AB BC

 

A.

16

. B.

9

. C.

10



. D.

9



.

Lời giải

Chọn D

Ta có:









4; 3 , 6; 5

AB BC

    

 

.

Do đó:













. 4. 6 3 . 5 9.

AB BC

      

 

Câu 40. Cho hai véctơ

a



,

b



khác véctơ-không thỏa mãn

1

.

2

a b a b

 

   

. Góc giữa hai véctơ

a



,

b



là:

A.

60



. B.

120



. C.

150



. D.

30



.

Lời giải

Chọn A





. .cos ,

a b a b a b



     





. os ,

a b c a b

 

   

1

2

a b

 

 





1

cos ,

2

a b

 

 





, 60

a b

  

 

.

Câu 41. Tìm tất cả các giá trị của tham số

m

để hàm số









1 2

y m x m

    đồng biến trên



.

A.

1

m



. B.

1

m



. C.

1

m



. D.

1

m



.

Lời giải

Chọn C













1 2 1 2

y m x m m x m

       . Hàm số đồng biến trên



khi và chỉ khi

1 0 1

m m

   

.

Câu 42. Cho tam giác đều

ABC

, gọi

D

là điểm thỏa mãn

2

DC BD



 

. Gọi

R

,

r

lần lượt là bán kính

đường tròn ngoại tiếp và nội tiếp tam giác

ADC

. Tính tỉ số

R

r

.

A.

7 5 7

9



. B.

5 7 7

9



. C.

7 5 5

9



. D.

5

2

.

Lời giải

Chọn A

Giả sử cạnh tam giác đều

ABC

là

a

,





0

a



.

2 2

2 2 3 3

.

3 3 4 6

ACD ABC

a a

S S  

 

;

2 2

3 3

a

CD BC  .

2 2 2

2 . .cos60

AD AC CD AC CD

   

2

2 2 1 7

2 . .

3 3 2 9

a a a

a a

 

   

 

 

7

3

a

AD  .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 20

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

2

7 2

. .

. . 21

3 3

4. 9

3

4.

6

ACD

a a

a

AD CD AC a

R

S

a

  



;

 

7 2

5 7

3 3

2 2 6

a a

a

AD CD AC

p

 



 

   .

 

2

3

6

5 7

6

ACD

a

S a

r

p

a

  





;

7 5 7

9

R

r



 .

Câu 43. Phương trình

2

2 1 2 1 2

x x x x x

       

có số nghiệm là

A.

1

. B.

3

. C.

2

. D.

0

.

Lời giải

Chọn D

Điều kiện xác định

2 0 2

x x

   

.

Với điều kiện trên, phương trình đã cho tương đương với

2

1 2 1 (1)

x x x    .

2 2 2

0

(1) 1 4 4 1 3 3 0 3 ( 1) 0

1

x

x x x x x x x x

x





            







Do

0

x



,

1

x



không thỏa mãn điều kiện bài toán nên phương trình đã cho vô nghiệm.

Câu 44. Cho tam giác

ABC

có

2

AB



,

3

AC



,

ˆ

60

A

 

. Tính độ dài đường phân giác trong góc

A

của tam giác

ABC

.

A.

12

5

. B.

6 2

5

. C.

6 3

5

. D.

6

5

.

Lời giải

Chọn C

Giả sử đường phân giác trong góc

A

của tam giác

ABC

cắt cạnh BC tại điểm

D

.

Với

S

là kí hiệu diện tích tam giác ta có

 

1 1 1

. .sin . sin . .sin

2 2 2 2 2

2 . .sin .cos .sin .

2 2 2

.

2cos . (1)

2

ABC ADB ADC

S S S

A A

AB AC A AD AB AD AC

A A A

AB AC AD AB AC

A AB AC

AD

AB AC

 

 



Áp dụng công thức

(1)

với

2

AB



,

3

AC



,

ˆ

60

A

 

ta được

6 3

5

AD  .

Câu 45. Tính diện tích tam giác

ABC

biết

3

AB



,

5

BC



,

6

CA



.

A.

8

. B.

48

. C.

6

. D.

56

.

Lời giải

Chọn D

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 21

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Đặt

AB c



,

BC a



,

CA b



và

p

là kí hiệu nửa chu vi tam giác

ABC

,

2

a b c

p

 

 .

Với

S

là kí hiệu diện tích tam giác ta có

( )( )( )

ABC

S p p a p b p c

   

(công thức Heron).

Áp dụng công thức trên với

7

p



,

5

a



,

6

b



,

3

c



ta được

56

ABC

S  .

Câu 46. Cho

ABC



có

3, 5

AB BC

 

và độ dài trung tuyến

13

BM  . Tính độ dài

AC

.

A.

9

2

. B.

11

. C.

4

. D.

10

.

Lời giải

Chọn C

Từ công thức tính độ dài đường trung tuyến của tam giác ta có:





2 2 2 2

4 2

BM AB BC AC

  





 

2 2 2

2 4 2 9 25 4.13 4

AC AB BC BM

       

.

Câu 47. Cho

ABC



vuông ở

A

, biết



30 , 3

C AB

  

. Tính độ dài đường trung tuyến

AM

.

A.

4

. B.

3

. C.

5

2

. D.

7

2

.

Lời giải

Chọn B

+)

ABC



vuông ở

A

nên ta có:

3

6

1

sin30

2

AB

BC

  



.

+)

AM

là trung tuyến kẻ từ đỉnh góc vuông

3

2

BC

AM

  

.

Câu 48. Tìm tất cả các giá trị của ham số

m

để phương trình









2 2

1 1 3 0

m x m x

    

có hai

nghiệm trái dấu

A.

1

m



. B.

0

m



. C.

0

m



. D.

1

m



.

Lời giải

Chọn A

Phương trình có 2 nghiệm trái dấu









0 1 3 0 1 0 1

ac m m m

          

.

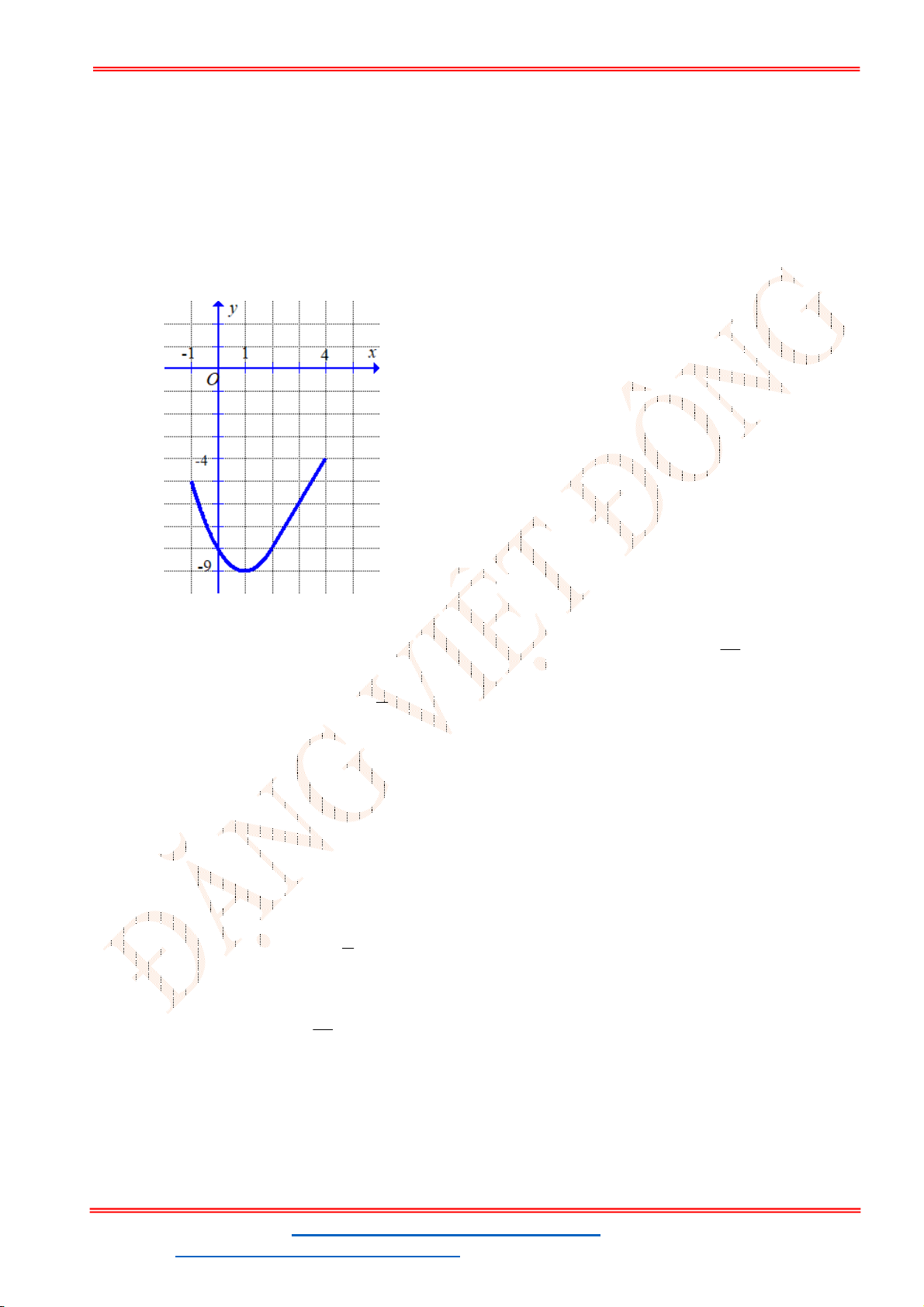
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 22

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 49. Cho hàm số

2

2 8 khi 2

2 12 khi 2

x x x

y

x x



  





 



. Gọi

M

,

m

lần lượt là giá trị lớn nhất và giá trị nhỏ

nhất của hàm số khi





1;4

x  . Tính

M m



.

A.

14



. B.

13



. C.

4



. D.

9



.

Lời giải

Chọn B

Ta có đồ thị của hàm số khi





1;4

x  như hình vẽ dưới đây:

Dựa vào đồ thị ta có

4

M

 

,

9

m

 

13

M m

   

.

Câu 50. Biết hệ phương trình

2 4

2 3

y x xy

 





 



có nghiệm





0 0

;

x y

với

0

x



. Tỉ số

0

y

x

bằng:

A.

2

. B.

1

2

. C.

1



. D.

1

.

Lời giải

Chọn A

Ta có:

2 4

2 3

y x xy

 





 



3 6 12

8 4 12

y x xy

 







 



2 4

5 10 0

y x xy

y x

 







  



2 4

2

y x xy

y x

 











2 2 4 .2

2

x x x x

y x

 











2

4 8

2

x x

y x













0

1

2

1

x

y

x

y

 





































.

Vì

0

x



nên tỉ số

0

2

y

x



.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 9 Môn Toán – Lớp 10

(Th

ời gian l

àm bài 90 phút)

Không k

ể thời gian phát đề

I. TRẮC NGHIỆM

Câu 1. Có bao nhiêu số nguyên

m

để phương trình

2 3

4 10 4

x mx x x

   

có

4

nghiệm

phân biệt.

A.

7

.

B.

8

. C.

6

.

D.

5

Câu 2. Tính độ dài hai cạnh góc vuông của một tam giác vuông, biết rằng khi ta tăng độ dài mỗi cạnh

đó

2

cm

thì diện tích của tam giác tăng

2

17

cm

, còn khi ta giảm độ dài cạnh này

3

cm

và cạnh kia

1

cm

thì

diện tích tam giác giảm

2

11

cm

.

A.

5

cm

và

6

cm

B.

2

cm

và

3

cm

. C.

4

cm

và

7

cm

.

D.

5

cm

và

10

cm

.

Câu 3. Cho các phương trình có tham số

m

sau:





2 2

3 1 0 1

m x m  









2

2 1 0 2

m x m   









2

3 3

m m x x   









2

1 2 1 4

m x x  

Phương trình luôn có nghiệm duy nhất vói mọi giá trị m là:

A. Phương trình (1). B. Phương trình (3). C. Phương trình (2).

D.

Phương trình (4).

Câu 4. Tìm tập hợp tất cả các giá trị m để phương trình





2 2

3 1 2 2 0

x m x m m

    

có hai nghiệm

phân biệt

1 2

;

x x

thỏa mãn

1 2

2 .

x x

 

A.

1 3

m

 

.

B.

2 4

m

 

. C.

2

m



.

D.

1 3

m

  

.

Câu 5: Trong mặt phẳng tọa độ

Oxy

, cho hai vectơ

4 6

a i j

 

  

và

3 7

b i j

 

  

. Tính tích vô hướng

.

a b

 

.

A.

. 43

ab



 

. B.

. 30

a b

 

 

. C.

. 3

a b



 

. D.

. 30

a b



 

.

Câu 6: Có bao nhiêu giá trị nguyên của tham số

m

thuộc đoạn





10;10

 để phương trình

2

4 0

x x m

  

vô nghiệm?

A.

7

. B.

19

. C.

6

. D.

10

.

Câu 7: Có bao nhiêu giá trị nguyên của tham số

m

thuộc đoạn





5;5

 để phương trình

2

1 1

x m x

x x

 



 

có nghiệm?

A.

8

. B.

11

. C.

9

. D.

10

.

Câu 8: Cho phương trình

0

mx n

 

, với

,

m n

là các số thực đã cho. Tìm mệnh đề đúng trong các

mệnh đề sau:

A. Nếu

0

m



thì tập nghiệm của phương trình là

S

 

.

B. Nếu

0

m



thì tập nghiệm của phương trình là

n

S

m

 

 

 

 

.

C. Nếu

0

n



thì tập nghiệm của phương trình là

n

S

m

 

 

 

 

.

D. Nếu

0

m



thì tập nghiệm của phương trình là

S





.

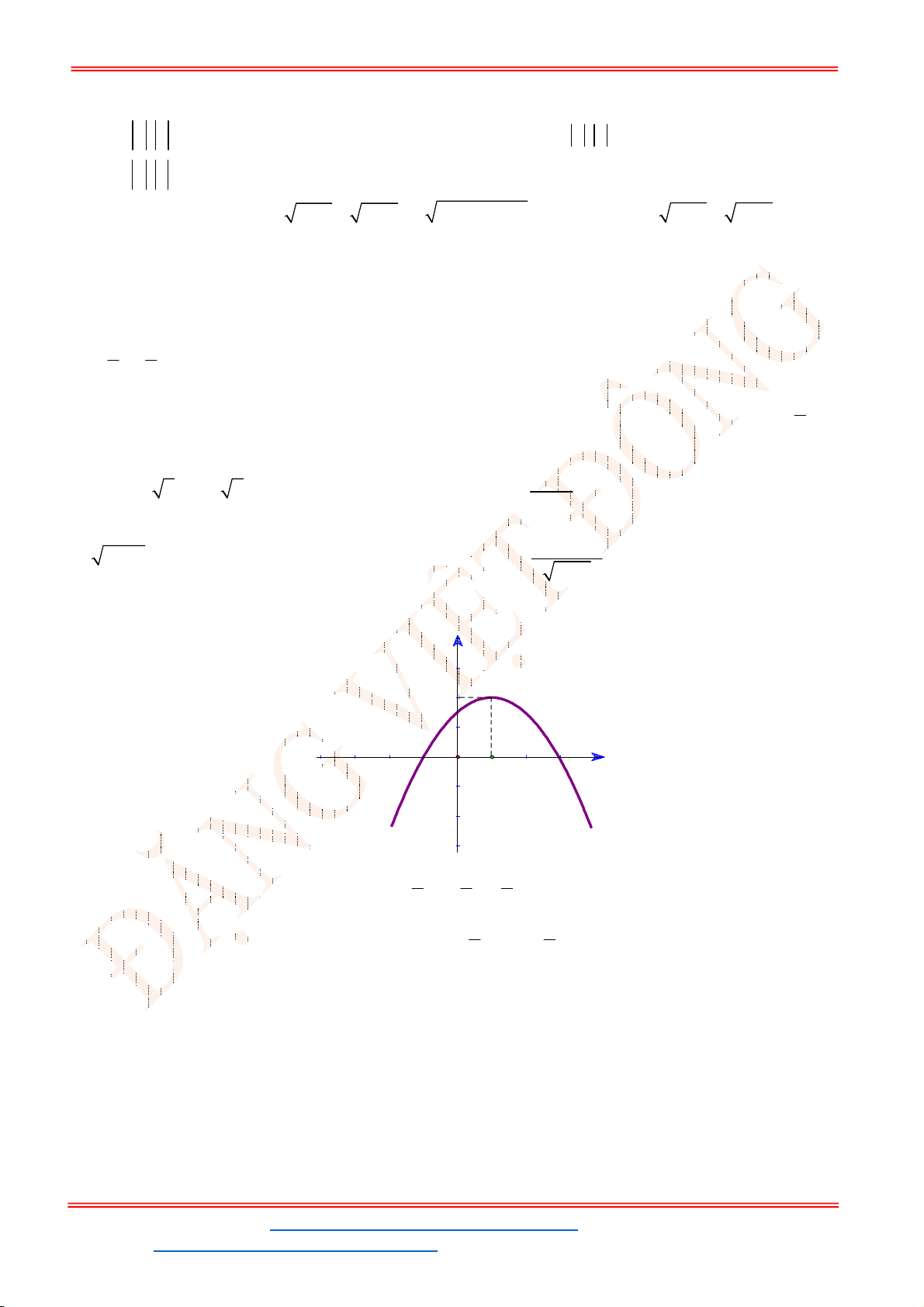
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 9: Cho hai vectơ

a



và

b



đều khác vectơ

0



. Xác định mệnh đề đúng.

A.





. . cos ,

a b a b a b



     

. B.





. . cos ,

a b a b a b



   

.

C.





. . sin ,

a b a b a b



     

. D.





. . .cos ,

a b a b a b



   

.

Câu 10: Cho phương trình

2

5 4 2 20 3

x x x x

       

. Nếu đặt





5 4 0

t x x t

    

thì

ta được phương trình nào sau đây?

A.

2

12 0

t t

   

. B.

2

2 15 0

t t

  

. C.

2

6 0

t t

  

. D.

2

12 0

t t

  

.

Câu 11: Hàm số bậc hai nào sau đây có đồ thị hàm số là parabol đi qua điểm





1; 9

A  và có tọa độ đỉnh

là

3 7

;

2 2

I

 



 

 

?

A.

2

2 6 1

y x x

  

. B.

2

3 5

y x x

  

. C.

2

2 6 13

y x x

  

. D.

2

5

3

4

y x x

  

.

Câu 12: Trong các phương trình sau, phương trình nào có nghiệm?

A. 2 3

x x x x

    . B.

3 1

1

x





.

C.

3 1 4

x

  

. D.

2

0

2

x x

x

 





.

Câu 13: Parabol ở hình vẽ bên là đồ thị của hàm số nào sau đây?

x

y

O

1

2

3

-1

A.

2

2 3

y x x

   

. B.

2

1 1 3

4 2 4

y x x

   

.

C.

2

2 3

y x x

  

. D.

2

1 3

2 2

y x x

   

.

Câu 14: Trong mặt phẳng tọa độ

Oxy

, cho véctơ





9;3

a 



. Véctơ nào sau đây không vuông góc với

vecto

a



?

A.





2

2; 6

v

 



. B.





1

1; 3

v

 



. C.





3

1;3

v 



. D.





4

1;3

v  



.

Câu 15: Hệ phương trình

1 0

2 7 0

x y

  





  



có nghiệm là:

A.





2;0

. B.





2; 3

 

. C.





2;3

. D.





3; 2



.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 16: Cho

 

2

sin cos 1

cot sin .cos

P

 

  

 





. Xác định mệnh đề đúng

A.

2

2tan

P



 . B.

2

2sin

P



 . C.

2

2cot

P



 . D.

2

2cos

P



 .

Câu 17: Cho parabol









2 2

: 2 1 2

P y x m x m m

     và đường thẳng

: 2

d y x

 

. Gọi

S

là tập hợp

các giá trị thực của tham số

m

để đường thẳng

d

cắt





P

tại hai điểm phân biệt

A

và

B

thoả mãn

OA OB



( với

O

là gốc toạ độ). Tính tổng tất cả các phần tử của

S

.

A.

1

. B.

6

. C.

2

. D.

4



.

Câu 18: Trong mặt phẳng cho hình vuông

ABCD

cạnh

a

. Với

M

là một điểm bất kì trên cạnh

BC

,

tính tích vô hướng

.

MA AB

 

.

A.

2

a

 . B.

2

a

. C.

2

a



. D.

2

a

.

Câu 19: Cho hàm số

2

y ax bx c

  

với

0

a



, có đồ thị là parabol





P

. Toạ độ đỉnh của





P

là

A. ;

4 2

b

I

a a



 

 

 

. B. ;

4

b

I

a a

 

 

 

 

. C. ;

2 4

b

I

a a

 

 

 

 

. D. ;

4 4

b

I

a a

 

 

 

 

.

Câu 20: Biết rằng trước đây

2

năm thì tuổi cha gấp

7

lần tuổi con và

3

năm sau nữa thì tuổi cha chỉ

còn gấp

4

lần tuổi con. Tuổi của cha và con hiện nay là

A.

28

và

4

. B.

32

và

8

. C.

37

và

7

. D.

38

và

8

.

Câu 21: Tính tổng các nghiệm của phương trình





2

2 3 16 4

x x x

   

.

A.

1



. B.

5

. C.

3

. D.

1

.

Câu 22: Cho tam giác

ABC

đều. Tập hợp tất cả các điểm

M

sao cho

. .

MC MA MC MB



   

là ?

A. Đường trung trực của đoạn

AB

. B. Đường tròn đường kính

AB

.

C. Trung điểm của đoạn

AB

. D. Điểm

C

.

Câu 23: Hệ phương trình nào sau đây vô nghiệm?

A.

3

x y

 





   



. B.

1

2 0

x y

 





 



. C.

0

2 2 6

x y

  





  



D.

4 3 1

2 0

x y

 





 



.

Câu 24: Cho phương trình

2

0

x bx c

  

với

b

,

c

là các số thực đã cho. Mệnh đề nào sau đây sai?

A. Phương trình có nghiệm kép khi

2

4

b c



.

B. Phương trình có hai nghiệm trái dấu khi

0

c



.

C. Phương trình có hai nghiệm phân biệt khi

2

4 0

b c

 

.

D. Phương trình có hai nghiệm cùng dấu khi

0

bc



.

Câu 25: Tìm số nghiệm của phương trình

2

5 4 4

x x x

   

.

A.

3

. B.

1

. C.

2

. D.

0

.

Câu 26: Giá trị của

tan30 cot30

  

bằng bao nhiêu?

A.

1 3

3



. B.

4

3

. C.

2

3

. D.

2

.

Câu 27: Cho hai vectơ

,

a b

 

đều khác vectơ

0



. Xác định góc



giữa hai vectơ

a



và

b



khi

a b a b

  

   

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

45



 

. B.

0



 

. C.

90



 

. D.

180



 

.

Câu 28: Cho hệ phương trình





2 2 1

1

m x my m

x y

   







  





(

m

là tham số).

Có bao nhiêu giá trị nguyên của tham số

m

để phương trình có nghiệm duy nhất





0 0

,

x y

và

0 0

,

x y

đều là

các số nguyên?

A.

4

. B.

0

. C.

2

. D.

1

.

Câu 29: Phương trình

2

4 1 0

mx x

  

có hai nghiệm phân biệt khi

A.

4

0

m











. B.

16

m

 

. C.

16

0

m











. D.

4

0

m

 









.

Câu 30: Cho phương trình













1 1 2 2 6 1

m m x x m     . Có bao nhiêu số nguyên

m

thuộc khoảng





10;10

 để phương trình





1

có nghiệm?

A.

18

. B.

17

. C.

19

. D.

20

.

Câu 31: Cho hai góc nhọn



và



trong đó

 



. Khẳng định nào sau đây là sai?

A.

sin sin

 



. B.

tan tan 0

 

 

. C.

cot cot

  

. D.

cos cos

 



.

Câu 32: Cho tam giác

ABC

với













2;3 , 1; 1 , 10; 3

A B C

  

. Điểm





;

M a b

nằm trên cạnh

BC

sao

cho

DE

có độ dài nhỏ nhất với

,

D E

lần lượt là hình chiếu vuông góc của

M

lên

,

AC AB

. Xác định

mệnh đề đúng.

A.

1

5

a b

  

. B.

1

5

a b

 

. C.

13

5

a b

 

. D.

13

5

a b

  

Câu 33. Trong các phương trình sau, phương trình nào tương đương với phương trình

2

4

x



?

A.

2

x



. B.

2

6 8 0

x x

  

. C.





2 2 0

x x

  

. D.





2

4 0

x x

 

.

Câu 34. Cho phương trình









2

1 : 4 4 2

m x m x

  

(

m

là tham số ). Tìm mệnh đề sai trong các mệnh

đề sau:

A. Khi

3

m



thì phương trình





1

có nghiệm duy nhất.

B. Khi

2

m

 

thì phương trình





1

vô nghiệm.

C. Khi

2

m



thì phương trình





1

có nghiệm duy nhất.

D. Khi

2

m



thì phương trình





1

có vô số nghiệm.

Câu 35. Giá trị lớn nhất

M

và giá trị nhỏ nhất

m

của hàm số

2

6 8

y x x

  

trên đoạn





1;4

là:

A.

1, 3

M m

  

. B.

3, 1

M m

 

. C.

0, 1

M m

  

. D.

3, 1

M m

  

.

II. TỰ LUẬN

Bài 1. Giải các phương trình sau:

a)

2

2 2 1 5

x x x

   

. b)

1 2 5 2

x x

  

.

Bài 2. Cho

tan 3



 

với

90 180



   

. Tính giá trị của

cos



.

Bài 3. Trong mặt phẳng với hệ trục tọa độ

Oxy

, cho điểm





1; 3

A



,





2;0

B  và





3;9

C  . Tính

côsin góc giữa hai vectơ

BA



và

BC



.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG HDG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 9 Môn Toán – Lớp 10

(Th

ời gian l

àm bài 90 phút)

Không k

ể thời gian phát đề

I. TRẮC NGHIỆM

Câu 1. Có bao nhiêu số nguyên

m

để phương trình

2 3

4 10 4

x mx x x

   

có

4

nghiệm phân biệt.

A.

7

.

B.

8

. C.

6

.

D.

5

Lời giải

Chọn B

+) Điều kiện của phươg trình :





3 2

4 0 4 0 0

x x x x x

      

.

+) Ta thấy

0

x



không là nghiệm của phương trình.

+) Nếu

0

x



thì phương trình tương đương

4 4

10x m x

x x

   

+) Đặt

2 2 2

4 4

2 4 0

t x t x x t x

x x

         

có

4

16

t

  

ta thấy

2

t



không thỏa

mãn bài toán

2

t

 

.

Khi đó phương trình đã cho trở thành :

2

10 (*)

t t m  . Yêu cầu bài toán tương đương với tìm

m

để phương trình (*) có hai nghiệm phân biệt

2

t



.

Xét hàm số





2

( ) 10 , 2

f t t t t

  

, ta có bảng biến thiên

Để phương trình (*) có hai nghiệm phân biệt

2

t



khi và chỉ khi đường thẳng

:

d y m



cắt đồ

thị hàm số

( )

y f t



tại hai điểm phân biệt. Dựa vào BBT ta có

25 16

m

   

mà





24, 23,...., 17

m m     



. Vậy có

8

giá trị nguyên

m

.

Câu 2. Tính độ dài hai cạnh góc vuông của một tam giác vuông, biết rằng khi ta tăng độ dài mỗi cạnh

đó

2

cm

thì diện tích của tam giác tăng

2

17

cm

, còn khi ta giảm độ dài cạnh này

3

cm

và cạnh

kia

1

cm

thì diện tích tam giác giảm

2

11

cm

.

A.

5

cm

và

6

cm

B.

2

cm

và

3

cm

. C.

4

cm

và

7

cm

.

D.

5

cm

và

10

cm

.

Lời giải

Chọn D

Gọi hai cạnh góc vuông của tam giác vuông là

,

a b

điều kiện

0, 0

a b

 

Khi đó diện tích tam giác vuông là

1

2

S ab



t

2

5



( )

f t

16



25





ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Theo bài ra ta có hệ phương trình:









  

2 2

1

17

5

2 2

10

3 1

1

11

2 2

a b

ab

b

a

a b

ab

 

 











 



 





 





.

Vậy hai cạnh góc vuông của tam giác vuông là

5

cm

và

10

cm

.

Câu 3. Cho các phương trình có tham số

m

sau:





2 2

3 1 0 1

m x m  









2

2 1 0 2

m x m   









2

3 3

m m x x   









2

1 2 1 4

m x x  

Phương trình luôn có nghiệm duy nhất vói mọi giá trị m là:

A. Phương trình (1). B. Phương trình (3). C. Phương trình (2).

D. Phương trình (4).

Lời giải

Chọn B

   

2 2

2

3

3 1 3

1

m m x x m m x x

m m

         

 

(vì

2

1 0,m m m

    



)

Câu 4. Tìm tập hợp tất cả các giá trị m để phương trình





2 2

3 1 2 2 0

x m x m m

    

có hai nghiệm

phân biệt

1 2

;

x x

thỏa mãn

1 2

2 .

x x

 

A.

1 3

m

 

.

B.

2 4

m

 

. C.

2

m



.

D.

1 3

m

  

.

Lời giải

Chọn A

Ta có

 





 

2 2

2

3 1 4 2 2 1 .

m m m m       Phương trình có hai nghiệm phân biệt

1 2

;

x x

khi

0 1.

m

    

Theo vi – ét :

2

1 2 1 2

3 1; 2 2

x x m x x m m

     .

Mặt khác:













 

1 2 1 2 1 2 1 2

2

2 1 1 0 2 4 0

2 2 2 3 1 4 0

2 8 6 0

1 3.

x x x x x x x x

m m m

m m

m

          

     

   

  

Câu 5: Trong mặt phẳng tọa độ

Oxy

, cho hai vectơ

4 6

a i j

 

  

và

3 7

b i j

 

  

. Tính tích vô hướng

.

a b

 

.

A.

. 43

ab



 

. B.

. 30

a b

 

 

. C.

. 3

a b



 

. D.

. 30

a b



 

.

Lời giải

Chọn B

Ta có:

   

4;6 ; 3; 7

a b

  

 

. Nên

. 4.3 6.7 30

a b

   

 

.

Câu 6: Có bao nhiêu giá trị nguyên của tham số

m

thuộc đoạn





10;10

 để phương trình

2

4 0

x x m

  

vô nghiệm?

A.

7

. B.

19

. C.

6

. D.

10

.

Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Chọn C

Phương trình

2

4 0

x x m

  

vô nghiệm khi và chỉ khi

2

0 2 0 4

m m



      

.

Mà

m

nguyên thuộc đoạn





10;10

 nên

5 10

m

  

có

6

giá trị

m

thỏa mãn.

Câu 7: Có bao nhiêu giá trị nguyên của tham số

m

thuộc đoạn





5;5

 để phương trình

2

1 1

x m x

x x

 



 

có nghiệm?

A.

8

. B.

11

. C.

9

. D.

10

.

Lời giải

Chọn C

Điều kiện:

1

x

 

.

       

2

. 1 1 . 2

1 1

x m x

x m x x x

x x

 

      

 





2 1

mx m   .

+) Nếu

0

m



thì phương trình vô nghiệm.

+) Nếu

0

m



thì phương trình





1

có nghiệm duy nhất.

Nên để phương trình đã cho có nghiệm thì phương trình





1

phải có nghiệm

1

x

 

2

1

2 1

m m m

m

m m m

  

 

    

 

    

 



.

Mà





5;5

m  nên





5; 4; 3; 2;1;2;3;4;5

m     . Vậy chọn C.

Câu 8: Cho phương trình

0

mx n

 

, với

,

m n

là các số thực đã cho. Tìm mệnh đề đúng trong các

mệnh đề sau:

A. Nếu

0

m



thì tập nghiệm của phương trình là

S

 

.

B. Nếu

0

m



thì tập nghiệm của phương trình là

n

S

m

 

 

 

 

.

C. Nếu

0

n



thì tập nghiệm của phương trình là

n

S

m

 

 

 

 

.

D. Nếu

0

m



thì tập nghiệm của phương trình là

S





.

Lời giải

Chọn B

Câu 9: Cho hai vectơ

a



và

b



đều khác vectơ

0



. Xác định mệnh đề đúng.

A.





. . cos ,

a b a b a b



     

. B.





. . cos ,

a b a b a b



   

.

C.





. . sin ,

a b a b a b



     

. D.





. . .cos ,

a b a b a b



   

.

Lời giải

Chọn A

Câu 10: Cho phương trình

2

5 4 2 20 3

x x x x

       

. Nếu đặt





5 4 0

t x x t

    

thì

ta được phương trình nào sau đây?

A.

2

12 0

t t

   

. B.

2

2 15 0

t t

  

. C.

2

6 0

t t

  

. D.

2

12 0

t t

  

.

Lời giải

Chọn D

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Đặt





5 4 0

t x x t

    

  

2

5 4 2 5 4

t x x x x

       

  

2 2

9 2 5 4 2 20

t x x x x

        

Phương trình đã cho trở thành:

2 2

9 3 12 0

t t t t

      

.

Câu 11: Hàm số bậc hai nào sau đây có đồ thị hàm số là parabol đi qua điểm





1; 9

A  và có tọa độ đỉnh

là

3 7

;

2 2

I

 



 

 

?

A.

2

2 6 1

y x x

  

. B.

2

3 5

y x x

  

. C.

2

2 6 13

y x x

  

. D.

2

5

3

4

y x x

  

.

Lời giải

Chọn A

Cách 1

Parabol có tọa độ đỉnh là

3 7

;

2 2

I

 



 

 

nên loại đáp án B và đáp án C.

Parabol đi qua điểm





1; 9

A  nên loại đáp án D

Vậy đáp án A đúng

Cách 2: Giả sử parabol có dạng





2

0

y ax bx c a

   

.

Parabol đi qua điểm





1; 9

A  và có tọa độ đỉnh là

3 7

;

2 2

I

 



 

 

nên ta có hệ

3

2 2

2

9 3 7

6

4 2 2

1

9

b

a

a b c b

c

a b c



 









 

      

 

 





  





.

Vậy

2

2 6 1

y x x

  

.

Câu 12: Trong các phương trình sau, phương trình nào có nghiệm?

A. 2 3

x x x x

    . B.

3 1

1

x





.

C.

3 1 4

x

  

. D.

2

0

2

x x

x

 





.

Lời giải

Chọn B

0

3 1 1

1

3 1

2

x

x x

x







    



 



.

Vậy phương trình

3 1

1

x





có nghiệm.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 13: Parabol ở hình vẽ bên là đồ thị của hàm số nào sau đây?

x

y

O

1

2

3

-1

A.

2

2 3

y x x

   

. B.

2

1 1 3

4 2 4

y x x

   

.

C.

2

2 3

y x x

  

. D.

2

1 3

2 2

y x x

   

.

Lời giải

Chọn D

Giả sử (P):

2

, ( 0)

y ax bx c a

   

Từ đồ thị hàm số ta xác định được Parabol có đỉnh





1;2

I và đồ thị đi qua hai điểm









1;0 , 3;0

A B . Do đó ta có hệ:

Ta có :

1

2

1

9 3 0

3

0

2

b

a

a b c

b

a b c

c

a b c







 



  

 

 

 

  

 



  







. Vậy có parabol:

2

1 3

2 2

y x x

   

.

Câu 14: Trong mặt phẳng tọa độ

Oxy

, cho véctơ





9;3

a 



. Véctơ nào sau đây không vuông góc với

vecto

a



?

A.





2

2; 6

v

 



. B.





1

1; 3

v

 



. C.





3

1;3

v 



. D.





4

1;3

v  



.

Lời giải

Chọn C

Ta có

3

. 9 9 18 0

v a

   

 

nên

3

v



không vuông góc với vecto

a



.

Câu 15: Hệ phương trình

1 0

2 7 0

x y

  





  



có nghiệm là:

A.





2;0

. B.





2; 3

 

. C.





2;3

. D.





3; 2



.

Lời giải

Chọn C

1 0 1 2

2 7 0 2 7 3

x y x y x

x y x y y

      

  

 

  

     

  

. Vậy hệ có nghiệm là

(2;3)

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 16: Cho

 

2

sin cos 1

cot sin .cos

P

 

  

 





. Xác định mệnh đề đúng

A.

2

2tan

P



 . B.

2

2sin

P



 . C.

2

2cot

P



 . D.

2

2cos

P



 .

Lời giải

Chọn A

 

2

sin cos 1

cot sin .cos

P

 

  

 





2 2

sin cos 2sin .cos 1

cos

sin .cos

sin

   



 



  





 

2

2sin .cos .sin

cos 1 sin

  

 





2

2sin

cos



 

2

2tan



.

Câu 17: Cho parabol









2 2

: 2 1 2

P y x m x m m

     và đường thẳng

: 2

d y x

 

. Gọi

S

là tập hợp

các giá trị thực của tham số

m

để đường thẳng

d

cắt





P

tại hai điểm phân biệt

A

và

B

thoả

mãn

OA OB



( với

O

là gốc toạ độ). Tính tổng tất cả các phần tử của

S

.

A.

1

. B.

6

. C.

2

. D.

4



.

Lời giải

Chọn D.

Phương trình hoành độ giao điểm của hai đường trên là





2 2 2 2

2 1 2 2 2 2 2 0

x m x m m x x mx m m

           

Điều kiện để hai đường có hai giao điểm là phương trình có

0 2 2 0 1

m m



       

(1).

Khi đó hoành độ của

A

và

B

là nghiệm của phương trình nên thoả mãn

1 2

2

1 2

2

. 2 2

x x m

x x m m

 





  



,

suy ra có









1 1 2 2

; 2 , ; 2

A x x B x x

 

.

Điều kiện

OA OB











1 2 1 2

. 2 . 2 0

x x x x

    

 

2

1 2 1 2

0

2 . 2 4 0 2 2 2 2 0

4

m

x x x x m m m

m





           



 



(2).

Từ (1) và (2) ta có





4;0

S   , nên tổng tất cả các phần tử của

S

là

4



.

Câu 18: Trong mặt phẳng cho hình vuông

ABCD

cạnh

a

. Với

M

là một điểm bất kì trên cạnh

BC

,

tính tích vô hướng

.

MA AB

 

.

A.

2

a

 . B.

2

a

. C.

2

a



. D.

2

a

.

Lời giải

Chọn C.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

C

B

D

A

M

Có

   

2

. . . . . .

BM AB

MA AB AM AB AB BM AB AB AB BM AB AB AB a



           

 

         

   

.

Câu 19: Cho hàm số

2

y ax bx c

  

với

0

a



, có đồ thị là parabol





P

. Toạ độ đỉnh của





P

là

A. ;

4 2

b

I

a a



 

 

 

. B. ;

4

b

I

a a

 

 

 

 

. C. ;

2 4

b

I

a a

 

 

 

 

. D. ;

4 4

b

I

a a

 

 

 

 

.

Lời giải

Chọn C.

Câu 20: Biết rằng trước đây

2

năm thì tuổi cha gấp

7

lần tuổi con và

3

năm sau nữa thì tuổi cha chỉ

còn gấp

4

lần tuổi con. Tuổi của cha và con hiện nay là

A.

28

và

4

. B.

32

và

8

. C.

37

và

7

. D.

38

và

8

.

Lời giải

Chọn C.

Gọi tuổi của cha và con hiện tại là

,

x y

với

, *

x y





Điều kiện bài toán tương đương với





 

2 7 2

7 12 37

4 9 7

3 4 3

x y

x y x

x y y

x y

  

   

 



 

  

  

  

 





.

Câu 21: Tính tổng các nghiệm của phương trình





2

2 3 16 4

x x x

   

.

A.

1



. B.

5

. C.

3

. D.

1

.

Lời giải

Chọn B

ĐK:

16

3

x   .

 

2

2 2

2

2 2

2 3 16 4

3 16 2

3 16 4 4 12 0

x x

x

x x

x x x

x x

x x x x x

 

 

 





 



 

 

      

 

 



   

 



 

      

 

 

 

 

2

3

x















: thỏa điều kiện.

Vậy tổng các nghiệm của phương trình bằng

5

.

Câu 22: Cho tam giác

ABC

đều. Tập hợp tất cả các điểm

M

sao cho

. .

MC MA MC MB



   

là ?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A. Đường trung trực của đoạn

AB

. B. Đường tròn đường kính

AB

.

C. Trung điểm của đoạn

AB

. D. Điểm

C

.

Lời giải

Chọn A





. . . . 0 0 . 0

MC MA MC MB MC MA MC MB MC MA MB MC BA

        

          

     

.

Suy ra tập hợp các điểm

M

là đường thẳng đi qua

C

và vuông góc với

AB

.

Vì tam giác

ABC

đều nên đó chính là đường trung trực của

AB

.

Câu 23: Hệ phương trình nào sau đây vô nghiệm?

A.

3

x y

 





   



. B.

1

2 0

x y

 





 



. C.

0

2 2 6

x y

  





  



D.

4 3 1

2 0

x y

 





 



.

Lời giải

Chọn C

Câu 24: Cho phương trình

2

0

x bx c

  

với

b

,

c

là các số thực đã cho. Mệnh đề nào sau đây sai?

A. Phương trình có nghiệm kép khi

2

4

b c



.

B. Phương trình có hai nghiệm trái dấu khi

0

c



.

C. Phương trình có hai nghiệm phân biệt khi

2

4 0

b c

 

.

D. Phương trình có hai nghiệm cùng dấu khi

0

bc



.

Lời giải

Chọn D

Ta có

2

4

b c

  

.

Phương trình có nghiệm kép khi

2

0 4

b c

   

.

Phương trình có hai nghiệm trái dấu khi

1. 0

c



.

Phương trình có hai nghiệm phân biệt khi

2

0 4 0

b c

   

.

Phương trình có hai nghiệm cùng dấu khi

2

0

4 0

0

b c

c



 



 



 



 

 











.

Câu 25: Tìm số nghiệm của phương trình

2

5 4 4

x x x

   

.

A.

3

. B.

1

. C.

2

. D.

0

.

Lời giải

Chọn A

Ta có

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

 

2

4

4 0

5 4 4

x

x x x x x x

x x x

 



 







     

   

 

   



 



    





4

0

2

x

 



 





 







  











 







 





Câu 26: Giá trị của

tan30 cot30

  

bằng bao nhiêu?

A.

1 3

3



. B.

4

3

. C.

2

3

. D.

2

.

Lời giải

Chọn B

Ta có

4

tan30 cot30

3

   

.

Câu 27: Cho hai vectơ

,

a b

 

đều khác vectơ

0



. Xác định góc



giữa hai vectơ

a



và

b



khi

a b a b

  

   

.

A.

45



 

. B.

0



 

. C.

90



 

. D.

180



 

.

Lời giải

Chọn D

Ta có













cos , cos , 1 , 180

a b a b a b a b a b a b a b

            

             

.

Câu 28: Cho hệ phương trình





2 2 1

1

m x my m

x y

   







  





(

m

là tham số).

Có bao nhiêu giá trị nguyên của tham số

m

để phương trình có nghiệm duy nhất





0 0

,

x y

và

0 0

,

x y

đều là các số nguyên?

A.

4

. B.

0

. C.

2

. D.

1

.

Lời giải

Chọn C

Ta có

 

   

1

2 2 1

2

2 1 2 1

2 1

1

y x

m x my m

m x m x m

x

x y

m

 



 

   

 

  

 

  

    

 

  

 

 







.

Để nghiệm

0

x

nguyên thì

   

 

2

1 1;1; 2;2 2;0; 3;1

1

3;1

2 2

2

1 2 1 2

1 2

1 1

1

m m

m

m m

m



       

 



  



    

  

 

  



  









 



.

Câu 29: Phương trình

2

4 1 0

mx x

  

có hai nghiệm phân biệt khi

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

4

0

m











. B.

16

m

 

. C.

16

0

m











. D.

4

0

m

 









.

Lời giải

Chọn D

Phương trình

2

4 1 0

mx x

  

có hai nghiệm phân biệt khi:

0 0

' 4 0 4

m m

 

 



 

     

 

.

Câu 30: Cho phương trình













1 1 2 2 6 1

m m x x m     . Có bao nhiêu số nguyên

m

thuộc khoảng





10;10

 để phương trình





1

có nghiệm?

A.

18

. B.

17

. C.

19

. D.

20

.

Lời giải

Chọn A

Phương trình













1 1 2 2 6 1

m m x x m    





2 2

2 6

m m x m m

     





















1 2 3 2 2

m m x m m      .

Nếu

  

1

1 2 0

2

m

m m

m

 



   







thì





2

có nghiệm duy nhất

3

1

m

x

m







.

Nếu

1

m

 

thì





2

có dạng

0 6

x

 

vô nghiệm.

Nếu

2

m



thì





2

có dạng

0 0

x



nghiệm đúng với mọi

x

.

Vậy





1

có nghiệm khi

1

m

 

. Khi đó có

18

giá trị thỏa mãn.

Câu 31: Cho hai góc nhọn



và



trong đó

 



. Khẳng định nào sau đây là sai?

A.

sin sin

 



. B.

tan tan 0

 

 

. C.

cot cot

  

. D.

cos cos

 



.

Lời giải

Chọn D

Khi



và



hai góc nhọn trong đó

 



thì ta có:

0 sin sin

0 tan tan

0 cot cot

0 cos cos

 

 

 





 





 



 



Vậy D sai.

Câu 32: Cho tam giác

ABC

với













2;3 , 1; 1 , 10; 3

A B C

  

. Điểm





;

M a b

nằm trên cạnh

BC

sao

cho

DE

có độ dài nhỏ nhất với

,

D E

lần lượt là hình chiếu vuông góc của

M

lên

,

AC AB

.

Xác định mệnh đề đúng.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

1

5

a b

  

. B.

1

5

a b

 

. C.

13

5

a b

 

. D.

13

5

a b

  

Lời giải

Chọn A

A

B

C

M

D

E

Ta có













3; 4 , 8; 6 , 11; 2 . 0

AB AC BC AB AC

       

    

.

Vậy tam giác

ABC

vuông tại

A

ADME



là hình chữ nhật

DE AM

 

.

DE



nhỏ nhất khi

AM

nhỏ nhất

M



là hình chiếu vuông góc của

A

trên

BC

.

Phương trình đường thẳng

: 2 11 13 0

BC x y

  

.

Gọi

d

là đường thẳng qua

A BC

 

phương trình

:11 2 16 0

d x y

  

.

Hình chiếu vuông góc của

A

trên

BC

là

6

6 7

5

;

7

5 5

5

a

H d BC

b







 

    



 

 



 





.

Câu 33. Trong các phương trình sau, phương trình nào tương đương với phương trình

2

4

x



?

A.

2

x



. B.

2

6 8 0

x x

  

. C.





2 2 0

x x

  

. D.





2

4 0

x x

 

.

Lời giải

Chọn C

Phương trình

2

4 2

x x

   

. Tập nghiệm là





2;2

S   .

+ Phương trình

2

x



. Phương trình có tập nghiệm





1

2

S  .

+ Phương trình

2

6 8 0

4

x

x x

x





   







. Phương trình có tập nghiệm





2

2;4

S  .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

+ Phương trình

 

2 2

2

2 2 0

2 0 2

2

2 0 2

x x

x

x x

x

x x

   

 





 

     

  

 

 



 



 

 

   

 

 

. Phương trình có tập

nghiệm





3

2;2

S   .

+ Phương trình

 

2

0

2

4 0 2

4 0

0

x

x x x

x











     



 



 











 







. Phương trình có tập

nghiệm





4

0;2

S  .

Vì

3

S S



nên phương trình

2

4

x



tương đương với phương trình





2 2 0

x x

  

.

Câu 34. Cho phương trình









2

1 : 4 4 2

m x m x

  

(

m

là tham số ). Tìm mệnh đề sai trong các mệnh

đề sau:

A. Khi

3

m



thì phương trình





1

có nghiệm duy nhất.

B. Khi

2

m

 

thì phương trình





1

vô nghiệm.

C. Khi

2

m



thì phương trình





1

có nghiệm duy nhất.

D. Khi

2

m



thì phương trình





1

có vô số nghiệm.

Lời giải

Chọn C

Phương trình













2 2

1 : 4 4 2 4 4 8

m x m x m x m

       

.

+

2

4 0 2

m m

    

: Phương trình





1

có nghiệm duy nhất.

+

2

m



: Phương trình





1

0 0

x

 

(thoả mãn

x

 



) do đó phương trình





1

có vô số

nghiệm.

+

2

m

 

: Phương trình





1

0 16

x

 

(vô lí) do đó phương trình





1

vô nghiệm.

Vậy khi

2

m



thì phương trình





1

có nghiệm duy nhất là mệnh đề sai.

Câu 35. Giá trị lớn nhất

M

và giá trị nhỏ nhất

m

của hàm số

2

6 8

y x x

  

trên đoạn





1;4

là:

A.

1, 3

M m

  

. B.

3, 1

M m

 

. C.

0, 1

M m

  

. D.

3, 1

M m

  

.

Lời giải

Chọn D

+ Parabol

2

6 8

y x x

  

có hoành độ đỉnh

 

3 1;4

2

b

x

a



   .

+ Tính













1 3, 3 1, 4 0

y y y

   

.

Vậy

3, 1

M m

  

.

II. TỰ LUẬN

Bài 1. Giải các phương trình sau:

a)

2

2 2 1 5

x x x

   

. b)

1 2 5 2

x x

  

.

Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

a)

2

2 2 1 5

x x x

   

.

TH1:

2 1 0

x

 

1

2

x

 

. Phương trình trở thành:





2

2 2 1 5

x x x

   

2

4 0

x

  





 

2

x TM

x KTM







 





.

TH2:

2 1 0

x

 

1

2

x

 

. Phương trình trở thành:





2

2 2 1 5

x x x

    

2

4 6 0

x x

   

 

2 10

x TM

x KTM



  







  



.

Vậy tập nghiệm của phương trình là:





2 10;2

S   

.

b) ĐK:

2 5 0

x

 

5

2

x

  

.

Ta có:

1 2 5 2

x x

  





2 5 2 5 6 0

x x

     

.

Đặt

2 5

t x

 





0

t



. Phương trình trở thành:

2

6 0

t t

  





 

3

2

t TM

t KTM







 





.

Với

3

t



2 5 3

x

  

2 5 9

x

  

2

x

 

.

Vậy phương trình có nghiệm là

2

x



.

Bài 2. Cho

tan 3



 

với

90 180



   

. Tính giá trị của

cos



.

Lời giải

Vì

90 180



   

cos 0



 

.

Ta có:

2

1

1 tan 10

cos



  

10

cos

10



   .

Bài 3. Trong mặt phẳng với hệ trục tọa độ

Oxy

, cho điểm





1; 3

A



,





2;0

B  và





3;9

C  . Tính

côsin góc giữa hai vectơ

BA



và

BC



.

Lời giải

Ta có:





3; 3

BA

 



 

2

3 3 3 2

BA    



.





1;9

BC  



 

2

1 9 82

BC    



.

Vậy

 

.

cos ,

.

BA BC



 









3. 1 3 .9

3 2. 82

  



5 41

41

 .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 10 Môn Toán – Lớp 10

(Th

ời gian l

àm bài 90 phút)

Không k

ể thời gian phát đề

Câu 1: Điều kiện xác định của phương trình

5

1

2

x







là.

A.

5

x

 

. B.

5

2

x

 









. C.

5

2

x

 









. D.

2

x



.

Câu 2: Cho hai vectơ









2; 1 , 3;4

u v   

 

. Tích

.

u v

 

là ?

A.

11

. B.

10



. C.

5

. D.

2



.

Câu 3: Gọi

S

là tập hợp các giá trị của tham số

m

để hệ phương trình





 

1 2

m x y m

mx m y

   







   





có

nghiệm là





0

2;

y

. Tổng các phần tử của tập

S

bằng

A.

0

. B.

1

. C.

2

. D.

3

.

Câu 4: Cho góc





90 ;180





 

. Khẳng định nào sau đây đúng?

A.

sin



và

cot



cùng dấu. B. Tích

sin .cot

 

mang dấu âm.

C. Tích

sin .cos

 

mang dấu dương. D.

sin



và

tan



cùng dấu.

Câu 5: Cho tam giác

ABC

cân tại

C

. Tập hợp các điểm

M

thỏa mãn

2

MA MB MC

 

  

là

A. Đường thẳng song song với

AB

. B. Đường thẳng vuông góc với

AB

.

C. Một điểm. D. Một đường tròn.

Câu 6: Hệ phương trình

2

4 6

mx y m

x my m

 





  



vô nghiệm khi giá trị

m

bằng

A.

2

m



. B.

2

m

 

. C.

1

m



. D.

1

m

 

.

Câu 7: Tọa độ đỉnh của parabol

2

2 4 6

y x x

   

là

A.





1;8

I  . B.





1;0

I . C.





2; 10

I  . D.





1;6

I  .

Câu 8: Số nghiệm của phương trình

2

3 9 7 2

x x x

   

là:

A.

3

. B.

1

. C.

0

. D.

2

.

Câu 9: Cho tam giác vuông tại

A

có

, 3

AB a AC a

 

và

AM

là trung tuyến. Tính tích vô hướng

.

BM AM

 

?

A.

2

a

. B.

2

a

. C.

2

a



. D.

2

a



.

Câu 10: Số nghiệm của phương trình

2

1 4

2 4

x

x x





 

là

A.

0

. B.

2

. C.

3

. D.

1

.

Câu 11: Cho tam giác ABC với













1;4 2;2, ,

4;0

BA C

. Tìm tọa độ vectơ

AM



với

M

là trung

điểm

BC

.

A.





3;0

AM 



. B.





0;3

AM 



. C.





0; 3

AM 





. D.





3;0

AM 



.

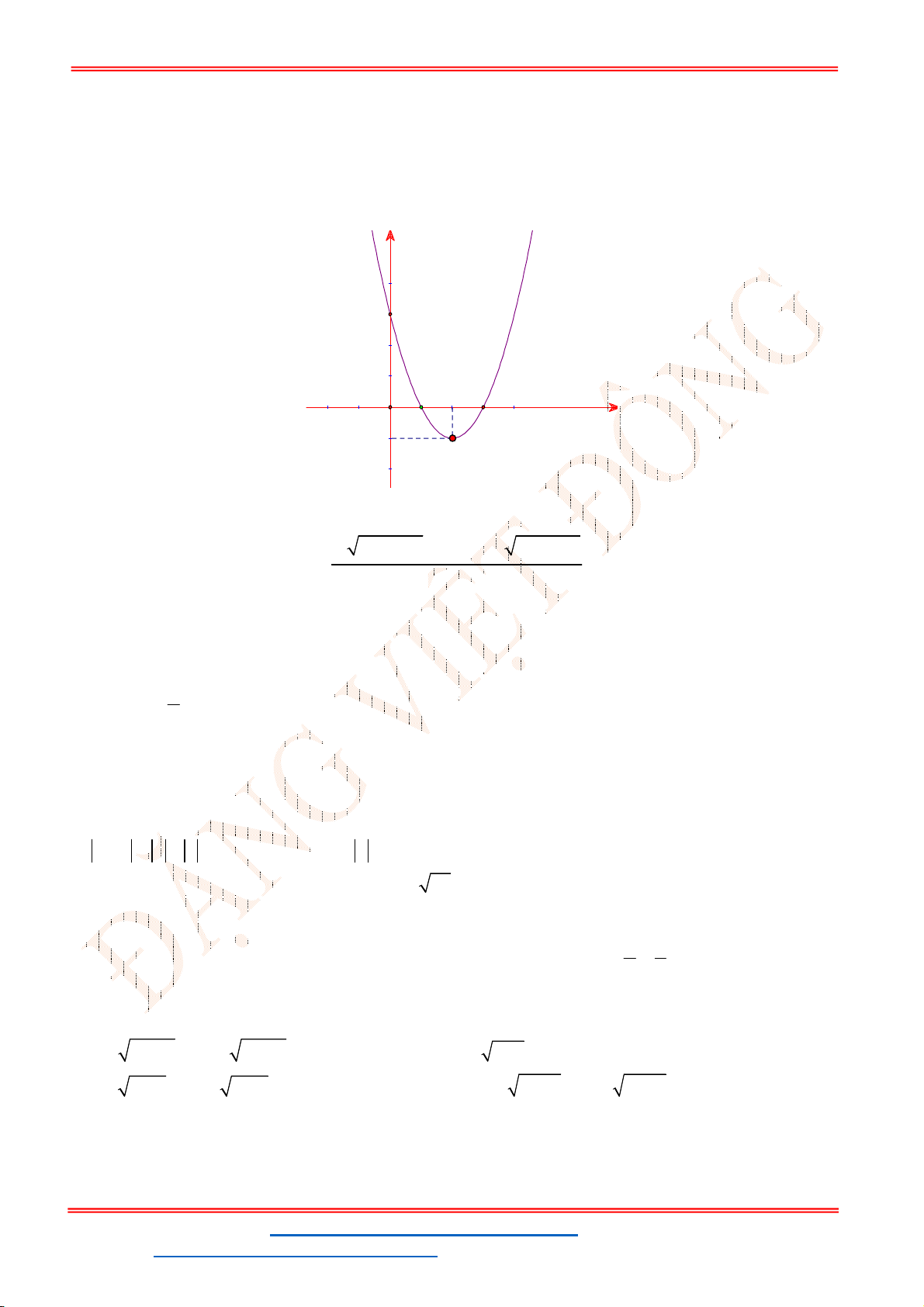
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 12: Cho hệ phương trình :

3

2 1

mx y

x my m

 





  



,

m

là tham số. Có bao nhiêu giá trị nguyên âm

của tham số

m

để hệ phương trình có nghiệm





;

x y

với

,

x y

là các số nguyên ?

A.

3

B.

1

C.

2

D.

0

Câu 13: Cho hàm số

2

y ax bx c

  

có đồ thị là đường cong trong hình vẽ dưới đây ?

x

y

3

2

3

-1

O

1

Giá trị của tổng

4 2

T a b c

  

là :

A.

2

T



. B.

1

T

 

. C.

4

T



. D.

3

T



.

Câu 14: Cho hàm số

 





 

2

2018 2 2018

1

m x m x

y f x

m x

   

 



có đồ thị là





m

C

(

m

là tham số).

Số giá trị của

m

để đồ thị





m

C

nhận

Oy

làm trục đối xứng là:

A.

0

. B.

1

. C.

2

. D.

3

.

Câu 15: Cho hình vuông

ABCD

cạnh

a

, tâm

O

. Tính độ dài của vecto

OA OB



 

.

A.

2

a

. B.

2

a

. C.

a

. D.

3

a

.

Câu 16: Trên đường thẳng cho điểm

B

nằm giữa hai điểm

A

và

C

, với

2

AB a



,

6

AC a



. Đẳng

thức nào sau đây đúng?

A.

2

BC BA

 

 

. B.

2

BC AB

 

 

. C.

4

BC AB



 

. D.

BC AB



 

.

Câu 17: Tìm mệnh đề sai trong các mệnh đề sau?

A.





, ,a b a b a b    



. B.





, 0

x a a x a a

     

.

C.





,a b ac bc c    



. D.





2 , 0, 0

a b ab a b

   

.

Câu 18: Cho

,

a b

là các số thực bất kì. Trong các mệnh đề sau, mệnh đề nào sai?

A.

0

a b a b

   

. B.

1 1

0a b

a b

   

.

C.

3 3

a b a b

  

. D.

2 2

a b a b

  

.

Câu 19: Phép biến đổi nào sau đây là phép biến đổi tương đương.

A.

2 2 2 2

2 2

x x x x x x

      

. B.

2

1 1

x x x x

    

.

C.

2 2

x x x x x x

      

. D.

2 2 2 2

3 3

x x x x x x

      

.

Câu 20: Phương trình





2

4 3 6

m x m

  

có nghiệm duy nhất khi và chỉ khi

A.

2

m

 

,

3

m

 

. B.

2

m

 

. C.

2

m



. D.

2

m

 

.

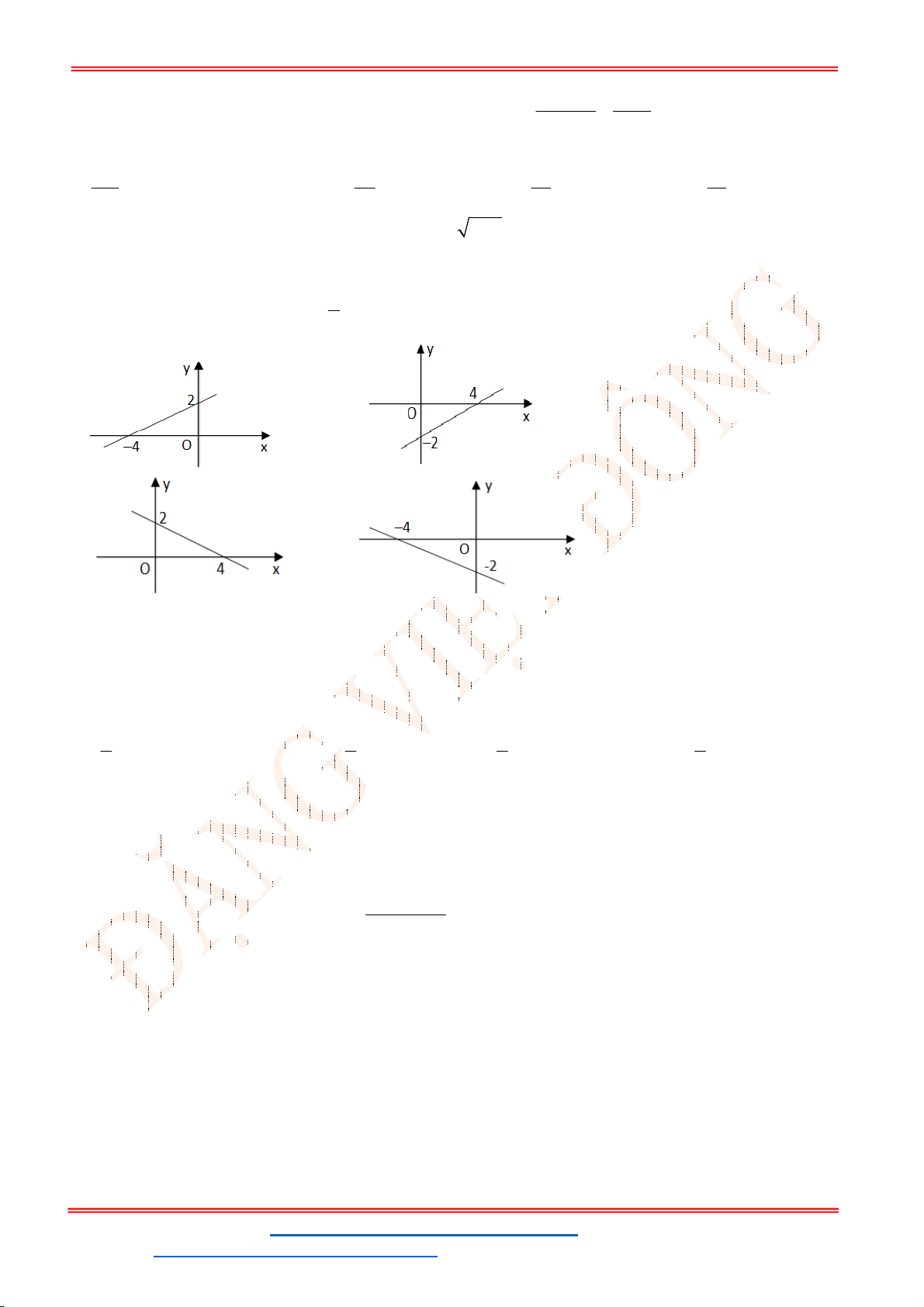
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 21: Gọi

S

là tập các giá trị của

m

để phương trình

2 3 2

3

2 1

x m x

x x

 

 

 

vô nghiệm. Tính bình

phương của tổng các phần tử của tập

S

.

A.

121

9

. B.

40

9

. C.

65

9

. D.

16

9

Câu 22: Tập nghiệm của phương trình





2

2 1 0

x x x

   

là:

A.





1;2

. B.





1;1;2

 . C.





1;2

. D.





1;2



Câu 23: Đồ thị của hàm số

2

x

y

  

là hình nào dưới đây?

A. . B. .

C. . D. .

Câu 24: Có bao nhiêu giá trị nguyên của

m

để phương trình





 

2

4 3 2 0

x x x m

    

có

4

nghiệm phân biệt?

A.

30

. B. Vô số. C.

28

. D.

0

.

Câu 25: Hàm số

2

3 2

y x x

   

nghịch biến trên khoảng

A.

1

; .

6

 



 

 

B.

1

; .

6

 

 

 

 

C.

1

; .

6

 

 

 

 

D.

1

; .

6

 



 

 

Câu 26: Cho hai đường thẳng

1

: 4

y mxd

 

và

2

: 4

d y mx

  

. Gọi

S

là tập hợp các giá trị nguyên

dương của

m

để tam giác tạo thành bởi

1 2

,

d d

và trục hoành có diện tích lớn hơn

8

. Số phần tử của tập

S

là

A.

1

. B.

3

. C.

2

. D.

4

.

Câu 27: Tập xác định của hàm số

2

1

3 4

x

y

x x





 

là

A.

D





. B.





\ 1;4

D  



. C.





\ 1; 4

D

 



. D.





\ 4

D

 



.

Câu 28: Hệ phương trình

2 3

3

2 2 2

x y z

x y x

x x z

   





  





   



có 1 nghiệm là:

A.









; ;z 8; 1;12

x y    . B.









; ;z 8;1; 12

x y   .

C.









; ;z 4; 1;8

x y    . D.









; ;z 4; 1; 6

x y

   

.

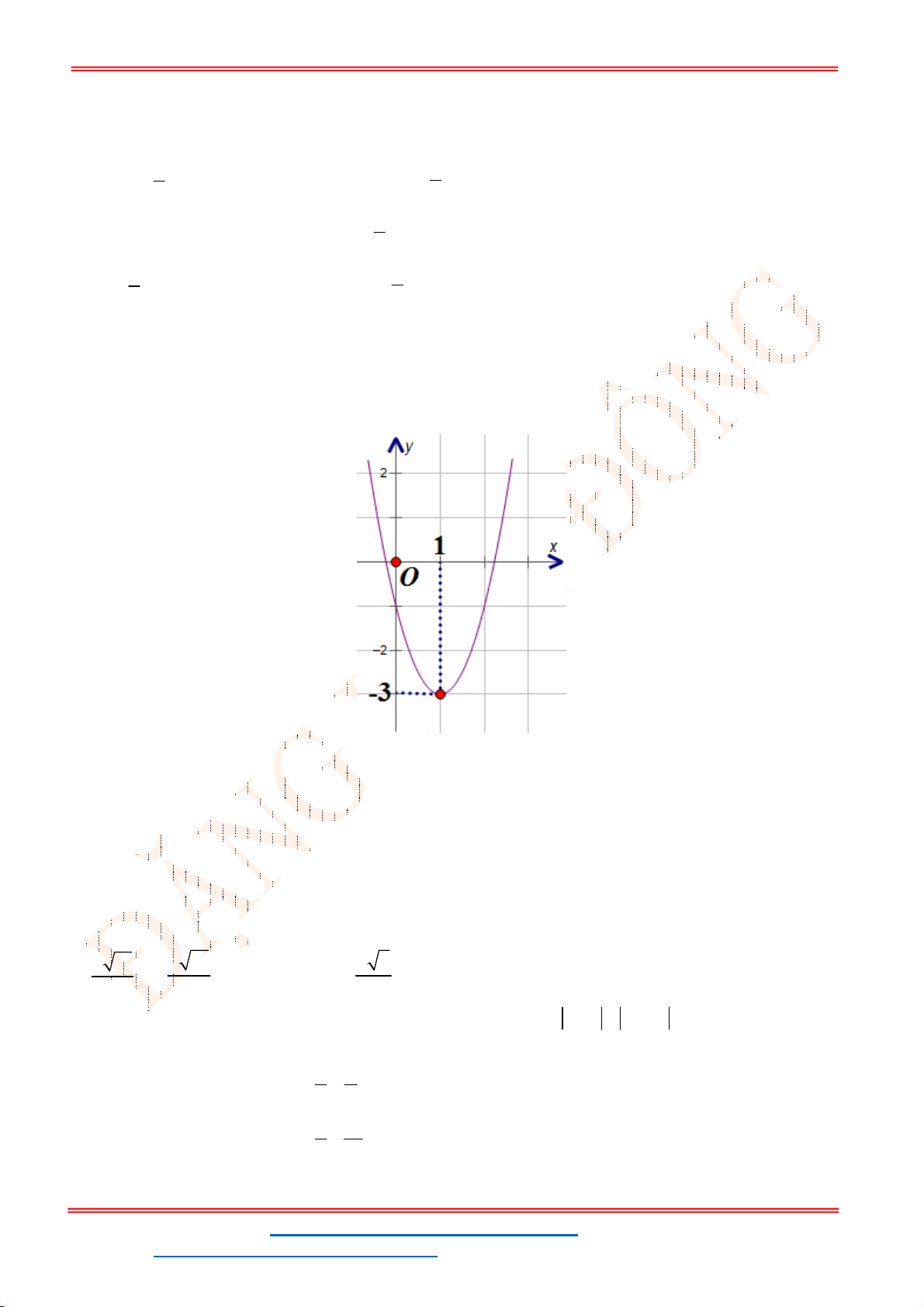
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 29: Trong mặt phẳng tọa độ

Oxy

, cho tam giác

ABC

. Biết





3; 1

A



;





1;2

B  và





1; 1

I



là trọng

tâm tam giác

ABC

. Trực tâm

H

của tam giác

ABC

có tọa độ





;

a b

. Tính

3

a b



.

A.

2

3

a b

 

. B.

4

3

a b

  

. C.

3 1

a b

 

. D.

3 2

a b

  

.

Câu 30: Trong hệ tọa độ

Oxy

, cho

1

5

2

u i j

 

  

. Tọa độ vectơ

u



là

A.

1

;5

2

u

 



 

 



. B.

1

; 5

2

u

 

 

 

 



. C.





1;10

u  



. D.





1; 10

u  



.

Câu 31: Cho tứ giác

ABCD

và điểm

M

tùy ý. Gọi

,

I J

lần lượt là trung điểm của

,

AC BC

. Khi đó

4 3

u MA MB MC

  

   

bằng

A. 3

u AI AJ

 

  

. B.

2

u BI



 

. C. 3

u AC AB

 

  

. D.

3

u BA BC

 

  

.

Câu 32: Cho parabol

2

y ax bx c

  

có đồ thị như hình sau:

Phương trình của parabol này là:

A.

2

1

y x x

   

. B.

2

2 4 1

y x x

  

. C.

2

2 1

y x x

  

. D.

2

2 4 1

y x x

  

.

Câu 33: Có bao nhiêu giá trị của tham số m để hệ phương trình

2 2

2

1

x xy y m

x y xy m

   





  



có nghiệm duy nhất.

A.

1

. B.

0

. C.

3

. D.

2

.

Câu 34: Cho hình bình hành

ABCD

có

,

AB a



,

AB BD





0

60 .

BAD 

Gọi

,

E F

lần lượt là trung điểm

của

, .

BD AD

Độ dài vec tơ

BE AF



 

là

A.

13

2

a

. B.

10

2

a

. C.

7

2

a

. D.

2

a

.

Câu 35: Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số

2 4 4 3

y x x

    

trên đoạn





2;2

 là

A.

24

. B.

21

. C.

23

. D.

26

.

Câu 36: Biết hệ phương trình

6 5

3

9 10

1

x y



 







 





có nghiệm





;

x y

. Hiệu

y x



là

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

2



. B.

2

15



. C.

2

. D.

2

15

.

Câu 37: Cho tam giác đều ABC. Tính

os(AB, ) os(BC, ) os(CA, ).

P c BC c CA c AB

  

     

A.

3 3

2

P  B.

3

2

P



C.

3

2

P

 

D.

3 3

2

P  

Câu 38: Cho hàm số

2

( )

y f x ax bx c

   

có đồ thị

( )

C

(như hình vẽ)

x

y

-5 -4 -3 -2 -1 5432O 1

Có bao nhiêu giá trị nguyên của tham số

m

để phương trình

2

( ) ( 2) ( ) 3 0

f x m f x m

    

có 6

nghiệm phân biệt ?

A. 1 B. 4 C. 3 D. 2

Câu 39: Tìm tất cả các giá trị của tham số

m

để phương trình

2 5 2 3

x m x m

   có nghiệm.

A.





0;m

 

. B.





0;m

 

. C.





;0

m  . D.





;m

  

.

Câu 40: Trong mặt phẳng tọa độ

Oxy

cho ba điểm













1; 2 , 3;2 , 4; 1

A B C

  

. Biết





;

E a b

di động

trên đường thẳng

AB

sao cho

2 3

EA EB EC

 

  

đạt giá trị nhỏ nhất. Tính

2 2

a b



?

A.

2 2

2

a b

 

. B.

2 2

1

a b

 

. C.

2 2

2

3

a b

 

. D.

2 2

3

2

a b

 

.

Câu 41: Cho hai tập hợp





2;4;6;9

A  ,





1;2;3;4

B  . Tập

A

\

B

bằng tập hợp nào sau đây?

A.





2;4

. B.





1;3

. C.





6;9

. D.





6;9;1;3

.

Câu 42: Cho hệ phương trình





1 3

2 2

2 4

mx m y m

x my m

x y

  



  





 



. Biết hệ phương trình có nghiệm khi tham số

0

m m



. Giá trị của

0

m

thuộc khoảng nào dưới đây?

A.





0

2;4

m  . B.





0

4; 2

m

  

. C.





0

1;2

m   . D.





0

2; 1

m

  

.

Câu 43: Trong mặt phẳng tọa độ

Oxy

cho điểm





3;1

M . Giả sử





;0

A a

và





0;

B b

( với

,

a b

là các số

thực không âm) là hai điểm sao cho tam giác

MAB

vuông tại

M

và có diện tích nhỏ nhất. Tính giá trị

biểu thức

2 2

T a b

 

.

A.

10

T



. B.

9

T



. C.

5

T



. D.

17

T



.

Câu 44: Có bao nhiêu giá trị của tham số

m

để phương trình









2 2

2 2 1 1 0

m x m mx m

     

có

hai nghiệm phân biệt và là hai số đối nhau?

A.

0

. B.

1

. C.

3

. D.

2

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 45: Cho

0 1

x y z

   

và

3 2 4

x y z

  

. Tìm giá trị lớn nhất của biểu thức

2 2 2

3 2

S x y z

  

.

A.

3

. B.

4

. C.

8

3

. D.

10

3

.

Câu 46: Cho tam giác

ABC

có

1 3

2 2

AM AB AC

  

  

. Tỉ số diện tích

ABM

ACM

S



là

A.

3

4

. B.

1

4

. C.

1

3

. D.

3

.

Câu 47: Cho hàm số





2018 2018

y f x x x     . Mệnh đề nào sau đây sai?

A. Hàm số





y f x

 có tập xác định là



.

B. Đồ thị hàm số





y f x

 nhận trục tung làm trục đối xứng.

C. Hàm số





y f x

 là hàm số chẵn.

D. Đồ thị hàm số





y f x

 nhận gốc tọa độ

O

làm tâm đối xứng.

Câu 48: Cho

ABC



có trọng tâm

G

và trung tuyến

AM

. Khẳng định nào sau đây sai ?

A.

0

  

   

GA GB GC

. B.

2 0

GA GM

 

  

.

C.

2

AM MG

 

 

. D.

3

OA OB OC OG

  

   

, với mọi điểm

O

.

Câu 49: Với giá trị nào của

a

và

b

thì đồ thị hàm số

y ax b

 

đi qua các điểm





2;1

A  ,





1; 2

B



?

A.

2

a



và

1

b



. B.

1

a

 

và

1

b

 

. C.

2

a

 

và

1

b

 

. D.

1

a



và

1

b



.

Câu 50: Cho các vectơ

a



,

b



,

c



thỏa mãn

a x





,

b y





,

c z





và

3 0

a b c

  

   

. Tính

. . .

A a b b c c a

  

     

.

A.

2 2 2

3

2

x z y

A

 

 . B.

2 2 2

3

2

z x y

A

 

 . C.

2 2 2

3

2

y x z

A

 

 . D.

2 2 2

3

2

z x y

A

 

 .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG HDG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 10 Môn Toán – Lớp 10

(Th

ời gian l

àm bài 90 phút)

Không k

ể thời gian phát đề

Câu 1: Điều kiện xác định của phương trình

5

1

2

x







là.

A.

5

x

 

. B.

5

2

x

 









. C.

5

2

x

 









. D.

2

x



.

Lời giải

Chọn C

Ta có phương trình có nghĩa khi và chỉ khi

5

2

x

 









.

Câu 2: Cho hai vectơ









2; 1 , 3;4

u v   

 

. Tích

.

u v

 

là ?

A.

11

. B.

10



. C.

5

. D.

2



.

Lời giải

Chọn B

Ta có









. 2. 3 1 .4 10

u v

     

 

Câu 3: Gọi

S

là tập hợp các giá trị của tham số

m

để hệ phương trình





 

1 2

m x y m

mx m y

   







   





có

nghiệm là





0

2;

y

. Tổng các phần tử của tập

S

bằng

A.

0

. B.

1

. C.

2

. D.

3

.

Lời giải

Chọn B

Do





0

2;

y

là nghiệm của hệ phương trình đã cho nên:

 

0

00 0

0

2

0

1

2 1 2

1

2 1 2

2 0 1

2

1

m

y m

ym y m y m

y m

m

m m m

m m y m m m

m

y

  











 

    





   



   

 



   



   

       

















 















1;2

S  

Vậy: Tổng các phần tử của tập

S

bằng

1

.

Câu 4: Cho góc





90 ;180





 

. Khẳng định nào sau đây đúng?

A.

sin



và

cot



cùng dấu. B. Tích

sin .cot

 

mang dấu âm.

C. Tích

sin .cos

 

mang dấu dương. D.

sin



và

tan



cùng dấu.

Lời giải

Chọn B

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Với





90 ;180





 

thì

sin 0;cos 0;tan 0;cot 0

   

   

.

Suy ra : Tích

sin .cot

 

mang dấu âm.

Câu 5: Cho tam giác

ABC

cân tại

C

. Tập hợp các điểm

M

thỏa mãn

2

MA MB MC

 

  

là

A. Đường thẳng song song với

AB

. B. Đường thẳng vuông góc với

AB

.

C. Một điểm. D. Một đường tròn.

Lời giải

Chọn A

Gọi

I

là trung điểm của

AB

CI AB

 

.

Ta có:

2

MA MB MC

 

  

2 2

MI MC MI MC

   

 

.

Suy ra tập hợp các điểm

M

là đường trung trực



của đoạn thẳng

CI

;

//

AB



.

Câu 6: Hệ phương trình

2

4 6

mx y m

x my m

 





  



vô nghiệm khi giá trị

m

bằng

A.

2

m



. B.

2

m

 

. C.

1

m



. D.

1

m

 

.

Lời giải

Chọn B

Cách 1:

Hệ vô nghiệm

1 2

4 6

m m



  

 

2

m

  

.

Cách 2:

Hệ vô nghiệm

2

2 2

0

4 0

2

3

0 0

2;

2 6 0

2

x y

m m

D

m

D D

x x

m m

   







  

 

    

  

  

  

   





 



Câu 7: Tọa độ đỉnh của parabol

2

2 4 6

y x x

   

là

A.





1;8

I  . B.





1;0

I . C.





2; 10

I  . D.





1;6

I  .

Lời giải

Chọn A

Ta có

 

; 1;8

2 2

b b

I f I

a a

 

   

  

 

.

Câu 8: Số nghiệm của phương trình

2

3 9 7 2

x x x

   

là:

A.

3

. B.

1

. C.

0

. D.

2

.

Lời giải

Chọn C

Điều kiện

2 0 2

x x

   

.

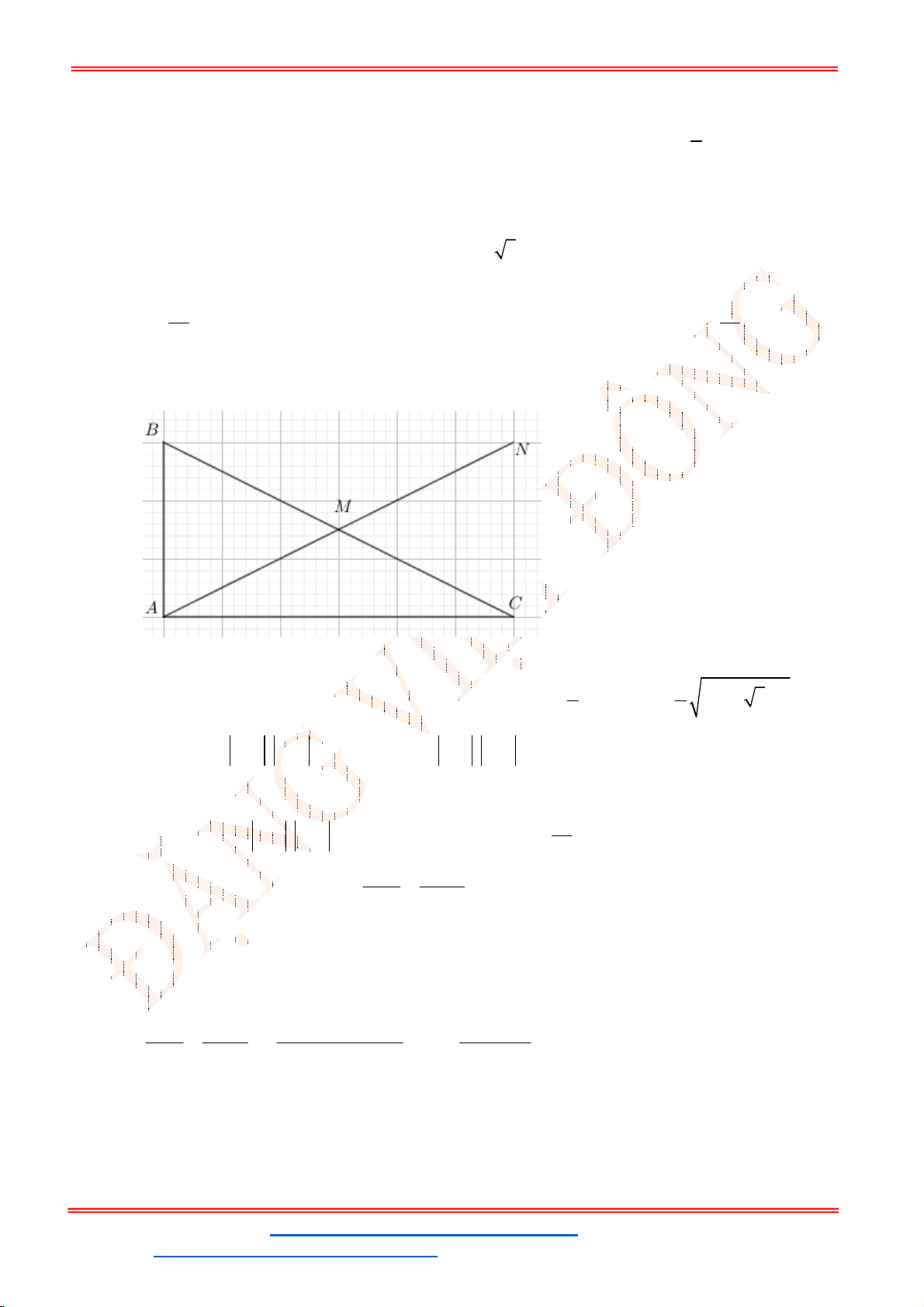
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Phương trình trở thành

 

2

3 9 7 2

x x x   

2

2 5 3 0

x x

   

1

3

2

x















.

So điều kiện, không có nghiệm nào thõa mãn

Vậy phương trình vô nghiệm.

Câu 9: Cho tam giác vuông tại

A

có

, 3

AB a AC a

 

và

AM

là trung tuyến. Tính tích vô hướng

.

BM AM

 

?

A.

2

a

. B.

2

a

. C.

2

a



. D.

2

a



.

Lời giải

Chọn A

Vẽ

MN AM



 

Tam giác vuông tại

A

có

AM

là trung tuyến

 

2

1 1

3

2 2

AM BC BM a a a

     













. . cos . . cos .

BM AM BM AM BM AM MC MN MC MN

 

       

 

BAM



có

AB AM MC a ABM

    

đều



0

60

NMC 







2

0

. . cos . . .cos60

2

a

BM AM MC MN MC MN a a   

     

Câu 10: Số nghiệm của phương trình

2

1 4

2 4

x

x x





 

là

A.

0

. B.

2

. C.

3

. D.

1

.

Lời giải

Chọn D

Đk:

2

4 0 2

x x

    









2

2 2 2

3

1 2 4

1 4 6

0 0 6 0

2( )

2 4 4 4

x

x x

x x x

x x

x l

x x x x

 

  



  

         





   



Câu 11: Cho tam giác ABC với













1;4 2;2, ,

4;0

BA C

. Tìm tọa độ vectơ

AM



với

M

là trung điểm

BC

.

A.





3;0

AM 



. B.





0;3

AM 



. C.





0; 3

AM 





. D.





3;0

AM 



.

Lời giải

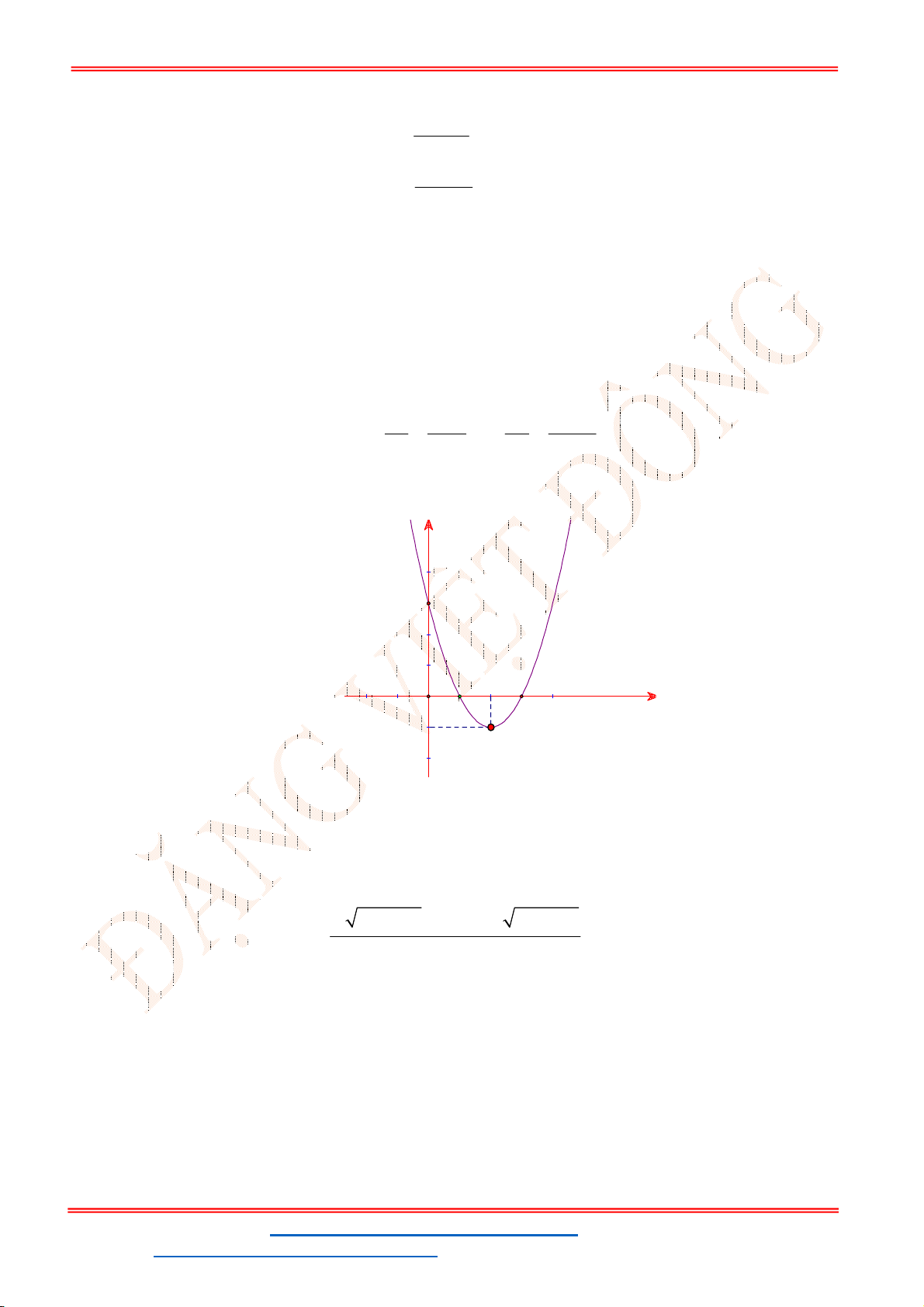
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Chọn C

Vì

M

là trung điểm

BC

nên

1

2

.

1

2

C B

M

C B M

M

x x

x

y y y

y

















 

 











Suy ra





0; 3

AM 





.

Câu 12: Cho hệ phương trình :

3

2 1

mx y

x my m

 





  



,

m

là tham số. Có bao nhiêu giá trị nguyên âm của

tham số

m

để hệ phương trình có nghiệm





;

x y

với

,

x y

là các số nguyên ?

A.

3

B.

1

C.

2

D.

0

Lời giải

Chọn A.

Ta có :

2

1



D m ,

1

 

x

D m ,

2

2 3

  

y

D m m

Hệ phương trình có nghiệm

1 2 1

,

1 1



   

 

y

x

D

m

x y

D m D m

Hệ phương trình có nghiệm nguyên khi

0; 2

  

m m .

Câu 13: Cho hàm số

2

y ax bx c

  

có đồ thị là đường cong trong hình vẽ dưới đây ?

x

y

3

2

3

-1

O

1

Giá trị của tổng

4 2

T a b c

  

là :

A.

2

T



. B.

1

T

 

. C.

4

T



. D.

3

T



.

Lời giải

Chọn B.

Đồ thị đã cho đi qua điểm





2; 1

I



, ta có:

4 2 1

a b c

   

. Vậy

1

T

 

.

Câu 14: Cho hàm số

 





 

2

2018 2 2018

1

m x m x

y f x

m x

   

 



có đồ thị là





m

C

(

m

là tham số).

Số giá trị của

m

để đồ thị





m

C

nhận

Oy

làm trục đối xứng là:

A.

0

. B.

1

. C.

2

. D.

3

.

Lời giải

Chọn B.

ĐKXĐ :

 

2

2018

1 0

x

m x



 









 





.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Đồ thị





m

C

nhận

Oy

làm trục đối xứng





y f x

  là hàm số chẵn.

+

2

1 0 1

m m

    

thì TXĐ:









2018;2018 \ 0

D   là tập đối xứng (1).

+ Khi đó









f x f x

 





 





 

2 2

2018 2 2018 2018 2 2018

1 1

m x m x m x m x

m x m x

       

 

  

2

1

2

m

m m

m





    



 



(2).

Từ (1), (2) ta được:

2

m

 

.

Câu 15: Cho hình vuông

ABCD

cạnh

a

, tâm

O

. Tính độ dài của vecto

OA OB



 

.

A.

2

a

. B.

2

a

. C.

a

. D.

3

a

.

Lời giải

Chọn C.

OA OB CO OB CB CB a

     

    

.

Câu 16: Trên đường thẳng cho điểm

B

nằm giữa hai điểm

A

và

C

, với

2

AB a



,

6

AC a



. Đẳng

thức nào sau đây đúng?

A.

2

BC BA

 

 

. B.

2

BC AB

 

 

. C.

4

BC AB



 

. D.

BC AB



 

.

Lời giải

Chọn A.

Ta có:

2

AB a



;

4

BC a



2 2

BC AB BC BA

    

   

.

Câu 17: Tìm mệnh đề sai trong các mệnh đề sau?

A.





, ,a b a b a b    



. B.





, 0

x a a x a a

     

.

C.





,a b ac bc c    



. D.





2 , 0, 0

a b ab a b

   

.

Lời giải

Chọn C





, 0

a b ac bc c

    

nên mệnh đề sai là





,a b ac bc c    



.

Câu 18: Cho

,

a b

là các số thực bất kì. Trong các mệnh đề sau, mệnh đề nào sai?

A.

0

a b a b

   

. B.

1 1

0a b

a b

   

.

C.

3 3

a b a b

  

. D.

2 2

a b a b

  

.

Lời giải

Chọn D

2 2

0

a b a b

   

nên mệnh đề sai là

2 2

a b a b

  

.

Câu 19: Phép biến đổi nào sau đây là phép biến đổi tương đương.

A.

2 2 2 2

2 2

x x x x x x

      

. B.

2

1 1

x x x x

    

.

C.

2 2

x x x x x x

      

. D.

2 2 2 2

3 3

x x x x x x

      

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Lời giải

Chọn D

Phép biến đổi

2 2 2 2

3 3

x x x x x x

      

là phép biến đổi tương vì

2

3

x



xác định

với

x

 



.

Câu 20: Phương trình





2

4 3 6

m x m

  

có nghiệm duy nhất khi và chỉ khi

A.

2

m

 

,

3

m

 

. B.

2

m

 

. C.

2

m



. D.

2

m

 

.

Lời giải

Chọn D

Phương trình có nghiệm duy nhất

2

4 0

2

m

 



   



 



.

Câu 21: Gọi

S

là tập các giá trị của

m

để phương trình

2 3 2

3

2 1

x m x

x x

 

 

 

vô nghiệm. Tính bình

phương của tổng các phần tử của tập

S

.

A.

121

9

. B.

40

9

. C.

65

9

. D.

16

9

Lời giải

Chọn C

Điều kiện xác định:

1, 2

x x

 

Với điều kiện trên, phương trình tương đương với:

























2 3 1 2 2 3 1 2

x m x x x x x

       





7 3 10 3 (1)

m x m   

Phương trình ban đầu vô nghiêm khi phương trình (1) hoặc vô nghiệm hoặc có nghiệm

1

x



hoặc có nghiệm

2

x



. Ta xét 3 trường hợp:

• Phương trình trình (1) vô nghiệm

7 3 0

7

10 3 0

3

m

 



  



 



• Phương trình (1) có nghiệm

1

x



: 7 3 10 3m m

    

không có

m

thỏa mãn.

• Phương trình (1) có nghiệm

2

x



:

4

14 6 10 3 3 4

3

m m m m

       

Thử lại với

4

3

m



: phương trình (1) có nghiệm

2

x



. Nghiệm này không phải là nghiệm của

phương trình ban đầu vì không thỏa mãn điều kiện.

Vậy

7 4

;

3 3

S

 



 

 

. Ta có

2 2

7 4 65

3 3 9

   

 

   

   

.

Câu 22: Tập nghiệm của phương trình





2

2 1 0

x x x

   

là:

A.





1;2

. B.





1;1;2

 . C.





1;2

. D.





1;2



Lời giải

Chọn A

Điều kiện xác định

1

x



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

 

2

1

2 0

2 1 0 2

1 0

1

x

x x

x x x x

x

 



  



      



 









Nghiệm

1

x

 

loại do không thỏa mãn điều kiện xác định. Phương trình đã cho có hai nghiệm

1

x



và

2

x



.

Câu 23: Đồ thị của hàm số

2

x

y

  

là hình nào dưới đây?

A. . B. .

C. . D. .

Lời giải

Chọn C.

Đồ thị của hàm số

2

x

y

  

đi qua









0;2 ; 4;0

nên chọn đáp án C.

Câu 24: Có bao nhiêu giá trị nguyên của

m

để phương trình





 

2

4 3 2 0

x x x m

    

có

4

nghiệm phân biệt?

A.

30

. B. Vô số. C.

28

. D.

0

.

Lời giải

Chọn A.

Ta có:





 









2 2

2

2 2 2

4 3 2 0 4 3 4 12 0

x x x m x x x x m

           

.

Đặt

2

4

t x x

 

với

4

t

 

.

Phương trình trở thành

2 2

3 12 0 3 12

t t m m t t

        

(1)

Phương trình đã cho có

4

nghiệm phân biệt



PT (1) có hai nghiệm phân biệt lớn hơn

4





Đường thẳng

y m



cắt đồ thị hàm số

2

3 12

y t t

   

trên





4;

 

tại hai điểm phân

biệt.

Bảng biến thiên của hàm số

2

3 12

y t t

   

trên





4;

 

như sau:

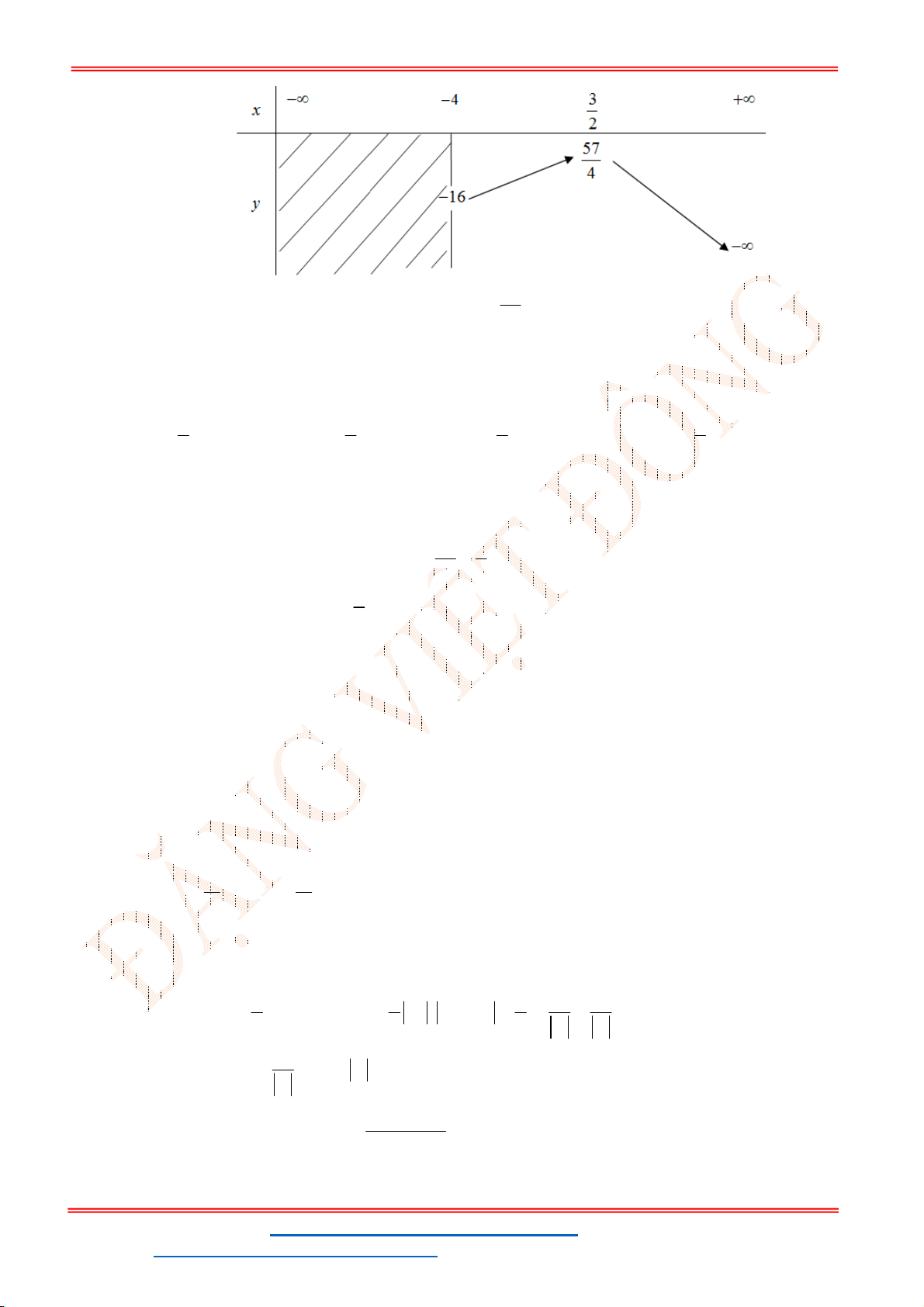
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Dựa vào bảng biến thiên ta thấy với

57

16;

4

m

 

 

 

 

thì phương trình đã cho có 4 nghiệm phân

biệt. Do

m

nguyên nên





15; 14;...;13;14

m   , có

30

giá trị của

m

thỏa mãn.

Câu 25: Hàm số

2

3 2

y x x

   

nghịch biến trên khoảng

A.

1

; .

6

 



 

 

B.

1

; .

6

 

 

 

 

C.

1

; .

6

 

 

 

 

D.

1

; .

6

 



 

 

Lời giải

Chọn A

Hàm số:

2

( ) 3 2

y f x x x

    

có:

1

2a 6

b

 

và hệ số

3 0

a

  

nên hàm số

( )

y f x



nghịch biến trên

1

; .

6

 



 

 

Câu 26: Cho hai đường thẳng

1

: 4

y mxd

 

và

2

: 4

d y mx

  

. Gọi

S

là tập hợp các giá trị nguyên

dương của

m

để tam giác tạo thành bởi

1 2

,

d d

và trục hoành có diện tích lớn hơn

8

. Số phần

tử của tập

S

là

A.

1

. B.

3

. C.

2

. D.

4

.

Lời giải

Chọn A

Ta có:

1

: 4

y mxd

 

;

2

: 4

d y mx

  

cắt nhau và cùng cắt trục Ox khi

0

m



.

Gọi

4 4

;0 , ;0

A B

m m

   



   

   

lần lượt là giao điểm của

1 2

;

d d

với trục hoành. Phương trình hoành

độ giao điểm của

1 2

;

d d

:

x 4 x 4 0.

m m x

     

Gọi

C

là giao điểm của

1 2

;

d d

thì





0; 4

C



.

Ta có

 

1 1 1 8 16

,Ox . . .4.

2 2 2

ABC C A B

S d C AB y x x

m m



     .

Có:

*

16

8 8 2, 1.

ABC

S m m N m

m



       

Vậy





1

S  .

Câu 27: Tập xác định của hàm số

2

1

3 4

x

y

x x





 

là

A.

D





. B.





\ 1;4

D  



. C.





\ 1; 4

D

 



. D.





\ 4

D

 



.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Lời giải

Chọn C

Hàm số xác định

2

1

3 4 0 .

4

x

x x

x





    



 



Vậy tập xác định của hàm số là:





\ 1; 4

D

 



.

Câu 28: Hệ phương trình

2 3

3

2 2 2

x y z

x y x

x x z

   





  





   



có 1 nghiệm là:

A.









; ;z 8; 1;12

x y    . B.









; ;z 8;1; 12

x y   .

C.









; ;z 4; 1;8

x y    . D.









; ;z 4; 1; 6

x y

   

.

Lời giải

Chọn A

2 3 2 3 2 3 2 3 8

3 2 2 2 6 3 9 12 1.

2 2 2 2 2 2 1 1 12

x y z x y z x y z x y z x

x y z x y z y z z y

x y z x y z y y z

                 

    

    

              

    

    

            

    

Vậy hệ phương trình có nghiệm là:









; ;z 8; 1;12

x y    .

Câu 29: Trong mặt phẳng tọa độ

Oxy

, cho tam giác

ABC

. Biết





3; 1

A



;





1;2

B  và





1; 1

I



là trọng

tâm tam giác

ABC

. Trực tâm

H

của tam giác

ABC

có tọa độ





;

a b

. Tính

3

a b



.

A.

2

3

a b

 

. B.

4

3

a b

  

. C.

3 1

a b

 

. D.

3 2

a b

  

.

Lời giải

Chọn A

Ta có:

3 1

3 4

C I A B

x x x x

y y y y

   





    



Suy ra





1; 4

C



Ta có:





4;3

AB  



;





2; 3

AC

  



;





2; 6

BC

 



;





3; 1

AH a b

  



;





1; 2

BH a b

  



Ta có:

     

    

10

1 2 2 3 0

. 0 2 3 4

3

2 6 12 8

3 .2 1 6 0

. 0

9

a

a b

BH AC a b

a b

AH BC

b









     

  



  

  

   

 

    









 





 

Vậy

2

3

a b

 

.

Câu 30: Trong hệ tọa độ

Oxy

, cho

1

5

2

u i j

 

  

. Tọa độ vectơ

u



là

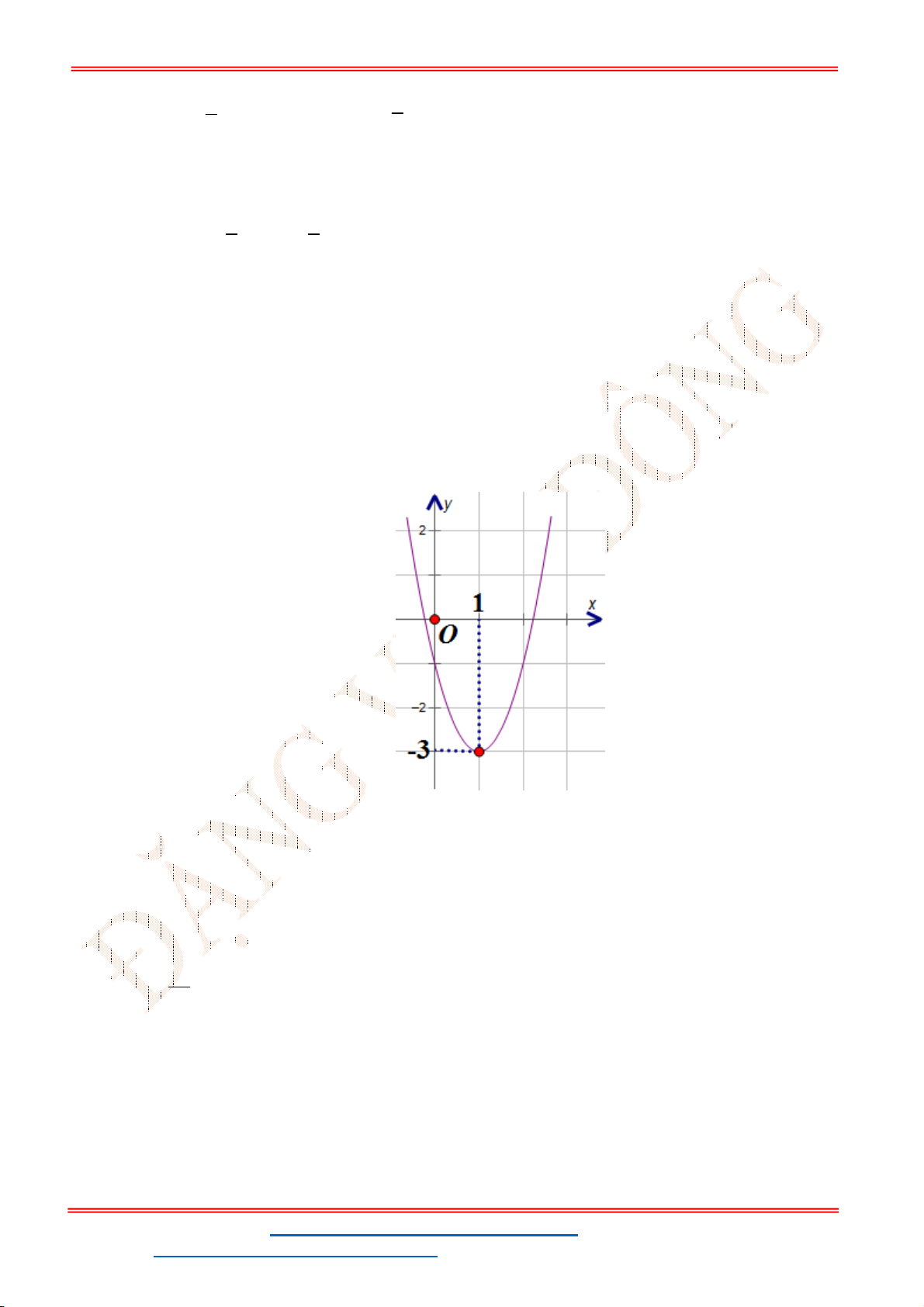
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

1

;5

2

u

 



 

 



. B.

1

; 5

2

u

 

 

 

 



. C.





1;10

u  



. D.





1; 10

u  



.

Lời giải

Chọn B

Ta có:

1 1

5 ; 5

2 2

u i j

 

   

 

 

  

.

Câu 31: Cho tứ giác

ABCD

và điểm

M

tùy ý. Gọi

,

I J

lần lượt là trung điểm của

,

AC BC

. Khi đó

4 3

u MA MB MC

  

   

bằng

A. 3

u AI AJ

 

  

. B.

2

u BI



 

. C. 3

u AC AB

 

  

. D.

3

u BA BC

 

  

.

Lời giải

Chọn D





4 3 3 3

u MA MB MC MA MB MC MB BA BC

        

         

.

Câu 32: Cho parabol

2

y ax bx c

  

có đồ thị như hình sau:

Phương trình của parabol này là:

A.

2

1

y x x

   

. B.

2

2 4 1

y x x

  

. C.

2

2 1

y x x

  

. D.

2

2 4 1

y x x

  

.

Lời giải

Chọn D

Dựa vào đồ thị





1; 3

I



là đỉnh của Parabol và Parabol đi qua điểm





0; 1



nên:

3

3 2

1 2 0 4

2

1 1

1

a b c

a b c a

b

a b b

a

c c

c

   



    

 



  

       

  

  

   

 

 





Vậy parabol có phương trình:

2

2 4 1

y x x

  

.

Câu 33: Có bao nhiêu giá trị của tham số m để hệ phương trình

2 2

2

1

x xy y m

x y xy m

   





  



có nghiệm duy

nhất.

A.

1

. B.

0

. C.

3

. D.

2

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Lời giải

Chọn D

Đặt:

x y S

xy P

 









khi đó hệ phương trình trở thành

2

( 4 )

1

S P m

S P

SP m

  







 



Vì vai trò của

,

x y

là như nhau nên để hệ có nghiệm duy nhất thì điều kiện cần là

x y



Thay

x y



vào hệ ta được

2

3

2 2

2 1

x x m

x m



  





 





Trừ vế ta được:

3 2

2 2 1 0

x x x

   

1 1

1 3

2 4

x m





  



     





  





+) Nếu

1

m



ta được

3 2, 1 2

1

2 1, 2( ) 1

S P S P x y

x y

SP S P l xy

     

  

    

 



   

  

(t/m).

+) Nếu

3

m

 

ta được

1 2, 1

2 1, 2

S P S P

SP S P

     

 







    

 

(loại vì hệ không phải có nghiệm duy

nhất).

+) Nếu

3

4

m



 ta được

5 1

1

1,

1

4 4

1

1 1

2

, 1( )

4

4 4

x y

S P S P

x y

xy

SP S P l

 

 

   



 

 

    



 





 

  







 

(t/m).

Vầy có

2

giá trị

m

thỏa mãn.

Câu 34: Cho hình bình hành

ABCD

có

,

AB a



,

AB BD





0

60 .

BAD 

Gọi

,

E F

lần lượt là trung điểm

của

, .

BD AD

Độ dài vec tơ

BE AF



 

là

A.

13

2

a

. B.

10

2

a

. C.

7

2

a

. D.

2

a

.

Lời giải

Chọn A

Ta có:

.tan60 3.

o

BD a a 

2

2 2 2

13

3

4 2

a a

GD BD BG a    

( ) 2

BE AF DE DF DH DG

       

     

13

2

a

BE AF DG   

 

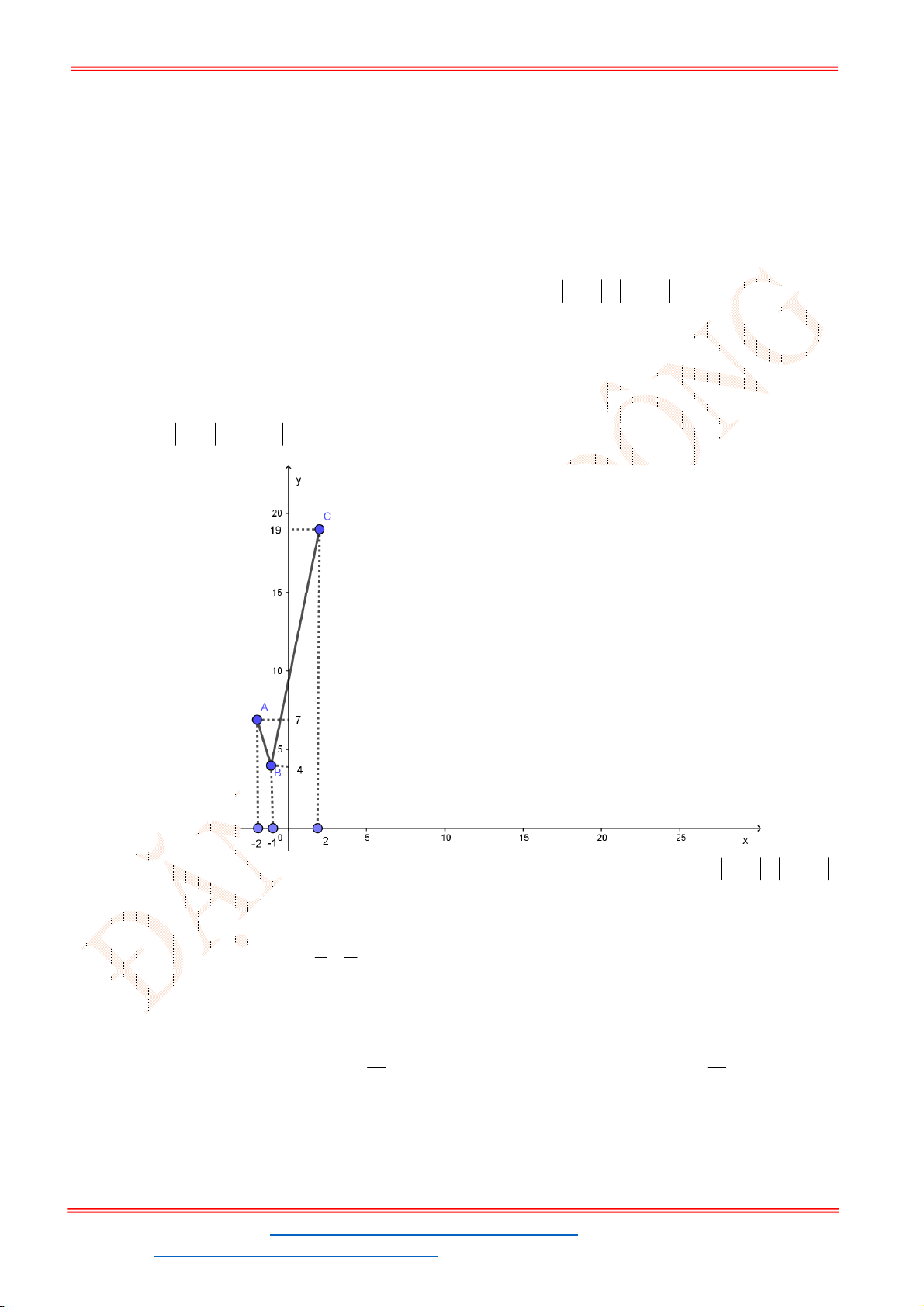
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Ta có





4 3 2 2 2

5 20 15 5 4 3

y x x x x x x



     





 

0 1 2

0 1 1 2

3 1 2

x ;

y x ;

x ;

   





    



  



















0 1; 1 2; 1 10; 2 7

y y y y

      

. Vậy

 

1;2

min 10, max 2

x

y y

 

  

.

Câu 35: Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số

2 4 4 3

y x x

    

trên đoạn





2;2

 là

A.

24

. B.

21

. C.

23

. D.

26

.

Lời giải

Chọn C

3 1 2 1

2 4 4 3

5 9 1 2

x khi x

y x x

x khi x

     



     



   



Dựa vào đồ thị ta thấy giá trị lớn nhất và giá trị nhỏ nhất của hàm số

2 4 4 3

y x x

    

trên đoạn





2;2

 lần lượt là

19

và

4

.

Câu 36: Biết hệ phương trình

6 5

3

9 10

1

x y



 







 





có nghiệm





;

x y

. Hiệu

y x



là

A.

2



. B.

2

15



. C.

2

. D.

2

15

.

Lời giải

Chọn C

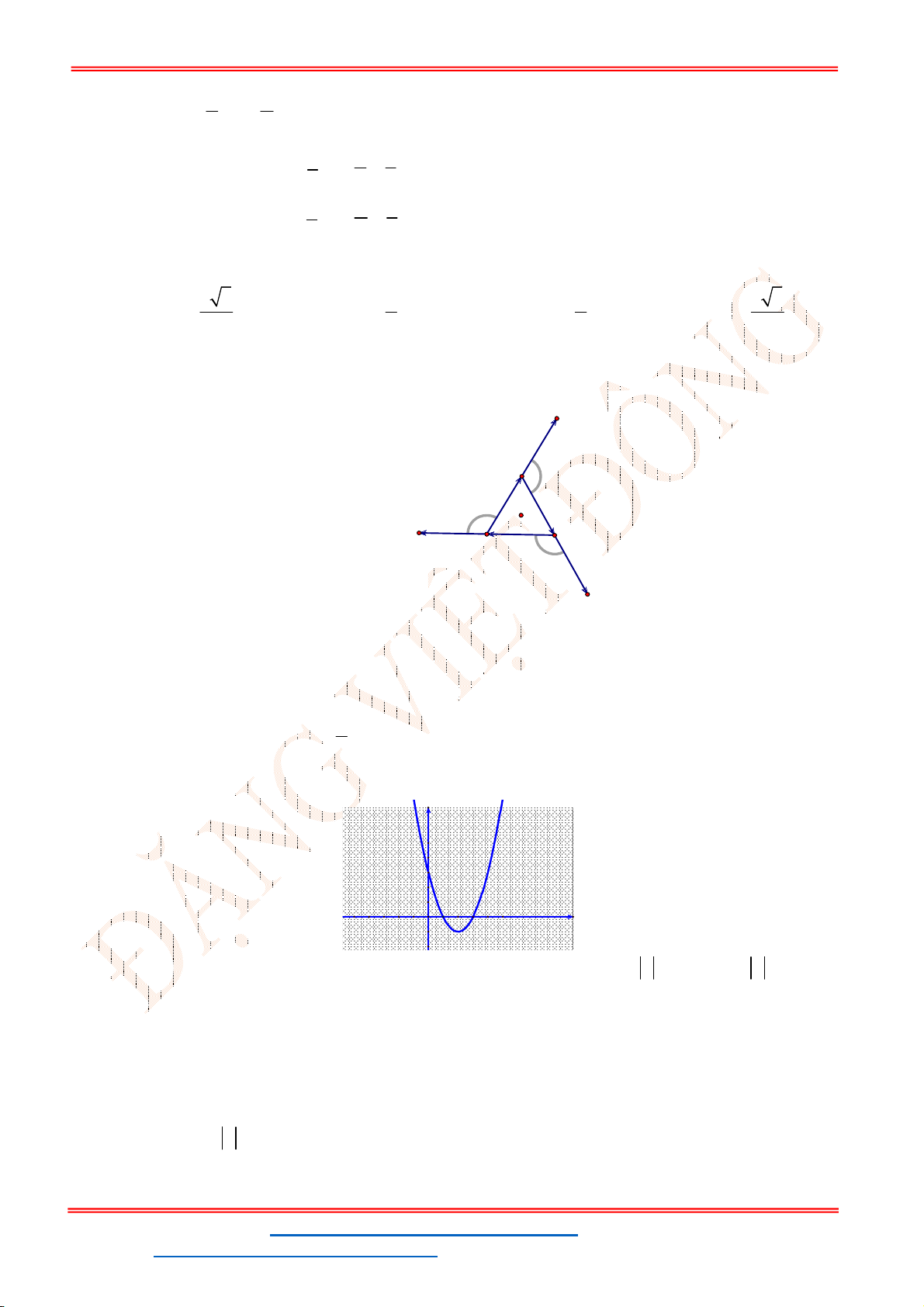
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Đặt

1 1

; a b

x y

 

ta được:

1 1

1

6 5 3 3

3

2

1 1

9 10 1 1 5

5

a

a b x

x

y x

a b y

b

y







  

 

 

     

   

  

 

 







.

Câu 37: Cho tam giác đều ABC. Tính

os(AB, ) os(BC, ) os(CA, ).

P c BC c CA c AB

  

     

A.

3 3

2

P  B.

3

2

P



C.

3

2

P

 

D.

3 3

2

P  

Lời giải

Chọn C

A'

C'

B'

A

B

C

Có



0

( , ) ( ', ) ' 120

AB BC BB BC B BC  

   

Có



0

( , ) ( ', ) ' 120

BC CA CC CA C CA  

   

Có



0

( , ) ( ', ) ' 120

CA AB AA AB A AB  

   

Suy ra

0

3

3.cos120

2

P

  

Câu 38: Cho hàm số

2

( )

y f x ax bx c

   

có đồ thị

( )

C

(như hình vẽ)

x

y

-5 -4 -3 -2 -1 5432O 1

Có bao nhiêu giá trị nguyên của tham số

m

để phương trình

2

( ) ( 2) ( ) 3 0

f x m f x m

    

có 6 nghiệm phân biệt ?

A. 1 B. 4 C. 3 D. 2

Lời giải

Chọn C

Đặt

( )

t f x

 , pttt

2

1

( 2) 3 0

3

t

t m t m

t m

 



     



 



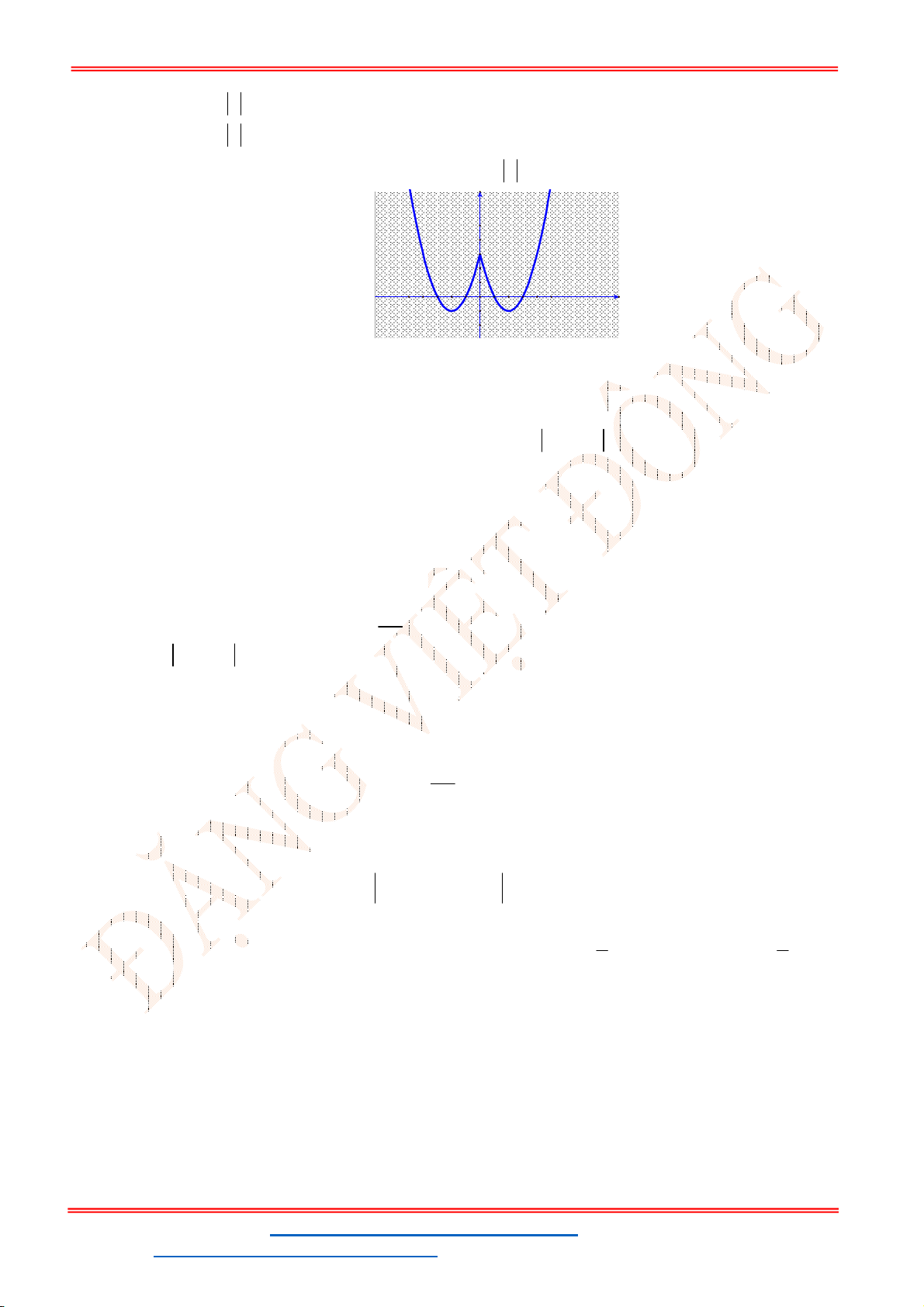
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 20

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Suy ra

( ) 1 (1)

( ) 3 (2)

f x

f x m

  



 





Từ đồ thị của

( )

y f x



suy ra đồ thị của

( )

y f x



x

y

-1

3

-5 -4 -3 -2 -1 5432

O

1

Có (1) cho 2 nghiệm là -2 và 2

ycbt <=> (2) có 4 nghiệm pb <=>

1 3 3 0 4

m m

      

.

Vậy có 3 giá trị nguyên m là 1; 2; 3

Câu 39: Tìm tất cả các giá trị của tham số

m

để phương trình

2 5 2 3

x m x m

   có nghiệm.

A.





0;m

 

. B.





0;m

 

. C.





;0

m  . D.





;m

  

.

Lời giải

Chọn B.

Có

3

2

2 5 2 3

0 2

2

m

x

x m x m

x m







   



















.

Để phương trình có nghiệm thì

0

3

2

m







 







.

Câu 40: Trong mặt phẳng tọa độ

Oxy

cho ba điểm













1; 2 , 3;2 , 4; 1

A B C

  

. Biết





;

E a b

di động

trên đường thẳng

AB

sao cho

2 3

EA EB EC

 

  

đạt giá trị nhỏ nhất. Tính

2 2

a b



?

A.

2 2

2

a b

 

. B.

2 2

1

a b

 

. C.

2 2

2

3

a b

 

. D.

2 2

3

2

a b

 

.

Lời giải

Chọn D.

Phương trình đường thẳng









: , 1; 2 , 3;2 : 1

AB y ax b A AB B AB AB y x

        

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 21

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay





; 1.

E a b AB b a

   

có

 

2 2 2 ; 4 2

3 9 3 ;6 3

4 ; 1

EA a b

EB a b

EC a b



    



  





   











2 3 3 4 ;3 4

EA EB EC a b

     

  





3 4 ;7 4

a a

   .

   

2 2

2 3 3 4 7 4 8

EA EB EC a a

      

  

khi

5

4

t



2 2

5

3

4

1

2

4

a

a b

b







   











.

Câu 41: Cho hai tập hợp





2;4;6;9

A  ,





1;2;3;4

B  . Tập

A

\

B

bằng tập hợp nào sau đây?

A.





2;4

. B.





1;3

. C.





6;9

. D.





6;9;1;3

.

Lời giải

Chọn C

Ta có:

A

\

B





6;9

 .

Câu 42: Cho hệ phương trình





1 3

2 2

2 4

mx m y m

x my m

x y

  



  





 



. Biết hệ phương trình có nghiệm khi tham số

0

m m



. Giá trị của

0

m

thuộc khoảng nào dưới đây?

A.





0

2;4

m  . B.





0

4; 2

m

  

. C.





0

1;2

m   . D.





0

2; 1

m

  

.

Lời giải

Chọn C

Ta có :





1 3

2 2

2 4

mx m y m

x my m

x y

  



  





 







 

1 3

4 2

mx m y m

x m x m

x y

  



    





  



 

2

5 2

1

2

1

2 4

1

m

x

m

m m

y

m

x y

m



























 



 



.

Suy ra:

 

2

5 2 2

2 4

1

m m m

m

 

 

 

 



 

  





 

2

5 2 1 2 2 4 1

m m m m m

      

.

2

1

5 3 2 0

2

5

m

m m

m







    



 



.

Với

1

m



hệ vô nghiệm.

Với

2

5

m

 

thì hệ phương trình có nghiệm thỏa hệ.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 22

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Do đó

 

0

2

1;2

5

m m     .

Câu 43: Trong mặt phẳng tọa độ

Oxy

cho điểm





3;1

M . Giả sử





;0

A a

và





0;

B b

( với

,

a b

là các số

thực không âm) là hai điểm sao cho tam giác

MAB

vuông tại

M

và có diện tích nhỏ nhất.

Tính giá trị biểu thức

2 2

T a b

 

.

A.

10

T



. B.

9

T



. C.

5

T



. D.

17

T



.

Lời giải

Chọn A

Ta có:









3; 1 , 3; 1

MA a MB b

     

 

.

. 0

MA MB



 











3. 3 1. 1 0

a b

    



10 3

b a

 

.

3 1

1

3 1

2

MAB

a

S

b



 



 

  

1

3 1 3

2

a b

   

  

1

3 9 3 3

2

a a

   

 

2

3

3 1

2

a

  

3

,

2

a

 

Vậy

MAB

S



đạt giá trị nhỏ nhất nếu

3

a



, suy ra

1

b



.

Khi đó

2 2

T a b

 

10



.

Câu 44: Có bao nhiêu giá trị của tham số

m

để phương trình









2 2

2 2 1 1 0

m x m mx m

     

có

hai nghiệm phân biệt và là hai số đối nhau?

A.

0

. B.

1

. C.

3

. D.

2

.

Lời giải

Chọn D

Giả sử phương trình









2 2

2 2 1 1 0

m x m mx m

     

có hai nghiệm

1 2

,

x x

phân biệt thỏa

mãn

1 2

0

x x

 

.

Theo định lý viet thì :

2

m

 

và





2

1 2

2 1

2

m m

x x

m



 



, nên ta có :

1 2

0

x x

 







2

2 1

0

2

m m

m









0

1

m











 



.

+ Với

0

m



, phương trình có dạng

2

2 1 0

x

 



1

2

x  

( thỏa mãn yêu cầu)

+ Với

1

m



, phương trình có dạng

2

3 0 0

x x

  

(không thỏa mãn yêu cầu)

+ Với

1

m

 

, phương trình có dạng

2

2 0 2

x x    

(thỏa mãn yêu cầu)

Vậy có hai giá trị của tham số m thỏa mãn yêu cầu đề bài.

Câu 45: Cho

0 1

x y z

   

và

3 2 4

x y z

  

. Tìm giá trị lớn nhất của biểu thức

2 2 2

3 2

S x y z

  

.

A.

3

. B.

4

. C.

8

3

. D.

10

3

.

Lời giải

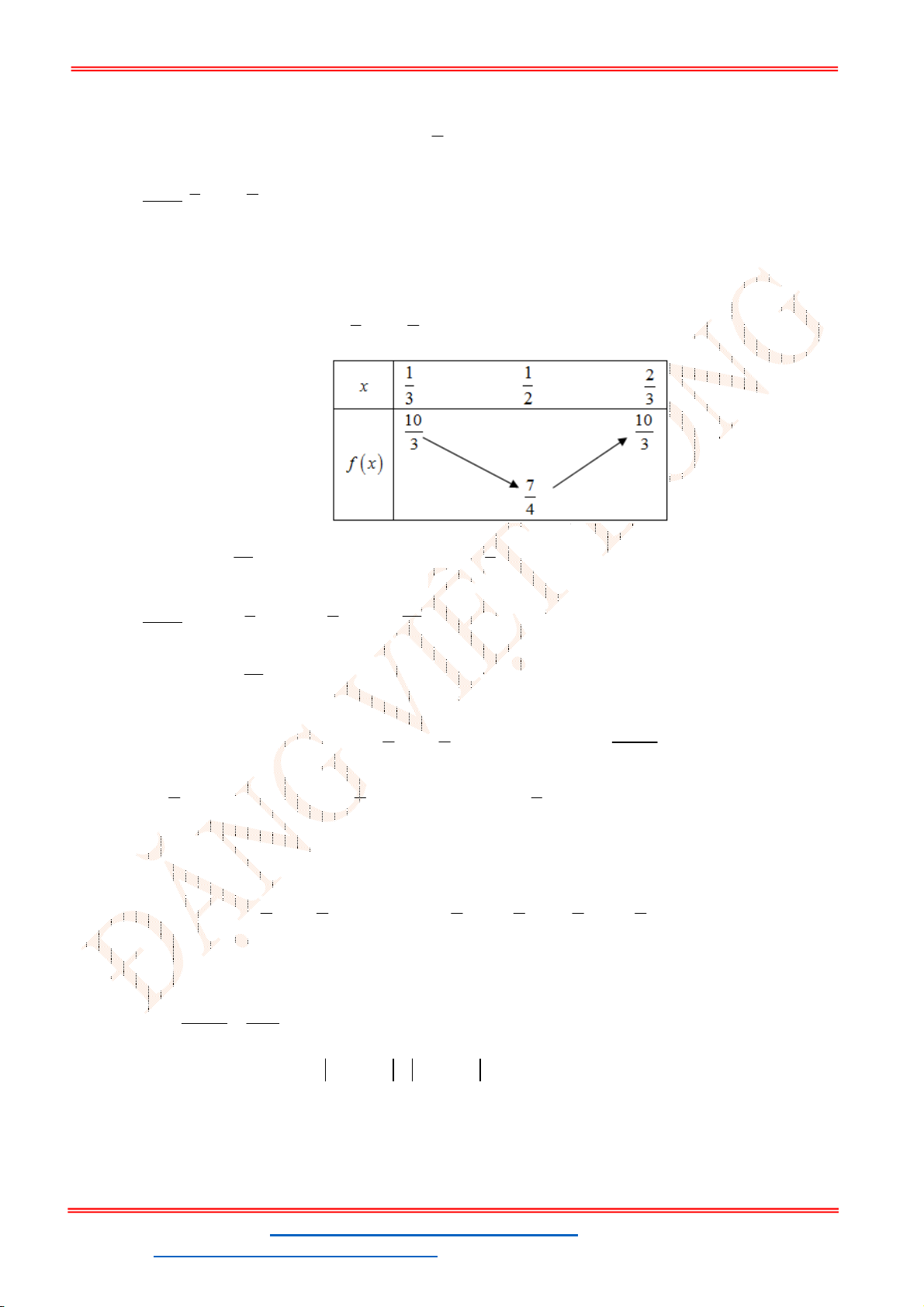
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 23

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Chọn D.

Ta có:

4 3 2 6

x y z x

   

2

0

3

x

  

.

TH1:

1 2

3 3

x

 

.

Vì

0 1

y z

  

2

y y

z z

















2 2

3 2 3 3 4

S x y z x x

      

.

Đặt





2

3 3

f x x x

  

với

1 2

3 3

x

 

. Lập bảng biến thiên:

Suy ra:

10

3

S



. Dấu đẳng thức xảy ra

1

3

x

 

;

1

y z

 

.

TH2:

1

0

3

x

 

1 10

3. 1 1

9 3

S     .

Vậy

10

maxS

3

 .

Câu 46: Cho tam giác

ABC

có

1 3

2 2

AM AB AC

  

  

. Tỉ số diện tích

ABM

ACM

S



là

A.

3

4

. B.

1

4

. C.

1

3

. D.

3

.

Lời giải

Chọn D.

Ta có:

1 3

2 2

AM AB AC

  

  

1 1 3 3

2 2 2 2

AM AM MB AM MC

     

    

3

MB MC

 

 

3

M BC

MB MC













.

Vậy

3

ABM

ACM

S BM

S CM



 

.

Câu 47: Cho hàm số





2018 2018

y f x x x     . Mệnh đề nào sau đây sai?

A. Hàm số





y f x

 có tập xác định là



.

B. Đồ thị hàm số





y f x

 nhận trục tung làm trục đối xứng.

C. Hàm số





y f x

 là hàm số chẵn.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 24

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

D. Đồ thị hàm số





y f x

 nhận gốc tọa độ

O

làm tâm đối xứng.

Lời giải

Chọn D





2018 2018

y f x x x    

TXĐ :

D





,

x D x D

   

.









2018 2018 2018 2018

f x x x x x f x

           

Do đó hàm số





y f x

 là hàm số chẵn .

Câu 48: Cho

ABC



có trọng tâm

G

và trung tuyến

AM

. Khẳng định nào sau đây sai ?

A.

0

  

   

GA GB GC

. B.

2 0

GA GM

 

  

.

C.

2

AM MG

 

 

. D.

3

OA OB OC OG

  

   

, với mọi điểm

O

.

Lời giải

Chọn C

M

A

B

C

G

C sai vì

3

AM MG

 

 

Câu 49: Với giá trị nào của

a

và

b

thì đồ thị hàm số

y ax b

 

đi qua các điểm





2;1

A  ,





1; 2

B



?

A.

2

a



và

1

b



. B.

1

a

 

và

1

b

 

. C.

2

a

 

và

1

b

 

. D.

1

a



và

1

b



.

Lời giải

Chọn B

Đồ thị hàm số

y ax b

 

đi qua các điểm





2;1

A  ,





1; 2

B



2 1

2

a b

  







  



1

a

b

 







 



.

Câu 50: Cho các vectơ

a



,

b



,

c



thỏa mãn

a x





,

b y





,

c z





và

3 0

a b c

  

   

. Tính

. . .

A a b b c c a

  

     

.

A.

2 2 2

3

2

x z y

A

 

 . B.

2 2 2

3

2

z x y

A

 

 . C.

2 2 2

3

2

y x z

A

 

 . D.

2 2 2

3

2

z x y

A

 

 .

Lời giải

Chọn B

Ta có

3 0

a b c

  

   

2

a b c c

    

   









2 2

2

a b c c

    

   

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 25

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay





2 2 2 2

2 . . . 4

a b c a b b c c a c

      

         





2 2 2

2 . . . 3

x y a b b c c a z

     

     

2 2 2

3

. . .

2

z x y

a b b c c a

 

   

     

.

---HẾT---

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 11 Môn Toán – Lớp 10

(Th

ời gian l

àm bài 90 phút)

Không k

ể thời gian phát đề

I. PHẦN TRẮC NGHIỆM

Câu 1. Cho các tập hợp:





2;4;6

A 

,





2;6

B  ,





4;6

C  ,





4;6;8

D  . Khẳng định nào sau đây

đúng?

A.

A D



. B.

B D



. C.

B C



. D.

C D



.

Câu 2. Cho hàm số





3 2

f x x

 

. Giá trị của hàm số tại điểm

1

x

 

bằng

A.

1

. B.

3

. C.

5

. D. 5.

Câu 3. Trong các hàm số sau, hàm số nào có đồ thị nhận đường

2020

x



làm trục đối xứng?

A.

2

2 2020 1

y x x

   

. B.

2

2 2020 5

y x x

  

.

C.

2

2020 2

y x x

  

. D.

2

1

2020 2

2

y x x

  

.

Câu 4. Điều kiện xác định của phương trình

2

4

1

 



x

là

A.





1;

  

x

. B.









1; \ 1

  x . C.









1; \ 1

  x . D.





1;1

 x .

Câu 5. Trong các phương trình sau, phương trình nào tương đương với phương trình

2

9

x



A.

2

3 4 0

x x

  

. B.

2

3 4 0

x x

  

.

C.

3

x



. D.

2

9

x x x

  

.

Câu 6. Có bao nhiêu giá trị của tham số

m

để phương trình





2

2 4 0

m x m

   

vô nghiệm?

A.

0

. B.

1

. C.

2

. D.

3

.

Câu 7. Cho tam giác  có trọng tâm 

và trung tuyến . Khẳng định nào sau đây là sai?

A. 

󰇍



+ 2

󰇍



=0

󰇍



. B.

󰇍



+ 

󰇍



+ 

󰇍



=3

󰇍



, ∀.

C. 

󰇍



=−2

󰇍



. D.

󰇍



+ 

󰇍



+ 

󰇍



=0

󰇍



.

Câu 8. Cho tam giác

ABC

đều có độ dài cạnh bằng

a

. Độ dài

AB BC



 

bằng

A.

2

a

. B.

3

a

. C.

3

2

a

. D.

a

.

Câu 9. Cho





1; 5

a 



,





2; 1

b  



. Tính

3 2

c a b

 



 

.

A.





7; 13

c 



. B.





1; 17

c 



. C.





1; 17

c  



. D.





1; 16

c 



.

Câu 10. Cho góc



thỏa mãn

0 0

90 180



 

. Khẳng định nào sau đây là khẳng định đúng?

A.

cos 0





. B.

sin 0





. C.

tan 0





. D.

cot 0





.

Câu 11. Cho





2; 1

OM

  



,





3; 1

ON

 



. Tính góc của





,

OM ON

 

A.

o

135

. B.

2

 . C.

o

135



. D.

2

.

Câu 12. Cho mệnh đề: “

2

, 3 5 0

x x x

    



”. Mệnh đề phủ định của mệnh đề trên là

A.

2

, 3 5 0

x x x

    



. B.

2

, 3 5 0

x x x

    



.

C.

2

, 3 5 0

x x x

    



. D.

2

, 3 5 0

x x x

    



.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 13. Cho tập hợp





1;2;3;4

A  . Hỏi có bao nhiêu tập hợp con của tập hợp

A

có chứa phần tử

1

?

A.

1

. B.

16

. C.

7

. D.

8

.

Câu 14. Cho tam giác

ABC

vuông tại

A

, trọng tâm

G

,

6, 8

AB AC

 

. Độ dài véc-tơ

AG



bằng

A. 10. B.

5 3

. C.

20

3

. D.

10

3

.

Câu 15. Cho hàm số





2 2 3

y m x m

   

số giá trị

m

nguyên thuộc đoạn





2021;2021

 để hàm số

nghịch biến trên



là

A.

2019

. B.

2020

. C.

2018

. D.

2021

.

Câu 16. Cho hai hàm số





3

2 3

f x x x

  

và





2021

3

g x x

 

. Mệnh đề nào sau đây đúng?

A.





f x

là hàm số lẻ;





g x

là hàm số lẻ.

B.





f x

là hàm số chẵn;





g x

là hàm số chẵn.

C. Cả





f x

và





g x

đều là hàm số không chẵn, không lẻ.

D.





f x

là hàm số lẻ;





g x

là hàm số không chẵn, không lẻ.

Câu 17. Phương trình

2

2 3 5

x x x

   

có tổng các nghiệm nguyên là

A.

2



. B.

3



. C.

1



. D.

4



.

Câu 18. Tổng các nghiệm của phương trình

   

2 5 5 2 1 0

x x là:

A.

5

. B.

0

. C.

15

4

. D.

15

2

.

Câu 19. Nghiệm của hệ phương trình

3 2 1

2 2 3 0

x y



  





 





là

A.





3; 2 2

 

B.





3;2 2

C.





3;2 2



D.





3; 2 2



Câu 20. Cho tam giác

ABC

. Điểm

M

nằm trên cạnh

BC

sao cho 2



MB MC

. Hãy phân tích vectơ



AM

theo hai vectơ 





u AB

,







v AC

.

A.

1 2

3 3

AM u v

 



 

. B.

1 2

3 3

 

AM u v



 

. C.

1 2

3 3

AM u v

  



 

. D.

4 2

3 3

AM u v

 



 

.

Câu 21. Trong mặt phẳng

Oxy

, cho









2; 1 , 5;4

a b   

 

và





3; 2

c

 



. Phân tích véc tơ

b



qua véc tơ

a



và

c



ta được:

A.

2 3

b a c

 

  

B.

2 3

b c a

  

  

C.

2 3

b c a

 

  

D.

3 2

b c a

 

  

Câu 22. Cho biết

2

tan

3



 

. Giá trị của biểu thức

3sin 2cos

5sin cos

E

 







bằng

A.

19

13



. B.

1

. C.

25

13

. D.

12

7

.

Câu 23. Trong mặt phẳng tọa độ

Oxy

, cho













1;2 , 2;6 , 9;8

A B C . Gọi





;

H a b

là hình chiếu của

A

lên cạnh

BC

. Khi đó

2

b a



bằng

A.

6



. B.

13

. C.

13



. D.

6

.

Câu 24. Biết rằng hàm số





2

0

y ax bx c a

   

đạt giá trị nhỏ nhất bằng

4

tại

2

x



và có đồ thị hàm

số đi qua điểm





0;6

A . Tính tích

.

P abc



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

6

P

 

. B.

6

P



. C.

3

P

 

. D.

3

2

P



.

Câu 25. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

4 2

4 3

y x x

  

trên





1;2



là

a

và

b

. Khi đó

P a b

 

bằng

A.

7

. B.

4



. C.

10



. D.

10



.

Câu 26. Tìm tất cả các giá trị của tham số

m

để đường thẳng : 2

y x m

  

cắt





2

: 4 1

P y x x

  

tại

hai điểm phân biệt có hoành độ dương.

A.

8 1

m

  

. B.

8

m

 

. C.

1

m



. D.

8 1

m

  

.

Câu 27. Cho hình thang





//

ABCD AB CD

, có 2

CD AB



,

H

là trung điểm của cạnh

DC

,

M

là điểm

thỏa mãn đẳng thức

MH AD MH HD

  

   

. Khẳng định nào sau đây là đúng?

A. Quỹ tích điểm

M

là đường trung trực của đoạn thẳng

BC

..

B. Quỹ tích điểm

M

là đường trung trực của đoạn thẳng

HD

. .

C. Quỹ tích điểm

M

là đường trung trực của đoạn thẳng

AB

.

D. Quỹ tích điểm

M

là đường trung trực của đoạn thẳng

BD

.

Câu 28. Có bao nhiêu số nguyên

m

thuộc nửa khoảng





2020; 2020

 để phương trình

2

2 3x 4 3

x m x

   

có nghiệm.

A.

2017

. B.

2018

. C.

2019

. D.

2020

.

II. PHẦN TỰ LUẬN

Câu 1a. Tìm tập xác định của hàm số

 

3

2

x

f x

x







.

Câu 1b. Xét tính chẵn, lẻ của hàm số





2020 2020

f x x x

   

.

Câu 2. Cho hệ phương trình

3

2 2 9

mx y

x y







 

 

a) Giải hệ phương trình khi

2

m



.

b) Tìm

m

để hệ có nghiệm duy nhất





0 0

;

x y

thỏa mãn điều kiện

0 0

2 4

x y

 

.

Câu 3a. Cho tam giác ABC, gọi M là trung điểm của BC và I là trung điểm của AM. Chứng minh rằng:

2 0

IA IB IC

  

   

.

Câu 3b. Cho hình thang cân

ABCD

biết đáy lớn

3

CD a



,

AB a



và

2

BC a

 . Gọi

H

là hình chiếu vuông

góc của

A

lên cạnh

CD

. Tính





.

BH AC AD



  

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG HDG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 11 Môn Toán – Lớp 10

(Th

ời gian l

àm bài 90 phút)

Không k

ể thời gian phát đề

I. PHẦN TRẮC NGHIỆM (7,0 điểm)

Câu 1. Cho các tập hợp:





2;4;6

A 

,





2;6

B  ,





4;6

C  ,





4;6;8

D  . Khẳng định nào sau đây

đúng?

A.

A D



. B.

B D



. C.

B C



. D.

C D



.

Lời giải

Ta có:

+





2 2;4;6

A 

và





2 4;6;8

D 

nên

A D



. Đáp án A sai.

+





2 2;6

B 

và





2 4;6;8

D 

nên

B D



. Đáp án B sai.

+





2 2;6

B 

và





2 4;6

C 

nên

B C



. Đáp án C sai.

+





4;6 4;6

C 

và





4;6 4;6;8

D 

nên

C D



. Đáp án D đúng.

Câu 2. Cho hàm số





3 2

f x x

 

. Giá trị của hàm số tại điểm

1

x

 

bằng

A.

1

. B.

3

. C.

5

. D. 5.

Lời giải

Thay

1

x

 

vào hàm số





3 2

f x x

 

, ta được

   

1 3 2 1 5

f     

Vậy giá trị của hàm số tại điểm

1

x

 

bằng

5

.

Câu 3. Trong các hàm số sau, hàm số nào có đồ thị nhận đường

2020

x



làm trục đối xứng?

A.

2

2 2020 1

y x x

   

. B.

2

2 2020 5

y x x

  

.

C.

2

2020 2

y x x

  

. D.

2

1

2020 2

2

y x x

  

.

Lời giải

Trục đối xứng của parabol





2

0

y ax bx c a

   

có phương trình

2

b

x

a

  .

Áp dụng vào các đáp án, chọn D.

Câu 4. Điều kiện xác định của phương trình

2

4

1

 



x

là

A.





1;

  

x

. B.









1; \ 1

  x . C.









1; \ 1

  x . D.





1;1

 x .

Lời giải

Đk

2

1 1

1 0

1 1

1 0

  



 

 

 

  

   

 

 



x x

x

x x

x

.









1; \ 1

   x .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 5. Trong các phương trình sau, phương trình nào tương đương với phương trình

2

9

x



A.

2

3 4 0

x x

  

. B.

2

3 4 0

x x

  

.

C.

3

x



. D.

2

9

x x x

  

.

Lời giải



2

9 3.

x x

   



3 3.

x x

   

Hai phương trình này có cùng tập nghiệm nên chúng tương đương. Suy ra đáp án C.

Câu 6. Có bao nhiêu giá trị của tham số

m

để phương trình





2

2 4 0

m x m

   

vô nghiệm?

A.

0

. B.

1

. C.

2

. D.

3

.

Lời giải

Phương trình





2

2 4 0

m x m

   

vô nghiệm khi

2

2 0

4 0

m

 





  



2

m

 



  



 



Không có giá trị nào của tham số

m

để phương trình vô nghiệm.

Câu 7. Cho tam giác  có trọng tâm 

và trung tuyến . Khẳng định nào sau đây là sai?

A. 

󰇍



+ 2

󰇍



=0

󰇍



. B.

󰇍



+ 

󰇍



+ 

󰇍



=3

󰇍



, ∀.

C. 

󰇍



=−2

󰇍



. D.

󰇍



+ 

󰇍



+ 

󰇍



=0

󰇍



.

Lời giải

A đúng vì 

󰇍



=−2

󰇍



⇒ 

󰇍



+ 2

󰇍



=0

󰇍



.

B đúng theo tính chất trọng tâm.

C sai vì 

󰇍



=−3

󰇍



.

D đúng theo tính chất trọng tâm. Suy ra: Đáp án C.

Câu 8. Cho tam giác

ABC

đều có độ dài cạnh bằng

a

. Độ dài

AB BC



 

bằng

A.

2

a

. B.

3

a

. C.

3

2

a

. D.

a

.

Lời giải

G

M

A

B

C

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Ta có:

AB BC AC AC a

   

  

.

Câu 9. Cho





1; 5

a 



,





2; 1

b  



. Tính

3 2

c a b

 



 

.

A.





7; 13

c 



. B.





1; 17

c 



. C.





1; 17

c  



. D.





1; 16

c 



.

Lời giải

Ta có:

3 (3;15)

2 ( 4;2)

a

b









 







Do đó

3 2 ( 1;17)

c a b   



 

.

Câu 10. Cho góc



thỏa mãn

0 0

90 180



 

. Khẳng định nào sau đây là khẳng định đúng?

A.

cos 0





. B.

sin 0





. C.

tan 0





. D.

cot 0





.

Lời giải

Ta có

0 0

90 180 sin 0, cos 0, tan 0, cot 0

    

      

.

Do đó đáp án đúng là

A

.

Câu 11. Cho





2; 1

OM

  



,





3; 1

ON

 



. Tính góc của





,

OM ON

 

A.

o

135

. B.

2

 . C.

o

135



. D.

2

.

Lời giải

Ta có

   

o

. 5 2

cos , , 135

2

5. 10

.

OM ON

OM ON OM ON

OM ON



     

 

   



.

Câu 12. Cho mệnh đề: “

2

, 3 5 0

x x x

    



”. Mệnh đề phủ định của mệnh đề trên là

A.

2

, 3 5 0

x x x

    



. B.

2

, 3 5 0

x x x

    



.

C.

2

, 3 5 0

x x x

    



. D.

2

, 3 5 0

x x x

    



.

Lời giải

Câu 13. Cho tập hợp





1;2;3;4

A  . Hỏi có bao nhiêu tập hợp con của tập hợp

A

có chứa phần tử

1

?

A.

1

. B.

16

. C.

7

. D.

8

.

Lời giải

Các tập hợp con của tập hợp

A

có chứa phần tử

1

là





1

,





1;2

,





1;3

,





1;4

,





1;2;3

,





1;2;4

,





1;3;4

,





1;2;3;4

.

Vậy có tất cả

8

tập hợp con của tập hợp

A

có chứa phần tử

1

.

Câu 14. Cho tam giác

ABC

vuông tại

A

, trọng tâm

G

,

6, 8

AB AC

 

. Độ dài véc-tơ

AG



bằng

A. 10. B.

5 3

. C.

20

3

. D.

10

3

.

Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Tam giác

ABC

vuông tại

A

nên

2 2

10

BC AB AC

  

Gọi

M

là trung điểm của

5

2

BC

BC AM

  

G

là trọng tâm tam giác nên

2 10

3 3

AG AM

 

Vậy

10

3

AG AG

 



Câu 15. Cho hàm số





2 2 3

y m x m

   

số giá trị

m

nguyên thuộc đoạn





2021;2021

 để hàm số

nghịch biến trên



là

A.

2019

. B.

2020

. C.

2018

. D.

2021

.

Lời giải

Hàm số nghịch biến trên

2 2 0 1

m m

    



Vậy số giá trị nguyên của





2021;2021

m  là





2;3;4;...;2021

Do đó số giá trị nguyên là 2020 giá trị

Câu 16. Cho hai hàm số





3

2 3

f x x x

  

và





2021

3

g x x

 

. Mệnh đề nào sau đây đúng?

A.





f x

là hàm số lẻ;





g x

là hàm số lẻ.

B.





f x

là hàm số chẵn;





g x

là hàm số chẵn.

C. Cả





f x

và





g x

đều là hàm số không chẵn, không lẻ.

D.





f x

là hàm số lẻ;





g x

là hàm số không chẵn, không lẻ.

Lời giải



Xét





3

2 3

f x x x

  

có TXĐ:

D





nên

D D.

x x

    

Ta có

         

3

2 3 2 3

f x x x x x f x f x

           là hàm số lẻ.



Xét





2021

3

g x x

 

có TXĐ:

D





nên

D, D.

x x

   

Ta có

     

2021

3 3

g x x x g x

         , do đó hàm số





g x

không chẵn, không

lẻ.

Vậy





f x

là hàm số lẻ;





g x

là hàm số không chẵn, không lẻ.

Câu 17. Phương trình

2

2 3 5

x x x

   

có tổng các nghiệm nguyên là

A.

2



. B.

3



. C.

1



. D.

4



.

Lời giải

+ TH1:

2

2 3 0

x x

  

3

1

x

 











. Khi đó phương trình trở thành:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

2

2 3 5

x x x

   

2

8 0

x x

   

1 33

2

1 33

2

x



 









 







.

+ TH2:

2

2 3 0

x x

  

3 1

x

   

. Khi đó phương trình trở thành:

2

2 3 5

x x x

    

2

3 2 0

x x

   

1

2

x

 







 



.

Vậy tổng các nghiệm nguyên là:

1 2 3

T

    

.

Câu 18. Tổng các nghiệm của phương trình

   

2 5 5 2 1 0

x x là:

A.

5

. B.

0

. C.

15

4

. D.

15

2

.

Lời giải

Ta có:

   

 





        



  







 



 

 

    

 

 

 

 





2

2 5 0

2 5 5 2 1 0 5 2 1 2 5

25 2 1 2 5

5

15

2

0; .

2

15 2

4 30 0

0;

2

x

x x x x

x x

x

x x

Do đó :

15 15

0

2 2

 

.

Câu 19. Nghiệm của hệ phương trình

3 2 1

2 2 3 0

x y



  





 





là

A.





3; 2 2

 

B.





3;2 2

C.





3;2 2



D.





3; 2 2



Lời giải

Ta có:

3 2 1 3 6 3 3

2 2 3 0 4 6 0 2 2

x y x y x

x y x y y

  

      

  

 

  

     

  

  

.

Câu 20. Cho tam giác

ABC

. Điểm

M

nằm trên cạnh

BC

sao cho 2



MB MC

. Hãy phân tích vectơ



AM

theo hai vectơ 





u AB

,







v AC

.

A.

1 2

3 3

AM u v

 



 

.

B.

1 2

3 3

 

AM u v



 

.

C.

1 2

3 3

AM u v

  



 

.

D.

4 2

3 3

AM u v

 



 

.

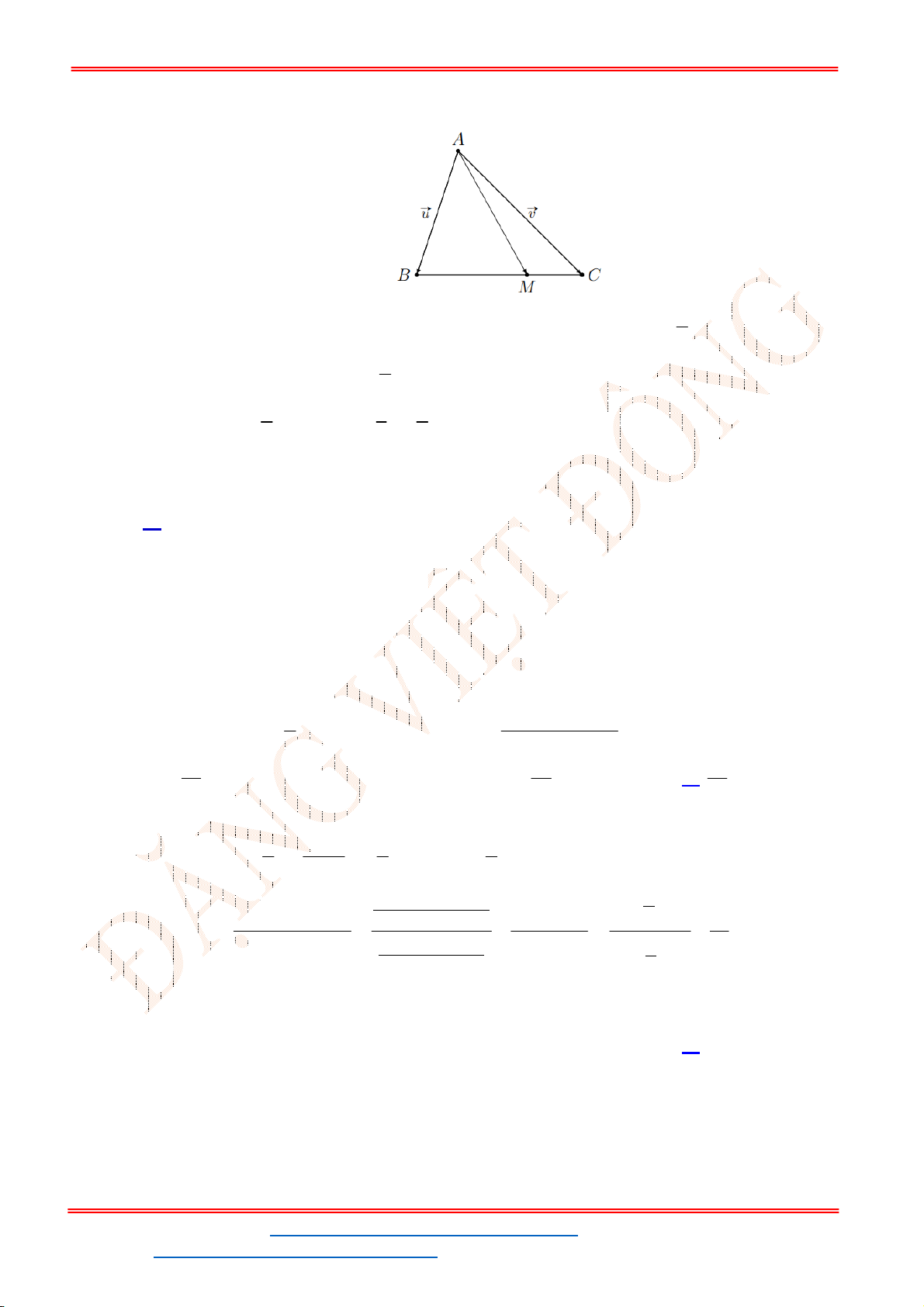
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Lời giải

Từ giả thiết 2



MB MC

và điểm

M

nằm giữa 2 điểm

,

B C

nên

2

3

BM BC



 

.

Do đó

2

3

   

    

AM AB BM AB BC

mà

 

  

BC AC AB







2 1 2

3 3 3

    

   

 

AM AB AC AB u v

.

Câu 21. Trong mặt phẳng

Oxy

, cho









2; 1 , 5;4

a b   

 

và





3; 2

c

 



. Phân tích véc tơ

b



qua véc tơ

a



và

c



ta được:

A.

2 3

b a c

 

  

B.

2 3

b c a

  

  

C.

2 3

b c a

 

  

D.

3 2

b c a

 

  

Lời giải

Gọi





2 3 ; 2

b ma nc m n m n

     

  

,

Ta có :

2 3 5 2

2 4 3

m n m

m n n

   

 



 

    

 

.

Vậy

2 3

b a c

 

  

Câu 23. Cho biết

2

tan

3



 

. Giá trị của biểu thức

3sin 2cos

5sin cos

E

 







bằng

A.

19

13



. B.

1

. C.

25

13

. D.

12

7

.

Lời giải

Ta có

2 sin 2 2

tan sin cos

3 cos 3 3



  



       

Do đó:

3sin 2cos

5sin cos

E

 



 



3sin 2cos

3tan 2

cos

5sin cos

5tan 1

cos

 



 









2

3 2

12

3

2

7

5 1

3

 

 

 

 

 

 

 

 

 

.

Câu 23. Trong mặt phẳng tọa độ

Oxy

, cho













1;2 , 2;6 , 9;8

A B C . Gọi





;

H a b

là hình chiếu của

A

lên cạnh

BC

. Khi đó

2

b a



bằng

A.

6



. B.

13

. C.

13



. D.

6

.

Lời giải

Gọi





;

H a b

là hình chiếu của

A

lên cạnh

BC

.

Ta có

     

1; 2 , 2; 6 , 11;2

AH x y BH x y BC   

  

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

   

. 0 11 1 2 2 0

AH BC AH BC x y

       

 

Hay

11 2 15 0

x y

  

(1)

Mặt khác ,

BH BC

 

cùng phương nên

2 6

2 11 70 0

11 2

x y

 

    

(2)

Từ (1) và (2) suy ra

1 32

,

5 5

x y 

Vậy hình chiếu của A lên BC là

1 32

;

5 5

H

 

 

 

.

Suy ra

1

5

2 6

32

5

a

b a

b







  









.

Câu 24. Biết rằng hàm số





2

0

y ax bx c a

   

đạt giá trị nhỏ nhất bằng

4

tại

2

x



và có đồ thị hàm

số đi qua điểm





0;6

A . Tính tích

.

P abc



A.

6

P

 

. B.

6

P



. C.

3

P

 

. D.

3

2

P



.

Lời giải

Hàm số đạt giá trị nhỏ bằng

4

tại

2

x



nên

0

2

4

a

b

a









 









 





.

Đồ thị hàm số đi qua điểm





0;6

A nên ta có

6

c



.

Từ đó ta có hệ:

2 2

2

1

4 4

2

4 16 16 8 0

4

2

4

6 6

6

0 0

0

b

b a b a

a

b ac a a a

b

a

c c

c

a a

a



 





   

 





 



    

  

 

    

   

 

   



   

 

 









.

Suy ra

6

P abc

  

.

Câu 25. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

4 2

4 3

y x x

  

trên





1;2



là

a

và

b

. Khi đó

P a b

 

bằng

A.

7

. B.

4



. C.

10



. D.

10



.

Lời giải

Đặt

2

t x



. Với





1;2

x  

ta có





0;4

t 

. Hàm số trở thành





2

4 3

f t t t

  

với





0;4

t 

.

Bảng biến thiên:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Dựa vào bảng biến thiên, ta có

 





 

1;2

0;4

max max 3

x

t

y f t

 



  

khi

0

4

t











hay

0

2

x











.

 





 

1;2

0;4

min min 7

x

t

y f t

 



  

khi

2

t



hay

2

x  .

Câu 26. Tìm tất cả các giá trị của tham số

m

để đường thẳng : 2

y x m

  

cắt





2

: 4 1

P y x x

  

tại

hai điểm phân biệt có hoành độ dương.

A.

8 1

m

  

. B.

8

m

 

. C.

1

m



. D.

8 1

m

  

.

Lời giải

Phương trình hoành độ giao điểm của





P

và



là:





2 2

4 1 2 6 1 0 *

x x x m x x m        

Đường thẳng



cắt





P

tại hai điểm phân biệt có hoành độ dương





*

 có hai nghiệm

dương phân biệt

'

0 8 0

0 6 0 8 1.

0 1 0

m

S m

P m



   



 

       

 

 

  



Câu 27. Cho hình thang





//

ABCD AB CD

, có 2

CD AB



,

H

là trung điểm của cạnh

DC

,

M

là điểm

thỏa mãn đẳng thức

MH AD MH HD

  

   

. Khẳng định nào sau đây là đúng?

A. Quỹ tích điểm

M

là đường trung trực của đoạn thẳng

BC

..

B. Quỹ tích điểm

M

là đường trung trực của đoạn thẳng

HD

. .

C. Quỹ tích điểm

M

là đường trung trực của đoạn thẳng

AB

.

D. Quỹ tích điểm

M

là đường trung trực của đoạn thẳng

BD

.

Lời giải

Ta có:

1

2

AB DH HC DC

  

.

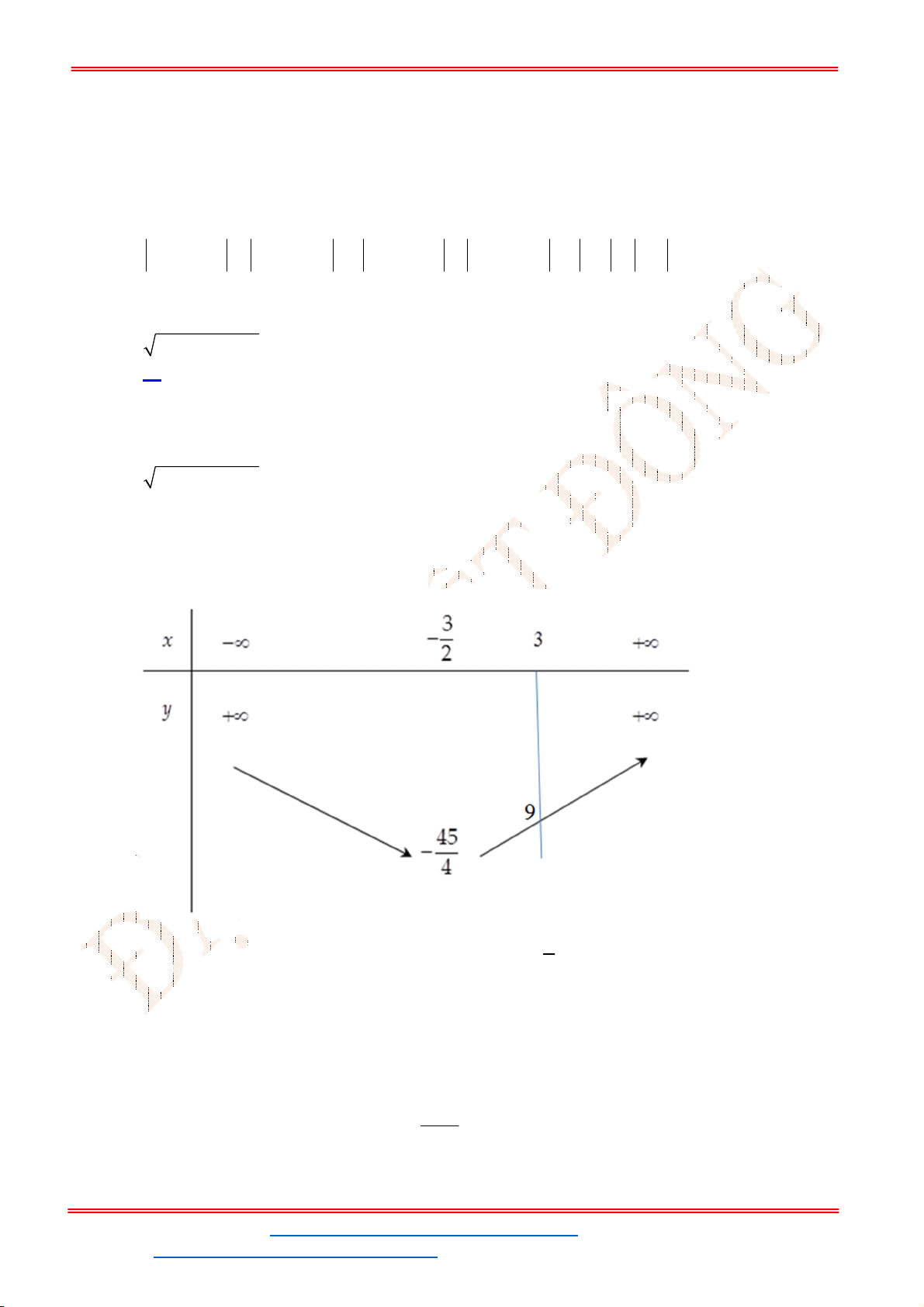
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Xét tứ giác ABHD , ta có:

/ /

AB DH















Tứ giác ABHD là hình bình hành.

HB DA 

 

.

Ta có:

MH AD MH HD  

   

MH HB MH HC   

   

MB MC 

 

MB MC  .

Suy ra: Quỹ tích điểm M là đường trung trực của đoạn thẳng BC .

Câu 28. Có bao nhiêu số nguyên m thuộc nửa khoảng





2020; 2020 để phương trình

2

2 3x 4 3x m x    có nghiệm.

A. 2017 . B. 2018. C. 2019 . D. 2020 .

Lời giải

Ta có :

2

2 2 2

3 3

2 3x 4 3

2x 3x 4 6x 9 3x 9 4

x x

x m x

m x x m

 

 

     

 

       

 

.

Xét hàm số :

2

3x 9y x  

.

Bảng biến thiên :

Để phương trình đã cho có nghiệm thì

9

4 9

4

m m   .

Do m ,





2020;2020m  nên

 

3;4;5...;2019m .

Vậy có 2017 giá trị nguyên của m thỏa mãn đề bài.

II. PHẦN TỰ LUẬN

Câu 1a. Tìm tập xác định của hàm số

 

3

2

x

f x

x







.

Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Điều kiện xác định của hàm số:

2 0 2

x x

   

.

Vậy tập xác định của hàm số là:





\ 2

D



.

Câu 1b. Xét tính chẵn, lẻ của hàm số





2020 2020

f x x x

   

.

Lời giải

Tập xác định của hàm số là:

D





.

Ta có

 

x D

thì

 

x D

và

















           2020 2020 2020 2020

f x x x x x f x

.

Vậy hàm số đã cho là hàm số chẵn.

Câu 2. Cho hệ phương trình

3

2 2 9

mx y

x y







 

 

a) Giải hệ phương trình khi

2

m



.

b) Tìm

m

để hệ có nghiệm duy nhất





0 0

;

x y

thỏa mãn điều kiện

0 0

2 4

x y

 

.

Lời giải

a) Với

2

m



hệ đã cho có dạng

5

2 3 2 3

2

2 2 9 2

2

x y x y

x

x y y

y



   



 



 

  

  

 







Vậy hệ có nghiệm duy nhất

 

5

; ;2

2

x y

 



 

 

.

b) Từ phương trình (1) rút ra :

3

y mx

 

, thế vào phương trình thứ (2) ta được:





2 2 3 9

x mx

  





2 2 15

m x

  

(3)

Để hệ có nghiệm duy nhất thì phương trình (3) có nghiệm duy nhất

1

m

  

.

Khi đó hệ có nghiệm là

 

0 0

15 9 6

; ;

2 2 2 2

m

x y

m m



 



 

 

 

Theo giả thiết

0 0

15 9 6 1

2 4 2. 4

2 2 2 2 2

m

x y m

m m



      

 

(thỏa mãn).

Câu 3a. Cho tam giác ABC, gọi M là trung điểm của BC và I là trung điểm của AM. Chứng minh rằng:

2 0

IA IB IC

  

   

.

Lời giải

I

M

A

C

B

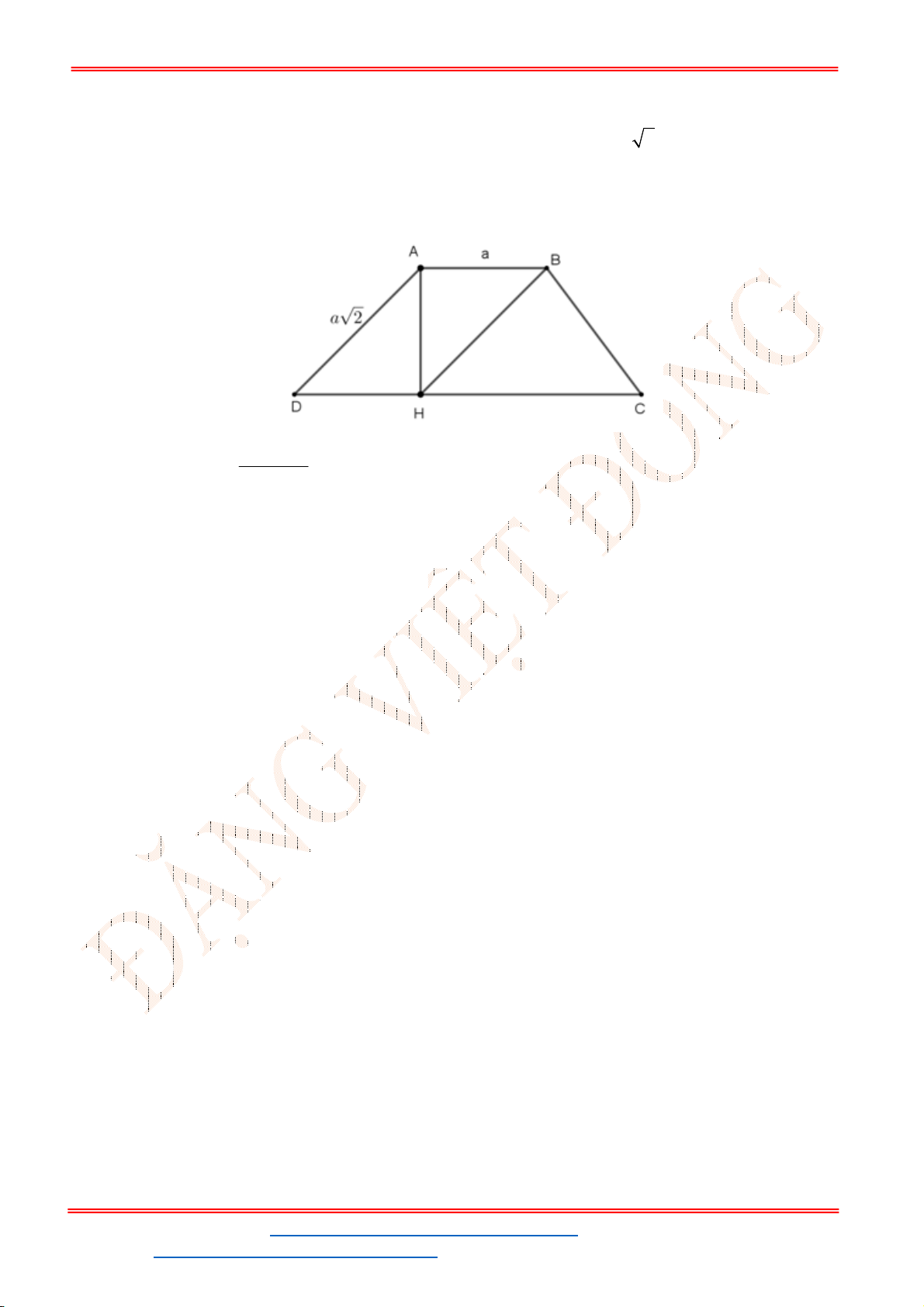
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Ta có:





2 2 2 2

VT IA IB IC IA IB IC IA IM

       

       





2 2.0 0

IA IM VP

    

   

.

Câu 3b. Cho hình thang cân

ABCD

biết đáy lớn

3

CD a



,

AB a



và

2

BC a

 . Gọi

H

là hình chiếu vuông

góc của

A

lên cạnh

CD

. Tính





.

BH AC AD



  

.

Lời giải

Ta có

2

CD AB

DH a



  

ABHD

là hình bình hành và

AH a



Khi đó:





. . .

BH AC AD BH AC BH AD

  

      









2

.

AH AB AH HC AD

   

    

2 2

.

AH AB HC AD

  

 

2 0 2

.2 .cos0 2

a a a a

  

2

a



.

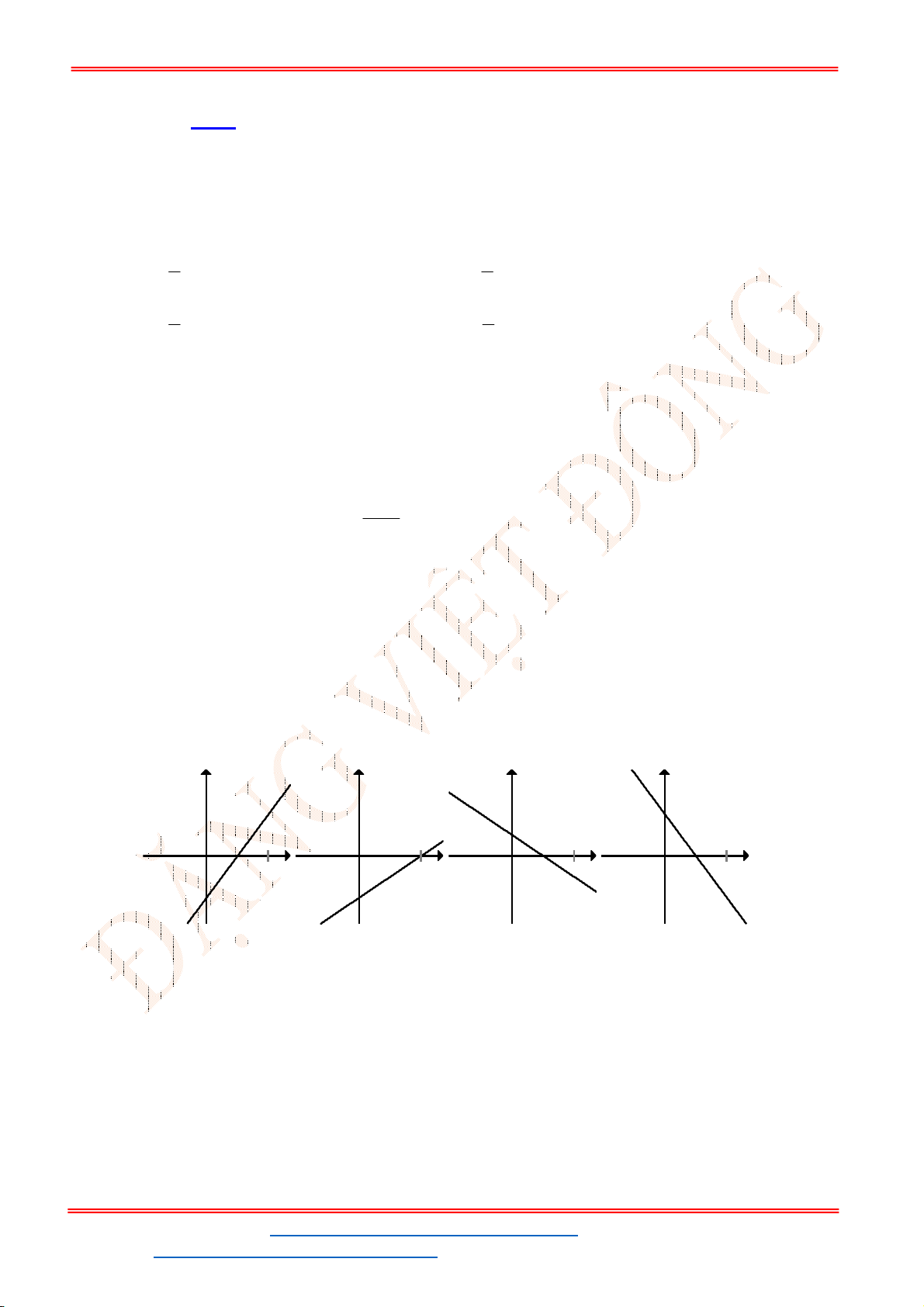
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 12 Môn Toán – Lớp 10

(Thời gian làm bài 90 phút)

Không k

ể thời gian phát đề

PHẦN I. TRẮC NGHIỆM

Câu 1. Mệnh đề nào sau đây là mệnh đề phủ định của mệnh đề

2

:" , 0"

P x R x

  

A.

2

:" , 0"

P x R x

  

. B.

2

:" , 0"

P x R x

  

.

C.

2

:" , 0"

P x R x

  

. D.

2

:" , 0"

P x R x

  

.

Câu 2. Phát biểu nào sau đây là một mệnh đề

A. Hôm nay là thứ mấy? B. Việt Nam là một nước thuộc Châu Á.

C. Các bạn hãy học đi! D. An học lớp mấy?

Câu 5. Tập xác định của hàm số

3

2

x

y

x







là

A.



2;D

 





. B.





\ 2

D 



. C.





;2

D  

. D.





\ 2

D

 



.

Câu 6. Hàm số





4 2

2 1

y f x x x

   

là hàm số

A. lẻ. B. không chẵn, không lẻ.

C. vừa chẵn, vừa lẻ. D. chẵn.

Câu 7. Hàm số

2 1

y x

 

có đồ thị là hình nào trong bốn hình sau ?

x

y

O

1



x

y

O

1



x

y

O

1



x

y

O

1



A. B. C. D.

Câu 8. Parabol

2

2 3

y x x

  

có phương trình trục đối xứng là

A.

1

x

 

. B.

2

x



. C.

1

x



. D.

2

x

 

.

Câu 9. Hàm số nào sau đây có đồ thị là parabol có đỉnh





1;3

I 

A.

2

2 4 5

y x x

  

. B.

2

2 2

y x x

  

.

C.

2

2 4 3

y x x

  

. D.

2

2 2 1

y x x

  

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 10. Cho phương trình

2

2 7 4 0x x  

 

*

. Hãy chọn kết luận đúng.

A. Phương trình

 

*

vô nghiệm.

B. Phương trình

 

*

có hai nghiệm phân biệt.

C. Phương trình

 

*

có nghiệm duy nhất.

D. Phương trình

 

*

có vô số nghiệm.

Câu 11. Hệ phương trình nào sau đây nhận

 

1; 2

là nghiệm?

A.

1 0

2 3 4 0

x y

  





  



. B.

1 0

2 3 8 0

x y

  





  



. C.

1 0

2 3 1 0

x y

  





  



. D.

1 0

2 3 4 0

x y

  





  



.

Câu 12. Cho 3 điểm , ,A B C bất kỳ. Hãy chọn khẳng định SAI

A. AB BC AC 

  

. B. AB AC CB 

  

. C. BA AC BC 

  

. D.

BC BA CA 

  

.

Câu 13. Cho các vectơ

, ,AB CD EF

  

như hình vẽ bên dưới. Phát biểu nào sau đây đúng?

A. AB



và

EF



là hai vectơ cùng hướng. B. AB



và

EF



là hai vectơ cùng phương.

C.

CD



và

EF



là hai vectơ cùng hướng. D. AB



và

CD



là hai vectơ bằng nhau.

Câu 14. Trong mặt phẳng

Oxy

, cho hai điểm

 

1;1A và

 

2;5B  . Tọa độ vectơ

AB



là

A.

 

3; 4AB  



. B.

 

3; 4AB   



. C.

 

3;4AB  



. D.

 

3;4AB 



.

Câu 15. Trong mặt phẳng Oxy cho

2 5OA i j 

  

. Khi đó

A.

 

2; 3 .A  

B.

 

2; 5A 

. C.

 

2; 3A 

. D.

 

2;3A

.

Câu 16. Mệnh đề nào sau đây là phủ định của mệnh đề “Mọi động vật đều di chuyển”?

A. Có ít nhất một động vật không di chuyển.

B. Mọi động vật đều không di chuyển.

C. Mọi động vật đều đứng yên.

D. Có ít nhất một động vật di chuyển.

Câu 17. Cho tập hợp

 

2

3 4 0A x x x    

, khẳng định nào sau đây là đúng?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A. Tập hợp

A

 

. B. Tập hợp





0

A 

.

C. Tập hợp

A

có

2

phần tử. D. Tập hợp

A

có vô số phần tử.

Câu 18. Tìm tập xác định

D

của hàm số

 

1

3 2 1

x

y

x x





 

?

A.

 

1

D ; \ 3

2

 

 

 

 

. B.

D





.

C.

 

1

D ; \ 3

2

 

  

 

 

. D.

 

1

D ; \ 3

2

 

 





 

.

Câu 19. Một hàm số bậc nhất





y f x

 có









1 2, 2 3

f f

   

. Hỏi hàm số đó là:

A.

2 3

y x

  

B.

5 1

3

x

y

 



C.

2 3

y x

 

D.

5 1

3

x

y

 



Câu 20. Giá trị nào của

m

thì đồ thị hàm số

2

3

y x x m

  

cắt trục hoành tại hai điểm phân biệt ?

A.

9

.

4

m

 

B.

9

.

4

m

 

C.

9

.

4

m



D.

9

.

4

m



Câu 21. Tọa độ giao điểm của hai đường thẳng

2

y x

 

và

3

4

y x

  

là:

A.

4 18

;

7 7

 

 

 

. B.

4 18

;

7 7

 



 

 

. C.

4 18

;

7 7

 



 

 

. D.

4 18

;

7 7

 

 

 

 

.

Câu 22. Tìm

m

để phương trình





2 2

– 4 3 – 3 2

m m x m m

  

có nghiệm duy nhất.

A.

1

m



. B.

3

m



. C.

1

3

m











. D.

1

3

m











.

Câu 23. Cho hình chữ nhật

ABCD

tâm

O

. Gọi

M

,

N

lần lượt là trung điểm của

OA

và

CD

. Biết

. .

MN a AB b AD

 

  

. Tính

a b



.

A.

1

a b

 

. B.

1

2

a b

 

. C.

3

4

a b

 

. D.

1

4

a b

 

.

Câu 24. Trong mặt phẳng tọa độ

Oxy

, cho hình bình hành

ABCD

có





4;5

B

và

13

0;

3

G

 



 

 

là trọng

tâm tam giác

ADC

. Tìm tọa độ đỉnh

D

.

A.





2;1

D

. B.





1;2

D 

. C.





2; 9

D

 

. D.





2;9

D

.

Câu 25. Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai điểm









1; 2 , 4; 5

A B 

. Tìm tọa độ điểm

M

trên trục

Oy

sao cho ba điểm

, ,

M A B

thẳng hàng.

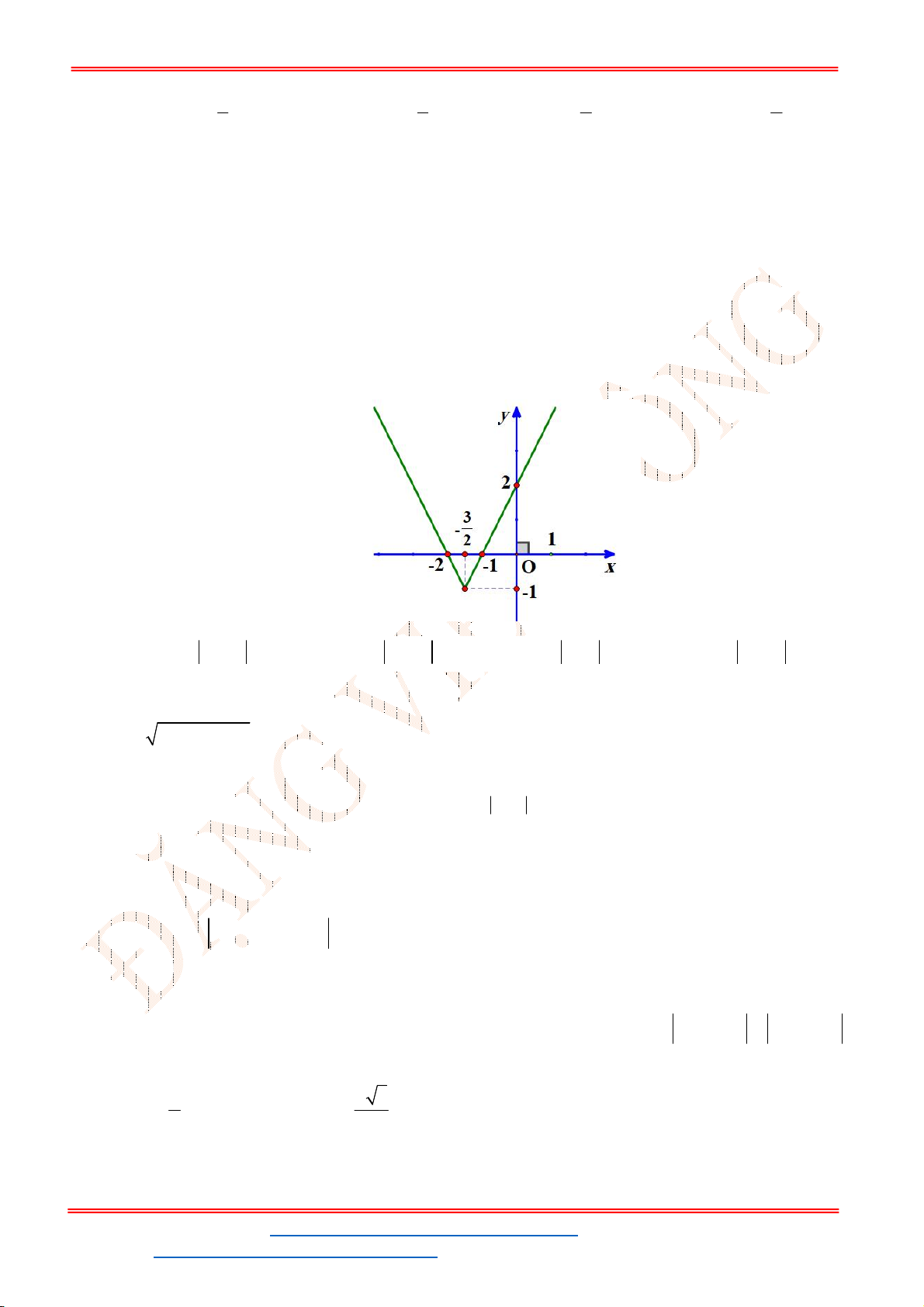
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

3

0;

5

M

 

 

 

. B.

3

0;

5

M

 



 

 

. C.

2

0;

5

M

 

 

 

. D.

2

0;

5

M

 



 

 

.

Câu 26. Cho hai tập hợp





4;3

A  

và





7;

B m m

 

. Tìm tất cả các giá trị thực của tham số

m

sao

cho

B A



.

A.

3

m



. B.

3

m



. C.

3

m



. D.

3

m



.

Câu 27. Tìm tất cả các giá trị của tham số

m

để hàm số









3 2 2

2 2 4 4 3 6

y x m x m x m

      

là

một hàm số lẻ.

A.

2

m

 

. B.

2

m



. C.

4

m

 

. D.

2

m

 

.

Câu 28. Đồ thị cho bởi hình vẽ là của hàm số nào dưới đây?

A.

2 3

 

y x

. B.

2 3 1

  

y x

. C.

2

 

y x

. D.

3 2 1

  

y x

Câu 29. Có bao nhiêu giá trị nguyên của tham số

m

thuộc đoạn





20;20



để tập nghiệm của phương trình

2

2 8 1

x x m x

   

có đúng một phần tử?

A.

27

. B.

1

. C.

26

. D.

2

.

Câu 30. Tổng các nghiệm của phương trình

 

2

1 3 1 2 0

x x

    

là

A.

5



. B.

4



. C.

6



. D.

0

.

Câu 31. Trong hệ tọa độ

Oxy

, cho













1;2 , 3;2 , 4; 1

A B C

 

. Tìm tọa độ điểm

M

thuộc trục

Ox

sao

cho

T MA MB MC

  

  

nhỏ nhất.

A.





4;0

M B.





4;0

M  C.





2;0

M D.





2;0

M 

Câu 32. Cho đoạn thẳng

AB

có độ dài bằng

a

. Một điểm

M

di động sao cho

  

   

MA MB MA MB

.

Gọi

H

là hình chiếu của

M

lên

AB

. Tính độ dài lớn nhất của

MH

?

A.

.

2

a

B.

3

.

2

a

C.

.

a

D.

2 .

a

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 33. Gọi

1 2

,

x x

là hai nghiệm của phương trình





2 2

2 1 2 3 1 0

     

x m x m m

(

m

là tham số). Giá

trị lớn nhất

max

P

của biểu thức

1 2 1 2

  

P x x x x

là

A.

max

1

4



P

. B.

max

1



P . C.

max

9

8



P

. D.

max

9

16

P

.

Câu 34. Tìm tất cả các giá trị thực của tham số

m

để phương trình

2 2

2 2 3 2 0

x mx m x m m m

      

có nghiệm.

A.









; 3 1; .

m

    

B.





3

; 3 ;

2

m

 

    





 

.

C.





1;m

 

. D.

3

;

2

m

 

 





 

.

Câu 35. Cho tam giác đều

ABC

có tâm

O

. Gọi

I

là một điểm tùy ý bên trong tam giác

ABC

. Hạ

, ,

ID IE IF

tương ứng vuông góc với

, ,

BC CA AB

. Giả sử

a

ID IE IF IO

b

  

   

(với

a

b

là phân

số tối giản). Khi đó

a b



bằng

A.

6

. B.

7

. C.

5

. D.

4

.

PHẦN II. TỰ LUẬN

Câu 1. Tìm hàm số bậc hai

2

  

y ax bx c

, biết rằng đồ thị là một đường Parabol đi qua điểm





1;0

A 

và có đỉnh





1;2

I

.

Câu 2. Cho tam giác

ABC

vuông tại

A

có

AB a



,

2

BC a



.

a) Tính

. , .

BA BC BC CA

   

b) Tính

. . .

AB BC BC CA CA AB

 

     

Câu 3. Số các giá trị nguyên của tham số





2018;2018

m 

để phương trình:

 

2 3

2 4 4 4

x m x x x

    

có nghiệm là

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG HDG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 12 Môn Toán – Lớp 10

(Thời gian làm bài 90 phút)

Không k

ể thời gian phát đề

PHẦN I. TRẮC NGHIỆM

Câu 1. Mệnh đề nào sau đây là mệnh đề phủ định của mệnh đề

2

:" , 0"

P x R x

  

A.

2

:" , 0"

P x R x

  

. B.

2

:" , 0"

P x R x

  

.

C.

2

:" , 0"

P x R x

  

. D.

2

:" , 0"

P x R x

  

.

Lời giải

Mệnh đề phủ định của mệnh đề

2

:" , 0"

P x R x

  

là

2

:" , 0"

P x R x

  

.

Vậy chọn đáp án B.

Câu 2. Phát biểu nào sau đây là một mệnh đề

A. Hôm nay là thứ mấy? B. Việt Nam là một nước thuộc Châu Á.

C. Các bạn hãy học đi! D. An học lớp mấy?

Lời giải

Phát biểu “Việt Nam là một nước thuộc Châu Á” là một mệnh đề.

Vậy chọn đáp án B.

Câu 3 . Số phần tử của tập hợp





2

4 3 0

A x R x x

    

là

A.

2

. B.

1

. C.

0

. D.

3

.

Lời giải

Ta có:

2

1

4 3 0

3

x

x x

x





   







. Vậy tập

A

có 2 phần tử.

Câu 4 . Chọn khẳng định sai trong các khẳng định sau

A.

Q R Q

 

. B.

* *

N R N

  . C.

Z Q Q

 

. D.

*

N N Z

 

.

Lời giải

Đáp án D sai vì

*

N N N

 

.

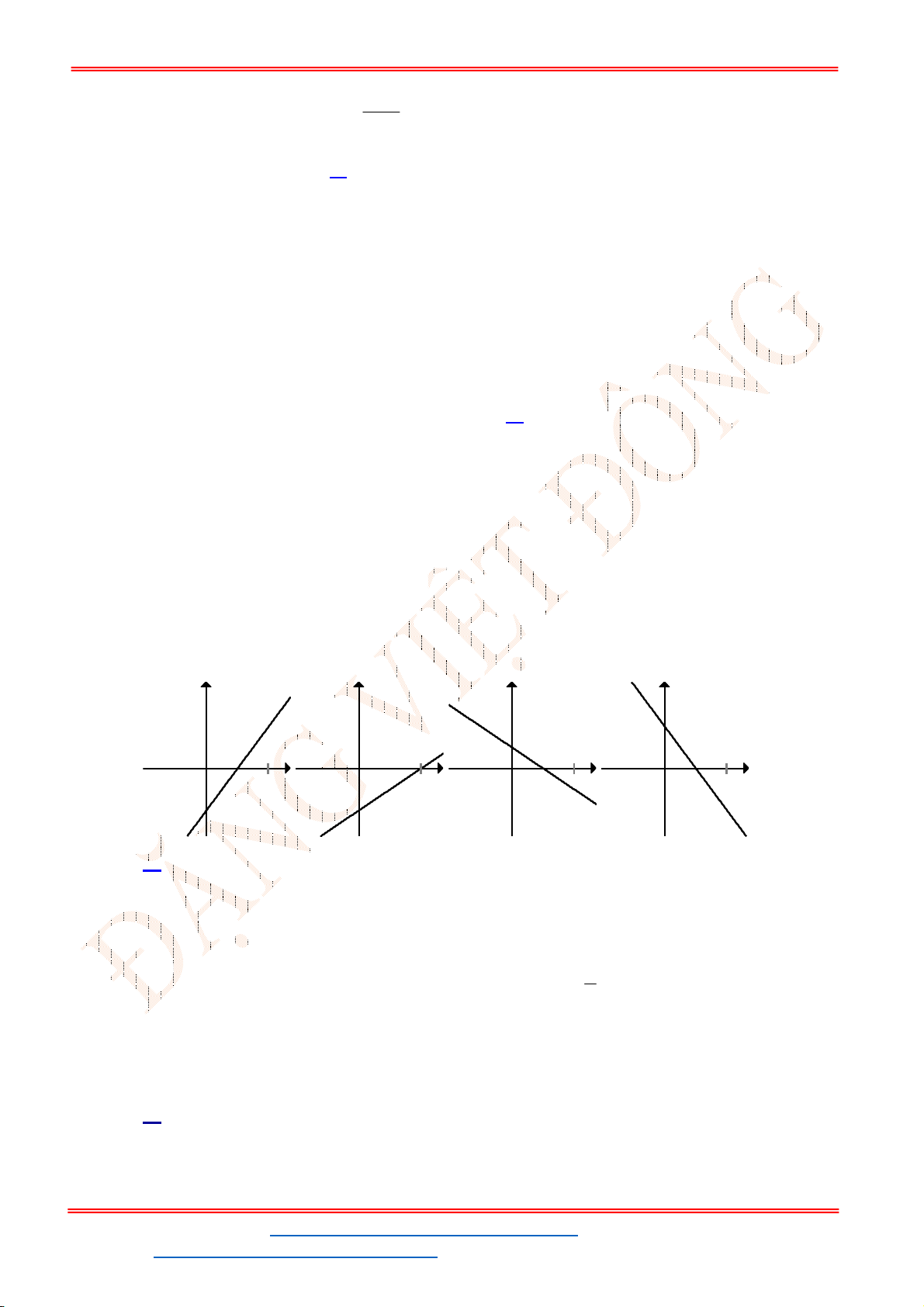
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 5. Tập xác định của hàm số

3

2

x

y

x







là

A.



2;D

 





. B.





\ 2

D 



. C.





;2

D  

. D.





\ 2

D

 



.

Lời giải

Điều kiện:

2 0

x

 

2

x

 

.

Vậy





\ 2

D 



.

Câu 6. Hàm số





4 2

2 1

y f x x x

   

là hàm số

A. lẻ. B. không chẵn, không lẻ.

C. vừa chẵn, vừa lẻ. D. chẵn.

Lời giải

Tập xác định:

D





.

x D

 

thì

x D

 

.

       

4 2

2 1 2 1

f x x x x x f x

         

.

Hàm số





y f x

 là hàm chẵn.

Câu 7. Hàm số

2 1

y x

 

có đồ thị là hình nào trong bốn hình sau ?

x

y

O

1



x

y

O

1



x

y

O

1



x

y

O

1



A. B. C. D.

Lời giải

Đáp án C, D loại vì đó là đồ thị của hàm số có hệ số góc âm.

Giao điểm của đồ thị hàm số

2 1

y x

 

với trục hoành là

1

;0

2

 

 

 

nên loại B.

Giao điểm của đồ thị hàm số

2 1

y x

 

với trục tung là





0; 1



nên chỉ có A thỏa mãn.

Câu 8. Parabol

2

2 3

y x x

  

có phương trình trục đối xứng là

A.

1

x

 

. B.

2

x



. C.

1

x



. D.

2

x

 

.

Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Parabol

2

2 3

y x x

  

có trục đối xứng là đường thẳng

2

b

x

a

 

1

x

  

.

Câu 9. Hàm số nào sau đây có đồ thị là parabol có đỉnh





1;3

I 

A.

2

2 4 5

y x x

  

. B.

2

2 2

y x x

  

.

C.

2

2 4 3

y x x

  

. D.

2

2 2 1

y x x

  

.

Lời giải

Tọa độ đỉnh

( , )

2 4

b

I

a a



 

nên chọn A.

Câu 10. Cho phương trình

2

2 7 4 0

x x

  





*

. Hãy chọn kết luận đúng.

A. Phương trình





*

vô nghiệm.

B. Phương trình





*

có hai nghiệm phân biệt.

C. Phương trình





*

có nghiệm duy nhất.

D. Phương trình





*

có vô số nghiệm.

Lời giải

Ta có

 

2

2 0

7 4.2.4 49 32 17 0

a  







      





Do đó phương trình





*

luôn có hai nghiệm phân biệt.

Câu 11. Hệ phương trình nào sau đây nhận





1; 2



là nghiệm?

A.

1 0

2 3 4 0

x y

  





  



. B.

1 0

2 3 8 0

x y

  





  



. C.

1 0

2 3 1 0

x y

  





  



. D.

1 0

2 3 4 0

x y

  





  



.

Lời giải

Thay

1, 2

x y

  

và 4 hệ ta thấy chỉ có đáp án D là đúng.

Câu 12. Cho 3 điểm

, ,

A B C

bất kỳ. Hãy chọn khẳng định SAI

A.

AB BC AC

 

  

. B.

AB AC CB

 

  

. C.

BA AC BC

 

  

. D.

BC BA CA

 

  

.

Lời giải

D sai vì

BC BA AC

 

  

.

Câu 13. Cho các vectơ

, ,

AB CD EF

  

như hình vẽ bên dưới. Phát biểu nào sau đây đúng?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A. AB



và

EF



là hai vectơ cùng hướng. B. AB



và

EF



là hai vectơ cùng phương.

C.

CD



và

EF



là hai vectơ cùng hướng. D. AB



và

CD



là hai vectơ bằng nhau.

Lời giải

Dựa theo hình vẽ ta có AB



và

EF



là hai vectơ cùng phương.

Câu 14. Trong mặt phẳng

Oxy

, cho hai điểm

 

1;1A và

 

2;5B  . Tọa độ vectơ

AB



là

A.

 

3; 4AB  



. B.

 

3; 4AB   



. C.

 

3;4AB  



. D.

 

3;4AB 



.

Lời giải

Áp dụng công thức

 

;

B A B A

AB x x y y  



.

Ta có:

 

3;4AB  



.

Câu 15. Trong mặt phẳng Oxy cho

2 5OA i j 

  

. Khi đó

A.

 

2; 3 .A  

B.

 

2; 5A 

. C.

 

2; 3A 

. D.

 

2;3A

.

Lời giải

Tọa độ của điểm

 

2; 5A 

Câu 16. Mệnh đề nào sau đây là phủ định của mệnh đề “Mọi động vật đều di chuyển”?

A. Có ít nhất một động vật không di chuyển.

B. Mọi động vật đều không di chuyển.

C. Mọi động vật đều đứng yên.

D. Có ít nhất một động vật di chuyển.

Lời giải

Phủ định của mệnh đề “Mọi động vật đều di chuyển” là “Có ít nhất một động vật không di

chuyển”.

Câu 17. Cho tập hợp

 

2

3 4 0A x x x    

, khẳng định nào sau đây là đúng?

A. Tập hợp

A  

. B. Tập hợp

 

0A 

.

C. Tập hợp A có 2 phần tử. D. Tập hợp A có vô số phần tử.

Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Ta có phương trình

2

3 4 0

x x

  

vô nghiệm (vì

2

3 4.1.4 7 0

     

).

Câu 18. Tìm tập xác định

D

của hàm số

 

1

3 2 1

x

y

x x





 

?

A.

 

1

D ; \ 3

2

 

 

 

 

. B.

D





.

C.

 

1

D ; \ 3

2

 

  

 

 

. D.

 

1

D ; \ 3

2

 

 





 

.

Lời giải

Hàm số xác định khi

3

3 0

.

1

2 1 0

2

x





 







 

 









Vậy tập xác định của hàm số là

 

1

D ; \ 3

2

 

 

 

 

.

Câu 19. Một hàm số bậc nhất





y f x

 có









1 2, 2 3

f f

   

. Hỏi hàm số đó là:

A.

2 3

y x

  

B.

5 1

3

x

y

 



C.

2 3

y x

 

D.

5 1

3

x

y

 



Lời giải

Gọi hàm số bậc nhất là:





( 0)

y f x ax b a

   

. Khi đó





1 2 2

f a b

     





2 3 2 3

f a b

     

Ta có hệ phương trình

5

2

3

2 3 1

3

a

a b

b



 



  







 

  











. Vậy hàm số đã cho là

5 1

3

x

y

 



Câu 20. Giá trị nào của

m

thì đồ thị hàm số

2

3

y x x m

  

cắt trục hoành tại hai điểm phân biệt ?

A.

9

.

4

m

 

B.

9

.

4

m

 

C.

9

.

4

m



D.

9

.

4

m



Lời giải

Đồ thị hàm số

2

3

y x x m

  

cắt trục hoành tại hai điểm phân biệt khi và chỉ khi phương

trình

2

3 0

x x m

  

có hai nghiệm phân biệt

9

0 9 4 0 .

4

m m

       

Câu 21. Tọa độ giao điểm của hai đường thẳng

2

y x

 

và

3

4

y x

  

là:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

4 18

;

7 7

 

 

 

. B.

4 18

;

7 7

 



 

 

. C.

4 18

;

7 7

 



 

 

. D.

4 18

;

7 7

 

 

 

 

.

Lời giải

Chọn A

Phương trình hoành độ giao điểm của hai đường thẳng:

3 4

2 3

4 7

x x x

     

.

Thế

4

7

x



vào

2

y x

 

suy ra

18

7

y 

. Vậy tọa độ giao điểm của hai đường thẳng là

4 18

;

7 7

 

 

 

.

Câu 22. Tìm

m

để phương trình





2 2

– 4 3 – 3 2

m m x m m

  

có nghiệm duy nhất.

A.

1

m



. B.

3

m



. C.

1

3

m











. D.

1

3

m











.

Lời giải

Chọn C

Phương trình có nghiệm duy nhất khi





2

0

– 4 3m m 



1

3

m













.

Câu 23. Cho hình chữ nhật

ABCD

tâm

O

. Gọi

M

,

N

lần lượt là trung điểm của

OA

và

CD

. Biết

. .

MN a AB b AD

 

  

. Tính

a b



.

A.

1

a b

 

. B.

1

2

a b

 

. C.

3

4

a b

 

. D.

1

4

a b

 

.

Lời giải

   

1 1 1 1 1 1 1 3

4 2 4 2 4 2 4 4

MN MO ON AC AD AB BC AD AB AD AD AB AD

           

         

   

.

1

4

a

 

;

3

4

b



. Vậy

1

a b

 

.

N

M

O

D

C

B

A

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 24. Trong mặt phẳng tọa độ

Oxy

, cho hình bình hành

ABCD

có





4;5

B

và

13

0;

3

G

 



 

 

là trọng

tâm tam giác

ADC

. Tìm tọa độ đỉnh

D

.

A.





2;1

D

. B.





1;2

D 

. C.





2; 9

D

 

. D.





2;9

D

.

Lời giải

Gọi





;

D a b

. Vì

13

0;

3

G

 



 

 

là trọng tâm tam giác

ADC

nên

3

2

BD BG

 

 

 

3

4 0 4

2

3 13

9

5 5

2 3

a

b



  



 







 



 

 





  

 



 







2; 9

D

  

.

Câu 25. Trong mặt phẳng với hệ tọa độ

Oxy

, cho hai điểm









1; 2 , 4; 5

A B 

. Tìm tọa độ điểm

M

trên trục

Oy

sao cho ba điểm

, ,

M A B

thẳng hàng.

A.

3

0;

5

M

 

 

 

. B.

3

0;

5

M

 



 

 

. C.

2

0;

5

M

 

 

 

. D.

2

0;

5

M

 



 

 

.

Lời giải

Gọi





0;

M y Oy



, ta có:









1; 2 , 5; 7

AM y AB    

 

.

, ,

M A B

thẳng hàng

,

AM AB



 

cùng phương

1 2 3

5 7 5

y

 

    



.

Vậy

3

0;

5

M

 



 

 

.

Câu 26. Cho hai tập hợp





4;3

A  

và





7;

B m m

 

. Tìm tất cả các giá trị thực của tham số

m

sao

cho

B A



.

A.

3

m



. B.

3

m



. C.

3

m



. D.

3

m



.

Lời giải

4 7 3

3

3 3

m m

B A m

m m

   

 

    

 

 

 

.

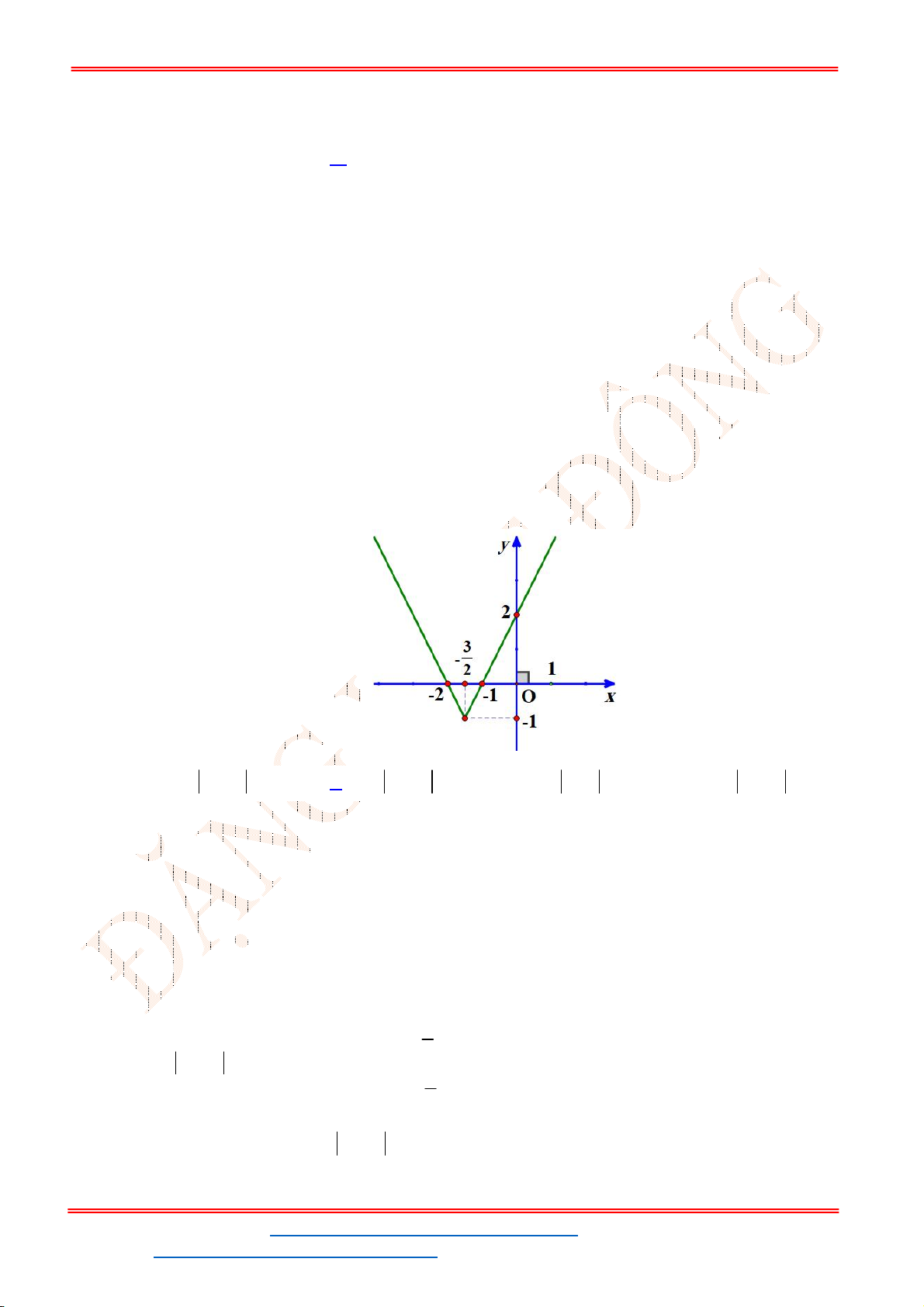
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 27. Tìm tất cả các giá trị của tham số

m

để hàm số









3 2 2

2 2 4 4 3 6

y x m x m x m

      

là

một hàm số lẻ.

A.

2

m

 

. B.

2

m



. C.

4

m

 

. D.

2

m

 

.

Lời giải













3 2 2

2 2 4 4 3 6

y f x x m x m x m

       

.

TXĐ:

D





Ta có

x x

    

 

Hàm số





y f x



là hàm số lẻ









,f x f x x

     



















3 2 2 3 2 2

2 2 4 4 3 6 2 2 4 4 3 6 ,x m x m x m x m x m x m x

 

                 

 











2 2

2 4 3 6 0,m x m x

      



2

4 0

2.

3 6 0m

m











 

 



Câu 28. Đồ thị cho bởi hình vẽ là của hàm số nào dưới đây?

A.

2 3

 

y x

. B.

2 3 1

  

y x

. C.

2

 

y x

. D.

3 2 1

  

y x

Lời giải

Ta có:

Giao điểm của đồ thị hàm số với trục hoành là





2;0

A

nên loại phương án

A

và

C

.

Giao điểm của đồ thị hàm số với trục tung là





0;2

B

nên loại phương án

D

.

Xét phương án

B

:

3

2 2 khi

2

2 3 1

3

2 4 khi

2



  



   





   





x x

y x

x x

.

Khi đó đồ thị hàm số

2 3 1

  

y x

bao gồm:

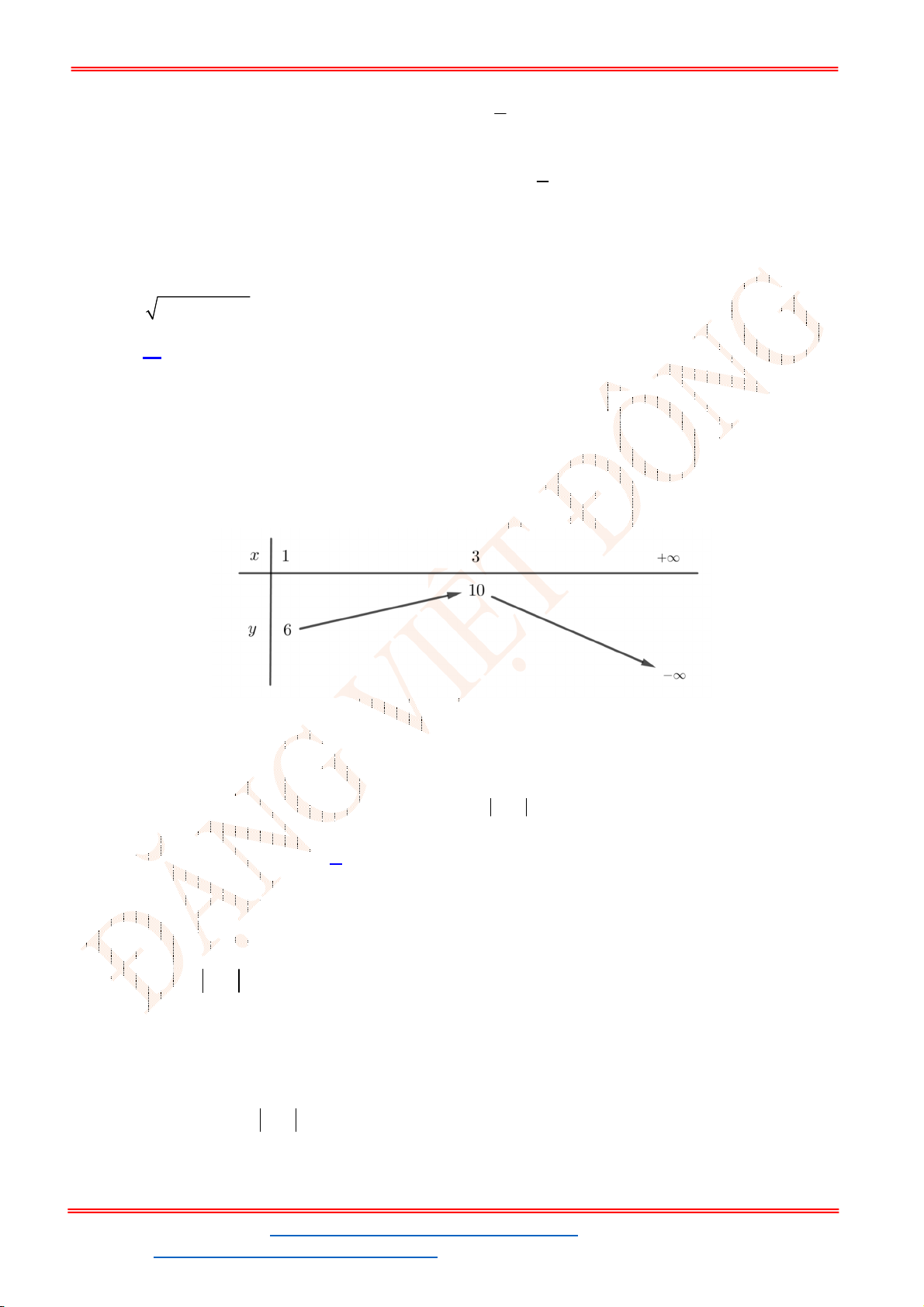
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

+) Phần đường thẳng

1

: 2 2 d y x khi

3

;

2

 

   





 

x

+) Phần đường thẳng

2

: 2 4  d y x khi

3

;

2

 

  

 

 

x

Đồ thị này khớp với đồ thị cho ở hình vẽ trên.

Câu 29. Có bao nhiêu giá trị nguyên của tham số

m

thuộc đoạn

 

20;20

để tập nghiệm của phương trình

2

2 8 1x x m x    có đúng một phần tử?

A.

27

. B. 1. C.

26

. D. 2 .

Lời giải

Phương trình đã cho tương đương với

 

2

1

6 1

2 8 1

x

m x x

x x m x













 

   

   





.

Xét hàm số

2

6 1y x x    trên





1; 

có bảng biến thiên như hình dưới đây.

Dựa vào bảng biến thiên ta thấy phương trình có một nghiệm khi và chỉ khi

6

10

m











.

Vậy có 27 giá trị của

m

thỏa mãn yêu cầu bài toán.

Câu 30. Tổng các nghiệm của phương trình

 

2

1 3 1 2 0x x     là

A.

5

. B. 4 . C.

6

. D.

0

.

Lời giải

Chọn B

Đặt

1t x 

,

0t 

.

Phương trình trở thành:

2

1( )

3 2 0

2( )

t n

t t

t n





   







Với

1t 

ta có

0

1 1 1 1

2

x

x x

x





      



 



.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Với

2

t



ta có

1

1 2 1 2

3

x

x x

x





      



 



.

Phương trình có tập nghiệm là





3; 2;0;1

S   

Tổng các nghiệm của phương trình là:









3 2 0 1 4

      

Câu 31. Trong hệ tọa độ

Oxy

, cho













1;2 , 3;2 , 4; 1

A B C

 

. Tìm tọa độ điểm

M

thuộc trục

Ox

sao

cho

T MA MB MC

  

  

nhỏ nhất.

A.





4;0

M B.





4;0

M  C.





2;0

M D.





2;0

M 

Lời giải

Chọn C

Ta có:





3

MA MB MC MG GA GC GC

     

      

. Chọn điểm





0 0

;

G x y

sao cho

0 0 0 0

1 3 4 0 2

0

2 2 1 0 1

x x x x

GA GC GC

y y y y

       

 

    

 

      

 

  



Với





2;1 3 3

G MA MB MC MG T MG

     

   

. Do





O ;0

M x M a

 

 

2

3 2 1 3

T a

    

.

Vậy

T MA MB MC

  

  

nhỏ nhất bằng

3

khi

2

a



. Suy ra





2;0

M

Câu 32. Cho đoạn thẳng

AB

có độ dài bằng

a

. Một điểm

M

di động sao cho

  

   

MA MB MA MB

.

Gọi

H

là hình chiếu của

M

lên

AB

. Tính độ dài lớn nhất của

MH

?

A.

.

2

a

B.

3

.

2

a

C.

.

a

D.

2 .

a

Lời giải

Chọn A

N

H

O

A

B

M

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Gọi

N

là đỉnh thứ 4 của hình bình hành

MANB

. Khi đó

MA MB MN

 

  

.

Ta có

MA MB MA MB MN BA

    

     

hay

MN AB



.

Suy ra

MANB

là hình chữ nhật nên



90

o

AMB 

.

Do đó

M

nằm trên đường tròn tâm

O

đường kính

AB

.

MH

lớn nhất khi

H

trùng với tâm

O

hay

max .

2 2

AB a

MH MO

  

Học sinh có thể nhầm lẫn độ dài lớn nhất bằng bán kính hoặc 2 lần bán kính, hoặc độ dài đường

cao của tam giác đều.

Câu 33. Gọi

1 2

,

x x

là hai nghiệm của phương trình





2 2

2 1 2 3 1 0

     

x m x m m

(

m

là tham số). Giá

trị lớn nhất

max

P

của biểu thức

1 2 1 2

  

P x x x x

là

A.

max

1

4



P

. B.

max

1



P . C.

max

9

8



P

. D.

max

9

16

P

.

Lời giải

Chọn C.

Ta có

 





 

2

2 2

' 1 2 3 1 1          

m m m m m m m

.

Để phương trình có hai nghiệm

' 0 0 1

     

m

.





*

Theo định lý Viet, ta có





1 2

2

1 2

2 1

. 2 3 1

  





  





x x m

x x m m

.

Khi đó

 

2

2 2

1 2 1 2

1 1 9

. 2 1 2 3 1 2 2

2 2 4 16

 

             

 

 

m

P x x x x m m m m m

.

Vì

2 2

1 1 3 1 9 1 9

0 1 0

4 4 4 4 16 4 16

   

             

   

   

m m m m

.

Do đó

2 2 2

1 9 9 1 9 1 9

2 2 2

4 16 16 4 8 4 8

 

     

         

 

     

 

     

 

P m m m

.

Dấu

'' ''



xảy ra khi và chỉ khi

1

4



m

: thỏa mãn





*

.

Câu 34. Tìm tất cả các giá trị thực của tham số

m

để phương trình

2 2

2 2 3 2 0

x mx m x m m m

      

có nghiệm.

A.









; 3 1; .

m

    

B.





3

; 3 ;

2

m

 

    





 

.

C.





1;m

 

. D.

3

;

2

m

 

 





 

.

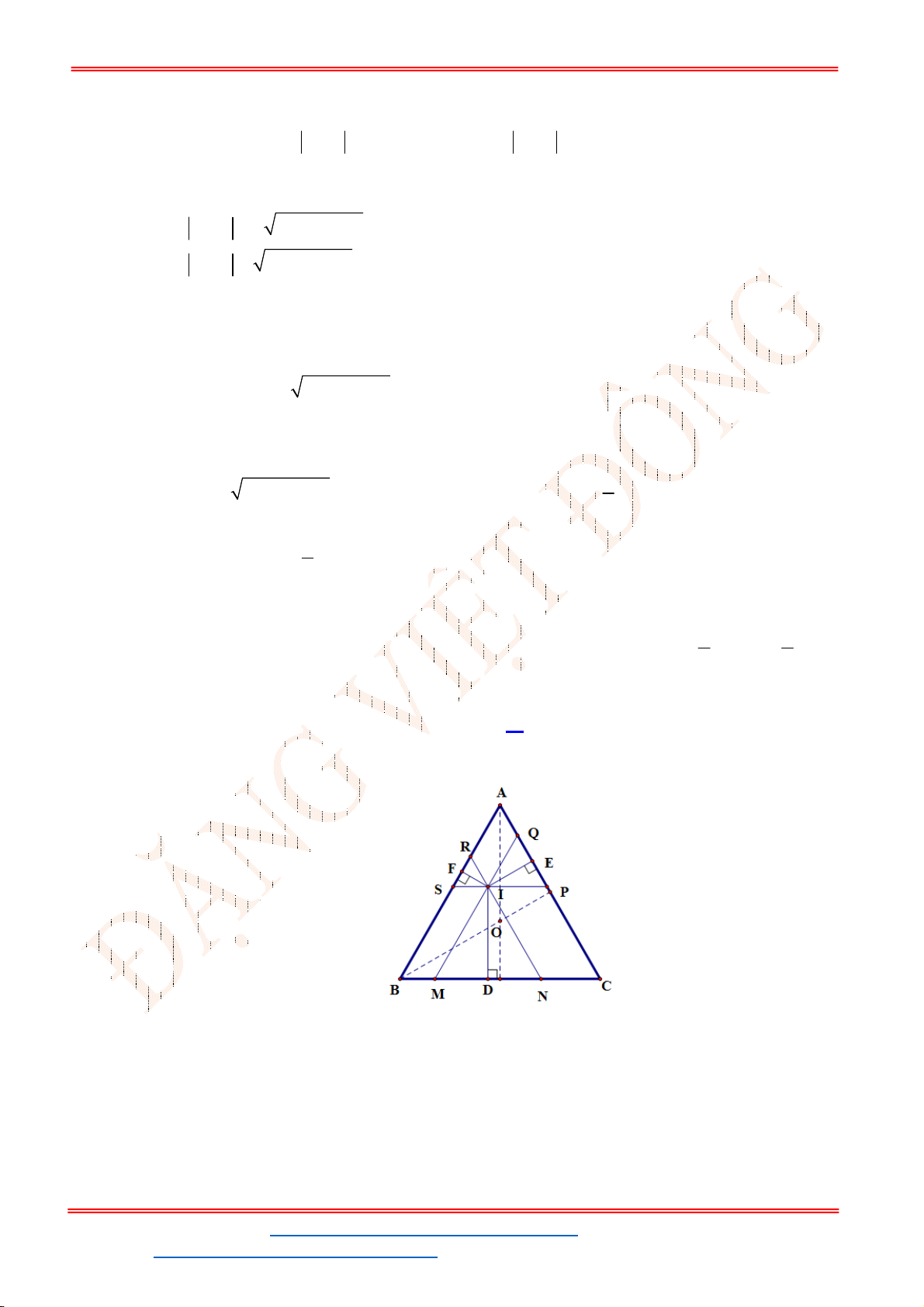
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Lời giải

Ta có





2

2 2 2

2 2 3 2 0 2 3

x mx m x m m m x m m m m

            

 

2

0

2 3 1

2 3 2

2 3

.

x m m m m

x

m m

m m m m





     



    



 















Ta có

2

0 .

2

3

1

3

m

m m

 



 







 



Nếu

3

m

 

, thì

2

,

2 3

0

m m m  



suy ra (2) có nghiệm, do đó phương trình đã cho có

nghiệm.



Nếu

1

m



thì (1) vô nghiệm, do đó phương trình đã cho có nghiệm khi và và chỉ khi (2) có

nghiệm

2 22

3

0 2 3 .

2

2 3m mm mm m m    

 

 

Vậy





3

; 3 ; .

2

m

 

    





 

Câu 35. Cho tam giác đều

ABC

có tâm

O

. Gọi

I

là một điểm tùy ý bên trong tam giác

ABC

. Hạ

, ,

ID IE IF

tương ứng vuông góc với

, ,

BC CA AB

. Giả sử

a

ID IE IF IO

b

  

   

(với

a

b

là phân

số tối giản). Khi đó

a b



bằng

A.

6

. B.

7

. C.

5

. D.

4

.

Lời giải

Qua điểm

I

dựng các đoạn

/ / , / / , / /

MQ AB PS BC NR CA

. Vì

ABC

là tam giác đều nên các

tam giác , ,

IMN IPQ IRS

cũng là tam giác đều. Suy ra

, ,

D E F

lần lượt là trung điểm của

, ,

MN PQ RS

. Khi đó:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

1 1 1

( ) ( ) ( )

2 2 2

ID IE IF IM IN IP IQ IR IS

       

        

1 1

( ) ( ) ( ) ( )

2 2

IQ IR IM IS IN IP IA IB IC

 

        

 

        

1 3

.3 3, 2

2 2

IO IO a b

    

 

. Do đó:

5

a b

 

.

PHẦN II. TỰ LUẬN

Câu 1. Tìm hàm số bậc hai

2

  

y ax bx c

, biết rằng đồ thị là một đường Parabol đi qua điểm





1;0

A 

và có đỉnh





1;2

I

.

Lời giải

Theo giả thiết ta có hệ:

0

1 .

2

  





 





  





a b c

b

a

a b c

với

0



a

1

0

1

2

3

2







  





 

     

 

 

  











b

a b c

b a a

a b c

c

Vậy hàm bậc hai cần tìm là

2

1 3

2 2

   

y x x

Câu 2. Cho tam giác

ABC

vuông tại

A

có

AB a



,

2

BC a



.

a) Tính

. , .

BA BC BC CA

   

b) Tính

. . .

AB BC BC CA CA AB

 

     

Lời giải

a) Ta có

2 2

3

AC BC AB a

   .

0 2

1

. =BA.BC.cos60 = .2 . = ;

2

3

. . . os150 2 . 3. 3 .

2

BA BC a a a

BC CA BC CAc a a a

    

 

b) Ta có

2

. .

. = 3

. 0

. . . = 4 .

AB BC BA BC a

BC CA a

CA AB

AB BC BC CA CA AB a

   





   

   

 

     

Câu 3. Số các giá trị nguyên của tham số





2018;2018

m 

để phương trình:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

 

2 3

2 4 4 4

x m x x x

    

có nghiệm là

Lời giải

ĐK:

0

x



Ta có

 

2 3

2 4 4 4

x m x x x

    

 





2 2

4 2 4 4 (1)

x m x x x     

Với

0

x



không phải là nghiệm của phương trình.

Với

0

x



phương trình

(1)

trở thành

 

2 2

4 4

2 4 (2)

x x

m

x x

 

   

Đặt

2

4 4

2 4 2 2

x

t x t

x x



      

Phương trình (2) trở thành:

2

4 2 0

t t m

   

.

2

4 2 (*)

t t m   

Để phương trình đã cho có nghiệm thì phương trình (*) có nghiệm lớn hơn

2

.

Số nghiệm của phương trình (*) là số giao điểm của đồ thị hàm

2

4 2

y t t

  

và đường thẳng

y m



Xét hàm số

2

4 2

y t t

  

có đồ thị như hình vẽ

Dựa vào đồ thị hàm số, để phương trình đã cho có nghiệm thì phương trình (*) có nghiệm lớn

hơn hoặc bằng

2

suy ra

2

m

 

.

Suy ra số các giá trị nguyên của tham số





2018;2018

m 

để phương trình có nghiệm là 2021.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 13 Môn Toán – Lớp 10

(Thời gian làm bài 90 phút)

Không k

ể thời gian phát đề

I. TRẮC NGHIỆM

Câu 1. Câu nào sau đây không là mệnh đề?

A.

5.

x



B.

4 5.



C.

10 5 5.

 

D.

5

là một số hữu tỉ.

Câu 2. Cho









0;1;3;4;5 , 4;5;6;8 .

A B  Tập hợp

\

A B

bằng

A.





0;1;3;4;5 .

B.





6;8 .

C.





4;5 .

D.





0;1;3 .

Câu 3. Khi sử dụng máy tính bỏ túi ta được:

5 2,236067977



. Giá trị gần đúng của

5

quy tròn đến

hàng phần trăm là

A.

2,23.

B.

2,20.

C.

2,236.

D.

2,24.

Câu 4. Cho hàm số

 

1

4

1

f x x

x

  



và các điểm





1; 5

A 

,

1

4;

5

B

 

 

 

,

3

3;

4

C



 

 

 

,

5

5;

6

D

 

 

 

. Số

điểm trong các điểm trên thuộc đồ thị hàm số đã cho là:

A.

4

. B.

3

. C.

2

. D.

1

.

Câu 5. Tìm

m

để hàm số





3 2

y m x

  

nghịch biến trên



.

A.

0

m



. B.

3

m



. C.

3

m



. D.

3

m



.

Câu 6. Hàm số nào sau đây có tập xác định là



?

A.

2

1

x

y

x





. B.

3

3 2 3

y x x

  

. C.

3

3 2 3

y x x

  

. D.

2

1

x

y

x





.

Câu 7. Trong mặt phẳng

Oxy

cho





1;3

a  



,





5; 7

b

 



. Tọa độ vectơ

3

2b

a



 

là:

A.





13; 29

 . B.





6;10

 . C.





13;23

 . D.





6; 19

 .

Câu 8. Trong mặt phẳng với hệ trục tọa độ

,

Oxy

cho vecto

(1; 2).

a

 



Trong các vectơ dưới đây, vectơ

nào cùng phương với

.

a



A.

(1;2).

b 



B.

( 1; 2).

c

  



C.

( 2;4).

d  



D.

(2;1).

e 



Câu 9. Trong mặt phẳng tọa độ

Oxy

cho





3;1

a  



,





2;0

b 



và





1;1

c 



. Đẳng thức nào sau đây

đúng?

A.

2 0

a b

 

  

. B.

0

a b c

  

   

.

C.

0

a b

 

  

. D.

2 0

a b c

  

   

.

Câu 10. Cho hình vuông

ABCD

có độ dài cạnh bằng

10

. Tính giá trị

.

ABCD

 

.

A.

100

. B.

10

.

C.

0

. D.

100



.

Câu 11. Cho

ABC



có

1

AB AC

 

,

0

120

BAC 

,

M AB



sao cho

1

3

AM



. Khi đó

.

AM AC

 

bằng:

A.

3

8



. B.

1

6



. C.

3

2



. D.

1

2

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 12. Điều kiện xác định của phương trình

5

1

2

x







là

A.

5.

x



B.

5

.

2

x



 













C.

5

.

2

x

















D.

2.

x



Câu 13. Tập nghiệm của phương trình

1

x x x

  

là

A.

S





. B.

S

 

. C.





0

S



. D.





1

S

 

.

Câu 14. Cho các khẳng định sau:

A:

2017 2017

( ) ( ) ( ) ( )

f x g x f x g x

  

B:

2 2

( ) ( ) ( ) ( )

f x g x f x g x

  

C:

( ) ( ) 0 ( ) ( )

f x g x f x g x

   

D:

2018 2018

( ) ( ) ( ) ( )

f x g x f x g x

  

Số các khẳng định đúng là:

A.

0

. B.

1

. C.

2

. D.

3

.

Câu 15. Trong các khẳng định sau đây ,khẳng định nào sai?

A.

o o

cos45 sin 45



. B.

o o

cos45 sin135



C.

o o

cos30 sin120



. D.

o o

cos60 sin120



.

Câu 16. Cho hai vectơ

a



và

b



thỏa mãn

1

a b

 

 

và hai vectơ

2 15

u a b

 

 



và

v a b

 

 



vuông góc

với nhau. Xác định góc



giữa hai vectơ

a



và

.

b



A.

o

90





. B.

o

180





. C.

o

60





. D.

o

45





.

Câu 17. Tam giác

ABC

có



60 , 45

B C

   

và

5

AB



. Tính độ dài cạnh

AC

.

A.

5 6

.

2

AC  B.

5 3.

AC



C.

5 6

.

3

AC 

D.

5 6

.

4

AC 

Câu 18. Trong mặt phẳng tọa độ cho hình vuông có và Tìm tọa độ điểm

, biết có tung độ âm.

A. B. C.





2; 1

D



D.

Câu 19. Mệnh đề phủ định của mệnh đề

2

:" : 2 0"

P x x x

    



là:

A.

2

:" : 2 0"

P x x x

    



B.

2

:" : 2 0"

P x x x

    



C.

2

:" : 2 0"

P x x x

    



D.

2

:" : 2 0"

P x x x

    



Câu 20. Cho hai tập





0;6

A  ;





: 3

B x x

  

 . Khi đó hợp của

A

và

B

là

A.





0;3

B.

(0;3)

C.





3;6

 D.





3;6



Câu 21. Cho tập hợp





; 3

A m m

 

;





2;4

B   . Tìm tất cả các giá trị

m

để

A B



?

A.

2

m

 

hoặc

1.

m



B.

2.

m

 

C.

1.

m



D.

2 1.

m

  

Câu 22. Cho Parabol





2

: 3 6 1

P y x x

   

. Chọn khẳng định sai?

A.





P

có đỉnh





1;2

I . B.





P

cắt trục hoành tại điểm





0; 1

A



.

C.





P

hướng bề lõm lên trên. D.





P

có trục đối xứng

1

x



.

Câu 23. Bảng biến thiên sau là của hàm số nào dưới đây?

,

Oxy

ABCD





1; 1

A







3;0 .

B

D





0; 1 .

D







2; 3 .

D







2; 3 .

D

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

2

2 4 4

y x x

  

. B.

2

3 6 1

y x x

   

.

C.

2

2 1

y x x

  

. D.

2

2 2

y x x

  

.

Câu 24. Cho hình bình hành

ABCD

tâm

O

. Khi biểu diễn vectơ

AI



theo vectơ

AB



và

AD



với

I

là

trung điểm của

BO

thì ta có

. .

AI a AB b AD

 

  

. Tính

a b



.

A.

1

a b

 

. B.

6

5

a b

 

. C.

2

a b

 

. D.

5

3

a b

 

.

Câu 25. Cho tam giác

ABC

có









10;13 ; 13;6

B C . Gọi

,

M N

lần lượt là trung điểm của

, .

AB AC

Biết

điểm

( 2;3)

M



. Xác định tọa độ điểm

N

.

A.

1 1

;

2 2

N

 

 

 

 

. B.

1 1

;

2 2

N

 



 

 

. C.

1 1

;

2 2

N

 



 

 

. D.

1 1

;

2 2

N

 

 

 

.

Câu 26. Tính tổng tất cả các nghiệm của phương trình

2

2 3 2 2

x x x

   

A.

3

2

. B. 1. C. 3. D. 2.

Câu 27. Số nghiệm của phương trình

2

1 4

2

4

x







là

A.

0

. B.

2

. C.

3

. D.

1

.

Câu 28. Trong mặt phẳng tọa độ

Oxy

, cho tam giác

ABC

có













4;3 , 1;2 , 3; 2

A B C

 

. Gọi

G

là

trọng tâm tam giác

ABC

. Tìm tọa độ điểm

M

sao cho

3 0

MB MC MG

  

   

.

A.

8 3

;

5 5

M

 

 

 

 

. B.

8 3

;

5 5

M

 

 

 

. C.

4 1

;

5 5

M

 

 

 

 

. D.

4 1

;

5 5

M

 

 

 

.

Câu 29. Có bao nhiêu giá trị nguyên của

m

để phương trình





 

2

4 3 2 0

x x x m

    

có

4

nghiệm phân biệt?

A.

30.

B. vô số. C.

28.

D.

0.

Câu 30. Tìm tất cả các giá trị của tham số

m

để phương trình

2 5 2 3

x m x m

   có nghiệm.

A.





0;m

 

. B.





0;m

 

. C.





;0

m  . D.





;m

  

.

Câu 31. Cho đường tròn tâm

O

bán kính

R

và điểm

M

thỏa mãn

3

MO R



. Một đường kính

AB

thay

đổi trên đường tròn. Giá trị nhỏ nhất của biểu thức

S MA MB

 

.

A.

min 6

S R



. B.

min 4

S R



. C.

min 2

S R



. D.

min

S R



.

Câu 32. Trong mặt phẳng tọa độ

Oxy

, cho Parabol





2

f x ax bx c

  

có đồ thị như hình vẽ. Có bao

nhiêu số nguyên dương

m

để đường thẳng

1

y m

 

cắt đồ thị





3

y f x

 

tại

4

điểm phân

biệt.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

1

. B.

2

. C.

3

. D.

4

.

Câu 33. Lớp 10A có

10

HS giỏi Toán,

11

HS giỏi Lý,

9

HS giỏi Hoá,

3

HS giỏi cả Toán và Lý,

4

HS

giỏi cả Toán và Hoá,

2

HS giỏi cả Lý và Hoá,

1

HS giỏi cả

3

môn Toán , Lý, Hoá. Hỏi số HS

giỏi ít nhất một môn Toán , Lý , Hoá của lớp 10A là?

A.

22

B.

18.

C.

20.

D.

19.

Câu 34. Gọi

S

là tập hợp tất cả các giá trị thực của tham số

m

để giá trị nhỏ nhất của hàm số





2 2

4

mx m m

y f x x











trên đoạn

3;0

 



 

 

bằng

11

. Bình phương của tổng tất cả các

phần tử của

S

bằng

A.

15

. B.

16

. C.

20

. D.

25

.

Câu 35. Trong mặt phẳng

Oxy

, cho hai điểm





1;2

A và





3; 1

B



. Điểm





;

M x y

thuộc trục hoành và

thỏa mãn

MA MB



nhỏ nhất. Khi đó tính giá trị của biểu thức

2

9 3 2

T x x y

  

.

A.

144

49

T 

. B.

56

T



. C.

49

144

T 

. D.

65

T



.

II. TỰ LUẬN

Câu 36. Cho 3 tập hợp:





1 2

A x x

    

 ,





3 5

B x x

   

 ,





1 4

C x x

   

 . Xác định tập

hợp





\

A B C

 và biểu diễn tập hợp đó trên trục số.

Câu 37. Cho Parabol





2

:

P y x mx n

  

(

,

m n

tham số). Xác định

,

m n

để





P

nhận đỉnh





2; 1

I



.

Câu 38. Trong mặt phẳng

Oxy

, cho tam giác

ABC

có





1;1

A ,





3;2

B ,





4; 1

C



. Tìm toạ độ điểm

D

nằm trên trục hoành sao cho tứ giác

ABCD

là hình thang.

Câu 39. Trên mặt phẳng tọa độ

Oxy

, cho



ABC

biết





2;2

A ;





2; 4

 

B ;





6;0

C .

a) Tìm tọa độ trọng tâm

G

, trực tâm

H

và tâm

I

đường tròn ngoại tiếp



ABC

. Chứng minh 3

điểm

, ,

G H I

thẳng hàng.

b) Tìm điểm

K

là hình chiếu của

A

lên

BC

.

Câu 40. Tập nghiệm

S

của phương trình

2 3 3

x x

  

là

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG HDG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 13 Môn Toán – Lớp 10

(Thời gian làm bài 90 phút)

Không k

ể thời gian phát đề

Câu 1. Câu nào sau đây không là mệnh đề?

A.

5.

x



B.

4 5.



C.

10 5 5.

 

D.

5

là một số hữu tỉ.

Lời giải

Chọn A

Vì “

5

x



”

là mệnh đề chứa biến, không phải mệnh đề.

Câu 2. Cho









0;1;3;4;5 , 4;5;6;8 .

A B  Tập hợp

\

A B

bằng

A.





0;1;3;4;5 .

B.





6;8 .

C.





4;5 .

D.





0;1;3 .

Lời giải

Chọn D

Vì





\

A B x x A B

và x   nên





\ 0;1;3

A B  .

Câu 3. Khi sử dụng máy tính bỏ túi ta được:

5 2,236067977



. Giá trị gần đúng của

5

quy tròn đến

hàng phần trăm là

A.

2,23.

B.

2,20.

C.

2,236.

D.

2,24.

Lời giải

Chọn D

Theo quy tắc quy tròn số.

Câu 4. Cho hàm số

 

1

4

1

f x x

x

  



và các điểm





1; 5

A 

,

1

4;

5

B

 

 

 

,

3

3;

4

C



 

 

 

,

5

5;

6

D

 

 

 

. Số

điểm trong các điểm trên thuộc đồ thị hàm số đã cho là:

A.

4

. B.

3

. C.

2

. D.

1

.

Lời giải

Từ điều kiện

4;

x



1

x

 

loại

A

và

C

Thay tọa độ các điểm B, D vào hàm số để kiểm tra thấy chỉ có B thỏa mãn.

Câu 5. Tìm

m

để hàm số





3 2

y m x

  

nghịch biến trên



.

A.

0

m



. B.

3

m



. C.

3

m



. D.

3

m



.

Lời giải

Hàm số





3 2

y m x

  

nghịch biến trên



khi và chỉ khi

3 0 3

m m

   

.

Câu 6. Hàm số nào sau đây có tập xác định là



?

A.

2

1

x

y

x





. B.

3

3 2 3

y x x

  

. C.

3

3 2 3

y x x

  

. D.

2

1

x

y

x





.

Lời giải

Điều kiện để các hàm số:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

+

2

1

x

y

x





có nghĩa là:

1

x

 

.

+

3

3 2 3

y x x

  

có nghĩa với

x

 



.

+

3

3 2 3

y x x

  

có nghĩa với

0

x



.

+

2

1

x

y

x





có nghĩa với

0

x



.

Câu 7. Trong mặt phẳng

Oxy

cho





1;3

a  



,





5; 7

b

 



. Tọa độ vectơ

3

2b

a



 

là:

A.





13; 29

 . B.





6;10

 . C.





13;23

 . D.





6; 19

 .

Lời giải

Chọn C

 

1;3 3 3;9

3 13;23

5; 7 2 10; 14

2b

a a

b

a

b

 

   

 

  

 

  













 

.

Câu 8. Trong mặt phẳng với hệ trục tọa độ

,

Oxy

cho vecto

(1; 2).

a

 



Trong các vectơ dưới đây, vectơ

nào cùng phương với

.

a



A.

(1;2).

b 



B.

( 1; 2).

c

  



C.

( 2;4).

d  



D.

(2;1).

e 



Lời giải

Chọn C

Ta có:

( 2;4) 2 .

d a

   

 

Do đó,

d



cùng phương với

.

a



Câu 9. Trong mặt phẳng tọa độ

Oxy

cho





3;1

a  



,





2;0

b 



và





1;1

c 



. Đẳng thức nào sau đây

đúng?

A.

2 0

a b

 

  

. B.

0

a b c

  

   

.

C.

0

a b

 

  

. D.

2 0

a b c

  

   

.

Lời giải

Chọn D

Ta có





2 4;0

b 







2 1;1

a b  

 





2 0;0

a b c   

  

Vậy

2 0

a b c

  

   

.

Câu 10. Cho hình vuông

ABCD

có độ dài cạnh bằng

10

. Tính giá trị

.

ABCD

 

.

A.

100

. B.

10

.

C.

0

. D.

100



.

Lời giải

Chọn D

0

. . cos180 100

ABCD AB CD  

   

Câu 11. Cho

ABC



có

1

AB AC

 

,

0

120

BAC 

,

M AB



sao cho

1

3

AM



. Khi đó

.

AM AC

 

bằng:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

3

8



. B.

1

6



. C.

3

2



. D.

1

2

.

Lời giải

Chọn B

Ta có.





0

1 1

. . cos , .1.cos120

3 6

AM AC AM AC AM AC

   

     

.

Câu 12. Điều kiện xác định của phương trình

5

1

2

x







là

A.

5.

x



B.

5

.

2

x



 













C.

5

.

2

x

















D.

2.

x



Lời giải

Chọn C

Phương trình xác định khi và chỉ khi

5 0 5

.

2 0 2

x x

 

  

 



 

 

  

 

 

Câu 13. Tập nghiệm của phương trình

1

x x x

  

là

A.

S





. B.

S

 

. C.





0

S



. D.





1

S

 

.

Lời giải

Chọn B

Điều kiện:

0

x



.

1 1

x x x x

     

(loại).

Vây tập nghiệm của phương trình đã cho là

S

 

.

Câu 14. Cho các khẳng định sau:

A.

2017 2017

( ) ( ) ( ) ( )

f x g x f x g x

   B.

2 2

( ) ( ) ( ) ( )

f x g x f x g x

  

C.

( ) ( ) 0 ( ) ( )

f x g x f x g x

    D.

2018 2018

( ) ( ) ( ) ( )

f x g x f x g x

  

Số các khẳng định đúng là:

A.

0

. B.

1

. C.

2

. D.

3

.

Lời giải

Chọn C

2017 2017

( ) ( ) ( ) ( )

f x g x f x g x

   : Khẳng định đúng.

2 2

( ) ( ) ( ) ( )

f x g x f x g x

   : Khẳng định sai vì thiếu điều kiện

( ), ( )

f x g x

cùng không âm

hoặc cùng không dương.

( ) ( ) 0 ( ) ( )

f x g x f x g x

    : Khẳng định đúng.

2018 2018

( ) ( ) ( ) ( )

f x g x f x g x

   : Khẳng định sai vì thiếu điều kiện

( ), ( )

f x g x

cùng không

âm hoặc cùng không dương.

Vậy số khẳng định đúng là

2

.

Câu 15. Trong các khẳng định sau đây ,khẳng định nào sai?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

o o

cos45 sin 45



. B.

o o

cos45 sin135



C.

o o

cos30 sin120



. D.

o o

cos60 sin120



.

Lời giải

Chọn D

Vì

o o

1 3

cos60 ,sin120

2 2

 

nên

o o

cos60 sin120



Câu 16. Cho hai vectơ

a



và

b



thỏa mãn

1

a b

 

 

và hai vectơ

2 15

u a b

 

 



và

v a b

 

 



vuông góc

với nhau. Xác định góc



giữa hai vectơ

a



và

.

b



A.

o

90





. B.

o

180





. C.

o

60





. D.

o

45





.

Lời giải

Chọn B

Ta có









2 2

. 0 2 15 0 2 13 . 15 0

u v u v a b a b a a b b

          

       

   

1

. 1

a b

 

  

 

Suy ra

   

0

.

cos , 1 , 180

.

a b

a b a b

a b

    



   



Câu 17. Tam giác

ABC

có



60 , 45

B C

   

và

5

AB



. Tính độ dài cạnh

AC

.

A.

5 6

.

2

AC  B.

5 3.

AC



C.

5 6

.

3

AC 

D.

5 6

.

4

AC 

Lời giải

Chọn A

Theo định lí sin ta có:

0

5 5 6

sin sin 2

sin45

sin60

AB AC AC

AC

C B

    

.

Câu 18. Trong mặt phẳng tọa độ cho hình vuông có và Tìm tọa độ điểm

, biết có tung độ âm.

A. B. C.





2; 1

D



D.

Lời giải

Chọn B

Vì

ABCD

là hình vuông nên

. 0

AB AD



















 

.

,

Oxy

ABCD





1; 1

A







3;0 .

B

D





0; 1 .

D







2; 3 .

D







2; 3 .

D

 

A

B

D

C

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Gọi

( ; ) ( 0)

D x y y



. Ta có:

(2; 1). 5. ( 1; 1)

AB AB AD x y

     

 

.

 

2

2 2 1 0

2, 3

. 0

0, 1

( 1) 1 5

x y

AB AD

x y

AB AD

x y



   









  

 

 



 

 



 

 



   

  







 

Vì

0

y



nên

Câu 19. Mệnh đề phủ định của mệnh đề

2

:" : 2 0"

P x x x

    



là:

A.

2

:" : 2 0"

P x x x

    



B.

2

:" : 2 0"

P x x x

    



C.

2

:" : 2 0"

P x x x

    



D.

2

:" : 2 0"

P x x x

    



Lời giải

Chọn D

Theo định nghĩa mệnh đề phủ định của một mệnh đề, ta chọn D.

Câu 20. Cho hai tập





0;6

A  ;





: 3

B x x

  

 . Khi đó hợp của

A

và

B

là

A.





0;3

B.

(0;3)

C.





3;6

 D.





3;6



Lời giải

Chọn D





0;6

A 









: 3 3;3

B x x    

( 3;6]

A B

  

Câu 21. Cho tập hợp





; 3

A m m

 

;





2;4

B   . Tìm tất cả các giá trị

m

để

A B



?

A.

2

m

 

hoặc

1.

m



B.

2.

m

 

C.

1.

m



D.

2 1.

m

  

Lời giải

Chọn D

2

2 1.

3 4

m

A B m

m

 



     



 



Câu 22. Cho Parabol





2

: 3 6 1

P y x x

   

. Chọn khẳng định sai?

A.





P

có đỉnh





1;2

I . B.





P

cắt trục hoành tại điểm





0; 1

A



.

C.





P

hướng bề lõm lên trên. D.





P

có trục đối xứng

1

x



.

Lời giải

Chọn C

Dễ thấy

3 0

a

  

nên hướng bề lõm quay xuống dưới.

Ta có

1

2

4

b

a



 









 





nên





P

có tọa độ đỉnh là





1;2

I và trục đối xứng

1

x



.





2; 3 .

D



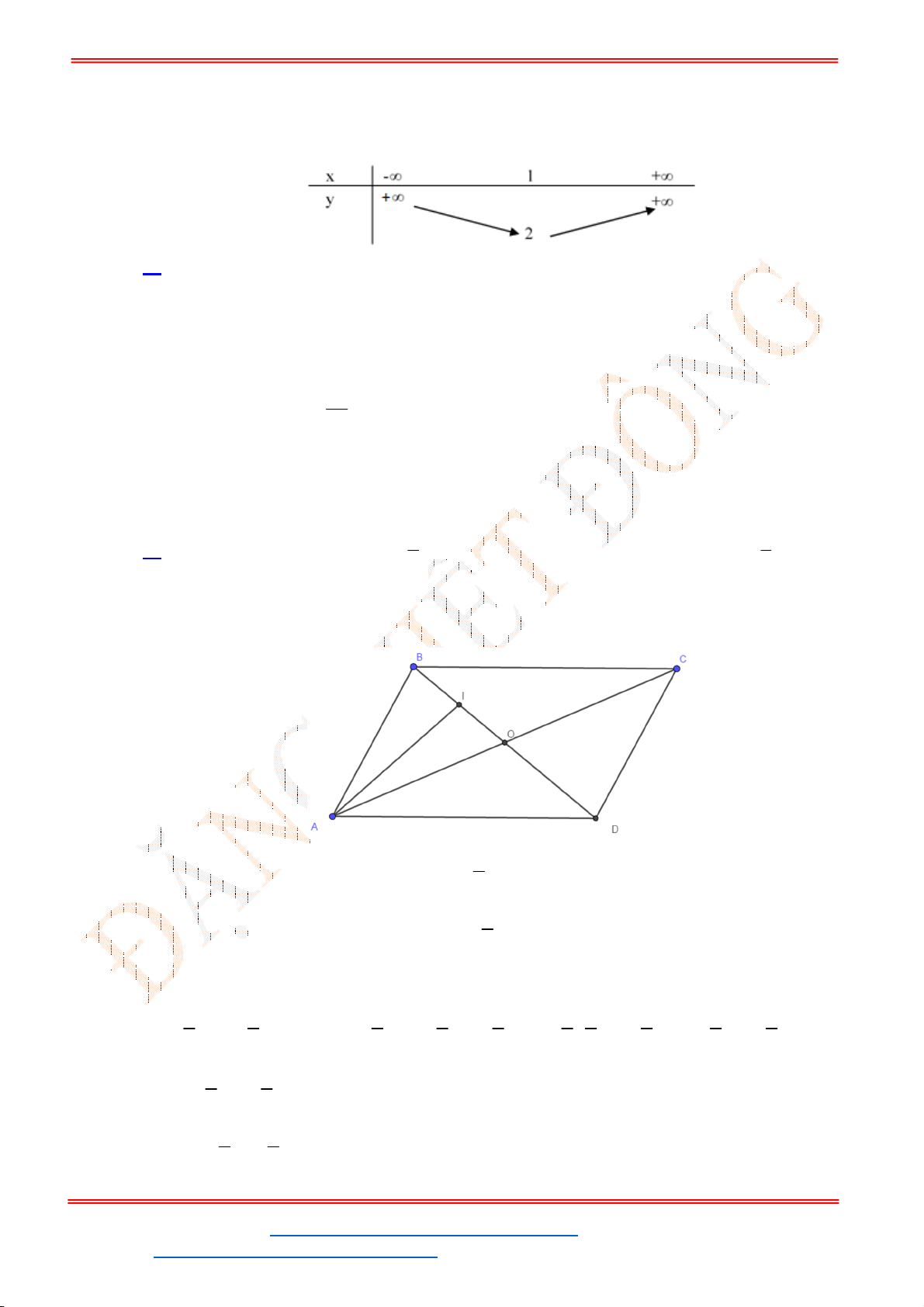
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Mặt khác

 

0; 1A  thuộc

 

P nên , ,A B D đúng.

Câu 23. Bảng biến thiên sau là của hàm số nào dưới đây?

A.

2

2 4 4y x x   . B.

2

3 6 1y x x    .

C.

2

2 1y x x   . D.

2

2 2y x x   .

Lời giải

Dựa vào bảng biến thiên ta thấy

0a 

. Loại

.B

Tọa độ đỉnh

 

1;2I

1 0

2

b

a

   

. Suy ra

0b 

. Loại

.C

Thay 1 2x y   . Loại

.D

Câu 24. Cho hình bình hành

ABCD

tâm

O

. Khi biểu diễn vectơ AI



theo vectơ AB



và AD



với I là

trung điểm của

BO

thì ta có

. .AI a AB b AD 

  

. Tính

a b

.

A.

1a b 

. B.

6

5

a b 

. C.

2a b 

. D.

5

3

a b 

.

Lời giải

Chọn A

Vì I là trung điểm của

BO

nên ta có:

 

1

2

AI AB AO 

  

Vì

O

là trung điểm của BD nên ta có:

 

1

2

AO AB AD 

  

Thay

 

2 vào

 

1 ta được:

 

1 1 1 1 1 1 3 1 3 1

2 2 2 2 2 2 2 2 4 4

AI AB AB AD AB AB AD AB AD AB AD

     

         

   

 

     

          

.

3 1

4 4

AI AB AD  

  

.

Ta có

3 1

, 1

4 4

a b a b    

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 25. Cho tam giác

ABC

có









10;13 ; 13;6

B C . Gọi

,

M N

lần lượt là trung điểm của

, .

AB AC

Biết

điểm

( 2;3)

M



. Xác định tọa độ điểm

N

.

A.

1 1

;

2 2

N

 

 

 

 

. B.

1 1

;

2 2

N

 



 

 

. C.

1 1

;

2 2

N

 



 

 

. D.

1 1

;

2 2

N

 

 

 

.

Lời giải

Chọn A

Vì

MN

là đường trung bình của tam giác

ABC

nên ta có

1

2

MN BC



 

.

Ta có





3; 7

BC

 



nên

1 1

( 2) .3

2 2

1 1

3 .( 7)

2 2

N N

x x

y y

 

    

 



 

 

    

 

 

.

Vậy

1 1

;

2 2

N

 

 

 

 

.

Câu 26. Tính tổng tất cả các nghiệm của phương trình

2

2 3 2 2

x x x

   

A.

3

2

. B. 1. C. 3. D. 2.

Lời giải

Chọn C

2

2 3 2 2

x x x

   





 

2

2 3 2 2

x x x    

4 2 3 2 2

4 9 4 12 8 12 4 4

x x x x x x x

        

4 3

4 12 8 0

x x x

   





3 2

4 12 8 0

x x x

   









2

4 1 2 2 0

x x x x

    

0

1 3

1

x







 







 









0 (1 3) (1 3) 1 3

S

       

.

Câu 27. Số nghiệm của phương trình

2

1 4

2

4

x







là

A.

0

. B.

2

. C.

3

. D.

1

.

Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Chọn D

Điều kiện

2

4 0 2

x x

    

.

Khi đó

  



    



2

1 4

1 2 4

2

4

x

x x

x

2

3

6 0

2

x

x x

x

 



    







Đối chiếu với điều kiện ta được

3

x

 

thỏa mãn và

2

x



bị loại.

Vậy phương trình đã cho có một nghiệm là

3

x

 

.

Câu 28. Trong mặt phẳng tọa độ

Oxy

, cho tam giác

ABC

có













4;3 , 1;2 , 3; 2

A B C

 

. Gọi

G

là

trọng tâm tam giác

ABC

. Tìm tọa độ điểm

M

sao cho

3 0

MB MC MG

  

   

.

A.

8 3

;

5 5

M

 

 

 

 

. B.

8 3

;

5 5

M

 

 

 

. C.

4 1

;

5 5

M

 

 

 

 

. D.

4 1

;

5 5

M

 

 

 

.

Lời giải

Chọn B

Tọa độ trọng tâm

G

là trọng tâm tam giác

ABC

là





2;1

.

Gọi





;

M x y

, ta có





1 ;2

MB x y

   



;





3 ; 2

MC x y

   



;





2 ;1

MG x y

  



.





3 8 5 ;3 5

MB MC MG x y

     

  

.

Vì

3 0

MB MC MG

  

   

nên

8

8 5 0

5

3 5 0 3

5

x

y







 







 

 











.

Câu 29. Có bao nhiêu giá trị nguyên của

m

để phương trình





 

2

4 3 2 0

x x x m

    

có

4

nghiệm phân biệt?

A.

30.

B. vô số. C.

28.

D.

0.

Lời giải

Chọn A

Ta có





   

2

2 2 2 2

4 3 2 0 ( 4) 3( 2) 0 1

x x x m x x x m           .

Đặt

2 4

2

a x

x a

  



  



 



Khi đó (1) có dạng :

2 2 2 4 2

( 2) ( 2) 3 0 11 16 0

a a a m a a m

         

(2)

Đặt

2

0

t a

 

khi đó (2)

2

11 16 0

t t m

    

(*)

Yêu cầu bài toán



(*) có hai nghiệm dương phân biệt



2

11 4(16 ) 0

11 0 16 14,25

16 0

m

S m

P m



  



     





  



mà

m

nguyên nên suy ra có

30

giá trị

m

thỏa mãn.

Câu 30. Tìm tất cả các giá trị của tham số

m

để phương trình

2 5 2 3

x m x m

   có nghiệm.

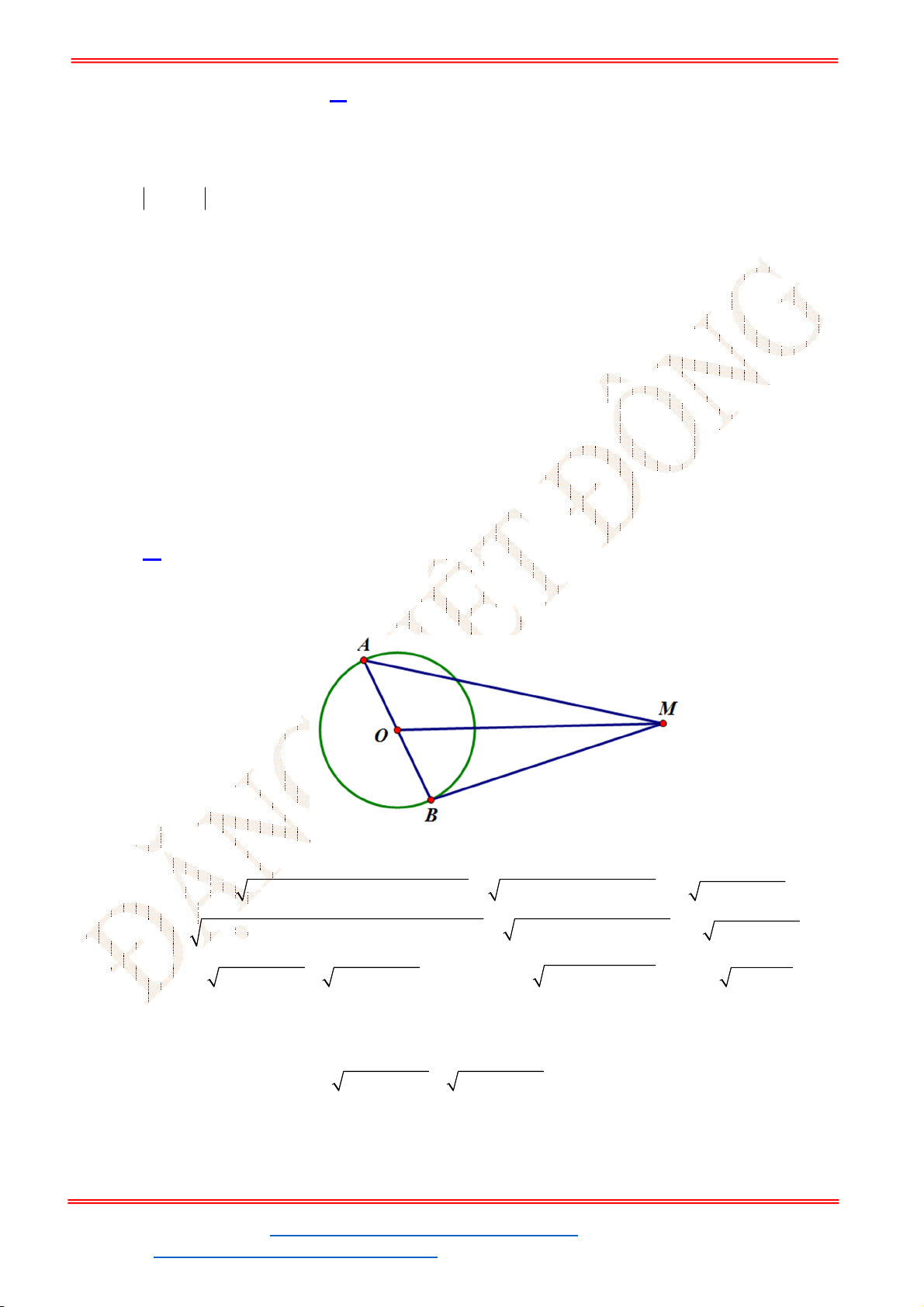
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

 

0;m  . B.





0;m  . C.

 

;0m  . D.

 

;m   .

Lời giải

Chọn B

2 5 2 3x m x m   (1)

Điều kiện để phương trình đã cho có nghiệm là

2 3 0x m 

(2)

Với điều kiện (2), ta có:

(1)

2 5 2 3

x m x m

  







   



2 0 (3)

2 (4)

m

x m













Phương trình (3) có nghiệm

x 

0m 

. Kết hợp điều kiện (2), suy ra

2 3.0 0x  

0x 

.

Nghiệm của phương trình (4) là nghiệm của phương trình (1)

2 3 0x m   2.2 3 0m m  

0m 

.

Vậy phương trình (1) có nghiệm khi và chỉ khi





0;m  .

Câu 31. Cho đường tròn tâm

O

bán kính

R

và điểm

M

thỏa mãn

3MO R

. Một đường kính

AB

thay

đổi trên đường tròn. Giá trị nhỏ nhất của biểu thức

S MA MB 

.

A.

min 6S R

. B.

min 4S R

. C.

min 2S R

. D.

min S R

.

Lời giải

Chọn A

Gọi



180MOA MOB

 

    

.

Ta có

2 2 2 2 2

2 . .cos 9 6 cos 10 6cosMA MO AO MO AO R R R R

  

       

.

 

2 2 2 2 2

2 . .cos 180 9 6 cos 10 6cosMB MO BO MO BO R R R R

  

         .

Xét

10 6cos 10 6cosC

 

   

2 2

20 2 100 36cos 20 2 100 36 36C



       

.

Suy ra

6C 

. Dấu

" "

xẩy ra khi

2

cos 1 0

cos 1

cos 1 180

 



 

  

 

  

 

   

 

.

Ta có

 

10 6cos 10 6cos 6S MA MB R R

 

      

.

Suy ra

min 6S R

khi và chỉ khỉ

A

,

O

,

B

,

M

thẳng hàng.

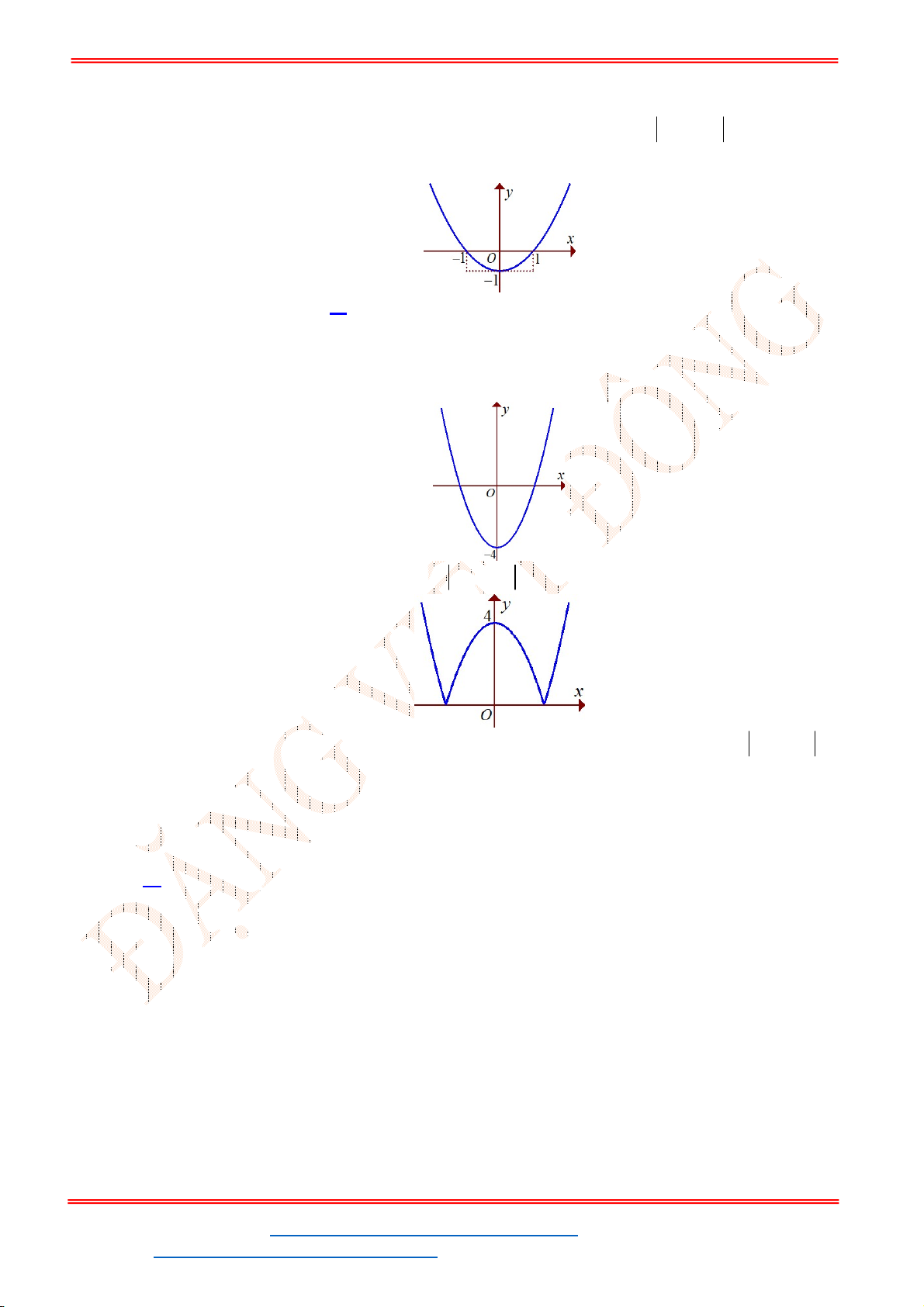
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 32. Trong mặt phẳng tọa độ

Oxy

, cho Parabol





2

f x ax bx c

  

có đồ thị như hình vẽ. Có bao

nhiêu số nguyên dương

m

để đường thẳng

1

y m

 

cắt đồ thị





3

y f x

 

tại

4

điểm phân

biệt.

A.

1

. B.

2

. C.

3

. D.

4

.

Lời giải

Chọn B

Ta có đồ thị hàm số





3

y f x

 

như hình vẽ (1):

Lấy trị tuyệt đối, ta có đồ thị hàm số





3

y f x

 

như hình vẽ (2):

Dựa vào đồ thị trên, ta nhận thấy để đường thẳng

1

y m

 

cắt đồ thị hàm số





3

y f x

 

tại 4

điểm phân biệt khi và chỉ khi

0 1 4 1 3

m m

      

.Vì

m

nguyên dương nên





1;2

m .

Câu 33. Lớp 10A có

10

HS giỏi Toán,

11

HS giỏi Lý,

9

HS giỏi Hoá,

3

HS giỏi cả Toán và Lý,

4

HS

giỏi cả Toán và Hoá,

2

HS giỏi cả Lý và Hoá,

1

HS giỏi cả

3

môn Toán , Lý, Hoá. Hỏi số HS

giỏi ít nhất một môn Toán , Lý , Hoá của lớp 10A là?

A.

22

B.

18.

C.

20.

D.

19.

Lời giải

Chọn A

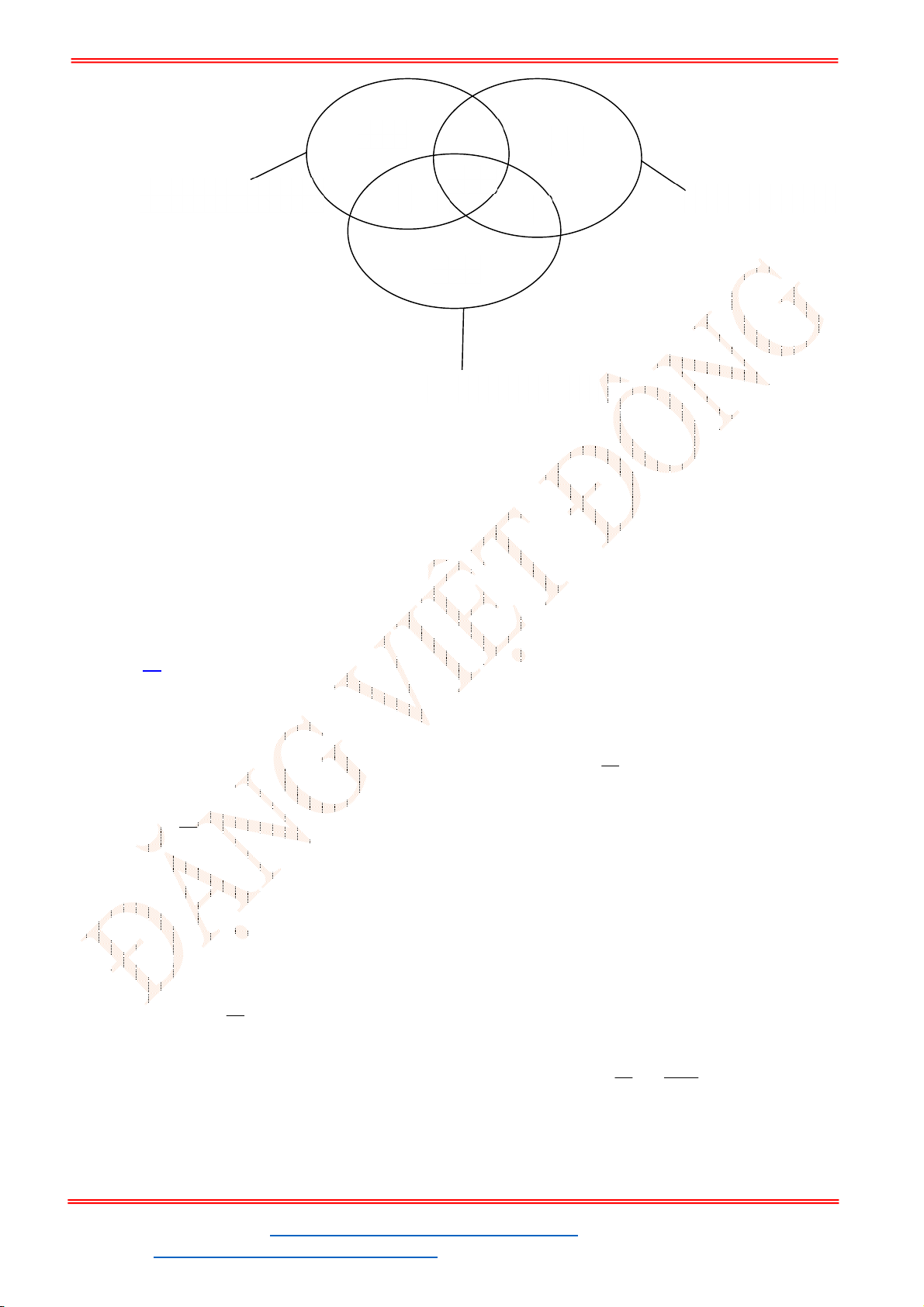
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Số học sinh chỉ học giỏi môn Toán là

10 4 3 1 4   

Số học sinh chỉ học giỏi môn Lý là

11 3 2 1 7   

Số học sinh chỉ học giỏi môn Hóa là

9 4 2 1 4   

Số học sinh học giỏi ít nhất 1 môn Toán, Lý, Hóa là

4 7 4 3 2 1 1 22      

Chú ý: Công thức nhanh

10 11 9 4 3 2 1 22.      

Câu 34. Gọi S là tập hợp tất cả các giá trị thực của tham số m để giá trị nhỏ nhất của hàm số

 

2 2

4mx m my f x x    trên đoạn 3;0

 



 

 

bằng 11. Bình phương của tổng tất cả các

phần tử của S bằng

A.

15

. B.16. C.20. D.25.

Lời giải

Chọn A

Nhận xét: Parabol có bề lõm hướng lên. Hoành độ đỉnh



2

I

m

x

.

Nếu

    3 6

2

m

thì

  3 0

I

x

. Suy ra

 

f x đồng biến trên đoạn

 



 

 

3;0 .

Do đó

   

 



 

 

    

2

3;0

min 3 9f x f m m

.

Theo yêu cầu bài toán:



 



       









2 2

1

9 11 2 0

2

m

m m m m

m

(loại).

Nếu

      3 0 6 0

2

m

thì

 

 

 

 

3;0

I

x .

Suy ra

 

f x đạt giá trị nhỏ nhất tại đỉnh. Do đó

 

 



 

 

 









 











 

2

3;0

3

m

2

4in

4

m

m m

f x f

.

a

c

2

-

1

4

-

1

10 HS GIỎI TOÁN

9 HS GI

Ỏ

I HÓA

11 HS GI

Ỏ

I LÝ

3

-

1

b

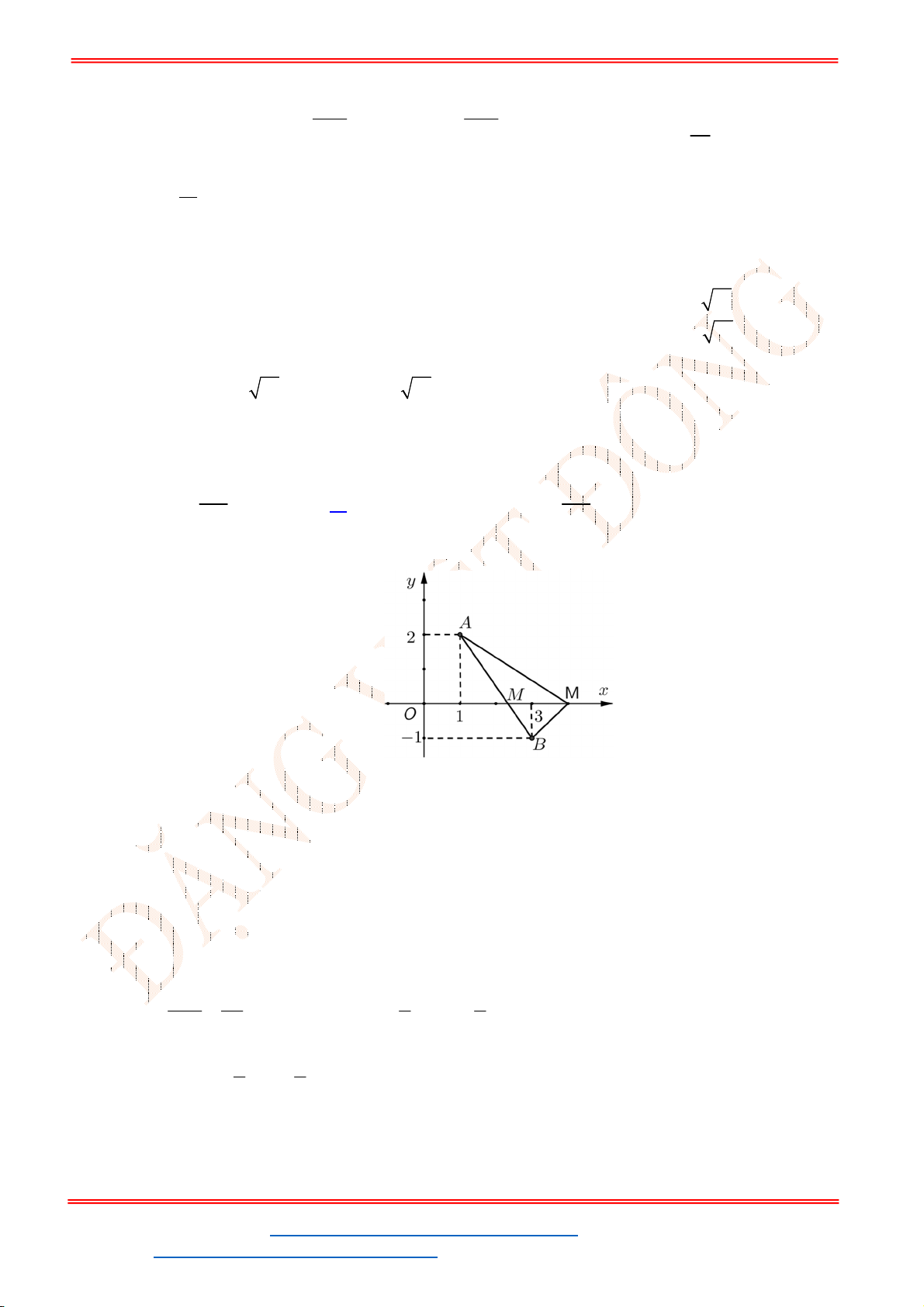
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Theo yêu cầu bài toán

(l)

(t/m)

2 2

2

4 11 4 11 0

22

3

4 4

m

m m

m



 



      









.

Nếu

  0 0

2

m

thì   0 3

I

x . Suy ra

 

f x nghịch biến trên đoạn

 



 

 

3;0 .

Do đó

   

 



 

 

  

3;0

2

4 .min 0f x m mf

Theo yêu cầu bài toán:

 

2 2

2 15

4 11 4 11 0 .

2 15 /

m

m l

m m

m t m

m



 



      



 



   

       

2

2;2 15 2 2 15 15S

.

Câu 35. Trong mặt phẳng Oxy , cho hai điểm

 

1;2A và

 

3; 1B  . Điểm

 

;M x y thuộc trục hoành và

thỏa mãn MA MB nhỏ nhất. Khi đó tính giá trị của biểu thức

2

9 3 2T x x y   .

A.

144

49

T 

. B.

56T 

. C.

49

144

T 

. D.

65T 

.

Lời giải

Do

 

;M x y Ox nên 0y  hay

 

;0M x .

Ta có

 

2; 3AB  



,

 

1; 2AM x  



.

Vì . 0

A B

y y  nên A , B nằm về hai phía so với trục

Ox

.

Do đó, với mọi điểm

M Ox

ta luôn có MA MB AB  .

Khi đó

 

min

MA MB AB  khi và chỉ khi ba điểm , ,A M B thẳng hàng.

Ta có , ,A M B thẳng hàng khi và chỉ khi AB



và AM



cùng phương

1 2 7

3 3 4

2 3 3

x

x x

 

      



7

;0

3

M

 



 

 

.

Vậy

2

7 7

9. 3. 2.0 56

3 3

T

 

   

 

 

.

II. TỰ LUẬN

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 36. Cho 3 tập hợp:





1 2

A x x

    

 ,





3 5

B x x

   

 ,





1 4

C x x

   

 . Xác định tập

hợp





\

A B C

 và biểu diễn tập hợp đó trên trục số.

Lời giải

Ta có









1 2 1;2

A x x      









3 5 3;5

B x x    









1 4 1;4

C x x    









1;2 3;5

A B   













\ 1;1 4;5

A B C    

Câu 37. Cho Parabol





2

:

P y x mx n

  

(

,

m n

tham số). Xác định

,

m n

để





P

nhận đỉnh





2; 1

I



.

Lời giải

Parabol





2

:

P y x mx n

  

nhận





2; 1

I



là đỉnh, khi đó ta có

4 2 1

2 5 3

4 4

2

m n

m n n

m

m m

   



   

 



 

  

   

 

 





.

Vậy

4, 3

m n

  

.

Câu 38. Trong mặt phẳng

Oxy

, cho tam giác

ABC

có





1;1

A ,





3;2

B ,





4; 1

C



. Tìm toạ độ điểm

D

nằm trên trục hoành sao cho tứ giác

ABCD

là hình thang.

Lời giải





;0

D

Ox D x

  .

Trường hợp 1.

//

AB

CD

.









2;1 , 4 ; 1 .

AB DC x

   

 

ABCD

là hình thang

,

AB DC



 

cùng hướng

4 1

0

2 1

x

 

  

(vô lý).

Loại trường hợp 1.

Trường hợp 2.

//

AD

BC

.









1; 1 , 1; 3 .

AD x BC

    

 

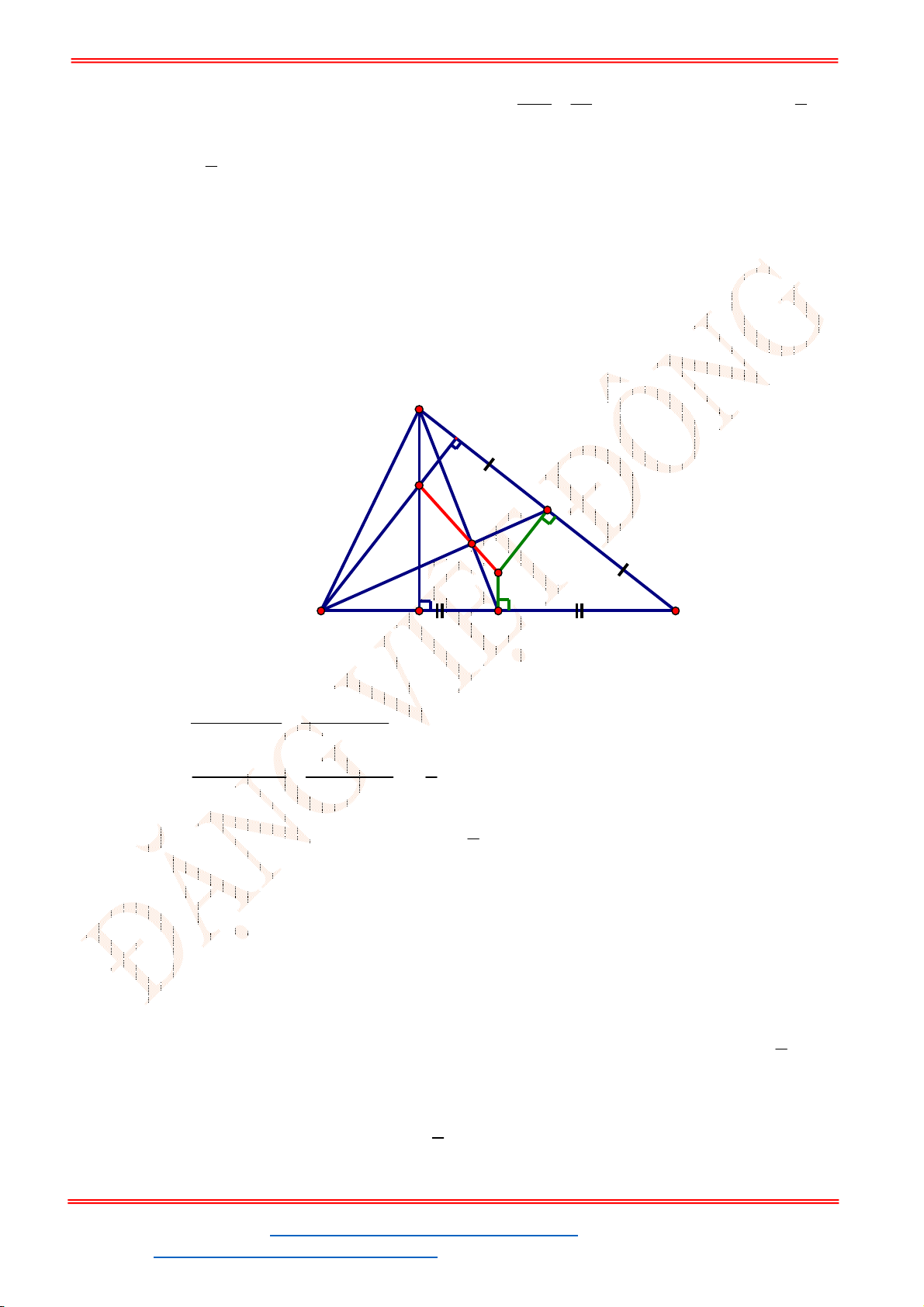
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ABCD

là hình thang

,

AD BC



 

cùng hướng

1 1 4

0 3 3 1

1 3 3

x

x x

 

         



.

Vậy

4

;0.

3

D

 

 

 

.

Câu 39. Trên mặt phẳng tọa độ

Oxy

, cho



ABC

biết





2;2

A ;





2; 4

 

B ;





6;0

C .

a) Tìm tọa độ trọng tâm

G

, trực tâm

H

và tâm

I

đường tròn ngoại tiếp



ABC

. Chứng minh 3

điểm

, ,

G H I

thẳng hàng.

b) Tìm điểm

K

là hình chiếu của

A

lên

BC

.

Lời giải

a) + Vì

G

là trọng tâm của



ABC

nên ta có:





 

2 2 6

2

3 3

2 4 0

2

3 3 3

  

 

  





  

 



   





A B C

G

A B C

G

x x x

x

y y y

y

Vậy tọa độ trọng tâm của



ABC

là

2

2;

3

 



 

 

G

.

+ Vì

H

là trực tâm



ABC

nên ta có:

. 0















 

AH BC

BH CA

.

Mà





2; 2

  



H H

AH x y ;





8;4





BC ;





2; 4

  



H H

BH x y ;





4;2

 



CA .

Nên:

   

     

3

2 .8 2 .4 0

8 4 24

. 0

2

4 2 0

2 . 4 4 .2 0

. 0

3



   

 





  

  

   

  

    













 

H H

H

H H

H

x y

AH BC

x

x y

BH CA

y

Vậy tọa độ trực tâm của



ABC

là

3

;3

2

 

 

 

H

.

I

G

N

M

K

H

B

C

A

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

+ Gọi





2; 2



M ;





4;1

N lần lượt là trung điểm của

BC

và

AC

.

Do

I

là tâm đường tròn ngoại tiếp



ABC

nên

. 0



 







 











 

 

IM BC IM BC

IN AC

IN CA

.

Mà





2 ; 2   



I I

IM x y

;





4 ;1  



I I

IN x y

Nên:

   

     

9

2 .8 2 .4 0

8 4 8

. 0

4

4 2 14 5

4 . 4 1 .2 0

. 0

2







    

   





  

  

   

 

    









 





 

 

I

I I

I

x

x y

IM BC

x y

IN AC

y

Vậy tọa độ tâm đường tròn ngoại tiếp



ABC

là

9 5

;

4 2

 



 

 

I

.

+ Ta có:

3 11

;

4 2

 

 

 

 



IH

;

1 11

;

4 6

 

 

 

 



IG

Ta thấy

3



 

IH IG

nên



IH

và



IG

cùng phương với nhau.

, ,



I G H

thẳng hàng.

b) Gọi





;

K K

K x y

là chân đường cao kẻ từ

A

lên

BC

, ta có

. 0

.















 

AK BC

BK k BC

.





2 ; 2

  



K K

AK x y

,





2 ; 4

  



K K

BK x y

.

Do đó

   

18

2 .8 2 .4 0

8 4 24

5

4 8 24 6

4. 2 8. 4 0

5







   

 



 

 

  

 

   







 





K

K K

K

x

x y

y

.

Vậy

18 6

;

5 5

 



 

 

K .

Câu 40. Tập nghiệm

S

của phương trình

2 3 3

x x

  

là

Lời giải

2 3 3

x x

  

 

2

3 0

2 3 3

x

x x

 









  





2

3

2 3 6 9

x

x x x









   



2

3

8 12 0

x

x x









  



3

6

2

x

xx

x







  

















.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 14 Môn Toán – Lớp 10

(Thời gian làm bài 90 phút)

Không k

ể thời gian phát đề

PHẦN I: TRẮC NGHIỆM

Câu 1. Trong các câu sau, câu nào không phải là mệnh đề?

A. Buồn ngủ quá!

B. Hình thoi có hai đường chéo vuông góc với nhau.

C.

8

là số chính phương.

D. Băng Cốc là thủ đô của Mianma.

Câu 2. Lập mệnh đề phủ định của mệnh đề: “Số

6

chia hết cho 2 và

3

”.

A. Số

6

chia hết cho 2 hoặc

3

.

B. Số

6

không chia hết cho 2 và

3

.

C. Số

6

không chia hết cho 2 hoặc

3

.

D. Số

6

không chia hết cho 2 và chia hết cho

3

.

Câu 3. Cho tập hợp

 

| 2 5A x x  

. Khi đó tập hợp

A

được viết dưới dạng liệt kê là

A.

 

0A 

. B.

 

1;2A 

. C.

 

0;2A 

. D.

 

0;1;2A 

.

Câu 4. Cho tập hợp

 

 

2 2

/ 2 2 4 0,A x R x m x m m R       

. Tìm số giá trị nguyên của

m

thuộc

đoạn

 

2020;2021 để tập hợp A

có đúng 4 tập hợp con

A.

2018

. B.

2019

. C.

2020

. D.

2021

.

Câu 5. Cho tập hợp

    



4;4 7;9 1;7A    

. Khẳng định nào sau đây đúng?

A.





4;7 .A   B.

 

4;9 .A   C.

 

1;8 .A  D.





6;2 .A  

Câu 6. Hình vẽ sau đây (phần không bị gạch) minh họa cho một tập con của tập số thực. Hỏi tập đó là

tập nào?

A.





\ 3; .  B.





\ 3;3 . C.

 

\ ; 3 .  D.

 

\ 3;3 .

Câu 7. Cho

 





2

3; , ; 1 2;

4

m

A m B



 

      





 

. Tìm

m

để

A B  

A.

14

2

3

m 

. B.

2 6m 

. C.

2 6m 

. D.

14

2

3

m 

.

Câu 8. Tập xác định của hàm số

2

3 4

x

y

x x





 

là

A.

 

D \ 1 

. B.

 

D \ 1; 4 

. C.

 

D \ 4 

. D. D   .

Câu 9. Tìm tập xác định của hàm số

 

2

2 2

2

, 0

4 5

x x

y m

x m x mx m



 

   

.

A.

 

;m 

. B.





;m  . C.





;m . D.

 

;m

.

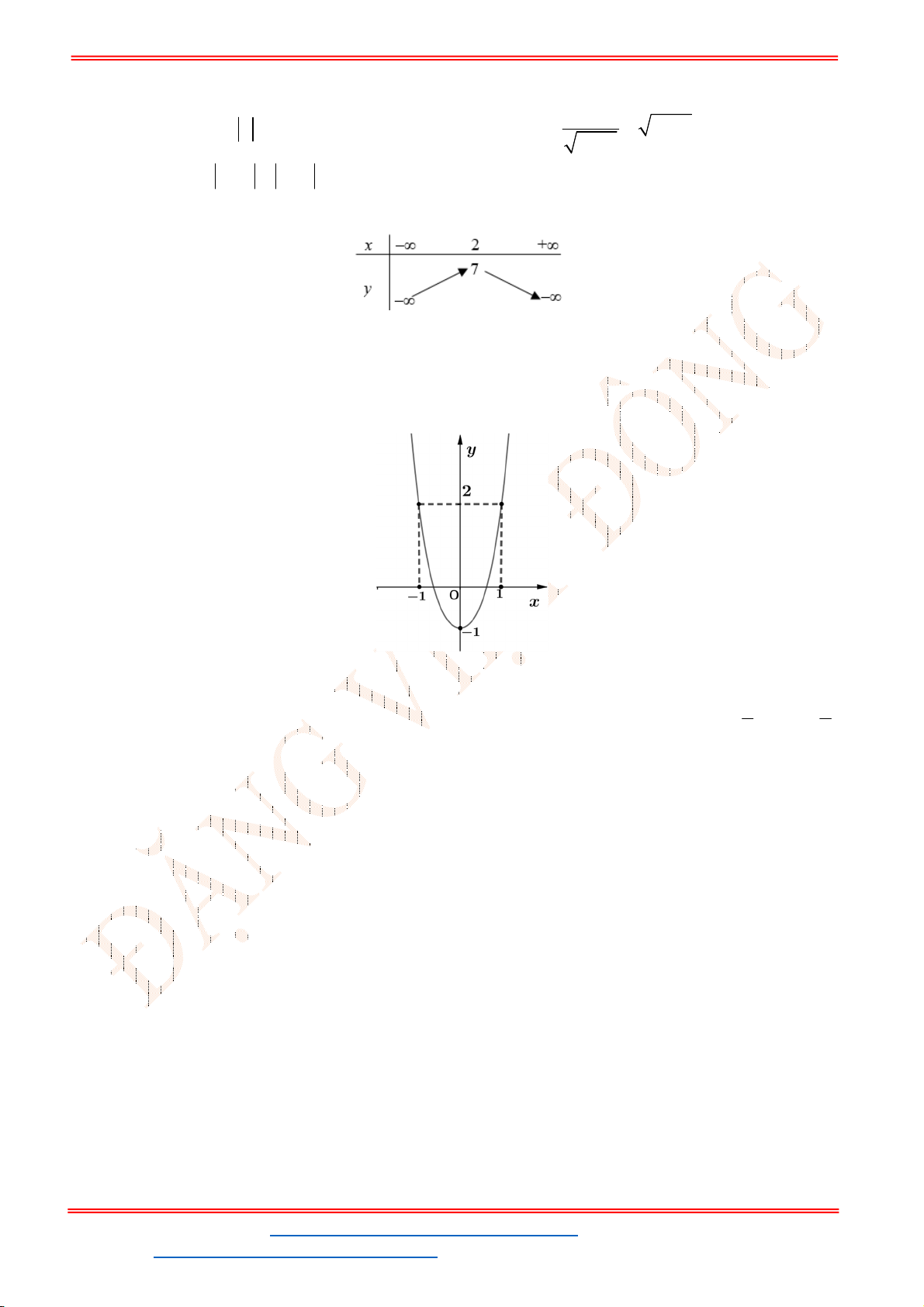
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 10. Trong các hàm sau đây hàm nào là hàm số chẵn?

A.

4

2y x x   . B.

2

x

y x

x



  



.

C.

1 1y x x    

. D.

3

3y x x 

.

Câu 11. Cho bảng biến thiên:

Bảng biến thiên trên là của hàm số nào?

A.

2

4 11  y x x

.

B.

2

4 3   y x x

.

C.

2

2 7  y x x . D.

2

4 7   y x x .

Câu 12. Đồ thị sau là của hàm số nào?

A.

2

3 1 y x . B.

2

3 1 y x . C.

2

1  y x x . D.

2

1  y x x .

Câu 13. Xác định hàm số

 

2

0y ax bx c a   

biết hàm số đạt giá trị lớn nhất bằng

1

4

tại

3

2

x  và

đồ thị hàm số cắt trục hoành tại 2 điểm

1 2

,x x thỏa mãn

3 3

1 2

9.x x 

A.

2

3 2.y x x    B.

2

3 2.y x x    C.

2

3 2.y x x   D.

2

3 2.y x x  

Câu 14. Tìm tọa độ giao điểm M của đồ thị

 

2

: 2P y x x  

và đường thẳng

 

: 3 2d y x 

biết rằng

0.

M

x 

A.

 

0;2 .M B.

 

0; 2 .M 

C.

 

4; 10 .M  D.

 

4;10 .M

Câu 15. Cho parabol

 

2

: 4 3P y x x  

và đường thẳng : 3d y mx  . Tìm giá trị của tham số

m

để

d

cắt

 

P

tại hai điểm phân biệt ,A B có hoành độ

1 2

,x x thỏa mãn

3 3

1 2

8x x  .

A.

2m 

. B.

4m 

. C. Không có

m

. D.

2m  

.

Câu 16. Phương trình đường thẳng đi qua một điểm

 

1; 1A 

và song song với trục Ox là

A. 1y  . B.

1x 

. C.

1x  

. D.

1y  

.

Câu 17. Với 3 điểm , ,A B C phân biệt. Trong các khẳng định sau đây, khẳng định nào sai?

A.

AB CB AC 

  

. B.

CD CM MD 

  

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

C.

B AC

AB CB

BA BC





  







 

. D.

2

AB BC



 

thì 2 điểm

, ,

A B C

thẳng hàng.

Câu 18. Cho ngũ giác lồi

ABCDE

, có bao nhiêu véc tơ khác véc tơ không mà có điểm đầu và điểm cuối

đều là các điểm đã cho.

A.

10

. B.

4

. C.

8

. D.

20

.

Câu 19. Cho bốn điểm

, , ,

A B C D

. Mệnh đề nào dưới đây sai?

A.

AB BC AC

 

  

. B.

AC CD DA

 

  

. C.

AB AD DB

 

  

. D.

BC BD DC

 

  

.

Câu 20. Cho hình bình hành

ABCD

tâm

O

. Mệnh đề nào dưới đây sai?

A.

0

OA OB OC OD

   

    

. B.

4

AB AC AD AO

  

   

.

C.

3

CA CB CD CA

  

   

. D.

0

AB CD

 

  

.

Câu 21 Trong hệ tọa độ

,

Oxy

cho





2; 3

A



,





4; 7

B

. Tìm tọa độ trung điểm

I

của đoạn thẳng

AB

A.





6; 4

. B.





2; 10

. C.





8; 21



. D.





3; 2

.

Câu 22 Trong mặt phẳng

Oxy

cho tam giác

A

BC

biết













1;3 2;0, ,

6;2

B CA    

. Tìm tọa độ

D

sao cho A

BCD

là hình bình hành.

A.





9; 1



. B.





3;5

. C.





5;3

. D.





1;9



.

Câu 23. Cho

(3, 4)

a

 



,

( 1,2)

b  



. Tìm tọa độ của

a b



 

A.

( 4,6)



. B.

(2, 2)



. C.

(4, 6)



. D.

( 3, 8)

 

Câu 24. Trong hệ trục tọa độ Oxy, có

,

i j

 

là hai véc tơ đơn vị. khi đó

2020 2021

u i j

 

  

có tọa độ là

A.

(2020, 2021)



. B.

(2020,2021)

. C.

( 2021,2020)



. D.

(2021, 2020)



.

Câu 25. Cho hình vuông

ABCD

có cạnh

a

. Tính .

AB AD

 

A.

0

. B.

a

. C.

2

a

. D.

2

a

.

Câu 26. Cho ba điểm

, ,

A B C

phân biệt. Tập hợp những điểm

M

thỏa mãn

. .

CM CB CACB



   

là

A.Đường tròn đường kính

AB

.

B.Đường thẳng đi qua

A

và vuông góc với

BC

.

C.Đường thẳng đi qua

B

và vuông góc với

AC

.

D.Đường thẳng đi qua

C

và vuông góc với

AB

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 27. Cho hàm số

2

y ax bx c  

 

P

có đồ thị như hình vẽ dưới đây. Trong các số , ,a b c có bao

nhiêu số dương?

A.1 . B. 2 . C.

3

. D.

0

.

Câu 28. Có bao nhiêu giá trị nguyên của

 

0;2021m

để hàm số

 

2y x m x m   

đồng biến trên 

.

A.

2019

. B.

2020

. C.

2021

. D.

2022

.

Câu 29. Tìm tất cả các giá trị của tham số

m

để hàm số

 

2

2 3

2 1

y x x m

m

   



đồng biến trên khoảng

 

0; 

.

A.

1

;

2

m

 





 

 

. B.

1

;

2

m

 

 





 

. C.

1

;

2

m

 



 

 

 

. D.

1

2

x 

.

Câu 30. Sức mạnh của động cơ (tính bằng đơn vị mã lực) sinh ra từ máy của một Canô ở tốc độ quay r

vòng/phút được tính bởi công thức

2

( ) 0,0000147 0,18 251P r r r    . Vậy sức mạnh lớn nhất

của động cơ đạt được bằng bao nhiêu?

A.

300000

49

. B.

145000

49

. C.

160453

49

. D.

14701

49

.

PHẦN II: TỰ LUẬN.

Câu 1. a) Giải phương trình:

  

2 10 50

1

x 2 x 3 2 x x 3

  

   

b) Giải phương trình:

2

2 6 2 3x x x   

c) Cho phương trình

2 2

2 2 2 0x mx m m    

. Tìm

m

để phương trình có hai nghiệm phân

biệt

1 2

,x x thỏa mãn hệ thức:

2

1 2 2

1 2

16 3x x x

x x

 



1

x .

Câu 2. Cho hàm số

2

( ): 2

m

P y x x m  

.

a/ Vẽ đồ thị hàm số khi

3m  

.

b/ Tìm các giá trị của

m

để đồ thị hàm số

( )

m

P

cắt đường thẳng

( ): 3 2d y x 

tại 2 điểm phân

biệt nằm về 2 phía của trục hoành .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 3 . Cho tam giác

ABC

. Gọi

M

là trung điểm của

AB

và

N

là một điểm trên cạnh

AC

sao cho

2

NA NC



. Gọi

K

là trung điểm của

MN

. Gọi

P

là điểm trên cạnh

BC

kéo dài sao cho

2 .

PB PC



 

a) Phân tích vec tơ

AK



theo

AB



và

AC



.

b) Chứng minh

, ,

K N P

thẳng hàng.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG HDG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 14 Môn Toán – Lớp 10

(Thời gian làm bài 90 phút)

Không k

ể thời gian phát đề

Câu 1. Trong các câu sau, câu nào không phải là mệnh đề?

A. Buồn ngủ quá!

B. Hình thoi có hai đường chéo vuông góc với nhau.

C.

8

là số chính phương.

D. Băng Cốc là thủ đô của Mianma.

Lời giải

Câu không phải là mệnh đề là “Buồn ngủ quá!”.

Câu 2. Lập mệnh đề phủ định của mệnh đề: “Số

6

chia hết cho

2

và

3

”.

A. Số

6

chia hết cho

2

hoặc

3

.

B. Số

6

không chia hết cho

2

và

3

.

C. Số

6

không chia hết cho

2

hoặc

3

.

D. Số

6

không chia hết cho

2

và chia hết cho

3

.

Lời giải

Phủ định của mệnh đề “Số

6

chia hết cho

2

và

3

” là “Số

6

không chia hết cho

2

hoặc

3

”.

Câu 3. Cho tập hợp





| 2 5

A x x

  



. Khi đó tập hợp

A

được viết dưới dạng liệt kê là

A.





0

A 

. B.





1;2

A 

. C.





0;2

A 

. D.





0;1;2

A 

.

Lời giải

Ta có

5

2 5

2

x x

  

,





0;1;2

x x  



. Chọn D.

Câu 4. Cho tập hợp









2 2

/ 2 2 4 0,

A x R x m x m m R

       

. Tìm số giá trị nguyên của

m

thuộc

đoạn





2020;2021

 để tập hợp

A

có đúng 4 tập hợp con

A.

2018

. B.

2019

. C.

2020

. D.

2021

.

Lời giải

Để tập hợp

A

có đúng 4 tập hợp con thì tập hợp

A

phải có đúng hai phần tử, tức là phương

trình





2 2

2 2 4 0

x m x m

    

có đúng hai nghiệm phân biệt

 





2

' 2 4 0 4 0 0

m m m m

          

Ta có









2020;2021 , 1;2;3;...;2021

m m m    



. Do đó có 2021 giá trị

m

thỏa. Chọn D.

Câu 5. Cho tập hợp













4;4 7;9 1;7

A    

. Khẳng định nào sau đây đúng?

A.





4;7 .

A   B.





4;9 .

A   C.





1;8 .

A  D.





6;2 .

A  

Lời giải

Chọn B

Câu 6. Hình vẽ sau đây (phần không bị gạch) minh họa cho một tập con của tập số thực. Hỏi tập đó là

tập nào?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.





\ 3; .  B.





\ 3;3 . C.

 

\ ; 3 .  D.

 

\ 3;3 .

Lời giải

Chọn B

Câu 7. Cho

 





2

3; , ; 1 2;

4

m

A m B



 

      





 

. Tìm

m

để

A B  

A.

14

2

3

m 

. B.

2 6m 

. C.

2 6m 

. D.

14

2

3

m 

.

Lời giải

14

2

3

4

14

3 1 2 2

3

2 6

2

4

m

A B m m m

m m







 





           

 

 

 

 





.

Câu 8. Tập xác định của hàm số

2

3 4

x

y

x x





 

là

A.

 

D \ 1 

. B.

 

D \ 1; 4 

. C.

 

D \ 4 

. D. D   .

Lời giải

Hàm số xác định khi

2

1

3 4 0

4

x

x x

x





   



 



Tập xác định của hàm số là

 

D \ 1; 4 

.

Câu 9. Tìm tập xác định của hàm số

 

2

2 2

2

, 0

4 5

x x

y m

x m x mx m



 

   

.

A.

 

;m 

. B.





;m  . C.





;m . D.

 

;m

.

Lời giải

Điều kiện:

 

2 2

0

4 5 0 *

4 5 0

x m

x mx m

x m x mx m



 



  





    



.

Do

 

2

2 2 2

4 5 2 0, 0x mx m x m m m       

 

* 0x m x m    

.

Tập xác định:





;D m  .

Câu 10. Trong các hàm sau đây hàm nào là hàm số chẵn?

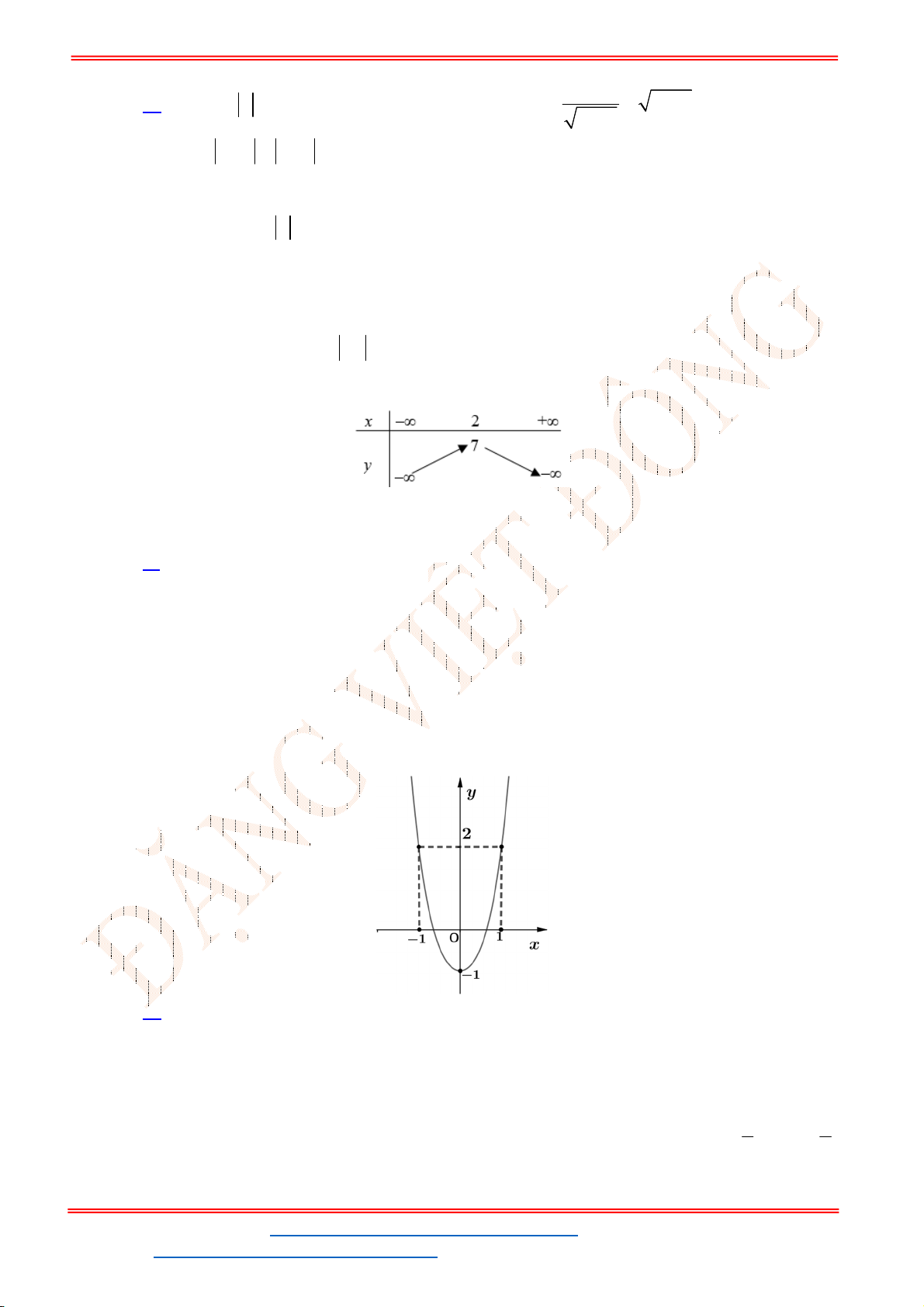
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

4

2y x x   . B.

2

x

y x

x



  



.

C.

1 1y x x    

. D.

3

3y x x 

.

Lời giải

Hàm số

4

2y x x   là hàm chẵn vì:

 Tập xác định: D   .



x D x D    

.



     

4

2f x x x f x      

.

Câu 11. Cho bảng biến thiên:

Bảng biến thiên trên là của hàm số nào?

A.

2

4 11  y x x

.

B.

2

4 3y x x   

.

C.

2

2 7  y x x .

D.

2

4 7   y x x .

Lời giải

Ta thấy dạng của bảng biến thiên



hệ số

0 a

loại đáp án A, C.

Tọa độ đỉnh

 

2;7 I

chọn đáp án B.

Câu 12. Đồ thị sau là của hàm số nào?

A.

2

3 1 y x . B.

2

3 1 y x . C.

2

1  y x x . D.

2

1  y x x .

Lời giải

Ta thấy tọa độ đỉnh

 

0; 1 I

loại đáp án B, C, D.

Câu 13. Xác định hàm số

 

2

0y ax bx c a   

biết hàm số đạt giá trị lớn nhất bằng

1

4

tại

3

2

x  và

đồ thị hàm số cắt trục hoành tại 2 điểm

1 2

,x x thỏa mãn

3 3

1 2

9.x x 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

2

3 2.

y x x

   

B.

2

3 2.

y x x

   

C.

2

3 2.

y x x

  

D.

2

3 2.

y x x

  

Lời giải

Hàm số





2

0

y ax bx c a

   

đạt giá trị lớn nhất bằng

1

4

tại

3

2

x



nên ta có

3

, 0

2 2

9 3 1

4 2 4

b

a

a b c





  







  





Theo giả thiết:

3 3

1 2

9

x x

 

   

3

Viet

1 2 1 2 1 2

3 9 3 9

b b c

x x x x x x

a a a

    

  

  

         

  

  

  

  

    

.

Từ đó ta có hệ:

 

2

3

2 2

1

9 3 1 9 3 1

3 : 3 2.

4 2 4 4 2 4

2

3 9

b

b a

a

a b c a b c b P y x x

c

b b c

a

a a a





 





 





 



 



             



 

 

 



 

 







    





  

  



   

  

  



  

  





    





Câu 14. Tìm tọa độ giao điểm M của đồ thị





2

: 2

P y x x

  

và đường thẳng





: 3 2

d y x

 

biết rằng

0.

M

x



A.





0;2 .

M B.





0; 2 .

M



C.





4; 10 .

M  D.





4;10 .

M

Lời giải

Phương trình hoành độ giao điểm

2 2

0

2 3 2 4 0

4

x

x x x x x

x





       







Theo bài ra

0

M

x



nên ta có





4;10 .

M

Câu 15. Cho parabol





2

: 4 3

P y x x

  

và đường thẳng

: 3

d y mx

 

. Tìm giá trị của tham số

m

để

d

cắt





P

tại hai điểm phân biệt

,

A B

có hoành độ

1 2

,

x x

thỏa mãn

3 3

1 2

8

x x

 

.

A.

2

m



. B.

4

m



. C. Không có

m

. D.

2

m

 

.

Lời giải

Phương trình hoành độ giao điểm của





P

và

d

là

2

4 3 3

x x mx

   

 

0

4 0

4

x

x x m

x m





    



 



.

Để

d

cắt





P

tại hai điểm phân biệt

,

A B

khi và chỉ khi

4 0 4

m m

    

.

Khi đó, ta có

 

3

3 3

1 2

8 0 4 8 4 2 2

x x m m m

           

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 16. Phương trình đường thẳng đi qua một điểm





1; 1

A



và song song với trục Ox là

A.

1

y



. B.

1

x



. C.

1

x

 

. D.

1

y

 

.

Lời giải

Ta có





/ / : 0

d Ox d y b b

  

mà d qua





1; 1 1 : y 1

A b d

      

.

Câu 17. Với 3 điểm

, ,

A B C

phân biệt. Trong các khẳng định sau đây, khẳng định nào sai?

A.

AB CB AC

 

  

. B.

CD CM MD

 

  

.

C.

B AC

AB CB

BA BC





  







 

. D.

2

AB BC



 

thì 2 điểm

, ,

A B C

thẳng hàng.

Lời giải

AB CB AC CB AC AB CB BC

      

       

( Đẳng thức sai với

B C



)

Câu 18. Cho ngũ giác lồi

ABCDE

, có bao nhiêu véc tơ khác véc tơ không mà có điểm đầu và điểm cuối

đều là các điểm đã cho.

A.

10

. B.

4

. C.

8

. D.

20

.

Lời giải

Cứ 1 cặp điểm gồm 2 điểm phân biệt tạo thành 2 véc tơ. Nên số véc tơ tạo thành theo yêu cầu

bài toán là :

2.10 20



Câu 19. Cho bốn điểm

, , ,

A B C D

. Mệnh đề nào dưới đây sai?

A.

AB BC AC

 

  

. B.

AC CD DA

 

  

. C.

AB AD DB

 

  

. D.

BC BD DC

 

  

.

Lời giải

Ta có

AB BC AC

 

  

.

AC CD AD

 

  

.

AB AD DB

 

  

.

BC BD DC

 

  

.

Vậy mệnh đề sai là

AC CD DA

 

  

.

Câu 20. Cho hình bình hành

ABCD

tâm

O

. Mệnh đề nào dưới đây sai?

A.

0

OA OB OC OD

   

    

.

B.

4

AB AC AD AO

  

   

.

C.

3

CA CB CD CA

  

   

.

D.

0

AB CD

 

  

.

Lời giải

Ta có

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay









0

OA OB OC OD OA OC OB OD

       

        

.





2 4

AB AC AD AB AD AC AC AC AC AO

        

         

.





2

CA CB CD CA CB CD CA CA CA

       

        

.

0

AB CD

 

  

.

Vậy mệnh đề sai là

3

CA CB CD CA

  

   

.

Câu 21. Trong hệ tọa độ

,

Oxy

cho





2; 3

A



,





4; 7

B

. Tìm tọa độ trung điểm

I

của đoạn thẳng

AB

A.





6; 4

. B.





2; 10

. C.





8; 21



. D.





3; 2

.

Lời giải

Ta có

 

2 4 3 7

; 3; 2

2 2

I

  

 

 

 

 

.

Câu 22. Trong mặt phẳng

Oxy

cho tam giác

A

BC

biết













1;3 2;0, ,

6;2

B CA    

. Tìm tọa độ

D

sao cho A

BCD

là hình bình hành.

A.





9; 1



. B.





3;5

. C.





5;3

. D.





1;9



.

Lời giải

ABCD

là hình bình hành khi

AB DC



 

.

Ta có













3; 3 , 6 ;2 , ;

AB DC x y D x y

    

 

.

Nên

 

6 3 3

3;5

2 3 5

x x

AB DC D

y y

  

 

   

 

   

 

 

.

Câu 23. Cho

(3, 4)

a

 



,

( 1,2)

b  



. Tìm tọa độ của

a b



 

A.

( 4,6)



. B.

(2, 2)



. C.

(4, 6)



. D.

( 3, 8)

 

Lời giải

(3 1, 4 2) (2, 2)

a b

      

 

Câu 24. Trong hệ trục tọa độ Oxy, có

,

i j

 

là hai véc tơ đơn vị. khi đó

2020 2021

u i j

 

  

có tọa độ là

A.

(2020, 2021)



. B.

(2020,2021)

. C.

( 2021,2020)



. D.

(2021, 2020)



.

Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

2020 (2020,0)i 



;

2021 (0, 2021)j  



(2020, 2021)u  



Câu 25. Cho hình vuông

ABCD

có cạnh

a

. Tính .AB AD

 

A.

0

. B.

a

. C.

2

a

. D.

2

a

.

Lời giải

Vì . 0AB AD AB AD  

   

.

Câu 26. Cho ba điểm , ,A B C phân biệt. Tập hợp những điểm M thỏa mãn

. .CM CB CACB

   

là

A.Đường tròn đường kính AB .

B.Đường thẳng đi qua A và vuông góc với

BC

.

C.Đường thẳng đi qua B và vuông góc với

AC

.

D.Đường thẳng đi qua

C

và vuông góc với AB .

Lời giải

Có:

. . . . 0CM CB CACB CM CB CACB   

       

 

. 0 . 0CM CA CB AM CB    

    

.

Tập hợp điểm M là đường thẳng đi qua A và vuông góc với

BC

.

Câu 27. Cho hàm số

2

y ax bx c  

 

P

có đồ thị như hình vẽ dưới đây. Trong các số , ,a b c có bao

nhiêu số dương?

A.1 . B. 2 . C.

3

. D.

0

.

Lời giải

Nhận xét: 1. Đồ thị hàm số có hướng quay lên

0a 

2. Đồ thị hàm số có trục đối xứng

nằm ở bên trái trục Oy nên

0 0

2

b

x b

a

    

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

3. Đồ thị hàm số cắt trục Oy tại điểm có tung độ âm

0c 

Câu 28. Có bao nhiêu giá trị nguyên của

 

0;2021m

để hàm số

 

2y x m x m   

đồng biến trên  .

A.

2019

. B.

2020

. C.

2021

. D.

2022

.

Lời giải

Biến đổi hàm số

   

2

2 2y x m x m m x m      

.

Yêu cầu của bài toán xảy ra khi

2 0 2

3 2021

0 2021 0 2021

m m

m

m m

m

m m

  

 

 



 

     

  





 

 

 



 

Vậy có

2021 3 1 2019  

giá trị

m

thỏa mãn.

Câu 29. Tìm tất cả các giá trị của tham số

m

để hàm số

 

2

2 3

2 1

y x x m

m

   



đồng biến trên

khoảng

 

0; 

.

A.

1

;

2

m

 





 

 

. B.

1

;

2

m

 

 





 

. C.

1

;

2

m

 



 

 

 

. D.

1

2

x 

.

Lời giải

Hàm số

 

2

2 3

2 1

y x x m

m

   



đồng biến trên khoảng

 

2 1;m   

và nghịch biến trên

khoảng

 

;2 1m 

.

Do đó ta phải có

1

2 1 0 .

2

m m   

Vậy

1

;

2

m

 

 





 

là các giá trị cần tìm.

Câu 30. Sức mạnh của động cơ (tính bằng đơn vị mã lực) sinh ra từ máy của một Canô ở tốc độ quay r

vòng/phút được tính bởi công thức

2

( ) 0,0000147 0,18 251P r r r    . Vậy sức mạnh lớn nhất

của động cơ đạt được bằng bao nhiêu?

A.

300000

49

. B.

145000

49

. C.

160453

49

. D.

14701

49

.

Lời giải

Xét hàm số

2

( ) 0,0000147 0,18 251.P r r r   

Ta có

14701

Max

4 49

P

a



 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Đạt tại

300000

.

2 49

b

r

a



 

TỰ LUẬN.

Câu 1. a) Giải phương trình:

  

2 10 50

1

x 2 x 3 2 x x 3

  

   

b) Giải phương trình:

2

2 6 2 3

x x x

   

c) Cho phương trình

2 2

2 2 2 0

x mx m m

    

. Tìm

m

để phương trình có hai nghiệm phân

biệt

1 2

,

x x

thỏa mãn hệ thức:

2

1 2 2

1 2

16 3

x x x

x x

 



1

x



.

Lời giải

a) Ta có

  





   

2

x 3;2

2 10 50

1

x 2 x 3 2 x x 3

x x 6 2 x 3 10 x 2 50 0

  









  

   

      













 

2

x 3;2

x 14

x 3;14

x 11x 42 0

 

 

   

 

 

  





.

b)

2

2 2

2 3 0

2 6 2 3

2 6 4 12 9

x

x x x

x x x x

 



    



    



2

3

2

5

3;

3 14 15 0

3

x

x x















 



  

 





 

 

  









.

KL: Phương trình đã cho có tập nghiệm là

5

3;

3

S

 



 

 

.

c)

' 2 2

m

  

.

Phương trình có hai nghiệm phân biệt

' 0 2 2 0

m

     





1 *

m  

.

Theo vi ét ta có:

1 2

2

1 2

2

2 2

x x m

x x m m

 







  





.

2

1 2 2

1

1 2

16 3x x x

x

x x

 





2 2

1 2 2 1 1 2

16 3

x x x x x x

     với

1 2

2 0

x x m

  

 

2

1 2 1 2

4 16 0

x x x x

    





2 2

4 4 2 2 16 0

m m m

     

8 8 0

m

  

1

m

 

(thỏa

mãn *).

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 2. Cho hàm số

2

( ): 2

m

P y x x m

  

.

a/ Vẽ đồ thị hàm số khi

3

m

 

.

b/ Tìm các giá trị của

m

để đồ thị hàm số

( )

m

P

cắt đường thẳng

( ): 3 2

d y x

 

tại 2 điểm phân

biệt nằm về 2 phía của trục hoành .

Lời giải

a/ Khi

3

m

 

hàm số trở thành

2

2 3

y x x

  

.

Tọa độ đỉnh





1; 4

I



.

Trục đối xứng là đường thẳng

1

x



.

Đồ thị hàm số cắt trục

Ox

tại các điểm









1;0 ; 3;0



và cắt trục

Oy

tại điểm





0; 3



.

b/ Phương trình hoành độ giao điểm của

( )

m

P

và

( )

d

:

2

2 3 2

x x m x

   



2

5 2 0

x x m

   

(*).

+) Để

( )

m

P

cắt

( )

d

tại 2 điểm phân biệt thì phương trình (*) có 2 nghiệm phân biệt .

Do đó

0

 



25 4( 2) 0

m

  



17

4

m



(1).

+) Gọi





1 1

;

A x y

và





2 2

;

B x y

là giao điểm của

( )

m

P

và

( )

d

.

Ta có

1 1

3 2;

y x

 

2 2

3 2

y x

 

với

1 2

;

x x

là nghiệm của phương trình (*).

Hai điểm

;

A B

nằm về 2 phía của trục hoành

1 2

. 0

y y

 









1 2

3 2 3 2 0

x x

   





1 2 1 2

9 . 6 4 0

x x x x

    





9 2 6.5 4 0

m

    

8

9

m

 

(2).

Từ (1) và (2) suy ra giá trị

m

cần tìm là

8

9

m



.

Câu 3 . Cho tam giác

ABC

. Gọi

M

là trung điểm của

AB

và

N

là một điểm trên cạnh

AC

sao cho

2

NA NC



. Gọi

K

là trung điểm của

MN

. Gọi

P

là điểm trên cạnh

BC

kéo dài sao cho

2 .

PB PC



 

a) Phân tích vec tơ

AK



theo

AB



và

AC



.

b) Chứng minh

, ,

K N P

thẳng hàng.

Lời giải

4

2

4

10 5 5 10

I

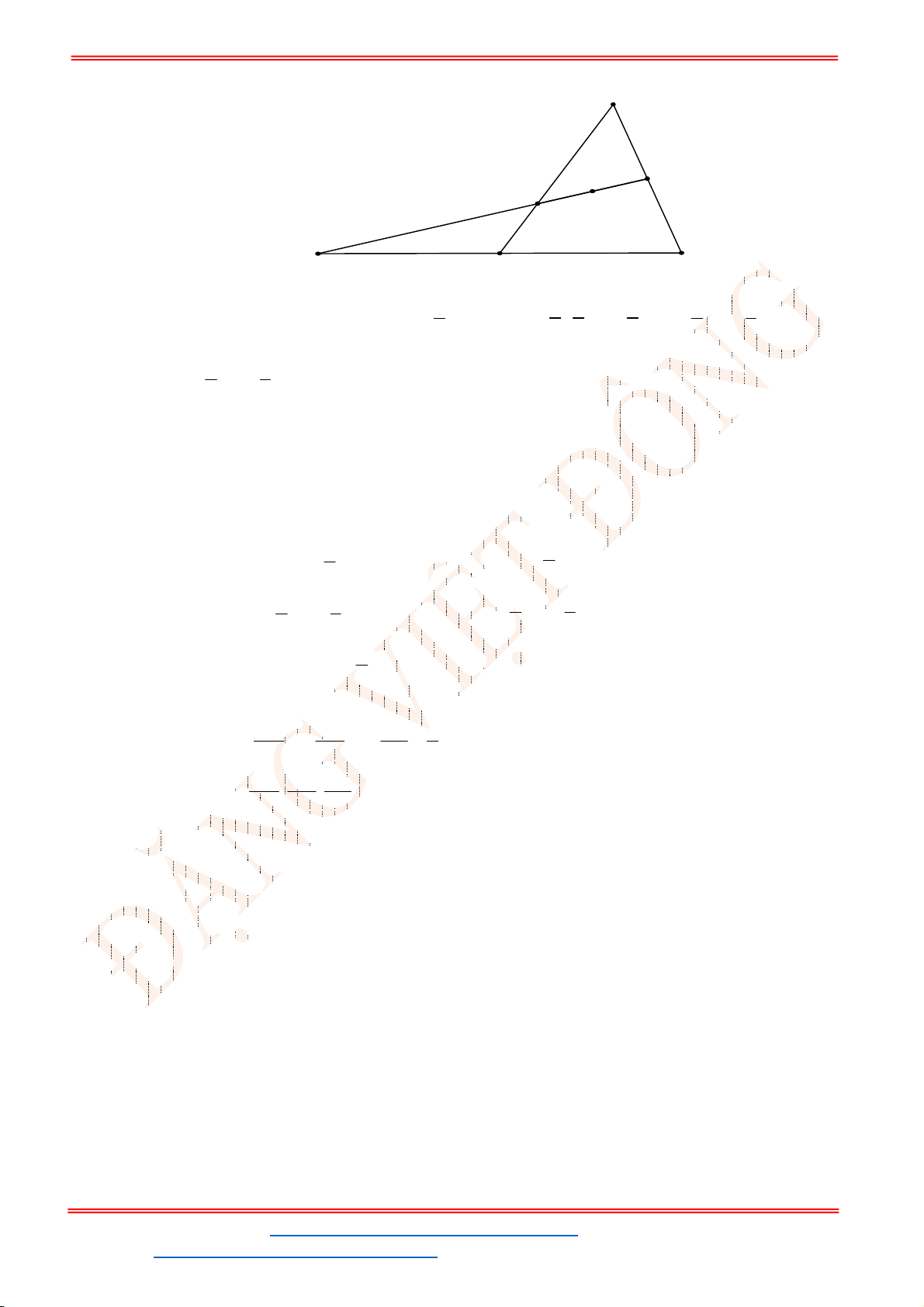
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

a) Vì

K

là trung điểm của

MN

nên

AK



=





1

2

AM AN



 

=

1 1 2

2 2 3

AB AC

 



 

 

 

=

1 1

4 3

AB AC



 

Vậy

1 1

.

4 3

AK AB AC

 

  

b) Cách 1:

Từ gt

2

PB PC



 







2

AB AP AC AP

  

   



2 .

AP AB AC

  

  

Ta có

PN AN AP

 

  





2

3

AC AB AC

   

  

4

3

AB AC

 

 

. (1)

PK AK AP

 

  





1 1

2

4 3

AB AC AB AC

    

   

5 5

4 3

AB AC

 

 

. (2)

Từ (1) và (2) ta được:

4

.

5

PN PK



 

(đpcm)

Cách 2:

Từ gt, ta được

1

1; 2;

2

MB NA PC

MA NC PB

  

Do đó:

. . 1

MB NA PC

MA NC PB



theo Menelauyt ba điểm

, ,

P M N

thẳng hàng mà

K

là trung điểm

của

MN

nên ba điểm

, ,

P K N

thẳng hàng. (đpcm)

K

N

M

C

P

B

A

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

ĐẶNG VIỆT ĐÔNG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 15 Môn Toán – Lớp 10

(Th

ời gian l

àm bài 90 phút)

Không k

ể thời gian phát đề

PHẦN I: TRẮC NGHIỆM

Câu 1. Tìm mệnh đề sai.

A.

2

" , 2 3 0"

x x x

    



. B.

2

" , "

x x x

  



.

C.

2

" , 5 6 0"

x x x

    



. D.

1

" , "

x x

x

  

.

Câu 2. Cho hai tập hợp khác rỗng





1;4

A m 

và





2;2 2 , .

B m m

   



Có bao nhiêu giá trị

nguyên dương của

m

để

A B

  

?

A.

5

. B.

6

. C.

4

. D. 3.

Câu 3. Xét tính chẵn – lẻ của hàm số

4 2

3

y x x

  

.

A. Hàm số vừa chẵn, vừa lẻ. B. Hàm số không chẵn, không lẻ.

C. Hàm số lẻ. D. Hàm số chẵn.

Câu 4. Tập xác định của hàm số

1

3

y x

x

  



là

A.





\ 3

D 



. B.





3;D

 

. C.





3;D

 

. D.





;3 .

D  

Câu 5. Xác định đường thẳng

y ax b

 

, biết hệ số góc bằng

2



và đường thẳng qua





1; 3

A

 

.

A.

2 1

y x

  

. B.

2 7

y x

 

. C.

2 2

y x

 

. D.

2 5

y x

  

.

Câu 6. Cho hàm số





2

2 1

y m x m

   

. Có bao nhiêu giá trị của tham số

m

để đồ thị hàm số đã cho

song song với đường thẳng

: 2 3

d y x

 

A.

0

. B.

1

. C.

2

. D.

3

.

Câu 7. Parabol

2

3 2 1

y x x

  

có đỉnh là

A.

1 2

;

3 3

I

 



 

 

. B.

1 2

;

3 3

I

 



 

 

. C.

1 2

;

3 3

I

 

 

 

. D.

1 2

;

3 3

I

 

 

 

 

Câu 8. Xét tính đồng biến, nghịch biến của hàm số





2

4 5

f x x x

  

?

A. Hàm số nghịch biến trên





;2



, đồng biến trên





2;

 

.

B. Hàm số nghịch biến trên các khoảng





;2



và





2;

 

.

C. Hàm số đồng biến trên





;2



, nghịch biến trên





2;

 

.

D. Hàm số đồng biến trên các khoảng





;2



và





2;

 

.

Câu 9. Biết đồ thị





2

:

P y ax bx c

  

cắt trục tung tại điểm bằng có tung độ bằng 7, đi qua điểm





3;1

A

và có tung độ đỉnh bằng 9. Xác định parabol





P

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

2

( ): 2 8 7

P y x x

   

. B.

2

( ): 2 4 7

P y x x

   

.

C.

2

( ): 4 2 7

P y x x

   

. D.

2

( ): 4 7

P y x x

   

.

Câu 10. Tập xác định của phương trình

2

1

4 2020 0

x

   

là:

A.









; 2 2;

   

. B.





2;

  

.

C.





0;

 

. D.





2;



.

Câu 11. Nghiệm của phương trình

2

5 6 0

x x

  

là:

A.

2

3

x

 









. B.

2

3

x







 



. C.

2

3

x











. D.

2

3

x

 





 



..

Câu 12. Hai phương trình được gọi là tương đương khi:

A. Có cùng tập hợp nghiệm. B. Cùng là phương trình bậc hai.

C. Có cùng tập xác định. D. Có cùng bậc.

Câu 13. Phương trình nào dưới đây có một nghiệm là

1

x

 

?

A.

1 0

x

 

. B.

2

1

0

1

x







.

C.





1 1 0

x x

  

. D.

3

2 1 1 0

x x

   

.

Câu 14. Tập xác định của phương trình

2

1 5 2

2

2 1

x

x x







 

là

A.

 

5

; \ 1;2

2

D

 

 





 

. B.

 

5

1; \ 2

2

D

 







 

.

C.





(1; )\ 2

D  

. D.

5

;

2

D

 

 





 

.

Câu 15. Phương trình nào sau đây tương đương với phương trình

2

4 0

x

 

?

A.









2

2 2 1 0

x x x

    

. B.









2

2 3 2 0

x x x

   

.

C.

2

3 1

x

 

. D.

2

4 4 0

x x

  

.

Câu 16. Tập nghiệm

S

của phương trình

1 0

x

 

là

A.





S

 

. B.





0

S 

. C.





1;S

   

. D.





1

S

 

.

Câu 17 . Số nghiệm của phương trình

4 1 1 2

x x x

     là

A. 0. B. 1. C. 2. D. 3.

Câu 18. Gọi

S

là tổng các nghiệm của phương trình

2 2

3 21 18 2 7 7 2

x x x x

     

Khi đó

S

bằng:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

2

3

S



 . B.

1

S

 

. C.

5

3

S



 . D.

7

S

 

.

Câu 19. Có bao nhiêu giá trị nguyên của tham số

m

thuộc đoạn





10;10



để phương trình









2

9 3 3

m x m m

  

có nghiệm duy nhất.

A.

3

. B.

19

. C.

20

. D.

18

.

Câu 20. Nghiệm của hệ phương trình

2 2 0

1 0

x y

  





  



là

A.





1;0

. B.





0; 2

. C.





1;0

. D.





1;0

.

Câu 21. Nghiệm của hệ phương trình

2 3 5 0

2 7 3 0

2 5 6 1 0

x y z

   





   





   



là

A.





11;9;4

. B.





9;11;4

. C.





9; 11; 4

  

. D.





11; 9; 4

  

.

Câu 22. Cho hệ phương trình

2 2

48

6

a b ab

a b



 



 



. Biết hệ phương trình có nghiệm là

( ; ) ( ; )

a b u v



. Tính

A u v

 

.

A.

5

. B.

4

. C.

3

. D.

2

.

Câu 23. Số các giá trị nguyên dương của tham số

m

với

9

m



, để hệ phương trình

2 2 2

2

1

1x y m

x y m m

  





  





có nghiệm

A.

0

. B.

4

. C.

1

. D.

2

.

Câu 24. Cho tam giác

OAB

. Gọi

,

M

N

lần lượt là trung điểm

,

OA

OB

. Tìm mệnh đề đúng?

A.

MN OA OB

 

  

. B.

1 1

2 2

MN OA OB

 

  

.

C.

1 1

2 2

MN OA OB

 

  

. D.

1 1

2 2

MN OB OA

 

  

.

Câu 25. Cho

G

là trọng tâm của tam giác

ABC

và

M

là trung điểm của đoạn

BC

. Khẳng định nào sau

đây là khẳng định sai?

A.

0

BM MC

 

  

. B.

2

AB AC AM

 

  

.

C.

0

GA GB GC

  

   

. D.

2

GB GC GM

 

  

.

Câu 26. Trong hệ tọa độ Oxy, cho





1;3 ,

A





4;0 ,

B

(2; 5)

C



. Tìm tọa độ điểm M thỏa mãn hệ thức

3 0

MA MB MC

  

   

?

A.





1;18

M

. B.





1;18

M 

. C.





1; 18

M 

. D.





18;1

M 

.

Câu 27. Cho





1;2

A

,





2;6

B 

. Tìm tọa độ điểm

M

thuộc trục

Oy

sao cho ba điểm

A

,

B

,

M

thẳng

hàng?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.





0;3

M

. B.

10

0;

3

M

 

 

 

. C.

5

;0

2

M

 

 

 

. D.

5

0;

2

M

 

 

 

.

Câu 28. Cho



là góc tù. Khẳng định nào sau đây là đúng?

A.

sin 0





. B.

cos 0





. C.

tan 0





. D.

cot 0





.

Câu 29. Cho biết

1

sin cos

2

 

 

thì

3 3

sin cos

 



bằng

A.

3 2

8

. B.

2

8

. C.

5 2

8

. D.

5

8

.

Câu 30. Gọi

G

là trọng tâm tam giác đều

ABC

có cạnh bằng

a

. Mệnh đề nào sau đây sai?

A.

2

1

.

2

AB AC a



 

. B.

2

1

.

2

AC CB a

 

 

. C.

2

.

6

a

GAGB 

 

. D.

2

1

.

2

AB AG a



 

.

Câu 31. Cho tam giác

ABC

vuông tại

A

có

3; 4

AB AC

 

. Trên đoạn thẳng

BC

lấy điểm

M

sao cho

2

MB MC



. Tính tích vô hướng

.

AM BC

 

.

A.

41

3

. B.

23

3

. C.

8

. D.

23



.

Câu 32. Cho









2;3 , 4; 1

u v

   

 

. Tính

2 .

u v

 

.

A.

11



. B.

11

2



. C.

22



. D.

22

.

Câu 33. Trong mặt phẳng tọa độ

Oxy

, cho điểm









1; 2 ; 3; 5

A B

 

. Tìm tọa độ điểm

C

trên trục

Ox

sao cho tam giác

ABC

vuông tại

A

.

A.





4;0



. B.





2;0



. C.





2;0

. D.





4;0

.

Câu 34. Trên mặt phẳng

Oxy

, cho tam giác

ABC

có





1;2

A 

,





5;4

B 

và





2;4

C

. Tìm tọa độ chân

đường cao

H

dựng từ

C

của

ABC



.

A.

6 3

;

5 5

H

 

 

 

. B.

6 3

;

5 5

H

 

 

 

 

. C.

3 6

;

5 5

H

 

 

 

 

. D.

3 6

;

5 5

H

 

 

 

.

Câu 35. Cho tam giác

ABC

có

2 3, 2

BC AC AB

 

và độ dài đường cao

2

AH



. Tính độ dài cạnh

AB

.

A.

2

AB



. B.

2 3

3

AB  .

C.

2

AB



hoặc

2 3

3

AB  . D.

2

AB



hoặc

2 21

3

AB  .

PHẦN II: TỰ LUẬN

Câu 36: Cho hàm số

2

2 4 3

y x x

   

có đồ thị là parabol





P

. Lập bảng biến thiên của hàm số đã

cho và vẽ parabol





P

.

Câu 37. Cho tứ giác

ABCD

. Gọi

M

,

N

,

P

,

Q

lần lượt là trung điểm của

AB

,

BC

,

CD

,

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

DA

. Gọi

O

là giao điểm của

MP

và

NQ

,

G

là trọng tâm của tam giác

BCD

. Chứng minh

rằng ba điểm

A

,

O

,

G

thẳng hàng.

Câu 38. Giải phương trình sau:

2

16 4

1 4

1

x

x x

x



  



.

Câu 39. Cho tam giác

ABC

. Chứng minh rằng:

3

cos2 cos 2 cos 2

2

A B C

   

.

ĐẶNG VIỆT ĐÔNG HDG ĐỀ ÔN TẬP KIỂM TRA HỌC KỲ I

Đề 15 Môn Toán – Lớp 10

(Th

ời gian l

àm bài 90 phút)

Không kể thời gian phát đề

PHẦN I: TRẮC NGHIỆM

Câu 1. Tìm mệnh đề sai.

A.

2

" , 2 3 0"

x x x

    



. B.

2

" , "

x x x

  



.

C.

2

" , 5 6 0"

x x x

    



. D.

1

" , "

x x

x

  

.

Lời giải

Chọn B

Chọn

2

1

2

x x x

  

. Vậy mệnh đề

2

" , "

x x x

  



sai.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 2. Cho hai tập hợp khác rỗng





1;4

A m 

và





2;2 2 , .

B m m

   



Có bao nhiêu giá trị

nguyên dương của

m

để

A B

  

?

A.

5

. B.

6

. C.

4

. D. 3.

Lời giải

Chọn C

Ta có

,

A B

là hai tập khác rỗng nên



1 4 5

2 5

2 2 2 2

m m

m

m m

  

    

    

(*).

Ta có

1 2 2 3

A B m m m

         

.

Đối chiếu với điều kiện (*), ta được

2 5

m

  

. Do

m







nên





1;2;3;4

m

.

Vậy có 4 giá trị nguyên dương của

m

thỏa mãn yêu cầu.

Câu 3. Xét tính chẵn – lẻ của hàm số

4 2

3

y x x

  

.

A. Hàm số vừa chẵn, vừa lẻ. B. Hàm số không chẵn, không lẻ.

C. Hàm số lẻ. D. Hàm số chẵn.

Lời giải

Chọn D

Đặt





4 2

3

f x x x

  

. Tập xác định

D





.

Với mọi

x D



, ta có

x D

 

và

     

4 2

3

f x x x

     

4 2

3

x x

  





f x



Vậy hàm số đã cho là hàm số chẵn.

Câu 4. Tập xác định của hàm số

1

3

y x

x

  



là

A.





\ 3

D 



. B.





3;D

 

. C.





3;D

 

. D.





;3 .

D  

Lời giải

Chọn C

Hàm số xác định khi

3 0 3

3

3 0 3

x x

x

x x

  

 

  

 

  

 

.

Suy ra tập xác định





3;D

 

.

Câu 5. Xác định đường thẳng

y ax b

 

, biết hệ số góc bằng

2



và đường thẳng qua





1; 3

A

 

.

A.

2 1

y x

  

. B.

2 7

y x

 

. C.

2 2

y x

 

. D.

2 5

y x

  

.

Lời giải

Chọn D

Đường thẳng

y ax b

 

có hệ số góc bằng

2



suy ra

2

a

 

.

Đường thẳng đi qua





1; 3

A

 

nên ta có:









3 2 . 1 5

b b

       

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Vậy đường thẳng cần tìm là:

2 5

y x

  

.

Câu 6. Cho hàm số





2

2 1

y m x m

   

. Có bao nhiêu giá trị của tham số

m

để đồ thị hàm số đã cho

song song với đường thẳng

: 2 3

d y x

 

A.

0

. B.

1

. C.

2

. D.

3

.

Lời giải

Chọn B

Đồ thị hàm số





2

2 1

y m x m

   

song song với đường thẳng

: 2 3

d y x

 

2 2

2 2 4

1 3 2

m m

 

  

 

 

    

 

2

m

 







  

 







 



.

Vậy có một giá trị của

m

để đồ thị ham số





2

2 1

y m x m

   

song song với đường thẳng

: 2 3

d y x

 

.

Câu 7. Parabol

2

3 2 1

y x x

  

có đỉnh là

A.

1 2

;

3 3

I

 



 

 

. B.

1 2

;

3 3

I

 



 

 

. C.

1 2

;

3 3

I

 

 

 

. D.

1 2

;

3 3

I

 

 

 

 

Lời giải

Chọn C

Đỉnh parabol

;

2 4

b

I

a a



 

 

 

 

1 2

;

3 3

I

 



 

 

.

(thay hoành độ đỉnh

1

2 3

b

a

 

vào phương trình parabol tìm tung độ đỉnh).

Câu 8. Xét tính đồng biến, nghịch biến của hàm số





2

4 5

f x x x

  

?

A. Hàm số nghịch biến trên





;2



, đồng biến trên





2;

 

.

B. Hàm số nghịch biến trên các khoảng





;2



và





2;

 

.

C. Hàm số đồng biến trên





;2



, nghịch biến trên





2;

 

.

D. Hàm số đồng biến trên các khoảng





;2



và





2;

 

.

Lời giải

Xét hàm số





2

4 5

f x x x

  

TXĐ:

D





.

Tọa độ đỉnh





2;1

I

.

Bảng biến thiên:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Hàm số nghịch biến trên





;2



, đồng biến trên





2;

 

.

Câu 9. Biết đồ thị





2

:

P y ax bx c

  

cắt trục tung tại điểm bằng có tung độ bằng 7, đi qua điểm





3;1

A

và có tung độ đỉnh bằng 9. Xác định parabol





P

.

A.

2

( ): 2 8 7

P y x x

   

. B.

2

( ): 2 4 7

P y x x

   

.

C.

2

( ): 4 2 7

P y x x

   

. D.

2

( ): 4 7

P y x x

   

.

Lời giải

Ta có





P

cắt trục tung tại điểm bằng 7 nên

7

c



.

Ta có





2

3;1 ( ): 1 .3 3 7

A P a b

   

9a 3 6

b

   

2

. (1)

3

b

a

 

 

Tung độ đỉnh

2

4.7.

9

4a 4a

b a

y

  

  

2

28a 36a

b

  

2

8 0

b a

  

.

Thay

(1)

vào phương trình trên ta được:

2

3 8 16 0

b b

  

4 2

3 9

4 2

b a

 

 

   

 

 

 

  

 

 

.

Vậy

2

( ): 2 4 7

P y x x

   

hoặc

2

2 2

( ): 7

9 3

P y x x

   

.

Câu 10. Tập xác định của phương trình

2

1

4 2020 0

x

   

là:

A.









; 2 2;

   

. B.





2;

  

.

C.





0;

 

. D.





2;



.

Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Điều kiện xác định:

2

4 0

0

x



 







2

0

x

xx

x

 







  

 











TXĐ:





2;D

 

.

Câu 11. Nghiệm của phương trình

2

5 6 0

x x

  

là:

A.

2

3

x

 









. B.

2

3

x







 



. C.

2

3

x











. D.

2

3

x

 





 



.

Lời giải

Xét phương trình









2

5 6 0 2 3 0

x x x x

      

2

3

x

 







 



.

Câu 12. Hai phương trình được gọi là tương đương khi:

A. Có cùng tập hợp nghiệm. B. Cùng là phương trình bậc hai.

C. Có cùng tập xác định. D. Có cùng bậc.

Lời giải

Hai phương trình được gọi là tương đương khi chúng có cùng tập nghiệm.

Câu 13. Phương trình nào dưới đây có một nghiệm là

1

x

 

?

A.

1 0

x

 

. B.

2

1

0

1

x







.

C.





1 1 0

x x

  

. D.

3

2 1 1 0

x x

   

.

Lời giải

Thay

1

x

 

vào phương trình

3

2 1 1 0

x x

   

thấy thỏa mãn.

Câu 14. Tập xác định của phương trình

2

1 5 2

2

2 1

x

x x







 

là

A.

 

5

; \ 1;2

2

D

 

 





 

. B.

 

5

1; \ 2

2

D

 







 

.

C.





(1; )\ 2

D  

. D.

5

;

2

D

 

 





 

.

Lời giải

Điều kiện:

2

2 1 0

5 2 0

2 0

x x

x



  



 





 



 

2

1 0

2 5

2

x



 



 











1

5

2

x







 











.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Từ đó suy ra tập xác định của phương trình là:

 

5

; \ 1;2

2

D

 

 





 

.

Ghi chú: Nhấn mạnh cho học sinh chỗ giải điều kiện

 

2

1 0

x

 

tương đương với

1 0

x

 

1

x

 

.

Câu 15. Phương trình nào sau đây tương đương với phương trình

2

4 0

x

 

?

A.









2

2 2 1 0

x x x

    

. B.









2

2 3 2 0

x x x

   

.

C.

2

3 1

x

 

. D.

2

4 4 0

x x

  

.

Lời giải

Thao định nghĩa, hai phương trình tương đương khi chúng có cùng một tập nghiệm.

Xét phương trình ban đầu:

2

4 0 2

x x

    

.

Xét từng đáp án:









2

2 2 1 0

x x x

    

2

1 2

x





 



 











2

2 3 2 0

x x x

   

2

1

2

x







  



 



2

3 1

x

 

2

3 1 2

x x

     

2

4 4 0

x x

  

2

x

 

Đáp án C thỏa mãn yêu cầu đề bài.

Câu 16. Tập nghiệm

S

của phương trình

1 0

x

 

là

A.





S

 

. B.





0

S 

. C.





1;S

   

. D.





1

S

 

.

Lời giải

Ta có

1 0

x

 

1 0 1

x x

     

.

Câu 17 . [Mức độ 2] Số nghiệm của phương trình

4 1 1 2

x x x

     là

A. 0. B. 1. C. 2. D. 3.

Lời giải

Điều kiện:

 

4 0

1

1 0 4 *

2

1 2 0

x

x x

x

 





     





 



.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Với điều kiện





*

thì phương trình tương đương

4 1 2 1 . 1 2 1 2

x x x x x

       

(1 )(1 2 ) 2 1

x x x

    



2

2 1 0

(1 )(1 2 ) (2 1)

x

x x x

 





   





2

1

2

2 7 0

x

x x



 







 





1/ 2

0 ( )

7 / 2 ( )

x

x n

x l

 















 





x 0

 

.

Kết luận: so với điều kiện





*

phương trình có 1 nghiệm

0

x



.

Câu 18. Gọi

S

là tổng các nghiệm của phương trình

2 2

3 21 18 2 7 7 2

x x x x

     

Khi đó

S

bằng:

A.

2

3

S



 . B.

1

S

 

. C.

5

3

S



 . D.

7

S

 

.

Lời giải

Ta có

2

7 21

2

7 7 0

7 21

2

x

x x

x



 





   



 







Phương trình

2 2 2 2

3 21 18 2 7 7 2 3( 7 7) 2 7 7 3 2

x x x x x x x x

             

2 2

3( 7 7) 2 7 7 5 0

x x x x

       

(1)

Đặt

2

7 7 ; 0

x x t t

   

phương trình

(1)

trở thành

2

1

3 2 5 0

5

3

t

t t

t







   









Với

5

0

3

t



 

loại

Với

2 2

1

1 7 7 1 7 6 0

6

x

t x x x x

x

 



         



 



thỏa mãn

Vậy tổng nghiệm của phương trình

6 ( 1) 7

s

     

.

Câu 19. Có bao nhiêu giá trị nguyên của tham số

m

thuộc đoạn





10;10



để phương trình









2

9 3 3

m x m m

  

có nghiệm duy nhất.

A.

3

. B.

19

. C.

20

. D.

18

.

Lời giải

Phương trình đã cho có nghiệm duy nhất khi:

2

9 0 3

m m

    

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Vì





10;10

m

  













nên





10; 9;...; 4; 2;...;2;4;...;10

m    

.

Vậy có

19

giá trị của tham số

m

thỏa mãn yêu cầu bài toán.

Câu 20. Nghiệm của hệ phương trình

2 2 0

1 0

x y

  





  



là

A.





1;0

. B.





0; 2

. C.





1;0

. D.





1;0

.

Lời giải

Ta có

2 2 0

1 0

x y

  





  



2 2 0

3 3 0

x y

x

  







 



0

1

y

x













.

Câu 21. Nghiệm của hệ phương trình

2 3 5 0

2 7 3 0

2 5 6 1 0

x y z

   





   





   



là

A.





11;9;4

. B.





9;11;4

. C.





9; 11; 4

  

. D.





11; 9; 4

  

.

Lời giải

Sử dụng máy tính cầm tay để tính nghiệm của hệ phương trình.

Lưu ý hằng số tự do trong quá trình bấm máy để sau dấu bằng.

Câu 22. Cho hệ phương trình

2 2

48

6

a b ab

a b



 



 



. Biết hệ phương trình có nghiệm là

( ; ) ( ; )

a b u v



. Tính

A u v

 

.

A.

5

. B.

4

. C.

3

. D.

2

.

Lời giải

2 2

48

6

a b b a

a b



 



 





( ) 48

6

ab a b

a b

 





 





6 48

6

ab

a b







 





8

6

ab

a b







 



.

Đặt ;

S a b P ab

  

ta được:

6

8

S

P











.

Khi đó

;

a

b

là nghiệm của phương trình:

2

6 8 0

X X

  



2

4

X











.

Suy ra:

2

4

a

b











hoặc

4

2

a

b











.

Suy ra

2 4 2

A u v

    

hoặc

4 2 2

A u v

    

.

Vậy

2

A u v

  

.

Câu 23. Số các giá trị nguyên dương của tham số

m

với

9

m



, để hệ phương trình

2 2 2

2

1

1x y m

x y m m

  





  





có nghiệm

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

0

. B.

4

. C.

1

. D.

2

.

Lời giải

Ta có:

2 2 2

2

1

1x y m

x y m m

  





  





2 2

2 2 1

1

( ) 0

x y

x m

m

y xy m

  





  











2 2

2

1

( 1 2

) 0

1x

x y m

m y m m

  





  











22

2 2 1 2 1

1x

xy m m m m

y m  





     





2

1

2 4xy

x y m

m

  





 





1

2xy

m

x y

  





 





.

Đặt

S x y

 

,

P xy



ta được:

1

2 1

S m

P m

 





 



.

Khi đó





;

x y

là nghiệm của phương trình:





2

1 +2 1=0

X m X m  





1

.

Hệ phương trình có nghiệm khi và chỉ khi phương trình





1

có nghiệm

Tức là:





2

( 1) 4(2 1) 0

m m

    

2

2 1 8 4 0

m m m

     

.

2

6 3 0

m m

   

.

3 2 3

m



 





 





.

Mà

m





,

0

m



và

9

m



nên





7;8

m

.

Vậy có

2

giá trị

m

thỏa mãn.

Câu 24. Cho tam giác

OAB

. Gọi

,

M

N

lần lượt là trung điểm

,

OA

OB

. Tìm mệnh đề đúng?

A.

MN OA OB

 

  

. B.

1 1

2 2

MN OA OB

 

  

.

C.

1 1

2 2

MN OA OB

 

  

. D.

1 1

2 2

MN OB OA

 

  

.

Lời giải

Gọi

I

là trung điểm

AB

.

Phương án A sai vì

2

OA OB OI MN

  

   

.

Phương án B sai vì

1 1

2 2

OA OB OI MN

  

   

.

Phương án C sai vì

1 1 1

2 2 2

OA OB BA NM MN

   

    

.

Phương án D đúng vì

1 1 1

2 2 2

OB OA AB MN

  

   

.

I

N

M

B

A

O

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Câu 25. Cho

G

là trọng tâm của tam giác

ABC

và

M

là trung điểm của đoạn

BC

. Khẳng định nào sau

đây là khẳng định sai?

A.

0

BM MC

 

  

. B.

2

AB AC AM

 

  

.

C.

0

GA GB GC

  

   

. D.

2

GB GC GM

 

  

.

Lời giải

Phương án A sai vì

0

BM MC BC

  

   

.

Phương án B đúng vì

M

là trung điểm

BC

nên

2

AB AC AM

 

  

.

Phương án C đúng vì

G

là trọng tâm của tam giác

ABC

nên

0

GA GB GC

  

   

.

Phương án D đúng vì

M

là trung điểm

BC

nên

2

GB GC GM

 

  

.

Câu 26. Trong hệ tọa độ Oxy, cho





1;3 ,

A





4;0 ,

B

(2; 5)

C



. Tìm tọa độ điểm M thỏa mãn hệ thức

3 0

MA MB MC

  

   

?

A.





1;18

M

. B.





1;18

M 

. C.





1; 18

M 

. D.





18;1

M 

.

Lời giải

Gọi tọa độ





;

M x y

.

Suy ra

(1 ;3 )

MA x y

  



,

(4 ; )

MB x y

  



,

(2 ; 5 )

MC x y

   



.

Ta có

3 0

MA MB MC

  

   













 

1 4 3 2 0

3 3 5 0

x x x

y y y

     









     





1

.

18

x

y









 



Câu 27. Cho





1;2

A

,





2;6

B 

. Tìm tọa độ điểm

M

thuộc trục

Oy

sao cho ba điểm

A

,

B

,

M

thẳng

hàng?

B.





0;3

M

. B.

10

0;

3

M

 

 

 

. C.

5

;0

2

M

 

 

 

. D.

5

0;

2

M

 

 

 

.

Lời giải

Vì

M

thuộc trục

Oy

nên





0;

M y

.

Suy ra

( 3;4)

AB  



,

( 1; 2)

AM y

  



. Để ba điểm

A

,

B

,

M

thẳng hàng thì

1 2

3 4

y

 





.

4 3 6

y

  

10

3

y

 

.

G

A

M

C

B

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Vậy

10

0;

3

M

 

 

 

.

Câu 28. Cho



là góc tù. Khẳng định nào sau đây là đúng?

A.

sin 0





. B.

cos 0





. C.

tan 0





. D.

cot 0





.

Lời giải

Góc tù có điểm biểu diễn thuộc góc phần tư thứ II, có giá trị

sin 0





,

cos 0





,

tan 0





,

cot 0





.

Câu 29. Cho biết

1

sin cos

2

 

 

thì

3 3

sin cos

 



bằng

A.

3 2

8

. B.

2

8

. C.

5 2

8

. D.

5

8

.

Lời giải

Ta có

 

2

1 1

sin cos sin cos

2

   

    

1

1 2sin .cos

2

 

  

1

sin .cos

4

 

  

.

Khi đó:

 

3 3 2 2

1 1 5 2

sin cos sin cos sin sin .cos cos . 1

4 8

2

       

 

       

 

 

.

Vậy

3 3

5 2

sin cos

8

 

  .

Câu 30. Gọi

G

là trọng tâm tam giác đều

ABC

có cạnh bằng

a

. Mệnh đề nào sau đây sai?

A.

2

1

.

2

AB AC a

 

. B.

2

1

.

2

AC CB a 

 

. C.

2

.

6

a

GAGB 

 

. D.

2

1

.

2

AB AG a

 

.

Lời giải

Ta có:



Xác định được góc

 

,AB AC

 

là góc



BAC nên

 

0

, 60AB AC 

 

.

Do đó

 

2

0

. . .cos , . .cos60

2

a

AB AC AB AC AB AC a a   

   

A đúng.



Xác định được góc

 

,AC CB

 

là góc bù của góc



ACB

nên

 

0

, 120AC CB 

 

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Do đó

 

2

0

. . .cos , . .cos120

2

a

AC CB AC CB AC CB a a    

   

B đúng.



Xác định được góc

 

,GA GB

 

là góc



AGB

nên

 

0

, 120GA GB 

 

.

Do đó

 

2

0

. . .cos , . .cos120

6

3 3

a a a

GAGB GAGB GA GB    

   

C sai.



Xác định được góc

 

,AB AG

 

là góc



GAB

nên

 

0

, 30AB AG 

 

.

Do đó

 

2

0

. . .cos , . .cos30

2

3

a a

AB AG AB AG AB AG a   

   

D đúng.

Câu 31. Cho tam giác

ABC

vuông tại A có 3; 4AB AC  . Trên đoạn thẳng

BC

lấy điểm M sao cho

2MB MC

. Tính tích vô hướng

.AM BC

 

.

A.

41

3

. B.

23

3

. C. 8. D.

23

.

Lời giải

Ta có:

0AB AC AB AC   

   

.

2MB MC 

 

 

2AB AM AC AM    

   

1 2

3 3

AM AB AC  

  

.

Do đó:

 

2 2

1 2 1 1 2

.

3 3 3 3 3

AM BC AB AC AC AB AB AB AC AC

 

        

 

 

         

2 2 2 2

1 2 1 2 23

3 4

3 3 3 3 3

AB AC        

.

Hướng biến đổi khác

Ta có

2

3

AM AB BC 

  

.

Suy ra

2

. .

3

AM BC AB BC BC 

    

 

2

. cos

3

AB BC B BC  

2 2

2 2 23

9 .25

3 3 3

AB BC       .

Câu 32. Cho

   

2;3 , 4; 1u v   

 

. Tính

2 .u v

 

.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

A.

11



. B.

11

2



. C.

22



. D.

22

.

Lời giải

Ta có

2 . 2( 2.4 3.( 1)) 22

u v

     

 

.

Câu 33. Trong mặt phẳng tọa độ

Oxy

, cho điểm









1; 2 ; 3; 5

A B

 

. Tìm tọa độ điểm

C

trên trục

Ox

sao cho tam giác

ABC

vuông tại

A

.

A.





4;0



. B.





2;0



. C.





2;0

. D.





4;0

.

Lời giải

Do

C Ox



nên gọi tọa độ điểm

C

là:





;0

C x

.

Ta có





2; 3

AB

 



;





1;2

AC x 



.

Tam giác

ABC

vuông tại

A

nên

. 0

AB AC AB AC

  

   





2 1 6 0

x

   





2 1 6 4

x x

    

.

Vậy





4;0

C

.

Câu 34. Trên mặt phẳng

Oxy

, cho tam giác

ABC

có





1;2

A 

,





5;4

B 

và





2;4

C

. Tìm tọa độ chân

đường cao

H

dựng từ

C

của

ABC



.

A.

6 3

;

5 5

H

 

 

 

. B.

6 3

;

5 5

H

 

 

 

 

. C.

3 6

;

5 5

H

 

 

 

 

. D.

3 6

;

5 5

H

 

 

 

.

Lời giải

Gọi





;

H a b

.

Ta có:





2; 4

CH a b

  



;





4;2

AB  



.

Mà:

CH AB



nên

. 0

CH AB



 

.













4 . 2 2. 4 0

a b

     

4 2 0

a b

   

2

b a

 





1

Ta có:





1; 2

AH a b

  



.

Vì

H AB



nên

;

AH AB

 

cùng phương, do đó ta có hệ thức:

1 2

4 2

a b

 





1

2

a

b



  



1 2 4

a b

    





2

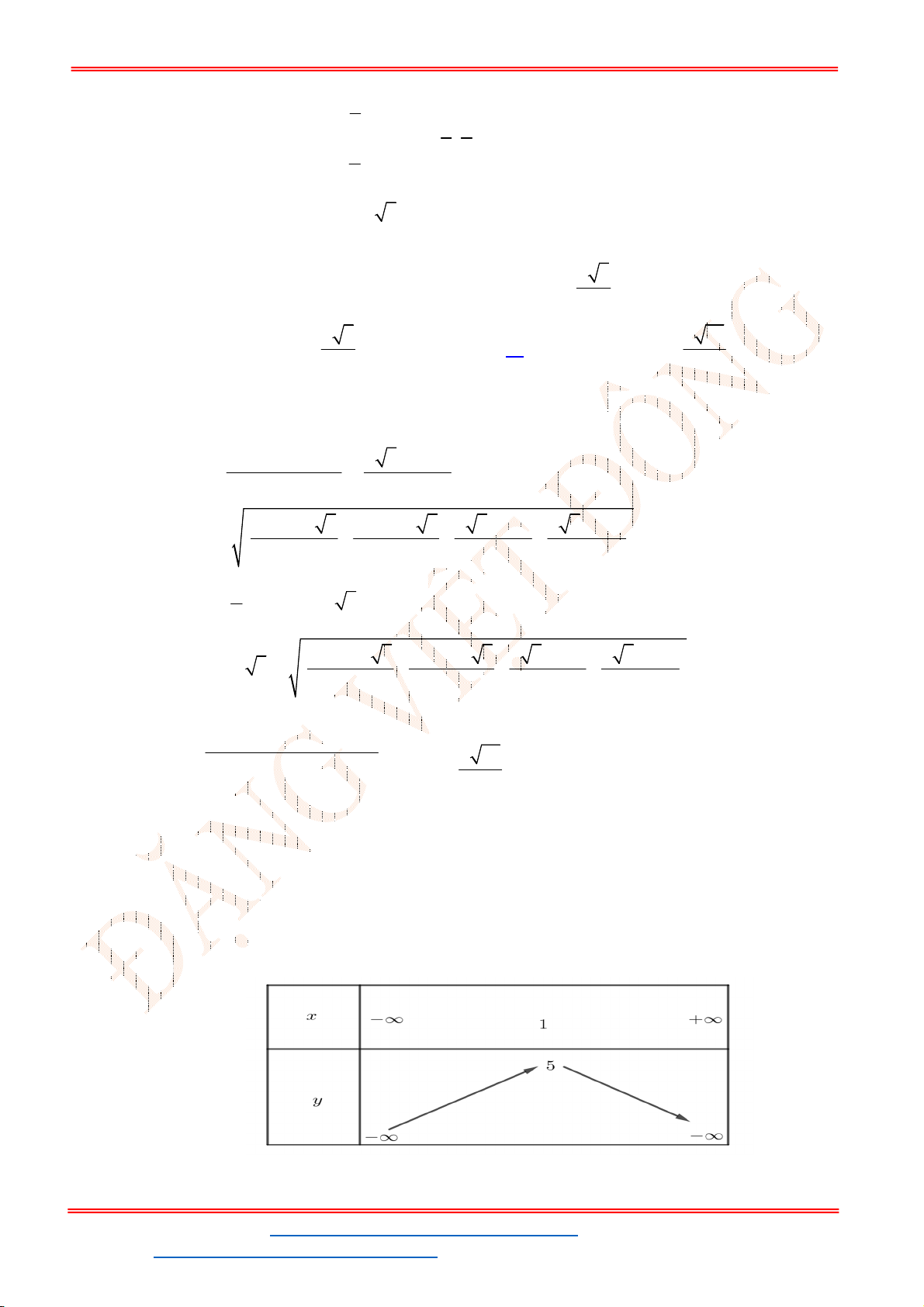
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Từ

 

1

và

 

2

suy ra:

3

5

6

5

a

b

















. Vậy

3 6

;

5 5

H

 

 

 

.

Câu 35. Cho tam giác

ABC

có

2 3, 2BC AC AB 

và độ dài đường cao 2AH  . Tính độ dài cạnh

AB .

A. 2AB  . B.

2 3

3

AB  .

C. 2AB  hoặc

2 3

3

AB  . D. 2AB  hoặc

2 21

3

AB  .

Lời giải

Ta có

2 3 3

2 2

AB BC CA AB

p

  

  .

Suy ra

3 2 3 3 2 3 2 3 2 3

2 2 2 2

AB AB AB AB

S

    

   

   

   

   

    

   

   

   

   

    

.

Lại có

1

. 2 3.

2

S BC AH 

Từ đó ta có

3 2 3 3 2 3 2 3 2 3

2 3

2 2 2 2

AB AB AB AB

    

   

   

   

   

    

   

   

   

   

    

  

2 2

2

9 12 12

12 .

2 21

16

3

AB

AB AB

AB





 



  









PHẦN II: TỰ LUẬN

Câu 36: Cho hàm số

2

2 4 3y x x    có đồ thị là parabol





P

. Lập bảng biến thiên của hàm số đã

cho và vẽ parabol

 

P

.

Lời giải

* BBT của hàm số

2

2 4 3y x x    .

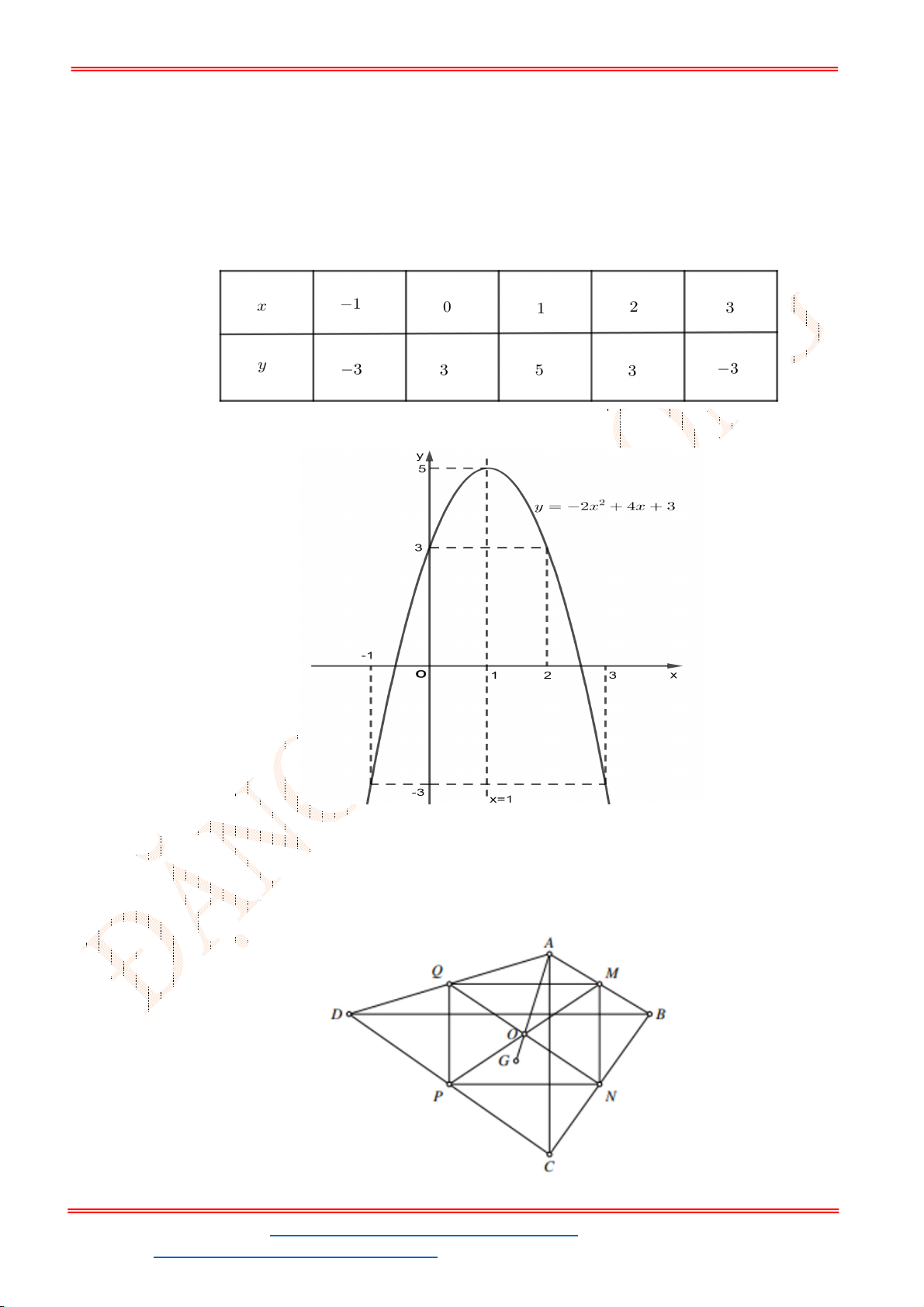
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

* Vẽ

 

2

: 2 4 3P y x x   

.

TXĐ: D   .

Đỉnh

 

1;5I

.

Trục đối xứng là đường thẳng

1x 

.

Bảng giá trị

Đồ thị:

Câu 37. Cho tứ giác

ABCD

. Gọi M ,

N

, P, Q lần lượt là trung điểm của AB ,

BC

,

CD

,

DA . Gọi

O

là giao điểm của MP và NQ ,

G

là trọng tâm của tam giác

BCD

. Chứng minh

rằng ba điểm A,

O

,

G

thẳng hàng.

Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 20

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

MN

,

PQ

lần lượt là đường trung bình của

ABC



,

ACD



// //

1

2

MN PQ AC









 





Do đó tứ giác

MNPQ

là hình bình hành

O



là trung điểm của

MP

.

Ta có:

















OA OB OC OD OM MA OM MB OP PC OP PD

          

         

  





2

OM OP

 

 

0





.

G

là trọng tâm



BCD

3

OB OC OD OG

   

   

.

Khi đó:

0

OA OB OC OD

   

    

3 0

OA OG

  

  



3

OA OG

 

 

.

Vậy ba điểm

A

,

O

,

G

thẳng hàng (đpcm).

Câu 38. Giải phương trình sau:

2

16 4

1 4

1

x

x x

x



  



.

Lời giải

Điều kiện:

1

x

 

.

Khi đó:

2

16 4

1 4

1

x

x x

x



  



2

1 4 1 16 4

x x x x

     

2

4 2.2 1 1 16

x x x x

     





2

2 1 16

x x

   

2 1 4 (1)

2 1 4 (2)

x x



  





   





.

(1)

1 2 4

x x

   

 

2

2 4 0

1 2 4

x

x x

 









  





2

4 17 15 0

x

x x









  



2

3

5

4

x







 



  

















(TMĐK).

(2)

1 2 4

x x

   

 

2

2 4 0

1 2 4

x

x x

 









  





2

4 15 15 0

x

x x

 







  



(vô nghiệm).

Vậy tập nghiệm của phương trình đã cho là





3

T 

.

Câu 39. Cho tam giác

ABC

. Chứng minh rằng:

3

cos2 cos 2 cos 2

2

A B C

   

.

Lời giải:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn Tập HKI

ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 21

Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông

ID Tik Tok: dongpay

Gọi





;

O R

là đường tròn ngoại tiếp

ABC



.

Ta có:





2

0

OA OB OC

  

  

2 2 2

2 . 2 . 2 . 0

OA OB OC OA OB OB OC OC OA

      

     













2 2 2 2

3 2 cos , 2 cos , 2 cos , 0

R R OA OB R OB OC R OC OA

    

     

2 2 2 2

3 2 cos2 2 cos2 2 cos2 0

R R C R A R B

    





3 2 cos2 cos2 cos2 0

C A B

    

3

cos2 cos 2 cos 2

2

A B C

    

.

Dấu bằng xảy ra khi

0

OA OB OC O

   

   

là trọng tâm

ABC ABC

  

đều.

 HẾT 

O

B

C

A

TOP15 đề ôn tập học kỳ 1 Toán 10 năm học 2020 – 2021 – Đặng Việt Đông

Đề HK1 Toán 10 412 tài liệu

Toán 10 2.8 K tài liệu

Bình luận

TOP15 đề ôn tập học kỳ 1 Toán 10 năm học 2020 – 2021 – Đặng Việt Đông