Trắc nghiệm bài 4 phương trình lượng giác cơ bản

TRẮC NGHIỆM PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN MỨC VẬN DỤNG
Câu 1: Tìm tất cả các giá trị thực của tham số m để cặp phương trình sau tương đương: 2
mx - (m - ) x + m- = ( ) (m- ) 2 2 2 1 2 0 1 và
2 x -3x + m -15 = 0(2). A. m = 5 - . B. m = 5; - m = 4.
C. m = 4 . D. m = 5 .
Câu 2: Tìm giá trị thực của tham số m để cặp phương trình sau tương đương: 2 x + mx - = ( ) 3 x + (m+ ) 2 2 2 0 1 và 2 4 x + 2(m- ) 1 x - 4 = 0(2). 1
A. m = 2 .
B. m = 3 . C. m = 2 - . D. m = . 2
Câu 3: Cho phương trình f (x) = 0 có tập nghiệm S = ;2 m m -1 g (x) = 0 1 { } và phương trình có tập nghiệm S = 1;2 m g (x) = 0 2
[ ]. Tìm tất cả các giá trị để phương trình
là phương trình hệ quả của phương
trình f (x) = 0. 3 3
A. 1 < m < .
B. 1 £ m £ 2 .
C. m ÎÆ . D. 1 £ m £ . 2 2
Câu 4: Xác định m để hai phương trình sau tương đương: 2 x + x + = ( ) 2 x - (m+ ) 2 2 0 1 và 2
1 x + m + m - 2 = 0
Dễ thấy phương trình (1) vô nghiệm. A. m < 3 - B. m £ 3 - C. m £ 6 - D. m ³ 6 - æ p ö æ 3p ö
Câu 5: Cho phương trình sin 2x - = sin x +
. Tính tổng các nghiệm thuộc khoảng (0;p ) của ç ÷ ç ÷ è 4 ø è 4 ø phương trình trên. 7p p p A. . B. p 3 . C. . D. . 2 2 4 p
Câu 6: Tìm giá trị thực của tham số m để phương trình (m - 2)sin2x = m + 1 nhận x = làm nghiệm. 12 2( 3 + ) 1
A. m ¹ 2 . B. m = . C. m = 4 - . D. m = 1 - . 3 - 2 æ p ö 3 æ p ö
Câu 7: Phương trình sin 3x + = -
có bao nhiêu nghiệm thuộc khoảng 0; ? ç ÷ è 3 ø 2 ç ÷ è 2 ø A. 3 . B. 4 . C. 1 . D. 2 .
Câu 8: Số nghiệm của phương trình 2sinx - 3 = 0 trên đoạn đoạn [0;2p .] A. 3 . B. 1 . C. 4 . D. 2 . æ p ö 3 æ p ö
Câu 9: Phương trình sin 3x + = -
có bao nhiêu nghiệm thuộc khoảng 0; ? ç ÷ è 3 ø 2 ç ÷ è 2 ø A. 3 . B. 4 . C. 1 . D. 2 . 3
Câu 10: Phương trình sin2x = -
có hai công thức nghiệm dạng a + p k , b + p
k (k ÎZ) với a, b 2 æ p p ö thuộc khoảng - ; . Khi đó, a + b bằng ç ÷ è 2 2 ø p p p A. . B. - . C. p . D. - . 2 2 3 Trang 1 1 é p p ù
Câu 11: Tính tổng S của các nghiệm của phương trình sinx = trên đoạn - ; . 2 ê 2 2 ú ë û 5p p p p A. S = . B. S = . C. S = . D. S = . 6 3 2 6 æ p ö
Câu 12: Số nghiệm của phương trình sin x +
= 1 thuộc đoạn [p;2p ] là: ç ÷ è 4 ø A. 3 . B. 2 . C. 0 . D. 1 .
Câu 13: Phương trình sin5x - sinx = 0 có bao nhiêu nghiệm thuộc đoạn [ 2018 - p;2018p ] ? Ta có A. 20179 . B. 20181 . C. 16144 . D. 16145 . é 3p ù
Câu 14: Số nghiệm thực của phương trình 2sinx +1 = 0 trên đoạn - ;10p là: ê 2 ú ë û A. 12 . B. 11 . C. 20 . D. 21 . æ p ö
Câu 15: Phương trình: 2sin 2x -
- 3 = 0 có mấy nghiệm thuộc khoảng (0;3p ). ç ÷ è 3 ø A. 8 . B. 6 . C. 2 . D. 4 . æ p p ö
Câu 16: Tổng các nghiệm thuộc khoảng - ; của phương trình 2 4sin 2x -1 = 0 bằng: ç ÷ è 2 2 ø p p A. p . B. . C. 0 . D. . 3 6 1 p p
Câu 17: Biết các nghiệm của phương trình cos2x = - có dạng x =
+ kp và x = - + kp ,k ÎZ ; với 2 m n ,
m n là các số nguyên dương) Khi đó m + n bằng Chọn A. 4 . B. 3 . C. 5 . D. 6 . E. æ p ö
Câu 18: Phương trình 2cos x +
=1 có số nghiệm thuộc đoạn [0;2p ]là ç ÷ è 3 ø A. 1 B. 2 C. 0 D. 3
Câu 19: Nghiệm lớn nhất của phương trình 2cos2x -1 = 0 trong đoạn [0;p ] là: 11p 2p 5p
A. x = p . B. x = . C. x = . D. x = . 12 3 6
Câu 20: Tìm số đo ba góc của một tam giác cân biết rằng có số đo của một góc là nghiệm của phương 1 trình cos2x = - . 2 ì2p p p ü ìp p p ü ì2p p p ü A. í , , ý. B. í , , ý;í , , ý. î 3 6 6 þ î 3 3 3 þ î 3 6 6 þ ìp p p ü ìp p p ü ìp p p ü
C. í , , ý;í , , ý. D. í , , ý . î 3 3 3 þ î 4 4 2 þ î 3 3 3 þ 1
Câu 21: Số nghiệm của phương trình cosx = thuộc đoạn [ 2 - p;2p ] là? 2 A. 4 . B. 2 . C. 3 . D. 1 .
Câu 22: Phương trình cos2x + cosx = 0 có bao nhiêu nghiệm thuộc khoảng ( p - ;p ) ? A. 2 . B. 3 . C. 1 . D. 4 . Trang 2
Câu 23: Tổng tất cả các nghiệm của phương trình cos2x - cosx = 0 trên khoảng (0;2p ) bằng T . Khi đó T có giá trị là: 7p 4p A. T = .
B. T = 2p . C. T = . D. T = p . 6 3 é 5p ù
Câu 24: Số nghiệm của phương trình 2cosx = 3 trên đoạn 0; là ê 2 ú ë û A. 2 . B. 1 . C. 4 . D. 3 .
Câu 25: Tính tổng các nghiệm trong đoạn [0;30] của phương trình: tanx = tan3x p p A. 55p 171 . B. . C. 45p 190 . D. . 2 2 - 3
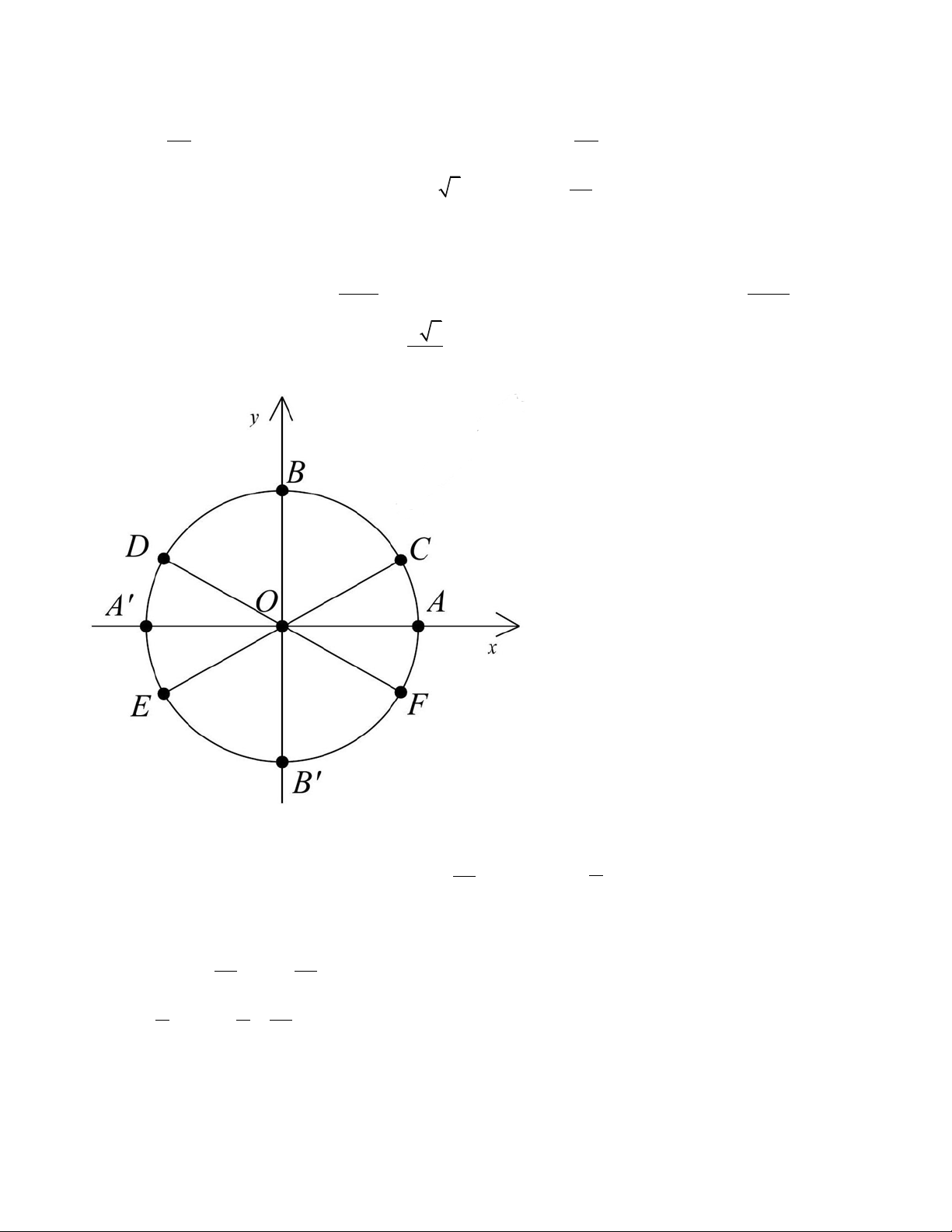
Câu 26: Nghiệm của phương trình tanx =
được biểu diễn trên đường tròn lượng giác ở hình bên là 3 những điểm nào?
A. Điểm F , điểm D .
B. Điểm C , điểm F .
C. Điểm C , điểm D , điểm E , điểm F .
D. Điểm E , điểm F . 3p æ p ö
Câu 27: Số nghiệm của phương trình tanx = tan trên khoảng ;2p là? ç ÷ 11 è 4 ø Lời giải 3p 3p Ta có tanx = tan Û x =
+ kp (k ÎZ ) . 11 11 æ p ö p 3p Do x Î ;2p ® < + kp < 2p ç ÷ è 4 ø 4 11 CASIO 0,027 kÎ ¾¾¾®- ¾¾¾ !®k Î Xap xi {0; } 1 A. 4 . B. 1 . C. 2 . D. 3 .
Câu 28: Tổng các nghiệm của phương trình tan5x - tanx = 0 trên nửa khoảng [0;p ) bằng: Trang 3 5p p A. . B. p 3 . C. . D. 2p . 2 2
Câu 29: Tính tổng các nghiệm của phương trình tan(2 -15! x ) =1 trên khoảng ( 90 - !;90! ) bằng) A. 0 0 . B. 0 30 - . C. 30!. D. -60!. æ p ö p kp k
Câu 30: Nghiệm của phương trình cot x + = 3 có dạng * x = - + , k ÎZ, , m n Î N và là ç ÷ è 3 ø m n n
phân số tối giản. Khi đó m - n bằng A. 3 . B. 5 . C. -3 . D. -5 .
Câu 31: Hỏi trên đoạn [0;2018p ], phương trình 3cotx -3 = 0 có bao nhiêu nghiệm? A. 2018 . B. 6340 . C. 2017. D. 6339 .
Câu 32: Số nghiệm của phương trình ( - ! x ) 3 sin 2 40 = với 180 - ! £ £180! x là ? 2 A. 2 . B. 4 . C. 6 . D. 7 . æ p ö
Câu 33: Tìm nghiệm dương nhỏ nhất của phương trình 2sin 4x - -1 = 0. ç ÷ è 3 ø p 7p p p A. x = . B. x = . C. x = . D. x = . 4 24 8 12
(2cosx - )1(sin2x -cosx) é p ù
Câu 34: Tính tổng T tất cả các nghiệm của phương trình = 0 trên 0; ta sinx -1 ê 2 ú ë û được kết quả là:
Điều kiện xác định sinx ¹ 1. 2p p p A. T = . B. T = .
C. T = p . D. T = . 3 2 3
Câu 35: Phương trình sinx = cosx có số nghiệm thuộc đoạn [ p - ;p ] là: . A. 3 B. 5 C. 2 D. 4 æ x öæ x ö
Câu 36: Giải phương trình 2cos -1 sin + 2 = 0 ç ÷ç ÷ è 2 øè 2 ø 2p p A. x = ±
+ k2p ,(k ÎZ)
B. x = ± + k2p ,(k ÎZ) 3 3 p 2p
C. x = ± + k4p ,(k ÎZ) D. x = ± + k4p ,(k ÎZ) 3 3
Câu 37: Phương trình 8×cos2x×sin2x×cos4x = - 2 có nghiệm là Ta có: é p - p é p p x = + ê k x = + ê k A. 32 4 ê (k ÎZ) . B. 16 8 ê (k ÎZ). 5 ê p p 3 ê p p x = + ê k x = + k ë 32 4 êë 16 8 é p p é p p x = + ê k x = + ê k C. 8 8 ê (k ÎZ). D. 32 4 ê (k ÎZ). 3 ê p p 3 ê p p x = + ê k x = + k ë 8 8 êë 32 4
Câu 38: Tìm số nghiệm của phương trình sin (cos2x) = 0 trên [0;2p .] Trang 4 A. 2 . B. 1 . C. 4 . D. 3 .
Câu 39: Trong khoảng (0;p ), phương trình cos4x + sinx = 0 có tập nghiệm là S . Hãy xác định S . ìp 2p 3p 7p ü ìp 3p ü A. S = í ; ; ; ý . B. S = í ; ý. î 3 3 10 10 þ î 6 10 þ ìp p 7p ü ìp 5p 3p 7p ü C. S = í ; ; ý. D. S = í ; ; ; ý. î 6 10 10 þ î 6 6 10 10 þ
Câu 40: Phương trình cos3x × tan5x = sin7x nhận những giá trị sau của x làm nghiệm p p p p A. x = .
B. x = 10p ; x = .
C. x = 5p; x = .
D. x = 5p; x = 2 10 10 20 2 1+ sin x
Câu 41: Giải phương trình 2 - tan x = 4. 2 1- sin x p p p p
A. x = ± + k2p .
B. x = ± + k2p .
C. x = ± + kp .
D. x = ± + kp . 3 6 3 6 cosx(1- 2sinx)
Câu 42: Giải phương trình = 3 . 2 2cos x - sinx -1 p p
A. x = - + k2p .
B. x = ± + k2p . 6 6 p p p C. x = + k2p .
D. x = - + k2p , x = - + k2p . 6 6 2
Câu 43: Giải phương trình sinx×cosx(1+ tanx)(1+ cotx) =1. p
A. Vô nghiệm.
B. x = k2p . C. = k x .
D. x = kp . 2
Câu 44: Phương trình sin2x + cosx = 0 có tổng các nghiệm trong khoảng (0;2p ) bằng A. 2p . B. 3p . C. 5p . D. 6p . æ p 3p ö
Câu 45: Số nghiệm chung của hai phương trình 2
4cos x - 3 = 0 và 2sinx +1 = 0 trên khoảng - ; ç ÷ è 2 2 ø bằng A. 2 . B. 4 . C. 3 . D. 1 .
Câu 46: Giải phương trình sin si x n7x = sin3 si x n5x . kp kp kp
A. x = kp , k ÎZ . B. x = , k Î Z . C. x = , k Î Z . D. x = , k Î Z . 6 4 2
Câu 47: Tìm số nghiệm của phương trình sinx = cos2x thuộc đoạn [0;20p ]. A. 20 . B. 40 . C. 30 . D. 60 .
Câu 48: Biểu diễn tập nghiệm của phương trình cosx + cos2x + cos3x = 0 trên đường tròn lượng giác ta
được số điểm cuối là A. 6 B. 5 C. 4 D. 2 Trang 5