Trắc nghiệm lượng giác có lời giải chi tiết trong các đề thi thử Toán 2018

Tài liệu gồm 145 trang tổng hợp câu hỏi và bài tập trắc nghiệm lượng giác có lời giải chi tiết trong các đề thi thử Toán 2018 của các trường THPT và sở Giáo dục – Đào tạo

31 16 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Hàm số lượng giác và phương trình lượng giác (KNTT)

Môn: Toán 11

Thông tin:

145 trang 7 tháng trước

Tác giả:

Profile Kim Oanh
Câu 1:
(THPT Chuyên Hùng Vương-Phú Thọ-lần 1-NH2017-2018)
Nghiệm của phương trình
2sin 1 0
x
được biểu diễn trên đường tròn lượng giác ở hình bên là những điểm nào ?
A. Điểm
E
, điểm
D
. B. Điểm
C
, điểm
F
. C. Điểm
D
, điểm
C
. D. Điểm
E
, điểm
F
.
Lời giải
Chọn D
Ta có:
2sin 1 0
x
1
sin
2
x
2
6
7
2
6
x k
k
x k
.
Vậy chỉ có hai điểm
E
và
F
thỏa mãn.
Câu 2:
(THPT Chuyên Hùng Vương-Phú Thọ-lần 1-NH2017-2018)
Khẳng định nào dưới đây là sai ?
A. Hàm số
cosy x
là hàm số lẻ. B. Hàm số
là hàm số lẻ.
C. Hàm số
siny x
là hàm số lẻ. D. Hàm số
tany x
là hàm số lẻ.
Lời giải
Chọn A
Ta có các kết quả sau:
+ Hàm số
cosy x
là hàm số chẵn.
+ Hàm số
là hàm số lẻ.
+ Hàm số
là hàm số lẻ.
+ Hàm số
tany x
là hàm số lẻ.
Câu 3:
(THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018)
Nghiệm của phương trình
tan 3 tanx x
là
A.
, .
2
k
x k
B.
,x k k
. C.
2 , .
x k k
D.
, .
6
k
x k
Lời giải
Chọn B
Ta có
tan3 tan 3 , .
2
k
x x x x k x k
Trình bày lại
ĐK:
cos3x 0
6 3
cosx 0
2
k
x
x k

*
O
x
y
A
B
A
B
E
D
C
F
Ta có
tan3 tan 3 , .
2
k
x x x x k x k
Kết hợp điều kiện
*
suy ra
,x k k
Câu 4:
(THPT Chuyên Thái Bình-lần 1-năm 2017-2018)
Cho hàm số
y f x
có đồ thị như hình
bên. Mệnh đề nào dưới đây đúng?
A. Hàm số có giá trị cực tiểu bằng
2
.
B. Hàm số có giá trị lớn nhất bằng
2
và giá trị nhỏ nhất bằng
2
.
C. Hàm số đạt cực đại tại
0
x
và cực tiểu tại
2
x
.
D. Hàm số có ba điểm cực trị.
Lời giải
Chọn C
Câu 5:
(THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018)
Tìm tất cả các giá trị thực của tham số
m
để
phương trình
sin 1
x m
có nghiệm?
A.
2 0.
m
B.
0.
m
C.
1.
m
D.
0 1.
m
Lời giải
Chọn A
Ta có
sin 1 sin 1.
x m x m
Khi đó YCBT
1 1 1 2 0.
m m
Câu 6:
(THPT Sơn Tây-Hà Nội-lần 1-năm 2017-2018)
Giải phương trình
sin 1
2
x
.
A.
4 ,x k k
. B.
2 ,x k k
. C.
2 ,x k k
. D.
2 ,
2
x k k
.
Lời giải
Chọn A
Ta có
sin 1 2 4 ,
2 2 2
x x
k x k k
.
Vậy nghiệm của phương trình là
,
.
4x k k
Câu 7:
(THPT Sơn Tây-Hà Nội-lần 1-năm 2017-2018)
Trong các hàm số sau hàm số nào là hàm số chẵn?
A.
1 siny x
. B.
siny x
. C.
cos
3
y x
. D.
sin cosy x x
.
Lời giải
Chọn B
TXĐ:
D
.
:
x D x D x D
1
Ta có
sin sin sin
f x x x x f x
2
.
Từ
1
và
2
suy ra hàm số
siny x
là hàm chẵn.
O
x
y
2
2
2
Câu 8:
(THPT Yên Lạc-Vĩnh Phúc-lần 1-năm 2017-2018)
Nghiệm của phương trình
1
cos
2
x
là
A.
2
2
3
x k
. B.
6
x k
. C.
2
3
x k
. D.
2
6
x k
.
Lời giải
Chọn A
1 2
cos cos cos
2
2 ,
2 3 3
kx kx x
.
Câu 9:
(THPT Yên Lạc-Vĩnh Phúc-lần 1-năm 2017-2018)
Trong các hàm số sau đây, hàm số nào là
hàm số tuần hoàn?
A.
1y x
. B.
2
y x
. C.
1
2
x
y
x
. D.
.
Lời giải
Chọn D
Hàm số
tuần hoàn với chu kì
2
.
Câu 10:
(THPT Yên Lạc-Vĩnh Phúc-lần 1-năm 2017-2018)
Công thức tính số tổ hợp là:
A.
!
!
k
n
n
C
n k
. B.
!
! !
k
n
n
C
n k k
. C.
!
!
k
n
n
A
n k
. D.
!
! !
k
n
n
A
n k k
.
Lời giải
Chọn B
Câu 11:
(THPT Yên Lạc-Vĩnh Phúc-lần 1-đề 2-năm 2017-2018)
Nghiệm của phương trình
1
cos
2
x
là
A.
2
2
3
x k
. B.
6
x k
. C.
2
3
x k
. D.
2
6
x k
.
Lời giải
Chọn A
1 2
cos cos cos
2
2 ,
2 3 3
kx kx x
.
Câu 12:
(THPT Yên Lạc-Vĩnh Phúc-lần 1-đề 2-năm 2017-2018)
Trong các hàm số sau đây, hàm số nào
là hàm số tuần hoàn?
A.
1y x
. B.
2
y x
. C.
1
2
x
y
x
. D.
.
Lời giải
Chọn D
Hàm số
tuần hoàn với chu kì
2
.
Câu 13:
(THPT Yên Lạc 2-Vĩnh Phúc-lần 1-năm 2017-2018)
Giá trị lớn nhất và nhỏ nhất của hàm
số
5cos2 1
2
x
y
là
A.
1
và
2
. B.
3
và
2
. C.
3
và
2
. D.
3
và
1
.
Lời giải
Chọn C
1 cos 2 1 5 5cos 2 5
x x
4 5cos 2 1 6
x
5cos2 1
2 3
2
x
.
Vậy giá trị lớn nhất của hàm số là
3
và giá trị nhỏ nhất của hàm số là
2
.
Câu 14:
(THPT Yên Lạc 2-Vĩnh Phúc-lần 1-năm 2017-2018)
Tập xác định của hàm số
cotf x x
là
A.
\ |k k
. B.
\ 2 |k k
.
C.
\ 2 1 |k k
. D.
\ 2 1 |
2
k k
.
Lời giải
Chọn A
f x
xác định khi và chỉ khi
sin 0x x k k
.
Câu 15:
(THPT Yên Lạc 2-Vĩnh Phúc-lần 1-năm 2017-2018)
Điều kiện xác định của hàm số
sin cos
cos
x x
y
x
là
A.
2
x k
. B.
2x k
. C.
2
x k
. D.
x k
.
Lời giải
Chọn A
Hàm số xác định
cos 0
x
2
x k
.
Câu 16:
(THPT Hai Bà Trưng-Vĩnh Phúc-lần 1-năm 2017-2018)
Trong các khẳng định sau khẳng định
nào đúng?
A. Phương trình
cos x a
có nghiệm với mọi số thực
a
.
B. Phương trình
và phương trình
có nghiệm với mọi số thực
a
.
C. Phương trình
sin
x a
có nghiệm với mọi số thực
a
.
D. Cả ba đáp án trên đều sai.
Lời giải
Chọn B
Cách 1: Ta có hàm
cosy x
và
siny x
nhận giá trị trên đoạn
1;1
nên A và C sai suy ra D cũng
sai.
Cách 2: Hàm
tany x
và
nhận giá trị trên tập số thực nên B đúng.
Câu 17:
(THPT Hai Bà Trưng-Vĩnh Phúc-lần 1-năm 2017-2018)
Trong các hàm số sau hàm số nào
tuần hoàn với chu kỳ
?
A.
sin 2 .y x
B.
tan 2 .y x
C.
cos .y x
D.
cot .
2
x
y
Lời giải
Chọn A
sin 2 sin 2 2
x x
sin 2x
; Giả sử có số
T
sao cho
0 T
và
sin 2 sin 2 x, x .
x T
Chọn
4
x
, ta được
sin 2 sin 1 cos2T 1.
4 2
T
Điều này trái giả thiết
0 T
. Vậy
là chu kỳ của hàm số
sin 2 .y x
Câu 18:
(THPT Việt Trì-Phú Thọ-lần 1-năm 2017-2018)
Phương trình
tan 0
3
x
có nghiệm là
A.
2 ,
3
k k
. B.
,
2
k k
. C.
,
3
k k
. D.
,
3
k k
.
Lời giải
Chọn D
ĐK:
cos 0
3
x
6
x k
Ta có
tan 0
3 3
x x k
,
3
x k k
.
Câu 19:
(THPT Bình Xuyên-Vĩnh Phúc-năm 2017-2018)
Hàm số
coty x
tuần hoàn với chu kỳ:
A.
T k
. B.
2
T
. C.
2T k
. D.
T
.
Lời giải
Chọn D
Theo tính chất trong sgk
11
thì hàm số
coty x
tuần hoàn với chu kì
.
Câu 20:
(THPT Bình Xuyên-Vĩnh Phúc-năm 2017-2018)
Trong các hàm số sau đây, hàm nào có đồ thị
nhận trục tung làm trục đối xứng?
A.
2
cos siny x x
. B.
tany x
. C.
3
sin cosy x x
. D.
.
Lời giải
Chọn A
Trong 4 hàm số trên chỉ có hàm số
2
cos siny x x
là hàm số chẵn nên có đồ thị nhận trục
tung làm trục đối xứng.
Thật vậy:
Tập xác định của hàm số là
D
nên
x
x
.
Và
2
cos sin
y x x x
2
cos sin
x x y x
Nên hàm số
2
cos siny x x
là hàm số chẵn.
Câu 21:
(THPT Nguyễn Đức Thuận-Nam Định-lần 1-năm 2017-2018)
Xét bốn mệnh đề sau:
1
: Hàm số
có tập xác định là
.
2
: Hàm số
cosy x
có tập xác định là
.
3
: Hàm số
tany x
có tập giá trị là
.
4
: Hàm số
có tập xác định là
.
Tìm số phát biểu đúng.
A.
3
. B.
2
. C.
4
. D.
1
.
Lời giải.
Chọn A
Dễ thấy các phát biểu
1
;
2
;
3
đúng.
Xét
4
:
cos
cot
sin
x
y x
x
ĐKXĐ:
sinx 0 \ ;x k D k k
.
Câu 22: [2D-3]
(THPT Nguyễn Đức Thuận-Nam Định-lần 1-năm 2017-2018)
Cho hàm số
3 2
3 1
3
m
y x mx x
(
m
là tham số thực). Tìm giá trị nhỏ nhất của
m
để hàm số đồng biến
trên
.
A.
3
m
. B.
2
m
. C.
1
m
. D.
0
m
.
Lời giải.
Chọn D
Ta có:
D
.
2
2 3y mx mx
.
Hàm số đồng biến trên
0,
y x R
2
2 3 0, *
mx mx x
Trường hợp 1:
0 3 0
m y
Hàm số đồng biến trên
0
R m
thỏa yêu cầu.
Trường hợp 2:
2
0
* 0 3
3 0
m
m
m m
.
Kết hợp hai trường hợp ta có
0 3
m
nên
0
m
thỏa yêu cầu đề bài.
Câu 23:
(THPT Hậu Lộc 2-Thanh Hóa-ần 1-năm 2017-2018)
Trong các hàm số sau, hàm số nào tuần hoàn
với chu kì
2
?
A.
cos2y x
. B.
siny x
. C.
tany x
. D.
.
Lời giải
Chọn B
Theo định nghĩa, hàm số
siny x
tuần hoàn với chu kì
2
, các hàm số lượng giác còn lại
tany x
,
,
cos2y x
tuần hoàn với chu kì
.
Xét
cos 2y x
: ta có
cos2 cos 2 2 cos 2
y x x x x y x
nên
cos2y x
tuần hoàn với chu kì
.
Câu 24:
(THPT Chuyên Lam-Thanh Hóa-lần 1-năm 2017-2018)
Nghiệm phương trình
2sin 1x
có
dạng nào dưới đây?
A.
2
3
2
2
3
x k
k
x k
. B.
2
6
5
3
6
x k
k
x k
.
C.
2
6
5
2
6
x k
k
x k
. D.
2
6
2
6
x k
k
x k
.
Lời giải
Chọn C
Ta có:
2
6
2sin 1 sin sin
5
6
2
6
x k
x x k
x k
.
Câu 25:
(THPT Cổ Loa-Hà Nội-lần 1-nawm-2018)
Tập xác định của hàm số
tany x
là
A.
. B.
\ ,
2
k k
.
C.
\ ,
k k
. D.
\ ,
2 2
k k
.
Lời giải
Chọn B
Hàm số xác định khi
,
2
x k k
.
Vậy tập xác định của hàm số đã cho là
\ ,
2
k k
.
Câu 26:
(THPT Cổ Loa-Hà Nội-lần 1-nawm-2018)
Phương trình
3
tan 3 30
3
x
có tập nghiệm
là
A.
180 ,
k k
. B.
60 ,
k k
. C.
360 ,
k k
. D.
90 ,
k k
.
Lời giải
Chọn B
3
tan 3 30
3
x
tan 3 30 tan 30
x
3 30 30 180
x k
60 ,
x k k
.
Câu 27:
(THPT Cổ Loa-Hà Nội-lần 1-nawm-2018)
Nghiệm của phương trình
cos 2 5sin 3 0
x x
là
A.
2
6
,
7
2
6
x k
k
x k
. B.
2
3
,
7
2
3
x k
k
x k
.
C.
6
,
7
6
x k
k
x k
. D.
3
,
7
3
x k
k
x k
.
Lời giải
Chọn A
cos2 5sin 3 0
x x
2
1 2sin 5sin 3 0
x x
2
2sin 5sin 2 0
x x
1
sin ( )
2
sin 2( )
x n
x l
2
6
sin sin ,
7
6
2
6
x k
x k
x k
.
Câu 28:
(THPT Chuyên Lê Hồng Phong-Nam Định-lần 2 năm 2017-2018)
Tìm tập xác định
D
của hàm
số
tan 1
cos
sin 3
x
y x
x
.
A.
\ ,D k k
. B.
\ ,
2
k
D k
.
C.
\ ,
2
D k k
. D.
D
.
Lời giải
Chọn B
Hàm số
tan 1
cos
sin 3
x
y x
x
xác định khi:
sin 0
sin 2 0 2
cos 0
2
x
k
x x k x
x
,
( )
k
.
Câu 29:
(SGD Vĩnh Phúc-KSCL lần 1 năm 2017-2018)
Phương trình
3
cos
2
x
có tập nghiệm là:
A.
;
6
k k
. B.
2 ;
6
k k
.
C.
;
3
k k
. D.
2 ;
3
k k
.
Lời giải
Chọn B
3
cos cos
2 6
x
2 ; .
6
x k k
Câu 30:
(THPT Triệu Sơn 3-Thanh Hóa năm 2017-2018)
Nghiệm của phương trình
sin 1
x
là:
A.
2 2
k
x
. B.
2
2
x k
. C.
2x k
. D.
2
x k
.
Lời giải
Chọn B
Ta có:
sin 1 2 ,
2
x x k k
.
Câu 31:
(THPT Triệu Sơn 3-Thanh Hóa năm 2017-2018)
Chu kì tuần hoàn của hàm số
sin 2y x
là:
A.
3
. B.
2
. C.
2
. D.
.
Lời giải
Chọn D
Ta có
sin 2 sin 2 2 sin 2y x x x
. Suy ra chu kì của hàm số là
T
.
Giải nhanh: Hàm số
sin
y ax b
là
2 2
2
T
a
.
Câu 1:
(THPT Chuyên Vĩnh Phúc-MĐ 903 lần 1-năm 2017-2018)
Phương trình
tan 3
x có tập
nghiệm là
A.
2 ,
3
k k
. B.
. C.
,
3
k k
. D.
,
6
k k
.
Lời giải
Chọn A
Ta có
tan 3
x
tan tan
3
x
3
x k
,
k
.
Câu 2:
(THPT Chuyên Vĩnh Phúc-lần 1 MĐ 904 năm 2017-2018)
Phương trình
2cos 1 0
x
có một
nghiệm là
A.
6
x
. B.
2
3
x
. C.
3
x
. D.
5
6
x
.
Lời giải
Chọn C
Phương trình
2cos 1 0
x
1
cos
2
x
2
3
x k
.
Vậy các nghiệm của phương trình là
2
3
x k
,
k
.
Câu 3:
(THPT Kiến An-Hải Phòng năm 2017-2018)
Có bao nhiêu số nguyên
m
để phương trình
5sin 12cos
x x m
có nghiệm?
A.
13
. B. Vô số. C.
26
. D.
27
.
Lời giải
Chọn D
Phương trình
5sin 12cos
x x m
có nghiệm khi và chỉ khi
2
2 2
5 12
m
2
169
m
13 13
m
.
Suy ra có
27
số nguyên
m
để phương trình
5sin 12cos
x x m
có nghiệm.
Câu 4:
(THPT Kiến An-Hải Phòng năm 2017-2018)
Tìm tất cả các nghiệm của phương trình
tan x m
,
m
.
A.
arctan
x m k
hoặc
arctan
x m k
,
k
.
B.
arctan
x m k
,
k
.
C.
arctan 2x m k
,
k
.
D.
arctan
x m k
,
k
.
Lời giải
Chọn D
Ta có:
tan arctan
x m x m k
,
k
.
Câu 5:
(THPT Chuyên Lương Văn Tụy-Ninh Bình lần 1 năm 2017-2018)
Tập xác định của hàm số
tany x
là:
A.
\ ,
2
D k k
. B.
\ ,D k k
.
C.
\ 2 ,D k k
. D.
\ 2 ,
2
D k k
.
Lời giải
Chọn A
Hàm số
tany x
xác định khi:
2
x k
,
k
.
Vậy tập xác định của hàm số là:
\ ,
2
D k k
.
Câu 6:
(THPT Hà Huy Tập-Hà Tĩnh-lần 1 năm 2017-2018)
Phương án nào sau đây là sai?
A.
cos 1 2x x k
. B.
cos 0 2
2
x x k
.
C.
cos 0
2
x x k
. D.
cos 1 2x x k
.
Lời giải
Chọn B
Ta có
cos 0
2
x x k
,
k
. Do đó đáp án B sai.
Câu 7:
(THPT Triệu Thị Trinh-lần 1 năm 2017-2018)
Nghiệm của phương trình
cos 1
x
là:
A.
2
x k
,
k
. B.
2x k
,
k
.
C.
2x k
,
k
. D.
x k
,
k
.
Lời giải
Chọn C
Phương trình
cos 1
x
2x k
,
k
.
Câu 8:
(THPT Thạch Thành 2-Thanh Hóa-lần 1 năm 2017-2018)
Khẳng định nào dưới đây là sai?
A. Hàm số
là hàm số lẻ. B. Hàm số
cosy x
là hàm số lẻ.
C. Hàm số
tany x
là hàm số lẻ. D. Hàm số
là hàm số lẻ.
Lời giải
Chọn B
B sai vì hàm số
cosy x
là hàm số chẵn.
Câu 9:
(THPT Yên Lạc-Vĩnh Phúc-lần 3 năm 2017-2018)
Nghiệm của phương trình
sin 1x
là
A.
2
k
,
k
. B.
2
k
,
k
. C.
2
2
k
,
k
. D.
2
2
k
,
k
.
Lời giải
Chọn D
Ta có
sin 1x
2
2
x k
,
k
.
Câu 10:
(SGD Bắc Ninh năm 2017-2018)
Tập giá trị của hàm số
sin 2y x
là:
A.
2;2
. B.
0;2
. C.
1;1
. D.
0;1
.
Lời giải
Chọn C
Ta có
1 sin 2 1
x
,
x
.
Vậy tập giá trị của hàm số đã cho là
1;1
.
Câu 11:
(SGD Ninh Bình năm 2017-2018)
Mệnh đề nào dưới đây sai?
A. Hàm số
tany x
tuần hoàn với chu kì
. B. Hàm số
cosy x
tuần hoàn với chu kì
.
C. Hàm số
tuần hoàn với chu kì
. D. Hàm số
sin 2y x
tuần hoàn với chu kì
.
Lời giải
Chọn B
Hàm số
tany x
;
coty x
tuần hoàn với chu kì
Hàm số
siny x
;
cosy x
tuần hoàn với chu kì
2
Hàm số
sin 2 sin 2 2 sin 2y x x x
. Vậy hàm số tuần hoàn với chu kì
.
Vậy đáp án B sai.
Câu 12:
(THPT Chuyên Thái Bình-lần 3 năm 2017-2018)
Số nghiệm thực của phương trình
2sin 1 0
x
trên đoạn
3
;10
2
là:
A.
12
. B.
11
. C.
20
. D.
21
.
Hướng dẫn giải
Chọn A
Phương trình tương đương:
1
sin
2
x
2
6
7
2
6
x k
x k
, (
k
)
+ Với
2
6
x k
,
k
ta có
3
2 10
2 6
k
,
k
2 61
3 12
k
,
k
0 5
k
,
k
. Do đó phương trình có
6
nghiệm.
+ Với
7
2
6
x k
,
k
ta có
3 7
2 10
2 6
k
,
k
4 53
3 12
k
,
k
1 4
k
,
k
. Do đó, phương trình có
6
nghiệm.
+ Rõ ràng các nghiệm này khác nhau từng đôi một, vì nếu
7 2
2 2
6 6 3
k k k k
(vô lí, do
k
,
k
).
Vậy phương trình có
12
nghiệm trên đoạn
3
;10
2
.
Câu 13:
(THPT Chuyên Vĩnh Phúc - lần 3 năm 2017-2018)
Phương trình
3
cos
2
x
có tập nghiệm
là
A.
;
6
x k k
. B.
5
2 ;
6
x k k
.
C.
;
3
x k k
. D.
2 ;
3
x k k
.
Lời giải
Chọn B
Ta có
3
cos
2
x
5
cos cos
6
π
x
5
2 ,
6
π
x k π k
.
Câu 14:
(THPT Chuyên Vĩnh Phúc-lần 3 MĐ 234 năm học 2017-2018)
Phương trình
2
cos
2
x
có
tập nghiệm là
A.
2 ;
3
x k k
. B.
;
4
x k k
.
C.
3
2 ;
4
x k k
. D.
;
3
x k k
.
Hướng dẫn giải
Chọn C
2
cos
2
x
3
cos cos
4
x
3
2 ,
4
x k k
.
Vậy tập nghiệm của phương trình là
3
2 ;
4
S x k k
.
Câu 15:
(THPT Chuyên Vĩnh Phúc-lần 3 MĐ 234 năm học 2017-2018)
Giá trị lớn nhất và giá trị nhỏ
nhất của hàm số
3sin 2 5y x
lần lượt là:
A.
3
;
5
. B.
2
;
8
. C.
2
;
5
. D.
8
;
2
.
Hướng dẫn giải
Chọn B
Ta có
1 sin 2 1x
8 3sin 2 5 2
x
8 2
y
.
Vậy giá trị lớn nhất và giá trị nhỏ nhất của hàm số lần lượt là
2; 8
.
Câu 16:
(THPT Hồng Quang-Hải Dương năm 2017-2018)
Tìm nghiệm của phương trình
2sin 3 0
x
.
A.
x
. B.
3
arcsin 2
2
3
arcsin 2
2
x k
k
x k
.
C.
3
arcsin 2
2
3
arcsin 2
2
x k
k
x k
. D.
x
.
Lời giải
Chọn A
Ta có:
3
2sin 3 0 sin 1
2
x x
nên phương trình vô nghiệm.
Câu 17:
(THPT Hồng Quang-Hải Dương năm 2017-2018)
Khẳng định nào sau đây sai ?
A.
tany x
nghịch biến trong
0;
2
. B.
cosy x
đồng biến trong
; 0
2
.
C.
siny x
đồng biến trong
; 0
2
. D.
coty x
nghịch biến trong
0;
2
.
Lời giải
Chọn A
Trên khoảng
0;
2
thì hàm số
tany x
đồng biến.
Câu 18:
(THPT Kinh Môn 2-Hải Dương năm 2017-2018)
Tập xác định của hàm số
tan 2
3
y x
là:
A.
5
\
12 2
k
,
k
. B.
5
\
12
k
,
k
.
C.
5
\
6 2
k
,
k
. D.
5
\
6
k
,
k
.
Lời giải
Chọn A
Hàm số đã cho xác định khi
cos 2 0
3
x
2
3 2
x k
5
12 2
x k
,
k
.
Vậy TXĐ:
5
\
12 2
D k
,
k
.
Câu 19:
(THPT Kinh Môn 2-Hải Dương năm 2017-2018)
Phương trình
2
3 tan 1 sin 1 0
x x
có
nghiệm là:
A.
2
3
x k
. B.
6
x k
. C.
6
x k
. D.
2
6
x k
.
Lời giải
Chọn B
Điều kiện
x
2
x k
,
k
.
Do
2
sin 1 0,x x
nên phương trình đã cho tương đương với
3 tan 1 0
x
1
tan
3
x
tan tan
6
x
6
x k
,
k
(nhận).
Câu 20:
(THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018)
Phương trình
cos 1x
có nghiệm là
A.
2x k
. B.
2
x k
. C.
x k
. D.
2
2
x k
.
Lời giải
Chọn A
Phương trình
cos 1x
2x k
,
k
.
Câu 21:
(THPT Phan Đăng Lưu-Huế-lần 1 năm 2017-2018)
Phương trình
2cos 2 0
x
có tất cả
các nghiệm là
A.
3
2
4
,
3
2
4
x k
k
x k
. B.
2
4
,
2
4
x k
k
x k
.
C.
2
4
,
3
2
4
x k
k
x k
. D.
7
2
4
,
7
2
4
x k
k
x k
.
Lời giải
Chọn B
2cos 2 0
x
2
cos
2
x
2
4
,
2
4
x k
k
x k
.
Câu 22:
(THPT Quãng Xương 1-Thanh Hóa năm 2017-2018)
Tìm điều kiện xác định của hàm số
tan cot .y x x
A.
2
k
x
,
k
. B.
2
x k
,
k
. C.
x
. D.
x k
,
k
.
Lời giải
Chọn A
Điều kiện:
sin .cos 0 sin 2 0 2
2
k
x x x x k x
k
.
Câu 23:
(THPT Trần Hưng Đạo-TP HCM năm 2017-2018)
Đường cong trong hình dưới đây là đồ thị
của một hàm số trong bốn hàm số được liệt kê ở bốn phương án
A
,
B
,
C
,
D
. Hỏi hàm số đó là
hàm số nào?
A.
1 siny x
. B.
1 siny x
. C.
siny x
. D.
cosy x
.
Lời giải
Chọn D
Dựa vào lý thuyết đây là đồ thị của hàm
cosy x
.
Câu 24:
(THPT Trần Hưng Đạo-TP HCM năm 2017-2018)
Mệnh đề nào dưới đây đúng?
A. Hàm số
siny x
là hàm số chẵn. B. Hàm số
cosy x
là hàm số chẵn.
C. Hàm số
tany x
là hàm số chẵn. D. Hàm số
coty x
là hàm số chẵn.
Lời giải
Chọn B
Các hàm số
,
tany x
,
là hàm số lẻ, hàm số
cosy x
là hàm số chẵn.
Câu 25:
(THPT Trần Hưng Đạo-TP HCM năm 2017-2018)
Giải phương trình
3 tan2 3 0
x
.
A.
3 2
x k k
. B.
3
x k k
.
C.
6 2
x k k
. D.
6
x k k
.
Lời giải
Chọn C
3 tan 2 3 0 tan 2 3
x x
2
3
x k
6 2
x k k
.
Câu 26:
(THPT Chuyên Hoàng Văn Thụ-Hòa Bình năm 2017-2018)
Tập giá trị của hàm số
cosy x
là ?
A.
. B.
;0

. C.
0;

. D.
1;1
.
Lời giải
Chọn D
Với
x
, ta có
cos 1;1
x
.
Tập giá trị của hàm số
cosy x
là
1;1
.
Câu 27:
(THPT Hậu Lộc 2-Thanh Hóa năm 2017-2018)
Chọn khẳng định đúng trong các khẳng định
sau:
A. Hàm số
tany x
tuần hoàn với chu kì
2
.
B. Hàm số
cosy x
tuần hoàn với chu kì
.
C. Hàm số
siny x
đồng biến trên khoảng
0;
2
.
D. Hàm số
coty x
nghịch biến trên
.
Lời giải
Chọn C
Hàm số
tany x
tuần hoàn với chu kì
đáp án A sai.
Hàm số
cosy x
tuần hoàn với chu kì
2
đáp án B sai.
Hàm số
nghịch biến trên mỗi khoảng
;
k k
,
k
đáp án D sai.
Câu 1:
(SGD Bà Rịa Vũng Tàu-đề 2 năm 2017-2018)
Tập nghiệm của phương trình
2sin 2 1 0
x
là
A.
7
, ,
12 12
S k k k
. B.
7
2 , 2 ,
6 12
S k k k
.
C.
7
2 , 2 ,
12 12
S k k k
. D.
7
, ,
6 12
S k k k
.
Lời giải
Chọn A
Ta có:
2sin 2 1 0
x
1
sin 2
2
x
sin 2 sin
6
x
2 2
6
,
7
2 2
6
x k
k
x k
12
,
7
12
x k
k
x k
.
Vậy tập nghiệm của phương trình là
7
, ,
12 12
S k k k
.
Câu 2:
(THPT Hà Huy Tập-Hà Tĩnh-lần 2 năm 2017-2018)
Điều kiện xác định của hàm số
1 sin
cos
x
y
x
là
A.
5
12
x k
,
k
. B.
5
12 2
x k
,
k
.
C.
6 2
x k
,
k
. D.
2
x k
,
k
.
Lời giải
Chọn D
Hàm số xác định khi
cos 0
x
2
x k
,
k
.
Câu 3:
(THPT Hà Huy Tập-Hà Tĩnh-lần 2 năm 2017-2018)
Đồ thị hàm số
2 3
1
x
y
x
có các đường
tiệm cận đứng và tiệm cận ngang lần lượt là
A.
1
x
và
3
y
. B.
1
x
và
3
y
.
C.
1x
và
2
y
. D.
2
x
và
1y
.
Lời giải
Chọn C
Ta có
2 3
lim lim
1
x x
x
y
x
 
3
2
lim 2
1
1
x
x
x

nên đường thẳng
2
y
là tiệm cận ngang.
1 1
2 3
lim lim
1
x x
x
y
x

suy ra đường thẳng
1x
là tiệm cận đứng.
Câu 4:
(THPT Lý Thái Tổ-Bắc Ninh-lần 1 năm 2017-2018)
Tập xác định của hàm số
tan 2y x
là
A.
\ ,
4 2
D k k
. B.
\ ,
2
D k k
.
C.
\ ,
2
D k k
. D.
\ ,
4
D k k
.
Lời giải
Chọn A
Hàm số
tan 2y x
xác định khi
cos2 0
x
2
2
x k
,
4 2
x k k
.
Vậy tập xác định của hàm số là
\ ,
4 2
D k k
Câu 5:
(THPT Lý Thái Tổ-Bắc Ninh-lần 1 năm 2017-2018)
Cho phương trình:
3cos cos2 cos3 1 2sin .sin 2x x x x x
. Gọi
là nghiệm lớn nhất thuộc khoảng
0;2
của
phương trình. Tính
sin
4
.
A.
2
2
. B.
2
2
. C.
0
. D.
1
.
Lời giải
Chọn A
Phương trình tương đương:
3cos cos2 cos3 1 cos cos3x x x x x
2cos cos2 1 0
x x
2
cos cos 0
x x
cos 0
cos 1
x
x
2
2
x k
x k
.
Vì
0;2
x
nên
3
; ,
2 2
x
. Nghiệm lớn nhất của phương là
3
2
.
Vậy
sin
4
3
sin
2 4
5
sin
4
2
2
.
Câu 6:
(THPT Phan Đình Phùng-Hà Tĩnh-lần 1 năm 2017-2018)
Xét bốn mệnh đề sau:
(1) Hàm số
siny x
có tập xác định là
.
(2) Hàm số
cosy x
có tập xác định là
.
(3) Hàm số
tany x
có tập xác định là
\
2
D k k
.
(4) Hàm số
coty x
có tập xác định là
\
2
D k k
.
Số mệnh đề đúng là
A.
3
. B.
2
. C.
1
. D.
4
.
Lời giải
Chọn A
Các mệnh đề đúng là
(1) Hàm số
siny x
có tập xác định là
.
(2) Hàm số
cosy x
có tập xác định là
.
(3) Hàm số
tany x
có tập xác định là
\
2
D k k
.
Câu 7:
(SGD Hà Nội-lần 11 năm 2017-2018)
Phương trình
sin 1
3
x
có nghiệm là
A.
2
3
x k
. B.
5
6
x k
. C.
5
2
6
x k
. D.
2
3
x
.
Lời giải
Chọn C
sin 1
3
x
2
3 2
x k
5
2
6
x k
k
.
Câu 8: (THPT Yên Lạc – Vĩnh Phúc – lần 4 - năm 2017 – 2018) Phương trình
sin 1x
có một
nghiệm là
A.
x
. B.
2
x
. C.
2
x
. D.
3
x
.
Lời giải
Chọn C
Ta có
sin 1x
2
2
x k
k
.
Do đó
2
x
là một nghiệm của phương trình
sin 1x
.
Câu 9: Cho hàm số
f x
liên tục trên
và có đồ thị như hình vẽ dưới đây, hàm số
f x
đồng biến
trên khoảng nào?
A.
;0

. B.
; 1
.
C.
1;

. D.
1;1
.
Câu 10:
(THPT Chuyên Ngữ – Hà Nội - Lần 1 năm 2017 – 2018)
Cho hàm số
f x
liên tục trên
và có đồ
thị như hình vẽ dưới đây, hàm số
f x
đồng biến trên khoảng nào?
A.
;0

. B.
; 1
. C.
1;

. D.
1;1
.
Lời giải
Chọn B
Dựa vào đồ thị ta thấy hàm số nghịch biến trên các khoảng
; 1
và
0;1
.
Vậy chỉ có phương án B thỏa mãn.
Câu 11: (THPT Chuyên Vĩnh Phúc – Vĩnh Phúc - Lần 4 năm 2017 – 2018)Tìm nghiệm của
phương trình
sin 2 1x
.
A.
2
2
x k
. B.
4
x k
. C.
2
4
x k
. D.
2
k
x
.
Lời giải
Chọn B
Ta có:
sin 2 1 2 2
2 4
x x k x k
.
O
x
y
1
1
1
O
x
y
1
1
1
Câu 12: (THPT Trần Phú – Hà Tĩnh - Lần 2 năm 2017 – 2018)Trong mặt phẳng
Oxy
, cho điểm
3;0
A
và vectơ
1;2
v
. Phép tịnh tiến
v
T
biến
A
thành
A
. Tọa độ điểm
A
là
A.
4;2
A
. B.
2; 2
A
. C.
2;2
A
. D.
2; 1
A
.
Lời giải
Chọn A
Biểu thức tọa độ của phép tịnh tiến
v
T
là
1
2
x x
y y
nên ảnh của điểm
3;0
A
là điểm
4;2
A
.
Câu 13: (SGD Quảng Nam – năm 2017 – 2018) Tìm tất cả các nghiệm của phương trình
sin 1
6
x
.
A.
3
x k
k
. B.
2
6
x k
k
.
C.
2
3
x k
k
. D.
5
2
6
x k
k
.
Lời giải
Chọn C
Ta có
sin 1
6
x
2
6 2
x k
2
3
x k
k
.
Câu 14: (THPT Trần Phú – Đà Nẵng - Lần 2 – năm 2017 – 2018) Giải phương trình
2cos 1 0
x
A.
3
,x k k
. B.
2
3
,
2
2
3
x k
x k
k
.
C.
3
,2x k k
. D.
3
,
2
3
x
k
k
k
x
.
Lời giải
Chọn C
TXĐ:
D
. Ta có
2cos 1 0
x
1
cos
2
x
2
3
x k
,
k
.
Câu 1:
(SGD Thanh Hóa – năm 2017 – 2018)
Cho các mệnh đề sau
I
Hàm số
2
sin
1
x
f x
x
là hàm số chẵn.
II
Hàm số
3sin 4cosf x x x
có giá trị lớn nhất là
5
.
III
Hàm số
tanf x x
tuần hoàn với chu kì
2
.
IV
Hàm số
cosf x x
đồng biến trên khoảng
0;
.
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn A
* Xét hàm số
2
sin
1
x
f x
x
.
Tập xác định:
D
.
x D
, ta có:
x D
và
2
sin
1
x
f x
x
2
sin
1
x
x
.
Vậy hàm số
2
sin
1
x
f x
x
là hàm số lẻ.
Do đó
I
sai.
* Xét hàm số
3sin 4cosf x x x
.
Tập xác định:
D
.
Ta có:
3sin 4cosf x x x
3 4
5 sin cos
5 5
x x
Đặt
3
sin
5
,
4
cos
5
. Ta có
5sin 5
f x x
max 5
f x
khi
sin 1
x
2
2
x k
,
k
.
Vậy hàm số
3sin 4cosf x x x
có giá trị lớn nhất là
5
.
Do đó
II
đúng.
* Xét hàm số
tanf x x
. Ta có hàm số
f x
tuần hoàn với chu kì
.
Do đó
III
sai.
* Xét hàm số
cosf x x
. Ta có
f x
nghịch biến trên mỗi khoảng
2 ; 2
k k
với
k
.
Do đó
IV
sai.
Vậy trong bốn mệnh đề đã cho có một mệnh đề đúng.
Câu 2:
(THPT Chuyên Hùng Vương – Gia Lai – Lần 2 năm 2017 – 2018)
Hàm số
siny x
đồng biến
trên mỗi khoảng nào dưới đây.
A.
2 ; 2
2 2
k k
,
k
. B.
3
2 ; 2
2 2
k k
,
k
.
C.
2 ; 2
k k
,
k
. D.
2 ; 2
k k
,
k
.
Lời giải
Chọn A
Câu 3: (THPT Nghèn – Hà Tĩnh – Lần 2 năm 2017 – 2018) Phương trình
sin
x m
vô nghiệm khi và
chỉ khi:
A.
1
1
m
m
. B.
1 1
m
. C.
1
m
. D.
1
m
.
Lời giải
Chọn A
Do
1 sin 1x
,
x
nên phương trình
sin
x m
vô nghiệm khi và chỉ khi
1
1
m
m
.
Câu 4:
(THPT Chuyên Võ Nguyên Giáp – Quảng Bình - năm 2017-2018)
Nghiệm của phương trình
sin 2 1x
là.
A.
2
2
x k
. B.
4
x k
. C.
2
4
x k
. D.
2
k
x
.
Hướng dẫn giải
Chọn B
Ta có:
sin 2 1x
2 2
2
x k
4
x k
.
Câu 5:
(SGD Bắc Ninh – Lần 2 - năm 2017-2018)
Trong các phương trình sau phương trình nào vô
nghiệm?
A.
tan 2018
x
. B.
sin x
. C.
2017
cos
2018
x
. D.
sin cos 2
x x
.
Lời giải
Chọn B
*
tan 2018
x
arctan 2018
x k
,
k
.
*
sin x
(vô nghiệm do
1
).
*
2017
cos
2018
x
2017
arccos 2
2018
x k
,
k
.
*
sin cos 2
x x
sin 1
4
x
2
4
x k
,
k
.
Câu 6:
(Chuyên Lê Hồng Phong – Nam Đinh - năm 2017-2018)
Tập xác định của hàm số
tan 2y x
là?
A.
\ ,
4
D k k
. B.
\ ,
4 2
D k k
.
C.
\ ,
2
D k k
. D.
\ ,
2
D k k
.
Hướng dẫn giải
Chọn B
Điều kiện:
cos 2 0
x
2
2
x k
,
4 2
x k k
.
Vậy tập xác định là
\ ,
4 2
D k k
.
Câu 7: Phương trình
sin sin
x
(hằng số
) có nghiệm là
A.
,x k x k k
. B.
2 , 2x k x k k
.
C.
2 , 2x k x k k
. D.
,x k x k k
.
Câu 8: Phương trình
sin sin
x
(hằng số
) có nghiệm là
A.
,x k x k k
. B.
2 , 2x k x k k
.
C.
2 , 2x k x k k
. D.
,x k x k k
.
Lời giải
Chọn C
Câu 9: Nghiệm của phương trình
2
sin 4sin 3 0
x x
là
A.
2 ,
2
x k k
. B.
2 ,
x k k
.
C.
2 ,
2
x k k
. D.
2 ,
x k k
Câu 10: Nghiệm của phương trình
2
sin 4sin 3 0
x x
là
A.
2 ,
2
x k k
. B.
2 ,
x k k
.
C.
2 ,
2
x k k
. D.
2 ,
x k k
Lời giải
Chọn C
2
sin 4sin 3 0
x x
sin 1
sin 3
x
x
.
Với
sin 1x
2 ,
2
x k k
.
Với
sin 3
x
phương trình vô nghiệm.
Câu 11: Tập nghiệm của phương trình
sin 2 sinx x
là
A.
π
2π; 2π
3
S k k k
.
B.
π 2π
2π;
3 3
k
S k k
.
C.
π
2π; 2π
3
S k k k
. D.
2π;π 2πS k k k
.
Câu 12: Tập nghiệm của phương trình
sin 2 sinx x
là
A.
π
2π; 2π
3
S k k k
.
B.
π 2π
2π;
3 3
k
S k k
.
C.
π
2π; 2π
3
S k k k
. D.
2π;π 2πS k k k
.
Lời giải
Chọn B
Ta có
sin 2 sinx x
2 2π
2
π 2π
x x k
x x k
2π
π 2π
3 3
x k
k
x
k
.
Câu 13: Tìm tập xác định
D
của hàm số
2
tan 5
1 sin
x
y
x
.
A.
π
\ π,
2
D k k
. B.
D
.
C.
π
\ 2π,
2
D k k
. D.
\ π π,D k k
.
Câu 14: Tìm tập xác định
D
của hàm số
2
tan 5
1 sin
x
y
x
.
A.
π
\ π,
2
D k k
. B.
D
.
C.
π
\ 2π,
2
D k k
. D.
\ π π,D k k
.
Lời giải
Chọn A
Điều kiện:
2
cos 0
sin 1
x
x
cos 0
x
π
π,
2
x k k
.
Vậy:
π
\ π,
2
D k k
.
Câu 15: Phương trình nào sau đây vô nghiệm?
A.
2cos 3
x
. B.
2sin 3
x
. C.
3tan 2
x
. D.
2 cot 3
x
.
Câu 16: Phương trình nào sau đây vô nghiệm?
A.
2cos 3
x
. B.
2sin 3
x
. C.
3tan 2
x
. D.
2 cot 3
x
.
Lời giải
Chọn A
2cos 3
x
3
cos
2
x
, phương trình vô nghiệm.
Câu 17: Tìm tất cả các giá trị thực của tham số
m
để phương trình
sin
x m
có nghiệm thực.
A.
0
m
. B.
1 1
m
. C.
1 1
m
. D.
0
m
.
Câu 18: Tìm tất cả các giá trị thực của tham số
m
để phương trình
sin
x m
có nghiệm thực.
A.
0
m
. B.
1 1
m
. C.
1 1
m
. D.
0
m
.
Lời giải
Chọn B
Do
1 sin 1, x x
nên phương trình
sin
x m
có nghiệm khi và chỉ khi
1 1
m
.
Câu 19: Với giá trị nào của
m
thì phương trình
sin
x m
có nghiệm?
A.
1
m
. B.
1
m
. C.
1
m
. D.
1 1
m
.
Câu 20: Với giá trị nào của
m
thì phương trình
sin
x m
có nghiệm?
A.
1
m
. B.
1
m
. C.
1
m
. D.
1 1
m
.
Hướng dẫn giải
Chọn D
Vì
1 sin 1x
nên phương trình
sin
x m
có nghiệm khi và chỉ khi
1 1
m
.
Câu 21: Chu kì tuần hoàn của hàm số
là
A.
π
2
. B.
2
π
. C.
π
. D.
πk
k
.
Câu 22: Phương trình
2cot 3 0
x
có nghiệm là
A.
3
arccot
2
x k k
. B.
6
x k k
.
C.
2
6
2
6
x k
k
x k
. D.
2
3
x k k
Câu 23: Chu kì tuần hoàn của hàm số
là
A.
π
2
. B.
2
π
. C.
π
. D.
πk
k
.
Lời giải
Chọn C
Chu kì tuần hoàn của hàm số
coty x
là
π
.
Câu 24: Phương trình
2cot 3 0
x
cónghiệmlà
A.
3
arccot
2
x k k
. B.
6
x k k
.
C.
2
6
2
6
x k
k
x k
. D.
2
3
x k k
Lời giải
Chọn A
Ta có
3
2cot 3 0 cot
2
x x
3
arccot
2
kx k
Câu 25: Tập xác định của hàm số
tany x
là:
A.
\ 0
. B.
\ ,
2
k k
.C.
. D.
\ ,k k
.
Câu 26: Tập xác định của hàm số
tany x
là:
A.
\ 0
. B.
\ ,
2
k k
.C.
. D.
\ ,k k
.
Lời giải
Chọn B
Điều kiện xác định:
x
2
x k
,
k
.
Vậy tập xác định là
\ ,
2
k k
.
Câu 27: Cho hàm số
y f x
xác định trên
và có bảng biến thiên sau:
Hỏi mệnh đề nào sau đây là mệnh đề sai?
A. Hàm số nghịch biến trên khoảng
;0

.
B. Hàm số có ba điểm cực trị.
C. Đồ thị hàm số
y f x
không có tiệm cận ngang.
D. Điểm cực tiểu của đồ thị hàm số là
0
x
.
Câu 28: Cho hàm số
y f x
xác định trên
và có bảng biến thiên sau:
Hỏi mệnh đề nào sau đây là mệnh đề sai?
A. Hàm số nghịch biến trên khoảng
;0

.
B. Hàm số có ba điểm cực trị.
C. Đồ thị hàm số
y f x
không có tiệm cận ngang.
D. Điểm cực tiểu của đồ thị hàm số là
0
x
.
Lời giải
Chọn B
Dựa vào bảng biến thiên hàm số có ba điểm cực trị là sai.
Câu 29: Hàm số
tuần hoàn với chu kỳ bằng
A.
. B.
2
. C.
. D.
2
.
Câu 30: Hàm số
tuần hoàn với chu kỳ bằng
A.
. B.
2
. C.
. D.
2
.
Lời giải
Chọn B
Hàm số
tuần hoàn với chu kỳ bằng
2
.
Câu 31: Phương trình nào trong số các phương trình sau có nghiệm?
A.
sin 3cos 6
x x
. B.
2sin 3cos 1x x
.
C.
sin 2
x
. D.
cos 3 0
x
.
Câu 32: Phương trình nào trong số các phương trình sau có nghiệm?
A.
sin 3cos 6
x x
. B.
2sin 3cos 1x x
.
C.
sin 2
x
. D.
cos 3 0
x
.
Hướng dẫn giải
Chọn B
x
f x

f x
1
0
1

0
0

1
3

x
f x

f x
1
0
1

0
0

1
3

Ta có
1 sin 1
1 cos 1
x
x
nên hai phương trình ở C và D vô nghiệm.
Phương trình lượng giác dạng
sin cos
a x b x c
có nghiệm khi
2 2 2
a b c
.
Đáp án A:
2 2 2
1 3 6
nên phương trình vô nghiệm.
Đáp án B:
2
2
2 3 1
nên phương trình có nghiệm.
Câu 1:
(THPT Chuyên Hùng Vương-Phú Thọ-lần 1-NH2017-2018)
Phương trình
sin 2 3cos 0
x x
có bao nhiêu nghiệm trong khoảng
0;
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải.
Chọn B
sin 2 3cos 0
x x
2sin .cos 3cos 0
x x x
cos . 2sin 3 0
x x
cos 0
2
3
sin
2
loai vì sin 1;1
x x k k
x x
Theo đề:
0; 0
2
x k x
.
Câu 2:
(THTT Số 1-484 tháng 10 năm 2017-2018)
Cho phương trình
5
cos2 4cos
3 6 2
x x
.
Khi đặt
cos
6
t x
, phương trình đã cho trở thành phương trình nào dưới đây?
A.
2
4 8 3 0
t t
. B.
2
4 8 3 0
t t
. C.
2
4 8 5 0
t t
. D.
2
4 8 5 0
t t
.
Lời giải
Chọn A
Phương trình tương đương với:
5
cos2 4cos 0
6 6 2
x x
2
4cos 8cos 3 0
6 6
x x
, nên nếu đặt
cos
6
t x
phương trình trở thành
2 2
4 8 3 0 4 8 3 0
t t t t
.
Câu 3:
(THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018)
Nghiệm của phương trình
2
cos
4 2
x
là
A.
2
2
x k
k
x k
. B.
2
x k
k
x k
.
C.
2
2
x k
k
x k
. D.
2
2
2
x k
k
x k
.
Lời giải
Chọn D
Phương trình
2
2
cos cos cos
4 2 4 4
2
2
x k
x x k
x k
.
Câu 4:
(THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018)
Tìm tập xác định
D
của
hàm số
tan 2y x
:
A.
\ 2 |
4
D k k
. B.
\ |
2
D k k
.
C.
\ |
4
D k k
. D.
\ |
4 2
D k k
.
Giải:
Chọn D
Hàm số xác định khi
cos2 0 2
2 4 2
x x k x k k
.
Tập xác định của hàm số là:
\ |
4 2
D k k
.
Câu 5:
(THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018)
Chọn phát biểu đúng:
A. Các hàm số
,
cosy x
,
coty x
đều là hàm số chẵn.
B. Các hàm số
siny x
,
cosy x
,
đều là hàm số lẻ.
C. Các hàm số
,
coty x
,
tany x
đều là hàm số chẵn
D. Các hàm số
,
coty x
,
tany x
đều là hàm số lẻ.
Giải:
Chọn D
Hàm số
cosy x
là hàm số chẵn, hàm số
,
coty x
,
tany x
là các hàm số lẻ.
Câu 6:
(THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018)
Phương trình
cos 2 4sin 5 0
x x
có bao nhiêu nghiệm trên khoảng
0;10
?
A.
5
. B.
4
. C.
2
. D.
3
.
Lời giải
Chọn A
PT đã cho
2
2sin 4sin 6 0
x x
sin 1
sin 3
x
x VN
2 ,
2
x k k
.
Theo đề:
0;10
x
0 2 10
2
k
1 21
4 4
k
.
Vì
k
nên
1;2;3;4;5
k
. Vậy PT đã cho có 5 nghiệm trên khoảng
0;10
.
Câu 7:
(THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018)
Tìm góc
; ; ;
6 4 3 2
để phương trình
cos2 3 sin 2 2cos 0
x x x
tương đương với phương trình
cos 2 cosx x
.
A.
6
. B.
4
. C.
2
. D.
3
.
Lời giải
Chọn D
2
2 2
cos 2 cos
3 3
2 2
2
k
x x k
x
x x
x x k
x k
cos2 3 sin 2 2cos 0
x x x
1 3
cos2 sin 2 cos
2 2
x x x
cos 2 cos
3
x x
2
3
2
9 3
x k
k
x
Để hai phương trình tương đương cần có
3 9
3
3
.
Câu 8:
(THPT Hoa Lư A-Ninh Bình-lần 1-năm 2017-2018)
Tìm tập xác định
D
của hàm số
1
sin cos
y
x x
.
A.
\ |D k k
. B.
\ |
2
D k k
.
C.
\ |
4
D k k
. D.
\ 2 |D k k
.
Lời giải
Chọn C
Hàm số đã cho xác định khi và chỉ khi
sin cos 0 sin 0 ,
4 4
x x x x k k
.
Câu 9:
(THPT Hoa Lư A-Ninh Bình-lần 1-năm 2017-2018)
Tìm tập giá trị của hàm số
3 sin cos 2
y x x
.
A.
2; 3
. B.
3 3; 3 1
. C.
4;0
. D.
2;0
Lời giải
Chọn C
Xét
3 sin cos 2
y x x
2 sin .cos cos .sin 2
6 6
x x
2sin 2
6
x
Ta có
1 sin 1
6
x
4 2sin 2 0
6
x
4 0
y
với mọi
x
Vậy tập giá trị của hàm số là
4;0
.
Câu 10:
(THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018)
Trong bốn hàm số:
(1) cos2y x
,
(2) siny x
;
(3) tan 2y x
;
(4) cot 4y x
có mấy hàm số tuần hoàn với chu kỳ
?
A.
1
. B.
0
. C.
2
. D.
3
.
Lời giải
Chọn A
Do hàm số
cosy x
tuần hoàn với chu kỳ
2
nên hàm số
(1) cos2y x
tuần hoàn chu kỳ
.
Hàm số
(2) siny x
tuần hoàn với chu kỳ
2
.
Do hàm số
tany x
tuần hoàn với chu kỳ
nên hàm số
(3) tan 2y x
tuần hoàn chu kỳ
2
.
Do hàm số
coty x
tuần hoàn với chu kỳ
nên hàm số
(4) cot 4y x
tuần hoàn chu kỳ
4
.
Câu 11:
(THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018)
Giải phương trình
2
2sin 3 sin 2 3
x x
.
A.
2
3
x k
. B.
3
x k
. C.
4
3
x k
. D.
5
3
x k
.
Lời giải
Chọn B
Cách 1: Xét
cos 0:
x
Phương trình tương đương
2 3
ktm
Xét
cos 0
x
, chia cả hai vế cho
2
cos x
ta có:
2 2 2
2 tan 2 3 tan 3 tan 1 tan 2 3 tan 3 0
x x x x x
tan 3
x
,
3
x k k

Cách 2:
2
1 2 sin 3 sin 2 2
pt x x
2sin 2 2
6
x
3
x k
.
Câu 12:
(THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018)
Tính tổng
S
của các nghiệm của phương
trình
1
sin
2
x
trên đoạn
;
2 2
.
A.
5
6
S
. B.
3
S
. C.
2
S
. D.
6
S
.
Lời giải
Chọn D
Ta có:
2
1
6
sin
5
2
2
6
x k
x
x k
k
.
Vì
;
2 2
x
nên
6 6
x S
.
Câu 13:
(THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018)
Giải phương trình
sin3 4sin cos2 0.
x x x
A.
2
3
2
3
k
x
x k
B.
2
4
k
x
x k
C.
2
3
x k
x k
D.
6
x k
x k
Lời giải
Chọn D
Cách 1: ĐK:
x
(*)
Phương trình
2
sin 3 4sin 4sin cos 2 0
x x x x
1 cos2
sin 3 4. 4cos 2 0 sin 1 2cos2 0
2
x
x x x x
sin 0
1
cos2 cos 2 2
2 3 3 6
x x k x k
k
x x k x k
thỏa mãn (*).
Cách 2: Phương trình
sin 3 2 sin 3 sin 0
x x x
sin 3 2 sin 0
x x
2
sin 4sin 1 0
x x
sin 1 2cos2 0
x x
6
x k
x k
Câu 14:
(THPT Xuân Hòa-Vĩnh Phúc-năm 2017-2018)
Phương trình
3
sin 2 sin
4 4
x x
có
tổng các nghiệm thuộc khoảng
0;
bằng
A.
7
2
. B.
. C.
3
2
. D.
4
.
Lời giải
Chọn B
Ta có
3
sin 2 sin
4 4
x x
3
2 2
4 4
2 2
4 4
x x k
x x l
2
,
2
6 3
x k
k l
x l
.
Họ nghiệm
2x k
không có nghiệm nào thuộc khoảng
0;
.
2
0;
6 3
x l
2
0
6 3
l
0; 1
l
.
Vậy phương trình có hai nghiệm thuộc khoảng
0;
là
6
x
và
5
6
x
. Từ đó suy ra tổng
các nghiệm thuộc khoảng
0;
của phương trình này bằng
.
Câu 15:
(THPT Xuân Hòa-Vĩnh Phúc-năm 2017-2018)
Chu kỳ của hàm số
3sin
2
x
y
là số nào sau
đây?
A.
0
. B.
2
. C.
4
. D.
.
Lời giải
Chọn C
Chu kì của hàm số
2
4
1
2
T
.
Câu 16:
(THPT Xuân Hòa-Vĩnh Phúc-năm 2017-2018)
Tập
\
2
k
D k
là tập xác định của
hàm số nào sau đây?
A.
coty x
. B.
cot 2y x
. C.
tany x
. D.
tan 2y x
Lời giải
Chọn B
Hàm số
cot 2y x
xác định khi
2
x k
2
k
x
.
Câu 17:
(THPT Xuân Hòa-Vĩnh Phúc-năm 2017-2018)
Khi
x
thay đổi trong khoảng
5 7
;
4 4
thì
siny x
lấy mọi giá trị thuộc
A.
2
1;
2
. B.
2
;0
2
C.
1;1
. D.
2
;1
2
.
Lời giải
Chọn A
Trong nửa khoảng
5 3
;
4 2
:
Hàm số
siny x
giảm nên
3 5 2
sin sin sin 1 sin
2 4 2
x x
.
Trong nửa khoảng
3 7
;
2 4
:
Hàm số
siny x
tăng nên
3 7 2
sin sin sin 1 sin
2 4 2
x x
.
Vậy khi
x
thay đổi trong khoảng
5 7
;
4 4
thì
lấy mọi giá trị thuộc
2
1;
2
.
Câu 18:
(THPT Sơn Tây-Hà Nội-lần 1-năm 2017-2018)
Tìm số điểm phân biệt biểu diễn các nghiệm của
phương trình
2
sin 2 cos 2 1 0
x x
trên đường tròn lượng giác.
A.
1
. B.
3
. C.
2
. D.
4
.
Lời giải
Chọn C
2 2
sin 2 cos 2 1 0 cos 2 cos 2 2 0
x x x x
cos2 1
cos2 2
x
x k k
x VN
.
Vậy có hai điểm phân biệt biểu diễn nghiệm của phương trình trên đường tròn lượng giác.
Câu 19:
(THPT Sơn Tây-Hà Nội-lần 1-năm 2017-2018)
Giải phương trình
cos 3 sin
0
2sin 1
x x
x
.
A.
5
2 , .
6
x k k
B.
5
, .
6
x k k
C.
2 , .
6
x k k
D.
, .
6
x k k
Lời giải
Chọn A
Điều kiện
2
1
6
sin , .
5
2
2
6
x k
x k
x k
Với điều kiện trên ta có
1 3
cos 3 sin 0 cos sin 0
2 2
os 0 , .
3 3 2 6
x x x x
c x x l x l l
Đối chiếu với điều kiện ta có nghiệm của phương trình là
5
2 , .
6
x k k
Câu 20:
(THPT Chuyên ĐH Vinh-GK1-năm 2017-2018)
Phương trình
2cos 2 0
x
có tất cả các
nghiệm là
A.
2
4
,
3
2
4
x k
k
x k
. B.
7
2
4
,
7
2
4
x k
k
x k
.
C.
3
2
4
,
3
2
4
x k
k
x k
. D.
2
4
,
2
4
x k
k
x k
.
Lời giải
Chọn C
Ta có
3
2
2 3
4
2cos 2 0 cos cos ,
3
2 4
2
4
x k
x x k
x k
.
Câu 21:
(THPT Chuyên ĐH Vinh-GK1-năm 2017-2018)
Nghiệm của phương trình
8.cos2 .sin 2 .cos4 2
x x x
là
A.
8 8
3
8 8
x k
k
x k
. B.
32 8
3
32 8
x k
k
x k
.
C.
16 8
3
16 8
x k
k
x k
. D.
32 4
3
32 4
x k
k
x k
.
Hướng dẫn giải
Chọn D
Cách 1:
8.cos2 .sin 2 .cos4 2
x x x
4sin 4 .cos4 2
x x
2sin 8 2
x
2
sin8
2
x
8 2
4
3
8 2
4
x k
x k
32 4
3
32 4
x k
k
x k
.
Cách 2: Hàm số
8.cos2 .sin 2 .cos 4 4sin 4 .cos 4 2sin8y x x x x x x
có chu kỳ
2
8 4
T
nên
trong công thức nghiệm có
4
k
. Do vậy, chọn D
Câu 22:
(THPT Chuyên ĐH Vinh-GK1-năm 2017-2018)
Phương trình
tan cotx x
có tất cả các
nghiệm là:
A.
4 4
x k k
. B.
4 2
x k k
.
C.
2
4
x k k
. D.
4
x k k
.
Lời giải
Chọn B
ĐK:
2
x k
ta có:
2
tan cot tan 1 0
x x x
.
1
4
4
x k
x k
4 2
x k k
.
Kết hợp điều kiện vậy phương trình có nghiệm:
4 2
x k k
Câu 23:
(THPT Yên Lạc-Vĩnh Phúc-lần 1-năm 2017-2018)
Hệ số góc của tiếp tuyến của đồ thị hàm số
4 2
1
4 2
x x
y
tại điểm có hoành độ
0
1
x
bằng
A.
2
. B. Đáp số khác. C.
2
. D.
0
.
Lời giải
Chọn A
3
1 2
y x x y
.
Câu 24:
(THPT Yên Lạc-Vĩnh Phúc-lần 1-năm 2017-2018)
Tìm
m
để phương trình
2
2sin .sin 2 2x m x m
vô nghiệm.
A.
0;
m
4
3
m
. B.
0;
m
4
3
m
. C.
4
0
3
m
. D.
0
m
hoặc
4
3
m
.
Lời giải
Chọn D
Xét phương trình
sin cos 0
a x b x c
có nghiệm khi
2 2 2
a b c
. Vậy để phương trình vô
nghiệm thì
2 2 2
a b c
.
Ta có:
2
2sin .sin 2 2x m x m
1 cos2 .sin 2 2x m x m
.sin 2 cos2 2 1 0
m x x m
.
Để phương trình
vô nghiệm thì
2 2
2
1 2 1
m m
2
3 4 0
m m
0
4
3
m
m
.
Câu 25:
(THPT Yên Lạc-Vĩnh Phúc-lần 1-năm 2017-2018)
Tìm nghiệm của phương trình
2
sin sin 0
x x
thỏa mãn điều kiện
.
2 2
x
A.
.
2
x
B.
.x
C.
0.
x
D.
.
3
x
Lời giải
Chọn C
Ta có
2
sin sin 0
x x
sin 0
sin 1
x
x
;
2
2
x k
k
x k
Đối chiếu với điều kiện
.
2 2
x
Ta được nghiệm của phương trình là
0.
x
Câu 26:
(THPT Yên Lạc-Vĩnh Phúc-lần 1-đề 2-năm 2017-2018)
Tìm
m
để phương trình
2
2sin .sin 2 2x m x m
vô nghiệm.
A.
0;
m
4
3
m
. B.
0;
m
4
3
m
. C.
4
0
3
m
. D.
0
m
hoặc
4
3
m
.
Lời giải
Chọn D
Xét phương trình
sin cos 0
a x b x c
có nghiệm khi
2 2 2
a b c
. Vậy để phương trình vô
nghiệm thì
2 2 2
a b c
.
Ta có:
2
2sin .sin 2 2x m x m
1 cos2 .sin 2 2x m x m
.sin 2 cos2 2 1 0
m x x m
.
Để phương trình
vô nghiệm thì
2 2
2
1 2 1
m m
2
3 4 0
m m
0
4
3
m
m
.
Câu 27:
(THPT Yên Lạc-Vĩnh Phúc-lần 1-đề 2-năm 2017-2018)
Tìm nghiệm của phương trình
2
sin sin 0
x x
thỏa mãn điều kiện
.
2 2
x
A.
.
2
x
B.
.x
C.
0.
x
D.
.
3
x
Lời giải
Chọn C
Ta có
2
sin sin 0
x x
sin 0
sin 1
x
x
;
2
2
x k
k
x k
Đối chiếu với điều kiện
.
2 2
x
Ta được nghiệm của phương trình là
0.
x
Câu 28:
(THPT Yên Lạc 2-Vĩnh Phúc-lần 1-năm 2017-2018)
Phương trình
x
có bao nhiêu
nghiệm thuộc khoảng
0;2018
?
A.
2017
. B.
2018
. C.
2019
. D.
1009
.
Lời giải
Chọn B
Ta có
cos 0
2
x x k
với
k
. Nghiệm thuộc khoảng
0;2018
thì
0 2018
2
k
1 4035
2 2
k
0,1,2,...,2017
k
.
Vậy phương trình có
2018
nghiệm thuộc khoảng
0;2018
.
Câu 29:
(THTT Số 2-485 tháng 11-năm học 2017-2018)
Hãy nêu tất cả các hàm số trong các hàm số
siny x
,
cosy x
,
tany x
,
thỏa mãn điều kiện đồng biến và nhận giá trị âm trong
khoảng
2
.
A.
tany x
. B.
sin , coty x y x
.
C.
siny x
,
tany x
. D.
tany x
,
cosy x
.
Lời giải
Chọn C
Vì hàm số
coty x
luôn nghịch biến trên từng khoảng xác định nên loại ngay đáp án B.
Dựa vào đồ thị của các hàm số lượng giác
siny x
,
cosy x
và
tany x
trên khoảng
;0
2
ta thấy hàm
và
tany x
thỏa.
Câu 30:
(THPT Việt Trì-Phú Thọ-lần 1-năm 2017-2018)
Trên đoạn
5
2 ;
2
, đồ thị hai hàm số
siny x
và
cosy x
cắt nhau tại bao nhiêu điểm?
A.
2
. B.
5
. C.
4
. D.
3
.
Lời giải
Chọn B
Phương trình hoành độ giao điểm của hai đồ thị hàm số là
sin cos tan 1
4
x x x x k k
.
Do
5
2 ;
4 2
x k
nên
5
2
4 2
k
9 9
4 4
k
2; 1;0;1;2
k
.
Vậy đồ thị hai hàm số đã cho cắt nhau tại
5
điểm trên đoạn
5
2 ;
2
.
Câu 31:
(THPT Thạch Thành-Thanh Hóa-năm 2017-2018)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của
hàm số
2sin 3
y x
.
A.
max 5,
y
min 1y
. B.
max 5,
y
min 2 5
y
.
C.
max 5,
y
min 2
y
. D.
max 5,
y
min 3
y
.
Lời giải
Chọn A
Ta có
1 sinx 1; x
1 2sinx+3 5; x
1 5; y x
Câu 32:
(THPT Thạch Thành-Thanh Hóa-năm 2017-2018)
Tìm chu kỳ cơ sở (nếu có) của hàm số
tan 2f x x
.
A.
0
2
T
. B.
0
2
T
. C.
0
T
. D.
0
3
T
.
Lời giải
Chọn B
Ta có
tan 2
2
f x k x k
tan 2x
; , f x x k
0
2
T
Câu 33:
(THPT Thạch Thành-Thanh Hóa-năm 2017-2018)
Hàm số
siny x
đồng biến trên mỗi
khoảng:
A.
2 ; 2
2 2
k k
với
k
. B.
3 5
2 ; 2
2 2
k k
với
k
.
C.
5
2 ; 2
2 2
k k
với
k
. D.
2 ; 2
2
k k
với
k
.
Lời giải
Chọn A
Nhìn vào đồ thị hàm số
ta thấy đồ thị hàm số là đường cong đi lên từ trái qua phải
trong các khoảng
2 ; 2
2 2
k k
với
k
nên đáp án là A.
Câu 34:
(THPT Thạch Thành-Thanh Hóa-năm 2017-2018)
Phương trình
sin 3 cos 1x x
chỉ có các
nghiệm là:
A.
2
2
( )
7
2
6
x k
k
x k
. B.
2
2
( )
7
2
6
x k
k
x k
.
C.
2
2
( )
7
2
6
x k
k
x k
. D.
2
2
( )
7
2
6
x k
k
x k
.
Lời giải
Chọn A
1
sin 3 cos 1 2sin sin sin
3 3 2 6
x x x x
2
3 6
5
2
3 6
x k
x k
2
2
7
2
6
x k
x k
Câu 35:
(THPT Thạch Thành-Thanh Hóa-năm 2017-2018)
Phương trình
2 2
sin 4sin cos + 3cos 0
x x x x
có tập nghiệm trùng với nghiệm của phương trình nào sau
đây?
A.
cos 0
x
. B.
cot 1x
. C.
tan 3
x
. D.
tan 1
1
cot
3
x
x
.
Lời giải
Chọn D
Dễ thấy với
x
không là nghiệm của phương trình đầu.
Với
cos 0
x
, chia 2 vế cho
2
cos x
, ta có:
2
tan 4 tan 3 0
x x
tan 1
tan 3
x
x
tan 1
1
cot
3
x
x
Câu 36:
(THPT Thạch Thành-Thanh Hóa-năm 2017-2018)
Giải phương trình
1
sin 2
3 2
x
A.
4
( )
5
12
x k
k
x k
. B.
4
( )
5
12
x k
k
x k
.
C.
4
( )
12
x k
k
x k
. D.
4 2
( )
12 2
x k
k
x k
.
Lời giải
Chọn A
Phương trình
sin 2 sin
3 6
x
2 2
3 6
2 2
3 6
x k
x k
4
,
5
12
x k
k
x k
Câu 37:
(THPT Chuyên Vĩnh Phúc-lần 2-năm 2017-2018)
Tìm tất cả các giá trị của tham số m để phương
trình
2
cos 1
x m
có nghiệm.
A.
1 2
m
. B.
2
m
. C.
1 2
m
. D.
1
m
.
Lời giải
Chọn C
Ta có:
2
0 cos 1 x
nên
0 1 1 1 2
m m
thì phương trình có nghiệm.
Câu 38:
(THPT Quãng Xương-Thanh Hóa-lần 1-năm 2017-2018)
Tìm điều kiện của tham số
m
để
phương trình
3sin cos 5
x m x
vô nghiệm
A.
4;4
m
. B.
; 4 4;m

.
C.
; 4
m

. D.
4;m

.
Lời giải
Chọn A
Để phương trình đã cho vô nghiệm thì
2 2 2
3 5
m
2
16
m
4 4
m
.
Câu 39:
(THPT Quãng Xương-Thanh Hóa-lần 1-năm 2017-2018)
Cho các hàm số
cosy x
,
siny x
,
tany x
,
coty x
. Trong các hàm số trên, có bao nhiêu hàm số chẵn?
A.
2
. B.
1
. C.
3
. D.
4
.
Lời giải
Chọn B

cosy f x x
là hàm số chẵn vì:
Tập xác định
D
, nên
x D x D
và
cos cos
f x x x f x
.

siny g x x
là hàm số lẻ vì:
Tập xác định
D
, nên
x D x D
và
sin sin
g x x x g x
.

tany h x x
là hàm số lẻ vì:
Tập xác định
\ |
2
D k k
, nên
x D x D
và
tan tan
h x x x h x
.

coty k x x
là hàm số lẻ vì:
Tập xác định
\ |D k k
, nên
x D x D
và
cot cot
k x x x k x
.
Câu 40:
(THPT Ngô Sĩ Liên-Bắc Giang-lần 1-năm 2017-2018)
Giải phương trình
sin 3 sinx x
ta được
tập nghiệm của phương trình là
A.
4
k k
. B.
,
4 2
k k l l

.
C.
2 ,
4
k k
. D.
2k k
.
Lời giải
Chọn B
3 2
3 2
x x k
x x l
,
4 2
x k
l
x
,k l
.
Vậy tập nghiệm của phương trình là:
,
4 2
k k l l

Câu 41:
(THPT Ngô Sĩ Liên-Bắc Giang-lần 1-năm 2017-2018)
Gọi
X
là tập nghiệm của phương trình
cos 15 sin
2
x
x
. Mệnh đề nào dưới đây đúng?
A.
290
X
. B.
220
X
. C.
240
X
. D.
200
X
.
Lời giải
Chọn A
Xét phương trình:
cos 15 sin cos 15 cos 90
2 2
x x
x x
3
15 90 360 75 360
50 120
2 2
210 720
15 90 360 105 360
2 2
x x
x k k
x k
x x x k
x k k
,
k
Vậy
290 50 2.120
X
.
Câu 42:
(THPT Nguyễn Đức Thuận-Nam Định-lần 1-năm 2017-2018)
Phương trình lượng giác:
2cos 2 0
x
có nghiệm là:
A.
2
4
2
4
x k
x k
. B.
3
2
4
3
2
4
x k
x k
. C.
2
4
3
2
4
x k
x k
. D.
7
2
4
7
2
4
x k
x k
.
Lời giải
Chọn B
Phương trình tương đương với
2 3 3
cos cos 2
2 4 4
x x k
Câu 43:
(THPT Hậu Lộc 2-Thanh Hóa-ần 1-năm 2017-2018)
Tìm số nghiệm thuộc khoảng
0;
của
phương trình
cos 0
4
x
.
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn B
Ta có:
cos 0 ;
4 4 2
x x k k
;
4
x k k
Do
1 3
0; 0 0
4 4 4
x x k k
.
Mà
0
4
k k x
Phương trình đã cho có duy nhất một nghiệm trong khoảng
0;
.
Câu 44:
(THPT Chuyên Lam-Thanh Hóa-lần 1-năm 2017-2018)
Hàm số nào dưới đây đồng biến trên
khoảng
5
0;
6
?
A.
siny x
. B.
cosy x
. C.
sin
3
y x
. D.
sin
3
y x
.
Lời giải
Chọn C
Ta có
5
0; ; ;
6 3 3 2 2 2
x x
nên hàm số
sin
3
y x
đồng biến.
Câu 45:
(THPT Chuyên Lam-Thanh Hóa-lần 1-năm 2017-2018)
Viết phương trình tiếp tuyến của
3 2
1
: 2
3
C y x x
tại điểm có hoành độ là nghiệm của phương trình
0.
y
A.
7
3 .
3
y x
B.
1
.
3
y x
C.
7
.
3
y x
D.
11
.
3
y x
Lời giải
Chọn C
2
2 2 2
y x x y x
0 2 2 0 1
y x x
4
3
y
Hệ số góc
1 1
k y
(loại A)
Phương trình tiếp tuyến cần tìm là
4 7
1 1
3 3
y x x
.
Câu 46:
(THPT Chuyên Lam-Thanh Hóa-lần 1-năm 2017-2018)
Cho phương
trình
2
sin 1 sin 2 sin cos
x x m x m x
. Tìm tập
S
tất cả các giá trị thực của tham số
m
để
phương trình có nghiệm trên khoảng
0;
6
.
A.
3
0;
2
S
. B.
0;1
S
. C.
1
0;
2
S
. D.
3
1;
2
S
.
Lời giải
Chọn A
Ta có:
2
sin 1 sin 2 sin cos
x x m x m x
*
sin 1 sin 2 sin sin 0
x x m x m m x
sin 1
sin 2 2
x
x m
Để phương trình
*
có nghiệm trên khoảng
0;
6
khi phương trình
2
có nghiệm trên
khoảng
0;
6
hay
0
6
x
0 2
3
x
3
0
2
m
.
Câu 47:
(THPT Cổ Loa-Hà Nội-lần 1-nawm-2018)
Nghiệm của phương trình
3 cos sin 2
x x là
A.
5
2
6
,
2
6
x k
k
x k
. B.
5
2 ,
6
x k k
.
C.
5
2 ,
6
x k k
. D.
2 ,
2
x k k
.
Lời giải
Chọn B
Ta có
3 cos sin 2
x x
3 1
cos sin 1
2 2
x x
sin 1
3
x
2
3 2
x k
5
2 , .
6
x k k
Câu 48:
(THPT Chuyên Lê Hồng Phong-Nam Định-lần 2 năm 2017-2018)
Khẳng định nào sau đây là
khẳng định sai?
A.
cos 1 2x x k
. B.
cos 0
2
x x k
.
C.
cos 1 2x x k
. D.
cos 0 2
2
x x k
.
Lời giải
Chọn D
Ta có:
cos 1 2x x k
k
. Suy ra A. đúng.
cos 0
2
x x k
k
. Suy ra B. đúng.
cos 1 2x x k
k
. Suy ra C. đúng.
Câu 49:
(THPT Chuyên Lê Hồng Phong-Nam Định-lần 2 năm 2017-2018)
Có bao nhiêu số tự nhiên có
ba chữ số dạng
abc
với
a
,
b
,
c
0;1;2;3;4;5;6
sao cho
a b c
.
A.
120
. B.
30
. C.
40
. D.
20
.
Lời giải
Chọn D
Vì số tự nhiên có ba chữ số dạng
abc
với
a
,
b
,
c
0;1;2;3;4;5;6
sao cho
nên
a
,
b
,
c
1;2;3;4;5;6
. Suy ra số các số có dạng
abc
là
3
6
20
C
.
Câu 50:
(THPT Chuyên Lê Hồng Phong-Nam Định-lần 2 năm 2017-2018)
Giải phương trình
cos 2 5sin 4 0
x x
. Mệnh đề nào sau đây đúng?
A.
2
x k
. B.
2
x k
. C.
2x k
. D.
2
2
x k
.
Lời giải
Chọn D
Ta có
cos 2 5sin 4 0
x x
2
1 2sin 5sin 4 0
x x
2
2sin 5sin 3 0
x x
2sin 3 sin 1 0
x x
sin 1x
( vì
1 sin 1x
).
Vậy phương trình có họ nghiệm là
2
2
x k
,
k
.
Câu 51:
(SGD Vĩnh Phúc-KSCL lần 1 năm 2017-2018)
Tìm tất cả các giá trị của
m
để phương trình
cos 2 sin 2 1 2x m x m
vô nghiệm, kết quả là:
A.
4
0
3
m
. B.
4
0
3
m
.
C.
4
;0 ;
3
m

. D.
4
;0 ;
3
m

.
Lời giải
Chọn C
Phương trình
cos 2 sin 2 1 2x m x m
vô nghiệm khi:
2
2 2
0
1 1 2 3 4 0
4
3
x
m m m m
x
.
Vậy
4
;0 ;
3
m

.
Câu 52:
(SGD Vĩnh Phúc-KSCL lần 1 năm 2017-2018)
Phương trình
2 2 2 2
cos cos 2 cos 3 cos 4 2
x x x x
tương đương với phương trình
A.
sin .sin 2 .sin 5 0
x x x
. B.
sin .sin 2 .sin 4 0
x x x
.
C.
cos .cos 2 .cos5 0
x x x
. D.
cos .cos 2 .cos 4 0
x x x
.
Lời giải
Chọn C
Ta có:
2 2 2 2
cos cos 2 cos 3 cos 4 2
x x x x
1 cos2 1 cos4 1 cos6 1 cos8
2
2 2 2 2
x x x x
cos8 cos 2 cos 6 cos4 0
x x x x
2cos5 cos3 2cos5 cos 0
x x x x
2cos5 cos3 cos 0
x x x
2cos5 .2cos 2 .cos 0
x x x
cos .cos 2 .cos5 0
x x x
.
Câu 53:
(THPT Lục Ngạn-Bắc Ninh-lần 1 năm 2017-2018)
Phương trình
2
sin 5 sin 9 2sin 1 0
x x x
có một họ nghiệm là:
A.
2
42 7
k
x
. B.
2
42 3
k
x
. C.
2
5
x k
. D.
3
7
x k
.
Lời giải
Chọn A
2
sin 5 sin 9 2sin 1 0
x x x
2sin 7 cos2 cos 2 0
x x x
2sin 7 1 cos2 0
x x
1
sin 7
2
cos2 0
x
x
7 2
6
5
7 2
6
2
2
x k
x k
x k
2
42 7
5 2
,
42 7
4 2
k
x
k
x k
k
x
.
Câu 54:
(THPT Lê Văn Thịnh-Bắc Ninh-lần 1 năm 2017-2018)
Hàm số nào sau đây là hàm số chẵn?
A.
sin cos3y x x
. B.
cos2y x
. C.
siny x
. D.
sin cosy x x
.
Lời giải
Chọn B
Hàm số
sin cos3y x x
có TXĐ:
D
, nên
x x
và có
sin cos 3 sin cos3
y x x x x x y x
suy ra hàm số
sin cos3y x x
là hàm số lẻ.
Hàm số
cos2y x
là hàm số chẵn vì TXĐ:
D
, nên
x x
và
cos 2 cos 2
y x x x y x
.
Xét tương tự ta có hàm số
là hàm số lẻ, hàm số
sin cosy x x
không chẵn cũng
không lẻ.
Câu 55:
(THPT Lê Văn Thịnh-Bắc Ninh-lần 1 năm 2017-2018)
Phương trình
2
sin 2
2
x
có bao
nhiêu nghiệm thuộc khoảng
0;
?
A.
4
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn C
Ta có
2
8
sin 2
5
2
8
x k
x
x l
với
k
,
l
.
Trên khoảng
0;
ta có
2
nghiệm thỏa mãn tương ứng
1
k
và
0l
.
Câu 56:
(THPT Lê Văn Thịnh-Bắc Ninh-lần 1 năm 2017-2018)
Tìm tập xác định của hàm số sau
cot
2sin 1
x
y
x
.
A.
\ , 2 , 2 ;
6 6
D k k k k
. B.
5
\ 2 , 2 ;
6 6
D k k k
.
C.
5
\ , 2 , 2 ;
6 6
D k k k k
. D.
2
\ , 2 , 2 ;
3 3
D k k k k
.
Lời giải
Chọn C
Hàm số
cot
2sin 1
x
y
x
xác định khi:
sin 0
sin 0
2 ,
1
2sin 1 0
6
sin
2
5
2
6
x k
x
x
x k k
x
x
x k
.
Câu 1:
(THPT Triệu Sơn 1-lần 1 năm 2017-2018)
Giá trị nhỏ nhất
m
và giá trị lớn nhất
M
của hàm số
sin 2cos 1
sin cos 2
x x
y
x x
là
A.
1
2
m
;
1M
. B.
1
m
;
2M
. C.
2
m
;
1M
. D.
1
m
;
2M
.
Lời giải
Chọn C
Ta có
sin 2cos 1
1 sin 2 cos 1 2
sin cos 2
x x
y y x y x y
x x
*
Phương trình
*
có nghiệm
2 2 2
2
1 2 1 2 2 0 2 1y y y y y y
.
Vậy
2
m
;
1M
.
Câu 2:
(THPT Chuyên Vĩnh Phúc-MĐ 903 lần 1-năm 2017-2018)
Tất cả các họ nghiệm của phương
trình
sin cos 1x x
là
A.
2
2
2
x k
x k
,
k
. B.
2x k
,
k
.
C.
2
4
x k
,
k
. D.
2
4
2
4
x k
x k
,
k
.
Lời giải
Chọn A
Ta có:
1
sin cos 1 2 sin 1 sin sin sin
4 4 4 4
2
x x x x x
2
2
4 4
3
2
2
2
4 4
x k
x k
x k
x k
k
.
Câu 3:
(THPT Chuyên Vĩnh Phúc-lần 1 MĐ 904 năm 2017-2018)
Tất cả các họ nghiệm của phương
trình
2cos2 9sin 7 0
x x
là
A.
2
x k k
. B.
2
x k k
.
C.
2
2
x k k
. D.
2
2
x k k
.
Lời giải
Chọn D
Ta có
2cos2 9sin 7 0
x x
2
2 1 2sin 9sin 7 0
x x
2
4sin 9sin 5 0
x x
sin 1x
,
5
sin
4
x
(vô nghiệm)
2
2
x k k
.
Câu 4:
(THPT Chuyên Vĩnh Phúc-lần 1 MĐ 904 năm 2017-2018)
Có bao nhiêu số tự nhiên lẻ có 4
chữ số khác nhau?
A.
2240.
B.
2520.
C.
2016.
D.
256.
Lời giải
Chọn A
Giả sử số tự nhiên lẻ có bốn chữ số khác nhau là
abcd
. Khi đó:
d
có
5
cách chọn.
a
có
8
cách chọn.
Số các số là:
2
8
5.8. 2240
A
(số).
Vậy số các số tự nhiên lẻ có bốn chữ số khác nhau là
2240
số.
Câu 5:
(THPT Kim Liên-Hà Nội năm 2017-2018)
Gọi
S
là tổng các nghiệm thuộc khoảng
0;2
của
phương trình
3cos 1 0
x
. Tính giá trị của
S
.
A.
0
S
. B.
4
S
. C.
3
S
. D.
2
S
.
Lời giải
Chọn D
Ta có:
3cos 1 0
x
1
cos
3
x
1
arccos 2
3
x k
,
k
.
Trong khoảng
0;2
phương trình
3cos 1 0
x
có hai nghiệm là
1
1
arccos
3
x
và
2
1
arccos
3
x
.
Vậy tổng các nghiệm là
1 2
1 1
arccos arccos 0
3 3
S x x
.
Câu 6:
(THPT Kim Liên-Hà Nội năm 2017-2018)
Tìm tất cả các nghiệm của phương trình
cos3 sin 2 sin 4 0x x x
.
A.
2
6 3
x k
,
k
.
B.
6 3
x k
,
k
.
C.
3
x k
;
2
6
x k
;
5
2
6
x k
,
k
.
D.
6 3
x k
;
2
3
x k
,
k
.
Lời giải
Chọn B
Ta có:
cos3 sin 2 sin 4 0x x x
cos3 2cos3 .sin 0 cos3 1 2sin 0
x x x x x
6 3
cos3 0
cos3 0
2
1
1 2sin 0
6
sin
2
5
2
6
x k
x
x
x k
x
x
x k
,
k
6 3
x k
,
k
.
Câu 7:
(THPT Kim Liên-Hà Nội năm 2017-2018)
Gọi
0
x
là nghiệm dương nhỏ nhất của phương trình
2 2
3sin 2sin cos cos 0
x x x x
. Chọn khẳng định đúng?
A.
0
3
; 2
2
x
. B.
0
3
;
2
x
. C.
0
;
2
x
. D.
0
0;
2
x
.
Lời giải
Chọn D
Ta thấy
cos 0
x
không thỏa phương trình. Chia hai vế phương trình cho
2
cos 0
x
ta được:
2
3tan 2 tan 1 0
x x
tan 1
1
tan
3
x
x
4
1
arctan
3
x k
x l
,
, k l
.
Vậy nghiệm dương nhỏ nhất của phương trình là
1
arctan 0;
3 2
.
Câu 8:
(THPT Kiến An-Hải Phòng năm 2017-2018)
Tìm số nghiệm của phương trình
cos 2 cos 2 0
x x
,
0;2
x
.
A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn C
cos 2 cos 2 0
x x
2
2cos cos 3 0
x x
3
cos
2
cos 1
x VN
x
2x k
k
.
Với
0;2
x
, ta có
0 2 2
k
0
k
.
Vậy phương trình đã cho có một nghiệm thỏa mãn yêu cầu bài toán.
Câu 9:
(THPT Chuyên Lương Văn Tụy-Ninh Bình lần 1 năm 2017-2018)
Đường cong trong hình vẽ
bên dưới là đồ thị của một trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây.
Hỏi hàm số đó là hàm số nào?
A.
cos 1y x
. B.
2 siny x
. C.
2cosy x
. D.
2
cos 1y x
.
Lời giải
Chọn A
Do đồ thị đi qua ba điểm
;0
,
0;2
,
;0
nên chọn phương án A.
Câu 10:
(THPT Chuyên Lương Văn Tụy-Ninh Bình lần 1 năm 2017-2018)
Nghiệm của phương trình
3
tan
3
x
được biểu diễn trên đường tròn lượng giác ở hình bên là những điểm nào?
y
x
B'
A'
B
D
F
O
A
C
E
A. Điểm
F
, điểm
D
. B. Điểm
C
, điểm
F
.
C. Điểm
C
, điểm
D
, điểm
E
, điểm
F
. D. Điểm
E
, điểm
F
.
Lời giải:
Chọn A
3
tan ,
3 3
x x k k
.
Với
0 2
3
x x
hoặc
2
3
x
.
Câu 11:
(THPT Chuyên Lương Văn Tụy-Ninh Bình lần 1 năm 2017-2018)
Nghiệm của phương trình
sin cos cos 2 0
x x x
là:
A.
k k
. B.
2
k k
. C.
4
k k
. D.
8
k k
.
Lời giải
Chọn C
Ta có
sin 0
sin cos cos2 0 cos 0
2 4
cos2 0
4 2
x k
x
x x x x x k x k k
x
x k
.
Câu 12:
(THPT Chuyên Trần Phú-Hải Phòng lần 1 năm 2017-2018)
Phương trình
3
sin 2
2
x
có
hai công thức nghiệm dạng
k
,
k
k
với
,
thuộc khoảng
;
2 2
. Khi
đó,
bằng
A.
3
. B.
2
. C.
2
. D.
.
Lời giải
Chọn B
Ta có:
3
sin 2 sin
2 3
x
2 2
3
4
2 2
3
x k
x k
6
2
3
x k
x k
6
3
x k
x k
.
Vậy
6
và
3
. Khi đó
2
.
Câu 13:
(THPT Đoàn Thượng-Hải Dương-lần 2 năm 2017-2018)
Phương trình nào trong số các phương
trình sau có nghiệm?
A.
cos 3 0
x
. B.
sin 2
x
. C.
2sin 3cos 1x x
. D.
sin 3cos 6
x x
.
Lời giải
Chọn C
Ta có
2sin 3cos 1x x
có
2 2 2
4 9 13 1
a b c
nên phương trình có nghiệm.
Câu 14:
(THPT Hà Huy Tập-Hà Tĩnh-lần 1 năm 2017-2018)
Tìm tất cả các giá trị của tham số
m
để
phương trình
sin 3cos 5
m x x
có nghiệm.
A.
4
m
. B.
4 4
m
. C.
34
m
. D.
4
4
m
m
.
Lời giải
Chọn D
Phương trình
sin 3cos 5
m x x
có nghiệm
2 2 2
3 5
m
2
16
m
4
4
m
m
.
Câu 15:
(THPT Hà Huy Tập-Hà Tĩnh-lần 1 năm 2017-2018)
Tìm tập xác định của hàm số
tan
cos 1
x
y
x
.
A.
\ 2
D k
. B.
\ 2
2
D k
.
C.
\ ; 2
2
D k k
. D.
\ 2 ;
2
D k x k
.
Lời giải
Chọn C
Hàm số
tan
cos 1
x
y
x
xác định khi:
cos 0
,
2
cos 1 0
2
x
x k
k
x
x k
.
Vậy tập xác định là
\ ; 2 ,
2
D k k k
.
Câu 16:
(THPT Hà Huy Tập-Hà Tĩnh-lần 1 năm 2017-2018)
Phương trình
3
sin
2
x
có nghiệm là
A.
2
3
x k
. B.
3
x k
. C.
6
5
6
x k
x k
. D.
2
3
2
2
3
x k
x k
.
Lời giải
Chọn D
Ta có
2
33
sin
2
2
2
3
x k
x
x k
, với
k
.
Câu 17:
(THPT Hà Huy Tập-Hà Tĩnh-lần 1 năm 2017-2018)
Tính tổng
T
các nghiệm của phương trình
2 2
cos sin 2 2 cos
2
x x x
trên khoảng
0;2
.
A.
7
8
T
. B.
21
8
T
. C.
11
4
T
. D.
3
4
T
.
Lời giải
Chọn C
Ta có
2 2
cos sin 2 2 cos
2
x x x
2 2
cos sin 2 2 sinx x x
cos2 sin 2 2
x x
cos 2 1
4
x
2 2
4
x k
,
k
8
x k
,
k
Vì
0 2
x
0 2
8
k
1 17
8 8
k
Vì
k
nên
k
1 2
7 15
;
8 8
x x
Vậy
1 2
11
4
x x
.
Câu 18:
(THPT Triệu Thị Trinh-lần 1 năm 2017-2018)
Tổng tất cả các nghiệm của phương trình
sin 5 cos7 cos4 sin8x x x x
trên
0;2
bằng
A.
19
3
. B.
9
2
. C.
5
. D.
7
.
Lời giải
Chọn D
Ta có phương trình
sin 5 cos7 cos4 sin8x x x x
1 1
sin12 sin 2 sin12 sin 4
2 2
x x x x
sin 4 sin 2 0
x x
2sin 3 cos 0
x x
sin3 0
cos 0
x
x
3
2
k
x
x k
I
.
Vì
0;2
x
nên từ
I
suy ra
2 4 5 3
, , , , , ,
3 3 3 3 2 2
x
.
Vậy tổng tất cả các nghiệm của phương trình là
2 4 5 3
7
3 3 3 3 2 2
.
Câu 19:
(THPT Thạch Thành 2-Thanh Hóa-lần 1 năm 2017-2018)
Phương trình
sin 2 3cos 0
x x
có
bao nhiêu nghiệm trong khoảng
0;
?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn B
Phương trình tương đương với
cos 2sin 3 0
x x
cos 0
3
sin
2
x
x L
2
x k
,
k
.
Vậy phương trình chỉ có một nghiệm duy nhất
2
x
.
Câu 20:
(THPT Thạch Thành 2-Thanh Hóa-lần 1 năm 2017-2018)
Nghiệm của phương trình
2sin 1 0
x
được biểu diễn trên đường tròn lượng giác ở hình bên là những điểm nào?
A. Điểm
D
, điểm
C
. B. Điểm
E
, điểm
F
.
C. Điểm
C
, điểm
F
. D. Điểm
E
, điểm
D
.
Lời giải
Chọn B
Ta có
2sin 1 0
x
2
1
6
sin
7
2
2
6
x k
x
x k
k
Với
0
6
k x
hoặc
7
6
x
.
Điểm biểu diễn của
6
x
là
F
, điểm biểu diễn
7
6
x
là
E
.
Câu 21:
(THPT Chuyên Thái Bình-lần 2 năm học 2017-2018)
Cho phương trình:
2
cos 1 cos 2 cos sinx x m x m x
. Phương trình có đúng hai nghiệm thuộc đoạn
2
0;
3
khi?
A.
1
m
. B.
1
m
. C.
1 1
m
. D.
1
1
2
m
.
Lời giải
Chọn D
Ta có
2
cos 1 cos 2 cos sinx x m x m x
cos 1 cos2 cos cos 1 0
x x m x m x
cos 1 cos 2 0
x x m
cos2 1
cos 1 2
x m
x
Phương trình
2 2x k
,
k
. Vì
2
0;
3
x
nên không tồn tại
k
thỏa mãn.
A
A
B
B
x
y
C
D
E
F
O
Theo đề phương trình có đúng hai nghiệm thuộc đoạn
2
0;
3
nên phương trình
1
có đúng
hai nghiệm thuộc đoạn
2
0;
3
.
Ta có
2
0;
3
x
nên
4
2 0;
3
x
.
Do đó
1
có hai nghiệm phân biệt khi
1
1;
2
m
.
Cách khác:
Xét hàm số
cos2y x
với
2
0;
3
x
. Khi đó
2sin 2 0
2
k
y x x
,
k
.
Do
2
0;
3
x
nên
0
x
hoặc
2
x
.
Bảng biến thiên:
Từ bảng biến thiên ta thấy
1
1;
2
m
thì đường thẳng
y m
cắt đồ thị
cos2y x
tại hai
điểm.
Câu 22:
(THPT Chuyên Thái Bình-lần 2 năm học 2017-2018)
Mệnh đề nào dưới đây đúng?
A.
cos 1
x
2x k
,
k
. B.
x
2
2
x k
,
k
.
C.
sin 0
x
2x k
,
k
. D.
tan 0
x
2x k
,
k
.
Lời giải
Chọn A
Mệnh đề A. đúng vì
cos 1
x
2x k
,
k
.
B. sai
cos 0
x
2
x k
,
k
.
C. sai vì
sin 0
x
x k
,
k
.
D. sai vì
x
x k
,
k
.
O
y
x
1
1
2
x
0
2
2
3
y
0
y
1
1
1
2
Câu 23:
(THPT Chuyên ĐHSP-Hà Nội-lần 1 năm 2017-2018)
Cho hai phương trình
cos3 1 0
x
(1);
1
cos2
2
x
(2). Tập các nghiệm của phương trình (1) đồng thời là nghiệm của phương trình
(2) là
A.
2
3
x k
,
k
. B.
2x k
,
k
.
C.
2
3
x k
,
k
D.
2
2
3
x k
,
k
.
Lời giải
Chọn D
Ta có
cos3 1 0
x
cos3 1x
2
3
x k
,
k
.
1
cos2
2
x
2
2 2
3
x k
3
x k
,
k
.
Biểu diễn các nghiệm trên đường tròn lượng giác ta có tập các nghiệm của phương trình (1)
đồng thời là nghiệm của phương trình (2) là
2
3
x k
,
k
.
Câu 24:
(THPT Chuyên ĐHSP-Hà Nội-lần 1 năm 2017-2018)
Phương trình
cos3 .tan5 sin 7x x x
nhận những giá trị sau của
x
làm nghiệm
A.
2
x
. B.
10 ;
10
x x
. C.
5
10
x x
. D.
5
20
x x
Lời giải
Chọn D
Điều kiện
5
2
k
x
,
k
(*)
Phương trình tương đương
cos3 .sin 5 sin 7 cos5 0 sin 2 0
2
k
x x x x x x
.
Ta thấy
,
2 10
x x
không thỏa mãn điều kiện (*) nên loại đáp án A, B, C.
Vậy đáp án đúng là D.
Câu 25:
(THPT Chuyên ĐHSP-Hà Nội-lần 1 năm 2017-2018)
Tìm số đo ba góc của một tam giác cân
biết rằng có số đo của một góc là nghiệm của phương trình
1
cos2
2
x
.
A.
2
, ,
3 6 6
. B.
, ,
3 3 3
;
2
, ,
3 6 6
.
C.
, ,
3 3 3
;
, ,
4 4 2
. D.
, ,
3 3 3
.
Lời giải
Chọn B
Ta có:
1 2
cos2 2 2
2 3 3
x x k x k
,
k
.
Do số đo một góc là nghiệm nên
3
x
hoặc
2
3
x
thỏa mãn.
Vậy tam giác có số đo ba góc là
, ,
3 3 3
hoặc
2
, ,
3 6 6
.
Câu 26:
(THPT Chuyên ĐHSP-Hà Nội-lần 1 năm 2017-2018)
Cho biểu thức
10
3
2
3
1 1
1
x x
P
x x
x x
với
0
x
,
1x
. Tìm số hạng không chứa
x
trong khai triển
Niu-tơn của
P
.
A.
200
. B.
160
. C.
210
. D.
100
.
Lời giải
Chọn C
Ta có
3 3
3 2
3
1 1 1 1
1
1
x x x
x x
x x x x
x x
.
Nên
10
10
3
3
2
3
1 1 1
1
x x
P x
x x x
x x
.
Số hạng tổng quát của khai triển là
10 20 5
3 6
10 10
1
. 1
k
k k
k
k k
C x C x
x
.
Khi
4
k
thì số hạng không chứa
x
là
4
4
10
1 210
C
.
Câu 27:
(THPT Chuyên ĐHSP-Hà Nội-lần 1 năm 2017-2018)
Số nghiệm thuộc khoảng
0;3
của
phương trình
2
5
cos cos 1 0
2
x x
là
A.
4
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn B
+ Ta có:
2
1
cos
5
2cos cos 1 0
2
cos 2
x n
x x
x l
.
Suy ra:
2
2
1 2
3
cos cos cos
2
2 3
2
3
x k
x x k
x k
+ Với
2
2
3
x k
,
k
. Vì
0;3
x
nên
2
0 2 3
3
k
,
k
1 7
3 6
k
,
k
. Suy ra:
0;1
k
2 8
;
3 3
x
.
+ Với
2
2
3
x k
,
k
. Vì
0;3
x
nên
2
0 2 3
3
k
,
k
1 11
3 6
k
,
k
. Suy ra:
1
k
4
3
x
.
Do đó
2 4 8
; ;
3 3 3
x
.
Vậy số nghiệm của phương trình là
3.
Câu 28:
(THPT Yên Lạc-Vĩnh Phúc-lần 3 năm 2017-2018)
Tìm tất cả các giá trị của tham số
m
để
phương trình
sin cos 5
2 2
x x
m
có nghiệm.
A.
2
2
m
m
. B.
2
2
m
m
. C.
2 2
m
. D.
2 2
m
.
Lời giải
Chọn A
Điều kiện có nghiệm của phương trình là:
2
2 2 2
2
1 5 4
2
m
m m
m
.
Câu 29:
(THTT Số 4-487 tháng 1 năm 2017-2018)
Tập giá trị của hàm số.
cos 1
sin 1
x
y
x
. trên
0;
2
là
A.
1
;2
2
. B.
1
;2
2
. C.
1
;2
2
. D.
1
;2
2
.
Lời giải
Chọn A
cos 1
sin 1
x
y
x
.
Vì
0;
2
x
nên
sin 0;1
x
. Do đó hàm số đã cho xác định trên
0;
2
.
2 2
2 2
cos 1 sin cos 1
0
sin 1
sin 1 sin 1
x x x
y y
x
x x
,
0;
2
x
.
Suy ra hàm số luôn nghịch biến trên
0;
2
.
Do đó:
0;
2
max 0 2
y y
;
0;
2
1
min
2
y
.
Vậy tập giá trị của hàm số đã cho là
1
;2
2
.
Câu 30:
(THTT Số 4-487 tháng 1 năm 2017-2018)
Phương trình
sin 2 cos sin 7 cos 4x x x x
có các họ
nghiệm là
A.
2
5
k
x
;
12 6
k
x
k
. B.
5
k
x
;
12 3
k
x
k
.
C.
5
k
x
;
12 6
k
x
k
. D.
2
5
k
x
;
12 3
k
x
k
.
Lời giải
Chọn C
sin 2 cos sin 7 cos 4x x x x
1 1
sin sin 3 sin 3 sin11
2 2
x x x x
sin sin11x x
11 2
11 2
x x k
x x k
5
12 6
k
x
k
x
k
.
Câu 31:
(THTT Số 4-487 tháng 1 năm 2017-2018)
Tổng tất cả các nghiệm của phương trình
cos sin 1
x
trên
0;2
bằng
A.
0
. B.
. C.
2
. D.
3
.
Lời giải
Chọn B
Ta có
0;2
x
sin 1;1
x
Khi đó:
cos sin 1 sin 2x x k
k
với
1 2 1 0
k k
.
Phương trình trở thành
0
sin 0
x
x x m
x
m
.
Vậy tổng tất cả các nghiệm của phương trình
cos sin 1
x
trên
0;2
bằng
.
Câu 32:
(THTT Số 4-487 tháng 1 năm 2017-2018)
Xét phương trình
sin 3 3sin 2 cos 2 3sin 3cos 2
x x x x x
. Phương trình nào dưới đây tương đương với phương
trình đã cho?
A.
2
2sin 1 2cos 3cos 1 0
x x x
. B.
2sin cos 1 2cos 1 0
x x x
.
C.
2sin 1 2cos 1 cos 1 0
x x x
. D.
2sin 1 cos 1 2cos 1 0
x x x
.
Lời giải
Chọn C
Ta có:
sin 3 3sin 2 cos 2 3sin 3cos 2
x x x x x
sin 3 sin 2sin 2 sin 2 2sin cos2 3cos 2 0
x x x x x x x
2sin 2 cos 1 2sin cos 1 cos 1 2cos 1 0
x x x x x x
cos 1 2sin 2 2sin 2cos 1 0
x x x x
cos 1 2cos 1 2sin 1 0
x x x
.
Câu 33:
(SGD Bắc Ninh năm 2017-2018)
Phương trình
3sin 2 cos2 2
x x
có tập nghiệm là
A.
|
3 2
k
S k
. B.
2
2 |
3
S k k
.
C.
|
3
S k k
. D.
5
|
12
S k k
.
Lời giải
Chọn C
Ta có:
3sin 2 cos2 2
x x
3 1
sin 2 cos 2 1
2 2
x x
sin 2 1
6
x
2 2
6 2
x k
3
x k
k
.
Vậy tập nghiệm của phương trình đã cho là
|
3
S k k
.
Câu 34:
(SGD Bắc Ninh năm 2017-2018)
Trong các hàm số
tany x
;
sin 2y x
;
siny x
;
coty x
,
có bao nhiêu hàm số thỏa mãn tính chất
f x k f x
,
x
,
k
.
A.
3
. B.
2
. C.
1
. D.
4
.
Lời giải
Chọn C
Ta có hàm số
tany x
có tập xác định là
\ ,
2
k k
và hàm số
có tập
xác định là
\ ,
k k
nên cả hai hàm số này đều không thỏa yêu cầu.
 Xét hàm số
sin 2y x
: Ta có
sin 2 sin 2 2 sin 2
x k x k x
,
x
,
k
.
 Hàm số
siny x
là hàm số tuần hoàn với chu kỳ
2
nên không thỏa yêu cầu.
Câu 35:
(SGD Ninh Bình năm 2017-2018)
Gọi
S
là tổng các nghiệm trong khoảng
0;
của phương
trình
1
sin
2
x
. Tính
S
.
A.
0
S
. B.
3
S
. C.
S
. D.
6
S
.
Lời giải
Chọn C
Ta có:
1
sin
2
x
sin sin
6
x
6
5
6
x k
x k
,
k
.
Với điều kiện
0;
x
.
Ta có:
0
π
6
k
1 5
6 6
k
0
k
, khi đó:
6
x
.
5
0
π
6
k
5 1
6 6
k
0
k
, khi đó:
5
6
x
.
Vậy
5
6 6
S
.
Câu 36:
(SGD Ninh Bình năm 2017-2018)
Cho phương trình
tan tan 1
4
x x
. Diện tích của đa
giác tạo bởi các điểm trên đường tròn lượng giác biểu diễn các họ nghiệm của phương trình gần
với số nào nhất trong các số dưới đây?
A.
0,948
. B.
0,949
. C.
0,946
. D.
0,947
.
Lời giải
Chọn B
Điều kiện
cos 0
cos 0
4
x
x
2
,
4
x k
k
x k
.
Với điều kiện trên, phương trình trở thành
tan 1
tan 1
1 tan
x
x
x
2
tan tan 0
x x
tan 0
tan 1
x
x
,
4
x m
m
x m
(thỏa điều kiện)
Gọi
1;0
A
,
2 2
;
2 2
B
,
C
và
2 2
;
2 2
D
là các điểm biểu diễn tập nghiệm của
phương trình đã cho
Ta có tứ giác
ABCD
là hình chữ nhật có
2 2
AB
;
2 2
AD
.
Khi đó
. 2 1,41
ABCD
S AB AD
.
Câu 37:
(THPT Chuyên Hạ Long-Quảng Ninh-lần 1 năm 2017-2018)
Tìm chu kì của hàm số
3
sin 2cos
2 2
x x
f x
.
A.
5
.
B.
2
.
C.
4
.
D.
2
Hướng dẫn giải
Chọn C
Chu kỳ của
sin
2
x
là
1
2
4
1
2
T
và Chu kỳ của
3
cos
2
x
là
2
2 4
3
3
2
T
Chu kì của hàm ban đầu là bội chung nhỏ nhất của hai chu kì
1
T
và
2
T
vừa tìm được ở trên.
Chu kì của hàm ban đầu
4
T
Câu 38:
(THPT Chuyên Hạ Long-Quảng Ninh-lần 1 năm 2017-2018)
Tính tổng tất cả các nghiệm
thuộc khoảng
0;
của phương trình:
2 cos3 sin cosx x x
.
A.
2
. B.
3
. C.
3
2
. D.
.
Hướng dẫn giải
Chọn C
Ta có:
2 cos3 sin cosx x x
cos3 cos
4
x x
8
16 2
x k
k
x k
.
Vì
0;
x
nên nhận
7
8
x
,
16
x
,
9
16
x
.
O
x
y
4
0
5
4
B
A
D
C
Câu 39:
(THPT Chuyên Phan Bội Châu-Nghệ An- lần 1 năm 2017-2018)
Số nghiệm thuộc đoạn
5
0;
2
của phương trình
2sin 1 0
x
là:
A.
2
. B.
3
. C.
1
. D.
4
.
Lời giải
Chọn B
+ Phương trình tương đương
1
sin
2
x
sin sin
6
x
2
6
5
2
6
x k
x k
,
k
.
+ Với
2
6
x k
,
k
.
Vì
5
0;
2
x
nên
5
0 2
6 2
k
,
k
1 7
12 6
k
,
k
0;1
k
.
Suy ra:
3
;
6 6
x
.
+ Với
5
2
6
x k
,
k
.
Vì
5
0;
2
x
nên
5 5
0 2
6 2
k
,
k
5 5
12 6
k
,
k
0
k
.
Suy ra:
5
6
x
.
Do đó
5 3
; ;
6 6 6
x
.
Vậy số nghiệm của phương trình là
3
.
Câu 40:
(THPT Chuyên Quốc Học-Huế năm 2017-2018)
Tính tổng tất cả các nghiệm thuộc khoảng
0;2
của phương trình
4 4
5
sin cos
2 2 8
x x
.
A.
9
8
. B.
12
3
. C.
9
4
. D.
2
.
Lời giải
Chọn B
4 4
5
sin cos
2 2 8
x x
2
2 2 2 2
5
sin cos 2sin .cos
2 2 2 2 8
x x x x
2
1 5
1 sin
2 8
x
1 5
1 1 cos 2
4 8
x
1
cos2
2
x
3
x k
,
k
.
Mà
0;2
x
nên
2 4 5
; ; ;
3 3 3 3
x
.
Khi đó tổng các nghiệm thuộc khoảng
0;2
của phương trình là
0
x
.
Câu 41:
(THPT Chuyên Quốc Học-Huế năm 2017-2018)
Tìm tập xác định
D
của hàm số
tan 2
4
y x
.
A.
3
\ ,
8 2
k
D k
. B.
3
\ ,
4
D k k
.
C.
3
\ ,
4 2
k
D k
. D.
\ ,
2
D k k
.
Lời giải
Chọn A
Hàm số
tan 2
4
y x
xác định khi và chỉ khi
cos 2 0 2
4 4 2
x x k
.
Suy ra
3
8 2
k
x
.
Vậy tập xác định của hàm số là
3
\ ,
8 2
k
D k
.
Câu 42:
(THPT Chuyên Quốc Học-Huế năm 2017-2018)
Cho hàm số
sin cosf x x x
có đồ thị
C
. Trong các hàm số sau, hàm số nào có đồ thị không thể thu được bằng cách tịnh tiến đồ thị
C
?
A.
sin cosy x x
. B.
2 sin 2
y x
. C.
sin cosy x x
. D.
sin
4
y x
.
Lời giải
Chọn D
Ta có
max sin cos 2
x
x x M
,
min sin cos 2
x
x x m
,
2 2
M m
. Vì phép
tịnh tiến không làm thay đổi khoảng cách giữa giá trị lớn nhất và giá trị nhỏ nhất nên chọn đáp
án D (chênh lệch giữa giá trị lớn nhất và giá trị nhỏ nhất bằng
2
).
Câu 43:
(THPT Chuyên Thái Bình-lần 3 năm 2017-2018)
Tập xác định của hàm số
tan cos
2
y x
là:
A.
\ 0
. B.
\ 0;
. C.
\
2
k
. D.
\
k
.
Hướng dẫn giải
Chọn D
Hàm số xác định:
cos cos 0
2
x
cos
2 2
x k
cos 1 2x k
cos 1
x
sin 0
x
x k k
.
Câu 44:
(THPT Chuyên Thái Bình-lần 3 năm 2017-2018)
Giải phương trình
2
2sin 3 sin 2 3
x x
.
A.
3
x k
. B.
3
x k
. C.
2
2
3
x k
. D.
4
x k
.
Hướng dẫn giải
Chọn B
2
2sin 3 sin 2 3
x x
1 cos 2 3sin 2 3
x x
3sin 2 cos2 2
x x
3 1
sin 2 cos2 1
2 2
x x
sin 2 1
6
x
2 2
6 2
x k
,
3
x k k
.
Câu 45:
(THPT Chuyên Vĩnh Phúc - lần 3 năm 2017-2018)
Giá trị lớn nhất và giá trị nhỏ nhất của hàm
số
trên đoạn
;
2 3
lần lượt là:
A.
1
2
;
3
2
. B.
3
2
;
1
. C.
3
2
;
2
. D.
2
2
;
3
2
.
Lời giải
Chọn B
Cách 1: Ta có:
2 3
x
sin sin sin
2 3
x
3
1 sin
2
x
.
Vậy
;
2 3
3
max sin
3 2
y
;
;
2 3
min sin 1
2
y
.
Cách 2: Xét hàm số
trên đoạn
;
2 3
+ Ta có:
cos 0
y x
,
;
2 3
x
;
0
2
y x
.
Hàm số đồng biến trên khoảng
;
2 3
.
Vậy
;
2 3
3
max sin
3 2
y
,
;
2 3
min sin 1
2
y
.
Câu 46:
(THPT Hoài Ân-Hải Phòng năm 2017-2018)
Tìm tập xác định
D
của hàm số
1 sin
1 sin
x
y
x
.
A.
\ 2 ; 2 ;
2 2
D k k k
. B.
\ ;D k k
.
C.
\ 2 ;
2
D k k
. D.
\ 2 ;
2
D k k
.
Lời giải
Chọn C
Ta có:
1 sin 1x
1 sin 0
1 sin 0
x
x
.
Hàm số xác định khi
1 sin 0
x
sin 1
x
2
2
x k
,
k
.
Vậy tập xác định của hàm số là:
\ 2 ;
2
D k k
.
Câu 47:
(THPT Hoài Ân-Hải Phòng năm 2017-2018)
Tìm nghiệm của phương trình
cos 3sin
0
2sin 1
x x
x
.
A.
6
x k
;
k
. B.
7
2
6
x k
;
k
.
C.
7
6
x k
;
k
. D.
2
6
x k
;
k
.
Lời giải
Chọn B
TXĐ:
5
\ 2 , 2 ,
6 6
D k k k
.
Phương trình trở thành:
3sin cos 0
x x
2sin 0
6
x
2
6
x k
k
.
Vậy nghiệm của phương trình là
7
2
6
x k
k
.
Câu 48:
(THPT Hồng Quang-Hải Dương năm 2017-2018)
Nghiệm của phương trình
cot 3
3
x
có dạng
k
x
m n
,
k
,
m
,
*
n
và
k
n
là phân số tối giản. Khi đó
m n
bằng
A.
5
. B.
3
. C.
5
. D.
3
.
Lời giải
Chọn A
Ta có
cot 3
3
x
cot cot
3 6
x
3 6
x k
6
x k
,
k
.
Vậy
6
1
m
n
5
m n
.
Câu 49:
(THPT Hồng Quang-Hải Dương năm 2017-2018)
Số vị trí biểu diễn các nghiệm của phương
trình
2
4cos 4cos 3 0
x x
trên đường tròn lượng giác là ?
A.
2
. B.
0
. C.
1
. D.
4
.
Lời giải
Chọn A
Ta có
2
4cos 4cos 3 0
x x
3
cos
2
1
cos
2
x L
x N
.
Với
1
cos
2
x
2
cos cos
3
x
2
2
3
x k
k
.
Vậy số vị trí biểu diễn các nghiệm của phương trình trên đường tròn lượng giác là
2
.
Câu 50:
(THPT Hồng Quang-Hải Dương năm 2017-2018)
Tìm các giá trị thực của tham số
m
để
phương trình
2 1 sin 3 cos3 3 1
m x m x m
có nghiệm.
A.
1
0;
2
m
. B.
1
;0 ;
2
m
 
.
C.
1
;0 ;
2
m
 
. D.
1
0;
2
m
.
Lời giải
Chọn A
Phương trình
2 1 sin 3 cos3 3 1
m x m x m
có nghiêm khi
2 2
2
2 1 3 1
m m m
2
4 2 0
m m
1
0
2
m
Câu 51:
(THPT Kinh Môn 2-Hải Dương năm 2017-2018)
Hàm số
sin 2y x
có chu kỳ là
A.
2
T
. B.
2
T
. C.
T
. D.
4
T
.
Lời giải
Chọn C
Hàm số
sin 2y x
tuần hoàn với chu kỳ
2
T
nên hàm số
sin 2y x
tuần hoàn với chu kỳ
T
.
Câu 52:
(THPT Kinh Môn 2-Hải Dương năm 2017-2018)
Phương trình lượng giác:
cos3 cos2 9sin 4 0
x x x
trên khoảng
0;3
. Tổng số nghiệm của phương trình trên là:
A.
25
6
. B.
6
. C. Kết quả khác. D.
11
3
.
Lời giải
Chọn B
Ta có
cos3 cos 2 9sin 4 0
x x x
3 2
4cos 3cos 2sin 9sin 5 0
x x x x
2
cos 1 4sin 2sin 1 sin 5 0
x x x x
2sin 1 cos 2sin cos sin 5 0
x x x x x
2sin 1 0 1
sin cos 2sin cos 5 0 2
x
x x x x
Giải
1
, ta có
2
1
6
1 sin
5
2
2
6
x k
x
x k
.
Với
0;3
x
nên
1
có các nghiệm thoả bài toán là:
6
x
,
13
6
x
,
5
6
x
,
17
6
x
.
Giải
2
, đặt
sin cos 2 sin
4
t x x x
với
2
t
.
Khi đó
2 2
1 2sin cos 2sin cos 1
t x x x x t
;
Phương trình
2
trở thành
2 2
1 5 0 4 0
t t t t
phương trình vô nghiệm.
Vậy tổng các nghiệm là:
13 5 17
6
6 6 6 6
.
Câu 53:
(THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018)
Số nghiệm của phương trình
sin 1
4
x
thuộc đoạn
;2
là:
A.
3
. B.
2
. C.
0
. D.
1
.
Lời giải
Chọn D
Ta có
sin 1 2 2
4 4 2 4
x x k x k
,
k
.
Suy ra số nghiệm thuộc
;2
của phương trình là
1
.
Câu 54:
(THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018)
Cho phương trình
5
cos2 4cos
3 6 2
x x
. Khi đặt
cos
6
t x
, phương trình đã cho trở thành
phương trình nào dưới đây ?
A.
2
4 8 5 0
t t
. B.
2
4 8 3 0
t t
. C.
2
4 8 3 0
t t
. D.
2
4 8 5 0
t t
.
Lời giải
Chọn C
Ta có:
5
cos2 4cos
3 6 2
x x
2
5
1 2sin 4cos
3 6 2
x x
2
5
1 2cos 4cos
6 6 2
x x
.
Đặt
cos
6
t x
,
1t
ta được phương trình:
2
5
1 2 4
2
t t
2
4 8 3 0
t t
.
Câu 55:
(THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018)
Số vị trí điểm biểu diễn các nghiệm của
phương trình
sin 2 2cos sin 1
0
tan 3
x x x
x
trên đường tròn lượng giác là:
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C
Điều kiện xác định:
tan 3
x
.
Phương trình tương đương:
2sin cos 2cos sin 1 0
x x x x
2cos 1 sin 1 0
x x
1
cos
2
sin 1
x
x
2
3
2
3
2
2
x k
x k
x k
. Do
tan 3
x
nên
2
3
x k
loại.
2
3
x k
biểu diễn trên đường tròn lượng giác có
1
điểm.
2
2
x k
biểu diễn trên đường tròn lượng giác có
1
điểm.
Vậy có
2
vị trí biểu diễn nghiệm của phương trình trên đường tròn lượng giác.
Câu 56:
(THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018)
Tính tổng
T
tất cả các nghiệm của
phương trình
2cos 1 sin 2 cos
0
sin 1
x x x
x
trên
0;
2
ta được kết quả là:
A.
2
3
T
. B.
2
T
. C.
T
. D.
3
T
.
Lời giải
Chọn B
Điều kiện xác định
sin 1x
.
Phương trình tương đương
2cos 1 cos . 2sin 1 0
x x x
1
cos
2
cos 0
1
sin
2
x
x
x
.
Vì
0;
2
x
và
sin 1x
nên
3
6
x
x
. Do đó
2
T
.
Câu 57:
(THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018)
Giá trị lớn nhất của hàm số
2
3sin 4
12
y x
bằng.
A.
7
. B.
1
. C.
3
. D.
4
.
Lời giải
Chọn A
Ta có
2 2 2
sin 1 3sin 3 3sin 4 7
12 12 12
x x x
.
Vậy giá trị lớn nhất của hàm số bằng
7
.
Câu 58:
(THPT Phan Đăng Lưu-Huế-lần 1 năm 2017-2018)
Giải phương trình
2
3sin 2cos 2 0
x x
.
A.
,
2
x k k
. B.
,x k k
. C.
2 ,x k k
. D.
2 ,
2
x k k
.
Lời giải
Chọn C
Ta có
2
3sin 2cos 2 0
x x
2
3cos 2cos 5 0
x x
cos 1x
2 ,x k k
.
Câu 59:
(THPT Phan Đăng Lưu-Huế-lần 1 năm 2017-2018)
Tìm tất cả các nghiệm của phương trình
tan 3 cot 3 1 0
x x
là:
A.
4
,
3
x k
k
x k
. B.
4
,
6
x k
k
x k
.
C.
2
4
,
2
6
x k
k
x k
. D.
4
,
6
x k
k
x k
.
Lời giải
Chọn A
ĐK
sin 0
sin 2 0 ,
cos 0
2
x
k
x x k
x
.
Phương trình tương đương
2
tan 1
4
tan 3 1 tan 3 0 ,
tan 3
3
x k
x
x x k
x
x k
.
Câu 60:
(THPT Phan Đăng Lưu-Huế-lần 1 năm 2017-2018)
Phương trình
sin 3 cos 1x x
có tập
nghiệm là:
A.
;
6 2
k k
, với
k
. B.
2 ; 2
6 2
k k
, với
k
.
C.
2 ; 2
6 2
k k
, với
k
. D.
7
2 ; 2
6 2
k k
, với
k
.
Lời giải
Chọn B
Ta có
sin 3 cos 1x x
1 3 1
sin cos
2 2 2
x x
sin sin
3 6
x
2
3 6
2
3 6
x k
x k
2
6
2
2
x k
k
x k
.
Câu 61:
(THPT Phan Đăng Lưu-Huế-lần 1 năm 2017-2018)
Tìm giá trị lớn nhất
M
của hàm số
5 3
5 20 2
y f x x x x
trên đoạn
1;3
.
A.
26
M
. B.
46
M
. C.
46
M
. D.
50
M
.
Lời giải
Chọn D
Ta có
4 2
5 15 20
f x x x
,
0
f x
4 2
5 15 20 0
x x
2
2
4
1
x
x
. Do
2
0
x
2
4
x
2
x
.
Mà
1;3
x
nên
2
x
.
Ta có
1 26
f
,
2 46
f
,
3 50
f
.
So sánh các giá trị ta được giá trị lớn nhất của hàm số là
50
M
.
Câu 62:
(THPT Thanh Miện 1-Hải Dương-lần 1 năm 2017-2018)
Cho phương trình
2sin 3 0
x
. Tổng
các nghiệm thuộc
0;
của phương trình là:
A.
. B.
3
. C.
2
3
. D.
4
3
.
Lời giải
Chọn A
2sin 3 0
x
3
sin sin
2 3
x
2
2
2
3
3
x k
x k
.
Các nghiệm của phương trình trong đoạn
0;
là
3
;
2
3
nên có tổng là
2
3 3
.
Câu 63:
(THPT Thanh Miện 1-Hải Dương-lần 1 năm 2017-2018)
Phương trình
sin 3 cos 0
x x
có
bao nhiêu nghiệm thuộc
2 ;2
.
A.
5
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn D
Ta có
sin 3 cos 0
x x
sin 0
3
x
,
3
x k k Z
Vì
2 ;2
x
nên
7 5
2 2
3 3
x k
. Do đó có
4
giá trị
k
, tương ứng có bốn
nghiệm
x
.
Câu 64:
(THPT Thanh Miện 1-Hải Dương-lần 1 năm 2017-2018)
Diện tích hình phẳng giới hạn bởi
hai đồ thị
3
3 2
f x x x
;
2
g x x
là:
A.
8
S
. B.
4
S
. C.
12
S
. D.
16
S
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm của hai đồ thị
3 3
0
3 2 2 4 0
2
x
x x x x x
x
Diện tích cần tìm
0 2
3 3
2 0
4 d 4 dS x x x x x x
0 2
3 3
2 0
4 d 4 dx x x x x x
4 4
2 2
0 2
2 2 8
2 0
4 4
x x
x x
.
Câu 65:
(THPT Trần Hưng Đạo-TP HCM năm 2017-2018)
Tìm số nghiệm của phương trình
sin cos2x x
thuộc đoạn
0;20
.
A.
40
. B.
30
. C.
60
. D.
20
.
Lời giải
Chọn B
Ta có
sin cos2x x
2
sin 1 2sinx x
1
sin
2
sin 1
x
x
.
1
sin
2
x
2
6
5
2
6
x k
x k
k
.
sin 1
x
2
2
x k
k
Xét
0;20
x
:
Với
2
6
x k
, ta có
0 2 20
6
k
1 119
12 12
k
, do
k
nên (có 10 giá trị
k
).
Với
5
2
6
x k
, ta có
5
0 2 20
6
k
5 115
12 12
k
, do
k
nên (có 10 giá trị
k
).
Với
2
2
x k
, ta có
0 2 20
2
k
1 41
4 4
k
, do
k
nên (có 10 giá trị
k
).
Vậy phương trình đã cho có
30
nghiệm thuộc đoạn
0;20
.
Câu 66:
(THPT Trần Hưng Đạo-TP HCM năm 2017-2018)
Cho phương trình
sin 4cos 2 5
m x x m
với
m
là tham số. Có bao nhiêu giá trị nguyên của
m
để phương trình có nghiệm?
A.
4
. B.
7
. C.
6
. D.
5
.
Lời giải
Chọn C
Điều kiện để phương trình
sin 4cos 2 5
m x x m
có nghiệm là
2
2 2
10 73 10 73
16 2 5 3 20 9 0
3 3
m m m m m
.
Câu 67:
Vậy
1,2,3,4,5,6
m
.
(THPT Tứ Kỳ-Hải Dương năm 2017-2018)
Số nghiệm thuộc
3
;
2
của phương trình
3
3 sin cos 2
2
x x
là:
A.
3
. B.
1
. C.
2
. D.
0
.
Hướng dẫn giải
Chọn C
Ta có
3
3sin cos 2
2
x x
3 sin sin 2x x
3 sin sin 2 3 sin 2sin cosx x x x x
sin 0
5
3 5
2
cos cos
6
2 6
x
x k
x k
x
k
.
Bài ra
3
;
2
x
nên
3
; 1
2
k k x
.
5 3 7
2 ; 1
6 2 6
k k x
.
5 3
2 ;
6 2
k k x
.
Do đó số nghiệm thuộc
3
;
2
của phương trình đã cho là
2
.
Câu 68:
(THPT Tứ Kỳ-Hải Dương năm 2017-2018)
Biết
3
sin
2
và
2
. Giá trị của
cos 2
3
P
là:
A.
0
P
. B.
1P
. C.
1
2
P
. D.
3
2
P
.
Hướng dẫn giải
Chọn B
Ta có
3
sin
2
2 2
3 1 1
cos 1 sin 1 cos
4 4 2
.
Từ
cos 0
2
nên
1
cos
2
.
Do đó
cos 2 cos2 cos sin 2 sin
3 3 3
P
2 2
1 3 1
2cos 1 . 2sin cos . cos 3 sin cos 1
2 2 2
.
Câu 69:
(THPT Xuân Trường-Nam Định năm 2017-2018)
Phương trình
2cos 1 0
x
có nghiệm là:
A.
2
6
x k
,
k
. B.
2
3
x k
,
k
.
C.
2
6
x
,
k
. D.
3
x k
,
k
.
Lời giải
Chọn B
Phương trình
2cos 1 0
x
1
cos
2
x
2
3
x k
,
k
.
Câu 70:
(THPT Xuân Trường-Nam Định năm 2017-2018)
Tất cả các nghiệm của phương trình
sin 3 cos 1x x
là:
A.
2
6
x k
,
k
. B.
2
6
2
2
x k
x k
,
k
.
C.
5
6
x k
,
k
. D.
5
2
6
x k
,
k
.
Lời giải
Chọn B
Ta có
sin 3 cos 1x x
1
sin
3 2
x
2
6
2
2
x k
x k
,
k
.
Vậy tất cả các nghiệm của phương trình đã cho là
2
6
2
2
x k
x k
,
k
.
Câu 71:
(THPT Lương Văn ChasnhPhus Yên năm 2017-2018)
Cho phương trình
2
2 sin cos 4 cos 5
m x x x m
, với
m
là một phần tử của tập hợp
3; 2; 1;0;1;2
E
. Có
bao nhiêu giá trị của
m
để phương trình đã cho có nghiệm ?
A.
3
. B.
2
. C.
6
. D.
4
.
Lời giải
Chọn A
Ta có
2
2 sin cos 4cos 5
m x x x m
1 cos 2
sin 2 4 5
2
x
m x m
sin 2 2cos2 3
m x x m
.
Phương trình trên có nghiệm khi và chỉ khi
2
2
5
4 3
9
m m m
.
Vậy có ba giá trị của
m E
để phương trình đã cho có nghiệm.
Câu 72:
(THPT Chuyên Biên Hòa-Hà Nam-lần 1 năm 2017-2018)
Phương trình 1cossin3 xx
tương đương với phương trình nào sau đây?
A.
2
1
6
sin
x
. B.
2
1
6
sin
x
. C.
1
6
sin
x
. D.
2
1
3
cos
x
.
Lời giải
Chọn A
Ta có 1cossin3 xx
3 1 1
sin cos
2 2 2
x x
1
sin
6 2
x
.
Câu 73:
(THPT Chuyên Biên Hòa-Hà Nam-lần 1 năm 2017-2018)
Số nghiệm của phương trình
2
2sin 2 cos 2 1 0
x x
trong
0;2018
là
A.
1008
. B.
2018
. C.
2017
. D.
1009
.
Lời giải
Chọn B
Ta có
2
2sin 2 cos 2 1 0
x x
2 2 2
8sin cos 2cos 0
x x x
2 2 2
2cos 4sin 1 0 cos 0 cos 0
2
x x x x x k
k
.
Bài ra
0;2018
x
nên
0;2018 0; 1; 2; 3;...; 2017
2
k k
.
Do đó số nghiệm của phương trình
2
2sin 2 cos 2 1 0
x x
trong
0;2018
là
2018
.
Câu 74:
(THPT Chuyên Biên Hòa-Hà Nam-lần 1 năm 2017-2018)
Tìm tập xác định của hàm số
tan 2
3
y x
.
A.
\
12 2
D k k
. B.
\
6
D k k
.
C.
\
12
D k k
. D.
\
6 2
D k k
.
Lời giải
Chọn A
Hàm số
tan 2
3
y x
xác định khi và chỉ khi
cos 2 0
3
x
2
3 2
x k
12 2
x k k
.
Câu 75:
(THPT Trần Nhân Tông-Quảng Ninh-lần 1 năm 2017-2018)
Giải phương trình
cos 2 2cos 3 0
x x
.
A.
2 , x k k
.
B.
2 , x k k
.
C.
2 ,
2
x k k
.
D.
2 ,
2
x k k
.
Hướng dẫn giải
Chọn B
Ta có
cos2 2cos 3 0
x x
2
2cos 1 2cos 3 0
x x
2
cos cos 2 0
x x
cos 1
cos 2
x
x
.
Vì
1 cos 1x
nên
cos 1x
2x k k
Vậy tập nghiệm của phương trình là:
2x k k
.
Câu 76:
(THPT Yên Định-Thanh Hóa-lần 1 năm 2017-2018)
Nghiệm của phương trình
sin 3 cos 2sin 3x x x
là
A.
6
x k
hoặc
2
6 3
x k
,
k
.
B.
2
3
x k
hoặc
2
2
3
x k
,
k
.
C.
2
3
x k
hoặc
4
2
3
x k
,
k
.
D.
3 2
x k
,
k
.
Hướng dẫn giải
Chọn D
Ta có
sin 3 cos 2sin 3x x x
1 3
sin cos sin3
2 2
x x x
cos sin sin cos sin 3
3 3
x x x
sin sin 3
3
x x
3 2
3
3 2
3
x x k
x x k
6
3 2
x k
x k
,
3 2
x k k
.
Câu 77:
(THTT số 5-488 tháng 2 năm 2018)
Phương trình
3 cos sin 2
x x
có bao nhiêu nghiệm
trên đoạn
0;4035
?
A.
2016
. B.
2017
. C.
2011
. D.
2018
.
Lời giải
Chọn B
Ta có
3 cos sin 2
x x
3 1
cos sin 1
2 2
x x
sin 1
3
x
3
2
3 2
x k
k
7
2
6
x k
k
.
Trên đoạn
0;4035
, các giá trị
k
thỏa bài toán thuộc tập
0;1;2; ;2016
.
Do đó có
2017
nghiệm của phương trình thuộc đoạn
0;4035
.
Câu 78:
(THPT Mộ Đức-Quãng Ngãi-lần 1 năm 2017-2018)
Phương trình
2sin 1 0
x
có bao nhiêu
nghiệm
0;2
x
?
A. 2 nghiệm. B. 1 nghiệm. C. 4 nghiệm. D. Vô số nghiệm.
Lời giải
Chọn A
Ta có:
2sin 1 0
x
1
sin
2
x
2
6
5
2
6
x k
x k
k
.
Do
0;2
x
nên ta có
5
;
6 6
x x
.
Câu 79:
(THPT Mộ Đức-Quãng Ngãi-lần 1 năm 2017-2018)
Cho phương trình:
cos 2 sin 1 0
x x
*
. Bằng cách đặt
sint x
1 1
t
thì phương trình
*
trở thành phương trình nào sau
đây?
A.
2
2 0
t t
. B.
2
2 0
t t
. C.
2
2 2 0
t t
. D.
2
0
t t
.
Lời giải
Chọn A
2 2 2
cos2 sin 1 0 1 2sin sin 1 0 2sin sin 0 2 0x x x x x x t t
.
Câu 1:
(SGD Bà Rịa Vũng Tàu-đề 1 năm 2017-2018)
Số giá trị nguyên dương của tham số
m
để phương
trình
4 3 cos sin 2 1 0
x x m
có nghiệm là
A.
6
. B.
5
C.
4
D.
3
Lời giải
Chọn C
Phương trình
4 3 cos sin 2 1 0
x x m
có nghiệm khi và chỉ khi:
2
2
2
4 3 1 2 1
m
2
4 4 48 0
m m
3 4
m
.
Vì
m
là số nguyên dương nên
1;2;3;4
m
.
Vậy có 4 giá trị nguyên dương của
m
thỏa yêu cầu bài toán.
Câu 2:
(SGD Bà Rịa Vũng Tàu-đề 1 năm 2017-2018)
Tập nghiệm của phương trình
2cos 2 1 0
x
là
A.
2 , 2 ,
3 3
S k k k
. B.
2 2
2 , 2 ,
3 3
S k k k
.
C.
, ,
3 3
S k k k
. D.
, ,
6 6
S k k k
.
Lời giải
Chọn C
Ta có
2cos 2 1 0
x
1 2
cos2 cos
2 3
x
2
2 2
3
x k
3
x k k
.
Câu 3:
(SGD Bà Rịa Vũng Tàu-đề 2 năm 2017-2018)
Cho
0
x
là nghiệm của phương trình
sin cos 2 sin cos 2
x x x x
thì giá trị của
0
3 sin 2P x
là
A.
3
P
. B.
2
3
2
P
. C.
0
P
. D.
2P
.
Lời giải
Chọn A
Đặt
sin cost x x
,
2 2
t
. Khi đó:
2
1
sin cos
2
t
x x
, phương trình đã cho trở thành:
2
1
2 2
2
t
t
2
4 5 0
t t
1
5
t
t
.
Với
5
t
loại do
2 2
t
.
Với
1t
ta có:
sin cos 1x x
2 sin 1
4
x
1
sin
4
2
x
2
4 4
3
2
4 4
x k
x k
2
2
2
x k
x k
.
Với
0
2x k
thì
3 sin 2 2 3
P k
.
Với
0
2
2
x k
thì
3 sin 2 2 3
2
P k
.
Vậy
3
P
.
Cách khác.
Khi
1t
thì
0
x
là nghiệm của pt
sin cos 1x x
. Suy ra
0 0
sin cos 1
x x
0
1 sin 2 1
x
0
sin 2 0
x
3
P
.
Câu 4:
(THPT Hà Huy Tập-Hà Tĩnh-lần 2 năm 2017-2018)
Nghiệm của phương trình
2
cos cos 0
x x
thỏa điều kiện
0 x
là
A.
2
x
. B.
2
x
. C.
6
x
. D.
4
x
.
Lời giải
Chọn A
Ta có
2
cos cos 0
x x
cos 0
cos 1
x
x
2
2
x k
x k
k
.
Do
0 x
2
x
.
Câu 5:
(THPT Phan Châu Trinh-DakLak-lần 2 năm 2017-2018)
Tổng các nghiệm của phương trình
sin cos sin cos 1
x x x x
trên khoảng
0;2
là
A.
2
. B.
4
. C.
3
. D.
.
Lời giải
Chọn C
Đặt
sin cost x x
, (
0 2
t
)
2
1 2sin .cost x x
2
1
sin .cos
2
t
x x
. Phương trình đã cho trở thành:
2
2 3 0
t t
1t
(thỏa mãn) hoặc
3
t
(loại).
Với
1t
sin 2 0
x
2
k
x
.
Trong khoảng
0;2
các nghiệm của phương trình là
3
; ;
2 2
.
Suy ra tổng các nghiệm của phương trình trong khoảng
0;2
là
3
.
Câu 6:
(THPT Kinh Môn-Hải Dương lần 1 năm 2017-2018)
Tập xác định của hàm số
tan 2
cos
x
y
x
là
tập nào sau đây?
A.
D
. B.
\
2
D k
,k
.
C.
\ ,
4 2
D k k
. D.
\ ; ,
4 2 2
D k k k
.
Lời giải
Chọn D
Hàm số xác định khi
2
cos2 0
2
cos 0
2
x k
x
x
x k
4 2
,
2
x k
k
x k
Vậy tập xác định là
\ ; ,
4 2 2
D k k k
.
Câu 7:
(THPT Kinh Môn-Hải Dương lần 1 năm 2017-2018)
Tìm tất cả các số thực của tham số
m
sao
cho hàm số
2sin 1
sin
x
y
x m
đồng biến trên khoảng
0;
2
.
A.
1
0
2
m
hoặc
1
m
. B.
1
2
m
.
C.
1
2
m
. D.
1
0
2
m
hoặc
1
m
.
Lời giải
Chọn D
0;
2
x
sinx 0;1
. Hàm số xác định trong khoảng
0;
2
khi
m 0;1
hay
0
1
m
m
1
.
Ta có
2
cos 2 1
sinx
x m
y
m
. Hàm số đồng biến trong khoảng
0;
2
khi và chỉ khi
0
y
với
x D
2 1 0
m
1
2
m
.
Kết hợp
1
ta có
1
0
2
m
hoặc
1
m
.
Câu 8:
(THPT Kinh Môn-Hải Dương lần 1 năm 2017-2018)
Số đường tiệm cận của đồ thị hàm số
2
2
1
x x
y
x
.
A.
1
. B.
4
. C.
3
. D.
2
.
Lời giải
Chọn C
Tập xác định
; 2 1;D

.

2
2
lim 1
1
x
x x
x

Đồ thị hàm số có tiệm cận ngang là đường thẳng
1y
.

2
2
lim 1
1
x
x x
x

Đồ thị hàm số có tiệm cận ngang là đường thẳng
1
y
.

2
1
2
lim 1
1
x
x x
x
1
1 2
lim
1
x
x x
x
1
2
lim
1
x
x
x

Đồ thị hàm số có tiệm cận
đứng là đường thẳng
1x
.
Vậy đồ thị hàm số có
3
đường tiệm cận.
Câu 9:
(THPT Can Lộc-Hà Tĩnh-lần 1 năm 2017-2018)
Tổng tất cả các giá trị nguyên của
m
để phương
trình
4sin 4 cos 2 5 0
x m x m
có nghiệm là
A.
5
. B.
6
. C.
10
. D.
3
.
Lời giải
Chọn C
4sin 4 cos 2 5 0
x m x m
4sin 4 cos 2 5
x m x m
.
Phương trình có nghiệm khi
2 2
2
4 4 2 5 0
m m
2
3 12 7 0
m m
6 57 6 57
3 3
m
Vì
m
nên
0,1,2,3,4
m
.
Vây tổng tất cả các giá trị nguyên của
m
để phương trình có nghiệm là
10
.
Câu 10:
(THPT Can Lộc-Hà Tĩnh-lần 1 năm 2017-2018)
Số nghiệm của phương trình
9 15
sin 2 3cos 1 2sin
2 2
x x x
với
0;2
x
là
A.
6
. B.
5
. C.
3
. D.
4
.
Lời giải
Chọn B
9 15
sin 2 3cos 1 2sin
2 2
x x x
sin 2 3cos 1 2sin
2 2
x x x
cos 2 3sin 1 2sinx x x
2
2sin sin 0
x x
sin 0
2
1
6
sin
2
5
2
6
x k
x
x k k
x
x k
Do
0;2
x
nên
5
0; ;2 ; ;
6 6
x
. Vậy có
5
nghiệm.
Câu 11:
(THPT Lê Quý Đôn-Hải Phòng lần 1 năm 2017-2018)
Hàm số
siny x
đồng biến trên khoảng
nào sau đây?
A.
5 7
;
4 4
. B.
9 11
;
4 4
. C.
7
;3
4
. D.
7 9
;
4 4
.
Lời giải
Chọn D
Dựa vào định nghĩa đường tròn lượng giác ta thấy hàm số lượng giác cơ bản
đồng
biến ở góc phần tư thứ nhất và góc phần tư thứ tư.
Dễ thấy khoảng
7 9
;
4 4
là phần thuộc góc phần tư thứ tư và thứ nhất nên hàm số đồng biến.
Câu 12: (THPT Lê Quý Đôn-Quãng Trị-lần 1 năm 2017-2018) Giải phương trình:
cos3 .tan 4 sin 5x x x
.
A.
2
3
x k
,
16 8
x k
. B.
2x k
,
3
16 8
x k
.
C.
x k
,
16 8
x k
. D.
2
x k
,
3
16 8
x k
.
Lời giải
Chọn C
Điều kiện xác định:
cos 4 0
x
.
cos3 .tan 4 sin 5x x x
cos3 .sin 4 sin 5 .cos 4x x x x
1 1
sin 7 sin sin 9 sin
2 2
x x x x
sin 9 sin 7x x
9 7 2
9 7 2
x x k
x x k
16 8
x k
x k
.
Thử qua điều kiện xác định ta thấy
x k
và
16 8
x k
thỏa mãn.
Vậy nghiệm phương trình là
16 8
x k
x k
.
Câu 13:
(THPT Chuyên Tiền Giang-lần 1 năm 2017-2018)
Phương trình nào dưới đây có tập nghiệm
trùng với tập nghiệm của phương trình
sin 0
x
?
A.
cos 1
x
. B.
cos 1x
. C.
tan 0
x
. D.
cot 1x
.
Lời giải
Chọn C
sin 0
x
;x k k
.
cos 1
x
2 ;x k k
.
cos 1x
2 ;x k k
.
tan 0
x
;x k k
.
Câu 14:
(THPT Phan Đình Phùng-Hà Tĩnh-lần 1 năm 2017-2018)
Số nghiệm của phương trình
2cos 3
x
trên đoạn
5
0;
2
là
A.
2
. B.
1
. C.
4
. D.
3
.
Lời giải
Chọn D
2cos 3
x
3
cos
2
x
2 ,
6
x k k
.
Mà
5
0;
2
x
và
k
nên
11 13
; ;
6 6 6
x
.
Câu 15:
(THPT Phan Đình Phùng-Hà Tĩnh-lần 1 năm 2017-2018)
Giá
trị nhỏ nhất của hàm số
2
2cos sin 2 5
y x x
.
A.
2
. B.
2
. C.
6 2
. D.
6 2
.
Lời giải
Chọn C
Ta có
2
2cos sin 2 5
y x x
cos 2 sin 2 6
x x
2 cos 2 6
4
x
.
Do
2 2 cos 2 2
4
x
nên
2 6 2 cos 2 6 2 6
4
x
.
Vậy giá trị nhỏ nhất của hàm số
2
2cos sin 2 5
y x x
là
6 2
.
Câu 16:
(THPT Lục Ngạn-Bắc Giang-lần 1 năm 2017-2018)
Phương trình
3sin cos
x x m
, với
m
là
tham số có nghiệm khi giá trị của
m
bằng
A.
2
2
m
m
. B.
1
1
m
m
. C.
2 2
m
. D.
1 1
m
.
Lời giải
Chọn C
Phương trình
3sin cos
x x m
có nghiệm khi
2
2
3 1
m
2
4
m
2 2
m
.
Câu 17:
(THPT Lục Ngạn-Bắc Giang-lần 1 năm 2017-2018)
Phương trình
sin 2 cosx x
có nghiệm là
A.
6 3
2
2
k
x
k
x k
. B.
6 3
2
3
k
x
k
x k
.
C.
2
6
2
2
x k
k
x k
. D.
2
6 3
2
2
k
x
k
x k
.
Lời giải
Chọn A
6 3
sin 2 cos sin 2 sin
2
2
2
k
x
x x x x k
x k
.
Câu 18: (THTT số 6-489 tháng 3 năm 2018) Tìm giá trị dương của
k
để
2
3 1 1
lim 9 2
x
k x
f
x

với
2
ln 5
f x x
:
A.
12
k
. B.
2
k
. C.
5
k
. D.
9
k
.
Lời giải
Chọn C
Ta có:
2
2
5
x
f x
x
4
2
9
f
.
Ta có:
2
3 1 1
lim
x
k x
x

2
1
3 1
lim
x
x k
x
x

2
1
3 1
lim
x
x k
x
x

2
1
lim 3 1 3 1
x
k k
x

.(Theo đề bài
0
k
).
Theo đề bài:
4
3 1 9. 5
9
k k
.
Câu 19: (THTT số 6-489 tháng 3 năm 2018) Với giá trị lớn nhất của
a
bằng bao nhiêu để phương trình
2 2
sin 2sin 2 3 cos 2
a x x a x
có nghiệm?
A.
2
. B.
11
3
. C.
4
. D.
8
3
.
Lời giải
Chọn D
Ta có:
2 2
sin 2sin 2 3 cos 2
a x x a x
1 cos2 1 cos2
2sin 2 3 2
2 2
x x
a x a
4sin 2 2 cos2 4 4 *x a x a
.
Phương trình
*
có nghiệm
2
2
16 4 4 4a a
2
12 32 0
a a
8
0
3
a
.
Câu 20: (THPT Đặng Thúc Hứa-Nghệ An-lần 1 năm 2017-2018) Cho các giả thiết sau đây. Giả thiết
nào kết luận đường thẳng
a
song song với mặt phẳng
?
A.
//a b
và
b
. B.
//a
và
//
.
C.
//a b
và
//b
. D.
a
.
Lời giải
Chọn D
Câu 21:
(THPT Chuyên Hạ Long-Quãng Ninh lần 2 năm 2017-2018)
Cho phương trình
cos2 2 3 cos 1 0
x m x m
(
m
là tham số). Tìm tất cả các giá trị thực của tham số
m
để
phương trình có nghiệm thuộc khoảng
3
;
2 2
.
A.
1 2
m
. B.
2
m
. C.
1
m
. D.
1
m
.
Lời giải
Chọn A
cos2 2 3 cos 1 0
x m x m
2
2cos 2 3 cos 2 0
x m x m
2cos 1 cos 2 0
x x m
cos 2 0
x m
, vì
3
;
2 2
x
cos 2
x m
Ycbt
1 2 0
m
1 2
m
Câu 22:
(THPT Chuyên Hùng Vương-Gia Lai-lần 1 năm 2017-2018)
Tính tổng tất cả các nghiệm của
phương trình
3 cos sin 1x x
trên
0;2
.
A.
6
. B.
11
6
. C.
5
3
. D.
3
2
.
Lời giải
Chọn C
Ta có
1
3 cos sin 1 cos
6 2
x x x
2
6
2
2
x k
k
x k
.
Do đó các nghiệm trên
0;2
của phương trình là
6
x
,
3
2
x
.
Vậy tổng tất cả các nghiệm của phương trình trên
0;2
bằng
3 5
6 2 3
.
Câu 23:
(THPT Chuyên Trần Phú-Hải Phòng-lần 2 năm 2017-2018)
Điều kiện của tham số thực
m
để
phương trình
sin 1 cos 2
x m x
vô nghiệm là
A.
0
2
m
m
. B.
2
m
. C.
2 0
m
. D.
0
m
.
Lời giải
Chọn C
Để phương trình
sin 1 cos 2
x m x
vô nghiệm thì
2
2
2
1 1 2 2 0
m m
.
Câu 24: (THPT Tây Thụy Anh – Thái Bình – lần 1 - năm 2017 – 2018) Tìm tất cả các giá trị của
tham số
m
để phương trình
2
1
cos x m
có nghiệm.
A.
2
m
. B.
1 2
m
. C.
1
m
. D.
1 2
m
.
Lời giải
Chọn D
Do
2
cos
0 1x
với
x
nên phương trình có nghiệm khi
0 1 1
m
1 2
m
Câu 25: (THPT Tây Thụy Anh – Thái Bình – lần 1 - năm 2017 – 2018) Đồ thị hàm số
3
3y x x
cắt:
A. Đường thẳng
3
y
tại hai điểm. B. Đường thẳng
5
3
y
tại ba điểm.
C. Đường thẳng
4
y
tại hai điểm. D. Trục hoành tại một điểm.
Lời giải
Chọn B
3
3 .y x x
2
3 3 0 1.
y x x
Bảng biến thiên:
Dựa vào bảng biến thiên ta chọn đáp án B.
Câu 26:
(THPT Yên Lạc – Vĩnh Phúc – lần 4 - năm 2017 – 2018)
Tập tất cả các nghiệm của phương trình
2
sin 2 2sin 6sin 2cos 4 0
x x x x
là
A.
2
3
x k
,
k
. B.
2
2
x k
,
k
.
C.
2
2
x k
,
k
. D.
2
x k
,
k
.
Lời giải
Chọn C
Cách 1: Ta có:
2
sin 2 2sin 6sin 2cos 4 0
x x x x
2
2sin cos 2cos 2sin 6sin 4 0
x x x x x
2cos sin 1 2 sin 2 sin 1 0
x x x x
sin 1 sin cos 2 0
x x x
sin 1
sin cos 2
x
x x
2
2
sin 2
4
x k
x VN
2
2
x k
,
k
.
Cách 2: Dùng MTCT thử lần lượt các đáp án, thấy C là đáp án đúng.
Câu 27: (THPT Chuyên Vĩnh Phúc – Vĩnh Phúc - Lần 4 năm 2017 – 2018)Tìm số nghiệm của phương trình
sin cos 0
x
trên đoạn
0;2
x
.
A.
0
. B.
1
. C.
2
. D. Vô số.
Lời giải
Chọn C
Ta có:
sin cos 0 cos
x x k
k
Vì
cos 1
x
nên
0
k
. Do đó phương trình
cos 0
2
x x m m
Vì
0;2
x
nên
2
x
,
3
2
x
.
Câu 28:
(ĐHQG TPHCM – Cơ Sở 2 – năm 2017 – 2018)
Giả sử
M
là giá trị lớn nhất và
m
là giá trị
nhỏ nhất của hàm số
2 3 sin cosy x x
. Khi đó
M m
bằng
A.
3 3
. B.
0
. C.
1 3
. D.
1
.
Lời giải
Chọn B
Ta có:
2 2
2 3 1 2 3 sin cos 2 3 1
x x
.
Vậy
0
M m
.
Câu 29:
(SGD Nam Định – năm 2017 – 2018)
Mệnh đề nào sau đây đúng?
A. Hàm số
siny x
tuần hoàn với chu kỳ
T
.
B. Hàm số
đồng biến trên
0;
2
.
C. Hàm số
siny x
là hàm số chẵn.
D. Đồ thị hàm số
có tiệm cận ngang.
Lời giải
Chọn B
Mệnh đề A sai vì hàm số
siny x
tuần hoàn với chu kỳ
2
T
.
Mệnh đề C sai vì hàm số
siny x
là hàm số lẻ.
Mệnh đề D sai vì hàm số
siny x
không có tiệm cận ngang.
Mệnh đề B đúng vì hàm số
siny x
đồng biến trên khoảng
2 ; 2
2 2
k k
.
Câu 1:
(SGD Thanh Hóa – năm 2017 – 2018)
Có tất cả bao nhiêu giá trị nguyên của tham số
m
để
phương trình
3 2 2
cos 2 cos 2 sinx x m x
có nghiệm thuộc khoảng
0;
6
?
A.
3
. B.
0
. C.
2
. D.
1
.
Lời giải
Chọn D
Ta có:
3 2 2
cos 2 cos 2 sinx x m x
2 2
cos 2 cos 2 1 sinx x m x
2 2
sin 2cos 2 0
x x m
2
2cos 2 0
x m
cos4 1
x m
.
Có
0;
6
x
2
4 0;
3
x
1
cos4 1
2
x
Để phương trình có nghiệm
0;
6
x
thì
1
1 1
2
m
1
2
2
m
.
Do
m
nên
1
m
.
Câu 2:
(THPT Chuyên Nguyễn Quang Diệu – Đồng Tháp – Lần 5 năm 2017 – 2018)
Tìm giá trị nguyên
lớn nhất của
a
để phương trình
2 2
sin 2sin 2 3 cos 2
a x x a x
có nghiệm
A.
3
a
. B.
2
a
. C.
1
a
. D.
1
a
.
Lời giải
Chọn B
2 2
sin 2sin 2 3 cos 2
a x x a x
1 cos2 1 cos2
2sin 2 3 2
2 2
x x
a x a
cos 2 4sin 2 3 3 cos 2 4
a a x x a a x
4sin 2 2 cos 2 4 4x a x a
*
*
có nghiệm khi
2
2 2
4 4 4 4a a
2
12 32 0
a a
2
12 32 0
a a
8
0
3
a
.
Do
a
và là số lớn nhất nên
2
a
.
Câu 3:
(THPT Chuyên Hùng Vương – Gia Lai – Lần 2 năm 2017 – 2018)
Phương trình
3
sin 3
3 2
x
có bao nhiêu nghiệm thuộc khoảng
0;
2
?
A.
3
. B.
4
. C.
1
. D.
2
.
Lời giải
Chọn D
Ta có:
3
sin 3
3 2
x
3 2
3 3
4
3 2
3 3
x k
x k
k
2
3 2
3
3 2
x k
x k
k
2 2
9 3
2
3 3
x k
x k
k
.
Vì
0;
2
x
nên
3
x
,
4
9
x
.
Vậy phương trình đã cho có hai nghiệm thuộc khoảng
0;
2
.
Câu 4: (SGD Hà Tĩnh – Lần 2 năm 2017 – 2018) Tổng các nghiệm của phương trình
2
2cos 3 sin 2 3
x x
trên
5
0;
2
là:
A.
7
6
. B.
7
3
. C.
7
2
. D.
2
.
Hướng dẫn giải
Chọn C
2
2cos 3 sin 2 3
x x
cos2 3 sin 2 2
x x
cos 2 1
3
x
2 2
3
x k
6
x k
k
.
Xét
5
0
2
x
5
0
6 2
k
0
k
,
1
k
,
2
k
.
Với
0
6
k x
;
7
1
6
k x
;
13
2
6
k x
.
Vậy tổng các nghiệm bằng
7
2
.
Câu 5:
(THPT Chu Văn An – Hà Nội - năm 2017-2018)
Gọi
M
,
m
tương ứng là giá trị lớn nhất và giá
trị nhỏ nhất của hàm số
2cos 1
cos 2
x
y
x
. Khẳng định nào sau đây đúng?
A.
9 0
M m
. B.
9 0
M m
. C.
9 0
M m
. D.
0
M m
.
Lời giải
Chọn C
Ta có
2cos 1 5
2
cos 2 cos 2
x
y
x x
,
mà
1 cos 1x
3 cos 2 1
x
5 5
5
3 cos 2x
1 5
2 3
3 cos 2x
1
3
3
y
. Vậy
1
3
M
và
1 cos 1x
9 0
M m
.
Câu 6: Phương trình
2 2
4sin 2 3sin 2 cos2 cos 2 0
x x x x
có bao nhiêu nghiệm trong khoảng
0;
?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 7: Phương trình
2 2
4sin 2 3sin 2 cos2 cos 2 0
x x x x
có bao nhiêu nghiệm trong khoảng
0;
?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn D
Dễ thấy
cos2 0
x
không thỏa mãn phương trình. Do đó, phương trình đã cho tương đương
với:
2
4tan 2 3tan 2 1 0
x x
tan 2 1
1
tan 2
4
x
x
1
8 2
1 1
arctan 2
2 4 2
x k
x k
Xét
1
, vì
0;
x
0
8 2
k
1
k
(do
k
).
Xét
2
, vì
0;
x
1 1
0 arctan
2 4 2
k
1;2
k
(do
k
).
Do đó, trong khoảng
0;
thì phương trình đã cho có
3
nghiệm.
Câu 8: Cho hàm số
3 2
1
2 1
3
y x x
có đồ thị
C
và đường thẳng
:
d y m
. Tìm tập hợp tất cả các giá trị của tham số
m
để
d
cắt
C
tại ba điểm phân biệt.
A.
29
;1
3
. B.
29
1;
3
. C.
29
1;
3
. D.
29
;1
3
.
Câu 9: Số nghiệm thuộc đoạn
0;
của phương trình
cos cos2 cos3 1 0
x x x
là
A.
4
. B.
3
. C.
1
. D.
2
.
Câu 10: Cho hàm số
3 2
1
2 1
3
y x x
có đồ thị
C
và đường thẳng
:
d y m
. Tìm tập hợp tất cả các giá trị của tham số
m
để
d
cắt
C
tại ba điểm phân biệt.
A.
29
;1
3
. B.
29
1;
3
. C.
29
1;
3
. D.
29
;1
3
.
Lời giải
Chọn A
2
4y x x
.
4
0
0
x
y
x
.
BBT
x

0
4

y
0
0
y

1
29
3

Để
d
cắt
C
tại ba điểm phân biệt thì
29
;1
3
m
.
Câu 11: Số nghiệm thuộc đoạn
0;
của phương trình
cos cos2 cos3 1 0
x x x
là
A.
4
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn B
Ta có
cos cos2 cos3 1 0
x x x
2 3
cos 2cos 1 4cos 3cos 1 0
x x x x
3 2
4cos 2cos 4cos 2 0
x x x
.
cos 1
cos 1
1
cos
2
x
x
x
0;
0
2
3
x
x
x
x

.
Câu 12: Số nghiệm thuộc khoảng
;
của phương trình:
2sin 1x
là:
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 13: Số nghiệm thuộc khoảng
;
của phương trình:
2sin 1x
là:
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn B
Ta có:
2
1
6
sin
5
2
2
6
x k
x
x k
.
Mà
5
; ;
6 6
x x x
. Vậy phương trình có hai nghiệm thỏa mãn đề bài.
Câu 14: Nghiệm của phương trình
2cos 2 9sin 7 0
x x
là
A.
2 ,
2
x k k
. B.
,
2
x k k
.
C.
,
2
x k k
. D.
2 ,
2
x k k
.
Câu 15: Nghiệm của phương trình
2cos 2 9sin 7 0
x x
là
A.
2 ,
2
x k k
. B.
,
2
x k k
.
C.
,
2
x k k
. D.
2 ,
2
x k k
.
Hướng dẫn giải
Chọn D
2cos 2 9sin 7 0
x x
2
4sin 9sin 5 0
x x
5
sin
4
sin 1
x VN
x
2 ,
2
x k k
.
Câu 16: Tổng tất cả các nghiệm của phương trình
3cos 1 0
x
trên đoạn
0;4
là
A.
15
2
. B.
6
. C.
17
2
. D.
8
.
Câu 17: Tổng tất cả các nghiệm của phương trình
3cos 1 0
x
trên đoạn
0;4
là
A.
15
2
. B.
6
. C.
17
2
. D.
8
.
Lời giải
Chọn D
Ta có:
3cos 1 0
x
1
cos
3
x
2
2
x k
x k
( với
0;
2
,
k
).
Mà
0;4
x
nên
; 2 ; 2 ; 4
x
.
Vậy tổng các nghiệm thỏa mãn đề bài là
2 2 4 8
.
Câu 18: Số điểm biểu diễn các nghiệm của phương trình
1
sin 2
3 2
x
trên đường tròn lượng giác là
A.
6
. B.
1
. C.
4
. D.
2
.
Câu 19: Số điểm biểu diễn các nghiệm của phương trình
1
sin 2
3 2
x
trên đường tròn lượng giác là
A.
6
. B.
1
. C.
4
. D.
2
.
Lời giải
Chọn C
Ta có
1
sin 2
3 2
x
2 2
3 6
5
2 2
3 6
x k
k
x k
12
4
x k
k
x k
.
Mỗi họ nghiệm biểu diễn trên đường tròn lượng giác
2
điểm và các điểm khác nhau nên số
điểm biểu diễn các nghiệm là
4
.
Câu 20: Một phương trình có tập nghiệm được biểu diễn trên đường tròn lượng giác là hai điểm
M
và
N
trong hình dưới.
y
x
N
M
O
-1
-1
1
1
Phương trình đó là
A.
2cos 1 0
x
. B.
2cos 3 0
x
. C.
2sin 3 0
x
. D.
2sin 1 0
x
.
Câu 21: Giá trị lớn nhất của hàm số
2
2sin sin 2 10
f x x x
là
A.
10
. B.
11 2
. C.
11 2
. D.
9 2
.
Câu 22: Một phương trình có tập nghiệm được biểu diễn trên đường tròn lượng giác là hai điểm
M
và
N
trong hình dưới.
y
x
N
M
O
-1
-1
1
1
Phương trình đó là
A.
2cos 1 0
x
. B.
2cos 3 0
x
. C.
2sin 3 0
x
. D.
2sin 1 0
x
.
Lời giải
Chọn A
Hai điểm
M
,
N
đối xứng qua trục
Ox
nên loại đáp án C, D.
MN
cắt
Ox
tại điểm có hoành độ bằng
1
2
.
Ta có
2cos 1 0
x
1
cos
2
x
, suy đáp án A đúng.
Câu 23: Giá trị lớn nhất của hàm số
2
2sin sin 2 10
f x x x
là
A.
10
. B.
11 2
. C.
11 2
. D.
9 2
.
Lời giải
Chọn C
Ta có
2
2sin sin 2 10
f x x x
11 sin 2 cos 2x x
11 2 sin 2
4
x
.
Do
1 sin 2 1
4
x
2 2 sin 2 2
4
x
nên
11 2 sin 2 11 2
4
x
.
Dấu
" ''
xảy ra khi
3
sin 2 1
4 8
x x k
,
k
. Vậy
max 11 2
f x
.
Câu 24: Giá trị lớn nhất của
m
để phương trình
2018
cos sin 5 0
x x m
có nghiệm là:
A.
1
. B.
0
. C.
1
. D.
3
2
.
Câu 25: Giá trị lớn nhất của
m
để phương trình
2018
cos sin 5 0
x x m
có nghiệm là:
A.
1
. B.
0
. C.
1
. D.
3
2
.
Hướng dẫn giải
Chọn C
Phương trình tương đương:
2018
cos sin 5
x x m
.
Ta có:
2018
2018
cos 1
cos sin 5 1
sin 5 0
x
x x
x
.
Dấu đẳng thức xảy ra khi
cos 1
sin 5 0
x
x
.
cos 1
π+ 2πx x k
. Khi đó
sin 5 sin 5
π 2π sin 5π 0
x k
thỏa mãn.
Phương trình có nghiệm thì
1 1
m m
.
Vậy giá trị lớn nhất của
m
là
1
m
.
Câu 26: Giải phương trình
1
sin .cos
2
x x
trên đoạn
;2018
ta được số nghiệm là:
A.
2016
nghiệm. B.
2017
nghiệm. C.
2018
nghiệm. D.
2019
nghiệm.
Câu 27: Giải phương trình
1
sin .cos
2
x x
trên đoạn
;2018
ta được số nghiệm là:
A.
2016
nghiệm. B.
2017
nghiệm. C.
2018
nghiệm. D.
2019
nghiệm.
Lời giải
Chọn B
Ta có
1
sin .cos sin 2 1
2 4
x x x x k k
.
Khi đó
3 8071
2018 1 2017
4 4
x k k
(Do
k
là số nguyên).
Vậy trên đoạn
;2018
phương trình đã cho có
2017
nghiệm.
Câu 28: Phương trình
sin5 sin 0
x x
có bao nhiêu nghiệm thuộc đoạn
2018 ;2018
?
A.
20179
. B.
20181
. C.
16144
. D.
16145
.
Câu 29: Phương trình
sin 5 sin 0
x x
có bao nhiêu nghiệm thuộc đoạn
2018 ;2018
?
A.
20179
. B.
20181
. C.
16144
. D.
16145
.
Lời giải
Chọn B
Ta có
sin 5 sin 0
x x
sin 5 sinx x
π
2
π π
6 3
k
x
k
x
,
(
k
).
Vì
2018
π;2018π
x
nên
+ Với
π
2
k
x
ta có
π
2018
π 2018π
2
k
4036 4036
k
. Suy ra có
8073
nghiệm.
+ Với
π π
6 3
k
x
ta có
π π
2018
π 2018π
6 3
k
12109 12107
2 2
k
. Suy ra có
12108
nghiệm.
Vậy có
8073 12108 20181
nghiệm thuộc đoạn
2018 ;2018
.
Câu 30: Phương trình
3
sin 2 sin
4 4
x x
có tổng các nghiệm thuộc khoảng
0;
bằng
A.
7
2
. B.
. C.
3
2
. D.
4
.
Câu 31: Phương trình
3
sin 2 sin
4 4
x x
có tổng các nghiệm thuộc khoảng
0;
bằng
A.
7
2
. B.
. C.
3
2
. D.
4
.
Lời giải
Chọn B
Ta có
3
sin 2 sin
4 4
x x
3
2 2
4 4
2 2
4 4
x x k
x x l
2
,
2
6 3
x k
k l
x l
.
Họ nghiệm
2x k
không có nghiệm nào thuộc khoảng
0;
.
2
0;
6 3
x l
2
0
6 3
l
0; 1
l
.
Vậy phương trình có hai nghiệm thuộc khoảng
0;
là
6
x
và
5
6
x
. Từ đó suy ra tổng
các nghiệm thuộc khoảng
0;
của phương trình này bằng
.
Câu 32: Tìm tập nghiệm của phương trình:
2cos 3 3 0
4
x
A.
7 2 13 2
;
36 3 36 3
k k k
. B.
5
2
6
k k
.
C.
7 2 13 2
;
36 3 36 3
k k k
. D.
7 13
2 ; 2
36 36
k k k
Câu 33: Tìm tập nghiệm của phương trình:
2cos 3 3 0
4
x
A.
7 2 13 2
;
36 3 36 3
k k k
. B.
5
2
6
k k
.
C.
7 2 13 2
;
36 3 36 3
k k k
. D.
7 13
2 ; 2
36 36
k k k
Lời giải
Chọn C
Ta có:
2cos 3 3 0
4
x
3 5
cos 3 cos 3 cos
4 2 4 6
x x
5 7 2
3 2
4 6 36 3
;
5 13 2
3 2
4 6 36 3
x k x k
k
x k x k
Câu 34: Cho phương trình
2 2
4 3
sin .tan cos .cot 2sin cos
3
x x x x x x
. Tính hiệu nghiệm âm lớn nhất
và nghiệm dương nhỏ nhất của phương trình.
A.
3
2
. B.
5
6
. C.
5
6
. D.
.
Câu 35: Cho phương trình
2 2
4 3
sin .tan cos .cot 2sin cos
3
x x x x x x
. Tính hiệu nghiệm âm lớn nhất
và nghiệm dương nhỏ nhất của phương trình.
A.
3
2
. B.
5
6
. C.
5
6
. D.
.
Hướng dẫn giải
Chọn C
Điều kiện:
sin 2 0
2
k
x x
.
Phương trình
3 3
sin cos 4 3
2sin cos
cos sin 3
x x
x x
x x
4 4 2 2
4 3
sin cos 2sin cos sin cos
3
x x x x x x
2
2 2
2 3
sin cos sin 2
3
x x x
3
sin 2
2
x
6
3
x k
k
x k
.
Suy ra nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình lần lượt là
2
3
và
6
Ta có:
2 5
3 6 6
.
Câu 36: Tìm tập xác định của hàm số
sin 2 2
1 cos
x
f x
x
.
A.
D
. B.
\ 2
π
D k
. C.
2
π
D k
. D.
\
πD k
.
Câu 37: Tìm tập xác định của hàm số
sin 2 2
1 cos
x
f x
x
.
A.
D
. B.
\ 2
π
D k
. C.
2
π
D k
. D.
\
πD k
.
Lời giải
Chọn B
Hàm số xác định
sin 2 2
0
1 cos
x
x
1 cos 0 2
πx x k
,
k
.
Vậy tập xác định của hàm số là
\ 2
π
D k
,
k
.
Câu 38: Số nghiệm của phương trình
3cos 2 2
x
trên
3
;
2 2
là
A.
4
. B.
3
. C.
2
. D.
1
.
Câu 39: Số nghiệm của phương trình
3cos 2 2
x
trên
3
;
2 2
là
A.
4
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn A
Cách 1:
2
3cos 2 2 os2
3
x c x
2
2 arccos 2
3
2
2 arccos 2
3
x k
x k
1 2
arccos
2 3
1 2
arccos
2 3
x k
x k
.
Xét trên
3
;
2 2
ta có
1 2
arccos
2 3
1 2
arccos
2 3
1 2
arccos
2 3
1 2
arccos
2 3
x
x
x
x
.
Vậy phương trình đã cho có bốn nghiệm trên
3
;
2 2
.
Cách 2: Dùng Casio.
Dùng chức năng TABLE.
Nhập hàm:
Cho Start =
4
, End =
3
2
, Step =
12
.
Kết quả có bốn lần đổi dấu như sau:
Chú ý: Tắt đi hàm
g X
như sau:
Bấm SHIFT, MODE, di chuyển xuống, chọn 5: TABLE
Sau đó chọn 1:
Câu 1:
(THTT Số 1-484 tháng 10 năm 2017-2018)
Tính tổng
S
các nghiệm của phương trình
4 4
2cos 2 5 sin cos 3 0
x x x
trong khoảng
0;2
.
A.
11
6
S
. B.
4
S
. C.
5
S
. D.
7
6
S
.
Lời giải
Chọn B
Ta có:
4 4 2 2
2cos 2 5 sin cos 3 0 2cos 2 5 sin cos 3 0
x x x x x x
2
1
2cos2 5 cos 2 3 0 2cos (2 ) 5cos 2 3 0 cos 2
2
x x x x x
.
1 5 7 11
cos2 ; ; ;
2 6 6 6 6 6
x x k k x
.
Do đó:
5 7 11
4 .
6 6 6 6
S
Câu 2:
(THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018)
Nghiệm của phương trình
cos2 3sin 2
0
cos
x x
x
là:
A.
2
2
6
5
6
x k
x k
x k
k
. B.
6
5
6
x k
x k
k
.
C.
2
2
2
6
5
2
6
x k
x k
x k
k
. D.
2
6
5
2
6
x k
x k
k
.
Lời giải
Chọn D
Cách 1: Điều kiện xác định:
cos 0
2
x x l
với
l
.
Khi đó phương trình trở thành
cos2 3sin 2 0
x x
2
2sin 3sin 1 0
x x
sin 1 (1)
1
sin (2)
2
x
x
Đối chiếu điều kiện ta loại phương trình
(1)
. Giải phương trình
(2)
được
2
6
5
2
6
x k
x k
với
k
.
Cách 2: Dùng máy tính
Bước 1: nhập vế trái của phương trình.
Bước 2: nhấn CALC thay X bằng các kết quả trong mỗi phương án.
Bước 3: chọn đáp án nào đều trả về kết quả bằng hoặc rất “gần”
0
.
(chú ý đơn vị ra-đi-an).
Câu 3:
(THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018)
Tập giá trị của hàm số
sin 2 3 cos2 1y x x
là đoạn
; .a b
Tính tổng
.T a b
A.
1.
T
B.
2.
T
C.
0.
T
D.
1.
T
Lời giải
Chọn B
Cách 1:
sin 2 3 cos 2 1 sin 2 3 cos2 1y x x x x y
Để phương trình trên có nghiệm thì
2
2
2 2
1 3 1 2 3 0 1 3
y y y y
.
Suy ra
1;3
y
. Vậy
1 3 2.
T
Cách 2: Ta có
1 sin 2 3 cos2 .y x x
Mặt khác áp dụng bất đẳng thức Bunhiacopskii ta có
2
2
2 2
1 sin 2 3 os2 1 3 sin 2 os 2 4 2 1 2 1 3.
y x c x x c x y y
Vậy
1 3 2.
T
Cách 3:
sin 2 3 cos2 1 2sin 2 1
3
y x x x
Do
sin 2 1;1
3
x
nên
2sin 2 1 1;3
3
x
.
Vậy
1 3
y
.( Ta thấy
1
y
khi
sin 2 1
3
x
,
3
y
khi
sin 2 1
3
x
).sss
Câu 4:
(THPT Sơn Tây-Hà Nội-lần 1-năm 2017-2018)
Gọi
K
là tập hợp tất cả các giá trị của tham số
m
để phương trình
sin 2 2 sin 2
4
x x m
có đúng hai nghiệm thuộc khoảng
3
0;
4
.
Hỏi
K
là tập con của tập hợp nào dưới đây?
A.
2 2
;
2 2
. B.
1 2; 2
. C.
2
2;
2
. D.
2
; 2
2
.
Lời giải
Chọn C
Cách 1: Đặt
2 sin sinx cos
4
t x x
,
2; 2
t
.
Suy ra
2
1 sin 2t x
2
3
t t m
Xét hàm số
2
3y f t t t
,
2; 2
t
2 1f t t
0
f t
1
2
t
2; 2
Phương trình
sin 2 2 sin 2
4
x x m
có đúng hai nghiệm thuộc khoảng
3
0;
4
Phương trình
2
3
t t m
có đúng một nghiệm
1; 2
t
Dựa vào bảng biến thiên ta thấy
1; 2 1
K
2
2;
2
Cách 2 : Xét hàm số
sin 2 2 sin 2
4
f x x x
với
3
0;
4
x
.
Ta có
2cos 2 2 cos
4
f x x x
, vậy
2 2
0 2cos 2 2 cos 0
4
2 cos sin cos sin 0
cos sin 0
2 cos sin 1 0
3
0;
4 4
2 2 sin 1 0 *
4
f x x
x
x
x x x
x x
x x
x
x
Vì trong khoảng
3
0;
4
thì
sin
4
0
x
nên phương trình
*
vô nghiệm trên
3
0;
4
.
Lập bảng biến thiên
Vậy để phương trình đã cho có hai nghiệm phân biệt trên khoảng
3
0;
4
thì
2
2;1; 2
2
1m
.
Câu 5:
(THPT Yên Lạc-Vĩnh Phúc-lần 1-năm 2017-2018)
Hằng ngày, mực nước của con kênh lên
xuống theo thủy triều. Độ sâu
m
h
của mực nước trong kênh tính theo thời gian
ht
được
cho bởi công thức
3cos 12
6 3
t
h
.
Khi nào mực nước của kênh là cao nhất với thời gian ngắn nhất?
A.
22 h
t
. B.
15 h
t
. C.
14 h
t
. D.
10 h
t
.
Lời giải
Chọn D
x
0
4
3
4
f x
0
f x
1
2 1
3
t
1
2
f t
f t
1
2 1
Ta có:
1 cos 1
6 3
t
9 15
h
. Do đó mực nước cao nhất của kênh là
15m
đạt
được khi
cos 1
6 3
t
2
6 3
t k
2 12t k
Vì
0t
2 12 0
k
k
Chọn số
k
nguyên dương nhỏ nhất thoả
1
6
k
là
1 10
k t
.
Câu 6:
(THPT Yên Lạc-Vĩnh Phúc-lần 1-đề 2-năm 2017-2018)
Hằng ngày, mực nước của con kênh lên
xuống theo thủy triều. Độ sâu
m
h
của mực nước trong kênh tính theo thời gian
ht
được
cho bởi công thức
3cos 12
6 3
t
h
.
Khi nào mực nước của kênh là cao nhất với thời gian ngắn nhất?
A.
22 h
t
. B.
15 h
t
. C.
14 h
t
. D.
10 h
t
.
Lời giải
Chọn D
Ta có:
1 cos 1
6 3
t
9 15
h
. Do đó mực nước cao nhất của kênh là
15m
đạt
được khi
cos 1
6 3
t
2
6 3
t k
2 12t k
Vì
0t
2 12 0
k
k
Chọn số
k
nguyên dương nhỏ nhất thoả
1
6
k
là
1 10
k t
.
Câu 7:
(THPT Yên Lạc 2-Vĩnh Phúc-lần 1-năm 2017-2018)
Cho phương trình
cos5 3 5
x m
. Gọi
đoạn
;a b
là tập hợp tất cả các giá trị của
m
để phương trình có nghiệm. Tính
3
a b
.
A.
5
. B.
2
. C.
19
3
. D.
6
.
Giải:
Chọn D
Phương trình đã cho có nghiệm khi
4
1 3 5 1 4 3 6 2
3
m m m
.
Khi đó tập hợp tất cả các giá trị của
m
để phương trình có nghiệm là
4
;2
3
.
Ta được
4
3
a
;
2
b
. Suy ra
3 6
a b
.
Câu 8:
(THPT Hai Bà Trưng-Vĩnh Phúc-lần 1-năm 2017-2018)
Trong các hàm số sau hàm số nào
đồng biến trên khoảng
;
2 2
?
A.
coty x
. B.
tany x
. C.
cosy x
. D.
.
Lời giải
Chọn D
[Phương pháp tự luận]
Hàm số
siny x
đồng biến trên các khoảng
2 ; 2
2 2
k k
với mọi
k
. Chọn
0
k
, ta được hàm số
siny x
đồng biến trên khoảng
;
2 2
.
Xét A: Hàm số
coty x
không xác định tại
0 ;
2 2
x
nên không thể đồng biến trên
khoảng
;
2 2
Xét B:Ta thấy
4 3
tan tan
4 3
Hàm số
tany x
không thể đồng biến trên
;
2 2
Xét C: Ta thấy
4 3
cos cos
4 3
Hàm số
cosy x
không thể đồng biến trên
;
2 2
[Phương pháp trắc nghiệm]
Thực hiện chuyển đơn vị: Shift mode 4.Rad.
Vào mode 7, nhập hàm
, START
2
, END
2
, STEP
19
. Nhìn bảng thấy giá trị
hàm số luôn giảm nên sai.
Tương tự với các hàm còn lại, chọn kết quả
có giá trị hàm số luôn tăng.
Câu 9:
(THPT Hai Bà Trưng-Vĩnh Phúc-lần 1-năm 2017-2018)
Phương trình
2
2cos 1x
có số
nghiệm trên đoạn
2 ;2
là
A.
2.
B.
4.
C.
6.
D.
8.
Lời giải
Chọn D
Ta có
2 2
2cos 1 2cos 1 0 os2 0 ; .
4 2
k
x x c x x k
Vì
2 ;2
x
nên ta có
9 7
2 2 .
4 2 2 2
k
k
Mặt khác
k
nên
k
nhận các giá trị
4; 3; 2; 1;0;1;2;3.
Vậy phương trình đã cho có tám nghiệm trên
2 ;2
.
Câu 10:
(THTT Số 2-485 tháng 11-năm học 2017-2018)
Cho hàm số
y f x
. Đồ thị hàm số
y f x
nhận gốc tọa độ làm tâm đối xứng như hình vẽ sau
Khẳng định nào sau đây SAI?
O
x
y
2
2
A. Đồ thị hàm số
y f x
có ba điểm cực trị.
B. Đồ thị hàm số
y f x
nhận trục tung làm trục đối xứng.
C. Đồ thị hàm số
y f x
cắt trục hoành tại
4
điểm.
D. Đồ thị hàm số
y f x
có hai điểm uốn.
Lời giải
Chọn C
Ta có dựa vào đồ thị thì
'y
là hàm số bậc
3
. Do
y f x
là hàm số lẻ và
0
f x
có
3
nghiệm phân biệt nên nó có dạng
3
0, 0
y ax cx a c
. Do đó
4 2 2
2
2
4 2 4
x x x
y a c ax c m
.
Dễ thấy
f x
đổi dấu qua
3
nghiệm nên hàm số có 3 cực trị nên đáp án A. đúng.
Hàm số
4 2 2
2
2
4 2 4
x x x
y a c ax c m
là hàm số chẵn nên đồ thị nhận trục tung làm trục
đối xứng, nên đáp án B. đúng.
Ta có
2
3
y ax c
vì
0, 0
a c
nên phương trình
0
y
có hai nghiệm phân biệt nên hàm
số luôn có hai điểm uốn, do đó đáp án D. đúng.
Câu 11:
(THTT Số 2-485 tháng 11-năm học 2017-2018)
Để giải phương trình:
tan tan 2 1x x
có ba bạn
An, Lộc, Sơn giải tóm tắt ba cách khác nhau như sau:
+ An: Điều kiện
2
,
4 2
x k
k
x k
.
Phương trình
tan tan 2 1 tan 2 cot tan
2 6 3
k
x x x x x x
Nên nghiệm phương trình là
,
6 3
k
x k
.
+ Lộc: Điều kiện
tan 1
x
.
Phương trình
I
1
tan ,
6
3
x x k k
là nghiệm.
+ Sơn: Điều kiện
2
cos 0
cos 0
1
cos2 0
sin
2
x
x
x
x
.
Ta có
2
sin sin 2
tan tan 2 1 . 1 2sin .cos cos cos 2
cos cos 2
x x
x x x x x x
x x
2 2 2 2
1
2sin cos 2 1 2sin sin sin 2 ,
4 6 6
x x x x x k k
là nghiệm.
Hỏi, bạn nào sau đây giải đúng?
A. An. B. Lộc. C. Sơn. D. An, Lộc, Sơn.
Lời giải
Chọn B
+ An: Giải sai do không kiểm tra lại điều kiện để loại nghiệm
,
2
x k k
.
+ Sơn: Giải sai ở bước biến đổi:
2 2
1
sin sin 2 ,
4 6 6
x x k k
.
Do đó chọn đáp án B.
Câu 12:
(THTT Số 2-485 tháng 11-năm học 2017-2018)
Tập nghiệm
S
của phương trình
cos2 5cos5 3 10cos2 cos3x x x x
là
A.
2 ,
3
S k k
. B.
2 ,
6
S k k
.
C.
,
3
S k k
. D.
2 ,
3
S k k
.
Lời giải
Chọn D
Ta có
cos2 5cos5 3 10cos2 cos3x x x x
1
cos2 5cos5 3 10 cos5 cos
2
x x x x
2
2cos 1 5cos5 3 5cos5 5cosx x x x
2
2cos 5cos 2 0
x x
cos 2 1 ( )
1
cos 2 ,
1
2 3
cos
2
x L
x x k k
x
.
Câu 13:
(THTT Số 2-485 tháng 11-năm học 2017-2018)
Số nghiệm của phương trình
2
cos 2cos3 .sin 2 0
x x x
trong khoảng
0;
là
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn A
Ta có
2
cos 2cos3 .sin 2 0,
x x x
0;
x
.
2
1
2cos3 .sin 1 sin 2cos3 sin
sin
x x x x x
x
1
Do
0;
x
nên
sin 0
x
, áp dụng bất đẳng thức Cauchy cho hai số dương
sin x
và
1
sin x
ta
có
1 1
sin 2 sin 2
sin sin
x x
x x
.
Mặt khác, ta có
2cos3 2
x
với mọi
x
.
Vậy
1
xảy ra
cos3 1
sin 1
x
x
Từ
sin 1
2
x x
(do
0;
x
); lúc đó
3
cos3 cos 0
2
x
. Hệ trên vô nghiệm.
Vậy phương trình đã cho không có nghiệm thuộc khoảng
0;
.
Câu 14:
(THTT Số 2-485 tháng 11-năm học 2017-2018)
Có bao nhiêu giá trị của tham số thực
a
để
hàm số
cos sin 1
cos 2
x a x
y
x
có giá trị lớn nhất
1y
.
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C
Do
1 cos 1x
nên
cos 2 1
x
với mọi giá trị thực của
x
, vậy hàm số xác định với mọi
x
.
Ta có
cos sin 1
sin 1 cos 2 1
cos 2
x a x
y a x y x y
x
1
.
Điều kiện để
1
có nghiệm là
2 2
2 2
2 2 2
1 1 3 1 1 3
1 2 1 3 2 0
3 3
a a
a y y y y a y
.
Vậy giá trị lớn nhất của
y
bằng
2
1 1 3
3
a
. Theo giả thiết, ta có
2
2 2 2
1
1 1 3
1 1 3 2 3 1 4 1
1
3
a
a
a a a
a
.
Vậy có hai giá trị thực của tham số
a
thỏa mãn yêu cầu bài toán.
Câu 15:
(THPT Chuyên Vĩnh Phúc-lần 2-năm 2017-2018)
Tính tổng tất cả các nghiệm của phương
trình
sin 2 4sin 2cos 4 0
x x x
trong đoạn
0;100
của phương trình.
A.
100
. B.
2476
. C.
25
. D.
2475
.
Lời giải
Chọn D
Ta có
sin 2 4sin 2cos 4 0 2sin cos 4sin 2cos 4 0
x x x x x x x
2sin cos 2 2 cos 2 0 cos 2 sin 1 0
x x x x x
sin 1
2 .
cos 2
2
x
x k k
x VN
Cách 1: Trong đoạn
0;100
, phương trình có các nghiệm
; 2 ; 4 ; 6 ;...; 98
2 2 2 2 2
Tổng các nghiệm bằng
2 4 6 ... 98 50. 2 4 6 ... 98 .
2 2 2 2 2 2
S
2 98 .49
25 . 2475
2
S
.
Cách 2: Tìm
k
thỏa mãn
0 2 100 0 49
2
k k
Bấm máy
49
0
2 2475
2
k
S k
.
Câu 16:
(THPT Bình Xuyên-Vĩnh Phúc-năm 2017-2018)
Giá trị nhỏ nhất của hàm số của hàm số
2
1 2sin cos cos 2y x x x
là:
A.
5
4
. B.
1
4
. C.
1
. D.
0
.
Lời giải
Chọn B
Tập xác định
D
.
2
1 2sin cos cos 2y x x x
2
1 sin 2 cos 2x x
2
sin 2 sin 2x x
2
1 1 1
sin 2
2 4 4
y x
. Dấu
" "
xảy ra khi
1
12
sin 2 ,
7
2
12
x k
x k
x k
.
Vậy giá trị nhỏ nhất bằng
1
4
đạt được khi
7
; ,
12 12
x k x k k
.
Câu 17:
(THPT Bình Xuyên-Vĩnh Phúc-năm 2017-2018)
Tìm
m
để hàm số
3 2
3 sin sin sin 2
y m x x x m
đồng biến trên khoảng
2
?
A.
3
m
. B.
0
m
. C.
1
3
m
. D.
1
3
m
.
Lời giải
Chọn D
Tập xác định
D
.
Đặt
sint x
, vì
;0
2
x
nên
1;0
t
.
Khi đó hàm số trở thành
3 2
3 2, 1;0 1
y mt t t m t
2
9 2 1y mt t
Để hàm số
1
đồng biến thì
0
y
1;0
t
2
9 2 1 0 1;0 2
mt t t
2
2 1
9
t
m
t
đặt
2
2 1
9
t
f t
t
Ta có
3
2 2
0
9
t
f t
t
1;0
t
Do đó
1
1
3
m f
Vậy
1
3
m
.
Câu 18:
(THPT Bình Xuyên-Vĩnh Phúc-năm 2017-2018)
Phương trình
2
sin sin 2 sin sin 2 sin 3x x x x x
tương đương với phương trình nào sau đây:
A.
sin sin 2 sin3 cos cos2 0
x x x x x
. B.
sin sin 3 sin 0
x x x
.
C.
sin sin 2 sin3 sin sin 2 0
x x x x x
. D.
sin sin3 sin3 0
x x x
.
Lời giải
Chọn D
Ta có
2 2 2 2
sin sin 2 sin sin 2 sin 3 sin sin 2 sin 3x x x x x x x x
2
1 cos2 1 cos4
sin 3
2 2
x x
x
2
1
cos4 cos2 sin 3
2
x x x
2
sin 3 .sin sin 3x x x
sin 3 sin sin 3 0
x x x
.
Câu 19:
(THPT Nguyễn Khuyến-TPHCM-năm 2017-2018)
Một đường thẳng cắt đồ thị hàm số
4 2
2y x x
tại bốn điểm
M
,
N
,
P
,
Q
. Biết hai điểm
M
,
N
có hoành độ lần lượt là
0
và
1
. Tính
P Q
S x x
với
P
x
,
Q
x
là hoành độ điểm
P
và điểm
Q
.
A.
1
S
. B.
1
S
. C.
2
S
. D.
1
S
.
Lời giải
Chọn C
Giả sử
:
d y ax b
là đường thẳng cắt đồ thị hàm số nói trên tại bốn điểm
, , ,M N P Q
. Ta có phương
trình hoành độ giao điểm
4 2
2 1x x ax b
. Vì
0
x
là nghiệm của
1
nên
0
b
.
Lại vì
1x
là nghiệm của
1
nên
1
a
. Do đó, phương trình
4 2 2
1 2 0 1 1 0
x x x x x x x
.
Suy ra
,
p Q
x x
là nghiệm của phương trình
2
1 0
x x
. Từ đó ta có
1
P Q
S x x
.
Câu 20:
(THPT Cổ Loa-Hà Nội-lần 1-nawm-2018)
Số nghiệm của phương trình
2
4 .cos3 0
x x
là
A.
7
. B.
2
. C.
4
. D.
6
.
Lời giải
Chọn D
Điều kiện
2
4 0 2 2
x x
.
Khi đó
2
2
2
4 0
4 .cos3 0
,
cos3 0
6 3
x
x
x x
x k k
x
.
So với điều kiện, ta thấy
2
x
(thỏa điều kiện).
Với
,
6 3
x k k
, ta có
2 2
6 3
k
, vì
k
nên
2
k
;
1
k
;
0
k
;
1
k
.
Vậy phương trình đã cho có
6
nghiệm.
Câu 21:
(THPT Cổ Loa-Hà Nội-lần 1-nawm-2018)
Gọi
M
và
N
lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của hàm số
1 2cos 2 3 sin cos
y x x x
trên
. Biểu thức
2
M N
có
giá trị bằng
A.
0
. B.
4 2 3
. C.
2
. D.
2 3 2
.
Lời giải
Chọn C
Ta có
1 2cos 2 3 sin cos
y x x x
2
1 2 2 3 sin cos 2cos
x x x
2
2 3 sin 2 2cos 1
x x
2 3 sin 2 cos 2
x x
6 2 1
6 2 sin 2 cos2
4
6 2
x x
6 2 sin 2
x
(với
6 2
cos
4
;
1
sin
6 2
)
Suy ra
6 2 6 2
y
. Do đó max 6 2
y M
;
min 6 2
y N
.
Vậy
2 2
M N
.
Câu 22:
(THPT Cổ Loa-Hà Nội-lần 1-nawm-2018)
Tìm tất cả các giá trị của tham số
m
để phương
trình
2 2
cos4 cos 3 sin
x x m x
có nghiệm
0;
12
x
.
A.
1
0;
2
m
. B.
1
;2
2
m
. C.
0;1
m
. D.
1
1;
4
m
.
Lời giải
Chọn C
Ta có
2 2
cos4 cos 3 sin
x x m x
2
2 2cos 2 1 1 cos6 cos 2
x x m m x
2 3
4cos 2 2 1 4cos 2 3cos 2 cos2
x x x m m x
3 2
4cos 2 4cos 2 3 cos2 3 0
x x m x m
2
4cos 2 cos2 1 3 cos 2 1 0
x x m x
2
cos2 1 4cos 2 3 0
x x m
2
cos2 1
4cos 2 3
x
x m
.
Với
cos 2 1
x x k
không thỏa yêu cầu bài toán.
Phương trình có nghiệm
0;
12
x
suy ra
3
cos 2 1
2
x
3 3
1
4 4
m
3 3 4
m
0 1
m
.
Câu 23:
(THTT Số 3-486 tháng 12 năm 2017-2018)
Tìm số nghiệm thuộc
3
;
2
của phương trình
3
3 sin cos 2
2
x x
.
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn B
Ta có
3 3 3
3 sin cos 2 cos cos 2 sin sin 2 3 sin 0
2 2 2
x x x x x
sin 0
sin 2cos 3 0
5
3
2
cos
6
2
x
x k
x x
x k
x
với
k
.
Trên
3
;
2
ta nhận được nghiệm duy nhất
5 7
2
6 6
x
.
Câu 24:
(THPT Lục Ngạn-Bắc Ninh-lần 1 năm 2017-2018)
Giá trị lớn nhất của hàm số
sin cos 1
sin cos 3
x x
y
x x
bằng?
A.
3
. B.
1
. C.
1
7
. D.
1
7
.
Lời giải
Chọn D
Tập xác định
D
.
Ta có
sin cos 1
sin cos 3
x x
y
x x
sin cos 3 sin cos 1y x x x x
1 sin 1 cos 1 3y x y x y
Để
có nghiệm
2 2 2
1 1 1 3y y y
2 2
2 2 1 6 9y y y
2
7 6 1 0
y y
1
1
7
y
.
Vậy
1
max
7
y
.
Câu 1:
(THPT Triệu Sơn 1-lần 1 năm 2017-2018)
Số nghiệm nằm trong đoạn
;
2 2
của phương
trình
sin5 sin3 sin 4x x x
là
A.
5
. B.
7
. C.
9
. D.
3
.
Lời giải
Chọn A
sin5 sin3 sin 4x x x
2sin 4 cos sin 4x x x
sin 4 0
1
cos
2
x
x
4
2
3
2
3
k
x
x k
x k
k
.
Trường hợp
1
:
4
k
x
, với
;
2 2
x
, ta được
;0;
4 4
x
.
Trường hợp
2
:
2
3
x k
, với
;
2 2
x
, ta được
3
x
.
Trường hợp
3
:
2
3
x k
, với
;
2 2
x
, ta được
3
x
.
Vậy phương trình đã cho có 5 nghiệm nằm trong đoạn
;
2 2
.
Câu 2:
(THPT Triệu Sơn 1-lần 1 năm 2017-2018)
Hàm số
cosy x
là hoàn tuần hoàn với chu kì là
A.
.
2
B.
.
4
C.
0
. D.
.
Lời giải
Chọn D
Ta có
2
1 cos2
cos cos
2
x
y x x
nên hàm số tuần hoàn với chu kỳ
2
2
T
.
Câu 3:
(THPT Chuyên Vĩnh Phúc-MĐ 903 lần 1-năm 2017-2018)
Tất cả các giá trị của
m
để phương
trình
cos2 2 1 cos 1 0
x m x m
có đúng
2
nghiệm
;
2 2
x
là
A.
1 1m
. B.
1 0m
. C.
0 1m
. D.
0 1m
.
Lời giải
Chọn C
Ta có
cos2 2 1 cos 1 0
x m x m
2
2cos 2 1 cos 0
x m x m
2cos 1 cos 0
x x m
1
cos
2
cos
x
x m
.
Phương trình đã cho có đúng 2 nghiệm
;
2 2
x
khi và chỉ khi
0 cos 1x
nên loại
1
cos
2
x
Vậy
phương trình đã cho có đúng
2
nghiệm
;
2 2
x
khi
và chỉ khi
0 1m
.
Câu 4:
(THPT Kim Liên-Hà Nội năm 2017-2018)
Hàm số
2cos3 3sin 3 2
y x x
có tất cả bao nhiêu
giá trị nguyên?
A.
7
. B.
3
. C.
5
. D.
6
.
Lời giải
Chọn A
TXD:
D
2cos3 3sin 3 2
y x x
2 3
13 cos3 sin 3 2
13 13
x x
3
13sin 3 arccos 2
13
y x
Để hàm số
y
có giá trị nguyên
3
13 sin 3 arccos
13
x
nguyên
3
sin 3 arccos
13 13
n
x
( với
n
là một số nguyên)
Mà:
3
sin 3 arccos 1;1
13
x
1 1 13 13
13
n
n
Mà:
n
0; 1; 2 3
n
y
có
7
giá trị nguyên.
Câu 5:
(THPT Chuyên Lương Văn Tụy-Ninh Bình lần 1 năm 2017-2018)
Số giá trị nguyên của tham
số
m
thuộc đoạn
2018; 2018
để phương trình
2
1 sin sin 2 cos 2 0
m x x x
A.
4037
. B.
4036
. C.
2019
. D.
2020
.
Lời giải
Chọn D
2
1 sin sin 2 cos 2 0
1 cos2
1 sin 2 cos 2 0
2
1 1
cos2 sin 2
2 2
m x x x
x
m x x
m m
x x
Điều kiện có nghiệm của phương trình
2 2
2
1 1
1 1
2 2
m m
m
Suy ra
2018 1
m
Suy ra có
2020
giá trị nguyên của
m
để phương trình có nghiệm.
Câu 6:
(THPT Chuyên Trần Phú-Hải Phòng lần 1 năm 2017-2018)
Phương trình
sin 1
2
x
x
có bao
nhiêu nghiệm?
A. Vô số nghiệm. B. Vô nghiệm. C.
3
nghiệm. D.
2
nghiệm.
Lời giải
Chọn D
Tập xác định:
\ 0
D
.
Phương trình tương đương với
2sin
x x
1
.
Số nghiệm của phương trình
1
là số giao điểm của đồ thị hai hàm số
2siny x
và
y x
.
Trên hệ trục
Oxy
vẽ đồ thị các hàm số
2siny x
và
y x
Từ đồ thị ta thấy, đồ thị hai hàm số chỉ cắt nhau tại ba điểm trong đó có một điểm có hoành
độ
0
x
không thỏa mãn phương trình. Do vậy, phương trình có hai nghiệm phân biệt.
Câu 7:
(THPT Đoàn Thượng-Hải Dương-lần 2 năm 2017-2018)
Phương trình
2
3
cos 2 cos2 0
4
x x
có bao nhiêu nghiệm
2 ;7
x
?
A.
16
. B.
20
. C.
18
. D.
19
.
Lời giải
Chọn C
Ta có:
2
3 1
cos 2 cos 2 0 cos 2
4 2
x x x
hoặc
3
cos2
2
x
(loại).
Với
1
cos2 2 2
2 3 6
x x k x k k
.
Phương trình có nghiệm
2 ;7
x
khi và chỉ khi
2 7
6
k
.
+ Trường hợp 1:
13 41
2 7
6 6 6
k k
. Vì
k
nên
2; 1;0;1;2;3;4;5;6
k
do đó có
9
nghiệm thuộc khoảng
2 ;7
.
+ Trường hợp 2:
11 43
2 7
6 6 6
k k
. Vì
k
nên
1;0;1;2;3;4;5;6;7
k
do đó có
9
nghiệm thuộc khoảng
2 ;7
. Vậy có tất cả
18
nghiệm thỏa mãn bài toán.
Câu 8:
(THPT Triệu Thị Trinh-lần 1 năm 2017-2018)
Tìm
m
để phương trình sau có nghiệm
cos 2sin 3
2cos sin 4
x x
m
x x
:
y
O
x
y x
2siny x
A.
2 0
m
. B.
2 1
m
. C.
0 1
m
. D.
2
2
11
m
.
Lời giải
Chọn D
Có
2cos sin 4 0,x x x
.
2cos sin 4 cos 2sin 3PT m x x x x
2 1 cos 2 sin 4 3 0
m x m x m
.
Phương trình trên có nghiệm khi
2 2 2
2 1 2 4 3
m m m
2
11 24 4 0
m m
2
2
11
m
.
Câu 9:
(THPT Chuyên Thái Bình-lần 2 năm học 2017-2018)
Cho phương trình
cos sin 2
1 0
cos3
x x
x
.
Khẳng định nào dưới đây là đúng:
A. Phương trình đã cho vô nghiệm.
B. Nghiệm âm lớn nhất của phương trình là
2
x
.
C. Phương trình tương đương với phương trình
sin 1 2sin 1 0
x x
.
D. Điều kiện xác định của phương trình là
2
cos 3 4cos 0
x x
.
Lời giải
Chọn A
Điều kiện:
cos3 0 3
2 6 3
x x k x k k
.
Ta có
2
cos sin 2
1 0
cos3
cos sin 2 cos3
0
cos3
cos 1 2sin 4cos 3
0
cos3
x x
x
x x x
x
x x x
x
2
2
cos 1 2sin 4cos 3 0
cos 4sin 2sin 2 0
x x x
x x x
cos 0
sin 1
1
sin
2
x
x
x
Ta có
2
cos3 cos 4cos 3
x x x
nên ta loại
cos 0
x
và
sin 1x
.
Ngoài ra
2 2
1 1 3
sin cos 1 4cos 3 0
2 4 4
x x x
nên ta loại tiếp
1
sin
2
x
.
Vậy phương trình đã cho vô nghiệm.
Câu 10:
(THPT Chuyên Thái Bình-lần 2 năm học 2017-2018)
Phương trình
cos4
tan 2
cos2
x
x
x
có bao nhiêu
nghiệm thuộc khoảng
0,
2
?
A.
1
. B.
3
. C.
4
. D.
2
.
Lời giải
Chọn D
Điều kiện
cos 2 0
x
2
2
x k
4 2
x k
,
k
.
Phương trình tương đương với
cos4 sin 2x x
2
2sin 2 sin 2 1 0
x x
sin 2 1
1
sin 2
2
x L
x N
2 2
6
5
2 2
6
x k
x k
12
5
12
x k
x k
,
k
. Do
0;
2
x
nên phương trình chỉ có hai
nghiệm là
12
x
và
5
12
x
.
Câu 11:
(THPT Chuyên ĐHSP-Hà Nội-lần 1 năm 2017-2018)
Số nghiệm thuộc khoảng
4
;
3 2
của phương trình
cos 3 sin sin 3
2
x x x
là
A.
4
. B.
3
. C.
6
. D.
2
.
Lời giải
Chọn C
Ta có:
cos 3 sin sin 3
2
x x x
cos 3 sin cos3x x x
2sin 2 sin 3 sin 0
x x x
sin 2sin 2 3 0
x x
sin 0
3
sin 2
2
x
x
6
3
x k
x k
x k
,
k
.
 Với
x k
, trên nửa khoảng
4
;
3 2
ta có:
4
3 2
k
4 1
3 2
k
1;0
k
. Suy ra các nghiệm là
x
,
0
x
.
 Với
6
x k
, trên nửa khoảng
4
;
3 2
ta có:
4
3 6 2
k
3 1
2 3
k
1;0
k
. Suy ra các nghiệm là
5
6
x
,
6
x
.
 Với
3
x k
, trên nửa khoảng
4
;
3 2
ta có:
4
3 3 2
k
5 1
3 6
k
1;0
k
. Suy ra các nghiệm là
2
3
x
,
3
x
.
Suy ra số nghiệm trên nửa khoảng
4
;
3 2
của phương trình là
6
.
Câu 12:
(THTT Số 4-487 tháng 1 năm 2017-2018)
Số nghiệm trên khoảng
0;2
của phương trình
4
27cos 8sin 12
x x
là
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn D
Ta có:
4
27cos 8sin 12
x x
4 2
27sin 54sin 8sin 15 0
x x x
2 2
3sin 2sin 3 9sin 6sin 5 0
x x x x
2
2
3sin 2sin 3 0
9sin 6sin 5 0
x x
x x
2
3sin 2sin 3 0
x x
1 10
sin 1;1
3
1 10
sin 1;1
3
x
x
Với
1 10
sin
3
x
trên khoảng
0;2
phương trình có
2
nghiệm.(dựa vào số giao điểm
giữa đồ thị hàm số
siny x
và đường thẳng
1 10
3
y
).
2
9sin 6sin 5 0
x x
1 6
sin 1;1
3
1 6
sin 1;1
3
x
x
Với
1 6
sin
3
x
trên khoảng
0;2
phương trình có
2
nghiệm.(dựa vào số giao điểm giữa
đồ thị hàm số
và đường thẳng
1 6
3
y
).
Vậy trên khoảng
0;2
phương trình đã cho có
4
nghiệm.
Câu 13:
(THPT Chuyên Phan Bội Châu-Nghệ An- lần 1 năm 2017-2018)
Có bao nhiêu giá trị nguyên
của tham số
m
để hàm số
5 sin 1 cosy m x m x
xác định trên
?
A.
6
. B.
8
. C.
7
. D.
5
.
Lời giải
Chọn B
Hàm số xác định trên
5 sin 1 cos 0m x m x x
sin 1 cos 5m x m x x
Max sin 1 cos 5
x
m x m x
.
2
2 2
1 25 12 0 4;3
m m m m m
.
Vậy có
8
giá trị nguyên của
m
thỏa mãn.
Câu 14:
(THPT Chuyên Phan Bội Châu-Nghệ An- lần 1 năm 2017-2018)
Cho đa giác đều
20
đỉnh.
Lấy ngẫu nhiên
3
đỉnh. Tính xác suất để
3
đỉnh đó là
3
đỉnh của
1
tam giác vuông không cân.
A.
2
35
. B.
17
114
. C.
8
57
. D.
3
19
.
Lời giải
Chọn C
Số cách chọn
3
đỉnh
3
20
n C
Gọi
O
là đường tròn ngoại tiếp đa giác đều
20
cạnh, đường tròn này có
10
đường kính tạo
thành từ
20
đỉnh của đa giác đó.
Chọn một đường kính bất kì, đường kính này chia đường tròn này thành
2
phần, mỗi phần có
9
đỉnh của đa giác
Khi đó mỗi phần có
8
tam giác vuông không cân (trừ đỉnh chính giữa)
Vậy số tam giác vuông không cân được tạo thành từ
20
đỉnh của đa giác là
8.2.10 160
n A
Vậy xác suất cần tìm là
8
57
p A
Câu 15:
(THPT Chuyên Thái Bình-lần 3 năm 2017-2018)
Số các giá trị thực của tham số
m
để
phương trình
2
sin 1 2cos 2 1 cos 0
x x m x m
có đúng
4
nghiệm thực thuộc đoạn
0;2
là:
A.
1
. B.
2
. C.
3
. D. vô số.
Hướng dẫn giải
Chọn B
Ta có phương trình tương đương
2
sin 1
2cos 2 1 cos 0
x
x m x m
sin 1
2cos 1 cos 0
x
x x m
sin 1
1
cos
2
cos
x
x
x m
Với
0;2
x
. Ta có:
sin 1
2
x x
vì
0;2
x
nên
2
x
(thỏa mãn).
1
3
cos cos cos
5
2 3
2
3 3
x
x x
x
vì
0;2
x
nên
3
5
3
x
x
(thỏa mãn).
 Với
1 1
m
, đặt
cosm
,
0;
.
Nhận xét: Với
0;2
x
thì phương trình
cos cos cos
2
x
x m x
x
*
.
Do đó, phương trình có
4
nghiệm thực phân biệt khi và chỉ khi phương trình
*
có
đúng một nghiệm hoặc có
2
nghiệm phân biệt và một nghiệm bằng
2
.
Trường hợp 1:
2
(thỏa vì khác
2
,
3
,
5
3
). Suy ra
cos 1
m
.
Trường hợp 3:
3
2
2 2
(thỏa). Suy ra
cos 0
2
m
.
Vậy
0; 1
m
nên có
2
giá trị
m
.
Câu 16:
(THPT Hoài Ân-Hải Phòng năm 2017-2018)
Tìm giá trị lớn nhất
M
của hàm số
sin 2cos 1
sin cos 2
x x
y
x x
.
A.
2M
. B.
3
M
. C.
3
M
. D.
1M
.
Lời giải
Chọn D
Ta có
sin cos 2 0
x x
,
x
.
Biến đổi hàm số về dạng phương trình ta được:
sin cos 2 sin 2cos 1 1 sin 2 cos 1 2y x x x x y x y x y
.
1
Phương trình
1
có nghiệm khi:
2 2 2
2
1 2 1 2 2 2 4 0 2 1y y y y y y
.
Vậy giá trị lớn nhất
1M
.
Câu 17:
(THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018)
Số nghiệm của phương trình
cos2 3 cos 1 0
x x
trong đoạn
;
2 2
là:
A.
4
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn C
Ta có:
cos2 3 cos 1 0
x x
2
2cos 3 cos 2 0
x x
.
Đặt
cost x
,
0 1t
, ta được phương trình:
2
2 3 2 0
t t
2
1
2
t
t
1
2
t
. (vì
0 1t
)
Với
1
2
t
, ta có:
1
cos
2
x
1
cos
2
1
cos
2
x
x
2
3
2
2
3
x k
x k
3
x k
k
.
Trên đoạn
;
2 2
phương trình có nghiệm là
3
x
.
Câu 18:
(THPT Ninh Giang-Hải Dương năm 2017-2018)
Phương trình:
2sin 2 3 0
3
x
có
mấy nghiệm thuộc khoảng
0;3
.
A.
6
. B.
2
. C.
4
. D.
8
.
Lời giải
Chọn A
Ta có
2sin 2 3 0
3
x
3
2sin 2
3 2
x
2 2
3 3
2 2
3 3
x k
x k
3
,
2
x k
k
x k
. Vì
0;3
x
nên
4 7 3 5
; ; ; ; ;
3 3 3 2 2 2
x
.
Câu 19:
(THPT Phan Đăng Lưu-Huế-lần 1 năm 2017-2018)
Số nghiệm của phương trình
2
sin sin 2 2sin cos sin cos
3 cos 2
sin cos
x x x x x x
x
x x
trong khoảng
;
là:
A.
2
. B.
4
. C.
3
. D.
5
.
Lời giải
Chọn A
Điều kiện
sin cos 0
x x
sin 0
4
x
4
x k
,
4
x k k
.
Ta có:
2
sin sin 2 2sin cos sin cos
3 cos 2
sin cos
x x x x x x
x
x x
sin 2 sin cos sin cos
3 cos2
sin cos
x x x x x
x
x x
sin 2 1 sin cos
3 cos 2
sin cos
x x x
x
x x
sin 2 3 cos 2 1
x x
sin 2 sin
3 6
x
2 2
3 6
2 2
3 6
x k
x k
12
3
4
x k
k
x k
.
Thử lại điều kiện, phương trình đã cho có nghiệm là:
12
x k k
.
Trên
;
phương trình đã cho có các nghiệm là:
11
;
12 12
.
Câu 20:
(THPT Quãng Xương 1-Thanh Hóa năm 2017-2018)
Tổng
S
các nghiệm của phương trình:
2
2cos 2 5cos 2 3 0
x x
trong khoảng
0;2
là
A.
5
S
. B.
7
6
S
. C.
4
S
. D.
11
6
S
.
Lời giải
Chọn C
Ta có
2
2cos 2 5cos 2 3 0
x x
cos2 3 1
1
cos2
2
x
x
.
Với
1
cos2
2
x
2 2
3
2 2
3
x k
x k
6
6
x k
k
x k
.
Do
0;2
x
nên ta có các nghiệm
6
x
,
7
6
x
,
5
6
x
,
11
6
x
.
Tổng các nghiệm của phương trình
7 5 11
4
6 6 6 6
S
.
Câu 21:
(THPT Đô Lương 4-Nghệ An năm 2017-2018)
Biết phương trình
3 2
0
ax bx cx d
với
0
a
có đúng hai nghiệm thực. Hỏi đồ thị hàm số
3 2
y ax bx cx d
có bao nhiêu điểm cực
trị?
A.
3
. B.
5
. C.
2
. D.
4
.
Lời giải
Chọn A
Vì phương trình
3 2
0
ax bx cx d
với
0
a
có đúng hai nghiệm thực nên đồ thị hàm số
3 2
y ax bx cx d
có hai điểm cực trị trong đó một điểm cực trị nằm trên trục hoành. Các dạng
của đồ thị hàm số
3 2
y ax bx cx d
trong trường hợp này được mô tả như sau:
Trường hợp 1:
0
a
Trường hợp 2:
0
a
Vậy với
0
a
đồ thị hàm số
3 2
y ax bx cx d
luôn có ba điểm cực trị.
Câu 22:
(THPT Hậu Lộc 2-Thanh Hóa năm 2017-2018)
Nghiệm lớn nhất của phương trình
2cos2 1 0
x
trong đoạn
0;
là:
A.
x
. B.
11
12
x
. C.
2
3
x
. D.
5
6
x
.
Lời giải
Chọn D
Phương trình
2cos2 1 0
x
1
cos2
2
x
2 2
3
2 2
3
x k
x k
6
6
x k
x k
.
Xét
0;
x
0
6
0
6
k
k
1 5
6 6
1 7
6 6
k
k
mà
k
suy ra
0
1
k
k
6
5
6
x
x
.
Vậy nghiệm lớn nhất của phương trình
2cos2 1 0
x
trong đoạn
0;
là
5
6
x
.
Câu 23:
(THPT Hậu Lộc 2-Thanh Hóa năm 2017-2018)
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số
sin cos
2sin cos 3
x x
y
x x
lần lượt là:
A.
1
1;
2
m M
. B.
1; 2
m M
. C.
1
; 1
2
m M
. D.
1; 2
m M
.
Lời giải
Chọn B
Ta có:
2sin cos 3 0
x x
với
x
.
sin cos
2sin cos 3
x x
y
x x
2sin cos 3 sin cosy x x x x
.
2 1 sin 1 cos 3y x y x y
(*).
Hàm số
sin cos
2sin cos 3
x x
y
x x
xác định với
x
nên (*) có nghiệm.
2 2 2
2 1 1 3y y y
.
1 2
y
.
Nên giá trị nhỏ nhất và giá trị lớn nhất của hàm số
sin cos
2sin cos 3
x x
y
x x
lần lượt là:
1; 2
m M
.
Câu 24:
(THPT Hoàng Hoa Thám-Hưng Yên-lần 1 năm 2017-2018)
Cho phương trình
sin 1 cos
cos
m
m x m x
x
. Số các giá trị nguyên dương của
m
nhỏ hơn
10
để phương trình
có nghiệm là:
A.
9
. B.
8
. C.
10
. D.
7
.
Lời giải
Chọn A
sin 1 cos
cos
m
m x m x
x
2
sin cos 1 cosm x x m x m
1
sin 2 1 cos 2
2 2
m m
x x m
sin 2 1 cos2 1 0
m x m x m
có nghiêm khi và chỉ
khi
2 2
2
1 1m m m
2
4
4 0
0
m
m m
m
. Do đó số các giá trị nguyên dương của
m
nhỏ hơn
10
là
9
.
Câu 1:
(SGD Bà Rịa Vũng Tàu-đề 1 năm 2017-2018)
Cho
0
x
là nghiệm của phương trình
sin cos 2 sin cos 2
x x x x
thì giá trị của
0
sin
4
P x
là
A.
2
2
P
. B.
1P
. C.
1
2
P
. D.
2
2
P
.
Lời giải
Chọn A
Đặt
sin cost x x
2 sin
4
x
,
2; 2
t
.
Ta có
2 2 2
sin cos 2sin .cost x x x x
1 2sin .cosx x
, suy ra
2
1
sin .cos
2
t
x x
.
Phương trình đã cho trở thành
2
2
1
1
2 2 4 5 0
5 2; 2
2
t
t
t t t
t
.
Từ đó ta có
2 sin 1
4
x
2
sin
4 2
x
.
Như vậy
0
2
sin
4 2
P x
.
Câu 2:
(SGD Bà Rịa Vũng Tàu-đề 2 năm 2017-2018)
Số giá trị nguyên của tham số
m
để phương trình
4 3 cos sin 2 1 0
x x m
có nghiệm là
A.
8
. B.
6
. C.
9
. D.
7
.
Lời giải
Chọn A
Ta có:
4 3 cos sin 2 1 0
x x m
sin 4 3 cos 1 2x x m
.
Phương trình có nghiệm khi
2 2 2
a b c
2
2
1 4 3 1 2
m
2
4 4 48 0
m m
3 4
m
3; 2; 1;0;1;2;3;4
m
.
Vậy có
8
giá trị nguyên của
m
để phương trình đã cho có nghiệm.
Câu 3:
(THPT Hà Huy Tập-Hà Tĩnh-lần 2 năm 2017-2018)
Để phương trình
2 2 2
2
sin 2
1 tan cos2
a x a
x x
có nghiệm, tham số
a
phải thỏa mãn điều kiện:
A.
3
a
. B.
1
3
a
a
. C.
4
a
. D.
1
a
.
Lời giải
Chọn B
* ĐKXĐ:
cos 0
cos2 0
x
x
2
2
sin 1
1
sin
2
x
x
* Ta có:
2 2 2
2
sin 2
1 tan cos2
a x a
x x
2 2 2 2
cos sin 2
a x x a
2 2 2
sin sin 2
a x x
2
2
2
sin
1
x
a
Để phương trình đã cho có nghiệm điều kiện là
2
2
2
2
0;1
1
2
1
1
2 1
1 2
a
a
a
2
2
2
0;1
1
2 1
1 2
a
a
2
2
1 2
1 4
a
a
1
3
a
a
.
Câu 4:
(THPT Lý Thái Tổ-Bắc Ninh-lần 1 năm 2017-2018)
Tính tổng tất cả các giá trị nguyên của hàm
số
3sin cos 4
2sin cos 3
x x
y
x x
.
A.
8
. B.
5
. C.
6
. D.
9
.
Lời giải
Chọn C
3sin cos 4
2sin cos 3
x x
y
x x
2sin cos 3 3sin cos 4
x x y x x
2 3 sin 1 cos 3 4 0
y x y x y
Điều kiện phương trình có nghiệm:
2 2 2
2 3 1 4 3y y y
2 2 2
4 12 9 2 1 16 24 9y y y y y y
2
4 14 6 0
y y
1
3
2
y
.
Vậy tổng tất cả các giá trị nguyên của hàm số bằng
6
.
Câu 5:
(THPT Kinh Môn-Hải Dương lần 1 năm 2017-2018)
Cho phương trình
2018 2018 2020 2020
sin cos 2 sin cos
x x x x
. Tính tổng các nghiệm của phương trình trong
khoảng
0;2018
A.
2
1285
4
. B.
2
643
. C.
2
642
. D.
2
1285
2
.
Lời giải
Chọn D
2018 2018 2020 2020
sin cos 2 sin cos
x x x x
2018 2 2018 2
sin 1 2sin cos 1 2cos 0
x x x x
2018 2018
sin .cos 2 cos cos 2 0
x x x x
2018 2018
cos2 0
sin cos
x
x x
.

cos2 0
x
2
2
x k
4 2
k
x k
1

2018 2018
sin cos
x x
2018
tan 1x
(
2
x k
không là nghiệm)
tan 1
x
4
x k k
2
. Từ
1
và
2
ta có
4 2
k
x k
là nghiệm của pt.
Do
0;2018
x
0 2018
4 2
k
0 1284,k k
.
Vậy tổng các nghiệm của phương trình trong khoảng
0;2018
bằng
.1285 1 2 ... 1284
4 2
1284.1285
.1285
4 4
2
1285
2
.
Câu 6:
(THPT Lê Quý Đôn-Hải Phòng lần 1 năm 2017-2018)
Biểu diễn tập nghiệm của phương trình
cos cos 2 cos3 0
x x x
trên đường tròn lượng giác ta được số điểm cuối là
A.
6
. B.
5
. C.
4
. D.
2
.
Lời giải
Chọn A
Ta có
cos cos2 cos3 0 cos3 cos cos2 0
x x x x x x
2cos 2 .cos cos 2 0 cos 2 2cos 1 0
x x x x x
2
2 4 2
cos2 0
2 2
2 2 ,
1
3 3
cos
2
2 2
2 2
3 3
x k x k
x
x k x k k
x
x k x k
Vậy biểu diễn tập nghiệm của phương trình
cos cos 2 cos3 0
x x x
trên đường tròn lượng
giác ta được số điểm cuối là
6
.
Câu 7:
(THPT Đức THọ-Hà Tĩnh-lần 1 năm 2017-2018)
Số nghiệm của phương trình
2 2
cos sin 2 2 cos
2
x x x
trên khoảng
0;3
là
A.
2
. B.
3
. C.
4.
D.
1
.
Lời giải
Chọn B
2 2
cos sin 2 2 cos
2
x x x
2 2
cos sin 2 2 sinx x x
cos2 sin 2 2
x x
2 cos 2 2
4
x
cos 2 1
4
x
2 2
4
x k
8
x k
k
Trên
0;3
7
8
x
,
15
8
x
,
23
8
x
.
Câu 8:
(SGD Hà Nội-lần 11 năm 2017-2018)
Số nghiệm chung của hai phương trình
2
4cos 3 0
x
và
2sin 1 0
x
trên khoảng
3
;
2 2
bằng
A.
2
. B.
4
. C.
3
. D.
1
.
Lời giải
Chọn A
Trên khoảng
3
;
2 2
phương trình
1
2sin 1 0 sin
2
x x
có hai nghiệm là
6
và
7
6
.
 Cả hai nghiệm này đều thỏa phương trình
2
4cos 3 0
x
.
 Vậy hai phương trình có
2
nghiệm chung.
Câu 9: (THTT số 6-489 tháng 3 năm 2018) Số giờ có ánh sáng của một thành phố X ở vĩ độ
40
bắc
trong ngày thứ
t
của một năm không nhuận được cho bởi hàm số:
3sin 80 12
182
d t t
,
t
và
0 365
t
. Vào ngày nào trong năm thì thành phố X
có nhiều giờ ánh sáng nhất?
A.
262
. B.
353
. C.
80
. D.
171
.
Lời giải
Chọn D
Ta có:
3sin 80 12
182
d t t
3 12 15
Dấu bằng xảy ra khi
sin 80 1
182
t
80 2
182 2
t k k
t k  
.
Mặt khác
0;365
t
nên
365
k
 
171 194
364 364
k
.
Mà
k
nên
0
k
.
Vậy
171
t
.
Câu 10:
(THPT Nguyễn Trãi-Đà Nẵng-lần 1 năm 2017-2018)
Cho phương trình
4sin cos
3 6
x x
2
3sin 2 cos2a x x
1
. Gọi
n
là số giá trị nguyên của tham số
a
để phương trình
1
có nghiệm. Tính
n
.
A.
5
n
. B.
3
n
. C.
2
n
. D.
1
n
.
Lời giải
Chọn A
Ta có
1
2 sin 2 1
6
x
2
3sin 2 cos2a x x
sin 2 1
6
x
2
sin 2
2 6
a
x
2
cos 2 1
2
a
x
.
Phương trình
1
có nghiệm
2
1 1
2
a
2 2
a
, Do
a
nên
0; 1; 2
a a a
Vậy
5
n
.
Câu 11:
(THPT Chuyên Hà Tĩnh-lần 1 năm 2017-2018)
Tổng tất cả các giá trị của tham số thực
m
sao
cho đồ thị hàm số
3 2 3
3 4y x mx m
có điểm cực đại và cực tiểu đối xứng với nhau qua
đường phân giác của góc phần tư thứ nhất là
A.
2
2
. B.
1
2
. C.
0
. D.
1
4
.
Lời giải
Chọn C
Ta có:
2
3 6y x mx
,
0
0
2
x
y
x m
.
Để hàm số có cực đại cực tiểu thì
0
m
.
Khi đó các điểm cực trị của đồ thị hàm số là
3
0;4
A m
,
2 ;0
B m
.
Ta có
3
;2
I m m
là trung điểm của đoạn thẳng
AB
.
Đường phân giác của góc phần tư thứ nhất là
: 0
d x y
.
Do đó để điểm cực đại và cực tiểu đối xứng với nhau qua
d
thì:
3
2
3
2 4 0
2
1 2 0
2
2 0
m m
m m
m m
.
Vậy tổng tất cả các giá trị của tham số thực
m
là
0
.
Câu 12:
(PTNK-ĐHQG TP HCM-lần 1 năm 2017-2018)
Giả sử
M
là giá trị lớn nhất và
m
là giá trị
nhỏ nhất của hàm số
sin 2cos 1
sin cos 2
x x
y
x x
trên
. Tìm
M m
.
A.
1 2
. B.
0
. C.
1
. D.
1
.
Lời giải
Chọn D
Tập xác định:
D
.
Ta có
sin 2cos 1
sin cos 2
x x
y
x x
1 sin 2 cos 1 2y x y x y
(*).
Hàm số đạt giá trị lớn nhất, nhỏ nhất khi (*) có nghiệm
2 2 2
1 2 1 2
y y y
2
2 2 4 0
y y
2 1y
.
Do đó
2
m
,
1M
.
Câu 13:
(PTNK-ĐHQG TP HCM-lần 1 năm 2017-2018)
Tìm
m
để phương trình
1
1 sin sin
2
x x m
có nghiệm.
A.
1 6
2 2
m
. B.
0 1
m
. C.
0 3
m
. D.
6
3
2
m
.
Lời giải
Chọn D
Đặt
sint x
1
1
2
t
, phương trình trở thành
1
1
2
t t m
Nhận xét phương trình ban đầu có nghiệm
x
khi và chỉ khi phương trình
*
có nghiệm
1
;
2
t
. Xét hàm
1
1
2
f t t t
, với
1
;1
2
t
.
Ta có:
1
1
1
2
1 1
2
2
2 1 1 1
1 1
2 2 1
2 1 1
2 2
2 2
t t
t
f t
t
t t t
t t t t
1
0
4
f t t
.
Ta có bảng biến thiên:
Dựa vào bảng biến thiên, phương trình đã cho có nghiệm
6
3
2
m
.
Câu 14: (THPT Hồng Bàng – Hải Phòng – năm 2017 – 2018) Gọi
M
,
m
lần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của hàm số
2 cosy x x
trên đoạn
0;
2
. Tính
M m
.
A.
1 2
4
. B.
2
2
. C.
1
4
. D.
1 2
4
.
Lời giải
Chọn A
Xét hàm
2 cosy x x
trên đoạn
0;
2
.
1 2 siny x
.
0
y
1
sin
2
x
2
4
3
2
4
x k
x k
.
Do
0;
2 4
x x
.
Ta có
0 2
y
;
1
4 4
y
;
2 2
y
.
Vậy
0;
2
max 1
4 4
M y y
;
0;
2
min 0 2
m y y
.
Nên
1 2
4
M m
.
Câu 15: (THPT Quảng Xương I – Thanh Hóa – năm 2017 – 2018) Tìm tổng tất cả các nghiệm
thuộc đoạn
0;10
của phương trình
2
sin 2 3sin 2 2 0
x x
.
A.
105
2
. B.
.
S ABCD
. C.
297
4
. D.
299
4
.
Lời giải
Chọn A
Ta có:
2
sin 2 3sin 2 2 0
x x
sin 2 1
sin 2 2
x
x
(loaïi)
sin 2 1
x
4
x k
,
k
.
Theo đề bài:
0 10
4
k
1 41
4 4
k
1,2,...,10
k
.
t
1
2
1
4
1
f t
||
0
||
f t
6
2
3
6
2
Vậy tổng các nghiệm là
3 3 3
... 9
4 4 4
S
105
2
.
Câu 16:
(THPT Chuyên Thoại Ngọc Hầu – An Giang - Lần 3 năm 2017 – 2018)
Có bao nhiêu giá trị
nguyên của tham số
m
để phương trình
6 6
sin cos 3sin cos 2 0
4
m
x x x x
có nghiệm
thực?
A.
13
. B.
15
. C.
7
. D.
9
.
Lời giải
Chọn A
Ta có
6 6
sin cos 3sin cos 2 0
4
m
x x x x
2 2
1 3sin cos 3sin cos 2 0
4
m
x x x x
Đặt
sin 2t x
,
1 1t
.
PT trở thành
2
3 6 12
t t m
.
Xét hàm số
2
3 6 12
f t t t
,
1 1t
Phương trình
6 6
sin cos 3sin cos 2 0
4
m
x x x x
có nghiệm thực khi
3 15
m
.
Vậy có
13
giá trị nguyên của tham số
m
.
Câu 17: (THPT Chuyên ĐHSP – Hà Nội - Lần 1 năm 2017 – 2018) Cho hai điểm
A
,
B
thuộc đồ
thị hàm số
trên đoạn
0; .
Các điểm
C
,
D
thuộc trục
Ox
thỏa mãn
ABCD
là hình
chữ nhật và
2
3
CD
. Độ dài cạnh
BC
bằng
A.
3
2
. B.
1
. C.
1
2
. D.
2
2
.
Lời giải
Chọn C
Gọi
;
A A
A x y
,
;
B B
B x y
. Ta có:
2
2
1
3
3
sin sin 2
B A
B A
B AB A
x x
x x
x x
y y
Thay
1
vào
2
, ta được:
2 2
sin sin 2
3 3 6
A A A A A
x x x x k x k
k
t
1
1
f t
f t
3
15
O
x
y
D
C
A
B
Do
0;
x
nên
1
sin
6 6 2
A
x BC AD
.
Câu 18: (THPT Kim Liên – Hà Nội - Lần 2 năm 2017 – 2018)Một vật nặng treo bởi một chiếc lò xo,
chuyển động lên xuống qua vị trí cân bằng (hình vẽ). Khoảng cách
h
từ vật đến vị trí cân bằng
ở thời điểm
t
giây được tính theo công thức
h d
trong đó
5sin 6 4cos6d t t
với
d
được
tính bằng centimet.
Ta quy ước rằng
0
d
khi vật ở trên vị trí cân bằng,
0
d
khi vật ở dưới vị trí cân bằng. Hỏi
trong giây đầu tiên, có bao nhiêu thời điểm vật ở xa vị trí cân bằng nhất?
A.
0
. B.
4
. C.
1
. D.
2
.
Lời giải
Chọn D
Ta có
5sin 6 4cos6 41 sin 6 41
h d t t t
, với
5
cos
41
4
sin
41
.
Do đó vật ở xa vị trí cân bằng nhất
max
41
h
khi
sin 6 1 cos 6 0
t t
6
2 6 12 6
t k t k
.
Trong giây đầu tiên,
1 6 1
0 1 0 1 0;1
6 12 6 2 2
t k k k
.
Vậy có
2
lần vật ở xa vị trí cân bằng nhất.
Câu 19: (THPT Trần Phú – Đà Nẵng - Lần 2 – năm 2017 – 2018) Cho phương trình
3 tan 1 sin 2cos sin 3cosx x x m x x
. Có tất cả bao nhiêu giá trị nguyên tham số
m
thuộc đoạn
2018;2018
để phương trình trên có nghiệm duy nhất
0;
2
x
?
A.
2018
. B.
2015
. C.
4036
. D.
2016
.
Lời giải
Chọn A
Với
0;
2
x
thì
cos 0
x
, chia hai vế cho
cos x
, ta được:
3 tan 1 sin 2cos sin 3cosx x x m x x
3 tan 1 tan 2 tan 3
x x m x
3 tan 1 tan 2
tan 3
x x
m
x
.
1
Vị trí cân bằng
h
Đặt
tan 1t x
,
0; 0;
2
x t
. Khi đó:
1
2
2
3 1
2
t t
g t m
t
.
2
Xét hàm
2
2
3 1
2
t t
g t
t
trên
0;
.
4 2
2
2
3 15 6
0, 0
2
t t
g t t
t
.
Suy ra để thỏa yêu cầu bài toán
0 0
m g
. Mà
2018;2018
m
m
.
Suy ra
1;2;3;...;2018
m
.
Câu 1:
(Tạp chí THTT – Tháng 4 năm 2017 – 2018)
Phương trình 1 sin 1 cos
x x m
có nghiệm
khi và chỉ khi
A.
2 2
m
. B.
1 4 2 2
m
. C.
1 2
m
. D.
0 1
m
.
Lời giải
Chọn B
TXĐ:
D
.
Đặt
1 sin 1 cosP x x
,
0
P
. Suy ra
2
2 sin cos 2 1 sin cos sin cosP x x x x x x
.
Đặt
sin cost x x
2 sin
4
x
2 ; 2
t
.
Khi đó
2
1 2sin cost x x
2
1
sin cos
2
t
x x
.
Do đó
2
2
1
2 2 1
2
t
P t t
2 2 1t t
.
TH1:
2 1
t
thì
2
1 2 2 2
P t
. Khi đó
2
1 4 2 2
P
.
TH2:
1 2
t
thì
2
1 2 2 2
P t
. Khi đó
2
1 4 2 2
P
.
Do đó
2
1 4 2 2
P
mà
0
P
nên
1 4 2 2
P
.
Phương trình có nghiệm khi
1 4 2 2
m
.
Câu 2:
(THPT Chu Văn An – Hà Nội - năm 2017-2018)
Phương trình
cos 2 .sin 5 1 0
x x
có bao
nhiêu nghiệm thuộc đoạn
π
;2
π
2
?
A.
2
. B.
1
. C.
4
. D.
3
.
Lời giải
Chọn B
cos 2 .sin 5 1 0
x x
sin 7 sin 3 2
x x
sin 7 1
sin 3 1
x
x
π 2π
14 7
π 2π
6 3
x k
x h
,h k
Do
π
;2
π
2
x
0;1;2;3
h
.
Ta có
π 2π π 2π
14 7 6 3
k h
28 4
12
h
k
, do
k
nên chỉ có
1
h
thỏa mãn.
Vậy phương trình đã cho có một nghiệm thỏa yêu cầu bài toán.
Câu 3:
(SGD Bắc Ninh – Lần 2 - năm 2017-2018)
Gọi
S
là tổng tất cả các nghiệm thuộc
0;20
của
phương trình
2
2cos sin 1 0
x x
. Khi đó, giá trị của
S
bằng :
A.
570
S
. B.
295
S
. C.
590
S
. D.
200
3
S
.
Lời giải
Chọn B
2
2cos sin 1 0
x x
2
2sin sin 1 0
x x
sin 1
1
sin
2
x
x
1
2
3
2
2
2
6
5
2
6
x k
x k
x k
1 2 3
, ,k k k
Do
0;20
x
nên:
1
2
3
0 2 20
2
0 2 20
6
5
0 2 20
6
k
k
k
1
2
3
1 41
4 4
1 119
12 12
5 115
12 12
k
k
k
1
2
3
1;2;3;...;10
0;1;2;...;9
0;1;2;...;9
k
k
k
Vậy tổng các nghiệm của phương trình trong đoạn
0;20
là:
1
10
1
1
2
2
k
S k
2
9
2
0
2
6
k
k
2
9
3
0
5
2
6
k
k
295
.
Câu 4:
(THPT Đặng Thúc Hứa – Nghệ An - năm 2017-2018)
Gọi
S
là tập hợp các nghiệm thuộc khoảng
0;100
của phương trình
2
sin cos 3 cos 3
2 2
x x
x
. Tổng các phần tử của
S
là
A.
7400
3
. B.
7525
3
. C.
7375
3
. D.
7550
3
.
Lời giải
Chọn C
Ta có
2
sin cos 3cos 3
2 2
x x
x
1 sin 3 cos 3
x x
sin 3cos 2
x x
1 3
sin cos 1
2 2
x x
sin 1
3
x
2 ,
6
x k k
.
Theo đề bài cho ta có
0 100
x
0 2 100
6
k
1 599
12 12
k
Mà
0;1;2;3;4,....;48;49
k k
Vậy
2 2 2 ...... 49 2
6 6 6 6
S
50
2 1 2 3 4 ..... 49
6
49 49 1
50 7375
2
6 2 3
.
Câu 5: Gọi
S
là tập hợp tất cả các nghiệm thuộc khoảng
0;2018
của phương trình sau:
3 1 cos2 sin 2 4cos 8 4 3 1 sinx x x x
Tính tổng tất cả các phần tử của
S
.
A.
103255
. B.
310408
3
. C.
312341
3
. D.
102827
.
Câu 6: Gọi
S
là tập hợp tất cả các nghiệm thuộc khoảng
0;2018
của phương trình sau:
3 1 cos2 sin 2 4cos 8 4 3 1 sinx x x x
Tính tổng tất cả các phần tử của
S
.
A.
103255
. B.
310408
3
. C.
312341
3
. D.
102827
.
Lời giải
Chọn B
Ta có
3 1 cos 2 sin 2 4cos 8 4 3 1 sinx x x x
2
2 3sin 2sin cos 4cos 4 3 sin 4sin 8 0
x x x x x x
2sin 3 sin cos 2 4 3 sin cos 2 0
x x x x x
2 sin 2 3 sin cos 2 0
x x x
3sin cos 2 0
x x
π
sin 1
6
x
2
3
x k
,
k
.
Vì
0;2018
x
nên
0 2 2018
3
k
1 1009 1
6 π 6
k
k
0;1;2;...;321
.
Suy ra
; 2 ; 2.2 ;...; 321.2
3 3 3 3
S
Vậy tổng tất cả các phần tử của
S
là
322. 2 1 2 3 ... 321
3
T
310408
3
.
Câu 7: Tìm tập hợp tất cả các giá trị của tham số thực
m
để phương trình
2
2 1 sin 4 1 cos 0
m x m x
có nghiệm thuộc khoảng
π 3π
;
2 2
.
A.
1
;
2

. B.
1
;0
2
. C.
1
;0
2
. D.
0;

.
Câu 8: Tìm tập hợp tất cả các giá trị của tham số thực
m
để phương trình
2
2 1 sin 4 1 cos 0
m x m x
có nghiệm thuộc khoảng
π 3π
;
2 2
.
A.
1
;
2

. B.
1
;0
2
. C.
1
;0
2
. D.
0;

.
Lời giải
Chọn B
Đặt
cost x
,
1;0
t
thì phương trình đã cho trở thành
2
2 4 1 0m t m t
2
2 4 2
t t m t
2 1 2 2 1
t t m t
2t m
(do
1
2
t
)
Phương trình có nghiệm khi
2 1;0
m
1
;0
2
m
.
Câu 9: Cho hàm số
sin 1
cos 2
m x
y
x
. Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
5;5
để giá
trị nhỏ nhất của
y
nhỏ hơn
1
.
A.
6
. B.
3
. C.
4
. D.
5
.
Câu 10: Cho hàm số
sin 1
cos 2
m x
y
x
. Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
5;5
để
giá trị nhỏ nhất của
y
nhỏ hơn
1
.
A.
6
. B.
3
. C.
4
. D.
5
.
Lời giải
Chọn A
Do
cos 2 0,x x
nên hàm số xác định trên
.
Ta có
sin 1
cos 2
m x
y
x
sin cos 2 1m x y x y
.
Do phương trình có nghiệm nên
2
2 2 2 2
2 1 3 4 1 0
m y y y y m
2 2
2 3 1 2 3 1
3 3
m m
y
.
Vậy GTNN của
y
bằng
2
2 3 1
3
m
.
Do đó yêu cầu bài toán
2
2 2
2 2
2 3 1
1 3 1 25 8
3
2 2
m
m
m m
m
.
Do
m
thuộc đoạn
5;5
nên
5; 4; 3;3;4;5
m
.
Câu 11: Có bao nhiêu giá trị nguyên dương của
m
để phương trình
2 2
sin 2 2sin cos cos sinx x x x m x
có nhiều hơn một nghiệm trong khoảng
0;2
π
?
A.
3
. B.
2
. C.
4
. D.
5
.
Câu 12: Có bao nhiêu giá trị nguyên dương của
m
để phương trình
2 2
sin 2 2sin cos cos sinx x x x m x
có nhiều hơn một nghiệm trong khoảng
0;2
π
?
A.
3
. B.
2
. C.
4
. D.
5
.
Lời giải
Chọn B
2 2
sin 2 2sin cos cos sinx x x x m x
2 2
2sin cos 2sin cos cos 1 cos 0
x x x x x m x
cos 1 2sin 1 cos 0
x x m x m
cos 1 0 1
2sin 1 cos 0 2
x
x m x m
Giải
1
:
cos 1 0
x
cos 1
x
π 2πx k
,
k
. Trong khoảng
0;2
π
thì
1
có
một nghiệm là:
πx
.
Giải
2
:
2sin 1 cos 0
x m x m
.
Để phương trình đã cho có nhiều hơn một nghiệm trong khoảng
0;2
π
thì
2sin 1 cos 0
x m x m
có nghiệm
2
2 2
2 1
m m
5
2
m
Vậy có hai giá trị nguyên dương
1
m
,
2
m
thỏa mãn điều kiện bài toán.
Câu 13: Tìm số tất cả các giá trị nguyên của tham số thực
m
để phương trình
3 2
2sin 2 sin 2 2 4 4cos 2x m x m x
có nghiệm thuộc
0;
6
.
A.
4
. B.
3
. C.
1
.
D.
6
.
Câu 14: Tìm số tất cả các giá trị nguyên của tham số thực
m
để phương trình
3 2
2sin 2 sin 2 2 4 4cos 2x m x m x
có nghiệm thuộc
0;
6
.
A.
4
. B.
3
. C.
1
.
D.
6
.
Lời giải
Chọn C
3 2
2sin 2 sin 2 2 4 4cos 2x m x m x
3 2
2sin 2 4sin 2 sin 2 2 0
x x m x m
.
Đặt
sin 2
x t
, với
3
0; 0;
6 2
x t
.
Khi đó, bài toán trở thành:
Tìm
m
để
3 2
2 4 2 0
t t mt m
có nghiệm trên khoảng
3
0;
2
t
.
3 2 2
2 4 2 0 2t t mt m m t
,
3
0;
2
t
.
Lập bảng biến thiên của hàm số
2
2y t t
trên khoảng
3
0;
2
t
.
Dựa vào bảng biến thiên ta thấy
3
;0
2
m
.
Vậy có
1
giá trị nguyên.
Câu 15: Phương trình
sin cos sin 2cos 3 0
x x x x
có tất cả bao nhiêu nghiệm thực thuộc
khoảng
3
;
4
?
A.
3
. B.
0
. C.
1
. D.
2
.
Câu 16: Phương trình
sin cos sin 2cos 3 0
x x x x
có tất cả bao nhiêu nghiệm thực thuộc
khoảng
3
;
4
?
A.
3
. B.
0
. C.
1
. D.
2
.
Lời giải
Chọn C
Ta có:
sin cos sin 2cos 3 0
x x x x
sin cos 0 1
sin 2cos 3 2
x x
x x
Giải
1
:
sin cos 0
x x
tan 1
x
4
x k
,
k
Do
3
;
4
x
nên
4
x
Giải
2
:
sin 2 cos 3
x x
vô nghiệm vì
2 2 2
1 2 3
Vậy phương trình đã cho có đúng một nghiệm thuộc khoảng
3
;
4
.
Câu 17: Cho phương trình
2 2
3 2 2
3 3
sin sin 2 sin
x m x m x m
. Gọi
;S a b
là tập hợp tất cả
các giá trị thực của tham số
m
để phương trình trên có nghiệm thực. Tính giá trị của
2 2
P a b
.
A.
162
49
P
. B.
49
162
P
. C.
4P
. D.
2P
.
Câu 18: Cho phương trình
2 2
3 2 2
3 3
sin sin 2 sin
x m x m x m
. Gọi
;S a b
là tập hợp tất cả
các giá trị thực của tham số
m
để phương trình trên có nghiệm thực. Tính giá trị của
2 2
P a b
.
A.
162
49
P
. B.
49
162
P
. C.
4P
. D.
2P
.
Lời giải
Chọn A
TH1:
sin
x m
thì ta có
2
3
2 0 0
m m
. Khi đó phương trình có nghiệm
x k
,
k
.
TH2:
sin
x m
thì phương trình đã cho tương đương
2
3 3
sin sin
2 0
sin sin
x m x m
x m x m
.
Giải ra ta được
3
3
sin
sin
1
1
0
sin
sin
sin 9sin 7
sin
8
2
sin
sin
x m
x m
m
x m
x m
x m x m
x m
x m
x m
.
Do đó để phương trình có nghiệm thực thì
7
9
9 9
7 7
m
m
m
0
9 9
7 7
m
m
KL: Hợp hai trường hợp suy ra tập hợp tất cả các giá trị thực của tham số
m
cần tìm là
7 7
;
9 9
S
2 2
2 2
9 9 162
7 7 49
P a b
.
Câu 19: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
3
3
3 3cos cosm m x x
có
nghiệm thực?
A.
2
. B.
7
. C.
5
. D.
3
.
Câu 20: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
3
3
3 3cos cosm m x x
có
nghiệm thực?
A.
2
. B.
7
. C.
5
. D.
3
.
Lời giải
Chọn C
Ta có
3
3
3 3cos cosm m x x
3
3
3 3cos cos
m x x m
1
Đặt
cos x u
. Điều kiện
1 1
u
và
3
3
3cos 3m x v v m u
2
1
trở thành
3
3u m v
3
Từ
3
và
2
suy ra
3 3
3 3u v v u
2 2
( )( 3) 0
u v u uv v
u v
Do
2
2
2 2
1 3
3 3 0
2 4
v
u uv v u v
,
,u v
Suy ra:
3
3
3 3m u u m u u
với
1;1
u
.
Xét hàm số
3
3f u u u
với
1;1
u
. Ta có
2
3 3
f u u
;
0 1
f u u
do
1;1
u
.
Suy ra
-1;1
max 2
f u
;
1;1
min 2
f u
Do đó phương trình có nghiệm khi và chỉ khi
2 2
m
, mà
m
nên
0; 1; 2
m
.
Câu 1:
(THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018)
Cho hàm số
2
1, 1
2 , 1.
x x
y f x
x x
Mệnh đề sai là
A.
1 2
f
. B.
f
không có đạo hàm tại
0
1.
x
C.
0 2.
f
D.
2 4.
f
Lời giải
Chọn B
Ta có
1 1
2
1 1 1
1
2 2
lim lim 2;
1 1
1
1 2
lim lim lim 1 2.
1 1
x x
x x x
f x f
x
x x
f x f
x
x
x x
Vậy
1 1 1 2.
f f f
Suy ra hàm số có đạo hàm tại
0
1.
x
Vậy B sai.
Câu 2:
(THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018)
Giám đốc một nhà hát A đang phân vân trong
việc xác định mức giá vé xem các chương trình được trình chiếu trong nhà hát. Việc này rất
quan trọng nó sẽ quyết định nhà hát thu được bao nhiêu lợi nhuận từ các buổi trình chiếu. Theo
những cuốn sổ ghi chép của mình, ông ta xác định được rằng: nếu giá vé vào cửa là
20
USD/người thì trung bình có
1000
người đến xem. Nhưng nếu tăng thêm
1
USD/người thì sẽ
mất
100
khách hàng hoặc giảm đi
1
USD/người thì sẽ có thêm
100
khách hàng trong số trung
bình.Biết rằng, trung bình, mỗi khách hàng còn đem lại
2
USD lợi nhuận cho nhà hát trong các
dịch vụ đi kèm. Hãy giúp giám đốc nhà hát này xác định xem cần tính giá vé vào cửa là bao
nhiêu để thu nhập là lớn nhất.
A.
18
USD/người. B.
19
USD/người. C.
14
USD/người. D.
25
USD/người.
Lời giải
Chọn C
Gọi giá vé sau khi điều chỉnh là
20
x
20 0
x
Số khách là:
1000 100x
Tổng thu nhập
2
20 .1 2 1000 100 22 1000 100 100 1200 22000
f x x x x x x x
Bảng biến thiên
20;
max 6
f x f

.Suy ra giá vé là:
20 20 6 14
x
USD
Câu 3:
(THPT Hai Bà Trưng-Vĩnh Phúc-lần 1-năm 2017-2018)
Tổng các nghiệm của phương trình
2cos3 2cos2 1 1
x x
trên đoạn
4 ;6
là:
A.
61
. B.
72
. C.
50
. D.
56
.
Lời giải
x
20
6

f x
0
f x

6
f

Chọn C
Xét
sin 0
x x m
: Thay vào phương trình thấy không thỏa mãn
Xét
sin 0
x x m
2cos3 2cos2 1 1
x x
2 cos5 cos 2cos3 1x x x
2sin cos5 2sin cos3 2sin cos sinx x x x x x x
sin 6 sin 4 sin 4 sin 2 sin 2 sinx x x x x x
sin 6 sinx x
2
5
,
2
7 7
k
x
k l
l
x
x m
.
Trước tiên ta cần chỉ ra giữa hai họ nghiệm
2
5
k
x
và
2
7 7
l
x
không có giá trị trùng
nhau.
Thật vậy: Giả sử
2 2
7 7 5
l k
,k l
14 5 10k l
: Vô lí vì
14k
là số nguyên chẵn và
5 10l
là số nguyên lẻ.
Với
2
5
4 ;6
k
x
x m
x
10; 9; 8;...14;15
10; 5;0;5,10,15
k
k
các giá trị
x
cần loại bỏ là
4 ,
2 ,
0,
2 ,
4 ,
6
.Tổng các giá trị này là
6
Với
2
7 7
4 ;6
l
x
x m
x
14; 13; 12;...19;20
4; 11;3;10;17
l
l
các giá trị
x
cần loại bỏ là
,
3 ,
,
3 ,
5
. Tổng các giá trị này là
5
Vậy tổng nghiệm
15 20
10 14
2 2
6 5 50
5 7 7
k l
k l
S
.
Câu 4:
(THPT Thạch Thành-Thanh Hóa-năm 2017-2018)
Cho
, 0;
2
x y
thỏa
cos2 cos2 2sin 2
x y x y
. Tìm giá trị nhỏ nhất của
4 4
sin cosx y
P
y x
A.
3
minP
. B.
2
min P
. C.
2
min
3
P
. D.
5
min P
.
Lời giải
Chọn B
Ta có:
2 2
cos2 cos2 2sin 2 sin sin sin
x y x y x y x y
Suy ra:
2
x y
Áp dụng bđt:
2
2 2
a b
a b
m n m n
Suy ra:
2 2
sin sin
2
x y
P
x y
. Đẳng thức xảy ra
4
x y
.
Do đó:
2
min P
.
Câu 1:
(THPT Chuyên Vĩnh Phúc-lần 1 MĐ 904 năm 2017-2018)
Số nghiệm thuộc đoạn
0;2017
của
phương trình
1 cos 1 cos
4cos
sin
x x
x
x
là
A.
1283.
B.
1285.
C.
1284.
D.
1287.
Lời giải
Chọn C
Điều kiện
0; sis
n .co 0
i snx x x
1 cos 1 cos
4cos 1 cos 1 cos 4sin cos
sin
x x
x x x x x
x
2 2 2 2
2 2 1 cos 1 cos 16sin cos 1 sin 8sin 1 sin 1
x x x x x x x
TH1:
sin 0
x
sin 0
3 2
sin 1
1
sin
1
2
1 1 sin 8sin 8sin 1 0 sin
2
1 5
sin
1 5
4
sin
4
x
x
x
x x x x
x
x
*
2
1
6
sin
2
2
5
6
x k
x
x k
vì
sin .cos 0
x x
nên
2
6
x k
.
*
arcsin
1 5
2
4
1 5
sin
4
1
arcs
5
in
2
4
x k
x
x k
vì
sin .cos 0
x x
nên
arcsi
5
4
n
1
2x k
.
TH2:
sin 0
x
sin 0
3 2
sin 1
1
sin
1
2
1 1 sin 8sin 8sin 1 0 sin
2
1 5
sin
1 5
4
sin
4
x
x
x
x x x x
x
x
*
2
1
6
sin
2
2
6
7
x k
x
x k
vì
sin .cos 0
x x
nên
2
6
7
x k
.
*
arcsin
1 5
2
4
1 5
sin
4
1 5
2
4
arcsin
x k
x
x k
vì
sin .cos 0
x x
nên
1 5
2
4
arcsin
x k
.
Xét nghiệm thuộc đoạn
0;2017
:
*Với
2 2
0 20 7 0 320
6
1
6
kx k k
có
321
nghiệm.
*Với
1 5 3 3
2 2 2
4 10
arcsin 0 2017 0 320
10
kx k k k
có
321
nghiệm.
*Với
7 7
0 2017 02 2
6
320
6
x k k k
có
321
nghiệm.
*Với
1 5 13 13
2 2 2
4 1
arcsin 0 2017 0 3
1
0
0 0
2
x k k k k
có
321
nghiệm.
*Vậy có tổng cộng
321.4 1284
nghiệm thỏa yêu cầu bài toán.
Câu 2:
(SGD Bắc Ninh năm 2017-2018)
Gọi
M
,
m
lần lượt là giá lớn nhất, giá trị nhỏ nhất của hàm số
2018 2018
sin cos
y x x
trên
. Khi đó:
A.
2M
,
1008
1
2
m
. B.
1M
,
1009
1
2
m
. C.
1M
,
0
m
. D.
1M
,
1008
1
2
m
.
Lời giải
Chọn D
Ta có:
2018 2018
y sin cos
x x
1009 1009
2 2
sin 1 sinx x .
Đặt
2
sint x
,
0 1t
thì hàm số đã cho trở thành
1009
1009
1y t t
.
Xét hàm số
1009
1009
1f t t t
trên đoạn
0;1
.
Ta có:
1008
1008
1009. 1009. 1f t t t
0
f t
1008
1008
1009 1009 1 0
t t
1008
1
1
t
t
1
1
t
t
1
2
t
Mà
1 0 1
f f
,
1008
1 1
2 2
f
.
Suy ra
0;1
max 0 1 1
f t f f
,
1008
0;1
1 1
min
2 2
f t f
Vậy
1M
,
1008
1
2
m
.
Câu 3:
(THPT Hoài Ân-Hải Phòng năm 2017-2018)
Tìm
m
để phương trình
2
2sin 2 1 sin 2 1 0
x m x m
có nghiệm thuộc khoảng
;0
2
.
A.
1 0
m
. B.
0 1
m
. C.
1 2
m
. D.
1 1
2 2
m
.
Lời giải
Chọn. D.
Đặt
sint x
,
1;0
t
, phương trình trở thành:
2
2 (2 1) 2 1 0
t m t m
Theo yêu cầu bài toán ta tìm
m
để phương trình
2
2 (2 1) 2 1 0
t m t m
có nghiệm
1;0
t
2
2 (2 1) 2 1 0
t m t m
2
2 1 2 2 0
t t m t
2
2 1
2 2
t t
m
t
2 1
2
t
Đặt
2 1
2
t
f t
,
1;0
t
,
f t
là hàm đồng biến nên
1 0
f m f
1 1
2 2
m
.
Câu 4:
(THPT Thanh Miện 1-Hải Dương-lần 1 năm 2017-2018)
Cho các số thực dương
x
,
y
,
z
thỏa
mãn
x y xyz z
. Giá trị lớn nhất của biểu thức
2
2
2
3
2
1
2
1
1
x yz
x
P
y z x
x
thuộc khoảng
nào trong các khoảng sau:
A.
1,3;1, 4
. B.
0,8;0,9
. C.
1,7;1,8
. D.
.
Lời giải
Chọn D
Từ giả thiết
1 1
. . 1x y xyz z x y xy
z z
.
Đặt
tan
2
A
x
,
tan
2
B
y
và
1
tan
2
C
z
thay vào hệ thức trên ta được
tan tan tan tan tan tan 1
2 2 2 2 2 2
A B B C C A
, suy ra
A
,
B
,
C
là ba góc của tam giác.
Từ đó ta có
2
3
2
2
2sin cos
2 2
1
x A A
x
và
2
2
2
sin
2
1
x A
x
.
2
2
tan tan
1
2 2
tan tan 1
2 2
C B
yz
B C
y z
cos cos tan tan 2 tan tan
2 2 2 2 2 2
cos cos tan tan 1
2 2 2 2
B C B C B C
B C B C
sin sin sin
2
cos
2
B C
B C
B C
1
cos cos cos
2 2
cos
2
A
B C B C
B C
2 2
cos cos 1 cos
2 2 2
cos
2
A B C A
B C
2
cos 1 1 cos
2 2
2cos
1 2
A A
A
.
Vậy
2 2
2sin cos 2sin cos
2 2 2 2
A A A A
P
sin sin cos
2 2
A A
A
2 sin .sin 2
2 4
A
A
.
Dấu bằng đạt được khi sin 1
sin 1
2 4
B C
A
A
2
4
A
B C
1
2 1
2 1
x
y
z
.
Câu 5:
(THPT Chuyên Hoàng Văn Thụ-Hòa Bình năm 2017-2018)
Số các giá trị nguyên của
m
để
phương trình
2
cos cos
x x m m
có nghiệm là:
A.
4
. B.
2
. C.
3
. D.
5
.
Lời giải
Chọn A
Ta có:
2
cos cos
x x m m
suy ra
0
m
.
Đặt
cos
x m t
,
0t
. Phương trình trở thành:
2
2
cos
cos
x t m
t x m
2 2
cos cos 0
x t t x
cos cos 1 0
x t x t
cos
cos 1 0
x t
x t
.
Trường hợp
1
:
cos x t
cos cosx m x
2
cos 0
cos cos
x
x x m
.
Đặt
cosu x
1 0
u
.
Xét
2
f u u u
, ta có
2 1f u u
;
1
0
2
f u u
.
Do đó với
1 0
u
suy ra
0
f u
với mọi
1;0
u
.
Suy ra
1 0
f f u f
2 0
f u
.
Để phương trình có nghiệm thì
0;2
m
. Vì
m
nên
0;1;2
m
.
Trường hợp
2
:
cos 1 0
x t
cos 1 cosx m x
2
cos cos 1
x x m
.
Đặt
cosv x
,
1 1v
. Ta có
2
1
m v v g v
,
1
2 1 0
2
g v v v
.
Vẽ bảng biến thiên ta được:
Để phương trình có nghiệm thì
3
;3
4
m
. Vì
m
nên
1;2;3
m
.
Vậy có tất cả
4
số nguyên
m
thỏa mãn bài toán.
Câu 6:
(THPT Trần Nhân Tông-Quảng Ninh-lần 1 năm 2017-2018)
Số nghiệm của phương trình:
2015 2016 2017 2018
sin cos 2 sin cos cos 2x x x x x
trên
10;30
là:
v
1
1
2
1
g v
0
g v
1
3
4
3
A.
46
. B.
51
. C.
50
. D.
44
.
Hướng dẫn giải
Chọn D
Ta có:
2015 2016 2017 2018
sin cos 2 sin cos cos 2x x x x x
2015 2 2016 2
sin 1 2sin cos 2cos 1 cos2x x x x x
2015 2016
sin .cos 2 cos .cos 2 cos 2x x x x x
2015 2016
cos2 0
sin cos 1
x
x x
.
Với
cos 2 0
x
,
4 2
x k k
Vì
10;30
x
10 30
4 2
k
20 1 60 1
2 2
k
6 18
k
.
Với
2015 2016
sin cos 1x x
. Ta có
2015 2 2016 2
sin sin ;cos cosx x x x
.
Do đó
2015 2016 2 2
1 sin cos sin cos 1x x x x
suy ra
sin 0,cos 1
sin 1,cos 0
x x
x x
.
Nếu
sin 0 ,x x k k
.
Vì
10;30
x
10 30
k
10 30
3 9
k
.
Nếu
sin 1 2 ,
2
x x k k
.
Vì
10;30
x
10 2 30
2
k
5 1 15 1
4 4
k
1 4
k
.
Vậy số nghiệm của phương trình đã cho là:
13 6 25 44
.
Câu 1:
(THPT Lê Quý Đôn-Hà Nội năm 2017-2018)
Có bao nhiêu giá trị nguyên của
m
để phương
trình
3
sin 2 sin 2
x m x
có nghiệm.
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải
Chọn A
Ta có
3
sin 2 sin 2
x m x
.
Đặt
3
sin 2
1 3
sin
u x
u
v m x
 . Khi đó
2
3
sin 2
sin
u x
v m x
2 3
2
u v m
(*).
Ta lại có
2 2
u v v u
.
(*) trở thành
3
2
2 2 1
u u m

3 2
5 12 10
m u u u f u
,
1 3
u
.
Trên
, ta có
2
3 14 12
f u u u
,
7 13
0 1; 3
3
f u u
Để phương trình đã cho có nghiệm thì
1
có nghiệm
1 3
u
hay
7 13
3
3
f m f
0;1
m
) Vì
m
nguyên ).
Vậy có
2
giá trị nguyên của
m
thỏa đề bài.
Câu 2:
(THPT Hồng Lĩnh-Hà Tĩnh-lần 1 năm 2017-2018)
Số giá trị nguyên của tham số
m
để phương
trình
sin 2 2 sin 2
4
x x m
có đúng một nghiệm thực thuộc khoảng
3
0;
4
?
A.
3
. B.
2
. C.
0
. D.
1
.
Lời giải
Chọn B
Ta có
3
0;
4
x
4 4
x
0 sin 1
4
x
0 2 sin 2
4
x
.
Mặt khác
2 sin sin cos
4
x x x
.
Đặt
sin cos
x x t
với
0; 2
t
2 2 2
sin cos 2sin .cos
x x x x t
2
sin 2 1
x t
.
Phương trình đã cho trở thành
2 2
1 2 3
t t m t t m
*
.
Xét
2
3f t t t
với
0; 2
t
.
Ta có
2 1f t t
. Do đó
1
0
2
f t t
(loại).
Bảng biến thiên
Dựa vào bảng biến thiên ta có phương trình
*
có nhiều nhất một nghiệm
t
. Do đó để phương
trình đã cho có đúng một nghiệm thực
x
thuộc khoảng
3
0;
4
thì
2
0 1
t
t
.
Với
2
t
thay vào phương trình
*
:
2 2 3
m
2 1m
.
Với
0 1t
ta có bảng biến thiên
Vậy
3 1
m
có
2
giá trị nguyên của
m
là
2
và
1
.
Câu 3: Có bao nhiêu giá trị nguyên âm của
m
để hàm số
1
5
2
m
y x
x
đồng biến trên
5;
?
A.
10
. B.
8
. C.
9
. D.
11
.
Câu 4: Cho hàm số
3 2
3y x x
có đồ thị
C
và điểm
; 4
M m
. Hỏi có bao nhiêu số nguyên
m
thuộc đoạn
10;10
sao cho qua điểm
M
có thể kẻ được ba tiếp tuyến đến
C
.
A.
20
. B.
15
. C.
17
. D.
12
.
Câu 5:
(THPT Chuyên Ngữ – Hà Nội - Lần 1 năm 2017 – 2018)
Có bao nhiêu giá trị nguyên âm của
m
để
hàm số
1
5
2
m
y x
x
đồng biến trên
5;
?
A.
10
. B.
8
. C.
9
. D.
11
.
Lời giải
Chọn B
Tập xác định:
\ 2
D
. Đạo hàm:
2
2 2
1 4 3
1
2 2
m x x m
y
x x
.
Xét hàm số
2
4 3f x x x
trên
5;
.
Đạo hàm:
2 4
f x x
. Xét
0 2 1
f x x y
. Ta có:
5 8
f
.
Bảng biến thiên:
Do
2
2 0
x
với mọi
5;x
nên
0
y
,
5;x
khi và chỉ khi
f x m
,
5;x
. Dựa vào bảng biến thiên ta có:
8 8
m m
.
Mà
m
nguyên âm nên ta có:
8; 7; 6; 5; 4; 3; 2; 1
m
.
x

2
5

y
0
0
y

1
8

Vậy có
8
giá trị nguyên âm của
m
để hàm số
1
5
2
m
y x
x
đồng biến trên
5;
.
Câu 6:
(THPT Chuyên Ngữ – Hà Nội - Lần 1 năm 2017 – 2018)
Cho hàm số
3 2
3y x x
có đồ thị
C
và
điểm
; 4
M m
. Hỏi có bao nhiêu số nguyên
m
thuộc đoạn
10;10
sao cho qua điểm
M
có thể kẻ được ba tiếp tuyến đến
C
.
A.
20
. B.
15
. C.
17
. D.
12
.
Lời giải
Chọn C
Tập xác định:
D
. Đạo hàm:
2
3 6y x x
.
Ta nhận thấy các đường thẳng
x a
với
a
không phải là tiếp tuyến của
C
và một
đường thẳng không thể tiếp xúc với đồ thị hàm số bậc ba tại hai điểm phân biệt.
Giả sử phương trình đường thẳng đi qua
; 4
M m
là
:d
4
y k x m
với
k
là hệ số
góc của đường thẳng.
Qua
M
có thể kẻ được ba tiếp tuyến đến
C
khi và chỉ khi hệ phương trình
2
3 2
3 6
4 3
k x x
k x m x x
có ba nghiệm phân biệt
2 3 2
3 6 3x x x m x x
có ba nghiệm phân biệt
3 2
2 3 1 6 0
x m x mx
có ba nghiệm phân biệt
2
2 3 1 6 0
x x m x m
có ba nghiệm phân biệt
2
2 3 1 6 0
x m x m
có hai nghiệm phân biệt khác
0
2
2
1
9 30 9 0
3
9 1 48 0
3
0
0
0
m
m m
m m
m
m
m
m
.
Với điều kiện trên và với
10;10
m
m
ta có
10; 9;...; 1;4;5;...;10
m
.
Vậy có
17
số thỏa mãn yêu cầu bài toán.
Câu 7: (THPT Quỳnh Lưu 1 – Nghệ An – Lần 2 năm 2017 – 2018) Có bao nhiêu giá trị nguyên m
để phương trình
3
3
8sin 162sin 27x m x m
có nghiệm thỏa mãn
0
3
x
?
A.
2
. B.
3
. C.Vô số. D.
1
.
Lời giải
Chọn A
Đặt
2sint x
, với
0
3
x
thì
0; 3
t
.
Phương trình đã cho trở thành
3
3
81 27t m t m
.
Đặt
3
u t m
3
t u m
.
Khi đó ta được
3
3
27 3
3 27
u t m
t u m
3
3
3 27 3
u t t u
3
3
27 3 27.3u u t t
*
Xét hàm số
3
27f v v v
liên tục trên
có nên hàm số đồng biến.
Do đó
*
3u t
3
3
t t m
1
Xét hàm số
3
3f t t t
trên khoảng
0; 3
.
có
2
3 3
f t t
;
0 1f t t
(vì
0t
).
Bảng biến thiên
Dựa vào bảng biến thiên ta thấy phương trình
1
có nghiệm khi.
Vậy có hai giá trị nguyên của
m
thỏa yêu cầu bài toán.
Câu 1: (THPT Chuyên Thái Bình – Thái Bình – Lần 5 năm 2017 – 2018) Cho phương trình
2
1 cos cos 4 cos sinx x m x m x
. Tìm tất cả các giá trị của
m
để phương trình có đúng
3
nghiệm phân biệt thuộc
2
0;
3
.
A.
1 1
;
2 2
m
. B.
; 1 1;m

.
C.
1;1
m
. D.
1
;1
2
m
.
Lời giải
Chọn D
Ta có:
2 2
1 cos cos 4 cos sin 1 cos cos 4 cos 1 cos 0
x x m x m x x x m x m x
1 cos cos4 cos 1 cos 0
x x m x m x
cos 1
cos 4
x
x m
.
Xét phương trình
cos 1 2x x k
k
.
Phương trình
cos 1
x
không có nghiệm trong đoạn
2
0;
3
.
Cách 1:
Xét phương trình
cos 4
x m
. Đặt
cos 4f x x
. Ta có:
4sin 4f x x
.
Xét
0 sin 4 0 4
4
f x x x k x k
k
.
Xét trong đoạn
2
0;
3
thì ta có:
0; ;
4 2
x
.
Bảng biến thiên:
Dựa vào bảng biến thiên, ta thấy phương trình
cos 4
x m
có đúng
3
nghiệm phân biệt trong
đoạn
2
0;
3
khi và chỉ khi
1
1
2
m
.
Cách 2:
Xét
cos 4
x m
. Ta có
2 8
0; 4 0;
3 3
x x
.
Với
4 0;2 \x
và
1;1
m
phương trình
cos 4
x m
có
2
nghiệm.
Với
8
4 2 ;
3
x
và
1
;1
2
m
phương trình
cos 4
x m
có
1
nghiệm.
x
0
4
2
2
3
f x
0
0
0
f x
1
1
1
1
2
Vậy phương trình có
3
nghiệm phân biệt thuộc
2
0;
3
khi
1
;1
2
m
.
Câu 2: Khẳng định nào sau đây là đúng về phương trình
2 2
80
sin cos 0
6 2 32 332
x
x x x
?
A. Số nghiệm của phương trình là
8
. B. Tổng các nghiệm của phương trình là
8
.
C. Tổng các nghiệm của phương trình là
48
. D. Phương trình có vô số nghiệm thuộc
.
Câu 3: Khẳng định nào sau đây là đúng về phương trình
2 2
80
sin cos 0
6 2 32 332
x
x x x
?
A. Số nghiệm của phương trình là
8
. B. Tổng các nghiệm của phương trình là
8
.
C. Tổng các nghiệm của phương trình là
48
. D. Phương trình có vô số nghiệm thuộc
.
Hướng dẫn giải
Chọn C
Phương trình đã cho tương đương với
2 2
80
sin sin
6 32 332
x
x x x
.
Ta biết rằng hàm số
siny x
đồng biến trên khoảng
;
2 2
. Ta chỉ ra rằng các hàm số
2
6
x
f x
x
và
2
80
32 332
g x
x x
nhận giá trị trong khoảng này.
Thật vậy, ta có
2
2
1
6
2 6
2 6
x x
x
x
và
2
2
80 80 80
0
32 332 76 2
16 76
x x
x
.
Từ các đánh giá trên,
xảy ra khi và chỉ khi
2 2
80
6 32 332
x
x x x
3 2
48 332 480 0
x x x
2
6
40
x
x
x
.
Tổng các nghiệm của phương trình đã cho là
2 6 40 48
.
| 1/145
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Câu 1: (THPT Chuyên Hùng Vương-Phú Thọ-lần 1-NH2017-2018) Nghiệm của phương trình
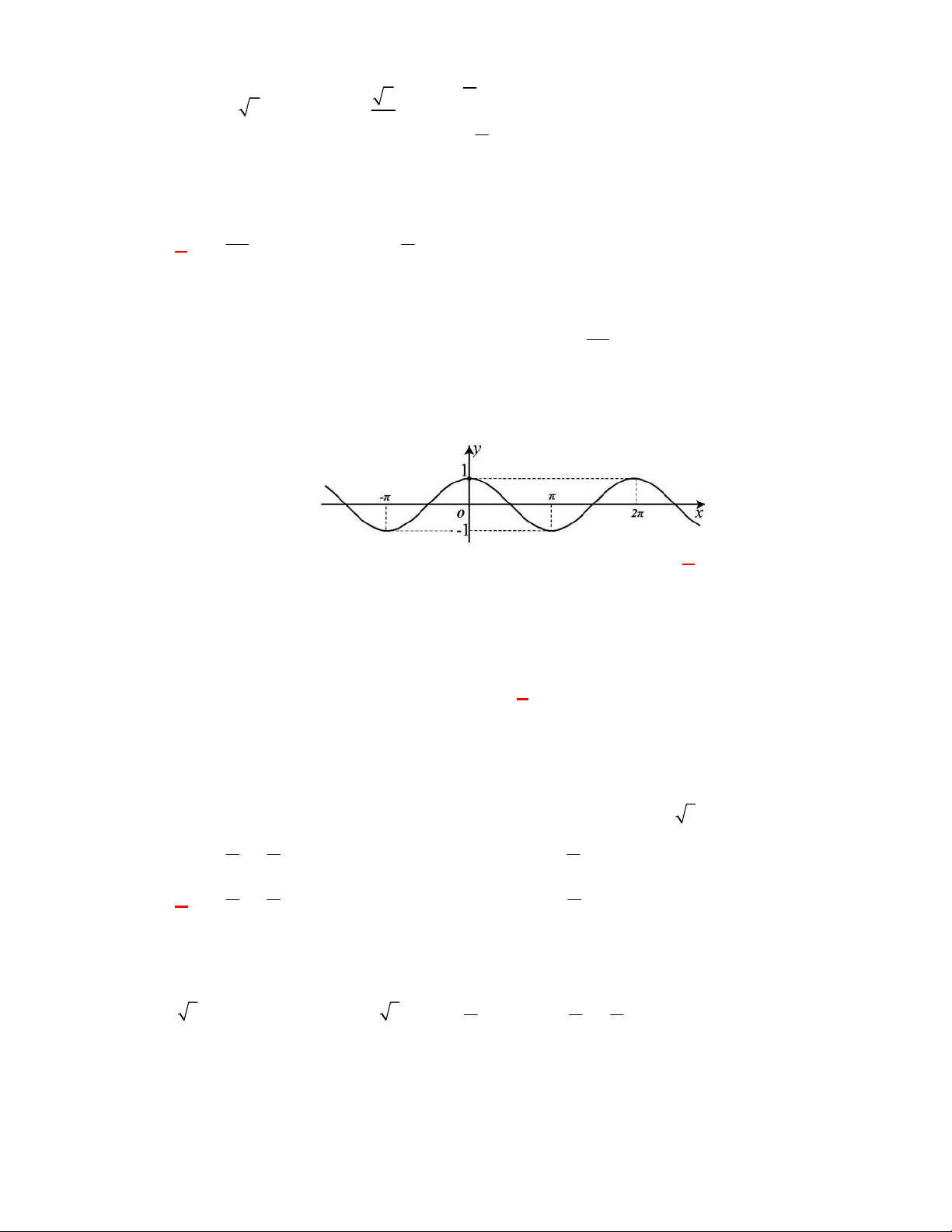
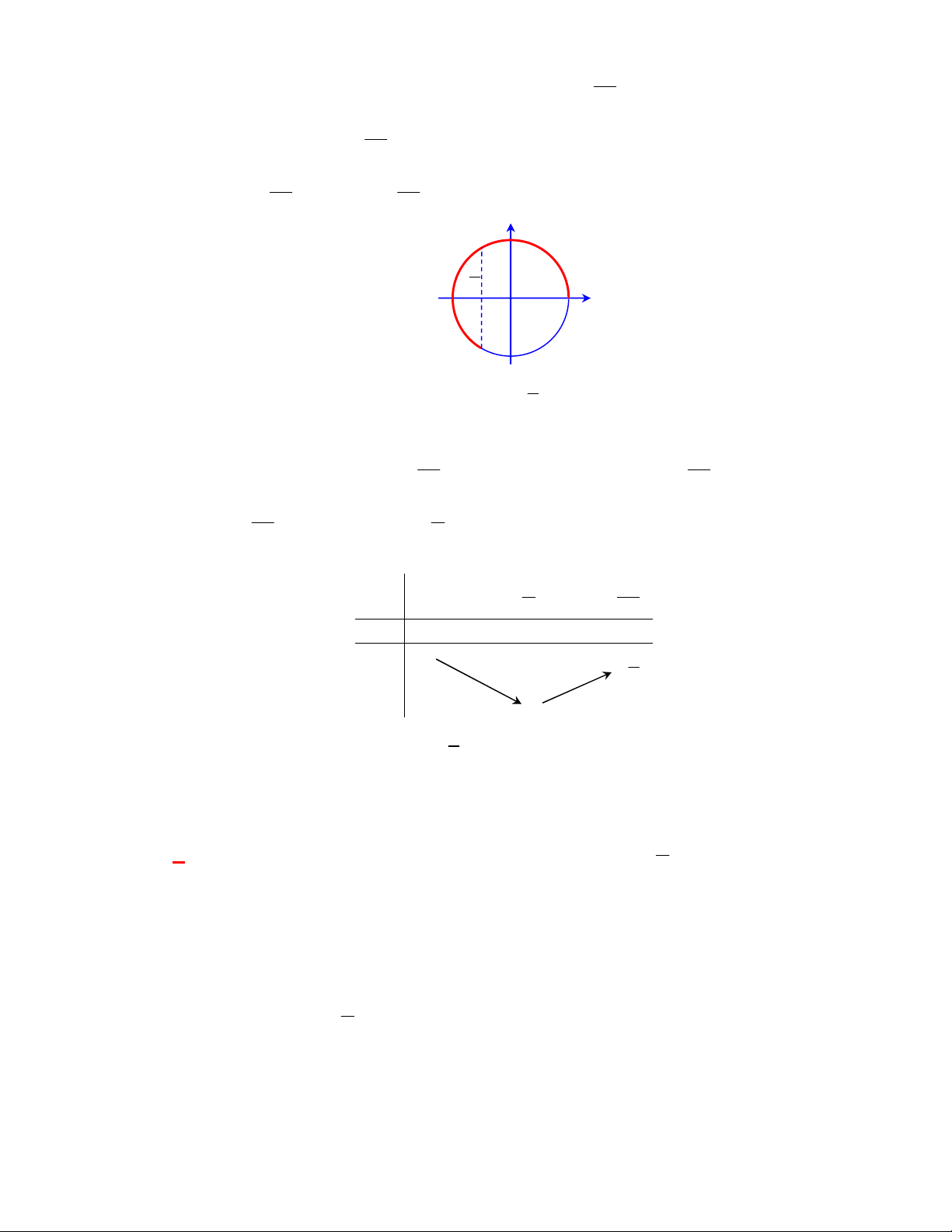
2 sin x 1  0 được biểu diễn trên đường tròn lượng giác ở hình bên là những điểm nào ? y B D C AO x A E F B
A. Điểm E , điểm D .
B. Điểm C , điểm F . C. Điểm D , điểm C . D. Điểm E , điểm F . Lời giải
Chọn D   x    k 2 1  6
Ta có: 2 sin x 1  0  sin x     k  . 2 7 x   k 2  6
Vậy chỉ có hai điểm E và F thỏa mãn.
Câu 2: (THPT Chuyên Hùng Vương-Phú Thọ-lần 1-NH2017-2018) Khẳng định nào dưới đây là sai ?
A. Hàm số y  cos x là hàm số lẻ.
B. Hàm số y  cot x là hàm số lẻ.
C. Hàm số y  sin x là hàm số lẻ.
D. Hàm số y  tan x là hàm số lẻ. Lời giải Chọn A
Ta có các kết quả sau:
+ Hàm số y  cos x là hàm số chẵn.
+ Hàm số y  cot x là hàm số lẻ.
+ Hàm số y  sin x là hàm số lẻ.
+ Hàm số y  tan x là hàm số lẻ.
Câu 3: (THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018) Nghiệm của phương trình
tan 3x  tan x là kkA. x  , k  . 
B. x k , k   .
C. x k 2 , k  .  D. x  , k  .  2 6
Lời giải Chọn B k
Ta có tan 3x  tan x  3x x k  x  , k  .  2 Trình bày lại   kx   cos3x  0   6 3 ĐK:    * cosx  0   x   k   2 k
Ta có tan 3x  tan x  3x x k  x  , k  .
 Kết hợp điều kiện * suy ra x k , k  2
Câu 4: (THPT Chuyên Thái Bình-lần 1-năm 2017-2018) Cho hàm số y f x có đồ thị như hình
bên. Mệnh đề nào dưới đây đúng? y 2 2 O x 2 
A. Hàm số có giá trị cực tiểu bằng 2 .
B. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng 2  .
C. Hàm số đạt cực đại tại x  0 và cực tiểu tại x  2 .
D. Hàm số có ba điểm cực trị. Lời giải Chọn C
Câu 5: (THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018) Tìm tất cả các giá trị thực của tham số m để
phương trình sin x m  1 có nghiệm? A. 2   m  0. B. m  0. C. m  1.
D. 0  m  1. Lời giải Chọn A
Ta có sin x m  1  sin x m 1. Khi đó YCBT  1
  m 1  1  2   m  0. x
Câu 6: (THPT Sơn Tây-Hà Nội-lần 1-năm 2017-2018) Giải phương trình sin  1. 2 
A. x    k 4 , k   . B. x k 2 , k   .
C. x    k 2 , k   . D. x
k 2 , k   . 2 Lời giải Chọn A x x  Ta có sin  1  
k 2  x    k 4 , k   . 2 2 2
Vậy nghiệm của phương trình là x    k 4 , k  . 
Câu 7: (THPT Sơn Tây-Hà Nội-lần 1-năm 2017-2018) Trong các hàm số sau hàm số nào là hàm số chẵn?   
A. y  1 sin x .
B. y  sin x .
C. y  cos x    .
D. y  sin x  cos x .  3  Lời giải Chọn B TXĐ: D   . x
  D : x D  x D   1
Ta có f x  sin x   sin  x  sin  x  f x 2 . Từ  
1 và 2 suy ra hàm số y  sin x là hàm chẵn. 1
Câu 8: (THPT Yên Lạc-Vĩnh Phúc-lần 1-năm 2017-2018) Nghiệm của phương trình cos x   là 2 2    A. x    k 2 . B. x    k . C. x    k 2 . D. x    k 2 . 3 6 3 6 Lời giải
Chọn A 1 2 2
cos x    cos x  cos  x  
k 2 , k   . 2 3 3
Câu 9: (THPT Yên Lạc-Vĩnh Phúc-lần 1-năm 2017-2018) Trong các hàm số sau đây, hàm số nào là
hàm số tuần hoàn? x 1
A. y x 1. B. 2 y x . C. y  .
D. y  sin x . x  2 Lời giải Chọn D
Hàm số y  sin x tuần hoàn với chu kì 2 .
Câu 10: (THPT Yên Lạc-Vĩnh Phúc-lần 1-năm 2017-2018) Công thức tính số tổ hợp là: n n n n k ! k ! k ! k ! A. C  . B. C  . C. A  . D. A  . nn k ! n
n k !k! nn k ! n
n k !k! Lời giải
Chọn B 1
Câu 11: (THPT Yên Lạc-Vĩnh Phúc-lần 1-đề 2-năm 2017-2018) Nghiệm của phương trình cos x   2 là 2    A. x    k 2 . B. x    k . C. x    k 2 . D. x    k 2 . 3 6 3 6 Lời giải
Chọn A 1 2 2
cos x    cos x  cos  x  
k 2 , k   . 2 3 3
Câu 12: (THPT Yên Lạc-Vĩnh Phúc-lần 1-đề 2-năm 2017-2018) Trong các hàm số sau đây, hàm số nào
là hàm số tuần hoàn? x 1
A. y x 1. B. 2 y x . C. y  .
D. y  sin x . x  2 Lời giải Chọn D
Hàm số y  sin x tuần hoàn với chu kì 2 .
Câu 13: (THPT Yên Lạc 2-Vĩnh Phúc-lần 1-năm 2017-2018) Giá trị lớn nhất và nhỏ nhất của hàm 5 cos 2x 1 số y  là 2 A. 1 và 2 . B. 3 và 2 . C. 3 và 2  . D. 3  và 1. Lời giải Chọn C 5 cos 2x 1
1  cos 2x  1  5
  5 cos 2x  5  4
  5 cos 2x 1  6  2   3 . 2
Vậy giá trị lớn nhất của hàm số là 3 và giá trị nhỏ nhất của hàm số là 2  .
Câu 14: (THPT Yên Lạc 2-Vĩnh Phúc-lần 1-năm 2017-2018) Tập xác định của hàm số f x  cot x là
A.  \ k | k    .
B.  \ k 2 | k    .    C.  \   2k   1  | k    . D.  \   2k   1 | k   .  2  Lời giải Chọn A
f x xác định khi và chỉ khi sin x  0  x k k   .
Câu 15: (THPT Yên Lạc 2-Vĩnh Phúc-lần 1-năm 2017-2018) Điều kiện xác định của hàm số sin x  cos x y  là cos x   A. x   k .
B. x k 2 .
C. x k .
D. x k . 2 2 Lời giải Chọn A
Hàm số xác định  cos x  0  x   k . 2
Câu 16: (THPT Hai Bà Trưng-Vĩnh Phúc-lần 1-năm 2017-2018) Trong các khẳng định sau khẳng định nào đúng?
A. Phương trình cos x a có nghiệm với mọi số thực a .
B. Phương trình tan x a và phương trình cot x a có nghiệm với mọi số thực a .
C. Phương trình sin x a có nghiệm với mọi số thực a .
D. Cả ba đáp án trên đều sai. Lời giải Chọn B
Cách 1: Ta có hàm y  cos x và y  sin x nhận giá trị trên đoạn 1 
;1 nên A và C sai suy ra D cũng sai.
Cách 2: Hàm y  tan x và y  cot x nhận giá trị trên tập số thực nên B đúng.
Câu 17: (THPT Hai Bà Trưng-Vĩnh Phúc-lần 1-năm 2017-2018) Trong các hàm số sau hàm số nào
tuần hoàn với chu kỳ  ? x A. y  sin 2 . x B. y  tan 2 . x C. y  cos . x D. y  cot . 2 Lời giải Chọn A
sin 2  x     sin 2x  2   
 sin 2x ; Giả sử có số T sao cho 0  T   và
sin 2  x T   sin 2 x, x  .          Chọn x  , ta được sin 2  T  sin  1  cos 2 T  1.    4   4  2 
Điều này trái giả thiết 0  T   . Vậy  là chu kỳ của hàm số y  sin 2 . x   
Câu 18: (THPT Việt Trì-Phú Thọ-lần 1-năm 2017-2018) Phương trình tan x   0   có nghiệm là  3      A.
k 2 , k   . B.
k , k   . C.
k , k   . D.
k , k   . 3 2 3 3 Lời giải Chọn D     ĐK: cos x   0    x   k  3  6      Ta có tan x   0  x   k    x  
k , k   .  3  3 3
Câu 19: (THPT Bình Xuyên-Vĩnh Phúc-năm 2017-2018) Hàm số y  cotx tuần hoàn với chu kỳ:
A. T k . B. T  2 .
C. T k 2 . D. T   . Lời giải Chọn D
Theo tính chất trong sgk 11 thì hàm số y  cotx tuần hoàn với chu kì  .
Câu 20: (THPT Bình Xuyên-Vĩnh Phúc-năm 2017-2018) Trong các hàm số sau đây, hàm nào có đồ thị
nhận trục tung làm trục đối xứng? A. 2
y  cos x  sin x .
B. y  tan x . C. 3
y  sin x cos x .
D. y  sin x . Lời giải Chọn A
Trong 4 hàm số trên chỉ có hàm số 2
y  cos x  sin x là hàm số chẵn nên có đồ thị nhận trục
tung làm trục đối xứng. Thật vậy:
Tập xác định của hàm số là D   nên x
    x   .
Và y x  x 2 cos  sin x 2
 cos x  sin x y x Nên hàm số 2
y  cos x  sin x là hàm số chẵn.
Câu 21: (THPT Nguyễn Đức Thuận-Nam Định-lần 1-năm 2017-2018) Xét bốn mệnh đề sau:  
1 : Hàm số y  sin x có tập xác định là .
2 : Hàm số y  cos x có tập xác định là .
3 : Hàm số y  tan x có tập giá trị là .
4 : Hàm số y  cot x có tập xác định là .
Tìm số phát biểu đúng. A. 3 . B. 2 . C. 4 . D. 1. Lời giải. Chọn A
Dễ thấy các phát biểu   1 ; 2 ; 3 đúng. cos x
Xét 4 : y  cot x
 ĐKXĐ: s inx  0  x k  D \ k ; k   . sin x
Câu 22: [2D-3](THPT Nguyễn Đức Thuận-Nam Định-lần 1-năm 2017-2018) Cho hàm số m 3 2 y
x mx  3x 1 ( m là tham số thực). Tìm giá trị nhỏ nhất của m để hàm số đồng biến 3 trên . A. m  3 . B. m  2 . C. m  1. D. m  0 . Lời giải. Chọn D
Ta có: D . 2
y  mx  2mx  3 .
Hàm số đồng biến trên y  0, x   R 2
mx  2mx  3  0, x   *
Trường hợp 1: m  0  y  3  0  Hàm số đồng biến trên R m  0 thỏa yêu cầu. m  0
Trường hợp 2: *    0  m  3 . 2
  m  3m  0 
Kết hợp hai trường hợp ta có 0  m  3 nên m  0 thỏa yêu cầu đề bài.
Câu 23: (THPT Hậu Lộc 2-Thanh Hóa-ần 1-năm 2017-2018) Trong các hàm số sau, hàm số nào tuần hoàn với chu kì 2 ?
A. y  cos 2x .
B. y  sin x .
C. y  tan x .
D. y  cot x . Lời giải Chọn B
Theo định nghĩa, hàm số y  sin x tuần hoàn với chu kì 2 , các hàm số lượng giác còn lại
y  tan x , y  cot x , y  cos 2x tuần hoàn với chu kì  .
Xét y  cos 2x : ta có y x     cos 2 x     cos 2x  2   cos 2x y x nên y  cos 2x
tuần hoàn với chu kì  .
Câu 24: (THPT Chuyên Lam-Thanh Hóa-lần 1-năm 2017-2018) Nghiệm phương trình 2 sin x  1 có dạng nào dưới đây?     x   k 2  x   k 2 3  6 A.  k  . B.  k   . 2  5 x   k 2 x   k3  3  6     x   k 2  x   k 2 6  6 C.  k  . D.  k . 5   x   k 2
x    k2  6  6 Lời giải Chọn C   x   k 2     6
Ta có: 2 sin x  1  sin x  sin     k  .  6  5  x   k 2  6
Câu 25: (THPT Cổ Loa-Hà Nội-lần 1-nawm-2018) Tập xác định của hàm số y  tan x là   A.  .
B.  \   k , k  .  2    
C.  \ k , k    .
D.  \   k , k   .  2 2  Lời giải Chọn B
Hàm số xác định khi x
k , k   . 2  
Vậy tập xác định của hàm số đã cho là  \   k , k .  2  3
Câu 26: (THPT Cổ Loa-Hà Nội-lần 1-nawm-2018) Phương trình tan 3x  30   có tập nghiệm 3 là A.  180 k ,  k    . B.k60 ,  k    . C.k360 ,  k    . D.k90 ,  k    . Lời giải Chọn B 3
tan 3x  30  
 tan 3x  30  tan  30   3  3x  30  30    180 k
  x k60 ,  k   .
Câu 27: (THPT Cổ Loa-Hà Nội-lần 1-nawm-2018) Nghiệm của phương trình cos 2x  5sin x  3  0 là     x    k 2   x    k 2 6  3 A.  , k   . B.  , k   . 7   7 x   k 2 x   k 2  6  3     x     kx    k 6  3 C.  , k   . D.  , k   . 7   7 x   k x   k  6  3 Lời giải Chọn A
cos 2x  5sin x  3  0 2
 1 2sin x  5sin x  3  0 2
 2 sin x  5sin x  2  0    1 x    k 2
sin x   (n)      6  2  sin x  sin    , k   .     6  7 sin x  2(  l)   x   k 2  6
Câu 28: (THPT Chuyên Lê Hồng Phong-Nam Định-lần 2 năm 2017-2018) Tìm tập xác định D của hàm tan x 1    số y   cos x    . sin x  3   k 
A. D   \ k , k    .
B. D   \  , k   .  2   
C. D   \   k , k   . D. D   .  2  Lời giải Chọn B tan x 1    Hàm số y   cos x    xác định khi: sin x  3  sin  x  0 k 
 sin 2x  0  2x k  x  , (k  ) . cos x  0 2  3
Câu 29: (SGD Vĩnh Phúc-KSCL lần 1 năm 2017-2018) Phương trình cos x  có tập nghiệm là: 2       A. 
k ; k   . B. 
k 2 ; k   .  6   6        C. 
k ; k   . D. 
k 2 ; k   .  3   3  Lời giải Chọn B 3   cos x   cos  x  
k 2 ; k  .  2 6 6
Câu 30: (THPT Triệu Sơn 3-Thanh Hóa năm 2017-2018) Nghiệm của phương trình sin x  1 là:   k     A. x   . B. x   k 2 . C. x     k 2 . D. x   k . 2 2 2 2 Lời giải
Chọn B
Ta có: sin x  1  x  
k 2 , k . 2
Câu 31: (THPT Triệu Sơn 3-Thanh Hóa năm 2017-2018) Chu kì tuần hoàn của hàm số y  sin 2x là:  A. 3 . B. . C. 2 . D.  . 2 Lời giải Chọn D
Ta có y  sin 2x  sin 2x  2   sin 2 x    . Suy ra chu kì của hàm số là T   . 2 2
Giải nhanh: Hàm số y  sin ax b là T     . a 2
Câu 1: (THPT Chuyên Vĩnh Phúc-MĐ 903 lần 1-năm 2017-2018) Phương trình tan x  3 có tập nghiệm là      
A.   k2 , k   . B.  .
C.   k , k   . D.   k , k   .  3   3   6  Lời giải Chọn A  
Ta có tan x  3  tan x  tan  x
k , k . 3 3
Câu 2: (THPT Chuyên Vĩnh Phúc-lần 1 MĐ 904 năm 2017-2018) Phương trình 2 cos x 1  0 có một nghiệm là  2  5 A. x  . B. x  . C. x  . D. x  . 6 3 3 6 Lời giải Chọn C 1 
Phương trình 2 cos x 1  0  cos x   x    k 2 . 2 3 
Vậy các nghiệm của phương trình là x  
k 2 , k   . 3
Câu 3: (THPT Kiến An-Hải Phòng năm 2017-2018) Có bao nhiêu số nguyên m để phương trình
5sin x 12 cos x m có nghiệm? A. 13 . B. Vô số. C. 26 . D. 27 . Lời giải Chọn D
Phương trình 5sin x 12 cos x m có nghiệm khi và chỉ khi   2 2 2 5 12  m  2 m  169
 13  m  13 .
Suy ra có 27 số nguyên m để phương trình 5sin x 12 cos x m có nghiệm.
Câu 4: (THPT Kiến An-Hải Phòng năm 2017-2018) Tìm tất cả các nghiệm của phương trình tan x m , m   .
A. x  arctan m k hoặc x    arctan m k , k  .
B. x   arctan m k , k  .
C. x  arctan m k 2 , k  .
D. x  arctan m k , k  . Lời giải Chọn D
Ta có: tan x m x  arctan m k , k  .
Câu 5: (THPT Chuyên Lương Văn Tụy-Ninh Bình lần 1 năm 2017-2018) Tập xác định của hàm số
y   tan x là:  
A. D   \   k , k   .
B. D   \ k , k    .  2   
C. D   \ k2 , k    .
D. D   \   k 2 , k   .  2  Lời giải Chọn A
Hàm số y   tan x xác định khi: x
k , k   . 2  
Vậy tập xác định của hàm số là: D   \   k , k   .  2 
Câu 6: (THPT Hà Huy Tập-Hà Tĩnh-lần 1 năm 2017-2018) Phương án nào sau đây là sai?  A. cosx  1
  x    k 2 .
B. cosx  0  x   k 2 . 2 
C. cosx  0  x   k .
D. cosx  1  x k 2 . 2 Lời giải Chọn B
Ta có cosx  0  x
k , k   . Do đó đáp án B sai. 2
Câu 7: (THPT Triệu Thị Trinh-lần 1 năm 2017-2018) Nghiệm của phương trình cos x  1  là:  A. x
k , k   .
B. x k 2 , k   . 2
C. x    k 2 , k   .
D. x k , k   . Lời giải Chọn C
Phương trình cos x  1
  x    k 2 , k   .
Câu 8: (THPT Thạch Thành 2-Thanh Hóa-lần 1 năm 2017-2018) Khẳng định nào dưới đây là sai?
A. Hàm số y  sin x là hàm số lẻ.
B. Hàm số y  cos x là hàm số lẻ.
C. Hàm số y  tan x là hàm số lẻ.
D. Hàm số y  cot x là hàm số lẻ. Lời giải Chọn B
B sai vì hàm số y  cos x là hàm số chẵn.
Câu 9: (THPT Yên Lạc-Vĩnh Phúc-lần 3 năm 2017-2018) Nghiệm của phương trình sin x  1 là     A.
k , k   . B.
k , k   . C.
k 2 , k   . D.
k 2 , k   . 2 2 2 2 Lời giải Chọn D
Ta có sin x  1  x
k 2 , k   . 2
Câu 10: (SGD Bắc Ninh năm 2017-2018) Tập giá trị của hàm số y  sin 2x là: A.  2  ; 2. B. 0;2. C.  1  ;  1 . D. 0;  1 . Lời giải Chọn C
Ta có 1  sin 2x  1, x .
Vậy tập giá trị của hàm số đã cho là  1  ;  1 .
Câu 11: (SGD Ninh Bình năm 2017-2018) Mệnh đề nào dưới đây sai?
A. Hàm số y  tan x tuần hoàn với chu kì  .
B. Hàm số y  cos x tuần hoàn với chu kì  .
C. Hàm số y  cot x tuần hoàn với chu kì  .
D. Hàm số y  sin 2x tuần hoàn với chu kì  . Lời giải Chọn B
Hàm số y  tan x ; y  cot x tuần hoàn với chu kì 
Hàm số y  sin x ; y  cos x tuần hoàn với chu kì 2
Hàm số y  sin 2x  sin 2x  2   sin 2 x    
 . Vậy hàm số tuần hoàn với chu kì  . Vậy đáp án B sai.
Câu 12: (THPT Chuyên Thái Bình-lần 3 năm 2017-2018) Số nghiệm thực của phương trình  3 
2 sin x 1  0 trên đoạn  ;10  là: 2    A. 12 . B. 11. C. 20 . D. 21. Hướng dẫn giải Chọn A    x   k 2 1  6
Phương trình tương đương: sin x     , ( k   ) 2 7 x   k 2  6  3   + Với x  
k 2 , k   ta có   
k 2  10 , k   2 61   k  , k   6 2 6 3 12
 0  k  5 , k   . Do đó phương trình có 6 nghiệm. 7 3 7  + Với x
k 2 , k   ta có  
k 2  10 , k   4 53   k  , k   6 2 6 3 12
 1  k  4 , k   . Do đó, phương trình có 6 nghiệm.
+ Rõ ràng các nghiệm này khác nhau từng đôi một, vì nếu  7 2   k 2   k 2
   k k 
(vô lí, do k , k   ). 6 6 3  3 
Vậy phương trình có 12 nghiệm trên đoạn  ;10  . 2    3
Câu 13: (THPT Chuyên Vĩnh Phúc - lần 3 năm 2017-2018) Phương trình cos x   có tập nghiệm 2 là     5  A.x    k ; k   . B.x    k 2 ; k   .  6   6        C.x    k ; k    . D.x    k 2 ; k   .  3   3  Lời giải
Chọn B 3 5π 5π Ta có cos x    cos x  cos  x  
k 2π, k   . 2 6 6 2
Câu 14: (THPT Chuyên Vĩnh Phúc-lần 3 MĐ 234 năm học 2017-2018) Phương trình cos x   có 2 tập nghiệm là       A.x  
k 2 ; k   . B.x  
k ; k   .  3   4   3     C.x  
k 2 ; k   . D.x  
k ; k   .  4   3 
Hướng dẫn giải Chọn C 2  3  3 cos x    cos x  cos    x  
k 2 , k   . 2  4  4  3 
Vậy tập nghiệm của phương trình là S  x  
k 2 ; k   .  4 
Câu 15: (THPT Chuyên Vĩnh Phúc-lần 3 MĐ 234 năm học 2017-2018) Giá trị lớn nhất và giá trị nhỏ
nhất của hàm số y  3sin 2x  5 lần lượt là: A. 3 ; 5 . B. 2  ; 8  . C. 2 ; 5  . D. 8 ; 2 .
Hướng dẫn giải Chọn B
Ta có 1  sin 2x  1  8
  3sin 2x  5  2  8   y  2  .
Vậy giá trị lớn nhất và giá trị nhỏ nhất của hàm số lần lượt là 2;  8 .
Câu 16: (THPT Hồng Quang-Hải Dương năm 2017-2018) Tìm nghiệm của phương trình 2 sin x  3  0 .   3  x  arcsin  k 2     2  A. x   . B.  k  .   3  x    arcsin  k 2      2    3  x  arcsin  k 2     2  C.  k  . D. x   .   3  x   arcsin  k 2      2  Lời giải Chọn A 3
Ta có: 2 sin x  3  0  sin x
 1 nên phương trình vô nghiệm. 2
Câu 17: (THPT Hồng Quang-Hải Dương năm 2017-2018) Khẳng định nào sau đây sai ?      
A. y  tan x nghịch biến trong 0;   .
B. y  cos x đồng biến trong  ; 0   .  2   2       
C. y  sin x đồng biến trong  ; 0   .
D. y  cot x nghịch biến trong 0;   .  2   2  Lời giải Chọn A    Trên khoảng 0; 
 thì hàm số y  tan x đồng biến.  2    
Câu 18: (THPT Kinh Môn 2-Hải Dương năm 2017-2018) Tập xác định của hàm số y  tan 2x     3  là: 5   5  A.  \   k
 , k . B.  \ 
k  , k .  12 2   12  5   5  C.  \   k
 , k . D.  \ 
k  , k .  6 2   6  Lời giải Chọn A      5 
Hàm số đã cho xác định khi cos 2x   0    2x  
k  x   k , k .  3  3 2 12 2 5  
Vậy TXĐ: D   \   k
 , k .  12 2 
Câu 19: (THPT Kinh Môn 2-Hải Dương năm 2017-2018) Phương trình  x   2 3 tan 1 sin x   1  0 có nghiệm là:     A. x   k 2 . B. x    k . C. x   k . D. x    k 2 . 3 6 6 6 Lời giải Chọn B
Điều kiện cos x  0  x
k , k . 2 Do 2
sin x 1  0, x
  nên phương trình đã cho tương đương với 1    
3 tan x 1  0  tan x    tan x  tan     x  
k , k (nhận). 3  6  6
Câu 20: (THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018) Phương trình cos x  1 có nghiệm là  
A. x k 2 . B. x   k .
C. x k . D. x   k 2 . 2 2 Lời giải Chọn A
Phương trình cos x  1  x k 2 , k   .
Câu 21: (THPT Phan Đăng Lưu-Huế-lần 1 năm 2017-2018) Phương trình 2 cos x  2  0 có tất cả các nghiệm là  3   x   k 2  x   k 2 4  4 A.  , k   . B.  , k   . 3   x    k 2
x    k2  4  4    7 x   k 2  x   k 2 4  4 C.  , k   . D.  , k   . 3  7 x   k 2 x    k 2  4  4 Lời giải Chọn B   x   k 2 2  4
2 cos x  2  0  cos x    , k   . 2 
x    k2  4
Câu 22: (THPT Quãng Xương 1-Thanh Hóa năm 2017-2018) Tìm điều kiện xác định của hàm số
y  tan x  cot . x k  A. x  , k . B. x
k , k . C. x .
D. x k , k . 2 2 Lời giải Chọn A k Điều kiện: sin .
x cos x  0  sin 2x  0  2x k  x
k  . 2
Câu 23: (THPT Trần Hưng Đạo-TP HCM năm 2017-2018) Đường cong trong hình dưới đây là đồ thị
của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A , B , C , D . Hỏi hàm số đó là hàm số nào?
A. y  1 sin x .
B. y  1 sin x .
C. y  sin x .
D. y  cos x . Lời giải Chọn D
Dựa vào lý thuyết đây là đồ thị của hàm y  cos x .
Câu 24: (THPT Trần Hưng Đạo-TP HCM năm 2017-2018) Mệnh đề nào dưới đây đúng?
A. Hàm số y  sin x là hàm số chẵn.
B. Hàm số y  cos x là hàm số chẵn.
C. Hàm số y  tan x là hàm số chẵn.
D. Hàm số y  cot x là hàm số chẵn. Lời giải Chọn B
Các hàm số y  sin x , y  tan x , y  cot x là hàm số lẻ, hàm số y  cos x là hàm số chẵn.
Câu 25: (THPT Trần Hưng Đạo-TP HCM năm 2017-2018) Giải phương trình 3 tan 2x  3  0 .    A. x   kk  . B. x
k k   . 3 2 3    C. x   kk  . D. x
k k   . 6 2 6 Lời giải
Chọn C   
3 tan 2x  3  0  tan 2x  3  2x
k  x   kk  . 3 6 2
Câu 26: (THPT Chuyên Hoàng Văn Thụ-Hòa Bình năm 2017-2018) Tập giá trị của hàm số y  cos x là ? A.  . B.  ;  0 . C. 0;  . D.  1   ;1 . Lời giải Chọn D Với x
   , ta có cos x  1  ;  1 .
Tập giá trị của hàm số y  cos x là 1  ;1 .
Câu 27: (THPT Hậu Lộc 2-Thanh Hóa năm 2017-2018) Chọn khẳng định đúng trong các khẳng định sau:
A. Hàm số y  tan x tuần hoàn với chu kì 2 .
B. Hàm số y  cos x tuần hoàn với chu kì  .   
C. Hàm số y  sin x đồng biến trên khoảng 0;   .  2 
D. Hàm số y  cot x nghịch biến trên  . Lời giải Chọn C
Hàm số y  tan x tuần hoàn với chu kì   đáp án A sai.
Hàm số y  cos x tuần hoàn với chu kì 2  đáp án B sai.
Hàm số y  cot x nghịch biến trên mỗi khoảng k ;  k  , k    đáp án D sai.
Câu 1: (SGD Bà Rịa Vũng Tàu-đề 2 năm 2017-2018) Tập nghiệm của phương trình 2 sin 2x 1  0 là   7    7  A. S    k ,
k , k   . B. S    k 2 ,
k 2 , k   .  12 12   6 12    7    7  C. S    k 2 ,
k 2 , k   . D. S    k ,
k , k   .  12 12   6 12  Lời giải Chọn A   2x    k 2 1     6
Ta có: 2 sin 2x 1  0  sin 2x    sin 2x  sin      , k 2  6  7 2x   k 2  6   x    k  12   , k . 7 x   k  12   7 
Vậy tập nghiệm của phương trình là S    k ,
k , k   .  12 12 
Câu 2: (THPT Hà Huy Tập-Hà Tĩnh-lần 2 năm 2017-2018) Điều kiện xác định của hàm số 1 sin x y  là cos x 5 5  A. x
k , k . B. x   k , k . 12 12 2    C. x   k , k . D. x
k , k . 6 2 2 Lời giải Chọn D
Hàm số xác định khi cos x  0  x
k , k . 2 2x  3
Câu 3: (THPT Hà Huy Tập-Hà Tĩnh-lần 2 năm 2017-2018) Đồ thị hàm số y  có các đường x 1
tiệm cận đứng và tiệm cận ngang lần lượt là A. x  1  và y  3 . B. x  1  và y  3 .
C. x  1 và y  2 .
D. x  2 và y  1. Lời giải Chọn C 3 2  2x  3 Ta có lim y  lim  lim
x  2 nên đường thẳng y  2 x x x 1 là tiệm cận ngang. x 1 1 x 2x  3 lim y  lim
  suy ra đường thẳng x  1 là tiệm cận đứng. x 1 x 1   x 1
Câu 4: (THPT Lý Thái Tổ-Bắc Ninh-lần 1 năm 2017-2018) Tập xác định của hàm số y  tan 2x là     
A. D   \   k , k  .
B. D   \   k , k   .  4 2   2      
C. D   \ k , k   .
D. D   \   k , k   .  2   4  Lời giải Chọn A   
Hàm số y  tan 2x xác định khi cos 2x  0  2x
k  x   k , k   . 2 4 2   
Vậy tập xác định của hàm số là D   \   k , k    4 2 
Câu 5: (THPT Lý Thái Tổ-Bắc Ninh-lần 1 năm 2017-2018) Cho phương trình:
3cosx  cos2x  cos3x 1  2sin .
x sin 2x . Gọi  là nghiệm lớn nhất thuộc khoảng 0; 2  của   
phương trình. Tính sin     .  4  2 2 A.  . B. . C. 0 . D. 1. 2 2 Lời giải Chọn A
Phương trình tương đương: 3cosx  cos2x  cos3x 1  cosx  cos3x  2cosx  cos2x 1  0   cosx  0 x   k 2
 cos x  cosx  0     2 . cosx  1 
x   k2   3  3
Vì x 0;2  nên x   ; ,
 . Nghiệm lớn nhất của phương là   .  2 2  2     3   5 2 Vậy sin      sin     sin   .  4   2 4  4 2
Câu 6: (THPT Phan Đình Phùng-Hà Tĩnh-lần 1 năm 2017-2018) Xét bốn mệnh đề sau:
(1) Hàm số y  sin x có tập xác định là  .
(2) Hàm số y  cos x có tập xác định là  .  
(3) Hàm số y  tan x có tập xác định là D   \   kk   .  2    
(4) Hàm số y  cot x có tập xác định là D   \ k k   .  2  Số mệnh đề đúng là A. 3 . B. 2 . C. 1. D. 4 . Lời giải Chọn A Các mệnh đề đúng là
(1) Hàm số y  sin x có tập xác định là  .
(2) Hàm số y  cos x có tập xác định là  .  
(3) Hàm số y  tan x có tập xác định là D   \   kk   .  2    
Câu 7: (SGD Hà Nội-lần 11 năm 2017-2018) Phương trình sin x   1   có nghiệm là  3   5 5  A. x   k 2 . B. x   k . C. x   k 2 . D. x   2 . 3 6 6 3 Lời giải Chọn C      5 sin x   1    x  
k 2  x
k 2 k   .  3  3 2 6
Câu 8: (THPT Yên Lạc – Vĩnh Phúc – lần 4 - năm 2017 – 2018) Phương trình sin x  1 có một nghiệm là    A. x   . B. x   . C. x  . D. x  . 2 2 3 Lời giải Chọn C
Ta có sin x  1  x
k 2 k   . 2  Do đó x
là một nghiệm của phương trình sin x  1. 2
Câu 9: Cho hàm số f x liên tục trên  và có đồ thị như hình vẽ dưới đây, hàm số f x đồng biến trên khoảng nào? y A.  ;  0 . B.  ;    1 . C. 1; . D. 1  ;1 . 1
Câu 10: (THPT Chuyên Ngữ – Hà Nội - Lần 1 năm 2017 – 2018) Cho hàm số f x liên tục trên  và có đồ 1  O x 1
thị như hình vẽ dưới đây, hàm số f x đồng biến trên khoảng nào? y 1 1 O x 1 A.  ;  0 . B.  ;    1 . C. 1;  . D.  1   ;1 . Lời giải Chọn B
Dựa vào đồ thị ta thấy hàm số nghịch biến trên các khoảng  ;    1 và 0;  1 .
Vậy chỉ có phương án B thỏa mãn.
Câu 11: (THPT Chuyên Vĩnh Phúc – Vĩnh Phúc - Lần 4 năm 2017 – 2018)Tìm nghiệm của
phương trình sin 2x  1 .    kA. x   k 2 . B. x   k . C. x   k 2 . D. x  . 2 4 4 2 Lời giải Chọn B  
Ta có: sin 2x  1  2x
k 2  x   k . 2 4
Câu 12: (THPT Trần Phú – Hà Tĩnh - Lần 2 năm 2017 – 2018)Trong mặt phẳng Oxy , cho điểm 
A3;0 và vectơ v  1; 2 . Phép tịnh tiến T biến A thành A . Tọa độ điểm A là v
A. A 4; 2 .
B. A 2; 2 .
C. A 2; 2 .
D. A 2;   1 . Lời giải Chọn A
x  x  1
Biểu thức tọa độ của phép tịnh tiến T là
nên ảnh của điểm A3;0 là điểm v
y  y  2  A 4; 2 .
Câu 13: (SGD Quảng Nam – năm 2017 – 2018) Tìm tất cả các nghiệm của phương trình    sin x   1   .  6    A. x
k k   . B. x  
k 2 k   . 3 6  5 C. x
k 2 k   . D. x
k 2 k   . 3 6 Lời giải Chọn C       Ta có sin x   1    x  
k 2  x
k 2 k   .  6  6 2 3
Câu 14: (THPT Trần Phú – Đà Nẵng - Lần 2 – năm 2017 – 2018) Giải phương trình 2 cos x 1  0   x   k 2   3 A. x    k ,  k   . B.  , k   . 3 2   x   k 2  3   x   k   3 C. x    k 2 ,  k   . D.  , k   . 3 2   x   k  3 Lời giải Chọn C 1 
TXĐ: D   . Ta có 2 cos x 1  0  cos x   x  
k 2 , k   . 2 3
Câu 1: (SGD Thanh Hóa – năm 2017 – 2018) Cho các mệnh đề sau sin x
I  Hàm số f x  là hàm số chẵn. 2 x 1
II  Hàm số f x  3sin x  4cos x có giá trị lớn nhất là 5 .
III  Hàm số f x  tan x tuần hoàn với chu kì 2 .
IV  Hàm số f x  cos x đồng biến trên khoảng 0;   .
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng? A. 1. B. 2 . C. 3 . D. 4 . Lời giải
Chọn A sin x
* Xét hàm số f x  . 2 x 1
Tập xác định: D   . sin x  sin x x
  D , ta có: x D và f x  
  f x .  2 x2 1 x 1 sin x
Vậy hàm số f x  là hàm số lẻ. 2 x 1 Do đó  I  sai.
* Xét hàm số f x  3sin x  4cos x .
Tập xác định: D   .  3 4 
Ta có: f x  3sin x  4cos x  5 sin x  cos x    5 5  3 4 Đặt sin   , cos 
. Ta có f x  5sin  x     5 5 5 
 max f x  5 khi sin  x     1  x
  k 2 , k   . 2
Vậy hàm số f x  3sin x  4cos x có giá trị lớn nhất là 5 .
Do đó  II  đúng.
* Xét hàm số f x  tan x . Ta có hàm số f x tuần hoàn với chu kì  .
Do đó  III  sai.
* Xét hàm số f x  cos x . Ta có f x nghịch biến trên mỗi khoảng k 2 ;   k 2  với k   .
Do đó  IV  sai.
Vậy trong bốn mệnh đề đã cho có một mệnh đề đúng.
Câu 2: (THPT Chuyên Hùng Vương – Gia Lai – Lần 2 năm 2017 – 2018) Hàm số y  sin x đồng biến
trên mỗi khoảng nào dưới đây.       3  A.   k 2 ;  k 2   , k   . B.k 2 ;  k 2   , k   .  2 2   2 2  C.  
  k 2 ; k 2  , k   .
D.k2 ;  k2  , k   . Lời giải Chọn A
Câu 3: (THPT Nghèn – Hà Tĩnh – Lần 2 năm 2017 – 2018) Phương trình sin x m vô nghiệm khi và chỉ khi: m  1 A.  .
B. 1  m  1 . C. m  1  . D. m  1. m  1  Lời giải Chọn A m  1
Do 1  sin x  1, x
   nên phương trình sin x m vô nghiệm khi và chỉ khi  . m  1 
Câu 4: (THPT Chuyên Võ Nguyên Giáp – Quảng Bình - năm 2017-2018) Nghiệm của phương trình sin 2x  1 là.    kA. x   k 2 . B. x   k . C. x   k 2 . D. x  . 2 4 4 2
Hướng dẫn giải Chọn B  
Ta có: sin 2x  1  2x
k 2  x   k . 2 4
Câu 5: (SGD Bắc Ninh – Lần 2 - năm 2017-2018) Trong các phương trình sau phương trình nào vô nghiệm? 2017
A. tan x  2018 .
B. sin x   . C. cos x  .
D. sin x  cos x  2 . 2018 Lời giải Chọn B
* tan x  2018  x  arctan 2018  k , k   .
* sin x   (vô nghiệm do   1). 2017 2017 * cos x   x   arccos
k 2 , k   . 2018 2018    
* sin x  cos x  2  sin x   1    x
k 2 , k   .  4  4
Câu 6: (Chuyên Lê Hồng Phong – Nam Đinh - năm 2017-2018) Tập xác định của hàm số y  tan 2x là?     
A. D   \   k , k   .
B. D   \   k , k   .  4   4 2      
C. D   \ k , k   .
D. D   \   k , k   .  2   2 
Hướng dẫn giải Chọn B   
Điều kiện: cos 2x  0  2x
k  x   k , k   . 2 4 2   
Vậy tập xác định là D   \   k , k  .  4 2 
Câu 7: Phương trình sin x  sin  (hằng số    ) có nghiệm là
A. x    k , x     k k  .
B. x    k2 , x  
  k2 k  .
C. x    k 2 , x     k2 k   .
D. x    k , x  
  k k  .
Câu 8: Phương trình sin x  sin  (hằng số    ) có nghiệm là
A. x    k , x     k k  .
B. x    k2 , x  
  k2 k  .
C. x    k 2 , x     k2 k   .
D. x    k , x  
  k k  . Lời giải Chọn C
Câu 9: Nghiệm của phương trình 2
sin x  4 sin x  3  0 là A. x  
k 2 , k   .
B. x    k 2 , k   . 2  C. x
k 2 , k   .
D. x k 2 , k   2
Câu 10: Nghiệm của phương trình 2
sin x  4 sin x  3  0 là A. x  
k 2 , k   .
B. x    k 2 , k   . 2  C. x
k 2 , k   .
D. x k 2 , k   2 Lời giải Chọn C sin x  1 2
sin x  4 sin x  3  0   . sin x  3  
Với sin x  1  x
k 2 , k   . 2
Với sin x  3 phương trình vô nghiệm.
Câu 11: Tập nghiệm của phương trình sin 2x  sin x là  π   π k 2π 
A. S  k2π;  k 2π k   .
B. S  k 2π;  k   .  3   3 3   π 
C. S  k2π;   k 2π k   .
D. S  k2π; π  k2π k    .  3 
Câu 12: Tập nghiệm của phương trình sin 2x  sin x là  π   π k 2π 
A. S  k2π;  k 2π k   .
B. S  k 2π;  k   .  3   3 3   π 
C. S  k2π;   k2π k   .
D. S  k2π; π  k2π k    .  3  Lời giải Chọn B x k 2π
2x x k 2π
Ta có sin 2x  sin x     π
k 2π k   .
2x  π  x k 2π  x    3 3 tan x  5
Câu 13: Tìm tập xác định D của hàm số y  . 2 1 sin x  π 
A. D   \   π
k , k   . B. D   .  2   π 
C. D   \   k 2π, k   .
D. D   \ π  π k , k    .  2  tan x  5
Câu 14: Tìm tập xác định D của hàm số y  . 2 1 sin x  π 
A. D   \   π
k , k   . B. D   .  2   π 
C. D   \   k 2π, k   .
D. D   \ π  π k , k    .  2  Lời giải Chọn A cos x  0 π Điều kiện: 
 cos x  0  x   π k , k   . 2 sin x  1  2  π 
Vậy: D   \   π
k , k   .  2 
Câu 15: Phương trình nào sau đây vô nghiệm?
A. 2 cos x  3 .
B. 2 sin x  3 .
C. 3 tan x  2 .
D. 2 cot x  3 .
Câu 16: Phương trình nào sau đây vô nghiệm?
A. 2 cos x  3 .
B. 2 sin x  3 .
C. 3 tan x  2 .
D. 2 cot x  3 . Lời giải Chọn A 3
2 cos x  3  cos x
, phương trình vô nghiệm. 2
Câu 17: Tìm tất cả các giá trị thực của tham số m để phương trình sin x m có nghiệm thực. A. m  0 .
B. 1  m  1 .
C. 1  m  1 . D. m  0 .
Câu 18: Tìm tất cả các giá trị thực của tham số m để phương trình sin x m có nghiệm thực. A. m  0 .
B. 1  m  1 .
C. 1  m  1 . D. m  0 . Lời giải Chọn B
Do 1  sin x  1, x
   nên phương trình sin x m có nghiệm khi và chỉ khi 1  m  1 .
Câu 19: Với giá trị nào của m thì phương trình sin x m có nghiệm? A. m  1. B. m  1  . C. m  1  .
D. 1  m  1 .
Câu 20: Với giá trị nào của m thì phương trình sin x m có nghiệm? A. m  1. B. m  1  . C. m  1  .
D. 1  m  1 .
Hướng dẫn giải Chọn D
Vì 1  sin x  1 nên phương trình sin x m có nghiệm khi và chỉ khi 1  m  1 .
Câu 21: Chu kì tuần hoàn của hàm số y  cot x là π A. . B. 2π . C. π . D. π
k k   . 2
Câu 22: Phương trình 2 cot x  3  0 có nghiệm là 3  A. x  arccot
k k   . B. x
k k   . 2 6   x   k 2  6  C.  k . D. x
k 2 k     3 x    k 2  6
Câu 23: Chu kì tuần hoàn của hàm số y  cot x là π A. . B. 2π . C. π . D. π
k k   . 2 Lời giải Chọn C
Chu kì tuần hoàn của hàm số y  cot x là π .
Câu 24: Phương trình 2 cot x  3  0 cónghiệmlà 3  A. x  arccot
k k   . B. x
k k   . 2 6   x   k 2  6  C.  k . D. x
k 2 k     3 x    k 2  6 Lời giải Chọn A 3 3
Ta có 2 cot x  3  0  cot x   x  arccot
k k   2 2
Câu 25: Tập xác định của hàm số y  tan x là:   A.  \   0 .
B.  \   k ,k   .C.  .
D.  \ k ,k    .  2 
Câu 26: Tập xác định của hàm số y  tan x là:   A.  \   0 .
B.  \   k ,k   .C.  .
D.  \ k ,k    .  2  Lời giải Chọn B
Điều kiện xác định: cos x  0  x
k , k   . 2  
Vậy tập xác định là  \   k ,k   .  2 
Câu 27: Cho hàm số y f x xác định trên  và có bảng biến thiên sau: x  1 0 1  f  x  0    0   f x 3 1 
Hỏi mệnh đề nào sau đây là mệnh đề sai?
A. Hàm số nghịch biến trên khoảng  ;  0 .
B. Hàm số có ba điểm cực trị.
C. Đồ thị hàm số y f x không có tiệm cận ngang.
D. Điểm cực tiểu của đồ thị hàm số là x  0 .
Câu 28: Cho hàm số y f x xác định trên  và có bảng biến thiên sau: x  1 0 1  f  x  0    0   f x 3 1 
Hỏi mệnh đề nào sau đây là mệnh đề sai?
A. Hàm số nghịch biến trên khoảng  ;  0 .
B. Hàm số có ba điểm cực trị.
C. Đồ thị hàm số y f x không có tiệm cận ngang.
D. Điểm cực tiểu của đồ thị hàm số là x  0 . Lời giải Chọn B
Dựa vào bảng biến thiên hàm số có ba điểm cực trị là sai.
Câu 29: Hàm số y  sin x tuần hoàn với chu kỳ bằng A.  . B. 2 . C.   . D. 2 .
Câu 30: Hàm số y  sin x tuần hoàn với chu kỳ bằng A.  . B. 2 . C.   . D. 2 . Lời giải Chọn B
Hàm số y  sin x tuần hoàn với chu kỳ bằng 2 .
Câu 31: Phương trình nào trong số các phương trình sau có nghiệm?
A. sin x  3cos x  6 .
B. 2sin x  3cos x  1. C. sin x  2 .
D. cos x  3  0 .
Câu 32: Phương trình nào trong số các phương trình sau có nghiệm?
A. sin x  3cos x  6 .
B. 2sin x  3cos x  1. C. sin x  2 .
D. cos x  3  0 .
Hướng dẫn giải Chọn B  1   sin x  1 Ta có 
nên hai phương trình ở C và D vô nghiệm. 1   cos x  1 
Phương trình lượng giác dạng a sin x b cos x c có nghiệm khi 2 2 2
a b c .
Đáp án A: 2 2 2
1  3  6 nên phương trình vô nghiệm.
Đáp án B:   2 2 2 3
 1 nên phương trình có nghiệm.
Câu 1: (THPT Chuyên Hùng Vương-Phú Thọ-lần 1-NH2017-2018) Phương trình sin 2x  3cos x  0
có bao nhiêu nghiệm trong khoảng 0;  A. 0 . B. 1. C. 2 . D. 3 . Lời giải.
Chọn B
sin 2x  3cos x  0  2 sin .
x cos x  3cos x  0  cos .
x 2sin x  3  0  
cos x  0  x   k k   2   3 sin x  
loai vì sin x 1;  1   2 
Theo đề: x  0;   k  0  x  . 2       5
Câu 2: (THTT Số 1-484 tháng 10 năm 2017-2018) Cho phương trình cos 2 x   4 cos  x      .  3   6  2    Khi đặt t  cos  x
 , phương trình đã cho trở thành phương trình nào dưới đây?  6  A. 2
4t  8t  3  0 . B. 2
4t  8t  3  0 . C. 2
4t  8t  5  0 . D. 2
4t  8t  5  0 . Lời giải Chọn A       5
Phương trình tương đương với:  cos 2  x  4 cos  x   0      6   6  2        2    4 cos  x  8 cos  x  3  0    
, nên nếu đặt t  cos  x
 phương trình trở thành  6   6   6  2 2
4t  8t  3  0  4t  8t  3  0 .
Câu 3: (THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018) Nghiệm của phương trình    2 cos x     là  4  2 x k 2 x kA.   k  . B.   k  . x    k x    k  2  2 x k x k 2 C.   k  . D.   k  . x    k 2 x    k 2  2  2 Lời giải
Chọn D x k 2    2       Phương trình cos x cos x cos         k         .  4  2  4   4   x    k 2  2
Câu 4: (THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018) Tìm tập xác định D của
hàm số y  tan 2x :    
A. D   \   k2 | k  .
B. D   \   k | k   .  4   2      
C. D   \   k | k   .
D. D   \   k | k   .  4   4 2  Giải:
Chọn D   
Hàm số xác định khi cos 2x  0  2x
k  x   kk  . 2 4 2   
Tập xác định của hàm số là: D   \   k | k  .  4 2 
Câu 5: (THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018) Chọn phát biểu đúng:
A. Các hàm số y  sin x , y  cos x , y  cot x đều là hàm số chẵn.
B. Các hàm số y  sin x , y  cos x , y  cot x đều là hàm số lẻ.
C. Các hàm số y  sin x , y  cot x , y  tan x đều là hàm số chẵn
D. Các hàm số y  sin x , y  cot x , y  tan x đều là hàm số lẻ. Giải: Chọn D
Hàm số y  cos x là hàm số chẵn, hàm số y  sin x , y  cot x , y  tan x là các hàm số lẻ.
Câu 6: (THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018) Phương trình
cos 2x  4 sin x  5  0 có bao nhiêu nghiệm trên khoảng 0;10  ? A. 5 . B. 4 . C. 2 . D. 3 . Lời giải
Chọn A sin x  1   PT đã cho 2  2
 sin x  4sin x  6  0    x  
k 2 , k   .
sin x  3 VN   2  1 21
Theo đề: x  0;10   0  
k 2  10   k  . 2 4 4
Vì k   nên k 1; 2;3;4; 
5 . Vậy PT đã cho có 5 nghiệm trên khoảng 0;10  .     
Câu 7: (THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018) Tìm góc    ; ; ;   6 4 3 2  để phương trình
cos 2x  3 sin 2x  2 cos x  0 tương đương với phương trình
cos 2x    cos x .     A.   . B.   . C.   . D.   . 6 4 2 3 Lời giải
Chọn D   k 2
2x   x k 2 x  
cos 2x   cos x      3 3 
2x   x k 2  
x    k 2  1 3
cos 2x  3 sin 2x  2 cos x  0  cos 2x
sin 2x  cos x 2 2   x   k 2     3  cos 2x   cos x      3   k 2 x    9 3      3 9 
Để hai phương trình tương đương cần có     .  3      3
Câu 8: (THPT Hoa Lư A-Ninh Bình-lần 1-năm 2017-2018) Tìm tập xác định D của hàm số 1 y  . sin x  cos x  
A. D   \ k | k  
. B. D   \   k | k  .  2   
C. D   \   k | k  .
D. D   \ k2 | k    4  . Lời giải Chọn C
Hàm số đã cho xác định khi và chỉ khi    
sin x  cos x  0  sin x   0  x
k , k     .  4  4
Câu 9: (THPT Hoa Lư A-Ninh Bình-lần 1-năm 2017-2018) Tìm tập giá trị của hàm số
y  3 sin x  cos x  2 . A. 2; 3 .
B.  3  3; 3 1 . C.  4  ;0 . D.  2  ;0     Lời giải Chọn C       
Xét y  3 sin x  cos x  2  2 sin . x cos  cos . x sin  2    2 sin x   2    6 6   6       
Ta có 1  sin x   1    4   2 sin x   2  0  
 4  y  0 với mọi x    6   6 
Vậy tập giá trị của hàm số là  4  ;0 .
Câu 10: (THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018) Trong bốn hàm số: (1) y  cos 2x ,
(2) y  sin x ; (3) y  tan 2x ; (4) y  cot 4x có mấy hàm số tuần hoàn với chu kỳ  ? A. 1. B. 0 . C. 2 . D. 3 . Lời giải Chọn A
Do hàm số y  cos x tuần hoàn với chu kỳ 2 nên hàm số (1) y  cos 2x tuần hoàn chu kỳ  .
Hàm số (2) y  sin x tuần hoàn với chu kỳ 2 . 
Do hàm số y  tan x tuần hoàn với chu kỳ nên hàm số (3) y  tan 2x tuần hoàn chu kỳ . 2 
Do hàm số y  cot x tuần hoàn với chu kỳ  nên hàm số (4) y  cot 4x tuần hoàn chu kỳ . 4
Câu 11: (THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018) Giải phương trình 2
2 sin x  3 sin 2x  3 . 2  4 5 A. x   k . B. x   k . C. x   k . D. x   k . 3 3 3 3 Lời giải
Chọn B
Cách 1: Xét cos x  0 : Phương trình tương đương 2  3ktm
Xét cos x  0 , chia cả hai vế cho 2 cos x ta có: 2 x x   2 x   2 2 tan 2 3 tan 3 tan
1  tan x  2 3 tan x  3  0 
 tan x  3  x
k , k 3    
Cách 2: pt    2
1  2 sin x   3 sin 2x  2  2sin 2x   2    x   k .  6  3
Câu 12: (THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018) Tính tổng S của các nghiệm của phương 1     trình sin x  trên đoạn  ; . 2  2 2    5    A. S  . B. S  . C. S  . D. S  . 6 3 2 6 Lời giải Chọn D   x   2k 1  6 Ta có: sin x    k   . 2 5 x   2k  6       Vì x   ;  nên x   S  . 2 2    6 6
Câu 13: (THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018) Giải phương trình sin 3x  4sin x cos 2x  0.  k 2  kx   x   x k 2  x k 3  2 A.B.C.   D.   2    x    k  x    kx    k
x    k   3  6  3  4 Lời giải
Chọn D
Cách 1: ĐK: x   (*) Phương trình  x  2 sin
3  4 sin x   4 sin x cos 2x  0  1 cos 2x   sin x 3  4.
 4 cos 2x  0  sin x  
1 2cos 2x  0  2  sin x  0 x k x k     1     
k   thỏa mãn (*). cos 2x   cos 2x    k 2 x    k  2 3  3  6
Cách 2: Phương trình  sin 3x  2 sin 3x  sin x  0
  sin 3x  2 sin x  0  x  2 sin 4 sin x   1  0 x k
 sin x 1 2 cos 2x  0    x    k  6     3 
Câu 14: (THPT Xuân Hòa-Vĩnh Phúc-năm 2017-2018) Phương trình sin 2x   sin x      có  4   4 
tổng các nghiệm thuộc khoảng 0;  bằng 7 3  A. . B.  . C. . D. . 2 2 4 Lời giải Chọn B   3 2x   x   k 2
x    k 2     3   4 4 Ta có sin 2x   sin x          
2 k, l   .  4   4     x   l 2x    x l2   6 3  4 4
Họ nghiệm x    k 2 không có nghiệm nào thuộc khoảng 0;   .  2  2 x   l  0;   0   l
   l 0;  1 . 6 3 6 3  5
Vậy phương trình có hai nghiệm thuộc khoảng 0;   là x  và x  . Từ đó suy ra tổng 6 6
các nghiệm thuộc khoảng 0;   của phương trình này bằng  . x
Câu 15: (THPT Xuân Hòa-Vĩnh Phúc-năm 2017-2018) Chu kỳ của hàm số y  3sin là số nào sau 2 đây? A. 0 . B. 2 . C. 4 . D.  . Lời giải Chọn C 2
Chu kì của hàm số T   4 . 1 2  k 
Câu 16: (THPT Xuân Hòa-Vĩnh Phúc-năm 2017-2018) Tập D   \ 
k   là tập xác định của  2  hàm số nào sau đây?
A. y  cot x .
B. y  cot 2x .
C. y  tan x .
D. y  tan 2x Lời giải Chọn B k
Hàm số y  cot 2x xác định khi 2x k  x  . 2  5 7 
Câu 17: (THPT Xuân Hòa-Vĩnh Phúc-năm 2017-2018) Khi x thay đổi trong khoảng ;   thì  4 4 
y  sin x lấy mọi giá trị thuộc  2   2   2  A. 1  ;    . B.  ; 0   C. 1  ;1 . D. ;1   . 2    2   2   Lời giải Chọn A  5 3   Trong nửa khoảng ;  : 4 2    3 5 2
Hàm số y  sin x giảm nên sin  sin x  sin  1   sin x   . 2 4 2 3 7   Trong nửa khoảng ;   :  2 4  3 7 2
Hàm số y  sin x tăng nên sin  sin x  sin  1   sin x   . 2 4 2  5 7  2   
Vậy khi x thay đổi trong khoảng ; 
 thì y  sin x lấy mọi giá trị thuộc 1  ;    .  4 4  2   
Câu 18: (THPT Sơn Tây-Hà Nội-lần 1-năm 2017-2018) Tìm số điểm phân biệt biểu diễn các nghiệm của phương trình 2
sin 2x  cos 2x 1  0 trên đường tròn lượng giác. A. 1. B. 3 . C. 2 . D. 4 . Lời giải Chọn C cos 2x  1 2 2
sin 2x  cos 2x 1  0  cos 2x  cos 2x  2  0 
x k k    .
cos 2x  2 VN  
Vậy có hai điểm phân biệt biểu diễn nghiệm của phương trình trên đường tròn lượng giác.
cos x  3 sin x
Câu 19: (THPT Sơn Tây-Hà Nội-lần 1-năm 2017-2018) Giải phương trình  0 . 2 sin x 1 5 5 A. x  
k 2 , k  .  B. x  
k , k  .  6 6   C. x
k 2 , k  .  D. x
k , k  .  6 6 Lời giải Chọn A   x   k 2 1   6
Điều kiện sin x    , k  .  2 5 x   k 2   6
Với điều kiện trên ta có 1 3
cos x  3 sin x  0  cos x  sin x  0 2 2        os c x   0  x  
l  x
l ,l  .     3  3 2 6 5
Đối chiếu với điều kiện ta có nghiệm của phương trình là x  
k 2 , k  .  6
Câu 20: (THPT Chuyên ĐH Vinh-GK1-năm 2017-2018) Phương trình 2 cos x  2  0 có tất cả các nghiệm là    7 x   k 2  x   k 2 4  4 A.  , k   . B.  , k   . 3  7 x   k 2 x    k 2  4  4  3   x   k 2  x   k 2 4  4 C.  , k   . D.  , k   . 3   x    k 2
x    k2  4  4 Lời giải Chọn C  3 x   k 2 2 3    4
Ta có 2 cos x  2  0  cos x    cos     , k   . 2  4  3 x    k 2  4
Câu 21: (THPT Chuyên ĐH Vinh-GK1-năm 2017-2018) Nghiệm của phương trình 8.cos 2 . x sin 2 .
x cos 4x  2 là       x   kx   k 8 8  32 8 A.
k  . B.
k  . 3   3  x   kx   k  8 8  32 8       x   kx   k 16 8  32 4 C.
k  . D.
k  . 3   3  x   kx   k  16 8  32 4 Hướng dẫn giải Chọn D 2
Cách 1: 8.cos 2 . x sin 2 .
x cos 4x  2  4sin 4 .
x cos 4x  2  2sin 8x  2  sin 8x  2      8x   k 2  x   k 4  32 4    
k  . 3 3  8  x   k 2 x   k  4  32 4 2 
Cách 2: Hàm số y  8.cos 2 . x sin 2 .
x cos 4x  4 sin 4 .
x cos 4x  2sin 8x có chu kỳ T   nên 8 4 
trong công thức nghiệm có k . Do vậy, chọn D 4
Câu 22: (THPT Chuyên ĐH Vinh-GK1-năm 2017-2018) Phương trình tan x  cot x có tất cả các nghiệm là:     A. x   kk  . B. x   kk . 4 4 4 2   C. x
k 2 k   . D. x
k k   . 4 4 Lời giải Chọn B  ĐK: x k ta có: 2 2
tan x  cot x  tan x 1  0 .   x   k      4 1    x   kk  .   4 2 x    k  4  
Kết hợp điều kiện vậy phương trình có nghiệm: x   kk  4 2
Câu 23: (THPT Yên Lạc-Vĩnh Phúc-lần 1-năm 2017-2018) Hệ số góc của tiếp tuyến của đồ thị hàm số 4 2 x x y  
1 tại điểm có hoành độ x  1  bằng 4 2 0 A. 2 .
B. Đáp số khác. C. 2 . D. 0 . Lời giải
Chọn A 3
y  x x y  1  2  .
Câu 24: (THPT Yên Lạc-Vĩnh Phúc-lần 1-năm 2017-2018) Tìm m để phương trình 2 2 sin x  .
m sin 2x  2m vô nghiệm. 4 4 4 4
A. m  0; m  .
B. m  0; m  . C. 0  m  .
D. m  0 hoặc m  . 3 3 3 3 Lời giải Chọn D
Xét phương trình a sin x b cos x c  0 có nghiệm khi 2 2 2
a b c . Vậy để phương trình vô nghiệm thì 2 2 2
a b c . Ta có: 2 2 sin x  .
m sin 2x  2m  1 cos 2x  .
m sin 2x  2m  .
m sin 2x  cos 2x  2m 1  0  . m  0 2 2
Để phương trình  vô nghiệm thì 2 m    1   2  m   1 2
 3m  4m  0   4 . m   3
Câu 25: (THPT Yên Lạc-Vĩnh Phúc-lần 1-năm 2017-2018) Tìm nghiệm của phương trình   2
sin x  sin x  0 thỏa mãn điều kiện   x  . 2 2   A. x  . B. x  . C. x  0. D. x  . 2 3 Lời giải
Chọn C x k sin x  0 Ta có 2
sin x  sin x  0     ; k    sin x  1    x    k 2  2  
Đối chiếu với điều kiện   x
. Ta được nghiệm của phương trình là x  0. 2 2
Câu 26: (THPT Yên Lạc-Vĩnh Phúc-lần 1-đề 2-năm 2017-2018) Tìm m để phương trình 2 2 sin x  .
m sin 2x  2m vô nghiệm. 4 4 4 4
A. m  0; m  .
B. m  0; m  . C. 0  m  .
D. m  0 hoặc m  . 3 3 3 3 Lời giải Chọn D
Xét phương trình a sin x b cos x c  0 có nghiệm khi 2 2 2
a b c . Vậy để phương trình vô nghiệm thì 2 2 2
a b c . Ta có: 2 2 sin x  .
m sin 2x  2m  1 cos 2x  .
m sin 2x  2m  .
m sin 2x  cos 2x  2m 1  0  . m  0 2 2
Để phương trình  vô nghiệm thì 2 m    1   2  m   1 2
 3m  4m  0   4 . m   3
Câu 27: (THPT Yên Lạc-Vĩnh Phúc-lần 1-đề 2-năm 2017-2018) Tìm nghiệm của phương trình   2
sin x  sin x  0 thỏa mãn điều kiện   x  . 2 2   A. x  . B. x  . C. x  0. D. x  . 2 3 Lời giải
Chọn C x k sin x  0 Ta có 2
sin x  sin x  0     ; k    sin x  1    x    k 2  2  
Đối chiếu với điều kiện   x
. Ta được nghiệm của phương trình là x  0. 2 2
Câu 28: (THPT Yên Lạc 2-Vĩnh Phúc-lần 1-năm 2017-2018) Phương trình cos x  0 có bao nhiêu
nghiệm thuộc khoảng 0; 2018  ? A. 2017 . B. 2018 . C. 2019 . D. 1009 . Lời giải Chọn B  Ta có
cos x  0  x   k với
k   . Nghiệm thuộc khoảng 0;2018  thì 2  1 4035 0 
k  2018    k
k 0,1, 2,..., 201  7 . 2 2 2
Vậy phương trình có 2018 nghiệm thuộc khoảng 0; 2018  .
Câu 29: (THTT Số 2-485 tháng 11-năm học 2017-2018) Hãy nêu tất cả các hàm số trong các hàm số
y  sin x , y  cos x , y  tan x , y  cot x thỏa mãn điều kiện đồng biến và nhận giá trị âm trong    khoảng  ; 0   .  2 
A. y  tan x .
B. y  sin x, y  cot x .
C. y  sin x , y  tan x .
D. y  tan x , y  cos x . Lời giải Chọn C
Vì hàm số y  cot x luôn nghịch biến trên từng khoảng xác định nên loại ngay đáp án B.
Dựa vào đồ thị của các hàm số lượng giác y  sin x , y  cos x và y  tan x trên khoảng     ; 0 
 ta thấy hàm y  sin x và y  tan x thỏa.  2   5 
Câu 30: (THPT Việt Trì-Phú Thọ-lần 1-năm 2017-2018) Trên đoạn 2   ;  , đồ thị hai hàm số 2   
y  sin x và y  cos x cắt nhau tại bao nhiêu điểm? A. 2 . B. 5 . C. 4 . D. 3 . Lời giải Chọn B
Phương trình hoành độ giao điểm của hai đồ thị hàm số là 
sin x  cos x  tan x  1  x
k k   . 4   5   5 9 9 Do x   k  2 ; nên 2   k     k   k  2  ; 1; 0;1;  2 . 4  2    4 2 4 4  5 
Vậy đồ thị hai hàm số đã cho cắt nhau tại 5 điểm trên đoạn 2   ;  . 2   
Câu 31: (THPT Thạch Thành-Thanh Hóa-năm 2017-2018) Tìm giá trị lớn nhất, giá trị nhỏ nhất của
hàm số y  2 sin x  3 .
A. max y  5, min y  1.
B. max y  5, min y  2 5 .
C. max y  5, min y  2 .
D. max y  5, min y  3 . Lời giải Chọn A
Ta có 1  s inx  1; x
    1  2 s inx+3  5; x
    1  y  5; x   
Câu 32: (THPT Thạch Thành-Thanh Hóa-năm 2017-2018) Tìm chu kỳ cơ sở (nếu có) của hàm số
f x  tan 2x .   A. T  2 . B. T  . C. T   . D. T  . 0 0 2 0 0 3 Lời giải Chọn B     Ta có f x k  tan  
2x k   tan 2x  f x; x   , k     T  0  2  2
Câu 33: (THPT Thạch Thành-Thanh Hóa-năm 2017-2018) Hàm số y  sin x đồng biến trên mỗi khoảng:      3 5  A.   k 2 ;  k 2   với k   . B.   k 2 ;  k 2   với k   .  2 2   2 2    5     C.k 2 ;  k 2   với k   . D.
k 2 ;   k 2   với k   .  2 2   2  Lời giải Chọn A
Nhìn vào đồ thị hàm số y  sin x ta thấy đồ thị hàm số là đường cong đi lên từ trái qua phải     trong các khoảng   k 2 ;  k 2 
 với k   nên đáp án là A.  2 2 
Câu 34: (THPT Thạch Thành-Thanh Hóa-năm 2017-2018) Phương trình sin x  3 cos x  1 chỉ có các nghiệm là:     x   k 2  x    k 2 2  2 A.  (k  ) . B.  (k  ) . 7  7 x   k 2 x    k 2  6  6     x    k 2  x   k 2 2  2 C.  (k  ) . D.  (k  ) . 7  7 x   k 2 x    k 2  6  6 Lời giải Chọn A       1 
sin x  3 cos x  1  2 sin x   sin x    sin      3   3  2 6      x    k 2  x   k 2 3 6  2      5  7 x    k 2 x   k 2  3 6  6 Câu 35: (THPT Thạch Thành-Thanh Hóa-năm 2017-2018) Phương trình 2 2
sin x  4 sin x cos x+ 3cos x  0 có tập nghiệm trùng với nghiệm của phương trình nào sau đây? tan x  1
A. cos x  0 . B. cot x  1.
C. tan x  3 . D.  1 . cot x   3 Lời giải Chọn D
Dễ thấy với cos x  0 không là nghiệm của phương trình đầu.
Với cos x  0 , chia 2 vế cho 2 cos x , ta có: 2
tan x  4 tan x  3  0 tan x  1 tan x  1     1 tan x  3  cot x   3    1
Câu 36: (THPT Thạch Thành-Thanh Hóa-năm 2017-2018) Giải phương trình sin 2x       3  2     x    k  x   k 4  4 A.  (k  ) . B.  (k  ) . 5  5 x   k x   k  12  12      x   k  x    k 4  4 2 C.  (k  ) . D.  (k  ) .     x   k x   k  12  12 2 Lời giải Chọn A      
Phương trình  sin 2x   sin       3   6       2x     k 2  x    k 3 6  4     , k      5 2x      k 2 x   k  3 6  12
Câu 37: (THPT Chuyên Vĩnh Phúc-lần 2-năm 2017-2018) Tìm tất cả các giá trị của tham số m để phương trình 2
cos x m 1 có nghiệm.
A. 1  m  2 . B. m  2 .
C. 1  m  2 . D. m  1. Lời giải Chọn C Ta có: 2
0  cos x  1 nên 0  m 1  1  1  m  2 thì phương trình có nghiệm.
Câu 38: (THPT Quãng Xương-Thanh Hóa-lần 1-năm 2017-2018) Tìm điều kiện của tham số m để
phương trình 3sin x m cos x  5 vô nghiệm A. m   4  ; 4 .
B. m   ;  4  4;  . C. m   ;  4   .
D. m  4;  . Lời giải Chọn A
Để phương trình đã cho vô nghiệm thì 2 2 2 3  m  5  2
m  16  4  m  4 .
Câu 39: (THPT Quãng Xương-Thanh Hóa-lần 1-năm 2017-2018) Cho các hàm số y  cos x ,
y  sin x , y  tan x , y  cot x . Trong các hàm số trên, có bao nhiêu hàm số chẵn? A. 2 . B. 1. C. 3 . D. 4 . Lời giải Chọn B 
y f x  cos x là hàm số chẵn vì:
Tập xác định D   , nên x
  D  x D và f x  cos x  cos x f x . 
y g x  sin x là hàm số lẻ vì:
Tập xác định D   , nên x
  D  x D và g x  sin x   sin x  g x . 
y h x  tan x là hàm số lẻ vì:  
Tập xác định D   \   k | k  , nên  2  x
  D  x D và h x  tan x   tan x  h x . 
y k x  cot x là hàm số lẻ vì:
Tập xác định D   \ k | k    , nên x
  D  x D và k x  cot x   cot x  k x .
Câu 40: (THPT Ngô Sĩ Liên-Bắc Giang-lần 1-năm 2017-2018) Giải phương trình sin 3x  sin x ta được
tập nghiệm của phương trình là       
A.   k k  .
B.k k     l ,l   .  4   4 2     C.   k2 ,  k   .
D.k2 k     .  4  Lời giải Chọn Bx k
3x x k 2      l ,
k  ,l   .
3x    x l2  x    4 2    
Vậy tập nghiệm của phương trình là: k k     l ,l    4 2 
Câu 41: (THPT Ngô Sĩ Liên-Bắc Giang-lần 1-năm 2017-2018) Gọi X là tập nghiệm của phương trình  x  cos 15  sin x  
. Mệnh đề nào dưới đây đúng?  2 
A. 290  X .
B. 220  X .
C. 240  X .
D. 200  X . Lời giải Chọn Ax   x  Xét phương trình: cos
15  sin x  cos 15  cos     90  x  2   2   x 3x
15  90  x k360  75  k360    x  50  120 2 2 k        , k   x x
x  210  k720  15 90 x k360           105  k360    2  2
Vậy 290  50  2.120  X .
Câu 42: (THPT Nguyễn Đức Thuận-Nam Định-lần 1-năm 2017-2018) Phương trình lượng giác:
2 cos x  2  0 có nghiệm là:    3    7 x   k 2  x   k 2 x   k 2 x   k 2 4  4  4  4 A.  . B.  . C.  . D.  .   3 3 7 x    k 2 x    k 2 x   k 2 x    k 2  4  4  4  4 Lời giải
Chọn B 2 3 3
Phương trình tương đương với cos x    cos  x    k 2 2 4 4
Câu 43: (THPT Hậu Lộc 2-Thanh Hóa-ần 1-năm 2017-2018) Tìm số nghiệm thuộc khoảng 0;   của   
phương trình cos x   0   .  4  A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn B       Ta có: cos x   0  x    k ; k      x
k ; k    4  4 2 4  1 3
Do x  0;    0  x    0 
k      k  . 4 4 4 
Mà k    k  0  x  4
 Phương trình đã cho có duy nhất một nghiệm trong khoảng 0;   .
Câu 44: (THPT Chuyên Lam-Thanh Hóa-lần 1-năm 2017-2018) Hàm số nào dưới đây đồng biến trên  5  khoảng 0;   ?  6       
A. y  sin x .
B. y  cos x .
C. y  sin x    .
D. y  sin x    .  3   3  Lời giải Chọn C  5              Ta có x  0;  x    ;   ;     
 nên hàm số y  sin x    đồng biến.  6  3  3 2   2 2   3 
Câu 45: (THPT Chuyên Lam-Thanh Hóa-lần 1-năm 2017-2018) Viết phương trình tiếp tuyến của 1 C 3 2 : y
x x  2 tại điểm có hoành độ là nghiệm của phương trình y  0. 3 7 1 7 11 A. y  3  x  .
B. y  x  .
C. y  x  .
D. y  x  . 3 3 3 3 Lời giải Chọn C 2
y  x  2x y  2x  2 4
y  0  2x  2  0  x  1  y   3
Hệ số góc k y  1  1  (loại A)  4  7
Phương trình tiếp tuyến cần tìm là y  1   x   1    x    .  3  3 Câu 46: (THPT Chuyên Lam-Thanh Hóa-lần 1-năm 2017-2018) Cho phương trình  x   x m x 2 sin 1 sin 2 sin
m cos x . Tìm tập S tất cả các giá trị thực của tham số m để   
phương trình có nghiệm trên khoảng 0;   .  6   3   1   3  A. S   0;  .
B. S  0  ;1 . C. S  0; .
D. S   1; .     2       2  2   Lời giải Chọn A Ta có:  x   x m x 2 sin 1 sin 2 sin
m cos x * sin x  1   sin x  
1 sin 2x msin x m msin x  0  
sin 2x m 2    
Để phương trình * có nghiệm trên khoảng 0; 
 khi phương trình 2 có nghiệm trên  6       3 khoảng 0;   hay 0  x   0  2x   0  m  .  6  6 3 2
Câu 47: (THPT Cổ Loa-Hà Nội-lần 1-nawm-2018) Nghiệm của phương trình 3 cos x  sin x  2 là  5 x    k 2   6 5 A.  , k   . B. x  
k 2 , k   .   6 x   k 2  6 5  C. x  
k 2 , k   . D. x  
k 2 , k   . 6 2 Lời giải Chọn B 3 1   
Ta có 3 cos x  sin x  2  cos x  sin x  1   sin x   1    2 2  3    5  x   
k 2  x  
k 2 , k  .  3 2 6
Câu 48: (THPT Chuyên Lê Hồng Phong-Nam Định-lần 2 năm 2017-2018) Khẳng định nào sau đây là khẳng định sai? 
A. cos x  1  x    k 2 .
B. cos x  0  x   k . 2 
C. cos x  1  x k 2 .
D. cos x  0  x   k 2 . 2 Lời giải Chọn D
Ta có: cos x  1  x    k 2 k   . Suy ra A. đúng. 
cos x  0  x
k k   . Suy ra B. đúng. 2
cos x  1  x k 2 k   . Suy ra C. đúng.
Câu 49: (THPT Chuyên Lê Hồng Phong-Nam Định-lần 2 năm 2017-2018) Có bao nhiêu số tự nhiên có
ba chữ số dạng abc với a , b , c 0;1; 2;3;4;5; 
6 sao cho a b c . A. 120 . B. 30 . C. 40 . D. 20 . Lời giải Chọn D
Vì số tự nhiên có ba chữ số dạng abc với a , b , c 0;1;2;3; 4;5; 
6 sao cho a b c nên a , b , c 1; 2;3;4;5; 
6 . Suy ra số các số có dạng abc là 3 C  20 . 6
Câu 50: (THPT Chuyên Lê Hồng Phong-Nam Định-lần 2 năm 2017-2018) Giải phương trình
cos 2x  5sin x  4  0 . Mệnh đề nào sau đây đúng?    A. x   k . B. x    k .
C. x k 2 . D. x   k 2 . 2 2 2 Lời giải Chọn D
Ta có cos 2x  5sin x  4  0 2
 1 2 sin x  5sin x  4  0 2
 2sin x  5sin x  3  0
 2sin x  3sin x  
1  0  sin x  1 ( vì 1  sin x  1 ). 
Vậy phương trình có họ nghiệm là x
k 2 , k   . 2
Câu 51: (SGD Vĩnh Phúc-KSCL lần 1 năm 2017-2018) Tìm tất cả các giá trị của m để phương trình
cos 2x m sin 2x  1 2m vô nghiệm, kết quả là: 4 4 A. 0  m  . B. 0  m  . 3 3  4   4 
C. m   ;  0  ;     . D. m   ;  0  ;     .  3   3  Lời giải Chọn C
Phương trình cos 2x m sin 2x  1 2m vô nghiệm khi:  x  0 1 m 1 2m2 2 2 3m 4m 0         4 .  x   3  4  Vậy m   ;  0  ;     .  3 
Câu 52: (SGD Vĩnh Phúc-KSCL lần 1 năm 2017-2018) Phương trình 2 2 2 2
cos x  cos 2x  cos 3x  cos 4x  2 tương đương với phương trình A. sin . x sin 2 .
x sin 5x  0 . B. sin . x sin 2 .
x sin 4x  0 . C. cos . x cos 2 .
x cos 5x  0 . D. cos . x cos 2 .
x cos 4x  0 . Lời giải Chọn C Ta có: 2 2 2 2
cos x  cos 2x  cos 3x  cos 4x  2 1 cos 2x 1 cos 4x 1 cos 6x 1 cos 8x      2 2 2 2 2
 cos 8x  cos 2x  cos 6x  cos 4x  0  2 cos 5x cos 3x  2 cos 5x cos x  0
 2 cos 5x cos 3x  cos x  0  2 cos 5 .2 x cos 2 .
x cos x  0  cos . x cos 2 .
x cos 5x  0 .
Câu 53: (THPT Lục Ngạn-Bắc Ninh-lần 1 năm 2017-2018) Phương trình 2
sin 5x  sin 9x  2 sin x 1  0 có một họ nghiệm là:  k 2  k 2  3 A. x   . B. x   . C. x   k 2 . D. x   k . 42 7 42 3 5 7 Lời giải Chọn A 2
sin 5x  sin 9x  2 sin x 1  0
 2 sin 7x cos 2x  cos 2x  0  2sin 7x   1 cos 2x  0     k 2 7x   k 2  x   6  42 7  1   sin 7x   5 5 k 2    2  7x
k 2  x   , k   .   6  42 7 cos 2x  0       k 2x   k x    2  4 2
Câu 54: (THPT Lê Văn Thịnh-Bắc Ninh-lần 1 năm 2017-2018) Hàm số nào sau đây là hàm số chẵn?
A. y  sin x cos 3x .
B. y  cos 2x .
C. y  sin x .
D. y  sin x  cos x . Lời giải Chọn B
Hàm số y  sin x cos 3x có TXĐ: D   , nên x
    x   và có
y x  sin x cos  3
x   sin x cos 3x   y x suy ra hàm số y  sin x cos 3x là hàm số lẻ.
Hàm số y  cos 2x là hàm số chẵn vì TXĐ: D   , nên x
    x   và
y x  cos 2x  cos 2x y x .
Xét tương tự ta có hàm số y  sin x là hàm số lẻ, hàm số y  sin x  cos x không chẵn cũng không lẻ. 2
Câu 55: (THPT Lê Văn Thịnh-Bắc Ninh-lần 1 năm 2017-2018) Phương trình sin 2x   có bao 2
nhiêu nghiệm thuộc khoảng 0;  ? A. 4 . B. 3 . C. 2 . D. 1. Lời giải Chọn C   x    k 2  8 Ta có sin 2x    
với k , l   . 2 5 x   l  8
Trên khoảng 0;  ta có 2 nghiệm thỏa mãn tương ứng k  1 và l  0 .
Câu 56: (THPT Lê Văn Thịnh-Bắc Ninh-lần 1 năm 2017-2018) Tìm tập xác định của hàm số sau cot x y  . 2 sin x 1      5 
A. D   \ k ,  k 2 , 
k 2 ; k  .
B. D   \   k2 ,
k 2 ; k  .  6 6   6 6    5    2 
C. D   \ k ,  k 2 ,
k 2 ; k  .
D. D   \ k ,  k 2 ,
k 2 ; k  .  6 6   3 3  Lời giải Chọn C cot x Hàm số y  xác định khi: 2sin x 1  x k sin  x  0  sin  x  0       1  x
k 2 , k  . 2 sin x 1  0 sin x  6     2  5 x   k 2   6
Câu 1: (THPT Triệu Sơn 1-lần 1 năm 2017-2018) Giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số
sin x  2 cos x 1 y  là
sin x  cos x  2 1 A. m   ; M  1 .
B. m  1; M  2 . C. m  2  ; M  1 . D. m  1  ; M  2 . 2 Lời giải Chọn C
sin x  2 cos x 1 Ta có y    y  
1 sin x   y  2 cos x  1 2 y *
sin x  cos x  2 2 2 2
Phương trình * có nghiệm   y     y      y 2 1 2 1 2
y y  2  0  2  y  1 . Vậy m  2  ; M  1 .
Câu 2: (THPT Chuyên Vĩnh Phúc-MĐ 903 lần 1-năm 2017-2018) Tất cả các họ nghiệm của phương
trình sin x  cos x  1 là  x k 2 A.   , k   .
B. x k 2 , k   .  x   k 2  2   x   k 2   4 C. x
k2 , k   . D.  , k   . 4 
x    k2  4 Lời giải Chọn A       1    
Ta có: sin x  cos x  1  2 sin x   1  sin x    sin x   sin        4   4  2  4  4    x    k 2 x k 2  4 4      k   .  3 x   k 2 x    k 2  2  4 4
Câu 3: (THPT Chuyên Vĩnh Phúc-lần 1 MĐ 904 năm 2017-2018) Tất cả các họ nghiệm của phương
trình 2 cos 2x  9sin x  7  0 là   A. x  
k k   . B. x
k k   . 2 2   C. x  
k 2 k   . D. x
k 2 k   . 2 2 Lời giải Chọn D
Ta có 2 cos 2x  9sin x  7  0   2
2 1 2 sin x  9sin x  7  0 5   2
4 sin x  9 sin x  5  0  sin x  1, sin x
(vô nghiệm)  x
k 2 k   . 4 2
Câu 4: (THPT Chuyên Vĩnh Phúc-lần 1 MĐ 904 năm 2017-2018) Có bao nhiêu số tự nhiên lẻ có 4 chữ số khác nhau? A. 2240. B. 2520. C. 2016. D. 256. Lời giải Chọn A
Giả sử số tự nhiên lẻ có bốn chữ số khác nhau là abcd . Khi đó: d có 5 cách chọn. a có 8 cách chọn. Số các số là: 2 5.8.A  2240 (số). 8
Vậy số các số tự nhiên lẻ có bốn chữ số khác nhau là 2240 số.
Câu 5: (THPT Kim Liên-Hà Nội năm 2017-2018) Gọi S là tổng các nghiệm thuộc khoảng 0; 2  của
phương trình 3cos x 1  0 . Tính giá trị của S . A. S  0 . B. S  4 . C. S  3 . D. S  2 . Lời giải Chọn D 1 1
Ta có: 3cos x 1  0  cos x
x   arccos  k 2 , k   . 3 3 1
Trong khoảng 0; 2  phương trình 3cos x 1  0 có hai nghiệm là x   arccos và 1 3 1 x  arccos . 2 3 1 1
Vậy tổng các nghiệm là S x x   arccos  arccos  0 . 1 2 3 3
Câu 6: (THPT Kim Liên-Hà Nội năm 2017-2018) Tìm tất cả các nghiệm của phương trình
cos3x  sin 2x  sin 4x  0 .  2 A. x   k , k   . 6 3   B. x   k , k   . 6 3   5
C. x k ; x
k 2 ; x
k 2 , k   . 3 6 6    D. x   k ; x  
k 2 , k   . 6 3 3 Lời giải Chọn B
Ta có: cos 3x  sin 2x  sin 4x  0  cos 3x  2 cos 3 .
x sin x  0  cos 3x 1 2sin x  0    x   k  6 3 cos3x  0  cos 3x  0         x   k 2 1  
, k    x   k , k   . 1 2sin x  0 sin x   6  6 3  2  5  x   k 2  6
Câu 7: (THPT Kim Liên-Hà Nội năm 2017-2018) Gọi x là nghiệm dương nhỏ nhất của phương trình 0 2 2
3sin x  2sin x cos x  cos x  0 . Chọn khẳng định đúng?  3   3        A. x  ; 2 . B. x   ; . C. x  ;  . D. x  0; . 0   0   0   0    2   2   2   2  Lời giải Chọn D
Ta thấy cos x  0 không thỏa phương trình. Chia hai vế phương trình cho 2
cos x  0 ta được: 2
3 tan x  2 tan x 1  0   tan x  1  x    k   4  1  
, k, l   . tan x  1   3 x  arctan  l  3 1   
Vậy nghiệm dương nhỏ nhất của phương trình là arctan  0;   . 3  2 
Câu 8: (THPT Kiến An-Hải Phòng năm 2017-2018) Tìm số nghiệm của phương trình
cos 2x  cos x  2  0 , x 0; 2  . A. 0 . B. 2 . C. 1. D. 3 . Lời giải Chọn C  3 cos x  VN
cos 2x  cos x  2  0 2
 2 cos x  cos x  3  0   2
x    k 2 k   . cos x  1 
Với x 0; 2  , ta có 0    k2  2  k  0 .
Vậy phương trình đã cho có một nghiệm thỏa mãn yêu cầu bài toán.
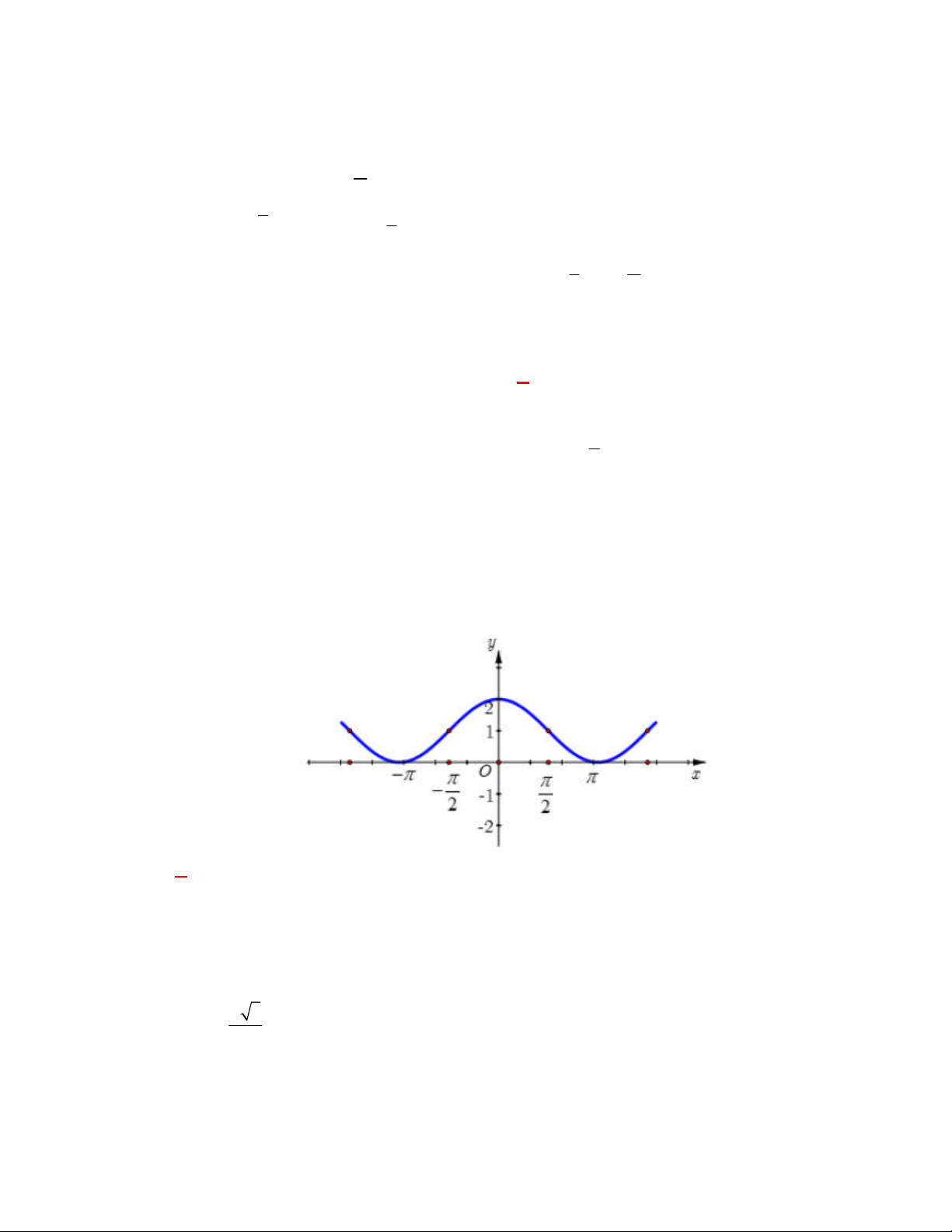
Câu 9: (THPT Chuyên Lương Văn Tụy-Ninh Bình lần 1 năm 2017-2018) Đường cong trong hình vẽ
bên dưới là đồ thị của một trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây.
Hỏi hàm số đó là hàm số nào?
A. y  cos x 1 .
B. y  2  sin x .
C. y  2 cos x . D. 2
y  cos x 1. Lời giải Chọn A
Do đồ thị đi qua ba điểm  
 ; 0 , 0; 2 ,  ;0 nên chọn phương án A.
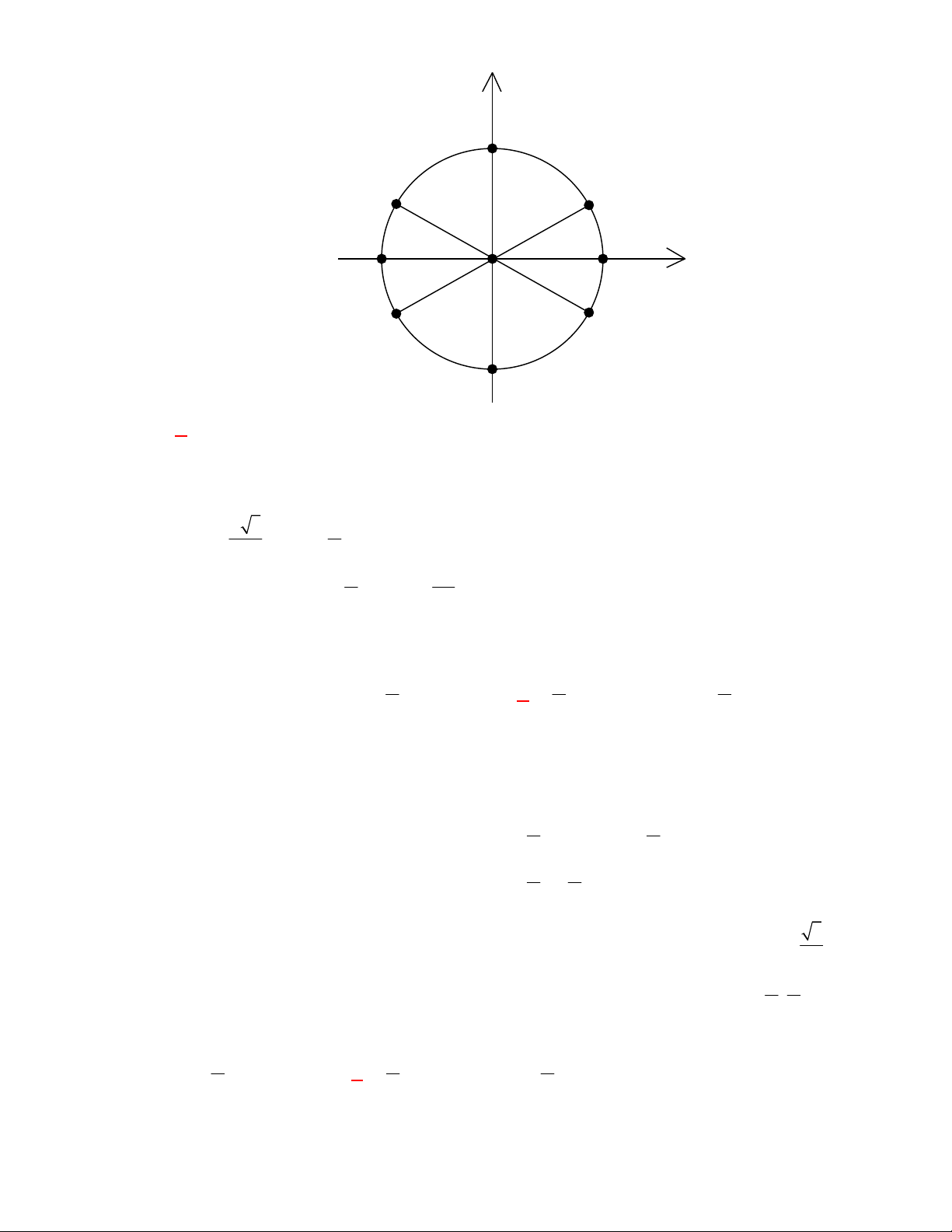
Câu 10: (THPT Chuyên Lương Văn Tụy-Ninh Bình lần 1 năm 2017-2018) Nghiệm của phương trình  3 tan x
được biểu diễn trên đường tròn lượng giác ở hình bên là những điểm nào? 3 y B D C A' O A x E F B'
A. Điểm F , điểm D .
B. Điểm C , điểm F .
C. Điểm C , điểm D , điểm E , điểm F .
D. Điểm E , điểm F . Lời giải: Chọn A  3  tan x   x  
k , k   . 3 3  2
Với 0  x  2  x   hoặc x  . 3 3
Câu 11: (THPT Chuyên Lương Văn Tụy-Ninh Bình lần 1 năm 2017-2018) Nghiệm của phương trình
sin x cos x cos 2x  0 là:   
A. k k   . B. kk  . C. kk  . D. kk  . 2 4 8 Lời giải Chọn C   x k sin x  0    
Ta có sin x cos x cos 2x 0 cos x 0      x
k  x kk  .   2 4 cos 2x  0      x   k  4 2 3
Câu 12: (THPT Chuyên Trần Phú-Hải Phòng lần 1 năm 2017-2018) Phương trình sin 2x   có 2    
hai công thức nghiệm dạng   k ,   k k   với  ,  thuộc khoảng  ;   . Khi  2 2  đó,    bằng    A.  . B.  . C. . D.  . 3 2 2 Lời giải Chọn B       2x    k 2 x    kx    k 3     3  6  6 Ta có: sin 2x    sin          . 2  3  4  2  2x   k 2 x   k
x    k  3  3  3    Vậy    và    . Khi đó      . 6 3 2
Câu 13: (THPT Đoàn Thượng-Hải Dương-lần 2 năm 2017-2018) Phương trình nào trong số các phương trình sau có nghiệm?
A. cos x  3  0 .
B. sin x  2 .
C. 2 sin x  3cos x  1 . D. sin x  3cos x  6 . Lời giải Chọn C
Ta có 2 sin x  3cos x  1có 2 2 2
a b  4  9  13  c  1 nên phương trình có nghiệm.
Câu 14: (THPT Hà Huy Tập-Hà Tĩnh-lần 1 năm 2017-2018) Tìm tất cả các giá trị của tham số m để
phương trình m sin x  3cos x  5 có nghiệm. m  4 A. m  4 .
B. 4  m  4 . C. m  34 . D.  . m  4  Lời giải Chọn Dm  4 
Phương trình m sin x  3cos x  5 có nghiệm 2 2 2  m  3  5 2  m  16   . m  4  tan x
Câu 15: (THPT Hà Huy Tập-Hà Tĩnh-lần 1 năm 2017-2018) Tìm tập xác định của hàm số y  . cos x 1  
A. D   \ k2 .
B. D   \   k2  .  2     
C. D   \   k ; k 2  .
D. D   \   k2 ; x k  .  2   2  Lời giải Chọn C   tan x cos x  0 x   k Hàm số y  xác định khi:    2 , k . cos x 1 cos x 1  0  x k2   
Vậy tập xác định là D   \   k ; k2 , k  .  2  3
Câu 16: (THPT Hà Huy Tập-Hà Tĩnh-lần 1 năm 2017-2018) Phương trình sin x  có nghiệm là 2    x   k x   k 2   6 3 A. x    k 2 . B. x   k . C.  . D.  . 3 3  5  2 x   kx   k 2  6  3 Lời giải Chọn D  x   k 2 3 3 Ta có sin x    , với k   .  2 2  x   k 2  3
Câu 17: (THPT Hà Huy Tập-Hà Tĩnh-lần 1 năm 2017-2018) Tính tổng T các nghiệm của phương trình   2 2 
cos x  sin 2x  2  cos  x
 trên khoảng 0; 2  .  2  7 21 11 3 A. T  . B. T  . C. T  . D. T  . 8 8 4 4 Lời giải Chọn C    Ta có 2 2
cos x  sin 2x  2  cos  x    2 2
cos x  sin 2x  2  sin x  2     
 cos 2x  sin 2x  2  cos 2x   1    2x
k 2 , k    4  4   x  
k , k   8  1 17
Vì 0  x  2  0    k  2   k  8 8 8 7 15
Vì k   nên k 1;  2  x  ; x  1 2 8 8 11
Vậy x x  . 1 2 4
Câu 18: (THPT Triệu Thị Trinh-lần 1 năm 2017-2018) Tổng tất cả các nghiệm của phương trình
sin 5x cos 7x  cos 4x sin 8x trên 0; 2  bằng 19 9 A. . B. . C. 5 . D. 7 . 3 2 Lời giải Chọn D 1 1
Ta có phương trình sin 5x cos 7x  cos 4x sin 8x
sin12x  sin 2x  sin12x  sin 4x 2 2  kx  sin 3x  0  3
 sin 4x  sin 2x  0  2 sin 3x cos x  0     I  . cos x  0  
x   k  2  2 4 5  3 
Vì x  0; 2  nên từ  I  suy ra x   , , , , , ,  .  3 3 3 3 2 2   2 4 5  3
Vậy tổng tất cả các nghiệm của phương trình là         7 . 3 3 3 3 2 2
Câu 19: (THPT Thạch Thành 2-Thanh Hóa-lần 1 năm 2017-2018) Phương trình sin 2x  3cos x  0 có
bao nhiêu nghiệm trong khoảng 0;  ? A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn B cos x  0
Phương trình tương đương với cos x 2sin x  3  0   3
sin x    L  2   x
k , k   . 2 
Vậy phương trình chỉ có một nghiệm duy nhất x  . 2
Câu 20: (THPT Thạch Thành 2-Thanh Hóa-lần 1 năm 2017-2018) Nghiệm của phương trình
2 sin x 1  0 được biểu diễn trên đường tròn lượng giác ở hình bên là những điểm nào? y B D CA A x O E FB
A. Điểm D , điểm C .
B. Điểm E , điểm F .
C. Điểm C , điểm F .
D. Điểm E , điểm D . Lời giải Chọn B   x    k 2 1  6
Ta có 2 sin x 1  0  sin x     k   2 7  x   k 2  6  7
Với k  0  x   hoặc x  . 6 6  7
Điểm biểu diễn của x  
là F , điểm biểu diễn x  là E . 6 6
Câu 21: (THPT Chuyên Thái Bình-lần 2 năm học 2017-2018) Cho phương trình:  2   x   x m x 2 cos 1 cos 2 cos
m sin x . Phương trình có đúng hai nghiệm thuộc đoạn 0;  3    khi? 1 A. m  1. B. m  1  .
C. 1  m  1 .
D. 1  m   . 2 Lời giải Chọn D Ta có  x   x m x 2 cos 1 cos 2 cos
m sin x  cos x  
1 cos 2x m cos x m cos x   1   0   cos 2x m   1  cos x  
1 cos 2x m  0   cos x  1  2   2 
Phương trình 2  x    k2 , k   . Vì x  0; 
nên không tồn tại k thỏa mãn. 3     2 
Theo đề phương trình có đúng hai nghiệm thuộc đoạn 0;  nên phương trình   1 có đúng 3     2 
hai nghiệm thuộc đoạn 0;  . 3     2   4  Ta có x  0;  nên 2x  0; . 3       3  y 1  1  2 O x  1  Do đó  
1 có hai nghiệm phân biệt khi m  1  ;   . 2    Cách khác:  2  k
Xét hàm số y  cos 2x với x  0;  
. Khi đó y  2 sin 2x  0  x  , k   . 3    2  2   Do x  0; 
nên x  0 hoặc x  . 3    2 Bảng biến thiên:  2 x 0 2 3 y  0  1 1  y 2 1  1 
Từ bảng biến thiên ta thấy m  1  ;  
thì đường thẳng y m cắt đồ thị y  cos 2x tại hai 2    điểm.
Câu 22: (THPT Chuyên Thái Bình-lần 2 năm học 2017-2018) Mệnh đề nào dưới đây đúng?  A. cos x  1
  x    k 2 , k   .
B. cos x  0  x
k 2 , k   . 2
C. sin x  0  x k 2 , k   .
D. tan x  0  x k 2 , k   . Lời giải Chọn A
Mệnh đề A. đúng vì cos x  1
  x    k 2 , k   . 
B. sai cos x  0  x
k , k   . 2
C. sai vì sin x  0  x k , k   .
D. sai vì tan x  0  x k , k   .
Câu 23: (THPT Chuyên ĐHSP-Hà Nội-lần 1 năm 2017-2018) Cho hai phương trình cos 3x 1  0 (1); 1 cos 2x  
(2). Tập các nghiệm của phương trình (1) đồng thời là nghiệm của phương trình 2 (2) là  A. x
k 2 , k   .
B. x k 2 , k   . 3  2 C. x  
k 2 , k   D. x  
k 2 , k   . 3 3 Lời giải Chọn D 2
Ta có cos 3x 1  0  cos 3x  1  x k , k   . 3 1 2  cos 2x    2x  
k 2  x  
k , k   . 2 3 3
Biểu diễn các nghiệm trên đường tròn lượng giác ta có tập các nghiệm của phương trình (1) 2
đồng thời là nghiệm của phương trình (2) là x  
k , k   . 3
Câu 24: (THPT Chuyên ĐHSP-Hà Nội-lần 1 năm 2017-2018) Phương trình cos 3 .
x tan 5x  sin 7x
nhận những giá trị sau của x làm nghiệm     A. x  .
B. x  10 ; x  .
C. x  5  x  .
D. x  5  x  2 10 10 20 Lời giải Chọn D k Điều kiện 5x  , k   (*) 2 k
Phương trình tương đương cos 3 .
x sin 5x  sin 7x cos 5x  0  sin 2x  0  x  . 2   Ta thấy x  , x
không thỏa mãn điều kiện (*) nên loại đáp án A, B, C. 2 10
Vậy đáp án đúng là D.
Câu 25: (THPT Chuyên ĐHSP-Hà Nội-lần 1 năm 2017-2018) Tìm số đo ba góc của một tam giác cân 1
biết rằng có số đo của một góc là nghiệm của phương trình cos 2x   . 2  2   
     2    A.  , ,  . B.  , ,  ;  , ,  .  3 6 6   3 3 3   3 6 6 
           
C.  , ,  ;  , ,  . D.  , ,  .  3 3 3   4 4 2   3 3 3  Lời giải Chọn B 1 2  Ta có: cos 2x    2x  
k 2  x  
k , k   . 2 3 3  2
Do số đo một góc là nghiệm nên x  hoặc x  thỏa mãn. 3 3      2   
Vậy tam giác có số đo ba góc là  , ,  hoặc  , ,  .  3 3 3   3 6 6  Câu 26:
(THPT Chuyên ĐHSP-Hà Nội-lần 1 năm 2017-2018) Cho biểu thức 10  x 1 x 1  P   
 với x  0 , x  1 . Tìm số hạng không chứa x trong khai triển 3 2 3  x x 1 x x  Niu-tơn của P . A. 200 . B. 160 . C. 210 . D. 100 . Lời giải Chọn C x 1 x 1 x 1 1 Ta có 3 3   x 1  x  . 3 2 3 x x 1 x x x x 10 10  x 1 x 1   1  Nên 3 P    x      . 3 2 3  x x 1 x x   x  10 kk 205   k 1 kk
Số hạng tổng quát của khai triển là 3 C x .      k 6 1 C x . 10 10  x
Khi k  4 thì số hạng không chứa x là  4 4 1 C  210 . 10
Câu 27: (THPT Chuyên ĐHSP-Hà Nội-lần 1 năm 2017-2018) Số nghiệm thuộc khoảng 0;3  của 5 phương trình 2 cos x  cos x 1  0 là 2 A. 4 . B. 3 . C. 1. D. 2 . Lời giải Chọn B  1 5 cos x   n + Ta có: 2 cos x cos x 1 0      2 . 2  cos x  2  l   2 x   k 2 1 2    3 Suy ra: cos x    cos x  cos     k  2  3  2 x    k 2  3 2 2 + Với x
k 2 , k   . Vì x  0;3  nên 0 
k 2  3 , k   3 3 1 7  2 8     k
, k   . Suy ra: k 0;  1  x   ;  . 3 6  3 3  2 2 + Với x  
k 2 , k   . Vì x  0;3  nên 0  
k 2  3 , k   3 3 1 11 4   k
, k   . Suy ra: k  1  x  . 3 6 3  2 4 8  Do đó x   ; ;  .  3 3 3 
Vậy số nghiệm của phương trình là 3.
Câu 28: (THPT Yên Lạc-Vĩnh Phúc-lần 3 năm 2017-2018) Tìm tất cả các giá trị của tham số m để x x phương trình m sin  cos  5 có nghiệm. 2 2 m  2 m  2 A.  . B.  .
C. 2  m  2 .
D. 2  m  2 . m  2  m  2  Lời giải Chọn A 2 m  2
Điều kiện có nghiệm của phương trình là: 2 2 2
m 1  5  m  4   . m  2   cos x 1   
Câu 29: (THTT Số 4-487 tháng 1 năm 2017-2018) Tập giá trị của hàm số. y  . trên 0; là sin x 1  2     1   1   1   1  A. ; 2  . B. ; 2  . C. ; 2   . D. ; 2   . 2      2   2   2  Lời giải
Chọn A cos x 1 y  . sin x 1       Vì x  0;  nên sin x 0 
;1 . Do đó hàm số đã cho xác định trên 0; . 2       2  2 2 cos x 1
 sin x  cos x 1     y   y    0 , x   0; . sin x 1    sin x  2 1 sin x  2 1  2    
Suy ra hàm số luôn nghịch biến trên 0;  . 2    1
Do đó: max y y 0  2 ; min y  .       0; 2  0; 2       2   1 
Vậy tập giá trị của hàm số đã cho là ; 2  . 2   
Câu 30: (THTT Số 4-487 tháng 1 năm 2017-2018) Phương trình sin 2x cos x  sin 7x cos 4x có các họ nghiệm là k 2  kk  kA. x  ; x   k   . B. x  ; x   k   . 5 12 6 5 12 3 k  kk 2  kC. x  ; x   k   . D. x  ; x   k   . 5 12 6 5 12 3 Lời giải
Chọn C 1 1
sin 2x cos x  sin 7x cos 4x
sin x  sin 3x  sin 3x  sin11x  sin x  sin11x 2 2  kx  11 
x x k 2  5     k   .
11x    x k 2   k x    12 6
Câu 31: (THTT Số 4-487 tháng 1 năm 2017-2018) Tổng tất cả các nghiệm của phương trình cos sin x  1
trên 0; 2  bằng A. 0 . B.  . C. 2 . D. 3 . Lời giải
Chọn B
Ta có x 0; 2   sin x  1   ;1
Khi đó: cos sin x  1  sin x k2 k   với 1  k2  1  k  0 . x  0
Phương trình trở thành sin x  0  x m   m   . x   
Vậy tổng tất cả các nghiệm của phương trình cos sin x  1 trên 0; 2  bằng  . Câu 32: (THTT Số 4-487 tháng 1 năm 2017-2018) Xét phương trình
sin 3x  3sin 2x  cos 2x  3sin x  3cos x  2 . Phương trình nào dưới đây tương đương với phương trình đã cho? A.x   2 2 sin
1 2 cos x  3cos x   1  0 .
B. 2sin x  cos x   1 2cos x   1  0 .
C. 2sin x   1 2 cos x   1 cos x   1  0 .
D. 2sin x   1 cos x   1 2cos x   1  0 . Lời giải Chọn C
Ta có: sin 3x  3sin 2x  cos 2x  3sin x  3cos x  2
 sin 3x  sin x  2sin 2x   sin 2x  2sin x   cos 2x  3cos x  2  0
 2 sin 2x cos x  
1  2 sin x cos x   1  cos x   1 2cos x   1  0  cos x  
1 2sin 2x  2sin x  2cos x   1  0  cos x   1 2cos x   1 2sin x   1  0 .
Câu 33: (SGD Bắc Ninh năm 2017-2018) Phương trình 3 sin 2x  cos 2x  2 có tập nghiệm là  k   2  A. S    | k   . B. S  
k 2 | k   .  3 2   3    5 
C. S    k | k   . D. S  
k | k   .  3   12  Lời giải Chọn C 3 1   
Ta có: 3 sin 2x  cos 2x  2  sin 2x
cos 2x  1  sin 2x   1   2 2  6      2x  
k 2  x
k k  . 6 2 3  
Vậy tập nghiệm của phương trình đã cho là S    k | k   .  3 
Câu 34: (SGD Bắc Ninh năm 2017-2018) Trong các hàm số y  tan x ; y  sin 2x ; y  sin x ; y  cot x ,
có bao nhiêu hàm số thỏa mãn tính chất f x k   f x , x   , k   . A. 3 . B. 2 . C. 1. D. 4 . Lời giải Chọn C  
Ta có hàm số y  tan x có tập xác định là  \   k , k   và hàm số y  cot x có tập  2 
xác định là  \ k , k  
 nên cả hai hàm số này đều không thỏa yêu cầu.
Xét hàm số y  sin 2x : Ta có sin 2 x k   sin 2x k 2   sin 2x , x   , k   .
Hàm số y  sin x là hàm số tuần hoàn với chu kỳ 2 nên không thỏa yêu cầu.
Câu 35: (SGD Ninh Bình năm 2017-2018) Gọi S là tổng các nghiệm trong khoảng 0;  của phương 1 trình sin x  . Tính S . 2   A. S  0 . B. S  . C. S   . D. S  . 3 6 Lời giải Chọn C   x   k 1   6 Ta có: sin x   sin x  sin   , k . 2 6 5 x   k  6
Với điều kiện x 0;  . Ta có:  1 5  0   k  π    k
k  0 , khi đó: x  . 6 6 6 6 5 5 1 5 0   k  π    k
k  0 , khi đó: x  . 6 6 6 6  5 Vậy S     . 6 6   
Câu 36: (SGD Ninh Bình năm 2017-2018) Cho phương trình tan x  tan x   1   . Diện tích của đa  4 
giác tạo bởi các điểm trên đường tròn lượng giác biểu diễn các họ nghiệm của phương trình gần
với số nào nhất trong các số dưới đây? A. 0, 948 . B. 0, 949 . C. 0, 946 . D. 0, 947 . Lời giải Chọn B   cos x  0 x   k    2 Điều kiện       , k   . cos x   0        4  x   k   4 tan x 1
Với điều kiện trên, phương trình trở thành tan x   1 1 tan xx m tan x  0 2
 tan x  tan x  0     , m
  (thỏa điều kiện) tan x  1  x    m  4 y 5 4 BA C O 0 x D   4  2 2   2 2 
Gọi A1;0 , B   ;  , C  1  ; 0 và D  ; 
là các điểm biểu diễn tập nghiệm của   2 2      2 2   phương trình đã cho
Ta có tứ giác ABCD là hình chữ nhật có AB  2  2 ; AD  2  2 . Khi đó SA . B AD  2  1, 41. ABCD
Câu 37: (THPT Chuyên Hạ Long-Quảng Ninh-lần 1 năm 2017-2018) Tìm chu kì của hàm số x 3x
f x  sin  2 cos . 2 2  A. 5 . B. . C. 4 . D. 2 2
Hướng dẫn giải Chọn C x 2 3x 2 4 Chu kỳ của sin là T
 4 và Chu kỳ của cos là T   2 1 1 2 2 3 3 2 2
Chu kì của hàm ban đầu là bội chung nhỏ nhất của hai chu kì T và T vừa tìm được ở trên. 1 2
Chu kì của hàm ban đầu T  4
Câu 38: (THPT Chuyên Hạ Long-Quảng Ninh-lần 1 năm 2017-2018) Tính tổng tất cả các nghiệm
thuộc khoảng 0;  của phương trình:
2 cos 3x  sin x  cos x .  3 A. . B. 3 . C. . D.  . 2 2
Hướng dẫn giải Chọn C   x    k     8
Ta có: 2 cos 3x  sin x  cos x  cos 3x  cos x      k   .  4    x   k  16 2 7  9
Vì x  0;  nên nhận x  , x  , x  . 8 16 16
Câu 39: (THPT Chuyên Phan Bội Châu-Nghệ An- lần 1 năm 2017-2018) Số nghiệm thuộc đoạn  5 0;  của phương trình  là:  2 sin x 1 0 2    A. 2 . B. 3 . C. 1. D. 4 .
Lời giải
Chọn B
x   k2 1  6
+ Phương trình tương đương sin x   sin x  sin   , k  . 2 6  5x   k2  6 + Với x
k2, k  . 6  5 5 Vì x  0;  nên    ,     ,   .  0 k 2 k   1 7 k k   k 0;  1 2    6 2 12 6 3     Suy ra: x   ;   .  6 6    5 + Với x
k2, k  . 6  5 5 5 Vì x  0;            nên 0 k 2 , k   5 5 k , k   k 0 . 2    6 2 12 6 5 Suy ra: x  . 6 53     Do đó x   ; ;   .  6 6 6   
Vậy số nghiệm của phương trình là 3 .
Câu 40: (THPT Chuyên Quốc Học-Huế năm 2017-2018) Tính tổng tất cả các nghiệm thuộc khoảng x x 5
0;2  của phương trình 4 4 sin  cos  . 2 2 8 9 12 9 A. . B. . C. . D. 2 . 8 3 4 Lời giải Chọn B 2 x x 5  x x x x 5 4 4 sin  cos  2 2 2 2  sin  cos  2 sin .cos    2 2 8  2 2  2 2 8 1 5 1 5 1   2  1 sin x   1
1 cos 2x   cos 2x   x  
k , k   . 2 8 4 8 2 3  2 4 5 
Mà x 0; 2  nên x   ; ; ;  .  3 3 3 3 
Khi đó tổng các nghiệm thuộc khoảng 0; 2  của phương trình là x  0 .
Câu 41: (THPT Chuyên Quốc Học-Huế năm 2017-2018) Tìm tập xác định D của hàm số    y  tan 2x    .  4  3 k  3 
A. D   \   , k   .
B. D   \ 
k , k   .  8 2   4  3 k   
C. D   \   , k   .
D. D   \   k , k  .  4 2   2  Lời giải Chọn A        
Hàm số y  tan 2x  
 xác định khi và chỉ khi cos 2x   0  2x    k   .  4   4  4 2 3 k Suy ra x   . 8 2 3 k 
Vậy tập xác định của hàm số là D   \   , k   .  8 2 
Câu 42: (THPT Chuyên Quốc Học-Huế năm 2017-2018) Cho hàm số f x  sin x  cos x có đồ thị
C  . Trong các hàm số sau, hàm số nào có đồ thị không thể thu được bằng cách tịnh tiến đồ thị C  ?   
A. y  sin x  cos x . B. y
2 sin x  2 . C. y   sin x  cos x . D. y  sin x    .  4  Lời giải Chọn D
Ta có max sin x  cos x  2  M , min sin x  cos x   2  m , M m  2 2 . Vì phép x x
tịnh tiến không làm thay đổi khoảng cách giữa giá trị lớn nhất và giá trị nhỏ nhất nên chọn đáp
án D (chênh lệch giữa giá trị lớn nhất và giá trị nhỏ nhất bằng 2 ).   
Câu 43: (THPT Chuyên Thái Bình-lần 3 năm 2017-2018) Tập xác định của hàm số y  tan cos x    2  là:    A.  \   0 . B.  \ 0; .
C.  \ k  .
D.  \ k .  2  Hướng dẫn giải Chọn D Hàm số xác định:       cos cos x  0    cos x
k  cos x  1 2k  cos x  1  sin x  0  2  2 2
x k k   .
Câu 44: (THPT Chuyên Thái Bình-lần 3 năm 2017-2018) Giải phương trình 2
2 sin x  3 sin 2x  3 .   2  A. x    k . B. x   k . C. x   k 2 . D. x   k . 3 3 3 4 Hướng dẫn giải Chọn B 2
2 sin x  3 sin 2x  3  1 cos 2x  3 sin 2x  3 3 1 
3 sin 2x  cos 2x  2  sin 2x  cos 2x  1 2 2        sin 2x   1    2x  
k 2  x
k , k   .  6  6 2 3
Câu 45: (THPT Chuyên Vĩnh Phúc - lần 3 năm 2017-2018) Giá trị lớn nhất và giá trị nhỏ nhất của hàm    
số y  sin x trên đoạn  ;   lần lượt là: 2 3    1 3 3 3 2 3 A.  ;  . B.  ; 1. C.  ; 2  . D.  ;  . 2 2 2 2 2 2 Lời giải
Chọn B         3 Cách 1: Ta có:   x    sin   sin x  sin    
  1  sin x   . 2 3  2   3  2    3    Vậy max y  sin      ; min y  sin   1   .          ;  3  2    2   ; 2 3       2 3     
Cách 2: Xét hàm số y  sin x trên đoạn  ;   2 3        
+ Ta có: y  cos x  0 , x    ;   
; y  0  x   . 2 3    2    
 Hàm số đồng biến trên khoảng  ;    .  2 3     3    Vậy max y  sin      , min y  sin   1   .          ;  3  2    2   ; 2 3       2 3  1 sin x
Câu 46: (THPT Hoài Ân-Hải Phòng năm 2017-2018) Tìm tập xác định D của hàm số y  . 1 sin x    
A. D   \   k 2 ;
k 2 ; k   .
B. D   \ k ; k    .  2 2      
C. D   \ 
k 2 ; k  .
D. D   \   k 2 ;k   .  2   2  Lời giải Chọn C 1   sin x  0
Ta có: 1  sin x  1   . 1 sin x  0  
Hàm số xác định khi 1 sin x  0  sin x  1  x  
k 2 , k   . 2   
Vậy tập xác định của hàm số là: D   \ 
k 2 ; k  .  2 
Câu 47: (THPT Hoài Ân-Hải Phòng năm 2017-2018) Tìm nghiệm của phương trình
cos x  3 sin x  0 . 2 sin x  1  7 A. x
k ; k   . B. x
k 2 ; k   . 6 6 7  C. x
k ; k   . D. x
k 2 ; k   . 6 6 Lời giải Chọn B  5 
TXĐ: D   \   k2 ,
k 2 , k   .  6 6  Phương trình trở thành:    
3 sin x  cos x  0  2 sin x   0    x
k 2 k   .  6  6 7
Vậy nghiệm của phương trình là x
k 2 k   . 6   
Câu 48: (THPT Hồng Quang-Hải Dương năm 2017-2018) Nghiệm của phương trình cot x   3    3   kk có dạng x   
, k   , m , * n   và
là phân số tối giản. Khi đó m n bằng m n n A. 5 . B. 3  . C. 5  . D. 3 . Lời giải Chọn A           Ta có cot x   3    cot x   cot    x  
k  x  
k , k   .  3   3  6 3 6 6 m  6 Vậy 
m n  5 . n  1 
Câu 49: (THPT Hồng Quang-Hải Dương năm 2017-2018) Số vị trí biểu diễn các nghiệm của phương trình 2
4 cos x  4 cos x  3  0 trên đường tròn lượng giác là ? A. 2 . B. 0 . C. 1. D. 4 . Lời giải Chọn A  3 cos x   L  2 Ta có 2
4 cos x  4 cos x  3  0   . 1
cos x   N   2 1 2 2 Với cos x    cos x  cos  x  
k 2 k   . 2 3 3
Vậy số vị trí biểu diễn các nghiệm của phương trình trên đường tròn lượng giác là 2 .
Câu 50: (THPT Hồng Quang-Hải Dương năm 2017-2018) Tìm các giá trị thực của tham số m để
phương trình 2m  
1 sin 3x m cos 3x  3m 1 có nghiệm.  1   1  A. m  0;  .
B. m   ;  0  ;    . 2     2   1   1 
C. m   ;  0  ;    . D. m  0;   .  2   2  Lời giải Chọn A
Phương trình 2m  
1 sin 3x m cos 3x  3m 1 có nghiêm khi 1
m  2  m   m  2 2 2 1 3 1  2
4m  2m  0  0  m  2
Câu 51: (THPT Kinh Môn 2-Hải Dương năm 2017-2018) Hàm số y  sin 2x có chu kỳ là A. T  2 . B. T  . C. T   . D. T  4 . 2 Lời giải Chọn C
Hàm số y  sin 2x tuần hoàn với chu kỳ T  2 nên hàm số y  sin 2x tuần hoàn với chu kỳ T   .
Câu 52: (THPT Kinh Môn 2-Hải Dương năm 2017-2018)Phương trình lượng giác:
cos 3x  cos 2x  9 sin x  4  0 trên khoảng 0;3  . Tổng số nghiệm của phương trình trên là: 25 11 A. . B. 6 . C. Kết quả khác. D. . 6 3 Lời giải Chọn B
Ta có cos 3x  cos 2x  9 sin x  4  0 3 2
 4 cos x  3cos x  2 sin x  9 sin x  5  0  x  2 cos
1 4 sin x  2sin x  
1 sin x  5  0  2sin x  
1  cos x  2sin x cos x  sin x  5  0 2 sin x 1  0   1  
sin x  cos x  2 sin x cos x  5  0 2    x   k 2 1  6 Giải   1 , ta có   1  sin x    . 2 5 x   k 2  6  13 5 17
Với x  0;3  nên  
1 có các nghiệm thoả bài toán là: x  , x  , x  , x  . 6 6 6 6   
Giải 2 , đặt t  sin x  cos x  2 sin x    với t  2 .  4  Khi đó 2 2
t  1 2 sin x cos x  2 sin x cos x  1 t ;
Phương trình 2 trở thành 2 2
t 1 t  5  0  t t  4  0 phương trình vô nghiệm.  13 5 17
Vậy tổng các nghiệm là:     6 . 6 6 6 6
Câu 53: (THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018) Số nghiệm của phương trình    sin x   1  
thuộc đoạn  ; 2  là:  4  A. 3 . B. 2 . C. 0 . D. 1. Lời giải Chọn D       Ta có sin x   1  x  
k 2  x   k 2   , k   .  4  4 2 4
Suy ra số nghiệm thuộc  ;2  của phương trình là 1.
Câu 54: (THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018) Cho phương trình       5    cos 2 x   4 cos  x      . Khi đặt t  cos  x
 , phương trình đã cho trở thành  3   6  2  6 
phương trình nào dưới đây ? A. 2
4t  8t  5  0 . B. 2
4t  8t  3  0 . C. 2
4t  8t  3  0 . D. 2
4t  8t  5  0 . Lời giải Chọn C       5       5 Ta có: cos 2 x   4 cos  x  2      1 2sin x   4 cos  x       3   6  2  3   6  2       5 2  1 2 cos  x  4 cos  x      .  6   6  2    5 Đặt t  cos  x
 , t  1 ta được phương trình: 2
1 2t  4t  2
 4t  8t  3  0 .  6  2
Câu 55: (THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018) Số vị trí điểm biểu diễn các nghiệm của
sin 2x  2 cos x  sin x 1 phương trình
 0 trên đường tròn lượng giác là: tan x  3 A. 4 . B. 1. C. 2 . D. 3 . Lời giải Chọn C
Điều kiện xác định: tan x   3 .
Phương trình tương đương: 2 sin x cos x  2 cos x  sin x 1  0  2cos x   1 sin x   1  0   x   k 2  3  1  cos x       2  x  
k 2 . Do tan x   3 nên x    k 2 loại.   3 3 sin x  1   
x    k2  2  x
k 2 biểu diễn trên đường tròn lượng giác có 1 điểm. 3  x  
k 2 biểu diễn trên đường tròn lượng giác có 1 điểm. 2
Vậy có 2 vị trí biểu diễn nghiệm của phương trình trên đường tròn lượng giác.
Câu 56: (THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018) Tính tổng T tất cả các nghiệm của 2cos x  
1 sin 2x  cos x    phương trình  0 trên 0; ta được kết quả là: sin x 1  2    2   A. T  . B. T  . C. T   . D. T  . 3 2 3 Lời giải Chọn B
Điều kiện xác định sin x  1 .  1 cos x   2 
Phương trình tương đương 2 cos x   1 cos .
x 2sin x   1  0  cos x  0  .  1 sin x   2   x      3  Vì x  0; 
và sin x  1 nên  . Do đó T  . 2      2 x   6
Câu 57: (THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018) Giá trị lớn nhất của hàm số   2  y  3sin x   4   bằng.  12  A. 7 . B. 1. C. 3 . D. 4 . Lời giải Chọn A          Ta có 2 2 2 sin x   1  3sin x   3  3sin x   4  7       .  12   12   12 
Vậy giá trị lớn nhất của hàm số bằng 7 . Câu 58:
(THPT Phan Đăng Lưu-Huế-lần 1 năm 2017-2018) Giải phương trình 2
3sin x  2 cos x  2  0 .   A. x
k , k   .
B. x k , k   .
C. x k 2 , k   . D. x
k 2 , k   . 2 2 Lời giải Chọn C Ta có 2
3sin x  2 cos x  2  0 2
 3cos x  2 cos x  5  0  cos x  1  x k 2 , k   .
Câu 59: (THPT Phan Đăng Lưu-Huế-lần 1 năm 2017-2018) Tìm tất cả các nghiệm của phương trình
tan x  3 cot x  3 1  0 là:     x   k  x    k 4  4 A.  , k   . B.  , k   .    x   k
x   k  3  6     x   k 2  x   k 4  4 C.  , k   . D.  , k   .    x   k 2
x   k  6  6 Lời giải Chọn A sin  x  0 k ĐK 
 sin 2x  0  x  , k   . cos x  0 2  Phương trình tương đương      tan  1 x k x  2 x     4 tan
3 1 tan x  3  0     , k   . tan x  3  
x   k  3
Câu 60: (THPT Phan Đăng Lưu-Huế-lần 1 năm 2017-2018) Phương trình sin x  3 cos x  1 có tập nghiệm là:         A.   k ; 
k  , với k . B.   k 2 ;
k 2  , với k .  6 2   6 2      7   C.   k 2 ; 
k 2  , với k . D.   k 2 ;
k 2  , với k .  6 2   6 2  Lời giải Chọn B 1 3 1    
Ta có sin x  3 cos x  1  sin x  cos x   sin x   sin   2 2 2  3  6      x    k 2  x    k 2 3 6  6    
k  .     x      k 2
x   k2  3 6  2
Câu 61: (THPT Phan Đăng Lưu-Huế-lần 1 năm 2017-2018) Tìm giá trị lớn nhất M của hàm số
y f x 5 3
x  5x  20x  2 trên đoạn 1;  3 . A. M  26 . B. M  46 .
C. M  46 . D. M  50 . Lời giải Chọn D
Ta có f  x 4 2
 5x 15x  20 , 2  x  4
f  x  0 4 2
 5x 15x  20  0  2  . Do 2
x  0  x  4  x  2 . 2 x  1   Mà x 1;  3 nên x  2 . Ta có f  
1  26 , f 2  4
 6 , f 3  50 .
So sánh các giá trị ta được giá trị lớn nhất của hàm số là M  50 .
Câu 62: (THPT Thanh Miện 1-Hải Dương-lần 1 năm 2017-2018) Cho phương trình 2 sin x  3  0 . Tổng
các nghiệm thuộc 0;  của phương trình là:  2 4 A.  . B. . C. . D. . 3 3 3 Lời giải
Chọn A   x   k 2 3   3
2 sin x  3  0  sin x   sin   . 2 3 2 x   k 2  3  2  2
Các nghiệm của phương trình trong đoạn 0;  là ; nên có tổng là    . 3 3 3 3
Câu 63: (THPT Thanh Miện 1-Hải Dương-lần 1 năm 2017-2018) Phương trình sin x  3 cos x  0 có
bao nhiêu nghiệm thuộc 2 ; 2  . A. 5 . B. 2 . C. 3 . D. 4 . Lời giải
Chọn D    
Ta có sin x  3 cos x  0  sin x   0    x
k , k Z  3  3 7 5
Vì x 2 ; 2  nên 2  x  2    k  . Do đó có 4 giá trị k , tương ứng có bốn 3 3 nghiệm x .
Câu 64: (THPT Thanh Miện 1-Hải Dương-lần 1 năm 2017-2018) Diện tích hình phẳng giới hạn bởi
hai đồ thị f x 3
x  3x  2 ; g x  x  2 là: A. S  8 . B. S  4 . C. S  12 . D. S  16 . Lời giải
Chọn A x  0
Phương trình hoành độ giao điểm của hai đồ thị 3 3
x  3x  2  x  2  x  4x  0   x  2  Diện tích cần tìm 0 2 0 2 3 3 S
x  4x dx
x  4x dx      3
x  4x dx   3
x  4xdx 2 0 2 0 4 4  x  0  x  2 2 2   2x   2x  8     . 4 2  4 0    
Câu 65: (THPT Trần Hưng Đạo-TP HCM năm 2017-2018) Tìm số nghiệm của phương trình sin x  cos 2x
thuộc đoạn 0; 20 . A. 40 . B. 30 . C. 60 . D. 20 . Lời giải
Chọn B  1 sin x
Ta có sin x  cos 2x 2
 sin x  1 2 sin x   2 . sin x  1     x   k 2 1  6 sin x    k  . 2 5  x   k 2  6  sin x  1   x  
k 2 k   2
Xét x 0;20  :   1 119 Với x
k 2 , ta có 0 
k 2  20    k
, do k   nên (có 10 giá trị k ). 6 6 12 12 5 5 5 115 Với x
k 2 , ta có 0 
k 2  20    k
, do k   nên (có 10 giá trị 6 6 12 12 k ).   1 41 Với x  
k 2 , ta có 0  
k 2  20   k
, do k   nên (có 10 giá trị k ). 2 2 4 4
Vậy phương trình đã cho có 30 nghiệm thuộc đoạn 0; 20 .
Câu 66: (THPT Trần Hưng Đạo-TP HCM năm 2017-2018) Cho phương trình msin x  4cos x  2m  5
với m là tham số. Có bao nhiêu giá trị nguyên của m để phương trình có nghiệm? A. 4 . B. 7 . C. 6 . D. 5 . Lời giải
Chọn C
Điều kiện để phương trình msin x  4cos x  2m  5 có nghiệm là 10  73 10  73
m  16  2m  52 2 2
 3m  20m  9  0   m  . 3 3
Câu 67: Vậy m 1, 2,3, 4,5, 
6 .(THPT Tứ Kỳ-Hải Dương năm 2017-2018) Số nghiệm thuộc  3   3   ;   
của phương trình 3 sin x  cos  2x   là: 2     2  A. 3 . B. 1. C. 2 . D. 0 . Hướng dẫn giải Chọn C  3  Ta có 3 sin x  cos  2x
  3 sin x  sin 2x     2 
 3 sin x   sin 2x  3 sin x  2
 sin x cos x sin x  0 x k    3 5  5 k   . cos x    cos x    k 2  2 6  6  3   3  Bài ra x   ;    nên k   ;    k  1   x    . 2       2  5  3  7  k 2   ;    k  1   x   . 6  2    6 5  3    k 2   ;  
k    x   . 6  2     3 
Do đó số nghiệm thuộc  ;   
của phương trình đã cho là 2 . 2    3 
Câu 68: (THPT Tứ Kỳ-Hải Dương năm 2017-2018) Biết sin   và
    . Giá trị của 2 2    P  cos 2    là:  3  1 3 A. P  0 . B. P  1  . C. P  . D. P   . 2 2 Hướng dẫn giải Chọn B 3 3 1 1 Ta có sin   2 2
 cos   1 sin   1   cos   . 2 4 4 2  1 Từ
     cos  0 nên cos   . 2 2     
Do đó P  cos 2   cos 2 cos  sin 2 sin    3  3 3   1 3 1 2 2 cos    2 1 .  2sin cos.  cos  
 3 sin  cos  1. 2 2 2
Câu 69: (THPT Xuân Trường-Nam Định năm 2017-2018) Phương trình 2 cos x 1  0 có nghiệm là:   A. x  
k 2 , k   . B. x  
k 2 , k   . 6 3   C. x  
 2 , k   . D. x  
k , k   . 6 3 Lời giải Chọn B 1 
Phương trình 2 cos x 1  0  cos x   x  
k 2 , k   . 2 3
Câu 70: (THPT Xuân Trường-Nam Định năm 2017-2018) Tất cả các nghiệm của phương trình
sin x  3 cos x  1 là:   x    k 2   6 A. x
k 2 , k   . B.  , k   . 6 
x   k2  2 5 5 C. x
k , k   . D. x
k 2 , k   . 6 6 Lời giải Chọn B   x    k 2    1  6
Ta có sin x  3 cos x  1  sin x       , k   .  3  2 
x   k2  2   x    k 2  6
Vậy tất cả các nghiệm của phương trình đã cho là  , k   . 
x   k2  2
Câu 71: (THPT Lương Văn ChasnhPhus Yên năm 2017-2018) Cho phương trình 2
2m sin x cos x  4 cos x m  5 , với m là một phần tử của tập hợp E   3  ;  2; 1; 0;1;  2 . Có
bao nhiêu giá trị của m để phương trình đã cho có nghiệm ? A. 3 . B. 2 . C. 6 . D. 4 . Lời giải Chọn A 1 cos 2x Ta có 2
2m sin x cos x  4 cos x m  5  m sin 2x  4  m  5 2
msin 2x  2 cos 2x m  3. 5 
Phương trình trên có nghiệm khi và chỉ khi m  4  m  32 2  m  . 9
Vậy có ba giá trị của m E để phương trình đã cho có nghiệm.
Câu 72: (THPT Chuyên Biên Hòa-Hà Nam-lần 1 năm 2017-2018) Phương trình 3 sin x  cos x  1
tương đương với phương trình nào sau đây?    1    1       1 A. sin x    . B. sin  x   . C. sin x    1. D. cos x    .  6  2  6  2  6   3  2 Lời giải Chọn A 3 1 1    1
Ta có 3 sin x  cos x  1  sin x  cos x   sin x     . 2 2 2  6  2
Câu 73: (THPT Chuyên Biên Hòa-Hà Nam-lần 1 năm 2017-2018) Số nghiệm của phương trình 2
2 sin 2x  cos 2x 1  0 trong 0; 2018 là A. 1008 . B. 2018 . C. 2017 . D. 1009 . Lời giải Chọn B Ta có 2
2 sin 2x  cos 2x 1  0 2 2 2
 8sin x cos x  2 cos x  0  2  x  2 x   2 2 cos 4sin
1  0  cos x  0  cos x  0  x
k k   . 2 
Bài ra x 0; 2018 nên  k 0; 2018  k 0; 1; 2; 3;  ...; 2017 . 2
Do đó số nghiệm của phương trình 2
2 sin 2x  cos 2x 1  0 trong 0; 2018 là 2018 .
Câu 74: (THPT Chuyên Biên Hòa-Hà Nam-lần 1 năm 2017-2018) Tìm tập xác định của hàm số    y  tan 2x    .  3       
A. D   \   k k   .
B. D   \   kk   . 12 2   6        
C. D   \ 
kk   .
D. D   \   k k   . 12   6 2  Lời giải Chọn A   
Hàm số y  tan 2x  
 xác định khi và chỉ khi  3         cos 2x   0    2x  
k  x   kk  .  3  3 2 12 2
Câu 75: (THPT Trần Nhân Tông-Quảng Ninh-lần 1 năm 2017-2018) Giải phương trình
cos 2x  2 cos x  3  0 .
A. x    k 2 , k   .
B. x k 2 , k   .   C. x  
k 2 , k   . D. x
k 2 , k   . 2 2
Hướng dẫn giải Chọn B
Ta có cos2x  2 cos x  3  0 2
 2cos x 1 2 cos x  3  0 cosx  1 2
 cos x  cos x  2  0   . cosx  2  
Vì 1  cosx  1 nên cosx  1  x k 2 k  
Vậy tập nghiệm của phương trình là: x k 2 k   .
Câu 76: (THPT Yên Định-Thanh Hóa-lần 1 năm 2017-2018) Nghiệm của phương trình
sin x  3 cos x  2 sin 3x là   2 A. x
k hoặc x   k , k   . 6 6 3  2 B. x
k 2 hoặc x
k 2 , k   . 3 3  4 C. x  
k 2 hoặc x
k 2 , k   . 3 3   D. x   k , k   . 3 2
Hướng dẫn giải Chọn D
Ta có sin x  3 cos x  2 sin 3x 1 3  sin x
cos x  sin 3x 2 2    cos sin x  sin
cos x  sin 3x 3 3     sin x   sin 3x    3    x
 3x k 2  3   
x     3x k2  3   x    k  6      x   k , k   .    3 2 x   k  3 2
Câu 77: (THTT số 5-488 tháng 2 năm 2018) Phương trình 3 cos x  sin x  2 có bao nhiêu nghiệm
trên đoạn 0; 4035 ? A. 2016 . B. 2017 . C. 2011. D. 2018 . Lời giải Chọn B 3 1   
Ta có 3 cos x  sin x  2  cos x  sin x  1   sin x   1    2 2  3   3   x  
k 2 k   7   x
k 2 k   . 3 2 6
Trên đoạn 0; 4035  , các giá trị k   thỏa bài toán thuộc tập 0;1; 2;; 201  6 .
Do đó có 2017 nghiệm của phương trình thuộc đoạn 0; 4035 .
Câu 78: (THPT Mộ Đức-Quãng Ngãi-lần 1 năm 2017-2018) Phương trình 2 sin x 1  0 có bao nhiêu
nghiệm x  0; 2  ? A. 2 nghiệm. B. 1 nghiệm. C. 4 nghiệm. D. Vô số nghiệm. Lời giải Chọn A   x   k 2 1  6
Ta có: 2 sin x 1  0  sin x   
k  . 2 5 x   k 2  6  5
Do x  0; 2  nên ta có x  ; x  . 6 6
Câu 79: (THPT Mộ Đức-Quãng Ngãi-lần 1 năm 2017-2018) Cho phương trình: cos 2x  sin x 1  0  
* . Bằng cách đặt t  sin x 1  t  
1 thì phương trình * trở thành phương trình nào sau đây? A. 2 2
t t  0 . B. 2
t t  2  0. C. 2 2
t t  2  0. D. 2 t   t  0 . Lời giải Chọn A 2 2 2
cos 2x  sin x 1  0  1 2 sin x  sin x 1  0  2 sin x  sin x  0  2
t t  0 .
Câu 1: (SGD Bà Rịa Vũng Tàu-đề 1 năm 2017-2018) Số giá trị nguyên dương của tham số m để phương
trình 4 3 cos x  sin x  2m 1  0 có nghiệm là A. 6 . B. 5 C. 4 D. 3 Lời giải Chọn C
Phương trình 4 3 cos x  sin x  2m 1  0 có nghiệm khi và chỉ khi: 
2    m 2 2 4 3 1 2 1 2
 4m  4m  48  0  3   m  4 .
Vì m là số nguyên dương nên m 1; 2;3;  4 .
Vậy có 4 giá trị nguyên dương của m thỏa yêu cầu bài toán.
Câu 2: (SGD Bà Rịa Vũng Tàu-đề 1 năm 2017-2018) Tập nghiệm của phương trình 2 cos 2x 1  0 là     2 2 
A. S    k2 , 
k 2 , k   . B. S    2k , 
 2k , k   .  3 3   3 3       
C. S    k , 
k , k   .
D. S    k , 
k , k   .  3 3   6 6  Lời giải Chọn C 1 2
Ta có 2 cos 2x 1  0  cos 2x    cos 2 3 2   2x  
k 2  x  
k k   . 3 3
Câu 3: (SGD Bà Rịa Vũng Tàu-đề 2 năm 2017-2018) Cho x là nghiệm của phương trình 0
sin x cos x  2 sin x  cos x  2 thì giá trị của P  3  sin 2x là 0 2 A. P  3 . B. P  3  . C. P  0 . D. P  2 . 2 Lời giải Chọn A 2 t 1
Đặt t  sin x  cos x ,  2  t  2 . Khi đó: sin x cos x
, phương trình đã cho trở thành: 2 2 t 1 t  1  2t  2 2
t  4t  5  0   . 2 t  5  
Với t  5 loại do  2  t  2 .       1
Với t  1ta có: sin x  cos x  1  2 sin x   1    sin x      4   4  2    x    2k     x 2k 4 4      .  3  x   2kx    2k   2  4 4
Với x  2k thì P  3  sin 2 2k   3. 0     Với x
 2k thì P  3  sin 2  2k  3 . 0   2  2  Vậy P  3 . Cách khác.
Khi t  1 thì x là nghiệm của pt sin x  cos x  1 . Suy ra 0
sin x  cos x  1  1 sin 2x  1  sin 2x  0  P  3 . 0 0 0 0
Câu 4: (THPT Hà Huy Tập-Hà Tĩnh-lần 2 năm 2017-2018) Nghiệm của phương trình 2
cos x  cos x  0 thỏa điều kiện 0  x   là     A. x  . B. x   . C. x  . D. x  . 2 2 6 4 Lời giải Chọn A    cos x  0 x   k Ta có 2
cos x  cos x  0     2 k   .  cos x  1   x k 2 
Do 0  x    x  . 2
Câu 5: (THPT Phan Châu Trinh-DakLak-lần 2 năm 2017-2018) Tổng các nghiệm của phương trình
sin x cos x  sin x  cos x  1 trên khoảng 0;2  là A. 2 . B. 4 . C. 3 . D.  . Lời giải Chọn C
Đặt t  sin x  cos x , ( 0  t  2 ) 2 t 1 2  t  1 2 sin .
x cos x  sin . x cos x
. Phương trình đã cho trở thành: 2 2
t  2t  3  0  t  1 (thỏa mãn) hoặc t  3 (loại). k
Với t  1  sin 2x  0  x  . 2  3 
Trong khoảng 0; 2  các nghiệm của phương trình là  ; ;  .  2 2 
Suy ra tổng các nghiệm của phương trình trong khoảng 0;2  là 3 . tan 2x
Câu 6: (THPT Kinh Môn-Hải Dương lần 1 năm 2017-2018) Tập xác định của hàm số y  là cos x tập nào sau đây?   A. D   .
B. D   \   k  , k  .  2        
C. D   \   k  , k   .
D. D   \   k ;
k , k   .  4 2   4 2 2  Lời giải Chọn D      2x   kx   k cos 2x  0   2   4 2 Hàm số xác định khi      , k   cos x  0     x   k x   k   2   2    
Vậy tập xác định là D   \   k ;  k , k   .  4 2 2 
Câu 7: (THPT Kinh Môn-Hải Dương lần 1 năm 2017-2018) Tìm tất cả các số thực của tham số m sao 2  s inx 1    cho hàm số y
đồng biến trên khoảng 0;   . s inx m  2  1 1 A.
m  0 hoặc m  1. B. m   . 2 2 1 1 C. m   . D.
m  0 hoặc m  1. 2 2 Lời giải Chọn D       x  0;    s inx  0; 
1 . Hàm số xác định trong khoảng 0;   khi m  0;  1 hay  2   2  m  0    1 . m  1 
cos x 2m   1    Ta có y 
. Hàm số đồng biến trong khoảng 0; 
 khi và chỉ khi y  0 với sinx  m2  2  1 x
  D  2m 1  0  m   . 2 1 Kết hợp   1 ta có 
m  0 hoặc m  1. 2
Câu 8: (THPT Kinh Môn-Hải Dương lần 1 năm 2017-2018) Số đường tiệm cận của đồ thị hàm số 2 x x  2 y  . x 1 A. 1. B. 4 . C. 3 . D. 2 . Lời giải Chọn C
Tập xác định D   ;
  2  1;   . 2 x x  2  lim
 1  Đồ thị hàm số có tiệm cận ngang là đường thẳng y  1. x x 1 2 x x  2  lim
 1  Đồ thị hàm số có tiệm cận ngang là đường thẳng y  1. x x 1 2 x x  2  x   1  x  2 x  2  lim  1  lim  lim
   Đồ thị hàm số có tiệm cận x 1  x 1 x 1  x 1 x 1  x 1
đứng là đường thẳng x  1 .
Vậy đồ thị hàm số có 3 đường tiệm cận.
Câu 9: (THPT Can Lộc-Hà Tĩnh-lần 1 năm 2017-2018) Tổng tất cả các giá trị nguyên của m để phương
trình 4 sin x  m  4 cos x  2m  5  0 có nghiệm là A. 5 . B. 6 . C. 10 . D. 3 . Lời giải Chọn C
4 sin x  m  4 cos x  2m  5  0  4sin x  m  4 cos x  2m  5 . 2 2
Phương trình có nghiệm khi 2
4  m  4  2m  5  0 2
 3m 12m  7  0 6  57 6  57   m  3 3
Vì m   nên m 0,1, 2,3,  4 .
Vây tổng tất cả các giá trị nguyên của m để phương trình có nghiệm là 10 .
Câu 10: (THPT Can Lộc-Hà Tĩnh-lần 1 năm 2017-2018) Số nghiệm của phương trình  9   15  sin 2x   3cos x   1 2sin x    
với x 0; 2  là  2   2  A. 6 . B. 5 . C. 3 . D. 4 . Lời giải Chọn B  9   15  sin 2x   3cos x   1 2sin x      2   2         sin 2x   3cos x   1 2sin x    
 cos 2x  3sin x  1 2 sin x  2   2   x k sin x  0   2
 2 sin x  sin x  0  1    x
k 2 k   sin x   6  2  5 x   k 2  6   5 
Do x 0; 2  nên x  0; ; 2 ; ;  . Vậy có 5 nghiệm.  6 6 
Câu 11: (THPT Lê Quý Đôn-Hải Phòng lần 1 năm 2017-2018) Hàm số y  sin x đồng biến trên khoảng nào sau đây?  5 7   9 11   7   7 9  A. ;   . B. ;   . C. ;3   . D. ;   .  4 4   4 4   4   4 4  Lời giải Chọn D
Dựa vào định nghĩa đường tròn lượng giác ta thấy hàm số lượng giác cơ bản y  sin x đồng
biến ở góc phần tư thứ nhất và góc phần tư thứ tư.  7 9  Dễ thấy khoảng ; 
 là phần thuộc góc phần tư thứ tư và thứ nhất nên hàm số đồng biến.  4 4 
Câu 12: (THPT Lê Quý Đôn-Quãng Trị-lần 1 năm 2017-2018) Giải phương trình: cos 3 .
x tan 4x  sin 5x . 2    3
A. x k  , x   k .
B. x k 2 , x   k . 3 16 8 16 8     3
C. x k , x   k .
D. x k , x   k . 16 8 2 16 8 Lời giải Chọn C
Điều kiện xác định: cos 4x  0 . 1 1 cos 3 .
x tan 4x  sin 5x  cos 3 .
x sin 4x  sin 5 . x cos 4x
sin 7x  sin x  sin 9x  sin x 2 2 x k
9x  7x k 2
sin 9x  sin 7x       .
9x    7x k 2  x   k  16 8  
Thử qua điều kiện xác định ta thấy x k và x   k thỏa mãn. 16 8 x k
Vậy nghiệm phương trình là    . x   k  16 8
Câu 13: (THPT Chuyên Tiền Giang-lần 1 năm 2017-2018) Phương trình nào dưới đây có tập nghiệm
trùng với tập nghiệm của phương trình sin x  0 ? A. cos x  1  . B. cos x  1.
C. tan x  0 . D. cot x  1. Lời giải Chọn C
sin x  0  x k ;k   . cos x  1
  x    k 2 ;k   .
cos x  1  x k 2 ;k   .
tan x  0  x k ;k   .
Câu 14: (THPT Phan Đình Phùng-Hà Tĩnh-lần 1 năm 2017-2018) Số nghiệm của phương trình  5 
2 cos x  3 trên đoạn 0;  là 2    A. 2 . B. 1. C. 4 . D. 3. Lời giải Chọn D 3 
2 cos x  3  cos x   x  
k 2 , k   . 2 6  5   11 13  Mà x  0; 
và k   nên x   ; ;  . 2     6 6 6 
Câu 15: (THPT Phan Đình Phùng-Hà Tĩnh-lần 1 năm 2017-2018) Giá trị nhỏ nhất của hàm số 2
y  2 cos x  sin 2x  5 . A. 2 . B.  2 . C. 6  2 . D. 6  2 . Lời giải Chọn C    Ta có 2
y  2 cos x  sin 2x  5  cos 2x  sin 2x  6  2 cos 2x   6   .  4       
Do  2  2 cos 2x   2  
nên  2  6  2 cos 2x   6  2  6   .  4   4 
Vậy giá trị nhỏ nhất của hàm số 2
y  2 cos x  sin 2x  5 là 6  2 .
Câu 16: (THPT Lục Ngạn-Bắc Giang-lần 1 năm 2017-2018) Phương trình 3 sin x  cos x m , với m là
tham số có nghiệm khi giá trị của m bằng m  2 m  1 A.  . B.  .
C. 2  m  2 .
D. 1  m  1 . m  2  m  1  Lời giải Chọn C
Phương trình 3 sin x  cos x m có nghiệm khi  2 2 3 1  m 2  m  4  2   m  2 .
Câu 17: (THPT Lục Ngạn-Bắc Giang-lần 1 năm 2017-2018) Phương trình sin 2x  cos x có nghiệm là   k   kx    x   6 3  6 3 A.  k  . B.  k  .    x   k 2
x   k2  2  3     k 2 x   k 2  x   6  6 3 C.  k  . D.  k  .    x   k 2
x   k2  2  2 Lời giải Chọn A   kx       6 3
sin 2x  cos x  sin 2x  sin  x     k  .  2  
x   k2  2  k   2 3 1 x 1
Câu 18: (THTT số 6-489 tháng 3 năm 2018) Tìm giá trị dương của k để lim  9 f 2 x x
với f x   2 ln x  5 : A. k  12 . B. k  2 . C. k  5 . D. k  9 . Lời giải Chọn C 2x 4
Ta có: f  x   f 2  . 2 x  5 9 1 1  k   2 3 1 x 1 x 3k   1  x 3k   1  2 x 2 x Ta có: lim  lim  lim x x x x x x 1  lim 3k   1 
 3k 1 .(Theo đề bài k  0 ). 2 x x 4
Theo đề bài: 3k 1  9.  k  5 . 9
Câu 19: (THTT số 6-489 tháng 3 năm 2018) Với giá trị lớn nhất của a bằng bao nhiêu để phương trình 2 2
a sin x  2 sin 2x  3a cos x  2 có nghiệm? 11 8 A. 2 . B. . C. 4 . D. . 3 3 Lời giải Chọn D 1 cos 2x 1 cos 2x Ta có: 2 2
a sin x  2 sin 2x  3a cos x  2  a
 2 sin 2x  3a  2 2 2
 4 sin 2x  2a cos 2x  4  4a   * . 8
Phương trình * có nghiệm 
a    a2 2 16 4 4 4  2
12a  32a  0  0  a  . 3
Câu 20: (THPT Đặng Thúc Hứa-Nghệ An-lần 1 năm 2017-2018) Cho các giả thiết sau đây. Giả thiết
nào kết luận đường thẳng a song song với mặt phẳng   ?
A. a // b và b    .
B. a //   và    //   .
C. a // b và b //   .
D. a      . Lời giải Chọn D
Câu 21: (THPT Chuyên Hạ Long-Quãng Ninh lần 2 năm 2017-2018) Cho phương trình
cos 2x  2m  3 cos x m 1  0 ( m là tham số). Tìm tất cả các giá trị thực của tham số m để   3 
phương trình có nghiệm thuộc khoảng ;   .  2 2 
A. 1  m  2 . B. m  2 . C. m  1. D. m  1. Lời giải Chọn A
cos 2x  2m  3 cos x m 1  0 2
 2 cos x  2m  3cos x m  2  0   3   2 cos x  
1 cos x  2  m  0  cos x  2  m  0 , vì x  ;    2 2 
 cos x m  2 Ycbt  1
  m  2  0  1  m  2
Câu 22: (THPT Chuyên Hùng Vương-Gia Lai-lần 1 năm 2017-2018) Tính tổng tất cả các nghiệm của
phương trình 3 cos x  sin x  1 trên 0; 2 .  11 5 3 A. . B. . C. . D. . 6 6 3 2 Lời giải Chọn C   x   k 2    1  6
Ta có 3 cos x  sin x  1  cos x      
k  .  6  2 
x    k2  2  3
Do đó các nghiệm trên 0; 2  của phương trình là x  , x  . 6 2  3 5
Vậy tổng tất cả các nghiệm của phương trình trên 0; 2  bằng   . 6 2 3
Câu 23: (THPT Chuyên Trần Phú-Hải Phòng-lần 2 năm 2017-2018) Điều kiện của tham số thực m để
phương trình sin x  m   1 cos x  2 vô nghiệm là m  0 A.  . B. m  2  .
C. 2  m  0 . D. m  0 . m  2  Lời giải Chọn C
Để phương trình sin x  m   1 cos x  2 vô nghiệm thì
 m     2 2 2 1 1 2  2  m  0 .
Câu 24: (THPT Tây Thụy Anh – Thái Bình – lần 1 - năm 2017 – 2018) Tìm tất cả các giá trị của
tham số m để phương trình 2
cos x m 1 có nghiệm. A. m  2 .
B. 1  m  2 . C. m  1.
D. 1  m  2 . Lời giải Chọn D Do 2
0  cos x  1 với x
   nên phương trình có nghiệm khi 0  m 1  1  1  m  2
Câu 25: (THPT Tây Thụy Anh – Thái Bình – lần 1 - năm 2017 – 2018) Đồ thị hàm số 3
y x  3x cắt: 5
A. Đường thẳng y  3 tại hai điểm.
B. Đường thẳng y  tại ba điểm. 3
C. Đường thẳng y  4 tại hai điểm.
D. Trục hoành tại một điểm. Lời giải Chọn B 3 y x  3 . x 2
y  3x  3  0  x  1  . Bảng biến thiên:
Dựa vào bảng biến thiên ta chọn đáp án B.
Câu 26: (THPT Yên Lạc – Vĩnh Phúc – lần 4 - năm 2017 – 2018) Tập tất cả các nghiệm của phương trình 2
sin 2x  2 sin x  6sin x  2 cos x  4  0 là   A. x  
k 2 , k   . B. x  
k 2 , k   . 3 2   C. x
k 2 , k   . D. x
k , k   . 2 2 Lời giải Chọn C
Cách 1: Ta có: 2
sin 2x  2 sin x  6 sin x  2 cos x  4  0   x x x   2 2 sin cos 2 cos
2 sin x  6 sin x  4  0
 2 cos x sin x  
1  2 sin x  2sin x  
1  0  sin x  
1 sin x  cos x  2  0   x   k 2 sin x  1  2       x
k 2 , k   .
sin x  cos x  2      2 sin x   2   VN    4 
Cách 2: Dùng MTCT thử lần lượt các đáp án, thấy C là đáp án đúng.
Câu 27: (THPT Chuyên Vĩnh Phúc – Vĩnh Phúc - Lần 4 năm 2017 – 2018)Tìm số nghiệm của phương trình
sin cos x  0 trên đoạn x 0; 2  . A. 0 . B. 1. C. 2 . D. Vô số. Lời giải Chọn C
Ta có: sin cos x  0  cos x k k  
Vì cos x  1 nên k  0 . Do đó phương trình  cos x  0  x
m m   2  3
Vì x 0; 2  nên x  , x  . 2 2
Câu 28: (ĐHQG TPHCM – Cơ Sở 2 – năm 2017 – 2018) Giả sử M là giá trị lớn nhất và m là giá trị
nhỏ nhất của hàm số y  2  3sin x  cos x . Khi đó M m bằng A. 3  3 . B. 0 . C. 1  3 . D. 1. Lời giải Chọn B 2 2
Ta có:  2  3 1  2  3sin x  cos x  2  3 1 .
Vậy M m  0 .
Câu 29: (SGD Nam Định – năm 2017 – 2018) Mệnh đề nào sau đây đúng?
A. Hàm số y  sin x tuần hoàn với chu kỳ T   .   
B. Hàm số y  sin x đồng biến trên 0;   .  2 
C. Hàm số y  sin x là hàm số chẵn.
D. Đồ thị hàm số y  sin x có tiệm cận ngang. Lời giải Chọn B
Mệnh đề A sai vì hàm số y  sin x tuần hoàn với chu kỳ T  2 .
Mệnh đề C sai vì hàm số y  sin x là hàm số lẻ.
Mệnh đề D sai vì hàm số y  sin x không có tiệm cận ngang.     
Mệnh đề B đúng vì hàm số y  sin x đồng biến trên khoảng  k 2 ;  k 2   .  2 2 
Câu 1: (SGD Thanh Hóa – năm 2017 – 2018) Có tất cả bao nhiêu giá trị nguyên của tham số m để    phương trình 3 2 2
cos 2x  cos 2x m sin x có nghiệm thuộc khoảng 0;   ?  6  A. 3 . B. 0 . C. 2 . D. 1. Lời giải Chọn D Ta có: 3 2 2
cos 2x  cos 2x m sin x 2  x x   2 cos 2 cos 2 1  m sin x 2  x  2 sin
2 cos 2x m  0 2
 2 cos 2x m  0  cos 4x  m 1.     2  1 Có x  0;    4x  0;      cos 4x  1  6   3  2    1 1
Để phương trình có nghiệm x  0;   thì 
 m 1  1  2  m   .  6  2 2
Do m   nên m  1.
Câu 2: (THPT Chuyên Nguyễn Quang Diệu – Đồng Tháp – Lần 5 năm 2017 – 2018) Tìm giá trị nguyên
lớn nhất của a để phương trình 2 2
a sin x  2 sin 2x  3a cos x  2 có nghiệm A. a  3. B. a  2 . C. a  1 . D. a  1  . Lời giải Chọn B 1 cos 2x 1 cos 2x 2 2
a sin x  2 sin 2x  3a cos x  2  a
 2 sin 2x  3a  2 2 2
a a cos 2x  4sin 2x  3a  3a cos 2x  4  4 sin 2x  2a cos 2x  4  4a * 8 * có nghiệm khi
a    a2 2 2 4 4 4 4 2
 12a  32a  0 2
 12a  32a  0  0  a  . 3
Do a   và là số lớn nhất nên a  2 .
Câu 3: (THPT Chuyên Hùng Vương – Gia Lai – Lần 2 năm 2017 – 2018) Phương trình    3    sin 3x     
có bao nhiêu nghiệm thuộc khoảng 0;   ?  3  2  2  A. 3 . B. 4 . C. 1. D. 2 . Lời giải Chọn D    3x     k 2    3  3 3 Ta có: sin 3x        k   3  2  4 3x    k 2  3 3  2 2  2 x    k 3x    k 2   9 3  3 k    k  .   2
3x    k 2   x   k  3 3     4 Vì x  0;   nên x  , x  .  2  3 9   
Vậy phương trình đã cho có hai nghiệm thuộc khoảng 0;   .  2 
Câu 4: (SGD Hà Tĩnh – Lần 2 năm 2017 – 2018) Tổng các nghiệm của phương trình  5 2 
2 cos x  3 sin 2x  3 trên 0;  là: 2    7 7 7 A. . B. . C. . D. 2 . 6 3 2
Hướng dẫn giải Chọn C   2 
2 cos x  3 sin 2x  3  cos 2x  3 sin 2x  2  cos 2x   1    3     2x
k 2  x
k k   . 3 6 5  5 Xét 0  x   0   k 
k  0 , k  1 , k  2 . 2 6 2  7 13
Với k  0  x
; k  1  x
; k  2  x  . 6 6 6 7
Vậy tổng các nghiệm bằng . 2
Câu 5: (THPT Chu Văn An – Hà Nội - năm 2017-2018) Gọi M , m tương ứng là giá trị lớn nhất và giá 2 cos x 1
trị nhỏ nhất của hàm số y
. Khẳng định nào sau đây đúng? cos x  2
A. M  9m  0 .
B. 9M m  0 .
C. 9M m  0 .
D. M m  0 . Lời giải
Chọn C 2 cos x 1 5 Ta có y   2  , cos x  2 cos x  2 5 5 1 5
mà 1  cos x  1  3  cos x  2  1     5   2   3 3 cos x  2 3 cos x  2 1 1 
y  3 . Vậy M
và 1  cos x  1  9M m  0 . 3 3
Câu 6: Phương trình 2 2
4 sin 2x  3sin 2x cos 2x  cos 2x  0 có bao nhiêu nghiệm trong khoảng 0;  ? A. 1. B. 2 . C. 3 . D. 4 .
Câu 7: Phương trình 2 2
4 sin 2x  3sin 2x cos 2x  cos 2x  0 có bao nhiêu nghiệm trong khoảng 0;  ? A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn D
Dễ thấy cos 2x  0 không thỏa mãn phương trình. Do đó, phương trình đã cho tương đương với:    tan 2x  1 x   k   1  8 2 2
4 tan 2x  3 tan 2x 1  0   1   tan 2x    1  1    4 x  arctan   k   2  2   4  2   Xét  
1 , vì x  0;   0   k
   k   1 (do k   ). 8 2 1  1  
Xét 2 , vì x 0;   0  arctan   k      k 1;  2 (do k   ). 2  4  2
Do đó, trong khoảng 0;  thì phương trình đã cho có 3 nghiệm. 1 Câu 8: Cho hàm số 3 2 y x  2x  1 có đồ thị C và đường thẳng 3
d : y  m . Tìm tập hợp tất cả các giá trị của tham số m để d cắt C  tại ba điểm phân biệt.  29   29   29   29  A.  ;1   . B. 1;   . C. 1  ;   . D.  ;1   .  3   3   3   3 
Câu 9: Số nghiệm thuộc đoạn 0;  của phương trình cos x  cos 2x  cos3x 1  0 là A. 4 . B. 3 . C. 1. D. 2 . 1 Câu 10: Cho hàm số 3 2 y x  2x  1 có đồ thị C  và đường thẳng 3
d : y  m . Tìm tập hợp tất cả các giá trị của tham số m để d cắt C  tại ba điểm phân biệt.  29   29   29   29  A.  ;1   . B. 1;   . C. 1  ;   . D.  ;1   .  3   3   3   3  Lời giải Chọn A 2
y  x  4x . x  4 y  0   . x  0  BBT x  0 4  y  0  0  1  y 29   3  29 
Để d cắt C  tại ba điểm phân biệt thì m   ;1   .  3 
Câu 11: Số nghiệm thuộc đoạn 0;  của phương trình cos x  cos 2x  cos3x 1  0 là A. 4 . B. 3 . C. 1. D. 2 . Lời giải Chọn B
Ta có cos x  cos 2x  cos 3x 1  0  x   2 x     3 cos 2 cos 1
4 cos x  3cos x 1  0 3 2
 4 cos x  2 cos x  4 cos x  2  0 .  x  0 cos x  1   x  2  cos x  1  0;    x  .  3  1 cos x   x     2
Câu 12: Số nghiệm thuộc khoảng  
 ;  của phương trình: 2sin x  1 là: A. 1. B. 2 . C. 3 . D. 4 .
Câu 13: Số nghiệm thuộc khoảng  
 ;  của phương trình: 2sin x  1 là: A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn B   x   k 2 1  6 Ta có: sin x    . 2 5 x   k 2  6  5 Mà x     ;   x  ; x
. Vậy phương trình có hai nghiệm thỏa mãn đề bài. 6 6
Câu 14: Nghiệm của phương trình 2 cos 2x  9 sin x  7  0 là   A. x  
k 2 , k   . B. x  
k , k   . 2 2   C. x
k , k   . D. x
k 2 , k   . 2 2
Câu 15: Nghiệm của phương trình 2 cos 2x  9 sin x  7  0 là   A. x  
k 2 , k   . B. x  
k , k   . 2 2   C. x
k , k   . D. x
k 2 , k   . 2 2
Hướng dẫn giải Chọn D  5 sin x  VN  
2 cos 2x  9 sin x  7  0 2
 4sin x  9 sin x  5  0   4  x
k 2 , k   .  2 sin x  1 
Câu 16: Tổng tất cả các nghiệm của phương trình 3cos x 1  0 trên đoạn 0; 4  là 15 17 A. . B. 6 . C. . D. 8 . 2 2
Câu 17: Tổng tất cả các nghiệm của phương trình 3cos x 1  0 trên đoạn 0; 4  là 15 17 A. . B. 6 . C. . D. 8 . 2 2 Lời giải Chọn D 1
x    k 2   
Ta có: 3cos x 1  0  cos x    ( với   0;   , k   ). 3 x     k 2   2 
Mà x 0; 4  nên x ; 
  2 ;  2 ;    4  .
Vậy tổng các nghiệm thỏa mãn đề bài là    
   2    2       4  8 .    1
Câu 18: Số điểm biểu diễn các nghiệm của phương trình sin 2x    
trên đường tròn lượng giác là  3  2 A. 6 . B. 1. C. 4 . D. 2 .    1
Câu 19: Số điểm biểu diễn các nghiệm của phương trình sin 2x    
trên đường tròn lượng giác là  3  2 A. 6 . B. 1. C. 4 . D. 2 . Lời giải Chọn C      2x    k 2 x    k    1  3 6  12 Ta có sin 2x       k    k  .  3  2  5   2x    k 2
x   k  3 6  4
Mỗi họ nghiệm biểu diễn trên đường tròn lượng giác 2 điểm và các điểm khác nhau nên số
điểm biểu diễn các nghiệm là 4 .
Câu 20: Một phương trình có tập nghiệm được biểu diễn trên đường tròn lượng giác là hai điểm M và
N trong hình dưới. y 1 M x -1 O 1 N -1
Phương trình đó là
A. 2 cos x 1  0 .
B. 2 cos x  3  0 .
C. 2 sin x  3  0 .
D. 2sin x 1  0 .
Câu 21: Giá trị lớn nhất của hàm số f x 2
 2sin x  sin 2x 10 là A. 10 . B. 11 2 . C. 11 2 . D. 9  2 .
Câu 22: Một phương trình có tập nghiệm được biểu diễn trên đường tròn lượng giác là hai điểm M và
N trong hình dưới. y 1 M x -1 O 1 N -1
Phương trình đó là
A. 2 cos x 1  0 .
B. 2 cos x  3  0 .
C. 2 sin x  3  0 .
D. 2 sin x 1  0 . Lời giải Chọn A
Hai điểm M , N đối xứng qua trục Ox nên loại đáp án C, D. 1
MN cắt Ox tại điểm có hoành độ bằng . 2 1
Ta có 2 cos x 1  0  cos x
, suy đáp án A đúng. 2
Câu 23: Giá trị lớn nhất của hàm số f x 2
 2 sin x  sin 2x 10 là A.10 . B.11 2 . C. 11 2 . D. 9  2 . Lời giải Chọn C   
Ta có f x 2
 2 sin x  sin 2x 10  11 sin 2x  cos 2x  11 2 sin 2x    .  4           Do 1  sin 2x   1     2  2 sin 2x   2  
nên 11 2 sin 2x   11 2   .  4   4   4     3
Dấu "  ' xảy ra khi sin 2x   1   x    k  
, k   . Vậy max f x  11 2 .  4  8
Câu 24: Giá trị lớn nhất của m để phương trình 2018 cos x  sin
5x m  0 có nghiệm là: 3 A. 1. B. 0 . C. 1. D. . 2
Câu 25: Giá trị lớn nhất của m để phương trình 2018 cos x  sin
5x m  0 có nghiệm là: 3 A. 1. B. 0 . C. 1. D. . 2
Hướng dẫn giải Chọn C
Phương trình tương đương: 2018 cos x  sin 5x  m . cos x  1  Ta có: 2018   cos x  sin 5x  1. 2018 sin 5x  0  cos x  1 
Dấu đẳng thức xảy ra khi  . sin 5x  0  cos x  1
  x  π+k 2π . Khi đó sin 5x  sin 5π  k2π  sin 5π  0   thỏa mãn.
Phương trình có nghiệm thì m  1  m  1.
Vậy giá trị lớn nhất của m là m  1. 1
Câu 26: Giải phương trình sin . x cos x
trên đoạn ; 2018  ta được số nghiệm là: 2 A. 2016 nghiệm. B. 2017 nghiệm. C. 2018 nghiệm. D. 2019 nghiệm. 1
Câu 27: Giải phương trình sin . x cos x
trên đoạn ; 2018  ta được số nghiệm là: 2 A. 2016 nghiệm. B. 2017 nghiệm. C. 2018 nghiệm. D. 2019 nghiệm. Lời giải
Chọn B 1 
Ta có sin x.cos x
 sin 2x  1  x
k  k   . 2 4 3 8071
Khi đó   x  2018   k
 1  k  2017 (Do k là số nguyên). 4 4
Vậy trên đoạn ; 2018  phương trình đã cho có 2017 nghiệm.
Câu 28: Phương trình sin 5x  sin x  0 có bao nhiêu nghiệm thuộc đoạn  2
 018 ; 2018  ? A. 20179 . B. 20181. C. 16144 . D. 16145 .
Câu 29: Phương trình sin 5x  sin x  0 có bao nhiêu nghiệm thuộc đoạn  2
 018 ; 2018  ? A. 20179 . B. 20181 . C. 16144 . D. 16145 . Lời giải Chọn B  π k x   2
Ta có sin 5x  sin x  0  sin 5x  sin x   ,( k   ). π π kx    6 3
Vì x 2018π;2018π nên π k π k + Với x  ta có 2018π   2018π  4036 
k  4036 . Suy ra có 8073 nghiệm. 2 2 π kπ π π k 12109 12107 + Với x   ta có 2  018π    2018π    k  . Suy ra có 12108 6 3 6 3 2 2 nghiệm.
Vậy có 8073 12108  20181 nghiệm thuộc đoạn  2  018 ; 2018  .     3 
Câu 30: Phương trình sin 2x   sin x    
 có tổng các nghiệm thuộc khoảng 0;  bằng  4   4  7 3  A. . B.  . C. . D. . 2 2 4     3 
Câu 31: Phương trình sin 2x   sin x    
 có tổng các nghiệm thuộc khoảng 0;  bằng  4   4  7 3  A. . B.  . C. . D. . 2 2 4 Lời giải Chọn B   3 2x   x   k 2
x    k 2     3   4 4 Ta có sin 2x   sin x          
2 k, l   .  4   4     x   l 2x    x l2   6 3  4 4
Họ nghiệm x    k 2 không có nghiệm nào thuộc khoảng 0;   .  2  2 x   l  0;   0   l
   l 0;  1 . 6 3 6 3  5
Vậy phương trình có hai nghiệm thuộc khoảng 0;   là x  và x  . Từ đó suy ra tổng 6 6
các nghiệm thuộc khoảng 0;   của phương trình này bằng  .   
Câu 32: Tìm tập nghiệm của phương trình: 2 cos 3x   3  0    4   7 2 13 2   5  A.   k ;  k k   . B. 
k 2 k   . 36 3 36 3    6  7 2 13 2   7 13  C.   k ;   k k   . D.   k 2 ; 
k 2 k   36 3 36 3    36 36    
Câu 33: Tìm tập nghiệm của phương trình: 2 cos 3x   3  0    4   7 2 13 2   5  A.   k ;  k k   . B. 
k 2 k   . 36 3 36 3    6  7 2 13 2   7 13  C.   k ;   k k   . D.   k 2 ; 
k 2 k   36 3 36 3    36 36  Lời giải Chọn C       3    5 Ta có: 2 cos 3x   3  0    cos 3x     cos 3x   cos      4   4  2  4  6   5  7 2 3x    k 2 x   k  4 6  36 3     ; k    5 13 2 3x k 2      x    k  4 6    36 3 4 3
Câu 34: Cho phương trình 2 2 sin . x tan x  cos .
x cot x  2sin x cos x
. Tính hiệu nghiệm âm lớn nhất 3
và nghiệm dương nhỏ nhất của phương trình. 3 5 5 A.  . B. . C.  . D.  . 2 6 6 4 3
Câu 35: Cho phương trình 2 2 sin . x tan x  cos .
x cot x  2sin x cos x
. Tính hiệu nghiệm âm lớn nhất 3
và nghiệm dương nhỏ nhất của phương trình. 3 5 5 A.  . B. . C.  . D.  . 2 6 6
Hướng dẫn giải Chọn C k
Điều kiện: sin 2x  0  x  . 2 3 3 sin x cos x 4 3 Phương trình  
 2 sin x cos x  cos x sin x 3 4 3 2 3 4 4 2 2
 sin x  cos x  2sin x cos x
sin x cos x  sin x  cos x2 2 2  sin 2x 3 3   x   k 3  6  sin 2x    k . 2 
x   k  3 2 
Suy ra nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình lần lượt là  và 3 6 2  5 Ta có:     . 3 6 6 sin 2x  2
Câu 36: Tìm tập xác định của hàm số f x  . 1 cos x
A. D   .
B. D   \ k 2  π .
C. D  k 2π .
D. D   \ k  π . sin 2x  2
Câu 37: Tìm tập xác định của hàm số f x  . 1 cos x
A. D   .
B. D   \ k 2  π .
C. D  k 2π .
D. D   \ k  π . Lời giải Chọn B sin 2x  2 Hàm số xác định 
 0  1 cos x  0  x k 2π , k   . 1 cos x
Vậy tập xác định của hàm số là D   \ k 2  π , k   .   3 
Câu 38: Số nghiệm của phương trình 3cos 2x  2 trên  ;  là 2 2    A. 4 . B. 3 . C. 2 . D. 1.   3 
Câu 39: Số nghiệm của phương trình 3cos 2x  2 trên  ;  là 2 2    A. 4 . B. 3 . C. 2 . D. 1. Lời giải Chọn A Cách 1:  2  1 2 2x  arc cos  k 2 x  arccos  k 2  3  2 3 3cos 2x  2  os c 2x      . 3 2  1 2 2x  arc cos  k 2
x   arccos  k  3  2 3  1 2 x  arccos  2 3  1 2 x  arccos    3   2 3 Xét trên  ;  ta có  . 2 2    1 2 x   arccos  2 3  1 2 x   arccos    2 3   3 
Vậy phương trình đã cho có bốn nghiệm trên  ;  . 2 2    Cách 2: Dùng Casio. Dùng chức năng TABLE. Nhập hàm:  3  Cho Start =  , End = , Step = . 4 2 12
Kết quả có bốn lần đổi dấu như sau:
Chú ý: Tắt đi hàm g X  như sau:
Bấm SHIFT, MODE, di chuyển xuống, chọn 5: TABLE Sau đó chọn 1:
Câu 1: (THTT Số 1-484 tháng 10 năm 2017-2018) Tính tổng S các nghiệm của phương trình  x   4 4 2 cos 2
5 sin x  cos x  3  0 trong khoảng 0;2  . 11 7 A. S  . B. S  4 . C. S  5 . D. S  . 6 6 Lời giải Chọn B Ta có:  x   4 4 x x     x   2 2 2 cos 2 5 sin cos 3 0 2 cos 2
5 sin x  cos x  3  0 1
  2cos 2x  5 2
cos 2x  3  0  2
 cos (2x)  5 cos 2x  3  0  cos 2x  . 2 1   5 7 11  cos 2x   x  
k k    x   ; ; ;  . 2 6  6 6 6 6   5 7 11 Do đó: S      4 . 6 6 6 6
Câu 2: (THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018) Nghiệm của phương trình
cos 2x  3sin x  2  0 là: cos x   x   k 2  2    x   k   6 A.x   k k  . B.
k  .  6 5   x   k 5    6 x   k  6   x   k 2  2    x   k 2   6 C.x   k 2 k  . D.
k  .  6 5   x   k 2 5    6 x   k 2  6 Lời giải Chọn D
Cách 1: Điều kiện xác định: cos x  0  x
l với l   . 2
Khi đó phương trình trở thành sin x  1 (1)
cos 2x  3sin x  2  0 2
 2 sin x  3sin x 1  0   1 sin x  (2)  2   x   k 2  6
Đối chiếu điều kiện ta loại phương trình (1) . Giải phương trình (2) được  5 x   k 2  6 với k   .
Cách 2: Dùng máy tính
Bước 1: nhập vế trái của phương trình.
Bước 2: nhấn CALC thay X bằng các kết quả trong mỗi phương án.
Bước 3: chọn đáp án nào đều trả về kết quả bằng hoặc rất “gần” 0 .
(chú ý đơn vị ra-đi-an).
Câu 3: (THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018) Tập giá trị của hàm số
y  sin 2x  3 cos 2x 1 là đoạn a; b. Tính tổng T a  . b A. T  1. B. T  2. C. T  0. D. T  1. Lời giải
Chọn B
Cách 1: y  sin 2x  3 cos 2x 1  sin 2x  3 cos 2x y 1 2 2
Để phương trình trên có nghiệm thì 2      y   2 1 3 1
y  2 y  3  0  1   y  3 . Suy ra y  1  ;  3 . Vậy T  1   3  2.
Cách 2: Ta có y 1  sin 2x  3 cos 2 .
x Mặt khác áp dụng bất đẳng thức Bunhiacopskii ta có 2  y  2   x c x     2 2 1 sin 2 3 os2 1 3 sin 2x  os c 2x  4  2
  y 1  2  1  y  3.
Vậy T  1 3  2.   
Cách 3: y  sin 2x  3 cos 2x 1  2 sin 2x  1    3        Do sin 2x     1;  1 nên 2 sin 2x  1    1  ;  3 .  3   3       
Vậy 1  y  3 .( Ta thấy y  1 khi sin 2x   1   
, y  3 khi sin 2x   1   ).sss  3   3 
Câu 4: (THPT Sơn Tây-Hà Nội-lần 1-năm 2017-2018) Gọi K là tập hợp tất cả các giá trị của tham số     3 
m để phương trình sin 2x  2 sin x   2  m  
có đúng hai nghiệm thuộc khoảng 0;   .  4   4 
Hỏi K là tập con của tập hợp nào dưới đây?  2 2   2   2  A.   ;  . B. 1 2; 2  . C.   2; . D.   ; 2 .    2 2      2   2   Lời giải Chọn C   
Cách 1: Đặt t  2 sin x   s inx  cos x  
, t   2; 2  .  4    Suy ra 2
t  1 sin 2x  2
t t  3  m
Xét hàm số y f t  2
t t  3 , t   2; 2   
f t   2t 1 1
f t   0  t     2; 2  2       3 
Phương trình sin 2x  2 sin x   2  m  
có đúng hai nghiệm thuộc khoảng 0;    4   4   Phương trình 2
t t  3  m có đúng một nghiệm t  1; 2  t 1 2
f t  2 1
f t 1  2 
Dựa vào bảng biến thiên ta thấy K  1; 2   1    2;   2        3 
Cách 2 : Xét hàm số f x  sin 2x  2 sin x   2   với x  0;   .  4   4    
Ta có f  x  2 cos 2x  2 cos x    , vậy  4    
f  x  0  2cos 2x  2 cos x   0    4   2  2 2
cos x  sin x  cos x  sin x  0
cos x  sin x  0
 2cos x sin x1 0     3  x   0;    4  4        2 2 sin x  1  0    *   4   3      3  Vì trong khoảng 0;   thì sin x   0  
nên phương trình * vô nghiệm trên 0;   .  4   4   4  Lập bảng biến thiên  3 x 0 4 4
f  x  0  2 1
f x 1 3   3 
Vậy để phương trình đã cho có hai nghiệm phân biệt trên khoảng 0;   thì  4    m   1  ; 2   2 1    2; .   2   
Câu 5: (THPT Yên Lạc-Vĩnh Phúc-lần 1-năm 2017-2018) Hằng ngày, mực nước của con kênh lên
xuống theo thủy triều. Độ sâu h m của mực nước trong kênh tính theo thời gian t h được   t  
cho bởi công thức h  3cos  12    6 3  .
Khi nào mực nước của kênh là cao nhất với thời gian ngắn nhất?
A. t  22 h .
B. t  15h .
C. t  14 h .
D. t  10h . Lời giải
Chọn D     Ta có: 1  cos t   1  
 9  h  15 . Do đó mực nước cao nhất của kênh là 15m đạt  6 3        được khi cos t   1    t
k 2  t  2  12k  6 3  6 3 1 Vì t  0  2
 12k  0  k  6 1
Chọn số k nguyên dương nhỏ nhất thoả k
là k  1  t  10 . 6
Câu 6: (THPT Yên Lạc-Vĩnh Phúc-lần 1-đề 2-năm 2017-2018) Hằng ngày, mực nước của con kênh lên
xuống theo thủy triều. Độ sâu h m của mực nước trong kênh tính theo thời gian t h được   t  
cho bởi công thức h  3cos  12    6 3  .
Khi nào mực nước của kênh là cao nhất với thời gian ngắn nhất?
A. t  22 h .
B. t  15h .
C. t  14 h .
D. t  10 h . Lời giải
Chọn D     Ta có: 1  cos t   1  
 9  h  15 . Do đó mực nước cao nhất của kênh là 15m đạt  6 3        được khi cos t   1    t
k 2  t  2  12k  6 3  6 3 1 Vì t  0  2
 12k  0  k  6 1
Chọn số k nguyên dương nhỏ nhất thoả k
là k  1  t  10 . 6
Câu 7: (THPT Yên Lạc 2-Vĩnh Phúc-lần 1-năm 2017-2018) Cho phương trình cos 5x  3m  5 . Gọi đoạn  ;
a b là tập hợp tất cả các giá trị của m để phương trình có nghiệm. Tính 3a b . 19 A. 5 . B. 2  . C. . D. 6 . 3 Giải: Chọn D 4
Phương trình đã cho có nghiệm khi 1  3m  5  1  4  3m  6   m  2 . 3  4 
Khi đó tập hợp tất cả các giá trị của m để phương trình có nghiệm là ; 2  . 3    4 Ta được a
; b  2 . Suy ra 3a b  6 . 3
Câu 8: (THPT Hai Bà Trưng-Vĩnh Phúc-lần 1-năm 2017-2018) Trong các hàm số sau hàm số nào    
đồng biến trên khoảng  ;   ?  2 2 
A. y  cot x .
B. y   tan x .
C. y  cos x .
D. y  sin x . Lời giải Chọn D
[Phương pháp tự luận]    
Hàm số y  sin x đồng biến trên các khoảng   k 2 ;  k 2 
 với mọi k   . Chọn  2 2     
k  0 , ta được hàm số y  sin x đồng biến trên khoảng  ;   .  2 2     
Xét A: Hàm số y  cot x không xác định tại x  0   ; 
 nên không thể đồng biến trên  2 2      khoảng  ;    2 2       4 3     Xét B:Ta thấy 
 Hàm số y   tan x không thể đồng biến trên  ;       2 2   tan   tan   4 3      4 3     Xét C: Ta thấy 
 Hàm số y  cos x không thể đồng biến trên  ;       2 2  cos  cos   4 3
[Phương pháp trắc nghiệm]
Thực hiện chuyển đơn vị: Shift mode 4.Rad.   
Vào mode 7, nhập hàm y  cot x , START  , END , STEP
. Nhìn bảng thấy giá trị 2 2 19
hàm số luôn giảm nên sai.
Tương tự với các hàm còn lại, chọn kết quả y  sin x có giá trị hàm số luôn tăng.
Câu 9: (THPT Hai Bà Trưng-Vĩnh Phúc-lần 1-năm 2017-2018) Phương trình 2 2 cos x  1 có số nghiệm trên đoạn  2   ; 2  là A. 2. B. 4. C. 6. D. 8. Lời giải Chọn Dk Ta có 2 2
2 cos x  1  2 cos x 1  0  os c
2x  0  x   ; k  .  4 2  k 9 7 Vì x  2
  ; 2  nên ta có 2      2    k  . 4 2 2 2
Mặt khác k   nên k nhận các giá trị 4  ; 3  ;  2; 1;0;1; 2;3.
Vậy phương trình đã cho có tám nghiệm trên  2   ; 2  .
Câu 10: (THTT Số 2-485 tháng 11-năm học 2017-2018) Cho hàm số y f x . Đồ thị hàm số y f
x nhận gốc tọa độ làm tâm đối xứng như hình vẽ sau y 2  O 2 x
Khẳng định nào sau đây SAI?
A. Đồ thị hàm số y f x có ba điểm cực trị.
B. Đồ thị hàm số y f x nhận trục tung làm trục đối xứng.
C. Đồ thị hàm số y f x cắt trục hoành tại 4 điểm.
D. Đồ thị hàm số y f x có hai điểm uốn. Lời giải
Chọn C
Ta có dựa vào đồ thị thì y ' là hàm số bậc 3 . Do y f  x là hàm số lẻ và f  x  0 có 3 nghiệm phân biệt nên nó có dạng 3
y  ax cx a  0, c  0 . Do đó 4 2 2 x x x y ac   2
ax  2c  m . 4 2 4
Dễ thấy f  x đổi dấu qua 3 nghiệm nên hàm số có 3 cực trị nên đáp án A. đúng. 4 2 2 x x x
Hàm số y ac   2
ax  2c  m là hàm số chẵn nên đồ thị nhận trục tung làm trục 4 2 4
đối xứng, nên đáp án B. đúng. Ta có 2
y  3ax c vì a  0, c  0 nên phương trình y  0 có hai nghiệm phân biệt nên hàm
số luôn có hai điểm uốn, do đó đáp án D. đúng.
Câu 11: (THTT Số 2-485 tháng 11-năm học 2017-2018) Để giải phương trình: tan x tan 2x  1 có ba bạn
An, Lộc, Sơn giải tóm tắt ba cách khác nhau như sau:   x   k   2
+ An: Điều kiện  , k .   x   k   4 2     k
Phương trình tan x tan 2x  1  tan 2x  cot x  tan  x x      2  6 3  k
Nên nghiệm phương trình là x   , k . 6 3
+ Lộc: Điều kiện tan x  1  . Phương trình I 1   tan x    x  
k , k là nghiệm. 3 6 cos x  0 cos x  0 
+ Sơn: Điều kiện    1 . 2 cos 2x  0 sin x     2 sin x sin 2x Ta có 2
tan x tan 2x  1  .  1  2sin .
x cos x  cos x cos 2x cos x cos 2x 1   2 2 2 2
 2 sin x  cos 2x  1 2 sin x  sin x   sin  x  
k 2 , k là nghiệm. 4 6 6
Hỏi, bạn nào sau đây giải đúng? A. An. B. Lộc. C. Sơn. D. An, Lộc, Sơn. Lời giải
Chọn B
+ An: Giải sai do không kiểm tra lại điều kiện để loại nghiệm x
k , k . 2 1  
+ Sơn: Giải sai ở bước biến đổi: 2 2 sin x   sin  x  
k 2 , k . 4 6 6
Do đó chọn đáp án B.
Câu 12: (THTT Số 2-485 tháng 11-năm học 2017-2018) Tập nghiệm S của phương trình
cos 2x  5cos 5x  3  10 cos 2x cos3x là     
A. S    k2 , k   . B. S  
k 2 , k   .  3   6        C. S  
k , k   . D. S  
k 2 , k   .  3   3  Lời giải Chọn D
Ta có cos 2x  5cos5x  3  10 cos 2x cos 3x 1
 cos 2x  5 cos 5x  3  10  cos 5x  cos x 2 2
 2 cos x 1 5 cos 5x  3  5 cos 5x  5 cos x 2
 2 cos x  5 cos x  2  0
cos x  2  1 (L) 1    1  cos x   x  
k 2 , k   . cos x  2 3  2
Câu 13: (THTT Số 2-485 tháng 11-năm học 2017-2018) Số nghiệm của phương trình 2 cos x  2 cos 3 .
x sin x  2  0 trong khoảng 0;  là A. 0 . B. 1. C. 2 . D. 3 . Lời giải
Chọn A Ta có 2 cos x  2 cos 3 .
x sin x  2  0, x 0;  . 1 2  2 cos 3 .
x sin x  1 sin x  2 cos 3x  sin x    1 sin x 1
Do x 0;   nên sin x  0, áp dụng bất đẳng thức Cauchy cho hai số dương sin x và ta sin x 1 1 có sin x   2 sin x   2 . sin x sin x
Mặt khác, ta có 2 cos 3x  2 với mọi x . cos 3x  1 Vậy   1 xảy ra   sin x  1   3
Từ sin x  1  x
(do x 0;  ); lúc đó cos 3x  cos
 0 . Hệ trên vô nghiệm. 2 2
Vậy phương trình đã cho không có nghiệm thuộc khoảng 0;  .
Câu 14: (THTT Số 2-485 tháng 11-năm học 2017-2018) Có bao nhiêu giá trị của tham số thực a để
cos x a sin x 1 hàm số y
có giá trị lớn nhất y  1. cos x  2 A. 0 . B. 1. C. 2 . D. 3 .
Lời giải
Chọn C Do 1
  cos x  1 nên cos x  2  1 với mọi giá trị thực của x , vậy hàm số xác định với mọi x   .
cos x a sin x 1 Ta có y
a sin x  1 y cos x  2 y 1   1 . cos x  2 Điều kiện để   1 có nghiệm là 2 2 1 1 3a 1 1 3a
a  1 y2  2y  2 2 2 2 1
 3y  2 y a  0   y  . 3 3 2 1 1 3a
Vậy giá trị lớn nhất của y bằng . Theo giả thiết, ta có 3 2 1 1 3aa  1 2 2 2
 1  1 3a  2  3a 1  4  a  1   . 3 a  1  
Vậy có hai giá trị thực của tham số a thỏa mãn yêu cầu bài toán.
Câu 15: (THPT Chuyên Vĩnh Phúc-lần 2-năm 2017-2018) Tính tổng tất cả các nghiệm của phương
trình sin 2x  4 sin x  2 cos x  4  0 trong đoạn 0;100  của phương trình.
A. 100 . B. 2476 . C. 25 . D. 2475 . Lời giải Chọn D
Ta có sin 2x  4 sin x  2 cos x  4  0  2 sin x cos x  4 sin x  2 cos x  4  0
 2 sin x cos x  2  2cos x  2  0  cos x  2sin x   1  0  sin x  1    x
k 2 k   .
cos x  2VN  2 
Cách 1: Trong đoạn 0;100  , phương trình có các nghiệm      ;  2 ;  4 ;  6 ;...;  98 2 2 2 2 2 Tổng các nghiệm bằng       S    2   4   6  ...   98  50.
 2  4  6  ...  98. 2 2 2 2 2 2 2  98.49 S  25  .  2475 . 2 
Cách 2: Tìm k thỏa mãn 0 
k 2  100  0  k  49 2 49    Bấm máy S   k 2  2475   . k 0  2 
Câu 16: (THPT Bình Xuyên-Vĩnh Phúc-năm 2017-2018) Giá trị nhỏ nhất của hàm số của hàm số 2
y  1 2 sin x cos x  cos 2x là: 5 1 A.  . B.  . C. 1. D. 0 . 4 4 Lời giải Chọn B
Tập xác định D   . 2
y  1 2sin x cos x  cos 2x 2
 1 sin 2x  cos 2x 2
 sin 2x  sin 2x   2 x    k  1  1 1 1  12 y   sin 2x     
. Dấu "  " xảy ra khi sin 2x     , k .  2  4 4 2 7  x   k  12 1  7
Vậy giá trị nhỏ nhất bằng 
đạt được khi x    k ; x
k , k . 4 12 12 Câu 17: (THPT Bình Xuyên-Vĩnh Phúc-năm 2017-2018) Tìm m để hàm số   3 2 
y  3m sin x  sin x  sin x m  2 đồng biến trên khoảng  ; 0   ?  2  1 1 A. m  3 . B. m  0 . C. m  . D. m   . 3 3 Lời giải Chọn D
Tập xác định D   .   
Đặt t  sin x , vì x   ;0   nên t   1  ; 0 .  2 
Khi đó hàm số trở thành 3 2
y  3mt t t m  2, t  1;0   1 2
y  9mt  2t 1 Để hàm số  
1 đồng biến thì y  0 t    1  ; 0 2
 9mt  2t 1  0 t    1  ; 0 2 2t 1 2t 1  m
đặt f t   2 9t 2 9t 2t  2
Ta có f t    0 t    1  ; 0 3 9t 1
Do đó m f   1   3 1 Vậy m   . 3 Câu 18: (THPT Bình Xuyên-Vĩnh Phúc-năm 2017-2018) Phương trình  x x x x 2 sin sin 2 sin sin 2
 sin 3x tương đương với phương trình nào sau đây:
A. sin x  sin 2x  sin 3xcos x  cos 2x  0 . B. sin x  sin 3xsin x  0 .
C. sin x  sin 2x  sin 3xsin x  sin 2x  0 . D. sin x  sin 3xsin 3x  0 . Lời giải Chọn D Ta có  x x x x 2 2 2 2 sin sin 2 sin sin 2
 sin 3x  sin x  sin 2x  sin 3x 1 cos 2x 1 cos 4x 1 2    sin 3x
cos 4x  cos 2x 2  sin 3x 2 2 2 2   sin 3 .
x sin x  sin 3x  sin 3x sin x  sin 3x  0 .
Câu 19: (THPT Nguyễn Khuyến-TPHCM-năm 2017-2018) Một đường thẳng cắt đồ thị hàm số 4 2
y x  2x tại bốn điểm M , N , P , Q . Biết hai điểm M , N có hoành độ lần lượt là 0 và
1. Tính S x x với x , x là hoành độ điểm P và điểm Q . P Q P Q A. S  1 . B. S  1. C. S  2  . D. S  1. Lời giải Chọn C
Giả sử d : y ax b là đường thẳng cắt đồ thị hàm số nói trên tại bốn điểm M , N , P,Q . Ta có phương
trình hoành độ giao điểm 4 2
x  2x ax b  
1 . Vì x  0 là nghiệm của   1 nên b  0 .
Lại vì x  1 là nghiệm của   1 nên a  1
 . Do đó, phương trình   4 2
x x x
x x   2 1 2 0
1 x x   1  0 .
Suy ra x , x là nghiệm của phương trình 2
x x 1  0 . Từ đó ta có S x x  1. p Q P Q
Câu 20: (THPT Cổ Loa-Hà Nội-lần 1-nawm-2018) Số nghiệm của phương trình 2
4  x .cos 3x  0 là A. 7 . B. 2 . C. 4 . D. 6 . Lời giải Chọn D Điều kiện 2 4  x  0  2   x  2 .  x   2 2 4  x  0 Khi đó 2 4 x .cos 3x 0         . cos 3x  0  x   k , k     6 3
So với điều kiện, ta thấy x   2 (thỏa điều kiện).     Với x   k
, k   , ta có 2   k
 2 , vì k   nên k  2  ; k  1
 ; k  0 ; k  1. 6 3 6 3
Vậy phương trình đã cho có 6 nghiệm.
Câu 21: (THPT Cổ Loa-Hà Nội-lần 1-nawm-2018) Gọi M và N lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của hàm số y 1 2 cos  x 2 3 sin x cos      
x trên  . Biểu thức M N  2 có   giá trị bằng A. 0 . B. 4 2  3 . C. 2 . D. 2  3  2 . Lời giải Chọn C Ta có y 1 2 cos  x 2 3 sin x cos       x       2 1 2 2
3 sin x cos x  2 cos x       x   2 2 3 sin 2 2 cos x  
1  2  3sin 2x  cos 2x     6  2 1  6 2 sin 2x  cos 2 
x   6  2 sin 2x   4 6  2   6  2 1 (với  cos ;  sin ) 4 6  2
Suy ra  6  2  y  6  2 . Do đó max y  6  2  M ; min y   6  2  N .  
Vậy M N  2  2 .
Câu 22: (THPT Cổ Loa-Hà Nội-lần 1-nawm-2018) Tìm tất cả các giá trị của tham số m để phương    trình 2 2
cos 4x  cos 3x m sin x có nghiệm x  0;   .  12   1   1   1  A. m  0;   . B. m  ; 2   .
C. m  0;  1 . D. m  1  ;   .  2   2   4  Lời giải Chọn C Ta có 2 2
cos 4x  cos 3x m sin x   2 2 2 cos 2x  
1  1 cos 6x m m cos 2x 2 3
 4 cos 2x  2  1 4 cos 2x  3cos 2x m m cos 2x 3 2
 4 cos 2x  4 cos 2x  m  3 cos 2x m  3  0 2
 4 cos 2x cos 2x  
1  m  3cos 2x   1  0 cos 2x  1   x   2 cos 2
1 4 cos 2x m  3  0   . 2
4 cos 2x m  3 
Với cos 2x  1  x k không thỏa yêu cầu bài toán.    3
Phương trình có nghiệm x  0;   suy ra  cos 2x  1  12  2 3 m  3  
 1  3  m  3  4  0  m  1. 4 4  3 
Câu 23: (THTT Số 3-486 tháng 12 năm 2017-2018) Tìm số nghiệm thuộc ;     của phương trình  2   3  3 sin x  cos  2  x  .  2  A. 0 . B. 1. C. 2 . D. 3 . Lời giải
Chọn B  3  3 3 Ta có 3 sin x  cos  2x  cos cos 2x  sin
sin 2x  3 sin x  0    2  2 2 sin x  0  x   k sin x 2cos x 3  0        3  5   với k   . cos  x x   k 2  2  6  3  5 7   Trên ;   
 ta nhận được nghiệm duy nhất x   2  .  2  6 6
Câu 24: (THPT Lục Ngạn-Bắc Ninh-lần 1 năm 2017-2018) Giá trị lớn nhất của hàm số
sin x  cos x 1 y  bằng?
sin x  cos x  3 1 1 A. 3 . B. 1. C.  . D. . 7 7 Lời giải Chọn D
Tập xác định D   .
sin x  cos x 1 Ta có y
sin x  cos x  3
y sin x  cos x  3  sin x  cos x 1   y  
1 sin x   y  
1 cos x  1 3y  2 2 2
Để  có nghiệm   y   1   y   1   1   3y  2 2
2 y  2  1 6 y  9 y  2
7 y  6 y 1  0 1  1  y  . 7 1 Vậy max y  .  7    
Câu 1: (THPT Triệu Sơn 1-lần 1 năm 2017-2018) Số nghiệm nằm trong đoạn  ;  của phương 2 2   
trình sin 5x  sin 3x  sin 4x là A. 5 . B. 7 . C. 9 . D. 3 . Lời giải Chọn Akx   4 sin 4x  0  
sin 5x  sin 3x  sin 4x  2sin 4x cos x  sin 4x    1  x   k 2 k  . cos x   3  2    x    k 2  3 k        
Trường hợp 1: x  , với x   ;
, ta được x   ;0;  . 4  2 2     4 4        
Trường hợp 2 : x
k 2 , với x   ;
, ta được x   . 3  2 2     3         
Trường hợp 3 : x  
k 2 , với x   ;
, ta được x    . 3  2 2     3     
Vậy phương trình đã cho có 5 nghiệm nằm trong đoạn  ;  . 2 2   
Câu 2: (THPT Triệu Sơn 1-lần 1 năm 2017-2018) Hàm số y  cos x là hoàn tuần hoàn với chu kì là   A. . B. . C. 0 . D. . 2 4 Lời giải Chọn D 1 cos 2x 2 Ta có 2
y  cos x  cos x
nên hàm số tuần hoàn với chu kỳ T    . 2 2
Câu 3: (THPT Chuyên Vĩnh Phúc-MĐ 903 lần 1-năm 2017-2018) Tất cả các giá trị của m để phương  
trình cos 2x  2m  
1 cos x m 1  0 có đúng 2 nghiệm   x   ; là   2 2 
A. 1  m  1.
B. 1  m  0 .
C. 0  m  1.
D. 0  m  1. Lời giải Chọn C Ta có
cos 2x  2m  
1 cos x m 1  0 2
 2 cos x  2m  
1 cos x m  0  1 cos x    2cos x  
1 cos x m  0   2 . cos x m    1
Phương trình đã cho có đúng 2 nghiệm   x   ;
khi và chỉ khi 0  cos x  1 nên loại cos x     2 2  2  
Vậy phương trình đã cho có đúng 2 nghiệm   x   ;
khi và chỉ khi 0  m  1 .   2 2 
Câu 4: (THPT Kim Liên-Hà Nội năm 2017-2018) Hàm số y  2 cos 3x  3sin 3x  2 có tất cả bao nhiêu giá trị nguyên? A. 7 . B. 3 . C. 5 . D. 6 . Lời giải Chọn A TXD: D    2 3 
y  2 cos 3x  3sin 3x  2  13 cos 3x  sin 3x  2    13 13   3 
y  13 sin 3x  arccos  2    13   3 
Để hàm số y có giá trị nguyên  13 sin 3x  arccos   nguyên  13   3  n  sin 3x  arccos   
( với n là một số nguyên)  13  13  3  Mà: sin 3x  arccos    1  ;1  13  n  1  
 1   13  n  13 13 Mà: n  
n  0; 1; 2   3
y có 7 giá trị nguyên.
Câu 5: (THPT Chuyên Lương Văn Tụy-Ninh Bình lần 1 năm 2017-2018) Số giá trị nguyên của tham
số m thuộc đoạn 2018; 201  8 để phương trình m   2
1 sin x  sin 2x  cos 2x  0 A. 4037 . B. 4036 . C. 2019 . D. 2020 . Lời giải Chọn Dm   2
1 sin x  sin 2x  cos 2x  0 1 cos 2x  m   1
 sin 2x  cos 2x  0 2  1 m m 1 
cos 2x  sin 2x      2  2 2 2  1 m  2  m 1 
Điều kiện có nghiệm của phương trình      1    m  1    2   2 
Suy ra 2018  m  1
Suy ra có 2020 giá trị nguyên của m để phương trình có nghiệm. sin x 1
Câu 6: (THPT Chuyên Trần Phú-Hải Phòng lần 1 năm 2017-2018) Phương trình  có bao x 2 nhiêu nghiệm? A. Vô số nghiệm. B. Vô nghiệm. C. 3 nghiệm. D. 2 nghiệm. Lời giải
Chọn D
Tập xác định: D   \   0 .
Phương trình tương đương với 2sin x x   1 .
Số nghiệm của phương trình  
1 là số giao điểm của đồ thị hai hàm số y  2 sin x và y x .
Trên hệ trục Oxy vẽ đồ thị các hàm số y  2sin x và y x y y x y  2 sin x x O
Từ đồ thị ta thấy, đồ thị hai hàm số chỉ cắt nhau tại ba điểm trong đó có một điểm có hoành
độ x  0 không thỏa mãn phương trình. Do vậy, phương trình có hai nghiệm phân biệt. 3
Câu 7: (THPT Đoàn Thượng-Hải Dương-lần 2 năm 2017-2018) Phương trình 2
cos 2x  cos 2x   0 4
có bao nhiêu nghiệm x   2   ; 7  ? A. 16 . B. 20 . C. 18 . D. 19 . Lời giải Chọn C 3 1 3 Ta có: 2
cos 2x  cos 2x   0  cos 2x  hoặc cos 2x   (loại). 4 2 2 1   Với cos 2x   2x  
k 2  x  
k k  . 2 3 6 
Phương trình có nghiệm x  2
  ; 7  khi và chỉ khi 2    k  7 . 6  13 41
+ Trường hợp 1: 2 
k  7    k  . Vì k   nên 6 6 6
k 2; 1;0;1; 2;3; 4;5; 
6 do đó có 9 nghiệm thuộc khoảng 2 ;7  .  11 43
+ Trường hợp 2: 2  
k  7    k  . Vì k   nên 6 6 6
k 1;0;1; 2;3;4;5;6; 
7 do đó có 9 nghiệm thuộc khoảng 2 ;7  . Vậy có tất cả 18
nghiệm thỏa mãn bài toán.
Câu 8: (THPT Triệu Thị Trinh-lần 1 năm 2017-2018) Tìm m để phương trình sau có nghiệm
cos x  2 sin x  3 m  :
2 cos x  sin x  4 2
A. 2  m  0 .
B. 2  m  1  .
C. 0  m  1 . D.m  2 . 11 Lời giải Chọn D
Có 2 cos x  sin x  4  0, x    .
PT m 2 cos x  sin x  4  cos x  2sin x  3  2m  
1 cos x  m  2sin x  4m  3  0 . 2 2 2
Phương trình trên có nghiệm khi 2m  
1  m  2  4m  3 2 2
 11m  24m  4  0   m  2 . 11 cos x  sin 2x
Câu 9: (THPT Chuyên Thái Bình-lần 2 năm học 2017-2018) Cho phương trình 1  0 . cos 3x
Khẳng định nào dưới đây là đúng:
A. Phương trình đã cho vô nghiệm. 
B. Nghiệm âm lớn nhất của phương trình là x   . 2
C. Phương trình tương đương với phương trình sin x   1 2sin x   1  0 .
D. Điều kiện xác định của phương trình là x  2 cos
3  4 cos x  0 . Lời giải Chọn A   
Điều kiện: cos 3x  0  3x
k  x   kk  . 2 6 3 Ta có
cos x  sin 2x 1 0 cos 3x
cos x  sin 2x  cos 3x   0 cos 3x cos x  2
1 2 sin x  4 cos x  3   0 cos 3x  cos x  2
1 2 sin x  4 cos x  3  0  cos x  2 4
 sin x  2 sin x  2  0   cos x  0   sin x  1   1 sin x    2 Ta có x x  2 cos 3 cos
4 cos x  3 nên ta loại cos x  0 và sin x  1. 1 1 3 1 Ngoài ra 2 2 sin x    cos x  1 
 4 cos x  3  0 nên ta loại tiếp sin x   . 2 4 4 2
Vậy phương trình đã cho vô nghiệm. cos 4x
Câu 10: (THPT Chuyên Thái Bình-lần 2 năm học 2017-2018) Phương trình
 tan 2x có bao nhiêu cos 2x    nghiệm thuộc khoảng 0,   ?  2  A. 1. B. 3 . C. 4 . D. 2 . Lời giải Chọn D   
Điều kiện cos 2x  0  2x
k  x   k , k   . 2 4 2
Phương trình tương đương với cos 4x  sin 2x 2
 2 sin 2x  sin 2x 1  0 sin 2x  1   L   1 sin 2x   N   2     2x   k 2  x   k 6  12       
, k   . Do x  0; 
 nên phương trình chỉ có hai 5  5  2  2x   k 2 x   k  6  12  5 nghiệm là x  và x  . 12 12  4  
Câu 11: (THPT Chuyên ĐHSP-Hà Nội-lần 1 năm 2017-2018) Số nghiệm thuộc khoảng  ;    3 2    
của phương trình cos   x  3 sin x  sin 3x    là  2  A. 4 . B. 3 . C. 6 . D. 2 . Lời giải Chọn C Ta có:   
cos   x  3 sin x  sin 3x  
   cos x  3 sin x   cos 3x  2 
 2sin 2x sin x  3 sin x  0  sin x 2sin 2x  3  0  x k sin x  0      3  x
k , k   . sin 2x   6  2   x   k  3  4   4  4 1 
Với x k , trên nửa khoảng  ;   ta có:   k     k   3 2  3 2 3 2  k 1; 
0 . Suy ra các nghiệm là x    , x  0 .   4   4   3 1  Với x
k , trên nửa khoảng  ;   ta có:    k     k  6  3 2  3 6 2 2 3 5   k 1; 
0 . Suy ra các nghiệm là x   , x  . 6 6   4   4   5 1  Với x
k , trên nửa khoảng  ;   ta có:    k     k  3  3 2  3 3 2 3 6 2   k 1; 
0 . Suy ra các nghiệm là x   , x  . 3 3  4  
Suy ra số nghiệm trên nửa khoảng  ; 
 của phương trình là 6 .  3 2 
Câu 12: (THTT Số 4-487 tháng 1 năm 2017-2018) Số nghiệm trên khoảng 0;2  của phương trình 4
27 cos x  8sin x  12 là A. 1. B. 2 . C. 3 . D. 4 . Lời giải
Chọn D Ta có: 4
27 cos x  8sin x  12 4 2
 27 sin x  54 sin x  8sin x 15  0   2 x x   2 3sin 2sin
3 9 sin x  6 sin x  5  0 2
3sin x  2sin x  3  0   2
9 sin x  6sin x  5  0   1   10 sin x   1;  1  3 2
3sin x  2 sin x  3  0    1   10 sin x    1   ;1  3 1 10 Với sin x
trên khoảng 0; 2  phương trình có 2 nghiệm.(dựa vào số giao điểm 3 1   10
giữa đồ thị hàm số y  sin x và đường thẳng y  ). 3  1 6 sin x    1   ;1  3 2
9 sin x  6 sin x  5  0    1 6 sin x   1;  1  3 1 6 Với sin x
trên khoảng 0;2  phương trình có 2 nghiệm.(dựa vào số giao điểm giữa 3 1 6
đồ thị hàm số y  sin x và đường thẳng y  ). 3
Vậy trên khoảng 0; 2  phương trình đã cho có 4 nghiệm.
Câu 13: (THPT Chuyên Phan Bội Châu-Nghệ An- lần 1 năm 2017-2018) Có bao nhiêu giá trị nguyên
của tham số m để hàm số y  5  m sin x  m  
1 cos x xác định trên  ? A. 6 . B. 8 . C. 7 . D. 5 . Lời giải Chọn B
Hàm số xác định trên 
 5  m sin x  m   1 cos x  0 x
    m sin x  m   1 cos x  5 x   
 Max msin x  m   1 cos x  5 . x
m  m  2 2 2 1
 25  m m 12  0  m 4;  3 .
Vậy có 8 giá trị nguyên của m thỏa mãn.
Câu 14: (THPT Chuyên Phan Bội Châu-Nghệ An- lần 1 năm 2017-2018) Cho đa giác đều 20 đỉnh.
Lấy ngẫu nhiên 3 đỉnh. Tính xác suất để 3 đỉnh đó là 3 đỉnh của 1 tam giác vuông không cân. 2 17 8 3 A. . B. . C. . D. . 35 114 57 19 Lời giải Chọn C
Số cách chọn 3 đỉnh n  3  C 20
Gọi O là đường tròn ngoại tiếp đa giác đều 20 cạnh, đường tròn này có 10 đường kính tạo
thành từ 20 đỉnh của đa giác đó.
Chọn một đường kính bất kì, đường kính này chia đường tròn này thành 2 phần, mỗi phần có 9 đỉnh của đa giác
Khi đó mỗi phần có 8 tam giác vuông không cân (trừ đỉnh chính giữa)
Vậy số tam giác vuông không cân được tạo thành từ 20 đỉnh của đa giác là
n A  8.2.10  160 8
Vậy xác suất cần tìm là p A  57
Câu 15: (THPT Chuyên Thái Bình-lần 3 năm 2017-2018) Số các giá trị thực của tham số m để phương trình  x   2 sin
1 2 cos x  2m  
1 cos x m  0 có đúng 4 nghiệm thực thuộc đoạn 0;2  là: A. 1. B. 2 . C. 3 . D. vô số. Hướng dẫn giải Chọn B sin x  1
Ta có phương trình tương đương  2
2 cos x  2m  
1 cos x m  0  sin x  1 sin x  1  1    cos x  2cos x  
1 cos x m  0   2 cos x m
Với x 0; 2  . Ta có:  
sin x  1  x
vì x 0; 2  nên x  (thỏa mãn). 2 2     x x  1   3  3 cos x   cos x  cos  
vì x 0; 2  nên  (thỏa mãn). 2 3  5  5 x    2  x   3 3  3
Với 1  m  1 , đặt m  cos ,  0;  .
Nhận xét: Với x 0; 2  thì phương trình  x  
cos x m  cos x  cos   * . x     2 
Do đó, phương trình có 4 nghiệm thực phân biệt khi và chỉ khi phương trình * có 
đúng một nghiệm hoặc có 2 nghiệm phân biệt và một nghiệm bằng . 2   5 Trường hợp 1:   
  2     (thỏa vì khác , ,
). Suy ra m  cos  1. 2 3 3  3  Trường hợp 3:       2 
(thỏa). Suy ra m  cos  0 . 2 2 2
Vậy m 0;  
1 nên có 2 giá trị m .
Câu 16: (THPT Hoài Ân-Hải Phòng năm 2017-2018) Tìm giá trị lớn nhất M của hàm số
sin x  2 cos x 1 y  .
sin x  cos x  2 A. M  2 . B. M  3 . C. M  3 . D. M  1 . Lời giải Chọn D
Ta có sin x  cos x  2  0 , x    .
Biến đổi hàm số về dạng phương trình ta được:
y sin x  cos x  2  sin x  2 cos x 1   y  
1 sin x   y  2 cos x  1 2 y .   1 2 2 2 Phương trình  
1 có nghiệm khi:  y     y      y 2 1 2 1 2
 2 y  2 y  4  0  2   y  1.
Vậy giá trị lớn nhất M  1 .
Câu 17: (THPT Lê Hoàn-Thanh Hóa-lần 1 năm 2017-2018) Số nghiệm của phương trình    
cos 2x  3 cos x 1  0 trong đoạn  ;  là: 2 2    A. 4 . B. 3 . C. 2 . D. 1. Lời giải Chọn C
Ta có: cos 2x  3 cos x 1  0 2
 2 cos x  3 cos x  2  0 .
Đặt t  cos x , 0  t  1 , ta được phương trình: t  2  1 2
2t  3t  2  0   1  t  . (vì 0  t  1 ) t  2  2  1   cos x x    k 2 1 1  2  3  Với t  , ta có: cos x       x  
k k   . 2 2 1  2 3 cos x   x    k 2  2  3      Trên đoạn  ; 
phương trình có nghiệm là x   . 2 2    3   
Câu 18: (THPT Ninh Giang-Hải Dương năm 2017-2018) Phương trình: 2 sin 2x   3  0   có  3 
mấy nghiệm thuộc khoảng 0;3  . A. 6 . B. 2 . C. 4 . D. 8 . Lời giải Chọn A    2x    k 2       3  3 3 Ta có 2 sin 2x   3  0    2 sin 2x        3   3  2  
2x      k2  3 3   x   k  3
 4 7  3 5   
, k   . Vì x  0;3  nên x   ; ; ; ; ;  .    3 3 3 2 2 2  x   k  2
Câu 19: (THPT Phan Đăng Lưu-Huế-lần 1 năm 2017-2018) Số nghiệm của phương trình 2
sin x sin 2x  2 sin x cos x  sin x  cos x  3cos2x trong khoảng    ;  là: sin x  cos x A. 2 . B. 4 . C. 3 . D. 5 . Lời giải Chọn A     
Điều kiện sin x  cos x  0  sin x   0    x
k  x  
k ,k  .  4  4 4 2
sin x sin 2x  2 sin x cos x  sin x  cos x Ta có:  3 cos 2x sin x  cos x
sin 2x sin x  cos x  sin x  cos x   3 cos 2x sin x  cos x sin 2x  
1 sin x  cos x   3 cos 2x sin x  cos x      
 sin 2x  3 cos 2x  1  sin 2x   sin       3   6       2x     k 2  x   k 3 6  12    
k  .    3 2x      k 2 x   k  3 6  4 
Thử lại điều kiện, phương trình đã cho có nghiệm là: x
k k  . 12  11 Trên  
 ;  phương trình đã cho có các nghiệm là: ;  . 12 12
Câu 20: (THPT Quãng Xương 1-Thanh Hóa năm 2017-2018) Tổng S các nghiệm của phương trình: 2
2 cos 2x  5 cos 2x  3  0 trong khoảng 0; 2  là 7 11 A. S  5 . B. S  . C. S  4 . D. S  . 6 6 Lời giải Chọn C cos 2x  3   1  Ta có 2
2 cos 2x  5 cos 2x  3  0  1 . cos 2x   2     2x   k 2 x   k 1  3  6 Với cos 2x      k  . 2    2x    k 2
x    k  3  6  7 5 11
Do x  0; 2  nên ta có các nghiệm x  , x  , x  , x  . 6 6 6 6  7 5 11
Tổng các nghiệm của phương trình S      4 . 6 6 6 6
Câu 21: (THPT Đô Lương 4-Nghệ An năm 2017-2018) Biết phương trình 3 2
ax bx cx d  0 với
a  0 có đúng hai nghiệm thực. Hỏi đồ thị hàm số 3 2
y ax bx cx d có bao nhiêu điểm cực trị? A. 3 . B. 5 . C. 2 . D. 4 . Lời giải Chọn A Vì phương trình 3 2
ax bx cx d  0 với a  0 có đúng hai nghiệm thực nên đồ thị hàm số 3 2
y ax bx cx d có hai điểm cực trị trong đó một điểm cực trị nằm trên trục hoành. Các dạng của đồ thị hàm số 3 2
y ax bx cx d trong trường hợp này được mô tả như sau:
Trường hợp 1: a  0
Trường hợp 2: a  0
Vậy với a  0 đồ thị hàm số 3 2
y ax bx cx d luôn có ba điểm cực trị.
Câu 22: (THPT Hậu Lộc 2-Thanh Hóa năm 2017-2018) Nghiệm lớn nhất của phương trình
2 cos 2x 1  0 trong đoạn 0;  là: 11 2 5 A. x   . B. x  . C. x  . D. x  . 12 3 6 Lời giải Chọn D     2x   k2 x   k 1  3  6
Phương trình 2 cos 2x 1  0  cos 2x      . 2    2x    k 2
x    k  3  6    1 5   0   k     k x  6  6 6 k  0  6
Xét x 0;      mà k   suy ra   .    1 7 k  1 5 0    k     k    x   6 6 6  6 5
Vậy nghiệm lớn nhất của phương trình 2 cos 2x 1  0 trong đoạn 0;  là x  . 6
Câu 23: (THPT Hậu Lộc 2-Thanh Hóa năm 2017-2018) Giá trị nhỏ nhất và giá trị lớn nhất của hàm số sin x  cos x y  lần lượt là:
2 sin x  cos x  3 1 1
A. m  1; M  .
B. m  1; M  2 .
C. m   ; M  1 .
D. m  1; M  2 . 2 2 Lời giải Chọn B
Ta có: 2 sin x  cos x  3  0 với x   . sin x  cos x y
y 2sin x  cos x  3  sin x  cos x .
2 sin x  cos x  3  2y  
1 sin x   y  
1 cos x  3y (*). sin x  cos x Hàm số y  xác định với x
   nên (*) có nghiệm.
2 sin x  cos x  3
  y  2   y  2   y2 2 1 1 3 .  1  y  2 . sin x  cos x
Nên giá trị nhỏ nhất và giá trị lớn nhất của hàm số y  lần lượt là:
2 sin x  cos x  3
m  1; M  2 .
Câu 24: (THPT Hoàng Hoa Thám-Hưng Yên-lần 1 năm 2017-2018) Cho phương trình m
m sin x  m   1 cos x
. Số các giá trị nguyên dương của m nhỏ hơn 10 để phương trình cos x có nghiệm là: A. 9 . B. 8 . C. 10 . D. 7 . Lời giải Chọn A m
m sin x  m   1 cos x   m x
x  m   2 sin cos
1 cos x m  cos x m m 1 sin 2x
1 cos 2x  m msin 2x  m  
1 cos 2x m 1  0 có nghiêm khi và chỉ 2 2 khi m  4 
m  m  2    m2 2 1 1  2
m  4m  0  
. Do đó số các giá trị nguyên dương của m m  0  nhỏ hơn 10 là 9 .
Câu 1: (SGD Bà Rịa Vũng Tàu-đề 1 năm 2017-2018) Cho x là nghiệm của phương trình 0   
sin x cos x  2 sin x  cos x  2 thì giá trị của P  sin x   là 0   4  2 1 2 A. P  . B. P  1 . C. P  . D. P   . 2 2 2 Lời giải Chọn A   
Đặt t  sin x  cos x  2 sin x  
 , t   2; 2  .  4    2 t 1 Ta có 2 2 2
t  sin x  cos x  2 sin .
x cos x  1 2 sin .
x cos x , suy ra sin . x cos x  . 2
Phương trình đã cho trở thành 2 t  1 t 1 2
 2t  2  t  4t  5  0   . 2
t  5   2; 2           2
Từ đó ta có 2 sin x   1    sin x     .  4   4  2    2
Như vậy P  sin x    . 0   4  2
Câu 2: (SGD Bà Rịa Vũng Tàu-đề 2 năm 2017-2018) Số giá trị nguyên của tham số m để phương trình
4 3 cos x  sin x  2m 1  0 có nghiệm là A. 8 . B. 6 . C. 9 . D. 7 . Lời giải Chọn A
Ta có: 4 3 cos x  sin x  2m 1  0  sin x  4 3 cos x  1 2m . 2 2
Phương trình có nghiệm khi 2 2 2
a b c  1 4 3  1 2m 2
 4m  4m  48  0  3
  m  4  m  3  ; 2  ; 1  ;0;1; 2;3;  4 .
Vậy có 8 giá trị nguyên của m để phương trình đã cho có nghiệm. Câu 3:
(THPT Hà Huy Tập-Hà Tĩnh-lần 2 năm 2017-2018) Để phương trình 2 2 2 a
sin x a  2 
có nghiệm, tham số a phải thỏa mãn điều kiện: 2 1 tan x cos 2xa  1 
A. a   3 . B.  . C. a  4 . D. a  1 . a  3   Lời giải Chọn B 2 sin  x  1 cosx  0  * ĐKXĐ:    1 cos2x  0 2  sin x    2 * Ta có: 2 2 2 a
sin x a  2  2 2 2 2
a cos x  sin x a  2 2 2 2
 a sin x  sin x  2 2 1 tan x cos 2x 2 2  sin x  2 1 a
Để phương trình đã cho có nghiệm điều kiện là  2  0;1  2   1 a  2   0;1  2   2  2 1   a 1    a  2  a  1    1     . 2   1 a 2  2 1  1   a  4 a  3      2 1 2 1    a 2   2 1   a 2
Câu 4: (THPT Lý Thái Tổ-Bắc Ninh-lần 1 năm 2017-2018) Tính tổng tất cả các giá trị nguyên của hàm
3sin x  cos x  4 số y  .
2 sin x  cos x  3 A. 8 . B. 5 . C. 6 . D. 9 . Lời giải Chọn C
3sin x  cos x  4 y
 2sin x  cos x  3 y  3sin x  cos x  4
2 sin x  cos x  3
 2y  3sin x   y  
1 cos x  3y  4  0 2 2 2
Điều kiện phương trình có nghiệm: 2 y  3   y   1  4  3y 1 2 2 2
 4 y 12 y  9  y  2 y 1  16  24 y  9 y 2  4
y 14 y  6  0   y  3 . 2
Vậy tổng tất cả các giá trị nguyên của hàm số bằng 6 .
Câu 5: (THPT Kinh Môn-Hải Dương lần 1 năm 2017-2018) Cho phương trình 2018 2018 x x   2020 2020 sin cos 2 sin x  cos
x . Tính tổng các nghiệm của phương trình trong khoảng 0; 2018 2 2  1285   1285  A.    . B.  2 643  . C.  2 642  . D.    .  4   2  Lời giải Chọn D 2018 2018 x x   2020 2020 sin cos 2 sin x  cos x 2018  x  2  x 2018  x  2 sin 1 2 sin cos 1 2 cos x  0 cos 2x  0 2018 2018  sin . x cos 2x  cos
x cos 2x  0   . 2018 2018 sin x  cos x    k
 cos 2x  0  2x
k  x   k     1 2 4 2   2018 2018 sin x  cos x 2018  tan x  1 ( x
k không là nghiệm)  tan x  1  2   k  x  
k k   2 . Từ  
1 và 2 ta có x  
k  là nghiệm của pt. 4 4 2  k
Do x 0;2018  0  
 2018  0  k  1284, k   . 4 2
Vậy tổng các nghiệm của phương trình trong khoảng 0; 2018 bằng 2    1284.1285  1285 
.1285  1 2  ... 1284  .1285       . 4 2 4 4  2 
Câu 6: (THPT Lê Quý Đôn-Hải Phòng lần 1 năm 2017-2018) Biểu diễn tập nghiệm của phương trình
cos x  cos 2x  cos 3x  0 trên đường tròn lượng giác ta được số điểm cuối là A. 6 . B. 5 . C. 4 . D. 2 . Lời giải Chọn A
Ta có cos x  cos 2x  cos 3x  0  cos 3x  cos x  cos 2x  0  2 cos 2 .
x cos x  cos 2x  0  cos 2x 2cos x   1  0      2x   kx   k  2  4 2 cos 2x  0   2 2     1  x   k 2  x   k 2 , k   cos x    3  3  2   2 2  x    k 2  x    k 2  3  3
Vậy biểu diễn tập nghiệm của phương trình cos x  cos 2x  cos 3x  0 trên đường tròn lượng
giác ta được số điểm cuối là 6 .
Câu 7: (THPT Đức THọ-Hà Tĩnh-lần 1 năm 2017-2018) Số nghiệm của phương trình   2 2 
cos x  sin 2x  2  cos  x
 trên khoảng 0;3  là  2  A. 2 . B. 3 . C. 4. D. 1. Lời giải
Chọn B   2 2 
cos x  sin 2x  2  cos  x 2 2 
  cos x  sin 2x
2  sin x  cos 2x  sin 2x  2  2           2 cos 2x   2    cos 2x   1    2x
k 2  x  
k k    4   4  4 8 7 15 23
Trên 0;3   x  , x  , x  . 8 8 8
Câu 8: (SGD Hà Nội-lần 11 năm 2017-2018) Số nghiệm chung của hai phương trình 2
4 cos x  3  0 và   3 
2sin x 1  0 trên khoảng  ;   bằng  2 2  A. 2 . B. 4 . C. 3 . D. 1. Lời giải Chọn A   3  1  Trên khoảng  ; 
 phương trình 2 sin x 1  0  sin x   có hai nghiệm là  và  2 2  2 6 7 . 6
Cả hai nghiệm này đều thỏa phương trình 2 4 cos x  3  0 .
Vậy hai phương trình có 2 nghiệm chung.
Câu 9: (THTT số 6-489 tháng 3 năm 2018) Số giờ có ánh sáng của một thành phố X ở vĩ độ 40 bắc
trong ngày thứ t của một năm không nhuận được cho bởi hàm số:   
d t   3sin t  80 12 
, t   và 0  t  365 . Vào ngày nào trong năm thì thành phố X 182   
có nhiều giờ ánh sáng nhất? A. 262 . B. 353 . C. 80 . D. 171. Lời giải Chọn D   
Ta có: d t   3sin t  80 12   3 12  15 182         Dấu bằng xảy ra khi sin t  80  1   t  80 
k 2 k   182    182 2
t    k . 171 194
Mặt khác t 0;365 nên     k  365    k  . 364 364
Mà k   nên k  0 . Vậy t  171.
Câu 10: (THPT Nguyễn Trãi-Đà Nẵng-lần 1 năm 2017-2018) Cho phương trình       4 sin x  cos x  2   
  a  3 sin 2x  cos 2x  
1 . Gọi n là số giá trị nguyên của tham số  3   6 
a để phương trình  
1 có nghiệm. Tính n . A. n  5 . B. n  3 . C. n  2 . D. n  1 . Lời giải Chọn A      Ta có   1  2 sin 2x  1 2   
  a  3 sin 2x  cos 2x   6   2 2    a    a  sin 2x  1     sin 2x     cos 2x  1 .  6  2  6  2 2 a Phương trình   1 có nghiệm  1  1  2
  a  2 , Do a   nên a  0; a  1; a  2 2 Vậy n  5 .
Câu 11: (THPT Chuyên Hà Tĩnh-lần 1 năm 2017-2018) Tổng tất cả các giá trị của tham số thực m sao cho đồ thị hàm số 3 2 3
y x  3mx  4m có điểm cực đại và cực tiểu đối xứng với nhau qua
đường phân giác của góc phần tư thứ nhất là 2 1 1 A. . B. . C. 0 . D. . 2 2 4 Lời giải Chọn Cx  0 Ta có: 2
y  3x  6mx , y  0   . x  2m
Để hàm số có cực đại cực tiểu thì m  0 .
Khi đó các điểm cực trị của đồ thị hàm số là A 3
0; 4m  , B 2m;0 . Ta có I  3
m ; 2m  là trung điểm của đoạn thẳng AB .
Đường phân giác của góc phần tư thứ nhất là d : x y  0 .
Do đó để điểm cực đại và cực tiểu đối xứng với nhau qua d thì: 3 
2m  4m  0 2 2 
 1 2m  0  m   . 3
m  2m  0 2 
Vậy tổng tất cả các giá trị của tham số thực m là 0 .
Câu 12: (PTNK-ĐHQG TP HCM-lần 1 năm 2017-2018) Giả sử M là giá trị lớn nhất và m là giá trị
sin x  2 cos x 1
nhỏ nhất của hàm số y
trên  . Tìm M m .
sin x  cos x  2 A. 1 2 . B. 0 . C. 1. D. 1  . Lời giải Chọn D
Tập xác định: D   .
sin x  2 cos x 1 Ta có y    y  
1 sin x   y  2 cos x  1 2y (*).
sin x  cos x  2
Hàm số đạt giá trị lớn nhất, nhỏ nhất khi (*) có nghiệm
   y2   y  2   y  2 1 2 1 2 2
 2 y  2 y  4  0  2  y  1.
Do đó m  2 , M  1 .
Câu 13: (PTNK-ĐHQG TP HCM-lần 1 năm 2017-2018) Tìm m để phương trình 1
1 sin x  sin x   m có nghiệm. 2 1 6 6 A.m  .
B. 0  m  1 .
C. 0  m  3 . D.m  3 . 2 2 2 Lời giải Chọn D  1   1
Đặt t  sin x t  1 
 , phương trình trở thành 1 t t   m  2  2
Nhận xét phương trình ban đầu có nghiệm x khi và chỉ khi phương trình * có nghiệm  1  1  1  t   ; 
. Xét hàm f t   1 t t  , với t   ;1 . 2      2  2  1 1 1 t t   2t 1 1
Ta có: f t  2 2      2 1 t 1 1 1  1  2 t  2 1 t t  2 1 t t
 1 t t   2 2 2 2   1
f t   0  t  . 4 Ta có bảng biến thiên: 1 1 t  1 2 4
f t ||  0  || 3
f t 6 6 2 2 6
Dựa vào bảng biến thiên, phương trình đã cho có nghiệm   m  3 . 2
Câu 14: (THPT Hồng Bàng – Hải Phòng – năm 2017 – 2018) Gọi M , m lần lượt là giá trị lớn nhất   
và giá trị nhỏ nhất của hàm số y x  2 cos x trên đoạn 0; 
. Tính M m . 2        A. 1 2 . B.  2 . C. 1 . D. 1 2 . 4 2 4 4 Lời giải Chọn A   
Xét hàm y x  2 cos x trên đoạn 0;  . 2   
y  1 2 sin x .   x   k 2 1  4
y  0  sin x    . 2 3 x   k 2  4     Do x  0;  x   . 2    4        
Ta có y 0  2 ; y  1   ; y    .  4  4  2  2    
Vậy M  max y y  1  
; m  min y y 0  2 .       0;  4  4  0; 2       2   Nên M m  1 2 . 4
Câu 15: (THPT Quảng Xương I – Thanh Hóa – năm 2017 – 2018) Tìm tổng tất cả các nghiệm
thuộc đoạn 0;10  của phương trình 2
sin 2x  3sin 2x  2  0 . 105 297 299 A. .
B. S.ABCD . C. . D. . 2 4 4 Lời giải Chọn A sin 2x  1  Ta có: 2
sin 2x  3sin 2x  2  0  
 sin 2x  1  x  
k , k   . sin 2x  2  (loaïi) 4  1 41 Theo đề bài: 0    k  10   k
k  1, 2,...,10 . 4 4 4 3  3   3  105
Vậy tổng các nghiệm là S      ...   9      . 4  4   4  2
Câu 16: (THPT Chuyên Thoại Ngọc Hầu – An Giang - Lần 3 năm 2017 – 2018) Có bao nhiêu giá trị m
nguyên của tham số m để phương trình 6 6
sin x  cos x  3sin x cos x   2  0 có nghiệm 4 thực? A. 13 . B. 15 . C. 7 . D. 9 . Lời giải
Chọn A m m Ta có 6 6
sin x  cos x  3sin x cos x   2  0  2 2
1 3sin x cos x  3sin x cos x   2  0 4 4
Đặt t  sin 2x , 1   t  1. PT trở thành 2
3t  6t 12  m .
Xét hàm số f t  2  3
t  6t 12 , 1   t  1 t 1 1 f t   15 f t  3 m Phương trình 6 6
sin x  cos x  3sin x cos x
 2  0 có nghiệm thực khi 3  m  15 . 4
Vậy có 13 giá trị nguyên của tham số m .
Câu 17: (THPT Chuyên ĐHSP – Hà Nội - Lần 1 năm 2017 – 2018) Cho hai điểm A , B thuộc đồ
thị hàm số y  sin x trên đoạn 0; . Các điểm C , D thuộc trục Ox thỏa mãn ABCD là hình 2 chữ nhật và CD
. Độ dài cạnh BC bằng 3 y A BO D C x 3 1 2 A. . B. 1. C. . D. . 2 2 2 Lời giải Chọn C  2  2 x x x x B AB A   1
Gọi Ax ; y , B x ; y . Ta có:  3   3 B B A A   y y sin  x  sin xB AB A  2 Thay   1 vào 2 , ta được:  2  2  sin x
 sin x x
   x k 2  x   k  k   A   3 A A  3 A A 6   1
Do x 0;  nên x
BC AD  sin  . A 6 6 2
Câu 18: (THPT Kim Liên – Hà Nội - Lần 2 năm 2017 – 2018)Một vật nặng treo bởi một chiếc lò xo,
chuyển động lên xuống qua vị trí cân bằng (hình vẽ). Khoảng cách h từ vật đến vị trí cân bằng
ở thời điểm t giây được tính theo công thức h d trong đó d  5sin 6t  4 cos 6t với d được tính bằng centimet. h Vị trí cân bằng
Ta quy ước rằng d  0 khi vật ở trên vị trí cân bằng, d  0 khi vật ở dưới vị trí cân bằng. Hỏi
trong giây đầu tiên, có bao nhiêu thời điểm vật ở xa vị trí cân bằng nhất? A. 0 . B. 4 . C. 1. D. 2 . Lời giải
Chọn D  5 cos    41
Ta có h d  5sin 6t  4 cos 6t  41 sin 6t     41 , với  . 4 sin      41
Do đó vật ở xa vị trí cân bằng nhất h
 41 khi sin 6t     1  cos 6t    0 max      6t   
k  t     k . 2 6 12 6     1 6  1
Trong giây đầu tiên, 0  t  1  0     k  1    k     k 0  ;1 . 6 12 6  2   2
Vậy có 2 lần vật ở xa vị trí cân bằng nhất.
Câu 19: (THPT Trần Phú – Đà Nẵng - Lần 2 – năm 2017 – 2018) Cho phương trình
3 tan x 1sin x  2cos x  msin x  3cos x . Có tất cả bao nhiêu giá trị nguyên tham số m   
thuộc đoạn 2018; 201 
8 để phương trình trên có nghiệm duy nhất x  0;   ?  2  A. 2018 . B. 2015 . C. 4036 . D. 2016 . Lời giải
Chọn A    Với x  0; 
 thì cos x  0 , chia hai vế cho cos x , ta được:  2 
3 tan x 1sin x  2 cos x  m sin x  3cos x  3 tan x 1 tan x  2  m tan x  3
3 tan x 1  tan x  2   m .   1 tan x  3 2    3t t   1 Đặt t
tan x 1 , x  0;  t  0;      . Khi đó:  
1  g t    m . 2 2  2  t  2 3t  2 t   1 4 2 3t 15t  6
Xét hàm g t  
trên 0;  . gt    0, t   0 . 2 t  2 t  22 2 m   
Suy ra để thỏa yêu cầu bài toán  m g 0  0 . Mà  . m   2018;2018 
Suy ra m 1; 2;3;...; 201  8 .
Câu 1: (Tạp chí THTT – Tháng 4 năm 2017 – 2018) Phương trình 1 sin x  1 cos x m có nghiệm khi và chỉ khi
A. 2  m  2 . B. 1  m
4  2 2 . C. 1  m  2 .
D. 0  m  1 . Lời giải Chọn B TXĐ: D   .
Đặt P  1 sin x  1 cos x , P  0 . Suy ra 2
P  2  sin x  cos x  2 1 sin x  cos x  sin x cos x .   
Đặt t  sin x  cos x  2 sin x  
  t   2 ; 2  .  4    2 t 1 Khi đó 2
t  1 2 sin x cos x  sin x cos x  . 2 2 t 1 Do đó 2
P  2  t  2 1 t
 2  t  2 t 1 . 2 TH1:  2  t  1  thì 2
P  1 2t  2  2 . Khi đó 2
1  P  4  2 2 .
TH2: 1  t  2 thì 2
P  1 2 t  2  2 . Khi đó 2
1  P  4  2 2 . Do đó 2
1  P  4  2 2 mà P  0 nên 1  P  4  2 2 .
Phương trình có nghiệm khi 1  m  4  2 2 .
Câu 2: (THPT Chu Văn An – Hà Nội - năm 2017-2018) Phương trình cos 2 .
x sin 5x 1  0 có bao  π 
nhiêu nghiệm thuộc đoạn  ; 2π  ? 2    A. 2 . B. 1. C. 4 . D. 3 . Lời giải
Chọn B  π 2π x    k si  n 7x  1   14 7 cos 2 .
x sin 5x 1  0  sin 7x  sin 3x  2       , h k   sin 3x 1  π 2π
x    h   6 3  π  Do x   ; 2π   h 0;1; 2;  3 . 2    π 2π π 2π 28h  4 Ta có   k    hk
, do k   nên chỉ có h  1 thỏa mãn. 14 7 6 3 12
Vậy phương trình đã cho có một nghiệm thỏa yêu cầu bài toán.
Câu 3: (SGD Bắc Ninh – Lần 2 - năm 2017-2018) Gọi S là tổng tất cả các nghiệm thuộc 0;20  của phương trình 2
2 cos x  sin x 1  0 . Khi đó, giá trị của S bằng : 200 A. S  570 . B. S  295 . C. S  590 . D. S   . 3 Lời giải Chọn B   x    k 2 1  2 sin x  1    2
2 cos x  sin x 1  0 2  2
 sin x  sin x 1  0    1  x   k 2  2 sin x   6  2  5  x   k 2 3  6
k ,k , k  1 2 3 
Do x 0;20  nên:   1 41 0    k 2  20  k  1  2 1  4 4   k  1; 2;3;...;10 1      1 119  0   k 2  20    k
 k  0;1; 2;...;9 2   2 6 2  12 12    5  5 115 k  0;1; 2;...;9  3   0   k 2  20   k  3  3   6  12 12
Vậy tổng các nghiệm của phương trình trong đoạn 0;20  là: 10    9    9  5  S    k 2    k 2   k 2  295 . 1    2    3  k   6 k   6 k   2    1 1 2 0 2 0
Câu 4: (THPT Đặng Thúc Hứa – Nghệ An - năm 2017-2018) Gọi S là tập hợp các nghiệm thuộc khoảng 2  x x  
0;100  của phương trình sin  cos  3 cos x  3  
. Tổng các phần tử của S là  2 2  7400 7525 7375 7550 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn C 2  x x  Ta có sin  cos  3 cos x  3  
 1  sin x  3 cos x  3  sin x  3 cos x  2  2 2  1 3      sin x
cos x  1  sin x   1    x
k 2 , k   . 2 2  3  6  1 599
Theo đề bài cho ta có 0  x  100  0 
k 2  100    k  6 12 12
Mà k    k 0;1;2;3;4,....;48;  49     50 Vậy S    2   2  2  ......   49  2 
 2 1 2  3  4  .....  49 6 6 6 6 6 50 4949   1 7375   2  . 6 2 3
Câu 5: Gọi S là tập hợp tất cả các nghiệm thuộc khoảng 0; 2018 của phương trình sau:
3 1 cos 2x  sin 2x  4 cos x  8  4 3   1 sin x
Tính tổng tất cả các phần tử của S . 310408 312341 A. 103255 . B. . C. . D. 102827 . 3 3
Câu 6: Gọi S là tập hợp tất cả các nghiệm thuộc khoảng 0; 2018 của phương trình sau:
3 1 cos 2x  sin 2x  4 cos x  8  4 3   1 sin x
Tính tổng tất cả các phần tử của S . 310408 312341 A. 103255 . B. . C. . D. 102827 . 3 3 Lời giải Chọn B
Ta có 3 1 cos 2x  sin 2x  4 cos x  8  4 3   1 sin x 2
 2 3 sin x  2sin x cos x  4 cos x  4 3 sin x  4sin x  8  0
 2 sin x  3 sin x  cos x  2  4 3 sin x  cos x  2  0
 2 sin x  2 3 sin x  cos x  2  0  π  
 3 sin x  cos x  2  0  sin x   1    x
k 2 , k .  6  3  1 1009 1
Vì x  0; 2018 nên 0 
k 2  2018    k  
k  0;1; 2;...;  321 . 3 6 π 6     
Suy ra S   ;  2 ;  2.2 ;...;  321.2   3 3 3 3   310408
Vậy tổng tất cả các phần tử của S là T  322.
 2 1 2  3  ...  321  . 3 3
Câu 7: Tìm tập hợp tất cả các giá trị của tham số thực
m để phương trình   π 3π 2 
2 m 1 sin x  4m  
1 cos x  0 có nghiệm thuộc khoảng ;   .  2 2   1   1   1  A. ;     . B.  ; 0   . C.  ; 0   . D. 0; .  2   2   2 
Câu 8: Tìm tập hợp tất cả các giá trị của tham số thực
m để phương trình   π 3π 2 
2 m 1 sin x  4m  
1 cos x  0 có nghiệm thuộc khoảng ;   .  2 2   1   1   1  A. ;     . B.  ; 0   . C.  ; 0   . D. 0; .  2   2   2  Lời giải Chọn B
Đặt t  cos x , t  1
 ; 0 thì phương trình đã cho trở thành  2
2 m t   4m   1 t  0 1 2
 2t t m 4t  2  t 2t  
1  2m 2t  
1  t  2m (do t  ) 2  1  
Phương trình có nghiệm khi 2m 1;0  m  ; 0   .  2  m sin x 1
Câu 9: Cho hàm số y
. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn 5;  5 để giá cos x  2
trị nhỏ nhất của y nhỏ hơn 1. A. 6 . B. 3 . C. 4 . D. 5 . m sin x 1
Câu 10: Cho hàm số y
. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn 5;  5 để cos x  2
giá trị nhỏ nhất của y nhỏ hơn 1  . A. 6 . B. 3 . C. 4 . D. 5 . Lời giải Chọn A
Do cos x  2  0, x
   nên hàm số xác định trên  . m sin x 1 Ta có y
m sin x y cos x  2 y 1. cos x  2
Do phương trình có nghiệm nên 2 2 2  3m 1 2  3m 1
m y   y  2 2 2 2 2 2 1
 3y  4 y 1 m  0   y  . 3 3 2 2  3m 1
Vậy GTNN của y bằng . 3 2 2  3m 1 m  2 2 Do đó yêu cầu bài toán 2 2   1
  3m 1  25  m  8   . 3 m  2 2 
Do m thuộc đoạn 5; 
5 nên m 5; 4;3;3; 4;  5 .
Câu 11: Có bao nhiêu giá trị nguyên dương của m để phương trình 2 2
sin 2x  2 sin x  cos x  cos x m sin x có nhiều hơn một nghiệm trong khoảng 0; 2π ? A. 3 . B. 2 . C. 4 . D. 5 .
Câu 12: Có bao nhiêu giá trị nguyên dương của m để phương trình 2 2
sin 2x  2 sin x  cos x  cos x m sin x có nhiều hơn một nghiệm trong khoảng 0; 2π ? A. 3 . B. 2 . C. 4 . D. 5 . Lời giải Chọn B 2 2
sin 2x  2 sin x  cos x  cos x m sin x 2  x x x x x m  2 2 sin cos 2 sin cos cos 1 cos x  0  cos x  
1 2 sin x  m  
1 cos x m  0  
cos x 1  0  1  
2 sin x  m  
1 cos x m  02  Giải  
1 : cos x 1  0  cos x  1
  x  π  k 2π , k   . Trong khoảng 0; 2π thì   1 có
một nghiệm là: x  π .
Giải 2 : 2sin x  m  
1 cos x m  0 .
Để phương trình đã cho có nhiều hơn một nghiệm trong khoảng 0; 2π thì 5
2 sin x  m  
1 cos x m  0 có nghiệm   m  2 2 2 2 1  m m  2
Vậy có hai giá trị nguyên dương m  1, m  2 thỏa mãn điều kiện bài toán.
Câu 13: Tìm số tất cả các giá trị nguyên của tham số thực m để phương trình 3 2   
2sin 2x msin 2x  2m  4  4 cos 2x có nghiệm thuộc 0; .    6  A. 4 . B. 3 . C. 1. D. 6 .
Câu 14: Tìm số tất cả các giá trị nguyên của tham số thực m để phương trình 3 2   
2sin 2x msin 2x  2m  4  4 cos 2x có nghiệm thuộc 0; .    6  A. 4 . B. 3 . C. 1. D. 6 . Lời giải Chọn C 3 2
2sin 2x msin 2x  2m  4  4 cos 2x 3 2
 2sin 2x  4sin 2x m sin 2x  2m  0 .   3   
Đặt sin 2x t , với x  0;  t     0;  6  2    .  
Khi đó, bài toán trở thành:  3  Tìm m để 3 2
2t  4t mt  2m  0 có nghiệm trên khoảng t   0;  .  2      3 2 2 3
2t  4t mt  2m  0  m  2  t , t    0;  .  2     3 
Lập bảng biến thiên của hàm số y t  2  2
t trên khoảng t   0;   2  .    3 
Dựa vào bảng biến thiên ta thấy m   ; 0   .  2 
Vậy có 1 giá trị nguyên.
Câu 15: Phương trình sin x  cos xsin x  2cos x  3  0 có tất cả bao nhiêu nghiệm thực thuộc  3  khoảng  ;   ?  4  A. 3 . B. 0 . C. 1. D. 2 .
Câu 16: Phương trình sin x  cos xsin x  2 cos x  3  0 có tất cả bao nhiêu nghiệm thực thuộc  3  khoảng  ;   ?  4  A. 3 . B. 0 . C. 1. D. 2 . Lời giải Chọn C
sin x  cos x  0   1
Ta có: sin x  cos xsin x  2 cos x  3  0  
sin x  2 cos x  3 2   Giải  
1 : sin x  cos x  0  tan x  1  x
k , k   4  3   Do x   ;   nên x   4  4 Giải  
2 : sin x  2 cos x  3 vô nghiệm vì 2 2 2 1  2  3  3 
Vậy phương trình đã cho có đúng một nghiệm thuộc khoảng  ;   .  4  2 2
Câu 17: Cho phương trình  x m 3 2 2 3 3 sin
 sin x m  2 sin x m . Gọi S   ;
a b là tập hợp tất cả
các giá trị thực của tham số m để phương trình trên có nghiệm thực. Tính giá trị của 2 2
P a b . 162 49 A. P  . B. P  . C. P  4 . D. P  2 . 49 162 2 2
Câu 18: Cho phương trình  x m 3 2 2 3 3 sin
 sin x m  2 sin x m . Gọi S   ;
a b là tập hợp tất cả
các giá trị thực của tham số m để phương trình trên có nghiệm thực. Tính giá trị của 2 2
P a b . 162 49 A. P  . B. P  . C. P  4 . D. P  2 . 49 162 Lời giải Chọn A
TH1: sin x m thì ta có  m2 3 2
 0  m  0 . Khi đó phương trình có nghiệm x k , k   .
TH2: sin x m thì phương trình đã cho tương đương 2
 sin x m  sin x m 3 3   2  0   .
 sin x m  sin x m  sin x m sin x m 3  1   1 sin x m   m  0 sin x m Giải ra ta được      .  sin x m 9sin x  7 sin m x m   3  8   2 sin  sin x m x m 7m m  m  0  9 
Do đó để phương trình có nghiệm thực thì    9 9 9 9    m    m    7 7   7 7
KL: Hợp hai trường hợp suy ra tập hợp tất cả các giá trị thực của tham số m cần tìm là 2 2  7 7   9   9  162 S  ; 2 2 
P a b        . 9 9     7   7  49
Câu 19: Có bao nhiêu giá trị nguyên của tham số m để phương trình 3 3
m  3 m  3cos x  cos x có nghiệm thực? A. 2 . B. 7 . C. 5 . D. 3 .
Câu 20: Có bao nhiêu giá trị nguyên của tham số m để phương trình 3 3
m  3 m  3cos x  cos x có nghiệm thực? A. 2 . B. 7 . C. 5 . D. 3 . Lời giải Chọn C Ta có 3 3
m  3 m  3cos x  cos x 3 3
 3 m  3cos x  cos x m   1
Đặt cos x u . Điều kiện 1  u  1 và 3 3
m  3cos x v v m  3u 2   1 trở thành 3
u m  3v 3
Từ 3 và 2 suy ra 3 3
u  3v v  3u 2 2
 (u v)(u uv v  3)  0  u v 2 2  1  3v Do 2 2
u uv v  3  u v   3  0   , u  , v    2  4 Suy ra: 3 3
m  3u u m u  3u với u  1   ;1 .
Xét hàm số f u 3
u  3u với u  1  
;1 . Ta có f u 2
 3u  3 ; f u  0  u  1  do u  1   ;1 .
Suy ra max f u  2 ; min f u  2 -1;  1  1  ;  1
Do đó phương trình có nghiệm khi và chỉ khi 2  m  2 , mà m   nên m 0; 1  ;   2 .
Câu 1: (THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018) Cho hàm số 2
x 1, x  1
y f x   Mệnh đề sai là 2x, x  1.  A. f   1  2 .
B. f không có đạo hàm tại x  1. 0
C. f 0  2.
D. f 2  4.
Lời giải
Chọn B
f x  f   1 2x  2 lim  lim  2; x 1  x 1 x 1   x 1 Ta có
f x  f   2 1 x 1 2 lim  lim  lim  x   1  2. x 1  x 1  x 1 x 1 x 1  
Vậy f 1   f 1     f  
1  2. Suy ra hàm số có đạo hàm tại x  1. Vậy B sai. 0
Câu 2: (THPT Chuyên Bắc Ninh-lần 1-năm 2017-2018) Giám đốc một nhà hát A đang phân vân trong
việc xác định mức giá vé xem các chương trình được trình chiếu trong nhà hát. Việc này rất
quan trọng nó sẽ quyết định nhà hát thu được bao nhiêu lợi nhuận từ các buổi trình chiếu. Theo
những cuốn sổ ghi chép của mình, ông ta xác định được rằng: nếu giá vé vào cửa là 20
USD/người thì trung bình có 1000 người đến xem. Nhưng nếu tăng thêm 1 USD/người thì sẽ
mất 100 khách hàng hoặc giảm đi 1 USD/người thì sẽ có thêm 100 khách hàng trong số trung
bình.Biết rằng, trung bình, mỗi khách hàng còn đem lại 2 USD lợi nhuận cho nhà hát trong các
dịch vụ đi kèm. Hãy giúp giám đốc nhà hát này xác định xem cần tính giá vé vào cửa là bao
nhiêu để thu nhập là lớn nhất. A. 18 USD/người. B. 19 USD/người. C. 14 USD/người. D. 25 USD/người. Lời giải Chọn C
Gọi giá vé sau khi điều chỉnh là 20  x x  20  0
Số khách là:1000 100x Tổng thu nhập
f x    x    x    x  x 2 20 .1 2 1000 100 22 1000 100
 100x 1200x  22000 Bảng biến thiên x 2  0 6 
f  x  0  f 6
f x  
max f x  f 6 .Suy ra giá vé là: x  20  20  6 14 USD  20  ;
Câu 3: (THPT Hai Bà Trưng-Vĩnh Phúc-lần 1-năm 2017-2018) Tổng các nghiệm của phương trình
2 cos 3x 2cos 2x   1  1 trên đoạn  4   ;6  là: A. 61 . B. 72 . C. 50 . D. 56 . Lời giải Chọn C
Xét sin x  0  x m : Thay vào phương trình thấy không thỏa mãn
Xét sin x  0  x m
2 cos 3x 2cos 2x   1  1
 2cos5x  cos x  2cos 3x  1
 2 sin x cos 5x  2 sin x cos 3x  2 sin x cos x  sin x
 sin 6x  sin 4x  sin 4x  sin 2x  sin 2x  sin x
 sin 6x  sin x  k 2 x   5     l2 
k,l  . x    7 7 x m  k 2  l2
Trước tiên ta cần chỉ ra giữa hai họ nghiệm x  và x   không có giá trị trùng 5 7 7 nhau.  l2 k 2 Thật vậy: Giả sử  
k,l   7 7 5
 14k  5 10l : Vô lí vì 14k là số nguyên chẵn và 5 10l là số nguyên lẻ.  k 2 x   5  k    1  0; 9  ; 8  ;...14;1  5
Với x m    k    1  0; 5  ; 0;5,10,1  5
x 4 ;6    
 các giá trị x cần loại bỏ là 4 , 2
  , 0, 2 , 4 , 6 .Tổng các giá trị này là 6   l2 x    7 7  l     1  4; 1  3; 1  2;...19; 2  0
Với x m    l    4  ; 1  1;3;10;1  7 x  4   ; 6    
 các giá trị x cần loại bỏ là   , 3
  ,  , 3 , 5 . Tổng các giá trị này là 5 15 20   k 2      l2  
Vậy tổng nghiệm S       6     5  50       . k  5   l  7 7 10 14      Câu 4: (THPT Thạch Thành-Thanh Hóa-năm 2017-2018) Cho x, y  0;   thỏa  2  4 4 sin x cos y
cos 2x  cos 2 y  2 sin  x y  2 . Tìm giá trị nhỏ nhất của P   y x 3 2 2 5 A. minP  . B. min P  . C. min P  . D. min P  .   3  Lời giải Chọn B Ta có: x y   x y 2 2 cos 2 cos 2 2sin
 2  sin x  sin y  sin  x y 
Suy ra: x y  2 a b   2 2 2 a b Áp dụng bđt:   m n m n  2 2
sin x  sin y 2  Suy ra: P  
. Đẳng thức xảy ra  x y  . x y  4 2 Do đó: min P  . 
Câu 1: (THPT Chuyên Vĩnh Phúc-lần 1 MĐ 904 năm 2017-2018) Số nghiệm thuộc đoạn 0;2017 của
1  cos x  1  cos x phương trình  4cos x là sin x A. 1283. B. 1285. C. 1284. D. 1287. Lời giải Chọn C
Điều kiện sinx  0; sin . x cos x  0
1  cos x  1  cos x  4cos x  1 cos x  1 cos x  4sin xcos x sin x     x  x 2 2 2  x x   x x  2 2 2 1 cos 1 cos 16 sin cos 1 sin 8sin 1  sin x   1
TH1: sin x  0  sin x  1  1  sin x  sin x0 1   2  
1  1 sin x 3 2
8sin x  8sin x   1  0  sin x     2  1 5  sin x   1 5    4 sin x   4   x   k 2 1  6  * sin x    vì sin .
x cos x  0 nên x   k 2 . 2 5  6 x   k 2  6   1 5  x  arcsin    k 2  4  1 5    * sin x   vì sin .
x cos x  0 nên 4   1 5 
x    arcsin    k 2   4      1 5  x  arcsin    k 2 .  4   
TH2: sin x  0  sin x  1  1  sin x   sin x0 1   2  
1  1 sin x 3 2
8sin x  8sin x  
1  0  sin x      2  1   5  sin x   1 5     4 sin x   4   x    k 2 1  6 7 * sin x     vì sin .
x cos x  0 nên x   k 2 . 2 7  6 x   k 2  6   1   5   x  arcsin    k 2  4  1   5    * sin x   4   1   5 
x    arcsin    k 2   4      1   5  vì sin .
x cos x  0 nên x    arcsin    k 2 .  4   
Xét nghiệm thuộc đoạn 0;2017 :   *Với x   k 2  0 
k 2  2017  0  k  320 có 321 nghiệm. 6 6  1 5  3 3 *Với x  arcsin    k 2   k 2  0 
k 2  2017  0  k  320 có 321  4  10 10   nghiệm. 7 7 *Với x   k 2  0 
k 2  2017  0  k  320 có 321 nghiệm. 6 6  1 5  13 13
*Với x    arcsin    k 2   k 2  0 
k 2  2017  0  k  320 có  4  10 10   321 nghiệm.
*Vậy có tổng cộng 321.4  1284 nghiệm thỏa yêu cầu bài toán.
Câu 2: (SGD Bắc Ninh năm 2017-2018) Gọi M , m lần lượt là giá lớn nhất, giá trị nhỏ nhất của hàm số 2018 2018 y  sin x  cos
x trên  . Khi đó: 1 1 1
A. M  2 , m  .
B. M  1 , m
. C. M  1 , m  0 .
D. M  1 , m  . 1008 2 1009 2 1008 2 Lời giải Chọn D 1009 1009 Ta có: 2018 2018 y  sin x  cos x   2 x   2 sin 1 sin x . Đặt 2
t  sin x , 0  t  1 thì hàm số đã cho trở thành y t    t 1009 1009 1 .
Xét hàm số f t   t    t 1009 1009 1 trên đoạn 0;  1 .
Ta có: f t   t    t 1008 1008 1009. 1009. 1
f t   0  t    t 1008 1008 1009 1009 1  0 1008  1 t  1 t 1   1     1  t   t t 2  1  1 Mà f  
1  f 0  1, f    . 1008  2  2  1  1
Suy ra max f t   f 0  f  
1  1 , min f t   f    0;  1   1008 0;1  2  2 1
Vậy M  1 , m  . 1008 2 Câu 3:
(THPT Hoài Ân-Hải Phòng năm 2017-2018) Tìm
m để phương trình   2 
2 sin x  2m  
1 sin x  2m 1  0 có nghiệm thuộc khoảng  ; 0   .  2  1 1
A.  1  m  0 .
B. 0  m  1 .
C. 1  m  2 . D.   m  . 2 2 Lời giải Chọn. D.
Đặt t  sin x , t   1
 ; 0 , phương trình trở thành: 2
2t  (2m 1)t  2m 1  0
Theo yêu cầu bài toán ta tìm m để phương trình 2
2t  (2m 1)t  2m 1  0 có nghiệm t   1  ; 0 2 2t t 1 2t 1 2
2t  (2m 1)t  2m 1  0 2
 2t t 1 m  2
t  2  0  m   2t  2 2 2t 1 1 1
Đặt f t   , t   1
 ; 0 , f t  là hàm đồng biến nên f  
1  m f 0    m  . 2 2 2
Câu 4: (THPT Thanh Miện 1-Hải Dương-lần 1 năm 2017-2018) Cho các số thực dương x , y , z thỏa x 1 2  yz x 2 2
mãn x y xyz z . Giá trị lớn nhất của biểu thức P   thuộc khoảng 2  3 2
y zx x    1 1
nào trong các khoảng sau: A. 1,3;1, 4 . B. 0,8;0,9 . C. 1, 7;1,8 . D. 1, 4;1,5 . Lời giải
Chọn D 1 1
Từ giả thiết x y xyz z  . x  . yxy  1 . z z A B 1 C Đặt x  tan , y  tan và  tan
thay vào hệ thức trên ta được 2 2 z 2 A B B C C A tan tan  tan tan  tan tan
 1, suy ra A , B , C là ba góc của tam giác. 2 2 2 2 2 2 2x A A 2 x A Từ đó ta có 2  2 sin cos và 2  sin . 2  x 1 2 x  3 2 2 2 1   2  C B B C B C B C     cos cos  tan  tan  2 tan tan yz 2 tan tan 1    2 2   2 2 2 2 2 2      y zB C B C B C  tan tan 1 cos cos tan tan 1 2 2   2 2  2 2  B C A 1 sin  sin B sin C cos 
cos  B C   cos  B C    2 2 2   B C B C cos cos 2 2 A 2 B C 2 A A A cos  cos 1 cos 2 cos  11 cos 2 2 2 2 2 A    2 cos . B C 1 2 cos 2 A A A AA A   A   Vậy 2 2 P  2 sin cos  2 sin cos  sin A sin  cos    2 sin . A sin   2   . 2 2 2 2  2 2   2 4   B C   x  1  A     2 
Dấu bằng đạt được khi si  n A  1     y  2 1.      A   B C z  2 1 si  n   1      4    2 4 
Câu 5: (THPT Chuyên Hoàng Văn Thụ-Hòa Bình năm 2017-2018) Số các giá trị nguyên của m để phương trình 2
cos x  cos x m m có nghiệm là: A. 4 . B. 2 . C. 3 . D. 5 . Lời giải Chọn A Ta có: 2
cos x  cos x m m suy ra m  0 . 2 
cos x t m
Đặt cos x m t , t  0 . Phương trình trở thành:  2
t  cos x m  cos x t    2 2
cos x t   t  cos x  0  cos x tcos x t   1  0   .
cos x t 1  0  cos x  0
Trường hợp 1 : cos x t  
cos x m   cos x   . 2
cos x  cos x m
Đặt u  cos x 1  u  0 . 1 Xét   2
f u u u , ta có f u  2u 1; f u  0  u  . 2
Do đó với 1  u  0 suy ra f u  0 với mọi u 1;0 . Suy ra f  
1  f u  f 0  2  f u  0 .
Để phương trình có nghiệm thì m 0; 2 . Vì m  nên m 0;1;  2 .
Trường hợp 2 : cos x t 1  0  cos x m  1 cos x 2
 cos x  cos x 1  m . 1
Đặt v  cos x , 1  v  1. Ta có 2
m v v 1  g v , gv  2v 1  0  v   . 2
Vẽ bảng biến thiên ta được: 1 v 1   1 2
gv  0  1 3
g v 3 4  3 
Để phương trình có nghiệm thì m  ;3 
. Vì m   nên m 1; 2;  3 . 4   
Vậy có tất cả 4 số nguyên m thỏa mãn bài toán.
Câu 6: (THPT Trần Nhân Tông-Quảng Ninh-lần 1 năm 2017-2018) Số nghiệm của phương trình: 2015 2016 x x   2017 2018 sin cos 2 sin x  cos
x  cos 2x trên 10;30 là: A. 46 . B. 51. C. 50 . D. 44 .
Hướng dẫn giải Chọn D Ta có: 2015 2016 x x   2017 2018 sin cos 2 sin x  cos
x  cos 2x 2015  x  2  x 2016  x  2 sin 1 2 sin cos 2 cos x   1  cos 2x cos 2x  0 2015 2016  sin . x cos 2x  cos .
x cos 2x  cos 2x   . 2015 2016 sin x  cos x  1   
Với cos 2x  0  x   k , k   4 2   20 1 60 1
Vì x 10;30  10    k  30     k    6   k  18 . 4 2  2  2 Với 2015 2016 sin x  cos x  1 . Ta có 2015 2 2016 2 sin x  sin ; x cos x  cos x .
sin x  0, cos x  1  Do đó 2015 2016 2 2 1  sin x  cos
x  sin x  cos x  1 suy ra  .
sin x  1, cos x  0 
Nếu sin x  0  x k , k   . 10  30
Vì x 10;30  10   k  30      3   k  9 .   
Nếu sin x  1  x
k 2 , k   . 2  5 1 15 1
Vì x 10;30  10  
k 2  30     k    1   k  4 . 2  4  4
Vậy số nghiệm của phương trình đã cho là: 13  6  25  44 .
Câu 1: (THPT Lê Quý Đôn-Hà Nội năm 2017-2018) Có bao nhiêu giá trị nguyên của m để phương trình 3
sin x  2  m  sin x  2 có nghiệm. A. 2 . B. 3. C. 1. D. 0 . Lời giải
Chọn A Ta có 3
sin x  2  m  sin x  2 .  2
u  sin x  2 u    sin x  2 Đặt  
 1  u  3 . Khi đó  2 3
u v m  2 (*). 3 3 v m  sin x
v m  sin x
Ta lại có u v  2  v  2  u . 3 (*) trở thành 2
u  u  2  m  2    1 3 2
m u  5u 12u 10  f u  , 1  u  3 . 7  13
Trên  , ta có f  u 2  3
u 14u 12 , f u  0  u   1  ; 3 3  
Để phương trình đã cho có nghiệm thì  
1 có nghiệm 1  u  3 hay  7  13  f    m fm 0  ;1 ) Vì m nguyên ).    3 3  
Vậy có 2 giá trị nguyên của m thỏa đề bài.
Câu 2: (THPT Hồng Lĩnh-Hà Tĩnh-lần 1 năm 2017-2018) Số giá trị nguyên của tham số m để phương     3 
trình sin 2x  2 sin x   2  m  
có đúng một nghiệm thực thuộc khoảng 0;   ?  4   4  A. 3 . B. 2 . C. 0 . D. 1. Lời giải Chọn B  3          Ta có x  0;     x
   0  sin x   1    0  2 sin x   2   .  4  4 4  4   4     Mặt khác 2 sin x
 sin x  cos x   .  4 
Đặt sin x  cos x t với t  0; 2 2 2 2
 sin x  cos x  2 sin .
x cos x t 2
 sin 2x t 1. 
Phương trình đã cho trở thành 2 2
t 1 t  2  m t t  3  m * . Xét f t  2
t t  3 với t  0; 2 .  1
Ta có f t   2t 1. Do đó f t   0  t   (loại). 2 Bảng biến thiên
Dựa vào bảng biến thiên ta có phương trình * có nhiều nhất một nghiệm t . Do đó để phương  3  t  2
trình đã cho có đúng một nghiệm thực x thuộc khoảng 0;   thì  .  4  0  t  1 
Với t  2 thay vào phương trình * : 2  2  3  m m  2 1  .
Với 0  t  1 ta có bảng biến thiên Vậy 3  m  1
  có 2 giá trị nguyên của m là 2 và 1  . 1 m
Câu 3: Có bao nhiêu giá trị nguyên âm của m để hàm số y x  5 
đồng biến trên 5;   ? x  2 A. 10 . B. 8 . C. 9 . D. 11.
Câu 4: Cho hàm số 3 2
y x  3x có đồ thị C  và điểm M m;  4 . Hỏi có bao nhiêu số nguyên m
thuộc đoạn 10;10 sao cho qua điểm M có thể kẻ được ba tiếp tuyến đến C  . A. 20 . B. 15 . C. 17 . D. 12 .
Câu 5: (THPT Chuyên Ngữ – Hà Nội - Lần 1 năm 2017 – 2018) Có bao nhiêu giá trị nguyên âm của m để 1 m
hàm số y x  5 
đồng biến trên 5;   ? x  2 A. 10 . B. 8 . C. 9 . D. 11. Lời giải Chọn B 2 m 1
x  4x m  3
Tập xác định: D   \  
2 . Đạo hàm: y  1  .  x  22  x  22
Xét hàm số f x 2
x  4x  3 trên 5;   .
Đạo hàm: f  x  2x  4 . Xét f  x  0  x  2  y  1. Ta có: f 5  8 . Bảng biến thiên: x  2 5  y  0  0    y 8 1  Do  x  2 2
 0 với mọi x 5;   nên y  0 , x
 5;   khi và chỉ khi f x  m , x
 5;  . Dựa vào bảng biến thiên ta có: m  8  m  8  .
Mà m nguyên âm nên ta có: m 8; 7;  6;  5;  4;  3; 2;   1 . 1 m
Vậy có 8 giá trị nguyên âm của m để hàm số y x  5 
đồng biến trên 5;  . x  2
Câu 6: (THPT Chuyên Ngữ – Hà Nội - Lần 1 năm 2017 – 2018) Cho hàm số 3 2
y x  3x có đồ thị C  và
điểm M m;  4 . Hỏi có bao nhiêu số nguyên m thuộc đoạn 10;10 sao cho qua điểm M
có thể kẻ được ba tiếp tuyến đến C  . A. 20 . B. 15 . C. 17 . D. 12 . Lời giải Chọn C
Tập xác định: D   . Đạo hàm: 2
y  3x  6x .
Ta nhận thấy các đường thẳng x a với a   không phải là tiếp tuyến của C  và một
đường thẳng không thể tiếp xúc với đồ thị hàm số bậc ba tại hai điểm phân biệt.
Giả sử phương trình đường thẳng đi qua M m;  4 là d : y k x m  4 với k   là hệ số góc của đường thẳng.
Qua M có thể kẻ được ba tiếp tuyến đến C  khi và chỉ khi hệ phương trình 2
k  3x  6x   có ba nghiệm phân biệt k
  x m 3 2
 4  x  3x    2
x x x m 3 2 3 6
x  3x có ba nghiệm phân biệt 3
x  m   2 2 3
1 x  6mx  0 có ba nghiệm phân biệt 2
x 2x  3m  
1 x  6m  0   có ba nghiệm phân biệt 2
 2x  3m  
1 x  6m  0 có hai nghiệm phân biệt khác 0  1 m  
  9m  2 2 1  48m  0 9m 30m 9 0        3        . m  3 m  0 m  0     m  0   m  10  ;10
Với điều kiện trên và với 
ta có m 10;  9;...; 1; 4;5;...  ;10 . m   
Vậy có 17 số thỏa mãn yêu cầu bài toán.
Câu 7: (THPT Quỳnh Lưu 1 – Nghệ An – Lần 2 năm 2017 – 2018) Có bao nhiêu giá trị nguyên m  để phương trình  x m3 3 8sin
 162 sin x  27m có nghiệm thỏa mãn 0  x  ? 3 A. 2 . B. 3 . C.Vô số. D. 1. Lời giải Chọn A
Đặt t  2sin x , với 0  x  thì t  0; 3. 3
Phương trình đã cho trở thành t m3 3
 81t  27m . Đặt 3
u t m 3
t u m . 3 u
 27 3t m  3 Khi đó ta được 3 
u  3t   273t u   u u   t 3 3 27 3  27.3t * 
 3t 3  27 u m 
Xét hàm số f v 3
v  27v liên tục trên  có nên hàm số đồng biến.
Do đó *  u  3t 3
t  3t m   1
Xét hàm số f t  3
t  3t trên khoảng 0; 3 .
có f t  2
 3t  3 ; f t   0  t  1 (vì t  0 ). Bảng biến thiên
Dựa vào bảng biến thiên ta thấy phương trình   1 có nghiệm khi.
Vậy có hai giá trị nguyên của m thỏa yêu cầu bài toán.
Câu 1: (THPT Chuyên Thái Bình – Thái Bình – Lần 5 năm 2017 – 2018) Cho phương trình   x x m x 2 1 cos cos 4 cos
m sin x . Tìm tất cả các giá trị của m để phương trình có đúng 3  2 
nghiệm phân biệt thuộc 0;  . 3     1 1  A. m   ;  .
B. m  ;  1  1;   . 2 2     1  C. m   1;   1 . D. m   ;1   .  2  Lời giải
Chọn D Ta có:   x x m x 2  m x    x x m x  m  2 1 cos cos 4 cos sin 1 cos cos 4 cos 1 cos x  0 cos x  1
 1 cos x cos 4x m cos x m1 cos x  0     . cos 4x m
 Xét phương trình cos x  1  x    k 2 k   .  2 
Phương trình cos x  1
 không có nghiệm trong đoạn 0;  . 3    Cách 1:
 Xét phương trình cos 4x m . Đặt f x  cos 4x . Ta có: f  x  4  sin 4x . 
Xét f  x  0  sin 4x  0  4x k  x kk   . 4  2      Xét trong đoạn 0; 
thì ta có: x  0; ;  . 3     4 2  Bảng biến thiên:   2 x 0 4 2 3
f  x 0  0  0  1 1
f x 1  1 2
Dựa vào bảng biến thiên, ta thấy phương trình cos 4x m có đúng 3 nghiệm phân biệt trong  2  1 đoạn 0;  khi và chỉ khi   m  1. 3    2 Cách 2:  2   8 
 Xét cos 4x m . Ta có x  0;  4x  0;  . 3   3     
Với 4x 0; 2  \  và m  
1;1 phương trình cos 4x m có 2 nghiệm.  8   1  Với 4x  2 ;  và m   ;1 
 phương trình cos 4x m có 1 nghiệm. 3     2   2   1 
Vậy phương trình có 3 nghiệm phân biệt thuộc 0;  khi m   ;1   . 3     2   x    80 
Câu 2: Khẳng định nào sau đây là đúng về phương trình sin  cos   0  ? 2   2   x  6   2
x  32x  332 
A. Số nghiệm của phương trình là 8 .
B. Tổng các nghiệm của phương trình là 8 .
C. Tổng các nghiệm của phương trình là 48 .
D. Phương trình có vô số nghiệm thuộc  .  x    80 
Câu 3: Khẳng định nào sau đây là đúng về phương trình sin  cos   0  ? 2   2   x  6   2
x  32x  332 
A. Số nghiệm của phương trình là 8 .
B. Tổng các nghiệm của phương trình là 8 .
C. Tổng các nghiệm của phương trình là 48 .
D. Phương trình có vô số nghiệm thuộc  .
Hướng dẫn giải Chọn C x   80 
Phương trình đã cho tương đương với sin  sin       . 2 2  x  6 
x  32x  332     
Ta biết rằng hàm số y  sin x đồng biến trên khoảng  ; 
 . Ta chỉ ra rằng các hàm số  2 2  x 80 f x 
và g x 
nhận giá trị trong khoảng này. 2 x  6 2
x  32x  332 x x 1 Thật vậy, ta có   2 2 x  6 2 6x 2 6 80 80 80  và 0     . 2
x  32x  332
x 162  76 76 2
Từ các đánh giá trên,  xảy ra khi và chỉ khi x  2 x 80   3 2
x  48x  332x  480  0  x  6 . 2 2 x  6
x  32x  332  x  40 
Tổng các nghiệm của phương trình đã cho là 2  6  40  48 .
Document Outline

  • Chương 1 - HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC - Mức độ 1 Phần 1
  • Chương 1 - HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC - Mức độ 1 Phần 2
  • Chương 1 - HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC - Mức độ 1 Phần 3
  • Chương 1 - HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC - Mức độ 1 Phần 4
  • Chương 1 - HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC - Mức độ 2 Phần 1
  • Chương 1 - HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC - Mức độ 2 Phần 2
  • Chương 1 - HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC - Mức độ 2 Phần 3
  • Chương 1 - HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC - Mức độ 2 Phần 4
  • Chương 1 - HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC - Mức độ 3 Phần 1
  • Chương 1 - HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC - Mức độ 3 Phần 2
  • Chương 1 - HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC - Mức độ 3 Phần 3
  • Chương 1 - HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC - Mức độ 3 Phần 4
  • Chương 1 - HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC - Mức độ 4 Phần 1
  • Chương 1 - HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC - Mức độ 4 Phần 2
  • Chương 1 - HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC - Mức độ 4 Phần 3
  • Chương 1 - HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC - Mức độ 4 Phần 4