Tuyển Chọn Các Câu Cuối Hình Học 9 Tuyển Sinh Vào 10 Theo Từng dạng Có Đáp Án
Chứng minh giao điểm hai đường thẳng nằm trên đường thẳng AH. Chứng minh rằng tứ giác nội tiếp. Chứng minh là tứ giác nội tiếp. Chứng minh thẳng hàng. Cho tam giác ABC có ba góc nhọn và đường cao BE. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi Toán 9 206 tài liệu
Môn: Toán 9 2.9 K tài liệu
Tác giả:
Preview text:
BỘ ĐỀ CÂU CUỐI HÌNH HỌC TUYỂN SINH VÀO LỚP 10
MÔN TOÁN THPT CÁC TỈNH TRÊN CẢ NƯỚC
PHẦN 1: CHỨNG MINH 3 ĐIỂM THẲNG HÀNG, ĐỒNG QUY CẦN THƠ
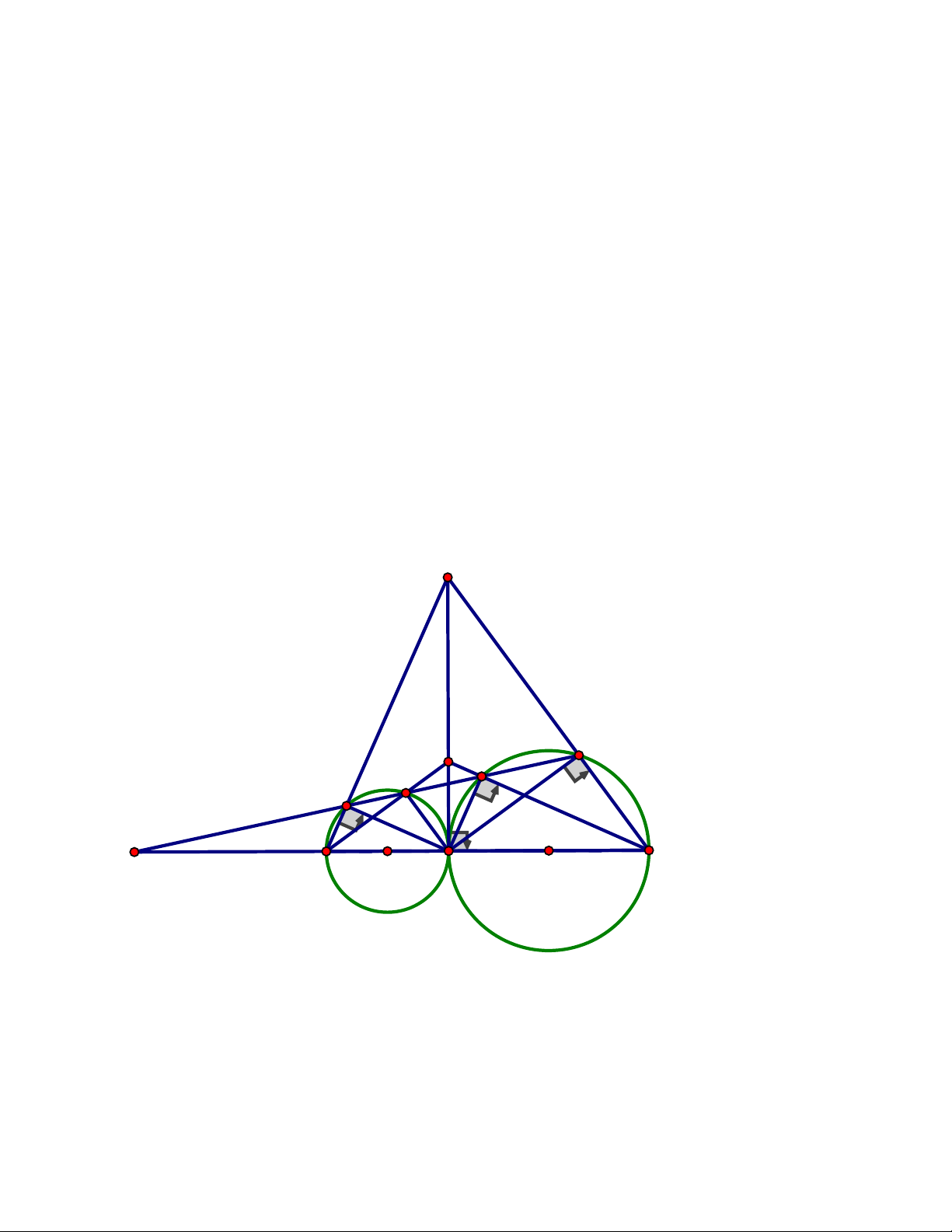
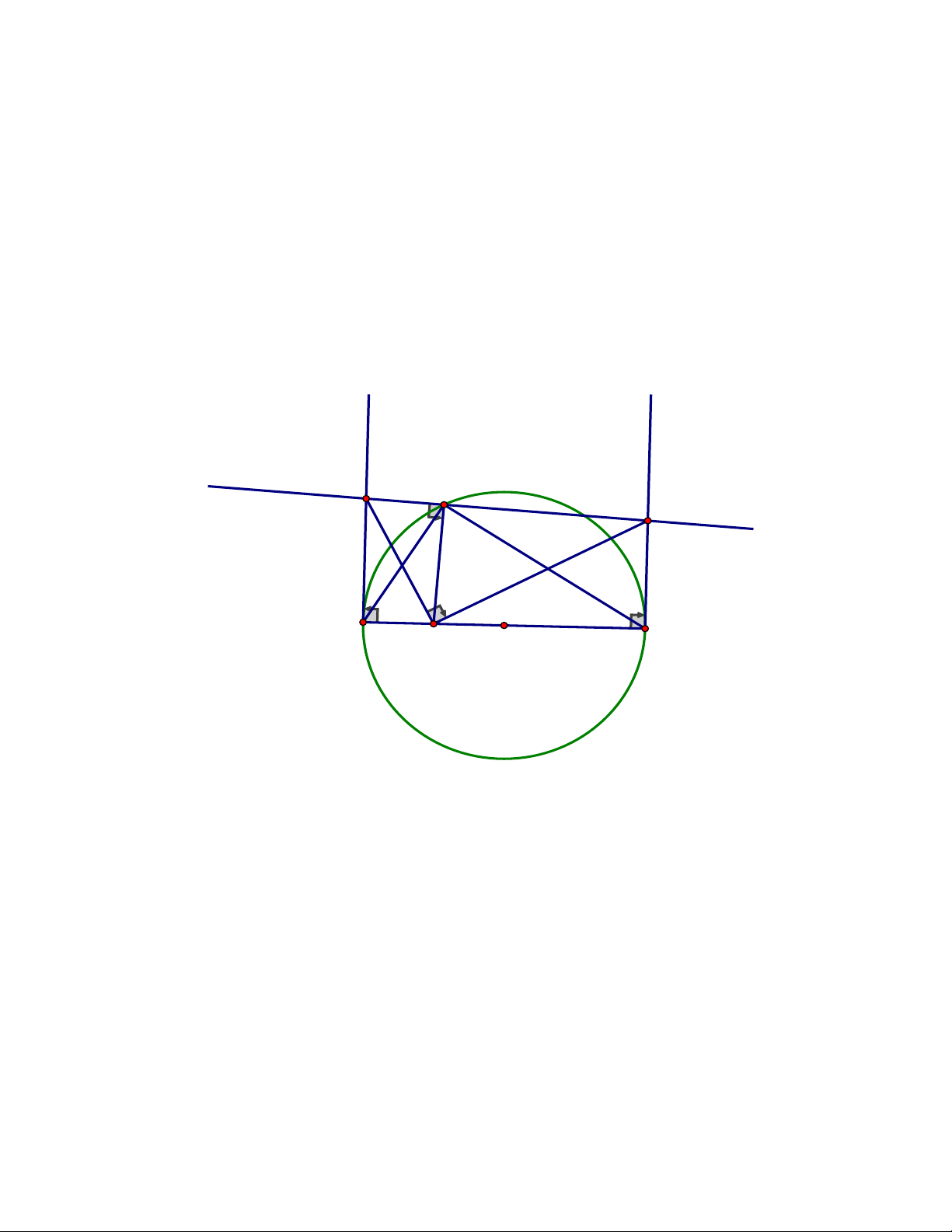
Câu 4. (2,5 điểm) Cho tam giác ABC có ba góc nhọn và AB AC. Vẽ đường cao AH ,
đường tròn đường kính HB cắt AB tại D và đường tròn đường kính HC cắt AC tại E
a) Chứng minh rằng tứ giác ADHE nội tiếp
b) Gọi I là giao điểm của hai đường thẳng DE và BC.Chứng minh 2 IH = I . D IE
c) Gọi M , N lần lượt là giao điểm của đường thẳng DE với đường tròn đường kính
HB và đường tròn đường kính HC. Chứng minh rằng giao điểm của hai đường
thẳng BM và CN nằm trên đường thẳng AH. ĐÁP ÁN Câu 4. A K N E M D I B H C
a) Chứng minh rằng tứ giác ADHE nội tiếp
Ta có: BDH là góc nội tiếp chắn nửa đường tròn đường kính 0 BH BDH = 90
CEH là góc nội tiếp chắn nửa đường tròn đường kính 0 CH CEH = 90
Xét tứ giác ADHE ta có: 0 0 0
ADH + AEH = 90 + 90 =180 ADHE là tứ giác nội tiếp b) Chứng minh: 2 IH = I . D IE
Ta có: ADHE là tứ giác nội tiếp (cmt) D AH = D
EH (cùng chắn DH ) Trang 1 Hay BAH = I
EH ,lại có BAH = BHD (cùng phụ với D BH )
BHD = IEH (= BAH )hay BHD = IEH
Xét IDH và IHE ta có: I chung; IHD = IEH (cmt) ID IH 2 I DH I
HE(g.g) = I .
D IE = IH (dfcm) IH IE
c) Chứng minh giao điểm hai đường thẳng BM ,CN nằm trên đường thẳng AH
Gọi giao điểm của BM và CN là K Ta có: BM
H là góc nội tiếp chắn nửa đường tròn đường kính BH 0 BM H = 90
Hay MH ⊥ BK , chứng minh tương tự NH ⊥ KC
Vì ADHE là tứ giác nội tiếp (cmt) nên DAH = DEH (cùng chắn cung DH ) hay BAH = MEH
Vì BDMH là tư giác nội tiếp đường tròn đường kính BD, MH
HME = DBH (góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện)
Hay EMH = ABH mà 0 0
BAH + ABH = 90 MBH + HME = 90 0
MHE = 90 hay MH ⊥ HE
Mà HE ⊥ AC MH / / AC
Lại có: MH ⊥ BK (cmt ) BK ⊥ AC , chứng minh tương tự: CK ⊥ AB
K là trực tâm ABC
K AH (dfcm) ĐỒNG NAI
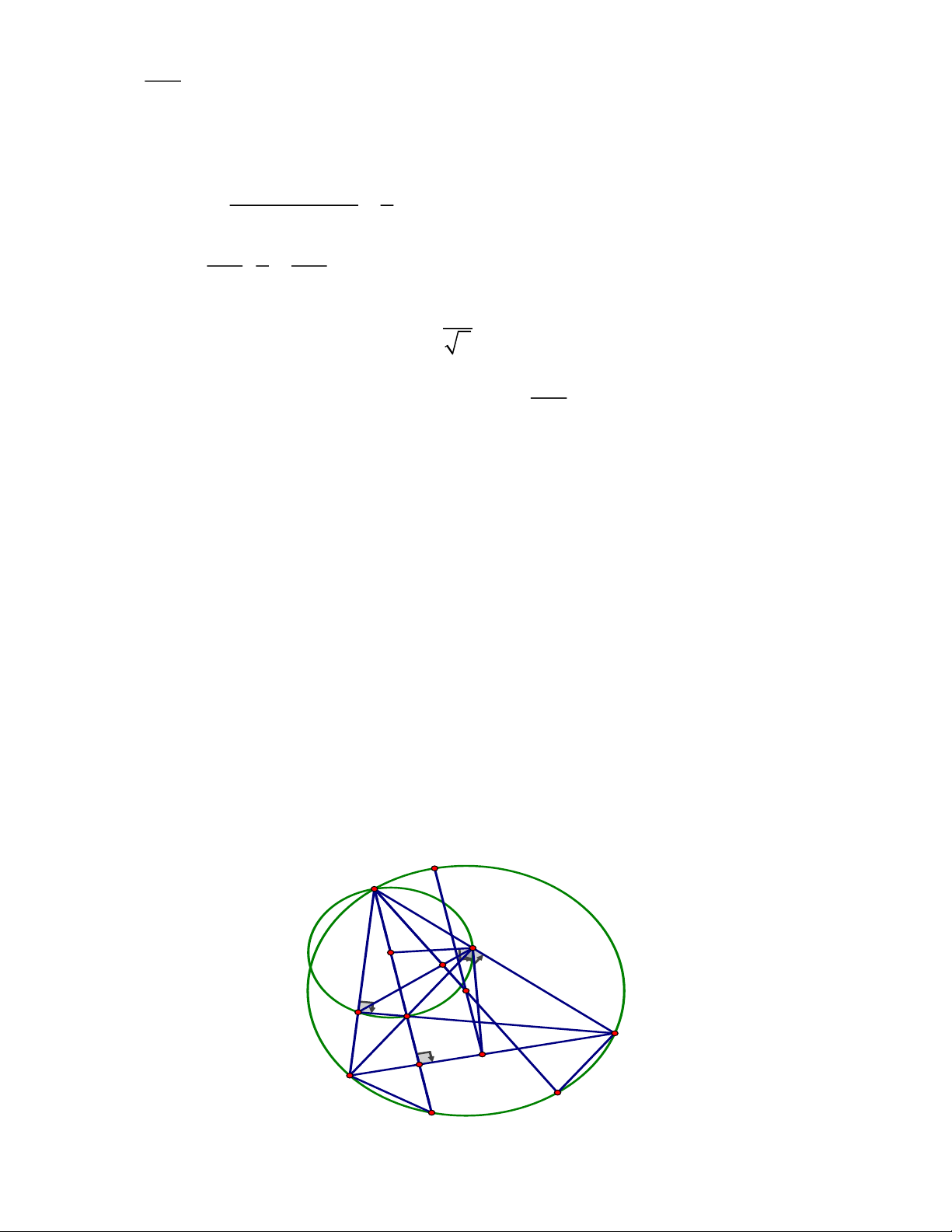
Câu 5. (2,75 điểm) Cho tam giác nhọn ABC nội tiếp đường tròn (O) có hai đường cao
BE,CF cắt nhau tại trực tâm H , AB AC. Vẽ đường kính AD của (O).Gọi K là giao
điểm của đường thẳng AH với đường tròn (O), K khác .
A Gọi L, P lần lượt là giao điểm
của đường thẳng AH với đường tròn (O), K khác .
A Gọi L, P lần lượt là giao điểm của
hai đường thẳng BC và EF, AC và KD
1) Chứng minh tứ giác EHKP nội tiếp đường tròn và tâm I của đường tròn này
thuộc đường thẳng BC
2) Gọi M là trung điểm của đoạn thẳng BC.Chứng minh AH = 2OM
3) Gọi T là giao điểm của đường tròn (O) với đường tròn ngoại tiếp tam giác
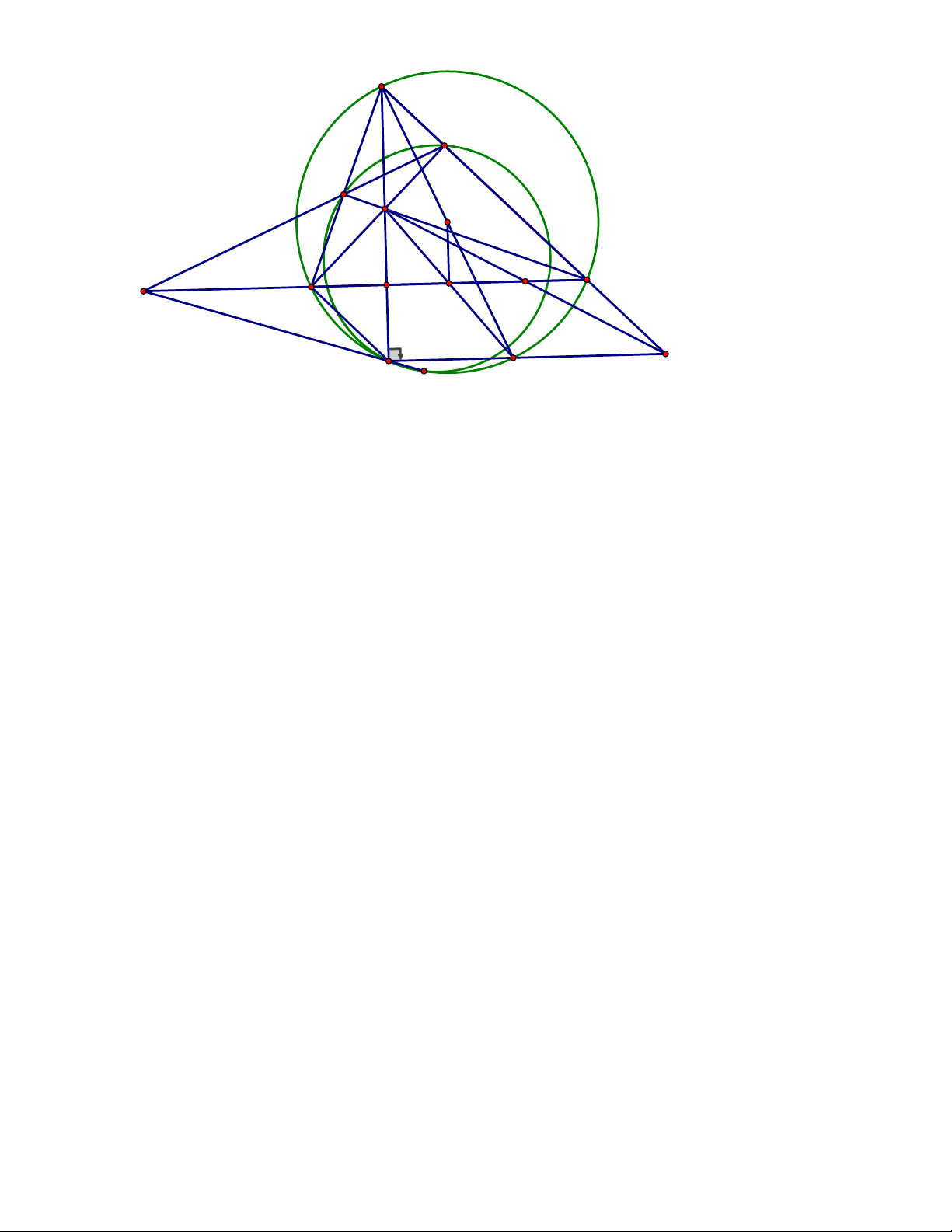
EFK ,T khác K.Chứng minh rằng ba điểm L, K ,T thẳng hàng. ĐÁP ÁN Câu 5. Trang 2 A E F H O L B J M I C P K D T'
1) Chứng minh EHKP là tứ giác nội tiếp
Ta có: BE là đường cao của ABC BE ⊥ AC hay 0 BEC = H EC = 90
AKD là góc nội tiếp chắn nửa đường tròn 0 AKD = 90
Xét tứ giác EHKP có: 0 0 0 H EP + H
KP = 90 + 90 =180 , mà hai góc này đối diện
nên EHKP là tứ giác nội tiếp (đpcm) Có 0
HKP = 90 là góc nội tiếp chắn cung HP HP là đường kính của đường tròn
ngoại tiếp tứ giác EHKP Tâm I của đường tròn này là trung điểm của HP
Gọi J là giao điểm của AK và BC
Ta có: HBJ = HAC (cùng phụ với ACB)
KBC = KAC (hai góc nôi tiếp cùng chắn cung KC) hay J BK = HAC H BJ = J BK (= H
AC) BJ là phân giác của HBK
Ta có: AH là đường cao của A
BC AH ⊥ BC = J BJ là đường cao BHK
Xét BHK ta có: BJ vừa là đường cao, vừa là đường phân giác từ đỉnh B của tam giác
BHK cân tại B và BJ là đường trung tuyến của BHK J là trung điểm của HK
Gọi I ' là giao điểm của BC và HP
Ta có: AJ ⊥ BC = Jmà KP ⊥ AH = K BC / /KP hay JI '/ /KP
Xét HKP ta có: J là trung điểm của HK (cmt); IJ / /KP(cmt) I ' J là đường trung
bình của HKP I 'là trung điểm của HP I I ' hay I BC(dfcm)
2) Chứng minh AH = 2OM AB ⊥ BD Ta có: 0 AB D = ACD
= 90 (góc nội tiếp chắn nửa đường tròn) AC ⊥ CD
AB ⊥ EF(gt) C F / /BD BH / /CD Mà hay
BDCH là hình bình hành
BE ⊥ AC(gt) BE / /CD CH / /BD Trang 3
BCcắt HD tại trung điểm mỗi đường, lại có M là trung điểm của BC(gt)
M cũng là trung điểm của .
HD Xét AHD ta có:
O, M lần lượt là trung điểm của AD, HD OM là đường trung bình AHD O M / / AH 1
AH = 2OM (dfcm) OM = AH 2
3) Chứng minh L, K ,T thẳng hàng
Gọi T ' là giao điểm của tia LK với đường tròn (O)
Xét tứ giác BFEC ta có: 0 BFC = B
EC = 90 . mà đỉnh F, E là các đỉnh kề nhau
Nên BFEC là tứ giác nội tiếp LFB = LCE (góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện)
Xét LFB và LCE ta có: L chung; LF LB L FB = L
CE(cmt) L FB L
CE(g.g) = L . E LF = L . B LC LC LE
Ta có tứ giác BCT ' K nội tiếp đường tròn (O) L KB = L
CT '(góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối diện)
Xét LBK và LCT 'ta có: L chung; LKB = LCT '(cmt) LB K LT
'C(g − g) LB LK = LF LK .
LB LC = LK.LT ' LE.LF = LK.LT '(= L . B LC) = LT ' LC LT ' LE
Xét LFK và LT ' E ta có: LF LK ELT ' chung; = L FK L
T 'E(c − g − c) LFK = LET ' LT ' LE
EFKT ' là tứ giác nội tiếp (tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện)
T 'thuộc đường tròn ngoại tiếp tam giác EFK
T T ' L, K,T thẳng hàng.(đpcm) HÀ NỘI Bài IV. (3,0 điểm)
Cho tam giác ABC có ba góc nhọn và đường cao BE.Gọi H và K lần lượt là
chân các đường vuông góc kẻ từ điểm E đến đường thẳng AB, BC
1) Chứng minh tứ giác BHEK là tứ giác nội tiếp
2) Chứng minh BH.BA = BK.BC
3) Gọi F là chân đường vuông góc kẻ từ điểm C đến đường thẳng AB và I là trung
điểm của đoạn thẳng EF.Chứng minh ba điểm H , I , K là ba điểm thẳng hàng ĐÁP ÁN Bài IV. Trang 4 A H 1 2 1 I E 2 1 F O B K C
1) Chứng minh BHEK là tứ giác nội tiếp Ta có : 0 BHE = (doEH ⊥ AB) 0 90 ,
BKE = 90 (do EK ⊥ BC) Tứ giác BHEK có 0 0 0
BHE + BKE = 90 + 90 =180 nên là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng 0 180 )(dfcm)
2) Chứng minh BH.BA = BK.BC
Theo câu a) tứ giác BHEK nội tiếp nên BKH = BEH (cùng chắn cung BH ) Ta có: 0
BEH + EBH = 90 (do B HE vuông tại H) 0
BAE + EBH = 90 (do A
BE vuông tại E) nên BEH = BAE (cùng phụ với EBH )
Mà BKH = BEH (cmt) nên BKH = BAE (= BEH )
Xét BHK và BCAcó:
ABC chung; BKH = BAE = BAC(cmt) B HK B C ( A g.g) BH BK =
(hai cặp cạnh tương ứng tỉ lệ) BH.BA = BC.BK BC BA
a) Chứng minh H , I , K thẳng hàng
Gọi I ' là giao điểm của HK và EF
Xét tứ giác BFEC có : 0
BFC = BEC = 90 (gt) nên là tứ giác nội tiếp (tứ giác có 2 đỉnh
kề nhau nhìn 1 cạnh dưới các góc bằng nhau) B = F (cùng chắn EC) 1 1
Ta có: EH / /CF (cùng vuông góc với AB) F = E (so le trong) do đó B = E 1 1 1 ( ) 1 1 Trang 5
Theo câu a, tứ giác BHEK nội tiếp nên B = H (cùng chắn EK )(2) 1 1
Từ (1) và (2) ta suy ra H = E 1 1
I 'HE có H = E nên là tam giác cân I 'H = I 'E (3) 1 1 Lại có: 0
H + H = BHE = 90 ; 0
F + E = 90 (do H FE vuông tại H) 1 2 2 1
Nên H = F hay tam giác I ' HF cân tại I ' I ' H = I ' F (4) 2 2
Từ (3)và (4) I 'E = I 'F hay I là trung điểm EF
Do đó I ' I nên ba điểm H , I , K thẳng hàng (đpcm)
CHUYÊN KHOA HỌC TỰ NHIÊN (HÀ NỘI) Câu III. (3 điểm)
Cho tam giác ABC có BAC là góc nhỏ nhất trong ba góc của tam giác và nội tiếp đường
tròn (O). Điểm D thuộc cạnh BC sao cho AD là phân giác BAC. Lấy các điểm M , N
thuộc (O) sao cho đường thẳng CM , BN cùng song song với đường thẳng AD
1) Chứng minh rằng AM = AN
2) Gọi giao điểm của đường thẳng MN với các đường thẳng AC, AB lần lượt là
E, F.Chứng minh rằng bốn điểm B,C, E, F cùng thuộc một đường tròn
3) Gọi P,Q theo thứ tự là trung điểm của các đoạn thẳng AM , AN. Chứng minh
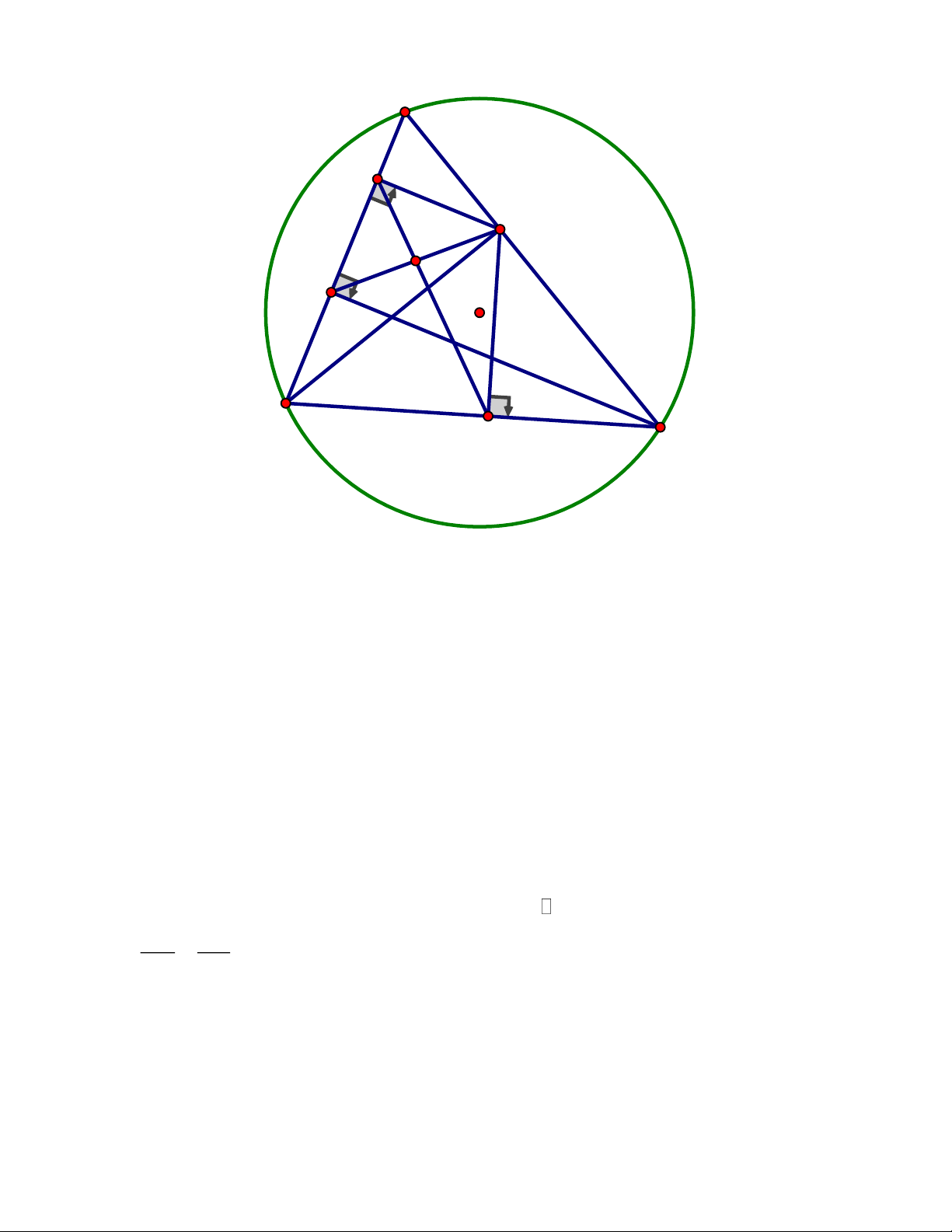
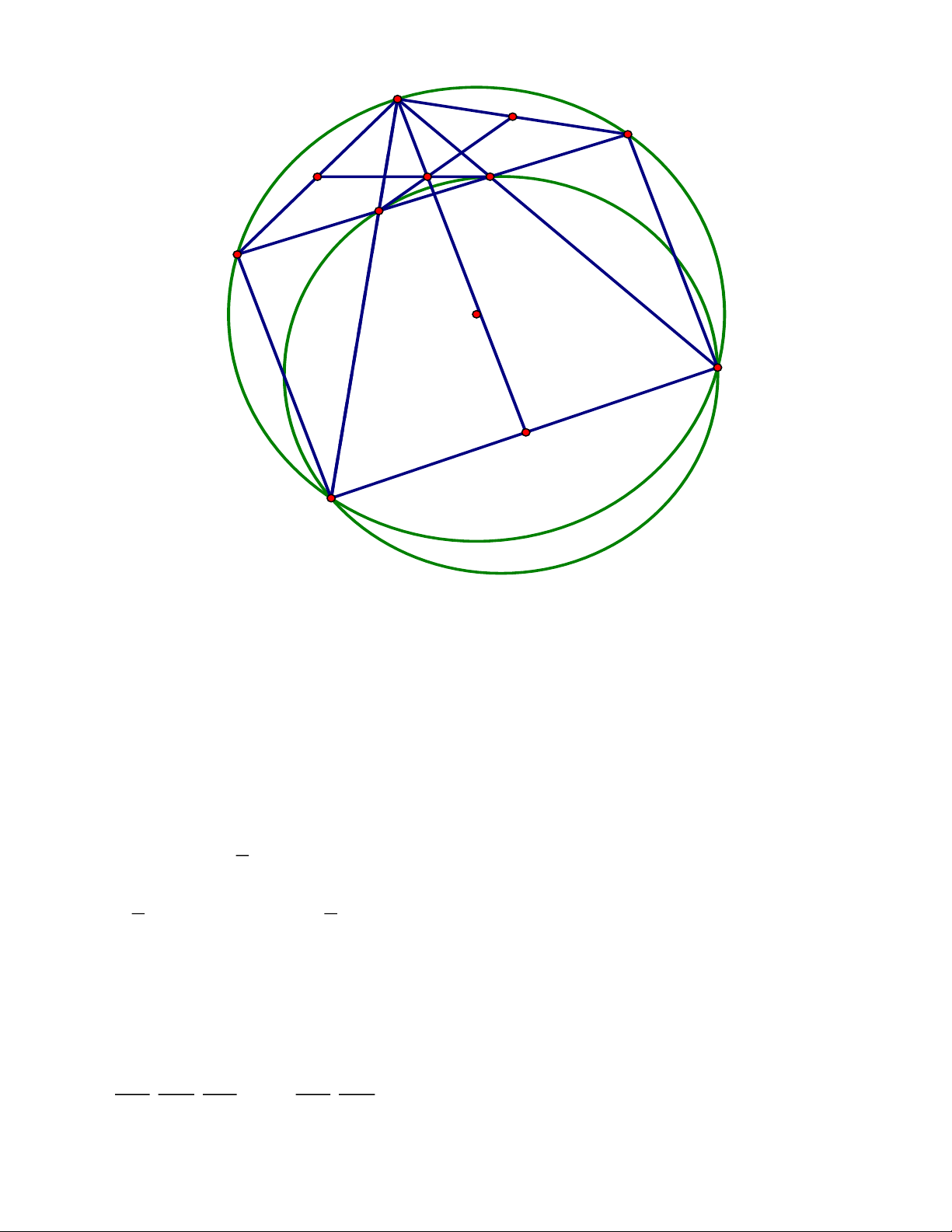
rằng các đường thẳng EQ, FP, AD đồng quy. ĐÁP ÁN Câu III. Trang 6 A P M Q K E F N O C D B
1) Chứng minh rằng AM = AN
Ta có: NBA = DAB (so le trong do BN / / AD)
DAB = DAC(gt) ; DAC = ACM (so le trong do CM / / AD)
NBA = MCA sd AN = sd AM (trong một đường tròn, hai góc nội tiếp bằng nhau
thì chắn hai cung bằng nhau).
Vậy AM = AN (trong một đường tròn, hai dây bằng nhau căng hai cung bằng nhau)
2) Chứng minh rằng 4 điểm B,C, E, F cùng thuộc một đường tròn. 1
Ta có: AEF = (sd AN + sdCM )(góc có đỉnh ở bên trong đường tròn) 2 1 = (sd AM + 1
sdCM ) = sd AC = ABC (góc nội tiếp bằng nửa số đo cung bị chắn) 2 2
Vậy tứ giác BCEF là tứ giác nội tiếp (tứ giác có góc ngoài và góc trong tại đỉnh đối diện
bằng nhau) hay B,C, E,F cùng thuộc một đường tròn.
3) Chứng minh các đường thẳng EQ, FP, AD đồng quy
Áp dụng định lý Mê-lê-na-uýt trong tam giác AHN , cát tuyến EKQ , ta có: EN KH QA EN KH . . =1 .
=1(do Q là trung điểm của AN (gt)nên QA = QN) EH KA QN EH KA Trang 7 EN KA = (I ) EH KH
Gọi AD PE = K '.Ta đi chứng minh K ' K
Áp dụng định lý Mê-lê-na-uýt trong tam giác AHM , cát tuyến PKF ta có: FM K 'H PA FM K 'H . . =1 .
=1(Do P là trung điểm của AM (gt) nên FH K ' A PM FH K ' A PA = PM ) FM K ' A = (II ) FH K 'H EN FM FM FH FM − FH HM Ta sẽ chứng minh = = = = ( ) * (tính chất dãy tỉ EH FH EN EH EN − EH HN số bằng nhau) HM DC
Vì BN / / AD / /CM nên áp dụng định lý Ta – let ta có: = HN DB DC AC HM AC Lại có : =
(định lý đường phân giác), do đó: = ( )1 DB AB HN AB
Xét AEF và ABC có: AEF = ABC(cmt), BAC chung ( AC AF AEF ABC g.g ) = (2) AB AE HM AF Từ (1) và (2) = (3) HN AE AF HF
Tiếp tục áp dụng định lý đường phân giác trong tam giác AEF ta có: = (4) AE HE HM HF EN FM Từ (3) và (4) ta suy ra =
,do đó (*) được chứng minh, tức là = (III ) HN HE EH FH KA K ' A
Từ (I ),(II ),(III )suy ra =
, do đó K K ' KH K 'H
Vậy EQ, FP, AD đồng quy tại K KHÁNH HÒA
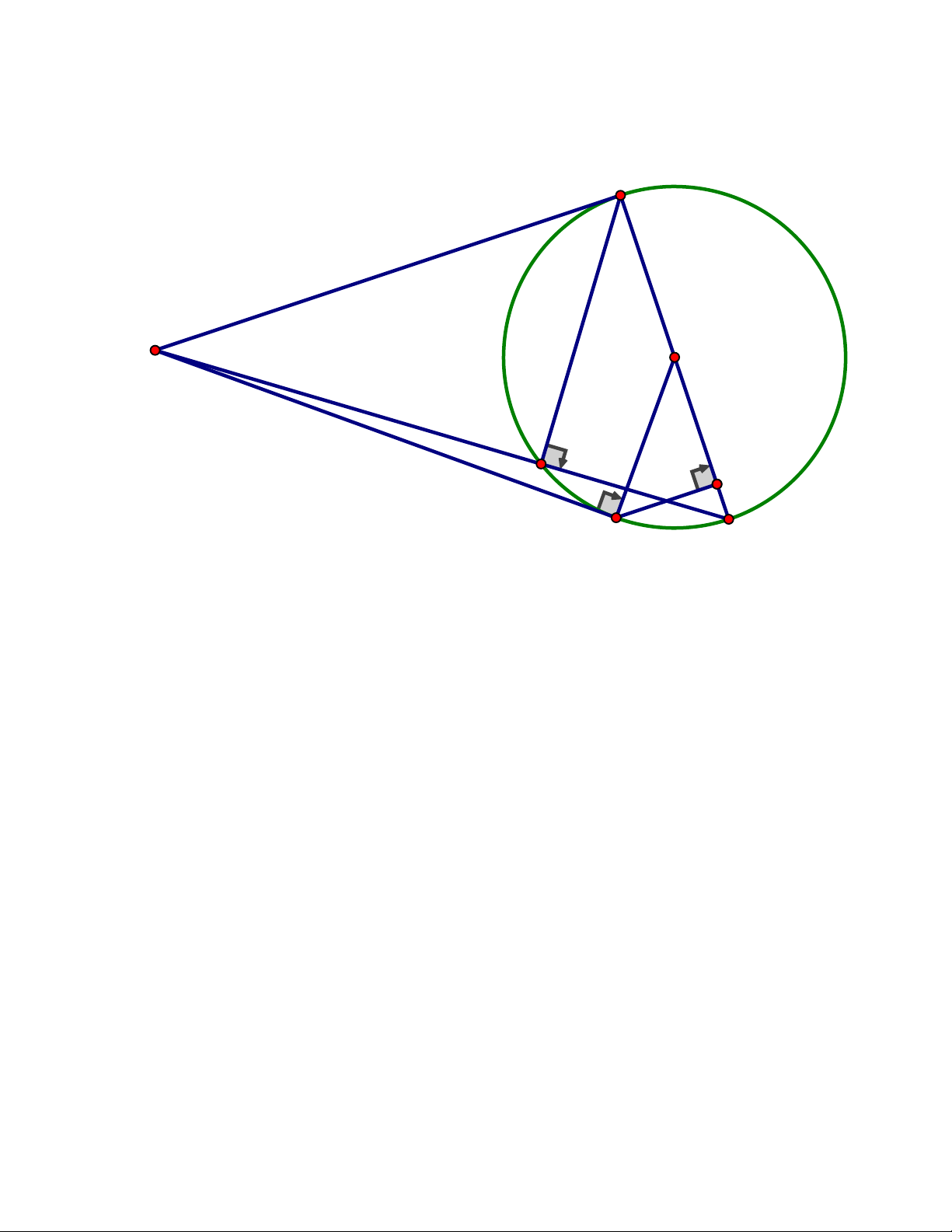
Câu 4. (3,00 điểm) Cho đường tròn (O) và một điểm I nằm ngoài đường tròn. Qua I kẻ
hai tiếp tuyến IM và IN với đường tròn (O).Gọi K là điểm đối xứng với M qua O.
Đường thẳng IK cắt đường tròn (O) tại H
a) Chứng minh tứ giác IMON nội tiếp đường tròn
b) Chứng minh IM .IN = IH.IK
c) Kẻ NP vuông góc với MK. Chứng minh đường thẳng IK đi qua trung điểm của . NP Trang 8 ĐÁP ÁN Câu 4. M O I H P K N
a) Chứng minh IMON là tứ giác nội tiếp
Ta có: IM , IN là các tiếp tuyến của (O) tại 0
M , N IMO = INO = 90
Xét tứ giác IMON ta có: 0 0 0
IMO + INO = 90 + 90 =180
Mà hai góc này là hai góc đối diện nên IMON là tứ giác nội tiếp đường tròn
b) Chứng minh IM .IN = IH.IK
Ta có: K là điểm đối xứng của M qua O O là trung điểm của MK và MK là đường kính của (O)
Ta có: MHK là góc nội tiếp chắn nửa đường tròn (O) 0
MHK = 90 hay MH ⊥ HK
Áp dụng hệ thức lượng vào IMK vuông tại M có đường cao MH Ta có: 2
IM = IH.IK
Mà IM = IN (tính chất hai tiếp tuyến cắt nhau) 2
IM = IN.IM = IH.IK(dfcm)
c) Chứng minh đường thẳng IK đi qua trung điểm của NP
Gọi IK NP = J
IK M = E Trang 9
Ta có: IM = IN (cmt) nên tam giác IMN cân tại I INM = IMN (hai góc đáy tam giác cân)
Lại có: MNP = IMN (so le trong do NP / /MI − cùng vuông góc với MK )
INM = MNP (cùng bằng IMN) NE là phân giác trong INJ
Lại có : MNK là góc nội tiếp chắn nửa đường tròn (O) nên 0 MNK = 90 , do đó
NK ⊥ NE nên NK là phân giác ngoài của INJ NI EI KI
Áp dụng tính chất đường phân giác ta có: = = NJ EJ KJ EI MI KI MI
Áp dụng định lý Ta let do NP / /MI ta có: = ; = EJ NJ KJ JP MI MI Từ đó suy ra =
NJ = JP J là trung điểm của NP NJ JP
Vậy đường thẳng IK đi qua trung điểm của NP(dfcm) THÁI NGUYÊN
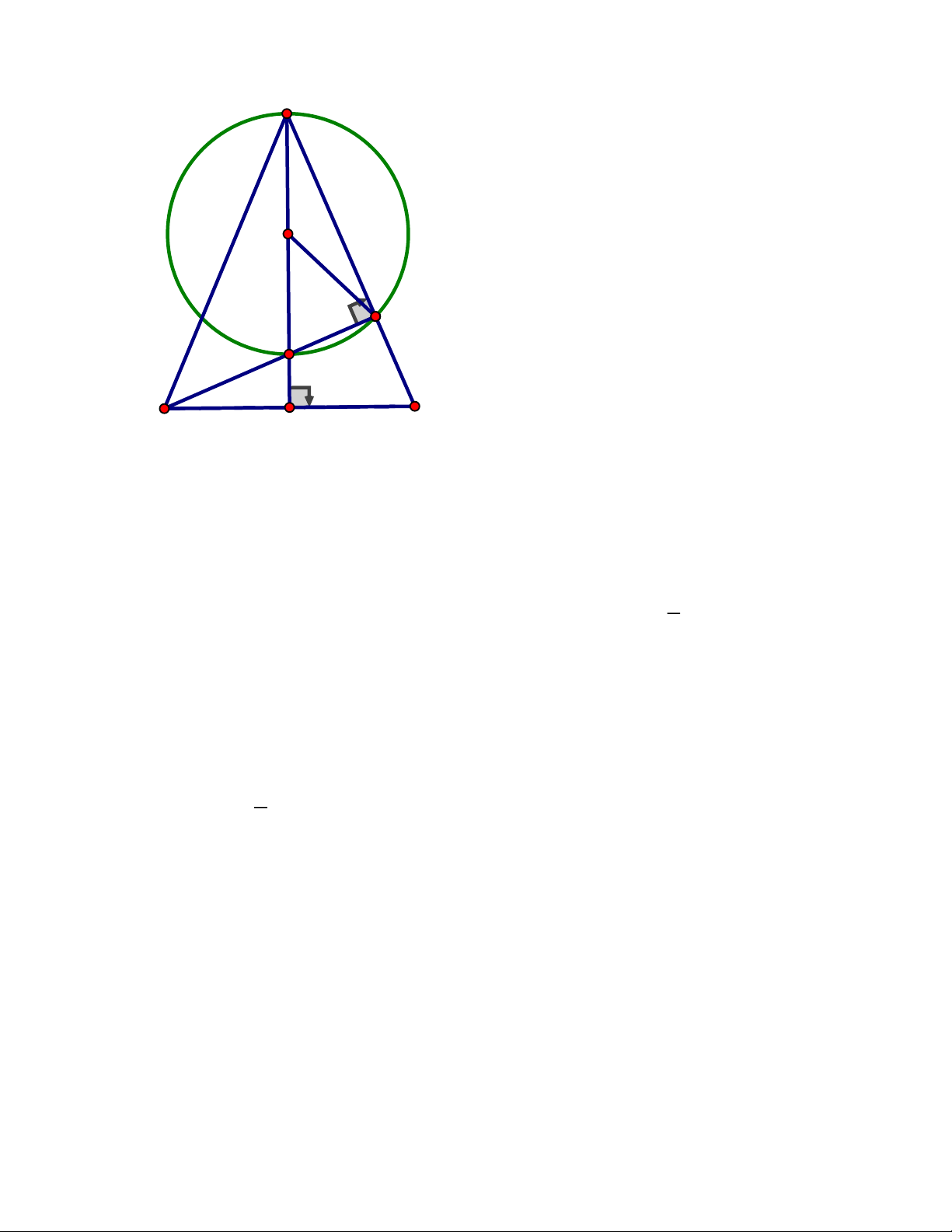
Câu 9. Cho tam giác ABC cân tại ,
A các đường cao AM , BN cắt nhau tại H.Chứng
minh MN là tiếp tuyến của đường tròn đường kính AH
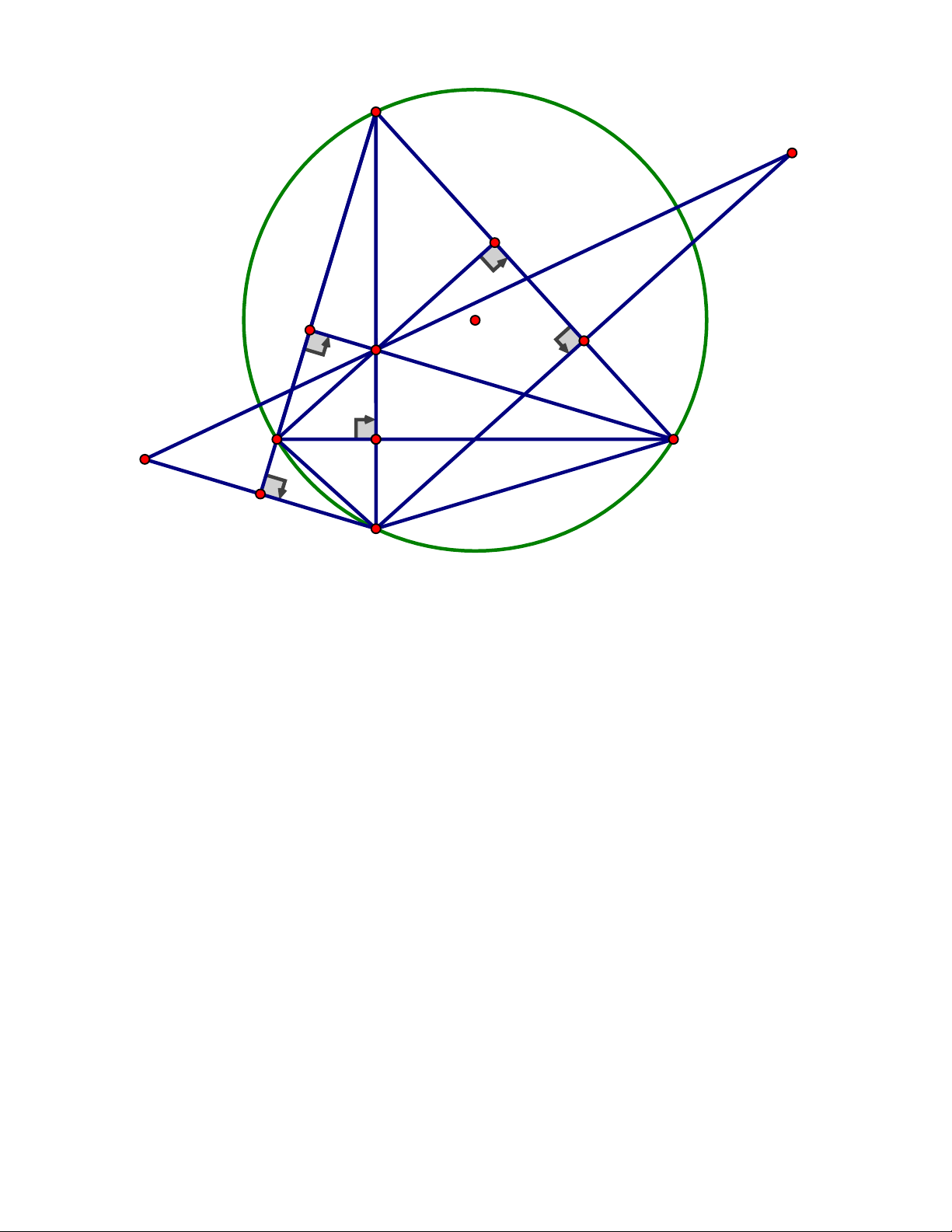
Câu 10. Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O), các đường cao
AD, BE,CF cắt nhau tại H.Đường thẳng AD cắt đường tròn (O)tại M khác A
a) Chứng minh tam giác BHM cân
b) Gọi P,Q lần lượt là điểm đối xứng với M qua AB và AC. Chứng minh ba điểm
P, H ,Q thẳng hàng. ĐÁP ÁN Câu 9. Trang 10 A O N H B M C
Gọi O là trung điểm của AH O là tâm của đường tròn đường kính AH
Ta có: BN là đường cao của 0 A
BC BN ⊥ AC HNA = 90 A NH vuông tại
N N (O)(*) 1
Xét ANH vuông tại N có đường trung tuyến ON ON = OH = AH (đường trung 2
tuyến ứng với cạnh huyền trong tam giác vuông). ON
H cân tại O ONH = OHN ( ) 1
Vì ABC cân tại A, có đường cao AM M là trung điểm BC
Xét BCN vuông tại N có đường trung tuyến NM 1
MN = BM = BC (đường trung tuyến ứng với cạnh huyền) 2 MBN = MNB (2)
Mặt khác BHM = OHN (hai góc đối đỉnh) 0
OHN + HBM = 90 (3) Từ (1), (2), (3) suy ra 0
MBN + HNO = 90 hay MN ⊥ ON (**)
Từ (*),(**) MN là tiếp tuyến của đường tròn đường kính AH. Câu 10. Trang 11 A Q E F H J O B D C P I M
a) Chứng minh BHM cân C F ⊥ AB
Ta có: AD,CF là hai đường cao của 0 ABC
AFC = ADC = 90 AD ⊥ BC
Xét tứ giác ACDF có : 0 A FC = E
DC = 90 , Mà đỉnh F, D là hai đỉnh kề nhau nên
ACDF là tứ giác nội tiếp DAC = DFC (cùng chắn DC) hay M AC = D FC ( ) 1
Xét đường tròn (O) ta có: MBC = MAC (2) (hai góc nội tiếp cùng chắn MC)
Xét tứ giác BFHD có: 0 0 0
BFH + BDH = 90 + 90 = 180 BFHD là tứ giác nội tiếp
HFD = HBD (hai góc nội tiếp cùng chắn HD) hay CF D = H BD (3)
Từ (1), (2), (3) suy ra HBD = CBM hay HBD = DBM BD là đường phân giác của BHM
Xét HBM ta có: BD vừa là đường cao, vừa là đường phân giác BHM cân tại B (dfcm)
b) Chứng minh P, H ,Q thẳng hàng Trang 12
Gọi I là giao điểm của AB và PM , J là giao điểm của AC và AB ⊥ PM = I MQ AC ⊥ MQ = J
Xét tứ giác IBDM có: 0 0 0
BIM + BDM = 90 + 90 =180 mà hai góc này là hai góc đối
diện nên IBDM là tứ giác nội tiếp IMB = IDB (hai góc nội tiếp cùng chắn IB)
Xét tứ giác MDJC ta có: 0
MDC = MJC = 90 mà hai góc này kề nhau nên MDJC là tứ
giác nội tiếp JDC = JMC (hai góc nội tiếp cùng chắn JC)
Tứ giác ABMC là tứ giác nội tiếp đường tròn (O) IBM = ACM (góc ngoài tại 1
đỉnh bằng góc trong tại đỉnh đối diện) ( ) 1
Ta có: BIM vuông tại 0
I IBM + IMB = 90 (2) JMC vuông tại 0
J JMC + JCM = 90 (3) Từ ( )
1 ,(2),(3) BMI = BDI = J DC = J
MC BDI, JDC là hai góc đối đỉnh nên
I, D, J thẳng hàng.
Ta có: BHD là tam giác cân tại B(cmt) có đường cao BD đồng thời là đường trung
tuyến D là trung điểm của HM . Xét PHM có:
D, I lần lượt là trung điểm của MH ,MP DI là đường trung bình của PHM
DI / /PH PH / /IJ (4)
Xét MHQ ta có: D, J lần lượt là trung điểm của MH , MQ
DJ là đường trung bình M
HQ DJ / /HQ HQ / /JI (5)
Từ (4) và (5) P, H,Q thẳng hàng.
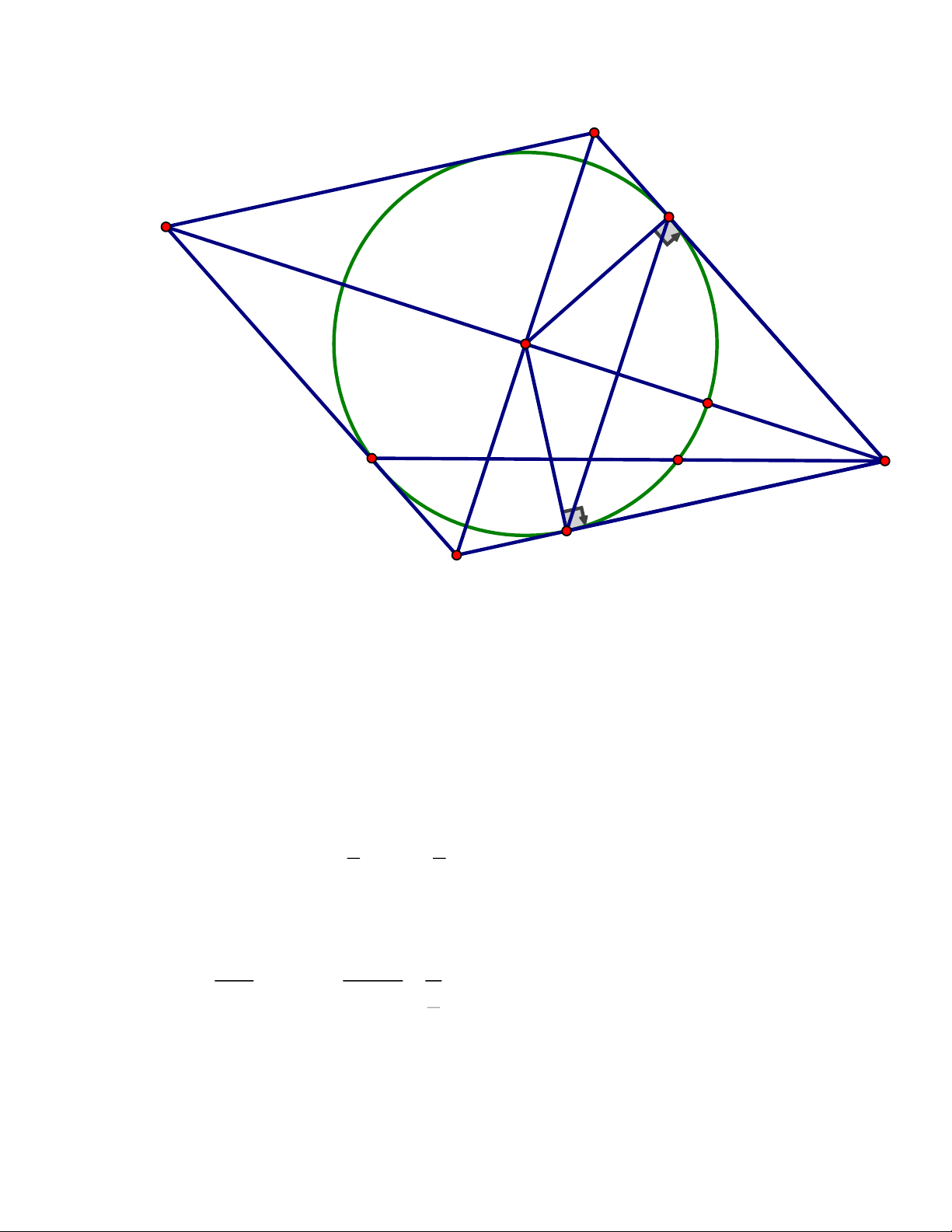
PHẦN 2: CỰC TRỊ HÌNH HỌC BẮC GIANG
Câu 4. (2,0 điểm) Cho đường tròn tâm O, bán kính R = 3c . m Gọi ,
A B là hai điểm phân
biệt cố định trên đường tròn (O; R)( AB không là đường kính). Trên tia đối của tia BA
lấy một điểm M ( M khác B) . Qua M kẻ hai tiếp tuyến MC, MD với đường tròn đã cho
(C, D là hai tiếp điểm)
a) Chứng minh tứ giác OCMD nội tiếp trong một đường tròn
b) Đoạn thẳng OM cắt đường tròn (O; R)tại điểm E. Chứng minh rằng khi 0
CMD = 60 thì E là trọng tâm của tam giác MCD
c) Gọi N là điểm đối xứng của M qua O. Đường thẳng đi qua O vuông góc với
MN cắt các tia MC, MD lần lượt tại các điểm P và Q. Khi M di động trên tia đối của tia ,
BA tìm vị trí của điểm M để tứ giác MPNQ có diện tích nhỏ nhất ĐÁP ÁN Trang 13 Câu 4. Q D N O E A B M P C
a) Chứng minh tứ giác OCMD nội tiếp
Xét đường tròn tâm O có MC, MD là các tiếp tuyến 0
OCM = ODM = 90 Tứ giác OCMD có: 0 0 0
OCM + ODM = 90 + 90 =180 OCMD là tứ giác nội tiếp
b) Chứng minh E là trọng tâm MCD
Xét đường tròn (O) có MC, MD là hai tiếp tuyến cắt nhau tại M nên MC = MD và
MO là tia phân giác của CMD 1 1 Mà 0 0 0
CMD = 60 OMD = CMD = .60 = 30 2 2 Xét ODM vuông có 0
OD = R = 3c , m OMD = 30 Ta có: OD OD 3 sin DMO = OM = =
= 6 cm EM = OM − OE = 6 − 3 = 3 cm 0 ( ) ( ) OM sin 30 1 2 MD = MC Lại có:
nên OM là đường trung trực của đoạn DC. Gọi I là giao điểm OD = OC = R
của OM và DC OM ⊥ DC tại I
Theo hệ thức lượng trong tam giác ODM vuông ta có: Trang 14 2 2 2 OD 3 3
OD = OI.OM OI = = = 3 9
IM = OM − OI = 6 − = OM 6 2 2 2 ME 3 2 2 Từ đó ta có: = = ME = MI MI 9 3 3 2
Xét tam giác MCD có MC = MD và 0
CMD = 60 nên MCD là tam giác đều có MI là
đường phân giác nên MI 2
cũng là trung tuyến. Lại có ME = MI (cmt) nên E là trọng 3
tâm tam giác MCD(dfcm)
c) Tìm vị trí của M để S min MNPQ
Vì N đối xứng với M qua O nên OM = ON
Xét hai tam giác vuông O QM , O
PM có cạnh OM chung, OMQ = OMP Suy ra O QM = O PM (g. .
c g) OP = OQ
Diện tích tứ giác MPNQ là : 1 1 1 S
= MN.PQ = .2OM.2OQ = 4. OM.OQ = 4S = 4.O . D MQ = 4 . R MQ MPNQ 2 2 2 OQM
Xét OQM vuông tại O có OD là đường cao, theo hệ thức lượng trong tam giác vuông ta có: 2 2 OD = D .
Q DM R = D . Q DM
Áp dụng bất đằng thức Cô si ta có: 2
QM = DQ + DM 2 D .
Q DM = 2 R = 2R Hay QM
= 2R QD = DM = R min Từ đó S nhỏ nhất là 2
8R MQ = 2R MPNQ
Khi đó: Xét MDB & MAD
có: DMB chung; MDB = MAD (cùng chắn BD) MD MB 2 2 M DB M
AD(g − g) = MD = M . A MB M . A MB = R MA MD
Đặt AB = a, MB = x ( a không đổi, a, x 0) Ta có: 2 2 − + + 2
A MB = R x(x + a) 2 2 2 a a 4R M .
= R x + ax − R = 0 x = (do x 0) 2
Vậy điểm M thuộc tia đối của tia AB và cách B một khoảng bằng 2 2
−a + a + 4R MB =
không đổi thì tứ giác MPNQ có diện tích nhỏ nhất là 2 8R 2 BẠC LIÊU Câu 4. (6,0 điểm) Trang 15
Cho đường tròn tâm O đường kính AB = 2 .
R Gọi I là trung điểm của đoạn thẳng O ,
A E là điểm thay đổi trên đường tròn (O)sao cho E không trùng với A và . B Dựng
đường thẳng d và d lần lượt là các tiếp tuyến của đường tròn (O)tại A và B. Gọi d 1 2
đường thẳng qua E và vuông góc với EI.Đường thẳng d cắt d ,d lần lượt tại M , N 1 2
a) Chứng minh tứ giác AMEI nội tiếp
b) Chứng minh IAE đồng dạng với NBE.Từ đó chứng minh I .
B NE = 3IE.NB
c) Khi điểm E thay đổi, chứng minh tam giác MNI vuông tại I và tìm giá trị nhỏ
nhất của diện tích tam giác MNI theo R ĐÁP ÁN Câu 4. d1 d2 d M E N A I O B
a) Chứng minh tứ giác AMEI nội tiếp
Vì d là tiếp tuyến của (O)tại A nên 0 IAM = 90 1
Vì d ⊥ EI tại E nên 0 IEM = 90
Xét tứ giác AMEI có 0 0 0
IAM + IEM = 90 + 90 = 180
Vậy tứ giác AMEI là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 0 180 )
b) Chứng minh IAE đồng dạng với NBE.Từ đó chứng minh I .
B NE = 3IE.NB
Vì AEB là góc nội tiếp chắn nửa đường tròn nên 0 AEB = 90 Ta có: 0 0
AEI + IEB = AEB = 90 ; BEN + IEB = IEN = 90 (dod ⊥ IE)
AEI = BEN (cùng phụ với IEB) Trang 16
Xét IAE và NBE có: AEI = BEN (cmt); IAE = NBE (góc nội tiếp và góc tạo bởi
tiếp tuyến và dây cung cùng chắn BE) IE IA I AE N
BE(g.g) =
(hai cạnh tương ứng) I .
A NE = IE.NB (1) NE NB
Mà I là trung điểm của O (
A gt) OA = 2IA
Lại có O là trung điểm của AB AB = 2OA = 4IA
IB = AB − IA = 4IA − IA = 3IA. Khi đó ta có: ( ) 1 3I .
A NE = 3IE.NB (nhân cẩ 2 vế với 3) I .
B NE = 3IE.NB(dfcm)
c) Chứng minh MNI vuông tại I và tìm GTNN của S theo R MNI
Xét tứ giác BNEI có: 0
IEN = 90 (do d ⊥ IE tại E) 0
IBN = 90 (do d là tiếp tuyến của đường tròn (O) tại B) 2 0 0 0
IEN + IBN = 90 + 90 =180
Tứ giác BNEI là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 0 180 )
INE = IEB = ABE (hai góc nội tiếp cùng chắn cung IE)
Lại có : Tứ giác AMEI là tứ giác nội tiếp (ý a)
IME = IAE = BAE (hai góc nội tiếp cùng chắn cung IE)
Xét tam giác MNI có: 0
INE + IME = ABE + BAE = 90 (do 0
AEB = 90 (cmt) nên AEB vuông tại E) MN
I vuông tại I (tam giác có tổng hai góc nhọn bằng 0 90 ) 1 Ta có: S = IM.IN M NI 2 Đặt AIM = ( 0 ) 0 0
90 BIN = 90 − AI AI
Xét AIM vuông ta có: cos = IM = IM cos BI BI BI
Xét BIN vuông ta có: cos( 0 90 − ) = IN = = IN cos( 0 90 − ) sin 1 1 AI BI AI.BI S = IM.IN = . . = M NI 2 2 cos sin sin.cos 1 R 3 3R
Ta có: AB = 4AI (cmt) AI = AB = , BI = AB = 4 2 4 2 2 3R 4 S = M NI sin.cos Trang 17 2 3R Do
không đổi nên diện tích tam giác MNI đạt giá trị nhỏ nhất sin.cos đạt 4 giá trị lớn nhất. Vì 0 0
0 90 nên sin,cos 0. Áp dụng BĐT Cô – si ta có: 2 2 sin + cos 1 sin.cos = ( ) 2 2 2 2 3R 1 3R S : = .Dấu " = " xảy ra A MI 4 2 2 s in = cos 1 0 sin = cos = = 45 2 2 s in = cos 2 2 3R
Vậy giá trị nhỏ nhất của diện tích tam giác MNI là , đạt được khi 0 AIM = 45 . 2 HÀ NAM
Câu 4. (4,0 điểm) Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn (O; R). Hai
đường cao BE,CF của tam giác ABC cắt nhau tại H. Đường thẳng AH cắt BC tại D và
cắt đường tròn (O; R)tại điêm thứ hai là M
1) Chứng minh tứ giác AEHF nội tiếp
2) Chứng minh BC là tia phân giác của EBM
3) Gọi I là tâm đường tròn ngoại tiếp tứ giác AEHF . Chứng minh IE là tiếp tuyến
của đường tròn ngoại tiếp BCE
4) Khi hai điểm B,C cố định và điểm A di động trên đường tròn (O; R)nhưng vẫn
thỏa mãn điều kiện tam giác ABC có ba góc nhọn. Chứng minh OA ⊥ EF.Xác
định vị trí của điểm A để tổng DE + EF + FD đạt giá trị lớn nhất. ĐÁP ÁN Câu 4. A' A E I K F O H C D N B P M Trang 18
1) Chứng minh AEHF là tứ giác nội tiếp
Ta có: BE,CF là các đường cao của ABC BE ⊥ AC = E 0 = = C F ⊥ AB = F AFC AEB 90
Xét tứ giác AEHF ta có : 0 0 0
AEH + AFH = 90 + 90 =180 AEHF là tứ giác nội tiếp
2) Chứng minh BC là tia phân giác của BEM 0 DAC + ACD = 90 Ta có:
DAC = EBC (cùng phụ góc DAC) 0 EBC + ECB = 90
Hay MAC = EBC
Lại có: MAC = MBC (cùng chắn cung MC)
MBC = EBC (= MAC) BC là phân giác của E BM (dfcm)
3) Chứng minh IE là tiếp tuyến của đường tròn ngoại tiếp BCE Ta có : 0
AEH = 90 là góc nội tiếp chắn cung AH
AH là đường kính của đường tròn ngoại tiếp tứ giác AEHF
I là trung điểm của AH
Ta có: BEC là tam giác vuông tại E
Đường tròn ngoại tiếp BEC có tâm là trung điểm của BC
Gọi N là trung điểm của BC N là tâm đường tròn ngoại tiếp BEC 1
NB = NE = BC (tính chất tiếp tuyến của tam giác vuông) 2 BN
E cân tại N N BE = N EB hay DBE = N EB 1
Ta có IE là đường trung tuyến của AEH vuông tại E EI = IH = AH I EH 2
cân tại I IEH = IHE mà IHE = BHD (hai góc đối đỉnh) IEH = BHD Lại có : 0 0 H BD + BH D = 90 I EH + BE N = 90
Hay IE ⊥ EN IE là tiếp tuyến của đường tròn ngoại tiếp BEC(dfcm)
4) Xác định vị trí điểm A………
Gọi EF OA = K
Kẻ đường kính AP
Khi đó ta có ACP là góc nội tiếp chắn nửa đường tròn 0 ACP = 90 0 0 A PC + P
AC = 90 hay O AC + A PC = 90
Xét tứ giác BCEF có: 0
BFC = BEC = 90 , mà hai đỉnh E, F kề nhau BCEF là tứ giác
nội tiếp FBC = AEF (góc ngoài bằng góc trong tại đỉnh đối diện) Hay ABC = AEB mà APC = ABC (cùng chắn ccung AC) 0 A EF = A PC A PC + O AE = A EF + E AO = 90 Trang 19
Hay AO ⊥ EF = K(dfcm)
Chứng minh tương tự ta có: OB ⊥ FD,OC ⊥ ED 1 Ta có: S = O .
A EF (tứ giác có hai đường chéo vuông góc) OEAF 2 1 1 Tương tự: S = O . B FD ; S = OC.DE OFBD 2 ODCE 2 1 1 1 S + S + S = . OA EF + .
OB FD + OC.DE OEAF OFBD ODCE 2 2 2 1 S
= R(EF + FE + DE) 2SABC
EF + FE + DE = ABC 2 R
Kéo dài ON cắt (O) tại A' A' N ⊥ BC (do ON ⊥ BC ) 1 1 Khi đó ta có: S = A .
D BC A' N.BC ABC 2 2 Đặt BC = a
Áp dụng định lý Pytago trong tam giác vuông ONC ta có: 2 2 2 2 a
ON = OC − CN = R − 4 2 2 2 a a 2 a
A'N = OA'+ ON = R + R − S
R + R − 4 ABC 2 4 2 2 a
a R + R − 4 EF FD DE + + R
Dấu " = " xảy ra A A', khi đó điểm A là điểm chính giữa của cung lớn BC HÀ NAM (CHUYÊN) Câu 4. (3,5 điểm)
Cho đường tròn (O), đường kính AB cố định. Điểm H cố định nằm giữa hai điểm
A và O sao cho AH OH. Kẻ dây cung MN vuông góc với AB tại H. Gọi C là điểm
tùy ý thuộc cung lớn MN sao cho C không trùng với M , N và .
B Gọi K là giao điểm của AC và MN.
1) Chứng minh tứ giác BCKH nội tiếp
2) Chứng minh tam giác AMK đồng dạng với tam giác ACM
3) Cho độ dài đoạn thẳng AH = .
a Tính AK.AC − . HA HB theo a
4) Gọi I là tâm đường tròn ngoại tiếp tam giác MKC.Xác định vị trí của điểm C để
độ dài đoạn thẳng IN nhỏ nhất ĐÁP ÁN Câu 4. Trang 20