Tuyển tập một số đề thi học kì 1 Toán 11 năm 2020 – 2021 – Bùi Đình Thông

Tài liệu gồm 32 trang, được biên soạn bởi thầy giáo Bùi Đình Thông, tuyển tập một số đề thi học kì 1 Toán 11 năm học 2020 – 2021, giúp học sinh khối 11 ôn tập để chuẩn bị cho kỳ thi học kì 1 Toán 11 sắp tới.

28 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 11

Môn: Toán 11

Thông tin:

32 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
11
Gv: Bùi Đình Thông
facebook: Thông Đình Đình
Tuyển tập một số đề thi học kì hay trên cả nước
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
S ABCD.
ABCD
M
BC
( )
P
M
AC SB,
( )
P
S ABCD.
=xsin 1
= +
π
xkπk2,
2
= − +
π
xkπk,
2
= +
π
xkπk,
2
= − +
π
xkπk2,
2
11B
25
10
15
3
26
3
3
2
1
3
115
7
920
9
92
27
92
( )
=
+
x
fx
x
2
sin
1
( )
=+f x x x3sin 4cos
5
( )
=f x xtan
π2
( )
=f x xcos
( )
π0;
3
1
4
2
ABCD
O
O
−1
ABD
CDB
O
π
2
OBC
OCD
O
=k 1
OBC
ODA
AD
ABD
DCB
2
a
b
a //b
2
a
b
a
b
2
a
b
a //b
0
1
2
3
10
5
C
5
10
5!
A
5
10
10 !
2!
10
3
3
2
7
15
7
10
73
120
29
60
ABCD
G
ABDΔ
M
BC
=BM MC2
MG
( )
BCD
( )
ABC
( )
ACD
( )
ABD
10
5
ÔN THI THPT QUỐC GIA 2020-2021
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
C
5
10
5!
A
5
10
10 !
2!
10
3
3
2
7
15
7
10
73
120
29
60
ABCD
G
ABDΔ
M
BC
=BM MC2
MG
( )
BCD
( )
ABC
( )
ACD
( )
ABD
20
18
CC
21
20 18
C
2
38
A
2
38
CC
11
20 18
.
0,8
0,9
0,95
0,98
0,89
0,85
Oxy
( )
−A 3;1
A
( )
O
V
;2
( )
−−A ' 6; 2
( )
−A ' 6; 2
( )
−A ' 6;2
( )
A ' 6;2
M
=−y x x3 sin 2 cos 2
=−M 31
=M 2
=M 3
=−M 2
=
−
x
y
x
2
2sin
tan 1

= + +


ππ
D R kπ k π\ , 2
24
( )
kZ

= +


π
D R kπ\
4
( )
kZ

= + +


ππ
D R k π kπ\ 2 ,
24
( )
kZ

= + +


ππ
D R kπ kπ\,
24
( )
kZ
x
15

−


x
x
10
2
2
180
80
−80
4
a
+ + =a x x a x
22
sin 2sin2 3 cos 2
=a 3
=a 1
=−a 1
=a 2
= X x x:7
X
3
5
45
60
50
55
Oxy
( )
C
+=xy
22
1
( )
=−v 1; 2
( )
C
v
T
( )
C
( ) ( )
− + − =xy
22
1 2 1
( )
C
( ) ( )
− + + =xy
22
1 2 1
( )
C
( ) ( )
+ + − =xy
22
1 2 1
( )
C
( ) ( )
+ + + =xy
22
1 2 1
Oxy
( )
+ + =d x y
1
: 2 3 1 0
( )
+ − =d x y
2
: 2 3 2 0
d
1
d
2
4
0
1
Oxy
( ) ( )
−AB1,0 , 3,2
B
A
( )
−−B 5; 2
( )
B 7;4
( )
B 10;4
( )
−B 7; 4
( )
n
u
=−
n
n
u 34
( )
n
v
=−
n
n
v
1
4
3
( )
n
a
+
=
+
n
n
a
n
4
2
( )
n
b
=
n
b
n
1
( )
n
v
( )
n
a
( )
n
b
( )
n
u
Oxy
( )
+ − =d x y: 1 0
d

−


π
O
Q
;
2
( )
d
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
( )
− − =d x y: 1 0
( )
− + =d x y: 1 0
( )
+ + =d x y: 1 0
( )
− − =d x y: 2 1 0
n
( )
+
++
n n n22
6 3 3
11
+=xx
22
sin cos 3 1
S ABCD.
ABCD
O
AC
BD
M
AB
N
SC
=SN NC
1
2
( )
SMC
( )
SBD
MN
( )
SBD
E
F
CD
SD
( )
MN AEF//
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
4
3
2
4
1
P
2
P
8
21
=
P
3
7
=
P
10
21
=
P
4
9
=
12
5
7
12
3
2
1
70
105
220
10
π[0; ]
x
1
sin
3
=
yxsin2=
2−
1−
0
1
xtan 3=
( )
π
xkπk
6
= +
( )
π
xkπk
3
= +
( )
π
xkπk
3
= − +
( )
π
xkπk
6
= − +
Oxy
d
xy2 1 0− + =
d
O
φ
0
90=−
xy2 1 0+ − =
xy2 1 0+ + =
xy2 1 0− + =
xy2 1 0− − =
4
3
3
3
4
Oxy
( )
v 2; 1=−
( )
M 3;2−
M
v
M '
M '
( )
M ' 5;3
( )
M ' 1;1−
( )
M ' 1;1
( )
M ' 1; 1−
Oxy
v (2; 1)=−
M( 3;2)−
M
v
(5;3)
( 1;1)−
(1;1)
(1; 1)−
Oxy
F
k 2=
( )
M 0;1
( )
N 1;0
M
N
MN

ÔN THI THPT QUỐC GIA 2020-2021
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
2
22
1
2
2
x
π
π
3
;2
2



xsin 0
xcos 0
xsin 0
xcos 0
xsin 0
xcos 0
xsin 0
xcos 0
x
0
1
cos( 20 )
2
−=
x k x k
0 0 0 0
50 .360 , 10 .360= + = − +
kZ()
x k x k
0 0 0 0
40 .360 , 40 .360= + = − +
kZ()
x k x k
0 0 0 0
80 .360 , 40 .360= + = +
kZ()
x k x k
0 0 0 0
80 .360 , 40 .360= + = − +
kZ()
Oxy
A( 1;0)−
M(2; 1)−
M
A
k 2=
M '
M '
M '( 5;2)−
M '(5; 2)−
M '(5;2)
M '(3; 2)−
S C C C C
0 1 2 2016
2016 2016 2016 2016
...= + + + +
S
2016
2=
S
2016
21=−
S
2016
21
2
−
=
S
2015
21=+
( )
ABCD
M N K,,
AB BC CD,,
MNK()
ABD()
AD
MN
BD
MK
AC
AD
MNK()
A
B
A
1
3
B
1
5
P
A
B
P
8
15
=
P
3
4
=
P
1
15
=
P
2
15
=
a
b
a
b
a
b
P
P
8
15
=
P
2
9
=
P
7
15
=
P
1
5
=
a
x
3
( )
x
5
1+
a 15=
a 6=
a 24=
a 10=
5
3
2
5
12
24
120
16
x αsin( ) 1− = −
π
x α kπ
2
= − +
kZ
π
x α k π2
2
= − − +
kZ
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
π
x α k π2
2
= − +
kZ
x α π k π2= + +
kZ
π
xcos 2 cos
6
=
xx3 sin cos 2+=
n
n
Cn
1
2 30+=
x
6
x
10
1
2
2

+


x 0
S ABCD.
AB
CD
M,
N
SC
SA
MN
ABCD()
DMN()
ABCD()
O
ABCD
SO
MAB()
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
=yxcos

−


ππ
;
22



π
0;
2
( )
−π;0
( )
−ππ;
5
6
8
19
118
20
240
( )
n
u
( )
−
=
+
n
n
u
n
1
25
−
1
27
1
27
1
25
−
1
7
( )
n
u
=−u
1
2
=d 3
10
S
10
( )
n
u
155
115
145
165
Oxy
( )
A 2;0
A
( )
O
Q
;90
( )
M 0;2
( )
−N 0; 2
( )
−P 2;0
( )
Q 1;1
a
b
1
2
3
4
( )
−=xxsin 3 cot 1 0

+

π
kπ kπ k,,
6

+

π
kπk,
6

+

π
kπk,
3

+

π
kπ kπ k,,
3

+


n
x
x
2
1
4096
x
195
118
2020
495
1
10
1
2
56
506
3
16
S ABCD.
O
M
SA
( )
P
M
SC
AD
S ABCD.
( )
P
Oxy
a
b
a
O
=−k 2
Oy
b
+ + =xy2 16 0
a
ÔN THI THPT QUỐC GIA 2020-2021
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
− − =xy2 8 0
− − =xy2 32 0
− + =xy2 32 0
− + =xy2 8 0
( )
n
u
=u
1
1
+
=+
nn
uu
2
1
2
n
*
= + + + +S u u u u
2 2 2 2
1 2 3 1001
...
1002001
1001001
1001002
1002002
50
A
25
A
( )
n
u
=u
1
3
=d 5
u
2
u
7
S
8
S ABCD.
ABCD
P M N,,
SA BC,
AD
( )
SAC
( )
SBD
( )
SAB
( )
PMN
SC
( )
PMN
( )
n
u
( )
−
=
n
n π
u
21
cos
3
+
=
nn
uu
3
n 1
17
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
50
20
3
1
CC
21
30 20
.
−CC
33
50 20
−CC
33
50 30
CC
33
50 30
.
=−yx3sin 2 2
4
1
5
−5
( )
( )
=
Ok
V M M
,
=OM kOM
=OM kOM
=−OM kOM
=OM k OM
=−x
3
cos
2
= +
π
xkπ
5
2
6
k
= +
π
xkπ
2
2
3
k
= +
π
xkπ2
3
k
= +
π
xkπ
6
k
( )
−M 1;2
=−k
1
2
( )
( )
=
Ok
V M M
,
O
M

−


M
1
;1
2

−


M
1
1;
2

−


M
1
;1
2

−


M
1
1;
2

=−


π
yxtan
3

= +


π
Dkπk\;
3

= +


π
Dkπk\ 2 ;
3

= +


π
Dkπk\;
3

= +


π
Dkπk
5
\;
6
−=xx
2
cos cos 0
− πx0
=
π
x
6
=
π
x
4
=−
π
x
2
=
π
x
2
+=xx3 sin cos 0
= − +
π
xkπ
6
k
= − +
π
xkπ2
3
k
= − +
π
xkπ
3
k
=+
π
xkπ
3
k
S ABCD.
=AC BD M
=AB CD N
( )
SAC
( )
SBD
SM
SA
MN
SN
Oxy
( )
−M 1; 2
( )
= − −v 3; 3
M
M
M
( )
−M 2; 5
( )
−M 4; 1
( )
M 2;5
( )
−−M 2; 5
15
13
20
280
1
2
3
5
6
ÔN THI THPT QUỐC GIA 2020-2021
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
22644
24642
26442
44622

− − =


π
x2sin 3 0
6
− = −xxsin 3 cos 2
=A 1;2;3; 4;5;6;7
A
A11
Oxy
( )
=−v 2; 1
+ − =d x y: 3 0
d
d
v
ABCD
G
BCD
M
CD
I
AG
( )
ABG
( )
ACD
J
BI
( )
ACD
AI
AG
ACD
JCD
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
x

−


x
x
9
2
1
3
3
x 0
2268
−2268
84
−27
2
2
3
2
3
25
2
5
3
10
7
10
S ABC.
GK,
ABC
SBC
E
AC
( )
GKE
SC
M
MS
MC
1
2
2
3
1
2
Oxy
Δ'
+ − =xyΔ : 2 1 0
( )
=−v 1; 1
+ − =xyΔ ' : 2 3 0
+=xyΔ ' : 2 0
+ + =xyΔ ' : 2 1 0
+ + =xyΔ ' : 2 2 0
Oxy
− + =d x y: 2 3 3 0
− − =d x y' : 2 3 5 0
v
d
d '
d
v
=−


v
64
;
13 13
=−


v
12
;
13 13
= − −


v
16 24
;
13 13
=−


v
16 24
;
13 13
ABCD
a
AB,
CD
a 3
2
a 2
2
a
2
a 5
2
ABCD
S
( )
ABCD
S
A B C D, , ,
3
4
5
6
kπk\|
−
=
x
y
x
1 cos
sin
+
=
x
y
x
1 cos
sin 2
+
=
x
y
x
1 cos
sin
−
=
x
y
x
1 cos
2sin
=yxcos
−x ππ;
( )
−π;0
( )
π0;
( )
−π;0
( )
π0;
( )
−π;0
( )
π0;
( )
−π;0
( )
π0;
cm cm cm cm1 ,3 ,5 ,7
cm9.
3
10
1
20
1
15
7
10
1,3,5,7,9
135
ÔN THI THPT QUỐC GIA 2020-2021
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
5
.
6
1
.
60
1
.
6
59
.
60
=yxcot 2
.

+


π
kπk\ | .
2

+


π kπ
k\ | .
42



π
kk\ | .
2
=−yx2sin
( )
−x3sin
=−yx2cos
=−y x xsin cos
=−
π
xsin2 sin
3
αβ,
−
ππ
αβ
3
,.
44
αβ.
−
π
2
9
−
π
2
4
9
π
2
9
−
π
9
= − +y x x x
2
2cos 2 3 sin .cos 1
+33
−33
Oxy
( )
I 1;0
( )
+=C x y
22
:4
I
( )
− + =xy
2
2
24
( ) ( )
− + − =xy
22
2 2 4
( )
+ − =xy
2
2
24
( ) ( )
− + − =xy
22
2 1 4
12
13
418
455
1
13
1
2
=xxtan3 tan
π0;10
n
*
( )
−
=
n
nn
CC
13
5*
x
5

−


n
nx
x
2
1
14
x 0
−16
35
−3
16
−35
16
−16
3
11
103
231
215
462
118
231
115
231
ABC
ABMN
ACPQ
O
1
O
2
ABMN
ACPQ
I
BC
IO O
12
I
AI
NQ
=AI NQ
1
2
=+x x x
2
tan cot 4cos 2
8
8
2
8
A
B
4
ABCD A B C D.
ABCD
O
==AA AB a22
EF,

ADD BB C,
EF
( )
ABCD
ABCD A B C D.
( )
OEF
ABCD A B C D.
( )
OEF
a
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
AB
C
I
AC
=AI BC
I
( )
+ − +
=
−
x x x x
x
sin2 cos 3 cos 2 sin
0
2sin2 3
ABCD A B C D.
ABCD
AB
CD
=AB CD2.
A
BB CC DD,,
M N P, , .
AMNP
AP
MN
+=BM DP CN2 2 .
ABC

ABB ACC,
IJ,

B C C B,
AIJ
+ − −
=
+
x x x
x
sin2 2cos sin 1
0.
tan 3
ABCD A B C D.
ABCD
AB
CD
=AB CD2
A
BB CC DD,,
M N P,,
AMNP
AP
MN
BM DP CN22+=
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
S
( )
−x
17
34
=−S 1
=S 1
=S 0
=S 8192
h
t
=hd
( )

=−


π
dt3cos 2 1
3
d 0
d 0
10
13
12,5
10,5
11
39
40
39
3
40
5
8
3
5
15
10
35
10
7
45
10
10
=A 1;2;3; 4;5;6
3
125
120
6
10
− + +
+ + + = + + +
n n n n
n n n n n n
C C C C C C
0 1 1 1 2 2
2 2 2 2 2 2
... ...
− + +
+ + + = + + +
n n n n
n n n n n n
C C C C C C
0 1 2 1 2 2
2 2 2 2 2 2
... ...
+ + +
+ + + = + + +
n n n n
n n n n n n
C C C C C C
0 1 1 1 2 2
2 2 2 2 2 2
... ...
++
+ + + = + + +
n n n n
n n n n n n
C C C C C C
0 1 1 2 2
2 2 2 2 2 2
... ...
16
1
16
9
16
1
2
3
8
7
16
52
K
1
6497400
4
6497400
1
270725
4
270725

−=


π
x
5
cos 1
6
=+
π
xkπ
3
=+
π
xkπ2
3
=+
π
xkπ
5
6
=+
π
xkπ
5
2
6
6
4
2
7
15
4
9
8
15
7
45
ÔN THI THPT QUỐC GIA 2020-2021
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
35
10
20
500
45
25
M
m
= + −y x xcos 2 cos 2
−Mm
−=Mm
25
8
−=Mm4
−=Mm
21
8
−=Mm2
=A 1;2;3;4;5;6;7;8
1111
384
345
3840
1920
Oxy
+ − =d x y: 2 3 0
( )
I 4;3
+ − =xy2 17 0
+ − =xy2 7 0
+ + =xy2 17 0
+ − =xy2 15 0
+=a x b x csin cos
+a b c
22
+a b c
2 2 2
+a b c
22
+a b c
2 2 2
O
=yx
2
sin
=yxcos
=yxtan
=yx
2
cot
3
10
P
2
C
3
10
P
10
A
3
10
n
n n n n
S C C C C
0 1 2 2
2 2 2 2
...= + + + +
=
n
S
2
2
=−
n
S
2
21
=
n
S 2
=+
n
S
2
21
6
6.7!
2.7!
−8! 7!
+2! 6!
ABCD
I
M
N
AD
DC
AMI
MDN
AC
AM
NI
MN
d
d
x
5
( )
+ x
11
1
55440
462
246
252
( )
α
( )
β
( )
γ
( ) ( )
α β d
1
=
( ) ( )
β γ d
2
=
( ) ( )
γ α d
3
=
d
1
d
2
d
3
= SS NNΩ,
= SNΩ,
= SS SN NS NNΩ , , ,
= SN NSΩ,
− + =xx
2
cos 3cos 2 0
( )( )
− + = −x x x x x2cos 1 2sin cos sin2 sin
S ABCD.
ABCD
AD
E
F
SA
SD
( )
SAC
( )
SBD
( )
SAD
( )
SBC
( )
EF // ABCD
( )
EF // SBC
K
AB
CD
M
N
SB
( )
CDE
SC
( )
EFM
( )
KEF
=AD BC2
KMN
KEF
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
30
1
30
10
5
5
1
10
99
667
0,1
48
105
0,17
x
2
( )
−
n
x13
90
n
S ABCD.
5
31
10
Oxy
( ) ( ) ( )
− + − =C x y
22
: 3 2 16
( )
C
( )
A 2;3
( ) ( )
− + − =xy
22
7 8 16
( ) ( )
− + + =xy
22
1 2 16
( ) ( )
+ + − =xy
22
1 1 16
( ) ( )
− + − =xy
22
1 4 16
S ABCD.
=AC BD M
=AB CD N.
( )
SAB
( )
SCD
MN
SN
SA
SM
( )
+xx
20
3
2 5 4
20
12
20
22 .
+ + + +C C C C
0 1 2 20
20 20 20 20
... .
+ + +C C C
0 20 0 1 19 1 20 0 20
20 20 20
2 .5 2 .5 ... 2 .5 .
A
B
C
D
AB
AD
M
N
MN
BD
I
I
( )
BCD
( )
ABD
( )
MNC
( )
ACD
( )
+
n
ab
−−k n k n k
n
C a b
−+k n k k
n
C a b
1
−k n k k
n
C a b
− + +k n k k
n
C a b
11
11
12
15
1
1
180
27
165
12
ÔN THI THPT QUỐC GIA 2020-2021
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
=yxsin
=yxsin
=yxsin
=−yxsin
=−yxsin2
=−y x xcos sin
=y x xcos .sin
=+y x x
2
cos sin
m
+=m x xsin 12cos 13
m 5
−
m
m
5
5
− m55
−m 5
4
6
3
720
42
120
80
ABCD
+AB AD
T
C
B
B
C
A
C
C
A
ab,
a
AB,
b
CD,
AD
BC

=−


π
yxsin 2
4
x
−+
π
kπ
8
−+
ππ
k
82
+
ππ
k
3
82
+
π
kπ
3
8
7
1
6
2
9
7
36
5
36
Oxy
( )
M 4;6
( )
I 2;3
( )
I
V
;2
Ox
( )
M 4;6
( )
−−6; 9
( )
6; 9
( )
−6; 9
( )
−6;9
=
+
x
x
sin
0
cos 1
ππ;4
1
2
3
4
5
4
48
240
120
24
+ + =xx
2
2sin 5cos 1 0
+ + + =
ππ
x x xsin cos 2 sin5
33
+ − =x x x
22
4sin 2 3 3 sin 4 2cos 2 4
0,6; 0,7; 0,8
S ABCD.
AB
=O AC BD
M
N
SAD
SBC
( )
SAC
( )
SBD
AC
( )
SMN
S ABCD.
( )
OMN
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
Oxy
− − =xyΔ : 2 3 5 0
Δ
( )
=−u 1;2
− + =xy2 3 13 0
− − =xy2 3 3 0
− − =xy2 3 13 0
− + =xy2 3 3 0
=X 1;2;4;5;7;8
6
4
A
4
6
C
4
6
4
6
6
( )
+xy
10
2
2
8064
xy
86
3360
3360
xy
10 5
8064
=x
1
cos2
2
(
0 ;360
8
6
2
4
ABCD
M
N
AB
CD
G
MN
I
AG
( )
BCD
GI
GA
=
GI
GA
1
4
=
GI
GA
1
5
=
GI
GA
1
2
=
GI
GA
1
3
3
5
2018
408.242
407.231
407.232
408.422
Oxy
( )
M 0;3
( )
N 0;4
M
N
M
N
O
90

MN
5
7
1
25
( )
− − − =xx
2
tan 3 3 1 tan3 3 0
( )
= − +
=+
ππ
xk
k
ππ
xk
12 3
93
( )
= − +
ππ
x k k
12 3
( )
= − +
=+
ππ
xk
k
ππ
xk
2
12 3
22
93
( )
= − +
=+
ππ
xk
k
ππ
xk
12 3
18 3
m
−=xmsin3 0
−m 1;1
−m 3;3
(
)
− − +m ; 1 1;
( ) ( )
− − +m ; 3 3;
Oxy
=−OA i j7
A
O
−3
( )
−A
4
0; 21
( )
−A
1
3; 21
( )
A
3
0;21
( )
−A
2
3;21
ÔN THI THPT QUỐC GIA 2020-2021
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
Oxy
( ) ( ) ( )
− + + =C x y
22
: 1 3 9
( )
C
( )
I 3;2
2
( ) ( )
+ + + =xy
22
1 8 36
( ) ( )
− + + =xy
22
4 1 36
( ) ( )
− + − =xy
22
1 8 36
( ) ( )
− + + =xy
22
2 6 36
( )
n
u
( )
+
−
=
n
n
n
u
1
1
2
( )
n
u
−
1
10
1
10
1
32
−
1
32
ABCDEF
O
O
0
120
O
−1
OBC
OBC
OEFΔ
OABΔ
ODEΔ
OCDΔ
x

−


n
x
x
2
2
2
−−
+ + + + + =
n n n n
n n n n n
C C C C C
1 2 2 3 3 1 1
3. 3 3 ... 3 3 65535
nx
*
,0
1120
−1120
112
−112
3255
49875
53130
756756
S ABCD.
ABCD
O
AC
BD
M
AB
CD
N
AD
BC
( )
SAB
( )
SCD
SA
SN
SM
SO
+
=
−
x
y
x
sin 1
cos 2 1
k πk\ 2 ,
kπk\,

+


π
kπk\,
2



π
kk\,
2
13
1
13
6
6
2
14
143
212
429
175
429
217
429
S ABC.
MN,
SB AB,
=
SM
SB
1
4
=NB NA3
MN
( )
SAB
( )
SBC
( )
ABC
( )
SAC
A
F
B
C
D
O
E
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
m
( )( )
+ − − =x x x msin cos 1 sin4 0



ππ5
;
86
)
m a b c;\
++a b c
2
2
7
2
7
4
11
4
9
4
+=x2sin 3 0
8
7
9
9
5
m
x

−


x
x
15
3
2
−
+=
m
mm
AC
22
4 60
+
mx;0
S ABCD.
AD BC
==AB BC a
=AD a3
=BAD
0
60
M
SD
N
SA
=SN NA2
H
MN
( )
ABCD
SAB
( )
α
G
AB AD,
( )
α
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
− − =xx3 sin2 cos 2 3 0
=+
π
xkπ
4
=+
π
xkπ
5
12
( )
k
=+
π
xkπ2
4
=+
π
xkπ
5
2
12
( )
k
=+
π
xkπ
12
=+
π
xkπ
4
( )
k
= − +
π
xkπ
12
=+
π
xkπ
3
4
( )
k
ABCΔ
A
=AB 6
=AC 8
A
5
4
B
B
C
C
R

AB CΔ
=R
25
2
=R
25
4
=R 5
=R
15
4
kn1
k
n
k
n
( )
−
n
nk
!
!
k !
n
k
!
!
( )
−
n
k n k
!
!!
S ABCD.
ABCD
M
N
K
SB
CD
AD
( )
SA// MNK
( )
AC// MNK
( )
SC// MNK
( )
SD// MNK
12
7
5
5
3
792
95040
350
210
Oxy
( )
−M 3; 1
M
M
( )
=−v 1;3
( )
−M 2; 4
( )
M 2;2
( )
−M 4; 4
( )
−M 2; 4
a
b
a
b
D
=yxcot

= +


π
Dkπk\,
2
=Dkπk\ 2 ,
=D
=Dkπk\,
0
1
2
3
4
5
5
20
40
36
60

+


x
x
18
2
2
x
0
x
9
C
33
18
2
C
3
18
C
66
18
2
C
6
18
=x
3
cos
4
( )
π0;2
1
0
2
4
ÔN THI THPT QUỐC GIA 2020-2021
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
d
d
( )
A
Q
,90
d
d
d
d
d
d
d
d
18
10
10
8
30
11
20
10
3
3
2785
8648
985
8648
225
1081
3915
8648
=yxcos5
−1
−5
5
1
AB,
T
A
1
2
B
1
5
A
B
( )
=AB
1
P.
10
( )
=AB
7
P.
10
( )
=AB
3
P.
10
( )
=AB
9
P.
10
=x
2
sin
2
− − =xxcos2 cos 2 0
S ABCD.
ABCD
AD
BC
=AD BC2
O
AC
BD
M,
N
SB
SD
( )
SAD
( )
SBC
SC
( )
AMN
G
SCD
OG
( )
SBC
11
2
1
5
5
5
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
=−y x x
3
sin2 tan

= +

π
D x x kπk|,
2

=

π
D x x k k|,
2

= +

π
D x x k πk| 2 ,
2
= D x x kπk|,
6
50
50
6
6
50
C
6
50
A
6
50
35
8
6
12
10
Oxy
d
− + =xy2 1 0
v
d
v
( )
=v 2;4
( )
=−v 2; 1
( )
=v 4;2
( )
=−v 1;2
x
5
( ) ( )
− + −x x x
68
2 1 3 1
−13368
13368
−13848
13848
Oxy
( )
C
( ) ( )
− + − =xy
22
2 2 4
O
=k
1
2
O
180
( )
C
( ) ( )
− + − =xy
22
1 1 1
( ) ( )
− + − =xy
22
1 1 4
( ) ( )
+ + + =xy
22
1 1 1
( ) ( )
+ + + =xy
22
1 1 4
S ABCD.
ABCD
M
N
AD
BC
( )
SMN
( )
SAC
SD
SO
O
ABCD
SG
G
AB
SF
F
CD
= + + + +S C C C C
1 2 3 1009
2019 2019 2019 2019
2019
2
+
2018
21
−
2018
21
2018
2
0,8
0,6
0,95
0,92
0,48
0,96
m
+ = +x x x m
6 6 2
sin cos cos 2



π
x 0;
8
m
1
0
8
− m
11
88
m
1
8
− m
1
0
8
30
1
30
1
28
2
15
1
15
ÔN THI THPT QUỐC GIA 2020-2021
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
ABCD
a
G
ABC
( )
CGD
a
2
2
6
a
2
3
4
a
2
2
4
a
2
3
2
+
=
−+
xx
y
xx
2sin2 cos 2
sin2 cos 2 3
4
2
3
1
16
1
16
4
4
1
26
1
25
1
21
1
27
ABCD
M
N
P
AB
BC
CD
( )
mp MNP
S ABCD.
M
N
SAB
SAD
P
BC
( )
MN // SCD
( )
MN // SBD
( )
MN // SAP
( )
MN // SDP
− − =x
x
2
3
2 3 cot 6 0
sin
( )

− − − +


=
−
π
cos x cos x πx
x
7
2 3 2 3 2cos
2
0
1 2sin
a
b
c
x
2
x
4
x
6

−


x
m
12
4
2
m
=a bc
A11
10
5
5
7
15
5
2
A11
S ABCD.
ABCD
=BC a2
==AD AB a
( )
SAD
M
AB
( )
α
M
SA
BC
( )
α
CD
SC
SB
N
P
Q
PN
( )
SAD
E
MQ
NP
E
=AM x
( )
xa0
( )
α
S ABCD.
a
x
M
n
n 2
−
−

−

−

n
n
nn
n n n n n
C C C C C
n
1
0 1 2 1
22
. . ... .
1
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
π
x
2
2cos 1 0
3

− − =


xx
2
2sin 3cos 3 0+ − =
xxsin2 3 cos 2 3+=
A 1;2;3;4;5;6;7;8=
x
x
x
12
4
2
3
2

−


ABCD
SA
SD
( )
SAC
( )
SBD
MN
BC
I
CM
SO
G
ABC
IG
( )
SAB
ABCD
G
ABC
MN,
AD
DM MN NA==
E
A
G
( ) ( )
MCE NBG //
ÔN THI THPT QUỐC GIA 2020-2021
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
x2sin 1 0+=
xx3 cos sin 2 0+ + =
x x x xcos cos2 cos3 cos4 0+ + + =
( )
( )
π
x x x
x
x
sin 1 sin cos 2
1
4
1 tan
cos
2

+ + +


=+
A 1;2;3;4;5;6;7;8=
10
1
1
3
x
n
x
x
3
2

−


nn
nn
CC
12
78
−−
+=
x 0
7
6
4
1;2;...;12
Oxy
( )
v 2;3=−
( )
A 1; 1−
v
ABC A B C.
N
AC
AC
MN
( )
BCC B

S ABCD.
ABCD
a
SC SD a 3==
a
AM
3
=
( )
GJ SAB// .
xxcos5 sin 0−=
x
8
x
x
21
3
2
2

−


n
nn
P C A
22
32
. 42
−
+=
( )
n
u
n
n
un23=−
n
u()
uu
S
15
4
20
14
+=
=
S ABCD.
ABCD
O
M,
N,
P
SB,
OC
SD
MP
( )
ABCD
( )
MNP
( )
ABCD
( )
MNP
S ABCD.
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
xx3 cos 2 sin2 2 0− − =
x x x xsin2 cos2 2sin 2cos 1− = − +
nn
A C n
12
+=
uu
uu
17
34
29
22
−=
+=
u
1
d
x
x
x
10
3
2
2
3

−


0;1;2;3;4;5;6;7;8;9
S ABCD.
O
MN,
CD BC,
E
SA
ME
SBC()
( )
MEO
( )
SAD
( )
P
O
CD SC,
( )
P
S ABCD.
π
x
2
cos 3
62

− = −


xxsin2 3 cos 2 2−=
x x xcos 3 cos 3 cos 2+=
x
20
( )
x
20
2
32−
S ABCD.
ABCD
O
M,
N
SA SB,
G
SAD
( )
SAC
( )
SBD
( )
OMN
( )
ABCD
I
CM
( )
SBD
( )
IG ABCD//
( )
MBC
S ABCD.
C C C C
2014
0 2 2 4 4 2014 2014
2014 2014 2014 2014
31
2 2 2
2
+
+ + ++ =
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
π
x
1
sin 2
32

−=


( )
3;1−
xcos2 3sinx + 4 = 0−
x
20
( )
x
20
2
32−
( )
x
8
2
2+
nn
A C n
2 2 2
2 80+ = +
n
xx
x
4
2
,0

−


( )
n
u
uu
S
73
4
36
22
+=
=
S ABCD.
ABCD
EF,
BC AD,
BE BC
3
5
=
AF AD
2
5
=
H
SF J;
AE
CD
( )
SAD
( )
SBC
CH
( )
SBD
FC
( )
SAE
BH
ED
AE
I
JE
JI
10
19
=
9
2
9
A
Z
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
x2sin2 1 0− + =
xx6 sin 2 2 cos2 2 2−=
x
xx
18
12 2
13

−



S ABCD.
ABCD
AC
BD
O
M
SA
N
SC
SN NC2=
( )
BMN
( )
ABCD
H
SD
( )
BMN
I
B
C
( )
SBC
J
IN
SB
( )
MNJ
S ABCD.
x x x x
22
2sin 2 3 sin cos 4cos 1 0+ − + =
X
X
n
n
u n n
3
10 2 2= − − +
n
S C C C C C
1 2018 2 2017 2 3 2016 3 2018 1 2018 2019 2019
2019 2019 2019 2019 2019
.3 .2 .3 .2 .3 .2 ... .3 .2 .2= − + − − +
S ABCD.
ABCD
O
SA CD=
SB AC=
E
F
BC
SD
( )
SAB
( )
SCD
H
CF
( )
SAB
( ) ( )
OEF SAB//
( )
OEF
AD
SC
L
I
OLFI
M
N
SB
OA
BM AN=
( )
MN SCD//
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
π
x
3
cos
32

+=


x x x
22
2sin 3sin2 6cos 1− + =
x
x
x
15
2
1
2

−


A 0;1;2;3;4;5=
4
A
8
3
0
8
3
12323112
S ABCD.
ABCD
MN,
BC
SA
( )
SAD
( )
SBC
( )
MN SDC//
K
MN
( )
SBD
KM
KN
π
x2cos 2 3
4

+=


xx3 sin cos 2+=
1;2;3;4;5;6
( )
n
n
n
x a a x a x a x
2
0 1 2
1 3 ...− = + + + +
a a a
0 1 2
376+ + =
a
3
( )
n
u
nn
u
u u n
1
1
1
2
+
=
=+
( )
n
v
nn
v u n 1= + +
nn
S u u u
12
...= + + +
n
S
n
S ABCD.
ABCD
M N P,,
CD AD SA,,
MD MC NA ND PA PS2 , 3 , 3= = =
G
SBC
K
BM
( )
SAC
( )
NKP
( )
SCD
MG
( )
SAD
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468
–
0987.154.555
| 1/32
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Tuyển tập một số đề thi học kì hay trên cả nước Gv: Bùi Đình Thông 11
facebook: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555
ÔN THI THPT QUỐC GIA 2020-2021
Lớp toán thầy Thông Đình Đình: ------------- DẠY THẬT – HỌC THẬT – GIÁ TRỊ THẬT--------------- PHẦN ĐỀ - TM1
I – PHẦN TRẮC NGHIỆM Câu 1: Cho hình chóp S A
. BCD có đáy ABCD là hình bình hành, M là trung điểm của BC . Gọi (P ) là
mặt phẳng qua M và song song với AC,SB . Thiết diện tạo bởi (P ) và S A
. BCD là hình gì? A. Tam giác. B. Tứ giác. C. Ngũ giác. D. Lục giác. Câu 2:
Phương trình sinx =1 có nghiệm là: π π π π A. x = + k π 2 ,k .
B. x = − + kπ,k  . C. x =
+ kπ,k . D. x = − + k π 2 ,k  . 2 2 2 2 Câu 3:
Lớp 11B có 25 đoàn viên trong đó 10 nam và 15 nữ. Chọn ngẫu nhiên 3 đoàn viên trong lớp
để tham dự hội trại ngày 26 tháng 3 . Tính xác suất để 3 đoàn viên được chọn có 2 nam và 1 nữ. 3 7 9 27 A. . B. . C. . D. . 115 920 92 92 Câu 4: Cho các mệnh đề sau sin x
(I) Hàm số f (x ) = là hàm số chẵn. x2 +1
(II) Hàm số f (x ) = 3sin x + 4cos x có giá trị lớn nhất là 5 .
(III) Hàm số f (x ) = tan x tuần hoàn với chu kì π 2 .
(IV) Hàm số f (x ) = cos x đồng biến trên khoảng (0; π ) .
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng? A. 3 . B. 1. C. 4 . D. 2 . Câu 5:
Cho hình thoi ABCD tâm O . Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
A. Phép vị tự tâm O , tỉ số −1 biến tam giác ABD thành tam giác CDB . π
B. Phép quay tâm O , góc biến tam giác OBC thành tam giác OCD . 2
C. Phép vị tự tâm O , tỉ số k =1 biến tam giác OBC thành tam giác ODA .
D. Phép tịnh tiến theo véc tơ AD biến tam giác ABD thành tam giác DCB . Câu 6: Cho các mệnh đề:
(I) Trong không gian, nếu 2 đường thẳng a và b không có điểm chung thì a //b .
(II) Trong không gian, nếu 2 đường thẳng a và b vuông góc nhau thì a cắt b .
(III) Trong không gian, nếu 2 đường thẳng a và b cùng song song với đường thẳng thứ ba thì a //b .
Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng? A. 0 . B. 1. C. 2 . D. 3 . Câu 7:
Cho tập hợp A có 10 phần tử. A có bao nhiêu tập hợp con có 5 phần tử? 10 ! A. C5 . B. 5!. C. A5 . D. . 10 10 2! Câu 8:
Có 10 người xếp thành một hàng dọc (vị trí của mỗi người trong hàng là cố định). Chọn ngẫu
nhiên 3 người trong hàng. Tính xác suất để 3 người được chọn không có 2 người nào đứng cạnh nhau. 7 7 73 29 A. . B. . C. . D. . 15 10 120 60 Câu 9:
Cho tứ diện ABCD , G là trọng tâm A
Δ BD và M là điểm trên cạnh BC sao cho BM = M 2 C . Đường
thẳng MG song song với mặt phẳng A. (BCD) . B. (ABC ) . C. (ACD) . D. (ABD) .
Câu 10: Cho tập hợp A có 10 phần tử. A có bao nhiêu tập hợp con có 5 phần tử? Trang 1 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555 10 ! A. C5 . B. 5!. C. A5 . D. . 10 10 2!
Câu 11: Có 10 người xếp thành một hàng dọc (vị trí của mỗi người trong hàng là cố định). Chọn ngẫu
nhiên 3 người trong hàng. Tính xác suất để 3 người được chọn không có 2 người nào đứng cạnh nhau. 7 7 73 29 A. . B. . C. . D. . 15 10 120 60
Câu 12: Cho tứ diện ABCD , G là trọng tâm A
Δ BD và M là điểm trên cạnh BC sao cho BM = M 2 C . Đường
thẳng MG song song với mặt phẳng A. (BCD) . B. (ABC ) . C. (ACD) . D. (ABD) .
Câu 13: Trong một buổi khiêu vũ có 20 nam và 18 nữ. Hỏi có bao nhiêu cách chọn ra một đôi nam nữ để khiêu vũ?
A. C2 C1 . B. C2 . C. A2 . D. C1 C1 . . 20 18 38 38 20 18
Câu 14: Hai người cùng bắn vào một bia (mỗi người bắn 1 phát duy nhất). Biết xác suất bắn trúng bia
của người 1 và người 2 lần lượt là 0,8 và 0,9 . Tính xác suất sao cho bia bị bắn trúng. A. 0,95 . B. 0,98 . C. 0,89 . D. 0,85 .
Câu 15: Trong mặt phẳng Oxy cho A (−3; )
1 . Ảnh của A qua phép vị tự V( là : O;2)
A. A '(−6;−2) .
B. A '(6;−2) .
C. A '(−6;2) .
D. A '(6;2) .
Câu 16: Ký hiệu M là giá trị lớn nhất y = 3 sin x 2 − cos x 2 . Ta có: A. M = 3 −1. B. M = 2 . C. M = 3 . D. M = −2 . 2sin x
Câu 17: Tập xác định của hàm số y = là: 2 tan x −1 A. π ππ
D = R \  + kπ, + k π
2  , (k Z ) . B.  
D = R \  + kπ , (k Z ) . 2 4   4  π π π π C.  
D = R \  + k π 2 ,
+ kπ , (k Z ) . D.  
D = R \  + kπ, + kπ  (k Z ) . 2 4  2 4   2 2 10
Câu 18: Hệ số của x15 trong khai triển nhị thức Newton của x −   là:  x A. 180 . B. 80 . C. −80 . D. 4 .
Câu 19: Tìm giá trị nguyên lớn nhất của a để phương trình a 2 x + x + a 2 sin 2sin2
3 cos x = 2 có nghiệm. A. a = 3 . B. a =1. C. a = −1. D. a = 2 .
Câu 20: Cho tập hợp X = x  : x  
7 . Từ X có thể lập được bao nhiêu số tự nhiên có 3 chữ số phân
biệt đôi một và chia hết cho 5 ? A. 45 . B. 60 . C. 50 . D. 55 .
Câu 21: Trong mặt phẳng Oxy cho (C ) : x2 + y2 = 1 và v = (1;− )
2 . Ảnh của (C ) qua phép tịnh tiến T là v
A. (C ) : (x − )2 + (y − )2 1 2 =1.
B. (C ) : (x − )2 + (y + )2 1 2 =1.
C. (C ) : (x + )2 + (y − )2 1 2 =1.
D. (C ) : (x + )2 + (y + )2 1 2 =1.
Câu 22: Trong mặt phẳng với hệ tọa độ Oxy , cho hai đường thẳng (d : 2 3 1 0 và 1 ) x + y + = (d : 2 3
2 0 . Có bao nhiêu phép tịnh tiến biến d thành d . 2 ) x + y − = 1 2 A. 4 . B. Vô số. C. 0 . D. 1.
Câu 23: Trong Oxy cho A (−1,0), B (3,2) . Ảnh của B qua phép vị tự tâm A , tỉ số 2 là :
A. B(−5;−2) . B. B(7;4) . C. B(10;4) .
D. B(7;−4) .
Câu 24: Cho 4 dãy số : ( 1
u với u = n
3 − 4 , (v với v = − 4 n ) n ) n n n 3 ( n + 4 1 a với a = , (b với b = n ) n ) n n + 2 n n
Trong các dãy số trên, dãy số nào là dãy số tăng ? A. (v . B. (a . C. (b . D. (u . n ) n ) n ) n )
Câu 25: Trong Oxy cho (d ) : x + y −1 = 0 . Ảnh của d qua phép quay Q
là đường thẳng (d) :  π O;−    2  Trang 2 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555
A. (d) : x − y −1 = 0 .
B. (d) : x − y +1 = 0 . C. (d) : x + y +1 = 0 . D. (d) : x − y 2 −1 = 0 . II – PHẦN TỰ LUẬN Câu 1:
Chứng minh rằng n  , ta có ( n2 n+ + 2 6 3 + n 3 ) chia hết cho 11. Câu 2: Giải phương trình: 2 x + 2 sin cos x 3 =1. Câu 3: Cho hình chóp S A
. BCD có đáy ABCD là hình bình hành, O là giao điểm của AC và BD . Gọi 1
M là trung điểm AB , N là điểm thuộc đoạn SC sao cho SN = NC . 2
a. Tìm giao tuyến của 2 mặt phẳng (SMC ) và (SBD) .
b. Tìm giao điểm của đường thẳng MN và (SBD) .
c. Gọi E , F lần lượt là trung điểm CD ,SD . Chứng minh: MN //(AEF ) . ----Hết---- Trang 3 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555
ÔN THI THPT QUỐC GIA 2020-2021
Lớp toán thầy Thông Đình Đình: ------------- DẠY THẬT – HỌC THẬT – GIÁ TRỊ THẬT--------------- PHẦN ĐỀ- TM2 I- PHẦN TRẮC NGHIỆM Câu 1:
Trong các khẳng định sau, khẳng định nào sai?
A. Phép dời hình biến đường tròn thành đường tròn có cùng bán kính.
B. Phép dời hình là phép đồng nhất.
C. Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
D. Phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kỳ. Câu 2:
Cho hai hộp bi, hộp thứ nhất có 4 bi đỏ và 3 bi trắng, hộp thứ hai có 2bi đỏ và 4 bi trắng. Chọn
ngẫu nhiên mỗi hộp ra 1 viên bi. Tính xác suất P để chọn được 2 viên bi cùng màu. A. 8 3 10 4 P = . B. P = . C. P = . D. P = . 21 7 21 9 Câu 3:
Có 12 học sinh gồm 5 nam và 7 nữ. Hỏi có bao nhiêu cách chọn từ 12 học sinh đó ra 3 học sinh gồm 2 nam và 1 nữ. A. 70 cách. B. 105 cách. C. 220 cách. D. 10 cách. 1 Câu 4:
Tìm số nghiệm thuộc đoạn [0 π
; ] của phương trình sin x = . 3 A. 0 nghiệm. B. 1 nghiệm. C. 3 nghiệm. D. 2 nghiệm. Câu 5:
Giá trị nhỏ nhất của hàm số y = sin x 2 là A. 2 − . B. 1 − . C. 0 D. 1. Câu 6:
Tìm nghiệm của phương trình tan x = 3 . A. π π x =
+ kπ (k  ) . B. x =
+ kπ (k  ) . 6 3 C. π π x = −
+ kπ (k  ) .
D. x = − + kπ (k  ) . 3 6 Câu 7:
Trong mặt phẳng tọa độ Oxy , cho đường thẳng d có phương trình x
2 − y +1 = 0 . Ảnh của đường
thẳng d qua phép quay tâm O góc quay φ 0 = 90 −
là đường thẳng có phương trình là: A. x + y 2 −1 = 0 . B. x + y 2 +1 = 0 .
C. x − y 2 +1 = 0 .
D. x − y 2 −1 = 0 . Câu 8:
Trong các khẳng định sau, khẳng định nào đúng ?
A. Hình tứ diện đều là hình có 4 cạnh bằng nhau.
B. Hình chóp tam giác là hình có 3 đỉnh, 3 cạnh và 3 mặt.
C. Hình chóp tam giác là hình tứ diện.
D. Hình chóp tứ giác là hình có 4 mặt là tứ giác. Câu 9:
Trong mặt phẳng tọa độ Oxy , cho v = (2;− ) 1 và điểm M ( 3
− ;2) . Ảnh của M qua phép tịnh tiến
theo véc tơ v là điểm M ' . Tìm tọa độ điểm M ' . A. M '(5;3) . B. M '( 1 − ; ) 1 . C. M '(1; ) 1 . D. M '(1; ) 1 − .
Câu 10: Trong các khẳng định sau, khẳng định nào đúng?
A. Hình tứ diện đều là hình có 4 cạnh bằng nhau.
B. Hình chóp tam giác là hình có 3 đỉnh, 3 cạnh và 3 mặt.
C. Hình chóp tam giác là hình tứ diện.
D. Hình chóp tứ giác là hình có 4 mặt là tứ giác.
Câu 11: Trong mặt phẳng tọa độ Oxy , cho v = (2; −1) và điểm M( 3
− ;2). Ảnh của M qua phép tịnh tiến
theo vectơ v là điểm M’. Tìm tọa độ điểm M’. A. M’(5;3). B. M’( 1 − ;1) . C. M’(1;1) . D. M’(1; 1 − ) .
Câu 12: Trong mặt phẳng tọa độ Oxy , phép đồng dạng F tỉ số k = 2 biến hai điểm M (0; ) 1 và N (1;0)
lần lượt thành M và N  . Tính độ dài đoạn thẳng MN   . Trang 4 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555 A. 2 . B. 2 2 . C. 1 . D. 2. 2  3 
Câu 13: Cho x thuộc khoảng π π ;2 
. Trong các khẳng định sau, khẳng định nào đúng? 2   
A. sinx  0 , cos x  0 .
B. sinx  0, cos x  0 .
C. sinx  0, cos x  0 .
D. sinx  0 , cos x  0 . 1
Câu 14: Phương trình cos x 0
( − 20 ) = có các nghiệm là 2 A. x 0 = + k 0 x 0 = − + k 0 50 .360 , 10 .360 k (  Z ) B. x 0 = + k 0 x 0 = − + k 0 40 .360 , 40 .360 k (  Z ) . C. x 0 = + k 0 x 0 = + k 0 80 .360 , 40 .360 k (  Z ) . D. x 0 = + k 0 x 0 = − + k 0 80 .360 , 40 .360 k (  Z ) .
Câu 15: Trong mặt phẳng tọa độ Oxy , cho điểm A( 1 − ;0) và M(2; 1
− ) Ảnh của M qua phép vị tự tâm A tỉ
số k = 2 là điểm M ' . Tìm tọa độ điểm M ' . A. M '( 5 − ;2). B. M '(5; 2 − ). C. M '(5;2). D. M '(3; 2 − ). Câu 16: 0 1 2 2016
Tính S = C + C + C + ... + C 2016 2016 2016 2016 2016 − A. 2 1 S 2016 = 2 . B. S 2016 = 2 −1. C. S = . D. S 2015 = 2 +1. 2
Câu 17: Cho tứ diện (ABCD) gọi M,N,K lần lượt là trung điểm của AB,BC,CD . Trong các khẳng định
sau, khẳng định nào đúng?
A. Giao tuyến của mặt phẳng M
( NK ) và mặt phẳng (ABD) đi qua trung điểm của AD .
B. Hai đường thẳng MN và BD cắt nhau.
C. Hai đường thẳng MK và AC cắt nhau.
D. AD song song với mặt phẳng M ( NK ) .
Câu 18: Mỗi đội bóng đá có 11 cầu thủ ra sân. Trước một trận thi đấu bóng đá, mỗi cầu thủ của đội
này đều bắt tay với 11 cầu thủ của đội kia và 3 trọng tài. Tính tổng số cái bắt tay. A. 154. B. 275. C. 308. D. 187.
Câu 19: A và B là hai biến cố độc lập, xác suất xảy ra biến cố A là 1 , xác suất xảy ra biến cố B là 3
1 . Tính xác suất P để xảy ra biến cố A và B . 5 A. 8 3 1 2 P = . B. P = . C. P = . D. P = . 15 4 15 15
Câu 20: Cho hai đường thẳng song song a và b . Trên đường thẳng a có 5 điểm phân biệt, trên đường
thẳng b có 7 điểm phân biệt. Tính số tam giác có 3 đỉnh lấy từ các điểm trên hai đường thẳng a và b . A. 175 tam giác. B. 220 tam giác. C. 45 tam giác. D. 350 tam giác.
Câu 21: Từ các số 1, 3, 5, 7, 9 lập được bao nhiêu số tự nhiên có 5 chữ số khác nhau mà chữ số đầu tiên là chữ số 3? A. 4 số. B. 6 số. C. 24 số. D. 12 số.
Câu 22: Một tổ có 4 học sinh nam và 6 học sinh nữ. Chọn ngẫu nhiên từ tổ này 2 học sinh. Tính xác suất
P để chọn được 2 học sinh cùng giới. A. 8 2 7 1 P = . B. P = . C. P = . D. P = . 15 9 15 5 Câu 23: 5
Hệ số a của số hạng chứa x 3 trong khai triển (1 + x ) là: A. a =15 . B. a = 6. C. a = 24 . D. a =10 .
Câu 24: Có 5 quyển sách khác nhau gồm 3 quyển sách Văn và 2 quyển sách Toán. Hỏi có bao nhiêu
cách sắp xếp 5 quyển sách trên kệ sách dài (xếp hàng ngang) sao cho tất cả quyển sách cùng
môn phải đứng cạnh nhau? A. 12 cách. B. 24 cách. C. 120 cách. D. 16 cách.
Câu 25: Tìm nghiệm của phương trình sin x ( − α) = 1 − . A. π x = α −
+ kπ (với k Z ). B. π x = α − − + k π
2 (với k Z ). 2 2 Trang 5 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555 C. π x = α − + k π
2 (với k Z ).
D. x = α + π + k π
2 (với k Z ). 2 II- PHẦN TỰ LUẬN Bài 1:
Giải các phương trình sau: a. π cos x 2 = cos .
b. 3 sinx + cos x = 2 . 6 Bài 2:
a. Tìm số nguyên dương n thỏa: C1 + n 2 = 30 . n 10  1
b. Tìm số hạng chứa 
x6 trong khai triển của x 2 +  , với x  0. 2    Bài 3:
Cho hình chóp tứ giác S A
. BCD có AB và CD không song song với nhau. Gọi M, N lần
lượt là trung điểm của SC và SA .
a. Chứng minh đường thẳng MN song song với mặt phẳng (ABCD) ; tìm giao tuyến của mặt phẳng DMN (
) và mặt phẳng (ABCD) .
b. Gọi O là điểm nằm ở miền trong của tứ giác ABCD . Tìm giao điểm của đường thẳng SO và mặt phẳng M ( AB). Bài 4:
Có 10 người ngồi xung quanh bàn tròn, mỗi người cầm một đồng xu như nhau. Tất cả 10
người cùng tung đồng xu của họ, người có đồng xu ngửa thì đứng, người có đồng xu úp thì
ngồi. Tính xác suất để có đúng 4 người cùng đứng trong đó có đúng 2 người đứng liền kề.
--------- Hết--------- Trang 6 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555
ÔN THI THPT QUỐC GIA 2020-2021
Lớp toán thầy Thông Đình Đình: ------------- DẠY THẬT – HỌC THẬT – GIÁ TRỊ THẬT--------------- PHẦN ĐỀ- SỐ 03 I- PHẦN TRẮC NGHIỆM Câu 1:
Hàm số y = cos x nghịch biến trên khoảng: A.π π  − π  ; . B.   0;  . C. (−π;0) .
D. (−π;π ) .  2 2   2  Câu 2:
Trên giá sách có 5 quyển sách Toán khác nhau, 6 quyển sách Anh khác nhau và 8 quyển
sách Văn khác nhau. Số cách chọn ra ba quyển sách có đủ ba môn là : A. 19 . B. 118 . C. 20 . D. 240 . (− )n 1 Câu 3:
Cho dãy số (u với u =
. Số hạng thứ mười một của dãy số bằng n ) n n 2 + 5 A. − 1 . B. 1 . C. 1 . D. − 1 . 27 27 25 7 Câu 4:
Cho cấp số cộng (u với u = −2 và công sai d = 3. Tổng 10 số hạng đầu tiên S của (u là: n ) n ) 1 10 A. 155 . B. 115 . C. 145 . D. 165 . Câu 5:
Trong mặt phẳng toạ độ Oxy , cho điểm A (2;0) . Ảnh của A qua phép quay Q( có toạ độ là: O;90) A. M (0;2) .
B. N (0;− 2) . C. P (−2;0) . D. Q (1; ) 1 . Câu 6:
Trong không gian, có bao nhiêu vị trí tương đối giữa hai đường thẳng phân biệt a và b ? A. 1. B. 2. C. 3 . D. 4 . Câu 7:
Tập nghiệm của phương trình sin x ( 3 cot x − ) 1 = 0 là: A.ππ
kπ, + kπ,k   . B.   
+ kπ,k   .  6   6  π C.π  
+ kπ,k   . D.  
kπ, + kπ,k   .  3   3  n 1 Câu 8:
Tổng các hệ số trong khai triển  2  x + 
 là 4096 . Hệ số của số hạng không chứa x trong khai  x  triển là A. 195 . B. 118 . C. 2020 . D. 495. Câu 9:
Từ một hộp chứa 16 cái thẻ đánh số từ 1 đến 16. Chọn ngẫu nhiên 3 thẻ. Xác suất để được 3 thẻ đều là số lẻ là A. 1 . B. 1 . C. 56 . D. 3 . 10 2 506 16
Câu 10: Cho hình chóp S A
. BCD có đáy là hình bình hành tâm O , M là trung điểm cạnh SA . Gọi (P ) là
mặt phẳng đi qua M đồng thời song song với SC và AD . Thiết diện của hình chóp S A . BCD cắt bởi (P ) là một A. hình thang.
B. hình bình hành. C. tứ giác. D. ngũ giác.
Câu 11: Trong mặt phẳng Oxy cho đường thẳng a . Gọi b là ảnh của a qua phép đồng dạng có được
bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = −2 và phép đối xứng trục Oy . Biết đường
thẳng b có phương trình là x
2 + y +16 = 0 , khi đó phương trình đường thẳng a là Trang 7 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555 A. x 2 − y − 8 = 0 . B. x 2 − y − 32 = 0 . C. x 2 − y + 32 = 0 . D. x 2 − y + 8 = 0 .
Câu 12: Cho dãy số (u xác định bởi u = 1 và u
= u2 + 2 , n  * . Tổng S = u2 + u2 + u2 + ... + u2 n ) 1 n +1 n 1 2 3 1001 bằng A. 1002001. B. 1001001. C. 1001002 . D. 1002002 . II- PHẦN TỰ LUẬN Câu 1:
Ngân hàng đề thi học kỳ I môn Văn của trường Y có 50 câu hỏi. Mỗi đề gồm bốn câu hỏi được
lấy ngẫu nhiên từ ngân hàng đề thi. Thí sinh A đã học thuộc 25 câu trong ngân hàng đề thi.
Tính xác suất để khi thí sinh A nhận đề thì có ít nhất ba câu đã học thuộc. Câu 2:
Cho cấp số cộng (u có số hạng đầu u = 3 và công sai d = 5. Tính u , u và S . n ) 1 2 7 8 Câu 3: Cho hình chóp S A
. BCD có đáy ABCD là hình bình hành. Gọi P,M,N lần lượt là trung điểm của
SA,BC và AD .
a) Tìm giao tuyến của các cặp mặt phẳng: (SAC ) và (SBD) ; (SAB ) và (PMN ) .
b) Chứng minh rằng SC song song với mặt phẳng (PMN ) . ( n 2 − ) 1 π Câu 4:
Cho dãy số (u với u = cos . n ) n 3
a) Chứng minh rằng u = u với mọi n 1. n n +3
b) Hãy tính tổng của 17 số hạng đầu tiên của dãy số đã cho. --------- HẾT--------- Trang 8 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555
ÔN THI THPT QUỐC GIA 2020-2021
Lớp toán thầy Thông Đình Đình: ------------- DẠY THẬT – HỌC THẬT – GIÁ TRỊ THẬT--------------- PHẦN ĐỀ - TM4 I - PHẦN TRẮC NGHIỆM
Câu 1. Lớp có 50 học sinh trong đó có 20 học sinh nữ. Chọn 3 bạn tham gia đội văn nghệ. Số cách
chọn sao cho có ít nhất 1 nam là A. C2 C1 . .
B. C3 − C3 .
C. C3 − C3 . D. C3 C3 . . 30 20 50 20 50 30 50 30
Câu 2. Giá trị nhỏ nhất của hàm số y = 3sin x 2 − 2 bằng A. 4 . B. 1. C. 5 . D. −5 .
Câu 3. Trong mặt phẳng, biết V M
M . Chọn kết luận đúng. O k , ( ) =  ( )
A. OM = kOM  .
B. OM  = kOM .
C. OM  = −kOM .
D. OM = k OM . 3
Câu 4. Tập nghiệm của phương trình cos x = − là 2 π 5 π 2 A. x =  + k π 2 , k  . B. x =  + k π 2 , k  . 6 3 π π
C. x =  + k π 2 , k  .
D. x =  + kπ , k  . 3 6 1
Câu 5. Trong mặt phẳng tọa độ, cho M (−1;2) , k = − , V M
M , O là gốc tọa độ. Khi đó M có tọa O k , ( ) =  2 ( ) độ là 1 1 1 1 A.   M  −  ;1 . B.   M  1;−   . C.   M  ; −  1 . D.   M  −  1;  .  2   2   2   2  π
Câu 6. Tập xác định của hàm số   y = tan x −   là  3  π π A.   D =
\  + kπ ;k   . B.   D = \  + k π 2 ;k   .  3  3  π π 5 C.   D =
\  + kπ ;k  . D.   D = \ 
+ kπ ;k   . 3   6 
Câu 7. Nghiệm của phương trình 2
cos x − cos x = 0 thỏa điều kiện −π x  0 là A. = π x . B. = π x . C. = − π x . D. = π x . 6 4 2 2
Câu 8. Tập nghiệm của phương trình 3 sin x + cos x = 0 là π π
A. x = − + kπ , k  .
B. x = − + k π 2 , k  . 6 3 π π
C. x = − + kπ , k  . D. x = + kπ , k  . 3 3
Câu 9. Cho hình chóp S A
. BCD có AC BD = M và AB CD = N . Giao tuyến của mặt phẳng (SAC ) và (SBD) là A. SM . B. SA . C. MN . D. SN .
Câu 10. Trong mặt phẳng tọa độ Oxy , cho điểm M (1;− 2) phép tịnh tiến theo vectơ v = (−3;− 3) biến điểm
M thành M . Tọa độ M là
A. M (2;− 5). B. M (4;− ) 1 .
C. M  (2;5).
D. M (−2;− 5) .
Câu 11. Trên giá sách có 7 quyển sách Toán khác nhau, 5 quyển sách Vật lý khác nhau, 8 quyển sách
Hóa học khác nhau. Số cách chọn 1 quyển sách để đọc là A. 15 . B. 13 . C. 20 . D. 280 .
Câu 12. Cho 5 chữ số 1, 2 , 3 , 5 , 6 . Lập các số tự nhiên gồm 3 chữ số đôi một khác nhau từ 5 chữ số
đã cho. Tổng tất cả các số lập được bằng Trang 9 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555 A. 22644 . B. 24642. C. 26442. D. 44622 . II - PHẦN TỰ LUẬN
Bài 1. Giải các phương trình sau a)π  2sin x − − 3 =   0 .  6 
b) sin x − 3 cos x = − 2 .
Bài 2. a) Cho tập hợp A = 1;2;3;4;5;6; 
7 . Từ A có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số đôi một khác nhau? b) Lớp A
11 có 15 học sinh nữ, 20 học sinh nam. Có bao nhiêu cách chọn 5 học sinh tham gia
văn nghệ trong đó có ít nhất 3 học sinh nữ?
Bài 3. 1) Trong mặt phẳng Oxy , cho vectơ v = (2;− )
1 và đường thẳng d : x + y − 3 = 0 . Viết phương trình
đường thẳng d là ảnh của đường thẳng d qua phép tịnh tiến theo vectơ v .
2) Cho tứ diện ABCD , gọi G là trọng tâm tam giác BCD , M là trung điểm CD , I là điểm trên đoạn thẳng AG .
a) Xác định giao tuyến của mặt phẳng (ABG ) với mặt phẳng (ACD) .
b) Xác định giao điểm J của BI với mặt phẳng (ACD) . Tính tỉ số giữa AI và AG để diện tích
tam giác ACD bằng 2 lần diện tích tam giác JCD .
Bài 4. Có bao nhiêu số tự nhiên có 6 chữ số sao cho số đó chia hết cho 13 và có chữ số tận cùng bằng 2? ------- Hết ------ Trang 10 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555
ÔN THI THPT QUỐC GIA 2020-2021
Lớp toán thầy Thông Đình Đình: ------------- DẠY THẬT – HỌC THẬT – GIÁ TRỊ THẬT--------------- PHẦN ĐỀ - TM5
I - PHẦN TRẮC NGHIỆM 9 1 Câu 1:
Số hạng không chứa x trong khai triển   3x −  (với x  0) là 2   3x A. 2268 . B. −2268 . C. 84 . D. −27 . Câu 2:
Chọn ngẫu nhiên 2viên bi từ một hộp có 2 viên bi đỏ và 3 viên bi xanh. Xác suất để chọn được 2 viên bi xanh là: 3 2 3 7 A. . B. . C. . D. . 25 5 10 10 Câu 3: Cho hình chóp S A
. BC có G,K lần lượt là trọng tậm các tam giác ABC và SBC . Gọi E là trung MS
điểm cạnh AC . Mặt phẳng (GKE ) cắt SC tại M . Tỉ số bằng: MC 2 1 A. 1. B. 2. C. . D. . 3 2 Câu 4:
Trong mặt phẳng tọa độ Oxy , viết phương trình đường thẳng Δ ' là ảnh của đường thẳng Δ : x + y
2 −1 = 0 qua phép tịnh tiến theo vectơ v = (1;− ) 1 .
A. Δ' : x + y 2 − 3 = 0 .
B. Δ' : x + y 2 = 0 .
C. Δ' : x + y
2 +1 = 0 . D. Δ' : x + y 2 + 2 = 0 . Câu 5:
Trong mặt phẳng tọa độ Oxy , cho hai đường thẳng d : x 2 − y
3 + 3 = 0 ; d ' : x 2 − y 3 − 5 = 0 . Tìm
tọa độ véc tơ v có phương vuông góc với đường thẳng d sao cho d ' là ảnh của d qua phép tịnh
tiến theo véc tơ v . 6 4 1 2 16 24 16 24 A.   v = −  ;  . B.   v = −  ;  . C.   v = − ;−   . D.   v = ;−   .  13 13   13 13   13 13  13 13  Câu 6:
Cho tứ diện đều ABCD có cạnh bằng a . Đoạn thẳng nối trung điểm hai cạnh AB, CD có độ dài bằng: a A. a 3 . B. a 2 . C. . D. a 5 . 2 2 2 2 Câu 7:
Cho tứ giác lồi ABCD và điểm S không thuộc mặt phẳng (ABCD) . Có bao nhiêu mặt phẳng qua
S và hai trong số bốn điểm A,B,C,D ? A. 3 . B. 4 . C. 5 . D. 6 . Câu 8: Tập hợp \kπ k
|   không phải là tập xác định của hàm số nào sau đây? 1 − cos 1 + cos 1 + cos 1 − cos A. = x y . B. = x y . C. = x y . D. = x y . sin x sin x 2 sin x 2sin x Câu 9:
Xét hàm số y = cos x với x  −π;π  . Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên (−π;0) và đồng biến trên (0;π ) .
B. Hàm số nghịch biến trên các khoảng (−π;0) và (0;π ) .
C. Hàm số đồng biến trên (−π;0) và nghịch biến trên (0;π ) ..
D. Hàm số đồng biến trên các khoảng (−π;0) và (0;π ) . .
Câu 10: Chọn ngẫu nhiên ba đoạn thẳng trong 5 đoạn thẳng có độ dài c 1 m, c 3 m, c 5 m, c 7 m và cm 9 .
Xác suất để ba đoạn thẳng được chọn là ba cạnh của một tam giác là: 3 1 1 7 A. . B. . C. . D. . 10 20 15 10
Câu 11: Xét tất cả các số tự nhiên gồm 5 chữ số khác nhau được lập từ các số 1,3,5,7,9 . Xác suất để
tìm được số không bắt đầu từ 135 là Trang 11 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555 5 1 1 59 A. . B. . C. . D. . 6 60 6 60
Câu 12: Tập xác định của hàm số y = cot x 2 là A. π . B.   \  + kπ k |  . 2  C.π kππ \  + k |  . D.   \ k k |  . 4 2   2 
Câu 13: Hàm số nào sau đây là hàm số chẵn ?
A. y = −2sin x .
B. 3sin(−x ) .
C. y = −2cos x .
D. y = sinx − cos x . π π 3
Câu 14: Phương trình sin2 = − π x
sin có nghiệm α, β với −  α, β
. Giá trị α.β bằng 3 4 4 A. − π2 . B. − π 2 4 . C. π 2 . D. − π . 9 9 9 9
Câu 15: Giá trị lớn nhất của hàm số y = 2
2cos x − 2 3 sin x.cos x +1 bằng A. 0. B. 4. C. 3 + 3 . D. 3 − 3 . Câu 16:
Trong mặt phẳng tọa độ Oxy , cho điểm I (1;0) . Phương trình ảnh của đường tròn
(C) x2 + y2 :
= 4 qua phép đối xứng tâm I là
A. (x − )2 + y2 2 = 4.
B. (x − )2 + (y − )2 2 2 = 4 .
C. x + (y − )2 2 2 = 4.
D. (x − )2 + (y − )2 2 1 = 4 .
Câu 17: Một hộp đựng 15 viên bi trong đó có 7 viên bi xanh và 8 viên bi đỏ. Lấy ngẫu nhiên 3 viên bi từ
hộp. Xác suất để trong 3 viên bi lấy ra có ít nhất 1 viên bi màu đỏ là 12 418 1 1 A. . B. . C. . D. . 13 455 13 2
Câu 18: Số nghiệm của phương trình tan x
3 = tanx trong 0;1 π 0  là A.10. B.20. C.21. D.11.
Câu 19: Cho n  * thỏa mãn n − C 1 = C3 5
* . Hệ số của số hạng chứa x5 trong khai triển nhị thức Newton n n ( )  2 1 n nx của 
−  với x  0là  14 x  −16 −3 −35 −16 A. . B. . C. . D. . 35 16 16 3
Câu 20: Một hộp chứa 11 viên bi được đánh số từ 1 đến 11. Chọn ngẫu nhiên 6 viên bi từ hộp. Tính xác
suất để tổng các số trên các viên bi là một số lẻ? 103 215 118 115 A. . B. . C. . D. . 231 462 231 231
II - PHẦN TỰ LUẬN DÀNH CHO LỚP A Câu 1:
Dựng về phía ngoài tam giác nhọn ABC các hình vuông ABMN , ACPQ . Gọi O , O lần lượt là 1 2
tâm của hình vuông ABMN , ACPQ và I là trung điểm BC . Câu 2:
Chứng minh tam giác IO O vuông cân tại I . 1 2 1 Câu 3:
Chứng minh AI vuông góc với NQ và AI = NQ . 2 Câu 4: Giải phương trình x = x + 2 tan cot 4cos x 2 . Câu 5:
Giải bóng đá khu vực có 8 đội bóng của 8 quốc gia tham gia trong đó có 2 đội Việt Nam và Thái
Lan. Ban tổ chức bốc thăm ngẫu nhiên 8 đội chia thành hai bảng A và B , mỗi bảng có 4 đội.
Tính xác suất để hai đội Việt Nam và Thái Lan không cùng thuộc một bảng. Câu 6:
Cho lăng trụ ABCD. 
A BCD có đáy ABCD là hình vuông tâm O và A A = A 2 B = a 2 .
Gọi E ,F lần lượt là trọng tâm tam giác ADD, BBC . Câu 7:
Chứng minh EF song song với mặt phẳng (ABCD) và xác định thiết diện của lăng trụ ABCD. 
A BCD cắt bởi mặt phẳng (OEF ) . Câu 8:
Tính chu vi thiết diện của lăng trụ ABCD. 
A BCD cắt bởi mặt phẳng (OEF ) theo a . DÀNH CHO LỚP B Trang 12 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555 Câu 1:
Cho nửa đường tròn đường kính AB . Gọi C là điểm chuyển động trên nửa đường tròn và I là
điểm trên tia AC sao cho AI = BC . Chứng minh I di động trên một đường tròn cố định. sin x
2 + cos x − 3 (cos x 2 + sin x ) Câu 2: Giải phương trình = 0 . 2sin x 2 − 3 Câu 3:
An và Bình tham gia thi hai môn trắc nghiệm Vật lý và Hóa học. Đề thi của mỗi môn gồm 6 mã
khác nhau và các môn khác nhau có mã khác nhau. Đề thi được sắp xếp và phát cho các thí
sinh một cách ngẫu nhiên. Tính xác suất để trong 2 môn thi đó An và Bình có chung đúng 1 mã đề. Câu 4:
Cho hình lăng trụ ABCD. 
A BCD có đáy ABCD là hình thang thỏa AB song song với CD và AB = C
2 D. Mặt phẳng qua A và cắt các cạnh BB,CC,DD lần lượt tại các điểm M,N,P. Câu 5:
Tứ giác AMNP là hình gì? Chứng minh giao điểm của hai đường thẳng AP và MN thuộc một
đường thẳng cố định. Câu 6:
Chứng minh BM + D 2 P = C 2 N. DÀNH CHO LỚP D Câu 1:
Dựng về phía ngoài tam giác nhọn ABC các tam giác đều ABB,ACC . Gọi I,J lần lượt là trung
điểm BC,CB . Chứng minh tam giác AIJ đều. sin x
2 + 2cos x − sin x −1 Câu 2: Giải phương trình = 0. tan x + 3 Câu 3:
Người ta chọn ngẫu nhiên 4 câu hỏi trong 15 câu hỏi của ngân hàng đề thi. Biết rằng bạn Thùy
đã học thuộc 8 câu trong số 15 câu hỏi của ngân hàng đề. Tính xác suất để chọn được ít nhất
hai 2 câu mà bạn Thùy đã thuộc. Câu 4:
Cho hình lăng trụ ABCD. 
A BCD có đáy ABCD là hình thang thỏa AB song song với CD và AB = C
2 D . Mặt phẳng qua A và cắt các cạnh BB, CC, DD lần lượt tại M, N, P . Câu 5:
Tứ giác AMNP là hình gì? Chứng minh giao điểm của các đường thẳng AP và MN thuộc một
đường thẳng cố định. Câu 6:
Chứng minh BM + D 2 P = C 2 N . ---- Hết ---- Trang 13 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555
ÔN THI THPT QUỐC GIA 2020-2021
Lớp toán thầy Thông Đình Đình: ------------- DẠY THẬT – HỌC THẬT – GIÁ TRỊ THẬT--------------- PHẦN ĐỀ - TM6
I - CÂU HỎI TRẮC NGHIỆM Câu 1: 17
Tính tổng S tất cả các hệ số trong khai triển ( x 3 − ) 4 . A. S = −1. B. S =1. C. S = 0. D. S = 8192 . Câu 2:
Làng Duyên Yên, xã Ngọc Thanh, huyện Kim Động, tỉnh Hưng Yên nổi tiếng với trò chơi dân gian
đánh đu. Trong trò chơi này, khi nhún đều thì cây đu sẽ đưa người chơi dao động qua lại ở vị trí
cân bằng. Nghiên cứu trò chơi này, người ta thấy khoảng cách h (tính bằng mét) từ người chơi
đến vị trí cân bằng được biểu diễn qua thời gian t (tính bằng giây) bởi hệ thức h = d với π d 3cos ( t 2 ) = − 
1  , trong đó quy ước rằng d  0 khi vị trí cân bằng ở phía sau lưng người chơi 3 
đu và d  0 trong trường hợp trái lại. Tìm thời điểm đầu tiên sau 10 giây mà người chơi ở xa vị trí cân bằng nhất. A. Giây thứ 13 . B. Giây thứ 12,5 . C. Giây thứ 10,5 . D. Giây thứ 11. Câu 3:
Bạn An muốn mua một chiếc áo sơ mi cỡ 39 hoặc 40 . Biết áo cỡ 39 có 3 màu khác nhau, áo
cỡ 40 có 5 màu khác nhau. Hỏi bạn An có bao nhiêu lựa chọn để mua một chiếc áo? A. 8 . B. 3 . C. 5 . D. 15 . Câu 4:
Số đường chéo của đa giác 10 cạnh là A. 35 . B. 10 7 . C. 45 . D. 10 10 . Câu 5:
Từ các chữ số của tập A = 1;2;3;4;5; 
6 có thể lập được bao số tự nhiên có 3 chữ số mà các chữ số đôi một khác nhau? A. 125 . B. 120 . C. 6 . D. 10 . Câu 6:
Trong các mệnh đề sau, mệnh đề nào sai?
A. Hai đường thẳng phân biệt không cắt nhau và không song song thì chéo nhau.
B. Hai đường thẳng phân biệt không chéo nhau thì hoặc cắt nhau hoặc song song.
C. Hai đường thẳng không có điểm chung thì chéo nhau.
D. Hai đường thẳng chéo nhau thì không có điểm chung. Câu 7:
Mệnh đề nào dưới đây là đúng? A. 0 1 n −1 n +1 n +
C + C + ... + C = C + C 2 + ... + n C2 . n 2 n 2 n 2 n 2 n 2 n 2 B. 0 1 n −2 n +1 n +
C + C + ... + C = C + C 2 + ... + n C2 . n 2 n 2 n 2 n 2 n 2 n 2 C. 0 1 n +1 n +1 n +
C + C + ... + C = C + C 2 + ... + n C2 . n 2 n 2 n 2 n 2 n 2 n 2 D. 0 1 n n +1 n +
C + C + ... + C = C + C 2 + ... + n C2 . n 2 n 2 n 2 n 2 n 2 n 2 Câu 8:
Chọn ngẫu nhiên một thẻ từ một hộp chứa 16 thẻ được đánh số từ 1 đến 16 . Tính xác suất để
nhận được thẻ đánh số lẻ. 9 1 3 7 A. . B. . C. . D. 16 2 8 16 Câu 9:
Từ cỗ bài tú lơ khơ 52 quân, rút ngẫu nhiên cùng một lúc bốn quân bài. Tính xác suất sao cho
cả bốn quân đều là K . 1 4 1 4 A. . B. . C. . D. 6497400 6497400 270725 270725 π 5
Câu 10: Phương trình   cos x − =   1 có nghiệm là  6  π π π 5 π 5 A. x = + kπ . B. x = + k π 2 . C. x = + kπ . D. x = + k π 2 . 3 3 6 6
Câu 11: Một hộp chứa 6 quả cầu đỏ khác nhau và 4 quả cầu xanh khác nhau. Chọn ngẫu nhiên cùng
một lúc 2 quả cầu từ hộp. Tính xác suất của biến cố “Lấy được hai quả cùng màu”. 7 4 8 7 A. . B. . C. . D. . 15 9 15 45 Trang 14 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555
Câu 12: Lớp 11A có 35 học sinh nam và 10 học sinh nữ. Hỏi có bao nhiêu cách chọn ngẫu nhiên một bạn trong lớp? A. 20 . B. 500 . C. 45 . D. 25 .
Câu 13: Gọi M là giá trị lớn nhất, m là giá trị nhỏ nhất của hàm số y = cos x
2 + cos x − 2 . Tìm M −m . 25 21
A. M − m = .
B. M −m = 4.
C. M − m = .
D. M − m = 2. 8 8
Câu 14: Có bao nhiêu số tự nhiên có 8 chữ số đôi một khác nhau được thành lập từ tập
A = 1;2;3;4;5;6;7; 
8 sao cho số đó chia hết cho 1111. A. 384 . B. 345 . C. 3840 . D. 1920.
Câu 15: Trong mặt phẳng tọa độ Oxy , ảnh của đường thẳng d : x + y
2 − 3 = 0 qua phép đối xứng tâm I (4;3) là A. x + y 2 −17 = 0 . B. x + y 2 − 7 = 0 . C. x + y 2 +17 = 0 . D. x + y 2 −15 = 0 .
Câu 16: Điều kiện cần và đủ để phương trình a sinx + b cos x = c có nghiệm là
A. a2 + b2  c .
B. a2 + b2  c2 .
C. a2 + b2  c .
D. a2 + b2  c2 .
Câu 17: Hàm số nào trong các hàm số dưới đây có đồ thị nhận gốc tọa độ O làm tâm đối xứng A. y = 2 sin x .
B. y = cos x .
C. y = tanx . D. y = 2 cot x .
Câu 18: Có bao nhiêu cách lấy ngẫu nhiên cùng lúc 3 quả cầu từ một hộp chứa 10 quả cầu khác nhau? A. P . B. C3 . C. P . D. A3 . 2 10 10 10 Câu 19: Tính tổng: 0 1 2 n
S = C + C + C + ... + C2 . n 2 n 2 n 2 n 2 A. = n S 2 2 . B. = n S 2 2 −1. C. = n S 2 . D. = n S 2 2 +1.
Câu 20: Cô dâu và chú rể mời 6 người ra chụp ảnh kỷ niệm, người thợ chụp hình có bao nhiêu cách sắp
xếp sao cho cô dâu, chú rể đứng cạnh nhau. A. 6.7! . B. 2.7! . C. 8 − ! 7! . D. 2 + ! 6! .
Câu 21: Cho hình vuông ABCD tâm I . Gọi M , N lần lượt là trung điểm của AD , DC . Phép tịnh tiến
theo vectơ nào sau đây biến tam giác AMI thành MDN . A. AC . B. AM . C. NI . D. MN .
Câu 22: Cho hai đường thẳng cắt nhau d và d . Có bao nhiêu phép đối xứng trục biến đường thẳng này thành đường thẳng kia? A. Vô số. B. Hai. C. Không có. D. Một. Câu 23: 11
Hệ số của x 5 trong khai triển (1+ x ) là A. 55440 . B. 462. C. 246 . D. 252 .
Câu 24: Cho ba mặt phẳng phân biệt (α) , ( β) , (γ ) có (α)  ( β) = d , ( β)  (γ ) = d và (γ )  (α) = d . Khi 1 2 3
đó, ba đường thẳng d , d và d 1 2 3
A. đôi một song song. B. đồng qui.
C. đôi một cắt nhau.
D. đôi một song song hoặc đồng qui.
Câu 25: Hãy mô tả không gian mẫu của phép thử: “ Gieo một đồng xu cân đối và đồng chất hai lần liên tiếp”.
A. Ω = SS,NN .
B. Ω = S,N.
C. Ω = SS,SN,NS,NN .
D. Ω = SN,NS .
II - CÂU HỎI TỰ LUẬN Câu 1:
Giải các phương trình sau a. 2
cos x − 3cos x + 2 = 0 . b. (2cos x − )
1 (2sin x + cos x ) = sin x 2 − sin x . Câu 2: Cho hình chóp S A
. BCD , đáy ABCD là hình thang có đáy lớn AD . Gọi E , F lần lượt là trung
điểm của SA , SD .
a) Tìm giao tuyến của các cặp mặt phẳng: (SAC ) và (SBD ) , (SAD ) và (SBC ) .
b) Chứng minh EF // (ABCD ) và EF // (SBC ) .
c) Gọi K là giao điểm của AB và CD . Tìm M , N lần lượt là giao điểm của SB và (CDE ) ; SC và
(EFM ) . Từ đó, tìm thiết diện của hình chóp cắt bởi mặt phẳng (KEF ) .
d) Cho AD = B
2 C . Tính tỉ số diện tích của tam giác KMN và tam giác KEF . ---- Hết ---- Trang 15 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555
ÔN THI THPT QUỐC GIA 2020-2021
Lớp toán thầy Thông Đình Đình: ------------- DẠY THẬT – HỌC THẬT – GIÁ TRỊ THẬT--------------- PHẦN ĐỀ - TM7
I – PHẦN TRẮC NGHIỆM
Câu 1: Có 30 tấm thẻ đánh số từ 1 đến 30 . Chọn ngẫu nhiên 10 tấm thẻ. Tính xác suất để có 5 tấm
thẻ mang số lẻ, 5 tấm thẻ mang số chẵn, trong đó có đúng 1 thẻ mang số chia hết cho 10 . 99 48 A. . B. 0,1 . C. . D. 0,17 . 667 105 Câu 2: n
Biết hệ số của x2 trong khai triển (1− x
3 ) là 90 , ta có n bằng giá trị nào sau đây? A. S A . BCD . B. 5 . C. 31. D. 10 . Câu 3: 2 2
Trong mặt phẳng Oxy cho đường tròn (C):(x − ) 3 + (y − )
2 =16. Ảnh của (C ) qua phép đối
xứng tâm A (2;3) là đường tròn có phương trình:
A. (x − )2 + (y − )2 7 8 =16 .
B. (x − )2 + (y + )2 1 2 =16.
C. (x + )2 + (y − )2 1 1 =16 .
D. (x − )2 + (y − )2 1 4 =16 .
Câu 4: Cho hình chóp S A
. BCD có AC BD = M và AB CD = N. Giao tuyến của hai mặt phẳng (SAB )
và (SCD ) là đường thẳng: A. MN . B.SN . C. SA . D. SM . 20
Câu 5: Tổng các hệ số của khai triển ( x3 2 + 5 4x ) bằng: A. 20 12 . B. 20 22 .
C. C0 + C1 + C2 + ... + C20. D. C0 20 0 2 .5 + C1 19 1 2 .5 + ... + C20 0 20 2 .5 . 20 20 20 20 20 20 20
Câu 6: Trong không gian cho bốn điểm A , B , C , D không cùng nằm trên một mặt phẳng. Trên các
đoạn AB , AD lần lượt lấy các điểm M , N sao cho MN cắt BD tại I . Khi đó điểm I không
thuộc mặt phẳng nào sau đây? A. (BCD) . B. (ABD) . C. (MNC ) . D. (ACD) .
Câu 7: Hình nào sau đây có tâm đối xứng nhưng không có trục đối xứng ? A. Hình vuông.
B. Hình bình hành. C. Tam giác cân. D. Hình tròn. Câu 8: n
Khai triển (a + b) có số hạng tổng quát là:
A. k n−k n−k C a b .
B. k n−k k+ C a b 1.
C. k n−k k C a b
D. k n−k+ k+ C a b 1 1 . n n n n
Câu 9: Bài kiểm tra tập trung môn Toán của khối 11 ở một trường THPT tỉnh A gồm hai loại đề tự luận
và trắc nghiệm. Có tất cả 12 đề tự luận và 15 để trắc nghiệm. Học sinh phải chọn 1 đề tự luận
và 1 đề trắc nghiệm. Hỏi mỗi học sinh có bao nhiêu sự lựa chọn cho một bài kiểm tra? A. 180 . B. 27 . C. 165 D. 12 .
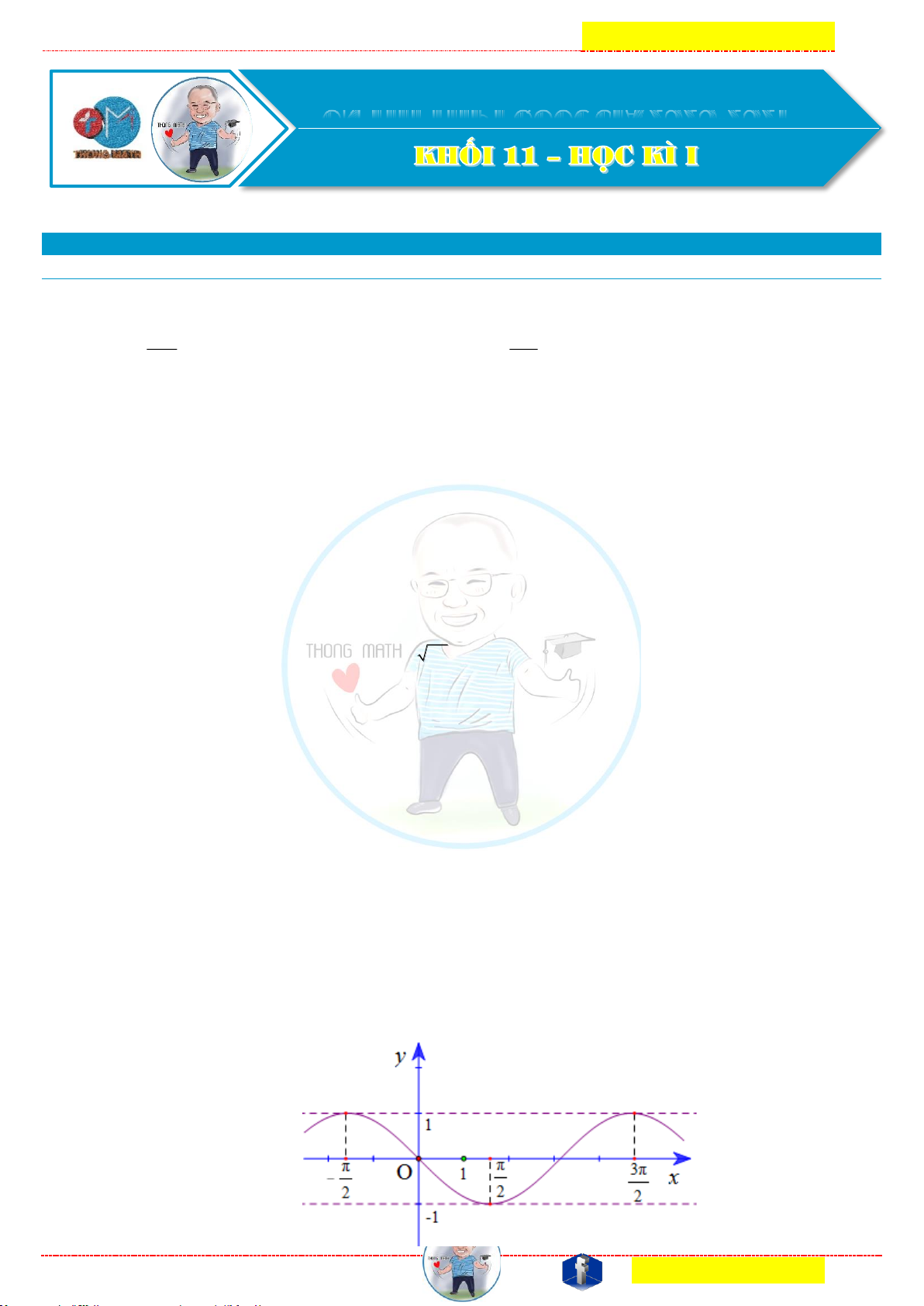
Câu 10: Đồ thị được cho là đồ thị của hàm số nào? Trang 16 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555
A. y = sin x .
B. y = sin x .
C. y = sin x
D. y = −sin x .
Câu 11: Hàm số nào sau đây là hàm chẵn?
A. y = −sin x 2 .
B. y = cos x − sinx .
C. y = cos x.sinx . D. y = x + 2 cos sin x .
Câu 12: Tất cả các giá trị của m để phương trình msinx +12cos x =13 có nghiệm là: m  −5 A. m  5 . B. .
C. −5  m  5 . D. m  −5. m  5
Câu 13: Một bình đựng 4 bi xanh và 6 bi đỏ. Lấy ngẫu nhiên 3 viên bi thì số phần tử của không gian mẫu là: A. 720 . B. 42 . C. 120 D. 80 .
Câu 14: Cho hình bình hành ABCD . Phép tịnh tiến T sẽ biến ? AB +AD
A. C thành B .
B. B thành C .
C. A thành C .
D. C thành A .
Câu 15: Trong không gian cho hai đường thẳng a,b chéo nhau. Trên a lấy hai điểm A,B và trên b lấy
hai điểm C,D . Khi đó hai đường thẳng AD và BC có vị trí tương đối nào sau đây? A. Chéo nhau.
B. Song song hoặc cắt nhau. C. Song song. D. Cắt nhau. π Câu 16: Hàm số   y = sin x 2 − 
 đạt giá trị lớn nhất tại x nhận giá trị nào sau đây?  4  π π π π 3 π π 3 A. − + kπ . B. − + k . C. + k . D. + kπ . 8 8 2 8 2 8
Câu 17: Gieo hai con xúc xắc cân đối. Xác suất để tổng số chấm trên mặt xuất hiện của hai con xúc xắc bằng 7 là : 1 2 7 5 A. . B. . C. . D. . 6 9 36 36
Câu 18: Trong mặt phẳng Oxy cho hai điểm M (4;6) và I (2;3) . Hợp của phép vị tự V( và phép đối I ;2)
xứng trục Ox sẽ biến điểm M (4;6) thành điểm có toạ độ: A. (−6;−9) . B. (6;9) . C. (6;−9) . D. (−6;9) . sin x
Câu 19: Số nghiệm của phương trình
= 0 trên đoạn π π ;4  là: cos x +1 A. 1. B. 2. C. 3 . D. 4 .
Câu 20: Có bao nhiêu số tự nhiên chẵn gồm 5 chữ số đều lớn hơn 4 và đôi một khác nhau? A. 48 . B. 240 . C. 120 . D. 24 . II – PHẦN TỰ LUẬN
Câu 1: Giải các phương trình lượng giác sau: a) 2
2sin x + 5cos x +1 = 0 . π π b)     sin x + + cos x + =     2 sin5x .  3   3  c) 2 x + x − 2 4sin 2 3 3 sin4 2cos x 2 = 4 .
Câu 2: Ba xạ thủ cùng bắn một viên đạn vào bia một cách độc lập.
Xác suất để ba xạ thủ bắn trúng bia lần lượt là 0,6; 0,7; 0,8 . Tính xác suất để:
a) Có ít nhất một xạ thủ bắn trúng bia.
b) Có đúng một xạ thủ bắn trúng bia.
Câu 3: Cho hình chóp S A
. BCD có đáy là hình thang, AB là đáy lớn và O = AC BD . Gọi M , N lần lượt
là trọng tâm của tam giác SAD và SBC .
a) Tìm giao tuyến của (SAC ) và (SBD ) .
b) Tìm giao điểm của AC và (SMN ) .
c) Xác định thiết diện của hình chóp S A
. BCD cắt bởi mặt phẳng (OMN ) . Trang 17 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555
ÔN THI THPT QUỐC GIA 2020-2021
Lớp toán thầy Thông Đình Đình: ------------- DẠY THẬT – HỌC THẬT – GIÁ TRỊ THẬT--------------- PHẦN ĐỀ - TM8 I – TRẮC NGHIỆM
Câu 1: Trong mặt phẳng Oxy , cho đường thẳng Δ : x 2 − y
3 − 5 = 0 . Ảnh của đường thẳng Δ qua phép
tịnh tiến theo vectơ u = (−1; ) 2 là đường thẳng nào? A. x 2 − y 3 +13 = 0 . B. x 2 − y 3 − 3 = 0 . C. x 2 − y 3 −13 = 0 . D. x 2 − y 3 + 3 = 0 .
Câu 2: Từ các chữ số của tập X = 1;2;4;5;7; 
8 có thể lập được bao nhiêu số tự nhiên có bốn chữ số đôi một khác nhau ? A. 6 4 . B. A4 . C. C 4 . D. 4 6 . 6 6 Câu 3: 10
Hệ số của số hạng thứ 6 trong khai triển biểu thức ( x2 2 + y) bằng A. 8064. B. x8y6 3360 . C. 3360 D. x10y5 8064 . 1
Câu 4: Số nghiệm của phương trình cos x 2 = trên nửa khoảng (  0 ;36  0  là 2 A. 8 . B. 6 . C. 2 D. 4 .
Câu 5: Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm của các cạnh AB , CD ; G là trung điểm GI
của MN , I là giao điểm của đường thẳng AG và mặt phẳng (BCD) . Tính tỉ số . GA GI 1 GI 1 GI 1 GI 1 A. = . B. = . C. = D. = . GA 4 GA 5 GA 2 GA 3
Câu 6: Ông Nam đã trồng cây ca cao trên mảnh đất của mình có dạng hình tam giác, ông trồng trồng ở
hàng đầu tiên 3 cây ca cao, kể từ hàng thứ hai trở đi số cây ca cao phải trồng ở mỗi hàng nhiều
hơn 5 cây so với số cây đã trồng ở hàng trước đó và ở hàng cuối cùng ông đã trồng 2018 cây
ca cao. Số cây ca cao ông Nam đã trồng trên mảnh đất của mình là A. 408.242 cây. B. 407.231 cây. C. 407.232 cây. D. 408.422 cây.
Câu 7: Trong mặt phẳng Oxy , cho hai điểm M (0;3) và N (0;4) . Gọi M , N lần lượt là ảnh của M , N
qua phép quay tâm O , góc quay 
90 . Độ dài đoạng thẳng MN bằng A. 5 . B. 7 . C. 1 D. 25 .
Câu 8: Nghiệm của phương trình 2 tan x 3 − ( 3 − ) 1 tan x 3 − 3 = 0 là
x = − π + πk π π A.  12 3 (k  ) . B. x = − + k (k  ) .  12 3
x = π + πk  9 3  2  π π x = − π + πk x = − +  k C.  12 3 (k  ). D.  12 3 (k  ) .  2 2 π π x = π + π   k x = + k  9 3  18 3
Câu 9: Tìm tất cả các giá trị của tham số m để phương trình sin x
3 − m = 0 có nghiệm.
A. m −1;  1 .
B. m  −3;3 .
C. m  (−;−  1  1;+)
D. m  (−;−3)  (3;+) .
Câu 10: Trong mặt phẳng Oxy , cho vectơ OA = i − 7 j . Ảnh của điểm A qua phép vị tự tâm O , tỉ số −3 là A. A 0; 21 . B. A 3; 21 . C. A 0;21 D. A 3;21 . 2 ( − ) 3 ( ) 1 ( − ) 4 ( − ) Trang 18 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555 Câu 11: 2 2
Trong mặt phẳng Oxy , cho đường tròn (C) : (x − ) 1 + (y + )
3 = 9 . Ảnh của đường tròn (C ) qua
phép vị tự tâm I (3;2) , tỉ số 2 là đường tròn có phương trình
A. (x + )2 + (y + )2 1 8 = 36 .
B. (x − )2 + (y + )2 4 1 = 36 .
C. (x − )2 + (y − )2 1 8 = 36 .
D. (x − )2 + (y + )2 2 6 = 36. ( )n+ − 1 1
Câu 12: Dãy sô (u có số hạng tổng quá u =
. Số hạng thứ 5 của (u là n ) n ) n n 2 1 1 A. − 1 . B. . C. . D. − 1 . 10 10 32 32
Câu 13: Cho lục giác đều ABCDEF tâm O như hình vẽ. Thực hiện liên tiếp phép quay tâm O , góc quay 0
120 và phép vị tự tâm O tỉ số −1 đối với một tam giác trong lục giác đều trên ta được ảnh là
tam giác OBC . Tạo ảnh của tam giác OBC là D E C O F B A A. O Δ EF . B. O Δ AB . C. O Δ DE . D. O Δ CD . n 2
Câu 14: Tìm số hạng không chứa x trong khai triển của biểu thức  2  x −  biết 2   x  1 2 2 3 3 n −1 n − C + C + C + + C 1 3. 3 3 ... 3 + n n
3 C = 65535 với n  *,x  0 . n n n n n A. 1120. B. −1120 . C. 112 . D. −112 .
Câu 15: Trong đề cương ôn tập bộ môn Toán có 15 câu hỏi Đại số và 10 câu hỏi Hình học. Hỏi có bao
nhiêu cách chọn ngẫu nhiên 5 câu hỏi có cả Đại số và Hình học để lập một đề kiểm tra 15 phút. A. 3255 . B. 49875 . C. 53130 . D. 756756 .
Câu 16: Cho hình chóp S A
. BCD có đáy ABCD là tứ giác lồi. Gọi O là giao điểm của AC và BD , M là
giao điểm của AB và CD , N là giao điểm của AD và BC . Giao tuyến của hai mặt phẳng (SAB ) và (SCD ) là A. SA . B. SN . C. SM . D. SO . sin x +1
Câu 17: Tập xác định của hàm số y = là cos x 2 −1 π π A. \k π 2 ,k   .
B. \kπ,k   . C.  
\  + kπ,k   . D.  
\ k ,k   . 2   2 
Câu 18: Trong hộp có 13 quả bóng bàn được đánh số từ 1 đến 13 . Lấy ngẫu nhiên cùng lúc 6 quả
bóng trong hộp. Xác suất để tổng các số ghi trên 6 quả bóng bàn được lấy ra không chia hết cho 2 là 14 212 175 217 A. . B. . C. . D. . 143 429 429 429 SM 1
Câu 19: Cho hình chóp S A
. BC . Lấy hai điểm M,N lần lượt nằm trên các cạnh SB, AB sao cho = SB 4 và NB = N
3 A. Khi đó đường thẳng MN song song với mặt phẳng A. (SAB ) . B. (SBC ) . C. (ABC ) . D. (SAC ) . Trang 19 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555
Câu 20: Giá trị của tham số m để phương trình (sin x + cos x − ) 1 (sin x
4 − m) = 0 có đúng bốn nghiệm
phân biệt thuộc đoạn π π 5  2  ;
 là m a;b)\c . Khi đó giá trị biểu thức a + b 2 + c bằng 8 6  7 7 11 9 A. . B. . C. . D. . 2 4 4 4 II - TỰ LUẬN
Câu 1: Giải phương trình 2sin x + 3 = 0 .
Câu 2: a) Đoàn học sinh tham gia Hội thao Giáo dục quốc phòng và an ninh học sinh THPT cấp tỉnh lần
thứ V năm 2018 của một trường THPT gồm có 8 học sinh nam và 7 học sinh nữ. Chọn ngẫu
nhiên 9 học sinh để tham gia môn thi điều lệnh. Tính xác suất để trong 9 học sinh được chọn
ra có đúng 5 học sinh nam. 15 2
b) Tìm số hạng chứa m
x trong khai triển biểu thức  3  x −   biết 2 m− A + C 2 4 = 60 với  x m m + m  ;x  0 .
Câu 3: Cho hình chóp S A
. BCD có đáy là hình thang, AD BC , AB = BC = a , AD = a 3 , BAD = 0 60 .
a) Gọi M là trung điểm của SD . Lấy điểm N trên cạnh SA sao cho SN = N
2 A . Tìm giao điểm H
của MN và (ABCD) .
b) Gọi là trọng tâm tam giác SAB . Mặt phẳng (α) đi qua G và song song với hai đường thẳng
AB, AD . Tính chu vi thiết diện của hình chóp khi cắt bởi (α) .
---------Hết--------- Trang 20 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555
ÔN THI THPT QUỐC GIA 2020-2021
Lớp toán thầy Thông Đình Đình: ------------- DẠY THẬT – HỌC THẬT – GIÁ TRỊ THẬT--------------- PHẦN ĐỀ - TM9
I – PHẦN TRẮC NGHIỆM
Câu 1: Phương trình 3 sin x 2 − cos x
2 − 3 = 0 có tất cả các nghiệm là: π 5 π 5 A. π π x = + kπ và x =
+ kπ (k  ) . B. x = + k π 2 và x = + k π 2 (k  ) . 4 12 4 12 π π π π 3 C. x = + kπ và x =
+ kπ (k  ) . D. x = − + kπ và x =
+ kπ (k  ) . 12 4 12 4 5 Câu 2: Cho A
Δ BC vuông tại A , AB = 6, AC = 8. Phép vị tự tâm A tỉ số biến B thành B , biến C 4
thành C . Tính bán kính R của đường tròn ngoại tiếp A Δ BC . 25 25 15 A. R = . B. R = . C. R = 5. D. R = . 2 4 4
Câu 3: Cho 1  k n ; k , n  . Số chỉnh hợp chập k của n phần tử được xác định bởi công thức nào sau đây? n ! n ! n ! A. ( . B. k ! . C. . D. . n − k )! k !
k !(n − k )!
Câu 4: Cho hình chóp S A
. BCD có đáy ABCD là hình bình hành. Gọi M , N , K lần lượt là trung điểm
của SB , CD , AD . Mệnh đề nào sau đây đúng?
A. SA// (MNK ) .
B. AC// (MNK ) .
C. SC// (MNK ) .
D. SD// (MNK ) .
Câu 5: Một hộp đựng 12 viên bi khác nhau, trong đó có 7 viên bi xanh và 5 viên bi đỏ. Có bao nhiêu
cách chọn từ hộp đó ra 5 viên bi gồm hai viên bi xanh và 3 viên bi đỏ? A. 792 . B. 95040 . C. 350 . D. 210 .
Câu 6: Trong mặt phẳng tọa độ Oxy , cho điểm M (3;− )
1 . Tìm tọa độ điểm M là ảnh của điểm M qua
phép tịnh tiến theo véctơ v = (−1; ) 3 .
A. M (2;− 4) . B. M (2;2) .
C. M (4;− 4) .
D. M (−2;4) .
Câu 7: Khẳng định nào sau đây đúng?
A. Hai đường thẳng song song nhau nếu chúng không có điểm chung.
B. Không có mặt phẳng nào chứa cả hai đường thẳng a và b thì ta nói a và b song song.
C. Hai đường thẳng cùng song song với một mặt phẳng thì song song với nhau.
D. Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.
Câu 8: Tìm tập xác định D của hàm số y = cot x . A. π
D = \  + kπ,k   .
B. D = \k π 2 ,k   . 2  C. D = .
D. D = \kπ,k   .
Câu 9: Từ các chữ số 0 , 1, 2, 3 , 4 , 5 lập được tất cả bao nhiêu số tự nhiên có ba chữ số đôi một khác
nhau và số đó chia hết cho 5 ? A. 20 số. B. 40 số. C. 36 số. D. 60 số. 18 2
Câu 10: Trong khai triển nhị thức Niutơn của biểu thức   x + 
(với x khác 0 ), tìm hệ số của số hạng 2   x  chứa x9 . A. C 3 3 2 . B. C3 . C. C 6 6 2 . D. C6 . 18 18 18 18 3
Câu 11: Phương trình cos x = có bao nhiêu nghiệm trong khoảng (0; π 2 ) ? 4 A. 1. B. 0 . C. 2. D. 4 . Trang 21 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555
Câu 12: Trong mặt phẳng, đường thẳng d là ảnh của đường thẳng d qua phép quay Q( . Mệnh đề A,90) nào sau đây đúng?
A. d song song với d .
B. d trùng với d .
C. d vuông góc với d .
D. d song song hoặc với d .
Câu 13: Trong đợt xét kết nạp Đoàn đầu năm của trường THPT A, kết quả có 18 học sinh khối 10 gồm
10 học sinh nam và 8 học sinh nữ. 30 học sinh khối 11 gồm 20 học sinh nam và 10 học sinh
nữ được kết nạp. Chọn ngẫu nhiên từ các học sinh được kết nạp ra 3 học sinh đại diện lên nhận
Huy hiệu Đoàn. Tính xác suất để trong 3 học sinh được chọn, có cả học sinh của hai khối, có cả
học sinh nam và học sinh nữ, đồng thời số học sinh nam nhiều hơn số học sinh nữ. A. 2785 . B. 985 . C. 225 . D. 3915 8648 8648 1081 8648
Câu 14: Tìm giá trị lớn nhất của hàm số y = cos 5x trên tập xác định của nó. A. −1. B. −5 . C. 5 . D. 1. 1
Câu 15: Cho A,B là hai biến cố độc lập cùng liên quan tới phép thử T ; xác suất xảy ra biến cố A là , 2 1
xác xuất xảy ra biến cố B là . Xác xuất để xảy ra biến của A và B là. 5 1 7 3 9 A. P (A B . ) = . B. P (A B . ) = . C. P (A B . ) = . D. P (A B . ) = 10 10 10 10 II – PHẦN TỰ LUẬN
Câu 16: Giải các phương trình sau. a) 2 sin x = . 2 b) cos x 2 − cos x − 2 = 0
Câu 17: Cho hình chóp S A
. BCD có đáy ABCD là hình thang, biết AD song song với BC và AD = B 2 C ,
O là giao điểm của AC và BD . Gọi M, N lần lượt là trung điểm SB và SD .
a) Cho Xác định giao tuyến của hai mặt phẳng (SAD ) và (SBC ) .
b) Cho Xác định giao điểm SC với mặt phẳng (AMN ) .
c) Cho Gọi G là trọng tâm SCD . Chứng minh rằng OG song song mặt phẳng (SBC ) .
Câu 18: Sau vòng đấu bảng AFF CUP 2018, một tờ báo tại khu vực đã bình chọn đội hình tiêu biểu gồm
11 cầu thủ, trong đó: các đội tuyển Việt Nam, Malaysia, Thái Lan, Philippines mỗi đội có 2 cầu
thủ; các tuyển Singapore, Myanmar, Indonesia mỗi đội có 1 cầu thủ. Tại buổi hộp báo trước khi
vào vòng đấu loại trực tiếp, Ban tổ chức chọn ra ngẫu nhiên 5 cầu thủ trong đội hình tiêu biểu
giao lưu cùng khán giả. Tính xác suất để 5 cầu thủ đó đến từ 5 đội tuyển khác nhau. ----HẾT---- Trang 22 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555
ÔN THI THPT QUỐC GIA 2020-2021
Lớp toán thầy Thông Đình Đình: ------------- DẠY THẬT – HỌC THẬT – GIÁ TRỊ THẬT--------------- PHẦN ĐỀ I - PHẦN TRẮC NGHIỆM Câu 1:
Tập xác định của hàm số y = 3 sin x 2 − tan x là: A. ππ
D = x  |x  + kπ,k  . B.  
D = x  |x k ,k   .  2   2  C.π
D = x  |x  + k π 2 ,k   .
D. D = x  |x kπ,k  .  2  Câu 2:
Có bao nhiêu cách chọn 6 học sinh vào đổi trực nhật từ một lớp có 50 học sinh? A. 50 6 . B. 6 50 . C. C6 . D. A6 . 50 50 Câu 3:
Một đa giác lồi có 35 đường chéo. Hỏi đa giác đó có bao nhiêu đỉnh? A. 8 . B. 6 . C. 12 . D. 10 . Câu 4:
Trong hệ trục tọa độ Oxy , cho đường thẳng d có phương trình x
2 − y +1 = 0 , phép tịnh tiến
theo vectơ v biến d thành chính nó thì v phải là vectơ nào trong các vectơ sau: A. v = (2;4) . B. v = (2;− ) 1 . C. v = (4;2) .
D. v = (−1;2) . Câu 5: 6 8
Hệ số của x5 trong khai triển biểu thức x ( x 2 − ) 1 + ( x 3 − ) 1 bằng A. −13368 . B. 13368 . C. −13848 . D. 13848 . Câu 6: 2 2
Trong hệ trục tọa độ Oxy , cho đường tròn (C ) có phương trình (x − ) 2 + (y − ) 2 = 4 . Hỏi phép 1
đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = và phép quay 2 tâm O góc quay 
180 sẽ biến đường tròn (C ) thành đường tròn nào trong các đường tròn có phương trình sau:
A. (x − )2 + (y − )2 1 1 =1.
B. (x − )2 + (y − )2 1 1 = 4 .
C. (x + )2 + (y + )2 1 1 =1.
D. (x + )2 + (y + )2 1 1 = 4 . Câu 7: Cho hình chóp S A
. BCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm của
AD và BC . Giao tuyến của hai mặt phẳng (SMN ) và (SAC ) là đường thẳng A. SD .
B. SO (O là tâm hình bình hành ABCD ).
C. SG (G là trung điểm AB ).
D. SF ( F là trung điểmCD ). Câu 8: Tổng S = C1 + C2 + C3
+    + C1009 bằng 2019 2019 2019 2019 A. 2019 2 . B. 2018 2 +1 . C. 2018 2 −1 . D. 2018 2 . Câu 9:
Có hai xạ thủ cùng bắn vào bia. Xác suất để người thứ nhất bắn trúng bia là 0,8 ; người thứ hai
bắn trúng bia là 0,6 . Xác suất để có ít nhất một người bắn trúng bia là A. 0,95 . B. 0,92 . C. 0,48 . D. 0,96 . π
Câu 10: Tìm các giá trị của tham số m để phương trình 6 x + 6 x = 2 sin cos cos x 2 + m có nghiệm   x  0;   8 1 1 1 1 1
A. 0  m  .
B. −  m  . C. m  .
D. −  m  0 . 8 8 8 8 8
Câu 11: Một lớp học có 30 học sinh được xếp thành một hàng dọc. Tính xác suất để hai bạn An và Hà đứng cạnh nhau. 1 1 2 1 A. . B. . C. . D. . 30 28 15 15 Trang 23 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555
Câu 12: Cho tứ diện ABCD đều cạnh a . Gọi G là trọng tâm tam giác ABC , mặt phẳng (CGD) cắt tứ
diện theo một thiết diện có diện tích là. A. a2 2 . B. a2 3 . C. a2 2 . D. a2 3 . 6 4 4 2 2sin x 2 + cos x 2
Câu 13: Tập giá trị của hàm số y =
có tất cả bao nhiêu giá trị nguyên? sin x 2 − cos x 2 + 3 A. 4 . B. 2. C. 3 . D. 1.
Câu 14: Từ một hộp chứa 16 thẻ được đánh số từ 1 đến 16 , chọn ngẫu nhiên 4 thẻ. Tính xác suất để 4
thẻ được chọn đều đánh số chẵn. 1 1 1 1 A. . B. . C. . D. . 26 25 21 27
Câu 15: Cho tứ diện ABCD . Gọi M , N , P lần lượt là trung điểm của AB , BC và CD . Thiết diện của tứ
diện cắt bởi mp (MNP ) là hình gì trong các hình sau? A. Hình thoi. B. Hình vuông. C. Hình chữ nhật. D. Hình bình hành.
Câu 16: Cho hình chóp tứ giác S A
. BCD . Gọi M , N lần lượt là trọng tâm của tam giác SAB , SAD . Gọi P
là trung điểm của BC . Mệnh đề nào sau đây đúng?
A. MN // (SCD ) .
B. MN // (SBD ) .
C. MN // (SAP ) .
D. MN // (SDP ) . II - PHẦN TỰ LUẬN Câu 1: Giải các phương trình:  π 7  cos − x 2 −   c 3 os ( x 2 − π 3 ) + 2cos x 3 a)
− 2 3 cot x − 6 = 0 . b)  2  = 0 2 sin x 1 − 2sin x Câu 2:
a) Gọi a ,b ,c lần lượt là hệ số của các số hạng chứa x2 , số hạng chứa x4 và số hạng chứa x6 x 12 trong khai triển   −  m
4  thành đa thức . Tìm m để a = bc .  2  b) Lớp A
11 có 10 học sinh nữ và một số học sinh nam. Cần chọn 5 học sinh tham gia đội văn 7
nghệ của trường. Biết xác suất cả 5 học sinh được chọn toàn nam bằng xác suất để trong 15
5 học sinh được chọn có 2 nữ. Hỏi lớp A 11 có bao nhiêu học sinh? Câu 3: Cho hình chóp S A
. BCD có đáy là hình thang ABCD với đáy lớn BC = a
2 , AD = AB = a . Mặt bên
(SAD) là tam giác đều. Gọi M là điểm bất kỳ thuộc cạnh AB . Mặt phẳng (α) qua điểm M song
song với SA , BC và (α) cắt CD , SC , SB lần lượt tại N , P , Q .
a) Chứng minh rằng: PN song song với mặt phẳng (SAD ) .
b) Gọi E là giao điểm của MQ và NP . Chứng minh rằng: E luôn nằm trên một đường thẳng cố định.
c) Giả sử AM = x , (0  x a ) . Tính diện tích thiết diện tạo bởi mặt phẳng (α) với hình chóp S A
. BCD theo a và x . Tìm vị trí của M để diện tích thiết diện đạt giá trị lớn nhất? n −  n 1 2 2 0 1 2 n 1 n −  Câu 4:
Cho n  , n  2. Chứng minh rằng: − C C . C . .. C . C .  . n n n n n    n −1 
---------HẾT--------- Trang 24 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555
ÔN THI THPT QUỐC GIA 2020-2021
Lớp toán thầy Thông Đình Đình: ------------- DẠY THẬT – HỌC THẬT – GIÁ TRỊ THẬT---------------
PHẦN ĐỀ TỰ LUẬN - TM11  2  Câu 1. Giải phương trình: π 2cos x − −1 = 0  . 3    Câu 2. Giải phương trình: 2
2sin x + 3cos x − 3 = 0 . Câu 3.
Giải phương trình sin x 2 + 3 cos x 2 = 3 . Câu 4.
Cho tập A = 1;2;3;4;5;6;7; 
8 . Có bao nhiêu số tự nhiên có 4 chữ số khác nhau chia hết cho 5
được lấy từ tập A. Câu 5.
Trong một hộp có 10 viên bi màu xanh, 12 viên bi màu đỏ. Chọn ngẫu nhiên 5 viên bi. Tính
xác suất để chọn được các viên bi có đủ hai màu? 12  3  Câu 6.
Tìm số hạng không chứa x trong khai triển của nhị thức x4 2 −  . x2    Câu 7.
Cho hình chóp SABCD đáy là hình bình hành ABCD tâm O. Gọi M , N lần lượt là trung điểm
của SA và SD .
a) Tìm giao tuyến của hai mặt phẳng (SAC ) và (SBD )
b) Chứng minh MN song song BC .
c) Gọi I là giao điểm của CM với SO và G là trọng tâm của tam giác ABC .Chứng minh IG
song song với mặt phẳng (SAB ) . Câu 8.
Cho tứ diện ABCD . Gọi G là trọng tâm tam giác ABC . Gọi M ,N thuộc cạnh AD sao cho
DM = MN = NA . Gọi E là điểm đối xứng của của A qua G . Chứng minh (MCE ) // (NBG ) . Trang 25 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555 PHẦN ĐỀ-TM12 Câu 1.
Giải phương trình sau: a/ 2sinx +1 = 0
b/ 3 cos x + sin x + 2 = 0 π sinx
+ (1+ sinx + cos x 2 ) c/  4  1 cos x + cos x 2 + cos x 3 + cos x 4 = 0 d/ = (1+ tanx) cos x 2 Câu 2.
a/ Cho tập A = 1;2;3;4;5;6;7; 
8 . Từ A có thể lập được bao nhiêu số tự nhiên lẻ gồm có 4 chữ số.
b/ Có bao nhiêu cách xếp 5 nam và 5 nữ ngồi vào 1 băng ghế dài .
c/ Một tập thể có 10 học sinh ưu tú, người ta cần cử một đoàn đi dự trại hè quốc tế, trong đó
có 1 trưởng đoàn, 1 phó đoàn và 3 đoàn viên. Hỏi có bao nhiêu cách cử như vậy. n
d/ Tìm hệ số không chứa  2 
x trong khai triển: x3 −  , biết n 1 − n C
+ C −2 = 78 với x  0 x    n n Câu 3.
a/ Gieo một con súc sắc cân đối và đồng chất. Tính xác suất để xuất hiện mặt lẻ chấm.
b/ Một hộp chứa 7 bi trắng, 6 bi xanh, 4 bi đen. Chọn ngẫu nhiên cùng lúc 3 bi từ hộp.
Tính xác suất để 3 bi được chọn có ít nhất 1 bi trắng.
c/ Chọn ngẫu nhiên 3 số từ tập 1;2;...; 
12 . Tính xác suất để tổng ba số là số lẻ
d/ Gọi X là tập hợp các số lẻ có 4 chữ số đôi một khác nhau được lập từ các chữ số 0; 1; 2; 3;
4; 5. Lấy ngẫu nhiên 1 số từ tập hợp X. Tính xác suất để số được chọn nhỏ hơn 2014. Câu 4.
a/ Trong mặt phẳng tọa độ Oxy , cho v = ( 2 − ; )
3 . Hãy tìm ảnh của điểm A (1; ) 1 − qua phép tịnh
tiến theo vectơ v .
b/ Cho hình lăng trụ ABC A . BC
 . Gọi M, N lần lượt là trung điểm của AC và AC . Chứng
minh MN song song với mặt phẳng (BCC B  ) . Câu 5. Cho hình chóp S A
. BCD có đáy ABCD là hình vuông cạnh a . Mặt bên SAB là tam giác đều.
Cho SC = SD = a 3 . Gọi M thuộc AD sao cho a AM = . 3
a/ Xác định giao tuyến của mặt phẳng (SAD) và (SBC).
b/ Gọi G; J lần lượt là trọng tâm của tam giác SCD và tam giác ADC. Chứng minh rằng GJ // (SAB ).
c/ Mặt phẳng (P) đi qua M, song song với AB và SD. Xác định thiết diện của hình chóp S.ABCD
cắt bởi mặt phẳng (P). Tính diện tích thiết diện vừa tìm được theo a. PHẦN ĐỀ-TM13 Câu 1.
Giải phương trình cos x 5 − sinx = 0. Câu 2.
Lớp 11A có 30 học sinh trong đó có 20 nam và 10 nữ. Có bao nhiêu cách chọn ra một nhóm 7
học sinh của lớp 11A gồm 4 học sinh nam và 3 học sinh nữ? 21  2  Câu 3.
Tìm hệ số của số hạng chứa x8 trong khai triển nhị thức − x3  . x2    Câu 4. Giải phương trình n P C −2 . + 42 = A2 . 3 n n 2 Câu 5.
Trường X tổ chức kiểm tra tập trung 3 môn Toán, Văn và Ngoại ngữ cho học sinh khối 11 trong
thời gian một tuần (không tổ chức kiểm tra vào ngày chủ nhật). Biết rằng mỗi ngày học sinh chỉ
kiểm tra một môn. Tính xác suất để môn Toán kiểm tra đầu tiên và các môn không kiểm tra
vào hai ngày liên tiếp nhau. Câu 6.
Xét tính tăng, giảm của dãy số (u có số hạng tổng quát n u = n 2 − 3 . n ) n u  + u 2 = 0 Câu 7. 1 5 Cho cấp số cộng u ( ) thỏa mãn
. Tìm số hạng thứ 15 của cấp số cộng đó. nS =14  4 Câu 8. Cho hình chóp S A
. BCD có đáy ABCD là hình bình hành tâm O . Gọi M, N, P lần lượt là
trung điểm của SB, OC và SD .
a) Chứng minh đường thẳng MP song song với mặt phẳng (ABCD) .
b) Tìm giao tuyến của mặt phẳng (MNP ) và mặt phẳng (ABCD) .
c) Tìm thiết diện tạo bởi mặt phẳng (MNP ) và hình chóp S A . BCD . Trang 26 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555 PHẦN ĐỀ-TM14 Câu 1.
Giải các phương trình sau: a) 3 cos x 2 − sin x 2 − 2 = 0 . b) sin x 2 − cos x
2 = 2sinx − 2cos x +1. c) A1 C2 + = n . n nu − u 2 = 9 Câu 2.
a) Cho cấp số cộng: 1 7 
. Tìm số hạng đầu u và công sai d . u + u 2 = 2  1 3 4 10
b) Tìm số hạng không chứa  2 
x trong khai triển nhị thức 3x3 −  . x2    Câu 3.
Từ các chữ số 0;1;2;3;4;5;6;7;8;9 lập được bao nhiêu số tự nhiên lẻ, có 6 chữ số; trong đó chữ
số 2 xuất hiện 3 lần, các chữ số còn lại xuất hiện không quá 1 lần và không có hai chữ số 2 nào đứng cạnh nhau. Câu 4.
Có 5 học sinh nữ và 10 học sinh nam, chọn một đội có 4 học sinh đi dự hội trại. Tính xác suất
sao cho đội có cả nam lẫn nữ Câu 5. Cho hình chóp S A
. BCD đáy là hình bình hành tâm O . Gọi M,N lần lượt là trung điểm của các
cạnh CD,BC . Lấy điểm E trên cạnh SA .
a) Tìm giao điểm của ME với mặt phẳng S ( BC) .
b) Tìm giao tuyến của hai mặt phẳng (MEO ) và mặt phẳng (SAD )
c) Gọi (P ) là mặt phẳng qua O và song song với CD,SC . Tìm thiết diện cắt bởi (P ) và hình chóp S A . BCD . PHẦN ĐỀ-TM15 Câu 1.
Giải các phương trình: π  2 a. cos 3x − = −  . 6    2 b. sin x 2 − 3 cos x 2 = 2 . c. cos x
3 + cos x = 3 cos x 2 . Câu 2. 20
Tìm số hạng x20 trong khai triển: ( x2 3 − 2) . Câu 3.
Một đề cương ôn tập gồm 10 câu hỏi, trong đó có 5 câu dễ, 3 câu trung bình và 2 câu khó.
Chọn ngẫu nhiên một đề thi gồm 4 câu. Tính xác suất sao cho chọn được đề thi:
a. Chỉ có câu hỏi dễ?
b. Có đủ 3 loại câu hỏi? Câu 4. Cho hình chóp S A
. BCD có đáy ABCD là hình bình hành tâm O . Gọi M, N lần lượt là trung
điểm của SA,SB và G là trọng tâm tam giác SAD
a) Tìm giao tuyến của (SAC ) và (SBD ) ; (OMN ) và (ABCD) .
b) Tìm giao điểm I của CM và (SBD ) . Chứng minh IG//(ABCD ) .
c) Xác định thiết diện của mặt phẳng (MBC ) và hình chóp S A . BCD . 2014 3 +1 Chứng minh rằng: C0 2 + 2 C2 4 + 2 C4 2014 + + 2 C2014 = 2014 2014 2014 2014 2 Trang 27 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555 PHẦN ĐỀ-TM16 Câu 1.
Giải các phương trình:   1 a. π sin x 2 − = 
. Phương trình có bao nhiêu nghiệm trong khoảng ( 3 − ; ) 1 ? 3    2 b. cos x 2 − 3s inx + 4 = 0 . Câu 2. 20
Tìm số hạng x20 trong khai triển: ( x2 3 − 2) .
a. Tìm hệ số của số hạng chứa x 8
8 trong khai triển của nhị thức: (x2 + 2) .
b. Cho số nguyên dương n thỏa A2 + C2 = n2 2
+ 80 . Tìm số hạng không chứa x trong khai triển n n n của nhị thức:  2  x − , x  0  x4    . Câu 3.
Một túi chứa 14 quả cầu khác nhau gồm 7 quả cầu màu đỏ, 4 quả cầu màu xanh và 3 quả cầu
màu vàng. Chọn ngẫu nhiên đồng thời 3 quả cầu. Tính xác suất để:
a. 3 quả cầu được chọn đều là màu đỏ.
b. 3 quả cầu được chọn có nhiều hơn 1 màu. u  + u = 36 Câu 4. 7 3
Tìm số hạng đầu và công sai của cấp số cộng (u biết n ) S = 22  4 Câu 5. Cho hình chóp S A
. BCD có ABCD là hình bình hành. Gọi E,F lần lượt thuộc cạnh BC, AD sao cho 3 2
BE = BC , AF = AD ; H là trung điểm SF;J là giao điểm của AE và CD . 5 5
a) Tìm giao tuyến của hai mặt phẳng (SAD ) và (SBC ) .
b) Tìm giao điểm của đường thẳng CH và mặt phẳng (SBD ) .
c) Chứng minh đường thẳng FC song song với mặt phẳng (SAE ) . c) Một mặt phẳng chứa 10
BH và song song ED cắt AE tại I . Chứng minh JE = . JI 19 Câu 6.
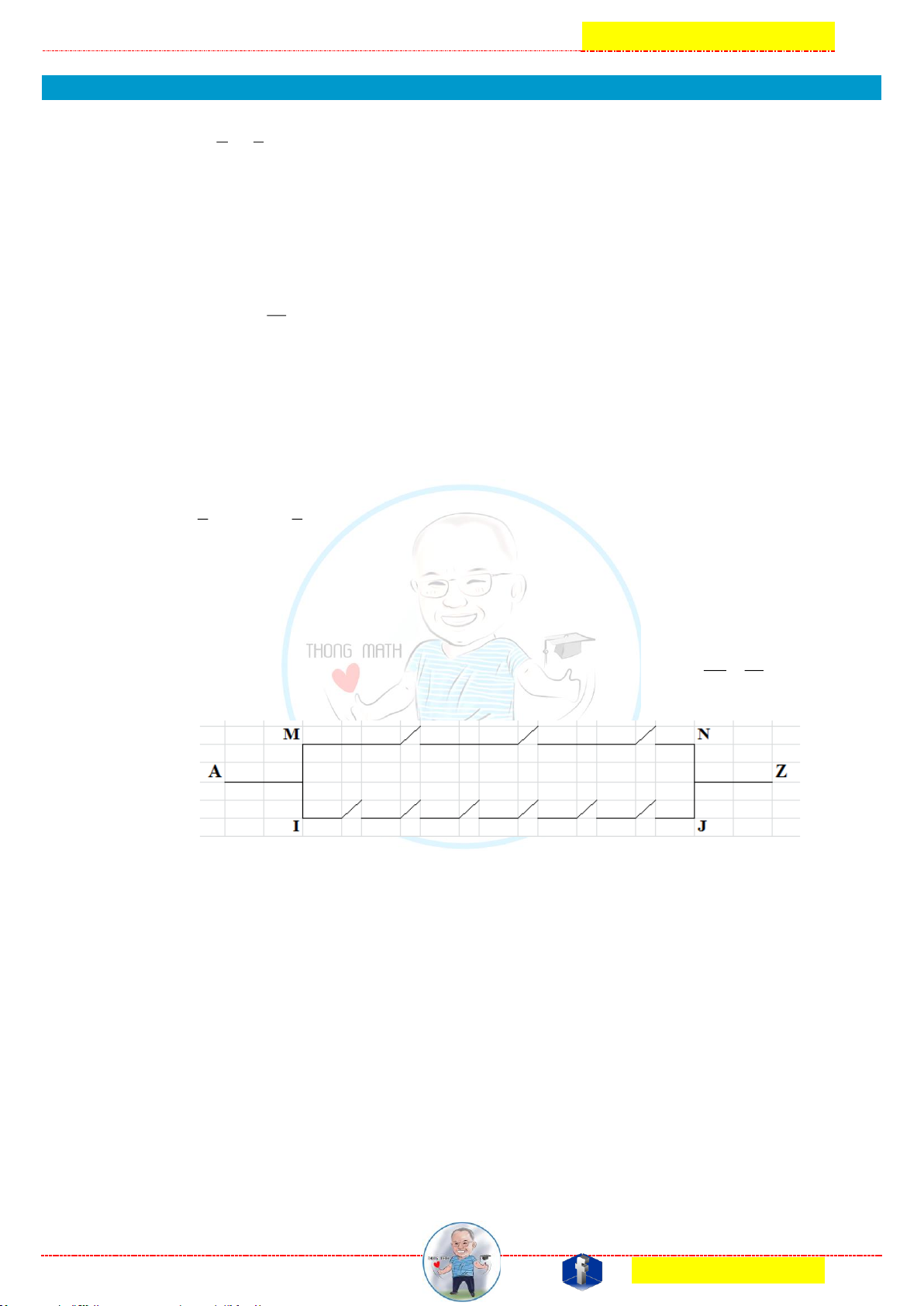
Cho sơ đồ mạch điện có 9 công tắc, mỗi công tắc có 2 trạng thái đóng và mở.
Hỏi có bao nhiêu cách đóng – mở 9 công tắc trên để mạng điện thông mạch từ A đến Z ? Trang 28 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555 PHẦN ĐỀ-TM17 Câu 1.
Giải các phương trình sau: a) 2 − sin x 2 +1 = 0. b) 6 sin x 2 − 2 cos x 2 = 2 2 Câu 2.
Từ ngày 15/09/2018, các nhà mạng điện thoại đã bắt đầu thay đổi đầu số dành cho các thuê
bao 11 số thành các thuê bao 10 số. Ví dụ, đầu số 0122-xxx-xxxx đã được đổi thành đầu số
077-xxx-xxxx với các chữ số phía sau không đổi. Hãy cho biết nhà mạng có thể thiết lập tối đa
bao nhiêu số điện thoại với đầu số 077. Câu 3.
Trong một hộp chứa năm que gỗ được đánh các số: 1, 2, 3, 5, 7. Một người chơi được bốc ngẫu
nhiên đồng thời hai que (không quan tâm thứ tự).
a) Mô tả không gian mẫu và tính số phần tử không gian mẫu của phép thử trên.
b) Người chơi đó sẽ chiến thắng nếu như tổng các số được đánh trên hai que là một số lẻ.
Tính xác suất chiến thắng của người đó. Câu 4.
a) Một lớp có 5 học sinh nam và 7 học sinh nữ. Hỏi có bao nhiêu cách sắp xếp 12 học sinh trên
thành một hàng sao cho không có hai học sinh nam nào đứng liền kề nhau? 18  
b) Tìm số hạng không chứa x trong khai triển 1 3 x −  . x12  x2    Câu 5. Cho hình chóp S A
. BCD có đáy ABCD là hình bình hành, hai đường chéo AC và BD cắt nhau
tại O . Gọi M là trung điểm của SA và N là một điểm trên cạnh SC sao cho SN = N 2 C .
a) Tìm giao tuyến của mặt phẳng (BMN ) và mặt phẳng (ABCD) .
b) Tìm giao điểm H của đường thẳng SD và mặt phẳng (BMN ) .
c) Gọi I là điểm đối xứng của B qua C . Trong mặt phẳng (SBC ) , gọi J là giao điểm của IN và
SB . Định hình tính thiết diện tạo bởi mặt phẳng (MNJ ) và hình chóp S A . BCD . PHẦN ĐỀ-TM18 Câu 1. Giải phương trình: 2 x + x x 2 2sin
2 3 sin cos − 4cos x +1 = 0 . Câu 2.
a) Gọi X là tập hợp các số tự nhiên gồm 3 chữ số khác nhau được lập nên từ các chữ số 1; 2;
4; 6; 8; 9. Lấy ngẫu nhiên 1 phần tử của X . Tính xác suất để chọn được số chia hết cho 2.
b) Xác suất bắn trúng đích của 4 xạ thủ đều bằng 0,7. Bốn xạ thủ cùng bắn vào mục tiêu. Tính
xác suất để có ít nhất 3 xạ thủ bắn trúng đích. Câu 3.
Một đa giác có độ dài các cạnh lập thành một cấp số cộng có công sai bằng 4(cm), cạnh nhỏ
nhất bằng 6(cm) và chu vi của đa giác bằng 126(cm). Tính độ dài cạnh lớn nhất của đa giác. Câu 4.
Dùng phương pháp quy nạp, hãy chứng minh: n u = − n3 10 2
− n + 2 luôn chia hết cho 3 với mọi n
số nguyên dương n . Câu 5.
Tính tổng: S = C1 2018 .3 .2 − C2 2017 2 .3 .2 + C3 2016 3 .3
.2 − ... − C2018 1 2018 .3 .2 + C2019 2019 .2 . 2019 2019 2019 2019 2019 Câu 6. Cho hình chóp S A
. BCD có đáy ABCD là hình bình hành tâm O . Biết SA = CD và SB = AC . Gọi
E , F lần lượt là trung điểm của BC và SD .
a) Xác định giao tuyến của hai mặt phẳng (SAB ) và (SCD ) . Từ đó tìm giao điểm H của đường
thẳng CF và mặt phẳng (SAB ) .
b) Chứng minh: (OEF ) //(SAB ) .
c) Mặt phẳng (OEF ) cắt AD và SC lần lượt tại L và I . Chứng minh: tứ giác OLFI là hình thoi.
d) Gọi M và N là các điểm lần lượt trên các cạnh SB và OA sao cho BM = AN . Chứng minh: MN //(SCD ) . Trang 29 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555 PHẦN ĐỀ-TM19 Câu 1.
Giải các phương trình sau: a.π  3 cos x + =  b. 2 x − x 2 2sin 3sin2 + 6cos x =1 3    2 15  1  Câu 2.
Tìm số hạng không chứa x trong khai triển x2 2 −  x    Câu 3.
Cho A = 0;1;2;3;4; 
5 , có bao nhiêu số tự nhiên lẻ có 4 chữ số phân biệt thuộc A ? Câu 4.
Có bao nhiêu số tự nhiên có 8 chữ số trong đó có 3 chữ số khác nhau và không có chữ số 0 ?
(Một số có 8 chữ số trong đó có 3 chữ số khác nhau là 12323112) Câu 5.
Một bài trắc nghiệm gồm 50 câu hỏi, mỗi câu hỏi có 4 phương án trả lời trong đó có đúng một
phương án đúng, mỗi câu trả lời đúng học sinh được 0.2 điểm. Một học sinh làm đúng 35 câu
đầu tiên và chọn ngẫu nhiêu 15 câu cuối. Tính xác xuất để học sinh đạt 10 điểm. Câu 6.
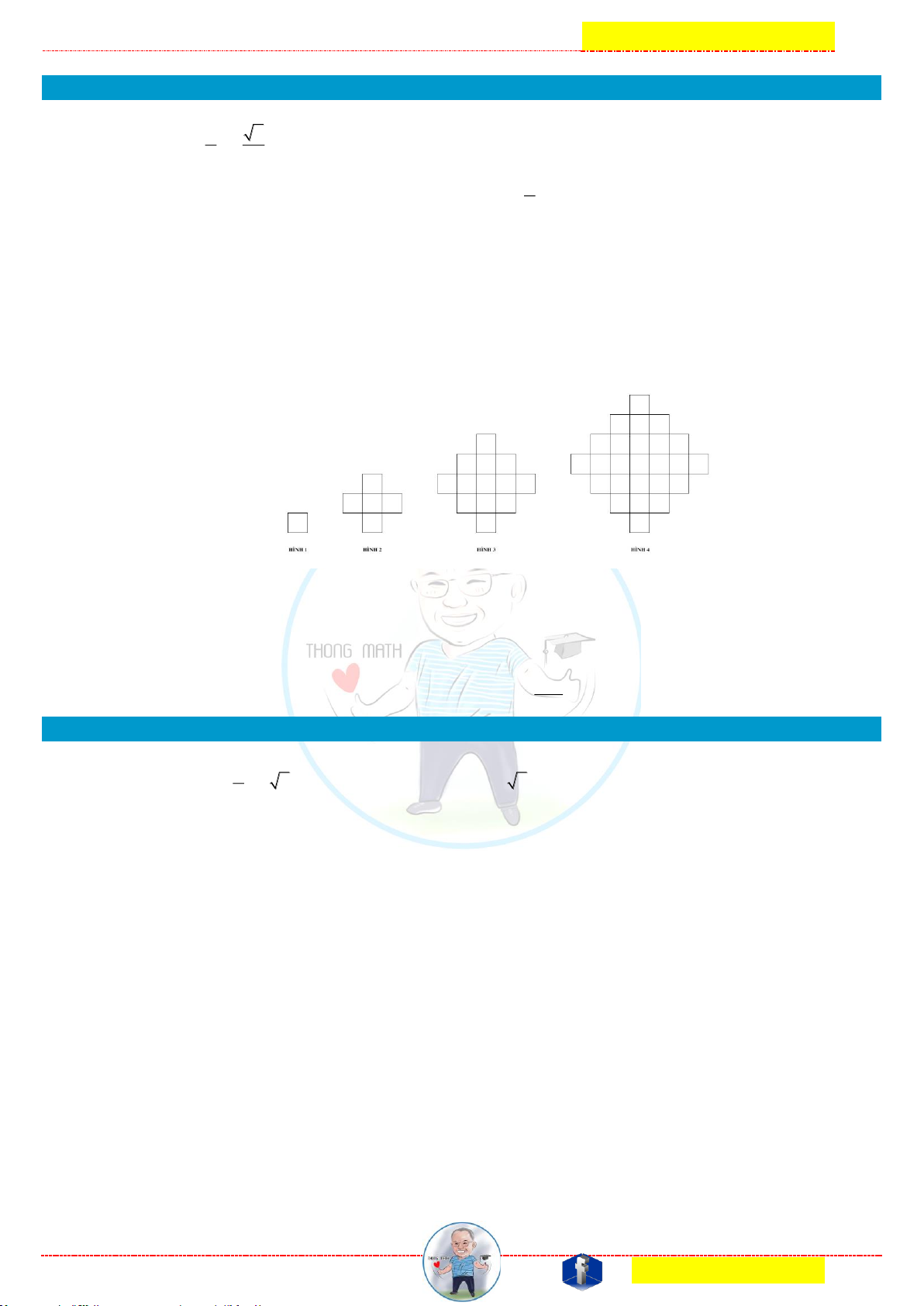
Các hình 1, 2, 3 và 4 có các hình vuông không chồng lấp lần lượt là 1, 5, 13 và 25. Nếu mô
hình được tiếp tục, có bao nhiêu hình vuông không chồng lấp sẽ có trong hình 100? Tại sao? Câu 7. Cho hình chóp S A
. BCD có đáy ABCD là hình bình hành. Gọi M,N lần lượt là trung điểm của BC và SA
a) Tìm giao tuyến của hai mặt phẳng (SAD ) và (SBC ) .
b) Chứng minh MN //(SDC )
c) Gọi K là giao điểm của MN với (SBD ) . Tính tỉ số KM ? KN PHẦN ĐỀ-TM20 Câu 1.
Giải các phương trình sau a) π  2cos x 2 + = 3 
b) 3 sinx + cos x = 2 4    Câu 2.
Gieo một con súc sắc cân đối đồng chất hai lần. Tính xác suất để số chấm xuất hiện trong hai lần gieo là khác nhau. Câu 3.
Từ các chữ số 1;2;3;4;5;6 có thể lập được bao nhiêu số chẵn có 4 chữ số khác nhau? Câu 4.
Khai triển nhị thức (1− x 3 )n 2 n
= a + a x + a x + ... + a x . Biết a + a + a = 376 . Tính a . 0 1 2 n 0 1 2 3 u  = 1 Câu 5. 1
Cho dãy số (u thoả mãn . n ) u = u 2 + nn 1 + n
a) Chứng minh dãy số (v
với v = u + n +1 là một cấp số nhân. n ) n n
b) Đặt S = u + u + ... + u . Tính S theo n . n 1 2 n n Câu 6.
Một số nguyên dương gọi là đối xứng nếu ta viết các chữ số theo thứ tự ngược lại thì được số
bằng số ban đầu, chẳng hạn như số 1221. Chọn ngẫu nhiên một số đối xứng có 4 chữ số, tính
xác suất chọn được số chia hết cho 7. Câu 7.
Cho hình chóp tứ giác S A
. BCD có đáy ABCD là hình bình hành. Gọi M,N,P lần lượt là các
điểm trên các cạnh CD,AD,SA thỏa MD = M
2 C,NA = N
3 D,PA = P
3 S . Gọi G là trọng tâm tam giác SBC .
a) Tìm giao điểm K của đường thẳng BM và mặt phẳng (SAC ) .
b) Chứng minh mặt phẳng (NKP ) song song với mặt phẳng (SCD ) .
c) Chứng minh đường thẳng MG song song với mặt phẳng (SAD ) .
--------- Hết--------- Trang 30 |
bs & st: Thông Đình Đình
Tương lai khóc hay cười là phụ thuộc vào độ lười của ngày hôm nay”!
09411.02468 – 0987.154.555
Chúc các bạn học sinh thân yêu một mùa giáng sinh an lành – hạnh phúc - ấm áp
Ôn thi tốt để đạt kết quả học kì như ý! --- Bùi Đình Thông --- Trang 31 |
bs & st: Thông Đình Đình