Vẻ đẹp lời giải hình học qua các bài toán lượng giác

NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Trao đổi kinh nghiệm dạy học theo định
hướng tiếp cận năng lực người học
Vẻ đẹp lời giải hình học qua các bài toán lượng giác Ths. HOÀNG MINH QUÂN
GV Trường THPT chuyên Nguyễn Huệ, Hà Nội
Trong chương trình toán THPT, để chứng minh một số hệ thức lượng giác, ta thường
sử dụng các biến đổi lượng giác. Câu hỏi đặt ra, ngoài các cách biến đổi lượng giác thì ta có cách
tiếp cận nào khác để giải quyết vấn đề không? Để trả lời câu hỏi này, bài viết sau đây mời bạn
đọc cùng đến với hướng tiếp cận hình học cho chứng minh một số hệ thức lượng giác.
I. CÁC ĐẲNG THỨC LƯỢNG GIÁC
Bài 1. Chứng minh rằng với x + y   , ta có
sin ( x + y) = sin x cos y + cos x sin . y
Chứng minh 1. Gọi z là góc thỏa mãn x + y + z =  . Ta có x, y, z là ba góc của một
tam giác. Không mất tổng quát, giả sử tam giác đó nội tiếp đường tròn bán kính 1 r = . 2 c 1 Ta có sin z = :
= c , tương tự sin x = a , sin y = b . 2 2
Từ công thức c = a cos y + b cos x , ta có
sin z = sin x cos y + cos x sin y
 sin (x + y) = sin xcos y + cos xsin . y
Chứng minh 2.
Vẽ tam giác ABC với H là chân đường
cao hạ từ đỉnh A lên cạnh . BC Đặt BAH = ; x CAH = y và AB = ; a AC = ; b AH = . h Ta có S = S + S A  BC A  BH A  CH 1  ab (x + y) 1 1 sin
= ahsin x + bhsin y 2 2 2 1  ab (x + y) 1 1 sin = abcos . y sin x + ba cos . x sin y 2 2 2
 sin (x + y) = sin xcos y + cos xsin . y
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Chứng minh 3.
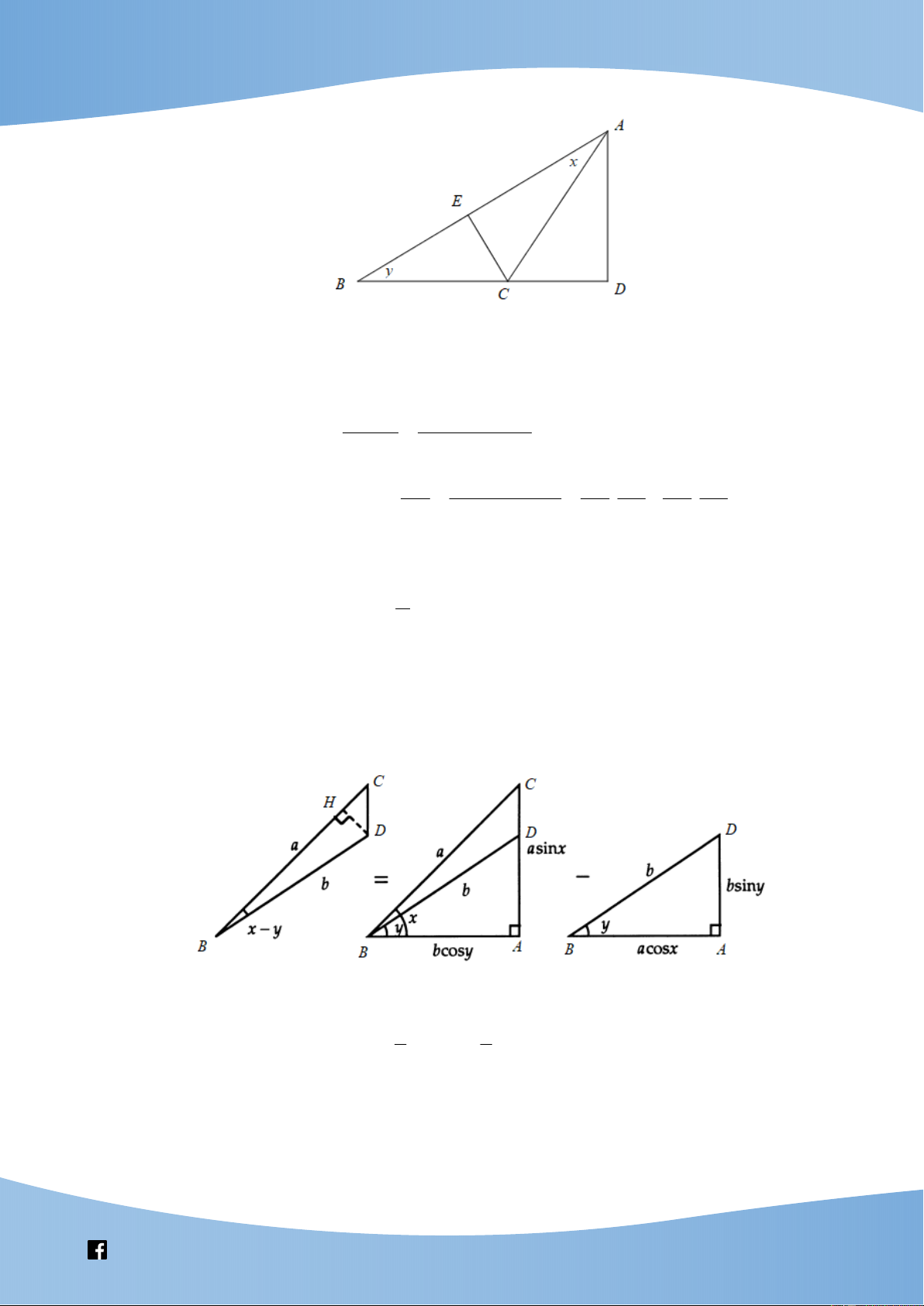
Vẽ tam giác ABC với D là chân đường cao hạ từ đỉnh A , E là chân đường cao hạ từ đỉnh C ,  
BAC  x, ABC  y . Khi đó 
ACD  x  y . CE.AB
CE. AE  EB Ta có A .
D BC  CE.AB  AD   . BC BC AD
CE. AE  EB AE CE CE EB
Mặt khác, lại có sin  x  y     sin ACD    .  . AC AC.BC AC BC AC BC
hay sin  x  y  cos x sin y  sin x cos . y   
Bài 2. Chứng minh rằng với ; x y  0; 
 và x  y ta có  2 
sin  x  y  sin x cos y  cos x sin . y
Chứng minh 1. Dựng tam giác ABC vuông tại A , gọi D là điểm thuộc cạnh AC sao cho  
ABC  x, ABD  . y Đặt BC  ;
a BD  b . Ta có AB  b cos y  a cos ;
x AD  a sin x  b sin y . 1 1 Mặt khác ta có S  S  S  A . B AC  A . B AD B  CD A  BC A  BD 2 2  B .
D BC.sin  x  y  A . B AC  A . B AD  . b .
a sin  x  y  b cos .
y a sin x  a cos . x b sin y
 sin  x  y  cos .
y sin x  cos . x sin . y Chứng minh 2.
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
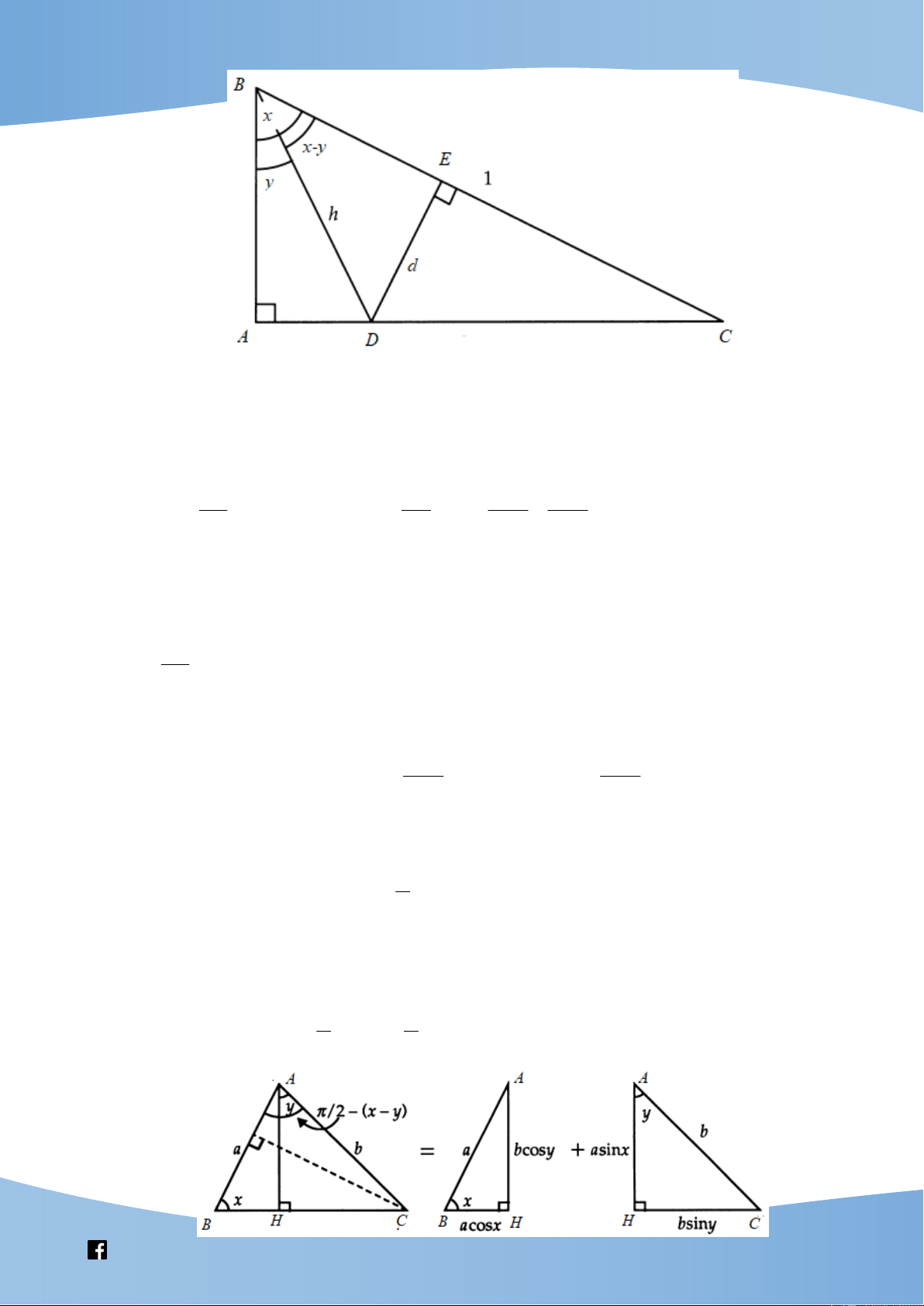
Vẽ tam giác ABC vuông tại A , độ dài BC  1. Trên cạnh AC lấy điểm D , đặt    ABC  ;
x ABD  y  DBC  x  .
y Gọi E là hình chiếu của D lên cạnh BC . Đặt BD  ; h DE  d . AB AB AB cos x Ta có cos x   AB  cos ; x cos y   h   . BC AD cos y cos y
Trong tam giác vuông EBD có d  h sin  x  y .
Mặt khác, CD  CA  AD  sin x  hsin .
y Do đó trong tam giác vuông EDC , ta có d sin C   d  C .
D sin C  C .
D cos x  sin x  hsin y cos . x CD
Vậy ta có d  h sin  x  y  sin x  hsin y cos x cos x  cos x 
 h sin  x  y  sin x  hsin y cos x 
sin  x  y  sin x  sin y cos x   cos y cos y  
 sin  x  y  cos .
y sin x  cos . x sin . y   
Bài 3. Chứng minh rằng với ; x y  0;   , ta có  2 
cos  x  y  cos x cos y  sin x sin . y (3)
Chứng minh 1. Dựng tam giác ABC có đường cao AH , đặt AB  a; AC  b và góc     
ABC  x; HAC  y  BAC   x  y 
  x  y. 2 2
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 1 1 1 Ta có  S  S  S  A . B AC.sin BAC  H . A HB  H . A HC ABC HAB HAC 2 2 2     ab sin  
 x  y  a cos .
x b cos y  a sin . x b sin y   2 
 cos  x  y  cos .
x cos y  sin . x sin . y Chứng minh 2.
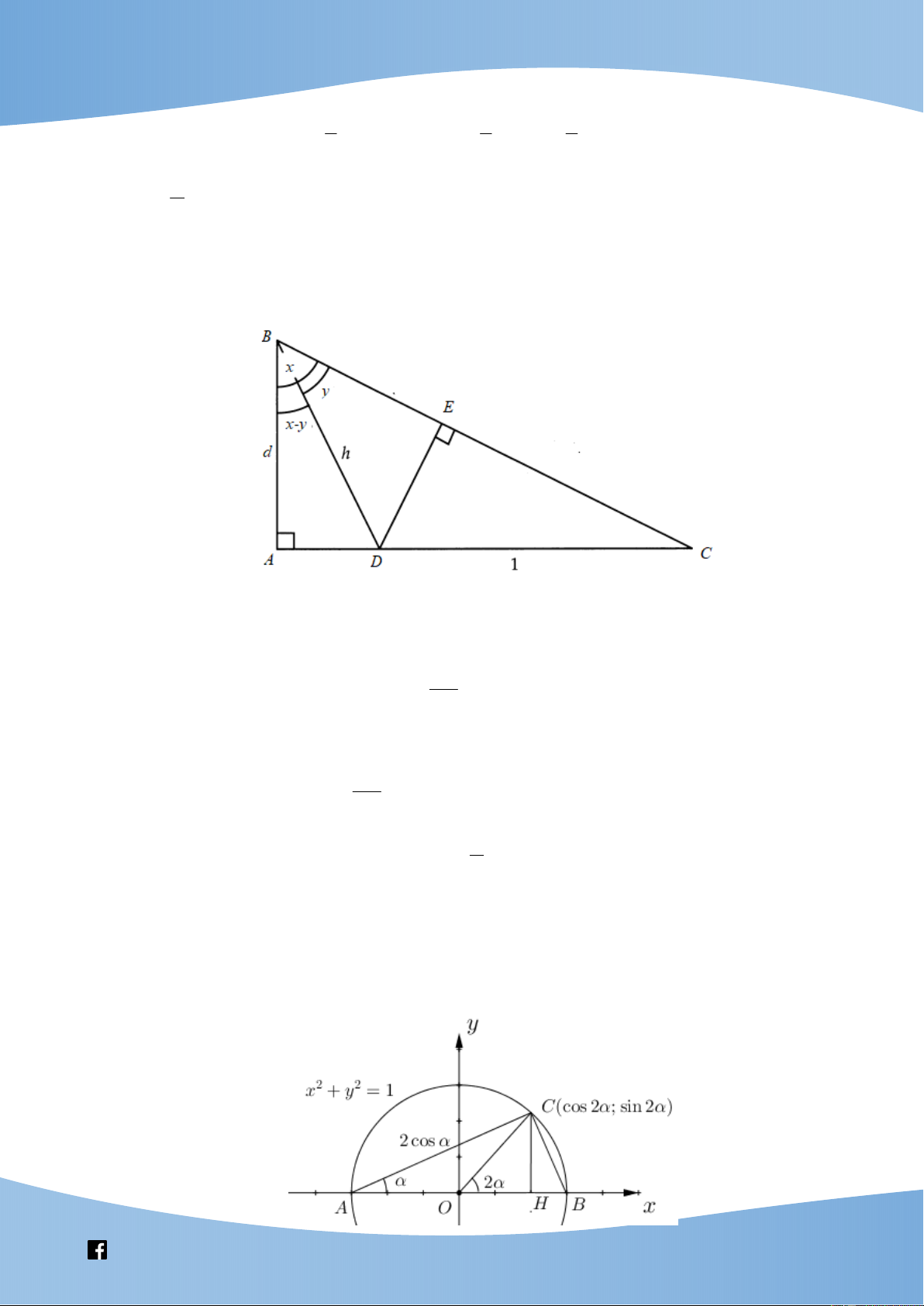
Vẽ tam giác ABC vuông tại A , trên cạnh AC lấy điểm D , đặt    ABC  ;
x CBD  y  DBA  x  . y
Gọi E là hình chiếu của D lên cạnh BC . Đặt CD  1; BD  ; h AB  d . EB
Trong tam giác BDE vuông, ta có cos y 
 BE  h cos y . BD
Trong tam giác CDE vuông, ta có ED sin C   DE  C .
D sin C  C .
D cos x  cos x . CD d
Trong tam giác ABD vuông, ta có cos  x  y 
 d  h cos  x  y. h
Bài 4. Chứng minh công thức nhân đôi
sin 2  2 sin  cos ; 2 cos 2  2 cos  1.
Chứng minh.
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Trên đường tròn lượng giác với điểm A 1
 ; 0; B 1;0 và điểm C sao cho 
BAC   . Gọi H là
chân đường cao hạ từ đỉnh C đến cạnh AB . Ta có
CH  OC.sin 2  sin 2 ;OH  OC.cos 2  cos 2 .
Khi đó C cos 2;sin 2  . Vì A  CH ∽ A
 BC nên ta có CH BC sin 2 2sin   
 sin 2  2sin cos. AC AB 2 cos 2 Mặt khác, từ A  CH ∽ A
 BC nên ta cũng có AH AC 1 cos 2 2 cos 2   
 cos 2  2 cos  1. AC AB 2 cos 2
Bài 5. Chứng minh công thức nhân ba a) 3
sin 3x  3sin x  4 sin x ; b) 3
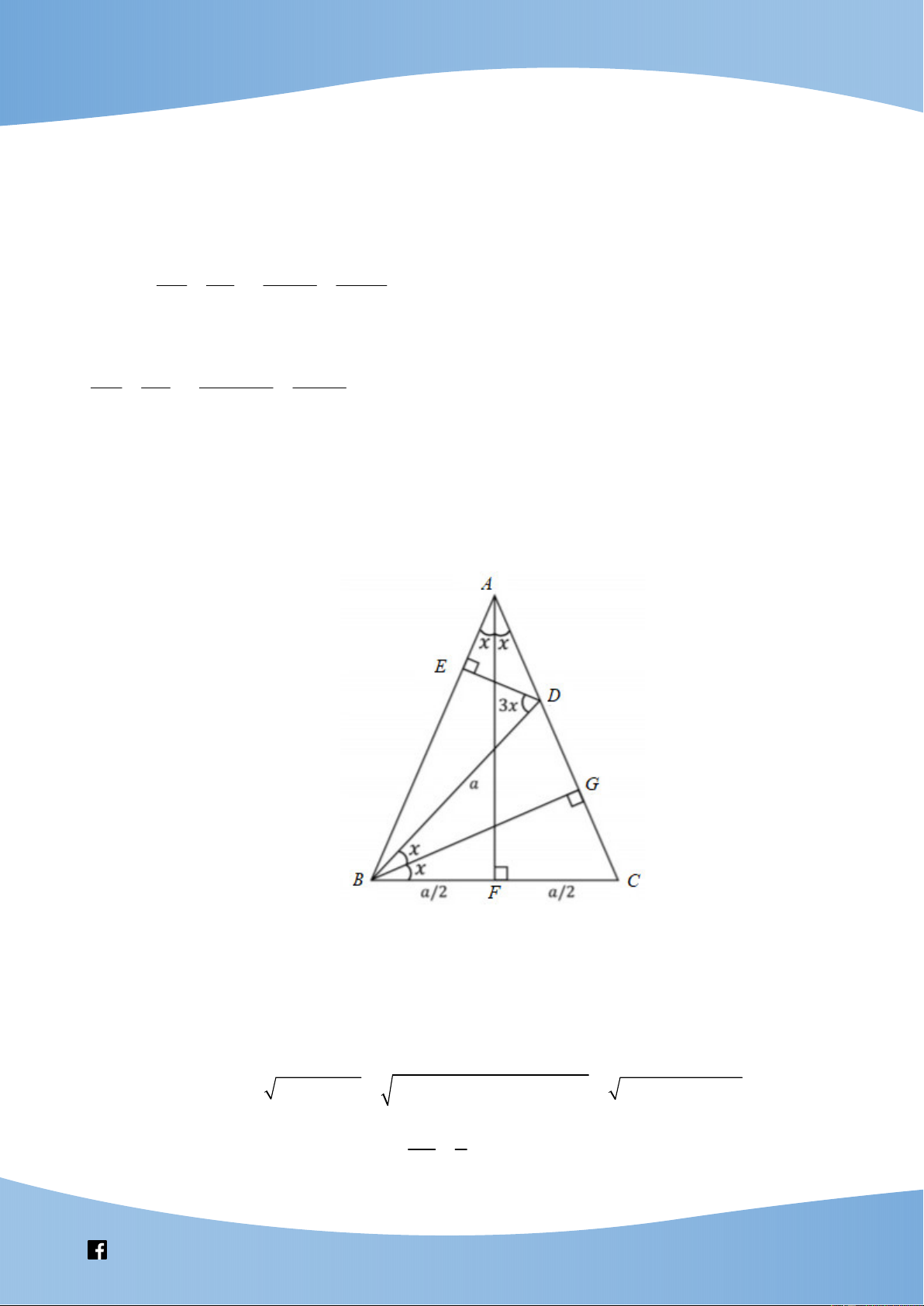
cos 3x  4 cos x  3cos x . Chứng minh1 Vẽ A  BC cân với 
AB  AC  1, BC  a, BAC  2x .
Lấy điểm D trên cạnh AC sao cho BD  BC  a . Gọi E là hình chiếu của D lên AB , G là hình
chiếu của B lên AC và F là trung điểm cạnh BC .
Ta có DE  a cos 3x, BE  a sin 3x  AE  1 a sin 3x và AD 
AE  DE    a x2  a x2 2 2 2 1 sin 3 cos 3
 1 a  2a sin 3x . BF a
Trong tam giác vuông ADE , có sin x    a  2 sin . x (1) AB 2
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 2 GC AC  AD
1 1 a  2a sin 3x
Mặt khác, ta có sin x    . (2) BC 2BC 2a Từ (1) và (2), ta có 2 a
1 1 a  2a sin 3x 2 2 
 a  1 1 a  2a sin 3x 2 2a  1 a 2 2 2
 1 a  2a sin 3x 4 2
 a  3a  2a sin 3x  0 3
 a  3a  2 sin 3x  0 3
 8sin x  6 sin x  2 sin 3x  0 3
 sin 3x  3sin x  4 sin . x Chứng minh2.
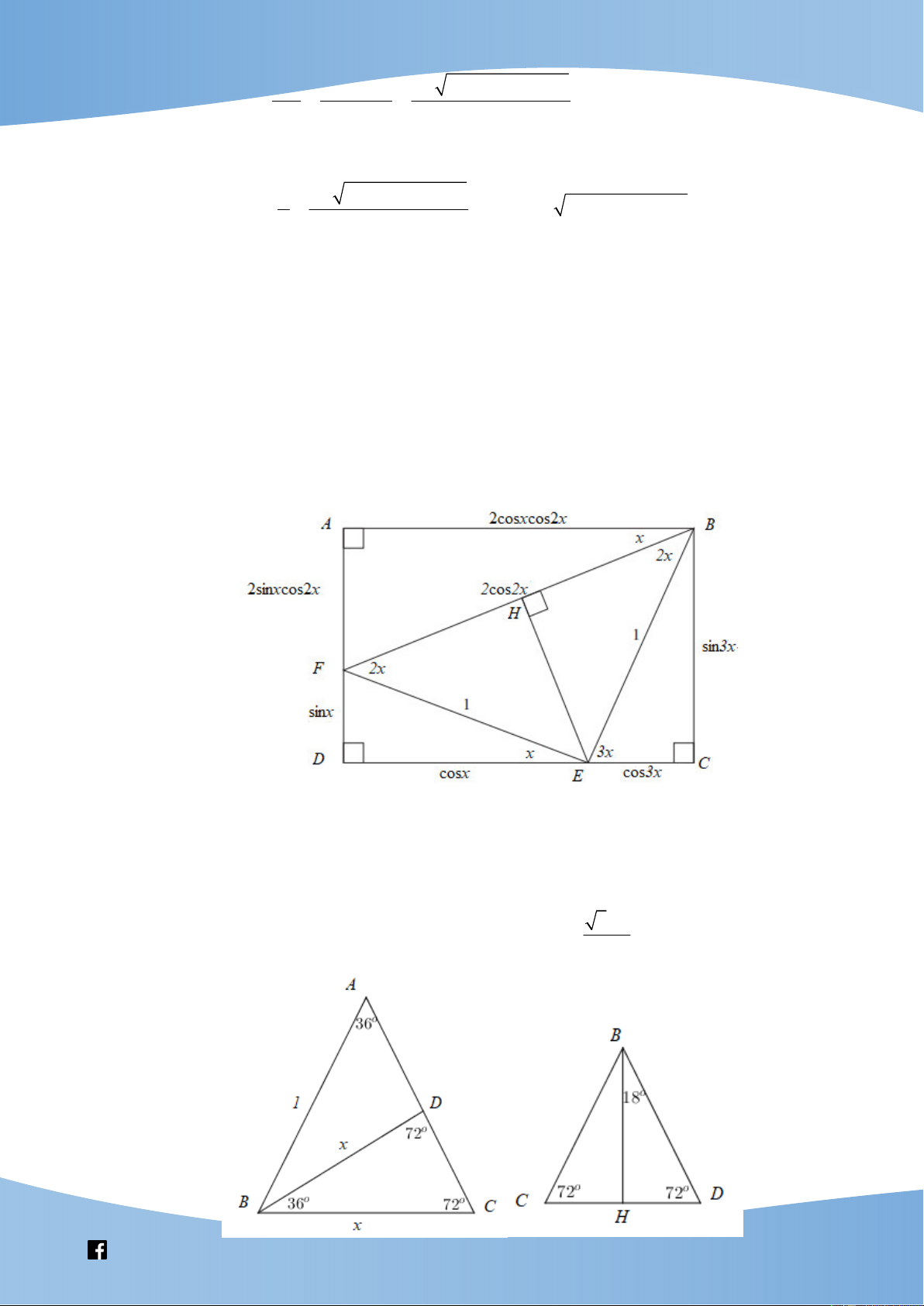
Dựng hình chữ nhật ABCD với các điều kiện như hình vẽ. Ta có x  x x  x  x  2  x 3 sin 3 2 sin cos 2 sin 2 sin 1 2 sin
 sin x  3sin x  4 sin . x b) x  x  x  x  2 x   3 cos 3 2 cos cos 2 cos 2 cos 2 cos
1  cos x  4 cos x  3cos . x 5 1
Bài 6. Không sử dụng lượng giác, hãy chứng minh o sin18  . 4
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
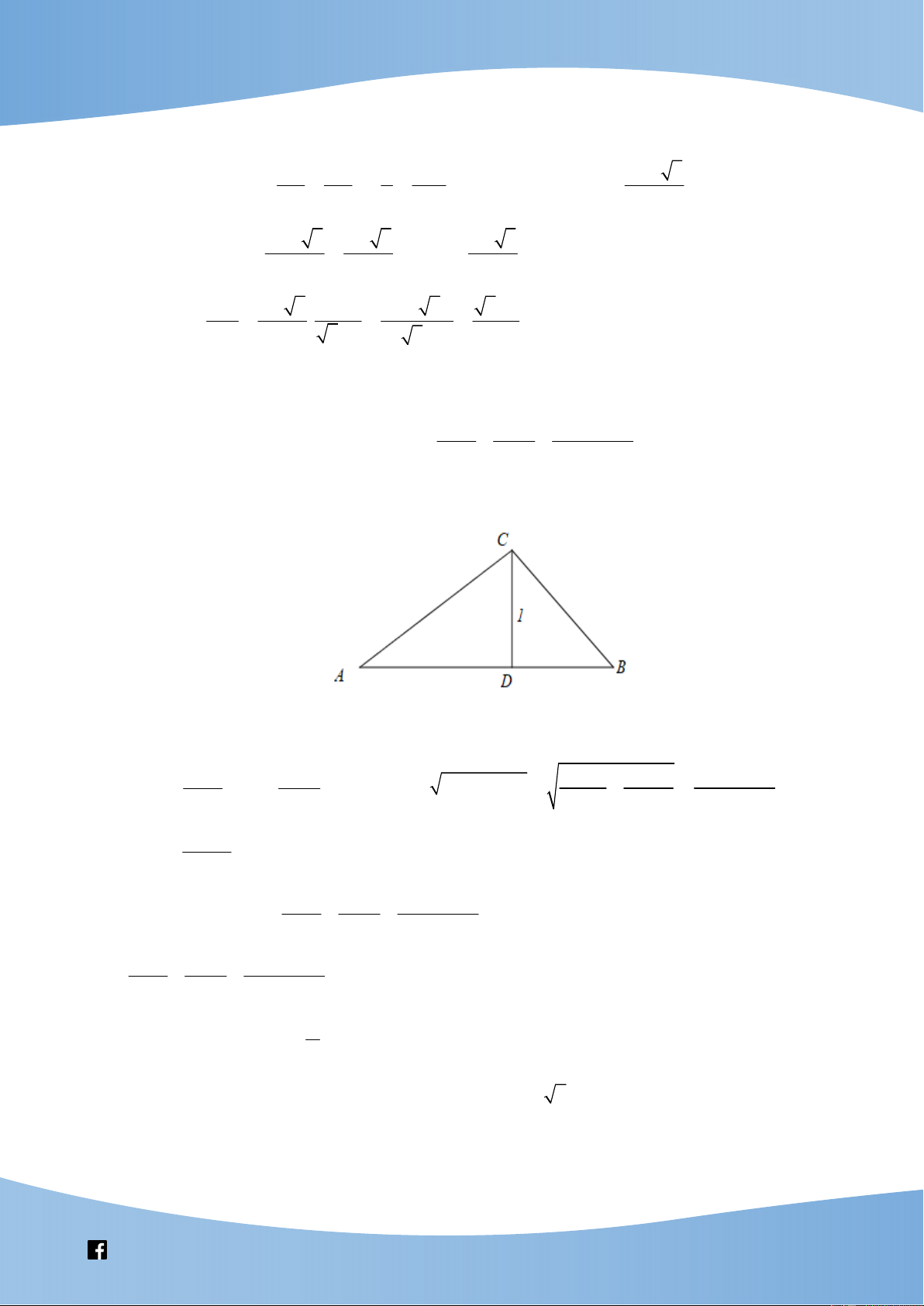
Dựng tam giác cân ABC , với  o
BAC  36 , đặt AB  1, BC  x .
Ta có tam giác ABC đồng dạng tam giác BCD nên AB BC 1 x 1   5 2   
 x  x 1  0  x  . BC CD x 1 x 2 1   5 3  5 3  5
Suy ra CD  1 x  1   DH  . 2 2 4 DH 3  5 2 3  5 5 1 Ta có o sin18   .   . BD 4 5 1 2  5   1 4 I.
BẤT ĐẲNG THỨC LƯỢNG GIÁC 1 1 1
Bài 7. Với góc  nhọn. Chứng minh rằng    4. sin  cos sin  cos Chứng minh
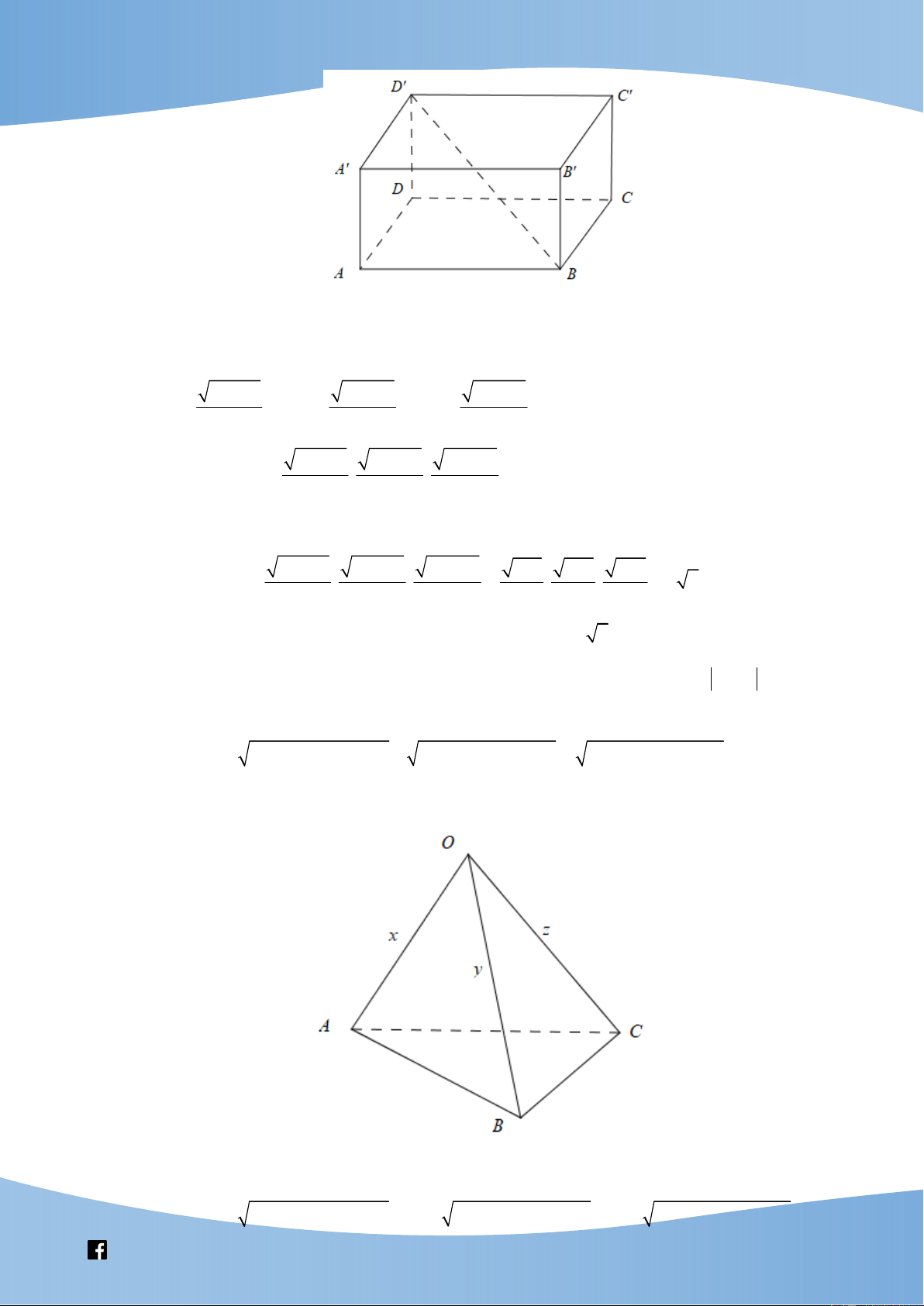
Vẽ tam giác ABC vuông ở C , có 
ABC   ,CD  1với D là hình chiếu của C lên cạnh AB . 1 1 1 1 1 Ta có BC  ; AC  , suy ra 2 2 AB  AC  BC    . sin  cos 2 2 sin  cos  sin cos 2 Ta có AB 
 2 . Áp dụng bất đẳng thức tam giác, ta có sin 2 1 1 1
BC  AC  AB  2 AB     2 AB  4. sin  cos sin  cos 1 1 1 Vậy    4. sin  cos sin  cos   
Bài 8. Với góc  ,  ,  0;   thoả mãn 2 2 2
cos   cos   cos   1 . Chứng minh rằng  2 
tan  tan  tan   2 2. Chứng minh
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
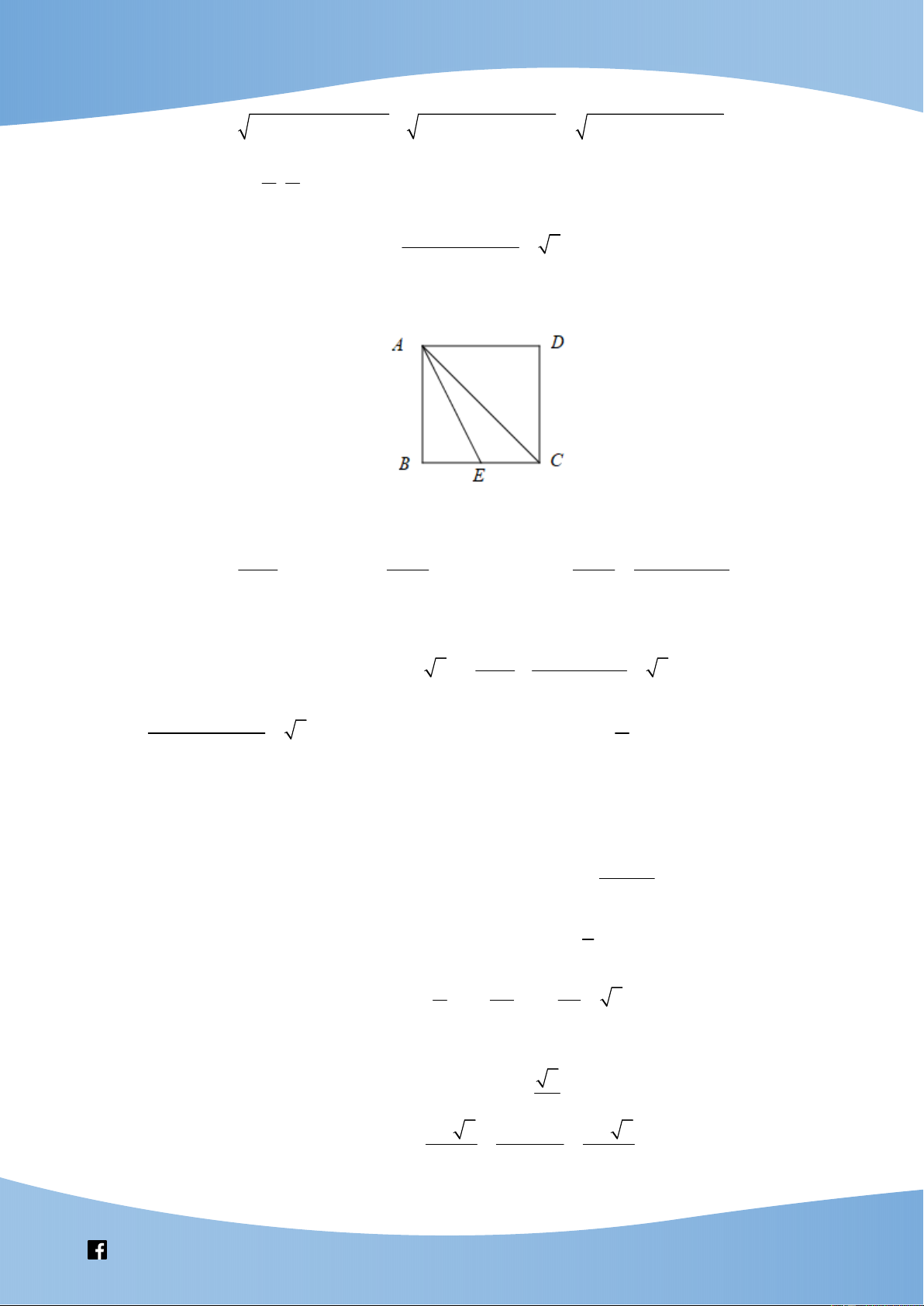
Dựng hình hộp chữ nhật ABCD.AB C  D
  với AB  a; AA  ; b BC  c và   
ABD   , B B
 D   , CBD   2 2 2 2 2 2 b  c a  c b  a Ta có tan  , tan   , tan   . a b c 2 2 2 2 2 2 b  c a  c b  a
Từ đó tan tan  tan   . . . a b c
Áp dụng bất đẳng thức Cauchy, ta có 2 2 2 2 2 2 b  c a  c b  a 2bc 2ac 2ba . .  . .  2 2. a b c a b c
Đẳng thức xảy ra khi và chỉ khi a  b  c        arctan 2.
Bài 9. Cho x, y, z   , các góc  ,  ,  0;  thoả mãn 0        2 và          . Chứng minh rằng 2 2 2 2 2 2
x  2xy cos  y 
x  2xz cos   z 
y  2 yz cos   z . Chứng minh
Dựng hình chóp O.ABC với OA  x,OB  y,OC  z , đặt   
AOB   , AOC   , BOC   . Khi đó ta có 2 2 2 2 2 2 AB 
x  2xy cos  y ; AC 
x  2xz cos   z ; BC 
y  2 yz cos   z .
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Áp dụng bất đẳng thức tam giác ta có AB  AC  BC hay 2 2 2 2 2 2
x  2xy cos  y 
x  2xz cos   z 
y  2 yz cos   z .  
Bài 10. Cho góc    ;   . Chứng minh rằng  4 2 
1 sin   cos  2. sin  Chứng minh
Dựng hình vuông ABCD cạnh bằng 1 và lấy điểm E trên cạnh BC , góc  AEB   . 1 cos cos sin   cos Khi đó ta có AE  ; BE  cot   . Suy ra EC  1  . sin  sin  sin  sin 
Xét tam giác AEC , theo bất đẳng thức tam giác, ta có 1 sin   cos
AE  EC  AC  2    2 . sin  sin  1 sin   cos  Suy ra 
2. Đẳng thức xảy ra khi và chỉ khi   . sin  4 II. BÀI TẬP TỰ LUYỆN 1
Bài 1. Không sử dụng biến đổi lượng giác, hãy tính giá trị o S   tan10 . o cos 50 1
Bài 2. Sử dụng hình học chứng minh rằng o o cos 36  cos 72  . 2  2 3
Bài 3. Sử dụng hình học, chứng minh cot  cot  cos  7. 7 7 7
Bài 4. Cho các góc  ,  , thoả mãn 2 2 2
cos   cos   cos   1 . Chứng minh rằng 2 cot  cot  cos   . 4 4  7 2  sin  4  7
Bài 5. Cho góc    . Chứng minh rằng   . 3 2  cos 3
https://www.facebook.com/groups/toanvd.vdc