Xác suất và phép đếm | Đại học Ngoại Ngữ - Tin Học Thành Phố Hồ Chí Minh
Xác suất và phép đếm | Đại học Ngoại Ngữ - Tin Học Thành Phố Hồ Chí Minh được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem
Thông tin :
Môn:
Trường:
Đại học Ngoại ngữ - Tin học Thành phố Hồ Chí Minh
Tác giả:
Tài liệu liên quan:
Preview text:
BUỔI 5: Xác suất và phép đếm A – LÝ THUYẾT
1. Biến cố - Xác suất
1.1. Phép thử: thực hiện một nhóm các điều kiện cơ bản để quan sát một hiện tượng nào đó xảy ra hay không
VD: Tung một con xúc xắc, tung 1 đồng xu
1.2. Biến cố: Kết quả của phép thử (hiện tượng, sự việc)
VD: “Gieo được mặt 6 chấm” 1.3. Phân loại
a. Ngẫu nhiên . VD: “Giao được mặt 6 chấm”
b. Không thể có. VD: “Gieo được mặt 7 chấm”
c. Chắc chắn VD: “Mã vàng (con ngựa màu vàng – trong cờ cá ngựa) di chuyển” 1.4. Xác suất:
Xác suất của một biến cố là một con số đặc trưng cho khả năng khách quan xuất hiện biến cố đó
VD: 0<= P(a) <=1 ; P(b)=0 ; P(c) = 1 1.5. Công thức P(A) = M N Trong đó,
N: tổng số kết cục duy nhất, đồng khả năng
M: tổng số kết cục thuận lợi cho A
2. Định lý nhân xác suất
Ω: “bạn trong lớp” A: “bạn nữ”
B: “bạn có người yêu”
AB: “bạn nữ có người yêu”
a. Nếu A và B độc lập
P(A và B) = P(AB) = P(A) * P(B)
Tổng quát: Nếu A ,
1 A2, A3, …, An độc lập toàn phần thì P(A1, A2, A , …, 3
An) = P(A1)*P(A2)*P(A3) * ... * P(An)
b. Nếu A, B phụ thuộc n
P(A và B) = P(AB) ≠ P(A) * P(B) P(AB) = P(A) * AB nA n
Trong đó: AB = số nữ có người yêu nA tổng số nữ
P(AB) = P(A) *P(B|A) = P(B)*P(A|B)
P(B|A) = P (AB) P( A)
Tổng quát: P(A1A2A3. . .An) = P(A1)*P(A |A 2
1) * . . . * P(An|A1A2A3…An-1)
c. Xác suất ít nhất - Nếu A1, A2, A3, …, An không xung khắc và độc lập toàn phần thì n n P(∑ A ¿= P ¿ ¿ i 1− ∏ i=1 i=1 3. Định lý cộng Nếu A, B xung khắc
P(A or B) = P(A+B) = P(A) + P(B)
Nếu A, B không xung khắc (bất kỳ)
P(A or B) = P(A+B) = P(A) + P(B) – P(AB) B – BÀI TẬP
Phần I – Không gian mẫu và xác suất
Câu 1. Trả lời các câu hỏi sau: a. Phép thử là gì? b. Không gian mẫu là gì?
c. Sự khác nhau giữa biến cố (event) và kết quả (outcome).
Câu 2. Một trung tâm thương mai tổ chức 1 sự kiện khuyến mãi. Với mỗi hóa đơn trên
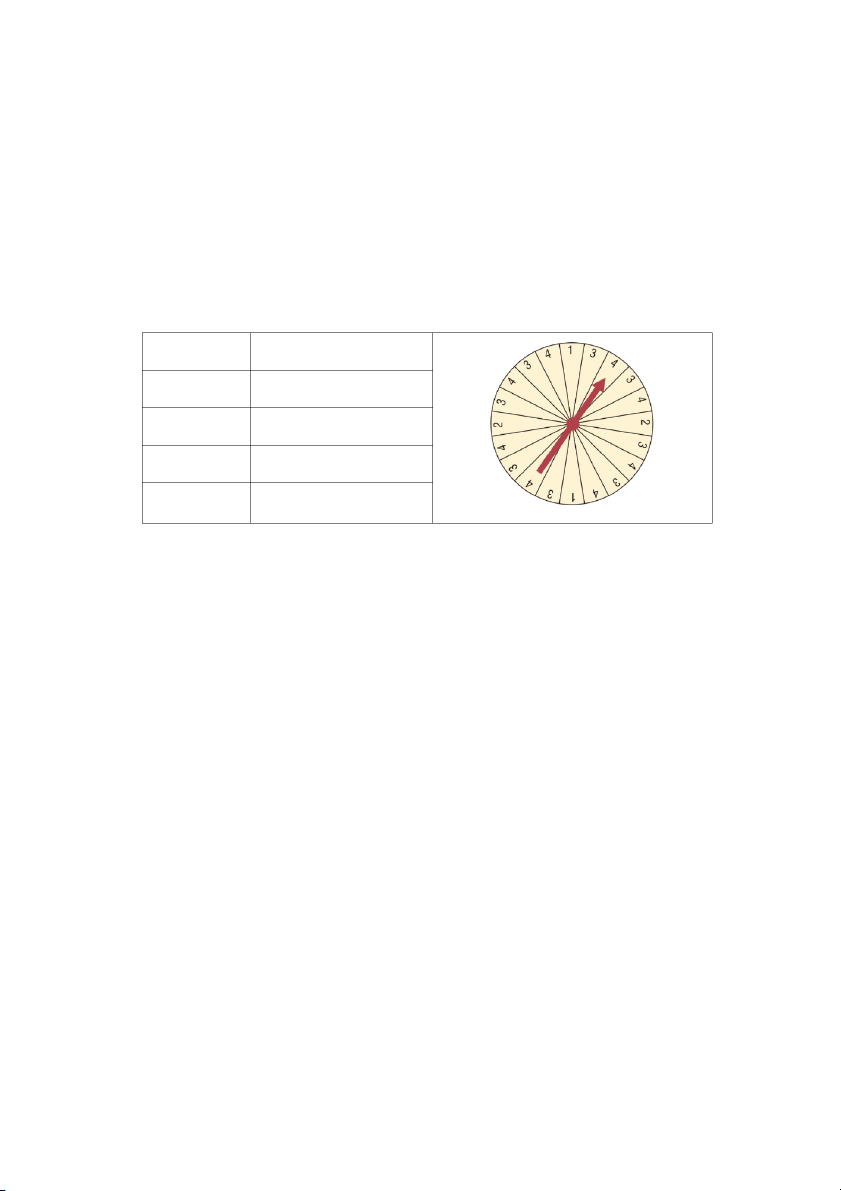
50$ khách hàng sẽ được thực hiện 1 vòng quay may mắn. Tùy theo kết quả của vòng
quay, khách hàng sẽ nhận được 1 phần qua tương ứng. Giá trị Quà 1 10$ 2 4$ 3 Discount coupon 4 Discount coupon
Hãy tính các xác suất sau: N=20
a. Khách hàng nhận được 10$.
Khả năng quay được số 1: M=2Xác suất P=M/N=2/20=1/10=0.1
b. Khách hàng nhận được tiền.
Khả năng nhận được tiền (quay trúng số 1 hoặc số 2) :M=4 Xác suất P=M/N=4/20=1/5=0.2
c. Khách hàng nhận được coupon
Khả năng quay được coupon (quay trúng số 3 và số 4) : M=16 Xác suất P=M/N=16/20=4/5=0.8
Câu 3. Tung 1 viên súc sắc, tính các xác suất sau: N=6
a. Được giá trị 2 , M=1P(a)=1/6=0.167
b. Được giá trị lớn hơn 6, M=0P(b)=0/6=0
c. Được giá trị chẵn, M=3P(c)=3/6=0.5
d. Được giá trị 4 hoặc giá trị lẻ, M=4P(d)=4/6=0.67
e. Được mặt giá trị nhỏ hơn 7,M=7 P(e)=7/6=1.17
f. Được giá trị lớn hơn hoặc bằng 3,M=3 P(f)=3/6=0.5
g. Được giá trị chẵn lớn hơn 2, M=2P(g)=2/6=1/3=0.33
Câu 4. Tung đồng thời 2 viên súc sắc, tính các xác suất sau: N=36
a. Được giá trị 9, M=4 ,P(a)=4/36=1/9=0.11
b. Được giá trị 7 hoặc 11, M=8, P(b)=8/36=0.222
c. 2 mặt giống nhau,M=6 , P(c)=6/36=0.167
d. Được giá trị nhỏ hơn 9, M=26,P(d)=26/36=13/18
e. Được giá trị lớn hơn hoặc bằng 10, M=6,P(e)= 6/36=1/6
Câu 5. Số nguyên tố là các số chỉ chia hết cho 1 và chính nó. Bên dưới là danh sách các
số nguyên tố nhỏ hơn 100. Lấy ngẫu nhiên 1 số, tính các xác suất sau: 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 N=25
a. Nhận được số chẵn,M=1 Xác suất :M/N=1/25
b. Tổng các chữ số là số chẵn (ví dụ số 53 – ta có 5 + 3 = 8),M=13 Xác suất :M/N=13/25
c. Giá trị lớn hơn 50,M=10Xác suất :M/N=10/25=2/5
Câu 6. Các trường cấp 1 và cấp 2 được phân vào các lớp dựa trên số lượng máy tính mà
họ có. Số liệu thống kê được biểu diễn trong bảng phân bố tần số bên dưới. Chọn ngẫu
nhiên 1 trường, tính xác suất: Số máy tính 1 – 10 11 – 20 21 – 50 51 – 100 100+ Số trường học 3170 4590 16.741 23.753 34.803
N=3170+4590+16741+23753+34803=83057
a. Có tối đa 50 máy, M=3170+4590+16741=24501 Xác suất P=M/N=24501/83057=0.295
b. Có nhiều hơn 100 máy, M=34803, P(b)=34803/83057=0.419
c. Không nhiều hơn 20 máy,M=3170+4590=7760, P(c)=7760/83057=0.093
Phần II – Quy tắc đếm
Câu 7. Rút ngẫu nhiên 1 lá bài từ bộ bài tây, tính xác suất các trường hợp sau: N=52
a. Rút được 1 lá J, Q hay K
Rút được 1 lá J , M1=4P(M1)=4/52
Rút được 1 lá Q, M2=4P(M2)=4/52
Rút được 1 lá K, M3=4P(M3)=4/52
P(M1 or M2 or M3) = P(M1)+P(M2)+P(M3)=4/52+4/52+4/52=12/52=3/13
b. Rút được 1 lá bài cơ (), chuồn () hoặc bích ( )
Rút được 1 lá bài cơ , M1=13P(M1)=13/52
Rút được 1 lá chuồn , M2=13P(M2)=13/52
Rút được 1 lá bích , M3=13P(M3)=13/52
P(M1 or M2 or M3)=13/52+13/52+13/52=3/4=0.75
c. Rút được 1 lá K hoặc Q hoặc rô ()
Rút được 1 lá K , M1=4P(M1)=4/52
Rút được 1 lá Q, M2=4P(M2)=4/52 Rút được 1 lá rô , M3=
P(M1 or M2 or M3) = P(M1)+P(M2)+P(M3)=
d. Rút được 1 lá Át (Xì) hoặc rô () hoặc cơ ()
e. Rút được 1 lá 9 hoặc 10 hoặc chuồn () hoặc bích ( )
Câu 8. Một nhân viên tiếp thị chào bán hàng tại nhà. Thống kê kết quả bán hàng trong
một ngày của anh ta được biểu diễn trong bảng phân bố tần số bên dưới. Tính các xác suất:
Số sản phẩm bán được Tần số 0 8 1 10 2 3 3 2 4 1
Tổng số kết quả N=8+10+3+2+1=24
a. Bán được 1 sản phẩm, M=10,P=M/N=10/24
b. Bán được nhiều hơn 2 sản phẩm.
P(bán 3 sp or 4 sp )=P( bán 3sp )+P(bán 4sp )=2/24+1/24=3/24=1/8=
c. Bán được ít nhất 1 sản phẩm.
d. Bán được nhiều nhất 3 sản phẩm.
Câu 9. Trong một thống kê dân số, người ta thống kê các thanh niên đang sống tại nhà
hoặc ký túc xá của trường học tại một thành phố. Kết quả được biểu diễn trong bảng phân
bố tần số bên dưới. Chọn ngẫu nhiên 1 người, tính xác suất: Tuổi từ 18 – 24 Tuổi từ 25 - 34 Nam 7922 2534 Nữ 5779 995 N=7922+5779+2534+995=17230
a. Nữ trong độ tuổi 25 – 34., M=995-->P=995/17230
b. Nam hoặc 1 người trong độ tuổi 18 – 24.
P( Nam or 1 người trong độ tuổi 18 -24 (không phải là Nam ))=P(Nam)+P(1 người
trong độ tuổi 18-24(không phải là Nam ))=P(Nam)-->M1=7922+2534=10456-- >P(Nam)=10456/17230
P(1 người trong độ tuổi 18-24( không phải là Nam ))=P(1 người Nư trong độ tuổi 18- 24)=5779/17230
P(Nam or 1 người trong độ tuổi 18-24)=10456/17230+5779/17230=16235/17230 c. Nữ dưới 25 tuổi
Câu 10. Danh sách dưới đây mô tả các loài động vật có nguy cơ tuyệt chủng và bị đe dọa
tại nước Mỹ và bên ngoài nước Mỹ. Chọn ngẫu nhiên 1 loài và tính xác suất:
Nguy cơ tuyệt chủng Bị đe dọa Mỹ Bên ngoài Mỹ Mỹ Bên ngoài Mỹ Động vật có vú 68 251 10 20 Chim 77 175 13 6 Bò sát 14 64 22 16 Lưỡng cư 11 8 10 1
a. Đang bị đe dọa tại Mỹ.
b. Một loài chim có nguy cơ tuyệt chủng không thuộc về nước Mỹ.
c. Một động vật có vú hoặc các loài đang bị đe dọa bên ngoài nước Mỹ.
Phần III – Quy tắc nhân và xác suất có điều kiện
Câu 11. Khảo sát sinh viên của một trường Đại học nhận được kết quả 25% sinh viên tập
thể dục thường xuyên. Chọn ra 3 sinh viên ngẫu nhiên, tính xác suất để cả 3 sinh viên này
đều tập thể dục thường xuyên.
Với xác suất này, bạn hãy nhận xét xem biến cố này có thể xảy ra không? Tại sao?
P( 1 SV tập thể dục thường xuyên )=25%=0.25 3SV : SV A , SV B , SV C
P( A tập thể dục thường xuyên và B tập thể dục thường xuyên và C tập thể dục thường
xuyên )=P( A tập thể dục thường xuyên ) * P( B tập thể dục thường xuyên ) *P( C tập thể
dục thường xuyên )=0.25*0.25*0.25=0.0156
Xác xuất quá nhỏ để có thể xảy ra .
Câu 12. Khảo sát cho thấy 69% trẻ em ở thành phố X chơi video game mỗi ngày. Chọn
ngẫu nhiên 3 bạn trẻ, tính xác suất:
a. Không có bạn nào chơi video game mỗi ngày. P(chơi game )=69%=0.69
P(không chơi game )= 100%-69%=31%=0.31
P( A không chơi game và B không chơi game và C không chơi game )= P( A không
chơi game )*P( B không chơi game )*P( C không chơi game )=0.31*0.31*0.31=0.0297
b. Cả 3 bạn đều chơi video game mỗi ngày. P=0.69*0.69*0.69=0.328509
Câu 13. Khảo sát một trường đại học X, có khoảng 54.3% sinh viên năm nhất sở hữu
laptop. Chọn ngẫu nhiên 3 sinh viên, tính xác suất:
a. Không bạn nào có laptop. P(có laptop ) =54,3%=0.543
P( không có laptop )= 100% -54.3%= 45.7%=0.457
P( A không có laptop và B không có laptop và C không có laptop) = P(A không có
laptop)* P( B không có laptop) *P( C không có laptop )= 0.457*0.457*0.457= 0.0954
b. Có l ít nhất 1 bạn có laptop.
P( có ít nhất 1 bạn có laptop )= 1-P( không có laptop)= 1- 0.0954=0.9046
c. Cả 3 bạn đều có laptop.
P( cả 3 đều có laptop )= 0.543*0.543*0.53= 0.1601
Câu 14. Một báo cáo chỉ ra rằng, tại tập đoàn X có 72% phụ nữ sử dụng máy tính trong
công việc hàng ngày. Chọn ra ngẫu nhiên 5 phụ nữ, tính xác suất:
a. Có ít nhất 1 người không sử dụng máy tính trong công việc hàng ngày.
P( 5 người đều sử dụng máy tính ) = 0.72*0.72*0.72*0.72*0.72=0.193
P( 1 người không sử dụng máy tính )= 1-0.193=0.875
b. Cả 5 người đều sử dụng máy tính trong công việc mỗi ngày.
Câu 15. Rút ngẫu nhiên (không hoàn lại) 4 lá bài trong bộ bài tây. Tính xác suất: a. Được 4 lá K b. Được 4 lá rô ()
c. Được 4 lá đỏ ( hoặc )
Câu 16. Trong một bình hoa lớn có 8 bông hồng, 5 bông cúc, 12 bông Lily và 9 bông hoa
Lan. Lấy ra ngẫu nhiên 4 bông (không hoàn lại), tính xác suất để lấy được tối thiểu 1 bông hoa hồng.
Với xác suất tính được, bạn có nghĩ biến cố này có thể xảy ra không? Tại sao?