











Preview text:
ĐỀ KIỂM TRA GIỮA KÌ I TOÁN 11 FORM 2025
Thời gian: 90 phút (Không kể thời gian phát đề)
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí
sinh chỉ chọn một phương án.
Câu 1: Trong mặt phẳng tọa độ Oxy, đường tròn lượng giác là đường tròn
A. có tâm trùng với gốc tọa độ và bán kính bằng 1.
B. có tâm trùng với gốc tọa độ.
C. bán kính bằng 1.
D. có tâm trùng với gốc tọa độ và bán kính bằng 2. π
Câu 2: Cho tanα = 3. Tính tan α − . 3 A. 1− 3 . B. 3+ 3 . C. 1− 3 . D. 3− 3 . 1+ 3 1− 3 3 1+ 3 3 1+ 3 3 Câu 3: 1
Nếu sinx + cos x = thì sin 2x bằng 3 − A. 3 . B. 3 . C. 2 . D. 8 . 4 8 2 9 Câu 4: 2025
Tìm tập xác định D của hàm số y = . sin x A. D = . B. D = \{ } 0 . π
C. D = \{kπ,k ∈ } . D. D \ kπ ,k = + ∈. 2
Câu 5: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua trục tung? π
A. y = sin xcos 2 .x B. 5
y sin .xcos x = − . 2 C. tan x y = . D. 3
y = cos xsin .x 2 tan x +1
Câu 6: Tất cả nghiệm của phương trình 3 cos x = − là 2 π π
A. x = + k2π ,k ∈ . B. 5 x =
+ k2π ,k ∈. 6 6 π π
C. x = ± + k2π ,k ∈ . D. 5 x = ±
+ k2π ,k ∈ . 6 6 + Câu 7: n 1
Cho dãy số (u với u = . Tính u . n ) n n 3 A. 5. B. 5 . C. 6 . D. 4 . 4 5 3 Câu 8: 1
Cho một cấp số cộng (u có u = , u = 26. Tìm công sai d n ) 1 3 8 A. 11 d = . B. 10 d = . C. 3 d = . D. 3 d = . 3 3 10 11 Câu 9: 1 Cho cấp số nhân u u = u =16 u n có 2 ,
. Tìm công bội q và số hạng đầu . 4 5 1
Trang 1/13 – Nhom làm đề lớp 11 A. 1 q = 1 1 1 1 , u = . B. 1
q = − , u = − . C. q = 4 − , u = −
. D. q = 4 , u = . 2 1 2 2 1 2 1 16 1 16
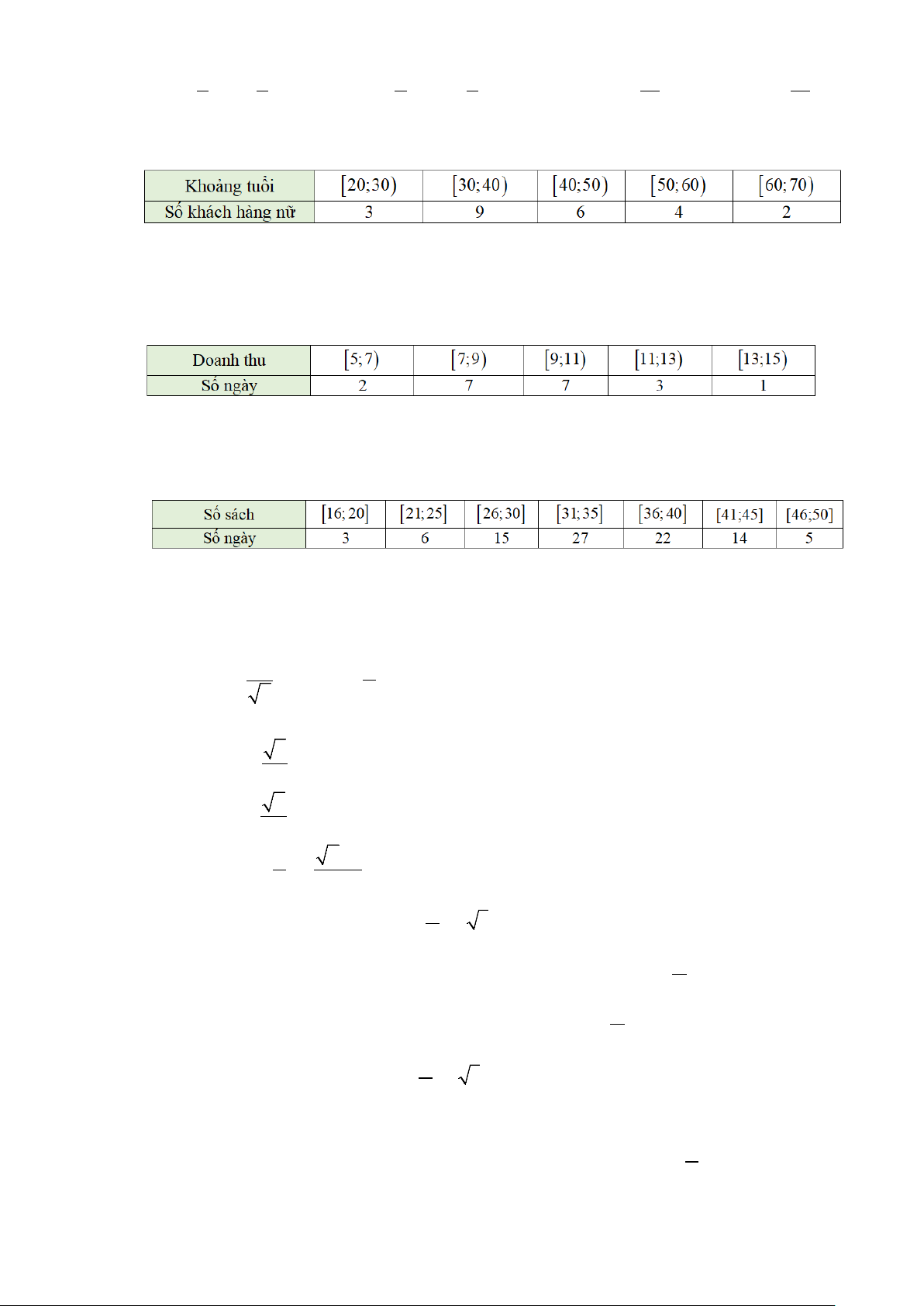
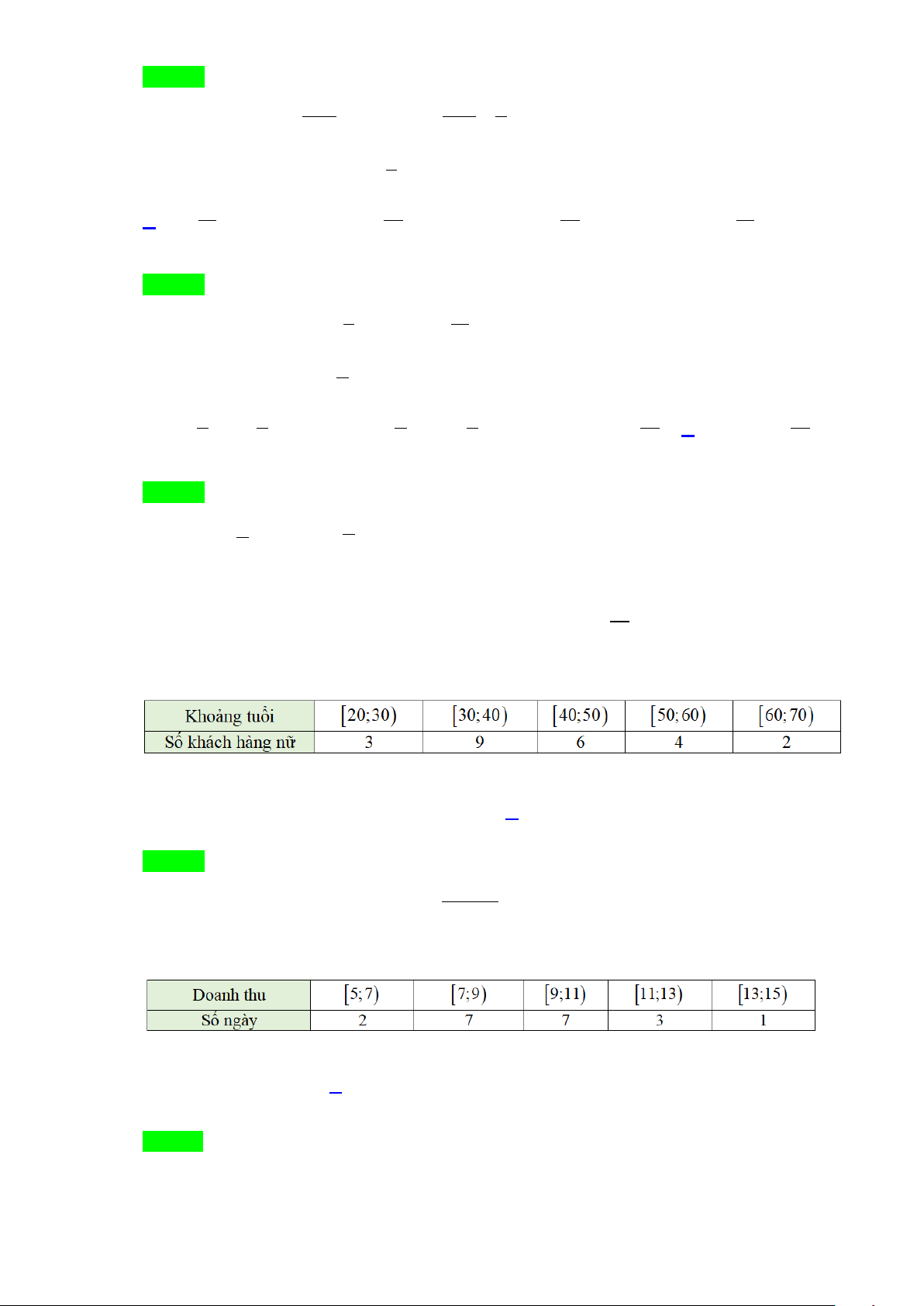
Câu 10: Số lượng khách hàng nữ mua bảo hiểm nhân thọ trong một ngày được thống kê trong bảng tần số ghép nhóm sau:
Giá trị đại diện của nhóm [30;40) là: A. 40 . B. 30. C. 35. D. 9.
Câu 11: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở
bảng sau (đơn vị: triệu đồng)
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng sau đây? A. [7;9) . B. [9;1 ) 1 . C. [11;13) . D. [13;15).
Câu 12: Một thư viện thống kê số lượng sách được mượn mỗi ngày trong 3 tháng ở bảng sau:
Trong 3 tháng trên số sách được mượn mỗi ngày cao nhất gần bằng giá trị nào sau đây? A. 32,5 . B. 32. C. 33,5 . D. 34.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S). Câu 1: Cho biết 1 sinx = và π
0 < x < . Khi đó các mệnh đề sau đúng sai? 3 2
a) [NB] cosx >0 b) [TH] 3 tanx = 3 c) [TH] 6 cosx = 3 d) [VD] π 6 - 3
cos x+ = . 3 8
Câu 2: Cho phương trình lượng giác π 2cos x − − 3 =
0 , khi đó các mệnh đề dưới đây đúng hay sai: 6
a) [NB] Phương trình đã cho có các nghiệm là: π
x = k2π (k ∈) và x = + k2π (k ∈) . 3 π
b) [TH] Phương trình đã cho có nghiệm dương nhỏ nhất bằng . 3
c) [TH] Đồ thị hàm số π y 2cos x = − −
3 giao với trục hoành tại gốc toạ độ. 6
d) [VD] Số nghiệm của phương trình đã cho trong khoảng ( π
− ;π ) là 3 nghiệm .
Câu 3: a) [NB] Công thức số hạng tổng quát của cấp số cộng đã cho là n u = 1+ . n 3
b) [TH] Số 5 là số hạng thứ 8 của cấp số cộng đã cho.
Trang 2/13 – Nhóm làm đề lớp 11 15
c) [TH] Số là một số hạng của cấp số cộng đã cho. 4
d) [VD] Tổng 100 số hạng đầu của cấp số cộng (u trên bằng 2620 . n )
Câu 4: Kết quả khảo sát cân nặng của 25 quả cam ở mỗi lô hàng ,
A B được cho ở bảng sau: Cân nặng (gam)
[150;155) [155;160) [160;165) [165;170) [170;175)
Số quả cam ở lô hàng A 2 6 12 4 1
Số quả cam ở lô hàng B 1 3 7 10 4
a) [NB] Giá trị đại diện nhóm [150;155) bằng 152,5
b) [TH] Nhóm chứa mốt của số liệu ở lô hàng A là [155;160) .
c) [TH] Nhóm chứa mốt của số liệu ở lô hàng B là [160;165) .
d) [VD] Theo số trung bình thì cam ở lô hàng B nặng hơn cam ở lô hàng A .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Bánh xe của người đi xe đạp quay được 10 vòng trong 5 giây. Tính độ dài quãng đường mà người
đi xe đã đi được trong 1 phút( đơn vị tính bằng mét và làm tròn kết quả đến hàng đơn vị, lấy π = 3,14 ),
biết rằng đường kính của bánh xe đạp là 0,68m.
Câu 2: Một cái cổng vào một trung tâm thương mại có hình dạng là một phần của đồ thị hàm số 2cos x y = + x 2 . Gọi ,
A B là hai điểm nằm trên cổng(trên đồ thị hàm số y = 2cos +
2 ) và C, D là hai 2 2
điểm nằm trên mặt nền của cổng sao cho ABCD là hình chữ nhật. Người quản lí trung tâm thương mại
muốn lắp một cái cửa kính tự động vào hình chữ nhật ABCD . Tính diện tích của cái cửa cần lắp biết chiều
cao của cái cửa là AD = 3 mét(kết quả làm tròn đến một chữ số thập phân, lấy π = 3,14 ).
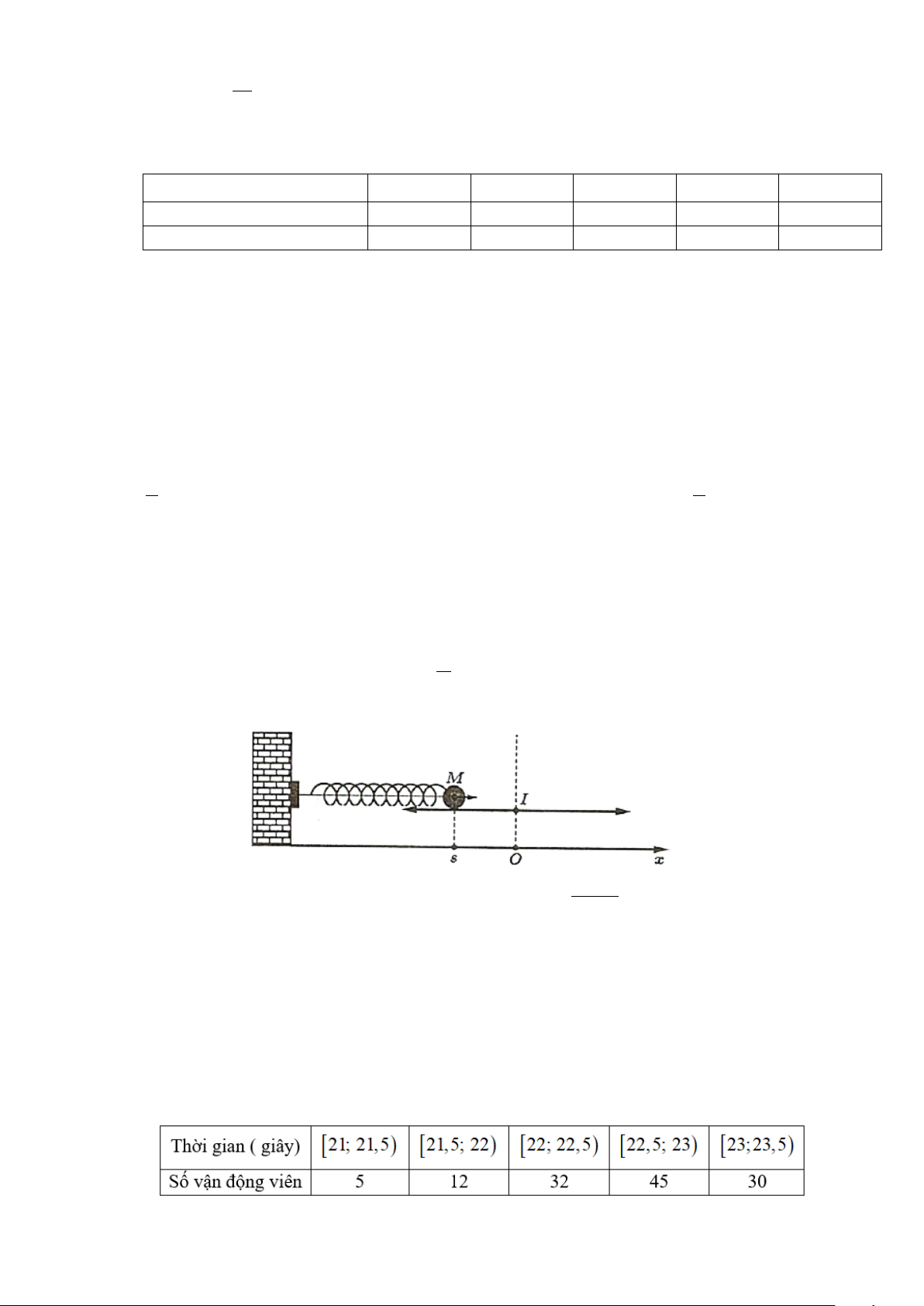
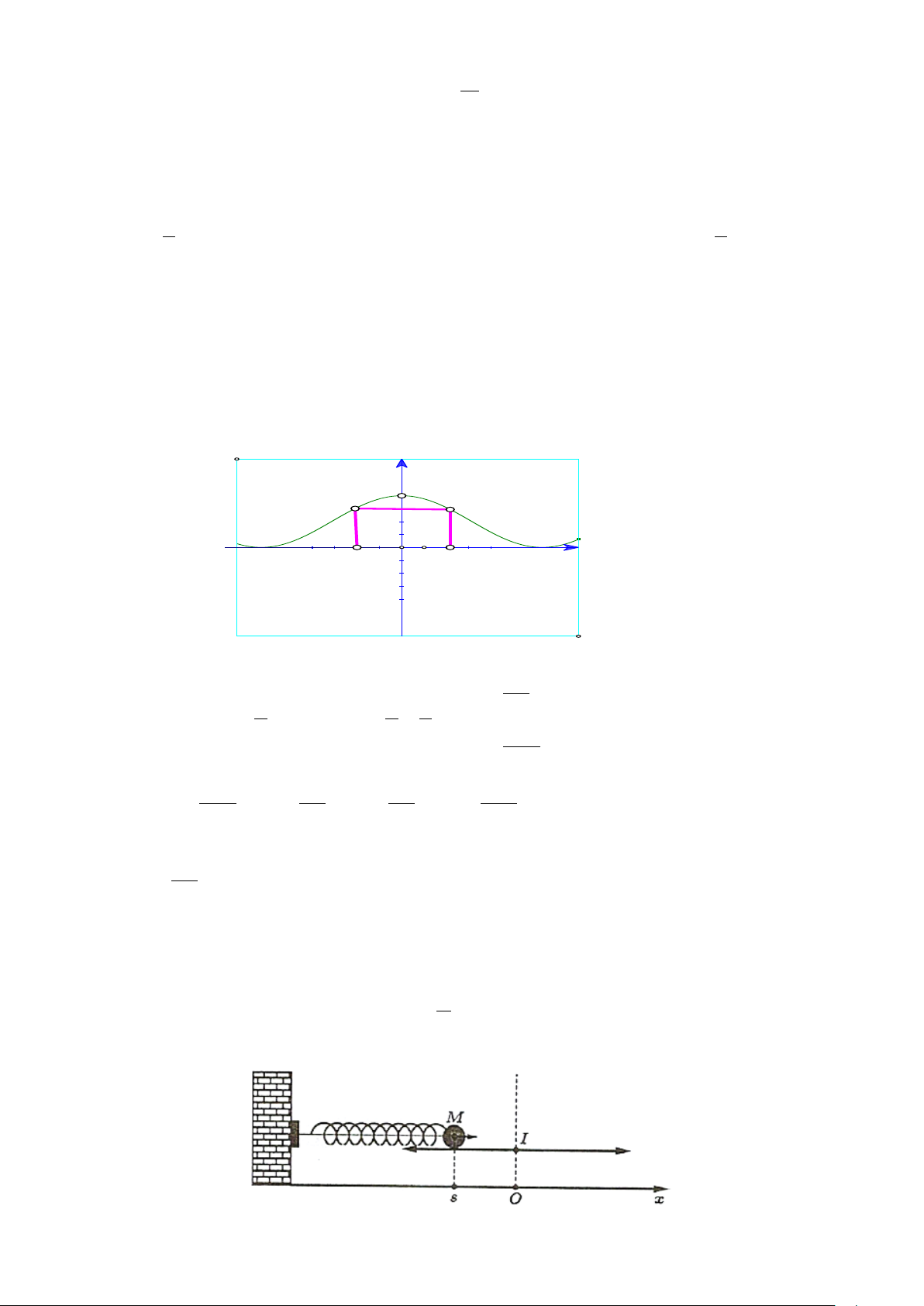
Câu 3: Một vật M được gắn vào đầu lò xo và dao động quanh vị trí cân bằng I , biết rằng O là hình
chiếu vuông góc của I trên trục Ox , toạ độ điểm M trên Ox tại thời điểm t (giây) là đại lượng s (đơn vị: π
cm ) được tính bởi công thức s 8,6cos 8t = +
. Tại mấy thời điểm trong khoảng 2 giây đầu tiên thì 2 s = 4,3 cm? − Câu 4: mn 1
Tìm giá trị nguyên lớn nhất của m để dãy số (u với u = là dãy số giảm. n ) n n +1
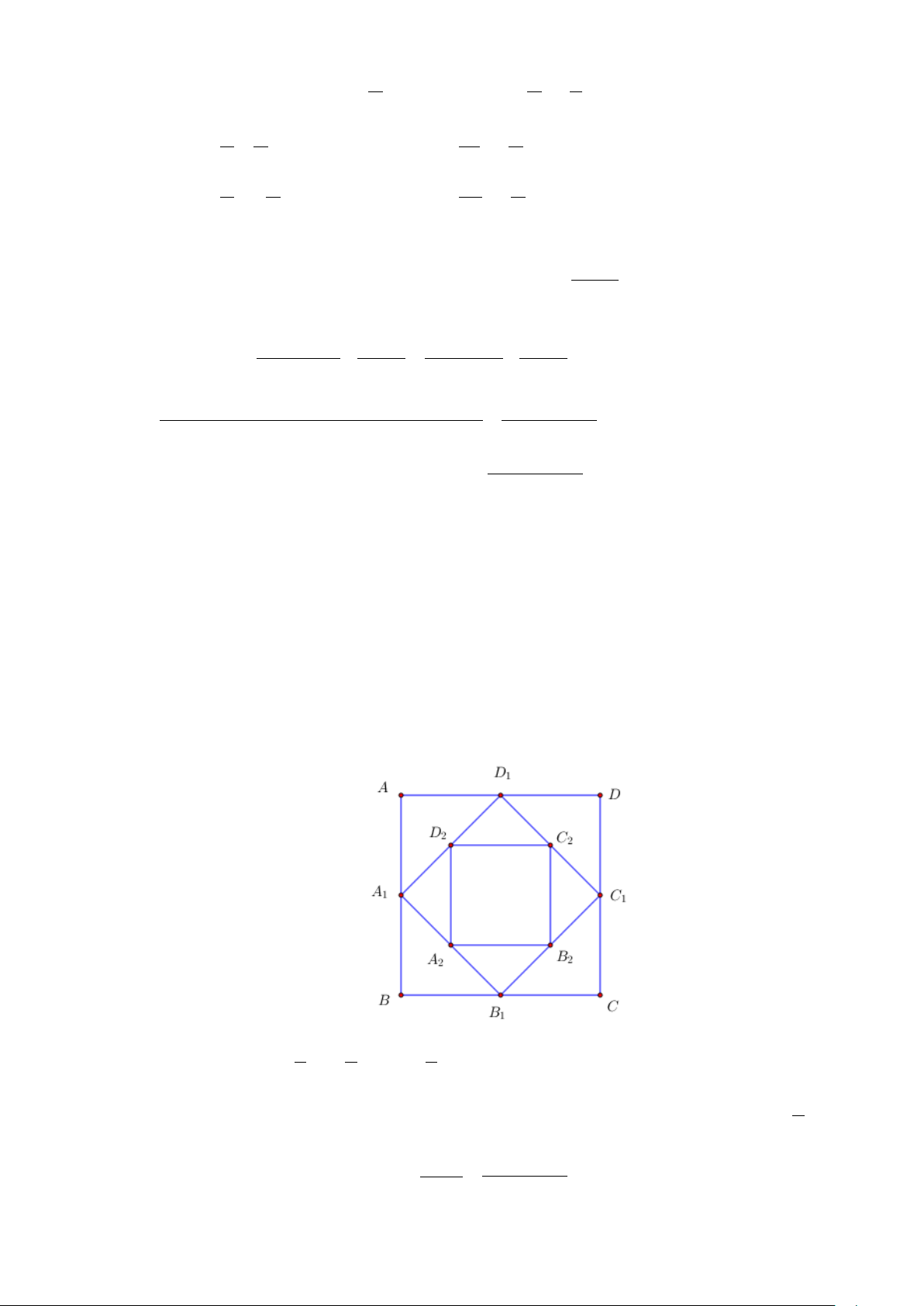
Câu 5: Cho hình vuông ABCD có cạnh bằng 4 và có diện tích S A B C D
1 . Nối 4 trung điểm 1 , 1 , 1 , 1 theo
thứ tự của 4 cạnh AB , BC , CD , DA ta được hình vuông thứ hai có diện tích S2 . Tiếp tục làm
như thế, ta được hình vuông thứ ba là A B C D S
2 2 2 2 có diện tích 3 , …và cứ tiếp tục làm như thế,
ta tính được các hình vuông lần lượt có diện tích S S S 4 , 5 ,…, 100 . Tính tổng
S = S + S + S +...+ S 1 2 3 100 .
Câu 6: Trong một hội thao, thời gian chạy 200m của một nhóm vận động viên được ghi lại trong bảng sau: Trang 3/13 - WordToan
Dựa vào bảng dữ liệu trên, ban tổ chức muốn chọn ra khoảng 50% số vận động viên chạy
nhanh nhất để tiếp tục thi vòng 2. Ban tổ chức nên chọn các vận động viên có thời gian chạy
không quá bao nhiêu giây? ( Kết quả làm tròn đến hàng phần mười).
-------------- Hết --------------
Trang 4/13 – Nhóm làm đề lớp 11 ĐÁP ÁN
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
(Mỗi câu trả lời đúng thí sinh được 0,25 điểm)
BẢNG ĐÁP ÁN TRẮC NGHIỆM Câu 1 2 3 4 5 6 7 8 9 10 11 12 Chọn A D D C B D D A D C B D
PHẦN II. Câu trắc nghiệm đúng sai.
Điểm tối đa của 01 câu hỏi là 1 điểm
-Thí sinh chỉ lựa chọn chính xác 01 ý trong 1 câu hỏi được 0,1 điểm.
-Thí sinh chỉ lựa chọn chính xác 02 ý trong 1 câu hỏi được 0,25 điểm.
-Thí sinh chỉ lựa chọn chính xác 03 ý trong 1 câu hỏi được 0,5 điểm.
-Thí sinh lựa chọn chính xác cả 04 ý trong 1 câu hỏi được 1,0 điểm. Câu 1 Câu 2 Câu 3 Câu 4 a) Đ a) Đ a) S a) Đ b) S b) Đ b) Đ b) S c) Đ c) S c) S c) S d) S d) S d) S d) Đ
PHẦN III. Câu trắc nghiệm trả lời ngắn.
(Mỗi câu trả lời đúng thí sinh được 0,5 điểm) Câu 1 2 3 4 5 6 Chọn 256 12,5 4 -2 32 22,6
LỜI GIẢI CHI TIẾT
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí
sinh chỉ chọn một phương án.
Câu 1: Trong mặt phẳng tọa độ Oxy, đường tròn lượng giác là đường tròn
A. có tâm trùng với gốc tọa độ và bán kính bằng 1.
B. có tâm trùng với gốc tọa độ.
C. bán kính bằng 1.
D. có tâm trùng với gốc tọa độ và bán kính bằng 2. Lời giải Chọn A
Theo SGK trong mặt phẳng tọa độ Oxy, đường tròn lượng giác là đường tròn có tâm trùng với
gốc tọa độ và bán kính bằng 1. Trên đường tròn này chọn điểm A(1;0) làm gốc, chiều dương là
chiều ngược kim đồng hồ và chiều âm là cùng chiều kim đồng hồ. π
Câu 2: Cho tanα = 3. Tính tan α − . 3 A. 1− 3 . B. 3+ 3 . C. 1− 3 . D. 3− 3 . 1+ 3 1− 3 3 1+ 3 3 1+ 3 3 Lời giải Chọn D tan − tan π α π 3 3− 3 Ta có: tan α − = = . 3 π 1+3 3 1+ tanα tan 3 Trang 5/13 - WordToan Câu 3: 1
Nếu sinx + cos x = thì sin 2x bằng 3 − A. 3 . B. 3 . C. 2 . D. 8 . 4 8 2 9 Lời giải Chọn D 1 8
Ta có sin x + cos x = 2 2 1
⇔ sin x + 2sin xcos x + cos x = sin 2x − ⇔ = 3 9 9 Câu 4: 2025
Tìm tập xác định D của hàm số y = . sin x A. D = . B. D = \{ } 0 . π
C. D = \{kπ,k ∈ } . D. D \ kπ ,k = + ∈. 2 Lời giải Chọn C
Hàm số xác định khi và chỉ khi sin x ≠ 0 ⇔ x ≠ kπ , k ∈ .
Vật tập xác định D = \{kπ,k ∈ } .
Câu 5: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua trục tung? π
A. y = sin xcos 2 .x B. 5
y sin .xcos x = − . 2 C. tan x y = . D. 3
y = cos xsin .x 2 tan x +1 Lời giải Chọn B
Ta dễ dàng kiểm tra được A, C, D là các hàm số lẻ nên có đồ thị đối xứng qua gốc tọa độ O . π
Xét đáp án B, ta có y = f (x) 5 5 6 = sin . x cos x − = sin . x sin x =
sin x . Kiểm tra được đây là 2
hàm số chẵn nên có đồ thị đối xứng qua trục tung.
Câu 6: Tất cả nghiệm của phương trình 3 cos x = − là 2 π π
A. x = + k2π ,k ∈ . B. 5 x =
+ k2π ,k ∈. 6 6 π π
C. x = ± + k2π ,k ∈ . D. 5 x = ±
+ k2π ,k ∈ . 6 6 Lời giải Chọn D π Vì 3 5 cos x = − ⇔ x = ±
+ k2π ,k ∈ . 2 6 + Câu 7: n 1
Cho dãy số (u với u = . Tính u . n ) n n 3 A. 5. B. 5 . C. 6 . D. 4 . 4 5 3 Lời giải
Trang 6/13 – Nhóm làm đề lớp 11 Chọn D n +1 3 1 4
Thay n = 3 vào u = ta được u + = = . n n 3 3 3 Câu 8: 1
Cho một cấp số cộng (u có u = , u = 26. Tìm công sai d n ) 1 3 8 A. 11 d = . B. 10 d = . C. 3 d = . D. 3 d = . 3 3 10 11 Lời giải Chọn A 1 11
Ta có u = u + 7d ⇔ 26= + 7d ⇔ d = 8 1 . 3 3 Câu 9: 1 Cho cấp số nhân u u = u =16 u n có 2 ,
. Tìm công bội q và số hạng đầu . 4 5 1 A. 1 q = , 1 u = . B. 1 q = − , 1
u = − . C. q 1 1 = 4 − , u = −
. D. q = 4 , u = . 2 1 2 2 1 2 1 16 1 16 Lời giải Chọn D 1 1 = u .q = 1 1 ( ) Ta có u2 4 ⇔ 4 . u = 16 4 u .q =16 2 1 ( ) 5 1
Chia hai vế của (2) cho ( ) 1 ta được 3
q = 64 ⇔ q = 4 ⇒ u = 1 . 16
Câu 10: Số lượng khách hàng nữ mua bảo hiểm nhân thọ trong một ngày được thống kê trong bảng tần số ghép nhóm sau:
Giá trị đại diện của nhóm [30;40) là: A. 40 . B. 30. C. 35. D. 9. Lời giải Chọn C 30 + 40
Ta có giá trị đại diện nhóm [30;40) là: = 35. 2
Câu 11: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở
bảng sau (đơn vị: triệu đồng)
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng sau đây? A. [7;9) . B. [9;1 ) 1 . C. [11;13) . D. [13;15). Lời giải Chọn B Ta có bảng sau: Trang 7/13 - WordToan 2.6 7.8 7.10 3.12 1.14 Khi đó x + + + + = = 9,4 . 20
Câu 12: Một thư viện thống kê số lượng sách được mượn mỗi ngày trong 3 tháng ở bảng sau:
Trong 3 tháng trên số sách được mượn mỗi ngày cao nhất gần bằng giá trị nào sau đây? A. 32,5 . B. 32. C. 33,5 . D. 34. Lời giải Chọn D
Do số sách là số nguyên nên ta hiệu chỉnh lại như sau:
Ta có nhóm chứa mốt của mẫu số liệu trên là nhóm [30,5;35,5) . Do đó u = n = n = n = u − = − = . + u m m 35,5 30,5 5 m , + 22 m , m 27 , − 15 m 30,5, 1 1 1
Mốt của mẫu số liệu ghép nhóm là: 27 −15 1157 M = 30,5 + .5 = ≈ 34 . 0 (27 −15) + (27 − 22) 34
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S). Câu 1: Cho biết 1 sinx = và π
0 < x < . Khi đó các mệnh đề sau đúng sai? 3 2
a) [NB] cosx >0 b) [TH] 3 tanx = 3 c) [TH] 6 cosx = 3 d) [VD] π 6 - 3
cos x+ = . 3 8 Lời giải a) Đúng Vì π
0 < x < nên cosx >0 . 2 b) Sai Ta có: 1 2 1 6 sinx =
⇒ cosx = 1- sin x = 1- = . Suy ra sin x 2 tan x = = 3 3 3 cos x 2 c) Đúng 1 2 1 6 sinx =
⇒ cosx = 1- sin x = 1- = 3 3 3 d) Sai π π π 6 1 1 3 6 - 3
cos x+ = cosx.cos - sinx.sin = . - . = . 3 3 3 3 2 3 2 6
Câu 2: Cho phương trình lượng giác π 2cos x − − 3 =
0 , khi đó các mệnh đề dưới đây đúng hay sai: 6
Trang 8/13 – Nhóm làm đề lớp 11
a) [NB] Phương trình đã cho có các nghiệm là: π
x = k2π (k ∈) và x = + k2π (k ∈) . 3 π
b) [TH] Phương trình đã cho có nghiệm dương nhỏ nhất bằng . 3
c) [TH] Đồ thị hàm số π y 2cos x = − −
3 giao với trục hoành tại gốc toạ độ. 6
d) [VD] Số nghiệm của phương trình đã cho trong khoảng ( π
− ;π ) là 3 nghiệm . Lời giải a) π π π π Đúng Ta có: 3 2cos x − − 3 = 0 ⇔ cos x − = ⇔ cos x − = cos 6 6 2 6 6 π π x − = + k2π π 6 6 x = + k2π ,(k ) ⇔ ∈ ⇔ 3 ,(k ∈) π π
x − = − + k2π x = k2π 6 6
Vậy phương trình đã cho có nghiệm là: π
x = k2π ,(k ∈) và x = + k2π ,(k ∈) . 3
b) Đúng Phương trình đã cho có nghiệm là: π
x = k2π ,(k ∈) và x = + k2π ,(k ∈) . Suy Phương 3 π
trình có nghiệm dương nhỏ nhất bằng . 3
c) Sai Thay toạ độ O(0;0) vào π y 2cos x = − −
3 không thoả mãn nên đồ thị hàm số 6 π y 2cos x = − −
3 không đi qua gốc toạ độ. 6
d) Sai Với x∈( π
− ;π ) ta xét 2 trường hợp π
* Khi x = + k2π , π x ∈( π − ;π ) , ta có: π
− < + k2π < π ,(k ∈) 3 3 1
⇔ − < + k < (k ∈) 2 1 1 2 1,
⇔ − < k < ,(k ∈) 3 3 3 ⇒ k = 0 π ⇒ x = 3
* Khi x = k2π , x∈( π − ;π ) , ta có π
− < k π < π k ∈ ⇔ − < k < (k ∈) 1 1 2 ,( ) 1 2 1,
⇔ − < k < ,(k ∈) 2 2 ⇒ k = 0 ⇒ x = 0
Vậy số nghiệm của phương trình trong khoảng ( π π
− ;π ) là x = 0 và x = . 3 3 1
Câu 3: Cho cấp số cộng (u có số hạng đầu u = , công sai d = . Khi đó các mệnh đề dưới đây đúng n ) 1 2 2 hay sai:
a) [NB] Công thức số hạng tổng quát của cấp số cộng đã cho là n u = 1+ . n 3
b) [TH] Số 5 là số hạng thứ 8 của cấp số cộng đã cho. Trang 9/13 - WordToan 15
c) [TH] Số là một số hạng của cấp số cộng đã cho. 4
d) [VD] Tổng 100 số hạng đầu của cấp số cộng (u trên bằng 2620 . n ) Lời giải 3 1 a) Sai. Ta có: = + 1 1 1 2 1
( − ) = + ( − )⋅ = + n u u n d n (n ∈ ;n ≥ . n ) 2 2 2 b)Đúng. Xét n *
5 = 1+ ⇒ n = 8∈ ; suy ra số 5 là số hạng thứ 8 của cấp số cộng đã cho. 2 15 11 15 c) Sai. Xét n * = 1+ ⇒ n =
∉ ; suy ra số không là một số hạng của cấp số cộng đã 4 2 2 4 cho.
d) Sai. Tổng 100 số hạng đầu của cấp số cộng là: 3 100 2 (100 ) 1 ⋅ + − 1 ⋅ 2 2 S = = 2625. 100 2
Câu 4: Kết quả khảo sát cân nặng của 25 quả cam ở mỗi lô hàng ,
A B được cho ở bảng sau: Cân nặng (gam)
[150;155) [155;160) [160;165) [165;170) [170;175)
Số quả cam ở lô hàng A 2 6 12 4 1
Số quả cam ở lô hàng B 1 3 7 10 4
a) [NB] Giá trị đại diện nhóm [150;155) bằng 152,5
b) [TH] Nhóm chứa mốt của số liệu ở lô hàng A là [155;160) .
c) [TH] Nhóm chứa mốt của số liệu ở lô hàng B là [160;165) .
d) [VD] Theo số trung bình thì cam ở lô hàng B nặng hơn cam ở lô hàng A . Lời giải
a) Đúng. Giá trị đại diện nhóm [150;155) là 150 +155 =152,5 2
b) Sai. Nhóm chứa mốt của số liệu là [160;165) .
c) Sai. Nhóm chứa mốt của số liệu là [165;170) .
d) Đúng. Bảng thống kê số lượng cam theo giá trị đại diện:
Cân nặng đại diện (gam) 152,5 157,5 162,5 167,5 172,5
Số quả cam ở lô hàng A 2 6 12 4 1
Số quả cam ở lô hàng B 1 3 7 10 4
Cân nặng trung bình của mỗi quả cam ở lô A là:
152,5 2 157,5 6 162,5 12 167,5 4 172,5 1 x ⋅ + ⋅ + ⋅ + ⋅ + ⋅ = = A 161,7 (gam). 25
Cân nặng trung bình của mỗi quả cam ở lô B là:
152,5 1 157,5 3 162,5 7 167,5 10 172,5 4 x ⋅ + ⋅ + ⋅ + ⋅ + ⋅ = = B 165,1 (gam). 25
Ta thấy x < x A
B . Vậy nếu so sánh theo số trung bình thì cam ở lô hàng B nặng hơn cam ở lô hàng A .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Bánh xe của người đi xe đạp quay được 10 vòng trong 5 giây. Tính độ dài quãng đường mà người
đi xe đã đi được trong 1 phút( đơn vị tính bằng mét và làm tròn kết quả đến hàng đơn vị, lấy
π = 3,14 ), biết rằng đường kính của bánh xe đạp là 0,68m. Lời giải
Chu vi bánh xe: C = π.d = 3,14.0,68(m)
Trang 10/13 – Nhóm làm đề lớp 11 10
Trong 1 giây bánh xe quay được số vòng: = 2, 5
Số vòng bánh xe quay được trong 1 phút là: 60.2 =120 (vòng)
Vậy quãng đường mà người đi xe đã đi được trong 1 phút là:
S = 3,14.0,68.120 ≈ 256(m)
Câu 2: Một cái cổng vào một trung tâm thương mại có hình dạng là một phần của đồ thị hàm số 2cos x y = + x 2 . Gọi ,
A B là hai điểm nằm trên cổng(trên đồ thị hàm số y = 2cos +
2 ) và C, D 2 2
là hai điểm nằm trên mặt nền của cổng sao cho ABCD là hình chữ nhật. Người quản lí trung tâm
thương mại muốn lắp một cái cửa kính tự động vào hình chữ nhật ABCD . Tính diện tích của cái cửa
cần lắp biết chiều cao của cái cửa là AD = 3 mét( kết quả làm tròn đến một chữ số thập phân, lấy π = 3,14 ). Lời giải
Chọn hệ trục tọa độ như hình vẽ y A B 1 x D O C 2π x = + k4π x x 1 3
AD = 3 ⇔ 2cos + 2 = 3 ⇔ cos = ⇔ (k ∈) 2 2 2 2 − π x = + k4π 3 2
− π 2π 2π 2 − π Chọn : A ;3;B ;3;C ;0;D ;0 3 3 3 3 4π 2 AB = ; AD = 3 ⇒ S = π m ABCD 4 ( ) 3
Câu 3: Một vật M được gắn vào đầu lò xo và dao động quanh vị trí cân bằng I , biết rằng O là hình
chiếu vuông góc của I trên trục Ox , toạ độ điểm M trên Ox tại thời điểm t (giây) là đại lượng s (đơn vị: π
cm ) được tính bởi công thức s 8,6cos 8t = +
. Tại mấy thời điểm trong khoảng 2 giây đầu tiên 2
thì s = 4,3 cm? Lời giải Trang 11/13 - WordToan Khi s = 4,3 thì π π 1 8,6cos 8t + = 4,3 ⇒ cos8t + = 2 2 2 π π π π 8t + = + k2π t = − + k 2 3 48 4 ⇔ (k ∈) ⇔ (k ∈). π π 5π π
8t + = − + k2π t = − + k 2 3 48 4
Vì t ∈(0;2) nên có 4 giá trị t thoả mãn là: t ≈ 0,72 s;t ≈1,51 s;t ≈ 0,46 s;t ≈ 0,1,24 s 1 2 3 4 . − Câu 4: mn 1
Tìm giá trị nguyên lớn nhất của m để dãy số (u với u = là dãy số giảm. n ) n n +1 Lời giải + − − + − − Xét
m(n 1) 1 mn 1 mn m 1 mn 1 u − = − = − + u n 1 n (n +1) +1 n +1 n + 2 n +1 2
mn + mn + m − n − − ( 2 2
1 mn + 2mn − n − 2) m +1 = = (n + 2)(n +1) (n + 2)(n +1) +
Dãy số đã cho là dãy giảm m 1 * ⇔ u − < ⇔ < ∀ ∈ ⇔ < − + u n m n n 0 0, 1 1 (n + 2)(n +1) ( *
do (n + 2)(n +1) > 0, n ∀ ∈ ).
Với m là số nguyên lớn nhất và m < 1 − suy ra m = 2 − .
Câu 5: Cho hình vuông ABCD có cạnh bằng 4 và có diện tích S A B C D
1 . Nối 4 trung điểm 1 , 1 , 1 , 1 theo
thứ tự của 4 cạnh AB , BC , CD , DA ta được hình vuông thứ hai có diện tích S2 . Tiếp tục làm
như thế, ta được hình vuông thứ ba là A B C D S
2 2 2 2 có diện tích 3 , …và cứ tiếp tục làm như thế,
ta tính được các hình vuông lần lượt có diện tích S S S 4 , 5 ,…, 100 . Tính tổng
S = S + S + S +...+ S 1 2 3 100 . Lời giải 1 1 1 Ta có 2
S = 4 S = 4 = S S = .S 1 ; 2 2 1 ; ,… 2 2 3 2 2 1 Do đó S S S S u = S = 4 q =
1 , 2 , 3 ,…, 100 là cấp số nhân với số hạng đầu 2 1 1 và công bội . 2 n 2 4 ( 100 2 − ) 1
Suy ra S = S + S + S +...+ S 1− q = = 1 2 3 100 = S . 32 . 1 1− q 99 2
Trang 12/13 – Nhóm làm đề lớp 11
Câu 6: Trong một hội thao, thời gian chạy 200m của một nhóm vận động viên được ghi lại trong bảng sau:
Dựa vào bảng dữ liệu trên, ban tổ chức muốn chọn ra khoảng 50% số vận động viên chạy
nhanh nhất để tiếp tục thi vòng 2. Ban tổ chức nên chọn các vận động viên có thời gian chạy
không quá bao nhiêu giây? ( Kết quả làm tròn đến hàng phần mười). Lời giải
Cỡ mẫu là n = 5+12+32+ 45+30 =124
Gọi x ,...., x là thời gian chạy của 124 vận động viên tham gia hội thao và giả sử dãy này 1 124
được sắp xếp theo thứ tự tăng dần. x + x Khi đó, trung vị là 62
63 . Do hai giá trị x , x thuộc nhóm [22,5;23) nên nhóm này chứa 2 62 63 trung vị.
Suy ra p = 4;a = 22,5; m = 45;m + m + m = 5 +12 + 32 = 49; a − a = 23− 22,5 = 0,5 4 4 1 2 3 5 4 124 −49 Ta có trung vị 2 M = + ≈ . e 22,5 .0,5 22,6 45
Vậy ban tổ chức nên chọn vận động viên có thời gian chạy không quá 22,6 giây.
-------------- Hết -------------- Trang 13/13 - WordToan
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 MÔN THI: TOÁN 11
Thời gian: 90 phút (Không kể thời gian phát đề)
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí
sinh chỉ chọn một phương án. π π π π
Câu 1: Cho bốn cung (trên một đường tròn định hướng): 5 25 19 α = − , β = ,γ = ,δ = , các cung 6 3 3 6
có điểm cuối trùng nhau là
A. β và γ ; α và δ . B. α, β,γ . C. β,γ ,δ .
D. α và β ; γ và δ .
Câu 2: Trong các công thức sau, công thức nào sai? A. 2 2
cos 2a = cos a – sin . a B. 2 2
cos 2a = cos a + sin . a C. 2
cos 2a = 2cos a –1. D. 2 cos 2a =1– 2sin . a Câu 3: Cho tanα π = 2 . Tính tan α − ? 4 A. 1 . B. 2 . C. 1. D. 1 − . 3 3 3
Câu 4: Trong các hàm số cho dưới đây, hàm số nào là hàm số tuần hoàn?
A. y = tan x . B. 2
y = x + tan x . C. 2 y = x . D. 2
y = x tan x .
Câu 5: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
A. y = cos x . B. 2
y = sin x .
C. y = cot 4x .
D. y = tan x + cos x .
Câu 6: Nghiệm của phương trình 1 cos x = − là 2 π π π π A. 2 x = ± + k2π .
B. x = ± + kπ .
C. x = ± + k2π . D. x = ± + k2π . 3 6 3 6 n 1 −
Câu 7: Cho dãy số (u 1 1 1 1; ; ;....;
;.... . Mệnh đề nào sau đây đúng? n ) : 2 4 2
A. Dãy số (u tăng.
B. Dãy số (u giảm. n ) n )
C. Dãy số (u không tăng, không giảm.
D. Dãy số (u không đổi. n ) n )
Câu 8: Trong các dãy số sau, dãy số nào là một cấp số cộng? A. 1; 2 − ; 4 − ; 6 − ; 8 − . B. 1; 3 − ; 6 − ; 9 − ; 1 − 2. C. 1; 3 − ; 7 − ; 1 − 1; 1 − 5. D. 1; 3 − ; 5 − ; 7 − ; 9 − .
Câu 9: Cho cấp số nhân (u có số hạng đầu u =12 và công bội q = − . Số hạng thứ sáu của cấp số n ) 1 2
nhân đã cho có giá trị bằng A. 384 − . B. 2 . C. 24 − . D. 34 − .
Câu 10: Cho mẫu số liệu về chiều cao (cm) của các học sinh nữ trong khối 11 của một trường như sau: Chiều cao
[145;150) [150;155) [155;160) [160;165) [165;170) [170;175) Số học sinh 20 45 34 27 15 4
Mẫu số liệu trên có bao nhiêu số liệu, bao nhiêu nhóm?
A. 145 số liệu; 6 nhóm.
B. 30 số liệu; 5 nhóm.
C. 6 số liệu; 145 nhóm.
D. 5 số liệu; 30 nhóm.
Trang 1/14 – Nhom làm đề lớp 11
Câu 11: Khảo sát thời gian chạy bộ trong một ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Thời gian (phút)
[0;20) [20;40) [40;60) [60;80) [80;100) Số học sinh 5 9 12 10 6
Quan sát mẫu số liệu trên và cho biết mệnh đề nào sau đây là đúng?
A. Độ dài mỗi nhóm của mẫu số liệu trên là 25 .
B. Mẫu số liệu đã cho gồm 5 nhóm có độ dài không bằng nhau.
C. Nhóm có nhiều học sinh nhất là nhóm [40;60) .
D. Nhóm có ít học sinh nhất là nhóm [80;100) .
Câu 12: Cho mẫu số liệu ghép nhóm về thống kê thời gian hoàn thành (phút) một bài kiểm tra trực tuyến
của 100 học sinh, ta có bảng số liệu sau: Thời gian (phút) [33;35) [35;37) [37;39) [39; ) 41 [41;43) [43;45) Số học sinh 4 13 38 27 14 4
Thời gian trung bình để 100 học sinh hoàn thành bài kiểm tra là: A. 38,92 phút. B. 38,29 phút. C. 39,28 phút. D. 39,82 phút.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng (Đ) hoặc sai (S).
Câu 13: Cho tam giác ABC có ba góc A , B ,C thỏa mãn sin A = cos B + cosC
B + C π A
a) [NB] Tam giác ABC có = − . 2 2 2 B + C A b) [TH] cos = cos 2 2 c) [TH] sin cos cos cos A cos B C A B C − = + ⇔ = 2 2
d) [VD] Tam giác ABC là tam giác cân. Câu 14: Cho hàm số π π y sin x = − và hàm số y = cos − x , khi đó: 4 2
a) [NB] Phương trình hoành độ giao điểm của hai đồ thị hàm số đã cho : π π sin x cos x − = − 4 2
b) [TH] Hoành độ giao điểm của hai đồ thị hàm số đã cho là 5π x =
+ k2π (k ∈) 8
c) [TH] Điểm 5π 5π M ;sin
là một giao điểm của hai đồ thị hàm số đã cho trên [0;2π ] 8 8
d) [VD] Khi x∈[0;3π ] thì hai đồ thị hàm số đã cho cắt nhau tại ba điểm lần lượt ,
A B,C gọi I là π π
trung điểm của AC thì 13 13 I ;sin 16 4 Câu 15:
Khi kí kết hợp đồng lao động với người lao động, một doanh nghiệp đề xuất hai phương án trả lương như sau:
Phương án 1: Năm thứ nhất, tiền lương là 120 triệu đồng. Kể từ năm thứ hai trở đi, mỗi năm tiền lương
được tăng 18 triệu đồng.
Trang 2/14 – Nhóm làm đề lớp 11
Phương án 2: Quý thứ nhất, tiền lương là 24 triệu đồng. Kể từ quý thứ hai trở đi, mỗi quý tiền lương
được tăng 1,8 triệu đồng.
a) [NB] Với phương án 1, tiền lương người lao động nhận được ở năm thứ hai là 138 triệu đồng.
b) [TH] Với phương án 2, tổng số tiền lương người lao động nhận được ở năm thứ nhất là 101,4 triệu đồng.
c) [TH] Với phương án 1, để người lao động nhận được tổng số tiền lương trên 1 tỷ đồng thì người lao
động đó phải làm việc cho doanh nghiệp ít nhất 6 năm.
d) [VD] Nếu người lao động kí hợp đồng với doanh nghiệp ít nhất 4 năm thì người lao động kí hợp
đồng theo phương án 2 sẽ nhận được số tiền lương nhiều hơn so với phương án 1.
Câu 16: Kết quả đo chiều cao (đơn vị: mét) của 100 cây keo 3 năm tuổi tại một nông trường được cho ở bảng sau:
Chiều cao (m) [8,4;8,6) [8,6;8,8) [8,8;9,0) [9,0;9,2) [9,2;9,4) Số cây 5 12 25 44 14
a) [NB] Mẫu số liệu ghép nhóm trên có 5 nhóm số liệu.
b) [TH] Số trung bình của mẫu số liệu ghép nhóm là x = 8,9(m) .
c) [TH] Số cây keo có chiều cao khoảng 9,1(m) là nhiều nhất.
d) [VD] Hiệu giữa tứ phân vị thứ ba và tứ phân vị thứ nhất bằng 2,06 .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. π α α Câu 17: Cho cotα = 3
− 2 với < α < π . Khi đó giá trị tan + cot bằng bao nhiêu ? (kết quả làm 2 2 2
tròn đến hàng phần trăm)
Câu 18: Số giờ có ánh sáng của thành phố T ở vĩ độ 40° bắc trong ngày thứ t của một năm không nhuận π
được cho bởi hàm số d(t) 3 sin (t 80) = ⋅ − +12
với t ∈ và 0 < t ≤ 365. Bạn An muốn đi tham quan 182
thành phố T nhưng lại không thích ánh sáng mặt trời, vậy bạn An nên chọn đi vào ngày nào trong năm để
thành phố T có ít giờ có ánh sáng mặt trời nhất? Câu 19.
Một vận động viên bắn súng nằm trên mặt đất để gắm bắn các mục tiêu khác nhau trên một
bức tường thẳng đứng. Vận động viên bắn trúng một mục tiêu cách mặt đất 25(m) tại một góc ngắm (góc
hợp bởi phương ngắm với phương ngang). Nếu giảm góc ngắm đi một nửa thì vận động viên bắn trúng mục
tiêu cách mặt đất 10(m) . Tính khoảng cách từ vận động viên đến bức tường? u = 1;u = 2
Câu 20 . Cho dãy số (u biết 1 2 n ) * u = + − ∀ ∈ + au + a u n n n (1 ) n, 2 1
Tìm giá trị nguyên dương của a nhỏ nhất để dãy số (u tăng. n )
Câu 21: Bạn định mua một chiếc xe máy theo phương thức trả góp. Theo phương thức này sau một tháng kể
từ khi nhận xe bạn phải trả đều đặn mỗi tháng một lượng tiền nhất định nào đó, liên tiếp trong 24 tháng. Giả sử
giá xe máy thời điểm bạn mua là 16 triệu đồng và giả sử lãi suất ngân hàng là 1% một tháng. Với mức phải trả
hàng tháng là bao nhiêu nghìn đồng thì việc mua trả góp là chấp nhận được? (làm tròn đến hàng nghìn)
Câu 22: Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 50 học sinh lớp 11A . Trang 3/14 - WordToan
Số học sinh có chiều cao bao nhiêu centimet là nhiều nhất? (Làm tròn đến hàng đơn vị)
-------------- Hết --------------
Trang 4/14 – Nhóm làm đề lớp 11 ĐÁP ÁN
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
(Mỗi câu trả lời đúng thí sinh được 0,25 điểm)
BẢNG ĐÁP ÁN TRẮC NGHIỆM Câu 1 2 3 4 5 6 7 8 9 10 11 12 Chọn A B A A C A B C A A C A
PHẦN II. Câu trắc nghiệm đúng sai.
Điểm tối đa của 01 câu hỏi là 1 điểm
-Thí sinh chỉ lựa chọn chính xác 01 ý trong 1 câu hỏi được 0,1 điểm.
-Thí sinh chỉ lựa chọn chính xác 02 ý trong 1 câu hỏi được 0,25 điểm.
-Thí sinh chỉ lựa chọn chính xác 03 ý trong 1 câu hỏi được 0,5 điểm.
-Thí sinh lựa chọn chính xác cả 04 ý trong 1 câu hỏi được 1,0 điểm. Câu 13 Câu 14 Câu 15 Câu 16 a) Đ a) Đ a) Đ a) Đ b) S b) S b) S b) S c) Đ c) Đ c) S c) Đ d) S d) Đ d) Đ d) S
PHẦN III. Câu trắc nghiệm trả lời ngắn.
(Mỗi câu trả lời đúng thí sinh được 0,5 điểm) Câu 17 18 19 20 21 22 Chọn 8,72 353 22,4 2 753 153
LỜI GIẢI CHI TIẾT
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí
sinh chỉ chọn một phương án. π π π π
Câu 1: Cho bốn cung (trên một đường tròn định hướng): 5 25 19 α = − , β = ,γ = ,δ = , các cung 6 3 3 6
có điểm cuối trùng nhau là
A. β và γ ; α và δ . B. α, β,γ . C. β,γ ,δ .
D. α và β ; γ và δ . Lời giải Chọn A
Ta có: δ −α = 4π ⇒ 2 cung α và δ có điểm cuối trùng nhau.
γ − β = 8π ⇒ hai cung β và γ có điểm cuối trùng nhau.
Câu 2: Trong các công thức sau, công thức nào sai? A. 2 2
cos 2a = cos a – sin . a B. 2 2
cos 2a = cos a + sin . a C. 2
cos 2a = 2cos a –1. D. 2 cos 2a =1– 2sin . a Lời giải Chọn B Ta có 2 2 2 2
cos 2a = cos a – sin a = 2cos a −1 =1− 2sin a . Câu 3: Cho tanα π = 2 . Tính tan α − ? 4 Trang 5/14 - WordToan A. 1 . B. 2 . C. 1. D. 1 − . 3 3 3 Lời giải Chọn A tan − tan π α π Ta có 4 1 tan α − = = . 4 π 3 1+ tanα tan 4 .
Câu 4: Trong các hàm số cho dưới đây, hàm số nào là hàm số tuần hoàn?
A. y = tan x . B. 2
y = x + tan x . C. 2 y = x . D. 2
y = x tan x . Lời giải Chọn A
Xét hàm số y = tan x có tập xác định π D \ kπ , = + k ∈ . 2
Với mọi số thực x ta có x − kπ ∈ D, x + kπ ∈ D và tan(x + kπ ) = tan .x
Vậy y = tan x là hàm số tuần hoàn.
Câu 5: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
A. y = cos x . B. 2
y = sin x .
C. y = cot 4x .
D. y = tan x + cos x . Lời giải Chọn C
+ Đồ thị của hàm số lẻ đối xứng qua gốc tọa độ.
+ Trong 4 hàm số đã cho ta nhận thấy hàm số y = cot 4x là hàm số lẻ nên có đồ thị đối xứng qua gốc tọa độ.
Câu 6: Nghiệm của phương trình 1 cos x = − là 2 π π π π A. 2 x = ± + k2π .
B. x = ± + kπ .
C. x = ± + k2π . D. x = ± + k2π . 3 6 3 6 Lời giải Chọn A Ta có: 1 2π 2π
cos x = − ⇔ cos x = cos ⇔ x = ± + k2π (k ∈ Ζ ) 2 3 3 n−1 Câu 7: Cho dãy số ( 1 1 1 u ) : 1; ; ;....;
;.... . Mệnh đề nào sau đây đúng? n 2 4 2
A. Dãy số (u tăng.
B. Dãy số (u giảm. n ) n )
C. Dãy số (u không tăng, không giảm.
D. Dãy số (u không đổi. n ) n ) Lời giải Chọn B
Dãy số (u là dãy giảm. n )
Câu 8: Trong các dãy số sau, dãy số nào là một cấp số cộng?
Trang 6/14 – Nhóm làm đề lớp 11 A. 1; 2 − ; 4 − ; 6 − ; 8 − . B. 1; 3 − ; 6 − ; 9 − ; 1 − 2. C. 1; 3 − ; 7 − ; 1 − 1; 1 − 5. D. 1; 3 − ; 5 − ; 7 − ; 9 − . Lời giải Chọn C
Dãy số (u có tính chất u = + thì được gọi là một cấp số cộng. + u d n ) n 1 n Ta thấy dãy số: 1; 3 − ; 7 − ; 1 − 1; 1
− 5 là một cấp số cộng có số hạng đầu là 1 và công sai bằng 4. −
Câu 9: Cho cấp số nhân (u có số hạng đầu u = và công bội q = − . Số hạng thứ sáu của cấp số n ) 12 1 2 nhân đã cho bằng A. 384 − . B. 2 . C. 24 − . D. 34 − . Lời giải Chọn A Ta có 5
u = u .q =12. 2 − = 384 − . 6 1 ( )5
Câu 10: Cho mẫu số liệu về chiều cao (cm) của các học sinh nữ trong khối 11 của một trường như sau: Chiều cao
[145;150) [150;155) [155;160) [160;165) [165;170) [170;175) Số học sinh 20 45 34 27 15 4
Mẫu số liệu trên có bao nhiêu số liệu, bao nhiêu nhóm?
A. 145 số liệu; 6 nhóm.
B. 30 số liệu; 5 nhóm.
C. 6 số liệu; 145 nhóm.
D. 5 số liệu; 30 nhóm. Lời giải Chọn A
Mẫu số liệu (T ) có:
20 + 45 + 34 + 27 +15 + 4 =145 (số liệu).
6 nhóm: [145;150);[150;155);[155;160);[160;165);[165;170);[170;175).
Câu 11: Khảo sát thời gian chạy bộ trong một ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Thời gian (phút)
[0;20) [20;40) [40;60) [60;80) [80;100) Số học sinh 5 9 12 10 6
Quan sát mẫu số liệu trên và cho biết mệnh đề nào sau đây là đúng?
A. Độ dài mỗi nhóm của mẫu số liệu trên là 25 .
B. Mẫu số liệu đã cho gồm 5 nhóm có độ dài không bằng nhau.
C. Nhóm có nhiều học sinh nhất là nhóm [40;60) .
D. Nhóm có ít học sinh nhất là nhóm [80;100) . Lời giải Chọn C.
Mẫu số liệu đã cho gồm 5 nhóm có độ dài là 20.
Nhóm có nhiều học sinh nhất là nhóm [40;60) .
Nhóm có ít học sinh nhất là nhóm [0;20) .
Câu 12: Cho mẫu số liệu ghép nhóm về thống kê thời gian hoàn thành (phút) một bài kiểm tra trực tuyến
của 100 học sinh, ta có bảng số liệu sau: Thời gian (phút) [33;35) [35;37) [37;39) [39; ) 41 [41;43) [43;45) Số học sinh 4 13 38 27 14 4 Trang 7/14 - WordToan




