-
Thông tin
-
Quiz
05 đề ôn tập giữa học kì 1 Toán 11 cấu trúc trắc nghiệm mới
Tài liệu 05 đề ôn tập giữa học kì 1 Toán 11 cấu trúc trắc nghiệm mới gồm 67 trang, tuyển tập 05 đề ôn tập kiểm tra giữa học kì 1 môn Toán 11 theo cấu trúc trắc nghiệm mới nhất do Bộ Giáo dục và Đào tạo công bố, áp dụng từ năm học 2024 – 2025, có đáp án và lời giải chi tiết. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây nhé.
Chủ đề: Đề giữa HK1 Toán 11 291 tài liệu
Môn: Toán 11 3.3 K tài liệu
Thông tin:
Tác giả:
Preview text:
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 11
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI
MÔN: TOÁN 11 – ĐỀ SỐ: 01
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1: Cấp số cộng (u với = có công sai d bằng n ) u n n 3 A. d = 2 . B. d = 3. C. d =1.
D. d = 4 .
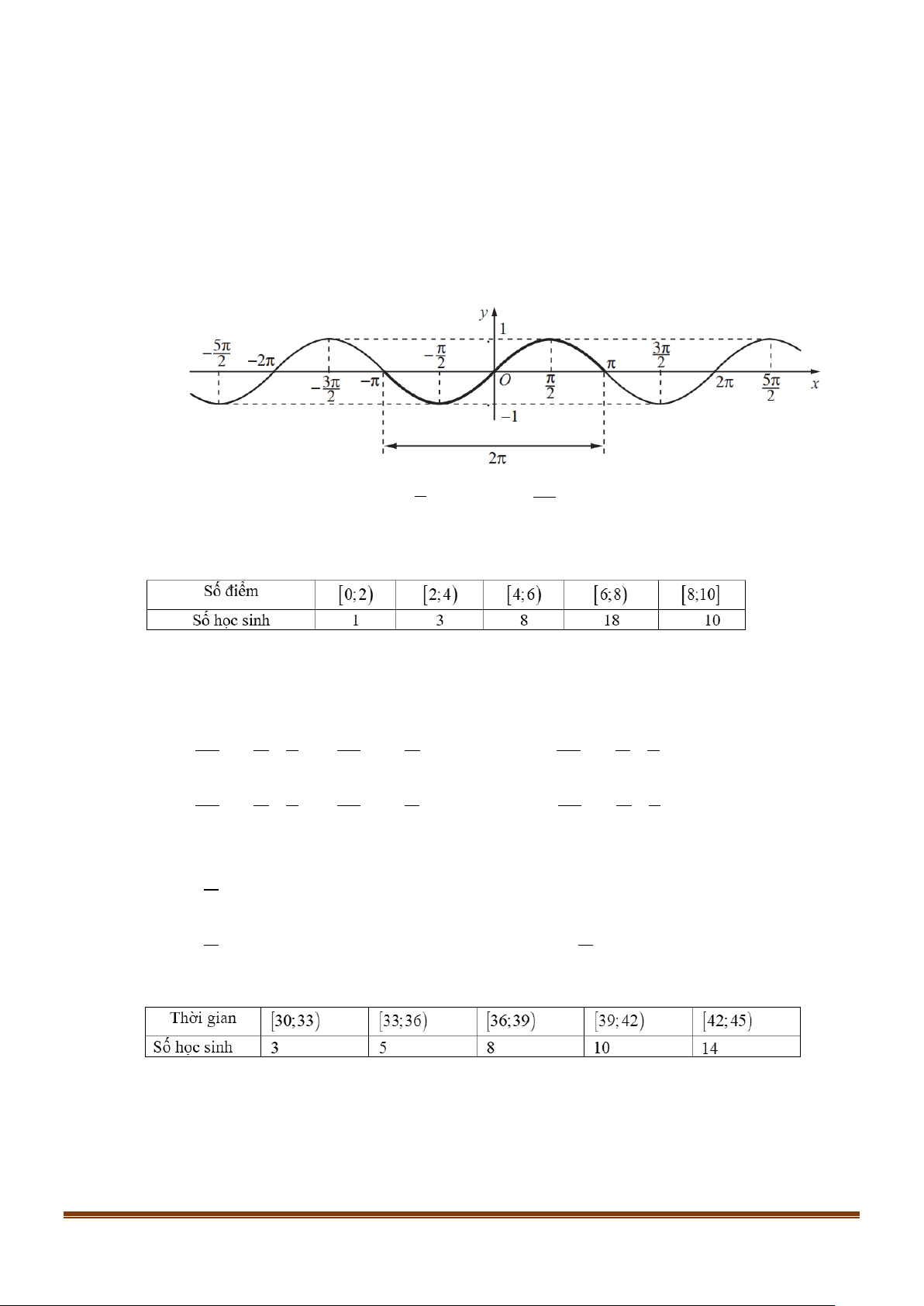
Câu 2: Biết rằng hàm số y = sin x có đồ thị như hình bên dưới.
Số nghiệm của phương trình 1
sin x = trên đoạn 3π ;π − là 2 2 A. 4 . B. 3. C. 6 . D. 2 .
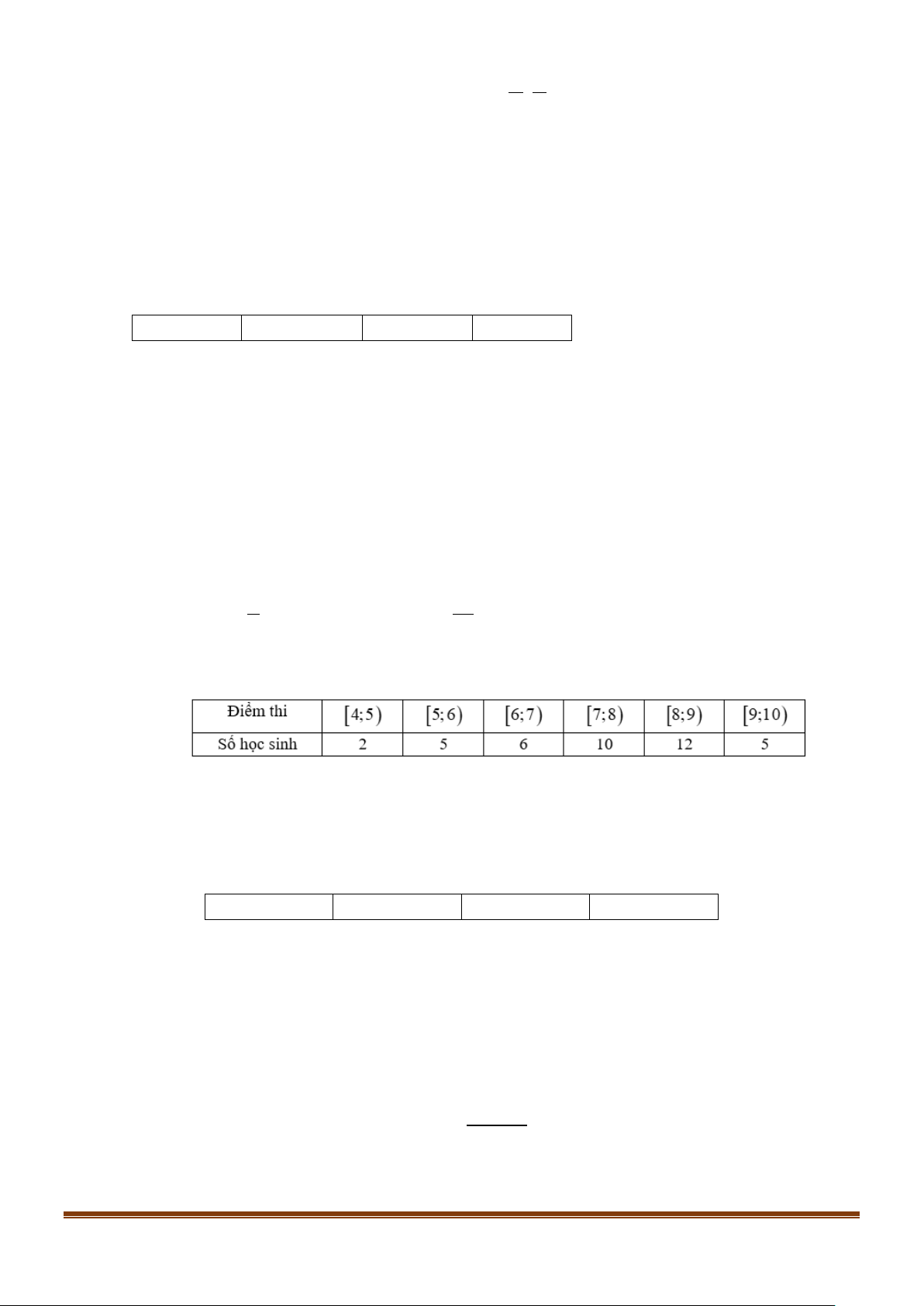
Câu 3: Điểm kiểm tra giữa học kì I của lớp 11A được thống kê theo bảng sau :
Trong các nhóm sau đây, nhóm nào chứa mốt của bảng số liệu ghép nhóm trên ? A. [8;10] B. [4;6) C. [6;8) D. [2;4)
Câu 4: Với góc lượng giác có số đo bằng α tùy ý. Đẳng thức nào sau đây luôn đúng? A. 3α α 1 3α α α α cos .cos 3 1 cos cos = + . B. cos
.cos = (cos 2α + cosα ) . 2 2 2 2 2 2 2 2 C. 3α α 1 3α α α α cos .cos 3 1 cos cos = − . D. cos
.cos = (cos 2α − cosα ) . 2 2 2 2 2 2 2 2
Câu 5: Tập xác định của hàm số y = tan x là A. π \ k2π | k + ∈.
B. \{kπ | k ∈ } . 2 C. π π \ kπ | k + ∈.
D. \ k | k ∈. 2 2
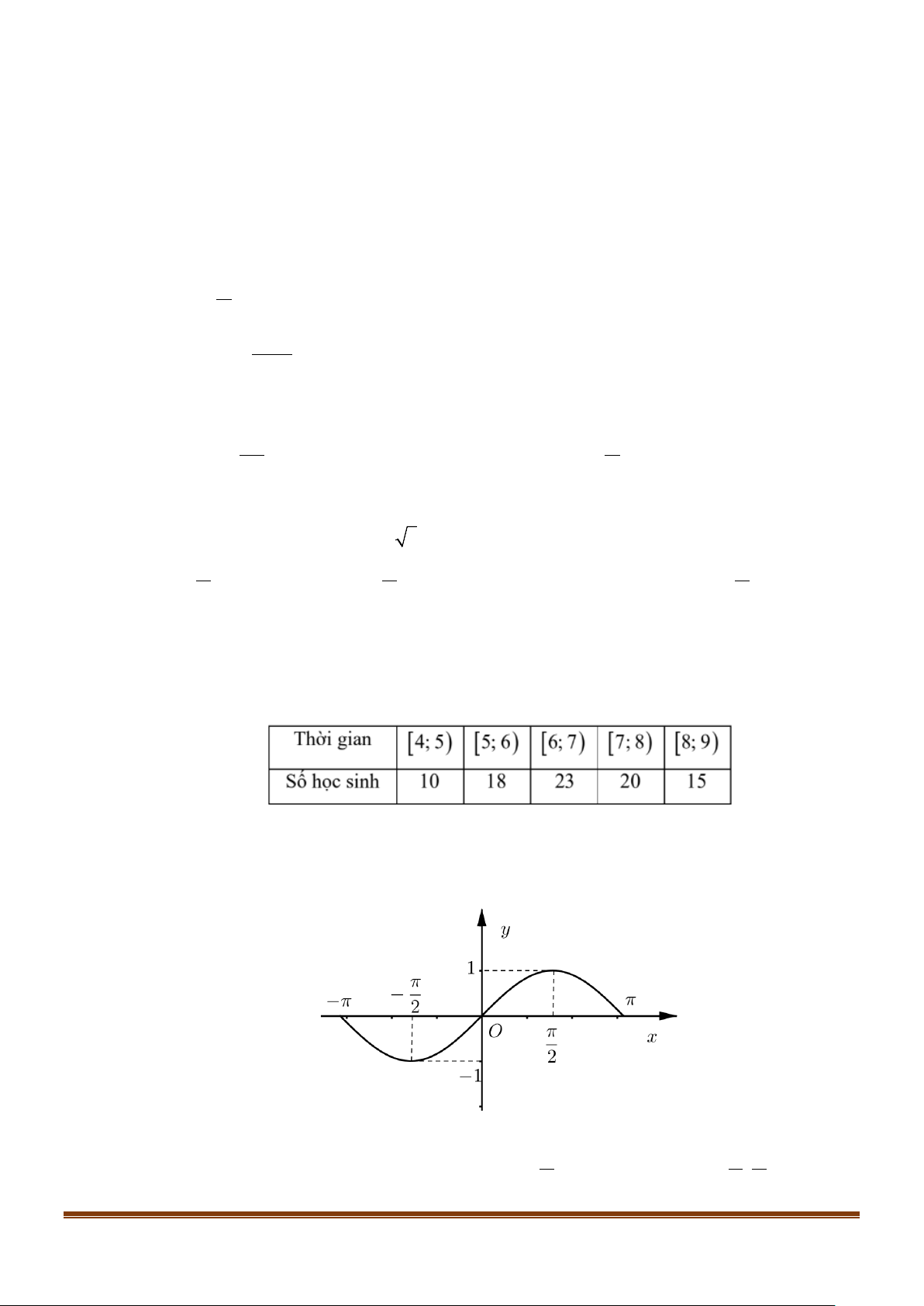
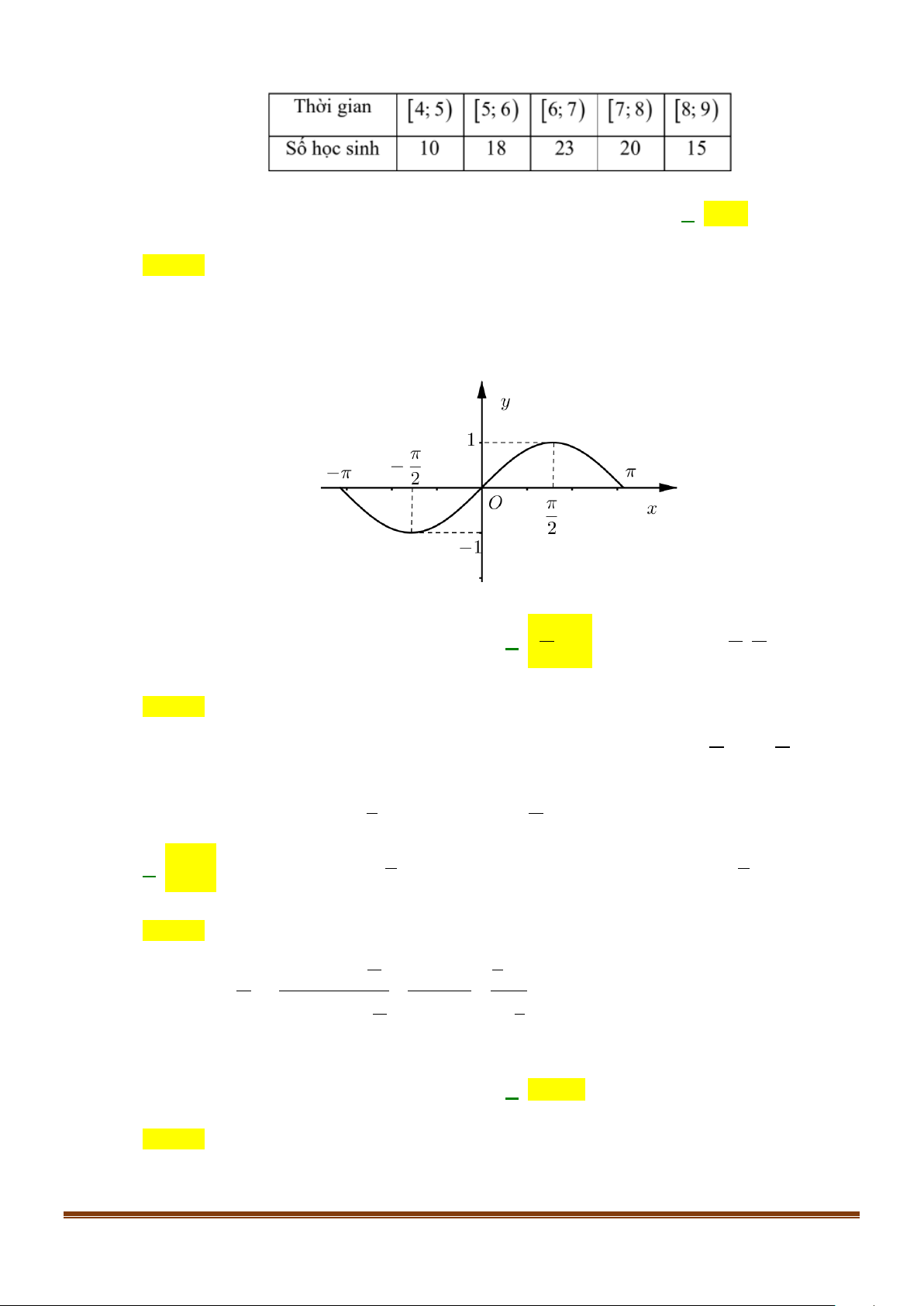
Câu 6: Thời gian hoàn thành bài kiểm tra 45 phút môn toán của 40 học sinh được cho trong bảng sau:
Nhóm chứa tứ phân vị thứ nhất Q là 1 A. [30;33) B. [39;42) C. [33;36) D. [36;39) Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 11
Câu 7: Cho góc hình học uOv có số đo 50o (hình vẽ). Xác định số đo của các góc lượng giác(Ou;Ov) . v 50° O u
A. sd ( ; ) = 50o + 360o Ou Ov k ,k ∈ .
B. sd ( ; ) = 50o + 180o Ou Ov k ,k ∈ .
C. sd ( ; ) = 50o − + 360o Ou Ov k ,k ∈ .
D. sd ( ; ) = 50o − + 180o Ou Ov k ,k ∈ .
Câu 8: Khảo sát thời gian tham gia câu lạc bộ trong một tuần của 100 bạn học sinh, thu được kết quả sau:
Nhóm chứa trung vị của mẫu số liệu trên là A. [90;120). B. [30;60). C. [60;90). D. [120;150).
Câu 9: Biến đổi sin 6x + sin 4x thành tích là
A. 2sin 6 .xcos 4x .
B. 2sin .xcos5x .
C. 2sin 5 .xcos x .
D. 2sin10 .xcos 2x .
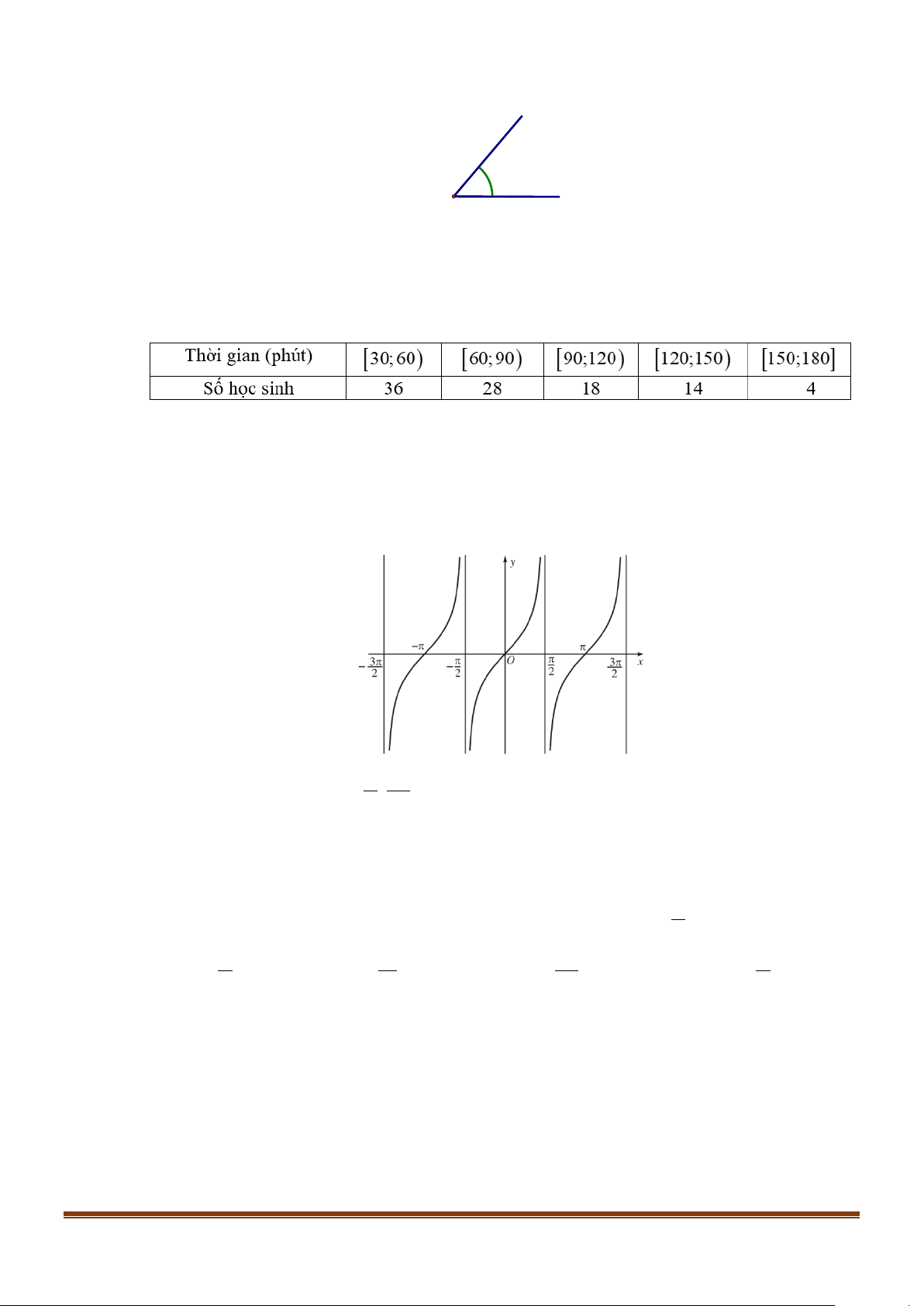
Câu 10: Cho hàm số y = tan x có đồ thị như hình bên dưới π π
Số giá trị của x trên đoạn 3 ; −
để hàm số y = tan x nhận giá trị bằng 0 là 2 2 A. 0. B. 2. C. 1. D. 3.
Câu 11: Một cấp số nhân có số hạng thứ nhất và thứ hai theo thứ tự là 16 và 36. Số hạng thứ ba là A. 64. B. 56. C. 81. D. 720.
Câu 12: Cho một đường tròn có bán kính 5cm . Tính độ dài cung tròn có số đo π . 3 A. π π π l = 5 + (cm). B. 15 l = (cm). C. 5 l = (cm).
D. l = 5 − (cm). 3 π 3 3 Page 2
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 11
PHẦN II: Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai. Câu 1: Cho biết 12 π cos x = − và 3 π < x < . 13 2
a) sin x > 0. b) 5 sin x = − . 13 c) 5 cot x = . 12 d) π 5 −12 3 sin − x = . 3 26
Câu 2: Cho phương trình 2sin x = − 2 (1).
a) Phương trình (1) tương đương với phương trình π sin x sin = − . 4 π π
b) Phương trình (1) có các nghiệm là: x = − + k2π; x = + k2π (k ∈ ) . 4 4 π
c) Phương trình (1) có nghiệm dương nhỏ nhất bằng . 4
d) Số nghiệm của phương trình (1) trong khoảng π π ; − là 1 nghiệm. 2 2 u
+ u − u = 7 −
Câu 3: Cho cấp số cộng biết: 2 4 6 . u −u = 2u 8 7 4
a) Số hạng đầu của cấp số cộng là: u = 5 − . 1
b) Số hạng thứ 20 của cấp số cộng là: 32.
c) Tổng 30 số hạng đầu của cấp số cộng là: 750 .
d) Số 201 là một số hạng của cấp số cộng.
Câu 4: Điểm thi môn Toán trong kì thi TNTHPT của lớp 12A được thống kê như sau:
a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là 10.
b) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm trên lớn hơn 8 .
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là 2 .
d) Phương sai của mẫu số liệu bằng 1,9.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. π π Câu 1: Cho góc 3 α ;2π ∈ sao cho 2
cosα = . Tính giá trị củacos α + . 2 3 3
Câu 2: Trong một hoạt động thiện nguyện, các bạn học sinh lớp 11B đã tiến hành tặng sách cho các
trẻ em vùng khó khăn. Kết quả hoạt động được ghi nhận ở bảng sau:
Tìm tứ phân vị thứ 3 của mẫu số liệu ghép nhóm trên. Page 3
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 11
Câu 3: Số giờ có ánh sáng mặt trời của một thành phố X ở vĩ độ 40° bắc trong ngày thứ t của một năm π
không nhuận được cho bởi hàm số d (t) 3sin (t 80) = − +12,
t ∈, 0 < t ≤ 365 . Vào ngày 182
thứ mấy trong năm thì thành phố X có nhiều giờ có ánh sáng mặt trời nhất?
Câu 4: Một công ty xây dựng mua một chiếc máy ủi với giá 3 tỉ đồng. Cứ sau mỗi năm sử dụng, giá trị
của chiếc máy ủi này lại giảm 20% so với giá trị của nó trong năm liền trước đó. Tìm giá trị còn
lại của chiếc máy ủi đó sau 5 năm sử dụng (làm tròn kết quả đến hàng phần trăm theo đơn vị tỉ đồng).
Câu 5: Một chiếc đu quay có tâm của vòng quay ở độ cao 35m so với mặt đất, khoảng cách từ tâm vòng
quay đến vị trí gắn các cabin là 30m . Thời gian thực hiện mỗi vòng của đu quay là 3 phút 20
giây. Một hành khách vào cabin số 1 được gắn tại vị trí A, thấp nhất của vòng quay (tham khảo
hình vẽ), sau t giây kể từ lúc quay, vị trí A cách mặt đất h(t) mét. Biết rằng h(t) có dạng
h(t) = a cos(ωt) + b ( a,b,ω là hằng số). Xác định a,b,ω và tính thời gian ngắn nhất kể từ lúc
quay để vị trí A cách mặt đất 25m (thời gian làm tròn đến hàng đơn vị).
Câu 6: Tỉ lệ tăng dân số mỗi năm của một tỉnh X từ năm 2010 đến năm 2019 là 0,4% . Vì thực hiện
các chính sách về dân số nên tỉnh X dự kiến từ năm 2020 đến 2030 tỉ lệ tăng dân số mỗi năm
chỉ còn lại 0,35% . Theo thống kê số dân tỉnh X năm 2021 nhiều hơn năm 2017 là 30400
người. Hỏi số dân tỉnh X năm 2030 khoảng bao nhiêu triệu người? (kết quả làm tròn đến hàng phần trăm)
---------- HẾT ---------- Page 4
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 11
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1: Cấp số cộng (u với = có công sai d bằng n ) u n n 3 A. d = 2 . B. d = 3. C. d =1.
D. d = 4 . Lời giải Chọn B Ta có u − = + − = nên d = 3. + u n n n n 3 1 3 3 1 ( )
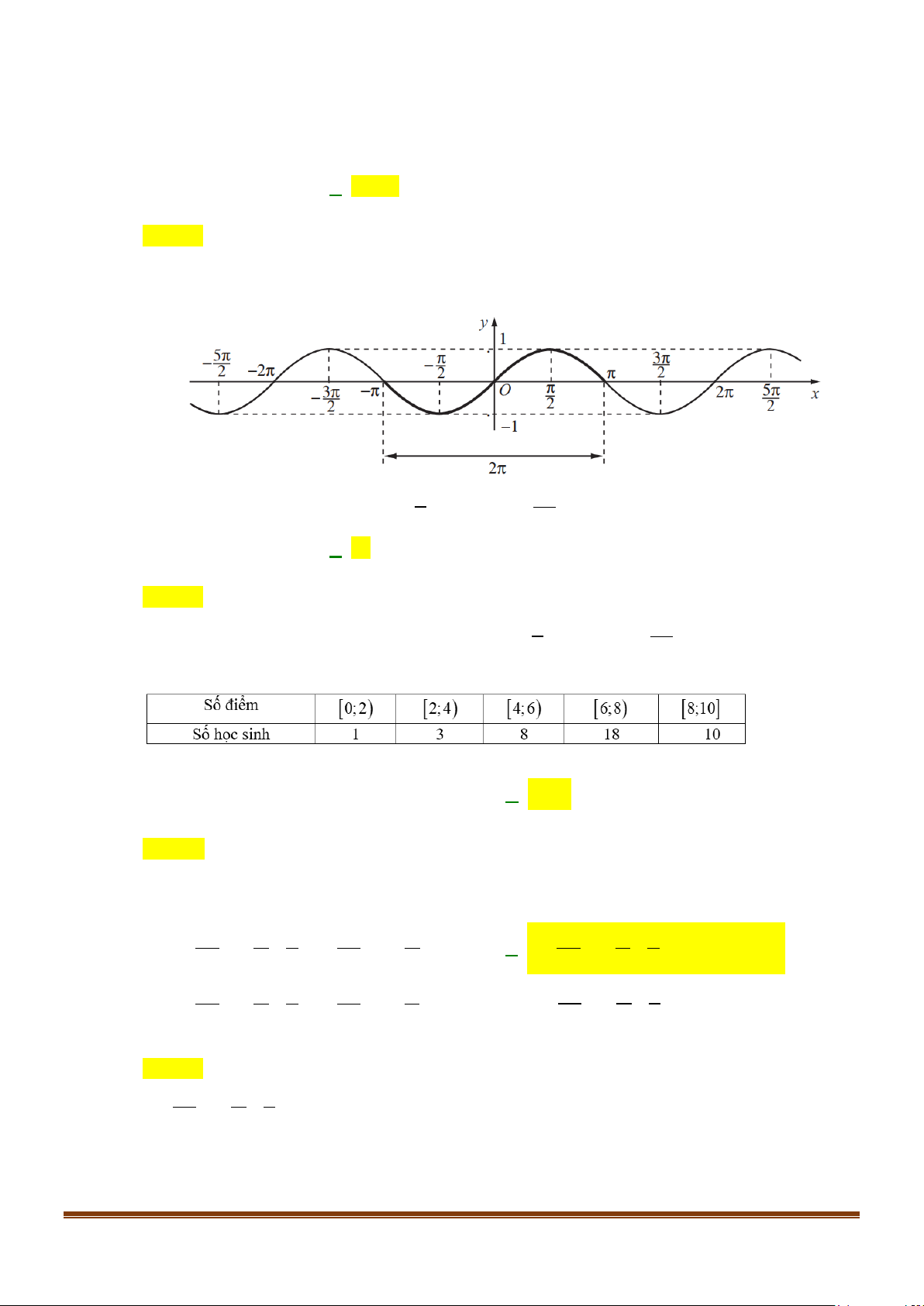
Câu 2: Biết rằng hàm số y = sin x có đồ thị như hình bên dưới.
Số nghiệm của phương trình 1 sin x π = trên đoạn 3 ;π − là 2 2 A. 4 . B. 3. C. 6 . D. 2 . Lời giải Chọn B
Dựa vào đồ thị, số nghiệm của phương trình 1
sin x = trên đoạn 3π ;π − là 3. 2 2
Câu 3: Điểm kiểm tra giữa học kì I của lớp 11A được thống kê theo bảng sau :
Trong các nhóm sau đây, nhóm nào chứa mốt của bảng số liệu ghép nhóm trên ? A. [8;10] B. [4;6) C. [6;8) D. [2;4) Lời giải Chọn C
Nhóm chứa mốt của bảng số liệu ghép nhóm trên là [6;8) .
Câu 4: Với góc lượng giác có số đo bằng α tùy ý. Đẳng thức nào sau đây luôn đúng? A. 3α α 1 3α α α α cos .cos 3 1 cos cos = + . B. cos
.cos = (cos 2α + cosα ) . 2 2 2 2 2 2 2 2 C. 3α α 1 3α α α α cos .cos 3 1 cos cos = − . D. cos
.cos = (cos 2α − cosα ) . 2 2 2 2 2 2 2 2 Lời giải Chọn B 3α α 1 cos
.cos = (cos 2α + cosα ) . 2 2 2
Câu 5: Tập xác định của hàm số y = tan x là Page 5
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 11 A. π \ k2π | k + ∈.
B. \{kπ | k ∈ } . 2 C. π π \ kπ | k + ∈.
D. \ k | k ∈. 2 2 Lời giải Chọn C
Tập xác định của hàm số π
y = tan x là \ kπ | k + ∈.. 2
Câu 6: Thời gian hoàn thành bài kiểm tra 45 phút môn toán của 40 học sinh được cho trong bảng sau:
Nhóm chứa tứ phân vị thứ nhất Q là 1 A. [30;33) B. [39;42) C. [33;36) D. [36;39) Lời giải Chọn D
Mẫu số liệu này có 40 giá trị nửa đầu có 20 giá trị; do đó 1 Q
x x mà x ; x thuộc 1 10 11 2 10 11
nhóm 36;39 vậy nhóm chứa tứ phân vị thứ nhất là nhóm 36;39.
Câu 7: Cho góc hình học uOv có số đo 50o (hình vẽ). Xác định số đo của các góc lượng giác(Ou;Ov) . v 50° O u
A. sd ( ; ) = 50o + 360o Ou Ov k ,k ∈ .
B. sd ( ; ) = 50o + 180o Ou Ov k ,k ∈ .
C. sd ( ; ) = 50o − + 360o Ou Ov k ,k ∈ .
D. sd ( ; ) = 50o − + 180o Ou Ov k ,k ∈ . Lời giải Chọn A
Số đo của các góc lượng giác (Ou;Ov) là: sñ ( ; ) = 50o + 360o Ou Ov k ,k ∈ .
Câu 8: Khảo sát thời gian tham gia câu lạc bộ trong một tuần của 100 bạn học sinh, thu được kết quả sau:
Nhóm chứa trung vị của mẫu số liệu trên là A. [90;120). B. [30;60). C. [60;90). D. [120;150). Lời giải Chọn C
Ta có cỡ mẫu n = 36 + 28 +18 +14 + 4 =102 nên trung vị của mẫu số liệu trên là trung bình cộng
của giá trị thứ 51 và 52. Page 6
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 11
Mà giá trị thứ 51 và 52 thuộc nhóm [60;90) nên nhóm này chính là nhóm chứa trung vị của mẫu số liệu đã cho.
Câu 9: Biến đổi sin 6x + sin 4x thành tích là
A. 2sin 6 .xcos 4x .
B. 2sin .xcos5x .
C. 2sin 5 .xcos x .
D. 2sin10 .xcos 2x . Lời giải Chọn C
sin 6x + sin 4x = 2sin 5x cos x
Câu 10: Cho hàm số y = tan x có đồ thị như hình bên dưới π π
Số giá trị của x trên đoạn 3 ; −
để hàm số y = tan x nhận giá trị bằng 0 là 2 2 A. 0. B. 2. C. 1. D. 3. Lời giải Chọn B π π Trên đoạn 3 ; −
đồ thị hàm số y = tan x cắt trục Ox tại 2 điểm phân biệt nên số giá trị của 2 2 π π x trên đoạn 3 ; −
để hàm số y = tan x nhận giá trị bằng 0 là 2. 2 2
Câu 11: Một cấp số nhân có số hạng thứ nhất và thứ hai theo thứ tự là 16 và 36. Số hạng thứ ba là A. 64. B. 56. C. 81. D. 720. Lời giải Chọn C
Gọi q là công bội của cấp số nhân. u =16 1 u =16 u =16 Ta có 1 1 9 ⇒ ⇒
9 ⇒ u = u .q = 36. = 81 3 2 . u = 36 u q = 36 q = 4 2 1 4
Câu 12: Cho một đường tròn có bán kính 5cm . Tính độ dài cung tròn có số đo π . 3 A. π π π l = 5 + (cm). B. 15 l = (cm). C. 5 l = (cm).
D. l = 5 − (cm). 3 π 3 3 Lời giải Chọn C Độ dài cung tròn là π 5π l = . Rα = 5. = (cm). 3 3
PHẦN II: Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai. Page 7
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 11 Câu 1: Cho biết 12 π cos x = − và 3 π < x < . 13 2
a) sin x > 0. b) 5 sin x = − . 13 c) 5 cot x = . 12 d) π 5 −12 3 sin − x = . 3 26 Lời giải a) Sai b) Đúng c) Sai d) Đúng π a) Vì 3 π < x < nên sin x < 0 . 2 2 b) Ta có: 12 2 12 5 cos x = −
⇒ sin x = − 1− cos x = − 1− − = − . 13 13 13 c) cos x 12 cot x = = sin 5 d) π π π
3 12 1 5 5 −12 3 sin − x =
sin cos x − cos sin x = − − − = 3 3 3 2 13 2 13 26
Câu 2: Cho phương trình 2sin x = − 2 (1).
a) Phương trình (1) tương đương với phương trình π sin x sin = − . 4 π π
b) Phương trình (1) có các nghiệm là: x = − + k2π; x = + k2π (k ∈ ) . 4 4 π
c) Phương trình (1) có nghiệm dương nhỏ nhất bằng . 4
d) Số nghiệm của phương trình (1) trong khoảng π π ; − là 1 nghiệm. 2 2 Lời giải a) Đúng b) Sai c) Sai d) Đúng a) − π Ta có: 2 2sin x 2 sin x sin x sin = − ⇔ = ⇔ = − (2) 2 4 π π x = − + k2π x = − + k2π b) (2) 4 4 ⇔ (k ∈ ) ⇔ (k ∈ ). π 5π x = π + + k2π x = + k2π 4 4 π π
Vậy phương trình có các nghiệm là: 5
x = − + k2π; x =
+ k2π (k ∈ ) . 4 4 π
c) Phương trình có nghiệm dương nhỏ nhất bằng 5 . 4 Page 8
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 11
d) Số nghiệm của phương trình trong khoảng π π ; − là 1 nghiệm. 2 2 u
+ u − u = 7 −
Câu 3: Cho cấp số cộng biết: 2 4 6 . u −u = 2u 8 7 4
a) Số hạng đầu của cấp số cộng là: u = 5 − . 1
b) Số hạng thứ 20 của cấp số cộng là: 32.
c) Tổng 30 số hạng đầu của cấp số cộng là: 750 .
d) Số 201 là một số hạng của cấp số cộng. Lời giải a) Đúng b) Sai c) Sai d) Đúng u
+ u − u = 7 − Ta có: 2 4 6 ( ) 1 . u − u = 2u 8 7 4 u +
d + u + 3d − u + 5d = 7 − 1 1 ( 1 ) ( ) u − d = 7 − u = 5 − 1 1 1 ⇔ ⇔ ⇔ . u
+ 7d − u + 6d = 2 u + d u + d = d = l 3 2 5 0 2. 1 ( 1 ) ( ) 1
Vậy cấp số cộng có u = 5
− , d = 2 , u = u + n − d = − + n − = n − . n ( 1) 5 ( 1).2 2 7 1 1
a) Số hạng đầu của cấp số cộng là: u = 5 − nên mệnh đề đúng. 1
b) Ta có u = n − nên u = 2.20 − 7 = 33 . Vậy mệnh đề sai. n 2 7 20 c) Ta có n S =
u + n − d nên 30 S = [2.( 5 − ) + (30 −1).2] = 7 0 2 . Vậy mệnh đề sai. n [2 ( 1) ] 1 2 30 2
d) Ta có: u = n − = ⇔ n =
. Suy ra u 201. Vậy mệnh đề đúng. n 2 7 201 104 104
Câu 4: Điểm thi môn Toán trong kì thi TNTHPT của lớp 12A được thống kê như sau:
a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là 10.
b) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm trên lớn hơn 8 .
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là 2 .
d) Phương sai của mẫu số liệu bằng 1,9. Lời giải a) Sai b) Đúng c) Sai d) Đúng
Cỡ của mẫu số liệu là: n = 2 + 5 + 6 +10 +12 + 5 = 40
Gọi x , x ,..., x là điểm thi Toán của 40 bạn học sinh lớp 12A trong kì thi TNTHPT và giả sử 1 2 40
dãy số liệu gốc này đã được sắp xếp theo thứ tự tăng dần. a) Sai
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: R =10 − 4 = 6 b) Đúng +
Tứ phân vị thứ ba của mẫu số liệu gốc là x x 30
31 nên nhóm chứa tứ phân vị thứ ba là nhóm 2 [8;9) nên ta có Page 9
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 11 3.40 (2 5 6 10) − + + + 4 103 Q = 8 + .1 = ≈ 8,58 3 12 12 c) Sai +
Tứ phân vị thứ nhất của mẫu số liệu gốc là x x 10
11 nên nhóm chứa tứ phân vị thứ nhất là nhóm 2 [6;7) nên ta có 40 (2 5) − + 4 13 Q = 6 + .1 = = 6,5 1 6 2
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là: 103 13 25 ∆ = Q − Q = − = Q 3 1 12 2 12 d) Đúng Ta có:
4,5 2 5,5 5 6,5 6 7,5 10 8,5 12 9,5 5 x × + × + × + × + × + × = = 7,5 40
m x − x + m x − x + m x − x + m x − x 2 1 ( 1 )2 2 ( 2 )2 3 ( 3 )2 4 ( 4 )2 Phương sai: s = = 1,9 32
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. π π Câu 1: Cho góc 3 α ;2π ∈ sao cho 2
cosα = . Tính giá trị củacos α + . 2 3 3 Lời giải Trả lời: 0,98 2 2 2 2 5 sin α =1− cos α =1− = . 3 9 3π α ;2π ∈ ⇒ sinα < 0 ⇒ 5 sinα = − 2 3 π π π 2 1 − 5 3 2 + 15 cos α +
= cosα.cos − sinα.sin = . − . = ≈ 0,98 . 3 3 3 3 2 3 2 6
Câu 2: Trong một hoạt động thiện nguyện, các bạn học sinh lớp 11B đã tiến hành tặng sách cho các
trẻ em vùng khó khăn. Kết quả hoạt động được ghi nhận ở bảng sau:
Tìm tứ phân vị thứ 3 của mẫu số liệu ghép nhóm trên. Lời giải Trả lời: 5,75
Ta có n =10 +13+ 8 + 5 + 4 = 40.
Tứ phân vị thứ 3 của mẫu số liệu ghép nhóm trên. Page 10
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 11 3.40 −(10+13) 4 23 Q = 4 + 6 − 4 = = 5,75. 3 ( ) 8 4
Câu 3: Số giờ có ánh sáng mặt trời của một thành phố X ở vĩ độ 40° bắc trong ngày thứ t của một năm π
không nhuận được cho bởi hàm số d (t) 3sin (t 80) = − +12,
t ∈, 0 < t ≤ 365 . Vào ngày 182
thứ mấy trong năm thì thành phố X có nhiều giờ có ánh sáng mặt trời nhất? Lời giải Trả lời: 171 π Vì 1 − ≤ sinα ≤ 1, α
∀ nên ta có: d (t) = 3sin
(t −80) +12 ≤ 3.1+12 =15 . 182 π π π Suy ra d (t) =15 sin t − 80 =1 ⇔
t − 80 = + k2π max đạt được khi ( ) ( ) 182 182 2
⇔ t = 171+ 364k , k ∈ . −
Vì 0 < t ≤ 365 nên ta có: 171 194
0 <171+ 364k ≤ 365 ⇒ < k ≤
do k ∈ nên k = 0 . 364 364
Vậy vào ngày thứ 171 trong năm thì thành phố X có nhiều giờ có ánh sáng mặt trời nhất.
Câu 4: Một công ty xây dựng mua một chiếc máy ủi với giá 3 tỉ đồng. Cứ sau mỗi năm sử dụng, giá trị
của chiếc máy ủi này lại giảm 20% so với giá trị của nó trong năm liền trước đó. Tìm giá trị còn
lại của chiếc máy ủi đó sau 5 năm sử dụng (làm tròn kết quả đến hàng phần trăm theo đơn vị tỉ đồng). Lời giải Đáp án: 1,23
Giá trị còn lại của chiếc máy ủi lập thành một cấp số nhân với số hạng đầu u = 3 và công bội 1 q = 80% = 0,8 .
Khi đó giá trị còn lại của chiếc máy ủi đó sau 5 năm sử dụng là: 4 u = 3.0,8 =1,2288. 5
Vậy giá trị còn lại của chiếc máy ủi đó sau 5 năm sử dụng là 1,23 (tỉ đồng).
Câu 5: Một chiếc đu quay có tâm của vòng quay ở độ cao 35m so với mặt đất, khoảng cách từ tâm vòng
quay đến vị trí gắn các cabin là 30m . Thời gian thực hiện mỗi vòng của đu quay là 3 phút 20
giây. Một hành khách vào cabin số 1 được gắn tại vị trí A, thấp nhất của vòng quay (tham khảo
hình vẽ), sau t giây kể từ lúc quay, vị trí A cách mặt đất h(t) mét. Biết rằng h(t) có dạng
h(t) = a cos(ωt) + b ( a,b,ω là hằng số). Xác định a,b,ω và tính thời gian ngắn nhất kể từ lúc
quay để vị trí A cách mặt đất 25m (thời gian làm tròn đến hàng đơn vị). Lời giải Trả lời: 39 Page 11
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI – TOÁN 11
Ta có 3 phút 20 giây bằng 200 giây.
Ta có chu kì của vòng quay là 2π π = 200 ⇔ ω = . ω 100
Ta có −a ≤ a cos(ωt) ≤ a ⇔ −a + b ≤ acos(ωt) + b ≤ a + b ⇔ −a + b ≤ h(t) ≤ a + b .
Mặt khác, theo đề bài ta có chiều cao h(t) = a cos(ωt) + b có chiều cao thấp nhất và cao nhất lần −a + b = 5 a = 30
lượt là 5 và 65 nên ta có hệ phương trình ⇔ . a b 65 + = b = 35 Khi đó π h(t) 30cos t = + 35 . 100
Để cabin A cách mặt đất π π 25 − m thì 1 30cos t + 35 = 25 ⇔ cos t = 100 100 3 π 1 − 100 1 t arccos k2π t arccos − = + = + 200k 100 3 π 3 ⇔ ⇔ (k ∈)(*) . π 1 − 100 1 t arccos k2π t arccos − = − + = − + 200k 100 3 π 3
Khi đó, ta có được thời gian ngắn nhất từ lúc bắt đầu đến khi cabin A cách mặt đất 25m là
nghiệm dương nhỏ nhất của ( − *) hay 100 1 t arccos = ≈ 39 . π 3
Vậy thời gian thời gian ngắn nhất từ lúc bắt đầu đến khi cabin A cách mặt đất 25m là 39 giây.
Câu 6: Tỉ lệ tăng dân số mỗi năm của một tỉnh X từ năm 2010 đến năm 2019 là 0,4% . Vì thực hiện
các chính sách về dân số nên tỉnh X dự kiến từ năm 2020 đến 2030 tỉ lệ tăng dân số mỗi năm
chỉ còn lại 0,35% . Theo thống kê số dân tỉnh X năm 2021 nhiều hơn năm 2017 là 30400
người. Hỏi số dân tỉnh X năm 2030 khoảng bao nhiêu triệu người? (kết quả làm tròn đến hàng phần trăm) Lời giải Trả lời: 2,11
Gọi dân số của tỉnh X vào năm 2010 là a (người, a ∈ *).
Khi đó số dân mỗi năm của tỉnh X từ năm 2010 đến năm 2019 là một cấp số nhân có u = a 1 và q = 1+ 0,4% .
Khi đó số dân năm 2017 và số dân năm 2019 là u = a(1+ 0,4%)7 và u = a 1+ 0,4% . Từ 10 ( )9 8
đó số dân của tỉnh X năm 2020 là a( + )9 1 0,4% (1+ 0,35%).
Khi đó số dân mỗi năm của tỉnh X từ năm 2020 đến năm 2030 là một cấp số nhân có
u * = a(1+ 0,4%)9 1+ 0,35% và + nên số dân năm 1 ( ) * q = 1 0,35% 2021 là a( + )9 ( + )2 1 0,4% 1 0,35% .
Theo đề bài, ta có a( + )9 ( + )2 − a( + )7 1 0,4% 1 0,35%
1 0,4% = 30400 ⇔ a = 1959782 (người).
Khi đó, số dân tỉnh X năm 2030 là ( + )9 ( + )11
1959782 1 0,4% 1 0,35% ≈ 2,11 triệu người.
---------- HẾT ---------- Page 12
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI –TOÁN 11
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI
MÔN: TOÁN 11 – ĐỀ SỐ: 02
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1: Dãy số nào sau đây là cấp số nhân? u 1 u 1 A. 1 . . u B. 1 u u n n n 1, 1 u n n 3 n, 1 1 1 u 1 2 u 2 C. . D. 1 . u u u n n 2 n 3, 1 n 1 n sin , 1 n 1
Câu 2: Hàm số y = cot x có tập xác định là π A. π \ k D | k = ∈ ⋅
B. D = \ + kπ | k ∈. 2 2
C. D = \ {k2π | k ∈ } ⋅
D. D = \ {kπ | k ∈ } ⋅
Câu 3: Phương trình lượng giác 3tan x − 3 = 0 có nghiệm là π π π
A. x = + kπ,k ∈ . B. x = + kπ, k ∈. C. Vô nghiệm.
D. x = + k2π ,k ∈ . 6 3 6
Câu 4: Trong các dãy số (u dưới đây, dãy số nào bị chặn dưới? n )
A. u = n − . B. 2
u = −n − n .
C. u = − n . D. u = − n . n ( )n 2 1 . n 1 2 n 6 n 2
Câu 5: Phỏng vấn một số học sinh khối 11 về thời gian ngủ (giờ) của một buổi tối thu được kết quả sau
75% số học sinh ngủ ít nhất bao nhiêu giờ trong một buổi tối? A. 5,92 . B. 7,68 . C. 6,65. D. 5,64.
Câu 6: Trên khoảng ( π
− ;π ) , đồ thị hàm số y = sin x được cho như hình vẽ.
Hàm số y = sin x nghịch biến trong khoảng nào sau đây? π π π A. ( π − ;0) . B. (0;π ) . C. ;π . D. − ; . 2 2 2 Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI –TOÁN 11 π
Câu 7: Cho góc α thỏa mãn 3
tanα = . Tính P tan α = + . 5 4 A. P = 4 . B. 8 P = . C. P = 3. D. 3 P = . 5 5
Câu 8: Biết bốn số 2;8; ;
x 128 theo thứ tự lập thành một cấp số nhân. Giá trị của x bằng
A. x = 64 .
B. x = 24 .
C. x = 32 .
D. x =16 .
Câu 9: Tính tổng S của các nghiệm của phương trình 1
sin x = trên đoạn π ;π − . 2 2 2 π π π π A. S = . B. S = . C. S = . D. 5 S = . 2 6 3 6
Câu 10: Tìm giá trị nhỏ nhất m của hàm số y = − 2 sin(2023x + 2024) . A. m = 1 − .
B. m 2023 2 . C. m 2 .
D. m 2024 2 .
Câu 11: Người ta ghi lại tuổi thọ của một số con muỗi cái trong phòng thí nghiệm cho kết quả như sau:
Muỗi cái có tuổi thọ khoảng bao nhiêu ngày là nhiều nhất? A. 76 ngày. B. 90ngày. C. 80 ngày. D. 66 ngày.
Câu 12: Cho cấp số cộng (u có số hạng đầu u = 5
− và công sai d = 3. Số 94 là số hạng thứ mấy của n ) 1 cấp số cộng? A. 33. B. 20 . C. 34. D. 35.
PHẦN II: Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai. π
Câu 1: Cho góc lượng giác α thỏa mãn cotα = 3 − α 0 − < < . 2 a) sinα > 0. α − α b) cos sin 10 = . 3 3 cos α + 3sin α + 2 o c sα 21 π c) 5 sin α + = − . 4 5 π π d) 2 2 2 2 2 3 cos α + cos +α + cos −α = . 3 3 2 Page 2
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI –TOÁN 11
Câu 2: Cho phương trình 2sin x = m .
a) Khi m = 5 phương trình đã cho có nghiệm.
b) Phương trình đã cho có nghiệm khi và chỉ khi m∈[ 1; − ] 1 . π
c) Khi m = 2 phương trình đã cho có nghiệm x = ± + k2π ,k ∈ . 4 π d) Khi m = 1
− phương trình đã cho có nghiệm 2 x = ±
+ k2π ,k ∈ . 3
Câu 3: Một rạp hát có 20 hàng ghế. Hàng thứ nhất có 20 ghế, số ghế ở các hàng sau đều hơn số ghế hàng
ngay trước đó một ghế. Cho biết rạp hát đã bán hết vé với giá mỗi vé là 60 nghìn đồng. Rạp hát
dự định quyên góp cho quỹ Be Flower 35000000 đồng để hỗ trợ các em nhỏ vùng khó khăn
được tiếp bước đến trường. Gọi u là số ghế ở hàng thứ n . n
a) Dãy số (u tạo thành cấp số cộng với u = 20 và d =1. n ) 1
b) Dãy số (u tạo thành cấp số cộng, công thức số hạng tổng quát là u = + n . n 19 . n )
c) Tổng số ghế có trong rạp hát là 590 ghế.
d) Tổng số tiền vé thu được đủ để rạp hát quyên góp vào quỹ BE Flower.
Câu 4: Số lượng người đi xem bộ phim Lật Mặt 7 của Lý Hải theo độ tuổi trong một rạp chiếu phim
(sau 1 h đầu công chiếu) được ghi lại theo bảng số liệu sau:
a) Cỡ mẫu của mẫu số liệu là 74 .
b) Độ tuổi được dự báo là ít xem phim Lật Mặt 7 nhất là thuộc nhóm [50;60) .
c) Trung vị của mẫu số liệu là 26,42 (kết quả làm tròn đến hàng phần trăm).
d) Độ tuổi được dự báo là thích xem phim Lật Mặt 7 nhiều nhất là 29 tuổi.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Bánh xe của người đi xe đạp quay được 10 vòng trong 5 giây. Tính độ dài quãng đường mà người
đi xe đã đi được trong 1 phút( đơn vị tính bằng mét và làm tròn kết quả đến hàng đơn vị, lấy
π = 3,14 ), biết rằng đường kính của bánh xe đạp là 0,68m.
Câu 2: Số nghiệm phương trình: (2sin x + 2)(2cos x − 3) = 0 trên [0;21π ] là Page 3
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI –TOÁN 11
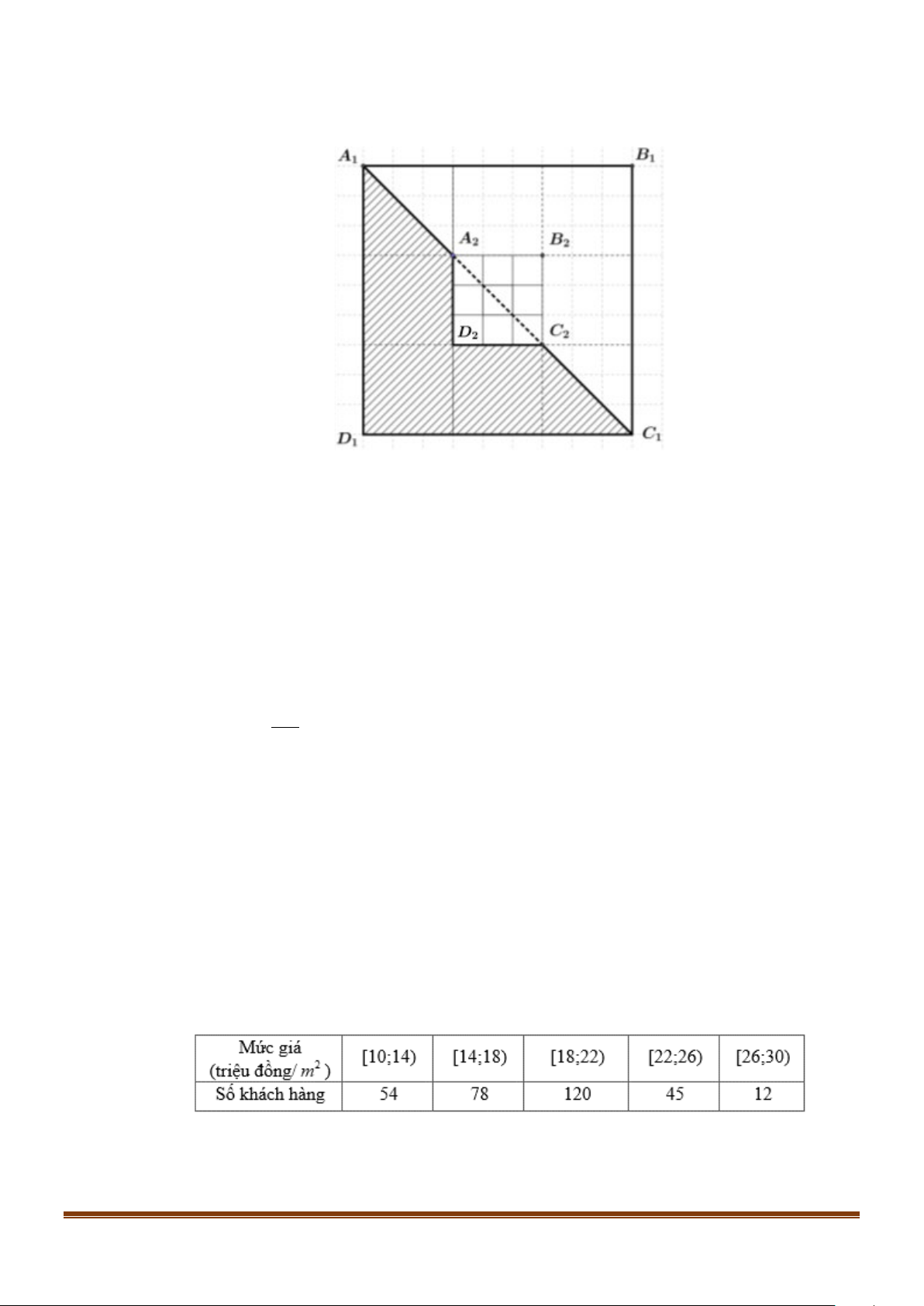
Câu 3: Với hình vuông A B C D như hình vẽ dưới đây, cách tô màu như phần gạch sọc được gọi là 1 1 1 1
cách tô màu “đẹp”. Một nhà thiết kế tiến hành tô màu cho một hình vuông như hình bên, theo quy trình sau:
Bước 1: Tô màu “đẹp” cho hình vuông A B C D . 1 1 1 1
Bước 2: Tô màu “đẹp” cho hình vuông A B C D là hình vuông ở chính giữa khi chia hình 2 2 2 2
vuông A B C D thành 9 phần bằng nhau như hình vẽ. 1 1 1 1
Bước 3: Tô màu “đẹp” cho hình vuông A B C D là hình vuông ở chính giữa khi chia hình 3 3 3 3
vuông A B C D thành 9 phần bằng nhau… 2 2 2 2
Cứ tiếp tục như vậy. Hỏi cần ít nhất bao nhiêu bước để tổng diện tích phần được tô màu chiếm ít
nhất 49,99% diện tích hình vuông A B C D . 1 1 1 1
Câu 4: Số giờ có ánh sáng mặt trời của thành phố A trong ngày thứ t của năm 2023 được cho bởi hàm số π y 9 2cos (t ) 61 = − − , *
t ∈ . Vào ngày thứ bao nhiêu trong năm 2023 thì thành phố 118
A có số giờ có ánh sáng mặt trời nhiều nhất?
Câu 5: Anh Thắng kí quỹ hợp đồng thi công xây dựng tòa chung cư với Công ty Cổ phần Xây dựng
ADP tại Ngân hàng TMCP Kỹ Thương Việt Nam (Techcombank). Theo đó, hai bên cam kết
khoản thanh toán lần đầu là 5 tỉ đồng. Sau đó, mỗi tháng nghiệm thu đúng tiến độ, sẽ tiếp tục
thanh toán một khoản giảm 200 triệu đồng so với tháng trước cho đến bàn giao xong tòa chung
cư. Gọi s (triệu đồng) là số tiền mà công ty ADP nhận được vào lần thứ n , khi đó: n s = s −
∀ ≥ Số tiền công ty ADP nhận được vào tháng thứ 18 kể từ khi thi công là − n n n 200, 2. 1
a (triệu đồng). Tính giá trị của a , biết công ty ADP chậm tiến độ 1 tháng.
Câu 6: Một công ty xây dựng khảo sát khách hàng xem họ có nhu cầu mua nhà ở mức giả nào. Kết quả
khảo sát được ghi lại ở bảng sau:
Hỏi công ty nên xây nhà ở mức giá nào để nhiều người có nhu cầu mua nhất?
---------- HẾT ---------- Page 4
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI –TOÁN 11
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Câu 1: Dãy số nào sau đây là cấp số nhân? u 1 u 1 A. 1 . . u B. 1 u u n n n 1, 1 u n n 3 n, 1 1 1 u 1 2 u 2 C. . D. 1 . u u u n n 2 n 3, 1 n 1 n sin , 1 n 1 Lời giải Chọn A Đáp án A có: un 1 u = − ⇒
= − không đổi, suy ra dãy số ở đáp án A là một cấp số nhân. + u + n 3 n 3 1 un
Câu 2: Hàm số y = cot x có tập xác định là π A. π \ k D | k = ∈ ⋅
B. D = \ + kπ | k ∈. 2 2
C. D = \ {k2π | k ∈ } ⋅
D. D = \ {kπ | k ∈ } ⋅ Lời giải Chọn D
Điều kiện xác định: cos x ≠ 0 ⇔ x ≠ kπ ,k ∈ .
Tập xác định của hàm số là D = \ {kπ | k ∈ } ⋅
Câu 3: Phương trình lượng giác 3tan x − 3 = 0 có nghiệm là π π π
A. x = + kπ,k ∈ . B. x = + kπ, k ∈. C. Vô nghiệm.
D. x = + k2π ,k ∈ . 6 3 6 Lời giải Chọn A 3tan x − 3 = 0 3 ⇔ tan x = 3 π ⇔ tan x = tan 6 π
⇔ x = + kπ ,k ∈ 6
Câu 4: Trong các dãy số (u dưới đây, dãy số nào bị chặn dưới? n )
A. u = n − . B. 2
u = −n − n .
C. u = − n . D. u = − n . n ( )n 2 1 . n 1 2 n 6 n 2 Lời giải Chọn A
u = n − ≥ − , n ∗ ∀ ∈
u bị chặn dưới. n 2 1 nên n Page 5
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI –TOÁN 11
Câu 5: Phỏng vấn một số học sinh khối 11 về thời gian ngủ (giờ) của một buổi tối thu được kết quả sau
75% số học sinh ngủ ít nhất bao nhiêu giờ trong một buổi tối? A. 5,92 . B. 7,68 . C. 6,65. D. 5,64. Lời giải Chọn D
Tứ phân vị thứ nhất của mẫu số liệu trên là Q ≈ 5,64 nên 75% số học sinh ngủ ít nhất 5,64 1
giờ trong một buổi tối.
Câu 6: Trên khoảng ( π
− ;π ) , đồ thị hàm số y = sin x được cho như hình vẽ.
Hàm số y = sin x nghịch biến trong khoảng nào sau đây? π π π A. ( π − ;0) . B. (0;π ) . C. ;π . D. − ; . 2 2 2 Lời giải Chọn C π π
Dựa vào đồ thị suy ra hàm số y = sin x nghịch biến trên các khoảng π; − − và ;π 2 2 π
Câu 7: Cho góc α thỏa mãn 3
tanα = . Tính P tan α = + . 5 4 A. P = 4 . B. 8 P = . C. P = 3. D. 3 P = . 5 5 Lời giải Chọn A π 3 tanα + tan +1 π α Có 4 tan +1 5 tan α + = = = = 4. 4 π 1− tanα 3 1− tanα.tan 1− 4 5
Câu 8: Biết bốn số 2;8; ;
x 128 theo thứ tự lập thành một cấp số nhân. Giá trị của x bằng
A. x = 64 .
B. x = 24 .
C. x = 32 .
D. x =16 . Lời giải Chọn C Ta có 2;8; ;
x 128 lập thành 1 cấp số nhân nên 2
8 2.x x 32 Kiểm tra lại ta thấy 2 32 8.128( thỏa mãn ). Page 6
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI –TOÁN 11
Câu 9: Tính tổng S của các nghiệm của phương trình 1
sin x = trên đoạn π ;π − . 2 2 2 π π π π A. S = . B. S = . C. S = . D. 5 S = . 2 6 3 6 Lời giải Chọn B π
x k2 Ta có 1
sin x = ⇔ sin x = sin 6
( với k;l Z ) 2 6 5 x l2 6
+Xét bất phương trình 1 1 1 1 1 k2 2k k 2 6 2 2 6 2 3 6 Do k Z k 0 x 6 + 5 1 5 1 2 1 l2 2l l 2 6 2 2 6 2 3 6 Do l
Z nên không có giá trị l nguyên để 5 l2 2 6 2 Vậy x π π
là nghiệm duy nhất của phương trình thuộc ; − 6 2 2 Vậy S . 6
Câu 10: Tìm giá trị nhỏ nhất m của hàm số y = − 2 sin(2023x + 2024) . A. m = 1 − .
B. m 2023 2 . C. m 2 .
D. m 2024 2 . Lời giải Chọn C
Ta có x , 1 sinx 1
Suy ra 1 sin2023x 20241
⇔ 2 2 sin2023x 2024 2
Vậy giá trị nhỏ nhất m của hàm số y 2 sin2023x 2024 là m 2 .
Câu 11: Người ta ghi lại tuổi thọ của một số con muỗi cái trong phòng thí nghiệm cho kết quả như sau:
Muỗi cái có tuổi thọ khoảng bao nhiêu ngày là nhiều nhất? A. 76 ngày. B. 90ngày. C. 80 ngày. D. 66 ngày. Lời giải Chọn A
Số ngày muỗi cái có tuổi thọ nhiều nhất là mốt của mẫu số liệu.
Nhóm có tần số nhiều nhất là nhóm 4. Vì vậy nhóm chứa mốt là nhóm 4: [60;80) . Page 7
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI –TOÁN 11
Ta có j = 4,a = 60,m = 31,m = 23,m = 29,h = 20. 4 4 3 5 Do đó 31 23 M − = + = . o 60 ( − )+( − ).20 76 31 23 31 29
Vậy Muỗi cái có tuổi thọ khoảng 76 ngày là nhiều nhất.
Câu 12: Cho cấp số cộng (u có số hạng đầu u = 5
− và công sai d = 3. Số 94 là số hạng thứ mấy của n ) 1 cấp số cộng? A. 33. B. 20 . C. 34. D. 35. Lời giải Chọn C
Áp dụng công thức u = u + n − d n 1 . 1 ( ) Suy ra 94 = 5 − + (n − )
1 .3 ⇔ 3n =102 ⇔ n = 34 .
Vậy số 94 là số hạng thứ 34 của cấp số cộng (u . n )
PHẦN II: Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai. π
Câu 1: Cho góc lượng giác α thỏa mãn cotα = 3 − α 0 − < < . 2 a) sinα > 0. α − α b) cos sin 10 = . 3 3 cos α + 3sin α + 2 o c sα 21 π c) 5 sin α + = − . 4 5 π π d) 2 2 2 2 2 3 cos α + cos +α + cos −α = . 3 3 2 Lời giải a) Sai b) Đúng c) Sai d) Đúng π
a) Sai: Do − < α < 0 nên sinα < 0 . 2 α − α b) Đúng: cos sin 10 = 3 3 cos α + 3sin α + 2 os c α 21 α − α Xét biểu thức cos sin P = 3 3 cos α + 3sin α + 2c s o α cosα 1 − 2 2 3 2 cotα α (1+cot α)−(1+cot α α ) Chia cả tử và mẫu cho 3 sin α ta được sin sin P = = 3 3 cos α o c sα cot α + 3+ 2cotα ( 2 1+ cot α ) + 3+ 2 3 3 sin α sin α Thay cotα = 3
− vào P ta được 10 P = . 21 Page 8
Sưu tầm và biên soạn