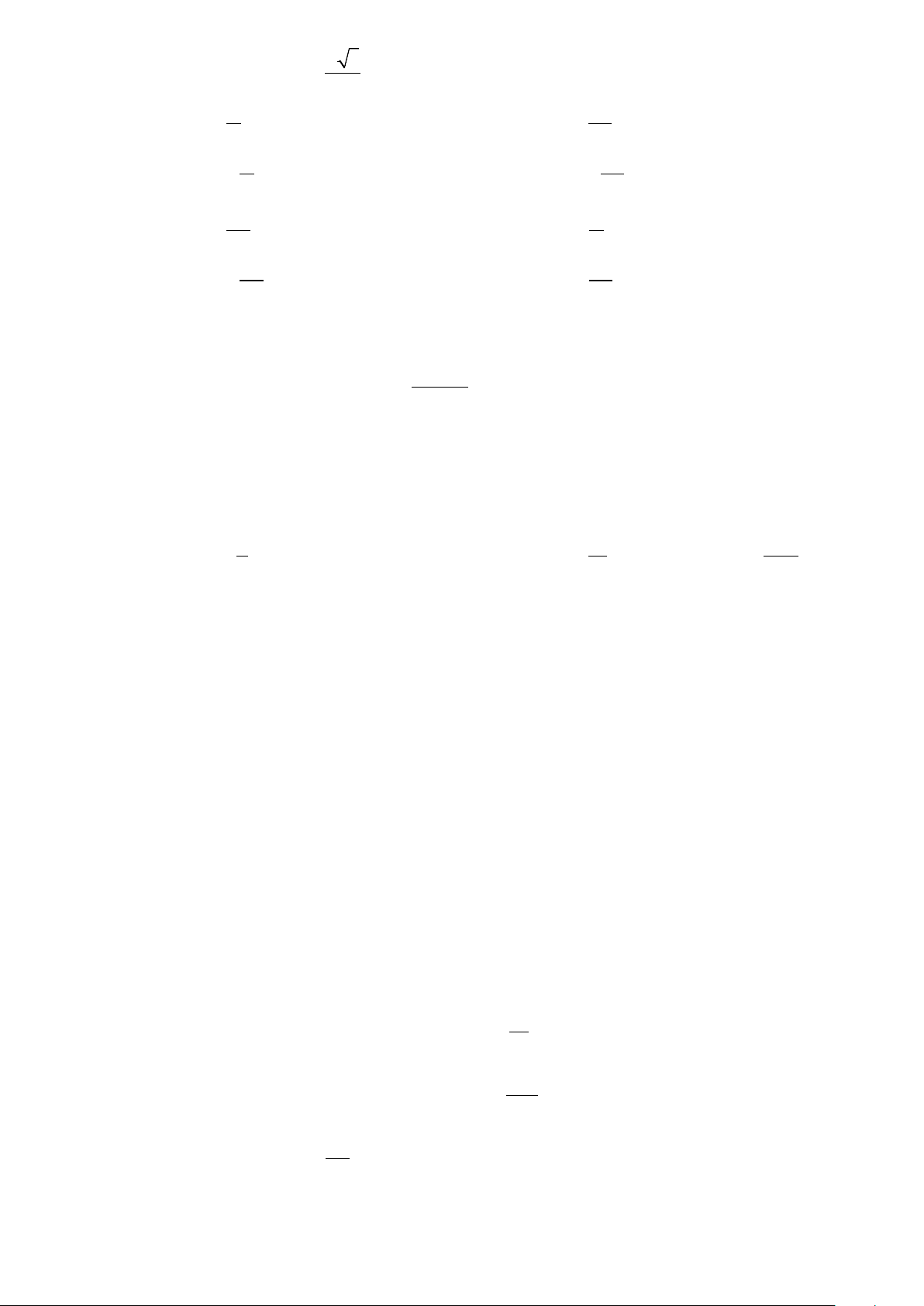








Preview text:
C C HƯ HƯ C HƯ S ƠN ON ƠN ƠN G. G S G. G Ch DÃY S I G. ÁC ủ Q ON LƯ đ UAN H ề G Ợ T Ố NG ổ ng s Ệ
ố câu s Đư s Ha không gi Đi C C D gi P H lư C m Gi ong m ong ấ ấ ã ờ i ể á hư à ợ á ộ p s p s y s m c m ng t đ ơ ng gi c á t phé góc M tr ư , đ ố ố ố ng s p ờ ng t ư nhâ c ố ị A TR N a ộ lư á lư n ờ ộ ng c h n t n r ợ p ợ i ẳ g, ng h ì ng gi bi n dung Ậ nh g ẳ N m ng gi ế p t á n á Đ l s s r ư c c Ề ong ong ong ợ c đ T ng ổ ủ i a HI GI 1 2 1 1 1 2 2 1 1 qua Ph ầ Ữ n n 1. T A K (m M ức Ô Ỳ đ rắ N: 1 ộ c 12 – 1 nghi TO Đ - Ị 2) ÁN 1 NH ệm D khá 1 Ạ NG ch TR 1 1 1 1 (m Ph Ắ ứ ầ c n 2. T C N đ N hó ộ GHI 1 m r – ắ c c 2 â Ệ nghi u h M 4 - 3) ỏ 20 ệ i m 25 đú ng sai 1 1 1 1 1 1 (m Ph ứ ầ c n 3. T đ ộ 3 6 - r ả 4) l ời ng ắn
ĐỀ KIỂM TRA GIỮA KỲ 1. TOÁN 11. ĐỀ SỐ 1
Phần 1. Câu trắc nghiệm nhiều phương án chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.
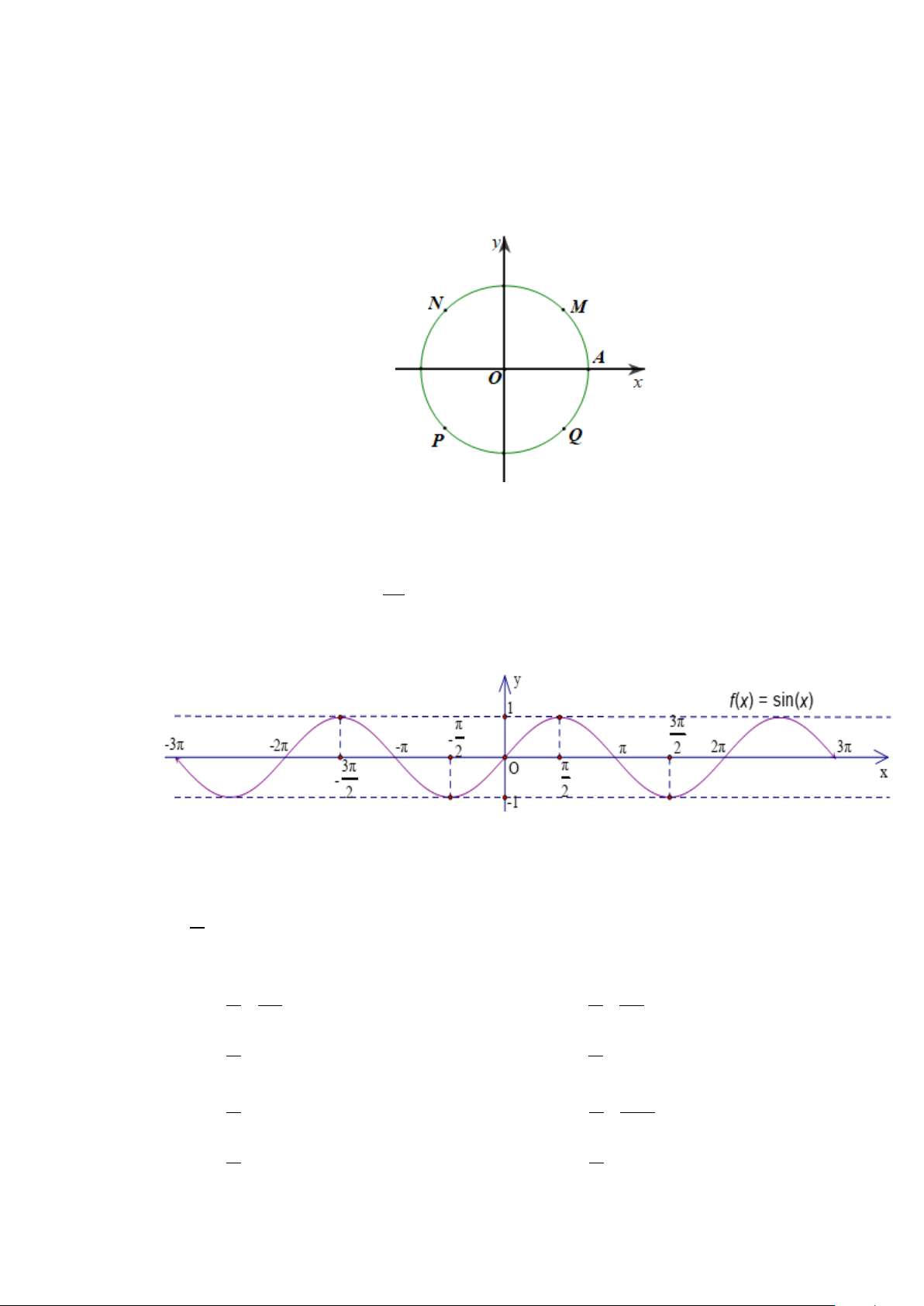
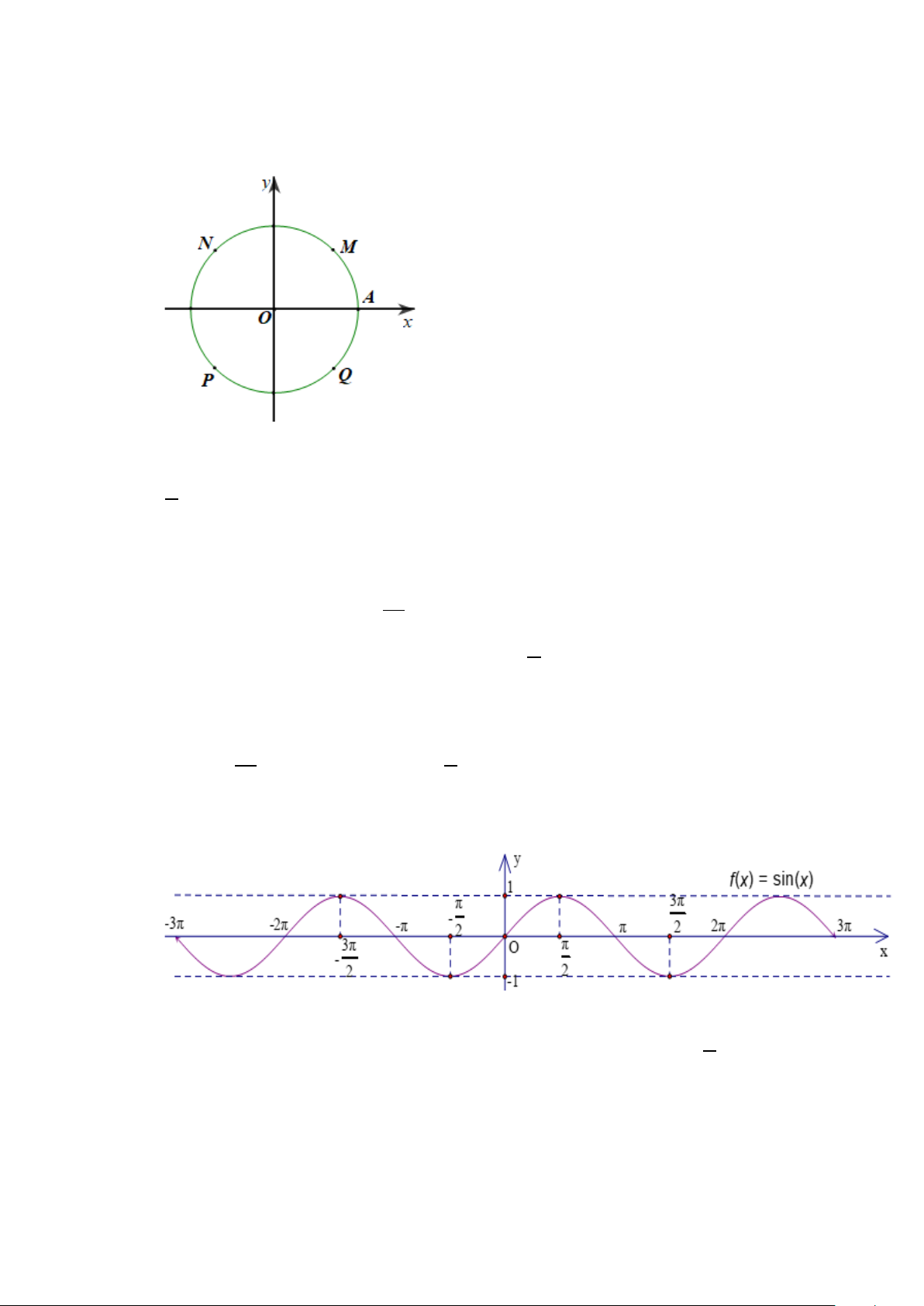
Câu 1. Trong mặt phẳng tọa độ Oxy , trên đường tròn lượng giác cho các điểm M, N, P, Q ở chính giữa
các cung trong 4 góc phần tư như hình vẽ.
Cho góc lượng giác có tia đầu là OA và số đo là 225°. Tia cuối của góc lượng giác đã cho là tia nào sau đây? A. OP . B. OQ . C. OM . D. ON .
Câu 2. Đơn giản biểu thức 9 A cos π α = + + sin (α + π ) ta được 2
A. A = 0
B. A = cosα + sinα C. A = 2 − sinα D. A = 2sinα
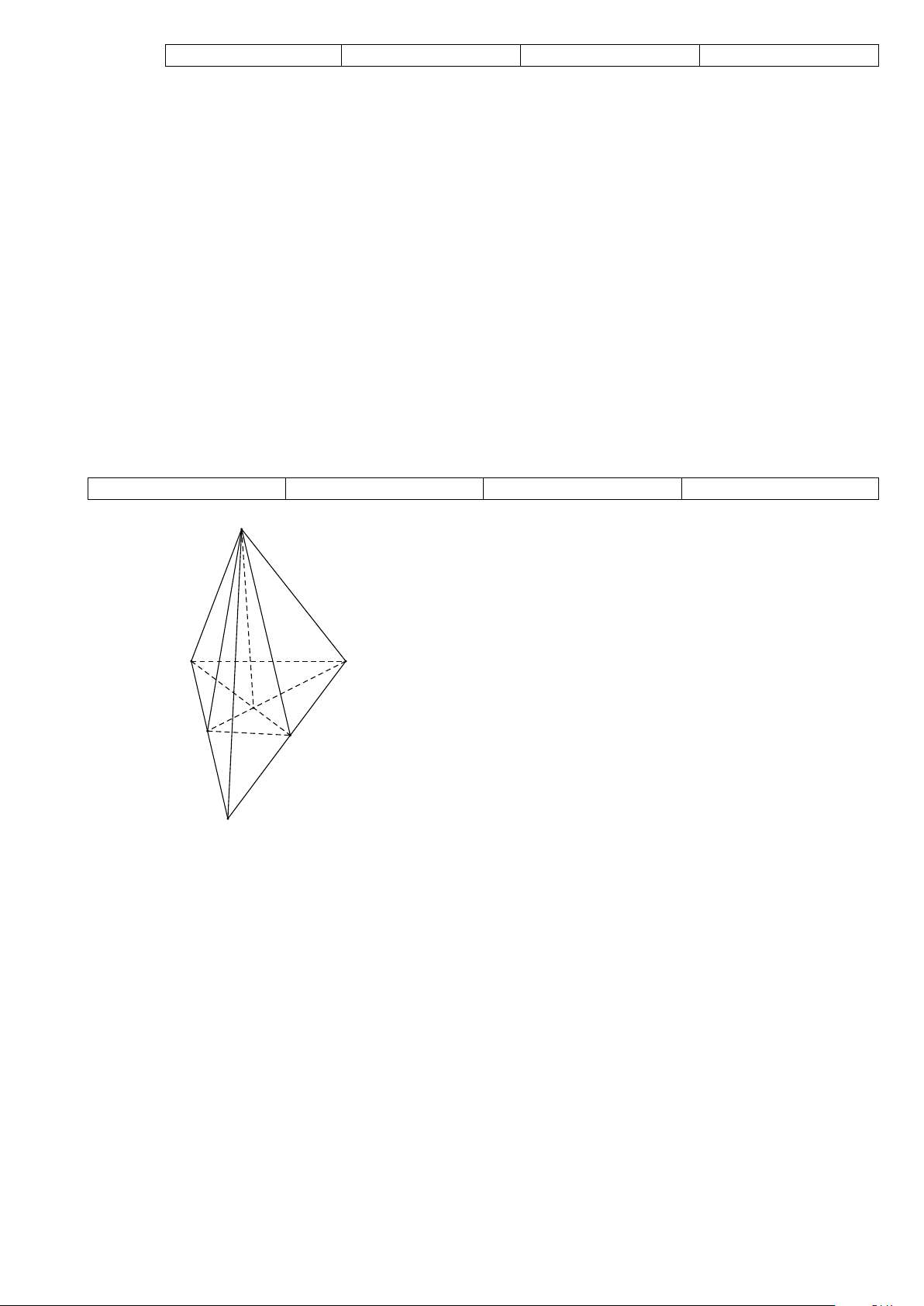
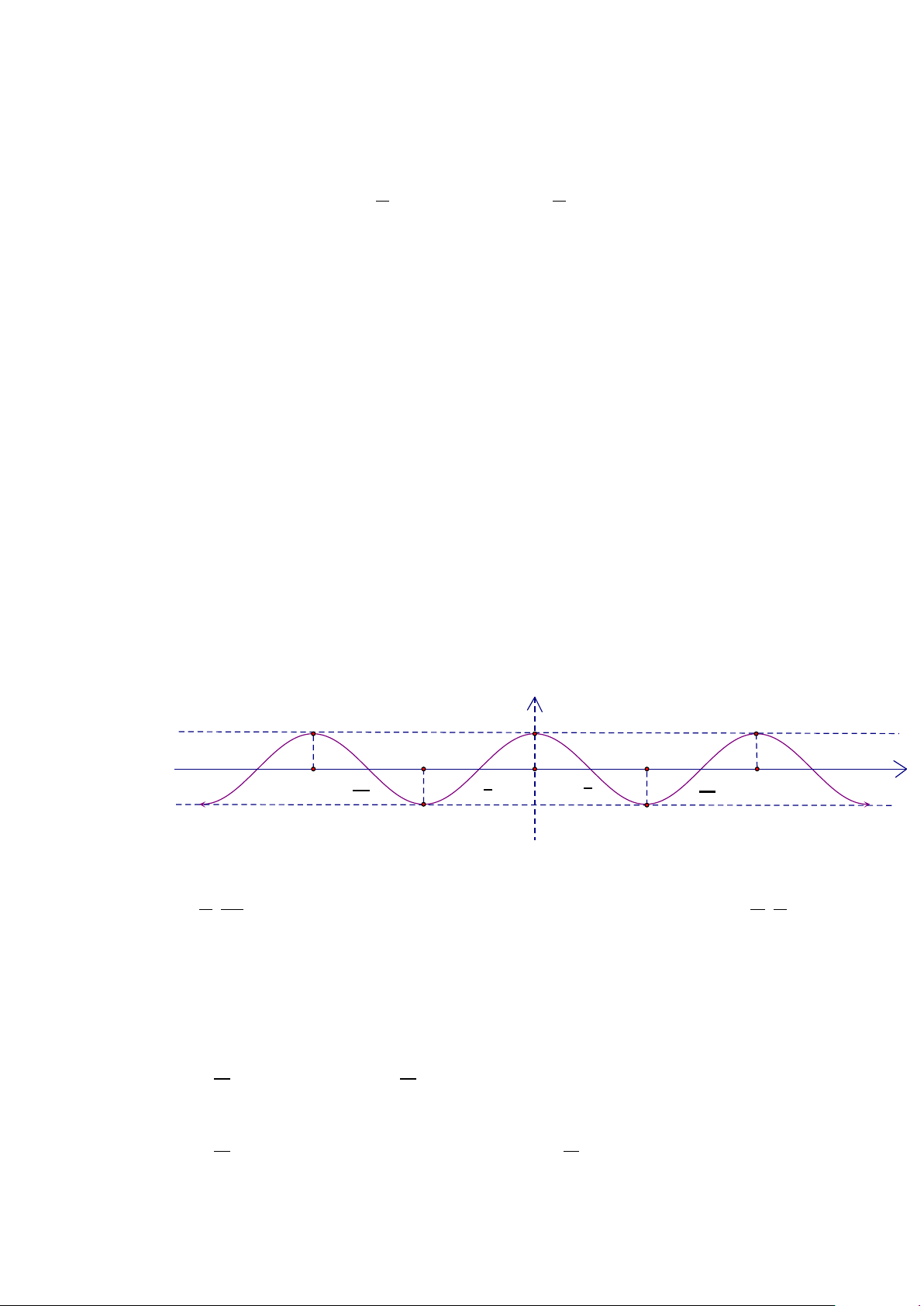
Câu 3. Cho đồ thị hàm số y = sin x :
Từ đồ thị trên hãy chỉ ra số nghiệm của phương trình sin x =1 trên [ 3 − π;3π ]? A. 6 B. 7 C. 1 D. 3
Câu 4. Chu kỳ của hàm số y = sin x là: π A. . B. π . C. 2π .
D. k2π , k ∈ . 2
Câu 5. Phương trình sin 2x = cos x có nghiệm là π kπ π π x = + k x = + A. 6 3 (k ∈) . B. 6 3 (k ∈) . π π x = + k2π x = + k2π 2 3 π π π x = + k2π k2 x = + C. 6 (k ∈) . D. 6 3 (k ∈) . π π x = + k2π x = + k2π 2 2 1
Câu 6. Phương trình 3 cos x − =
có hai họ nghiệm là: 2 π π x = + k2π 5 x = + k2π A. 3 ,k ∈ 6 ,k ∈ π B. π x = − + k2π 5 x = − + k2π 3 6 2π π x = + k2π x = + k2π C. 3 ,k ∈ D. 6 ,k ∈ 2π π x = − + k2π 5 x = + k2π 3 6
Câu 7. Trong các dãy số (u cho bởi công thức số hạng tổng quát u sau, dãy số nào là một cấp số n ) n nhân?
A. u = 3− 2 .n B. 3 u = C. u =
D. u = − n n 4 5 . n 5.2 .n n . n 2(n +1)
Câu 8. Cấp số cộng ( u ) có số hạng đầu u = − 2, công sai d = 3. Công thức của số hạng tổng quát u n 1 n là:
A. u = n −
B. u = + n
C. u = n −
D. u = − + n n 2 3 n 3 8. n 5 3 . n 3 5.
Câu 9. Trong các dãy số (u cho bởi số hạng tổng quát u dưới đây, dãy số nào là dãy số tăng? n ) n A. 1 u = − n ; u = n + . u = . u = . n . B. C. 1 D. 1 n 2 2 n 3n n n +1
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt
phẳng (SAD) và (SBC) . Khẳng định nào sau đây đúng?
A. d đi qua S và song song với BD .
B. d đi qua S và song song với DC .
C. d đi qua S và song song với AB .
D. d đi qua S và song song với BC .
Câu 11. Cho biết mệnh đề nào sau đây là sai ?
A. Có một và chỉ một mặt phẳng đi qua hai đường thẳng song song.
B. Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
C. Có một và chỉ một mặt phẳng đi qua một đường thẳng và một điểm không thuộc nó.
D. Có một và chỉ một mặt phẳng đi qua hai đường thẳng cho trước.
Câu 12. Cho năm điểm phân biệt ,
A B,C, D, E, trong đó không có bốn điểm nào ở trên cùng một mặt
phẳng. Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong số năm điểm đã cho? A. 14. B. 10. C. 12. D. 8.
Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai
Câu 1. Xác định tính đúng, sai của các mệnh đề sau π
a) Ta đổi số đo của góc 15° sang radian bằng 12 π b) 13
Ta đổi số đo của góc 65° sang radian bằng 36 π c) 4 Đổi số đo của góc
sang độ bằng 48° 15 2 π d) 19 Đổi số đo của góc −
sau đây sang độ bằng 427,5° − 8
Câu 2. Cho hàm số f (x) = tan 2x −1. Khi đó:
a) Giá trị của hàm số tại π x = bằng 0 8
b) Giá trị của hàm số tại π
x = bằng − 3 −1 3
c) Có ba giá trị x thuộc [0;π ] khi hàm số đạt giá trị bằng 2 − .
d) Hàm số đã cho là hàm tuần hoàn.
Câu 3. Cho dãy số (u . Khi đó: n )
a) Nếu (u giảm thì (u bị chặn. n ) n )
b) Nếu (u giảm thì (u bị chặn trên. n ) n )
c) Nếu (u tăng thì (u bị chặn dưới. n ) n )
d) Nếu (u bị chặn trên và bị chặn dưới thì (u bị chặn. n ) n )
Câu 4. Cho hình chóp S.ABCD có đáy là hình thang ABCD ( AB CD).
Các mệnh đề sau đúng hay sai?
a) Hình chóp S.ABCD có 4 mặt bên.
b) Giao tuyến của hai mặt phẳng (SAC) và (SBD) là SO (O là giao điểm của AC và BD).
c) Giao tuyến của hai mặt phẳng (SAD) và (SBC) là SI (I là giao điểm của AD và BC).
d) Giao tuyến của hai mặt phẳng (SAB) và (SAD) là đường trung bình của ABC . D
Phần 3. Câu trả lời ngắn.
Thí sinh trả lời đáp án từ câu 1 đến câu 6.
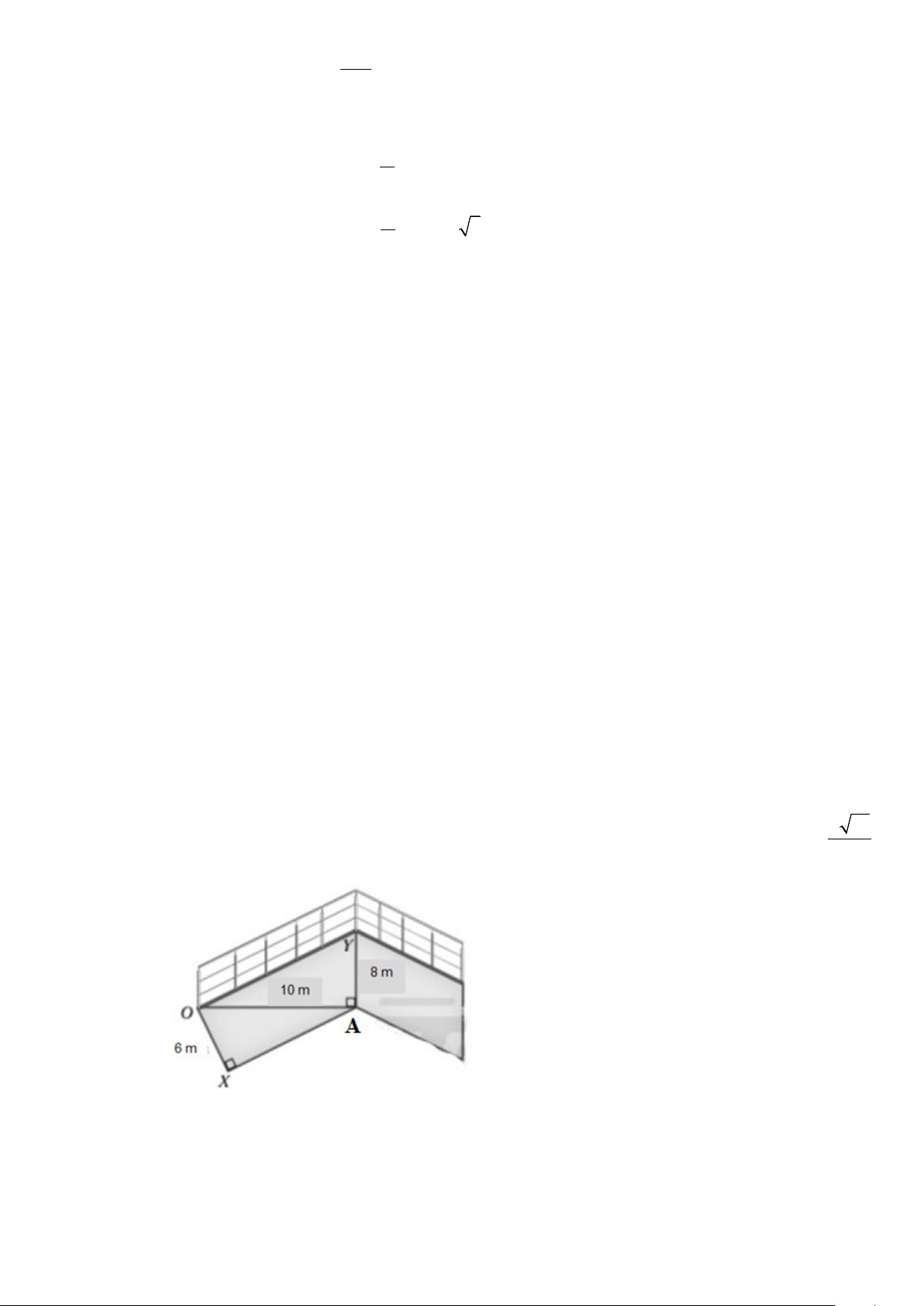
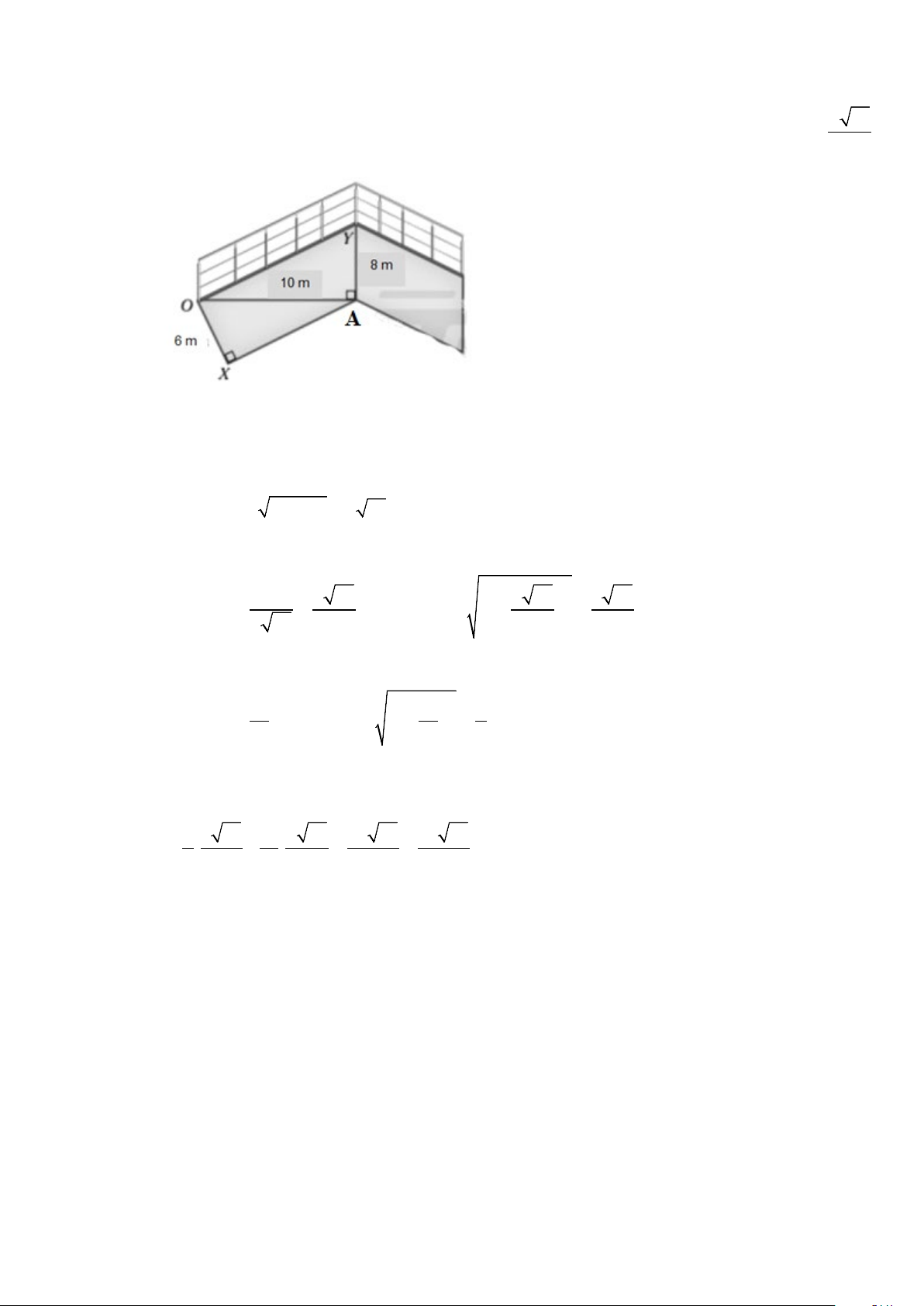
Câu 1. Sơ đồ cho thấy một phần cấu trúc kim loại của một cây cầu. Giá trị của
sin XOY bằng a 41 . 205 Tìm a
Câu 2. Tập giá trị của hàm số: y = 5 + 4sin 2xcos 2x là T = [ ;
a b] , tính b − a
Câu 3. Hỏi có bao nhiêu giá trị nguyên của m để các phương trình lượng giác sau có nghiệm:
2sin 3x = m −1. 3 u = 4
Câu 4. Cho dãy số (u xác định bởi hệ thức truy hồi 1
. Số hạng thứ bốn của dãy số bằng? n ) u = + + u n n 1 n
Câu 5. Một cầu thang bằng gạch có tổng cộng 30 bậc. Để xây xong bậc dưới cùng cần 100 viên gạch.
Mỗi bậc tiếp theo cần ít hơn hai viên gạch so với bậc ngay trước nó. Hỏi cần tất cả bao nhiêu
viên gạch để xây xong cầu thang đó?
Câu 6. Trong mặt phẳng (α ) , cho 3 điểm ,
A B,C trong đó không có 3 điểm nào thẳng hàng. Điểm
S ∉(α ) , hỏi có bao nhiêu mặt phẳng tạo bởi S và các điểm đã cho? PHIẾU TRẢ LỜI 4
LỜI GIẢI THAM KHẢO
Phần 1. Câu trắc nghiệm nhiều phương án chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.
Câu 1. Trong mặt phẳng tọa độ Oxy , trên đường tròn lượng giác cho các điểm M, N, P, Q ở chính giữa
các cung trong 4 góc phần tư như hình vẽ.
Cho góc lượng giác có tia đầu là OA và số đo là 225°. Tia cuối của góc lượng giác đã cho là tia nào sau đây? A. OP . B. OQ . C. OM . D. ON . Lời giải Chọn A
Câu 2. Đơn giản biểu thức 9 A cos π α = + + sin (α + π ) ta được 2
A. A = 0
B. A = cosα + sinα C. A = 2 − sinα D. A = 2sinα Lời giải Chọn A 9 A cos π α sin (α ) cos π 4 α = + + + π = + π + − sinα 2 2
A = −sin (4π +α ) − sinα = −sinα − sinα = 2 − sinα
Câu 3. Cho đồ thị hàm số y = sin x :
Từ đồ thị trên hãy chỉ ra số nghiệm của phương trình sin x =1 trên [ 3 − π;3π ]? A. 6 B. 7 C. 1 D. 3 Lời giải Chọn D Trên đoạn [ 3
− π;3π ] đường thẳng y =1 cắt đồ thị y = sin x tại 3 điểm nên số nghiệm của phương trình là 3.
Câu 4. Chu kỳ của hàm số y = sin x là: 5 A. π . B. π . C. 2π .
D. k2π , k ∈ . 2 Lời giải Chọn C
Câu 5. Phương trình sin 2x = cos x có nghiệm là π kπ π π x = + k x = + A. 6 3 (k ∈) . B. 6 3 (k ∈) . π π x = + k2π x = + k2π 2 3 π π π x = + k2π k2 x = + C. 6 (k ∈) . D. 6 3 (k ∈) . π π x = + k2π x = + k2π 2 2 Lời giải Chọn D
Câu 6. Phương trình 3 cos x − =
có hai họ nghiệm là: 2 π π x = + k2π 5 x = + k2π A. 3 ,k ∈ 6 ,k ∈ π B. π x = − + k2π 5 x = − + k2π 3 6 2π π x = + k2π x = + k2π C. 3 ,k ∈ D. 6 ,k ∈ 2π π x = − + k2π 5 x = + k2π 3 6 Lời giải Chọn B
Câu 7. Trong các dãy số (u cho bởi công thức số hạng tổng quát u sau, dãy số nào là một cấp số n ) n nhân?
A. u = 3− 2 .n B. 3 u = C. u =
D. u = − n n 4 5 . n 5.2 .n n . n 2(n +1) Lời giải Chọn C Ta có: n 1 u :u = 5.2 +
= nên chọn đáp án C. + :5.2n n n 2 1
Câu 8. Cấp số cộng ( u ) có số hạng đầu u = − 2, công sai d = 3. Công thức của số hạng tổng quát u n 1 n là:
A. u = n −
B. u = + n
C. u = n −
D. u = − + n n 2 3 n 3 8. n 5 3 . n 3 5. Lời giải Chọn A
Số hạng tổng quát: u = − + n − = n − . n 2 ( ) 1 .3 3 5 6
Câu 9. Trong các dãy số (u cho bởi số hạng tổng quát u dưới đây, dãy số nào là dãy số tăng? n ) n A. 1 u = − n ; u = n + . u = . u = . n . B. C. 1 D. 1 n 2 2 n 3n n n +1 Lời giải Chọn A
Ta có: u − = + + − + = > ⇒ u = n + là dãy số tăng. n 2 + u n n n n 1 2 2 1 0 1 ( )
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt
phẳng (SAD) và (SBC) . Khẳng định nào sau đây đúng?
A. d đi qua S và song song với BD .
B. d đi qua S và song song với DC .
C. d đi qua S và song song với AB .
D. d đi qua S và song song với BC . Lời giải Chọn D
Câu 11. Cho biết mệnh đề nào sau đây là sai ?
A. Có một và chỉ một mặt phẳng đi qua hai đường thẳng song song.
B. Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
C. Có một và chỉ một mặt phẳng đi qua một đường thẳng và một điểm không thuộc nó.
D. Có một và chỉ một mặt phẳng đi qua hai đường thẳng cho trước. Lời giải Chọn D
Câu 12. Cho năm điểm phân biệt ,
A B,C, D, E, trong đó không có bốn điểm nào ở trên cùng một mặt
phẳng. Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong số năm điểm đã cho? A. 14. B. 10. C. 12. D. 8. Lời giải Chọn B
Với 3 điểm phân biệt không thẳng hàng, ta luôn tạo được 1 mặt phẳng xác định. Ta có 3
C cách chọn 3 điểm trong 5 điểm đã cho để tạo được 1 mặt phẳng xác định. Vậy số mặt 5
phẳng tạo được là 10.
Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai
Câu 1. Xác định tính đúng, sai của các mệnh đề sau π
a) Ta đổi số đo của góc 15° sang radian bằng 12 π b) 13
Ta đổi số đo của góc 65° sang radian bằng 36 π c) 4 Đổi số đo của góc
sang độ bằng 48° 15 π d) 19
Đổi số đo của góc −
sau đây sang độ bằng 427,5° − 8 7 Lời giải a) Đúng b) Đúng c) Đúng d) Đúng
Câu 2. Cho hàm số f (x) = tan 2x −1. Khi đó:
a) Giá trị của hàm số tại π x = bằng 0 8
b) Giá trị của hàm số tại π
x = bằng − 3 −1 3
c) Có ba giá trị x thuộc [0;π ] khi hàm số đạt giá trị bằng 2 − .
d) Hàm số đã cho là hàm tuần hoàn. Lời giải a) Đúng b) Đúng c) Sai d) Đúng a) b) Ta có: π π f tan 2 = ⋅ −1 =1−1 = 0 8 8 π π f tan 2 = ⋅ −1 = − 3 − 1 3 3
c) Ta có: f (x) = 2 − ⇔ tan 2x −1 = 2 − ⇔ tan 2x = 1 − π π π
⇔ 2x = − + kπ (k ∈) ⇔ x = − + k (k ∈). 4 8 2 Vì x∈[0;π ] nên 3π 7π x ; ∈
(khi đó k =1;k = 2 ). 8 8
d) Tập xác định hàm số là: π π D \ = + k k ∣ ∈ . 4 2 Với mọi π
x ∈ D , ta có: x ± ∈ D và 2 π π f x tan 2 x + = +
−1 = tan(2x +π ) −1 = tan 2x −1 = f (x). 2 2
Vậy hàm số đã cho là hàm tuần hoàn.
Câu 3. Cho dãy số (un ) .
a) Nếu (u giảm thì (u bị chặn. n ) n )
b) Nếu (u giảm thì (u bị chặn trên. n ) n )
c) Nếu (u tăng thì (u bị chặn dưới. n ) n )
d) Nếu (u bị chặn trên và bị chặn dưới thì (u bị chặn. n ) n ) Lời giải 8 a) Sai b) Đúng c) Đúng d) Đúng
+ Nếu (u giảm thì (u là dãy số bị chặn trên bởi u . n ) n ) 1
+ Nếu (u tăng thì (u là dãy số bị chặn dưới bởi u . n ) n ) 1
+ Nếu (u vừa bị chặn trên vừa bị chặn dưới thì (u là dãy số bị chặn. n ) n )
+ Nếu (u giảm thì (u có thể không bị chặn dưới nên khẳng định bị chặn là sai. n ) n )
Câu 4. Cho hình chóp S.ABCD có đáy là hình thang ABCD ( AB CD).
Các mệnh đề sau đúng hay sai?
a) Hình chóp S.ABCD có 4 mặt bên.
b) Giao tuyến của hai mặt phẳng (SAC) và (SBD) là SO (O là giao điểm của AC và BD).
c) Giao tuyến của hai mặt phẳng (SAD) và (SBC) là SI (I là giao điểm của AD và BC).
d) Giao tuyến của hai mặt phẳng (SAB) và (SAD) là đường trung bình của ABC . D Lời giải. a) Đúng b) Đúng c) Đúng d) Sai S A B O D C I
• Hình chóp S.ABCD có 4 mặt bên: (SAB), (SBC), (SCD), (SAD). Do đó a đúng.
• S là điểm chung thứ nhất của hai mặt phẳng (SAC) và (SBD). O ∈
AC ⊂ (SAC) ⇒ O∈(SAC)
là điểm chung thứ hai của hai mặt phẳng (SAC) và ∈ ⊂ ( ) ⇒ ∈( ) ⇒ O O BD SBD O SBD (SBD).
→(SAC) ∩(SBD) = . SO Do đó b đúng.
• Tương tự, ta có (SAD) ∩(SBC) = SI. Do đó c đúng.
• (SAB) ∩(SAD) = SA mà SA không phải là đường trung bình của hình thang ABC . D Do đó d sai. 9
Phần 3. Câu trả lời ngắn.
Thí sinh trả lời đáp án từ câu 1 đến câu 6.
Câu 1. Sơ đồ cho thấy một phần cấu trúc kim loại của một cây cầu. Giá trị của
sin XOY bằng a 41 . 205 Tìm a Lời giải Trả lời: 32 Ta có 2 2 OY = 10 + 8 = 2 41 Mặt khác ta có: 2 8 4 41 = = ⇒ 4 41 5 41 sin AOY cos AOY = 1− = (vì góc
AOY là góc nhọn nên 2 41 41 41 41 cos AOY > 0 ) 2 6 = ⇒ 6 4 cos XOA sin XOA = 1− = (vì góc
XOA là góc nhọn nên sin XOA > 0 ) 10 10 5 Ta lại có = + XOY
(XOA AOY)= + sin sin sin X .
OA cos AOY cos X . OA sin AOY 4 5 41 6 4 41 64 41 32 41 = . + . = = . 5 41 10 41 410 205
Câu 2. Tập giá trị của hàm số: y = 5 + 4sin 2xcos 2x là T = [ ;
a b] , tính b − a Lời giải Trả lời: 4
y = 5 + 4sin 2xcos 2x .
Hàm số có tập xác định D = .
Ta có y = 5 + 4sin 2xcos 2x = 5 + 2sin 4x . Do 1
− ≤ sin 4x ≤1 ⇔ 2
− ≤ 2sin 4x ≤ 2 ⇔ 3 ≤ 5 + 2sin 4x ≤ 7 ⇔ 3 ≤ y ≤ 7 .
Vậy giá trị của hàm số là T = [3;7] .
Câu 3. Hỏi có bao nhiêu giá trị nguyên của m để các phương trình lượng giác sau có nghiệm:
2sin 3x = m −1. Lời giải 10 Trả lời: 5 m 1 2sin 3x m 1 sin 3x − = − ⇔ = . 2 Điều kiện có nghiệm: m −1 1 − ≤ ≤ 1 ⇔ 1 − ≤ m ≤ 3. 2
Với m∈ → m∈{ 1; − 0;1;2; } 3 u = 4
Câu 4. Cho dãy số (u xác định bởi hệ thức truy hồi 1
. Số hạng thứ bốn của dãy số bằng? n ) u = + + u n n 1 n Lời giải Trả lời: 10
Có u = u +1 = 5;u = u + 2 = 7;u = u + 3 =10 2 1 3 2 4 3
Câu 5. Một cầu thang bằng gạch có tổng cộng 30 bậc. Để xây xong bậc dưới cùng cần 100 viên gạch.
Mỗi bậc tiếp theo cần ít hơn hai viên gạch so với bậc ngay trước nó. Hỏi cần tất cả bao nhiêu
viên gạch để xây xong cầu thang đó? Lời giải
Trả lời: 2130.
Số viên gạch xây xong mỗi bậc là dãy số cấp số cộng với u =100 và công sai d = 2 − . 1
Số viên gạch để xây xong 30 bậc cầu thang là 30.29 S = 30.100 + . 2 − = 2130. 30 ( ) 2
Câu 6. Trong mặt phẳng (α ) , cho 3 điểm ,
A B,C trong đó không có 3 điểm nào thẳng hàng. Điểm
S ∉(α ) , hỏi có bao nhiêu mặt phẳng tạo bởi S và các điểm đã cho? Lời giải Trả lời: 3
Số mặt phẳng tạo bởi S và các điểm đã cho là 3 mặt phẳng: (SAB),(SAC),(SBC). 11
ĐỀ KIỂM TRA GIỮA KỲ 1 – TOÁN 11 – ĐỀ SỐ 2
Phần 1. Câu trắc nghiệm nhiều phương án chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.
Câu 1. Góc lượng giác α xác định điểm M ( ;
x y) trên đường tròn lượng giác sao cho α = ( , OA OM ) .
Giá trị lượng giác cotα là: A. y
B. x ( y ≠ 0)
C. y (x ≠ 0) D. x y x
Câu 2. Rút gọn M = cos xcos(x − y) + sin xsin(x − y) ta được :
A. M = sin .x
B. M = cos y
C. M = sin(2x − y) D. M = cos(2x − y)
Câu 3. Khẳng định nào sau đây là sai?
A. Hàm số y = sin x là hàm số chẵn;
B. Hàm số y = cos x là hàm số chẵn;
C. Hàm số y = tan x là hàm số lẻ;
D. Hàm số y = cot x là hàm số lẻ.
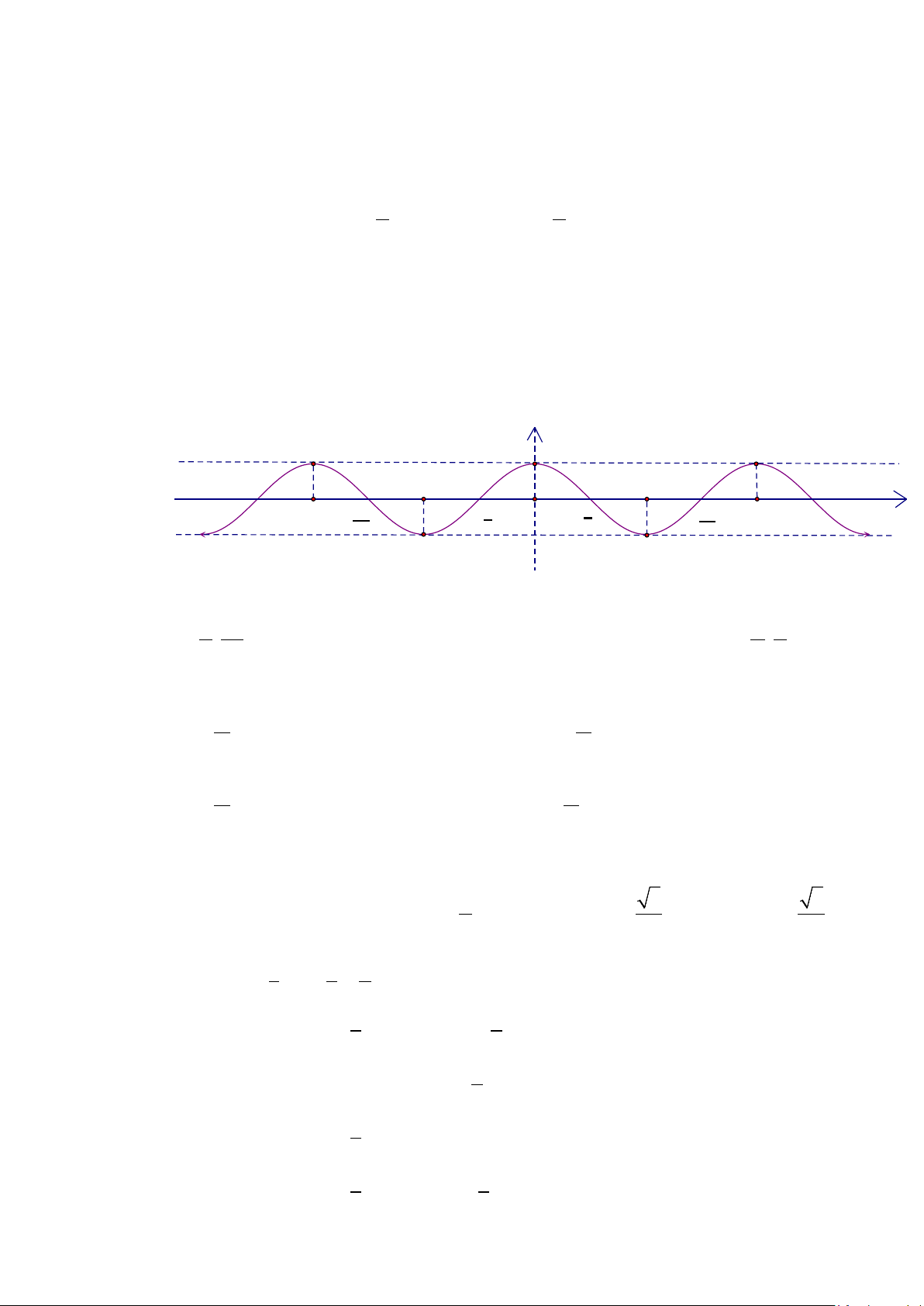
Câu 4. Cho hàm số y = cos x có đồ thị như hình vẽ dưới đây: y 1
f(x) = cos(x) -3π -π π 3π -2π 3π π O π 3π 2π x - - 2 2 2 2 -1
Hàm số y = cos x đồng biến trên khoảng nào trong các khoảng sau: A. π π ; 3π π B. (0;π ) C. (π;2π ) D. − ; 2 2 2 2
Câu 5. Tập nghiệm của phương trình tan x = 1 − là π π A. kπ , k − + ∈ .
B. − + kπ ,k ∈. 4 2 π π C. k2π , k − + ∈ .
D. + kπ , k ∈. 4 4
Câu 6. Trong các phương trình sau, phương trình nào vô nghiệm? 2 3 5
A. cos 2x = 0.
B. cos2x = − . C. cos2x = − . D. cos2x = . 3 4 2 1 5 7
Câu 7. Cho dãy số − ;−1;− ;− ;−3;... là cấp số cộng với: 3 3 3 1 2
A. Số hạng đầu tiên là − và công sai là − 3 3 2
B. Số hạng đầu tiên là −1 và công sai là 3 1
C. Số hạng đầu tiên là − và công sai là −1 3 1 2
D. Số hạng đầu tiên là − và công sai là 3 3 1
Câu 8. Trong các dãy số sau, dãy số nào không phải cấp số nhân?
A. 5;5;5;5;5;5. B. 4
− ;−16;−64;− 256;−1024;− 4094. 1 1 1 1 1 C. 2;−1; ;− ; ; − .
D. − ; 1;−3; 9; −27; 81. 2 4 8 16 3 u = −1
Câu 9. Cho dãy số (u , biết 1
với n ≥1. Ba số hạng đầu tiên của dãy số đó là lần lượt là n ) u = + + u n n 4 1
những số nào dưới đây? A. 1; − 3;7. B. 1; − 4;7. C. −1;4;6 D. 1 − ;3;5.
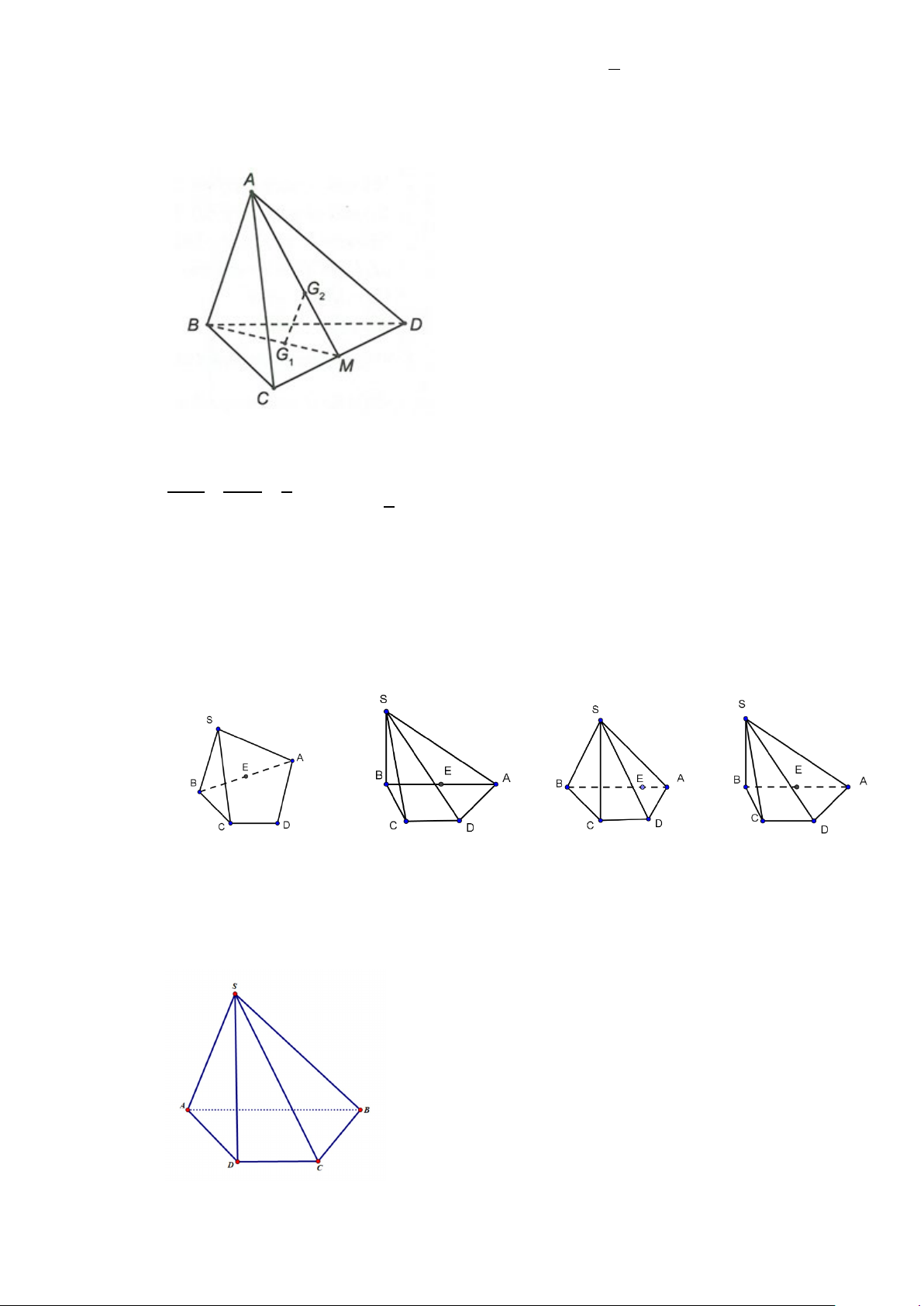
Câu 10. Cho tứ diện ABCD . Gọi G và G lần lượt là trọng tâm các tam giác BCD và ACD . 1 2
Chọn khẳng định sai trong các khẳng định sau:
A. G G // ABD .
B. G G // ABC . 1 2 ( ) 1 2 ( ) 2
C. BG , AG và CD đồng qui.
D. G G = AB . 1 2 1 2 3
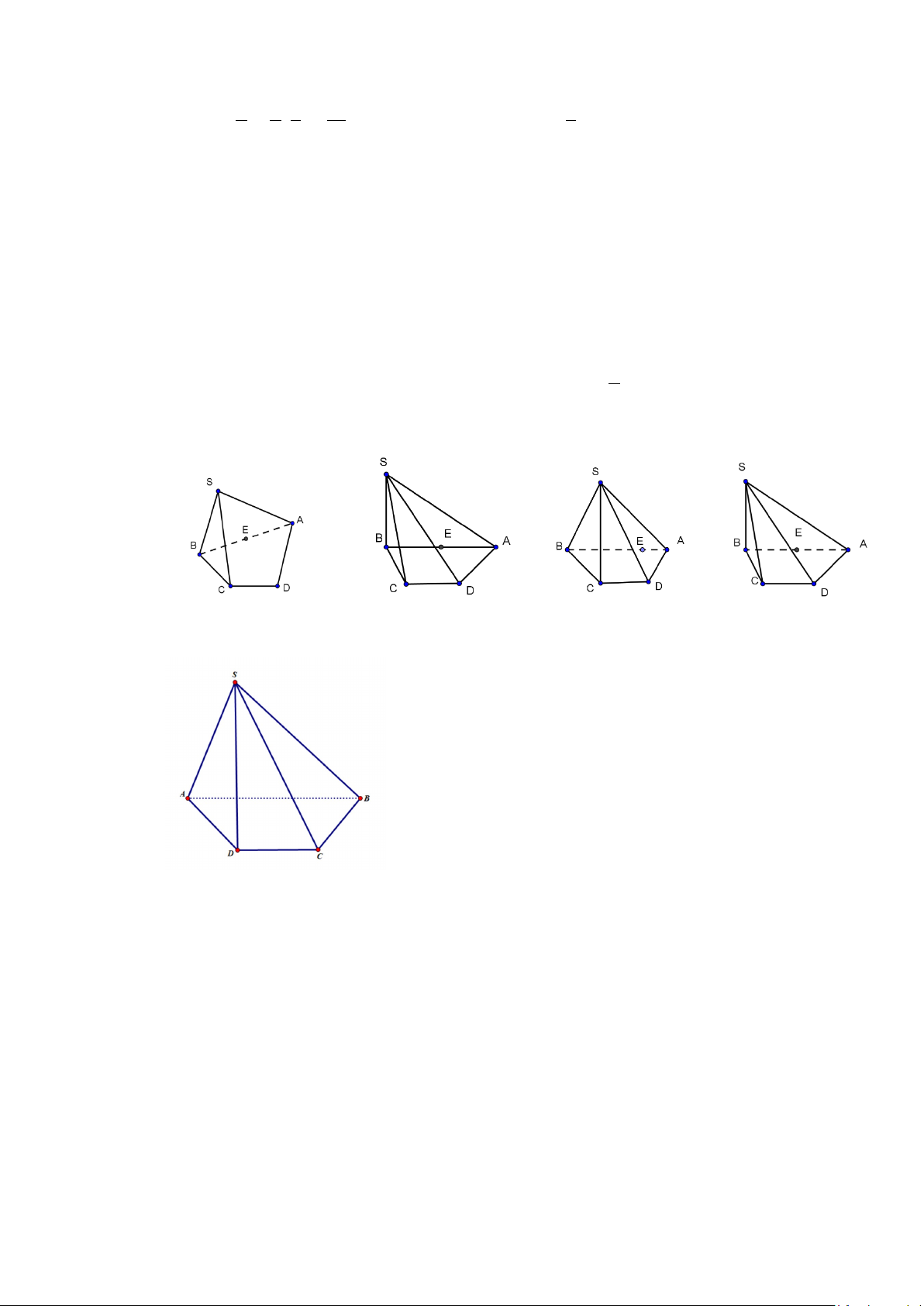
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB gấp đôi đáy nhỏ CD, E là
trung điểm của đoạn AB . Hình vẽ nào sau đây vẽ đúng quy tắc ? A. B. C. D.
Câu 12. Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy lớn A .
B Gọi I là giao điểm của
AD và BC ; O là giao điểm của AC và B . D
Khẳng định nào sau đây sai?
A. Giao tuyến của hai mặt phẳng (SAB) và (SAD) là SI .
B. Giao tuyến của hai mặt phẳng (SAC) và (SBD) là SO .
C. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là SI .
D. Hình chóp S.ABCD có 4 mặt bên.
Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai
Câu 1. Một đường tròn có bán kính 36m . Khi đó:
a) Cung tròn bán kính R có số đo α (0 ≤ α ≤ 2π ) , có số đo 0
a (0 ≤ a ≤ 360) và có độ dài là l thì: 2 a l = Rα = .R 180 3π
b) Độ dài của cung trên đường tròn có số đo là ≈ 84,8m 4
c) Độ dài của cung trên đường tròn có số đo 0
51 là ≈ 32,04m 1
d) Độ dài của cung trên đường tròn có số đo là 22m 3 Câu 2. π
Cho hàm số y 3 sin 2x = − + , khi đó: 4
a) Hàm số có tập xác định D = .
b) Giá trị nhỏ nhất của hàm số bằng 2
c) Giá trị lớn nhất của hàm số bằng 4
d) Tập giá trị của hàm số là T = [2;4]
Câu 3. Cho dãy số (u có số hạng tổng quát 2n +1 u = . n ) n n + 2
a) Tổng của năm số hạng đầu của dãy là 941. 140
b) Số hạng thứ 100: 67 u = . Số hạng thứ 200: 401 u = 100 34 200 202
c) Số 167 là số hạng thứ 230 84
d) Dãy số có duy nhất một số hạng là số nguyên
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I , J lần lượt là trung điểm SA
và SB . Các mệnh đề sau đúng hay sai?
a) IJCD là hình thang.
b) (SAB)∩(IBC) = IB .
c) (SBD) ∩(JCD) = JD .
d) (IAC) ∩(JBD) = AO , O là tâm hình bình hành ABCD .
Phần 3. Câu trả lời ngắn.
Thí sinh trả lời đáp án từ câu 1 đến câu 6.
Câu 1. Tính góc lượng giác (đơn vị độ) mà kim phút quay được từ 0 giờ đến 2 giờ 15 phút?
Câu 2. Huyết áp là áp lực máu cần thiết tác động lên thành động mạch nhằm đưa máu đi nuôi dưỡng các
mô trong cơ thể. Nhờ lực co bóp của tim và sức cản của động mạch mà huyết áp được tạo ra. Giả
sử huyết áp của một người thay đổi theo thời gian được cho bởi công thức: 3
p(t) =120 +15cos150πt, trong đó p(t) là huyết áp tính theo đơn vị mmHg (milimét thuỷ ngân)
và thời gian t tính theo đơn vị phút.
Huyết áp cao nhất và huyết áp thấp nhất lần lượt được gọi là huyết áp tâm thu và huyết áp tâm
trương. Tìm chỉ số huyết áp của người đó (biết tỉ số huyết áp bằng huyết áp tâm thu ) (làm tròn huyết áp tâm trương
kết quả đến hàng phần mười) Câu 3. π
Có bao nhiêu giá trị nguyên của m để phương trình sin 2x = 7m + 3 có nghiệm 7 x 0 ; ∈ . 12
Câu 4. Cho dãy số n u , biết 2 5 u
. Số 7 là số hạng thứ mấy của dãy số? n n 5n 4 12
Câu 5. Giả sử một chiếc xe ô tô lúc mới mua là 700 triệu đồng. Cứ sau mỗi năm sử dụng, giá của chiếc
xe ô tô giảm 45 triệu đồng. Hỏi giá còn lại của chiếc xe sau 6 năm sử dụng là bao nhiêu triệu đồng ?
Câu 6. Cho năm điểm phân biệt ,
A B,C, D, E, trong đó không có bốn điểm nào ở trên cùng một mặt
phẳng. Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong số năm điểm đã cho? PHIẾU TRẢ LỜI 4
LỜI GIẢI THAM KHẢO
Phần 1. Câu trắc nghiệm nhiều phương án chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.
Câu 1. Góc lượng giác α xác định điểm M ( ;
x y) trên đường tròn lượng giác sao cho α = ( , OA OM ) .
Giá trị lượng giác cotα là: A. y
B. x ( y ≠ 0)
C. y (x ≠ 0) D. x y x Lời giải Chọn B
Câu 2. Rút gọn M = cos xcos(x − y) + sin xsin(x − y) ta được :
A. M = sin .x
B. M = cos y
C. M = sin(2x − y) D. M = cos(2x − y) Lời giải Chọn B
M = cos x cos(x − y) + sin xsin(x − y)
M = cos(x − x + y) = cos y
Câu 3. Khẳng định nào sau đây là sai?
A. Hàm số y = sin x là hàm số chẵn;
B. Hàm số y = cos x là hàm số chẵn;
C. Hàm số y = tan x là hàm số lẻ;
D. Hàm số y = cot x là hàm số lẻ. Lời giải Chọn A
Câu 4. Cho hàm số y = cos x có đồ thị như hình vẽ dưới đây: y 1
f(x) = cos(x) -3π -π π 3π -2π 3π π O π 3π 2π x - - 2 2 2 2 -1
Hàm số y = cos x đồng biến trên khoảng nào trong các khoảng sau: A. π π ; 3π π B. (0;π ) C. (π;2π ) D. − ; 2 2 2 2 Lời giải Chọn C
Câu 5. Tập nghiệm của phương trình tan x = 1 − là π π A. kπ , k − +
∈ . B. − + kπ ,k ∈. 4 2 π π C. k2π , k − + ∈ .
D. + kπ , k ∈. 4 4 Lời giải 5 Chọn A π π Ta có tan x = 1 − tan x tan ⇔ = −
⇔ x = − + kπ ,(k ∈). 4 4
Câu 6. Trong các phương trình sau, phương trình nào vô nghiệm? 2 3 5
A. cos 2x = 0.
B. cos2x = − . C. cos2x = − . D. cos2x = . 3 4 2 Lời giải Chọn D 5 Ta có: cos 2x =
> 1 nên phương trình này vô nghiệm. 2 1 5 7
Câu 7. Cho dãy số − ;−1;− ;− ;−3;... là cấp số cộng với: 3 3 3 1 2
A. Số hạng đầu tiên là − và công sai là − 3 3 2
B. Số hạng đầu tiên là −1 và công sai là 3 1
C. Số hạng đầu tiên là − và công sai là −1 3 1 2
D. Số hạng đầu tiên là − và công sai là 3 3 Lời giải Chọn A
Câu 8. Trong các dãy số sau, dãy số nào không phải cấp số nhân?
A. 5;5;5;5;5;5. B. 4
− ;−16;−64;− 256;−1024;− 4094. 1 1 1 1 1 C. 2;−1; ;− ; ; − .
D. − ; 1;−3; 9; − 27; 81. 2 4 8 16 3 Lời giải Chọn B u = −1
Câu 9. Cho dãy số (u , biết 1
với n ≥1. Ba số hạng đầu tiên của dãy số đó là lần lượt là n ) u = + + u n n 4 1
những số nào dưới đây? A. 1; − 3;7. B. 1; − 4;7. C. −1;4;6 D. 1 − ;3;5. Lời giải Chọn A
Câu 10. Cho tứ diện ABCD . Gọi G và G lần lượt là trọng tâm các tam giác BCD và ACD . 1 2
Chọn khẳng định sai trong các khẳng định sau:
A. G G // ABD .
B. G G // ABC . 1 2 ( ) 1 2 ( ) 6 2
C. BG , AG và CD đồng qui.
D. G G = AB . 1 2 1 2 3 Lời giải Chọn D
Gọi M là trung điểm của CD . Xét ABM , ta có: G G / / AB 1 2 MG MG 1 1 2 = = ⇒ 1 MB MA 3 G G = AB 1 2 3
G G / / AB ⇒ G G / /(ABD) 1 2 1 2
G G / / AB ⇒ G G / /(ABC) 1 2 1 2
Ba đường BG , AG ,CD đồng quy tại M => B đúng. 1 2
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB gấp đôi đáy nhỏ CD, E là
trung điểm của đoạn AB . Hình vẽ nào sau đây vẽ đúng quy tắc ? A. B. C. D. Lời giải Chọn D
Câu 12. Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy lớn A .
B Gọi I là giao điểm của
AD và BC ; O là giao điểm của AC và B . D
Khẳng định nào sau đây sai? 7
A. Giao tuyến của hai mặt phẳng (SAB) và (SAD) là SI .
B. Giao tuyến của hai mặt phẳng (SAC) và (SBD) là SO .
C. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là SI .
D. Hình chóp S.ABCD có 4 mặt bên. Lời giải Chọn A
Ta có: (SAB) ∩(SAD) = SA nên chọn#A.
Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai
Câu 1. Một đường tròn có bán kính 36m . Khi đó:
a) Cung tròn bán kính R có số đo α (0 ≤ α ≤ 2π ) , có số đo 0
a (0 ≤ a ≤ 360) và có độ dài là l thì: a l = Rα = .R 180 3π
b) Độ dài của cung trên đường tròn có số đo là ≈ 84,8m 4
c) Độ dài của cung trên đường tròn có số đo 0
51 là ≈ 32,04m 1
d) Độ dài của cung trên đường tròn có số đo là 22m 3 Lời giải a) Sai b) Đúng c) Đúng d) Sai π a) a
Theo công thức tính độ dài cung tròn ta có l = Rα = .R 180 3π
b) Ta có l = Rα = 36.
= 27π ≈ 84,8m 4 π a π 51 51π c) Ta có l = .R = .36 = ≈ 32,04m 180 180 5 1
d) Ta có l = Rα = 36. =12m 3 Câu 2. π
Cho hàm số y 3 sin 2x = − + , khi đó: 4
a) Hàm số có tập xác định D = .
b) Giá trị nhỏ nhất của hàm số bằng 2
c) Giá trị lớn nhất của hàm số bằng 4
d) Tập giá trị của hàm số là T = [2;4] Lời giải a) Đúng b) Đúng c) Đúng d) Đúng 8




