10 Đề Trắc Nghiệm Ôn Tập Chương 1 Khảo Sát Hàm Số Giải Tích 12 Có Đáp Án

10 đề trắc nghiệm ôn tập Chương 1 Khảo Sát Hàm Số Giải Tích 12 được biên soạn dưới dạng file PDF gồm 33 trang. Mỗi đề thi là kiến thức từ cơ bản đến nâng cao khác nhau và kèm sẵn đáp án để các em học sinh dễ dàng so sánh kết quả sao cho chuẩn xác nhất. Mời các em tham khảo thêm nh

42 21 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

33 trang 8 tháng trước

Tác giả:

Profile ha phan
Trang1
ĐỀ 1
ĐỀ ÔN TẬP CHƯƠNG I
GIẢI TÍCH 12
Câu 1: Gi
m
là giá tr nh nht ca hàm s
3
3y x x
n
0;38 .
Tìm giá tr
m
.
A.
0.m
B.
1.m
C.
2.m
D.
Câu 2: (ĐỀ THI TỐT NGHIỆP THPT 2020-ĐỢT 1) Cho hàm s
fx
có bng bi
Giá tr cc tiu ca hàm s ng
A.
2
.
B.
2
.
C.
3
.
D.
1
.
Câu 3: Gi
12
,xx
m cc tr ca hàm s
32
1
32
3
y x x x

22
12
xx
bng:
A. 4. B. 10. C. 16. D. 9.
Câu 4: Tìm s m c th hàm s
42
41 y x x
ng thng
3.y
A.
0.
B.
2.
C.
3.
D.
4.
Câu 5: (ĐỀ THI TỐT NGHIỆP THPT 2021-ĐỢT 1) Cho hàm s
()y f x
có bng xét du co

S m cc tr ca hàm s 
A.5 . B. 3 . C.2 . D.
4
.
Câu 6: Hàm s
32
39 y x x x
ng bin trên kho
A.
1;3
. B.
. C.
3; 1
. D.
1;3
.
Câu 7: Tìm tt c các giá tr thc ca tham s m   th hàm s
2
1
x2

x
y
xm
có hai tim cn
ng.
A.
3.m
B.
2 2;2 2 .m
C.
; 2 2 2 2; \ 3 . m
D.
; 2 2 2 2; . m
Câu 8: Cho hàm s
32
5 4. y x x x
M đúng?
A. Hàm s ng bin trên
5
;.
3




B. Hàm s nghch bin trên
5
;1 .
3



C. Hàm s ng bin trên
1; .
D. Hàm s ng bin trên
5
;1 .
3



Câu 9:  th hàm s
32
+c +y ax bx x d
m cc tiu là
0;0O
m ci là
1;1 .M
Giá tr ca
, , ,a b c d
lt là?
Trang2
A.
3;0;2;0.
B.
2;3;0;0.
C.
2;0;0;3.
D.
3;0; 2;0.
Câu 10: 
2
3
:
9
x
Cy
x
?
A. 3. B. 1. C. 2. D. 4.
Câu 11: Bit r th hàm s
3
1
x
y
x
ng thng
2yx
ct nhau tm phân bit
;
AA
A x y
và
; .
BB
B x y
Tính
.
AB
yy
A.
2.
AB
yy
B.
2.
AB
yy
C.
4.
AB
yy
D.
0.
AB
yy
Câu 12: Cho hàm s:
1
21
C
x
y
x
. Tìm tt c các giá tr thc ca tham s m  ng thng
1
2
:

m
y mxd
c th
C
tm phân bit A, B sao cho
22
OA OB
t giá tr nh
nht?
A.
0.m
B.
1.m
C.
1.m
D.
Câu 13: Cho hàm s
42
82 y x x
 th
()C
m
M
thuc
()C
 bng
2
. Tìm
h s góc
k
ca tip tuyn v th
()C
ti
M
.
A.
6 2.k
B.
9 2.k
C.
7 2.k
D.
8 2.k
Câu 14: Tip tuyn c th hàm s
32
4 4 1 y x x x
tm
3; 2M
c th tm th
hai là
.N
Tìm t m
.N
A.
2;1 .N
B.
2; 3 .N
C.
2;33 .N
D.
1;0 .N
Câu 15: Cho hàm s
32
y ax bx cx d
 th  bên. M 
A.
0, 0, 0, 0 a b c d
.
B.
0, 0, 0, 0 a b c d
.
C.
0, 0, 0, 0 a b c d
.
D.
0, 0, 0, 0 a b c d
.
Câu 16: Cho hàm s
()y f x
nh, liên tc trên
R
 th ng cong trong hình v bên.
Kh
A. Hàm s ng bin trên khong
0;1
.
B. Hàm s ng bin trên khong
4;2
.
C. Hàm snghch bin trên khong
1;0 2;3
.
D. Hàm snghch bin trên khong
4;1
.
Câu 17: Cho hàm s
()y f x
nh và liên tc trên
 th ng cong trong hình v
m cc tiu c th hàm s
()y f x
là:
-2
-4
1
O
3
-1
2
Trang3
A.
(0; 2).M
B.
0.x
C.
( 2;2).M
D.
2.x
Câu 18: Cho hàm s
32
( ) 6 9 2 y f x x x x
 th ng cong trong hình v bên. Tìmtt c
các giá tr thc ca tham s
m

()f x m
có sáu nghim thc phân bit.
A.
1 2.m
B.
2.m
C.
2 2. m
D.
2 2. m
Câu 19: Cho hàm s
()y f x
nh trên
\0
, liên tc trên mi khonh và có bng bin

Tìm tp hp tt c các giá tr thc ca tham s
m

()f x m

nghim thc?
A.
( ; 1) {2}.
B.
( ;2).
C.
( ;2].
D.
( ; 1] 2 .
Câu 20:
( ĐỀ THI TỐT NGHIỆP THPT 2021-ĐỢT 1) Cho hàm s bc ba
()y f x
 th ng cong
trong hình bên. S nghim thc phân bit c
( ( )) 1f f x
là
A. 9 . B.
7
. C.
3.
D. 6 .
---------------------------------------------
----------- HT ----------
x
y
2
2
-2
-1
1
-2
O
Trang4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
C
D
B
B
D
A
D
C
D
B
C
D
D
D
C
D
A
A
D
B
ĐỀ 2
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG I
GIẢI TÍCH 12
Câu 1: Vip tuyn c th
42
( ): 2C y x x
t bng
2.
A.
24 40. yx
B.
24 40.yx
C.
24 40. yx
D.
24 40.yx
Câu 2: Cho hàm s
1
xm
y
x
(m là tham s thc) tha mãn
2;4
min 3y
. M ?
A.
1 3.m
B.
1.m
C.
4.m
D.
3 4.m
Câu 3: Bit rng thng
5 yx
c th hàm s
32
32 y x x
tm duy nht. Kí hiu
00
( ; )xy
là t 
00
( ; ).xy
A.
00
( ; ) 3;8 .xy
B.
00
( ; ) 2;3 .xy
C.
00
( ; ) 2;7 .xy
D.
00
( ; ) 3;2 .xy
Câu 4: Vip tuyn c th hàm s
21
( ):
1
x
Cy
x
, bit rng tip tuyn song song
vng thng
3 2.yx
A.
31yx
và
3 11.yx
B.
32yx
và
3 11.yx
C.
31 yx
và
3 11. yx
D.
31yx
và
3 11. yx
Câu 5: Vip tuyn c th (C):
32
( ) 3 9 2 y f x x x x
t
0
x
, bit rng
//
0
( ) 6.fx
A.
9 6.yx
B.
3 2.yx
C.
9 6.yx
D.
6.yx
Câu 6: Tìm tt c giá tr thc ca m   th hàm s
4 2 2
( ): 2 1 C y x m x
có ba cc tr nh
ca mt tam giác vuông cân.
A.
1m
hoc
2.m
B.
2.m
C.
1.m
D.
1m
hoc
2.m
Câu 7: Tìm tt c các giá tr thc ca tham s m  giá tr nh nht ca hàm s
2
()
1

x m m
fx
x
trên
n
0;1
bng
2.
A.
1; 2. mm
B.
1; 2. mm
C.
1; 2.mm
D.
1, 2. mm
Câu 8: Hàm s ng bin trên khong
;? 
A.
3
3 1. y x x
B.
3
6. y x x
C.
21
.
1
x
y
x
D.
42
2.y x x
Câu 9: Cho hàm s
()y f x
có bng bi
Trang5
Tìm giá tr ci
CÑ
y
và giá tr cc tiu
CT
y
ca
hàm s 
A.
0
CÑ
y
và
1.
CT
y
B.
0
CÑ
y
và
4.
CT
y
C.
3
CÑ
y
và
1.
CT
y
D.
3
CÑ
y
và
4.
CT
y
Câu 10: Cho hàm s
()y f x
có
lim ( ) 1


x
fx
và
lim ( ) 1

x
fx
. M ?
A.  th hàm s m cng thng
1y
và
1.y
B.  th hàm s t tim cn ngang.
C.  th hàm s m cng thng
1x
và
1.x
D.  th hàm s m cn ngang.
Câu 11: ng cong  th ca mt trong bn hàm s  
nào?
A.
B.
C.
D.
Câu 12: Cho hàm s
1
.
2
x
y
x
M ?
A. Hàm s ng bin trên khong
;2 .
B. Hàm s nghch bin trên khong
;2 .
C. Hàm s nghch bin trên khong
2; .
D. Hàm s nghch bin trên khong
;. 
Câu 13: Cho hàm s
()y f x
o hàm
2
( ) 3 1, .
f x x x
M ?
A. Hàm s nghch bin trên khong
1
;.
3




B. Hàm s ng bin trên khong
;. 
C. Hàm s nghch bin trên khong
;. 
D. Hàm s ng bin trên khong
11
;.
33



Câu 14:  th hàm s
32
35 y x x
m cc tr A và B. Tính din tích S ca tam giác
OAB
vi O là gc t.
A.
10.S
B.
9.S
C.
10
.
3
S
D.
5.S
Câu 15: Hàm s
32
1
x
y
x
có bao nhiêu cc tr?
A. 2. B. 0. C. 1. D. 3.
Câu 16: Cho hàm s
32
31 y x x
 th
( ).C
Tìm nhng giá tr thc ca tham s
m
 th
ng thng
ym
ct
C
tm phân bit.
A.
3 1. m
B.
1m
hoc
1.m
C.
D.
3.m
1
0
0
_
+
+
+
x
y'
y
+
3
0
4
3
3 1.y x x
32
3 1.y x x
.y x x
3
31
3
3 1.y x x
Trang6
Câu 17: Cho hàm s vi
, , ,a b c d
là các s th th hàm s  bên.
M ?
A.
và
B.
và
C.
và
D.
và
Câu 18: Tìm giá tr nh nht m ca hàm s
42
13 y x x
n
2;3 .
A.
49
.
4
m
B.
51
.
2
m
C.
13.m
D.
51
.
4
m
Câu 19: ng cong c th ca hàm s
ax b
y
cx d
vi
, , ,a b c d
là các s thc. M
?
A.
0, 1.
yx
B.
0, 1.
yx
C.
0, .
yx
D.
0, .
yx
Câu 20: Tìm s tim cn c th hàm s
2
2
56
.
4

xx
y
x
A.
3.
B.
2.
C.
1.
D.
0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
ĐỀ 3
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG I
GIẢI TÍCH 12
Câu 1: Vip tuyn c th hàm s
2
( ):
2
Cy
x
, tm c th (C) và
 th ca hàm s
2
1.yx
A.
1
1
2
yx
và
2.yx
B.
1
2
2
yx
và
3.yx
C.
1
2
yx
và
.yx
D.
1
1
2
yx
và
2.yx
32
y ax bx cx d
0, 0, 0 a b c
0.d
0, 0, 0 abc
0.d
0, 0, 0 a b c
0.d
0, 0, 0 a b c
0.d
Trang7
Câu 2: ng cong c th ca hàm s
ax b
y
cx d
vi
, , ,a b c d
là các s thc. M
?
A.
0, 2.
yx
B.
0, 2.
yx
C.
0, 1.
yx
D.
0, 1.
yx
Câu 3: Cho hàm s
5
mx m
y
xm
vi m là tham s. Gi S là tp hp tt c các giá tr nguyên ca m 
hàm s ng bin trên các khonh. Tìm s phn t ca S.
A. 4. B. 6. C. 5. D. 3.
Câu 4: Cho hàm s
42
23 y x x
có giá tr ci
CÑ
y
và giá tr cc tiu
CT
y
. M i
?
A.
3 15.
CT
CÑ
yy
B.
2 3.
CT
CÑ
yy
C.
2 5.
CT
CÑ
yy
D.
12.
CT
CÑ
yy
Câu 5: Cho hàm s
32
3.y x x
M úng?
A. Hàm s nghch bin trên khong
2; .
B. Hàm s nghch bin bin trên khong
;0 .
C. Hàm s nghch bin trên khong
0;2 .
D. Hàm s ng bin trên khong
Câu 6: Cho hàm s
42
2 y x x
 th 
Tìm tt c các giá tr thc ca tham s m  
42
20 x x m
có bn nghim phân bit.
A.
0 1.m
B.
0.m
C.
0 1.m
D.
1.m
Câu 7: Mt vt chuyng theo qui lut
32
1
6
2
s t t
vit (giây) là khong thi gian tính t khi vt
bu chuyng và s ng vt di chuyc trong khong th
Hi trong khong thi gian 6 giây, k t khi bu chuyng, vn tc ln nht ca vt
c bng bao nhiêu?
A.
64( / ).ms
B.
24( / ).ms
C.
108( / ).ms
D.
18( / ).ms
Câu 8:  th ca hàm s nào trong các hàm s m cng?
A.
4
1
.
1
y
x
B.
2
1
.
1

y
xx
C.
1
.y
x
D.
2
1
.
1
y
x
Câu 9: 
()y f x

H th hàm s ng tim
cn?
A.
1.
B.
2.
C.
4.
D.
3.
_
+
0
1
+
∞
-
∞
-2
0
+
∞
-
∞
y
y'
x
Trang8
Câu 10: ng thm cc tr c th hàm s
32
2 1. y x x
A.
9 8.yx
B.
8
1.
9
yx
C.
8 9. yx
D.
3 4.yx
Câu 11: Hàm s ch bin trên khong
;? 
A.
42
2.y x x
B.
4
.
2
x
y
x
C.
3
3. y x x
D.
42
2 3. y x x
Câu 12: 
()y f x

M ?
A. Hàm s ng bin trên khong
1; .
B. Hàm s nghch bin trên khong
5;1 .
C. Hàm s ng bin trên khong
(1;2).
D. Hàm s nghch bin trên khong
;1 .
Câu 13: Vip tuyn c th
42
( ): 2 3 C y x x
t bng
2.
A.
2 4.yx
B.
24 43.yx
C.
2 2. yx
D.
24 43. yx
Câu 14: Cho bit hàm s
32
y ax bx cx d
  th       nh sau,
kh?
A.
2
0
.
30

a
b ac
B.
2
0
.
30

a
b ac
C.
2
0
.
30

a
b ac
D.
2
0
.
30

a
b ac
Câu 15: Vi   p tuyn c  th (C):
42
13
( ) 3
22
f x x x
t     là
nghim c
//
( ) 0.fx
A.
4 3. yx
B.
3 5. yx
C.
4 3.yx
D.
4 3. yx
Câu 16: Cho hàm s
2
22 y x x
 th
()C
. M ?
A.
()C
ct trc hoành tm. B.
()C
ct trc hoành ti mm.
C.
()C
ct trc hoành tm. D.
()C
không ct trc hoành.
Câu 17: Tìm tp hp tt c các giá tr ca tham sm  hàm s
2
1
x mx
y
xm
t ci ti
2.x
A.
2.m
B.
0 1.m
C.
2.m
D.
1 3. m
Câu 18: ng cong trong hình v  th ca mt hàm s trong bn hàm s c lit kê bn

, , ,A B C D
i hàm s  nào?
_
_
+
+
0
0
2
0
1
+
y'
x
y
x
O
Trang9
A.
42
3 3. y x x
B.
42
2 3. y x x
C.
42
2 3. y x x
D.
42
2 3. y x x
Câu 19: Cho hàm s
1
mx
y
mx
(m là tham s thc) tha mãn
1;3
max 4y
. M ?
A.
5 7.m
B.
12.m
C.
10.m
D.
9 12.m
Câu 20: Cho hàm s
()y f x
nh, liên tc trên khonh và có bng bi
M ?
A. Hàm s t cc tiu ti
0x
t c i ti
1.x
B. Giá tr ci bng
1
và giá tr cc tiu bng
0.
C. Hàm s nghch bin trên khong
( 1;0).
D. Hàm s t giá tr ln nht bng 1 và giá tr nh
nht bng 0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
ĐỀ 4
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG I
GIẢI TÍCH 12
Câu 1: Tìm tt c các giá tr ca tham s m   th hàm s
4 2 2
21 y x m x
m cc tr to
nh ca mt tam giác vuông cân.
A.
1;0;1 .m
B.
1.m
C.
D.
2.m
Câu 2: Vip tuyn c th hàm s
3
32 y x x
t bng 0.
A.
3 2. yx
B.
3 2.yx
C.
3 2.yx
D.
2;0 , 2; . 
Câu 3: Tìm tt c các giá tr ca m  ng thng
1 y x m
c th hàm s
21
1
x
y
x
ti hai
m phân bit A, B sao cho
2;0 , 0;2 .
A.
4 10.m
B.
4 3.m
C.
2 3.m
D.
2 10.m
Câu 4: Cho hàm s
42
21 y x mx
 th
0x
tip tuyn c th
(C)
có h s t giá
tr ln nht khi nào?
A.
0a
 tim là
.
3

b
x
a
y
x
O
3
4
1
1
3
3
1
+
∞
∞
y
y'
x
+
+
+
∞
∞
0
1
_
0
0
Trang10
B.
1 0. m
 tim là
.
3

b
x
a
C. tip tuym u m un là nghim c
1.m
D.  tim là
.
3

b
x
a
Câu 5:  th sau là ca hàm s nào?
A.
32
3 1. y x x
B.
5.
C.
32
2 6 1. y x x
D.
32
3 1. y x x
Câu 6: S m chung c th hàm s
32
2 3( 1) 6( 2) 2017 y x m x m
  th hàm s
;ab
là bao nhiêu?
A. 0. B. 3. C. 1. D. 2.
Câu 7: Tìm tt c các giá tr ca tham s m  th hàm s
9.m
không có tim cng.
A. không có giá tr nào ca m. B.
10.m
C.
0m
D.
10.m
Câu 8: Giá tr ln nht ca hàm s
3
( ) 3 2 f x x x
n
2
22
.
1

xx
y
x
là bao nhiêu?
A. 0. B. 4. C. 2. D.
2.
Câu 9: Cho hàm s
3
6
42

x x m
y
x
Kh
A. Hàm s nghch bin trên
16.m
B. Hàm s nghch bin trên
.
C. Hàm s nghch bin trên các khong
( ;1)
và
D. Hàm s ng bin trên khong
( ;1)
và nghch bin trên khong
(1; ).
Câu 10: Hàm s
2
2 y x x
ng bin trên kho
A.
0;1 .
B.
;1 .
C.
1; .
D.
1;2 .
Câu 11: Cho hàm s
( 0)

ax b
ya
cx d
 th
 bên. M nà

A.
0, 0, 0. b c d
B.
0, 0, 0. b c d
C.
0, 0, 0. b c d
D.
0, 0, 0. b c d
6
-6
-2
1
-4
-3
-1
4
3
2
-5
-4
-3
-2
-1
5
4
3
2
O
1
x
y

0
0
Trang11
Câu 12:  th a hàm s nào?
A.
42
2.y x x
B.
24
2.y x x
C.
42
2 1. y x x
D.
42
2.y x x
Câu 13: Hàm s
32
32 y x x x
t cc tiu t
A.
33
.
3
x
B.
9 5 3
.
9

x
C.
0.x
D.
33
.
3
x
Câu 14: Cho hàm s
32
1
( ) ( 1) ( 3) 4.
3
f x x m x m x m
u kin ca tham s
m
  th hàm
s
(| |)y f x
m cc tr là gì?
A.
3 1. m
B.
4.m
C.
0.m
D.
Câu 15: Gi M là giá tr ln nht và m là giá tr nh nht ca hàm s
2
2
2 4 5
,
1

xx
y
x

Mm
bng bao nhiêu?
A. 4. B. 3. C. 7. D. 1.
Câu 16: Tìm tp hp tt c các giá tr ca tham s
m
 hàm s
32
33 y x x mx
nghch bin trên
(2; ).
A.
;0 .
B.
; 3 .
C.
; 3 .
D.
;0 .
Câu 17: Tìm tt c các giá tr ca tham s m  hàm s
3
22
( 1) 1
3
x
y mx m m x
t ci ti
1.x
A. 2. B. 2. C.
2.
D. 1.
Câu 18: Hàm s
32
34 y x x
nghch bin trên kho
A.
;2
và
0; .
B.
;0
và
2; .
C.
0;2 .
D.
2;0 .
Câu 19: Cho hàm s
23
.
1
x
y
x
Tìm tt c các giá tr ca tham s m   th hàm s tip xúc vi
ng thng
2?y x m
A.
8.m
B.
.m
C.
2 2.m
D.
Câu 20:  th hàm s
2
2
32
56


xx
y
xx
có bao nhiêu tim cn?
A. Mt tim cn ngang và mt tim cng.
B. Mt tim cn ngang và hai tim cng.
C. Ch có hai tim cng.
D. Hai tim cn ngang và mt tim cng.
-----------------------------------------------
----------- HT ----------
1
-1
3
2
-2
-1
2
O
1
x
y
Trang12
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
ĐỀ 5
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG I
GIẢI TÍCH 12
Câu 1: Cho hàm s
42
y ax bx c
  th
.
M 
A.
0, 0, 0. a b c
B.
0, 0, 0. abc
C.
0, 0, 0. abc
D.
0, 0, 0. a b c
Câu 2: Cho hàm s
2
2 1 1
32


x
y
xx
 th
( ).C
Kh
A.
()C
có 2 tim cng. B.
()C
không có tim cn ngang.
C.
()C
có 1 tim cn ngang. D.
()C
không có tim cng.
Câu 3: Tìm tt c các giá tr ca tham s m  ng thng
2ym
c th hàm s
42
23 y x x
tm phân bit.
A.
2 3.m
B.
2 3.m
C.
3
1.
2
m
D.
3
1.
2
m
Câu 4: Giá tr ln nht ca hàm s
21
1
x
y
x
n
1;2
là giá tr 
A.
1;2
max 1.y
B.
1;2
1
max .
2
y
C.
1;2
1
max .
2
y
D.
1;2
1
max .
3
y
Câu 5: Tìm tp giá tr ca hàm s
2
.y x x
A.
0;2 .
B.
0;1 .
C.
1
0; .
2



D.
1
0; .
4



Câu 6: Cho hàm s
32
3 ( 1) 1 y x x m x
 th
( ).C
Tìm
m
 ng thng
: y 1dx
ct
 th
()C
tm phân bit
(0;1), ,P M N
ng tròn ngoi tip tam giác
OMN
bng
52
.
2
A.
3.m
B.
9
.
4
m
C.
0.m
D.
y
x
Trang13
Câu 7: Cho hàm s
32
21 y x x m x m
 th
( ).C
Tìm m 
()C
ct trc hoành tm
phân bi
1 2 3
,,x x x
tha mãn
222
1 2 3
4. xxx
A.
1
1.
4
m
B.
1
.
0
m
m
C.
1
1.
4
m
D.
1
1
.
4
0
m
m
Câu 8: Hàm s
2
2 y x x x
nghch bin trên kho
A.
1;2 .
B.
1; .
C.
;1 .
D.
0;1 .
Câu 9: Hàm s
3 2 2
1
(m 1) 1
3
y x mx m x
t cc tiu ti
1x
khi m bng my?
A.
1.m
B.
2.m
C.
1.m
D.
2.m
Câu 10: Cho hàm s
1
1
x
y
x
 th
( ).C
Gi
d
là tip tuyn ca
()C
t bng 3.
Tìm h s góc
k
ca
.d
A.
1
.
2
B.
1
.
2
C.
2.
D. 2.
Câu 11:  th sau là ca hàm s nào?
A.
32
3 1. y x x
B.
32
3 1. y x x
C.
32
3 1. y x x
D.
32
1
1.
3
y x x
Câu 12: Cho hàm s
42
8 4. y x x
Các khong bin ca hàm s là các kho
A.
; 2 , 0;2 .
B.
2;0 , 2; . 
C.
; 2 , 2; . 
D.
2;0 , 0;2 .
Câu 13: Hàm s ng bin trên
?
A.
42
2 5. y x x
B.
1. yx
C.
3
3 1. y x x
D.
1
.
1
x
y
x
Câu 14: Hàm s
42
21 y x mx
t cc tiu ti
0x
khi m thu ki
A.
0.m
B.
0.m
C.
1 0. m
D.
1.m
Câu 15: Hàm s
42
10 9 y x x
t c i, cc tiu l t ti
12
,.xx
    biu thc
12
||xx
bng bao nhiêu?
A. 5. B.
5.
C. 4. D.
2 5.
Câu 16: Tìm tt c các giá tr thc ca tham s
m
 hàm s
32
2 3( 1) 6( 2) 2017 y x m x m
nghch bin trên khong
;ab
sao cho
3.ba
A.
0.m
B.
9.m
C.
6.m
D.
0m
hoc
6.m
-2
1
-4
-3
-1
3
2
-2
-1
4
3
2
O
1
x
y
Trang14
Câu 17: Cho hàm s
2
22
.
1

xx
y
x
Bing thng
y ax b
tip xúc v th hàm s tm
 bng 3. Giá tr ca
T a b
là bao nhiêu?
A.
1.
B. 2. C. 3. D. 1.
Câu 18: Cho tham s
m
 th hàm s
3
6
42

x x m
y
x
không có tim cng. Khnh

A.
16.m
B.
2.m
C.
D.
23
.
8
m
Câu 19:  th a hàm s nào?
A.
1
.
21
x
y
x
B.
1
.
21
x
y
x
C.
1
.
12
x
y
x
D.
1
.
21
x
y
x
Câu 20: Cho hàm s
32
3 3 1. y x x x
Vip tuyn c th tm c
th vi trc tung.
A.
3.yx
B.
3 1. yx
C.
3 3. yx
D.
0.y
-----------------------------------------------
----------- HT ----------
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
ĐỀ 6
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG I
GIẢI TÍCH 12
Câu 1:
Hàm s
22
4 2 3 2 y x x x x
t giá tr ln nht ti x
1;
x
2
.

1
x
2
có giá tr là
A.
1
B. - 1 C.
2
D. 2
Câu 2: Tìm tt c ng tim cng c th hàm s
2
3 1 3
23

xx
y
xx
A.
3x
B. .
1x
.
và
3x
C.
3x
D.
1x
và
3x
Câu 3: Vi giá tr nào ca m  ng thng
1 yx
c th hàm s
32
2 3 1 1 y x mx m x
tm phân bit?
A.
8
0;
9



m
B.
0m
hoc
8
9
m
C.
0m
hoc
D.
8
; 0;
9

 


m
6
-6
-2
1
6
-4
-3
-1
5
4
3
2
-5
-4
-3
-2
-1
5
4
3
2
O
1
x
y
Trang15
Câu 4:  th ca hàm s nào?
A.
23
1
x
y
x
B.
23
1
x
y
x
C.
23
1

x
y
x
D.
23
1

x
y
x
Câu 5: Cho hàm s
42
24 y x x
 
22
23 x x m
có hai nghim phân
bit
A.
3m
B.
2m
C.
3m
D.
3m
hoc m=2
Câu 6: ng thng
1y
c th hàm s
42
13
3
22
y x x
ti mm?
A. 4 B. 3 C. 2 D. 1
Câu 7: Cho hàm s
32
y x ax bx c
. Bit r th hàm s m
0; 1A
m
ci là
2;3M
. Tính
2 Q a b c
A.
0Q
B.
4Q
C.
1Q
D.
2Q
Câu 8: Hàm s
2
2y x x
nghch bin trên khong
A. (0; 1) B.
(1; )
C.
( ;1)
D. (1;2)
Câu 9: Vi tt c các giá tr thc nào ca tham s
m
thì hàm s
32
3 1 3 2 y x m x m m x
nghch bin
0;1
?
A.
10 m
B.
0m
C.
10 m
D.
1m
Câu 10: Cho hàm s
32
3 9 5 y x x x
 th (C ). Tip tuyn c th (C ) tm cc tiu là
ng thng:
A. Trùng vi trc hoành B. Song song vi trc hoành
C.
5 yx
D. Song song vi trc tung
Câu 11:  th hàm s
32
( ): 3 2 C y x x
. S tip tuyn c th (C) bit tip tuyn song song
vng thng
97yx
là:
A.
1
B.
2
C.
1
D.
0
Câu 12: Cho hàm s
21
1
x
y
x
.M 
A. Tip tuyn c th hàm s tm có hoành
2x
có h s góc bng 1
B. Hàm s nghch bin trên tng khong nh
C. Hàm s có tnh là
\{1} D
D.  th hàm s m A (2; 3)
Câu 13: Bng bia hàm s nào?
x
20
 - 0 + 0-
Trang16
y
A.
3
2
2
3
x
yx
B.
2
1
1


xx
y
x
C.
3
2
1
3
x
yx
D.
2
1
1

xx
y
x
Câu 14: Vi giá tr nào ca tham s m thì hàm s
32
( 2) 3 5 y m x x mx
có ci và cc tiu
A. m > - 3 B.
( 3;1)m
C.
( ; 3) (1; )  m
D.
( 3;1) \{ 2} m
Câu 15: Cho hàm s
3
2
2(5 8) 1
3
x
y mx m x
.Tìm các giá tr ca tham s m  hàm s t cc tiu
ti
2x
A. Vi mi giá tr m B.
6
7
m
C.
6
7
m
D. Không có giá tr m nào
Câu 16: Cho hàm s
42
y ax bx c
 th  bên.
Kh
A.
0, 0, 0 abc
B.
0, 0, 0 a b c
C.
0, 0, 0 a b c
D.
0, 0, 0 abc
Câu 17:  th hàm s
23
( ):
1

x
Cy
x
. p tuyn c th (C) tm ca
(Cng thng
3yx
là:
A.
3 yx
và
1 yx
B.
3 yx
và
1 yx
C.
3yx
và
1yx
D.
3 yx
và
1 yx
Câu 18: Cho hàm s
4 2 4
2 2 . y x mx m m
Vi giá tr nào ca
m
 th
m
C
m cc tr,
ng thm cc tr o thành mt tam giác có din tích bng 2.
A.
3
16m
B.
5
4m
. C.
5
16m
. D.
16m
.
Câu 19: Gi
,Mm
l t là giá tr ln nht và giá tr nh nht ca hàm s
2
3
2
x
y
x
 n
3
1;
2



.
M 
A.
13
6
Mm
B.
7
2
Mm
C.
8
3
Mm
D.
4
3
Mm
Câu 20: Tìm tt c các giá tr thc ca tham s  th ca hàm s
2
1
1
x
y
mx
có hai tim
cn ngang.
A. m 0.
B. Không có giá tr thc nào ca m tha mãn yêu c bài.
C. m 0.
D. m 0.
Trang17
-----------------------------------------------
----------- HT ----------
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
ĐỀ 7
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG I
GIẢI TÍCH 12
Câu 1:  th a hàm s
32
34 y x x
. Vi giá tr nào ca tham s m 
32
3 4 0 x x m
có nghim duy nht.
A.
40 m hay m
B.
42 m hay m
C.
40 m hay m
D.
40 m
Câu 2: Trong các hàm s sau, hàm s t cc tiu tm
1?x
A.
22
( 1)yx
B.
3
2 yx
C.
2
23 y x x
D.
3
2
3
x
y x x
Câu 3: Cho hàm s
xb
y
cx d
 th . Kh
A.
0, 0, 0. b c d
B.
0, 0, 0. b c d
C.
0, 0, 0. b c d
D.
0, 0, 0. b c d
Câu 4: Cho hàm s
2
3 10 y x x
. Trong các m sau, chn m 
A. Hàm s t giá tr ln nht bng 10 ti
3x
B. Hàm s t giá tr ln nht bng 10 ti
3x
C. Hàm s t giá tr nh nht bng
3 10
ti
10x
D. Hàm s t giá tr nh nht bng
3 10
ti
10x
Câu 5: Giá tr ln nht ca hàm s
2
4 y x x
trên
3;3
là.
A.
4
B.
0
C.
2
D.
2
-2
-4
1
O
3
-1
2
Trang18
Câu 6: Cho hàm s
32
3 1 4 y mx mx m x
. Tìm tt c các giá tr thc ca tham s
m
 hàm
s không có cc tr
A.
1
0
4
m
B.
1
4
m
C.
1
0
3
m
D.
1
0
4
m
Câu 7: Cho hàm s
y f x
nh, liên tn
1;3
 th ng cong trong
hình v bên. Tp hp
T
tt c các giá tr thc ca tham s
m
 
f x m
có 3
nghim phân bit thun
1;3
là
A.
4;1T
. B.
3;0T
.
C.
4;1T
. D.
3;0T
.
Câu 8: Hàm s nào có bng bi
X

1

'( )fx
()fx
2


2
A.
21
2
x
y
x
B.
22
1
x
y
x
C.
22
1
x
y
x
D.
23
1
x
y
x
Câu 9: Cho hàm s
32
3
6
3 2 4
xx
yx
. M 
A. Hàm s nghch bin trên khong
;2
B. Hàm s ng bin trên khong
2;3
.
C. Hàm s ng bin trên khong
2; 
D. Hàm s nghch bin trên khong
2;3
Câu 10:  th hàm s
42
1
( ) 2
4
f x x x
p tuyn c th (C) tm
0
x
bit
//
0
( ) 1fx
là:
A.
5
3
4
yx
và
5
3
4
yx
B.
5
3
4
yx
và
5
3
4
yx
C.
35 yx
và
35yx
D.
5
4
yx
và
5
3
4
yx
Câu 11: Cho hàm s
3
31
4
a
 th (C). Kh
A. (C) có hai tim cng thng
3
15a
và mt tim cng thng
3
17a
B. (Ct tim cng thng
3
12a
và mt tim cng thng
3
C. (C) có mt tim cng thng
3a
và không có tim cn ngang
D. (C) có hai tim cng thng
5a
và không có tim cn ngang
Câu 12: Hàm s
32
34 y x x mx
nghch bin trên khong
0;
, ng vi các giá tr thc ca
tham s m là
O
1
O
1
2
3
x
y
4
3
Trang19
A.
;0
B.
0;
C.
;1
D.
0;
Câu 13: Tìm tt c các giá tr ca
m
 hàm s
32
1
3 2 1
3
y x mx m x
ng bin trên
.
A.
1
2


m
m
B.
21 m
C.
1
2


m
m
D.
21 m
Câu 14: Tìm tt c các giá tr thc ca tham s m   th hàm s
32
3 y x m x
m cc tr A
và B sao cho
2 5.AB
A.
2m
B.
2m
C.
1m
D.
1m
Câu 15: Hàm s
3
3yx
A. Có cc tiu
B. Có ci và cc tiu
C. Có ci
D. Không có cc tr
Câu 16:  th ca hàm s
3
1

x
y
x
m vng thng
1 y mx
, ng vi giá tr
thc ca tham s m là
A.
0 16m
B.
0 16m
C.
0 16m
D.
0 16m
Câu 17: 










 
(3; 1)
A.
B.
C.
D.
Câu 18: Tìm tt c các giá tr thc ca tham s m  th ca hàm s
42
2( ) 1 y x mx
m
cc tr to thành mu.
A.
6
3m
B.
6
3m
hoc
6
3m
C.
0m
hoc
6
3m
D.
6
3m
hoc
6
3m
hoc
0m
Câu 19:  th hàm s
32
y x ax bx c
m
1;3A
,
0;7B
,
3; 35C

trình ca hàm s là
A.
32
27 y x x x
B.
32
27 y x x x
C.
32
27 y x x x
D.
3
27 y x x
Câu 20: Tip tuyn ca
42
( ): 2 3 C y x x
tm ca
()C
và trc hoành có h s góc là?
A.
53
B.
73
C.
83
D.
33
-----------------------------------------------
----------- HT ----------
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
2
1
2
mx
y
x
1m 
3m
1m 
3m 
Trang20
ĐỀ 8
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG I
GIẢI TÍCH 12
Câu 1: Cho hàm s  th .
M đúng?
A.
B.
C.
D.
0, 0, 0. abc
Câu 2: Vi các giá tr nào ca
m
 th hàm s
2
23
x x m
y
xm
không có tim cng?
A.
1m
. B.
1m
hoc
2m
. C.
0m
. D.
0m
hoc
1m
.
Câu 3: Có bao nhiêu s nguyên m  
42
8 3 0 x x m
có 4 nghim phân bit
A. 15. B. 16. C. Không có. D. Vô s.
Câu 4: Tìm giá tr ln nht ca hàm s n
A.
B.
C.
D.
Câu 5: Bit hàm s có giá tr nh nhn bng 2. Kh
A.
11 m
. B.
1m
.
C.
15m
. D.
5m
.
Câu 6: Tìm tt c các giá tr ca tham s m  ng thng
:2 d y x m
c  th hàm s
2
1
x
y
x
tm phân bit A và B  dài AB ngn nht.
A.
3m
. B.
1m
. C.
3m
. D.
1m
.
Câu 7: ng thng
:4d y x
c th hàm s
32
2 3 4 y x mx m x
tm phân bit
0;4A
, B, C sao cho tam giác MBC có din tích bng 4, vi
1;3M
. Tp tt c các giá tr ca
m nhc là:
A.
2m
hoc
3m
. B.
3m
.
C.
2m
hoc
3m
. D.
2m
hoc
3m
.
Câu 8: Cho hàm s
3
32 y x x
. M 
A. Hàm s ng bin trên khong
( ;0)
và nghch bin trên khong
(0; )
.
B. Hàm s nghch bin trên khong
( ;0)
ng bin trên khong
(0; )
.
C. Hàm s ng bin trên khong
( ; ) 
.
D. Hàm s nghch bin trên khong
( ; ) 
.
42
y ax bx c
0, 0, 0.abc
0, 0, 0.a b c
0, 0, 0.a b c
3
3y x x
0;2 .
0;2
max 2.y
0;2
max 2.y
0;2
max 1.y
0;2
max 0.y
32
3y x x m
0;1
Trang21
Câu 9:  th ca hàm s
32
y x x
m cc tr A và B. Tính din tích S ca tam
giác OAB vi O là gc t.
A.
3
9
8
a
V
. B.
60
. C.
10
3
S
. D.
3
8
a
V
.
Câu 10: Cho hàm s
32
4 6 1 y x x
 th (C). Ltip tuyn ca (C) m
1; 9M
.
A.
24 15yx
. B.
24 15yx
hoc
15 21
.
44
yx
C.
24 33yx
. D.
15 21
.
44
yx
Câu 11:  th hình bên là ca hàm s nào?
A.
2
1 y x x
.
B.
3
31 y x x
.
C.
42
1 y x x
.
D.
3
31 y x x
.
Câu 12: Hàm s
2
2
1
y
x
nghch bin trên kho
A.
( ; ) 
. B.
(0; )
. C.
( ;0)
. D.
.
Câu 13: Tìm m  hàm s
42
2y x mx
nghch bin trên
( ;0)
ng bin trên
(0; )
.
A.
0m
. B.
0m
. C.
0m
. D. .
21
:
1
x
Cy
x
.
.
Câu 14: m ci c th hàm s
32
6 9x xyx
m nào?
A.
1;4
. B.
3x
. C.
3;0
. D.
1x
.
Câu 15: Tìm tham s m  th hàm s
42
21y x mx
  m cc tr
( )
0;1 , , A B C
tha mãn
4BC
.
A.
4m 
. B.
4m
. C.
2m
. D.
2m 
.
Câu 16: Bit r th hàm s  th hàm s ct nhau tm
duy nht có t Tìm
A.
B.
C.
D.
Câu 17: Cho hàm s
32
69y x x x
 th (C). Ltip tuyn ca (C) song song
vng thng
:9d y x
.
A.
9 32yx
. B.
9 40yx
. C.
9 32yx
. D.
9 40yx
.
Câu 18: Tìm s tim cn c th hàm s
3
2
1
54
x
y
xx

.
A.
4
( 1;2;0)u 
. B.
24V
. C.
32V
. D.
1
(0;2;0)u
.
Câu 19:  th sau là ca hàm s nào?
32
2y x x x
2
5y x x
00
;.xy
0
.y
0
3.y
0
4.y
0
1.y 
0
0.y
Trang22
A.
B.
C.
D.
Câu 20: Cho hàm s  th Gi là tip tuyn ca t bng 3.
Tìm h s góc ca
A.
B.
C.
D. 2.
-----------------------------------------------
----------- HT ----------
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
ĐỀ 9
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG I
GIẢI TÍCH 12
Câu 1: Tìm m  hàm s t cc tiu ti .
A.
B.
C.
D.
Câu 2: S tim cn c th hàm s là bao nhiêu?
A. 3. B. 1. C. 2. D. 0.
Câu 3: Tìm tt c các giá tr ca tham s m ng thng
:d y x m
c th hàm s
21
:
1
x
Cy
x
tm phân bit M và N sao cho din tích tam giác IMN bng 4, vi I
i xng ca (C).
A.
3; 1mm
. B.
3; 3mm
. C.
3; 5mm
. D.
3; 1mm
.
Câu 4: Cho hàm s Vip tuyn c th tm ca
 th vi trc trung.
A.
B.
C.
D.
2
.
1
x
y
x
3
.
1
x
y
x
1
.
1
x
y
x
21
.
1
x
y
x
1
1
x
y
x
( ).C
d
()C
k
.d
1
.
2
2.
1
.
2
3 2 2
1
(m 1) 1
3
y x mx m x
1x
1.m
1.m
2.m
2.m
2
2
1
2
x
y
x
32
3 3 1.y x x x
3 1.yx
0.y
3 3.yx
3.yx
Trang23
Câu 5: Cho hàm s
32
31y x x
 th là (C). Gi
là tip tuyn ca (C) tm
1;5A
và
B m th hai ca
vi (C). Din tích tam giác OAB bng bao nhiêu?
A. 12. B.
6 82
. C. 6. D. 5.
Câu 6: Có bao nhiêu s nguyên  ng thng c th hàm s ti 4
m phân bit?
A. 1. B. Không có.
C. 2.
D. 4.
Câu 7: Cho hàm s có giá tr nh nh  n bng 2. Khnh nào

A.
13m
.
B.
1m 
.
C.
3m
.
D.
11 m
.
Câu 8:  th sau là ca hàm s nào?
A.
B.
C.
D.
Câu 9: Cho hàm s
2
21yx
. M 
A. Hàm s ng bin trên khong
( ;0)
.
B. Hàm s nghch bin trên khong
(0; )
.
C. Hàm s nghch bin trên khong
( 1;1)
.
D. Hàm s ng bin trên khong
(0; )
.
Câu 10: Cho hàm s
y f x
có bng xét d:
M 
A. Hàm s ng bin trên khong
( 2;0)
.
B. Hàm s nghch bin trên khong
( ; 2)
.
C. Hàm s ng bin trên khong
( ;0)
.
D. Hàm s nghch bin trên khong
(0;2)
.
Câu 11:  th hình bên là ca hàm s nào?
A.
42
23y x x
.
B.
42
23y x x
.
C.
42
23y x x
.
D.
42
23y x x
.
m
21ym
42
22y x x
32
36y x mx
0;3
32
2 6 1. y x x
32
3 1. y x x
32
3 1. y x x
3
2
1.
3
x
yx
x
'y

2
0
2

0
0
Trang24
Câu 12: Cho hàm s
21
1
x
y
x
  th (C). Gi d là tip tuyn ca (C), bit d   m
4; 1A
. Gi M là tim ca d và (C). Tìm t m M.
A.
2;5 , 0; 1MM
. B.
2;5 , 2;1MM
.
C.
0; 1 , 2;1MM
. D.
3
1; , 2;1
2




MM
.
Câu 13: Hàm s t ci tm nào?
A.
B.
C.
D.
Câu 14: Cho hàm s  th Tìm  ng thng ct
 th tm phân bit ng tròn ngoi tip tam giác
bng
A.
B.
C.
D.
Câu 15: Cho hàm s  th  bên. M đúng?
A.
B.
C.
D.
Câu 16: Gi M, N   m c ng thng
:1d y x
 ng cong
24
:
1
x
Cy
x
. Tìm
 m I cn thng MN.
A.
5
2
. B. 2. C. 1. D.
5
2
.
Câu 17: Tìm tt c các giá tr ca tham s m   th hàm s m cc tr to
nh ca mt tam giác vuông cân.
A.
B.
C.
D.
Câu 18: Tìm tt c các giá tr ca tham s m  ng bin trên mi khonh.
A.
2 2. mm
B.
2 2. mm
C. D.
Câu 19: Tìm tt c các giá tr ca tham s m   th hàm s ng tim
cn.
A.
B.
C.
D.
Câu 20: Gi lt là giá tr ln nht, giá tr nh nht ca hàm s trên tp xác
nh.
3
32 y x x
1.x
0.x
2.x
1.x
32
3 ( 1) 1y x x m x
( ).C
m
:1d y x
()C
(0;1), ,P M N
OMN
52
.
2
0.m
1.m
3.m
9
.
4
m
( 0)
ax b
ya
cx d

0, 0, 0.b c d
0, 0, 0.b c d
0, 0, 0.b c d
0, 0, 0.b c d
4 2 2
21y x m x
1.m
1;0;1 .m
2.m
1.m
2
2
mx
y
xm
2 2.m
2 2.m
2
2
32
xm
y
xx

1.m
4.m
1, 4.mm
0.m
, Mm
2
1y x x
y
x
O
Trang25
 bng bao nhiêu?
A. 2. B. 1. C. 3. D. 4.
-----------------------------------------------
----------- HT ----------
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
ĐỀ 10
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG I
GIẢI TÍCH 12
Câu 1: Cho hàm s
3 2 2 3
3 y x m x m
 th
C
. Tìm tt c các giá tr thc ca tham s
m

tip tuyn c th
C
t
0
1x
song song vng thng
: 3 .d y x
A.
1.m
B.
1.m
C.
1
.
1

m
m
D. Không có giá tr ca
.m
Câu 2: Giá tr ln nht M và giá tr nh nht m ca hàm s
42
23 y x x
trên
0;2
là:
A.
11, 3.Mm
B.
5, 2.Mm
C.
3, 2.Mm
D.
11, 2.Mm
Câu 3: S ng tim cn c th hàm s
2
2
32
4

xx
y
x
là:
A. 4. B. 1. C. 2. D. 3.
Câu 4: Cho hàm s
21
1
x
y
x
 th m
M
 th (C) sao cho khong cách t
m
(2;4)A
và
( 4; 2)B
n tip tuyn ca (C) ti
M
là bng nhau
A.
(0;1).M
B.
35
(1; ), (2; ).
23
MM
C.
3
(1; ).
2
M
D.
3
(0;1); (1; ); ( 2;3).
2
M M M
Câu 5: Tng các giá tr thc ca tham s
m
ng thng
yx
c th hàm s
5
x
y
xm
tm A và B sao cho
42AB
là
A. 2 B. 5 C. 7 D. 9
Câu 6:
Tìm tt c các giá tr thc ca tham s
m
 ng thng
: d y x m
c th hàm s (C):
21
2
x
y
x
tm phân bit
A.
1 4. m
B.
.m
C.
4.m
D.
1m
hoc
4.m
Câu 7: Chohàms
()y f x
co hàm
2
'( ) 1.f x x
Mnnào dâyúng?
Mm
Trang26
A. Hàms nghch bin trênkhong
(.1;1)
B. Hàms nghch bin trên khong
(1; ).
C. Hàms nghch bin trênkhong
( ).;0
D. Hàms ngbin trênkhong
.; () 
Câu 8: Tìm tt c các giá tr thc ca tham s
m
  th hàm s
42
1 y x m x m
ct trc
hoành ti bm phân bit có t bng
8.
A.
1.m
B.
1 2 2. m
C.
7.m
D.
3.m
Câu 9: Cho hàm s
1
2
x
y
x
 th (C). Tip tuyn ca (C) tm ca (C) và trc hoành có

A.
3.yx
B.
11
.
33
yx
C.
3 3.yx
D.
3.yx
Câu 10:  ng cong
2
2
36
( ):


xx
Cy
x ax a
ng tim cng thì giá tr ca
a
là
A.
0
.
4
a
a
B.
1
.
2
a
a
C.
1.a
D.
2.a
Câu 11: Cho
2
2
1
4 5 4

x
f x x
xx
. Gi
0;3
0;3
max ; minM f x m f x

Mm
bng
A.
3
.
5
B. 1. C.
7
.
5
D.
9
.
5
Câu 12: Cho hàms
2
21yx
.
Mnh nàây úng?
A. Hàms nghch bin trênkhong
(0; ).
B. Hàms ngbin trênkhong
( ).; 0
C. Hàms nghch bin trênkhong
(.1;1)
D. Hàms ng bin trênkhong
(0; ).
Câu 13: S m ci c th hàm s
42
1
( ) 2 4
4
f x x x
là:
A. 1 B. 3 C. 2 D. 0
Câu 14: Cho hàms
()y f x
có bng bin thiêau
Mn nàodâysai?
A. Hàms cógiátrcibng 0
B. Hàms cóbaimcc tr.
C. Hàms có haimcctiu.
D. Hàms cógiátrcibng
3
.
Câu 15: Giá tr cc tiu ca hàm s
3
1
1
3
y x x
là:
A. 1 B.
1
3
C.
5
3
D.
1
Trang27
Câu 16: Cho hàm s
42
y ax bx c
, vi
0a
, có bng bi
Khđúng:
A.
0a
và
0b
B.
0a
và
0b
C.
0a
và
0b
D.
0a
và
0b
Câu 17: Hàm s
2
2
1
xx
y
x
ng bin trên khong:
A.
( ;2).
B.
( ;1) (1; ). và
C.
( 1; ). 
D.
(0; ).
Câu 18: Cho hàm s
y f x
o hàm
'( )fx
 th hàm s
()y f x

Khđúng:
A. Hàm s
y f x
ng bin trên khong
(0;1).
B. Hàm s
y f x
ng bin trên khong
( ;2).
C. Hàm s
y f x
m cc tr.
D. Hàm s
y f x
ng bin trên khong
( ; 1).
Câu 19: Cho hàm s
y f x
 th tt c các giá tr thc ca tham s
m


2f x m
có bn nghim phân bit.
A.
43 m
.
B.
43 m
.
C.
65 m
.
D.
65 m
.
.
-----------------------------------
Câu 20:  th hàm s
32
32 y x x
có dng:
A.
B.
C.
D.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
----------- HT ----------
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
B
D
C
D
C
B
D
D
B
A
D
D
D
A
C
A
B
D
D
C
1
-1
-3
-4
y
x
O
Trang28
ĐỀ 11
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG I
GIẢI TÍCH 12
Câu 1: 

42
y ax bx c
. 


đu
ng?
A.
( ;1).
B.
(1;3).
C.
0, 0, 0. a b c
D.
0, 0, 0. a b c
Câu 2: 

32
3 1. y x x



(3;1)A
là:
A.
9 20.yx
B.
9 28 0. xy
C.
13
.
2
m
D.
13
.
2
m
Câu 3: Cho hàm s
3 2 2
y x m x m
 th
C
. Tìm tt c các giá tr thc ca tham s
m
 tip
tuyn c th
C
t
0
1x
song song vng thng
: 5 .d y x
A.
2.m
B.
2.m
C. Không có giá tr ca
.m
D.
3;2
min 1.
y
Câu 4: Tìm giá tr ln nht ca hàms
2
4
x
y
x
n
1;3
.
A.
1;3
max 4.y
B.
, .AB
C.
12
kk
D.
1.
Câu 5: S m cng cong
32
2 2 1 y x x x
ng thng
1yx
bng:
A. 0. B. 2. C. 3. D. 1.
Câu 6: Tìm tt c các giá tr thc ca tham s
m
  th hàm s
42
1 y x m x m
ct trc
hoành ti bm phân bit có t bng
2 2.
A.
3.m
B.
42
2.f x x x
C.
42
2.f x x x
D.
1 2. m
Câu 7: Cho hàm s
2
1
x
y
x
. :
1) Hàm s ch bin trên
;1 1; . 
2) Hàm s ng bin trên
;1 .
3) Hàm s ch bin trên tnh.
4) Hàm s ch bin trên các khong
;1
và
1; .
S 


A.
1.
B.
3.
C.
2.
D.
4.
Câu 8: Tp tt c các giá tr thc ca tham s
m
 hàm s
32
1 3 1 y x m x x
ng bin trên
khong
; 
là
A.
x
B.
; 2 4; . 
Trang29
C.
2;4 .
D.
; 2 4; . 
Câu 9: , 










2
4 y x x
. 
A.
4.Mm
B.
2 2 2. Mm
C.
2 2.Mm
D.
2 2 2. Mm
Câu 10: Cho hàm s
3
1 y x x
 th (C). Vip tuyn ca (C) tm ca
(C) vi trc tung.
A.
2 2.yx
B.
2 1.yx
C.
1. yx
D.
1. yx
Câu 11: Giá tr thc ca tham s
, ab
 hàm s
1
ax b
y
x
 th 
A.
1, 2. ab
B.
1, 2. ab
C.
1, 2.ab
D.
1, 2. ab
Câu 12: Hàm s
2
2 y x x x
nghch bin trên khong
A.
;1 .
B.
1; .
C.
0;1 .
D.
1;2 .
Câu 13: Gi
12
,xx
m cc tr ca hàm s
32
1
5
3
y x x x
. Giá tr biu thc
22
12
12
11

xx
S
xx
bng
A. 4. B. 2. C. 1. D. 3.
Câu 14: Khong cách t m ci c th hàm s
32
21 y x x x
n trc hoành là
A.
23
.
27
B.
( ) 1. f a b c
C. 1. D.
1
.
9
Câu 15: Cho hàm s có bng bi
x

-2 0

'y
+ 0 - 0 +
y
3


-1
A. Giá tr cc tiu ca hàm s là 0.
B. Hàm s t cc tiu ti
1x
t ci ti
3.x
C. Giá tr ci ca hàm s là
2.
D. Hàm s t ci ti
2x
t cc tiu ti
0.x
Câu 16: Tp hp giá tr thc ca tham s
m
  th hàm s
2
62
2

mx x
y
x
có tim cng là
A.
.
B.
7
.
2



C.
\ 0 .
D.
7
\.
2



Câu 17: 
3
32 y x x
?
Trang30
A.
;1
và
1; .
B.
; 1 1; . 
C.
1; . 
D.
1;1 .
Câu 18: :
1)  th hàm s
1
23
y
x
có mng tim cng và mng tim cn ngang.
2)  th hàm s
2
1
x x x
y
x
ng tim cn ngang và mng tim cng.
3)  th hàm s
2
21
1

xx
y
x
có mng tim cng tim cng.
S 


A.
2
. B.
3
. C.
1
. D.
0
.
Câu 19: Tìm tt c m thu th hàm s
21
1
x
y
x
có khon trc hoành bng 1
A.
0; 1 , 2;1 .MN
B.
2;1 .M
C.
0; 1 , 1; 1 . MN
D.
0; 1 .M
-------------------------------------------
Câu 20: Hình v  th ca hàm s nào?
A.
21
.
1
x
y
x
B.
12
.
1
x
y
x
C.
21
.
1
x
y
x
D.
12
.
1
x
y
x
----------- HT ----------
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
C
B
B
C
D
D
A
A
B
D
C
D
A
A
D
D
A
A
A
A
ĐỀ 12
Thuvienhoclieu.Com
ĐỀ ÔN TẬP CHƯƠNG I
GIẢI TÍCH 12
Câu 1: Cho hàm s
ax b
y
cx d
 th : Kh
4
2
-2
-5
5
y
x
O
1
-1
Trang31
A.
0
.
0
ad
bc
B.
0
.
0
ad
bc
C.
0
.
0
ad
bc
D.
0
.
0
ad
bc
Câu 2: Vip tuyn v th hàm s
24
4
x
y
x
t bng
3.
A.
4 5 0. xy
B.
4 20 0. xy
C.
4 5 0. xy
D.
4 20 0. xy
Câu 3: 
 :
32
4 6 1 y x x
   p tuyn c  th bi    m
1; 9M
là:
A.
24 15yx
hoc
15 21
.
44
yx
B.
24 15.yx
C.
15 21
.
44
yx
D.
10x
hoc
24 15.yx
Câu 4: Gi
l t là giá tr ln nht và giá tr nh nht ca hàm s
2
3
2
x
y
x


3
1;
2



. M nào 
A.
8
.
3
Mm
B.
4
.
3
Mm
C.
7
.
2
Mm
D.
16
.
3
Mm
Câu 5: Tìm s m
n
c th
42
32 y x x
và
2
2yx
.
A.
0.n
B.
1.n
C.
4.n
D.
2.n
Câu 6: Tìm tt c các giá tr ca tham s thc
m
 ng thng
21yx



.
1
xm
y
x
A.
3
1.
2
m
B.
3
.
2
m
C.
3
1.
2
m
D.
3
.
2
m
Câu 7: Cho hàm s
32
1
2 3 1.
3
y x x x
M 
A. Hàm s ng bin trên khong
(1;3).
B. Hàm s nghch bin trên khong
(1; ).
C. Hàm s ng bin trên khong
( ;1).
D. Hàm s nghch bin trên khong
(1;3).
Câu 8: Tìm tt c các giá tr thc ca tham s
m
 hàm s
32
22 y x mx x
ng bin trên khong
2;0 .
A.
2 3.m
B.
2 3.m
C.
13
.
2
m
D.
13
.
2
m
Trang32
Câu 9: Tìm giá tr nh nht ca hàm s
2
1yx
n
3;2 .
A.
3;2
min 8.
y
B.
3;2
min 3.
y
C.
3;2
min 1.
y
D.
3;2
min 3.
y
Câu 10: Cho hàm s
1
21

x
y
x
(C). Gi
, AB
m cng
y x m
v th (C) và
12
,kk
là h s góc ca tip tuyn v th tm
, .AB

12
kk
t giá tr ln
nht bng:
A. 2. B. 1. C.
1.
D.
2.
Câu 11: : 

y f x
. 
fx



 , B, C, 
 . 
fx
A.
42
2.f x x x
B.
42
2.f x x x
C.
42
2 1. f x x x
D.
42
2. f x x x
Câu 12: Da vào hình v. Tìm kh
A. Hàm s nghch bin trên
(0; ),
ng bin trên
( ;0)
và có
hai cc tr.
B. Hàm s ng bin trên
(0; ),
nghch bin trên
( ;0)
và có hai cc tr.
C. Hàm s luôn nghch bin trên tng khonh và
không có cc tr.
D. Hàm s ng bin trên tng khonh và
không có cc tr.
Câu 13: Cho hàm s
()y f x
liên tc trên ℝo hàm
23
'( ) ( 1) ( 1) . f x x x x
Hàm s 
bao nhm cc tr?
A. Ch m cc tr. B. Không có cc tr.
C. m cc tr D. m cc tr.
Câu 14:
Tìm các s thc
p
và
q
sao cho hàm s
()
1
q
f x x p
x
t c i ti
2x
và
( 2) 2. f
A.
1, 1. pq
B.
1, 1.pq
C.
1, 1. pq
D.
1, 1. pq
Câu 15: 

y f x

22
'4f x x x
,
x
. 



?
A. Hàm s m cc tr. B. Hàm s m cc tr.
C. Hàm s t ci ti
2.x
D. Hàm s t cc tiu ti
2.x
Câu 16: 

a

2
2
xa
y
x ax
3 


A.
0.a
B.
0, 1. aa
C.
0, 1. aa
D.
0, 1.aa
Trang33
Câu 17: 

y f x
. 


sai?
x

1 2

'y
+ 0 - 0 +
y
3


0
A. Hàm s ng bin trên khong
;1 .
B. Hàm s nghch bin trên khong
0;3 .
C. Hàm s nghch bin trên khong
3
1; .
2



D. Hàm s ng bin trên khong
2; .
Câu 18: S ng tim cng c th hàm s
2
32
1

x
y
x
là:
A.
2.
B.
1.
C.
3.
D.
0.
Câu 19: Cho hàm s
4 2 4
2 2 . y x mx m m
Tìm tt c các giá tr tham s thc
m
 th có 3
m cc trng thm cc tr o thành mt tam giác có din tích bng 2.
A.
5
4.m
B.
16.m
C.
5
16.m
D.
3
16.m
Câu 20:
Bit rng hàm s
42
() y f x ax bx c
 th ng cong trong hình v bên. Tính giá
tr
( ).f a b c
A.
( ) 1. f a b c
B.
( ) 2. f a b c
C.
( ) 2. f a b c
D.
( ) 1. f a b c
-----------------------------------------------
----------- HT ----------
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
C
D
A
A
D
D
A
B
C
D
D
D
C
B
B
B
B
B
A
A
| 1/33
| | Tải xuống

Có thể bạn quan tâm:

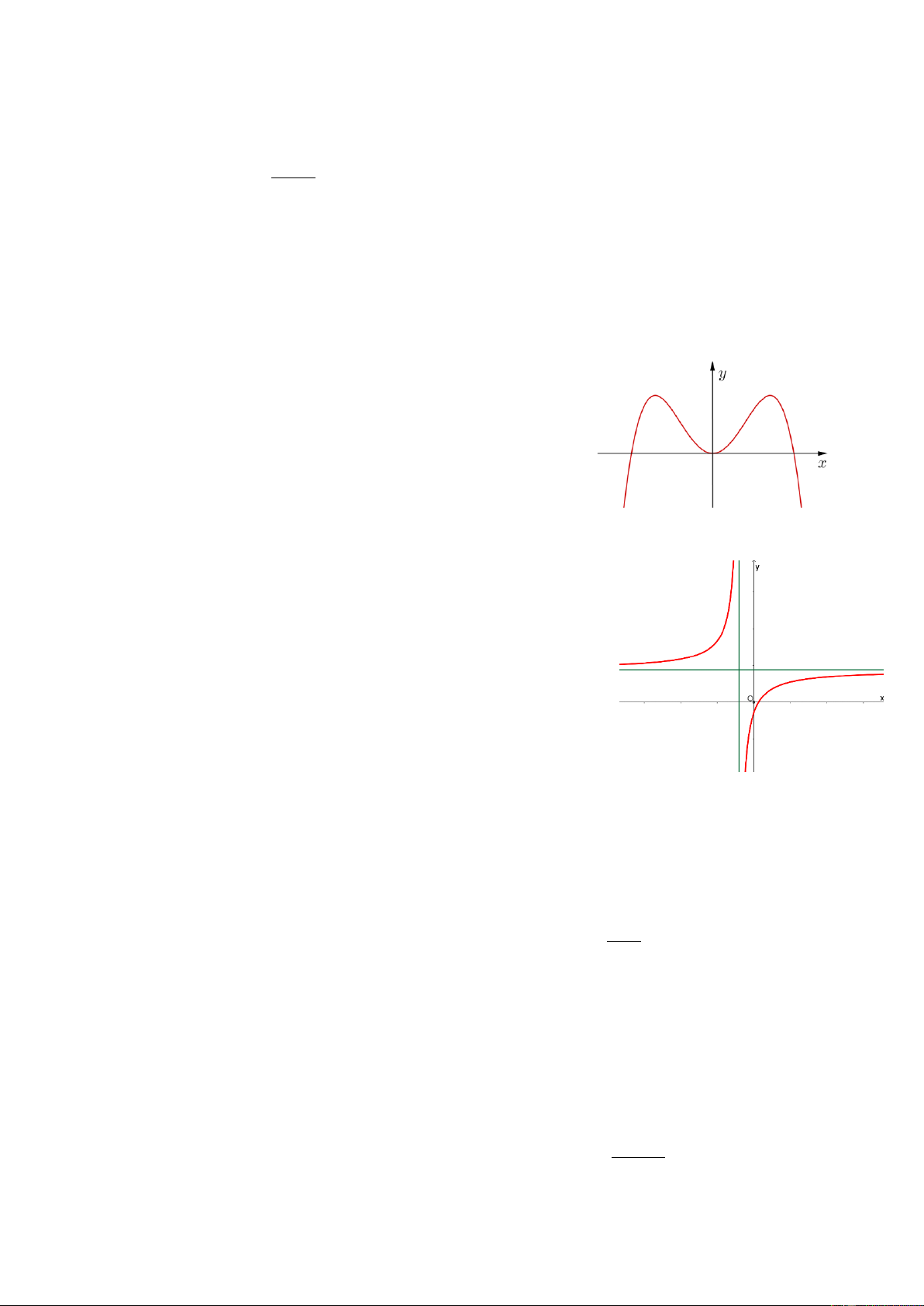
Preview text:

ĐỀ 1
ĐỀ ÔN TẬP CHƯƠNG I GIẢI TÍCH 12 Câu 1:
Gọi m là giá trị nhỏ nhất của hàm số 3
y x  3x trên đoạn 0;3 
8 . Tìm giá trị m . A. m  0. B. m  1.  C. m  2.  D. m 1. Câu 2:
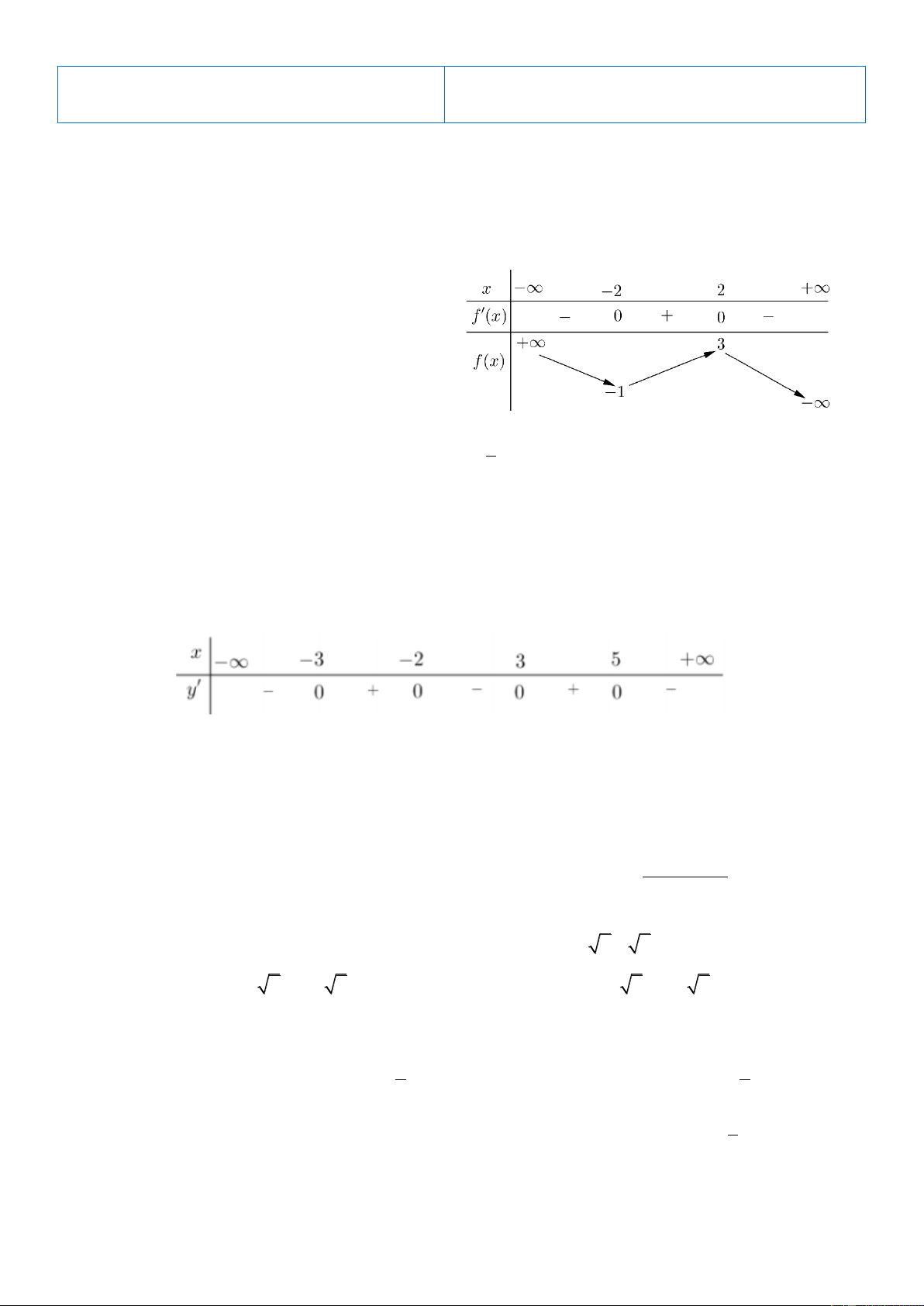
(ĐỀ THI TỐT NGHIỆP THPT 2020-ĐỢT 1) Cho hàm số f x có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng A. 2 . B. 2  . C. 3 . D. 1. 1 Câu 3:
Gọi x , x là hai điểm cực trị của hàm số 3 2 y
x x  3x  2 khi đó 2 2 x x bằng: 1 2 3 1 2 A. 4. B. 10. C. 16. D. 9. Câu 4:
Tìm số giao điểm của đồ thị hàm số 4 2
y x  4x 1 và đường thẳng y  3. A. 0. B. 2. C. 3. D. 4. Câu 5:
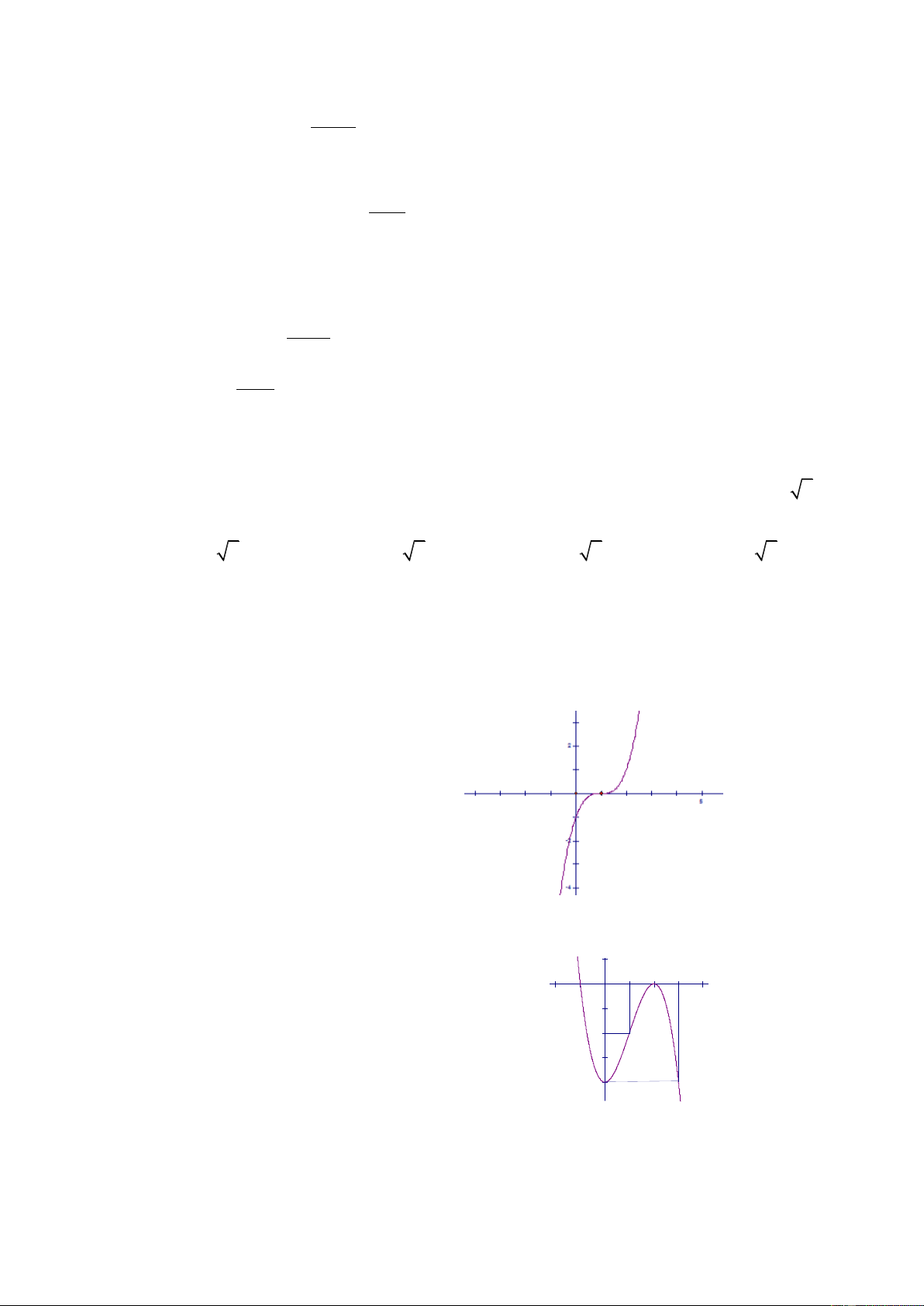
(ĐỀ THI TỐT NGHIỆP THPT 2021-ĐỢT 1) Cho hàm số y f (x) có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là A.5 . B. 3 . C.2 . D. 4 . Câu 6: Hàm số 3 2
y  x  3x  9x đồng biến trên khoảng nào sau đây? A. 1;3 . B.  . C.  3  ;  1 . D. 1;3 . x 1 Câu 7:
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y  có hai tiệm cận 2 x  x m  2 đứng. A. m  3. B. m 2  2;2 2. C. m ;  2
 22 2;\  3 . D. m ;  2  22 2;. Câu 8: Cho hàm số 3 2
y  x x  5x  4. Mệnh đề nào sau đây đúng?  5   5 
A. Hàm số đồng biến trên  ;   .  
B. Hàm số nghịch biến trên  ;1 .    3   3   5 
C. Hàm số đồng biến trên 1; .
D. Hàm số đồng biến trên  ;1 .    3  Câu 9: Đồ thị hàm số 3 2
y ax bx +cx+d có điểm cực tiểu là O 0;0 và điểm cực đại là M 1  ;1 .
Giá trị của a, b, c, d lần lượt là? Trang1 A. 3; 0; 2; 0. B. 2;3; 0; 0. C. 2; 0; 0;3. D. 3; 0; 2; 0. x  3
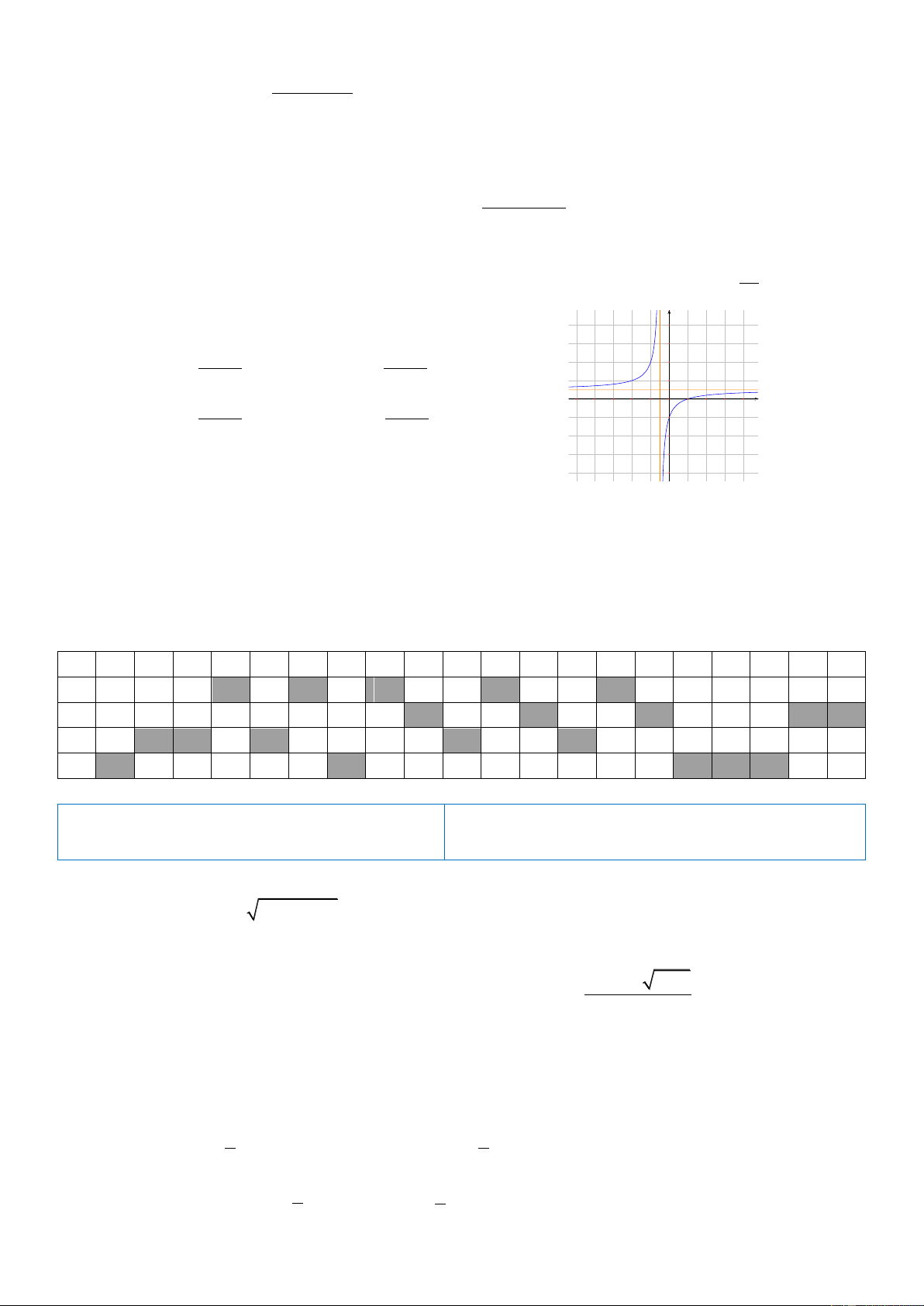
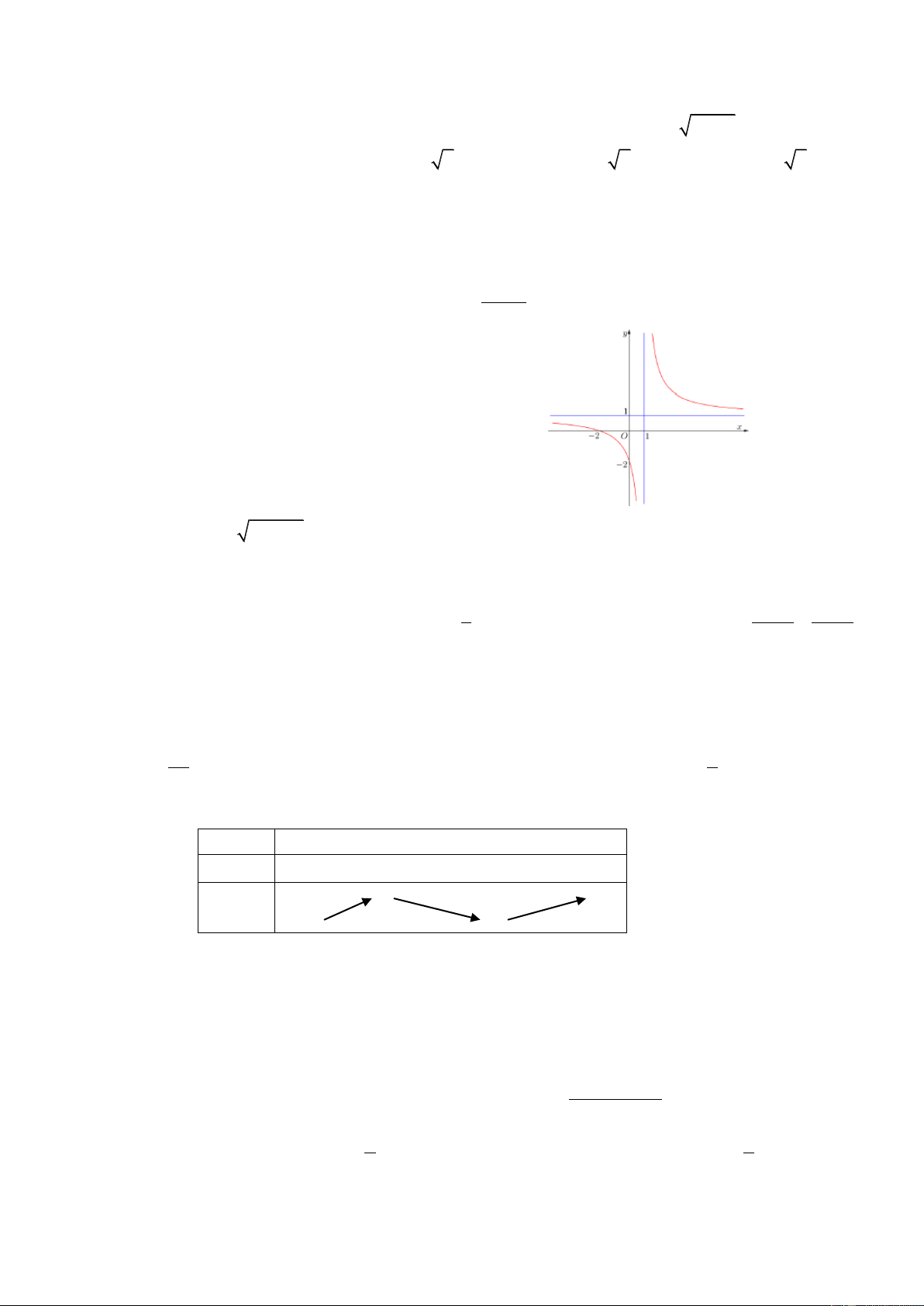
Câu 10: Đường cong C  : y
có bao nhiêu đường tiệm cận? 2 x  9 A. 3. B. 1. C. 2. D. 4. x  3
Câu 11: Biết rằng đồ thị hàm số y
và đường thẳng y x  2 cắt nhau tại hai điểm phân biệt x 1
Ax ; y và Bx ; y
Tính y y . B B . A A A B
A. y y  2  .
B. y y  2.
C. y y  4.
D. y y  0. A B A B A B A B x 1
Câu 12: Cho hàm số: y
C . Tìm tất cả các giá trị thực của tham số m để đường thẳng 2x 1 1 d :   m y mx
cắt đồ thị C tại hai điểm phân biệt A, B sao cho 2 2
OA OB đạt giá trị nhỏ 2 nhất? A. m  0. B. m  1.  C. m  1.  D. m  1. Câu 13: Cho hàm số 4 2
y x  8x  2 có đồ thị (C) và điểm M thuộc (C) có hoành độ bằng 2 . Tìm
hệ số góc k của tiếp tuyến với đồ thị (C) tại M . A. k  6  2. B. k  9  2. C. k  7  2. D. k  8  2.
Câu 14: Tiếp tuyến của đồ thị hàm số 3 2
y x  4x  4x 1 tại điểm M  3  ; 2
  cắt đồ thị tại điểm thứ
hai là N. Tìm tọa độ điểm N. A. N  2  ;  1 . B. N 2; 3  .
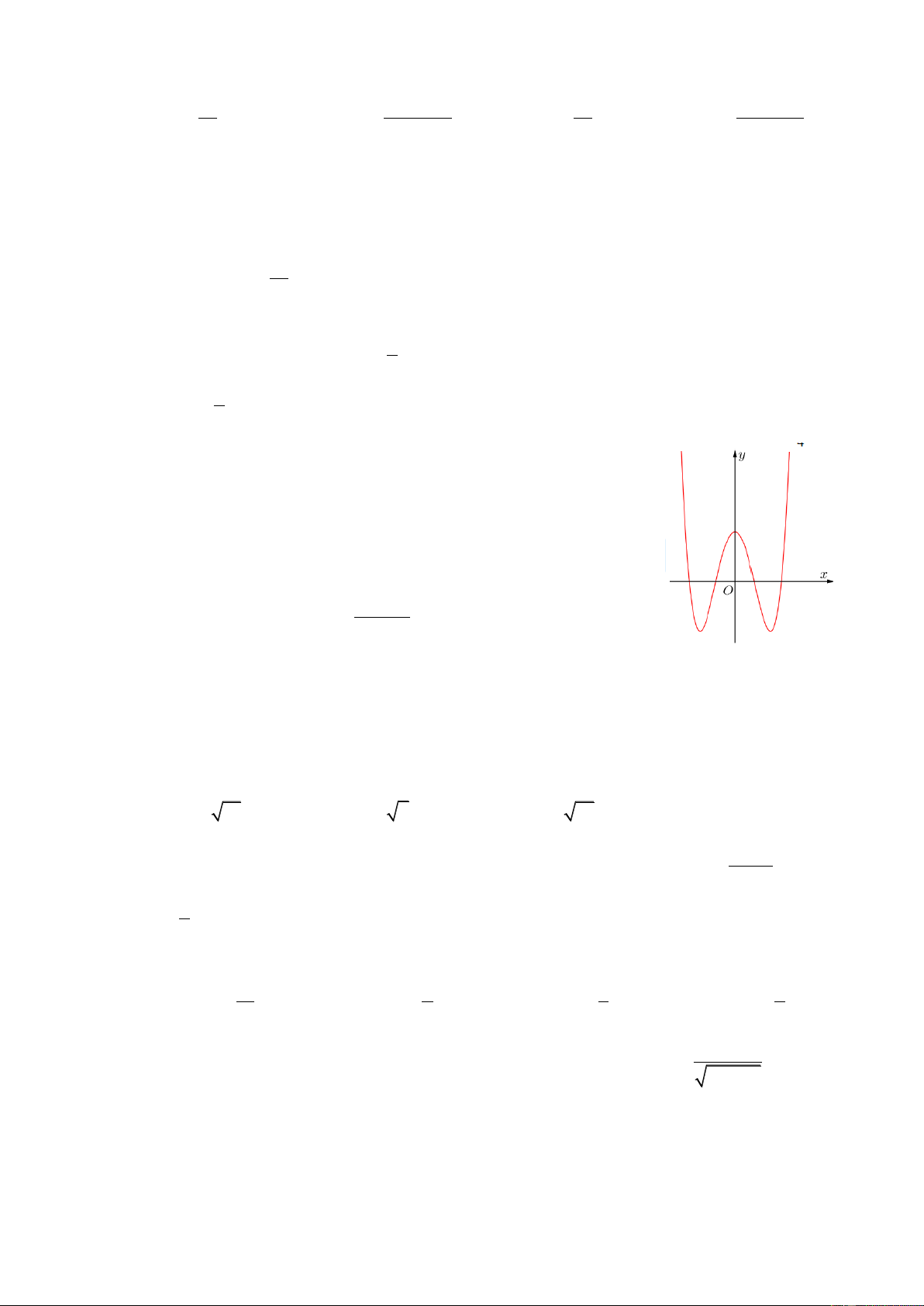
C. N 2;33. D. N  1  ;0. Câu 15: Cho hàm số 3 2
y ax bx cx d có đồ thị nhưhình vẽ bên. Mệnh đề nào dưới đây đúng? A.
a  0, b  0, c  0, d  0 .
B. a  0, b  0, c  0, d  0 .
C. a  0, b  0, c  0, d  0 .
D. a  0, b  0, c  0, d  0 .
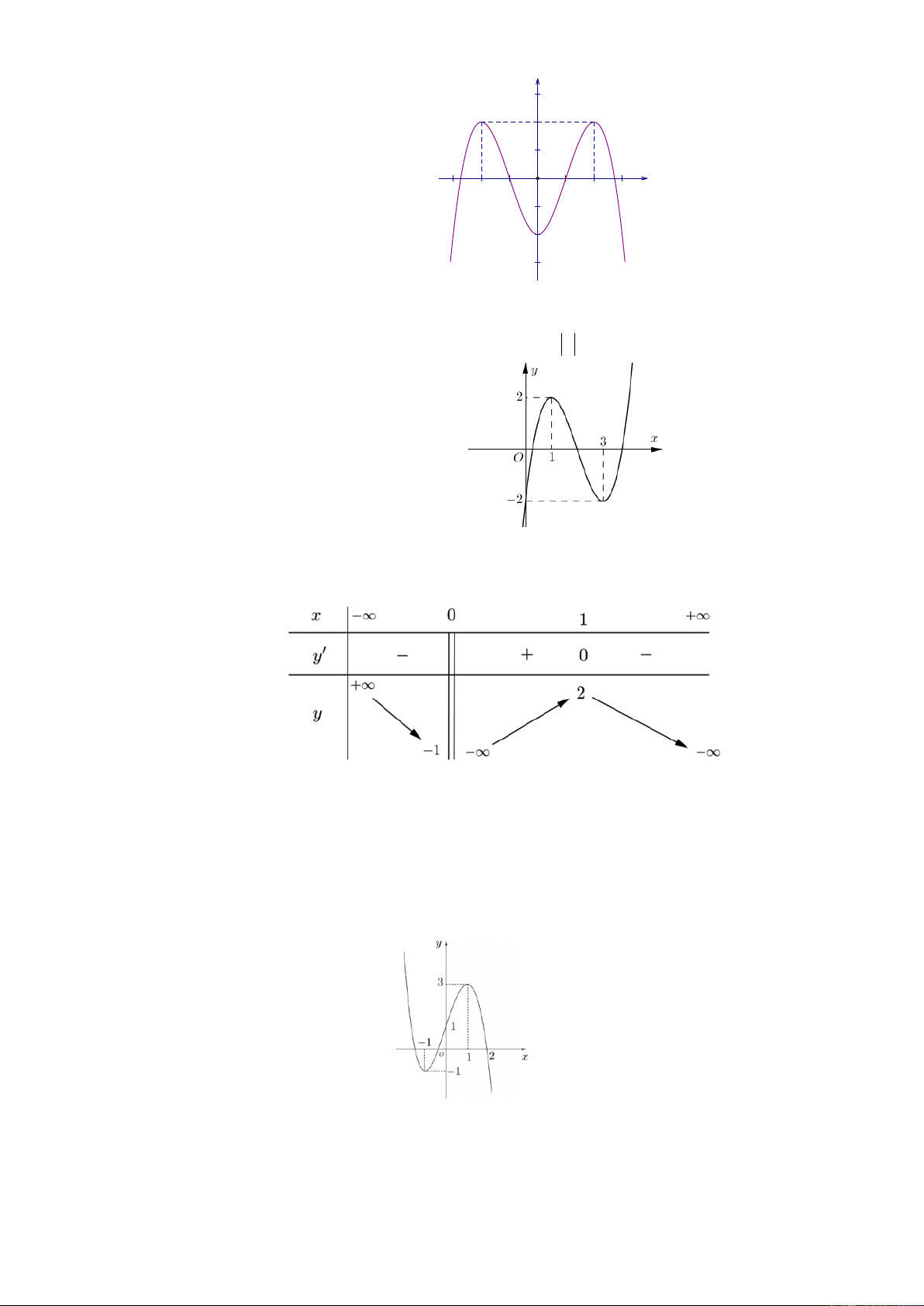
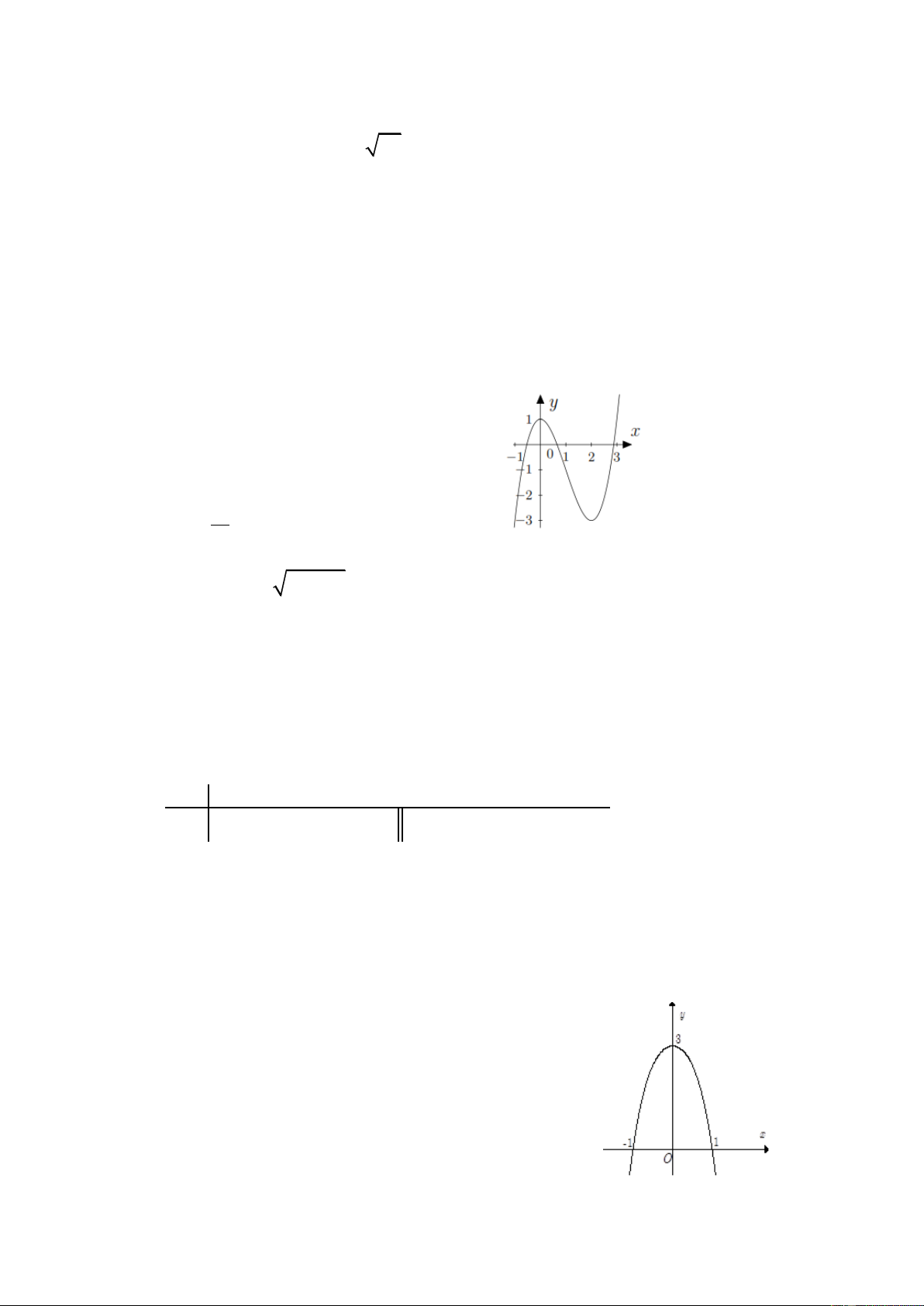
Câu 16: Cho hàm số y f (x) xác định, liên tục trên R và có đồ thị là đường cong trong hình vẽ bên.
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số đồng biến trên khoảng 0;  1 . 1 O 3 -1 2
B. Hàm số đồng biến trên khoảng  4  ;2 . -2
C. Hàm sốnghịch biến trên khoảng  1  ;02;3 .
D. Hàm sốnghịch biến trên khoảng  4   ;1 . -4
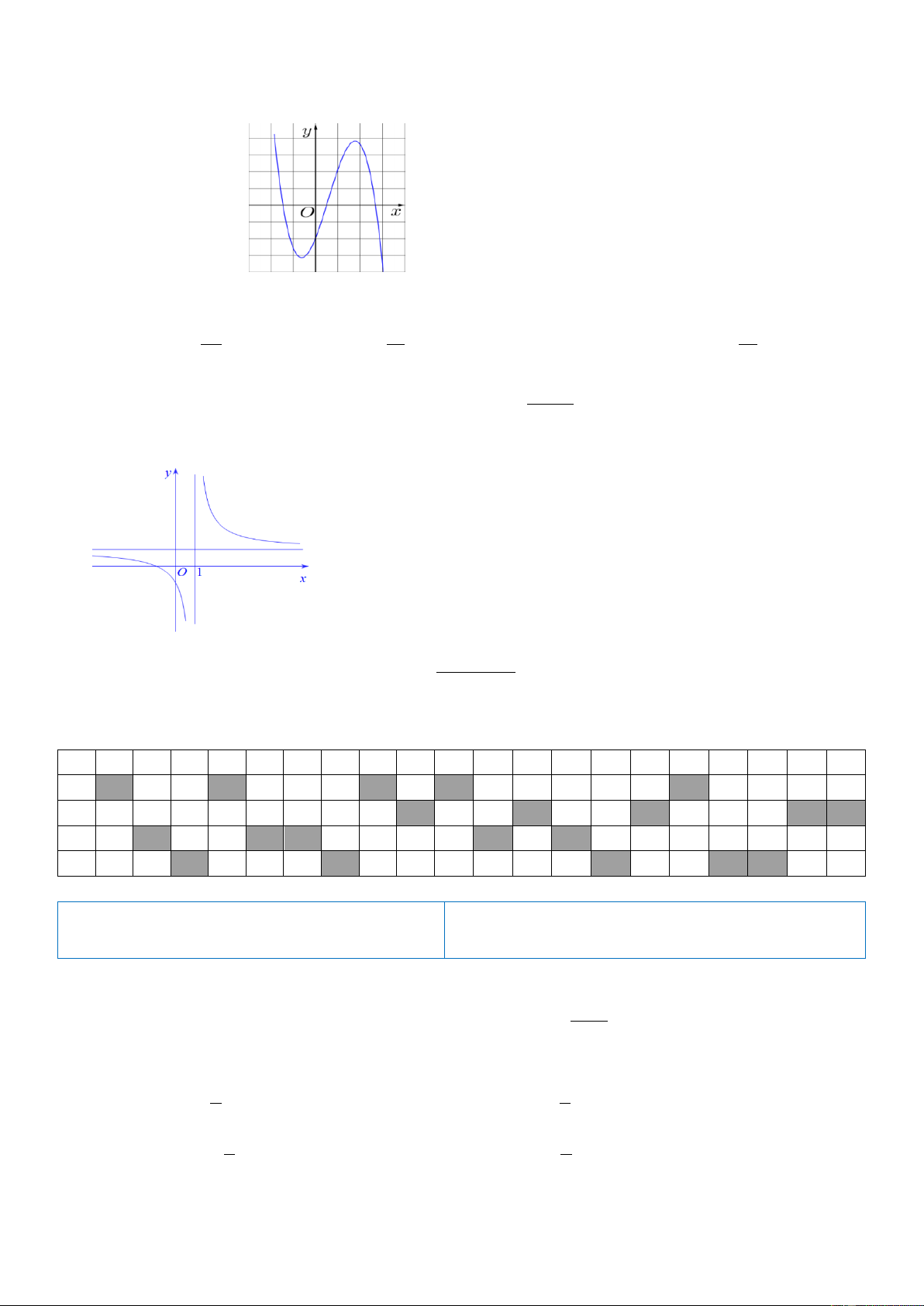
Câu 17: Cho hàm số y f (x) xác định và liên tục trên  và có đồ thị là đường cong trong hình vẽ
bên. Điểm cực tiểu của đồ thị hàm số y f (x) là: Trang2 y A. M (0; 2). 2 B. x  0. C. M (2; 2). D. x  2.  x O 2 -2 -1 1 -2 Câu 18: Cho hàm số 3 2
y f (x)  x  6x  9x  2 có đồ thị là đường cong trong hình vẽ bên. Tìmtất cả
các giá trị thực của tham số m sao cho phương trình f ( x )  m có sáu nghiệm thực phân biệt.
A. 1 m  2. B. m  2. C. 2   m  2. D. 2   m  2.
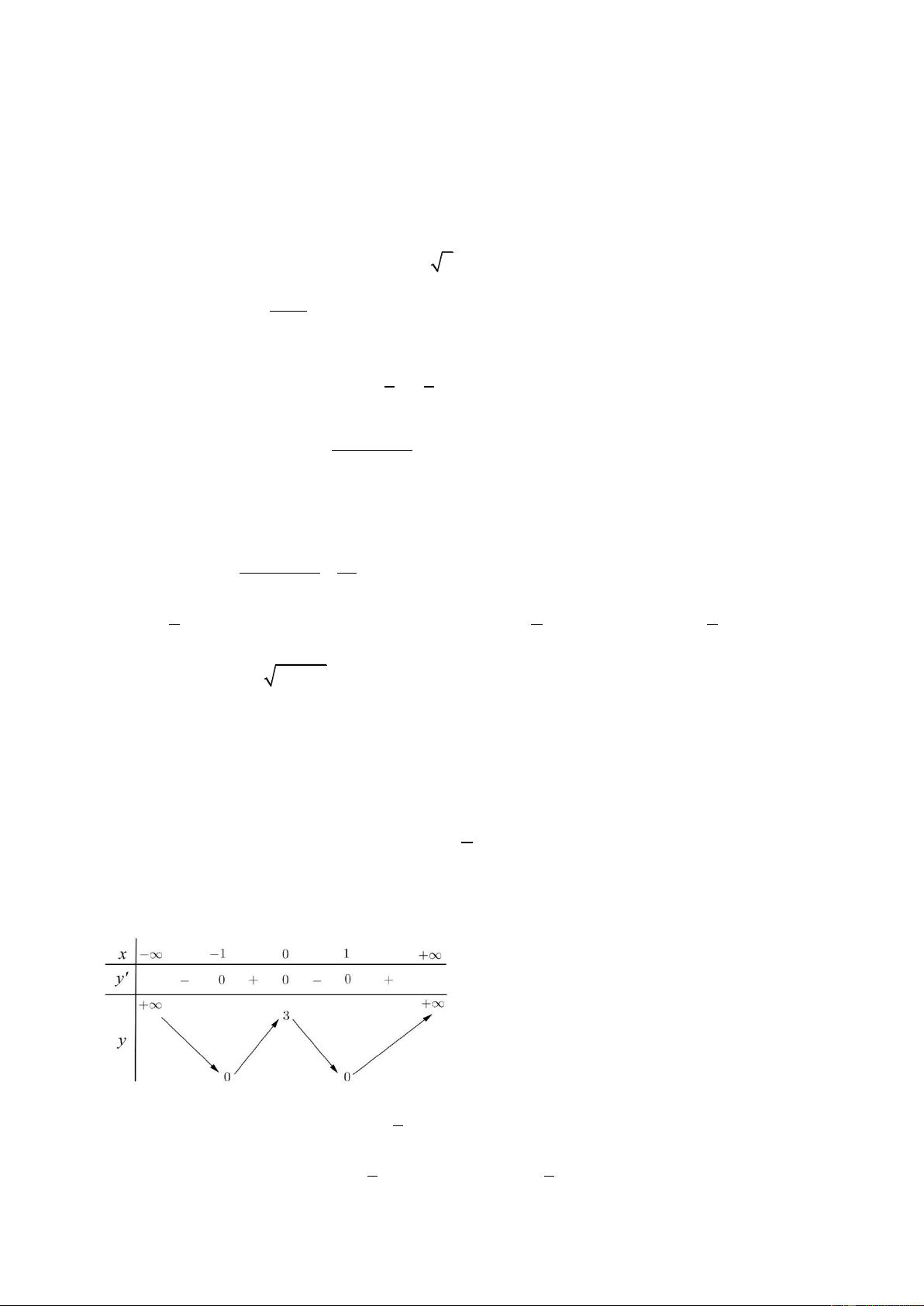
Câu 19: Cho hàm số y f (x) xác định trên  \  
0 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau
Tìm tập hợp tất cả các giá trị thực của tham số m sao cho phương trình f (x)  m có đúng hai nghiệm thực? A. ( ;  1) {2}. B. ( ;  2). C. ( ;  2]. D. ( ;  1  ]  2 . Câu 20:
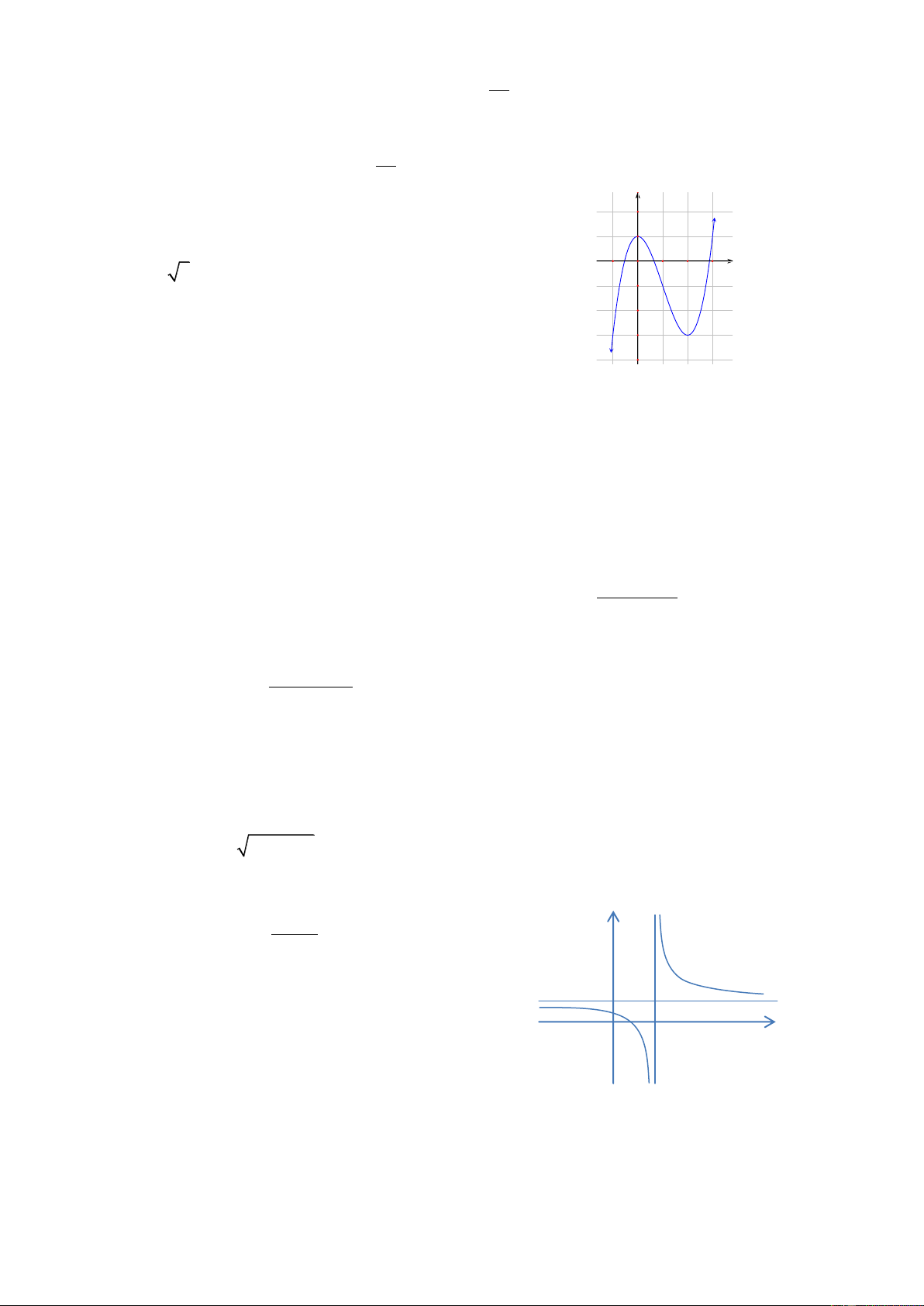
( ĐỀ THI TỐT NGHIỆP THPT 2021-ĐỢT 1) Cho hàm số bậc ba y f (x) có đồ thị là đường cong
trong hình bên. Số nghiệm thực phân biệt của phương trình f ( f (x))  1 là A. 9 . B. 7 . C. 3. D. 6 .
--------------------------------------------- ----------- HẾT ---------- Trang3 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 C D B B D A D C D B C D D D C D A A D B ĐỀ 2
ĐỀ ÔN TẬP CHƯƠNG I Thuvienhoclieu.Com GIẢI TÍCH 12 Câu 1:
Viết phương trình tiếp tuyến của đồ thị 4 2
(C) : y x  2x tại điểm có hoành độ bằng 2.  A. y  24  x  40.
B. y  24x  40. C. y  24  x  40.
D. y  24x  40. x m Câu 2: Cho hàm số y
(m là tham số thực) thỏa mãn min y  3 . Mệnh đề nào dưới đây đúng? x 1 2;4
A. 1 m  3. B. m  1.  C. m  4.
D. 3  m  4. Câu 3:
Biết rằng đường thẳng y  x  5 cắt đồ thị hàm số 3 2
y x  3x  2 tại điểm duy nhất. Kí hiệu
(x ; y ) là tọa độ điểm đó. Tìm (x ; y ). 0 0 0 0
A. (x ; y )  3  ;8 .
B. (x ; y )  2;3 .
C. (x ; y )  2
 ;7 . D. (x ; y )  3;2 . 0 0   0 0   0 0   0 0   x Câu 4:
Viết phương trình tiếp tuyến của đồ thị hàm số 2 1 (C) : y
, biết rằng tiếp tuyến song song x 1
với đường thẳng y  3x  2.
A. y  3x 1 và y  3x 11.
B. y  3x  2 và y  3x 11.
C. y  3x 1và y  3  x 11.
D. y  3x 1và y  3  x 11. Câu 5:
Viết phương trình tiếp tuyến của đồ thị (C): 3 2
y f (x)  x  3x  9x  2 tại điểm có hoành độ x , biết rằng // f (x )  6  . 0 0
A. y  9x  6.
B. y  3x  2.
C. y  9x  6.
D. y x  6. Câu 6:
Tìm tất cả giá trị thực của m để đồ thị hàm số 4 2 2
(C) : y x  2m x 1 có ba cực trị là ba đỉnh
của một tam giác vuông cân.
A. m 1 hoặc m  2. B. m  2.  C. m  1.  D. m  1  hoặc m  2.  2
x m m Câu 7:
Tìm tất cả các giá trị thực của tham số m để giá trị nhỏ nhất của hàm số f (x)  trên x 1 đoạn 0  ;1 bằng 2.  A. m  1  ;m  2. 
B. m  1; m  2.
C. m  1; m  2.
D. m  1, m  2. Câu 8:
Hàm số nào dưới đây đồng biến trên khoảng  ;  ? 2x 1 A. 3
y x  3x 1. B. 3
y  x  6 . x C. y  . D. 4 2
y x  2x . x 1 Câu 9:
Cho hàm số y f (x) có bảng biến thiên như sau Trang4
Tìm giá trị cực đại y
và giá trị cực tiểu y của CÑ CT x ∞ 1 3 +∞ hàm số đã cho. + 0 _ y' 0 + A. y  0 và y  1.  CÑ CT +∞ 0 y B. y  0 và y  4.  CÑ CT ∞ 4 C. y  3 và y  1.  CÑ CT D. y  3 và y  4.  CÑ CT
Câu 10: Cho hàm số y f (x) có lim f (x)  1
 và lim f (x) 1. Mệnh đề nào dưới đây đúng? x x
A. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y  1 và y  1.
B. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x 1 và x  1. 
D. Đồ thị hàm số đã cho không có tiệm cận ngang.
Câu 11: Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là ham số nào? 3    A. y x 3x 1. 3 2     B. y x 3x 1.   3  3  C. y x x . 1 3     D. y x 3x 1. x 1
Câu 12: Cho hàm số y
. Mệnh đề nào dưới đây đúng? x  2
A. Hàm số đồng biến trên khoảng  ;  2.
B. Hàm số nghịch biến trên khoảng  ;  2.
C. Hàm số nghịch biến trên khoảng 2; .
D. Hàm số nghịch biến trên khoảng  ;  .
Câu 13: Cho hàm số y f (x) có đạo hàm 2 f (  x)  3
x 1,x  . Mệnh đề nào dưới đây đúng?  1 
A. Hàm số nghịch biến trên khoảng ;  . 
B. Hàm số đồng biến trên khoảng  ;  .  3 
C. Hàm số nghịch biến trên khoảng  ;  .  1 1 
D. Hàm số đồng biến trên khoảng  ; .    3 3 
Câu 14: Đồ thị hàm số 3 2
y  x  3x  5 có hai điểm cực trị A và B. Tính diện tích S của tam giác OAB
với O là gốc tọa độ. 10 A. S 10. B. S  9. C. S  . D. S  5. 3 3x  2
Câu 15: Hàm số y  có bao nhiêu cực trị? x 1 A. 2. B. 0. C. 1. D. 3. Câu 16: Cho hàm số 3 2
y x  3x 1 có đồ thị (C). Tìm những giá trị thực của tham số m đểđồ thị
đường thẳng y m cắt C tại ba điểm phân biệt. A. 3   m 1.
B. m 1 hoặc m  1.  C. m 1. D. m  3.  Trang5 Câu 17: Cho hàm số 3 2
với a, b, c, d là các số thực, có đồ thị hàm số như hình vẽ bên.
y ax bx cx d
Mệnh đề nào dưới đây là đúng?
a  0, b  0, c  0 d  0. A. và
a  0, b  0, c  0 d  0. B. và
a  0, b  0, c  0 d  0. C. và
a  0, b  0, c  0 d  0. D. và
Câu 18: Tìm giá trị nhỏ nhất m của hàm số 4 2
y x x 13 trên đoạn  2  ;  3 . 49 51 51 A. m  . B. m  . C. m 13. D. m  . 4 2 4 ax b
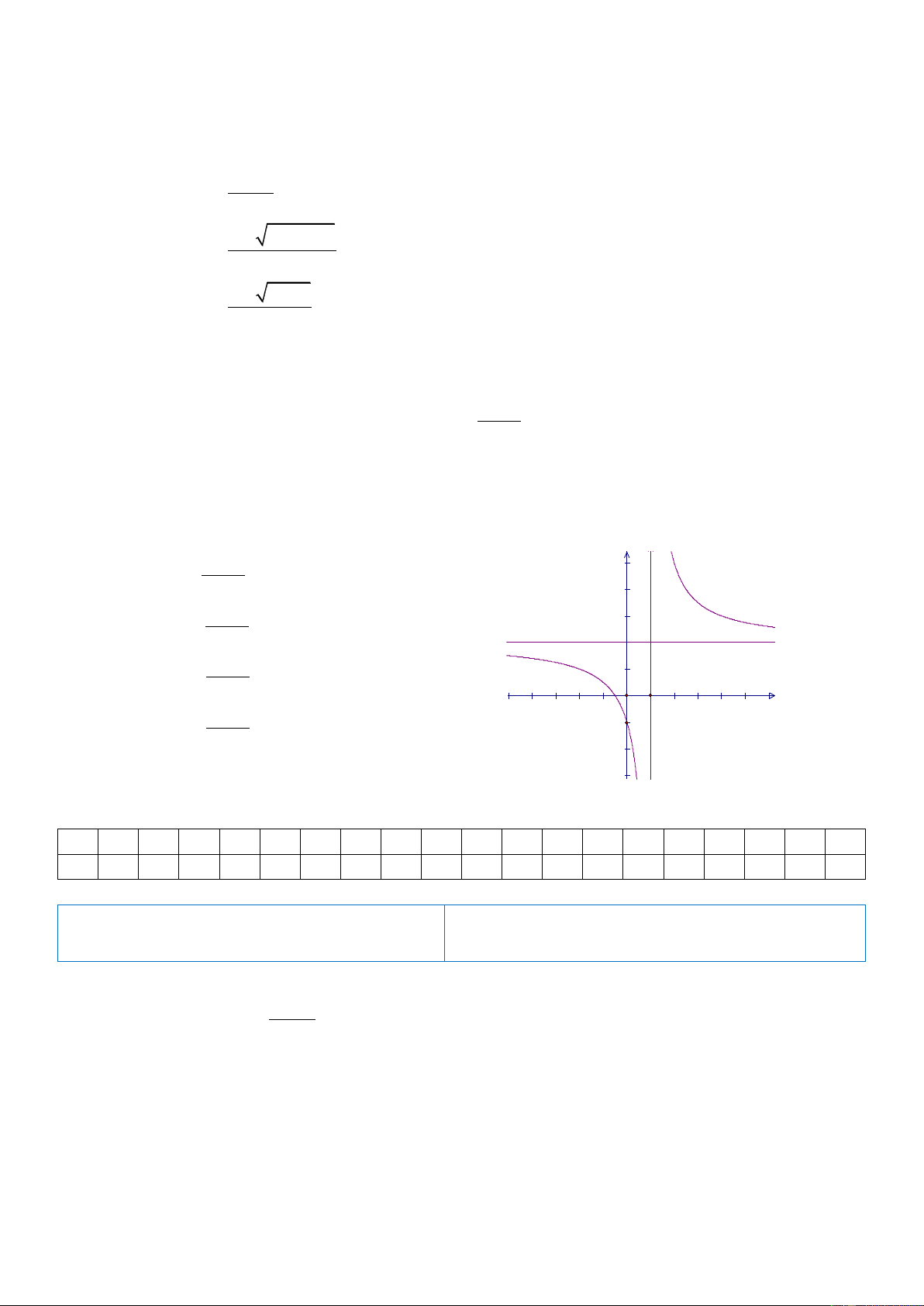
Câu 19: Đường cong của hình bên là đồ thị của hàm số y
với a, b, c, d là các số thực. Mệnh đề cx d nào đưới đây đúng?
A. y  0, x  1.
B. y  0,x  1.
C. y  0, x   .
D. y  0, x   . 2 x  5x  6
Câu 20: Tìm số tiệm cận của đồ thị hàm số y  . 2 x  4 A. 3. B. 2. C. 1. D. 0. 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D ĐỀ 3
ĐỀ ÔN TẬP CHƯƠNG I Thuvienhoclieu.Com GIẢI TÍCH 12 Câu 1:
Viết phương trình tiếp tuyến của đồ thị hàm số 2 (C) : y
, tại giao điểm của đồ thị (C) và 2  x đồ thị của hàm số 2 y x 1. 1 1 A. y  
x 1 và y  2  . x B. y
x  2 và y  3 . x 2 2 1 1
C. y x  và y  . x D. y
x 1 và y  2 . x 2 2 Trang6 ax b Câu 2:
Đường cong của hình bên là đồ thị của hàm số y
với a, b, c, d là các số thực. Mệnh đề cx d nào đưới đây đúng?
A. y  0, x  2. B.
y  0, x  2.
C. y  0,x  1. D.
y  0, x  1. mx  5m Câu 3: Cho hàm số y
với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để x m
hàm số đồng biến trên các khoảng xác định. Tìm số phần tử của S. A. 4. B. 6. C. 5. D. 3. Câu 4: Cho hàm số 4 2
y  x  2x  3 có giá trị cực đại y
và giá trị cực tiểu y . Mệnh đề nào dưới CÑ CT đây đúng? A. y  3y 15. B. y
y  2 3. C. 2y y  5. D. yy  12. CÑ CT CT CÑ CÑ CT CÑ CT Câu 5: Cho hàm số 3 2
y x  3x . Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng 2; .
B. Hàm số nghịch biến biến trên khoảng  ;  0.
C. Hàm số nghịch biến trên khoảng 0; 2.
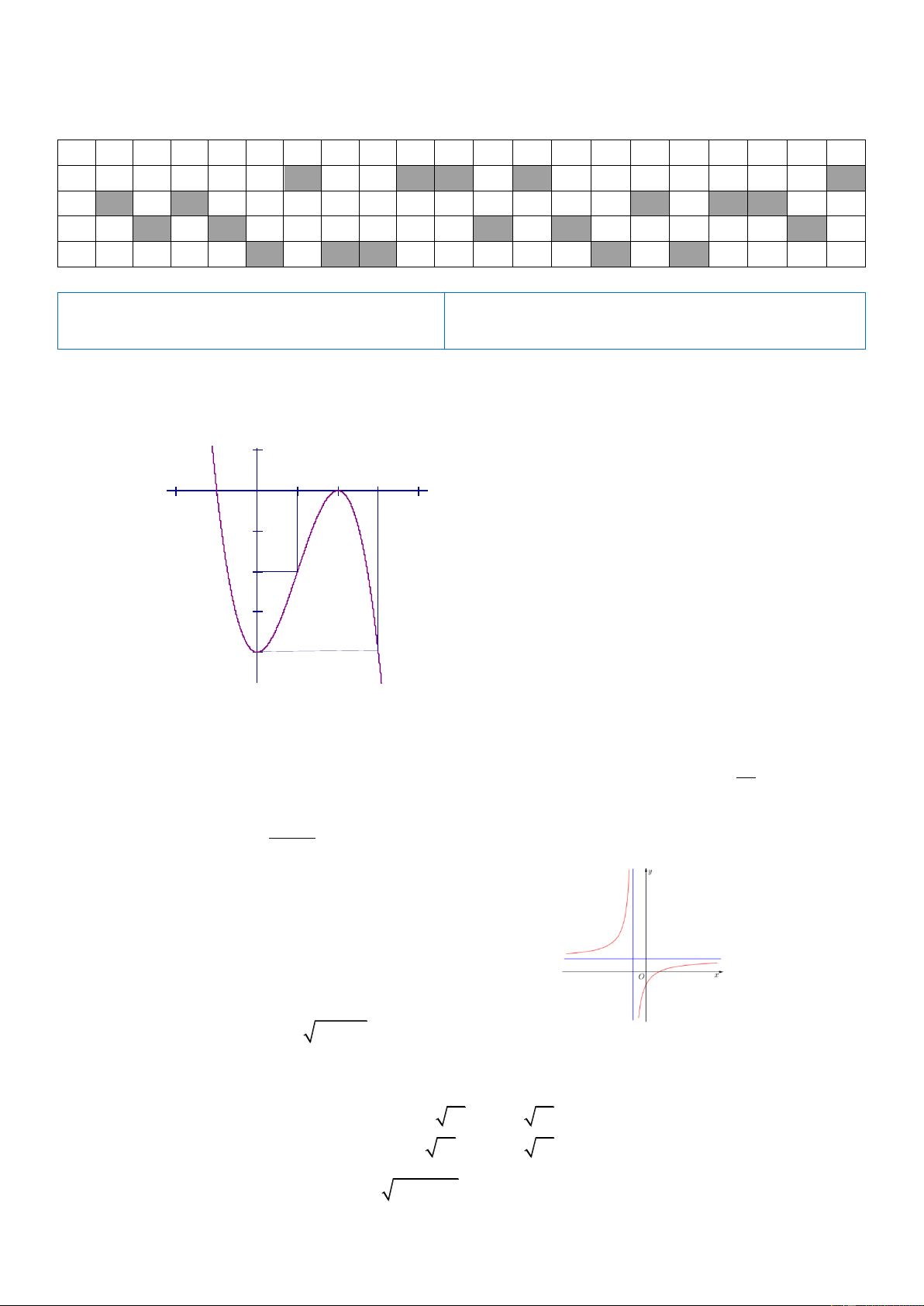
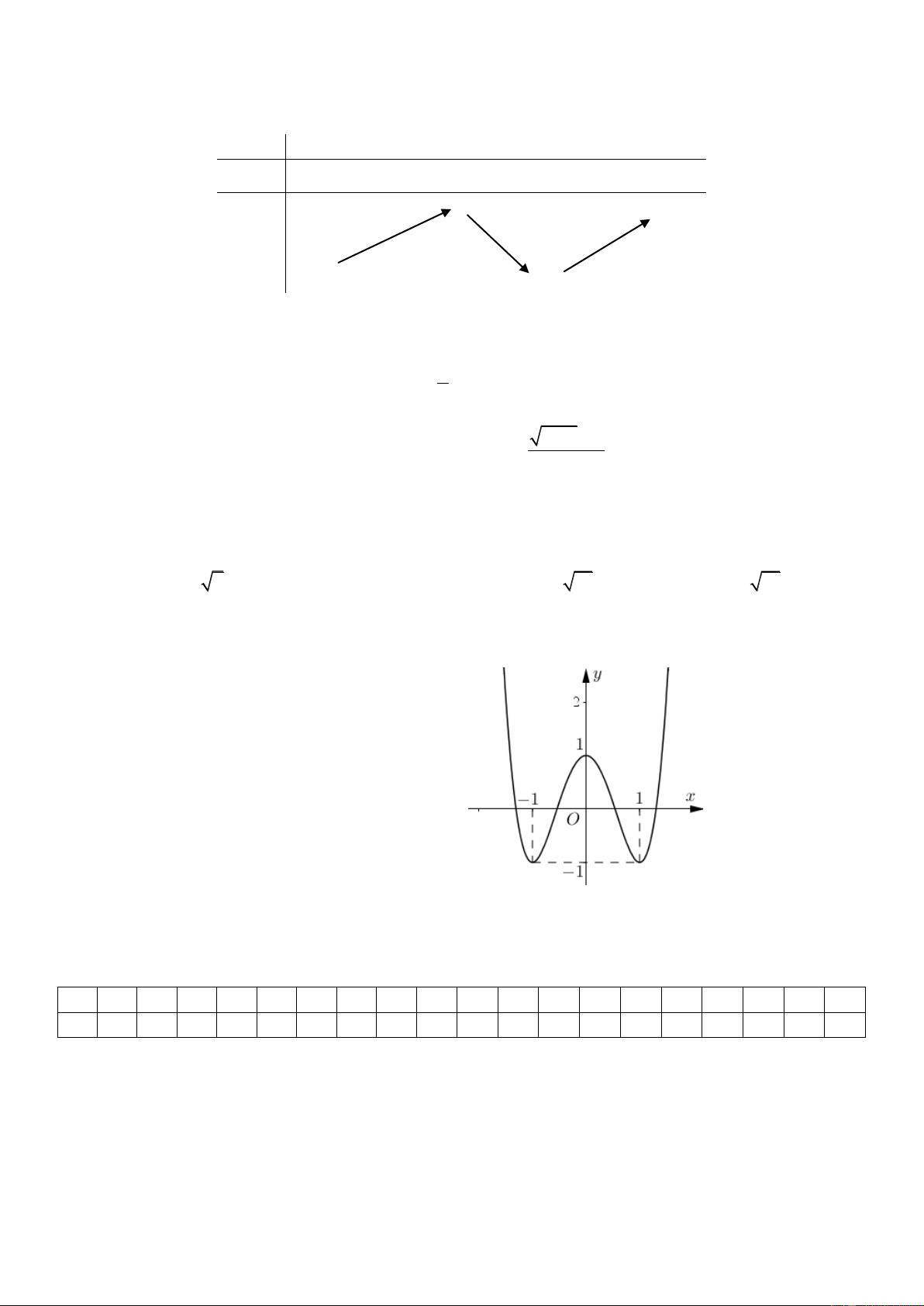
D. Hàm số đồng biến trên khoảng 0; 2. Câu 6: Cho hàm số 4 2
y  x  2x có đồ thị như hình bên.
Tìm tất cả các giá trị thực của tham số m để phương trình 4 2
x  2x m  0 có bốn nghiệm phân biệt.
A. 0  m 1. B. m  0.
C. 0  m 1. D. m 1. 1 Câu 7:
Một vật chuyển động theo qui luật 3 2 s  
t  6t vớit (giây) là khoảng thời gian tính từ khi vật 2
bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó.
Hỏi trong khoảng thời gian 6 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
A. 64(m / s).
B. 24(m / s).
C. 108(m / s).
D. 18(m / s). Câu 8:
Đồ thị của hàm số nào trong các hàm số dưới đây có tiệm cận đứng? 1 1 1 1 A. y  . B. y  . C. y  . D. y  . 4 x  1 2 x x 1 x 2 x  1 Câu 9:
Cho hàm số y f (x) có bảng biến thiên dưới đây.
Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm x -∞ -2 0 +∞ _ cận? y' + A. 1. B. 2. +∞ 1 y C. 4. D. 3. 0 -∞ Trang7
Câu 10: Tìm phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3 2
y x  2x 1. 8
A. y  9x  8. B. y   x 1.
C. y  8x  9.
D. y  3x  4. 9
Câu 11: Hàm số nào dưới đây nghịch biến trên khoảng  ;  ? x  4 A. 4 2
y x  2x . B. y  . C. 3
y  x  3 . x D. 4 2
y x  2x  3. x  2
Câu 12: Cho hàm số y f (x) có bảng xét dấu đạo hàm như sau x ∞ 0 1 2 +∞ _ y' _ 0 + + 0
Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng 1; .
B. Hàm số nghịch biến trên khoảng  5  ;  1 .
C. Hàm số đồng biến trên khoảng (1; 2).
D. Hàm số nghịch biến trên khoảng  ;   1 .
Câu 13: Viết phương trình tiếp tuyến của đồ thị 4 2
(C) : y  x  2x  3 tại điểm có hoành độ bằng 2.
A. y  2x  4.
B. y  24x  43. C. y  2  x  2. D. y  24  x  43.
Câu 14: Cho biết hàm số 3 2
y ax bx cx d có đồ thị như hình bên. Trong các khẳng định sau, khẳng định nào đúng? ya  0 A.  . B. 2
b  3ac  0 O xa  0  . 2
b  3ac  0 a  0 C.  . 2
b  3ac  0 a  0 D.  . 2
b  3ac  0 1 3
Câu 15: Viết phương trình tiếp tuyến của đồ thị (C): 4 2 f (x)  x  3x
tại điểm có hoành độ là 2 2
nghiệm của phương trình // f (x)  0.
A. y  4x  3.
B. y  3x  5.
C. y  4x  3.
D. y  4x  3.
Câu 16: Cho hàm số y   x   2 2
x  2 có đồ thị (C) . Mệnh đề nào dưới đây đúng?
A. (C) cắt trục hoành tại hai điểm.
B. (C) cắt trục hoành tại một điểm.
C. (C) cắt trục hoành tại ba điểm.
D. (C) không cắt trục hoành. 2 x mx 1
Câu 17: Tìm tập hợp tất cả các giá trị của tham sốm để hàm số y
đạt cực đại tại x  2. x m A. m  2. 
B. 0  m 1. C. m  2. D. 1   m  3.
Câu 18: Đường cong trong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án ,
A B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? Trang8 y A. 4 2
y  x  3x  3. B. 4 2
y x  2x  3. 4 3 C. 4 2
y  x  2x  3. D. 4 2
y  x  2x  3. 3 1 O 1 3 x mx 1
Câu 19: Cho hàm số y
(m là tham số thực) thỏa mãn max y  4 . Mệnh đề nào dưới đây đúng? m x 1; 3
A. 5  m  7. B. m 12. C. m 10.
D. 9  m 12.
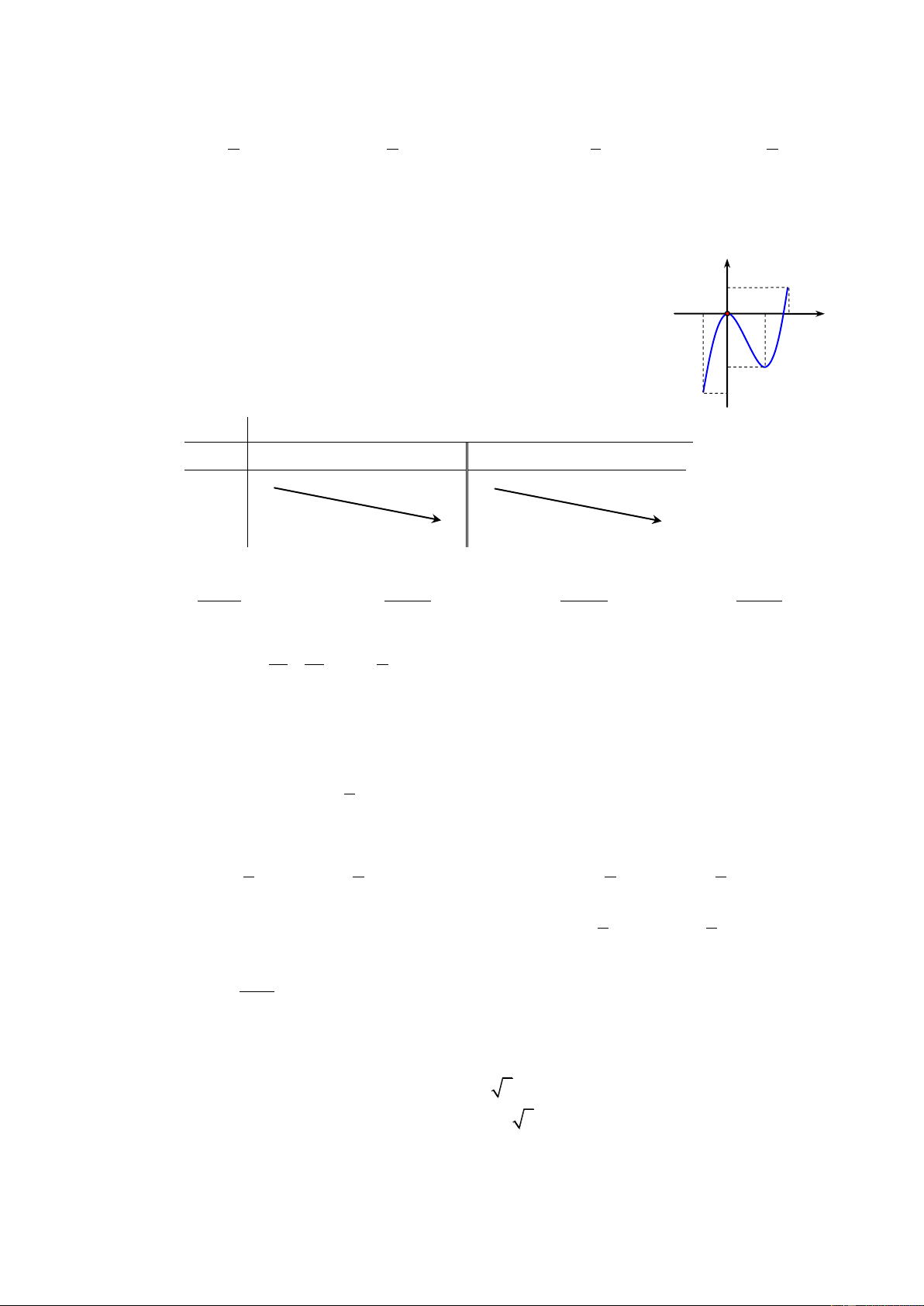
Câu 20: Cho hàm số y f (x) xác định, liên tục trên khoảng xác định và có bảng biến thiên dưới đây.
Mệnh đề nào dưới đây sai? x ∞ 1 0 +∞
A. Hàm số đạt cực tiểu tại x  0 vàđạt cực đại tại y' + _ + 0 x  1.  +∞ 1 y
B. Giá trị cực đại bằng 1 và giá trị cực tiểu bằng 0. 0 ∞
C. Hàm số nghịch biến trên khoảng ( 1; 0).
D. Hàm số đạt giá trị lớn nhất bằng 1 và giá trị nhỏ nhất bằng 0. 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D ĐỀ 4
ĐỀ ÔN TẬP CHƯƠNG I Thuvienhoclieu.Com GIẢI TÍCH 12 Câu 1:
Tìm tất cả các giá trị của tham số m để đồ thị hàm số 4 2 2
y x  2m x 1 có 3 điểm cực trị tạo
thành 3 đỉnh của một tam giác vuông cân. A. m  1  ;0;  1 . B. m  1.  C. m  1. D. m  2.  Câu 2:
Viết phươmg trình tiếp tuyến của đồ thị hàm số 3
y x  3x  2 tại điểm có hoành độ bằng 0.
A. y  3x  2.
B. y  3x  2.
C. y  3x  2. D.  2  ;0, 2;. 2x 1 Câu 3:
Tìm tất cả các giá trị của m để đường thẳng y x m 1 cắt đồ thị hàm số y  tại hai x 1
điểm phân biệt A, B sao cho  2  ;0, 0;2.
A. m  4  10.
B. m  4  3.
C. m  2  3.
D. m  2  10. Câu 4: Cho hàm số 4 2
y  x  2mx 1 có đồ thị x  0 tiếp tuyến của đồ thị (C) có hệ số góc đạt giá trị lớn nhất khi nào?
A. a  0 và hoành độ tiếp điểm là   b x . 3a Trang9 B. 1
  m  0. và hoành độ tiếp điểm là   b x . 3a
C. tiếp tuyến đi qua điểm uốn (hoành độ điểm uốn là nghiệm của phương trình m  1. 
D. hoành độ tiếp điểm là   b x . 4 3a 3 y Câu 5:
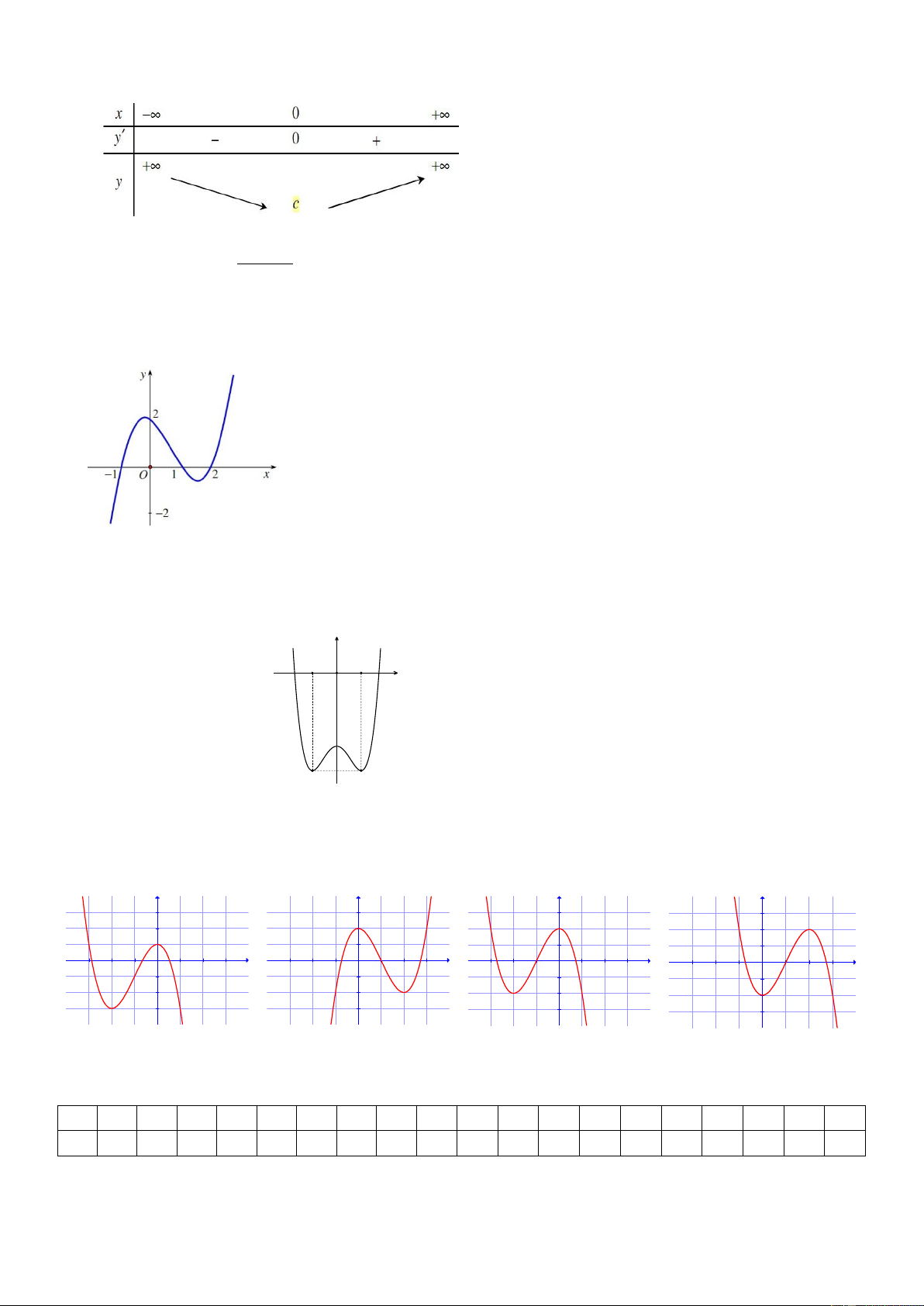
Đồ thị sau là của hàm số nào? 2 A. 3 2
y  x  3x 1. 1 O x B. 5. -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 -1 C. 3 2
y  2x  6x 1. -2 D. 3 2
y x  3x 1. -3 -4 Câu 6:
Số điểm chung của đồ thị hàm số 3 2
y  2x  3(m 1)x  6(m  2)  2017 và đồ thị hàm số
a;b là bao nhiêu? A. 0. B. 3. C. 1. D. 2. Câu 7:
Tìm tất cả các giá trị của tham số m sao cho đồ thị hàm số m  9. không có tiệm cận đứng.
A. không có giá trị nào của m. B. m  10.  C. m  0 D. m  10.  2 x  2x  2 Câu 8:
Giá trị lớn nhất của hàm số 3
f (x)  x  3x  2 trên đoạn y  . là bao nhiêu? x 1 A. 0. B. 4. C. 2. D. 2.  3
x  6x m Câu 9: Cho hàm số y
Khẳng định nào sau đây là đúng? 4x  2
A. Hàm số nghịch biến trên m 16.
B. Hàm số nghịch biến trên  .
C. Hàm số nghịch biến trên các khoảng ( ;  1) và m 1.
D. Hàm số đồng biến trên khoảng ( ;
 1) và nghịch biến trên khoảng (1;). Câu 10: Hàm số 2 y
x  2x đồng biến trên khoảng nào sau đây? A. 0  ;1 . B.  ;   1 . C. 1; . D. 1; 2. ax b 
Câu 11: Cho hàm số y
(a  0) có đồ thị cx d
như hình vẽ bên. Mệnh đề nào dưới đây đúng?
A. b  0, c  0, d  0. 0
B. b  0, c  0, d  0. 0
C. b  0, c  0, d  0.
D. b  0, c  0, d  0. Trang10 3 y
Câu 12: Đồ thị sau đây là của hàm số nào? 2 A. 4 2
y x  2x . B. 2 4
y x  2x . 1 x C. 4 2
y x  2x 1. O -2 -1 1 2 D. 4 2
y x  2x . -1 Câu 13: Hàm số 3 2
y x  3x  2x đạt cực tiểu tại điểm nào sau đây? 3  3 9  5 3 3  3 A. x  . B. x  . C. x  0. D. x  . 3 9 3 1 Câu 14: Cho hàm số 3 2 f (x) 
x  (m 1)x  (m  3)x m  4. Điều kiện của tham số m để đồ thị hàm 3
số y f (| x |) có 5 điểm cực trị là gì? A. 3   m  1  . B. m  4. C. m  0. D. m  1. 2 2x  4x  5
Câu 15: Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số y
, khi đó M m 2 x 1 bằng bao nhiêu? A. 4. B. 3. C. 7. D. 1.
Câu 16: Tìm tập hợp tất cả các giá trị của tham số m để hàm số 3 2
y  x  3x mx  3 nghịch biến trên (2; ). A.  ;  0. B.  ;  3  . C.  ;    3 . D.  ;  0. 3 x
Câu 17: Tìm tất cả các giá trị của tham số m để hàm số 2 2 y
mx  (m m 1)x 1 đạt cực đại tại 3 x  1. A. –2. B. 2. C. 2.  D. 1. Câu 18: Hàm số 3 2
y x  3x  4 nghịch biến trên khoảng nào sau đây? A.  ;  2
  và 0;. B.  ;0
  và 2;. C. 0; 2. D.  2  ;0. 2x  3
Câu 19: Cho hàm số y
. Tìm tất cả các giá trị của tham số m để đồ thị hàm số tiếp xúc với x 1
đường thẳng y  2x m? A. m  8. B. m . C. m  2  2. D. m  1. 2 x  3x  2
Câu 20: Đồ thị hàm số y  có bao nhiêu tiệm cận? 2 x  5x  6
A. Một tiệm cận ngang và một tiệm cận đứng.
B. Một tiệm cận ngang và hai tiệm cận đứng.
C. Chỉ có hai tiệm cận đứng.
D. Hai tiệm cận ngang và một tiệm cận đứng.
----------------------------------------------- ----------- HẾT ---------- Trang11 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D ĐỀ 5
ĐỀ ÔN TẬP CHƯƠNG I Thuvienhoclieu.Com GIẢI TÍCH 12 Câu 1: Cho hàm số 4 2
y ax bx c có đồ thị y như hình vẽ.
Mệnh đề nào sau đây là đúng?
A. a  0,b  0,c  0. x
B. a  0,b  0,c  0.
C. a  0,b  0,c  0.
D. a  0,b  0,c  0. 2x 1 1 Câu 2: Cho hàm số y
có đồ thị (C). Khẳng định nào sau đây là đúng? 2 x  3x  2
A. (C) có 2 tiệm cận đứng.
B. (C) không có tiệm cận ngang.
C. (C) có 1 tiệm cận ngang.
D. (C) không có tiệm cận đứng. Câu 3:
Tìm tất cả các giá trị của tham số m để đường thẳng y  2m cắt đồ thị hàm số 4 2
y x  2x  3 tại 4 điểm phân biệt. 3 3
A. 2  m  3.
B. 2  m  3. C. 1  m  . D. 1  m  . 2 2 2x 1 Câu 4:
Giá trị lớn nhất của hàm số y
trên đoạn 1; 2 là giá trị nào sau đây? x 1 1 1 1 A. max y  1. B. max y  .
C. max y   .
D. max y   . 1;2 1;2 2 1;2 2 1;2 3 Câu 5:
Tìm tập giá trị của hàm số 2 y x x .  1  1 A. 0;2. B. 0  ;1 . C. 0; .   D. 0; .    2   4 Câu 6: Cho hàm số 3 2
y x  3x  (m 1)x 1 có đồ thị (C). Tìm m để đường thẳng d : y  x 1 cắt
đồ thị (C) tại 3 điểm phân biệt P(0;1), M , N sao cho bán kính đường tròn ngoại tiếp tam giác 5 2 OMN bằng . 2 9 A. m  3.  B. m  . C. m  0. D. m  1. 4 Trang12 Câu 7: Cho hàm số 3 2
y x  2x  1 mx m có đồ thị (C). Tìm m để (C) cắt trục hoành tại 3 điểm
phân biệt có hoành độ x , x , x thỏa mãn 2 2 2
x x x  4. 1 2 3 1 2 3  1 1 m 1 1   m 1 A. m  1. B.  . C.   m  1. D.  4 . 4 m  0 4 m  0 Câu 8: Hàm số 2 y
2x x x nghịch biến trên khoảng nào sau đây? A. 1; 2. B. 1; . C.  ;   1 . D. 0  ;1 . 1 Câu 9: Hàm số 3 2 2 y  
x mx  (m  m 1)x 1đạt cực tiểu tại x 1 khi m bằng mấy? 3 A. m  1. B. m  2. C. m  1.  D. m  2.  x 1
Câu 10: Cho hàm số y
có đồ thị (C). Gọi d là tiếp tuyến của (C) tại điểm có tung độ bằng 3. x 1
Tìm hệ số góc k của d. 1 1 A.  . B. . C. 2.  D. 2. 2 2 3 y
Câu 11: Đồ thị sau là của hàm số nào? 2 A. 3 2
y x  3x 1. 1 B. 3 2
y x  3x 1. x O C. 3 2
y  x  3x 1. -2 -1 1 2 3 4 -1 1 D. 3 2 y   x x 1. -2 3 -3 -4 Câu 12: Cho hàm số 4 2
y x  8x  4. Các khoảng đồng biến của hàm số là các khoảng nào sau đây? A.  ;  2  , 0;2. B.  2
 ;0, 2;.C.  ;  2  , 2;. D.  2  ;0, 0;2.
Câu 13: Hàm số nào sau đây đồng biến trên  ? x 1 A. 4 2
y x  2x  5.
B. y  x 1. C. 3
y x  3x 1. D. y  . x 1 Câu 14: Hàm số 4 2
y  x  2mx 1 đạt cực tiểu tại x  0 khi m thỏa mãn điều kiện nào sau đây? A. m  0. B. m  0. C. 1   m  0. D. m  1.  Câu 15: Hàm số 4 2
y x 10x  9 đạt cực đại, cực tiểu lần lượt tại x , x . Khi đó giá trị biểu thức 1 2
| x x | bằng bao nhiêu? 1 2 A. 5. B. 5. C. 4. D. 2 5.
Câu 16: Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y  2x  3(m 1)x  6(m  2)  2017
nghịch biến trên khoảng a;b sao cho b a  3. A. m  0. B. m  9.
C. m  6. D. m  0 hoặc m  6. Trang13 2 x  2x  2
Câu 17: Cho hàm số y
. Biết đường thẳng y ax b tiếp xúc với đồ thị hàm số tại điểm x 1
có hoành độ bằng 3. Giá trị của T a b là bao nhiêu? A. 1.  B. 2. C. 3. D. 1. 3
x  6x m
Câu 18: Cho tham số m sao cho đồ thị hàm số y
không có tiệm cận đứng. Khẳng định 4x  2 nào sau đây là đúng? 23 A. m 16. B. m  2. C. m 1. D. m  . 6 8 5 y
Câu 19: Đồ thị sau đây là của hàm số nào? 4 3 x  1 x 1 A. y  . B. y  . 2 2x 1 2x 1 1 O x x 1 x 1 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 C. y  . D. y  . -1 1  2x 2x 1 -2 -3 -4 Câu 20: Cho hàm số 3 2
y  x  3x  3x 1. Viết phương trình tiếp tuyến của đồ thị tại giao điểm của đồ thị với trục tung. A. y  3 . x
B. y  3x 1.
C. y  3x  3. D. y  0.
----------------------------------------------- ----------- HẾT ---------- 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D ĐỀ 6
ĐỀ ÔN TẬP CHƯƠNG I Thuvienhoclieu.Com GIẢI TÍCH 12 y
x x   x Câu 1: Hàm số 2 2 4 2 3 2
x đạt giá trị lớn nhất tại x1;x2. khi đó tíchx1 x2có giá trị là A. 1 B. - 1 C. 2  D. 2
3x 1 x  3 Câu 2:
Tìm tất cả các đường tiệm cận đứng của đồ thị hàm số y  2 x  2x  3 A. x  3 B. . x  1
 . và x  3 C. x  3 
D. x 1 và x  3  Câu 3:
Với giá trị nào của m thì đường thẳng
y  x 1 cắt đồ thị hàm số 3 2
y  2x  3mx  m  
1 x 1 tại ba điểm phân biệt?  8  8 A. m  0;  
B. m  0 hoặc m   9  9 8  8 
C. m  0 hoặc m D. m   ;   0;    9  9  Trang14 Câu 4:
Đây là đồ thị của hàm số nào? 2x  3 A. y x 1 2x  3 B. y x 1 2x  3 C. y x 1 2x  3 D. y x 1 Câu 5: Cho hàm số 4 2
y x  2x  4 .Tìm m để phương trình 2 x  2
x  2  3  m có hai nghiệm phân biệt A. m  3 B. m  2 C. m  3
D. m  3 hoặc m=2 1 3 Câu 6:
Đường thẳng y  1 cắt đồ thị hàm số 4 2 y x  3x  tại mấy điểm? 2 2 A. 4 B. 3 C. 2 D. 1 Câu 7: Cho hàm số 3 2
y  x ax bx c . Biết rằng đồ thị hàm số đi qua điểm A0; 1  và có điểm
cực đại là M 2;3 . Tính Q a  2b c A. Q  0 B. Q  4 C. Q  1 D. Q  2 Câu 8: Hàm số 2 y
2x x nghịch biến trên khoảng A. (0; 1) B. (1; ) C. ( ;  1) D. (1;2) Câu 9:
Với tất cả các giá trị thực nào của tham số m thì hàm số 3
y x  m   2 3
1 x  3mm  2 x
nghịch biến trên đoạn 0  ;1 ? A. 1   m  0 B. m  0 C. 1   m  0 D. m  1  Câu 10: Cho hàm số 3 2
y x  3x  9x  5 có đồ thị (C ). Tiếp tuyến của đồ thị (C ) tại điểm cực tiểu là đường thẳng:
A. Trùng với trục hoành B. Song song với trục hoành
C. y  x  5
D. Song song với trục tung
Câu 11: Cho đồ thị hàm số 3 2
(C) : y x  3x  2 . Số tiếp tuyến của đồ thị (C) biết tiếp tuyến song song
với đường thẳng y  9x  7 là: A. 1 B. 2 C. 1 D. 0 2x 1
Câu 12: Cho hàm số y
.Mệnh đề nào sau đây sai? x 1
A. Tiếp tuyến của đồ thị hàm số tại điểm có hoành x  2 có hệ số góc bằng 1
B. Hàm số nghịch biến trên từng khoảng xác định
C. Hàm số có tập xác định là D   \ {1}
D. Đồ thị hàm số qua điểm A (2; 3)
Câu 13: Bảng biến thiên sau đây của hàm số nào? x   2 0   y’ - 0 + 0- Trang15 y 3 x 2 x x 1 3 x 2 x x 1 A. 2 y   x  2 B. y C. 2 y    x 1 D. y  3 x 1 3 x 1
Câu 14: Với giá trị nào của tham số m thì hàm số 3 2
y  (m  2)x  3x mx  5 có cực đại và cực tiểu A. m > - 3
B. m  (3;1) C. m  ( ;  3)  (1;) D. m  ( 3  ;1) \{ 2  } 3 x Câu 15: Cho hàm số 2 y
mx  2(5m  8)x 1.Tìm các giá trị của tham số m để hàm số đạt cực tiểu 3 tại x  2 6
A. Với mọi giá trị m B. m  7 6 C. m  
D. Không có giá trị m nào 7 Câu 16: Cho hàm số 4 2
y ax bx c có đồ thị như hình vẽ bên.
Khẳng định nào sau đây đúng?
A. a  0, b  0, c  0
B. a  0, b  0, c  0
C. a  0, b  0, c  0
D. a  0, b  0, c  0  x
Câu 17: Cho đồ thị hàm số 2 3 (C) : y
. Phương trình tiếp tuyến của đồ thị (C) tại giao điểm của x 1
(C) và đường thẳng y x  3 là:
A. y  x  3 và y  x 1
B. y  x  3 và y  x 1
C. y x  3 và y x 1 D. y  x  3 và y  x 1 Câu 18: Cho hàm số 4 2 4
y x  2mx  2m m . Với giá trị nào của m thì đồ thị C có 3 điểm cực trị, m
đồng thời 3 điểm cực trị đó tạo thành một tam giác có diện tích bằng 2. A. 3 m   16 B. 5 m  4 . C. 5 m  16 . D. m 16 . 2 x  3
Câu 19: Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  trên đoạn x  2  3  1  ;   .  2 
Mệnh đề nào sau đây là đúng? 13 7 8 4
A. M m
B. M m
C. M m
D. M m  6 2 3 3 x 1
Câu 20: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y  có hai tiệm 2 mx 1 cận ngang. A. m  0.
B. Không có giá trị thực nào của m thỏa mãn yêu cầu đề bài. C. m  0. D. m  0. Trang16
----------------------------------------------- ----------- HẾT ---------- 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D ĐỀ 7
ĐỀ ÔN TẬP CHƯƠNG I Thuvienhoclieu.Com GIẢI TÍCH 12 Câu 1:
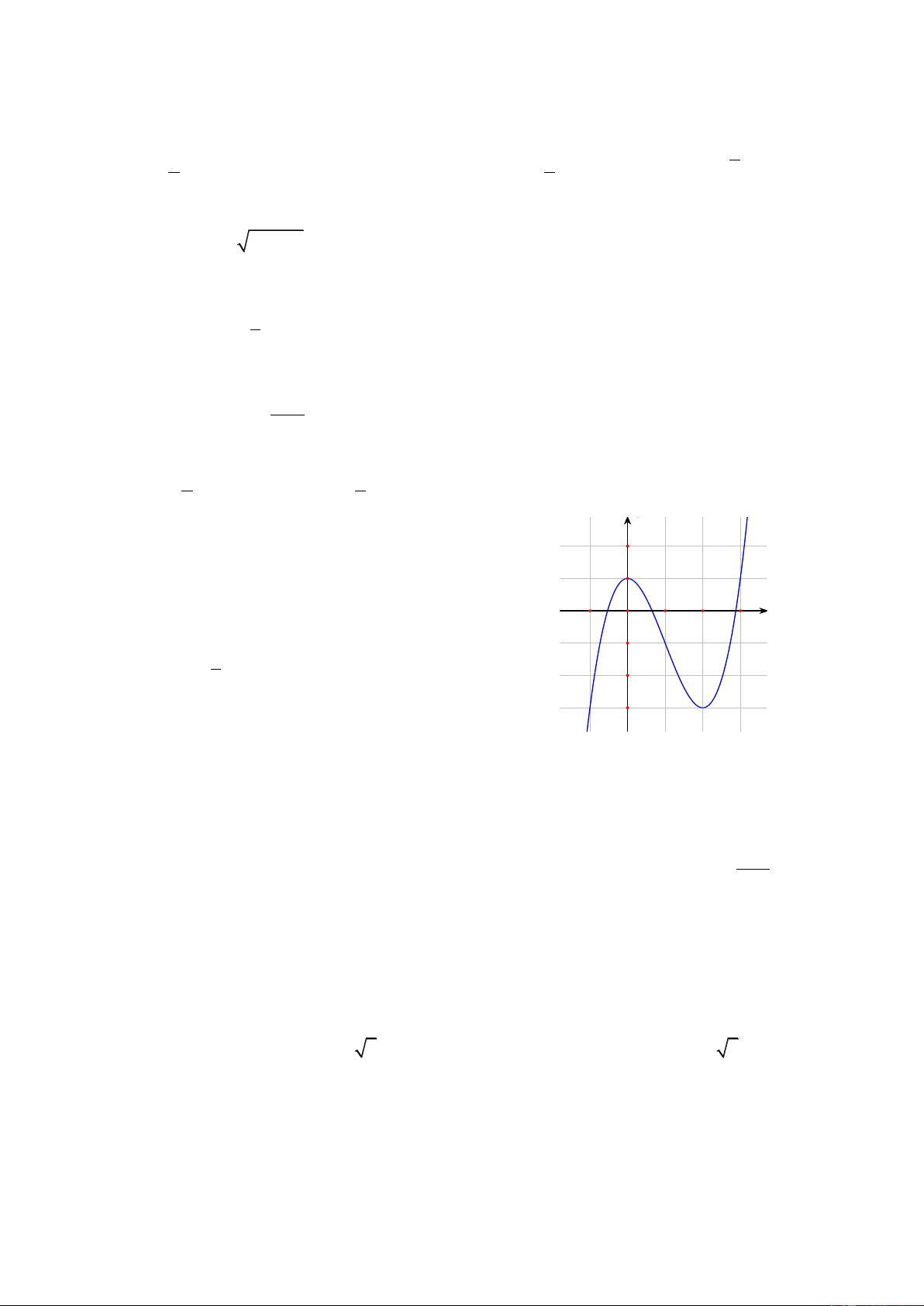
Đồ thị sau đây là của hàm số 3 2
y  x  3x  4 . Với giá trị nào của tham số m thì phương trình 3 2
x  3x  4  m  0 có nghiệm duy nhất. 1 O 3 -1 2 -2 -4
A. m  4 hay m  0
B. m  4 hay m  2 C. m  4
hay m  0 D. 4   m  0 Câu 2:
Trong các hàm số sau, hàm số nào đạt cực tiểu tại điểm x  1? 3 x A. 2 2 y  (x 1) B. 3
y  x  2 C. 2
y  x  2x  3 D. 2 y   x x 3 x b Câu 3: Cho hàm số y
có đồ thị như hình vẽ. Khẳng định nào sau đây là đúng? cx d
A. b  0, c  0, d  0.
B. b  0, c  0, d  0.
C. b  0, c  0, d  0.
D. b  0, c  0, d  0. Câu 4: Cho hàm số 2
y  3x  10  x . Trong các mệnh đề sau, chọn mệnh đề đúng:
A. Hàm số đạt giá trị lớn nhất bằng 10 tại x  3 
B. Hàm số đạt giá trị lớn nhất bằng 10 tại x  3
C. Hàm số đạt giá trị nhỏ nhất bằng 3  10 tại x  10
D. Hàm số đạt giá trị nhỏ nhất bằng 3 10 tại x   10 Câu 5:
Giá trị lớn nhất của hàm số 2 y
x  4x trên  3  ;3 là. A. 4 B. 0 C. 2  D. 2 Trang17 Câu 6: Cho hàm số 3 2
y mx  3mx  m  
1 x  4 . Tìm tất cả các giá trị thực của tham số m để hàm
số không có cực trị 1 1 1 1 A. 0  m B. m C. 0  m D. 0  m  4 4 3 4 Câu 7:
Cho hàm số y f x xác định, liên tục trên đoạn  1  ; 
3 và có đồ thị là đường cong trong
hình vẽ bên. Tập hợp T tất cả các giá trị thực của tham số m để phương trình f x  m có 3
nghiệm phân biệt thuộc đoạn  1  ;  3 là y A. T   4  ;  1 . B. T   3  ;0. 1O 1  2 O 3 x C. T   4  ;  1 . D. T   3  ;0 . 3  4  Câu 8:
Hàm số nào có bảng biến thiên sau đây? X  1  f '(x) − − 2  f (x)  2 2x 1 2x  2 2x  2 2x  3 A. y B. y C. y D. y x  2 x 1 1  x x 1 3 2 x x 3 Câu 9: Cho hàm số y  
 6x  . Mệnh đề nào dưới đây đúng? 3 2 4
A. Hàm số nghịch biến trên khoảng  ;  2
  B. Hàm số đồng biến trên khoảng  2  ;3 .
C. Hàm số đồng biến trên khoảng  2;  
D. Hàm số nghịch biến trên khoảng  2  ;3 1
Câu 10: Cho đồ thị hàm số 4 2 f (x) 
x  2x . Phương trình tiếp tuyến của đồ thị (C) tại điểm x biết 4 0 // f (x )  1  là: 0 5 5 5 5
A. y  3x
và y  3x
B. y  3x
và y  3x  4 4 4 4 5 5
C. y  3x  5 và y  3x  5
D. y  x
và y  3x  4 4 3 31a Câu 11: Cho hàm số
có đồ thị (C). Khẳng định nào sau đây là đúng? 4
A. (C) có hai tiệm cận đứng là đường thẳng 3
15a và một tiệm cận ngang là đường thẳng 3 17a
B. (C) có đúng một tiệm cận đứng là đường thẳng 3
12a và một tiệm cận ngang là đường thẳng 3
C. (C) có một tiệm cận đứng là đường thẳng a 3 và không có tiệm cận ngang
D. (C) có hai tiệm cận đứng là hai đường thẳng a 5 và không có tiệm cận ngang Câu 12: Hàm số 3 2
y  x  3x mx  4 nghịch biến trên khoảng 0;  , ứng với các giá trị thực của tham số m là Trang18  ;0   0; C.  ;    1 D. 0;  A. B. 1
Câu 13: Tìm tất cả các giá trị của m để hàm số 3 2 y
x mx  3m  2 x 1 đồng biến trên  . 3 m  1 m  1 A. B. 2   m  1  C. D. 2   m  1  m  2 m  2
Câu 14: Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 3 2
y  x  3m x có hai điểm cực trị A
và B sao cho AB  2 5. A. m  2  B. m  2 C. m  1  D. m 1
Câu 15: Hàm số y    x3 3 A. Có cực tiểu
B. Có cực đại và cực tiểu C. Có cực đại
D. Không có cực trị x  3
Câu 16: Đồ thị của hàm số y
không có giao điểm với đường thẳng y  mx 1, ứng với giá trị x 1 thực của tham số m là
A. 0  m 16
B. 0  m 16
C. 0  m 16
D. 0  m 16 2 m x  1
Câu 17: Với giá tri ̣ nào của m thì tiê ̣m câ ̣n ngang của đồ thi ̣ hàm số y  đi qua điểm A(3; 1) x  2   A. m  1 B. m  3 C. m  1 D. m   3
Câu 18: Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số 4 2
y x  2(mx) 1 có ba điểm
cực trị tạo thành một tam giác đều. A. 6 m  3 B. 6 m  3 hoặc 6 m   3
C. m  0 hoặc 6 m  3 D. 6 m  3 hoặc 6
m   3 hoặc m  0
Câu 19: Đồ thị hàm số 3 2
y x ax bx c đi qua ba điểm A 1
 ;3 , B0;7 , C  3  ; 3  5 thì phương trình của hàm số là A. 3 2
y  x x  2x  7 B. 3 2
y x x  2x  7 C. 3 2
y x x  2x  7 D. 3
y x  2x  7
Câu 20: Tiếp tuyến của 4 2
(C) : y x  2x  3 tại giao điểm của (C) và trục hoành có hệ số góc là? A. 5  3 B. 7  3 C. 8  3 D. 3 3
----------------------------------------------- ----------- HẾT ---------- 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D Trang19 ĐỀ 8
ĐỀ ÔN TẬP CHƯƠNG I Thuvienhoclieu.Com GIẢI TÍCH 12 Câu 1: Cho hàm số 4 2
y ax bx c có đồ thị như hình vẽ.
Mệnh đề nào sau đây là đúng?
a  0, b  0, c  0.
a  0, b  0, c  0. A. B.
a  0, b  0, c  0. a b c C. D. 0, 0, 0. 2
2x  3x m Câu 2:
Với các giá trị nào của m thì đồ thị hàm số y
không có tiệm cận đứng? x m A. m 1.
B. m 1hoặc m  2 . C. m  0 .
D. m  0 hoặc m 1. Câu 3:
Có bao nhiêu số nguyên m để phương trình 4 2
x  8x m  3  0 có 4 nghiệm phân biệt A. 15. B. 16. C. Không có. D. Vô số. Câu 4:
Tìm giá trị lớn nhất của hàm số 3
y  x  3x trên đoạn 0; 2. max y  2. max y  2  . max y  1. max y  0. A. 0;  2 B. 0;2 C. 0;  2 D. 0;  2 Câu 5: Biết hàm số 3 2
y x  3x m có giá trị nhỏ nhất trên đoạn 0; 
1 bằng 2. Khẳng định nào đúng? A. 1   m 1. B. m  1  . 1 m  5. D. m  5 . C. Câu 6:
Tìm tất cả các giá trị của tham số m để đường thẳng d : y x m  2 cắt đồ thị hàm số 2  x y
tại hai điểm phân biệt A và B sao cho độ dài AB ngắn nhất. x 1 A. m  3  . B. m  1  . C. m  3 . D. m 1. Câu 7:
Đường thẳng d : y x  4 cắt đồ thị hàm số 3 2
y x  2mx  m  3 x  4 tại ba điểm phân biệt
A0; 4 , B, C sao cho tam giác MBC có diện tích bằng 4, với M 1;3 . Tập tất cả các giá trị của m nhận được là:
A. m  2 hoặc m  3 . B. m  3 . C. m  2
 hoặc m  3. D. m  2  hoặc m  3  . Câu 8: Cho hàm số 3
y x  3x  2 . Mệnh đề nào dưới đây là đúng?
A. Hàm số đồng biến trên khoảng (; 0) và nghịch biến trên khoảng (0; ) .
B. Hàm số nghịch biến trên khoảng (; 0) và đồng biến trên khoảng (0; ) .
C. Hàm số đồng biến trên khoảng (; ) .
D. Hàm số nghịch biến trên khoảng (; ) . Trang20 Câu 9: Đồ thị của hàm số 3 2
y  – x  3x  5 có hai điểm cực trị A và
B. Tính diện tích S của tam
giác OAB với O là gốc tọa độ. 3 9 10 3 A. a V . B. 60 . C. S  . D. a V . 8 3 8 Câu 10: Cho hàm số 3 2
y  4x  6x 1 có đồ thị (C). Lập phương trình tiếp tuyến của (C) đi qua điểm M  1  ;9 . 15 21
A. y  24x 15 .
B. y  24x 15 hoặc y x  . 4 4 15 21
C. y  24x  33 . D. y x  . 4 4
Câu 11: Đồ thị hình bên là của hàm số nào? A. 2
y  x x 1. B. 3
y  x  3x 1. C. 4 2
y x x 1. D. 3
y x  3x 1. 2
Câu 12: Hàm số y
nghịch biến trên khoảng nào dưới đây? 2 x 1 A. (; ) . B. (0; ) . C. (; 0) . D. (1;1) .
Câu 13: Tìm m để hàm số 4 2
y x  2mx nghịch biến trên (; 0) và đồng biến trên (0; ) . x A. m  0. B. m  0 . C. m  0 . D. . C  2 1 : y  .. x 1 3 2
Câu 14: Điểm cực đại của đồ thị hàm số y x  6x  9x là điểm nào? A. 1;4 . B. x  3. C. 3;0 . D. x  1. 4 2
Câu 15: Tìm tham số m đồ thị hàm số y x  2mx  1 có ba điểm cực trị A(0; ) 1 , ,
B C thỏa mãn BC  4. A. m  4  . B. m  4 . C. m  2 .
D. m   2 .
Câu 16: Biết rằng đồ thị hàm số 3 2
y x x x  2 và đồ thị hàm số 2
y  x x  5 cắt nhau tại điểm
duy nhất có tọa độ  x ; y . y . 0 0  Tìm 0 y  3. y  4. y  1.  y  0. A. 0 B. 0 C. 0 D. 0 3 2
Câu 17: Cho hàm số y x  6x  9x có đồ thị (C). Lập phương trình tiếp tuyến của (C) song song
với đường thẳng d : y  9x .
A. y  9x  32 .
B. y  9x  40 .
C. y  9x  32 .
D. y  9x  40 . 3 x 1
Câu 18: Tìm số tiệm cận của đồ thị hàm số y  2 x  5x  . 4   A. u  ( 1  ;2;0) . B. V  24 . C. V  32 .
D. u  (0;2;0) . 4 1
Câu 19: Đồ thị sau là của hàm số nào? Trang21 x  2 y  . A. x 1 x  3 y  . B. 1  x x 1 y  . C. x 1 2x 1 y  . D. x 1 x  1
Câu 20: Cho hàm số y  có đồ thị ( )
C . Gọi d là tiếp tuyến của (C) tại điểm có tung độ bằng 3. x 1
Tìm hệ số góc k của . d 1  . B. 2.  1 . D. 2. A. 2 C. 2
----------------------------------------------- ----------- HẾT ---------- 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D ĐỀ 9
ĐỀ ÔN TẬP CHƯƠNG I Thuvienhoclieu.Com GIẢI TÍCH 12 1 Câu 1: Tìm m để hàm số 3 2 2
y   x mx  (m  m1)x 1 đạt cực tiểu tại x 1. 3   A. m  1. B. m  1. C. m  2. D. m  2. 2 x  1 Câu 2:
Số tiệm cận của đồ thị hàm số y  là bao nhiêu? 2 x  2 A. 3. B. 1. C. 2. D. 0. Câu 3:
Tìm tất cả các giá trị của tham số m sao cho đường thẳng d : y x m cắt đồ thị hàm số   C  2x 1
: y x tại hai điểm phân biệt M và N sao cho diện tích tam giác IMN bằng 4, với I 1
là tâm đối xứng của (C).
A. m  3; m  1  .
B. m  3; m  3  .
C. m  3; m  5  . D. m  3  ;m  1  . Câu 4: Cho hàm số 3 2
y  x  3x  3x  1. Viết phương trình tiếp tuyến của đồ thị tại giao điểm của
đồ thị với trục trung.
y  3x  1. y  0. y  3  x  3. y  3 . x A. B. C. D. Trang22 Câu 5: Cho hàm số 3 2
y x  3x 1 có đồ thị là (C). Gọi  là tiếp tuyến của (C) tại điểm A1;5và
B là giao điểm thứ hai của  với (C). Diện tích tam giác OAB bằng bao nhiêu? A. 12. B. 6 82 . C. 6. D. 5. Câu 6:
Có bao nhiêu số nguyên m để đường thẳng y  2m  1 cắt đồ thị hàm số 4 2
y x  2x  2 tại 4 điểm phân biệt? A. 1. B. Không có. C. 2. D. 4. Câu 7: Cho hàm số 3 2
y x  3mx  6 có giá trị nhỏ nhất trên đoạn 0; 
3 bằng 2. Khẳng định nào đúng? A. 1 m 3  . B. m  1. C. m 3 . D. 1   m1. Câu 8:
Đồ thị sau là của hàm số nào? 3 2
y x x A. 2 6 1. 3 2
y x x B. 3 1. 3 2
y  x x C. 3 1. 3 x 2 y    x 1. D. 3 Câu 9: Cho hàm số 2
y  2x 1 . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng ( ;  0) .
B. Hàm số nghịch biến trên khoảng (0; ) .
C. Hàm số nghịch biến trên khoảng ( 1  ;1) .
D. Hàm số đồng biến trên khoảng (0; ) .
Câu 10: Cho hàm số y f x có bảng xét dấu đạo hàm như sau: x  2  0 2  y '   0  0 
Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng (2;0) .
B. Hàm số nghịch biến trên khoảng ( ;  2  ).
C. Hàm số đồng biến trên khoảng ( ;  0) .
D. Hàm số nghịch biến trên khoảng (0; 2) .
Câu 11: Đồ thị hình bên là của hàm số nào? A. 4 2
y  x  2x  3. 4 2
B. y x  2x  3 . C. 4 2
y  x  2x  3. 4 2
D. y  x  2x  3. Trang23 2x 1
Câu 12: Cho hàm số y x  có đồ thị (C). Gọi d là tiếp tuyến của (C), biết d đi qua điểm 1 A4; 
1 . Gọi M là tiếp điểm của d và (C). Tìm tọa độ điểm M.
A. M 2;5, M 0;  1
 . B. M 2;5, M  2  ;  1 .  3 
C. M 0;   1 , M  2  ;  1 . D. M 1  ; , M  2     ;1 .  2  Câu 13: Hàm số 3
y x  3x  2 đạt cực đại tại điểm nào? x x x x   A. 1. B. 0. C. 2. D. 1. Câu 14: Cho hàm số 3 2
y x  3x  (m1)x 1 có đồ thị ( )
C . Tìm m để đường thẳng d : y x 1 cắt
đồ thị (C) tại 3 điểm phân biệt (
P 0;1), M, N sao cho bán kính đường tròn ngoại tiếp tam giác 5 2 OMN bằng . 2  9 A. m 0. B. m  1. C. m  3. m  . D. 4 ax b
Câu 15: Cho hàm số y
(a  0) có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng? cx d y
b  0, c  0, d  0. A.
b  0, c  0, d  0. B.
b  0, c  0, d  0. C.
b  0, c  0, d  0. O D. x x
Câu 16: Gọi M, N là giao điểm của đường thẳng d : y x 1 và đường cong C  2 4 : y  . Tìm x 1
hoành độ trung điểm I của đoạn thẳng MN. 5 5 A. . B. 2. C. 1. D.  . 2 2
Câu 17: Tìm tất cả các giá trị của tham số m để đồ thị hàm số 4 2 2
y x  2m x 1 có 3 điểm cực trị tạo
thành 3 đỉnh của một tam giác vuông cân.  m 1  ;0   A. m  1. ;1 . m  2. m1. B. C. D. mx  2
Câu 18: Tìm tất cả các giá trị của tham số m để y
đồng biến trên mỗi khoảng xác định. 2x m       A. m  2
  m  2. B. m  2
  m  2.C. 2 m 2. D. 2 m 2. 2 x m
Câu 19: Tìm tất cả các giá trị của tham số m để đồ thị hàm số y
có đúng 2 đường tiệm 2 x  3x  2 cận.   A. m  1. B. m 4. m 1, m 4. m 0. C. D.
Câu 20: Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2
y x 1  x trên tập xác định. Trang24
Khi đó M m bằng bao nhiêu? A. 2. B. 1. C. 3. D. 4.
----------------------------------------------- ----------- HẾT ---------- 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 A B C D ĐỀ 10
ĐỀ ÔN TẬP CHƯƠNG I Thuvienhoclieu.Com GIẢI TÍCH 12 Câu 1: Cho hàm số 3 2 2 3
y x  3m x m có đồ thị C . Tìm tất cả các giá trị thực của tham số m để
tiếp tuyến của đồ thị C tại điểm có hoành độ x  1 song song với đường thẳng d : y  3 . x 0 A. m  1. B. m  1.  m 1 C. . 
D. Không có giá trị của m. m  1  Câu 2:
Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số 4 2
y x  2x  3 trên0; 2 là:
A. M  11, m  3.
B. M  5, m  2.
C. M  3, m  2.
D. M  11, m  2. 2 x  3x  2 Câu 3:
Số đường tiệm cận của đồ thị hàm số y  là: 2 4  x A. 4. B. 1. C. 2. D. 3. x Câu 4: Cho hàm số 2 1 y
có đồ thị (C). Tìm các điểm M trên đồ thị (C) sao cho khoảng cách từ x 1 hai điểm (
A 2; 4) và B(4; 2) đến tiếp tuyến của (C) tại M là bằng nhau 3 5 A. M (0;1).
B. M (1; ) , M (2; ). 2 3 3 3 C. M (1; ).
D. M (0;1); M (1; ); M ( 2  ;3). 2 2 x  5 Câu 5:
Tổng các giá trị thực của tham số m sao cho đường thẳng y x cắt đồ thị hàm số y x m
tại hai điểm A và B sao cho AB  4 2 là A. 2 B. 5 C. 7 D. 9 Câu 6:
Tìm tất cả các giá trị thực của tham số m để đường thẳng d : y  x m cắt đồ thị hàm số (C): 2x 1 y
tại hai điểm phân biệt x  2 A. 1   m  4. B. m . C. m  4. D. 1
  m hoặc m  4. Câu 7:
Chohàmsố y f (x) có đạo hàm 2
f '(x)  x 1. Mệnhđềnào dướiđâyđúng? Trang25
A. Hàmsố nghịch biến trênkhoảng (1;1).
B. Hàmsố nghịch biến trên khoảng (1; ).
C. Hàmsố nghịch biến trênkhoảng ( ;  0).
D. Hàmsố đồngbiến trênkhoảng (; ). Câu 8:
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 4
y x  m   2
1 x m cắt trục
hoành tại bốn điểm phân biệt có tổng bình phương các hoành độ bằng 8. A. m  1. B. m  1   2 2. C. m  7. D. m  3. x 1 Câu 9: Cho hàm số y
có đồ thị (C). Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có x  2 phương trình là: 1 1 A. y  3 . x B. y x  .
C. y  3x  3.
D. y x  3. 3 3 2 x  3x  6
Câu 10: Để đường cong (C) : y
có đúng 1 đường tiệm cận đứng thì giá trị của a là 2
x ax aa  0 a 1 A. .  B. .  C. a  1. D. a  2. a  4 a  2 1 x
Câu 11: Cho f x 2  
x . Gọi M  max f x;m  min f x , khi đó: M – m bằng 2 x  4x  5 4 0; 3 0; 3 3 7 9 A. . B. 1. C. . D. . 5 5 5 Câu 12: Cho hàmsố 2 y
2x 1 . Mệnh đềnào dướiđây đúng?
A. Hàmsố nghịch biến trênkhoảng (0; ).
B. Hàmsố đồngbiến trênkhoảng (; 0).
C. Hàmsố nghịch biến trênkhoảng (1;1).
D. Hàmsố đồng biến trênkhoảng (0; ). 1
Câu 13: Số điểm cực đại của đồ thị hàm số 4 2 f (x) 
x  2x  4 là: 4 A. 1 B. 3 C. 2 D. 0
Câu 14: Cho hàmsố y f (x) có bảng biến thiênnhư sau
Mệnh đề nàodướiđâysai?
A. Hàmsố cógiátrịcực đạibằng 0
B. Hàmsố cóbađiểmcực trị.
C. Hàmsố có haiđiểmcựctiểu.
D. Hàmsố cógiátrịcực đạibằng3. 1
Câu 15: Giá trị cực tiểu của hàm số 3 y  
x x 1 là: 3 1 5 A. 1 B. C. D. 1 3 3 Trang26 Câu 16: Cho hàm số 4 2
y ax bx c , với a  0 , có bảng biến thiên như hình sau:
Khẳng định nào sau đây đúng:
A. a  0 và b  0
B. a  0 và b  0
C. a  0 và b  0
D. a  0 và b  0 2 x  2x
Câu 17: Hàm số y
đồng biến trên khoảng: x 1 A. ( ;  2). B. ( ;1
 ) và (1;). C. ( 1  ;). D. (0; ).
Câu 18: Cho hàm số y f x xác định và có đạo hàm f '(x) . Đồ thị hàm số y f (x) như hình bên.
Khẳng định nào sau đây đúng:
A. Hàm số y f x đồng biến trên khoảng (0;1).
B. Hàm số y f x đồng biến trên khoảng ( ;  2).
C. Hàm số y f x có 3 điểm cực trị.
D. Hàm số y f x đồng biến trên khoảng ( ;  1  ).
Câu 19: Cho hàm số y f x có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số m để
phương trình f x  m  2 có bốn nghiệm phân biệt. y -1 1 x O A. 4   m  3  . B. 4   m  3  . C. 6   m  5  . -3 D. 6   m  5  . -4 .
-----------------------------------
Câu 20: Đồ thị hàm số 3 2
y  x  3x  2 có dạng: A. B. C. D. y y y y 3 3 3 3 2 2 2 2 1 1 1 1 x x x x -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -3 -2 -1 1 2 3 -1 -1 -1 -1 -2 -2 -2 -2 -3 -3 -3 -3 ----------- HẾT ---------- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 B D C D C B D D B A D D D A C A B D D C Trang27 ĐỀ 11
ĐỀ ÔN TẬP CHƯƠNG I Thuvienhoclieu.Com GIẢI TÍCH 12 Câu 1: Cho hàm số 4 2
y ax bx c có đồ thị như hình vẽ bên. Khẳng đi ̣nh nào sau đây đúng? A. ( ;  1). B. (1;3).
C. a  0, b  0, c  0.
D. a  0, b  0, c  0. Câu 2: Cho hàm số 3 2
y  x  3x 1. Phương trình tiếp tuyến ta ̣i điểm A(3;1) là: 13 13
A. y  9x  20.
B. 9x y  28  0. C. m  . D. m   . 2 2 Câu 3: Cho hàm số 3 2 2
y x m x m có đồ thị C . Tìm tất cả các giá trị thực của tham số m để tiếp
tuyến của đồ thị C tại điểm có hoành độ x  1song song với đường thẳng d : y  5  . x 0 A. m  2.  B. m  2.
C. Không có giá trị của m. D. min y  1.   3;  2 2  4 Câu 4:
Tìm giá trị lớn nhất của hàmsố  x y trên đoạn 1;  3 . x A. max y  4. B. , A B.
C. k k D. 1.   1 2 1;  3 Câu 5:
Số giao điểm của đường cong 3 2
y x  2x  2x 1 và đường thẳng y  1 x bằng: A. 0. B. 2. C. 3. D. 1. Câu 6:
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số 4
y x  m   2
1 x m cắt trục
hoành tại bốn điểm phân biệt có tổng bình phương các hoành độ bằng 2 2. A. m  3.
B. f x 4 2
x  2x . C. f x 4 2
x  2x . D. m  1   2. x  2 Câu 7: Cho hàm số y  . Xét các mệnh đề sau: x 1
1) Hàm số đã cho nghịch biến trên  ;   1  1; .
2) Hàm số đã cho đồng biến trên  ;   1 .
3) Hàm số đã cho nghịch biến trên tập xác định.
4) Hàm số đã cho nghịch biến trên các khoảng   ;1  và 1;.
Số mê ̣nh đề đúng là A. 1. B. 3. C. 2. D. 4. Câu 8:
Tập tất cả các giá trị thực của tham số m để hàm số 3
y x  m   2
1 x  3x 1 đồng biến trên khoảng  ;   là A. x  B.  ;  2  4;. Trang28 C.  2  ;4. D.  ;  2  4;. Câu 9:
Gọi M, m lần lươ ̣t là giá tri ̣ lớn nhất giá tri ̣ nhỏ nhất của hàm số 2
y x  4  x . Khi đó
A. M m  4.
B. M m  2 2  2. C. M m  2 2.
D. M m  2 2  2. Câu 10: Cho hàm số 3
y x x 1 có đồ thị (C). Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục tung.
A. y  2x  2.
B. y  2x 1.
C. y  x 1.
D. y  x 1. ax b
Câu 11: Giá trị thực của tham số a, b để hàm số y
có đồ thị như hình bên là x 1
A. a  1, b  2. B. a  1  ,b  2. 
C. a  1, b  2.
D. a  1, b  2.  Câu 12: Hàm số 2 y
2x x x nghịch biến trên khoảng A.  ;   1 . B. 1; . C. 0  ;1 . D. 1; 2. 1 2 2 x 1 x 1
Câu 13: Gọi x , x là điểm cực trị của hàm số 3 2 y
x x x  5 . Giá trị biểu thức 1 2 S   1 2 3 x x 1 2 bằng A. 4. B. 2. C. 1. D. 3.
Câu 14: Khoảng cách từ điểm cực đại của đồ thị hàm số 3 2
y x  2x x 1 đến trục hoành là 23 1 A. .
B. f (a b c)  1. C. 1. D. . 27 9
Câu 15: Cho hàm số có bảng biến thiên dưới đây. Phát biểu nào là đúng? x  -2 0  y ' + 0 - 0 + y 3   -1
A. Giá trị cực tiểu của hàm số là 0.
B. Hàm số đạt cực tiểu tại x  1
 và đạt cực đại tại x  3.
C. Giá trị cực đại của hàm số là 2. 
D. Hàm số đạt cực đại tại x  2
 và đạt cực tiểu tại x  0. 2 mx  6x  2
Câu 16: Tập hợp giá trị thực của tham số m để đồ thị hàm số y  có tiệm cận đứng là x  2 7  7  A.  . B.  . C.  \   0 . D.  \  . 2 2 Câu 17: Hàm số 3
y  x  3x  2 nghịch biến trên các khoảng nào sau đây? Trang29 A.  ;   
1 và 1; . B.  ;    1  1; . C.  1  ;. D.  1  ;  1 .
Câu 18: Xét các mệnh đề sau: 1
1) Đồ thị hàm số y
có một đường tiệm cận đứng và một đường tiệm cận ngang. 2x  3 2   1 2) Đồ thị hàm số  x x x y
có hai đường tiệm cận ngang và một đường tiệm cận đứng. x x  2x 1
3) Đồ thị hàm số y
có một đường tiệm cận ngang và hai đường tiệm cận đứng. 2 x 1
Số mê ̣nh đề đúng là A. 2 . B. 3 . C. 1. D. 0 . 2x 1
Câu 19: Tìm tất cả các điểm thuộc đồ thị hàm số y
có khoảng cách đến trục hoành bằng 1 x 1
A. M 0;   1 , N  2  ;  1 . B. M  2   ;1 .
C. M 0;   1 , N  1  ; 
1 . D. M 0; 
1 .-------------------------------------------
Câu 20: Hình vẽ bên là đồ thị của hàm số nào? 2x 1 y A. y  . x 1 4 1  2x B. y  . x  1 2 2x 1 C. y  . x 1 -5 O 1 5 x 1  2x D. y  . -1 x 1 -2 ----------- HẾT ---------- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 C B B C D D A A B D C D A A D D A A A A ĐỀ 12
ĐỀ ÔN TẬP CHƯƠNG I Thuvienhoclieu.Com GIẢI TÍCH 12 ax b Câu 1: Cho hàm số y
có đồ thị như hình vẽ: Khẳng định nào sau đây đúng? cx d Trang30 ad  0 ad  0 A.  . B.  . bc  0 bc  0 ad  0 ad  0 C.  . D.  . bc  0 bc  0 2x  4 Câu 2:
Viết phương trình tiếp tuyến với đồ thị hàm số y
tại điểm có tung độ bằng 3. x  4
A. 4x y  5  0.
B. 4x y  20  0.
C. x  4 y  5  0.
D. x  4 y  20  0. Câu 3: Cho hàm số : 3 2
y  4x  6x 1 (C). Phương trình tiếp tuyến của đồ thị biết nó đi qua điểm M  1  ;9 là: 15 21
A. y  24x 15 hoặc y x  .
B. y  24x 15. 4 4 15 21 C. y x  .
D. x 1  0 hoặc y  24x 15. 4 4 2 x  3 Câu 4:
Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  trên đoa ̣n x  2  3  1  ; 
 . Mệnh đề nào sau đây là đúng?  2  8 4 7 16
A. M m  .
B. M m  .
C. M m  .
D. M m  . 3 3 2 3 Câu 5:
Tìm số giao điểm n của hai đồ thị 4 2
y x  3x  2 và 2 y x  2 . A. n  0. B. n  1. C. n  4. D. n  2. Câu 6:
Tìm tất cả các giá trị của tham số thực m để đường thẳng y  2x 1 cắt đồ thi ̣ hàm số x   m y . x 1 3 3 3 3 A.   m  1. B. m   . C.   m  1. D. m   . 2 2 2 2 1 Câu 7: Cho hàm số 3 2 y  
x  2x  3x 1. Mệnh đề nào dưới đây đúng? 3
A. Hàm số đồng biến trên khoảng (1;3).
B. Hàm số nghịch biến trên khoảng (1; ).
C. Hàm số đồng biến trên khoảng ( ;  1).
D. Hàm số nghịch biến trên khoảng (1;3). Câu 8:
Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y  2x mx  2x đồng biến trên khoảng  2  ;0. 13 13 A. m  2  3. B. m  2  3. C. m  . D. m   . 2 2 Trang31 Câu 9:
Tìm giá trị nhỏ nhất của hàm số 2
y x 1 trên đoạn  3  ;2. A. min y  8. B. min y  3.  C. min y  1.  D. min y  3.  3  ;2  3;  2  3;  2  3  ;2 x 1
Câu 10: Cho hàm số y  (C). Gọi ,
A B là hai giao điểm của đường y x m với đồ thị (C) và 2x 1
k , k là hệ số góc của tiếp tuyến với đồ thị tại hai điểm ,
A B. Khi đó k k đạt giá trị lớn 1 2 1 2 nhất bằng: A. 2. B. 1. C. 1.  D. 2. 
Câu 11: : Cho hàm số y f x có đồ thị như hình vẽ bên. Biết rằng f x là một trong bốn hàm được
đưa ra trong các phương án A , B, C, D dưới đây . Tìm f x
A. f x 4 2  x  2x .
B. f x 4 2  x  2x .
C. f x 4 2
 x  2x 1.
D. f x 4 2
 x  2x .
Câu 12: Dựa vào hình vẽ. Tìm khẳng định đúng.
A. Hàm số nghịch biến trên (0; ), đồng biến trên (; 0) và có hai cực trị.
B. Hàm số đồng biến trên (0; ), nghịch biến trên
(; 0) và có hai cực trị.
C. Hàm số luôn nghịch biến trên từng khoảng xác định và không có cực trị.
D. Hàm số luôn đồng biến trên từng khoảng xác định và không có cực trị.
Câu 13: Cho hàm số y f (x) liên tục trên ℝ, có đạo hàm 2 3
f '(x)  x(x 1) (x 1) . Hàm số đã cho có
bao nhiêu điểm cực trị?
A. Chỉ có 1 điểm cực trị. B. Không có cực trị.
C. Có 2 điểm cực trị
D. Có 3 điểm cực trị.
f x x p q x  
Câu 14: Tìm các số thực p và q sao cho hàm số ( ) đạt cực đại tại 2 và x 1 f (2)  2.
A. p  1, q  1.
B. p  1, q  1. C. p  1  , q  1. 
D. p  1, q  1.
Câu 15: Cho hàm số y f x có đạo hàm f x 2  x  2 '
x  4 , x . Mê ̣nh đề nào sau đây là đúng?
A. Hàm số đã cho có 3 điểm cực trị.
B. Hàm số đã cho có 2 điểm cực trị.
C. Hàm số đã cho đạt cực đại tại x  2.
D. Hàm số đã cho đạt cực tiểu tại x  2.  2 x a
Câu 16: Tìm tất cả các giá trị thực của tham số a để đồ thị hàm số y
có 3 đường tiê ̣m câ ̣n 2 x ax A. a  0.
B. a  0, a  1. 
C. a  0, a  1. 
D. a  0, a  1. Trang32
Câu 17: Cho hàm số y f x có bảng biến thiên như hình vẽ bên. Mê ̣nh đề nào sau đây là sai? x  1 2  y ' + 0 - 0 + y 3   0
A. Hàm số đồng biến trên khoảng  ;   1 .
B. Hàm số nghịch biến trên khoảng 0;3.  3 
C. Hàm số nghịch biến trên khoảng 1; .  
D. Hàm số đồng biến trên khoảng 2; .  2  x  3  2
Câu 18: Số các đường tiệm cận đứng của đồ thị hàm số y  là: 2 x 1 A. 2. B. 1. C. 3. D. 0. Câu 19: Cho hàm số 4 2 4
y x  2mx  2m m . Tìm tất cả các giá trị tham số thực m thì đồ thị có 3
điểm cực trị, đồng thời 3 điểm cực trị đó tạo thành một tam giác có diện tích bằng 2. A. 5 m  4. B. m 16. C. 5 m  16. D. 3 m   16.
y f x ax bx
Câu 20: Biết rằng hàm số 4 2 ( )
c có đồ thị là đường cong trong hình vẽ bên. Tính giá
trị f (a b c).
A. f (a b c)  1.
B. f (a b c)  2.
C. f (a b c)  2.
D. f (a b c)  1.
----------------------------------------------- ----------- HẾT ---------- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 C D A A D D A B C D D D C B B B B B A A Trang33