








Preview text:
KĨ THUẬT GIẢI NHANH BÀI TOÁN CỰC TRỊ HÀM TRÙNG PHƯƠNG
Phương pháp chung:
MỘT SỐ DẠNG TOÁN CƠ BẢN VỀ HÀM BẬC 4 TRÙNG PHƯƠNG
y Ax4 Bx2 C
Lý thuyết: y Ax4 Bx2 C
TXĐ: D = R
y ' 4ax3 2bx
Hàm số có 3 CT khi y’ = 0 có 3 nghiệm pb.
x 0
x1 0
y1 c
b2
b
2a
A(0; c)
b
2a
b2
2x 2ax2 b 0 b x y c
B ; c
x 0
2 2
2
2a
4a 4a
b2 b b2
b
2a
x3 y2 4a c C 2a ; 4a c
+) Hàm số bậc 4 trùng phương khi có 3 CT thì luôn tạo thành tam giác cân tại A(0;c).
b4 b
b
2a
+) AB AC
b
2a
; BC 2.
16a2 2a
3
+) Phương trình đường thẳng qua BC:
+) Gọi góc BAC = ta luôn có:
y và AB;AC:
4a
y
x c
3 b3 8a 2 b5
8a(1 cos ) b (1 cos ) 0 cos b3 8a ; S
32a3
+) Bán kính đường tròn ngoại tiếp tam giác ABC:
b3 8a
R
8 a .b
=> 3 CỰC TRỊ TẠO THÀNH TAM GIÁC ĐỀU: AB=BC
 3 CỰC TRỊ TẠO THÀNH TAM GIÁC VUÔNG: AB.AC 0
3 CỰC TRỊ TẠO THÀNH TAM GIÁC VUÔNG: AB.AC 0
CÔNG THỨC TÍNH NHANH:
DỮ KIỆN | CÔNG THỨC THỎA MÃN: a.b<0 |
1. Tam giác vuông cân tại A | 8a b3 0 |
2. Tam giác ABC đều | 24a b3 0 |
3. Tam giác có góc BAC= | b3 8a cos hoặc 8a b3. tan2 b3 8a 2 |
4. Tam giác có SABC S0 | 32a3.S 2 b5 0 0 |
5. Tam giác có max(S0 ) | b5 S0 32a3 |
6. Tam giác có độ dài cạnh BC = t | at2 2b 0 |
7. Tam giác có độ dài AB=AC = t | 16a2t2 b4 8ab 0 |
8.Tam giác cùng điểm O tạo hình thoi | b2 2ac 0 |
9. Tam giác có cực trị B;C Ox | b2 4ac 0 |
10. Tam giác có trọng tâm O | b2 6ac 0 |
11. Tam giác có điểm cực trị cách đều Ox | b2 8ac 0 |
12.Tam giác có bán kính đường tròn ngoại tiếp : RABC R0 | b3 8a R0 8 a .b |
(BÀI TẬP VỀ CỰC TRỊ VỚI HÌNH HỌC CƠ BẢN)
Câu 1: Cho y x4 2mx2 m2 m cos 3 cực trị sao cho khoảng cách 2 điểm cực tiểu
bằng 2 . Tìm m.
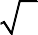
2
A.1 B.2 C.3. D.4
Giải:
a.b 0
- 0
1
2m 0
Hàm số có 2 CT, 1CĐ thỏa mãn:
a 0
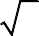 at 2 2b 0 2
at 2 2b 0 2
m 2
Tương tự 2 CĐ, 1CT thỏa mãn:
a.b 0
a 0
at 2 2b 0
1.2 2
2(2m) 0
Câu 53. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số y
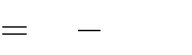
x4
2mx2
có ba điểm cực trị tạo thành một tam giác vuông ?
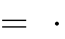
1
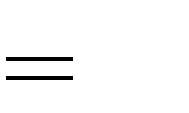
2.
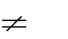
0.
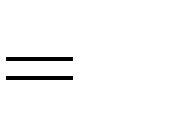
3.
A. m
B. m
C. m
D. m
Câu 54. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số
y có ba điểm cực trị tạo thành một tam giác vuông cân ?
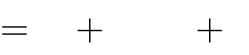
x4
2mx2
1
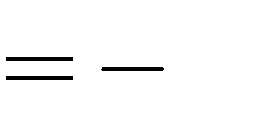
1.
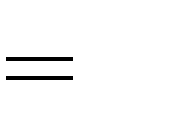
1.
A. m

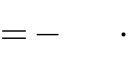
1
3 9
B. m
C. m
D. m
Câu 56. Với giá trị nào của tham số m thì đồ thị hàm số y
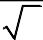
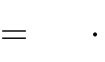
1
3 9
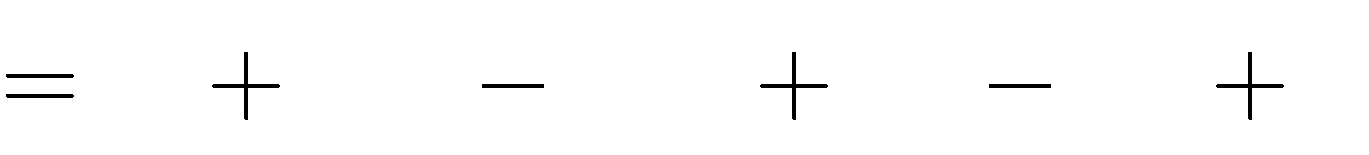
x4
2(m 2)x2
m2
5m
5
có ba điểm cực trị tạo thành một tam giác vuông cân ?
1.
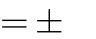
1.
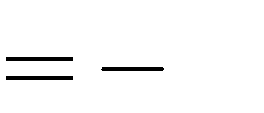
1.
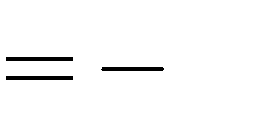
2.
A. m
B. m
C. m
D. m
Câu 57. Với giá trị nào của tham số m thì đồ thị hàm số y
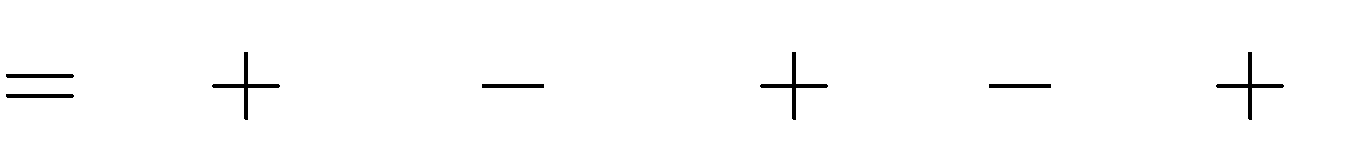
x4
2(m 2)x2
m2
5m
5
có ba điểm cực trị tạo thành một tam giác đều ?
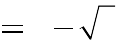
2 3.
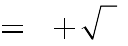
2
3.
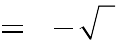
2 3 3.
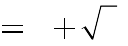
2 3 3.
A. m
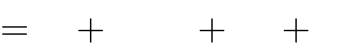
x4
2mx2
m2
m
B. m
C. m
D. m
Câu 58. Với giá trị nào của tham số m thì đồ thị hàm số điểm cực trị tạo thành một tam giác có một góc bằng 1200
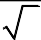

1
3 3

0
y
?
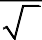
1
3 3
có ba
A. m
0
hoặc
m
B. m
hoặc m
 C. m D. m
C. m D. m
0.
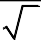
3 3
1
Câu 59. Với giá trị nào của tham số m thì đồ thị hàm số
y
có ba
điểm cực trị tạo thành một tam giác có bán kính đường tròn ngoại tiếp bằng 1 ?

x4
2mx2
m 1
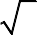


1 5
2
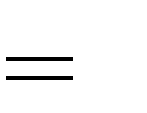
1
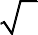
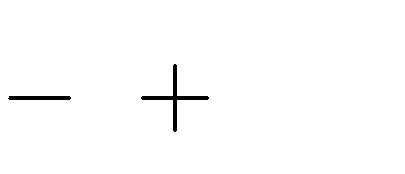

1 5
2
A. m
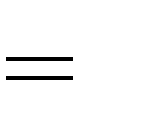
1
hoặc
m
B. m
hoặc m
C. m
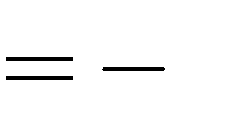
1
hoặc
m
D. m
hoặc m
Câu 61. Với giá trị nào của tham số m thì đồ thị hàm số y có
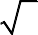
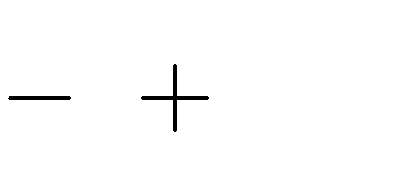

1 5
2
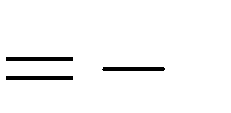
1
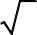


1 5
2
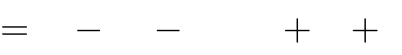
x4
2(1 m2 )x2
m 1
ba điểm cực trị tạo thành một tam giác có diện tích lớn nhất ?
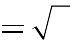
2.
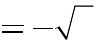
2.
0.
2.
A. m
B. m
C. m
D. m
Câu 62. Với giá trị nào của tham số m thì đồ thị hàm số y
1 x4
4
(3m 1)x2
2m 2
có ba điểm cực trị tạo thành một tam giác có trọng tâm là gốc tọa độ O ?
2
3
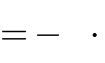
1
3
A. m
C. m
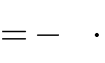
2
3
hoặc
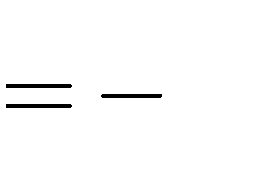
2
3
m
B. m
D. m
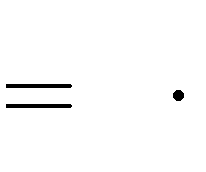
1
3
hoặc m
Câu 63. Với giá trị nào của tham số m thì đồ thị hàm số
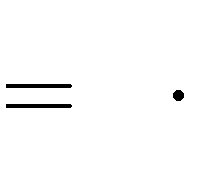
1
3
y
có ba
điểm cực trị tạo thành tam giác cân sao cho độ dài cạnh đáy bằng 2
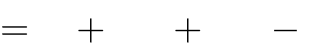
x4
(3m 1)x2
3
3
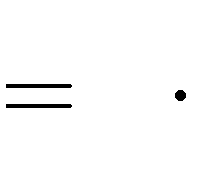
5
3
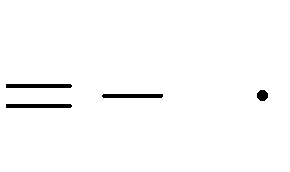
5
3
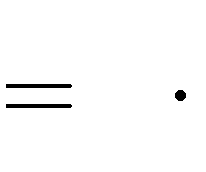
3
5
độ dài cạnh bên?
A. m
B. m
C. m
D. m
Câu 64. Với giá trị nào của tham số m thì đồ thị hàm số
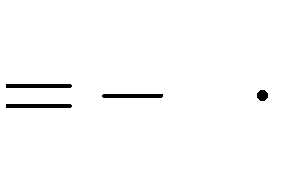
3
5
y
có ba
điểm cực trị A, B, C sao cho bốn điểm A, B, C, O là bốn đỉnh một hình thoi với O là gốc tọa độ ?

2x4
m2x2
m2
1
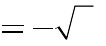
2.
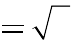
2.
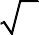
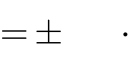
2
2
A. m
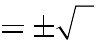
2.
B. m
C. m
D. m
Câu 66. Với m bằng bao nhiêu thì đồ thị hàm số thỏa mãn tam giác ABC vuông tại A(2;2) ?
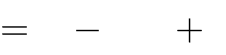
x3
3mx 1
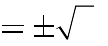
2.
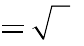
2.
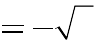
2.
y
có hai cực trị B, C
A. m
B. m
C. m
D. Đáp án kháC.
Câu 67. Với m bằng bao nhiêu thì đồ thị hàm số
y
có hai
cực trị A, B thỏa mãn AB ?
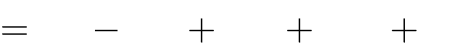
2x3 3(m 1)x2 6mx
m3
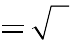
2
A. | m | 0. 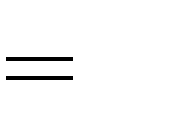 | B. | m | 2. 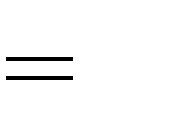 | |||||||
C. | m | 0 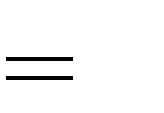 | hoặc | m | 2. 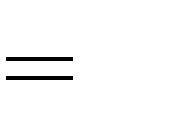 | D. | m 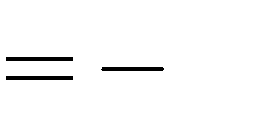 | 2. | hoặc | m | 0. 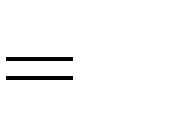 | |
BÀI TẬP TỰ LUYỆN
Câu 1: Giá trị cực tiểu của hàm số 𝑦 = 𝑥3 − 3𝑥 là:
- B. -2 C. 2 D. -4
Câu 2: Cho hàm số y x3 3mx2 3 1 m2 x m3 m2 có hai điểm cực trị A, B. Tìm
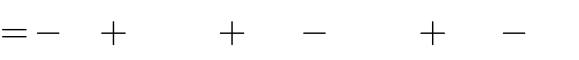
m để đường thẳng AB đi qua điểm M 0; 2
2
A. m
C. m
hoặc m
hoặc m
0
0
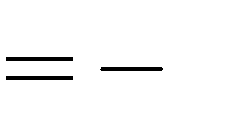
2
B. m
D. m
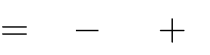
x3
mx 1
hoặc m
hoặc m
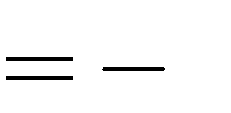
1
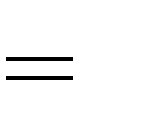
2
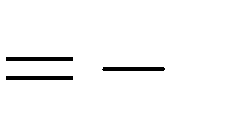
1
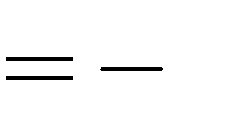
2
Câu 3. Với giá trị nào của m thì hàm số
y
có hai cực trị:
A. m 0 B. m 0  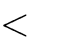 Câu 4. Với giá trị nào của m thì hàm số | y 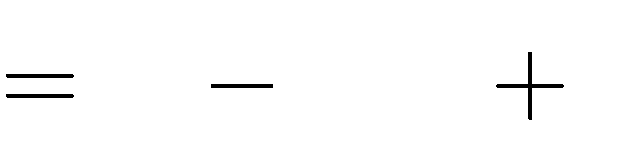 | x3 | C. m 2mx |
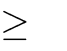
| 0 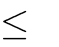 1 : 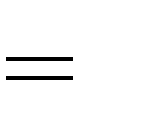 |
A. m 3 B. m 3 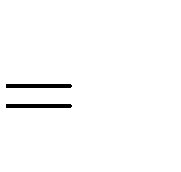  | C. m | 2 D. m  | 2  | ||
2 2 | 3 | 3 |
Câu 5. Cho hàm số
y
có hai điểm cực trị là
x , x . Khi đó tích
x1.x2 bằng:
1 x3
3
4x2
5x 17
1 2
- B.-5 C.8 D.
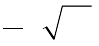
2 11
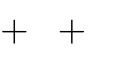


x2
x
x 1
2
Câu 6.Cho hàm số
y
. Hàm số có hai điểm cực trị
x , x .Tích
x .x bằng
A.- 3 B. 2 C.- 2 D. 3
1 2
1 2
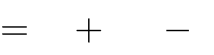 Câu 7.Cho hàm số y x3 3x2 1. Biểu thức liên hệ giữa giá trị cực đại (y ) và giá trị cực tiểu (y ) là:
Câu 7.Cho hàm số y x3 3x2 1. Biểu thức liên hệ giữa giá trị cực đại (y ) và giá trị cực tiểu (y ) là:
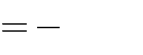
3.yCT

3.yCT
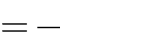
3.yCD
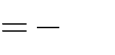
yCT
CT
CD
- yCD
- yCD
- yCT
- yCD
Câu 8:Hàm số y
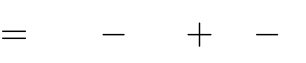
1 x3
3
mx m 5
bằng bao nhiêu?
- m
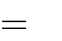
4
- m
đạt cực tiểu tại x
- m
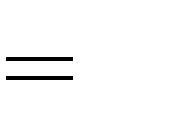
2
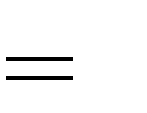
1
khi tham số m lấy giá trị
- m
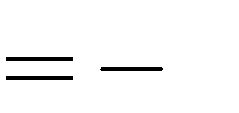
3
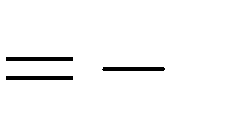
1
Câu 9.Tìm tất cả các giá trị của tham số m sao cho hàm số y
x3 x2
mx 5
cực trị. Chọn kết quả đúng:
có hai
A. m
B. m
C. m
D. m
Câu 10.Gọi A,B là hai điểm cực trị của đồ thị hàm sốy
1
3
1
3
1
3
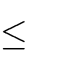
1
3
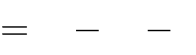
x3
3x 1
thẳng AB bằng :
.Khi đó đoạn
A. 2
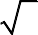
5
B. 3
C. 2
D. 3
Câu 11. Tìm tất cả các giá trị thực của tham số m để hàm số
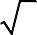
5
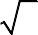
2
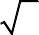
2
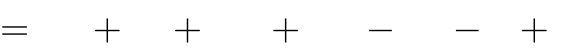 y 2x3 (m 1)x2 (m2 4)x m 1đạt cực tiểu tại x = 0
y 2x3 (m 1)x2 (m2 4)x m 1đạt cực tiểu tại x = 0
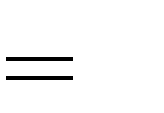
2
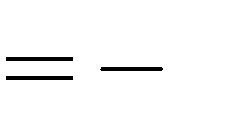
2
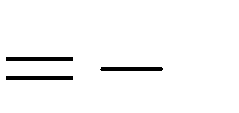
3
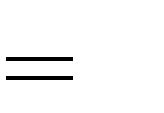
3
A. m
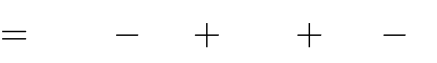
m x3
3
m 1 x2
mx 7
B. m
C. m
D. m
Câu 12.Hàm số
y
có hai cực trị khi và chỉ khi:
A. m
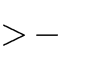
1
2
và m
B. m
C. m
D. m
Câu 13.Cho hàm số y
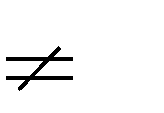
0
đây là sai
1 x3
 3
3
mx2
(2m 1)x 1 , m là tham số thực. Mệnh đề nào sau
- Hàm số luôn luôn có cực đại và cực tiểu với mọi m
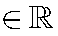
- Hàm số có hai điểm cực trị khi m
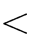
1
- Hhàm số luôn luôn có cực đại và cực tiểu khi m
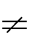
1
- Hàm số có cực trị khi m
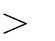
1
Câu 14.Hàm số y x3 mx 1 , m là tham số thực, có 2 cực trị khi :
- m 0
D. m 0
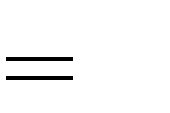
2
- m 0
- m 0
Câu 15.Hàm số mãn:
y x3 3x2 mx
đạt cực tiểu tại x
khi giá trị của tham số m thỏa
A. m 0
- m 0
B. m 0
C. m 0
Câu 16.Tìm tất cả các giá trị của tham số m sao cho hàm số y
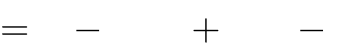
x3
3mx2
3(m2 1)
 đạt cực đại tại x 1 . Kết quả nào đúng?
đạt cực đại tại x 1 . Kết quả nào đúng?
1
2
A. Không có giá trị m B. m
3
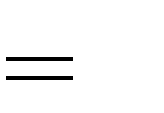
0
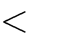
5
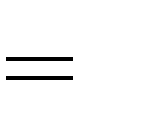
2
C. m
D. m
Câu 17: Điểm cực tiểu của đồ thị hàm số y là
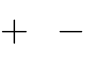

x2
x 1
x 2
A. | 1;  | 1 và | 3; | 5 . | B. | 3;  | 5 . |
C. | 1;  | 1 . | D. | 1; 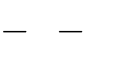 | 3 . |
Câu 18: Điểm cực đại của hàm số y là .
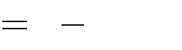
x sin 2x

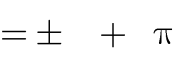
6
k

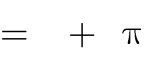
6
k

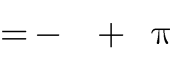
6
k
- x

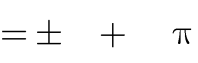
3
k2
. B. x
. C. x
. D. x .
Câu 19: Hàm số y
chỉ khi.




m 1
m 3
1 x3
 3
3
(m2
m 2)x2
(3m2
1)x 1 đạt cực tiểu tại x = - 2 khi và
A.
. B.
. C. m 1. D. m 3 .
 Câu 20: Đồ thị hàm số y x3 3mx2 2m có hai điểm cực trị đối xứng nhau qua
Câu 20: Đồ thị hàm số y x3 3mx2 2m có hai điểm cực trị đối xứng nhau qua



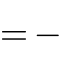

m
m
1
3

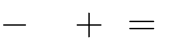
đường thẳng x 2y 1 0 khi và chỉ khi :
A. m | { 1;0;1}. B. m 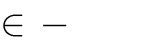 | 1. 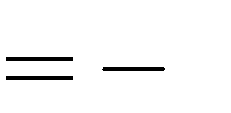 | C. m 1 . D. m 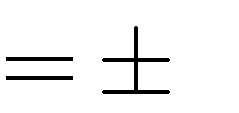 |
Câu 21. Giá trị tam giác đều. | m để đồ thị hàm | y x4 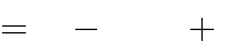 | 2mx2 1 có ba điểm cực trị tạo thành một |
A. m | 1 B. m 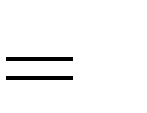 | 3 3 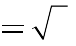 | C. m 3 3 D. m 1 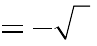 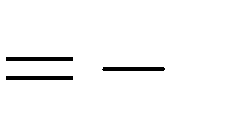 |
Câu 22. Giá trị | m để đồ thị hàm | y x4 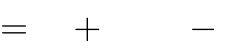 | 2mx2 1 có ba điểm cực trị tạo thành một |
tam giác có diện tích bằng 4
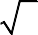
2
2
1
A. m
2
x4
4x2 1
B. m
C. m
D. m
Câu 23. Ba điểm cực trị của hàm số diện tích S bằng
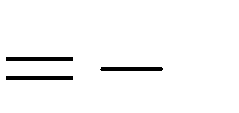
4
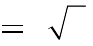
2 2
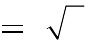
8 2
y
tạo thành một tam giác cân có
A. S
B. S
C. S
D. S
Câu 24. Cho hàm số y
1 x3
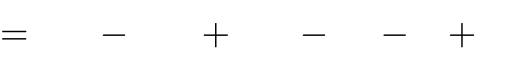 3
3
mx2
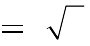
3 2
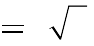
4 2
(2m 1)x m 2 có cực đại, cực tiểu và hoành độ
các điểm cực trị dương thì tập giá trị của m bằng
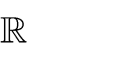


1
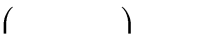


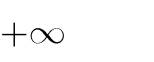




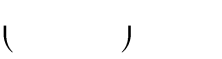


1 ;
2
1
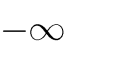
;0
A.

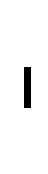

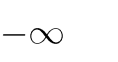
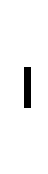

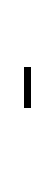


; 1
2
B.
C.
D. ”
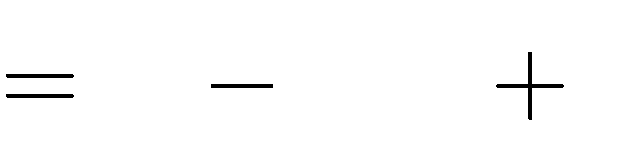 Câu 25. Cho hàm số y x3 2mx 1. Tìm tất cả các giá trị của m để hàm số đạt cực tiểu tại x = 1.
Câu 25. Cho hàm số y x3 2mx 1. Tìm tất cả các giá trị của m để hàm số đạt cực tiểu tại x = 1.
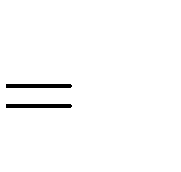
3
2
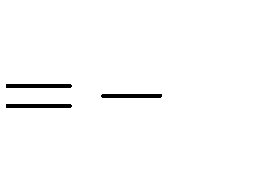
3
2
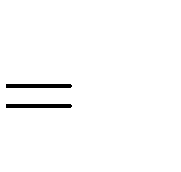
2
3
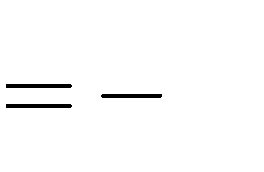
2
3
A. m
B. m
C. m
D. m
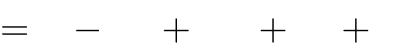 Câu 26. Cho hàm số y x3 3x2 3(m 1)x 2 . Tìm tất cả các giá trị của mđể hàm số có cực trị.
Câu 26. Cho hàm số y x3 3x2 3(m 1)x 2 . Tìm tất cả các giá trị của mđể hàm số có cực trị.
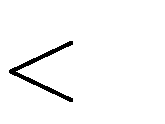
2
2
0
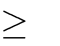
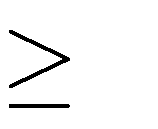
A. m
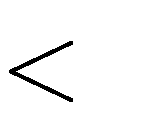
0
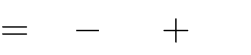
x3
3x2
mx
B. m
C. m
D. m
Câu 27. Tìm tất cả các giá trị thực của tham số m để hàm số tiểu tại x = 2 .
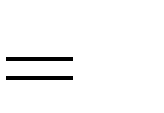
0
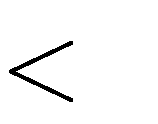
0
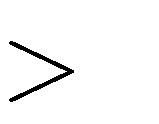
0
y
đạt cực
A. m
B. m
C. m
D. m
Câu 28. Tìm tất cả các giá trị thực của tham số m để hàm số
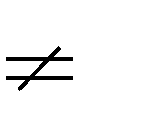
0
y
A. m
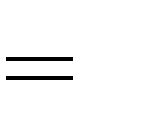
2
đạt cực đại tại x 2 .
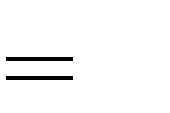 B. m
B. m
x3
(m 1)x2
2m 1
1
C. m
5
D. m
Câu 29. Tìm tất cả các giá trị thực của tham số m để hàm số y
3
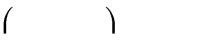


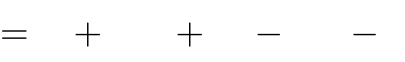




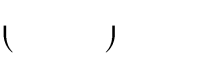
x3
mx2
m
2 x
3
7
có cực trị tại x = 1.
A. m
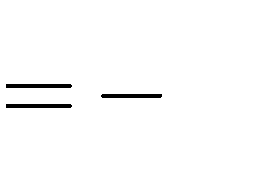
7
9
B. m
C. m
D. m
 Câu 30. Cho hàm số y x3 3x2 1 . Viết phương trình đường thẳng đi qua điểm cực
Câu 30. Cho hàm số y x3 3x2 1 . Viết phương trình đường thẳng đi qua điểm cực
3
7
7
đại và điểm cực tiểu của đồ thị hàm số đã cho.

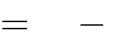

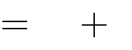 A. y 2x 1 . B. y 2x 1. C. y 2x 1. D. y 2x 1.
A. y 2x 1 . B. y 2x 1. C. y 2x 1. D. y 2x 1.
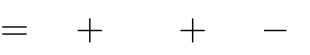
x4
3mx
m2
1
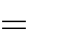 Câu 31. Tìm tất cả các giá trị thực của tham số m để hàm số cực tiểu tại x 0 .
Câu 31. Tìm tất cả các giá trị thực của tham số m để hàm số cực tiểu tại x 0 .
y
đạt
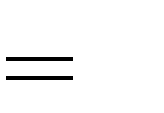 m 0 . B. Không có giá trị thực nào của m thỏa mãn yêu cầu đề bài.
m 0 . B. Không có giá trị thực nào của m thỏa mãn yêu cầu đề bài.
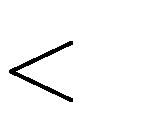
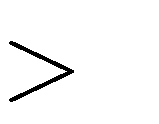 C. m 0 . D. m 0 .
C. m 0 . D. m 0 .
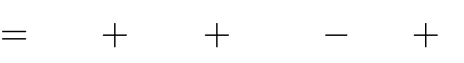
1 x3
3
mx2
2 5m 8 x 1
Câu 32. Tất cả các giá trị của m để hàm số và cực tiểu.
y
đạt cực đại
A.
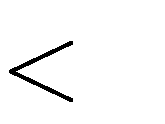
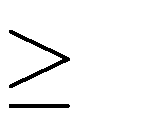
m 2
8
m
Câu 33. Hàm số
hoặc m 8 B. 2
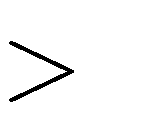 y
y
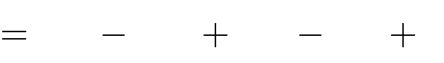
1 x3
3
mx2
m2
4 x
5
C. 2
đạt cực tiểu tại x
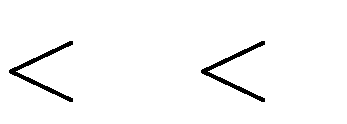
m 8
D. m
khi:
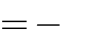
1
hoặc
A. m
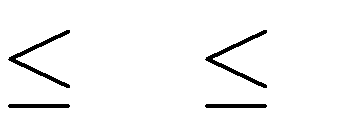
m 8
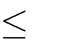
2
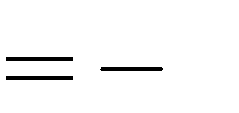
3
B. m
C. m
D. m
Câu 34. Tìm tất cả giá trị m sao cho điểm I(1;0) thuộc đường thẳng qua 2 điểm cực
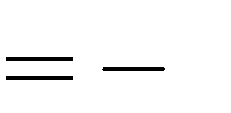
1
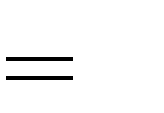
0
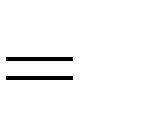
1
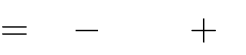
x3
3mx2
2
trị của đồ thị hàm số y
A. m
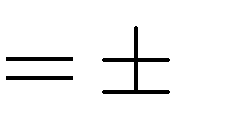
1
- m
- m=0 D.
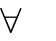
m
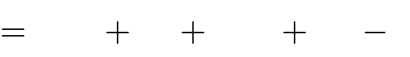
mx4 (m 3)x2 2m 1
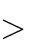
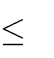




m 3
m 0
Câu 35. Tìm tất cả giá trị mđể hàm số không có cực tiểu
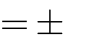
2
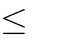
0
y
chỉ đạt cực đại mà
A. m
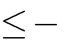
3
B. m
C.
D. m
Câu 36. Tìm tất cả giá trị m để hàm số điểm cực trị

m – 1 x4
m2 – 2m x 2
m2

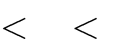




0 m 1
m 2




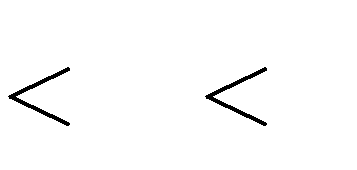

1
m
m
0
2
y
có ba
-
- D.
Câu 37. Tìm tất cả giá trị mđể hàm số

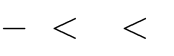


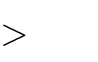

1 m 1
m 2

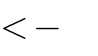


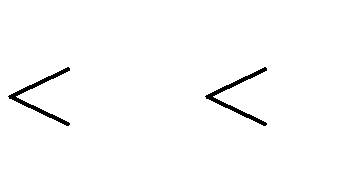

m 1
1 m 2
y
có hai điểm cực trị
- B. 0 < m < 8 C. D.
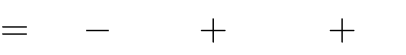
x3
3mx2
6mx m




m 0
m 2




m 0
m 8

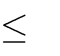


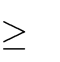

m 0
m 2
Câu 38. Hàm số y = x3 – mx + 1 có hai cực trị khi:
A. m < 0 B. m > 0 C. m = 0 D. m
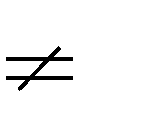
0
 Câu 39: Cho hàm số y x4 2mx2 2m 1 . Với giá trị nào của m thì hàm số có 3 điểm cực trị:
Câu 39: Cho hàm số y x4 2mx2 2m 1 . Với giá trị nào của m thì hàm số có 3 điểm cực trị:
A. y B. m < 0 C. m = 0 D. m
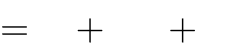
x4
4x2
2
0
Câu 40: Giá trị của m để haøm soá y = x3 – 2mx + 1 ñaït cöïc tieåu taïi x = 1 là:
- m = - 2
3
; B. m = 2 3
; C. m = - 3 2
; D. m = 3 2
ĐÁP ÁN:

3
1B | 2B | 3A | 4A | 5A | 6A | 7A | 8A | 9A | 10A |
11A | 12 | 13A | 14A | 15A | 16A | 17 | 18 | 19 | 20 |
21 | 22 | 23 | 24C | 25A | 26A | 27A | 28A | 29A | 30A |
31A | 32A | 33A | 34A | 35A | 36B | 37A | 38B | 39A | 40D |
Trên đây là toàn bộ phương pháp giải nhanh cực trị hàm bậc 4 trùng phương
 .
.



