Ôn kiến thức, luyện kỹ năng bài giảng tính đơn điệu của hàm số

Tài liệu gồm 46 trang, được biên soạn bởi thầy giáo Đặng Công Đức (Giang Sơn), tuyển chọn các bài tập trắc nghiệm ôn kiến thức, luyện kỹ năng bài giảng tính đơn điệu của hàm số môn Toán 12 THPT (kết hợp ba bộ sách giáo khoa Toán 12 chương trình mới: Cánh Diều, Chân Trời Sáng Tạo, Kết Nối Tri Thức Với Cuộc Sống). Mời bạn đọc đón xem!

29 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

46 trang 1 tháng trước

Tác giả:

Profile Lê Phương
1
T
T
À
À
I
I
L
L
I
I
Ệ
Ệ
U
U
T
T
H
H
A
A
M
M
K
K
H
H
Ả
Ả
O
O
T
T
O
O
Á
Á
N
N
H
H
Ọ
Ọ
C
C
P
P
H
H
Ổ
Ổ
T
T
H
H
Ô
Ô
N
N
G
G
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Ô
Ô
N
N
K
K
I
I
Ế
Ế
N
N
T
T
H
H
Ứ
Ứ
C
C
T
T
O
O
Á
Á
N
N
1
1
2
2
T
T
H
H
P
P
T
T
B
B
À
À
I
I
G
G
I
I
Ả
Ả
N
N
G
G
T
T
Í
Í
N
N
H
H
Đ
Đ
Ơ
Ơ
N
N
Đ
Đ
I
I
Ệ
Ệ
U
U
C
C
Ủ
Ủ
A
A
H
H
À
À
M
M
S
S
Ố
Ố
(
(
K
K
Ế
Ế
T
T
H
H
Ợ
Ợ
P
P
3
3
B
B
Ộ
Ộ
S
S
Á
Á
C
C
H
H
G
G
I
I
Á
Á
O
O
K
K
H
H
O
O
A
A
)
)
T
T
H
H
Â
Â
N
N
T
T
Ặ
Ặ
N
N
G
G
T
T
O
O
À
À
N
N
T
T
H
H
Ể
Ể
Q
Q
U
U
Ý
Ý
T
T
H
H
Ầ
Ầ
Y
Y
C
C
Ô
Ô
V
V
À
À
C
C
Á
Á
C
C
E
E
M
M
H
H
Ọ
Ọ
C
C
S
S
I
I
N
N
H
H
T
T
R
R
Ê
Ê
N
N
T
T
O
O
À
À
N
N
Q
Q
U
U
Ố
Ố
C
C
C
C
R
R
E
E
A
A
T
T
E
E
D
D
B
B
Y
Y
G
G
I
I
A
A
N
N
G
G
S
S
Ơ
Ơ
N
N
(
(
F
F
A
A
C
C
E
E
B
B
O
O
O
O
K
K
)
)
G
G
A
A
C
C
M
M
A
A
1
1
4
4
3
3
1
1
9
9
8
8
8
8
@
@
G
G
M
M
A
A
I
I
L
L
.
.
C
C
O
O
M
M
(
(
G
G
M
M
A
A
I
I
L
L
)
)
;
;
T
T
E
E
L
L
0
0
3
3
9
9
8
8
0
0
2
2
1
1
9
9
2
2
0
0
T
T
H
H
À
À
N
N
H
H
P
P
H
H
Ố
Ố
T
T
H
H
Á
Á
I
I
B
B
Ì
Ì
N
N
H
H
–
–
T
T
H
H
Á
Á
N
N
G
G
7
7
/
/
2
2
0
0
2
2
4
4
2
Ô
Ô
N
N
K
K
I
I
Ế
Ế
N
N
T
T
H
H
Ứ
Ứ
C
C
T
T
O
O
Á
Á
N
N
1
1
2
2
T
T
H
H
P
P
T
T
T
T
Í
Í
N
N
H
H
Đ
Đ
Ơ
Ơ
N
N
Đ
Đ
I
I
Ệ
Ệ
U
U
C
C
Ủ
Ủ
A
A
H
H
À
À
M
M
S
S
Ố
Ố
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
DUNG
LƯỢNG
NỘI DUNG
1 FILE
TÍNH ĐƠN ĐIỆU CÁC HÀM SỐ THƯỜNG GẶP
1 FILE
TÍNH ĐƠN ĐIỆU CÁC HÀM SỐ PHỨC TẠP
1 FILE
CÁC BÀI TOÁN CHỨA THAM SỐ
3
PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI TOÁN KHẢO SÁT HÀM SỐ LỚP 12 THPT
LÝ THUYẾT TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
_____________________________________
TÍNH ĐƠN ĐIỆU CÙA HÀM SỐ.
1) Cách nhận biết tính đơn điệu của hàm số bằng dấu của đạo hàm.
Cách 1: Cho hàm số
y f x
có đạo hàm trên tập
K
, trong đó
K
là một khoảng, đoạn hoặc nửa
khoảng.
Nếu
0
f x
với mọi
x
thuộc
K
thì hàm số
f x
đồng biến trên
K
.
Nếu
0
f x
với mọi
x
thuộc
K
thì hàm số
f x
nghịch biến trên
K
.
Cách 2: Cho hàm số
y f x
có đạo hàm trên tập
, trong đó
K
là một khoång, đoạn hoặc nửa
khoảng. Nếu
0
f x
(hoặc
0
f x
) với mọi
x
thuộc
K
và
0
f x
chỉ tại một số hữu hạn điểm của
K
thì hàm số
f x
đồng biến (hoặc nghịch biến) trên
K
.
2) Chú ý:
Nếu hàm số
y f x
đồng biến trên tập
K
hoặc nghịch biến trên tập
K
thì hàm số
y f x
còn được gọi là
đơn điệu trên tập
K
.
3) Cách xét tính đơn điệu của hàm số bằng dấu của đạo hàm.
Đế xét tính đồng biến, nghịch biến của hàm số
y f x
, ta có thể thực hiện các bước sau:
Bước 1. Tìm tập xác định của hàm số
y f x
.
Bước 2. Tính đạo hàm
f x
. Tìm các điểm
1,2, ,
i
x i n
mà tại đó hàm số có đạo hàm bằng 0 hoặc không
tồn tại.
Bước 3. Sắp xếp các điểm
i
x
theo thư tự tăng dần và lập bảng biến thiên.
Bước 4. Căn cứ vào bảng biến thiên, nêu kết luận vể các khoảng đồng biến, nghịch biến của hàm số.
4
PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI TOÁN KHẢO SÁT HÀM SỐ LỚP 12 THPT
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
TÍNH ĐƠN ĐIỆU CÁC HÀM SỐ THƯỜNG GẶP
_____________________________________
XÉT DẤU ĐẠO HÀM VÀ QUAN SÁT ĐỒ THỊ HÀM SỐ, BẢNG BIẾN THIÊN
Bài toán 1. Cho hàm số
y f x
có
2
2 1 1
f x x x x
. Hàm số
y f x
đồng biến trên khoảng
nào sau đây?
A.
1;1
. B.
0;

. C.
; 2
. D.
2; 1
.
Lời giải
2
2
2 1 1 1 1 2
f x x x x x x x
. Dễ thấy hàm số đồng biến trên khoảng
; 2
.
Bài toán 2. Cho hàm số
f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
; 1
. B.
0;1
. C.
1;1
. D.
1;0
Lời giải. Hàm số đã cho đồng biến trên khoảng
1;0
và
1;
Bài toán 3. Cho hàm số
( )y f x
có bảng xét dấu đạo hàm như sau:
Hỏi mệnh đề nào sai ?
A. Hàm số đã cho đồng biến trên khoảng
(2; ).
B. Hàm số đã cho đồng biến trên khoảng
(3; ).
C. Hàm số đã cho đồng biến trên khoảng
( ;1).
D. Hàm số đã cho nghịch biến trên khoảng
(0;3).
Bài toán 4. Cho hàm số
y f x
có bảng xét dấu đạo hàm như sau:
Khoảng nghịch biến của hàm số
y f x
là
A.
( ;3)
. B.
(1; )
. C.
(1;3)
. D.
( ;1)
.
Bài toán 5. Cho hàm số
( )y f x
có đồ thị như hình vẽ
Hàm số đã cho đồng biến trên khoảng nào
A.
0;3
. B.
3;

. C.
;2

. D.
1;3
.
Bài toán 6. Cho hàm số
y f x
có đạo hàm
2
2, .
f x x x
Mệnh đề nào dưới đây là đúng?
A.
1 1f f
. B.
1 1f f
. C.
1 1f f
. D.
1 1f f
.
Lời giải
5
Từ
2
2,f x x x
Hàm số đồng biến trên
.
. Mà
1 1 1 1 .
f f
Bài toán 7. Cho hàm số
y f x
có đạo hàm
2
2f x x x
,
x
. Hàm số
2
y f x
đồng biến trên
khoảng
A.
0;2
. B.
2;

. C.
; 2
. D.
.
Lời giải
Ta có:
2
2 2 4 0 0;2
y f x x x x
.Suy ra: hàm số
2
y f x
đồng biến trên khoảng
0;2
Bài toán 8. Cho hàm số
( )y f x
có đạo hàm
1 3 ,f x x x x
. Hàm số đã cho nghịch biến trên
khoảng nào dưới đây?
A.
0;3
. B.
3;

. C.
;2

. D.
1;3
.
Lời giải
Ta xét:
1
0 1 3 0
3
x
f x x x
x
.
Bảng xét dấu
f x
:
Suy ra hàm số nghịch biến trên khoảng
1;3
.
Bài toán 9. Đường cong ở hình bên là đồ thị của hàm số
ax b
y
cx d
với
, , ,a b c d
là các số thực. Mệnh đề nào
dưới đây đúng ?
A.
0,y x
B.
0,y x
C.
0, 1y x
D.
0, 1y x
Lời giải
Dựa vào hình dáng của đồ thị ta được:
+ Điều kiện
1x
+ Đây là đồ thị của hàm nghịch biến
Từ đó ta được
0, 1.y x
Bài toán 10. Cho hàm số
y f x
xác định và liên tục trên
, có bảng đạo hàm
f x
thỏa mãn:
Hàm số
( )y f x
nghịch biến trên khoảng nào dưới đây
A.
1;3
. B.
1;1
. C.
2; 1
. D.
1;
.
Bài toán 11. Cho đồ thị hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ bên dưới.
Khẳng định nào sau đây là đúng ?
A. Hàm số đồng biến trên khoảng
1;3
. B. Hàm số nghịch biến trên khoảng
6;

.
C. Hàm số đồng biến trên khoảng
;3

. D. Hàm số nghịch biến trên khoảng
3;6
.
6
TÍNH ĐƠN ĐIỆU HÀM SỐ ĐA THỨC
Bài toán 1. Tìm khoảng nghịch biến của hàm số
3
2 6 1y x x
.
A.
1;1
B.
1
;
2

. C.
0;

. D.
1
;
2

.
Lời giải
+
2
6 6
y x
. Giải
2
1
0 6 6 0
1
x
y x
x
.
+ Bảng biến thiên của hàm số như sau
Vậy hàm số đồng biến trên các khoảng
; 1
và
1;
; nghịch biến trên khoảng
1;1
.
Bài toán 2. Tìm các khoảng nghịch biến của hàm số
3 2
2 3 5y x x x
.
A.
;
 
B.
1
;
2

. C.
0;

. D.
1
;
2

.
Lời giải
+
2
2
2 5
3 4 3 3 0,
3 3
y x x x x
. Vậy hàm số nghịch biến
.
Bài toán 3. Hàm số nào dưới đây đồng biến trên
?
A.
1
2
x
y
x
. B.
2
2y x x
. C.
3 2
y x x x
. D.
4 2
3 2
y x x
.
Lời giải
2
3 2 2
1 2
' 3 2 1 3 0
3 3
y x x x y x x x x
Vậy hàm số đồng biến trên
.
Bài toán 4. Hàm số nào dưới đây nghịch biến trên
A.
3
y x x
. B.
4 2
y x x
. C.
3
y x x
. D.
2
1
x
y
x
.
Lời giải
Hàm số
3
y x x
có tập xác định
D
, đạo hàm
2 2
3 1 3 1 0,y x x x
Suy ra, hàm số nghịch biến trên
.
Bài toán 5. Hàm số nào dưới đây đồng biến trên
?
A.
4 2
y x x
. B.
3
y x x
. C.
1
2
x
y
x
. D.
3
y x x
.
Lời giải
Ta có:
3 2
3 1 0y x x y x x
.
Bài toán 6. Hỏi hàm số
4
2 1
y x
đồng biến trên khoảng nào?
A.
;0 .

B.
1
;
2

. C.
0;

. D.
1
;
2

.
Lời giải
4
2 1
y x
. Tập xác định:
D
. Ta có:
3
8y x
;
3
0 8 0 0
y x x
suy ra
0 1
y
Giới hạn:
lim
x
y


;
lim
x
y


. Bảng biến thiên:
7
Vậy hàm số đồng biến trên khoảng
0;

.
Bài toán 7. Cho hàm số
4 2
2y x x
. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
 ; 2
B. Hàm số đồng biến trên khoảng
1;1
C. Hàm số nghịch biến trên khoảng
1;1
D. Hàm số đồng biến trên khoảng
 ; 2
Lời giải
3 3
0
4 4 ; 0 4 4 0 1
1
x
y x x y x x x
x
Suy ra hàm số đồng biến trên các khoảng
,
1;
; hàm số nghịch biến trên các khoảng
 ; 1
,
0;1
. Vậy hàm số nghịch biến trên khoảng
 ; 2
.
Bài toán 8. Hàm số
3
3
y x x m
nghịch biến trên khoảng nào?
A.
; 1
. B.
;
 
. C.
1;1
. D.
0;

.
Lời giải
Tập xác định
D
. Ta có
2
3 3;
y x
1
0
1
x
y
x
.
Ta có bảng xét dấu
y
:
Từ bảng xét dấu ta thấy hàm số nghịch biến trên khoảng
1;1
.
Bài toán 9. Cho hàm số
3 2
3 1
y x x
, kết luận nào sau đây về tính đơn điệu của hàm số là đúng nhất:
A. Hàm số đồng biến trên khoảng
0;2
và nghịch biến trên các khoảng
;0

;
2;

;
B. Hàm số đồng biến trên khoảng
0;2
;
C. Hàm số nghịch biến trên khoảng
0;2
và đồng biến trên các khoảng
;0

;
2;

;
D. Hàm số nghịch biến trên các khoảng
;0

và
2;

.
Lời giải
Ta có hàm số xác định trên
.
3 2
3 1
y x x
2
3 6 0
y x x
0
2
x
x
.
Bảng biến thiên
Vậy đáp án A là đúng nhất.
8
TÍNH ĐƠN ĐIỆU HÀM SỐ PHÂN THỨC HỮU TỶ
Bài toán 1. Hàm số nào dưới đây đồng biến trên từng khoảng xác định
A.
1
2
x
y
x
B.
3
y x x
C.
3
3y x x
D.
1
3
x
y
x
Lời giải. Ta có
2
1 2
0, 3
3 ( 3)
x
y y x
x x
Bài toán 2. Hàm số nào dưới đây đồng biến trên từng khoảng xác định
A.
1
2
x
y
x
. B.
2
1
x
y
x
. C.
3
3 3 2
y x x
. D.
2
2
1
y
x
.
Lời giải. Đạo hàm
2
2 3
0, 1
1 ( 1)
x
y y x
x x
nên đồng biến trên từng khoảng xác định.
Bài toán 3. Hàm số
2
2
1
y
x
nghịch biến trên khoảng nào dưới đây?
A.
 ( ; )
B.
(0; )
C.
( ; 0)
D.
( 1;1)
Lời giải. Ta có
2
2
4
0 0
1
x
y x
x
.
Bài toán 4. Hàm số
2
4
1
x x
y
x
đồng biến trên khoảng nào
A.
 ( ; )
B.
(0; )
C.
 ( ; 2)
D.
( 1;1)
Lời giải
Tập xác định:
\ 1
D
. Ta có
2
2
2
1
2 3
, 0 2 3 0
3
1
x
x x
y y x x
x
x
.
Bảng xét dấu đạo hàm
Từ bảng xét dấu
y
ta có :
+ Hàm số đồng biến trên mỗi khoảng
; 1
và
3;

.
Bài toán 5. Hàm số
5 2
2024
3
x
y
x
nghịch biến trên
A.
R\ 3
. B.
R
. C.
; 3
. D.
3;

.
Lời giải
Hàm số
5 2
2024
3
x
y
x
có tập xác định là
\ 3
D
. Đạo hàm
2
11
' 0,
3
y
x
với
x D
.
Vậy hàm số đã cho nghịch biến trên các khoảng
; 3
và
3;

.
Bài toán 6. Cho hàm số
1
.
1
x
y
x
Khẳng định nào sau đây là đúng?
A. Hàm số đã cho nghịch biến trên khoảng
.
B. Hàm số đã cho đồng biến trên khoảng
và khoảng
1;
.
C. Hàm số đã cho đồng biến trên khoảng
0;

.
D. Hàm số đã cho nghịch biến trên tập
\ 1
.
Lời giải
TXĐ:
\ 1
D
. Ta có:
2
2
0
1
y
x
với
1x
. Hàm số nghịch biến trên từng khoảng xác định.
Bài toán 7. Tìm một khoảng đồng biến nào đó của hàm số
2
1
1
x x
y
x
.
9
A.
R\ 3
. B.
R
. C.
; 3
. D.

1
;
2
.
Lời giải. Hàm số đã cho có tập xác định là .
⬩Ta có: với ; Giải
⬩Bảng biến thiên của hàm số như sau:
Bài toán 8. Hàm số
2
2 2
1
x x
y
x
đồng biến trên khoảng nào
A.
 ( ; )
B.
(0; )
C.
( ; 0)
D.
( 1;1)
Lời giải.
2 2
2
2 2 2
; 0 0; 2
1
( 1)
x x x x
y y y x x
x
x
. Bảng biến thiên
Hàm số đồng biến trên
(0; )
Bài toán 9. Cho các hàm số
2
3
1 5
,
2 2
, ,
1 51
3
x x
y y
x x
y x x y
x xx
.
Có bao nhiêu hàm số đồng biến trên từng khoảng xác định.
A.3 B. 2 C. 1 D. 4
Lời giải
Ta thấy hàm
5
5
x
y
x
có đạo hàm
2
10
0, 5
( 5)
y x
x
nên đồng biến trên từng khoảng xác định.
Hàm số
2
2 2
1
x x
y
x
có đạo hàm
2
2
2
; 0 0; 2
( 1)
x x
y y x x
x
.
Hàm đa thức
3
3y x x
có
2
3 3
y x
, có nghiệm.
Bài toán 10. Cho hàm số
2
2 5
1
x x
y
x
. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
1;1 1;3
. B. Hàm số nghịch biến trên khoảng
1;3 \ 1
.
C. Hàm số nghịch biến trên mỗi khoảng
1;1
và
1;3
. D. Hàm số nghịch biến trên khoảng
; 1
.
Lời giải
Tập xác định:
\ 1
D
.
Ta có
2
2
2 2
2 2 1 2 5
2 3
1 1
x x x x
x x
y
x x
. Giải phương trình
1
0
3
x
y
x
.
Bảng biến thiên
Từ bảng biến thiên suy ra: Hàm số nghịch biến trên mỗi khoảng
1;1
và
1;3
.
10
TÍNH ĐƠN ĐIỆU HÀM SỐ LƯỢNG GIÁC, HÀM SỐ MŨ, HÀM SỐ LOGARIT
Bài toán 1. Chọn khẳng định sai trong các khẳng định sau:
A. Hàm số
2
logy x
đồng biến trên
.
B. Hàm số
1
2
logy x
nghịch biến trên tập xác định của nó.
C. Hàm số
2
x
y
đồng biến trên
.
D. Hàm số
2
y x
có tập xác định là
0;

.
Lời giải
Hàm số
2
logy x
đồng biến trên khoảng
0;

.
Bài toán 2. Hàm số nào dưới đây nghịch biến trên tập xác định của nó?
A.
3
log
y x
B.
2
log 1
y x
C.
4
logy x
D.
3
x
y
Lời giải
Xét hàm số
4
logy x
có tập xác định:
0;D

.
Nhận thấy cơ số
1
4
nên
4
logy x
nghịch biến trên tập xác định.
Bài toán 3. Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập số thực
R
.
A.
3
x
y
B.
2
4
log 2 1
y x
C.
2
x
y
e
D.
2
3
logy x
Lời giải
Vì
2
1
e
nên
2
x
y
e
nghịch biến trên
R
.
Bài toán 4. Hàm số
2
3
log 2y x x
nghịch biến trên khoảng nào?
A.
2;
. B.
;0

. C.
1;
. D.
0;1
.
Lời giải
Hàm số
2
3
log 2y x x
có tập xác định
;0 2;D

.
Ta có
2
2 2
2 ln3
x
y
x x
. Khi đó
0
y
1x
.
Bảng biến thiên:
Dựa vào bảng biến thiên ta có hàm số
y
nghịch biến trên
;0

.
Bài toán 5. Cho hàm số
ln
f x x x
. Khẳng định nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
0;1
.
B. Hàm số đồng biến trên khoảng
0;
.
C. Hàm số đồng biến trên các khoảng
;0
và
1;
.
D. Hàm số đồng biến trên khoảng
1;
.
Lời giải
Tập xác định của hàm số
f x
:
0;D

11
Ta có
1 1
1
x
f x
x x
và
0 1f x x
. Bảng xét dấu
f x
:
Bài toán 6. Trong các hàm số sau,hàm số nào luôn nghịch biến trên tập xác định của nó?
A.
2
1
2
y
. B.
logy x
. C.
2
x
y
. D.
2
3
x
y
.
Lời giải
Ta thấy hàm số
2
3
x
y
là hàm số mũ có có tập xác định là
cơ số
2
1
3
a
nên nghịch biến trên tập xác
định của nó.
Bài toán 7. Cho các hàm số
3 2
cos 5 3; sin 2 3 ; 2 5 6y x x y x x m y x x x
.
Có bao nhiêu hàm số đồng biến trên
?
A.3 B. 4 C. 1 D. 2
Lời giải
Ta có các đạo hàm
3 2 2
cos 5 3 sin 5 0,
sin 2 3 2cos2 3 0,
2 5 6 3 4 5 0,
y x x y x x
y x x m y x x
y x x x y x x x
Kết luận 3 hàm số đồng biến trên
Bài toán 8. Cho các hàm số
3 2
1
; 3 1; ; sin 3
1
x
x
y y x x y e y x x
x
.
Số lượng hàm số đồng biến trên
là
A.3 B. 2 C. 1 D. 4
Lời giải
Ta có các đạo hàm
2
3 2 2
1 2
1 ( 1)
3 1 3 6 3 ( 2)
0,
sin 3 cos 3 0,
x x
x
y y
x x
y x x y x x x x
y e y e x
y x x y x x
Kết luận có 2 hàm số đồng biến trên
.
Bài toán 9. Tìm khoảng đồng biến của hàm số
2
ln 1
x
y e e
.
A.
;

. B.
1;0
. C.
1;1
. D.
0;1
.
Lời giải
Ta có
2
2
2
2 2
1
2
ln 1 0,
1 1
x
x
x
x x
e
e
y e e x
e e
.
Khoảng đồng biến là
;

.
Bài toán 10. Khoảng đồng biến của hàm số
2
x x
y e
là
A.
1
;
2

. B.
1; 0
. C.
1;1
. D.
 
;
Lời giải
Ta có
2 2 2
'
2
1
0
2
. 2 1
x x x x x x
e e x x ey x x
.
Bài toán 11. Khoảng đồng biến của hàm số
2
3
log 1
y x x
là
A.
1
;
2

. B.
1; 0
. C.
1;1
. D.
0;1
.
Lời giải
12
2
2 2
1 '
2 1 1
' 0
2
1 ln3 1 ln3
x x
x
y x
x x x x
. Suy ra khoảng đồng biến là
1
;
2

.
Bài toán 12. Khoảng đồng biến của hàm số
sin 2 6y x x
là
A.
;
2 2
B.
2
;
2 3
C.
0;2
D.
;

Lời giải
Ta có
2cos 2 6 0,y x x
nên khoảng đồng biến là
;

Bài toán 13. Tìm khoảng đồng biến của hàm số
2
2
log 1 2024
f x x
.
A.
B.
;4

C.
D.
0;

Lời giải
Hàm số đồng biến khi
2
2
0 0
1 .ln 2
x
f x x
x
.
Bài toán 14. Trong các hàm số sau hàm số nào nghịch biến trên
?
A.
2
3
log
x
B.
3
log
y x
C.
e
4
x
y
D.
2
5
x
y
Lời giải
Hàm số mũ
x
y a
với
0 1a
nghịch biến trên
.
Ta có
e
0 1
4
nên hàm số
e
4
x
y
nghịch biến trên
.
Bài toán 15. Hàm số nào sau đây đồng biến trên
.
A.
1
.
1
x
y
x
B.
sin 2y x x
C.
6
x
y e x
D.
2
2
y x
Lời giải
Hàm số
sin 2 cos 2 0,y x x y x x
. Hàm số đồng biến trên
.
Bài toán 16. Tìm hàm số đồng biến trên
.
A.
3
x
f x
. B.
3
x
f x
. C.
1
3
x
f x
. D.
3
3
x
f x
.
Lời giải
Hàm số
x
f x a
đồng biến trên
nếu
1
a
và nghịch biến trên
nếu
0 1a
.
Vậy hàm số
3
x
f x
là hàm số đồng biến trên
.
Bài toán 17. Hàm số nào sau đây đồng biến trên
.
A.
1
6
x
y
x
B.
cos 5 3y x x
C.
6
x
y e x
D.
2
2y x x
Lời giải
Hàm số
cos 5 3 sin 5 0,y x x y x x
. Hàm số đồng biến trên
Bài toán 18. Hàm số nào dưới đây đồng biến trên khoảng
(0; )
?
A.
3
log
y x
. B.
6
logy x
. C.
3
log
e
y x
. D.
1
4
logy x
.
Lời giải
Hàm số
log
a
y x
đồng biến trên khoảng
(0; )
⇔
1
a
⇒ Chọn A
Bài toán 19. Hàm số nào dưới đây nghịch biến trên tập xác định của nó?
A.
4
3 2
x
y
B.
3
2
x
y
C.
e
2
x
y
D.
1
6 5
x
y
Lời giải
Ta có
3
1
2
nên hàm số
3
2
x
y
nghịch biến trên TXĐ.
13
Bài toán 20. Tập tất cả các giá trị của tham số
a
để hàm số
2
x
y a
nghịch biến trên
là
A.
;3

. B.
2;3
. C.
;1

. D.
3;
.
Lời giải
Hàm số
2
x
y a
nghịch biến trên
0 2 1 2 3 2;3
a a a
.
Bài toán 21. Hàm số nào sau đây đồng biến trên tập xác định của nó
A.
2
2
log
y x
. B.
e
3
logy x
. C.
4
logy x
. D.
e
2
logy x
.
Lời giải
Ta thấy
e
0
3
,
4
,
2
nên các hàm số ở
A
,
B
,
D
nghịch biến.
Vậy hàm số
e
2
log x
đồng biến trên tập xác định của nó, vì
e
1
2
.
Bài toán 22. Chọn mệnh đề sai trong các mệnh đề sau
A. Hàm số
0,2
log
y x
nghịch biến trên
0;

.
B. Hàm số
2
logy x
đồng biến trên
0;

.
C. Hàm số
2
logy x
đồng biến trên
0;

.
D. Hàm số
2
log 1
y x
đồng biến trên
0;

.
Lời giải
Phương án D đúng.
Vì hàm số
2
log 1
y x
có
1
1 1 1
. . 0, 0
ln 2 ln 2
1
2 1
x
y x
x
x x
.
Phương án A đúng. Vì hàm số
0,2
log
y x
có
0,2 1
a
.
Phương án B đúng. Vì hàm số
2
logy x
có
2 1
a
.
Phương án C sai. Vì hàm số
2
logy x
có tập xác định là
0;D

.
Bài toán 23. Trong các hàm số sau, hàm số nào đồng biến trên
R
?
A.
3
x
e
y
. B.
2
3
x
y
. C.
3
logy x
. D.
1
5
logy x
.
Lời giải
2 3
3 2
x x
y
có tập xác định
R
.
Do
3
1
2
nên hàm số
2
3
x
y
đồng biến trên
R
.
Bài toán 24. Trong các hàm số sau hàm số nào nghịch biến trên
?
A.
e
4
x
y
. B.
2
5
x
y
. C.
3
log
y x
. D.
2
3
log
x
.
Lời giải
Hàm số
3
log
y x
có tập xác đinh là
0;
.
Hàm số
2
3
log
y x
có tập xác đinh là
.
Do đó hai hàm số đó không thể nghịch biến trên
được.
Mặt khác hàm số
2 5
5 2
x x
y
là hàm số có tập xác định là
nhưng có cơ số
5
1
2
nên hàm số đồng
biến trên
.
Hàm số
e
4
x
y
là hàm số có tập xác định là
và có cơ số
1
4
e
nên hàm số nghịch biến trên
14
TÍNH ĐƠN ĐIỆU HÀM SỐ CHỨA CĂN
Bài toán 1. Hàm số
2
2018
y x x
nghịch biến trên khoảng nào trong các khoảng sau đây?
A.
1010;2018
. B.
2018;

. C.
0;1009
. D.
1;2018
.
Lời giải
TXĐ:
0;2018
D
2
2 2
2018 2 1009
2018 ; 0 1009
2 2018 2018
x x
y x x y x
x x x x
' 0 1009;2018
y x
, suy ra hàm số nghịch biến trên khoảng
1009;2018
, suy ra hàm số nghịch biến trên
khoảng
1010;2018
, chọn A.
Bài toán 2. Cho hàm
2
6 5
y x x
. Mệnh đề nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng
5; .
B. Hàm số đồng biến trên khoảng
3; .
C. Hàm số đồng biến trên khoảng
;1 .

D. Hàm số nghịch biến trên khoảng
;3 .

Lời giải
Tập xác định:
;1 5;D
 
. Ta có
2
3
0
6 5
x
y
x x
,
5;x

.
Vậy hàm số đồng biến trên khoảng
5; .
Bài toán 3. Cho hàm số
2
2 1
y x
. Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
0;
B. Hàm số đồng biến trên khoảng
;0
C. Hàm số nghịch biến trên khoảng
0;
D. Hàm số nghịch biến trên khoảng
1;1
Lời giải
Ta có
D
,
2
2
2 1
x
y
x
;
0 0
y x
.
Vậy hàm số nghịch biến trên khoảng
;0
và đồng biến trên khoảng
0;
.
Bài toán 4. Hàm số
2
4
y x
đồng biến trên khoảng nào?
A.
2;
. B.
0;2
. C.
2;2
. D.
2;0
.
Lời giải
+ Tập xác định
2; 2
D
. Đạo hàm
2
4
x
y
x
. Giải
0 0
y x
.
+ Bảng xét dấu của đạo hàm như sau
Vậy hàm số đồng biến trên khoảng
2;0
.
Bài toán 5. Cho hàm số
2
3
y x x
. Hàm số đồng biến trên khoảng nào?
A.
3
0;
2
. B.
0;3
. C.
3
;3
2
. D.
3
;
2

.
Lời giải
Điều kiện
0 3
x
và đạo hàm
2
2
3 2 3
3 0
2
2 3
x
y x x y x
x x
.
Kết luận hàm đồng biến trên
3
0;
2
.
Bài toán 6. Tìm các khoảng nghịch biến của hàm số
3 1y x x
.
A.
1;3
. B.
0;3
. C.
3
;3
2
. D.
3
;
2

.
Lời giải
15
+) Tập xác định:
1;3
D
.
+)
1 1 3 1
2 3 2 1 2 3 . 1
x x
y
x x x x
.
+)
0 3 1 0 3 1.
y x x x x
1 1
1.
3 1 2 2
x x
x
x x x
+) Bảng biến thiên
Vậy hàm số đồng biến trên khoảng
1;1
, nghịch biến trên khoảng
1;3
.
Bài toán 7. Cho hàm số
2
8 7 4
y x x
. Mệnh đề nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng
17; .
B. Hàm số đồng biến trên khoảng
3;

C. Hàm số đồng biến trên khoảng
;1 .

D. Hàm số nghịch biến trên khoảng
;3 .

Lời giải
Tập xác định:
;1 7;D
 
.
Ta có
2
2 8
0 4
8 7
x
y x
x x
. Vậy hàm số đồng biến trên khoảng
17; .
Bài toán 8. Khoảng đồng biến của hàm số
2
6 7
y x x
chứa bao nhiêu số nguyên nhỏ hơn 20
A.18 B. 5 C. 10 D. 12
Lời giải
Điều kiện
2
1
6 7 0
7
x
x x
x
Hàm số đồng biến khi
2
2
2 6
6 7 0 3 1
2 6 7
x
y x x y x x
x x
.
Suy ra có 18 số nguyên.
Bài toán 9. Hàm số
2
8 7y x x
có khoảng đồng biến là
A.
 
;
B.
; 1
. C.
0;

. D.
0;8
.
Lời giải
Ta có
2
2
2 2
8
8 7 1 0
8 8
x x x
y x x y
x x
(do
2
8
x x
).
Bài toán 10.
Hai hàm số
2 2
4 ; 6 5
y x x y x x
có khoảng đồng biến lần lượt là
; , ;a b c d
. Tính giá
trị biểu thức
a c b d
.
A.1 B. 0 C. – 1 D. – 2
Lời giải
Xét tập xác định
2
2
4 2
0;4 ; 4 0 2 ; 0;2
2 4
x
y x x y x a b
x x
.
Xét tập xác định
2
2
6 2
1;5 ; 6 5 0 3 ; 1;3
2 6 5
x
y x x y x c d
x x
.
Như vậy
0 1 2 3 2
a c b d
.
16
PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI TOÁN KHẢO SÁT HÀM SỐ LỚP 12 THPT
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
TÍNH ĐƠN ĐIỆU CÁC HÀM SỐ PHỨC TẠP
_____________________________________
Bài toán 1. Tìm khoảng đồng biến của hàm số
2
ln 1
x
y e e
.
A.
;

. B.
1;0
. C.
1;1
. D.
0;1
.
Lời giải
Ta có
2
2
2
2 2
1
2
ln 1 0,
1 1
x
x
x
x x
e
e
y e e x
e e
.
Khoảng đồng biến là
;

.
Bài toán 2. Cho hàm số
y f x
thỏa mãn:
Hàm số
2024 ( ) 2
y f x
đồng biến trên khoảng nào sau đây ?
A.
3;
. B.
;0

. C.
2;2
. D.
2;
.
Lời giải
Hàm số
2024 ( ) 2
y f x
cùng khoảng đồng biến với hàm số
y f x
.
Ta chọn
3;
.
Bài toán 3. Cho hàm số
( )y f x
có bảng biến thiên như sau
Hàm số
3
2 1
y x x f x
đã cho nghịch biến trên khoảng nào dưới đây?
A.
0;1
B.
;0

C.
1;
D.
1;0
Lời giải
Hàm số
3
2 1
y x x f x
có cùng khoảng nghịch biến với hàm số đã cho. Ta có
0;1
.
Bài toán 4. Khoảng nghịch biến của hàm số
2
(2 5 2)
x
y x x e
là
;a b
. Tính
5a b ab
.
A.6 B. 8 C. 7 D. 4
Lời giải
2 2 2
(2 5 2) (2 5 2) (4 5) (2 3)
x x x x
y x x e y x x e x e x x e
2
1 3
0 2 3 0 5 5. 8
2 2
y x x a b ab
(Theo hệ thức Viet).
Bài toán 5. Cho hàm số
( )y f x
. Hàm số
'( )y f x
có đồ thị như hình bên. Hàm số
3 ( )y f x
đồng biến trên
khoảng
A.
2;
B.
2;1
C.
; 2
D.
4;

Lời giải
17
Giá trị đạo hàm dương, hàm số đồng biến trên
4;

.
Bài toán 6. Tìm khoảng đồng biến của hàm số
2
4 5
x x
y e e
.
A.
2;1
B.
ln 2;

C.
ln 2;5
D.
1;ln 2
Lời giải
2
2 2
2
2 4
0 ln 2
2 4 5 4 5
x x
x x
x x x x
e e
e e
y x
e e e e
. Ta thu được khoảng đồng biến
ln 2;

.
Bài toán 7. Cho hàm số
f x
, bảng xét dấu của
'f x
như sau:
Hàm số
3
y x f x
nghịch biến trên khoảng nào dưới đây?
A.
1;1 .
B.
2;4 .
C.
1;2 .
D.
4; .
Lời giải
Hàm số
3
y x f x
có cùng khoảng nghịch biến với hàm số đã cho. Ta chọn
1;1 .
Bài toán 8. Cho hàm số
( )y f x
. Hàm số
'( )y f x
có đồ thị như hình bên. Hàm số
(2 ) y f x
đồng biến
trên khoảng
A.
2;
B.
2;1
C.
; 2
D.
1;3
Lời giải
Cách 1:
Ta thấy
'( ) 0
f x
với
(1; 4)
1
x
x
nên
( )f x
nghịch biến trên
1;4
và
; 1
suy ra
( ) ( )g x f x
đồng biến
trên
( 4; 1)
và
1;

. Khi đó
(2 )f x
đồng biến biến trên khoảng
( 2;1)
và
3;

Bài toán 9. Cho các hàm số
2 3 2 3
1 3 3 1 2 3
; ; ;
x x x x x x
y e y e y e y e
. Số lượng hàm số đồng biến trên
là
A.3 B. 2 C. 1 D. 4
Lời giải
2 2
3 2 3 2 3 2
3 3
1 1
2
3 3 1 2 3 3 1 3 3 1
2 2
3 2 3
2
3 6 3 3 1 0, ;
2
3 0,
x x
x x x x x x x x x
x x
x x
y e y xe
y e y x x e x e x
y e y e
y e y x e x
Như vậy có 2 hàm số đồng biến trên
.
Bài toán 10. Tìm khoảng đồng biến của hàm số
3 2
3 3 7
y x x x
.
A.
1;4
B.
2;1
C.
3;

D.
4;7
Lời giải
Điều kiện xác định
3
x
.
Ta có
2
2
3 2 3 2
3 1
3 6 3
0, 3
2 3 3 9 2 3 3 9
x
x x
y x
x x x x x x
. Khoảng đồng biến là
3;

.
Bài toán 11. Hàm số
2
1
1
x
y
x x
có khoảng đồng biến là
A.
; 2
. B.
;1
. C.
; 2
. D.
;
.
Lời giải
18
2
2
2
2 2 2
2 1
1 .( 1)
1 3 3
2 1
1
1 2 1 1
x
x x x
x x
x x
y y
x x
x x x x x x
.
0 1y x
. Khoảng đồng biến của hàm số là
;1
.
Bài toán 12. Hàm số
2
ln 1
y x x
có khoảng đồng biến là
A.
; 2
. B.
;1
. C.
; 2
. D.
;
.
Lời giải
2
1 0
x x x x
nên hàm số luôn xác định
.
2
2 2
1
1 : 1 0,
1 1
x
y x x x
x x
. Khoảng đồng biến của hàm số là
;
.
Bài toán 13. Cho hàm số bậc bốn
( )y f x
có đồ thị của hàm số
( )y f x
như hình vẽ bên.
x
y
O
-4
-2 2-3
-3
1
-1
-2
Hàm số
3 2
3 ( ) 6 9y f x x x x
đồng biến trên khoảng nào trong các khoảng sau đây?
A.
0;2
. B.
1;1
. C.
1;

. D.
2;0
.
Lời giải
Hàm số
4 3 2
( ) ,( 0)
f x ax bx cx dx e a
;
3 2
( ) 4 3 2
f x ax bx cx d
.
Đồ thị hàm số
( )y f x
đi qua các điểm
( 4;0),( 2;0),(0; 3),(2;1)
nên ta có:
5
96
256 48 8 0
7
32 12 4 0
24
3
7
32 12 4 1
24
3
a
a b c d
a b c d
b
d
c
a b c d
d
Do đó hàm số
3 2 2 3 2
5 15 55
3 ( ) 6 9 ; 3 ( ) 4 3 3
24 8 12
y f x x x x y f x x x x x x
11
0 0
2
x
y x
x
. Hàm số đồng biến trên các khoảng
( 11;0)
và
2;

.
Bài toán 14. Cho hàm số
f x
có đạo hàm liên tục trên
và có đồ thị của hàm số
y f x
như hình vẽ.
Xét hàm số
2
2
g x f x
. Mệnh đề nào dưới đây sai?
19
A. Hàm số
g x
nghịch biến trên
0;2
. B. Hàm số
g x
đồng biến trên
2;

.
C. Hàm số
g x
nghịch biến trên
1;0
. D. Hàm số
g x
nghịch biến trên
; 2
.
Lời giải
Ta có
2 2 2
2 . 2 2 . 2
g x x f x x f x
.
Hàm số nghịch biến khi
0
g x
2
. 2 0
x f x
2
2
0
2 0
0
2 0
x
f x
x
f x
Từ đồ thị hình của hàm số
y f x
như hình vẽ, ta thấy
0 2
f x x
và
0
f x
2
x
.
+ Với
2
0
2 0
x
f x
2
0
2 2
x
x
2
0
4
x
x
0
2
2
x
x
x
2
x
.
+ Với
2
0
2 0
x
f x
2
0
2 2
x
x
2
0
4
x
x
0 2
x
.
Như vậy hàm số nghịch biến trên mỗi khoảng
; 2
,
0;2
; suy ra hàm số đồng biến trên
2;0
và
2;

. Do
1;0 2;0
nên hàm số đồng biến trên
1;0
. Vậy C sai.
Bài toán 15. Cho hàm số
y f x
. Biết rằng hàm số
y f x
có đồ thị như hình vẽ bên dưới.
Hàm số
2
3
y f x
đồng biến trên khoảng
A.
0;1
. B.
1;0
. C.
2;3
. D.
2; 1
.
Lời giải
Cách 1:
Đặt
2
3
y g x f x
. Ta có:
2
2 . 3
g x x f x
.
2
0 2 . 3 0
g x x f x
2
0
3 0
x
f x
2
2
2
0
3 6
3 1
3 2
x
x
x
x
0
3
2
1
x
x
x
x
.
Bảng xét dấu của
g x
:
x
g x
3
0
0
2
0
1
0
0
0
1
2
3
0
0
Suy ra hàm số
2
3
y f x
đồng biến trên mỗi khoảng:
3; 2 , 1;0 , 1;2 , 3;

.
Vậy hàm số
2
3
y f x
đồng biến trên khoảng
1;0
.
Bài toán 16. Cho hàm số
( )f x
có bảng xét dấu như sau:
20
Hàm số
2
2y f x x
nghịch biến trên khoảng nào dưới đây?
A.
2;1
. B.
4; 3
. C.
0;1
. D.
2; 1
.
Lời giải
Ta có: Đặt:
2
( ) 2y g x f x x
;
2 2
( ) ( 2 ) 2 2 . ( 2 )g x f x x x f x x
2
( ) 0 2 2 . ( 2 ) 0
g x x f x x
2
2 2
2
1
1
1 2
2 2 0 2 2( )
1 2
( 2 ) 0 2 1
1
2 3
3
x
x
x
x x x VN
x
f x x x x
x
x x
x
(Trong đó:
1 2 ; 1 2
x x
là các nghiệm bội chẵn của PT:
2
2 1
x x
)
+ Ta có bảng biến thiên
Dựa vào bảng biến thiên, suy ra hàm số
2
2y f x x
nghịch biến trên khoảng
2; 1
.
Bài toán 17. Cho hàm số
y f x
có bảng xét dấu đạo hàm như sau:
Hàm số
3 2
x
g x f
đồng biến trên khoảng nào sau đây
A.
3;

. B.
; 5
. C.
1;2
. D.
2;7
.
Lời giải
Ta có
' 2 ln 2. ' 3 2
x x
g x f
. Để
( ) 3 2
x
g x f
đồng biến thì
' 2 ln 2. ' 3 2 0
x x
g x f
' 3 2 0 5 3 2 2 0 3
x x
f x
.
Vậy hàm số đồng biến trên
1;2
.
Bài toán 18. Cho hàm số
f x
có bảng xét dấu đạo hàm như sau:
Hàm số
2
2 1 1
y f x x x
nghịch biến trên những khoảng nào dưới đây
A.
; 2
. B.
;1

. C.
2;0
. D.
3; 2
.
Lời giải.
2
2 1 1
1
x
y f x
x
. Có
2
1 0
1
x
x
,
2;0
x
.
Bảng xét dấu:
2 1 0, 2;0
f x x
2
2 1 1 0, 2;0
1
x
f x x
x
.
| 1/46
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


TÀI LIỆU THAM KHẢO TOÁN HỌC PHỔ THÔNG
______________________________________________________________
------------------------------------------------------------------------------------------
ÔN KIẾN THỨC TOÁN 12 THPT BÀI GIẢNG
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
(KẾT HỢP 3 BỘ SÁCH GIÁO KHOA)
THÂN TẶNG TOÀN THỂ QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TRÊN TOÀN QUỐC
CREATED BY GIANG SƠN (FACEBOOK)
GACMA1431988@GMAIL.COM (GMAIL); TEL 0398021920
THÀNH PHỐ THÁI BÌNH – THÁNG 7/2024 1
ÔN KIẾN THỨC TOÁN 12 THPT
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
__________________________ DUNG NỘI DUNG LƯỢNG 1 FILE
TÍNH ĐƠN ĐIỆU CÁC HÀM SỐ THƯỜNG GẶP 1 FILE
TÍNH ĐƠN ĐIỆU CÁC HÀM SỐ PHỨC TẠP 1 FILE
CÁC BÀI TOÁN CHỨA THAM SỐ 2
PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI TOÁN KHẢO SÁT HÀM SỐ LỚP 12 THPT
LÝ THUYẾT TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
_____________________________________
TÍNH ĐƠN ĐIỆU CÙA HÀM SỐ.
1) Cách nhận biết tính đơn điệu của hàm số bằng dấu của đạo hàm.
 Cách 1: Cho hàm số y f x có đạo hàm trên tập K   , trong đó K là một khoảng, đoạn hoặc nửa khoảng.
Nếu f  x  0 với mọi x thuộc K thì hàm số f x đồng biến trên K .
Nếu f  x  0 với mọi x thuộc K thì hàm số f x nghịch biến trên K .
 Cách 2: Cho hàm số y f x có đạo hàm trên tập K   , trong đó K là một khoång, đoạn hoặc nửa
khoảng. Nếu f  x  0 (hoặc f  x  0 ) với mọi x thuộc K và f  x  0 chỉ tại một số hữu hạn điểm của
K thì hàm số f x đồng biến (hoặc nghịch biến) trên K . 2) Chú ý:
Nếu hàm số y f x đồng biến trên tập K hoặc nghịch biến trên tập K thì hàm số y f x còn được gọi là
đơn điệu trên tập K   .
3) Cách xét tính đơn điệu của hàm số bằng dấu của đạo hàm.
Đế xét tính đồng biến, nghịch biến của hàm số y f x , ta có thể thực hiện các bước sau:
Bước 1. Tìm tập xác định của hàm số y f x .
Bước 2. Tính đạo hàm f  x . Tìm các điểm x i 1, 2, ,
n mà tại đó hàm số có đạo hàm bằng 0 hoặc không i  tồn tại.
Bước 3. Sắp xếp các điểm x theo thư tự tăng dần và lập bảng biến thiên. i
Bước 4. Căn cứ vào bảng biến thiên, nêu kết luận vể các khoảng đồng biến, nghịch biến của hàm số. 3
PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI TOÁN KHẢO SÁT HÀM SỐ LỚP 12 THPT
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
TÍNH ĐƠN ĐIỆU CÁC HÀM SỐ THƯỜNG GẶP
_____________________________________
XÉT DẤU ĐẠO HÀM VÀ QUAN SÁT ĐỒ THỊ HÀM SỐ, BẢNG BIẾN THIÊN
Bài toán 1. Cho hàm số y f x có f  x   x   x   2 2 1 x  
1 . Hàm số y f x đồng biến trên khoảng nào sau đây? A. 1;  1 . B. 0;  . C. ; 2 . D. 2;   1 . Lời giải
f  x   x   x   x     x  2 2 2 1 1 1  x  
1  x  2 . Dễ thấy hàm số đồng biến trên khoảng ; 2 .
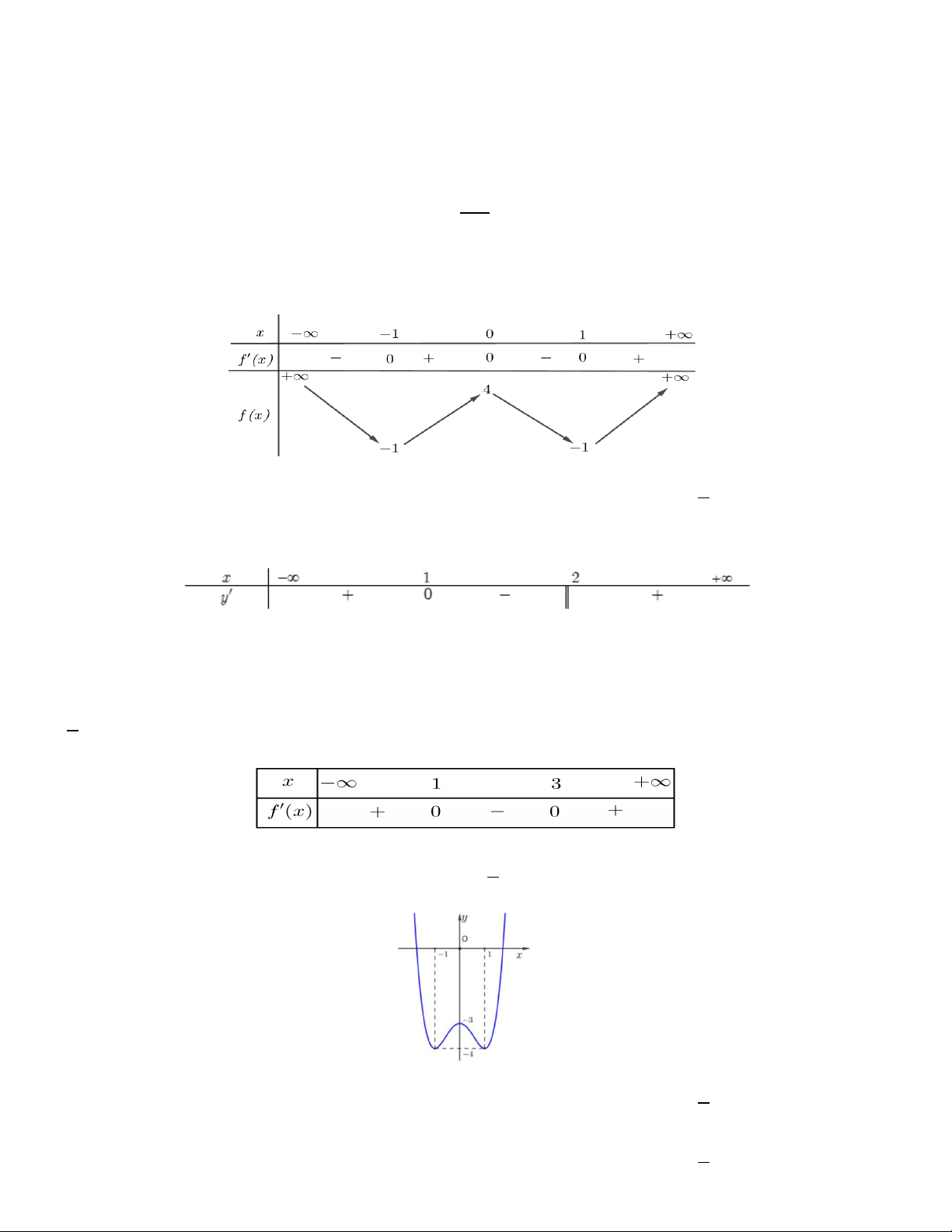
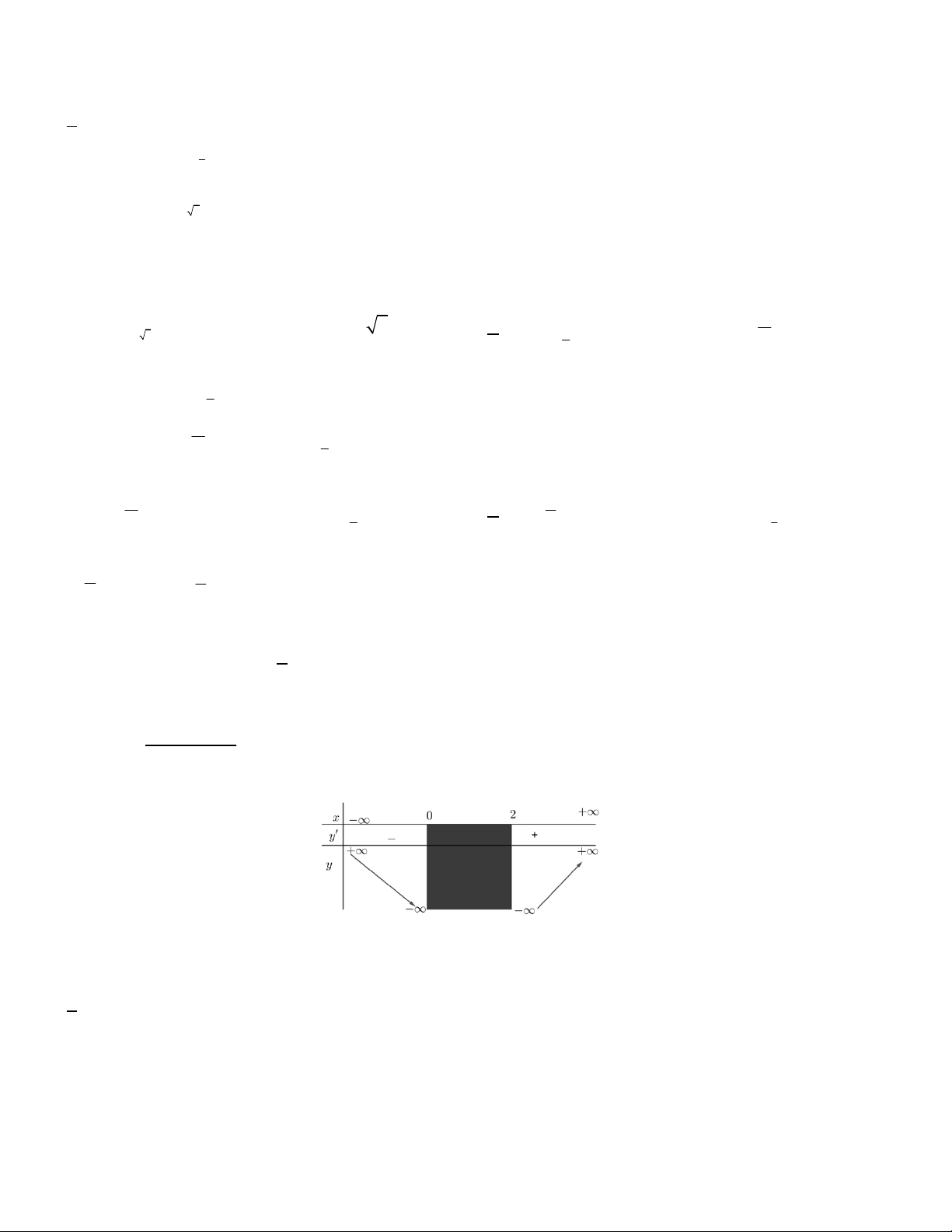
Bài toán 2. Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A.  ;    1 . B. 0  ;1 . C.  1   ;1 . D.  1  ; 0
Lời giải. Hàm số đã cho đồng biến trên khoảng  1
 ; 0 và 1; 
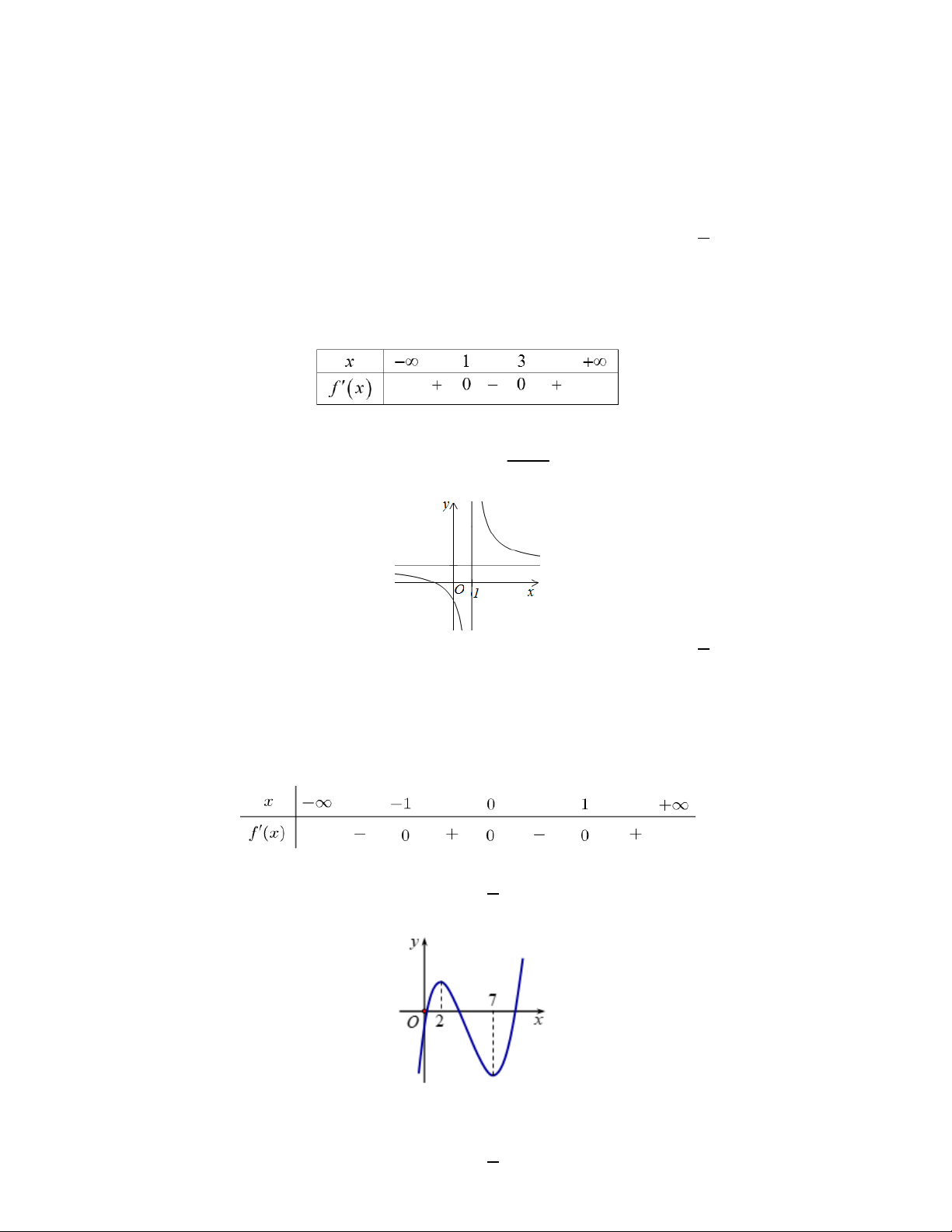
Bài toán 3. Cho hàm số y f (x) có bảng xét dấu đạo hàm như sau: Hỏi mệnh đề nào sai ?
A. Hàm số đã cho đồng biến trên khoảng (2; )  .
B. Hàm số đã cho đồng biến trên khoảng (3;  )  .
C. Hàm số đã cho đồng biến trên khoảng ( ;  1).
D. Hàm số đã cho nghịch biến trên khoảng (0;3).
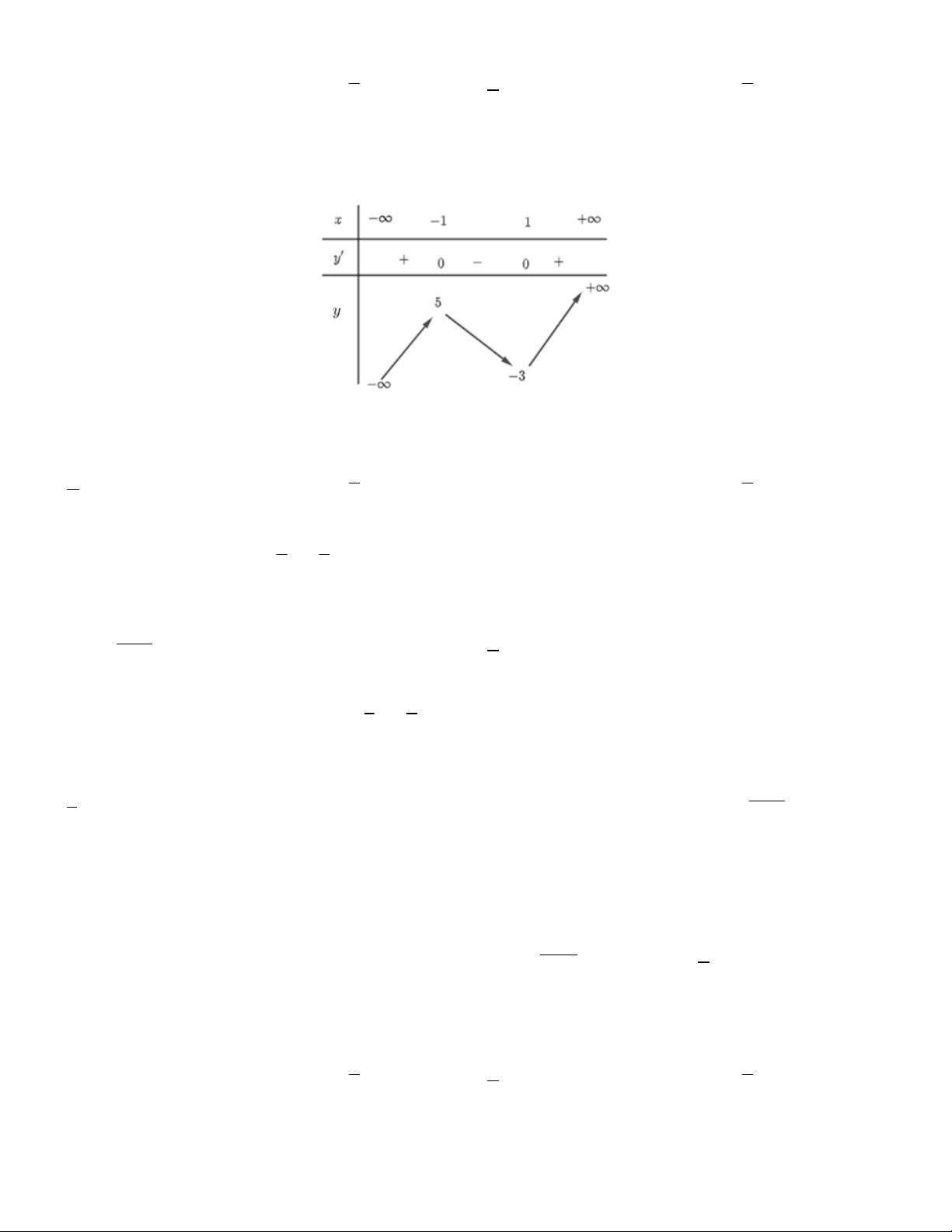
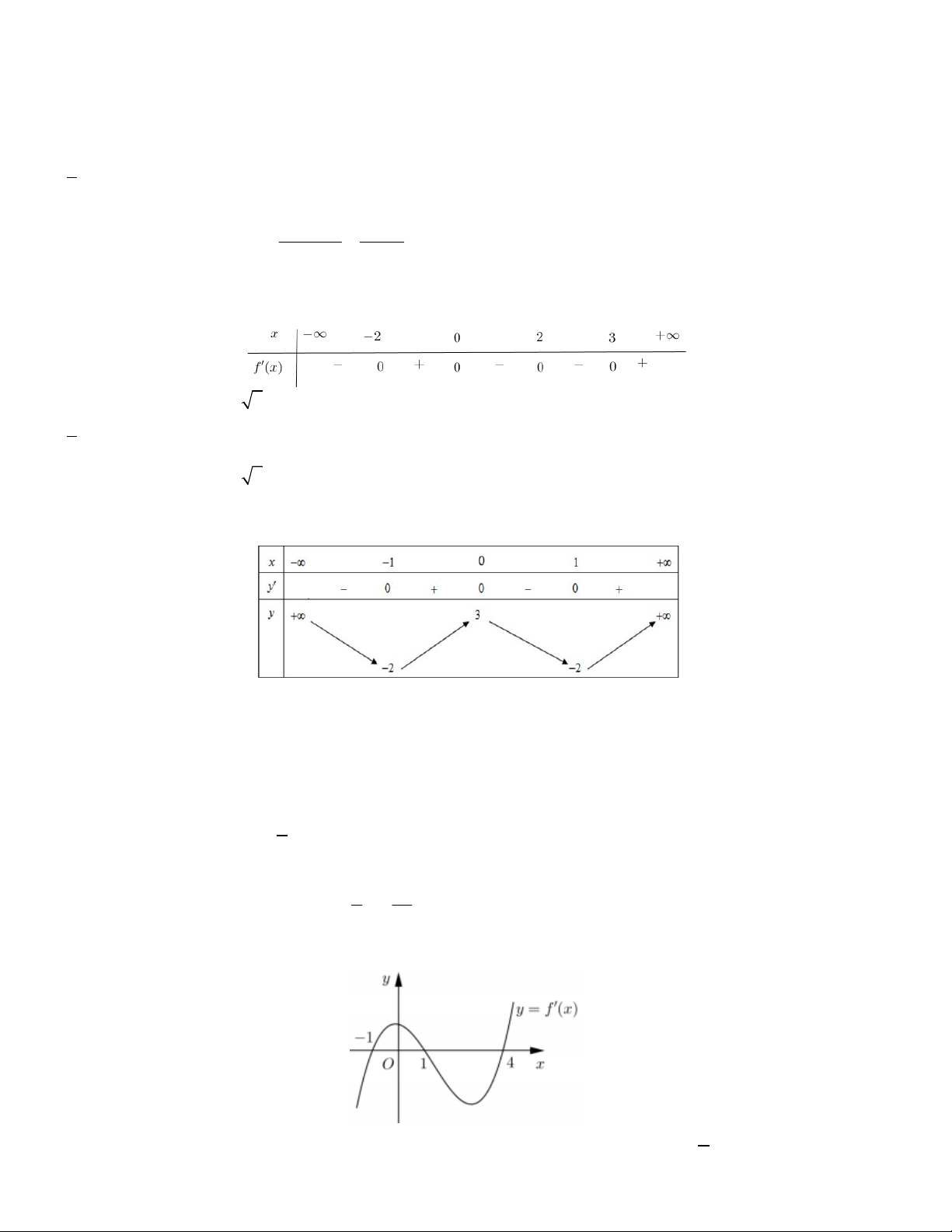
Bài toán 4. Cho hàm số y f x có bảng xét dấu đạo hàm như sau:
Khoảng nghịch biến của hàm số y f x là A. ( ;  3) . B. (1; ) . C. (1;3) . D. ( ;1  ) .
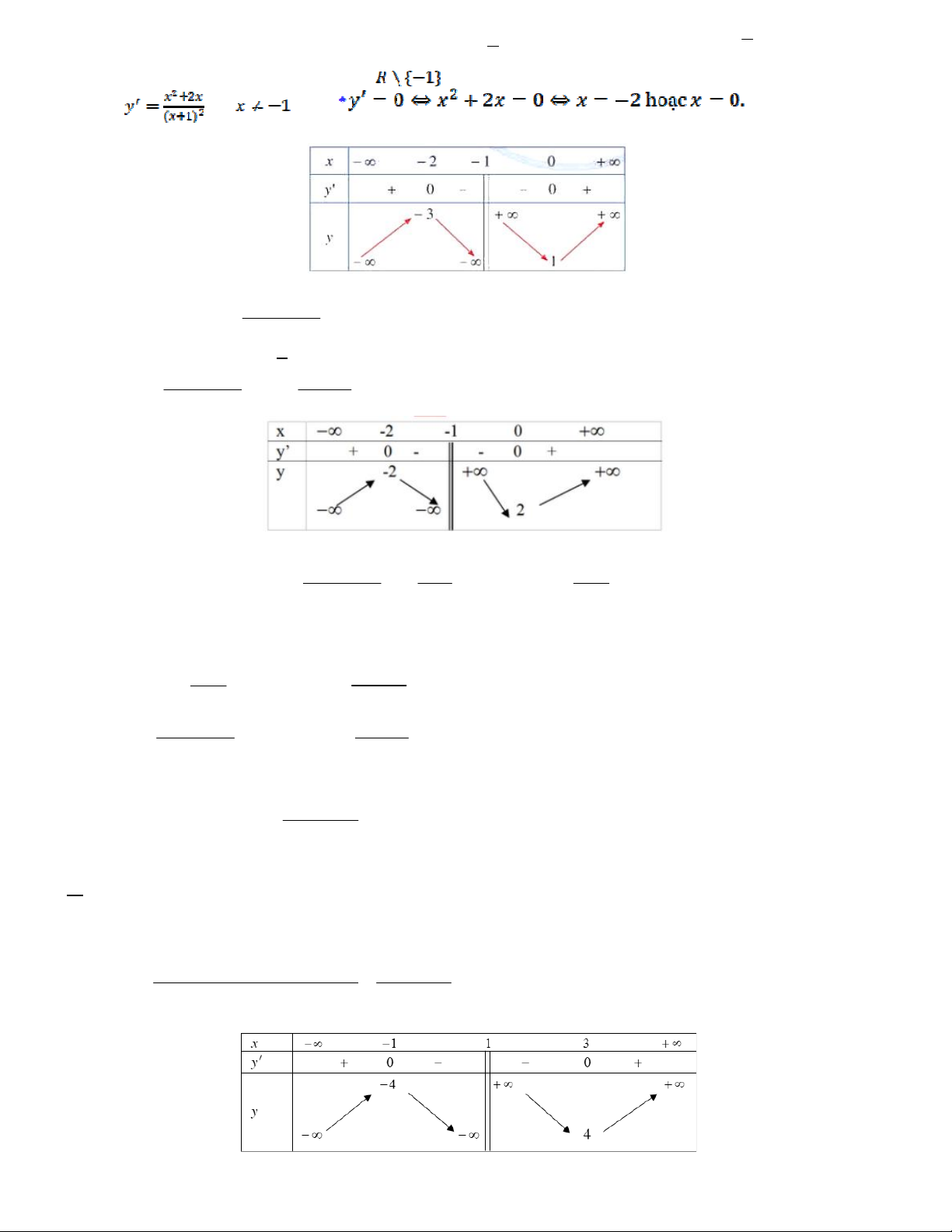
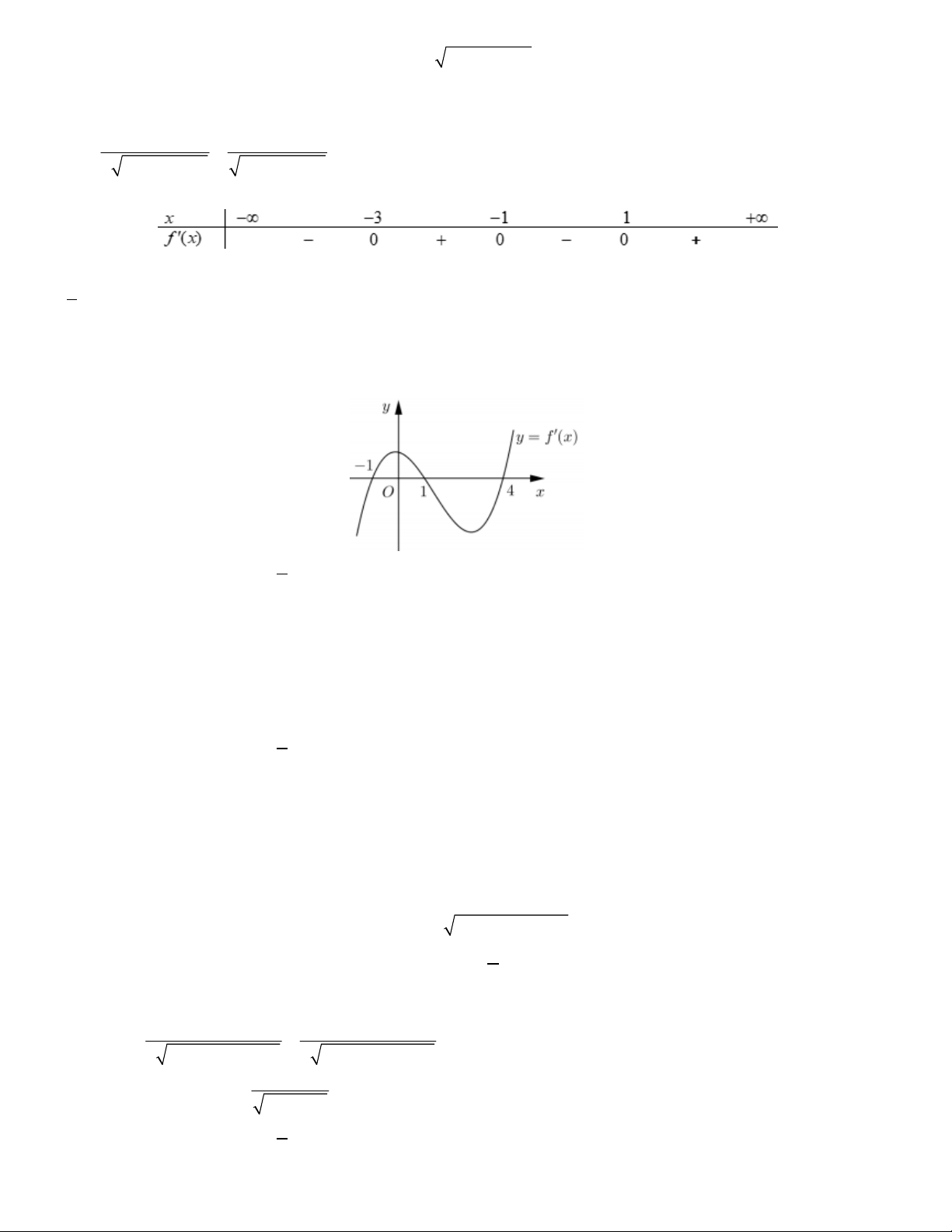
Bài toán 5. Cho hàm số y f (x) có đồ thị như hình vẽ
Hàm số đã cho đồng biến trên khoảng nào A. 0;3 . B. 3;  . C. ; 2 . D. 1;3 .
Bài toán 6. Cho hàm số y f x có đạo hàm f  x 2  x  2, x   .
 Mệnh đề nào dưới đây là đúng? A. f   1  f   1 . B. f   1  f   1 . C. f   1  f   1 . D. f   1  f   1 . Lời giải 4
Từ f  x 2  x  2, x
    Hàm số đồng biến trên .  . Mà 1
  1  f   1  f   1 .
Bài toán 7. Cho hàm số y f x có đạo hàm f  x 2
x  2x , x
   . Hàm số y  2
f x đồng biến trên khoảng A. 0; 2 . B. 2;  . C.  ;  2   . D.  2  ;0 . Lời giải
Ta có: y   f  x 2 2  2
x  4x  0  x 0; 2 .Suy ra: hàm số y  2
f x đồng biến trên khoảng 0; 2
Bài toán 8. Cho hàm số y f (x) có đạo hàm f  x   x  
1  x  3, x
   . Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. 0;3 . B. 3; . C. ; 2 . D. 1;3 . Lời giải x  1
Ta xét: f  x  0   x  
1  x  3  0   . x  3 
Bảng xét dấu f  x :
Suy ra hàm số nghịch biến trên khoảng 1;3 . ax b
Bài toán 9. Đường cong ở hình bên là đồ thị của hàm số y
với a,b,c,d là các số thực. Mệnh đề nào cx d dưới đây đúng ?
A. y  0,x  
B. y  0,x  
C. y  0,x  1
D. y  0,x  1 Lời giải
Dựa vào hình dáng của đồ thị ta được:
+ Điều kiện x  1
+ Đây là đồ thị của hàm nghịch biến Từ đó ta được 
y  0,x  1.
Bài toán 10. Cho hàm số y f x xác định và liên tục trên  , có bảng đạo hàm f  x thỏa mãn:
Hàm số y f (x) nghịch biến trên khoảng nào dưới đây A.  1  ;3 . B. 1  ;1 . C.  2  ;   1 . D. 1; .
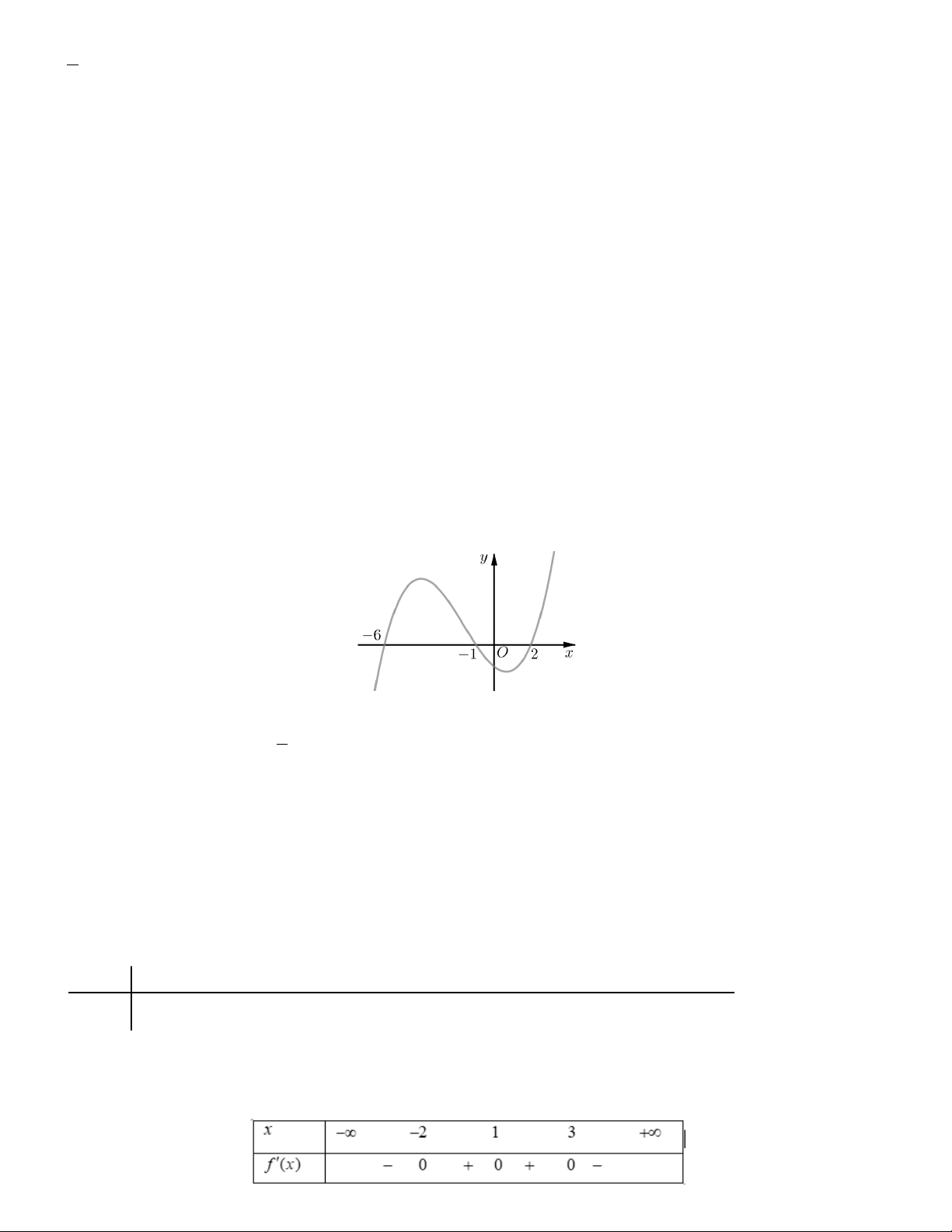
Bài toán 11. Cho đồ thị hàm số y f x liên tục trên  và có đồ thị như hình vẽ bên dưới.
Khẳng định nào sau đây là đúng ?
A. Hàm số đồng biến trên khoảng 1;3 .
B. Hàm số nghịch biến trên khoảng 6;  .
C. Hàm số đồng biến trên khoảng  ;  3 .
D. Hàm số nghịch biến trên khoảng 3;6 . 5
TÍNH ĐƠN ĐIỆU HÀM SỐ ĐA THỨC
Bài toán 1. Tìm khoảng nghịch biến của hàm số 3
y  2x  6x 1.  1   1  A.  1   ;1 B. ;    . C. 0;  . D.  ;    .  2   2  Lời giải x  1 + 2
y  6x  6 . Giải 2
y  0  6x  6  0   . x  1  
+ Bảng biến thiên của hàm số như sau
Vậy hàm số đồng biến trên các khoảng  ;   
1 và 1;   ; nghịch biến trên khoảng  1   ;1 .
Bài toán 2. Tìm các khoảng nghịch biến của hàm số 3 2
y  x  2x  3x  5 .  1   1  A.  ;   B. ;    . C. 0;  . D.  ;    .  2   2  Lời giải 2  2  5 + 2 y  3
x  4x  3  3  x    0, x    
 . Vậy hàm số nghịch biến  .  3  3
Bài toán 3. Hàm số nào dưới đây đồng biến trên  ? x 1 A. y  . B. 2
y x  2x . C. 3 2
y x x x . D. 4 2
y x  3x  2 . x  2 Lời giải 2  1  2 3 2 2
y x x x y '  3x  2x 1  3 x    0 x       3  3
Vậy hàm số đồng biến trên  .
Bài toán 4. Hàm số nào dưới đây nghịch biến trên  x  2 A. 3
y  x x . B. 4 2
y  x x . C. 3
y  x x . D. y  . x 1 Lời giải Hàm số 3
y  x x có tập xác định D   , đạo hàm 2
y   x     2 3 1 3x   1  0, x   
Suy ra, hàm số nghịch biến trên  .
Bài toán 5. Hàm số nào dưới đây đồng biến trên  ? x 1 A. 4 2
y x x . B. 3
y x x . C. y  . D. 3
y x x . x  2 Lời giải Ta có: 3 2
y x x y  3x 1  0 x    .
Bài toán 6. Hỏi hàm số 4
y  2x 1 đồng biến trên khoảng nào?  1   1  A.  ;  0. B. ;    . C. 0;  . D.  ;    .  2   2  Lời giải 4
y  2x 1 . Tập xác định: D   . Ta có: 3 y  8x ; 3
y  0  8x  0  x  0 suy ra y 0  1
Giới hạn: lim y   ; lim y   . Bảng biến thiên: x x 6
Vậy hàm số đồng biến trên khoảng 0;  .
Bài toán 7. Cho hàm số y  4 x  2
2x . Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng ;  2
B. Hàm số đồng biến trên khoảng 1;1
C. Hàm số nghịch biến trên khoảng 1;1
D. Hàm số đồng biến trên khoảng ;  2 Lời giải x  0 3 3 
y  4x  4x; y  0  4x  4x  0  x   1 x    1
Suy ra hàm số đồng biến trên các khoảng 1; 0 , 1;   ; hàm số nghịch biến trên các khoảng ;  1,
0;1. Vậy hàm số nghịch biến trên khoảng ;  2 .
Bài toán 8. Hàm số 3
y x  3x m nghịch biến trên khoảng nào? A.  ;    1 . B. ; . C.  1  ;  1 . D. 0; . Lời giải x  1 
Tập xác định D   . Ta có 2
y  3x  3; y  0   . x  1 
Ta có bảng xét dấu y :
Từ bảng xét dấu ta thấy hàm số nghịch biến trên khoảng 1;  1 .
Bài toán 9. Cho hàm số 3 2
y  x  3x 1, kết luận nào sau đây về tính đơn điệu của hàm số là đúng nhất:
A. Hàm số đồng biến trên khoảng 0; 2 và nghịch biến trên các khoảng ;0 ; 2;  ;
B. Hàm số đồng biến trên khoảng 0; 2 ;
C. Hàm số nghịch biến trên khoảng 0; 2 và đồng biến trên các khoảng  ;
 0 ; 2;  ;
D. Hàm số nghịch biến trên các khoảng ;0 và 2;  . Lời giải
Ta có hàm số xác định trên  .  x  0 3 2
y  x  3x 1 2
y  3x  6x  0   . x  2  Bảng biến thiên
Vậy đáp án A là đúng nhất. 7
TÍNH ĐƠN ĐIỆU HÀM SỐ PHÂN THỨC HỮU TỶ
Bài toán 1. Hàm số nào dưới đây đồng biến trên từng khoảng xác định x 1 x 1 A. y  B. 3
y x x C. 3
y  x  3x D. y x  2 x  3 x 1 2
Lời giải. Ta có y   y   0, x   3  2 x  3 (x  3)
Bài toán 2. Hàm số nào dưới đây đồng biến trên từng khoảng xác định x 1 x  2 2 A. y  . B. y  . C. 3
y  3x  3x  2 . D. y  . x  2 x 1 2 x  1 x  2 3
Lời giải. Đạo hàm y   y   0, x   1
 nên đồng biến trên từng khoảng xác định. 2 x 1 (x 1) 2
Bài toán 3. Hàm số y
nghịch biến trên khoảng nào dưới đây? 2 x  1 A. (; ) B. (0; ) C. (; 0) D. (1;1) 4x
Lời giải. Ta có y 
 0  x  0 .  2 2 x  1 2 x x  4
Bài toán 4. Hàm số y
đồng biến trên khoảng nào x 1 A. (; ) B. (0; ) C. (; 2) D. (1;1) Lời giải 2 x  2x  3  x  1
Tập xác định: D   \   1 . Ta có 2 y 
, y  0  x  2x  3  0   .  x  2 1 x  3  Bảng xét dấu đạo hàm
Từ bảng xét dấu y ta có :
+ Hàm số đồng biến trên mỗi khoảng  ;    1 và 3; . 5  2x
Bài toán 5. Hàm số y
 2024 nghịch biến trên x  3 A. R\   3  . B. R . C.  ;  3   . D. 3; . Lời giải 5  2x 11  Hàm số y
 2024 có tập xác định là D   \   3 . Đạo hàm y ' 
 0, với x D . x  3  x  32
Vậy hàm số đã cho nghịch biến trên các khoảng  ;  3   và  3  ; . x 1
Bài toán 6. Cho hàm số y
. Khẳng định nào sau đây là đúng? x 1
A. Hàm số đã cho nghịch biến trên khoảng  ;   1 .
B. Hàm số đã cho đồng biến trên khoảng  ;  
1 và khoảng 1; .
C. Hàm số đã cho đồng biến trên khoảng 0; .
D. Hàm số đã cho nghịch biến trên tập  \   1 . Lời giải 2
TXĐ: D   \   1 . Ta có: y   0 với x
  1. Hàm số nghịch biến trên từng khoảng xác định.  x  2 1 2 x x  1
Bài toán 7. Tìm một khoảng đồng biến nào đó của hàm số y  . x  1 8  1  A. R\   3  . B. R . C.  ;  3   . D.  ;    .  2 
Lời giải. Hàm số đã cho có tập xác định là . ⬩Ta có: với ; Giải
⬩Bảng biến thiên của hàm số như sau: 2 x  2x  2
Bài toán 8. Hàm số y
đồng biến trên khoảng nào x  1 A. (; ) B. (0; ) C. (; 0) D. (1;1) 2 x  2x  2 2 x  2x
Lời giải. y   y 
; y  0  x  0; x  2 . Bảng biến thiên x  1 (x  2 1)
Hàm số đồng biến trên (0; ) 2 x  2x  2 x  1 x  5
Bài toán 9. Cho các hàm số y  , y  , y  3
x  3x, y  . x  1 x  1 x  5
Có bao nhiêu hàm số đồng biến trên từng khoảng xác định. A.3 B. 2 C. 1 D. 4 Lời giải x  5 10 Ta thấy hàm y
có đạo hàm y 
 0,x  5 nên đồng biến trên từng khoảng xác định. x  5 (x  2 5) 2 x  2x  2 2 x  2x Hàm số y
có đạo hàm y 
; y  0  x  0; x  2 . x  1 (x  2 1) Hàm đa thức y  3
x  3x có y  2
3x  3 , có nghiệm. 2 x  2x  5
Bài toán 10. Cho hàm số y
. Mệnh đề nào dưới đây đúng? x 1
A. Hàm số nghịch biến trên khoảng  1  ;  1  1;3 .
B. Hàm số nghịch biến trên khoảng  1  ;  3 \  1 .
C. Hàm số nghịch biến trên mỗi khoảng  1  ; 
1 và 1;3 . D. Hàm số nghịch biến trên khoảng  ;    1 . Lời giải
Tập xác định: D  \  1 .
2x  2 x   1   2
x  2x  5 2 x  2x  3 x  1 Ta có y  
. Giải phương trình y  0   .  x  2 1  x  2 1 x  3  Bảng biến thiên
Từ bảng biến thiên suy ra: Hàm số nghịch biến trên mỗi khoảng  1   ;1 và 1;3 . 9
TÍNH ĐƠN ĐIỆU HÀM SỐ LƯỢNG GIÁC, HÀM SỐ MŨ, HÀM SỐ LOGARIT
Bài toán 1. Chọn khẳng định sai trong các khẳng định sau:
A. Hàm số y  log x đồng biến trên  . 2
B. Hàm số y  log x nghịch biến trên tập xác định của nó. 1 2 C. Hàm số 2x y  đồng biến trên  . D. Hàm số 2 y x
có tập xác định là 0;  . Lời giải
Hàm số y  log x đồng biến trên khoảng 0;  . 2
Bài toán 2. Hàm số nào dưới đây nghịch biến trên tập xác định của nó? x    A. y  log x B. y  log x 1 C. y  log x D. y  2   3     3 4  Lời giải
Xét hàm số y  log x có tập xác định: D  0;  .  4  Nhận thấy cơ số
 1 nên y  log x nghịch biến trên tập xác định. 4  4
Bài toán 3. Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập số thực R . x x     2  A. y  2  
B. y  log 2x   1 C. y  D. y  log x    2  3  e 4   3 Lời giải 2 x  2  Vì
 1 nên y    nghịch biến trên R . ee
Bài toán 4. Hàm số y  log  2
x  2x nghịch biến trên khoảng nào? 3  A. 2;  . B. ;0 . C. 1;   . D. 0;  1 . Lời giải
Hàm số y  log  2
x  2x có tập xác định D  ;0  2;   . 3  2x  2 Ta có y 
. Khi đó y  0  x  1 .  2 x  2xln 3 Bảng biến thiên:
Dựa vào bảng biến thiên ta có hàm số y nghịch biến trên  ;0 .
Bài toán 5. Cho hàm số f x  ln x x . Khẳng định nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng 0;  1 .
B. Hàm số đồng biến trên khoảng 0; .
C. Hàm số đồng biến trên các khoảng  ;  0 và 1; .
D. Hàm số đồng biến trên khoảng 1; . Lời giải
Tập xác định của hàm số f x : D  0; 10 1 1 x
Ta có f  x  1 
và f  x  0  x 1. Bảng xét dấu f  x : x x
Bài toán 6. Trong các hàm số sau,hàm số nào luôn nghịch biến trên tập xác định của nó? 2 x  1   2  A. y    .
B. y  log x . C. 2x y  . D. y    .  2   3  Lời giải x  2  2
Ta thấy hàm số y    là hàm số mũ có có tập xác định là  cơ số a   1 nên nghịch biến trên tập xác  3  3 định của nó.
Bài toán 7. Cho các hàm số 3 2
y  cos x  5x  3; y  sin 2x  3x  ; m
y x  2x  5x  6 .
Có bao nhiêu hàm số đồng biến trên  ? A.3 B. 4 C. 1 D. 2 Lời giải Ta có các đạo hàm
y  cos x  5x  3  y  sin x  5  0, x
y  sin 2x  3x m y  2 cos 2x  3  0, x  3 2 2
y x  2x  5x  6  y  3x  4x  5  0, x
Kết luận 3 hàm số đồng biến trên  x 1
Bài toán 8. Cho các hàm số 3 2 y
; y  x  3x 1; x y e ;
y  sin x  3x . x 1
Số lượng hàm số đồng biến trên  là A.3 B. 2 C. 1 D. 4 Lời giải Ta có các đạo hàm x 1 2 y   y  2 x 1 (x 1) 3 2 2
y  x  3x 1  y  3x  6x  3  x(x  2) x x
y e y  e  0, x
y  sin x  3x y  cos x  3  0, x
Kết luận có 2 hàm số đồng biến trên  .
Bài toán 9. Tìm khoảng đồng biến của hàm số   2 ln 1 x y
e   e . A. ;  . B. 1; 0 . C. 1;1 . D. 0 ;1 . Lời giải  1 xee x 2 x 2  2  2
Ta có y  ln 1 e   e    0, x  . 2 x 2   1 e 1 xe
Khoảng đồng biến là  ;  . 2
Bài toán 10. Khoảng đồng biến của hàm số x x y e   là  1  A.  ;    . B. 1; 0  . C. 1;1 . D. ;   2  Lời giải 2 2 ' 2  x x x x x x 1
Ta có y  e
  e . 2x x  2x  1e  0  x   . 2
Bài toán 11. Khoảng đồng biến của hàm số y  log  2
x x 1 là 3   1  A.  ;    . B. 1; 0  . C. 1;1 . D. 0 ;1 .  2  Lời giải 11  2 x x   1 ' 2x 1 1  1  y '    0  x  
. Suy ra khoảng đồng biến là  ;  .  2   x x   1 ln 3  2 x x   1 ln 3 2  2 
Bài toán 12. Khoảng đồng biến của hàm số y  sin 2x  6x là       2  A.  ;   B.  ;   C. 0; 2 D. ;    2 2   2 3  Lời giải
Ta có y  2 cos 2x  6  0, x
 nên khoảng đồng biến là ;  
Bài toán 13. Tìm khoảng đồng biến của hàm số f x  log  2 x 1  2024 . 2  A.   ;1  B.  ;  4 C.   ;1  D. 0;   Lời giải 2x
Hàm số đồng biến khi f  x   0  x  0 .  2 x   1 .ln 2
Bài toán 14. Trong các hàm số sau hàm số nào nghịch biến trên  ? xx  e   2  A. 2 log x B. y   3 log x  C. y  D. y  3      4   5  Lời giải Hàm số mũ x
y a với 0  a  1 nghịch biến trên  . x e  e  Ta có 0 
 1 nên hàm số y    nghịch biến trên  . 4  4 
Bài toán 15. Hàm số nào sau đây đồng biến trên  . x 1 A. y  .
B. y  sin x  2x C. x
y e  6x D. 2 y x  2 x 1 Lời giải
Hàm số y  sin x  2x y  cos x  2  0, x
 . Hàm số đồng biến trên  .
Bài toán 16. Tìm hàm số đồng biến trên  . x  1  3 A.   3x f x  . B.   3 x f x   .
C. f x    .
D. f x  .  3  3x Lời giải Hàm số   x
f x a đồng biến trên  nếu a  1 và nghịch biến trên  nếu 0  a  1. Vậy hàm số   3x f x
là hàm số đồng biến trên  .
Bài toán 17. Hàm số nào sau đây đồng biến trên  . x 1 A. y
B. y  cos x  5x  3 C. x
y e  6x D. 2
y x  2x x  6 Lời giải
Hàm số y  cos x  5x  3  y  sin x  5  0, x
 . Hàm số đồng biến trên 
Bài toán 18. Hàm số nào dưới đây đồng biến trên khoảng (0;  ) ? A. y  log x .
B. y  log x .
C. y  log x .
D. y  log x . 3  e 1 6 3 4 Lời giải
Hàm số y  log x đồng biến trên khoảng (0;  ) ⇔ a  1 ⇒ Chọn A a
Bài toán 19. Hàm số nào dưới đây nghịch biến trên tập xác định của nó? x x x x  4     3   e   1  A. y    B. y    C. y    D. y     3  2   2   2   6  5  Lời giải x   3    3  Ta có
 1 nên hàm số y  
 nghịch biến trên TXĐ. 2  2  12 x
Bài toán 20. Tập tất cả các giá trị của tham số a để hàm số y  a  2 nghịch biến trên  là A. ;3 . B. 2;3 . C. ;  1 . D. 3;   . Lời giải x
Hàm số y  a  2 nghịch biến trên   0  a  2  1  2  a  3  a 2;3 .
Bài toán 21. Hàm số nào sau đây đồng biến trên tập xác định của nó A. y  log x .
B. y  log x .
C. y  log x .
D. y  log x . 2 e  e 2 3 4 2 Lời giải e  2 Ta thấy 0  , ,
 1 nên các hàm số ở A , B , D nghịch biến. 3 4 2 e
Vậy hàm số log x đồng biến trên tập xác định của nó, vì  1. e 2 2
Bài toán 22. Chọn mệnh đề sai trong các mệnh đề sau A. Hàm số y  log
x nghịch biến trên 0;  . 0,2
B. Hàm số y  log x đồng biến trên 0;  . 2
C. Hàm số y  log x đồng biến trên 0;  . 2 D. Hàm số y  log
x 1 đồng biến trên 0;  . 2   Lời giải
 Phương án D đúng.   x   1 1 1 1 Vì hàm số y  log
x 1 có y  .  .  0, x   0 . 2   ln 2 x 1
ln 2 2 x x   1
 Phương án A đúng. Vì hàm số y  log x có a  0, 2 1. 0,2
 Phương án B đúng. Vì hàm số y  log x có a  2 1. 2
 Phương án C sai. Vì hàm số y  log x có tập xác định là D  0; . 2
Bài toán 23. Trong các hàm số sau, hàm số nào đồng biến trên R ? xxe   2  A. y    . B. y    .
C. y  log x .
D. y  log x . 3 1  3   3  5 Lời giải x x  2   3   y    
  có tập xác định R .  3   2   x 3  2  Do
 1 nên hàm số y    đồng biến trên R . 2  3 
Bài toán 24. Trong các hàm số sau hàm số nào nghịch biến trên  ? xx  e   2  A. y  3   . B. y    .
C. y  log  x  . D. 2 log x . 3  4   5  Lời giải Hàm số y   3
log x  có tập xác đinh là 0;  .
Hàm số y  log  2 x
có tập xác đinh là  \   0 . 3 
Do đó hai hàm số đó không thể nghịch biến trên  được.  x x  2   5  5
Mặt khác hàm số y    
  là hàm số có tập xác định là  nhưng có cơ số  1 nên hàm số đồng  5   2  2 biến trên  . x  e  e
Hàm số y    là hàm số có tập xác định là  và có cơ số  1 nên hàm số nghịch biến trên   4  4 13
TÍNH ĐƠN ĐIỆU HÀM SỐ CHỨA CĂN
Bài toán 1. Hàm số 2
y  2018x x nghịch biến trên khoảng nào trong các khoảng sau đây? A. 1010; 2018 . B. 2018;  . C. 0;1009 . D. 1; 2018 . Lời giải
TXĐ: D  0; 201  8    y   2018 2x 1009 x 2
2018x x   
; y  0  x  1009 2 2 2 2018x x 2018x x
y '  0  x 1009;2018 , suy ra hàm số nghịch biến trên khoảng 1009; 2018 , suy ra hàm số nghịch biến trên
khoảng 1010; 2018 , chọn A. Bài toán 2. Cho hàm 2 y
x  6x  5 . Mệnh đề nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng 5; . B. Hàm số đồng biến trên khoảng 3; .
C. Hàm số đồng biến trên khoảng  ;  
1 . D. Hàm số nghịch biến trên khoảng  ;  3. Lời giải x  3
Tập xác định: D   ;  
1 5; . Ta có y   0 , x  5;  . 2 x  6x  5
Vậy hàm số đồng biến trên khoảng 5; .
Bài toán 3. Cho hàm số 2 y
2x  1 . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng 0;  
B. Hàm số đồng biến trên khoảng ; 0
C. Hàm số nghịch biến trên khoảng 0;  
D. Hàm số nghịch biến trên khoảng 1;1 Lời giải 2x
Ta có D   , y 
; y  0  x  0. 2 2x  1
Vậy hàm số nghịch biến trên khoảng ; 0 và đồng biến trên khoảng 0;   .
Bài toán 4. Hàm số 2
y  4  x đồng biến trên khoảng nào? A. 2;   . B. 0; 2 . C. 2; 2 . D. 2; 0 . Lời giải x
+ Tập xác định D  2; 2 . Đạo hàm y 
. Giải y  0  x  0 . 2 4  x
+ Bảng xét dấu của đạo hàm như sau
Vậy hàm số đồng biến trên khoảng 2;0 .
Bài toán 5. Cho hàm số 2
y  3x x . Hàm số đồng biến trên khoảng nào?  3   3   3  A. 0;   . B.  0;3  . C. ;3   . D. ;   .  2   2   2  Lời giải 3  2x 3
Điều kiện 0  x  3 và đạo hàm 2
y  3x x y   0  x  . 2 2 2 3x x  3 
Kết luận hàm đồng biến trên 0;   .  2 
Bài toán 6. Tìm các khoảng nghịch biến của hàm số y  3  x x 1 .  3   3  A.  1;3  . B.  0;3  . C. ;3   . D. ;   .  2   2  Lời giải 14
+) Tập xác định: D  1;  3 . 1  1
3  x x 1 +) y    . 2 3  x 2 x 1 2 3  . x x 1 +) y  0 
3  x x 1  0  3  x x 1. x  1  x  1       x  1.
3  x x 1 2x  2   +) Bảng biến thiên
Vậy hàm số đồng biến trên khoảng  1  
;1 , nghịch biến trên khoảng 1;3 .
Bài toán 7. Cho hàm số 2 y
x  8x  7  4 . Mệnh đề nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng  17;.
B. Hàm số đồng biến trên khoảng 3; 
C. Hàm số đồng biến trên khoảng  ;   1 .
D. Hàm số nghịch biến trên khoảng  ;  3. Lời giải
Tập xác định: D    ;1 7; . 2x  8 Ta có y 
 0  x  4 . Vậy hàm số đồng biến trên khoảng  17;. 2 x  8x  7
Bài toán 8. Khoảng đồng biến của hàm số 2 y
x  6x  7 chứa bao nhiêu số nguyên nhỏ hơn 20 A.18 B. 5 C. 10 D. 12 Lời giải x  1 Điều kiện 2
x  6x  7  0   x  7  2x  6 Hàm số đồng biến khi 2 y
x  6x  7  y   0  x  3   x  1. 2 2 x  6x  7 Suy ra có 18 số nguyên.
Bài toán 9. Hàm số 2 y
x  8  x  7 có khoảng đồng biến là A. ;  B.  ;    1 . C. 0;  . D. 0;8 . Lời giải 2 x x x  8 Ta có 2 y
x  8  x  7  y  1   0 (do 2 x x  8 ). 2 2 x  8 x  8
Bài toán 10. Hai hàm số 2 2
y  4x x ; y  x  6x  5 có khoảng đồng biến lần lượt là  ; a b, ; c d  . Tính giá
trị biểu thức a c b d . A.1 B. 0 C. – 1 D. – 2 Lời giải 4  2x
Xét tập xác định 0; 4 2 ; y
4x x y 
 0  x  2   ;
a b  0; 2 . 2 2 4x x 6  2x
Xét tập xác định 1;  2 5 ;
y  x  6x  5  y 
 0  x  3   ;
c d   1;3 . 2
2 x  6x  5
Như vậy a c b d  0 1 2  3  2  . 15
PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI TOÁN KHẢO SÁT HÀM SỐ LỚP 12 THPT
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
TÍNH ĐƠN ĐIỆU CÁC HÀM SỐ PHỨC TẠP
_____________________________________
Bài toán 1. Tìm khoảng đồng biến của hàm số   2 ln 1 x y
e   e . A. ;   . B. 1; 0  . C. 1;1 . D. 0 ;1 . Lời giải  1 xee x 2 x 2  2  2
Ta có y  ln 1 e   e    0, x  . 2 x 2   1 e 1 xe
Khoảng đồng biến là  ;  .
Bài toán 2. Cho hàm số y f x thỏa mãn:
Hàm số y  2024 f (x)  2 đồng biến trên khoảng nào sau đây ? A. 3;  . B.  ;0 . C.  2  ; 2 . D. 2;   . Lời giải
Hàm số y  2024 f (x)  2 cùng khoảng đồng biến với hàm số y f x . Ta chọn 3;  .
Bài toán 3. Cho hàm số y f (x) có bảng biến thiên như sau Hàm số y   3 x  2x  
1 f x đã cho nghịch biến trên khoảng nào dưới đây? A. 0;  1 B. ;0 C. 1;  D. 1;0 Lời giải Hàm số y   3 x  2x  
1 f x có cùng khoảng nghịch biến với hàm số đã cho. Ta có 0;  1 .
Bài toán 4. Khoảng nghịch biến của hàm số 2  (2  5  2) x y x x e là  ;
a b . Tính a b  5ab . A.6 B. 8 C. 7 D. 4 Lời giải 2 x 2 x x 2  (2  5  2)    (2  5  2)  (4  5)  (2   3) x y x x e y x x e x e x x e 1 3  2
y  0  2x x  3  0  a b  5ab   5.
 8 (Theo hệ thức Viet). 2 2
Bài toán 5. Cho hàm số y f (x) . Hàm số y f '(x) có đồ thị như hình bên. Hàm số y  3 f (x) đồng biến trên khoảng A. 2;  B.  2  ;  1 C.  ;  2   D. 4;  Lời giải 16
Giá trị đạo hàm dương, hàm số đồng biến trên 4;  .
Bài toán 6. Tìm khoảng đồng biến của hàm số 2 x   4 x y e e  5 . A.  2  ;  1 B. ln 2;  C. ln 2;5 D. 1;ln 2 Lời giải 2 x e eex x x e  2 2 4  y  
 0  x  ln 2 . Ta thu được khoảng đồng biến ln 2; . 2 x x 2 2 e  4e  5 x e  4 x e  5
Bài toán 7. Cho hàm số f x , bảng xét dấu của f ' x như sau: Hàm số 3
y x f x nghịch biến trên khoảng nào dưới đây? A.  1;   1 . B. 2; 4. C. 1;2. D. 4; . Lời giải Hàm số 3
y x f x có cùng khoảng nghịch biến với hàm số đã cho. Ta chọn  1;   1 .
Bài toán 8. Cho hàm số y f (x) . Hàm số y f '(x) có đồ thị như hình bên. Hàm số y f (2  x) đồng biến trên khoảng A. 2; B.  2  ;  1 C.  ;  2   D. 1;  3 Lời giải Cách 1:  x  (1; 4)
Ta thấy f '(x)  0 với 
nên f (x) nghịch biến trên 1; 4 và  ;   
1 suy ra g(x)  f (x) đồng biến x  1 
trên (4; 1) và 1;  . Khi đó f (2  x) đồng biến biến trên khoảng (2;1) và 3;  2 3 2 3
Bài toán 9. Cho các hàm số x 1 
x 3x 3x 1  2 x x 3 y e ; y e ; y e ; y e
. Số lượng hàm số đồng biến trên  là A.3 B. 2 C. 1 D. 4 Lời giải 2 2 x 1  x 1 y e
y  2xe  3 2
x x x y e
  y  3x  6x  3 3 2
x x x e   3 x   3 2 2 3 3 1 2 3 3 1
x 3x 3x 1 1 e   0, x  ; 2 x 2 y ey  2 x e 3 3 x 3 2 x 3 y e
y  3x e  0, x
Như vậy có 2 hàm số đồng biến trên  .
Bài toán 10. Tìm khoảng đồng biến của hàm số 3 2 y
x  3x  3x  7 . A. 1; 4 B.  2  ;  1 C. 3;  D. 4;7 Lời giải
Điều kiện xác định x  3 . 3x  6x  3 3 x  2 2 1 Ta có y    0, x
  3 . Khoảng đồng biến là 3; . 3 2 3 2
2 x  3x  3x  9
2 x  3x  3x  9 x 1
Bài toán 11. Hàm số y
có khoảng đồng biến là 2 x x 1 A.  ;  2   . B.   ;1  . C.  ;  2  . D.  ;   . Lời giải 17 2x 1 2 x x 1  .(x 1) 2 x 1 2 x x 1 3  x  3 y   y   . 2 2 x x 1 x x 1 2  2 x x   2 1 x x 1
y  0  x  1 . Khoảng đồng biến của hàm số là   ;1  .
Bài toán 12. Hàm số y   2 ln x
x 1 có khoảng đồng biến là A.  ;  2   . B.   ;1  . C.  ;  2  . D.  ;   . Lời giải 2
x 1  x x x  0 nên hàm số luôn xác định.  xy  1  :  1 2 x x 1   0, x
 . Khoảng đồng biến của hàm số là  ;   . 2  2  x 1  x 1
Bài toán 13. Cho hàm số bậc bốn y f (x) có đồ thị của hàm số y f (
x) như hình vẽ bên. y 1 O -4 -3 -2 2 x -1 -2 -3 Hàm số 3 2
y  3 f (x)  x  6x  9x đồng biến trên khoảng nào trong các khoảng sau đây? A. 0; 2 . B. 1;  1 . C. 1;  . D. 2; 0 . Lời giải Hàm số 4 3 2
f (x)  ax bx cx dx  , e (a  0) ; 3 2 f (
x)  4ax  3bx  2cx d .
Đồ thị hàm số y f (
x) đi qua các điểm ( 4  ; 0), ( 2
 ; 0), (0; 3), (2;1) nên ta có:  5 a   96
256a  48b  8c d  0   7
 32a 12b 4c d 0 b            24 d  3    7 3  2 12  4   1 c a b c d    24  d  3   5 15 55  Do đó hàm số 3 2
y  3 f (x)  x  6x  9 ; x y  3 2 f (
x)  x  4x  3 3 2  3 x x x    24 8 12  x  1  1 
y  0  x  0
. Hàm số đồng biến trên các khoảng ( 1  1;0) và 2; .  x  2 
Bài toán 14. Cho hàm số f x có đạo hàm liên tục trên  và có đồ thị của hàm số y f  x như hình vẽ.
Xét hàm số g x  f  2
x  2 . Mệnh đề nào dưới đây sai? 18
A. Hàm số g x nghịch biến trên 0;2 .
B. Hàm số g x đồng biến trên 2; .
C. Hàm số g x nghịch biến trên  1  ;0 .
D. Hàm số g x nghịch biến trên  ;  2   . Lời giải
Ta có g x   2
x   f  2
x    x f  2 2 . 2 2 . x  2 . x  0   f    2 x  2  0 
Hàm số nghịch biến khi g x  0  x f  2 .
x  2  0   x  0   f    2 x  2  0 
Từ đồ thị hình của hàm số y f  x như hình vẽ, ta thấy
f  x  0  x  2 và f  x  0  x  2 . x  0 x  0  x  0 x  0  + Với     
 x  2  x  2 . f  2 2   2 x  2  0  x  2  2  x  4   x  2  x  0  x  0 x  0 + Với       0  x  2 . f  2 2   2 x  2  0  x  2  2  x  4 
Như vậy hàm số nghịch biến trên mỗi khoảng  ;  2
  , 0;2 ; suy ra hàm số đồng biến trên  2  ;0 và 2; . Do  1  ;0   2
 ;0 nên hàm số đồng biến trên  1  ;0 . Vậy C sai.
Bài toán 15. Cho hàm số y f x . Biết rằng hàm số y f  x có đồ thị như hình vẽ bên dưới.
Hàm số y f  2
3  x  đồng biến trên khoảng A. 0;  1 . B.  1  ;0 . C. 2;3 . D.  2  ;   1 . Lời giải Cách 1:
Đặt y g x  f  2
3  x  . Ta có: g x   x f  2 2 . 3  x  .  x  0 x  0  x  0 2 3  x  6   x  3 
g x    x f  2 0 2 .
3  x   0      . f  2    2 3  x   0   3  x  1 x  2    2 3  x  2  x  1  
Bảng xét dấu của g x : x  3  2  1  0 1 2 3  gx  0  0  0  0  0  0  0 
Suy ra hàm số y f  2
3  x  đồng biến trên mỗi khoảng:  3  ; 2  ,  1
 ;0, 1; 2, 3;  .
Vậy hàm số y f  2
3  x  đồng biến trên khoảng  1  ;0 .
Bài toán 16. Cho hàm số f (
x) có bảng xét dấu như sau: 19
Hàm số y f  2
x  2x nghịch biến trên khoảng nào dưới đây? A.  2  ;  1 . B.  4  ; 3   . C. 0;  1 . D.  2  ;   1 . Lời giải
Ta có: Đặt: y g x f  2 ( ) x  2x  ; 2
gx   f x x    x   2 ( ) ( 2 ) 2 2 . f (  x  2x)   x  1 x  1 x  1 2   2 2x  2  0
x  2x  2(VN )
gx    x   2 ( ) 0 2 2 . f (
x  2x)  0      x  1 2  2 2 f (x 2x) 0     x  2x  1    x  1 2
x  2x  3   x  3  (Trong đó: x  1   2 ; x  1
  2 là các nghiệm bội chẵn của PT: 2
x  2x  1 ) + Ta có bảng biến thiên
Dựa vào bảng biến thiên, suy ra hàm số y f  2
x  2x nghịch biến trên khoảng  2  ;   1 .
Bài toán 17. Cho hàm số y f x có bảng xét dấu đạo hàm như sau: Hàm số    3  2x g x f
đồng biến trên khoảng nào sau đây A. 3;  . B.  ;  5   . C. 1;2 . D. 2;7 . Lời giải Ta có
'   2x ln 2. '3  2x g x f
. Để ( )  3 2x g x f  đồng biến thì '   2
x ln 2. '3  2x g x f
  0  '3 2x   0  5  3 2x f
 2  0  x  3 .
Vậy hàm số đồng biến trên 1;2 .
Bài toán 18. Cho hàm số f x có bảng xét dấu đạo hàm như sau: Hàm số y f   x 2 2 1 
x  1  x nghịch biến trên những khoảng nào dưới đây A.  ;  2 . B.  ;  1 . C. 2;0 . D. 3;  2 . Lời giải. x x y  2
f 1 x  1. Có
1  0 , x  2;0 . 2 x 1 2 x 1 Bảng xét dấu: x
 2 f  1 x  0, x  2; 0  2 f 1 x  1  0, x    2  ; 0 . 2 x 1 20