



















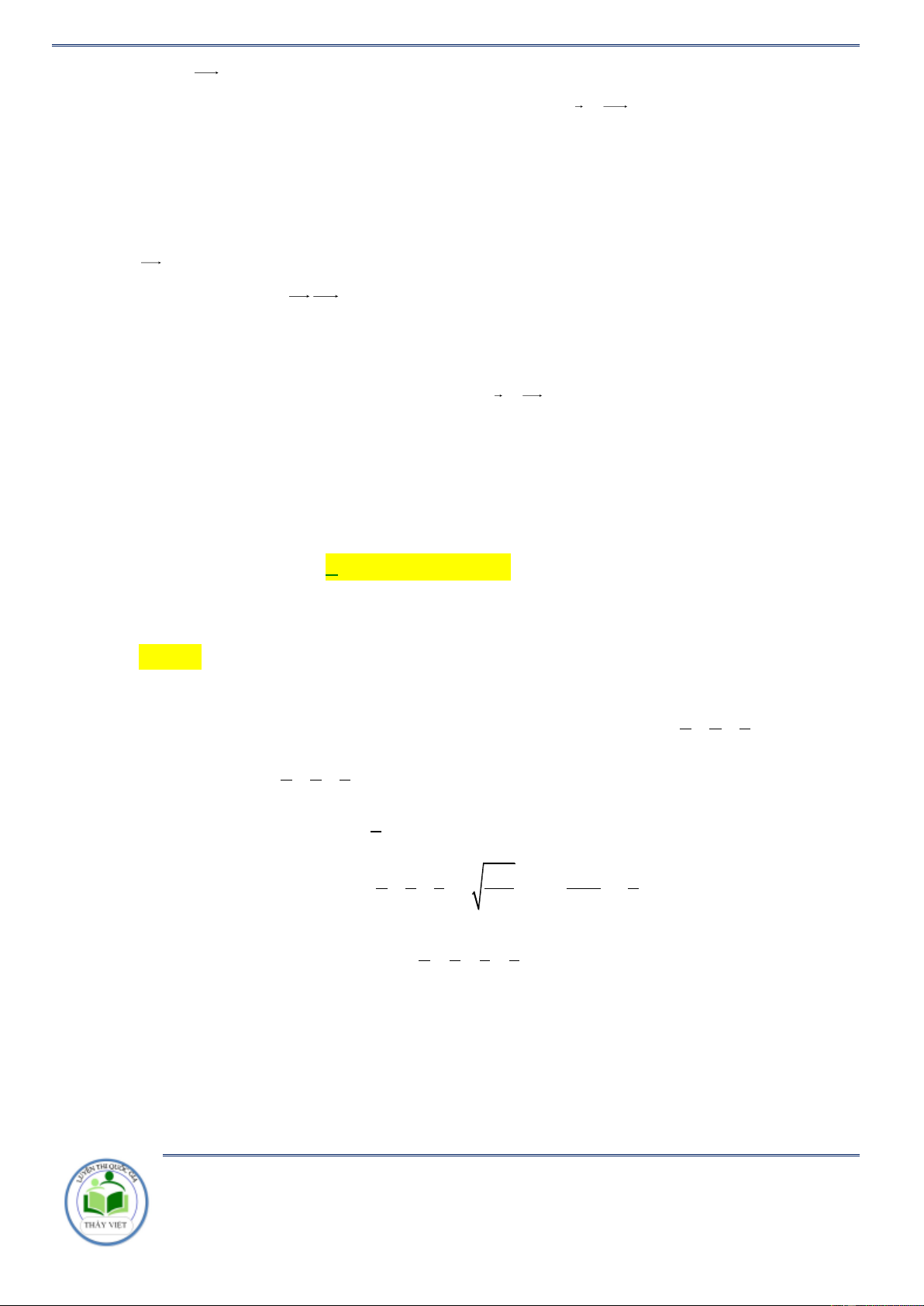





















































Preview text:
Chuyên đề: Cực trị hình giải tích T r a n g 1/ 8 5 x −1 y z + 2 Câu 1: Cho đường thẳng : = = và hai điểm ( A 0; 1 − ;3), B(1; 2
− ;1).Tìm tọa độ điểm M 2 1 1 −
thuộc đường thẳng sao cho 2 2
MA + 2MB đạt giá trị nhỏ nhất. A. M (1;0; 2) − .
B. M (3;1; −3). C. M ( 1 − ; 1 − ; 1 − ). D. M (5; 2; 4). − Lời giải Chọn C Ta có 2 2 2
M M (1+ 2t;t; 2 − −t)nên ta có 2
MA = (− − t ) + (− − t ) + ( + t ) 2 1 2 1 5 = 6t +16t + 27 ;
MB = (− t )2 + (− − t )2 + ( + t )2 2 2 2 2 3 = 6t +10t +13 Suy ra 2 2 2
MA + 2MB = 18t + 36t + 53 = ( 2 18 t + 2t + ) 1 + 35 = (t + )2 18 1 + 35 35 nên 2 2 MA + 2MB đạt
giá trị nhỏ nhất khi t = 1 − suy ra M ( 1 − ; 1 − ; 1 − ) . x y −1 z + 2 Câu 2: Cho đường thẳng : = = và ba điểm ( A 1;3; 2 − ), B(0;4; 5 − ), C(1;2; 4) − . Biết điểm 1 1 2 − M ( ; a ;
b c) thuộc đường thẳng sao cho 2 2 2
MA + MB + 2MC đạt giá trị nhỏ nhất. Khi đó, tổng
a + b + c bằng bao nhiêu? A. 0 . B. 1. C. 3 . D. 4 . Lời giải Chọn B Ta có 2 2 2
M M (t;1+ t; 2 − − 2t)nên ta có 2
MA = ( − t ) + ( − t ) + ( t ) 2 1 2 2
= 6t − 6t + 5 ; MB = ( t
− )2 + ( − t)2 + (− + t)2 2 2 3 3 2
= 6t −18t +18 .
MC = ( − t )2 + ( − t )2 + (− + t )2 2 2 1 1 2 2 = 6t −12t + 6 2 2
2MC = 12t − 24t +12 Suy ra 2 2 2 2
MA + MB + 2MB = 24t − 48t + 35 = ( 2 24 t − 2t + ) 1 +11 = (t − )2 24 1 +11 11nên 2 2 2
MA + MB + 2MC đạt giá trị nhỏ nhất khit =1suy ra M (1;2; 4
− ) nên a =1;b = 2;c = 3 − . Khi đó
a + b + c = 1 − x y z −1 Câu 3:
Trong không gian với hệ tọa độ Oxyz , cho đường thẳng : = = và hai điểm 2 1 − 1 − A( 1 − ; 1 − ;6), B(2; 1
− ;0) . Biết điểm M thuộc đường thẳng sao cho biểu thức 2 2 MA + 3MB
đạt giá trị nhỏ nhất là T . Khi đó, T bằng bao nhiêu? min min 1 25 A. T = . B. T = 25 . C. T = . D. T = 39 . min 2 min min 2 min Lời giải Chọn D
Đường thẳng đi qua điểm M (0;0; )
1 và có véc tơ chỉ phương u = (2; 1 − ;− ) 1 nên có o
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 2 / 8 5 x = 2t
phương trình tham số: y = − t (t ). z =1− t
Vì M thuộc đường thẳng nên M (2t;−t;1−t) . 2 2 2 2 2 2 Ta có 2 2
MA + 3MB = (2t + ) 1 + (t − ) 1 + (t + 5) + 3 (
2t − 2) +(t − ) 1 + (t − ) 1 45 2 2
= 24t − 24t + 45 = 6 4t − 4t + 6 ( t − )2 39 = 6 2 1 + = 6(2t − )2
1 + 39 39, t . 6 1 1 − 1 Vậy ( 2 2
min MA + 3MB ) = 39 t = hay M 1; ; . 2 2 2 x −1 y z + 2 Câu 4:
Cho đường thẳng d : = = và A(1; 1 − ;0), B(0; 1 − ;2),C( 1
− ;1;0) . Tìm tọa độ điểm 1 − 1 1
M thuộc đường thẳng d sao cho MA + 2MB − MC đạt giá trị nhỏ nhất. 1 2 4 A. M ; ; − .
B. M (0;1;− ) 1 . 3 3 3 2 1 5
C. M − ; ; − .
D. M (2; 1 − ; 4 − ). 3 3 3 Lời giải Chọn A
Gọi M có tọa độ là: M (1−t;t; 2 − +t) .
Ta có: MA = (t; t
− −1;2 −t),2MB = (2t − 2; 2
− t − 2;8− 2t),MC = (t − 2;1−t;2 −t).
Do đó: MA + 2MB − MC = (2t; 2
− t − 4;8− 2t) . 2 224
Suy ra: MA + 2MB − MC = 4t + (2t + 4)2 + (2t − 8)2 2 2
=12t −16t + 80 . 3 4 42
MA + 2MB − MC . 3 2 1 2 4
Dấu " = " xảy ra t = hay M ; ; − . 3 3 3 3 x y +1 z −1 Câu 5: Cho đường thẳng : = = và hai điểm ( A 1; 0;1), B( 1
− ;1;2). Biết điểm M ( ; a ; b c) 2 1 1 −
thuộc sao cho MA − 3MB đạt giá trị nhỏ nhất. Khi đó, tổng a + 2b + 4c bằng bao nhiêu? A. 0 . B. −1. C. 1. D. 2 . Lời giải Chọn D
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 3/ 8 5
Do M M (2t; 1 − + t;1−t)
MA = (1− 2t;1− t;t) MB = ( 1
− − 2t;2 −t;1+ t) 3MB = ( 3
− − 6t;6 −3t;3+ 3t)
MA − 3MB = (4 + 4t; 5 − + 2t; 3 − − 2t) 1 2 2 MA − 3MB = 24t + 24t + 50 = 24(t + ) + 44 44 2
MA − 3MB đạt giá trị nhỏ nhất bằng 44 khi 1 t = − 2
Khi đó điểm M có tọa độ là 3 3 M ( 1
− ;− ; ) và a + 2b + 4c = 1 − − 3+ 6 = 2 2 2 x +1 y −1 z + 2 Câu 6: Cho đường thẳng : = = và (
A 1;1; 0), B(3; 1
− ;4), C(−1;0;1). Tìm tọa độ điểm 1 1 − 2
M thuộc đường thẳng sao cho 2 2 2
MA − MB + 4MC đạt giá trị nhỏ nhất. 1 1 2 1 1 A. M (0;0;0) .
B. M − ; ; − .
C. M ( 2 − ;2; 4) − .
D. M − ; − ;0 . 3 3 3 2 2 Lời giải Chọn B
Do M M ( 1
− + t;1− t; 2 − + 2t)
MA = (2 − t;t; 2 − 2t) MB = (4 − t; 2
− + t;6 − 2t) MC = ( t − ; 1
− + t;3− 2t) 2 2 2 2 2 2 2 2 2 2 2 2
MA − MB + 4MC = (2 − t) + t + (2 − 2t) − 4[(4 - t) + (t − 2) + (6 − 2t) ] +[t + (t −1) + (3 − 2t) ] 2 2 2
= 6t −12t + 8 − (6t − 36t + 56) + 4(6t −14t +10) 2 7 7 2 2
= 24t − 32t − 8 = 24[(t − ) − ] − 3 9 9 2 2 2
MA − MB + 4MC đạt giá trị nhỏ nhất bằng 7 − khi 2 t = 9 3 Suy ra điểm 1 1 2 M (− ; ; − ) 3 3 3 x +1 y −1 z + 2 Câu 7: Cho đường thẳng : = =
. Tìm tọa độ điểm M thuộc đường thẳng sao cho 1 1 − 2
MA + MB − 3MC đạt giá trị nhỏ nhất với A(2;1;− 2), B(6;−1; ) 1 ,C (1;1;− 2) . 3 3 1 1 2
A. M − ; ; −3 . B. M ; − ; . C. M ( 3 − ;3; 6) − . D. M ( 1 − ;1; 2 − ) . 2 2 3 3 3 Lời giải Chọn C
Gọi I là điểm thỏa mãn IA + IB − 3IC = 0 I ( 5 − ;3; 5 − ).
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 4 / 8 5
Ta có: P = MA + MB − 3MC = MI + IA + MI + IB − 3MI − 3IC = MI = IM .
M M ( −1+ t ;1− t ;− 2 + 2t) 2 2 2 2 2
IM = (t + 4) + ( t
− − 2) + (2t + 3) = 6t + 24t + 29 = 6(t + 2) + 5 5 . Do đó P = 5 khi t = 2 − M ( 3 − ;3; 6) − . min x y −1 z +1 Câu 8: Cho đường thẳng : = = và hai điểm (
A 1; 0; −1), B(2;1; 1
− ). Biết điểm M thuộc 1 1 − 1
đường thẳng sao cho T = MA + 2MB đạt giá trị nhỏ nhất là T . Khi đó, T bằng bao min min nhiêu? A. T = 4. B. T = 3 . C. T = 14 . D. T = 6 . min min min min Lời giải Chọn C 5 2
Gọi I là điểm thỏa mãn IA + 2IB = 0 I ; ; −1 . 3 3
Ta có: P = MA + 2MB = MI + IA + 2MI + 2IB = 3MI = 3.IM .
M M (t ;1− t ;−1+ t) 2 2 2 5 1 26 2 14 14 2 2 IM = t − + t − +
+ t = 3t − 4t + = 3 t − + . 3 3 9 3 9 3 2 Do đó: P = 14 khi t = . min 3
Nhận xét: Ở Câu 7,8 này, ta có thể giải trực tiếp khi biểu diễn điểm M theo tham số t mà
không cần tìm tâm tỉ cự của hệ điểm như Lời giải trên. Câu 9:
Cho mặt phẳng ( ) : x + 2 y + 2z + 9 = 0 và ba điểm (
A 1; 2; 0), B(2; 0; 1
− ), C(3;1;1). Tìm tọa độ
điểm M ( ) sao cho 2 2 2
2MA + 3MB − 4MC đạt giá trị nhỏ nhất. A. M (1; 2 − ; 3 − ). B. M ( 3 − ;1; 4 − ). C. M ( 3 − ;2; 5 − ).
D. M (1; 3 − ; 2 − ). Lời giải Chọn C
Giả sử I ( x ; y ; z là điểm thỏa mãn: 2IA+ 3IB − 4IC = 0 (1) 0 0 0 )
2(1− x + 3 2 − x − 4 3− x = 0 − − = = − 0 ) ( 0 ) ( 0 ) x 4 0 x 4 0 0
(1) 2(2 − y + 3 − y − 4 1− y = 0 − y = 0
y = 0 I 4 − ;0; 7 − 0 ) ( 0) ( 0 ) 0 0 ( ) 2 (−z ) + 3( 1
− − z ) − 4(1− z ) = 0 −z − 7 = 0 z = 7 − 0 0 0 0 0 2 2 2 Ta có: 2 2 2
2MA + 3MB − 4MC = 2MA + 3MB − 4MC
= (MI + IA)2 + (MI + IB)2 − (MI + IC)2 2 3 4
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 5/ 8 5 = ( 2 2 MI +
MI IA + IA ) + ( 2 2 MI +
MI IB + IB ) − ( 2 2 2 2. . 3 2. .
4 MI + 2.MI.IC + IC ) 2 2 2 2
= MI + 2IA + 3IB − 4IC + 2MI.(2IA+3IB −4IC) 2 2 2 2
= MI + 2IA +3IB − 4IC + 2MI.0 2 2 2 2
= MI + 2IA + 3IB − 4IC Khi đó, để 2 2 2
2MA + 3MB − 4MC đạt giá trị nhỏ nhất thì MI có độ dài ngắn nhất
Mà M ( ) M là hình chiếu vuông góc của I lên ( ) .
Gọi d là đường thẳng qua I và vuông góc ( ) d có 1 VTCP u = (1;2;2) x = 4 − + t
Phương trình đường thẳng d : y = 2t z = 7 − + 2t
Giả sử tọa độ điểm M ( 4 − +t;2t; 7 − + 2t) Do M ( ) ( 4
− + t) + 2.2t + 2( 7
− + 2t)+9 = 0 9t −9 = 0 t =1 M ( 3 − ;2; 5 − ). x +1 y −1 z + 2
Câu 10: Cho đường thẳng : = = và (
A 1;1; 0), B(3; 1
− ;4). Tìm tọa độ điểm M thuộc 1 1 − 2
sao cho MA + MB đạt giá trị nhỏ nhất. 1 1 3 3 A. M ( 1 − ;1; 2) − . B. M ; − ;1 .
C. M − ; ; −3 .
D. M (1; 1 − ;2). 2 2 2 2 Lời giải Chọn D x +1 y −1 z + 2 : = = có 1 VTCP u (1; 1 − ;2) 1 1 − 2 (
A 1;1; 0), B(3; 1 − ;4) AB(2; 2 − ;4) 1+1 1−1 Ta có: AB (2; 2
− ;4) cùng phương với u(1; 1 − ;2) và ( A 1;1; 0) (do ) 1 −1
AB // AB và đồng phẳng .
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 6/ 8 5
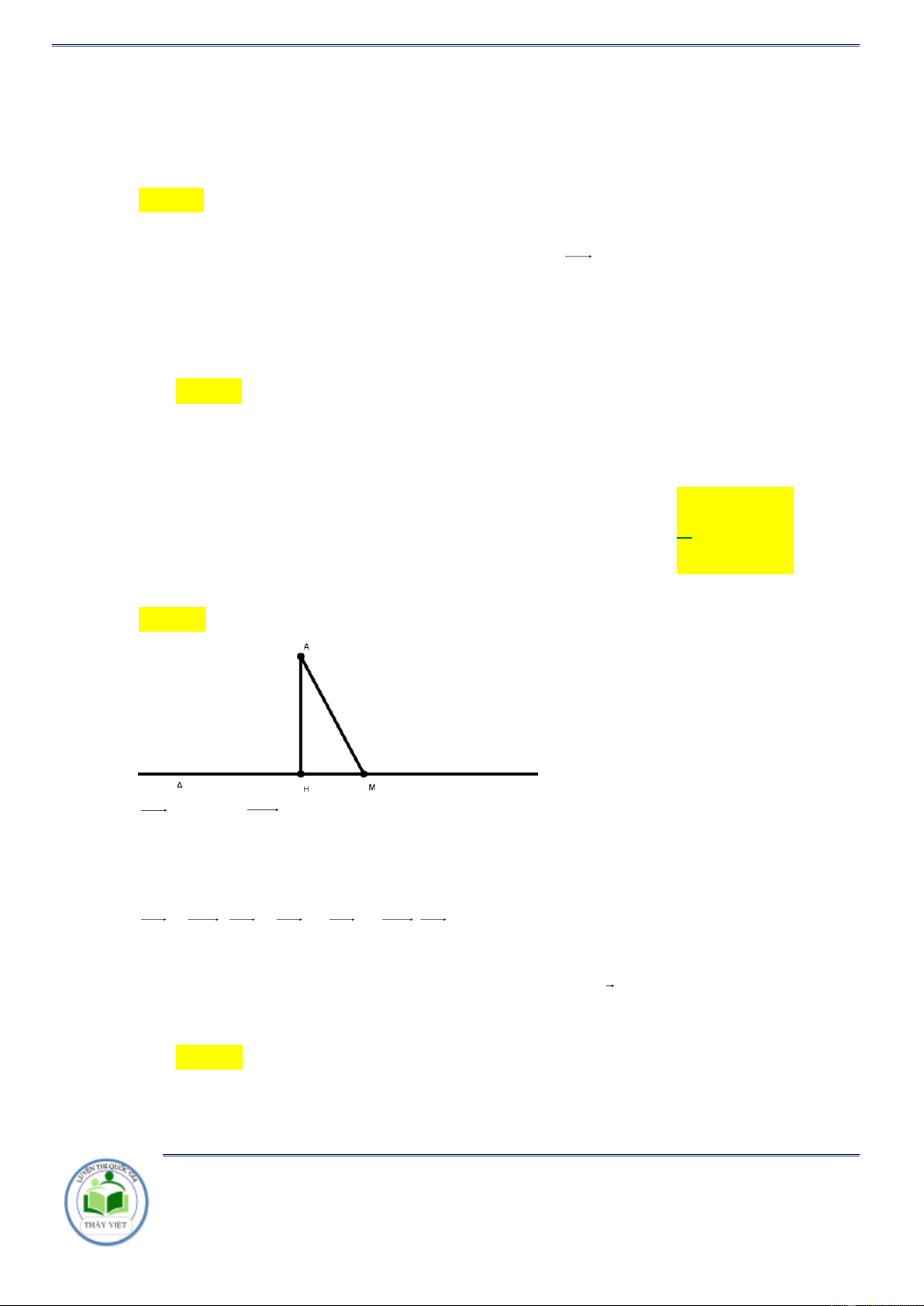
* Xét mặt phẳng chứa AB và :
Gọi A là điểm đối xứng của A qua ; ( ) là mặt phẳng qua A , vuông góc với
Khi đó, giao điểm H của với ( ) là trung điểm của AA () có 1 VTPT n(1; 1 − ;2) , đi qua (
A 1;1; 0) , có phương trình: ( 1 x − ) 1 − ( 1 y − )
1 + 2( z − 0) = 0 x − y + 2z = 0 x +1 y −1 z + 2 H : = = Giả sử H ( 1 − +t;1−t; 2 − + 2t) 1 1 − 2 H ( ) ( 1
− +t)−(1−t)+ 2( 2
− + 2t) = 0 6t −6 = 0 t =1 H (0;0;0)
2x = x + x = + = − 2.0 1 x x 1 H A A A A
H là trung điểm của AA 2y = y + y = + = − − − 2.0 1 y y 1 A H A A A A ( 1; 1;0)
2z = z + z = + = 2.0 0 z z 0 H A A A A
Ta có: MA+ MB = MA + MB A B
(MA+ MB) = A B
khi và chỉ khi M trùng với M là min 0
giao điểm của AB và x = 1 − + t A B = (4;0;4) A B có 1 VTCP (1;0; ) 1 và đi qua A( 1 − ; 1
− ;0) , có phương trình: y = 1 − z = t x = 1 − + t
Mà : y = 1− t z = 2 − + 2t 1 − + t = 1 − + t t = t t = 2 Giải hệ phương trình: 1 − t = 1 − t = 2 t = 2 2 − + 2t = t 2 − + 2t = t M 1; 1 − ;2 0 ( )
Vậy, để MA + MB đạt giá trị nhỏ nhất thì M (1; 1 − ;2) . x y −1 z +1 = = − − −
Câu 11: Cho đường thẳng : và hai điểm (
A 1;1; 2), B( 1;0; 1). Biết điểm M 1 − 1 1
thuộc sao cho biểu thức T = MA + MB đạt giá trị nhỏ nhất là T . Khi đó tính T . min min 1 1 1 1 T = 2 1− T = 2 + T = 2 − T = 2 1+ min min min min A. 3 . B. 3 . C. 3 . D. 3 . Lời giải Chọn D
Vì điểm M thuộc nên ta có M ( t
− ;t +1;t −1) . Lúc đó
T = MA + MB = (t + )2 + t + (t + )2 + (t − )2 + t + (t + )2 2 2 1 1 1 1 2 2
= 3t + 4t + 2 + 3t + 2
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 7 / 8 5 2 2 2 2 2 2 2 = 3 t + + + t + . 3 3 3 2 2 2
Đặt u = t + ; , v = t − ;
. Ta cóT = 3( u + v ) 3 u + v . 3 3 3 2 2 2 2 2 1 Tứclà T 3. + + = 2 1+ . 3 3 3 3 2 2 t + 1
Đẳng thức xảy ra khi và chỉ khi 3 3 = t = 1 − + . t − 2 3 3 1 Vậy T = 2 1+ . min 3 x +1 y −1 z + 2
Câu 12: Cho đường thẳng : = = và hai điểm ( A 1;1; 0), B( 1 − ;0;1). 1 1 − 2 Biết điểm M ( ; a ; b c) = − − +
thuộc sao cho biểu thức T
MA MB đạt giá trị lớn nhất. Khi đó tổng a b c bằng: 33 4 33 A. 8 . B. 8 + 33 . C. 8 + . D. 8 + . 3 3 Lời giải Chọn D qua C( 1
− ;1;− 2), và có vectơ chỉ phươngu = (1; 1 − ;2) AB = ( 2 − ;−1;1); AC = ( 2 − ;0;− 2) . A ; B u AC 0 nên ;
AB không đồng phẳng
Vì điểm M thuộc nên ta có M ( 1
− + t ;1− t ;− 2 + 2t), t . Lúc đó
P = MA − MB =
(t − )2 +t +( t − )2 − ( t
− )2 + (t − )2 + ( t − )2 2 2 2 2 1 2 3 2 2
= 6t −12t + 8 − 6t −14t +10 . 2 P = (t − )2 1 7 11 6 1 + − t − + 3 6 6 3 7 11
Đặt u = t −1; ,
v = t − ;
. Ta có | u | − | v | u − v . 3 6 6 2 2 1 3 11 Tức là P 6. + − . 6 3 6
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 8 / 8 5 3 t −1 33
Đẳng thức xảy ra khi và chỉ khi 3 = t = 3+ . 7 11 3 t − 6 6 4 33
Với ta có a − b + c = 4t − 4 = 8 + . 3 x y −1 z
Câu 13: Cho đường thẳng : = = và hai điểm ( A 0;1; 3 − ), B( 1
− ;0;2). Biết điểm M thuộc 1 1 1
sao cho biểu thức T = MA − MB đạt giá trị lớn nhất là T .Khi đó, T bằng bao nhiêu? max max A. T = 3 . B. T = 2 3 . C. T = 3 3 . D. T = 2 . max max max max Lời giải Chọn C x = t − Ta có AB = ( 1
− ; −1; 5), phương trình đường thẳng AB là y =1−t (t ) . z = 3 − + 5t 1 1 1
Xét vị trí tương đối giữa AB và ta có AB cắt tại C − ; ;− . 2 2 2 1 1 5 1 Suy ra AC = − ; − ;
AC = AB C là trung điểm AB . 2 2 2 2
T = MA − MB AB . Dấu “=” xảy ra khi M A hoặc M B . Do đó T = AB = 27 = 3 3 . max
Câu 14: Cho mặt phẳng ( ) :x + 2y + 2z + 9 = 0 và ba điểm A(1;2;0), B(2;0;− ) 1 , C (3;1; ) 1 . Tìm tọa độ
điểm M ( ) sao cho 2 2 2
2MA + 3MB − 4MC đạt giá trị nhỏ nhất. A. M (1; 2 − ;− ) 3 . B. M ( 3 − ;1; 4 − ) . C. M ( 3 − ;2; 5 − ) .
D. M (1; 3 − ; 2 − ) . Lời giải Chọn C
Ta đi tìm tọa độ điểm I ( ; a ;
b c) sao cho 2IA+ 3IB − 4IC = 0 . Ta có IA = (1− ; a 2 − ;
b − c); IB = (2 − ; a − ;
b −1− c); IC = (3 − ; a 1− ; b 1− c)
2IA + 3 IB − 4 IC = ( 4 − − ; a − ;
b − 7 − c) = 0 a = 4
− ; b = 0; c = 7 − Suyra I ( 4 − ; 0; −7)() . 2 2 2 Khiđó 2 2 2
T = 2MA + 3MB − 4MC = 2(MA) +3(MB) − 4(MC)
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 9 / 8 5
= (MI + IA)2 + (MI + IB)2 − (MI + IC)2 2 2 2 2 2 3 4
= MI + 2IA + 3IB − 4IC + 2MI (2IA+3IB−4IC) 2 2 2 2
= MI + 2IA + 3IB − 4IC
Do đó T nhỏ nhất khi MI ngắn nhất, khi và chỉ khi M là hình chiếu vuông góc của I trên mặt phẳng ( ) .
Đường thẳng d qua I và vuông góc với ( ) có vectơ chỉ phương u = (1; 2; 2) x = 4 − + t
Do đó phương trình của d là y = 2t (t ) z = 7 − + 2t x = 4 − + t y = 2t
Khi đó tọa độ M thỏa mãn hệ
t =1 M ( 3 − ;2; 5 − ). z = 7 − + 2t
x + 2y + 2z +9 = 0
Câu 15: Cho mặt phẳng (P) :5x − y + z − 2 = 0 và hai điểm A(0; 1 − ;0), B( 2 − ;1;− ) 1 . Biết điểm M
thuộc mặt phẳng (P) sao cho 2 2
MA − 2MB đạt giá trị lớn nhất. Khi đó điểm M có hoành độ x bằng bao nhiêu? M A. x = 1 .
B. x = 2 . C. x = 1 −
D. x = 3. M M M M Lời giải Chọn A
Gọi I là điểm thỏa mãn: IA − 2IB = 0 I ( 4 − ;3;− 2) . Khi đó 2 2 2 2 2
T = MA − 2MB = −MI + IA − 2.IB T MI
M là hình chiếu của I lên mặt max min
phẳng (P). Khi đó đường thẳng MI đi qua I ( 4
− ;3;− 2) và vuông góc với (P) nên nhận VTPT x = 4 − + 5t
n (5; −1;1) của (P) làm VTCP, phương trình là y = 3 − t (t R) . z = 2 − + t Ta có
M = IM (P) Tọa độ M là nghiệm của hệ x = 4 − + 5t t =1 y = 3− t x =1
M (1;2;−1) x =1. z = 2 − + t y = 2 M 5
x − y + z − 2 = 0 z = −1
Câu 16: Cho mặt phẳng (P) :x + y − 3z + 7 = 0 và ba điểm A(2; 1 − ;0), B(0; 1 − ;2),C(2;3;− ) 1 . Biết
điểm M ( x ; y ; z thuộc mặt phẳng (P) sao cho 2 2 2
MA + 3MB − 2MC đạt giá trị nhỏ nhất. 0 0 0 )
Khi đó tổng T = x + 3y − 2z bằng bao nhiêu? 0 0 0 A. T = 0 . B. T = 4 − .
C. T = 1.
D. T = 14 − . Lời giải
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 10 / 8 5 Chọn D
Gọi I là điểm thỏa mãn: IA + 3IB − 2IC = 0 I ( 1 − ;− 5;4) . Khi đó 2 2 2 2 2 2 2
T = MA + 3MB − 2MC = 2MI + IA + 3IB − 2IC T MI
M là hình chiếu mim max
của I lên mặt phẳng (P). Khi đó đường thẳng MI đi qua I ( 1
− ;− 5;4) và vuông góc với (P) x = 1 − + t
nên nhận VTPT n (1;1; 3
− ) của (P) làm VTCP, phương trình là y = 5
− + t (t R) . z = 4−3t Ta có
M = IM (P) Tọa độ M là nghiệm của hệ x = 1 − + t t =1 y = 5 − + t x = 0
M (0;− 4;1) T = 1 − 4. z = 4 − 3t y = 4 − 5
x − y + z − 2 = 0 z =1
Câu 17: Cho mặt phẳng ( ) :2x + 6y −3z −1 = 0 và ba điểm A(1; 1 − ; 5
− ), B(0;1;2),C(2;3;− ) 1 . Biết
điểm M thuộc mặt phẳng ( ) sao cho 2 2 2
P = MA + 2MB − 2MC đạt giá trị nhỏ nhất là P . min
Khi đó P bằng bao nhiêu? min A. 16 . B. 17 . C. 18 . D. 19 . Lời giải Chọn B Gọi I ( ; a ;
b c) sao cho IA+ 2IB − 2IC = 0 .
OI = OA+ 2OB − 2OC . I ( 3 − ; 5 − ;− ) 3 . 2 2 2 Ta có 2 2 2
P = MA + 2MB − 2MC = (MI + IA) + 2(MI + IB) − 2(MI + IC ) 2 2 2 2
= MI + IA + 2IB − 2IC + 2(IA+ 2IB − 2IC) 2 2 2 2
= MI + IA + 2IB − 2IC . Do 2 2 2
IA + 2IB − 2IC = 36 + 70 − 93 = 13 không đổi nên m P in MImin 2. 3 − + 6. 5 − − 3 3 − −1 Và MI
= d (I,(P)) ( ) ( ) ( ) = = min 4 . 4 + 36 + 9 Vậy m P = + = in 4 13 17 .
Câu 18: Cho mặt phẳng ( ) :2x − y −3z +1= 0 và ba điểm A(1;1;− ) 1 , B( 3 − ;1;0),C( 2 − ;1;− ) 1 . Tìm tọa
độ điểm M ( ) sao cho 2MA + 5MB − 6MC đạt giá trị nhỏ nhất. A. M (0;1;0) .
B. M (2; 1 − ;2).
C. M (1;0; ) 1 . D. M ( 1 − ;2;− ) 1 . Lời giải Chọn C
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 11/ 8 5 Gọi I ( ; a ;
b c) sao cho 2IA+ 5IB − 6IC = 0
OI = 2OA+5OB −6OC . I ( 1 − ;1;4).
2MA + 5MB − 6MC = 2(MI + IA) + 5(MI + IB) − 6(MI + IC) = MI .
Nên 2MA + 5MB − 6MC đạt giá trị nhỏ nhất khi MI đạt giá trị nhỏ nhất khi và chỉ khi M là
hình chiếu của I trên (P) .
Do I (P) MI ⊥ (P). x = 1 − + 2t
MI : y =1−t M ( 1
− + 2t;1−t;4 −3t). z = 4−3t
Mà M (P) 2( 1
− + 2t)−(1−t)−3(4−3t)+1= 0 t =1. M (1;0; ) 1 .
Câu 19: Cho mặt phẳng (P) :x − y − z −1 = 0 và hai điểm A( 5 − ;1;2), B(1; 2
− ;2) . Trong tất cả các điểm
M thuộc mặt phẳng ( P) , điểm để MA + 2MB đạt giá trị nhỏ nhất có tung độ y là M A. y = 1. B. y = 2 − .
C. y = 0. D. y = 1 − . M M M M Lời giải Chọn A
Gọi I là điểm thỏa mãn: IA + 2IB = 0 I ( 1 − ;−1;2) .
Khi đó T = MA + 2MB = 3MI T MI
M là hình chiếu của I lên mặt phẳng (P). min min
Khi đó đường thẳng MI đi qua I ( 1
− ;−1;2) và vuông góc với (P) nên nhận VTPT x = 1 − + t n (1; 1 − ; 1
− ) của (P) làm VTCP, phương trình là y = 1
− − t (t R) . z = 2−t Ta có
M = IM (P) Tọa độ M là nghiệm của hệ x = 1 − + t t =1 y = 1 − − t x = 0
M (0;− 2;1) y = 2 − . z = 2 − t y = 2 M −
x − y − z −1= 0 z =1
Câu 20: Cho mặt phẳng ( ) :2x + y −3z − 6 = 0 và hai điểm A(0; 1 − ; ) 1 , B (1; 2
− ;0). Biết điểm M thuộc
mặt phẳng ( ) sao cho P = 2MA − MB đạt giá trị nhỏ nhất là P . Khi đó P bằng bao min min nhiêu? A. P = 2 3 . B. P = 14 . C. P = 3. D. P = 21 . min min min min
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 12 / 8 5 Lời giải Chọn D
Gọi I là điểm thỏa mãn: 2IA − IB = 0 I ( 1 − ;0;2) .
Khi đó P = 2MA − MB = MI P MI
M là hình chiếu của I lên mặt phẳng (P). Khi min min 2 − − 6 − 6 đó P = d(I / ()) = = 14. min 2 2 2 2 +1 + 3
Câu 21: Cho mặt phẳng ( ) :x − y + 2z −1= 0 và hai điểm A(0; 1 − ; ) 1 , B(1;1; 2
− ). Biết M ( ) sao cho
MA + MB đạt giá trị nhỏ nhất. Khi đó, hoành độ x M M của điểm là 1 2 A. x = . B. x = 1 − . C. x = 2 − . D. x = . M 3 M M M 7 Lời giải Chọn D
Ta có: ( x − y + 2z − )
1 ( x − y + 2z − ) 1 = (0 +1+ 2.1− ) 1 (1−1− 4 − )
1 0 nên hai điểm A và A A A B B B
B nằm khác phía so với mặt phẳng ( ) .
Nên MA + MB đạt giá trị nhỏ nhất khi M = AB ( ) . x = t
Phương trình đường thẳng AB : y = 1
− + 2t , do đó tọa độ điểm M là nghiệm của hệ z =1−3t 2 t = 7 x = t 2 = x y = 1 − + 2t 7 2 3 1 2 phương trình . Do đó M ; − ; , x = z = 1− 3t M 3 . = − 7 7 7 7 y
x − y + 2z −1 = 0 7 1 z = 7
Câu 22: Cho mặt phẳng ( ) :x − y + z +1 = 0 và hai điểm A(1;1;0), B(3; 1
− ;4). Gọi M là điểm thuộc
mặt phẳng ( ) sao cho P = MA + MB đạt giá trị nhỏ nhất. Khi đó giá trị của P là: A. P = 5.
B. P = 6 .
C. P = 7 .
D. P = 8. Lời giải Chọn B
Ta có: ( x − y + z + )
1 ( x − y + z + ) 1 = (1−1+ 0 + ) 1 (3+1+ 4 + )
1 0 nên hai điểm A và B A A A B B B
cùng nằm về một phía của mặt phẳng ( ) .
Gọi H là hình chiếu vuông góc của A lên mặt phẳng ( ) .
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 13/ 8 5 x = 1+ t
Phương trình đường thẳng AH : y = 1− t . z = t 1 t = − 3 x = 1+ t 2 = x y = 1− t 3
Do đó tọa độ điểm H là nghiệm của hệ phương trình . z = t 4 = y
x − y + z +1 = 0 3 1 z = − 3 2 4 1 Do đó H ; ; − . 3 3 3 1 5 2
Gọi A đối xứng với A qua ( ) , suy ra A ; ; − . 3 3 3
Ta có MA+ MB = MA + MB A B P = A B = 6 .
Câu 23: Cho mặt phẳng ( ) :x + y −3z −5 = 0 và hai điểm A(1; 1 − ;2), B( 5 − ; 1 − ;0). Biết M ( ; a ; b c)
thuộc mặt phẳng ( ) sao cho MA + MB đạt giá trị nhỏ nhất. Khi đó, giá trị của biểu thức
T = a + 2b + 3c bằng bao nhiêu? A. T = 5 . B. T = 3 − . C. T = 7 − . D. T = 9 − . Lời giải Chọn C
Ta có: ( x + y −3z −5)(x + y −3z −5) = (1−1−3.2 −5)( 5
− −1−3.0−5) 0 nên hai điểm A A A A B B B
và B cùng nằm về một phía của mặt phẳng ( ) .
Gọi H là hình chiếu vuông góc của A lên mặt phẳng ( ) . x =1+ t
Phương trình đường thẳng AH : y = 1 − + t . z = 2−3t x = 1+ t t =1 y = 1 − + t x = 2
Do đó tọa độ điểm H là nghiệm của hệ phương trình . z = 2 − 3t y = 0
x + y −3z −5 = 0 z = 1 − Do đó H (2;0;− ) 1 .
Gọi A đối xứng với A qua ( ) , suy ra A(3;1;− 4) .
Ta có MA + MB = MA + MB A B
nên MA+ MB nhỏ nhất khi M = A B ().
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 14 / 8 5 x = 3− 4t
Phương trình đường thẳng AB : y = 1− t . z = 4 − + 3t 12 t = 11 x = 3 − 4t 15 = − x y = 1− t Do đó tọa độ điểm 11
M là nghiệm của hệ phương trình . z = 4 − + 3t 1 = − y
x + y − 3z − 5 = 0 11 20 z = − 11 15 1 20 Do đó M − ; − ; −
, T = a + 2b +3c = 7 − . 11 11 11
Câu 24: Cho A(1;1;0), B(3; 1
− ;4) và mặt phẳng ():x − y + z +1= 0. Tìm tọa độ điểm M ( ) sao cho
MA − MB đạt giá trị lớn nhất. 3 5 1 1 2 2 A. M (1;3;− ) 1 . B. M ; ; − . C. M ; ; − .
D. M (0;2; ) 1 . 4 4 2 3 3 3 Lời giải Chọn B
Ta có: ( x − y + z + )
1 ( x − y + z + ) 1 = (1−1+ 0 + ) 1 (3+1+ 4 + )
1 0 nên hai điểm A và B A A A B B B
cùng nằm về một phía của mặt phẳng ( ) .
Ta có MA − MB AB = 2 6 , nên MA − MB lớn nhất khi và chỉ khi M = AB ( ) . x =1+ 2t
Phương trình đường thẳng AB : y = 1− 2t , do đó tọa độ điểm M là nghiệm của hệ z = 4t 1 t = − 8 x = 1+ 2t 3 = x y = 1− 2t 3 5 1 phương trình 4 . Do đó M ; ; − . z = 4t 5 = 4 4 2 y
x − y + z +1 = 0 4 1 z = − 2 x −1 y z +1
Câu 25: Cho hai điểm A(1; 1
− ;2), B(0;1;6) và đường thẳng d : = = 2 1 1
− . Biết điểm M thuộc.
đường thẳng d sao cho biểu thức T = AM.BM đạt giá trị nhỏ nhất bằng T . Khi đó giá trị min T bằng bao nhiêu? min
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 15/ 8 5 A. T =14 . B. T = 3 . C. T = 3 2 . D. T = 2 3 . min min min min Lời giải Chọn A Vì M d M 2t 1;t; t 1 AM 2t;t 1; t 3 BM 2t 1;t 1; t 7 AM.BM 2t 2t 1 t 1 t 1 t 1 t 3 2 2 6t 12t 20 6 t 1 14 14. x +1 y z −1
Câu 26: Cho hai điểm A(0; 1
− ;2), B(1;1;2) và đường thẳng d : = = . Biết điểm M ( ; a ; b c) 1 1 1
thuộc đường thẳng d sao cho tam giác MAB có diện tích nhỏ nhất. Khi đó, giá trị
T = a + 2b + 3c bằng bao nhiêu? A. T = 5 .
B. T = 3.
C. T = 4 .
D. T =10 . Lời giải Chọn D M d M t 1;t;t 1 AM t 1;t 1;t 1 Mà AB 1;2; 0 AB AB 5. AM;AB 2 2t;t 1;t 3 Mà 1 2 2 2 S AM;AB 2 2t t 1 t 3 MAB 2 2 4 10 10 2 6t 16t 14 6 t 3 3 3 1 a 3 4 1 4 7 4
Dấu bằng xảy ra khi t M ; ; b T a 2b 3c 10. 3 3 3 3 3 7 c 3
Câu 27: Viết phương trình đường thẳng đi qua M (1;0; 1
− ) và tạo với mặt phẳng
():2x− y +3z −6 = 0 góc lớn nhất.
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 16/ 8 5 x =1+ 2t x =1− 2t x =1+ 2t x = 2 + t
A. y = t − .
B. y = t − .
C. y = t − .
D. y = 1 − . x = 1 − + 3t z = 1 − + 3t z = 1 − − 3t z = 3 − t Lời giải Chọn A
Đường thẳng đi qua M (1;0; 1
− ) tạo với ( ) góc lớn nhất max( ,
()) = 90 ⊥ ().
Khi đó đường thẳng đi qua nhận M (1;0; 1 − ) và n 2; 1
− ;3 làm véc tơ chỉ phương nên ( ) ( ) x =1+ 2t
phương trình đường thẳng có dạng: y = t − x = 1 − + 3t Vậy Chọn A
Câu 28: Viết phương trình đường thẳng đi qua M (4; 2 − ; )
1 , song song với mặt phẳng
():3x−4y + z −12 = 0 và cách điểm A( 2
− ;5;0) một khoảng lớn nhất. x =1+ 4t x = 4 + t x = 4 − t x = 4 + t
A. y = 1− 2t .
B. y = 2 − + t .
C. y = 2 − + t .
D. y = 2 − + t x = 1 − + t z = 1− t z = 1+ t z = 1 − + t Lời giải Chọn D n − − (3; 4; ) ( ) 1 , AM (6; 7; ) 1
Gọi H là hình chiếu của A trên đường thẳng suy ra d ( ; A ) = AH Ta có:
AH AM max (d ( ;
A )) = AM H M . Khi đó u
⊥ AM , u ⊥ n u = AM ,n = − − − = − ( 3; 3; 3) 3(1;1; ) ( ) ( ) ( ) ( ) ( ) 1 x = 4 + t
Đường thẳng đi qua M (4; 2 − ; )
1 có véc tơ chỉ phương u (1;1; ) 1 có dạng: y = 2 − + t z =1+t Vậy Chọn D
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 17 / 8 5 x = t
Câu 29: Viết phương trình đường thẳng đi qua A(1;1; )
1 , vuông góc với đường thẳng ' : y = 1+ t z =1+ 2t và cách điểm B (2;0; )
1 một khoảng lớn nhất. x = 1− t x = 1+ t x = 1+ t x =1+ t
A. y = 1+ t .
B. y = 1+ t .
C. y = 1− t .
D. y = 1+ t . z = 1+ t z = 1− t z = 1+ t z = 1 − + t Lời giải Chọn B
Giả sử , ' có VTCP lần lượt là u = , u 1;1; 2 ' ( )
Do ⊥ ' nên u ⊥ u ( ) 1 '
Gọi H là hình chiếu của B trên .
Do A nên BH BA .
Suy ra cách B một khoảng lớn nhất khi và chỉ khi H A hay ⊥ AB u ⊥ AB = − (2) (1; 1;0) . Từ ( )
1 và (2) nên ta chọn một VTCP của : u = u ; AB = 2;2; 2 − = 2 1;1; 1 − ' ( ) ( ) . x =1+ t
Vậy : y = 1+ t . z =1−t
Câu 30: Trong không gian với hệ tọa độ Oxyz , viết phương trình đường thẳng qua A(1;1;2) và x −1 y − 2 z vuông góc với d : =
= đồng thời tạo với trục Oz góc lớn nhất. 2 1 2 x =1 x =1− t x =1+ t x = 1+ t
A. y = 1+ t .
B. y = 1 .
C. y = 1− 2t .
D. y = 2 − + t . z = 2 − 2t z = 2 + t z = 2 z = 2t Lời giải Chọn C
d có VTCP là u = (2;1;2 . d )
Oz có VTCP là k = (0;0; ) 1 .
Gọi u là VTCP của .
Do ⊥ d nên u ⊥ u ( ) 1 d
tạo với Oz một góc lớn nhất khi và chỉ khi ⊥ Oz hay u ⊥ k . (2)
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 18 / 8 5 Từ ( )
1 và (2) nên ta chọn một VTCP của : u = u ;k = − (1; 2;0 d ) . x =1+ t
Vậy : y = 1− 2t . z = 2
Câu 31: Trong không gian với hệ tọa độ Oxyz viết phương trình đường thẳng qua A (1;1; 2) , nằm
trong ( ) : x + 2y − z − 1 = 0 , đồng thời tạo với trục Oz góc nhỏ nhất. x = 5 + 2t x = 1+ 5t x = 1+ 2t x = 1+ t
A. y = 2 + t .
B. y = 1+ t .
C. y = 1+ 5t .
D. y = 1+ 2t . z = 1 + t z = 2 + 2t z = 2 + t z = 2 + 5t Lời giải Chọn D
Gọi VTCP của là u = (a; ; b c) với 2 2 2
a + b + c 0 .
VTPT của ( ) là n = (1;2;− ) 1
Do u ⊥ n nên a + 2b − c = 0 c = a + 2b . Từ đó u = ( ; a ; b a + 2b) .
Trục Oz có VTCP là u = (0;0; ) 1 .
Gọi là góc tạo bởi và trục Oz . a + 2 2 a + 2b b t + 2 t + 4t + 4 cos = = = = . + + + + + + + a b (a 2b) 2 2 2 2 2 2 2t 4t 5 a a 2t 4t 5 2 + 4 + 5 b b 2 t + 4t + 4 Ta đặt y = 2
2t + 4t + . Ta đi tìm Min, Max của biểu thức này. 5 2 t + 4t + 4 y = (2y − ) 2
1 t + 4y − 4 t + 5y − 4 = 0 2 ( ) 2t + 4t + . (1) 5 1 3 + TH1: Nếu y = thì t = − . 2 4 1 + TH1: Nếu y
thì (1) là phương trình bậc hai.Có 2 ' = 6 − y + 5y . 2 5
Để phương trình có nghiệm thì 2 ' = 6
− y + 5y 0 0 y . 6 1
Ta có min, khi và chỉ khi cos max. Khi đó t = 2
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 19 / 8 5 a 1 Suy ra
= . Từ đó chọn a =1;b = 2 c = 5. b 2
Vậy u = (1;2;5) . Chọn D x − 1 y 2 z
Câu 32: Cho A(1; 4; 2) , B(−1; 2; 4) + ,d : =
= . Viết phương trình đường thẳng qua A , cắt −1 1 2 d sao cho d ( ,
B ) là nhỏ nhất. x = 1+ t x = 1+ t x = 15 + t x = 1+ 15t
A. y = 4 − t .
B. y = −1 + 4t .
C. y = 18 + 4t .
D. y = 4 + 18t . z = 2 − 3t z = −3 + 2t z = −19 − 2t z = 2 − 19t Lời giải Chọn D
d đi qua M (1; 2
− ;0) và có một VTCP là u = ( 1 − ;1;2) .
Gọi (P) là mặt phẳng chứa A và d .
Kẻ BK ⊥ và BH ⊥ ( )
P . Ta có BK BH . Khi đó d ( ,
B ) = BK đạt GTNN khi K H . Khi đó qua , A H .
Lập phương trình mặt phẳng (P) chứa A và d . n = ; u AM = (10; 2 − ;6 n = 5; 1 − ;3 . P ) . Chọn P ( )
Suy ra phương trình (P) : 5x − y + 3z − 7 = 0 .
Ta tìm toạ độ điểm H là hình chiếu vuông góc của B lên (P) . x = 1 − + 5t
Phương trình đường thẳng BH : y = 2 − t . z = 4 + 3t Gọi H ( 1
− + 5t;2 −t;4 +3t) . Cho H (P) ta được:
(− + t) −( −t) + ( + t) 2 5 1 5 2 3 4 3 − 7 = 0 t = . 35 5 − 68 146
Toạ độ điểm H là H ; ; . 7 35 35 x = 1+15t
Khi đó phương trình đường thẳng qua ,
A H là : y = 4 +18t . z = 2 −19t x − y + z Câu 33: Cho A( ) B(− ) 1 2 1; 4; 2 , 1; 2; 4 , d : = = A 1 −
. Viết phương trình đường thẳng a đi qua , cắt 1 2 d sao cho d ( , B a) là lớn nhất.
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 2 0 / 8 5 x =1+ t x =1+ t x =15 + t x =1+15t
A. y = 4 − 4t . B. y = 1 − + 4t .
C. y =18 + 4t .
D. y = 4 +18t . z = 2 − 3t z = 3 − + 2t z = 1 − 9 − 2t z = 2 −19t Lời giải Chọn A C (1; 2
− ;0)d , AC = (0; 6 − ; 2 − ) , u = ( 1
− ;1;2) là vecto chi phương của d nên vecto pháp tuyến 1
của mp(A,d) là p = n, − AC = ( 5 − ;1; 3 − ) 2 1 AB = ( 2 − ; 2
− ;2) n = − AB, p = (−2;8;6) 2
Gọi H là hình chiếu của B lên mặt phẳng (A,d), K là hình chiếu của H lên a, vậy d(B,a)=BK,
Dễ thấy BK lớn nhất khi K trùng A, khi đó BK=AB. Tại vị trí này,a nằm trong mp(A,d) và 1
vuông góc với AB nên vecto chỉ phương của a là − n = (1; −4; −3) . Phương trình đường 2 x =1+ t
thẳng cần tìm là: y = 4 − 4t z = 2−3t
Câu 34: Trong không gian với hệ tọa độ Oxyz , cho 2 điểm A(1;5;0), B(3;3;6) và đường thẳng x +1 y −1 z : =
= . Gọi d là đường thẳng qua B và cắt tại điểm C sao cho S đạt giá 2 1 − 2 ABC trị nhỏ nhất. x =1− 4t x =1− 2t x = 2 − + t x = 3 +10t A. y = 2 − t B. y = 3 − t . C. y = 3 − .
D. y = 3 − 3t . z = 2 − 3t z = 2 − 4t z = 4 − + 2t z = 6 +11t Lời giải Chọn D Ta thấy được S
nhỏ nhất khi d đi qua hình chiếu H của A lên mp(B, ) . ABC
Ta có phương trình mp(B, ) là 5x + 2 y − 4z + 3 = 0 21 8
Hình chiếu của A lên mp(B, ) là H −1; ; 5 5 5
Vecto chi phương của d là u = BH = (10; 3 − ) ;1 2 x = 3 +10t
Phương trình d là y = 3 − 3t z = 6+11t
Câu 35: Trong không gian Oxyz , gọi (P) là mặt phẳng song song với mặt phẳng (Oxz) và cắt mặt
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 2 1/ 8 5
cầu ( x − )2 + ( y + )2 2 1 2
+ z = 12 theo đường tròn có chu vi lớn nhất. Phương trình của (P) là
A. x − 2 y +1 = 0 .
B. y − 2 = 0 . C. y +1 = 0 .
D. y + 2 = 0 . Lời giải Chọn D
Mặt cầu (S ) theo đề bài có tâm I (1; 2
− ;0) và bán kính R = 2 3 .
(P)/ /(Oxz) (P): y +d = 0 (d 0).
(P) cắt (S) theo một đường tròn có chu vi lớn nhất khi (P) đi qua I (1; 2 − ;0)
Suy ra: d = 2 (nhận).
Vậy (P) : y + 2 = 0.
Câu 36: Trong không gian Oxyz , cho điểm M (1;2;3) . Gọi ( ) là mặt phẳng chứa trục Oy và cách
điểm M một khoảng lớn nhất. Phương trình mặt phẳng ( ) là
A. x + 3z = 0 .
B. x + 2z = 0.
C. x −3z = 0.
D. x = 0 . Lời giải Chọn A
Gọi H , K (0;2;0) lần lượt là hình chiếu của M trên ( ) và trục Oy thì MH MK = 10 .
Do đó, d (M,( )) = MH lớn nhất khi H K hay ( ) ⊥ MK .
Khi đó, ( ) đi qua O(0;0;0) và có một véctơ pháp tuyến là KM = (1;0;3) .
Phương trình mặt phẳng ( ) là x + 3z = 0 .
Câu 37: Trong không gian với hệ tọa độ Oxyz , cho mặt cầu 2 2 2
(S) : (x −1) + ( y − 2) + (z − 3) = 9 , điểm (
A 0;0; 2) . Phương trình mặt phẳng (P) đi qua A và cắt mặt cầu (S ) theo thiết diện là hình
tròn (C) có diện tích nhỏ nhất là:
A. x + 2 y + 3z − 6 = 0 . B. x + 2 y + z − 2 = 0 .
C. 3x + 2 y + 2z − 4 = 0 .
D. x − 2 y + 3z − 6 = 0 . Lời giải
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 2 2 / 8 5 Chọn B
Mặt cầu (S) có tâm I (1; 2;3) bán kính R = 3. IA = ( 1 − ; 2 − ; 1
− ) IA = 6 3 điểm (
A 0;0; 2) nằm trong mặt cầu (S) .
Gọi H là hình chiếu của I lên (P)
(C ) có diện tích nhỏ nhất khi và chỉ khi d I;( )
P = IH lớn nhất.
Ta có: IHA vuông tại H IH
= IA IA ⊥ (P) n = IA = ( 1 − ; 2 − ; 1 − ) max ( P)
Phương trình mặt phẳng (P) qua (
A 0;0; 2) và có vtpt n = IA = ( 1 − ; 2 − ; 1 − ) là: 1
− (x − 0) − 2(y − 0) −1(z − 2) = 0 x + 2y + z − 2 = 0
Câu 38: Trong không gian với hệ tọa độ Oxyz , cho ba điểm (
A 2;1;3) , B(3;0; 2) , C(0; −2;1) . Viết
phương trình mặt phẳng (P) đi qua ,
A B và cách C một khoảng lớn nhất?
A. 3x + 2y + z −11 = 0 . B. 3x + y + 2z −13 = 0 .
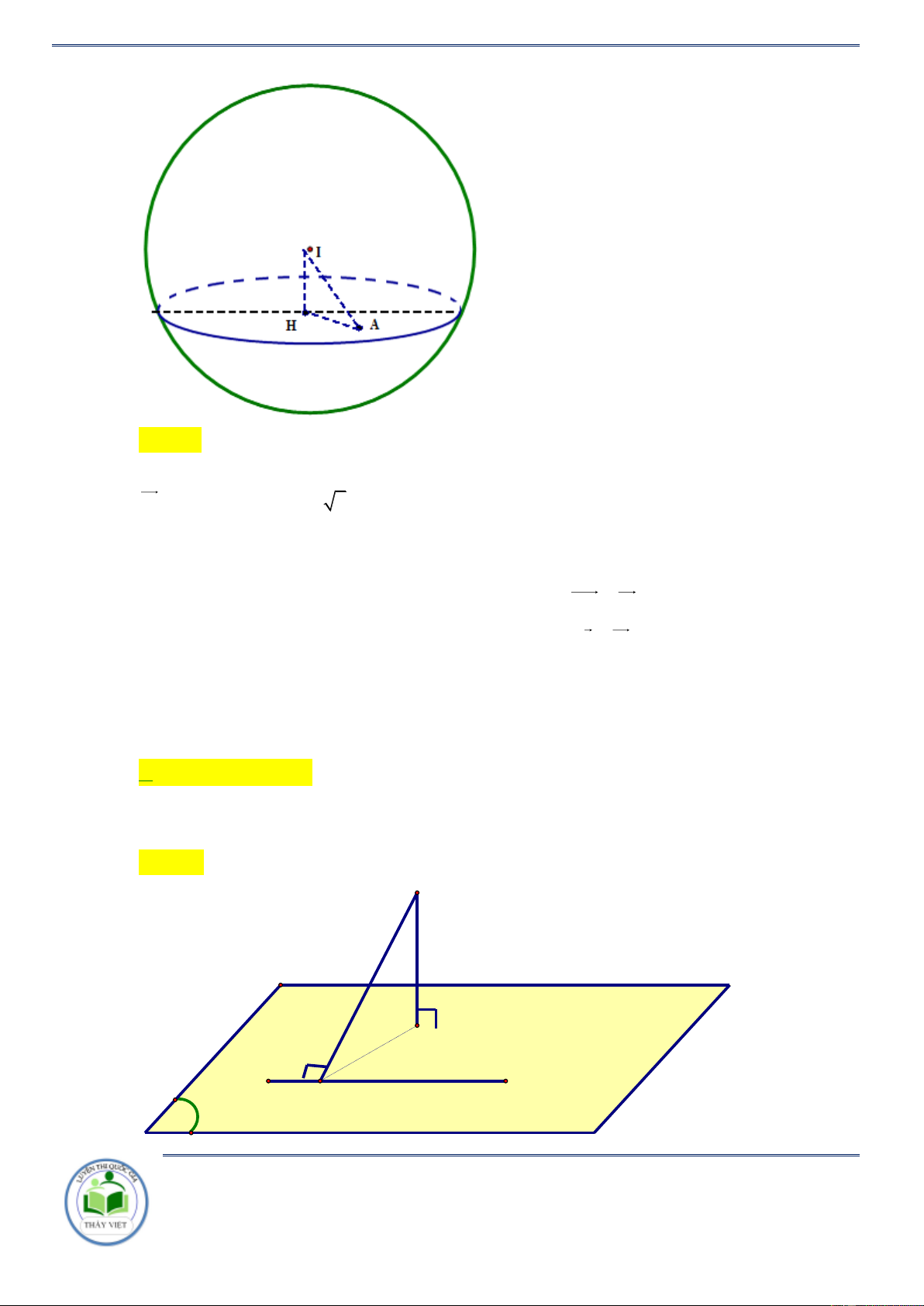
C. 2x − y + 3z −12 = 0 . D. x + y − 3 = 0 . Lời giải Chọn A C H A B I (P)
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 2 3/ 8 5 Ta có: AB = (1; 1 − ; 1 − ) .
Phương trình đường thẳng AB qua: (
A 2;1;3) có vtcp u = AB = (1; 1 − ; 1 − ) có dạng: x = 2 + t y =1− t . z = 3− t
Gọi I là hình chiếu của C lên AB I AB I (2 + t;1− t;3 − t)
CI = (2 + t;3 − t; 2 − t)
Ta có: CI ⊥ AB CI.AB = 0 2 + t −3+ t − 2 + t = 0 t =1 I (3;0;2)
Gọi H là hình chiếu C lên mặt phẳng (P) d C;( )
P = CH CI d C;( ) P
= CI CI ⊥ (P) max
Phương trình mặt phẳng (P) qua I có vtpt n = IC = (3;2;1) có dạng:
3(x − 3) + 2( y − 0) +1(z − 2) = 0 3x + 2 y + z −11 = 0
Câu 39: Trong không gian với hệ tọa độ Oxyz , cho điểm M (1;2;3) . Mặt phẳng (P) qua M cắt các
tia Ox,Oy,Oz lần lượt tại ,
A B,C sao cho thể tích khối tứ diện OABC nhỏ nhất có phương trình là:
A. 6x + 3y + 2z = 0 .
B. 6x + 3y + 2z −18 = 0 .
C. x + 2 y + 3z −14 = 0 . D. x + y + z − 6 = 0 . Lời giải Chọn B Giả sử ( A ; a 0;0) , B(0; ;
b 0) , C(0;0;c) với (a,b, c 0) x y z
Khi đó, phương trình mặt phẳng (P) qua 3 điểm ,
A B,C có dạng: + + = 1. a b c 1 2 3 Ta có: M (P) + + = 1. a b c 1
Thể tích tứ diện OABC: V = abc . 6 1 2 3 6 27.6 1 Áp dụng BDT Côsi ta có: 3 1 = + + 3 1
abc 27 V 27 . a b c abc abc 6 a = 3 1 2 3 1
V đạt giá trị nhỏ nhất là:V = 27 = = = b = 6 a b c 3 c = 9
Vậy (P) : 6x + 3y + 2z −18 = 0 . − −
Câu 40: Trong không gian với hệ tọa độ Oxyz , cho tứ diện ABCD có (
A 1;1;1) , B(2;0;2) ; C( 1; 1;0) , D(0;3; 4) B C
. Trên các cạnh AB, AC, AD lần lượt lấy các điểm phẳng , , D sao cho
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 2 4 / 8 5
AB + AC + AD =
BCD
4 . Viết phương trình mặt phẳng (
) biết tứ diện A B C D có thể tích A B AC A D nhỏ nhất.
A. 16x + 40y − 44z + 39 = 0 .
B. 16x + 40y + 44z − 39 = 0 .
C. 16x − 40y − 44z + 39 = 0 .
D. 16x − 40 y − 44z − 39 = 0 . Lời giải Chọn A AB AC AD A . B AC.AD
Áp dụng bất đẳng thức Cauchy ba s ta có: 3 4 = + + 3 A B AC A D
AB .AC .A D
AB .AC .A D 27 V A B AC A D 27
ABCD . . 27 = V V A . B AC.AD 64 V A . B AC.AD 64
AB 'C ' D ' 64 ABCD ABCD A B AC A D 3 3 7 1 7 Để V
nhỏ nhất khi và chỉ khi = = = AB = AB B ; ;
AB 'C ' D ' AB AC AD 4 4 4 4 4 7 1 7 Lúc đó mặt phẳng ( B C
D ) song song với mặt phẳng (BCD) và đi qua B ; ; 4 4 4 Ta có: BC = ( 3 − ; 1 − ; 2) − ;BD = ( 2
− ;3;2) BC;BD = (4;10; 1 − 1) 7 1 7
Phương trình mặt phẳng ( B C D ) qua B ; ;
có vtpt n = BC;BD = (4;10; 1 − 1) là: 4 4 4
16x + 40 y − 44z + 39 = 0 . x −1 y z +1
Câu 41: Trong không gian Oxyz , cho đường thẳng : = =
. Viết phương trình mặt 2 1 1 −
phẳng ( ) chứa hai điểm M (1;1; ) 1 , N ( 1 − ;− 2;− )
1 và tạo với đường thẳng một góc lớn nhất.
A. 16x +10y −11z −15 = 0 .
B. 16x +10y −11z + 5 = 0 .
C. x − y + z −1 = 0 .
D. 24x + 2 y − 27z +1 = 0 . Lời giải Chọn D Gỉa sử n = ( ; a ;
b c) là vec-tơ pháp tuyến của ( ) .
Do mặt phẳng ( ) chứa hai điểm M (1;1; ) 1 , N ( 1 − ;− 2;− )
1 nên n ⊥ MN . n MN = 0 a + b 2
− a −3b−2c = 2 3 0 c = − . 2 Gọi là góc giữa ( ) và . Khi đó 2 2 . n u
2a + b − c 6a + 5b 1
36a + 60ab + 25b sin = = = = . . 2 2 2 2 2 2 2 n . u
a + b + c . 6
6. 8a +12ab +13b 6
8a +12ab +13b
lớn nhất sin đạt giá trị lớn nhất.
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 2 5/ 8 5 3
Nếu b = 0 sin = . 2 a 2 2 2
36a + 60ab + 25b 36t + 60t + 25
Nếu b 0 , đặt t = thì = = f (t) . b 2 2 2
8a +12ab +13b 8t +12t +13 77 a
Khi đó Max f (t) =
t =12 . Do đó = 12 . Chọn a = 24, b = 2 c = 2 − 7 . 17 b
Mặt phẳng ( ) đi qua M (1;1; ) 1 , nhận n = (24;2; 2
− 7) làm vec-tơ pháp tuyến, nên có
phương trình là 24(x −1) + 2( y −1) − 27(z −1) = 0 24x + 2 y − 27z +1 = 0 .
Câu 42: Trong không gian Oxyz , cho điểm M (1;− 2;3) . Gọi (P) là mặt phẳng qua M và cắt các trục
tọa độ lần lượt tại ,
A B, C . Viết phương trình mặt phẳng (P) biết biểu thức 1 1 1 + +
đạt giá trị nhỏ nhất. 2 2 2 OA OB OC
A. x − 2 y + z − 8 = 0 .
B. 2x + y − 3z + 9 = 0 .
C. x − 2y + 3z −14 = 0 . D. 2x − 4 y + z −10 = 0 . Lời giải Chọn C
Gọi H là trực tâm của tam giác ABC . Khi đó OH ⊥ ( ABC) . 1 1 1 1
Do OH là đường cao của tứ diện . O ABC = + + . 2 2 2 2 OH OA OB OC 1 1 1 Suy ra + +
đạt giá trị nhỏ nhất khi OH đạt giá trị lớn nhất OH = OM . 2 2 2 OA OB OC
Mặt phẳng (P) đi qua M và vuông góc với OM nên nhận OM = (1; 2 − ;3) làm vec-tơ pháp
tuyến, có phương trình là 1(x −1) − 2(y+ 2) + 3(z− 3) = 0 x − 2 y + 3z −14 = 0 .
Câu 43: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;5;0), B(3;3;6) và đường thẳng x = 1 − + 2t
d y = 1− t
. Một điểm M thay đổi trên đường thẳng sao cho chu vi tam giác MAB nhỏ z = 2t
nhất. Khi đó tọa độ điểm M và chu vi tam giác MAB là
A. M (1;0;2); P = 2( 11 + 29) .
B. M (1;2;2); P = 2( 11 + 29) .
C. M (1;0;2); P = ( 11 + 29) .
D. M (1;2;2); P = ( 11 + 29) . Lời giải Chọn A Độ dài 2 2 2
AB = 2 + 2 + 6 = 2 11 .
Chu vi tam giác MAB nhỏ nhất khi MA + MB nhỏ nhất.
Gọi tọa độ của M là ( 1 − + 2 ; a 1− ; a 2a) .
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 2 6/ 8 5
MA + MB = (− + a)2 + (− − a)2 + a + (− + a)2 + (− − a)2 + ( a − )2 2 2 2 4 4 4 2 2 2 6 MA + MB = a + + a − a + = ( a) + ( )2 + ( − a) +( )2 2 2 2 2 9 20 9 36 56 3 20 6 3 20 Xét véc tơ u = ( ; a b);v = ( ; c d ) . Ta có + + + + + ( + )2 + ( + )2 2 2 2 2 u v u v a b c d a c b d .
MA + MB ( a + − a) + ( + )2 2 3 6 3 20 20 = 2 29 . 3a 20 Dấu bằng xảy ra khi =
=1 a =1 M (1;0;2) P = 2( 11+ 29) 6 − 3a 20 x + 2 y − 3 z −1
Câu 44: Cho hai điểm A( 1 − ;2; ) 3 và B(7; 2 − ; )
3 và đường thẳng d : = = . Gọi I là điểm 3 2 − 2
trên d sao cho AI + BI nhỏ nhất. Tìm tổng các tọa độ của I . A. 11. B. 9 C. 7 . D. 5 . Lời giải Chọn D
Do điểm I d nên toạ độ điểm I có dạng I (3a − 2; 2 − a +3;2a + ) 1 .
P = AI + BI = ( a − )2 + ( − a)2 + ( a − )2 + ( a − )2 + ( − a)2 + ( a − )2 3 1 1 2 2 2 3 9 5 2 2 2 2 2
P = 17a −18a + 6 + 17a −82a +110 18 6 82 110 2 2 P = 17 a − a + + a − a + 17 17 17 17 2 2 9 21 41 189 P = 17 a − + + a − + 17 289 17 289 2 2 2 2 9 21 41 3 21 P = 17 a − + + − a + 17 17 17 17 Xét véc tơ u = ( ; a b);v = ( ; c d ) . 2 2 Ta có 2 2 2 2
u + v u + v a + b + c + d (a + c) + (b + d ) . 2 2 2 9 41 21 3 21 32 16.21 Do đó P 17 a − + − a + + = 17 + = 4 5. 2 2 17 17 17 17 17 17 9 21 a − 1 9 41 17 17 Dấu bằng xảy ra khi = = 3 a − = − a a = 1 . 41 3 21 3 17 17 − a 17 17
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 2 7 / 8 5
Vậy tổng các toạ độ của I là 3.1− 2 − 2.1+ 3+ 2.1+1= 5. x −1 y z Câu 45: Cho d : = =
và các điểm A(3;0;0) ; B(0; 6
− ;0) ; C(0;0;6). M là điểm thuộc d sao 2 1 1
cho MA + MB + MC nhỏ nhất. Khi đó 2 MA bằng: A. 2 . B. 3 . C. 4 . D. 5 . Lời giải Chọn C x =1+ 2t x −1 y z d : = = y = t 2 1 1 z = t
Điểm M d M (1+ 2t;t;t ) . Ta có
MA = (2 − 2t; t − ; t − ) MB = ( 1
− − 2t;6 − t; t − ) MC = ( 1 − − 2t; t − ;6 − t)
MA + MB + MC = ( 6 − t, 6
− − 3t;6 −3t)
Do đó: MA + MB + MC = (− t)2 + (− − t )2 + ( − t )2 2 6 6 3 6 3 = 54t + 72 72
Dấu “=” xảy ra t = 0 MA = (2;0;0) Vậy 2 MA = 4 x = 4 + 3t
Câu 46: Trong không gian với hệ tọa độ Oxyz cho đường thẳng có phương trình d : y = 1− t và ba z = 5+ 2t điểm A(1 1 ; ;2) ; B( 1 − 1 ; ; ) 1 ; C (3 1
; ;0) . M là điểm thuộc d sao cho biểu thức 2 2 2
P = MA + MB + MC đạt giá trị nhỏ nhất. Khi đó tổng các tọa độ của M là: 36 55 A. . B. 11. C. 12 . D. . 7 7 Lời giải Chọn A
Điểm M d M (4 + 3t 1
; − t;5 + 2t ) . Ta có MA = ( 3 − − 3t; t − ; 3 − − 2t) MB = ( 5 − − 3t; t
− ;−4 − 2t) MC = ( 1 − − 3t; t − ; 5 − − 2t) 2 17 323 323 Do đó 2 2 2 2
P = MA + MB + MC = 42t +102t + 85 = 42 t + + 14 14 14
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 2 8 / 8 5 323 17 5 31 18 P = t = − M ; ; min 14 14 14 14 7 36
Vậy tổng các tọa độ của M là . 7 x 1 t
Câu 47: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng có phương trình d : y 2 t và ba z t
điểm A 6;0;0 , B 0;3;0 , C 0;0;4 . M là điểm thuộc d sao cho biểu thức 2 2 2 P MA 2MB
3MC đạt giá trị nhỏ nhất. Khi đó tổng bình phương các tọa độ của M là: A. 6 . B. 7 . C. 8 . D. 9 . Lời giải Chọn A 6x x 2x 3x x 1 I A B C I
Gọi I là điểm thỏa IA 2IB 3IC 0 6 y y 2 y 3y y 1 I 1;1; 2 . I A B C I 6z z 2z 3z z 2 I A B C I 2 2 2 Ta có: 2 2 2 P MA 2MB 3MC MI IA 2 MI IB 3 MI IC 2 2 2 2 2 2 2 2 6IM 2MI. IA 2IB 3IC IA 2IB 3IC 6IM IA 2IB 3IC .
Khi đó P đạt giá trị nhỏ nhất 2 6IM nhỏ nhất 2 IM nhỏ nhất. Vì M d M 1 t; 2
t; t . Suy ra IM t;1 t; t 2 . Ta có 2 2 2 2 2 2 IM t 1 t t 2 3t 6t 5 3 t 1 2 2. Dấu ' ' xảy ra t 1. Suy ra M 2;1;1 .
Vậy tổng bình phương các tọa độ của M là: 6 . x 1 t
Câu 48: Trong không gian với hệ tọa độ Oxyz , cho đường thẳng có phương trình d : y 2 t và z 2t
hai điểm A 1;4;2 , B
1; 2; 4 . M là điểm thuộc d sau cho diện tích tam giác MAB nhỏ
nhất. Khi đó hoành độ của M là: 12 12 11 11 A. . B. . C. . D. . 7 7 7 7 Lời giải Chọn A Vì M d M 1 ; m 2 ; m 2m AM ; m m 6; 2m 2 và AB 2; 2; 2 .
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 2 9 / 8 5 Khi đó A ; B AM 6m 16; 2m 4; 4m 12 . 2 1 1 19 24 42
Ta có diện tích MAB là: S A ; B AM 8 7m . MAB 2 2 7 7 7 42 19 19 Do đó: min S . Dấu " " xảy ra 7m 0 m . MAB 7 7 7 19 12
Vậy khi diện tích tam giác MAB nhỏ nhất thì hoành độ của M là: 1 . 7 7
Câu 49: Cho mặt phẳng (P) : x + y + z − 4 = 0 . Tìm điểm M (P) sao cho MA + MB nhỏ nhất, biết,
A(1;0;0), B(1;2;0) . 3 1 A. M (1;1;2)
B. M (0;1;3)
C. M (2;0;2) D. M ; 2; 2 2 Lời giải B A I M (P) A ' Chọn D
Ta thấy rằng điểm A và B nằm cùng phía so với mặt phẳng (P) nên ta sẽ lấy điểm A’ đối
xứng với điểm A qua mặt phẳng (P) . Vecto chỉ phương của đường thẳng AA’ là u (1;1; ) 1 . x = t +1
Suy ra phương trình đường thẳng AA’ là AA' : y = t
, tọa độ I là giao điểm của đường z = t
thẳng AA’ và mặt phẳng (P) là I (2;1; ) 1 A'(3;2;2)
Ta có MA + MB = MA'+ MB A' B . Dấu “=” xảy ra khi và chỉ khi điểm M = A' B (P) x = 3+ 2t 3 1
Ta có phương trình đường thẳng A' B : y = 2 M ; 2; 2 2 z = 2 + 2 t + + − =
Câu 50: Cho mặt phẳng (P) : x y z 4 0 . Tìm điểm M
(P) sao cho MA − MB lớn nhất, biết (
A 1;1;1) , B(1;1;0) .
A. M (1; 2;1) .
B. M (0; 2; 2) .
C. M (1;1; 2) .
D. M (3;1;0) .
Lời giải
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
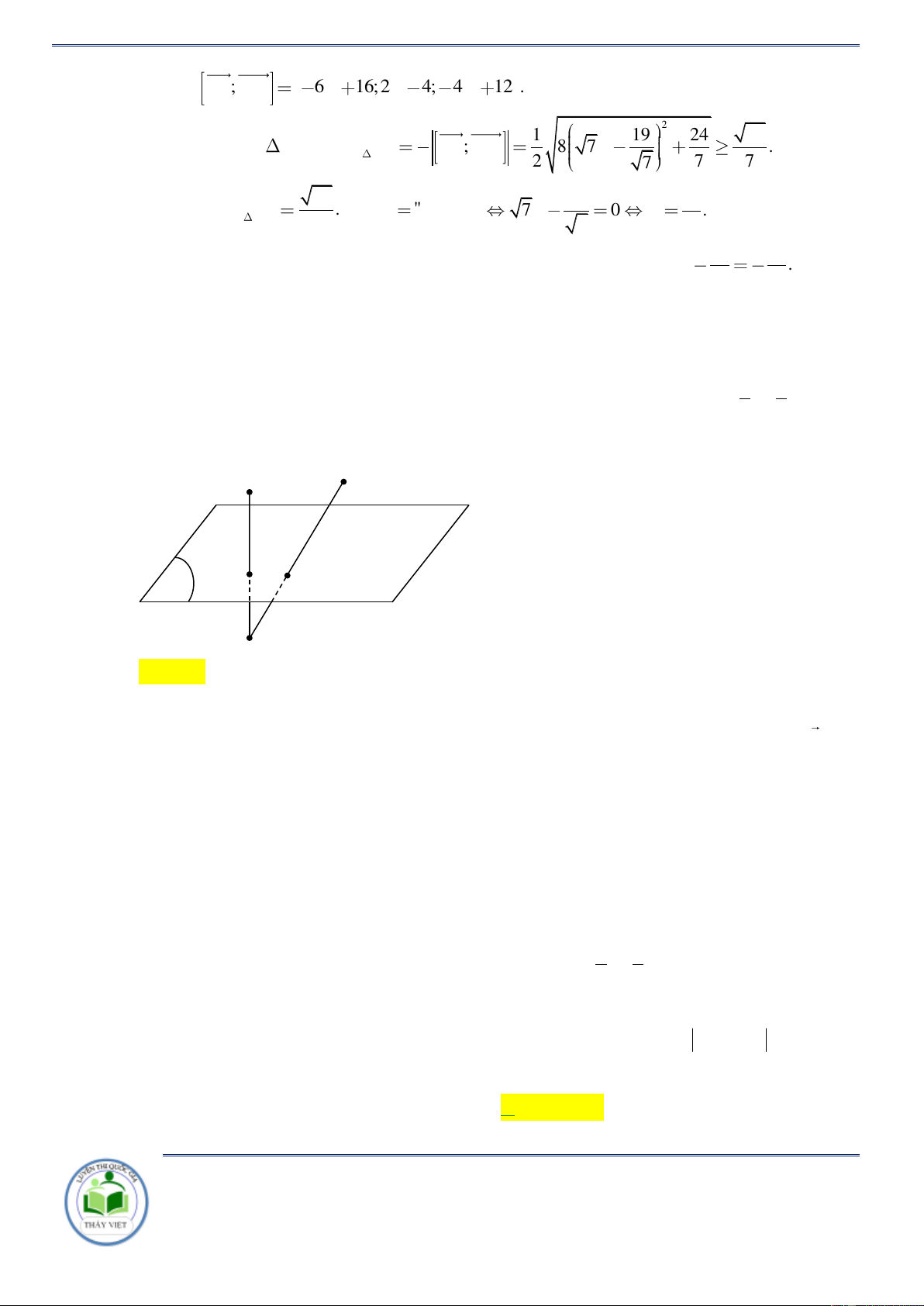
Chuyên đề: Cực trị hình giải tích T r a n g 30 / 8 5 Chọn C A B (P) M
Ta có (1+1+1− 4).(1+1+ 0 − 4) 0 nên M = AB ( P) . Minh nghỉ đoạn này thầy giải thích
vì sao M là giao của AB với (P) băng cách sử dụng bất đẳng thức tam giác
Đường thẳng ( AB) qua điểm (
A 1;1;1) và có vecto chỉ phương AB 0; 0; 1 . x = 1 x = 1 x = 1 y = 1
Phương trình ( AB) : y = 1 . Xét hệ y =1 . z = 1− t z = 1− t z = 2
x + y + z − 4 = 0 Suy ra M (1;1; 2) . + + − =
Câu 51: Cho mặt phẳng (P) : x y z 4 0 . Tìm điểm M
(P) sao cho MA − MB lớn nhất, biết (
A 1;1;1) , B(0;1;5) . 1 1 10 5 5 2 5 7 10 7 5 A. M ; ; . B. M ; ; . C. M ; 0; . D. M ; ; − . 3 3 3 3 3 3 3 3 3 3 3 Lời giải Chọn D A M (P) I A' B
Ta có (1+1+1− 4).(0 +1+ 5 − 4) 0 nên A và B nằm khác phía so với mặt phẳng (P).
Gọi A là điểm đối xứng với ( A 1;1;1) .
MA − MB MA − MB AB do đó MA − MB lớn nhất khi M = AB ( P) . x 1 t Gọi là đường thẳng qua (
A 1;1;1) và vuông góc với P . Phương trình : y 1 t z 1 t
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 31/ 8 5 4 x x 1 t 3 y 1 t 4 4 4 4 Gọi I P . Xét hệ y I ; ; . z 1 t 3 3 3 3 4 x y z 4 0 z 3 5 5 5
Khi đó I là trung điểm AA suy ra tọa độ A ; ; . 3 3 3 5 2 10
Đường thẳng BA qua điểm B(0;1;5) và có vecto chỉ phương BA' = ; ; − . 3 3 3 5 x t 3 2
Phương trình BA : y 1 t 3 10 z 5 t 3 5 x t 10 3 x 3 2 y 1 t 7 Xét hệ phương trình 3 y . 3 10 z 5 t 5 3 z 3 x y z 4 0 10 7 5 Suy ra M ; ; − . 3 3 3
Câu 52: Cho mặt phẳng (P) : x + y + z − 4 = 0 . Tìm điểm M (P) sao cho 2 2
MA + 2MB nhỏ nhất, biết A(1;2; ) 1 , B (0;1;2) . 5 14 17 5 1 4 11 7 A. M ; ; . B. M ; ; 2 . C. M (1;1;2) . D. M ; ; . 9 9 9 3 3 9 9 3 Lời giải Chọn A 1 4 5
- Gọi I là điểm thỏa mãn: IA + 2IB = 0 I = ; ; 3 3 3 2 2 2 2 - Khi đó: 2 2
MA + 2MB = MA + 2MB = (MI + IA) + 2(MI + IB) 2 2 2 2
= 3MI + IA + 2IB = 3MI + 2 2 2
MA + 2MB nhỏ nhất khi và chỉ khi MI nhỏ nhất khi và chỉ khi M là hình chiếu vuông
góc của I trên mặt phẳng (P) . Khi đó MI là đường thẳng đi qua I và nhận vectơ pháp
tuyến của (P) làm vectơ chỉ phương
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 32 / 8 5 1 x = + t 3 4
Suy ra MI có phương trình y = + t . 3 5 z = + t 3 2 1 t = x = + t 9 3 5 4 x = y = + t 9 5 14 17
- Điểm M có tọa độ là nghiệm của hệ 3 M = ; ; . 14 9 9 9 5 y = z = + t 9 3 17
x + y + z − 4 = 0 z = 9
Câu 53: Cho mặt phẳng (P) : x + y + z − 4 = 0 . Tìm điểm M (P) sao cho 2 2
MA + 2MB nhỏ nhất, biết A(1;2; ) 1 , B (0;1;4) . 1 10 25 4 8 4 5 A. M ; ; .
B. M 0; ; . C. M 1; ; .
D. M (1;1;2) . 9 9 9 3 3 3 3 Lời giải Chọn A 1 4
- Gọi I là điểm thỏa mãn: IA + 2IB = 0 I = ; ;3 3 3 - Khi đó: 2 2 2 2 22
MA + 2MB = MA + 2MB = (MI + IA)2 + 2(MI + IB)2 2 2 2 2
= 3MI + IA + 2IB = 3MI + 3 2 2
MA + 2MB nhỏ nhất khi và chỉ khi MI nhỏ nhất khi và chỉ khi M là hình chiếu vuông
góc của I trên mặt phẳng (P) . Khi đó MI là đường thẳng đi qua I và nhận vectơ pháp
tuyến của (P) làm vectơ chỉ phương 1 x = + t 3 4
Suy ra MI có phương trình y = + t . 3 z = 3 + t
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 33/ 8 5 2 t = − 1 9 x = + t 3 1 x = 4 9 1 10 25
- Điểm M có tọa độ là nghiệm của hệ y = + t M = ; ; . 3 10 9 9 9 y = z = 3 + t 9
x + y + z − 4 = 0 25 z = 9
Câu 54: Cho mặt phẳng (P) : x + y + z − 4 = 0. Tìm điểm M (P) sao cho MA + 3MB + 2MC nhỏ nhất, biết A(1;1; )
1 , B (1;2;0) , C (0;0;3) . 3 3 2 5 5 3 3 A. M (1;1;2) .
B. M 1; ; . C. M ; ; . D. M ;1; 2 2 3 3 3 3 2
Lời giải Chọn B 2 7 7
- Gọi I là điểm thỏa mãn: IA + 3IB + 2IC = 0 I = ; ; 3 6 6
- Khi đó: MA + 3MB + 2MC = 6MI + IA + 3IB + 2IC = 6 MI = 6.IM
MA+ 3MB + 2MC nhỏ nhất khi và chỉ khi MI nhỏ nhất khi và chỉ khi M là hình chiếu
vuông góc của I trên mặt phẳng (P) .Khi đó MI là đường thẳng đi qua I và nhận vectơ
pháp tuyến của (P) làm vectơ chỉ phương 2 x = + t 3 7
Suy ra MI có phương trình y = + t . 6 7 z = + t 6 2 1 x = + t t = 3 3 7 x = 1 y = + t 3 3
- Điểm M có tọa độ là nghiệm của hệ 6 M = 1; ; 3 . y = 2 2 7 2 z = + t 6 3 z =
x + y + z − 4 = 0 2
Câu 55: Cho mặt phẳng (P) : x + y + z − 4 = 0. Tìm điểm M (P) sao cho MA + 3MB + 4MC nhỏ nhất, biết A(1;2; )
1 , B (1;2;0) , C (0;0;3) .
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 34 / 8 5 17 7 1 5 19 31 23 A. M (1;1;2) . B. M ; ;1 . C. M ; ;3 . D. M ; ; . 12 12 6 5 24 24 12 Lời giải Chọn D 1 13
- Gọi I là điểm thỏa mãn: IA + 3IB + 4IC = 0 I = ;1; 2 8
- Khi đó: MA + 3MB + 4MC = 8MI + IA + 3IB + 4IC = 8 MI = 8.IM
MA+ 3MB + 4MC nhỏ nhất khi và chỉ khi MI nhỏ nhất khi và chỉ khi M là hình chiếu
vuông góc của I trên mặt phẳng (P) . Khi đó MI là đường thẳng đi qua I và nhận vectơ
pháp tuyến của (P) làm vectơ chỉ phương 1 x = + t 2
Suy ra MI có phương trình y = 1+ t . 13 z = + t 8 7 t = 1 24 x = + t 2 19 x = y = 1+ t 24 19 31 23
- Điểm M có tọa độ là nghiệm của hệ M = ; ; . 13 31 24 24 12 z = + t y = 8 24
x + y + z − 4 = 0 23 z = 12 x − 5 y +1 z −11
Câu 56: Trong không gian với hệ trục Oxyz , cho hai đường chéo nhau d : = = 1 1 2 1 − x + 4 y − 3 z − 4 d : = =
,. Tìm điểm I không thuộc d ; d sao cho d (I;d + d I;d nhỏ nhất. 1 ) ( 2) 2 7 − 2 3 1 2 A. I (5;2;5) .
B. I (7;3;9) C. I (7; 2 − ; 1 − ) 1 . D. I ( 7 − ;2;1 ) 1 Lời giải Chọn A x = 5 + t x = 4 − − 7u
Phương trình tham số d là y = 1
− + 2t ; Phương trình tham số d là y = 3+ 2u ; 1 2 z = 11− t z = 4 + 3 u
d ; d lần lượt có vtcp là u 1;2; 1 − ,u 7
− ;2;3 . Gọi AB là đoạn vuông góc chung của d ;d 1 ( ) 2 ( ) 1 2 1 2 với A(5+ t; 1
− + 2t;11−t);B( 4 − −7 ; u 3 + 2 ; u 4 + 3u) . Ta có AB = ( 7
− u −t −9;2u − 2t + 4;3u + t − 7).
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 35/ 8 5 A . B u = 0 6
− u − 6t + 6 = 0 u = 1 − Mà 1
suy ra: A(7;3;9); B(3;1; ) 1 . AB u =
62u + 6t + 50 = 0 t = 2 . 0 2
d (I;d + d I;d AB đẳng thức xẩy ra khi I thuộc đoạn AB . Mà với I (5;2;5) thì 1 ) ( 2) 1 AI = AB . Chọn A 2
Câu 57: Trong không gian với hệ trục Oxyz , cho A( 1
− ;3;4), B(2;1;2) . Tìm điểm M sao cho biểu thức
P = MA + MB đạt giá trị nhỏ nhất. 1 3 3 A. M ; 2;3 . B M ; 1 − ; 1 − . C. M − ;1;1 . D. M ( 3 − ;2;2). 2 . 2 2 Lời giải Chọn A 1
Gọi I là trung điểm của AB suy ra tọa độ I ; 2;3 . 2
Ta có: P = MA + MB = 2MI = 2MI 0 đẳng thức xẩy ra khi M I Chọn A
Câu 58: Trong không gian với hệ trục Oxyz , cho tam giác ABC với A(2;0;− ) 3 ; B( 1 − ;− 2;4);
C (2;−1;2) . Tìm điểm E sao cho biểu thức P = EA + EB + EC đạt giá trị nhỏ nhất. A. E (1;1; ) 1 .
B. E (1;−1; ) 1 . C. E ( 1 − ;− 2;− ) 1 .
D. E (0;2;− ) 3 . Lời giải Chọn B
Gọi G là trọng tâm tam giác ABC G(1;−1; ) 1 .
Ta có: P = EA + EB + EC = 3EG = 3EG 0 P
= 0 khi E G(1;−1; ) 1 . min
Câu 59: Trong không gian với hệ trục Oxyz , cho 4 điểm A(0;1;5) ; B(2;0;0) ; C (0;0;6) ; D(2;4;− ) 3 .
Tìm điểm E sao cho biểu thức P = EA + EB − CE − DE đạt giá trị nhỏ nhất. 5 1 A. E 1; ; 2 .
B. E 0; − 3; . C. E ( 1 − ;−3;0) .
D. E (2;0;− ) 1 . 4 2 Lời giải Chọn A
Gọi G là điểm thỏa mãn GA+ GB + GC + GD = 5 0 G 1; ; 2 . 4
Ta có: P = EA + EB − CE − DE = EA + EB + EC + ED = 4EG = 4EG 0 5 P
= 0 khi E G 1; ;2 . min 4
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 36/ 8 5
Câu 60: Trong không gian với hệ tọa độ 2 2 2
Oxyz , cho mặt cầu (S ) : ( x − 3) + ( y + 2) + ( z − ) 1 =100 và mặt
phẳng (P) : 2x − 2y − z + 9 = 0 . Tìm M trên mặt cầu (S ) sao cho khoảng cách từ M đến ( P) lớn nhất. 29 26 7 11 − 14 13 29 26 7 29 26 7 A. M ; − ; −
. B. M ; ;
. C. M ; ; −
. D. M − ; ; . 3 3 3 3 3 3 3 3 3 3 3 3 Lời giải Chọn A
Mặt cầu (S ) có tâm I (3; 2 − ; )
1 và bán kính R = 10 . 2.3 − 2. 2 − −1.1+ 9
Khoảng cách từ I đến (P) là d (I,(P)) ( ) =
= 6 R nên (P) cắt (S) theo giao 2 2 + ( 2 − )2 + (− )2 1
tuyến là một đường tròn (C).
Với điểm M bất kì trên (S) thì ta có d (M,(P)) MI + d (I,(P)) =16 .
Dấu “=” xảy ra khi và chỉ khi M là giao điểm của (S) và đường thẳng d đi qua I và vuông góc với (P).
Đường thẳng d vuông góc với (P) nên có VTCP u = = − − ( n ) (2; 2; ) 1 P . x = 3 + 2t
Đường thẳng d có phương trình tham số là y = 2
− − 2t M (3+ 2t; 2
− − 2t;1− t)d . z =1−t
Lại có M (S ) 2 2 2 10
4t + 4t + t =100 t = . 3 10 29 2 − 6 7 − +) Với t = M ; ;
khi đó d (M,(P)) =16 (thỏa mãn). 3 3 3 3 10 1 − 1 14 13 +) Với t = − M ; ;
khi đó d (M,(P)) = 4 (không thỏa mãn). 3 3 3 3 29 26 7 Vậy M ; − ; − 3 3 3 .
Câu 61: Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC với A(2;3;4) ; B( 2 − ; 3 − ;0) ; C (2;3;0)
Gọi I là tâm mặt cầu đi qua đi 3 điểm A, B, C. Tìm I để mặt cầu có bán kính nhỏ nhất.
A. I (0;0;2) .
B. I (2;3;2) .
C. I (0;0;0) . D. I ( 2 − ;3;2) . Lời giải Chọn A
Ta có AB = 68 , AC = 4 , BC = 52 . Ta thấy 2 2 2
AB = AC + BC = 68 nên tam giác ABC vuông tại C.
Gọi J là tâm đường tròn ngoại tiếp tam giác ABC thì J là trung điểm của AB do đó J (0;0;2) .
Mặt cầu tâm I có bán kính R = IA JA = 17 nên mặt cầu có bán kính nhỏ nhất thỏa mãn đề
bài có tâm I trùng với điểm J. Vậy I (0;0;2) .
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 37 / 8 5
Câu 62: Trong không gian với hệ trục Oxyz, cho lăng trụ đứng ABC. A B C
,với A(0;0;0); B(0;1;0) 3 1 C ; ; 0
; A(0;0;2) .Tìm tọa độ điểm M thuộc cạnh AA sao cho diện tích tam giác 2 2 M C D
đạt giá trị lớn nhất, với D là trung điểm của B B . 1 A. M (0;0;0) .
B. M (0;0;2) .
C. M (0;0; ) 1 .
D. M 0;0; . 2 Lời giải Chọn A Ta có: , A A O
z , M A A, gọi M (0;0;m) , 0 m 2. Do ABC. A B C
lăng trụ đứng nên AA= BB= CC . 3 1
Suy ra, B(0;1;2) ; C ; ; 2
. Vì D là trung điểm của B B nên D(0;1; ) 1 . 2 2 3 1 Suy ra, MC = ; ; 2 − m
; MD = (0 ; 1 ;1− m) 2 2 1 3 3 3 3 1 MC, MD = m − ; m − ; = , do đó S MC ; MD 2 2 2 2 2 MC D 2 1 1 = ( 1 m − )2 3 + (m − )2 3 3 1 + = 2
4 m −12 m +15 . 2 4 4 4 4 3
Xét hàm số f (m) 2
= 4m −12m +15 trên 0;2 có f (m) = 8m −12 = 0 m = 0;2 . 2 Bảng biến thiên : x 3 0 2 2 15 7 f ( x) 6
Dựa vào bbt có diện tích tam giác M C D
đạt giá trị lớn nhất khi m = 0. Vậy M (0;0;0) . Câu 63: 2 2
Trong không gian với hệ trục Oxyz, cho mặt cầu ( S ) ( x + ) + ( y − ) 2 : 1 4
+ z = 8 và hai điểm
A(3;0;0) ; B(4;2; )
1 . Gọi M là điểm thuộc mặt cầu ( S ) . Tính giá trị nhỏ nhất của biểu thức MA+ 2MB A. 2 2 . B. 4 2 . C. 6 2 . D. 3 2 . Lời giải Chọn C
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 38 / 8 5 A E F I B M
Mặt cầu ( S ) có tâm I ( 1
− ;4;0) , bán kính R = 2 2 . Ta có 2 2
IA = 4 + 4 + 0 = 2 2 = 2R .
Gọi E (1;2;0) là trung điểm của IA E (S ). Gọi F (0;3;0) là trung điểm của IE . IF 1 IM
Xét tam giác IMF và tam giác IAM có = =
và góc MIA chung nên I MF I AM . IM 2 IA MF 1 Do đó
= AM = 2MF . AM 2 Ta có 2 2 2 M +
A 2MB = 2MF + 2MB 2BF = 2 4 +1 +1 = 6 2 .
Dấu bằng xảy ra khi M = BF (S ) .
Vậy giá trị nhỏ nhất của biểu thức MA+ 2MB là 6 2 .
Câu 64: Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(1;2;0) , B(3;4; ) 1 , D( 1 − ;3;2). Tìm tọa
độ điểm C sao cho ABCD là hình thang có hai cạnh đáy AB , CD và có góc C bằng 45 . A. C (5;9;5) .
B. C (1;5; ) 3 . C. C ( 3 − ;1; ) 1 .
D. C (3;7;4) . Lời giải Chọn D
Ta có AB = (2; 2;1), AD = ( 2 − ;1;2) .
Suy ra AB ⊥ AD và AB = AD .
Khi đó, tam giác ABD, BCD lần lượt là các tam giác vuông cân tại A và B nên
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 39 / 8 5
DC = BD 2 = 2AB
Suy ra DC = 2AB ( x +1; y − 3; z − 2) = (4;4;2) C(3;7;4) . C C C x = t x =1 x = 1 1
Câu 65: Trong không gian với hệ tọa độ Oxyz , cho ba đường thẳng d : y = 0 , d : y = t , d : y = 0 . 1 2 2 3 z = 0 z = 0 z = t 3
Viết phương trình mặt phẳng đi qua điểm H (3;2; )
1 và cắt ba đường thẳng d , d , d lần 1 2 3
lượt tại A , B , C sao cho H là trực tâm tam giác ABC .
A. 2x + 2y + z −11 = 0 . B. x + y + z − 6 = 0 .
C. 2x + 2 y − z − 9 = 0 . D. 3x + 2 y + z −14 = 0 . Lời giải Chọn A Gọi A( ; a 0;0) , B(1; ;
b 0) , C (1;0;c) . AB = (1− ; a ;
b 0), BC = (0; − ;
b c), CH = (2;2;1− c), AH = (3 − ; a 2; ) 1 . H là trực tâm tam giác ABC
AB, BC.CH = 0 2bc + 2c (a − )
1 + (1− c)b (a − ) 1 = 0 b = 0 2 3 A . B CH 0 a b 1 9b 2b 0 = = + − = 9 b = = c = 2 . 0 b BC AH 2
Nếu b = 0suy ra B C (loại). 9 11 9 Nếu b = , tọa độ A ; 0; 0 , B 1; ;0
, C (1;0;9) . Suy ra phương trình mặt phẳng ( ABC) 2 2 2
là 2x + 2y + z −11 = 0 .
Câu 66: (NGUYỄN KHUYẾN TP HCM) Trong không gian với hệ tọa độ Oxyz , cho hình hộp chữ nhật ABC . D A B C D
có A trùng với gốc tọa độ O , các đỉnh B( ; m 0; 0) , D(0; ; m 0) , A ( 0;0;n)
với m, n 0 và m + n = 4. Gọi M là trung điểm của cạnh CC . Khi đó thể tích tứ diện
BDAM đạt giá trị lớn nhất bằng 245 9 64 75 A. . B. . C. . D. . 108 4 27 32 Lời giải Chọn C
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 4 0 / 8 5 n Ta có A'(0;0; n); B( ; m 0; 0); D (0; ; m 0);C'( ; m ; m n);C ( ; m ; m 0); M ; m ; m với 0 , m n 4. 2 Khi đó ( n BD − ; m ; m 0); BA'(− ;
m 0; n); BM 0; ; m
; BD, BA ' = ( 3 2 m ; n m ; n m ) 2
; BD, BA ' BM = m .n Mặt 2 2 khác, 1 1 1 1 1 2 2 V = V
= BD, BA' BM = m .n = m − m =
−m + m V = − m + m BDA M (4 ) ( 3 2 4 ) ' ( 2 3 8 ' ) 6 4 4 4 4 m = 0 V ' = 0 8 m = 3 64 8 4
Lập bảng biến thiên, ta thấy V đạt giá trị lớn nhất là
tại m = , n = . 27 3 3
Câu 67: (NGUYỄN KHUYẾN TPHCM) Trong không gian với hệ tọa độ Oxyz , hai mặt phẳng
4x − 4 y + 2z − 7 = 0 và 2x − 2 y + z +1 = 0 chứa hai mặt của hình lập phương. Thể tích khối lập phương đó là 27 81 3 9 3 64 A. V = . B. V = . C. V = . D. V = . 8 8 2 27 Lời giải Chọn A
Gọi a là độ dài của cạnh của hình lập phương.
Gọi ( ) : 4x − 4y + 2z − 7 = 0,( ) : 2x − 2y + z +1 = 0.
Cạnh của hình lập phương là khoảng cách giữa hai mặt phẳng đã cho. 7 Lấy A 0;0;
thuộc mặt phẳng 4x − 4y + 2z − 7 = 0 . 2 7 2.0 − 2.0 + +1 2 9 3
Khi đó a = d ( ; A ( )) = = = . 4 + 4 +1 6 2
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 4 1/ 8 5 3 3 27
Vậy thể tích hình lập phương là: = . 2 8
Câu 68: Trong không gian với hệ trục tọa độ Oxyz, cho điểm (
A 2;3;0), B(0; − 6 2;0), M ; − 2; 2 và 5 x = t
đường thẳng d : y = 0
. Điểm C thuộc d sao cho chu vi tam giác ABC là nhỏ nhất thì độ z = 2−t dài CM bằng 2 6 A. 2 3 . B. 4 . C. 2 . D. . 5 Lời giải Chọn C Do hai điểm ,
A B cố định nên chu vi tam giác ABC nhỏ nhất khi CA + CB nhỏ nhất.
Gọi C (t;0;2 − t ) d , ta có CA = ( − t t − ) AC = t − t + = ( t − )2 2 2 ;3; 2 2 8 17 2 2 2 + 9 ; CB = ( t − − t − ) CB = t − t + = ( t − )2 2 ; 2; 2 2 4 6 2 2 + 4 .
Trong mặt phẳng Oxy xét hai vectơ u = ( 2t − 2 2;3) và v = ( 2 − 2t;2) . Ta luôn có 2 2 2
u + v u + v
( 2t −2 2) +9 + ( 2t− 2) +4 ( 2 −2 2) +25 . 2 − 2t 2 7 Dấu bằng xảy ra khi = t = . 2t − 2 2 3 5 7 7 3 1 7 1 49 Với t = thì C ;0;
CM = − ;− 2; CM = + 2 + = 2 . 5 5 5 5 5 25 29
Câu 69: Trong không gian với hệ trục tọa độ Oxyz , cho A(1;1; )
1 , B (0;1;2) , C ( 2 − ;0; ) 1
(P): x − y + z +1= 0. Tìm điểm N (P)sao cho 2 2 2
S = 2NA + NB + NC đạt giá trị nhỏ nhất. 1 5 3 3 1 3 1 A. N − ; ; . B. N ( 2 − ;0; ) 1 . C. N ; − ; 2 − . D. N ; − ; 2 − . 2 4 4 2 2 2 2 Lời giải Chọn A
2(1− x) − x − 2 − x = 0 Gọi I ( ;
x y; z ) là điểm thỏa mãn 2IA + IB + IC = 0 khi đó ta có 2(1− y) +1− y − y = 0 2
(1− z) + 2 − z +1− z = 0
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 4 2 / 8 5 x = 0 3 3 5
y = I 0; ; 4 4 4 5 z = 4 Ta có
S = NA + NB + NC = (NI + IA)2 + (NI + IB)2 + (NI + IC )2 2 2 2 2 2 2 2 2 2
= NI + IA + IB + IC + NI (IA+ IB + IC) 2 2 2 2 4 2
= 4NI + IA + IB + IC . Do I , ,
A B,C cố định nên 2 2 2 2
S = 4NI + IA + IB + IC nhỏ nhất khi NI nhỏ nhất hay N là
hình chiếu của I trên mặt phẳng ( P) . 3 5
Gọi là đường thẳng đi qua I 0; ;
và vuông góc với mặt phẳng (P) khi đó 4 4 x = t 3
: y = − t . 4 5 y = + t 4 3 5
x − y + z +1 = 0 t −
− t + t + +1 = 0 4 4 x = t x = t
Tọa độ điểm N là nghiệm của hệ phương trình 3 y = − t 3 4 y = − t 4 5 z = + t 5 4 z = + t 4 1 1 5 3
t = − N − ; ; . 2 2 4 4
Câu 70: (LẠNG GIANG SỐ 1) Trong không gian với hệ tọa độ Oxyz, cho ba đường thẳng x = 1 x = 2 x −1 y z −1
d : y = 1,t ; d : y = u , u ; : = =
. Viết phương trình mặt cầu tiếp xúc 1 2 1 1 1 z = t z = 1+ u
với cả d , d và có tâm thuộc đường thẳng ? 1 2 2 2 2 1 1 1 5
A. ( x − )2 + y + ( z − )2 2 1 1 = 1. B. x − + y + + z − = . 2 2 2 2 2 2 2 2 2 2 3 1 3 1 5 1 5 9 C. x − + y − + z − = . D. x − + y − + z − = . 2 2 2 2 4 4 4 16
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 4 3/ 8 5 Lời giải Chọn A
Ta có M 1;1;0 d , vec tơ chỉ phương của đường thẳng d là : u 0;0;1 . 1 ( ) 1 ( ) 1 1 M
2; 0;1 d , vec tơ chỉ phương của đường thẳng d là : u 0;1;1 . 2 ( ) 2 ( ) 2 2
Giả sử mặt cầu có tâm là I và bán kính R . Do I suy ra I (1+ t;t;1+ t ) . Ta tính được: M I t −1; t
− ;0 , M I 0;1− t;t −1 1 ( ) 2 ( )
Mặt cầu tiếp xúc với cả hai đường thẳng d và d nên ta có 1 2 M I,u M I,u 2 2 2 (t − ) 2 1 + t
(t − )1 +(t − )1
d ( I , d = d I , d = 1 1 2 2 R = = t = 0 1 ) ( 2) u u 1 2 1 2 Suy ra I (1;0; )
1 và bán kính của mặt cầu là: R = 1 .
Vậy phương trình của mặt cầu cần tìm là ( x − )2 + y + ( z − )2 2 1 1 = 1.
Câu 71: (LẠNG GIANG SỐ 1) Trong không gian với hệ tọa độ Oxyz cho hai điểm
A(1;0; 2); B (0; 1
− ;2) và mặt phẳng (P) : x + 2y − 2z +12 = 0 . Tìm tọa độ điểm M thuộc (P)
sao cho MA + MB nhỏ nhất? 6 18 25 A. M (2; 2;9) . B. M − ; − ; . 11 11 11 7 7 31 2 11 18 C. M ; ; .
D. M − ; − ; . 6 6 4 5 5 5 Lời giải Chọn D
Dễ kiểm tra được hai điểm ,
A B nằm cùng phía so với mặt phẳng ( P) .
Gọi A là điểm đối xứng với điểm A qua mặt phẳng ( P) , ta có:
MA + MB = MA + MB A B
. Dấu bằng xảy ra khi và chỉ khi M = AB (P). Ta có n (1; 2; 2
− ) là một vtpt của mặt phẳng (P) . Phương trình đường thẳng AA qua A nhận n (1; 2; 2 − ) làm vtcp, có dạng: x = 1+ t
AA : y = 2t . z = 2− 2t
Gọi H = AA ( P) , suy ra tọa độ điểm H là nghiệm của hệ phương trình : x = 1+ t x = 0 y = 2t y = 2 − H (0; 2 − ;4) z = 2 − 2t z = 4
2+ 2y − 2z +12 = 0 t = 1 −
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 4 4 / 8 5
Do A đối xứng với điểm A qua H A( 1 − ; 4 − ;6).
Ta có AB (1;3; 4) là vtcp của đường thẳng AB , nên phương trình đường thẳng AB có dạng : x = m
AB : y = 1 − + 3m . z = 2− 4m
Do M = AB ( P) , nên tọa độ của M là nghiệm của hệ phương trình: x = m y = 1 − + 3m 2 11 18
giải hệ ta tìm được M − ; − ; . z = 2 − 4m 5 5 5
x + 2y − 2z +12 = 0 x y −1 z − 2
Câu 72: Trong không gian với hệ tọa độ yz Ox , cho đường thẳng : = = và mặt phẳng 1 1 1 −
(P): x + 2y + 2z − 4 = 0 . Phương trình đường thẳng d nằm trong (P) sao cho d cắt và vuông góc với là x = 3 − + t x = 3t
A. d : y =1− 2t (t ) .
B. d : y = 2 + t (t ) . z = 1− t z = 2 + 2t x = 2 − − 4t x = 1 − − t
C. d : y = 1
− + 3t (t ) .
D. d : y = 3 − 3t (t ) . z = 4 − t z = 3 − 2t Lời giải Chọn C x = t
Phương trình tham số của đường thẳng : y = 1+ t (t ) . z = 2−t
Đặt A = d Ad mà d (P) A (P) A = (P) . x = t t = 2 − y =1+ t x = 2 −
Tọa độ A là nghiệm của hệ phương trình: A( 2 − ;−1;4). z = 2 − t y = 1 −
x + 2y + 2z − 4 = 0 z = 4
có vectơ chỉ phương u = (1;1;− )
1 , ( P) có vectơ pháp tuyến n = (1;2;2) . Gọi u là vectơ 1
chỉ phương của d . d (P) u ⊥ u Ta có: 1 , chọn u = , n u = 4 − ;3;−1 1 ( ) . d ⊥ u ⊥ n 1
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 4 5/ 8 5
Phương trình đường thẳng d qua A( 2
− ;−1;4) và có vectơ chỉ phương u = 4 − ;3;−1 : 1 ( ) x = 2 − − 4t y = 1
− + 3t (t ) . z = 4−t
Câu 73: Trong không gian cho điểm M (1; 3
− ;2). Có bao nhiêu mặt phẳng đi qua M và cắt các trục tọa độ tại ,
A B, C mà OA = OB = OC 0 . A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn C
Gọi (P) là mặt phẳng cần tìm. Giả sử A( ; a 0;0), B(0; ;
b 0), C (0;0;c), điều kiện: abc 0. x y z
Phương trình mặt phẳng ( P) : + + = 1. a b c 2 2 2
OA = OB = OC a = b = c a = b = c ( ) .
Trường hợp 1: a, b, c cùng dấu. x y z Từ ( )
a = b = c phương trình mặt phẳng (P) : + + =1 x + y + z − a = 0 . a a a M (1; 3
− ;2)(P) 1−3+ 2−a = 0 a = 0 (loại). Do đó: không tồn tại mặt phẳng (P) trong trường này.
Trường hợp 2: a cùng dấu b và trái dấu với c . x y z Từ ( )
a = b = c
− phương trình mặt phẳng (P) : + − =1 x + y − z − a = 0 . a a a M (1; 3
− ;2)(P) 1−3−2−a = 0 a = 4
− (P): x + y − z + 4 = 0 .
Trường hợp 3: a cùng dấu c và trái dấu với b . x y z Từ ( )
a = c = b
− phương trình mặt phẳng (P) : − + =1 x − y + z − a = 0 . a a a M (1; 3
− ;2)(P) 1+3+ 2−a = 0 a = 7 (P): x − y + z −7 = 0 .
Trường hợp 4: b cùng dấu c và trái dấu với a . x y z Từ ( )
b = c = −a phương trình mặt phẳng (P) : − + + =1 −x + y + z − a = 0 . a a a M (1; 3 − ;2)(P) 1
− −3+ 2 − a = 0 a = 2
− (P): −x + y + z + 2 = 0 .
Vậy từ các trường hợp trên có 3 mặt phẳng thỏa mãn.
Câu 74: Trong không gian với hệ tọa độ Oxyz cho điểm E(8;1;1) .Viết phương trình mặt phẳng ( )
qua E và cắt nửa trục dương Ox,Oy,Oz lần lượt tại ,
A B, C sao cho OG nhỏ nhất với G là
trọng tâm tam giác ABC
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 4 6/ 8 5
A. x + y + 2z −11 = 0 . B. 8x + y + z − 66=0 . C. 2x + y + z −18 = 0 . D. x + 2 y + 2z −12 = 0 . Lời giải Chọn D Giả sử A( ; a 0;0), B(0; ;
b 0),C (0;0;c), , a b, c 0 . x y z
Khi đó phương trình mặt phẳng ( ) là: + + = 1. a b c 8 1 1
Vì mặt phẳng ( ) đi qua điểm E (8;1; ) 1 nên ta có + + =1. a b c a b c
Trọng tâm G của tam giác ABC là G ; ; . 3 3 3 1 2 2 2 OG =
a + b + c . 3 4 1 1 ( + + )2 2 2 2 4 1 1 Ta có 1 = + +
2a + b + c 36 . 2a b c
2a + b + c 2 36
Ta có ( + + )(a + b + c ) ( a + b + c)2 2 2 2 2 2 2 2 1 1 2 2 2 2
a + b + c . 6 2 1 1 a =12 = =
Vậy OG nhỏ nhất khi a b c b = 6 .
2a +b +c = 36 c = 6
Vậy phương trình mặt phẳng ( ) là x + 2y + 2z −12 = 0.
Câu 75: (CHUYÊN PHAN BỘI CHÂU) Trong không gian với hệ tọa độ Oxyz , cho đường thẳng x − 2 y z 2 2 2 d : =
= và mặt cầu (S ) :(x − ) 1
+ ( y − 2) + (z − ) 1
= 2. Hai mặt phẳng (P) và(Q) 2 1 − 4
chứa d và tiếp xúc với (S ) . Gọi M , N là tiếp điểm. Tính độ dài đoạn thẳng MN. 4 A. 2 2 . B. . C. 6 . D. 4 . 3 Lời giải Chọn B
Mặt cầu (S ) có I (1;2; )
1 và bán kính R = 2 . IM ⊥ d Ta có
(IMN ) ⊥ d . IN ⊥ d
Phương trình mặt phẳng (IMN ) là 2( x − )
1 − ( y − 2) + 4( z − )
1 = 0 2x − y + 4z − 4 = 0 .
Mặt phẳng (IMN ) cắt đường thẳng d tại P . Khi đó tọa độ điểm P là nghiệm của hệ
2x − y + 4z − 4 = 0
phương trình x − 2 y z P(2;0;0). = = 2 1 − 4
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 4 7 / 8 5
Trong mặt phẳng (IMPN ) , gọi K = MN IP .
Ta có IP = 6; IM = 2 PM = 2 2 MK = 4 MN = . 3 3
Câu 76: (CHUYÊN PHAN BỘI CHÂU) Trong không gian với hệ tọa độ Oxyz , cho điểm M (1;2; ) 1 .
Mặt phẳng (P) thay đổi đi qua M lần lượt cắt các tia Ox,Oy,Oz tại ,
A B,C khác O . Tính
giá trị nhỏ nhất của thể tích khối tứ diện OABC . A. 54 B. 6 C. 9. D. 18 Lời giải Chọn C Giả sử A( ; a 0;0); B(0; ;
b 0);C (0;0;c) . Do cắt các tia nên: ; a ;
b c 0 . Khi đó, phương trình mặt x y z 1 2 1
phẳng (P) là: ( P) : + + = 1. (P) đi qua M (1;2; ) 1 nên:
+ + = 1. Áp dụng bất đẳng a b c a b c 1 2 1 1 2 1 2 thức Cauchy ta có: 3 3 1 = + + 3. . . = 3. V 9 a b c a b c 6V 1 2 1 1 Dấu " = " xảy ra khi:
= = = . Vậy, Chọn C a b c 3 x = 2 + t
x = 2 − 2t
Câu 77: (THTT – 477) Cho hai đường thẳng d : y = 1− t và d : y = 3 . Mặt phẳng cách đều 1 2 z = 2t z = t
hai đường thẳng d và d có phương trình là 1 2
A. x + 5y + 2z +12 = 0. B. x + 5y − 2z +12 = 0.
C. x − 5y + 2z −12 = 0. D. x + 5y + 2z −12 = 0 . Lời giải Chọn D Ta có d
M 2;1;0 có vtcp u 1;−1;2 , đường thẳng d M 2;3;0 1 ( ) 1 đi qua 1 ( ) 2 đi qua 2 ( ) có vtcp u 2
− ;0;1 . Gọi (P) là mặt phẳng song song với d và d 2 ( ) 1 2 thì n
= u u = −1;− 5;− 2 (P) : x + 5y + 2z + D = 0 . Mặt phẳng (P) cách đều d và d P 1 2 ( ) ( ) 1 2 D + 7 D +17
thì d (M ,(P) = d M ,(P) =
D = − . Vậy (P) : x + 5y + 2z-12=0. Chọn 1 ) ( 2 ) 30 30 12 D
Câu 78: (THTT – 477) Cho hai điểm A(3;3; ) 1 , B(0;2; )
1 và mặt phẳng ( ) : x + y + z − 7 = 0 . Đường
thẳng d nằm trên ( ) sao cho mọi điểm của d cách đều 2 điểm ,
A B có phương trình là
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 4 8 / 8 5 x = t x = t x = t − x = 2t
A. y = 7 − 3t .
B. y = 7 + 3t .
C. y = 7 − 3t .
D. y = 7 − 3t . z = 2t z = 2t z = 2t z = t Lời giải Chọn A
Vì (d ) cách đều A và B nên (d ) nằm trên mặt phẳng trung trực ( ) của AB. Gọi M là 3 5 trung điểm AB thì M ; ;1
mp( ) đi qua M và vuông góc với AB nên có vtpt 2 2 AB = ( 3 − ; 1
− ;0) , phương trình mp( ) : 3x + y − 7 = 0 . Đường thẳng (d ) là giao tuyến của
() và () nên tập hợp các điểm thuộc (d ) có toạ độ ( ;x y;z)thoả mãn hệ: x = t
x + y + z − 7 = 0
y = 7 −3t (t ). Vậy, Chọn A 3
x + y − 7 = 0 z = 2t
Câu 79: (SỞ GD HÀ NỘI) Trong không gian Oxyz, cho các điểm A(1;0;0), B( 2 − ;0;3), M (0;0; ) 1 và N (0;3; )
1 . Mặt phẳng (P) đi qua các điểm M , N sao cho khoảng cách từ điểm B đến (P)
gấp hai lần khoảng cách từ điểm A đến (P). Có bao mặt phẳng (P) thỏa mãn đầu bài?
A. Có vô số mặt phẳng (P).
B. Chỉ có một mặt phẳng (P).
C. Không có mặt phẳng (P) nào.
D. Có hai mặt phẳng (P). Lời giải Chọn A
Giả sử (P) có phương trình là: ax + by + c + d = ( 2 2 2 z
0 a + b + c 0)
Vì M (P) c + d = 0 d = − . c
Vì N (P) 3b + c + d = 0 hay b = 0 vì c + d = 0 (P) :ax + cz − c = 0.
Theo bài ra: d (B,(P)) = 2d ( , A ( P)) − + − − 2a 3c c a c = 2
a − c = a − c (luôn đúng) 2 2 2 2 a + c a + c
Vậy có vô số mặt phẳng (P) thỏa mãn đề bài. Chọn A 1 3
Câu 80: Trong không gian, cho điểm M ; ; 0 và mặt cầu 2 2 2
(S) : x + y + z = 8 . Đường thẳng d 2 2
thay đổi đi qua điểm M , cắt mặt cầu (S ) tại hai điểm A , B phân biệt. Tính diện tích lớn
nhất S của tam giác OAB . A. S = 7 .
B. S = 4 .
C. S = 2 7 .
D. S = 2 2 .
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 4 9 / 8 5 Lời giải Chọn A
Mặt cầu (S ) có tâm O(0;0;0) , bán kính R = 2 2 = OA = OB . 1
Kẻ OH ⊥ AB ( H trung điểm AB ). Ta có 2 S = A .
B OH = OH.AH = OH R − OH . OAB 2
Đặt OH = x ,ta có OH OM =1 x (0; 1 2 S = x 8 − x . OAB
Xét hàm số f ( x) 2
= x 8− x , x(0; 1 − f ( x) 2 2 x 8 2x 2 = 8 − x − = 0 x (0
;1 f ( x) đồng biến trên (0 ;1 . 2 2 8 − x 8 − x
max f (x) = f ( )
1 = 7 tại x = 1. Vậy diện tích S lớn nhất S = 7 . ( OAB 0; 1
Câu 81: Có bao nhiêu mặt phẳng đi qua điểm M (1;9;4) và cắt các trục tọa độ tại các điểm A , B , C
khác gốc tọa độ sao cho OA = OB = OC . A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn D
Mặt phẳng (P) cắt các trục tọa độ tại các điểm A( ; a 0;0) , B(0; ;
b 0) , C (0;0;c) có dạng: ( 1 9 4 P) x y z :
+ + = 1. Vì M (P) + + =1 (*) . a b c a b c
a = b = c
a = b = −c
Ta có OA = OB = OC a = b = c . a = b − = c a = b − = −c
Thử lại cả 4 trường hợp vào điều kiện ( )
* thấy thỏa mãn. Vậy có 4 mặt phẳng thỏa mãn
Câu 82: (BIÊN HÒA – HÀ NAM) Trong không gian với hệ tọa độ Oxyz , cho
A(a;0;0), B (0; ;
b 0), C (0;0;c) với a, , b c dương. Biết ,
A B, C di động trên các tia Ox, Oy, Oz
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 50 / 8 5
sao cho a + b + c = 2 . Biết rằng khi a, ,
b c thay đổi thì quỹ tích tâm hình cầu ngoại tiếp tứ
diện OABC thuộc mặt phẳng ( P) cố định. Tính khoảng cách từ M (2016;0;0) tới mặt phẳng ( P) . 2014 2016 2015 A. 2017 . B. . C. . D. . 3 3 3 Lời giải: Chọn B
Mặt cầu ngoại tiếp OABC có dạng 2 2 2
x + y + z -ax-by-cz=0 a b c a b c
Tâm mặt cầu là I ( ; ; ) luoon nằm trên mặt phẳng (P) :
+ + = 1 hay x + y + z − 2 = 0 2 2 2 2 2 2 2014
Do đó khoảng cách d (M;(P)) = 3
Câu 83: (SỞ BÌNH PHƯỚC) Trong không gian với hệ tọa độ Oxyz, cho điểm 1 2 3
A(a;0;0), B (0; ;
b 0), C (0;0;c), trong đó a 0 , b 0 , c 0 và + + = 7. Biết mặt phẳng a b c
(ABC) tiếp xúc với mặt cầu (S) (x − )2 +( y − )2 +(z − )2 72 : 1 2 3 =
. Thể tích của khối tứ diện 7 OABC là 2 1 3 5 A. . B. . C. . D. . 9 6 8 6 Lời giải Chọn A x y z
Ta có phương trình (ABC) là: + + = 1 a b c 6 2
Mặt cầu (S) có tâm I (1; 2;3) , bán kính R = 7 Do mặt phẳng (ABC) tiếp xúc với mặt cầu (S) nên 1 2 3 + + a b c 6 2 1 1 1 7 2 2 2 d (I; (ABC)) = R = ( ) + ( ) + ( ) = 1 1 1 7 a b c 2 2 2 2 ( ) + ( ) + ( ) a b c 1 2 3 2 ( + + ) 7 1 1 1 7 Theo BĐT bunhiacopski ta có 2 2 2 = ( ) + ( ) + ( ) a b c = 2 2 2 2 a b c (1 + 2 + 3 ) 2 2 abc 2
Do đó dấu bằng xảy ra khi a = 2;b = 1;c = V = = 3 OABC 6 9
Câu 84: Phương trình mặt phẳng nào sau đây đi qua điểm M (1;2;3) và cắt ba tia Ox,Oy,Oz lần lượt tại ,
A B, C sao cho thể tích tứ diện OABC là nhỏ nhất.
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 51/ 8 5
A. 6x + 3y + 2z +18 = 0 B. 6x + 3y + 3z − 21 = 0
C. 6x + 3y + 3z + 21 = 0 D. 6x + 3y + 2z −18 = 0 Lời giải Chọn D Gọi A( ; a 0;0) , B(0; ;
b 0) và C (0;0;c) AB(− ; a ;
b 0) và AC (− ; a 0;c) n = A , B AC = (b , c a , c ab) 1 1
Suy ra diện tích tam giác ABC là: S = AB, AC 2 2 2 2 2 2 = + + b c a c a b ( ) 1 2 2 x y z
Phương trình mặt phẳng ( ABC) là: + + = 1 a b c 1
Khoảng cách từ điểm O đến mặt phẳng ( ABC) là: h = d (O,( ABC)) = (2) 1 1 1 + + 2 2 2 a b c Từ ( )
1 và (2) suy ra thể tích tứ diện OABC là 1 1 1 1 2 2 2 2 2 2 V = .
b c + c a + a b . = abc (3) 3 2 1 1 1 6 + + 2 2 2 a b c 1 2 3
Vì điểm M ( ABC) nên ta có: + + = 1 a b c 1 2 3 6 6 1 3 1= + + 3 3 abc 162 (4) a b c abc abc 3 1
Từ (3) và (4) suy ra V = abc 27 6
Dấu “ = ” xảy ra a = 3;b = 6;c = 9 x y z
Suy ra phương trình mặt phẳng ( ABC) là: + + = 1 6x + 3y + 2z −18 = 0 3 6 9
Câu 85: Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng (P) có phương trình
3x + y − z + 5 = 0 và hai điểm A(1;0;2) , B(2; 1
− ;4) . Tập hợp các điểm M ( ; x ; y z) nằm trên
mặt phẳng (P) sao cho tam giác MAB có diện tích nhỏ nhất.
x − 7y − 4z + 7 = 0
x − 7y − 4z +14 = 0 A. B.
3x − y + z − 5 = 0
3x + y − z + 5 = 0
x − 7y − 4z + 7 = 0 3
x − 7y − 4z + 5 = 0 C. D.
3x + y − z + 5 = 0
3x + y − z + 5 = 0 Lời giải Chọn C
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 52 / 8 5 Ta có AB (1; 1
− ;2); véctơ pháp tuyến của mặt phẳng (Q) : n = (3;1;− ) 1 . P Vì A .
B n = 0 suy ra AB song song với mặt phẳng ( P) và hai điểm ,
A B nằm về cùng một P
phía với mặt phẳng (P) . Điểm M (P) sao cho tam giác ABM có diện tích nhỏ nhất, suy 1 ra S = .
AB d M AB là nhỏ nhất hay d (M , AB) là nhỏ nhất. ABC ( ; ) 2
Suy ra M = (P) (Q) , với (Q) là mặt phẳng đi qua AB và vuông góc với (P) .
Véctơ pháp tuyến của (Q) là: n = A , B n = ( 1 − ;7;4 Q P ) ( ) ( ) Phương trình tổng quát của mặt phẳng (Q) là: − ( 1 x − )
1 + 7 y + 4( z − 2) = 0 x − 7y − 4z + 7 = 0
x − 7y − 4z + 7 = 0
Vậy quỹ tích điểm M là
3x + y − z + 5 = 0
Câu 86: (CHUYÊN ĐH VINH) Trong không gian với hệ tọa độ Oxyz , cho hai điểm M ( 2 − ; 2 − ; ) 1 , x +1 y − 5 z A(1;2; 3
− ) và đường thẳng d : = =
. Tìm véc-tơ chỉ phương u của đường thẳng 2 2 1 −
đi qua M , vuông góc với đường thẳng d đồng thời cách điểm A một khoảng bé nhất.
A. u = (2;1;6) .
B. u = (1;0;2) .
C. u = (3;4; 4 − ) .
D. u = (2;2; − ) 1 . Lời giải Chọn D
Phương trình mặt phẳng ( ) đi qua M và vuông góc với d là
2( x + 2) + 2( y + 2) −( z − )
1 = 0 2x + 2y − z + 9 = 0.
Gọi H là hình chiếu vuông góc của A trên ( ) . Tọa độ điểm H là nghiệm của hệ x =1+ 2t x = 3 − y = 2 + 2t y = 2 − . Vậy H ( 3 − ; 2 − ;− ) 1 . z = 3 − − t z = 1 −
2x + 2y − z +9 = 0
Gọi là đường thẳng đi qua M và vuông góc với d . Khi đó, ( ) . Suy ra khoảng cách
từ A đến ngắn nhất khi và chỉ khi đi qua H . Ta có HA = (4;4; 2
− ) là một véc-tơ chỉ phương của .
Vậy véc-tơ chỉ phương cần tìm là u = (2;2; − ) 1 .
Câu 87: (MINH HỌA LẦN 2) Trong không gian với hệ tọa độ Oxyz , xét các điểm A(0;0; ) 1 , B( ; m 0;0) , C (0; ; n 0) , D(1;1; )
1 với m 0, n 0 và m + n =1. Biết rằng khi ,
m n thay đổi, tồn
tại một mặt cầu cố định tiếp xúc với mặt phẳng ( ABC) và đi qua D . Tính bán kính R của mặt cầu đó?
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 53/ 8 5 2 3 3 A. R = 1 . B. R = . C. R = . D. R = . 2 2 2 Lời giải Chọn A Gọi I ( ; a ;
b c) là tâm của mặt cầu. Khi đó, bán kính R = ID = d(I,( ABC)) . x y z
Phương trình theo đoạn chắn của mặt phẳng ( ABC) là + + = 1. m n 1 a b c + + −1 m n 1 2 2 2
Khi đó, d (I,( ABC)) =
và ID = (1− a) + (1− b) + (1− c) . 2 2 1 1 + +1 m n 2 2 2 2 2 1 1 1 1 2 1 2 1
Từ m + n =1 suy ra + +1 = + − +1 = − +1 = −1 . m n m n mn mn mn mn
an + bm + cmn − mn
an + bm + cmn − mn 2 m + n 1
Như thế d (I,( ABC )) = = (vì mn = ). 1− mn 1− mn 2 4
Nếu an + bm + cmn − mn 0 thì
an + bm + cmn − mn
d ( I,( ABC )) = R = R 1− mn
a(1− m) + bm + cm(1− m) − m(1− m) = R 1
− m(1− m) 2
m (1− c − R) + m(b + c − a −1+ R) + a − R = 0 ( ) 1 Vì đẳng thức ( )
1 đúng với mọi m(0; ) 1 nên 1
− c − R = 0 a = R b
+ c − a −1+ R = 0 b = R . a − R = 0 c = 1− R Mặt khác
ID = R (1− a)2 + (1− b)2 + (1− c)2 = R 2(1− R)2 2 + R = R . 2(1− R)2 = 0 R =1
Tương tự, nếu an + bm + cmn − mn 0 thì ta tìm được R = −1 (không thỏa mãn R 0 )
Vậy bán kính mặt cầu cần tìm là R = 1 .
Câu 88: Cho ba điểm A(3;1;0), B(0; 1 − ;0),C(0;0; 6
− ) . Nếu tam giác A'B'C' thỏa mãn hệ thức
A' A + B ' B + C 'C = 0 thì có tọa độ trọng tâm là: A. (1;0; 2 − ) . B. (2; 3 − ;0). C. (3; 2 − ;0). D. (3; 2 − ; ) 1 . Lời giải
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 54 / 8 5 Chọn A
Gọi G ,G lần lượt là trọng tâm AB C, A B C . 1 2 Thì A G + B G +C G
= 0 và G A+G B +G C = 0 2 2 2 1 1 1
Có A' A+ B' B + C 'C = 0 A G + B G +C G
+G A+G B +G C +3G G = 0 G G = 0 2 2 2 1 1 1 2 1 2 1 G G . 2 1
Nên hai tam giác ABC và A' B 'C ' có cùng trọng tâm G(1;0; 2
− ) là trọng tâm A 'B'C '.
Câu 89: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A( 2 − ; 2 − ; ) 1 , B(1;2;− ) 3 và đường thẳng x +1 y − 5 z d : = =
. Tìm véc tơ chỉ phương u của đường thẳng qua A , vuông góc với d 2 2 1 −
đồng thời cách điểm B một khoảng bé nhất.
A. u = (2;1;6) .
B. u = (2;2; − ) 1 .
C. u = (25; 2 − 9; 6
− ) . D. u = (1;0;2) . Lời giải Chọn D Gọi u = ( ; a ;
b c) là VTCP của với 2 2 2
a + b + c 0 .
⊥ d 2a + 2b−c = 0 c = 2a + 2b u = ( ; a ;
b 2a + 2b). AB = (3;4; 4
− ) AB u = (8a +12 ; b 1 − 0a − 6 ; b 4 − a + 3b) AB u
(8a +12b)2 +(10a +6b)2 +(4a −3b)2 2 2
180a + 288ab +189b Ta có: d ( ; B ) = = = 2 2 u + +
a + b + (2a + 2b)2 2 2 5a 8ab 5b
Nếu b = 0 thì d ( ; B ) = 6 . 180x + 288x +189 a
Nếu b 0 thì d ( ; B ) 2 = x = . 2 5x + 8x + với 5 b 180x + 288x +189
Xét hàm số f ( x) 2 = 2 5x + 8x + , tập xác đinh D = 5 Ta có BBT:
So sánh hai trường hợp trên ta thấy d ( ;
B ) nhỏ nhất bằng 6 khi b = 0 c = 2a nên có 1 VTCP u = (1;0;2) .
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 55/ 8 5
Cách 2: (Nguyễn Trí Chính) (d) B ( ) H A K (P)
Gọi (P) là mặt phẳng đi qua A( 2 − ; 2 − ; )
1 và có vec tơ pháp tuyến a = (2;2;− ) 1 ( a = (2;2;− ) 1
là véc tơ chỉ phương của d ), nên phương trình (P) là: 2x + 2y − z + 9 = 0
Gọi (D) là đường thẳng đi qua B(1;2; 3
− ) và vuông góc (P) thì phương trình (D) là: x =1+ 2t (
D) : y = 2 + 2t . z = 3 − − t
Vẽ BH ⊥ (P), H (P) .
Giải phương trình: 2(1+ 2t) + 2(2 + 2t) −( 3
− −t)+9 = 0 9t = 1 − 8 t = 2 − H ( 3 − ; 2 − − ) 1 + + +
Vẽ BK ⊥ , K , có d ( ,
B ) = BK , d (B (P)) 2 4 3 9 , = BH = = 6 3
Có BK BH = 6.
Do đó BK nhỏ nhất khi K H . Suy ra K ( 3 − ; 2 − − ) 1
Suy ra () đi qua A( 2 − ; 2 − ; ) 1 và K ( 3 − ; 2 − − ) 1 .
Nên véc tơ chỉ phương của đường thẳng () là KA = (1;0;2) . x − 2 y −1 z
Câu 90: Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d : = = . Viết phương 1 2 1 −
trình mặt phẳng (P) chứa đường thẳng d và cắt các trục Ox,Oy lần lượt tại A và B sao
cho đường thẳng AB vuông góc với d .
A. (P) : x + 2y + 5z − 4 = 0.
B. (P) : x + 2y + 5z −5 = 0 .
C. (P) : x + 2y − z − 4 = 0.
D. (P) : 2x − y −3 = 0 . Lời giải Chọn A
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 56/ 8 5 Gọi A( ; a 0;0), B(0; ;
b 0) AB = (− ; a ; b 0)
d đi qua M (2;1;0) và có 1 VTCP u = (1;2;− ) 1 .
AB ⊥ d A . B u = 0 a
− + 2b = 0 a = 2b AB = b( 2 − ;1;0) = .
b v với v = ( 2 − ;1;0) .
u v = (1; 2;5) nên (P) có 1 VTPT n = (1;2;5) . Vậy phương trình mặt phẳng (P) là:
x + 2 y + 5z − 4 = 0
Câu 91: Trong không gian với hệ tọa độ Oxyz , cho ba điểm M (3;0;0), N ( , m ,
n 0), P(0;0; p) . Biết 0
MN = 13, MON = 60 , thể tích tứ diện OMNP bằng 3 .Giá trị của biểu thức 2 2
A = m + 2n + p bằng: A. 29 . B. 27 . C. 28 . D. 30 . Lời giải P N O M Chọn A 2 2
OM = 3,ON = m + n , OP = p , MN = 13 . 1 Ta có: 2 2 2 0
MN = OM + ON − 2OM .ON.cos 60 2 2 2 2
13 = 9 + m + n − 2.3. m + n . 2 2 2 2 2
m + n −3 m + n − 4 = 0 , 2 2 m + n 0 2 2 m + n = 4 2 2
m + n =16 ( ) 1 .
MN = 13 (m − )2 2 3 + n = 13 2 2
m + n − 6m = 4 6m =12 m = 2 (2) . Từ ( ) 1 và (2) 2 n =12 (3) .
Có OP ⊥ OM ,OP ⊥ ON . Suy ra OP ⊥ (OMN ) , có OM = 3,ON = 4 , OP = p . 1 1 1 3 V = 3 0 .O . P
OM .ON.sin 60 = 3 p .3.4. = 3 p = 3 2 p = 3 (4) . OMNP 3 2 6 2 Từ (2),( ) 3 ,(4) 2 2
A = m + 2n + p = 29 .
Câu 92: Trong không gian Oxyz cho hình vuông ABCD ; B(3;0;8); D( 5 − ; 4
− ;0). Biết đỉnh A thuộc
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 57 / 8 5
mặt phẳng Oxy và có tọa độ là số nguyên. Khi đó CA + CB bằng A. 5 10 . B. 6 10 . C. 10 6 . D. 10 5 Lời giải Chọn B
Ta có CA + CB = CM = 2 CK
BD = (− − )2 + (− − )2 + ( − )2 5 3 4 0 0 8 =12 5 2 2
BD = 12 BC = 6 2 CK = CB + BK = CB = 3 10 2 CA + CB = 6 10 .
Câu 93: Trong không gian Oxyz cho điểm A(2;4;− ) 1 ; B(1;4;− )
1 ;C (2;4;3); D(2;2; − ) 1 . Biết M ( ; x ; y z) , để 2 2 2 2
MA + MB + MC + MD đạt giá trị nhỏ nhất thì x + y + z bằng? A. 7. B. 8. C. 9. D. 10 Lời giải Chọn A 7 14
Gọi G là trọng tâm của tứ diện . A BCD G ; ; 0 3 3
Ta có GA+ GB + GC + GD = 0 + + + = ( )2 +( )2 +( )2 +( )2 2 2 2 2 MA MB MC MD MA MB MC MD = ( + )2 +( + )2 +( + )2 +( + )2 MG GA MG GB MG GC MG GD 2
= MG + MG(GA+GB +GC +GD) 2 2 2 2 4 2.
+ GA + GB + GC + GD
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 58 / 8 5 2 2 2 2 2 = 4MG + 2.M .
G 0 + GA + GB + GC + GD Ta có G, ,
A B, C, D cố định nên 2 2 2 2
GA + GB + GC + GD là hằng số. Để 2 2 2 2
MA + MB + MC + MD đạt giá trị nhỏ nhất thì 2
MG đạt giá trị nhỏ nhất 7 14 Min
= 0 M G M ;
; 0 x + y + z = 7 2 MG 3 3 A( 2 − ;2;6) B( 3 − ;1;8) C( 1 − ;0;7) D(1;2;3)
Câu 94: Cho hình chóp S.ABCD biết , , , . Gọi H là trung SH ⊥ ( ABCD) 27 điểm của CD,
. Để khối chóp S.ABCD có thể tích bằng (đvtt) thì có hai 2
điểm S , S thỏa mãn yêu cầu bài toán. Tìm tọa độ trung điểm I của S S . 1 2 1 2 A. I (0; 1 − ; 5 − ) .
B. I (1;0;5) .
C. I (0;1;5) . D. I ( 1 − ;0; 5 − ). Lời giải Chọn C AB = ( 1 − ; 1 − ;2) A ; B AC = (3;3;3) Ta có AC = (1; 2 − ) ;1
AC; AD = (6;6;6) AD = (3;0; 3 − ) 1 1 S = S + S = ( A ;
B AC + AC; AD ) = (3 3 + 9 3 6 3 ) = . ABCD A BC A CD 2 2 2
CD có trung điểm H (0;1;5) . Vì SH ⊥ ( ABCD) nên đường thẳng SH có vtcp u = n(ABCD) x = t = A ; B AC = (3;3; )
3 vtcp khác của SH là (1;1; )
1 SH : y = 1+ t (t ) z = 5+t
S SH S (t;1+ t;5 + t ) HS = (t;t;t ) . 27 Theo giả thiết V = 1 27 SH.S = 1 9 3 27 3 t . = t = 3 S . ABCD 2 3 ABCD 2 3 2 2 t = 3 S 3;4;8 1 ( )
. Vậy S S có trung điểm I (0;1;5) . 1 2 t = 3 − S 3 − ; 2 − ;2 2 ( )
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 59 / 8 5 x −1 y − 6 z
Câu 95: Cho điểm I (1;7;5) và đường thẳng d : =
= . Phương trình mặt cầu có tâm I và 2 1 − 3
cắt đường thẳng d tại hai điểm ,
A B sao cho tam giác diện tích tam giác IAB bằng 2 6015 là 2 2 2 2 2 2 A. ( x − )
1 + ( y − 7) + ( z − 5) = 2018 .
B. ( x − )
1 + ( y − 7) + ( z − 5) = 2017 . 2 2 2 2 2 2
C. ( x − )
1 + ( y − 7) + ( z − 5) = 2016 .
D. ( x − )
1 + ( y − 7) + ( z − 5) = 2019 . Lời giải Chọn B
Gọi H là trung điểm của AB IH ⊥ AB .
d có vectơ chỉ phương u = (2; 1
− ;3) và đi qua M (1;6;0) Ta có IM = (0; 1 − ; 5
− ) u;IM = (8;10; 2 − ) . u; IM 2 2 2 8 +10 + ( 2 − )
Vậy IH = d (I;d ) = = = 2 3 u 2 + (− )2 2 2 1 + 3 Ta có S
= 2 6015 1 IH.AB = 1 2 6015
.2 3.AB = 2 6015 AB = 2 2005 I AB 2 2 HA = 2005 .
Mặt cầu (S ) cần tìm có bán kính 2 2 R = IA = HA + IH = 2005+12 = 2017
(S ) (x − )2 + ( y − )2 + (z − )2 : 1 7 5 = 2017 x = 1 − + t
Câu 96: Cho điểm I (0;0;3) và đường thẳng d : y = 2t
. Phương trình mặt cầu ( S ) có tâm I và cắt z = 2+ t
đường thẳng d tại hai điểm ,
A B sao cho tam giác IAB vuông là: 3 8
A. x + y + ( z − 3)2 2 2 = .
B. x + y + ( z − 3)2 2 2 = . 2 3 2 4
C. x + y + ( z − 3)2 2 2 = .
D. x + y + ( z − 3)2 2 2 = . 3 3 Lời giải
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 60 / 8 5 Chọn B
Tam giác IAB là tam giác vuông, mà IA = IB = R nên tam giác IAB vuông cân tại I . R
Khi đó IH = d (I;(d )) =
( Với H là hình chiếu của I trên đường thẳng d . 2 2 − 2 7 2 2 6 Ta có H ( 1
− +t;2t;2 +t), IH.u = 0 H ; ; IH = R = . d 3 3 3 3 3 8
Vậy phương trình mặt cầu (S ) x + y + ( z − 3)2 2 2 = . 3
Câu 97: Cho điểm A(2;5; )
1 và mặt phẳng (P) : 6x + 3y − 2z + 24 = 0 , H là hình chiếu vuông góc của
A trên mặt phẳng (P) . Phương trình mặt cầu (S) có diện tích 784 và tiếp xúc với mặt
phẳng (P) tại H , sao cho điểm A nằm trong mặt cầu là: 2 2 2
A. ( x − 8) + ( y − 8) + ( z + ) 1 = 196. 2 2 2
B. ( x + 8) + ( y + 8) + ( z − ) 1 =196 . 2 2 2
C. ( x +16) + ( y + 4) + ( z − 7) = 196 . 2 2 2
D. ( x −16) + ( y − 4) + ( z + 7) = 196 . Lời giải Chọn A x = 2 + 6t
Phương trình đường thẳng qua A và vuông góc với mặt phẳng (P) có dạng: y = 5 + 3t (d ) z =1−2t .
Khi đó H = d (P) H ( 4 − ;2; ) 3 . Ta có 2
S = 4 R R = 14 .
Do mặt cầu (S ) tiếp xúc với (P) tại H nên tâm I của mặt cầu thuộc đường thẳng d . = 2 2 2 t 1
Nên tọa độ I (2 + 6t;5 + 3t;1− 2t) và IH = 14 (6t + 6) + (3 + 3t ) + ( 2
− − 2t) =196 . t = 3 −
Khi đó ta được tọa độ điểm I (8;8;− ) 1 . ( Tâm I ( 1 − 6; 4
− ;7) loại do không thỏa mãn IA R ).
Vây phương trình mặt cầu ( 2 2 2
S ) có dạng: ( x − 8) + ( y − 8) + ( z + ) 1 = 196 . x − 2 y z −1
Câu 98: Cho mặt phẳng (P) : x − 2y − 2z +10 = 0 và hai đường thẳng : = = , 1 1 1 1 − x − 2 y z + 3 : = =
. Mặt cầu (S ) có tâm thuộc , tiếp xúc với và mặt phẳng (P) , có 2 2 1 1 4 1 phương trình: 2 2 2 11 7 5 81 A. 2 2 2
(x −1) + ( y +1) + (z − 2) = 9 hoặc x −
+ y − + z + = . 2 2 2 4
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 61/ 8 5 2 2 2 11 7 5 81 B. 2 2 2
(x +1) + ( y −1) + (z + 2) = 9 hoặc x +
+ y + + z − = . 2 2 2 4 C. 2 2 2
(x −1) + ( y +1) + (z − 2) = 9 . D. 2 2 2
(x −1) + ( y +1) + (z − 2) = 3 . Lời giải Chọn A x − 2 y z −1 t + Tâm I : = =
I (2+t;t;1−t) có d (I (P)) 10 ; = 1 1 1 1 − 3 Lấy M (2;0; 3
− ) MI = t;t;4 −t ; u = (1;1;4 tính MI ,u = (5t − 4;4 −5t;0 d ) d ) 2 ( ) 2 2 − d ( MI ,ud 5t 4 I; = = . 2 ) 2 u 3 d2 t = 1 − t − t + Ta có d ( I; = d I; P = 5 4 10 R = . 2 ) ( ( )) 7 3 3 t = 2 1 − :10 Với t = 1 − I (1; 1 − ;2); R =
= 3phương trình mặt cầu: 2 2 2
(x −1) + ( y +1) + (z − 2) = 9 3 7 +10 2 2 2 7 11 7 2 11 7 5 81 Với t = I ; ; 2 ; R =
= 3 phương trình mặt cầu: x − + y − + z + = 2 2 2 3 2 2 2 4
Câu 99: Trong không gian với hệ toạ độ Oxyz , cho (P) : x + 4y − 2z − 6 = 0, (Q) : x − 2y + 4z − 6 = 0 . Lập
phương trình mặt phẳng ( ) chứa giao tuyến của (P) , (Q) và cắt các trục tọa độ tại các điểm ,
A B, C sao cho hình chóp .
O ABC là hình chóp đều.
A. x + y + z + 6 = 0 .
B. x + y + z − 6 = 0 .
C. x + y − z − 6 = 0 .
D. x + y + z − 3 = 0 . Lời giải Chọn B Ta có n = (1;4; 2 − ; n = (1; 2
− ;4 , d = (P)(Q) chọn được u = n ,n = (12; 6 − ; 6 − d P Q ) Q ) P ) ( ) ( ) ( ) ( ) . Do .
O ABC là hình chóp đều nên là OA = OB = OC suy ra tọa độ của A( ; m 0;0) hoặc A( ; m − 0;0); của B(0; ; m 0) hoặc B(0; ; m
− 0) và C(0;0;m) hoặc C(0;0;−m) với m 0. Giả sử A( ; m 0;0); B(0; ;
m 0); C (0;0;m) theo phương trình đoạn chắn ta có ( ) x y z ABC : + +
= 1 x + y + z = m có vectơ pháp tuyến n = 1;1;1 , lập luận tương tự ta 1 ( ) m m m
có các vectơ pháp tuyến khác là n = 1 − ;1;1 , n = 1; 1 − ;1 , n = 1;1; 1 − . 4 ( ) 3 ( ) 2 ( )
Do ( ) ( ABC) là mặt phẳng xác định nên chỉ được nhận 1 trong 4 vectơ trên, ( ) chứa d
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 62 / 8 5 ta có n n = 1;1;1 . 1 ( ) ( n = ).u 0 suy ra d ( ) x = 0 x = 0
Tìm một điểm giao của (P) và (Q) ta có x = 0 xét hệ x + 4y − 2z − 6 = 0 y = 3 được tọa
x − 2 y + 4z − 6 = 0 z = 3 độ điểm M (0;3; ) 3 .
Phương trình mặt phẳng ( ) : ( 1 x − 0) + ( 1 y − ) 3 + ( 1 z − )
3 = 0 x + y + z − 6 = 0 .
Câu 100: Trong không gian với hệ trục toạ độ Oxyz ,cho tứ diện ABCD có điểm A(1;1; ) 1 , B (2;0;2), C ( 1 − ; 1
− ;0), D(0;3;4). Trên các cạnh AB, AC, AD lần lượt lấy các điểm B ,C , D thỏa: AB AC AD + + = 4 B C D
biết tứ diện AB C D có thể tích AB AC AD
. Viết phương trình mặt phẳng ( ) nhỏ nhất?
A. 16x + 40y − 44z + 39 = 0 .
B. 16x + 40y + 44z − 39 = 0 .
C. 16x − 40 y − 44z + 39 = 0 .
D. 16x − 40 y − 44z − 39 = 0 . Lời giải Face: Nguyễn Quân Chọn A V
AB AC AD
AB 'C ' D ' = . . . V AB AC AD ABCD AB AC AD AB AC AD Mặt khác 3 4 = + + 3. . . AB AC AD
AB AC AD AB AC AD 64 V 27 27 Suy ra . . V V
AB AC AD 27 V 64 64 AB AC AD 3 V = = = . min AB AC AD 4 1 3 7
Do đó (P) đi qua trọng tâm G ; ;
của tứ diện ABCD và song song với (BCD) 2 4 4
n = BC, BD = (4;10; 1 − ) 1
Vậy (P) :16x + 40y − 44z + 39 = 0 .
Câu 101: Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng
đi qua điểm M 1;2;3 và cắt các
trục Ox, Oy, Oz lần lượt tại A , B , C ( khác gốc toạ độ O ) sao cho M là trực tâm tam giác ABC . Mặt phẳng
có phương trình là: x y z A. x 2 y 3z 14 0 . B. 1 0 . 1 2 3 C. 3x 2 y z 10 0 . D. x 2 y 3z 14 0 . Lời giải
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 63/ 8 5 Face: Nguyễn Quân Chọn A
Tứ diện OABC vuông đỉnh O, M là trực tâm . ABC AB ⊥ OC
AB ⊥ (OCM ) AB ⊥ OM ( ) * AB ⊥ CM AC ⊥ OB
AC ⊥ (OBM ) AC ⊥ OM ( ) ** AC ⊥ BM Từ đó ( ) * , (* )
* suy ra OM ⊥ ( ABC)
(ABC) có vecto pháp tuyến là OM = (1;2;3).
(ABC) có phương trình: 1.(x − )
1 + 2( y − 2) + 3( z − )
3 = 0 x + 2y + 3z −14 = 0.
Câu 102: Trong không gian với hệ toạ độ Oxyz , cho điểm N (1;1; )
1 . Viết phương trình mặt phẳng
(P) cắt các trục Ox,Oy,Oz lần lượt tại ,AB,C (không trùng với gốc tọa độO) sao cho N là
tâm đường tròn ngoại tiếp tam giác ABC
A. (P) : x + y + z −3 = 0 . B. (P) : x + y − z +1= 0 .
C. (P) : x − y − z +1= 0 . D. (P) : x + 2y + z − 4 = 0 . Lời giải Face: Nguyễn Quân Chọn A x y z
Phương trình mặt phẳng ( P) : + + = 1, A(a;0;0), B(0;b;0),C (0;0;c) a b c N ( )(P) 1 1 1 1;1;1 + + = 1 (1) a b c NA = NB (a − )2 1 +1+1 = 1+ (b − )2 1 +1 a = b (2) NA = NC ( = a − )2 1 +1+1 = 1+1+ (c − )2 1 a c (do ABC
có 3 góc nhọn và có tâm đường tròn ngoại tiếp N (1;1; )
1 nên ta có a ,b , c 1)
Từ (1) và (2) ta có: a = b = c = 3.
Vậy phương trình mặt phẳng (P) : x + y + z −3 = 0
Câu 103: Trong không gian với hệ toạ độ Oxyz ,cho hai đường thẳng d , d lần lượt có phương trình 1 2 x − 2 y − 2 z − 3 x −1 y − 2 z −1 d : = = , d : = =
. Phương trình mặt phẳng ( ) cách đều hai 1 2 1 3 2 2 1 − 4
đường thẳng d , d là: 1 2
A. 7x − 2 y − 4z = 0 .
B. 7x − 2 y − 4z + 3 = 0 .
C. 2x + y + 3z + 3 = 0. D. 14x − 4y − 8z + 3 = 0 . Lời giải
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 64 / 8 5 Face: Nguyễn Quân Chọn D
d có vtcp u = 2;1;3 và đi qua điểm A 2; 2;3 . 1 ( ) 1 ( ) 1
d có vtcp u = 2; 1
− ;4 và đi qua điểm A 1;2;1 2 ( ) 2 ( ) 2
n = u ;u = 7; 2 − ; 4 − A A = 1 − ;0; 2 − ; u
;u .A A =1 0 1 2 ( ) , 1 2 ( ) 1 2 1 2
Suy ra d , d chéo nhau. 1 2 3
Do đó ( ) đi qua trung điểm I ; 2; 2
của A A có vtpt là n 2 1 2
Vậy phương trình ( ) là 14x − 4y − 8z + 3 = 0
Câu 104: Trong không gian với hệ tọa độ Oxyz, gọi d đi qua A(3; 1 − ; ) 1 , nằm trong mặt phẳng ( x y − 2 z
P) : x − y + z − 5 = 0 , đồng thời tạo với : = = một góc 0
45 . Phương trình đường 1 2 2 thẳng d là: x = 3 + 7t x = 3+ t A. y = 1 − −8t .
B. y = 1 − − t. z = 1 − −15 t z = 1 x = 3+ 7t x = 3+ t x = 3+ 7t
C. y = 1 − −8t.
D. y = 1
− − t và y = 1 − −8t. z = 1−15 t z = 1 z = 1−15 t Lời giải Chọn C
Gọi u = a b c là vtcp của d ( 2 2 2
a + b + c 0). d ( ; ; )
(P): x− y + z −5 = 0 có vtpt n = (1; 1 − P ) ( ) ;1 . x y − 2 z : = = có vtcp u = (1;2;2). 1 2 2
Vì d (P) nên u .n
= 0 a = b − . c d P (*) ( ) Ta có u .u d 2
a + 2b + 2c 0 cos 45 = = 2 2 2 u . u 2 a + b + c d 3 2
8c −15bc = 0
c = 0 a = b u = a d (1;1;0) − − = = = = b c b c b a b ud ( − − ). 15 7 8 15 7; 8; 15 8 8 8
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 65/ 8 5 x = 3+ t x = 3+ 7t
Vậy d : y = 1 − + t,t hay d : y = 1
− −8t,t . z = 1 z = 1−15 t
Câu 105: Trong không gian với hệ tọa độ Oxyz, gọi d đi qua điểm A(1; 1 − ;2), song song với ( x +1 y −1 z
P) : 2x − y − z + 3 = 0 , đồng thời tạo với đường thẳng : = = một góc lớn nhất. 1 2 − 2
Phương trình đường thẳng d là: x −1 y +1 z − 2 x −1 y +1 z − 2 A. = = . B. = = . 1 5 − 7 4 5 3 x −1 y +1 z − 2 x −1 y +1 z − 2 C. = = . D. = = . 4 5 7 1 5 − 7 − Lời giải Chọn B
(P):2x− y − z +3= 0 có vtpt n = (2; 1 − ;− P ) ( ) 1 . x +1 y −1 z : =
= có vtcp u = (1; 2 − ;2). 1 2 − 2
(d;) ⊥d. max qua A(1; 1 − ;2) Khi đó d
u = n ;u = P ( 4 − ; 5 − ; 3 − ) = − (4;5;3 ). vtcp d ( ) x −1 y +1 z − 2 Vậy d : = = . 4 5 3 x −1 y − 2 z + 2
Câu 106: Trong hệ tọa độ Oxyz gọi d đi qua A(-1;0;-1) cắt : = = sao cho góc giữa d 1 2 1 1 − x − 3 y − 2 z + 3 và : = =
là nhỏ nhất. Phương trình đường thẳng d là: 2 1 − 2 2 x +1 y z +1 x +1 y z +1 A. = = B. = = 2 2 1 − 4 5 2 − x +1 y z +1 x +1 y z +1 C. = = D. = = 4 5 − 2 − 2 2 1 Lời giải Chọn C
M = d M 1+ 2t; 2 + t; 2
− −t , AM (2t + 2;t + 2; t − − ) 1 1 ( ) có vtcp u ( 1 − ;2;2) . 2 2t
Gọi là góc giữa hai đường thẳng d, : cos = 2 2 3 6t +14t + 9
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 66/ 8 5
+) với t = 0 cos = 0 = 2 2 2 2 +) t 0 cos = = 2 14 9 5 5 3 7 3 6 + + + + 2 3 t t 9 t 3 2 9 cos − = , t = 5 7 − − + + 9 1 x 1 y z 1 khi t = AM = (4; 5 − ; 2 − ) d : = = Chọn C min 7 7 4 5 − 2 − x −1 y z + 2
Câu 107: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d : = = và 1 2 1 1 − x −1 y + 2 z − 2 d : = =
. Gọi là đường thẳng song song với (P) : x + y + z − 7 = 0 và cắt 2 1 3 2 −
d , d lần lượt tại A, B sao cho AB ngắn nhất. Phương trình đường thẳng là: 1 2 = − x 6 t x = 12 − t 5 A. y = 5
B. y = 2 z = 9 − + t 9 − z = + t 2 x = 6 x = 6 − 2t 5 5
C. y = − t
D. y = + t 2 2 9 − 9 − z = + t z = + t 2 2 Lời giải Chọn B
Ad A 1+ 2 ; a ; a 2
− − a ,Bd B 1+ ; b 2 − +3b;2 − 2b . 1 ( ) 2 ( ) AB (b − 2 ;
a 3b − a − 2; 2
− b + a + 4) . (P) có vtpt n(1;1; ) 1 . 2
/ / (P) A .
B n = 0 b = a − 2 AB (−a −1;2a − 5;−a + 6) 5 49 49 2 2
AB = 6a − 30a + 62 6 a − + 2 2 2 x = 6 − t 5 5 9 − 7 5 AB khi a = A 6; ; , AB = ( 1 − ;0 ) ;1 y = Chọn B min 2 2 2 2 2 9 − z = + t 2
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 67 / 8 5 x y − 1 z + 2
Câu 108: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d : = = 1 2 1 − và 1 x = 1 − + 2t
d : y = 1+ t
. Phương trình đường thẳng d vuông góc với (P) : 7x + y − 4z = 0 và cắt hai 2 z = 3
đường thẳng d , d là 1 2 x − 7 y z + 4 x − 2 y z +1 A. = = . B. = = . 2 1 1 7 1 4 − x + 2 y z −1 x − 2 y z +1 C. = = . D. = = . 7 − 1 − 4 7 1 4 Lời giải Chọn B
Gọi A , B lần lượt là giao điểm của đường thẳng d với d , d ; n = (7;1; 4 − ) là một véc tơ 1 2
pháp tuyến của (P).
Do Ad A 2 ; a 1− ; a 2
− + a , Bd B 1 − + 2 ; b 1+ ; b 3 2 ( ) 1 ( ) .
AB = (2b − 2a −1;a + ; b 5 − a) .
Theo giả thiết ta có đường thẳng d vuông góc với (P) nên AB và n cùng phương, khi đó 2
− a + 2b −1 = 7k
2a − 2b + 7k = 1 − a = 1
tồn tại số thực k sao cho AB = kn a + b = k
a +b − k = 0 b = 2 − . 5 − a = 4 − k a − 4k = 5 k = 1 − A(2;0;− ) 1 .
Vậy đường thẳng d đi qua điểm A(2;0;− )
1 và nhận n = (7;1; 4
− ) làm một véc tơ chỉ x − 2 y z +1 phương có phương trình: = = . 7 1 4 − x + 1 y − 2 z − 1
Câu 109: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng : = = và 1 3 1 2 x = 3 x −1 y z + 1 : = =
. Phương trình đường thẳng song song với d : y = 1 − + t và cắt hai 2 1 2 3 z = 4 + t
đường thẳng ; là 1 2 x = 2 x = 2 − x = 2 − x = 2
A. y = 3 − t .
B. y = 3 − − t . C. y = 3 − + t .
D. y = 3 − + t . z = 3 − t z = 3 − − t z = 3 − + t z = 3 + t Lời giải Chọn A
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 68 / 8 5
Gọi A , B lần lượt là giao điểm của đường thẳng với , ; u = (0;1 ) ;1 là một véc tơ chỉ 1 2
phương của đường thẳng d .
Do A A 3a −1;a + 2;2a +1 , B B 1+ ; b 2 ; b 3b −1 2 ( ) 1 ( ) . AB = ( 3
− a + b + 2;−a + 2b − 2; 2
− a + 3b − 2) .
Theo giả thiết ta có đường thẳng song song với đường thẳng d nên AB và u cùng phương, 3
− a + b + 2 = 0 3 − a + b = 2 − a =1
khi đó tồn tại số thực k sao cho AB = ku −a + 2b − 2 = k −a + 2b − k = 2 b =1 . 2
− a + 3b − 2 = k 2
− a + 3b − k = 2 k = 1 − A(2;3; ) 3 .
Vậy đường thẳng đi qua điểm A(2;3; ) 3 và nhận n = (0; 1 − ;− ) 1 làm một véc tơ chỉ x = 2
phương có phương trình: y = 3 − t . z = 3−t x − 12 y − 9 z − 1
Câu 110: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : = = , và mặt 4 3 1
thẳng (P): 3x + 5y − z − 2 = 0. Gọi d ' là hình chiếu của d lên (P). Phương trình tham số của d ' là x = 62 − t x = 62t x = 62t x = 62t
A. y = 25t . B. y = 25 − t . C. y = 25 − t . D. y = 25 − t . z = 2 − 61t z = 2 + 61t z = 2 − + 61t z = 2 + 61t Lời giải Chọn C
Ta có: d qua A(12;9; )
1 và có VTCP a = (4;3; ) 1 .
(P) có VTPT n = (3;5;− )1.
Gọi (Q) là mặt phẳng chứa d và vuông góc (P) .
(Q) qua A(12;9; ) 1 và có VPT n = ; a n = 8 − ;7;11 . 1 ( ) (Q): 8
− x + 7y +11z + 22 = 0.
d ' là hình chiếu của d lên ( P) nên d ' = (P) (Q) . Phương trình d ' là x = 62t 8
− x + 7y +11z + 22 = 0 y = 25 − t . 3
x + 5y − z − 2 = 0 z = 2 − + 61 t
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 69 / 8 5 x =1+ 2t
Câu 111: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : y = 2
− + 4t . Hình chiếu song z = 3+t x +1 y − 6 z − 2
song của d lên mặt phẳng (Oxz) theo phương : = = có phương trình là 1 − 1 − 1 x = 3+ 2t x = 3+ t x = 1 − − 2t x = 3+ 2t A. y = 0 . B y = 0 . C y = 0 . D. y = 0 . z = 1− 4t z = 1+ 2t z = 5 − 4t z = 1− 5t . . Lời giải Chọn D 7
Gọi A = d (Oxz) A 2;0; . 2 Lấy M (1; 2 − ; )
3 d . Gọi d là đường thẳng qua M và song song với . x =1− t
Phương trình d : y = 2 − − t . z = 3+t
Gọi B là hình chiếu song song của M lên (Oxz) theo phương B = d(Oxz) B(3;0; ) 1 .
Đường thẳng hình chiếu song song của d lên (Oxz) có vec tơ chỉ phương
u = 2AB = (2;0; 5 − ) x = 3+ 2t
Phương trình có dạng : y = 0 . z =1−5t
Câu 112: Trong không gian Oxyz , cho hai điểm A(3;0; 2) , B (1; 2; 4) và mặt cầu (S): 2 2 2
x + ( y + 2) + (z −1) = 25 . Phương trình mặt phẳng ( ) đi qua hai điểm A , B và cắt mặt
cầu ( S ) theo một đường tròn bán kính nhỏ nhất là
A. x − 4 y − 5z +17 = 0. B. 3x − 2 y + z − 7 = 0 .
C. x − 4 y + 5z −13 = 0. D. 3x + 2 y + z –11 = 0. Lời giải Chọn D (S) có tâm I (0; 2
− ;1) và bán kính R = 5. AB = ( 2
− ;2;2) ; IA = (3;2;1). 2 2 2
r = R − IH với H là hình chiếu vuông góc của I lên mặt phẳng ( ) .
Gọi K là hình chiếu vuông góc của I lên lên đường thẳng AB.
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 7 0 / 8 5 r IH
= IK H K IK ⊥ () . min max qua ( A 3; 0; 2) Khi đó ( ) . vtpt n
= AB, AB, IA = 12( − 3; 2;1) ( )
Vậy ( ) : 3x − 2 y + z −11 = 0 .
Câu 113: Trong không gian Oxyz , cho điểm M ( 3 − ;3; 3
− ) thuộc mặt phẳng ( ) : 2x – 2y + z +15 = 0 và mặt cầu (S ) 2 2 2
: (x− 2) + (y− 3) + (z− 5) = 100 . Đường thẳng qua M, nằm trên mặt phẳng
( ) cắt (S) tại hai điểm A và B . Để độ dài AB lớn nhất thì phương trình đường thẳng là x + 3 y − 3 z + 3 x + 3 y − 3 z + 3 A. = = . B. = = . 1 4 6 16 11 10 − x = 3 − + 5t x + 3 y − 3 z + 3
C. y = 3 . D. = = . 1 1 3 z = 3 − + 8 t Lời giải Chọn A
(S) có tâm I (2;3;5) và bán kính R = 10 .
( ):2x – 2y + z +15 = 0 có vtpt n = (2; 2 − ;1) . ( ) IM = ( 5 − ;0; 8 − ).
Gọi H là hình chiếu vuông góc của I lên ( ), K là hình chiếu vuông góc của I lên AB. 2 2 2 2
AB = 4KB = 4(R − IK ) . qua = H AB IK IH H K . max min qua M qua M ( 3 − ;3; 3 − ) Khi đó . vtcp u = n , n
, IM = (9;36;54) = 9(1; 4; 6) ( ) ( ) d x + 3 y − 3 z + 3 Vậy : = = . 1 4 6
Câu 114: Trong không gian Oxyz ,cho mặt phẳng
(P):2x − 2y − z +9 = 0 và mặt cầu 2 2 2
(S ) : (x − 3) + ( y + 2) + (z −1) = 100 . Tọa độ điểm M nằm trên mặt cầu (S) sao cho khoảng
cách từ điểm M đến mặt phẳng (P) đạt giá trị lớn nhất là 11 14 13 29 26 7 29 26 7 11 14 13 A. M − ; ; . B. M ; − ; −
. C. M − ; ; −
. D. M ; ; − . 3 3 3 3 3 3 3 3 3 3 3 3 Lời giải Chọn B
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 7 1/ 8 5 + − +
Mặt cầu (S ) có tâm I (3; 2 − ; )
1 và bán kính R = 100 = 10 . Ta có d ( I ( P)) 6 4 1 9 , = 3
= 6 R (P) cắt mặt cầu (S ) theo giao tuyến là một đường tròn.
Gọi H là hình chiếu vuông góc của I trên ( P) . Tia IH cắt mặt cầu (S ) tại Q và tia đối của
tia IH cắt mặt cầu (S ) tại K . Khi ấy, KQ là đường kính của mặt cầu (S ) . Gọi N, J lần
lượt là hình chiếu vuông góc của M trên ( P) và của M trên KQ . M
QK ⊥ tại M nên J
nằm trên cạnh KQ . Ta có MJHN là hình chữ nhật ( N = H = J = 90 ) MN = HJ và
0 HJ HK (Vì HK = 16 HQ = 4 ) max d (M ;( P)) = HK = 16 . Dấu " = " xảy ra khi M K . x = 3 + 2t (
IH ) đi qua I (3; 2 − ; ) 1 u = n = (2; 2
− ;− ) (IH ) : y = 2
− − 2t (t ) và có vtcp 1 . (P) z =1−t 2 2 2
K ( IH ) K (3 + 2t; 2
− − 2t;1− t ) . Ta lại có
K (S ) (2t ) + ( 2
− t) + (−t) =100 10 t = 100 2 3 t = 9 10 t = − 3 10 Với t = 29 26 7 K ; − ; −
d (M ;(P)) =16 (nhận). 3 3 3 3 10 Với t = − 11 14 13 K − ; ;
d (M ;(P)) = 4 (loại). 3 3 3 3
Nhận xét: Đề bài ban đầu yêu cầu tìm tọa độ điểm M nằm trên mặt cầu (S) sao cho
khoảng cách từ điểm M đến mặt phẳng (P) đạt giá trị nhỏ nhất. Trong quá trình lập luận
tôi thấy không phù hợp vì có vô số điểm M nên đã sửa đề lại như trên.
Câu 115: Trong không gian Oxyz , cho hình hộp chữ nhật ABC . D A B C D
có điểm A trùng với gốc
của hệ trục tọa độ, B( ; a 0; 0) , D(0; ; a 0) , A (
0;0;b) (a 0,b 0) . Gọi M là trung điểm của a
cạnh CC . Giá trị của tỉ số để hai mặt phẳng ( ABD) và (MBD) vuông góc với nhau là b
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 7 2 / 8 5 1 1 A. . B. . C. 1 − . D. 1. 3 2 Lời giải Chọn D
Ta có ABCD là hình bình hành nên AB = DC C (a; a;0) . Và ACC A
là hình bình hành nên CC = AA C(a;a;b) . b
CC có trung điểm M a; a; 2
BA = (−a;0;b) và BD = (−a; a;0) ( ABD) có vtpt BA BD = ( 2 ; − ; ab − ; ab −a ) vtpt khác a
của ( ABD) là n = 1;1; (vì b 0 ) 1 b b −ab −ab BM = 0; a; (MBD) có vtpt 2 BM; BD = ; ; a
vtpt khác của (MBD) là 2 2 2 2a n = 1;1; − (vì b 0 ). 2 b a = 2 1 a b
Theo giả thiết ( ABD) ⊥ (MBD) n ⊥ n n .n = 0 2 − 2 = 0 . 1 2 1 2 b a = 1 − (l) b
Câu 116: Trong không gian Oxyx , cho mặt phẳng (P) : x + 2 y + 2z + 4 = 0 và mặt cầu 2 2 2
(S) : x + y + z − 2x − 2 y − 2z −1 = 0 . Giá trị của điểm M trên (S) sao cho d (M , (P)) đạt giá trị nhỏ nhất là 5 7 7 1 1 − 1 − A. (1;1; ) 3 . B. ; ; . C. ; ; . D. (1; 2 − ; ) 1 . 3 3 3 3 3 3 Lời giải Chọn C
Ta có: x + y + z − x − y − z − = ( x − )2 2 2 2 2 2 2 2 2 1 0 1
+ (y −1) + (z −1) = 4
Mặt cầu (S) có tâm I (1;1;1) , bán kính R = 2
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 7 3/ 8 5 1+ 2 + 2 + 4
d (I , (P)) =
= 3 R . Do đó, (S) và (P) không giao nhau. 2 2 2 1 + 2 + 2
Vậy để khoảng cách từ M đến (P) đạt giá trị nhỏ nhất thì M thuộc đường thẳng d đi qua
tâm I của mặt cầu (S) và vuông góc với mặt phẳng (P) .
Mặt phẳng (P) có VTPT n = (1; 2; 2)
Đường thẳng d đi qua I và nhận n = (1; 2; 2) là VTCP nên d có phương trình là: x =1+ t y = 1+ 2t z =1+ 2t
M d M (1+ t;1+ 2t;1+ 2t)
M (S ) (1+ t − )2 2 2 2 2
1 + (1+ 2t −1) + (1+ 2t −1) = 4 9t = 4 t = 3 2 5 7 7 11 Với t =
M ( ; ; ) d(M ,(P)) = 3 3 3 3 3 2 1 1 − 1 − 1
Với t = − M ( ; ;
) d (M , (P)) = 3 3 3 3 3 1 1 − 1 − Vậy M ; ;
thỏa mãn yêu cầu bài toán. 3 3 3
Câu 117: Trong không gian với hệ trục tọa độ Oxyz , cho điểm ( A 10; 2; 1 − ) và đường thẳng x −1 y z −1 d : = =
. Gọi (P) là mặt phẳng đi qua điểm A , song song với đường thẳng d sao 2 1 3
cho khoảng cách giữa d và (P) lớn nhất. Khoảng cách từ điểm M (−1; 2;3) đến mặt phẳng (P) là 97 3 76 790 2 13 3 29 A. . B. . C. . D. . 15 790 13 29 Lời giải Chọn A
Gọi H là hình chiếu của A trên d , gọi I là hình chiếu của H trên (P) .
Mặt phẳng (P) đi qua điểm
A , song song với đường thẳng d nên
d (d, (P)) = d (H , (P)) = IH .
Ta có AH IH nên IH lớn nhất AH = IH A I .
Vậy mặt phẳng (P) thỏa mãn yêu cầu bài toán là mặt phẳng đi qua điểm A và nhận vectơ AH làm VTPT.
Ta có H d H (1+ 2t;t;1+ 3t) AH = (2t − 9;t − 2;3t + 2) x −1 y z −1 d : = = u = (2;1;3) 2 1 3 d Vì H là hình chiếu của A trên d nên
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 7 4 / 8 5
AH ⊥ d AH. u = 0 2(2t − 9) + (t − 2) + 3(3t + 2) = 0 t = 1 d
Do đó H (3;1; 4) AH = ( 7 − ; 1 − ;5)
Mặt phẳng (P) đi qua điểm ( A 10; 2; 1
− ) và có VTPT là AH = ( 7 − ; 1
− ;5) nên (P) có phương trình là: 7
− (x −10) − (y − 2) + 5(z +1) = 0 7x + y − 5z − 77 = 0 7 − + 2 − 5.3− 77 97 3
Vậy d (M ;(P)) = = . 2 2 + + − 15 7 1 ( 5)
Câu 118: Trong không gian với hệ trục toạ độ Oxyz, cho điểm A(2;5; ) 3 và đường thẳng x −1 y z − 2 d : = =
. Gọi (P) là mặt phẳng chứa đường thẳng d sao cho khoảng cách từ A 2 1 2
đến (P) lớn nhất. Tính khoảng cách từ điểm M (1;2;− )
1 đến mặt phẳng (P) . 11 18 11 4 A. . B. 3 2 . C. . D. . 18 18 3 Lời giải Chọn A
Kẻ AH ⊥ (P), AK ⊥ d .
Ta có K d K (1+ 2t, t, 2 + 2t) AK = (2t −1, t − 5, 2t − ) 1 . Ta có: u (2;1;2). d
AK ⊥ d AK.u = 0 2(2t −1) +1(t − 5) + 2(2t −1) = 0 t =1 K (3;1;4), AK = (1; 4 − ) ;1 . Do d
AH ⊥ (P), AK ⊥ d , d (P) nên AH ⊥ KH AH AK.
max AH = AK khi H K hay AK ⊥ (P).
(P) đi qua K (3;1;4) nhận AK làm VTPT nên phương trình (P) là: x − 4y + z −3 = 0. 11 18
d(M ,(P)) = . 18
Câu 119: Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng (P) : x + y − z + 2 = 0 và hai x =1+ t x = 3− t
đường thẳng d : y = t
; d : y = 1+ t . Biết rằng có 2 đường thẳng có các đặc điểm: z = 2 + 2t z = 1− 2t
song song với (P) ; cắt d, d và tạo với d góc O
30 . Tính cosin góc tạo bởi hai đường thẳng đó. 1 1 2 1 A. . B. . C. . D. . 5 2 3 2 Lời giải Chọn B
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 7 5/ 8 5
Gọi là đường thẳng thỏa mãn YCBT.
Gọi giao điểm của đường thẳng với hai đường thẳng d, d lần lượt là M , N.
Ta có: M (1+ t, t, 2 + 2t), N (3−t , 1+ t , 1− 2t).
MN = (2 −t−t, 1+t−t, −1− 2t− 2t). Có n = 1;1; 1 − , u (1;1;2). ( P) ( ) d
//(P) MN.n = 0 4 + 2t = 0 t = 2 − . ( P)
MN = (4 −t, -1−t, 3− 2t).
MN,u = ( 5 − , -5, 5). d ( MN , ud 1 d ) 0 , = 30 (d ) 0 sin , = sin30 = 2
6t −18t − 24 = 0 t = 4, t = 1 − . 1 2 MN . u 2 d MN = 0; 5 − ; 5 − = 5
− 0;1;1 , MN = 5;0;5 = 5 1;0;1 . 2 ( ) ( ) 1 ( ) ( )
Do đó 2 VTCP của hai đường thẳng , cần tìm là: u = 0;1;1 , u = 1;0;1 . 2 ( ) 1 ( ) 1 2 u ,u 3 1 sin ( , 1 2 = = os c
( , = ( do góc giữa hai đường thẳng là góc nhọn). 1 2 ) 1 2 ) u . u 2 2 1 2
Câu 120: Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(1; 0; )
1 , B (3; -2; 0) ; B (3; -2; 0) Gọi
(P)là mặt phẳng đi qua A sao cho tổng khoảng cách từ B và C đến (P) . lớn nhất. Biết
rằng ( P) không cắt BC . Khi đó, điểm nào sau đây thuộc mặt phẳng ( P) ? A. G ( 2 − ;0;3).
B. F (3;0; 2 − ) .
C. E (1;3; ) 1 .
D. H (0;3; ) 1 . Lời giải Chọn C
Gọi I là trung điểm của BC I (2;0; − ) 1
Theo giả thiết ( P) không cắt BC nên ;
B C nằm cùng phía với ( P) . Do đó d ( ;
B ( P)) + d (C;( P)) = BH + CK = 2IJ 2IA = 2 5
Trong đó H ; K; J lần lượt là hình chiếu vuông góc của B;C; I lên mặt phẳng ( P)
Dấu “=” xảy ra J A hay ( P) ⊥ IA .
Suy ra, Mặt phẳng ( P) có VTPT IA = ( 1 − ;0;2)
Do đó, Phương trình mặt phẳng ( P) qua A(1; 0; ) 1 và có VTPT n = ( 1 − ;0;2) là:
(P): x − 2z +1= 0 E(1;3; )1(P) .
Câu 121: Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(1; 0; 0) , B (0; b; 0) , C (0; 0; c) , trong đó ;
b c dương và mặt phẳng ( P) : y − z +1 = 0 . Biết rằng mặt phẳng ( ABC ) ⊥ ( P) và
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 7 6/ 8 5
d (O ( ABC )) 1 ;
= . Mệnh đề nào đúng? 3
A. b + c = 1.
B. b + c = 1.
C. b + c = 1.
D. b + c = 1. Lời giải Chọn A x y z
Phương trình mặt phẳng ( ABC ) : + + = 1 bcx + cy + bz = bc 1 b c Ta có n (0;1; − ) 1 ; n = ( ; bc c; b . Do mặt phẳng
( ABC) ⊥ (P) n ⊥ n P ABC ) ( ) P (ABC) n .n
= 0 b = c (* P ABC ) ( ) 1 bc 1 Mặt khác, d ( ; O ( ABC )) = = (**) 3 (bc)2 2 2 3 + b + c c = 0
Thay (*) vào (**) ta được: 2 4 2 4 2
3c = c + 2c 8c − 2c = 0 1 c = 2 1 Do ;
b c dương nên b = c = . 2
Vậy, b + c = 1.
Câu 122: Trong không gian với hệ trục toạ độ Oxyz, cho 3 điểm A(1;2; ) 3 , B(0;1; ) 1 , C (1;0; 2 − ).
Điểm M (P) : x + y + z + 2 = 0 sao cho giá trị của biểu thức 2 2 2
T = MA + 2MB + 3MC nhỏ
nhất. Khi đó, điểm M cách (Q) : 2x − y − 2z + 3 = 0 một khoảng bằng 121 2 5 91 A. 54 . B. 24 . C. 3 . D. 54 . Lời giải Chọn D 4 4 1 Gọi I là điểm thỏa mãn
IA + 2IB + 3IC = 0 I ; ; − . 6 6 6 2 2 2 2
T = IA + IB + IC + IM − IM (IA+ IB + IC) 2 2 2 2 2 3 6 2 2 3
= IA + 2IB + 3IC + 6IM .
T nhỏ nhất IM ngắn nhất M là hình chiếu của I trên (P) . 4 x = + t 6 4
d : y = + t t R là đường thẳng đi qua I và vuông góc với ( P) . 6 1 z = − + t 6 − − −
M = d ( P) 7 7 22 M
d (M (Q)) 91 ; ; , = . 18 18 18 54
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 7 7 / 8 5
Câu 123: (Đề minh họa L1) Trong không gian với hệ tọa độ Oxyz cho bốn điểm A(1; 2 − ;0), B(0; 1 − ; ) 1 C (2;1;− )
1 , D(3;1;4). Hỏi có tất cả bao nhiêu mặt phẳng cách đều bốn điểm đó? A. 1. B. 4. C. 7. D. Vô số. Lời giải Chọn C AB = ( 1 − ;1; ) 1 , AC = (1;3; − )
1 , AD = (2;3;4) A , B AC = ( 4 − ;0; 4 − ) A , B AC AD 0 , suy ra
bốn điểm A, B, C, D là bốn đỉnh của một tứ diện.
Xét mp(P) và hai điểm M, N không nằm trên (P), ta có: (P) cách đều hai điểm M, N khi và
chỉ khi (P) song song với MN hoặc (P) đi qua trung điểm của đoạn MN.
Vậy có 7 mặt phẳng cách đều 4 điểm A, B, C, D, trong đó có
4 mặt phẳng mà mỗi mặt phẳng đi qua trung điểm của ba cạnh chung một đỉnh.
3 mặt phẳng mà mỗi mặt phẳng song song với hai cạnh đối diện và đi qua trung điểm
của bốn cạnh còn lại. Chọn C
Câu 124: (Đề minh họa L1 )Cho Trong không gian với hệ tọa độ Oxyz cho điểm (
A 1; 0; 2) và đường x −1 y 2 +1
thẳng d có phương trình: = =
. Viết phương trình đường thẳng đi qua A , 1 1 2
vuông góc và cắt d . x −1 y 2 − 2 x −1 y z − 2 A. : = =
. B. : = = . 1 1 1 1 1 1 − x −1 y 2 − 2 x −1 y z − 2 C. : = =
. D. : = = . 2 1 1 1 3 − 1
Lời giải Chọn B Gọi B d
tọa độ B t 1;t; 2t 1 , AB t;t; 2t 3 . Ta có . AB u 0 t t 2. 2t 3 0 t 1 B 2;1; 1 d Đường thẳng
đi qua A 1;0; 2 , vecto chỉ phương AB 1;1; 1 . x −1 y z − 2
Suy ra phương trình đường thẳng : = = 1 1 1 − .
Câu 125: (Đề thử nghiệm 2017) Trong không gian với hệ tọa độ Oxyz , cho hai điểm A 2;3;1 và AM
B 5; 6; 2 . Đường thẳng AB cắt mặt phẳng Oxz tại điểm M . Tính tỉ số . BM AM 1 AM AM 1 AM A. = . B. = 2 . C. = . D. = 3. BM 2 BM BM 3 BM Lời giải Chọn A
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 7 8 / 8 5 A H2 (Oxz) H1 M B
Mặt phẳng Oxz có phương trình y 0 . AM d ( , A (Oxz)) 3 1 Ta có = = = . BM
d ( B,(Oxz)) 6 2
Câu 126: (Đề thử nghiệm 2017) Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng ( x − 2 y z x y −1 z − 2
P) song song và cách đều hai đường thẳng d : = = và d : = = . 1 1 − 1 1 2 2 1 − 1 −
A. 2x − 2z +1 = 0 .
B. 2 y − 2z +1 = 0 .
C. 2x − 2 y +1 = 0 .
D. 2 y − 2z −1 = 0 . Lời giải Chọn B u = ( 1 − ;1; ) 1 , v = (2; 1 − ;− )
1 lần lượt là véc tơ chỉ phương của d , d . u, v = (0;1; − ) 1 1 2 .
A(2;0;0)d , B 0;1;2 d AB = 2
− ;1;2 . u,v AB 0 d ,d chéo nhau suy ra có duy 1 ( ) 2 ( ) 1 2
nhất một mặt phẳng (P) song song và cách đều d , d . 1 2 ( 1
P) đi qua trung điểm I 1; ;1
của đoạn AB và nhận u,v = (0;1;− ) 1 2 làm VTPT.
Vậy (P) : 2y − 2z +1 = 0 . Chọn B
Câu 127: (Tạp chí THTT Lần 5) Trong không gian với hệ tọa độ Oxyz , cho điểm M (1;2;− ) 1 . Viết
phương trình mặt phẳng ( ) đi qua gốc tọa độ O(0;0;0) và cách M một khoảng lớn nhất. x y z
A. x + 2 y − z = 0 . B. + + = 1.
C. x − y − z = 0 .
D. x + y + z − 2 = 0 . 1 2 −1 Lời giải Chọn A M O H P
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 7 9 / 8 5
Gọi (P) là một mặt phẳng đi qua O, H là hình chiếu của M trên (P). Khi đó d (M,(P)) = MH.
Ta có MH OM MH lớn nhất khi và chỉ khi MH = OM H O OM ⊥ (P) .
Vây ( ) là mặt phẳng đi qua O và có VTPT OM = (1;2;− )
1 ( ) : x + 2y − z = 0 . Chọn A
Câu 128: (THPT Hai Bà Trưng Lần 1) Trong không gian với hệ tọa độ Oxyz , cho điểm A(2;0; 2 − ), B(3; 1 − ; 4 − ),C( 2
− ;2;0) . Tìm điểm D trong mặt phẳng (Oyz) có cao độ âm sao
cho thể tích của khối tứ diện ABCD bằng 2 và khoảng cách từ D đến mặt phẳng (Oxy)
bằng 1. Khi đó có tọa độ điểm D thỏa mãn bài toán là: A. D(0;3;− ) 1 B. D(0; 3 − ;− ) 1 .
C. D(0;1;− ) 1 .
D. D(0;2;− ) 1 . Lời giải Chọn A
Vì D(Oyz) nên D(0; ;
y z) , z 0 . Do d ( ,
D (Oxy)) =1 nên z =1 z = 1 − D(0; ; y − ) 1 Ta có AB = (1; 1 − ; 2 − ), AC = ( 4 − ;2;2) A , B AC = (2;6; 2 − ) ; AD = ( 2 − ; y ) ;1 . 1 1 V
= AB, AC.AD = 6y − 6 = y −1 ABCD . 6 6 y = 3 D(0;3;− ) 1 Theo giả thiết V = 2 y −1 = 2 . ABCD y = 1 − D (0; 1 − ;− ) 1
Câu 129: (THPT Hai Bà Trưng Lần 1) Trong không gian với hệ tọa độ Oxyz , cho điểm H (1;2; ) 3 .
Mặt phẳng (P) đi qua điểm H , cắt Ox,Oy,Oz tại ,
A B, C sao cho H là trực tâm của tam
giác ABC . Phương trình của mặt phẳng (P) là
A. (P) :3x + y + 2z −11= 0 .
B. (P) : 3x + 2y + z −10 = 0 .
C. (P) : x + 3y + 2z −13 = 0.
D. (P) : x + 2y + 3z −14 = 0 . Lời giải Chọn D
Do OABC là tam diện vuông và H là trực tâm tam giác ABC nên OH ⊥ ( ABC) . Suy ra (P) đi điểm H (1;2; )
3 và có véc tơ pháp tuyến OH = (1;2;3) nên ( P) có phương trình ( 1 x − )
1 + 2( y − 2) + 3( z − ) 3 = 0
Hay x + 2 y + 3z −14 = 0 .
Câu 130: Trong không gian với hệ tọa độ Oxyz , cho điểm A(0;0;4) , điểm M nằm trên mặt phẳng
(Oxy) và M O. Gọi D là hình chiếu vuông góc của O lên AM và E là trung điểm của
OM . Biết đường thẳng DE luôn tiếp xúc với một mặt cầu cố định. Tính bán kính mặt cầu đó.
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 8 0 / 8 5 A. R = 2 .
B. R = 1 .
C. R = 4 .
D. R = 2 . Lời giải Chọn A Ta có ODM
vuông tại D có DE là trung tuyến nên O
ED cân tại E , suy ra E OD = E DO ( )1.
Gọi I là trung điểm của OA , ta có ODA
vuông tại D và có DI là trung tuyến nên ODA
cân tại I , suy ra I OD = I DO (2). Từ (1) và (2) ta có: 0 E DI = E DO + I DO = E OD + I OD = I OE = 90 hay OA ED ⊥ DI =
= 2. Vậy đường thẳng DE luôn tiếp xúc với mặt cầu tâm I bán kính 2 OA R = = 2. 2 Câu 131: Cho điểm (
A 0;8; 2) và mặt cầu (S ) có phương trình 2 2 2
(S ) : (x − 5) + ( y + 3) + (z − 7) = 72 và điểm B(9; 7
− ;23) . Viết phương trình mặt phẳng (P) qua A tiếp xúc với (S) sao cho khoảng
cách từ B đến (P) là lớn nhất. Giả sử n = (1; ;
m n) là một vectơ pháp tuyến của (P) . Lúc đó A. . m n = 2. B. . m n = 2. − C. . m n = 4. D. . m n = 4. − Lời giải Chọn D + + + =
Gọi phương trình mặt phẳng (P) là: x my nz d 0 A ( P)
8m + 2n + d = 0 d = 8
− m − 2n (P): x + my + nz − (8m + 2n) = 0 Vì nên ta . 5 −11m + 5n (
d ( I;( P)) = R = 6 2 P) (S) 2 2 Do
tiếp xúc với mặt cầu nên 1+ m + n . − + − − − + + − + d ( m n m n m n m n ; B ( P)) 9 7 23 8 2 (5 11 5 ) 4(1 4 ) = = 2 2 2 2 Ta có: 1+ m + n 1+ m + n
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 8 1/ 8 5 ( − + − + − + 1 m 4n B ( P)) 5 11m 5n 1 m 4n d ; + 4 d ( ;
B ( P)) 6 2 + 4 2 2 2 2 1+ m + n 1+ m + n 2 2 1+ m + n 2 2 Cosi− + + + + Svac ( m n d ; B ( P)) (1 1 16)(1 ) 6 2 + 4 d ( ;
B ( P)) 18 2 . 2 2 1+ m + n n 1 = −m = m = 1 − 4 n = 4 5 −11m + 5n = 6 2 d = 0 2 2 + +
Dấu “=” xảy ra khi 1 m n . x − 3 y z +1
Câu 132: Trong không gian cho đường thẳng : = = và đường thẳng 1 2 3 x + 3 y −1 z + 2 d : = =
. Viết phương trình mặt phẳng ( P) đi qua và tạo với đường thẳng 3 1 2
d một góc lớn nhất.
A. 19x −17 y − 20z − 77 = . 0
B. 19x −17 y − 20z + 34 = . 0
C. 31x − 8y − 5z + 91 = . 0
D. 31x − 8y − 5z − 98 = . 0 Lời giải Chọn D
Cách 1: ( P) : ax + by + cz + d = 0 ( 3
a − c + d = 0 a = 2 − a − 3c
P) chứa nên ( P) đi qua A(3;0; − )
1 và n ⊥ u P
a + 2b + 3c = 0
d = c − 3a = 10c − 6b ( + d ( P)) 5b 7c sin , = 2
5b +10c + 2bc 14 Nếu c = (d (P)) 5 0 sin , = 14 b 5 + 7 c
Nếu c 0 sin (d,( P)) = 2 b b 5 +10 +12 14 c c 2 25t + 70t + 49 10t −1
Xét hàm số f (t ) = = 5 + = g t 2 2 ( ) 5t +12t +10 5t +12t + 10 8 t = − + + g (t ) 2 50t 10t 112 5 ' = ( = t + t + ) 0 2 2 7 5 12 10 t = − 5 (t) 75 8 maxg = t = 14 5
Chọn b = 8, c = 5 a = 31
− ;d = 98 . Vậy Chọn D
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 8 2 / 8 5 Câu 133: 2 2 2
Trong không gian Oxyz cho mặt cầu (S ) :( x − ) 1
+ ( y − 2) + (z − 3) = 9 và mặt phẳng
(P):2x−2y + z +3= 0.Gọi M ( ;a ;bc)là điểm trên mặt cầu (S) sao cho khoảng cách từ M
đến (P) là lớn nhất. Khi đó
A. a + b + c = 5.
B. a + b + c = 6.
C. a + b + c = 7.
D. a + b + c = 8. Lời giải Chọn C
Mặt cầu (S ) có tâm I (1;2;3) , bán kính R = 3.
d(I (P)) = 4 , R d (M,(P)) Ta có: 3
vậy (P) cắt (S ) . Khi đó
lớn nhất M d đi qua I, vuông x =1+ 2t
góc với (P) và cắt mặt cầu tại 2 điểm M , M . PTĐT d : y = 2 − 2t 1 2 z = 3+t d cắt (S)tại M , M nên tọa độ M , M là nghiệm của hệ 1 2 1 2 x =1+ 2t y = 2−2t t =1 z 3 t = + t = 1 − (x− )2
1 + ( y − 2)2 + ( z − 3)2 = 9 13
Với t = 1 M 3;0; 4 d M , P = 1 ( ) ( 1 ( )) 3 5 Với t = 1 − M 1
− ;4;2 d M , P = 2 ( ) ( 2 ( )) 3 13
Vậy khoảng cách từ M đến (P) lớn nhất bằng
khi M (3;0;4) a + b + c = 7. 3 x −1 y z + 3
Câu 134: Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d : = = và mặt cầu (S ) 1 − 2 1 −
tâm I có phương trình: (S ) ( x − )2 + ( y − )2 + ( z + )2 : 1 2 1
=18. Đường thẳng d cắt (S ) tại 2 điểm ,
A B. Tính diện tích tam giác IA . B 8 11 16 11 11 8 11 A. . B. . C. . D. . 3 3 6 9 Lời giải Chọn A x =1− t
Phương trình tham số của đường thẳng d :y = 2t z = 3 − − t
Đường thẳng d cắt (S ) tại 2 điểm ,
A B . Khi đó tọa độ ,
A B ứng với t là nghiệm của
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 8 3/ 8 5 t = 1 − phương trình: ( 1− t − )2 1 + (2t − 2)2 + ( 3 − − t + )2 1 = 18 5 t = 3 Với t = 1 − A(2; 2 − ; 2 − ) 5 2 10 14 Với t = B − ; ;− . 3 3 3 3
Mặt cầu (S ) có tâm I (1;2;− ) 1 . 1 8 11 Khi đó S = I , A IB = . I AB 2 3
Câu 135: Cho hình lập phương ABC . D A B C D
có cạnh bằng 2 . Tính khoảng cách giữa hai mặt phẳng ( AB D ) và (BC D ). 3 3 2 A. . B. 3 . C. . D. . 3 2 3 Lời giải Chọn D Ta có ( AB D ) / / (BC D ).
d (( AB' D'),(BC ' D)) = d ( ,
A (BC ' D))
Gắn hệ trục tọa độ ( Axyz) , trong đó A(0;0;0), B(2;0;0), D(0;2;0),C '(2;2;2) Mặt phẳng (BC D
) qua B(2;0;0) có vtpt n =BC',BD = ( 4 − ; 4 − ;4) pt (BC D ): 4
− (x − 2) − 4y + 4z = 0 x + y − z − 2 = 0
d ( A (BC D)) 2 , ' = 3 .
Câu 136: Trong không gian Oxyz , cho điểm A(2;0; 2 − ), B(3; 1 − ; 4 − ),C( 2
− ;2;0). Điểm D trong mặt
phẳng (Oyz) có cao độ âm sao cho thể tích của khối tứ diện ABCD bằng 2 và khoảng cách
từ D đến mặt phẳng (Oxy) bằng 1. Khi đó có tọa độ điểm D thỏa mãn bài toán là
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 8 4 / 8 5 A. D(0;3;− ) 1 .
B. D(0; 3 − ;− ) 1 .
C. D(0;1;− ) 1 .
D. D(0;2;− ) 1 . Lời giải Chọn A
D (Oyz) D (0; y; z ), z 0
d ( D, (Oxy)) = z = 1 z = 1
− D (0; y;− ) 1 Ta có A , B AC = (2;6; 2 − ), AD = ( 2 − ; ; y 1) 1 1 y = 3 V
= AB, AC.AD = 4 − + 6y − 2 = 2 ABCD 6 6 y = 1 − D (0;3; − ) 1 D (0; 1 − ;− ) 1
Câu 137: Trong không gian với hệ tọa độ Oxyz , cho điểm ( A 2;11; 5 − ) và mặt phẳng 2 2
(P) : 2mx + (m +1) y + (m −1)z −10 = 0 . Biết rằng khi m thay đổi, tồn tại hai mặt cầu cố định
tiếp xúc với mặt phẳng (P) và cùng đi qua A . Tìm tổng bán kính của hai mặt cầu đó. A. 2 2 . B. 5 2 . C. 7 2 . D. 12 2 . Lời giải Chọn D
Gọi I (x ; y ; z ) là tâm mặt cầu. Vì mặt cầu tiếp xúc với mặt phẳng nên ta có 0 0 0 2 2
2mx + (m +1) y + (m −1)z −10 1 − − 0 0 0 1 2mx 2z 10 0 0
d (I;(P)) = = y + z + = const với mọi 2 0 0 2 2 m +1 2 m +1 2x = 0 x = 0 1 m suy ra 0 0 I(0; y ; 5
− ) d(I,(P)) = y − 5 2 − z −10 = 0 z = 5 − 0 0 2 0 0 Mặt khác mặt cầu đi qua A nên y − 5 2 0
IA = d (I;(P)) 4 + ( y −11) = I(0;25; 5 − ); I(0;9; 5 − ) 0 2 Với I (0; 25; 5 − ) R =10 2 Với I (0;9; 5 − ) R = 2 2
Câu 138: Trong không gian với hệ tọa độ Oxyz , cho ba điểm (
A 5;5; 0), B(1; 2;3), C(3;5; 1 − ) và mặt
phẳng (P) : x + y + z + 5 = 0 . Tính thể tích V của khối tứ diện S.ABC biết đỉnh S thuộc mặt
phẳng (P) và SA = SB = SC . 145 45 127 A. V = .
B. V =145. C. V = . D. V = . 6 6 3 Lời giải Chọn A
Vì SA = SB = SC nên hình chiếu của đỉnh S xuống mặt phẳng đáy trùng với tâm đường
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688
Chuyên đề: Cực trị hình giải tích T r a n g 8 5/ 8 5
tròn ngoại tiếp tam giác ABC
Phương trình mặt phẳng ( ABC) :3x −10y − 6z + 35 = 0
Phương trình mặt phẳng trung trực cạnh AB : 4x + 3y − 3z −18 = 0 15
Phương trình mặt phẳng trung trực cạnh AC : 2x + z − = 0 2 7 3
Suy ra tọa độ tâm đường tròn ngoại tiếp I 3; ; 2 2 x = 3 + 3t 7
Phương trình đường thẳng
SI : y = −10t , do điểm S thuộc mặt phẳng 2 3 z = − 6t 2 14 9
(P) t = 1 S 6; − ; − SI = 145 2 2 145
AB = 34, BC = 29, AC = 5 S = ABC 2 1 145
Vậy V = .SI.S = . 3 ABC 6
Nguyễn Hoàng Việt - Website: http://luyenthitracnghiem.vn 0905193688




