







Preview text:
ĐỀ 1
ĐỀ THI HỌC KỲ II Môn Toán Lớp 9 Thời gian: 90 phút
A. Phần trắc nghiệm (3 điểm) Hãy khoanh vào đáp án đúng trong các câu sau: Câu 1: Hàm số 2 y = 3x − :
A. Nghịch biến trên R.
B. Đồng biến trên R.
C. Nghịch biến khi x>0, đồng biến khi x<0 D. Nghịch biến khi x<0, đồng biến khi x>0
Câu 2. Trong các hệ phương trình sau đây hệ phương trình nào vô nghiệm: 3 x − 2y = 5 x − y =1 3 x − 2y = 5 5 x − 3y =1 A. B. C. D. 5 x − 3y =1 2017x − 2017y = 2 6x − 4y =10 5 x + 2y = 2 3 x + 2y = 8
Câu 3. Hệ phương trình:
có nghiệm là: 5 x − 2y = 8 x = 2 x = 2 x = 2 − x = 2 A. B. C. D. y = 1 y = 1 − y = 1 y = 3
Câu 4: Tìm 2 số biết tổng của chúng bằng 27 và tích của chúng bằng 180. Hai số đó là: A. -12 và -15 B. 15 và 12 C. 9 và 20 D. 15 và -12
Câu 5: Tọa độ hai giao điểm của đồ thị hai hàm số 2 y = x và y = 3x − 2 là:
A. (1; -1) và (1; 2) B. (1; 1) và (1; 2) C. (1; 2) và (2; 4) D. (1; 1) và (2; 4)
Câu 6: Cho hình vẽ bên, biết số đo góc P o
MAN = 30 Số đo góc PCQ ở hình vẽ bên là: M A. o PCQ = 120 A B C ? B. o PCQ = 60 C. o PCQ = 30 N D. o PCQ = 240 Q
B.Phần tự luận (7 điểm) 3 x − 2y = 5
Câu 7 (1đ): Giải hệ phương trình 5 x + y =17
Câu 8 (1đ): Cho phương trình bậc hai ẩn x, ( m là tham số): 2 x − 4x + m = 0 (1) Trang 1
a, Giải phương trình với m = 3.
b, Tìm điều kiện của m để phương trình (1) luôn có 2 nghiệm phân biệt.
Câu 9 (1,5 đ): Một mảnh đất hình chữ nhật có chiều dài lớn hơn chiều rộng 17m và
diện tích của mảnh đất là 2
110m . Tính các kích thước của mảnh đất đó.
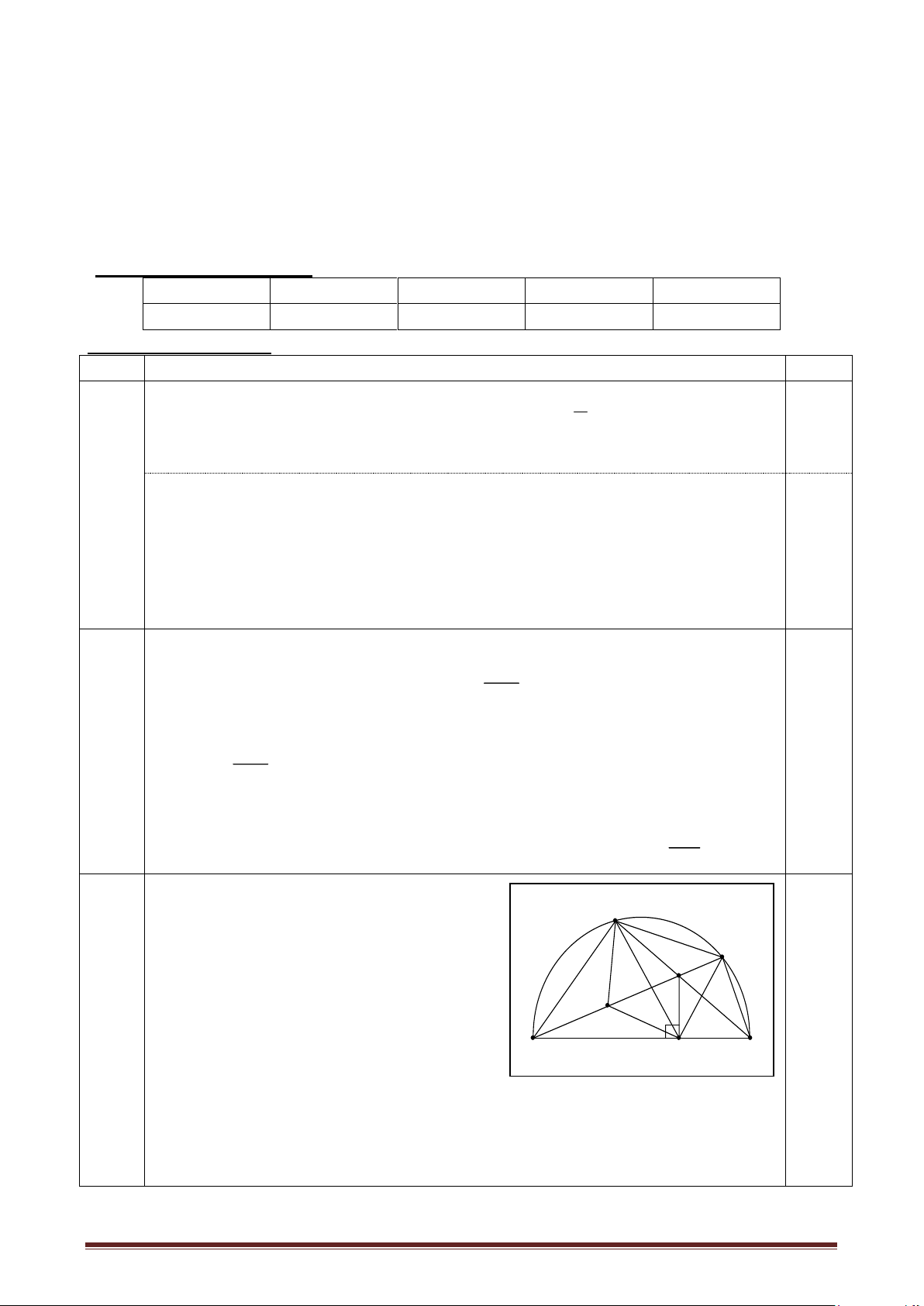
Câu 10 (3 đ): Cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD. Hai
đường chéo AC và BD cắt nhau tai E. Kẻ EF ⊥ AD. Gọi M là trung điểm của AE. Chứng minh rằng:
a. Tứ giác ABEF nội tiếp một đường tròn.
b. Tia BD là tia phân giác của góc CBF.
c. Tứ giác BMFC nội tiếp một đường tròn.
Câu 11 (0,5 đ): Tính diện tích xung quanh của một chiếc thùng phi hình trụ, biết
chiều cao của thùng phi là 1,2 m và đường kính của đường tròn đáy là 0,6m. Trang 2 III. ĐÁP ÁN
I. Trắc nghiệm (3 điểm) Mỗi ý chọn đúng đáp án được 0,5 điểm. Câu 1 2 3 4 5 6 Đáp án C B A B D A I.
Tự luận (7 điểm) II. Bài Nội dung Điểm 3 x − 2y = 5 3 x − 2y = 5 0,5 a, 5 x + y =17 1 0x + 2y = 34
Câu Cộng theo từng vế 2 phương trình trên ta được: 7
13x = 39 x = 3 thay vào PT tìm được y = 2 x = 3
Hệ có nghiệm duy nhất 0,5 y = 2
a, Với m = 3 phương trình (1) trở thành 2 x − 4x + 3 = 0
Có 1 + (-4) + 3 = không nên PT có 2 nghiệm x = 1 và x = 3 0,5 Câu 1 2 8 b, Ta có: 2 ' = ( 2 − ) − m = 4 − m
Để phương trình (1) có hai nghiệm phân biệt thì : 4-m>0 m < 4 0,5
Gọi chiều rộng của mảnh đất đó là x(m), x>0
Suy ra chiều dài của mảnh đất đó là x+17 (m) 0,5
Vì diện tích của mảnh đất là 2 110m nên ta có PT: Câu x(x+17) = 110 0,5 9 2 x +17x −110 = 0
Giải phương trình được x = 5 ( Thỏa mãn) và x = 22 − (loại) 1 2
Vậy chiều dài mảnh đất đó là 22 m, chiều rộng mảnh đất là 5 0,5 Hình vẽ: 0,25 B 2 1 C E M 1 1 A F D Câu 0,25 10 a.Chỉ ra · 0 ABD = 90 suy ra · 0 ABE = 90 EF ⊥ AD suy ra · 0 EFA = 90 0,25
Tứ giác ABEF có tổng hai góc đối bằng 900 nội tiếp được đường 0,25 tròn
b. Tứ giác ABEF nội tiếp suy ra ¶ ¶
B = A ( góc nội tiếp cùng chắn » EF) 0,25 1 1 Mà ¶ ¶
A = B ( nội tiếp cùng chắn cung CD) 1 2 0,25 Suy ra ¶ ¶
B = B suy ra BD là tia phân giác của góc CBF. 1 2 0,5 Trang 3
c. Chỉ ra tam giác AEF vuông tại F có trung tuyến FM AMF cân tại M suy ra ¶ ¶ M = 2A 0,25 1 1 Chỉ ra · ¶ CBF = 2A suy ra ¶ · M = CBF 1 1 0,25
Suy ra B và M cùng nhìn đoạn CF dưới một góc bằng nhau và chúng
cùng phía đối với CF nên suy ra tứ giác BMFC nội tiếp một đường tròn 0,5
Câu Diện tích xung quanh của thùng phi đó là: 11 S = 2 Rh
= dh = 0,6.1,2 = 0,72 (m2) 0,5 xq
Chú ý: Nếu học sinh làm cách khác mà đúng thì vẫn cho điểm tối đa theo từng phần. ĐỀ 2
ĐỀ THI HỌC KỲ II Môn Toán Lớp 9 Thời gian: 90 phút
A. PHẦN TRẮC NGHIỆM (2,0 điểm). Câu 1. Phương trình 2
x − 6x +1 = 0 có tổng hai nghiệm bằng A. -6 B. 6 C. 1 D. -1 3x − y = 2
Câu 2. Hệ phương trình có nghiệm bằng x + y = −6
A. (x;y)=(-1;5) B. (x;y)=(1;5) C. (x;y)=(-1;-5) D. (x;y)=(1;-5)
Câu 3. Cho tứ giác ABCD nội tiếp đường tròn tâm O, biết . Khi đó bằng A. B. C. D.
Câu 4. Phương trình 4 2
x + 3x − 4 = 0 có tổng các nghiệm bằng. A. 0 B. 3 C. 4 D. -3
B. PHẦN TỰ LUẬN (8,0 điểm). mx − y = 3
Câu 5. Cho hệ phương trình ( m là tham số) (*) 4x − my = 7
a, Giải hệ phương trình với m=1
b, Tìm m để hệ phương trình (*) có nghiệm duy nhất.
Câu 6. Cho phương trình bậc hai 2
x − 2x − 3m +1 = 0 (m là tham số) (**)
a, Giải phương trình với m=0
b, Tìm m để phương trình (**) có hai nghiệm phân biệt. Trang 4
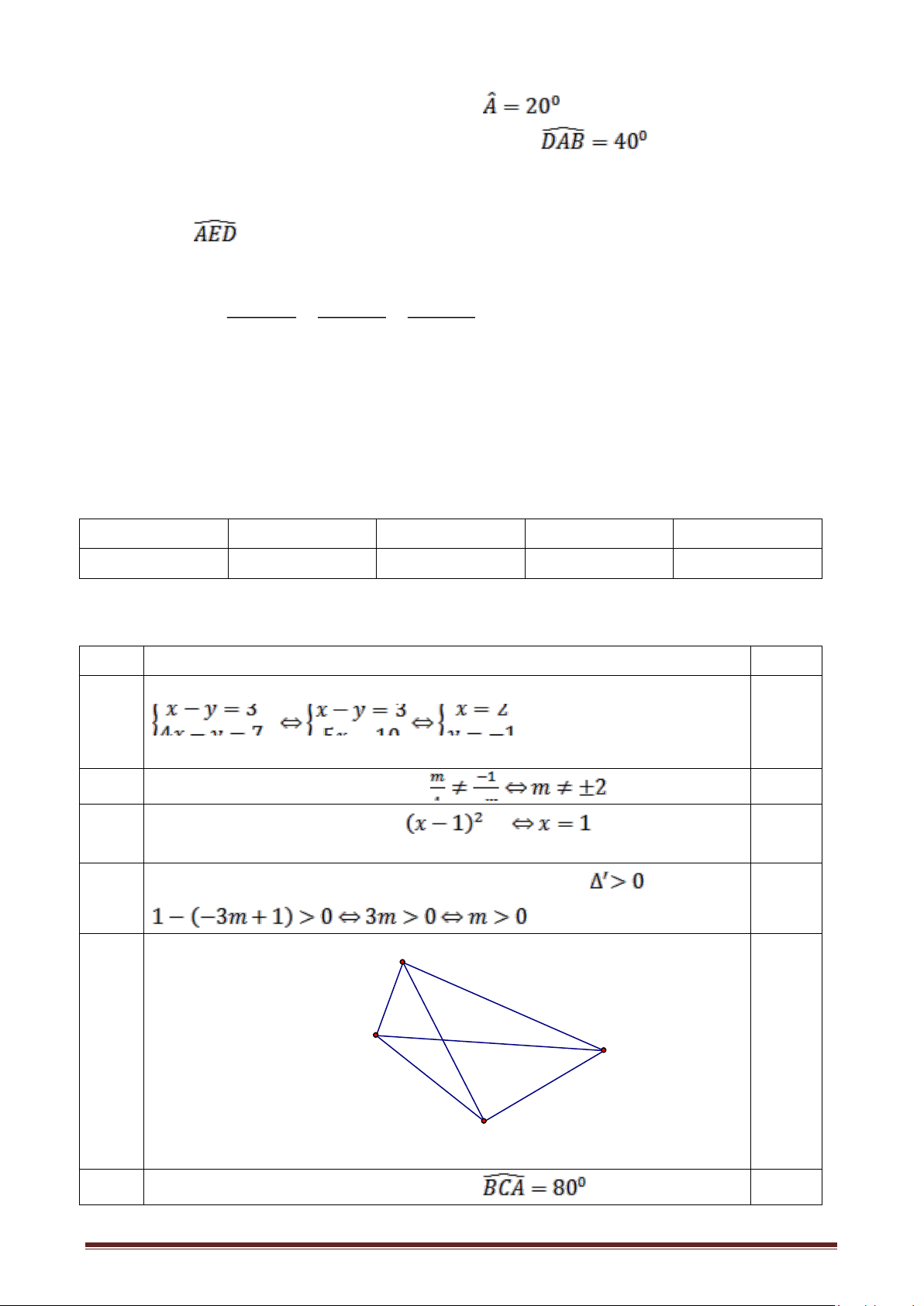
Câu 7. Cho tam giác cân ABC có đáy BC và
. Trên nửa mặt phẳng bờ AB
không chứa điểm C lấy điểm D sao cho DA=DB và . Gọi E là giao điểm của AB và CD.
a, Chứng minh ACBD là tứ giác nội tiếp. b, Tính .
Câu 8. Cho a,b,c là các số thực, không âm đôi một khác nhau. Chứng minh rằng: ( + + ) 1 1 1 ab bc ca . + + ( a b) 4 2 (b c)2 (c a)2 − − −
-------------------- Hết --------------------
(Cán bộ coi thi không giải thích gì thêm)
Họ và tên học sinh.…….......……………........................................SBD:…....................… ĐÁP ÁN A.
PHẦN TRẮC NGHIỆM ( Mỗi cấu đúng 0,5 điểm) Câu 1 2 3 4 Đáp án B C A A B. PHẦN TỰ LUẬN C. Câu Nội dung Điểm 5
a, Thay m=1 vào HPT ta được 1,5 2,5đ
Vậy nghiệm của HPT là (x;y)=(2;-1)
b, HPT có nghiệm duy nhất khi 1 6
a, Thay m=0 vào PT ta được =0 1,5 2,5đ
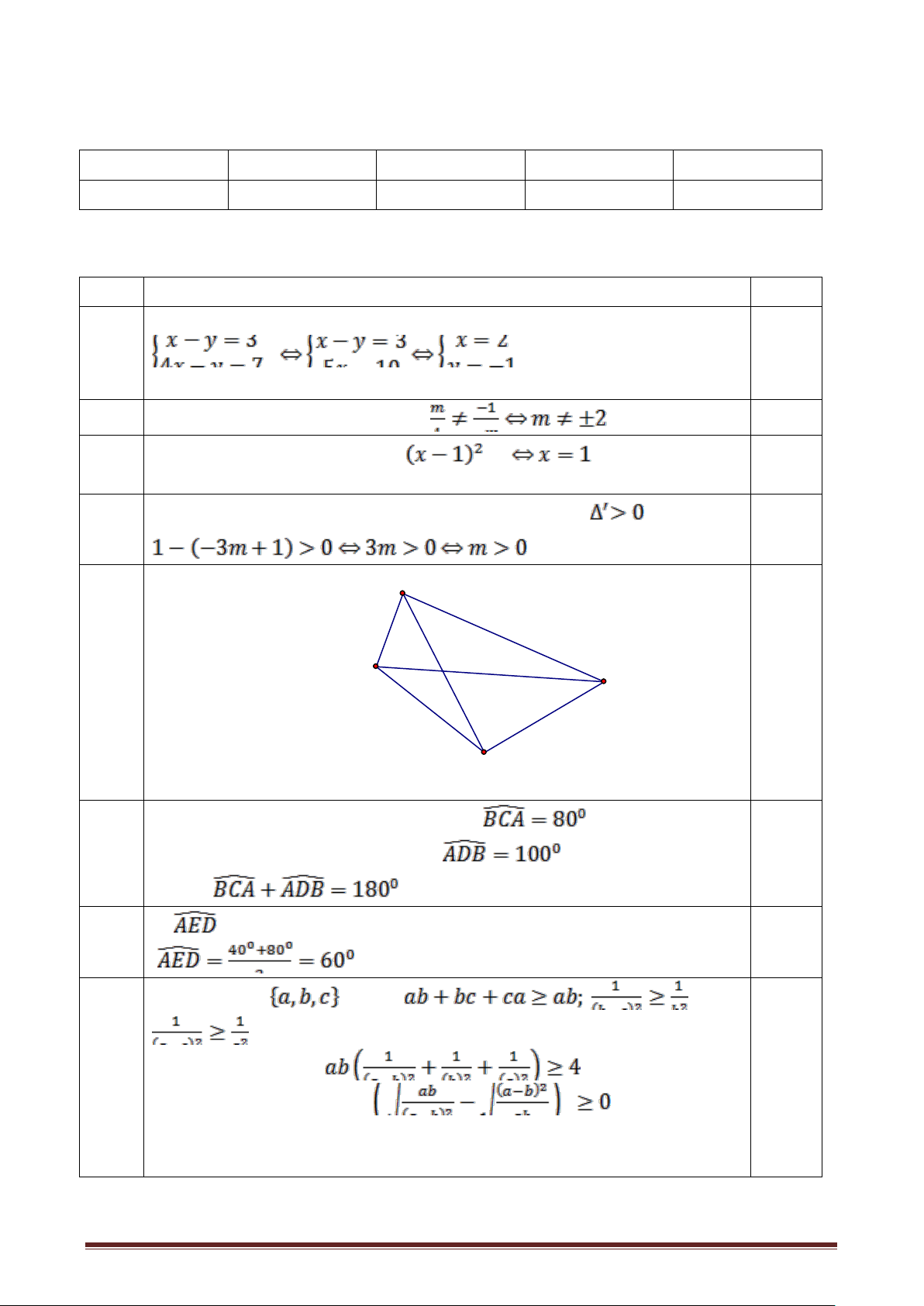
b, ĐK để phương trình có hai nghiệm phân biệt là 1 7 C 2,0đ E B A D
a, Từ tam giác ABC cân A, tính được 1 Trang 5
Từ tam giác cân ADB, tính được Suy ra
. Do đó tứ giác ACBD nội tiếp b,
Là góc có đỉnh bên trong đường tròn 1 8 Giả sử c=min khi đó ; 1đ 1đ Ta cần chứng minh . Bằng cách biến
đổi tương đương ta được ĐỀ 3
ĐỀ THI HỌC KỲ II Môn Toán Lớp 9 Thời gian: 90 phút
I - LÝ THUYẾT: (2 điểm) Học sinh chọn một trong hai đề sau:
Đề 1: Viết công thức nghiệm của phương trình bậc hai.
Đề 2: Câu 1. Nêu tính chất góc nội tiếp.
Câu 2. Nêu định nghĩa số đo cung.
II - BÀI TẬP : (8 điểm)
Bài 1: (2 điểm) Giải phương trình và hệ phương trình sau : 4x + 5y = 3 a) x2 + 5x – 6 = 0 b) 2x4 + 3x2 – 2 = 0 c) x − 3y = 5
Bài 2: (2 điểm) Một xe khách và một xe du lịch khởi hành đồng thời từ Hà Tiên đi
Rạch Sỏi. Xe du lịch có vận tốc lớn hơn xe khách là 20 km/h do đó đến Rạch Sỏi
trước xe khách 50 phút. Tính vận tốc mỗi xe. Biết khoảng cách từ Hà Tiên đến Rạch Sỏi là 100 km.
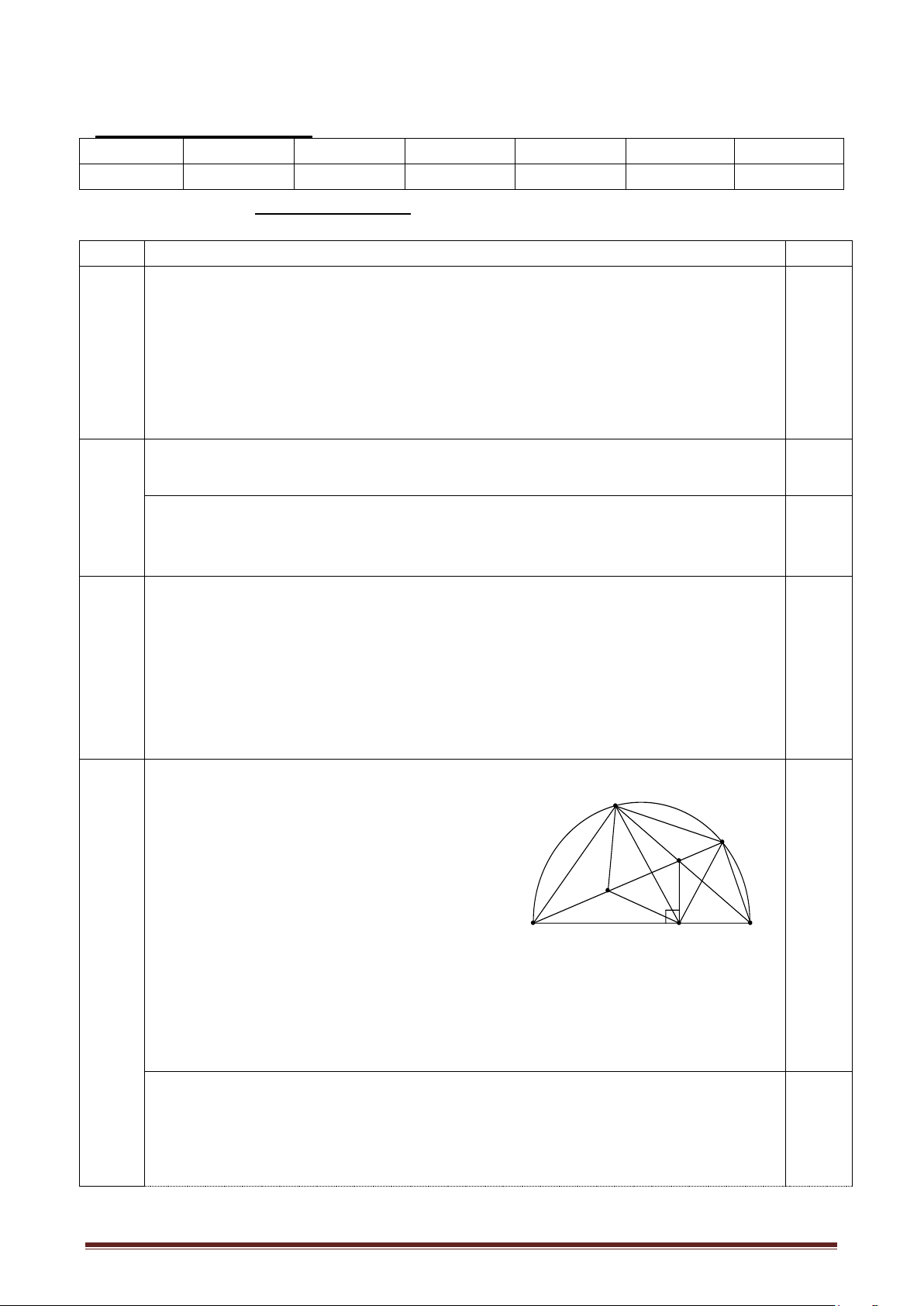
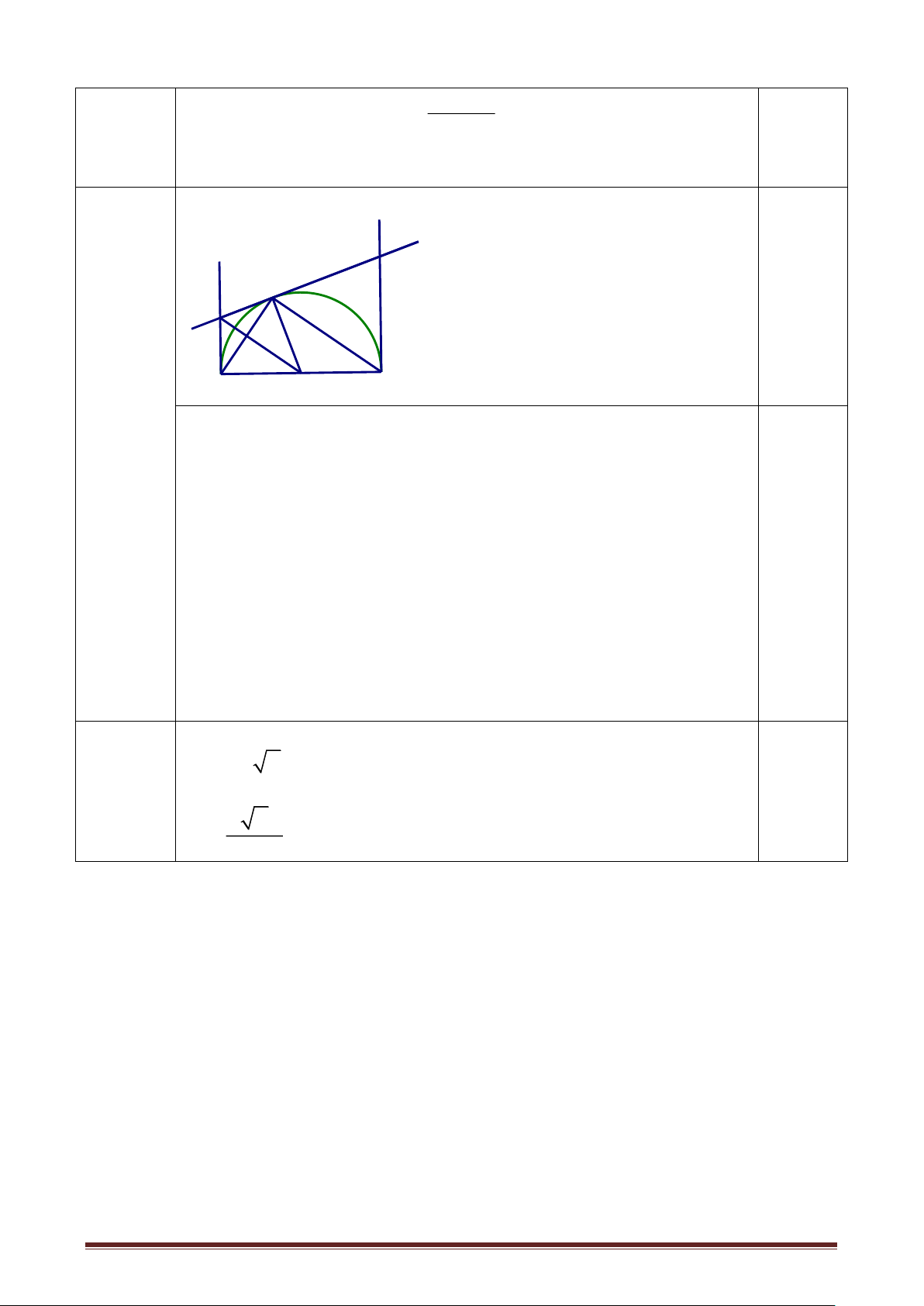
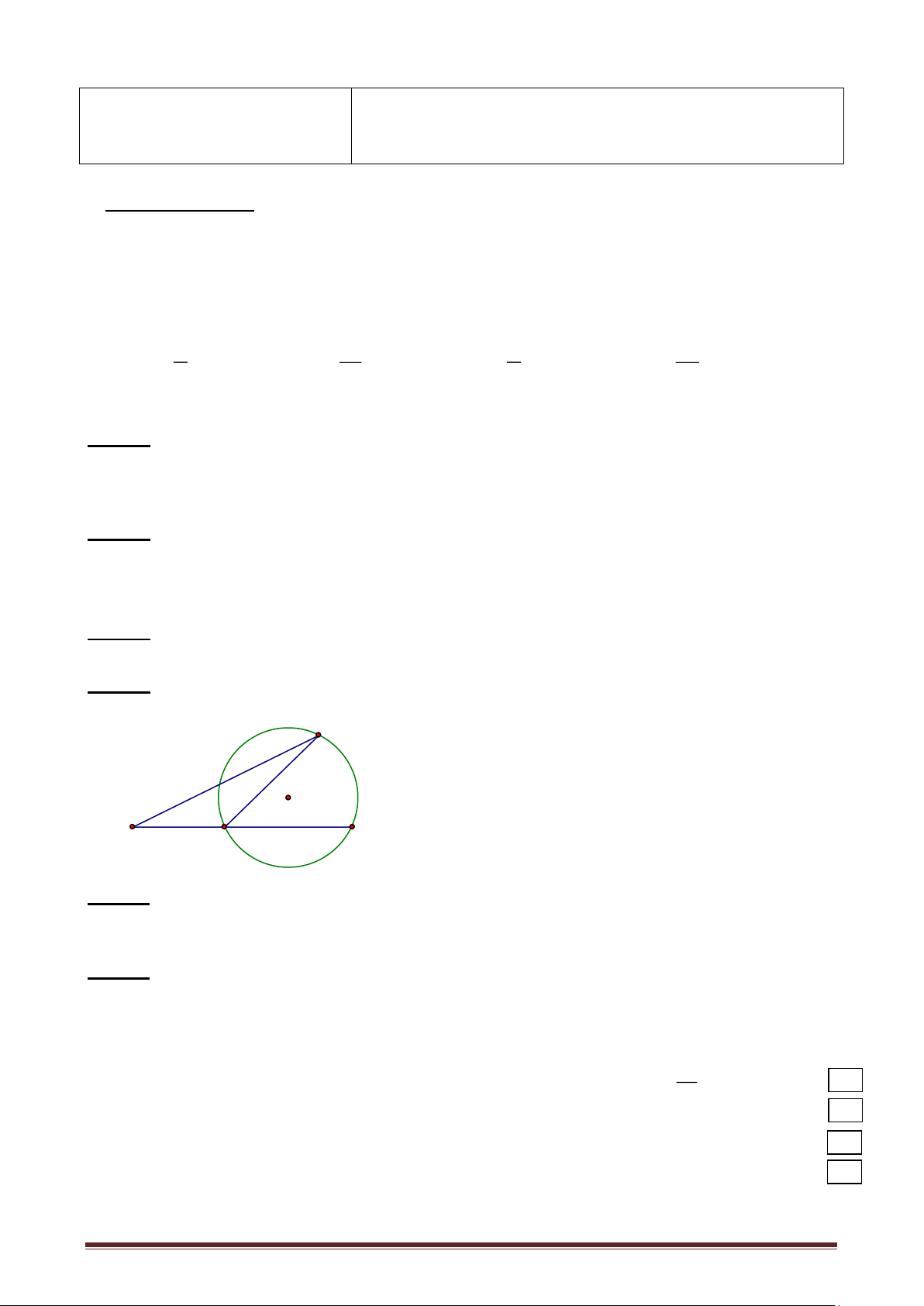
Bài 3: (3 điểm) Cho nửa đường tròn (O ; R) đường kính AB cố định. Qua A và B vẽ
các tiếp tuyến với nửa đường tròn tâm O. Từ một điểm M tùy ý trên nửa đường tròn
(M A và B) vẽ tiếp tuyến thứ 3 với nửa đường tròn cắt các tiếp tuyến tại A và B theo thứ tự là H và K.
a) Chứng minh tứ giác AHMO là tứ giác nội tiếp. b) Chứng minh AH + BK = HK.
c) Chứng minh tam giác HAO đồng dạng với tam giác AMB và HO . MB = 2R2
Bài 4: (1 điểm) Khi quay tam giác ABC vuông ở A một vòng quanh cạnh góc vuông
AC cố định, ta được một hình nón. Biết rằng BC = 4 cm, góc ACB bằng 300. Tính
diện tích xung quanh và thể tích hình nón.
+ ĐÁP ÁN VÀ THANG ĐIỂM: Câu Nội dung Điểm LÝ THUYẾT Trang 6 LT
Nêu đúng công thức nghiệm. 2 Đề 1 (2 điểm) LT
Câu 1. Nêu đúng tính chất góc nội tiếp. 1 Đề 2
Câu 2. Nêu đúng định nghĩa số đo cung. 1 (2 điểm) BÀI TẬP
a) x2 + 5x – 6 = 0 có a + b + c = 1 + 5+ (-6) = 0 0,25
Nên phương trình có 2 nghiệm là: x1 = 1 ; x2 = -6 0,25 b) 2x4 + 3x2 – 2 = 0 (b)
Đặt x2 = t (t 0) PT (b) trở thành 2t2 + 3t – 2 = 0 (b’)
= 32 – 4 . 2 . (-2) = 25 > 0 = 25 = 5 0,25
Phương trình (b’) có hai nghiệm t
1 = ½ (nhận) ; t2 = -2 (loại) 2 Với t1 = ½ x = 0,25 1,2 2 Bài 1 2
(2 điểm) Vậy PT (b) có hai nghiệm x = 0,25 1,2 2 4x + 5y = 3 c) x − 3y = 5 5 ( 4 + 3y) + 5y = 3 0,25 x = 5 + 3y 17y = −17 0,25 x = 5 + 3y y = −1 0,25 x = 2
Gọi vận tốc của xe khách là x (km/h); ĐK: x > 0 0,25
Vận tốc xe du lịch là: x + 20 (km/h) 0,25
Thời gian xe khách đi hết quãng đường là: 100 (h) x
Thời gian xe du lịch đi hết quãng đường là: 100 (h) x + 20 Đổi 50 phút = 5 h 6 Bài 2 100 5 100 0,25
(2 điểm) Theo bài ta có phương trình : - = x 6 x + 20
600(x + 20) – 5x(x + 20) = 600x 0,25
600x + 12 000 – 5x2 – 100x – 600x = 0 5x2 + 100x – 12 000 = 0 x2 + 20x – 2 400 = 0 0,25 '= 102 + 2 400 = 2 500 0,25 − 10 + 50 ' = 50 x1 = = 40 1 Trang 7 x −10 − 50 0,25 2 = = -60 ( loại) 1
Vậy vận tốc xe khách là 40 km/h và vận tốc xe du lịch là 60 0,25 km/h Vẽ hình ghi GT, KL 0,5 K M H A O R B
a) Chứng minh tứ giác AHMO là tứ giác nội tiếp Bài 3 Xét tứ giác AHMO có: (3 điểm)
OAH = OMH = 900 (tính chất tiếp tuyến) 0,5
OAH + OMH = 1800 0,5
Nên tứ giác AHMO nội tiếp đường tròn. b) Chứng minh AH + BK = HK
Theo tính chất hai tiếp tuyến cắt nhau 0,25 Ta có: AH = MH và MK = KB 0,25
Mà HM + MK = HK (vì M nằm giữa H và K) 0,25 AH + BK = HK 0,25 c) HAO ∽ A MB (g - g) 0,5 HO . MB = AB . AO = 2R2 AB = 2 cm 0,25 AC = 2 3 cm 0,25 Bài 4 S 0,25 (1 điểm) xq = 8 cm2 8 3 V = cm 0,25 3 Trang 8 ĐỀ 4
ĐỀ THI HỌC KỲ II Môn Toán Lớp 9 Thời gian: 90 phút
A. PHẦN TRẮC NGHIỆM (2,0 điểm). Câu 1. Phương trình 2
x − 6x +1 = 0 có tổng hai nghiệm bằng B. -6 B. 6 C. 1 D. -1 3x − y = 2
Câu 2. Hệ phương trình có nghiệm bằng x + y = −6
B. (x;y)=(-1;5) B. (x;y)=(1;5) C. (x;y)=(-1;-5) D. (x;y)=(1;-5)
Câu 3. Cho tứ giác ABCD nội tiếp đường tròn tâm O, biết . Khi đó bằng B. B. C. D.
Câu 4. Phương trình 4 2
x + 3x − 4 = 0 có tổng các nghiệm bằng. B. 0 B. 3 C. 4 D. -3
B. PHẦN TỰ LUẬN (8,0 điểm). mx − y = 3
Câu 5. Cho hệ phương trình ( m là tham số) (*) 4x − my = 7
a, Giải hệ phương trình với m=1
b, Tìm m để hệ phương trình (*) có nghiệm duy nhất.
Câu 6. Cho phương trình bậc hai 2
x − 2x − 3m +1 = 0 (m là tham số) (**)
a, Giải phương trình với m=0
b, Tìm m để phương trình (**) có hai nghiệm phân biệt.
Câu 7. Cho tam giác cân ABC có đáy BC và
. Trên nửa mặt phẳng bờ AB
không chứa điểm C lấy điểm D sao cho DA=DB và . Gọi E là giao điểm của AB và CD.
a, Chứng minh ACBD là tứ giác nội tiếp. b, Tính .
Câu 8. Cho a,b,c là các số thực, không âm đôi một khác nhau. Chứng minh rằng: ( + + ) 1 1 1 ab bc ca . + + ( a b) 4 2 (b c)2 (c a)2 − − −
-------------------- Hết --------------------
(Cán bộ coi thi không giải thích gì thêm)
Họ và tên học sinh.…….......……………........................................SBD:…....................… Trang 9 ĐÁP ÁN D.
PHẦN TRẮC NGHIỆM ( Mỗi cấu đúng 0,5 điểm) Câu 1 2 3 4 Đáp án B C A A E. PHẦN TỰ LUẬN F. Câu Nội dung Điểm 5
a, Thay m=1 vào HPT ta được 1,5 2,5đ
Vậy nghiệm của HPT là (x;y)=(2;-1)
b, HPT có nghiệm duy nhất khi 1 6
a, Thay m=0 vào PT ta được =0 1,5 2,5đ
b, ĐK để phương trình có hai nghiệm phân biệt là 1 7 C 2,0đ E B A D
a, Từ tam giác ABC cân A, tính được 1
Từ tam giác cân ADB, tính được Suy ra
. Do đó tứ giác ACBD nội tiếp b,
Là góc có đỉnh bên trong đường tròn 1 8 Giả sử c=min khi đó ; 1đ 1đ Ta cần chứng minh . Bằng cách biến
đổi tương đương ta được Trang 10 ĐỀ 5
ĐỀ THI HỌC KỲ II Môn Toán Lớp 9 Thời gian: 90 phút
I. TRẮC NGHIỆM : (3 điểm)
Chọn câu trả lời em cho là đúng nhất:
Câu 1: Trong các cặp số sau đây, cặp số nào là nghiệm của phương trình 3x + 5y = – 3? A. (–2; 1) B. (0; –1) C. (–1; 0) D. (1; 0)
Câu 2. Cho đường tròn (O; 2cm), độ dài cung 600 của đường tròn này là: A. cm. B. 3 cm C. cm D. 2 cm. 3 2 2 3 2x − 3y = 3
Câu 3: Nghiệm của hệ phương trình là: x + 3y = 6 A.(2;1) B.( 3;1) C(1;3) D.(3; -1)
Câu 4: Đường kính vuông góc với một dây cung thì:
A. Đi qua trung điểm của dây cung ấy.
B. không đi qua trung điểm của dây cung ấy
Câu 5: Phương trình x2 - 7x – 8 = 0. có tổng hai nghiệm là: A.8 B.-7 C.7 D.3,5 Câu 6: Cho hình vẽ: 0 0 P = 35 ; IMK = 25 m
Số đo của cung MaN bằng: 25 a A. 600 B. 700 i o 35 p k n C. 1200 D.1300 Câu 7:
Phương trình của parabol có đỉnh tại gốc tọa độ và đi qua điểm ( - 1 ; 3 ) là: A. y = x2 B. y = - x2 C. y = -3x2 D. y = 3x2 Câu 8:
Tứ giác ABCD nội tiếp đường tròn có A = 500; B = 700 . Khi đó C - D bằng: A. 300 B . 200 C . 1200 D . 1400
II. Điền đúng (Đ) hoặc sai (S) vào ô vuông ở cuối mỗi câu sau: (1 điểm)
1. Phương trình 7x2 – 12x + 5 = 0 có hai nghiệm là x − 1 = 1; x2 = 5 . 7
2. x2 + 2x = mx + m là một phương trình bậc hai một ẩn số với mọi m R.
3. Trong một đường tròn hai cung bị chắn giữa hai dây song song thì bằng nhau.
4. Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng số đo của góc nội tiếp. Trang 11
II. TỰ LUẬN (7 điểm) Bài 1. (2 điểm) 2x − 3y = 1
a. Giải hệ phương trình sau: x − 4 y = 7 −
b. Giải phương trình: x4 – 5x2 + 4 = 0 Bài 2. (1 điểm)
Tìm các giá trị của m để phương trình 2x2 – (4m + 3)x + 2m2 –1 = 0 có nghiệm ? Bài 3.(1 điểm)
Một xe khách và một xe du lịch khởi hành cùng một lúc từ A đến B. Xe du lịch
có vận tốc lớn hơn vận tốc của xe khách là 20 km/h, do đó nó đến B trước xe khách
25 phút. Tính vận tốc của mỗi xe, biết khoảng cách AB là 100 km. Bài 4. (3 điểm)
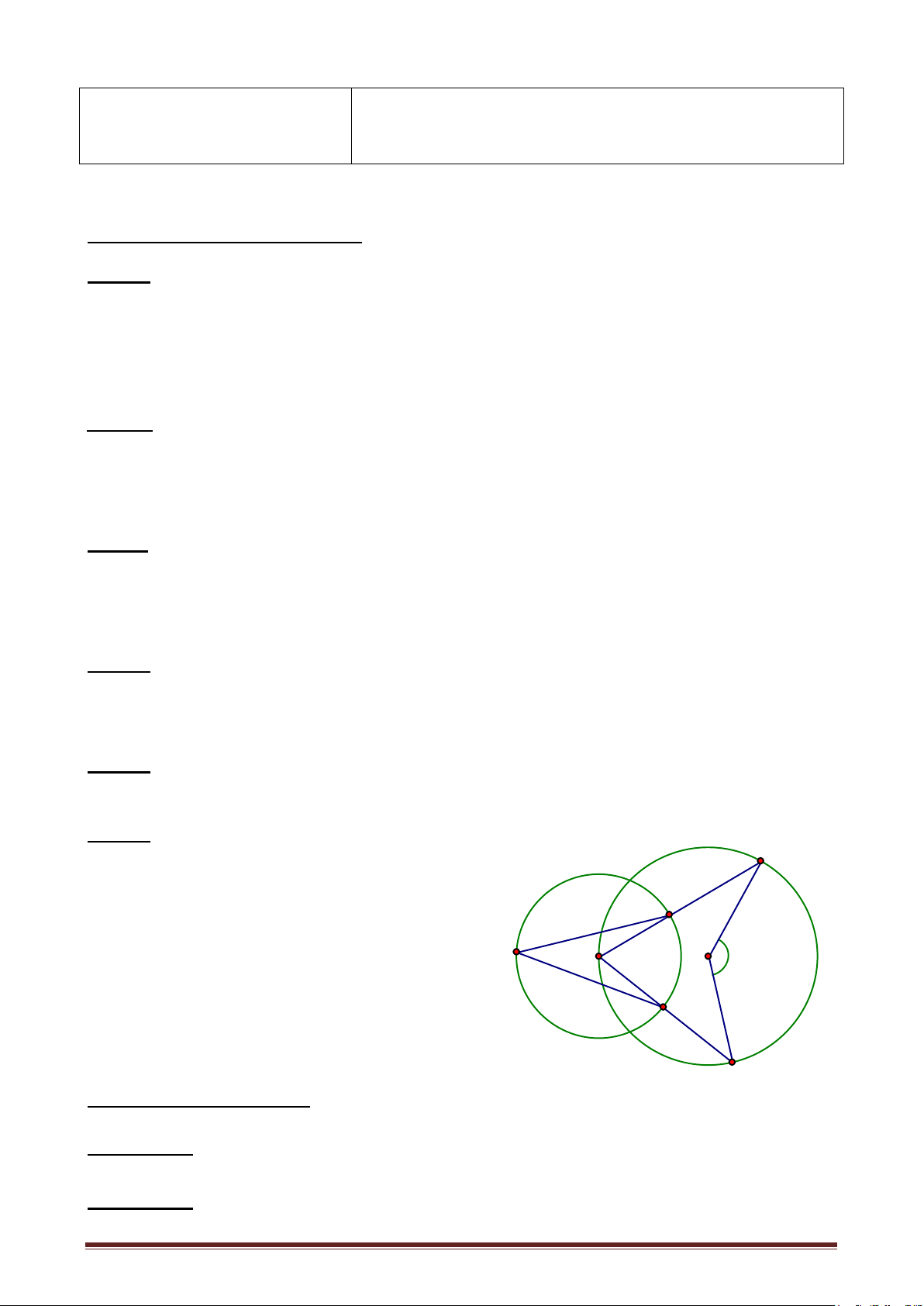
Cho tam giác ABC nội tiếp đường tròn tâm O. Gọi E, D lần lượt là giao điểm
của các tia phân giác trong và ngoài của hai góc B và C. Đường thẳng ED cắt BC tại
I, cắt cung nhỏ BC ở M. Chứng minh:
a. Ba điểm A, E, D thẳng hàng.
b.Tứ giác BECD nội tiếp được trong đường tròn. c. BI. IC = ID. IE
ĐÁP ÁN VÀ BIỂU ĐIỂM
MÔN TOÁN 9 - HỌC KÌ II
I/ TRẮC NGHIỆM ( 3 điểm):- Mỗi câu đúng được 0,25 điểm. Câu 1 2 3 4 5 6 7 8 Đáp án C D B A C C D A
II. Điền Đ hoặc S vào chỗ trống: 1- Sai 2 - Đúng 3 - Đúng 4 - Sai
II. TỰ LUẬN: (7 điểm). Câu Lời giải Điểm 2x − 3y =1
Giải hệ phương trình 0.5 x − 4y = 7 −
Từ PT (2) x = 4y - 7 (*)
thế vào PT (1) Ta có 2(4y - 7) - 3y = 1 8y - 14 - 3y = 1 5y = 15 y = 3.
Bài 1 ThÕ vµo (*) x = 4.3 - 7 = 5. 0.5
VËy HPT cã 1 nghiÖm: (x;y) = (5; 3)
2x2 – (4m + 3)x + 2m2 –1 = 0
Tìm được = 24m + 17 (0,25điểm) 0,75 Tìm được m 17 − (0,75 điểm) 0,25 24 Trang 12
Đặt t = x2 ( t>0). Phương trình trở thành t 2 -5t + 4 = 0 0.5
Bài 2 Giải ra t = 1, t = 4 (nhận)
Giải ra x = 1, x= -1, x= 2, x= -2. 0,5
Gọi vận tốc của xe khách là x (km/h), (ĐK: x > 0)
khi đó vận tốc của xe du lịch là x + 20 (km/h) 0.25 100
Thời gian đi từ A đến B của xe khách là : (giờ) x 0.25 100
Thời gian đi từ A đến B của xe du lịch là : (giờ) x + 20 Bài 5
Vì xe du lịch đến B trước xe khách 25 phút = giờ 3 12 100 100 5 nên ta có phương trình: - = x x + 20 12 => x1 = 60 0.25 x2 = -80 < 0 ( lo¹i)
VËy vËn tèc cña xe kh¸ch lµ 60 km/h; 0.25
VËn tèc cña xe du lÞch lµ 60 + 20 = 80 (km/h) a Hình vẽ 0.5 d
a)Vì E là giao điểm hai phân giác
góc B và C của tam giác ABC nên b c i
AE cũng là phân giác của góc A. 0.5
Khi đó AE và AD đều là phân
giác trong của góc BAC nên A, E, D thẳng hàng Bài 4 e
b) Ta có: EBD + ECD = 900 + 900 = 1800 0.5
Tứ giác BECD nội tiếp đường tròn 0.5
c) Xét hai tam giác BIE và tam giác DIC:
EBC = EDC (haigóc nội tiếp cùng chắn cung EC)
BIE = DIC ( đối đỉnh) 0.5 BI IE BIE DIC ( g-g) = ID IC Trang 13 BI. IC = IE. ID 0.5 ĐỀ 6
ĐỀ THI HỌC KỲ II Môn Toán Lớp 9 Thời gian: 90 phút
I. Trắc nghiệm (2 điểm) Hãy chọn đáp án đúng trong các câu sau:
Câu 1: Hàm số = ( − ) 2 y 1 2 x là:
A. Nghịch biến trên R.
B. Đồng biến trên R.
C. Nghịch biến khi x>0, đồng biến khi x<0 D. Nghịch biến khi x<0, đồng biến khi x>0
Câu 2. Trong các phương trình sau đây phương trình nào vô nghiệm:
A. x2-2x+1=0 B. -30x2+4x+2011 C. x2+3x-2010 D. 9x2-10x+10 Câu 3. Cho · 0
AOB = 60 là góc của đường tròn (O) chắn cung AB. Số đo cung AB bằng:
A. 1200 B. 600 C. 300 D. Một đáp án khác
Câu 4: Một hình trụ có chu vi đáy là 15cm, diện tích xung quanh bằng 360cm2.
Khi đó chiều cao của hình trụ là: A. 24cm B. 12cm C. 6cm D. 3cm
II. Tự luận (8 điểm) mx + 2y = 3
Bài 1 (2 đ): Cho hệ phương trình: ví i m lµ tham sè 2x − my = 11 a. Giải hệ khi m=2
b. Chứng tỏ rằng hệ luôn có nghiệm duy nhất với mọi giá trị của m.
Bài 2 (3 đ): Một mảnh đất hình chữ nhật có diện tích 720m2, nếu tăng chiều dài 6m
và giảm chiều rộng 4m thì diện tích của mảnh vườn không đổi. Tính các kích thước của mảnh vườn đó.
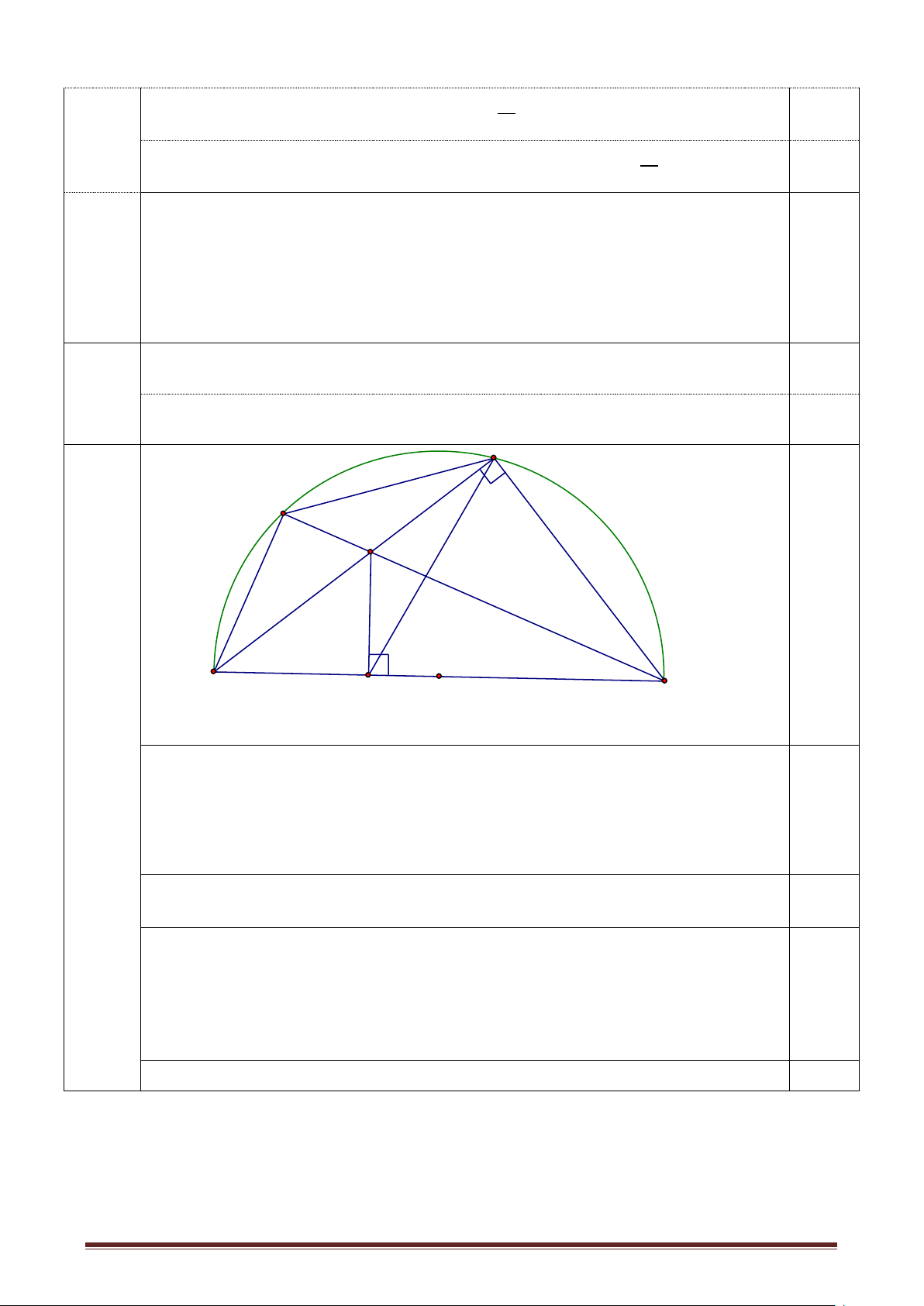
Bài 3 (3 đ): Cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD. Hai đường
chéo AC và BD cắt nhau tai E. Kẻ EF ⊥ AD. Gọi M là trung điểm của AE. Chứng minh rằng:
a. Tứ giác ABEF nội tiếp một đường tròn. Trang 14
b. Tia BD là tia phân giác của góc CBF.
c. Tứ giác BMFC nội tiếp một đường tròn
Hướng dẫn chấm Đề kiểm tra học kì ii
I. Trắc nghiệm (2 điểm) Mỗi ý chọn đúng đáp án được 0,5 điểm. Câu 1 2 3 4 Đáp án C D B A
II. Tự luận (8 điểm) Bài Nội dung Điểm 7 2x + 2y = 3 x =
a. Với m=2 hệ trở thành: 2 1,0 2x − 2y = 11 y = 2 − Bài 1 mx + 2y = 3 b) Xét hệ: ví i m lµ tham sè (2 đ) 2x − my = 11
Từ hai phương trình của hệ suy ra: ( 2 m + 4)x = 22− 3m (*) 0,5
Vì phương trình (*) luôn có nghiệm với mọi m nên hệ đã cho luôn có nghiệm với mọi m. 0,5
Gọi chiều dài của mảnh đất đó là x(m), x>0 720 0,5
Suy ra chiều rộng của mảnh đất đó là (m) x
Lý luận để lập được phương trình: Bài 2 (3 đ) ( + ) 720 x 6 − 4 = 720 x 1
Giải phương trình được x=30 1 720
Vậy chiều dài mảnh đất đó là 30m, chiều rộng mảnh đất là = 24m 30 0,5 Hình vẽ: 0,25 B 2 1 C E M 1 Bài 3 1 (3 đ) A F D a.Chỉ ra · 0 ABD = 90 suy ra · 0 ABE = 90 0,25 EF ⊥ AD suy ra · 0 EFA = 90 0,25
Tứ giác ABEF có tổng hai góc đối bằng 900 nội tiếp được đường 0,25 tròn Trang 15
b. Tứ giác ABEF nội tiếp suy ra ¶ ¶
B = A ( góc nội tiếp cùng chắn » EF) 0,25 1 1 Mà ¶ ¶
A = B ( nội tiếp cùng chắn cung CD) 1 2 0,25 Suy ra ¶ ¶
B = B suy ra BD là tia phân giác của góc CBF. 1 2 0,5
c. Chỉ ra tam giác AEF vuông tại F có trung tuyến FM AMF cân tại M suy ra ¶ ¶ M = 2A 0,25 1 1 Chỉ ra · ¶ CBF = 2A suy ra ¶ · M = CBF 1 1 0,25
Suy ra B và M cùng nhìn đoạn CF dưới một góc bằng nhau và chúng
cùng phía đối với CF nên suy ra tứ giác BMFC nội tiếp một đường tròn 0,5
Chú ý: Nếu học sinh làm cách khác mà đúng thì vẫn cho điểm tối đa theo từng phần. ĐỀ 7
ĐỀ THI HỌC KỲ II Môn Toán Lớp 9 Thời gian: 90 phút
Bài 1: ( 2 điểm ) Giải các phương trình và hệ phương trình sau: x + y = 5 a) b) 4 2
x − 5x + 4 = 0 3 x − y = 7
Bài 2 : ( 2 điểm ) Trên cùng một MFTĐ Oxy cho hai đồ thị Parabol (P) 2 : y = x và (d): y = 4 − x − 3 a) Vẽ (P)
b) Tìm tọa độ giao điểm của (P) và (d ) .
Bài 3 : ( 2 điểm ) Cho phương trình : 2
x − (m − 2) x − 2m = 0 (1)
a) Chứng tỏ phương trình (1) luôn có 2 nghiệm x ; x với mọi m . 1 2
b) Tìm m để phương trình có 2 nghiệm x ; x sao cho 2 2
x + x đạt giá trị nhỏ nhất. 1 2 1 2
Bài 4: ( 4 điểm ) Cho ABC nhọn nội tiếp (O;R) . Các đường cao AD; BE; CF cắt nhau tại H.
a) Chứng minh : Tứ giác AEHF nội tiếp.
b) Chứng minh : Tứ giác BFEC nội tiếp.
c) Chứng minh : OA ⊥ EF
d) Biết số đo cung AB bằng 90 0 và số đo cung AC bằng 120 0 .
Tính theo R diện tích phần hình tròn giới hạn bởi dây AB; cung BC và dây AC ------- Hết -------
ĐÁP ÁN VÀ BIỂU ĐIỂM Bài NỘI DUNG ĐIỂM x + y = 5 1,0đ a) Giải hpt 3 x − y = 7 Trang 16 4x =12 0,5 x + y = 5 x = 3 x = 3 0,5 3 + y = 5 y = 5 − 3 = 2 b) Giải pt 4 2
x − 5x + 4 = 0 (*) 1,0đ Đặt 2
x = t (t 0) . PT ( ) 2
* t − 5t + 4 = 0 0,25 = ( nhận ) ; ( nhận ) 0,25 1 t 1 t = 4 1 2 2
t = 1 x = 1 x = 1 Với 1 2
t = 4 x = 4 x = 2 0,25 2
Vậy phương trình đã cho có 4 nghiệm : x =1; x = 1
− ; x = 2; x = 2 − 0,25 1 2 3 4 a) Vẽ (P) 2 : y = x 1,0đ
+ Lập bảng giá trị đúng : 0,5 x -2 -1 0 1 2 y = x2 4 1 0 1 4 0,5 2 + Vẽ đúng đồ thị :
b)Tìm tọa độ giao điểm của (P) và (d ) . 1,0đ
+ Pt hoành độ giao điểm của (P) và (d ) : 2 x + 4x + 3 = 0 0,25 x = 1
− y =1: A 1 − ;1 0,25 1 1 ( ) + x = 3
− y = 9 : B 3 − ;9 0,25 2 2 ( )
Vậy tọa độ giao điểm của (P) và (d ) là A( 1 − ) ;1 ; B ( 3 − ;9) 0,25
a) Chứng tỏ phương trình (1) luôn có nghiệm với mọi m . 1,0đ
+ = −(m − )2 −
(− m) = m + m+ = (m+ )2 2 2 4.1. 2 4 4 2 0, m 0,75
+ Vậy phương trình (1) luôn có 2 nghiệm x ; x với mọi m . 0,25 1 2
b) Tìm m để phương trình có 2 nghiệm x ; x sao cho 2 2 x + x 1,0đ 1 2 1 2
đạt giá trị nhỏ nhất. 3
+ Theo vi-et : x + x = m − 2 1 2 0,25 x .x = 2 − m 1 2
+ x + x = x + x − 2x x 0,25 1 2 ( 1 2 )2 2 2 1 2 2 2
= (m − ) − (− m) 2 2 2. 2
= m + 8m + 4 = (m + 4) −12 1 − 2, m 0,25 + Vậy GTNN của 2 2
x + x là – 12 khi m + 4 = 0 m = −4 0,25 1 2
a) Chứng minh : Tứ giác AEHF nội tiếp. 1,0đ Trang 17 4 + Tứ giác AEHF có: · 0 · = = 0 AEH 90 ;AFH 90 (gt) 0,5 + · · + = 0 + 0 = 0 AEH AFH 90 90 180 0,25
+ Vậy tứ giác AEHF nội tiếp đường tròn đường kính AH 0,25
b) Chứng minh : Tứ giác BFEC nội tiếp. 1,0đ + Tứ giác BFEC có: · 0 · = = 0 BFC 90 ;BEC 90 (gt) 0,5
+ F và E là hai đỉnh kề nhau cùng nhìn BC dưới 1 góc 900 0,25
+ Vậy tứ giác BFEC nội tiếp đường tròn đường kính BC 0,25
c) Chứng minh : OA ⊥ EF 1,0đ
+ Kẻ tiếp tuyến x’Ax của (O) ·' ·
x AB = ACB ( Cùng chắn cung 0,25 AB ) + · ·
AFE = ACB ( BFEC nội tiếp ) 0,25 + ·' · = Þ ' x AB AFE x x //FE 0,25 + Vậy : OA ⊥ EF 0,25
d) Tính theo R diện tích phần hình tròn giới hạn bởi dây AB; 1,0đ cung BC và dây AC
+ Gọi S là diện tích phần hình tròn giới hạn bởi dây AB; cung 0,25 Ct BC và dây AC . S = S - S - S Ct ( ) O VFAB VFAC + p 2 2 R R S = S - S = - (đvdt) 0,25 VFAB quatOAB DOAB 4 2 + p 2 2 R R 3 S = S - S = - (đvdt) 0,25 VFAC quatOAC DOAC 3 4 + 0,25 æ 2 2 ö æ 2 2 ö p 2 2 2 R R R R 3 5 R 6R 3 3R 2 ç ÷ çp ÷ p - - S = S - S - S = pR - ç - ÷- ç ÷ - = Ct ( ) O VFAB VFAC ç ÷ ç ÷ ç 4 2 ÷ è ø ç ÷ ç 3 4 ÷ è ø 12 (đvdt) * Ghi chú :
- Hình vẽ sai không chấm điểm phần bài hình
- Mọi cách giải khác đúng vẫn đạt điểm tối đa của câu đó. ĐỀ 8
ĐỀ THI HỌC KỲ II Môn Toán Lớp 9 Thời gian: 90 phút
Bài 1: (1,0đ) Cho hàm số 1 2
y = f (x) = x .Tính f (2) ; f (−4) 2 3 x + y =10
Bài 2: (1,0đ): Giải hệ phương trình: x + y = 4 Trang 18 Bài 3: (1,5đ) Giải phương trình: 4 2
x + 3x − 4 = 0
Bài 4 : (1,0đ)
Với giá trị nào của m thì phương trình: x2 -2(m +1)x + m2 = 0 có hai nghiệm phân biệt. Bài 5: (1.5đ)
Tích của hai số tự nhiên liên tiếp lớn hơn tổng của chúng là 19. Tìm hai số đó
Bài 6: (1,0đ) Một hình trụ có bán kính đường tròn đáy là 6cm, chiều cao 9cm. Hãy tính:
a) Diện tích xung quanh của hình trụ.
b) Thể tích của hình trụ.
(Kết quả làm tròn đến hai chữ số thập phân; 3,14)
Bài 7: (3,0đ) Cho tứ giác ABCD nội tiếp đường tròn đường kính AD. Hai đường
chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc với AD tại F. Chứng minh rằng:
a) Chứng minh: Tứ giác DCEF nội tiếp được
b) Chứng minh: Tia CA là tia phân giác của BCˆF .
ĐÁP ÁN VÀ BIỂU ĐIỂM: Biểu Bài Đáp án điểm f(2)=2 0,5 1 f(-4)=8 0,5 (1,0đ)
Trừ hai PT ta được 2x=6 => x = 3, y = 1 0,75 2
(1,0đ) Vậy: Hệ phương trình có nghiệm duy nhất là ( 3; 1) 0,25 4 2
x + 3x − 4 = 0 Đặt x2 = t (ĐK t≥0) 0,5
Ta có PT : t2+3t-4 = 0 3
Có dạng: a + b + c = 1 +3+(-4) = 0
(1,5đ) t1 = 1 ; t2 = -4 (loại) 0,25
Với t = 1 x1 = 1, x2 = -1 0,5
Vậy: Phương trình đã cho có 2 nghiệm: x1 = 1; x2 = –1 0,25 4
Cho phương trình: x2 – 2(m+1)x + m2 = 0 (1)
(1,0đ) phương trình (1) luôn có 2 nghiệm phân biệt khi Trang 19 -1 0,75
∆ = (m+1)2 – m2 = 2m + 1 > 0 => m > 2 -1 0,25
Vậy: Phương trình (1) có hai nghiệm phân biệt khi m > 2
Gọi số tự nhiên thứ nhất là x (x N) =>Số thứ 2 là x+1 0.25
Tích của hai số tự nhiên liên tiếp là x(x+1) 5
Tổng của hai số đó là: x + x + 1 = 2x + 1 0.25
(1,5đ) Theo bài ra ta có PT: x2 – x – 20 = 0 0.25
Có nghiệm thỏa mãn x = 5 0.5
Vậy: Hai số tự nhiên liên tiếp cần tìm là 5 và 6 0.25
a) Diện tích xung quanh của hình trụ là: 0,5 6
Sxq = 2 r.h = 2.3,14.6.9 339,12 (cm2)
(1,0đ) b) Thể tích của hình trụ là: 0,5
V = r2h = 3,14 . 62 . 9 1017,36 (cm3) Hình vẽ: C 2 1 B E 0,5đ 1 A F D 7
a)Ta có: ACD = 900 ( góc nội tiếp chắn nửa đường tròn đường kính AD (3,0đ) ) Xét tứ giác DCEF có: 0,25 0,25
ECD = 900 ( cm trên )
và EFD = 900 ( vì EF ⊥ AD (gt) )
=> ECD + EFD = 1800 => Tứ giác DCEF là tứ giác nội tiếp ( 0,5 đpcm )
b) Vì tứ giác DCEF là tứ giác nội tiếp ( cm phần a ) 0,5
=> ˆC = ˆD ( góc nội tiếp cùng chắn cung EF ) (1) 1 1
Mà: ˆC = ˆD (góc nội tiếp cùng chắn cung AB ) (2) 0,5 2 1
Từ (1) và (2) => ˆC = ˆC hay CA là tia phân giác của BCˆF ( đpcm ) 0,5 1 2
( Lưu ý : Các cách làm khác đúng vẫn cho điểm tối đa) Trang 20




