50 bài tập trắc nghiệm sử dụng phương pháp tọa độ giải bài toán hình học không gian Toán 12

50 bài tập trắc nghiệm sử dụng phương pháp tọa độ giải bài toán hình học không gian Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Môn:

Toán 12 3.8 K tài liệu

Thông tin:
67 trang 1 năm trước
Tác giả:
Student
Mai Nguyệt
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

50 bài tập trắc nghiệm sử dụng phương pháp tọa độ giải bài toán hình học không gian Toán 12

50 bài tập trắc nghiệm sử dụng phương pháp tọa độ giải bài toán hình học không gian Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

43 22 lượt tải Tải xuống

Chủ đề: Chương 3: Phương pháp tọa độ trong không gian 143 tài liệu

Môn: Toán 12 3.8 K tài liệu

Thông tin:

67 trang 1 năm trước

Tác giả:

Profile Mai Nguyệt
Trang 1/69
50 BÀI TẬP TRẮC NGHIỆM VD - VDC
SỬ DỤNG PHƯƠNG PHÁP TỌA ĐỘ GIẢI BÀI TOÁN HÌNH HỌC KHÔNG GIAN
ĐỀ BÀI
DẠNG TOÁN 1: HÌNH CHÓP CÓ CẠNH BÊN HOẶC MỘT MẶT VUÔNG GÓC VỚI ĐÁY.
Câu 1: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
và
SA
vuông góc với mặt phẳng
đáy. Góc giữa mặt bên
( )SBC
với mặt phẳng đáy bằng
45
. Gọi
,M N
lần lượt là trung điểm
của
AB
và
. Tính theo
a
khoảng cách giữa hai đường thẳng
MD
và
CN
.
A.
3
4
a
. B.
21
3
a
. C.
2a
. D.
2 21
21
a
.
Câu 2: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
A
,
o
60
ABC
,
2BC a
. Gọi
D
là
điểm thỏa mãn
3 2SB SD
. Hình chiếu của
S
trên mặt phẳng
ABC
là điểm
H
thuộc đoạn
BC
sao cho
4
BC BH
. Tính góc giữa hai đường thẳng
AD
và
SC
biết
SA
tạo với mặt đáy
một góc
o
60
.
A.
o
60
. B.
o
45
. C.
o
90
. D.
o
30
.
Câu 3: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
5a
, cạnh bên
10SA a
và vuông
góc với mặt phẳng đáy. Gọi
M
là trung điểm cạnh
SD
. Tính
của góc tạo bởi hai mặt
phẳng
AMC
và
SBC
.
A.
3
2
. B.
2 3
3
. C.
5
5
. D.
2 5
5
.
Câu 4: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông, tam giác
SAB
đều. Hình chiếu của
S
lên mặt phẳng
ABCD
trùng với trung điểm
I
của
AB
. Gọi
,H K
lần lượt là trung điểm của
DC
và
, biết
7
2
a
SH
.Tính khoảng cách giữa
HK
và
SC
.
A.
3
8
. B.
15
2
. C.
15
8
D.
5
10
.
Câu 5: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật, cạnh bên
SA
vuông góc với
đáy,
, 2 , 3AB a AD a SA a
. Gọi
,M N
lần lượt là hình chiếu của
A
lên
,SB SD
và
P
là giao điểm của
SC
với mặt phẳng
AMN
. Tính thể tích khối chóp
.
S AMPN
.
A.
3
1869
140
a
. B.
3
5589
1820
a
. C.
3
181
120
a
. D.
3
1863
1820
a
.
Câu 6: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
2
,
SA
vuông góc với mặt
phẳng đáy
ABCD
và
2
SA
. Gọi
M
,
N
lần lượt là hai điểm thay đổi trên hai cạnh
AB
,
AD
sao cho mặt phẳng
SMC
vuông góc với mặt phẳng
SNC
. Thể tích khối chóp
.
S AMCN
đạt giá trị nhỏ nhất bằng
A.
4 3 4
3
. B.
8 3 8
3
. C.
2 3 2
. D.
4 3 4
3
.
Trang 2/69
Câu 7: Cho hình chóp
.
S ABCD
có đáy là hình thang vuông tại
A
và
B
,
AB BC a
,
2AD a
;
cạnh bên
SA
vuông góc với mặt phẳng đáy và
SA a
. Gọi
M
,
N
lần lượt là trung điểm của
,
CD
. Tính cosin của góc giữa
MN
và
SAC
.
A.
2
5
. B.
55
10
. C.
3 5
10
. D.
1
5
.
Câu 8: Cho hình chóp
.
S ABC
có
ABC
vuông tại
B
,
1, 3
AB BC
,
SAC
đều, mặt phẳng
SAC
vuông với đáy. Gọi
là góc giữa hai mặt phẳng
SAB
và
SBC
. Giá trị của
cos
bằng
A.
2 65
65
B.
65
20
C.
65
10
D.
65
65
Câu 9: Cho hình lập phương
.
ABCD A B C D
có các cạnh bằng
2
, gọi điểm
M
là tâm của mặt bên
ABB A
, các điểm
, , ,N P Q K
lần lượt là trung điểm của các cạnh
, , ,
AC DD D C B C
. Tính
cosine góc giữa hai mặt phẳng
MNP
và
AQK
.
A.
2
2
. B.
1
2
. C.
102
34
. D.
3
4
.
Câu 10: Cho hình chóp
.
S AB C D
có đáy
ABCD
là hình vuông cạnh bằng
a
.
S A
vuông góc với mặt
phẳng đáy.
H
và
K
là hai điểm lần lượt nằm trên hai cạnh
BC
và
CD
sao cho
3
4
a
BH
,
(0 )KD x x a
. Tìm giá trị của
x
để hai mặt phẳng
SAH
và
SAK
tạo với nhau một
góc bằng
45
.
A.
7
a
x
. B.
5
a
x
. C.
2
7
a
x
. D.
2
5
a
x
.
Câu 11: Trong không gian, cho tam giác
OAB
cân ở
O
có
4
5; tan
3
OA OB AOB
. Điểm
C
di
động trên tia
Oz
vuông góc
OAB
, gọi
H
là trực tâm của tam giác
ABC
. Khi
C
di động
trên tia
Oz
thì
H
luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng:
A.
5
4
. B.
3
2
. C.
5
2
. D.
.
Câu 12: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thoi tâm
O
cạnh
a
, góc
120
BCD
.
SA ABCD
. Thể tích khối chóp
.
S ABCD
là
3
3
3
a
. Gọi
M
là tâm đường tròn ngoại tiếp
tam giác
SOD
. Hãy tính khoảng cách
h
từ
M
tới mặt phẳng
SBC
theo
a
.
A.
57
19
a
h
. B.
57
38
a
h
. C.
2 5
5
a
h
. D.
2 5
19
a
h
.
Câu 13: Cho tam giác
ABC
vuông tại
A
và đường thẳng vuông góc với mặt phẳng
ABC
tại điểm
A
. Các điểm
,M N
thay đổi trên đường thẳng sao cho
MBC NBC
. Biết
,
AB b AC c
. Giá trị nhỏ nhất của thể tích tứ diện
MNBC
theo
b
và
c
bằng
A.
2 2
2 2
3
b c
b c
. B.
2 2
2 2
b c
b c
. C.
2 2
3
bc
b c
. D.
2 2
2 2
3
b c
b c
.
Trang 3/69
DẠNG TOÁN 2: HÌNH CHÓP ĐỀU VÀ HÌNH CHÓP DẠNG KHÁC.
Câu 14: Cho hình chóp tứ giác đều
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, tâm
O
. Gọi
M
và
N
lần lượt là trung điểm của hai cạnh
và
BC
. Biết
6
2
a
MN
, tính sin của góc giữa
đường thẳng
MN
và mặt phẳng
SBD
.
A.
2
5
. B.
3
3
. C.
5
5
. D.
3
.
Câu 15: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Gọi
M
và
N
lần lượt là trung
điểm các cạnh
AB
và
AD
;
H
là giao điểm của
CN
và
DM
. Biết
SH
vuông góc với mặt
phẳng
( )ABCD
và
3SH a
. Tính khoảng cách giữa hai đường thẳng
DM
và
SC
theo
a
.
A.
2 57
19
a
. B.
57
19
a
. C.
2 13
19
a
. D.
7
19
a
.
Câu 16: Cho hình chóp tứ giác đều
.
S ABCD
có tất cả các cạnh đều bằng nhau. Gọi
,E M
lần lượt là
trung điểm các cạnh
, ,BC SA
là góc tạo bởi đường thẳng
EM
và mặt phẳng
SBD
. Tính
sin
.
A.
6
sin
3
. B.
1
sin
2
. C.
3
sin
2
. D.
2
sin
2
.
Câu 17: Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a
và chiều cao bằng
h
. Gọi
I
là trung
điểm cạnh bên
SC
. Tính khoảng cách từ
S
đến mặt phẳng
AIB
.
A.
2 2
2
4 9
ah
h a
. B.
2 2
4
4 9
ah
h a
. C.
2 2
4 9
ah
h a
. D.
2 2
2
2 3
ah
h a
.
Câu 18: Cho hình chóp tứ giác đều
.
S ABCD
có đáy là hình vuông cạnh
a
, tâm
O
. Gọi
E
là điểm đối
xứng với
D
qua trung điểm của
SA
,
M
là trung điểm của
AE
,
N
là trung điểm của
BC
.
Tính khoảng cách giữa hai đường thẳng
MN
và
AC
.
A.
2
4
a
. B.
2
2
a
. C.
3
4
a
. D.
8
a
.
Câu 19: Cho hình lăng trụ
.
ABC A B C
có
.
A ABC
là tứ diện đều cạnh
a
. Gọi
M
,
N
lần lượt là trung
điểm của
AA
và
BB
. Tính tan của góc giữa hai mặt phẳng
ABC
và
CMN
.
A.
2
5
. B.
3 2
4
. C.
2 2
5
. D.
4 2
13
.
Câu 20: Cho hình chóp
SABC
có đáy
ABC
là tam giác cân tại
A
và
AB a
,
120
BAC
.
SA SB SC
. Gọi
là góc của hai mặt phẳng
SAB
và
SBC
sao cho
5
cos
7
. Khi đó
thể tích của khối chóp
SABC
là
A.
3
3
12
a
. B.
3
2a
. C.
3
3
a
. D.
3
2
5
a
.
Câu 21: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông cân tại
B
,
2AC a
, tam giác
SAB
và
tam giác
SCB
lần lượt vuông tại
A
,
C
. Khoảng cách từ
S
đến mặt phẳng
ABC
bằng
2a
.
Côsin của góc giữa hai mặt phẳng
SAB
và
SCB
bằng:
Trang 4/69
A.
1
2
. B.
1
3
. C.
1
2
. D.
1
3
.
Câu 22: Cho hình chóp đều
SABCD
có cạnh đáy bằng
2
, cạnh bên bằng
3 2
. Gọi
,M N
lần lượt là
các điểm thuộc
,SB SD
sao cho
3 , 3
SB SM SD DN
. Khoảng cách giữa
AM
và
CN
bằng
A.
40
857
. B.
72
857
. C.
24
153
. D.
40
257
.
Câu 23: Cho hình chóp tam giác đều
.
S ABC
có
2SA a
,
AB a
. Gọi
M
là trung điểm cạnh
BC
.
Tính khoảng cách
d
từ
M
tới mặt phẳng
SAB
.
A.
165
.
30
a
d
B.
15
.
3
a
d
C.
65
.
15
a
d
D.
65
.
10
a
d
Câu 24: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thang cân,
2 2 2 2AD AB BC CD a
. Hai
mặt phẳng
SAB
và
SAD
cùng vuông góc với mặt phẳng
ABCD
. Gọi
,M N
lần lượt là
trung điểm của
SB
và
CD
. Tính cosin góc giữa
MN
và
SAC
, biết thể tích khối chóp
.
S ABCD
bằng
3
3
4
a
.
A.
5
10
. B.
3 310
20
. C.
310
20
. D.
3 5
10
.
Câu 25: Cho hình chóp
SABC
có đáy
ABC
là tam giác vuông tại
A
,
3AB a
,
4AC a
. Các mặt bên
SAB
,
SAC
,
SBC
cùng tạo với đáy
ABC
một góc
0
45
. Biết chân đường vuông góc hạ
từ
S
xuống mặt phẳng
ABC
nằm ở miền trong tam giác
ABC
. Gọi góc tạo bởi hai mặt
phẳng
SAC
và
SBC
là
. Tính
cos
.
A.
1
cos
10
. B.
1
cos
5
. C.
3
cos
5
. D.
1
cos
15
.
Câu 26: Cho hình chóp
.
S ABC
có đáy là tam giác đều cạnh
.a
Hình chiếu vuông góc của
S
trên mặt
phẳng
ABC
là điểm
H
thuộc cạnh
AB
sao cho
2HA HB
. Góc giữa đường thẳng
SC
và
mặt phẳng
ABC
bằng
60
o
. Tính khoảng cách
h
giữa hai đường thẳng
SA
và
BC
theo
a
.
A.
42
8
a
. B.
42
12
a
. C.
42
4
a
. D.
42
24
a
.
DẠNG TOÁN 3: HÌNH LĂNG TRỤ TAM GIÁC.
Câu 27: Cho hình lăng trụ đứng
.
ABC A B C
có
AB AC a
, góc
30
ABC
, góc giữa đường thẳng
A B
và mặt phẳng
ABC
bằng
0
45
. Gọi
M
,
N
lần lượt là trung điểm của
B C
và
CC
.
Cosin của góc giữa mặt phẳng
AMN
và mặt phẳng
ABC
bằng
A.
1
2
. B.
3
2
. C.
13
4
. D.
3
4
.
Câu 28: Cho hình lăng trụ tam giác
. ' ' 'ABC A B C
có đáy
ABC
là tam giác đều cạnh
a
và các mặt bên
đều là các hình vuông cạnh
a
. Gọi
G
là trọng tâm của tam giác
ABC
và
I
là trung điểm của
đoạn thẳng
'CC
. Khoảng cách giữa hai đường thẳng
'A B
và
GI
bằng
Trang 5/69
A.
11
22
a
. B.
3 11
7
a
. C.
11
12
a
. D.
3 11
.
22
a
.
Câu 29: Cho lăng trụ đứng
. ' ' 'ABC A B C
có đáy là tam giác
ABC
vuông cân tại
A
, cạnh
6BC a
.
Góc giữa mặt phẳng
'AB C
và mặt phẳng
' 'BCC B
bằng
0
60
. Tính thể tích
V
của khối
lăng trụ
. ' ' 'ABC A B C
?
A.
3
2 3
.
3
a
V
B.
3
3
.
2
a
V
C.
3
3 3
.
4
a
V
D.
3
3 3
.
2
a
V
Câu 30: Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác cân, với
AB AC a
và góc
120
BAC
, cạnh bên
AA a
. Gọi
M
là trung điểm của
CC
. Cosin của góc tạo bởi hai mặt
phẳng
ABC
và
AB M
bằng
A.
11
11
. B.
33
11
. C.
10
10
. D.
30
10
.
Câu 31: Cho hình lăng trụ đứng có đáy là tam giác vuông tại
A
,
AB AC a
và có
cạnh bên bằng
2a
. Gọi
,M N
lần lượt là trung điểm
', 'BB CC
. Tính khoảng cách từ điểm
A
đến mặt phẳng
( ' )A MN
A.
a
. B.
2 3
3
a
. C.
3
2
a
. D.
3a
.
Câu 32: Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác cân tại
C
,
2AB a
,
AA a
,
góc giữa
BC
và
ABB A
bằng
60
. Gọi
N
là trung điểm
AA
và
M
là trung điểm
BB
.
Tính khoảng cách từ điểm
M
đến mặt phẳng
BC N
.
A.
2 74
37
a
. B.
74
37
a
. C.
2 37
37
a
. D.
37
37
a
.
Câu 33: Cho hình lăng trụ đứng
.
ABC A B C
có
AB AC a
, góc
BAC
bằng
120
,
AA a
. Gọi
M
,
N lần lượt là trung điểm
B C
và
CC
. Khoảng cách giữa 2 đường thẳng
MN
và
AH
là
A.
3
2
a
. B.
3
4
a
. C.
6
2
a
. D.
6
4
a
.
Câu 34: Cho hình lăng trụ
1 1 1
.
ABC A B C
có đáy là tam giác đều cạnh
a
.
1
2AA a
và vuông góc với mặt
phẳng
ABC
. Gọi
D
là trung điểm của
1
BB
,
M
di động trên cạnh
1
AA
. Giá trị lớn nhất của
diện tích
1
MC D
là
A.
2
15
4
a
. B.
2
15
6
a
. C.
2
5
4
a
. D.
2
10
4
a
.
Câu 35: Cho lăng trụ tam giác đều
. ' ' 'ABC A B C
có tất cả các cạnh bằng
a
,
M
là điểm di chuyển trên
đường thẳng
' 'A C
; Tính khoảng cách lớn nhất giữa
AM
và
'BC
A.
34
6
a
. B.
17
4
a
. C.
14
4
a
. D.
21
6
a
.
Câu 36: Cho lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông, , cạnh bên
. Gọi M là trung điểm của
BC
. Tính theo khoảng cách giữa hai đường thẳng
AM
và
B C
.
.
ABC A B C
AB BC a
' 2AA a
a
Trang 6/69
A. . B. . C. . D.
7
7
a
.
Câu 37: Cho lăng trụ đứng
ABCA B C
có đáy
ABC
là tam giác vuông tại
A
và
1, 2
AB AC
.Gọi
là góc tạo bởi đường thẳng
BC
và mặt phẳng
( )A BC
có số đo lớn nhất. Biết
sin
p
q
( với
,p q
nguyên tố cùng nhau ). Giá trị tổng
p q
là
A.
11
. B.
7
. C.
5
. D.
9
Câu 38: Cho hình lăng trụ tam giác đều
.
ABC A B C
có độ dài cạnh đáy bằng a. Góc giữa
A BC
và
ABC
bằng
60
. Gọi
,M N
là trung điểm của
BC
và
.CC
Tính khoảng cách giữa
A M
và
.AN
A.
6 97
97
a
. B.
3 97
.
97
a
C.
6 65
65
a
. D.
3 65
65
a
.
DẠNG TOÁN 4: HÌNH HỘP.
Câu 39: Cho lăng trụ tam giác đều
.
ABC A B C
có tất cả các cạnh bằng
a
.
M
là một điển thỏa mãn
1
2
CM AA
. Côsin của góc giữa hai mặt phẳng
A MB
và
ABC
bằng
A.
30
10
. B.
30
8
. C.
30
16
. D.
1
4
.
Câu 40: Cho hình hộp
.
ABCD A B C D
có thể tích bằng
V
. Gọi
M
,
N
,
P
lần lượt là trung điểm của
các cạnh
AB
,
A C
,
BB
. Tính thể tích khối tứ diện CMNP.
A.
5
48
V
. B.
1
8
V
. C.
7
48
V
. D.
1
6
V
.
Câu 41: Cho hình hộp
.
ABCD A B C D
, có đáy là hình thoi cạnh
2a
, tâm
O
,
0
60
BAD
và
2AA a
.
Hình chiếu vuông góc của
A
lên mặt phẳng
ABCD
trùng với tâm
O
. Gọi
M
là trung điểm
CD
. Khoảng cách giữa hai đường thẳng
A M
và
B D
bằng
A.
21
7
. B.
2 21
7
. C.
3 21
7
. D.
4 21
7
.
Câu 42: Cho hình hộp chữ nhật
.
ABCD A B C D
, có
, 2,
AB a AD a
góc giữa
A C
và mặt phẳng
ABCD
bằng
30
. Gọi
H
là hình chiếu vuông góc của
A
trên
A B
và
K
là hình chiếu vuông
góc của
A
trên
.A D
Tính góc giữa hai mặt phẳng
AHK
và
ABB A
.
A.
60
. B.
45
. C.
90
. D.
30
.
Câu 43: Cho lăng trụ
1 1 1 1
.
ABCD A B C D
có đáy
ABCD
là hình vuông cạnh
a
. Hình chiếu vuông góc của
1
A
lên
ABCD
trùng với giao điểm của
AC
và
BD
. Tính khoảng cách từ điểm
1
B
đến mặt
phẳng
1
A BD
.
A.
2
4
a
. B.
2
2
a
. C.
21
4
a
. D.
3
2
a
.
Câu 44: Cho hình lập phương
. ' ' ' 'ABCD A B C D
cạnh
a
. Gọi
K
là trung điểm của
'DD
. Tính khoảng
cách giữa hai đường thẳng
CK
và
'A D
.
3
7
a
21
7
a
7a
Trang 7/69
A.
3
a
. B.
4
a
. C.
5
a
. D.
2
a
.
Câu 45: Cho hình hộp chữ nhật
.
ABCD A B C D
có
3AB a
,
AD AA a
. Lấy điểm
M
thuộc đoạn
AB
, điểm
N
thuộc đoạn
A C
sao cho
AM A N x
,
0 10x a
. Tìm
x
theo
a
để
đoạn
MN
nhỏ nhất.
A.
0
. B.
30
3
a
. C.
10
2
a
. D.
10
3
a
.
Câu 46: Cho hình hộp chữ nhật
. ' ' ' 'ABCD A B C D
có
, 2 , ' 3 .AB a AD a AA a
Gọi
, , M N P
lần
lượt là trung điểm của
, ' ' '.BC C D và DD
Tính khoảng cách từ
A
đến mp
.MNP
A.
15
22
a
. B.
9
11
a
. C.
. D.
15
11
a
.
Câu 47: Cho hình lăng trụ đứng
.
ABC A B C
có đáy là tam giác vuông cân,
2AA a
,
AB AC a
.
Gọi
G
và
G
lần lượt là trọng tâm của tam giác
ABC
và tam giác
A B C
,
I
là tâm của hình
chữ nhật
ABB A
. Thể tích của khối
.
A IGCG
.
A.
3
2
a
. B.
3
6
a
. C.
3
5
6
a
. D.
3
5
30
a
.
Câu 48: Cho hình hộp
' ' ' 'ABCDA B C D
có đáy là hình vuông cạnh a. Mặt phẳng
( ' ')ABB A
vuông góc
với đáy, tam giác
'A AB
vuông tại
'A
, góc giữa
'BA
và đáy bằng
0
60
. Gọi
I
là tâm của hình
vuông
ABCD
. Tính khoảng cách giữa hai đường thẳng
'IA
và
'DB
.
A.
2 55
a
. B.
55
a
. C.
3
55
a
. D.
3
2
a
.
Câu 49: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
2SA a
và vuông góc
với mặt phẳng đáy. Gọi
M
là trung điểm cạnh
SD
. Tang của góc tạo bởi hai mặt phẳng
( )AMC
và
( )SBC
bằng
A.
3
2
. B.
2 5
5
. C.
2 3
3
. D.
5
5
.
Câu 50: Hai quả bóng hình cầu có kích thước khác nhau được đặt ở hai góc của một căn nhà hình hộp
chữ nhật sao cho mỗi quả bóng đều tiếp xúc với hai bức tường và nền của nhà đó. Biết rằng
trên bề mặt của hai quả bóng đều tồn tại một điểm có khoảng cách đến hai bức tường và nền
nhà mà nó tiếp xúc bằng
1; 2;4
. Tổng độ dài đường kính của hai quả bóng đó là?
A.
7
. B.
12
. C.
14
. D.
16
.
-------------------- HẾT --------------------
Trang 8/69
BẢNG ĐÁP ÁN
1.D 2.C 3.D 4.D 5.D 6.B 7.B 8.D 9.C 10.A
11.A 12.A 13.D 14.B 15.A 16.A 17.A 18.A 19.C 20.A
21.B 22.A 23.A 24.C 25.A 26.A 27.D 28.D 29.D 30.D
31.B 32.A 33.D 34.A 35.C 36.D 37.D 38.B 39.A 40.A
41.B 42.B 43.B 44.A 45.C 46.D 47.B 48.C 49.B 50.C
HƯỚNG DẪN GIẢI
Câu 1: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
và
SA
vuông góc với mặt phẳng
đáy. Góc giữa mặt bên
( )SBC
với mặt phẳng đáy bằng
45
. Gọi
,M N
lần lượt là trung điểm
của
AB
và
. Tính theo
a
khoảng cách giữa hai đường thẳng
MD
và
CN
.
A.
3
4
a
. B.
21
3
a
. C.
2a
. D.
2 21
21
a
.
Lời giải
Chọn D
Gọi
là giữa hai mặt phẳng
SBC
và
ABCD
.
Ta có
BC SBC ABCD
và
BC AB
BC SAB
BC SA
.
Suy ra
45
ABS
.
Do
SAB
vuông cân tại
A
nên
SA a
.
Chọn hệ trục tọa độ
Oxyz
(như hình vẽ) sao cho
(0;0;0), ;0;0
A O D a
0; ;0 ; 0;0;B a S a
.
Khi đó
; ;0 , 0; ; , 0; ;0
2 2 2
a a a
C a a N M
.
Suy ra
2 2
2
3
; ;0
2
; ; ;
4 2
; ;
2 2
. ;
0; ;0
2
a
MD a
a a
MD NC a
a a
NC a
a
CD MD NC
CD a
.
O
z
y
x
45°
N
M
C
A
B
D
S
Trang 9/69
3
2
. ,
2
2 21
,
21
21
,
4
a
CD MD NC
a
d MD NC
a
MD NC
.
Cách khác:
Dựng hình bình hành
DMEC
.
Ta có
//
MD CNE
nên
, , ,
d MD CN d MD CNE d M CNE
.
Gọi
I
là hình chiếu của
M
lên
CE
và
H
là hình chiếu của
M
lên
.
Suy ra
MH CNE
hay
, ,
d MD CN d M CNE MH
.
Gọi
là giữa hai mặt phẳng
SBC
và
ABCD
.
Ta có
BC SBC ABCD
và
BC AB
BC SAB
BC SA
.
Suy ra
45
ABS
.
Do
SAB
vuông cân tại
A
nên
SA a
.
Ta có
. 2
sin
5
MI BC BC ME a
MEC MI
ME CE CE
.
2 2
. 2 21
21
MI MN a
MH
MI MN
.
Câu 2: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
A
,
o
60
ABC
,
2BC a
. Gọi
D
là
điểm thỏa mãn
3 2SB SD
. Hình chiếu của
S
trên mặt phẳng
ABC
là điểm
H
thuộc đoạn
BC
sao cho
4
BC BH
. Tính góc giữa hai đường thẳng
AD
và
SC
biết
SA
tạo với mặt đáy
một góc
o
60
.
A.
o
60
. B.
o
45
. C.
o
90
. D.
o
30
.
Lời giải
Chọn C
O
y
x
z
B
S
A
C
D
Trang 10/69
Ta có
2 2 2 o
2. . .cos60
AH BH BA BH BA
2 2
2
1 3
2. . .
4 2 2 4
a a a
a a
3
2
a
AH
.
o
tan 60
SH
AH
. 3
SH AH
3
2
a
.
3
.sin 60 2 . 3
2
AC BC a a
,
3 3
4 2
a
HC BC
.
Ta có
2 2
2 2 2 2
9 3
3
4 4
a a
AH HC a AC
nên tam giác
AHC
vuông tại
H
, tức là
AH HC
.
Chọn
1
a
và chọn hệ trục tọa độ
Oxyz
(như hình vẽ) sao cho
0;0;0
O H
,
3
;0;0
2
C
,
3
0; ;0
2
A
,
3
0;0;
2
S
.
Suy ra
1
;0;0
2
B
.
1 3
;0;
2 2
SB
3 9
;0;
4 4
SD
3 3
;0;
4 4
D
.
Ta có
3 3 3
; ;
4 2 4
DA
3;2; 3
u
là một véctơ chỉ phương của
AD
.
3 3
;0;
2 2
SC
1;0; 1
v
là một véctơ chỉ phương của
SC
.
Ta có
. 0
u v
AD SC
.
Vậy góc giữa hai đường thẳng
AD
và
SC
bằng
o
90
.
Câu 3: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
5a
, cạnh bên
10SA a
và vuông
góc với mặt phẳng đáy. Gọi
M
là trung điểm cạnh
SD
. Tính
tan
của góc tạo bởi hai mặt
phẳng
AMC
và
SBC
.
A.
3
2
. B.
2 3
3
. C.
5
5
. D.
2 5
5
.
Lời giải
Chọn D
Chuẩn hóa với
1
a
.
Xét hệ trục tọa độ
Oxyz
như hình vẽ sau:
Trang 11/69
Chọn hệ trục tọa độ như hình vẽ.
5
0;0;0 ; 0;5;0 ; 5;0;0 ; 5;5;0 ; 0;0;10 ; 0; ;5
2
A D B C S M
.
0;5;0 , 5;0;10
BC BS
.
, 50;0;25BC BS
một véctơ pháp tuyến của
SBC
là
1
2;0;1
n
.
5
5;5;0 , 0; ;5
2
AC AM
.
25
, 25; 25;
2
AC AM
một véctơ pháp tuyến của
AMC
là
2
2; 2;1
n
.
Gọi
là góc giữa hai mặt phẳng
AMC
và
SBC
.
1 2
2
2 2 2 2 2
1 2
2.2 0. 2 1.1
.
5
cos
.
3 5
2 0 1 . 2 2 1
n n
n n
.
Suy ra:
2
2
1 1 2 5
tan 1 1
cos 5
5
3 5
.
Cách khác:
x
y
z
(0;
5
2
;5)
(0;0;10)
(5;5;0)
(0;5;0)
(5;0;0)
A≡O
M
C
D
B
S
Trang 12/69
Dựng hình bình hành
'SADS
. Khi đó
( ) ( )
SBC AMC S C
.
Dựng
AH SB
tại
H
và
//HK BC
(
K S C
).
Gọi
là góc giữa hai mặt phẳng
AMC
và
SBC
.
Khi đó ta có
( )
AHK S C
HKA
.
Ta có
2 2
.
2 5
AB AS
AH a
SA AB
.
Do đó
2 5
tan
5
AH
HK
.
Câu 4: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông, tam giác
SAB
đều. Hình chiếu của
S
lên mặt phẳng
ABCD
trùng với trung điểm
I
của
AB
. Gọi
,H K
lần lượt là trung điểm của
DC
và
, biết
7
2
a
SH
.Tính khoảng cách giữa
HK
và
SC
.
A.
3
8
. B.
15
2
. C.
15
8
D.
5
10
.
Lời giải
Chọn D
H
M
S'
B
C
A
S
K
Trang 13/69
Đặt
AB x
Ta có
2 2 2
SH SI IH
2 2
2
7 3
2 2
a x
x
x AB a
Chuẩn hóa
1
a
. Chọn hệ toạ độ
Oxyz
sao cho
0;0;0
O I
,
1
;0;0
2
B
,
1
;1;0
2
C
,
3
0;0;
2
S
(0;1;0)
H
,
1 3
;0;
4 4
K
1 3
; 1;
4 4
HK
,
1 3
;1;
2 2
SC
,
3
0; 1;
2
HS

3 3 3
, ; ;
4 4 4
HK SC
,
3 3 3 3 3
, . .0 . 1 .
4 4 4 2 8
HK SC HS

, .
5
,
10
,
HK SC HS
d HK SC
HK SC
.
Câu 5: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật, cạnh bên
SA
vuông góc với
đáy,
, 2 , 3AB a AD a SA a
. Gọi
,M N
lần lượt là hình chiếu của
A
lên
,SB SD
và
P
là giao điểm của
SC
với mặt phẳng
AMN
. Tính thể tích khối chóp
.
S AMPN
.
A.
3
1869
140
a
. B.
3
5589
1820
a
. C.
3
181
120
a
. D.
3
1863
1820
a
.
Lời giải
K
H
I
A
D
B
C
S
z
x
y
Trang 14/69
Chọn hệ trục tọa độ như hình vẽ.
Ta có tọa độ các điểm
0;0;0 , ;0;0 , 0;2 ;0 , ;2 ;0 , 0;0;3A B a D a C a a S a
.
Suy ra
;0; 3 , 0;2 ; 3 , ;2 ; 3SB a a SD a a SC a a a
.
Phương trình
: 0
3
x a t
SB y
z t
;0; 3 ;0; 3M a t t AM a t t
.
Mà
. 0 9 0
10
a
AM SB AM SB a t t t
9 3
;0;
10 10
a a
M
.
Tương tự vậy ta tìm được
18 12
0; ;
13 13
a a
N
.
Suy ra
2
1
27
, 1;2; 3
65
a
n AM AN
.
Do đó ta có phương trình của
: 2 3 0
AMN x y z
.
Phương trình
: 2
3 3
x t
SC y t
z a t
nên tọa độ điểm
P
là nghiệm của hệ
2
9 9 15 9 9 15
, , ; ;
3 3
14 7 14 14 7 14
2 3 0
x t
y t
a a a a a a
x y z P
z a t
x y z
.
Ta có:
2
27
, 1;2; 3
70
a
AM AP
,
2
27
, 1;2; 3
91
a
AN AP
Suy ra
2
1 621 14.
, ,
2 1820
AMPN
a
S AM AP AN AP
và
9
,
14
a
d S AMN
.
Vậy
2 3
.
1 9 621 14. 1863.
. .
3 1820 1820
14
S AMPN
a a a
V
.
Cách khác: (Công thức tính nhanh – trắc nghiệm)
1
SA
a
SA
;
2
2
10
9
SB SB
b
SM SA
;
SC
c
SP
;
2
2
13
9
SD SD
d
SN SA
.
y
z
x
C
B
S
A
D
N
M
P
Trang 15/69
Ta có
14
9
a c b d c
.
3
.
. .
.
1863 1863 1863 1 1863
. .
4 . . . 3640 3640 3640 3 1820
S AMPN
S AMPN S ABCD ABCD
S ABCD
V
a b c d
V V SA S a
V a b c d
.
Câu 6: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
2
,
SA
vuông góc với mặt
phẳng đáy
ABCD
và
2SA
. Gọi
M
,
N
lần lượt là hai điểm thay đổi trên hai cạnh
AB
,
AD
sao cho mặt phẳng
SMC
vuông góc với mặt phẳng
SNC
. Thể tích khối chóp
.S AMCN
đạt giá trị nhỏ nhất bằng
A.
4 3 4
3
. B.
8 3 8
3
. C.
2 3 2
. D.
4 3 4
3
.
Lời giải
Chọn B
Chọn hệ trục tọa độ
Oxyz
như hình vẽ trên sao cho
0;0;0A
,
2;0;0B
,
0;2;0D
,
0;0;2S
, suy ra
2;2;0C
.
Đặt
AM m
,
AN n
,
, 0;2m n
, suy ra
;0;0M m
,
0; ;0N n
.
;0; 2SM m
,
2;2; 2SC
,
0; ; 2SN n
.
, 4;2 4;2
SMC
n SM SC m m

,
, 4 2 ; 4; 2
SNC
n SN SC n n
.
Do
SMC SNC
nên
. 0 4 4 2 4 2 4 4 0
SMC SNC
n n n m mn
2 8mn m n
.
Mặt khác
2
2 2
2
m n
mn m n m n
nên ta có
2
2 8 0
4
m n
m n
4 3 4
4 3 4
m n
m n
. Do
, 0m n
nên
4 3 4m n
.
4 2 2 4 3 4
AMCN ABCD BMC DNC
S S S S m n m n
.
.
8 3 8
1 2
.
3 3 3
S AMCD AMCN
V SA S m n
.
Trang 16/69
Vậy thể tích nhỏ nhất của khối chóp
.
S AMCN
là
8 3 8
3
.
Câu 7: Cho hình chóp
.
S ABCD
có đáy là hình thang vuông tại
A
và
B
,
AB BC a
,
2AD a
;
cạnh bên
SA
vuông góc với mặt phẳng đáy và
SA a
. Gọi
M
,
N
lần lượt là trung điểm của
,
CD
. Tính cosin của góc giữa
MN
và
SAC
.
A.
2
5
. B.
55
10
. C.
3 5
10
. D.
1
5
.
Lời giải
Chọn B
Chọn hệ trục
Oxyz
như hình vẽ, với
O A
.
Tọa độ các đỉnh của hình chóp là :
0;0;0
A
,
;0;0
B a
,
; ;0C a a
,
0;2 ;0D a
,
0;0;S a
.
;0;
2 2
a a
M
,
3
; ;0
2 2
a a
N
.
Ta có:
1
0;0;1
SA u
a
;
1
1;1; 1
SC v
a
.
Một véc tơ pháp tuyến của mặt phẳng
SAC
là
, 1;1;0
n u v
.
Lại có:
2
0;3; 1
MN w
a
.
Gọi
là góc giữa
MN
và
SAC
ta có:
.
3
sin
.
2 5
n w
n w
55
cos
10
.
Câu 8: Cho hình chóp
.
S ABC
có
ABC
vuông tại
B
,
1, 3
AB BC
,
SAC
đều, mặt phẳng
SAC
vuông với đáy. Gọi
là góc giữa hai mặt phẳng
SAB
và
SBC
. Giá trị của
cos
bằng
A.
2 65
65
B.
65
20
C.
65
10
D.
65
65
Lời giải
Chọn D
a
2a
a
a
z
y
x
N
M
D
A
B
C
S
Trang 17/69
Gọi
, ,H M N
lần lượt là trung điểm của
, ,AC AB BC
.
SAC ABC
SH ABC
,
SH HM SH HN
.
ABC
vuông tại
B
HM HN
.
ABC
vuông tại
B
2
AC
3
SH
.
1 3
2 2
HM BC
;
1 1
2 2
HN AB
.
Chọn hệ trục tọa độ như sau:
0;0;0
H
;
0;0; 3
S
;
3
0; ;0
2
M
;
1
;0;0
2
N
,
1 3
; ;0
2 2
B
1
;0;0
2
1 3
; ; 3
2 2
BM
BS
3
0; ;0
2
1 3
; ; 3
2 2
BN
BS
1
3 3
, 0; ;
2 4
n BM BS
;
2
3 3
, ;0;
2 4
n BN BS
1 2
cos cos ;n n
3
65
16
65
3 3 9 3
.
4 16 4 16
.
Chú ý: Ta có thể chứng minh công thức tổng quát sau:
Cho hình chóp
.
S HMBN
có đáy
HMBN
là hình chữ nhật có
,
HM m HN n
và
( )SH HMBN
và
SH h
. Gọi
là góc giữa hai mặt phẳng
MSB
và
NSB
thì
2 2 2 2
cos
mn
m h n h
.
Trang 18/69
Ta có:
( )BN SHN
nên dựng
HE SN
tại
N
thì
( )HE SNB
.
Dựng hình bình hành
HEKM
( )MK SNB
Hình chiếu của
MSB
trên
SNB
là
KSB
.
Ta có:
2 2
1 1
.
2 2
MSB
S MB MS n m h
2 2
2
cos
KSB KSB
MSB
S S
S
n m h
Gọi
F EK SB
ta có:
. . . 1 .
KSB ESB
ESB NSB
S S
FK SE KE EF SE KE SE
S S FE SN FE SN EF SN
=
2 2
2 2 2 2
1 1
SN SE h n
SE SN n h n h
(vì
2 2
2 2 2 2
.SE SE SN SH h
SN SN SN n h
)
2 2 2 2 2
2 2 2 2
2 2
.
2
2
KSB NSB
n n m n h mn
S S
n h n h
n h
.
Vậy
2 2 2 2
cos
KSB
MSB
S
mn
S
m h n h
.
Áp dụng vào bài toán với
3 1
3, ,
2 2
h m n
ta được
65
cos
65
.
Câu 9: Cho hình lập phương
.
ABCD A B C D
có các cạnh bằng
2
, gọi điểm
M
là tâm của mặt bên
ABB A
, các điểm
, , ,N P Q K
lần lượt là trung điểm của các cạnh
, , ,
AC DD D C B C
. Tính
cosine góc giữa hai mặt phẳng
MNP
và
AQK
.
A.
2
2
. B.
1
2
. C.
102
34
. D.
3
4
.
Lời giải
Chọn C
m
n
h
K
F
N
M
B
H
S
E
Trang 19/69
Ta chọn hệ trục tọa độ
Oxyz
với gốc
A O
cạnh
A B
nằm trên
Ox
, cạnh
A D
nằm trên
Oy
và cạnh
A A
nằm trên
Oz
. Từ các dữ kiện đề bài đã cho ta tìm được tọa độ các điểm
1;0;1 , 1;1;2 , 0; 2;1 , 2;1;0 , 1;2;0 , 0;0;2
M N P K Q A
Ta có
0;1;1 , 1;1; 1 , 2;1; 2 , 1;2; 2
MN NP AK AQ
.
Gọi
1 2
,u u
lần lượt là 2 vector pháp tuyến của mặt phẳng
MNP
và
AQK
.
Như vậy ta tính được
1 2
2; 1;1 , 2;2;3
u u
.
Ta gọi góc giữa hai mặt phẳng
MNP
và
AQK
là
.
Như vậy
cos
được tính theo công thức
1 2
2 2 2 2 2 2
1 2
.
2.2 1.2 1.3
102
cos
34
2 1 1 2 2 3
u u
u u
.
Câu 10: Cho hình chóp
.
S A B C D
có đáy
ABCD
là hình vuông cạnh bằng
a
.
S A
vuông góc với mặt
phẳng đáy.
H
và
K
là hai điểm lần lượt nằm trên hai cạnh
BC
và
CD
sao cho
3
4
a
BH
,
(0 )KD x x a
. Tìm giá trị của
x
để hai mặt phẳng
SAH
và
SAK
tạo với nhau một
góc bằng
45
.
A.
7
a
x
. B.
5
a
x
. C.
2
7
a
x
. D.
2
5
a
x
.
Lời giải
Chọn A
M
N
K
Q
P
C
B
D
A
A'
D'
B'
C'
Trang 20/69
Ta chọn hệ tọa độ
Oxyz
như hình vẽ.
Khi đó
0;0;0 ; ;0;0 ; 0; ;0 ;A B a D a S Oz
.
Qua đó ta có tọa độ các điểm
3
; ;0 ; ; ;0 ; ; ;0
4
a
C a a H a K x a
.
Ta có:
3
; ;0 ; ; ;0
4
a
AH a AK x a

.
Ta có
0;0;1
3
; ;0
4
k
a
AH a
3
, ; ;0
4
a
k AH a
.
Gọi
n
là một véctơ pháp tuyến của mặt phẳng
SAH
thì
3
;1;0
4
n
.
Ta có
0;0;1
; ;0
k
AK x a

, ; ;0k AK a x
.
Gọi
n
là một véctơ pháp tuyến của mặt phẳng
SAK
thì
; ;0n a x
.
Gọi
là góc giữa hai mặt phẳng
SAH
và
SAK
, khi đó
2
2 2
2
2
2
3
.
3 25
4
cos cos 45 2
4 16
.
3
1.
4
a
x
n n
a
x a x
n n
a x
2 2
7 48 7 0 0 .
7
a
x ax a x do x
Vậy
7
a
x
.
Cách khác:
Ta có:
( )SA ABCD
,SA AH SA AK
.
Gọi
là góc giữa hai mặt phẳng
SAH
và
SAK
.
Suy ra
45HAK
.
Trang 21/69
Ta có
2
2
3 5
4 4
a a
AH a
;
2 2
AK a x
và
2
2
4
a
HK a x
.
Áp dụng định lí Cosin cho tam giác
AHK
ta có:
2 2 2 0
2 . cos 45
HK AH AK AH AK
2 2
2 2 2 2 2
25 5 2
( ) 2. . .
16 16 4 2
a a a
a x a x a x
2 2
3 5 2
2 .
2 4
a
x a x
2 2
5 2 6 8a x a x
2 2 2 2
50( ) 64 96 36x a x ax a
2 2
14 96 14 0
x ax a
2 2
7 48 7 0 0 .
7
a
x ax a x do x
Vậy
7
a
x
.
Câu 11: Trong không gian, cho tam giác
OAB
cân ở
O
có
4
5; tan
3
OA OB AOB
. Điểm
C
di
động trên tia
Oz
vuông góc
OAB
, gọi
H
là trực tâm của tam giác
ABC
. Khi
C
di động
trên tia
Oz
thì
H
luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng:
A.
5
4
. B.
3
2
. C.
5
2
. D.
.
Lời giải
Chọn A
Chọn hệ trục tọa độ
Oxyz
có gốc
O
, tia
trùng tia
OA
, tia
nằm trong mặt phẳng
OAB
sao cho tia
OB
nằm giữa hai tia
,Ox Oy
như hình vẽ. Khi đó
5;0;0
A
và
3;4;0
B
.
x
z
H
E
y
A
O
B
C
K
Trang 22/69
Giả sử
0;0;C c
. Dễ thấy tam giác
ABC
cân tại
C
. Gọi
4;2;0
E
là trung điểm của
AB
.
Ta có mặt phẳng
OCE
vuông góc với
AB
và là mặt phẳng cố định.
Gọi
K
là trực tâm tam giác
OAB
, do
A
,
B
và
K
cùng nằm trong mặt phẳng
Oxy
.
Giả sử
; ;0K x y
, ta có
. 0
. 0
OK AB
BK OA
. 2 .4 0
3 0
x y
x
3
3
2
x
y
. Tìm được
3
3; ;0
2
K
.
Do
AB OEC
HK AB
HK CA
CA BHK
90
KH CAB KH HE KHE
.
Do đó
H
thuộc mặt cầu đường kính
1 5
1
4 2
KE
và thuộc mặt phẳng
OCE
cố định.
Vậy
H
luôn thuộc một đường tròn cố định có bán kính
5
4
R
.
Cách khác:
Gọi
E
là trung điểm
AB
. Ta có
( )AB OCE
nên
AB CE
do đó
H
thuộc
CE
nên
H
luôn
nằm trong mặt phẳng
( )OCE
cố định.
Gọi
K
là trực tâm
OAB
, ta có:
( )
AK OB
AK OBC AK BC
AK OC
mà
AH BC
nên
( )BC AHK
HK BC
mà
HK AB
( )HK ABC
0
90
KHE
H
thuộc đường tròn đường kính
KE
nằm trong
( )OCE
cố định.
Ta có:
2
2
1 1 9
cos
16
25
1 tan
1
9
AOB
AOB
3
cos
5
AOB
3, 4
OM AM
.
1, 4, 2
MN ON NE
(N là trung điểm MB)
K
E
O
A
B
C
M
H
Trang 23/69
2 2
2 5
OE ON NE
.
Lại có
1 5
4 4 2
KE NM OE
KE
OE ON
.
Vậy bán kính của đường tròn đường kính
KE
là
5
2 4
KE
R
.
Câu 12: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thoi tâm
O
cạnh
a
, góc
120
BCD
.
SA ABCD
. Thể tích khối chóp
.
S ABCD
là
3
3
3
a
. Gọi
M
là tâm đường tròn ngoại tiếp
tam giác
SOD
. Hãy tính khoảng cách
h
từ
M
tới mặt phẳng
SBC
theo
a
.
A.
57
19
a
h
. B.
57
38
a
h
. C.
2 5
5
a
h
. D.
2 5
19
a
h
.
Lời giải
Chọn A
Cách 1: Phương pháp dựng hình
Tam giác
SOD
vuông tại
O
nên
M
là trung điểm của
.
Ta có
1 1
, ,
2 2
DM
d M SBC d D SBC
DS
;
//AD BC
.
1
, ,
2
//
AD SBC d D SBC d A SBC
. Vậy
1
, ,
2
d M SBC d A SBC
Gọi
H
là trung điểm của
BC
, do tam giác
ABC
đều nên
AH BC
, lại có
SA ABCD SA BC
nên
BC SAH SBC SAH
Dựng
,
AK SH AK SBC d A SBC AK
.
Diện tích hình thoi ABCD là:
2
0
3
. .sin 60
2
ABCD
a
S AB BC
Từ đó suy ra
.
3
2
S ABCD
ABCD
V
SA a
S
. Tính được
3
2
a
AH
Tam giác SAH vuông tại A, đường cao AK nên:
K
M
H
D
S
A
B
C
O
x
y
z
M
D
S
A
B
C
Trang 24/69
2 2 2 2 2 2
1 1 1 4 1 19 228
3 4 12 19
a
AK
AK AH SA a a a
.
Vậy
1 57
,
2 19
a
d M SBC AK
.
Cách 2: Phương pháp tọa độ
Không mất tính tổng quát, ta giả sử
1
a
.
Chọn hệ trục tọa độ như hình vẽ,
//Oz SA
. Khi đó ta có
1 3 1
0;0;0 , ;0;0 , 0; ;0 , ;0;0
2 2 2
O A B C
.
3 1 1 3
0; ;0 ;0;2 , ; ;1
2 2 4 4
D S M
.
1 3
; ; 2 , 1;0; 2
2 2
SB SC
.
Ta có
3
, 3; 1;
2
SBC
n SB SC
.
Phương trình mặt phẳng
SBC
là:
3 3
3 0
2 2
x y z
.
Suy ra
3
57
2
,
19
3
3 1
4
d M SBC
.
Vậy
57
,
19
a
d M SBC
.
Câu 13: Cho tam giác
ABC
vuông tại
A
và đường thẳng vuông góc với mặt phẳng
ABC
tại điểm
A
. Các điểm
,M N
thay đổi trên đường thẳng sao cho
MBC NBC
. Biết
,
AB b AC c
. Giá trị nhỏ nhất của thể tích tứ diện
MNBC
theo
b
và
c
bằng
A.
2 2
2 2
3
b c
b c
. B.
2 2
2 2
b c
b c
. C.
2 2
3
bc
b c
. D.
2 2
2 2
3
b c
b c
.
Lời giải
Chọn D
Chọn hệ trục tọa độ
Oxyz
sao cho
O A
, các tia
, , Ox Oy Oz
lần lượt trùng với các tia
, ,
AB AC AM
.
Đặt
, ,
AB b AC c AM m
(
, b c
không đổi).
Trang 25/69
Khi đó
0;0;0 , ;0;0 , 0; ;0 , 0; 0; A B b C c M m
. Giả sử
0; 0; .N n
Ta có:
:MBC
1 0
x y z
b c m
có một véctơ pháp tuyến là
1 1 1
; ;
b c m
.
:
NBC
1 0
x y z
b c n
có một véctơ pháp tuyến là
1 1 1
; ;
b c n
.
Vậy
MBC NBC
2 2
1 1 1
. 0 0
b c mn
2 2
2 2
.
.
b c
m n
b c
0
mn
.
Mặt khác
0
m
nên
0
n
. Vậy
M
và
N
nằm về hai phía của
A
.
Ta có
; ;0 , ;0; , ;0;BC b c BM b m BN b n
,
, 0; ;0 .
BM BN b n m
Vậy V
MNBC
=
1 1
. ,
6 6
BC BM BN bc n m
1
6
bc m n
.
Ta có
2 2
2 2
.
b c
m n
b c
không đổi.
Áp dụng bất đẳng thức Cauchy ta có V
MNBC
=
2 2
2 2
1 1 1
. .2 . .
6 6 3
b c
bc m n bc m n
b c
.
Dấu đẳng thức xảy ra khi và chỉ khi
m n
2 2
bc
b c
.
Vậy V
MNBC
nhỏ nhất khi
,M N
nằm về hai phía của
A
và
.AB AC
AM AN
BC
.
Khi đó giá trị nhỏ nhất của thể tích tứ diện
MNBC
bằng
2 2
2 2
1
.
3
b c
b c
.
Cách khác:
Trang 26/69
Dựng
AH BC
, ta có
( )BC MHN
nên
HMN
vuông tại H.
Do đó
2 2
2
2 2
.
b c
AM AN AH
b c
Khi đó thể tích tứ diện
MNBC
là
1 1
. .
3 3
MNBC MABC NABC ABC ABC
V V V AM S AN S
1
.
3
ABC
AM AN S
1
6
bc AM AN
2 2
2 2
1
.2 .
6
3
b c
bc AM AN
b c
.
Dấu “=” xảy ra
2 2
bc
AM AN
b c
.
Vậy
2 2
2 2
min
3
MNBC
b c
V
b c
.
Câu 14: Cho hình chóp tứ giác đều
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, tâm
O
. Gọi
M
và
N
lần lượt là trung điểm của hai cạnh
và
BC
. Biết
6
2
a
MN
, tính sin của góc giữa
đường thẳng
MN
và mặt phẳng
SBD
.
A.
2
5
. B.
3
3
. C.
5
5
. D.
3
.
Lời giải
Chọn B
H
N
M
C
B
A
Trang 27/69
Gọi
I
hình chiếu của
M
lên
ABCD
, suy ra
I
là trung điểm của
AO
.
Khi đó
3 3 2
4 4
a
CI AC
.
Áp dụng định lý cosin ta có:
2 2
2 2
9 3 2 2 10
2 . .cos45 2. . .
4 8 2 4 2 4
o
a a a a a
NI CN CI CN CI
.
Do
MIN
vuông tại
I
nên
2 2
2 2
3 5 14
2 8 4
a a a
MI MN NI
.
Mà
1 14
/ / ,
2 2
a
MI SO MI SO SO
.
Chọn hệ trục tọa độ
Oxyz
như hình vẽ.
Khi đó ta có tọa độ các điểm:
0;0;0
O
,
2
0; ;0
2
B
,
2
0; ;0
2
D
,
2
;0;0
2
C
,
2 2
; ;0
4 4
N
,
2
;0;0
2
A
,
14
0;0;
2
S
,
2 14
;0;
4 4
M
.
Khi đó
2 2 14
; ;
2 4 4
MN
,
2 14
0; ;
2 2
SB
,
2 14
0; ;
2 2
SD
.
Vectơ pháp tuyến mặt phẳng
SBD
:
, 7 ;0;0
n SB SD
.
Suy ra
2
. 7
.
2
3
sin ,
3
6
.
. 7
2
MN n
MN SBD
MN n
.
Trang 28/69
Câu 15: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Gọi
M
và
N
lần lượt là trung
điểm các cạnh
AB
và
AD
;
H
là giao điểm của
CN
và
DM
. Biết
SH
vuông góc với mặt
phẳng
( )ABCD
và
3SH a
. Tính khoảng cách giữa hai đường thẳng
DM
và
SC
theo
a
.
A.
2 57
19
a
. B.
57
19
a
. C.
2 13
19
a
. D.
7
19
a
.
Lời giải
Chọn A
Chọn hệ trục tọa độ như hình vẽ
Tọa độ các đỉnh:
(0;0;0), ;0;0 , (0; ;0), ( ; ;0), ;0;0 , 0; ;0
2 2
a a
A B a D a C a a M N
Suy ra
; ;0
2
a
DM a

phương trình
: 2 ; 2 ;0
0
x t
DM y a t H t a t
z
; 2 ;0 , ; ;0
2
a
CH t a t CN a
Vì
2 3 3
4 ; ;0 ; ; 3
5 5 5 5 5
2
t a t a a a a a
H CN t a t t H S a
a
a
Ta có:
2
2 2
4 2 3
; ; 3 , ;0;0 , 3; ;
5 5 2
a a a
SC a DC a DM SC a a
3
, . 3
DM SC DC a
.
Vậy
3
2
, .
3 2 57
,
19
19
,
2
DM SC DC
a a
d SC DM
a
DM SC
.
z
x
y
H
N
M
B
A
D
C
S
Trang 29/69
Câu 16: Cho hình chóp tứ giác đều
.
S ABCD
có tất cả các cạnh đều bằng nhau. Gọi
,E M
lần lượt là
trung điểm các cạnh
, ,BC SA
là góc tạo bởi đường thẳng
EM
và mặt phẳng
SBD
. Tính
sin
.
A.
6
sin
3
. B.
1
sin
2
. C.
3
sin
2
. D.
2
sin
2
.
Lời giải
Chọn A
Gọi
AC BD O
. Vì hình chóp tứ giác
.
S ABCD
là hình chóp đều nên
SO ABCD
.
Đặt
1
OA
. Vậy
2
AC
và đáy của hình chóp
.
S ABCD
là hình vuông có cạnh bằng
2
.
Do giả thiết hình chóp tứ giác đều
.
S ABCD
có tất cả các cạnh đều bằng nhau nên
2
SA
.
Xét tam giác
SAO
vuông tại
O
có
2
2 2 2
2 1 1
SO SA AO
.
Chọn hệ trục tọa độ
Oxyz
sao cho
, ,
Ox OC Oy OB Oz OS
.
Khi đó ta có:
1;0;0 , 1;0;0 , 0;1;0 , 0;0;1
C A B S
.
Do
,E M
lần lượt là trung điểm các cạnh
,BC SA
nên
1 1 1 1
; ;0 , ;0;
2 2 2 2
E M
.
AC SBD
nên mặt phẳng
SBD
nhận
2;0;0
AC
là một vectơ pháp tuyến.
Đường thẳng
EM
nhận
1 1
1; ;
2 2
ME
là một vectơ chỉ phương.
Gọi
là góc tạo bởi đường thẳng
EM
và mặt phẳng
SBD
.
Trang 30/69
Vậy ta có:
2 2
2
1 1
1.2 .0 .0
.
2 2
6
sin
. 3
1 1
1 .2
2 2
ME AC
ME AC

.
Câu 17: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
và chiều cao bằng
h
. Gọi
I
là trung
điểm cạnh bên
SC
. Tính khoảng cách từ
S
đến mặt phẳng
AIB
.
A.
2 2
2
4 9
ah
h a
. B.
2 2
4
4 9
ah
h a
. C.
2 2
4 9
ah
h a
. D.
2 2
2
2 3
ah
h a
.
Lời giải
Chọn A
Gọi
O
là giao điểm của
AC
và
BD
. Ta có
2
2
a
OA OB OC
.
Chọn hệ trục tọa độ
Oxyz
có gốc tọa độ
O
, tia
Ox
chứa
A
, tia
Oy
chứa
B
, tia
Oz
chứa
S
.
Khi đó:
2
;0;0
2
a
A
,
2
0; ;0
2
a
B
,
2
;0;0
2
a
C
,
0;0;S h
.
Gọi
M
là giao điểm của
SO
và
AI
. Tam giác
SAC
có
M
là giao điểm của hai đường trung
tuyến nên
M
là trọng tâm, do đó
0;0;
3
h
M
.
Mặt phẳng
AIB
đi qua
, ,MA B
nên có phương trình:
1
2 2
3
2 2
x y z
h
a a
.
2 2 3
1 0x y z
a a h
.
Trang 31/69
Do đó khoảng cách từ
S
đến mặt phẳng
AIB
là:
2 2
2 2 2
3
. 1
2
2 2 9
4 9
h
ah
h
d
h a
a a h
.
Câu 18: Cho hình chóp tứ giác đều
.
S ABCD
có đáy là hình vuông cạnh
a
, tâm
O
. Gọi
E
là điểm đối
xứng với
D
qua trung điểm của
SA
,
M
là trung điểm của
AE
,
N
là trung điểm của
BC
.
Tính khoảng cách giữa hai đường thẳng
MN
và
AC
.
A.
2
4
a
. B.
2
2
a
. C.
3
4
a
. D.
8
a
.
Lời giải
Chọn A
Chọn hệ trục tọa độ như hình vẽ. Đặt
SO h
và gọi
I
là trung điểm của
SA
.
Ta có tọa độ các đỉnh là:
2
0; ;0
2
a
A
,
2
;0;0
2
a
B
,
2
0; ;0
2
a
C
,
2
;0;0
2
a
D
0;0;S h
.
I
,
N
lần lượt là trung điểm
SA
,
BC
2
0; ;
4 2
a h
I
,
2 2
; ;0
4 4
a a
N
.
E
đối xứng với
D
qua
I
2 2
; ;
2 2
a a
E h
.
M
là trung điểm
AE
2 2
; ;
4 2 2
a a h
M
.
Do đó
3 2
0; ;
4 2
a h
MN
,
0; 2;0
AC a
,
2 3 2
; ;0
4 4
a a
AN
Trang 32/69
2
, ;0;0
2
ah
MN AC

2
, .
4
a h
MN AC AN
.
Vậy
, .
2
,
4
,
MN AC AN
a
d MN AC
MN AC
.
Câu 19: Cho hình lăng trụ
.
ABC A B C
có
.
A ABC
là tứ diện đều cạnh
a
. Gọi
M
,
N
lần lượt là trung
điểm của
AA
và
BB
. Tính tan của góc giữa hai mặt phẳng
ABC
và
CMN
.
A.
2
5
. B.
3 2
4
. C.
2 2
5
. D.
4 2
13
.
Lời giải
Chọn C
Không mất tính tổng quát ta chọn
1
a
.
Gọi
O
là trung điểm của
A B
. Gọi
H
là tâm của
ABC A H ABC
.
Chuẩn hóa và chọn hệ trục tọa độ như hình vẽ sao cho
0;0;0
O
.
Khi đó:
1
;0;0
2
A
,
1
;0;0
2
B
,
3
0; ;0
2
C
. Dễ thấy mp
ABC
có vtpt
1
0;0;1
n
.
Do:
3
0; ;0
6
H
,
6
3
A H
3 6
0; ;
6 3
A
. Ta có
AB A B
3 6
1; ;
6 3
B
.
M
là trung điểm
AA
1 3 6
; ;
4 12 6
M
,
N
là trung điểm
BB
3 3 6
; ;
4 12 6
N
z
y
x
H
M
N
O
B'
A'
C'
C
A
B
Trang 33/69
1;0;0
MN
,
1 5 3 6
; ;
4 12 6
CM
CMN
có vtpt
2
0;2 2;5
n
Đặt
,
ABC CMN
cos
1 2
1 2
.
5
5
1. 33 33
n n
n n
2
1
tan 1
cos
2 2
5
( do góc
nhọn).
Câu 20: Cho hình chóp
SABC
có đáy
ABC
là tam giác cân tại
A
và
AB a
,
120
BAC
.
SA SB SC
. Gọi
là góc của hai mặt phẳng
SAB
và
SBC
sao cho
5
cos
7
. Khi đó
thể tích của khối chóp
SABC
là
A.
3
3
12
a
. B.
3
2a
. C.
3
3
a
. D.
3
2
5
a
.
Lời giải
Chọn A
 Vì
SA SB SC
Hình chiếu của
S
lên
ABC
trùng với tâm đường tròn ngoại tiếp
ABC
là
D
(với
D
là đỉnh của hình thoi
ABDC
)
 Đặt
SD x
0
x
.
 Gắn hệ tọa độ:
0;0;0 , ;0;0 , 0;0;D B a S x
. Vì
3 3
0; ;0
2 2
a a
DI I
.
 Ta có
1 3
;0;0 , ; ;0
2 2 2
a a
DB a IA DB A
,
3
; ;0
2 2
a a
C
3 3
; ; , ;0; , ; ;
2 2 2 2
a a a a
SA x SB a x SC x

2
1
3 3
, ; ; 3; ; 3
2 2 2
ax xa a
SA SB n x x a

là một vecto pháp tuyến của
SAB
Trang 34/69
2
2
3
, 0; ; 0;2 ; 3
2
a
SA SC ax n x a
là vecto pháp tuyến của
SAC
2 2
1 2
2 2
1 2
.
2 3 5
os
4 3 7
.
n n
x a
c x a
x a
n n
2 3
1 1 3 3
. .
3 3 4 12
SABC ABC
V SD S a a a
.
Câu 21: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
B
,
2AC a
, tam giác
SAB
và
tam giác
SCB
lần lượt vuông tại
A
,
C
. Khoảng cách từ
S
đến mặt phẳng
ABC
bằng
2a
.
Côsin của góc giữa hai mặt phẳng
SAB
và
SCB
bằng:
A.
1
2
. B.
1
3
. C.
1
2
. D.
1
3
.
Lời giải
Chọn B
Chọn hệ trục tọa độ sao cho:
0;0;0B
,
2;0;0A a ,
0; 2;0C a ,
; ;S x y z
,
0z
.
Ta có
: 0ABC z
,
2;0;0AB a
,
0; 2;0CB a
,
2; ;AS x a y z
,
; 2;CS x y a z
.
Do
. 0AS AB
 
2 2 0x a a
2x a
.
. 0CS CB
 
2 2 0y a a
2y a
.
Mà
, 2d S ABC a
2z a
. Từ đó
2; 2;2S a a a .
Ta có
0; 2;2AS a a
,
2;0;2CS a a
,
2; 2; 2BS a a a
.
SBC
có 1 vtpt
2;0;1n
,
SAB
có 1 vtpt
0; 2; 1m
.
Vậy
cos
1
3. 3
1
3
.
Trang 35/69
Câu 22: Cho hình chóp đều
SABCD
có cạnh đáy bằng
2
, cạnh bên bằng
3 2
. Gọi
,M N
lần lượt là
các điểm thuộc
,SB SD
sao cho
3 , 3
SB SM SD DN
. Khoảng cách giữa
AM
và
CN
bằng
A.
40
857
. B.
72
857
. C.
24
153
. D.
40
257
.
Lời giải
Chọn A
Gọi
O
là giao điểm của
,AC BD
SO ABCD
.
2, 18 2 4
OA SO
.
Chọn hệ trục
Oxyz
như hình vẽ. (
// , // ,
Ox AB Oy AD Oz OS
)
Tọa độ điểm
1; 1;0
A
,
1; 1;0
B
,
1;1;0
C
,
1;1;0
D
,
0;0;4
S
.
Từ giả thiết ta có
1
1 0
3
1 1 1 1 8
1 0 ; ;
3 3 3 3 3
1
4 0 4
3
M
M
M
x
SM SB y M
z
.
Tương tự tọa độ điểm
2 2 4
; ;
3 3 3
N
.
Suy ra
4 2 8 5 1 4
; ; , ; ; , 2;2;0
3 3 3 3 3 3
AM CN AC
.
Chọn vectơ chỉ phương của đường thẳng
AM
là
1
2;1;4
u
, chọn vectơ chỉ phương của
đường thẳng
CN
là
2
5;1; 4
u
.
Ta có
1 2
; 8;28; 3
u u
.
Trang 36/69
Khoảng cách giữa hai đường thẳng
,AM CN
bằng
1 2
2 2
2
1 2
; .
16 56 0
40
;
857
;
8 28 3
u u AC
d AM CN
u u

.
Câu 23: Cho hình chóp tam giác đều
.
S ABC
có
2SA a
,
AB a
. Gọi
M
là trung điểm cạnh
BC
.
Tính khoảng cách
d
từ
M
tới mặt phẳng
SAB
.
A.
165
.
30
a
d
B.
15
.
3
a
d
C.
65
.
15
a
d
D.
65
.
10
a
d
Lời giải
Chọn A
Gọi
O
là hình chiếu của
S
trên
ABC
, ta suy ra
O
là trọng tâm tam giác
ABC
.
Do
M
là trung điểm
BC
nên
3
2
a
AM
. Suy ra
3
3
a
OA
và
3
6
a
OM
.
Xét tam giác
SOA
vuông tại
O
, ta có
2
2 2 2
33
4
3 3
a a
SO SA OA a
.
Ta chọn hệ trục tọa độ
Oxyz
như hình vẽ với
O
trùng với gốc tọa độ, khi đó ta được:
0;0;0
O
,
3
;0;0
3
a
A
,
33
0; 0;
3
a
S
,
3
;0;0
6
a
M
.
Suy ra
3
; ;0
6 2
a a
B
,
3
; ;0
6 2
a a
C
Ta có
3 33 3 33
;0; , ; ;
3 3 6 2 3
a a a a a
SA SB
Trang 37/69
Suy ra
2 2 2
33 11 3
; ; ;
6 2 6
SAB
a a a
n SA SB
.
Phương trình măt phẳng
SAB
là
33 11 3 11
0
6 2 6 6
a
x y z
.
Suy ra
33 3 11
6 6 6
165
,
30
33 11 3
36 4 36
a a
a
d M SAB
.
Câu 24: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thang cân,
2 2 2 2AD AB BC CD a
.
Hai mặt phẳng
SAB
và
SAD
cùng vuông góc với mặt phẳng
ABCD
. Gọi
,M N
lần
lượt là trung điểm của
SB
và
CD
. Tính cosin góc giữa
MN
và
SAC
, biết thể tích khối chóp
.
S ABCD
bằng
3
3
4
a
.
A.
5
10
. B.
3 310
20
. C.
310
20
. D.
3 5
10
.
Lời giải
Chọn C
Cách 1:
Vì
ABCD
là hình thang cân có
2 2 2 2AD AB BC CD a
2 ;
AD a AB BC CD a
3
2
a
CH
;
2
2 3 3 3
.
2 2 4
ABCD
a a a a
S
.
nên
2 3
1 3 3 3
. .SA
3 4 4
ABCD
a a
V
SA a
Gắn hình chóp vào hệ trục tọa độ như hình vẽ
Trang 38/69
Ta có:
0;0;0 ,
K
;0;0 ,
2
a
B
3
0; ;0 ,
2
a
C
3
0; ;0 ,
2
a
A
3
; ;0 ,
2 2
a a
N
3
0; ; ,
2
a
S a
3
; ;
4 4 2
a a a
M
3 3 3
; ;
4 4 2
a a a
MN
. Chọn
1
3;3 3; 2
u
cùng phương với
MN

Nhận xét:
BK SA
BK SAC
BK AC
;0;0
2
a
BK
là vtpt của
SAC
.Chọn
1
1;0;0
n
cùng phương với
BK
Gọi
là góc góc giữa
MN
và
SAC
. Ta có
1 1
1 2
.
3 10
sin
20
u n
u u
310
cos
20
.
Cách 2:
Gọi
là mp đi qua
MN
và song song với mp
SAD
. Khi đó
cắt
AB
tại
P
, cắt
SC
tại
Q
, cắt
AC
tại
K
. Gọi
I
là giao điểm của
MN
và
QK
I SAC
.
Suy ra:
P
,
Q
,
K
lần lượt là trung điểm của
AB
,
SC
và
AC
.
Lại có:
ABCD
là hình thang cân có
2 2 2 2AD AB BC CD a
2 ;
AD a AB BC CD a
3
2
a
CH
;
2
2 3 3 3
.
2 2 4
ABCD
a a a a
S
.
Nên
2 3
1 3 3 3
. .
3 4 4
ABCD
a a
V SA
SA a
1
2 2
a
MP SA
và
3
2
a
NP
.
Xét tam giác
MNP
vuông tại P:
2 2
3 10
2 2 2
a a a
MN
,MP KQ
lần lượt là đường trung bình của tam giác
,
SAB SAC
// //MP KQ SA
KN
là đường trung bình của tam giác
1
2
ACD KN AD a
.
Trang 39/69
Xét tam giác
AHC
vuông tại H:
2
2
3 3
3
2 2
a a
AC a
3
2
a
KC
Suy ra: tam giác
KNC
vuông tại
C
C
là hình chiếu vuông góc của
N
lên
SAC
.
góc giữa
MN
và
SAC
là góc
NIC
Khi đó:
2 2 2 10 10
. .
3 3 3 2 3
IN KN a a
IN MN
MN NP
Xét tam giác
NIC
vuông tại
C
:
10
;
2 3
a a
NC IN
2
2
10 31
3 2 6
a a a
IC
31 10 310
cos :
6 3 20
IC a a
NIC
IN
.
Câu 25: Cho hình chóp
SABC
có đáy
ABC
là tam giác vuông tại
A
,
3AB a
,
4AC a
. Các mặt bên
SAB
,
SAC
,
SBC
cùng tạo với đáy
ABC
một góc
0
45
. Biết chân đường vuông góc hạ
từ
S
xuống mặt phẳng
ABC
nằm ở miền trong tam giác
ABC
. Gọi góc tạo bởi hai mặt
phẳng
SAC
và
SBC
là
. Tính
cos
.
A.
1
cos
10
. B.
1
cos
5
. C.
3
cos
5
. D.
1
cos
15
.
Lời giải
Chọn A
Gọi
H
là hình chiếu của
S
lên mặt phẳng
ABC
. Gọi
, ,M N P
lần lượt là hình chiếu của
H
trên
AB
,
AC
và
BC
. Ta có góc giữa
( )SAB
và
( )BAC
là góc
SMH
. Tương tự ta có
0
45
SMH SNH SPH
Do đó
SMH SNH SPH HM HN HP
Mà
H
nằm ở miền trong tam giác
ABC
nên
H
là tâm đường tròn nội tiếp tam giác ABC.
Trang 40/69
Gọi
r
là bán kính đường tròn nội tiếp tam giác
ABC
, khi đó
1
.
3 .4
2
1
3 4 5
2
ABC
ABC
AB AC
S
a a
r a
p a a a
AB BC CA
.
Tam giác
SHM
vuông cân tại
H
nên
SH HM r
.
Chọn hệ trục Đề-các vuông góc
Axyz
như hình vẽ. Khi đó ta tìm được tọa độ các điểm như sau
0;0;0
A
,
3 ;0;0
B a
,
0;4 ;0C a
,
; ;0 ; ;0H r r a a
,
; ; ; ;
H H
S x y SH a a a
. Suy ra:
Mặt phẳng
SAC
có véc tơ pháp tuyến
1
2
1
, 1;0;1
4
n AS AC
a
Mặt phẳng
SBC
có véc tơ pháp tuyến
2
2
1
, 4;3;5
n AS AC
a
Do đó
2
2 2 2 2 2
1.4 0.3 1.5 1
cos
10
1 0 1 4 3 5
Câu 26: Cho hình chóp
.
S ABC
có đáy là tam giác đều cạnh
.a
Hình chiếu vuông góc của
S
trên mặt
phẳng
ABC
là điểm
H
thuộc cạnh
AB
sao cho
2HA HB
. Góc giữa đường thẳng
SC
và
mặt phẳng
ABC
bằng
60
o
. Tính khoảng cách
h
giữa hai đường thẳng
SA
và
BC
theo
a
.
A.
42
8
a
. B.
42
12
a
. C.
42
4
a
. D.
42
24
a
.
Lời giải
Chọn A
Chọn hệ trục tọa độ có gốc tại
M
, trục hoành là
MC
, trục tung là
MB
, trục cao là
/ /Mz HS
(xem hình vẽ).
Ta có:
2 2
7
6 6 3
AB a a
MH CH CM MH
Trang 41/69
o o
21
, 60 .tan 60
3
a
SC ABC SCH SH CH
Do đó tọa độ các điểm là
0; ;0
2
a
A
,
21
0; ;
6 3
a a
S
,
0; ;0
2
a
B
,
3
;0;0
2
a
C
2 21
0; ;
3 3
a a
SA
,
3
; ;0
2 2
a a
BC
,
0; ;0
AB a
2 2 2
21 7 3
, ; ;
6 2 3
a a a
SA BC
, .
42
,
8
,
SA BC AB
a
d SA BC
SA BC

.
Câu 27: Cho hình lăng trụ đứng
.
ABC A B C
có
AB AC a
, góc
30
ABC
, góc giữa đường thẳng
A B
và mặt phẳng
ABC
bằng
0
45
. Gọi
M
,
N
lần lượt là trung điểm của
B C
và
CC
.
Cosin của góc giữa mặt phẳng
AMN
và mặt phẳng
ABC
bằng
A.
1
2
. B.
3
2
. C.
13
4
. D.
3
4
.
Lời giải
Chọn D
Ta có
, ,
A B ABC A B AB ABA
45
nên
A AB
vuông cân tại
A
AA AB a
Gọi
H
là trung điểm
BC
.sin 30
2
a
AH BC AH AB
2 2
2 2 3BC BH AB AH a
.
z
y
x
N
M
H
A
C
B
A'
B'
C'
Trang 42/69
Lại có
,M H
lần lượt là trung điểm của
B C
và
BC
; //
MH BB AA a MH BB MH ABC
Chọn hệ trục tọa độ
Oxyz
như hình vẽ có
H O
, suy ra
0;0;0
H
,
;0;0
2
a
A
,
3
0; ;0
2
a
B
,
0;0;M a
.
3
0; ;0
2
a
C
,
3
0; ;
2 2
a a
N
.
3
;0; , ; ;
2 2 2 2
a a a a
AM a AN
2 2 2
3 3
, ; ;
2 4 4
a a a
AM AN
AMN
có một VTPT là
n
3 1 3
; ;
2 4 4
Ta có
HM
0;0;a
,
HM ABC
ABC
có một VTPT
1
0;0;1
n
Gọi
là góc giữa mặt phẳng
AMN
và mặt phẳng
ABC
.
từ đó
1
1
.
cos
.
n n
n n
2 2
2
3
4
3 1 3
.1
2 4 4
3
4
.
Câu 28: Cho hình lăng trụ tam giác
. ' ' 'ABC A B C
có đáy
ABC
là tam giác đều cạnh
a
và các mặt bên
đều là các hình vuông cạnh
a
. Gọi
G
là trọng tâm của tam giác
ABC
và
I
là trung điểm của
đoạn thẳng
'CC
. Khoảng cách giữa hai đường thẳng
'A B
và
GI
bằng
A.
11
22
a
. B.
3 11
7
a
. C.
11
12
a
. D.
3 11
.
22
a
.
Lời giải
Chọn D
Trang 43/69
Chọn hệ trục tọa độ sao cho
0;0;0 , ;0;0 , ' 0;0;A C a A a
trục
nằm trong mặt phẳng
ABC
và vuông góc với trục
. Khi đó gọi
,H K
lần lượt là hình chiếu của
B
lên các trục
,Ax Ay
khi đó góc
0
30
BAy
nên
0 0
3
cos30 ; cos60
2 2
a a
AK AB AH AB
nên
3
; ;0
2 2
a a
B
. Vì
G
là trọng tâm tam giác
ABC
nên ta có
3
; ;0
2 6
a a
G
. Đồng thời
I
là
trung điểm của
'CC
nên
, ;0;
2
a
I a
. Suy ra
3 3
' ; ; ; ; ; ; ' ;0;
2 2 2 6 2 2
a a a a a a
A B a IG A I a
.
Ta có
2 2 2 3
3 3 3 3
' , ; ; ' , '
12 4 3 4
a a a a
A B IG A B IG A I
và
2
33
' , .
6
a
A B IG
Vậy
' , '
3 11
' , .
22
' ,
A B IG A I
a
d A B GI
A B IG

Câu 29: Cho lăng trụ đứng
. ' ' 'ABC A B C
có đáy là tam giác
ABC
vuông cân tại
A
, cạnh
6BC a
.
Góc giữa mặt phẳng
'AB C
và mặt phẳng
' 'BCC B
bằng
0
60
. Tính thể tích
V
của khối
lăng trụ
. ' ' 'ABC A B C
?
A.
3
2 3
.
3
a
V
B.
3
3
.
2
a
V
C.
3
3 3
.
4
a
V
D.
3
3 3
.
2
a
V
Lời giải
Chọn D
Trang 44/69
Vì tam giác
ABC
vuông cân tại
A
, cạnh
6BC a
nên
3AB AC a
.
Chọn hệ trục tọa độ
Oxyz
sao cho
0;0;0A
,
3;0;0C a ,
0; 3;0B a ,
0;0;A z
0z
.
0; 3;B a z
;
3; 3;0
BC a a ,
0;0;BB z
.
VTPT của
BCC B
là:
1
1
, 1;1;0
3
n BC BB
za
.
3;0;0AC a
,
0; 3;AB a z
.
VTPT của mặt phẳng
BA C
là:
2
1
, 0; ; 3
3
n AC AB z a
a
.
Vì góc giữa mặt phẳng
'AB C
và mặt phẳng
' 'BCC B
bằng
0
60
nên:
1 2
60 ,cos cos n n
2 2
1
2
2 3
z
z a
3z a
.
Vậy thể tích của khối lăng trụ
. ' ' 'ABC A B C
là:
3
1 3 3
. .
2 2
a
V AC AB AA
.
Câu 30: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác cân, với
AB AC a
và góc
120BAC
, cạnh bên
AA a
. Gọi
M
là trung điểm của
CC
. Cosin của góc tạo bởi hai mặt
phẳng
ABC
và
AB M
bằng
A.
11
11
. B.
33
11
. C.
10
10
. D.
30
10
.
Lời giải
Chọn D
Trang 45/69
Cách 1:
Ta có
2 2 2
2 . .cosBC AB AC AB AC BAC
2 2
1
2. . .
2
a a a a
2
3a
3BC a
.
Trong tam giác vuông
B AB
, ta có
2 2
AB BB AB
2 2
a a
2a
.
Trong tam giác vuông
MAC
, ta có
2 2
MA MC AC
2
2
4
a
a
5
2
a
.
Trong tam giác vuông
MB C
,ta có
2 2
B M B C C M
2
2
3
4
a
a
13
2
a
.
Xét tam giác
MB A
có
2
2 2 2
5
2
4
a
B A MA a
2
13
4
a
2
B M
MB A
vuông tại
A
1
.
2
MB A
S AB AM
1 5
. 2.
2 2
a
a
2
10
4
a
.
Lại có
1
. .sin
2
ABC
S AB AC BAC
1 3
. .
2 2
a a
2
3
4
a
.
Gọi
là góc tạo bởi hai mặt phẳng
ABC
và
AB M
.
Ta có
ABC
là hình chiếu vuông góc của
AB M
trên mặt phẳng
ABC
.
Do đó
.cos
ABC MB A
S S
2 2
3 10
.cos
4 4
a a
30
cos
10
.
Cách 2: Chọn hệ trục tọa độ
Oxyz
như hình vẽ:
Trang 46/69
( trong đó gốc tọa độ
O
trùng với trung điểm của
BC
).
0; ;0
2
a
A
,
3
;0;
2
a
B a
,
3
;0;0
2
a
C
,
3
;0;
2
a
C a
,
3
;0;
2 2
a a
M
3
; ; 3; 1;2
2 2 2
a a a
AB a

;
3 1
; ; = 3; 1;1
2 2 2 2
a a a
AM a

.
Có:
2 2 2 2
3 3 3
; ; ; 1; 3 3; 2 3
4 4 2 4
a a a a
AB AM
Mặt phẳng
ABC
có véc tơ pháp tuyến là
1
0;0;1n k
.
Mặt phẳng
AB M
có véc tơ pháp tuyến là
2
; 1; 3 3; 2 3
4
a
AB AM
.
Chọn véc tơ pháp tuyến là
2
1; 3 3; 2 3n
1 2
2
2 2 2 2 2
1 2
0.1 0.( 3 3) 1. 2 3
.
30
cos ;
10
.
0 0 1 1 ( 3 3) 2 3
n n
ABC AB M
n n
.
Câu 31: Cho hình lăng trụ đứng có đáy là tam giác vuông tại
A
,
AB AC a
và có
cạnh bên bằng
2a
. Gọi
,M N
lần lượt là trung điểm
', 'BB CC
. Tính khoảng cách từ điểm
A
đến mặt phẳng
( ' )A MN
A.
a
. B.
2 3
3
a
. C.
3
2
a
. D.
3a
.
.
ABC A B C
Trang 47/69
Lời giải
Chọn B
Chọn hệ trục tọa độ
Oxyz
sao cho điểm
A
trùng với gốc tọa độ, điểm
B
nằm trên trục
Ax
,
điểm
C
nằm trên trục
Ay
, điểm
'A
nằm trên trục
Az
. Ta có:
(0;0;0),B( ;0;0),C(0; ;0),A'(0;0;2a),B'( ;0;2a),C'(0;a;2a)A a a a
Do
,M N
lần lượt là trung điểm
', ' M(a;0;a), N(0; ; )BB CC a a
2 2 2
' ( ;0; ), ' (0; ; )
' , ' ( ; ; )
A M a a A N a a
n A M A N n a a a
Suy ra :
1
(1;1;1)n
là một vecto pháp tuyến của mặt phẳng
( ' )A MN
Phương trình mặt phẳng
( ' )A MN
là :
1( 0) 1( 0) 1( 2 ) 0 2 0x y z a x y z a
Khoảng cách từ điểm
A
đến mặt phẳng
( ' )A MN
là:
(A;(A'MN))
2 2 2
2
2 3
3
1 1 1
a
a
d
Câu 32: Cho hình lăng trụ đứng .ABC A B C
có đáy ABC là tam giác cân tại C , 2AB a , AA a
,
góc giữa BC
và
ABB A
bằng
60
. Gọi N là trung điểm
AA
và
M
là trung điểm
BB
.
Tính khoảng cách từ điểm
M
đến mặt phẳng
BC N
.
A.
2 74
37
a
. B.
74
37
a
. C.
2 37
37
a
. D.
37
37
a
.
Lời giải
Chọn A
Trang 48/69
Gọi
,H K
lần lượt là là trung điểm cạnh
A B
và
AB
. Từ giả thiết ta có:
2 .tan 60 6
o
HB a HB a HC HB a
Mặt khác:
`
, v a HC HB HK
đôi một vuông góc nhau. Chọn hệ trục
Oxyz
như hình vẽ có
H O
Tọa độ hóa:
(0;0;0)H
,
(0; 6;0)C a
,
( ;0;0)A a
,
( ;0; )A a a
,
;0;
2
a
N a
,
( ;0;0)B a
,
( ;0; )B a a
,
;0;
2
a
M a
.
Xét mặt phẳng
( )BC N
có
( ; 6; )
( 6; 3; 4 6)
2 ;0;
2
C B a a a
vtpt n
a
BN a
Phương trình
( )BC N
là:
6( ) 3 4 6 0
2
a
x a y z
.
Khoảng cách từ M đến
( )BC N
là:
6( ) 3.0 4 6( )
2 6 2 74
2 2
( ;( ))
37
6 9 96 111
a a
a a
a a
d M BC N
.
Câu 33: Cho hình lăng trụ đứng
.ABC A B C
có
AB AC a
, góc
BAC
bằng
120
,
AA a
. Gọi
M
,
N lần lượt là trung điểm
B C
và
CC
. Khoảng cách giữa 2 đường thẳng
MN
và
AH
là
A.
3
2
a
. B.
3
4
a
. C.
6
2
a
. D.
6
4
a
.
Lời giải
Chọn D
Trang 49/69
Gọi
H
là trung điểm
BC
. Áp dụng định lí cosin cho tam giác
ABC
ta có:
2 2 2 2 2 2
2. . .cos 2. . .cos120 3 3BC AB AC AB AC BAC a a a a a BC a
2 2 2 2 2 2
2
2
2. 2. 3
4 4 4 2
AB AC BC a a a
a a
AH AH
Vì tam giác
ABC
cân tại
A
có
AH
là đường trung tuyến nên
AH BC
tại
H
hay 3 cạnh
MH
,
HA
và
HB
đôi một vuông góc với nhau. Ta chọn hệ trục tọa độ
Hxyz
sao cho điểm
A Hx
, điểm
B Hy
và điểm
M Hz
. Khi đó ta có tọa độ các điểm như sau:
0;0;0
H
,
;0;0
2
a
A
,
3
0; ;0
2
a
B
,
3
0; ;0
2
a
C
,
0;0;M a
,
3
0; ;
2 2
a a
N
.
Ta có:
3
0; ;
2 2
a a
MN
;
;0;0
2
a
AH
;
3
; ;
2 2 2
a a a
AN
Suy ra:
2 2
3
; 0; ;
4 4
a a
MN AH
Áp dụng công thức tính khoảng cách giữa hai đường thẳng chéo nhau, ta có:
6
4
3
, .
6
32
,
4
,
4
a
MN AH AN
a
d MN AH
a
MN AH

.
Câu 34: Cho hình lăng trụ
1 1 1
.
ABC A B C
có đáy là tam giác đều cạnh
a
.
1
2AA a
và vuông góc với mặt
phẳng
ABC
. Gọi
D
là trung điểm của
1
BB
,
M
di động trên cạnh
1
AA
. Giá trị lớn nhất của
diện tích
1
MC D
là
Trang 50/69
A.
2
15
4
a
. B.
2
15
6
a
. C.
2
5
4
a
. D.
2
10
4
a
.
Lời giải
Chọn A
+ Chọn hệ trục tọa độ
Oxyz
sao cho
A O
;
B Oy
;
1
A Oz
.
Khi đó
0;0;0
A
,
0; ;0B a
1
0;0;2A a
,
1
3
; ;2
2 2
a a
C a
và
0; ;D a a
Do
M
di động trên
1
AA
, tọa độ
0;0;M t
với
0;2t a
Ta có:
1
1
1
,
2
DC M
S DC DM
Ta có:
1
3
( ; ; )
2 2
(0; ; )
a a
DC a
DM a t a
1
,DC DM
( 3 ; 3( ); 3
2
a
t a t a a
2 2 2
1
, ( 3 ) 3( ) 3
2
a
DC DM t a t a a
1
2 2
2 2
4 12 15
2
1
. . 4 12 15
2 2
DC M
a
t at a
a
S t at a
Xét
2 2
4 – 12 15
f t t at a
(
0;2t a
)
' 8 – 12f t t a
Trang 51/69
3
'( ) 0
2
a
f t t
Lập BBT giá trị lớn nhất của
1
2
15
4
DC M
a
S
khi
0t
hay
M A
.
Câu 35: Cho lăng trụ tam giác đều
. ' ' 'ABC A B C
có tất cả các cạnh bằng
a
,
M
là điểm di chuyển trên
đường thẳng
' 'A C
; Tính khoảng cách lớn nhất giữa
AM
và
'BC
A.
34
6
a
. B.
17
4
a
. C.
14
4
a
. D.
21
6
a
.
Lời giải
Chọn C
Không mất tính tổng quát chọn
1a
; Chọn hệ trục tọa độ sao cho gốc tọa độ trùng
C'
;
Ox
trùng
' 'C A
;
Oz
trùng với
'C C
; Sao cho:
1 3 1 3
'(1;0;0); '(0;0;0); B'( ; ;0); (1;0;1); ( ; ;1); (0;0;1); M(m;0;0)
2 2 2 2
A C A B C
Khi đó:
, ' . '
( ; ' )
, '
AM C B AC
d AM C B
AM C B
Ta có:
1 3
( 1;0; 1); ' ; ;1 ; ' ( 1;0; 1)
2 2
AM m C B AC
2 2 2
3
2
( ; ' )
3 1 3
( ) ( ) ( 1) .
2 2 4
m
d AM C B
m m
=
2
2
3 3
2 2
7 5 7 7 1 5 1 7
. .
4 2 4 4 2 4
m
m m
m m
(
0m
vì nếu
0m
thì
M
trùng
'C
dẫn đến khoảng cách bằng 0)
Trang 52/69
Khoảng cách đó lớn nhất khi
2
7 1 5 1 7
. .
4 2 4m m
nhỏ nhất
1 5 7
7 5
m
m
; Khi đó: khoảng
cách lớn nhất là:
14
4
; Vậy: trong trường hợp tổng quát, khoảng cách lớn nhất là
14
4
a
khi
7
'
5
a
MC
.
Câu 36: Cho lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông, , cạnh bên
. Gọi M là trung điểm của
BC
. Tính theo khoảng cách giữa hai đường thẳng
AM
và
B C
.
A. . B. . C. . D.
7
7
a
.
Lời giải
Chọn D
Chọn hệ trục toạ độ Đêcac vuông góc như sau:
; A ; C ; B’ ; M
;0;0
2
a
; ;
Ta có:
+) Khoảng cách giữa
Vì: nên chéo nhau.
, ' '
, '
, '
AM B C AB
d AM B C
AM B C

3
4 4 4
7
2
7
1
2
2
a
a
a a a
AB BC a
' 2AA a
a
3
7
a
21
7
a
7a
Oxyz
(0;0;0)
B
0; ;0a
;0;0
a
0;0; 2
a
; ;0
2
a
AM a
' ;0; 2
B C a a
' 0; ; 2
AB a a
2
2 2
, ' 2; ;
2
a
AM B C a a
, 'AM B C
3
, ' '
2
a
AM B C AB
, 'AM B C
Trang 53/69
Câu 37: Cho lăng trụ đứng
ABCA B C
có đáy
ABC
là tam giác vuông tại
A
và
1, 2
AB AC
.Gọi
là góc tạo bởi đường thẳng
BC
và mặt phẳng
( )A BC
có số đo lớn nhất. Biết
sin
p
q
( với
,p q
nguyên tố cùng nhau ). Giá trị tổng
p q
là
A.
11
. B.
7
. C.
5
. D.
9
Lời giải
Chọn D
Giả sử
AA m
( 0)
m
. Chọn hệ trục tọa độ như hình vẽ:
(0;0;0), (1;0;0), (0;2;0), (0;2; ), (0;0; )A B C C m A m
Phương trình mặt phẳng
( )A BC
là:
1 2 2 2 0
1 2
x y z
mx my z m
m
véc tơ pháp tuyến mặt phẳng
( )A BC
là:
(2 ; ;2)
n m m
( 1;2; )BC m
là véc tơ chỉ phương của đường thẳng
BC
2 2 4 2
2 2
sin cos( ; )
5 4. 5 (5 20) 29
m m
n BC
m m m m
Áp dụng bất đẳng thức cô si cho 2 số
4
5m
và
20
:
2 2
4 2
2 2 2
sin
7
20 29
2. 5 .20 29
m m
m m
m m
Dấu “=” xảy ra khi
4
5 20 2
m m
. Vậy
2, 7 9
p q p q
.
Trang 54/69
Câu 38: Cho hình lăng trụ tam giác đều
.
ABC A B C
có độ dài cạnh đáy bằng a. Góc giữa
A BC
và
ABC
bằng
60
. Gọi
,M N
là trung điểm của
BC
và
.CC
Tính khoảng cách giữa
A M
và
.AN
A.
6 97
97
a
. B.
3 97
.
97
a
C.
6 65
65
a
. D.
3 65
65
a
.
Lời giải
Chọn B
Do
BC
vuông góc với mặt phẳng
A MA
nên góc giữa 2 mặt phẳng
ABC
và
A BC
là góc
A MA
bằng
60
,
Trong tam giác vuông
A AM
:
0
' 3 3
tan 60 ' . 3
2 2
AA a a
AA
AM
Trong mặt phẳng
ABC
kẻ đường thẳng
song song với
BC
, khi đó 3 đường
, ,
AM Ay A A
đôi một vuông góc với nhau.
Xét hệ tọa độ
Axyz
sao cho:
, '
M Ax A Az
Ta có:
3 3 3 3
(0;0;0), '(0;0; ), ( ;0;0), ( ; ; )
2 2 2 2 4
a a a a a
A A M N
suy ra:
2 2 2
3 3 3 3 3 9 3 3
' ( ;0; ), ( ; ; ) ' , ( ; ; )
2 2 2 2 4 4 8 4
a a a a a a a a
A M AN A M AN

Áp dụng công thức tính khoảng cách giữa 2 đường thẳng chéo nhau, ta có:
3
2
' , .
3 3 / 8 3 97
( ' , )
97
291 / 8
' ,
A M AN AM
a a
d A M AN
a
A M AN

Cách giải theo hình học cổ điển:
Trang 55/69
Kẻ
//A E AN E AC
//AN A ME
, , ,d A M AN d AN A ME d A A ME
.AK
Có
2 2 2
1 1 1
AK AA AH
+Có góc giữa
A BC
và
ABC
là
60 ' tan 60 .A MA A A AM
3 3
3. .
2 2
a a
+Dễ thấy
' 2AE A F AC
, với
'F A N AC
.
21
. ;
2
AME
AME
S
S AH EM AH
EM
mà
2
2 2 1 3
.3. .
3 3 2 4
AME MEC ABC ABC
a
S S S S
2 2
31
2 . .cos150 .
2
a
EM AE AM AE AM
53
31
a
AH
Vậy
2 2 2 2
1 1 1 97
9AK AH AA a
3 97
.
97
AK a
Câu 39: Cho lăng trụ tam giác đều
.ABC A B C
có tất cả các cạnh bằng
a
.
M
là một điển thỏa mãn
1
2
CM AA
. Côsin của góc giữa hai mặt phẳng
A MB
và
ABC
bằng
A.
30
10
. B.
30
8
. C.
30
16
. D.
1
4
.
Lời giải
Chọn A
Xét hình lăng trụ tam giác đều
.ABC A B C
có tất cả các cạnh bằng
a
. Gắn hệ trục như hình vẽ
quy ước
1a
( đơn vị ).
Trang 56/69
Gọi
D
là giao điểm của
A M
và
AC
.
Vì tam giác
A B C
là tam giác cân cạnh bằng
a
nên ta suy ra độ dài các đường trung tuyến là
3
2
a
. Suy ra tọa độ các điểm như hình vẽ.
Theo giả thiết ta có
1
2
CM AA
vậy
ADA CDM
2 2
AD
DA DC
CD
Vậy
tọa độ của điểm
D
là:
2
0; ;1
3
D
Ta có mặt phẳng (
ABC
) có phương trình
0 0;0;1
ABC
z n
Mặt khác mặt phẳng
A MB
là mặt phẳng đi qua ba điểm
A
, D
và
B
.
Ta có:
2
0; ;1
3
A D
và
3 1
; ;1
2 2
A B
1 3 3
n , ; ;
6 2 3
A BM
A D A B
Vậy
cô sin góc tạo bởi hai mặt phẳng
A MB
và
ABC
là:
cos ' , cos ,
A BM ABC
A BM ABC n n
.
3
3
3 30
10
1 3 1 10
. 1
36 4 3
.
Cách khác:
3 1
; ;1
2 2
A B
,
3
0;1;
2

A M
,
1 3 3 3 1
, ; ; 1;3 3; 2 3
4 4 2 4
A B A M
Trang 57/69
mp
A MB
có một vectơ pháp tuyến là
1;3 3; 2 3
A BM
n .
Mp(ABC) là mp(Oxy): z=0 có vtpt
0;0;1
ABC
n
2 3
30
cos ' , cos ,
10
1 27 12
A BM ABC
A BM ABC n n
Câu 40: Cho hình hộp
.
ABCD A B C D
có thể tích bằng
V
. Gọi
M
,
N
,
P
lần lượt là trung điểm của
các cạnh
AB
,
A C
,
BB
. Tính thể tích khối tứ diện
CMNP
.
A.
5
48
V
. B.
1
8
V
. C.
7
48
V
. D.
1
6
V
.
Lời giải
Chọn A
Đây là bài toán tổng quát, ta đưa về cụ thể, giả sử hình hộp đã cho là hình lập phương có cạnh
bằng
1
. Khi đó
1
V
.
Chọn hệ trục
Oxyz
như hình vẽ,
A
là gốc toạ độ, các trục
, ,Ox Oy Oz
nằm trên các cạnh
, ,
AB AD AA
.
Khi đó,
1;1;0
C
;
1
1;0;0 ;0;0
2
B M
;
1
1;0;1 1;0;
2
B P
;
1 1
0;0;1 , 1;1;1 ; ;1
2 2
A C N
.
Ta có
1
; 1;0
2
CM
,
1 1
; ;1
2 2
CN
,
1
0; 1;
2
CP
.
Khi đó
1 1 5 5
, .
6 6 8 48
CMNP
V CM CN CP
5
48
CMNP
V V
Trang 58/69
Câu 41: Cho hình hộp
.
ABCD A B C D
, có đáy là hình thoi cạnh
2a
, tâm
O
,
0
60
BAD
và
2AA a
.
Hình chiếu vuông góc của
A
lên mặt phẳng
ABCD
trùng với tâm
O
. Gọi
M
là trung điểm
CD
. Khoảng cách giữa hai đường thẳng
A M
và
B D
bằng:
A.
21
7
. B.
2 21
7
. C.
3 21
7
. D.
4 21
7
.
Lời giải
Chọn B
+) Đáy
ABCD
là hình thoi cạnh
2a
, tâm
O
,
0
60
BAD
nên tam giác
ABD
là tam giác đều
cạnh
2a
3
.2 3
2
AO a a
2 2 2 2
4 3
A O AA AO a a a
+) Giả sử
1
a
. Chọn hệ trục tọa độ như hình vẽ
0;0;0
O O
,
1;0;0
D Ox
,
0; 3 ;0
C Oy
và
0;0;1
A Oz
. Khi đó,
1;0;0
B
,
0; 3;0
A
Ta có:
0; 3 ;1
BB DD AA
nên tìm được
1; 3;1
B
và
1; 3;1
D
M
là trung điểm
CD
1 3
; ;0
2 2
M
+) Ta có:
; .
;
;
A M B D A B
d A M B D
A M B D


1 3
; ; 1
2 2
; 0; 2; 3
2;0;0
A M
A M B D
B D
z
y
x
M
C'
D'
B'
O
C
A
B
D
A'
Trang 59/69
Mà
1; 3 ;0
A B
nên
0 2 3 0
2 21
;
7
0 4 3
d A M B D
.
Câu 42: Cho hình hộp chữ nhật
.
ABCD A B C D
, có
, 2,
AB a AD a
góc giữa
A C
và mặt phẳng
ABCD
bằng
30
. Gọi
H
là hình chiếu vuông góc của
A
trên
A B
và
K
là hình chiếu vuông
góc của
A
trên
.A D
Tính góc giữa hai mặt phẳng
AHK
và
ABB A
.
A.
60
. B.
45
. C.
90
. D.
30
.
Lời giải
Chọn B
Do
.
ABCD A B C D
là hình hộp chữ nhật nên
' 'A C
là hình chiếu vuông góc của
'A C
trên
0
( ) ( ' ,( )) ( ' , ' ') ' ' 30 .
ABCD A C ABCD A C A C CA C
Ta có
2 2
'
3; tan ' ' ' .
' '
CC
AC AB AD a CA C CC a
A C
Kết hợp với giả thiết ta được
' 'ABB A
là hình vuông và có
H
là tâm.
Gọi
,E F
lần lượt là hình chiếu vuông góc của
K
trên
' '& ' .A D A A
Ta có
2 2 2
1 1 1 6
;
' 3
a
AK
AK A A AD
2 2
' ' ;
3
a
A K A A AK
2 2
2 2 2
1 1 1 2
; ' .
' 3 3
a a
KF KE A K KF KE
KF KA A K
Ta chọn hệ trục tọa độ
Oxyz
thỏa mãn
'O A
còn
, , D B A
theo thứ tự thuộc các tia
, , .Ox Oy Oz
Khi đó ta có tọa độ các điểm lần lượt là:
2 2 2
(0;0; ), '(0; ;0), (0; ; ), ( ;0; ), ( ;0;0), (0;0; ).
2 2 3 3 3 3
a a a a a a
A a B a H K E F
Mặt phẳng
' 'ABB A
là mặt phẳng
( )yOz
nên có VTPT là
1
(1;0;0);
n
Trang 60/69
Ta có
2
2 2
, , (2; 2; 2).
6
a
AK AH n n
Mặt phẳng
( )AKH
có VTPT là
2
(2; 2; 2);
n
Gọi
là góc giữa hai mặt phẳng
AHK
và
ABB A
.
Ta có
0
1 2
1
( , ) 45 .
2
cos cos n n
Câu 43: Cho lăng trụ
1 1 1 1
.
ABCD A B C D
có đáy
ABCD
là hình vuông cạnh
a
. Hình chiếu vuông góc của
1
A
lên
ABCD
trùng với giao điểm của
AC
và
BD
. Tính khoảng cách từ điểm
1
B
đến mặt
phẳng
1
A BD
.
A.
2
4
a
. B.
2
2
a
. C.
21
4
a
. D.
3
2
a
.
Lời giải
Chọn B
Chọn hệ trục toạ độ sao cho tâm O của hình vuông ABCD là gốc toạ độ, OA là trục Ox, OB là
trục Oy, OA
1
là trục Oz như hình vẽ
2
;0;0
2
a
A
Vì
1
( )
mp A BD mp Oyz
nên
1
mp A BD
có phương trình:
0
x
1
AB
cắt
1
mp A BD
tại trung điểm
1
AB
1 1 1
2 2
(B ;( )) ( ;( ))
2 2
a a
d A BD d A A BD
Câu 44: Cho hình lập phương
. ' ' ' 'ABCD A B C D
cạnh
a
. Gọi
K
là trung điểm của
'DD
. Tính khoảng
cách giữa hai đường thẳng
CK
và
'A D
.
A.
3
a
. B.
4
a
. C.
5
a
. D.
2
a
.
Lời giải
Trang 61/69
Chọn A
Chọn hệ trục tọa độ
Oxyz
với gốc
O
trùng với điểm
A
, các tia
Ox
,
Oy
,
Oz
lần lượt trùng với
các tia
AB
,
AD
,
'AA
. Khi đó
0;0;0
A
,
;0;0
B a
,
0; ;0D a
,
' 0;0;A a
,
' ;0;B a a
,
; ;0C a a
Gọi
M
là trung điểm của
'BB
;0;
2
a
M a
' ;0;
2
a
A M a

,
' 0; ;
A D a a
2 2
2 2
' , ' ; ; 1;2;2
2 2
a a
A M A D a a
Suy ra
'
A DM
nhận
1;2;2
n
làm vec tơ pháp tuyến và đi qua điểm
' 0;0;A a
'
A DM
:
2 2 2 0
x y z a
Do
M
là trung điểm của
'BB
nên
' / /A M CK
2 2 2
2 2
, ' , ' , '
3
1 2 2
a a a
a
d CK A D d CK A DM d C A DM
.
Câu 45: Cho hình hộp chữ nhật
.
ABCD A B C D
có
3 ,
AB a AD AA a
. Lấy điểm
M
thuộc đoạn
AB
, điểm
N
thuộc đoạn
A C
sao cho
, 0 10AM A N x x a
,. Tìm
x
theo
a
để
đoạn
MN
nhỏ nhất.
A.
0
. B.
30
3
a
. C.
10
2
a
. D.
10
3
a
.
Lời giải
Chọn C
Trang 62/69
Ta có
2 2 2 2
9 10AB AB BB a a a
.
Gọi
E
là hình chiếu của
M
lên
AB
.
Ta có
. 3 3
10 10
AE AM AB AM ax x
AE
AB AB AB
a
.
.
10 10
ME AM BB AM ax x
ME
BB AB AB
a
.
Gọi
F
là hình chiếu của
N
lên
A B
.
Tương tự ta tính được
10A C a
,
3
10
x
A F
,
10
x
NF
.
Chọn hệ trục tọa độ
Oxyz
sao cho
O A
, các điểm
B
,
D
,
A
lần lượt nằm trên các tia
Ox
,
Oy
,
Oz
. Khi đó ta có tọa các điểm lần lượt là:
0;0;0
A
,
3 ;0;0
B a
,
0; ;0D a
,
0;0;A a
,
3
;0;
10 10
x x
M
,
3
; ;
10 10
x x
N a
.
Ta có
2
2
2 2 2
2
2 2 2
10 10 2
10 10 10 2 2
x x x ax x a a a
MN a a
.
GTNN của
MN
là
2
a
khi
2 10
2
10 2
x a a
x
.
Câu 46: Cho hình hộp chữ nhật
. ' ' ' 'ABCD A B C D
có
, 2 , ' 3 .AB a AD a AA a
Gọi
, , M N P
lần
lượt là trung điểm của
, ' ' '.BC C D và DD
Tính khoảng cách từ
A
đến mp
.MNP
A.
15
22
a
. B.
9
11
a
. C.
. D.
15
11
a
.
Lời giải
Chọn D
D'
C'
B'
A'
F
N
M
E
z
y
x
D
C
B
A
Trang 63/69
Chọn hệ trục tọa độ
Oxyz
với gốc
O
trùng với điểm
B
, tia
; ;Ox Oy Oz
lần lượt trùng với tia
; ; '.BA BC BB
Khi đó
0;0;0 ; ;0;0 ; 0;2 ;0 ; ; 2 ;0 ; ' 0;2 ;3 ; ' ; 2 ;3 .B A a C a D a a C a a D a a a
Suy ra
3
0; ;0 ; ; 2 ;
2
;;2 3
2
a
M a
a
và Na
a a
P a
.
Ta có
3
; ; ; ; ;3
2 2
a a
MP a a MN a a

, vectơ pháp tuyến của
MNP
là:
2
2
3 9 1
; ; ; 6; 9;2
2 4 2 4
a
n MP MN a
Suy ra
:6 9 2 9 0; ;0;0
MNP x y z a A a
. Vậy
2 2 2
6 9
15
; .
11
6 9 2
a a
a
d A MNP
Câu 47: Cho hình lăng trụ đứng
.
ABC A B C
có đáy là tam giác vuông cân,
2AA a
,
AB AC a
.
Gọi
G
và
G
lần lượt là trọng tâm của tam giác
ABC
và tam giác
A B C
,
I
là tâm của hình
chữ nhật
ABB A
. Thể tích của khối
.
A IGCG
.
A.
3
2
a
. B.
3
6
a
. C.
3
5
6
a
. D.
3
5
30
a
.
Lời giải
Chọn B
Trang 64/69
Chọn hệ trục tọa độ
Oxyz
thỏa mãn
O
trùng với điểm
A
, các tia
Ox
,
Oy
,
Oz
trùng với các
tia
AB
,
AC
và
AA
.
Suy ra
0;0;0
A
,
;0;0
B a
,
0; ;0C a
,
0;0;2A a
,
;0;2B a a
,
0; ;2C a a
,
; ;0
3 3
a a
G
,
; ;2
3 3
a a
G a
,
;0;
2
a
I a
(vì
I
là trung điểm của
AB
và
A B
).
Ta có
; ;
6 3
a a
IG a
và
2
; ; 2
3 3
a a
G C a

. Suy ra
IG
và
G C
cùng phương.
Do đó bốn điểm
I
,
G
,
C
,
G
đồng phẳng.
Mặt khác
2
; ;0
3 3
a a
GC
Vì
2 2
4 2
, ; ;0
3 3
a a
G C GC
nên mặt phẳng
IGCG
có véc-tơ pháp tuyến
2;1;0
n
.
Vậy phương trình mặt phẳng
IGCG
:
2 0
x y a
.
Suy ra
5
d ,
5
4 1
a
a
h A IGCG
.
Diện tích tứ giác
IGCG
bằng
1
.d ,
2
IGCG
S IG G C IG G C
.
Trong đó
41
6
a
IG
,
41
3
a
G C
,
,
d , d ,
G C GC
IG G C G G C
G C
Vì
2 2
4 2
, ; ;0
3 3
a a
G C GC
 
nên
5
d , 2
41
IG G C a
.
Suy ra
2
1 41 41 5 5
.2
2 6 3 41 2
IGCG
a a a
S a
.
Thể tích cần tìm bằng
2
.
1 1 5 5
. .d , . .
3 3 2 5
A IGCG IGCG
a
V S A IGCG a
3
6
a
.
Cách khác:
Gọi
E , E
là trung điểm
AB, A B
, kẻ
AH
vuông góc
CE
tại
H
CEE C
là hình chữ nhật,
G'
I
E'
E
C'
B'
A'
G
C
B
A
Trang 65/69
2EE CC' a
,
2
2
5
4 2
a a
CE C E a
,
5
3
a
CG C G
,
5
6
a
GE G E
,
5
5
EA .AC a
AH
CE
2
5 1 5 1 5 5
2 2 2
2 2 6 2 3 2
IGCG CEE C IEG IE G CG C
a a a a
S S S S S a. a. . a.
2 3
.
1 1 5 5
. . . .
3 3 2 5 6
A IGCG IGCG
a a
V S AH a
Câu 48: Cho hình hộp
' ' ' 'ABCDA B C D
có đáy là hình vuông cạnh a. Mặt phẳng
( ' ')ABB A
vuông góc với đáy, tam giác
'A AB
vuông tại
'A
, góc giữa
'BA
và đáy bằng
0
6 0
.
Gọi
I
là tâm của hình vuông
ABCD
. Tính khoảng cách giữa hai đường thẳng
'IA
và
'DB
.
A.
2 55
a
. B.
55
a
. C.
3
55
a
. D.
3
2
a
.
Lời giải
Chọn C
Gọi
O
là hình chiếu vuông góc của
'A
lên cạnh
AB
. Vì mặt phẳng
( ' ')ABB A
vuông góc với
( )ABCD
nên
' ( )A O ABCD
.
Ta có góc giữa
'BA
và mặt phẳng
( )ABCD
là góc
'A BO
Ta có
0
' .cos 60
2
a
BA AB
,
0
' .cos 60
4
a
BO A B
,
0
3
' ' .sin60
4
a
OA A B
Chọn hệ tọa độ
Oxyz
như hình vẽ. Khi đó
(0; 0; 0)O
,
3
'(0;0; )
4
a
A
,
( ;0;0)
4
a
B
,
3 3
( ; ;0), ( ; ;0), '( ;0; )
4 2 4 4
a a a a
I D a B a
Ta có
3 7 3
' ; ; , ' ; ; ; ' ' ;0;0
4 2 4 4 4
a a a a a
IA DB a A B a
.
Trang 66/69
Khi đó:
2 2 2
3 3 3 5
'; ' ; ;
8 8 8
a a a
IA DB
.
Ta có:
3
3
2
4
3
'; ' . ' '
8
3 8 3
(A'I;DB') .
8
55 55
3 27 25
'; '
64 64 64
a
IA DB A B
a a
d
a
IA DB
a
 
.
Câu 49: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
2SA a
và vuông góc
với mặt phẳng đáy. Gọi
M
là trung điểm cạnh
SD
. Tang của góc tạo bởi hai mặt phẳng
( )AMC
và
( )SB C
bằng
A.
3
2
. B.
2 5
5
. C.
2 3
3
. D.
5
5
.
Lời giải
Chọn B
Để thuận tiện trong việc tính toán ta chọn
1a
.
Trong không gian, gắn hệ trục tọa độ
Oxyz
như hình vẽ sao cho gốc
O
trùng với điểm
A
, tia
O x
chứa đoạn thẳng
AB
, tia
O y
chứa đoạn thẳng
AD
, tia
Oz
chứa đoạn thẳng
AS
. Khi
đó:
(0 ; 0 ; 0)A
,
(1;0;0)B
,
(1;1;0)C
,
(0;0;2)S
,
(0;1;0)D
.
Vì
M
là trung điểm
SD
nên tọa độ
M
là
1
0; ;1
2
M
.
Ta có
(1;0; 2)
(0;1;0)
SB
BC
[ ; ] =(2;0;1)
SBC
n SB BC
.
Gọi
là góc giữa hai mặt phẳng
( )AMC
và
( )SB C
.
Suy ra
.
5
cos cos ;
3
.
SBC AMC
SBC AMC
SBC AMC
n n
n n
n n
.
Mặt khác,
2
2 2
1 1
1 tan tan 1
cos cos
.
Vậy
2
1 2 5
tan 1 .
5
5
3
Câu 50: Hai quả bóng hình cầu có kích thước khác nhau được đặt ở hai góc của một căn nhà hình hộp
chữ nhật sao cho mỗi quả bóng đều tiếp xúc với hai bức tường và nền của nhà đó. Biết rằng
Trang 67/69
trên bề mặt của hai quả bóng đều tồn tại một điểm có khoảng cách đến hai bức tường và nền
nhà mà nó tiếp xúc bằng
1; 2; 4
. Tổng độ dài đường kính của hai quả bóng đó là?
A.
7
. B.
12
. C.
14
. D.
16
.
Lời giải:
Chọn C
 Xét 1 quả bóng tại góc nhà
 Chọn hệ trục như hình vẽ, ở đó các trục
, ,O x O y O z
là ba mép tường nhà;
O
là góc nhà.
 Tâm của quả bóng là
; ;I a b c
.
Vì mỗi quả bóng đều tiếp xúc với hai bức tường và nền của nhà nên chúng tiếp xúc với ba
mặt
phẳng tọa độ, do đó
; ; ; 0
d I Oxy d I Oyz d I Oxz R a b c R
.
Gọi
; ;M x y z
là điểm nằm trên quả bóng có khoảng cách đến hai bức tường và nền nhà
mà nó
tiếp xúc bằng
1; 2; 4
, ta suy ra
1;2;4
M
.
 Điểm
M
nằm trên quả bóng khi:
2 2 2
1 2 4
IM R a a a a a
2
2 14 21 0
a a
7 7
2
7 7
2
a
a
 Vì hai quả bóng có vai trò và tính chất như nhau nên chúng lần lượt có bán kính là:
1 2
7 7 7 7
;
2 2
R R
 Vậy tổng đường kính của hai quả bóng là
1 2
2 14
d R R
.
-------------------- HẾT --------------------
a
a
a
z
y
x
O
I
| 1/67

Tài liệu khác của Toán 12

Preview text:

50 BÀI TẬP TRẮC NGHIỆM VD - VDC
SỬ DỤNG PHƯƠNG PHÁP TỌA ĐỘ GIẢI BÀI TOÁN HÌNH HỌC KHÔNG GIAN ĐỀ BÀI
DẠNG TOÁN 1: HÌNH CHÓP CÓ CẠNH BÊN HOẶC MỘT MẶT VUÔNG GÓC VỚI ĐÁY. Câu 1:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và SA vuông góc với mặt phẳng
đáy. Góc giữa mặt bên (SBC) với mặt phẳng đáy bằng 45 . Gọi M , N lần lượt là trung điểm
của AB và SB . Tính theo a khoảng cách giữa hai đường thẳng MD và CN . 3 a 21 2a 21 A. a . B. . C. 2a . D. . 4 3 21  Câu 2:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , o
ABC  60 , BC  2a . Gọi D là  
điểm thỏa mãn 3SB  2SD . Hình chiếu của S trên mặt phẳng  ABC  là điểm H thuộc đoạn
BC sao cho BC  4BH . Tính góc giữa hai đường thẳng AD và SC biết SA tạo với mặt đáy một góc o 60 . A. o 60 . B. o 45 . C. o 90 . D. o 30 . Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 5a , cạnh bên SA  10a và vuông
góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD . Tính tan của góc tạo bởi hai mặt
phẳng  AMC  và SBC . 3 2 3 5 2 5 A. . B. . C. . D. . 2 3 5 5 Câu 4:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, tam giác SAB đều. Hình chiếu của S
lên mặt phẳng  ABCD trùng với trung điểm I của AB . Gọi H , K lần lượt là trung điểm của a 7
DC và SB , biết SH
.Tính khoảng cách giữa HK và SC . 2 3 15 15 5 A. . B. . C. D. . 8 2 8 10 Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với
đáy, AB a, AD  2a, SA  3a . Gọi M , N lần lượt là hình chiếu của A lên SB, SD và
P là giao điểm của SC với mặt phẳng  AMN  . Tính thể tích khối chóp S.AMPN . 3 1869a 3 5589a 3 181a 3 1863a A. . B. . C. . D. . 140 1820 120 1820 Câu 6:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2 , SA vuông góc với mặt
phẳng đáy  ABCD và SA  2 . Gọi M , N lần lượt là hai điểm thay đổi trên hai cạnh AB ,
AD sao cho mặt phẳng SMC vuông góc với mặt phẳng SNC . Thể tích khối chóp
S.AMCN đạt giá trị nhỏ nhất bằng 4 3  4 8 3  8 4 3  4 A. . B. . C. 2 3  2 . D. . 3 3 3 Trang 1/69 Câu 7:
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B , AB BC a , AD  2a ;
cạnh bên SA vuông góc với mặt phẳng đáy và SA a . Gọi M , N lần lượt là trung điểm của
SB , CD . Tính cosin của góc giữa MN và SAC . 2 55 3 5 1 A. . B. . C. . D. . 5 10 10 5 Câu 8:
Cho hình chóp S.ABC có A
BC vuông tại B , AB  1, BC  3 , SAC đều, mặt phẳng
SAC vuông với đáy. Gọi  là góc giữa hai mặt phẳng SAB và SBC . Giá trị của cos bằng 2 65 65 65 65 A. B. C. D. 65 20 10 65 Câu 9:
Cho hình lập phương ABCD.AB CD
  có các cạnh bằng 2 , gọi điểm M là tâm của mặt bên ABB A
  , các điểm N, P, ,
Q K lần lượt là trung điểm của các cạnh AC, DD ,  D C  , B C   . Tính
cosine góc giữa hai mặt phẳng MNP và  AQK  . 2 1 102 3 A. . B. . C. . D. . 2 2 34 4
Câu 10: Cho hình chóp S . AB CD có đáy ABCD là hình vuông cạnh bằng a . S A vuông góc với mặt 3a
phẳng đáy. H và K là hai điểm lần lượt nằm trên hai cạnh BC và CD sao cho BH  , 4
KD x (0  x a) . Tìm giá trị của x để hai mặt phẳng  SAH  và  SAK  tạo với nhau một góc bằng 45 . a a 2a 2a A. x  . B. x  . C. x  . D. x  . 7 5 7 5
Câu 11: Trong không gian, cho tam giác OAB cân ở O có  4
OA OB  5; tan AOB  . Điểm C di 3
động trên tia Oz vuông góc OAB , gọi H là trực tâm của tam giác ABC . Khi C di động
trên tia Oz thì H luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng: 5 3 5 A. . B. . C. . D. 3 . 4 2 2  
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh a , góc BCD  120 . 3 a 3
SA   ABCD . Thể tích khối chóp S.ABCD là
. Gọi M là tâm đường tròn ngoại tiếp 3
tam giác SOD . Hãy tính khoảng cách h từ M tới mặt phẳng  SBC  theo a . a 57 a 57 2 5a 2 5a A. h  . B. h  . C. h  . D. h  . 19 38 5 19
Câu 13: Cho tam giác ABC vuông tại A và đường thẳng  vuông góc với mặt phẳng  ABC  tại điểm
A . Các điểm M , N thay đổi trên đường thẳng  sao cho MBC    NBC  . Biết
AB b, AC c . Giá trị nhỏ nhất của thể tích tứ diện MNBC theo b và c bằng 2 2 3b c 2 2 b c bc 2 2 b c A. . B. . C. . D. . 2 2 b c 2 2 b c 2 2 3 b c 2 2 3 b c Trang 2/69
DẠNG TOÁN 2: HÌNH CHÓP ĐỀU VÀ HÌNH CHÓP DẠNG KHÁC.
Câu 14: Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a , tâm O . Gọi M và a 6
N lần lượt là trung điểm của hai cạnh SA và BC . Biết MN  , tính sin của góc giữa 2
đường thẳng MN và mặt phẳng SBD . 2 3 5 A. . B. . C. . D. 3 . 5 3 5
Câu 15: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Gọi M và N lần lượt là trung
điểm các cạnh AB và AD ; H là giao điểm của CN và DM . Biết SH vuông góc với mặt
phẳng ( ABCD) và SH a 3 . Tính khoảng cách giữa hai đường thẳng DM và SC theo a . 2a 57 a 57 2a 13 a 7 A. . B. . C. . D. . 19 19 19 19
Câu 16: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng nhau. Gọi E, M lần lượt là
trung điểm các cạnh BC, S ,
A  là góc tạo bởi đường thẳng EM và mặt phẳng SBD . Tính sin  . 6 1 3 2 A. sin   . B. sin  . C. sin   . D. sin   . 3 2 2 2
Câu 17: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng h . Gọi I là trung
điểm cạnh bên SC . Tính khoảng cách từ S đến mặt phẳng  AIB . 2ah 4ah ah 2ah A. . B. . C. . D. . 2 2 4h  9a 2 2 4h  9a 2 2 4h  9a 2 2 2h  3a
Câu 18: Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông cạnh a , tâm O . Gọi E là điểm đối
xứng với D qua trung điểm của SA , M là trung điểm của AE , N là trung điểm của BC .
Tính khoảng cách giữa hai đường thẳng MN và AC . a 2 a 2 a 3 a A. . B. . C. . D. . 4 2 4 8
Câu 19: Cho hình lăng trụ ABC.AB C
  có A .ABC là tứ diện đều cạnh a . Gọi M , N lần lượt là trung
điểm của AA và BB . Tính tan của góc giữa hai mặt phẳng  ABC  và CMN  . 2 3 2 2 2 4 2 A. . B. . C. . D. . 5 4 5 13 
Câu 20: Cho hình chóp SABC có đáy ABC là tam giác cân tại A và AB a , BAC  120 .
SA SB SC 5
. Gọi  là góc của hai mặt phẳng  SAB và SBC sao cho cos  . Khi đó 7
thể tích của khối chóp SABC là 3 3a 3 a 3 2a A. . B. 3 2a . C. . D. . 12 3 5
Câu 21: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AC  2a , tam giác SAB và
tam giác SCB lần lượt vuông tại A , C . Khoảng cách từ S đến mặt phẳng  ABC bằng 2a .
Côsin của góc giữa hai mặt phẳng  SAB và SCB bằng: Trang 3/69 1 1 1 1 A. . B. . C. . D. . 2 3 2 3
Câu 22: Cho hình chóp đều SABCD có cạnh đáy bằng 2 , cạnh bên bằng 3 2 . Gọi M , N lần lượt là
các điểm thuộc SB, SD sao cho SB  3SM , SD  3DN . Khoảng cách giữa AM và CN bằng 40 72 24 40 A. . B. . C. . D. . 857 857 153 257
Câu 23: Cho hình chóp tam giác đều S.ABC có SA  2a , AB a . Gọi M là trung điểm cạnh BC .
Tính khoảng cách d từ M tới mặt phẳng  SAB  . a 165 a 15 a 65 a 65 A. d  . B. d  . C. d  . D. d  . 30 3 15 10
Câu 24: Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AD  2AB  2BC  2CD  2a . Hai
mặt phẳng  SAB và SAD cùng vuông góc với mặt phẳng  ABCD  . Gọi M , N lần lượt là
trung điểm của SB và CD. Tính cosin góc giữa MN và SAC  , biết thể tích khối chóp 3 a 3 S.ABCD bằng . 4 5 3 310 310 3 5 A. . B. . C. . D. . 10 20 20 10
Câu 25: Cho hình chóp SABC có đáy ABC là tam giác vuông tại A , AB  3a , AC  4a . Các mặt bên
SAB , SAC , SBC cùng tạo với đáy  ABC một góc 0
45 . Biết chân đường vuông góc hạ
từ S xuống mặt phẳng  ABC nằm ở miền trong tam giác ABC . Gọi góc tạo bởi hai mặt
phẳng SAC  và SBC  là  . Tính cos . 1 1 3 1 A. cos  . B. cos  . C. cos  . D. cos  . 10 5 5 15
Câu 26: Cho hình chóp S.ABC có đáy là tam giác đều cạnh .
a Hình chiếu vuông góc của S trên mặt
phẳng  ABC  là điểm H thuộc cạnh AB sao cho HA  2HB . Góc giữa đường thẳng SC và
mặt phẳng  ABC  bằng 60o . Tính khoảng cách h giữa hai đường thẳng SA và BC theo a . a 42 a 42 a 42 a 42 A. . B. . C. . D. . 8 12 4 24
DẠNG TOÁN 3: HÌNH LĂNG TRỤ TAM GIÁC.
Câu 27: Cho hình lăng trụ đứng AB . C A BC
  có AB AC a , góc 
ABC  30 , góc giữa đường thẳng
AB và mặt phẳng  ABC  bằng 0
45 . Gọi M , N lần lượt là trung điểm của B C   và CC .
Cosin của góc giữa mặt phẳng  AMN  và mặt phẳng  ABC bằng 1 3 13 3 A. . B. . C. . D. . 2 2 4 4
Câu 28: Cho hình lăng trụ tam giác AB .
C A' B'C ' có đáy ABC là tam giác đều cạnh a và các mặt bên
đều là các hình vuông cạnh a . Gọi G là trọng tâm của tam giác ABC và I là trung điểm của
đoạn thẳng CC ' . Khoảng cách giữa hai đường thẳng A' B và GI bằng Trang 4/69 a 11 3a 11 a 11 3a 11 A. . B. . C. . D. . . 22 7 12 22
Câu 29: Cho lăng trụ đứng AB .
C A' B 'C ' có đáy là tam giác ABC vuông cân tại A , cạnh BC a 6 .
Góc giữa mặt phẳng  AB 'C và mặt phẳng  BCC ' B ' bằng 0
60 . Tính thể tích V của khối lăng trụ AB .
C A' B 'C ' ? 3 2a 3 3 a 3 3 3a 3 3 3a 3 A. V  . B. V  . C. V  . D. V  . 3 2 4 2
Câu 30: Cho hình lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác cân, với AB AC a và góc 
BAC  120 , cạnh bên AA  a . Gọi M là trung điểm của CC . Cosin của góc tạo bởi hai mặt
phẳng  ABC và  AB M   bằng 11 33 10 30 A. . B. . C. . D. . 11 11 10 10
Câu 31: Cho hình lăng trụ đứng ABC.AB C
  có đáy là tam giác vuông tại A , AB AC a và có
cạnh bên bằng 2a . Gọi M , N lần lượt là trung điểm BB ',CC ' . Tính khoảng cách từ điểm A
đến mặt phẳng ( A ' MN ) 2a 3 3a A. a . B. . C. . D. a 3 . 3 2
Câu 32: Cho hình lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác cân tại C , AB  2a , AA  a ,
góc giữa BC và  ABB A
  bằng 60 . Gọi N là trung điểm AA và M là trung điểm BB .
Tính khoảng cách từ điểm M đến mặt phẳng  BC N   . 2a 74 a 74 2a 37 a 37 A. . B. . C. . D. . 37 37 37 37
Câu 33: Cho hình lăng trụ đứng ABC.AB C
  có AB AC a , góc BAC bằng 120 , AA  a . Gọi M ,
N lần lượt là trung điểm B C
  và CC . Khoảng cách giữa 2 đường thẳng MN và AH là a 3 a 3 a 6 a 6 A. . B. . C. . D. . 2 4 2 4
Câu 34: Cho hình lăng trụ ABC.A B C có đáy là tam giác đều cạnh a . AA  2a và vuông góc với mặt 1 1 1 1
phẳng  ABC . Gọi D là trung điểm của BB , M di động trên cạnh AA . Giá trị lớn nhất của 1 1 diện tích MC D là 1 2 a 15 2 a 15 2 a 5 2 a 10 A. . B. . C. . D. . 4 6 4 4
Câu 35: Cho lăng trụ tam giác đều AB .
C A' B'C ' có tất cả các cạnh bằng a , M là điểm di chuyển trên
đường thẳng A'C ' ; Tính khoảng cách lớn nhất giữa AM và BC ' a 34 a 17 a 14 a 21 A. . B. . C. . D. . 6 4 4 6
Câu 36: Cho lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông, AB BC a , cạnh bên
AA'  a 2 . Gọi M là trung điểm của BC . Tính theo a khoảng cách giữa hai đường thẳng AM và B C  . Trang 5/69 a 3 a 21 a 7 A. . B. . C. a 7 . D. . 7 7 7
Câu 37: Cho lăng trụ đứng ABCA BC
  có đáy ABC là tam giác vuông tại A và AB  1, AC  2 .Gọi  p
là góc tạo bởi đường thẳng BC và mặt phẳng ( ABC ) có số đo lớn nhất. Biết sin  ( với q
p, q nguyên tố cùng nhau ). Giá trị tổng p q là A. 11. B. 7 . C. 5 . D. 9
Câu 38: Cho hình lăng trụ tam giác đều AB . C A BC
  có độ dài cạnh đáy bằng a. Góc giữa  ABC và
ABC bằng 60 . Gọi M , N là trung điểm của BC và CC . Tính khoảng cách giữa A M  và AN. 6a 97 3a 97 6a 65 3a 65 A. . B. . C. . D. . 97 97 65 65
DẠNG TOÁN 4: HÌNH HỘP.
Câu 39: Cho lăng trụ tam giác đều AB . C A BC
  có tất cả các cạnh bằng a . M là một điển thỏa mãn  1  CM  
AA . Côsin của góc giữa hai mặt phẳng  AMB  và  ABC  bằng 2 30 30 30 1 A. . B. . C. . D. . 10 8 16 4
Câu 40: Cho hình hộp ABC . D A BCD
  có thể tích bằng V . Gọi M , N , P lần lượt là trung điểm của
các cạnh AB , A C
  , BB . Tính thể tích khối tứ diện CMNP. 5 1 7 1 A. V . B. V . C. V . D. V . 48 8 48 6
Câu 41: Cho hình hộp ABC . D A BCD
  , có đáy là hình thoi cạnh 2a , tâm O ,  0
BAD  60 và AA  2a .
Hình chiếu vuông góc của A lên mặt phẳng  ABCD trùng với tâm O . Gọi M là trung điểm
CD . Khoảng cách giữa hai đường thẳng A M
và BD bằng 21 2 21 3 21 4 21 A. . B. . C. . D. . 7 7 7 7
Câu 42: Cho hình hộp chữ nhật ABC . D A BCD
  , có AB a, AD a 2, góc giữa A C  và mặt phẳng
ABCD bằng 30. Gọi H là hình chiếu vuông góc của A trên AB và K là hình chiếu vuông
góc của A trên A . D
Tính góc giữa hai mặt phẳng  AHK  và  ABB A   . A. 60 . B. 45. C. 90 . D. 30 .
Câu 43: Cho lăng trụ ABCD.A B C D có đáy ABCD là hình vuông cạnh a . Hình chiếu vuông góc của 1 1 1 1
A lên  ABCD trùng với giao điểm của AC và BD . Tính khoảng cách từ điểm B đến mặt 1 1 phẳng  A BD . 1  a 2 a 2 a 21 a 3 A. . B. . C. . D. . 4 2 4 2
Câu 44: Cho hình lập phương ABC .
D A' B 'C ' D ' cạnh a . Gọi K là trung điểm của DD ' . Tính khoảng
cách giữa hai đường thẳng CK và A' D . Trang 6/69 a a a a A. . B. . C. . D. . 3 4 5 2
Câu 45: Cho hình hộp chữ nhật ABC . D A BCD
  có AB  3a , AD AA  a . Lấy điểm M thuộc đoạn
AB , điểm N thuộc đoạn A C
  sao cho AM A N
x , 0  x  10a . Tìm x theo a để
đoạn MN nhỏ nhất. 30a 10a 10a A. 0 . B. . C. . D. . 3 2 3
Câu 46: Cho hình hộp chữ nhật ABC .
D A' B 'C ' D' có AB a, AD  2a, AA '  3a. Gọi M , N , P lần
lượt là trung điểm của BC , C ' D ' và DD '. Tính khoảng cách từ A đến mp MNP. 15 9 3 15 A. a . B. a . C. a . D. a . 22 11 4 11
Câu 47: Cho hình lăng trụ đứng ABC.AB C
  có đáy là tam giác vuông cân, AA  2a , AB AC a .
Gọi G và G lần lượt là trọng tâm của tam giác ABC và tam giác AB C
  , I là tâm của hình chữ nhật ABB A
  . Thể tích của khối . A IGCG . 3 a 3 a 3 a 5 3 a 5 A. . B. . C. . D. . 2 6 6 30
Câu 48: Cho hình hộp ABCDA' B 'C ' D ' có đáy là hình vuông cạnh a. Mặt phẳng ( ABB ' A ') vuông góc
với đáy, tam giác A' AB vuông tại A' , góc giữa BA' và đáy bằng 0
60 . Gọi I là tâm của hình
vuông ABCD . Tính khoảng cách giữa hai đường thẳng IA' và DB ' . a a a 3 a 3 A. . B. . C. . D. . 2 55 55 55 2
Câu 49: Cho hình chóp .
S ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA  2a và vuông góc
với mặt phẳng đáy. Gọi M là trung điểm cạnh SD . Tang của góc tạo bởi hai mặt phẳng
(AMC) và (SBC) bằng 3 2 5 2 3 5 A. . B. . C. . D. . 2 5 3 5
Câu 50: Hai quả bóng hình cầu có kích thước khác nhau được đặt ở hai góc của một căn nhà hình hộp
chữ nhật sao cho mỗi quả bóng đều tiếp xúc với hai bức tường và nền của nhà đó. Biết rằng
trên bề mặt của hai quả bóng đều tồn tại một điểm có khoảng cách đến hai bức tường và nền
nhà mà nó tiếp xúc bằng 1; 2; 4 . Tổng độ dài đường kính của hai quả bóng đó là? A. 7 . B. 12 . C. 14 . D. 16 .
-------------------- HẾT -------------------- Trang 7/69 BẢNG ĐÁP ÁN 1.D 2.C 3.D 4.D 5.D 6.B 7.B 8.D 9.C 10.A 11.A 12.A 13.D 14.B 15.A 16.A 17.A 18.A 19.C 20.A 21.B 22.A 23.A 24.C 25.A 26.A 27.D 28.D 29.D 30.D 31.B 32.A 33.D 34.A 35.C 36.D 37.D 38.B 39.A 40.A 41.B 42.B 43.B 44.A 45.C 46.D 47.B 48.C 49.B 50.C HƯỚNG DẪN GIẢI Câu 1:
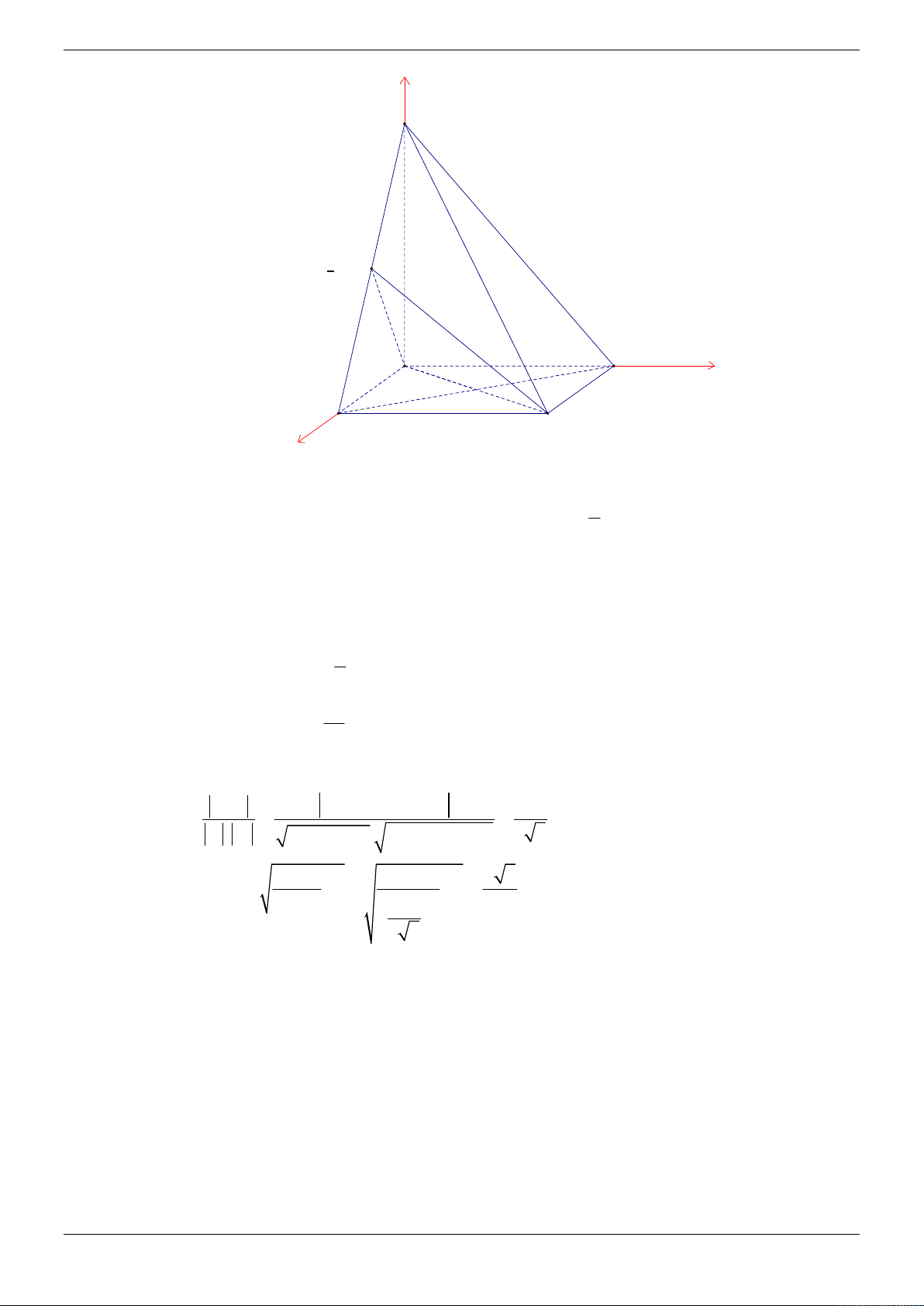
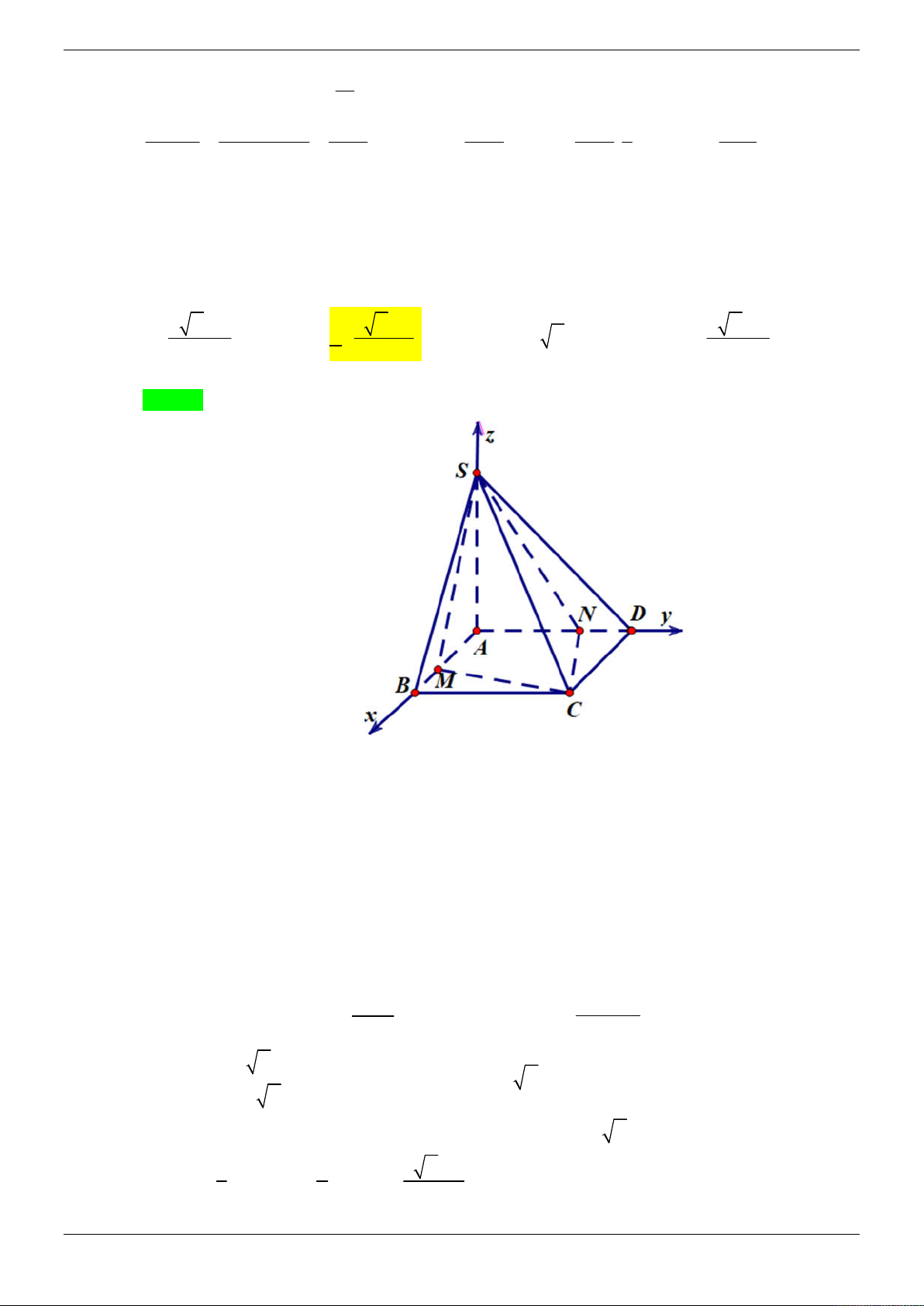
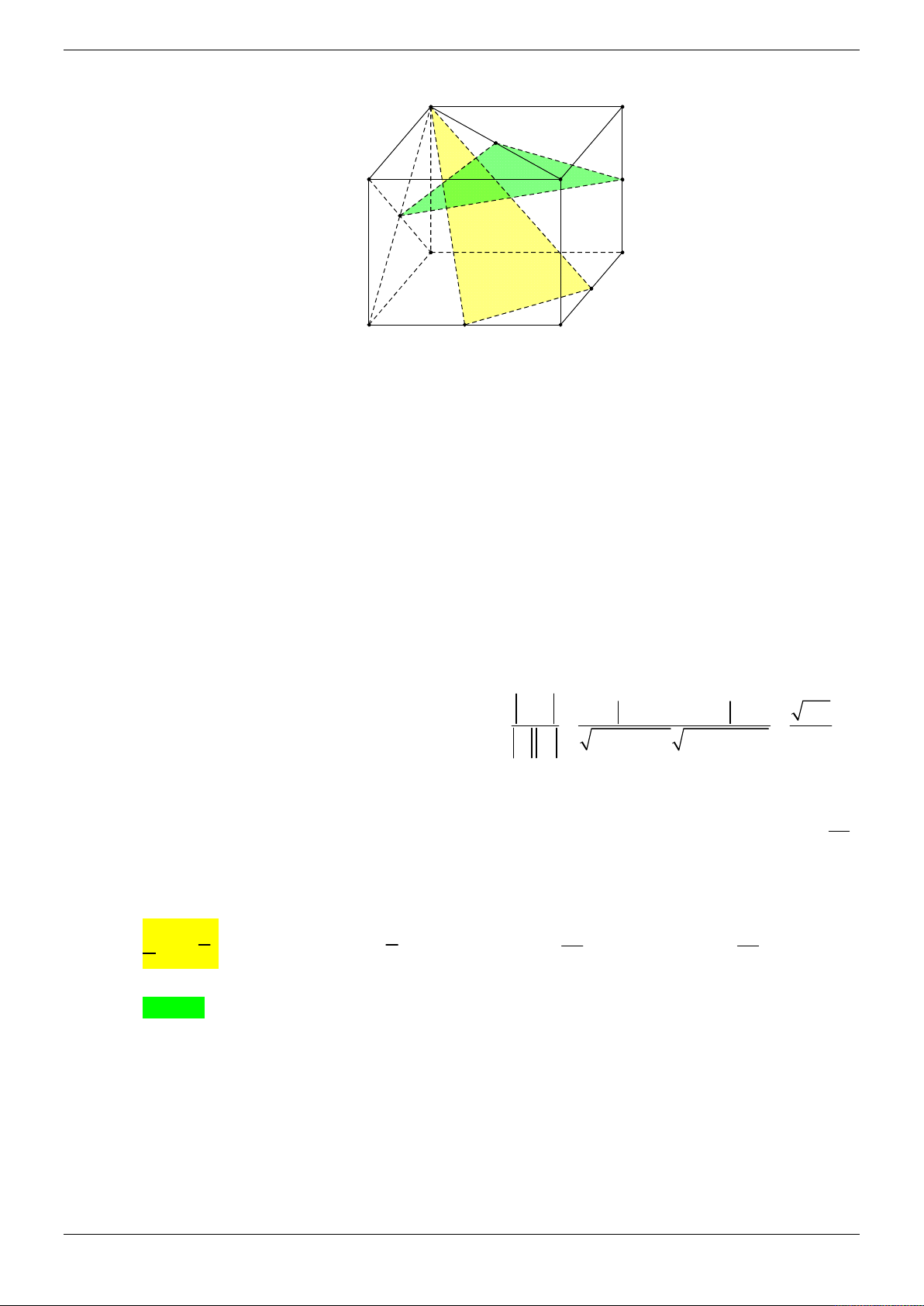
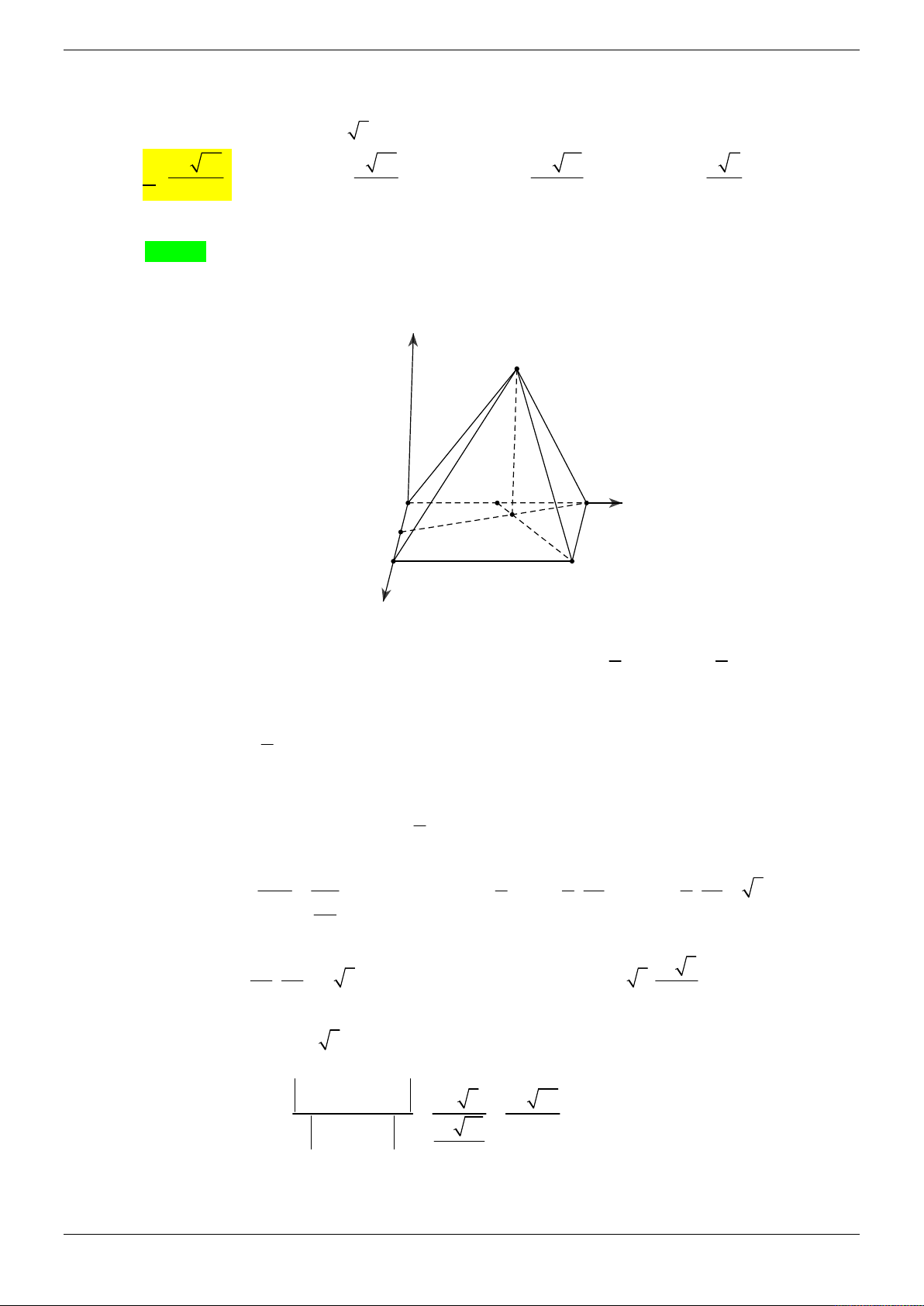
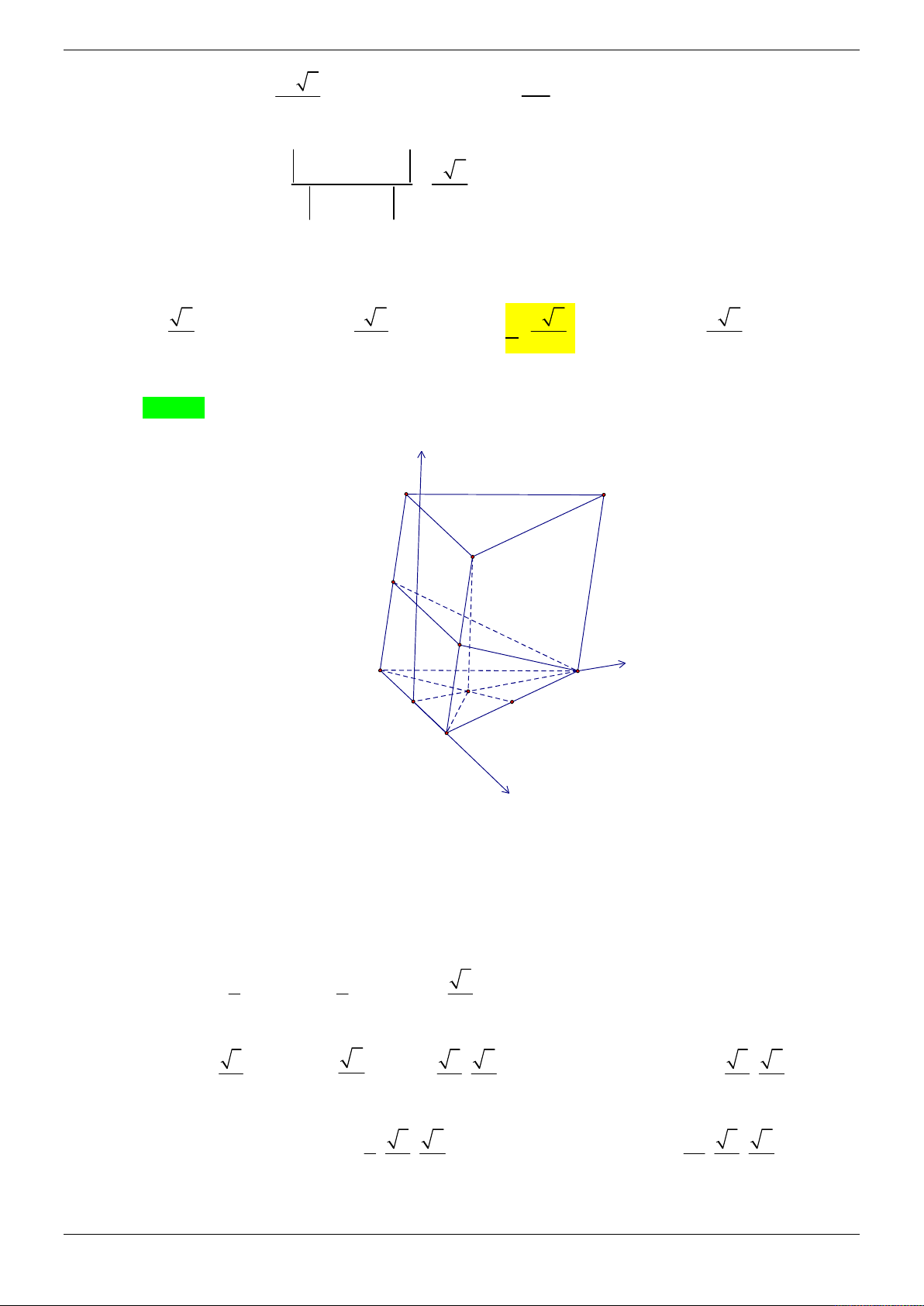
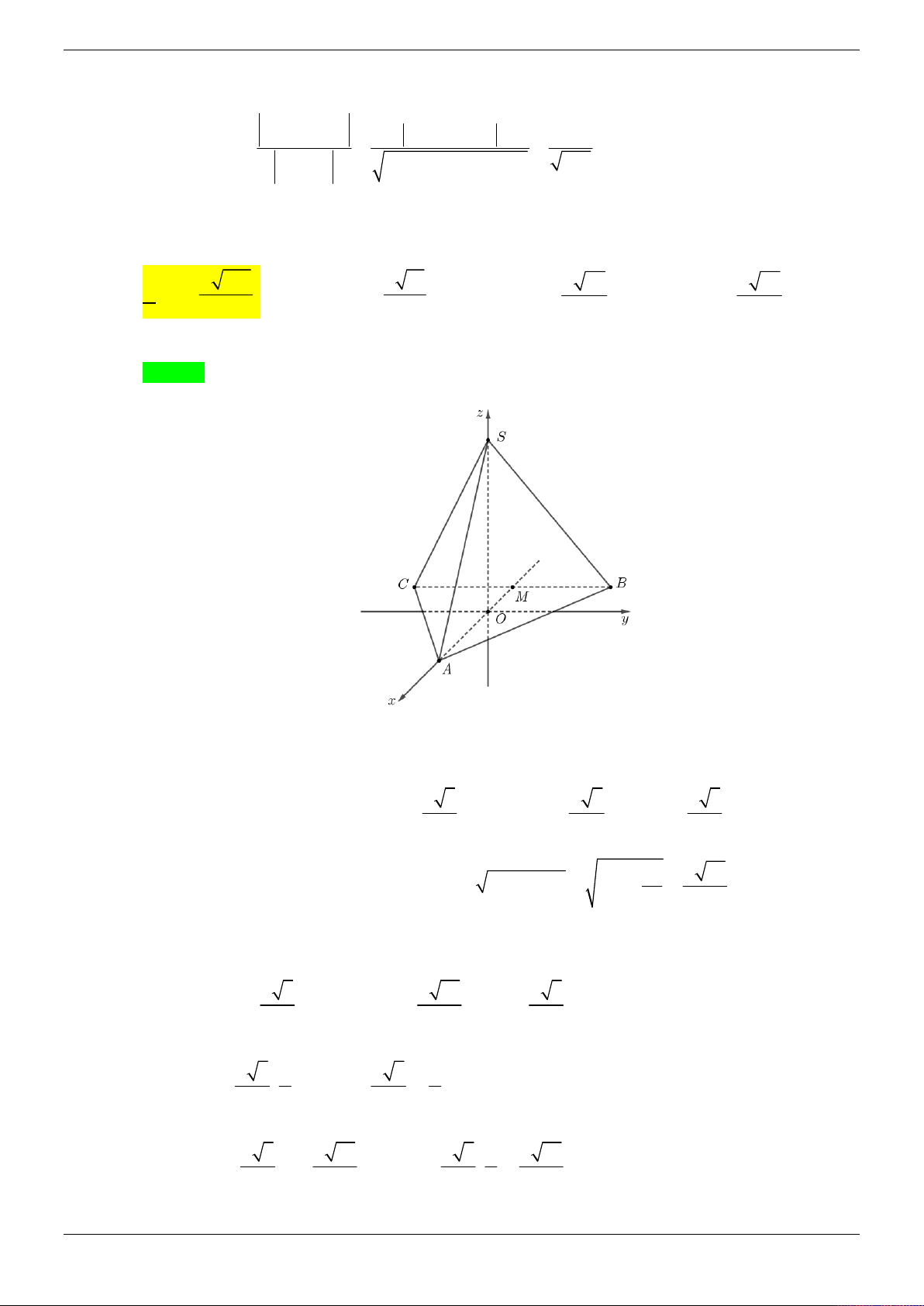
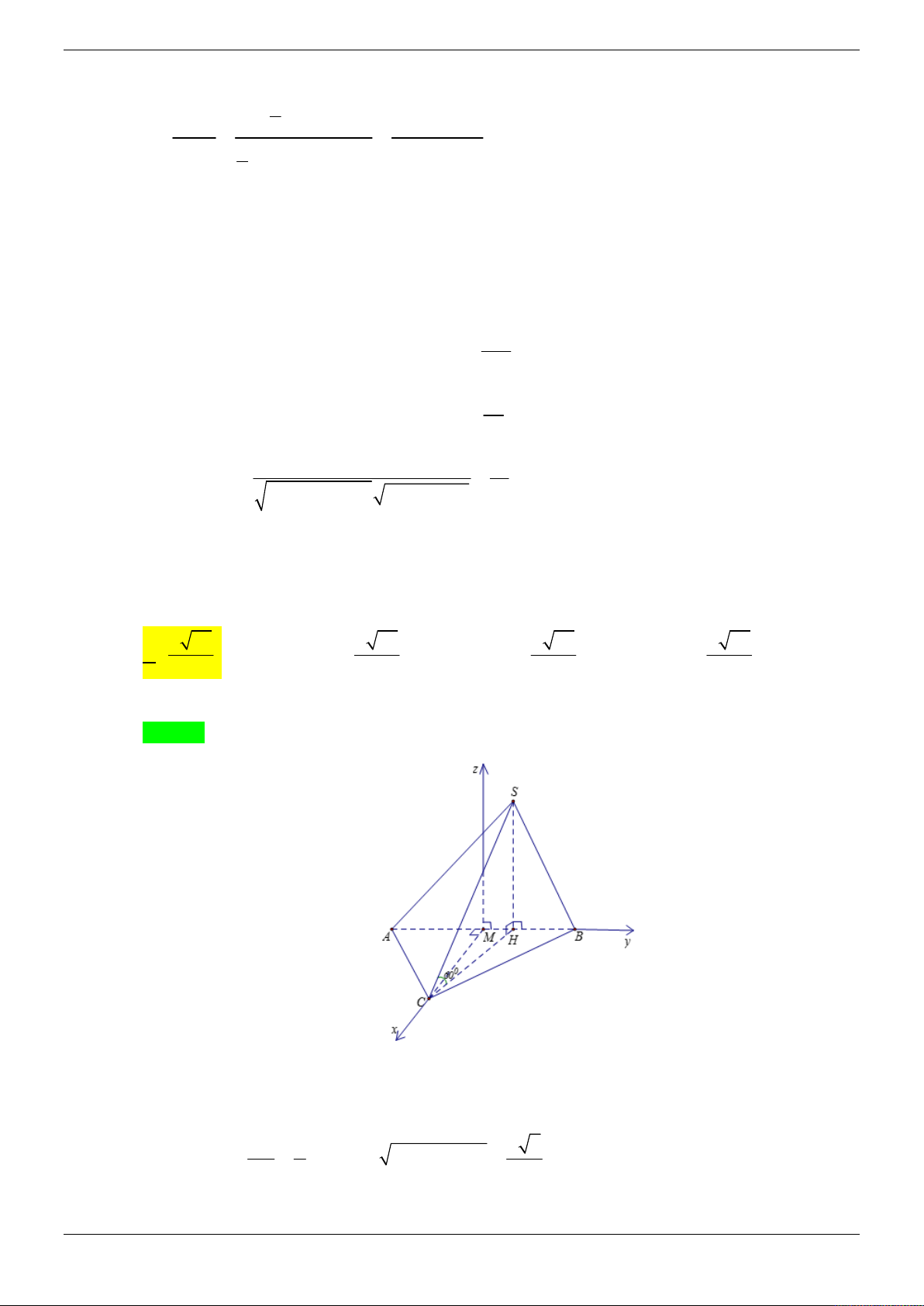
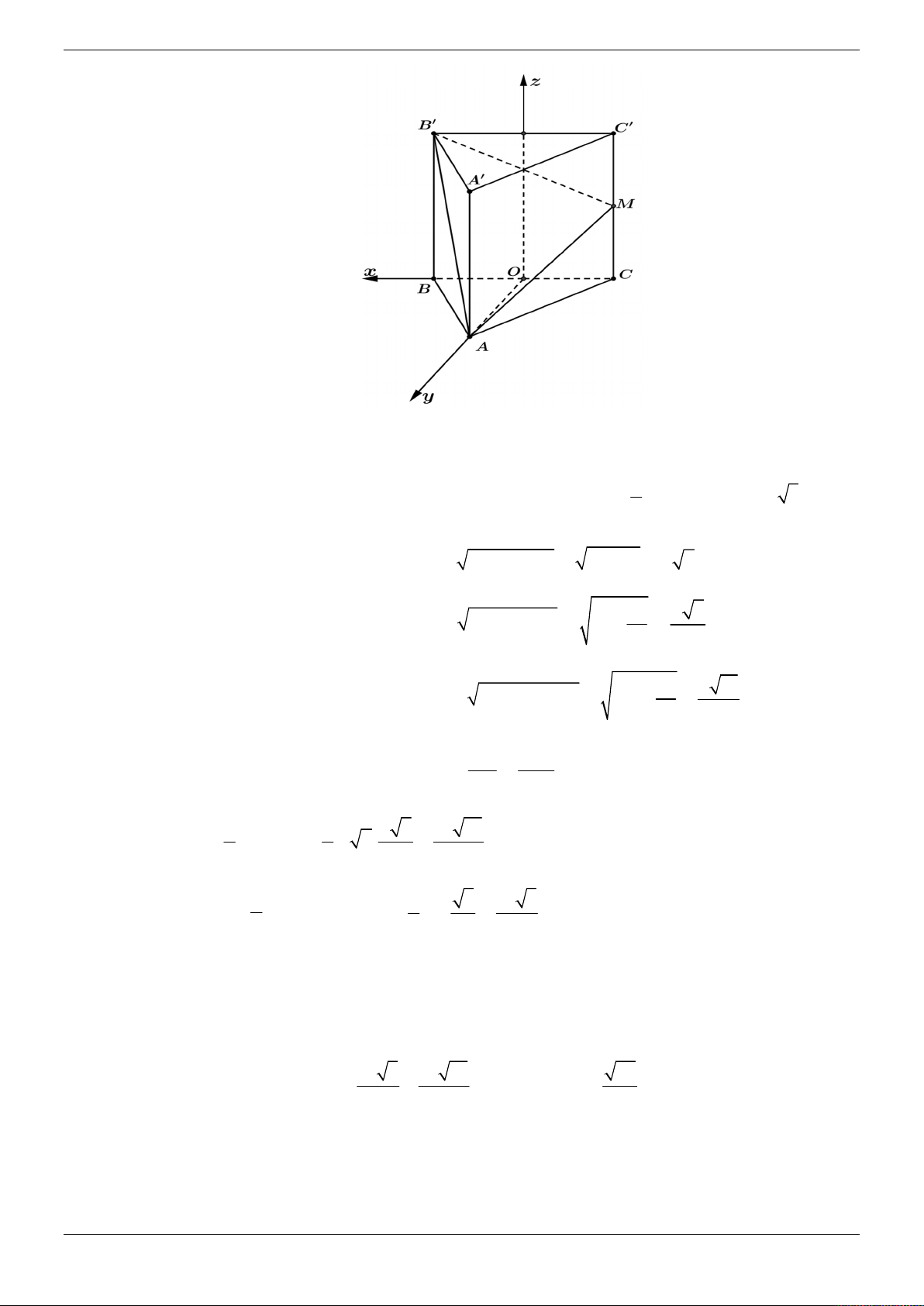
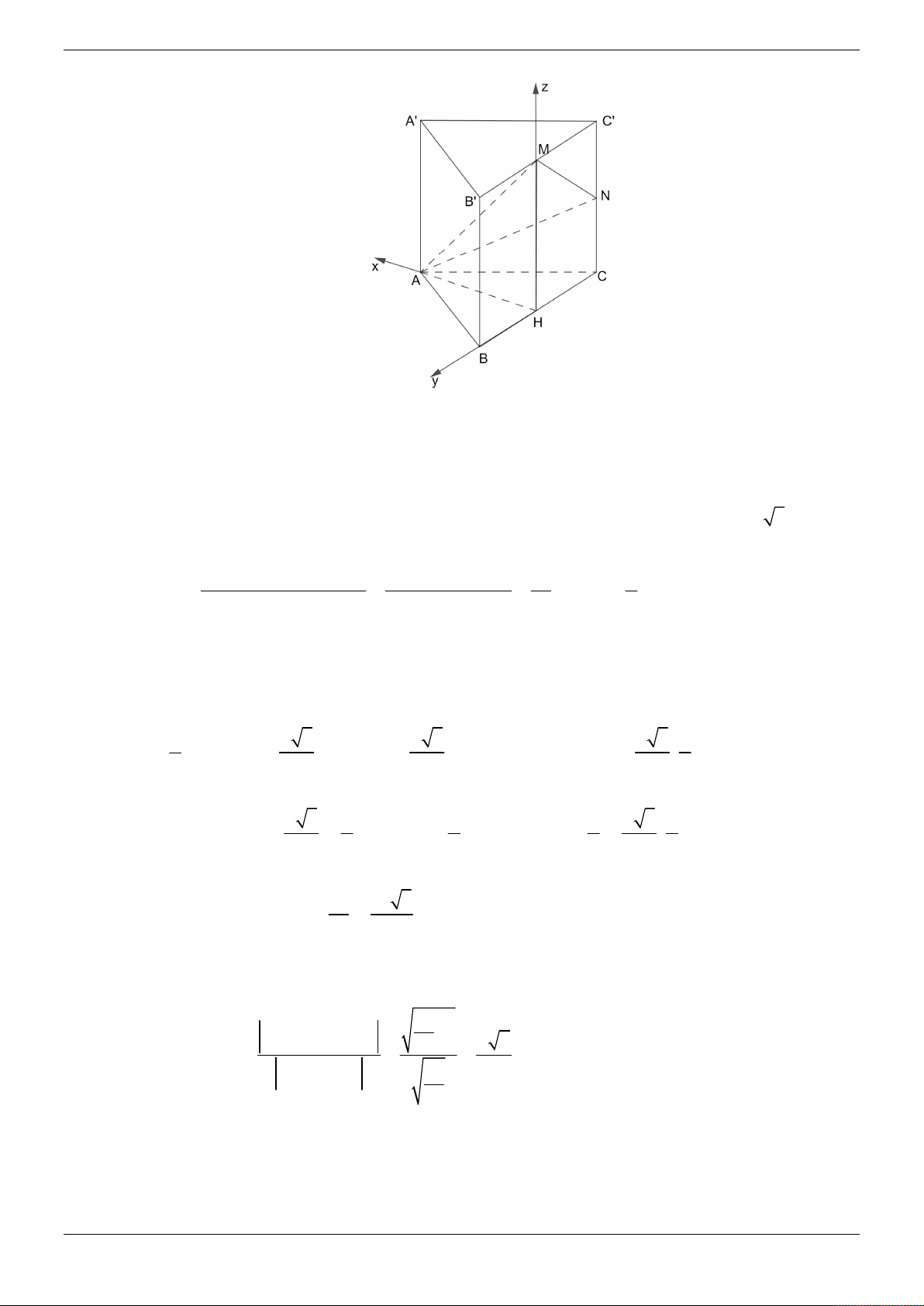
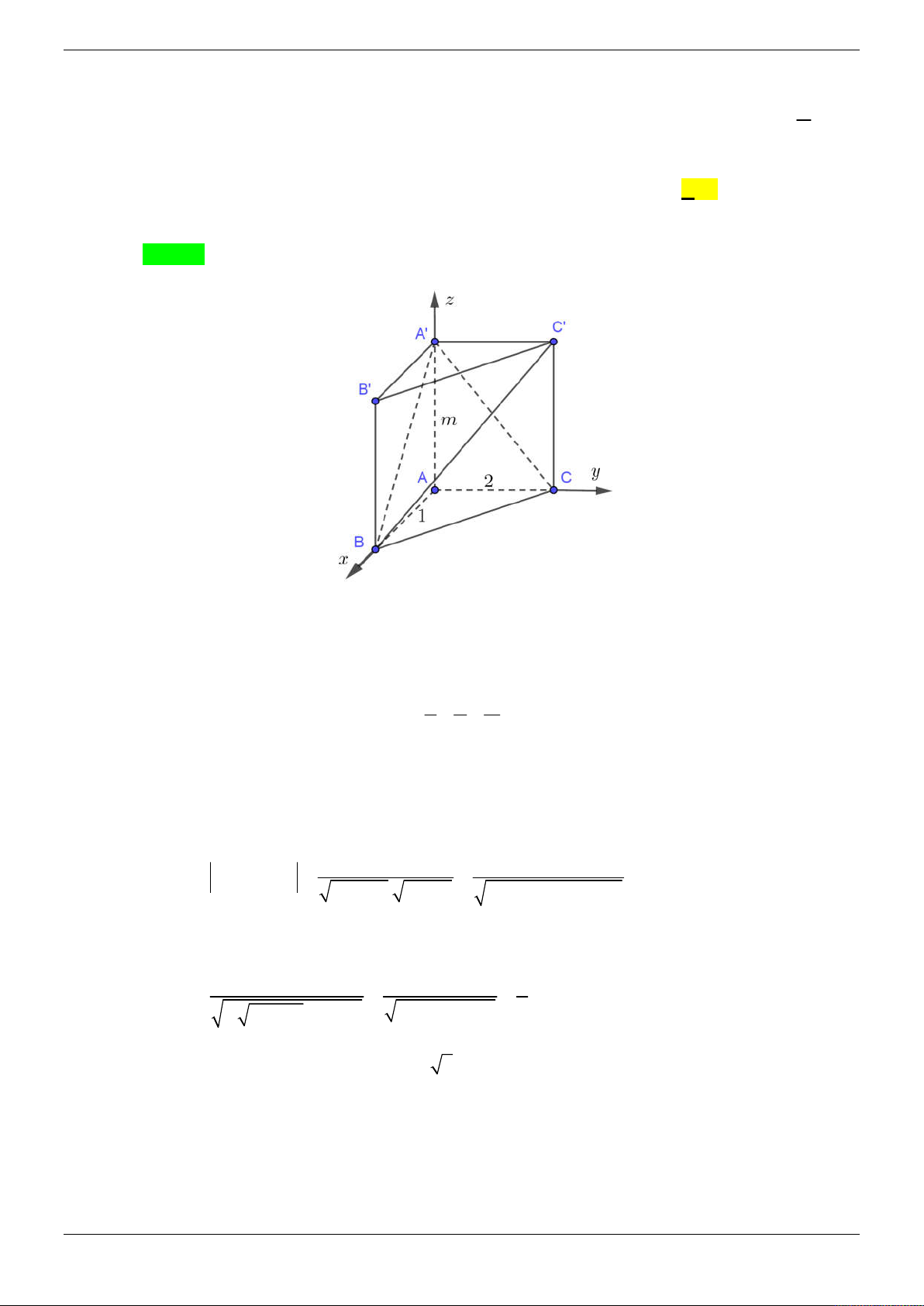
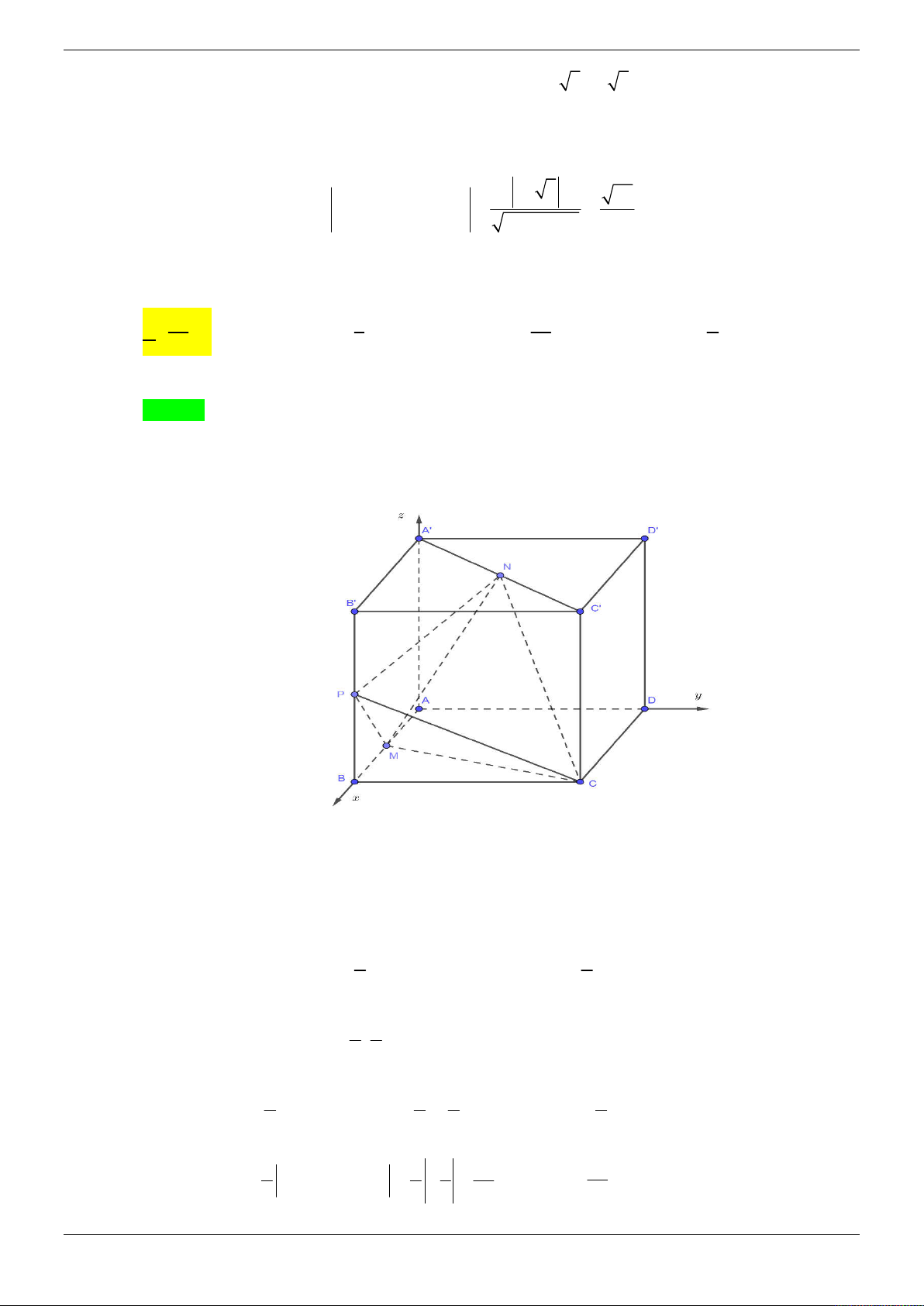
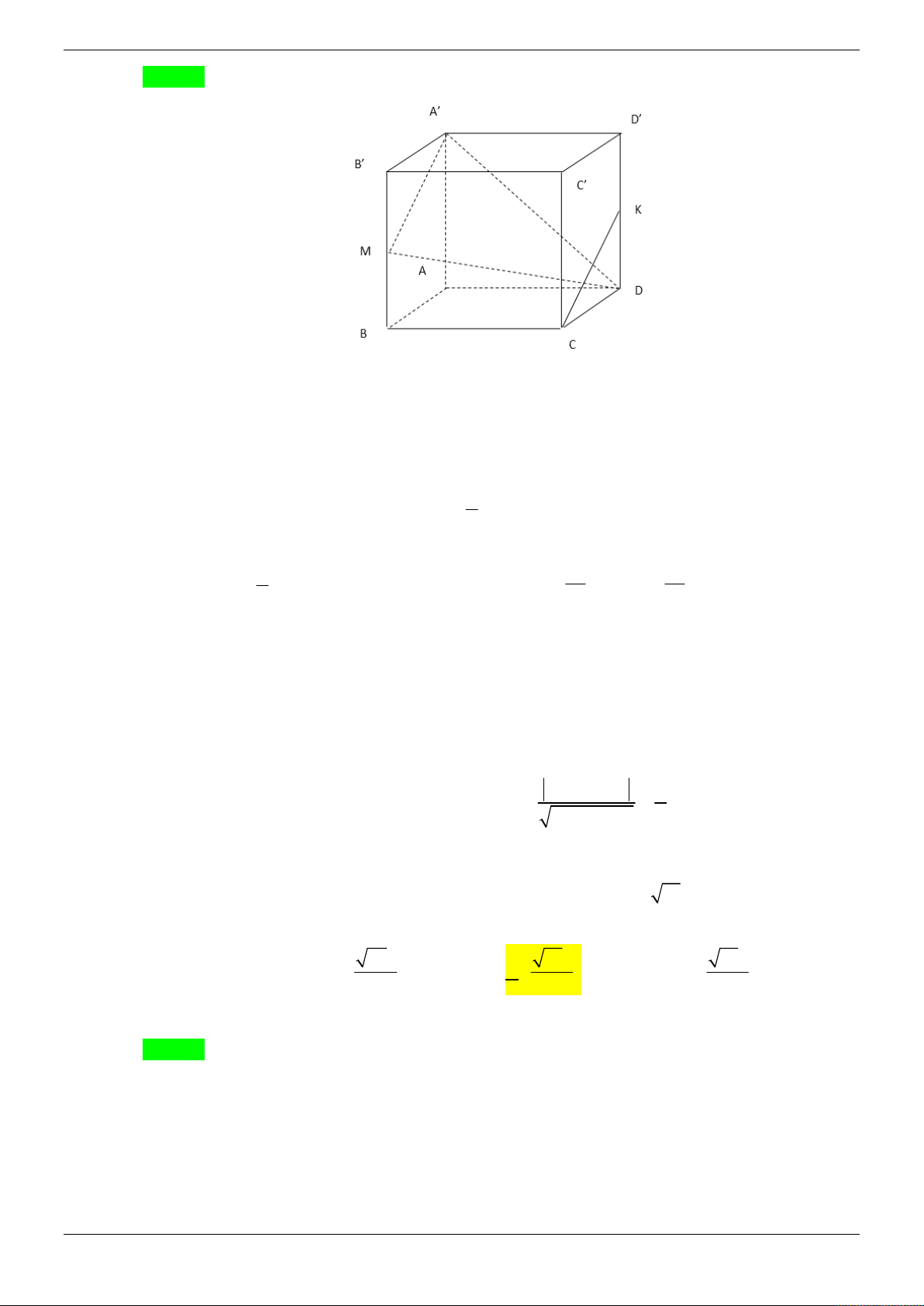
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và SA vuông góc với mặt phẳng
đáy. Góc giữa mặt bên (SBC) với mặt phẳng đáy bằng 45 . Gọi M , N lần lượt là trung điểm
của AB và SB . Tính theo a khoảng cách giữa hai đường thẳng MD và CN . 3 a 21 2a 21 A. a . B. . C. 2a . D. . 4 3 21 Lời giải Chọn D z S N A M B y O 45° D x C
Gọi  là giữa hai mặt phẳng SBC và  ABCD  . BC AB
Ta có BC  SBC  ABCD và 
BC  SAB . BC SA  Suy ra 
  ABS  45 . Do S
AB vuông cân tại A nên SA a .
Chọn hệ trục tọa độ Oxyz (như hình vẽ) sao cho A  ( O 0;0;0), D ;
a 0;0 B0; ;
a 0; S 0;0;a . a a   a
Khi đó C a; a;0, N 0; ; , M 0; ; 0     .  2 2   2    aMD  ; a ;0    2 2  2 
   a a  2  M ; D NC   ; ; a      a a       4 2 Suy ra NC ; a ;        . 3  2 2  
   a  C . D M ; D NC   CD 0; ; a 0       2   Trang 8/69 3
   a C .
D MD, NC    2 2a 21
d MD, NC       . 2 MD, NC a 21 21   4 Cách khác:
Dựng hình bình hành DMEC .
Ta có MD// CNE nên d M ,
D CN   d M ,
D CNE  d M ,CNE .
Gọi I là hình chiếu của M lên CE và H là hình chiếu của M lên NI .
Suy ra MH  CNE hay d M ,
D CN   d M ,CNE  MH .
Gọi  là giữa hai mặt phẳng SBC và  ABCD  . BC AB
Ta có BC  SBC  ABCD và 
BC  SAB . BC SA  Suy ra 
  ABS  45 . Do S
AB vuông cân tại A nên SA a .  MI BC BC.ME 2a Ta có sin MEC    MI   . ME CE CE 5 MI.MN 2a 21 MH   . 2 2 21 MI MNCâu 2:
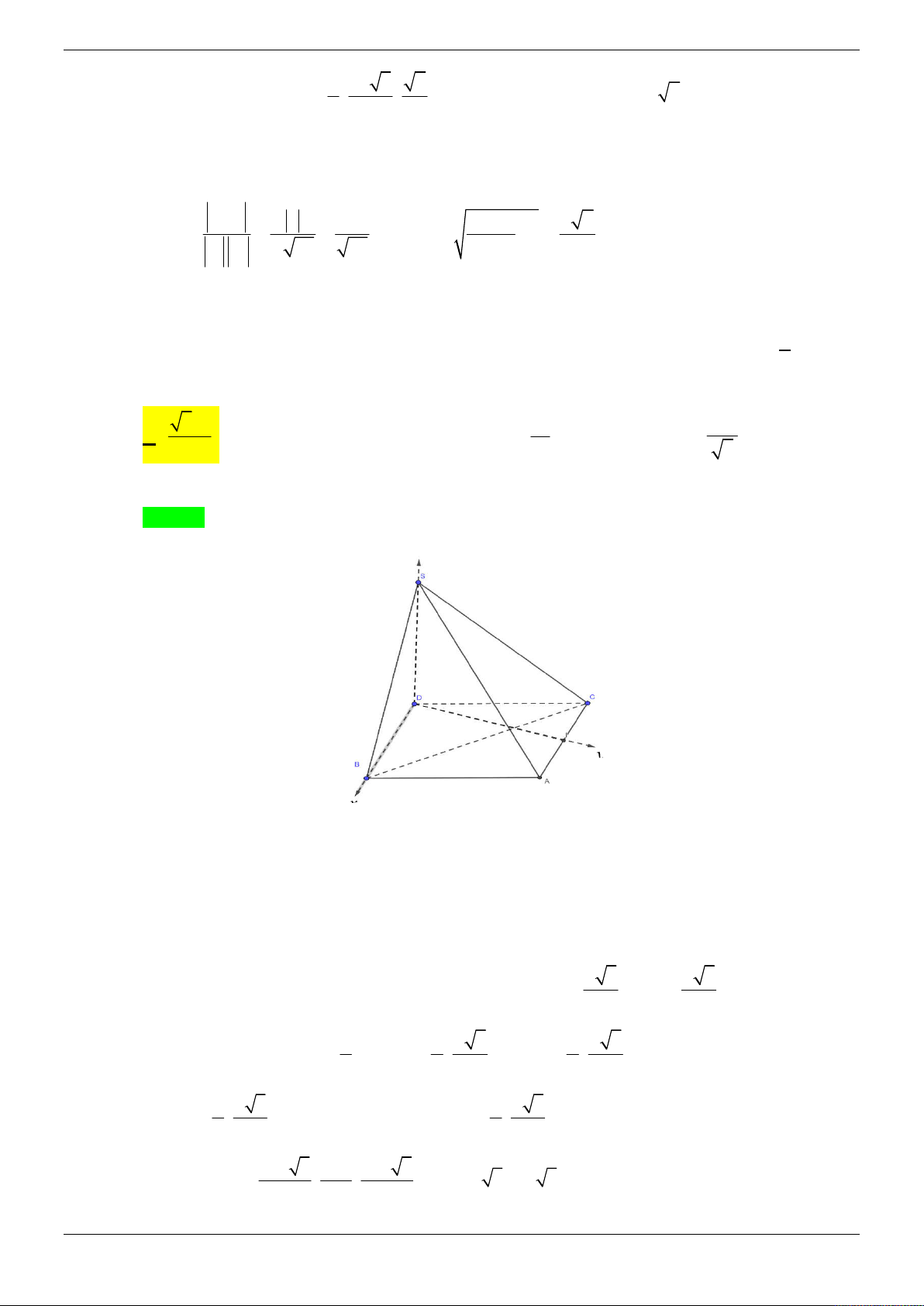
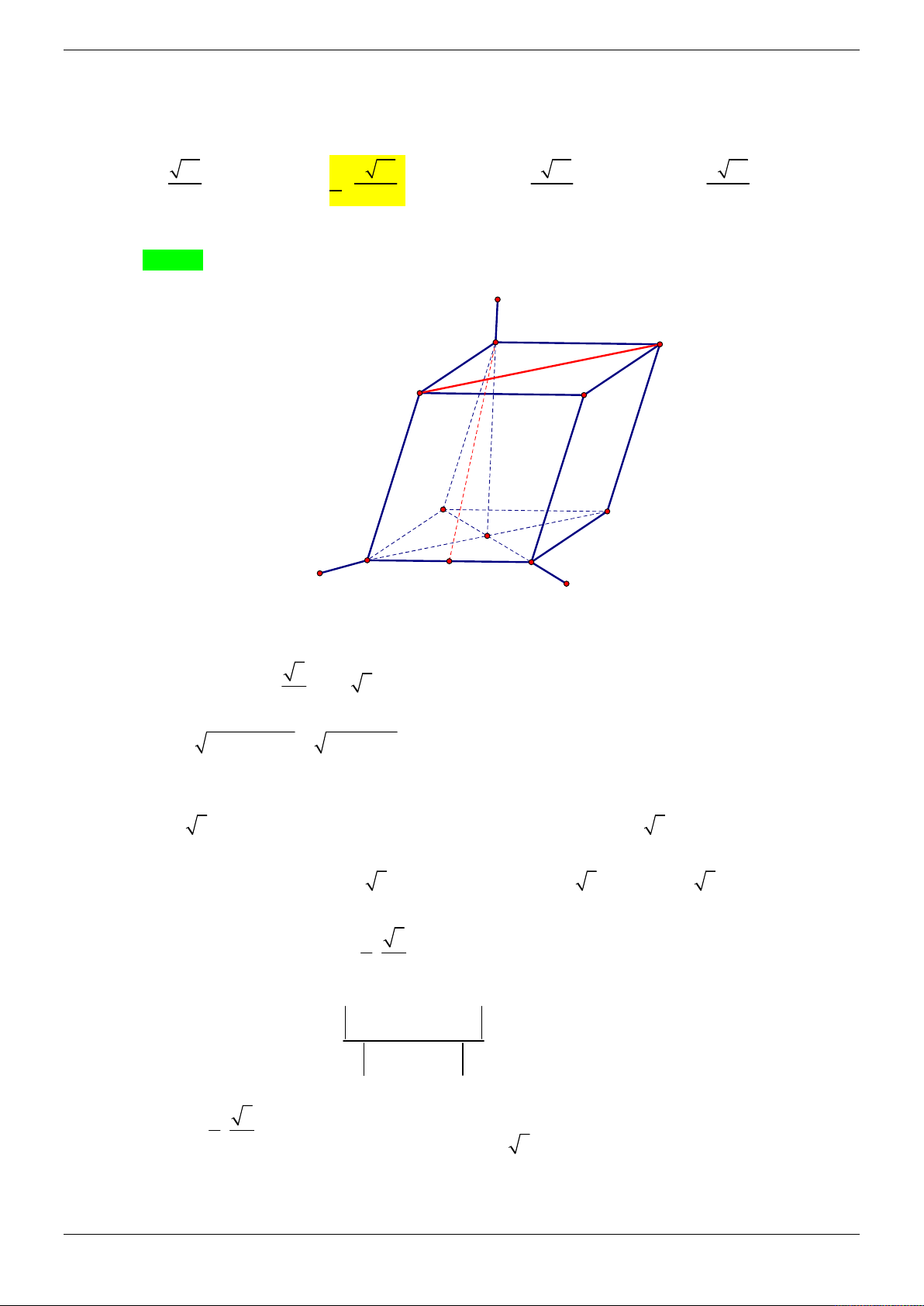
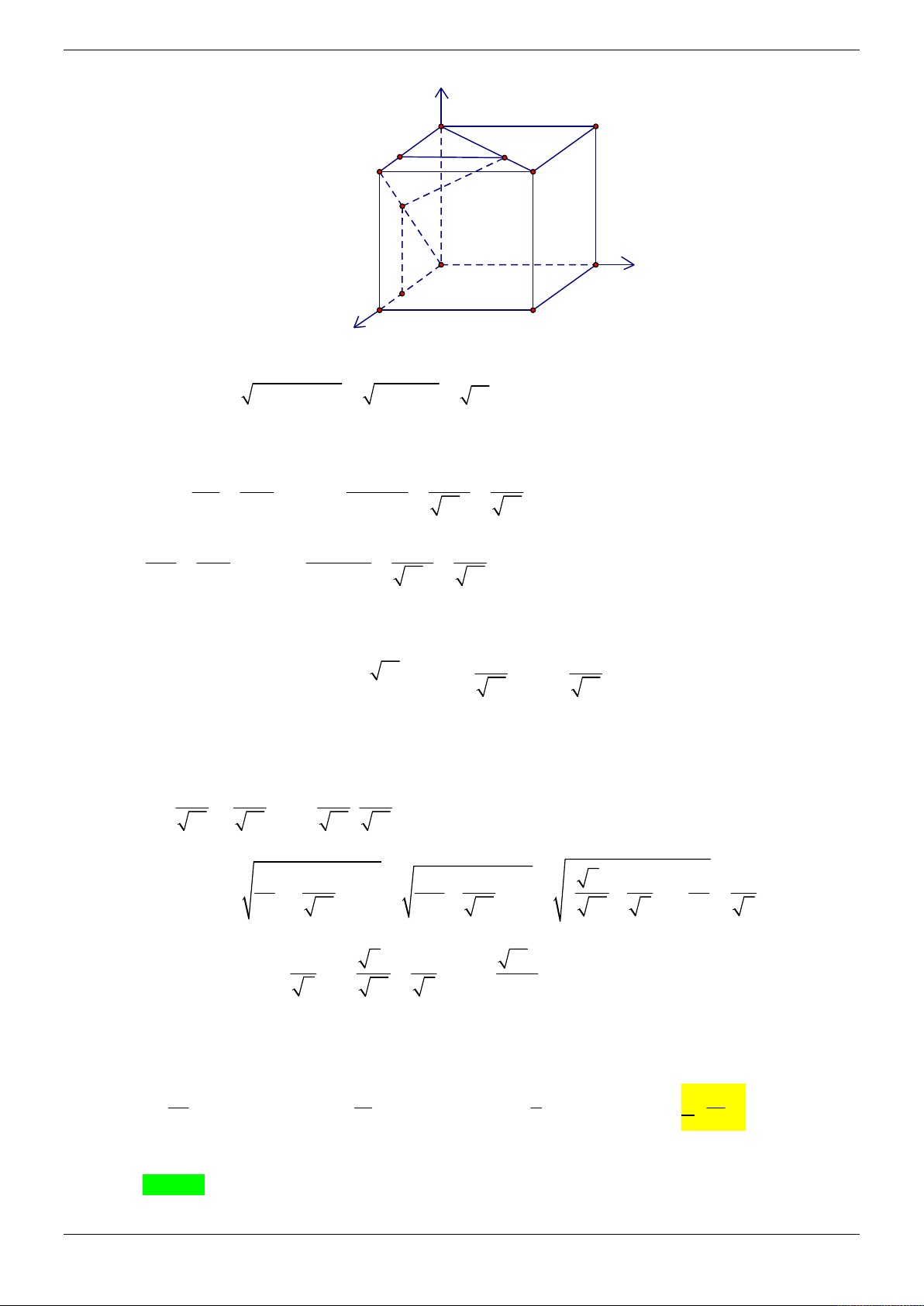
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , o
ABC  60 , BC  2a . Gọi D là  
điểm thỏa mãn 3SB  2SD . Hình chiếu của S trên mặt phẳng  ABC là điểm H thuộc đoạn
BC sao cho BC  4BH . Tính góc giữa hai đường thẳng AD và SC biết SA tạo với mặt đáy một góc o 60 . A. o 60 . B. o 45 . C. o 90 . D. o 30 . Lời giải Chọn C z S B O x H C D A y Trang 9/69 2 2 a a 1 3a a 3 Ta có 2 2 2 o
AH BH BA  2.BH .B . A cos 60 2   a  2. . . a   AH  . 4 2 2 4 2 SH 3a o tan 60 
SH AH. 3  . AH 2 3 3 3a
AC BC.sin 60  2 . aa 3 , HC BC  . 2 4 2 2 2 9a 3a Ta có 2 2 2 2 AH HC  
 3a AC nên tam giác AHC vuông tại H , tức là 4 4 AH HC .  3 
Chọn a  1 và chọn hệ trục tọa độ Oxyz (như hình vẽ) sao cho O H 0;0;0 , C ; 0; 0   ,  2   3   3  A 0; ; 0  , S 0; 0; .    2     2   1    1 3    3 9   3 3  Suy ra B  ; 0; 0 
 . SB   ; 0;  
  SD   ; 0;     D  ; 0;    .  2   2 2   4 4   4 4    3 3 3   Ta có DA   ;
;   u   3;2; 3 là một véctơ chỉ phương của AD .  4 2 4      3 3   SC  ; 0;  
  v  1;0;  
1 là một véctơ chỉ phương của SC .  2 2   
Ta có u.v  0  AD SC .
Vậy góc giữa hai đường thẳng AD và SC bằng o 90 . Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 5a , cạnh bên SA  10a và vuông
góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD . Tính tan của góc tạo bởi hai mặt
phẳng  AMC  và SBC . 3 2 3 5 2 5 A. . B. . C. . D. . 2 3 5 5 Lời giải Chọn D
Chuẩn hóa với a  1.
Xét hệ trục tọa độ Oxyz như hình vẽ sau: Trang 10/69 z
S (0;0;10) 5 (0; ;5) M 2 A≡O B (5;0;0) x (0;5;0) D C (5;5;0) y
Chọn hệ trục tọa độ như hình vẽ.  5 
A0;0;0; D 0;5;0; B 5;0;0;C 5;5;0; S 0;0;10; M 0; ;5   .  2   
BC  0;5;0, BS   5  ; 0;10 .   
BC, BS   50;0;25  SBC n  2;0;1  
một véctơ pháp tuyến của   là . 1      5 
AC  5;5;0, AM  0; ;5   .  2     25  
AC, AM   25;  25;    AMC n  2;  2;1  
một véctơ pháp tuyến của   là . 2    2 
Gọi  là góc giữa hai mặt phẳng  AMC  và SBC .   n .n 2.2  0.2 1.1 5 1 2 cos      . n . n
2  0 1 . 2  22 2 2 2 2 2 3 5 1 2 1 1 1 2 5 Suy ra: tan   1  1  . 2 2 cos  5  5     3 5  Cách khác: Trang 11/69 S S' M H K D A B C
Dựng hình bình hành SADS ' . Khi đó (SBC)  ( AMC)  S C  .
Dựng AH SB tại H và HK //BC ( K S C  ).
Gọi  là góc giữa hai mặt phẳng  AMC  và SBC . 
Khi đó ta có ( AHK )  S C     HKA . . AB AS Ta có AH   2 5a . 2 2 SA AB AH 2 5 Do đó tan    . HK 5 Câu 4:
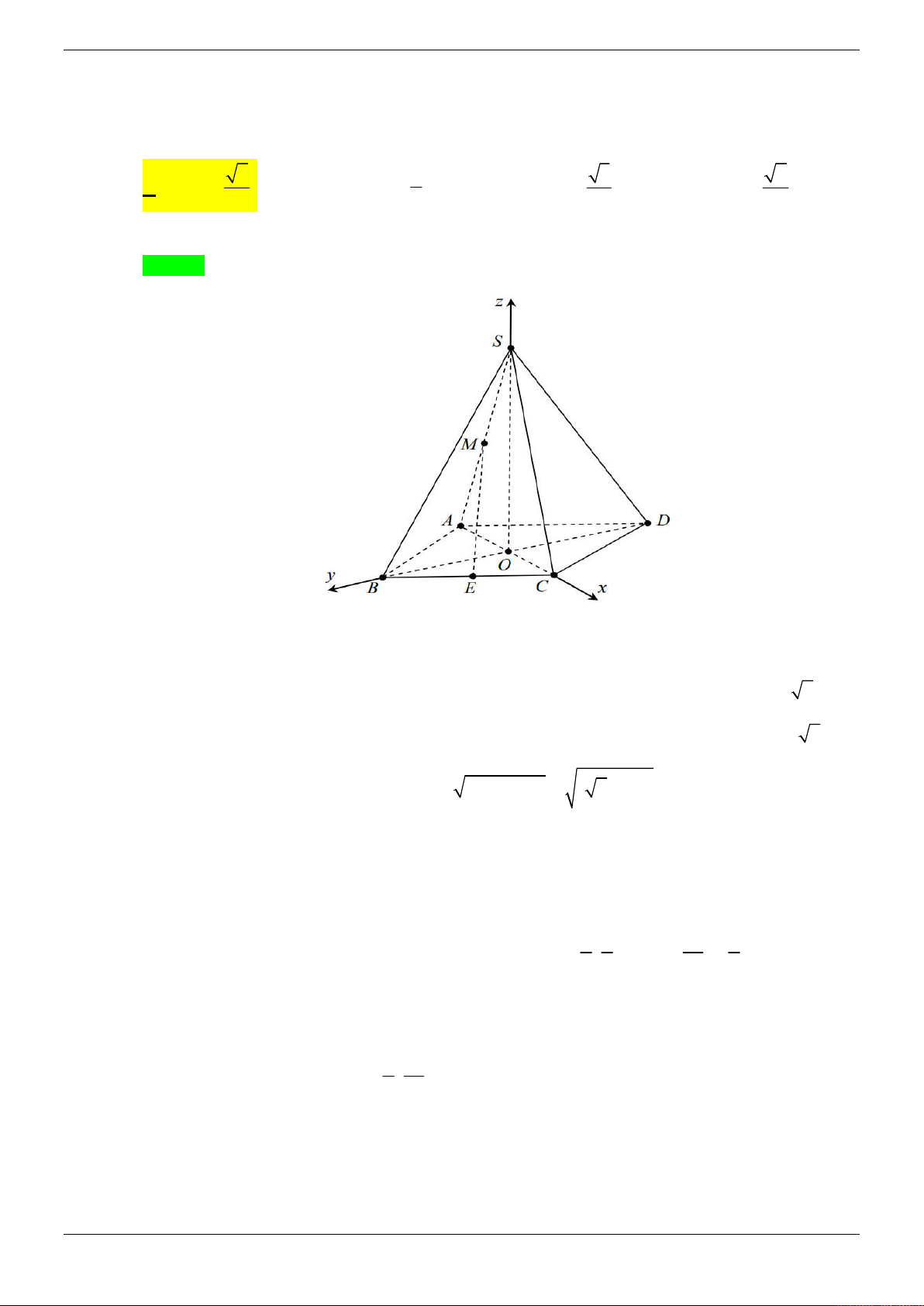
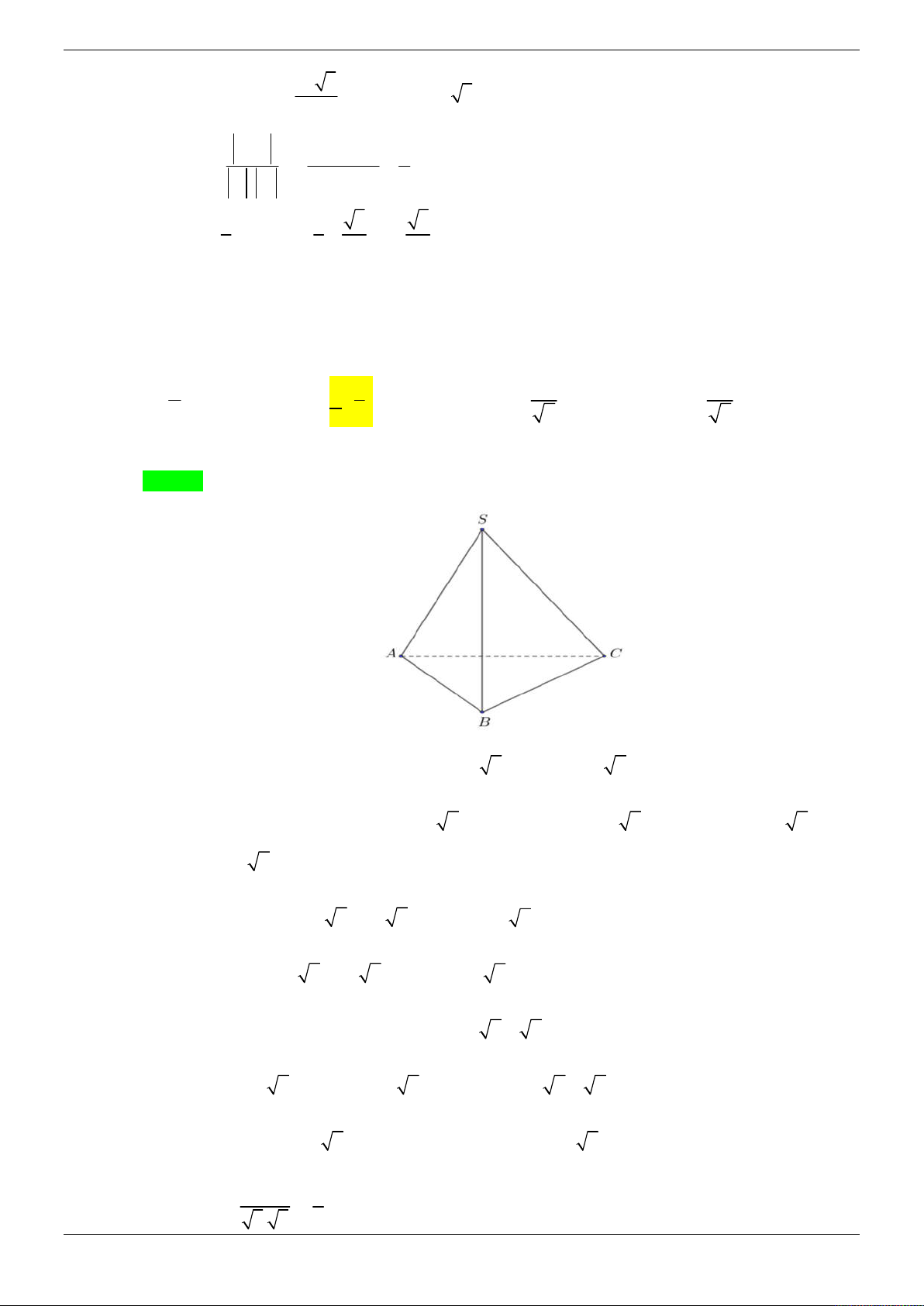
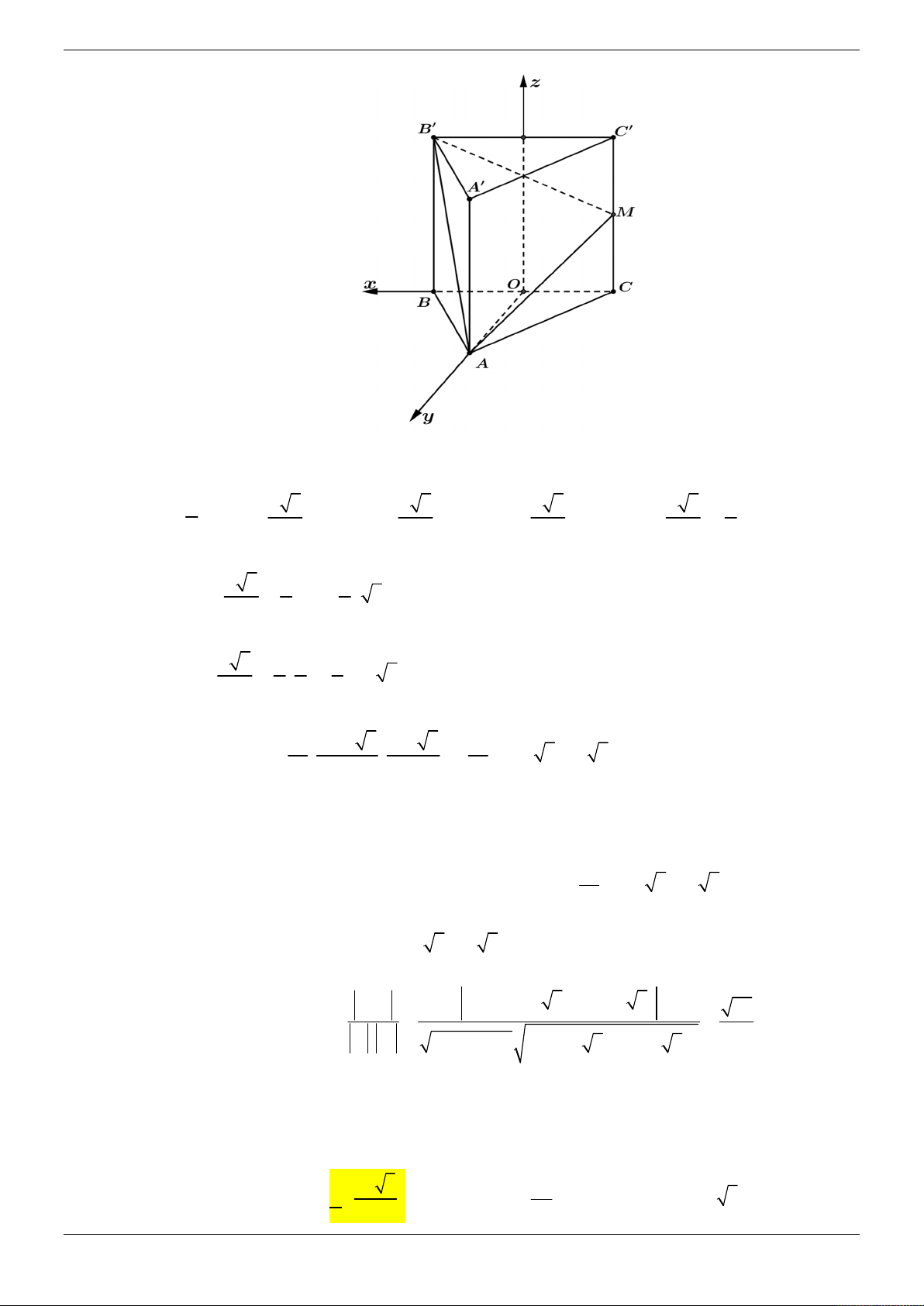
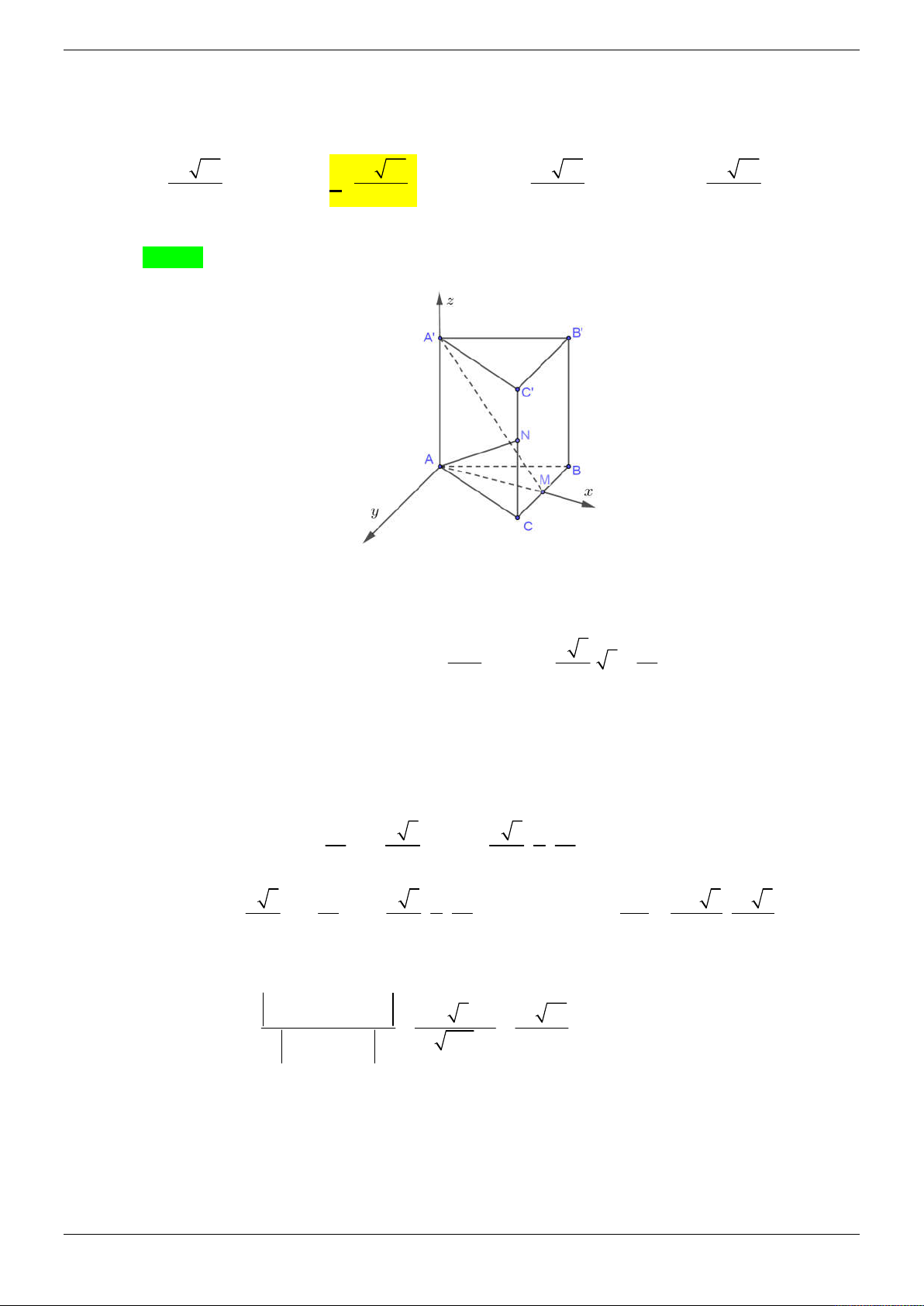
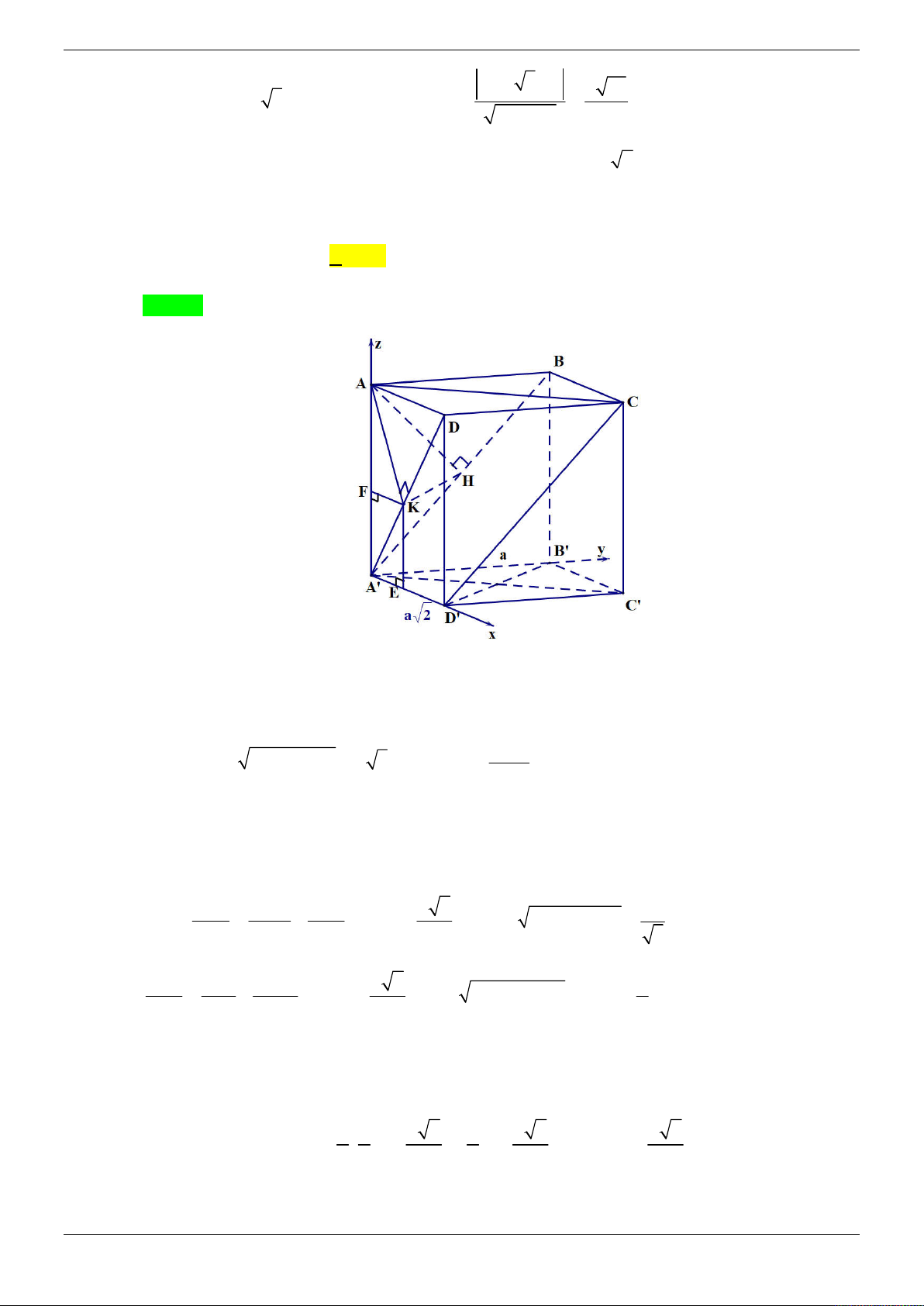
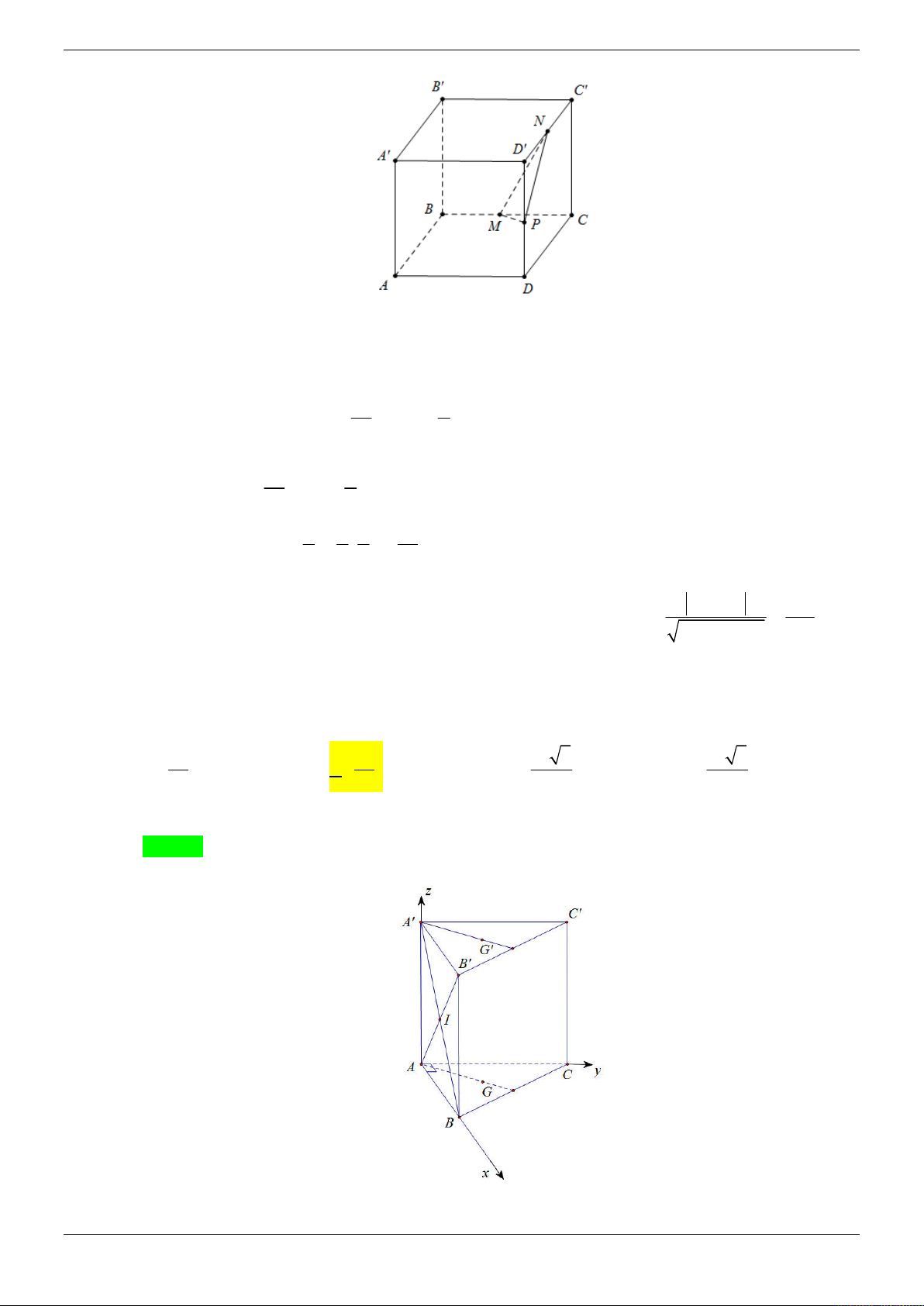
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, tam giác SAB đều. Hình chiếu của S
lên mặt phẳng  ABCD trùng với trung điểm I của AB . Gọi H , K lần lượt là trung điểm của a 7
DC và SB , biết SH
.Tính khoảng cách giữa HK và SC . 2 3 15 15 5 A. . B. . C. D. . 8 2 8 10 Lời giải Chọn D Trang 12/69 z S K A D y H I B C x
Đặt AB x 2 2  a 7   x 3  Ta có 2 2 2
SH SI IH 2     
  x x AB a  2   2     
Chuẩn hóa a  1. Chọn hệ toạ độ Oxyz sao cho  1  1  3 
O I 0;0;0   , B ; 0; 0   , C ;1; 0   , S  0; 0;   2   2   2     1 3 
H (0;1; 0) , K  ;0;   4 4      1 3    1 3    3  HK   ; 1;
, SC   ;1; 
, HS   0; 1;    4 4        2 2   2      3 3 3 
   3 3 3 3 3
HK, SC    ;
;  , HK , SC  .HS  .0  .  1  .     4 4 4      4 4 4 2 8
  
HK, SC  .HS   5
d HK, SC      .   10 HK , SC   Câu 5:
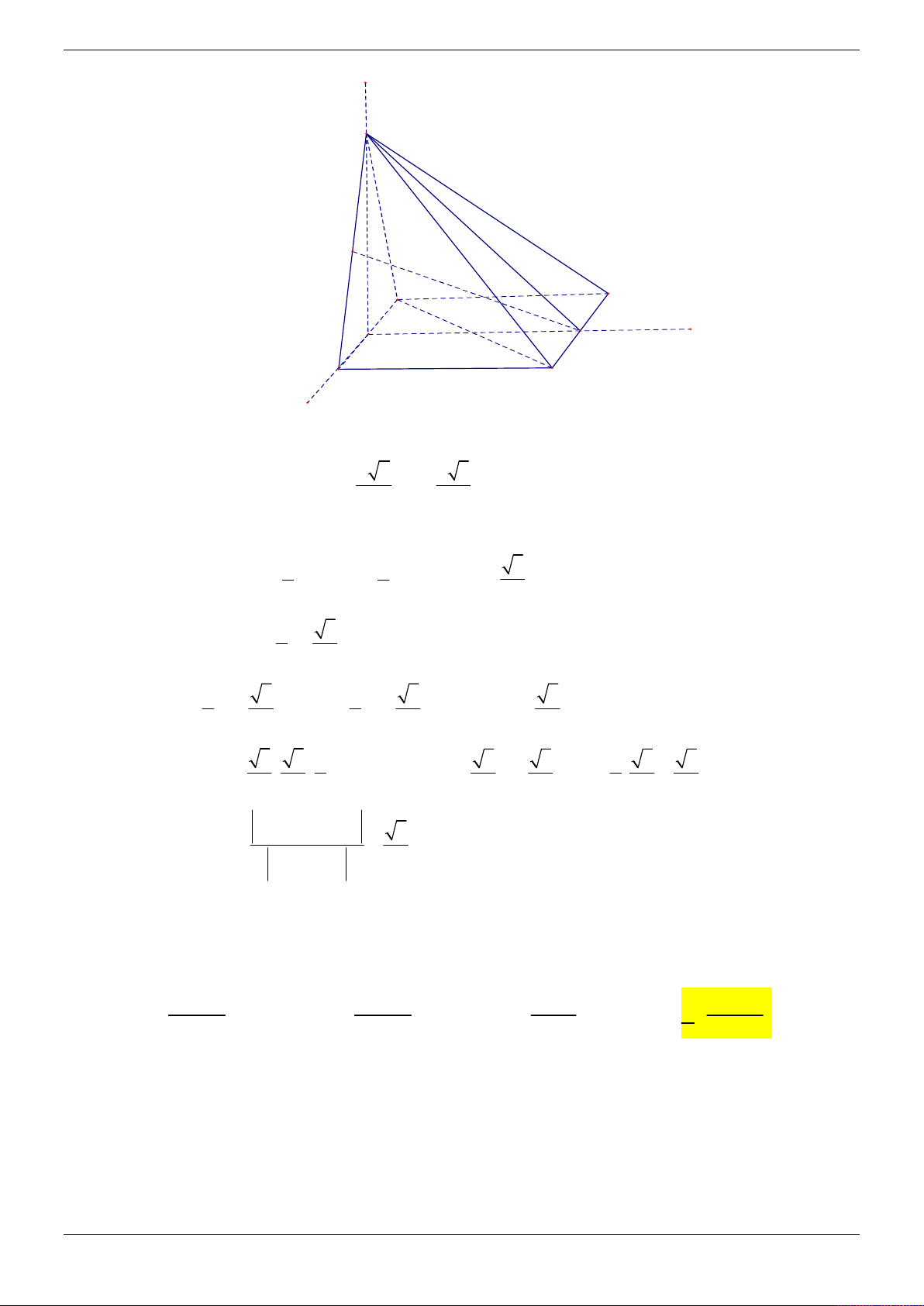
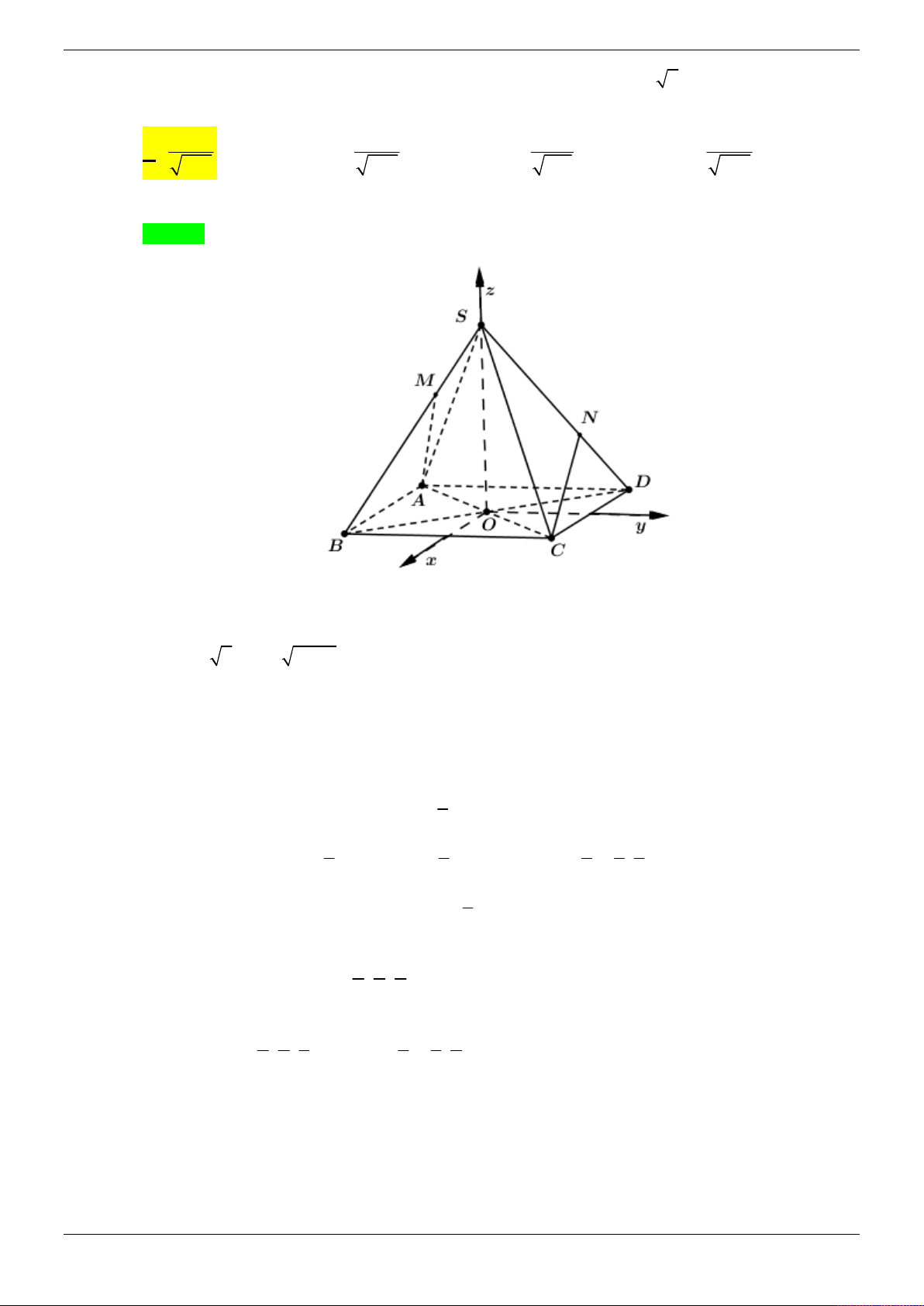
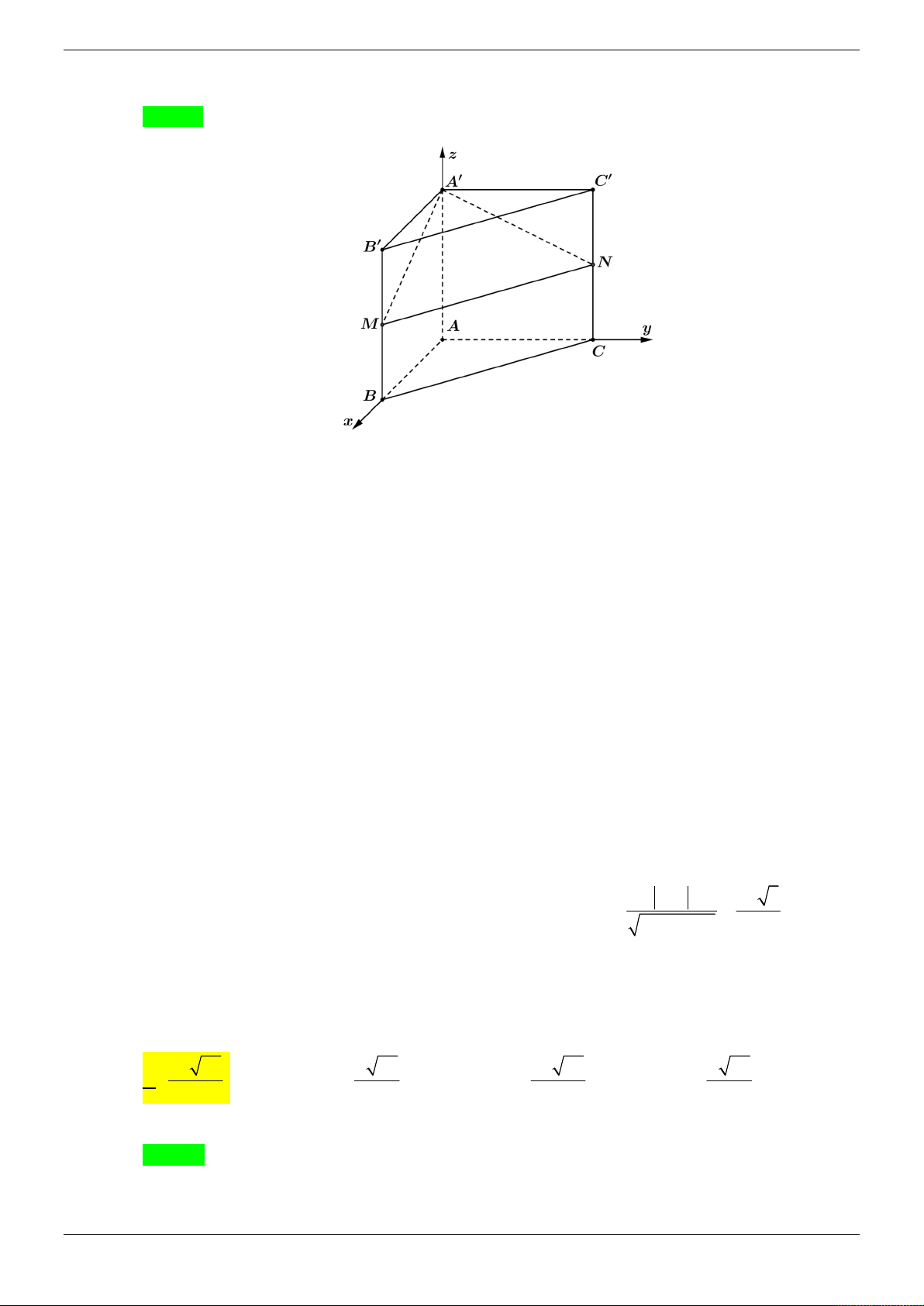
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với
đáy, AB a, AD  2a, SA  3a . Gọi M , N lần lượt là hình chiếu của A lên SB, SD và
P là giao điểm của SC với mặt phẳng  AMN  . Tính thể tích khối chóp S.AMPN . 3 1869a 3 5589a 3 181a 3 1863a A. . B. . C. . D. . 140 1820 120 1820 Lời giải Trang 13/69 z S P N M A y D B x C
Chọn hệ trục tọa độ như hình vẽ.
Ta có tọa độ các điểm A0;0;0, B  ;
a 0;0, D 0;2 ; a 0,C  ; a 2 ;
a 0, S 0;0;3a .   
Suy ra SB  a;0; 3
a, SD  0;2a; 3
a, SC  a;2a; 3  a .
x a t
Phương trình SB :  y  0  z  3t  
M a t;0; 3
t  AM  a t;0; 3  t .   a  9a 3a
Mà AM SB AM .SB  0  a t   9t  0  t   M ;0;   . 10  10 10   18a 12a
Tương tự vậy ta tìm được N 0; ;   .  13 13  2    27a
Suy ra n   AM , AN    1;2; 3  . 1     65
Do đó ta có phương trình của  AMN  : x  2 y  3z  0 .  x t
Phương trình SC :  y  2t
nên tọa độ điểm P là nghiệm của hệ
z  3a  3t   x t   y  2t 9a 9a 15a
 9a 9a 15a    x  , y  , z   P ; ;   .
z  3a  3t 14 7 14  14 7 14  
x  2 y  3z  0  2   27a 2   27a
Ta có:  AM , AP   1;2; 
3 ,  AN , AP  1;2;  3   70   91 2 1     621 14.a a Suy ra S  
AM , AP   AN , AP  
và d S AMN  9 ,  . AMPN 2       1820 14 2 3 1 9a 621 14.a 1863.a Vậy V  . .  . S . AMPN 3 14 1820 1820
Cách khác: (Công thức tính nhanh – trắc nghiệm) SA 2 SB SB 10 SC 2 SD SD 13 a   1; b    ; c  ; d    . SA 2 SM SA 9 SP 2 SN SA 9 Trang 14/69 14
Ta có a c b d c  . 9 V
a b c d 1863 1863 1863 1 1863 S . AMPN 3    VV  . . SA Sa . S . AMPN S . V 4 . a . b . c d 3640 3640 ABCD 3640 3 ABCD 1820 S . ABCD Câu 6:
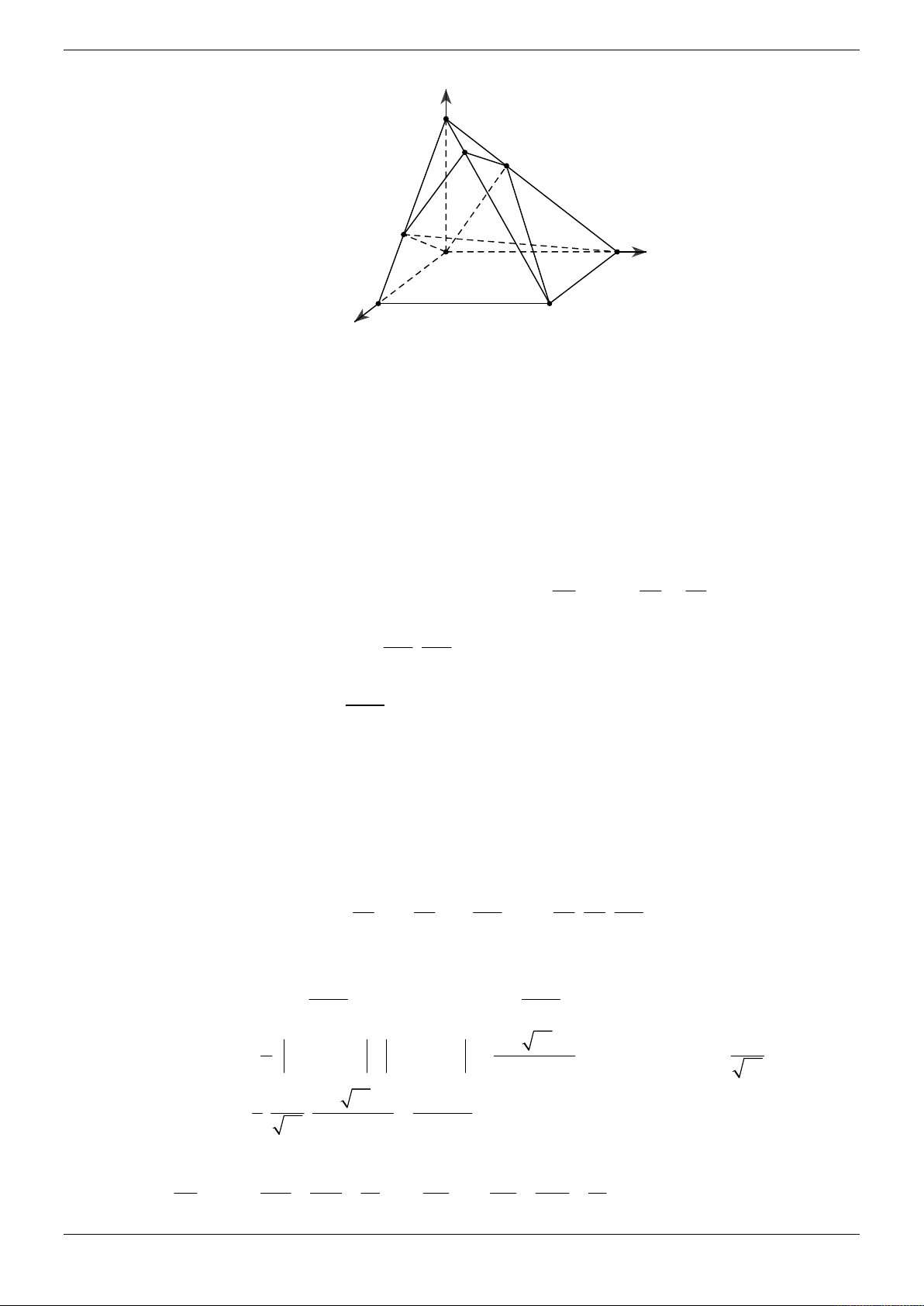
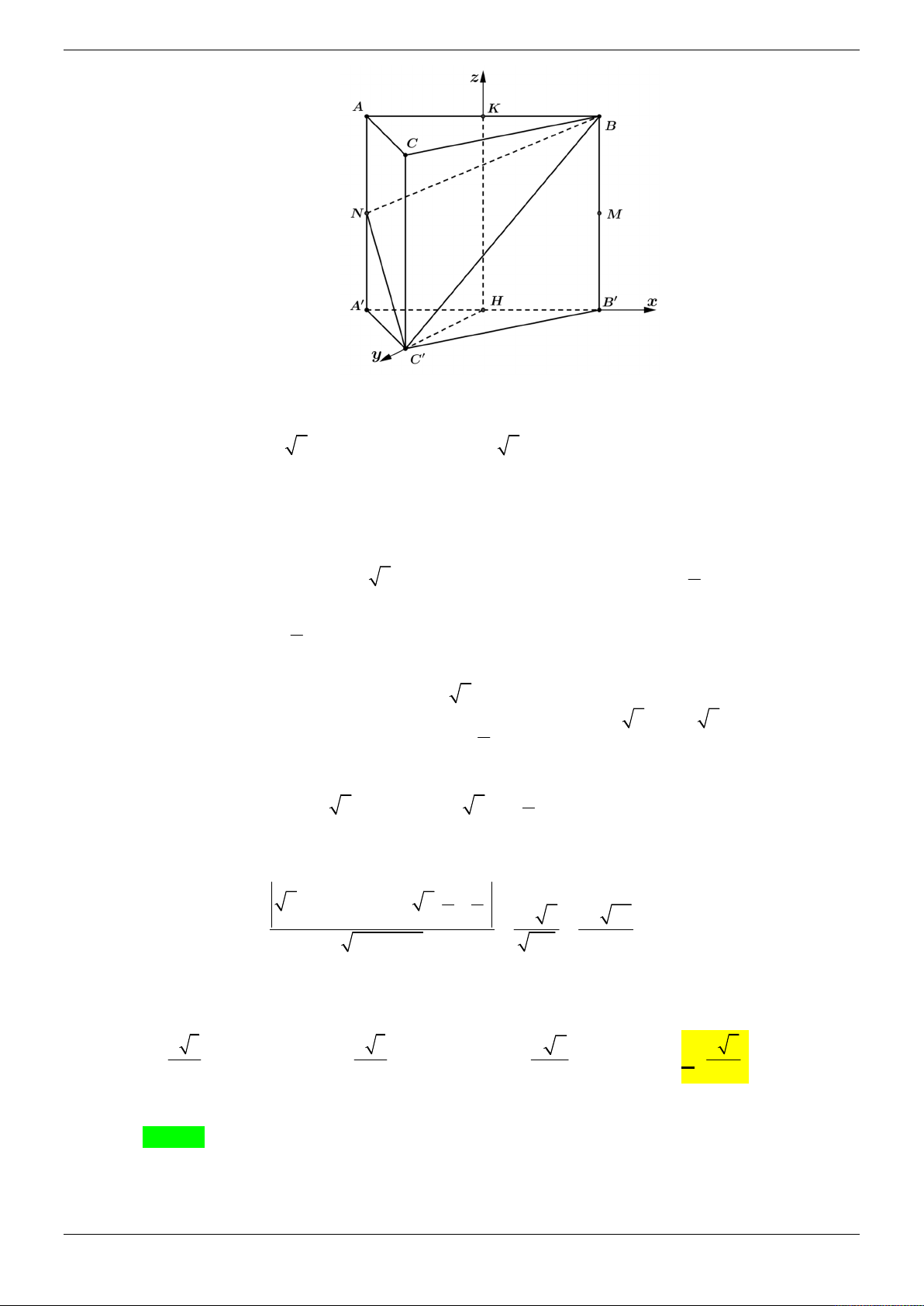
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2 , SA vuông góc với mặt
phẳng đáy  ABCD và SA  2 . Gọi M , N lần lượt là hai điểm thay đổi trên hai cạnh AB ,
AD sao cho mặt phẳng SMC vuông góc với mặt phẳng SNC . Thể tích khối chóp
S.AMCN đạt giá trị nhỏ nhất bằng 4 3  4 8 3  8 4 3  4 A. . B. . C. 2 3  2 . D. . 3 3 3 Lời giải Chọn B
Chọn hệ trục tọa độ Oxyz như hình vẽ trên sao cho A0;0;0 , B2;0;0 , D0;2;0 , S 0;0;2
, suy ra C 2;2;0 .
Đặt AM m , AN n , ,
m n 0;2, suy ra M  ;
m 0;0 , N 0; ; n 0 .    SM   ; m 0; 2
  , SC  2;2; 2
  , SN  0; ; n 2   .        n
 SM , SC   4; 2m  4; 2m , n
 SN , SC   4  2 ; n 4; 2n . SNCSMC         
 
Do SMC  SNC nên n .n  0  4  n m   mn SMC SNC 4 2  42 4 4 0    
mn  2m n  8. 2 2  m n  m n
Mặt khác mn  2m n   2  
m n nên ta có
 2m n  8  0  2  4
m n  4 3  4  
. Do m, n  0 nên m n  4 3  4 . m n  4  3  4  SSSS
 4  2  m  2  n  m n  4 3  4 . AMCN ABCD BMC DNC 1 2 8 3  8 V  . SA Sm n  . S . AMCD AMCN   3 3 3 Trang 15/69 8 3  8
Vậy thể tích nhỏ nhất của khối chóp S.AMCN là . 3 Câu 7:
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B , AB BC a , AD  2a ;
cạnh bên SA vuông góc với mặt phẳng đáy và SA a . Gọi M , N lần lượt là trung điểm của
SB , CD . Tính cosin của góc giữa MN và SAC . 2 55 3 5 1 A. . B. . C. . D. . 5 10 10 5 Lời giải Chọn B z S a M 2a y A D a N B a C x
Chọn hệ trục Oxyz như hình vẽ, với O A.
Tọa độ các đỉnh của hình chóp là : A0;0;0 , B ;
a 0;0 , C  ; a ;
a 0 , D0;2 ;
a 0 , S 0;0;a .  a a   a 3a   M ; 0;   , N ; ; 0   .  2 2   2 2  1   1   Ta có:  SA  0;0  ;1  u ; SC  1;1;   1  v . a a   
Một véc tơ pháp tuyến của mặt phẳng SAC là n  u,v   1  ;1;0 . 2   Lại có: MN  0;3;   1  w . a   n.w 3 55
Gọi  là góc giữa MN và SAC ta có: sin      cos  . n . w 2 5 10 Câu 8:
Cho hình chóp S.ABC có A
BC vuông tại B , AB  1, BC  3 , S
AC đều, mặt phẳng
SAC vuông với đáy. Gọi  là góc giữa hai mặt phẳng SAB và SBC . Giá trị của cos bằng 2 65 65 65 65 A. B. C. D. 65 20 10 65 Lời giải Chọn D Trang 16/69
Gọi H , M , N lần lượt là trung điểm của AC , AB, BC .
SAC   ABC  SH   ABC  SH HM , SH HN . A
BC vuông tại B HM HN . A
BC vuông tại B AC  2  SH  3 . 1 3 1 1 HM BC  ; HN AB  . 2 2 2 2  3   1 
Chọn hệ trục tọa độ như sau: H 0;0;0 ; S 0;0; 3 ; M 0; ; 0  ; N ; 0; 0 ,    2     2   1 3  B  ; ; 0   2 2       1   3  BM   ; 0; 0   BN   0;  ; 0   2   2      1 3     BS  1 3   ;  ; 3   BS    ;  ; 3 2 2      2 2        3 3      3 3 
n  BM , BS    0; ;
; n  BN , BS     ;0;  1      2 4  2       2 4   3    16 65
cos  cos n ;n   . 1 2  3 3 9 3 65  .  4 16 4 16
Chú ý: Ta có thể chứng minh công thức tổng quát sau:
Cho hình chóp S.HMBN có đáy HMBN là hình chữ nhật có HM m, HN n và
SH  (HMBN ) và SH h . Gọi  là góc giữa hai mặt phẳng  MSB và  NSB thì mn cos  . 2 2 2 2 m h n h Trang 17/69 S h E F H n N m K M B
Ta có: BN  (SHN ) nên dựng HE SN tại N thì HE  (SNB) .
Dựng hình bình hành HEKM MK  (SNB)  Hình chiếu của M
SB trên SNB là KSB . 1 1 S 2S Ta có: 2 2 SM . B MS
n m h  cos KSB KSB    MSB 2 2 2 2 SMSB n m h
Gọi F EK SB ta có: S S FK SE KE EF SEKESE KSB . ESB  .  .  1 .   S S FE SN FE SNEFSN ESB NSB 2 2  SNSE h n 2 2 SE SE.SN SH h = 1  1    (vì    ) 2 2 2 2 2 2 2 2  SESN n h n h SN SN SN n h 2 2 2 2 2 n n m n h mnSS  .  . KSB 2 2 NSB 2 2 2 2 n h n h 2 2 n h S mn Vậy cos KSB    . 2 2 2 2 SMSB m h n h 3 1 65
Áp dụng vào bài toán với h  3, m  , n  ta được cos  . 2 2 65 Câu 9:
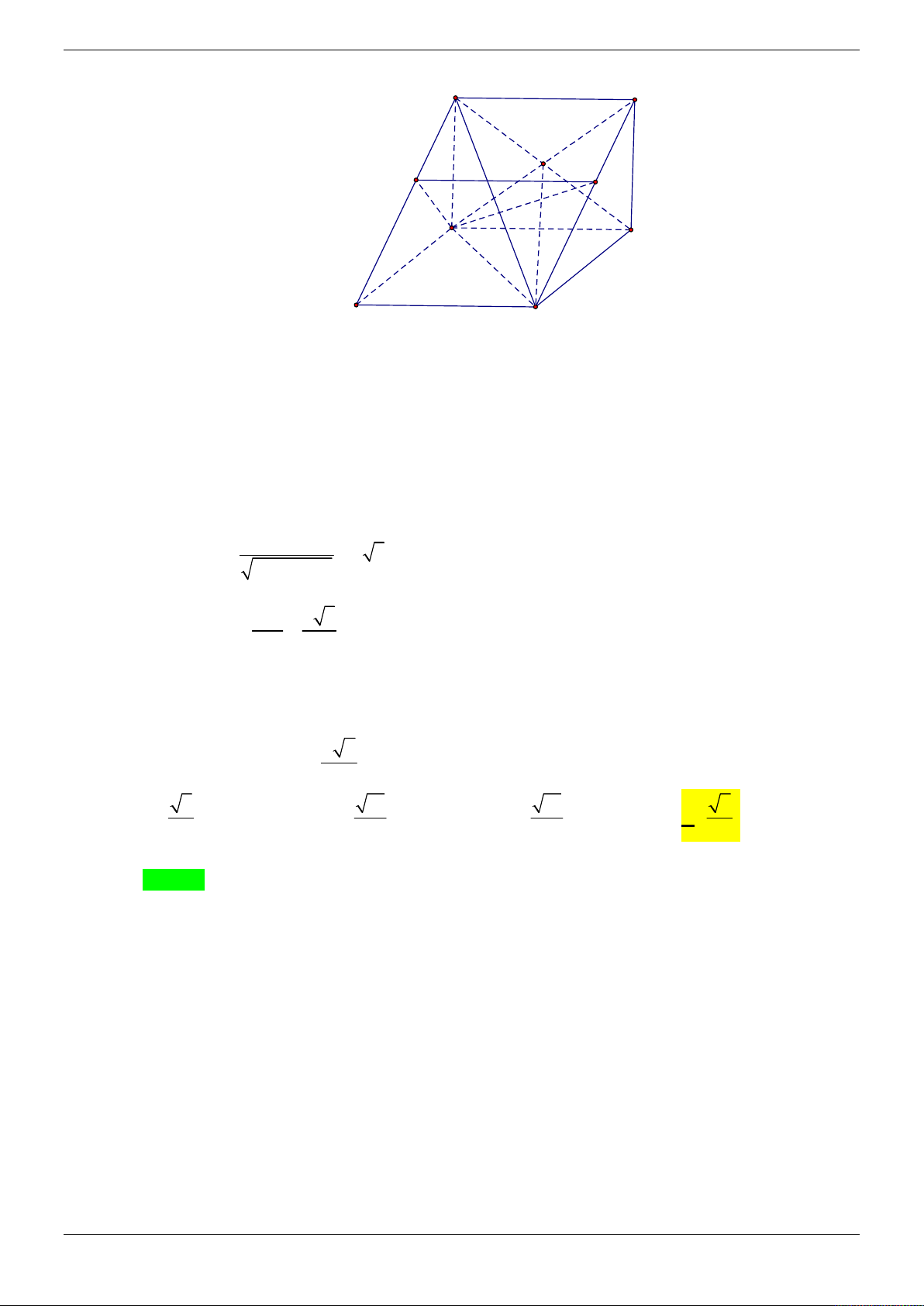
Cho hình lập phương ABCD.AB CD
  có các cạnh bằng 2 , gọi điểm M là tâm của mặt bên ABB A
  , các điểm N, P, ,
Q K lần lượt là trung điểm của các cạnh AC, DD ,  D C  , B C   . Tính
cosine góc giữa hai mặt phẳng MNP và  AQK  . 2 1 102 3 A. . B. . C. . D. . 2 2 34 4 Lời giải Chọn C Trang 18/69 A D N B P C M A' D' Q B' K C'
Ta chọn hệ trục tọa độ Oxyz với gốc A  O cạnh AB nằm trên Ox , cạnh A D
  nằm trên Oy
và cạnh AA nằm trên Oz . Từ các dữ kiện đề bài đã cho ta tìm được tọa độ các điểm M 1; 0; 
1 , N 1;1; 2, P 0; 2; 
1 , K 2;1; 0,Q 1; 2;0, A0;0; 2    
Ta có MN  0;1  ;1 , NP   1  ;1;   1 , AK  2;1; 2
 , AQ  1; 2; 2   .  
Gọi u ,u lần lượt là 2 vector pháp tuyến của mặt phẳng MNP và  AQK  . 1 2  
Như vậy ta tính được u 2  ; 1  ;1 ,u 2; 2;3 . 1   2  
Ta gọi góc giữa hai mặt phẳng MNP và  AQK  là  .   u .u 1 2 2.2  1.2 1.3 102
Như vậy cos  được tính theo công thức cos       . 2 2 2 2 2 2 u u 34 2 1 1 2  2  3 1 2
Câu 10: Cho hình chóp S . AB C D có đáy ABCD là hình vuông cạnh bằng a . S A vuông góc với mặt 3a
phẳng đáy. H và K là hai điểm lần lượt nằm trên hai cạnh BC và CD sao cho BH  , 4
KD x (0  x a) . Tìm giá trị của x để hai mặt phẳng  SAH  và  SAK  tạo với nhau một góc bằng 45 . a a 2a 2a A. x  . B. x  . C. x  . D. x  . 7 5 7 5 Lời giải Chọn A Trang 19/69
Ta chọn hệ tọa độ Oxyz như hình vẽ.
Khi đó A0;0;0; B ;
a 0;0; D0; ;
a 0; S Oz .  3a
Qua đó ta có tọa độ các điểm C  ; a ; a 0; H ; a ; 0 ; K    ; x ; a 0 .  4 
  3a  
Ta có: AH a; ; 0 ; AK     ; x a; 0 .  4   k  0;0;  1     a  Ta có  3     3ak, AH   ; a; 0   . AH a; ; 0       4    4     3 
Gọi n là một véctơ pháp tuyến của mặt phẳng  SAH  thì n  ;1; 0   .  4   k   0;0;  1   Ta có 
 k, AK   a; x;0 .  
AK   x; a; 0   
Gọi n là một véctơ pháp tuyến của mặt phẳng  SAK  thì n   ; a ; x 0 .
Gọi  là góc giữa hai mặt phẳng SAH  và  SAK  , khi đó   3a x 2 . n n 4  3a  25
cos     cos 45   2  x     2 2 a x  2 n . n  4  16  3  1.   a2 2  x  4  a 2 2
 7x  48ax  7a  0  x  do x  0. 7 a Vậy x  . 7 Cách khác:
Ta có: SA  ( ABCD)  SA AH , SA AK .
Gọi  là góc giữa hai mặt phẳng SAH  và  SAK  . 
Suy ra   HAK  45 . Trang 20/69 2 2  3a  5aa  2 Ta có 2 AH a     ; 2 2
AK a x và HK     a x .  4  4  4 
Áp dụng định lí Cosin cho tam giác AHK ta có: 2 2 2 0
HK AH AK  2 AH .AK cos 45 2 2 a 25a 5a 2  2 2 2 2 2
 (a x) 
a x  2. . a x . 16 16 4 2 3a 5 2  2 2 2x   . a x  2 2
5 2 a x  6a  8x 2 4  2 2 2 2
50(x a )  64x  96ax  36a a  2 2
14x  96ax 14a  0 2 2
 7x  48ax  7a  0  x  do x  0. 7 a Vậy x  . 7
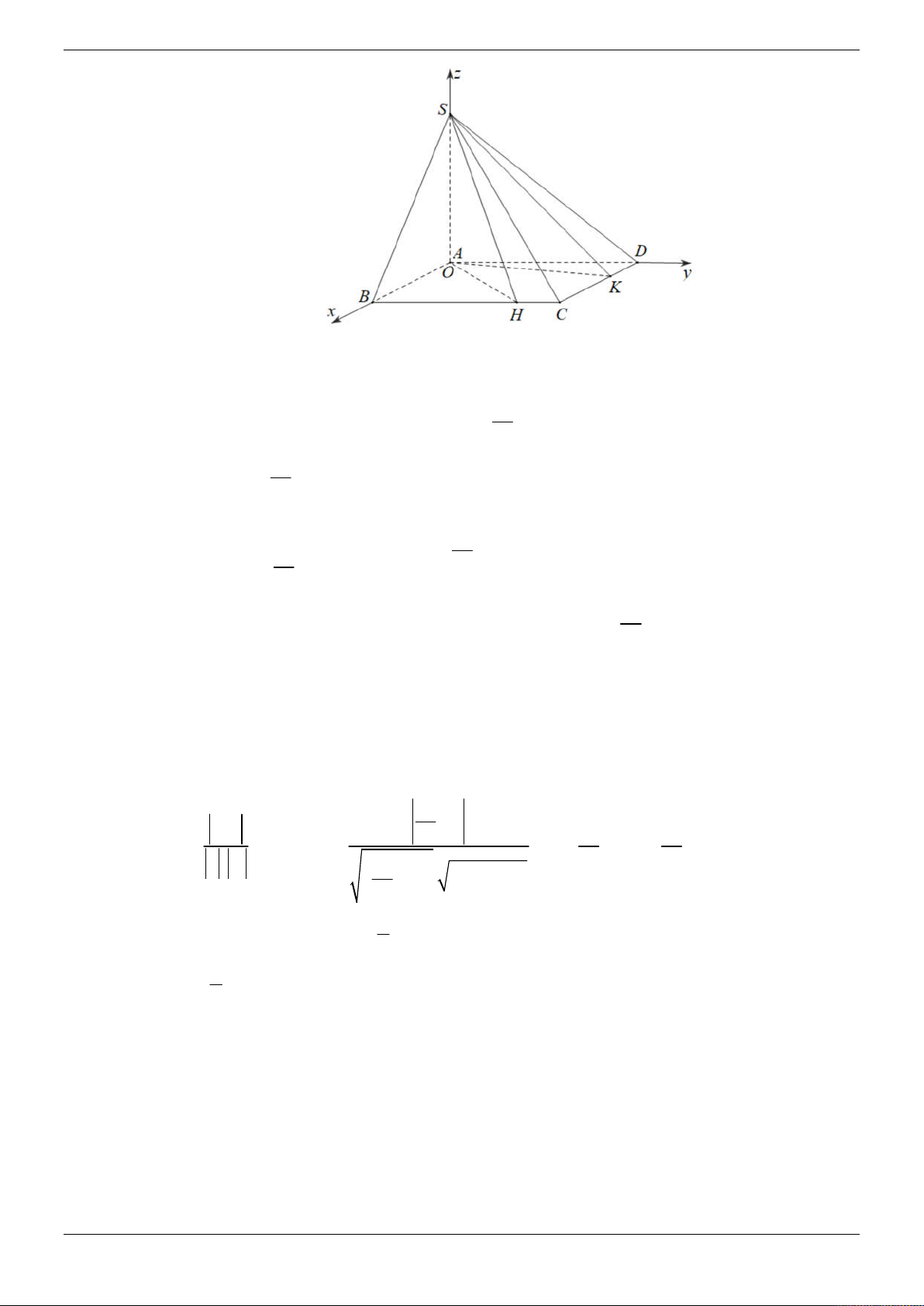
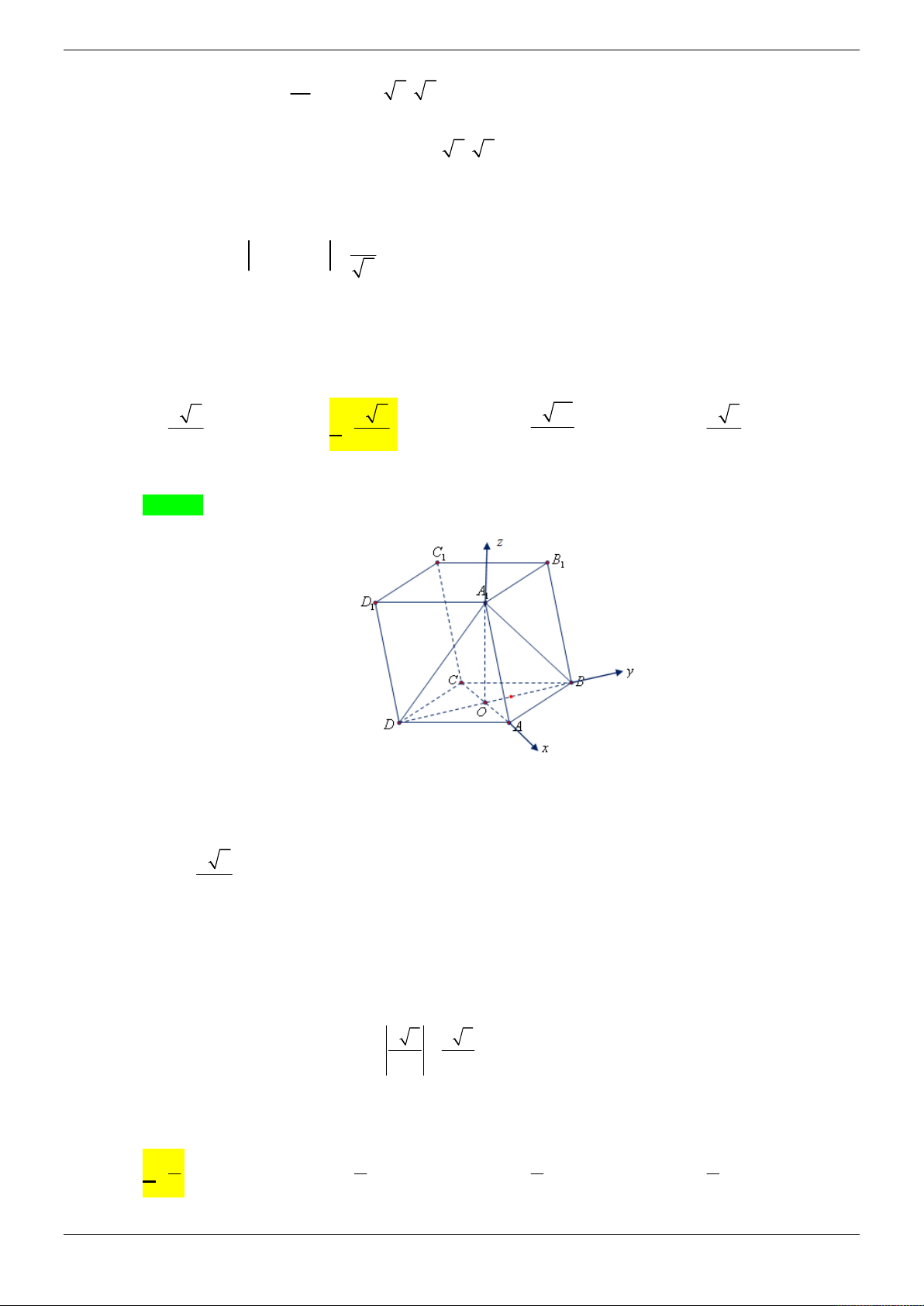
Câu 11: Trong không gian, cho tam giác OAB cân ở O có  4
OA OB  5; tan AOB  . Điểm C di 3
động trên tia Oz vuông góc OAB , gọi H là trực tâm của tam giác ABC . Khi C di động
trên tia Oz thì H luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng: 5 3 5 A. . B. . C. . D. 3 . 4 2 2 Lời giải Chọn A z C H y O K B E x A
Chọn hệ trục tọa độ Oxyz có gốc O , tia Ox trùng tia OA, tia Oy nằm trong mặt phẳng OAB
sao cho tia OB nằm giữa hai tia Ox, Oy như hình vẽ. Khi đó A5;0;0 và B3;4;0 . Trang 21/69
Giả sử C 0;0;c . Dễ thấy tam giác ABC cân tại C . Gọi E  4; 2;0 là trung điểm của AB .
Ta có mặt phẳng OCE  vuông góc với AB và là mặt phẳng cố định.
Gọi K là trực tâm tam giác OAB , do A , B và K cùng nằm trong mặt phẳng Oxy .    x  3  OK.AB  0   . x  2    .4 y  0   3  Giả sử K  ; x ;
y 0 , ta có      
3 . Tìm được K  3; ; 0   BK.OA  0  x  3  0  y    2   2 .  AB   OEC  HK AB Do   
KH  CAB 
KH HE KHE  90 . CA    BHK HK CA   1 5
Do đó H thuộc mặt cầu đường kính KE  1 
và thuộc mặt phẳng OCE  cố định. 4 2 5
Vậy H luôn thuộc một đường tròn cố định có bán kính R  . 4 Cách khác: C M N B O H K E A
Gọi E là trung điểm AB . Ta có AB  (OCE) nên AB CE do đó H thuộc CE nên H luôn
nằm trong mặt phẳng (OCE) cố định.
Gọi K là trực tâm OAB , ta có:  AK OB
AK  (OBC)  AK BC mà AH BC AK OC
nên BC  ( AHK )  HK BC mà HK AB HK  ( ABC)   0
KHE  90  H thuộc đường tròn đường kính KE nằm trong (OCE) cố định. 1 1 9 2   3 Ta có: cos AOB     cos AOB
OM  3, AM  4 . 2  16 1 tan AOB 25 5 1 9
MN  1, ON  4, NE  2 (N là trung điểm MB) Trang 22/69  2 2
OE ON NE  2 5 . KE NM 1 OE 5 Lại có    KE   . OE ON 4 4 2 KE 5
Vậy bán kính của đường tròn đường kính KE là R   . 2 4 
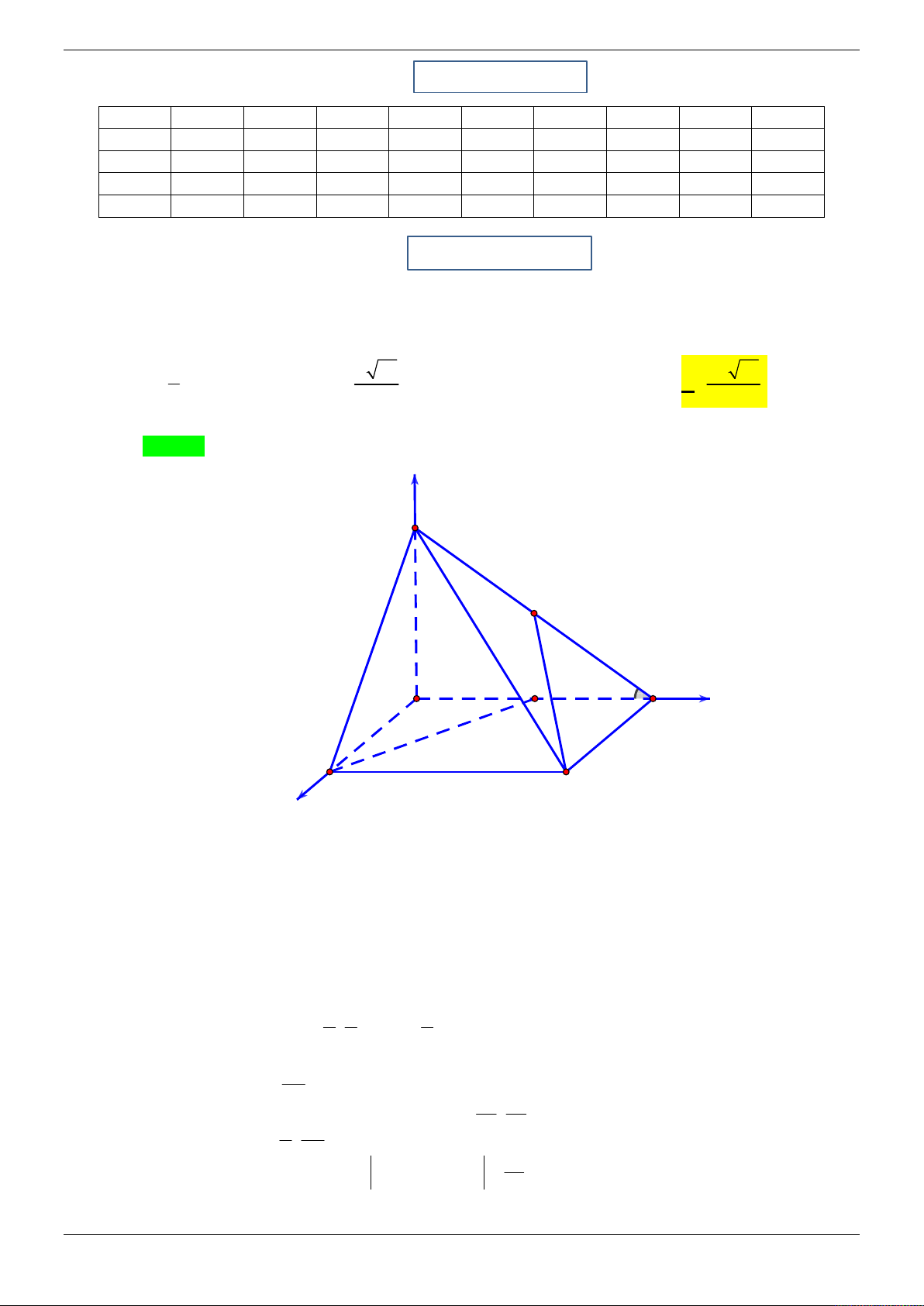
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh a , góc BCD  120 . 3 a 3
SA   ABCD . Thể tích khối chóp S.ABCD là
. Gọi M là tâm đường tròn ngoại tiếp 3
tam giác SOD . Hãy tính khoảng cách h từ M tới mặt phẳng SBC  theo a . a 57 a 57 2 5a 2 5a A. h  . B. h  . C. h  . D. h  . 19 38 5 19 Lời giải Chọn A S z S M M K y A D D A O B B x H C C
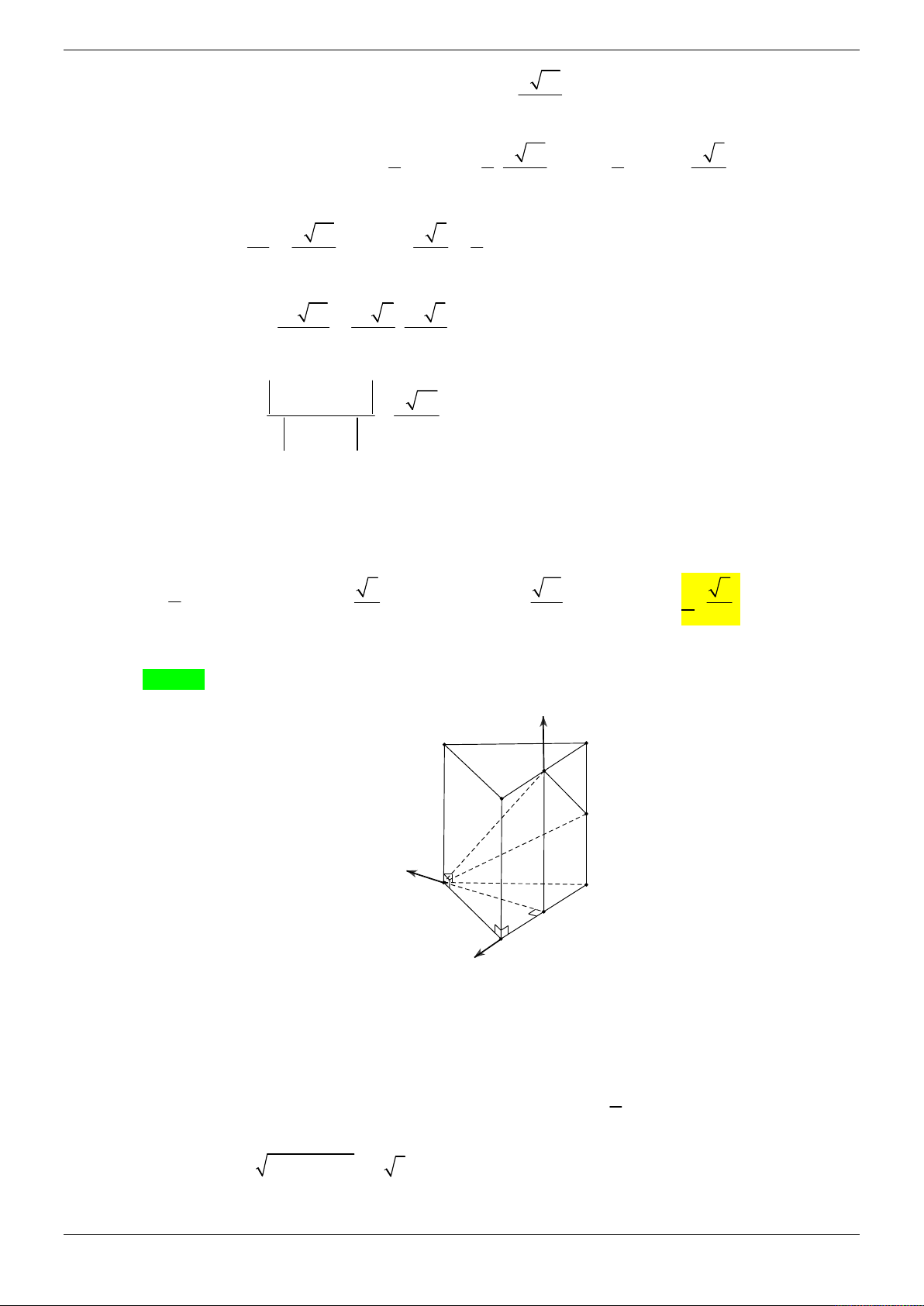
Cách 1: Phương pháp dựng hình
Tam giác SOD vuông tại O nên M là trung điểm của SD . DM 1 1 Ta có 
d M ,SBC  d D,SBC ; AD//BC . DS 2 2 1 1
AD// SBC   d D,SBC   d  ,
A SBC  . Vậy d M ,SBC   d  , A SBC  2 2
Gọi H là trung điểm của BC , do tam giác ABC đều nên AH BC , lại có
SA   ABCD   SA BC nên BC   SAH    SBC    SAH
Dựng AK SH AK  SBC   d  ,
A SBC   AK . 2 a 3
Diện tích hình thoi ABCD là: 0 SA . B BC.sin 60  ABCD 2 3V a 3 Từ đó suy ra S . ABCD SA
 2a . Tính được AH S 2 ABCD
Tam giác SAH vuông tại A, đường cao AK nên: Trang 23/69 1 1 1 4 1 19 a 228       AK  . 2 2 2 2 2 2 AK AH SA 3a 4a 12a 19 a
Vậy d M SBC  1 57 ,  AK  . 2 19
Cách 2: Phương pháp tọa độ
Không mất tính tổng quát, ta giả sử a  1.
Chọn hệ trục tọa độ như hình vẽ, Oz//SA. Khi đó ta có  1     3   1 
O 0; 0;0, A ; 0; 0 , B    0; ; 0  ,C ; 0; 0   . 2  2     2     3   1    1  3  D  0; ; 0   S ; 0; 2 , M    ; ;1 .  2  2  4 4          1  3    SB   ;
;  2  , SC  1;0;  2 .  2 2       3  Ta có n  S ,
B SC   3 ;1; . SBC     2    3 3
Phương trình mặt phẳng SBC là: 3x y z   0 . 2 2 3 57
Suy ra d M SBC  2 ,   . 3 19 3 1 4 a
Vậy d M SBC  57 ,  . 19
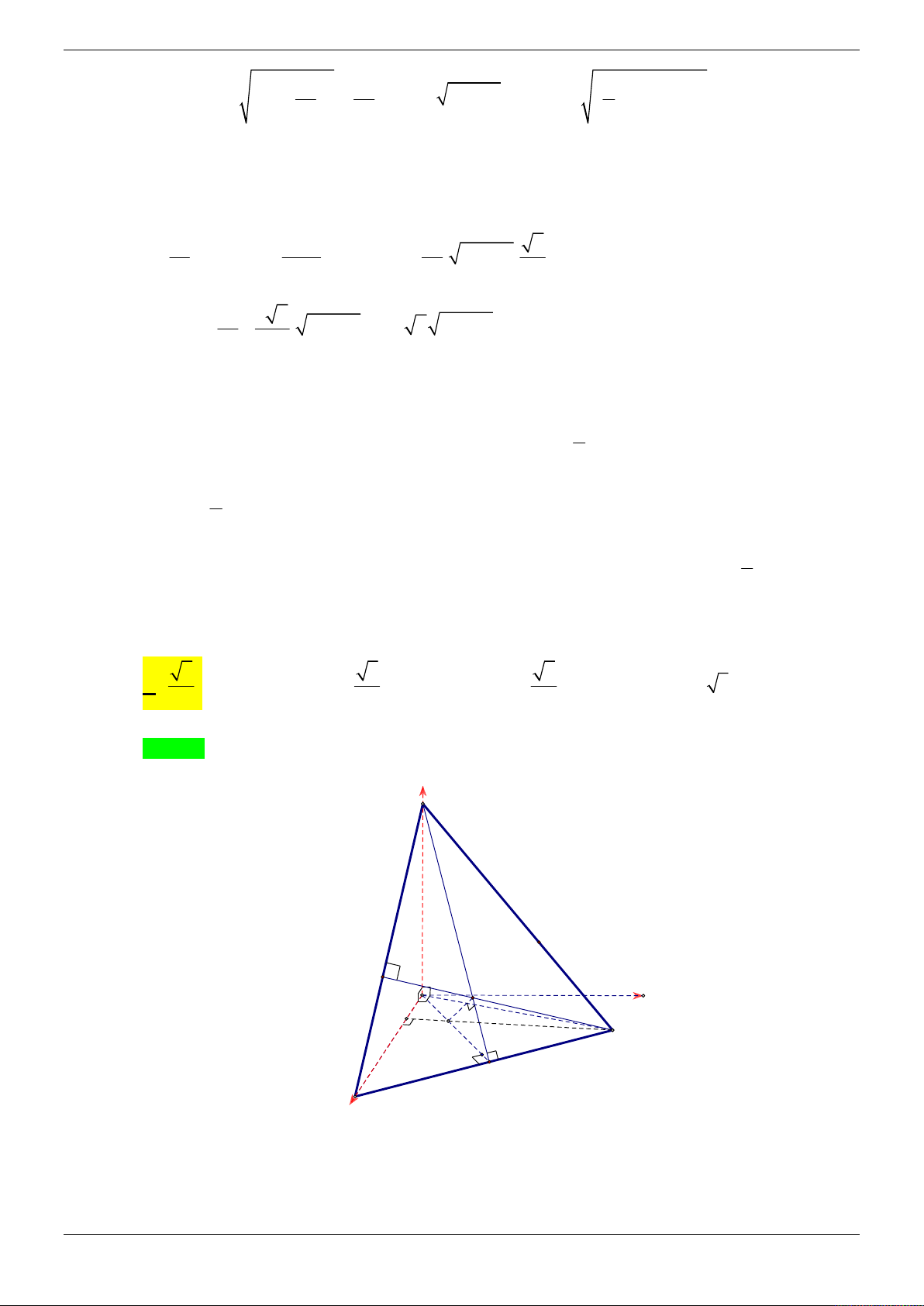
Câu 13: Cho tam giác ABC vuông tại A và đường thẳng  vuông góc với mặt phẳng  ABC tại điểm
A . Các điểm M , N thay đổi trên đường thẳng  sao cho  MBC   NBC . Biết
AB b, AC c . Giá trị nhỏ nhất của thể tích tứ diện MNBC theo b và c bằng 2 2 3b c 2 2 b c bc 2 2 b c A. . B. . C. . D. . 2 2 b c 2 2 b c 2 2 3 b c 2 2 3 b c Lời giải Chọn D
Chọn hệ trục tọa độ Oxyz sao cho OA , các tia Ox, Oy, Oz lần lượt trùng với các tia
AB, AC , AM .
Đặt AB b, AC c, AM m (b, c không đổi). Trang 24/69
Khi đó A0;0;0, B ;
b 0;0, C 0; ;
c 0, M 0; 0; m . Giả sử N 0; 0; n. Ta có:   x y z  1 1 1  MBC  :  
1  0 có một véctơ pháp tuyến là  ; ;   . b c mb c m    x y z  1 1 1 
NBC :   1  0 có một véctơ pháp tuyến là  ; ;   . b c nb c n    1 1 1 2 2 b .c
Vậy  MBC   NBC  .  0     0  . m n   mn  0. 2 2 b c mn 2 2 b c
Mặt khác m  0 nên n  0 . Vậy M và N nằm về hai phía của A .      Ta có BC   ; b ;
c 0, BM   ;
b 0; m, BN   ;
b 0; n , BM , BN   0;bn m;0.  
1    1 1 Vậy VMNBC =
BC. BM , BN  
bc n m  bc m n . 6   6 6 2 2 b c Ta có . m n  không đổi. 2 2 b c 2 2 1 1 1 b c
Áp dụng bất đẳng thức Cauchy ta có VMNBC = bc m n  .b . c 2 .
m n  . . 2 2 6 6 3 b c bc
Dấu đẳng thức xảy ra khi và chỉ khi m  n  . 2 2 b c A . B AC
Vậy VMNBC nhỏ nhất khi M , N nằm về hai phía của A và AM AN  . BC 2 2 1 b c
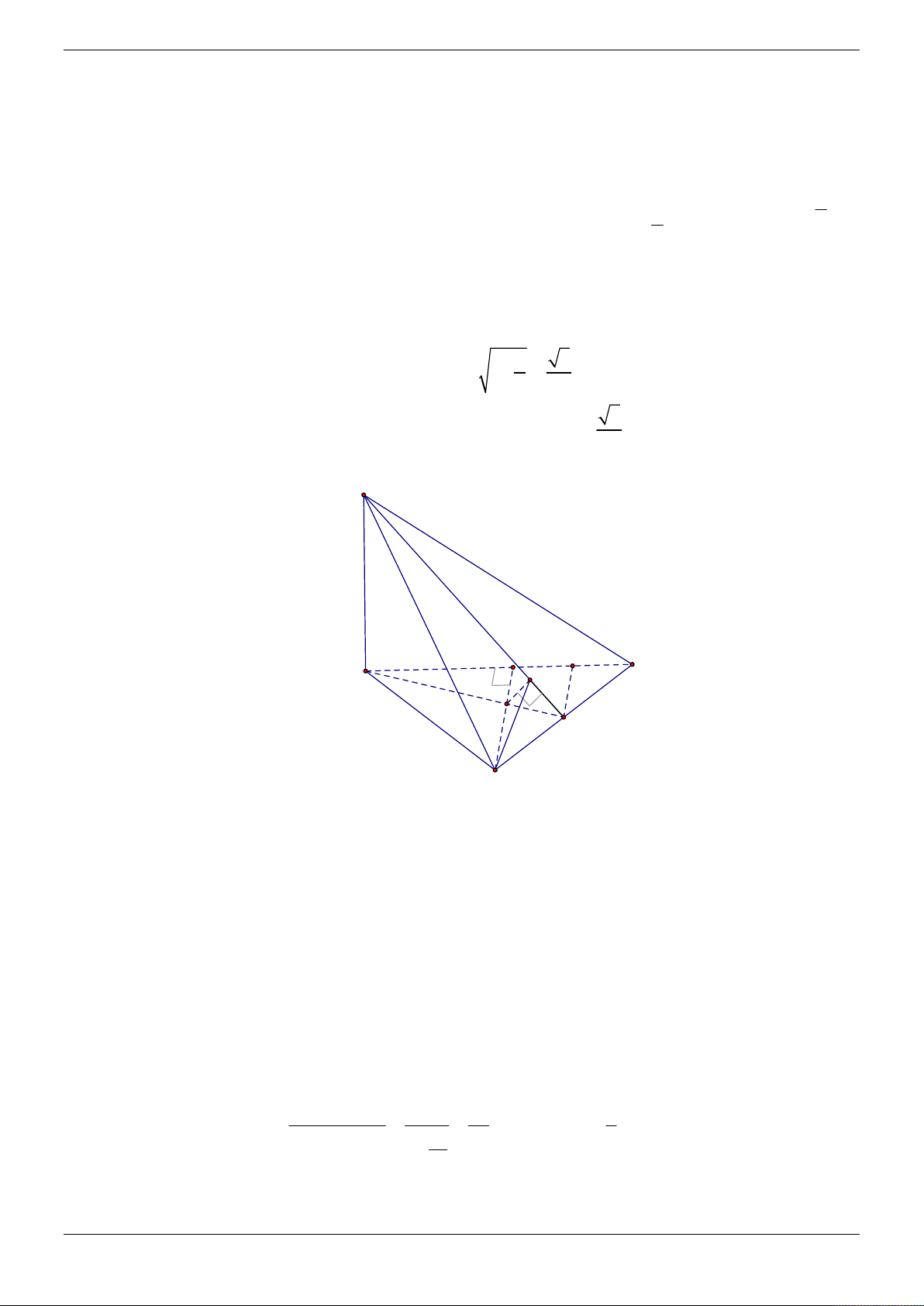
Khi đó giá trị nhỏ nhất của thể tích tứ diện MNBC bằng . . 2 2 3 b c Cách khác: Trang 25/69 M C A H B N
Dựng AH BC , ta có BC  (MHN ) nên H
MN vuông tại H. 2 2 b c Do đó 2
AM .AN AH  2 2 b c
Khi đó thể tích tứ diện MNBC là 1 1 1 1 VVVAM .SAN.S
  AM AN .S
bc AM AN MNBC MABC NABC 3 ABC 3 ABC 3 ABC 6 2 2 1 b c  .2 bc AM .AN  . 2 2 6 3 b c bc
Dấu “=” xảy ra  AM AN  . 2 2 b c 2 2 b c Vậy minV  . MNBC 2 2 3 b c
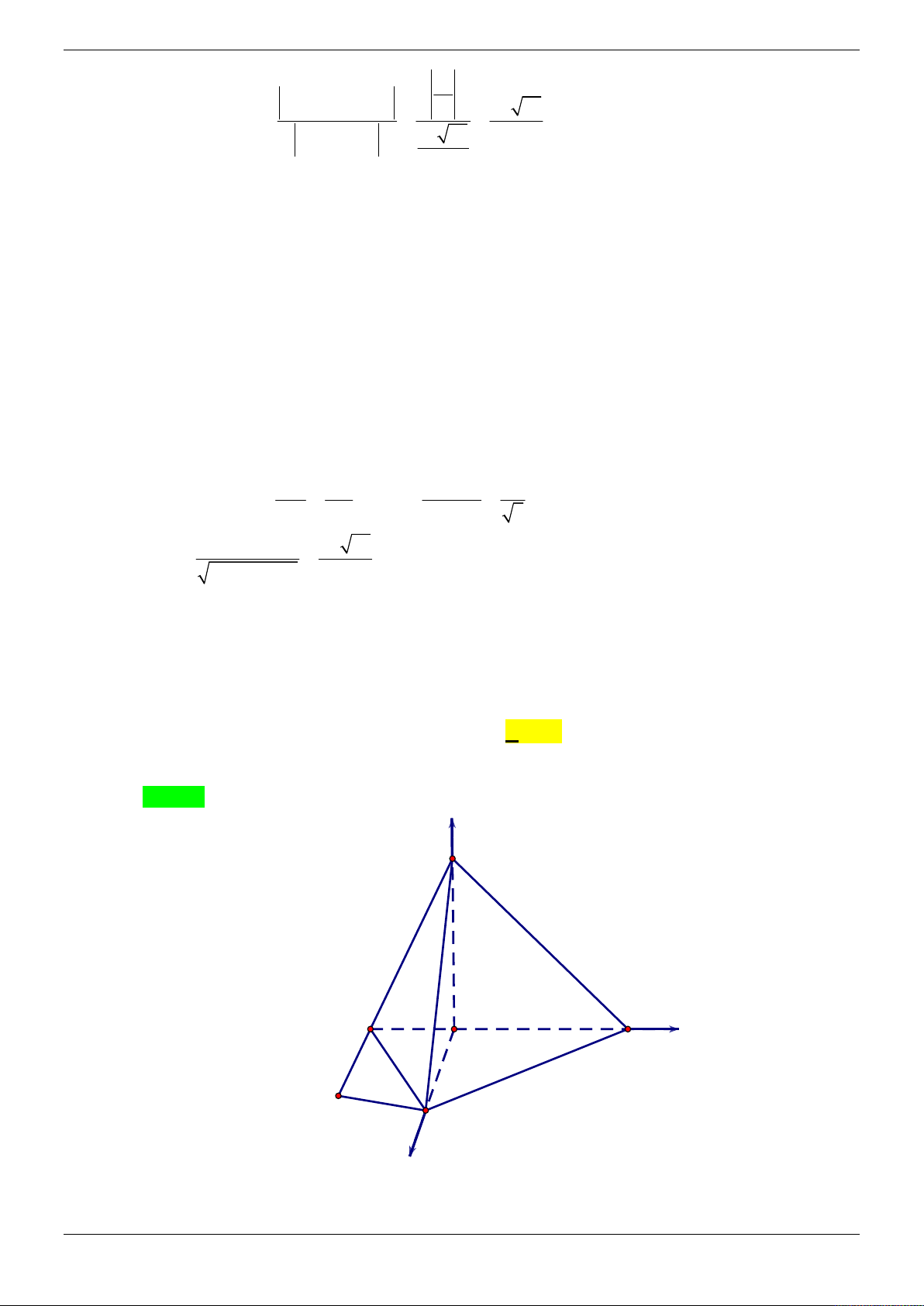
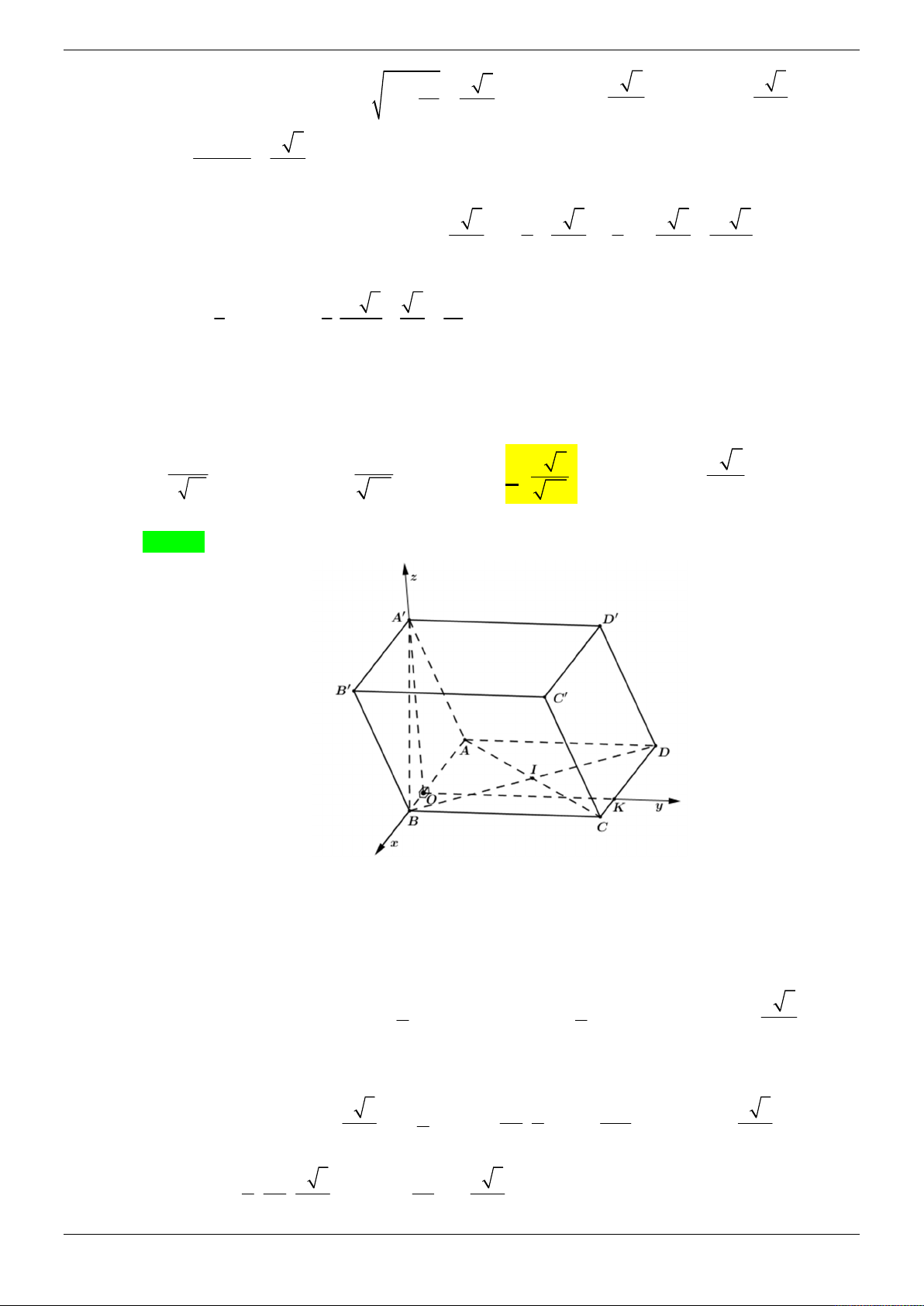
Câu 14: Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a , tâm O . Gọi M và a 6
N lần lượt là trung điểm của hai cạnh SA và BC . Biết MN  , tính sin của góc giữa 2
đường thẳng MN và mặt phẳng SBD . 2 3 5 A. . B. . C. . D. 3 . 5 3 5 Lời giải Chọn B Trang 26/69
Gọi I hình chiếu của M lên  ABCD , suy ra I là trung điểm của AO . 3 3a 2 Khi đó CI AC  . 4 4
Áp dụng định lý cosin ta có: 2 2 a a a a a o 9 3 2 2 10 2 2
NI CN CI  2CN.CI.cos 45    2. . .  . 4 8 2 4 2 4 2 2 3a 5a a 14 Do M
IN vuông tại I 2 2 nên MI MN NI    . 2 8 4 1 a 14
Mà MI / /SO, MI SO SO  . 2 2
Chọn hệ trục tọa độ Oxyz như hình vẽ.  2   2   2 
Khi đó ta có tọa độ các điểm: O 0;0;0 , B  0; ; 0  , D  0;  ; 0 , C  ; 0; 0 ,    2        2   2    2 2   2   14   2 14  N  ; ; 0  , A  ; 0; 0 , S  0;0; , M   ; 0 ; .     4 4          2   2   4 4     2 2 14    2 14    2 14  Khi đó MN   ; ;   , SB   0 ; ;  , SD   0;  ;  .    2 4 4        2 2   2 2     
Vectơ pháp tuyến mặt phẳng SBD : n  SB , SD  .    7 ;0;0 2   . 7  MN.n 2 3
Suy ra sin MN ,SBD      . MN . n 6 3 . 7 2 Trang 27/69
Câu 15: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Gọi M và N lần lượt là trung
điểm các cạnh AB và AD ; H là giao điểm của CN và DM . Biết SH vuông góc với mặt
phẳng ( ABCD) và SH a 3 . Tính khoảng cách giữa hai đường thẳng DM và SC theo a . 2a 57 a 57 2a 13 a 7 A. . B. . C. . D. . 19 19 19 19 Lời giải Chọn A
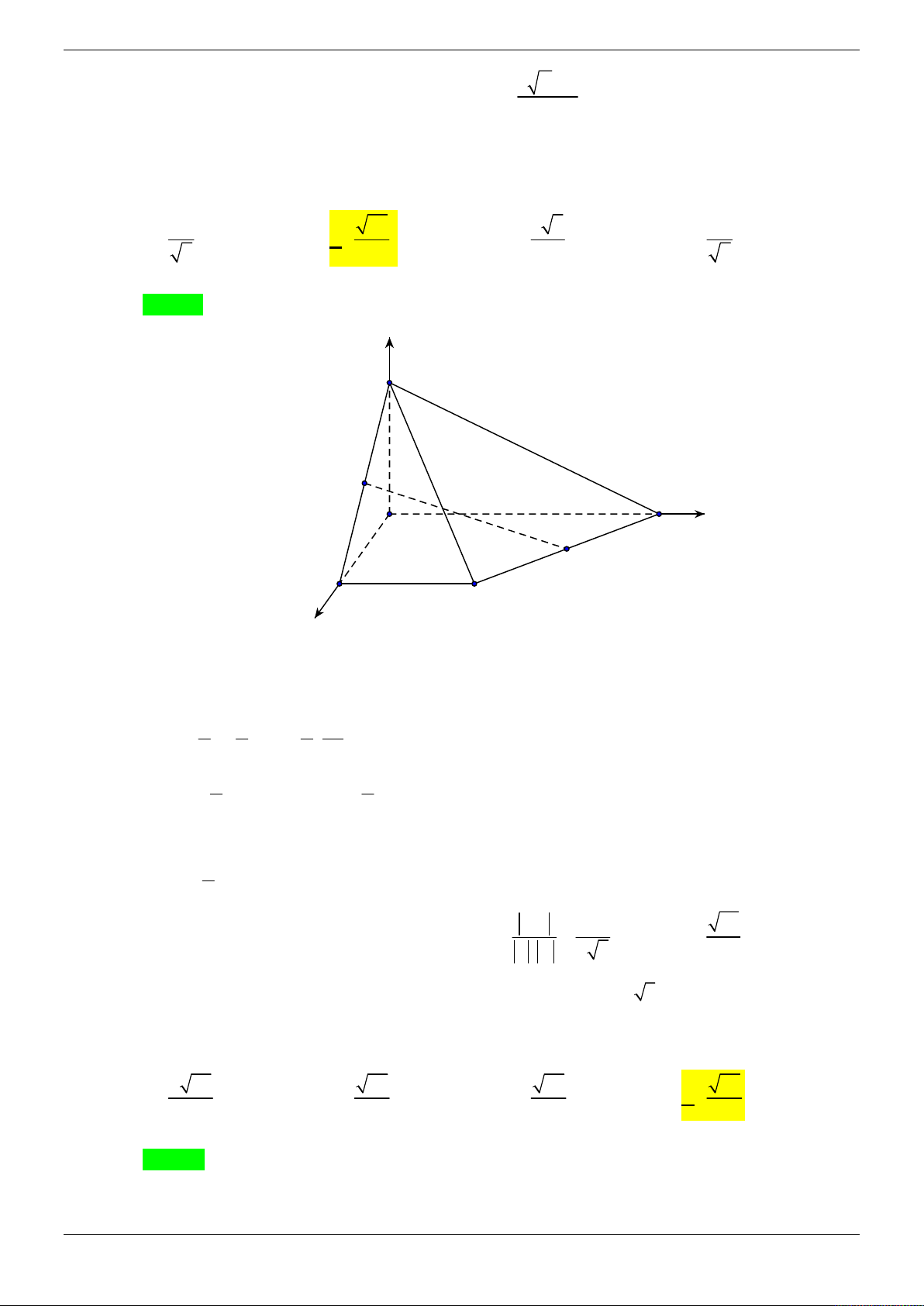
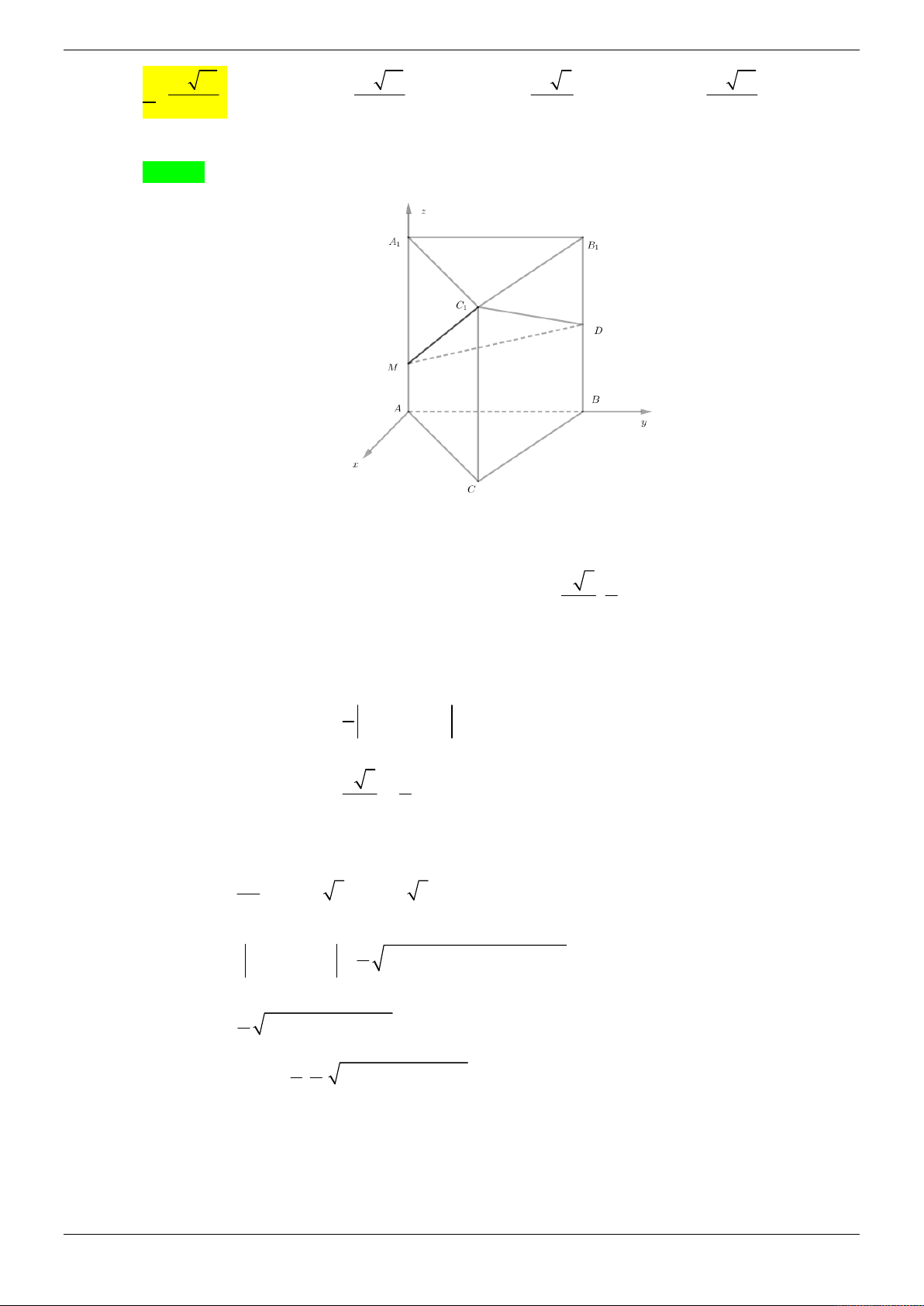
Chọn hệ trục tọa độ như hình vẽ z S N D A y H M B C xa   a  Tọa độ các đỉnh: (
A 0; 0; 0), B a;0;0, D(0; a;0),C( ; a a; 0), M ; 0; 0 , N 0; ; 0      2   2  x t   a   Suy ra DM  ; a; 0   
phương trình DM :  y a  2t H t; a  2t;0  2  z  0     a
CH  t a; 2t;0,CN  a;  ;0    2  t a 2  t aa 3a   a 3a  Vì H CN    t
  a  4t t   H ; ; 0  S ; ; a 3     aa 5  5 5   5 5  2 2  4a 2a     a 3    Ta có: SC  ;
; a 3 , DC    a;0;0 2 2
 DM , SC    a 3; ; a  5 5    2     
   3
 DM , SC .DC a 3   .
  
DM , SC.DC 3   a 3 2a 57
Vậy d SC, DM       . 2 DM , SCa 19 19   2 Trang 28/69
Câu 16: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng nhau. Gọi E, M lần lượt là
trung điểm các cạnh BC, S ,
A  là góc tạo bởi đường thẳng EM và mặt phẳng SBD . Tính sin  . 6 1 3 2 A. sin   . B. sin  . C. sin   . D. sin   . 3 2 2 2 Lời giải Chọn A
Gọi AC BD   
O . Vì hình chóp tứ giác S.ABCD là hình chóp đều nên SO   ABCD .
Đặt OA  1. Vậy AC  2 và đáy của hình chóp S.ABCD là hình vuông có cạnh bằng 2 .
Do giả thiết hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng nhau nên SA  2 .
Xét tam giác SAO vuông tại O có SO
SA AO   2 2 2 2 2 1  1 .
Chọn hệ trục tọa độ Oxyz sao cho Ox OC, Oy OB, Oz OS .
Khi đó ta có: C 1;0;0, A 1
 ;0;0, B0;1;0, S 0;0;  1 .  1 1   1 1 
Do E, M lần lượt là trung điểm các cạnh BC, SA nên E ; ; 0 , M ; 0;     .  2 2   2 2  
AC  SBD nên mặt phẳng SBD nhận AC 2;0;0 là một vectơ pháp tuyến.   1 1
Đường thẳng EM nhận ME 1; ; 
 là một vectơ chỉ phương.  2 2 
Gọi  là góc tạo bởi đường thẳng EM và mặt phẳng SBD . Trang 29/69   1  1  1.2  .0  .0 ME.AC   2  2  6 Vậy ta có: sin     . 2 2 ME.AC 3  1   1 2  1    .2      2   2 
Câu 17: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng h . Gọi I là trung
điểm cạnh bên SC . Tính khoảng cách từ S đến mặt phẳng  AIB . 2ah 4ah ah 2ah A. . B. . C. . D. . 2 2 4h  9a 2 2 4h  9a 2 2 4h  9a 2 2 2h  3a Lời giải Chọn A a 2
Gọi O là giao điểm của AC và BD . Ta có OA OB OC  . 2
Chọn hệ trục tọa độ Oxyz có gốc tọa độ O , tia Ox chứa A , tia Oy chứa B , tia Oz chứa S .  a 2   a 2   a 2  Khi đó: A  ; 0; 0  , B  0; ; 0 , C
; 0; 0 , S 0;0;h .    2        2   2  
Gọi M là giao điểm của SO và AI . Tam giác SAC có M là giao điểm của hai đường trung  h
tuyến nên M là trọng tâm, do đó M 0; 0;   .  3  x y z
Mặt phẳng  AIB đi qua ,
A B, M nên có phương trình:    1 . 2 2 h a a 3 2 2 2 2 3  x y z 1  0 . a a h Trang 30/69 3 .h 1 h 2ah
Do đó khoảng cách từ S đến mặt phẳng  AIB là: d   . 2 2 2 2 9 4h  9a   2 2 2 a a h
Câu 18: Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông cạnh a , tâm O . Gọi E là điểm đối
xứng với D qua trung điểm của SA , M là trung điểm của AE , N là trung điểm của BC .
Tính khoảng cách giữa hai đường thẳng MN và AC . a 2 a 2 a 3 a A. . B. . C. . D. . 4 2 4 8 Lời giải Chọn A
Chọn hệ trục tọa độ như hình vẽ. Đặt SO h và gọi I là trung điểm của SA .  a 2   a 2   a 2   a 2 
Ta có tọa độ các đỉnh là: A 0;  ; 0  , B  ; 0; 0 , C  0; ; 0 , D   ; 0; 0     2          2   2   2   S 0;0;h .  a 2 h   a 2 a 2 
I , N lần lượt là trung điểm SA , BC I  0;  ;  , N  ; ; 0 .   4 2      4 4    a 2 a 2 
E đối xứng với D qua I E  ;  ; h  .  2 2     a 2 a 2 h
M là trung điểm AE M  ;  ;  .  4 2 2   
  3a 2 h  
  a 2 3a 2  Do đó MN   0; ; 
 , AC  0; a 2;0 , AN   ; ; 0   4 2      4 4   Trang 31/69    ah 2  2
   a h
 MN , AC   
; 0; 0   MN, AC.AN  .    2      4
  
MN, AC  .AN   a 2
Vậy d MN, AC      .   4 MN , AC  
Câu 19: Cho hình lăng trụ ABC.AB C
  có A .ABC là tứ diện đều cạnh a . Gọi M , N lần lượt là trung
điểm của AA và BB . Tính tan của góc giữa hai mặt phẳng  ABC và CMN  . 2 3 2 2 2 4 2 A. . B. . C. . D. . 5 4 5 13 Lời giải Chọn C z B' C' A' N M B C y H O A x
Không mất tính tổng quát ta chọn a  1 .
Gọi O là trung điểm của A B . Gọi H là tâm của ABC A H    ABC .
Chuẩn hóa và chọn hệ trục tọa độ như hình vẽ sao cho O0;0;0 .   1   1   3  Khi đó: A ; 0; 0   , B  ; 0; 0   , C  0;
; 0  . Dễ thấy mp  ABC có vtpt n  0;0;1 . 1    2   2   2     3  6  3 6     3 6  Do: H  0;
; 0  , AH   A 0; ;
. Ta có AB A B
   B 1; ; .    6        3 6 3   6 3    1 3 6   3 3 6 
M là trung điểm AA  M  ; ;
 , N là trung điểm BB  N  ; ;   4 12 6      4 12 6   Trang 32/69 
  1 5 3 6   MN   1
 ;0;0 , CM   ; ;
  CMN  có vtpt n  0; 2 2;5 2    4 12 6   
Đặt    ABC ,CMN    n .n 1 2 5 5 1 2 2
cos       tan   1  ( do góc  nhọn). 2 n n 1. 33 33 cos  5 1 2 
Câu 20: Cho hình chóp SABC có đáy ABC là tam giác cân tại A và AB a , BAC  120 .
SA SB SC 5
. Gọi  là góc của hai mặt phẳng  SAB và SBC sao cho cos  . Khi đó 7
thể tích của khối chóp SABC là 3 3a 3 a 3 2a A. . B. 3 2a . C. . D. . 12 3 5 Lời giải Chọn A
Vì SA SB SC  Hình chiếu của S lên  ABC trùng với tâm đường tròn ngoại tiếp A
BC là D (với D là đỉnh của hình thoi ABDC )
Đặt SD x x  0 . a 3  a 3 
Gắn hệ tọa độ: D 0;0;0, B a;0;0, S 0;0; x . Vì DI   I  0; ; 0  . 2  2      1   a a 3   a a 3 
Ta có DB a;0;0, IA DB A ; ; 0  , C   ; ; 0  2  2 2      2 2     a a 3     a a 3  SA   ;
;  x  , SB  a; 0; x, SC    ; ;  x   2 2   2 2      2  
 ax 3 xa a 3    S , A SB   ; ;
  n x 3; x; a 3 là một vecto pháp tuyến của  SAB  1       2 2 2   Trang 33/69 2    a 3   S ,
A SC    0; ax;
  n 0; 2x; a 3 là vecto pháp tuyến của  SAC  2       2     2 2 n .n 1 2 2x  3a 5 os
c        x a 2 2 n . n 4x  3a 7 1 2 1 1 3 3 2 3 VS . D S  . a a a . SABC 3 ABC 3 4 12
Câu 21: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AC  2a , tam giác SAB và
tam giác SCB lần lượt vuông tại A , C . Khoảng cách từ S đến mặt phẳng  ABC bằng 2a .
Côsin của góc giữa hai mặt phẳng  SAB và SCB bằng: 1 1 1 1 A. . B. . C. . D. . 2 3 2 3 Lời giải Chọn B
Chọn hệ trục tọa độ sao cho: B0;0;0 , Aa 2;0;0 , C 0;a 2;0 , S  ; x ;
y z ,  z  0 .    Ta có
ABC : z  0 ,
AB  a 2;0;0 , CB  0;a 2;0 ,
AS   x a 2; y; z ,  CS   ;
x y a 2; z  .  
Do AS.AB  0  x a 2 a 2   0  x a 2 .  
CS.CB  0   y a 2 a 2   0  y a 2 .
Mà d S, ABC  2a z  2a . Từ đó S a 2;a 2;2a .   
Ta có AS  0;a 2;2a , CS  a 2;0;2a , BS  a 2;a 2;2a .  
SBC có 1 vtpt n   2;0 
;1 ,  SAB có 1 vtpt m  0; 2;  1 . 1 1 Vậy cos   . 3. 3 3 Trang 34/69
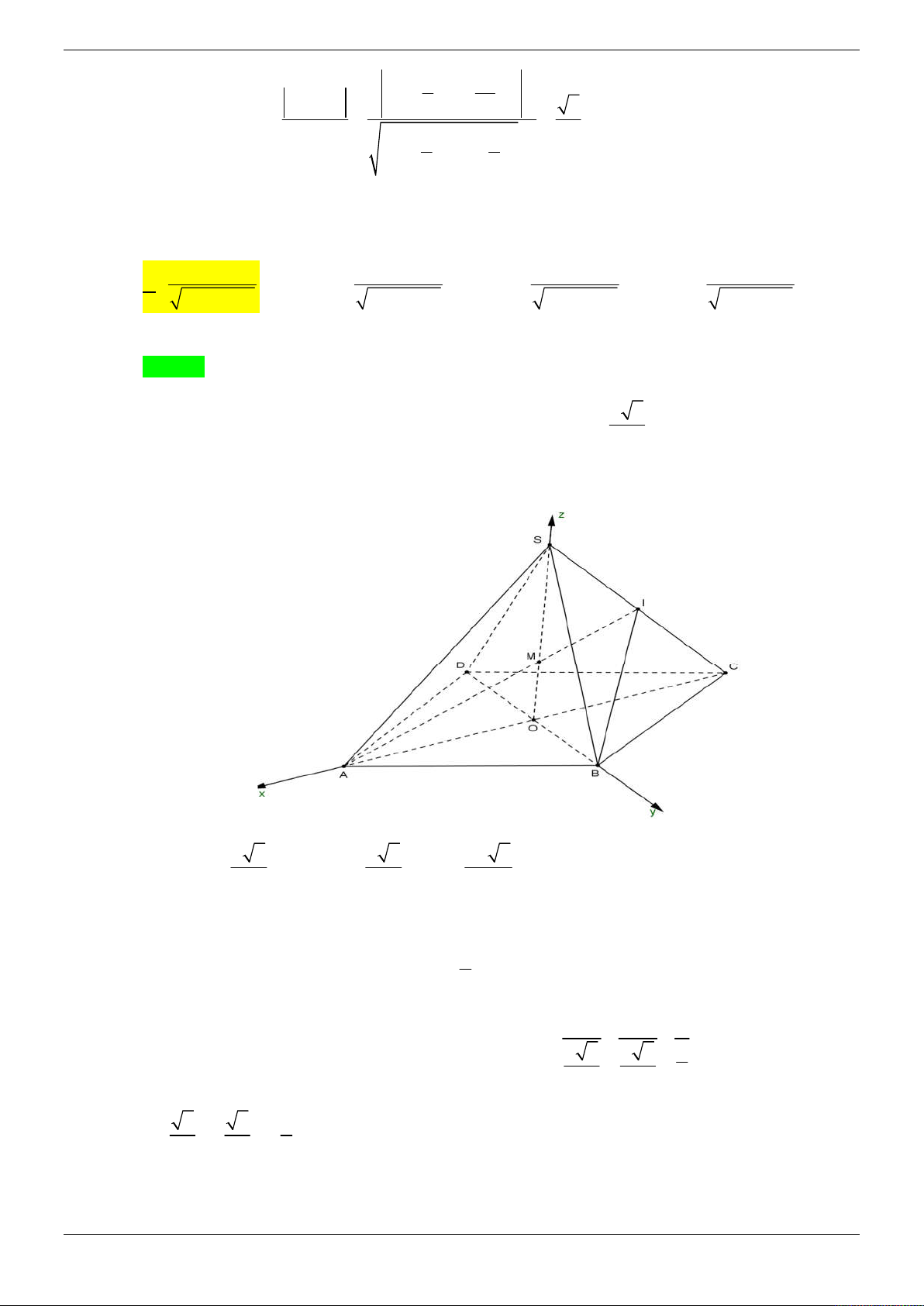
Câu 22: Cho hình chóp đều SABCD có cạnh đáy bằng 2 , cạnh bên bằng 3 2 . Gọi M , N lần lượt là
các điểm thuộc SB, SD sao cho SB  3SM , SD  3DN . Khoảng cách giữa AM và CN bằng 40 72 24 40 A. . B. . C. . D. . 857 857 153 257 Lời giải Chọn A
Gọi O là giao điểm của AC, BD SO   ABCD .
OA  2, SO  18  2  4 .
Chọn hệ trục Oxyz như hình vẽ. ( Ox//AB, Oy//AD, Oz OS )
Tọa độ điểm A 1; 1; 0 , B 1; 1; 0 , C 1;1; 0 , D 1;1; 0 , S 0; 0; 4 .  1 x   M 1 0  3   1   1  1 1 8 
Từ giả thiết ta có SM SB   y     M  . M  1 0 ; ;   3 3  3 3 3    1 z  4   M 0 4   3  2 2 4 
Tương tự tọa độ điểm N  ; ;   .  3 3 3 
  4 2 8    5 1 4   Suy ra AM  ; ; , CN   ;  ; , AC      2;2;0 .  3 3 3   3 3 3  
Chọn vectơ chỉ phương của đường thẳng AM là u  2;1; 4 , chọn vectơ chỉ phương của 1   
đường thẳng CN là u  5;1; 4  . 2    
Ta có u ;u   8; 28; 3  . 1 2     Trang 35/69
Khoảng cách giữa hai đường thẳng AM , CN bằng   
u ;u .AC 1 2 16  56  0   40
d AM ;CN       . u ;u
82  28  32 2 857 1 2  
Câu 23: Cho hình chóp tam giác đều S.ABC có SA  2a , AB a . Gọi M là trung điểm cạnh BC .
Tính khoảng cách d từ M tới mặt phẳng  SAB  . a 165 a 15 a 65 a 65 A. d  . B. d  . C. d  . D. d  . 30 3 15 10 Lời giải Chọn A
Gọi O là hình chiếu của S trên  ABC  , ta suy ra O là trọng tâm tam giác ABC . a 3 a 3 a 3
Do M là trung điểm BC nên AM  . Suy ra OA  và OM  . 2 3 6 2 a a 33
Xét tam giác SOA vuông tại O , ta có 2 2 2 SO
SA OA  4a   . 3 3
Ta chọn hệ trục tọa độ Oxyz như hình vẽ với O trùng với gốc tọa độ, khi đó ta được:  a 3   a 33   a 3 
O 0; 0; 0 , A ;0;0 , S  0; 0; , M   ; 0;0 .    3        3   6    a 3 a   a 3 a  Suy ra B   ; ; 0  , C   ;  ; 0   6 2      6 2     a 3 a 33    a 3 a a 33  Ta có SA   ; 0;   , SB    ; ;    3 3   6 2 3      Trang 36/69 2 2 2     a 33 a 11 a 3  Suy ra n   ; SA SB   ; ; . SAB     6 2 6    33 11 3 a 11
Phương trình măt phẳng  SAB  là x y z   0 . 6 2 6 6 33 a 3 a 11   6 6 6 a 165
Suy ra d M ,SAB   . 33 11 3 30   36 4 36
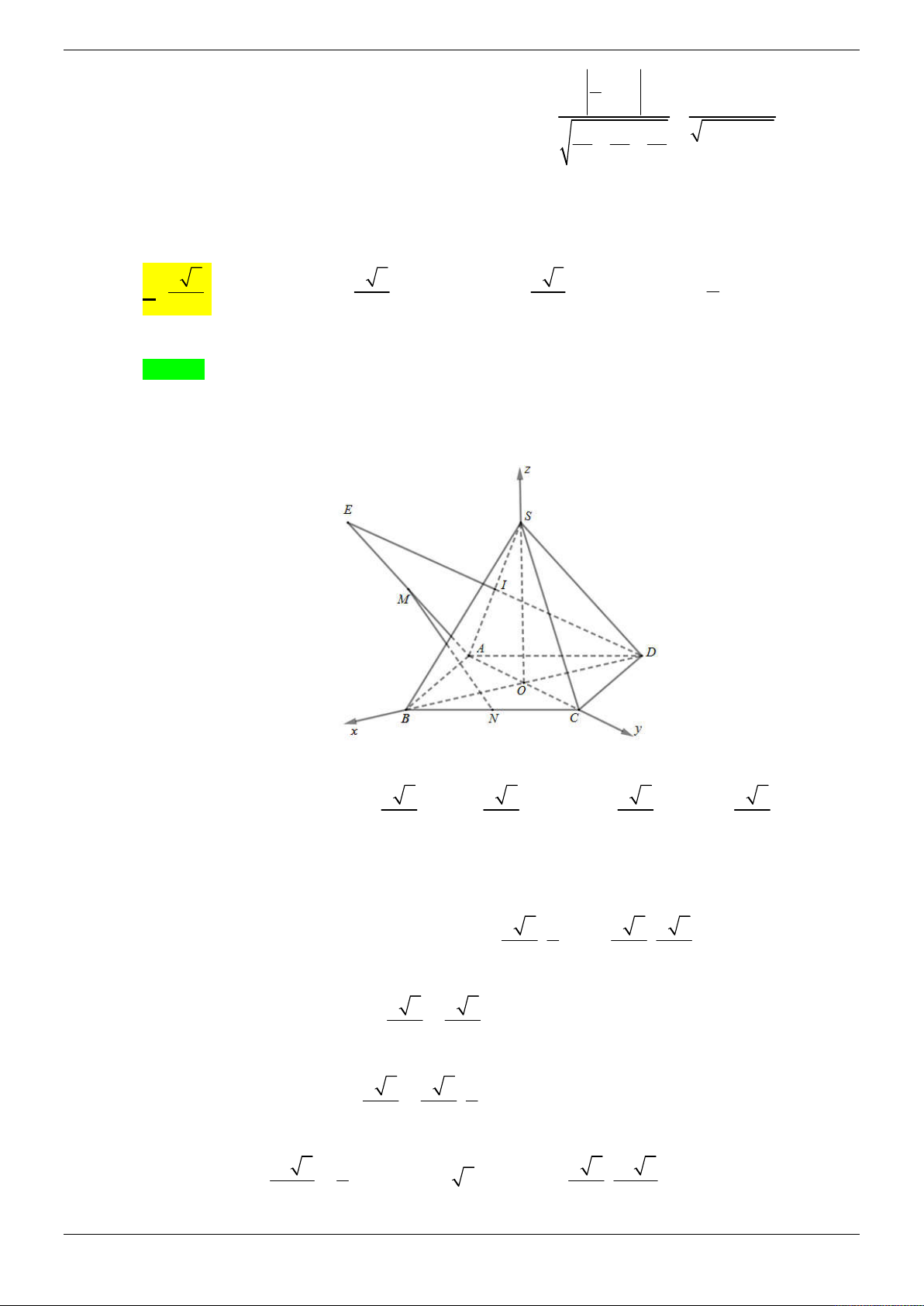
Câu 24: Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AD  2AB  2BC  2CD  2a .
Hai mặt phẳng  SAB và SAD cùng vuông góc với mặt phẳng  ABCD  . Gọi M , N lần
lượt là trung điểm của SB và CD. Tính cosin góc giữa MN và SAC  , biết thể tích khối chóp 3 a 3 S.ABCD bằng . 4 5 3 310 310 3 5 A. . B. . C. . D. . 10 20 20 10 Lời giải Chọn C Cách 1:
Vì ABCD là hình thang cân có AD  2AB  2BC  2CD  2a
AD  2a; AB BC CD a a 3 2 a  2a a 3 3 3aCH  ; S  .  . 2 ABCD 2 2 4 2 3 1 3 3a a 3 nên V  . .SA   SA a ABCD 3 4 4
Gắn hình chóp vào hệ trục tọa độ như hình vẽ Trang 37/69  a   a 3   a 3   a a 3 
Ta có: K 0; 0; 0, B ; 0; 0 ,   C  0; ;0, A 0;  ;0 , N  ; ; 0 ,  2   2        2   2 2    a 3   a a 3 a S  0; 
; a , M  ; ;   2      4 4 2     3
a 3a 3 a    MN   ; ;  . Chọn u  3
 ;3 3;  2 cùng phương với MN 1    4 4 2    BK SA Nhận xét: 
BK  SACBK AC     a   BK   ; 0; 0 
 là vtpt của  SAC  .Chọn n  1;0;0 cùng phương với BK 1    2    u .n 1 1 3 10
Gọi  là góc góc giữa MN và SAC  . Ta có sin    310   cos  . u u 20 20 1 2 Cách 2:
Gọi   là mp đi qua MN và song song với mp SAD . Khi đó   cắt AB tại P , cắt SC tại
Q , cắt AC tại K . Gọi I là giao điểm của MN và QK I  SAC  .
Suy ra: P , Q , K lần lượt là trung điểm của AB , SC và AC .
Lại có: ABCD là hình thang cân có AD  2AB  2BC  2CD  2a
AD  2a; AB BC CD a a 3 2 a  2a a 3 3 3aCH  ; S  .  . 2 ABCD 2 2 4 2 3 1 3 3a a 3 1 a 3a Nên V  . .SA
SA a MP SA  và NP  . ABCD 3 4 4 2 2 2 2 2  a   3a a 10
Xét tam giác MNP vuông tại P: MN         2   2  2
MP, KQ lần lượt là đường trung bình của tam giác SA , B S
AC MP//KQ//SA 1
KN là đường trung bình của tam giác ACD KN AD a . 2 Trang 38/69 2 2  a 3   3a a 3
Xét tam giác AHC vuông tại H: AC      a 3     KC  2   2    2
Suy ra: tam giác KNC vuông tại C C là hình chiếu vuông góc của N lên SAC .
 góc giữa MN và SAC  là góc  NIC IN KN 2 2 2 a 10 a 10 Khi đó:    IN  .MN  .  MN NP 3 3 3 2 3 2 2 a a 10  a 10   a a 31
Xét tam giác NIC vuông tại C : NC  ; IN   IC        2 3  3   2  6   IC a a   31 10 310 cos NIC   :  . IN 6 3 20
Câu 25: Cho hình chóp SABC có đáy ABC là tam giác vuông tại A , AB  3a , AC  4a . Các mặt bên
SAB , SAC , SBC cùng tạo với đáy  ABC một góc 0
45 . Biết chân đường vuông góc hạ
từ S xuống mặt phẳng  ABC nằm ở miền trong tam giác ABC . Gọi góc tạo bởi hai mặt
phẳng SAC và SBC là  . Tính cos . 1 1 3 1 A. cos  . B. cos  . C. cos  . D. cos  . 10 5 5 15 Lời giải Chọn A
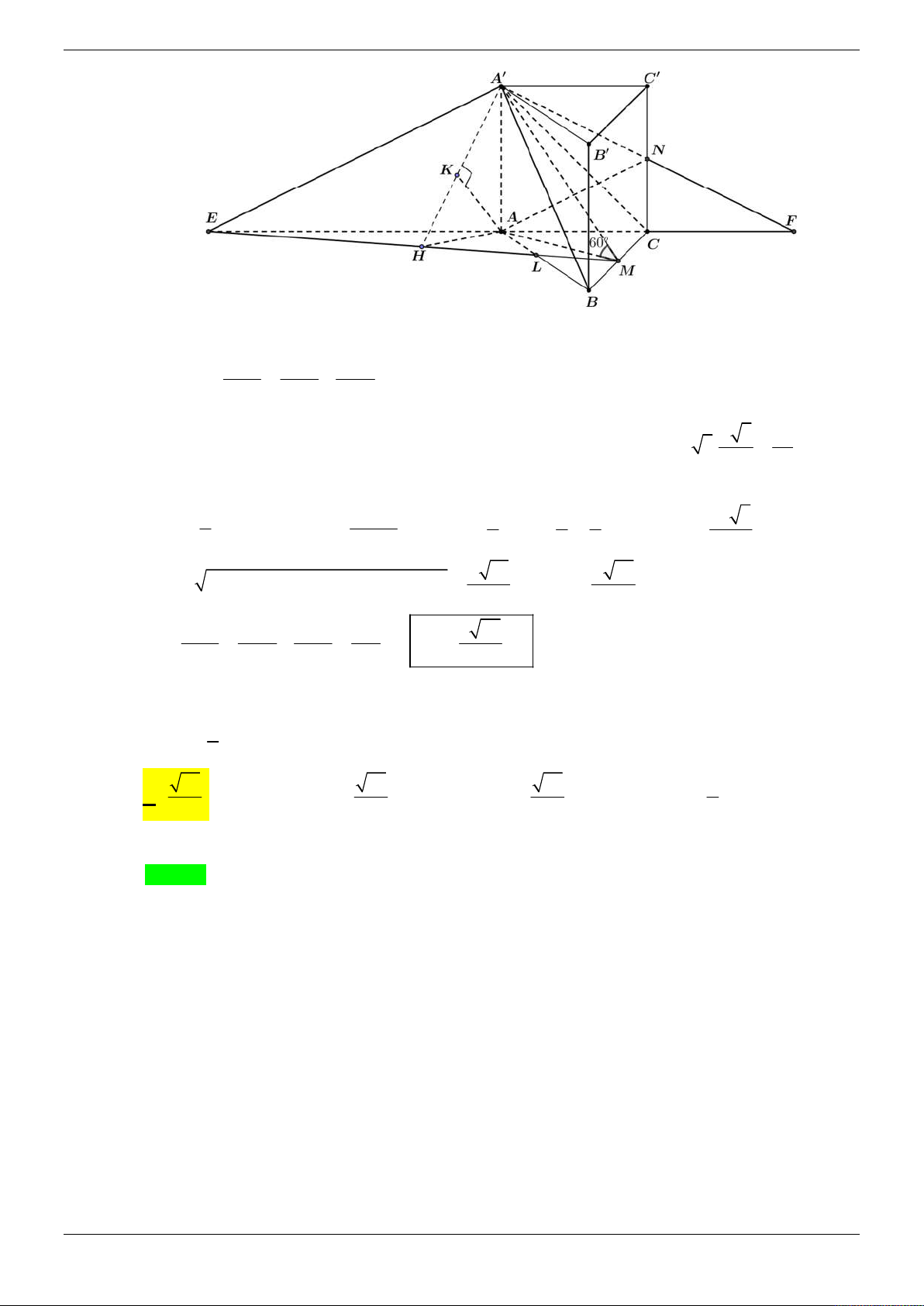
Gọi H là hình chiếu của S lên mặt phẳng  ABC . Gọi M , N , P lần lượt là hình chiếu của H
trên AB , AC và BC . Ta có góc giữa (SAB) và (BAC) là góc SMH . Tương tự ta có    0
SMH SNH SPH  45 Do đó SMH SNH S
PH HM HN HP
Mà H nằm ở miền trong tam giác ABC nên H là tâm đường tròn nội tiếp tam giác ABC. Trang 39/69 Gọi r là bán kính đường tròn nội tiếp tam giác ABC , khi đó 1 . AB AC S 3 .4 a aABC 2 r     a . p 1
a a a ABC
AB BC CA 3 4 5 2
Tam giác SHM vuông cân tại H nên SH HM r .
Chọn hệ trục Đề-các vuông góc Axyz như hình vẽ. Khi đó ta tìm được tọa độ các điểm như sau
A0;0;0 , B3 ;
a 0;0 , C 0;4 ;
a 0 , H r;r;0   ; a ;
a 0 , S x ; y ; SH    ; a ; a a . Suy ra: H H   1  
Mặt phẳng SAC có véc tơ pháp tuyến n
AS, AC  1  ;0;1 1 2   4a    1   
Mặt phẳng SBC có véc tơ pháp tuyến n
AS, AC  4;3;5 2 2   a   1.4  0.3 1.5 1 Do đó cos    2 2 2 2 2 2 10 1  0  1 4  3  5
Câu 26: Cho hình chóp S.ABC có đáy là tam giác đều cạnh .
a Hình chiếu vuông góc của S trên mặt
phẳng  ABC là điểm H thuộc cạnh AB sao cho HA  2HB . Góc giữa đường thẳng SC và
mặt phẳng  ABC bằng 60o . Tính khoảng cách h giữa hai đường thẳng SA và BC theo a . a 42 a 42 a 42 a 42 A. . B. . C. . D. . 8 12 4 24 Lời giải Chọn A
Chọn hệ trục tọa độ có gốc tại M , trục hoành là MC , trục tung là MB , trục cao là Mz / / HS (xem hình vẽ). AB a a 7 Ta có: 2 2 MH  
CH CM MH  6 6 3 Trang 40/69 a 21 SC,  ABC      o o
SCH  60  SH CH . tan 60  3  a   a a 21   a   a 3 
Do đó tọa độ các điểm là A 0;  ; 0   , S  0; ;  , B 0; ; 0   , C  ; 0; 0   2   6 3       2  2     2a a 21    a 3 a    SA   0;  ;   , BC   ; 
; 0 , AB  0; a;0   3 3      2 2   2 2 2    a 21 a 7 a 3   S , A BC     ;  ;     6 2 3   
    , SA BC  .AB   a 42  d  , SA BC      .   8 , SA BC  
Câu 27: Cho hình lăng trụ đứng AB . C A BC
  có AB AC a , góc 
ABC  30 , góc giữa đường thẳng
AB và mặt phẳng  ABC  bằng 0
45 . Gọi M , N lần lượt là trung điểm của B C   và CC .
Cosin của góc giữa mặt phẳng  AMN  và mặt phẳng  ABC bằng 1 3 13 3 A. . B. . C. . D. . 2 2 4 4 Lời giải Chọn D z A' C' M B' N x A C H y B
Ta có  AB ABC 
  AB AB   , ,
ABA  45 nên AA
B vuông cân tại A
AA  AB a a
Gọi H là trung điểm BC AH BC AH  . AB sin 30  2 2 2
BC  2BH  2 AB AH a 3 . Trang 41/69
Lại có M , H lần lượt là trung điểm của B C   và BC
MH BB  AA  ;
a MH // BB  MH   ABC  a
Chọn hệ trục tọa độ Oxyz như hình vẽ có H O , suy ra H 0;0;0 , A ; 0; 0   ,  2   a 3  B  0;
; 0  , M 0;0; a .  2     a 3   a 3 a   C  0;  ; 0  , N  0;  ; .   2      2 2    a
  a a 3 a    2 2 2    a 3 a a 3 
AM  ;0; a , AN     ; 
;    AM , AN    ;  ;  2  2 2 2          2 4 4     3 1  3 
  AMN  có một VTPT là n   ; ;   2 4 4     
Ta có HM  0;0;a , HM   ABC   ABC có một VTPT n  0;0;1 1  
Gọi  là góc giữa mặt phẳng  AMN  và mặt phẳng  ABC .   3 . n n1 3
từ đó cos    4   . n . n 2 2 2 4 1  3  1  3             .1 2  4  4    
Câu 28: Cho hình lăng trụ tam giác AB .
C A' B'C ' có đáy ABC là tam giác đều cạnh a và các mặt bên
đều là các hình vuông cạnh a . Gọi G là trọng tâm của tam giác ABC và I là trung điểm của
đoạn thẳng CC ' . Khoảng cách giữa hai đường thẳng A' B và GI bằng a 11 3a 11 a 11 3a 11 A. . B. . C. . D. . . 22 7 12 22 Lời giải Chọn D Trang 42/69
Chọn hệ trục tọa độ sao cho A0;0;0, C  ;
a 0;0, A'0;0;a trục Ay nằm trong mặt phẳng
ABC và vuông góc với trục Ax . Khi đó gọi H , K lần lượt là hình chiếu của B lên các trục a 3 a
Ax, Ay khi đó góc 0 BAy  30 nên 0 0
AK AB cos 30 
; AH AB cos 60  nên 2 2  a a 3   a a 3  B  ;
; 0 . Vì G là trọng tâm tam giác ABC nên ta có G  ;
;0 . Đồng thời I là   2 2      2 6    a
trung điểm của CC ' nên , I a; 0;   . Suy ra  2 
  a a 3    a a 3 a    a A' B   ;
; a ; IG    ; ;  ; A' I  ; a 0;    .  2 2   2 6 2   2      2 2 2 3    a 3 3a a 3 
   a 3 2   a 33
Ta có  A' B, IG    ; ;
   A' B, IGA' I  
và  A ' B, IG   .    12 4 3    4     6
  
A' B, IGA' I   3a 11
Vậy d A' B,GI      .   22 A' B, IG  
Câu 29: Cho lăng trụ đứng AB .
C A' B 'C ' có đáy là tam giác ABC vuông cân tại A , cạnh BC a 6 .
Góc giữa mặt phẳng  AB 'C và mặt phẳng  BCC ' B ' bằng 0
60 . Tính thể tích V của khối lăng trụ AB .
C A' B 'C ' ? 3 2a 3 3 a 3 3 3a 3 3 3a 3 A. V  . B. V  . C. V  . D. V  . 3 2 4 2 Lời giải Chọn D Trang 43/69
Vì tam giác ABC vuông cân tại A , cạnh BC a 6 nên AB AC a 3 .
Chọn hệ trục tọa độ Oxyz sao cho A0;0;0 , C a 3;0;0 , B 0;a 3;0 , A0;0; z  z  0.  
B0;a 3; z; BC  a 3; a 3;0 , BB  0;0; z .  1    VTPT của  BCC B   là: n
BC, BB  1;1;0 . 1   za 3    
AC  a 3;0;0 , AB  0;a 3; z .  1  
 VTPT của mặt phẳng  BA C   là: n
AC, AB  0;  z; a 3 . 2     a 3
Vì góc giữa mặt phẳng  AB 'C và mặt phẳng  BCC ' B ' bằng 0 60 nên:   z 1
cos60  cos n ,n    z a 3 . 1 2   2 2 z a  2 2 3 3 1 3a 3
Vậy thể tích của khối lăng trụ AB .
C A' B 'C ' là: V AC. . AB AA  . 2 2
Câu 30: Cho hình lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác cân, với AB AC a và góc 
BAC  120 , cạnh bên AA  a . Gọi M là trung điểm của CC . Cosin của góc tạo bởi hai mặt
phẳng  ABC và  AB M   bằng 11 33 10 30 A. . B. . C. . D. . 11 11 10 10 Lời giải Chọn D Trang 44/69 Cách 1: 2 2 2   1 
Ta có BC AB AC  2 A . B AC.cos BAC 2 2
a a  2. . a . a  2 
  3a BC a 3 .  2 
Trong tam giác vuông B AB , ta có 2 2 AB  BB  AB 2 2
a a a 2 . 2 a a 5
Trong tam giác vuông MAC , ta có 2 2
MA MC AC 2  a   . 4 2 2 a a 13
Trong tam giác vuông MB C   ,ta có 2 2 B M   B C    C M  2  3a   . 4 2 2 5a 2 13a Xét tam giác MB A  có 2 2 2 B A
MA  2a   2  B M   MB A  vuông tại A 4 4 1 1 a 5 2 a 10  SAB .AM  .a 2.  . MB A  2 2 2 4 1  1 3 2 a 3 Lại có SA . B AC.sin BAC  . a . a  . ABC 2 2 2 4
Gọi  là góc tạo bởi hai mặt phẳng  ABC và  AB M   .
Ta có ABC là hình chiếu vuông góc của AB M
trên mặt phẳng  ABC . 2 2 a 3 a 10 30 Do đó SS .cos   .cos  cos  . ABC MB A  4 4 10
Cách 2: Chọn hệ trục tọa độ Oxyz như hình vẽ: Trang 45/69
( trong đó gốc tọa độ O trùng với trung điểm của BC ).  a   a 3   a 3   a 3   a 3 a A 0; ;0   , B
; 0; a  , C  
; 0; 0  , C 
;0; a  , M   ; 0;   2   2          2   2   2 2     a 3 aaAB   ;  ; a   ;    3;1;2 2 2 2     a 3 a a  1 AM    ;  ;  = a .    3;1;  1 2 2 2 2   2 2 2 2    a 3  a 3 a 3  a Có:  AB ;  AM    ; ;       1;3 3; 2 3 4 4 2 4    
Mặt phẳng  ABC có véc tơ pháp tuyến là n k  0;0;1 . 1   2   a Mặt phẳng  AB M
 có véc tơ pháp tuyến là AB ; AM   .   1;3 3; 2 3 4 
Chọn véc tơ pháp tuyến là n  1;  3 3 ;  2 3 2     n .n 0.1  0.(3 3)  1. 2  3 1 2     30
cos  ABC ; AB M
      . n . n 0  0 1
1  (3 3)  2 32 2 2 2 2 2 10 1 2
Câu 31: Cho hình lăng trụ đứng ABC.AB C
  có đáy là tam giác vuông tại A , AB AC a và có
cạnh bên bằng 2a . Gọi M , N lần lượt là trung điểm BB ',CC ' . Tính khoảng cách từ điểm A
đến mặt phẳng ( A ' MN ) 2a 3 3a A. a . B. . C. . D. a 3 . 3 2 Trang 46/69 Lời giải Chọn B
Chọn hệ trục tọa độ Oxyz sao cho điểm A trùng với gốc tọa độ, điểm B nằm trên trục Ax , điểm C
nằm trên trục Ay , điểm A ' nằm trên trục Az . Ta có: (
A 0; 0; 0), B(a; 0; 0), C(0; a; 0), A'(0; 0; 2 a), B'(a; 0; 2 a), C'(0; a; 2 a)
Do M , N lần lượt là trung điểm BB ',CC '  M(a;0; a), N(0; a; a)   A' M  ( ;
a 0; a), A' N  (0; ; a a) 
   2 2 2
n   A' M , A' N   n  (a ; a ; a )    Suy ra : n  (1;1;1) A MN 1
là một vecto pháp tuyến của mặt phẳng ( ' )
Phương trình mặt phẳng ( A ' MN ) là :
1(x  0) 1( y  0) 1(z  2a)  0  x y z  2a  0 2  a 2a 3
Khoảng cách từ điểm A đến mặt phẳng ( A ' MN ) là: d   (A;(A'MN)) 2 2 2 3 1 1 1
Câu 32: Cho hình lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác cân tại C , AB  2a , AA  a ,
góc giữa BC và  ABB A
  bằng 60 . Gọi N là trung điểm AA và M là trung điểm BB .
Tính khoảng cách từ điểm M đến mặt phẳng  BC N   . 2a 74 a 74 2a 37 a 37 A. . B. . C. . D. . 37 37 37 37 Lời giải Chọn A Trang 47/69
Gọi H , K lần lượt là là trung điểm cạnh AB và AB . Từ giả thiết ta có:     2    .tan 60o HB a HB a HC HBa 6 ` Mặt khác: HC ,
HB v a HK đôi một vuông góc nhau. Chọn hệ trục Oxyz như hình vẽ có H O a
Tọa độ hóa: H (0;0;0) , C (
 0; a 6; 0) , A (   ; a 0; 0) , ( A  ;
a 0; a) , N a; 0;   , B (  ; a 0;0) ,  2   a
B(a; 0; a) , M a; 0;   .  2   CB
  (a; a 6; a)  
Xét mặt phẳng (BC N  ) có 
vtpt n  ( 6; 3; 4 6)  a BN  2  a; 0;       2   a  Phương trình (BC N
 ) là: 6(x a)  3y  4 6 z   0   .  2 
Khoảng cách từ M đến (BC N  ) là: a a
6 (a a)  3.0  4 6(  ) 2 2 2a 6 2a 74
d (M ; (BC N  ))    . 6  9  96 111 37
Câu 33: Cho hình lăng trụ đứng ABC.AB C
  có AB AC a , góc BAC bằng 120 , AA  a . Gọi M ,
N lần lượt là trung điểm B C
  và CC . Khoảng cách giữa 2 đường thẳng MN và AH là a 3 a 3 a 6 a 6 A. . B. . C. . D. . 2 4 2 4 Lời giải Chọn D Trang 48/69
Gọi H là trung điểm BC . Áp dụng định lí cosin cho tam giác ABC ta có: 2 2 2 
BC AB AC AB ACBAC 2 2 2 2. . .cos
a a  2.a. .
a cos120  3a BC a 3 2. AB ACBC 2. a a  3a a a 2  2 2  2  2 2  2 2 AH     AH  4 4 4 2
Vì tam giác ABC cân tại A có AH là đường trung tuyến nên AH BC tại H hay 3 cạnh
MH , HA và HB đôi một vuông góc với nhau. Ta chọn hệ trục tọa độ Hxyz sao cho điểm
A Hx , điểm B Hy và điểm M Hz . Khi đó ta có tọa độ các điểm như sau: H 0;0;0 ,  a   a 3   a 3   a 3 a A ; 0; 0   , B  0; ;0  , C  0; 
; 0  , M 0; 0; a , N  0;  ;  .  2   2        2   2 2     a 3 a     a   a a 3 a
Ta có: MN   0;  ;   ; AH  
; 0; 0 ; AN    ;  ;     2 2       2  2 2 2   2 2    a a 3 
Suy ra: MN; AH    0; ;      4 4   
Áp dụng công thức tính khoảng cách giữa hai đường thẳng chéo nhau, ta có:
   3 6  ,  . a MN AH AN   32 a 6
d MN, AH       . 4   4 MN , AH a   4
Câu 34: Cho hình lăng trụ ABC.A B C có đáy là tam giác đều cạnh a . AA  2a và vuông góc với mặt 1 1 1 1
phẳng  ABC . Gọi D là trung điểm của BB , M di động trên cạnh AA . Giá trị lớn nhất của 1 1 diện tích MC D là 1 Trang 49/69 2 a 15 2 a 15 2 a 5 2 a 10 A. . B. . C. . D. . 4 6 4 4 Lời giải Chọn A
+ Chọn hệ trục tọa độ Oxyz sao cho A O ; B Oy ; A Oz . 1  a 3 a
Khi đó A0;0;0 , B0; ;
a 0 A 0;0;2a , C
; ; 2a và D 0; ; a a 1   1   2 2   
Do M di động trên AA , tọa độ M 0;0;t với t 0;2a 1 1   Ta có: S  DC DM  1 , DC M 1 2    a 3 aDC
  1  ( ;  ; a) Ta có:  2 2
 DC , DM    1  
DM  (0;a;t a)  a
(t 3 ;a 3(t a);a 3 2
  a 2 2 2
 DC , DM  
(t  3a)  3(t a)  3a 1   2 a 2 2 
4t  12at  15a 2 1 a 2 2 S
. . 4t  12at  15a  1 DC M 2 2 Xét f t  2 2
 4t – 12at  15a ( t 0;2a)
f 't   8t – 12a Trang 50/69 3a
f '(t)  0  t  2 2 a 15
Lập BBT giá trị lớn nhất của S
khi t  0 hay M A . 1 DC M 4
Câu 35: Cho lăng trụ tam giác đều AB .
C A' B'C ' có tất cả các cạnh bằng a , M là điểm di chuyển trên
đường thẳng A'C ' ; Tính khoảng cách lớn nhất giữa AM và BC ' a 34 a 17 a 14 a 21 A. . B. . C. . D. . 6 4 4 6 Lời giải Chọn C
Không mất tính tổng quát chọn a  1; Chọn hệ trục tọa độ sao cho gốc tọa độ trùng C'; Ox  
trùng C ' A' ; Oz trùng với C 'C ; Sao cho: 1 3 1 3 A '(1; 0; 0); C '(0; 0; 0); B'( ; ; 0); ( A 1; 0;1); B( ;
;1); C(0; 0;1); M(m; 0; 0) 2 2 2 2
  
AM ,C ' B.AC '  
Khi đó: d ( AM ;C ' B) 
 
AM ,C ' B   
  1 3  
Ta có: AM  (m 1;0; 1
 ); C ' B   ; ;1; AC '  ( 1  ; 0; 1  )  2 2    3 m 3 3 2 m
d ( AM ;C ' B)  = 2 2  3 1 3 7 5 7 7 1 5 1 7 2 2 2 2 (
)  (  m)  (m 1) .  m m .  .  2 2 2 4 4 2 4 4 m 2 m 4
( m  0 vì nếu m  0 thì M trùng C ' dẫn đến khoảng cách bằng 0) Trang 51/69 7 1 5 1 7 1 5 7
Khoảng cách đó lớn nhất khi .  .  nhỏ nhất    m  ; Khi đó: khoảng 2 4 m 2 m 4 m 7 5 14 a 14 cách lớn nhất là:
; Vậy: trong trường hợp tổng quát, khoảng cách lớn nhất là khi 4 4 7a MC '  . 5
Câu 36: Cho lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông, AB BC a , cạnh bên
AA'  a 2 . Gọi M là trung điểm của BC . Tính theo a khoảng cách giữa hai đường thẳng AM và B C  . a 3 a 21 a 7 A. . B. . C. a 7 . D. . 7 7 7 Lời giải Chọn D
Chọn hệ trục toạ độ Đêcac vuông góc Oxyz như sau:  a
B(0;0;0) ; A 0; ; a 0 ; C  ;
a 0;0 ; B’ 0;0; a 2 ; M ; 0; 0      2    a    AM
; a; 0 ; B 'C  ;
a 0; a 2 ; AB '  0;  ; a a 2        2  2
   a  Ta có: 2 2
AM , B 'C  a 2; ; a      2 
+) Khoảng cách giữa AM , B 'C 3
   a
Vì:  AM , B 'C AB ' 
nên AM , B 'C chéo nhau.   2
   3 a
AM , B 'C AB '   2 a 7
d AM , B 'C  
   
AM , B 'C  1 7   4 4 4 2a a a 2 Trang 52/69
Câu 37: Cho lăng trụ đứng ABCA BC
  có đáy ABC là tam giác vuông tại A và AB  1, AC  2 .Gọi  p
là góc tạo bởi đường thẳng BC và mặt phẳng ( ABC ) có số đo lớn nhất. Biết sin  ( với q
p, q nguyên tố cùng nhau ). Giá trị tổng p q là A. 11. B. 7 . C. 5 . D. 9 Lời giải Chọn D
Giả sử AA  m (m  0) . Chọn hệ trục tọa độ như hình vẽ:
A(0; 0; 0), B(1; 0; 0), C(0; 2; 0), C (
 0; 2; m), A (  0; 0; m) x y z
Phương trình mặt phẳng ( ABC ) là:  
 1  2mx my  2z  2m  0 1 2 m
 véc tơ pháp tuyến mặt phẳng ( ABC) là: n(2 ; m ; m 2)  BC (
 1; 2; m) là véc tơ chỉ phương của đường thẳng BC   2m 2m sin   cos( ; n BC )    2 2 4 2
5m  4. m  5
(5m  20)  29m
Áp dụng bất đẳng thức cô si cho 2 số 4 5m và 20 : 2m 2m 2 sin    2 2 4 2 7 20m  29 2. 5 .20  29 m m m Dấu “=” xảy ra khi 4
5m  20  m  2 . Vậy p  2, q  7  p q  9 . Trang 53/69
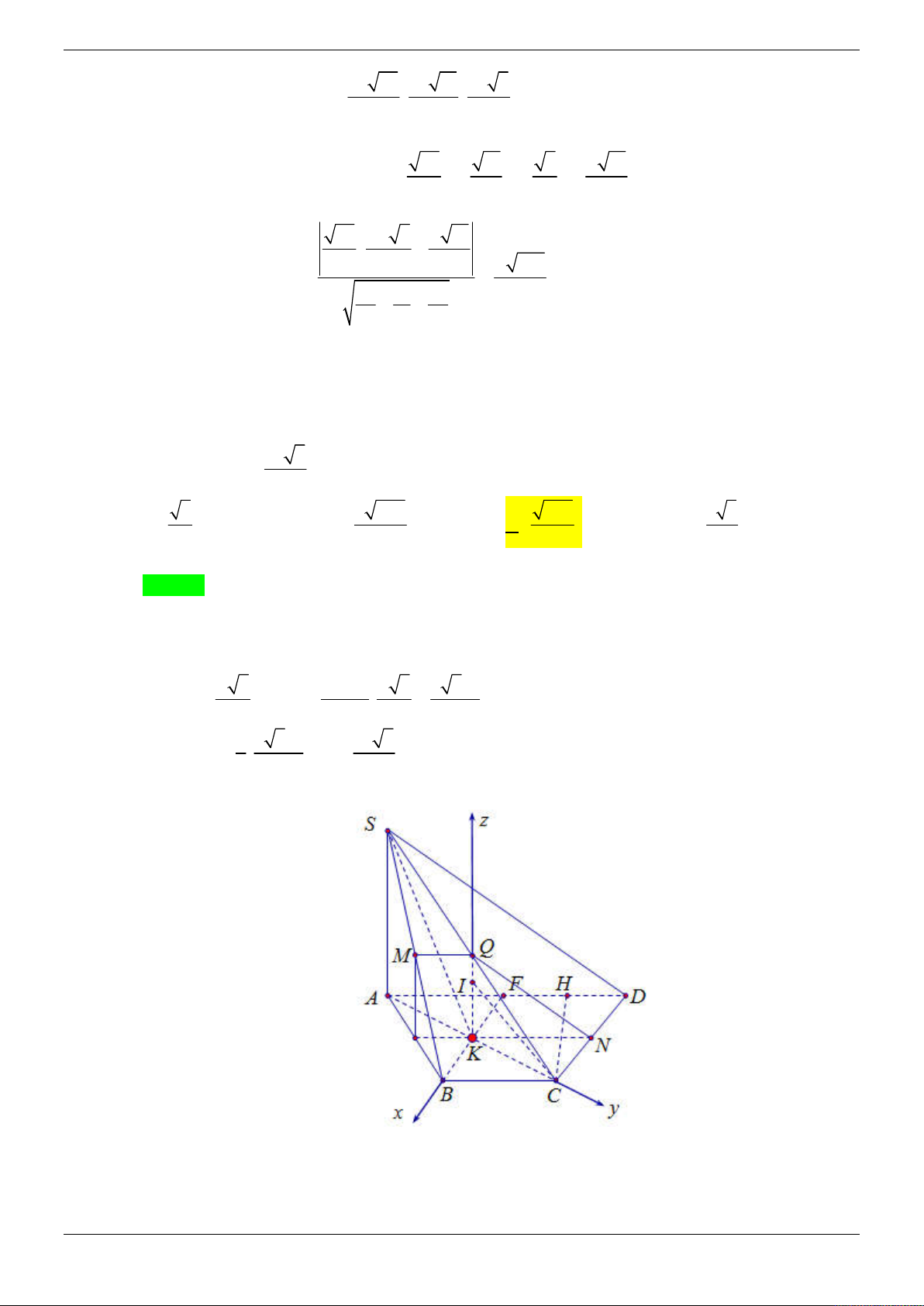
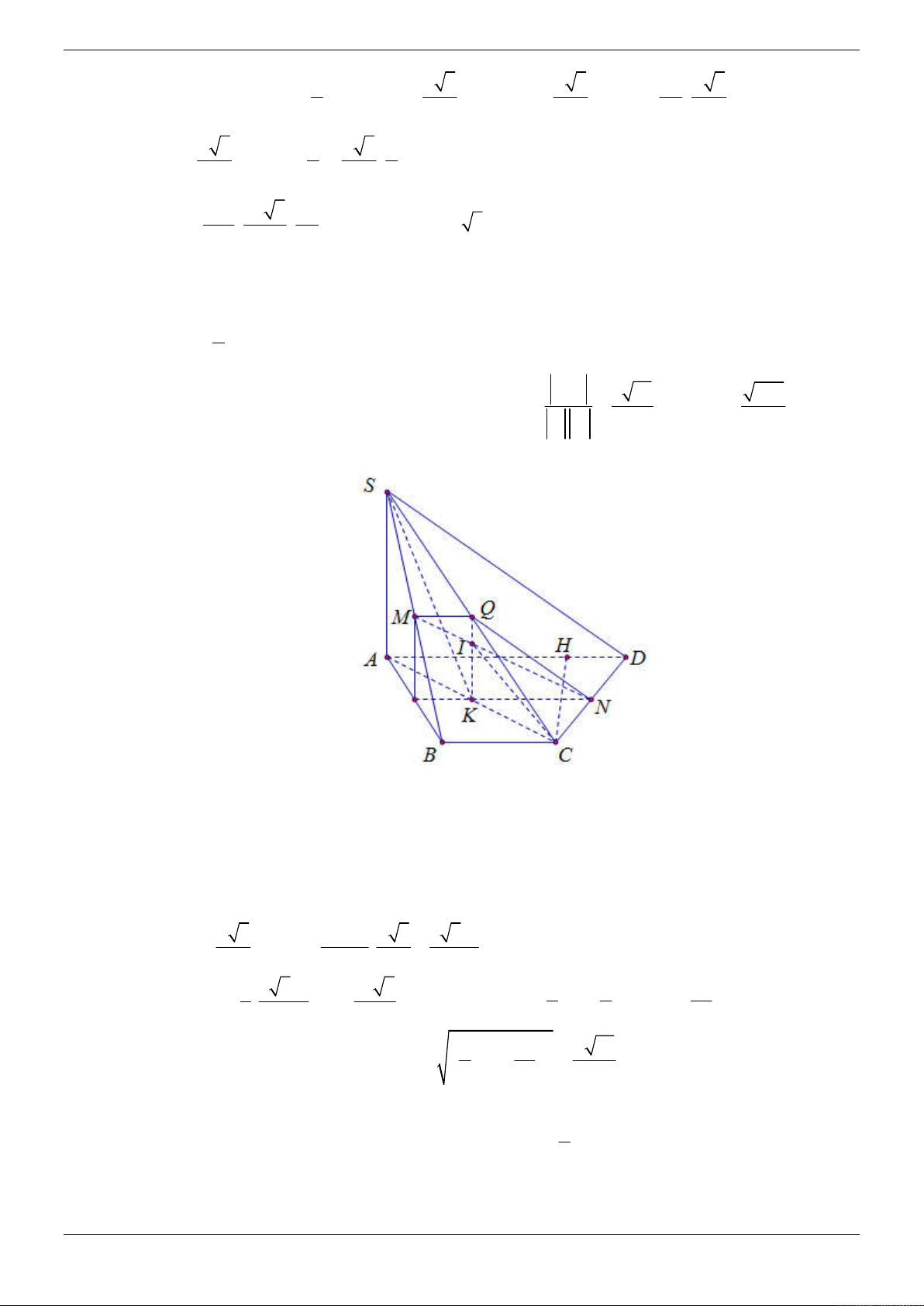
Câu 38: Cho hình lăng trụ tam giác đều AB . C A BC
  có độ dài cạnh đáy bằng a. Góc giữa  ABC và
ABC bằng 60 . Gọi M , N là trung điểm của BC và CC . Tính khoảng cách giữa A M  và AN. 6a 97 3a 97 6a 65 3a 65 A. . B. . C. . D. . 97 97 65 65 Lời giải Chọn B
Do BC vuông góc với mặt phẳng  AMA nên góc giữa 2 mặt phẳng  ABC  và  ABC  là góc
AMA bằng 60 , AA ' a 3 3a
Trong tam giác vuông AAM : 0 tan 60   AA '  . 3  AM 2 2
Trong mặt phẳng  ABC  kẻ đường thẳng Ay song song với BC , khi đó 3 đường
AM , Ay, A A
 đôi một vuông góc với nhau.
Xét hệ tọa độ Axyz sao cho: M Ax, A '  Az 3a a 3 a 3 a 3a Ta có: (
A 0; 0; 0), A '(0; 0; ), M ( ; 0; 0), N ( ; ; ) 2 2 2 2 4 2 2 2  a 3
3a  a 3 a 3a
  3a 9a 3 a 3 suy ra: A ' M ( ; 0;  ), AN ( ; ;
)   A ' M , AN   ( ;  ; ) 2 2 2 2 4   4 8 4
Áp dụng công thức tính khoảng cách giữa 2 đường thẳng chéo nhau, ta có:
  
A' M , AN  .AM 3   3a 3 / 8 3a 97
d ( A' M , AN ) 
    2
A' M , AN a 291 / 8 97  
Cách giải theo hình học cổ điển: Trang 54/69
Kẻ AE//AN E AC   AN //  AME   d AM , AN   d AN , AME   d  ,
A AME  1 1 1  AK. Có   2 2 2 AK AAAHa 3 3a
+Có góc giữa  ABC  và  ABC  là AMA  60  A' A  tan 60 .  AM  3.  . 2 2
+Dễ thấy AE A' F  2AC , với F A' N AC . 1 2S 2 2 2 1 a 3 SAH. AME EM AH  ; mà SS  .3. SS  . AME 2 EM AME 3 MEC 3 2 ABC ABC 4 a 31 a 53 2 2 EM
AE AM  2 AE.AM .cos150  .  AH  2 31 1 1 1 97 3 97 Vậy     AK a . 2 2 2 2 AK AH AA 9a 97
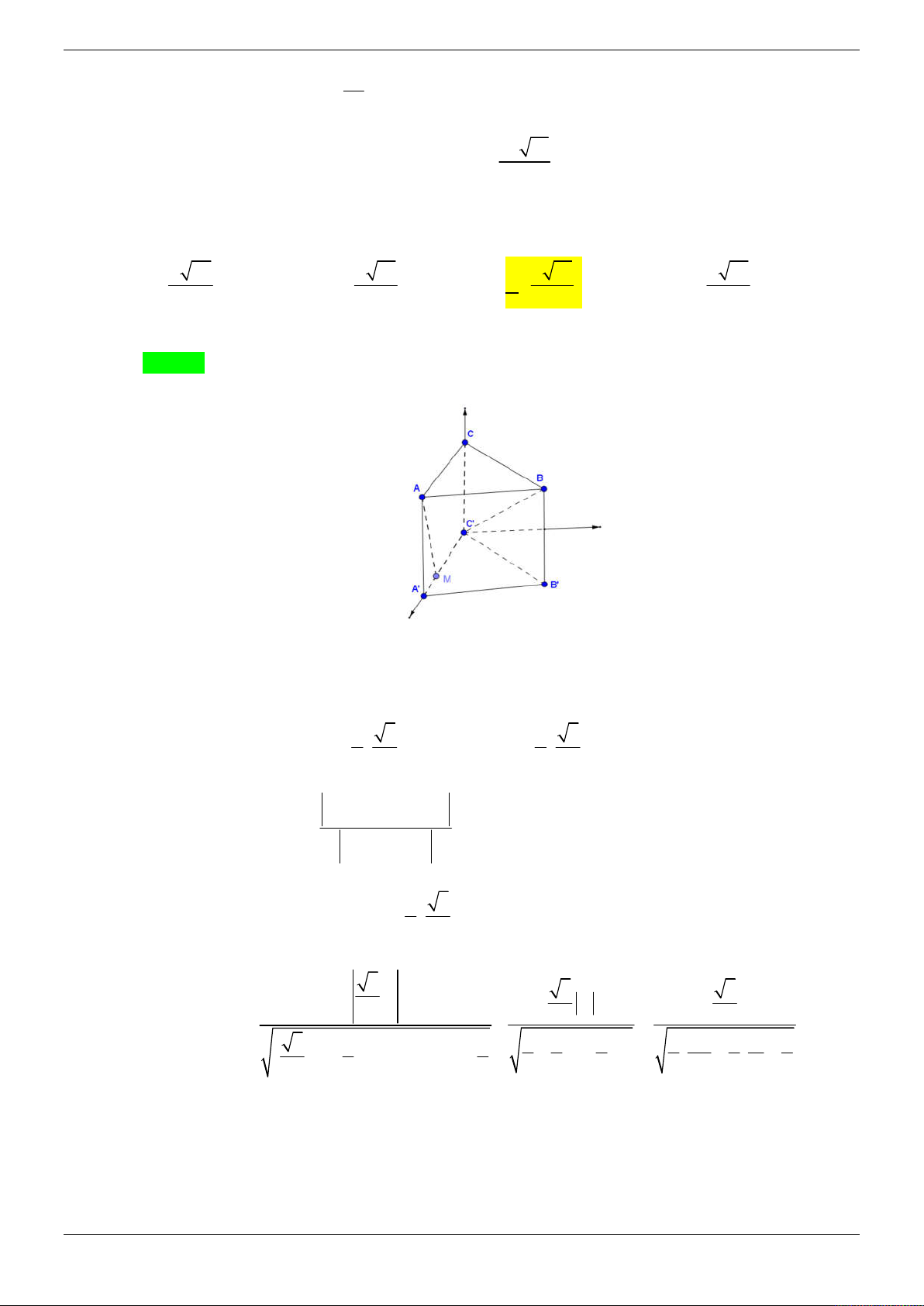
Câu 39: Cho lăng trụ tam giác đều AB . C A BC
  có tất cả các cạnh bằng a . M là một điển thỏa mãn  1  CM  
AA . Côsin của góc giữa hai mặt phẳng  AMB và  ABC  bằng 2 30 30 30 1 A. . B. . C. . D. . 10 8 16 4 Lời giải Chọn A
Xét hình lăng trụ tam giác đều AB . C A BC
  có tất cả các cạnh bằng a . Gắn hệ trục như hình vẽ
quy ước a 1 ( đơn vị ). Trang 55/69
Gọi D là giao điểm của A M  và AC . Vì tam giác A BC
  là tam giác cân cạnh bằng a nên ta suy ra độ dài các đường trung tuyến là
a 3 . Suy ra tọa độ các điểm như hình vẽ. 2  1  AD  
Theo giả thiết ta có CM  
AA vậy  ADA  CDM   2  DA  2  DC 2 CD  2 
Vậy tọa độ của điểm D là: D 0; ;1    3  
Ta có mặt phẳng ( ABC ) có phương trình z  0  nABC  0;0  ;1
Mặt khác mặt phẳng  AMB là mặt phẳng đi qua ba điểm A , D và B .  
   2   3 1    1 3  3 
Ta có: AD  0; ;1 
 và AB   ; ;1  n
  AD , AB    ; ;  A BM     3   2 2        6 2 3  
Vậy  cô sin góc tạo bởi hai mặt phẳng  AMB và  ABC  là:  3   3 3 30
A BM   ABC      n n .    . ABM ABC   cos ' , cos ,     1 3 1 10 10   . 1 36 4 3 Cách khác:
  3 1  
   3   1 3  3 3  1 AB   ; ;1 ,  A M  0;1; ,   A B ,  A M     ; ;        1;3 3; 2  3     2 2     2  4 4 2 4   Trang 56/69 
 mp  AMB có một vectơ pháp tuyến là n  . A BM 1;3 3; 2  3     
Mp(ABC) là mp(Oxy): z=0 có vtpt nABC  0;0;  1   
A BM   ABC     n n    A BM ABC   2 3 30 cos ' , cos ,     1 27 12 10
Câu 40: Cho hình hộp ABC . D A BCD
  có thể tích bằng V . Gọi M , N , P lần lượt là trung điểm của
các cạnh AB , A C
  , BB . Tính thể tích khối tứ diện CMNP . 5 1 7 1 A. V . B. V . C. V . D. V . 48 8 48 6 Lời giải Chọn A
Đây là bài toán tổng quát, ta đưa về cụ thể, giả sử hình hộp đã cho là hình lập phương có cạnh
bằng 1. Khi đóV  1 .
Chọn hệ trục Oxyz như hình vẽ, A là gốc toạ độ, các trục Ox, Oy, Oz nằm trên các cạnh
AB, AD, AA . Khi đó,  1   1 
C 1;1;0 ; B 1;0; 0  M ; 0 ; 0 
 ; B 1; 0 ;  1  P 1; 0 ;   ;  2   2   1 1  A 0; 0;  1 , C 1;1;  1  N ; ;1   .  2 2    1    1 1    1 
Ta có CM   ; 1; 0   , CN   ;  ;1   , CP  0 ; 1;   .  2   2 2   2 
1    1 5 5 5 Khi đó V
CM ,CN  .CP     VV CMNP CMNP 6   6 8 48 48 Trang 57/69
Câu 41: Cho hình hộp ABC . D A BCD
  , có đáy là hình thoi cạnh 2a , tâm O ,  0
BAD  60 và AA  2a .
Hình chiếu vuông góc của A lên mặt phẳng  ABCD trùng với tâm O . Gọi M là trung điểm
CD . Khoảng cách giữa hai đường thẳng A M
và BD bằng: 21 2 21 3 21 4 21 A. . B. . C. . D. . 7 7 7 7 Lời giải Chọn B z A' B' D' C' A B O D M C x y
+) Đáy ABCD là hình thoi cạnh 2a , tâm O ,  0
BAD  60 nên tam giác ABD là tam giác đều 3
cạnh 2a AO  .2a  3a 2 2 2 2 2 AO AA  AO
4a  3a a
+) Giả sử a  1. Chọn hệ trục tọa độ như hình vẽ O O 0;0; 0 , D 1; 0; 0  Ox ,
C 0; 3;0Oy và A0;0; 
1  Oz . Khi đó, B 1; 0;0 , A0; 3;0
  
Ta có: BB  DD  AA  0; 3 
;1 nên tìm được B 1;  3  ;1 và D1; 3  ;1  1 3 
M là trung điểm CD M  ; ;0   2 2   
  
AM ; B D
  .AB  
+) Ta có: d AM ; B D   
 
AM ; B D       1 3  AM   ; ; 1
   2 2  
   AM ; B D      0; 2; 3   B D    2;0;0   Trang 58/69  0  2 3  0 2 21
Mà AB  1; 3 ;0 nên d AM ; B D     . 0  4  3 7
Câu 42: Cho hình hộp chữ nhật ABC . D A BCD
  , có AB a, AD a 2, góc giữa A C  và mặt phẳng
ABCD bằng 30. Gọi H là hình chiếu vuông góc của A trên AB và K là hình chiếu vuông
góc của A trên A . D
Tính góc giữa hai mặt phẳng  AHK  và  ABB A   . A. 60 . B. 45. C. 90 . D. 30 . Lời giải Chọn B Do ABC . D A BCD
  là hình hộp chữ nhật nên A'C ' là hình chiếu vuông góc của A'C trên  0
( ABCD)  ( A 'C, ( ABCD))  ( A 'C, A 'C ')  CA 'C '  30 . CC ' 2 2  Ta có AC
AB AD a 3; tan CA 'C '   CC '  . a A 'C '
Kết hợp với giả thiết ta được ABB ' A' là hình vuông và có H là tâm.
Gọi E, F lần lượt là hình chiếu vuông góc của K trên A' D'& A' . A 1 1 1 a 6 a Ta có    AK  ; 2 2 A' K
A' A AK  ; 2 2 2 AK A' A AD 3 3 1 1 1 a 2 a 2 2    KF  ; KE
A' K KF KE  . 2 2 2 KF KA A' K 3 3
Ta chọn hệ trục tọa độ Oxyz thỏa mãn O A' còn D ,
B , A theo thứ tự thuộc các tia O , x O , y O .
z Khi đó ta có tọa độ các điểm lần lượt là: a a a 2 a a 2 a 2 (
A 0;0; a), B '(0; ;
a 0), H (0; ; ), K ( ; 0; ), E( ; 0;0), F (0; 0; ). 2 2 3 3 3 3 
Mặt phẳng  ABB ' A ' là mặt phẳng (yOz) nên có VTPT là 1 n  (1; 0; 0); Trang 59/69 2   a  
Ta có  AK , AH  
n2 , n2 (2; 2; 2).   6 
Mặt phẳng (AKH ) có VTPT là n2  (2; 2; 2 );
Gọi  là góc giữa hai mặt phẳng  AHK  và  ABB A   .   1 Ta có 0
cos  cos( 1 n , n2 )     45 . 2
Câu 43: Cho lăng trụ ABCD.A B C D có đáy ABCD là hình vuông cạnh a . Hình chiếu vuông góc của 1 1 1 1
A lên  ABCD trùng với giao điểm của AC và BD . Tính khoảng cách từ điểm B đến mặt 1 1 phẳng  A BD . 1  a 2 a 2 a 21 a 3 A. . B. . C. . D. . 4 2 4 2 Lời giải Chọn B
Chọn hệ trục toạ độ sao cho tâm O của hình vuông ABCD là gốc toạ độ, OA là trục Ox, OB là
trục Oy, OA1 là trục Oz như hình vẽ  a 2   A ; 0;0   2   
Vì mp A BD mp(Oyz) nên mp A BD có phương trình: x  0 1  1 
AB cắt mp A BD tại trung điểm AB 1  1 1 a 2 a 2
d (B ;( A BD))  d ( ; A ( A BD))   1 1 1 2 2
Câu 44: Cho hình lập phương ABC .
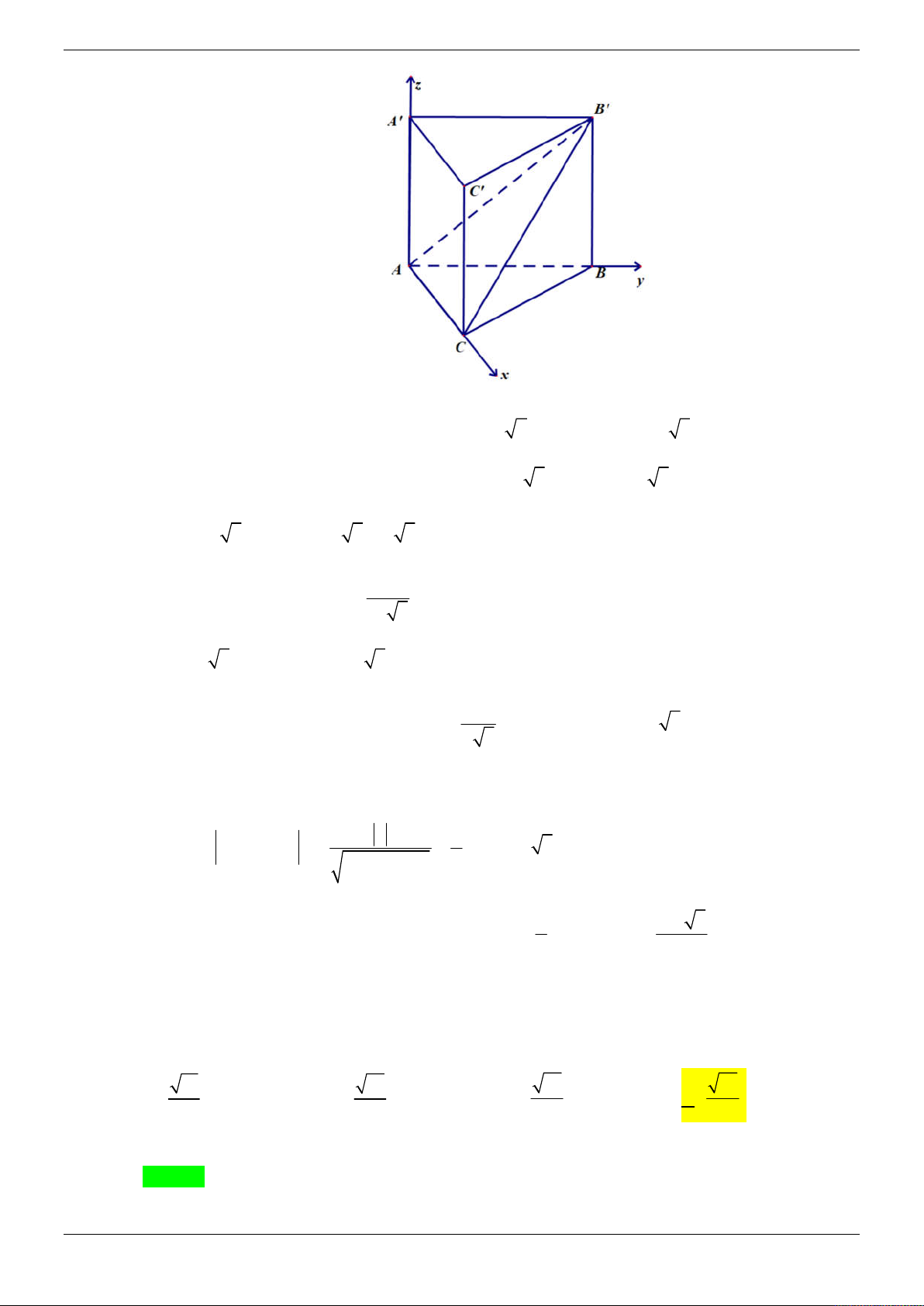
D A' B 'C ' D ' cạnh a . Gọi K là trung điểm của DD ' . Tính khoảng
cách giữa hai đường thẳng CK và A' D . a a a a A. . B. . C. . D. . 3 4 5 2 Lời giải Trang 60/69 Chọn A
Chọn hệ trục tọa độ Oxyz với gốc O trùng với điểm A , các tia Ox , Oy , Oz lần lượt trùng với
các tia AB , AD , AA ' . Khi đó A 0;0;0 , B a; 0; 0 , D 0; a;0 , A '0; 0; a , B 'a; 0; a  ,
C a; a;0  a
Gọi M là trung điểm của BB '  M a; 0;    2    2 2
   a   aa
A ' M a; 0;  2 2    
 , A' D  0; ; a a
A' M , A' D  ; a ; a    1;2;2    2  2 2   
Suy ra  A ' DM  nhận n  1; 2; 2 làm vec tơ pháp tuyến và đi qua điểm A '0; 0; a
A ' DM  : x  2 y  2z  2a  0
Do M là trung điểm của BB ' nên A' M / /CK
a  2a  2a a
d CK, A' D  d CK, A' DM   d C, A' DM    . 2 2 2 3 1  2  2
Câu 45: Cho hình hộp chữ nhật ABC . D A BCD
  có AB  3a, AD AA  a . Lấy điểm M thuộc đoạn
AB , điểm N thuộc đoạn A C
  sao cho AM AN x , 0  x  10a,. Tìm x theo a để
đoạn MN nhỏ nhất. 30a 10a 10a A. 0 . B. . C. . D. . 3 2 3 Lời giải Chọn C Trang 61/69 z A' D' F N B' C' M y A D B E C x Ta có 2 2 2 2 AB  AB BB 
9a a  10a .
Gọi E là hình chiếu của M lên AB . AE AM . AB AM 3ax 3x Ta có   AE    . AB ABAB 10a 10 ME AM BB .AM ax x   ME    . BBABAB 10a 10
Gọi F là hình chiếu của N lên AB . 3x x
Tương tự ta tính được AC   10a , AF  , NF  . 10 10
Chọn hệ trục tọa độ Oxyz sao cho O A , các điểm B , D , A lần lượt nằm trên các tia Ox ,
Oy , Oz . Khi đó ta có tọa các điểm lần lượt là: A 0;0;0 , B 3a;0;0 , D 0; a;0 , A0; 0; a  ,  3x x   3x xM ; 0;   , N ; ; a   .  10 10   10 10  2 2 2 2 2 xx  2x 2ax  2x a a a Ta có 2 MN    a    a         . 10  10 10  10  10 2  2 2   a 2x a 10a GTNN của MN là khi   x  . 2 10 2 2
Câu 46: Cho hình hộp chữ nhật ABC .
D A' B 'C ' D' có AB a, AD  2a, AA '  3a. Gọi M , N , P lần
lượt là trung điểm của BC , C ' D ' và DD '. Tính khoảng cách từ A đến mp MNP. 15 9 3 15 A. a . B. a . C. a . D. a . 22 11 4 11 Lời giải Chọn D Trang 62/69
Chọn hệ trục tọa độ Oxyz với gốc O trùng với điểm B , tia ; Ox ;
Oy Oz lần lượt trùng với tia B ;
A BC; BB '. Khi đó B 0; 0;0; Aa;0; 0;C 0; 2a;0; D a; 2a; 0;C '0; 2a;3a; D 'a; 2a;3a.  3a   a
Suy ra M 0; a; 0; P a; 2a; và N ; 2a; 3a     .  2   2   
3a    a  Ta có MP a; a; ; MN ; a; 3a   
 , vectơ pháp tuyến của  MNP là:  2   2  2     3 9 1  a 2
n  MP; MN   a ;  ;    6;9; 2    2 4 2  4 6a  9a 15a
Suy ra MNP :6x  9y  2z  9a  0; A ;
a 0;0 . Vậy d  ;
A MNP   . 2 2 2 11 6  9  2
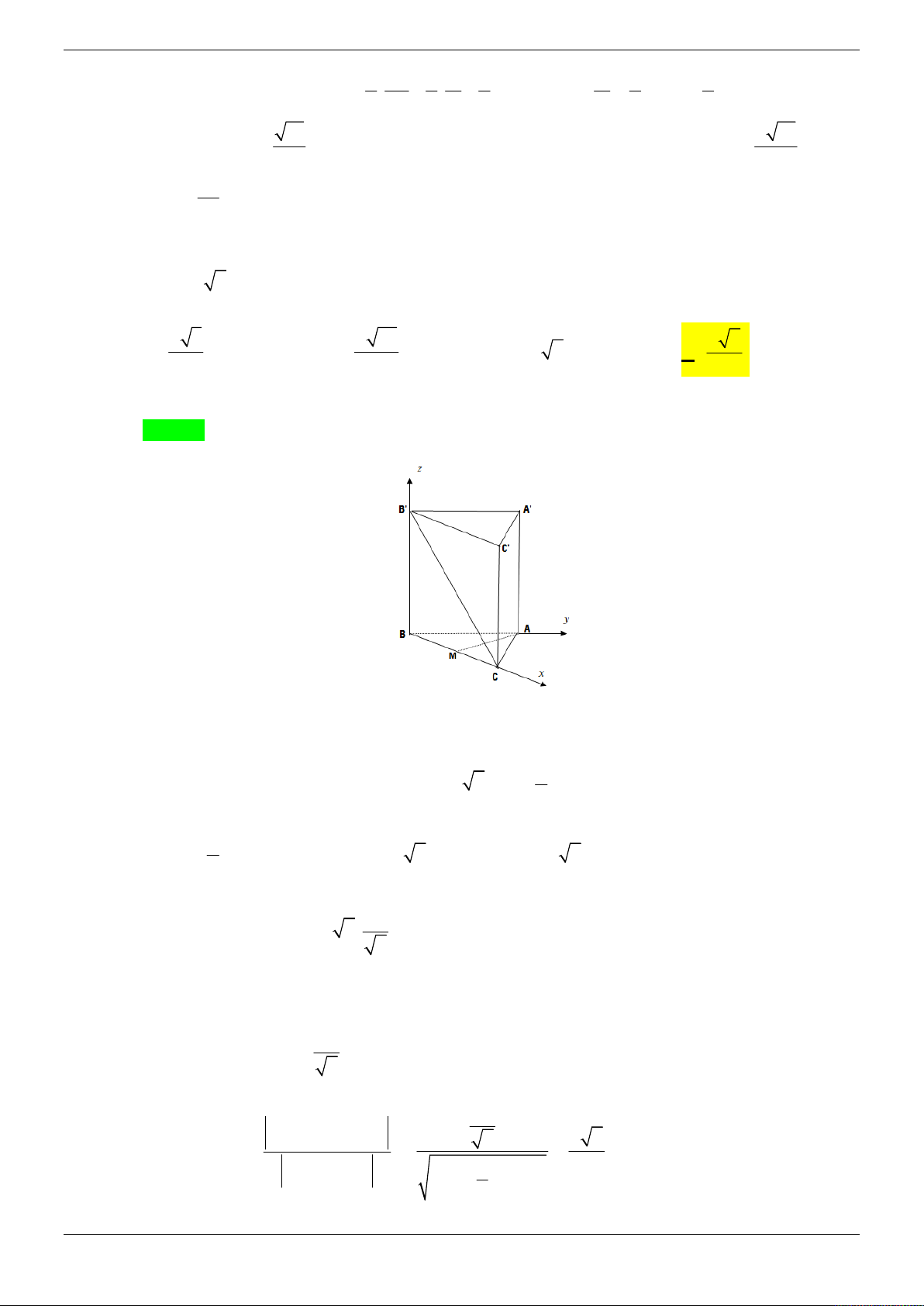
Câu 47: Cho hình lăng trụ đứng ABC.AB C
  có đáy là tam giác vuông cân, AA  2a , AB AC a .
Gọi G và G lần lượt là trọng tâm của tam giác ABC và tam giác AB C
  , I là tâm của hình chữ nhật ABB A
  . Thể tích của khối . A IGCG . 3 a 3 a 3 a 5 3 a 5 A. . B. . C. . D. . 2 6 6 30 Lời giải Chọn B Trang 63/69
Chọn hệ trục tọa độ Oxyz thỏa mãn O trùng với điểm A , các tia Ox , Oy , Oz trùng với các
tia AB , AC và AA .  a a
Suy ra A0;0;0 , B  ;
a 0;0 , C 0; ;
a 0 , A0;0;2a , B ;
a 0; 2a , C0; ;
a 2a , G ; ; 0   ,  3 3   a a   aG ; ; 2a   , I ; 0; a
 (vì I là trung điểm của AB và AB ).  3 3   2      a a
  a 2a  Ta có IG   ; ; a   và G C    ; ; 2a
 . Suy ra IG và G C  cùng phương.  6 3   3 3 
Do đó bốn điểm I , G , C , G đồng phẳng.
  a 2a
Mặt khác GC   ; ; 0    3 3  2 2    4a 2a   Vì GC  ,GC  ; ;0   IGCG   nên mặt phẳng 
 có véc-tơ pháp tuyến n  2;1;0 . 3 3  
Vậy phương trình mặt phẳng  IGCG : 2x y a  0 . a a
Suy ra h   A IGCG 5 d ,   . 4 1 5 1
Diện tích tứ giác IGCG bằng SIG G CIG G C  . IGCG   .d  ,  2   a 41 a 41 GC  ,GC   Trong đó IG  , G C   , d  I , G G C    d , G G C     6 3 G C  2 2    4a 2a  5 Vì G C  , GC   ; ; 0   nên d I , G G C    2a .   3 3   41 2 1  a 41 a 41  5 a 5 Suy ra S    .2aIGCG . 2  6 3  41 2   Thể tích cần tìm bằng A' G' C' 2 1 1 a 5 5 3 E' V  .S .d , A IGCG  . .a a . A IGCGIGCG     . 3 3 2 5 B' 6 Cách khác: I
Gọi E , E  là trung điểm AB, A B
  , kẻ AH vuông góc C E tại H CEE C
  là hình chữ nhật, A H C E G B Trang 64/69 2 a a 5 a 5 a 5
EE  CC'  2a , 2 CE C E    a   , CG C G    , GE G E    , 4 2 3 6 E A .AC a 5 AH   CE 5 2 a 5  1 a 5  1 a 5 a 5 SSSSS  2a.  2 a.   2 . a.IGCGCEE C   IEG IE G   CG C   2  2 6  2 3 2   2 3 1 1 a 5 5 a V  .S .AH  . .a  . A IGCG  3 IGCG 3 2 5 6 Câu 48:
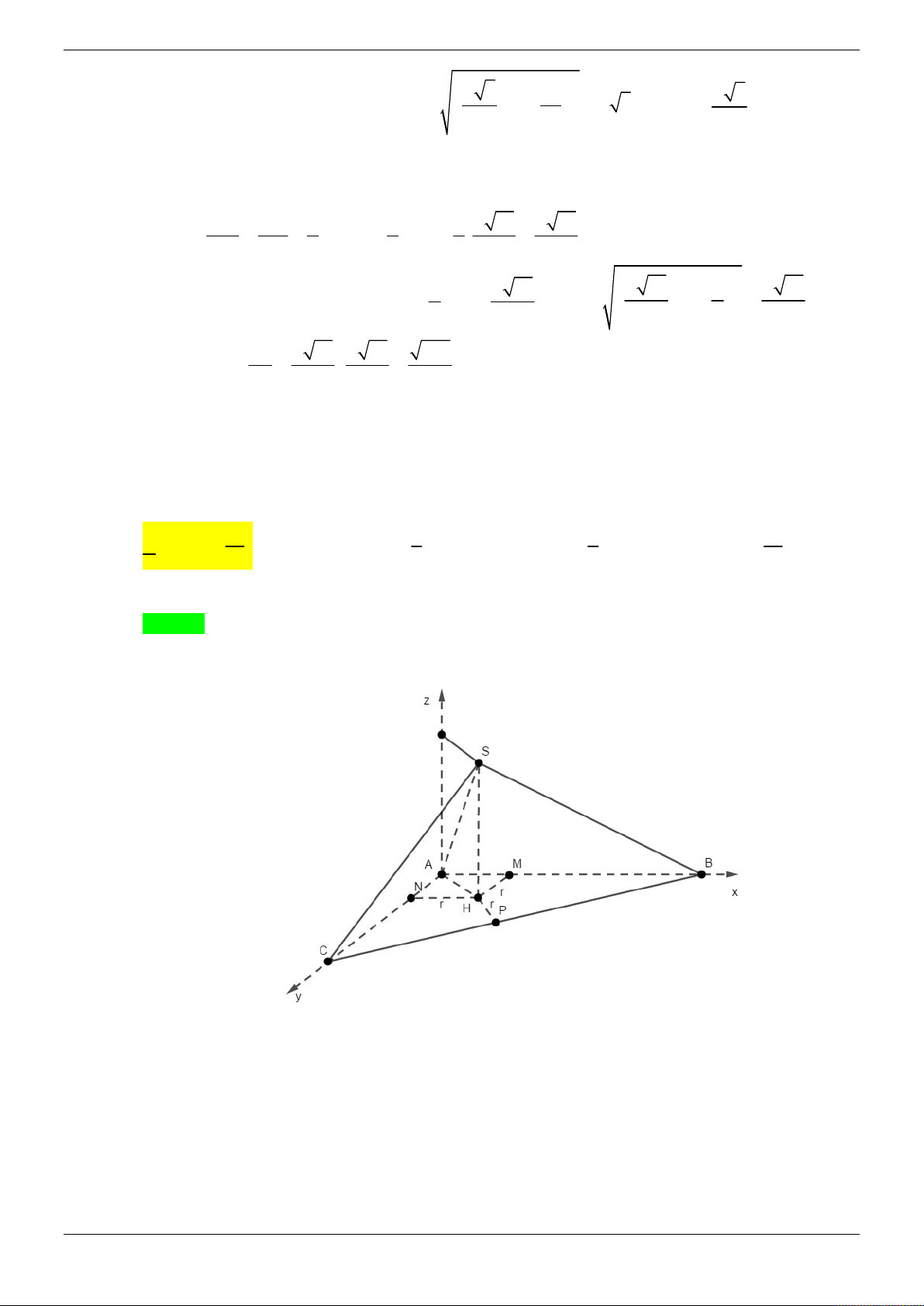
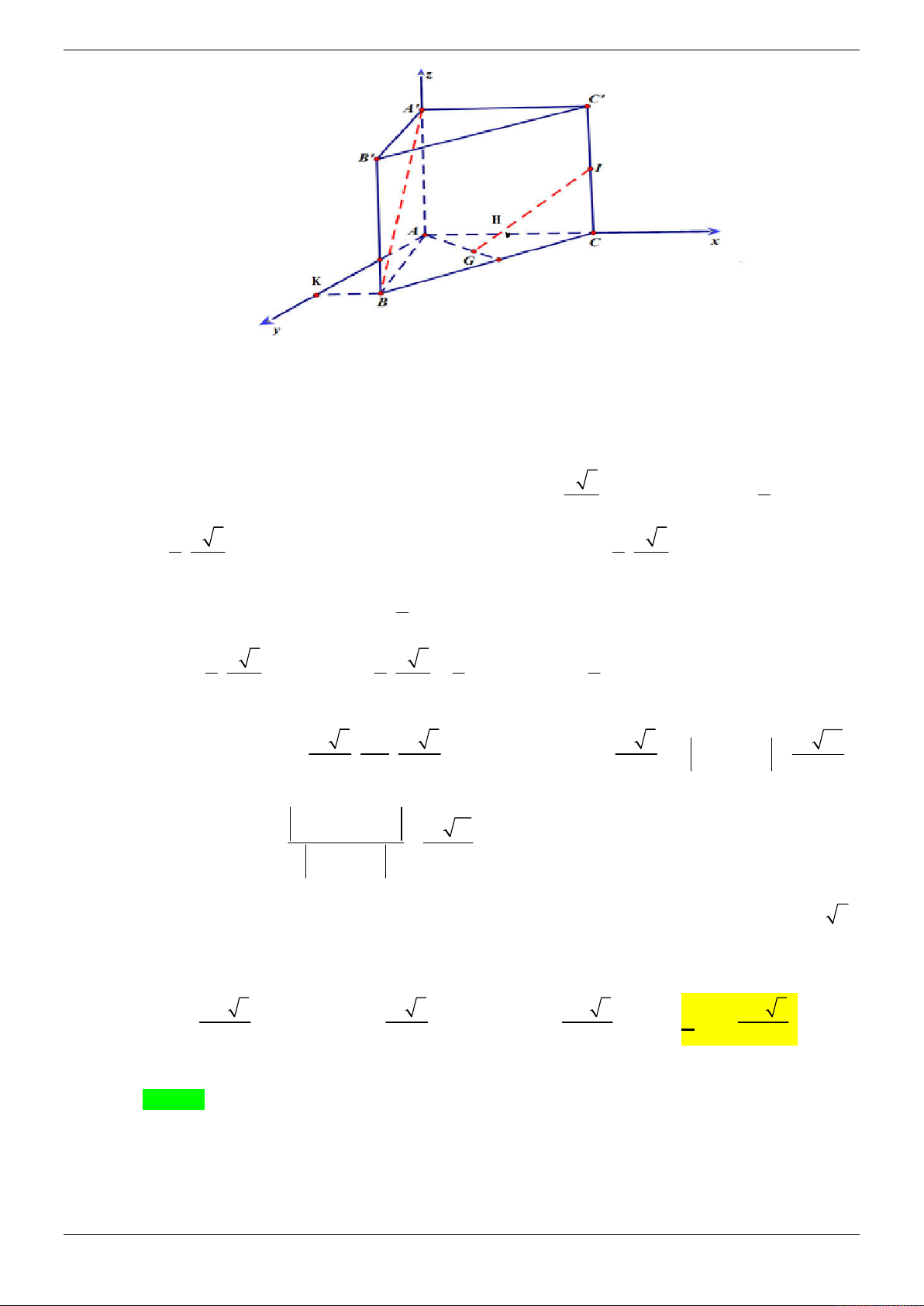
Cho hình hộp ABCDA' B 'C ' D ' có đáy là hình vuông cạnh a. Mặt phẳng ( ABB ' A ') BA
vuông góc với đáy, tam giác ' A AB vuông tại ' A , góc giữa ' và đáy bằng 0 6 0 .
Gọi I là tâm của hình vuông ABCD . Tính khoảng cách giữa hai đường thẳng IA ' và DB' . a a a 3 a 3 A. . B. . C. . D. . 2 55 55 55 2 Lời giải Chọn C
Gọi O là hình chiếu vuông góc của '
A lên cạnh AB . Vì mặt phẳng ( ABB ' A ') vuông góc với
( ABCD) nên A ' O  ( ABC D ) . 
Ta có góc giữa BA' và mặt phẳng ( ABCD) là góc A' BO a a a 3 0 Ta có 0
BA '  AB.cos 60  , 0
BO A ' B.cos 60  , OA'  A' . B sin 60  2 4 4
Chọn hệ tọa độ O xyz như hình vẽ. Khi đó a 3 a aa 3  a a 3
O (0; 0; 0 ) , A'(0;0;
) , B( ; 0; 0) , I( ; ;0), ( D ; ; a 0), B'( ; a 0; ) 4 4 4 2 4 4   a a
a 3    7a
a 3   Ta có IA'   ; ; , DB'   ; ; a
; A' B'   ; a 0;0  . 4 2 4   4 4      Trang 65/69 2 2 2  
a 3 3a 3 5a
Khi đó: IA'; DB'   ; ;     . 8 8 8    3 a 3
  
IA '; DB ' .A ' B ' 3 8   a 3 8 a 3
Ta có: d (A'I; DB')      .  . 2
IA '; DB '  3 27 25 8  a 55 55 4   a      64 64 64 
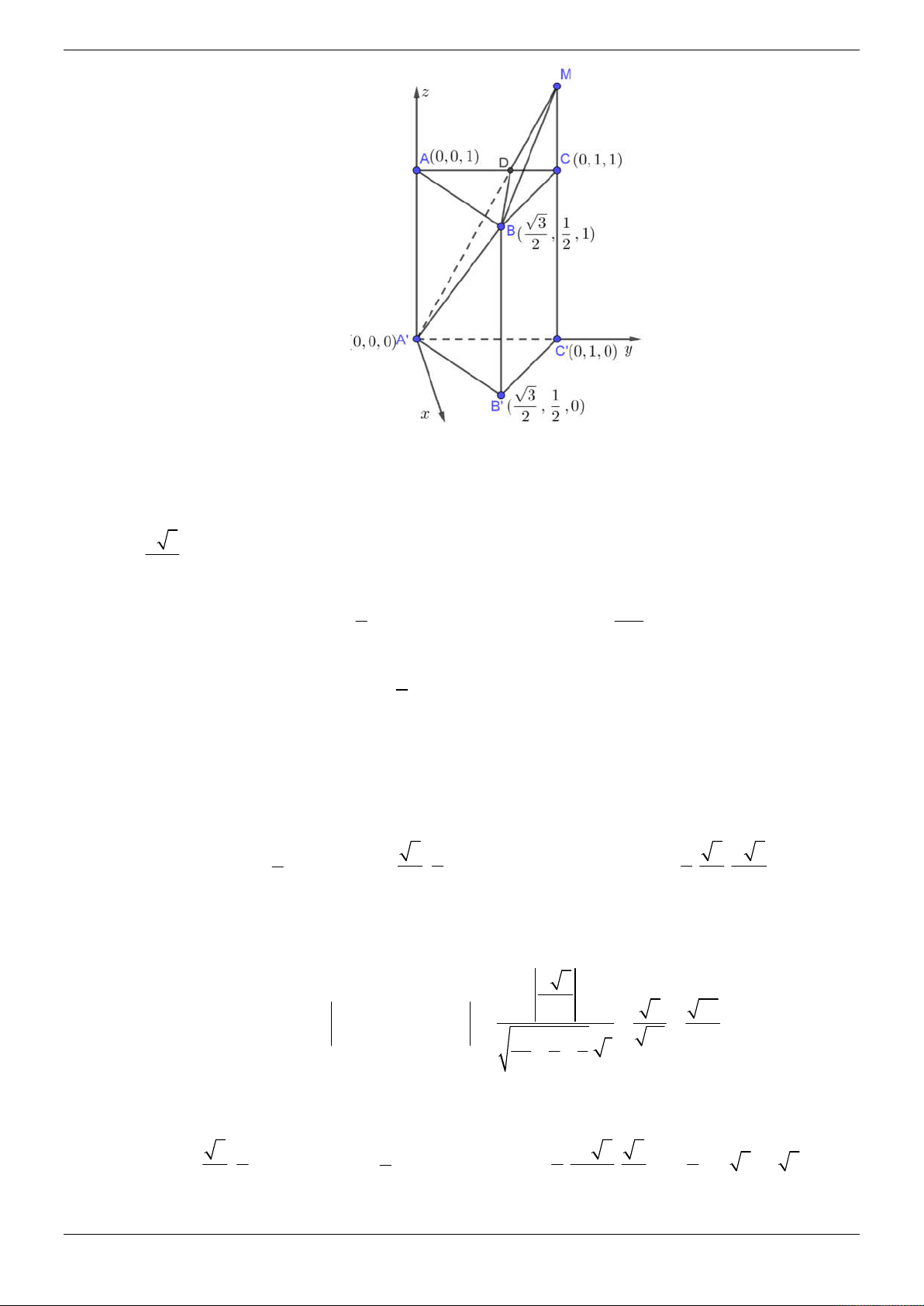
Câu 49: Cho hình chóp .
S ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA  2a và vuông góc
với mặt phẳng đáy. Gọi M là trung điểm cạnh SD . Tang của góc tạo bởi hai mặt phẳng
( AMC ) và ( S B C ) bằng 3 2 5 2 3 5 A. . B. . C. . D. . 2 5 3 5 Lời giải Chọn B
Để thuận tiện trong việc tính toán ta chọn a  1 .
Trong không gian, gắn hệ trục tọa độ Oxyz như hình vẽ sao cho gốc O trùng với điểm A , tia
O x chứa đoạn thẳng AB , tia O y chứa đoạn thẳng AD , tia Oz chứa đoạn thẳng AS . Khi
đó: A(0 ; 0 ; 0) , B(1; 0;0) , C (1;1; 0) , S(0;0; 2) , D(0;1;0) .  1 
Vì M là trung điểm SD nên tọa độ M là M 0; ;1   .  2     SB  (1; 0 ; 2)    Ta có   n  [ S ; B BC ] =(2;0;1) . SBC BC  (0 ;1; 0) 
Gọi  là góc giữa hai mặt phẳng ( AMC) và ( SB C ) .   n .n   SBC AMC 5
Suy ra cos  cos n ; n SBC AMC              . n . n 3 SBC  AMC 1 1 Mặt khác, 2 1 tan    tan  1 . 2 2 cos  cos  Vậy 1 2 5 tan   1  . 2 5  5    3  
Câu 50: Hai quả bóng hình cầu có kích thước khác nhau được đặt ở hai góc của một căn nhà hình hộp
chữ nhật sao cho mỗi quả bóng đều tiếp xúc với hai bức tường và nền của nhà đó. Biết rằng Trang 66/69
trên bề mặt của hai quả bóng đều tồn tại một điểm có khoảng cách đến hai bức tường và nền
nhà mà nó tiếp xúc bằng 1; 2; 4 . Tổng độ dài đường kính của hai quả bóng đó là? A. 7. B. 12 . C. 14 . D. 16 . Lời giải: Chọn C z a a y O I a x
Xét 1 quả bóng tại góc nhà
Chọn hệ trục như hình vẽ, ở đó các trục O x, O y , O z là ba mép tường nhà; O là góc nhà.
Tâm của quả bóng là I  ; a ; b c .
Vì mỗi quả bóng đều tiếp xúc với hai bức tường và nền của nhà nên chúng tiếp xúc với ba mặt
d I;Oxy  d I;Oyz  d I;Oxz  R a b c R  0 phẳng tọa độ, do đó . M  ; x ; y z Gọi
là điểm nằm trên quả bóng có khoảng cách đến hai bức tường và nền nhà mà nó M 1;2;  4
tiếp xúc bằng 1; 2; 4 , ta suy ra .
Điểm M nằm trên quả bóng khi:
IM R a  a  2 a  2 a  2 1 2 4  a 2
 2a  14a  21  0  7  7 a   2   7 7 a   2
Vì hai quả bóng có vai trò và tính chất như nhau nên chúng lần lượt có bán kính là: 7  7 7  7 R  ; R  1 2 2 2
Vậy tổng đường kính của hai quả bóng là d  2 R R 14. 1 2 
-------------------- HẾT -------------------- Trang 67/69