50 câu trắc nghiệm tổng ôn số phức có lời giải chi tiết – Lê Viết Nhơn Toán 12

50 câu trắc nghiệm tổng ôn số phức có lời giải chi tiết – Lê Viết Nhơn Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

31 16 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Số phức

Môn: Toán 12

Thông tin:

15 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Mã đê 04_Trang 1
Gv. LÊ VIẾT NHƠN KỲ THI TRUNG HỌC PHỔ THÔNG QUỐC GIA 2017
50 CÂU
TỔNG ÔN SỐ PHỨC
Bài thi: TOÁN
( Đề thi gồm có 7 trang ) Thời gian làm bài. 90 phút, không kể thời gian phát đề.
Họ, tên thí sinh. …………………………………………………………
Số báo danh. …………………………………………………………….
Câu 1: Tìm môđun của số phức
1w
z z
biết rằng số phức
z
thỏa mãn biểu thức:
2
3 2 2 4i z i i
.
A.
2w
. B.
10w
. C.
8w
. D.
2w
.
(TTLT ĐH DIỆU HIỀN_CẦN THƠ).
Hướng dẫn giải
Ta có
2
2
1
5
3 2 2 4 3 2 4 2 3 2 1 5
3 2
i
i z i i i z i i i z i z
i
1 5 3 2
1
3 2 3 2
i i
z z i
i i
Khi đó
1
1 1 1 3 10 w z z i i i w
Chọn B.
Câu 2: Cho số phức
2
3z i
. Tìm môđun của số phức
1w
i z z
.
A.
3w
. B.
5w
. C.
4w
. D.
7w
.
(TRƯỜNG THPT CHUYÊN KHTN_HÀ NỘI).
Hướng dẫn giải.
Ta có
1
2 3 2 3 3 4 5w i i i i w
.
Chọn B.
Câu 3: Cho số phức
,z
a bi a b
thỏa mãn
2
3 5 4 4i z i i
. Tính tổng
P
a b
.
A.
2
6
5
P
B.
8
3
P
C.
4P
D.
2P
(TRƯỜNG THPT CHUYÊN KHTN_HÀ NỘI).
Hướng dẫn giải
Ta có
4
4 3 5
2
3 5 4 4 3 3, 1
2
i
i
i z i i z i a b
i
.
Do đó
2P
.
Chọn D
Câu 4: Gọi
1
z
,
2
z
là 2 nghiệm của phương trình
2
1 0z z
. Tính giá trị
2017
2017
1 2
P
z z
A.
1P
. B.
1P
. C.
0P
. D.
2P
.
(TRƯỜNG THPT CHUYÊN KHTN_HÀ NỘI).
Hướng dẫn giải
Mã đề 04
Mã đê 04_Trang 2
Ta có:
2
3 3 2016 2017
1
1 1 1 1 1 1
1
0 1 0 1 1
z
z z z z z z
Chứng minh tương tự:
2017
2 2
z z
1
2
1P
z z
.
Chọn B.
Câu 5: Xác định số phức liên hợp
z
của số phức
z
biết
1
2
2 3 .
1 2
i z
i
i
A.
7
5
.
2 2
z i
B.
7
5
.
2 2
z i
C.
7
5
.
2 2
z i
D.
7
5
.
2 2
z i
(TRƯỜNG THPT GIA LỘC II)
Hướng dẫn giải
1 2
2 3 1 2 8
1 2
i z
i i z i
i
6
7 5
.
1 2 2
i
z
i
i
Vậy
7
5
.
2 2
z i
Chọn A.
Câu 6: Cho số phức
z
thỏa mãn
1
7
1 2
1 3
i
iz i
i
. Xác định điểm A biểu diễn số phức liên hợp
z
.
A.
1
;3A
. B.
1
; 3A
. C.
1
; 3A
. D.
1
;3A
.
(TRƯỜNG THPT GIA LỘC II)
Hướng dẫn giải
Ta có
1 7 3
1 2 1 2 ( 2 ) 3 1 3 1 3
1 3
i i
iz i iz i i iz i z i z i
i i
Chọn D
Câu 7: Gọi
1 2
,z
z
là hai nghiệm của phương trình
2
2 3 2 0z z
trên tập số phức. Tính giá trị
biểu thức
2
2
1 1 2 2
P
z z z z
.
A.
5
2
P
. B.
5
2
P
. C.
3
3
4
P
. D.
3
4
P
(TRƯỜNG THPT GIA LỘC II)
Hướng dẫn giải
Ta có
2
2
2
1 1 2 2 1 2 1 2
9
5
1
4 2
P z z z z z z z z
.
Chọn A.
Câu 8: Gọi
1
z
và
2
z
là hai nghiệm của phương trình
2
2
5 0z z
biết
1
2
z
z
có phần ảo là
số thực âm. Tìm phần thực của số phức
2
2
1 2
2w z
z
.
A.
4
.
B.
4
.
C.
9.
D.
9
.
(TRƯỜNG THPT HAI BÀ TRƯNG_HUẾ)
Mã đê 04_Trang 3
Hướng dẫn giải
Ta có
12
2
1 2
2 5 0
1 2
z i
z z
z i
(do
1
2
4z
z i
có phần ảo là
4
).
Do đó
2
2
92
zw
.
Vậy phần thực của số phức
2
2
1 2
2w
z z
là
9
.
Chọn D.
Câu 9: Tính
2
3 2017
1
009 2 3 ... 2017S i i i i
A.
S
2017 1009i.
B.
10
09 2017 .i
C.
20
17 1009 .i
D.
10
08 1009 .i
(TRƯỜNG THPT HAI BÀ TRƯNG_HUẾ)
Hướng dẫn giải
Chọn C
Ta có
2
3 4 2017
4 8 2016 5 9 2017
2
6 10 2014 3 7 11 2015
504
505 504 504
1 1 1 1
1008
2 3 4 ... 2017
1009 4 8 ... 2016 5 9 ... 2017
2 6 10 ...2014 3 7 11 ... 2015
1009 4 4 3 4 2 4 1
1009
n
n n n
S
i i i i i
i i i i i i i
i i i i i i i i
n i n n i n
509040
509545 508032 508536
2017 1009 .
i i
i
(TRƯỜNG THPT HAI BÀ TRƯNG_HUẾ)
Câu 10: Cho hai số phức
1
z
,
2
z
thỏa mãn
1
2
,
0
z
z
;
1
2
0
z
z
và
1
2 1 2
1
1 2
z z z z
. Tính
1
2
z
z
A.
2
2
. B.
3
2
. C.
2
3
. D.
2
3
.
(CHUYÊN QUANG TRUNG_BÌNH PHƯỚC)
Hướng dẫn giải.
Đặt
1
2
z
x
z
1
2
.z
x z
và
1
2
z
x
z
Từ giả thiết
1
2 1 2
1 1 2
z z z z
2
2 2 2
1 1 2
.
.
x
z z x z z
2
2
1
1 1
2
1z
x z x
1 1
2
1x
x
2
2 2 1 0
x x
1
1
2 2
x i
2
2
x
Chọn A.
Câu 11: Cho
1
2
,z
z
là hai nghiệm phức của phương trình
2
2 4 0
z z
. Tính
1
2
z
z
.
A.
2
3.
B.
4.
C.
4
3.
D.
5.
(CHUYÊN QUANG TRUNG_BÌNH PHƯỚC)
Hướng dẫn giải
Mã đê 04_Trang 4
Ta có
1
2
2
1 3
2 4 0
1 3
z i
z z
z i
.
Vậy
2
2
2 2
1 2
1
3 1 3 4z z
.
Chọn B.
Câu 12: Tính mô đun của số phức
4 3z i
.
A.
5.2z
B.
7.z
C.
5.z
D.
7.z
(TRƯỜNG THPT HÀ HUY TẬP_NGHỆ AN)
Hướng dẫn giải.
Ta có
2
2
.4
3 5z
Chọn C.
Câu 13: Cho hai số phức
1
3 3z i
và
2
1 2z i
. Phần ảo của số phức
1 2
2w z z
là:
A.
1.
B.
.1
C.
.7
D.
7.
(TRƯỜNG THPT HÀ HUY TẬP_NGHỆ AN)
Hướng dẫn giải
Ta có
1
2
2
3 3 2 1 2 1z z iw i i
.
Vậy phần ảo của số phức
1
2
2w z
z
là
1.
Chọn A.
Câu 14: Tìm số phức
z
thỏa mãn
1
1 2 3 2 0i z i i
.
A.
4
3z i
. B.
3
5
2 2
z i
. C.
5
3
2 2
z i
.
D.
4
3z i
.
(TRƯỜNG THPT HÀ HUY TẬP_NGHỆ AN)
Hướng dẫn giải
Chọn B.
Ta có
1 1 2 3 2 0i z i i
3 2 5 1
1 2
1 2 2
i
z i i
i
5 1 3 5
1 2
2 2 2 2
z i i i
.
Câu 15: Gọi
0
x
là nghiệm phức có phần ảo là số dương của phương trình
2
2 0x x
. Tìm số
phức
2
0
0
2
3z x x
.
A.
1
7z i
. B.
2
7z i
. C.
1 7
2
i
z
. D.
3 7
2
i
z
.
(THPT CHUYÊN LAM SƠN THANH HÓA)
Hướng dẫn giải.
Ta có:
2
0
1
7
2
0
2 2
x
x z i
2
0
0
1
7
2
3
2 2
z
x x i
Chọn C
Câu 16: Cho số phức
1
3z i
. Tính môđun của số phức
2
.w
z i z
.
A.
14
6w
. B.
5
2w
. C.
50w
. D.
10w
.
(THPT CHUYÊN LAM SƠN THANH HÓA)
Hướng dẫn giải.
Mã đê 04_Trang 5
Chọn B.
Câu 17: Mệnh đề nào dưới đây sai?
A. Số phức
5 3z i
có phần thực là
5
, phần ảo
3
.
B. Điểm
1
;2M
là điểm biểu diễn số phức
1 2z i
.
C. Mô đun của số phức
,z
a bi a b
là
2
2
a b
.
D. Số phức
2z
i
là số thuần ảo.
(THPT CHUYÊN LAM SƠN THANH HÓA)
Hướng dẫn giải
Mô đun của số phức
,z a bi a b
là
2
2
z a b
.
Chọn C.
Câu 18: Cho
( )P z
là một đa thức với hệ số thực. Nếu số phức
z
thỏa mãn
( ) 0P z
thì
A.
0P
z
. B.
1
0P
z
. C.
1
0P
z
. D.
(
) 0P z
.
(THPT CHUYÊN KHTN_HÀ NỘI)
Hướng dẫn giải
Giả sử
0 1
(
) ... 0
n
n
P
z a a z a z
0
1 0 1
...
0 ... 0 ( ) 0
n
n
n n
a
a z a z a a z a z P z
Chọn D.
Câu 19: Gọi
1
2
,z
z
là hai nghiệm phức của phương trình
2
1 0z z
. Giá trị của
1 2
z z
bằng
A.
0
.
B.
1.
C.
2
.
D.
4
.
(THPT CHUYÊN KHTN_HÀ NỘI)
Hướng dẫn giải:
2
1 0z z
1
2
1 3 1 3
2 2 2 2
z i z i
.
Khi đó:
1
2
1
3
2 2
4 4
z z
.
Chọn C.
Câu 20: Cho số phức
2 5 .z i
Tìm số phức
w
iz z
A.
7 3 .w i
B.
3 3 .w i
C.
3 7 .w i
D.
7 7w i
.
(THPT CHUYÊN KHTN_HÀ NỘI)
Hướng dẫn giải.
Ta có:
2
5 2 5 (2 5 ) 2 5 3 3 .z i z i w iz z i i i i
Chọn B
Câu 21: Kí hiệu
1
2 3
,
,z z z
và
4
z
là bốn nghiệm phức của phương trình
4
2
12 0z z
. Tính tổng
1
2 3 4
T
z z z z
A. T 4. B. T
2
3
C. T 4+
2
3
D. T 2 +
2
3
(THPT CHUYÊN KHTN_HÀ NỘI)
Hướng dẫn giải.
Mã đê 04_Trang 6
Ta có:
2
4
2
2
2
4
12
0
3
3
z
z
z z
z
i
z
1 2 3 4
4 2 3T z z z z
Chọn C
Câu 22: Cho số phức z = 3 – 2i. Tìm phần thực và phần ảo của số phức
z
A. Phần thực bằng –3 và Phần ảo bằng –2i. B. Phần thực bằng –3 và Phần ảo bằng –2.
C. Phần thực bằng 3 và Phần ảo bằng 2i. D. Phần thực bằng 3 và Phần ảo bằng 2.
(ĐỀ THI MINH HỌA)
Hướng dẫn giải.
3
2z i
phần thực là 3 và phần ảo là 2.
Câu 23: Cho số phức z thỏa mãn
2 3 1 2 7i z i z i
. Tìm môđun của z.
A.
5z
. B.
1z
. C.
3z
. D.
2z
.
(TRƯỜNG THPT CHUYÊN KHTN_HÀ NỘI).
Hướng dẫn giải
Đặt
z
a bi
,
,a b
.
2
3 1 2 7 2 3 1 2 7
2 3 3 2 2 2 7 5 3 7
5 7 2
3 1 1
i z i z i i a bi i a bi i
a b a b i a b a b i i a b a b i i
a b a
a b b
Vậy
2
2
2 1 5z
Chọn D.
Câu 24: Cho số phức
3z m m i
,
m
. Tìm
m
để điểm biểu diễn của số phức
z
nằm trên
đường phân giác của góc phần tư thứ hai và thứ tư.
A.
3
2
m
B.
1
2
m
C.
2
3
m
D.
0m
(TRƯỜNG THPT GIA LỘC II)
Hướng dẫn giải:
3
3
; 3 :
2
z
m m i M m m d y x m
.
Chọn A
Câu 25: Có bao nhiêu số phức
z
thoả mãn
2
2
z
z z
.
A.
3
.
B.
2
.
C.
1
.
D.
4
.
(TRƯỜNG THPT HAI BÀ TRƯNG_HUẾ)
Hướng dẫn giải
Gọi
z
a bi
với
;a b
.
Khi đó
22 2
2
2
2
2 0a bi a b az z bi b a bi abz i
Mã đê 04_Trang 7
2
2
0
0
2 0
2 0
1
1
2
0
1 2 0
2
2
b
a
b a
b a
b ab
b a
a b
.
Vậy có
3
số phức
z
thỏa mãn điều kiện đề bài là
0,z
1 1
,
2 2
z i
1 1
2 2
z i
.
Chọn A.
Câu 26: Cho hai số phức
1
z
,
2
z
thỏa mãn
1
2
,
0
z
z
;
1
2
0
z
z
và
1
2 1 2
1
1 2
z z z z
. Tính
1
2
z
z
A.
2
2
. B.
3
2
. C.
2
3
. D.
2
3
.
(CHUYÊN QUANG TRUNG_BÌNH PHƯỚC)
Hướng dẫn giải.
Đặt
1
2
z
x
z
1
2
.z x z
và
1
2
z
x
z
Từ giả thiết
1
2 1 2
1 1 2
z z z z
2
2 2 2
1 1 2
.
.
x
z z x z z
2
2
1
1 1
2
1z
x z x
1
1
2
1x
x
2
2 2 1 0
x x
1
1
2 2
x i
2
2
x
Chọn A.
Câu 27: Trên trường số phức
, cho phương trình
2
0
az bz c
,
, , 0
a
b c a
.
Chọn khảng định sai:
A. Phương trình luôn có nghiệm.
B. Tổng hai nghiệm bằng
b
a
.
C. Tích hai nghiệm bằng
c
a
.
D.
2
4 0
b ac
thì phương trình vô nghiệm.
(CHUYÊN QUANG TRUNG_BÌNH PHƯỚC)
Hướng dẫn giải.
Trên trường số phức
, phương trình bậc hai luôn có nghiệm
A đúng.
Tổng hai nghiệm
1 2
b
z
z
a
B đúng.
Tích hai nghiệm
1
2
.
c
z
z
a
C đúng.
2
4 0
b ac
Phương trình bậc hai có nghiệm phức
D sai.
Chọn D.
Câu 28: Cho thỏa mãn
z
thỏa mãn
10
2
1 2i z i
z
. Biết tập hợp các điểm biểu diễn
cho số phức
3 4 1 2w i z i
là đường tròn
I
, bán kính
R
. Khi đó.
A.
1
; 2
.,
5
I
R
B.
1
;2 ,
.5
I
R
C.
1
;2 , 5.
I
R
D.
1
; 2 , 5.
I
R
(CHUYÊN QUANG TRUNG_BÌNH PHƯỚC)
Mã đê 04_Trang 8
Hướng dẫn giải
Đặt
z
a bi
và
0z c
, với
; ;a b c
.
Lại có
1
2
3 4 1 2
3 4
w i
w i z i z
i
.
Gọi w x yi với
;x y
.
Khi đó
1
2
1 2
1 2 5
3 4 3 4
w i
w i
z c c c x yi i c
i i
2
2 2 2
2
1
2 5 1 2 25x y c x y c
.
Vậy tập hợp các điểm biểu diễn của số phức
w
là đường tròn
1
;2I
.
Khi đó chỉ có chọn C có khả năng đúng và theo đó
5
5 5 1R c c
.
Thử
1c
vào phương trình (1) thì thỏa mãn.
ChọnC.
(CHUYÊN QUANG TRUNG_BÌNH PHƯỚC)
Câu 29: Tìm số phức
z
thỏa mãn
2
4 4zi z i
.
A.
4
4z i
B.
3
4z i
C.
3
4z i
D.
4
4z i
(TRƯỜNG THPT HÀ HUY TẬP_NGHỆ AN)
Hướng dẫn giải
Chọn D.
Giả sử
z
a bi z a bi
. Khi đó
2
4 4zi z i
2 2 4 4a b i a b i
2
4 4
2 4 4
a b a
a b b
.
Câu 30: Có bao nhiêu số phức thỏa mãn đồng thời điều kiện và ?
A. . B. . C. . D. .
(THPT CHUYÊN LAM SƠN THANH HÓA)
Hướng dẫn giải
Đặt , ta có:
. Vậy có đúng một số phức thỏa đề.
Chọn D
Câu 31: Nếu số phức
z
thỏa mãn
1z
thì phần thực của
1
1 z
bằng
A.
1
2
. B.
1
2
. C.
2
. D. Một giá trị khác.
(THPT CHUYÊN LAM SƠN THANH HÓA)
Hướng dẫn giải
Gọi
; ,z x yi x y
.
2
2
1
1z x y
z
.
2
z
z z
2
z
2
4
3
1
,z
x yi x y
2
2
2
2
2 2
2 2
2 2
2
.
2
4 2
4 4
4
4
2
2
x
y x yi
z z z
x yi
x y
x y
x y
z
x y
2 2
8
16 0
2
0
4
x
x
y
x
y
z
Mã đê 04_Trang 9
2
2 2
2 2 2
1
1
1 1
1 1
1 1 1
x yi x
yi
z x yi
x y x y x y
.
2
2
2 2
1
1
2
2 2
1 1
x
yi yi
x
x y x y
.
Vậy phần thực của
1
1 z
bằng
1
2
.
Chọn A.
Câu 32: Cho
, ,a b c
là các số thực và
1
3
2 2
z i
. Giá trị của
2
2
a
bz cz a bz cz
bằng.
A.
a
b c
. B.
2
2 2
a b c ab bc ca
.
C.
2
2 2
a b c ab bc ca
. D.
0
.
(THPT CHUYÊN LAM SƠN THANH HÓA)
Hướng dẫn giải
Ta có
2
1
3 1 3
2 2 2 2
z i z i z
và
2
z z ,
1z z
,
1zz z
.
Khi đó
2
2
a
bz cz a bz cz a bz cz a bz cz
2
2 2 2 2
a
abz acz abz b z z bcz acz bcz c z z
2
2 2
a b c ab ac bc
.
Chọn B.
Câu 33: Gọi
1 2 3
, ,z z z
là ba số phức thỏa mãn
1 2 3
0z z z
và
1
2 3
1z z z
. Khẳng định nào
dưới đây là sai
A.
3
3 3
3 3 3
1 2 3 1 2 3
z
z z z z z
. B.
3
3 3
3 3 3
1 2 3 1 2 3
z
z z z z z
.
B.
3
3 3
3 3 3
1 2 3 1 2 3
z z z z z z
. D.
3
3 3
3 3 3
1 2 3 1 2 3
z z z z z z
.
(TRƯỜNG CHUYÊN KHTN_HÀ NỘI)
Hướng dẫn giải
1
2 3 3 1 2
3 3 3 3 3 3
1 2 3 1 2 1 2 1 2 1 2 1 2 3
0
( )
( ) 3 ( ) 3 3
z z z z z z
z z z z z z z z z z z z z z
mà
3
3 3
1 2 3 1 2 3
3 3z z z z z z
Chọn B
Câu 34: Phương trình có bao nhiêu nghiệm trong tập số phức?
A.
2
. B.
1
. C.
0
. D. Vô số.
(TRƯỜNG CHUYÊN KHTN_HÀ NỘI)
Hướng dẫn giải.
Ta đặt
z
a bi
, .
Khi đó
2
2 2
2 2
2
0
1 0 1 2 0
1 0
ab a
iz a b b a a i
a
z b
b b
2
1 0izz
,a b
Mã đê 04_Trang 10
TH1. .
TH2. vô nghiệm.
Chọn A.
Câu 35: Cho
1
2 3
,
,z z z
là các số phức thõa mãn
1
2 3
1z z z
. Khẳng định nào sau đây đúng?
A.
1
2 3 1 2 2 3 3 1
z
z z z z z z z z
. B.
1
2 3 1 2 2 3 3 1
z
z z z z z z z z
.
C.
1
2 3 1 2 2 3 3 1
z
z z z z z z z z
. D.
1
2 3 1 2 2 3 3 1
z
z z z z z z z z
.
(TRƯỜNG CHUYÊN KHTN_HÀ NỘI)
Hướng dẫn giải
Ta có
1
2 3 1 2 3
1
2 3
1
1 1
1
, ,z z z z z z
z
z z
Mặt khác ta có
2
3 1 2 3 1
1 2 3 1 2 3 1 2 2 3 3 1
1 2 3 1 2 3
1
1 1
z z z z z z
z z z z z z z z z z z z
z z z z z z
Chọn A.
(THPT CHUYÊN KHTN_HÀ NỘI)
Câu 36: Kí hiệu
1 2 3
,
,z z z
và
4
z
là bốn nghiệm phức của phương trình
4
2
1
2 0z z
. Tính tổng
1
2 3 4
T
z z z z
A. T 4. B. T
2
3
C. T 4+
2
3
D. T 2 +
2
3
Hướng dẫn giải.
Ta có:
2
4
2
2
2
4
12
0
3
3
z
z
z
z
z i
z
1
2 3 4
4
2 3T z z z z
Chọn C
Câu 37: Cho các số phức
z
thỏa mãn
4z
. Biết rằng tập hợp các điểm biểu diễn các số phức
(3 4 )w i z i
là một đường tròn. Tính bán kính r của đường tròn đó.
A. r 4. B. r 5. C. r 20. D. r 22.
Hướng dẫn giải.
Gọi
w
a bi
, ta có
2
(
1) (3 4 )
( 1)
(3 4 )
3 4 9 16
a b i i
a b i
w a bi i z i z
i i
2
2
(3
4 4) (3 4 3)
3 4 4 (3 4 3)
.
25 25 25
a b b a
a b b a
i z
Mà
z
= 4 nên
2
2 2 2 2
(3
4 4) (3 4 3) 100 2 399a b b a a b b
Theo giả thiết, tập hợp các điểm biểu diễn các số phức
(
3 4 )w i z i
là một đường tròn nên
ta có
2
2 2 2
2
399 ( 1) 400 400 20
a
b b a b r
Chọn C.
2
1
5
1
00
2
a b
bb
2
1
5
0
2 4
b
a
Mã đê 04_Trang 11
Câu 38: Gọi
,M N
lần lượt là các điểm biểu diễn của các số phức
1 i
,
2
3i
. Số phức
z
biểu diễn bởi điểm
Q
sao cho
3
0
M
N MQ
là:
A.
2
1
3 3
z i
. B.
2
1
3 3
z i
. C.
2
1
3 3
z i
. D.
2
1
3 3
z i
.
(TTLT ĐH DIỆU HIỀN_CẦN THƠ).
Hướng dẫn giải
Ta có điểm . Vectơ và .
Ta có khi chỉ khi . Vậy
Chọn B.
Câu 39: Cho hình vuông
A
BCD
có tâm
H
và
, , , ,A B C D H
lần lượt là điểm biểu diễn cho
các số phức
, , , , .a b c d h
Biết
2 ; 1 3a i h i
và số phức
b
có phần ảo dương. Khi đó, mô-đun
của số phức
b
là:
A.
13
. B.
10
. C.
26
. D.
37
.
(TTLT ĐH DIỆU HIỀN_CẦN THƠ).
Hướng dẫn giải
Do
AB
CD
là hình vuông và
H
là tâm hình vuông nên ta có
,
HB AH HB AH
Do điểm
A
biểu diễn bởi số phức
2
2;1
a
i A
, Điểm H biểu diễn bởi
1 3 1;3
h i H
Đường thẳng
B
H
nhận
3
;2
A
H
làm VTPT nên có phương trình là:
3
1 2 3 0 3 2 9 0
x
y x y
Do
9
2
;
, 0
3
m
B BH B m m
Ta có:
2
2
2 2 2 2
9
2
3
2 1 3
3
m
A
H BH m
2
0
1
3 78 0 6
6
m
m
m m
m
Vậy
1 6b i
, suy ra
mô-đun của số phức
b
là:
3
7
Chọn D.
(TTLT ĐH DIỆU HIỀN_CẦN THƠ).
Câu 40: Với các số phức
z
thỏa mãn
| 2 | 4
z i
, tập hợp các điểm biểu diễn các số phức
z
là
một đường tròn. Tìm bán kính
R
đường tròn đó
A.
8
R
B.
1
6
R
. C.
2R
. D.
4R
.
(TRƯỜNG THPT CHUYÊN KHTN_HÀ NỘI).
1
;1 , 2;3
M
N
1;2
MN
1
; 1
Q
Q
MQ
x y
3
0
M
N MQ
2
1 3 0
3
1
2
3
1
13 0
Q
Q
Q
Q
x
x
y
y
2 1
3 3
z i
Mã đê 04_Trang 12
Hướng dẫn giải.
Gọi
,z
x yi x y
. Khi đó
2
2
2
| 2 | 4 2 1 4z i x y
.
Tập hợp các điểm biểu diễn các số phức
z
là một đường tròn có tâm
2
; 1I
và bán kính
4R
Chọn D.
Câu 41: Với hai số phức
1
z
và
2
z
thỏa mãn
1
2
8
6 z z i
và
1
2
2
z z
. Tìm giá trị lớn nhất của
1
2
P z z
A.
5
3 5 P
. B.
2
26P
. C.
4
6P
. D.
34 3 2 P
.
(TRƯỜNG THPT CHUYÊN KHTN_HÀ NỘI).
Hướng dẫn giải:
Chọn chọn B.
Đặt
1
2
,
OA z OB z
( với
O
là gốc tọa độ,
,A B
là điểm biểu diễn của
1 2
,z
z
).
Dựng hình bình hành
O
ACB
, khi đó ta có
1
2 2 1
2, 10, 5 AB z z OC z z OM
Theo định lý đường trung tuyến ta có
2
2 2
2 2
2 2 2
1 2
2
52
52
4
OA OB AB
OM OA OB z z
Ta có
2
2
1 2 1 2 max
2
2 26 2 26
z z z z P
(TRƯỜNG THPT CHUYÊN KHTN_HÀ NỘI).
Câu 42: Cho số phức
z
thỏa mãn
2 1 2iz i i
. Biết rằng trong mặt phẳng tọa độ
Oxy
, tập hợp
các điểm biểu diễn số phức
z
là một đường tròn. Hãy xác định tọa độ tâm
I
của đường tròn đó.
A.
0
;2I
. B.
0
; 2I
. C.
2
;0I
. D.
2
;0I
.
(TRƯỜNG THPT GIA LỘC II)
Hướng dẫn giải
Giả sử z x iy suy ra là
;M x y
điểm biểu diễn cho số phức
z
.
Ta có
2
1 2 2 1 2 2 1 2iz i i i x iy i i y x i i
2
2
2 2 2 2
2
1 2 2 5.x y x y
Chọn D.
Câu 43: Cho số phức
z
thỏa mãn
4 3 1 iz i
. Tìm giá trị nhỏ nhất của
z
.
A.
6
. B.
4
. C.
3
. D.
5
.
(TRƯỜNG THPT GIA LỘC II)
Hướng dẫn giải
Ta có
3
4 5 53 11 4 4z i i z z z
.
Chọn B.
Mã đê 04_Trang 13
Câu 44: Tìm tập hợp các điểm
M
biểu diễn hình học số phức
z
trong mặt phẳng phức, biết số
phức
z
thỏa mãn điều kiện:
4
4 10.z z
A. Tập hợp các điểm cần tìm là đường tròn có tâm
0
;0
O
và có bán kính
4
.R
.
B. Tập hợp các điểm cần tìm là đường elip có phương trình
2
2
1.
9
25
x y
C. Tập hợp các điểm cần tìm là những điểm
;M x y
trong mặt phẳng
Oxy
thỏa mãn phương
trình
2
2
2 2
4
4 12.x y x y
D. Tập hợp các điểm cần tìm là đường elip có phương trình
2 2
1.
25
9
x
y
(TRƯỜNG THPT HAI BÀ TRƯNG_HUẾ)
Hướng dẫn giải
Ta có: Gọi
;M x y
là điểm biểu diễn của số phức .z x yi
Gọi
4
;0
A
là điểm biểu diễn của số phức
4
.z
Gọi
4
;0B
là điểm biểu diễn của số phức
4.z
Khi đó:
4
4 10 10.
z
z MA MB
(*)
Hệ thức trên chứng tỏ tập hợp các điểm
M
là elip nhận
,A B
là các tiêu điểm.
Gọi phương trình của elip là
2 2
2 2 2
2 2
1
, 0,
x y
a b a b c
a b
Từ (*) ta có:
2 10 5.a a
2
2 2
2 8 2 4 9AB c c c b a c
Vậy quỹ tích các điểm
M
là elip:
2
2
:
1.
25 9
x y
E
Chọn D.
Câu 45: Trong mặt phẳng phức gọi
M
là điểm biểu diễn cho số phức
z
a bi
, , 0a b ab
,
M
là diểm biểu diễn cho số phức
z
. Mệnh đề nào sau đây đúng?
A.
M
đối xứng với
M
qua
Oy
. B.
M
đối xứng với
M
qua
O
x
.
C.
M
đối xứng với
M
qua
O
. D.
M
đối xứng với
M
qua đường thẳng
y
x
.
(CH
UYÊN QUANG TRUNG_BÌNH PHƯỚC)
Hướng dẫn giải:
Ta có:
;M
a b
và
;M
a b
nên
M
đối xứng với
M
qua
Ox
.
Chọn B.
Câu 46: Cho thỏa mãn
z
thỏa mãn
10
2
1 2i z i
z
. Biết tập hợp các điểm biểu diễn
cho số phức
3
4 1 2w i z i
là đường tròn
I
, bán kính
R
. Khi đó.
A.
1
; 2 ., 5I R
B.
1
;2 , .5I R
C.
1
;2 , 5.I R
D.
1
; 2 , 5.I R
(CHUYÊN QUANG TRUNG_BÌNH PHƯỚC)
Hướng dẫn giải
Đặt
z
a bi
và
0z c
, với
; ;a b c
.
Mã đê 04_Trang 14
Lại có
1
2
3
4 1 2
3
4
w i
w
i z i z
i
.
Gọi w x yi với
;x y
.
Khi đó
1
2
1 2
1 2 5
3 4 3 4
w i
w i
z c c c x yi i c
i i
2
2 2 2
2
1
2 5 1 2 25x y c x y c
.
Vậy tập hợp các điểm biểu diễn của số phức
w
là đường tròn
1; 2I
.
Khi đó chỉ có chọn C có khả năng đúng và theo đó
5 5 5 1R c c
.
Thử
1c
vào phương trình (1) thì thỏa mãn.
ChọnC.
(CHUYÊN QUANG TRUNG_BÌNH PHƯỚC)
Câu 47: Cho số phức
z
thỏa mãn
1z
z i
. Tìm mô đun nhỏ nhất của số phức
w
2 2z i
.
A.
3
2
2
. B.
3
2
. C.
3 2
2
.
D.
3
2
.
(TRƯỜNG THPT HÀ HUY TẬP_NGHỆ AN)
Hướng dẫn giải
Chọn C.
Giả sử
z
a bi z a bi
. Khi đó
1z
z i
1 1a bi a b i
2 2
2 2
1 1a b a b
0a b
.
Khi đó
w
2 2z i
2
2 2 2 1a ai i a i a
.
2
2
2
3
2
w 2 2 2 1 8 4 5
2
a a a a
.
Vậy mô đun nhỏ nhất của số phức
w
là
3
2
2
.
Câu 48: Cho số phức
z
, tìm giá trị lớn nhất của
z
biết rằng
z
thỏa mãn điều kiện
2
3
1 1
3 2
i
z
i
.
A.
3
. B.
2
. C.
2
. D.
1
.
(THPT CHUYÊN LAM SƠN THANH HÓA)
Hướng dẫn giải.
Gọi
,z
x yi x y
Ta có:
2
2
2
3
1 1 1 1 1 1 1
3 2
i
z iz z i x y
i
.
Vậy tập hợp các điểm biểu diễn số phức
z
là đường tròn tâm
0; 1I
, bán kính
1R
.
Gọi
M
là điểm biểu diễn số phức
z
, ta có
1IM
.
Ta có:
2z
OM OI IM
.
Chọn C.
Câu 49: Cho các số phức
z
thỏa mãn
4z
. Biết rằng tập hợp các điểm biểu diễn các số phức
(
3 4 )w i z i
là một đường tròn. Tính bán kính r của đường tròn đó.
A. r 4. B. r 5. C. r 20. D. r 22.
Mã đê 04_Trang 15
Hướng dẫn giải.
Gọi
w
a bi
, ta có
2
( 1) (3 4 )
( 1)
(3 4 )
3 4 9 16
a b i i
a b i
w a bi i z i z
i i
2
2
(3
4 4) (3 4 3)
3 4 4 (3 4 3)
.
25 25 25
a b b a
a b b a
i z
Mà
z
= 4 nên
2
2 2 2 2
(3 4 4) (3 4 3) 100 2 399a b b a a b b
Theo giả thiết, tập hợp các điểm biểu diễn các số phức
(
3 4 )w i z i
là một đường tròn nên
ta có
2
2 2 2
2
399 ( 1) 400 400 20
a
b b a b r
Chọn C.
Câu 50:
Cho số phức
z
thỏa mãn
(
1 ) 3 .i z i
Hỏi điểm
biểu diễn của
z
là
điểm nào trong các điểm M, N, P, Q
ở hình bên ?
A. Điểm P. B. Điểm Q. \
C. Điểm M. D. Điểm N.
(ĐỀ THI MINH HỌA)
Hướng dẫn giải.
Gọi
(
, )z x yi x y
Khi đó:
(
1 ) 3 ( 3) ( 1) 0i z i x y x y i
3 0 1
(1; 2).
1 0 2
x y x
Q
x y y
Chọn A
| 1/15
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Gv. LÊ VIẾT NHƠN
KỲ THI TRUNG HỌC PHỔ THÔNG QUỐC GIA 2017
50 CÂU TỔNG ÔN SỐ PHỨC Bài thi: TOÁN
( Đề thi gồm có 7 trang )
Thời gian làm bài. 90 phút, không kể thời gian phát đề. Mã đề 04
Họ, tên thí sinh. …………………………………………………………
Số báo danh. …………………………………………………………….
Câu 1: Tìm môđun của số phức w  1 zz biết rằng số phức z thỏa mãn biểu thức:
  iz    i2 3 2 2  4  i .
A. w  2 . B. w  10 . C. w  8 . D. w  2 .
(TTLT ĐH DIỆU HIỀN_CẦN THƠ). Hướng dẫn giải Ta có  i
  iz    i2   i    iz   i    i2 1 5 3 2 2 4 3 2 4 2
 3  2iz  1  5i z  3 2i
1 5i3  2i  z
z  1  i
3  2i3  2i
Khi đó w  1 zz  11 i1 i  3  i w  10 Chọn B. Câu 2:
Cho số phức z  2  3i . Tìm môđun của số phức w  1 iz z . A. w  3 . B. w  5 . C. w  4 . D. w  7 .
(TRƯỜNG THPT CHUYÊN KHTN_HÀ NỘI). Hướng dẫn giải.
Ta có w  1 i2  3i  2  3i  3  4i w  5 . Chọn B. Câu 3:
Cho số phức z a bi a,b   thỏa mãn 2  iz  3  5i  4  4i . Tính tổng P a b . 26 8 A. P   B. P  C. P  4 D. P  2 5 3
(TRƯỜNG THPT CHUYÊN KHTN_HÀ NỘI). Hướng dẫn giải
4  4i  3  5i
Ta có 2  iz  3  5i  4  4i z
 3  i a  3,b  1  . 2  i Do đó P  2 . Chọn D Câu 4:
Gọi z , z là 2 nghiệm của phương trình 2
z z  1  0 . Tính giá trị 2017 2017 P zz 1 2 1 2 A. P 1. B. P  1  . C. P  0 . D. P  2 .
(TRƯỜNG THPT CHUYÊN KHTN_HÀ NỘI). Hướng dẫn giải Mã đê 04_Trang 1 Ta có: 2 3 3 2016 2017
z z 1  0  z 1  0  z  1  z  1  zz 1 1 1 1 1 1 1
Chứng minh tương tự: 2017 zz 2 2
P z z  1  . 1 2 Chọn B. i   1 z  2 Câu 5:
Xác định số phức liên hợp z của số phức z biết  2  3 . i 1 2i 7 5 7 5 7 5 7 5 A. z    . i B. z   . i C. z    . i D. z   . i 2 2 2 2 2 2 2 2 (TRƯỜNG THPT GIA LỘC II) Hướng dẫn giải i  
1 z  2  23i  i  1z  2 8i 1 2i 6  i 7 5  z     . i i 1 2 2 7 5 Vậy z    . i 2 2 Chọn A. 1 7i Câu 6:
Cho số phức z thỏa mãn iz  1 2i
. Xác định điểm A biểu diễn số phức liên hợp 1 3i z . A. A 1  ;3 . B. A 1  ; 3   . C. A1; 3   . D. A1;3 . (TRƯỜNG THPT GIA LỘC II) Hướng dẫn giải Ta có 1 7i 3  i
iz  1 2i
iz  1 2i  (2  i)  iz  3  i z
 1 3i z  1 3i 1 3i i Chọn D Câu 7:
Gọi z , z là hai nghiệm của phương trình 2
2z  3z  2  0 trên tập số phức. Tính giá trị 1 2 biểu thức 2 2 P
z z z z . 1 1 2 2 5 5 3 3 3 A. P  . B. P  . C. P  . D. P  2 2 4 4 (TRƯỜNG THPT GIA LỘC II) Hướng dẫn giải 9 5
Ta có P z z z z   z z 2 2 2  z z  1  . 1 1 2 2 1 2 1 2 4 2 Chọn A. Câu 8:
Gọi z và z là hai nghiệm của phương trình 2
z  2z  5  0 biết z z có phần ảo là 1 2  1 2
số thực âm. Tìm phần thực của số phức 2 2
w  2z z . 1 2 A. 4. B. 4. C. 9. D. 9.
(TRƯỜNG THPT HAI BÀ TRƯNG_HUẾ) Mã đê 04_Trang 2 Hướng dẫn giải
z  1  2i Ta có 2  1
z  2z  5  0  
(do z z  4i có phần ảo là 4 ). z  1  2i  1 2 2  Do đó 2 2
w  2z z  9   4i . 1 2
Vậy phần thực của số phức 2 2
w  2z z là 9. 1 2 Chọn D. Câu 9: Tính 2 3 2017
S  1009  i  2i  3i  ...  2017i A. S  2017 1009 i. B. 1009  2017 . i C. 2017  1009 . i D. 1008  1009 . i
(TRƯỜNG THPT HAI BÀ TRƯNG_HUẾ) Hướng dẫn giải Chọn C Ta có 2 3 4 2017
S  1008  i  2i  3i  4i  ...  2017i  1009   4 8 2016
4i  8i  ...  2016i  5 9 2017
i  5i  9i  ...  2017i    2 6 10 2014
2i  6i  10i  ...2014i  3 7 11 2015
3i  7i  11i  ...  2015i  504
 1009  4n 505
i4n  3 504  4n  2 504
i4n   1 n 1  n 1  n 1  n 1 
 1009  509040  509545i  508032  508536i  2017  1009i.
(TRƯỜNG THPT HAI BÀ TRƯNG_HUẾ) 1 1 2 z
Câu 10: Cho hai số phức z , z thỏa mãn z , z  0 ; z z  0 và   . Tính 1 1 2 1 2 1 2 z z z z z 1 2 1 2 2 2 3 2 A. . B. . C. 2 3 . D. . 2 2 3
(CHUYÊN QUANG TRUNG_BÌNH PHƯỚC) Hướng dẫn giải. z z Đặt 1 x   z  . x z và 1  x z 1 2 z 2 2 1 1 2 1 1 2 1 1  1  1 1 Từ giả thiết         2      2 z z z z . x z z . x z z z x 1 z x x 1 x 2   1 2 1 2 2 2 2 2 2  1 1 2  2
2x  2x 1  0  x    i x  2 2 2 Chọn A.
Câu 11: Cho z , z là hai nghiệm phức của phương trình 2
z  2z  4  0 . Tính z z . 1 2 1 2 A. 2 3. B. 4. C. 4 3. D. 5.
(CHUYÊN QUANG TRUNG_BÌNH PHƯỚC) Hướng dẫn giải Mã đê 04_Trang 3
z  1 i 3 Ta có 2 1
z  2z  4  0   .  z  1   i 3  2 2 2 2 2
Vậy z z  1   3  1    3  4 . 1 2         Chọn B.
Câu 12: Tính mô đun của số phức z  4  3i . A. z  5 2 . B. z  7. C. z  5. D. z  7.
(TRƯỜNG THPT HÀ HUY TẬP_NGHỆ AN) Hướng dẫn giải.
Ta có z  4   3  2 2  . 5 Chọn C.
Câu 13: Cho hai số phức z  3  3i và z  1 2i . Phần ảo của số phức w z  2z là: 1 2 1 2 A. 1. B. . 1  C. . 7  D. 7.
(TRƯỜNG THPT HÀ HUY TẬP_NGHỆ AN) Hướng dẫn giải
Ta có w z  2z  3  3i  2 1
  2i  1 i . 1 2    
Vậy phần ảo của số phức w z  2z là 1. 1 2 Chọn A.
Câu 14: Tìm số phức z thỏa mãn 1 i z 1 2i  3  2i  0 . 3 5 5 3
A. z  4  3i . B. z   i . C. z   i .
D. z  4  3i . 2 2 2 2
(TRƯỜNG THPT HÀ HUY TẬP_NGHỆ AN) Hướng dẫn giải Chọn B. 3  2i 5 1 5 1 3 5
Ta có 1 i z 1 2i  3  2i  0  z 1 2i    i z   i 1 2i   i . 1 i 2 2 2 2 2 2
Câu 15: Gọi x là nghiệm phức có phần ảo là số dương của phương trình 2
x x  2  0 . Tìm số 0 phức 2
z x  2x  3 . 0 0 1 7i 3   7i
A. z 1 7i . B. z  2  7i . C. z  . D. z  . 2 2
(THPT CHUYÊN LAM SƠN THANH HÓA) Hướng dẫn giải. 1 7 1 7 Ta có: 2
x x  2  0  z    i 2
z x  2x  3   i 0 2 2 0 0 2 2 Chọn C
Câu 16: Cho số phức z  1 3i . Tính môđun của số phức 2 w z  . i z . A. w  146 . B. w  5 2 . C. w  50 . D. w  10 .
(THPT CHUYÊN LAM SƠN THANH HÓA) Hướng dẫn giải. Mã đê 04_Trang 4 Chọn B.
Câu 17: Mệnh đề nào dưới đây sai?
A. Số phức z  5  3i có phần thực là 5, phần ảo 3  . B. Điểm M  1
 ; 2 là điểm biểu diễn số phức z  1   2i .
C. Mô đun của số phức z a bi a,b   là 2 2 a b .
D. Số phức z  2i là số thuần ảo.
(THPT CHUYÊN LAM SƠN THANH HÓA) Hướng dẫn giải
Mô đun của số phức z a bi a,b   là 2 2
z a b . Chọn C.
Câu 18: Cho P(z) là một đa thức với hệ số thực. Nếu số phức z thỏa mãn P(z)  0 thì  1   1 
A. Pz   0 . B. P    0 . C. P  0   . D. P(z)  0 .  z   z  (THPT CHUYÊN KHTN_HÀ NỘI) Hướng dẫn giải
Giả sử P(z)  a a z  ... na z  0 0 1 n
a a z  ... n
a z  0  a a z  ... n
a z  0  P(z)  0 0 1 n 0 1 n Chọn D.
Câu 19: Gọi z , z là hai nghiệm phức của phương trình 2
z z  1  0 . Giá trị của z z bằng 1 2 1 2 A. 0. B. 1. C. 2. D. 4. (THPT CHUYÊN KHTN_HÀ NỘI) Hướng dẫn giải: 1 3 1 3 2
z z  1  0  z   i z   i . 1 2 2 2 2 2 1 3
Khi đó: z z  2   2 . 1 2 4 4 Chọn C.
Câu 20: Cho số phức z  2  5 .
i Tìm số phức w iz z A. w  7  3 . i B. w  3  3 . i C. w  3  7 . i
D. w  7  7i . (THPT CHUYÊN KHTN_HÀ NỘI) Hướng dẫn giải.
Ta có: z  2  5i z  2  5i w iz z i(2  5i)  2  5i  3  3 . i Chọn B
Câu 21: Kí hiệu z , z , z và z là bốn nghiệm phức của phương trình 4 2
z z 12  0 . Tính tổng 1 2 3 4
T z z z z 1 2 3 4 A. T  4. B. T  2 3 C. T  4+ 2 3 D. T 2 + 2 3 (THPT CHUYÊN KHTN_HÀ NỘI) Hướng dẫn giải. Mã đê 04_Trang 5 2 z  4  z  2  Ta có: 4 2
z z 12  0     2 z  3  z  i 3  
T z z z z  4  2 3 1 2 3 4 Chọn C
Câu 22: Cho số phức z = 3 – 2i. Tìm phần thực và phần ảo của số phức z
A. Phần thực bằng –3 và Phần ảo bằng –2i.
B. Phần thực bằng –3 và Phần ảo bằng –2.
C. Phần thực bằng 3 và Phần ảo bằng 2i.
D. Phần thực bằng 3 và Phần ảo bằng 2. (ĐỀ THI MINH HỌA) Hướng dẫn giải.
z  3  2i  phần thực là 3 và phần ảo là 2.
Câu 23: Cho số phức z thỏa mãn 2  3iz  1 2iz  7  i . Tìm môđun của z.
A. z  5 . B. z 1. C. z  3 . D. z  2.
(TRƯỜNG THPT CHUYÊN KHTN_HÀ NỘI). Hướng dẫn giải
Đặt z a bi , a, b   .
2  3iz  1 2iz  7  i  2  3ia bi  1 2ia bi  7  i
 2a  3b  3a  2bi a  2b  2a bi  7  i a  5b  a  3bi  7  i
a  5b  7 a  2     a  3b  1  b  1    Vậy 2 2 z  2 1  5 Chọn D.
Câu 24: Cho số phức z m  m  3i , m  . Tìm m để điểm biểu diễn của số phức z nằm trên
đường phân giác của góc phần tư thứ hai và thứ tư. 3 1 2 A. m  B. m  C. m  D. m  0 2 2 3 (TRƯỜNG THPT GIA LỘC II) Hướng dẫn giải: 3
z m  m  3i M  ;
m m  3  d : y  x m  . 2 Chọn A 2
Câu 25: Có bao nhiêu số phức z thoả mãn 2
z z z . A. 3. B. 2. C. 1. D. 4.
(TRƯỜNG THPT HAI BÀ TRƯNG_HUẾ) Hướng dẫn giải
Gọi z a bi với a;b   . 2 Khi đó 2
z z z  a bi 2 2 2
a b a bi  2b a bi  2abi  0 Mã đê 04_Trang 6   2   2
b  0  a  0 2b a  0 2
b a  0           . b   ab b      a 1 1 2 0 1 2  0 a
    b      2 2 1 1 1 1
Vậy có 3 số phức z thỏa mãn điều kiện đề bài là z  0, z    ,
i z    i . 2 2 2 2 Chọn A. 1 1 2 z
Câu 26: Cho hai số phức z , z thỏa mãn z , z  0 ; z z  0 và   . Tính 1 1 2 1 2 1 2 z z z z z 1 2 1 2 2 2 3 2 A. . B. . C. 2 3 . D. . 2 2 3
(CHUYÊN QUANG TRUNG_BÌNH PHƯỚC) Hướng dẫn giải. z z Đặt 1 x   z  . x z và 1  x z 1 2 z 2 2 1 1 2 1 1 2 1 1  1  1 1 Từ giả thiết         2      2 z z z z . x z z . x z z z x 1 z x x 1 x 2   1 2 1 2 2 2 2 2 2  1 1 2  2
2x  2x 1  0  x    i x  2 2 2 Chọn A.
Câu 27: Trên trường số phức  , cho phương trình 2
az bz c  0 a, ,
b c  , a  0 . Chọn khảng định sai:
A. Phương trình luôn có nghiệm. b
B. Tổng hai nghiệm bằng  . a c
C. Tích hai nghiệm bằng . a D. 2
  b  4ac  0 thì phương trình vô nghiệm.
(CHUYÊN QUANG TRUNG_BÌNH PHƯỚC) Hướng dẫn giải.
Trên trường số phức  , phương trình bậc hai luôn có nghiệm  A đúng. b
Tổng hai nghiệm z z    B đúng. 1 2 a c
Tích hai nghiệm z .z   C đúng. 1 2 a  2
  b  4ac  0  Phương trình bậc hai có nghiệm phức  D sai. Chọn D. 10
Câu 28: Cho thỏa mãn z   thỏa mãn 2  iz
1 2i . Biết tập hợp các điểm biểu diễn z
cho số phức w  3  4iz 1 2i là đường tròn I , bán kính R . Khi đó. A. I  1  ; 2  , R  5.
B. I 1; 2, R  5. C. I  1  ; 2, R  5. D. I 1; 2  , R  5.
(CHUYÊN QUANG TRUNG_BÌNH PHƯỚC) Mã đê 04_Trang 7 Hướng dẫn giải
Đặt z a bi và z c  0 , với a;b;c   . w 1 2i
Lại có w  3  4iz 1 2i z  . 3  4i
Gọi w x yi với ; x y   . w 1 2i w 1 2i
Khi đó z c   c
c x yi 1 2i  5c 3  4i 3  4i
  x  2   y  2  c   x  2   y  2 2 1 2 5 1 2  25c .
Vậy tập hợp các điểm biểu diễn của số phức w là đường tròn I  1  ; 2 .
Khi đó chỉ có chọn C có khả năng đúng và theo đó R  5  5c  5  c  1.
Thử c  1 vào phương trình (1) thì thỏa mãn. ChọnC.
(CHUYÊN QUANG TRUNG_BÌNH PHƯỚC)
Câu 29: Tìm số phức z thỏa mãn zi  2z  4  4i .
A. z  4  4i
B. z  3  4i
C. z  3  4i
D. z  4  4i
(TRƯỜNG THPT HÀ HUY TẬP_NGHỆ AN) Hướng dẫn giải Chọn D.
Giả sử z a bi z a bi . Khi đó zi  2z  4  4i  a  2bi  2a b  4  4i
a  2b  4  a  4     . 2a b  4 b  4  
Câu 30: Có bao nhiêu số phức z thỏa mãn đồng thời điều kiện z.z z  2 và z  2 ? A. 2 . B. 4 . C. 3 . D. 1 .
(THPT CHUYÊN LAM SƠN THANH HÓA) Hướng dẫn giải
Đặt z x yi x, y   , ta có: 2 2
z.z z  2
x y x yi  2   
 4  x  yi  2   4  x2 2  y  4        2 2 2 2 2 2  z  2
x y  2 x y  4   x y  4   8  x 16  0 x  2     
. Vậy có đúng một số phức z thỏa đề. 2 2 x y  4 y  0   Chọn D 1
Câu 31: Nếu số phức z thỏa mãn z  1 thì phần thực của bằng 1 z 1 1 A. . B.  . C. 2 . D. Một giá trị khác. 2 2
(THPT CHUYÊN LAM SƠN THANH HÓA) Hướng dẫn giải
Gọi z x yi; x, y   . 2 2
z  1  x y  1 Mã đê 04_Trang 8 1 1
1 x  yi 1 xyi     . 1 z
1 x  yi 1 x2  y
1 x2  y 1 x2 2 2 2  y 1 xyi 1 yi     . 2  2x
1 x2  y 2 1 x2 2 2  y 1 1 Vậy phần thực của bằng . 1 z 2 Chọn A. 1 3
Câu 32: Cho a,b, c là các số thực và z    i . Giá trị của  2    2 a bz cz
a bz cz  bằng. 2 2
A. a b c . B. 2 2 2
a b c ab bc ca . C. 2 2 2
a b c ab bc ca . D. 0 .
(THPT CHUYÊN LAM SƠN THANH HÓA) Hướng dẫn giải 1 3 1 3 Ta có 2 z    iz    iz và 2
z z , z z  1 , z z z  1. 2 2 2 2 Khi đó  2    2 a bz cz
a bz cz   a bz cza bz cz 2 2 2 2 2
a abz acz abz b z z bcz ac z bc z c z z 2 2 2
a b c ab ac bc . Chọn B.
Câu 33: Gọi z , z , z là ba số phức thỏa mãn z z z  0 và z z z  1. Khẳng định nào 1 2 3 1 2 3 1 2 3 dưới đây là sai 3 3 3 3 3 3 A. 3 3 3
z z zzzz . B. 3 3 3
z z zzzz . 1 2 3 1 2 3 1 2 3 1 2 3 3 3 3 3 3 3 B. 3 3 3
z z zzzz . D. 3 3 3
z z zzzz . 1 2 3 1 2 3 1 2 3 1 2 3
(TRƯỜNG CHUYÊN KHTN_HÀ NỘI) Hướng dẫn giải
z z z  0  z  (z z ) 1 2 3 3 1 2 3 3 3 3 3 3
z z z
z z  (z z )  3
z z (z z )  3z z z  3 1 2 3 1 2 1 2 1 2 1 2 1 2 3 3 3 3 mà z zz  3 z z z  3 1 2 3 1 2 3 Chọn B Câu 34: Phương trình 2
z iz  1  0 có bao nhiêu nghiệm trong tập số phức? A. 2 . B. 1. C. 0 . D. Vô số.
(TRƯỜNG CHUYÊN KHTN_HÀ NỘI) Hướng dẫn giải.
Ta đặt z a bi , a,b   .
2ab a  0  Khi đó 2 2 2
z iz  1  0  a b b  1  2ab ai  0   2 2
a b b  1  0  Mã đê 04_Trang 9   TH1. 2 1 5
a  0  b b  1  0  b  . 2 1 5 TH2. 2 b    a   0 vô nghiệm. 2 4 Chọn A.
Câu 35: Cho z , z , z là các số phức thõa mãn z z z  1 . Khẳng định nào sau đây đúng? 1 2 3 1 2 3
A. z z z z z z z z z .
B. z z z z z z z z z . 1 2 3 1 2 2 3 3 1 1 2 3 1 2 2 3 3 1
C. z z z z z z z z z .
D. z z z z z z z z z . 1 2 3 1 2 2 3 3 1 1 2 3 1 2 2 3 3 1
(TRƯỜNG CHUYÊN KHTN_HÀ NỘI) Hướng dẫn giải 1 1 1
Ta có z z z  1  z  , z  , z  1 2 3 1 2 3 z z z 1 2 3 Mặt khác ta có 1 1 1
z z z z z z 2 3 1 2 3 1
z z z z z z    
z z z z z z 1 2 3 1 2 3 1 2 2 3 3 1 z z z z z z 1 2 3 1 2 3 Chọn A. (THPT CHUYÊN KHTN_HÀ NỘI)
Câu 36: Kí hiệu z , z , z và z là bốn nghiệm phức của phương trình 4 2
z z 12  0 . Tính tổng 1 2 3 4
T z z z z 1 2 3 4 A. T  4. B. T  2 3 C. T  4+ 2 3 D. T 2 + 2 3 Hướng dẫn giải. 2 z  4  z  2  Ta có: 4 2
z z 12  0     2 z  3  z  i 3  
T z z z z  4  2 3 1 2 3 4 Chọn C
Câu 37: Cho các số phức z thỏa mãn z  4 . Biết rằng tập hợp các điểm biểu diễn các số phức
w  (3  4i)z i là một đường tròn. Tính bán kính r của đường tròn đó. A. r  4. B. r  5. C. r  20. D. r  22. Hướng dẫn giải.
a  (b 1)i
a  (b 1)i(3 4i)
Gọi w a bi , ta có w a bi  (3  4i)z i z   2 3  4i 9 16i 2 2 3a  4b  4
(3b  4a  3)
(3a  4b  4)  (3b  4a  3)   .i z  25 25 25 Mà z = 4 nên 2 2 2 2 2
 (3a  4b  4)  (3b  4a  3)  100  a b  2b  399
Theo giả thiết, tập hợp các điểm biểu diễn các số phức w  (3  4i)z i là một đường tròn nên ta có 2 2 2 2
a b  2b  399  a  (b 1)  400  r  400  20 Chọn C. Mã đê 04_Trang 10 Câu 38:
Gọi M , N lần lượt là các điểm biểu diễn của các số phức 1 i , 2  3i . Số phức z   
biểu diễn bởi điểm Q sao cho MN  3MQ  0 là: 2 1 2 1 2 1 2 1 A. z   i . B. z   i .
C. z    i .
D. z    i . 3 3 3 3 3 3 3 3
(TTLT ĐH DIỆU HIỀN_CẦN THƠ). Hướng dẫn giải  
Ta có điểm M 1 
;1 , N 2;3 . Vectơ MN  1;2 và MQ   x 1; y   1 Q Q .  2    1 3     1 0 x x     QQ  3 2 1
Ta có MN  3MQ  0 khi chỉ khi    . Vậy z   i   3 y   3 3 Q  1 2 1 0   y Q   3 Chọn B. Câu 39:
Cho hình vuông ABCD có tâm H và ,
A B, C, D, H lần lượt là điểm biểu diễn cho
các số phức a,b, c, d , .
h Biết a  2  i ; h  1 3i và số phức b có phần ảo dương. Khi đó, mô-đun
của số phức b là: A. 13 . B. 10 . C. 26 . D. 37 .
(TTLT ĐH DIỆU HIỀN_CẦN THƠ). Hướng dẫn giải
Do ABCD là hình vuông và H là tâm hình vuông nên ta có HB AH , HB AH
Do điểm A biểu diễn bởi số phức a  2  i A2 
;1 , Điểm H biểu diễn bởi
h  1  3i H 1;3 
Đường thẳng BH nhận AH 3;2 làm VTPT nên có phương trình là: 3 x  
1  2  y  3  0  3x  2 y  9  0  9  2m
B BH B ; m , m  0   Do  3  2  9  2m
AH BH  3  2  1    m  32 2 2 2 2 Ta có:  3  m  0 2
 13m  78m  0   m  6 m  6  Vậy b  1
  6i , suy ra mô-đun của số phức b là: 37 Chọn D.
(TTLT ĐH DIỆU HIỀN_CẦN THƠ).
Câu 40: Với các số phức z thỏa mãn | z  2  i | 4 , tập hợp các điểm biểu diễn các số phức z là
một đường tròn. Tìm bán kính R đường tròn đó A. R  8 B. R  16 . C. R  2 . D. R  4 .
(TRƯỜNG THPT CHUYÊN KHTN_HÀ NỘI). Mã đê 04_Trang 11 Hướng dẫn giải. 2 2
Gọi z x yi  ,
x y  . Khi đó z   i    x     y   2 | 2 | 4 2 1  4 .
Tập hợp các điểm biểu diễn các số phức z là một đường tròn có tâm I 2; 
1 và bán kính R  4 Chọn D.
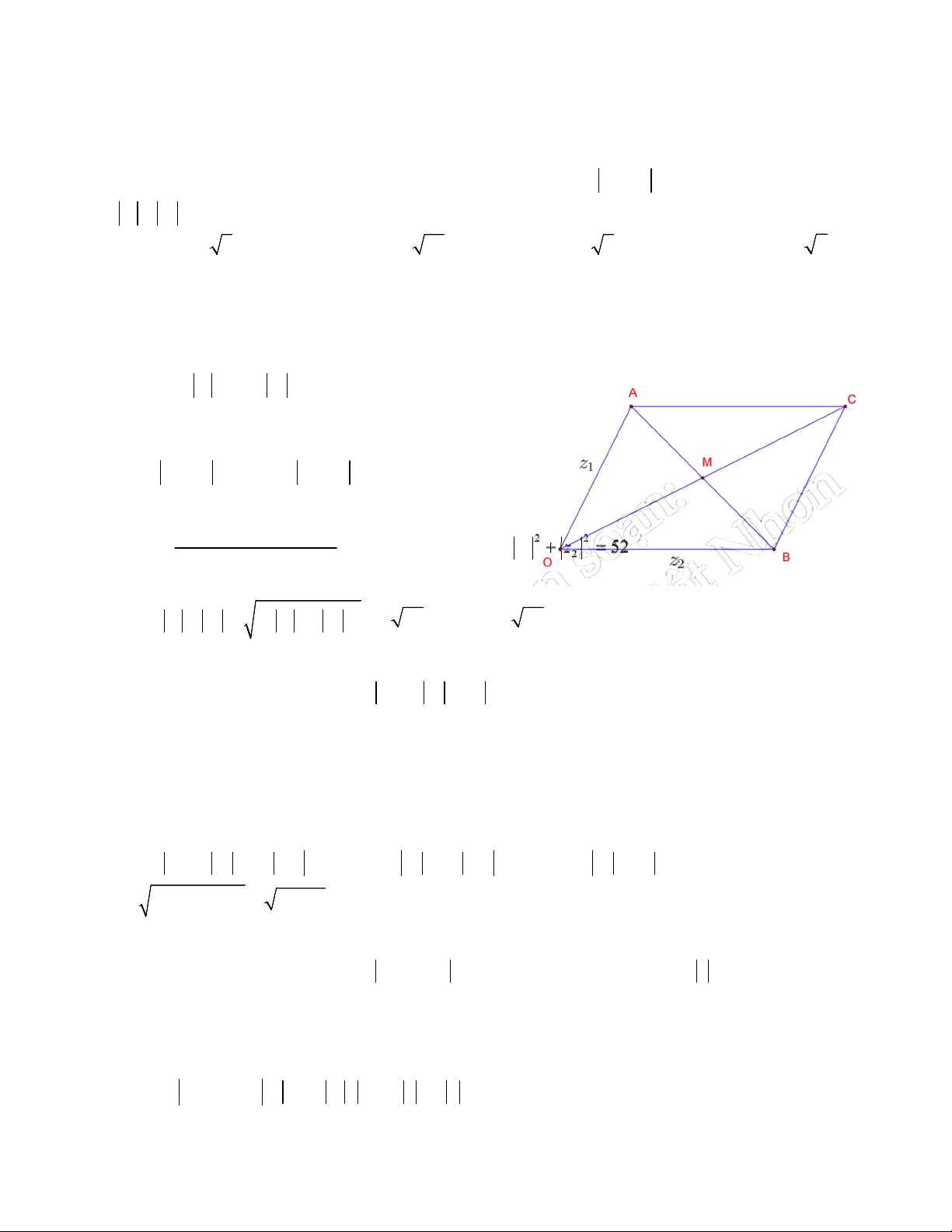
Câu 41: Với hai số phức z và z thỏa mãn z z  8  6i và z z  2 . Tìm giá trị lớn nhất của 1 2 1 2 1 2
P z z 1 2 A. P  5  3 5 . B. P  2 26 . C. P  4 6 . D. P  34  3 2 .
(TRƯỜNG THPT CHUYÊN KHTN_HÀ NỘI). Hướng dẫn giải: Chọn chọn B.
Đặt OA z ,OB z ( với O là gốc tọa độ, , A B 1 2
là điểm biểu diễn của z , z ). 1 2
Dựng hình bình hành OACB , khi đó ta có
AB z z  2,OC z z  10,OM  5 1 2 2 1
Theo định lý đường trung tuyến ta có 2  2 2 OA OB  2  AB 2 2 2 2 2 OM
OA OB  52  zz  52 1 2 4 2 2
Ta có z z  2 zz  2 26  P  2 26 1 2  1 2  max
(TRƯỜNG THPT CHUYÊN KHTN_HÀ NỘI).
Câu 42: Cho số phức z thỏa mãn iz  2i  1 2i . Biết rằng trong mặt phẳng tọa độ Oxy , tập hợp
các điểm biểu diễn số phức z là một đường tròn. Hãy xác định tọa độ tâm I của đường tròn đó. A. I 0; 2 . B. I 0; 2   . C. I  2  ;0 . D. I 2;0 . (TRƯỜNG THPT GIA LỘC II) Hướng dẫn giải
Giả sử z x iy suy ra là M  ;
x y  điểm biểu diễn cho số phức z .
Ta có iz  2i  1 2i i x iy  2i  1 2i   y   x  2i  1 2i
  x  2  y     x  2 2 2 2 2 2 1 2 2  y  5. Chọn D.
Câu 43: Cho số phức z thỏa mãn iz  4  3i  1. Tìm giá trị nhỏ nhất của z . A. 6 . B. 4 . C. 3. D. 5. (TRƯỜNG THPT GIA LỘC II) Hướng dẫn giải
Ta có 1  z  3  4i  3  4i z  5  z z  5 1  4 . Chọn B. Mã đê 04_Trang 12
Câu 44: Tìm tập hợp các điểm M biểu diễn hình học số phức z trong mặt phẳng phức, biết số
phức z thỏa mãn điều kiện: z  4  z  4  10.
A. Tập hợp các điểm cần tìm là đường tròn có tâm O 0;0 và có bán kính R  4. . 2 2 x y
B. Tập hợp các điểm cần tìm là đường elip có phương trình   1. 9 25
C. Tập hợp các điểm cần tìm là những điểm M x;y trong mặt phẳng Oxy thỏa mãn phương 2 2 trình x   2
y  x   2 4 4  y  12. 2 2 x y
D. Tập hợp các điểm cần tìm là đường elip có phương trình   1. 25 9
(TRƯỜNG THPT HAI BÀ TRƯNG_HUẾ) Hướng dẫn giải
Ta có: Gọi M x;y là điểm biểu diễn của số phức z x  . yi
Gọi A4;0 là điểm biểu diễn của số phức z  4.
Gọi B 4;0 là điểm biểu diễn của số phức z  4.
Khi đó: z  4  z  4  10  MA MB  10.(*)
Hệ thức trên chứng tỏ tập hợp các điểm M là elip nhận ,
A B là các tiêu điểm. 2 2 x y
Gọi phương trình của elip là   1, 2 2 2
a b  0,a b c 2 2  a b
Từ (*) ta có: 2a  10  a  5. 2 2 2
AB  2c  8  2c c  4  b a c  9 x y
Vậy quỹ tích các điểm M là elip: E  2 2 :   1. 25 9 Chọn D.
Câu 45: Trong mặt phẳng phức gọi M là điểm biểu diễn cho số phức z a bi a,b  , ab  0 ,
M  là diểm biểu diễn cho số phức z . Mệnh đề nào sau đây đúng?
A. M  đối xứng với M qua Oy .
B. M  đối xứng với M qua Ox .
C. M  đối xứng với M qua O .
D. M  đối xứng với M qua đường thẳng y x .
(CHUYÊN QUANG TRUNG_BÌNH PHƯỚC) Hướng dẫn giải: Ta có: M  ;
a b và M  ; a b
  nên M  đối xứng với M qua Ox . Chọn B. 10
Câu 46: Cho thỏa mãn z   thỏa mãn 2  iz
1 2i . Biết tập hợp các điểm biểu diễn z
cho số phức w  3  4iz 1 2i là đường tròn I , bán kính R . Khi đó. A. I  1  ; 2  , R  5.
B. I 1; 2, R  5. C. I  1  ; 2, R  5. D. I 1; 2  , R  5.
(CHUYÊN QUANG TRUNG_BÌNH PHƯỚC) Hướng dẫn giải
Đặt z a bi và z c  0 , với a;b;c   . Mã đê 04_Trang 13 w 1 2i
Lại có w  3  4iz 1 2i z  . 3  4i
Gọi w x yi với ; x y   . w 1 2i w 1 2i
Khi đó z c   c
c x yi 1 2i  5c 3  4i 3  4i
  x  2   y  2  c   x  2   y  2 2 1 2 5 1 2  25c .
Vậy tập hợp các điểm biểu diễn của số phức w là đường tròn I  1  ; 2 .
Khi đó chỉ có chọn C có khả năng đúng và theo đó R  5  5c  5  c  1.
Thử c  1 vào phương trình (1) thì thỏa mãn. ChọnC.
(CHUYÊN QUANG TRUNG_BÌNH PHƯỚC)
Câu 47: Cho số phức z thỏa mãn z 1  z i . Tìm mô đun nhỏ nhất của số phức w  2z  2  i . 3 3 2 3 A. . B. 3 2 . C. . D. . 2 2 2 2
(TRƯỜNG THPT HÀ HUY TẬP_NGHỆ AN) Hướng dẫn giải Chọn C.
Giả sử z a bi z a bi . Khi đó z 1  z i a 1 bi a  b   1 i
 a  2  b a  b  2 2 2 1 1
a b  0 .
Khi đó w  2z  2  i  2a ai  2  i  2a  2  i a   1 . 3 2
 w  2a  22  2a  2 2 1
 8a  4a  5  . 2 3 2
Vậy mô đun nhỏ nhất của số phức w là . 2 2   3i
Câu 48: Cho số phức z , tìm giá trị lớn nhất của z biết rằng z thỏa mãn điều kiện z 1  1. 3  2i A. 3. B. 2 . C. 2 . D. 1.
(THPT CHUYÊN LAM SƠN THANH HÓA) Hướng dẫn giải.
Gọi z x yi x, y   2  3i Ta có: z 1  1  iz
 1  1  z i  1  x   y  2 2 1  1 . 3  2i
Vậy tập hợp các điểm biểu diễn số phức z là đường tròn tâm I 0;  
1 , bán kính R  1 .
Gọi M là điểm biểu diễn số phức z , ta có IM  1 .
Ta có: z OM OI IM  2 . Chọn C.
Câu 49: Cho các số phức z thỏa mãn z  4 . Biết rằng tập hợp các điểm biểu diễn các số phức
w  (3  4i)z i là một đường tròn. Tính bán kính r của đường tròn đó. A. r  4. B. r  5. C. r  20. D. r  22. Mã đê 04_Trang 14 Hướng dẫn giải.
a  (b 1)i
a  (b 1)i(3 4i)
Gọi w a bi , ta có w a bi  (3  4i)z i z   2 3  4i 9 16i 2 2 3a  4b  4
(3b  4a  3)
(3a  4b  4)  (3b  4a  3)   .i z  25 25 25 Mà z = 4 nên 2 2 2 2 2
 (3a  4b  4)  (3b  4a  3)  100  a b  2b  399
Theo giả thiết, tập hợp các điểm biểu diễn các số phức w  (3  4i)z i là một đường tròn nên ta có 2 2 2 2
a b  2b  399  a  (b 1)  400  r  400  20 Chọn C.
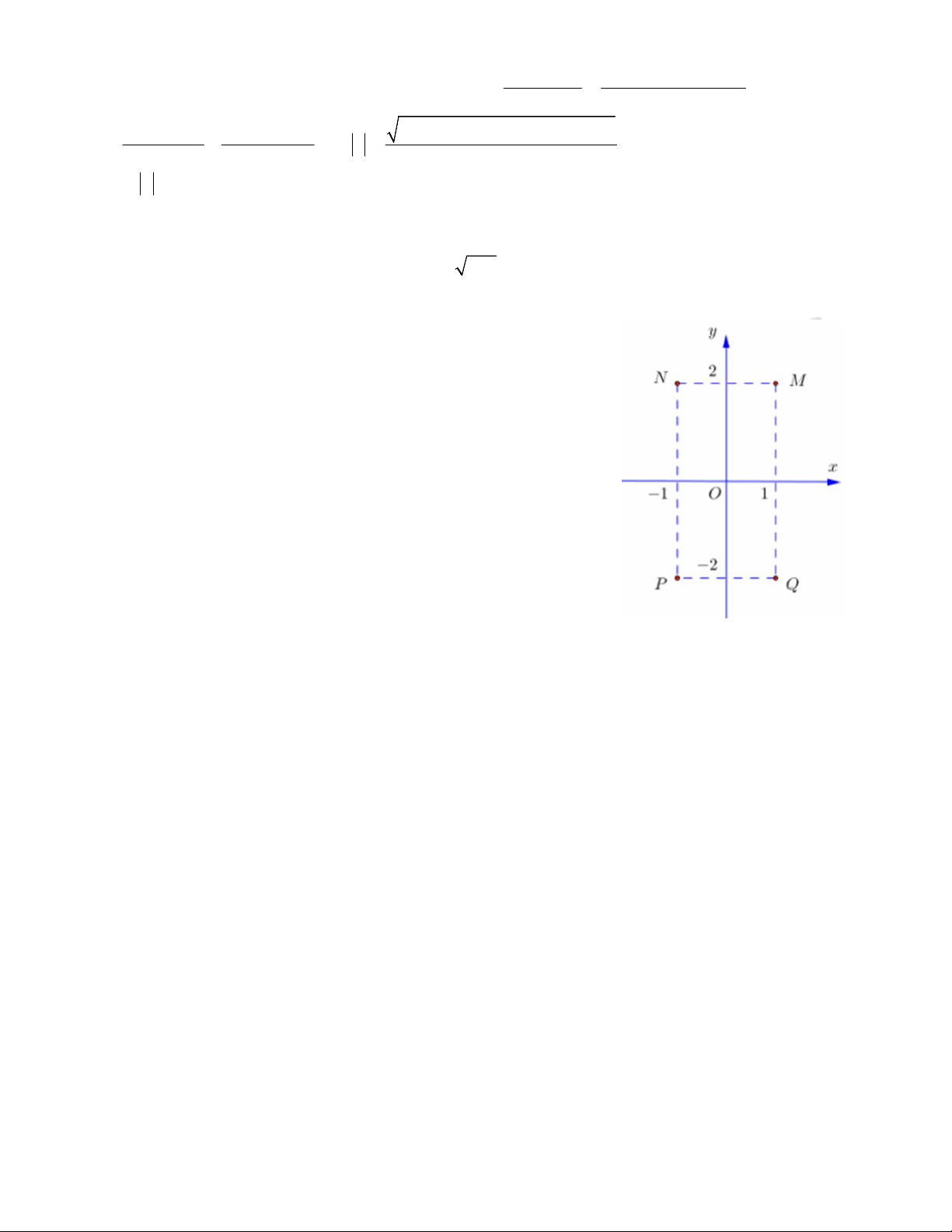
Câu 50: Cho số phức z thỏa mãn (1 i)z  3  .i Hỏi điểm
biểu diễn của z là điểm nào trong các điểm M, N, P, Q ở hình bên ? A. Điểm P. B. Điểm Q. \ C. Điểm M. D. Điểm N. (ĐỀ THI MINH HỌA) Hướng dẫn giải.
Gọi z x yi( , x y  )
Khi đó: (1 i)z  3  i  (x y  3)  (x y 1)i  0
x y  3  0 x  1      Q(1; 2)  .
x y 1  0 y  2    Chọn A Mã đê 04_Trang 15