650 câu hỏi trắc nghiệm chuyên đề phương pháp tọa độ trong không gian – Nhóm Toán 12

650 câu hỏi trắc nghiệm chuyên đề phương pháp tọa độ trong không gian – Nhóm Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

104 52 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Phương pháp tọa độ trong không gian

Môn: Toán 12

Thông tin:

114 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN
ĐỀ 001
C©u 1 :
Trong không gian với hệ tọa độ Oxyz cho tam giác ABC có A(1;0;0), B(0;-
2;3),C(1;1;1). Phương trình mặt phẳng (P) chứa A, B sao cho khoảng cách từ C tới (P)
là
2
3
A.
x+y+z-1=0 hoặc -23x+37y+17z+23=0
B.
x+y+2z-1=0 hoặc -2x+3y+7z+23=0
C.
x+2y+z-1=0 hoặc -2x+3y+6z+13=0
D.
2x+3y+z-1=0 hoặc 3x+y+7z+6=0
C©u 2 :
Trong không gian Oxyz mặt phẳng song song với hai đường thẳng




xt
x y z
yt
zt
12
2
21
: ; : 3 2
2 3 4
1
có một vec tơ pháp tuyến là
A.
B.

n
(5; 6;7)
C.
D.

n
( 5;6;7)
C©u 3 :
Trong không gian với hệ tọa độ Oxyz cho mặt cầu
2 2 2
( ):( 1) ( 2) ( 3) 9S x y z
và
đường thẳng
6 2 2
:
3 2 2
x y z
. Phương trình mặt phẳng (P) đi qua M(4;3;4),
song song với đường thẳng ∆ và tiếp xúc với mặt cầu (S)
A.
2x+y+2z-19=0
B.
x-2y+2z-1=0
C.
2x+y-2z-12=0
D.
2x+y-2z-10=0
C©u 4 :
Trong không gian với hệ tọa độ vuông góc Oxyz, cho mặt phẳng
(P) : x + 2y + z – 4 = 0 và đường thẳng
12
:.
2 1 3
x y z
d


Phương trình đường thẳng
∆ nằm trong mặt phẳng (P), đồng thời cắt và vuông góc với đường thẳng d là:
A.
1 1 1
5 1 3
x y z

B.
1 1 1
5 2 3
x y z

2
C.
1 1 1
5 1 2
x y z

D.
1 3 1
5 1 3
x y z

C©u 5 :
Trong không gian Oxyz đường thẳng d đi qua gốc tọa độ O và có vec tơ chỉ
phương
u
(1;2;3)
có phương trình:
A.
x
d y t
zt
0
:2
3
B.
x
dy
z
1
:2
3
C.
xt
d y t
zt
:3
2
D.



xt
d y t
zt
:2
3
C©u 6 :
Trong không gian Oxyz, cho tứ diện ABCD với A(1; 6; 2), B(5; 1; 3), C(4; 0; 6), D(5;
0; 4). phương trình mặt cầu (S) có tâm D và tiếp xúc với mặt phẳng (ABC).
A.
(S):
x y z
2 2 2
8
( 5) ( 4)
223
B.
(S):
x y z
2 2 2
8
( 5) ( 4)
223
C.
(S):
x y z
2 2 2
8
( 5) ( 4)
223
D.
(S):
x y z
2 2 2
8
( 5) ( 4)
223
C©u 7 :
Cho 3 điểm A(1; 6; 2), B(5; 1; 3), C(4; 0; 6) phương trình mặt phẳng (ABC) LÀ
A.
mp(ABC):
x y z+
14 13 9 110 0
B.
mp(ABC):
x y z
14 13 9 110 0
C.
mp(ABC):
x- y z
14 13 9 110 0
D.
mp(ABC):
x y z
14 13 9 110 0
C©u 8 :
Cho 3 điểm A(2; 1; 4), B(–2; 2; –6), C(6; 0; –1). Tích
AB AC
.
bằng:
A.
–67
B.
65
C.
67
D.
33
C©u 9 :
Cho hai đường thẳng
1
12
: 2 3
34
xt
d y t
zt



và
2
3 4 '
: 5 6 '
7 8 '
xt
d y t
zt



Trong các mệnh đề sa, mệnh đề nào đúng?
A.
12
dd
B.
12
dd
C.
12
dd
D.
12
và dd
chéo
nhau
C©u 10 :
Trong không gian Oxyz, cho ba vectơ
1,1,0 ; (1,1,0); 1,1,1a b c
. Trong các
mệnh đề sau, mệnh đề nào đúng?
A.
0abc
B.
,,abc
đồng
phẳng.
C.
6
cos ,
3
bc
D.
.1ab
C©u 11 :
Mặt phẳng (Q) song song với mp(P): x+2y+z-4=0 và cách D(1;0;3) một khoảng bằng
3
6
có phương trình là
A.
x+2y+z+2=0
B.
x+2y-z-10=0
C.
x+2y+z-10=0
D.
x+2y+z+2=0 và
x+2y+z-10=0
C©u 12 :
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;1;1) và mặt phẳng (P): 2x – y +
2z + 1 = 0. Phương trình mặt cầu tâm A tiếp xúc với mặt phẳng (P) là:
A.
: (x – 2)
2
+ (y –1)
2
+ (z – 1)
2
= 4
B.
(x –+2)
2
+ (y – 1)
2
+ (z – 1)
2
= 9
C.
: (x – 2)
2
+ (y –1)
2
+ (z – 1)
2
= 3
D.
: (x – 2)
2
+ (y – 1)
2
+ (z – 1)
2
= 5
C©u 13 :
Cho hai điểm A(1;-1;5) và B(0;0;1). Mặt phẳng (P) chứa A, B và song song với Oy có
phương trình là
A.
4 1 0x y z
B.
2 5 0xz
C.
4 1 0xz
D.
4 1 0yz
C©u 14 :
Trong mặt phẳng Oxyz Cho tứ diện ABCD có A(2;3;1), B(4;1;-2), C(6;3;7), D-5;-4;-8).
Độ dài đường cao kẻ từ D của tứ diện là
A.
11
B.
65
5
C.
5
5
D.
43
3
C©u 15 :
Cho hai điểm
A 1, 2,0
và
B 4,1,1
. Độ dài đường cao OH của tam giác OAB là:
A.
1
19
B.
86
19
C.
19
86
D.
19
2
C©u 16 :
Trong không gian Oxyz, cho bốn điểm
1,1,1 ; 1,3,5 ; 1,1,4 ; 2,3,2A B C D
. Gọi I,
J lần lượt là trung điểm của AB và CD. Câu nào sau đây đúng?
A.
IJAB
B.
IJCD
C.
AB và CD có
chung trung
điểm
D.
IJ ABC
C©u 17 :
Mặt cầu (S) có tâm I(1;2;-3) và đi qua A(1;0;4) có phương trình
A.
2 2 2
(x 1) (y 2) (z 3) 53
B.
2 2 2
(x 1) (y 2) (z 3) 53
C.
2 2 2
(x 1) (y 2) (z 3) 53
D.
2 2 2
(x 1) (y 2) (z 3) 53
C©u 18 :
Trong không gian toạ độ Oxyz, cho điểm
A 1,2,1
và hai mặt phẳng
2x 4: y 6z 5 0
,
x 2y 3: z0 
. Mệnh đề nào sau đây đúng ?
4
A.
không đi qua A và không song
song với
B.
đi qua A và song song với
C.
đi qua A và không song song với
D.
không đi qua A và song song với
C©u 19 :
Cho hai mặt phẳng song song (P):
nx y z
7 6 4 0
và (Q):
x my z
3 2 7 0
. Khi đó
giá trị của m và n là:
A.
mn
7
;1
3

B.
nm
7
;9
3

C.
mn
3
;9
7

D.
mn
7
;9
3

C©u 20 :
Vị trí tương đối của hai đường thẳng





x t x ts
d y t d y t
z t z t
12
1 2 7 3
: 2 3 ; : 2 2
5 4 1 2
là:
A.
Chéo nhau
B.
Trùng nhau
C.
Song song
D.
Cắt nhau
C©u 21 :
Trong không gian với hệ tọa độ Oxyz cho tam giác ABC có A(1;0;0), B(0;-
2;3),C(1;1;1). Phương trình mặt phẳng (P) chứa A, B sao cho khoảng cách từ C tới (P)
là
2
3
A.
x+y+z-1=0 hoặc -23x+37y+17z+23=0
B.
2x+3y+z-1=0 hoặc 3x+y+7z+6=0
C.
x+2y+z-1=0 hoặc -2x+3y+6z+13=0
D.
x+y+2z-1=0 hoặc -2x+3y+7z+23=0
C©u 22 :
Trong không gian Oxyz cho hai mặt phẳng (P): 2x+y-z-3=0 và
(Q): x+y+x-1=0. Phương trình chính tắc đường thẳng giao tuyến của hai mặt phẳng
(P) và (Q) là:
A.
21
2 3 1
x y z

B.
1 2 1
2 3 1
x y z


C.
1 2 1
2 3 1
x y z

D.
21
2 3 1
x y z


C©u 23 :
Cho đường thẳng


xt
dy
zt
:1
và 2 mp (P):
x y z
2 2 3 0
và (Q):
x y z
2 2 7 0
.
Mặt cầu (S) có tâm I thuộc đường thẳng (d) và tiếp xúc với hai mặt phẳng (P) và (Q)
5
có phương trình
A.
x y z
222
4
3 1 3
9
B.
x y z
2 2 2
4
3 1 3
9
C.
x y z
2 2 2
4
3 1 3
9
D.
x y z
2 2 2
4
3 1 3
9
C©u 24 :
Trong không gian Oxyz, cho ba vectơ
1,1,0 ; (1,1,0); 1,1,1a b c
. Cho hình
hộp OABC.O’A’B’C” thỏa mãn điều kiện
,,OA a OB b OC c
. Thể tích của hình
hộp nói trên bằng bao nhiêu?
A.
1
3
B.
2
3
C.
2
D.
6
C©u 25 :
Trong không gian với hệ tọa độ Oxyz cho mặt cầu
2 2 2
( ):( 1) ( 2) ( 3) 9S x y z
và
đường thẳng
6 2 2
:
3 2 2
x y z
. Phương trình mặt phẳng (P) đi qua M(4;3;4),
song song với đường thẳng ∆ và tiếp xúc với mặt cầu (S)
A.
2x+y+2z-19=0
B.
2x+y-2z-12=0
C.
x-2y+2z-1=0
D.
2x+y-2z-10=0
C©u 26 :
Trong không gian với hệ tọa độ Oxyz cho đường thẳng
22
( ):
1 1 2
x y z
d


và điểm
A(2;3;1). Viết phương trình mặt phẳng (P) chứa A và (d). Cosin của góc giữa mặt
phẳng (P) và mặt phẳng tọa độ (Oxy) là:
A.
2
6
B.
2
3
C.
26
6
D.
7
13
C©u 27 :
Cho mặt phẳng
:3x 2y z 6 0
và điểm
A 2, 1,0
. Hình chiếu vuông góc của
A lên mặt phẳng
là:
A.
1, 1,1
B.
1,1, 1
C.
3, 2,1
D.
5, 3,1
C©u 28 :
Cho điểm A(1;1;1) và đường thẳng
64
:2
12
xt
d y t
zt

.
Hình chiếu của A trên d có tọa độ là
A.
2; 3; 1
B.
2;3;1
C.
2; 3;1
D.
2;3;1
6
C©u 29 :
Trong hệ trục Oxyz , M’ là hình chiếu vuông góc của
M 3,2,1
trên Ox . M’ có toạ độ
là:
A.
0,0,1
B.
3,0,0
C.
3,0,0
D.
0,2,0
C©u 30 :
Trong không gian Oxyz cho các điểm A(3; -4; 0), B(0; 2; 4), C(4; 2; 1). Tọa độ điểm D
trên trục Ox sao cho AD = BC.
là:
A.
D(0;0;0) hoặc D(0;0;6)
B.
D(0;0;2) hoặc D(0;0;8)
C.
D(0;0;-3) hoặc D(0;0;3)
D.
D(0;0;0) hoặc D(0;0;-6)
C©u 31 :
Phương trình tổng quát của
qua A(2;-1;4), B(3;2;-1) và vuông góc với
: 2 3 0x y z
là:
A.
11x+7y-2z-21=0
B.
11x+7y+2z+21=0
C.
11x-7y-2z-21=0
D.
11x-7y+2z+21=0
C©u 32 :
Khoảng cách từ điểm M(-2; -4; 3) đến mặt phẳng (P) có phương trình 2x – y + 2z – 3
= 0 là:
A.
3
B.
1
C.
2
D.
Đáp án khác
C©u 33 :
Trong không gian Oxyz, cho điểm M(8,-2,4). Gọi A, B, C lần lượt là hình chiếu của
M trên các trục Ox, Oy, Oz. Phương trình mặt phẳng đi qua ba điểm A, B và C là:
A.
4 2 8 0x y z
B.
4 2 8 0x y z
C.
4 2 8 0x y z
D.
4 2 8 0x y z
C©u 34 :
Gọi H là hình chiếu vuông góc của A(2; -1; -1) đến mặt phẳng (P) có phương trình
16x – 12y – 15z – 4 = 0. Độ dài của đoạn thẳng AH là:
A.
11
25
B.
11
5
C.
22
25
D.
22
5
C©u 35 :
Trong không gian với hệ tọa độ Oxyz, cho vecto
AO 3 i 4j 2k 5j
. Tọa độ của
điểm A là
A.
3, 2,5
B.
3, 17,2
C.
3,17, 2
D.
3,5, 2
C©u 36 :
Cho tam giác ABC có A = (1;0;1), B = (0;2;3), C = (2;1;0). Độ dài đường cao của tam
giác kẻ từ C là
7
A.
26
B.
26
2
C.
26
3
D.
26
C©u 37 :
Cho 4 điềm A(3; -2; -2), B(3; 2; 0), C(0; 2; 1) và D(-1; 1; 2). Mặt cầu tâm A và tiếp xúc
với mặt phẳng (BCD) có phương trình là:
A.
2 2 2
( 3) ( 2) ( 2) 14x y z
B.
2 2 2
( 3) ( 2) ( 2) 14x y z
C.
2 2 2
( 3) ( 2) ( 2) 14x y z
D.
2 2 2
( 3) ( 2) ( 2) 14x y z
C©u 38 :
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1;2;2), B(5;4;4) và mặt
phẳng (P): 2x + y – z + 6 =0. Tọa độ điểm M nằm trên (P) sao cho MA
2
+ MB
2
nhỏ
nhất là:
A.
M(-1;1;5)
B.
M(1;-1;3)
C.
M(2;1;-5)
D.
M(-1;3;2)
C©u 39 :
Trong không gian Oxyz cho hai mặt phẳng (P): 2x+y-z-3=0 và
(Q): x+y+x-1=0. Phương trình chính tắc đường thẳng giao tuyến của hai mặt phẳng
(P) và (Q) là:
A.
21
2 3 1
x y z

B.
1 2 1
2 3 1
x y z


C.
21
2 3 1
x y z


D.
1 2 1
2 3 1
x y z

C©u 40 :
Mặt phẳng
()
đi qua M (0; 0; -1) và song song với giá của hai vectơ
(1; 2;3) và (3;0;5)ab
. Phương trình của mặt phẳng
()
là:
A.
5x – 2y – 3z -21 = 0
B.
-5x + 2y + 3z + 3 = 0
C.
10x – 4y – 6z + 21 = 0
D.
5x – 2y – 3z + 21 = 0
C©u 41 :
Cho (S) là mặt cầu tâm I(2; 1; -1) và tiếp xúc với mặt phẳng (P) có phương trình: 2x –
2y – z + 3 = 0. Khi đó, bán kính của (S) là:
A.
4
3
B.
2
C.
1
3
D.
3
C©u 42 :
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1;2;2), B(5;4;4) và mặt
phẳng (P): 2x + y – z + 6 =0. Tọa độ điểm M nằm trên (P) sao cho MA
2
+ MB
2
nhỏ
nhất là:
8
A.
M(-1;1;5)
B.
M(2;1;-5)
C.
M(1;-1;3)
D.
M(-1;3;2)
C©u 43 :
Trong không gian Oxyz, cho mặt phẳng (P)đi qua hai điểm A(4,-1,1), B(3,1,-1) và
song song với trục Ox. Phương trình nào sau đây là phương trình của mặt phẳng
(P):
A.
0x y z
B.
0xy
C.
0yz
D.
0xz
C©u 44 :
Trong không gian Oxyz mp (P) đi qua B(0;-2;3) ,song song với đường thẳng d:


xy
z
21
23
và vuông góc với mặt phẳng (Q):x+y-z=0 có phương trình ?
A.
2x-3y+5z-9=0
B.
2x-3y+5z-9=0
C.
2x+3y-5z-9=0
D.
2x+3y+5z-9=0
C©u 45 :
Trong không gian Oxyz, cho bốn điểm
1,0,0 ; 0,1,0 ; 0,0,1 ; 1,1,1A B C D
. Xác
định tọa độ trọng tâm G của tứ diện ABCD
A.
111
,,
222



B.
111
,,
333



C.
222
,,
333



D.
111
,,
444



C©u 46 :
Trong không gian Oxyz, gọi (P) là mặt phẳng cắt ba trục tọa độ tại ba điểm
8,0,0 ; 0, 2,0 ; 0,0,4A B C
. Phương trình của mặt phẳng (P) là:
A.
1
4 1 2
x y z
B.
0
8 2 4
x y z
C.
4 2 8 0x y z
D.
4 2 0x y z
C©u 47 :
Cho hai đường thẳng
1
13
:
1 2 3
x y z
d


và
2
2
: 1 4
26
xt
d y t
zt


Khẳng định nào sau đây là đúng?
A.
12
,dd
cắt nhau;
B.
12
,dd
trùng
nhau;
C.
12
//dd
;
D.
12
,dd
chéo nhau.
C©u 48 :
Trong không gian với hệ tọa độ Oxyz cho đường thẳng
22
( ):
1 1 2
x y z
d


và điểm
A(2;3;1). Viết phương trình mặt phẳng (P) chứa A và (d). Cosin của góc giữa mặt
phẳng (P) và mặt phẳng tọa độ (Oxy) là:
9
A.
2
6
B.
26
6
C.
7
13
D.
2
3
C©u 49 :
Trong không gian Oxyz cho hai điểm A(0;0;-3), B(2;0;-1) và mặt phẳng (P): 3x-8y+7z-
1=0. Gọi C là điểm trên (P) để tam giác ABC đều khi đói tọa độ điểm C là:
A.
( 3;1;2)C
B.
1 3 1
( ; ; )
222
C

C.
221
( ; ; )
3 3 3
C

D.
(1;2; 1)C
C©u 50 :
Trong không gian Oxyz mặt phẳng (P) đi qua điểm M(-1;2;0) và có VTPT

n
(4;0; 5)
có phương trình là:
A.
4x-5y-4=0
B.
4x-5z-4=0
C.
4x-5y+4=0
D.
4x-5z+4=0
C©u 51 :
Cho các vectơ
(1;2;3); ( 2;4;1); ( 1;3;4) a b c
. Vectơ
2 3 5v a b c
có toạ độ là:
A.
(7; 3; 23)
B.
(7; 23; 3)
C.
(23; 7; 3)
D.
(3; 7; 23)
C©u 52 :
Trong không gian với hệ tọa độ vuông góc Oxyz, cho mặt phẳng
(P) : x + 2y + z – 4 = 0 và đường thẳng
12
:.
2 1 3
x y z
d


Phương trình đường thẳng
∆ nằm trong mặt phẳng (P), đồng thời cắt và vuông góc với đường thẳng d là:
A.
1 1 1
5 1 3
x y z

B.
1 3 1
5 1 3
x y z

C.
1 1 1
5 1 2
x y z

D.
1 1 1
5 2 3
x y z

C©u 53 :
Tọa độ hình chiếu vuông góc của M(2; 0; 1) trên đường thằng
1
: 2
12
xy
z
là:
A.
(2; 2; 3)
B.
(1; 0; 2)
C.
(0; -2; 1)
D.
(-1; -4; 0)
C©u 54 :
Trong không gian Oxyz cho hai điểm A(0;0;-3), B(2;0;-1) và mặt phẳng (P): 3x-8y+7z-
1=0. Gọi C là điểm trên (P) để tam giác ABC đều khi đói tọa độ điểm C là:
A.
( 3;1;2)C
B.
(1;2; 1)C
C.
221
( ; ; )
3 3 3
C

D.
1 3 1
( ; ; )
222
C

C©u 55 :
Trong không gian Oxyz cho các điểm A(3; -4; 0), B(0; 2; 4), C(4; 2; 1). Tọa độ điểm D
trên trục Ox sao cho AD = BC.
là:
10
A.
D(0;0;0) hoặc D(0;0;6)
B.
D(0;0;2) hoặc D(0;0;8)
C.
D(0;0;-3) hoặc D(0;0;3)
D.
D(0;0;0) hoặc D(0;0;-6)
C©u 56 :
Trong không gian Oxyz, cho điểm I(2,6,-3) và các mặt phẳng:
: 2 0; : 6 0; : 3 0x y z
Trong các mệnh đề sau, tìm mệnh đề sai:
A.
B.
đi qua
điểm I
C.
//Oz
D.
// xOz
C©u 57 :
Cho đường thẳng d đi qua M(2; 0; -1) và có vectơ chỉ phương
(4; 6;2)a
. Phương
trình tham số của đường thẳng d là:
A.
22
3
1
xt
yt
zt


B.
22
3
1
xt
yt
zt


C.
42
63
2
xt
yt
zt


D.
24
6
12
xt
yt
zt


C©u 58 :
Trong không gian Oxyz mặt phẳng trung trực của đoạn thẳng AB có phương trình
là ,với A(1;2;-3),B(-3;2;9)
A.
-x-3z-10=0
B.
-4x+12z-10=0
C.
-x-3z-10=0
D.
-x+3z-10=0
C©u 59 :
Cho điểm M(2; 1; 0) và đường thẳng :
x y z
11
2 1 1


. Đ ường thẳng d đi qua điểm
M, cắt và vuông góc với có vec tơ chỉ phương
A.
(2; 1; 1)
B.
(2;1; 1)
C.
(1; 4;2)
D.
(1; 4; 2)
C©u 60 :
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;1;1) và mặt phẳng (P): 2x – y +
2z + 1 = 0. Phương trình mặt cầu tâm A tiếp xúc với mặt phẳng (P) là:
A.
: (x – 2)
2
+ (y –1)
2
+ (z – 1)
2
= 4
B.
: (x – 2)
2
+ (y – 1)
2
+ (z – 1)
2
= 5
C.
: (x – 2)
2
+ (y –1)
2
+ (z – 1)
2
= 3
D.
(x –+2)
2
+ (y – 1)
2
+ (z – 1)
2
= 9
C©u 61 :
Trong không gian toạ độ Oxyz, cho ba điểm
M 1,0,0
,
N 0,2,0
,
P 0,0,3
. Mặt phẳng
MNP
có phương trình là
A.
6x 3y 2z 1 0
B.
6x 3y 2z 6 0
C.
6x 3y 2z 1 0
D.
x y z 6 0
11
C©u 62 :
Gọi
()
là mặt phẳng cắt ba trục tọa độ tại 3 điểm M (8; 0; 0), N(0; -2; 0) , P(0; 0; 4).
Phương trình của mặt phẳng
()
là:
A.
0
8 2 4
x y z
B.
x – 4y + 2z – 8 =
0
C.
x – 4y + 2z = 0
D.
1
4 1 2
x y z
C©u 63 :
Cho điểm A(-1;2;1) và hai mặt phẳng (P) : 2x+4y-6z-5=0 và (Q) : x+2y-3z=0. Mệnh đề
nào sau đây là đúng ?
A.
mp (Q) không đi qua A và không song song với (P);
B.
mp (Q) đi qua A và không song song với (P);
C.
mp (Q) đi qua A và song song với (P) ;
D.
mp (Q) không đi qua A và song song với (P);
C©u 64 :
Trong hệ trục Oxyz , cho ba điểm
A 2,1,0
,
B 3,0,4
,
C 0,7,3
. Khi đó ,
cos AB,BC
bằng:
A.
14
3 118
B.
72
3 59
C.
14
57
D.
14
57
C©u 65 :
Khoảng cách giữa hai mặt phẳng (P):
x y z
2 3 5 0
và (Q):
x y z
2 3 1 0
bằng:
A.
6
14
B.
6
C.
4
D.
4
14
C©u 66 :
Cho bốn điểm A(1;1;1), B(1;2;1), C(1;1;2) và D(2;2;1). Tâm I của mặt cầu ngoại tiếp tứ
diện ABCD có tọa độ :
A.
3;3; 3
B.
3 3 3
;;
2 2 2



C.
333
;;
222



D.
3;3;3
C©u 67 :
Cho điểm A(0;-1;3) và đường thẳng d
12
2
1
xt
y
z


.
Khoảng cách từ A đến d bằng
A.
8
B.
3
C.
14
D.
6
C©u 68 :
Cho mặt cầu (S):
x y z x y z
2 2 2
8 4 2 4 0
. Bán kính R của mặt cầu (S) là:
12
A.
R =
17
B.
R =
88
C.
R = 2
D.
R = 5
C©u 69 :
Cho 2 điểm A(2; 4; 1), B(–2; 2; –3). Phương trình mặt cầu đường kính AB là:
A.
x y z
2 2 2
( 3) ( 1) 9
B.
x y z
2 2 2
( 3) ( 1) 9
C.
x y z
2 2 2
( 3) ( 1) 3
D.
x y z
2 2 2
( 3) ( 1) 9
C©u 70 :
Trong mặt phẳng Oxyz Cho tứ diện ABCD có A(2;3;1), B(4;1;-2), C(6;3;7), D-5;-4;-8).
Độ dài đường cao kẻ từ D của tứ diện là
A.
11
B.
65
5
C.
5
5
D.
43
3
C©u 71 :
Cho A(1;0;0), B(0;1;0), C(0;0;1) và D(-2;1;-1).Thể tích của tứ diện ABCD là
A.
1
B.
2
C.
1
2
D.
1
3
C©u 72 :
Trong không gian Oxyz, tam giác ABC có
1,0,0 ; 0,2,0 ; 3,0,4A B C
. Tọa độ
điểm M trên mặt phẳng Oyz sao cho MC vuông góc với (ABC) là:
A.
3 11
0, ,
22



B.
3 11
0, ,
22



C.
3 11
0, ,
22



D.
3 11
0, ,
22




C©u 73 :
Cho 3 điểm A(1; –2; 1), B(–1; 3; 3), C(2; –4; 2). Một VTPT
n
của mặt phẳng (ABC) là:
A.
n
( 1;9;4)
B.
n
(9;4;1)
C.
n
(4;9; 1)
D.
n
(9;4; 1)
C©u 74 :
Tọa độ giao điểm M của đường thẳng
12 9 1
:
4 3 1
x y z
d

và mặt phẳng (P): 3x +
5y – z – 2 = 0 là:
A.
(1; 0; 1)
B.
(0; 0; -2)
C.
(1; 1; 6)
D.
(12; 9; 1)
C©u 75 :
Trong không gian Oxyz, xác định các cặp giá trị (l, m) để các cặp mặt phẳng sau đây
song song với nhau:
2 3 5 0; 6 6 2 0x ly z mx y z
A.
3,4
B.
4; 3
C.
4,3
D.
4,3
C©u 76 :
: Cho 2 điểm A(1; 2; –3) và B(6; 5; –1). Nếu OABC là hình bình hành thì toạ độ điểm
13
C là:
A.
(–5;–3;–2)
B.
(–3;–5;–2)
C.
(3;5;–2)
D.
(5; 3; 2)
C©u 77 :
Bán kính của mặt cầu tâm I(3;3;-4), tiếp xúc với trục Oy bằng
A.
5
B.
4
C.
5
D.
5
2
C©u 78 :
Trong không gian toạ độ Oxyz, cho mặt phẳng
:2x y z 5 0
và đường thẳng
x 1 y 3 z 2
d:
3 1 3


. Toạ độ giao điểm của d và
là
A.
4,2, 1
B.
17,9,20
C.
17,20,9
D.
2,1,0
C©u 79 :
Cho mặt phẳng
:4x 2y 3z 1 0
và mặt cầu
2 2 2
S : x y z 2x 4y 6z 0
. Khi
đó, mệnh đề nào sau đây là một mệnh đề sai:
A.
cắt
S
theo một đường tròn
B.
tiếp xúc với
S
C.
có điểm chung với
S
D.
đi qua tâm của
S
C©u 80 :
Cho mặt phẳng
:2x y 2z 1 0
và đường thẳng
x 1 t
d : y 2t
z 2t 2



. Gọi
là góc giữa
đường thẳng d và mặt phẳng
. Khi đó, giá trị của
cos
là:
A.
4
9
B.
65
9
C.
65
4
D.
4
65
14
ĐÁP ÁN
01
) | } ~
28
{ | ) ~
55
) | } ~
02
{ | } )
29
{ ) } ~
56
{ | ) ~
03
) | } ~
30
) | } ~
57
{ ) } ~
04
) | } ~
31
{ | ) ~
58
{ | } )
05
{ | } )
32
{ ) } ~
59
{ | } )
06
{ | } )
33
{ | ) ~
60
) | } ~
07
{ | } )
34
{ ) } ~
61
{ ) } ~
08
{ | } )
35
{ ) } ~
62
{ ) } ~
09
{ ) } ~
36
{ | ) ~
63
{ | ) ~
10
{ | ) ~
37
{ ) } ~
64
{ ) } ~
11
{ | } )
38
) | } ~
65
{ | } )
12
) | } ~
39
) | } ~
66
{ | ) ~
13
{ | ) ~
40
{ ) } ~
67
{ | ) ~
14
) | } ~
41
{ ) } ~
68
{ | } )
15
{ ) } ~
42
) | } ~
69
{ | } )
16
{ | ) ~
43
{ | ) ~
70
) | } ~
17
{ | } )
44
{ | } )
71
{ | ) ~
18
{ ) } ~
45
{ | ) ~
72
{ | ) ~
19
{ | } )
46
{ | ) ~
73
{ | } )
20
{ | } )
47
{ | ) ~
74
{ ) } ~
21
) | } ~
48
) | } ~
75
{ | ) ~
22
) | } ~
49
) | } ~
76
{ | } )
23
{ | } )
50
{ | } )
77
{ | ) ~
24
{ | ) ~
51
{ | } )
78
{ ) } ~
25
) | } ~
52
) | } ~
79
{ ) } ~
26
) | } ~
53
{ ) } ~
80
{ ) } ~
27
{ ) } ~
54
) | } ~
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN
ĐỀ 002
C©u 1 :
Cho
(2;1; 1)A
,
(3;0;1)B
,
(2; 1;3)C
; điểm
D
thuộc
Oy
, và thể tích khối tứ diện
ABCD
bằng
5
. Tọa độ điểm
D
là:
A.
(0; 7;0)
hoặc
(0;8;0)
B.
(0; 7;0)
C.
(0;8;0)
D.
(0;7;0)
hoặc
(0; 8;0)
C©u 2 :
Cho đường thẳng
3
3
:
1 3 2
y
xz
d

,
( ) : 3 0mp x y z
và điểm
(1;2; 1)A
. Đường
thẳng
qua
A
cắt
d
và song song với
()mp
có phương trình là
A.
2
11
1 2 1
y
xz



B.
2
11
1 2 1
y
xz



C.
2
11
121
y
xz


D.
2
11
121
y
xz


C©u 3 :
Cho
(5;1;3)A
,
( 5;1; 1)B 
,
(1; 3;0)C
,
(3; 6;2)D
. Tọa độ điểm
A
đối xứng với điểm
A
qua
()mp BCD
là
A.
( 1;7;5)
B.
(1; 7; 5)
C.
(1;7;5)
D.
(1; 7;5)
C©u 4 :
Cho mặt cầu
2 2 2
( ): 2 4 6 2 0S x y z x y z
và mặt phẳng
( ) :4 3 12 10 0x y z
.
Mặt phẳng tiếp xúc với
()S
và song song với
()
có phương trình là:
A.
4 3 12 78 0x y z
B.
4 3 12 78 0x y z
hoặc
4 3 12 26 0x y z
C.
4 3 12 78 0x y z
hoặc
4 3 12 26 0x y z
D.
4 3 12 26 0x y z
C©u 5 :
Cho hai điểm
( 2;0; 3)A 
,
(2;2; 1)B
. Phương trình nào sau đây là phương trình mặt cầu
đường kính
AB
?
A.
2 2 2
2 4 1 0x y z y z
B.
2 2 2
2 4 1 0x y z x z
C.
2 2 2
2 4 1 0x y z y z
D.
2 2 2
2 4 1 0x y z y z
C©u 6 :
Đường thẳng
x 12 y 9 z 1
d:
4 3 1

cắt mặt phẳng
:3x 5y z 2 0
tại điểm có tọa
độ là :
A.
2;0;4
B.
0;1;3
C.
1;0;1
D.
0;0; 2
C©u 7 :
Cho
(2; 1;6)A
,
( 3; 1; 4)B
,
(5; 1;0)C
,
(1;2;1)D
. Thể tích tứ diện
ABCD
bằng:
A.
30
B.
50
C.
40
D.
60
C©u 8 :
Cho mặt cầu
2 2 2
( ): 2 6 4 0S x y z x y z
. Biết
OA
, (
O
là gốc tọa độ) là đường kính
của mặt cầu
()S
. Tìm tọa độ điểm
A
?
A.
( 1;3;2)A
B.
Chưa thể xác định được tọa độ điểm
A
vì
mặt cầu
()S
có vô số đường kính
C.
(2; 6; 4)A 
D.
( 2;6;4)A
C©u 9 :
Tìm điểm
A
trên đường thẳng
1
:
2 1 1
y
xz
d

sao cho khoảng cách từ điểm
A
đến
( ): 2 2 5 0mp x y z
bằng
3
. Biết
A
có hoành độ dương
A.
(0;0; 1)A
B.
( 2;1; 2)A 
C.
(2; 1;0)A
D.
(4; 2;1)A
C©u 10 :
Cho
()S
là mặt cầu tâm
(2;1; 1)I
và tiếp xúc mặt phẳng
( ) : 2 2 3 0x y z
. Khi đó bán
kính mặt cầu
()S
là:
A.
2
B.
2
3
C.
4
3
D.
2
9
C©u 11 :
Cho hai mặt phẳng
22
( ) : ( 2) 2 0m x y m z
và
2
( ) : 2 2 1 0x m y z
. Mặt phẳng
()
vuông góc với
()
khi
A.
2m
B.
2m
C.
1m
D.
3m
C©u 12 :
Trong không gian
Oxyz
, cho bốn điểm
(1;0;0)A
,
(0;1;0)B
,
(0;0;1)C
và
(1;1;1)D
. Gọi
,MN
lần lượt là trung điểm của
AB
và
CD
. Khi đó tọa độ trung điểm
G
của đoạn thẳng
MN
là:
A.
111
;;
222
G



B.
111
;;
333
G



C.
111
;;
444
G



D.
222
;;
333
G



C©u 13 :
Cho ba mặt phẳng
P :3x y z 4 0 ; Q :3x y z 5 0
và
R :2x 3y 3z 1 0
.
Xét các mệnh đề sau:
(I): (P) song song (Q) (II): (P) vuông góc (Q)
Khẳng định nào sau đây ĐÚNG ?
A.
(I) sai ; (II) đúng
B.
(I) đúng ; (II) sai
C.
(I) ; (II) đều sai
D.
(I) ; (II) đều đúng
C©u 14 :
Cho đường thẳng
13
:2
2
xt
d y t
z mt
và
( ): 2 2 6 0mp P x y z
. Giá trị của
m
để
()dP
là:
A.
2m
B.
2m 
C.
4m
D.
4m 
C©u 15 :
Cho hai đường thẳng
1
6
31
:
2 2 1
y
xz
d


và
2
:
2
xt
d y t
z


. Đường thẳng đi qua điểm
(0;1;1)A
, vuông góc với
1
d
và
2
d
có pt là:
A.
1
1
1 3 4
y
xz

B.
1
1
1 3 4
y
xz

C.
1
1
1 3 4
y
xz


D.
11
1 3 4
y
xz


C©u 16 :
Cho
(0;0;2)A
,
(3;0;5)B
,
(1;1;0)C
,
(4;1;2)D
. Độ dài đường cao của tứ diện
ABCD
hạ từ
đỉnh
D
xuống mặt phẳng
()ABC
là:
A.
11
11
B.
11
C.
1
D.
11
C©u 17 :
Cho
(0;0;1)A
,
( 1; 2;0)B 
,
(2;1; 1)C
. Đường thẳng
đi qua trọng tâm
G
của tam giác
ABC
và vuông góc với
()mp ABC
có phương trình:
A.
1
5
3
1
4
3
3
xt
yt
zt

B.
1
5
3
1
4
3
3
xt
yt
zt

C.
1
5
3
1
4
3
3
xt
yt
zt


D.
1
5
3
1
4
3
3
xt
yt
zt

C©u 18 :
Cho tứ diện OABC với
A 3;1; 2 ; B 1;1;1 ;C 2;2;1
. Tìm thể tích tứ diện OABC.
A.
8
(đvtt)
B.
8
3
(đvtt)
C.
4 (đvtt)
D.
4
3
(đvtt)
C©u 19 :
Cho mặt phẳng
( ) : 2 3 1 0x y z
và đường thẳng
.
Trong các mệnh đề sau, mệnh đề nào đúng?
A.
()d
B.
d
cắt
()
C.
()d
D.
()d
C©u 20 :
Cho tam giác ABC với
A 3;2; 7 ;B 2;2; 3 ; C 3;6; 2
. Điểm nào sau đây là trọng tâm
của tam giác ABC
A.
G 4;10; 12
B.
4 10
G ; ;4
33



C.
G 4; 10;12
D.
4 10
G ; ; 4
33




C©u 21 :
Cho hai đường thẳng chéo nhau :
x 1 y 7 z 3
d:
2 1 4

và
x 1 y 2 z 2
d' :
1 2 1

. Tìm
khoảng cách giữa (d) và (d’) :
A.
3
14
B.
2
14
C.
1
14
D.
5
14
C©u 22 :
Cho mặt cầu
2 2 2
S :x y z 2x 4y 6z 5 0
và mặt phẳng
:x y z 0
. Khẳng
định nào sau đây đúng ?
A.
đi qua tâm của (S)
B.
tiếp xúc với (S)
C.
cắt (S) theo 1 đường tròn và không đi
qua tâm của mặt cầu (S)
D.
và
S
không có điểm chung
C©u 23 :
Trong không gian
Oxyz
, cho ba vectơ
( 1;1;0)a 
,
(1;1;0)b
và
(1;1;1)c
. Trong các
mệnh đề sau, mệnh đề nào đúng?
A.
2
cos( , )
6
bc
B.
.1ac
C.
a
và
b
cùng
phương
D.
0a b c
C©u 24 :
Tọa độ hình chiếu vuông góc của điểm
(5; 1; 3)A 
lên mặt phẳng
( ) : 2x y 1 0
là điểm
nào trong các điểm sau?
A.
(1;1;3)
B.
(1; 1; 3)
C.
(1;1; 3)
D.
( 1; 1;3)
C©u 25 :
Cho hai điểm
(1;4;2)A
,
( 1;2;4)B
và đường thẳng
2
1
:
1 1 2
y
xz
. Điểm
M
mà
22
MA MB
nhỏ nhất có tọa độ là
A.
(1;0; 4)
B.
(0; 1;4)
C.
( 1;0;4)
D.
(1;0;4)
C©u 26 :
Trong không gian
,Oxyz
cho điểm
(1;1;1)G
, mặt phẳng qua
G
và vuông góc với đường
thẳng
OG
có phương trình:
A.
0x y z
B.
30xyz
C.
0xyz
D.
30x y z
C©u 27 :
Cho hai điểm
( 1;3;1)A
,
(3; 1; 1)B 
. Khi đó mặt phẳng trung trực của đoạn thẳng
AB
có
phương trình là
A.
2 2 0x y z
B.
2 2 0x y z
C.
2 2 0x y z
D.
2 2 1 0x y z
C©u 28 :
Cho
(0;2; 2)A
,
( 3;1; 1)B 
,
(4;3;0)C
và
(1;2; )Dm
. Tìm
m
để bốn điểm
, , ,A B C D
đồng
phẳng. Một học sinh giải như sau:
Bước 1:
( 3; 1;1)AB
;
(4;1;2)AC
;
(1;0; 2)AD m
Bước 2:
2 4 4 1
1 1 1 3 3 1
, ; ; ( 3;10;1)
11
AB AC





, . 3 2 5AB AC AD m m


Bước 3:
, , ,A B C D
đồng phẳng
, . 0 5 0AB AC AD m


Đáp số:
5m 
Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào?
A.
Sai ở bước 2
B.
Đúng
C.
Sai ở bước 1
D.
Sai ở bước 3
C©u 29 :
Trong không gian
Oxyz
, cho bốn điểm
(1;0;0)A
,
(0;1;0)B
,
(0;0;1)C
và
(1;1;1)D
. Khi đó
mặt cầu ngoại tiếp tứ diện
ABCD
có bán kính:
A.
3
2
B.
2
C.
3
4
D.
3
C©u 30 :
Trong không gian tọa độ
Oxyz
cho hai đường thẳng
1
3
: 1 2
4
xt
d y t t R
z

và
2
:1
32
xk
d y k k R
zk

.Khoảng cách giữa
1
d
và
2
d
bằng giá trị nào sau đây ?
A.
105
7
B.
1
2
C.
2
D.
5 21
7
C©u 31 :
Cho mặt phẳng
()
đi qua điểm
(0;0; 1)M
và song song với giá của hai vectơ
(1; 2;3)a 
và
(3;0;5)b
. Phương trình mặt phẳng
()
là:
A.
5 2 3 3 0x y z
B.
5 2 3 21 0x y z
C.
5 2 3 21 0x y z
D.
10 4 6 21 0x y z
C©u 32 :
Cho hai đường thẳng
1
2
23
:
2 1 1
y
xz
d


;
2
1
: 1 2
1
xt
d y t
zt

và điểm
(1;2;3)A
. Đường
thẳng
đi qua
A
, vuông góc với
1
d
và cắt
2
d
có phương trình là:
A.
2
13
1 3 5
y
xz


B.
2
13
1 3 5
y
xz



C.
2
13
1 3 5
y
xz


D.
2
13
1 3 5
y
xz


C©u 33 :
Trong không gian với hệ tọa độ
Oxyz
, cho (d):
1 3 1
3 2 2
x y z


và
:
3 4 0x y z
. Phương trình hình chiếu của (d) trên
là:
A.
3 1 1
2 1 1
x y z

B.
2 1 1
2 1 1
x y z

C.
5 1 1
2 1 1
x y z

D.
11
2 1 1
x y z

C©u 34 :
Trong không gian với hệ tọa độ Oxyz, phương trình mặt cầu (S) có tâm I(3;7;9) và tiếp xúc với mặt
phẳng (Oyz) là :
A.
2 2 2
3 7 9 3x y z
B.
2 2 2
3 7 9 9x y z
C.
2 2 2
3 7 9 81x y z
D.
2 2 2
3 7 9 9x y z
C©u 35 :
Cho mặt phẳng
( ): 3 4 5 8 0P x y z
và đường thẳng
d
là giao tuyến của hai mặt phẳng
( ) : 2 1 0xy
và
( ) : 2 3 0xz
. Gọi
là góc giữa đường thẳng
d
và
()mp P
. Khi đó
A.
0
45
B.
0
60
C.
0
30
D.
0
90
C©u 36 :
Cho đường thẳng
d
đi qua điểm
(1;2;3)A
và vuông góc với mặt phẳng
( ) : 4 3 7 1 0xyz
. Phương trình tham số của
d
là:
A.
14
23
37
xt
yt
zt


B.
18
26
3 14
xt
yt
zt
C.
13
24
37
xt
yt
zt


D.
14
23
37
xt
yt
zt
C©u 37 :
Tìm góc giữa hai mặt phẳng
:2x y z 3 0
;
:x y 2z 1
0
:
A.
0
30
B.
0
90
C.
0
45
D.
0
60
C©u 38 :
Cho lăng trụ tam giác đều
.ABC A B C
có cạnh đáy bằng
a
và
AB BC

. Tính thể tích
khối lăng trụ.
Một học sinh giải như sau:
Bước 1: Chọn hệ trục như hình vẽ:
;0;0
2
a
A



,
3
0; ;0
2
a
B




,
3
0; ;
2
a
Bh




,
;0;0
2
a
C



,
;0;
2
a
Ch



(
h
là chiều cao của
lăng trụ), suy ra
3
;;
22
aa
AB h




;
3
;;
22
aa
BC h



Bước 2:
.0AB BC AB BC
22
2
32
0
4 4 2
a a a
hh
Bước 3:
23
.
3 2 6
..
2 2 4
ABC A B C
a a a
V B h
Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào?
A.
Lời giải đúng
B.
Sai ở bước 1
C.
Sai ở bước 3
D.
Sai ở bước 2
C©u 39 :
Cho hai điểm
(0;0;3)A
và
(1; 2; 3)B 
. Gọi
AB

là hình chiếu vuông góc của đường thẳng
AB
lên mặt phẳng
()Oxy
. Khi đó phương trình tham số của đường thẳng
AB

là
A.
1
22
0
xt
yt
z
B.
1
22
0
xt
yt
z
C.
2
0
xt
yt
z


D.
2
0
xt
yt
z

C©u 40 :
Trong không gian với hệ tọa độ Oxyz, phương trình mặt cầu tâm A(1;2;1) và tiếp xúc với mặt phẳng
:
2 3 0x y z
là:
A.
2 2 2
1
1 2 1
6
x y z
B.
2 2 2
2 4 2 6 0x y z x y z
C.
2 2 2
1
1 2 1
6
x y z
D.
2 2 2
6 6 6 12 24 12 35 0x y z x y z
z
x
y
B'
A'
C
B
A
C'
C©u 41 :
Cho
(3;0;0)A
,
(0; 6;0)B
,
(0;0;6)C
và
( ) : 4 0mp x y z
. Tọa độ hình chiếu vuông góc
của trọng tâm tam giác
ABC
trên
()mp
là
A.
(2;1;3)
B.
(2; 1;3)
C.
( 2; 1;3)
D.
(2; 1; 3)
C©u 42 :
Cho
(1;1;3)A
,
( 1;3;2)B
,
( 1;2;3)C
. Khoảng cách từ gốc tọa độ
O
tới mặt phẳng
()ABC
bằng
A.
3
B.
3
C.
3
2
D.
3
2
C©u 43 :
Trong không gian với hệ tọa độ Oxyz, phương trình đường thẳng (d) đi qua N(5;3;7) và vuông góc
với mặt phẳng (Oxy) là :
A.
5
3
7
x
y t t R
z
B.
5
3
72
x
y t R
zt


C.
5
3
7
xt
y t R
z


D.
5
3
7
x
y t R
zt


C©u 44 :
Cho hai đường thẳng
1
2
:1
2
xt
d y t
zt

và
2
22
:3
xt
dy
zt
. Mặt phẳng cách đều
1
d
và
2
d
có
phương trình là
A.
5 2 12 0xyz
B.
5 2 12 0x y z
C.
5 2 12 0x y z
D.
5 2 12 0x y z
C©u 45 :
Cho 3 điểm
A 2; 1;5 ; B 5; 5;7
và
M x;y;1
. Với giá trị nào của x ; y thì A, B, M thẳng
hàng ?
A.
x 4 ; y 7
B.
x 4; y 7
C.
x 4;y 7
D.
x 4 ;y 7
C©u 46 :
Cho hai đường thẳng
1
52
:1
5
xt
d y t
zt


và
2
92
:
2
xt
d y t
zt
. Mặt phẳng chứa cả
1
d
và
2
d
có
phương trình là:
A.
3 5 25 0x y z
B.
3 5 25 0x y z
C.
3 5 25 0x y z
D.
3 25 0xyz
C©u 47 :
Khoảng cách từ điểm
( 1;2; 4)M 
đến
( ) : 2 2 8 0mp x y z
là:
A.
4
B.
3
C.
6
D.
5
C©u 48 :
Cho hai đường thẳng
1
3
79
:
1 2 1
y
xz
d


và
2
1
31
:
7 2 3
y
xz
d


. Phương trình
đường vuông góc chung của
1
d
và
2
d
là
A.
1
31
1 2 4
y
xz



B.
3
79
2 1 4
y
xz


C.
3
79
2 1 4
y
xz


D.
3
79
2 1 4
y
xz


C©u 49 :
Cho hai điểm
(1; 2; 4)M 
và
(5; 4;2)M
. Biết
M
là hình chiếu vuông góc của
M
lên
()mp
. Khi đó,
()mp
có phương trình là
A.
2 3 20 0x y z
B.
2 3 20 0x y z
C.
2 3 20 0x y z
D.
2 3 20 0x y z
C©u 50 :
Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
: 2 3 1 0x y z
và đường thẳng d có
phương trình tham số:
3
22
1
xt
yt
z

. Trong các mệnh đề sau, mệnh đề nào đúng ?
A.
d
B.
d//
C.
d cắt
D.
d
C©u 51 :
Trong không gian
Oxyz
, cho hình bình hành
OADB
có
( 1;1;0)OA 
,
(1;1;0)OB
(O là
gốc tọa độ). Khi đó tọa độ tâm hình hình
OADB
là:
A.
(0;1;0)
B.
(1;0;0)
C.
(1;0;1)
D.
(1;1;0)
C©u 52 :
Cho mặt cầu
2 2 2
( ):( 2) ( 1) 14S x y z
. Mặt cầu
()S
cắt trục
Oz
tại
A
và
B
( 0)
A
z
.
Phương trình nào sau đây là phương trình tiếp diện của
()S
tại
B
?
A.
2 3 9 0x y z
B.
2 3 0x y z
C.
2 3 9 0x y z
D.
2 3 0x y z
C©u 53 :
Cho đường thẳng
84
: 5 2
xt
d y t
zt

và điểm
(3; 2;5)A
. Tọa độ hình chiếu của điểm
A
trên
d
là:
A.
(4; 1; 3)
B.
(4; 1;3)
C.
( 4;1; 3)
D.
( 4; 1;3)
C©u 54 :
Trong không gian
,Oxyz
cho hình lập phương
.ABCD A B C D
với
(0;0;0)A
,
(1;0;0)B
,
(0;1;0)D
,
(0;0;1)A
. Gọi
,MN
lần lượt là trung điểm các cạnh
AB
và
CD
. Tính khoảng
cách giữa hai đường thẳng
AC
và
MN
.
Một học sinh giải như sau:
Bước 1: Xác định
(1;1; 1); (0;1;0)A C MN
Suy ra
, (1;0;1)A C MN


Bước 2: Mặt phẳng
()
chứa
AC
và song song với
MN
là mặt phẳng qua
(0;0;1)A
và có
vectơ pháp tuyến
(1;0;1) ( ): 1 0n x z
Bước 3:
2 2 1
1
01
2
1
( , ) ( ,( ))
22
1 0 1
d A C MN d M


Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào?
A.
Sai ở bước 3
B.
Lời giải đúng
C.
Sai ở bước 1
D.
Sai ở bước 2
C©u 55 :
Cho hai đường thẳng
1
1
23
:
1 2 2
y
xz
d


và
2
1
11
:
1 2 2
y
xz
d


.Khoảng cách giữa
1
d
và
2
d
là
A.
42
B.
42
3
C.
4
3
D.
43
2
C©u 56 :
Phương trình mặt phẳng
()P
chứa trục
Oy
và điểm
(1; 1;1)M
là:
A.
0xz
B.
0xz
C.
0xy
D.
0xy
C©u 57 :
Cho hai mặt phẳng
( ) : 3 2 2 7 0x y z
và
( ) : 5 4 3 1 0xyz
. Phương trình mặt
phẳng đi qua gốc tọa độ
O
và vuông góc cả
()
và
()
là:
A.
2 2 0x y z
B.
2 2 0x y z
C.
2 2 1 0x y z
D.
2 2 0x y z
C©u 58 :
Cho mặt cầu
2 2 2
( ): 8 2 2 3 0S x y z x y z
và đường thẳng
12
:
3 2 1
y
xz

. Mặt
phẳng
()
vuông góc với
và cắt
()S
theo giao tuyến là đường tròn
()C
có bán kính lớn
nhất. Phương trình
()
là
A.
3 2 5 0x y z
B.
3 2 5 0x y z
C.
3 2 15 0x y z
D.
3 2 15 0x y z
C©u 59 :
Cho
(2;0;0)A
,
(0;2;0)B
,
(0;0;2)C
,
(2;2;2)D
. Mặt cầu ngoại tiếp tứ diện
ABCD
có bán
kính
A.
3
B.
3
C.
2
3
D.
3
2
C©u 60 :
Cho ba điểm
(1;0;0)A
,
(0;1;0)B
,
(0;0;1)C
,
(0;0;0)O
. Khi đó mặt cầu ngoại tiếp tứ diện
OABC
có phương trình la:
A.
2 2 2
2 2 2 0x y z x y z
B.
2 2 2
0x y z x y z
C.
2 2 2
0x y z x y z
D.
2 2 2
2 2 2 0x y z x y z
C©u 61 :
Cho ba mặt phẳng
( ) : 2 1 0x y z
;
( ) : 2 0x y z
và
( ): 5 0xy
. Trong các
mệnh đề sau, mệnh đề nào sai?
A.
( ) ( )
B.
( ) ( )

C.
( ) ( )

D.
( ) ( )

C©u 62 :
Trong không gian
Oxyz
, cho ba vectơ
( 1;1;0)a 
,
(1;1;0)b
và
(1;1;1)c
. Trong các
mệnh đề sau, mệnh đề nào sai?
A.
bc
B.
3c
C.
2a
D.
ab
C©u 63 :
Trong không gian với hệ tọa độ Oxyz, phương trình mặt cầu (S) qua ba điểm A(1;-2;4); B(1;3;-1);
C(2;-2;-3) và có tâm nằm trên mặt phẳng (Oxy) là:
A.
2 2 2
4 2 21 0x y z x y
B.
2 2 2
4 2 3 21 0x y z x y z
C.
2 2 2
4 2 21 0x y z x y
D.
2 2 2
4 2 21 0x y z x y
C©u 64 :
Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng đi qua hai điểm E(1;3;-5); F(-2;-1;1)
và song song với trục
'
x Ox
là:
A.
3 2 1 0yz
B.
3 2 1 0yz
C.
2 3 2 1 0x y z
D.
3 2 1 0yz
C©u 65 :
Gọi
()
là mặt phẳng cắt ba trục tọa độ tại ba điểm
(8;0;0)M
,
(0; 2;0)N
và
(0;0;4)P
.
Phương trình mặt phẳng
()
là:
A.
4 2 8 0x y z
B.
0
8 2 4
y
xz
C.
1
4 1 2
y
xz
D.
4 2 0x y z
C©u 66 :
Trong không gian với hệ tọa độ Oxyz cho A(1;2;1), B(0;1;2) .Biết B là hình chiếu của A lên mặt
phẳng
.Phương trình mặt phẳng
là:
A.
10x y z
B.
10x y z
C.
10x y z
D.
10x y z
C©u 67 :
Cho đường thẳng
3
1
:
2 3 2
y
xz
d

và
( ): 2 2 1 0mp P x y z
. Mặt phẳng chứa
d
và
vuông góc với
()mp P
có phương trình
A.
2 2 8 0x y z
B.
2 2 8 0x y z
C.
2 2 8 0x y z
D.
2 2 8 0x y z
C©u 68 :
Cho hai đường thẳng
1
12
: 2 3
34
xt
d y t
zt


và
2
34
: 5 6
78
xt
d y t
zt


.
Trong các mệnh đề sau, mệnh đề nào đúng?
A.
12
dd
B.
12
dd
C.
1
d
và
2
d
chéo
nhau
D.
12
dd
C©u 69 :
Đường thẳng
1
3 2 1
y
xz


vuông góc với mặt phẳng nào trong các mặt phẳng sau đây?
A.
6 4 2 1 0xyz
B.
6 4 2 1 0x y z
C.
6 4 2 1 0x y z
D.
6 4 2 1 0xyz
C©u 70 :
Cho hai điểm
(3;3;1)A
,
(0;2;1)B
và
( ): 7 0mp P x y z
. Đường thẳng
d
nằm trên
()mp P
sao cho mọi điểm của
d
cách đều hai điểm
,AB
có phương trình là
A.
73
2
xt
yt
zt


B.
2
73
xt
yt
zt


C.
73
2
xt
yt
zt


D.
73
2
xt
yt
zt

C©u 71 :
Cho hai điểm
( 2;3;1)M
,
(5;6; 2)N
. Đường thẳng
MN
cắt mặt phẳng
()Oxz
tại điểm
A
.
Điểm
A
chia đoạn
MN
theo tỉ số
A.
1
2
B.
1
2
C.
2
D.
2
C©u 72 :
Cho điểm
M 2; 3;5
và đường thẳng
x 1 2t
d : y 3 t t
z 4 t


. Đường thẳng
đi qua M
và song song với
d
có phương trình chính tắc là :
A.
x 2 y 3 z 5
1 3 4

B.
x 2 y 3 z 5
1 3 4

C.
x 2 y 3 z 5
2 1 1

D.
x 2 y 3 z 5
2 1 1

C©u 73 :
Cho đường thẳng
1
12
:
2 1 1
y
xz
d


. Hình chiếu vuông góc của
d
trên mặt phẳng tọa
độ
()Oxy
là
A.
12
1
0
xt
yt
z

B.
12
1
0
xt
yt
z
C.
0
1
0
x
yt
z

D.
12
1
0
xt
yt
z
C©u 74 :
Cho ba điểm
(0;2;1)A
,
(3;0;1)B
,
(1;0;0)C
. Phương trình mặt phẳng
()ABC
là:
A.
2 3 4 2 0xyz
B.
4 6 8 2 0x y z
C.
2 3 4 2 0x y z
D.
2 3 4 1 0x y z
C©u 75 :
Cho đường thẳng
đi qua điểm
(2;0; 1)M
và có vectơ chỉ phương
(4; 6;2)a 
. Phương
trình tham số của
là:
A.
22
3
1
xt
yt
zt

B.
42
63
2
xt
yt
zt

C.
24
6
12
xt
yt
zt


D.
22
3
1
xt
yt
zt


C©u 76 :
Biết đường thẳng
d
là giao tuyến của hai mặt phẳng
( ) : 3 2 1 0x y z
và
( ) : 4 3 2 0x y z
. Khi đó, vectơ chỉ phương của đường thẳng
d
có tọa độ là:
A.
(0;4;5)
B.
(2; 4; 5)
C.
(1; 4; 5)
D.
( 1; 4;5)
C©u 77 :
Cho vectơ
(1;1; 2)u 
và
(1;0; )vm
. Tìm
m
để góc giữa hai vectơ
u
và
v
có số đo bằng
0
45
Một học sinh giải như sau:
Bước 1:
2
12
cos ,
6. 1
m
uv
m
Bước 2: Góc giữa
u
,
v
bằng
0
45
suy ra
2
1 2 1
2
6. 1
m
m
2
1 2 3. 1 (*)mm
Bước 3: phương trình (*)
2
(1 2 ) 3( 1)mm
2
26
4 2 0
26
m
mm
m


Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào?
A.
Sai ở bước 2
B.
Sai ở bước 3
C.
Bài giải đúng
D.
Sai ở bước 1
C©u 78 :
Cho đường thẳng
x 1 2t
d : y 2 4t
z 3 t



và mặt phẳng
P :x y z 1 0
Khẳng định nào sau đây đúng ?
A.
d / / P
B.
d
cắt
P
tại điểm
M 1;2;3
C.
dP
D.
d
cắt
P
tại điểm
M 1; 2;2
C©u 79 :
Trong không gian với hệ tọa độ
Oxyz
cho mặt cầu (S):
2 2 2
2 2 0x y z x z
và mặt phẳng
: 4 3 0x y m
. Xét các mệnh đề sau:
I.
cắt (S) theo một đường tròn khi và chỉ khi
4 5 2 4 5 2m
.
II.
tiếp xúc với (S) khi và chỉ khi
4 5 2m
.
III.
S
khi và chỉ khi
4 5 2m
hoặc
4 5 2m
.
Trong ba mệnh đề trên, những mệnh đề nào đúng ?
A.
II và III
B.
I và II
C.
I
D.
I,II,III
C©u 80 :
Trong không gian
Oxyz
, cho bốn điểm
(1;0;0)A
,
(0;1;0)B
,
(0;0;1)C
và
(1;1;1)D
.Trong các
mệnh đề sau, mệnh đề nào sai?
A.
Tam giác
BCD
là tam giác vuông
B.
Tam giác
ABD
là tam giác đều
C.
Bốn điểm
, , ,A B C D
tạo thành một tứ diện
D.
AB CD
ĐÁP ÁN
01
) | } ~
28
) | } ~
55
{ ) } ~
02
{ ) } ~
29
) | } ~
56
{ ) } ~
03
{ ) } ~
30
{ | } )
57
{ ) } ~
04
{ ) } ~
31
) | } ~
58
{ | ) ~
05
{ | ) ~
32
{ ) } ~
59
{ ) } ~
06
{ | } )
33
{ | } )
60
{ | ) ~
07
) | } ~
34
{ | } )
61
) | } ~
08
{ | ) ~
35
{ ) } ~
62
) | } ~
09
{ | ) ~
36
) | } ~
63
{ | } )
10
) | } ~
37
{ | } )
64
{ | } )
11
{ ) } ~
38
{ | ) ~
65
) | } ~
12
) | } ~
39
{ | ) ~
66
{ | } )
13
{ | } )
40
{ | } )
67
{ ) } ~
14
{ | ) ~
41
{ ) } ~
68
) | } ~
15
{ | ) ~
42
{ ) } ~
69
{ | ) ~
16
) | } ~
43
{ | } )
70
{ | ) ~
17
{ ) } ~
44
{ ) } ~
71
) | } ~
18
{ | } )
45
{ | } )
72
{ | } )
19
) | } ~
46
{ | ) ~
73
{ ) } ~
20
{ | } )
47
{ | ) ~
74
) | } ~
21
{ | } )
48
{ | ) ~
75
) | } ~
22
{ | } )
49
{ | ) ~
76
{ | ) ~
23
) | } ~
50
{ | } )
77
{ ) } ~
24
{ | ) ~
51
) | } ~
78
{ | } )
25
{ | ) ~
52
{ | ) ~
79
{ | } )
26
{ ) } ~
53
{ ) } ~
80
) | } ~
27
{ | ) ~
54
{ ) } ~
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN
ĐỀ 003
C©u 1 :
Tọa độ tâm mặt cầu đi qua 4 điểm
A(1;1;1);B(1;2;1);C(3;3;3);D(3; 3;3)
là :
A.
3 3 3
( ; ; )
2 2 2
B.
(3;3;3)
C.
(3; 3;3)
D.
333
( ; ; )
222
C©u 2 :
Trong hệ tọa độ Oxy cho các điểm A(1 ;0 ;0) ; B(0 ;1 ;0) ;C(0 ;0 ;1), D(1 ;1 ;1). Bán kính
mặt cầu đi qua bốn điểm ABCD là :
A.
3
4
B.
2
C.
3
D.
3
2
C©u 3 :
Cho mặt cầu
()S
có tâm
(2;1; 1)I
và tiếp xúc với mặt phẳng
()
có phương trình
2 2 3 0x y z
. Bán kính của mặt cầu
()S
là:
A.
2
9
B.
2
C.
2
3
D.
4
3
C©u 4 :
Cho ba điểm A(2;1;-1); B(-1;0;4);C(0;-2-1). Phương trình mặt phẳng nào đi qua A và
vuông góc BC
A.
x-2y-5z-5=0
B.
2x-y+5z-5=0
C.
x-3y+5z+1=0
D.
2x+y+z+7=0
C©u 5 :
Viết phương trình mặt cầu có tâm
(1;4; 7)I
và tiếp xúc với mặt phẳng
6 6 7 42 0xyz
.
A.
2 2 2
( 1) ( 3) ( 3) 1
x y z
B.
2 2 2
( 1) ( 4) ( 7) 121
x y z
C.
2 2 2
( 5) ( 3) ( 1) 18
x y z
D.
2 2 2
( 1) ( 2) ( 2) 9
x y z
C©u 6 :
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm
(2;1;0)A
,
(3;1; 1)B
,
(1;2;3)C
. Tọa độ điểm D để ABCD là hình bình hành là:
A.
(2;1;2)D
B.
C.
( 2;1;2)D
D.
(2;2;2)D
C©u 7 :
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng
2
1 2 3
:
2 1 2
x y z
d
mm
và mặt phẳng
( ) : 3 2 5 0P x y z
. Để đường thẳng
d vuông góc với (P) thì:
A.
0m
B.
1m
C.
2m
D.
1m
C©u 8 :
Phương trình chính tắc của đường thẳng d đi qua điểm M(2;0;-1) có vecto chỉ
phương
(4; 6;2)a 
là
A.
21
2 3 1
x y z

B.
21
4 6 2
x y z

C.
21
2 3 1
x y z

D.
4 6 2
2 3 1
x y z

C©u 9 :
Cho hai mặt phẳng
: 2 2 3 0, : 2 2 4 0P x y z Q x y x
và đường thẳng
24
:
1 2 3
x y z
d
.
Lp phương trình mặt cầu (S) có tâm
Id
và tiếp xc với hai mặt phẳng (P) và (Q).
A.
2 2 2 2 2 2
2
11 26 35 38 1 2 1 4x y z x y z
B.
2 2 2 2 2 2
2
11 26 35 38 1 2 1 4x y z x y z
C.
2 2 2 2 2 2
2
11 26 35 38 1 2 1 4x y z x y z
D.
2 2 2 2 2 2
2
11 26 35 38 1 2 1 4x y z x y z
C©u 10 :
Cho các điểm
A(2;0;0);B(0;2;0);C(0;0;1)
. Tọa độ trực tâm H của tam giác ABC là :
A.
11
H( ; ;1)
22
B.
1 2 2
H( ; ; )
3 3 3
C.
2 1 2
H( ; ; )
333
D.
1 1 2
H( ; ; )
3 3 3
C©u 11 :
Cho hai đường thẳng (d1):
1 2 3
2 3 4
x y z

và (d2)
3 5 7
4 6 8
x y z

. Mệnh đề nào
dưới đây đng?
A.
( 1) ( 2)dd
B.
( 1) ( 2)dd
C.
(d1) và (d2)
chéo nhau
D.
( 1) / /( 2)dd
C©u 12 :
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng
12
:
1 1 3
x y z
d
và mặt phẳng
( ) : 2 3 0P x y z
. Khi đó tọa độ giao điểm M của d và (P) là:
3
A.
3;1; 7M
B.
3 1 7
;;
2 2 2
M
C.
3 1 7
;;
2 2 2
M
D.
3 1 7
;;
2 2 2
M
C©u 13 :
Gọi
()
là mặt phẳng cắt trục tọa độ tại ba điểm
(8;0;0), (0; 2;0), (0;0;4)M N P
.
Phương trình mặt phẳng
()
là:
A.
0
8 2 4
x y z
B.
4 2 8 0x y z
C.
1
4 1 2
x y z
D.
4 2 0x y z
C©u 14 :
Cho
A(1;4;2),B(-1;2;4)
và đường thẳng d:
x -1
-1
=
y + 2
1
=
z
2
. Điểm M thuộc d, biết
MA
2
+ MB
2
nhỏ nhất. Điểm M có toạ độ là?
A.
M(1;0;4)
B.
M(0;-1;4)
C.
M(-1;0;4)
D.
M(1;0;-4)
C©u 15 :
Cho
2;0;0 , 1;1;1AM
. Viết phương trình mặt phẳng (P) đi qua A và M sao cho (P)
cắt trục Oy, Oz lần lưt tại hai điểm B, C tha mn:
a) Diện tích của tam giác ABC bng
46
.
A.
Cả ba đáp án trên
B.
1
: 2 4 0P x y z
C.
3
: 6 3 21 3 21 12 0P x y z
D.
2
: 6 3 21 3 21 12 0P x y z
C©u 16 :
Trong không gian với hệ trục tọa độ
Oxyz
, cho bốn điểm
3;3;0 , 3;0;3 , 0;3;3 , 3;3;3A B C D
. Viết phương trình mặt cầu đi qua bốn điểm A, B,
C, D.
A.
2 2 2
3 3 3 0x y z x y z
B.
2 2 2
3 3 3 0x y z x y z
C.
2 2 2
3 3 3 0x y z x y z
D.
2 2 2
3 3 3 0x y z x y z
C©u 17 :
Cho đường thẳng
83
:
1 4 2
x y z
và mặt phẳng
: 7 0P x y z
. Viết
phương trình hình chiếu của trên (P).
A.
84
15 5
xt
yt
zt
B.
84
15 5
xt
yt
zt
C.
84
15 5
xt
yt
zt
D.
84
15 5
xt
yt
zt
C©u 18 :
Trong không gian với hệ tọa độ
Oxyz
cho bốn điểm
(1;0;0)A
,
(0;1;0)B
,
(0;0;1)C
và
(1;1;1)D
. Trong các mệnh đề sau, mệnh đề nào sai ?
4
A.
Bốn điểm
, , ,A B C D
tạo thành một tứ
diện
B.
Tam giác
BCD
là tam giác vuông
C.
Tam giác
ABD
là một tam giác đều
D.
AB CD
C©u 19 :
Trong không gian với hệ trục tọa độ Oxyz, cho điểm
(2;2;2)M
. Khi đó mặt phảng
đi qua M cắt các tia Ox, Oy, Oz tại các điểm A, B, C sao cho diện tích tứ giác OABC
nh nhất có phương trình là:
A.
10x y z
B.
60x y z
C.
0x y z
D.
60x y z
C©u 20 :
Cho mặt phẳng
(P):x y 1 0
và mặt phẳng (Q). Biết hình chiếu cưa gốc O lên (Q)
là điểm
H(2; 1; 2)
. Khi đó góc giữa hai mặt phẳng (P) và (Q) có giá trị là:
A.
0
30
B.
0
60
C.
0
90
D.
0
45
C©u 21 :
Biết tam giác ABC có ba đỉnh A, B, C thuộc các trục tọa độ và trọng tâm tam giác là
G( 1; 3;2)
. Khi đó phương trình mặt phẳng (ABC) là :
A.
2x 3y z 1 0
B.
x y z 5 0
C.
6x 2y 3z 18 0
D.
6x 2y 3z 18 0
C©u 22 :
Trong các bộ ba điểm:
(I).
(1;3;1); B(0;1;2); C(0;0;1),A
(II).
M(1;1;1); ( 4;3;1); ( 9;5;1),NP
(III).
D(1;2;7); ( 1;3;4); (5;0;13),EF
bộ ba nào thẳng hàng?
A.
Chỉ III, I.
B.
Chỉ I, II.
C.
Chỉ II, III.
D.
Cả I, II, III.
C©u 23 :
Viết phương trình mặt phẳng trung trực của đoạn thẳng AB với
(1;2; 4), (5;4;2)AB
.
A.
10 9 5 70 0
x y z
B.
4 2 6 11 0
x y z
C.
2 3 6 0
x y z
D.
2 3 3 0
xz
C©u 24 :
Cho mặt cầu (S) x
2
+y
2
+z
2
-2x-4y-6z=0. Trong ba điểm (0;0;0); (1;2;3) và (2;-1;-1) thì có
bao nhiêu điểm nm trong mặt cầu (S)
5
A.
1
B.
3
C.
2
D.
0
C©u 25 :
Cho ba điểm
(0;2;1), (3;0;1),C(1;0;0)AB
. Phương trình mặt phẳng
()ABC
là:
A.
4 6 8 2 0x y z
B.
2 3 4 2 0xyz
C.
2 3 4 2 0x y z
D.
2 3 4 1 0x y z
C©u 26 :
Gọi H là hình chiếu vuông góc của A(2;-1;-1) trên (P):
16x -12y -15z - 4 = 0
. Độ dài đoạn
AH bằng?
A.
22
5
B.
11
5
C.
11
25
D.
55
C©u 27 :
Cho đường thẳng
đi qua điểm
(2;0; 1)M
và có vectơ chỉ phương
(4; 6;2)a 
.
Phương trình tham số của đường thẳng
là:
A.
22
3
1
xt
yt
zt


B.
22
3
1
xt
yt
zt


C.
24
6
12
xt
yt
zt


D.
42
6
2
xt
y
zt



C©u 28 :
Trong hệ tọa độ Oxy cho các điểm A(1 ;0 ;0) ; B(0 ;1 ;0) ;C(0 ;0 ;1), D(1 ;1 ;1). Trong
các mệnh đề sau mệnh đề nào sai :
A.
ABCD là một tứ diện
B.
AB vuông góc với CD
C.
Tam giác ABD là tam giác đều
D.
Tam giác BCD vuông
C©u 29 :
Trong không gian
Oxyz
cho ba vectơ
( 1;1;0), (1;1;0)ab
và
(1;1;1)c
. Trong các
mệnh đề sau, mệnh đề nào sai ?
A.
|a | 2
B.
bc
C.
| | 3c
D.
ab
C©u 30 :
Cho tứ diện ABCD với
(5;1;3), (1;6;2),C(5;0;4), D(4;0;6)AB
. Viết phương trình mặt
phẳng đi qua C, D và song song với AB.
A.
10 9 5 0
x z z
B.
5 3 2 0
x y z
C.
10 9 5 70 0
x y z
D.
10 9 5 50 0
x y z
C©u 31 :
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng
( ) : 3 2 7 0P x my z
và
( ) : 7 6 4 0Q nx y z
. Để (P) song song với (Q) thì:
A.
7; 9mn
B.
7
;9
3
mn
C.
7
;9
3
mn
D.
7
;9
3
mn
6
C©u 32 :
Trong không gian với hệ trục tọa độ Oxyz, cho
(1;1;2)u
,
( 1; ; 2)v m m
. Khi
đó
,4uv
thì :
A.
11
1;
5
mm
B.
11
1;
5
mm
C.
1m
D.
11
1;
5
mm
C©u 33 :
Viết phương trình mặt phẳng đi qua điểm B(1; 2; -1) và cách gốc tọa độ một khoảng
lớn nhất.
A.
2 6 0x y z
B.
2 2 7 0x y z
C.
2 5 0x y z
D.
2 5 0x y z
C©u 34 :
Trong không gian với hệ trục tọa độ Oxyz, cho điểm
(3;1;0)A
và mặt phẳng
( ) : 2 2 1 0P x y z
. Khi đó tọa độ điểm M là hình chiếu của điểm A trên (P) là:
A.
( 1;1;1)M
B.
(1;1;1)M
C.
(1;1; 1)M
D.
(1; 1;1)M
C©u 35 :
Gọi (P) là mặt phẳng đi qua M(3;-1;-5) và vuông góc với hai mặt phẳng (Q): 3x-
2y+2z+7=0 và (R): 5x-4y+3z+1=0
A.
2x+y-2z-15=0
B.
2x+y-2z+15=0
C.
x+y+z-7=0
D.
x+2y+3z+2=0
C©u 36 :
Cho ba mặt phẳng
( ) : 2 1 0, ( ) : 2 0,( ):x y 5 0x y z x y z
. Trong các
mệnh đề sau, mệnh đề nào sai ?
A.
( ) ( )

B.
()
//
()
C.
( ) ( )

D.
( ) ( )

C©u 37 :
Tìm tọa độ tâm J của đường tròn (C) là giao tuyến của mặt cầu
2 2 2
( ):( 2) ( 3) ( 3) 5S x y z
và mặt phẳng (P):
2 2 1 0x y z
A.



333
;;
242
J
B.
1;2;0J
C.




5 7 11
;;
3 3 3
J
D.
1;2;3J
C©u 38 :
Cho hai đường thẳng
d :
x - 3
-2
=
y - 6
2
=
z -1
1
;d ':
x = t
y = -t
z = 2
ì
í
ï
î
ï
. Đường thẳng đi qua A(0;1;1) cắt d’
và vuông góc d có phương trình là?
A.
x -1
-1
=
y
-3
=
z -1
4
B.
x
1
=
y -1
-3
=
z -1
4
C.
x
-1
=
y -1
-3
=
z -1
4
D.
x
-1
=
y -1
3
=
z -1
4
C©u 39 :
Cho
2 2 2
(S):x y z 2y 2z 2 0
và mặt phẳng
(P): x 2y 2z 2 0
. Mặt phẳng
(Q) song song với (P) đồng thời tiếp xúc với (S) có phương trình là :
7
A.
x 2y 2x 10 0
B.
x 2y 2x 10 0;x 2y 2z 2 0
C.
x 2y 2x 10 0;x 2y 2z 2 0
D.
x 2y 2x 10 0
C©u 40 :
Cho điểm A(0;-1;3) và đường thẳng d:
12
2
xt
y
zt


. Khoảng cách từ A đến d là:
A.
14
B.
8
C.
6
D.
3
C©u 41 :
Cho
d
là đường thẳng đi qua điểm
(1;2;3)A
và vuông góc với mặt phẳng
( ) : 4 3 7 1 0x y z
. Phương trình tham số của
d
là:
A.
14
23
37
xt
yt
zt
B.
14
23
37
xt
yt
zt



C.
13
24
37
xt
yt
zt



D.
18
26
3 14
xt
yt
zt
C©u 42 :
Cho mặt phẳng
:3 2 3 7 0P x y z
và đường thẳng
2 4 1
:
3 2 2
x y z
d
. Viết
phương trình đường thẳng đi qua A(-1; 0; 1) song song với mặt phẳng (P) và cắt
đường thẳng d.
A.
11
15 3 17
x y z
B.
11
15 3 17
x y z
C.
11
15 3 17
x y z
D.
11
15 3 17
x y z
C©u 43 :
Cho
A(0;2;1),B(3;0;1),C(1;0;0)
. Phương trình mặt phẳng (ABC) là?
A.
2x + 3y - 4z +2 = 0
B.
2x - 3y - 4z +1= 0
C.
2x + 3y - 4z -2 = 0
D.
2x + 3y + z - 7 = 0
C©u 44 :
Cho
d :
x -1
2
=
y +1
1
=
z - 2
1
. Hình chiếu vuông góc của d trên (Oxy) có dạng?
A.
x = 0
y = -1- t
z = 0
ì
í
ï
î
ï
B.
x = -1+ 2t
y =1+ t
z = 0
ì
í
ï
î
ï
C.
x = 1+ 2t
y = -1+ t
z = 0
ì
í
ï
î
ï
D.
x = -1+ 2t
y = -1+ t
z = 0
ì
í
ï
î
ï
C©u 45 :
Cho mặt cầu (S) có tâm I(4;2;-2), bán kính R. Biết (S) tiếp xúc (P): 12x – 5z – 19 =0. Bán
kính R là?
A.
R = 39
B.
R =13
C.
R = 3
D.
R = 3 13
C©u 46 :
Cho
(
a
):m
2
x - y +(m
2
-2)z + 2 = 0;(
b
):2x + m
2
y - 2z +1= 0
. Để hai mặt phẳng đã ch vuông
góc nhau, giá trị m bằng?
8
A.
m =1
B.
m = 2
C.
m = 2
D.
m = 3
C©u 47 :
Cho
A(a;0;0);B(0;b;0);C(0;0;c)
với
a,b,c 0
. Biết mặt phẳng (ABC) qua điểm
I(1;3;3)
và thể tích tứ diện OABC đạt giá trị nh nhất. Khi đó phương trình (ABC)
là :
A.
x 3y 3z 21 0
B.
3x y z 9 0
C.
3x 3y z 15 0
D.
3x y z 9 0
C©u 48 :
Cho hai đường thẳng
1
12
: 2 3
34
xt
d y t
zt



và
2
34
: 5 6
78
xt
d y t
zt



.
Trong các mệnh đề sau, mệnh đề nào đng ?
A.
12
dd
B.
12
dd
C.
1
d
//
2
d
D.
1
d
và
2
d
chéo
nhau
C©u 49 :
Mặt cầu (S) tâm I(1 ;2 ;2) và tiếp xúc với
(P): x 2y 2z 5 0
có bán kính là :
A.
3
2
B.
2
3
C.
4
3
D.
3
C©u 50 :
Trong không gian với hệ trục tọa độ Oxyz, cho điểm
(2; 0;1)A
và đường thẳng
11
:
2 1 1
x y z
d
. Khi đó tọa độ điểm M thuộc d tha mãn
3MA
là :
A.
(3; 1; 1)M
B.
(3; 1;0)M
C.
(5; 1; 1)M
D.
(3;1;0)M
C©u 51 :
Gọi (d) là giao tuyến của hai mặt phẳng
2 3 1 0x y z
và
2 3 1 0x y z
. Xác
định m để có mặt phẳng (Q) qua (d) và vuông góc với
( ;2; 3)am
A.
6
B.
85
3
C.
1
D.
1
2
C©u 52 :
Cho mặt phẳng
()
đi qua điểm
(0;0; 1)M
và song song với giá của hai vectơ
(1; 2;3), (3;0;5)ab
. Phương trình của mặt phẳng
()
là:
A.
5 2 3 21 0x y z
B.
5 2 3 3 0x y z
C.
10 4 6 21 0x y z
D.
5 2 3 21 0x y z
9
C©u 53 :
Cho
1 2 3
2 1 1 1
: 4 , : ; :
1 3 3 5 2 1
12
xt
x y z x y z
d y t d d
zt
Viết phương trình đường thẳng , biết cắt
1 2 3
,,d d d
lần lưt tại A, B, C sao cho AB
= BC.
A.
2
1 1 1
x y z
B.
21
1 1 1
x y z
C.
2
1 1 1
x y z
D.
2
1 1 1
x y z
C©u 54 :
Xác định m để cặp mặt phẳng sau vuông góc với nhau:
7 3 3 0; 3 4 5 0x y mz x y z
.
A.
6
B.
4
C.
1
D.
2
C©u 55 :
Phương trình mặt phẳng qua giao tuyến của hai mặt phẳng (P): x-3y+2z-1=0 và (Q):
2x+y-3z+1=0 và song song với trục Ox là
A.
7x+y+1=0
B.
7y-7z+1=0
C.
7x+7y-1=0
D.
x-3=0
C©u 56 :
Trong không gian với hệ trục tọa độ Oxyz, cho điểm
(1;0; 1)A
và đường thẳng
11
:
2 2 1
x y z
d
. Khi đó tọa độ điểm M là hình chiếu của điểm A trên d là :
A.
5 1 1
( ; ; )
333
M
B.
(5; 1; 1)M
C.
5 1 1
( ; ; )
333
M
D.
5 1 1
( ; ; )
333
M
C©u 57 :
Gọi (d) là đường thẳng đi qua điểm
(2;3;5)A
và vuông góc mặt phẳng (P):
2 3 17 0x y z
.Tìm giao điểm của (d) và trục Oz.
A.
0;0;6
B.
0;4;0
C.
0;0;4
D.
6
0;0;
7



C©u 58 :
Cho mặt cầu S :
2 2 2
( 1) ( 3) ( 2) 49x y z
phương trình nào sau đây là phương
trình của mặt phẳng tiếp xúc với mặt cầu S?
A.
2x+3y+6z-5=0
B.
6x+2y+3z-55=0
C.
x+2y+2z-7=0
D.
6x+2y+3z=0
C©u 59 :
Trong hệ Oxyz cho các điểm A(3;3;1); B(0;2;1) và
(P):x y z 7 0
. Gọi d là đường
thẳng nm trong (P) sao cho
d(A;d) d(B;d)
. Khi đó phương trình đường thẳng d
là:
10
A.
xt
y 7 3t
z 2t


B.
x 2t
y 7 3t
zt

C.
xt
y 7 3t
z 2t

D.
xt
y 7 3t
z 2t

C©u 60 :
Cho
d :
x -1
1
=
y
2
=
z - 3
3
;d ':
x = 2t
y =1+ 4t
z = 2 + 6t
ì
í
ï
î
ï
. Khẳng định nào sau đây đúng khi nói veef vị trí tương
đối của d và d’.
A.
d, d’ cắt nhau
B.
d, d’ trùng nhau
C.
d song song d’
D.
d, d’ chéo nhau
C©u 61 :
Cho A(0; 1; 2) và hai đường thẳng
1
1
1
: , ': 1 2
2 1 1
2
xt
y
xz
d d y t
zt


. Viết phương trình
mặt phẳng
P
đi qua A đồng thời song song với d và d’.
A.
3 5 13 0x y z
B.
2 6 10 11 0x y z
C.
2 3 5 13 0x y z
D.
3 5 13 0x y z
C©u 62 :
Trong không gian với hệ tọa độ
Oxyz
cho bốn điểm
(1;0;0)A
,
(0;1;0)B
,
(0;0;1)C
và
(1;1;1)D
. Mặt cầu ngoại tiếp tứ diện
ABCD
có bán kính là:
A.
3
B.
3
2
C.
2
D.
3
4
C©u 63 :
Trong mặt phẳng (Oxz), tìm điểm M cách đều ba điểm
(1;1;1),A
( 1;1;0), (3;1; 1)BC
.
A.



5 11
;0;
22
M
B.



9
;0;5
4
M
C.



57
;0;
66
M
D.
5;0; 7M
C©u 64 :
Cho mặt phẳng
( ) : 2 3 1 0x y z
và đường thẳng
3
: 2 2
1
xt
d y t
z

.
Trong các mệnh đề sau, mệnh đề nào đng ?
A.
()d
B.
()d
C.
d
cắt
()
D.
d
//
()
C©u 65 :
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng
( ) : 5 5 5 1 0P x y z
và
( ) : 1 0Q x y z
. Khi đó khoảng cách giữa (P) và
(Q) là:
A.
23
15
B.
2
5
C.
2
15
D.
23
5
11
C©u 66 :
Trong không gian với hệ tọa độ
Oxyz
cho bốn điểm
(1;0;0)A
,
(0;1;0)B
,
(0;0;1)C
và
(1;1;1)D
. Gọi
,MN
lần lưt là trung điểm của
AB
và
CD
. Tọa độ trung điểm
G
của
MN
là:
A.
222
;;
333
G



B.
111
;;
222
G



C.
111
;;
444
G



D.
111
;;
333
G



C©u 67 :
Cho hình bình hành OADB có
( 1;1;0), (1;1;0)OA OB
(O là gốc tọa độ). Tọa độ của
tâm hình bình hành OADB là:
A.
(1;0;1)
B.
(0;1;0)
C.
(1;0;0)
D.
(1;1;0)
C©u 68 :
Trong Oxyz cho A(3;4;-1), B(2;0;3), C(-3;5;4). Diện tích tam giác ABC là:
A.
1562
2
B.
29
2
C.
7
D.
379
2
C©u 69 :
Mặt cầu có tâm I(1;3;5) và tiếp xúc
d :
x = t
y = -1- t
z = 2 - t
ì
í
ï
î
ï
có phương trình là?
A.
x -1
( )
2
+ y - 3
( )
2
+ z - 5
( )
2
= 49
B.
x -1
( )
2
+ y - 3
( )
2
+ z - 5
( )
2
=14
C.
x -1
( )
2
+ y - 3
( )
2
+ z - 5
( )
2
= 256
D.
x -1
( )
2
+ y - 3
( )
2
+ z - 5
( )
2
= 7
C©u 70 :
Cho
d :
x - 5
2
=
y -1
-1
=
z - 5
-1
;d ':
x = 9 - 2t
y = t
z = -2+ t
ì
í
ï
î
ï
. Phương trình mặt phẳng chứa d và d’, có dạng?
A.
3x - 5y + z - 25 = 0
B.
3x + y + z - 25 = 0
C.
2x + 5y + z - 25 = 0
D.
2x - 5y - z + 25 = 0
C©u 71 :
Cho mặt phẳng (P) x-2y-3z+14=0. Tìm tọa độ M’ đối xứng với
M(1;-1;1) qua (P).
A.
M’(-1;3;7)
B.
M’(2;-3;-2)
C.
M’(1;-3;7)
D.
M’(2;-1;1)
C©u 72 :
Trong không gian
Oxyz
cho ba vectơ
( 1;1;0), (1;1;0)ab
và
(1;1;1)c
. Trong các
mệnh đề sau, mệnh đề nào đng ?
A.
.1ac
B.
2
cos( , )
6
bc
C.
0a b c
D.
,ab
cùng
phương
12
C©u 73 :
1) Cho điểm I(1; 2; -2), đường thẳng d:
52
22
xt
yt
zt
và mặt phẳng (P):
2 2 5 0x y z
.
Viết phương trình mặt cầu (S) có tâm là I, sao cho (P) cắt (S) theo đường tròn giao
tuyến có chu vi bng
8
.
A.
2 2 2
1 2 2 25x y z
B.
2 2 2
1 2 2 9x y z
C.
2 2 2
1 2 2 5x y z
D.
2 2 2
1 2 2 16x y z
C©u 74 :
Cho
12
1 1 1 1 2 1
: ; :
2 1 1 1 1 2
x y z x y z
dd
. Viết phương trình đường thẳng
là đoạn vuông góc chung của
1
d
và
2
d
.
A.
7
5
9
8
3,
9
10
7
9
xt
y t t
zt
B.
7
5
9
8
3,
9
10
7
9
xt
y t t
zt
C.
7
5
9
8
3,
9
10
7
9
xt
y t t
zt
D.
7
5
9
8
3,
9
10
7
9
xt
y t t
zt
C©u 75 :
Cho hình hộp ABCD.A’B’C’D’, biết
(1;0;1), (2;1;2), (1; 1;1),A B D
'(4;5; 5)C
.Tìm tọa
độ đỉnh A’ ?
A.
'( 2;1;1)
A
B.
'(3;5; 6)
A
C.
'(5; 1;0)
A
D.
'(2;0;2)
A
13
ĐÁP ÁN
01
{ | } )
28
{ | ) ~
55
{ ) } ~
02
{ | } )
29
{ ) } ~
56
{ | } )
03
{ ) } ~
30
{ | ) ~
57
{ | ) ~
04
) | } ~
31
{ | } )
58
) | } ~
05
{ ) } ~
32
{ | } )
59
{ | } )
06
{ | } )
33
) | } ~
60
{ | ) ~
07
{ | } )
34
{ | } )
61
) | } ~
08
) | } ~
35
) | } ~
62
{ ) } ~
09
) | } ~
36
{ ) } ~
63
{ | ) ~
10
{ | } )
37
{ | ) ~
64
{ ) } ~
11
) | } ~
38
{ | ) ~
65
{ | } )
12
{ | } )
39
{ | } )
66
{ ) } ~
13
{ ) } ~
40
) | } ~
67
{ ) } ~
14
{ | ) ~
41
{ ) } ~
68
) | } ~
15
) | } ~
42
) | } ~
69
{ | ) ~
16
) | } ~
43
{ | ) ~
70
{ | ) ~
17
) | } ~
44
{ | ) ~
71
) | } ~
18
{ ) } ~
45
{ | ) ~
72
{ ) } ~
19
{ | } )
46
{ | ) ~
73
) | } ~
20
{ | } )
47
{ | } )
74
) | } ~
21
{ | } )
48
{ ) } ~
75
{ ) } ~
22
{ | ) ~
49
{ | ) ~
23
{ | ) ~
50
{ | } )
24
) | } ~
51
{ | ) ~
25
{ ) } ~
52
{ ) } ~
26
{ | ) ~
53
) | } ~
27
{ ) } ~
54
{ ) } ~
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN
ĐỀ 005
C©u 1 :
Trong không gian Oxyz cho 2 đim A(1;2;3), B(4;4;5). Ta đ đim M
(Oxy) sao
cho tng
22
MA MB
nh nht l:
A.
17 11
( ; ;0)
84
M
.
B.
1
(1; ;0)
2
M
C.
1 11
( ; ;0)
84
M
D.
11
( ; ;0)
84
M
C©u 2 :
Trong hệ trục ta đ Oxyz cho hình bình hành ABCD với
1;0;1 , 2;1;2AB
và giao
đim của hai đường chéo là
33
;0;
22
I



. Diện tích của hình bình hành ABCD là:
A.
5
B.
6
C.
2
D.
3
C©u 3 :
Trong không gian với hệ trục ta đ Oxyz cho tam giác ABC với
1;2; 1 , 2; 1;3 , 4;7;5A B C
. Đường cao của tam giác ABC hạ từ A là:
A.
110
57
B.
1110
53
C.
1110
57
D.
111
57
C©u 4 :
Trong không gian với hệ toạ đ Oxyz, cho 3 đim A(3; 1; 1), B(7; 3; 9), C(2; 2; 2) . Tìm
ta đ trng tâm của tam giác ABC:
A.
6;3;6G
B.
4;2;4G
C.
D.
4;3; 4G
C©u 5 :
Ta đ giao đim của đường thẳng
11
:
1 2 4
x y z
d
và mặt phẳng
:3 2 1 0x y z
là:
A.
1,0,1
B.
1, 1,0
C.
1,1,0
D.
1,0, 1
C©u 6 :
Trong không gian với hệ trục Oxyz, cho (P): 2x-y+2z-4=0. Đim no sau đây thuc
(P).
A.
C(1;0; 2)
B.
(1; 1;1)A
C.
(2;0; 2)B
D.
(2;0;0)D
C©u 7 :
Cho mặt phẳng
:8 4 7 0P x y z
v đường thẳng d
2
2 4 0
3 2 0
x y z
d
x y z
. Gi (d’) l hình chiếu của (d) xuống (P). Phương trình (d’)
là:
A.
3 5 4 8 0
8 4 7 0
xyz
x y z
B.
4 3 5 8 0
8 4 7 0
x y z
x y z
C.
3 5 4 8 0
8 4 7 0
x y z
x y z
D.
3 5 4 8 0
8 4 7 0
x y z
x y z
C©u 8 :
Cho đim
1,4, 7A
và mặt phẳng
: 2 2 5 0P x y z
. Phương trình đường
thẳng đi qua A v vuông góc với mặt phẳng (P) là:
A.
1 4 7
1 2 2
x y z
B.
1 4 7
1 2 2
x y z
C.
1 4 7
1 2 7
x y z
D.
1 4 7
1 2 2
x y z
C©u 9 :
Trong không gian với hệ trục ta đ
,Oxyz
cho hai mặt phẳng
( ) : 3 4 0P x my z
và
( ) : 2 9 0Q x y nz
. Khi hai mặt phẳng
( ),( )PQ
song song với nhau thì giá trị
của
mn
bằng
A.
13
2
B.
4
C.
11
2
D.
1
C©u 10 :
Trong không gian
Oxyz
cho 3 đim
,,A B C
tha:
2 3 ; 2 ; 3 2OA i j k OB i j k OC i j k
với
;;i j k
l các vecto đơn vị. Xét
các mệnh đề:
1,1,4I AB
1,1,2II AC
Khẳng định no sau đây đúng?
A.
Cả (I) v (II) đều đúng
B.
(I) đúng, (II) sai
C.
Cả (I) v (II) đều sai
D.
(I) sai, (II) đúng
C©u 11 :
Cho ba vectơ
0;1; 2 , 1;2;1 , 4;3;a b c m
. Đ ba vectơ đồng phẳng thì giá trị của m
là?
3
A.
14
B.
5
C.
-7
D.
7
C©u 12 :
Phương trình đường thẳng đi qua đim
3;2;1A
vuông góc và cắt đường thẳng
3
2 4 1
x y z
là?
A.
3
:1
54
x
yt
zt
B.
3
:2
12
xt
yt
zt
C.
3
:1
54
x
yt
zt
D.
3
:2
13
x
yt
zt
C©u 13 :
Cho
: 2 3 14 0P x y z
và
1; 1;1M
Ta đ đim N đối xứng của M qua
P
là
A.
1; 3;7
B.
2; 1;1
C.
2; 3; 2
D.
1;3;7
C©u 14 :
Trong không gian với hệ trục ta đ Oxyz cho tứ diện ABCD với
2;3;1 , 1;2;0 , 1;1; 2 ; 2;3;4A B C D
. Th tích của tứ diện ABCD là:
A.
7
2
B.
7
6
C.
5
2
D.
7
3
C©u 15 :
Trong không gian với hệ toạ đ Oxyz, cho đường thẳng
x y z
d
1 2 2
:
3 2 2

và mặt
phẳng (P): x + 3y + 2z + 2 = 0. Lập phương trình đường thẳng song song với mặt
phẳng (P), đi qua M(2; 2; 4) và cắt đường thẳng (d).
A.
:

x y z
2 2 4
9 7 6
B.
:
x y z
2 2 4
9 7 6

C.
:

x y z
2 2 4
9 7 6
D.
:

x y z
2 2 4
3 2 2
C©u 16 :
Trong không gian với hệ ta đ Oxyz, cho hai đim A(1;0;1),B(2;1;2) và
(P):x+2y+3z+3=0. Viết phương trình mặt phẳng (Q) đi qua 2 đim A,B và vuông góc
với (P).
A.
( ) : x 2 2 0
Q y z
B.
( ) : x 2 2 0
Q y z
C.
( ) : x 2 2 0
Q y z
D.
( ) : x 2 2 0
Q y z
C©u 17 :
Cho
1; 1;2 , 2; 2;2 , 1;1; 1A B C
Phương trình của
chứa AB và vuông góc
với mặt phẳng (ABC)
A.
3 2 14 0x y z
B.
3 5 14 0x y z
4
C.
3 5 14 0x y z
D.
3 5 14 0xyz
C©u 18 :
Trong không gian với hệ trục Oxyz, cho mặt cầu
2 2 2
( ): 2 4 2 3 0S x y z x y z
.
Viết phương trình (P) chứa trục Ox và cắt (S) theo đường tròn có bán kính bằng 3.
A.
( ): 3 0P y z
B.
( ): 2 0P y z
C.
( ): 0P y z
D.
( ): 2 0P y z
C©u 19 :
Trong không gian với hệ trục ta đ
,Oxyz
cho tứ diện
ABCD
biết
(0; 1; 1)A 
,
(1;0;2)B
,
(3;0;4)C
,
(3;2; 1)D
. Th tích của tứ diện
ABCD
bằng ?
A.
1
6
B.
1
2
C.
3
D.
6
C©u 20 :
Trong không gian với hệ trục ta đ
,Oxyz
cho phương trình đường thằng
11
:
2 1 4
x y z
d


và mặt phẳng
( ) : 3 0P x y z
. Ta đ giao đim
A
của
d
và
()P
là:
A.
(3; 2;4)A
B.
( 3;1; 8)A 
C.
( 1;0; 4)A 
D.
( 1; 1; 5)A 
C©u 21 :
Phương trình mặt phẳng (P) đi qua 3 đim
3,4,1 , 1, 2,5 , 1,7,1A B C
là:
A.
3 2 6 7 0x y z
B.
3 2 6 23 0x y z
C.
3 2 6 23 0x y z
D.
3 2 6 5 0x y z
C©u 22 :
Trong không gian với hệ toạ đ Oxyz, cho ba đim A(0; 1; 2), B(2; –2; 1), C(–2; 0; 1).
Viết phương trình mặt phẳng (ABC)
A.
2 5 0x y z
B.
x y z
2 4 6 0
C.
x y z
2 4 1 0
D.
x y z
2 4 6 0
C©u 23 :
Cho đường thẳng (d) có phương trình tng quát là
20
2 1 0
x y z
x y z
. Phương
trình tham số của (d) là
A.
13
25
xt
yt
zt


B.
1
3
2
1
3
3
xt
yt
zt
C.
1
13
5
xt
yt
zt


D.
13
25
xt
yt
zt
5
C©u 24 :
Cho
0,2, 3A
,
1, 4,1B
. Phương trình mặt phẳng (P) đi qua
1,3, 2M
và vuông
góc với AB là:
A.
20x y z
B.
6 4 25 0x y z
C.
3 4 0x y z
D.
6 17 0xy
C©u 25 :
Phương trình mặt phẳng chứa đường thẳng
12
:
32
xt
yt
zt
v đi qua
2; 1;0M
là?
A.
3 1 0x y z
B.
4 2 0x y z
C.
4 2 0x y z
D.
3 1 0x y z
C©u 26 :
Trong không gian với hệ trục ta đ Oxyz cho tam giác ABC với
1;0;0 , 0;0;1 , 2;1;1A B C
. Diện tích của tam giác ABC là:
A.
6
4
B.
3
2
C.
6
2
D.
6
C©u 27 :
Phương trình mặt phẳng đi qua đim
3;1;0M
và vuông góc với đường thẳng
1 2 1
:
2 1 2
x y z
d

là:
A.
2 5 0x y z
B.
2 2 5 0x y z
C.
2 5 0x y z
D.
2 2 5 0x y z
C©u 28 :
Trong không gian với hệ trục Oxyz, cho (P): 2x-y+2z-4=0. Mặt phẳng no sau đây
song song với (P).
A.
2 1 0x y z
B.
2 1 0x y z
C.
2 2 4 0x y z
D.
4 2 4 1 0x y z
C©u 29 :
Trong không gian với hệ trục ta đ
,Oxyz
cho tam giác
ABC
biết
( 1;0;2)A
,
(1;3; 1)B
,
(2;2;2)C
. Trong các khẳng định sau khẳng định nào sai?
A.
Đim
25
; ;1
33
G



là trng tâm của tam
giác
ABC
.
B.
2AB BC
6
C.
AC BC
D.
Đim
31
0; ;
22
M



l trung đim của
cạnh
.AB
C©u 30 :
Cho
8; 3; 3M 
và mặt phẳng
:3 8 0x y z
Ta đ hình chiếu vuông góc
của A xuống
là
A.
1; 2; 5
B.
1;1;6
C.
1; 2; 6
D.
2; 1; 1
C©u 31 :
Trong không gian với hệ toạ đ Oxyz, cho hai đim A(1; 4; 2),B(–1; 2; 4) v đường
thẳng
:
x y z
12
1 1 2


. Tìm toạ đ đim M trên
sao cho:
MA MB
22
28
.
A.

M
( 1;0; 4)
B.
M
( 1;0;4)
C.
M
(1;0; 4)
D.
M
(1;0;4)
C©u 32 :
Trong không gian với hệ ta đ Oxyz, cho hai đim A(2;4;1), B(–1;1;3) và mặt phẳng
(P):
x y z
– 3 2 – 5 0
. Viết phương trình mặt phẳng (Q) đi qua hai đim A, B và
vuông góc với mặt phẳng (P).
A.
Q y z
( ) : 2 3 5 0
B.
Q y z
( ) : 2 3 11 0
C.
3 2 8 0x y z
D.
3 3 2 16 0x y z
C©u 33 :
Trong không gian với hệ trục ta đ Oxyz cho
4;0;0 , 6;6;0AB
Đim D thuc tia
Ox v đim E thuc tia Oz tha mãn th tích tứ diện ABDE bằng 20 và tam giác
ABD cân tại D có ta đ là:
A.
(14;0;0); (0;0;2)DE
B.
(14;0;0); (0;0; 2)DE
C.
(14;0;0); (0;0; 2)DE
D.
(14;2;0); (0;0;2)DE
C©u 34 :
Trong không gian với hệ toạ đ Oxyz, cho đường thẳng
x y z
d
1 1 2
:
2 1 3

và mặt
phẳng
P
:
x y z
10
. Viết phương trình đường thẳng đi qua
A
(1;1; 2)
, song
song với mặt phẳng
P
()
và vuông góc với đường thẳng
d
.
A.


x y z
112
:
1 1 1
B.
x y z
1 1 2
:
2 5 3

C.

x y z
1 1 2
:
2 5 3
D.


x y z
112
:
2 5 3
C©u 35 :
Trong không gian với hệ trục Oxyz, cho hai đim A(2;-2;1),B(3;-2;1) Ta đ đim C
đối xứng với A qua B là:
7
A.
C(1;2;1)
B.
D(1; 2; 1)
C.
D( 1;2; 1)
D.
C(1; 2;1)
C©u 36 :
Trong không gian với hệ trục ta đ Oxyz cho 3 đim
2;0;4 , 4; 3;5 , sin5 ;cos3 ;sin3A B C t t t
và O là gốc ta đ. với giá trị nào của t đ
AB OC
.
A.
2
3
()
24 4
tk
k
k
t

B.
2
3
()
24 4
tk
k
k
t


C.
3
()
24 4
tk
k
k
t


D.
2
3
()
24 4
tk
k
k
t



C©u 37 :
Trong không gian với hệ trục ta đ
,Oxyz
cho ba vectơ
(1;2;2)a
,
(0; 1;3)b 
,
(4; 3; 1)c
. Xét các mệnh đề sau:
(I)
3a
(II)
26c
(III)
ab
(IV)
bc
(V)
.4ac
(VI)
,ab
cùng phương (VII)
2 10
cos ,
15
ab
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng?
A.
1
B.
6
C.
4
D.
3
C©u 38 :
Trong không gian với hệ trục ta đ
,Oxyz
cho hai đim
(1; 1;3)A
,
( 3;0; 4)B 
.
Phương trình no sau đây l phương trình chính tắc của đường thẳng đi qua hai
đim
A
và
B
?
A.
34
4 1 7
x y y

B.
34
1 1 3
x y y

C.
1 1 3
4 1 7
x y y

D.
1 1 3
4 1 7
x y y

C©u 39 :
Cho đường thẳng d
1
2
12
xt
yt
zt



v mặt phẳng (
)
3 1 0x y z
. Trong các khẳng
định sau, tìm khẳng định đúng :
8
A.
/ /( )d
B.
()d
C.
()d
D.
(
) cắt d
C©u 40 :
Phương trình mặt cầu đường kính AB với
4, 3,7 , 2,1,3AB
là:
A.
2 2 2
3 1 5 9x y z
B.
2 2 2
3 1 5 9x y z
C.
2 2 2
3 1 5 35x y z
D.
2 2 2
3 1 5 35x y z
C©u 41 :
Cho
5;2; 6 , 5;5;1 , 2, 3, 2 , 1,9,7A B C D
. Bán kính mặt cầu ngoài tiếp tứ diện
ABCD là?
A.
15
B.
6
C.
9
D.
5
C©u 42 :
Trong không gian với hệ trục Oxyz, cho đim A(1;-2;1) và (P):x+2y-z-1=0. Viết
phương trình mặt phẳng (Q) đi qua A v song song với (P).
A.
(Q):x 2y z 4 0
B.
(Q):x 2y z 4 0
C.
(Q):x 2y z 2 0
D.
(Q):x 2y z 4 0
C©u 43 :
Tìm ta đ đim H trên đường thẳng d:
1
2
12
xt
yt
zt



sao cho MH nhắn nht, biết
M(2;1;4):
A.
H(2;3;3)
B.
H(1;3;3)
C.
H(2;2;3)
D.
H(2;3;4)
.
C©u 44 :
Khoảng cách giữa hai mặt phẳng
: 2 2 1 0P x y z
và
: 2 2 1 0Q x y z
là?
A.
2
3
B.
1
5
C.
3
2
D.
5
C©u 45 :
Cho 2 mặt phẳng
: 2 2 1 0, :6 2 5 0P x y z Q x y x
Phương trih2 mặt
phẳng
qua
1;2;1M
và vuông góc với cả 2 mặt phẳng (P) và (Q) là
A.
2 6 0x y z
B.
2 7 13 17 0x y z
C.
7 2 10 0x y z
D.
2 7 13 17 0x y z
C©u 46 :
Trong không gian với hệ ta đ Oxyz, cho hai đim A(2;4;1),B(-1;1;3) và (P):x-3y+2z-
5=0. Viết phương trình mặt phẳng (Q) đi qua 2 đim A,B và vuông góc với (P).
9
A.
( ) : 2 3 11 0
Q y z
B.
( ) : 2 3 11 0
Q y z
C.
( ) : 2 3 11 0
Q y z
D.
( ) : 2 3 11 0
Q y z
C©u 47 :
Cho phương trình mặt phẳng
: 2 3 1 0P x y x
. Trong các mệnh đề sau, mệnh
đề no đúng?
A.
Ba đim
1;0;0 , 0;1;1 , 3;1;2M N Q
cùng thuc mặt phẳng (P).
B.
Ba đim
1;0;0 , 0;1;1 , 0;0;1M N K
cùng thuc mặt phẳng (P).
C.
Ba đim
1;0;0 , 0;1;2 , 3;1;2M N Q
cùng thuc mặt phẳng (P).
D.
Ba đim
1;0;0 , 0;1;2 , 1;1;2M N K
cùng thuc mặt phẳng (P).
C©u 48 :
Cho mặt phẳng (P): 16x – 15y – 12z + 75 =0 v mặt cầu (S)
2 2 2
9x y z
. (P) tiếp xúc
với (S) tại đim:
A.
48 36
( ;11; )
25 25
B.
19
( 1;1; )
3
C.
36
( 1;1; )
25
D.
48 9 36
( ; ; )
25 5 25
C©u 49 :
Cho ba đim
1;2;0 , 2;3; 1 , 2;2;3
. Trong các đim
1;3;2 , 3;1;4 ,AB
0;0;1C
thì đim nào tạo với ba đim ban đầu thành hình bình hành là?
A.
Cả A và B
B.
Chỉ có đim C.
C.
Chỉ có đim A.
D.
Cả B và C.
C©u 50 :
Cho mặt phẳng
: 2 0P y z
v hai đường thẳng
1
:
4
xt
d y t
zt
và
2
' : 4
1
xt
d y t
z
.
Đường thẳng ở trong (P) cắt cả hai đường thẳng d v d’ l?
A.
1
4 2 1
x y z
B.
14
12
xt
yt
zt
C.
14
2
xt
yt
zt
D.
11
4 2 1
x y z
C©u 51 :
Cho hai đim
1;2; 1 , 0;1; 2MN
v vectơ
3; 1;2v
. Phương trình mặt phẳng
chứa M, N và song song với vectơ
v
là?
A.
3 4 9 0x y z
B.
3 4 7 0x y z
10
C.
3 3 7 0x y z
D.
3 3 9 0x y z
C©u 52 :
Trong không gian với hệ trục Oxyz, cho 3 đim A(1;0;0),B(0;2;0),C(0;0;3). Viết
phương trình mặt phẳng đi qua 3 đim A,B,C.
A.
( ):6x 3y 2z 6 0ABC
B.
( ):6x 3y 2z 6 0ABC
C.
( ):x 2y 3z 1 0ABC
D.
( ):6x 3y 2z 6 0ABC
C©u 53 :
Cho hai đường thẳng có phương trình sau:
1
2 5 0
:
5 2 4 1 0
xy
d
x y z
2
50
:
3 6 0
x y z
d
yz
Mệnh đề sau đây đúng:
A.
1
d
hợp với
2
d
góc
60
o
B.
1
d
cắt
2
d
C.
12
dd
D.
12
dd
C©u 54 :
Trong không gian với hệ trục Oxyz, cho (P): 2x-y+2z-4=0. Mặt phẳng no sau đây
vuông góc với (P).
A.
4 2 0x y z
B.
4 5 0x y z
C.
4 2 0x y z
D.
4 1 0x y z
C©u 55 :
Gi
l gác giữa hai đường thẳng d
1
:
3 2 6
234
x y z

v d
2
:
19
1 4 1
x y z

.
Khi đó cos
bằng:
A.
2
58
B.
2
5
C.
1
2
D.
2
58
.
C©u 56 :
Cho ba đim
2;5; 1 , 2;2;3 , 3;2;3A B C
. Mệnh đề no sau đây l sai?
A.
ABC
đều.
B.
,,A B C
không thẳng hàng.
C.
ABC
vuông.
D.
ABC
cân tại B.
C©u 57 :
Trong không gian với hệ trục ta đ
,Oxyz
cho ba đim
(1; 1;3)M
,
(1;1;5)N
,
(3;0;4)P
.
Phương trình no sau đây l phương trình mặt phẳng đi qua đim
M
và vuông góc
với đường thẳng
NP
?
A.
30x y z
B.
2 3 0x y z
C.
2 2 0x y z
D.
2 4 0x y z
11
C©u 58 :
Cho tam giác ABC có A(1;2;3), B(4;5;6), C(-3; 0 ;5). Gi G l trng tâm tam giác ABC,
I l trung đim AC, (
) l mặt phẳng trung trc của AB. Chn khẳng định đúng
trong các khẳng định sau:
A.
2 7 14 21
( ; ; ), I(1;1;4), ( ): x y 0
3 3 3 2
Gz
..
B.
2 7 14
( ; ; ), I( 1;1;4), ( ): 5x 5y 5 21 0
3 3 3
Gz
C.
(2;7;14), I( 1;1;4), ( ): 2x 2y 2 21 0Gz
D.
2 7 14
( ; ; ), I(1;1;4), ( ): 2x 2y 2 21 0
3 3 3
Gz
C©u 59 :
Trong không gian với hệ trục ta đ Oxyz cho
4;0;0 , ; ;0A B b c
. Với b,c là các số
thc dương tha mãn
2 10AB
và góc
0
45AOB
. Đim C thuc tia Oz tha mãn th
tích tứ diện OABC bằng 8 có ta đ là:
A.
(0;0; 2)C
B.
(0;0;3)C
C.
(0;0;2)C
D.
(0;1;2)C
C©u 60 :
Cho tam giác ABC có A(0;0;1), B(-1;-2;0), C(2; 1 ;-1).. Khi đó ta đ chân đường cao
H hạ từ A xuống BC:
A.
5 14 8
( ; ; )
19 19 19
H

B.
4
( ;1;1)
9
H
C.
8
(1;1; )
9
H
D.
3
(1; ;1)
2
H
C©u 61 :
Trong không gian với hệ toạ đ Oxyz, cho đim A(1; –2; 3) v đường thẳng d có
phương trình
x y z
1 2 3
2 1 1

. Viết phương trình mặt cầu tâm A, tiếp xúc với d.
A.
2 2 2
( –1) ( 2) ( – 3) 5
x y z
B.
x y z
2 2 2
( –1) ( 2) ( – 3) 50
C.
2 2 2
( 1) ( 2) ( 3) 50
x y z
D.
2 2 2
( –1) ( 2) ( – 3) 50
x y z
C©u 62 :
Trong các đim sau, đim nào là hình chiếu vuông góc của đim
1; 1;2M
trên
mặt phẳng
:2 2 2 0P x y z
.
A.
0,2,0
B.
1,0,0
C.
0,0, 1
D.
1,0, 2
C©u 63 :
Trong không gian với hệ trục ta đ
,Oxyz
cho hai đim
( 1;1;5)A
,
(1;2; 1)B
.
Phương trình no sau đây l phương trình mặt phẳng đi qua hai đim
A
,
B
và
vuông góc với mặt phẳng
()Oxy
?
A.
6 6 7 0x y z
B.
6 11 0yz
C.
2 3 0xy
D.
3 2 0xz
12
C©u 64 :
Trong không gian với hệ ta đ Oxyz. Cho tứ diện ABCD với
0;1;1 , 1;0;2 , 1;1; , (2;1; 2)0 DA B C 
. Th tích của tứ diện ABCD là:
A.
7
6
B.
11
6
C.
5
6
D.
5
18
C©u 65 :
Trong không gian với hệ trục ta đ Oxyz cho
0;0;4 , 3;0;0 , 0;4;0A B C
.Phương trình mp(ABC) l :
A.
4 3 - 3 – 12 0x y z
B.
4 3 3 – 12 0x y z
C.
4 3 3 + 12 0x y z
D.
4 - 3 3 – 12 0x y z
C©u 66 :
Cho
3; 1;2 , 4; 1; 1 , 2;0;2A B C
Phương trình mặt phẳng qua 3 đim A, B, C
là
A.
3 3 2 0x y z
B.
3 2 2 0x y z
C.
2 3 2 0x y z
D.
3 3 2 0x y z
C©u 67 :
Trong không gian với hệ trục ta đ
,Oxyz
cho mặt cầu
()S
có đường kính
AB
với
(3;2; 1)A
,
(1; 4;1)B
. Tìm mệnh đề sai trong các mệnh đề sau:
A.
Mặt cầu
()S
có bán kính
11R
.
B.
Mặt cầu
()S
đi qua đim
( 1;0; 1)M 
.
C.
Mặt cầu
()S
tiếp xúc với mặt phẳng
( ) : 3 11 0x y z
.
D.
Mặt cầu
()S
có tâm
(2; 1;0)I
.
C©u 68 :
Tìm trên trục tung những đim cách đều hai đim
1, 3,7A
và
5,7, 5B
A.
0,1,0M
và
0,2,0N
B.
0,2,0M
C.
0, 2,0M
D.
0,2,0M
và
0, 2,0N
C©u 69 :
Trong không gian với hệ trục ta đ
,Oxyz
cho tam giác
ABC
biết
(1;2;3)A
,
(2;0;2)B
,
(0;2;0)C
. Diện tích của tam giác
ABC
bằng ?
A.
7
2
B.
14
2
C.
14
D.
27
C©u 70 :
Đ 2 mặt phẳng có phương trình
2 3 5 0x ly z
và
6 6 2 0mx y z
song
13
song với nhau thì giá trị của m và l là:
A.
2, 6ml
B.
4, 3ml
C.
2, 6ml
D.
4, 3ml
C©u 71 :
Trong hệ trục ta đ Oxyz cho
4;3;4 , 2; 1;2 , 1;2;1wuv
.khi đó
, .wuv


là:
A.
2
B.
3
C.
0
D.
1
C©u 72 :
Phương trình mặt cầu đi qua 4 đim
3,0,0A
,
0,4,0B
,
0,0, 2C
và
0,0,0O
là:
A.
2 2 2
6 8 4 0x y z x y z
B.
2 2 2
3 4 2 0x y z x y z
C.
2 2 2
6 8 4 0x y z x y z
D.
2 2 2
3 4 2 0x y z x y z
C©u 73 :
Phương trình mặt phẳng đi qua 3 đim A(0;0;1), B(2;1;-1), C(-1;-2;0) l:
A.
5x – 4y + 3z – 3 = 0
B.
5x – 4y + 3z – 9 = 0
C.
5x – y + 3z – 33 = 0
D.
x – 4y + z – 6 = 0
C©u 74 :
Cho đường thẳng
13
:
2 3 2
x y z
d


v mặt phẳng (P)
2 2 1 0x y z
. Mặt phẳng
chứa đường thẳng d v vuông góc với (P) có phương trình :
A.
2x + 2y + z – 8 = 0
B.
2x – 2y + z – 8 = 0
C.
2x – 2y + z + 8 = 0
D.
2x + 2y - z – 8 = 0
C©u 75 :
Phương trình mặt phẳng đi qua đim
1; 1;2M
và song song với mặt phẳng
: 2 1 0P x x z
A.
2 1 0x y z
B.
2 1 0x y z
C.
2 2 0x y z
D.
2 1 0x y z
C©u 76 :
Khoảng cách từ A(- 1;3;2) đến mặt phẳng (BCD) với B(4;0;- 3),
C(5; - 1; 4), D(0; 6;1) bằng:
A.
72
786
B.
72
76
C.
72
87
D.
72
77
C©u 77 :
Trong không gian với hệ toạ đ Oxyz, cho mặt cầu (S) có phương trình:
x y z x y z
2 2 2
2 6 4 2 0
. Viết phương trình mặt phẳng (P) song song với giá
14
của véc tơ
v
(1;6;2)
, vuông góc với mặt phẳng
x y z
( ) : 4 11 0
và tiếp xúc với
(S).
A.
(P):
x y z
2 2 3 0
hoặc (P):
x y z
2 2 0
.
B.
(P):
x y z
2 2 3 0
hoặc (P):
x y z
2 2 21 0
.
C.
(P):
x y z
2 2 21 0
.
D.
(P):
x y z
2 2 3 0
C©u 78 :
Trong không gian với hệ trục ta đ Oxyz cho tam giác ABC với
1;2; 1 , 2; 1;3 , 4;7;5A B C
. Chân đường phần giác trong của góc B của tam
giác ABC l đim D có ta đ là:
A.
2 11
; ; 1
33
D




B.
2 11
; ;1
33
D




C.
2 11
; ;1
33
D



D.
2 11
; ;1
33
D



C©u 79 :
Trong không gian với hệ trục Oxyz, cho tam giác ABC có A(2;-2;1),B(3;-2;1),C(1;-2;-
2). Ta đ trng tâm G của tam giác ABC là
A.
(2;2;0)G
B.
( 2; 2;0)G 
C.
(2; 2;1)G
D.
(2; 2;0)G
C©u 80 :
Phương trình mặt phẳng (P) đi qua 2 đim
2, 1,4 , 3,2, 1AB
và vuông góc mặt
phẳng
: 2 3 0Q x y z
là:
A.
11 7 2 21 0x y z
B.
11 7 2 21 0x y z
C.
11 7 2 21 0x y z
D.
11 7 2 21 0x y z
C©u 81 :
Cho 2 đường thẳng lần lượt có phương trình
1
12
:2
xt
dy
zt


và
2
3'
: 4 '
4
xt
d y t
z


Đ di đoạn vuông góc chung của
1
d
và
2
d
là
A.
6
B.
4
C.
22
D.
26
15
ĐÁP ÁN
01
) | } ~
28
{ | } )
55
) | } ~
02
{ | ) ~
29
{ | ) ~
56
) | } ~
03
{ | ) ~
30
{ | } )
57
{ | ) ~
04
{ ) } ~
31
{ ) } ~
58
) | } ~
05
{ ) } ~
32
{ ) } ~
59
{ | ) ~
06
{ | } )
33
{ | ) ~
60
) | } ~
07
{ | } )
34
{ ) } ~
61
{ ) } ~
08
{ ) } ~
35
{ | } )
62
{ ) } ~
09
{ | ) ~
36
{ | ) ~
63
{ | ) ~
10
) | } ~
37
{ | ) ~
64
{ | ) ~
11
) | } ~
38
{ | ) ~
65
{ ) } ~
12
) | } ~
39
) | } ~
66
{ | } )
13
{ | } )
40
{ ) } ~
67
{ | ) ~
14
{ | ) ~
41
) | } ~
68
{ ) } ~
15
{ ) } ~
42
{ | } )
69
{ | ) ~
16
{ | } )
43
) | } ~
70
{ | } )
17
{ | } )
44
) | } ~
71
{ | ) ~
18
{ | } )
45
{ | } )
72
{ ) } ~
19
{ | ) ~
46
{ | } )
73
) | } ~
20
{ | ) ~
47
) | } ~
74
) | } ~
21
{ ) } ~
48
) | } ~
75
{ ) } ~
22
{ ) } ~
49
) | } ~
76
) | } ~
23
{ | } )
50
) | } ~
77
{ ) } ~
24
{ ) } ~
51
) | } ~
78
{ | ) ~
25
) | } ~
52
{ | } )
79
{ | } )
26
{ | ) ~
53
{ | } )
80
{ ) } ~
27
{ ) } ~
54
{ | } )
81
{ | } )
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN
ĐỀ 006
C©u 1 :
Cho
: 2x 1 0, : 4 6 10 0y z x y z

và
3
d : 4 3
2
x
yz
Khẳng định nào sau đây là đúng:
A.
//d
và
d
B.
d
và
//d
C.
d
và
d
D.
//d
và
//d
C©u 2 :
Trong không gian Oxyz, cho các điểm
3;0;4 , 1;2;3 , 9;6;4A B C
là 3 đỉnh của hình
bình hành ABCD. Tọa độ đỉnh D là:
A.
11;4;5D
B.
11; 4; 5D 
C.
11; 4;5D
D.
11; 4; 5D
C©u 3 :
Trong không gian với hệ tọa độ Oxyz, góc tạo bởi hai vectơ
( 4;2;4)a
và
2 2; 2 2;0b
là:
A.
0
30
B.
0
90
C.
0
135
D.
0
45
C©u 4 :
Trong không gian với hệ tọa độ
Oxyz
,đường thẳng
21
1 1 3
:
x y z

đi qua điểm
(2; ; )M m n
. Khi đó giá trị của m, n lần lượt là :
A.
2; 1mn
B.
2; 1mn
C.
4; 7mn
D.
0; 7mn
C©u 5 :
Mặt phẳng đi qua
( 2;4;3)A
A(-2;4;3), song song với mặt
( ): 3 2 1 0P x y z
có
phương trình dạng:
A.
3 2 4 0x y z
B.
3 2 4 0x y z
C.
3 2 4 0x y z
D.
3 4 0x y z
C©u 6 :
Cho
,,A B C
lần lượt là hình chiếu vuông góc của điểm
(4;1; 5)S
trên các mặt phẳng
,,Oxy Oyz Ozx
. Khoảng cách từ
S
đến mặt phẳng
ABC
bằng:
2
A.
A,B,C đều sai
B.
40
21
C.
20
21
D.
2 21
C©u 7 :
Trong không gian với hệ tọa độ
Oxyz
,gọi
M
là giao điểm của đường thẳng
21
3 1 2
:
x y z

và mặt phẳng
( ):x+2y-3z+2=0P
. Khi đó :
A.
(5; 1; 3)M 
B.
(2;0; 1)M
C.
( 1;1;1)M
D.
(1;0;1)M
C©u 8 :
Cho hình hộp
A
B
CD.A’
B’C’D’ biết: A
(
1
;
0
;
1
)
,
B
(
2
;
1
;
2
)
,
D
(
1
;
1
;
1
)
,
C
′
(
4
;
5
;
5
)
.
Thể tích khối
hộp là:
A.
9
B.
6
C.
7
D.
8
C©u 9 :
Trong không gian với hệ tọa độ Oxyz, cho điểm
A
(2; 1;1)
. phương trình mặt phẳng (P) đi
qua điểm A và cách gốc tọa độ O một khoảng lớn nhất là
A.
x y z
2 6 0
B.
2 6 0
x y z
C.
2 6 0
x y z
D.
2x+y-z+6=0
C©u 10 :
Cho
󰇍
󰇍
󰇛
  
󰇜
󰇍
󰇛  󰇜. Kết luận nào sai:
A.
󰇍
󰇍
󰇍

B.
󰇟
󰇍
󰇍
󰇍
󰇠
󰇛  󰇜
C.
󰇍
󰇍
và
󰇍
không cùng phương
D.
Góc của
󰇍
󰇍
và
󰇍
là 
C©u 11 :
Cho ba điểm
B
(
1
;
0
;
1
)
,
C
(
1
;
1
;
0
)
,
D
(
2
;
1
;
2
)
. Phương trình mặt phẳng qua B, C,
D
là:
A.
4x + 7y 3 = 0
B.
2y + 3z + 1 = 0
C.
2y + 3z  0
D.
4x 7y +  2 = 0
C©u 12 :
Trong không gian Oxyz, cho 3 điểm
0;1;2 , 2; 2;1 ; 2;1;0A B C
. Khi đó phương
trình mặt phẳng (ABC) là:
2 4 0ax y z d
. Hãy xác định a và d
A.
1; 6ad
B.
1; 6ad
C.
1; 6ad
D.
1; 6ad
C©u 13 :
Trong không gian
Oxyz
cho 4 điểm
(1;0;0), (0;1;0), (0;0;1), (1;1;1)A B C D
. Trong các mệnh
đề sau, mệnh đề nào sai:
A.
Bốn điểm A, B, C, D tạo thành một tứ
diện.
B.
AB vuông góc với CD
C.
Tam giác BCD vuông
D.
Tam giác ABD đều
3
C©u 14 :
Trong không gian Oxyz cho cc điểm
)2;4;3(,)0;2;1( BA
. Tìm tọa độ điểm I trên trc Ox
cch đu hai điểm A, B và viết phương trình mặt cu tâm I , đi qua hai điểm A, B.
A.
20)3(
222
zyx
B.
2 2 2
( 3) 20x y z
C.
2 2 2
( 1) ( 3) ( 1) 11/ 4x y z
D.
2 2 2
( 1) ( 3) ( 1) 20x y z
C©u 15 :
Trong không gian với hệ tọa độ Oxyz cho tam giác MNP biết
( 3;0;4)MN
và
( 1;0; 2)NP
. Độ dài đường trung tuyến MI của tam giác MNP bằng:
A.
9
2
B.
95
2
C.
85
2
D.
15
2
C©u 16 :
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x+ y+z+1=0.
a)Viết phương trình mặt cu có tâm I(1;1;0) và tiếp xúc với mp(P).
A.
22
2
1 1 3x y z
B.
22
2
1 1 3x y z
C.
22
2
1 1 3x y z
D.
22
2
1 1 3x y z
C©u 17 :
Cho và
󰇍
tạo với nhau một góc

. Biết

󰇍
thì
󰇍
bằng:
A.
B.
C.
D.
C©u 18 :
Trong hệ tọa độ Oxyz cho 2 điêm A(1;2;3) và B(2;1;2). Phương trình đường thẳng
nào dưới đây không phải là phương trình đường thẳng đi qua 2 điểm A và B
A.
1 2 3
1 1 1
x y z


B.
34
1 1 1
x y z


C.
2 1 2
1 1 1
x y z

D.
31
1 1 1
x y z

C©u 19 :
Cho
󰇛
 
󰇜
 
Gọi M là điểm trên trục tung và cách đều A và B thì:
A.
󰇛  󰇜
B.
󰇛  󰇜
C.
󰇛  󰇜
D.
󰇛  󰇜
C©u 20 :
Trong không gian với hệ tọa độ Oxyz cho đường thẳng
3 2 10 0
:
2 4 2 0
x y z
d
x y z
. Vectơ
chỉ phương của d có tọa độ là:
A.
6; 13;8
B.
6;13; 8
C.
6;13;8
D.
6;13; 8
C©u 21 :
Trong hệ tọa độ Oxyz, mặt phẳng
cắt ba trục Ox, Oy,Oz lần lượt tại ba điểm
A(-3;0;0), B(0;4;0), C(0;0;-2) có phương trình là:
4
A.
4 3 6 12 0x y z
B.
4 3 6 12 0xyz
C.
4 3 6 12 0x y z
D.
4 3 6 12 0x y z
C©u 22 :
Trong không gian Oxyz, đường thẳng d đi qua hai điểm
2;0;3 , 1;2;1AB
có
phương trình tham số là:
A.
1
22
14
xt
yt
zt



B.
2
2
34
xt
yt
zt

C.
22
4
38
xt
yt
zt


D.
2
2
34
xt
yt
zt

C©u 23 :
Cho
󰇍
có độ dài bằng 1 và 2. Biết
󰇍
. Thì
󰇍
bằng:
A.
B.
C.
D.
C©u 24 :
Trong không gian 0xyz cho mặt phẳng (P): 2x + 3y + z – 11 = 0. mặt cu (S) có tâm I(1; -2;
1) và tiếp xúc với (P) tại H. tọa độ tiếp điểm H là.
A.
H(3;1;2).
B.
H(5;4;3)
C.
H(1;2;3)
D.
H(2;3;-1)
C©u 25 :
Trong không gian với hệ tọa độ
Oxyz
, điểm
(1;2; 3)M
và mặt phẳng
( ): 2 2 3 0P x y z
. Khoảng cách từ điểm
M
đến mặt phẳng
()P
có giá trị là :
A.
3
B.
1
C.
2
D.
4
C©u 26 :
Cho
󰇛
 
󰇜
󰇛
 
󰇜
󰇛  󰇜 thì ABCD là hình bình hành khi:
A.
󰇛  󰇜
B.
󰇛  󰇜
C.
D.
A.
󰇛  󰇜
B.
󰇛  󰇜
C.
󰇛  󰇜
D.
󰇛  󰇜
C©u 27 :
Trong không gian với hệ tọa độ Oxyz cho điểm
(3;5; 8)M
và mặt phẳng
( ) : 6 3 2 28 0x y z
. Khoảng cách từ M đến
()
bằng:
A.
6
B.
47
7
C.
41
7
D.
45
7
C©u 28 :
Trong hệ tọa độ Oxyz, cho phương trình đường thẳng d:
5 2 4
11
2
x y z

và
phương trình mặt phẳng
: 2 7 0x y z
. Góc của đường thẳng d và mặt
5
phằng
là:
A.
0
45
B.
0
60
C.
0
90
D.
0
30
C©u 29 :
Cho hình bình hành
ABCD
với
1;1;3A
,
4;0;2B
,
1;5;1C
. Tọa độ điểm
D
là:
A.
4;6;4D
B.
4;6;2D
C.
2;3;1D
D.
2;6;2D
C©u 30 :
Trong không gian Oxyz, cho mặt cầu (S) có tâm
1;4;2I
và có thể tích
972V
.
Khi đó phương trình của mặt cầu (S) là:
A.
2 2 2
1 4 2 81x y z
B.
2 2 2
1 4 2 9x y z
C.
2 2 2
1 4 2 9x y z
D.
2 2 2
1 4 2 81x y z
C©u 31 :
Trong không gian với hệ tọa độ
Oxyz
,đường thẳng
1 2 1
2
:
11
x y z
song song với
mặt phẳng
( ): 0P x y z m
khi m thỏa :
A.
Cả 3 đáp án đều sai.
B.
0m
C.
0m
D.
Rm
C©u 32 :
Mặt phẳng chứa hai điểm
2;1;3 , 1; 2;1AB
và song song với đường thẳng d
1
2,
32
xt
y t t R
zt


đi qua điểm:
A.
2;1;1M
.
B.
0;0;19M
C.
0;1;1M
D.
2;1;0M
C©u 33 :
Cho và
󰇍
khác
󰇍
. Kết luận nào sau đây sai:
A.
󰇟
󰇍
󰇠
󰇍
󰇛
󰇍
󰇜
B.

󰇍
󰇟
󰇍
󰇠
C.

󰇍
󰇟
󰇍
󰇠
D.
 
󰇍
󰇟
󰇍
󰇠
6
C©u 34 :
Trong mặt phẳng Oxyz, cho A(1; 2; 3) và B(3; 2; 1). Mặt phẳng đi qua A và cách B
một khoảng lớn nhất là:
A.
x-z- 2 = 0
B.
x-z+ 2 = 0
C.
2 3 -10 0x y z
D.
3x + 2y + z-10 = 0
C©u 35 :
Cho A
(
2
,
1
,
1
)
và (P):
x
+
2
y
2
z
+
3
=
0
. (d) là đường thẳng đi qua
A
và
vuông góc với
(P).
Tìm tọa độ M thuộc (d) sao cho OM =

3
A.
(
1
,
1
,
1
)
o
󰉢
c
(
5/3; 1/3; -1/3
)
B.
(1;1;-1) ; (5/3; 1/3; -1/3)
C.
(1;-1;-1) ; (5/3; -1/3; 1/3)
D.
(1;-1;-1) ; (5/3; 1/3; 1/3)
C©u 36 :
Trong không gian với hệ tọa độ Oxyz cho điểm
(2;1;4).M
Điểm N thuộc đường
thẳng
1
( ) : 2 ( )
12
xt
y t t
zt
sao cho đoạn MN ngắn nhất có tọa độ là:
A.
(2;3;2)N
B.
(3;2;3)N
C.
(2;3;3)N
D.
(3;3;2)N
C©u 37 :
Trong hệ tọa độ Oxyz cho điêm M(1;1;1) N(-1;1;0) P(3;1;-1). Điểm Q thuộc mặt
phẳng Oxz cách đều 3 điểm M,N,P có tọa độ
A.
57
;0;
44



B.
51
;0;
66



C.
17
;0;
66



D.
57
;0;
66



C©u 38 :
Trong không gian
Oxyz
cho 3 véctơ
( 1;1;0), (1;1;0), (1;1;1)a b c
. Trong các mệnh đề
sau, mệnh đề nào sai:
A.
3c
B.
2a
C.
a b
D.
c b
C©u 39 :
7
A.
S
(9;9;9)
hoặc
S
( 7; 7; 7)
B.
S
(9;9;9)
hoặc
S
(7;7;7)
C.

S
( 9; 9; 9)
hoặc
S
(7;7;7)
D.

S
( 9; 9; 9)
hoặc
S
( 7; 7; 7)
C©u 40 :
Phương trình mặt phẳng chứa hai đường thẳng
1
73
: 2 2
12
xt
d y t
zt



và
2
1 2 5
:
2 3 4
x y z
d

A.
2 16 13 31 0x y z
B.
2 16 13 31 0x y z
C.
2 16 13 31 0x y z
D.
2 16 13 31 0x y z
C©u 41 :
Cho
1; 1;5 , 3; 3;1AB
. Phương trình mặt phẳng trung trực của đoạn
AB
là:
A.
2 2 0x y z
B.
2 2 0x y z
C.
2 2 0x y z
D.
2 7 0x y z
C©u 42 :
Cho mặt cầu (S):
2 2 2
2x 6 4z 9 0x y z y
. Khi đó tâm I và bán kính R của mặt
cầu (S) là:
A.
(1;3; 2),R 25I 
B.
(1;3; 2),R 5I 
C.
(1;3; 2),R 7I 
D.
( 1; 3; 2),R 5I
C©u 43 :
Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;3;-1) và đường thẳng
4 1 5
:
1 2 2
x y z
d
tọa độ hình chiếu vuông góc của M trên (d)
A.
2;5;1H
B.
H(2;3;-1)
C.
H(1;-2;2)
D.
H(4;1;5)
C©u 44 :
Cho
󰇛
 
󰇜
󰇛
 
󰇜
󰇛
 
󰇜
Kết luận nào sau đây là đúng:
A.
 
B.

󰇍
󰇍
󰇍
󰇍
󰇍

󰇍
󰇍
󰇍
󰇍
󰇍
󰇛  󰇜
C.
 thẳng hàng
D.

C©u 45 :
Trong hệ tọa độ Oxyz, phương trình mặt cầu có tâm I(1;2;3) và đi qua gốc O có
phương trình là
A.
2 2 2
1 2 3 14x y z
B.
2 2 2
2 3 0x y z x y z
8
C.
2 2 2
1 2 3 24x y z
D.
2 2 2
2 4 6 0x y z x y z
C©u 46 :
Trong không gian với hệ tọa độ Oxyz cho ba điểm
(1;0;1), (0;2;0), (0;0;3).A B C
Khoảng cách từ gốc tọa độ O đến mặt phẳng (ABC) bằng:
A.
3
4
B.
5
7
C.
6
7
D.
9
7
C©u 47 :
Trong không gian Oxyz, cho điểm
2;1; 1A
và mặt phẳng
: 2 2 3 0P x y z
.
Gọi
1;a;bH
là hình chiếu vuông góc của A lên mặt phẳng (P). Khi đó a bằng:
A.
1
B.
1
C.
2
D.
2
C©u 48 :
Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;3;-1) và đường thẳng
4 1 5
:
1 2 2
x y z
d
phương trình mp (P) qua M và vuông góc với đt (d) là.
A.
x-2y+2z+6=0
B.
x-2y+2z-16=0
C.
X-2y+2z=0
D.
x-2y+2z+16=0
C©u 49 :
Phương trình mặt phẳng
()P
đi qua hai điểm
1;2;3A
,
2; 1; 1B 
và vuông góc với
mặt phẳng
: 2z 3 0Q x y
là:
A.
60x y z
B.
20x y z
C.
40x y z
D.
20x y z
C©u 50 :
Phương trình
đi qua 3 điểm A(1;0;0), B(0; 2;0), C(0;0;3) là:
A.
2 3z 6 0xy
B.
z
1
1 2 3
y
x
C.
z
0
1 2 3
y
x
D.
6 3 2z 1 0xy
C©u 51 :
Trong các phương trình sau, phương trình nào là phương trình của mặt cầu:
A.
2 2 2
10xy 8 2z 1 0x y z y
B.
2 2 2
3 3 3 2x 6 4z 1 0x y z y
9
C.
2 2 2
2 2 2 2x 6 4z 9 0x y z y
D.
2
2
2x 4 z 9 0x y z y
C©u 52 :
Trong không gian với hệ tọa độ Oxyz cho tứ diện ABCD với
(1;0;0), (0;1;0), (0;0;1), ( 2;1; 1).A B C D
Thể tích tứ diện ABCD bằng:
A.
3
2
B.
4
3
C.
1
2
D.
2
3
C©u 53 :
Cho
󰇛
 
󰇜
󰇛  󰇜. Gọi là điểm sao cho 
󰇍
󰇍
󰇍
󰇍
󰇍
󰇍

󰇍
󰇍
󰇍
󰇍
󰇍
thì:
A.
󰇛  󰇜
B.
󰇛  󰇜
C.
󰇛  󰇜
D.
󰇛  󰇜
C©u 54 :
Trong không gian Oxyz, cho
5;7;2 , 3;0;4 , 6;1; 1a b c
. Tọa độ của vecto
5 6 4 3n a b c i
là:
A.
16;39;26n
B.
16; 39;26n 
C.
16;39;26n 
D.
16;39; 26n 
C©u 55 :
Cho
󰇛
 
󰇜
󰇛
 
󰇜
󰇛
 
󰇜
󰇛  󰇜 thì tứ giác ABCD là hình:
A.
Bình hành
B.
Vuông
C.
Chữ nhật
D.
Thoi
C©u 56 :
Phương trình mặt phẳng
()P
đi qua
1;2;3A
và song song với mặt phẳng
( ):2x 5 0Q y z
A.
2 2 0x y z
B.
2 3 0x y z
C.
2 1 0x y z
D.
2 3 0x y z
C©u 57 :
Trong không gian với hệ tọa độ Oxyz cho hai điểm
(2; 4;5)M
và
( 3;2;7)N
. Điểm P
trên trục Ox cách đều hai điểm M và N có tọa độ là:
A.
19
;0;0
10
P
B.
9
;0;0
10
P
C.
17
;0;0
10
P
D.
7
;0;0
10
P
10
C©u 58 :
Trong không gian với hệ tọa độ
Oxyz
,hai đường thẳng
1
11
2 3 1
:
x y z
d


và đường
thẳng
2
1 2 7
1 2 3
:
x y z
d


có vị trí tương đối là :
A.
Cắt nhau
B.
Trùng nhau
C.
Chéo nhau
D.
Song song.
C©u 59 :
Khoảng cách giữa hai điểm
1; 1; 3M
và
2; 2; 3N
bằng
A.
4MN
B.
3MN
C.
32MN
D.
25MN
C©u 60 :
Trong không gian với hệ tọa độ Oxyz cho ba điểm
(1;2;4), (2; 1;0), P( 2;3; 1)MN
.
Để tứ giác MNPQ là hình bình hành thì tọa độ đỉnh Q là:
A.
( 1;2;1)Q
B.
33
;3;
22
Q
C.
( 3;6;3)Q
D.
(3; 6; 3)Q
C©u 61 :
Mặt phẳng đi qua 3 điểm
(1;0;0), (0; 2;0), (0;0; 2)M N P
có phương trình là:
A.
2 1 0x y z
B.
2 2 2 0x y z
C.
1
1 2 2
x y z
D.
1 2 2
x y z


C©u 62 :
Trong hệ tọa độ Oxyz cho hình hộp MNPQ.M’N’P’Q’ có M(1;0;0) N(2;-1;1) Q(0;1;0)
M’(1;2;1). Điểm P’ có tọa độ:
A.
(3;1;0)
B.
(1;2;2)
C.
(0;3;1)
D.
(2;1;2)
C©u 63 :
Trong không gian Oxyz, cho mặt cầu
2 2 2
: 2 2 2 4 8 2 0S x y z x y
. Tọa độ tâm
I và bán kính R của mặt cầu là:
A.
1;2;0 ; 4IR
B.
1; 2;0 ; 2IR
C.
1;2;0 ; 2IR
D.
1;2;0 ; 4IR
C©u 64 :
Cho đường thẳng
1
qua điểm M có VTCP
1
u
, và
2
qua điểm N có VTCP
2
u
. Điều
11
kiện để
1
và
2
chéo nhau là:
A.
1
u
và
2
u
cùng phương.
B.
12
, . 0u u MN


C.
12
,uu


và
MN
cùng phương.
D.
12
, . 0u u MN


C©u 65 :
Trong không gian Oxyz, cho điểm
4; 3;2A
, và đường thẳng
22
:
3 2 1
x y z
d


.
Tọa độ hình chiếu vuông góc của A lên đường thẳng d là:
A.
1;0; 1H
B.
1;0;1H
C.
1;0; 1H 
D.
0;1; 1H
C©u 66 :
Trong không gian với hệ tọa độ
Oxyz
,mặt cầu
2 2 2
2 4 6 2() 0:x yz xzS y
có
tâm I, bán kính R là :
A.
( 2;4; 6), 58IR
B.
( 1;2; 3), 4IR
C.
(1; 2;3), 4IR
D.
(2; 4;6), 58IR
C©u 67 :
Giao điểm
A
của đường thẳng
13
:1
22
yz
x

và mặt phẳng
:2x 2 3 0P y z
có tọa độ:
A.
( 2; 1; 5)A
B.
( 2; 1;5)A 
C.
( 2;1;5)A
D.
(2; 1;5)A
C©u 68 :
Phương trình mặt phẳng
()P
đi qua gốc tọa độ
O
và vuông góc với hai mặt phẳng
( ):2 3 1 0Q x y z
,
( ): 2 0R x y z
:
A.
7 5 0x y z
B.
7 5 0x y z
C.
7 5 0x y z
D.
7 5 0x y z
C©u 69 :
Trong hệ tọa độ Oxyz, cho điểm M(1;2;-6) và đường thẳng d có phương trình:
22
1
3
xt
yt
zt


. Hình chiếu vuông góc của điểm M lên đường thẳng d có tọa độ là:
A.
(-2;0;4)
B.
4;0;2
12
C.
2;0;4
D.
0;2; 4
C©u 70 :
Trong không gian Oxyz, cho
1;0; 3 , 1; 3; 2 , 1;5;7A B C
. Gọi G là trong tâm của
tam giác ABC. Khi đó độ dài của OG là
A.
3
B.
5
C.
3
D.
5
C©u 71 :
Trong hệ tọa độ Oxyz, mặt phẳng
đi qua điểm M(2;-1;4) và chắn trên nửa trục
dương Oz gấp đôi đoạn chắn trên nửa trục Ox, Oy có phương trình là:
A.
2 6 0x y z
B.
2 6 0x y z
C.
2 2 6 0x y z
D.
2 2 6 0x y z
C©u 72 :
Trong không gian Oxyz, cho các điểm
1;3;2 , 1;2;1 , 1;1;3A B C
. Phương trình
đường thẳng đi qua trọng tâm G của tam giác ABC và vuông góc với mặt phẳng
(ABC) là:
A.
1
2
2
xt
y
z

B.
12
2
2
xt
yt
zt



C.
12
3
2
xt
yt
zt



D.
1
2
3
xt
y
z

C©u 73 :
Trong hệ tọa độ Oxyz cho các điêm M(1;2;3) N(2;2;3) P(1;3;3) Q(1;2;4) MNPQ là hình
gì:
A.
Tứ giác
B.
Hình bình hành
C.
Hình thang
D.
Tứ diện
C©u 74 :
Điều kiện cần và đủ để ba vec tơ
a, ,bc
khác
0
đồng phẳng là:
A.
a. . 0bc
B.
a, . 0bc


C.
Ba vec tơ đôi một vuông góc nhau.
D.
Ba vectơ có độ lớn bằng nhau.
C©u 75 :
Cho mặt phẳng
( ): 4 0P x y z
và điểm
(1; 2; 2)A 
. Tọa độ
'A
là đối xứng của
A
13
qua
()P
A.
'(3;4;8)A
B.
'(3;0; 4)A
C.
'(3;0;8)A
D.
'(3;4; 4)A
C©u 76 :
Cho
󰇛
 
󰇜
󰇛
 
󰇜
󰇛
 
󰇜
󰇛
  
󰇜
thì ABCD là hình:
A.
Bình hành
B.
Vuông
C.
Thoi
D.
Chữ nhật
C©u 77 :
Chọn phát biểu đúng: Trong không gian
A.
Vec tơ có hướng của hai vec tơ thì
cùng phương với mỗi vectơ đã cho.
B.
Tích có hướng của hai vec tơ là một
vectơ vuông góc với cả hai vectơ đã
cho.
C.
Tích vô hướng của hai vectơ là một
vectơ.
D.
Tích của vectơ có hướng và vô hướng
của hai vectơ tùy ý bằng 0
C©u 78 :
Trong hệ tọa độ Oxyz cho điêm M(3;1;-2). Điểm N đối xứng với M trục Ox có tọa
độ là:
A.
(-3;1;2)
B.
(-3;-1;-2)
C.
(3;1;0)
D.
(3;-1;2)
C©u 79 :
Trong không gian với hệ tọa độ Oxyz cho ba vectơ
(5;4; 1), ( 2; 5;3)ab
và
c
thỏa hệ thức
2a c b
. Tọa độ
c
là:
A.
3; 9;4
B.
39
; ; 2
22
C.
39
; ;2
22
D.
39
; ;1
44
C©u 80 :
Cho (S):
2 2 2
4x 2 10z+14 0x y z y
. Mặt phẳng (P):
x 4 0yz
cắt mặt cầu
(S) theo một đường tròn có chu vi là:
A.
8
B.
4
C.
43
D.
2
14
ĐÁP ÁN
01
{ ) } ~
28
{ | } )
55
{ | } )
02
) | } ~
29
{ ) } ~
56
{ ) } ~
03
{ | ) ~
30
) | } ~
57
{ | ) ~
04
{ | ) ~
31
{ | ) ~
58
{ | ) ~
05
{ | ) ~
32
{ ) } ~
59
{ ) } ~
06
{ ) } ~
33
{ | } )
60
{ | ) ~
07
{ | ) ~
34
{ ) } ~
61
{ | ) ~
08
) | } ~
35
) | } ~
62
{ | } )
09
) | } ~
36
{ | ) ~
63
) | } ~
10
{ | } )
37
{ | } )
64
{ ) } ~
11
) | } ~
38
{ | ) ~
65
) | } ~
12
) | } ~
39
) | } ~
66
{ | ) ~
13
{ | ) ~
40
{ ) } ~
67
{ ) } ~
14
) | } ~
41
{ ) } ~
68
{ ) } ~
15
{ | ) ~
42
{ ) } ~
69
{ | } )
16
) | } ~
43
) | } ~
70
) | } ~
17
{ | } )
44
{ | } )
71
{ | } )
18
{ | } )
45
{ | } )
72
) | } ~
19
{ | } )
46
{ | ) ~
73
{ | } )
20
{ | ) ~
47
) | } ~
74
{ ) } ~
21
{ | } )
48
) | } ~
75
{ ) } ~
22
) | } ~
49
{ ) } ~
76
{ | } )
23
{ | } )
50
{ ) } ~
77
{ ) } ~
24
) | } ~
51
{ ) } ~
78
{ | } )
25
{ | ) ~
52
{ | ) ~
79
{ | ) ~
26
{ | } )
53
{ | } )
80
{ ) } ~
27
{ | ) ~
54
) | } ~
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN
ĐỀ 007
C©u 1 :
Mặt phẳng nào sau đây chứa trục Oy?
A.
–y + z = 0
B.
-2x + z =0
C.
-2x – y + z =0
D.
-2x – y = 0
C©u 2 :
Cho lăng trụ tam giác đều ABC.A’B’C’ cạnh đáy bằng
a
và
. Tính thể
tích khối lăng trụ.
Một học sinh giải như sau:
Bước 1: Chọn hệ trục toạ độ như hình vẽ. Khi đó:
33
;0; 0 ; 0; ;0 ; ' 0; ; ;
2 2 2
;0; 0 ; ' ;0;
22
a a a
A B B h
aa
C C h
với
h
là chiều cao của lăng trụ, suy ra:
33
' ; ; ; ' ; ;
2 2 2 2
a a a a
AB h BC h
Bước 2:
22
2
32
' ' '. ' 0 0
4 4 2
a a a
AB BC AB BC h h
Bước 3:
l¨ng trô
23
3 2 6
..
2 2 4
a a a
V B h
O
z
y
x
A'
B'
C'
C
B
A
2
Bài giải này đã đúng chưa? Nếu sai thì sai ở bước nào?
A.
Sai ở bước 2
B.
Sai ở bước 1
C.
Sai ở bước 3
D.
Đúng
C©u 3 :
Trong không gian Oxyz cho mặt cầu
2 2 2
: 2 2 2 22 0S x y z x y z
, và mặt
phẳng
:3 2 6 14 0P x y z
. Khoảng cách từ tâm I của mặt cầu (S) đến mặt phẳng
(P) là
A.
2
B.
1
C.
3
D.
4
C©u 4 :
Trong không gian tọa độ Oxyz, cho điểm M=(3; 1; 2). Phương trình của mặt phẳng
đi qua hình chiếu của M trên các trục tọa độ là:
A.
-3x – y – 2z =0
B.
2x + 6y + 3z – 6 =0
C.
3x + y + 2z = 0
D.
-2x – 6y – 3z – 6 =0
C©u 5 :
Trong không gian Oxyz cho ba vectơ
1;1;0 , 1;1;0 , 1;1;1a b c
. Trong các
mệnh đề sau, mệnh đề nào sai?
A.
3c
B.
bc
C.
ab
D.
2a
C©u 6 :
Trong không gian (Oxyz). Cho đường thẳng
2
:1
13
xt
yt
zt


. và mặt phẳng (P):
3 1 0x y z
. Mặt phẳng (Q) chứa
và vuông góc với (P) có phương trình là:
A.
5 2 2 13 0x y z
B.
5 2 13 0x y z
C.
5 2 13 0x y z
D.
5 2 13 0x y z
C©u 7 :
Trong không gian (Oxyz). Cho điểm
1;1;2M
và đường thẳng
11
:
2 1 1
x y z
. Tọa độ hình chiếu vuông góc của M lên
là:
A.
1 1 2
;;
3 6 3



B.
1 1 2
;;
3 3 3




C.
1 1 2
;;
3 3 3




D.
1 1 2
;;
633



C©u 8 :
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
:3 2 12 0x y z
và
đường thẳng
: 6 3
3
xt
yt
zt
. Trong các mệnh đề sau, mệnh đề nào đúng.
3
A.

B.
cắt
C.

D.
//
C©u 9 :
Trong không gian Oxyz cho hai điểm
(–1;3;–2), (–3;7; –18)AB
và mặt phẳng (P):
2 – 1 0x y z
. Gọi
;;M a b c
là điểm trên (P) sao cho MA+MB nhỏ nhất. Giá trị
của
abc
là
A.
1
B.
3
C.
2
D.
4
C©u 10 :
Trong không gian với hệ tọa độ Oxyz, cho điểm
1, 1,1M
và hai đường thẳng
x y z
d
1
1
( ) :
1 2 3


và
x y z
d
2
14
( ) :
1 2 5


. Mệnh đề nào dưới đây là đúng.
A.
1
()d
,
1
()d
và M đồng phẳng
B.
1
Md
nhưng
2
Md
C.
2
Md
nhưng
1
Md
D.
1
()d
và
1
()d
vuông góc nhau
C©u 11 :
Cho hai đường thẳng
1
7 3 9
:
1 2 1
x y z
d
và
2
3 1 1
:
7 2 3
x y z
d
.
Phương trình đường vuông góc chung của
1
d
và
2
d
là:
A.
3 1 1
1 2 4
x y z
B.
7 3 9
2 1 4
x y z
C.
7 3 9
2 1 4
x y z
D.
7 3 9
2 1 4
x y z
C©u 12 :
Trong không gian với hệ tọa độ
Oxyz
cho 3 điểm
M 2;3; 1
,
N 1;1;1
,
P 1;m 1;2
. Với giá trị nào của
m
thì tam giác
MNP
vuông tại
N
?
A.
m3
B.
m2
C.
m1
D.
m0
C©u 13 :
Trong không gian (Oxyz).Cho 3 điểm
1;0; 1 , 2;1; 1 , 1; 1;2ABC
. Điểm M
thuộc đường thẳng AB mà
14MC
có tọa độ là:
A.
2;2; 1 , 1; 2; 1MM
B.
2;1; 1 , 1; 2; 1MM
C.
2;1; 1 , 1; 2; 1MM
D.
2;1;1 , 1;2; 1MM
C©u 14 :
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm
2, 1,5 ; 5, 5,7 ; 11, 1,6 ; 5,7,2A B C D
.Tứ giác là hình gì?
A.
Hình thang
B.
Hình bình hành
C.
Hình thoi
D.
Hình vuông
4
C©u 15 :
Trong không gian với hệ tọa độ Oxyz, cho ba mặt phẳng
:2 4 5 2 0, : 2 2 1 0, :4 0x y z x y z x my z n
Để
,,
có chung giao tuyến thì tổng
mn
là
A.
-4
B.
8
C.
-8
D.
4
C©u 16 :
Cho 4 điểm
M 2; 3;5
,
N 4;7; 9
,
P 3;2;1
,
Q 1; 8;12
. Bộ 3 điểm nào sau đây là
thẳng hàng:
A.
N,P,Q
B.
M,N,P
C.
M,P,Q
D.
M,N,Q
C©u 17 :
Cho các điểm A(1; -2; 1), B(2; 1; 3) và mặt phẳng (P) : x – y + 2z – 3 = 0. Đường thẳng
AB cắt mặt phẳng (P) tại điểm có tọa độ:
A.
(0;5;1)
B.
(0; 5;1)
C.
(0;5; 1)
D.
(0; 5; 1)
C©u 18 :
Mặt phẳng (Q) đi qua hai điêm A(1; 0; 1), B(2; 1; 2) và vuông góc với mặt phẳng
2 3 3 0
P x y z
( ) :
cắt trục oz tại điểm có cao độ
A.
2
B.
4
C.
3
D.
1
C©u 19 :
Cho hai điểm
(3;3;1), (0;2;1)AB
và mp(P):
70x y z
. Đường thẳng
d
nằm
trên mp(P) sao cho mọi điểm của
d
cách đều hai điểm A, B có phương trình là:
A.
73
2
xt
yt
zt
B.
73
2
xt
yt
zt
C.
73
2
xt
yt
zt
D.
2
73
xt
yt
zt
C©u 20 :
Góc giữa hai đường thẳng d :
4 3 1
2 1 1
x y z

và d’ :
5 7 3
2 4 2
x y z

là :
A.
30
o
B.
90
o
C.
45
o
D.
60
o
C©u 21 :
Cho hai đường thẳng
1
:d
d1:
1
x
=
3
2
y
=
1
3
z
, d2:
4
1
x
=
1
y
=
3
2
z
. Hai đường thẳng
đó:
A.
Chéo nhau
B.
Trùng nhau
C.
Cắt nhau
D.
Song song
C©u 22 :
Cho ba điểm A(1; 0; 1), B(-1; 1; 0), C(2; -1; -2). Phương trình mặt phẳng (ABC) là:
5
A.
x – 2y + 3z – 6 = 0
B.
- 4x – 7y + z – 2 = 0
C.
x – 2y + 3z + 1 = 0
D.
4x + 7y – z – 3 = 0.
C©u 23 :
Cho đường thẳng
13
:
2 3 2
x y z
d
và mp(P):
2 8 0x y z
. Mặt phẳng
chứa
d
và vuông góc với mp(P) có phương trình là:
A.
2 2 8 0x y z
B.
2 2 8 0x y z
C.
2 2 8 0x y z
D.
2 2 8 0x y z
C©u 24 :
Cho hai mặt phẳng
P : x y z 1 0, Q : x y z 5 0
. Điểm nằm trên
Oy
cách điều
P
và
Q
là:
A.
0;3;0
B.
0; 3;0
C.
0; 2;0
D.
0;2;0
C©u 25 :
Cho hai đường thẳng
1
2
:1
2
xt
d y t
zt
và
2
22
:3
xt
dy
zt
.
Mặt phẳng cách đều hai đường thẳng
1
d
và
2
d
có phương trình là:
A.
5 2 12 0x y z
B.
5 2 12 0x y z
C.
5 2 12 0x y z
D.
5 2 12 0x y z
C©u 26 :
Trong không gian toạ độ Oxyz, cho hai điểm A(1; -1; 0) và B(-2; 0; 1). Phương trình
mặt phẳng trung trực (P) của đoạn thẳng AB là:
A.
-3x + y + z +3 =0
B.
-6x + 2y + 2z – 3=0
C.
-6x + 2y + 2z + 3=0
D.
-3x + y + z -3 =0
C©u 27 :
Cho hai véctơ
,uv
khác
0
. Phát biểu nào sau đây không đúng?
A.
,uv


có độ dài là
cos ,u v u v
B.
,0uv


khi hai véctơ
,uv
cùng
phương.
C.
,uv


vuông góc với hai véctơ
,uv
D.
,uv


là một véctơ
C©u 28 :
Trong không gian (Oxyz). Cho điểm
1;0;2A
và mặt phẳng
6
(P):
2 3 0x y z
. Mặt cầu (S) tâm A tiếp xúc với mặt phẳng (P) tại điểm H có
tọa độ là:
A.
2 1 11
;;
3 6 6
H



B.
2 1 11
;;
3 6 6
H




C.
2 1 11
;;
3 6 3
H




D.
2 1 11
;;
3 6 6
H



C©u 29 :
Cho
A 2;2;0
,
B 2;4;0
,
C 4;0;0
và
D 0; 2;0
. Mệnh đề nào sau đây là đúng
A.
ABCD
tạo thành tứ diện
B.
Diện tích
ABC
bằng diện tích
DBC
C.
ABCD
là hình chóp đều
D.
ABCD
là hình vuông
C©u 30 :
Trong không gian Oxyz cho mặt cầu
2 2 2
: 1 3 2 49S x y z
. Phương trình
nào sau đây là phương trình của mặt phẳng tiếp xúc với mặt cầu (S) ?
A.
6 2 3 0x y z
B.
2 2 7 0x y z
C.
6 2 3 55 0x y z
D.
2 3 6 5 0x y z
C©u 31 :
Cho mặt phẳng (P) : 2x + y - 2z - 1 = 0 và đường thẳng d :
23
1 2 3
x y z

. Phương
trình mặt phẳng chứa d và vuông góc với (P) là :
3 1 1
1 2 3
x y z

A.
x + 8y + 5z + 31 = 0
B.
5x + y + 8z + 14 = 0
C.
5x + y + 8z = 0
D.
x + 8y + 5z +13 = 0
C©u 32 :
Mặt phẳng nào sau đây cắt các trục tọa độ Ox, Oy, Oz lần lượt tại A, B, C sao cho
tam giác ABC nhận điểm G(1; 2; 1) làm trọng tâm?
A.
x + 2y + 2z -6 =0
B.
2x + y + 2z – 6 =0
C.
2x + 2y + z – 6=0
D.
2x + 2y + 6z – 6 =0
C©u 33 :
Trong không gian (Oxyz). Cho mặt cầu
(S) :
2 2 2
4 5 0x y z x
. Điểm A thuộc mặt cầu (S) và có tọa độ thứ nhất bằng -
1. Mặt phẳng (P) tiếp xúc với (S) tại A có phương trình là:
A.
10xy
B.
10x 
C.
10y 
D.
10x 
7
C©u 34 :
Trong không gian với hệ tọa độ 0xyz, cho M(-2;1;0) và đường thẳng
2 1 1
:
1 1 2
x y z
. Điểm N thuộc
sao cho
11MN
. Tọa độ điểm N là:
A.
1,2, 1
B.
1,2,1
C.
2,1,1
D.
2, 1,1
C©u 35 :
Trong không gian với hệ toạ độ Oxyz, cho
2,0,0 , 1,1,1AB
. Mặt phẳng (P) thay đổi
qua A,B cắt các trục Ox, Oy lần lượt tại B(0; b; 0), C(0; 0; c) (b > 0, c > 0). Hệ thức nào
dưới đây là đúng.
A.
2bc b c
B.
11
bc
bc

C.
b c bc
D.
bc b c
C©u 36 :
Mặt cầu tâm I(1; -2; 3) tiếp xúc với mặt phẳng (P) : 2x – y + 2z – 1 = 0 có phương
trình :
A.
2 2 2
( 2) (( )31 3) yx z 
B.
2 2 2
( 2) (( )91 3) yx z 
C.
2 2 2
( 2) (( )31 3) yx z 
D.
2 2 2
( 2) (( )91 3) yx z 
C©u 37 :
Trong không gian với hệ toạ độ Oxyz, cho đường thẳng
x y z
d
1 1 2
:
2 1 3

và mặt
phẳng
P
:
x y z
10
.Đường thẳng qua
1,1,1A
song song với mặt phẳng
P
()
và vuông góc với đường thẳng d. Véctơ chỉ phương của là:
A.
1, 1, 1
B.
2, 5, 3
C.
2,1,3
D.
4,10, 6
C©u 38 :
Cho mặt phẳng (P) : 2x – 2y – z – 4 = 0 và mặt cầu (S) :
2 2 2
2 4 6 11 0yx x y zz
.
Bán kính đường tròn giao tuyến là:
A.
2
B.
5
C.
3
D.
4
C©u 39 :
Nếu mặt phẳng
(α)
qua ba điểm M(0; -1; 1), N(1; -1; 0), và P(1; 0; -2) thì nó có một
vectơ pháp tuyến là:
A.
n = (1; 1; 2)
B.
n = (1; 2; 1)
C.
n = (-1; 2; -1)
D.
n = (2; 1; 1)
C©u 40 :
Cho hai điểm
(1;4;2), ( 1;2;4)AB
và đường thẳng
12
:
1 1 2
x y z
. Điểm
M
mà
22
MA MB
nhỏ nhất có toạ độ là:
A.
(1;0;4)
B.
(0; 1; 4)
C.
( 1; 0;4)
D.
(1;0; 4)
C©u 41 :
Trong không gian (Oxyz). Cho mặt cầu
8
(S):
2 2 2
2 4 2 3 0x y z x y z
và mặt phẳng
(P):
2 2 1 0x y z m
( m là tham số). Mặt phẳng (P) tiếp xúc với mặt cầu (S)
ứng với giá trị m là:
A.
3
15
m
m


B.
3
15
m
m

C.
3
5
m
m

D.
3
15
m
m
C©u 42 :
Trong không gian (Oxyz). Cho tứ diện ABCD biết
1; 1; 2 , 0;3;0 ,AB
3;1; 4 , 2;1; 3CD
. Chiều cao của tứ diện hạ từ đỉnh A là:
A.
1
3
B.
2
3
C.
2
3
D.
4
9
C©u 43 :
Trong không gian với hệ tọa độ Oxyz, gọi
là góc hợp bởi đường thẳng
3 4 3
1 2 1
x y z

và mặt phẳng
2 1 0x y z
thì
cos
bằng:
A.
3
2
B.
1
2
C.
1
2
D.
3
2
C©u 44 :
Cho hai đường thẳng
1
2 1 3
:
1 2 2
x y z
d
và
2
1 1 1
:
1 2 2
x y z
d
.
Khoảng cách giữa
1
d
và
2
d
bằng:
A.
43
2
B.
42
C.
42
3
D.
4
3
C©u 45 :
Hai mặt phẳng
)(
: 3x + 2y – z + 1 = 0 và
)'(
: 3x + y + 11z – 1 = 0
A.
Song song với nhau;
B.
Vuông góc với nhau.
C.
Trùng nhau;
D.
Cắt nhau nhưng không vuông góc với
nhau;
C©u 46 :
Trong không gian Oxyz cho bốn điểm
1;0;0 , 0;1;0 , 0;0;1 , 1;1;1A B C D
Trong các
mệnh đề sau, mệnh đề nào sai ?
A.
AB CD
B.
Bốn điểm A, B, C, D tạo thành một tứ
diện
C.
Tam giác BCD đều
D.
Tam giác BCD vuông cân
9
C©u 47 :
Cho hai đường thẳng
1
3 6 1
:
2 2 1
x y z
d
và
2
:
2
xt
d y t
z
Đường thẳng đi qua
điểm
(0;1;1)A
, vuông góc với
1
d
và cắt
2
d
có phương trình là:
A.
11
1 3 4
x y z
B.
11
1 3 4
x y z
C.
11
1 3 4
x y z
D.
11
1 3 4
x y z
C©u 48 :
Cho ba điểm A(3; 2; -2) , B(1; 0; 1) và C(2; -1; 3). Phương trình mặt phẳng đi qua A
và vuông góc với BC là:
A.
2 3 0x y z
B.
2 5 0x y z
C.
2 1 0x y z
.
D.
2 3 0x y z
C©u 49 :
Cho đường thẳng
84
: 5 2
xt
d y t
zt
và điểm
(3; 2;5)A
. Toạ độ hình chiếu của điểm
A trên
d
là:
A.
(4; 1; 3)
B.
( 4; 1;3)
C.
(4; 1;3)
D.
( 4;1; 3)
C©u 50 :
Trong không gian Oxyz cho điểm
0; 1;3A
và đường thẳng
12
:2
xt
dy
zt


. Khoảng
cách từ A đến đường thẳng d bằng
.
A.
3
B.
6
C.
14
D.
8
C©u 51 :
Trong không gian Oxyz cho hai đường thẳng
1
13
:
1 2 3
x y z
d


và
2
2
: 1 4
26
xt
d y t
zt


.
Khẳng định nào sau đây là đúng ?
A.
12
,dd
trùng
nhau.
B.
12
,dd
cắt nhau.
C.
12
dd
D.
12
,dd
chéo
nhau.
C©u 52 :
Khoảng cách giữa hai mặt phẳng
: 2 1 0x y z
và
: 2 5 0x y z
là
10
A.
6
B.
4
C.
5
D.
3
C©u 53 :
Trong không gian với hệ tọa độ Oxyz, giả sử mặt cầu
2 2 2 2
: 4 4 2 4 0
m
S x y z mx y mz m m
có bán kính nhỏ nhất. Khi đó giá trị của
m là:
A.
1
2
B.
1
3
C.
3
2
D.
0
C©u 54 :
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(0; 1; 2), B(2; –2; 1), C(–2; 0; 1).
Gọi
;;M a b c
là điểm thuộc mặt phẳng (P):
2 2 – 3 0x y z
sao cho MA=MB=MC.
Giá trị của
abc
là
A.
-2
B.
0
C.
-1
D.
-3
C©u 55 :
Trong không gian (Oxyz).
Cho mặt cầu (S):
2 2 2
1 2 3 0x y z
. Gọi I là tâm của mặt cầu (S). Giao
điểm của OI và mặt cầu (S) có tọa độ là:
A.
1; 2; 3
và
3; 6;9
B.
1;2; 3
và
3; 6;9
C.
1;2; 3
và
3; 6; 9
D.
1;2; 3
và
3;6;9
C©u 56 :
Cho
A 2; 1;6
,
B 3; 1; 4
,
C 5; 1;0
tam giác
ABC
là
A.
Tam giác vuông
cân
B.
Tam giác cân
C.
Tam giác đều
D.
Tam giác vuông
C©u 57 :
Trong không gian với hệ toạ độ Oxyz, cho điểm M(0;1;1) và 2 đường thẳng (d1), (d2)
với: (d1):
12
3 2 1
x y z

; (d2) là giao tuyến của 2 mặt phẳng (P):
10x
và (Q):
20x y z
. Gọi (d) là đường thẳng qua M vuông góc (d1) và cắt (d2). Trong số các
điêm A(0;1;1),
B(-3;3;6), C(3;-1;-3), D(6;-3;0), có mấy điểm nằm trên (d)?
A.
2
B.
0
C.
1
D.
3
C©u 58 :
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
2 2 2
; 2 4 6 0S x y z x y z
và
ba điểm
0,0,0 ; 1,2,3 ; 2, 1, 1O A B 
. Trong ba điểm trên, số điểm nằm bên trong
mặt cầu là
A.
1
B.
2
C.
0
D.
3
11
C©u 59 :
Trên mặt phẳng
Oxy
, cho điểm E có hoành độ bằng 1, tung độ nguyên và cách đều
mặt phẳng
: x 2y z 1 0
và mặt phẳng
: 2x y z 2 0
. Tọa độ của E
là:
A.
1;4;0
B.
1;0; 4
C.
1;0;4
D.
1; 4;0
C©u 60 :
Trong không gian Oxyz cho mặt cầu
2 2 2
: 2 4 6 0S x y z x y z
. Trong ba
0;0;0 , 1;2;3 , 2; 1; 1
điểm có bao nhiêu điểm thuộc mặt cầu (S) ?
A.
2
B.
0
C.
1
D.
3
C©u 61 :
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):
2 2 4 0x y z
và mặt cầu
(S): x
2
+ y
2
+ z
2
– 2x – 4y – 6z – 11 = 0. Mặt phẳng (P) cắt mặt cầu (S) theo một đường
tròn có chu vi là
A.
8
B.
2
C.
4
D.
6
C©u 62 :
Trong không gian
Oxyz
cho các điểm
A 1;1; 6
,
B 0;0; 2
,
C 5;1;2
và
D' 2;1; 1
.
Nếu
ABCD.A'B'C'D'
là hình hộp thì thể tích của nó là:
A.
36 (đvtt)
B.
40 (đvtt)
C.
42 (đvtt)
D.
38 (đvtt)
C©u 63 :
Phương trình đường thẳng đi qua hai điểm A(1; 2; -3) và B(3; -1; 1) là:
A.
1 2 3
3 1 1
x y z

B.
3 1 1
1 2 3
x y z

C.
1 2 3
2 3 4
x y z

D.
1 2 3
2 3 4
x y z

C©u 64 :
Cho hai đường thẳng
1
52
:1
5
xt
d y t
zt
và
2
92
:
2
xt
d y t
zt
.
Mặt phẳng chứa hai đường thẳng
1
d
và
2
d
có phương trình là:
A.
3 5 25 0x y z
B.
3 25 0x y z
C.
3 5 25 0x y z
D.
3 5 25 0x y z
C©u 65 :
Trong không gian Oxyz cho ba vectơ
1;1;0 , 1;1;0 , 1;1;1a b c
. Trong các
mệnh đề sau, mệnh đề nào đúng?
12
A.
.1ac
B.
,ab
cùng
phương
C.
2
,
6
bc cos
D.
0abc
C©u 66 :
Trong không gian Oxyz cho tam giác ABC có
1;0;1 , 0;2;3 , 2;1;0A B C
. Độ dài
đường cao của tam giác kẻ từ C là
A.
26
B.
26
2
C.
26
3
D.
26
C©u 67 :
Trong không gian Oxyz cho điểm
1;1;1A
và đường thẳng
64
:2
12
xt
d y t
zt

. Hình chiếu
của A trên d có tọa độ là
A.
2; 3; 1
B.
2;3;1
C.
2; 3;1
D.
2;3;1
C©u 68 :
Mặt cầu có tâm I(1; 2; 3) và tiếp xúc với mp(Oxz) là:
A.
2 2 2
x + y + z - 2x - 4y - 6z + 10 = 0
B.
2 2 2
x + y + z + 2x + 4y + 6z - 10 = 0
C.
2 2 2
x + y + z - 2x - 4y + 6z + 10 = 0
D.
2 2 2
x + y + z + 2x + 4y + 6z - 10 = 0
C©u 69 :
Trong không gian với hệ tọa độ Oxyz, cho 3 điểm
(1;2; 1), (2;1;1), (0;1;2)A B C
. Gọi
;;H a b c
là trực tâm của tam giác. Giá trị của
abc
A.
4
B.
5
C.
7
D.
6
C©u 70 :
Cho (P) : 2x – y + 2z – 1 = 0 và A(1; 3; -2). Hình chiếu của A trên (P) là H(a; b; c). Giá
trị của a – b + c là :
A.
3
2
.
B.
3
2
.
C.
2
3
.
D.
2
3
C©u 71 :
Cho hai điểm A(1; 0; -3) và B(3; 2; 1). Phương trình mặt cầu đường kính AB là:
A.
2 2 2
x + y + z - 2x - y + z - 6= 0
B.
2 2 2
x + y + z - 4x - 2y + 2z = 0
C.
2 2 2
x + y + z + 4x - 2y + 2z = 0
D.
2 2 2
x + y + z - 4x - 2y + 2z + 6 = 0
C©u 72 :
Trong không gian Oxyz cho
1;2;1A
, và hai mặt phẳng
:2 4 6 5 0, : 2 3 0P x y z Q x y z
. Trong các mệnh đề sau, mệnh đề nào
đúng?
A.
Mặt phẳng (Q) đi qua A và không song song với (P).
13
B.
Mặt phẳng (Q) không đi qua A và song song với (P).
C.
Mặt phẳng (Q) đi qua A và song song với (P).
D.
Mặt phẳng (Q) không đi qua A và không song song với (P).
C©u 73 :
Trong không gian (Oxyz). Cho 2 điểm
1;2;3 , 0;3;5AB
và đường thẳng d:
11
2 1 3
x y z

. Mặt phẳng (P) chứa 2 điểm A, B và song song với d có phương
trình là:
A.
5 7 16 0x y z
B.
5 7 16 0x y z
C.
5 7 16 0x y z
D.
5 7 16 0x y z
C©u 74 :
Tọa độ hình chiếu vuông góc của điểm M(2; 0; 1) trên đường thẳng
d :
12
1 2 1
x y z

là :
A.
(-1; -4; 0)
B.
(0; -2; 1)
C.
(2; 2; 3)
D.
(1; 0; 2)
C©u 75 :
Trong không gian với hệ tọa độ
Oxyz
, cho điểm
2; 5;4M
. Trong các phát biểu sau,
phát biểu nào sai:
A.
Tọa độ điểm
'M
đối xứng với
M
qua trục
Oy
là
2; 5; 4M
.
B.
Khoảng cách từ
M
đến trục
Oz
bằng
29.
C.
Khoảng cách từ
M
đến mặt phẳng tọa
xOz
bằng
5
.
D.
Tọa độ điểm
'M
đối xứng với
M
qua mặt phẳng
yOz
là
2;5; 4M
.
C©u 76 :
Cho hai điểm A(-3; 1; 2) và B(1; 0; 4). Mặt phẳng đi qua A và vuông góc với đường
thẳng AB có phương trình là:
A.
4x + y + 2z + 7 =0
B.
4x – y + 2z + 9 =0
C.
4x – y + 2z – 9 = 0
D.
4x – y – 2z + 17 =0
C©u 77 :
Cho
A 1;2; 1
,
B 5;0;3
,
C 7,2,2
. Tọa độ giao điểm M của trục
Ox
với mặt phẳng
qua
ABC
là:
A.
M 1;0;0
B.
M 1;0;0
C.
M 2;0;0
D.
M 2;0;0
14
C©u 78 :
Cho ba điểm A(0;1;2), B(3;0;1), C(1;0;0). Phương trình mặt phăng (ABC) là
A.
2 3 4 2 0x y z
B.
2 3 4 2 0x y z
C.
4 6 8 2 0x y x
D.
2 3 4 1 0x y x
C©u 79 :
Trong không gian (Oxyz). Cho điểm
1;0;2I
và đường thẳng
: 1 2
xt
yt
zt

. Đường
thẳng qua I vuông góc và cắt có
phương trình là:
A.
13
0
2
xt
y
zt


B.
13
0
2
xt
y
zt


C.
16
0
2
xt
y
zt


D.
13
0
2
xt
y
zt


C©u 80 :
Vectơ nào sau đây vuông góc với vectơ pháp tuyến của mặt phẳng 2x - y –z =0?
A.
n = (2; 1; -1)
B.
n = (1; 2; 0)
C.
n = (0; 1; 2)
D.
n = (-2; 1; 1)
C©u 81 :
Trong không gian với hệ tọa độ
Oxyz
cho 3 điểm
A 1;0;0
,
B 0;0;1
,
C 2;1;1
. Diện
tích của tam giác
ABC
bằng:
A.
7
2
B.
11
2
C.
5
2
D.
6
2
15
ĐÁP ÁN
01
{ ) } ~
28
{ ) } ~
55
{ ) } ~
02
{ | ) ~
29
{ | } )
56
{ | } )
03
{ | ) ~
30
{ | ) ~
57
) | } ~
04
{ ) } ~
31
{ | } )
58
) | } ~
05
{ ) } ~
32
{ ) } ~
59
{ | } )
06
{ ) } ~
33
{ ) } ~
60
{ | ) ~
07
{ ) } ~
34
) | } ~
61
) | } ~
08
) | } ~
35
) | } ~
62
{ | } )
09
) | } ~
36
{ | } )
63
{ | } )
10
) | } ~
37
) | } ~
64
{ | ) ~
11
{ | ) ~
38
{ | } )
65
{ | ) ~
12
{ | } )
39
{ ) } ~
66
{ | ) ~
13
{ ) } ~
40
{ | ) ~
67
{ | ) ~
14
) | } ~
41
{ ) } ~
68
) | } ~
15
) | } ~
42
{ ) } ~
69
) | } ~
16
{ | } )
43
) | } ~
70
{ | } )
17
{ | } )
44
{ | ) ~
71
{ ) } ~
18
) | } ~
45
{ ) } ~
72
{ | ) ~
19
{ | ) ~
46
{ | ) ~
73
{ ) } ~
20
{ | } )
47
{ | ) ~
74
{ | } )
21
) | } ~
48
{ | } )
75
{ | } )
22
{ | } )
49
{ | ) ~
76
{ ) } ~
23
{ | ) ~
50
{ | ) ~
77
{ | } )
24
{ | } )
51
{ | ) ~
78
) | } ~
25
{ | ) ~
52
) | } ~
79
{ ) } ~
26
{ ) } ~
53
) | } ~
80
{ ) } ~
27
) | } ~
54
) | } ~
81
{ | } )
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN
ĐỀ 008
C©u 1 :
Góc giữa 2 vectơ
󰇛

󰇜
và
󰇍
󰇛󰇜 là:
A.
30
0
B.
60
0
C.
135
0
D.
45
0
C©u 2 :
Cho mặt phẳng
(P):k(x y z) (x y z) 0
và điểm A(1;2;3). Chọn khẳng định đúng:
A.
Hình chiếu của A trên (P) luôn thuộc một đường tròn cố định khi k thay đổi.
B.
(P) luôn chứa trục Oy khi k thay đổi.
C.
Hình chiếu của A trên (P) luôn thuộc một mặt phẳng cố định khi k thay đổi.
D.
(P) không đi qua một điểm cố định nào khi k thay đổi
C©u 3 :
Cho mặt cầu
󰇛
󰇜

 và mặt phẳng (P): 4x+3y+1=0. Tìm mệnh đề
đúng trong các mệnh đề sau:
A.
(P) đi qua tâm của (S)
B.
(P) cắt (S) theo một đường tròn
C.
(S) không có điểm chung với (P)
D.
(S) tiếp xúc với (P)
C©u 4 :
Trong không gian Oxyz, cho ba vectơ
1,1,0 ; (1,1,0); 1,1,1a b c
. Cho hình hộp
OABC.O’A’B’C” thỏa mãn điều kiện
,,OA a OB b OC c
. Thể tích của hình hộp nói
trên bằng bao nhiêu?
A.
6
B.
2
C.
2
3
D.
1
3
C©u 5 :
Cho hình hộp
' 'C'D'ABCDA B
.Hãy xác định 3 vecto nào đồng phẳng:
A.
', ', 'AA BB CC
B.
, ,AA'AB AD
C.
, ' ', 'AD A B CC
D.
', , 'BB AC DD
C©u 6 :
Trong không gian với hệ trục tọa độ Oxyz cho tọa độ 4 điểm
2; 1;1 ;A
1;0;0 ;B
3;1;0C
và
0;2;1D
. Cho các mệnh đề sau :
(1) Độ dài
2.AB
(2) Tam giác BCD vuông tại B
2
(3) Thể tích của tứ diện A.BCD bằng 6
Các mệnh đề đúng là :
A.
(1) ; (2)
B.
(3)
C.
(1) ; (3)
D.
(2)
C©u 7 :
Trong không gian Oxyz,cho 2 đường thẳng
12
;dd
và mặt phẳng
P
12
1 1 1 1
: , :
1 1 1 2 1 2
x y z x y z
dd
:2 3 2 4 0P x y z
.Viết phương trình đường
thẳng
nằm trong
P
và cắt
1
d
,và đồng thời vuông với
2
d
A.
22
1 2 2
x y z

B.
3 2 2
1 2 2
x y z


C.
2 2 2
3 2 2
x y z

D.
322
221
x x z

C©u 8 :
Trong không gian Oxyz, xác định các cặp giá trị (l, m) để các cặp mặt phẳng sau đây song
song với nhau:
2 3 5 0; 6 6 2 0x ly z mx y z
A.
3,4
B.
4,3
C.
4; 3
D.
4,3
C©u 9 :
Trong không gian
Oxyz
,cho điểm
1, 1,1A
, đường thẳng
11
:
2 1 1
x y z
,mặt phẳng
:2 2 1 0P x y z
.Viết phương trình mặt phẳng
Q
chứa
và khoảng cách từ A đến
Q
lớn nhất
A.
2 3 1 0x y z
B.
2 3 1 0x y z
C.
2 3 2 0x y z
D.
2 3 3 0x y z
C©u 10 :
Trong không gian Oxyz cho hình lập phương ABCD.A’B’C’D’ với A(0 ; 0; 0), B(1; 0 ;
0), D(0; 1; 0), A’(0; 0; 1). Gọi M và N lần lượt là trung điểm của các cạnh AB và CD.
Tính khoảng cách giữa hai đường thẳng A’C và MN.
A.
1
2
B.
1
2
C.
1
2
D.
1
22
C©u 11 :
Trong không gian với hệ trục tọa độ Oxyz cho tọa độ cho mặt cầu
2
22
: 2 9S x y z
và mặt phẳng
: 1 0P x y z
. Biết (P) cắt (S) theo một
đường tròn, bán kính của đường tròn là :
A.
1
B.
3
C.
3
D.
6
C©u 12 :
Trong không gian Oxyz, gọi (P) là mặt phẳng cắt ba trục tọa độ tại ba điểm
3
8,0,0 ; 0, 2,0 ; 0,0,4A B C
. Phương trình của mặt phẳng (P) là:
A.
1
4 1 2
x y z
B.
4 2 8 0x y z
C.
0
8 2 4
x y z
D.
4 2 0x y z
C©u 13 :
Trong không gian với hệ trục tọa độ Oxyz cho tọa độ điểm
1;1;0M
và đường thẳng
31
:
1 2 1
x y z
. Phương trình mặt phẳng chứa M và là:
A.
3 2 0x y z
B.
4 2 5 0x y z
C.
2 3 0xy
D.
2 3 0xy
C©u 14 :
Cho hai điểm A(1; 4; 2), B(1; 2; 4) và đường thẳng
x 1 y 2 z
:
1 1 2

. Điểm
M
mà MA
2
+ MB
2
nhỏ nhất có tọa độ là:
A.
1;0; 4
B.
1;0;4
C.
1;0;4
D.
0; 1;4
C©u 15 :
Trong không gian với hệ trục tọa độ Oxyz cho hình bình hành ABCD với
0;1; 2 ; 1;0;0AB
;
0;3;1C
. Tọa độ đỉnh D là:
A.
1;4;1D
B.
2; 1;3D
C.
2;1;3D
D.
1;4; 1D
C©u 16 :
Cho điểm
(1,2,3)M
.Gọi
,,A B C
lần lượt là hình chiếu của M trên các trục
,,Ox Oy Oz
.Viết
mặt phẳng
ABC
A.
6 3 2 6 0x y z
B.
6 3 2 6 0x y z
C.
6 3 2 3 0x y z
D.
6 3 2 3 0x y z
C©u 17 :
Trong không gian Oxyz,cho 2 đường thẳng
12
;dd
và mặt phẳng
P
12
1 1 1 1
: , :
1 1 1 2 1 2
x y z x y z
dd
:2 3 2 4 0P x y z
.Viết phương trình đường
thẳng
nằm trong
P
và cắt
12
,dd
A.
2 3 1
3 2 2
x y z

B.
3 2 2
6 2 3
x y z


C.
122
3 2 3
x y z

D.
3 2 2
623
x y z

C©u 18 :
Cho mặt phẳng
󰇛
󰇜
  và đường thẳng



. Gọi
󰇛
󰇜
là
4
mặt phẳng chứa d và song song với
󰇛
󰇜
. Khoảng cách giữa
󰇛
󰇜
và
󰇛
󰇜
là:
A.

B.

C.

D.

C©u 19 :
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;4;1), B(–1;1;3) và mặt phẳng
(P):
x y z
– 3 2 – 5 0
. Viết phương trình mặt phẳng (Q) đi qua hai điểm A, B và
vuông góc với mặt phẳng (P).
A.
10 4 5 0
x y z
B.
10 4 11 0
x y z
C.
x y z
10 4 19 0
D.
Đáp án khác
C©u 20 :
Trong không gian với hệ tọa độ Oxyz cho ba điểm A(2; 0; 1), B(1; 0; 0)c C(1; 1; 1) và
mặt phẳng (P): x + y + z 2 = 0. Phương trình mặt cầu đi qua ba điểm A, B, C và có
tâm thuộc mặt phẳng (P) có dạng là:
A.
2 2 2
x y z x 2z 1 0
B.
2 2 2
x y z x 2y 1 0
C.
2 2 2
x y z 2x 2y 1 0
D.
2 2 2
x y z 2x 2z 1 0
C©u 21 :
Cho mặt cầu
2 2 2
(S): (x 1) (y 2) (z 3) 25
và mặt phẳng
:2x y 2z m 0
. Tìm m
để α và (S) không có điểm chung
A.
9 m 21
B.
9 m 21
C.
m9
hoặc
m 21
D.
m9
hoặc
m 21
C©u 22 :
Trong không gian với hệ trục tọa độ Oxyz cho hai mặt phẳng
:2 3 0P x y z
;
:0Q x y z
. (S) là mặt cầu có tâm thuộc (P) và tiếp xúc với (Q) tại điểm
1; 1;0H
.
Phương trình của (S) là :
A.
22
2
: 2 1 1S x y z
B.
22
2
: 1 1 3S x y z
C.
22
2
: 1 2 1S x y z
D.
22
2
: 2 1 3S x y z
C©u 23 :
Phương trình mặt phẳng đi qua 2 điểm
1; 1;5 , 0;0;1AB
và song song với Oy là:
A.
4 1 0xz
B.
4 1 0yz
C.
4 1 0xy
D.
4 1 0xz
C©u 24 :
Phương trình của 2 mặt phẳng tiếp xúc với mặt cầu:
2 2 2
: 6 4 2 11 0S x y z x y z
và
song song với mặt phẳng
:4 3 17 0xz
là:
A.
4 3 40 0xz
và
4 3 10 0xz
B.
4 3 40 0xz
và
4 3 10 0xz
5
C.
4 3 20 0xy
và
4 3 5 0xz
D.
4 3 40 0xy
và
4 3 10 0xy
C©u 25 :
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng
: 2 5 0P x y z
và đường
thẳng
31
:
2 1 1
x y z
d
tọa độ giao điểm của (P) và d là :
A.
3;1;0
B.
0;2; 1
C.
1;1; 2
D.
5; 1;0
C©u 26 :
Trong không gian cho đường thẳng
x 3 y 1 z 1
d:
3 1 1

. và mặt phẳng
(P):x z 4 0
.
Hình chiếu vuông góc của d trên (P) có phương trình:
A.
x 3 t
y 1 t
z 1 t


B.
x 3 t
y1
z 1 t

C.
x 3 3t
y 1 t
z 1 t


D.
x 3 t
y 1 2t
z 1 t


C©u 27 :
Trong không gian với hệ tọa độ Oxyz, cho điểm
I
(1; 2;3)
. Viết phương trình mặt cầu
tâm I và tiếp xúc với trục Oy.
A.
2 2 2
( 1) ( 2) ( 3) 9
x y z
B.
2 2 2
( 1) ( 2) ( 3) 16
x y z
C.
x y z
2 2 2
( 1) ( 2) ( 3) 10
D.
2 2 2
( 1) ( 2) ( 3) 8
x y z
C©u 28 :
Trong không gian với hệ tọa độ Oxyz , cho hai điểm
AB
(3;5;4) , (3;1;4)
. Tìm tọa độ
điểm C thuộc mặt phẳng
P x y z
( ) : 1 0
sao cho tam giác ABC cân tại C và có diện
tích bằng
2 17
.
A.
Đáp án khác
B.
C(7; 3; 3)
C.
C(4; 3; 0) và C(7;
3; 3)
D.
C(4; 3; 0)
C©u 29 :
Toạ độ điểm M’ là hình chiếu vuông góc của điểm M(2; 0; 1) trên


là:
A.
M’(-1; -4; 0)
B.
M’ (2; 2; 3)
C.
M’(1; 0; 2)
D.
M’(0; -2; 1)
C©u 30 :
Trong không gian Oxyz, cho mặt phẳng (P)đi qua hai điểm A(4,-1,1), B(3,1,-1) và song song
với trục Ox. Phương trình nào sau đây là phương trình của mặt phẳng (P):
A.
0xy
B.
0yz
C.
0xz
D.
0x y z
C©u 31 :
Trong không gian với hệ trục tọa độ Oxyz cho các vectơ
1;1 2 ;a
3;0; 1b
và
điểm
0;2;1A
tọa độ điểm M thỏa mãn:
2AM a b
là :
A.
5;1;2M
B.
3; 2;1M
C.
1;4; 2M
D.
5;4; 2M
6
C©u 32 :
Cho
u(2; 1;1), v(m;3; 1), w(1;2;1).
Ba vectơ đồng phẳng khi giá trị của m là:
A.
8
B.
4
C.
7
3
D.
8
3
C©u 33 :
Góc giữa đường thẳng
và mp
󰇛
󰇜
là:
A.
60
0
B.
45
0
C.
30
0
D.
90
0
C©u 34 :
Trong không gian cho hai đường thẳng:
12
x 1 t
x 1 y z 2
d : y 2 ; d :
2 1 3
z 3 t



Phương trình của đường thẳng d đi qua O(0;0;0) và vuông góc với cả
1
d
và
2
d
là:
A.
xt
y 5t
zt

B.
xt
yt
zt
C.
xt
y 5t
zt
D.
x1
y 5t
z1

C©u 35 :
Cho 2 điểm
(1,2, 1), ( 2,1,3)AB
.Tìm điểm M thuộc
Ox
sao cho tam giác AMB có diện tích
nhỏ nhất
A.
( 7,0,0)M
B.
1
( ,0,0)
7
M
C.
1
( ,0,0)
3
M
D.
(3,0,0)M
C©u 36 :
Trong không gian Oxyz, cho bốn điểm
1,1,1 ; 1,3,5 ; 1,1,4 ; 2,3,2A B C D
. Gọi I, J lần
lượt là trung điểm của AB và CD. Câu nào sau đây đúng?
A.
IJCD
B.
AB và CD có
chung trung điểm
C.
IJ ABC
D.
IJAB
C©u 37 :
Trong không gian cho hai đường thẳng:
12
x 1 t
x 1 y z 2
d : y 2 ; d :
2 1 3
z 3 t



Mặt phẳng (P) chứa
1
d
và song song với
2
d
. Chọn câu đúng:
A.
(P): x 5y z 6 0
B.
(P): x 5y z 1 0
C.
(P):x z 2 0
D.
Có vô số đường thẳng d thỏa mãn.
7
C©u 38 :
Trong không gian với hệ trục tọa độ Oxyz cho tọa độ cho mặt cầu
2
22
: 2 9S x y z
và mặt phẳng
:0P x y z m
, m là tham số. Biết (P) cắt (S)
theo một đường tròn có bán kính
6r
. Giá trị của tham số m là :
A.
3; 4mm
B.
3; 5mm
C.
1; 4mm
D.
1; 5mm
C©u 39 :
Trong không gian với hệ toạ độ Oxyz, cho điểm A(1; –2; 3) và đường thẳng d có
phương trình
x y z
1 2 3
2 1 1

. Tính khoảng cách từ điểm A đến đường thẳng d.
A.
72
B.
62
C.
52
D.
42
C©u 40 :
Cho điểm H(2; 1; 3). Gọi K là điểm đối xứng của H qua gốc tọa độ O. Khi đó độ
dài đoạn thẳng HK bằng:
A.
56
B.
12
C.
12
D.
56
C©u 41 :
Cho (S) là mặt cầu tâm
I(1;2;3)
và tiếp xúc với mặt phẳng
(P):x 2y 2z 3 0
. Bán kính
của (S) là:
A.
2
B.
6
C.
1
D.
2
3
C©u 42 :
Cho hai mặt phẳng
:2 3 6 0, : 3 2 5 1 10 0x my z m m x y m z

,
2 mặt phẳng song song với nhau khi:
A.
Không có m
B.
6m
C.
1m
D.
0m
C©u 43 :
Cho mặt cầu
2 2 2
(S):x y z 2x 2y 2z 1 0
. Đường thẳng d đi qua
O(0;0;0)
cắt (S) theo
một dây cung có độ dài bằng 2. Chọn khẳng định đúng:
A.
d nằm trên một mặt nón.
B.
x y z
d:
1 1 1


C.
d nằm trên một mặt trụ.
D.
Không tồn tại đường thẳng d.
C©u 44 :
Viết phương trình mặt phẳng đi qua OA và vuông góc với mặt phẳng (P) biết A(0;
2; 0) và (P): 2x + 3y 4z 2 = 0
A.
2x y 0
B.
2x y 0
C.
2x z 0
D.
2x z 0
C©u 45 :
Trong không gian Oxyz, cho điểm M(8,-2,4). Gọi A, B, C lần lượt là hình chiếu của M trên
các trục Ox, Oy, Oz. Phương trình mặt phẳng đi qua ba điểm A, B và C là:
A.
4 2 8 0x y z
B.
4 2 8 0x y z
8
C.
4 2 8 0x y z
D.
4 2 8 0x y z
C©u 46 :
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(4; 5; 6). Viết phương trình
mặt phẳng (P) qua A, cắt các trục tọa độ lần lượt tại I, J, K mà A là trực tâm của tam
giác IJK.
A.
2 3 29 0
x y z
B.
15 0
x y z
C.
x y z
4 5 6 77 0
D.
Đáp án khác
C©u 47 :
Gọi d’ là hình chiếu của



trên mặt phẳng (P):
. Góc giữa
d và d’ là:
A.
45
0
B.
60
0
C.
30
0
D.
Đáp án khác
C©u 48 :
Cho mặt cầu
S
:
2 2 2
2 4 64 0x y z x y
,các đường thẳng :
1 2 1 1 2
: , ':
7 2 2 3 2 1
x y z x y z
dd
.Viết phương trình mặt phẳng
P
tiếp xúc với mặt
cầu
S
và song song với
,'dd
A.
2 8 12 0
2 8 12 0
x y z
x y z
B.
2 8 69 0
2 8 69 0
x y z
x y z
C.
2 8 6 0
2 8 6 0
x y z
x y z
D.
2 8 13 0
2 8 13 0
x y z
x y z
C©u 49 :
Cho
1;2;1 , 1;1;1 , 0;3;2A B C
.tọa độ của
,AB BC


là:
A.
1; 2;3
B.
1,2,3
C.
1; 2; 3
D.
1;2; 3
C©u 50 :
Trong không gian với hệ trục tọa độ Oxyz cho tứ diện A.BCD với tọa độ
1;0;0 ; 2;1;1AB
;
0;3; 2 ; 1;3;0CD
, thể tích của tứ diện đã cho là:
A.
1
B.
1
6
C.
1
2
D.
6
C©u 51 :
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(0; 1; 2), B(2; –2; 1), C(–2; 0; 1).
Viết phương trình mặt phẳng (ABC) và tìm điểm M thuộc mặt phẳng (P):
x y z
2 2 – 3 0
sao cho MA = MB = MC .
A.
M(2; 1; - 3 )
B.
M(0; 1; 1)
C.
M
(2;3; 7)
D.
M(1; 1; - 1)
C©u 52 :
Trong không gian Oxyz, đường thẳng d nằm trong mặt phẳng Oxy và cắt cả hai đường thẳng
9
12
x 1 t x 2 2t
d : y 2 3t; d : y 3 2t
z 3 t z 1 t





có phương trình là:
A.
x4
yt
z0
B.
x4
y 16t
zt
C.
x4
yt
zt
D.
x 4 t
y 11 t
z0


C©u 53 :
Trong không gian Oxyz, cho ba vectơ
1,1,0 ; (1,1,0); 1,1,1a b c
. Trong các mệnh
đề sau, mệnh đề nào đúng?
A.
0abc
B.
6
cos ,
3
bc
C.
.1ab
D.
,,abc
đồng
phẳng.
C©u 54 :
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
x y z
d
57
:
2 2 1


và điểm
M
(4;1;6)
. Đường thẳng d cắt mặt cầu (S), có tâm M, tại hai điểm A, B sao cho
AB
6
.
Viết phương trình của mặt cầu (S).
A.
222
( 4) ( 1) ( 6) 12
x y z
B.
222
( 4) ( 1) ( 6) 9
x y z
C.
x y z
2 2 2
( 4) ( 1) ( 6) 18
D.
222
( 4) ( 1) ( 6) 16
x y z
C©u 55 :
Cho hai mặt phẳng
(P):x 2y z 4 0; (Q):2x y z 4 0
và điểm M(2;0;1). Phương
trình mặt phẳng (R) qua M và giao tuyến của (P) và (Q) là:
A.
3x 3y 2z 8 0
B.
3x 3y 2z 8 0
C.
x 2y z 4 0
D.
x y 3z 1 0
C©u 56 :
Mặt phẳng (P) tiếp xúc với mặt cầu
󰇛
󰇜

󰇛
󰇜
󰇛
󰇜
󰇛
󰇜
 tại điểm
M(7; -1; 5) có phương trình là:
A.
3x+y+z-22=0
B.
6x+2y+3z-55=0
C.
6x+2y+3z+55=0
D.
3x+y+z+22=0
C©u 57 :
Trong không gian với hệ trục Oxyz, cho mặt cầu (S):
x y z x y z
2 2 2
– 2 4 2 – 3 0
.
Viết phương trình mặt phẳng (P) chứa trục Ox và cắt mặt cầu (S) theo một đường
tròn có bán kính
r
3
.
A.
y – 2z -1 = 0
B.
y – 2z - 2 = 0
C.
y – 2z = 0.
D.
y – 2z + 1 = 0
C©u 58 :
Cho 2 đường thẳng








. Trong các mệnh đề sau,
mệnh đề nào đúng:
10
A.
và
chéo nhau
B.
song song với
C.
trùng
D.
vuông góc với
C©u 59 :
Cho hai mặt phẳng
: x y 2 z 4 0
và
: x y 2 z 0.
Tìm góc hợp bởi α và β
A.
0
30
B.
0
45
C.
0
90
D.
0
60
C©u 60 :
Phương trình mặt phẳng đi qua 3 điểm
1;1;0 , 3;0;4 , 1; 1;2A B C
là:
A.
3 4 4 1 0x y z
B.
4 3 4 1 0x y z
C.
4 3 4 1 0x y z
D.
3 4 4 1 0x y z
C©u 61 :
Trong không gian cho đường thẳng
x 2 y 1 z
d:
2 1 1


. và mặt phẳng
(P): x y z 3 0
.
Khẳng định nào sau đây đúng:
A.
Đường thẳng d nằm trong mặt phẳng (P).
B.
Đường thẳng d cắt mặt phẳng (P).
C.
Đường thẳng d song song với mặt phẳng
(P).
D.
Đường thẳng d vuông góc với mặt phẳng
(P).
C©u 62 :
Cho đường thẳng

và mặt phẳng
󰇛
󰇜
 . Trong các mệnh
đề sau, mệnh đề nào đúng:
A.
d nằm trong (P)
B.
d cắt (P)
C.
d // (P)
D.
d vuông góc với
(P)
C©u 63 :
Cho hai đường thẳng
12
x 1 t
x 2 y 2 z 3
d : ; d : y 1 2t
2 1 1
z 1 t

và điểm A(1; 2; 3). Đường
thẳng đi qua A, vuông góc với d1 và cắt d2 có phương trình là
A.
x 1 y 2 z 3
1 3 5

B.
x 1 y 2 z 3
1 3 5

C.
x 1 y 2 z 3
1 3 5

D.
x 1 y 2 z 3
1 3 5


C©u 64 :
Trong không gian Oxyz, cho điểm I(2,6,-3) và các mặt phẳng:
: 2 0; : 6 0; : 3 0x y z
Trong các mệnh đề sau, tìm mệnh đề sai:
11
A.
B.
//Oz
C.
// xOz
D.
đi qua điểm
I
C©u 65 :
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(1; 4; 2),B(–1; 2; 4) và đường
thẳng
:
x y z
12
1 1 2


. Tìm toạ độ điểm M trên
sao cho:
MA MB
22
28
.
A.
M(0; -1; 2)
B.
M(1; - 2 ; 0
C.
M
( 1;0;4)
D.
Đáp án khác
C©u 66 :
Khoảng cách giữa 2 đường thẳng

và
󰆒



là:
A.
2
B.
C.
D.
4
C©u 67 :
Trong không gian với hệ trục tọa độ Oxyz cho tọa độ 4 điểm
2;0;0 ; 0;2;0AB
;
0;0;2C
và
2;2;2D
, M ; N lần lượt là trung điểm của AB và CD. Tọa độ trung điểm I của MN là:
A.
11
; ;1
22
I
B.
1;1;0I
C.
1; 1;2I
D.
1;1;1I
C©u 68 :
Cho điểm M(3; 3; 3). Gọi A, B, C lần lượt là hình chiếu của M trên các trục Ox, Oy,
Oz. Khẳng định nào sau đây đúng?
A.
ABC là tam giác vuông tại A
B.
ABC là tam giác vuông tại C
C.
ABC là tam giác vuông tại B
D.
ABC là tam giác đều
C©u 69 :
Cho
; ; 3 , 6; 2;4 , 3;7; 5A x y B C
. Giá trị x, y để 3 điểm A, B, C thẳng hàng là:
A.
1, 5xy
B.
1, 5xy
C.
D.
1, 5xy
C©u 70 :
Trong không gian với hệ trục tọa độ Oxyz cho tọa độ 4 điểm
1;0;0 ; 0;1;0AB
;
0;0;1C
và
1;1;1D
, trong các mệnh đề sau mệnh đề nào sai:
A.
Bốn điểm A, B, C,D tạo thành một tứ
diện.
B.
Tam giác ABD là tam giác đều.
C.
AB vuông góc với CD.
D.
Tam giác BCD là tam giác vuông.
C©u 71 :
Trong không gian cho hai đường thẳng:
12
x 1 3t
x 2 y 1 z
d: ; d': y 2 t
3 1 1
z 1 t


.
Vị trí tương đối của d và d’ là:
A.
Cắt nhau.
B.
Song song.
C.
Trùng nhau.
D.
Chéo nhau.
C©u 72 :
Trong không gian Oxyz, cho bốn điểm
1,0,0 ; 0,1,0 ; 0,0,1 ; 1,1,1A B C D
. Xác định
tọa độ trọng tâm G của tứ diện ABCD
A.
111
,,
222



B.
222
,,
333



C.
111
,,
444



D.
111
,,
333



C©u 73 :
Cho điểm
(1,2,3)M
.Gọi
,,A B C
lần lượt là hình chiếu của M trên các trục
,,Ox Oy Oz
.Viết
mặt phẳng
song song mặt phẳng
ABC
và đi qua
M
A.
6 3 2 6 0x y z
B.
6 3 2 18 0x y z
C.
6 3 2 6 0x y z
D.
6 3 2 7 0x y z
C©u 74 :
Phương trình mặt trình mặt cầu có đường kính AB với
6;2; 5 , 4;0;7AB
là:
A.
2 2 2
2 2 2 59 0x y z x y z
B.
2 2 2
2 2 2 59 0x y z x y z
C.
2 2 2
2 2 2 59 0x y z x y z
D.
2 2 2
2 2 2 59 0x y z x y z
C©u 75 :
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng
: 3 0P x y z
và điểm
1;0; 1M
. Tọa độ điểm M’ đối xứng với M qua (P) là :
A.
' 1;4; 1M
B.
' 2;0;1M
C.
' 4;2; 2M
D.
' 3;2;1M
C©u 76 :
Viết phương trình mặt cầu
S
có tâm
I
thuộc mặt phẳng
Oyz
và đi qua các điểm
0,0,4 , (2,1,3), 0,2,6A B C
A.
2
2
2
5
2 26
2
x y z



B.
22
2
5 7 13
2 2 2
x y z
C.
2 2 2
3 1 2 9x y z
D.
22
2
15
1 13
22
x y z
C©u 77 :
Trong không gian
Oxyz
,đường thẳng
11
:
2 1 1
x y z
,mặt phẳng
:2 2 1 0P x y z
.Viết phương trình mặt phẳng
Q
chứa
và tạo với
P
nhỏ nhất
13
A.
10 7 13 2 0x y z
B.
10 7 13 3 0x y z
C.
10 7 13 1 0yz
D.
10 7 13 3 0x y z
C©u 78 :
Mặt cầu
2 2 2
:3 3 3 6 3 15 2 0S x y z x y z
có tâm I và bán kính R là:
A.
1 5 7 6
1; ; ,
2 2 6
IR




B.
3 15 7 6
3; ; ,
2 2 2
IR



C.
3 15 7 6
3; ; ,
2 2 2
IR




D.
1 5 7 6
1; ; ,
2 2 6
IR



C©u 79 :
Cho
1;0;0 , 0;2;0 , 2;1;3A B C
.Diện tích tam giác ABC là
A.
36
2
B.
6
2
C.
3
2
D.
36
C©u 80 :
Trong không gian với hệ tọa độ Oxyz, cho điểm
A
(2; 1;1)
. Viết phương trình mặt
phẳng (P) đi qua điểm A và cách gốc tọa độ O một khoảng lớn nhất.
A.
2 1 0
x y z
B.
2 5 0
x y z
C.
x y z
2 6 0
D.
2 3 0
x y z
C©u 81 :
Viết phương trình mặt phẳng
đi qua gốc tọa độ O và vuông góc với hai mặt phẳng
( ): 2 3 4 0P x y z
,
:2 0Q x y z
A.
5 7 3 0x y z
B.
5 7 3 0x y z
C.
5 7 3 0x y z
D.
5 7 3 0x y z
14
ĐÁP ÁN
01
{ | ) ~
28
{ | ) ~
55
) | } ~
02
) | } ~
29
{ | ) ~
56
{ ) } ~
03
{ ) } ~
30
{ ) } ~
57
{ | ) ~
04
{ ) } ~
31
{ | } )
58
{ | ) ~
05
) | } ~
32
{ | } )
59
{ | } )
06
{ | } )
33
{ | ) ~
60
) | } ~
07
{ ) } ~
34
) | } ~
61
) | } ~
08
{ ) } ~
35
{ ) } ~
62
{ | ) ~
09
{ ) } ~
36
{ ) } ~
63
{ | } )
10
{ | } )
37
) | } ~
64
{ ) } ~
11
{ | } )
38
{ | } )
65
{ | ) ~
12
{ ) } ~
39
{ | ) ~
66
{ | ) ~
13
{ | } )
40
{ | } )
67
{ | } )
14
{ | } )
41
) | } ~
68
{ | } )
15
{ | } )
42
) | } ~
69
) | } ~
16
) | } ~
43
) | } ~
70
{ | } )
17
{ ) } ~
44
{ | } )
71
) | } ~
18
{ | ) ~
45
{ ) } ~
72
{ ) } ~
19
{ | ) ~
46
{ | ) ~
73
{ ) } ~
20
{ | } )
47
{ | ) ~
74
) | } ~
21
{ | } )
48
{ ) } ~
75
{ | } )
22
{ | } )
49
) | } ~
76
{ ) } ~
23
) | } ~
50
{ | ) ~
77
{ ) } ~
24
) | } ~
51
{ | ) ~
78
) | } ~
25
{ | ) ~
52
) | } ~
79
) | } ~
26
) | } ~
53
{ ) } ~
80
{ | ) ~
27
{ | ) ~
54
{ | ) ~
81
{ ) } ~
1
GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN
ĐỀ 004
C©u 1 :
Cho
0;0;1 , 3;0;0 , 0;2;0A B C
. Khi đó phương trình mặt phẳng (ABC) là :
A.
1
123
x y z
B.
1
2 3 1
x y z
C.
1
3 2 1
x y z
D.
1
1 3 2
x y z
C©u 2 :
Cho đường thẳng qua
1;0; 1A
và có véc tơ chỉ phương
2;4;6u
. Phương trình
tham số của đường thẳng là :
A.
B.
2
4
6
xt
y
zt
C.
D.
1
2
13
xt
yt
zt
C©u 3 :
Gọi M, N lần lượt là trung điểm của AB và CD. Tọa độ điểm G là trung điểm của
MN là:
A.
2
1
;
2
1
;
2
1
G
B.
4
1
;
4
1
;
4
1
G
C.
3
2
;
3
2
;
3
2
G
D.
3
1
;
3
1
;
3
1
G
C©u 4 :
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
(P):
4 4 0x y z
và mặt cầu (S):
2 2 2
4 10 4 0x y z x z
Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đ7ờng tròn có bán kính bằng:
A.
3
B.
7
C.
2
D.
4
C©u 5 :
Trong không gian với hệ tọa độ Oxyz, cho 2 đường thẳng
12
1 1 1 2 1
: ; :
2 3 2 2 1 3
x y z x y z m
dd
.
Để
1
d
cắt
2
d
thì m bằng
A.
3
4
B.
7
4
C.
1
4
D.
5
4
2
C©u 6 :
Cho đường thẳng
13
:
2 3 2
x y z
và
: 2 2 1 0P x y z
mặt phẳng chứa
và vuông góc với
P
có phương trình là :
A.
2 2 8 0x y z
B.
2 2 8 0x y z
C.
2 2 8 0x y z
D.
2 2 8 0x y z
C©u 7 :
Cho hai mặt phẳng (P): x+y-z+5=0 và (Q): 2x-z=0. Nhận xét nào sau đây là đúng
A.
Mặt phẳng (P) và mặt phẳng (Q) có giao tuyến là
B.
Mặt phẳng (P) và mặt phẳng (Q) có giao tuyến là
5
1 1 2
x y z

C.
Mặt phẳng (P) song song với mặt phẳng (Q)
D.
Mặt phẳng (P) vuông góc với mặt phẳng (Q)
C©u 8 :
Vị trí tương đối của hai đường thẳng
12
1 1 5 1 1 1
: , :
2 3 1 4 3 5
x y z x y z
là:
A.
Song song với nhau.
B.
Cắt nhau tại điểm
(3;2;6)M
C.
Cắt nhau tại điểm
(3;2; 6)M
D.
Chéo nhau.
C©u 9 :
Cho hai đường thẳng
12
12
12
: , : 1
2 1 1
3
xt
x y z
yt
z

. Phương trình đường thẳng
vuông góc với mặt phẳng (P):
7 4 0x y z
và cắt hai đường thẳng
1
và
2
là:
A.
57
:1
34
xt
yt
zt

B.
5 1 3
7 1 4
x y z

C.
57
:1
34
xt
yt
zt

D.
5 1 3
:.
6 1 4
x y z
C©u 10 :
Cho mặt phẳng
0132: zyx
và đường thẳng d có phương trình tham số:
1
22
3
z
ty
tx
. Trong các mệnh đề sau, mệnh đề nào đúng?
3
A.
d
B.
d cắt
()
C.
d
D.
//d
C©u 11 :
Gọi (S) là mặt cầu tâm I(2 ; 1 ; -1) và tiếp xúc với mặt phẳng (
)
có phương trình: 2x
– 2y – z + 3 = 0. Bán kính của (S) bằng bao nhiêu ?
A.
2
3
B.
2
9
C.
2
D.
4
3
C©u 12 :
Đường thẳng nào sau đây song song với (d):
2 4 4
1 2 3
x y z

A.
1 2 1
1 2 3
x y z

B.
2 4 4
1 1 1
x y z

C.
1 2 1
1 2 3
x y z


D.
1 2 1
1 2 3
x y z


C©u 13 :
Trong không gian Oxyz, cho các điểm
1;0;0M
;
0;1;0N
;
0;0;1C
. Khi đó thể tích
tứ diện OMNP bằng:
A.
1
B.
1
2
C.
1
.
6
D.
3
C©u 14 :
Trong không gian với hệ toạ độ Oxyz, cho đường thẳng d :
12
2 1 1
x y z

và điểm
A(1;-1;2). Tọa độ hình chiếu vuông góc H của A lên d là:
A.
H(0;- 1;- 2)
B.
H(0; 1; 2)
C.
H(0; 1;- 2)
D.
H(0;- 1; 2)
C©u 15 :
Cho mặt phẳng
( ):2 2 4 0P x y z
và mặt cầu
2 2 2
( ): 2 4 6 11 0S x y z x y z
. Giả
sử (P) cắt (S) theo thiết diện là đường tròn (C). Xác định tọa độ tâm và tính bán kính đường
tròn (C).
A.
Tâm
(3;0; 2), 3Ir
B.
Tâm
(3;0;2), 4Ir
C.
Tâm
(3;0;2), 5Ir
D.
Tất cả 3 đáp án trên đều sai.
C©u 16 :
Gọi (
)
là mặt phẳng cắt ba trục tọa độ tại ba điểm M(8; 0; 0), N(0; -2; 0), P(0; 0; 4).
Phương trình của (
)
là:
A.
4 1 2
x y z

B.
0
8 2 4
x y z
C.
x – 4y + 2z – 8 = 0
D.
x – 4y + 2z = 0
C©u 17 :
Mặt phẳng (P) chứa trục Oy và điểm
1; 1;1A
là :
4
A.
0xz
B.
0xy
C.
0xz
D.
0xy
C©u 18 :
Phương trình mặt cầu tâm I(1; 2; 3) và bán kính R=3 là:
A.
2 2 2
2 4 6 5 0x y z x y z
B.
B và C đều đúng.
C.
2 2 2
( 1) ( 2) ( 3) 9x y z
D.
2 2 2
( 1) ( 2) ( 3) 3x y z
C©u 19 :
Mặt phẳng qua 3 điểm A(1; 0; 0), B(0; -2; 0), C(0; 0; 3) có phương trình:
A.
2 3 1 0x y z
B.
6 3 2 6 0x y z
C.
2 3 1 0x y z
D.
Đáp án khác
C©u 20 :
Cho bốn điểm A(-1,1,1), B(5,1,-1) C(2,5,2) , D(0,-3,1). Nhận xét nào sau đây là đúng
A.
A,B,C,D là bốn đỉnh của một tứ diện
B.
Ba điểm A, B, C thẳng hàng
C.
Cả A và B đều đúng
D.
A,B,C,D là hình thang
C©u 21 :
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):
2 2 3 0x y z
và 2
điểm A(4; -4; 4), B(4; -2 ;6), C(3 ; -5; 7).
Mặt cầu (S) tiếp xúc với (P), đi qua điểm C và có tâm nằm trên đường thẳng AB.
Tâm I của mặt cầu (S) có tọa độ là:
A.
(-4; -3; 5)
B.
(4; -3; 5)
C.
(4; 3; 5)
D.
(4:3; -5)
C©u 22 :
Cho điểm A(0,0,3) , B(-1,-2,1) , C(-1,0,2)
Có bao nhiêu nhận xét đúng trong số các nhận xét sau
1. Ba điểm A,B,C thẳng hàng
2. Tồn tại duy nhất một mặt phẳng đi qua ba điểm ABC
3. Tồn tại vô số mặt phẳng đi qua ba điểm A,B,C
4. A,B,C tạo thành ba đỉnh một tam giác
5. Độ dài chân đường cao kẻ từ A là
35
5
6. Phương trình mặt phẳng (A,B,C) là 2x+y-2z+6=0
7. Mặt phẳng (ABC) có vecto pháp tuyến là (2,1,-2)
A.
5
B.
2
C.
4
D.
3
5
C©u 23 :
Mặt cầu có phương trình
2 2 2
2 1 0x y z x y
có tọa độ tâm I và bán kính r là:
A.
11
1; ;0 ;
22
Ir



B.
1
1; ;0 , 1
2
Ir




C.
11
1; ;0 ;
22
Ir




D.
1
1; ;0 , 1
2
Ir




C©u 24 :
Điểm nào nằm trên đường thẳng (d) là giao tuyến của x + 2y – z +3 = 0 và 2x – 3y –
2z + 6 = 0.
A.
(0; 1; 5)
B.
(-1; -1; 0)
C.
(1; 2; 1)
D.
( 1; 0; 4)
C©u 25 :
Đường thẳng có phương trình:
20
0
x y z
xz

có một vectơ pháp tuyến là:
A.
2; 1;1u
B.
1; 1;0u
C.
1;3;1u
D.
1;0; 1u
C©u 26 :
Trong không gian Oxyz, cho ba điểm
1;0;0A
;
1;1;0B
; C
0;1;1
. Khi đó tọa độ điểm
D để ABCD là hình bình hành:
A.
1;1;1D
B.
0;0;1D
C.
0;2;1D
D.
2;0;0D
C©u 27 :
Trong không gian với hệ toạ độ Oxyz, cho tam giác ABC có tọa độ A(-1;1;-1), B(2;0;-
1), C(3;1;-2). Độ dài đường cao kẻ từ B của tam giác ABC bằng:
A.
26
3
B.
26
17
C.
2 26
17
D.
26
3
C©u 28 :
Cho tam giác ABC với A(1;-4;2), B(-3;2;1), C(3;-1;4), trọng tâm G của tam giác ABC
có tọa độ bằng:
A.
(3; -9; 21)
B.
;;



17
2
22
C.
;;



17
1
33
D.
;;



1 1 7
4 4 4
C©u 29 :
Phương trình đường thẳng qua A( 1; 2; -1) và vuông góc với mặt phẳng (P): x + 2y –
3z +1 = 0 là:
A.
1 2 1
2 3 1
x y z

B.
1 2 1
1 2 3
x y z

C.
1 2 1
1 2 3
x y z

D.
2 4 4
1 2 3
x y z

C©u 30 :
Cho hai đường thẳng
85
:
4 2 1
x y z
và
3; 2;5A
. Tọa độ hình chiếu của A
trên là ?
6
A.
4; 1; 3
B.
4; 1;3
C.
4; 1;3
D.
4;1; 3
C©u 31 :
Phương trình chính tắc của đường thẳng đi qua điểm M(2 ; 0 ; -1) và có vectơ chỉ
phương
(4
a
;-6 ; 2) là
A.
21
4 6 2
x y z


B.
21
2 3 1
x y z


C.
4 6 2
2 3 1
x y z

D.
21
2 3 1
x y z


C©u 32 :
Tọa độ giao điểm I của đường thẳng
3
0
x y z
d
xy

và mặt phẳng
2 3 1 0xz
:
A.
1;1;0I
B.
2;1;0
C.
. 1;1;1I
D.
. 1;2;0I
C©u 33 :
Phương trình mặt phẳng đi qua M(1; 3; -3) và vuông góc đường thẳng d:
11
2 1 3
x y z

là:
A.
1 3 3
2 1 3
x y z

B.
2 3 10 0x y z
C.
Đáp án A và B đều đúng.
D.
3 3 10 0x y z
C©u 34 :
Mặt phẳng đi qua
2;0;0D
vuông góc với trục Oy có phương trình là:
A.
z = 0
B.
y = 2.
C.
y = 0
D.
z = 2
C©u 35 :
Khoảng cách từ điểm A(1;2;3) đến mặt phẳng (P): 2x – y +2z +6=0 bằng:
A.
5
B.
2
C.
3
D.
4
C©u 36 :
Trong không gian oxyz cho hai điểm A(5,3,-4) và điểm B(1,3,4) Tìm tọa độ điểm
(Ox )Cy
sao cho tam giác ABC cân tại C và có diện tích bằng
85
. Chọn câu trả lời
đúng nhất
A.
C(3,7,0) và C(3,-1,0)
B.
C(-3-7,0) và C(-3,-1,0)
C.
C(3,7,0) và C(3,1,0)
D.
C(-3,-7,0) và C(3,-1,0)
C©u 37 :
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có A(3; 1; 5), B(2; 6; 1), C(4;
0 ; 5) và D(6; 0; 4). Phương trình mặt cầu (S) ngoại tiếp tứ diện ABCD là:
7
A.
2 2 2
( 1) ( 1) ( 1) 25x y z
B.
2 2 2
( 1) ( 1) ( 1) 5x y z
C.
2 2 2
( 1) ( 1) ( 1) 25x y z
D.
2 2 2
( 1) ( 1) ( 1) 5x y z
C©u 38 :
Gọi
là mặt phẳng cắt 3 trục tọa độ tại 3 điểm M(8; 0; 0), N(0; -2; 0), P(0; 0; 4).
Phương trình của
là:
A.
x – 4y + 2z – 8 =
0
B.
0
214
zyx
C.
0
428
zyx
D.
x – 4y + 2z = 0
C©u 39 :
Cho
1;4;2 , 1;2;4AB
và
12
:
1 1 2
x y z
Điểm
M
mà
22
MA MB
nhỏ nhất có tọa độ là :
A.
1;0; 4
B.
0; 1;4
C.
1;0;4
D.
1;0; 4
C©u 40 :
Cho mặt phẳng
05:)(
02:)(
012:
yx
zyx
zyx
. Trong các mệnh đề sau, mệnh đề nào sai ?
A.
B.
C.
D.
C©u 41 :
Cho điểm I(3,4,0) và đường thẳng
1 2 1
:
1 1 4
x y z
Viết phương trình mặt cầu (S)
có tâm I và cắt
tại hai điểm A,B sao cho diện tích tam giác IAB bằng 12
A.
2 2 2
( 3) ( 4) 25x y z
B.
2 2 2
( 3) ( 4) 5x y z
C.
2 2 2
( 3) ( 4) 5x y z
D.
2 2 2
( 3) ( 4) 25x y z
C©u 42 :
Trong không gian với hệ tọa độ Oxyz, cho điểm H(2;1;1). Mặt phẳng (P) qua H , cắt
các trục tọa độ tại A,B,C và H là trực tâm của tam giác ABC. Phương trình mặt
phẳng (P) là:
A.
10
3 6 6
x y z
B.
10
3 6 6
x y z
C.
21x y z
D.
2 6 0x y x
C©u 43 :
Mặt phẳng qua A( 1; -2; -5) và song song với mặt phẳng (P):
10xy
cách (P) một
khoảng có độ dài là:
8
A.
2
B.
2
C.
4
D.
22
C©u 44 :
Trong không gian Oxyz cho
1;1;3 , 1;3;2 , 1;2;3A B C
Khoảng cách từ gốc tọa độ
O tới mặt phẳng (ABC) bằng :
A.
3
B.
3
2
C.
3
D.
3
2
C©u 45 :
Cho (P): x + 2y + 2z – 1 = 0 cắt mặt cầu (S) theo một đường tròn giao tuyến có bán
kính r = 1/3,biết tâm của (S) là I(1; 2; 2). Khi đó, bán kính mặt cầu (S) là:
A.
7
3
B.
1 2 2
3
C.
1 2 2
3
D.
1
C©u 46 :
Mặt phẳng (P) song song và cách đều hai mặt phẳng
( ):2 4 5 0, ( ):2 4 7 0x y z x y z

có phương trình là:
A.
Đáp án khác.
B.
2 4 6 0x y z
C.
2 4 0x y z
D.
2 4 12 0x y z
C©u 47 :
Khoảng cách từ A( 1; -2; 3) đến đường thẳng (d) qua B( 1; 2; -1) và vuông góc với
mặt phẳng (P): x + 2y + 3z + 5 = 0 là:
A.
3
2 14
B.
3
14
C.
3
4 14
D.
23
14
C©u 48 :
Giao điểm của đường thẳng
1
12
xt
yt
zt


và mặt phẳng
( ):2 3 5 0P x y z
là:
A.
(1; 3;4)M
B.
1 2 5
( ; ; )
3 3 3
M
C.
(1;3;4)M
D.
1 4 5
( ; ; )
3 3 3
M
C©u 49 :
Cho
2; 1;6 , 3; 1; 4 , 5; 1;0 , 1;2;1A B C D
thể tích của khối tứ diện ABCD là :
A.
50
B.
40
C.
30
D.
60
C©u 50 :
Tồn tại bao nhiêu mặt phẳng (P) vuông góc với hai mặt phẳng (α): x+y+z+1=0 , (β) :
2x-y+3z-4=0 sao cho khoảng cách từ gốc tọa độ đến mặt phẳng (P) bằng
26
A.
2
B.
0
C.
1
D.
Vô số
C©u 51 :
Giá trị cosin của góc giữa hai véctơ
(4;3;1)a
và
(0;2;3)b
là:
9
A.
5 26
26
B.
5 13
26
C.
52
26
D.
Kết quả khác.
C©u 52 :
Góc giữa đường thẳng
2 1 1
:
1 2 3
x y z
d

và mặt phẳng
2 3 0x y z
A.
0
90
B.
0
45
C.
0
0
D.
0
180
C©u 53 :
Cho mặt cầu (S):
2 2 2
2 4 1 0x y z x y
có tâm I và bán kính R là:
A.
1; 2;0 , 6IR
B.
1; 2;1 , 6IR
C.
1; 2;1 , 2IR
D.
1; 2;0 , 2IR
C©u 54 :
Mặt cầu ngoại tiếp tứ diện ABCD có bán kính là:
A.
2
3
B.
4
3
C.
3
D.
2
C©u 55 :
Trong không gian với hệ tọa độ Oxyz, cho điểm A(3; 0; -1) và
B(1;3; -2). M là điểm nằm trên trục hoành Ox và cách đều 2 điểm A,B.
Tọa độ điểm M là:
A.
(2; 0 ; 0)
B.
( -1; 0 ; 0)
C.
( -2; 0 ;0)
D.
( 1; 0 ; 0)
C©u 56 :
Cho mặt phẳng
qua điểm M(0; 0; -1) và song song với giá của hai vecto
a
= (1; -2;
3) và
b
= (3; 0; 5). Phương trình của mặt phẳng
là:
A.
-5x + 2y + 3z + 3 = 0
B.
5x – 2y – 3z – 21 = 0
C.
10x – 4y – 6z + 21 = 0
D.
5x – 2y – 3z + 21 = 0
C©u 57 :
Phương trình của mặt phẳng (P) đi qua điểm A và vuông góc với đường thẳng (d)
với A(1;-1;-1) và
2
:1
12
xt
d y t
zt


A.
x – y + 2z + 4=0
B.
x –y – 2z - 4=0
C.
x –y – 2z + 4=0
D.
x + y – 2z + 4=0
C©u 58 :
Góc giữa đường thẳng (d):
2 4 4
1 2 3
x y z

và mặt phẳng (P):
20x y z
là:
A.
45
o
B.
90
o
C.
180
o
D.
0
o
C©u 59 :
Phương trình đường thẳng AB với A(1; 1; 2) và B( 2; -1; 0) là:
10
A.
1 1 2
3 2 2
x y z

.
B.
1 1 2
1 2 2
x y z

.
C.
21
3 2 2
x y z

.
D.
34
1 2 2
x y z


.
C©u 60 :
Trong không gian với hệ toạ độ Oxyz, cho đường thẳng d :
12
2 1 1
x y z

, mặt
phẳng
( ):2 2 6 0P x y z
và điểm A(1;-1;2). Mặt phẳng (Q) đi qua điểm A và chứa
d thì phương trình của (Q) là:
A.
2 5 11 0x y z
B.
2 5 11 0x y z
C.
2 5 11 0x y z
D.
2 5 11 0x y z
C©u 61 :
Cho bốn điểm A(1,1,-1) , B(2,0,0) , C(1,0,1) , D (0,1,0) , S(1,1,1)
Nhận xét nào sau đây là đúng nhất
A.
ABCD là hình chữ nhật
B.
ABCD là hình bình hành
C.
ABCD là hình thoi
D.
ABCD là hình vuông
C©u 62 :
Cho hai đường thẳng
11
:
1 1 2
x y z
và
12
:2
34
xt
d y t
zt
. Trong các mệnh đề sau
, mệnh đề nào đúng ?
A.
và
d
cắt nhau
B.
và
d
song song
C.
và
d
trùng nhau
D.
và
d
chéo nhau
C©u 63 :
Cho d là đường thẳng đi qua điểm A(1; 2; 3) và vuông góc với mặt phẳng
01734: zyx
. Phương trình tham số của d là:
A.
14
23
37
xt
yt
zt



B.
tz
ty
tx
143
62
81
C.
tz
ty
tx
73
32
31
D.
tz
ty
tx
73
32
41
C©u 64 :
Cho 3 điểm A(0; 2; 1), B(3; 0; 1), C(1; 0; 0). Phương trình mặt phẳng (ABC) là:
A.
2x + 3y – 4z – 2 = 0
B.
2x – 3y – 4z + 1 = 0
11
C.
4x + 6y – 8z + 2 = 0
D.
2x – 3y – 4z + 2 = 0
C©u 65 :
Cho hai điểm A(2,0,3) , B(2,-2,-3) và đường thẳng
:
21
1 2 3
x y z

Nhận xét nào sau đây là đúng
A.
A , B và
cùng nằm trong một mặt
phẳng
B.
A và B cùng thuộc đường thẳng
C.
Tam giác MAB cân tại M với M (2,1,0)
D.
và đường thẳng AB là hai đường
thẳng chéo nhau
C©u 66 :
Cho mặt cầu (S) có phương trình
2 2 2
3 3 3 0x y z x y z
và mặt phẳng (P) :
x+y+z-6=0
Nhận xét nào sau đây là đúng
A.
Mặt phẳng (P) cắt mặt cầu (S) theo
đường tròn (C)
B.
Tâm mặt cầu (S) là I(3,3,3)
C.
Mặt cầu (S) và mặt phẳng (P) không có
điểm chung
D.
Mặt cầu (S) tiếp xúc với mặt phẳng (P)
C©u 67 :
Cho hai đường thẳng
12
1 ( 1)
1
: , : 1 (2 )
1 2 1
1 (2 1)
x m t
x y z m
y m t
z m t

. Tìm m để hai đường thẳng
trùng nhau.
A.
3, 1mm
B.
0m
C.
0, 1mm
D.
0, 2mm
C©u 68 :
Mặt cầu tâm
2; 1;2I
và đi qua điểm
2;0;1A
có phương trình là:
A.
2 2 2
2 1 2 2x y z
B.
2 2 2
2 1 2 2x y z
C.
2 2 2
2 1 2 1x y z
D.
2 2 2
2 1 2 1x y z
C©u 69 :
Phương trình đường thẳng d qua A(1; 2; 3), có véc tơ chỉ phương
(1;2; 3)u 
là:
A.
1 2 3
1 2 3
x y z

B.
1
22
33
xt
yt
zt



C.
2 3 4 0x y z
D.
1
22
33
xt
yt
zt


C©u 70 :
Cho hai đường thẳng
12
1 2 3 3 5 7
: , :
2 3 4 4 6 8
x y z x y z
dd
. Tìm khẳng định
12
đúng
A.
12
d d
B.
1
d
chéo
2
d
C.
12
//dd
D.
12
dd
C©u 71 :
Vị trí tương đối của 2 mặt phẳng:
:
2 3 0x y z
và
: 2x + y – z – 5 = 0.
A.
//

B.

C.
,

cắt
nhau
D.
,

chéo
nhau
C©u 72 :
Phương trình mặt phẳng qua A( 1; 1; 1), B(1; 0; 0), C( 1; -1; -1) là:
A.
10x y z
B.
30x y z
C.
3 3 0x 
D.
10x y z
C©u 73 :
Cho đường thẳng d đi qua điểm M(2; 0; -1) và có vecto chỉ phương
(4; 6;2)a 
.
Phương trình tham số của đường thẳng d là:
A.
tz
ty
tx
1
3
22
B.
tz
ty
tx
21
6
42
C.
tz
ty
tx
2
36
24
D.
tz
ty
tx
1
3
22
C©u 74 :
Cho ba điểm A(0 ; 2 ; 1), B(3 ; 0 ; 1), C(1; 0 ; 0). Phương trình mặt phẳng (ABC) là
A.
x – 4y + 2z – 8 = 0
B.
2x – 3y – 4z +2 = 0
C.
x – 4y + 2z = 0
D.
2x + 3y – 4z – 2 = 0
C©u 75 :
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d:
35
1 1 3
x y z

và mặt phẳng (P):
2 2 7 0x y z
. Mlà điểm trên d và cách (P)
một khoảng bằng 3. Tọa độ M là:
A.
(3;0;5)
B.
Cả 2 đáp án A) và B) đều đúng.
C.
Cả 2 đáp án A) và B) đều sai.
D.
(1;2;-1)
C©u 76 :
Cho 2 đường thẳng
tz
ty
tx
d
43
32
21
:
1
và
tz
ty
tx
d
87
65
43
:
2
. Trong các mệnh đề sau, mệnh
đề nào đúng ?
A.
21
dd
B.
21
// dd
C.
21
dd
D.
21
,dd
chéo nhau
C©u 77 :
Trong không gian Oxyz cho 3 vectơ
( 1;1;0),
a

(1;1;0)
b
và
(1;1;1)
c
. Trong
13
các mệnh đề sau, mệnh đề nào sai ?
A.
3
c
B.
ab
C.
2
a
D.
cb
C©u 78 :
Cho
2;0;0 , 0;2;0 , 0;0;2 , 2;2;2A B C D
mặt cầu ngoại tiếp tứ diện ABCD có bán
kính là :
A.
3
B.
2
3
C.
3
D.
3
2
C©u 79 :
Cho hai mặt phẳng (): 2x + 3y + 3z - 5 = 0; (): 2x + 3y + 3z - 1 = 0. Khoảng cách giữa
hai mặt phẳng này là:
A.
11
22
B.
4
C.
11
2
D.
2 22
11
C©u 80 :
Cho đường thẳng d:
8 5 8
1 2 1
x y z

và mặt phẳng (P) x+2y+5z+1=0 . Nhận xét nào
sau đây là đúng
A.
Đường thẳng d song song với mặt
phẳng (P)
B.
Đường thẳng d thuộc mặt phẳng (P)
C.
Đường thẳng d cắt mặt phẳng (P) tại
A(8,5,8)
D.
Đường thẳng d vuông góc với mặt
phẳng (P)
14
ĐÁP ÁN
01
{ | ) ~
28
{ | ) ~
55
{ ) } ~
02
{ | ) ~
29
{ | } )
56
) | } ~
03
) | } ~
30
{ | ) ~
57
{ | } )
04
{ ) } ~
31
{ | } )
58
{ | } )
05
{ ) } ~
32
{ | ) ~
59
{ | } )
06
{ | ) ~
33
{ ) } ~
60
{ ) } ~
07
) | } ~
34
{ | ) ~
61
) | } ~
08
{ ) } ~
35
{ | } )
62
{ | ) ~
09
{ ) } ~
36
) | } ~
63
) | } ~
10
) | } ~
37
{ ) } ~
64
) | } ~
11
{ | } )
38
) | } ~
65
) | } ~
12
{ | } )
39
{ | ) ~
66
) | } ~
13
{ | ) ~
40
) | } ~
67
{ ) } ~
14
{ ) } ~
41
) | } ~
68
{ | ) ~
15
{ ) } ~
42
{ ) } ~
69
{ ) } ~
16
{ | } )
43
{ | } )
70
{ | } )
17
{ | ) ~
44
{ | ) ~
71
{ | ) ~
18
{ ) } ~
45
{ | } )
72
{ | } )
19
{ ) } ~
46
{ ) } ~
73
) | } ~
20
) | } ~
47
{ | } )
74
{ | } )
21
{ ) } ~
48
{ ) } ~
75
{ ) } ~
22
) | } ~
49
{ | ) ~
76
) | } ~
23
{ | ) ~
50
) | } ~
77
{ | } )
24
{ | } )
51
{ | } )
78
{ | ) ~
25
{ | ) ~
52
{ | ) ~
79
{ | } )
26
{ | ) ~
53
{ | } )
80
) | } ~
27
{ ) } ~
54
) | } ~
| 1/114
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN ĐỀ 001
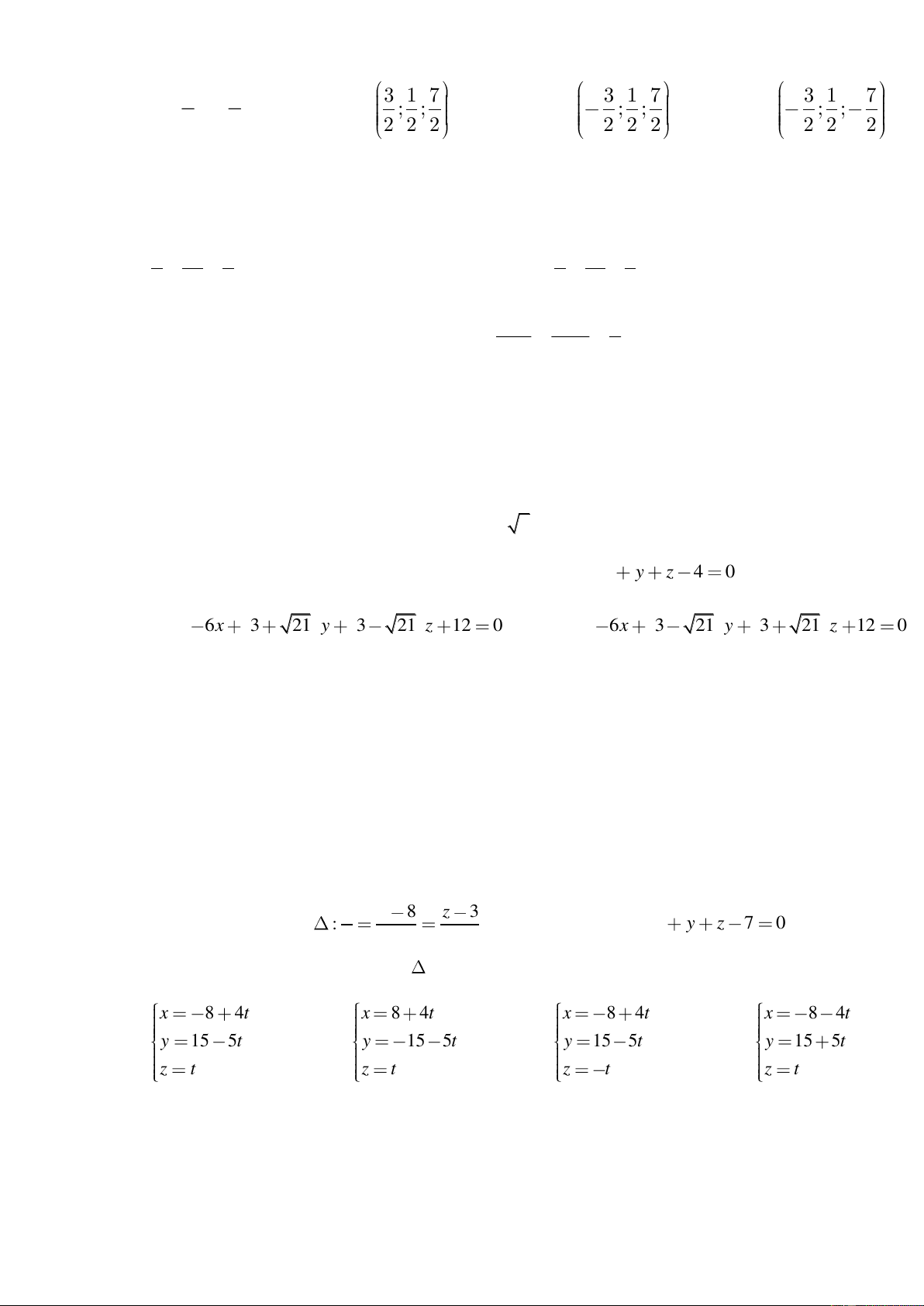
C©u 1 : Trong không gian với hệ tọa độ Oxyz cho tam giác ABC có A(1;0;0), B(0;-
2;3),C(1;1;1). Phương trình mặt phẳng (P) chứa A, B sao cho khoảng cách từ C tới (P) 2 là 3
A. x+y+z-1=0 hoặc -23x+37y+17z+23=0
B. x+y+2z-1=0 hoặc -2x+3y+7z+23=0
C. x+2y+z-1=0 hoặc -2x+3y+6z+13=0
D. 2x+3y+z-1=0 hoặc 3x+y+7z+6=0
C©u 2 : Trong không gian Oxyz mặt phẳng song song với hai đường thẳng x  2  t x 2 y 1 z    : ;    1 2 : y  3  2t 2
có một vec tơ pháp tuyến là 3 4 z 1  t
A. n  (5;6; 7) B. n  (5;6;7)
C. n  (5;6; 7) D. n  (5;6;7)
C©u 3 : Trong không gian với hệ tọa độ Oxyz cho mặt cầu 2 2 2
(S) : (x 1)  ( y  2)  (z  3)  9 và x  6 y  2 z  2 đường thẳng  :  
. Phương trình mặt phẳng (P) đi qua M(4;3;4), 3  2 2
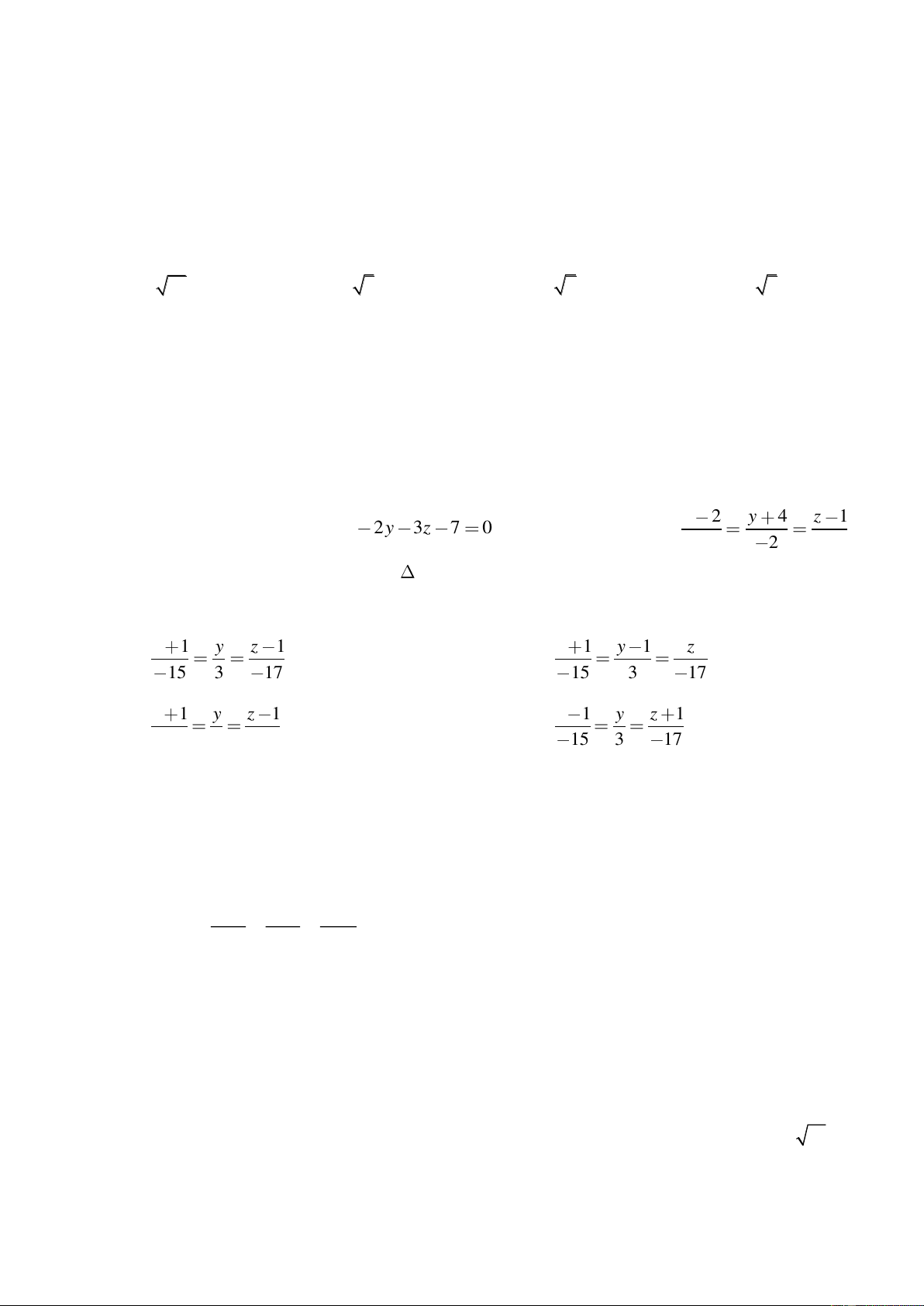
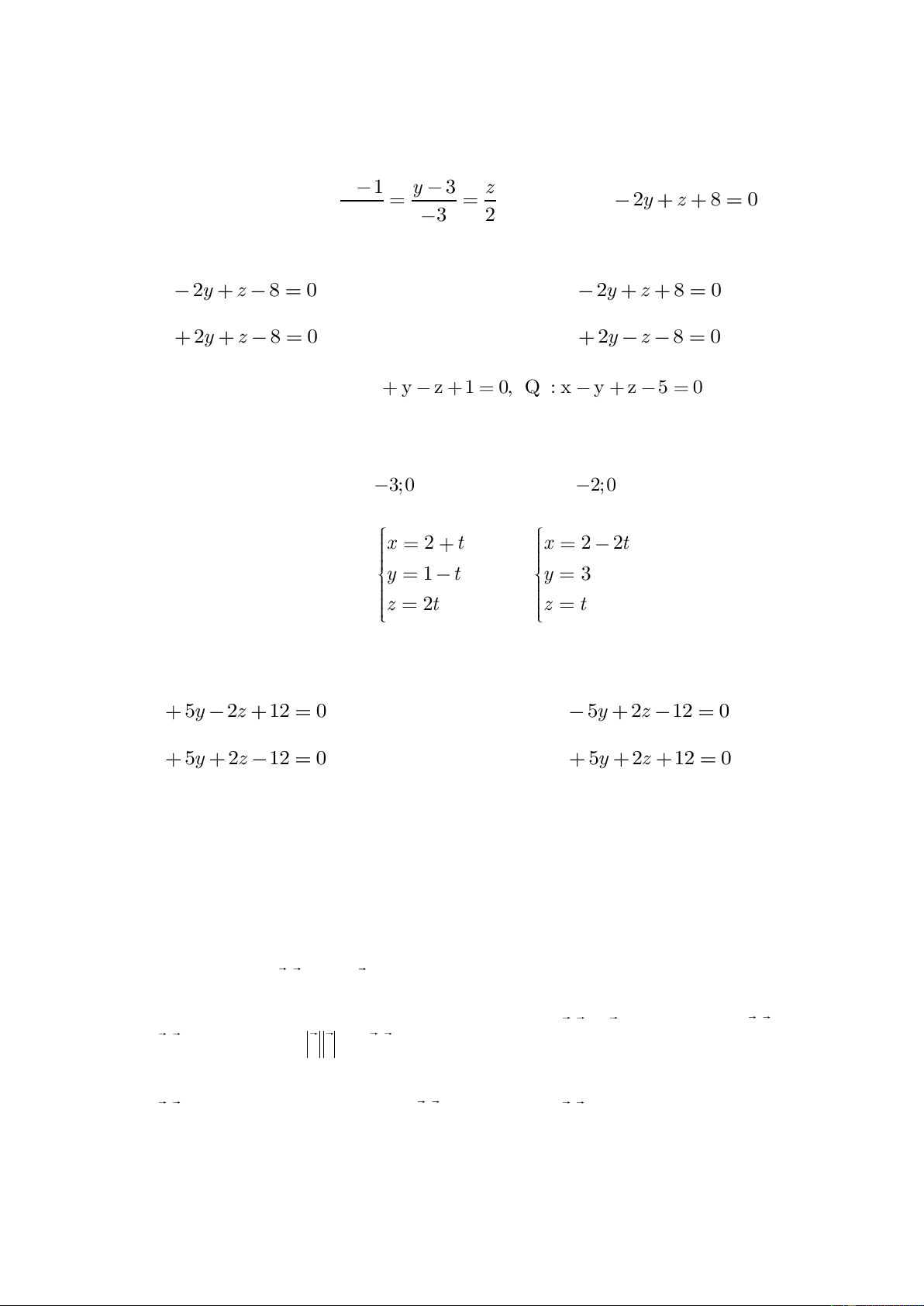
song song với đường thẳng ∆ và tiếp xúc với mặt cầu (S) x-2y+2z-1=0 A. 2x+y+2z-19=0 B. C. 2x+y-2z-12=0 D. 2x+y-2z-10=0
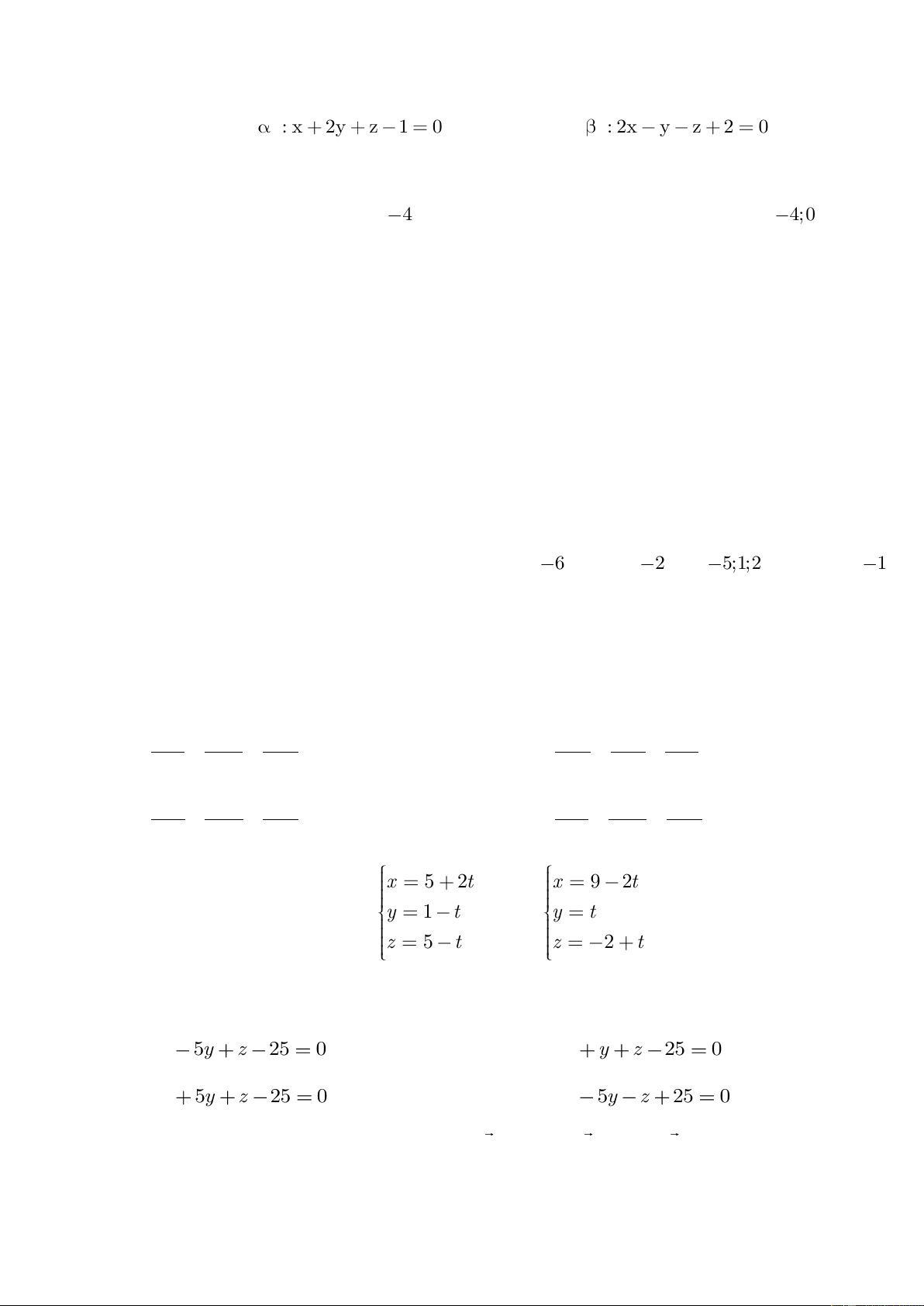
C©u 4 : Trong không gian với hệ tọa độ vuông góc Oxyz, cho mặt phẳng x 1 y z  2
(P) : x + 2y + z – 4 = 0 và đường thẳng d :  
. Phương trình đường thẳng 2 1 3
∆ nằm trong mặt phẳng (P), đồng thời cắt và vuông góc với đường thẳng d là: x 1 y 1 z 1 x 1 y 1 z 1 A.   B.   5 1  3 5 2 3 1 x 1 y 1 z 1 x 1 y  3 z 1 C.   D.   5 1  2 5 1  3
C©u 5 : Trong không gian Oxyz đường thẳng d đi qua gốc tọa độ O và có vec tơ chỉ
phương u(1;2;3) có phương trình: x  0 x  1 x  t x  t     A. d : y  2t B. d : y  2 C. d : y  t 3 D. d : y  2t z   t 3 z   3 z   2t z    t 3
C©u 6 : Trong không gian Oxyz, cho tứ diện ABCD với A(1; 6; 2), B(5; 1; 3), C(4; 0; 6), D(5;
0; 4). phương trình mặt cầu (S) có tâm D và tiếp xúc với mặt phẳng (ABC). 2 2 2 8 2 2 2 8
A. (S): (x  5)  y  (z  4)  (x 5) y (z 4) 223 B. (S):      223 2 2 2 8 2 2 2 8
C. (S): (x  5)  y  (z  4)  (  5)   (  4)  223 D. (S): x y z 223
C©u 7 : Cho 3 điểm A(1; 6; 2), B(5; 1; 3),
C(4; 0; 6) phương trình mặt phẳng (ABC) LÀ
A. mp(ABC): 14x 13y  9z+110  0
B. mp(ABC): 14x 13y  9z110  0
C. mp(ABC): 14x-13y  9z110  0
D. mp(ABC): 14x 13y  9z110  0
C©u 8 : Cho 3 điểm A(2; 1; 4), B(–2; 2; –6), C(6; 0; –1). Tích AB.AC bằng: A. –67 B. 65 C. 67 D. 33 C©u 9 : x 1 2t
x  3 4t '  
Cho hai đường thẳng d : y  2  3t và d : y  5  6t ' 1 2   z  3  4tz  7  8t ' 
Trong các mệnh đề sa, mệnh đề nào đúng? d và d chéo 1 2
A. d d d d d d 1 2 B. 1 2 C. 1 2 D. nhau
C©u 10 : Trong không gian Oxyz, cho ba vectơ a   1
 ,1,0;b  (1,1,0);c  1,1,  1 . Trong các
mệnh đề sau, mệnh đề nào đúng? a, , b c đồng
A. a b c  0 B. C. b c 6 cos ,  D. . a b  1 phẳng. 3
C©u 11 : Mặt phẳng (Q) song song với mp(P): x+2y+z-4=0 và cách D(1;0;3) một khoảng bằng 2 6 có phương trình là x+2y+z+2=0 và A. x+2y+z+2=0 B. x+2y-z-10=0 C. x+2y+z-10=0 D. x+2y+z-10=0
C©u 12 : Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;1;1) và mặt phẳng (P): 2x – y +
2z + 1 = 0. Phương trình mặt cầu tâm A tiếp xúc với mặt phẳng (P) là:
A. : (x – 2)2 + (y –1)2 + (z – 1)2 = 4
B. (x –+2)2 + (y – 1)2 + (z – 1)2 = 9
C. : (x – 2)2 + (y –1)2 + (z – 1)2 = 3
D. : (x – 2)2 + (y – 1)2 + (z – 1)2 = 5
C©u 13 : Cho hai điểm A(1;-1;5) và B(0;0;1). Mặt phẳng (P) chứa A, B và song song với Oy có phương trình là
A. 4x y z 1  0
B. 2x z 5  0
C. 4x z 1  0
D. y  4z 1  0
C©u 14 : Trong mặt phẳng Oxyz Cho tứ diện ABCD có A(2;3;1), B(4;1;-2), C(6;3;7), D-5;-4;-8).
Độ dài đường cao kẻ từ D của tứ diện là 6 5 5 4 3 A. 11 B. C. D. 5 5 3
C©u 15 : Cho hai điểm A1, 2  ,0 và B4,1, 
1 . Độ dài đường cao OH của tam giác OAB là: 1 86 19 19 A. B. C. D. 19 19 86 2
C©u 16 : Trong không gian Oxyz, cho bốn điểm A1,1, 
1 ; B1,3,5;C 1,1,4; D2,3,2 . Gọi I,
J lần lượt là trung điểm của AB và CD. Câu nào sau đây đúng? AB và CD có A. AB  IJ B. CD  IJ C. chung trung
D. IJ   ABC  điểm
C©u 17 : Mặt cầu (S) có tâm I(1;2;-3) và đi qua A(1;0;4) có phương trình A.  2   2   2 (x 1) (y 2) (z 3)  53 B.  2   2   2 (x 1) (y 2) (z 3)  53 C.  2   2   2 (x 1) (y 2) (z 3)  53 D.  2   2   2 (x 1) (y 2) (z 3)  53
C©u 18 : Trong không gian toạ độ Oxyz, cho điểm A 1  ,2,  1 và hai mặt phẳng
:2x 4y6z5  0 , : x 2y3z  0. Mệnh đề nào sau đây đúng ? 3
 không đi qua A và không song A.
B.  đi qua A và song song với  song với 
 đi qua A và không song song với
 không đi qua A và song song với C. D.  
C©u 19 : Cho hai mặt phẳng song song (P): nx  7y 6z 4  0 và (Q): 3x  my 2z 7  0 . Khi đó
giá trị của m và n là: 7 7 3 7 A. m  ; n  1  ;  9  ;  9  ;  9 3 B. n m 3 C. m n 7 D. m n 3 C©u 20 : x  1 2t x  7  ts 3  
Vị trí tương đối của hai đường thẳng d1 : y  2  t
3 ;d2 : y  2  2t là: z  5  4t z 1   2t A. Chéo nhau B. Trùng nhau C. Song song D. Cắt nhau
C©u 21 : Trong không gian với hệ tọa độ Oxyz cho tam giác ABC có A(1;0;0), B(0;-
2;3),C(1;1;1). Phương trình mặt phẳng (P) chứa A, B sao cho khoảng cách từ C tới (P) 2 là 3
A. x+y+z-1=0 hoặc -23x+37y+17z+23=0
B. 2x+3y+z-1=0 hoặc 3x+y+7z+6=0
C. x+2y+z-1=0 hoặc -2x+3y+6z+13=0
D. x+y+2z-1=0 hoặc -2x+3y+7z+23=0
C©u 22 : Trong không gian Oxyz cho hai mặt phẳng (P): 2x+y-z-3=0 và
(Q): x+y+x-1=0. Phương trình chính tắc đường thẳng giao tuyến của hai mặt phẳng (P) và (Q) là: x y  2 z 1 x 1 y  2 z 1 A.   B.   2 3  1 2  3  1 x 1 y  2 z 1 x y  2 z 1 C.   D.   2 3 1 2 3  1  C©u 23 : x  t 
Cho đường thẳng d :  y  1 và 2 mp (P): x  2y  2z 3  0 và (Q): x  2y  2z 7  0 .  z    t
Mặt cầu (S) có tâm I thuộc đường thẳng (d) và tiếp xúc với hai mặt phẳng (P) và (Q) 4 có phương trình 2 2 2 4 2 2 2 4
A.  x  3  y  1  z3 
x 3  y1  z 3  9 B.       9 2 2 2 4 2 2 2 4
C.  x  3  y  1  z3 
x  3  y1  z 3  9 D.       9
C©u 24 : Trong không gian Oxyz, cho ba vectơ a   1
 ,1,0;b  (1,1,0);c  1,1,  1 . Cho hình
hộp OABC.O’A’B’C” thỏa mãn điều kiện OA  , a OB  ,
b OC c . Thể tích của hình
hộp nói trên bằng bao nhiêu? 1 2 A. B. C. 2 D. 6 3 3
C©u 25 : Trong không gian với hệ tọa độ Oxyz cho mặt cầu 2 2 2
(S) : (x 1)  ( y  2)  (z  3)  9 và x  6 y  2 z  2 đường thẳng  :  
. Phương trình mặt phẳng (P) đi qua M(4;3;4), 3  2 2
song song với đường thẳng ∆ và tiếp xúc với mặt cầu (S) x-2y+2z-1=0 A. 2x+y+2z-19=0 B. 2x+y-2z-12=0 C. D. 2x+y-2z-10=0 C©u 26 : x  2 y  2 z
Trong không gian với hệ tọa độ Oxyz cho đường thẳng (d) :   và điểm 1  1 2
A(2;3;1). Viết phương trình mặt phẳng (P) chứa A và (d). Cosin của góc giữa mặt
phẳng (P) và mặt phẳng tọa độ (Oxy) là: 2 2 2 6 7 A. B. C. D. 6 3 6 13
C©u 27 : Cho mặt phẳng  :3x  2y  z  6  0 và điểm A2, 1
 ,0. Hình chiếu vuông góc của
A lên mặt phẳng  là: A. 1, 1  ,  1 B.  1  ,1,  1 C. 3, 2  ,  1 D. 5, 3  ,  1 C©u 28 :
x  6  4t
Cho điểm A(1;1;1) và đường thẳng d :y  2   t . z  1   2t
Hình chiếu của A trên d có tọa độ là A. 2; 3  ;  1 B. 2;3;  1 C. 2; 3  ;  1 D.  2  ;3;  1 5
C©u 29 : Trong hệ trục Oxyz , M’ là hình chiếu vuông góc của M3,2, 
1 trên Ox . M’ có toạ độ là: A. 0, 0,  1 B. 3,0,0 C.  3  ,0,0 D. 0, 2,0
C©u 30 : Trong không gian Oxyz cho các điểm A(3; -4; 0), B(0; 2; 4), C(4; 2; 1). Tọa độ điểm D
trên trục Ox sao cho AD = BC. là:
A. D(0;0;0) hoặc D(0;0;6)
B. D(0;0;2) hoặc D(0;0;8)
C. D(0;0;-3) hoặc D(0;0;3)
D. D(0;0;0) hoặc D(0;0;-6)
C©u 31 : Phương trình tổng quát của   qua A(2;-1;4), B(3;2;-1) và vuông góc với
 : x y  2z 3  0 là: A. 11x+7y-2z-21=0
B. 11x+7y+2z+21=0 C. 11x-7y-2z-21=0 D. 11x-7y+2z+21=0
C©u 32 : Khoảng cách từ điểm M(-2; -4; 3) đến mặt phẳng (P) có phương trình 2x – y + 2z – 3 = 0 là: A. 3 B. 1 C. 2 D. Đáp án khác
C©u 33 : Trong không gian Oxyz, cho điểm M(8,-2,4). Gọi A, B, C lần lượt là hình chiếu của
M trên các trục Ox, Oy, Oz. Phương trình mặt phẳng đi qua ba điểm A, B và C là:
A. x  4 y  2z  8  0
B. x  4 y  2z  8  0
C. x  4 y  2z  8  0
D. x  4 y  2z  8  0
C©u 34 : Gọi H là hình chiếu vuông góc của A(2; -1; -1) đến mặt phẳng (P) có phương trình
16x – 12y – 15z – 4 = 0. Độ dài của đoạn thẳng AH là: 11 11 22 22 A. B. C. D. 25 5 25 5
C©u 35 : Trong không gian với hệ tọa độ Oxyz, cho vecto AO  3i  4 j2k 5j . Tọa độ của điểm A là A. 3, 2  ,5 B.  3  , 1  7,2 C. 3,17, 2   D. 3,5, 2  
C©u 36 : Cho tam giác ABC có A = (1;0;1), B = (0;2;3), C = (2;1;0). Độ dài đường cao của tam giác kẻ từ C là 6 26 26 A. 26 B. C. D. 26 2 3
C©u 37 : Cho 4 điềm A(3; -2; -2), B(3; 2; 0), C(0; 2; 1) và D(-1; 1; 2). Mặt cầu tâm A và tiếp xúc
với mặt phẳng (BCD) có phương trình là: A. 2 2 2
(x  3)  ( y  2)  (z  2)  14 B. 2 2 2
(x  3)  ( y  2)  (z  2)  14 C. 2 2 2
(x  3)  ( y  2)  (z  2)  14 D. 2 2 2
(x  3)  ( y  2)  (z  2)  14
C©u 38 : Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1;2;2), B(5;4;4) và mặt
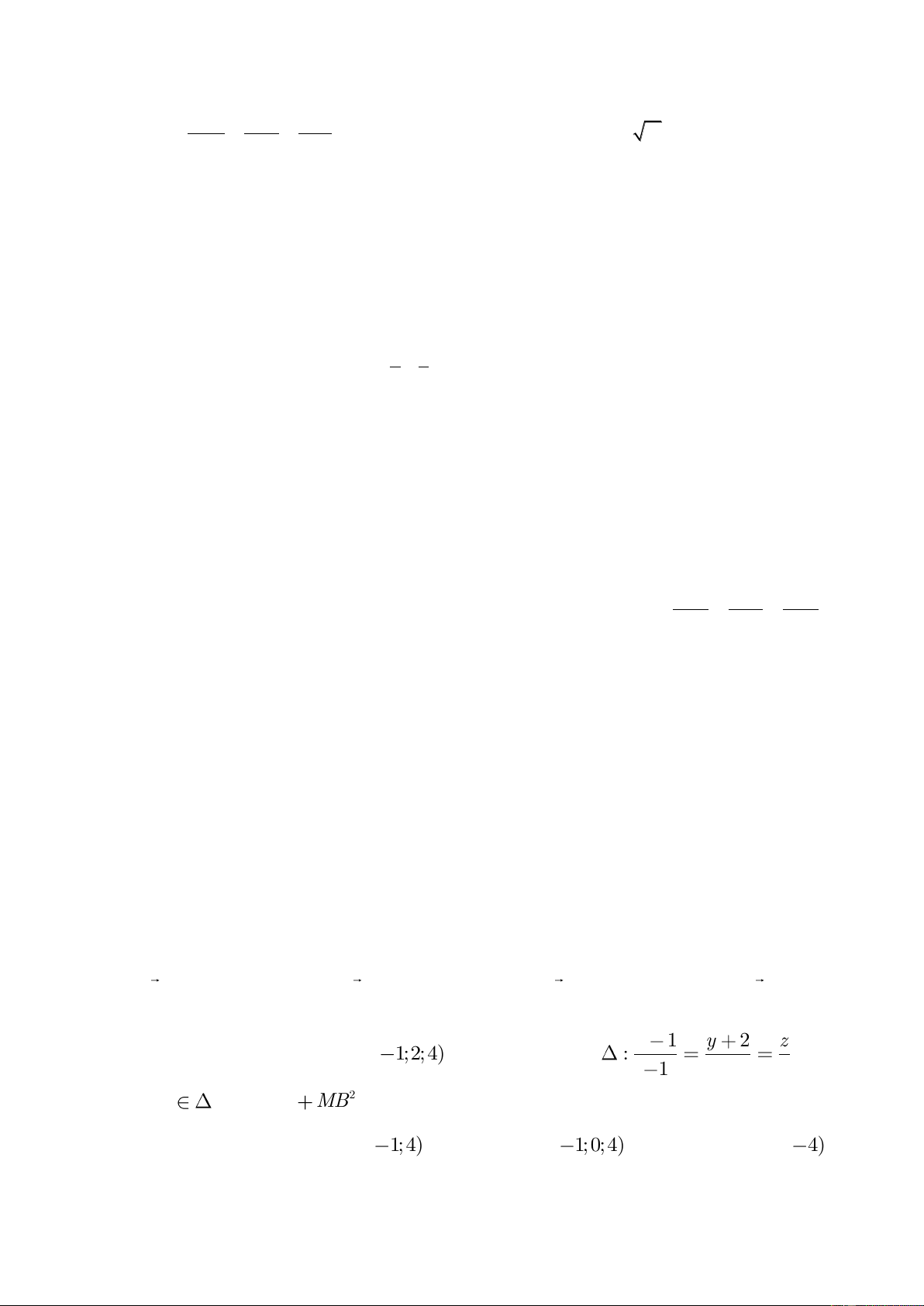
phẳng (P): 2x + y – z + 6 =0. Tọa độ điểm M nằm trên (P) sao cho MA2 + MB2 nhỏ nhất là: M(-1;1;5) A. B. M(1;-1;3) C. M(2;1;-5) D. M(-1;3;2)
C©u 39 : Trong không gian Oxyz cho hai mặt phẳng (P): 2x+y-z-3=0 và
(Q): x+y+x-1=0. Phương trình chính tắc đường thẳng giao tuyến của hai mặt phẳng (P) và (Q) là: x y  2 z 1 x 1 y  2 z 1 A.   B.   2 3  1 2  3  1 x y  2 z 1 x 1 y  2 z 1 C.   D.   2 3  1  2 3 1
C©u 40 : Mặt phẳng () đi qua M (0; 0; -1) và song song với giá của hai vectơ a(1; 2  ;3) và (
b 3;0;5) . Phương trình của mặt phẳng ( ) là:
A. 5x – 2y – 3z -21 = 0
B. -5x + 2y + 3z + 3 = 0
C. 10x – 4y – 6z + 21 = 0
D. 5x – 2y – 3z + 21 = 0
C©u 41 : Cho (S) là mặt cầu tâm I(2; 1; -1) và tiếp xúc với mặt phẳng (P) có phương trình: 2x –
2y – z + 3 = 0. Khi đó, bán kính của (S) là: 4 1 A. B. 2 C. D. 3 3 3
C©u 42 : Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1;2;2), B(5;4;4) và mặt
phẳng (P): 2x + y – z + 6 =0. Tọa độ điểm M nằm trên (P) sao cho MA2 + MB2 nhỏ nhất là: 7 M(-1;1;5) A. B. M(2;1;-5) C. M(1;-1;3) D. M(-1;3;2)
C©u 43 : Trong không gian Oxyz, cho mặt phẳng (P)đi qua hai điểm A(4,-1,1), B(3,1,-1) và
song song với trục Ox. Phương trình nào sau đây là phương trình của mặt phẳng (P):
A. x y z  0
B. x y  0
C. y z  0
D. x z  0
C©u 44 : Trong không gian Oxyz mp (P) đi qua B(0;-2;3) ,song song với đường thẳng d: x  2 y1   z 2 3
và vuông góc với mặt phẳng (Q):x+y-z=0 có phương trình ? A. 2x-3y+5z-9=0 B. 2x-3y+5z-9=0 C. 2x+3y-5z-9=0 D. 2x+3y+5z-9=0
C©u 45 : Trong không gian Oxyz, cho bốn điểm A1,0,0;B0,1,0;C0,0,  1 ; D1,1,  1 . Xác
định tọa độ trọng tâm G của tứ diện ABCD  1 1 1   1 1 1   2 2 2   1 1 1  A. , ,   , ,   C. , ,   , ,    B. D. 2 2 2   3 3 3   3 3 3   4 4 4 
C©u 46 : Trong không gian Oxyz, gọi (P) là mặt phẳng cắt ba trục tọa độ tại ba điểm
A8,0,0; B0, 2
 ,0;C0,0,4 . Phương trình của mặt phẳng (P) là: x y z x y z A.   1    4 1  B. 0 2 8 2  4
C. x  4 y  2z  8  0
D. x  4 y  2z  0 C©u 47 : x  2t x 1 y z  3 
Cho hai đường thẳng d :  
và d : y  1 4t 1 1 2 3 2  z  2  6t
Khẳng định nào sau đây là đúng? d , d 1 2 trùng d // d d , d A. d , d 1 2 cắt nhau; B. C. 1 2 ; D. 1 2 chéo nhau. nhau; C©u 48 : x  2 y  2 z
Trong không gian với hệ tọa độ Oxyz cho đường thẳng (d) :   và điểm 1  1 2
A(2;3;1). Viết phương trình mặt phẳng (P) chứa A và (d). Cosin của góc giữa mặt
phẳng (P) và mặt phẳng tọa độ (Oxy) là: 8 2 2 6 7 2 A. B. C. D. 6 6 13 3
C©u 49 : Trong không gian Oxyz cho hai điểm A(0;0;-3), B(2;0;-1) và mặt phẳng (P): 3x-8y+7z-
1=0. Gọi C là điểm trên (P) để tam giác ABC đều khi đói tọa độ điểm C là: 1  3 1  2  2  1  A. C( 3  ;1;2) B. C( ; ; ) C. C( ; ; ) D. C(1;2; 1  ) 2 2 2 3 3 3
C©u 50 : Trong không gian Oxyz mặt phẳng (P) đi qua điểm M(-1;2;0) và có VTPT
n  (4;0;5) có phương trình là: A. 4x-5y-4=0 B. 4x-5z-4=0 C. 4x-5y+4=0 D. 4x-5z+4=0
C©u 51 : Cho các vectơ a  (1;2;3); b  ( 2  ;4;1); c  ( 1
 ;3;4) . Vectơ v  2a 3b  5c có toạ độ là: A. (7; 3; 23) B. (7; 23; 3) C. (23; 7; 3) D. (3; 7; 23)
C©u 52 : Trong không gian với hệ tọa độ vuông góc Oxyz, cho mặt phẳng x 1 y z  2
(P) : x + 2y + z – 4 = 0 và đường thẳng d :  
. Phương trình đường thẳng 2 1 3
∆ nằm trong mặt phẳng (P), đồng thời cắt và vuông góc với đường thẳng d là: x 1 y 1 z 1 x 1 y  3 z 1 A.   B.   5 1  3 5 1  3 x 1 y 1 z 1 x 1 y 1 z 1 C.   D.   5 1  2 5 2 3 C©u 53 : x 1 y
Tọa độ hình chiếu vuông góc của M(2; 0; 1) trên đường thằng :   z  2 là: 1 2 A. (2; 2; 3) B. (1; 0; 2) C. (0; -2; 1) D. (-1; -4; 0)
C©u 54 : Trong không gian Oxyz cho hai điểm A(0;0;-3), B(2;0;-1) và mặt phẳng (P): 3x-8y+7z-
1=0. Gọi C là điểm trên (P) để tam giác ABC đều khi đói tọa độ điểm C là: 2  2  1  1  3 1  A. C( 3  ;1;2) B. C(1;2; 1  ) C. C( ; ; ) D. C( ; ; ) 3 3 3 2 2 2
C©u 55 : Trong không gian Oxyz cho các điểm A(3; -4; 0), B(0; 2; 4), C(4; 2; 1). Tọa độ điểm D
trên trục Ox sao cho AD = BC. là: 9
A. D(0;0;0) hoặc D(0;0;6)
B. D(0;0;2) hoặc D(0;0;8)
C. D(0;0;-3) hoặc D(0;0;3)
D. D(0;0;0) hoặc D(0;0;-6)
C©u 56 : Trong không gian Oxyz, cho điểm I(2,6,-3) và các mặt phẳng:
: x  2  0; : y 6  0; : z 3 0
Trong các mệnh đề sau, tìm mệnh đề sai:  đi qua 
A.    B. C. / /Oz
D.  / /  xOz điểm I
C©u 57 : Cho đường thẳng d đi qua M(2; 0; -1) và có vectơ chỉ phương a(4; 6  ;2) . Phương
trình tham số của đường thẳng d là: x  2   2t
x  2  2t
x  4  2tx  2   4t     A. y  3  t B. y  3  t C. y  6   3t D. y  6  t     z  1 tz  1   tz  2  tz 1 2t
C©u 58 : Trong không gian Oxyz mặt phẳng trung trực của đoạn thẳng AB có phương trình
là ,với A(1;2;-3),B(-3;2;9) A. -x-3z-10=0 B. -4x+12z-10=0 C. -x-3z-10=0 D. -x+3z-10=0 C©u 59 : x 1 y1 z
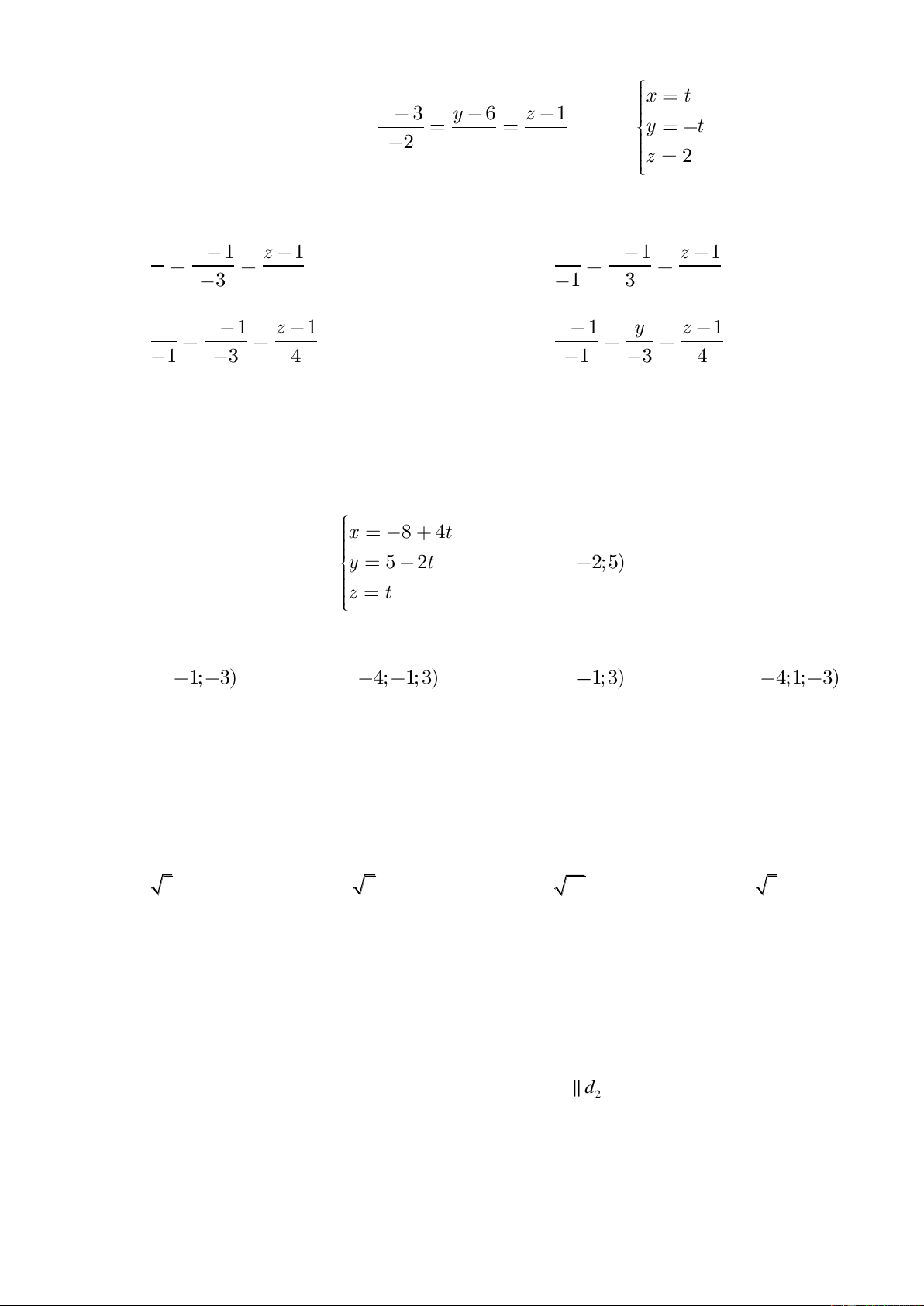
Cho điểm M(2; 1; 0) và đường thẳng :   2 1
1 . Đ ường thẳng d đi qua điểm
M, cắt và vuông góc với  có vec tơ chỉ phương A. (2; 1; 1) B. (2;1;1) C. (1; 4;2)
D. (1;4;2)
C©u 60 : Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;1;1) và mặt phẳng (P): 2x – y +
2z + 1 = 0. Phương trình mặt cầu tâm A tiếp xúc với mặt phẳng (P) là:
A. : (x – 2)2 + (y –1)2 + (z – 1)2 = 4
B. : (x – 2)2 + (y – 1)2 + (z – 1)2 = 5
C. : (x – 2)2 + (y –1)2 + (z – 1)2 = 3
D. (x –+2)2 + (y – 1)2 + (z – 1)2 = 9
C©u 61 : Trong không gian toạ độ Oxyz, cho ba điểm M1,0,0, N0,2,0 , P0,0,3 . Mặt phẳng
MNP có phương trình là
A. 6x  3y  2z 1  0
B. 6x  3y  2z  6  0
C. 6x  3y  2z 1  0
D. x  y  z  6  0 10
C©u 62 : Gọi () là mặt phẳng cắt ba trục tọa độ tại 3 điểm M (8; 0; 0), N(0; -2; 0) , P(0; 0; 4).
Phương trình của mặt phẳng ( ) là: x y z
x – 4y + 2z – 8 = x y z A.    0 B.
C. x – 4y + 2z = 0 D.   1 8 2  4 0 4 1  2
C©u 63 : Cho điểm A(-1;2;1) và hai mặt phẳng (P) : 2x+4y-6z-5=0 và (Q) : x+2y-3z=0. Mệnh đề nào sau đây là đúng ?
A. mp (Q) không đi qua A và không song song với (P);
B. mp (Q) đi qua A và không song song với (P);
C. mp (Q) đi qua A và song song với (P) ;
D. mp (Q) không đi qua A và song song với (P);
C©u 64 : Trong hệ trục Oxyz , cho ba điểm A 2  ,1,0, B 3
 ,0,4 , C0,7,3 . Khi đó , cos AB,BC bằng: 14 7 2 14 14 A. B. C. D.  3 118 3 59 57 57
C©u 65 : Khoảng cách giữa hai mặt phẳng (P): 2x  y z
3  5  0 và (Q): 2x y z 3 1  0 bằng: 6 4 A. B. 14 6 C. 4 D. 14
C©u 66 : Cho bốn điểm A(1;1;1), B(1;2;1), C(1;1;2) và D(2;2;1). Tâm I của mặt cầu ngoại tiếp tứ diện ABCD có tọa độ :  3 3 3   3 3 3  A. 3;3; 3   B. ;  ;   ; ;   3;3;3  C. D.   2 2 2   2 2 2  C©u 67 : x  1 2t
Cho điểm A(0;-1;3) và đường thẳng dy  2 . 
Khoảng cách từ A đến d bằng z  1   A. 8 B. 3 C. 14 D. 6
C©u 68 : Cho mặt cầu (S): x2  y2  z2 8x 4y 2z 4  0 . Bán kính R của mặt cầu (S) là: 11 A. R = 17 B. R = 88 C. R = 2 D. R = 5
C©u 69 : Cho 2 điểm A(2; 4; 1), B(–2; 2; –3). Phương trình mặt cầu đường kính AB là: A. x2  y 2   z 2 ( 3) ( 1)  9 B. x2  y 2   z 2 ( 3) ( 1)  9 C. x2  y 2   z 2 ( 3) ( 1)  3 D. x2  y 2   z 2 ( 3) ( 1)  9
C©u 70 : Trong mặt phẳng Oxyz Cho tứ diện ABCD có A(2;3;1), B(4;1;-2), C(6;3;7), D-5;-4;-8).
Độ dài đường cao kẻ từ D của tứ diện là 6 5 5 4 3 A. 11 B. C. D. 5 5 3
C©u 71 : Cho A(1;0;0), B(0;1;0), C(0;0;1) và D(-2;1;-1).Thể tích của tứ diện ABCD là 1 1 A. 1 B. 2 C. D. 2 3
C©u 72 : Trong không gian Oxyz, tam giác ABC có A1,0,0;B0,2,0;C3,0,4. Tọa độ
điểm M trên mặt phẳng Oyz sao cho MC vuông góc với (ABC) là:  3 11  3 11  3 11   3 11  A. 0, ,   B. 0, ,    C. 0,  ,   D. 0,  ,     2 2   2 2   2 2   2 2 
C©u 73 : Cho 3 điểm A(1; –2; 1), B(–1; 3; 3), C(2; –4; 2). Một VTPT n của mặt phẳng (ABC) là: A. n  ( 1  ;9;4) B. n  (9;4;1) C. n  (4;9; 1  ) D. n  (9;4; 1  ) C©u 74 : x 12 y  9 z 1
Tọa độ giao điểm M của đường thẳng d :  
và mặt phẳng (P): 3x + 4 3 1
5y – z – 2 = 0 là: A. (1; 0; 1) B. (0; 0; -2) C. (1; 1; 6) D. (12; 9; 1)
C©u 75 : Trong không gian Oxyz, xác định các cặp giá trị (l, m) để các cặp mặt phẳng sau đây
song song với nhau: 2x ly  3z  5  0;mx  6y  6z  2  0 A. 3, 4 B. 4; 3   C.  4  ,3 D. 4,3
C©u 76 : : Cho 2 điểm A(1; 2; –3) và B(6; 5; –1). Nếu OABC là hình bình hành thì toạ độ điểm 12 C là: A. (–5;–3;–2) B. (–3;–5;–2) C. (3;5;–2) D. (5; 3; 2)
C©u 77 : Bán kính của mặt cầu tâm I(3;3;-4), tiếp xúc với trục Oy bằng 5 A. 5 B. 4 C. 5 D. 2
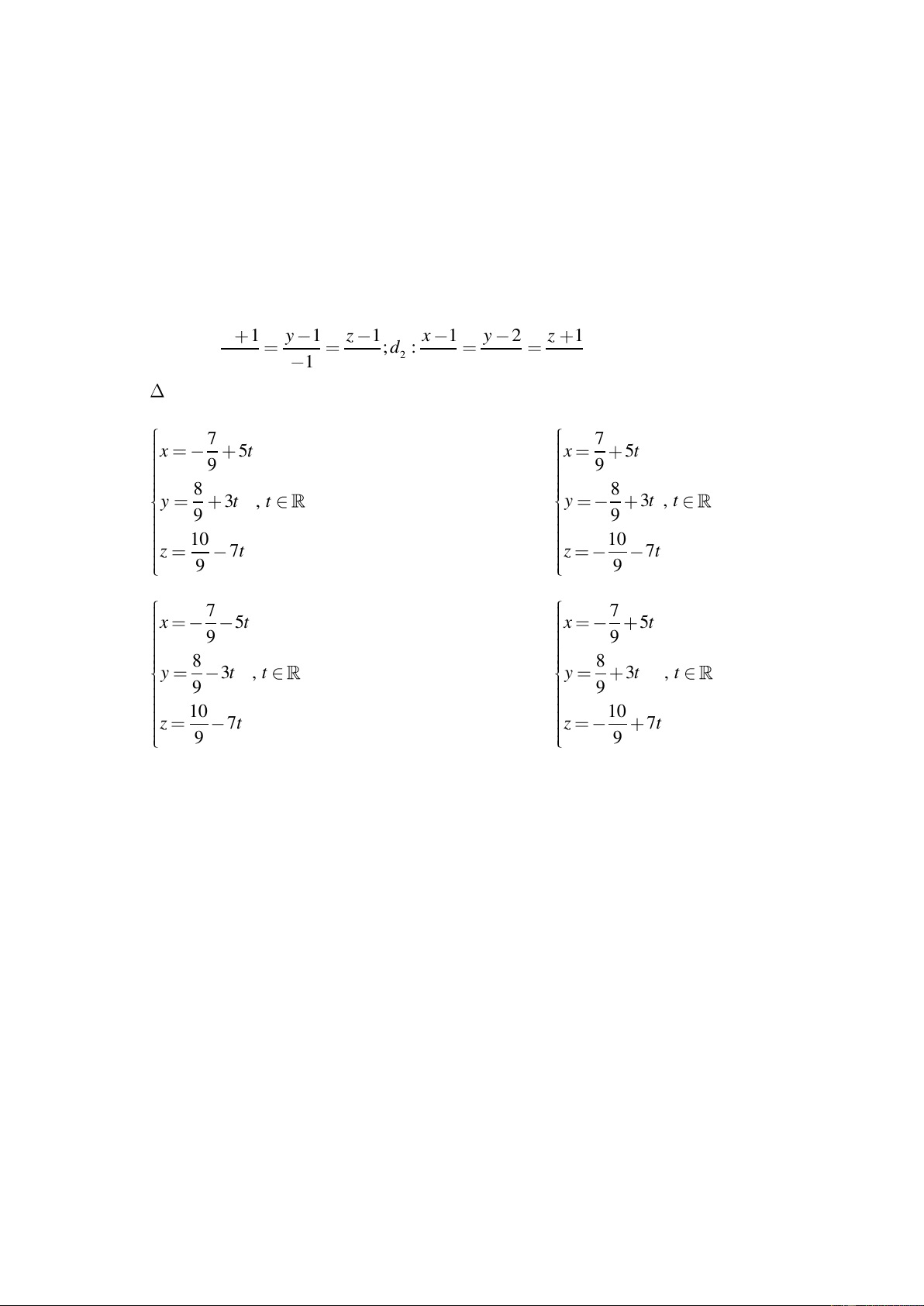
C©u 78 : Trong không gian toạ độ Oxyz, cho mặt phẳng  : 2x  y  z  5  0 và đường thẳng x 1 y  3 z  2 d :  
. Toạ độ giao điểm của d và  là 3 1  3  A. 4, 2,  1  B.  1  7,9,20 C.  1  7,20,9 D.  2  ,1,0
C©u 79 : Cho mặt phẳng  : 4x  2y  3z 1 0 và mặt cầu   2 2 2
S : x  y  z  2x  4y  6z  0 . Khi
đó, mệnh đề nào sau đây là một mệnh đề sai:
A.  cắt S theo một đường tròn
B.  tiếp xúc với S
C.  có điểm chung với S
D.  đi qua tâm của S C©u 80 : x 1 t 
Cho mặt phẳng  : 2x  y  2z 1  0 và đường thẳng d : y  2
 t . Gọi  là góc giữa z  2t  2 
đường thẳng d và mặt phẳng  . Khi đó, giá trị của cos là: 4 65 65 4 A. B. C. D. 9 9 4 65 13 ĐÁP ÁN 01 ) | } ~ 28 { | ) ~ 55 ) | } ~ 02 { | } ) 29 { ) } ~ 56 { | ) ~ 03 ) | } ~ 30 ) | } ~ 57 { ) } ~ 04 ) | } ~ 31 { | ) ~ 58 { | } ) 05 { | } ) 32 { ) } ~ 59 { | } ) 06 { | } ) 33 { | ) ~ 60 ) | } ~ 07 { | } ) 34 { ) } ~ 61 { ) } ~ 08 { | } ) 35 { ) } ~ 62 { ) } ~ 09 { ) } ~ 36 { | ) ~ 63 { | ) ~ 10 { | ) ~ 37 { ) } ~ 64 { ) } ~ 11 { | } ) 38 ) | } ~ 65 { | } ) 12 ) | } ~ 39 ) | } ~ 66 { | ) ~ 13 { | ) ~ 40 { ) } ~ 67 { | ) ~ 14 ) | } ~ 41 { ) } ~ 68 { | } ) 15 { ) } ~ 42 ) | } ~ 69 { | } ) 16 { | ) ~ 43 { | ) ~ 70 ) | } ~ 17 { | } ) 44 { | } ) 71 { | ) ~ 18 { ) } ~ 45 { | ) ~ 72 { | ) ~ 19 { | } ) 46 { | ) ~ 73 { | } ) 20 { | } ) 47 { | ) ~ 74 { ) } ~ 21 ) | } ~ 48 ) | } ~ 75 { | ) ~ 22 ) | } ~ 49 ) | } ~ 76 { | } ) 23 { | } ) 50 { | } ) 77 { | ) ~ 24 { | ) ~ 51 { | } ) 78 { ) } ~ 25 ) | } ~ 52 ) | } ~ 79 { ) } ~ 26 ) | } ~ 53 { ) } ~ 80 { ) } ~ 27 { ) } ~ 54 ) | } ~ 14 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN ĐỀ 002 C©u 1 : Cho ( A 2;1; 1  ) , ( B 3; 0;1) , ( C 2; 1
 ; 3); điểm D thuộc Oy , và thể tích khối tứ diện ABCD
bằng 5 . Tọa độ điểm D là: A. (0; 7  ;0) hoặc (0;8;0) B. (0; 7  ;0) C. (0; 8; 0)
D. (0; 7; 0) hoặc (0; 8  ;0) C©u 2 : x  3 y  3 z
Cho đường thẳng d :   , m (
p ) : x y z  3  0 và điểm ( A 1; 2; 1  ) . Đường 1 3 2
thẳng  qua A cắt d và song song với (
mp ) có phương trình là x  1 y  2 z  1 x  1 y  2 z  1 A.   B.   1  2  1 1 2  1  x  1 y  2 z  1 x  1 y  2 z  1 C.   D.   1 2 1 1 2 1 C©u 3 : Cho ( A 5;1; 3) , ( B 5  ;1; 1  ) , ( C 1; 3  ;0) , ( D 3; 6
 ; 2) . Tọa độ điểm A đối xứng với điểm A qua m ( p BC ) D là A. ( 1  ;7; 5) B. (1; 7  ; 5  ) C. (1; 7; 5) D. (1; 7  ; 5) C©u 4 : Cho mặt cầu 2 2 2 ( )
S : x y z  2x  4y  6z  2  0 và mặt phẳng () : 4x  3y 12z  10  0 .
Mặt phẳng tiếp xúc với (S) và song song với ( ) có phương trình là:
4x  3y 12z  78  0 hoặc
A. 4x  3y  12z  78  0
B. 4x3y12z26  0
4x  3y 12z  78  0 hoặc C.
D. 4x  3y  12z  26  0
4x  3y 12z  26  0 C©u 5 : Cho hai điểm ( A 2  ;0; 3  ) , ( B 2; 2; 1
 ) . Phương trình nào sau đây là phương trình mặt cầu đường kính AB ? A. 2 2 2
x y z  2y  4z 1  0 B. 2 2 2
x y z  2x  4z  1  0 C. 2 2 2
x y z  2y  4z 1  0 D. 2 2 2
x y z  2y  4z 1  0 C©u 6 :    Đường thẳng   x 12 y 9 z 1 d :  
cắt mặt phẳng  : 3x  5y  z  2  0 tại điểm có tọa 4 3 1 độ là : A. 2;0; 4 B. 0;1;3 C. 1;0;  1 D. 0;0; 2   C©u 7 : Cho ( A 2; 1  ;6) , ( B 3  ; 1  ; 4  ) , ( C 5; 1  ;0), (
D 1; 2;1) . Thể tích tứ diện ABCD bằng: A. 30 B. 50 C. 40 D. 60 C©u 8 : Cho mặt cầu 2 2 2 ( )
S : x y z  2x  6y  4z  0 . Biết OA , (O là gốc tọa độ) là đường kính
của mặt cầu (S) . Tìm tọa độ điểm A ?
Chưa thể xác định được tọa độ điểm A vì A. ( A 1  ; 3; 2)
B. mặt cầu (S) có vô số đường kính C. ( A 2; 6  ; 4  ) D. ( A 2  ;6; 4) C©u 9 : x y z  1
Tìm điểm A trên đường thẳng d :   2 1 
sao cho khoảng cách từ điểm A đến 1 m (
p ) : x  2y  2z  5  0 bằng 3 . Biết A có hoành độ dương A. ( A 0; 0; 1  ) B. ( A 2  ;1; 2  ) C. ( A 2; 1  ;0) D. ( A 4; 2  ;1)
C©u 10 : Cho (S) là mặt cầu tâm I(2;1; 1
 ) và tiếp xúc mặt phẳng () : 2x  2y z  3  0 . Khi đó bán
kính mặt cầu (S) là: 2 4 2 A. 2 B. C. D. 3 3 9
C©u 11 : Cho hai mặt phẳng 2 2
() : m x y  (m  2)z  2  0 và 2
( ) : 2x m y  2z  1  0 . Mặt phẳng
( ) vuông góc với ( ) khi A. m  2 B. m  2 C. m  1 D. m  3
C©u 12 : Trong không gian Oxyz , cho bốn điểm ( A 1; 0; 0) , ( B 0;1; 0) , ( C 0; 0;1) và (
D 1;1;1) . Gọi M, N
lần lượt là trung điểm của AB và CD . Khi đó tọa độ trung điểm G của đoạn thẳng MN là:  1 1 1   1 1 1   1 1 1   2 2 2 
A. G  ; ; 
B. G  ; ; 
C. G  ; ; 
D. G  ; ;   2 2 2   3 3 3   4 4 4   3 3 3 
C©u 13 : Cho ba mặt phẳng P:3x  y  z  4  0 ; Q:3x  y  z 5  0 và R: 2x 3y 3z 1 0 . Xét các mệnh đề sau:
(I): (P) song song (Q) (II): (P) vuông góc (Q)
Khẳng định nào sau đây ĐÚNG ?
A. (I) sai ; (II) đúng
B. (I) đúng ; (II) sai
C. (I) ; (II) đều sai
D. (I) ; (II) đều đúng C©u 14 : x  1 3t
Cho đường thẳng d : y  2t và m ( p )
P : 2x y  2z  6  0 . Giá trị của m để d  (P) là: z  2   mtA. m  2 B. m  2  C. m  4 D. m  4  C©u 15 : x t x  3 y  6 z  1 
Cho hai đường thẳng d :  
d : y t
 . Đường thẳng đi qua điểm 1 2  và 2 1 2 z  2  (
A 0;1;1) , vuông góc với d và d có pt là: 1 2 x y  1 z  1 x y  1 z  1 A.     1 3  B. 4 1  3 4 x y  1 z  1 x  1 y z  1 C.   D.   1  3  4 1  3  4 C©u 16 : Cho ( A 0; 0; 2) , ( B 3; 0; 5) , ( C 1;1; 0) , (
D 4;1; 2) . Độ dài đường cao của tứ diện ABCD hạ từ
đỉnh D xuống mặt phẳng (ABC) là: 11 A. B. 11 C. 1 D. 11 11 C©u 17 : Cho ( A 0; 0;1) , ( B 1  ; 2  ;0), ( C 2;1; 1
 ). Đường thẳng  đi qua trọng tâm G của tam giác
ABC và vuông góc với m (
p ABC) có phương trình:  1  1  1  1 x   5tx   5tx   5tx   5t  3  3  3  3   1  1  1  1
A. y    4t
B. y    4t
C. y    4t
D. y    4t 3  3  3  3  z  3tz  3tz  3  tz  3t    
C©u 18 : Cho tứ diện OABC với A 3  ;1; 2   ; B1;1;  1 ;C 2  ;2; 
1 . Tìm thể tích tứ diện OABC. 8 4 A. 8 (đvtt) B. (đvtt) C. 4 (đvtt) D. (đvtt) 3 3 C©u 19 : x  3   t
Cho mặt phẳng () : 2x y  3z  1  0 và đường thẳng d : y  2  2t . z  1 
Trong các mệnh đề sau, mệnh đề nào đúng? A. d  ( )
B. d cắt ( ) C. d ( ) D. d  ()
C©u 20 : Cho tam giác ABC với A 3  ;2; 7  ;B2;2; 3   ; C 3  ;6; 2
  . Điểm nào sau đây là trọng tâm của tam giác ABC  4 10   4 10  A. G  4  ;10;12 B. G ;  ; 4   C. G 4; 1  0;12 D. G  ; ;  4    3 3   3 3  C©u 21 :      
Cho hai đường thẳng chéo nhau :   x 1 y 7 z 3 d :   và   x 1 y 2 z 2 d ' :   . Tìm 2 1 4 1 2 1 
khoảng cách giữa (d) và (d’) : 3 2 1 5 A. B. C. D. 14 14 14 14
C©u 22 : Cho mặt cầu   2 2 2
S : x  y  z  2x  4y  6z  5  0 và mặt phẳng  : x  y  z  0 . Khẳng
định nào sau đây đúng ?
A.  đi qua tâm của (S)
B.  tiếp xúc với (S)
 cắt (S) theo 1 đường tròn và không đi C.
D.  và S không có điểm chung
qua tâm của mặt cầu (S)
C©u 23 : Trong không gian Oxyz , cho ba vectơ a  ( 1
 ;1;0), b  (1;1;0) và c  (1;1;1) . Trong các
mệnh đề sau, mệnh đề nào đúng? 2 a và b cùng
A. cos(b,c)  B. . a c  1 C.
D. a b c  0 6 phương
C©u 24 : Tọa độ hình chiếu vuông góc của điểm ( A 5; 1  ; 3
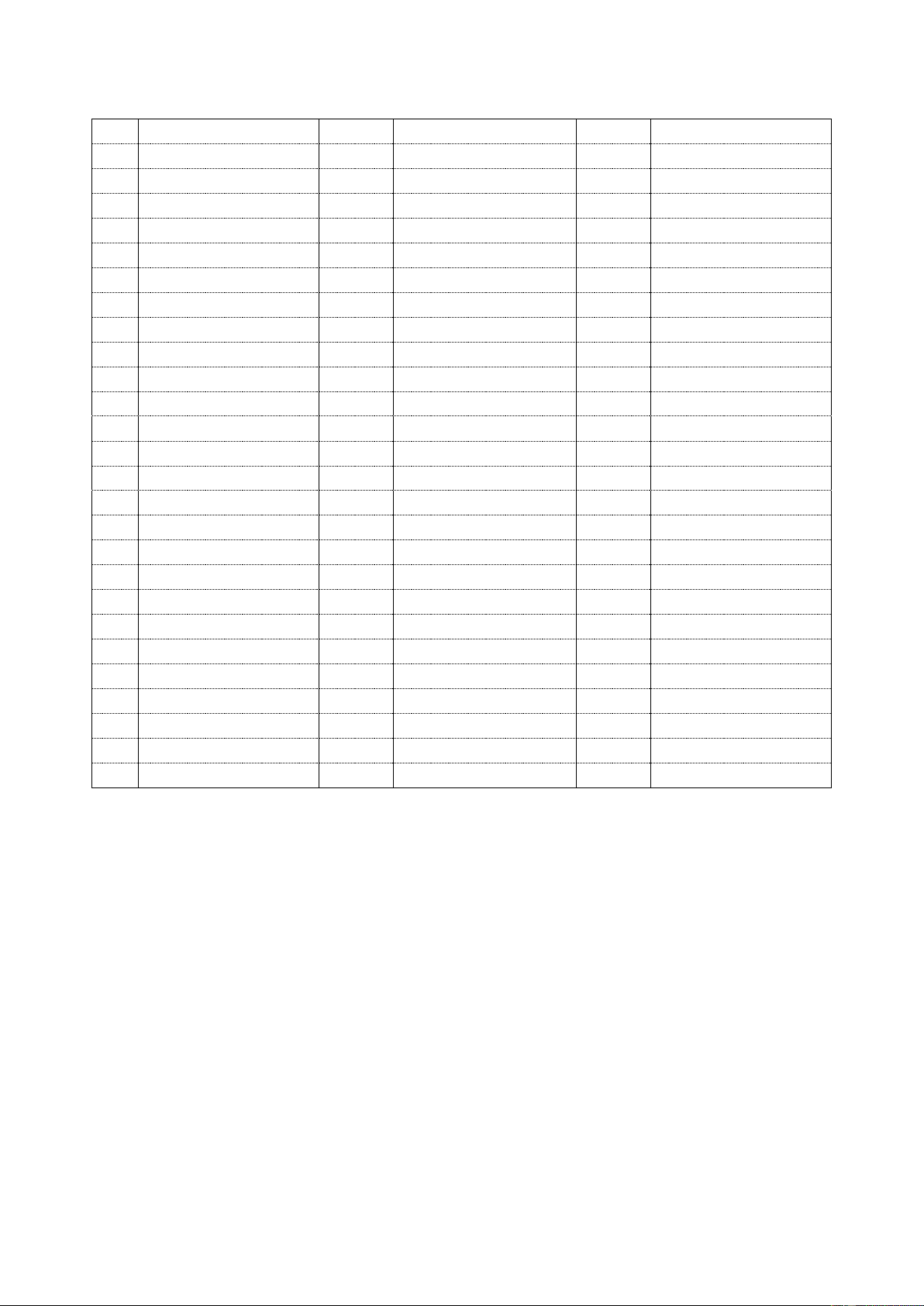
 ) lên mặt phẳng () : 2x y1  0 là điểm nào trong các điểm sau? A. (1;1; 3) B. (1; 1  ; 3  ) C. (1;1; 3  ) D. ( 1  ; 1  ; 3) C©u 25 : x  1 y  2 z Cho hai điểm ( A 1; 4; 2) , ( B 1
 ; 2; 4) và đường thẳng  :   1  . Điểm M  mà 1 2 2 2
MA MB nhỏ nhất có tọa độ là A. (1; 0; 4  ) B. (0; 1  ; 4) C. ( 1  ;0; 4) D. (1; 0; 4)
C©u 26 : Trong không gian Oxyz, cho điểm (
G 1;1;1) , mặt phẳng qua G và vuông góc với đường
thẳng OG có phương trình:
A. x y z  0
B. x y z  3  0
C. x y z  0
D. x y z  3  0 C©u 27 : Cho hai điểm ( A 1  ; 3;1), ( B 3; 1  ; 1
 ) . Khi đó mặt phẳng trung trực của đoạn thẳng AB có phương trình là
A. 2x  2y z  0
B. 2x  2y z  0
C. 2x  2y z  0
D. 2x  2y z  1  0 C©u 28 : Cho ( A 0; 2; 2  ), ( B 3  ;1; 1  ) , ( C 4; 3; 0) và ( D 1; 2; )
m . Tìm m để bốn điểm A, B,C, D đồng
phẳng. Một học sinh giải như sau: Bước 1: AB  ( 3  ; 1
 ;1) ; AC  (4;1;2) ; AD  (1;0;m 2)  1  1 1  3 3  1 
Bước 2: AB, AC         2 ; 4 ; 4 1 ( 3;10;1) 1 1   
AB, AC.AD  3  m  2  m  5  
Bước 3: A, B,C, D đồng phẳng  AB, AC .AD  0  m  5  0   Đáp số: m  5 
Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào? A. Sai ở bước 2 B. Đúng C. Sai ở bước 1 D. Sai ở bước 3
C©u 29 : Trong không gian Oxyz , cho bốn điểm ( A 1; 0; 0) , ( B 0;1; 0) , ( C 0; 0;1) và ( D 1;1;1) . Khi đó
mặt cầu ngoại tiếp tứ diện ABCD có bán kính: 3 3 A. B. 2 C. D. 3 2 4 C©u 30 : x  3  t
Trong không gian tọa độ Oxyz cho hai đường thẳng d :  y  1
  2t t R và 1    z  4  x k   d
:  y  1 k
k R .Khoảng cách giữa d và d bằng giá trị nào sau đây ? 2  1  2    z  3 2k  105 1 5 21 A. B. C. 2 D. 7 2 7
C©u 31 : Cho mặt phẳng () đi qua điểm ( M 0; 0; 1
 ) và song song với giá của hai vectơ a  (1; 2;  3)
và b  (3; 0; 5) . Phương trình mặt phẳng ( ) là: A. 5
x  2y  3z  3  0
B. 5x  2y  3z  21  0
C. 5x  2y  3z  21  0
D. 10x  4y  6z  21  0 C©u 32 : x  1 t x  2 y  2 z  3 
Cho hai đường thẳng d :  
d : y  1 2t và điểm ( A 1; 2; 3) . Đường 1 2 1  ; 1 2 z  1   t
thẳng  đi qua A , vuông góc với d và cắt d có phương trình là: 1 2 x  1 y  2 z  3 x  1 y  2 z  3 A.   B.   1 3 5  1 3  5  x  1 y  2 z  3 x  1 y  2 z  3 C.   D.   1  3  5  1 3 5 C©u 33 : x 1 y  3 z 1
Trong không gian với hệ tọa độ Oxyz , cho (d):   và 3  2 2 
 : x 3y z  4  0 . Phương trình hình chiếu của (d) trên  là: x  3 y  1 z 1 x  2 y  1 z 1 A.   B.   2 1  1 2  1 1 x  5 y  1 z 1 x y  1 z 1 C.   D.   2 1 1  2 1 1
C©u 34 : Trong không gian với hệ tọa độ Oxyz, phương trình mặt cầu (S) có tâm I(3;7;9) và tiếp xúc với mặt phẳng (Oyz) là : 2 2 2 2 2 2
A. x  3   y  7   z  9  3
B. x  3   y  7   z  9  9 2 2 2 2 2 2
C. x  3   y  7   z  9  81
D. x  3   y  7   z  9  9
C©u 35 : Cho mặt phẳng ( )
P : 3x  4y  5z  8  0 và đường thẳng d là giao tuyến của hai mặt phẳng
() : x  2y  1  0 và ( ) : x  2z  3  0 . Gọi  là góc giữa đường thẳng d và m ( p P) . Khi đó A. 0   45 B. 0   60 C. 0   30 D. 0   90
C©u 36 : Cho đường thẳng d đi qua điểm (
A 1; 2; 3) và vuông góc với mặt phẳng
() : 4x  3y  7z  1  0 . Phương trình tham số của d là: x  1 4t
x  1 8tx  1 3tx  1   4t    
A. y  2  3t B. y  2   6t
C. y  2  4t D. y  2   3t     z  3  7tz  3  14tz  3  7tz  3   7t
C©u 37 : Tìm góc giữa hai mặt phẳng  : 2x  y  z  3  0 ; : x  y  2z 1  0 : A. 0 30 B. 0 90 C. 0 45 D. 0 60
C©u 38 : Cho lăng trụ tam giác đều AB . C A BC
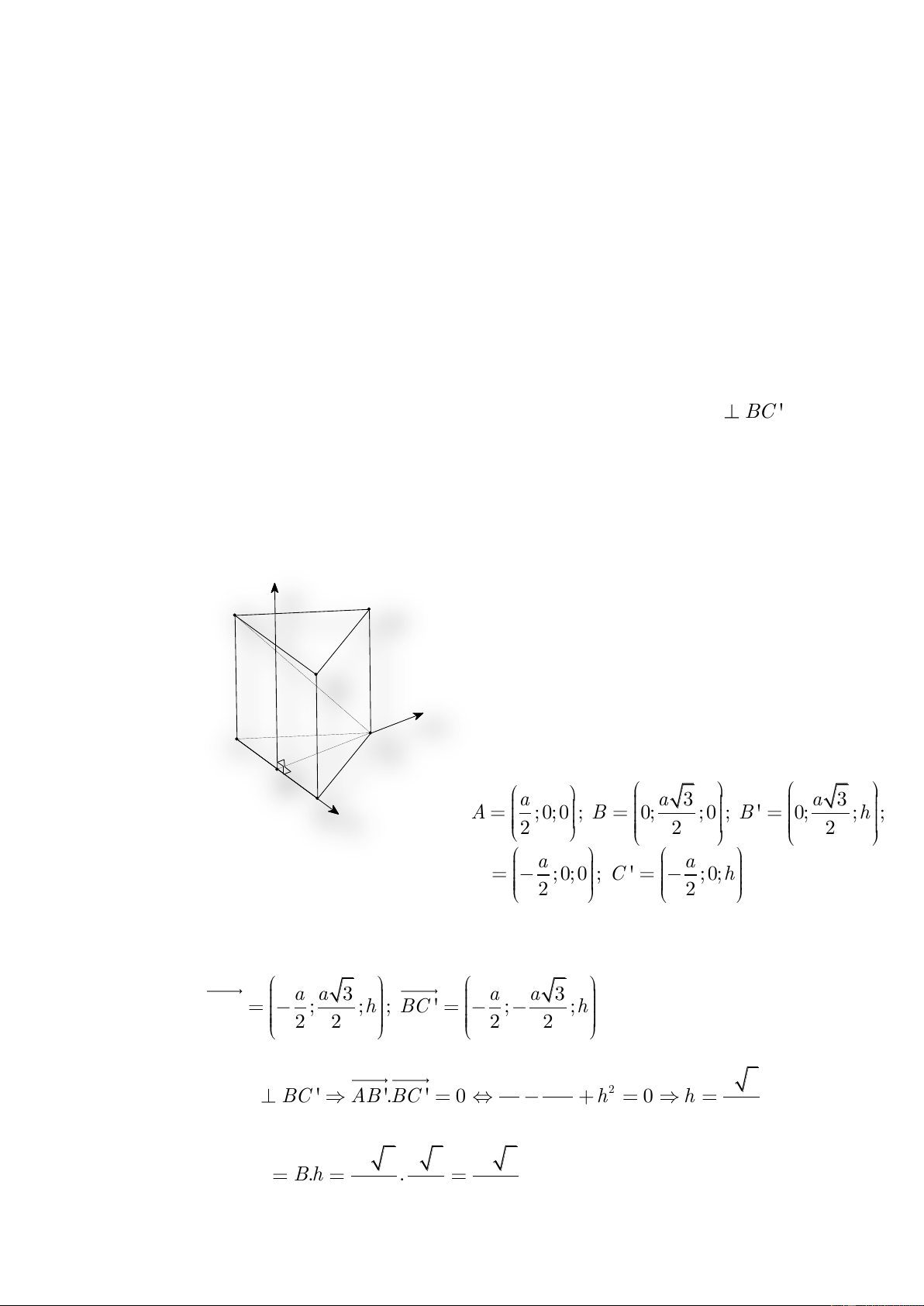
  có cạnh đáy bằng a và AB  BC. Tính thể tích khối lăng trụ.
Một học sinh giải như sau:
Bước 1: Chọn hệ trục như hình vẽ: z C' B' A' y C B x A  a   a 3   a 3   a   a
A ;0;0 , B0; ; 0  , B 0; ; h  , C   ; 0; 0  , C  
; 0; h  ( h là chiều cao của  2   2      2    2   2  lăng trụ), suy ra  a a 3   a a 3  AB    ; ; h    ; BC    ;  ; h  2 2      2 2  
Bước 2: AB  BC  AB .BC  0 2 2 a 3a 2 a 2  
h  0  h  4 4 2 2 3 a 3 a 2 a 6 Bước 3: V       . B h . ABC.A B C 2 2 4
Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào? A. Lời giải đúng B. Sai ở bước 1 C. Sai ở bước 3 D. Sai ở bước 2 C©u 39 : Cho hai điểm ( A 0; 0; 3) và ( B 1; 2  ; 3  ) . Gọi A B
  là hình chiếu vuông góc của đường thẳng
AB lên mặt phẳng (Oxy) . Khi đó phương trình tham số của đường thẳng A B   là x  1 tx  1 tx tx  t     A. y  2   2t B. y  2   2t C. y  2  t D. y  2  t     z  0  z  0  z  0  z  0 
C©u 40 : Trong không gian với hệ tọa độ Oxyz, phương trình mặt cầu tâm A(1;2;1) và tiếp xúc với mặt phẳng
 : x  2y z 3  0 là: 2 2 2 1 A. x   1
  y  2  z   1  B. 2 2 2
x y z  2x  4y  2z  6  0 6 2 2 2 1
C. 1  x  2  y  1  z   D. 2 2 2
6x  6y  6z 12x  24y 12z  35  0 6 C©u 41 : Cho ( A 3; 0; 0) , ( B 0; 6  ;0), (
C 0; 0; 6) và m (
p ) : x y z  4  0 . Tọa độ hình chiếu vuông góc
của trọng tâm tam giác ABC trên ( mp ) là A. (2;1; 3) B. (2; 1  ; 3) C. ( 2  ; 1  ; 3) D. (2; 1  ; 3  ) C©u 42 : Cho ( A 1;1; 3) , ( B 1  ; 3; 2) , ( C 1
 ; 2; 3). Khoảng cách từ gốc tọa độ O tới mặt phẳng (ABC) bằng 3 3 A. 3 B. 3 C. D. 2 2
C©u 43 : Trong không gian với hệ tọa độ Oxyz, phương trình đường thẳng (d) đi qua N(5;3;7) và vuông góc
với mặt phẳng (Oxy) là : x  5 x  5  
A. y  3  t t RB. y  3 t R   z  7  z  7  2t  x  5  tx  5   C. y  3 t RD. y  3 t R   z  7  z  7  t  C©u 44 : x  2  t
x  2  2t  
Cho hai đường thẳng d : y  1 t và d : y  3
. Mặt phẳng cách đều d và d có 1  2  1 2 z  2tz t  phương trình là
A. x  5y  2z  12  0
B. x  5y  2z  12  0
C. x  5y  2z  12  0
D. x  5y  2z  12  0
C©u 45 : Cho 3 điểm A2; 1  ;5 ; B5; 5  ;7 và Mx;y; 
1 . Với giá trị nào của x ; y thì A, B, M thẳng hàng ? A. x  4 ; y  7 B. x  4  ; y  7  C. x  4; y  7  D. x  4  ; y  7 C©u 46 :
x  5  2t
x  9  2t  
Cho hai đường thẳng d : y  1 t và d : y t
. Mặt phẳng chứa cả d và d có 1  2  1 2 z  5  tz  2   t  phương trình là:
A. 3x  5y z  25  0
B. 3x  5y z  25  0
C. 3x  5y z  25  0
D. 3x y z  25  0
C©u 47 : Khoảng cách từ điểm ( M 1  ;2; 4  ) đến m (
p ) : 2x  2y z  8  0 là: A. 4 B. 3 C. 6 D. 5 C©u 48 : x  7 y  3 z  9 x  3 y  1 z  1
Cho hai đường thẳng d :   d :   1 1 2 1  và 2 7  . Phương trình 2 3
đường vuông góc chung của d và d là 1 2 x  3 y  1 z  1 x  7 y  3 z  9 A.     1  2 4  B. 2 1  4 x  7 y  3 z  9 x  7 y  3 z  9 C.   D.   2 1 4 2 1 4  C©u 49 : Cho hai điểm ( M 1; 2  ; 4  ) và M (5; 4
 ; 2) . Biết M là hình chiếu vuông góc của M lên ( mp ) . Khi đó, (
mp ) có phương trình là
A. 2x y  3z  20  0
B. 2x y  3z  20  0
C. 2x y  3z  20  0
D. 2x y  3z  20  0
C©u 50 : Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng   : 2x y  3z 1  0 và đường thẳng d có phương trình tham số: x  3   t
y  2  2t . Trong các mệnh đề sau, mệnh đề nào đúng ? z 1 
A. d    B. d//   C. d cắt  
D. d   
C©u 51 : Trong không gian Oxyz , cho hình bình hành OADB có OA  ( 1
 ;1;0), OB  (1;1;0) (O là
gốc tọa độ). Khi đó tọa độ tâm hình hình OADB là: A. (0;1; 0) B. (1; 0; 0) C. (1; 0;1) D. (1;1; 0) C©u 52 : Cho mặt cầu 2 2 2 ( )
S : (x  2)  (y  1)  z  14 . Mặt cầu (S) cắt trục Oz tại A và B (z  0) . A
Phương trình nào sau đây là phương trình tiếp diện của (S) tại B ?
A. 2x y  3z  9  0
B. x  2y z  3  0
C. 2x y  3z  9  0
D. x  2y z  3  0 C©u 53 : x  8   4t
Cho đường thẳng d : y  5  2t và điểm ( A 3; 2
 ; 5). Tọa độ hình chiếu của điểm A trên d z t  là: A. (4; 1  ; 3  ) B. (4; 1  ; 3) C. ( 4  ;1; 3  ) D. ( 4  ; 1  ; 3)
C©u 54 : Trong không gian Oxyz, cho hình lập phương ABC . D A BCD   với ( A 0; 0; 0) , ( B 1; 0; 0) , ( D 0;1; 0) , A (
 0;0;1). Gọi M,N lần lượt là trung điểm các cạnh AB và CD . Tính khoảng
cách giữa hai đường thẳng A C  và MN .
Một học sinh giải như sau:
Bước 1: Xác định A C   (1;1; 1  ); MN  (0;1;0) Suy ra A C  ,MN  (1;0;1)  
Bước 2: Mặt phẳng ( ) chứa A C
 và song song với MN là mặt phẳng qua A (0;0;1) và có
vectơ pháp tuyến n  (1; 0;1)  () : x z 1  0 1  0 1 2 1 Bước 3: ( d A C  , MN)  ( d M,())   2 2 1 1  0  1 2 2
Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào? A. Sai ở bước 3 B. Lời giải đúng C. Sai ở bước 1 D. Sai ở bước 2 C©u 55 : x  2 y  1 z  3 x  1 y  1 z  1
Cho hai đường thẳng d :   và d :  
.Khoảng cách giữa d 1 1 2 2 2 1 2 2 1 và d là 2 4 2 4 4 3 A. 4 2 B. C. D. 3 3 2
C©u 56 : Phương trình mặt phẳng (P) chứa trục Oy và điểm ( M 1; 1  ;1) là:
A. x z  0
B. x z  0
C. x y  0
D. x y  0
C©u 57 : Cho hai mặt phẳng () : 3x  2y  2z  7  0 và () : 5x  4y  3z 1  0 . Phương trình mặt
phẳng đi qua gốc tọa độ O và vuông góc cả ( ) và ( ) là:
A. 2x y  2z  0
B. 2x y  2z  0
C. 2x y  2z  1  0 D. 2x y  2z  0 C©u 58 : x  1 y z  2 Cho mặt cầu 2 2 2 ( )
S : x y z  8x  2y  2z  3  0 và đường thẳng  :   3 2  1  . Mặt
phẳng ( ) vuông góc với  và cắt (S) theo giao tuyến là đường tròn (C) có bán kính lớn
nhất. Phương trình ( ) là
A. 3x  2y z  5  0
B. 3x  2y z  5  0
C. 3x  2y z  15  0
D. 3x  2y z  15  0 C©u 59 : Cho ( A 2; 0; 0) , ( B 0; 2; 0) , ( C 0; 0; 2) , (
D 2; 2; 2) . Mặt cầu ngoại tiếp tứ diện ABCD có bán kính 2 3 A. 3 B. 3 C. D. 3 2 C©u 60 : Cho ba điểm ( A 1; 0; 0) , ( B 0;1; 0) , ( C 0; 0;1) , (
O 0; 0; 0) . Khi đó mặt cầu ngoại tiếp tứ diện
OABC có phương trình la: A. 2 2 2
x y z  2x  2y  2z  0 B. 2 2 2
x y z x y z  0 C. 2 2 2
x y z x y z  0 D. 2 2 2
x y z  2x  2y  2z  0
C©u 61 : Cho ba mặt phẳng () : x y  2z 1  0 ; () : x y z  2  0 và ( ) : x y  5  0 . Trong các
mệnh đề sau, mệnh đề nào sai? A. ( ) ( ) B. ()  ( ) C. ( )  ( ) D. ()  ( )
C©u 62 : Trong không gian Oxyz , cho ba vectơ a  ( 1
 ;1;0), b  (1;1;0) và c  (1;1;1) . Trong các
mệnh đề sau, mệnh đề nào sai?
A. b c B. c  3 C. a  2
D. a b
C©u 63 : Trong không gian với hệ tọa độ Oxyz, phương trình mặt cầu (S) qua ba điểm A(1;-2;4); B(1;3;-1);
C(2;-2;-3) và có tâm nằm trên mặt phẳng (Oxy) là: A. 2 2 2
x y z  4x  2y  21  0 B. 2 2 2
x y z  4x  2y  3z  21  0 C. 2 2 2
x y z  4x  2y  21  0 D. 2 2 2
x y z  4x  2y  21  0
C©u 64 : Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng đi qua hai điểm E(1;3;-5); F(-2;-1;1) và song song với trục ' x Ox là:
2x  3y  2z 1  0
A. 3y  2z 1  0 B. 3
y  2z 1  0 C.
D. 3y  2z 1  0
C©u 65 : Gọi () là mặt phẳng cắt ba trục tọa độ tại ba điểm ( M 8; 0; 0) , ( N 0; 2  ;0) và ( P 0; 0; 4) .
Phương trình mặt phẳng ( ) là: x y z x y z
A. x  4y  2z  8  0 B.    0   
D. x  4y  2z  0 8 2  C. 1 4 4 1  2
C©u 66 : Trong không gian với hệ tọa độ Oxyz cho A(1;2;1), B(0;1;2) .Biết B là hình chiếu của A lên mặt
phẳng   .Phương trình mặt phẳng   là:
A. x y z 1  0
B. x y z 1  0
C. x y z 1  0
D. x y z 1  0 C©u 67 : x  1 y  3 z
Cho đường thẳng d :  
mp P x y z   . Mặt phẳng chứa d và 2 3  và ( ) : 2 2 1 0 2 vuông góc với m (
p P) có phương trình
A. 2x  2y z  8  0
B. 2x  2y z  8  0
C. 2x  2y z  8  0
D. 2x  2y z  8  0 C©u 68 : x  1 2t
x  3  4t  
Cho hai đường thẳng d : y  2  3t và d : y  5  6t . 1  2  z  3  4t
z  7  8t 
Trong các mệnh đề sau, mệnh đề nào đúng? d và d chéo 1 2
A. d d B. d d C.
D. d d 1 2 1 2 1 2 nhau C©u 69 : x  1 y z Đường thẳng   3  2 1
 vuông góc với mặt phẳng nào trong các mặt phẳng sau đây?
A. 6x  4y  2z  1  0
B. 6x  4y  2z  1  0
C. 6x  4y  2z  1  0
D. 6x  4y  2z  1  0 C©u 70 : Cho hai điểm ( A 3; 3;1) , (
B 0; 2;1) và m ( p )
P : x y z  7  0 . Đường thẳng d nằm trên m (
p P) sao cho mọi điểm của d cách đều hai điểm A, B có phương trình là x tx  2tx tx t     
A. y  7  3t
B. y  7  3t
C. y  7  3t
D. y  7  3t     z  2tz tz  2tz  2t  C©u 71 : Cho hai điểm ( M 2  ; 3;1) , ( N 5; 6; 2
 ). Đường thẳng MN cắt mặt phẳng (Oxz) tại điểm A .
Điểm A chia đoạn MN theo tỉ số 1 1 A. B. C. 2  D. 2 2 2 C©u 72 : x 1 2t  Cho điểm M2; 3
 ;5 và đường thẳng d:  y  3 t t   . Đường thẳng  đi qua M  z  4 t 
và song song với d có phương trình chính tắc là : x  2 y  3 z  5 x  2 y  3 z  5 A.   B.   1 3 4 1 3 4 x  2 y  3 z  5 x  2 y  3 z  5 C.   D.   2 1  1 2 1  1 C©u 73 : x  1 y  1 z  2
Cho đường thẳng d :  
. Hình chiếu vuông góc của d trên mặt phẳng tọa 2 1 1 độ (Oxy) là x  1   2tx  1 2tx  0 x  1   2t    
A. y  1  t B. y  1   t C. y  1   t D. y  1   t     z  0  z  0  z  0  z  0  C©u 74 : Cho ba điểm ( A 0; 2;1) , ( B 3; 0;1) , (
C 1; 0; 0) . Phương trình mặt phẳng (ABC) là:
A. 2x  3y  4z  2  0
B. 4x  6y  8z  2  0
C. 2x  3y  4z  2  0
D. 2x  3y  4z  1  0
C©u 75 : Cho đường thẳng  đi qua điểm ( M 2; 0; 1
 ) và có vectơ chỉ phương a  (4; 6;  2) . Phương
trình tham số của  là:
x  2  2t
x  4  2tx  2   4tx  2   2t     A. y  3  t B. y  6   3t C. y  6  t D. y  3  t     z  1   tz  2  tz  1  2tz  1  t
C©u 76 : Biết đường thẳng d là giao tuyến của hai mặt phẳng () : 3x  2y z 1  0 và
( ) : x  4y  3z  2  0 . Khi đó, vectơ chỉ phương của đường thẳng d có tọa độ là: A. (0; 4; 5) B. (2; 4  ; 5  ) C. (1; 4  ; 5  ) D. ( 1  ; 4  ; 5)
C©u 77 : Cho vectơ u  (1;1; 2)  và v  (1;0; )
m . Tìm m để góc giữa hai vectơ u và v có số đo bằng 0 45
Một học sinh giải như sau: 1 2m
Bước 1: cosu,v  2 6. m  1 1 2m 1
Bước 2: Góc giữa u , v bằng 0 45 suy ra  2 6. m  1 2 2
 1 2m  3. m 1 (*)
Bước 3: phương trình (*) 2  (1 2 )
m  3(m  1) m  2  6 2
m  4m  2  0   m  2   6
Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào? A. Sai ở bước 2 B. Sai ở bước 3 C. Bài giải đúng D. Sai ở bước 1 C©u 78 :  x 1 2t 
Cho đường thẳng d : y  2  4t và mặt phẳng P : x  y  z 1  0 z  3 t 
Khẳng định nào sau đây đúng ? A. d / / P
B. d cắt P tại điểm M 1; 2;3 C. d  P
D. d cắt P tại điểm M  1  ; 2  ;2
C©u 79 : Trong không gian với hệ tọa độ Oxyz cho mặt cầu (S): 2 2 2
x y z  2x  2z  0 và mặt phẳng
: 4x 3y m  0. Xét các mệnh đề sau:
I.   cắt (S) theo một đường tròn khi và chỉ khi 4   5 2  m  4   5 2 .
II.   tiếp xúc với (S) khi và chỉ khi m  4   5 2 .
III.    S    khi và chỉ khi m  4
  5 2 hoặc m  4   5 2 .
Trong ba mệnh đề trên, những mệnh đề nào đúng ? A. II và III B. I và II C. I D. I,II,III
C©u 80 : Trong không gian Oxyz , cho bốn điểm ( A 1; 0; 0) , ( B 0;1; 0) , ( C 0; 0;1) và ( D 1;1;1) .Trong các
mệnh đề sau, mệnh đề nào sai?
A. Tam giác BCD là tam giác vuông
B. Tam giác ABD là tam giác đều
C. Bốn điểm A, B,C, D tạo thành một tứ diện D. AB CD ĐÁP ÁN 01 ) | } ~ 28 ) | } ~ 55 { ) } ~ 02 { ) } ~ 29 ) | } ~ 56 { ) } ~ 03 { ) } ~ 30 { | } ) 57 { ) } ~ 04 { ) } ~ 31 ) | } ~ 58 { | ) ~ 05 { | ) ~ 32 { ) } ~ 59 { ) } ~ 06 { | } ) 33 { | } ) 60 { | ) ~ 07 ) | } ~ 34 { | } ) 61 ) | } ~ 08 { | ) ~ 35 { ) } ~ 62 ) | } ~ 09 { | ) ~ 36 ) | } ~ 63 { | } ) 10 ) | } ~ 37 { | } ) 64 { | } ) 11 { ) } ~ 38 { | ) ~ 65 ) | } ~ 12 ) | } ~ 39 { | ) ~ 66 { | } ) 13 { | } ) 40 { | } ) 67 { ) } ~ 14 { | ) ~ 41 { ) } ~ 68 ) | } ~ 15 { | ) ~ 42 { ) } ~ 69 { | ) ~ 16 ) | } ~ 43 { | } ) 70 { | ) ~ 17 { ) } ~ 44 { ) } ~ 71 ) | } ~ 18 { | } ) 45 { | } ) 72 { | } ) 19 ) | } ~ 46 { | ) ~ 73 { ) } ~ 20 { | } ) 47 { | ) ~ 74 ) | } ~ 21 { | } ) 48 { | ) ~ 75 ) | } ~ 22 { | } ) 49 { | ) ~ 76 { | ) ~ 23 ) | } ~ 50 { | } ) 77 { ) } ~ 24 { | ) ~ 51 ) | } ~ 78 { | } ) 25 { | ) ~ 52 { | ) ~ 79 { | } ) 26 { ) } ~ 53 { ) } ~ 80 ) | } ~ 27 { | ) ~ 54 { ) } ~ GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN ĐỀ 003
C©u 1 : Tọa độ tâm mặt cầu đi qua 4 điểm A(1;1;1);B(1;2;1);C(3;3;3);D(3; 3  ;3) là : 3 3 3 3 3 3 A. ( ;  ; ) B. (3;3;3) C. (3; 3  ;3) D. ( ; ; ) 2 2 2 2 2 2
C©u 2 : Trong hệ tọa độ Oxy cho các điểm A(1 ;0 ;0) ; B(0 ;1 ;0) ;C(0 ;0 ;1), D(1 ;1 ;1). Bán kính
mặt cầu đi qua bốn điểm ABCD là : 3 3 A. B. 2 C. 3 D. 4 2
C©u 3 : Cho mặt cầu (S) có tâm I(2;1; 1
 ) và tiếp xúc với mặt phẳng () có phương trình
2x  2 y z  3  0 . Bán kính của mặt cầu (S) là: 2 2 4 A. B. 2 C. D. 9 3 3
C©u 4 : Cho ba điểm A(2;1;-1); B(-1;0;4);C(0;-2-1). Phương trình mặt phẳng nào đi qua A và vuông góc BC A. x-2y-5z-5=0 B. 2x-y+5z-5=0 C. x-3y+5z+1=0 D. 2x+y+z+7=0
C©u 5 : Viết phương trình mặt cầu có tâm I(1;4;7) và tiếp xúc với mặt phẳng
6x  6y  7z  42  0 . 2 2 2 2 2 2
A. (x 1)  (y  3)  (z  3)  1
B. (x 1)  (y  4)  (z  7)  121 2 2 2 2 2 2
C. (x  5)  (y  3)  (z 1)  18
D. (x 1)  (y  2)  (z  2)  9
C©u 6 : Trong không gian với hệ trục tọa độ Oxyz, cho các điểm ( A 2;1; 0), ( B 3;1; 1),
C(1;2; 3). Tọa độ điểm D để ABCD là hình bình hành là: A. ( D 2;1;2) B. ( D 2; 2; 2) C. ( D 2;1;2) D. ( D 2;2;2)
C©u 7 : Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng 1 x 1 y 2 z 3 d :
và mặt phẳng (P) : x 3y 2z 5 0 . Để đường thẳng m 2m 1 2 d vuông góc với (P) thì: A. m 0 B. m 1 C. m 2 D. m 1
C©u 8 : Phương trình chính tắc của đường thẳng d đi qua điểm M(2;0;-1) có vecto chỉ phương a  (4; 6  ;2) là x  2 y z 1 x  2 y z 1 A.   B.   2 3  1 4 6  2 x  2 y z 1 x  4 y  6 z  2 C.   D.   2 3  1 2 3  1
C©u 9 : Cho hai mặt phẳng P : x 2y 2z 3 0, Q : 2x y 2x 4 0 và đường thẳng x 2 y z 4 d : . 1 2 3
Lập phương trình mặt cầu (S) có tâm I
d và tiếp xúc với hai mặt phẳng (P) và (Q). A. 2 2 2 2 2 2 2 x 11 y 26 z 35 38 x 1 y 2 z 1 4 2 2 2 2 2 2 B. 2 x 11 y 26 z 35 38 x 1 y 2 z 1 4 2 2 2 2 2 2 C. 2 x 11 y 26 z 35 38 x 1 y 2 z 1 4 D. 2 2 2 2 2 2 2 x 11 y 26 z 35 38 x 1 y 2 z 1 4
C©u 10 : Cho các điểm A(2;0;0);B(0;2;0);C(0;0;1) . Tọa độ trực tâm H của tam giác ABC là : 1 1 1 2 2 2 1 2 1 1 2 A. H( ; ;1) B. H( ; ; ) C. H( ; ; ) D. H( ; ; ) 2 2 3 3 3 3 3 3 3 3 3 C©u 11 : x 1 y  2 z  3 x  3 y  5 z  7
Cho hai đường thẳng (d1):   và (d2)   . Mệnh đề nào 2 3 4 4 6 8 dưới đây đúng? (d1) và (d2) A. ( 1 d )  (d 2) B. ( 1 d )  (d 2) C. D. ( 1 d ) / /(d 2) chéo nhau C©u 12 : x 1 y z 2
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d : 1 1 3
và mặt phẳng (P) : x 2y z 3
0 . Khi đó tọa độ giao điểm M của d và (P) là: 2 3 1 7 3 1 7 3 1 7 A. M 3;1; 7 B. M ; ; C. M ; ; D. M ; ; 2 2 2 2 2 2 2 2 2
C©u 13 : Gọi () là mặt phẳng cắt trục tọa độ tại ba điểm M(8;0;0), N(0; 2  ;0), (0 P ;0; 4) .
Phương trình mặt phẳng () là: x y z
x  4 y  2z  8  0 x y z A.    0 B. C.    1
D. x  4y  2z  0 8 2  4 4 1  2 C©u 14 : x -1
Cho A(1;4;2), B(-1;2;4) và đường thẳng d:
= y + 2 = z . Điểm M thuộc d, biết -1 1 2
MA2 + MB2 nhỏ nhất. Điểm M có toạ độ là? A. M (1;0; 4) B. M (0;-1; 4) C. M (-1;0; 4) D. M (1;0;-4)
C©u 15 : Cho A 2;0;0 , M 1;1;1 . Viết phương trình mặt phẳng (P) đi qua A và M sao cho (P)
cắt trục Oy, Oz lần lượt tại hai điểm B, C thỏa mãn:
a) Diện tích của tam giác ABC bằng 4 6 .
A. Cả ba đáp án trên B. P : 2x y z 4 0 1 P : 6x 3 21 y 3 21 z 12 0 P : 6x 3 21 y 3 21 z 12 0 3 2 C. D. C©u 16 : Trong không gian với hệ trục tọa độ Oxyz , cho bốn điểm
A3;3;0, B 3;0;3, C 0;3;3, D 3;3;3 . Viết phương trình mặt cầu đi qua bốn điểm A, B, C, D. A. 2 2 2
x y z  3x  3y  3z  0 B. 2 2 2
x y z  3x  3y  3z  0 C. 2 2 2
x y z  3x  3y  3z  0 D. 2 2 2
x y z  3x  3y  3z  0 C©u 17 : x y 8 z 3 Cho đường thẳng :
và mặt phẳng P : x y z 7 0 . Viết 1 4 2
phương trình hình chiếu của trên (P). x 8 4t x 8 4t x 8 4t x 8 4t A. y 15 5t B. y 15 5t C. y 15 5t D. y 15 5t z t z t z t z t
C©u 18 : Trong không gian với hệ tọa độ Oxyz cho bốn điểm (
A 1; 0; 0) , B(0;1;0) , C(0;0;1) và (
D 1;1;1) . Trong các mệnh đề sau, mệnh đề nào sai ? 3 Bốn điểm , A ,
B C, D tạo thành một tứ A.
B. Tam giác BCD là tam giác vuông diện
C. Tam giác ABD là một tam giác đều
D. AB CD
C©u 19 : Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(2;2;2) . Khi đó mặt phảng
đi qua M cắt các tia Ox, Oy, Oz tại các điểm A, B, C sao cho diện tích tứ giác OABC
nhỏ nhất có phương trình là: A. x y z 1 0 B. x y z 6 0 C. x y z 0 D. x y z 6 0
C©u 20 : Cho mặt phẳng (P) : x  y 1  0 và mặt phẳng (Q). Biết hình chiếu cưa gốc O lên (Q) là điểm H(2; 1  ; 2
 ). Khi đó góc giữa hai mặt phẳng (P) và (Q) có giá trị là: A. 0   30 B. 0   60 C. 0   90 D. 0   45
C©u 21 : Biết tam giác ABC có ba đỉnh A, B, C thuộc các trục tọa độ và trọng tâm tam giác là G( 1  ; 3
 ;2) . Khi đó phương trình mặt phẳng (ABC) là :
A. 2x  3y  z 1  0
B. x  y  z  5  0
C. 6x  2y  3z 18  0
D. 6x  2y  3z 18  0
C©u 22 : Trong các bộ ba điểm: (I). (
A 1; 3;1); B(0;1; 2); C(0;0;1), (II). M(1;1;1); ( N 4; 3;1); ( P 9; 5;1), (III). D(1;2;7); ( E 1; 3; 4); ( F 5;0;13), bộ ba nào thẳng hàng? A. Chỉ III, I. B. Chỉ I, II. C. Chỉ II, III. D. Cả I, II, III.
C©u 23 : Viết phương trình mặt phẳng trung trực của đoạn thẳng AB với ( A 1; 2; 4), ( B 5; 4; 2) .
A. 10x  9y  5z  70  0
B. 4x  2y  6z 11  0
C. 2x  y  3z  6  0
D. 2x  3z  3  0
C©u 24 : Cho mặt cầu (S) x2+y2+z2-2x-4y-6z=0. Trong ba điểm (0;0;0); (1;2;3) và (2;-1;-1) thì có
bao nhiêu điểm nằm trong mặt cầu (S) 4 A. 1 B. 3 C. 2 D. 0 C©u 25 : Cho ba điểm (0 A ; 2;1), (3
B ;0;1), C(1;0;0) . Phương trình mặt phẳng ( ABC) là:
A. 4x  6y  8z  2  0
B. 2x  3y  4z  2  0
C. 2x  3y  4z  2  0
D. 2x  3y  4z  1  0
C©u 26 : Gọi H là hình chiếu vuông góc của A(2;-1;-1) trên (P): 16x -12y -15z - 4 = 0 . Độ dài đoạn AH bằng? 22 11 11 A. B. C. D. 55 5 5 25
C©u 27 : Cho đường thẳng  đi qua điểm M(2;0; 1
 ) và có vectơ chỉ phương a  (4; 6  ;2) .
Phương trình tham số của đường thẳng  là: x  2   2t
x  2  2tx  2   4t
x  4  2t     A. y  3  t B. y  3  t C. y  6  t D. y  6      z  1  tz  1  tz  1  2tz  2  t
C©u 28 : Trong hệ tọa độ Oxy cho các điểm A(1 ;0 ;0) ; B(0 ;1 ;0) ;C(0 ;0 ;1), D(1 ;1 ;1). Trong
các mệnh đề sau mệnh đề nào sai :
A. ABCD là một tứ diện
B. AB vuông góc với CD
C. Tam giác ABD là tam giác đều
D. Tam giác BCD vuông
C©u 29 : Trong không gian Oxyz cho ba vectơ a  ( 1
 ;1;0),b  (1;1;0) và c  (1;1;1) . Trong các
mệnh đề sau, mệnh đề nào sai ? A. | a | 2
B. b c C. | c | 3
D. a b
C©u 30 : Cho tứ diện ABCD với ( A 5;1; 3), (
B 1;6; 2), C(5;0; 4), D(4;0;6) . Viết phương trình mặt
phẳng đi qua C, D và song song với AB.
A. 10x  9z 5z  0 x y z  B. 5 3 2 0
C. 10x  9y  5z 70  0 x  y z D. 10 9 5  50  0
C©u 31 : Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng (P) : 3x my 2z 7 0 và (Q) : nx 7y 6z 4
0. Để (P) song song với (Q) thì: 7 m ;n 9 7 7 A. m 7;n 9 B. 3 C. m ;n 9 D. m ;n 9 3 3 5
C©u 32 : Trong không gian với hệ trục tọa độ Oxyz, cho u (1;1;2) , v ( 1; ; m m 2). Khi đó , u v 4 thì : 11 11 m 1;m 11 A. m 1;m B. 5 C. m 1 m 1;m 5 D. 5
C©u 33 : Viết phương trình mặt phẳng đi qua điểm B(1; 2; -1) và cách gốc tọa độ một khoảng lớn nhất.
A. x  2y z  6  0
B. x  2y  2z  7  0 C. 2x y z 5  0
D. x y  2z 5  0
C©u 34 : Trong không gian với hệ trục tọa độ Oxyz, cho điểm (
A 3;1; 0) và mặt phẳng (P) : 2x 2y z 1
0 . Khi đó tọa độ điểm M là hình chiếu của điểm A trên (P) là: A. M( 1;1;1) B. M(1;1;1) C. M(1;1; 1) D. M(1; 1;1)
C©u 35 : Gọi (P) là mặt phẳng đi qua M(3;-1;-5) và vuông góc với hai mặt phẳng (Q): 3x-
2y+2z+7=0 và (R): 5x-4y+3z+1=0 A. 2x+y-2z-15=0 B. 2x+y-2z+15=0 C. x+y+z-7=0 D. x+2y+3z+2=0
C©u 36 : Cho ba mặt phẳng () : x y  2z 1  0, () : x y z  2  0,( ) :x y 5  0 . Trong các
mệnh đề sau, mệnh đề nào sai ? A. ()  ( ) B. () // ( ) C. ( )  ( ) D. ()  ( )
C©u 37 : Tìm tọa độ tâm J của đường tròn (C) là giao tuyến của mặt cầu S
x  2  y  2  z  2 ( ) : ( 2) ( 3) (
3)  5 và mặt phẳng (P): x  2y  2z  1  0  3 3 3   5 7 11
A. J  ; ; 
B. J 1; 2;0 C. J ;  ;   
D. J 1; 2; 3  2 4 2   3 3 3  C©u 38 : ìx = t x - ï Cho hai đườ 3 ng thẳng d : = y - 6 = z -1
íy = -t . Đường thẳng đi qua A(0;1;1) cắt d’ - ;d ' : 2 2 1 ïz î = 2
và vuông góc d có phương trình là? x -1 x x x A. = y = z -1 = y -1 = z -1 = y -1 = z -1 = y -1 = z -1 - B. C. D. 1 -3 4 1 -3 4 -1 -3 4 -1 3 4 C©u 39 : Cho 2 2 2
(S) : x  y  z  2y  2z  2  0 và mặt phẳng (P) : x  2y  2z  2  0. Mặt phẳng
(Q) song song với (P) đồng thời tiếp xúc với (S) có phương trình là : 6
A. x  2y  2x 10  0
B. x  2y  2x 10  0; x  2y  2z  2  0
C. x  2y  2x 10  0; x  2y  2z  2  0
D. x  2y  2x 10  0 C©u 40 : x  1 2t
Cho điểm A(0;-1;3) và đường thẳng d:  y  2
. Khoảng cách từ A đến d là: z t   A. 14 B. 8 C. 6 D. 3
C©u 41 : Cho d là đường thẳng đi qua điểm (
A 1; 2; 3) và vuông góc với mặt phẳng
() : 4x  3y  7z  1  0 . Phương trình tham số của d là: x  1   4t
x  1  4t
x  1  3tx  1   8t     A. y  2   3t
B. y  2  3t
C. y  2  4t D. y  2   6t     z  3   7tz  3  7tz  3  7tz  3   14t  C©u 42 : x 2 y 4 z 1
Cho mặt phẳng P : 3x 2y 3z 7
0 và đường thẳng d : . Viết 3 2 2
phương trình đường thẳng
đi qua A(-1; 0; 1) song song với mặt phẳng (P) và cắt đường thẳng d. x 1 y z 1 x 1 y 1 z A. B. 15 3 17 15 3 17 x 1 y z 1 x 1 y z 1 C. D. 15 3 17 15 3 17
C©u 43 : Cho A(0;2;1), B(3;0;1),C(1;0;0). Phương trình mặt phẳng (ABC) là?
A. 2x + 3y - 4z + 2 = 0
B. 2x - 3y - 4z +1 = 0
C. 2x + 3y - 4z - 2 = 0
D. 2x + 3y + z - 7 = 0 C©u 44 : x -1 Cho d :
= y +1 = z - 2 . Hình chiếu vuông góc của d trên (Oxy) có dạng? 2 1 1 ìx = 0 ìx = -1+ 2t ìx = 1+ 2t ìx = -1+ 2t ï ï ï ï
A. íy = -1- t
B. íy = 1+ t
C. íy = -1+ t
D. íy = -1+ t ïz ï ï ï î = 0 z î = 0 z î = 0 z î = 0
C©u 45 : Cho mặt cầu (S) có tâm I(4;2;-2), bán kính R. Biết (S) tiếp xúc (P): 12x – 5z – 19 =0. Bán kính R là? A. R = 39 B. R = 13 C. R = 3 D. R = 3 13
C©u 46 : Cho (a) : m2x - y + (m2 - 2)z + 2 = 0;(b) :2x + m2y - 2z +1 = 0. Để hai mặt phẳng đã ch vuông
góc nhau, giá trị m bằng? 7 A. m = 1 B. m = 2 C. m = 2 D. m = 3
C©u 47 : Cho A(a;0;0);B(0;b;0);C(0;0;c) với a,b,c  0 . Biết mặt phẳng (ABC) qua điểm
I(1;3;3) và thể tích tứ diện OABC đạt giá trị nhỏ nhất. Khi đó phương trình (ABC) là :
A. x  3y  3z  21  0
B. 3x  y  z  9  0
C. 3x  3y  z 15  0
D. 3x  y  z  9  0 C©u 48 :
x  1  2t
x  3  4t  
Cho hai đường thẳng d :  y  2  3t và d :  y  5  6t . 1 2   z  3  4tz  7  8t
Trong các mệnh đề sau, mệnh đề nào đúng ? d và d chéo 1 2
A. d d d d d // d 1 2 B. 1 2 C. D. 1 2 nhau
C©u 49 : Mặt cầu (S) tâm I(1 ;2 ;2) và tiếp xúc với (P) : x  2y  2z  5  0 có bán kính là : 3 2 4 A. B. C. D. 3 2 3 3
C©u 50 : Trong không gian với hệ trục tọa độ Oxyz, cho điểm (
A 2; 0;1) và đường thẳng x 1 y z 1 d :
. Khi đó tọa độ điểm M thuộc d thỏa mãn MA 3 là : 2 1 1 A. M(3; 1; 1) B. M(3; 1; 0) C. M(5; 1; 1) D. M(3;1; 0)
C©u 51 : Gọi (d) là giao tuyến của hai mặt phẳng x  2y  3z  1  0 và 2x  3y z  1  0 . Xác
định m để có mặt phẳng (Q) qua (d) và vuông góc với a  ( ; m 2; 3) 85 1 A. 6 B. C. 1 D. 3 2
C©u 52 : Cho mặt phẳng () đi qua điểm M (0;0; 1
 ) và song song với giá của hai vectơ a  (1; 2
 ;3), b  (3;0;5) . Phương trình của mặt phẳng () là:
A. 5x  2y  3z  21  0 B. 5
x  2y  3z  3  0
C. 10x  4 y  6z  21  0
D. 5x  2y  3z  21  0 8 C©u 53 : x t x y 2 z x 1 y 1 z 1 Cho d : y 4 t , d : ; d : 1 2 3 1 3 3 5 2 1 z 1 2t
Viết phương trình đường thẳng , biết cắt d , d , d lần lượt tại A, B, C sao cho AB 1 2 3 = BC. x y 2 z x y 2 z 1 x y 2 z x y 2 z A. B. C. D. 1 1 1 1 1 1 1 1 1 1 1 1
C©u 54 : Xác định m để cặp mặt phẳng sau vuông góc với nhau:
7x  3y mz  3  0; x  3y  4z  5  0 . A. 6 B. 4  C. 1 D. 2
C©u 55 : Phương trình mặt phẳng qua giao tuyến của hai mặt phẳng (P): x-3y+2z-1=0 và (Q):
2x+y-3z+1=0 và song song với trục Ox là A. 7x+y+1=0 B. 7y-7z+1=0 C. 7x+7y-1=0 D. x-3=0
C©u 56 : Trong không gian với hệ trục tọa độ Oxyz, cho điểm (
A 1; 0; 1) và đường thẳng x 1 y 1 z d :
. Khi đó tọa độ điểm M là hình chiếu của điểm A trên d là : 2 2 1 5 1 1 M( ; ; ) 5 1 1 5 1 1 A. 3 3 3 B. M(5; 1; 1) C. M( ; ; ) D. M( ; ; ) 3 3 3 3 3 3
C©u 57 : Gọi (d) là đường thẳng đi qua điểm (
A 2; 3; 5) và vuông góc mặt phẳng (P):
2x  3y z  17  0 .Tìm giao điểm của (d) và trục Oz.  6  A. 0;0;6 B. 0;4;0 C. 0;0;4 D. 0;0;  7   
C©u 58 : Cho mặt cầu S  : 2 2 2
(x 1)  ( y  3)  (z  2)  49 phương trình nào sau đây là phương
trình của mặt phẳng tiếp xúc với mặt cầu S? 6x+2y+3z-55=0 A. 2x+3y+6z-5=0 B. C. x+2y+2z-7=0 D. 6x+2y+3z=0
C©u 59 : Trong hệ Oxyz cho các điểm A(3;3;1); B(0;2;1) và (P) : x  y  z  7  0 . Gọi d là đường
thẳng nằm trong (P) sao cho d(A;d)  d(B;d) . Khi đó phương trình đường thẳng d là: 9 x  t x  2t x  t x  t     A. y  7  3t B. y  7  3t C. y  7  3t D. y  7  3t     z  2t  z  t  z  2t  z  2t  C©u 60 : ìx = 2t x -1 ï Cho d :
= y = z - 3;d ' : íy = 1+ 4t . Khẳng định nào sau đây đúng khi nói veef vị trí tương 1 2 3 ïz î = 2 + 6t đối của d và d’. A. d, d’ cắt nhau B. d, d’ trùng nhau C. d song song d’ D. d, d’ chéo nhau C©u 61 : x 1  t x y  1  
Cho A(0; 1; 2) và hai đường thẳng z 1 d :  
, d ' :  y  1
  2t . Viết phương trình 2 1 1  z  2  t
mặt phẳng P đi qua A đồng thời song song với d và d’.
A. x  3y  5z 13  0
B. 2x  6y 10z 11  0
C. 2x  3y  5z 13  0
D. x  3y  5z 13  0
C©u 62 : Trong không gian với hệ tọa độ Oxyz cho bốn điểm (
A 1; 0; 0) , B(0;1;0) , C(0;0;1) và (
D 1;1;1) . Mặt cầu ngoại tiếp tứ diện ABCD có bán kính là: 3 3 A. 3 B. C. 2 D. 2 4
C©u 63 : Trong mặt phẳng (Oxz), tìm điểm M cách đều ba điểm ( A 1;1;1), ( B 1;1;0), ( C 3;1; 1) .  5 11   9   5 7  A. M  ;0; 
B. M  ;0; 5 C. M ; 0;   
D. M5;0; 7  2 2   4   6 6  C©u 64 : x  3   t
Cho mặt phẳng () : 2x y  3z 1  0 và đường thẳng d :  y  2  2t . z  1 
Trong các mệnh đề sau, mệnh đề nào đúng ? A. d  () B. d  ()
C. d cắt ( ) D. d // ()
C©u 65 : Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng (P) : 5x 5y 5z 1 0 và (Q) : x y z 1
0 . Khi đó khoảng cách giữa (P) và (Q) là: 2 3 2 2 2 3 A. B. C. D. 15 5 15 5 10
C©u 66 : Trong không gian với hệ tọa độ Oxyz cho bốn điểm (
A 1; 0; 0) , B(0;1;0) , C(0;0;1) và (
D 1;1;1) . Gọi M , N lần lượt là trung điểm của AB và CD . Tọa độ trung điểm G của MN là:  2 2 2   1 1 1   1 1 1   1 1 1  A. G ; ;   G ; ;   G ; ;   G ; ;    B. C. D. 3 3 3   2 2 2   4 4 4   3 3 3
C©u 67 : Cho hình bình hành OADB có OA  ( 1
 ;1;0), OB  (1;1;0) (O là gốc tọa độ). Tọa độ của
tâm hình bình hành OADB là: A. (1;0;1) B. (0;1;0) C. (1;0;0) D. (1;1;0)
C©u 68 : Trong Oxyz cho A(3;4;-1), B(2;0;3), C(-3;5;4). Diện tích tam giác ABC là: 1562 29 379 A. B. C. 7 D. 2 2 2 C©u 69 : ìx = t ï
Mặt cầu có tâm I(1;3;5) và tiếp xúc d : íy = -1- t có phương trình là? ïz î = 2 - t
A. (x -1)2 + (y - 3)2 + (z - 5)2 = 49
B. (x -1)2 + (y - 3)2 + (z - 5)2 = 14
C. (x -1)2 + (y - 3)2 + (z - 5)2 = 256
D. (x -1)2 + (y - 3)2 + (z - 5)2 = 7 C©u 70 : ìx = 9 - 2t x - 5 ï Cho d :
= y -1 = z - 5;d ' : íy = t
. Phương trình mặt phẳng chứa d và d’, có dạng? 2 -1 -1 ïz î = -2 + t
A. 3x - 5y + z - 25 = 0
B. 3x + y + z - 25 = 0
C. 2x + 5y + z - 25 = 0
D. 2x - 5y - z + 25 = 0
C©u 71 : Cho mặt phẳng (P) x-2y-3z+14=0. Tìm tọa độ M’ đối xứng với M(1;-1;1) qua (P). A. M’(-1;3;7) B. M’(2;-3;-2) C. M’(1;-3;7) D. M’(2;-1;1)
C©u 72 : Trong không gian Oxyz cho ba vectơ a  ( 1
 ;1;0),b  (1;1;0) và c  (1;1;1) . Trong các
mệnh đề sau, mệnh đề nào đúng ? 2 a, b cùng A. . a c  1 B. cos( , b c) 
C. a b c  0 D. 6 phương 11 C©u 73 : x t1)
Cho điểm I(1; 2; -2), đường thẳng d:  y  5
  2t và mặt phẳng (P): 2x  2y z 5  0. z  2   2t
Viết phương trình mặt cầu (S) có tâm là I, sao cho (P) cắt (S) theo đường tròn giao
tuyến có chu vi bằng 8 . 2 2 2 2 2 2 A. x  
1   y  2   z  2  25 B. x  
1   y  2   z  2  9 2 2 2 2 2 2 C. x  
1   y  2   z  2  5 D. x  
1   y  2   z  2  16 C©u 74 : x 1 y 1 z 1 x 1 y 2 z 1 Cho d : ; d :
. Viết phương trình đường thẳng 1 2 2 1 1 1 1 2
là đoạn vuông góc chung của d và d . 1 2 7 7 x 5t x 5t 9 9 8 8 A. y 3t , t B. y 3t , t 9 9 10 10 z 7t z 7t 9 9 7 7 x 5t x 5t 9 9 8 8 C. y 3t , t D. y 3t , t 9 9 10 10 z 7t z 7t 9 9
C©u 75 : Cho hình hộp ABCD.A’B’C’D’, biết ( A 1;0;1), ( B 2;1;2), (
D 1; 1;1), C'(4;5;  5) .Tìm tọa độ đỉnh A’ ? A. '( A 2  ;1;1) B. '( A 3;5; 6  ) C. '( A 5; 1  ;0) D. '( A 2;0;2) 12 ĐÁP ÁN 01 { | } ) 28 { | ) ~ 55 { ) } ~ 02 { | } ) 29 { ) } ~ 56 { | } ) 03 { ) } ~ 30 { | ) ~ 57 { | ) ~ 04 ) | } ~ 31 { | } ) 58 ) | } ~ 05 { ) } ~ 32 { | } ) 59 { | } ) 06 { | } ) 33 ) | } ~ 60 { | ) ~ 07 { | } ) 34 { | } ) 61 ) | } ~ 08 ) | } ~ 35 ) | } ~ 62 { ) } ~ 09 ) | } ~ 36 { ) } ~ 63 { | ) ~ 10 { | } ) 37 { | ) ~ 64 { ) } ~ 11 ) | } ~ 38 { | ) ~ 65 { | } ) 12 { | } ) 39 { | } ) 66 { ) } ~ 13 { ) } ~ 40 ) | } ~ 67 { ) } ~ 14 { | ) ~ 41 { ) } ~ 68 ) | } ~ 15 ) | } ~ 42 ) | } ~ 69 { | ) ~ 16 ) | } ~ 43 { | ) ~ 70 { | ) ~ 17 ) | } ~ 44 { | ) ~ 71 ) | } ~ 18 { ) } ~ 45 { | ) ~ 72 { ) } ~ 19 { | } ) 46 { | ) ~ 73 ) | } ~ 20 { | } ) 47 { | } ) 74 ) | } ~ 21 { | } ) 48 { ) } ~ 75 { ) } ~ 22 { | ) ~ 49 { | ) ~ 23 { | ) ~ 50 { | } ) 24 ) | } ~ 51 { | ) ~ 25 { ) } ~ 52 { ) } ~ 26 { | ) ~ 53 ) | } ~ 27 { ) } ~ 54 { ) } ~ 13 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN ĐỀ 005
C©u 1 : Trong không gian Oxyz cho 2 điểm A(1;2;3), B(4;4;5). Tọa độ điểm M (Oxy) sao cho tổng 2 2
MA MB nhỏ nhất là: 17 11 1 1 11 1 1 A. M ( ; ; 0) M (1; ; 0) C. M ( ; ; 0) D. M ( ; ;0) 8 4 . B. 2 8 4 8 4
C©u 2 : Trong hệ trục tọa độ Oxyz cho hình bình hành ABCD với A  1;0; 
1 , B  2;1;2 và giao  3 3 
điểm của hai đường chéo là I ;0; 
 . Diện tích của hình bình hành ABCD là:  2 2  A. 5 B. 6 C. 2 D. 3
C©u 3 : Trong không gian với hệ trục tọa độ Oxyz cho tam giác ABC với A  1;2;  1 , B  2; 1  ;3, C   4
 ;7;5 . Đường cao của tam giác ABC hạ từ A là: 110 1110 1110 111 A. B. C. D. 57 53 57 57
C©u 4 : Trong không gian với hệ toạ độ Oxyz, cho 3 điểm A(3; 1; 1), B(7; 3; 9), C(2; 2; 2) . Tìm
tọa độ trọng tâm của tam giác ABC:
A. G 6;3;6
B. G 4;2;4 C. G  4  ; 3  ; 4   D. G 4;3; 4   C©u 5 : x 1 y 1 z
Tọa độ giao điểm của đường thẳng d : và mặt phẳng 1 2 4 : 3x 2y z 1 0 là: A.  1  ,0,  1 B. 1, 1  ,0 C.  1  ,1,0 D. 1,0, 1 
C©u 6 : Trong không gian với hệ trục Oxyz, cho (P): 2x-y+2z-4=0. Điểm nào sau đây thuộc (P). A. C(1;0; 2  ) B. ( A 1; 1  ;1) C. B(2;0; 2  ) D. ( D 2;0;0)
C©u 7 : Cho mặt phẳng P:8x  4y z  7  0 và đường thẳng d 1       d x y 2z 4 0 
. Gọi (d’) là hình chiếu của (d) xuống (P). Phương trình (d’)
x  3y z  2  0 là: 3
x  5y  4z  8  0
4x  3y  5z  8  0 A. B.  8
x  4y z  7  0 8
x  4y z  7  0  3
x  5y  4z  8  0 3
x  5y  4z  8  0 C. D.  8
x  4y z  7  0 8
x  4y z  7  0
C©u 8 : Cho điểm A 1,4, 7 và mặt phẳng P : x 2y 2z 5 0 . Phương trình đường
thẳng đi qua A và vuông góc với mặt phẳng (P) là: x 1 y 4 z 7 x 1 y 4 z 7 A. B. 1 2 2 1 2 2 x 1 y 4 z 7 x 1 y 4 z 7 C. D. 1 2 7 1 2 2
C©u 9 : Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng (P) : x my  3z  4  0
và (Q) : 2x y nz  9  0. Khi hai mặt phẳng (P),(Q) song song với nhau thì giá trị
của m n bằng 13 11 A. B. 4  C. D. 1  2 2 C©u 10 :
Trong không gian Oxyz cho 3 điểm , A , B C thỏa: OA 2i j 3k ; OB i 2 j k ; OC 3i 2 j k với ;
i j; k là các vecto đơn vị. Xét các mệnh đề: I AB 1,1, 4 II AC
1,1, 2 Khẳng định nào sau đây đúng?
A. Cả (I) và (II) đều đúng
B. (I) đúng, (II) sai
C. Cả (I) và (II) đều sai
D. (I) sai, (II) đúng
C©u 11 : Cho ba vectơ a 0;1; 2 , b 1;2;1 , c 4;3;m . Để ba vectơ đồng phẳng thì giá trị của m là? 2 A. 14 B. 5 C. -7 D. 7
C©u 12 : Phương trình đường thẳng đi qua điểm A 3;2;1 vuông góc và cắt đường thẳng x y z 3 là? 2 4 1 x 3 x 3 t x 3 x 3 A. : y 1 t B. : y 2 t C. : y 1 t D. : y 2 t z 5 4t z 1 2t z 5 4t z 1 3t
C©u 13 : Cho P: x  2y  3z 14  0 và M 1; 1  ; 
1 Tọa độ điểm N đối xứng của M qua P là A. 1; 3  ;7 B. 2; 1  ;  1 C. 2; 3  ; 2   D.  1  ;3;7
C©u 14 : Trong không gian với hệ trục tọa độ Oxyz cho tứ diện ABCD với A  2;3;  1 , B   1
 ;2;0, C  1;1; 2
 ;D  2;3;4 . Thể tích của tứ diện ABCD là: 7 7 5 7 A. B. C. D. 2 6 2 3 C©u 15 : x  y z
Trong không gian với hệ toạ độ Oxyz, cho đường thẳng d 1 2 2 :   3 2 và mặt  2
phẳng (P): x + 3y + 2z + 2 = 0. Lập phương trình đường thẳng  song song với mặt
phẳng (P), đi qua M(2; 2; 4) và cắt đường thẳng (d). x  2 y 2 z 4 x  2 y 2 z 4 A. :     9 7 6 B. : 9 7  6 x  2 y 2 z 4 x  2 y 2 z 4 C. :     9 7 6 D. : 3 2 2
C©u 16 : Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;0;1),B(2;1;2) và
(P):x+2y+3z+3=0. Viết phương trình mặt phẳng (Q) đi qua 2 điểm A,B và vuông góc với (P). A. ( ) Q : x 2y  z  2  0 B. ( ) Q : x 2y  z  2  0 C. ( ) Q : x 2y  z  2  0 D. ( ) Q : x 2y  z  2  0 C©u 17 : Cho A1; 1  ;2,B 2  ; 2
 ;2,C1;1; 
1 Phương trình của   chứa AB và vuông góc với mặt phẳng (ABC)
A. x  3y  2z 14  0
B. x  3y  5z 14  0 3
C. x  3y  5z 14  0
D. x  3y  5z 14  0
C©u 18 : Trong không gian với hệ trục Oxyz, cho mặt cầu 2 2 2
(S) : x y z  2x  4y  2z  3  0 .
Viết phương trình (P) chứa trục Ox và cắt (S) theo đường tròn có bán kính bằng 3.
A. (P) : y  3z  0
B. (P) : y  2z  0 C. ( )
P : y z  0
D. (P) : y  2z  0
C©u 19 : Trong không gian với hệ trục tọa độ Oxyz, cho tứ diện ABCD biết ( A 0;  1;  1) , (
B 1;0;2) , C(3;0;4), (
D 3;2;  1) . Thể tích của tứ diện ABCD bằng ? 1 1 A. B. C. 3 D. 6 6 2
C©u 20 : Trong không gian với hệ trục tọa độ Oxyz, cho phương trình đường thằng x  1 y  1 z d : 
 và mặt phẳng (P) : x y z  3  0 . Tọa độ giao điểm A của d và 2 1  4 (P)là: A. ( A 3; 2  ;4) B. ( A 3  ;1; 8  ) C. ( A 1  ;0; 4  ) D. ( A 1  ;1; 5  )
C©u 21 : Phương trình mặt phẳng (P) đi qua 3 điểm A 3,4,1 , B 1, 2,5 ,C 1,7,1 là:
A. 3x  2y  6z  7  0
B. 3x  2y  6z  23  0
C. 3x  2y  6z  23  0
D. 3x  2y  6z  5  0
C©u 22 : Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(0; 1; 2), B(2; –2; 1), C(–2; 0; 1).
Viết phương trình mặt phẳng (ABC)
A. x y  2z  5  0
B. x  2y  4z  6  0
C. x  2y  4z1  0
D. x  2y  4z 6  0 C©u 23 :
x  2y z  0
Cho đường thẳng (d) có phương trình tổng quát là  . Phương
2x y z 1 0
trình tham số của (d) là  1     x t x t
x  1 tx t  3   
A. y  1  3t
B. y  2t
C. y  1  3t D. y  1   3t     z  2  5t  1  z  5  tz  2   5tz    3t  3 4
C©u 24 : Cho A 0,2, 3 , B 1, 4,1 . Phương trình mặt phẳng (P) đi qua M 1,3, 2 và vuông góc với AB là: A. x y z 2 0 B. x 6y 4z 25 0 C. 3x y z 4 0 D. x 6y 17 0 C©u 25 : x 1 2t
Phương trình mặt phẳng chứa đường thẳng : y t
và đi qua M 2; 1;0 là? z 3 2t A. x 3y z 1 0 B. x 4y z 2 0 C. x 4y z 2 0 D. x 3y z 1 0
C©u 26 : Trong không gian với hệ trục tọa độ Oxyz cho tam giác ABC với
A  1;0;0, B  0;0;  1 , C  2;1; 
1 . Diện tích của tam giác ABC là: 6 3 6 A. B. C. D. 6 4 2 2
C©u 27 : Phương trình mặt phẳng đi qua điểm M 3;1;0 và vuông góc với đường thẳng x 1 y  2 z 1 d :   2 1  là: 2
A. x  2y z  5  0
B. 2x y  2z  5  0
C. x  2y z  5  0
D. 2x y  2z  5  0
C©u 28 : Trong không gian với hệ trục Oxyz, cho (P): 2x-y+2z-4=0. Mặt phẳng nào sau đây song song với (P).
A. x y  2z 1  0
B. 2x y z 1  0 C. 2
x y  2z  4  0
D. 4x  2y  4z 1  0
C©u 29 : Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC biết ( A 1  ;0;2), ( B 1;3; 1
 ), C(2;2;2). Trong các khẳng định sau khẳng định nào sai?  2 5 
Điểm G  ; ;1 là trọng tâm của tam A. 3 3  
B. AB  2BC giác ABC . 5  3 1 
Điểm M 0; ;  là trung điểm của
C. AC BC D. 2 2   cạnh . AB C©u 30 : Cho M 8; 3  ; 3
  và mặt phẳng  :3x y z 8  0 Tọa độ hình chiếu vuông góc
của A xuống   là A. 1; 2  ; 5   B.  1  ;1;6 C. 1; 2  ; 6   D. 2; 1  ;  1
C©u 31 : Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(1; 4; 2),B(–1; 2; 4) và đường x 1 y 2 z thẳng  :   2 2   28 1
. Tìm toạ độ điểm M trên  sao cho: MA MB .  1 2 A. M(1; 0; 4) B. M( 1  ;0;4) C. M(1; 0; 4) D. M(1;0;4)
C©u 32 : Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;4;1), B(–1;1;3) và mặt phẳng
(P): x – 3y  2z – 5  0 . Viết phương trình mặt phẳng (Q) đi qua hai điểm A, B và
vuông góc với mặt phẳng (P). A. Q ( ) : 2y z 3  5  0 B. Q ( ) : 2y z 3 11  0
C. x  3y  2z  8  0 D. 3
x 3y  2z 16  0
C©u 33 : Trong không gian với hệ trục tọa độ Oxyz cho A  4;0;0, B  6;6;0 Điểm D thuộc tia
Ox và điểm E thuộc tia Oz thỏa mãn thể tích tứ diện ABDE bằng 20 và tam giác
ABD cân tại D có tọa độ là: A. (
D 14;0;0); E(0;0;2) B. (
D 14;0;0); E(0;0; 2  ) C. (
D 14;0;0); E(0;0; 2  ) D. (
D 14;2;0); E(0;0;2) C©u 34 : x  y z
Trong không gian với hệ toạ độ Oxyz, cho đường thẳng d 1 1 2 :   2 1 3 và mặt
phẳng P : x  y  z1  0 . Viết phương trình đường thẳng  đi qua A(1;1; 2  ) , song
song với mặt phẳng (P) và vuông góc với đường thẳng d . x 1 y 1 z 2 x 1 y1 z 2 A.     :    :   1 1 1 B. 2 5 3  x 1 y 1 z 2 x 1 y 1 z 2 C.     :   : 2 5 3 D.       2 5 3
C©u 35 : Trong không gian với hệ trục Oxyz, cho hai điểm A(2;-2;1),B(3;-2;1) Tọa độ điểm C
đối xứng với A qua B là: 6 A. C(1; 2;1) B. D(1; 2  ; 1  ) C. D( 1  ;2; 1  ) D. C(1; 2  ;1)
C©u 36 : Trong không gian với hệ trục tọa độ Oxyz cho 3 điểm
A  2;0;4, B  4; 3;5, C  sin5t;cos3t;sin3t và O là gốc tọa độ. với giá trị nào của t để AB OC .  2  2 t    k  t   k  3 3 A.  (k  ) B.  (k  )   k   kt     t     24 4  24 4    2 t   k  t   k  3 3 C.  (k  ) D.  (k  )   k   kt     t    24 4  24 4
C©u 37 : Trong không gian với hệ trục tọa độ Oxyz, cho ba vectơ a  (1;2;2), b  (0; 1;3),
c  (4;  3;  1). Xét các mệnh đề sau:
(I) a  3 (II) c  26 (III) a b (IV) b c
(V) a.c  4 (VI) a, b cùng phương (VII) a b 2 10 cos ,  15
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng? A. 1 B. 6 C. 4 D. 3
C©u 38 : Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm ( A 1;  1;3), ( B 3  ;0;  4).
Phương trình nào sau đây là phương trình chính tắc của đường thẳng đi qua hai
điểm A và B ? x  3 y y  4 x  3 y y  4 A.   B.   4 1  7 1 1  3 x  1 y  1 y  3 x  1 y  1 y  3 C.   D.   4 1  7 4  1 7 C©u 39 : x 1 t
Cho đường thẳng d  y  2  t và mặt phẳng ( ) x  3y z 1 0 . Trong các khẳng z 1 2t
định sau, tìm khẳng định đúng : 7 A. d / /() B. d  () C. d  () D. ( ) cắt d
C©u 40 : Phương trình mặt cầu đường kính AB với A 4, 3,7 , B 2,1,3 là: 2 2 2 2 2 2 A. x 3 y 1 z 5 9 B. x 3 y 1 z 5 9 2 2 2 2 2 2 C. x 3 y 1 z 5 35 D. x 3 y 1 z 5 35
C©u 41 : Cho A 5;2; 6 , B 5;5;1 , C 2, 3, 2 , D 1,9,7 . Bán kính mặt cầu ngoài tiếp tứ diện ABCD là? A. 15 B. 6 C. 9 D. 5
C©u 42 : Trong không gian với hệ trục Oxyz, cho điểm A(1;-2;1) và (P):x+2y-z-1=0. Viết
phương trình mặt phẳng (Q) đi qua A và song song với (P).
A. (Q) : x 2 y z 4  0
B. (Q) : x 2 y z 4  0
C. (Q) : x 2 y z 2  0
D. (Q) : x 2 y z 4  0 C©u 43 : x 1 t
Tìm tọa độ điểm H trên đường thẳng d:  y  2  t sao cho MH nhắn nhất, biết z 1 2t  M(2;1;4): A. H(2;3;3) B. H(1;3;3) C. H(2; 2;3) D. H(2;3;4) .
C©u 44 : Khoảng cách giữa hai mặt phẳng P : 2x y 2z 1 0 và Q : 2x y 2z 1 0 là? 2 1 3 A. B. C. D. 5 3 5 2
C©u 45 : Cho 2 mặt phẳng P: x  2y  2z 1 0,Q: 6x y  2x  5  0 Phương trih2 mặt
phẳng   qua M 1;2; 
1 và vuông góc với cả 2 mặt phẳng (P) và (Q) là
A. x  2 y z  6  0
B. 2x  7 y 13z 17  0
C. 7x  2 y z 10  0
D. 2x  7 y 13z 17  0
C©u 46 : Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;4;1),B(-1;1;3) và (P):x-3y+2z-
5=0. Viết phương trình mặt phẳng (Q) đi qua 2 điểm A,B và vuông góc với (P). 8 A. ( ) Q : 2y  3z 11  0 B. ( ) Q : 2y  3z 11  0 C. ( ) Q : 2y  3z 11  0 D. ( ) Q : 2y  3z 11  0
C©u 47 : Cho phương trình mặt phẳng P : x 2y 3x 1
0 . Trong các mệnh đề sau, mệnh đề nào đúng? A. Ba điểm M
1;0;0 , N 0;1;1 ,Q 3;1;2 cùng thuộc mặt phẳng (P). B. Ba điểm M
1;0;0 , N 0;1;1 ,K 0;0;1 cùng thuộc mặt phẳng (P). C. Ba điểm M
1;0;0 , N 0;1;2 ,Q 3;1;2 cùng thuộc mặt phẳng (P). D. Ba điểm M
1;0;0 , N 0;1;2 ,K 1;1;2 cùng thuộc mặt phẳng (P).
C©u 48 : Cho mặt phẳng (P): 16x – 15y – 12z + 75 =0 và mặt cầu (S) 2 2 2
x y z  9 . (P) tiếp xúc với (S) tại điểm: 48 36 19 36 48 9 36 A. ( ;11; ) B. ( 1  ;1; ) C. ( 1  ;1; ) D. ( ; ; ) 25 25 3 25 25 5 25
C©u 49 : Cho ba điểm 1;2;0 , 2;3; 1 ,
2;2;3 . Trong các điểm A 1;3;2 , B 3;1;4 , C 0;0;1
thì điểm nào tạo với ba điểm ban đầu thành hình bình hành là? A. Cả A và B
B. Chỉ có điểm C.
C. Chỉ có điểm A. D. Cả B và C. C©u 50 : x 1 t x 2 t
Cho mặt phẳng P : y 2z
0 và hai đường thẳng d : y t và d ' : y 4 t . z 4t z 1
Đường thẳng ở trong (P) cắt cả hai đường thẳng d và d’ là? x 1 4t x 1 4t x 1 y z 1 x 1 y z A. B. y 1 2t C. y 2t D. 4 2 1 4 2 1 z t z t
C©u 51 : Cho hai điểm M 1;2; 1 , N 0;1; 2 và vectơ v 3; 1;2 . Phương trình mặt phẳng
chứa M, N và song song với vectơ v là? A. 3x y 4z 9 0 B. 3x y 4z 7 0 9 C. 3x y 3z 7 0 D. 3x y 3z 9 0
C©u 52 : Trong không gian với hệ trục Oxyz, cho 3 điểm A(1;0;0),B(0;2;0),C(0;0;3). Viết
phương trình mặt phẳng đi qua 3 điểm A,B,C.
A. (ABC) : 6 x 3y 2z 6  0
B. (ABC) : 6 x 3y 2z 6  0
C. (ABC) : x 2 y 3z1  0
D. (ABC) : 6 x 3y 2z 6  0
C©u 53 : Cho hai đường thẳng có phương trình sau:
x  2y  5  0
x y z  5  0 d :  d :  1 5
x  2y  4z 1 0 2 3
y z  6  0
Mệnh đề sau đây đúng:
d hợp với d 1 2 A.
B. d cắt d
C. d d D. d d 1 2 1 2 1 2 góc 60o
C©u 54 : Trong không gian với hệ trục Oxyz, cho (P): 2x-y+2z-4=0. Mặt phẳng nào sau đây vuông góc với (P).
A. x  4y z  2  0
B. x  4y z  5  0
C. x  4y z  2  0 D. x  4y z 1  0 C©u 55 : x  3 y  2 z  6 x y 19 z
Gọi  là gác giữa hai đường thẳng d :   và d :   . 1 2 3 4 2 1 4  1 Khi đó cos bằng: 2 2 1 2 A. B. C. D. 58 . 5 2 58
C©u 56 : Cho ba điểm A 2;5; 1 , B 2;2;3 , C
3;2;3 . Mệnh đề nào sau đây là sai? A. ABC đều. B. , A ,
B C không thẳng hàng. C. ABC vuông. D. ABC cân tại B.
C©u 57 : Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm M(1;1;3), N(1;1;5) , P(3;0;4).
Phương trình nào sau đây là phương trình mặt phẳng đi qua điểm M và vuông góc
với đường thẳng NP ?
A. x y z  3  0
B. x  2y z  3  0
C. 2x y z  2  0
D. 2x y z  4  0 10
C©u 58 : Cho tam giác ABC có A(1;2;3), B(4;5;6), C(-3; 0 ;5). Gọi G là trọng tâm tam giác ABC,
I là trung điểm AC, ( ) là mặt phẳng trung trực của AB. Chọn khẳng định đúng
trong các khẳng định sau: 2 7 14 21 A. G( ; ; ), I(1;1; 4),
( ) : x y z   0 3 3 3 2 .. 2 7 14 B. G( ; ; ), I( 1
 ;1;4), () : 5x 5 y 5z  21  0 3 3 3 C. ( G 2;7;14), I( 1
 ;1;4), () : 2x 2 y 2z 21  0 2 7 14 D. G( ; ; ), I(1;1; 4),
() : 2 x 2 y 2z  21  0 3 3 3
C©u 59 : Trong không gian với hệ trục tọa độ Oxyz cho A  4;0;0, B   ; b ;
c 0 . Với b,c là các số
thực dương thỏa mãn AB  2 10 và góc 0
AOB  45 . Điểm C thuộc tia Oz thỏa mãn thể
tích tứ diện OABC bằng 8 có tọa độ là: A. C(0;0; 2  ) B. C(0;0;3) C. C(0;0;2) D. C(0;1;2)
C©u 60 : Cho tam giác ABC có A(0;0;1), B(-1;-2;0), C(2; 1 ;-1).. Khi đó tọa độ chân đường cao H hạ từ A xuống BC: 5 1  4 8  4 8 3 A. H ( ; ; ) B. H ( ;1;1) H (1;1;  ) D. H (1; ;1) 19 19 19 9 C. 9 2
C©u 61 : Trong không gian với hệ toạ độ Oxyz, cho điểm A(1; –2; 3) và đường thẳng d có x 1 y 2 z 3 phương trình   2 1
1 . Viết phương trình mặt cầu tâm A, tiếp xúc với d.  A. 2 x  y 2  2 ( –1) ( 2) (z– 3)  5 B. x 2  y 2   z 2 ( –1) ( 2) ( – 3)  50 C. x 2  y 2  z 2 ( 1) ( 2) ( 3)  50 D. 2 x  y 2  2 ( –1) ( 2) (z– 3)  50
C©u 62 : Trong các điểm sau, điểm nào là hình chiếu vuông góc của điểm M 1; 1;2 trên
mặt phẳng P : 2x y 2z 2 0 . A. 0, 2, 0 B.  1  ,0,0 C. 0, 0,  1  D. 1,0, 2  
C©u 63 : Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm ( A 1  ;1;5) , ( B 1;2;  1).
Phương trình nào sau đây là phương trình mặt phẳng đi qua hai điểm A , B và
vuông góc với mặt phẳng (Oxy)? A.      
6x  6y z  7  0 B. 6y z 11 0 C. x 2y 3 0
D. 3x z  2  0 11
C©u 64 : Trong không gian với hệ tọa độ Oxyz. Cho tứ diện ABCD với A  0;1;  1 , B   1
 ;0;2, C   1  ;1;0, ( D 2;1; 2
 ) . Thể tích của tứ diện ABCD là: 7 11 5 5 A. B. C. D. 6 6 6 18
C©u 65 : Trong không gian với hệ trục tọa độ Oxyz cho A  0;0;4, B  3;0;0, C  0;4;0
.Phương trình mp(ABC) là :
A. 4x  3y - 3z – 12  0
B. 4x  3y  3z – 12  0
C. 4x  3y  3z + 12  0
D. 4x - 3y  3z – 12  0 C©u 66 : Cho A3; 1  ;2,B4; 1  ; 
1 ,C 2;0;2 Phương trình mặt phẳng qua 3 điểm A, B, C là
A. 3x  3y z  2  0
B. 3x  2 y z  2  0
C. 2x  3y z  2  0
D. 3x  3y z  2  0
C©u 67 : Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có đường kính AB với ( A 3;2;  1), (
B 1;  4;1) . Tìm mệnh đề sai trong các mệnh đề sau:
A. Mặt cầu (S) có bán kính R  11 .
B. Mặt cầu (S) đi qua điểm M( 1  ;0;  1).
Mặt cầu (S) tiếp xúc với mặt phẳng C.
D. Mặt cầu (S) có tâm I(2; 1  ;0).
( ) : x  3y z  11  0.
C©u 68 : Tìm trên trục tung những điểm cách đều hai điểm A 1, 3,7 và B 5,7, 5
A. M 0,1,0 và N 0, 2,0 B. M 0, 2,0 C. M 0, 2,0
D. M 0, 2,0 và N 0, 2,0
C©u 69 : Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC biết ( A 1;2;3) , ( B 2;0;2) ,
C(0;2;0). Diện tích của tam giác ABC bằng ? 7 14 A. B. C. 14 D. 2 7 2 2
C©u 70 : Để 2 mặt phẳng có phương trình 2x ly  3z  5  0 và mx  6y  6z  2  0 song 12
song với nhau thì giá trị của m và l là:
A. m  2,l  6
B. m  4,l  3 
C. m  2,l  6  D. m  4  ,l  3
C©u 71 : Trong hệ trục tọa độ Oxyz cho u  4;3;4, v  2; 1  ;2, w  1;2; 
1 .khi đó u,v.w   là: A. 2 B. 3 C. 0 D. 1
C©u 72 : Phương trình mặt cầu đi qua 4 điểm A 3,0,0 , B 0,4,0 , C 0,0, 2 và O 0,0,0 là: A. 2 2 2
x y z  6x  8y  4z  0 B. 2 2 2
x y z  3x  4y  2z  0 C. 2 2 2
x y z  6x  8y  4z  0 D. 2 2 2
x y z  3x  4y  2z  0
C©u 73 : Phương trình mặt phẳng đi qua 3 điểm A(0;0;1), B(2;1;-1), C(-1;-2;0) là:
A. 5x – 4y + 3z – 3 = 0
B. 5x – 4y + 3z – 9 = 0
C. 5x – y + 3z – 33 = 0
D. x – 4y + z – 6 = 0 C©u 74 : x 1 y  3 z
Cho đường thẳng d : 
 và mặt phẳng (P) x  2y  2z 1 0 . Mặt phẳng 2 3  2
chứa đường thẳng d và vuông góc với (P) có phương trình :
A. 2x + 2y + z – 8 = 0
B. 2x – 2y + z – 8 = 0
C. 2x – 2y + z + 8 = 0
D. 2x + 2y - z – 8 = 0
C©u 75 : Phương trình mặt phẳng đi qua điểm M 1; 1
 ;2 và song song với mặt phẳng
P: x  2x z 1 0
A. 2x y z 1  0
B. x  2y z 1 0
C. x  2y z  2  0
D. x  2y z 1 0
C©u 76 : Khoảng cách từ A(- 1;3;2) đến mặt phẳng (BCD) với B(4;0;- 3),
C(5; - 1; 4), D(0; 6;1) bằng: 72 72 72 72 A. B. C. D. 786 76 87 77
C©u 77 : Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S) có phương trình:
x2  y2  z2  2x  6y 4z 2  0 . Viết phương trình mặt phẳng (P) song song với giá 13
của véc tơ v  (1;6;2) , vuông góc với mặt phẳng () : x  4y  z11  0 và tiếp xúc với (S).
(P): 2x  y 2z3  0 hoặc (P):
(P): 2x  y  2z 3  0 hoặc (P): A. B. 2x  y 2z  0.
2x  y 2z 21  0 .
(P): 2x  y  2z 21  0 . C.
D. (P): 2x  y  2z  3  0
C©u 78 : Trong không gian với hệ trục tọa độ Oxyz cho tam giác ABC với A  1;2;  1 , B  2; 1  ;3, C   4
 ;7;5 . Chân đường phần giác trong của góc B của tam
giác ABC là điểm D có tọa độ là:  2 11   2 11   2 11   2 11  A. D  ; ; 1    D  ; ;1   C. D  ; ;1   D ; ;1    B. D. 3 3   3 3   3 3   3 3 
C©u 79 : Trong không gian với hệ trục Oxyz, cho tam giác ABC có A(2;-2;1),B(3;-2;1),C(1;-2;-
2). Tọa độ trọng tâm G của tam giác ABC là A. G(2; 2;0) B. G( 2  ; 2  ;0) C. G(2; 2  ;1) D. G(2; 2  ;0)
C©u 80 : Phương trình mặt phẳng (P) đi qua 2 điểm A 2, 1,4 , B 3,2, 1 và vuông góc mặt phẳng Q : x y 2z 3 0 là:
A. 11x  7 y  2z  21  0
B. 11x  7 y  2z  21  0
C. 11x  7 y  2z  21  0
D. 11x  7 y  2z  21  0
C©u 81 : Cho 2 đường thẳng lần lượt có phương trình x 1 2t
x  3  t '   d :  y  2
và d :  y  4  t ' 1 2   z t   z  4 
Độ dài đoạn vuông góc chung của d và d là 1 2 A. 6 B. 4 C. 2 2 D. 2 6 14 ĐÁP ÁN 01 ) | } ~ 28 { | } ) 55 ) | } ~ 02 { | ) ~ 29 { | ) ~ 56 ) | } ~ 03 { | ) ~ 30 { | } ) 57 { | ) ~ 04 { ) } ~ 31 { ) } ~ 58 ) | } ~ 05 { ) } ~ 32 { ) } ~ 59 { | ) ~ 06 { | } ) 33 { | ) ~ 60 ) | } ~ 07 { | } ) 34 { ) } ~ 61 { ) } ~ 08 { ) } ~ 35 { | } ) 62 { ) } ~ 09 { | ) ~ 36 { | ) ~ 63 { | ) ~ 10 ) | } ~ 37 { | ) ~ 64 { | ) ~ 11 ) | } ~ 38 { | ) ~ 65 { ) } ~ 12 ) | } ~ 39 ) | } ~ 66 { | } ) 13 { | } ) 40 { ) } ~ 67 { | ) ~ 14 { | ) ~ 41 ) | } ~ 68 { ) } ~ 15 { ) } ~ 42 { | } ) 69 { | ) ~ 16 { | } ) 43 ) | } ~ 70 { | } ) 17 { | } ) 44 ) | } ~ 71 { | ) ~ 18 { | } ) 45 { | } ) 72 { ) } ~ 19 { | ) ~ 46 { | } ) 73 ) | } ~ 20 { | ) ~ 47 ) | } ~ 74 ) | } ~ 21 { ) } ~ 48 ) | } ~ 75 { ) } ~ 22 { ) } ~ 49 ) | } ~ 76 ) | } ~ 23 { | } ) 50 ) | } ~ 77 { ) } ~ 24 { ) } ~ 51 ) | } ~ 78 { | ) ~ 25 ) | } ~ 52 { | } ) 79 { | } ) 26 { | ) ~ 53 { | } ) 80 { ) } ~ 27 { ) } ~ 54 { | } ) 81 { | } ) 15 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN ĐỀ 006 C©u 1 : 3  x
Cho   : 2x  y z 1  0,  : x  4y  6z 10  0 và d :
y  4  z  3 2
Khẳng định nào sau đây là đúng:
A. d / /   và d   
B. d    và d / /  
C. d    và d   
D. d / /   và d / /  
C©u 2 : Trong không gian Oxyz, cho các điểm A3;0;4,B 1;2;3,C 9;6;4 là 3 đỉnh của hình
bình hành ABCD. Tọa độ đỉnh D là:
A. D 11;4;5   D 11; 4  ;5 
B. D 11; 4; 5 C.
D. D 11;4; 5
C©u 3 : Trong không gian với hệ tọa độ Oxyz, góc tạo bởi hai vectơ a ( 4;2;4) và b 2 2; 2 2;0 là: A. 0 30 B. 0 90 C. 0 135 D. 0 45 C©u 4 : x y  2 z 1
Trong không gian với hệ tọa độ Oxyz ,đường thẳng  :   đi qua điểm 1 1  3 M (2; ; m )
n . Khi đó giá trị của m, n lần lượt là : A. m  2  ;n 1
B. m  2;n  1  C. m  4  ;n  7
D. m  0;n  7
C©u 5 : Mặt phẳng đi qua ( A 2
 ;4;3) A(-2;4;3), song song với mặt ( )
P : x  3y  2z 1  0 có phương trình dạng:
A. x  3y  2z  4  0
B. x  3y  2z  4  0
C. x  3y  2z  4  0
D. x  3y z  4  0 C©u 6 : Cho , A ,
B C lần lượt là hình chiếu vuông góc của điểm S(4;1; 5
 ) trên các mặt phẳng
Oxy,Oyz,Ozx. Khoảng cách từ S đến mặt phẳng ABC bằng: 1 40 20 A. A,B,C đều sai B. C. D. 2 21 21 21
C©u 7 : Trong không gian với hệ tọa độ Oxyz ,gọi M là giao điểm của đường thẳng x  2 y z 1  :   và mặt phẳng ( )
P : x+2y-3z+2=0 . Khi đó : 3  1 2 A. M (5; 1  ; 3  ) B. M (2;0; 1  ) C. M ( 1  ;1;1) D. M (1;0;1) C©u 8 :
Cho hình hộp ABCD.A’B’C’D’ biết: A(1;0;1),B(2;1;2),D(1;− 1;1),C′(4;5;−
5).Thể tích khối hộp là: A. 9 B. 6 C. 7 D. 8 C©u 9 :
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2; 1
 ;1) . phương trình mặt phẳng (P) đi
qua điểm A và cách gốc tọa độ O một khoảng lớn nhất là
A. 2x  y  z  6  0
B. 2x  y  z  6  0
C. 2x  y  z  6  0 D. 2x+y-z+6=0 C©u 10 : Cho 𝑚
⃗ = (1; 0; −1); 𝑛⃗ = (0; 1; 1). Kết luận nào sai: A. 𝑚 ⃗ . 𝑛⃗ = −1 B. [𝑚
⃗ , 𝑛⃗ ] = (1; −1; 1) C. 𝑚
⃗ và 𝑛⃗ không cùng phương D. Góc của 𝑚 ⃗ và 𝑛⃗ là 600
C©u 11 : Cho ba điểm B(1;0;1),C(− 1;1;0),D(2;− 1;− 2). Phương trình mặt phẳng qua B, C, D là:
A. 4x + 7y − z− 3 = 0
B. x − 2y + 3z + 1 = 0
C. x − 2y + 3z − 6 = 0
D. − 4x − 7y + z− 2 = 0
C©u 12 : Trong không gian Oxyz, cho 3 điểm A0;1;2,B 2; 2  ;  1 ;C  2
 ;1;0 . Khi đó phương
trình mặt phẳng (ABC) là: ax  2y  4z d  0 . Hãy xác định a và d
A. a  1;d  6    B. a  1  ;d  6 C. a  1  ;d  6  a d D. 1; 6
C©u 13 : Trong không gian Oxyz cho 4 điểm ( A 1;0;0), (
B 0;1;0),C(0;0;1), (
D 1;1;1) . Trong các mệnh
đề sau, mệnh đề nào sai:
A. Bốn điểm A, B, C, D tạo thành một tứ
B. AB vuông góc với CD diện.
C. Tam giác BCD vuông
D. Tam giác ABD đều 2
C©u 14 : Trong không gian Oxyz cho các điểm A ) 0 ; 2 ; 1 ( , ( B  ) 2 ; 4 ; 3
. Tìm tọa độ điểm I trên trục Ox
cách đều hai điểm A, B và viết phương trình mặt cầu tâm I , đi qua hai điểm A, B. A. (x  ) 3 2 2 2
y z  20 B. 2 2 2
(x  3)  y z  20 C. 2 2 2
(x 1)  ( y  3)  (z 1)  11 / 4 D. 2 2 2
(x 1)  ( y  3)  (z 1)  20
C©u 15 : Trong không gian với hệ tọa độ Oxyz cho tam giác MNP biết MN ( 3;0;4) và NP
( 1;0; 2) . Độ dài đường trung tuyến MI của tam giác MNP bằng: 9 95 85 15 A. 2 B. C. D. 2 2 2
C©u 16 : Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x+ y+z+1=0.
a)Viết phương trình mặt cầu có tâm I(1;1;0) và tiếp xúc với mp(P). A.  2 2
x  2   y  2 2 1 1  z  3
B. x     y   2 1 1  z  3 C.  2 2
x  2   y  2 2 1 1  z  3
D. x     y   2 1 1  z  3 C©u 17 : 2𝜋
Cho 𝑎 và 𝑏⃗ tạo với nhau một góc . Biết |𝑎 | = 3, |𝑏⃗ | = 5 thì |𝑎 − 𝑏⃗ | bằng: 3 A. 6 B. 5 C. 4 D. 7
C©u 18 : Trong hệ tọa độ Oxyz cho 2 điêm A(1;2;3) và B(2;1;2). Phương trình đường thẳng
nào dưới đây không phải là phương trình đường thẳng đi qua 2 điểm A và B x  1 y  2 z  3 x y  3 z  4 A.     1 1  1  B. 1 1  1  x  2 y  1 z  2 x  3 y z  1 C.     1  D. 1 1 1  1 1
C©u 19 : Cho 𝐴(3; 1; 0); 𝐵(−2; 4; √2). Gọi M là điểm trên trục tung và cách đều A và B thì: A. 𝑀(0; 0; 2) B. 𝑀(0; −2; 0) C. 𝑀(2; 0; 0) D. 𝑀(0; 2; 0) C©u 20 : 3x 2y z 10 0
Trong không gian với hệ tọa độ Oxyz cho đường thẳng d : . Vectơ x 2y 4z 2 0
chỉ phương của d có tọa độ là: A. 6; 13;8 B. 6;13; 8 C. 6;13;8 D. 6;13; 8
C©u 21 : Trong hệ tọa độ Oxyz, mặt phẳng   cắt ba trục Ox, Oy,Oz lần lượt tại ba điểm
A(-3;0;0), B(0;4;0), C(0;0;-2) có phương trình là: 3
A. 4x  3y  6z  12  0
B. 4x  3y  6z  12  0
C. 4x  3y  6z  12  0
D. 4x  3y  6z  12  0
C©u 22 : Trong không gian Oxyz, đường thẳng d đi qua hai điểm A2;0;3,B 1;2;  1 có
phương trình tham số là: x   1  t x   2  t x   2  2t x   2  t     A. y   2  2t        B. y 2t y 4t y 2t C. D. z   1  4t     z  3   4tz  3   8tz  3   4t
C©u 23 : Cho 𝑎 , 𝑏⃗ có độ dài bằng 1 và 2. Biết (𝑎 , 𝑏⃗ ) = − 𝜋. Thì |𝑎 + 𝑏⃗ | bằng: 3 3 3 A. 1 B. C. 2 D. √2 2 2
C©u 24 : Trong không gian 0xyz cho mặt phẳng (P): 2x + 3y + z – 11 = 0. mặt cầu (S) có tâm I(1; -2;
1) và tiếp xúc với (P) tại H. tọa độ tiếp điểm H là. A. H(3;1;2). B. H(5;4;3) C. H(1;2;3) D. H(2;3;-1)
C©u 25 : Trong không gian với hệ tọa độ Oxyz , điểm M (1;2; 3  ) và mặt phẳng ( )
P : x  2y  2z  3  0 . Khoảng cách từ điểm M đến mặt phẳng (P) có giá trị là : A. 3 B. 1 C. 2 D. 4
C©u 26 : Cho 𝐴(1; 0; 0); 𝐵(0; 0; 1); 𝐶(2; 1; 1) thì ABCD là hình bình hành khi: A. 𝐷(3; −1; 0) B. 𝐷(1; 1; 2) C. D. A. 𝐷(3; −1; 0) B. 𝐷(1; 1; 2) C. 𝐷(−1; 1; 2) D. 𝐷(3; 1; 0)
C©u 27 : Trong không gian với hệ tọa độ Oxyz cho điểm M (3;5; 8) và mặt phẳng
( ) : 6x 3y 2z 28 0 . Khoảng cách từ M đến ( ) bằng: A. 6 B. 47 7 C. 41 D. 45 7 7 C©u 28 : x  5 y  2 z  4
Trong hệ tọa độ Oxyz, cho phương trình đường thẳng d:   và 1 1 2
phương trình mặt phẳng   : x y  2z  7  0 . Góc của đường thẳng d và mặt 4 phằng   là: A. 0 45 B. 0 60 C. 0 90 D. 0 30
C©u 29 : Cho hình bình hành ABCD với A1;1;3 , B 4  ;0;2, C  1  ;5; 
1 . Tọa độ điểm D là: A. D4;6;4 B. D4;6;2 C. D2;3;  1 D. D2;6;2
C©u 30 : Trong không gian Oxyz, cho mặt cầu (S) có tâm I  1
 ;4;2 và có thể tíchV  972 .
Khi đó phương trình của mặt cầu (S) là: A.  2 2 2
x  2  y  2  z  2 1 4 2  81      
B. x 1 y 4 z 2 9 C.  2 2 2
x  2  y  2  z  2 1 4 2  9
D. x  1  y  4  z  2  81 C©u 31 : x 1 y  2 z 1
Trong không gian với hệ tọa độ Oxyz ,đường thẳng  :   song song với 2 1  1 mặt phẳng ( )
P : x y z m  0 khi m thỏa :
A. Cả 3 đáp án đều sai. B. m  0 C. m  0 D. m   R
C©u 32 : Mặt phẳng chứa hai điểm A2;1;3,B1; 2; 
1 và song song với đường thẳng d x  1   t
y  2t ,t R đi qua điểm: z  3 2tA. M  2;  1;  1
B. M 0;0;19 . C. M 0;1;  1 D. M  2;  1;0
C©u 33 : Cho 𝑎 và 𝑏⃗ khác 0⃗ . Kết luận nào sau đây sai:
A. |[𝑎 , 𝑏⃗ ]| = |𝑎 ||𝑏⃗ |sin (𝑎 , 𝑏⃗ )
B. [𝑎 , 3𝑏⃗ ] = 3[𝑎 ; 𝑏⃗ ]
C. [2𝑎 , 𝑏⃗ ] = 2[𝑎 , 𝑏⃗ ]
D. [2𝑎 , 2𝑏⃗ ] = 2[𝑎 , 𝑏⃗ ] 5
C©u 34 : Trong mặt phẳng Oxyz, cho A(1; 2; 3) và B(3; 2; 1). Mặt phẳng đi qua A và cách B
một khoảng lớn nhất là: A. x - z - 2 = 0 B. x - z + 2 = 0
C. x  2y  3z - 10  0
D. 3x + 2y + z - 10 = 0 C©u 35 :
Cho A(2,1,− 1) và (P): x + 2y − 2z + 3 = 0. (d) là đường thẳng đi qua A và
vuông góc với (P). Tìm tọa độ M thuộc (d) sao cho OM = √ 3
A. (1,− 1,1)ℎoặc (5/3; 1/3; -1/3)
B. (1;1;-1) ; (5/3; 1/3; -1/3)
C. (1;-1;-1) ; (5/3; -1/3; 1/3)
D. (1;-1;-1) ; (5/3; 1/3; 1/3)
C©u 36 : Trong không gian với hệ tọa độ Oxyz cho điểm M (2;1;4). Điểm N thuộc đường x 1 t thẳng ( ) : y 2 t (t
) sao cho đoạn MN ngắn nhất có tọa độ là: z 1 2t A. N (2;3;2) B. N (3;2;3) C. N (2;3;3) D. N (3;3;2)
C©u 37 : Trong hệ tọa độ Oxyz cho điêm M(1;1;1) N(-1;1;0) P(3;1;-1). Điểm Q thuộc mặt
phẳng Oxz cách đều 3 điểm M,N,P có tọa độ A.  5 7  B.  5 1  ;0;   ;0;    4 4   6 6  C.  1 7  D.  5 7  ;0;   ;0;    6 6   6 6 
C©u 38 : Trong không gian Oxyz cho 3 véctơ a  ( 1
 ;1;0),b  (1;1;0),c  (1;1;1) . Trong các mệnh đề sau, mệnh đề nào sai: A. c  3 B. a  2
C. a b
D. c b C©u 39 : 6
A. S(9;9;9) hoặc S( 7  ; 7  ; 7  )
B. S(9;9;9) hoặc S(7;7;7)
C. S(9; 9; 9) hoặc S(7;7;7)
D. S(9; 9; 9) hoặc S( 7  ; 7  ; 7  ) C©u 40 :
x  7  3t
Phương trình mặt phẳng chứa hai đường thẳng d : y  2  2t và 1 z 1 2tx 1 y  2 z  5 d :   2 2 3  4
A. 2x 16y 13z  31  0
B. 2x 16y 13z  31  0
C. 2x 16y 13z  31  0
D. 2x 16y 13z  31  0 C©u 41 : Cho A1; 1  ;5, B3; 3  ; 
1 . Phương trình mặt phẳng trung trực của đoạn AB là:
A. x y  2z  2  0
B. x y  2z  2  0
C. x  2y  2z  0
D. x y  2z  7  0
C©u 42 : Cho mặt cầu (S): 2 2 2
x y z  2x  6y  4z  9  0 . Khi đó tâm I và bán kính R của mặt cầu (S) là: A. I(1; 3; 2  ),R  25 B. I(1; 3; 2  ),R  5 C.     I(1; 3; 2  ),R  7 D. I( 1; 3; 2),R 5
C©u 43 : Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;3;-1) và đường thẳng x 4 y 1 z 5 d : 1 2 2
tọa độ hình chiếu vuông góc của M trên (d) A. H 2;5;  1 B. H(2;3;-1) C. H(1;-2;2) D. H(4;1;5)
C©u 44 : Cho 𝐴(0; 1; 1); 𝐵(−1; 0; 1); 𝐶(1; 1; 1). Kết luận nào sau đây là đúng:
A. 𝐴𝐵 ⊥ 𝐴𝐶 B. [𝐴𝐵 ⃗⃗⃗ , 𝐴𝐶 ⃗⃗⃗ ] = (0; 0; −1)
C. 𝐴, 𝐵, 𝐶 thẳng hàng
D. 𝑆∆𝐴𝐵𝐶 = 1 2
C©u 45 : Trong hệ tọa độ Oxyz, phương trình mặt cầu có tâm I(1;2;3) và đi qua gốc O có phương trình là
A. x  2   y  2  z  2 1 2 3 14 B. 2 2 2
x y z x  2y  3z  0 7
C. x  2   y  2  z  2 1 2 3  24 D. 2 2 2
x y z  2x  4y  6z  0
C©u 46 : Trong không gian với hệ tọa độ Oxyz cho ba điểm (
A 1;0;1), B(0;2;0), C(0;0;3).
Khoảng cách từ gốc tọa độ O đến mặt phẳng (ABC) bằng: A. 3 B. 5 4 7 C. 6 D. 9 7 7
C©u 47 : Trong không gian Oxyz, cho điểm A2;1; 
1 và mặt phẳng P : x  2y  2z  3  0 .
Gọi H 1;a;b là hình chiếu vuông góc của A lên mặt phẳng (P). Khi đó a bằng: A. 1  B. 1 C. 2  D. 2
C©u 48 : Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;3;-1) và đường thẳng x 4 y 1 z 5 d : 1 2 2
phương trình mp (P) qua M và vuông góc với đt (d) là. A. x-2y+2z+6=0 B. x-2y+2z-16=0 C. X-2y+2z=0 D. x-2y+2z+16=0
C©u 49 : Phương trình mặt phẳng (P) đi qua hai điểm A1;2;3 , B2; 1  ;  1 và vuông góc với
mặt phẳng Q : x y  2z 3  0 là:
A. x y z  6  0
B. x y z  2  0
C. x y z  4  0
D. x y z  2  0
C©u 50 : Phương trình   đi qua 3 điểm A(1;0;0), B(0; 2;0), C(0;0;3) là:
A. x  2y  3z  6  0 B. x y z    1 1 2 3 C. x y z       
D. 6x 3y 2z 1 0 0 1 2 3
C©u 51 : Trong các phương trình sau, phương trình nào là phương trình của mặt cầu: A. 2 2 2
x y z 10xy  8y  2z 1  0 B. 2 2 2
3x  3y  3z  2x  6y  4z 1  0 8 C. 2 2 2
2x  2y  2z  2x  6y  4z  9  0
D. x y z2 2
 2x  4y  z9  0
C©u 52 : Trong không gian với hệ tọa độ Oxyz cho tứ diện ABCD với (
A 1;0;0), B(0;1;0), C(0;0;1), D( 2;1; 1). Thể tích tứ diện ABCD bằng: A. 3 B. 4 2 3 C. 1 D. 2 2 3
C©u 53 : Cho 𝐴(−1; 2; 3); 𝐵(0; 1; −3). Gọi 𝑀 là điểm sao cho 𝐴𝑀 ⃗⃗⃗ = 2𝐵𝐴 ⃗⃗⃗ thì: A. 𝑀(1; 0; −9) B. 𝑀(−1; 0; 9) C. 𝑀(3; 4; 9) D. 𝑀(−3; 4; 15)
C©u 54 : Trong không gian Oxyz, cho a  5;7;2,b  3;0;4,c   6  ;1;   1 . Tọa độ của vecto
n  5a  6b  4c  3i là:
A. n  16;39;26
B. n  16; 3  9;26 C. n   1  6;39;26
D. n  16;39; 2  6
C©u 55 : Cho 𝐴(4; 2; 6); 𝐵(10; −2; 4); 𝐶(4; −4; 0); 𝐷(−2; 0; 2) thì tứ giác ABCD là hình: A. Bình hành B. Vuông C. Chữ nhật D. Thoi
C©u 56 : Phương trình mặt phẳng (P) đi qua A1;2;3 và song song với mặt phẳng ( )
Q : 2x  y z  5  0
A. 2x y z  2  0
B. 2x y z  3  0
C. 2x y z 1  0
D. 2x y z  3  0
C©u 57 : Trong không gian với hệ tọa độ Oxyz cho hai điểm M (2; 4;5) và N ( 3;2;7) . Điểm P
trên trục Ox cách đều hai điểm M và N có tọa độ là: A. 19 B. 9 P ;0;0 P ;0;0 10 10 C. 17 D. 7 P ;0;0 P ;0;0 10 10 9 C©u 58 : x 1 y z 1
Trong không gian với hệ tọa độ Oxyz ,hai đường thẳng d :   và đường 1 2  3 1 x 1 y  2 z  7 thẳng d :  
có vị trí tương đối là : 2 1  2 3  A. Cắt nhau B. Trùng nhau C. Chéo nhau D. Song song.
C©u 59 : Khoảng cách giữa hai điểm M 1; 1
 ; 3 và N  2; 2; 3 bằng A. MN  4 B. MN  3 C. MN  3 2 D. MN  2 5
C©u 60 : Trong không gian với hệ tọa độ Oxyz cho ba điểm M (1;2;4), N(2; 1;0), P( 2;3; 1) .
Để tứ giác MNPQ là hình bình hành thì tọa độ đỉnh Q là: A. Q( 1;2;1) B. 3 3 Q ;3; 2 2 C. Q( 3;6;3) D. Q(3; 6; 3)
C©u 61 : Mặt phẳng đi qua 3 điểm M(1;0;0), N(0; 2  ;0), ( P 0;0; 2
 ) có phương trình là:
A. 2x y z 1  0
B. x  2y  2z  2  0 C. x y z    x y z 1   1 2 2 D. 1 2  2 
C©u 62 : Trong hệ tọa độ Oxyz cho hình hộp MNPQ.M’N’P’Q’ có M(1;0;0) N(2;-1;1) Q(0;1;0)
M’(1;2;1). Điểm P’ có tọa độ: A. (3;1;0) B. (1;2;2) C. (0;3;1) D. (2;1;2)
C©u 63 : Trong không gian Oxyz, cho mặt cầu S  2 2 2
: 2x  2y  2z  4x  8y  2  0 . Tọa độ tâm
I và bán kính R của mặt cầu là: A. I  1  ;2;0;R  4 B. I 1; 2  ;0;R  2 C. I  1  ;2;0;R  2
D. I 1;2;0;R  4
C©u 64 : Cho đường thẳng  qua điểm M có VTCP u , và  qua điểm N có VTCP u . Điều 1 1 2 2 10
kiện để  và  chéo nhau là: 1 2
A. u và u cùng phương.
B. u ,u .MN  0 1 2 1 2  
C. u ,u
u ,u .MN  0 1 2 
 và MN cùng phương. D. 1 2   C©u 65 : x y z
Trong không gian Oxyz, cho điểm A4; 3
 ;2, và đường thẳng d 2 2 :   . 3 2 1 
Tọa độ hình chiếu vuông góc của A lên đường thẳng d là:
A. H 1;0;  1 
B. H  1;0;  1 C. H  1  ;0;   1  D. H 0;1;  1
C©u 66 : Trong không gian với hệ tọa độ Oxyz ,mặt cầu 2 2 2
(S) : x  y z  2x  4y  6z  2  0 có tâm I, bán kính R là : A. I( 2  ;4; 6  ), R  58 B. I ( 1  ;2; 3  ), R  4 C. I (1; 2  ;3), R  4 D. I(2; 4  ;6), R  58 C©u 67 : y 1 3  z
Giao điểm A của đường thẳng  : x 1   và mặt phẳng 2 2
P:2x 2y z 3  0 có tọa độ: A. ( A 2  ; 1  ; 5  ) B. ( A 2  ; 1  ;5) C. ( A 2  ;1;5) D. ( A 2; 1  ;5)
C©u 68 : Phương trình mặt phẳng (P) đi qua gốc tọa độ O và vuông góc với hai mặt phẳng ( )
Q : 2x y  3z 1  0 , ( )
R : x  2y z  0 :
A. 7x y  5z  0
B. 7x y  5z  0
C. 7x y  5z  0
D. 7x y  5z  0
C©u 69 : Trong hệ tọa độ Oxyz, cho điểm M(1;2;-6) và đường thẳng d có phương trình:
x  2  2t
y 1  t . Hình chiếu vuông góc của điểm M lên đường thẳng d có tọa độ là: z  3   tA. (-2;0;4) B.  4  ;0;2 11 C. 2;0;4 D. 0;2; 4  
C©u 70 : Trong không gian Oxyz, cho A1;0; 3  ,B  1  ; 3  ; 2
 ,C 1;5;7 . Gọi G là trong tâm của
tam giác ABC. Khi đó độ dài của OG là A. 3 B. 5 C. 3 D. 5
C©u 71 : Trong hệ tọa độ Oxyz, mặt phẳng   đi qua điểm M(2;-1;4) và chắn trên nửa trục
dương Oz gấp đôi đoạn chắn trên nửa trục Ox, Oy có phương trình là:
A. x y  2z  6  0
B. x y  2z  6  0
C. 2x  2y z  6  0
D. 2x  2y z  6  0
C©u 72 : Trong không gian Oxyz, cho các điểm A1;3;2,B 1;2; 
1 ,C 1;1;3 . Phương trình
đường thẳng đi qua trọng tâm G của tam giác ABC và vuông góc với mặt phẳng (ABC) là: A. x   1  t B. x   1  2t   y   2 y   2  t z   2   z  2  tC. x   1  2t D. x   1  t   y   3  t y   2 z   2  t   z  3 
C©u 73 : Trong hệ tọa độ Oxyz cho các điêm M(1;2;3) N(2;2;3) P(1;3;3) Q(1;2;4) MNPQ là hình gì: A. Tứ giác B. Hình bình hành C. Hình thang D. Tứ diện
C©u 74 : Điều kiện cần và đủ để ba vec tơ a,b,c khác 0 đồng phẳng là: A. a. . b c  0
B. a,b.c  0  
C. Ba vec tơ đôi một vuông góc nhau.
D. Ba vectơ có độ lớn bằng nhau.
C©u 75 : Cho mặt phẳng ( )
P : x y z  4  0 và điểm ( A 1; 2  ; 2
 ) . Tọa độ A' là đối xứng của A 12 qua (P) A. A'(3; 4;8) B. A'(3;0; 4  ) C. A'(3;0;8) D. A'(3; 4; 4  )
C©u 76 : Cho 𝐴(4; 2; −6); 𝐵(5; −3; 1); 𝐶(12; 4; 5); 𝐷(11; 9; −2) thì ABCD là hình: A. Bình hành B. Vuông C. Thoi D. Chữ nhật
C©u 77 : Chọn phát biểu đúng: Trong không gian
A. Vec tơ có hướng của hai vec tơ thì
B. Tích có hướng của hai vec tơ là một
cùng phương với mỗi vectơ đã cho.
vectơ vuông góc với cả hai vectơ đã cho.
C. Tích vô hướng của hai vectơ là một
D. Tích của vectơ có hướng và vô hướng vectơ.
của hai vectơ tùy ý bằng 0
C©u 78 : Trong hệ tọa độ Oxyz cho điêm M(3;1;-2). Điểm N đối xứng với M trục Ox có tọa độ là: A. (-3;1;2) B. (-3;-1;-2) C. (3;1;0) D. (3;-1;2)
C©u 79 : Trong không gian với hệ tọa độ Oxyz cho ba vectơ a (5;4; 1), b (2; 5;3) và c thỏa hệ thức a 2c
b . Tọa độ c là: A. 3; 9;4 B. 3 9 ; ; 2 2 2 C. 3 9 ; ;2 D. 3 9 ; ;1 2 2 4 4 C©u 80 : Cho (S): 2 2 2
x y z  4x  2y  10z+14  0 . Mặt phẳng (P): x  y z  4  0 cắt mặt cầu
(S) theo một đường tròn có chu vi là: A. 8 B. 4 C. D. 4 3 2 13 ĐÁP ÁN 01 { ) } ~ 28 { | } ) 55 { | } ) 02 ) | } ~ 29 { ) } ~ 56 { ) } ~ 03 { | ) ~ 30 ) | } ~ 57 { | ) ~ 04 { | ) ~ 31 { | ) ~ 58 { | ) ~ 05 { | ) ~ 32 { ) } ~ 59 { ) } ~ 06 { ) } ~ 33 { | } ) 60 { | ) ~ 07 { | ) ~ 34 { ) } ~ 61 { | ) ~ 08 ) | } ~ 35 ) | } ~ 62 { | } ) 09 ) | } ~ 36 { | ) ~ 63 ) | } ~ 10 { | } ) 37 { | } ) 64 { ) } ~ 11 ) | } ~ 38 { | ) ~ 65 ) | } ~ 12 ) | } ~ 39 ) | } ~ 66 { | ) ~ 13 { | ) ~ 40 { ) } ~ 67 { ) } ~ 14 ) | } ~ 41 { ) } ~ 68 { ) } ~ 15 { | ) ~ 42 { ) } ~ 69 { | } ) 16 ) | } ~ 43 ) | } ~ 70 ) | } ~ 17 { | } ) 44 { | } ) 71 { | } ) 18 { | } ) 45 { | } ) 72 ) | } ~ 19 { | } ) 46 { | ) ~ 73 { | } ) 20 { | ) ~ 47 ) | } ~ 74 { ) } ~ 21 { | } ) 48 ) | } ~ 75 { ) } ~ 22 ) | } ~ 49 { ) } ~ 76 { | } ) 23 { | } ) 50 { ) } ~ 77 { ) } ~ 24 ) | } ~ 51 { ) } ~ 78 { | } ) 25 { | ) ~ 52 { | ) ~ 79 { | ) ~ 26 { | } ) 53 { | } ) 80 { ) } ~ 27 { | ) ~ 54 ) | } ~ 14 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN ĐỀ 007
C©u 1 : Mặt phẳng nào sau đây chứa trục Oy? A. –y + z = 0 B. -2x + z =0 C. -2x – y + z =0 D. -2x – y = 0
C©u 2 : Cho lăng trụ tam giác đều ABC.A’B’C’ cạnh đáy bằng a và AB ' BC ' . Tính thể tích khối lăng trụ.
Một học sinh giải như sau:
Bước 1: Chọn hệ trục toạ độ như hình vẽ. Khi đó: z C' B' A' y C B O a a 3 a 3 A x A ; 0; 0 ; B 0; ; 0 ; B ' 0; ;h ; 2 2 2 a a C ; 0; 0 ; C ' ; 0;h 2 2
với h là chiều cao của lăng trụ, suy ra: a a 3 a a 3 AB ' ; ;h ; BC ' ; ;h 2 2 2 2 2 2 a 3a a 2 Bước 2: 2 AB ' BC ' AB '.BC ' 0 h 0 h 4 4 2 2 3 a 3 a 2 a 6 Bước 3: V . B h . l¨ng trô 2 2 4 1
Bài giải này đã đúng chưa? Nếu sai thì sai ở bước nào? A. Sai ở bước 2 B. Sai ở bước 1 C. Sai ở bước 3 D. Đúng
C©u 3 : Trong không gian Oxyz cho mặt cầu S 2 2 2
: x y z  2x  2y  2z  22  0 , và mặt
phẳng P : 3x  2y  6z 14  0 . Khoảng cách từ tâm I của mặt cầu (S) đến mặt phẳng (P) là A. 2 B. 1 C. 3 D. 4
C©u 4 : Trong không gian tọa độ Oxyz, cho điểm M=(3; 1; 2). Phương trình của mặt phẳng
đi qua hình chiếu của M trên các trục tọa độ là: A. -3x – y – 2z =0
B. 2x + 6y + 3z – 6 =0 C. 3x + y + 2z = 0
D. -2x – 6y – 3z – 6 =0
C©u 5 : Trong không gian Oxyz cho ba vectơ a   1
 ;1;0,b  1;1;0,c  1;1;  1 . Trong các
mệnh đề sau, mệnh đề nào sai? A. c  3
B. b c
C. a b D. a  2 C©u 6 :
x  2  t
Trong không gian (Oxyz). Cho đường thẳng  :  y  1 t . và mặt phẳng (P): z 13t
x  3y z 1 0. Mặt phẳng (Q) chứa  và vuông góc với (P) có phương trình là:
A. 5x  2y  2z 13  0
B. 5x  2 y z 13  0
C. 5x  2 y z 13  0
D. 5x  2 y z 13  0
C©u 7 : Trong không gian (Oxyz). Cho điểm M  1
 ;1;2 và đường thẳng x 1 y 1 z  :   2 1 
. Tọa độ hình chiếu vuông góc của M lên  là: 1  1 1 2   1 1 2   1 1 2   1 1 2  A.  ; ;   B.  ; ;   C.  ; ;   D.  ; ;    3 6 3   3 3 3   3 3 3   6 3 3 
C©u 8 : Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng   :3x  2y z 12  0 và x t
đường thẳng  : y  6  3t . Trong các mệnh đề sau, mệnh đề nào đúng. z  3t  2
A.    
B.  cắt  
C.    
D.  / /   C©u 9 :
Trong không gian Oxyz cho hai điểm ( A –1;3; –2), (
B –3;7; –18) và mặt phẳng (P):
2x – y z 1  0. Gọi M  ; a ;
b c là điểm trên (P) sao cho MA+MB nhỏ nhất. Giá trị
của a b c là A. 1 B. 3 C. 2 D. 4
C©u 10 : Trong không gian với hệ tọa độ Oxyz, cho điểm M 1, 1  ,  1 và hai đường thẳng x y1 z x y1 z (d  4 1) :   (d ) :   1 2 và
. Mệnh đề nào dưới đây là đúng.  3  2 1 2 5 A. ( 1 d ) , ( 1
d ) và M đồng phẳng B.
M d nhưng M d 2  1 
C. M d
nhưng M d
(d ) và (d ) vuông góc nhau 1  2  D. 1 1 C©u 11 : x 7 y 3 z 9 x 3 y 1 z 1
Cho hai đường thẳng d : và d : . 1 1 2 1 2 7 2 3
Phương trình đường vuông góc chung của d và d là: 1 2 x 3 y 1 z 1 x 7 y 3 z 9 A. B. 1 2 4 2 1 4 x 7 y 3 z 9 x 7 y 3 z 9 C. D. 2 1 4 2 1 4
C©u 12 : Trong không gian với hệ tọa độ Oxyz cho 3 điểm M 2;3; 1 , N 1;1;1 ,
P 1;m 1;2 . Với giá trị nào của m thì tam giác MNP vuông tại N ? A. m 3 B. m 2 C. m 1 D. m 0
C©u 13 : Trong không gian (Oxyz).Cho 3 điểm A1;0;  1 , B2;1;  1 ,C 1; 1  ;2 . Điểm M
thuộc đường thẳng AB mà MC  14 có tọa độ là: A. M  2  ;2;  1 , M  1  ; 2  ;  1
B. M 2;1;  1 , M  1  ; 2  ;  1
C. M 2;1;  1 , M 1; 2  ;  1 D. M 2;1;  1 , M  1  ;2;  1
C©u 14 : Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A2, 1  ,5;B5, 5  ,7;C11, 1
 ,6;D5,7,2 .Tứ giác là hình gì? A. Hình thang
B. Hình bình hành C. Hình thoi D. Hình vuông 3
C©u 15 : Trong không gian với hệ tọa độ Oxyz, cho ba mặt phẳng
:2x4y 5z 2  0, : x2y 2z 1 0, :4xmy z n  0
Để  , ,  có chung giao tuyến thì tổng m n là A. -4 B. 8 C. -8 D. 4
C©u 16 : Cho 4 điểm M 2; 3;5 , N 4;7; 9 , P 3;2;1 , Q 1; 8;12 . Bộ 3 điểm nào sau đây là thẳng hàng: A. N, P,Q B. M, N, P C. M, P,Q D. M, N,Q
C©u 17 : Cho các điểm A(1; -2; 1), B(2; 1; 3) và mặt phẳng (P) : x – y + 2z – 3 = 0. Đường thẳng
AB cắt mặt phẳng (P) tại điểm có tọa độ: A. (0;5;1) B. (0; 5  ;1) C. (0;5; 1  ) D. (0; 5  ; 1  )
C©u 18 : Mặt phẳng (Q) đi qua hai điêm A(1; 0; 1), B(2; 1; 2) và vuông góc với mặt phẳng
(P) : x  2y 3z 3  0 cắt trục oz tại điểm có cao độ A. 2 B. 4 C. 3 D. 1 C©u 19 : Cho hai điểm ( A 3; 3;1), (
B 0;2;1)và mp(P): x y z 7
0 . Đường thẳng d nằm
trên mp(P) sao cho mọi điểm của d cách đều hai điểm A, B có phương trình là: x t x t x t x 2t A. y 7 3t B. y 7 3t C. y 7 3t D. y 7 3t z 2t z 2t z 2t z t C©u 20 : x  4 y  3 z 1
Góc giữa hai đường thẳng d :   và d’ : 2 1 1  x  5 y  7 z  3   là : 2  4  2  A. 30o B. 90o C. 45o D. 60o C©u 21 : x y  3 z 1 x  4 y z  3
Cho hai đường thẳng d : d1: = = , d2: = = . Hai đường thẳng 1 1 2 3 1 1 2 đó: A. Chéo nhau B. Trùng nhau C. Cắt nhau D. Song song
C©u 22 : Cho ba điểm A(1; 0; 1), B(-1; 1; 0), C(2; -1; -2). Phương trình mặt phẳng (ABC) là: 4
A. x – 2y + 3z – 6 = 0
B. - 4x – 7y + z – 2 = 0
C. x – 2y + 3z + 1 = 0
D. 4x + 7y – z – 3 = 0. C©u 23 : x 1 y 3 z
Cho đường thẳng d : và mp(P): x 2y z 8 0 . Mặt phẳng 2 3 2
chứa d và vuông góc với mp(P) có phương trình là: A. 2x 2y z 8 0 B. 2x 2y z 8 0 C. 2x 2y z 8 0 D. 2x 2y z 8 0
C©u 24 : Cho hai mặt phẳng P : x y z 1 0, Q : x y z 5 0 . Điểm nằm trên Oy cách điều P và Q là: A. 0;3;0 B. 0; 3;0 C. 0; 2;0 D. 0;2;0 C©u 25 : x 2 t x 2 2t
Cho hai đường thẳng d : y
1 t và d : y 3 . 1 2 z 2t z t
Mặt phẳng cách đều hai đường thẳng d và d có phương trình là: 1 2 A. x 5y 2z 12 0 B. x 5y 2z 12 0 C. x 5y 2z 12 0 D. x 5y 2z 12 0
C©u 26 : Trong không gian toạ độ Oxyz, cho hai điểm A(1; -1; 0) và B(-2; 0; 1). Phương trình
mặt phẳng trung trực (P) của đoạn thẳng AB là: A. -3x + y + z +3 =0
B. -6x + 2y + 2z – 3=0 C. -6x + 2y + 2z + 3=0 D. -3x + y + z -3 =0
C©u 27 : Cho hai véctơ u,v khác 0 . Phát biểu nào sau đây không đúng? u,v  0  
khi hai véctơ u,v cùng
A. u,v 
 có độ dài là u v cosu,vB. phương.
C. u,v 
 vuông góc với hai véctơ u,v
D. u,v   là một véctơ
C©u 28 : Trong không gian (Oxyz). Cho điểm A 1  ;0;2 và mặt phẳng 5
(P): 2x y z  3  0. Mặt cầu (S) tâm A tiếp xúc với mặt phẳng (P) tại điểm H có tọa độ là:  2 1 11  2 1 11 A. H  ; ;   B. H  ; ;    3 6 6   3 6 6   2 1 11  2 1 11 C. H  ; ;   D. H ; ;    3 6 3   3 6 6 
C©u 29 : Cho A 2;2;0 , B 2;4;0 , C 4;0;0 và D 0; 2;0 . Mệnh đề nào sau đây là đúng
A. ABCD tạo thành tứ diện
B. Diện tích ABC bằng diện tích DBC
C. ABCD là hình chóp đều
D. ABCD là hình vuông
C©u 30 : Trong không gian Oxyz cho mặt cầu S x  2  y  2 z  2 : 1 3 2  49 . Phương trình
nào sau đây là phương trình của mặt phẳng tiếp xúc với mặt cầu (S) ?
A. 6x  2y  3z  0
B. x  2y  2z  7  0
C. 6x  2y  3z  55  0
D. 2x  3y  6z  5  0 C©u 31 : x  2 y z  3
Cho mặt phẳng (P) : 2x + y - 2z - 1 = 0 và đường thẳng d :   . Phương 1 2  3 x  3 y 1 z 1
trình mặt phẳng chứa d và vuông góc với (P) là :   1 2 3 
A. x + 8y + 5z + 31 = 0
B. 5x + y + 8z + 14 = 0 C. 5x + y + 8z = 0 D. x + 8y + 5z +13 = 0
C©u 32 : Mặt phẳng nào sau đây cắt các trục tọa độ Ox, Oy, Oz lần lượt tại A, B, C sao cho
tam giác ABC nhận điểm G(1; 2; 1) làm trọng tâm? A. x + 2y + 2z -6 =0
B. 2x + y + 2z – 6 =0 C. 2x + 2y + z – 6=0
D. 2x + 2y + 6z – 6 =0
C©u 33 : Trong không gian (Oxyz). Cho mặt cầu (S) : 2 2 2
x y z  4x  5  0 . Điểm A thuộc mặt cầu (S) và có tọa độ thứ nhất bằng -
1. Mặt phẳng (P) tiếp xúc với (S) tại A có phương trình là:
A. x y 1  0 B. x 1  0 C. y 1  0 D. x 1  0 6
C©u 34 : Trong không gian với hệ tọa độ 0xyz, cho M(-2;1;0) và đường thẳng
 x 2 y 1 z 1 :  
 sao cho MN  11 . Tọa độ điểm N là: 1 1  . Điểm N thuộc   2 A. 1, 2, 1  B.  1  ,2,  1 C. 2,1,  1 D. 2, 1  ,  1
C©u 35 : Trong không gian với hệ toạ độ Oxyz, cho A2,0,0, B1,1, 
1 . Mặt phẳng (P) thay đổi
qua A,B cắt các trục Ox, Oy lần lượt tại B(0; b; 0), C(0; 0; c) (b > 0, c > 0). Hệ thức nào dưới đây là đúng. 1 1
A. bc  2b cB. bc  
C. b c bc
D. bc b c b c
C©u 36 : Mặt cầu tâm I(1; -2; 3) tiếp xúc với mặt phẳng (P) : 2x – y + 2z – 1 = 0 có phương trình : A. 2 2 2
(x 1)  ( y  2)  (z  ) 3  3 B. 2 2 2
(x 1)  ( y  2)  (z  ) 3  9 C. 2 2 2
(x 1)  ( y  2)  (z  ) 3  3 D. 2 2 2
(x 1)  ( y  2)  (z  ) 3  9 C©u 37 : x  y z
Trong không gian với hệ toạ độ Oxyz, cho đường thẳng d 1 1 2 :   2 1 3 và mặt
phẳng P : x  y  z1  0 .Đường thẳng  qua A1,1, 
1 song song với mặt phẳng (P)
và vuông góc với đường thẳng d. Véctơ chỉ phương của  là: A. 1, 1  ,  1 B. 2, 5  , 3   C. 2,1,3 D. 4,10, 6  
C©u 38 : Cho mặt phẳng (P) : 2x – 2y – z – 4 = 0 và mặt cầu (S) : 2 2 2
x y z  2x  4y  6z 11  0 .
Bán kính đường tròn giao tuyến là: A. 2 B. 5 C. 3 D. 4
C©u 39 : Nếu mặt phẳng (α) qua ba điểm M(0; -1; 1), N(1; -1; 0), và P(1; 0; -2) thì nó có một vectơ pháp tuyến là: A. n = (1; 1; 2) B. n = (1; 2; 1) C. n = (-1; 2; -1) D. n = (2; 1; 1) C©u 40 : x 1 y 2 z Cho hai điểm ( A 1;4;2), (
B 1;2;4) và đường thẳng : . Điểm 1 1 2 M mà 2 2 MA
MB nhỏ nhất có toạ độ là: A. (1; 0; 4) B. (0; 1; 4) C. ( 1; 0; 4) D. (1; 0; 4)
C©u 41 : Trong không gian (Oxyz). Cho mặt cầu 7 (S): 2 2 2
x y z  2x  4y  2z  3  0 và mặt phẳng
(P): x  2y  2z m 1  0 ( m là tham số). Mặt phẳng (P) tiếp xúc với mặt cầu (S) ứng với giá trị m là:  m  3   m  3  m  3  m  3 A. B. C. D.  m  15  m  15  m  5  m 15
C©u 42 : Trong không gian (Oxyz). Cho tứ diện ABCD biết A1; 1  ; 2  ,B0;3;0, C 3;1; 4  ,D2;1; 3
 . Chiều cao của tứ diện hạ từ đỉnh A là: 1 2 2 4 A. B. C. D. 3 3 3 9
C©u 43 : Trong không gian với hệ tọa độ Oxyz, gọi  là góc hợp bởi đường thẳng x  3 y  4 z  3  
và mặt phẳng 2x y z 1  0 thì cos bằng: 1 2 1  3 1 1 3 A. B. C. D.  2 2 2 2 C©u 44 : x 2 y 1 z 3 x 1 y 1 z 1
Cho hai đường thẳng d : và d : . 1 1 2 2 2 1 2 2
Khoảng cách giữa d và d bằng: 1 2 4 3 4 2 4 A. B. 4 2 C. D. 2 3 3
C©u 45 : Hai mặt phẳng () : 3x + 2y – z + 1 = 0 và (') : 3x + y + 11z – 1 = 0
A. Song song với nhau;
B. Vuông góc với nhau. C. Trùng nhau;
D. Cắt nhau nhưng không vuông góc với nhau;
C©u 46 : Trong không gian Oxyz cho bốn điểm A1;0;0, B0;1;0,C 0;0;  1 , D 1;1;  1 Trong các
mệnh đề sau, mệnh đề nào sai ?
B. Bốn điểm A, B, C, D tạo thành một tứ
A. AB CD diện
C. Tam giác BCD đều
D. Tam giác BCD vuông cân 8 C©u 47 : x t x 3 y 6 z 1
Cho hai đường thẳng d : và d : y
t Đường thẳng đi qua 1 2 2 1 2 z 2 điểm (
A 0;1;1), vuông góc với d và cắt d có phương trình là: 1 2 x y 1 z 1 x y 1 z 1 A. B. 1 3 4 1 3 4 x y 1 z 1 x 1 y z 1 C. D. 1 3 4 1 3 4
C©u 48 : Cho ba điểm A(3; 2; -2) , B(1; 0; 1) và C(2; -1; 3). Phương trình mặt phẳng đi qua A và vuông góc với BC là:
A. x y  2z  3  0
B. x y  2z 5  0
C. x y  2z 1  0 .
D. x y  2z  3  0 C©u 49 : x 8 4t
Cho đường thẳng d : y 5 2t và điểm (
A 3; 2;5). Toạ độ hình chiếu của điểm z t A trên d là: A. (4; 1; 3) B. ( 4; 1; 3) C. (4; 1; 3) D. ( 4;1; 3) C©u 50 : x 1 2t
Trong không gian Oxyz cho điểm A0; 1
 ;3 và đường thẳng d : y  2 . Khoảng z t  
cách từ A đến đường thẳng d bằng . A. 3 B. 6 C. 14 D. 8 C©u 51 : x  2t x 1 y z  3 
Trong không gian Oxyz cho hai đường thẳng d :  
và d :  y  1 4t . 1 1 2 3 2 z  2 6t
Khẳng định nào sau đây là đúng ? d , d trùng d , d chéo 1 2 1 2 A.
B. d , d cắt nhau. C. d d D. 1 2 1 2 nhau. nhau.
C©u 52 : Khoảng cách giữa hai mặt phẳng  : x  2y z 1 0 và  : x  2y z  5  0 là 9 A. 6 B. 4 C. 5 D. 3
C©u 53 : Trong không gian với hệ tọa độ Oxyz, giả sử mặt cầu S  2 2 2 2
: x y z  4mx  4y  2mz m  4m  0 có bán kính nhỏ nhất. Khi đó giá trị của m m là: 1 1 3 A. B. C. D. 0 2 3 2
C©u 54 : Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(0; 1; 2), B(2; –2; 1), C(–2; 0; 1). Gọi M  ; a ;
b c là điểm thuộc mặt phẳng (P): 2x  2y z – 3  0 sao cho MA=MB=MC.
Giá trị của a b c là A. -2 B. 0 C. -1 D. -3
C©u 55 : Trong không gian (Oxyz). 2 2 2
Cho mặt cầu (S):  x   1
  y  2  z  3  0. Gọi I là tâm của mặt cầu (S). Giao
điểm của OI và mặt cầu (S) có tọa độ là: A.  1  ; 2  ; 3   3; 6  ;9   3; 6  ;9 và B.  1;2; 3 và C.  1  ;2; 3   3; 6  ; 9     3;6;9 và D.  1;2; 3 và
C©u 56 : Cho A 2; 1;6 , B 3; 1; 4 , C 5; 1;0 tam giác ABC là Tam giác vuông A. B. Tam giác cân C. Tam giác đều D. Tam giác vuông cân
C©u 57 : Trong không gian với hệ toạ độ Oxyz, cho điểm M(0;1;1) và 2 đường thẳng (d1), (d2) x 1 y  2 z với: (d1): 
 ; (d2) là giao tuyến của 2 mặt phẳng (P): x 1 0 và (Q): 3 2 1
x y z  2  0 . Gọi (d) là đường thẳng qua M vuông góc (d1) và cắt (d2). Trong số các điêm A(0;1;1),
B(-3;3;6), C(3;-1;-3), D(6;-3;0), có mấy điểm nằm trên (d)? A. 2 B. 0 C. 1 D. 3
C©u 58 : Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S 2 2 2
; x y z  2x  4y  6z  0 và
ba điểm O0,0,0; A1,2,3; B2, 1  , 
1 . Trong ba điểm trên, số điểm nằm bên trong mặt cầu là A. 1 B. 2 C. 0 D. 3 10
C©u 59 : Trên mặt phẳng Oxy , cho điểm E có hoành độ bằng 1, tung độ nguyên và cách đều mặt phẳng : x 2y z 1 0 và mặt phẳng : 2x y z 2 0 . Tọa độ của E là: A. 1; 4; 0 B. 1;0; 4 C. 1; 0; 4 D. 1; 4;0
C©u 60 : Trong không gian Oxyz cho mặt cầu S 2 2 2
: x y z  2x  4y  6z  0 . Trong ba
0;0;0,1;2;3,2; 1  ; 
1 điểm có bao nhiêu điểm thuộc mặt cầu (S) ? A. 2 B. 0 C. 1 D. 3
C©u 61 : Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x  2y z  4  0 và mặt cầu
(S): x2 + y2 + z2 – 2x – 4y – 6z – 11 = 0. Mặt phẳng (P) cắt mặt cầu (S) theo một đường tròn có chu vi là A. 8 B. 2 C. 4 D. 6
C©u 62 : Trong không gian Oxyz cho các điểm A 1;1; 6 , B 0;0; 2 , C 5;1;2 và D' 2;1; 1 .
Nếu ABCD.A'B'C'D' là hình hộp thì thể tích của nó là: A. 36 (đvtt) B. 40 (đvtt) C. 42 (đvtt) D. 38 (đvtt)
C©u 63 : Phương trình đường thẳng đi qua hai điểm A(1; 2; -3) và B(3; -1; 1) là: x 1 y  2 z  3 x  3 y 1 z 1 A.   B.   3 1  1 1 2 3  x 1 y  2 z  3 x 1 y  2 z  3 C.   D.   2 3  4 2 3  4 C©u 64 : x 5 2t x 9 2t
Cho hai đường thẳng d : y
1 t và d : y t . 1 2 z 5 t z 2 t
Mặt phẳng chứa hai đường thẳng d và d có phương trình là: 1 2 A. 3x 5y z 25 0 B. 3x y z 25 0 C. 3x 5y z 25 0 D. 3x 5y z 25 0
C©u 65 : Trong không gian Oxyz cho ba vectơ a   1
 ;1;0,b  1;1;0,c  1;1;  1 . Trong các
mệnh đề sau, mệnh đề nào đúng? 11 a,b cùng A. . a c  1 B. C. cosb c 2 , 
D. a b c  0 phương 6
C©u 66 : Trong không gian Oxyz cho tam giác ABC có A1;0; 
1 , B 0;2;3,C 2;1;0 . Độ dài
đường cao của tam giác kẻ từ C là 26 26 A. 26 B. C. D. 26 2 3 C©u 67 :
x  6  4t
Trong không gian Oxyz cho điểm A1;1; 
1 và đường thẳng d :  y  2
  t . Hình chiếu z  1   2t
của A trên d có tọa độ là A. 2; 3  ;  1 B.  2  ;3;  1 C. 2; 3  ;  1 D. 2;3;  1
C©u 68 : Mặt cầu có tâm I(1; 2; 3) và tiếp xúc với mp(Oxz) là: A. 2 2 2
x + y + z - 2x - 4y - 6z + 10 = 0 B. 2 2 2
x + y + z + 2x + 4y + 6z - 10 = 0 C. 2 2 2
x + y + z - 2x - 4y + 6z + 10 = 0 D. 2 2 2
x + y + z + 2x + 4y + 6z - 10 = 0
C©u 69 : Trong không gian với hệ tọa độ Oxyz, cho 3 điểm ( A 1; 2; 1  ), (
B 2;1;1),C(0;1; 2) . Gọi H  ; a ;
b c là trực tâm của tam giác. Giá trị của a b c A. 4 B. 5 C. 7 D. 6
C©u 70 : Cho (P) : 2x – y + 2z – 1 = 0 và A(1; 3; -2). Hình chiếu của A trên (P) là H(a; b; c). Giá trị của a – b + c là : 3 3 2 2 A.  . B. . C. . D.  2 2 3 3
C©u 71 : Cho hai điểm A(1; 0; -3) và B(3; 2; 1). Phương trình mặt cầu đường kính AB là: A. 2 2 2 x + y + z - 2x - y + z - 6= 0 B. 2 2 2 x + y + z - 4x - 2y + 2z = 0 C. 2 2 2 x + y + z + 4x - 2y + 2z = 0 D. 2 2 2
x + y + z - 4x - 2y + 2z + 6 = 0
C©u 72 : Trong không gian Oxyz cho A 1  ;2;  1 , và hai mặt phẳng
P:2x4y 6z 5  0, Q: x2y 3z  0. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Mặt phẳng (Q) đi qua A và không song song với (P). 12
B. Mặt phẳng (Q) không đi qua A và song song với (P).
C. Mặt phẳng (Q) đi qua A và song song với (P).
D. Mặt phẳng (Q) không đi qua A và không song song với (P).
C©u 73 : Trong không gian (Oxyz). Cho 2 điểm A1;2; 
3 , B0;3;5 và đường thẳng d: x 1 y 1 z   2 1 
. Mặt phẳng (P) chứa 2 điểm A, B và song song với d có phương 3 trình là:
A. 5x  7 y z 16  0
B. 5x  7 y z 16  0
C. 5x  7 y z 16  0
D. 5x  7 y z 16  0
C©u 74 : Tọa độ hình chiếu vuông góc của điểm M(2; 0; 1) trên đường thẳng x 1 y z  2 d :   là : 1 2 1 A. (-1; -4; 0) B. (0; -2; 1) C. (2; 2; 3) D. (1; 0; 2)
C©u 75 : Trong không gian với hệ tọa độ Oxyz , cho điểm M 2; 5;4 . Trong các phát biểu sau, phát biểu nào sai:
A. Tọa độ điểm M ' đối xứng với M qua trục Oy là M 2; 5; 4 .
B. Khoảng cách từ M đến trục Oz bằng 29.
C. Khoảng cách từ M đến mặt phẳng tọa xOz bằng 5 .
D. Tọa độ điểm M ' đối xứng với M qua mặt phẳng yOz là M 2;5; 4 .
C©u 76 : Cho hai điểm A(-3; 1; 2) và B(1; 0; 4). Mặt phẳng đi qua A và vuông góc với đường
thẳng AB có phương trình là: A. 4x + y + 2z + 7 =0
B. 4x – y + 2z + 9 =0
C. 4x – y + 2z – 9 = 0
D. 4x – y – 2z + 17 =0
C©u 77 : Cho A 1;2; 1 , B 5;0;3 , C 7,2,2 . Tọa độ giao điểm M của trục Ox với mặt phẳng qua ABC là: A. M 1;0;0 B. M 1;0;0 C. M 2; 0; 0 D. M 2;0;0 13
C©u 78 : Cho ba điểm A(0;1;2), B(3;0;1), C(1;0;0). Phương trình mặt phăng (ABC) là
A. 2x  3y  4z  2  0
B. 2x  3y  4z  2  0
C. 4x  6y  8x  2  0
D. 2x  3y  4x 1 0 C©u 79 :  x t
Trong không gian (Oxyz). Cho điểm I 1;0;2 và đường thẳng  :  y  1 2t . Đường  z t  
thẳng qua I vuông góc và cắt có  phương trình là: x 1 3tx 1 3tx 1 6tx 1 3t     A. y  0 B. y  0 C. y  0 D. y  0     z  2  tz  2  tz  2  tz  2  t
C©u 80 : Vectơ nào sau đây vuông góc với vectơ pháp tuyến của mặt phẳng 2x - y –z =0? A. n = (2; 1; -1) B. n = (1; 2; 0) C. n = (0; 1; 2) D. n = (-2; 1; 1)
C©u 81 : Trong không gian với hệ tọa độ Oxyz cho 3 điểm A 1;0;0 , B 0;0;1 , C 2;1;1 . Diện
tích của tam giác ABC bằng: 7 11 5 6 A. B. C. D. 2 2 2 2 14 ĐÁP ÁN 01 { ) } ~ 28 { ) } ~ 55 { ) } ~ 02 { | ) ~ 29 { | } ) 56 { | } ) 03 { | ) ~ 30 { | ) ~ 57 ) | } ~ 04 { ) } ~ 31 { | } ) 58 ) | } ~ 05 { ) } ~ 32 { ) } ~ 59 { | } ) 06 { ) } ~ 33 { ) } ~ 60 { | ) ~ 07 { ) } ~ 34 ) | } ~ 61 ) | } ~ 08 ) | } ~ 35 ) | } ~ 62 { | } ) 09 ) | } ~ 36 { | } ) 63 { | } ) 10 ) | } ~ 37 ) | } ~ 64 { | ) ~ 11 { | ) ~ 38 { | } ) 65 { | ) ~ 12 { | } ) 39 { ) } ~ 66 { | ) ~ 13 { ) } ~ 40 { | ) ~ 67 { | ) ~ 14 ) | } ~ 41 { ) } ~ 68 ) | } ~ 15 ) | } ~ 42 { ) } ~ 69 ) | } ~ 16 { | } ) 43 ) | } ~ 70 { | } ) 17 { | } ) 44 { | ) ~ 71 { ) } ~ 18 ) | } ~ 45 { ) } ~ 72 { | ) ~ 19 { | ) ~ 46 { | ) ~ 73 { ) } ~ 20 { | } ) 47 { | ) ~ 74 { | } ) 21 ) | } ~ 48 { | } ) 75 { | } ) 22 { | } ) 49 { | ) ~ 76 { ) } ~ 23 { | ) ~ 50 { | ) ~ 77 { | } ) 24 { | } ) 51 { | ) ~ 78 ) | } ~ 25 { | ) ~ 52 ) | } ~ 79 { ) } ~ 26 { ) } ~ 53 ) | } ~ 80 { ) } ~ 27 ) | } ~ 54 ) | } ~ 81 { | } ) 15 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN ĐỀ 008
C©u 1 : Góc giữa 2 vectơ 𝑎⃗(2; 5; 0) và 𝑏⃗ (3 ; −7; 0) là: A. 300 B. 600 C. 1350 D. 450
C©u 2 : Cho mặt phẳng (P) : k(x  y  z)  (x  y  z)  0 và điểm A(1;2;3). Chọn khẳng định đúng:
A. Hình chiếu của A trên (P) luôn thuộc một đường tròn cố định khi k thay đổi.
B. (P) luôn chứa trục Oy khi k thay đổi.
C. Hình chiếu của A trên (P) luôn thuộc một mặt phẳng cố định khi k thay đổi.
D. (P) không đi qua một điểm cố định nào khi k thay đổi
C©u 3 : Cho mặt cầu (𝑆): 𝑥2 + 𝑦2 + 𝑧2 − 2𝑥 − 2𝑧 = 0 và mặt phẳng (P): 4x+3y+1=0. Tìm mệnh đề
đúng trong các mệnh đề sau:
A. (P) đi qua tâm của (S)
B. (P) cắt (S) theo một đường tròn
C. (S) không có điểm chung với (P)
D. (S) tiếp xúc với (P)
C©u 4 : Trong không gian Oxyz, cho ba vectơ a   1
 ,1,0;b  (1,1,0);c  1,1,  1 . Cho hình hộp
OABC.O’A’B’C” thỏa mãn điều kiện OA  , a OB  ,
b OC c . Thể tích của hình hộp nói trên bằng bao nhiêu? 2 1 A. 6 B. 2 C. D. 3 3
C©u 5 : Cho hình hộp ABCDA' B 'C'D' .Hãy xác định 3 vecto nào đồng phẳng:
A. AA', BB ',CC ' B. A , B A , D AA' C. A ,
D A' B ',CC '
D. BB ', AC, DD '
C©u 6 : Trong không gian với hệ trục tọa độ Oxyz cho tọa độ 4 điểm A 2; 1;1 ; B 1;0;0 ; C 3;1;0
và D 0;2;1 . Cho các mệnh đề sau : (1) Độ dài AB 2 .
(2) Tam giác BCD vuông tại B 1
(3) Thể tích của tứ diện A.BCD bằng 6
Các mệnh đề đúng là : A. (1) ; (2) B. (3) C. (1) ; (3) D. (2)
C©u 7 : Trong không gian Oxyz,cho 2 đường thẳng d ;d và mặt phẳng P 1 2 x 1 y z x 1 y 1 z 1 d :   , d :  
P : 2x  3y  2z  4  0 .Viết phương trình đường 1 2 1  1 1  2 1  2
thẳng  nằm trong  P và cắt d ,và đồng thời vuông với d 1 2 x y  2 z  2 x  3 y  2 z  2 A.   B.   1 2  2 1 2  2  x  2 y  2 z  2 x  3 x  2 z  2 C.   D.   3 2  2 2 2 1
C©u 8 : Trong không gian Oxyz, xác định các cặp giá trị (l, m) để các cặp mặt phẳng sau đây song
song với nhau: 2x ly  3z  5  0;mx  6y  6z  2  0 A. 3, 4 B.  4  ,3 C. 4; 3   D. 4,3 C©u 9 : x 1 y z 1
Trong không gian Oxyz ,cho điểm A1, 1  ,  1 , đường thẳng  :   ,mặt phẳng 2 1 1 
P:2xy 2z 1 0 .Viết phương trình mặt phẳng Q chứa  và khoảng cách từ A đến Q lớn nhất
A. 2x y  3z 1  0
B. 2x y  3z 1  0
C. 2x y  3z  2  0
D. 2x y  3z  3  0
C©u 10 : Trong không gian Oxyz cho hình lập phương ABCD.A’B’C’D’ với A(0 ; 0; 0), B(1; 0 ;
0), D(0; 1; 0), A’(0; 0; 1). Gọi M và N lần lượt là trung điểm của các cạnh AB và CD.
Tính khoảng cách giữa hai đường thẳng A’C và MN. 1 1 1 1 A. B. C. D. 2 2 2 2 2
C©u 11 : Trong không gian với hệ trục tọa độ Oxyz cho tọa độ cho mặt cầu 2 2 2 S : x 2 y z
9 và mặt phẳng P :x y z 1
0 . Biết (P) cắt (S) theo một
đường tròn, bán kính của đường tròn là : A. 1 B. 3 C. 3 D. 6
C©u 12 : Trong không gian Oxyz, gọi (P) là mặt phẳng cắt ba trục tọa độ tại ba điểm 2
A8,0,0; B0, 2
 ,0;C0,0,4 . Phương trình của mặt phẳng (P) là: x y z A.   1
x y z   4 1  B. 4 2 8 0 2 x y z C.    0
x y z  8 2  D. 4 2 0 4
C©u 13 : Trong không gian với hệ trục tọa độ Oxyz cho tọa độ điểm M 1;1;0 và đường thẳng x y 3 z 1 :
. Phương trình mặt phẳng chứa M và là: 1 2 1 4x y 2z 5 0 A. x 3y z 2 0 B. C. x 2y 3 0 D. 2x y 3 0 C©u 14 : x 1 y  2 z
Cho hai điểm A(1; 4; 2), B(1; 2; 4) và đường thẳng  :   . Điểm M 1  1 2
mà MA2 + MB2 nhỏ nhất có tọa độ là: A. 1;0; 4   B. 1;0;4 C.  1  ;0;4 D. 0; 1  ;4
C©u 15 : Trong không gian với hệ trục tọa độ Oxyz cho hình bình hành ABCD với A 0;1; 2 ; B
1;0;0 ; C 0;3;1 . Tọa độ đỉnh D là: A. D 1;4;1 B. D 2; 1;3 C. D 2;1;3 D. D 1;4; 1
C©u 16 : Cho điểm M (1, 2,3) .Gọi , A ,
B C lần lượt là hình chiếu của M trên các trục O ,
x Oy,Oz .Viết
mặt phẳng  ABC
A. 6x  3y  2z  6  0
B. 6x  3y  2z  6  0
C. 6x  3y  2z  3  0
D. 6x  3y  2z  3  0
C©u 17 : Trong không gian Oxyz,cho 2 đường thẳng d ;d và mặt phẳng P 1 2 x 1 y z x 1 y 1 z 1 d :   , d :  
P : 2x  3y  2z  4  0 .Viết phương trình đường 1 2 1  1 1  2 1  2
thẳng  nằm trong  P và cắt d , d 1 2 x  2 y  3 z 1 x  3 y  2 z  2 A.   B.   3 2  2 6  2 3  x 1 y  2 z  2 x  3 y  2 z  2 C.   D.   3 2 3 6 2 3
C©u 18 : Cho mặt phẳng (𝛼): 3𝑥 − 2𝑦 − 𝑧 + 5 = 0 và đường thẳng 𝑑: 𝑥−1 = 𝑦−7 = 𝑧−3. Gọi (𝛽) là 2 1 4 3
mặt phẳng chứa d và song song với (𝛼). Khoảng cách giữa (𝛼) và (𝛽) là: 9 3 9 3 A. D. 14 B. 14 C. √14 √14
C©u 19 : Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;4;1), B(–1;1;3) và mặt phẳng
(P): x – 3y  2z – 5  0 . Viết phương trình mặt phẳng (Q) đi qua hai điểm A, B và
vuông góc với mặt phẳng (P).
A. 10x  4y  z  5  0
B. 10x  4y  z 11  0
C. 10x  4y  z 19  0 D. Đáp án khác
C©u 20 : Trong không gian với hệ tọa độ Oxyz cho ba điểm A(2; 0; 1), B(1; 0; 0)c C(1; 1; 1) và
mặt phẳng (P): x + y + z  2 = 0. Phương trình mặt cầu đi qua ba điểm A, B, C và có
tâm thuộc mặt phẳng (P) có dạng là: A. 2 2 2
x  y  z  x  2z 1  0 B. 2 2 2
x  y  z  x  2y 1  0 C. 2 2 2
x  y  z  2x  2y 1  0 D. 2 2 2
x  y  z  2x  2z 1  0 C©u 21 : Cho mặt cầu 2 2 2
(S) : (x1)  (y 2)  (z 3)  25 và mặt phẳng  : 2x  y  2z  m  0 . Tìm m
để α và (S) không có điểm chung m  9  hoặc m  9  hoặc A. 9   m  21 B. 9   m  21 C. D. m  21 m  21
C©u 22 : Trong không gian với hệ trục tọa độ Oxyz cho hai mặt phẳng P :2x y z 3 0 ; Q :x y z
0 . (S) là mặt cầu có tâm thuộc (P) và tiếp xúc với (Q) tại điểm H 1; 1;0 .
Phương trình của (S) là : 2 2 2 2 A. 2 S : x 2 y z 1 1 B. 2 S : x 1 y 1 z 3 2 2 2 2 C. 2 S : x 1 y 2 z 1 D. 2 S : x 2 y z 1 3
C©u 23 : Phương trình mặt phẳng đi qua 2 điểm A1; 1  ;5, B0;0;  1 và song song với Oy là:
A. 4x z 1  0
B. 4y z 1  0
C. 4x y 1  0
D. x  4z 1  0
C©u 24 : Phương trình của 2 mặt phẳng tiếp xúc với mặt cầu: S  2 2 2
: x y z  6x  4y  2z 11  0 và
song song với mặt phẳng   : 4x  3z 17  0 là:
4x  3z  40  0
4x  3z 10  0
4x  3z  40  0
4x  3z 10  0 A. và B. và 4
4x  3y  20  0
4x  3z  5  0
4x  3y  40  0
4x  3y 10  0 C. và D. và
C©u 25 : Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng P :x 2y z 5 0 và đường x 3 y z 1 thẳng d :
tọa độ giao điểm của (P) và d là : 2 1 1 A. 3;1;0 B. 0;2; 1 C. 1;1; 2 D. 5; 1;0 C©u 26 :    Trong không gian cho đườ x 3 y 1 z 1 ng thẳng d :  
. và mặt phẳng (P) : x  z  4  0 . 3 1 1 
Hình chiếu vuông góc của d trên (P) có phương trình: x  3  t x  3  t x  3  3t x  3  t     A. y  1 t B. y  1 C. y  1 t D. y  1 2t     z  1   t  z  1   t  z  1   t  z  1   t 
C©u 27 : Trong không gian với hệ tọa độ Oxyz, cho điểm I(1; 2
 ;3) . Viết phương trình mặt cầu
tâm I và tiếp xúc với trục Oy. 2 2 2 2 2 2
A. (x 1)  (y  2)  (z  3)  9
B. (x 1)  (y  2)  (z  3)  16 2 2 2 C. x 2   y 2   z 2 ( 1) ( 2) ( 3) 10
D. (x 1)  (y  2)  (z  3)  8
C©u 28 : Trong không gian với hệ tọa độ Oxyz , cho hai điểm A(3;5;4) , B(3;1;4) . Tìm tọa độ
điểm C thuộc mặt phẳng (P) : x  y  z1  0 sao cho tam giác ABC cân tại C và có diện tích bằng 2 17 . C(4; 3; 0) và C(7; A. Đáp án khác B. C(7; 3; 3) C. D. C(4; 3; 0) 3; 3)
C©u 29 : Toạ độ điểm M’ là hình chiếu vuông góc của điểm M(2; 0; 1) trên 𝑑: 𝑥−1 = 𝑦 = 𝑧−2 là: 1 2 1 A. M’(-1; -4; 0) B. M’ (2; 2; 3) C. M’(1; 0; 2) D. M’(0; -2; 1)
C©u 30 : Trong không gian Oxyz, cho mặt phẳng (P)đi qua hai điểm A(4,-1,1), B(3,1,-1) và song song
với trục Ox. Phương trình nào sau đây là phương trình của mặt phẳng (P):
A. x y  0
B. y z  0
C. x z  0
D. x y z  0
C©u 31 : Trong không gian với hệ trục tọa độ Oxyz cho các vectơ a 1;1 2 ; b 3;0; 1 và
điểm A 0;2;1 tọa độ điểm M thỏa mãn: AM 2a b là : A. M 5;1;2 B. M 3; 2;1 C. M 1;4; 2 D. M 5;4; 2 5 C©u 32 : Cho u(2; 1  ;1), v(m;3; 1
 ), w(1;2;1). Ba vectơ đồng phẳng khi giá trị của m là: 7 8 A. 8  B. 4 C. D.  3 3 C©u 33 : 𝑥 = 5 − 𝑡
Góc giữa đường thẳng 𝑑: { 𝑦 = 6 và mp (𝑃): 𝑦 − 𝑧 + 1 = 0 là: 𝑧 = 2 + 𝑡 A. 600 B. 450 C. 300 D. 900
C©u 34 : Trong không gian cho hai đường thẳng: x 1 t  x 1 y z  2 d : y  2 ; d :   1 2 2 1 3 z  3 t 
Phương trình của đường thẳng d đi qua O(0;0;0) và vuông góc với cả d và d là: 1 2 x  t x  t x  t x  1     A. y  5  t B. y  t C. y  5t D. y  5  t     z  t  z  t  z  t  z  1  C©u 35 : Cho 2 điểm ( A 1, 2, 1  ), ( B 2
 ,1,3) .Tìm điểm M thuộc Ox sao cho tam giác AMB có diện tích nhỏ nhất 1  1 A. M ( 7  ,0,0) B. M ( , 0, 0) C. M ( , 0, 0) D. M (3,0,0) 7 3
C©u 36 : Trong không gian Oxyz, cho bốn điểm A1,1, 
1 ; B1,3,5;C 1,1,4; D2,3,2 . Gọi I, J lần
lượt là trung điểm của AB và CD. Câu nào sau đây đúng? AB và CD có A. CD  IJ B. IJ  ABC AB  chung trung điể C.   D. IJ m
C©u 37 : Trong không gian cho hai đường thẳng: x 1 t  x 1 y z  2 d : y  2 ; d :   1 2 2 1 3 z  3 t 
Mặt phẳng (P) chứa d và song song với d . Chọn câu đúng: 1 2
A. (P) : x  5y  z  6  0
B. (P) : x  5y  z 1  0
C. (P) : x  z  2  0
D. Có vô số đường thẳng d thỏa mãn. 6
C©u 38 : Trong không gian với hệ trục tọa độ Oxyz cho tọa độ cho mặt cầu 2 2 2 S : x 2 y z
9 và mặt phẳng P :x y z m
0 , m là tham số. Biết (P) cắt (S)
theo một đường tròn có bán kính r
6 . Giá trị của tham số m là : A. m 3;m 4 B. m 3;m 5 C. m 1;m 4 D. m 1;m 5
C©u 39 : Trong không gian với hệ toạ độ Oxyz, cho điểm A(1; –2; 3) và đường thẳng d có x 1 y 2 z 3 phương trình   2 1
1 . Tính khoảng cách từ điểm A đến đường thẳng d.  A. 7 2 B. 6 2 C. 5 2 D. 4 2
C©u 40 : Cho điểm H(2; 1; 3). Gọi K là điểm đối xứng của H qua gốc tọa độ O. Khi đó độ
dài đoạn thẳng HK bằng: A. 56 B. 12 C. 12 D. 56
C©u 41 : Cho (S) là mặt cầu tâm I(1;2;3) và tiếp xúc với mặt phẳng (P) : x  2y  2z  3  0 . Bán kính của (S) là: 2 A. 2 B. 6 C. 1 D. 3
C©u 42 : Cho hai mặt phẳng   : 2x my  3z  6  m  0,  : m  3 x  2y  5m   1 z 10  0 ,
2 mặt phẳng song song với nhau khi: A. Không có m B. m  6 C. m  1 D. m  0 C©u 43 : Cho mặt cầu 2 2 2
(S) : x  y  z  2x  2y  2z 1  0 . Đường thẳng d đi qua O(0;0;0) cắt (S) theo
một dây cung có độ dài bằng 2. Chọn khẳng định đúng:
A. d nằm trên một mặt nón. x y z B. d :   1  1 1 
C. d nằm trên một mặt trụ.
D. Không tồn tại đường thẳng d.
C©u 44 : Viết phương trình mặt phẳng đi qua OA và vuông góc với mặt phẳng (P) biết A(0;
2; 0) và (P): 2x + 3y  4z  2 = 0 A. 2x  y  0 B. 2x  y  0 C. 2x  z  0 D. 2x  z  0
C©u 45 : Trong không gian Oxyz, cho điểm M(8,-2,4). Gọi A, B, C lần lượt là hình chiếu của M trên
các trục Ox, Oy, Oz. Phương trình mặt phẳng đi qua ba điểm A, B và C là:
A. x  4 y  2z  8  0
B. x  4 y  2z  8  0 7
C. x  4 y  2z  8  0
D. x  4 y  2z  8  0
C©u 46 : Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(4; 5; 6). Viết phương trình
mặt phẳng (P) qua A, cắt các trục tọa độ lần lượt tại I, J, K mà A là trực tâm của tam giác IJK.
A. 2x  3y  z  29  0
B. x  y  z 15  0
C. 4x  5y  6z  77  0 D. Đáp án khác
C©u 47 : Gọi d’ là hình chiếu của 𝑑: 𝑥−5 = 𝑦+2 = 𝑧−4 trên mặt phẳng (P):𝑥 − 𝑦 + √2𝑧 = 0. Góc giữa 1 1 √2 d và d’ là: A. 450 B. 600 C. 300 D. Đáp án khác
C©u 48 : Cho mặt cầu S  : 2 2 2
x y z  2x  4y  64  0 ,các đường thẳng : x 1 y  2 z x 1 y 1 z  2 d :   ,d ':  
.Viết phương trình mặt phẳng  P tiếp xúc với mặt 7 2 2 3 2 1
cầu S  và song song với d, d '
2x y  8z 12  0
2x y  8z  69  0 A. B.
2x y  8z 12  0
2x y  8z  69  0
2x y  8z  6  0
2x y  8z 13  0 C. D.
2x y  8z  6  0
2x y  8z 13  0 C©u 49 : Cho A 1  ;2;  1 , B 1;1; 
1 ,C 0;3;2 .tọa độ của  AB, BC   là: A.  1  ; 2  ;3 B. 1, 2,3 C.  1  ; 2  ; 3   D.  1  ;2; 3  
C©u 50 : Trong không gian với hệ trục tọa độ Oxyz cho tứ diện A.BCD với tọa độ
A 1;0;0 ; B 2;1;1 ; C 0;3; 2 ; D 1;3;0 , thể tích của tứ diện đã cho là: 1 1 A. 1 B. C. D. 6 6 2
C©u 51 : Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(0; 1; 2), B(2; –2; 1), C(–2; 0; 1).
Viết phương trình mặt phẳng (ABC) và tìm điểm M thuộc mặt phẳng (P):
2x  2y z– 3  0 sao cho MA = MB = MC . A. M(2; 1; - 3 ) B. M(0; 1; 1) C. M(2;3; 7  ) D. M(1; 1; - 1)
C©u 52 : Trong không gian Oxyz, đường thẳng d nằm trong mặt phẳng Oxy và cắt cả hai đường thẳng 8 x 1 t x  2  2t  
d : y  2  3t; d : y  3
  2t có phương trình là: 1 2   z  3  t z  1 t   x  4 x  4 x  4 x  4  t     A. y  t B. y  16t C. y  t D. y  11 t     z  0  z  t  z  t  z  0 
C©u 53 : Trong không gian Oxyz, cho ba vectơ a   1
 ,1,0;b  (1,1,0);c  1,1,  1 . Trong các mệnh
đề sau, mệnh đề nào đúng? a, , b c đồng
A. a b c  0 B. b c 6 cos ,  C. . a b  1 D. 3 phẳng. C©u 54 : x  y z
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d 5 7 :   2 2 và điểm  1
M(4;1;6) . Đường thẳng d cắt mặt cầu (S), có tâm M, tại hai điểm A, B sao cho AB  6.
Viết phương trình của mặt cầu (S). 2 2 2 2 2 2
A. (x  4)  (y 1)  (z  6)  12
B. (x  4)  (y 1)  (z  6)  9 2 2 2 C. x 2   y 2   z 2 ( 4) ( 1) (  6) 18
D. (x  4)  (y 1)  (z  6)  16
C©u 55 : Cho hai mặt phẳng (P) : x  2y  z  4  0; (Q) : 2x  y  z  4  0 và điểm M(2;0;1). Phương
trình mặt phẳng (R) qua M và giao tuyến của (P) và (Q) là:
A. 3x  3y  2z 8  0
B. 3x  3y  2z 8  0
C. x  2y  z  4  0
D. x  y  3z 1  0
C©u 56 : Mặt phẳng (P) tiếp xúc với mặt cầu (𝑆): (𝑥 − 1)2 + (𝑦 + 3)2 + (𝑧 − 2)2 = 49 tại điểm
M(7; -1; 5) có phương trình là: A. 3x+y+z-22=0 B. 6x+2y+3z-55=0 C. 6x+2y+3z+55=0 D. 3x+y+z+22=0
C©u 57 : Trong không gian với hệ trục Oxyz, cho mặt cầu (S): x2  y2  z2 – 2x  4y 2z– 3  0 .
Viết phương trình mặt phẳng (P) chứa trục Ox và cắt mặt cầu (S) theo một đường tròn có bán kính r  3. A. y – 2z -1 = 0 B. y – 2z - 2 = 0
C. y – 2z = 0. D. y – 2z + 1 = 0
C©u 58 : Cho 2 đường thẳng 𝑑1: 𝑥−1 = 𝑦−2 = 𝑧−3 ; 𝑑
= 𝑦−5 = 𝑧−7. Trong các mệnh đề sau, 2 3 4 2 : 𝑥−3 4 6 8 mệnh đề nào đúng: 9
A. 𝑑1 và 𝑑2 chéo nhau
B. 𝑑1 song song với 𝑑2 C. 𝑑1 trùng 𝑑2
D. 𝑑1 vuông góc với 𝑑2
C©u 59 : Cho hai mặt phẳng  : x  y 2  z  4  0 và : x  y 2  z  0. Tìm góc hợp bởi α và β A. 0 30 B. 0 45 C. 0 90 D. 0 60
C©u 60 : Phương trình mặt phẳng đi qua 3 điểm A1;1;0, B 3  ;0;4,C1; 1  ;2 là:
A. 3x  4y  4z 1  0
B. 4x  3y  4z 1  0
C. 4x  3y  4z 1  0
D. 3x  4y  4z 1  0 C©u 61 :   Trong không gian cho đườ x 2 y 1 z ng thẳng d :  
. và mặt phẳng (P) : x  y  z  3  0 . 2 1 1 
Khẳng định nào sau đây đúng:
A. Đường thẳng d nằm trong mặt phẳng (P).
B. Đường thẳng d cắt mặt phẳng (P).
C. Đường thẳng d song song với mặt phẳng
D. Đường thẳng d vuông góc với mặt phẳng (P). (P). C©u 62 : 𝑥 = 1 + 𝑡
Cho đường thẳng 𝑑: { 𝑦 = 2 − 𝑡 và mặt phẳng (𝑃): 𝑥 + 3𝑦 + 𝑧 + 1 = 0. Trong các mệnh 𝑧 = 1 + 2𝑡
đề sau, mệnh đề nào đúng: d vuông góc với A. d nằm trong (P) B. d cắt (P) C. d // (P) D. (P) C©u 63 : x 1 t x  2 y  2 z  3  Cho hai đường thẳng d :  
; d : y  1 2t và điểm A(1; 2; 3). Đường 1 2 2 1  1 z  1   t 
thẳng  đi qua A, vuông góc với d1 và cắt d2 có phương trình là x 1 y  2 z  3 x 1 y  2 z  3 A.   B.   1  3  5  1 3 5 x 1 y  2 z  3 x 1 y  2 z  3 C.   D.   1 3 5  1 3  5 
C©u 64 : Trong không gian Oxyz, cho điểm I(2,6,-3) và các mặt phẳng:
: x  2  0; : y 6  0; : z 3 0
Trong các mệnh đề sau, tìm mệnh đề sai: 10   đi qua điểm
A.    B. / /Oz
C.  / /  xOzD. I
C©u 65 : Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(1; 4; 2),B(–1; 2; 4) và đường x 1 y 2 z thẳng  :   2 2   28 1
. Tìm toạ độ điểm M trên  sao cho: MA MB .  1 2 A. M(0; -1; 2) B. M(1; - 2 ; 0 C. M( 1  ;0;4) D. Đáp án khác C©u 66 : 𝑥 = 1 + 𝑡 𝑥 = 2 + 𝑡′
Khoảng cách giữa 2 đường thẳng 𝑑: { 𝑦 = 2𝑡 và 𝑑′: { 𝑦 = 4𝑡′ là: 𝑧 = 2 + 𝑡 𝑧 = 1 + 2𝑡′ √2 A. 2 B. 2 C. √2 D. 4
C©u 67 : Trong không gian với hệ trục tọa độ Oxyz cho tọa độ 4 điểm A 2;0;0 ;B 0;2;0 ; C 0;0;2
và D 2;2;2 , M ; N lần lượt là trung điểm của AB và CD. Tọa độ trung điểm I của MN là: 1 1 A. I ; ;1 B. I 1;1;0 C. I 1; 1;2 D. I 1;1;1 2 2
C©u 68 : Cho điểm M(3; 3; 3). Gọi A, B, C lần lượt là hình chiếu của M trên các trục Ox, Oy,
Oz. Khẳng định nào sau đây đúng?
A. ABC là tam giác vuông tại A
B. ABC là tam giác vuông tại C
C. ABC là tam giác vuông tại B
D. ABC là tam giác đều C©u 69 : Cho A ; x ; y   3 , B 6; 2  ;4,C  3  ;7; 5
  . Giá trị x, y để 3 điểm A, B, C thẳng hàng là: A. x  1  , y  5
B. x 1, y  5  C. x  1  , y  5 
D. x 1, y  5
C©u 70 : Trong không gian với hệ trục tọa độ Oxyz cho tọa độ 4 điểm A 1;0;0 ;B 0;1;0 ; C 0;0;1
và D 1;1;1 , trong các mệnh đề sau mệnh đề nào sai:
A. Bốn điểm A, B, C,D tạo thành một tứ
B. Tam giác ABD là tam giác đều. diện.
C. AB vuông góc với CD.
D. Tam giác BCD là tam giác vuông.
C©u 71 : Trong không gian cho hai đường thẳng: 11 x  1   3t x  2 y 1 z  d :   ; d ' : y  2  t . 3 1 1  z 1 t 
Vị trí tương đối của d và d’ là: A. Cắt nhau. B. Song song. C. Trùng nhau. D. Chéo nhau.
C©u 72 : Trong không gian Oxyz, cho bốn điểm A1,0,0;B0,1,0;C0,0,  1 ; D1,1,  1 . Xác định
tọa độ trọng tâm G của tứ diện ABCD  1 1 1   2 2 2   1 1 1   1 1 1  A. , ,   B. , ,   C. , ,   D. , ,    2 2 2   3 3 3   4 4 4   3 3 3 
C©u 73 : Cho điểm M (1, 2,3) .Gọi , A ,
B C lần lượt là hình chiếu của M trên các trục O ,
x Oy,Oz .Viết
mặt phẳng   song song mặt phẳng  ABC và đi qua M
A. 6x  3y  2z  6  0
B. 6x  3y  2z 18  0
C. 6x  3y  2z  6  0
D. 6x  3y  2z  7  0
C©u 74 : Phương trình mặt trình mặt cầu có đường kính AB với A6;2; 5  , B 4  ;0;7 là: A. 2 2 2
x y z  2x  2y  2z  59  0        B. 2 2 2 x y z 2x 2y 2z 59 0 C. 2 2 2
x y z  2x  2y  2z  59  0 D. 2 2 2
x y z  2x  2y  2z  59  0
C©u 75 : Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng P :x y z 3 0 và điểm
M 1;0; 1 . Tọa độ điểm M’ đối xứng với M qua (P) là : A. M ' 1;4; 1 B. M ' 2;0;1 C. M ' 4;2; 2 D. M ' 3;2;1
C©u 76 : Viết phương trình mặt cầu S  có tâm I thuộc mặt phẳng Oyz và đi qua các điểm A0,0, 4, (
B 2,1,3),C 0, 2,6 2 2 2 2  5   5   7  13
A. x  2 2  y   z  26   B. 2 x y   z        2   2   2  2 2 2 2 2 2 2  1   5 
C. x  3   y  
1   z  2  9 D. x   1  y   z  13      2   2  C©u 77 : x 1 y z 1
Trong không gian Oxyz ,đường thẳng  :  
,mặt phẳng P : 2x y  2z 1  0 2 1 1 
.Viết phương trình mặt phẳng Q chứa  và tạo với  P nhỏ nhất 12
A. 10x  7y 13z  2  0
B. 10x  7y 13z  3  0
C. 10  7 y 13z 1  0
D. 10x  7y 13z  3  0
C©u 78 : Mặt cầu S 2 2 2
: 3x  3y  3z  6x  3y 15z  2  0 có tâm I và bán kính R là:  1 5  7 6  3 15  7 6 A. I 1; ;  , R    B. I 3  ; ; , R     2 2  6  2 2  2  3 15  7 6  1 5  7 6 C. I 3; ;  , R    D. I 1  ; ; , R     2 2  2  2 2  6
C©u 79 : Cho A1;0;0, B0;2;0,C 2;1;3.Diện tích tam giác ABC là 3 6 6 3 A. C. D. 3 6 2 B. 2 2
C©u 80 : Trong không gian với hệ tọa độ Oxyz, cho điểm A(2; 1
 ;1) . Viết phương trình mặt
phẳng (P) đi qua điểm A và cách gốc tọa độ O một khoảng lớn nhất.
A. 2x  y  z 1  0
B. 2x  y  z  5  0
C. 2x  y  z  6  0
D. 2x  y  z  3  0
C©u 81 : Viết phương trình mặt phẳng   đi qua gốc tọa độ O và vuông góc với hai mặt phẳng ( )
P : x  2y  3z  4  0 , Q : 2x y z  0
A. 5x  7 y  3z  0
B. 5x  7 y  3z  0
C. 5x  7 y  3z  0
D. 5x  7 y  3z  0 13 ĐÁP ÁN 01 { | ) ~ 28 { | ) ~ 55 ) | } ~ 02 ) | } ~ 29 { | ) ~ 56 { ) } ~ 03 { ) } ~ 30 { ) } ~ 57 { | ) ~ 04 { ) } ~ 31 { | } ) 58 { | ) ~ 05 ) | } ~ 32 { | } ) 59 { | } ) 06 { | } ) 33 { | ) ~ 60 ) | } ~ 07 { ) } ~ 34 ) | } ~ 61 ) | } ~ 08 { ) } ~ 35 { ) } ~ 62 { | ) ~ 09 { ) } ~ 36 { ) } ~ 63 { | } ) 10 { | } ) 37 ) | } ~ 64 { ) } ~ 11 { | } ) 38 { | } ) 65 { | ) ~ 12 { ) } ~ 39 { | ) ~ 66 { | ) ~ 13 { | } ) 40 { | } ) 67 { | } ) 14 { | } ) 41 ) | } ~ 68 { | } ) 15 { | } ) 42 ) | } ~ 69 ) | } ~ 16 ) | } ~ 43 ) | } ~ 70 { | } ) 17 { ) } ~ 44 { | } ) 71 ) | } ~ 18 { | ) ~ 45 { ) } ~ 72 { ) } ~ 19 { | ) ~ 46 { | ) ~ 73 { ) } ~ 20 { | } ) 47 { | ) ~ 74 ) | } ~ 21 { | } ) 48 { ) } ~ 75 { | } ) 22 { | } ) 49 ) | } ~ 76 { ) } ~ 23 ) | } ~ 50 { | ) ~ 77 { ) } ~ 24 ) | } ~ 51 { | ) ~ 78 ) | } ~ 25 { | ) ~ 52 ) | } ~ 79 ) | } ~ 26 ) | } ~ 53 { ) } ~ 80 { | ) ~ 27 { | ) ~ 54 { | ) ~ 81 { ) } ~ 14 GROUP NHÓM TOÁN
NGÂN HÀNG ĐỀ THI TRẮC NGHIỆM
CHUYÊN ĐỀ : PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN ĐỀ 004
C©u 1 : Cho A 0;0;1 ,B 3;0;0 ,C 0;2;0 . Khi đó phương trình mặt phẳng (ABC) là : x y z x y z x y z x y z A. 1 B. 1 C. 1 D. 1 1 2 3 2 3 1 3 2 1 1 3 2
C©u 2 : Cho đường thẳng qua A 1;0; 1 và có véc tơ chỉ phương u 2;4;6 . Phương trình
tham số của đường thẳng là : x 1 2t x 2 t x 1 t x 1 t A. y 4t B. y 4 C. y 2t D. y 2t z 1 6t z 6 t z 1 3t z 1 3t
C©u 3 : Gọi M, N lần lượt là trung điểm của AB và CD. Tọa độ điểm G là trung điểm của MN là:  1 1 1   1 1 1   2 2 2   1 1 1  A. G ; ;  G ; ; G ; ; G ; ;  B. C. D.  2 2 2   4 4 4   3 3 3   3 3 3
C©u 4 : Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
(P): x y  4z  4  0 và mặt cầu (S): 2 2 2
x y z  4x 10z  4  0
Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đ7ờng tròn có bán kính bằng: A. 3 B. 7 C. 2 D. 4
C©u 5 : Trong không gian với hệ tọa độ Oxyz, cho 2 đường thẳng x 1 y 1 z 1 x  2 y 1 z m     1 d : ; d2 : . 2 3 2 2 1 3 Để 1
d cắt d2 thì m bằng 3 7 1 5 A. B. C. D. 4 4 4 4 1 C©u 6 : x 1 y 3 z Cho đường thẳng : và P : x 2y 2z 1 0 mặt phẳng chứa 2 3 2
và vuông góc với P có phương trình là : A. 2x 2y z 8 0 B. 2x 2y z 8 0 C. 2x 2y z 8 0 D. 2x 2y z 8 0
C©u 7 : Cho hai mặt phẳng (P): x+y-z+5=0 và (Q): 2x-z=0. Nhận xét nào sau đây là đúng x y  5 z
A. Mặt phẳng (P) và mặt phẳng (Q) có giao tuyến là   1 1 2 x y  5 z
B. Mặt phẳng (P) và mặt phẳng (Q) có giao tuyến là   1 1 2
C. Mặt phẳng (P) song song với mặt phẳng (Q)
D. Mặt phẳng (P) vuông góc với mặt phẳng (Q) C©u 8 : x 1 y 1 z  5 x 1 y 1 z 1
Vị trí tương đối của hai đường thẳng  :   ,  :   là: 1 2 2 3 1 4 3 5
A. Song song với nhau.
B. Cắt nhau tại điểm M (3; 2;6)
C. Cắt nhau tại điểm M (3; 2;  6) D. Chéo nhau. C©u 9 : x  1   2t    Cho hai đườ x y 1 z 2 ng thẳng  :  
,  : y  1 t
. Phương trình đường thẳng  1 2 2 1  1 z  3 
vuông góc với mặt phẳng (P): 7x y  4z  0 và cắt hai đường thẳng  và  là: 1 2 x  5   7tx  5 y 1 z  3
A.  : y  1 t B.    7 1 4  z  3  4t  x  5   7tx  5 y 1 z  3
C.  : y  1   t D.  :   .  6 1 4 z  3  4t
C©u 10 : Cho mặt phẳng : 2x y  3z 1  0 và đường thẳng d có phương trình tham số:
x  3  t
y  2  2t . Trong các mệnh đề sau, mệnh đề nào đúng? z 1 2
A. d    B. d cắt ( )
C. d   
D. d // 
C©u 11 : Gọi (S) là mặt cầu tâm I(2 ; 1 ; -1) và tiếp xúc với mặt phẳng ( ) có phương trình: 2x
– 2y – z + 3 = 0. Bán kính của (S) bằng bao nhiêu ? 2 2 4 A. B. C. 2 D. 3 9 3 C©u 12 : x  2 y  4 z  4
Đường thẳng nào sau đây song song với (d):   1 2 3  x 1 y  2 z 1 x  2 y  4 z  4 A.   B.   1 2 3  1 1 1 x 1 y  2 z 1 x 1 y  2 z 1 C.   D.   1  2  3 1  2  3
C©u 13 : Trong không gian Oxyz, cho các điểm M 1;0;0 ; N 0;1;0; C 0;0;  1 . Khi đó thể tích tứ diện OMNP bằng: 1 1 A. 1 B. C. . D. 3 2 6 C©u 14 : x y 1 z  2
Trong không gian với hệ toạ độ Oxyz, cho đường thẳng d :   và điểm 2 1 1 
A(1;-1;2). Tọa độ hình chiếu vuông góc H của A lên d là: A. H(0;- 1;- 2) B. H(0; 1; 2) C. H(0; 1;- 2) D. H(0;- 1; 2)
C©u 15 : Cho mặt phẳng ( )
P :2x  2y z  4  0 và mặt cầu 2 2 2
(S) : x y z  2x  4y  6z 11  0 . Giả
sử (P) cắt (S) theo thiết diện là đường tròn (C). Xác định tọa độ tâm và tính bán kính đường tròn (C).
A. Tâm I (3;0; 2), r  3
B. Tâm I (3;0; 2), r  4
C. Tâm I (3;0; 2), r  5
D. Tất cả 3 đáp án trên đều sai.
C©u 16 : Gọi ( ) là mặt phẳng cắt ba trục tọa độ tại ba điểm M(8; 0; 0), N(0; -2; 0), P(0; 0; 4).
Phương trình của ( ) là: x y z x y z A.      4 1  B. 0 2 8 2  4
C. x – 4y + 2z – 8 = 0 D. x – 4y + 2z = 0
C©u 17 : Mặt phẳng (P) chứa trục Oy và điểm A 1; 1;1 là : 3 A. x z 0 B. x y 0 C. x z 0 D. x y 0
C©u 18 : Phương trình mặt cầu tâm I(1; 2; 3) và bán kính R=3 là: A. 2 2 2
x y z  2x  4y  6z  5  0
B. B và C đều đúng. C. 2 2 2
(x 1)  ( y  2)  (z  3)  9 D. 2 2 2
(x 1)  ( y  2)  (z  3)  3
C©u 19 : Mặt phẳng qua 3 điểm A(1; 0; 0), B(0; -2; 0), C(0; 0; 3) có phương trình:
6x  3y  2z  6  0
A. x  2y  3z 1  0 B.
C. x  2y  3z 1  0 D. Đáp án khác
C©u 20 : Cho bốn điểm A(-1,1,1), B(5,1,-1) C(2,5,2) , D(0,-3,1). Nhận xét nào sau đây là đúng
A. A,B,C,D là bốn đỉnh của một tứ diện
B. Ba điểm A, B, C thẳng hàng
C. Cả A và B đều đúng
D. A,B,C,D là hình thang
C©u 21 : Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x  2y  2z  3  0 và 2
điểm A(4; -4; 4), B(4; -2 ;6), C(3 ; -5; 7).
Mặt cầu (S) tiếp xúc với (P), đi qua điểm C và có tâm nằm trên đường thẳng AB.
Tâm I của mặt cầu (S) có tọa độ là: A. (-4; -3; 5) B. (4; -3; 5) C. (4; 3; 5) D. (4:3; -5)
C©u 22 : Cho điểm A(0,0,3) , B(-1,-2,1) , C(-1,0,2)
Có bao nhiêu nhận xét đúng trong số các nhận xét sau
1. Ba điểm A,B,C thẳng hàng
2. Tồn tại duy nhất một mặt phẳng đi qua ba điểm ABC
3. Tồn tại vô số mặt phẳng đi qua ba điểm A,B,C
4. A,B,C tạo thành ba đỉnh một tam giác 3 5
5. Độ dài chân đường cao kẻ từ A là 5
6. Phương trình mặt phẳng (A,B,C) là 2x+y-2z+6=0
7. Mặt phẳng (ABC) có vecto pháp tuyến là (2,1,-2) A. 5 B. 2 C. 4 D. 3 4
C©u 23 : Mặt cầu có phương trình 2 2 2
x y z  2x y 1  0 có tọa độ tâm I và bán kính r là:  1  1  1   1  1  1 
A. I 1; ;0 ; r    B. I 1  ; ;0 , r  1   C. I 1  ; ;0 ;r   
D. I 1; ;0 ,r 1    2  2  2   2  2  2 
C©u 24 : Điểm nào nằm trên đường thẳng (d) là giao tuyến của x + 2y – z +3 = 0 và 2x – 3y – 2z + 6 = 0. A. (0; 1; 5) B. (-1; -1; 0) C. (1; 2; 1) D. ( 1; 0; 4) C©u 25 :
2x y z  0
Đường thẳng có phương trình: 
có một vectơ pháp tuyến là: x z  0 A. u 2; 1  ;  1 B. u 1; 1  ;0 C. u 1;3;  1
D. u 1;0;  1
C©u 26 : Trong không gian Oxyz, cho ba điểm A1;0;0; B1;1;0; C 0;1 
;1 . Khi đó tọa độ điểm
D để ABCD là hình bình hành: A. D 1;1;  1 B. D0;0;  1
C. D 0; 2;  1 D. D2;0;0
C©u 27 : Trong không gian với hệ toạ độ Oxyz, cho tam giác ABC có tọa độ A(-1;1;-1), B(2;0;-
1), C(3;1;-2). Độ dài đường cao kẻ từ B của tam giác ABC bằng: 26 26 2 26 26 A. B. C. D. 3 17 17 3
C©u 28 : Cho tam giác ABC với A(1;-4;2), B(-3;2;1), C(3;-1;4), trọng tâm G của tam giác ABC có tọa độ bằng:  1 7   1 7   1 1 7  A. (3; -9; 21) B. ;  ;  2  C. ;  ;  1      2 2   3 3  D. ; ;  4 4 4 
C©u 29 : Phương trình đường thẳng qua A( 1; 2; -1) và vuông góc với mặt phẳng (P): x + 2y – 3z +1 = 0 là: x 1 y  2 z 1 x 1 y  2 z 1 A.   B.   2 3 1 1 2 3  x 1 y  2 z 1 x  2 y  4 z  4 C.   D.   1 2 3 1 2 3  C©u 30 : x 8 y 5 z Cho hai đường thẳng :
và A 3; 2;5 . Tọa độ hình chiếu của A 4 2 1 trên là ? 5 A. 4; 1; 3 B. 4; 1;3 C. 4; 1;3 D. 4;1; 3
C©u 31 : Phương trình chính tắc của đường thẳng đi qua điểm M(2 ; 0 ; -1) và có vectơ chỉ
phương a  (4 ;-6 ; 2) là x  2 y z  1 x  2 y z  1 A.   B.   4 6  2 2 3  1 x  4 y  6 z  2 x  2 y z  1 C.   D.   2 3  1 2 3  1 C©u 32 :
x y z
Tọa độ giao điểm I của đường thẳng d  3 
và mặt phẳng   2x 3z 1 0 : x y  0
A. I 1;1;0 B. 2;1;0 C. I.1;1;  1
D. I.1;2;0
C©u 33 : Phương trình mặt phẳng đi qua M(1; 3; -3) và vuông góc đường thẳng d: x 1 y z 1   là: 2 1  3 x 1 y  3 z  3 A.  
B. 2x y  3z 10  0 2 1  3
C. Đáp án A và B đều đúng.
D. x  3y  3z 10  0
C©u 34 : Mặt phẳng đi qua D2;0;0 vuông góc với trục Oy có phương trình là: A. z = 0 B. y = 2. C. y = 0 D. z = 2
C©u 35 : Khoảng cách từ điểm A(1;2;3) đến mặt phẳng (P): 2x – y +2z +6=0 bằng: A. 5 B. 2 C. 3 D. 4
C©u 36 : Trong không gian oxyz cho hai điểm A(5,3,-4) và điểm B(1,3,4) Tìm tọa độ điểm
C (Oxy) sao cho tam giác ABC cân tại C và có diện tích bằng 8 5 . Chọn câu trả lời đúng nhất
A. C(3,7,0) và C(3,-1,0)
B. C(-3-7,0) và C(-3,-1,0)
C. C(3,7,0) và C(3,1,0)
D. C(-3,-7,0) và C(3,-1,0)
C©u 37 : Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có A(3; 1; 5), B(2; 6; 1), C(4;
0 ; 5) và D(6; 0; 4). Phương trình mặt cầu (S) ngoại tiếp tứ diện ABCD là: 6 A. 2 2 2
(x 1)  ( y 1)  (z 1)  25 B. 2 2 2
(x 1)  ( y 1)  (z 1)  5 C. 2 2 2
(x 1)  ( y 1)  (z 1)  25 D. 2 2 2
(x 1)  ( y 1)  (z 1)  5
C©u 38 : Gọi   là mặt phẳng cắt 3 trục tọa độ tại 3 điểm M(8; 0; 0), N(0; -2; 0), P(0; 0; 4).
Phương trình của   là: x – 4y + 2z – 8 = x y z x y z A. B.    0 C.    0 D. x – 4y + 2z = 0 0 4 1 2 8  2 4 C©u 39 : x 1 y 2 z Cho A 1;4;2 ,B 1;2;4 và : Điểm M mà 1 1 2 2 2 MA
MB nhỏ nhất có tọa độ là : A. 1;0;4 B. 0; 1;4 C. 1;0;4 D. 1;0; 4 C©u 40 :
: x y  2z 1  0
Cho mặt phẳng ( ) : x y z  2  0 . Trong các mệnh đề sau, mệnh đề nào sai ?
( ) : x y  5  0
A.     
B.     
C.     
D.      C©u 41 : x 1 y  2 z 1
Cho điểm I(3,4,0) và đường thẳng  :  
Viết phương trình mặt cầu (S) 1 1 4 
có tâm I và cắt  tại hai điểm A,B sao cho diện tích tam giác IAB bằng 12 2 2 2
(x  3)  ( y  4)  z  5 A. 2 2 2
(x  3)  ( y  4)  z  25 B. 2 2 2
(x  3)  ( y  4)  z  25 C. 2 2 2
(x  3)  ( y  4)  z  5 D.
C©u 42 : Trong không gian với hệ tọa độ Oxyz, cho điểm H(2;1;1). Mặt phẳng (P) qua H , cắt
các trục tọa độ tại A,B,C và H là trực tâm của tam giác ABC. Phương trình mặt phẳng (P) là: x y z x y z A.   1  0 B.
  1  0 C. 2x y z 1
D. 2x y x  6  0 3 6 6 3 6 6
C©u 43 : Mặt phẳng qua A( 1; -2; -5) và song song với mặt phẳng (P): x y 1 0 cách (P) một khoảng có độ dài là: 7 A. 2 B. 2 C. 4 D. 2 2
C©u 44 : Trong không gian Oxyz cho A 1;1;3 ,B 1;3;2 ,C
1;2;3 Khoảng cách từ gốc tọa độ
O tới mặt phẳng (ABC) bằng : 3 3 A. 3 B. C. 3 D. 2 2
C©u 45 : Cho (P): x + 2y + 2z – 1 = 0 cắt mặt cầu (S) theo một đường tròn giao tuyến có bán
kính r = 1/3,biết tâm của (S) là I(1; 2; 2). Khi đó, bán kính mặt cầu (S) là: 7  1 2 2 A. B. 1 2 2 C. D. 1 3 3 3
C©u 46 : Mặt phẳng (P) song song và cách đều hai mặt phẳng
() :2x y  4z  5  0, ( ) :2x y  4z  7  0 có phương trình là:
2x y  4z 12  0 A. Đáp án khác.
B. 2x y  4z  6  0 C. 2x y  4z  0 D.
C©u 47 : Khoảng cách từ A( 1; -2; 3) đến đường thẳng (d) qua B( 1; 2; -1) và vuông góc với
mặt phẳng (P): x + 2y + 3z + 5 = 0 là: 3 3 3 2 3 A. B. C. D. 2 14 14 4 14 14 C©u 48 : x t
Giao điểm của đường thẳng y 1 t và mặt phẳng ( )
P :2x y  3z  5  0  là: z  1 2t  1  2 5 1  4 5
A. M (1;  3; 4) B. M ( ; ; ) C. M (1;3; 4) D. M ( ; ; ) 3 3 3 3 3 3
C©u 49 : Cho A 2; 1;6 ,B
3; 1; 4 ,C 5; 1;0 ,D 1;2;1 thể tích của khối tứ diện ABCD là : 50 40 60 A. B. C. 30 D.
C©u 50 : Tồn tại bao nhiêu mặt phẳng (P) vuông góc với hai mặt phẳng (α): x+y+z+1=0 , (β) :
2x-y+3z-4=0 sao cho khoảng cách từ gốc tọa độ đến mặt phẳng (P) bằng 26 A. 2 B. 0 C. 1 D. Vô số
C©u 51 : Giá trị cosin của góc giữa hai véctơ a  (4;3;1) và b  (0;2;3) là: 8 5 26 5 13 5 2 A. B. C. D. Kết quả khác. 26 26 26 C©u 52 : x y z
Góc giữa đường thẳng d  2 1 1 :  
và mặt phẳng    x  2y  3z  0 1 2  3 A. 0 90 B. 0 45 C. 0 0 D. 0 180
C©u 53 : Cho mặt cầu (S): 2 2 2
x y z  2x  4y 1  0 có tâm I và bán kính R là: A. I 1; 2
 ;0, R  6 B. I 1; 2  ;  1 , R  6 C. I 1; 2  ;  1 , R  2 D. I 1; 2  ;0, R  2
C©u 54 : Mặt cầu ngoại tiếp tứ diện ABCD có bán kính là: 3 3 A. B. C. 3 D. 2 2 4
C©u 55 : Trong không gian với hệ tọa độ Oxyz, cho điểm A(3; 0; -1) và
B(1;3; -2). M là điểm nằm trên trục hoành Ox và cách đều 2 điểm A,B. Tọa độ điểm M là: A. (2; 0 ; 0) B. ( -1; 0 ; 0) C. ( -2; 0 ;0) D. ( 1; 0 ; 0) 
C©u 56 : Cho mặt phẳng   qua điểm M(0; 0; -1) và song song với giá của hai vecto a = (1; -2; 
3) và b = (3; 0; 5). Phương trình của mặt phẳng   là:
A. -5x + 2y + 3z + 3 = 0
B. 5x – 2y – 3z – 21 = 0
C. 10x – 4y – 6z + 21 = 0
D. 5x – 2y – 3z + 21 = 0
C©u 57 : Phương trình của mặt phẳng (P) đi qua điểm A và vuông góc với đường thẳng (d) x  2  t 
với A(1;-1;-1) và d : y  1  t z  1   2t  A. x – y + 2z + 4=0 B. x –y – 2z - 4=0 C. x –y – 2z + 4=0 D. x + y – 2z + 4=0 C©u 58 : x  2 y  4 z  4
Góc giữa đường thẳng (d):  
và mặt phẳng (P): x y z  2  0 là: 1 2 3  A. 45o B. 90o C. 180o D. 0o
C©u 59 : Phương trình đường thẳng AB với A(1; 1; 2) và B( 2; -1; 0) là: 9 x 1 y 1 z  2 x 1 y 1 z  2 A.   . B.   . 3 2 2 1  2 2 x  2 y 1 z x y  3 z  4 C.   . D.   . 3 2  2 1 2  2  C©u 60 : x y 1 z  2
Trong không gian với hệ toạ độ Oxyz, cho đường thẳng d :   , mặt 2 1 1  phẳng ( )
P : 2x y  2z  6  0 và điểm A(1;-1;2). Mặt phẳng (Q) đi qua điểm A và chứa
d thì phương trình của (Q) là:
A. 2x y  5z 11  0
B. 2x y  5z 11  0 C. 2
x y  5z 11 0
D. 2x y  5z 11  0
C©u 61 : Cho bốn điểm A(1,1,-1) , B(2,0,0) , C(1,0,1) , D (0,1,0) , S(1,1,1)
Nhận xét nào sau đây là đúng nhất
A. ABCD là hình chữ nhật
B. ABCD là hình bình hành C. ABCD là hình thoi
D. ABCD là hình vuông C©u 62 : x 1 2t x y 1 z 1 Cho hai đường thẳng : và d : y 2t . Trong các mệnh đề sau 1 1 2 z 3 4t , mệnh đề nào đúng ? và d song song A. và d cắt nhau B. và d trùng nhau và d chéo nhau C. D.
C©u 63 : Cho d là đường thẳng đi qua điểm A(1; 2; 3) và vuông góc với mặt phẳng
: 4x  3y  7z 1  0. Phương trình tham số của d là: x 1 4t
x  1  t 8 x  1  t 3
x  1 4t    
A. y  2  3t
B. y  2  t 6
C. y  2  t 3
D. y  2  t 3     z  3  7t
z  3  14t
z  3  7t
z  3  t 7
C©u 64 : Cho 3 điểm A(0; 2; 1), B(3; 0; 1), C(1; 0; 0). Phương trình mặt phẳng (ABC) là:
A. 2x + 3y – 4z – 2 = 0
B. 2x – 3y – 4z + 1 = 0 10
C. 4x + 6y – 8z + 2 = 0
D. 2x – 3y – 4z + 2 = 0 C©u 65 : x  2 y 1 z
Cho hai điểm A(2,0,3) , B(2,-2,-3) và đường thẳng  :   1 2 3
Nhận xét nào sau đây là đúng
A , B và  cùng nằm trong một mặt A.
B. A và B cùng thuộc đường thẳng  phẳng
C. Tam giác MAB cân tại M với M (2,1,0)
 và đường thẳng AB là hai đường D. thẳng chéo nhau
C©u 66 : Cho mặt cầu (S) có phương trình 2 2 2
x y z  3x  3y  3z  0 và mặt phẳng (P) : x+y+z-6=0
Nhận xét nào sau đây là đúng
A. Mặt phẳng (P) cắt mặt cầu (S) theo
B. Tâm mặt cầu (S) là I(3,3,3) đường tròn (C)
C. Mặt cầu (S) và mặt phẳng (P) không có D. Mặt cầu (S) tiếp xúc với mặt phẳng (P) điểm chung C©u 67 :
x 1 (m 1)t    Cho hai đườ x y 1 z m ng thẳng  :  
,  : y  1 (2  )
m t . Tìm m để hai đường thẳng 1 2 1 2 1
z 1 (2m1)t  trùng nhau.
A. m  3, m 1 B. m  0
C. m  0, m  1 
D. m  0, m  2
C©u 68 : Mặt cầu tâm I 2; 1
 ;2 và đi qua điểm A2;0;  1 có phương trình là: 2 2 2 2 2 2
A. x  2   y  
1   z  2  2
B. x  2   y  
1   z  2  2 2 2 2 2 2 2
C. x  2   y  
1   z  2  1
D. x  2   y  
1   z  2  1
C©u 69 : Phương trình đường thẳng d qua A(1; 2; 3), có véc tơ chỉ phương u  (1;2;3) là: x 1 y  2 z  3 x  1 tx  1 t     A. 1 2 3
B. y  2  2t
C. x  2y  3z  4  0
D. y  2  2t   z  3  3tz  3   3t  C©u 70 : x 1 y  2 z  3 x  3 y  5 z  7
Cho hai đường thẳng d :   , d :   . Tìm khẳng định 1 2 2 3 4 4 6 8 11 đúng A. d  d d chéo d
C. d // d d d 1 2 B. D. 1 2 1 2 1 2
C©u 71 : Vị trí tương đối của 2 mặt phẳng:   : 2x y z 3  0 và   : 2x + y – z – 5 = 0. ,  cắt ,  chéo
A.   //  
B.      C. D. nhau nhau
C©u 72 : Phương trình mặt phẳng qua A( 1; 1; 1), B(1; 0; 0), C( 1; -1; -1) là:
A. x y z 1  0
B. x y z  3  0
C. 3x  3  0
D. x y z 1  0 C©u 73 : a  (4; 6  ;2)
Cho đường thẳng d đi qua điểm M(2; 0; -1) và có vecto chỉ phương .
Phương trình tham số của đường thẳng d là:
x  2  2t
x  2  t 4 x  4  t 2
x  2  t 2    
A. y   t 3
B. y   t 6
C. y  6  t 3
D. y   t 3      z  1  t
z  1  2tz  2  tz  1  t
C©u 74 : Cho ba điểm A(0 ; 2 ; 1), B(3 ; 0 ; 1), C(1; 0 ; 0). Phương trình mặt phẳng (ABC) là
A. x – 4y + 2z – 8 = 0
B. 2x – 3y – 4z +2 = 0 C. x – 4y + 2z = 0
D. 2x + 3y – 4z – 2 = 0
C©u 75 : Trong không gian với hệ tọa độ Oxyz, cho đường thẳng x  3 y z  5 d:  
và mặt phẳng (P): 2x y  2z  7  0 . Mlà điểm trên d và cách (P) 1 1  3
một khoảng bằng 3. Tọa độ M là: A. (3;0;5)
B. Cả 2 đáp án A) và B) đều đúng.
C. Cả 2 đáp án A) và B) đều sai. D. (1;2;-1) C©u 76 : x  1  t 2 x  3  t 4  
Cho 2 đường thẳng d : và d :
. Trong các mệnh đề sau, mệnh 2 y  5  t 6 1 y  2  t 3   z  3  t 4 z  7  t 8 đề nào đúng ?
A. d d d // d d d
d , d chéo nhau 1 2 B. 1 2 C. 1 2 D. 1 2
C©u 77 : Trong không gian Oxyz cho 3 vectơ a  ( 1
 ;1;0), b  (1;1;0) và c  (1;1;1). Trong 12
các mệnh đề sau, mệnh đề nào sai ? A. c  3 B. a  b C. a  2 D. c  b
C©u 78 : Cho A 2;0;0 ,B 0;2;0 ,C 0;0;2 ,D 2;2;2 mặt cầu ngoại tiếp tứ diện ABCD có bán kính là : 2 3 A. 3 B. C. 3 D. 3 2
C©u 79 : Cho hai mặt phẳng (): 2x + 3y + 3z - 5 = 0; (): 2x + 3y + 3z - 1 = 0. Khoảng cách giữa hai mặt phẳng này là: 22 2 2 22 A. B. 4 C. D. 11 11 11 C©u 80 : x  8 y  5 z  8 Cho đường thẳng d:  
và mặt phẳng (P) x+2y+5z+1=0 . Nhận xét nào 1 2 1  sau đây là đúng
A. Đường thẳng d song song với mặt
B. Đường thẳng d thuộc mặt phẳng (P) phẳng (P)
C. Đường thẳng d cắt mặt phẳng (P) tại
D. Đường thẳng d vuông góc với mặt A(8,5,8) phẳng (P) 13 ĐÁP ÁN 01 { | ) ~ 28 { | ) ~ 55 { ) } ~ 02 { | ) ~ 29 { | } ) 56 ) | } ~ 03 ) | } ~ 30 { | ) ~ 57 { | } ) 04 { ) } ~ 31 { | } ) 58 { | } ) 05 { ) } ~ 32 { | ) ~ 59 { | } ) 06 { | ) ~ 33 { ) } ~ 60 { ) } ~ 07 ) | } ~ 34 { | ) ~ 61 ) | } ~ 08 { ) } ~ 35 { | } ) 62 { | ) ~ 09 { ) } ~ 36 ) | } ~ 63 ) | } ~ 10 ) | } ~ 37 { ) } ~ 64 ) | } ~ 11 { | } ) 38 ) | } ~ 65 ) | } ~ 12 { | } ) 39 { | ) ~ 66 ) | } ~ 13 { | ) ~ 40 ) | } ~ 67 { ) } ~ 14 { ) } ~ 41 ) | } ~ 68 { | ) ~ 15 { ) } ~ 42 { ) } ~ 69 { ) } ~ 16 { | } ) 43 { | } ) 70 { | } ) 17 { | ) ~ 44 { | ) ~ 71 { | ) ~ 18 { ) } ~ 45 { | } ) 72 { | } ) 19 { ) } ~ 46 { ) } ~ 73 ) | } ~ 20 ) | } ~ 47 { | } ) 74 { | } ) 21 { ) } ~ 48 { ) } ~ 75 { ) } ~ 22 ) | } ~ 49 { | ) ~ 76 ) | } ~ 23 { | ) ~ 50 ) | } ~ 77 { | } ) 24 { | } ) 51 { | } ) 78 { | ) ~ 25 { | ) ~ 52 { | ) ~ 79 { | } ) 26 { | ) ~ 53 { | } ) 80 ) | } ~ 27 { ) } ~ 54 ) | } ~ 14