77 bài toán tính đơn điệu của hàm số trong đề thi THPT môn Toán (2016 – 2021)

77 bài toán tính đơn điệu của hàm số trong đề thi THPT môn Toán (2016 – 2021) được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

14 7 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

38 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 1
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Câu 1: (Câu 24 - MĐ 104 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Cho hàm số
( )
y f x=
có đồ thị là
đường cong trong hình bên.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Ⓐ.
( )
1;1−
.
Ⓑ.
( )
1; +∞
.
Ⓒ.
( )
;1−∞
.
Ⓓ.
( )
0;3
.
Lời giải
Chọn A
Quan sát đồ thị ta thầy hàm số đã cho nghịch biến trên khoảng
( )
1;1−
.
Câu 2: (Câu 15 - MĐ 103 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Cho hàm số
( )y f x=
có đồ thị là
đường cong trong hình bên. Hàm số đã cho đồng biến trong khoảng nào dưới đây?
Ⓐ.
( ;2)−∞
.
Ⓑ.
(0;2)
.
Ⓒ.
( 2;2)−
.
Ⓓ.
(2; )+∞
.
Lời giải
Chọn B
Dựa vào đồ thị suy ra hàm số đã cho đồng biến trong khoảng
(0;2)
.
Câu 3: (Câu 8 - MĐ 102 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Cho hàm số
( )
y f x=
có đồ thị là
đường cong như hình vẽ. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
BÀI TOÁN
TÍNH N I
U
TRONG  THI BGD
-
2021
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 2
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Ⓐ.
( )
1;1−
.
Ⓑ.
( )
;0−∞
.
Ⓒ.
( )
0;1
.
Ⓓ.
( )
0;+∞
.
Lời giải
Chọn C
Dựa vào đồ thị hàm số
( )
y f x=
ta thấy hàm số đồng biến trên khoảng
( )
0;1
.
Câu 4: (Câu 14 - MĐ 101 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Cho hàm số
( )
y f x=
có đồ thị là
đường cong trong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Ⓐ.
( )
0;1
.
Ⓑ.
( )
;0−∞
.
Ⓒ.
( )
0;+∞
.
Ⓓ.
( )
1;1−
.
Lời giải
Chọn A
Câu 5: (Câu 29 - MĐ 101 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Biết hàm số
1
x a
y
x
+
=
+
(
a
là số
thực cho trước,
1a ≠
) có đồ thị như trong hình bên.
Mệnh đề nào dưới đây đúng?
Ⓐ.
' 0, 1y x< ∀ ≠ −
.
Ⓑ.
' 0, 1y x> ∀ ≠ −
.
Ⓒ.
' 0,y x< ∀ ∈ℝ
.
Ⓓ.
' 0,y x> ∀ ∈ℝ
.
Lời giải
Chọn B
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 3
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Tập xác định:
\{ 1}D = −ℝ
.
Dựa vào đồ thị, ta có: Hàm số
1
x a
y
x
+
=
+
đồng biến trên
( ; 1)−∞ −
và
( 1; )− +∞
' 0, 1y x⇒ > ∀ ≠ −
.
Câu 6: (Câu 3 - Đề Tham Khảo - BGD&ĐT - Năm 2020 - 2021)
Cho hàm số
( )
f x
có bảng biến
thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào, trong các khoảng dưới đây?
Ⓐ.
( )
2;2−
.
Ⓑ.
( )
0;2
.
Ⓒ.
( )
2;0−
.
Ⓓ.
( )
2;+∞
.
Lời giải
Chọn B
Từ bảng biến thiên ta thấy hàm số đồng biến trên khoảng
( )
0;2
.
Câu 7: (Câu 19 - MĐ 103 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020)
Cho hàm số
( )y f x=
có đồ thị là
đường cong trong hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây
Ⓐ.
( )
1;0−
Ⓑ.
( )
; 1−∞ −
.
Ⓒ.
( )
0;+∞
.
Ⓓ.
( )
0;1
.
Lời giải
Chọn A
Trên khoảng
( )
1;0−
và
( )
1;+∞
hàm số có đồ thị là đường đi lên. Do đó hàm số đã cho đồng
biến trên các khoảng này.
Câu 8: (Câu 23 - MĐ 102 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020)
Cho hàm số
( )
y f x=
có đồ thị là
đường cong trong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 4
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Ⓐ.
( )
1; 0−
.
Ⓑ.
( )
; 1−∞ −
.
Ⓒ.
( )
0;1
.
Ⓓ.
( )
0;+∞
.
Lời giải
Chọn A
Trên khoảng
( )
1;0−
đồ thị hàm số đi xuống theo hướng từ trái sang phải nên hàm số nghịch
biến trên khoảng này.
Câu 9: (Câu 3 - MĐ 101 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) C
ho hàm số
( )
y f x=
có đồ thị là
đường cong trong hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Ⓐ.
( )
1;+ ∞
.
Ⓑ.
( )
1;0−
.
Ⓒ.
( )
0;1
.
Ⓓ.
( )
;0−∞
.
Lời giải
Chọn C
Hàm số đồng biến trên khoảng
( )
; 1−∞ −
và
( )
0;1
.
Câu 10: (Câu 16 - MĐ 104 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020)
Cho hàm số
( )
y f x=
có bảng
biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Ⓐ.
( )
3;0−
.
Ⓑ.
( )
3;3−
.
Ⓒ.
( )
0;3
.
Ⓓ.
( )
; 3−∞ −
Lời giải
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 5
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Chọn A
Từ BBT ta có hàm số
( )
f x
đồng biến trên hai khoảng
( )
3;0−
và
( )
3;+∞
Câu 11: (Câu 17 - MĐ 103 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020)
Cho hàm số
( )
f x
có bảng biến
thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây
Ⓐ.
( )
2;2−
.
Ⓑ.
( )
0;2
.
Ⓒ.
( )
2;0−
.
Ⓓ.
( )
2;+∞
.
Lời giải
Chọn B
Nhìn vào bảng biến thiên ta thấy hàm số đồng biến trên các khoảng:
( )
; 2−∞ −
và
( )
0;2
Câu 12: (Câu 17 - MĐ 102 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020)
Cho hàm số
( )
f x
có bảng biến
thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Ⓐ.
( )
1;+∞
.
Ⓑ.
( )
1;1−
.
Ⓒ.
( )
0;1
.
Ⓓ.
( )
1;0−
.
Lời giải
Chọn C
Dựa vào bảng biến thiên ta có hàm số đồng biến trên khoảng
( )
0;1
Câu 13: (Câu 4 - MĐ 101 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020)
Cho hàm số
( )
f x
có bảng biến
thiên như sau:
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 6
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Ⓐ.
( )
; 1− ∞ −
.
Ⓑ.
( )
0;1
.
Ⓒ.
( )
1;1−
.
Ⓓ.
( )
1; 0−
.
Lời giải
Chọn D
Dựa vào bảng biến thiên của hàm số
( )
f x
suy ra hàm số đã cho đồng biến trên khoảng
( )
1; 0 .−
Câu 14: (Câu 10 - ĐTK - BGD&ĐT - Lần 2 - Năm 2019 - 2020)
Cho hàm số
( )
f x
có bảng biến thiên
như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Ⓐ.
( )
; 1−∞ −
.
Ⓑ.
( )
0;1
.
Ⓒ.
( )
1;0−
.
Ⓓ.
( )
;0−∞
.
Lời giải
Chọn C
Nhìn vào bảng biến thiên ta thấy
( )
' 0f x <
trên các khoảng
( )
1;0−
và
( )
1;+∞ ⇒
hàm số
nghịch biến trên
( )
1;0−
.
Câu 15: (Câu 4 - ĐTK - BGD&ĐT - Lần 1 - Năm 2019 - 2020)
Cho hàm số
( )
f x
có bảng biến thiên
như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Ⓐ.
( )
1;+ ∞
.
Ⓑ.
( )
1;0−
.
Ⓒ.
( )
1;1−
.
Ⓓ.
( )
0;1
.
Lời giải
Chọn D
Hàm số đã cho đồng biến trên mỗi khoảng
( )
; 1−∞ −
và
( )
0;1
.
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 7
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Ta chọn phương án
D
Câu 16: (Câu 10 - MĐ 104 - BGD&ĐT - Năm 2018 - 2019)
Cho hàm số
( )
f x
có bảng biến thiên như
sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Ⓐ.
( )
0;1
.
Ⓑ.
( )
1;+∞
.
Ⓒ.
( )
1;0−
.
Ⓓ.
( )
0;+∞
.
Lời giải
Chọn A
Câu 17: (Câu 15 - MĐ 103 - BGD&ĐT - Năm 2018 - 2019)
Cho hàm số
( )
f x
có bảng biến thiên như
sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Ⓐ.
( )
1;0−
.
Ⓑ.
( )
1;− + ∞
.
Ⓒ.
( )
; 1−∞ −
.
Ⓓ.
( )
0;1
.
Lời giải
Chọn A
Nhìn BBT ta thấy hàm số đã cho đồng biến trên các khoảng
( )
1; 0−
và
( )
1; + ∞
. Đáp án A
đúng.
Câu 18: (Câu 14 - MĐ 102 - BGD&ĐT - Năm 2018 - 2019)
Cho hàm số
( )
f x
có bảng biến thiên sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Ⓐ.
( )
0;+∞
.
Ⓑ.
( )
0;2
.
Ⓒ.
( )
2;0−
.
Ⓓ.
( )
; 2−∞ −
.
Lời giải
Chọn C
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 8
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Dựa vào bảng biến thiên, hàm số đã cho đồng biến trên khoảng
( )
2;0−
và
( )
2;+∞
.
Căn cứ các phương án, ta chọn đáp án
D
.
Câu 19: (Câu 3 - MĐ 101 - BGD&ĐT - Năm 2018 - 2019)
Cho hàm số
( )
f x
có bảng biến thiên như
sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Ⓐ.
( )
2;0−
.
Ⓑ.
( )
2;+∞
.
Ⓒ.
( )
0;2
.
Ⓓ.
( )
0;+ ∞
.
Lời giải
Chọn C
Ta có
( ) ( ) ( )
0 0;2f x x f x
′
< ⇔ ∀ ∈ ⇒
nghịch biến trên khoảng
( )
0;2
.
Câu 20: (Câu 4 - ĐTK - BGD&ĐT - Năm 2018 - 2019)
Cho hàm số
( )
y f x=
có đồ thị như hình vẽ
bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Ⓐ.
( )
0;1
.
Ⓑ.
( )
; 1−∞ −
.
Ⓒ.
( )
1;1−
.
Ⓓ.
( )
1;0−
.
Lời giải
Chọn D
Nhìn đồ thị hàm số ta thấy hàm số
( )
y f x=
đồng biến trên khoảng
( )
1;0−
và
( )
1;+ ∞
.
Câu 21: (Câu 7 - MĐ 104 - BGD&ĐT - Năm 2017 - 2018)
Cho hàm số
( )
y f x=
có bảng biến thiên
như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 9
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Ⓐ.
( )
2;− + ∞
Ⓑ.
( )
2;3−
Ⓒ.
( )
3;+∞
Ⓓ.
( )
; 2−∞ −
Lời giải
Chọn B
Câu 22: (Câu 7 - MĐ 103 - BGD&ĐT - Năm 2017 - 2018)
Cho hàm số
( )
y f x=
có bảng biến thiên
như sau :
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Ⓐ.
( )
1;0−
.
Ⓑ.
( )
1; +∞
.
Ⓒ.
( )
;1−∞
.
Ⓓ.
( )
0;1
Lời giải
Chọn D
Câu 23: (Câu 12 - MĐ 102 - BGD&ĐT - Năm 2017 - 2018)
Cho hàm số
( )
y f x=
có bảng biến thiên
như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Ⓐ.
( )
1;− +∞
.
Ⓑ.
( )
1;+∞
.
Ⓒ.
( )
1;1−
.
Ⓓ.
( )
;1−∞
.
Lời giải
Chọn B
Câu 24: (Câu 4 - MĐ 101 - BGD&ĐT - Năm 2017 - 2018)
Cho hàm số
( )
y f x=
có bảng biến thiên
như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 10
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Ⓐ.
( )
0;1
Ⓑ.
( )
;0−∞
Ⓒ.
( )
1;+∞
Ⓓ.
( )
1;0−
Lời giải
Chọn A
Dựa vào bảng biến thiên ta có hàm số đã cho nghịch biến trên các khoảng
( )
0;1
và
( )
; 1−∞ −
.
Câu 25: (Câu 1 - MĐ 104 - BGD&ĐT - NĂM 2016 - 2017)
Cho hàm số
( )
y f x=
có bảng xét dấu đạo
hàm như sau
Mệnh đề nào dưới đây đúng?
Ⓐ.
Hàm số đồng biến trên khoảng
( )
2;0−
.
Ⓑ.
Hàm số đồng biến trên khoảng
( )
;0−∞
.
Ⓒ.
Hàm số nghịch biến trên khoảng
( )
0;2
.
Ⓓ.
Hàm số nghịch biến trên khoảng
( )
; 2−∞ −
.
Lời giải
Chọn C
Dễ thấy mệnh đề hàm số nghịch biến trên khoảng
( )
0;2
đúng.
Câu 26: (Câu 3 - MĐ 103 - BGD&ĐT - NĂM 2016 - 2017)
Cho hàm số
( )
y f x=
có đạo hàm
( )
2
1f x x
′
= +
,
x∀ ∈ℝ
. Mệnh đề nào dưới đây đúng?
Ⓐ.
Hàm số nghịch biến trên khoảng
( )
;0−∞
.
Ⓑ.
Hàm số nghịch biến trên khoảng
( )
1;+∞
.
Ⓒ.
Hàm số nghịch biến trên khoảng
( )
1;1−
.
Ⓓ.
Hàm số đồng biến trên khoảng
( )
;−∞ +∞
.
Lời giải
Chọn D
Ta có
( )
2
1 0, f x x x
′
= + > ∀ ∈ ⇒ℝ
Hàm số đồng biến trên khoảng
( )
;−∞ +∞
.
Câu 27: (Câu 3 - MĐ 102 - BGD&ĐT - Năm 2016 - 2017)
Hàm số nào dưới đây đồng biến trên khoảng
( )
;−∞ +∞
?
Ⓐ.
1
3
x
y
x
+
=
+
Ⓑ.
3
y x x= +
Ⓒ.
1
2
x
y
x
−
=
−
Ⓓ.
3
3y x x= − −
Lời giải
Chọn B
Vì
3
y x x= +
2
3 1 0,y x x
′
⇒ = + > ∀ ∈ℝ .
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 11
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Câu 28: (Câu 11 - MĐ 102 - BGD&ĐT - Năm 2016 - 2017)
Cho hàm số
3 2
3y x x= −
. Mệnh đề nào
dưới đây đúng?
Ⓐ.
Hàm số nghịch biến trên khoảng
( )
0;2
Ⓑ.
Hàm số nghịch biến trên khoảng
( )
2;+∞
Ⓒ.
Hàm số đồng biến trên khoảng
( )
0;2
Ⓓ.
Hàm số nghịch biến trên khoảng
( )
;0−∞
Lời giải
Chọn A
Ta có
2
3 6y x x
′
= −
;
0
0
2
x
y
x
=
′
= ⇔
=
.
Lập bảng biến thiên rồi suy ra hàm số nghịch biến trên khoảng
( )
0;2
Câu 29: (Câu 8 - MĐ 101 - BGD&ĐT - Năm 2016 - 2017)
Cho hàm số
3
3 2y x x= + +
. Mệnh đề nào
dưới đây là đúng?
Ⓐ.
Hàm số đồng biến trên khoảng
( ;0)−∞
và nghịch biến trên khoảng
(0; )+∞
.
Ⓑ.
Hàm số nghịch biến trên khoảng
( ; )−∞ +∞
.
Ⓒ.
Hàm số đồng biến trên khoảng
( ; )−∞ +∞
.
Ⓓ.
Hàm số nghịch biến trên khoảng
( ;0)−∞
và đồng biến trên khoảng
(0; )+∞
.
Lời giải
Chọn C
′
= + > ∀ ∈ℝ
2
3 3 0,y x x
⇒
Hàm số đồng biến trên
( )
;−∞ + ∞
Câu 30: (Câu 13 - MĐ 101 - BGD&ĐT - Năm 2016 - 2017)
Hàm số
2
2
1
y
x
=
+
nghịch biến trên khoảng
nào dưới đây?
Ⓐ.
(0; )+∞
Ⓑ.
( 1;1)−
Ⓒ.
( ; )−∞ +∞
Ⓓ.
( ;0)−∞
Lời giải
Chọn A
( )
′
= = −
+
ℝ
2
2
4
;
1
x
D y
x
. Cho
′
= ⇔ =
0 0y x
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 12
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Câu 31:
Hàm số nghịch biến trên khoảng
( )
0; + ∞
(Câu 33 - MĐ 104 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021)
Biết hàm số
1
x a
y
x
+
=
−
(
a
là số thực
cho trước và
1a ≠ −
) có đồ thị như trong hình bên.
Mệnh đề nào dưới đây đúng?
Ⓐ.
0,y x
′
< ∀ ∈
ℝ .
Ⓑ.
0, 1y x
′
< ∀ ≠
.
Ⓒ.
0,y x
′
> ∀ ∈
ℝ .
Ⓓ.
0, 1y x
′
> ∀ ≠
.
Lời giải
Chọn B
TXĐ:
{ }
\ 1D = ℝ
.
Khi đó:
2
1
1
( 1)
a
y x
x
− −
′
= ∀ ≠
−
.
Hai nhánh của đồ thị có chiều đi xuống nên
0, 1y x
′
< ∀ ≠
.
Câu 32: (Câu 38 - MĐ 103 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021)
Biết hàm số
1
x a
y
x
+
=
−
, có đồ thị
như trong hình bên. Mệnh đề nào dưới đây đúng?
Ⓐ.
0, 1y x
′
> ∀ ≠
.
Ⓑ.
0,y x
′
> ∀ ∈
ℝ
.
Ⓒ.
0,y x
′
< ∀ ∈
ℝ
.
Ⓓ.
0, 1y x
′
< ∀ ≠
.
Lời giải
Chọn A
Điều kiện
1x ≠
.
Dựa vào đồ thị ta thấy theo thứ tự từ trái qua phải đồ thị đi lên nên
0, 1y x
′
> ∀ ≠
.
Câu 33: (Câu 33 - MĐ 102 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021)
Biết hàm số
1
x a
y
x
+
=
+
(
a
là số
thực cho trước,
1a ≠
) có đồ thị như trong hình bên. Mệnh đề nào dưới đây đúng?
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 13
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Ⓐ.
0,y x
′
< ∀ ∈ℝ
.
Ⓑ.
0, 1y x
′
> ∀ ≠ −
.
Ⓒ.
0, 1y x
′
< ∀ ≠ −
.
Ⓓ.
0,y x
′
> ∀ ∈ℝ
.
Lời giải
Chọn C
Tập xác định:
{ }
\ 1D = −ℝ
nên loại đáp án A và
Ⓓ.
Dạng đồ thị đi xuống thì
0y
′
<
nên loại đáp án
Ⓑ.
Câu 34: (Câu 30 - Đề Tham Khảo - BGD&ĐT - Năm 2020 - 2021)
Hàm số nào dưới đây đồng biến
trên ℝ ?
Ⓐ.
1
2
x
y
x
+
=
−
.
Ⓑ.
2
2y x x= +
.
Ⓒ.
3 2
y x x x= − +
.
Ⓓ.
4 2
3 2y x x= − +
.
Lời giải
Chọn C
2
3 2 2
1 2
' 3 2 1 3 0
3 3
y x x x y x x x x
= − + ⇒ = − + = − + > ∀ ∈
ℝ
Vậy hàm số đồng biến trên
ℝ
.
Câu 35: (Câu 4 - MĐ 104 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020)
Cho hàm số
( )y f x=
có đồ thị là
đường cong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 14
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Ⓐ.
(1; )+∞
.
Ⓑ.
(0;1)
.
Ⓒ.
( 1;0)−
.
Ⓓ.
( ;0)−∞
.
Lời giải
Chọn B
Trên khoảng
(0;1)
đồ thị hàm số đi xuống nên hàm số đã cho nghịch biến trên
(0;1)
.
Câu 36: (Câu 40 - MĐ 101 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020)
Tập hợp tất cả các giá trị thực
của tham số
m
để hàm số
( )
3 2
3 4y x x m x= − + −
đồng biến trên khoảng
( )
2;+ ∞
là
Ⓐ.
(
]
;1−∞
.
Ⓑ.
(
]
;4−∞
.
Ⓒ.
( )
;1−∞
.
Ⓓ.
( )
;4−∞
.
Lời giải
Chọn B
Tập xác định:
D = ℝ
.
Ta có:
2
3 6 4y x x m
′
= − + −
.
Hàm số đồng biến trên khoảng
( )
2;+∞
( )
0, 2;y x
′
⇔ ≥ ∀ ∈ +∞
( )
2
3 6 4, 2;m x x x⇔ ≤ − + ∀ ∈ +∞
.
Xét hàm số
( )
2
3 6 4g x x x= − +
trên khoảng
( )
2;+∞
.
Ta có:
( )
6 6g x x
′
= −
;
( )
0 1g x x
′
= ⇔ =
.
Bảng biến thiên
Dựa vào bảng biến thiên ta có:
( )
( ), 2;m g x x≤ ∀ ∈ +∞
4m⇔ ≤
.
Vậy
4m ≤
thoả yêu cầu bài toán.
Câu 37: (Câu 39 - MĐ 102 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020)
Tập hợp các giá trị thực của tham
số
m
để hàm số
5x
y
x m
+
=
+
đồng biến trên khoảng
( )
; 8−∞ −
là
Ⓐ.
( )
5;+∞
.
Ⓑ.
(
]
5;8
.
Ⓒ.
[
)
5;8
.
Ⓓ.
( )
5;8
.
Lời giải
Chọn B
Tập xác định của hàm số là
{ }
\D m= −ℝ
.
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 15
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Hàm số
5x
y
x m
+
=
+
đồng biến trên khoảng
( )
; 8−∞ −
( )
0, ; 8y x
x m
′
> ∀ ∈ −∞ −
⇔
≠ −
( )
( )
( )
2
5
0, ; 8
; 8
m
x
x m
m
−
> ∀ ∈ −∞ −
+
⇔
− ∉ −∞ −
5 5
5 8
8 8
m m
m
m m
> >
⇔ ⇔ ⇔ < ≤
− ≥ − ≤
.
Vậy
(
]
5;8m ∈
thỏa mãn yêu cầu bài toán.
Câu 38: (Câu 34 - MĐ 104 - BGD&ĐT - Năm 2018 - 2019)
Cho hàm số
( )
f x
, có bảng xét dấu
( )
f x
′
như sau:
Hàm số
( )
5 2y f x= −
đồng biến trên khoảng nào dưới đây?
Ⓐ.
( )
; 3−∞ −
.
Ⓑ.
( )
4;5
.
Ⓒ.
( )
3;4
.
Ⓓ.
( )
1;3
.
Lời giải
Chọn B
Ta có
( )
2 5 2y f x
′ ′
= − −
.
Hàm số
( )
5 2y f x= −
đồng biến
( )
2 5 2 0f x
′
⇔ − − ≥
( )
5 2 0f x
′
⇔ − ≤
5 2 3
1 5 2 1
x
x
− < −
⇔
− < − <
4
2 3
x
x
>
⇔
< <
.
Vậy chọn đáp án
Ⓑ.
Câu 39: (Câu 33 - MĐ 103 - BGD&ĐT - Năm 2018 - 2019)
Cho hàm số
( )
f x
, bảng xét dấu của
( )
f x
′
như sau:
Hàm số
( )
3 2y f x= −
đồng biến trên khoảng nào dưới đây?
Ⓐ.
( )
3;4
.
Ⓑ.
( )
2;3
.
Ⓒ.
( )
; 3−∞ −
.
Ⓓ.
( )
0;2
.
Lời giải
Chọn A
Ta có:
( )
3 2y f x
′ ′
= −
( ) ( )
3 2 3 2x f x
′
′
= − −
( )
2 3 2f x
′
= − −
.
*) 0y
′
=
( )
2 3 2 0f x
′
⇔ − − =
( )
3 2 0f x
′
⇔ − =
3 2 3
3 2 1
3 2 1
x
x
x
− = −
⇔ − = −
− =
3
2
1
x
x
x
=
⇔ =
=
.
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 16
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
*) 0y
′
≥
( )
2 3 2 0f x
′
⇔ − − ≥
( )
3 2 0f x
′
⇔ − ≤
3 2 3
1 3 2 1
x
x
− ≤ −
⇔
− ≤ − ≤
3
1 2
x
x
≥
⇔
≤ ≤
.
Bảng xét dấu:
Hàm số
( )
3 2y f x= −
đồng biến trên khoảng
( )
3; +∞
nên đồng biến trên khoảng
( )
3;4
.
Câu 40: (Câu 30 - MĐ 102 - BGD&ĐT - Năm 2017 - 2018)
Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
6
5
x
y
x m
+
=
+
nghịch biến trên khoảng
( )
10;+∞
?
Ⓐ.
3
.
Ⓑ.
Vô số.
Ⓒ.
4
.
Ⓓ.
5
Lời giải
Chọn C
Tập xác định
{ }
\ 5D m= −R
.
( )
2
5 6
5
m
y
x m
−
′
=
+
Hàm số nghịch biến trên
( )
10;+∞
khi và chỉ khi
( )
0,
5 10;
y x D
m
′
< ∀ ∈
− ∉ +∞
5 6 0
5 10
m
m
− <
⇔
− ≤
6
5
2
m
m
<
⇔
≥ −
.
Mà
m∈ℤ
nên
{ }
2; 1;0;1m ∈ − −
.
Câu 41: (Câu 5 - ĐTK - BGD&ĐT - Năm 2017 - 2018)
Cho hàm số
( )
y f x=
có bảng biến thiên như
sau:
Hàm số
( )
y f x=
nghịch biến trên khoảng nào dưới đây?
Ⓐ.
( )
2;0
−
Ⓑ.
( )
; 2
−∞ −
Ⓒ.
( )
0;2
Ⓓ.
( )
0;
+∞
Lời giải
Chọn A
Câu 42: (Câu 30 - ĐTK - BGD&ĐT - Năm 2017 - 2018)
Có bao nhiêu giá trị nguyên âm của tham số
m
để hàm số
3
5
1
5
y x mx
x
= + −
đồng biến trên khoảng
( )
0;
+∞
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 17
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Ⓐ.
5
Ⓑ.
3
Ⓒ.
0
Ⓓ.
4
Lời giải
Chọn D
2
6
1
3y x m
x
′
= + +
Hàm số đồng biến trên
( )
0;
+∞
khi và chỉ khi
( )
2
6
1
3 0, 0;y x m x
x
′
= + + ≥ ∀ ∈ +∞
( )
2
6
1
3 , 0;x m x
x
⇔ − − ≤ ∀ ∈ +∞
. Xét hàm số
2
6
1
( ) 3g x x m
x
= − − ≤
,
( )
0;
x∈ +∞
8
7 7
6( 1)
( ) 6
6
− −
′
= − + =
x
g x x
x x
,
1
( ) 0
1(loai)
x
g x
x
=
′
= ⇔
= −
Bảng
biến
thiên:
Dựa vào BBT ta có
4m ≥ −
, suy ra các giá trị nguyên âm của tham số
m
là
4; 3; 2; 1− − − −
Câu 43: (Câu 21 - MĐ 104 - BGD&ĐT - NĂM 2016 - 2017)
Cho hàm số . Mệnh đề nào
dưới đây đúng?
Ⓐ.
Hàm số nghịch biến trên khoảng .
Ⓑ.
Hàm số đồng biến trên khoảng .
Ⓒ.
Hàm số đồng biến trên khoảng .
Ⓓ.
Hàm số nghịch biến trên khoảng .
Lời giải
Chọn B
Ta có , . Hàm số nghịch biến trên khoảng và đồng biến trên khoảng
.
Câu 44: (Câu 30 - MĐ 103 - BGD&ĐT - NĂM 2016 - 2017)
Cho hàm số
4 2
2y x x= −
. Mệnh đề nào
dưới đây đúng?
Ⓐ.
Hàm số đồng biến trên khoảng
( )
; 2−∞ −
.
Ⓑ.
Hàm số nghịch biến trên khoảng
( )
; 2−∞ −
.
Ⓒ.
Hàm số đồng biến trên khoảng
( )
1;1−
.
2
2 1
y x
= +
(
)
1;1
−
(
)
0;
+∞
(
)
;0
−∞
(
)
0;
+∞
D
=
ℝ
2
2
2 1
x
y
x
′
=
+
(
)
;0
−∞
(
)
0;
+∞
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 18
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Ⓓ.
Hàm sô nghịch biến trên khoảng
( )
1;1−
.
Lời giải
Chọn B
Ta có
3
4 4y x x
′
= −
.
0
0
1
x
y
x
=
′
= ⇔
= ±
.
Ta có bảng biến thiên:
Từ bảng biến thiên suy ra hàm số nghịch biến trên khoảng
( )
; 2−∞ −
.
Câu 45: (Câu 6 - ĐTK - BGD&ĐT - Năm 2016 - 2017)
Cho hàm số
2
1
x
y
x
−
=
+
. Mệnh đề nào dưới đây
đúng?
Ⓐ.
Hàm số nghịch biến trên khoảng
( )
; 1−∞ −
Ⓑ.
Hàm số đồng biến trên khoảng
( )
; 1−∞ −
Ⓒ.
Hàm số nghịch biến trên khoảng
( )
;−∞ +∞
Ⓓ.
Hàm số nghịch biến trên khoảng
( )
1;− +∞
Lời giải
Chọn B
Tập xác định:
{ }
1\ −
ℝ
.
Ta có
( )
2
3
' 0
1
y
x
= >
+
,
{ }
1\
x
∀ ∈ −
ℝ
.
Suy ra hàm số đồng biến trên các khoảng
( )
; 1−∞ −
và
( )
1;− +∞
.
Câu 46: (Câu 14 - ĐTK - BGD&ĐT - Năm 2016 - 2017)
Hàm số nào dưới đây đồng biến trên khoảng
( )
;−∞ +∞
?
Ⓐ.
3
3 3 2y x x= + −
.
Ⓑ.
3
2 5 1y x x= − +
.
Ⓒ.
4 2
3y x x= +
.
Ⓓ.
2
1
x
y
x
−
=
+
.
Lời giải
Chọn A
Hàm số
3
3 3 2y x x= + −
có TXĐ:
D = ℝ
.
2
9 3 0,y x x
′
= + > ∀ ∈
ℝ
, suy ra hàm số đồng biến trên khoảng
( )
;−∞ +∞
.
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 19
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Câu 47: (Câu 4 - ĐTN - BGD&ĐT - Năm 2016 - 2017)
Cho hàm số
3 2
2 1= − + +y x x x
. Mệnh đề nào
dưới đây đúng?
Ⓐ.
Hàm số nghịch biến trên khoảng
1
;1
3
Ⓑ.
Hàm số nghịch biến trên khoảng
1
;
3
−∞
Ⓒ.
Hàm số đồng biến trên khoảng
1
;1
3
Ⓓ.
Hàm số nghịch biến trên khoảng
( )
1;+∞
Lời giải
Chọn A
Ta có
2
1
3 4 1 0
1
3
x
y x x y
x
=
′ ′
= − + ⇒ = ⇔
=
Bảng biến thiên:
Vậy hàm số nghịch biến trên khoảng
1
;1
3
.
Câu 48: (Câu 3 - ĐMH - BGD&ĐT - Năm 2017 - 2018)
Hỏi hàm số
4
2 1
y x
= +
đồng biến trên khoảng
nào?
Ⓐ.
1
;
2
−∞ −
.
Ⓑ.
( )
0;+∞
.
Ⓒ.
1
;
2
− +∞
.
Ⓓ.
( )
;0 .−∞
Lời giải
Chọn B
4
2 1
y x
= +
. Tập xác định:
D = ℝ
Ta có:
3
8
y x
′
=
;
3
0 8 0 0
y x x
′
= ⇔ = ⇔ =
suy ra
( )
0 1
y
=
Giới hạn:
lim
x
y
→−∞
= +∞
;
lim
x
y
→+∞
= +∞
Bảng biến thiên:
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 20
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Câu 49:
Vậy hàm số đồng biến trên khoảng
( )
0; +∞
.
(Câu 42 - MĐ 104 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020)
Tập hợp tất cả các giá trị của
tham số
m
để hàm số
( )
3 2
3 1y x x m x= − + −
đồng biến trên khoảng
( )
2;+∞
là
Ⓐ.
( )
;2−∞
.
Ⓑ.
( )
;1−∞
.
Ⓒ.
( ; 2]−∞ −
.
Ⓓ.
( ;1]−∞
.
Lời giải
Chọn D
Ta có
2
' 3 6 1y x x m= − + −
.
Hàm số
( )
3 2
3 1y x x m x= − + −
đồng biến trên khoảng
( )
2;+∞
nên
( )
' 0 2;y x≥ ∀ ∈ +∞
Suy ra:
( )
( )
2 2
2;
3 6 1 2; (3 6 1) 1
x
x x m x Min x x m m
∈ +∞
− + ≥ ∀ ∈ +∞ ⇔ − + ≥ ⇔ ≥
.
Câu 50: (Câu 42 - MĐ 102 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020)
Tập hợp tất cả các giá trị thực của
tham số
m
để hàm số
( )
3 2
3 5y x x m x= − + −
đồng biến trên khoảng
( )
2;+∞
là
.
Ⓐ.
( )
;2−∞
.
Ⓑ.
( )
;5−∞
Ⓒ.
(
]
;5−∞
.
Ⓓ.
(
]
;2−∞
Lời giải
Chọn C
Ta có:
2
3 6 5y x x m
′
= − + −
Để hàm số
( )
3 2
3 5y x x m x= − + −
đồng biến trên khoảng
( )
2;+∞
thì
( )
0 2;y x
′
≥ ∀ ∈ +∞
[
)
2
3 6 5 0 2;x x m x⇔ − + − ≥ ∀ ∈ +∞
(do hàm số xác định trên
ℝ
nên xác định tại
2x =
)
[
)
2
3 6 5 2;x x m x⇔ − + ≥ ∀ ∈ +∞
( )
[
)
2;f x m x⇔ ≥ ∀ ∈ +∞
[
)
( )
2;
min f x m
+∞
⇔ ≥
Xét
( )
2
3 6 5f x x x= − +
[
)
2;x ∈ +∞
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 21
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
( )
[
)
6 6 0 2;f x x x
′
= − > ∀ ∈ +∞
⇒
Hàm số
( )
2
3 6 5f x x x= − +
đồng biến trên nữa khoảng
[
)
2;+∞
[
)
( ) ( )
2;
min 2 5f x f
+∞
⇒ = =
5m⇒ ≤
Câu 51: (Câu 42 - MĐ 104 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020)
Tập hợp tất cả các giá trị thực
của tham số
m
để hàm số
3
x
y
x m
+
=
+
đồng biến trên khoảng
( )
; 6−∞ −
là
Ⓐ.
(
]
3;6
.
Ⓑ.
( )
3;6
.
Ⓒ.
( )
3;+∞
.
Ⓓ.
[
)
3;6
.
Lời giải
Chọn A
TXĐ:
{ }
\ .D m= −ℝ
Ta có
( )
2
3
.
m
y
x m
−
′
=
+
Để hàm số đồng biến trên khoảng
( )
; 6−∞ −
( )
0 ; 6y x
′
⇔ > ∀ ∈ −∞ −
.
( )
3 0
3 3
3 6.
; 6
6 6
m
m m
m
m
m m
− >
> >
⇔ ⇔ ⇔ ⇔ < ≤
− ∉ −∞ −
− ≥− ≤
Câu 52: (Câu 41 - MĐ 103 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020)
Tìm
m
để hàm số
2x
y
x m
+
=
+
đồng biến trên khoảng
( )
; 5 .
−∞ −
Ⓐ.
(
]
2;5
.
Ⓑ.
[
)
2;5
.
Ⓒ.
( )
2;
+∞
.
Ⓓ.
( )
2;5
.
Lời giải
Chọn A
Điều kiện:
x m≠ −
.
Ta có:
( )
2
2
'
m
y
x m
−
=
+
.
Hàm số đồng biến trên khoảng
( )
( )
' 0
2 0
; 5 2 5.
; 5
5
y
m
m
m
m
>
− >
−∞ − ⇔ ⇔ ⇔ < ≤
− ∉ −∞ −
− ≥ −
Vậy
(
]
2;5
m∈
.
Câu 53: (Câu 40 - MĐ 101 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020)
Tập hợp tất cả các giá trị thực
của tham số
m
để hàm số
4x
y
x m
+
=
+
đồng biến trên khoảng
( )
; 7−∞ −
là
Ⓐ.
[
)
4;7
.
Ⓑ.
(
]
4;7
.
Ⓒ.
( )
4;7
.
Ⓓ.
( )
4;+ ∞
.
Lời giải
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 22
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Chọn B
Tập xác định:
{ }
\D m= −ℝ
.
( )
2
4
'
m
y
x m
−
=
+
.
Hàm số đồng biến trên khoảng
( )
;7−∞
⇔
( )
' 0
4
4 7
; 7
7
y
m
m
m
m
>
>
⇔ ⇔ < ≤
− ∉ −∞ −
− ≥ −
.
Vậy
(
]
4;7m ∈
thì hàm số đồng biến trên khoảng
( )
; 7−∞ −
.
Câu 54: (Câu 41 - ĐTK - BGD&ĐT - Lần 2 - Năm 2019 - 2020)
Có bao nhiêu giá trị nguyên của tham
số
m
sao cho hàm số
( )
3 2
1
4 3
3
f x x mx x= + + +
đồng biến trên
ℝ
?
Ⓐ.
5
.
Ⓑ.
4
.
Ⓒ.
3
.
Ⓓ.
2
.
Lời giải
Chọn A
* TXĐ:
D = ℝ
.
* Ta có:
( )
2
2 4f x x mx
′
= + +
Để hàm số đồng biến trên
ℝ
điều kiện là
( )
2
0; 4 0 2 2f x x m m
′ ′
≥ ∀ ∈ ⇔ ∆ = − ≤ ⇔ − ≤ ≤ℝ
mà
m∈ℤ
{ }
2; 1;0;1;2m⇒ ∈ − −
.
Câu 55: (Câu 39 - ĐTK - BGD&ĐT - Lần 1 - Năm 2019 - 2020)
Cho hàm số hàm số
( )
4mx
f x
x m
−
=
−
(
m
là tham số thực). Có bao nhiêu giá trị nguyên của
m
để hàm số đã cho đồng biến trên khoảng
( )
0;
+∞
?
Ⓐ.
5
.
Ⓑ.
4
.
Ⓒ.
3
.
Ⓓ.
2
.
Lời giải
Chọn D
Điều kiện xác định:
x m≠
.
Ta có
( )
2
2
4m
y
x m
− +
′
=
−
.
Để hàm số đồng biến trên khoảng
( )
0;
+∞
thì
( )
2
0
2 2
4 0
0;
0
0
y
m
m
m
m
m
′
>
− < <
− + >
⇔ ⇔ ⇔
∉ +∞
≤
≤
2 0m⇔ − < ≤
.
Do
m
nguyên nên
= − =1; 0m m
. Vậy có
2
giá trị nguyên của
m
thỏa mãn.
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 23
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Câu 56: (Câu 38 - MĐ 103 - BGD&ĐT - Năm 2018 - 2019)
Cho hàm số
( )
f x
, hàm số
( )
y f x
′
=
liên
tục trên
ℝ
và có đồ thị như hình vẽ bên.
Bất phương trình
( )
2f x x m< +
(
m
là tham số thực) nghiệm đúng với mọi
( )
0;2x ∈
khi và chỉ khi
Ⓐ.
( )
0
m f
>
.
Ⓑ.
( )
2 4m f> −
.
Ⓒ.
( )
0m f≥
.
Ⓓ.
( )
2 4
m f
≥ −
.
Lời giải
Chọn C
Ta có
( ) ( )
2 2f x x m m f x x< + ⇔ > −
( )
*
.
Xét hàm số
( ) ( )
2g x f x x= −
trên
( )
0;2
.
Ta có
( ) ( )
2 0g x f x
′ ′
= − <
( )
0;2x∀ ∈
nên hàm số
( )
g x
nghịch biến trên
( )
0;2
.
Do đó
( )
*
đúng với mọi
( )
0;2x ∈
khi
( ) ( )
0 0m g f≥ =
.
Câu 57: (Câu 35 - MĐ 102 - BGD&ĐT - Năm 2018 - 2019)
Cho hàm số
( )
f x
, bảng xét dấu
( )
f x
′
như sau:
Hàm số
( )
5 2y f x= −
nghịch biến trên khoảng nào dưới đây?
Ⓐ.
( )
2;3
.
Ⓑ.
( )
0;2
.
Ⓒ.
( )
3;5
.
Ⓓ.
( )
5;+∞
.
Lời giải
Chọn B
Xét hàm số
( )
5 2y f x= −
.
( ) ( )
5 2 2 5 2y f x f x
′
′ ′
= − = − −
.
Xét bất phương trình:
( )
3 5 2 1 3 4
0 5 2 0
5 2 1 2
x x
y f x
x x
− < − < − < <
′ ′
< ⇔ − > ⇔ ⇔
− > <
.
Suy ra hàm số
( )
5 2y f x= −
nghịch biến trên các khoảng
( )
;2−∞
và khoảng
( )
3;4
.
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 24
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Vì
( ) ( )
0;2 ;2⊂ −∞
nên chọn đáp án B
Câu 58: (Câu 35 - MĐ 101 - BGD&ĐT - Năm 2018 - 2019)
Cho hàm số
( )
f x
, bảng xét dấu của
( )
′
f x
như sau:
Hàm số
( )
3 2
= −y f x
nghịch biến trên khoảng nào dưới đây?
Ⓐ.
( )
4;
+ ∞
.
Ⓑ.
( )
2;1
−
.
Ⓒ.
( )
2;4
.
Ⓓ.
( )
1;2
.
Lời giải
Chọn B
Ta có
( ) ( )
3 3 2 1 3 2
2 3 2 0 3 2 0
3 2 1 1
− < − < − > >
′ ′ ′
= − − < ⇔ − > ⇔ ⇔
− > <
x x
y f x f x
x x
.
Vì hàm số nghịch biến trên khoảng
( )
;1
−∞
nên nghịch biến trên
( )
2;1
−
.
Câu 59: (Câu 36 - ĐTK - BGD&ĐT - Năm 2018 - 2019)
Tập hợp các giá trị thực của
m
để hàm số
( )
3 2
6 4 9 4
y x x m x= − − + − +
nghịch biến trên khoảng
( )
; 1
−∞ −
là
Ⓐ.
(
]
;0
−∞
.
Ⓑ.
3
;
4
− +∞
.
Ⓒ.
3
;
4
−∞ −
.
Ⓓ.
[
)
0;
+∞
Lời giải
Chọn C
+ TXĐ:
ℝ
.
Ta có
( )
' 2
3 12 4 9
y x x m= − − + −
.
Hàm số
( )
3 2
6x 4 9 4
y x m x= − − + − +
nghịch biến trên khoảng
( )
; 1
−∞ −
khi và chỉ khi
( ) ( )
2
3 12 4 9 0, ; 1
y x x m x
′
= − − + − ≤ ∀ ∈ −∞ −
( )
2
4 3 12 9, ; 1m x x x⇔ ≤ + + ∀ ∈ −∞ −
.
+ Xét hàm
( ) ( )
2
3 12 9, ; 1
g x x x x
= + + ∈ −∞ −
;
( ) ( )
6 12; g' 0 2
g x x x x
′
= + = ⇔ = −
.
+ BBT
+ Từ bảng biến thiên suy ra
3
4 3
4
m m
≤ − ⇔ ≤ −
.
Câu 60: (Câu 26 - MĐ 104 - BGD&ĐT - Năm 2017 - 2018)
Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
3
x
y
x m
+
=
+
đồng biến trên khoảng
( )
; 6−∞ −
?
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 25
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Ⓐ.
2
Ⓑ.
6
Ⓒ.
Vô số
Ⓓ.
1
Lời giải
Chọn A
Tập xác định:
( ) ( )
; 3 3 ;D m m= −∞ − ∪ − +∞
.
Ta có
( )
2
3 2
3
m
y
x m
−
′
=
+
Hàm số đổng biến trên khoảng
( )
; 6−∞ −
2
3 2 0
3
6 3
2
m
m
m
m
− >
>
⇔ ⇔
− ≤ −
≤
2
2
3
m
⇔ < ≤ .
Mà
m
nguyên nên
{ }
1;2m =
.
Câu 61: (Câu 31 - MĐ 103 - BGD&ĐT - Năm 2017 - 2018)
Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
1
3
x
y
x m
+
=
+
nghịch biến trên khoảng
( )
6;+∞
?.
Ⓐ.
3.
Ⓑ.
Vô số.
Ⓒ.
0 .
Ⓓ.
6
Lời giải
Chọn A
Tập xác định
{ }
\ 3
D m
= −
ℝ
;
( )
2
3 1
3
m
y
x m
−
′
=
+
.
Hàm số
1
3
x
y
x m
+
=
+
nghịch biến trên khoảng
( )
6;+∞
khi và chỉ khi:
( )
0
6;
y
D
′
<
+∞ ⊂
3 1 0
3 6
m
m
− <
⇔
− ≤
1
3
2
m
m
<
⇔
≥ −
1
2
3
m
⇔ − ≤ <
.
Vì
m ∈ ℤ
{ }
2; 1;0
m
⇒ ∈ − −
.
Câu 62: (Câu 35 - MĐ 101 - BGD&ĐT - Năm 2017 - 2018)
Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
5
x
y
x m
+
=
+
đồng biến trên khoảng
( )
; 10−∞ −
?
Ⓐ.
2
Ⓑ.
Vô số
Ⓒ.
1
Ⓓ.
3
Lời giải
Chọn A
TXĐ:
{ }
\ 5D m= −ℝ
.
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 26
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
( )
2
5 2
'
5
m
y
x m
−
=
+
.
Hàm số đồng biến trên khoảng
( )
; 10−∞ −
khi và chỉ khi
[
)
5 2 0
5 10;
m
m
− >
− ∈ − +∞
2
5
5 10
m
m
>
⇔
− ≥ −
2
2
5
m⇔ < ≤ .
Vì
m
nguyên nên
{ }
1;2m ∈
. Vậy có
2
giá trị của tham số
m
.
Câu 63: (Câu 39 - ĐTK - BGD&ĐT - Năm 2017 - 2018)
Cho hàm số
( )=y f x
. Hàm số
'( )=y f x
có
đồ thị như hình bên. Hàm số
(2 )= −y f x
đồng biến trên khoảng
Ⓐ.
( )
1;3
Ⓑ.
( )
2;
+∞
Ⓒ.
( )
2;1
−
Ⓓ.
( )
; 2
−∞ −
Lời giải
Chọn C
Cách
1:
Ta thấy
'( ) 0f x <
với
(1;4)
1
∈
< −
x
x
nên
( )f x
nghịch biến trên
( )
1;4
và
( )
; 1
−∞ −
suy ra
( ) ( )g x f x= −
đồng biến trên
( 4; 1)− −
và
( )
1;
+∞
. Khi đó
(2 )−f x
đồng biến biến trên khoảng
( 2;1)−
và
( )
3;
+∞
Cách
2:
Dựa vào đồ thị của hàm số
( )
y f x
′
=
ta có
( )
1
0
1 4
x
f x
x
< −
′
< ⇔
< <
.
Ta có
( )
( )
( ) ( ) ( )
2 2 . 2 2f x x f x f x
′
′
′ ′
− = − − = − −
.
Để hàm số
( )
2
y f x= −
đồng biến thì
( )
( )
( )
2 0 2 0f x f x
′
′
− > ⇔ − <
2 1 3
1 2 4 2 1
x x
x x
− < − >
⇔ ⇔
< − < − < <
.
Câu 64: (Câu 41 - MĐ 104 - BGD&ĐT - NĂM 2016 - 2017)
Cho hàm số
4mx m
y
x m
+
=
+
với
m
là tham
số. Gọi S là tập hợp tất cả các giá trị nguyên của
m
để hàm số nghịch biến trên các khoảng xác
định. Tìm số phần tử của
S
.
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 27
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Ⓐ.
5.
Ⓑ.
4
.
Ⓒ.
Vô số.
Ⓓ.
3.
Lời giải
Chọn D
{ }
\
D m
= −
ℝ
;
( )
2
2
4m m
y
x m
−
′
=
+
Hàm số nghịch biến trên các khoảng xác định khi
0,
y x D
′
< ∀ ∈
2
4 0
m m
⇔ − <
0 4m⇔ < <
Mà m∈ℤ nên có 3 giá trị thỏ
Ⓐ.
Câu 65: (Câu 31 - MĐ 103 - BGD&ĐT - NĂM 2016 - 2017)
Cho hàm số
2 3− −
=
−
mx m
y
x m
với m là
tham số. Gọi
S
là tập hợp tất cả các giá trị nguyên của
m
để hàm số đồng biến trên các khoảng
xác định. Tìm số phần tử của
S
.
Ⓐ.
5
.
Ⓑ.
4
.
Ⓒ.
Vô số.
Ⓓ.
3
.
Lời giải
Chọn D
Ta có
Để hàm số đồng biến trên từng khoảng xác định thì
Xét tại
thấy không thỏa mãn. Vậy
Câu 66: (Câu 38 - MĐ 101 - BGD&ĐT - Năm 2016 - 2017)
Cho hàm số
3 2
(4 9) 5y x mx m x= − − + + +
với m là tham số. Có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng
( ; )−∞ +∞
?
Ⓐ.
7
Ⓑ.
4
Ⓒ.
6
Ⓓ.
5
Lời giải
Chọn A
′
= = − − + +ℝ
2
, 3 2 4 9D y x mx m
Hàm số nghịch biến trên
( )
;
−∞ +∞
′ ′
⇔ ≤ ∀ ∈ ⇔ ∆ ≤
ℝ
0, 0y x
2
12 27 0 9 3m m m
⇔ + + ≤ ⇔ − ≤ ≤ −
Mà
{ }
∈ ⇒ ∈ − − − − − − −ℤ
9; 8; 7; 6; 5; 4; 3m m
Câu 67: (Câu 41 - ĐTK - BGD&ĐT - Năm 2016 - 2017)
Hỏi có bao nhiêu số nguyên
m
để hàm số
( )
( )
2 3 2
1 1 4y m x m x x= − + − − +
nghịch biến trên khoảng
( )
;−∞ +∞
.
Ⓐ.
2
Ⓑ.
1
Ⓒ.
0
Ⓓ.
3
Lời giải
Chọn A
2
2
2 3
'
( )
=
−
m m
y
x m
2
' 0 2 3 0 [-1;3]
≥ ⇔ − + + ≥ ⇔ ∈
y m m m
1; 3
= − =
m m
0; 1; 2.
= = =
m m m
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 28
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
TH1:
1m =
. Ta có:
4y x= − +
là phương trình của một đường thẳng có hệ số góc âm nên hàm
số luôn nghịch biến trên ℝ . Do đó nhận
1m =
.
TH2:
1m = −
. Ta có:
2
2 4y x x= − − +
là phương trình của một đường Parabol nên hàm số không
thể nghịch biến trên
ℝ
. Do đó loại
1m = −
.
TH3:
1m ≠ ±
. Khi đó hàm số nghịch biến trên khoảng
( )
;−∞ +∞
0y x
′
⇔ ≤ ∀ ∈ ℝ
, dấu “=” chỉ
xảy ra ở hữu hạn điểm trên
ℝ
.
( )
( )
2 2
3 1 2 1 1 0m x m x⇔ − + − − ≤
,
x∀ ∈ ℝ
( )
( )
( )( )
2
2
2
2
1 1
1 0
1 0
0
1
1
1
0
2
11 4 2 0
1 3 1 0
2
m
m
m
a
m
mm m
m m
− < <
− <
− <
<
⇔ ⇔ ⇔ ⇔ ⇔ − ≤ <
′
∆ ≤
− ≤ ≤− + ≤
− + − ≤
.
Vì
m∈ℤ
nên
0m =
.
Vậy có
2
giá trị
m
nguyên cần tìm là
0m=
hoặc
1m =
.
Câu 68: (Câu 9 - ĐTN - BGD&ĐT - Năm 2016 - 2017)
Tìm tập hợp tất cả các giá trị thực của tham số
m
để hàm số
( )
2
y ln 1 1x mx= + − +
đồng biến trên khoảng
( )
;−∞ +∞
Ⓐ.
(
]
; 1−∞ −
Ⓑ.
( )
; 1−∞ −
Ⓒ.
[ ]
1;1−
Ⓓ.
[
)
1;+∞
Lời giải
Chọn A
Ta có:
2
2
1
x
y m
x
′
= −
+
.
Hàm số
( )
2
ln 1 1y x mx= + − +
đồng biến trên khoảng
( )
;−∞ +∞
⇔
( )
0, ;
y x
′
≥ ∀ ∈ −∞ +∞
.
⇔
( )
2
2
( ) , ;
1
x
g x m x
x
= ≥ ∀ ∈ −∞ +∞
+
. Ta có
( )
2
2
2
2 2
( ) 0 1
1
x
g x x
x
− +
′
= = ⇔ = ±
+
Bảng biến thiên:
Câu 69:
Dựa vào bảng biến thiên ta có:
( )
2
2
( ) , ;
1
x
g x m x
x
= ≥ ∀ ∈ −∞ +∞
+
⇔
1m ≤ −
(Câu 43 - MĐ 101 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020)
Xét các số thực
,x y
thỏa mãn:
( )
2 2
1 2 2
2 2 2 .4
+ +
≤ + − +
x y x
x y x
. Giá trị nhỏ nhất của biểu thức
4
2 1
=
+ +
y
P
x y
gần nhất
với số
nào dưới đây?
Ⓐ.
2−
.
Ⓑ.
3−
.
Ⓒ.
5−
.
Ⓓ.
4−
.
Lời giải
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 29
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Chọn B
Ta có:
( )
2 2
2 2
1
1 2 2 2 2
2
2 2 2 .4 2 2
4
x y
x y x
x
x y x x y x
+ +
+ +
≤ + − + ⇔ ≤ + − +
( )
( )
2 2
2 1 2 2
2 2 1 1 0 *
x y x
x y x
+ − +
⇔ − + − + − ≤
.
Đặt
( )
2
2 2 2
2 1 1 0= + − + ⇔ = − + ≥t x y x t x y
. Khi đó
( )
*
trở thành
2 1 0
t
t− − ≤
.
Xét hàm số:
( )
2 1= − −
t
f t t
trên
[
)
0;+∞
( ) ( )
2
1
2 ln 2 1 0 log
ln 2
′ ′
= − ⇒ = ⇔ =
t
f t f t t
.
Bảng biến thiên:
Dựa vào bảng biến thiên ta có
( ) ( )
2
2
0 0 1 1 1≤ ⇔ ≤ ≤ ⇔ − + ≤f t t x y
.
Khi đó
2 1 0+ + >x y
và
( )
4
2 4 0
2 1
= ⇔ + − + =
+ +
y
P Px P y P
x y
.
Các cặp
( )
;x y
thỏa mãn:
( )
2
2
1 1− + ≤x y
là tọa độ các điểm
( )
;x y
thuộc hình tròn
( )
C
Tâm
( )
1;0I
, bán kính
1=R
.
Các cặp
( )
;x y
thỏa mãn:
( )
2 4 0+ − + =Px P y P
là tọa độ các điểm
( )
;x y
thuộc
đường thẳng
( ) ( )
: 2 4 0+ − + =d Px P y P
.
Do đó tồn tại giá trị nhỏ nhất của
P
khi đường thẳng
( )
d
phải có điểm chung với hình tròn
( )
C
( )
( )
2
;
2
2
3
1 2 4 0 1 5 1 5
4 4
⇔ ≤ ⇔ ≤ ⇔ + − ≤ ⇔ − − ≤ ≤ − +
+ −
I d
P
d R P P P
P P
.
Vậy
min 1 5 3,24= − − ≈ −P
.
Dấu bằng xảy ra khi
( )
;x y
là tọa độ tiếp điểm của đường thẳng
( )
d
với hình tròn
( )
C
.
Câu 70: (Câu 50 - MĐ 101 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020)
Có bao nhiêu cặp số nguyên
dương
( )
,m n
sao cho 14
m n
+ ≤ và ứng với mỗi cặp
( )
,m n
tồn tại đúng ba số thực
( )
1;1a ∈ −
thỏa mãn
(
)
2
2 ln 1
m
a n a a= + + ?
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 30
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Ⓐ.
14
.
Ⓑ.
12
.
Ⓒ.
11
.
Ⓓ.
13.
Lời giải
Chọn C
Xét phương trình:
(
)
( )
2
2 ln 1 1
m
a n a a= + +
.
+ Nhận xét:
0a =
là một nghiệm của phương trình
( )
1
.
+ Với
0a ≠
, phương trình
( )
(
)
( )
2
ln 1
2
1 *
m
a a
n a
+ +
⇔ =
.
Xét hàm số:
( )
( )
2
ln 1
m
a a
f a
a
+ +
=
trên
( )
1;1−
;
( )
(
)
2
2
1
ln 1
1
m
a
m a a
a
f a
a
+
− + +
+
′
=
.
Xét phương trình
(
)
( )
2
2
ln 1 0 2
1
a
m a a
a
− + + =
+
.
Xét hàm số
( )
(
)
2
2
ln 1
1
a
g a m a a
a
= − + +
+
trên
( )
1;1−
.
( )
(
)
( ) ( )
2
3
2
2
1
0, 1;1 ; *
1
1
m a
g a g a a m
a
a
−
′ ′
= − ⇒ ≤ ∀ ∈ − ∈
+
+
ℕ
.
Suy ra hàm số
( )
g a
nghịch biến trên khoảng
( )
1;1−
.
Do đó, phương trình
( )
2
có nghiệm duy nhất
0a =
.
+ Trường hợp 1:
m
chẵn.
Phương trình đã cho có 3 nghiệm phân biệt thuộc khoảng
( )
1;1−
khi và chỉ khi phương trình
( )
*
có
2
nghiệm phân biệt khác
0
thuộc khoảng
( )
1;1−
Dựa vào bảng biến thiên, ta thấy với
n
nguyên dương phương trình
( )
2
f a
n
=
không có hai
nghiệm phân biệt. Suy ra loại trường hợp
m
chẵn.
+ Trường hợp 2:
m
lẻ và
1m ≠
.
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 31
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Phương trình đã cho có
3
nghiệm phân biệt thuộc khoảng
( )
1;1−
khi và chỉ khi phương trình
( )
*
có hai nghiệm phân biệt khác
0
thuộc khoảng
( )
1;1−
( )
( )
1
2 2
ln 1 2
2
ln 1 2
n
n
n
n
=
⇔ > + ⇔ < ⇔
=
+
.
Với
1n =
,
m
lẻ và
1m ≠
, 1 14m + ≤ suy ra
{ }
3;5;7;9;11;13m ∈
.
Với
2n =
,
m
lẻ và
1m ≠
, 2 14m + ≤ suy ra
{ }
3;5;7;9;11m ∈
.
+ Trường hợp 3:
1m =
.
Phương trình đã cho có
3
nghiệm phân biệt thuộc khoảng
( )
1;1−
khi và chỉ khi phương trình
( )
*
có hai nghiệm phân biệt khác
0
thuộc khoảng
( )
1;1−
( )
( )
2 2
ln 1 2 1 2
ln 1 2
n
n
⇔ + < < ⇔ < <
+
suy ra không tồn tại số tự nhiên
n
thỏa mãn.
Vậy có 11 cặp
( )
;m n
thỏa mãn yêu cầu bài toán.
Câu 71: (Câu 50 - ĐTK - BGD&ĐT - Lần 1 - Năm 2019 - 2020)
Cho hàm số
( )
f x
. Hàm số
( )
y f x
′
=
có đồ thị như hình sau.
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 32
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Hàm số
( ) ( )
2
1 2g x f x x x= − + −
nghịch biến trên khoảng nào dưới đây?
Ⓐ.
3
1;
2
.
Ⓑ.
1
0;
2
.
Ⓒ.
( )
2; 1− −
.
Ⓓ.
( )
2;3
.
Lời giải
Chọn A
Ta có
( ) ( )
2 1 2 2 1g x f x x
′ ′
= − − + −
( ) ( ) ( )
2 1
0 2 1 2 2 1 0 1 2
2
x
g x f x x f x
−
′ ′ ′
< ⇔ − − + − < ⇔ − >
(*).
Đặt
1 2t x= −
, ta có đồ thị hàm số
( )
y f t
′
=
và
2
t
y = − như hình vẽ sau :
( ) ( )
1 3
2 0 2 1 2 0
2 2
*
4 1 2 4 3
2
2
x
t x
t
f t
t x
x
< <
− < < − < − <
′
⇔ > − ⇒ ⇔ ⇔
> − >
< −
.
⇒
hàm số nghịch biến trên khoảng
1 3
;
2 2
và
3
;
2
−∞ −
Cách
2:
Ta có:
( ) ( )
2
1 2g x f x x x= − + −
( ) ( )
2 1 2 2 1g x f x x
′ ′
⇒ = − − + −
.
( ) ( )
1 2
0 ' 1 2
2
x
g x f x
−
′
= ⇔ − = −
.
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 33
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Xét sự tương giao của đồ thị hàm số
( )
y f t
′
=
và
2
t
y = − .
Từ đồ thị ta có:
( )
2
' 0
2
4
t
t
f t t
t
= −
= − ⇔ =
=
. Khi đó:
( )
3
2
1 2 2
1
0 1 2 0
2
1 2 4
3
2
x
x
g x x x
x
x
=
− = −
′
= ⇔ − = ⇔ =
− =
= −
.
Ta có bảng xét dấu:
Câu 72:
Dựa vào bảng xét dấu, ta thấy: hàm số nghịch biến trên các khoảng
3
;
2
−∞ −
và
1 3
;
2 2
.
(Câu
48 - ĐTK - BGD&ĐT - Năm 2018 - 2019)
Cho hàm số
( )
y f x
=
có bảng xét dấu của đạo hàm
như sau:
Hàm số
( )
3
3 2 3
y f x x x
= + − +
đồng biến trên khoảng nào dưới đây?
Ⓐ.
( )
1; +∞
.
Ⓑ.
( )
; 1−∞ −
.
Ⓒ.
( )
1;0−
.
Ⓓ.
( )
0;2
.
Lời giải
Chọn C
Cách
1:
Ta có
( ) ( )
2 2
0 3 2 3 3 0 2 1y f x x f x x
′ ′ ′
> ⇔ + − + > ⇔ + > −
.
Đặt
2,t x= +
bất phương trình trở thành:
2
( ) ( 2) 1f t t
′
> − − .
Xét hệ bất phương trình
( )
( )
2
2 1 0
, .
( ) 0
t
I
f t
− − <
′
>
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 34
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Ta có
( )
1 2 1 1 3
1 2 1 2
1 2
2 3 2 3
2 3
4 4
t t
t t
t
I
t t
t
t t
− < − < < <
< < < <
< <
⇔ ⇔ ⇔
< < < <
< <
> >
.
Khi đó
1 2 2 1 0
2 2 3 0 1
x x
x x
< + < − < <
⇔
< + < < <
.
Vậy hàm số đã cho đồng biến trên các khoảng
( )
1;0−
.
Cách
2:
Xét hàm số
( )
3
3 2 3
y f x x x
= + − +
( ) ( )
( )
2 2
3 2 3 3 3 2 1y f x x f x x
′ ′ ′
= + − + = + + −
.
Ta có
3 7 5
3 0
2 2 4
y f
′ ′
= − <
nên loại đáp án A,
D
( ) ( )
2 3 0 3 0y f
′ ′
− = − <
nên loại đáp án B
Vậy ta chọn đáp án C
Câu 73: (Câu 46 - MĐ 104 - BGD&ĐT - Năm 2017 - 2018)
Cho hai hàm số
( )y f x=
,
( )y g x=
. Hai
hàm số
( )y f x
′
=
và
( )y g x
′
=
có đồ thị như hình vẽ dưới đây, trong đó đường cong đậm hơn là
đồ thị hàm số
( )y g x
′
=
. Hàm số
5
( ) ( 6) 2
2
h x f x g x
= + − +
đồng biến trên khoảng nào dưới
đây?
Ⓐ.
21
;
5
+∞
Ⓑ.
1
;1
4
Ⓒ.
21
3;
5
Ⓓ.
17
4;
4
Lời giải
Chọn B
Ta có
5
( ) ( 6) 2 2
2
h x f x g x
′ ′ ′
= + − +
.
Nhìn vào đồ thị của hai hàm số
( )y f x
′
=
và
( )y g x
′
=
ta thấy trên khoảng
(3;8)
thì
( ) 5g x
′
<
và
( ) 10f x
′
>
. Do đó
( ) 2 ( )f x g x
′ ′
>
.
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 35
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Như vậy:
5
2 5
2
g x
′
+ <
nếu
5 1 11
3 2 8
2 4 4
x x< + < ⇔ < <
.
( 6) 10f x
′
+ >
nếu 3 6 8 3 2x x< + < ⇔ − < < .
Suy ra trên khoảng
1
;2
4
thì
5
2 5
2
g x
′
+ <
và
( 7) 10f x
′
+ >
hay
( ) 0h x
′
>
.
Tức là trên khoảng
1
;1
4
hàm số
( )h x
đồng biến.
Câu 74: (Câu 44 - MĐ 103 - BGD&ĐT - Năm 2017 - 2018)
Cho hai hàm số
( )
y f x
=
,
( )
y g x
=
. Hai
hàm số
( )
y f x
′
=
và
( )
y g x
′
=
có đồ thị như hình vẽ bên
trong đó đường cong đậm hơn là đồ thị của hàm số
( )y g x
′
=
. Hàm số
( ) ( )
7
3 2
2
h x f x g x
= + − −
đồng
biến trên khoảng nào dưới đây?
Ⓐ.
13
;4
4
.
Ⓑ.
29
7;
4
.
Ⓒ.
36
6;
5
.
Ⓓ.
36
;
5
+∞
Lời giải
Chọn A
Cách 1. Ta thấy
'( ) 2 '( )f x g y>
với mọi
(3 8) ;x ∈
và mọi
y ∈ ℝ
.
Suy ra
7
'( 3) 2 ' 2 0
2
f x g x
+ − − >
với mọi
3 (3;8) x + ∈
hay
(0 5) ;x ∈
.
Cách 2. Ta có:
25
3 ;7 ( 7) 10
4
13
;4 ( ) 0
4
7 9 7
2 3; 2 5
2 2 2
x f x
x h x
x g x
′
+ ∈ ⇒ + >
′
∈ ⇒ ⇒ >
′
− ∈ ⇒ − <
( )
h x
⇒
đồng biến trên
13
;4
4
.
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 36
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Câu 75: (Câu 47 - MĐ 102 - BGD&ĐT - Năm 2017 - 2018)
Cho hai hàm số
( )
y f x
=
và
( )
y g x
=
.
Hai hàm số
( )
y f x
′
=
và
( )
y g x
′
=
có đồ thị như hình vẽ dưới đây, trong đó đường cong
đậm
hơn
là đồ thị hàm số
( )
y g x
′
=
. Hàm số
( ) ( )
9
7 2
2
h x f x g x
= + − +
đồng biến trên khoảng
nào dưới đây?
Ⓐ.
16
2;
5
.
Ⓑ.
3
;0
4
−
.
Ⓒ.
16
;
5
+∞
.
Ⓓ.
13
3;
4
Lời giải
Chọn B
Ta có
( ) ( )
9
7 2 2
2
h x f x g x
′ ′ ′
= + − +
.
Nhìn vào đồ thị của hai hàm số
( )
y f x
′
=
và
( )
y g x
′
=
ta thấy trên khoảng
( )
3;8
thì
( )
5
g x
′
<
và
( )
10
f x
′
>
. Do đó
( ) ( )
2
f x g x
′ ′
>
.
Như vậy:
9
2 5
2
g x
′
+ <
nếu
9 3 7
3 2 8
2 4 4
x x< + < ⇔ − < <
.
( )
7 10
f x
′
+ >
nếu
3 7 8 4 1x x< + < ⇔ − < <
.
Suy ra trên khoảng
3
;1
4
−
thì
9
2 5
2
g x
′
+ <
và
( )
7 10
f x
′
+ >
hay
( )
0
h x
′
>
.
Tức là trên khoảng
3
;0
4
−
hàm số
( )
h x
đồng biến.
Câu 76: (Câu 50 - MĐ 101 -
Ⓑ
G
Ⓓ
&ĐT - Năm 2017 - 2018)
Cho hai hàm số
( ) ( )
,y f x y g x= =
. Hai
hàm số
( )
y f x
′
=
và
( )
y g x
′
=
có đồ thị như hình vẽ bên, trong đó
đường
cong
đậm
hơn
là
đồ thị của hàm số
( )
y g x
′
=
.
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 37
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Hàm số
( ) ( )
3
4 2
2
h x f x g x
= + − −
đồng biến trên khoảng nào dưới đây?
Ⓐ.
31
5;
5
Ⓑ.
9
;3
4
Ⓒ.
31
;
5
+∞
Ⓓ.
25
6;
4
Lời giải
Chọn B
Ta có
( ) ( )
3
4 2 2
2
h x f x g x
′ ′ ′
= + − −
.
Hàm số
( ) ( )
3
4 2
2
h x f x g x
= + − −
đồng biến
( )
0h x
′
⇔ ≥
( )
3
4 2 2 0
2
f x g x
′ ′
⇔ + − − ≥
( )
3
4 2 2
2
f x g x
′ ′
⇔ + ≥ −
3 4 8
3
3 2 8
2
x
x
≤ + ≤
⇔
≤ − ≤
1 4
3 3
3 2 8
2 2
x
x
− ≤ ≤
⇔
+ ≤ ≤ +
1 4
9 19
2
2 2
x
x
− ≤ ≤
⇔
≤ ≤
1 4
9 19
4 4
x
x
− ≤ ≤
⇔
≤ ≤
9 19
4 4
x⇔ ≤ ≤
.
Câu 77:
Câu này giải em không biết chỉnh sửa như thế nào!
(Câu 11 - ĐMH - BGD&ĐT - Năm 2017 -
2018)
Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
tan 2
tan
x
y
x m
−
=
−
đồng biến trên
khoảng
0; .
4
π
Ⓐ.
0m ≤
hoặc1 2m≤ <
Ⓑ.
0m ≤
Ⓒ.
1 2m≤ <
Ⓓ.
2m ≥
Lời giải
Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
https://www.facebook.com/vietgold
Trang 38
Luyenthitracnghiem.vn
Nguy
%
n Hoàng Vi
)
t
Chọn A
Đặt
tant x=
, vì
( )
0; 0;1
4
x t
π
∈ ⇒ ∈
Xét hàm số
( ) ( )
2
0;1
t
f t t
t m
−
= ∀ ∈
−
. Tập xác định:
{ }
\
D m
=
ℝ
Ta có
( )
( )
2
2 m
f t
t m
−
′
=
−
.
Ta thấy hàm số
( )
tan=
t x x
đồng biến trên khoảng
0;
4
π
. Nên để hàm số
tan 2
tan
x
y
x m
−
=
−
đồng
biến trên khoảng
0;
4
π
khi và chỉ khi:
( ) ( )
0 0;1
f t t
′
> ∀ ∈
( )
( )
( )
(
] [
)
2
2
2 0
2
0 0;1 ;0 1;2
0
0;1
1
m
m
m
t m
m
m
t m
m
<
− >
−
⇔ > ∀ ∈ ⇔ ⇔ ⇔ ∈ −∞ ∪
≤
∉
−
≥
CASIO:
Đạo hàm của hàm số ta được
( ) ( )
( )
2 2
2
1 1
tan tan 2
cos cos
tan
x m x
x x
y
x m
− − −
′
=
−
Ta nhập vào máy tính thằng
y
′
\ CALC\Calc
8
x
π
=
( Chọn giá trị này thuộc
0;
4
π
)
\= \ ?m = 1 giá trị bất kỳ trong 4 đáp án.
Đáp án D 2m ≥ . Ta chọn 3m = . Khi đó
0,17 0y
′
= − <
( Loại)
Đáp án C 1 2m≤ < Ta chọn
1,5m =
. Khi đó
0, 49 0y
′
= >
(nhận)
Đáp án B
0m ≥
Ta chọn
0m =
. Khi đó
13,6 0y
′
= >
(nhận)
Vậy đáp án B và C đều đúng nên chọn đáp án
Ⓐ.
| 1/38
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 BÀI TOÁN TÍNH N I U L uy e TRONG THI BGD n thi t 2016 - 2021 ra cngh
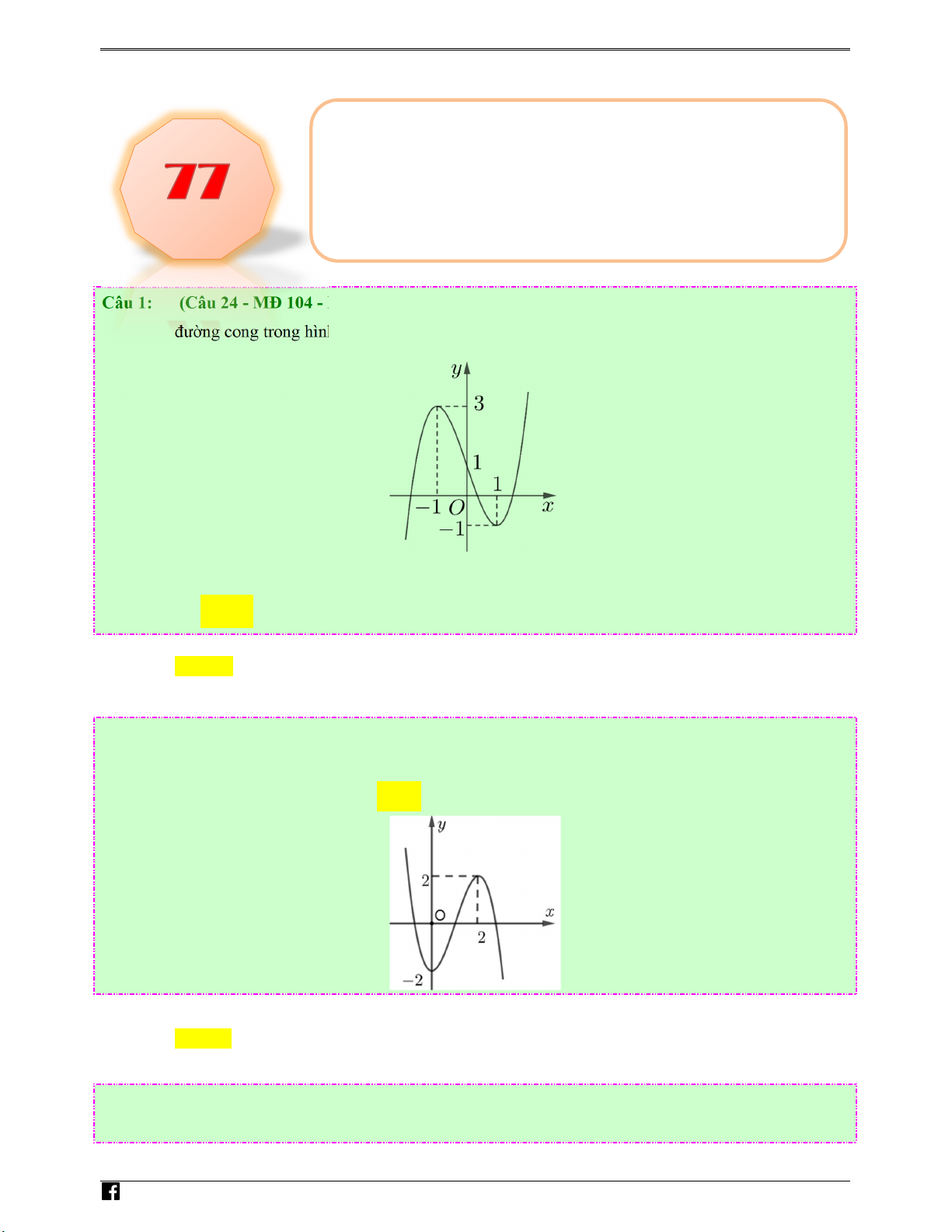
Câu 1: (Câu 24 - MĐ 104 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Cho hàm số y = f ( x) có đồ thị là iem
đường cong trong hình bên. .vn
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? Ⓐ. ( 1 − ; ) 1 . Ⓑ. (1;+∞). Ⓒ. (−∞; ) 1 . Ⓓ. (0;3). Lời giải N Chọn A gu
Quan sát đồ thị ta thầy hàm số đã cho nghịch biến trên khoảng ( 1 − ; ) 1 . y%n
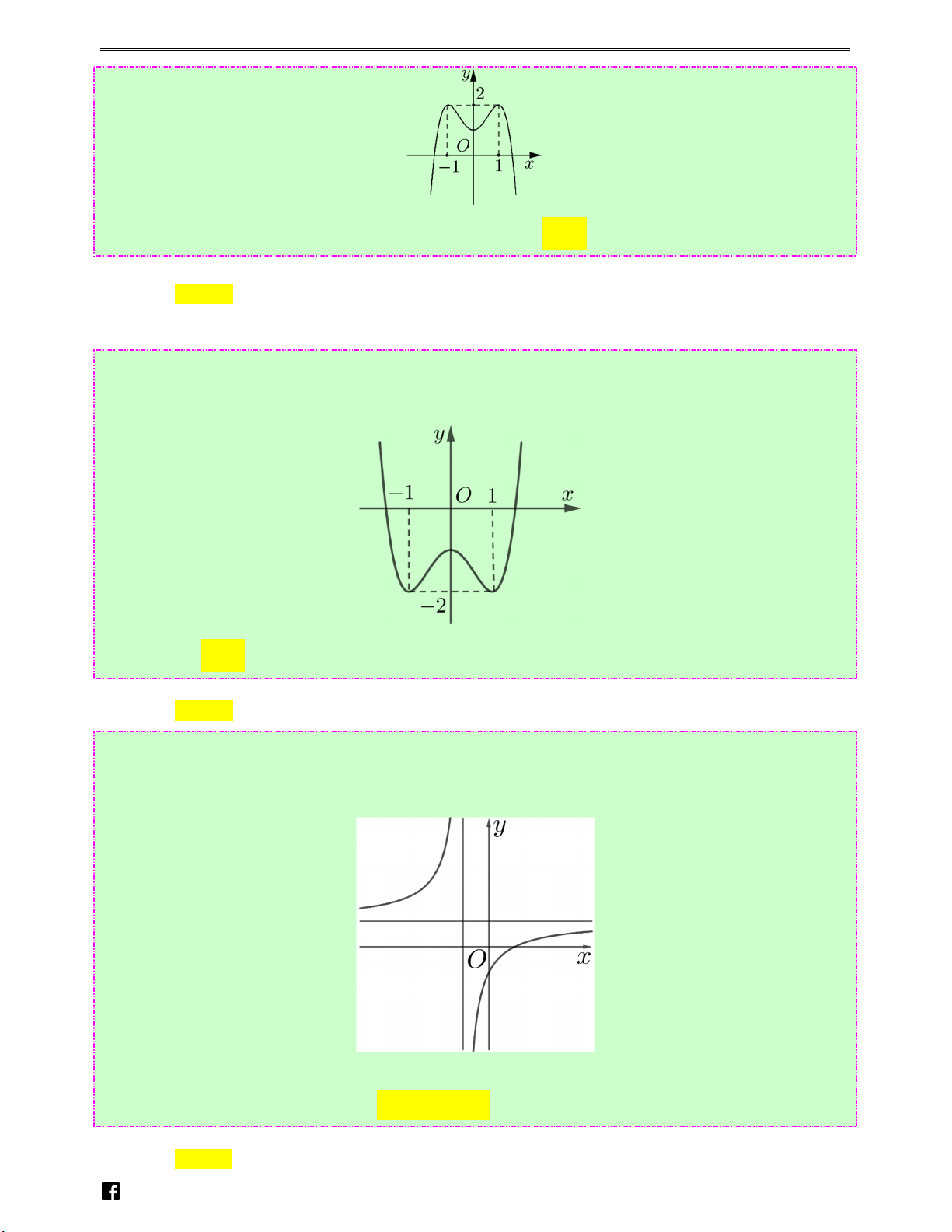
Câu 2: (Câu 15 - MĐ 103 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Cho hàm số y = f (x) có đồ thị là Ho
đường cong trong hình bên. Hàm số đã cho đồng biến trong khoảng nào dưới đây? àng −∞ − +∞ Ⓐ. ( ;2). Ⓑ. (0;2) . Ⓒ. ( 2;2) . Ⓓ. (2; ) . Vi)t Lời giải Chọn B
Dựa vào đồ thị suy ra hàm số đã cho đồng biến trong khoảng (0;2) .
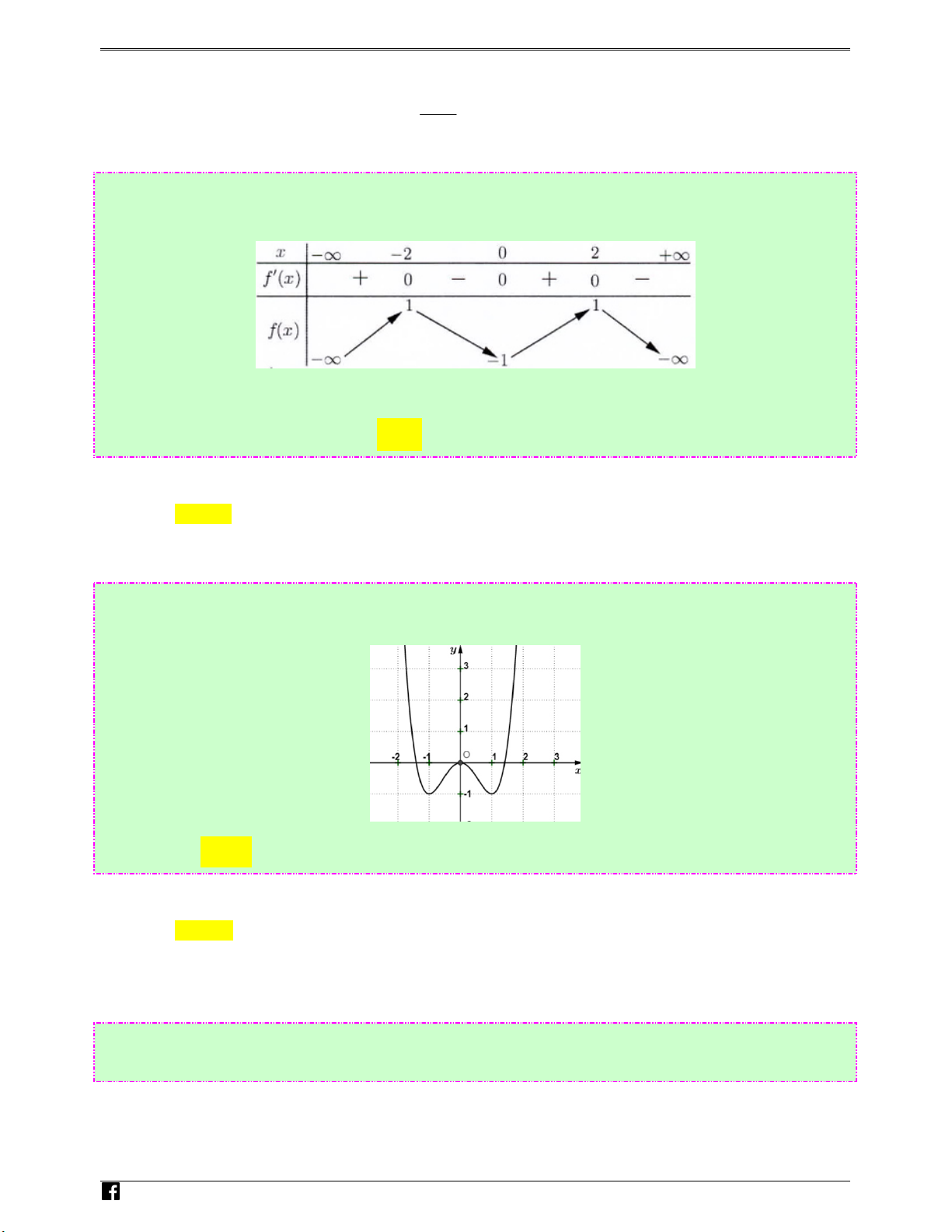
Câu 3: (Câu 8 - MĐ 102 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Cho hàm số y = f ( x) có đồ thị là
đường cong như hình vẽ. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
https://www.facebook.com/vietgold Trang 1 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 Luyen thi Ⓐ. (−1;1) . Ⓑ. (−∞;0). Ⓒ. (0;1) . Ⓓ. (0;+∞). trac Lời giải ng Chọn C hie
Dựa vào đồ thị hàm số y = f ( x) ta thấy hàm số đồng biến trên khoảng (0;1) . m .vn
Câu 4: (Câu 14 - MĐ 101 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Cho hàm số y = f ( x) có đồ thị là
đường cong trong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây? Ⓐ. (0; ) 1 . Ⓑ. (−∞;0). Ⓒ. (0;+∞). Ⓓ. ( 1 − ; ) 1 . N gu Lời giải y% Chọn A n H x + a o
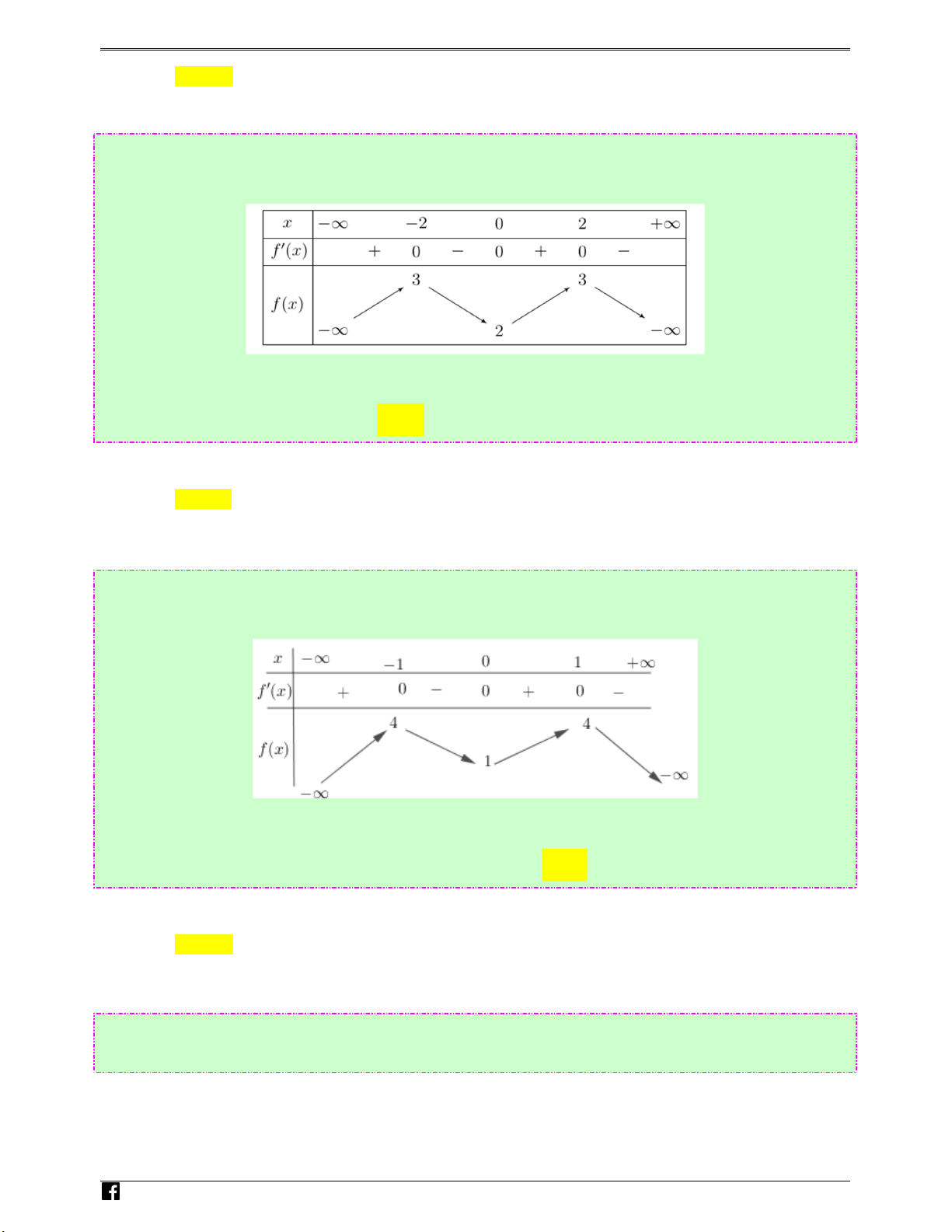
Câu 5: (Câu 29 - MĐ 101 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Biết hàm số y = ( a là số à x +1 ng
thực cho trước, a ≠ 1) có đồ thị như trong hình bên. Vi)t
Mệnh đề nào dưới đây đúng?
Ⓐ. y' < 0, x ∀ ≠ 1 − .
Ⓑ. y ' > 0, ∀x ≠ −1. Ⓒ. y ' < 0, x ∀ ∈ ℝ .
Ⓓ. y ' > 0, x ∀ ∈ ℝ . Lời giải Chọn B
https://www.facebook.com/vietgold Trang 2 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
Tập xác định: D = ℝ \{−1} . +
Dựa vào đồ thị, ta có: Hàm số x a y =
đồng biến trên (−∞; −1) và (−1; +∞) x +1
⇒ y ' > 0, ∀x ≠ −1. Luy
Câu 6: (Câu 3 - Đề Tham Khảo - BGD&ĐT - Năm 2020 - 2021) Cho hàm số có bảng biến e f ( x) nt thiên như sau: hitracnghiem.vn
Hàm số đã cho đồng biến trên khoảng nào, trong các khoảng dưới đây? Ⓐ. (−2;2) . Ⓑ. (0;2) . Ⓒ. (−2;0) . Ⓓ. (2;+∞) . Lời giải Chọn B
Từ bảng biến thiên ta thấy hàm số đồng biến trên khoảng (0;2) .
Câu 7: (Câu 19 - MĐ 103 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Cho hàm số y = f (x) có đồ thị là
đường cong trong hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây N guy%n H oàng Vi)t Ⓐ. (−1;0) Ⓑ. (−∞;− ) 1 . Ⓒ. (0;+∞). Ⓓ. (0; ) 1 . Lời giải Chọn A
Trên khoảng (−1;0) và (1; +∞) hàm số có đồ thị là đường đi lên. Do đó hàm số đã cho đồng
biến trên các khoảng này.
Câu 8: (Câu 23 - MĐ 102 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Cho hàm số y = f ( x) có đồ thị là
đường cong trong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
https://www.facebook.com/vietgold Trang 3 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 Luyenth itra −1; 0 . −∞; −1 . 0;1 . 0;+∞ . c Ⓐ. ( ) Ⓑ. ( ) Ⓒ. ( ) Ⓓ. ( ) ngh Lời giải iem Chọn A .vn
Trên khoảng (−1;0) đồ thị hàm số đi xuống theo hướng từ trái sang phải nên hàm số nghịch
biến trên khoảng này.
Câu 9: (Câu 3 - MĐ 101 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Cho hàm số y = f ( x) có đồ thị là
đường cong trong hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây? N guy Ⓐ. (1;+ ∞). Ⓑ. ( 1 − ;0) . Ⓒ. (0; ) 1 . Ⓓ. (−∞;0). %n H Lời giải oàn Chọn C g V
Hàm số đồng biến trên khoảng (−∞;− ) 1 và (0; ) 1 . i)t
Câu 10: (Câu 16 - MĐ 104 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Cho hàm số y = f ( x) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? Ⓐ. (−3;0) . Ⓑ. (−3;3) . Ⓒ. (0;3). Ⓓ. ( ; −∞ 3 − ) Lời giải
https://www.facebook.com/vietgold Trang 4 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 Chọn A
Từ BBT ta có hàm số f ( x) đồng biến trên hai khoảng (−3;0) và (3;+∞)
Câu 11: (Câu 17 - MĐ 103 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Cho hàm số f ( x) có bảng biến Luy thiên như sau: enthitracnghiem. vn
Hàm số đã cho đồng biến trên khoảng nào dưới đây Ⓐ. ( 2 − ;2) . Ⓑ. (0;2) . Ⓒ. ( 2 − ;0) . Ⓓ. (2;+∞) . Lời giải Chọn B
Nhìn vào bảng biến thiên ta thấy hàm số đồng biến trên các khoảng: (− ; ∞ 2 − ) và (0;2)
Câu 12: (Câu 17 - MĐ 102 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Cho hàm số f ( x) có bảng biến thiên như sau: N guy%n Hoàng Vi)
Hàm số đã cho đồng biến trên khoảng nào dưới đây? t Ⓐ. (1;+∞). Ⓑ. (−1; ) 1 . Ⓒ. (0; ) 1 . Ⓓ. (−1;0) . Lời giải Chọn C
Dựa vào bảng biến thiên ta có hàm số đồng biến trên khoảng (0; ) 1
Câu 13: (Câu 4 - MĐ 101 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Cho hàm số f ( x) có bảng biến thiên như sau:
https://www.facebook.com/vietgold Trang 5 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 Luy en
Hàm số đã cho đồng biến trên khoảng nào dưới đây? thitr − ∞; −1 . 0;1 . 1 − ;1 . −1; 0 . a Ⓐ. ( ) Ⓑ. ( ) Ⓒ. ( ) Ⓓ. ( ) cngh Lời giải iem Chọn D .vn
Dựa vào bảng biến thiên của hàm số f ( x) suy ra hàm số đã cho đồng biến trên khoảng ( 1 − ; 0).
Câu 14: (Câu 10 - ĐTK - BGD&ĐT - Lần 2 - Năm 2019 - 2020) Cho hàm số f (x) có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? Ⓐ. (− ; ∞ − ) 1 . Ⓑ. (0; ) 1 . Ⓒ. ( 1 − ;0) . Ⓓ. (− ; ∞ 0). N g Lời giải uy% Chọn C n H
Nhìn vào bảng biến thiên ta thấy f '( x) < 0 trên các khoảng ( 1
− ;0) và (1;+∞) ⇒ hàm số oàn nghịch biến trên ( 1 − ;0) . g Vi)
Câu 15: (Câu 4 - ĐTK - BGD&ĐT - Lần 1 - Năm 2019 - 2020) Cho hàm số f ( x) có bảng biến thiên t như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? Ⓐ. (1;+∞) . Ⓑ. ( 1 − ;0) . Ⓒ. ( 1 − ; ) 1 . Ⓓ. (0; ) 1 . Lời giải Chọn D
Hàm số đã cho đồng biến trên mỗi khoảng (−∞;− ) 1 và (0; ) 1 .
https://www.facebook.com/vietgold Trang 6 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 Ta chọn phương án D
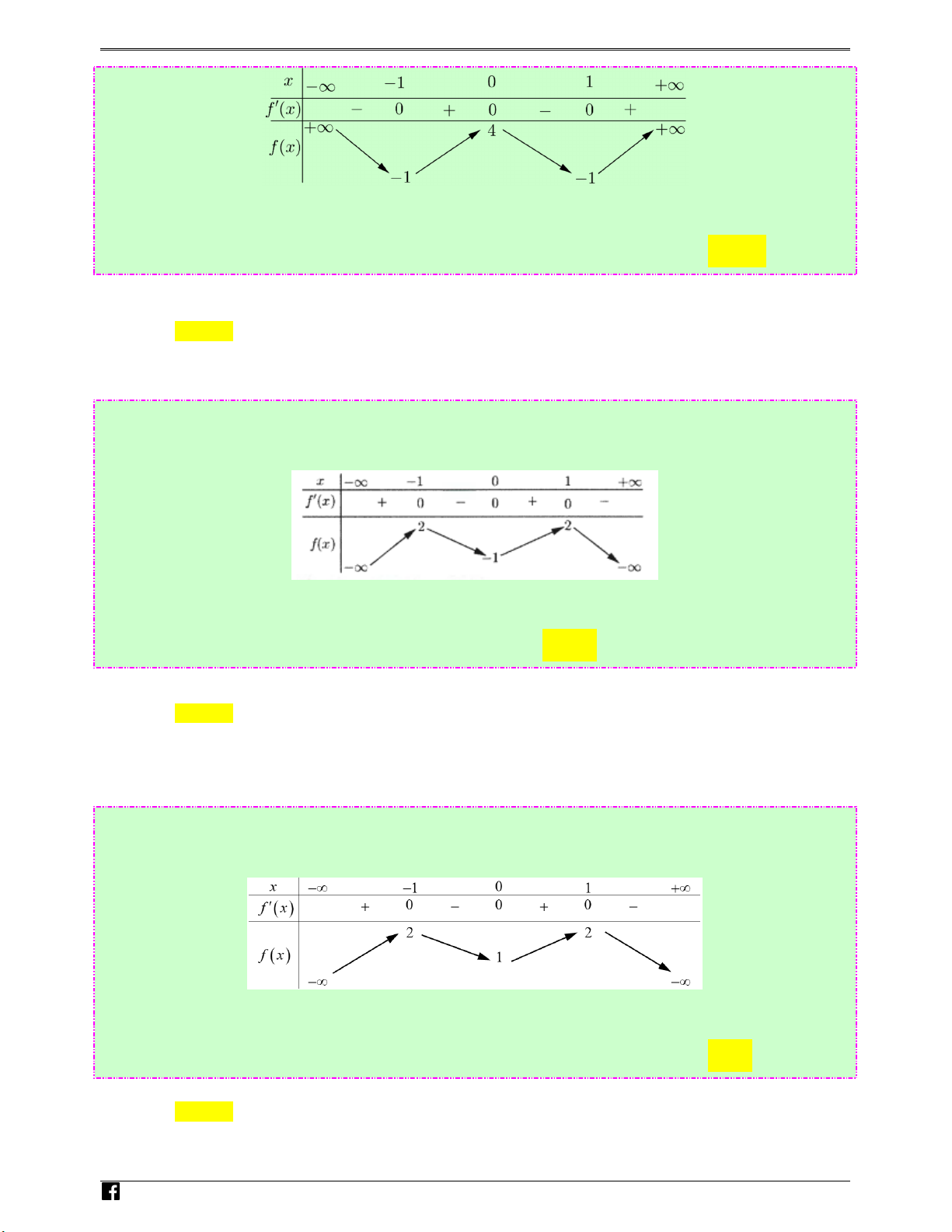
Câu 16: (Câu 10 - MĐ 104 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số f (x) có bảng biến thiên như sau: Luyenthitracn ghi
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? em .v Ⓐ. (0;1) . Ⓑ. (1;+∞). Ⓒ. (−1;0) . Ⓓ. (0;+∞). n Lời giải Chọn A
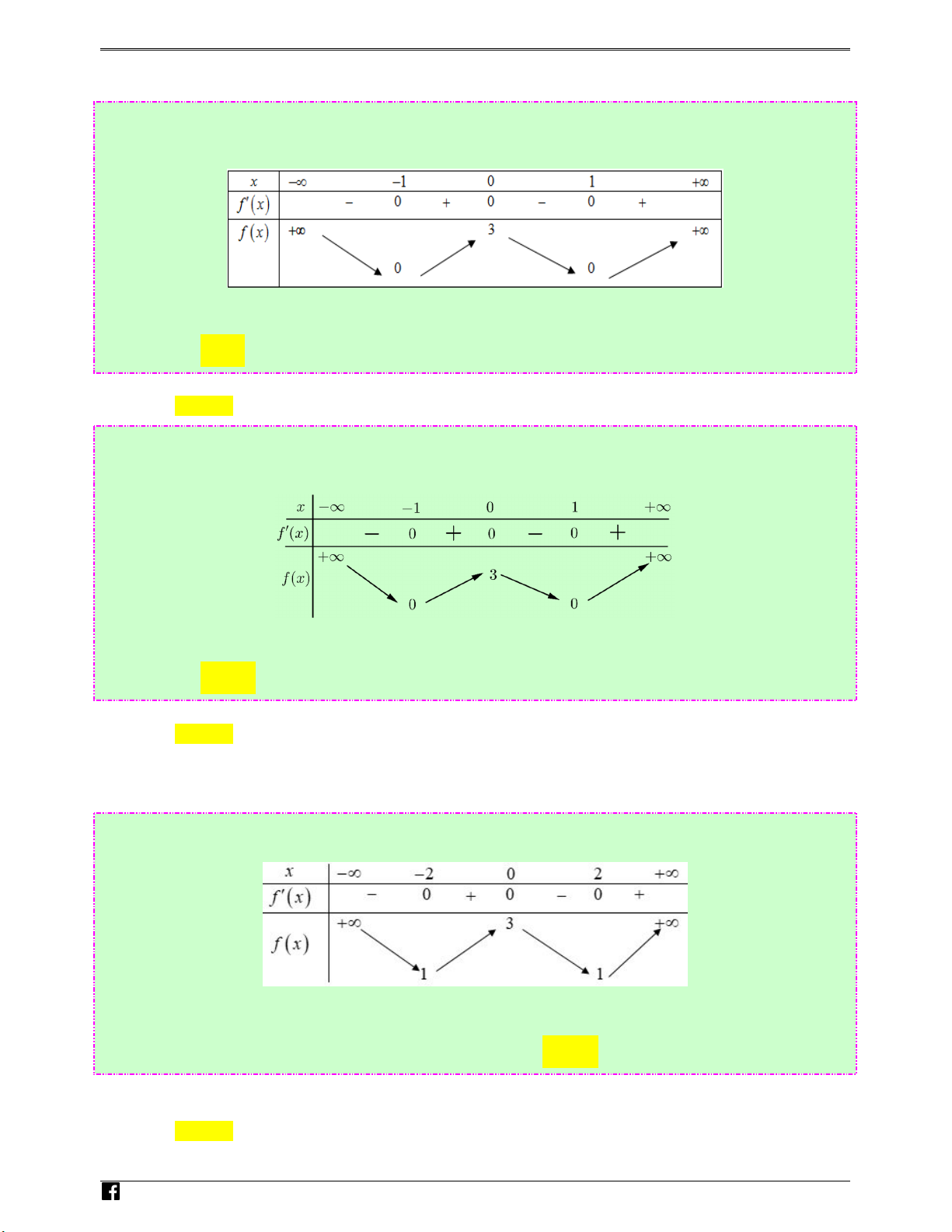
Câu 17: (Câu 15 - MĐ 103 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số f ( x) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? N g Ⓐ. ( 1 − ;0) . Ⓑ. (−1;+ ∞) . Ⓒ. (−∞;− ) 1 . Ⓓ. (0; ) 1 . uy% Lời giải n Chọn A H o
Nhìn BBT ta thấy hàm số đã cho đồng biến trên các khoảng (−1; 0) và (1; + ∞) . Đáp án A àng đúng. Vi)t
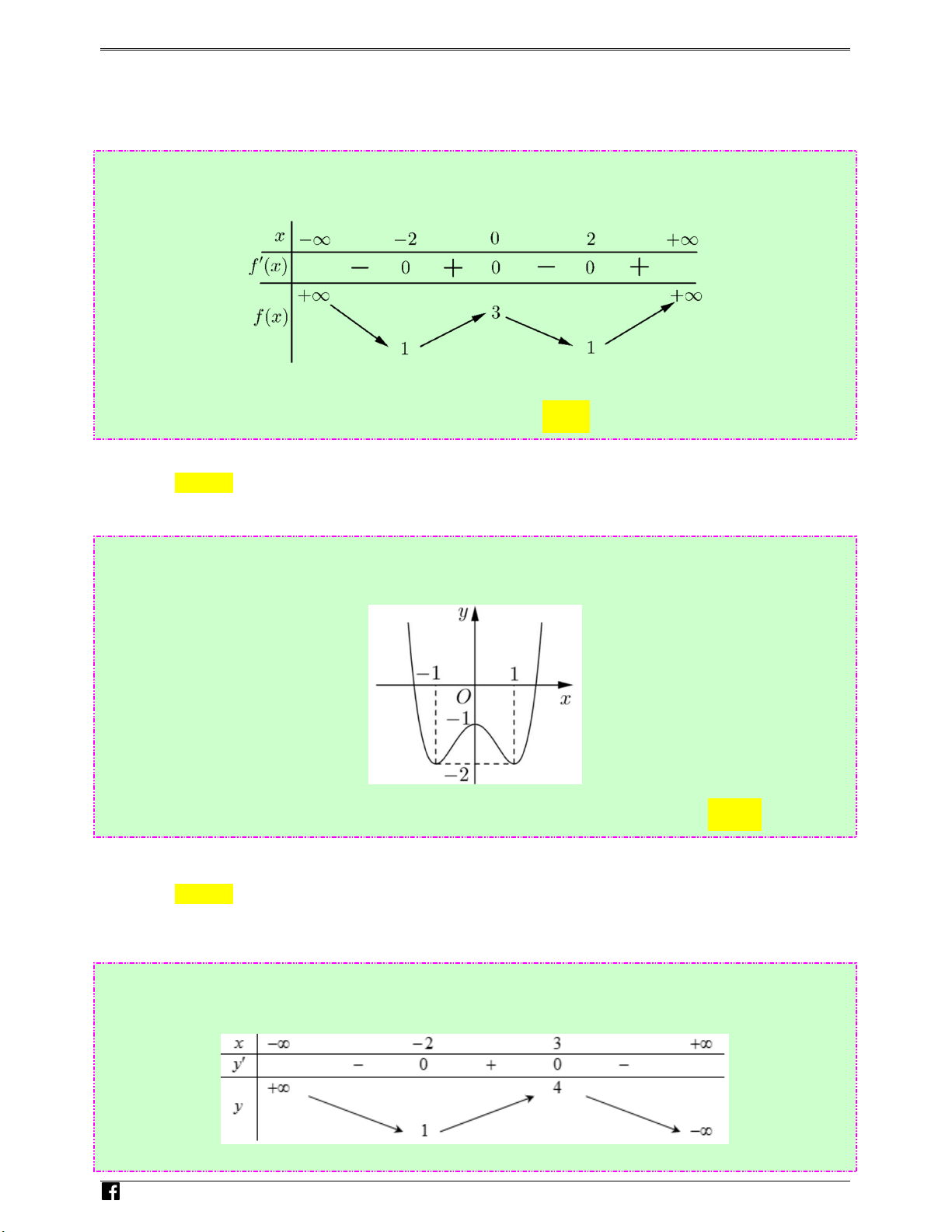
Câu 18: (Câu 14 - MĐ 102 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số f ( x) có bảng biến thiên sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? Ⓐ. (0;+∞) . Ⓑ. (0; ) 2 . Ⓒ. ( 2 − ; ) 0 . Ⓓ. (− ; ∞ 2 − ). Lời giải Chọn C
https://www.facebook.com/vietgold Trang 7 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
Dựa vào bảng biến thiên, hàm số đã cho đồng biến trên khoảng ( 2 − ; ) 0 và (2;+∞).
Căn cứ các phương án, ta chọn đáp án D . Lu
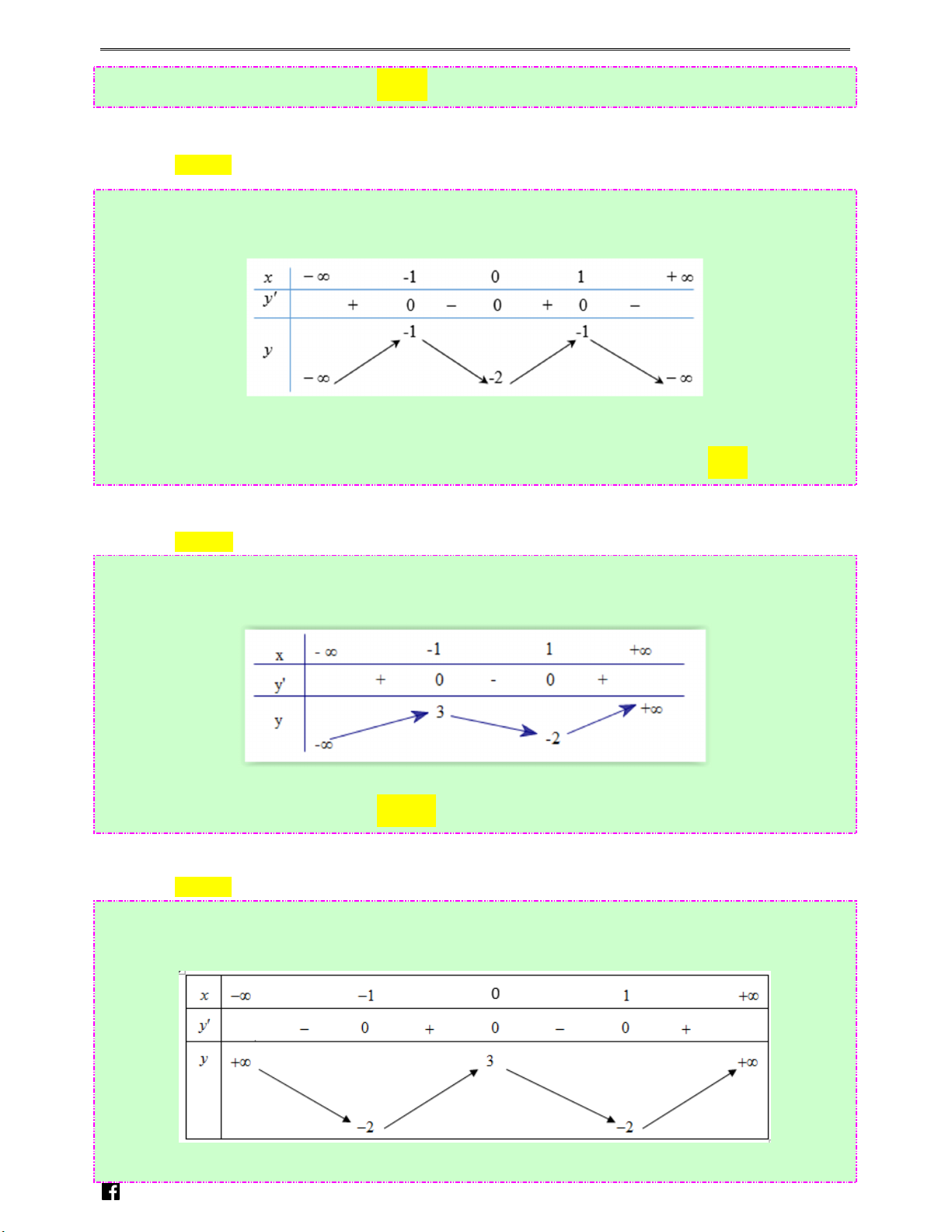
Câu 19: (Câu 3 - MĐ 101 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số f ( x) có bảng biến thiên như ye sau: nthitracnghiem.v n
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? Ⓐ. ( 2 − ;0) . Ⓑ. (2;+ ∞) . Ⓒ. (0;2). Ⓓ. (0;+ ∞) . Lời giải Chọn C
Ta có f ′(x) < 0 ⇔ x
∀ ∈(0;2) ⇒ f (x) nghịch biến trên khoảng (0;2).
Câu 20: (Câu 4 - ĐTK - BGD&ĐT - Năm 2018 - 2019) Cho hàm số y = f ( x) có đồ thị như hình vẽ
bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây? N guy%n Hoàng Vi Ⓐ. (0; ) 1 . Ⓑ. ( ; −∞ − ) 1 . Ⓒ. ( 1 − ; ) 1 . Ⓓ. ( 1 − ;0) . )t Lời giải Chọn D
Nhìn đồ thị hàm số ta thấy hàm số y = f (x ) đồng biến trên khoảng ( 1 − ;0) và (1;+ ∞) .
Câu 21: (Câu 7 - MĐ 104 - BGD&ĐT - Năm 2017 - 2018) Cho hàm số y = f ( x) có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
https://www.facebook.com/vietgold Trang 8 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 Ⓐ. ( 2 − ;+ ∞) Ⓑ. ( 2 − ; ) 3 Ⓒ. (3;+∞) Ⓓ. (− ; ∞ − 2) Lời giải L Chọn B uyen
Câu 22: (Câu 7 - MĐ 103 - BGD&ĐT - Năm 2017 - 2018) Cho hàm số y = f ( x) có bảng biến thiên thi như sau : tracnghiem.vn
Hàm số đã cho đồng biến trên khoảng nào dưới đây? Ⓐ. ( 1 − ;0) . Ⓑ. (1;+∞). Ⓒ. (−∞; ) 1 . Ⓓ. (0; ) 1 Lời giải Chọn D
Câu 23: (Câu 12 - MĐ 102 - BGD&ĐT - Năm 2017 - 2018) Cho hàm số y = f ( x) có bảng biến thiên như sau: N guy%n Ho àn
Hàm số đã cho đồng biến trên khoảng nào dưới đây? g V Ⓐ. (−1;+∞). Ⓑ. (1;+∞). Ⓒ. (−1; ) 1 . Ⓓ. (−∞;1). i)t Lời giải Chọn B
Câu 24: (Câu 4 - MĐ 101 - BGD&ĐT - Năm 2017 - 2018) Cho hàm số y = f ( x) có bảng biến thiên như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
https://www.facebook.com/vietgold Trang 9 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 Ⓐ. (0; ) 1 Ⓑ. (− ; ∞ 0) Ⓒ. (1;+∞) Ⓓ. ( 1 − ;0) Lời giải L Chọn A uyen
Dựa vào bảng biến thiên ta có hàm số đã cho nghịch biến trên các khoảng (0; ) 1 và (− ; ∞ − ) 1 . thitr
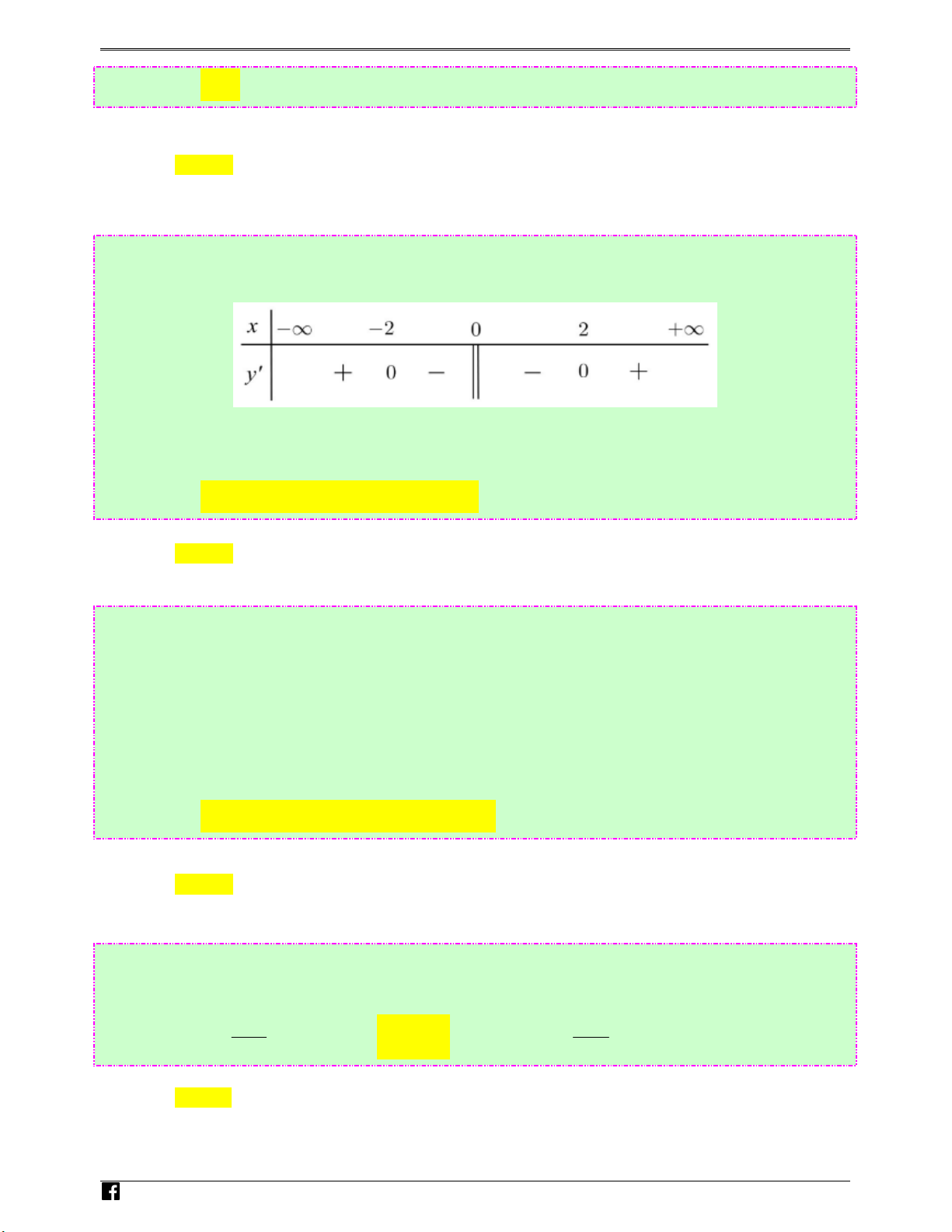
Câu 25: (Câu 1 - MĐ 104 - BGD&ĐT - NĂM 2016 - 2017) Cho hàm số y = f ( x) có bảng xét dấu đạo acn hàm như sau ghiem.vn
Mệnh đề nào dưới đây đúng?
Ⓐ. Hàm số đồng biến trên khoảng (−2;0) .
Ⓑ. Hàm số đồng biến trên khoảng (−∞;0).
Ⓒ. Hàm số nghịch biến trên khoảng (0;2) .
Ⓓ. Hàm số nghịch biến trên khoảng (−∞;−2) . Lời giải Chọn C
Dễ thấy mệnh đề hàm số nghịch biến trên khoảng (0;2) đúng.
Câu 26: (Câu 3 - MĐ 103 - BGD&ĐT - NĂM 2016 - 2017) Cho hàm số y = f ( x) có đạo hàm f ′( x) 2 = x +1, x
∀ ∈ ℝ . Mệnh đề nào dưới đây đúng? N guy
Ⓐ. Hàm số nghịch biến trên khoảng (− ; ∞ 0). %n H
Ⓑ. Hàm số nghịch biến trên khoảng (1;+∞). oàn
Ⓒ. Hàm số nghịch biến trên khoảng ( 1 − ; ) 1 . g Vi
Ⓓ. Hàm số đồng biến trên khoảng (− ; ∞ +∞) . )t Lời giải Chọn D Ta có f ′( x) 2 = x +1> 0, x
∀ ∈ℝ ⇒ Hàm số đồng biến trên khoảng (− ; ∞ +∞) .
Câu 27: (Câu 3 - MĐ 102 - BGD&ĐT - Năm 2016 - 2017) Hàm số nào dưới đây đồng biến trên khoảng (− ; ∞ +∞) ? + − Ⓐ. x 1 x y = Ⓑ. 3
y = x + x Ⓒ. 1 y = Ⓓ. 3
y = −x − 3x x + 3 x − 2 Lời giải Chọn B Vì 3 y = x + x 2
⇒ y′ = 3x +1 > 0, x ∀ ∈ℝ .
https://www.facebook.com/vietgold Trang 10 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
Câu 28: (Câu 11 - MĐ 102 - BGD&ĐT - Năm 2016 - 2017) Cho hàm số 3 2
y = x − 3x . Mệnh đề nào dưới đây đúng?
Ⓐ. Hàm số nghịch biến trên khoảng (0;2) Luy
Ⓑ. Hàm số nghịch biến trên khoảng (2;+∞) enth
Ⓒ. Hàm số đồng biến trên khoảng (0;2) itra
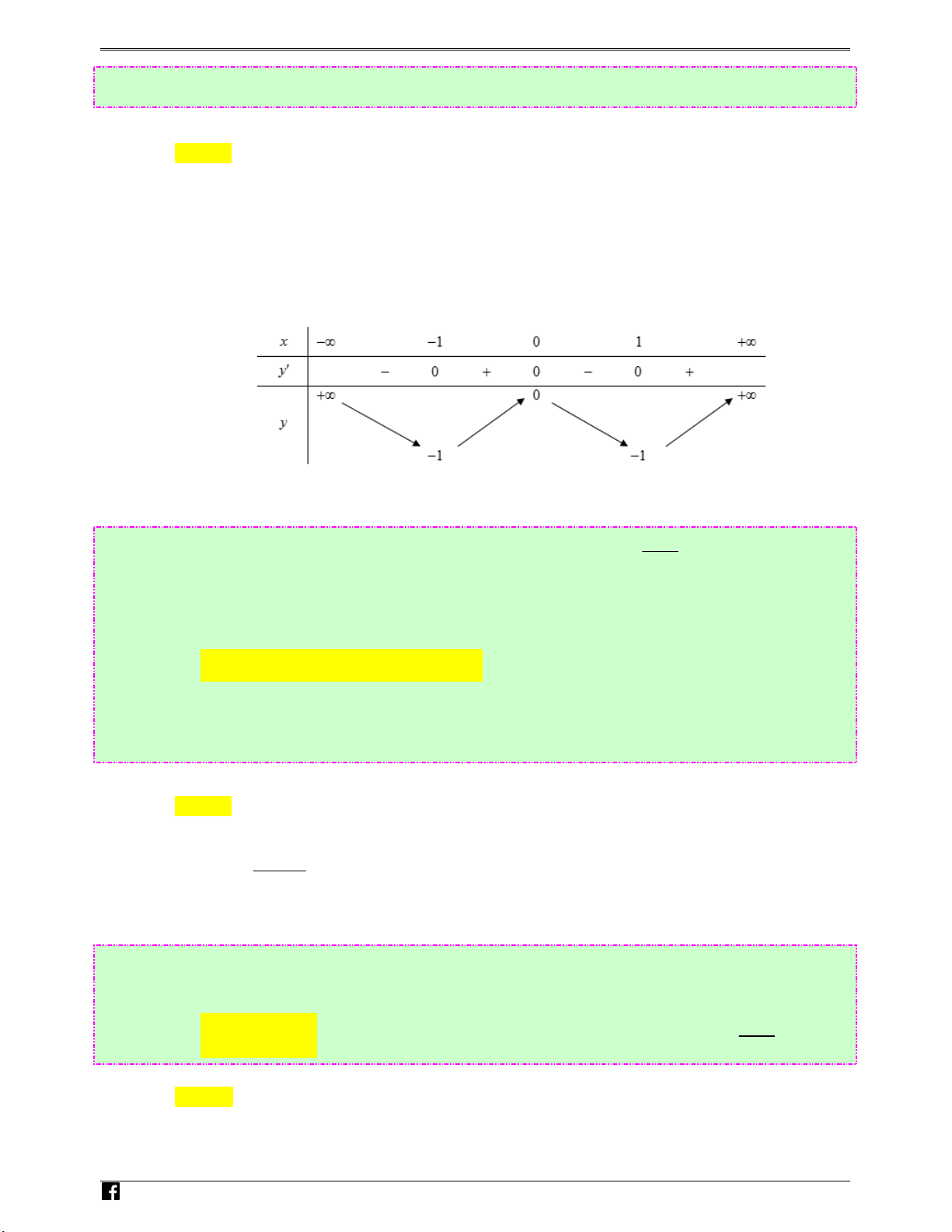
Ⓓ. Hàm số nghịch biến trên khoảng (− ; ∞ 0) cngh Lời giải iem Chọn A .vn x = 0 Ta có 2
y′ = 3x − 6x ; y′ = 0 ⇔  . x = 2 
Lập bảng biến thiên rồi suy ra hàm số nghịch biến trên khoảng (0;2)
Câu 29: (Câu 8 - MĐ 101 - BGD&ĐT - Năm 2016 - 2017) Cho hàm số 3
y = x + 3x + 2 . Mệnh đề nào dưới đây là đúng?
Ⓐ. Hàm số đồng biến trên khoảng (−∞;0) và nghịch biến trên khoảng (0;+∞) .
Ⓑ. Hàm số nghịch biến trên khoảng (− ; ∞ +∞) .
Ⓒ. Hàm số đồng biến trên khoảng (−∞;+∞) .
Ⓓ. Hàm số nghịch biến trên khoảng (−∞;0) và đồng biến trên khoảng (0;+∞) . N gu Lời giải y%n Chọn C 2 H ′
y = 3x + 3 > 0,∀x ∈ ℝ ⇒ Hàm số đồng biến trên (−∞;+ ∞) oàn 2 g
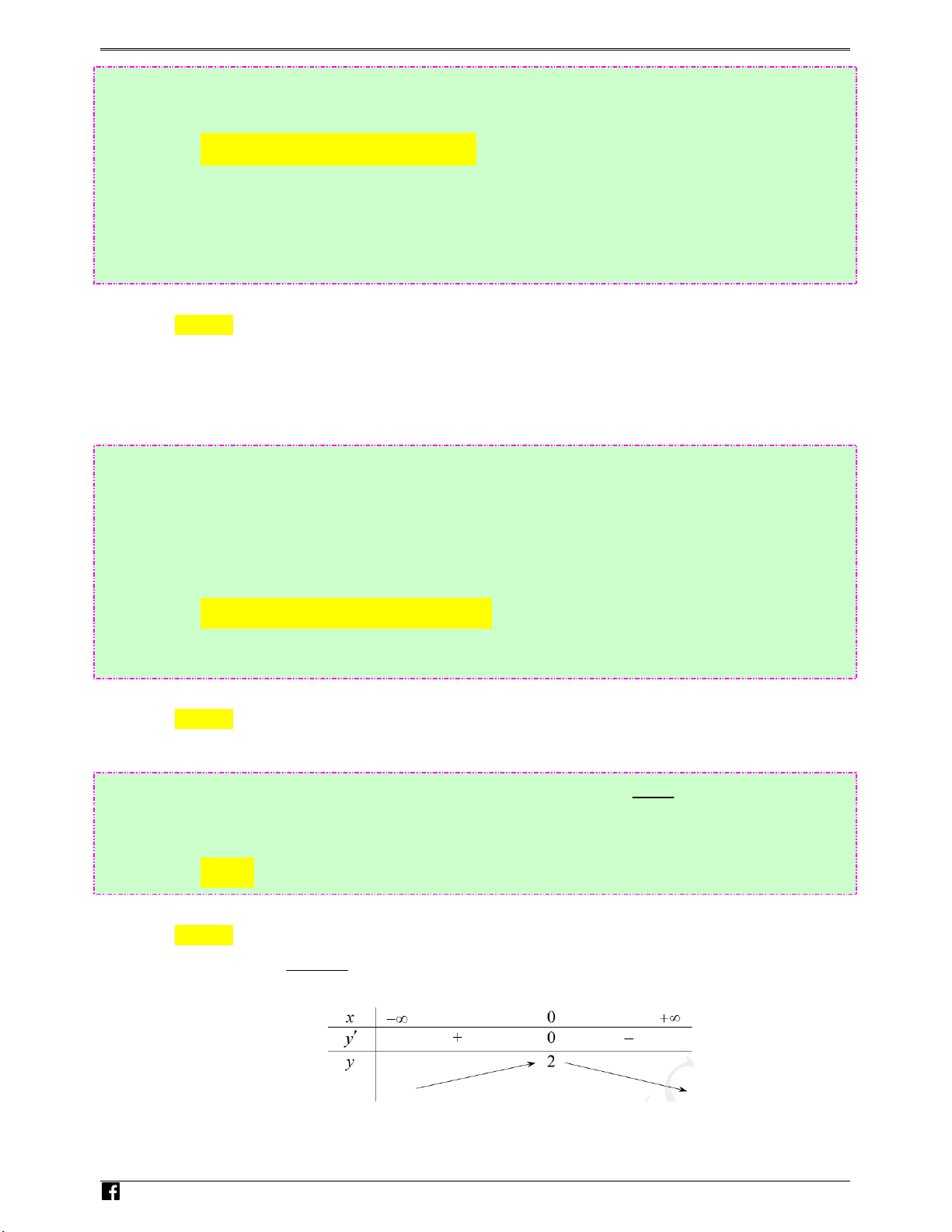
Câu 30: (Câu 13 - MĐ 101 - BGD&ĐT - Năm 2016 - 2017) Hàm số y =
nghịch biến trên khoảng 2 V x + 1 i)t nào dưới đây? Ⓐ. (0;+∞) Ⓑ. (−1;1) Ⓒ. (− ; ∞ +∞) Ⓓ. (−∞;0) Lời giải Chọn A D = 4x ℝ; y′ = − . Cho ′ y = 0 ⇔ x = ( 0 x + )2 2 1
https://www.facebook.com/vietgold Trang 11 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
Câu 31: Hàm số nghịch biến trên khoảng (0;+ ∞) x + a
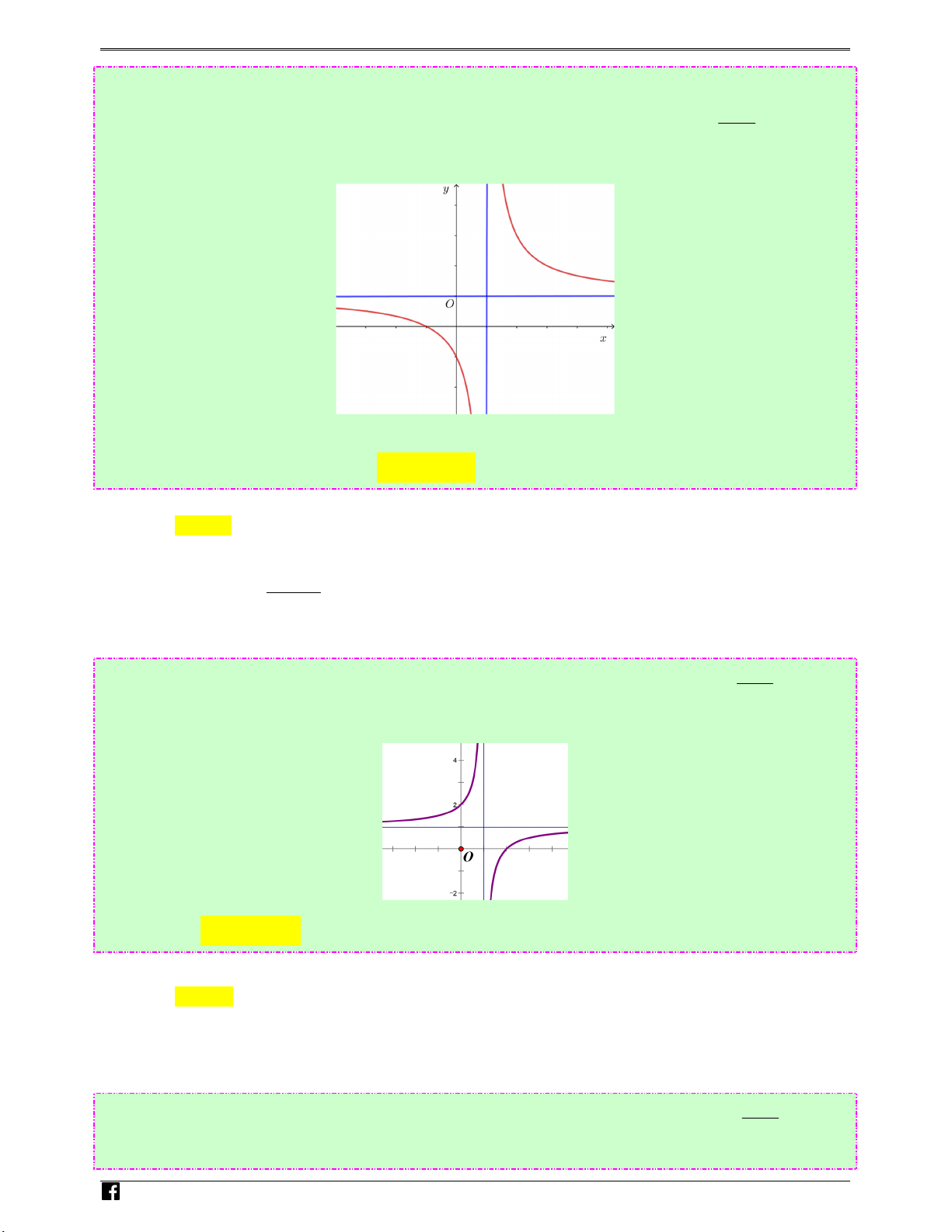
(Câu 33 - MĐ 104 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Biết hàm số y = ( a là số thực x −1 L
cho trước và a ≠ −1 ) có đồ thị như trong hình bên. uyenthitracnghiem.vn
Mệnh đề nào dưới đây đúng?
Ⓐ. y′ < 0, x ∀ ∈ℝ .
Ⓑ. y′< 0, x ∀ ≠1.
Ⓒ. y′ > 0, x ∀ ∈ℝ .
Ⓓ. y′ > 0, x ∀ ≠ 1. Lời giải Chọn B TXĐ: D = ℝ \{ } 1 . −1− Khi đó: a y′ = ∀x ≠ 1. 2 (x −1)
Hai nhánh của đồ thị có chiều đi xuống nên y′ < 0, x ∀ ≠1. N x + a g
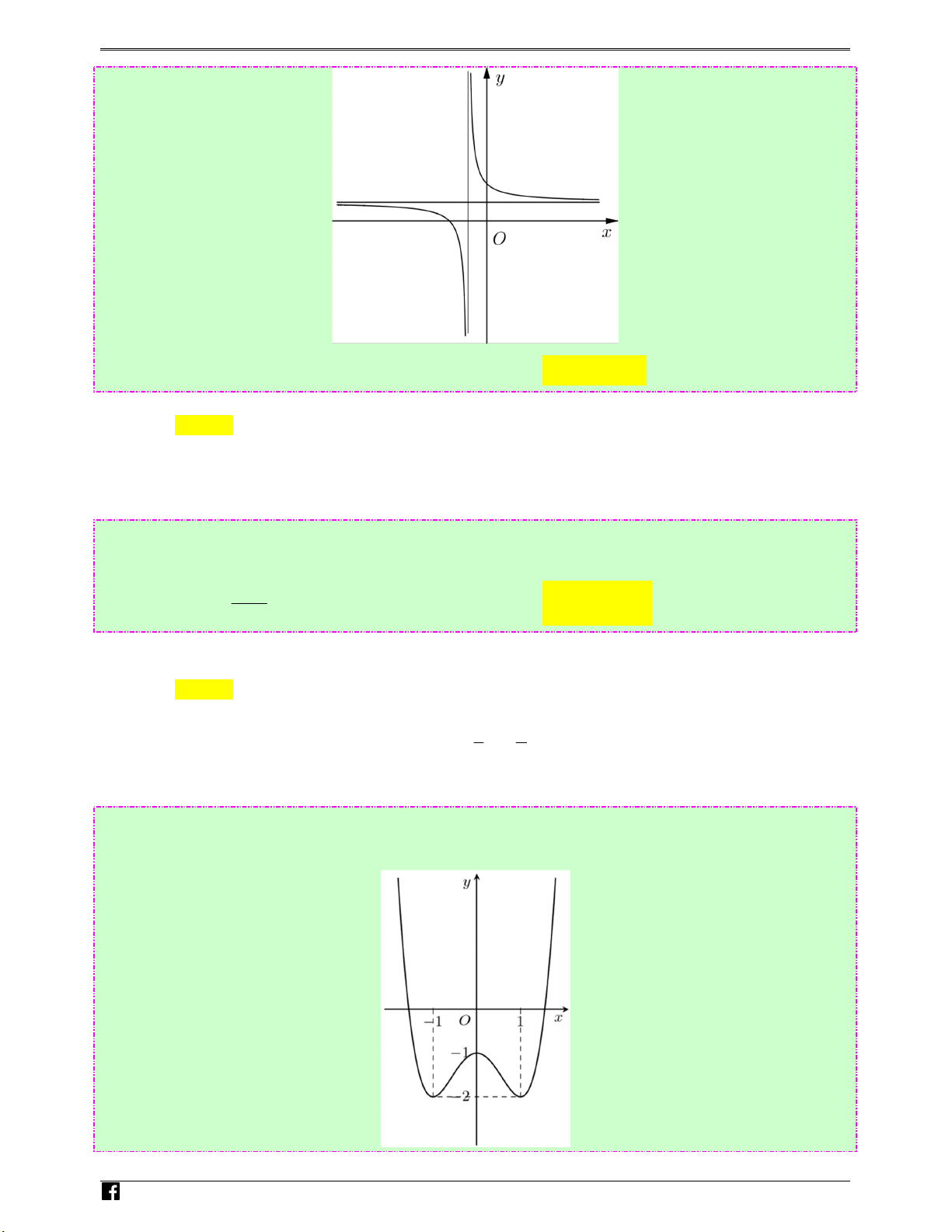
Câu 32: (Câu 38 - MĐ 103 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Biết hàm số y = , có đồ thị u x −1 y%
như trong hình bên. Mệnh đề nào dưới đây đúng? n Hoàng Vi)t
Ⓐ. y′ > 0, x ∀ ≠ 1.
Ⓑ. y′ > 0, x ∀ ∈ℝ .
Ⓒ. y′ < 0, x ∀ ∈ℝ .
Ⓓ. y′ < 0, x ∀ ≠ 1. Lời giải Chọn A
Điều kiện x ≠ 1.
Dựa vào đồ thị ta thấy theo thứ tự từ trái qua phải đồ thị đi lên nên y′ > 0, x ∀ ≠ 1. +
Câu 33: (Câu 33 - MĐ 102 - BGD&ĐT - Đợt 1 - Năm 2020 - 2021) Biết hàm số x a y = ( a là số x +1
thực cho trước, a ≠1) có đồ thị như trong hình bên. Mệnh đề nào dưới đây đúng?
https://www.facebook.com/vietgold Trang 12 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 Luyenthitracnghiem .vn
Ⓐ. y′ < 0, x ∀ ∈ℝ .
Ⓑ. y′ > 0, x ∀ ≠ 1 − .
Ⓒ. y′ < 0, x ∀ ≠ 1 − .
Ⓓ. y′ > 0, x ∀ ∈ℝ . Lời giải Chọn C
Tập xác định: D = ℝ \ {− }
1 nên loại đáp án A và Ⓓ.
Dạng đồ thị đi xuống thì y′ < 0 nên loại đáp án Ⓑ.
Câu 34: (Câu 30 - Đề Tham Khảo - BGD&ĐT - Năm 2020 - 2021) Hàm số nào dưới đây đồng biến trên ℝ ? + Ⓐ. x 1 y = . Ⓑ. 2
y = x + 2x . Ⓒ. 3 2
y = x − x + x . Ⓓ. 4 2
y = x − 3x + 2 . x − 2 Lời giải N gu Chọn C y%n 2  1  2 3 2 2 H
y = x − x + x ⇒ y ' = 3x − 2x +1 = 3 x − + > 0 x ∀ ∈   ℝ o  3  3 àn
Vậy hàm số đồng biến trên ℝ . g Vi
Câu 35: (Câu 4 - MĐ 104 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Cho hàm số y = f (x) có đồ thị là )t
đường cong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây
https://www.facebook.com/vietgold Trang 13 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 Ⓐ. (1;+∞) . Ⓑ. (0;1) . Ⓒ. (−1;0) . Ⓓ. (−∞;0) . Lời giải Chọn B Luy
Trên khoảng (0;1) đồ thị hàm số đi xuống nên hàm số đã cho nghịch biến trên (0;1) . enth
Câu 36: (Câu 40 - MĐ 101 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Tập hợp tất cả các giá trị thực itr của tham số 3 2
y = x − 3x + 4 −
đồng biến trên khoảng 2; + ∞ là a m để hàm số ( m) x ( ) cngh Ⓐ. (−∞; ] 1 . Ⓑ. (−∞;4]. Ⓒ. (−∞; ) 1 . Ⓓ. ( ; −∞ 4) . iem. Lời giải vn Chọn B
Tập xác định: D = ℝ . Ta có: 2
y′ = 3x − 6x + 4 − m .
Hàm số đồng biến trên khoảng (2;+∞) ⇔ y′ ≥ 0, x ∀ ∈(2;+∞) 2
⇔ m ≤ 3x − 6x + 4, x ∀ ∈(2;+∞) .
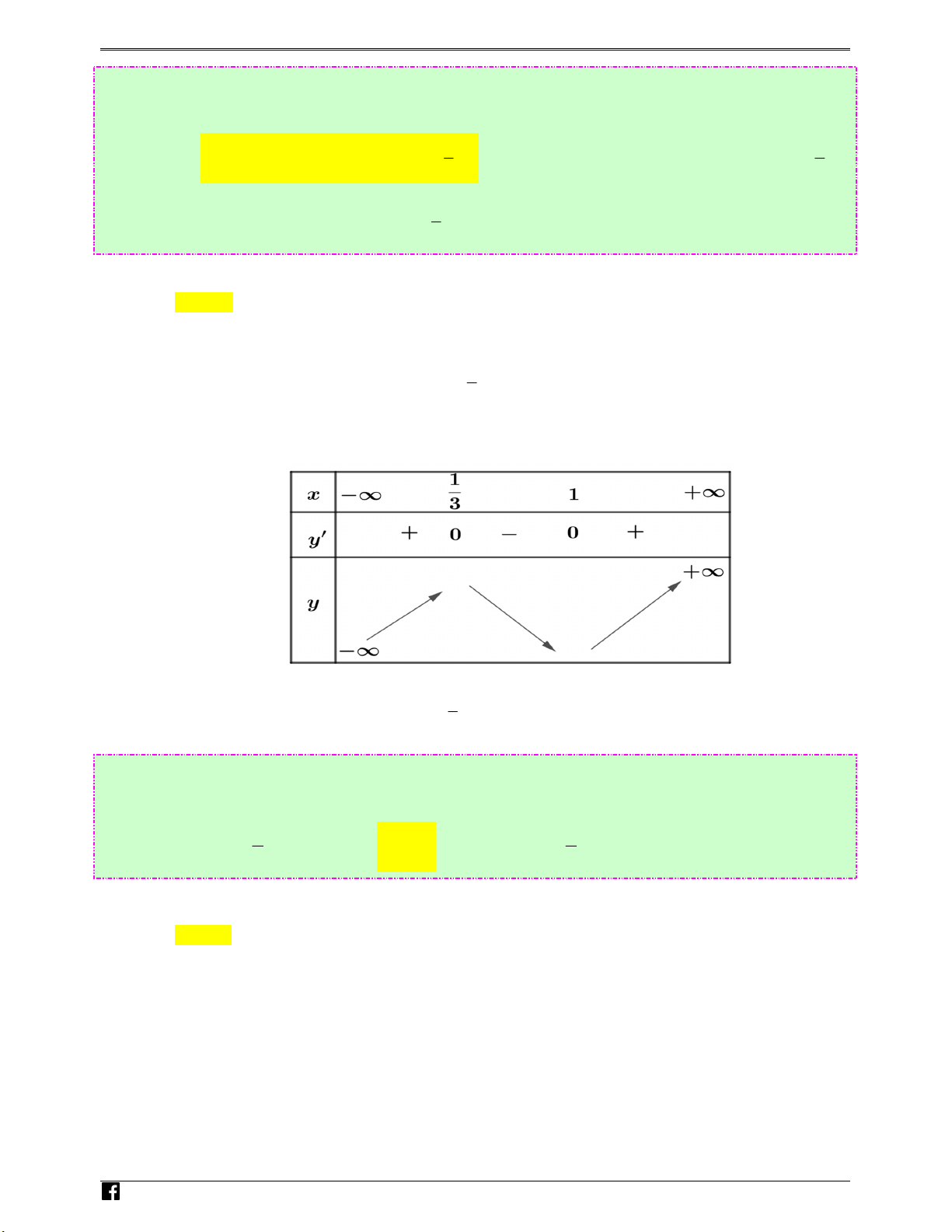
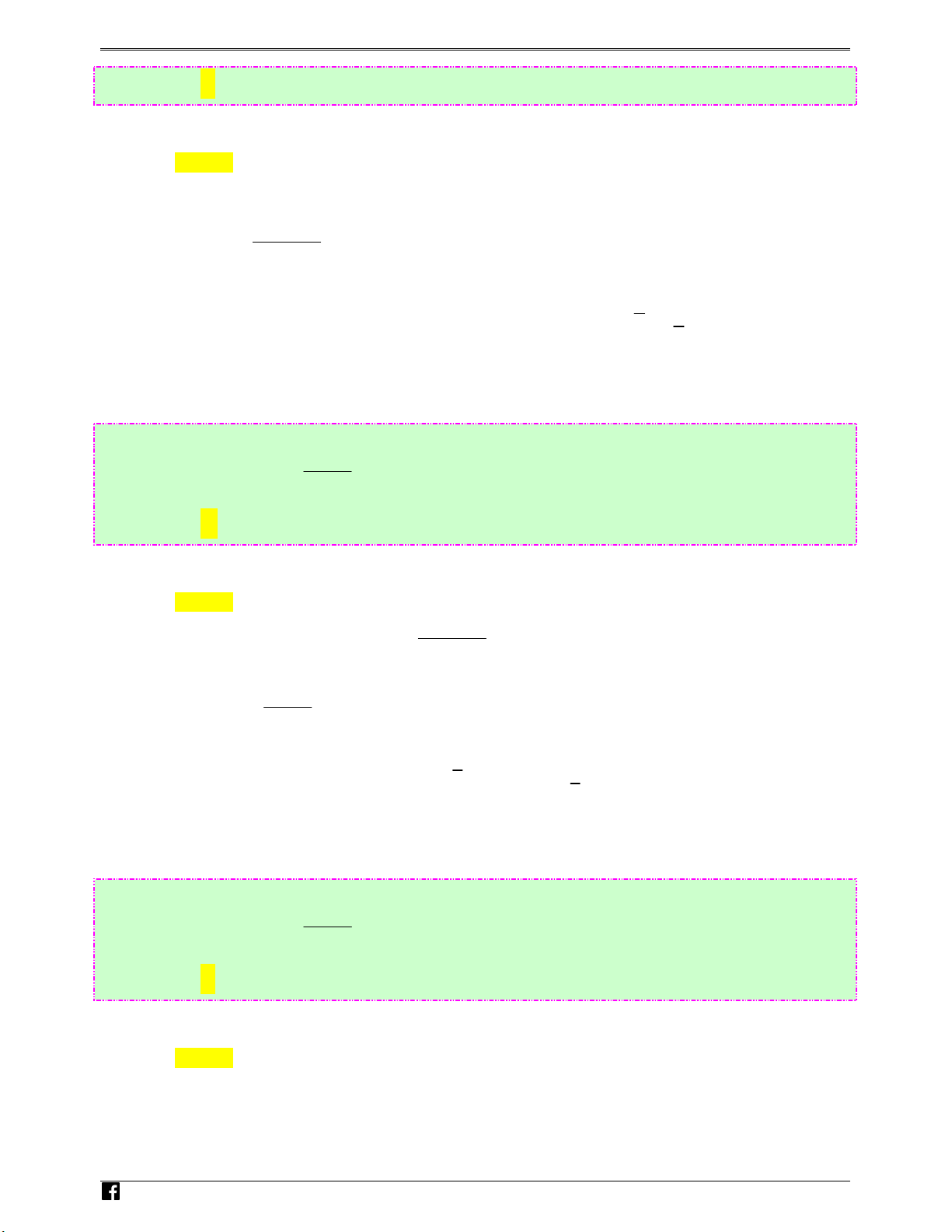
Xét hàm số g ( x) 2
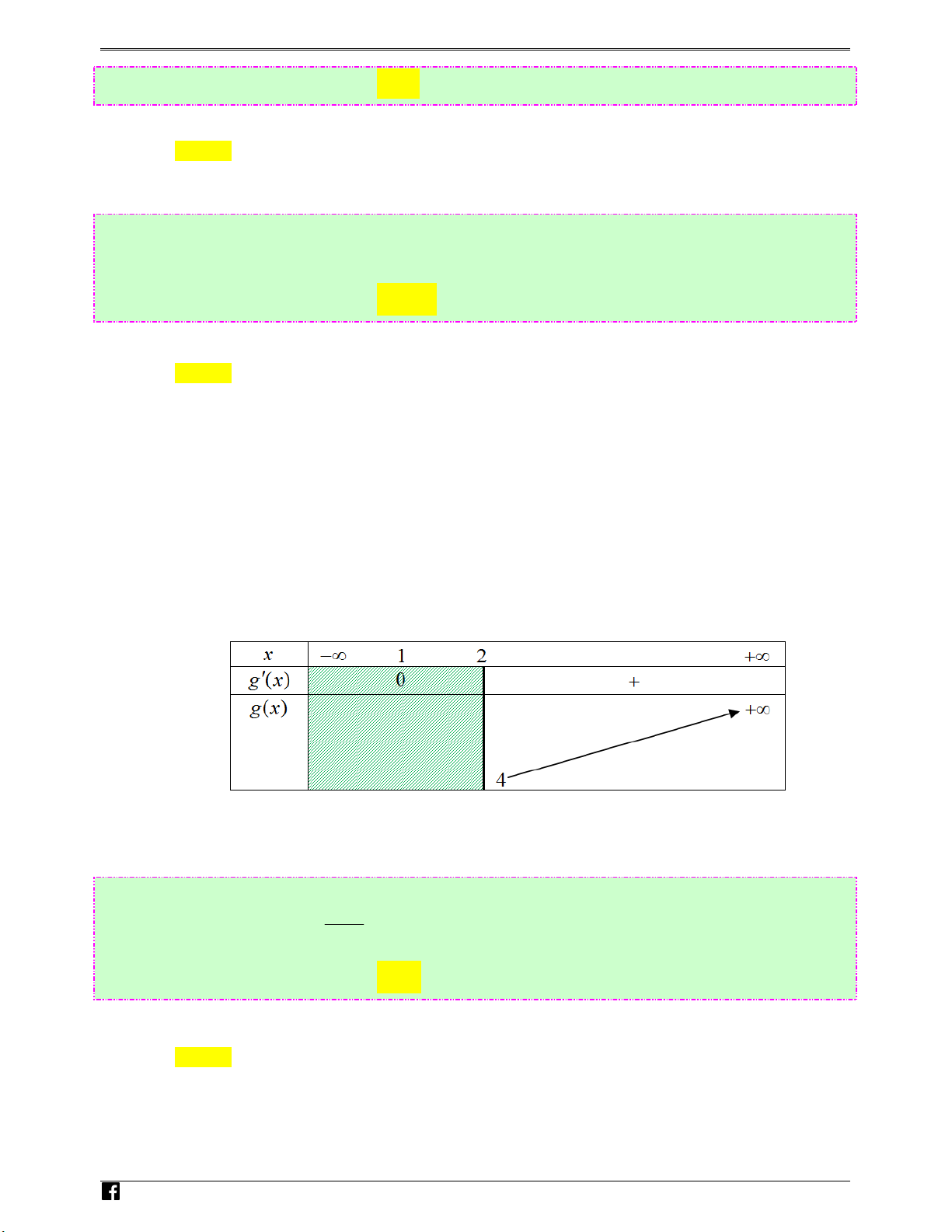
= 3x − 6x + 4 trên khoảng (2;+∞) .
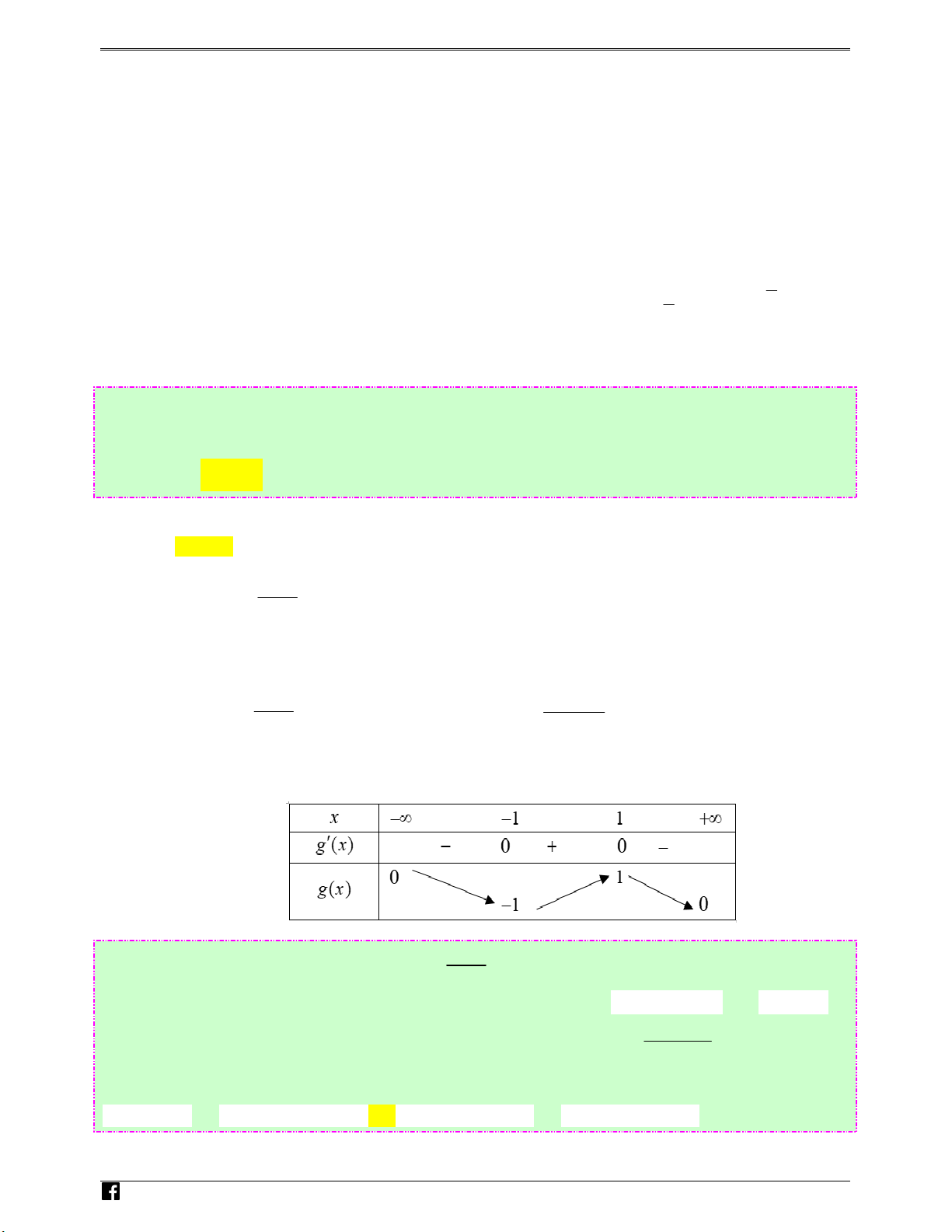
Ta có: g′( x) = 6x − 6 ; g′( x) = 0 ⇔ x = 1. Bảng biến thiên N guy%n Hoàng Vi
Dựa vào bảng biến thiên ta có: m ≤ g(x), x
∀ ∈(2;+∞) ⇔ m ≤ 4 . )t
Vậy m ≤ 4 thoả yêu cầu bài toán.
Câu 37: (Câu 39 - MĐ 102 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Tập hợp các giá trị thực của tham x + 5
số m để hàm số y =
đồng biến trên khoảng ( ; −∞ −8) là x + m Ⓐ. (5;+∞) . Ⓑ. (5;8]. Ⓒ. [5;8) . Ⓓ. (5;8) . Lời giải Chọn B
Tập xác định của hàm số là D = ℝ \ {− } m .
https://www.facebook.com/vietgold Trang 14 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 x + 5
y′ > 0, x ∀ ∈(−∞;−8) Hàm số y =
đồng biến trên khoảng ( ; −∞ 8 − ) ⇔  x + mx ≠ −m   m − 5 L > 0, x ∀ ∈ −∞; − 8  2 ( ) u m > 5 m > 5 y ⇔ ( x + m) ⇔  ⇔  ⇔ 5 < m ≤ 8. e −m ≥ 8 − m ≤ 8 n    −m ∉  (−∞;−8) thitra
Vậy m ∈ (5;8] thỏa mãn yêu cầu bài toán. cngh
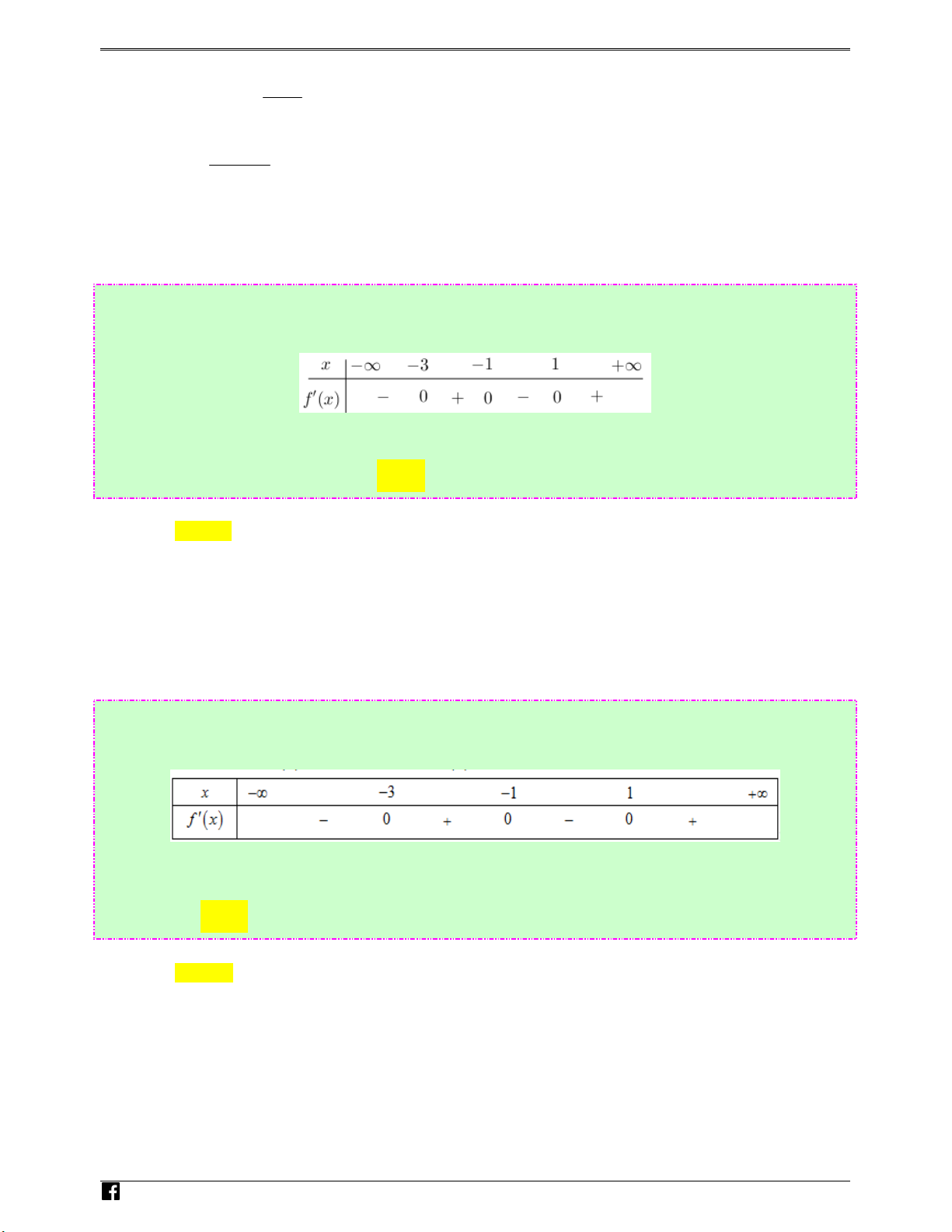
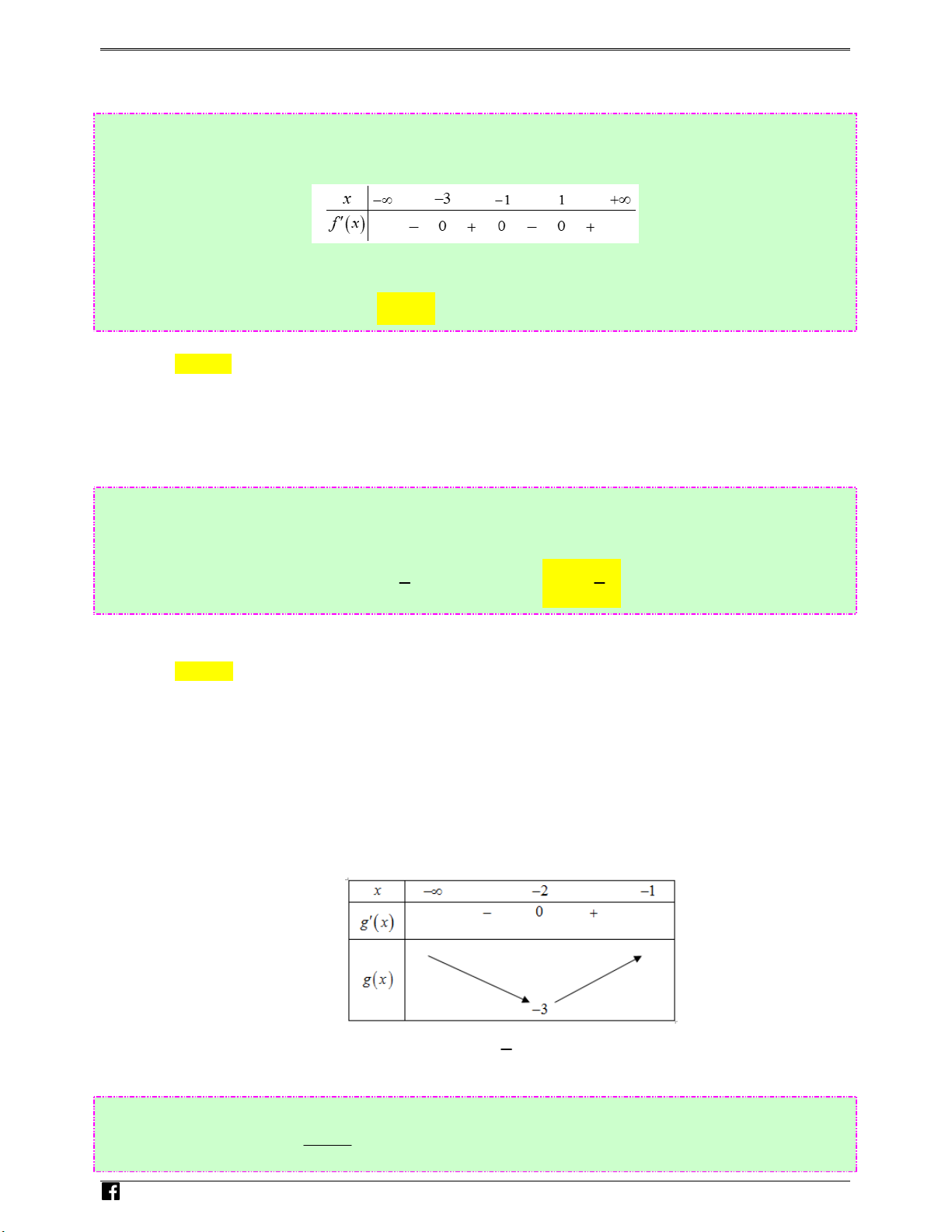
Câu 38: (Câu 34 - MĐ 104 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số f (x) , có bảng xét dấu f ′( x) iem như sau: .vn
Hàm số y = f (5 − 2x) đồng biến trên khoảng nào dưới đây? Ⓐ. (−∞;− 3) . Ⓑ. (4;5) . Ⓒ. (3;4) . Ⓓ. (1;3) . Lời giải Chọn B Ta có y′ = 2
− f ′(5 − 2x) .
Hàm số y = f (5 − 2x) đồng biến ⇔ 2
− f ′(5 − 2x) ≥ 0 ⇔ f ′(5 − 2x) ≤ 0 5 − 2x < 3 − x > 4 ⇔  ⇔ . 1 − < 5 − 2  x < 1  2 < x < 3  N
Vậy chọn đáp án Ⓑ. guy%
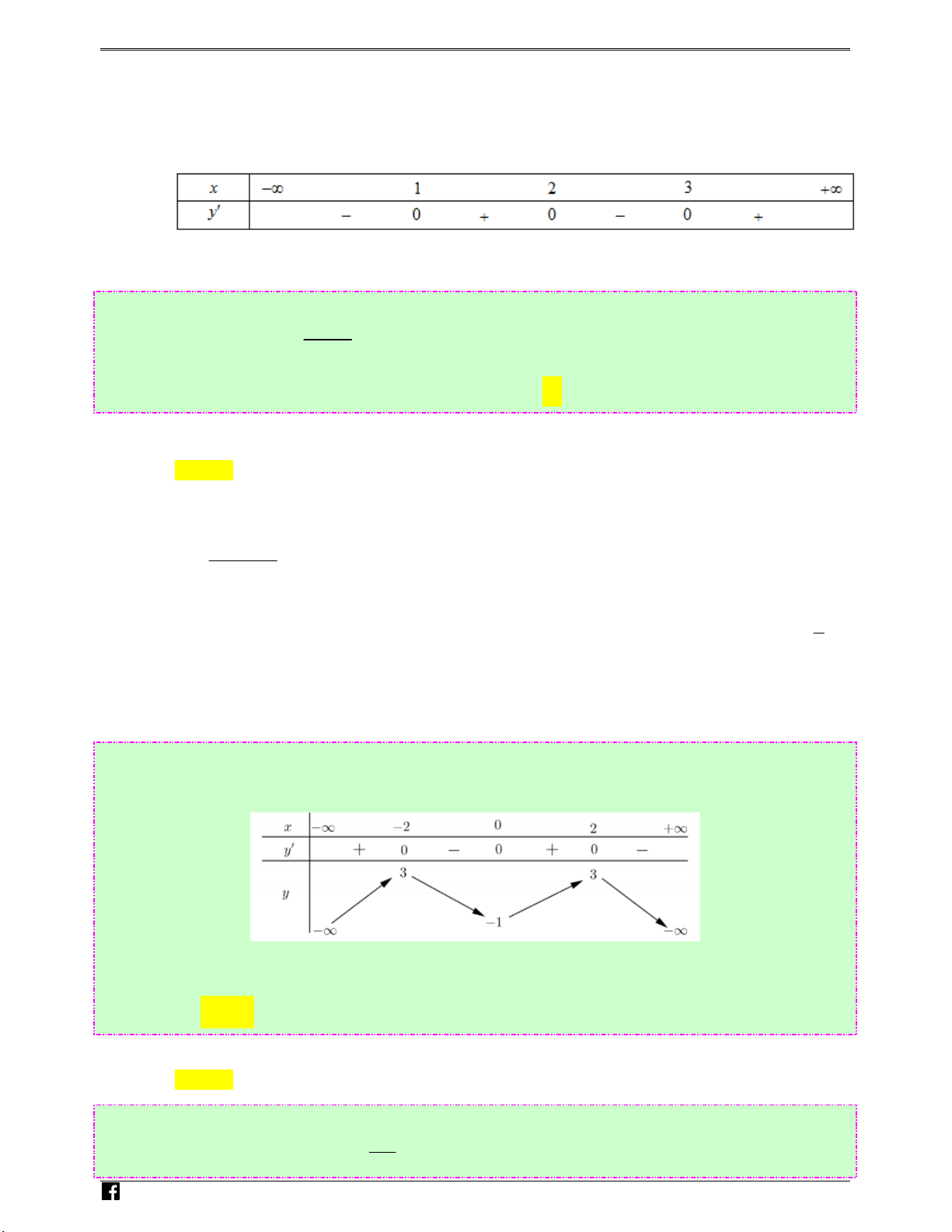
Câu 39: (Câu 33 - MĐ 103 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số f ( x) , bảng xét dấu của f ′( x) n H như sau: oàng Vi)t
Hàm số y = f (3− 2x) đồng biến trên khoảng nào dưới đây? Ⓐ. (3;4) . Ⓑ. (2;3) . Ⓒ. (−∞;−3) . Ⓓ. (0;2). Lời giải Chọn A
Ta có: y′ = f ′(3 − 2x) = (3 − 2 ′
x ) f ′(3 − 2x) = −2 f ′(3 − 2x) . 3 − 2x = −3 x = 3 *)   y′ = 0 ⇔ 2
− f ′(3 − 2x) = 0 ⇔ f ′(3 − 2x) = 0 ⇔ 3− 2x = −1  ⇔ x = 2  . 3 − 2x =1  x =1 
https://www.facebook.com/vietgold Trang 15 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 3− 2x ≤ 3 − x ≥ 3 *) y′ ≥ 0 ⇔ 2
− f ′(3 − 2x) ≥ 0 ⇔ f ′(3 − 2x) ≤ 0 ⇔  ⇔ . 1 − ≤ 3− 2  x ≤ 1  1≤ x ≤ 2  Bảng xét dấu: Luyenth itra
Hàm số y = f (3− 2x) đồng biến trên khoảng (3; +∞) nên đồng biến trên khoảng (3;4). cngh
Câu 40: (Câu 30 - MĐ 102 - BGD&ĐT - Năm 2017 - 2018) Có bao nhiêu giá trị nguyên của tham số iem x + 6
m để hàm số y =
nghịch biến trên khoảng (10; +∞) ? .v x + 5m n Ⓐ. 3. Ⓑ. Vô số. Ⓒ. 4 . Ⓓ. 5 Lời giải Chọn C
Tập xác định D = R \{−5 } m . 5m − 6 y′ = (x +5m)2   6 y′ < 0, x ∀ ∈ D  5  m − 6 < 0 m <
Hàm số nghịch biến trên (10;+∞) khi và chỉ khi  ⇔  ⇔  5 .  5 − m∉  (10;+∞) 5 − m ≤10  N m ≥ 2 −  guy%
Mà m∈ℤ nên m ∈{−2; −1;0; } 1 . n Ho
Câu 41: (Câu 5 - ĐTK - BGD&ĐT - Năm 2017 - 2018) Cho hàm số y = f ( x) có bảng biến thiên như àng sau: Vi)t
Hàm số y = f ( x) nghịch biến trên khoảng nào dưới đây? Ⓐ. ( 2 − ;0) Ⓑ. (− ; ∞ 2 − ) Ⓒ. (0; ) 2 Ⓓ. (0;+∞) Lời giải Chọn A
Câu 42: (Câu 30 - ĐTK - BGD&ĐT - Năm 2017 - 2018) Có bao nhiêu giá trị nguyên âm của tham số 1 m để hàm số 3
y = x + mx −
đồng biến trên khoảng (0;+∞) 5 5x
https://www.facebook.com/vietgold Trang 16 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 Ⓐ. 5 Ⓑ. 3 Ⓒ. 0 Ⓓ. 4 Lời giải Chọn D L 2 1 u
y′ = 3x + m + 6 y x en 2 1 t 0;+∞ ′ h
Hàm số đồng biến trên (
) khi và chỉ khi y = 3x + m + ≥ 0,∀x∈ 0;+∞ 6 ( ) i x tra 1 1 2 c ⇔ −3x −
≤ m,∀x ∈ 0; +∞ . Xét hàm số 2
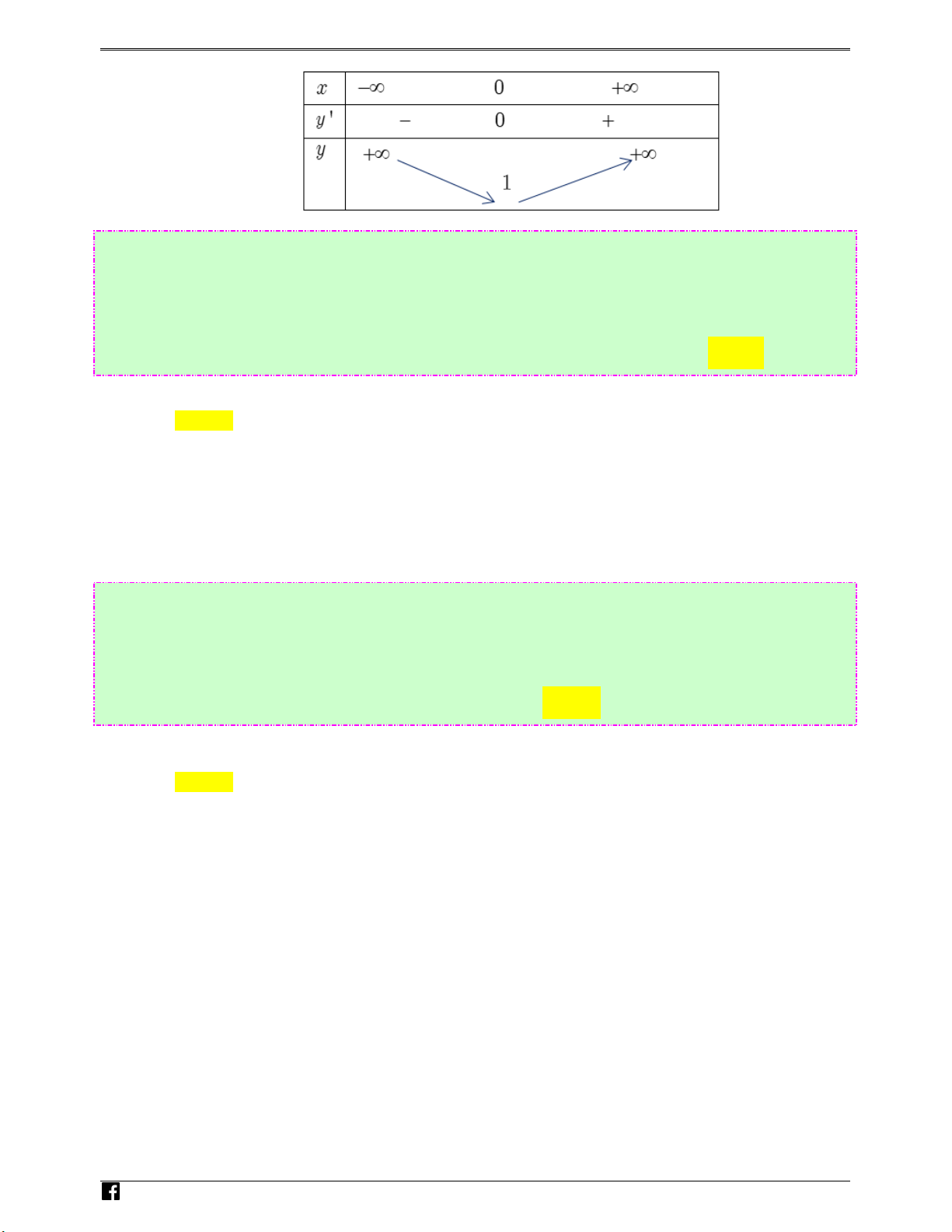
g ( x) = −3x −
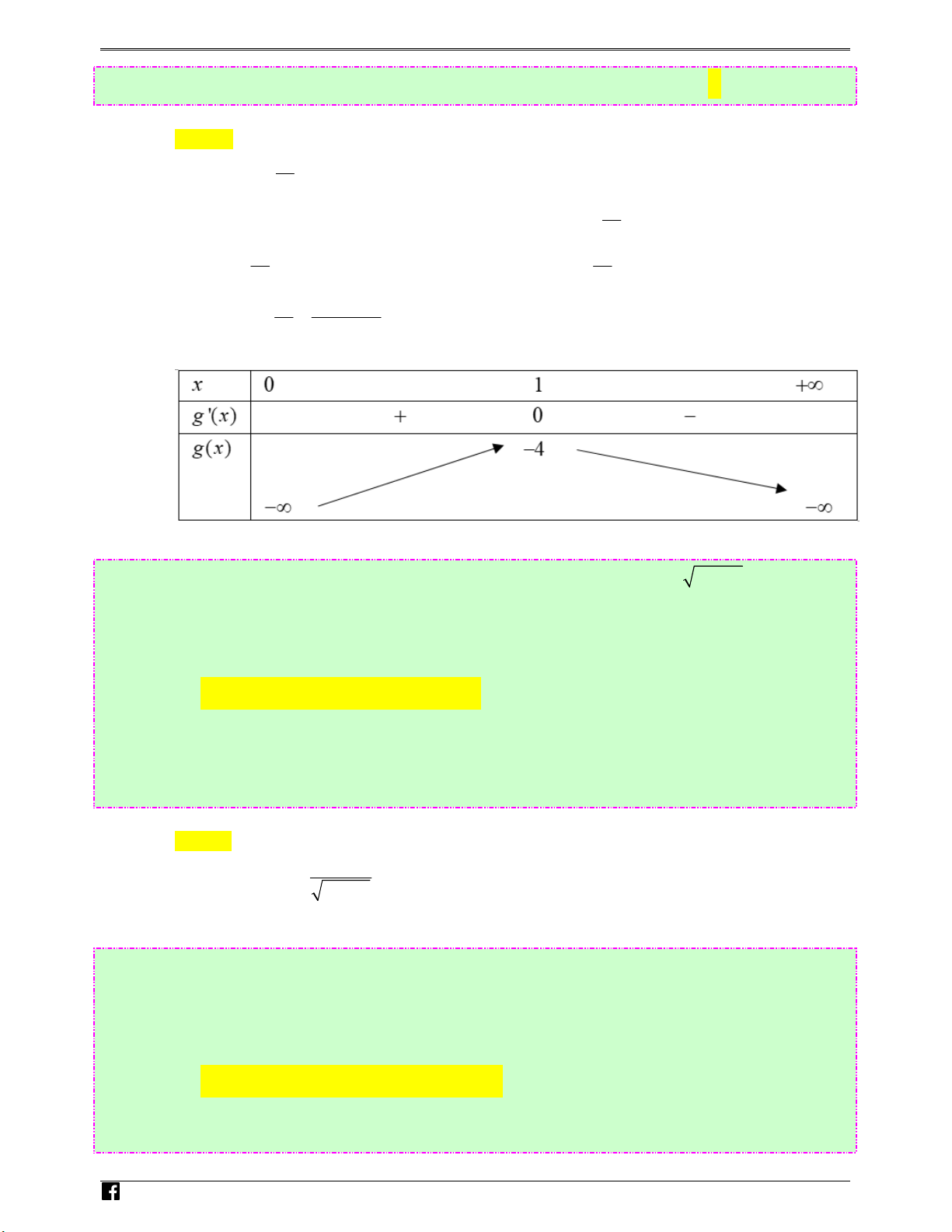
≤ m , x ∈(0;+∞) 6 ( ) 6 n x x gh 8 6 6 − ( −1) x = 1 i ′ e ( ′ ) = −6 + = x g x x
, g (x) = 0 ⇔ 7 7  m x x x = 1 − (loai)  .v
Bảng biến thiên: n
Dựa vào BBT ta có m ≥ −4 , suy ra các giá trị nguyên âm của tham số m là −4; −3; −2; −1
Câu 43: (Câu 21 - MĐ 104 - BGD&ĐT - NĂM 2016 - 2017) Cho hàm số 2
y = 2x +1 . Mệnh đề nào dưới đây đúng?
Ⓐ. Hàm số nghịch biến trên khoảng (−1;1) . N gu
Ⓑ. Hàm số đồng biến trên khoảng (0;+∞). y%n H
Ⓒ. Hàm số đồng biến trên khoảng (−∞;0). oàn
Ⓓ. Hàm số nghịch biến trên khoảng (0;+∞). g Vi Lời giải )t Chọn B 2x
Ta có D = ℝ , y′ =
. Hàm số nghịch biến trên khoảng (−∞;0) và đồng biến trên khoảng 2 2x +1 (0;+∞).
Câu 44: (Câu 30 - MĐ 103 - BGD&ĐT - NĂM 2016 - 2017) Cho hàm số 4 2
y = x − 2x . Mệnh đề nào dưới đây đúng?
Ⓐ. Hàm số đồng biến trên khoảng ( ; −∞ 2 − ) .
Ⓑ. Hàm số nghịch biến trên khoảng ( ; −∞ −2) .
Ⓒ. Hàm số đồng biến trên khoảng ( 1 − ; ) 1 .
https://www.facebook.com/vietgold Trang 17 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
Ⓓ. Hàm sô nghịch biến trên khoảng (−1; ) 1 . Lời giải Chọn B Luye Ta có 3
y′ = 4x − 4x . nthi x = 0 tr y′ = 0 ⇔  . a x = 1 ± c  ngh Ta có bảng biến thiên: iem.vn
Từ bảng biến thiên suy ra hàm số nghịch biến trên khoảng (− ; ∞ 2 − ) . x − 2
Câu 45: (Câu 6 - ĐTK - BGD&ĐT - Năm 2016 - 2017) Cho hàm số y =
. Mệnh đề nào dưới đây x + 1 đúng?
Ⓐ. Hàm số nghịch biến trên khoảng (−∞;− ) 1 N
Ⓑ. Hàm số đồng biến trên khoảng (−∞;− ) 1 guy
Ⓒ. Hàm số nghịch biến trên khoảng (−∞; +∞) %n H
Ⓓ. Hàm số nghịch biến trên khoảng (−1;+∞) oà Lời giải ng V Chọn B i) Tập xác định: ℝ − . t \ { } 1 3 Ta có y ' =
> 0, ∀x ∈ ℝ\{− } 1 . (x + )2 1
Suy ra hàm số đồng biến trên các khoảng (−∞;− ) 1 và (−1; +∞) .
Câu 46: (Câu 14 - ĐTK - BGD&ĐT - Năm 2016 - 2017) Hàm số nào dưới đây đồng biến trên khoảng (−∞;+∞) ? − Ⓐ. 3 x
y = 3x + 3x − 2 . Ⓑ. 3
y = 2x − 5x +1. Ⓒ. 4 2
y = x + 3x . Ⓓ. 2 y = . x + 1 Lời giải Chọn A Hàm số 3
y = 3x + 3x − 2 có TXĐ: D = ℝ . 2
y′ = 9x + 3 > 0, x
∀ ∈ ℝ , suy ra hàm số đồng biến trên khoảng (−∞; +∞) .
https://www.facebook.com/vietgold Trang 18 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
Câu 47: (Câu 4 - ĐTN - BGD&ĐT - Năm 2016 - 2017) Cho hàm số 3 2
y = x − 2x + x +1 . Mệnh đề nào dưới đây đúng?  1   1  L
Ⓐ. Hàm số nghịch biến trên khoảng ;1  
Ⓑ. Hàm số nghịch biến trên khoảng − ; ∞   u  3   3  yen  1  th
Ⓒ. Hàm số đồng biến trên khoảng ;1  
Ⓓ. Hàm số nghịch biến trên khoảng (1;+∞ ) i  3 t  rac Lời giải ngh Chọn A iem. x = 1 vn Ta có 2
y = 3x − 4x + 1 ⇒ y = 0  ′ ′ ⇔ 1 x =  3 Bảng biến thiên: N gu  1  y%
Vậy hàm số nghịch biến trên khoảng ;1   . n  3  Hoà
Câu 48: (Câu 3 - ĐMH - BGD&ĐT - Năm 2017 - 2018) Hỏi hàm số 4
y = 2x +1 đồng biến trên khoảng ng nào? Vi)t     Ⓐ. 1 − ; ∞ −  . Ⓑ. (0;+∞). Ⓒ. 1 − ;+∞ . Ⓓ. (−∞;0). 2       2  Lời giải Chọn B 4
y = 2x +1 . Tập xác định: D = ℝ Ta có: 3 y′ = 8x ; 3
y′ = 0 ⇔ 8x = 0 ⇔ x = 0 suy ra y (0) = 1
Giới hạn: lim y = +∞ ; lim y = +∞ x→−∞ x→+∞ Bảng biến thiên:
https://www.facebook.com/vietgold Trang 19 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 Luyen thitr
Câu 49: Vậy hàm số đồng biến trên khoảng (0;+∞) . acn
(Câu 42 - MĐ 104 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Tập hợp tất cả các giá trị của gh
tham số m để hàm số 3 2
y = x − 3x + (1− m) x 2; +∞ là i
đồng biến trên khoảng ( ) em .v Ⓐ. (−∞;2) . Ⓑ. (−∞; ) 1 . Ⓒ. (−∞;−2] . Ⓓ. (−∞;1] . n Lời giải Chọn D Ta có 2
y ' = 3x − 6x +1− m . Hàm số 3 2
y = x − 3x + (1− m) x đồng biến trên khoảng (2; +∞ ) nên y ' ≥ 0 x ∀ ∈ (2;+∞) Suy ra: 2
3x − 6x +1 ≥ m∀x ∈ (2; +∞) 2
⇔ Min (3x − 6x +1) ≥ m ⇔ 1 ≥ m . x ( ∈ 2;+∞)
Câu 50: (Câu 42 - MĐ 102 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Tập hợp tất cả các giá trị thực của
tham số m để hàm số 3 2
y = x − 3x + (5 − m) x đồng biến trên khoảng (2; +∞) là . N guy Ⓐ. (− ; ∞ 2) . Ⓑ. (−∞;5) Ⓒ. ( ; −∞ 5]. Ⓓ. (−∞;2] %n H Lời giải oàn Chọn C g Vi Ta có: 2
y′ = 3x − 6x + 5 − ) m t Để hàm số 3 2
y = x − 3x + (5 − m) x đồng biến trên khoảng (2; +∞) thì y′ ≥ 0 x ∀ ∈(2;+∞) 2
⇔ 3x − 6x + 5 − m ≥ 0 x
∀ ∈[2;+∞) (do hàm số xác định trên ℝ nên xác định tại x = 2 ) 2
⇔ 3x − 6x + 5 ≥ m ∀x ∈[2;+∞)
⇔ f ( x) ≥ m x ∀ ∈[2;+∞)
⇔ min f ( x) ≥ m [2;+∞) Xét f ( x) 2
= 3x − 6x + 5 x ∈[2;+∞)
https://www.facebook.com/vietgold Trang 20 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
f ′( x) = 6x − 6 > 0 x
∀ ∈[2;+∞) ⇒ Hàm số f ( x) 2
= 3x − 6x + 5 đồng biến trên nữa khoảng
[2;+∞) ⇒ min f (x) = f (2) = 5 ⇒ m ≤ 5 [2;+∞) L
Câu 51: (Câu 42 - MĐ 104 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Tập hợp tất cả các giá trị thực uy x + 3 e
của tham số m để hàm số y =
đồng biến trên khoảng (−∞;− 6) là n x + m thitr Ⓐ. (3;6] . Ⓑ. (3;6) . Ⓒ. (3;+∞ ) . Ⓓ. [3;6) . acng Lời giải hie Chọn A m .
TXĐ: D = ℝ \ { m − }. vn m − 3 Ta có y′ = . (x + m)2
Để hàm số đồng biến trên khoảng (−∞;− 6) ⇔ y′ > 0 ∀x ∈(−∞;−6) . m  −3> 0 m  > 3 m  > 3    ⇔  ⇔  ⇔  ⇔ 3 < m ≤ 6.  m − ∉ (−∞;− ) 6  m − ≥ 6 − m  ≤ 6    x + 2
Câu 52: (Câu 41 - MĐ 103 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Tìm m để hàm số y = x + m
đồng biến trên khoảng (− ; ∞ 5 − ). 2;5 2;5 2;+∞ 2;5 N Ⓐ. ( ]. Ⓑ. [ ) . Ⓒ. ( ) . Ⓓ. ( ) . guy Lời giải %n H Chọn A oàn
Điều kiện: x ≠ −m . g Vi − 2 ) Ta có: ' m y = . t (x + m)2  y ' > 0  m − 2 > 0
Hàm số đồng biến trên khoảng (− ; ∞ 5 − ) ⇔  ⇔  ⇔ < ≤ −m ∉  (−∞ − ) 2 m 5. ; 5 −m ≥ 5 −  Vậy m∈(2; ] 5 .
Câu 53: (Câu 40 - MĐ 101 - BGD&ĐT - Đợt 1 - Năm 2019 - 2020) Tập hợp tất cả các giá trị thực x + 4
của tham số m để hàm số y =
đồng biến trên khoảng (−∞;− 7) là x + m Ⓐ. [4;7) . Ⓑ. (4;7] . Ⓒ. (4;7) . Ⓓ. (4;+ ∞) . Lời giải
https://www.facebook.com/vietgold Trang 21 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 Chọn B
Tập xác định: D = ℝ \{− } m . L − 4 u ' m y = . y (x + m)2 enth  y ' > 0  m > 4 it
Hàm số đồng biến trên khoảng −∞ ;7 ⇔  ⇔  ⇔ 4 < m ≤ 7 . r ( ) a −m ∉  (−∞;− 7) −m ≥ 7 −  cngh
Vậy m ∈(4;7] thì hàm số đồng biến trên khoảng (−∞;− 7) . iem.
Câu 54: (Câu 41 - ĐTK - BGD&ĐT - Lần 2 - Năm 2019 - 2020) Có bao nhiêu giá trị nguyên của tham vn 1
số m sao cho hàm số f ( x) 3 2
= x + mx + 4x + 3 đồng biến trên ℝ ? 3 Ⓐ. 5. Ⓑ. 4. Ⓒ. 3. Ⓓ. 2. Lời giải Chọn A * TXĐ: D = ℝ .
* Ta có: f ′( x) 2 = x + 2mx + 4
Để hàm số đồng biến trên ℝ điều kiện là f ′( x) 2
≥ 0; ∀x ∈ ℝ ⇔ ∆′ = m − 4 ≤ 0 ⇔ 2 − ≤ m ≤ 2
mà m∈ℤ ⇒ m ∈{ 2 − ; 1 − ;0;1; } 2 . N guy mx − %
Câu 55: (Câu 39 - ĐTK - BGD&ĐT - Lần 1 - Năm 2019 - 2020) Cho hàm số hàm số f ( x) 4 = n x − m H
( m là tham số thực). Có bao nhiêu giá trị nguyên của m để hàm số đã cho đồng biến trên khoảng oàn (0;+∞)? g Vi) Ⓐ. 5 . Ⓑ. 4 . Ⓒ. 3 . Ⓓ. 2 . t Lời giải Chọn D
Điều kiện xác định: x ≠ m . 2 −m + 4 Ta có y′ = . (x − m)2
Để hàm số đồng biến trên khoảng (0;+∞) thì 2 y′ > 0  −m + 4 > 0  2 − < m < 2 ⇔  ⇔  ⇔ 
⇔ −2 < m ≤ 0 . m∉  (0;+∞) m ≤ 0 m ≤ 0  
Do m nguyên nên m = −1;m = 0 . Vậy có 2 giá trị nguyên của m thỏa mãn.
https://www.facebook.com/vietgold Trang 22 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
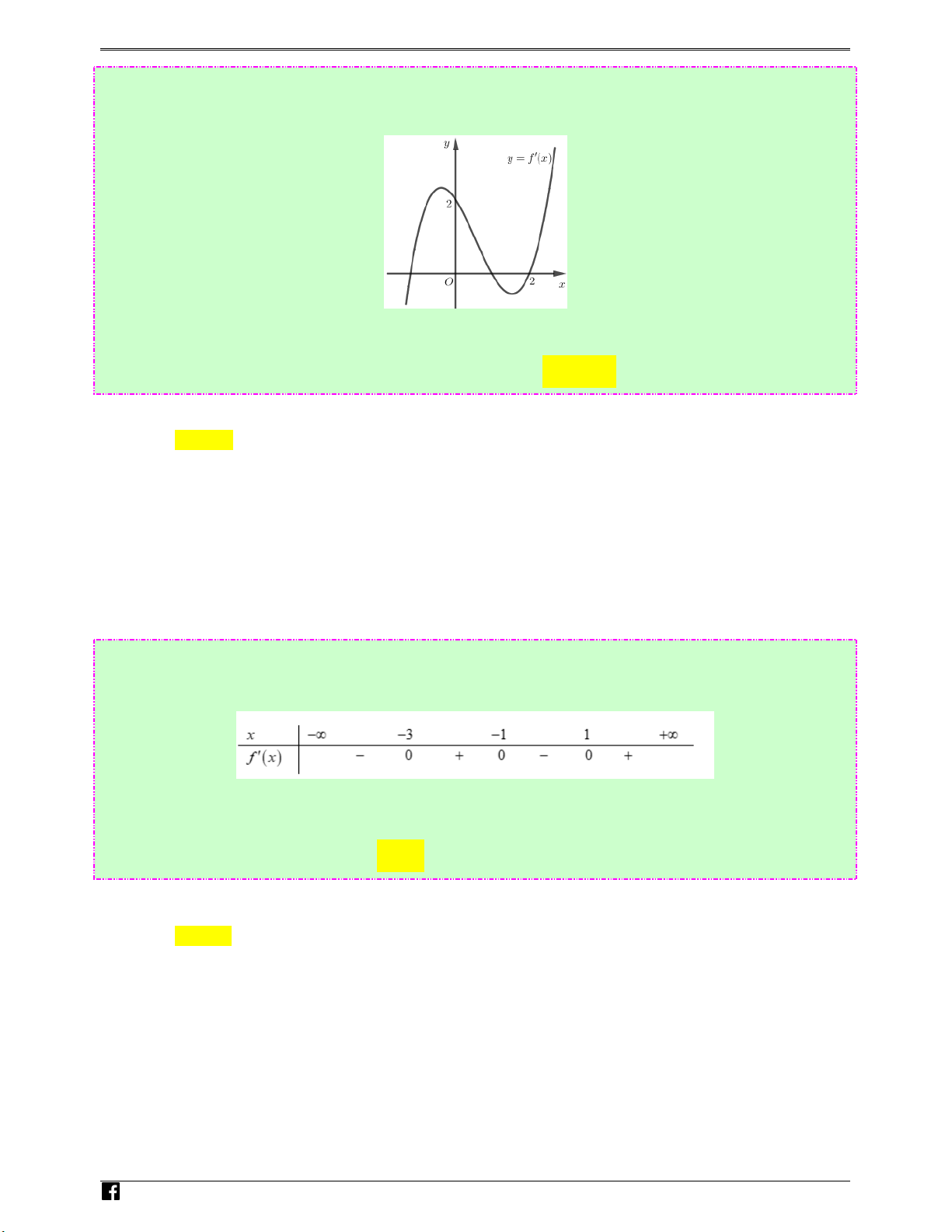
Câu 56: (Câu 38 - MĐ 103 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số f ( x) , hàm số y = f ′( x) liên
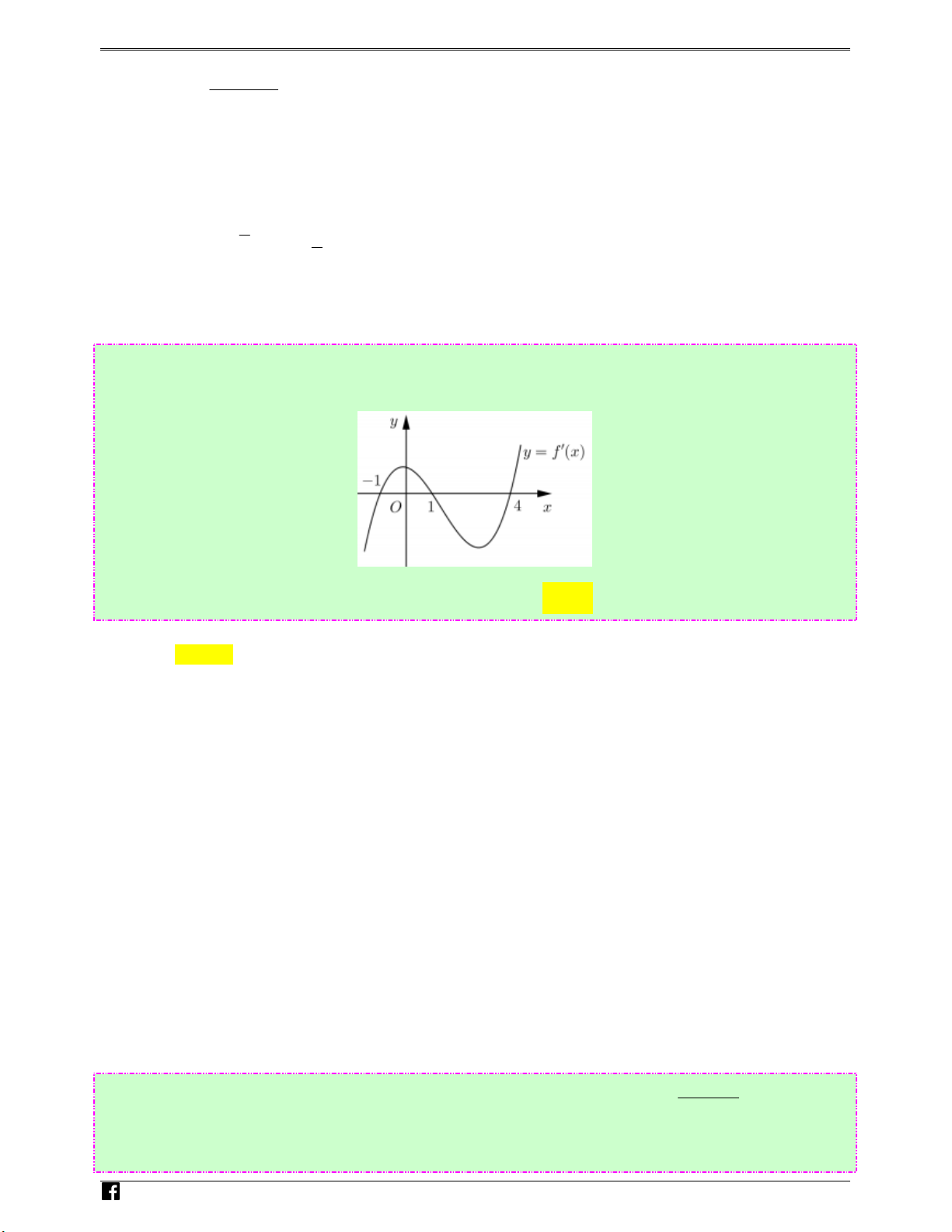
tục trên ℝ và có đồ thị như hình vẽ bên. Luyenthitracngh ie < + m
Bất phương trình f ( x) 2x m ( m là tham số thực) nghiệm đúng với mọi x ∈(0;2) khi và chỉ khi .vn
Ⓐ. m > f (0).
Ⓑ. m > f (2) − 4.
Ⓒ. m ≥ f (0) .
Ⓓ. m ≥ f (2) − 4 . Lời giải Chọn C
Ta có f ( x) < 2x + m ⇔ m > f ( x) − 2x ( ) * .
Xét hàm số g ( x) = f ( x) − 2x trên (0;2) .
Ta có g′( x) = f ′( x) − 2 < 0 x
∀ ∈(0;2) nên hàm số g ( x) nghịch biến trên (0;2) .
Do đó (*) đúng với mọi x ∈(0;2) khi m ≥ g (0) = f (0) .
Câu 57: (Câu 35 - MĐ 102 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số f ( x) , bảng xét dấu f ′( x ) N g như sau: uy%n Hoà ng V
Hàm số y = f (5− 2x) nghịch biến trên khoảng nào dưới đây? i)t Ⓐ. (2; ) 3 . Ⓑ. (0; ) 2 . Ⓒ. (3; ) 5 . Ⓓ. (5;+ ∞). Lời giải Chọn B
Xét hàm số y = f (5− 2x) . ′ y′ =  f  (5−2x) = 2 − f ′  (5−2x) .
− < − x < −  < x <
Xét bất phương trình: y′ < ⇔ f ′( − x) 3 5 2 1 3 4 0 5 2 > 0 ⇔ ⇔  . 5 2  − x >1 x < 2  
Suy ra hàm số y = f (5− 2x) nghịch biến trên các khoảng (− ; ∞ ) 2 và khoảng (3;4).
https://www.facebook.com/vietgold Trang 23 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 Vì (0;2) ⊂ (− ;
∞ 2) nên chọn đáp án B
Câu 58: (Câu 35 - MĐ 101 - BGD&ĐT - Năm 2018 - 2019) Cho hàm số f ( x) , bảng xét dấu của f ′( x) L như sau: uyenthit ra
Hàm số y = f (3− 2x) nghịch biến trên khoảng nào dưới đây? cnghi Ⓐ. (4;+ ∞) . Ⓑ. ( 2 − ; ) 1 . Ⓒ. (2;4) . Ⓓ. (1;2) . em Lời giải .vn Chọn B
− < − x < −  > x >
Ta có y′ = − f ′( − x) < ⇔ f ′( − x) 3 3 2 1 3 2 2 3 2 0 3 2 > 0 ⇔ ⇔  . 3 2x 1  − > x < 1  
Vì hàm số nghịch biến trên khoảng (− ; ∞ )
1 nên nghịch biến trên ( 2 − ; ) 1 .
Câu 59: (Câu 36 - ĐTK - BGD&ĐT - Năm 2018 - 2019) Tập hợp các giá trị thực của m để hàm số 3 2
y = −x − 6x + (4m −9) x + 4 nghịch biến trên khoảng (− ; ∞ − ) 1 là     Ⓐ. (− ; ∞ ] 0 . Ⓑ. 3 − ; +∞  . Ⓒ. 3 − ; ∞ −  . Ⓓ. [0;+∞)  4   4    Lời giải N Chọn C guy + TXĐ: ℝ . %n ' 2 Ta có y = 3
− x −12x +(4m−9) . H o 3 2 à
Hàm số y = −x − 6x + (4m−9) x + 4 nghịch biến trên khoảng (− ; ∞ − ) 1 khi và chỉ khi ng 2 2 ′ V y = 3
− x −12x + (4m−9) ≤ 0, x ∀ ∈(− ; ∞ − )
1 ⇔ 4m ≤ 3x +12x + 9, x ∀ ∈ ( ; −∞ − ) 1 . i) 2 t
+ Xét hàm g x = 3x +12x + 9, x ∈ −∞; −1 ; g′ x = 6x +12; g' x = 0 ⇔ x = −2 . ( ) ( ) ( ) ( ) + BBT 3
+ Từ bảng biến thiên suy ra 4m ≤ 3 − ⇔ m ≤ − . 4
Câu 60: (Câu 26 - MĐ 104 - BGD&ĐT - Năm 2017 - 2018) Có bao nhiêu giá trị nguyên của tham số x + 2
m để hàm số y =
đồng biến trên khoảng (−∞;−6) ? x + 3m
https://www.facebook.com/vietgold Trang 24 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 Ⓐ. 2 Ⓑ. 6 Ⓒ. Vô số Ⓓ. 1 Lời giải L Chọn A uye
Tập xác định: D = ( ; −∞ 3 − m) ∪( 3 − ; m +∞) . nth 3m − 2 it Ta có y′ = ra (x +3m)2 cngh  2 i 3m − 2 > 0 m > 2 em
Hàm số đổng biến trên khoảng (−∞;−6) ⇔  ⇔  3 ⇔ < m ≤ 2 . 6 − ≤ −3m  3 .  v m ≤ 2  n
Mà m nguyên nên m = {1; } 2 .
Câu 61: (Câu 31 - MĐ 103 - BGD&ĐT - Năm 2017 - 2018) Có bao nhiêu giá trị nguyên của tham số x +1
m để hàm số y =
nghịch biến trên khoảng (6; +∞) ?. x + 3m Ⓐ. 3. Ⓑ. Vô số. Ⓒ. 0 . Ⓓ. 6 Lời giải Chọn A 3m −1
Tập xác định D = ℝ\{−3m}; y′ = . (x +3m)2 N gu x +1 y Hàm số y =
nghịch biến trên khoảng (6; +∞) khi và chỉ khi: %n x + 3m Ho  1 à y′ < 0  3  m −1< 0 m < 1 n  ⇔  ⇔ 
3 ⇔ −2 ≤ m < . g (  6;+∞  ) ⊂ D 3 − m ≤ 6 3   V m ≥ 2 −  i)t
Vì m ∈ ℤ ⇒ m ∈{−2; −1; } 0 .
Câu 62: (Câu 35 - MĐ 101 - BGD&ĐT - Năm 2017 - 2018) Có bao nhiêu giá trị nguyên của tham số x + 2
m để hàm số y =
đồng biến trên khoảng ( ; −∞ −10) ? x + 5m Ⓐ. 2 Ⓑ. Vô số Ⓒ. 1 Ⓓ. 3 Lời giải Chọn A TXĐ: D = ℝ \ {−5 } m .
https://www.facebook.com/vietgold Trang 25 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 5m − 2 y ' = . (x +5m)2 5m − 2 > 0  L
Hàm số đồng biến trên khoảng ( ; −∞ 1 − 0) khi và chỉ khi u   5 − m ∈  [ 1 − 0;+∞) yenth  2 i m > 2 tr ⇔  5 ⇔ < m ≤ 2 . a 5 c  5 − m ≥ 1 − 0 n  ghi
Vì m nguyên nên m ∈ 1; 2 . Vậy có 2 giá trị của tham số m . e { } m .v
Câu 63: (Câu 39 - ĐTK - BGD&ĐT - Năm 2017 - 2018) Cho hàm số y = f (x) . Hàm số y = f '(x) có n
đồ thị như hình bên. Hàm số y = f (2 − x) đồng biến trên khoảng Ⓐ. (1; ) 3 Ⓑ. (2;+∞) Ⓒ. ( 2 − ; ) 1 Ⓓ. (− ; ∞ 2 − ) Lời giải Chọn C N g Cách 1: uy% x ∈ (1; 4) n
Ta thấy f '(x) < 0 với
nên f (x) nghịch biến trên (1;4) và (− ; ∞ − ) 1 suy ra  H x < −1  oà =
− đồng biến trên − − và 1;+∞ . Khi đó f −
đồng biến biến trên khoảng n g (x) f ( x) ( 4; 1) ( ) (2 x) g V (−2;1) và (3; +∞) i)t Cách 2: x < −
Dựa vào đồ thị của hàm số y = f ′( x) ta có f ′( x) 1 < 0 ⇔ . 1  < x < 4  Ta có ( ′ ′
f (2 − x)) = (2 − x) . f ′(2 − x) = − f ′(2 − x) . Để hàm số ′
y = f (2 − x) đồng biến thì ( f (2 − x)) > 0 ⇔ f ′(2 − x) < 0 2 − x < 1 − x > 3 ⇔ ⇔ . 1  2  < − x < 4 2 − < x < 1   mx + 4
Câu 64: (Câu 41 - MĐ 104 - BGD&ĐT - NĂM 2016 - 2017) Cho hàm số m y = với m là tham x + m
số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số nghịch biến trên các khoảng xác
định. Tìm số phần tử của S .
https://www.facebook.com/vietgold Trang 26 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 Ⓐ. 5. Ⓑ. 4 . Ⓒ. Vô số. Ⓓ. 3. Lời giải Chọn D L 2 m − 4m u D = ℝ \ {− } m ; y′ = y 2 e (x + m) nt 2 h
Hàm số nghịch biến trên các khoảng xác định khi y′ < 0, x
∀ ∈ D ⇔ m − 4m < 0 ⇔ 0 < m < 4 itra
Mà m ∈ ℤ nên có 3 giá trị thỏ Ⓐ. cngh mx − 2m − 3
Câu 65: (Câu 31 - MĐ 103 - BGD&ĐT - NĂM 2016 - 2017) Cho hàm số y = với i m là e x − m m .
tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số đồng biến trên các khoảng vn
xác định. Tìm số phần tử của S . Ⓐ. 5. Ⓑ. 4 . Ⓒ. Vô số. Ⓓ. 3. Lời giải Chọn D 2 −m + 2m + 3 Ta có y ' = 2 (x − m)
Để hàm số đồng biến trên từng khoảng xác định thì 2
y ' ≥ 0 ⇔ −m + 2m + 3 ≥ 0 ⇔ m ∈[-1;3] Xét tại m = 1
− ;m = 3 thấy không thỏa mãn. Vậy m = 0;m = 1;m = 2. N
Câu 66: (Câu 38 - MĐ 101 - BGD&ĐT - Năm 2016 - 2017) Cho hàm số 3 2
y = − x − mx + (4m + 9)x + 5 guy
với m là tham số. Có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng (− ; ∞ +∞) %n ? Hoà Ⓐ. 7 Ⓑ. 4 Ⓒ. 6 Ⓓ. 5 ng V Lời giải i)t Chọn A D = ℝ ′ y = − 2 ,
3x − 2mx + 4m + 9
Hàm số nghịch biến trên (− ; ∞ + ∞) ⇔ ′
y ≤ 0, ∀x ∈ ℝ ⇔ ′ ∆ ≤ 0 2
⇔ m +12m + 27 ≤ 0 ⇔ 9 − ≤ m ≤ 3 −
Mà m∈ℤ ⇒ m∈{−9;−8;−7;−6;−5;− 4;− } 3
Câu 67: (Câu 41 - ĐTK - BGD&ĐT - Năm 2016 - 2017) Hỏi có bao nhiêu số nguyên m để hàm số y = ( 2 m − ) 3 x + (m − ) 2 1
1 x − x + 4 nghịch biến trên khoảng (−∞; +∞) . Ⓐ. 2 Ⓑ. 1 Ⓒ. 0 Ⓓ. 3 Lời giải Chọn A
https://www.facebook.com/vietgold Trang 27 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
TH1: m =1. Ta có: y = − x + 4 là phương trình của một đường thẳng có hệ số góc âm nên hàm
số luôn nghịch biến trên ℝ . Do đó nhận m =1. TH2: m = 1 − . Ta có: 2 y = 2
− x − x + 4 là phương trình của một đường Parabol nên hàm số không L
thể nghịch biến trên ℝ . Do đó loại m = 1 − . u ⇔ ′ y TH3: m ≠ 1
± . Khi đó hàm số nghịch biến trên khoảng (−∞; +∞)
y ≤ 0 ∀x ∈ ℝ , dấu “=” chỉ en
xảy ra ở hữu hạn điểm trên ℝ . th 2 2 i ⇔ 3(m − ) 1 x + 2(m − )
1 x −1 ≤ 0 , ∀x ∈ ℝ trac 2 2  1 − < m < 1   < − < n a 0 m 1 0   m −1 < 0  1 g ⇔  ⇔  ⇔  ⇔  1 ⇔ − ≤ m < 1 . 2 h ∆′ ≤ 0  (m −  ) 1 + 3  ( 2 m − ) 1 ≤ 0 (  m −  ) 1 (4m + 2) ≤ 0 − ≤ m ≤ 1 2 i  e  2 m
Vì m∈ℤ nên m = 0 . .vn
Vậy có 2 giá trị m nguyên cần tìm là m = 0 hoặc m =1.
Câu 68: (Câu 9 - ĐTN - BGD&ĐT - Năm 2016 - 2017) Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số = ( 2 y ln x + )
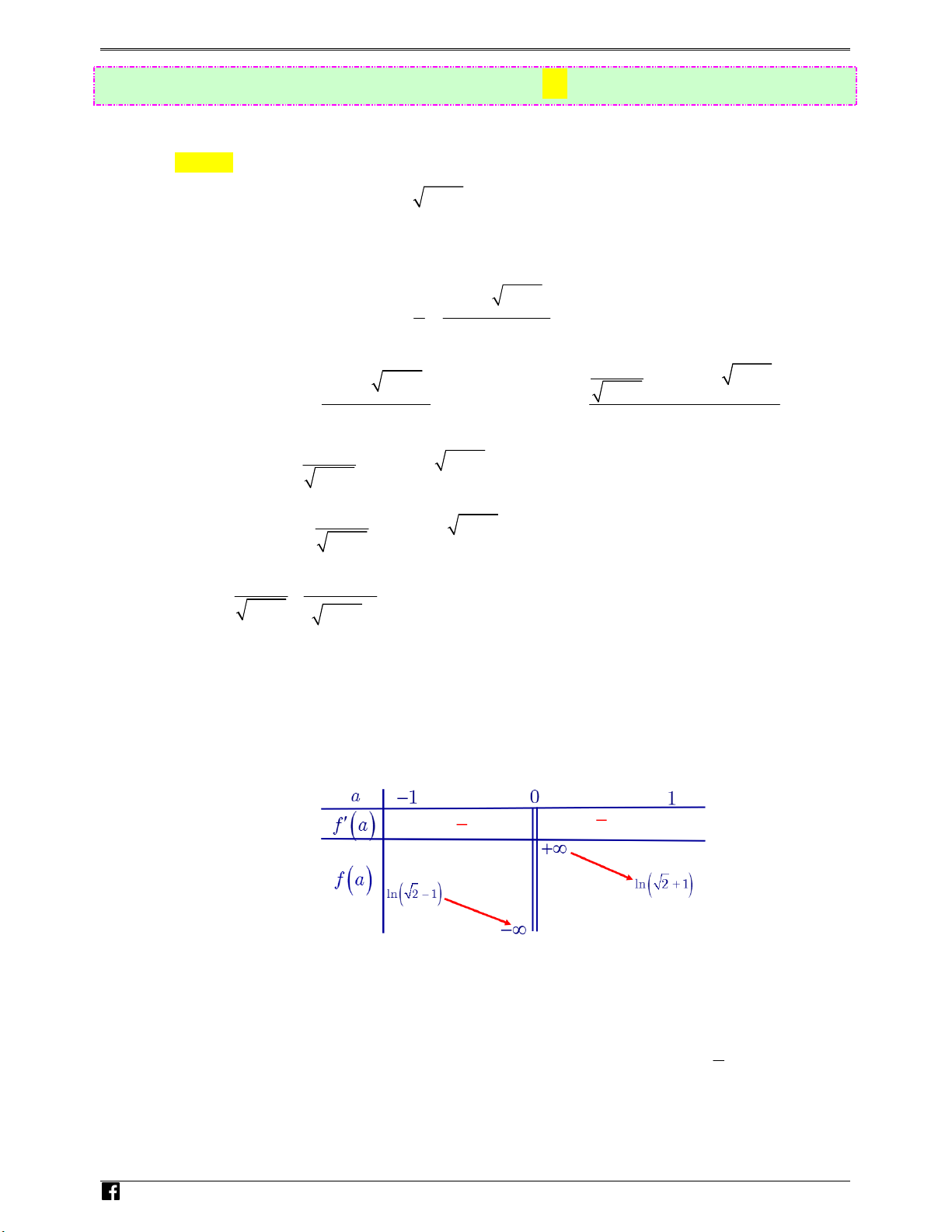
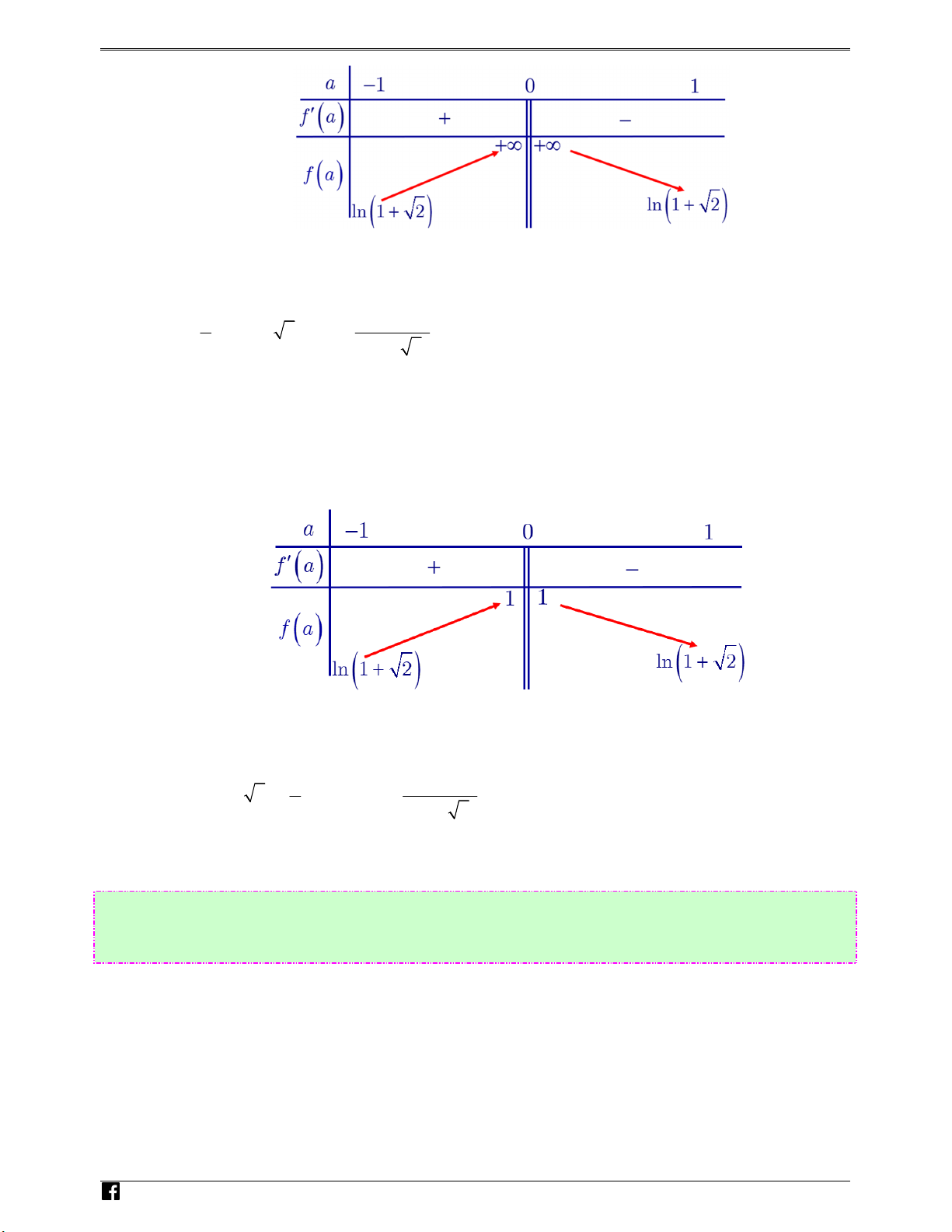
1 − mx +1 đồng biến trên khoảng (−∞;+∞) Ⓐ. (−∞;− ] 1 Ⓑ. (−∞;− ) 1 Ⓒ. [−1; ] 1 Ⓓ. [1;+∞) Lời giải Chọn A 2 Ta có: x y′ = − m . 2 x +1 Hàm số y = ( 2 ln x + )
1 − mx +1 đồng biến trên khoảng (− ;
∞ +∞) ⇔ y′ ≥ 0,∀x ∈(−∞;+∞) . N gu 2x 2 −2x + 2 y% ⇔ g(x) = ≥ , m x ∀ ∈ − ;
∞ +∞ . Ta có g (′x) = = 0 ⇔ x = ±1 2 ( ) 2 n x +1 ( 2x + )1 Hoà Bảng biến thiên: ng Vi)t 2
Câu 69: Dựa vào bảng biến thiên ta có: ( ) x g x = ≥ , m x ∀ ∈ − ; ∞ +∞ ⇔ m ≤ 1 − 2 ( ) x +1
(Câu 43 - MĐ 101 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Xét các số thực , x y thỏa mãn: 2 2 4y x + y 1 + ≤ ( 2 2 2 + − 2 + 2).4x x y x
. Giá trị nhỏ nhất của biểu thức P =
gần nhất với số 2x + y +1 nào dưới đây? Ⓐ. 2 − . Ⓑ. 3 − . Ⓒ. 5 − . Ⓓ. 4 − . Lời giải
https://www.facebook.com/vietgold Trang 28 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 Chọn B 2 2 x + y 1 + x + y + x 2 Ta có: 2 2 1 2 ≤ ( 2 2
x + y − 2x + 2) 2 2 .4 ⇔
≤ x + y − 2x + 2 4x L 2 2
x + y −2 x 1 + 2 2 u ⇔ 2
− (x + y − 2x + ) 1 −1 ≤ 0 (*) . yen t t
Đặt t = x + y − x + ⇔ t = ( x − )2 2 2 2 2 1
1 + y ≥ 0 . Khi đó (*) trở thành 2 − t −1≤ 0 . hitr
Xét hàm số: ( ) = 2t f t
− t −1 trên [0;+∞) acng t  1  h
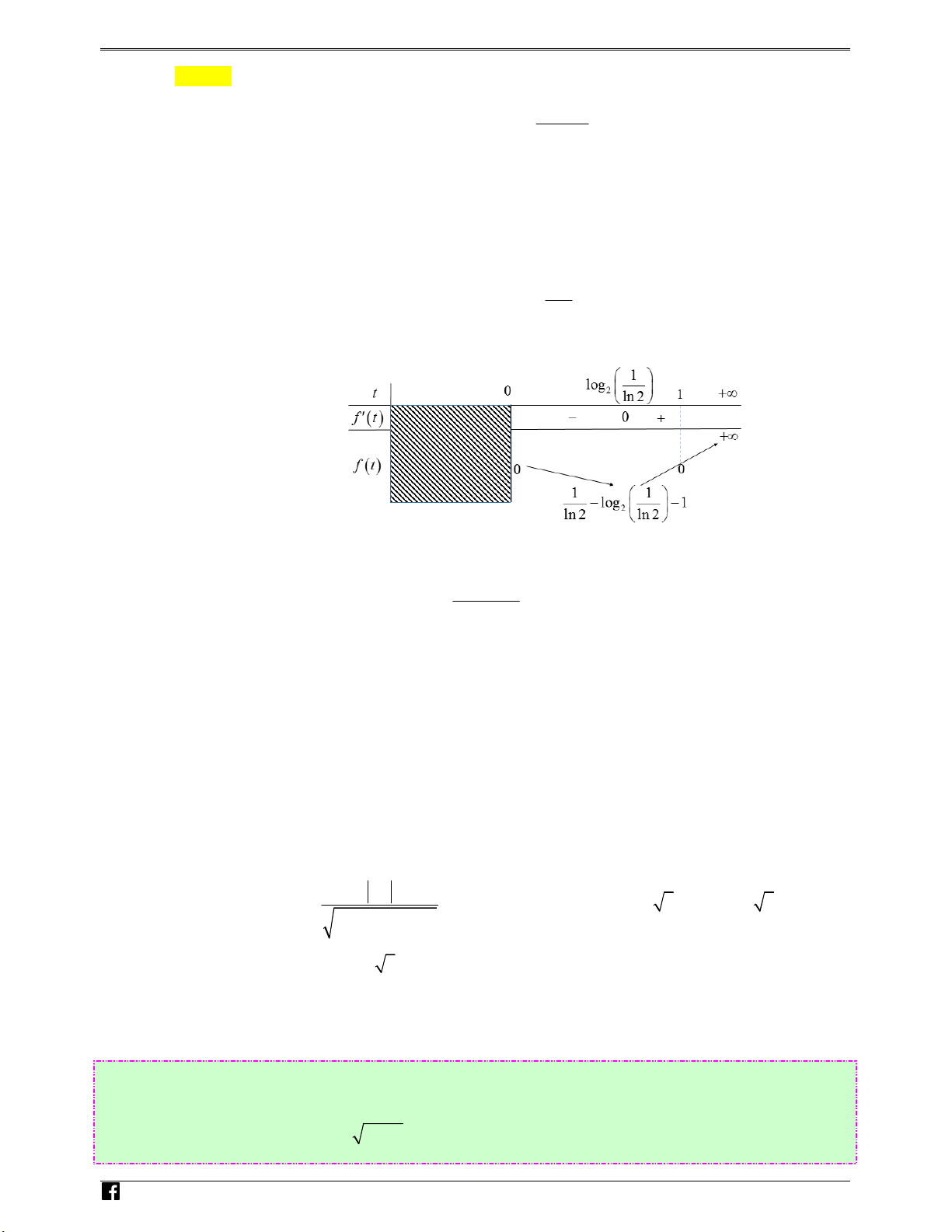
f ′(t ) = 2 ln 2 −1 ⇒ f ′(t ) = 0 ⇔ t = log . 2   i  ln 2 e  m . Bảng biến thiên: vn
Dựa vào bảng biến thiên ta có f (t) ≤ ⇔ ≤ t ≤ ⇔ ( x − )2 2 0 0 1 1 + y ≤ 1. 4y
Khi đó 2x + y +1 > 0 và P =
⇔ 2Px + (P − 4) y + P = 0. 2x + y +1 Các cặp ( ;
x y ) thỏa mãn: ( x − )2 2
1 + y ≤ 1 là tọa độ các điểm ( x; y) thuộc hình tròn N g (C ) uy%n
Tâm I (1;0) , bán kính R =1. Ho Các cặp ( ;
x y ) thỏa mãn: 2Px + ( P − 4) y + P = 0 là tọa độ các điểm ( ; x y ) thuộc àng đường thẳng Vi)
(d ) : 2Px + (P − 4) y + P = 0 . t
Do đó tồn tại giá trị nhỏ nhất của P khi đường thẳng (d ) phải có điểm chung với hình tròn 3 ( P 2 C ) ⇔ d( ≤ R ⇔
≤1 ⇔ P + 2P − 4 ≤ 0 ⇔ 1 − − 5 ≤ P ≤ 1 − + 5 . I ;d ) 4P + (P − 4)2 2 Vậy min P = 1 − − 5 ≈ 3 − , 24 .
Dấu bằng xảy ra khi ( x; y) là tọa độ tiếp điểm của đường thẳng (d ) với hình tròn (C ).
Câu 70: (Câu 50 - MĐ 101 - BGD&ĐT - Đợt 2 - Năm 2019 - 2020) Có bao nhiêu cặp số nguyên dương ( ,
m n) sao cho m + n ≤ 14 và ứng với mỗi cặp ( ,
m n) tồn tại đúng ba số thực a ∈( 1 − ; ) 1 thỏa mãn m a = n ( 2 2 ln a + a +1) ?
https://www.facebook.com/vietgold Trang 29 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 Ⓐ. 14. Ⓑ. 12. Ⓒ. 11. Ⓓ. 13. Lời giải L Chọn C uye m 2 n
Xét phương trình: 2a = n ln (a + a +1) ( ) 1 . thitr
+ Nhận xét: a = 0 là một nghiệm của phương trình ( ) 1 . acng 2 h ln (a + a +1 2 ) ie
+ Với a ≠ 0 , phương trình ( ) 1 ⇔ = ( ) * . m m n a .vn a 2 ( 2 ln
− mln a + a +1 2 ( ) a + a +1) Xét hàm số: a +1 f (a) = trên (−1; ) 1 ; f ′(a) = . m a m 1 a + Xét phương trình a − m ln ( 2
a + a +1 = 0 2 . 2 ) ( ) a +1 Xét hàm số ( ) a g a = − m ln ( 2
a + a +1 trên (−1; ) 1 . 2 ) a +1 2 ′( ) 1− m a g a = −
⇒ g′ a ≤ 0, a ∀ ∈ 1 − ;1 ;m∈ ℕ*. 2 a +1 ( 2a +1)3 ( ) ( ) N
Suy ra hàm số g (a) nghịch biến trên khoảng (−1; ) 1 . guy%
Do đó, phương trình (2) có nghiệm duy nhất a = 0 . n H + Trường hợp 1: o m chẵn. àng Vi)t
Phương trình đã cho có 3 nghiệm phân biệt thuộc khoảng (−1; )
1 khi và chỉ khi phương trình ( )
* có 2 nghiệm phân biệt khác 0 thuộc khoảng (−1; ) 1
Dựa vào bảng biến thiên, ta thấy với n nguyên dương phương trình ( ) 2 f a = không có hai n
nghiệm phân biệt. Suy ra loại trường hợp m chẵn.
+ Trường hợp 2: m lẻ và m ≠ 1.
https://www.facebook.com/vietgold Trang 30 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 Luyenth itra
Phương trình đã cho có 3 nghiệm phân biệt thuộc khoảng (−1; )
1 khi và chỉ khi phương trình cng ( )
* có hai nghiệm phân biệt khác 0 thuộc khoảng (−1; ) 1 hie 2 2 n = 1 m ⇔
> ln (1+ 2) ⇔ n < ⇔  . . n ln 1+ 2 n = 2 v ( )  n
Với n =1, m lẻ và m ≠1, m +1 ≤ 14 suy ra m ∈{3;5;7;9;11;1 } 3 .
Với n = 2 , m lẻ và m ≠ 1, m + 2 ≤ 14 suy ra m ∈{3;5;7;9;11}.
+ Trường hợp 3: m =1. N gu y%n
Phương trình đã cho có 3 nghiệm phân biệt thuộc khoảng (−1; )
1 khi và chỉ khi phương trình Ho ( )
* có hai nghiệm phân biệt khác 0 thuộc khoảng (−1; ) 1 àn 2 2 g
⇔ ln 1+ 2 < <1 ⇔ 2 < n <
suy ra không tồn tại số tự nhiên n thỏa mãn. ( ) V n ln 1+ 2 i ( ) )t
Vậy có 11 cặp (m;n) thỏa mãn yêu cầu bài toán. Câu 71:
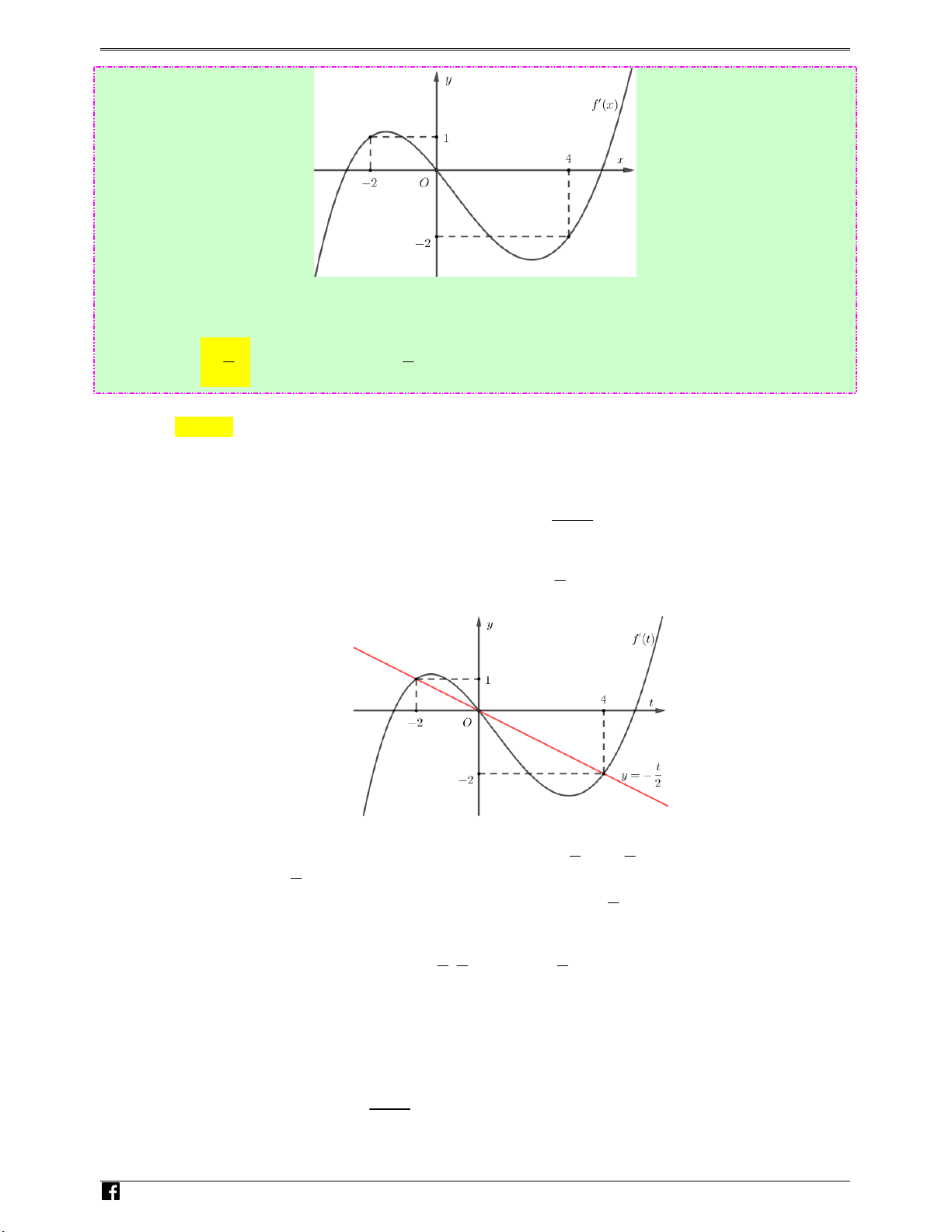
(Câu 50 - ĐTK - BGD&ĐT - Lần 1 - Năm 2019 - 2020) Cho hàm số f (x) . Hàm số
y = f ′( x) có đồ thị như hình sau.
https://www.facebook.com/vietgold Trang 31 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 Luyenthitrac ngh
Hàm số g ( x) = f ( − x) 2
1 2 + x − x nghịch biến trên khoảng nào dưới đây? iem.v     n Ⓐ. 3 1;   . Ⓑ. 1 0;   . Ⓒ. ( 2 − ;− ) 1 . Ⓓ. (2; ) 3 .  2   2  Lời giải Chọn A
Ta có g′( x) = 2
− f ′(1−2x) + 2x −1 −
g′( x) < ⇔ − f ′( − x) + x − < ⇔ f ′( − x) 2x 1 0 2 1 2 2 1 0 1 2 > (*). 2 Đặt t
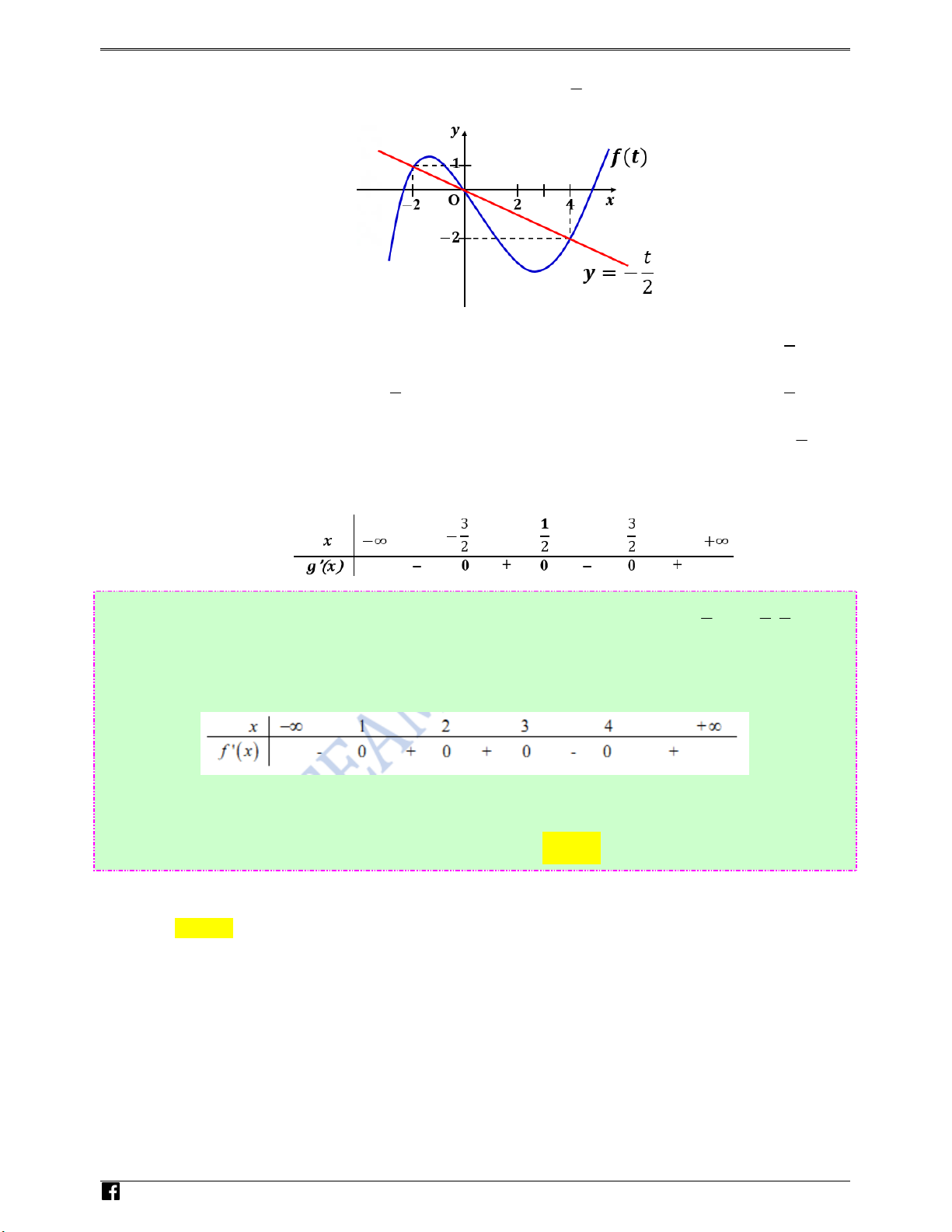
t = 1 − 2 x , ta có đồ thị hàm số y = f ′(t ) và y = − như hình vẽ sau : 2 N guy%n Hoàng V i)t 1 3 < x < − < < − < − <  ( ) ⇔ f ′(t) t 2 t 0 2 1 2x 0 2 2 * > − ⇒ ⇔ ⇔    . 2 t > 4 1− 2x > 4 3   x < −  2  1 3  3 ⇒  
hàm số nghịch biến trên khoảng ;  và − ; ∞ − 2 2       2  Cách 2:
Ta có: g ( x) = f ( − x) 2
1 2 + x − x ⇒ g′( x) = 2
− f ′(1−2x) + 2x −1. ′( ) = ⇔ ( − ) 1− 2 0 ' 1 2 x g x f x = − . 2
https://www.facebook.com/vietgold Trang 32 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
Xét sự tương giao của đồ thị hàm số t
y = f ′(t) và y = − . 2 Luyenthitracngh iem  3 . x = v  n  2 t = 2 − 1  − 2x = −2  t  1 Từ đồ thị ta có:  
f '(t ) = − ⇔ t = 0 . Khi đó: g′( x) = 0 ⇔ 1− 2x = 0 ⇔ x = . 2    2 t = 4  1  − 2x = 4   3 x = −  2 Ta có bảng xét dấu:  3   1 3 
Câu 72: Dựa vào bảng xét dấu, ta thấy: hàm số nghịch biến trên các khoảng −∞; −  và ; . (Câu 2       2 2 
48 - ĐTK - BGD&ĐT - Năm 2018 - 2019) Cho hàm số y = f ( x) có bảng xét dấu của đạo hà m N g như sau: uy%n Hoà ng
Hàm số y = f ( x + ) 3 3
2 − x + 3x đồng biến trên khoảng nào dưới đây? Vi)t Ⓐ. (1;+∞). Ⓑ. (−∞;− ) 1 . Ⓒ. (−1;0) . Ⓓ. (0;2) . Lời giải Chọn C Cách 1:
Ta có y′ > ⇔ f ′( x + ) 2
− x + > ⇔ f ′( x + ) 2 0 3 2 3 3 0 2 > x −1.
Đặt t = x + 2, bất phương trình trở thành: 2 f (
′ t) > (t − 2) −1. (  t − )2 2 −1 < 0
Xét hệ bất phương trình  ,( I ).
f (′t) > 0 
https://www.facebook.com/vietgold Trang 33 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020  1 − < t − 2 <1 1  < t < 3   1   < t < 2  1  < t < 2 1  < t < 2 Ta có (I ) ⇔  ⇔   ⇔ . 2   < t < 3 2 < t < 3 2 < t < 3     L  t  > 4  t  > 4   uyen 1  < x + 2 < 2  1 − < x < 0 t Khi đó ⇔ . h   i 2 < x + 2 < 3 0 < x < 1   tracn
Vậy hàm số đã cho đồng biến trên các khoảng ( 1 − ;0) . ghi
Cách 2: em .v
Xét hàm số y = f ( x + ) 3 3 2 − x + 3x n y′ = f ′( x + ) 2
− x + =  f ′( x + ) +  ( 2 3 2 3 3 3 2 1 − x ) .  3    7  5 Ta có y′ = 3 f ′ − < 0 
nên loại đáp án A, D 2     2  4     
y′(−2) = 3 f ′  (0) − 3 < 0  nên loại đáp án B Vậy ta chọn đáp án C
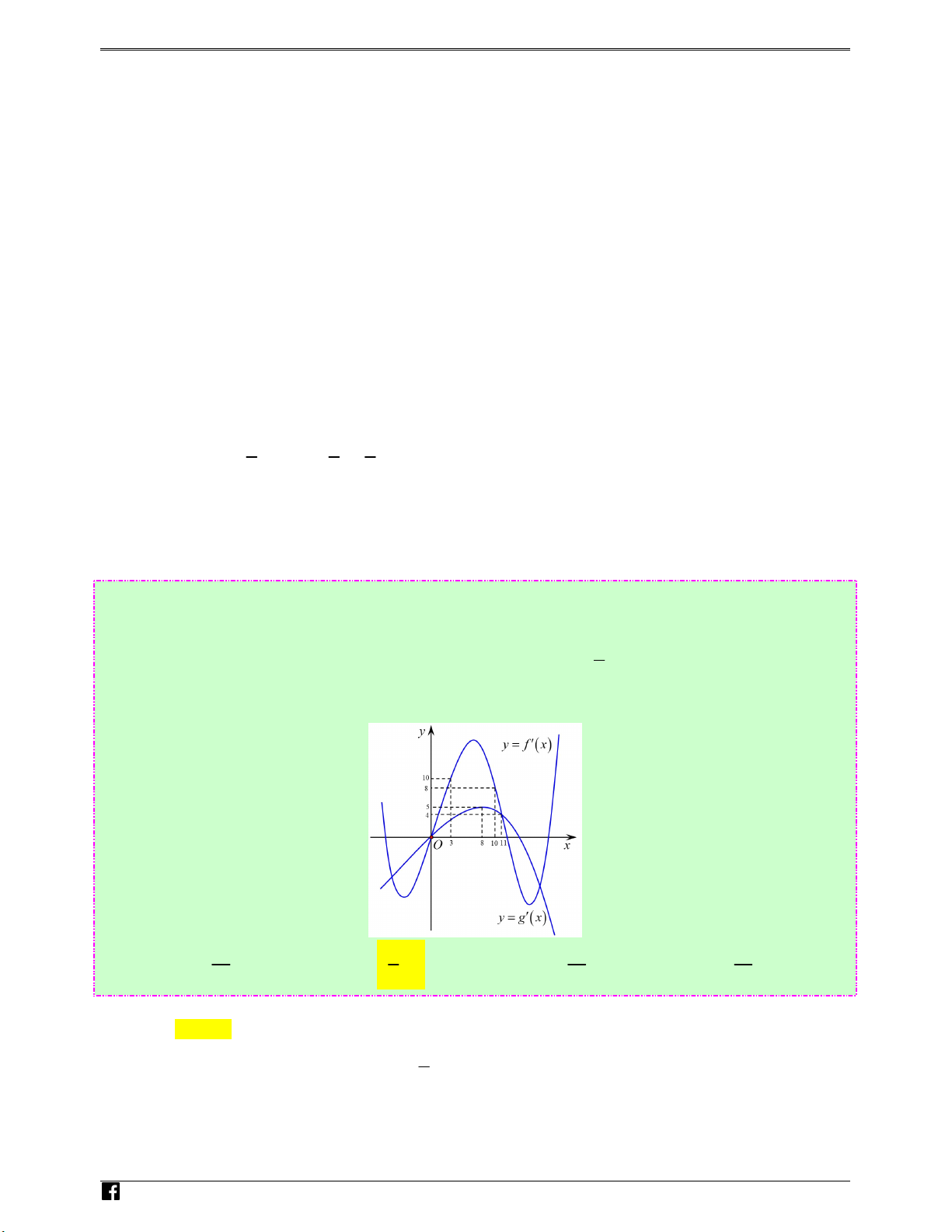
Câu 73: (Câu 46 - MĐ 104 - BGD&ĐT - Năm 2017 - 2018) Cho hai hàm số y = f (x) , y = g(x) . Hai
hàm số y = f (
′ x) và y = g (′x) có đồ thị như hình vẽ dưới đây, trong đó đường cong đậm hơn là  5 
đồ thị hàm số y = g (′x) . Hàm số h(x) = f (x + 6) − g 2x +
đồng biến trên khoảng nào dư ới N  2    gu đây? y%n Hoàng Vi)t         Ⓐ. 21;+∞  Ⓑ. 1 ;1 Ⓒ. 21 3; Ⓓ. 17 4; 5           4   5   4  Lời giải Chọn B  5  Ta có h (
′ x) = f (′x + 6) − 2g′ 2x +  . 2   
Nhìn vào đồ thị của hai hàm số y = f (′x) và y = g (′x) ta thấy trên khoảng (3;8) thì g (′x) < 5
và f (′x) > 10 . Do đó f (′x) > 2g (′x) .
https://www.facebook.com/vietgold Trang 34 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020  5  5 1 11
Như vậy: g′ 2x + < 5 
nếu 3 < 2x + < 8 ⇔ < x < . 2    2 4 4 f (
′ x + 6) > 10 nếu 3 < x + 6 < 8 ⇔ 3 − < x < 2 . L  1   5  u Suy ra trên khoảng ;2 
 thì g′ 2x + < 5  
và f (′x + 7) > 10 hay h (′x) > 0 . y  4   2  en  1  th Tức là trên khoảng ;1 
 hàm số h(x) đồng biến. i  4  tracn
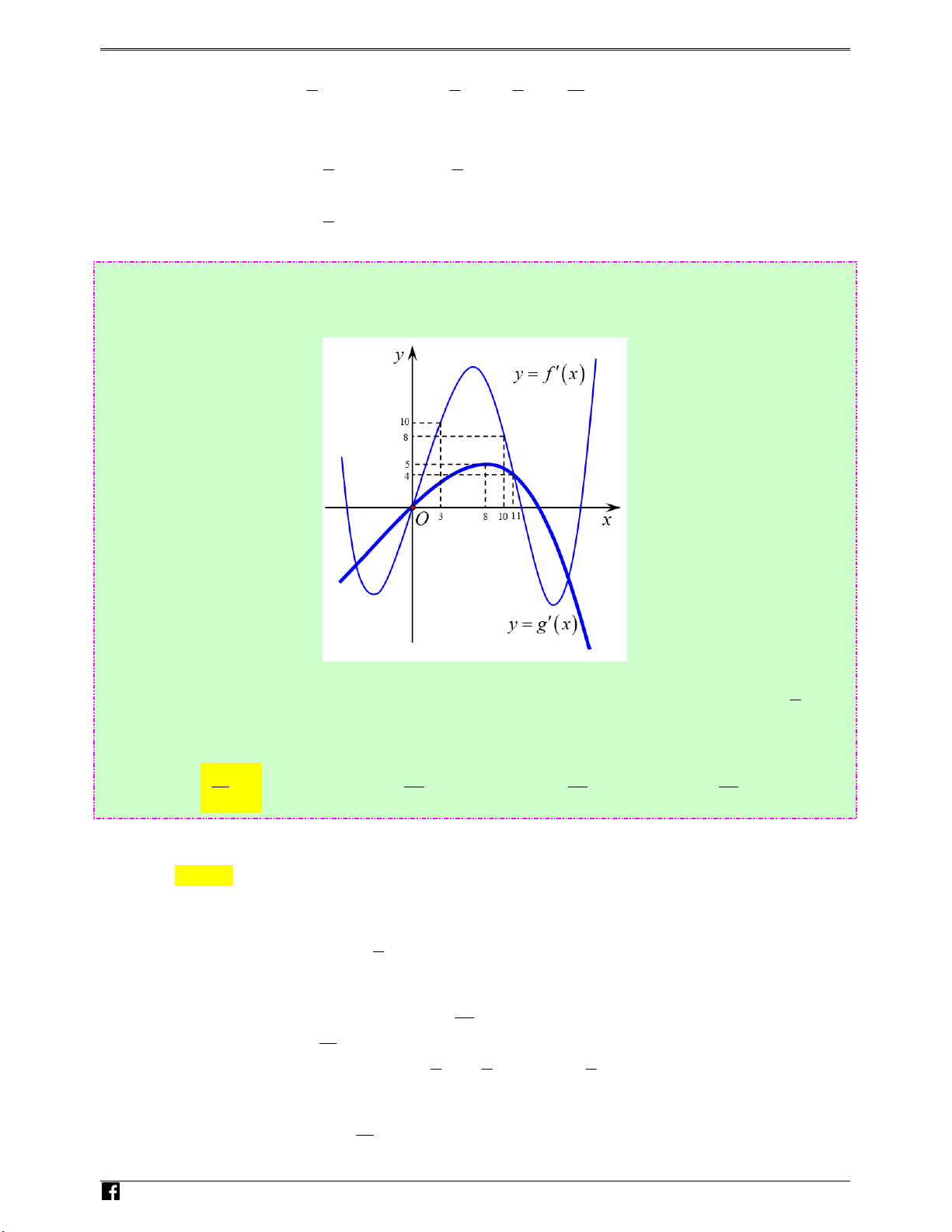
Câu 74: (Câu 44 - MĐ 103 - BGD&ĐT - Năm 2017 - 2018) Cho hai hàm số y = f ( x) , y = g ( x) . Hai gh
hàm số y = f ′ x và y = g′ x có đồ thị như hình vẽ bên i ( ) ( ) em .vn N gu  
trong đó đường cong đậm hơn là đồ thị của hàm số y = g′(x) . Hàm số h ( x) = f ( x + ) 7 3 − g 2x − đồng y   %  2  n
biến trên khoảng nào dưới đây? H oàn         Ⓐ. 13;4 . Ⓑ. 29 7; . Ⓒ. 36 6; . Ⓓ. 36 ;+∞ g          4   4   5   5  Vi)t Lời giải Chọn A
Cách 1. Ta thấy f '(x) > 2g '( y) với mọi x ∈ (3 ;8) và mọi y ∈ ℝ .  7 
Suy ra f '(x + 3) − 2g ' 2x − > 0 
với mọi x + 3∈ (3; 8) hay x ∈ (0 ;5) . 2      25  x + 3∈ ;7 ⇒ f ( ′ x + 7) > 10     13    4 
Cách 2. Ta có: x ∈ ; 4 ⇒   
⇒ h (′x) > 0  4  7   9   7  2x − ∈ 3; ⇒ g′ 2x − < 5  2  2   2        13 
⇒ h ( x) đồng biến trên ; 4  . 4   
https://www.facebook.com/vietgold Trang 35 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020
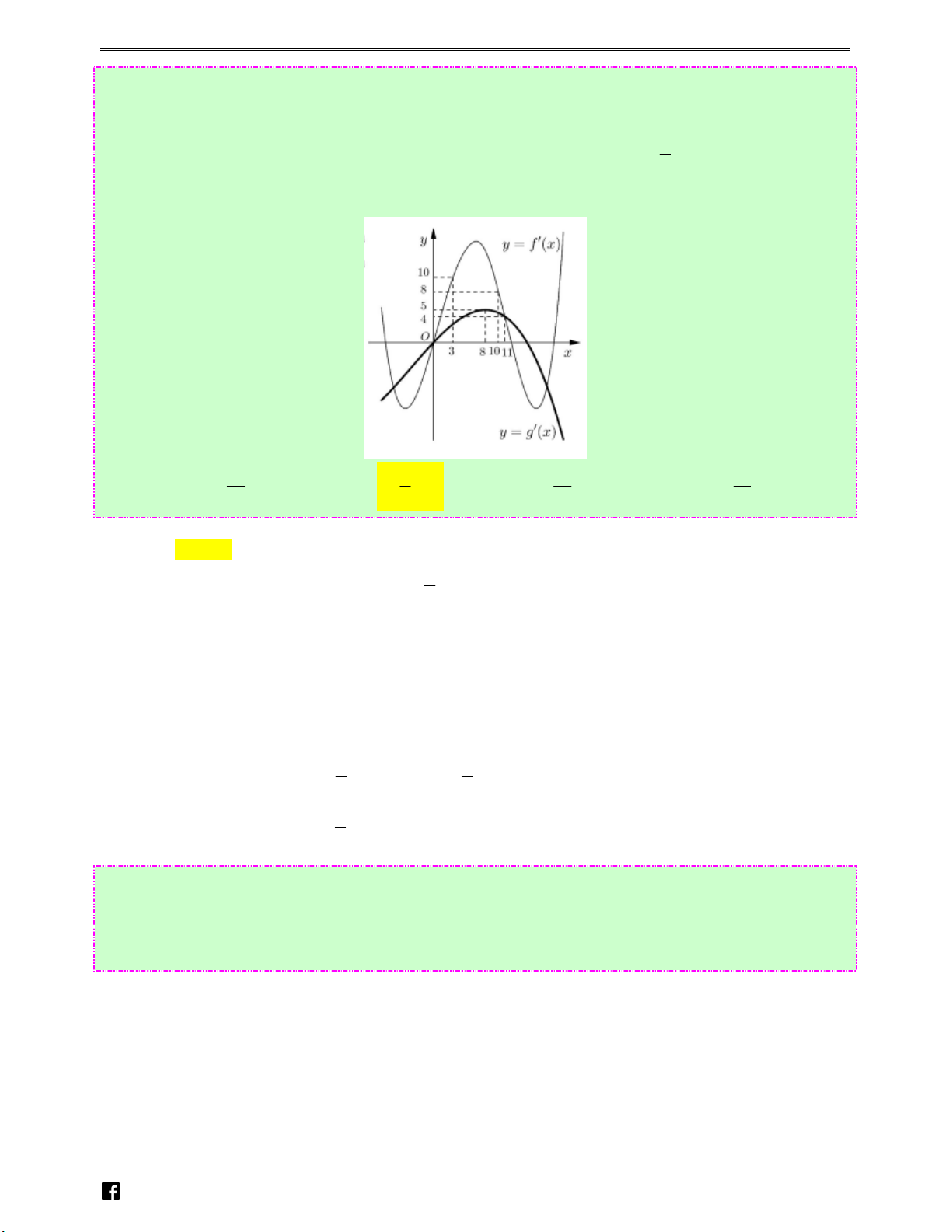
Câu 75: (Câu 47 - MĐ 102 - BGD&ĐT - Năm 2017 - 2018) Cho hai hàm số y = f ( x) và y = g ( x) .
Hai hàm số y = f ′( x) và y = g′( x) có đồ thị như hình vẽ dưới đây, trong đó đường cong đậm  
hơn là đồ thị hàm số = ′
. Hàm số h x = f x + − g x +
đồng biến trên khoảng L y g ( x) ( ) ( ) 9 7 2   u  2  ye nào dưới đây? nthitracnghiem.vn         Ⓐ. 16 2;  . Ⓑ. 3 − ;0 . Ⓒ. 16 ;+∞ . Ⓓ. 13 3; 5           4   5   4  Lời giải Chọn B  
Ta có h′( x) = f ′( x + ) 9 7 − 2g′ 2x +  . 2   
Nhìn vào đồ thị của hai hàm số y = f ′( x) và y = g′( x) ta thấy trên khoảng (3;8) thì g′( x) < 5
và f ′( x) > 10 . Do đó f ′( x) > 2g′( x) . N g  9  9 3 7 u
Như vậy: g′ 2x + < 5  
nếu 3 < 2x + < 8 ⇔ − < x < . y  2 2 4 4 %  n
f ′ ( x + 7) > 10 nếu 3 < x + 7 < 8 ⇔ 4 − < x < 1. H oà  3   9  ′ ′ ′ n Suy ra trên khoảng − ;1   thì g 2x + < 5  
và f ( x + 7) > 10 hay h ( x) > 0 . g  4   2  Vi  3  )
Tức là trên khoảng − ;0 hàm số h ( x) đồng biến. t    4 
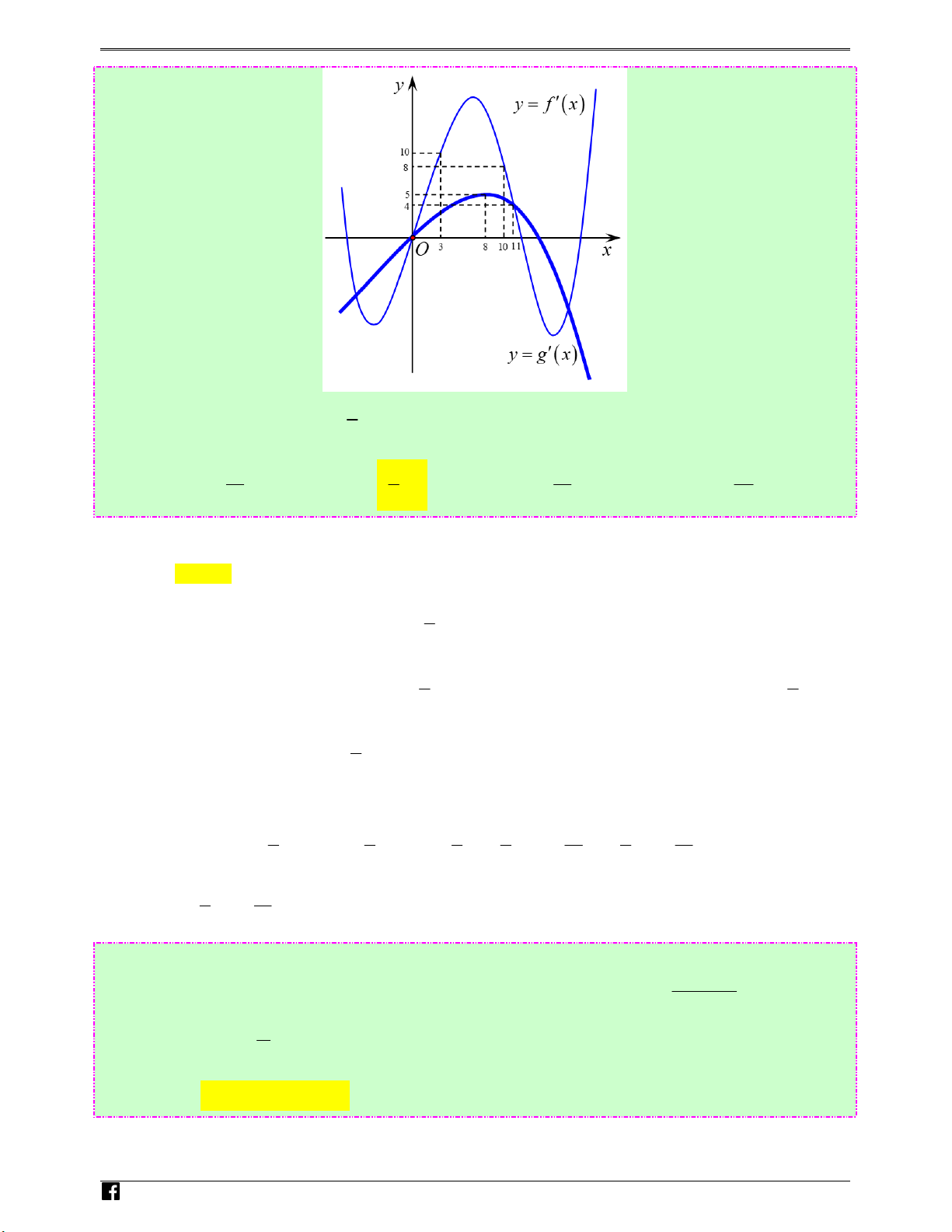
Câu 76: (Câu 50 - MĐ 101 - ⒷGⒹ&ĐT - Năm 2017 - 2018) Cho hai hàm số y = f ( x), y = g ( x) . Hai
hàm số y = f ′( x) và y = g′( x) có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là
đồ thị của hàm số y = g′( x) .
https://www.facebook.com/vietgold Trang 36 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 Luyenthitracnghiem.vn  
Hàm số h( x) = f ( x + ) 3 4 − g 2x − 
đồng biến trên khoảng nào dưới đây? 2            Ⓐ. 31 5;  Ⓑ. 9 ;3 Ⓒ. 31;+∞ Ⓓ. 25 6; 5           4   5   4  Lời giải Chọn B  
Ta có h′( x) = f ′( x + ) 3
4 − 2g′ 2x −  . 2    N g   = + − −   ⇔ ′ ⇔ ′ + − ′ − ≥ u
Hàm số h( x) f ( x ) 3 4 g 2x   đồng biến h ( x) ≥ 0 f ( x ) 3 4 2g 2x 0   y  2   2  %n H   ⇔ ′ + ≥ ′ − o f ( x ) 3 4 2g 2x   à  2  ng V  3 ≤ x + 4 ≤ 8  1 − ≤ x ≤ 4  1 − ≤ x ≤ 4  1 − ≤ x ≤ 4 i     ) ⇔ ⇔ ⇔ ⇔ t  3  3 3 9 19 9 19 3 ≤ 2x − ≤ 8  3 + ≤ 2x ≤ 8 + ≤ 2x ≤ ≤ x ≤  2  2 2 2 2 4 4 9 19 ⇔ ≤ x ≤ . 4 4
Câu 77: Câu này giải em không biết chỉnh sửa như thế nào! (Câu 11 - ĐMH - BGD&ĐT - Năm 2017 - tan x − 2
2018) Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = đồng biến trên tan x − m  π  khoảng 0; .  4   
Ⓐ. m ≤ 0 hoặc1≤ m < 2 Ⓑ. m ≤ 0
Ⓒ. 1≤ m < 2 Ⓓ. m ≥ 2 Lời giải
https://www.facebook.com/vietgold Trang 37 Luyenthitracnghiem.vn
77 BÀI TOÁN TRONG Đ THI BGD T 2016 - 2020 Chọn A  π 
Đặt t = tan x , vì x ∈ 0; ⇒ t ∈   (0; ) 1  4  Lu t − 2 y
Xét hàm số f (t) = ∀t ∈(0; )
1 . Tập xác định: D = ℝ \ m e { } n t − m thi 2 − t m r
Ta có f ′(t) = . ac (t − m)2 ngh  π  tan x − 2 ie
Ta thấy hàm số t ( x) = tan x đồng biến trên khoảng 0; 
 . Nên để hàm số y = đồng m  4  tan x − m .vn  π  biến trên khoảng 0;
khi và chỉ khi: f ′ t > 0 ∀t ∈ 0;1  ( ) ( ) 4    m < 2 2 − 2 − m > 0 m   ⇔ > 0 t ∀ ∈ 0;1 ⇔ 
⇔ m ≤ 0 ⇔ m∈ − ; ∞ 0 ∪ 1; 2 2 ( ) (t − m) m ∉  (0; ) ( ] [ ) 1 m ≥1  1 1
tan x − m − tan x − 2 2 ( ) ( ) 2
CASIO: Đạo hàm của hàm số ta được cos x cos x y′ = (tan x − m)2 π  π 
Ta nhập vào máy tính thằng y′ \ CALC\Calc x =
( Chọn giá trị này thuộc 0; ) 8  4    N
\= \ m = ? 1 giá trị bất kỳ trong 4 đáp án. guy
Đáp án D m ≥ 2 . Ta chọn m = 3 . Khi đó y′ = −0,17 < 0 ( Loại) %n H
Đáp án C 1 ≤ m < 2 Ta chọn m = 1,5 . Khi đó y′ = 0, 49 > 0 (nhận) oàn
Đáp án B m ≥ 0 Ta chọn m = 0 . Khi đó y′ = 13, 6 > 0 (nhận) g Vi)
Vậy đáp án B và C đều đúng nên chọn đáp án Ⓐ. t
https://www.facebook.com/vietgold Trang 38