

Bài tập trắc nghiệm số phức
Trang 2
MỤC LỤC
PHẦN 1. TÓM TẮT LÝ THUYẾT
PHẦN 2. SỐ PHỨC VÀ CÁC PHÉP TOÁN ( 453 CÂU)
A – BÀI TẬP ( 260 CÂU)
B – HƯỚNG DẪN GIẢI
C – BÀI TẬP TỰ LUYỆN ( 193 CÂU)
PHẦN 3. PHƯƠNG TRÌNH VÀ CÁC BÀI TẬP TÌM SỐ PHỨC THỎA MÃN ĐIỀU KIỆN (256 CÂU)
A – BÀI TẬP (130 CÂU)
B – HƯỚNG DẪN GIẢI
C – BÀI TẬP TỰ LUYỆN (126 CÂU)
PHẦN 4. BIỂU DIỄN HÌNH HỌC CỦA SỐ PHỨC, TÌM TẬP HỢP ĐIỂM (227 CÂU)
A – BÀI TẬP (138 CÂU)
B – HƯỚNG DẪN GIẢI
C – BÀI TẬP TỰ LUYỆN (89 CÂU)
Bài tập trắc nghiệm số phức
Trang 3
PHẦN 1. TÓM TẮT LÝ THUYẾT
1. Khái niệm số phức
• Tập hợp số phức:
• Số phức (dạng đại số) :
z a bi
= +
(a, b
R∈
, a là phần thực, b là phần ảo, i là đơn vị ảo, i
2
= –1)
• z là số thực ⇔ phần ảo của z bằng 0 (b = 0)
z là thuần ảo ⇔ phần thực của z bằng 0 (a = 0)
Số 0 vừa là số thực vừa là số ảo.
• Hai số phức bằng nhau:
a a'
a bi a’ b’i (a,b,a',b' R)
b b'
=
+=+ ⇔ ∈
=
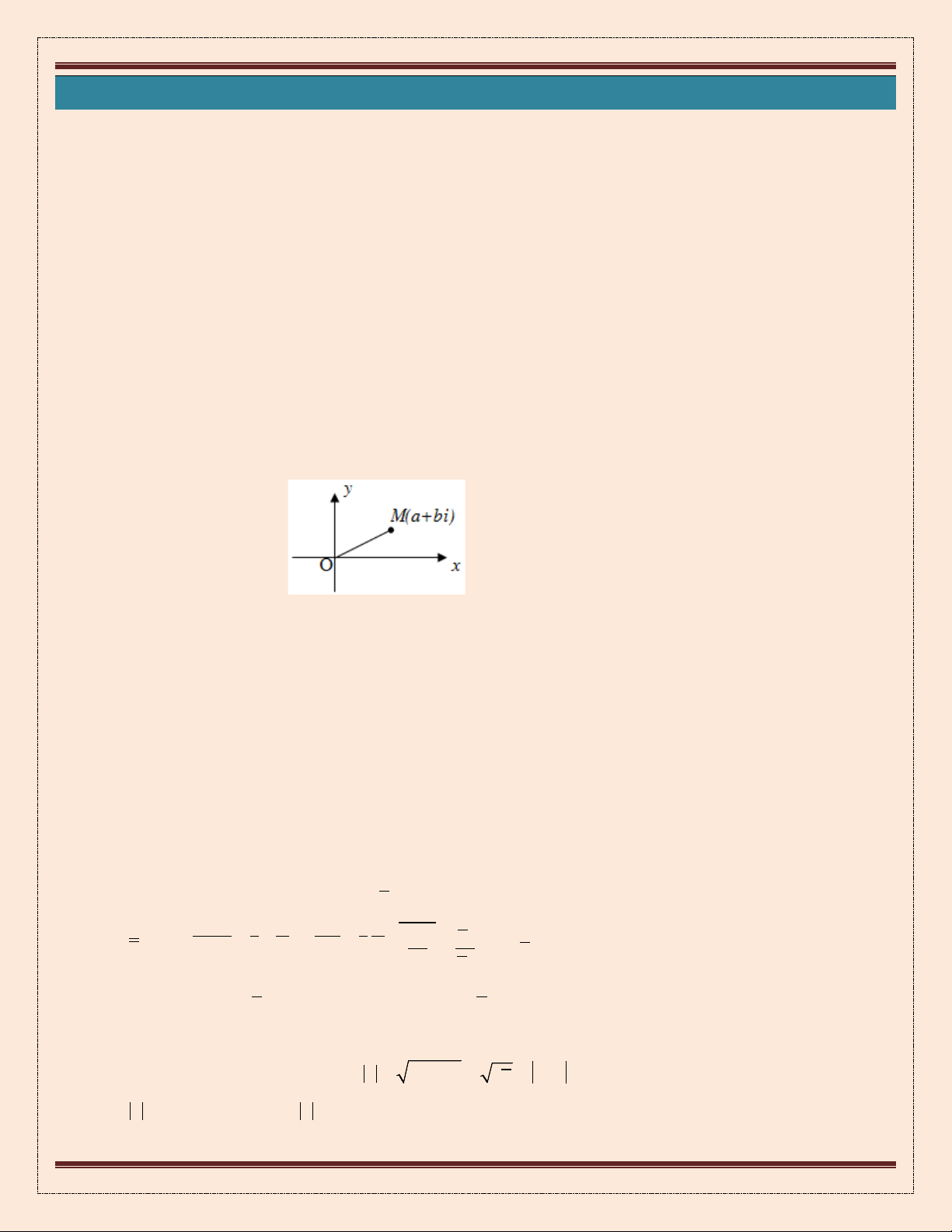
2. Biểu diễn hình học:
Số phức z = a + bi (a, b
R)∈
được biểu diễn bởi điểm M(a; b) hay bởi
u (a; b)=
trong mp(Oxy) (mp phức)
3. Cộng và trừ số phức:
•
( ) ( ) ( ) ( )
a bi a’ b’i a a’ b b’ i+++ =+++
•
( )
( ) ( )
( )
a bi a’ b’i a a’ b b’ i
+−+ =−+−
• Số đối của z = a + bi là –z = –a – bi
•
u
biểu diễn z,
u'
biểu diễn z' thì
u u'+
biểu diễn z + z’ và
u u'−
biểu diễn z – z’.
4. Nhân hai số phức :
•
( )
( ) (
) ( )
a bi a ' b'i aa’ – bb’ ab’ ba’ i+ += + +
•
k(a bi) ka kbi (k R)+=+ ∈
5. Số phức liên hợp
Số phức liên hợp của số phức z = a + bi là
z a bi= −
•
11
22
zz
z z; z z' z z'; z.z' z.z';
zz
= ±=± = =
;
22
z.z a b= +
• z là số thực ⇔
zz=
; z là số ảo ⇔
zz= −
6. Môđun của số phức :
Môđun của số phức : z = a + bi :
22
z a b zz OM= += =
•
z 0, z C , z 0 z 0≥ ∀∈ = ⇔ =

Bài tập trắc nghiệm số phức
Trang 4
•
z.z' z.z'=
•
zz
z' z'
=
•
z z' z z' z z'− ≤± ≤ +
7. Chia hai số phức:
•
1
2
1
zz
z
−
=
(z ≠ 0) •
1
2
z' z'.z z'.z
z'z
z z.z
z
−
= = =
•
z'
w z ' wz
z
=⇔=
8. Căn bậc hai của số phức:
•
z x yi= +
là căn bậc hai của số phức
w a bi= +
⇔
2
zw=
⇔
22
xya
2xy b
−=
=
• w = 0 có đúng 1 căn bậc hai là z = 0
• w
0≠
có đúng hai căn bậc hai đối nhau
• Hai căn bậc hai của a > 0 là
a
±
• Hai căn bậc hai của a < 0 là
a .i±−
9. Phương trình bậc hai Az
2
+ Bz + C = 0 (*) (A, B, C là các số phức cho trước, A
0
≠
).
2
B 4AC∆= −
•
0
∆≠
: (*) có hai nghiệm phân biệt
1,2
B
z
2A
− ±δ
=
, (
δ
là 1 căn bậc hai của ∆)
•
0∆=
: (*) có 1 nghiệm kép:
12
B
zz
2A
= = −
Chú ý: Nếu z
0
∈
C là một nghiệm của (*) thì
0
z
cũng là một nghiệm của (*).

Bài tập trắc nghiệm số phức
Trang 5
PHẦN 2. SỐ PHỨC VÀ CÁC PHÉP TOÁN (453 CÂU)
A – BÀI TẬP (260 CÂU)
Câu 1. Cho
( )
; ' ' ' , , ', 'z x iy z x iy x y x y=+=+ ∈
. Tìm mệnh đề không đúng trong các mệnh đề sau:
A.
(
)
( )
'' 'z z x x iy y±=± + ±
B.
( )
.' ' ' ' 'z z xx yy i xy x y=−+ +
C.
22 22
'' ' '
''' ''
z xx yy x y xy
i
zxy xy
+−
= +
++
D. phương án B và C sai.
Câu 2. Số
(
)
2345
iiii+++
bằng số nào dưới đây?
A. 0 B. i C. –i D. 2i
Câu 3. Tính
2009
i
A.
1−
B. 1 C.
i−
D.
i
Câu 4. Tính
( ) ( )
47 5 7ii− +− +
A.
11 12i−
B.
1 i−+
C.
12 11i+
D.
1−
Câu 5. Tìm phần thực, phần ảo của số phức sau
( ) ( ) ( )
4 23 5i ii−+ + − +
:
A. Số phức trên có phần thực là 1, phần ảo là
i
B. Số phức trên có phần thực là 1, phần ảo là –1
C. Số phức trên có phần thực là 1, phần ảo là 1 D. Số phức trên có phần thực là 1, phần ảo là
i−
Câu 6. Viết số phức
3
1
z
ở dạng chuẩn với
1
zi= +
A.
1
2
i
B.
11
44
i−−
C.
1
2
i−
D.
i
Câu 7. Cho
(
)
; ' ' ', ,z x iy z x iy x y
=+=+ ∈
. Trong các mệnh đề sau mệnh đề nào sai ?
A.
( ) ( )
'' 'z z x x iy y
±=± + ±
B.
(
)
. ' x' ' ' '
z z x yy i xy x y
=−+ +
C.
22 22
'' ' '
.
''' ''
z xx yy x y xy
i
zxy xy
+−
= +
++
D.
( )
'' 'zz xxi yy+ = + + −+
Câu 8. Tính
( )( )
53 35ii
+−
A.
15 15i−
B.
30 16i−
C.
25 30i+
D.
26 9i−
Câu 9. Cho số phức z thỏa mãn
( )
1 . 14 2iz i+=−
. Tính tổng phần thực và phần ảo của
z
A. –4 B. 14 C. 4 D. –14
Câu 10. Cho số phức z thỏa mãn
( )
13 1iz i z− ++=−
. Môdun của số phức
w 13z 2i= +
có giá trị bằng:
A. –2 B.
26
13
C.
10
D.
4
13
−

Bài tập trắc nghiệm số phức
Trang 6
Câu 11. Cho số phức
( )( )
12 43 28z ii i= − − −+
. Cho các phát biểu sau:
(1). Modun của z là một số nguyên tố
(2). z có phần thực và phần ảo đều âm
(3). z là số thuần thực
(4). Số phức liên hợp của z có phần ảo là 3i.
Số phát biểu sai là:
A. 1 B. 2 C. 3 D. 4
Câu 12. Cho số phức
(
)
,z ax bi a b=+∈
, mệnh đề nào sau đây là không đúng?
A. Đối với số phức z , a là phần thực
B. Điểm
( )
,M ab
trong một hệ tọa độ vuông góc của mặt phẳng phức được gọi là điểm biểu diễn số phức
z ax bi= +
C. Đối với số phức z , bi là phần ảo.
D. Số i được gọi là đơn vị ảo.
Câu 13. Cho số phức
76zi= +
, tính mô đun của số phức
2
1
21
3
z
z
+
=
A.
3217
B.
85
C. 3127 D. 85
Câu 14. Cho số phức
12
32, 65z iz i=+=+
. Tìm số phức liên hợp của số phức
12
56zz z= +
A.
51 40zi
= +
B.
51 40zi= −
C.
48 37zi= +
D.
48 37zi
= −
Câu 15. Trong các kết luận sau, kết luận nào sai ?
A. Mô đun của số phức
( )
,z a bi a b=+∈
được tính bằng
22
z ab= +
B. Mô đun của số phức z (với z là khác 0) là một số thực dương.
C. Mô đun của số phức z là một số phức.
D. A và B đúng.
Câu 16. Thu gọn biểu thức
2
( 2 3)zi= +
ta được:
A.
11 6zi= −
B.
1zi
=−−
C.
43zi
= +
D.
7 62zi=−+
Câu 17. Mô đun của số phức
6
5 2 (1 )z ii=+ −+
là :
A.
5 10
B.
61
C.
5
D.
55
Câu 18. Tìm số nghịch đảo của
32zi= +
A.
32i−
B.
32i−+
C.
32
13 13
i−
D.
32
13 13
i+

Bài tập trắc nghiệm số phức
Trang 7
Câu 19. Cho 3 số phức
1
13
22
zi
−
= +
;
2
3zi= +
và
3
12zi=−+
. Tìm môđun số phức
12 3
.
z zz z
= −
A. 4 B.
22
C.
2
D.
42
Câu 20. Số đối của số phức
25
zi= +
là:
A.
25
i
−
B.
25
i
−+
C.
25
i
−−
D.
25
29 29
i−
Câu 21. Phần ảo của số phức
2
23wz z=−+
biết
3zi= −
là:
A. –4 B. –4i C. 4 D. 4i
Câu 22. Các cặp số phức không là hai phân số liên hợp của nhau là:
A.
1; 1xy xy++ ++
B.
;xy xy
C.
;1xyxy− −−
D.
;
xx
yi
yi
+
+
Câu 23. Tìm modun của số phức z biết:
(
)
(
)( )
( )(
)
2424
1
22
abbai
zz
abbai
+−
+=
+−
?
A. 2 B. 1 C. 0 D. 3
Câu 24. Tìm số phức
z
thỏa mãn
2 13
12
ii
z
ii
+ −+
=
−+
A.
22 4
25 25
i+
B.
22 4
25 25
i
−
C.
22 4
25 25
i
+
D.
22 4
25 25
i−+
Câu 25. Tìm phần thực của số phức z biết:
2
10
z
z
z
+=
A. 10 B. 5 C. –5 D.
10
Câu 26. Cho số phức
z a bi= +
thỏa mãn
2. 3 3z iz i+=+
. Tính giá trị biểu thức:
2016 2017
Pa b= +
A. 0 B. 2 C.
4032 2017
2017
33
5
−
D.
4032 2017
2017
33
5
−
−
Câu 27. Nếu
23zi= +
thì
z
z
bằng:
A.
56
2
11
i
i
+
−
B.
5 12
13
i+
C.
5 12
13
i−
D.
34
7
i−
Câu 28. Số nào trong các số phức sau là số thực
A.
( )
( )
33ii+− −
B.
( )
( )
2 5 12 5ii+ +−
C.
( )( )
1 31 3ii+−
D.
2
2
i
i
+
−

Bài tập trắc nghiệm số phức
Trang 8
Câu 29. Tập hợp các nghiệm của phương trình
z
z
zi
=
+
là:
A.
{ }
0;1
i−
B.
{ }
0
C.
{ }
1 i−
D.
{ }
0;1
Câu 30. Cho hai số phức
12
1 2; 2 3
z iz i
=+=−
. Tổng của hai số phức là
A.
3 i−
B.
3 i
+
C.
35i−
D.
35i+
Câu 31. Môđun của số phức
( )( )
12
12
ii
z
i
+−
=
+
là:
A. 2 B. 3 C.
2
D.
3
Câu 32. Phần ảo của số phức z biết
( )
( )
2
2 .1 2zi i=+−
là:
A.
2
B.
2−
C. 5 D. 3
Câu 33. Cho số phức
1
1
3
zi= −
. Tính số phức
3w iz z
= +
.
A.
8
3
w =
B.
10
3
w =
C.
8
3
wi= +
D.
10
3
wi= +
Câu 34. Cho hai số phức
z a bi= +
và
' ''z a bi
= +
. Điều kiện giữa a,b,a’,b’ để
.'
zz
là một số thực là:
A.
' '0aa bb
+=
B.
' bb' 0aa −=
C.
ab' a'b 0+=
D.
ab' a'b 0−=
Câu 35. Cho số phức
z x yi= +
, biết rằng
,xy∈
thỏa
( ) ( ) ( ) ( )
32 21 1 5x y ix y i− + + = +− −
. Tìm số
phức
( )
6w z iz= +
A.
17 17
wi= +
B.
17wi= +
C.
1wi
= −
D.
1 17
wi= +
Câu 36. Cho số phức
126zi=−−
. Tìm phần thực và phần ảo của số phức
z
.
A. Phần thực bằng
1−
và phần ảo bằng
26i−
B. Phần thực bằng
1
−
và phần ảo bằng
26
C. Phần thực bằng 1 và phần ảo bằng
26
D. Phần thực bằng
1−
và phần ảo bằng
26i
Câu 37. Tính
ab+
biết rằng a, b là các số thực thỏa mãn
( )
2017
13
a bi i+=+
A.
( )
672
1 3 .8ab+= +
B.
( )
671
1 3 .8ab+= +
C.
( )
672
3 1 .8ab+= −
D.
( )
671
3 1 .8ab+= −
Câu 38. Cho số phức
13zi=−−
. Tìm phần thực và phần ảo của số phức
z
A. Phần thực bằng
1−
và phần ảo bằng 3. B. Phần thực bằng
1−
và phần ảo bằng
3i
C. Phần thực bằng 1 và phần ảo bằng 3. D. Phần thực bằng 1 và phần ảo bằng
3i
.

Bài tập trắc nghiệm số phức
Trang 9
Câu 39. Cho số phức
23zi= −
. Tìm số phức
1
zi
w
z
+
=
−
A.
1wi=−+
B.
71
55
wi=−−
C.
42
55
wi= +
D.
24
55
wi= −
Câu 40. Cho số phức
2016 2017zi
= −
. Tìm phần thực và phần ảo của số phức z.
A. Phần thực bằng 2016 và phần ảo bằng
2017i
−
. B. Phần thực bằng 2016 và phần ảo bằng –2017.
C. Phần thực bằng 2017 và phần ảo bằng
2016i−
. D. Phần thực bằng 2016 và phần ảo bằng 2017.
Câu 41. Cho các số phức
12
1 2, 1 3z iz i=−=−
. Tính mô–đun của số phức
12
zz
+
A.
12
5zz+=
B.
12
26zz
+=
C.
12
29zz+=
D.
12
23zz+=
Câu 42. Thu gọn số phức
32 1
1 32
ii
z
ii
+−
= +
−+
ta được:
A.
23 61
26 26
zi= +
B.
23 63
26 26
zi= +
C.
15 55
26 26
zi= +
D.
26
13 13
zi= +
Câu 43. Cho số phức
3
13
1
i
z
i
+
=
+
. Tìm phần thực và phần ảo của số phức
z
.
A. Phần thực bằng 2 và phần ảo bằng
2i−
B. Phần thực bằng 2 và phần ảo bằng
2−
C. Phần thực bằng 2 và phần ảo bằng
2i
D. Phần thực bằng 2 và phần ảo bằng 2
Câu 44. Cho số phức z thỏa mãn:
( ) ( )
2
32 2 4iz i i+ +− =+
. Hiệu phần thực và phần ảo của số phức z là:
A. 1 B. 0 C. 4 D. 6
Câu 45. Gọi x,y là hai số thực thỏa mãn biểu thức
32
1
x yi
i
i
+
= +
−
. Khi đó, tích số x.y bằng:
A.
.5xy=
B.
.5xy= −
C.
.1xy=
D.
.1xy= −
Câu 46. Cho số phức
( )
14 3zi=−+
. Tìm phần thực và phần ảo của số phức
z
.
A. Phần thực bằng
11−
và phần ảo bằng
4i
B. Phần thực bằng
11−
và phần ảo bằng 4
C. Phần thực bằng
11
−
và phần ảo bằng
4i
−
D. Phần thực bằng
11−
và phần ảo bằng
4−
Câu 47. Tìm mệnh đề sai trong các mệnh đề sau:
A. Số phức
z a bi= +
được biểu diễn bằng điểm M trong mặt phẳng phức Oxy.
B. Số phức
z a bi= +
có môđun là
2
ab+
C. Số phức
0
0
0
a
z a bi
b
=
=+=⇔
=
D. Số phức
z a bi= +
có số phức đối
' a biz = −
Câu 48. Cho hai số phức
z a bi= +
và
z' a' b'i= +
. Số phức z.z’ có phần thực là:

Bài tập trắc nghiệm số phức
Trang 10
A.
a a'+
B.
aa'
C.
aa' bb'
−
D.
2bb'
Câu 49. Phần thực của số phức
( )
2
z 23i= +
A. –7 B.
62
C.
2
D. 3
Câu 50. Cho số phức z thỏa
( )
( )
(
)
2
12 34 2zi ii−=+ −
. Khi đó, số phức z là:
A.
25z =
B.
5zi=
C.
25 50zi= +
D.
5 10zi= +
Câu 51. Cho hai số phức
3z a bi= −
và
( )
'2 ,z b ai a b=+∈
. Tìm a và b để
'6zz i−=−
A.
3; 2ab=−=
B.
6; 4ab= =
C.
6; 5ab=−=
D.
4; 1ab= = −
Câu 52. Tính môđun của số phức
( )
2016
1zi= +
A.
1008
2
B.
1000
2
C.
2016
2
D.
1008
2−
Câu 53. Tính A=3+2i+(6+i)(5+i).
A. 30+10i B. 32+13i C. 33+13i D. 33+12i
Câu 54. Cho z=1–i, môđun của số phức 4z–1 là:
A. 2 B. 3 C. 4 D. 5
Câu 55. Cho z=3+4i, tìm phần thực ảo của số phức :
A. Phần thực là , phần ảo là B. Phần thực là , phần ảo là
C. Phần thực là , phần ảo là D. Phần thực là , phần ảo là
Câu 56. Cho số phức . Tìm phần thực và phần ảo của số phức
A. Phần thực bằng 5, phần ảo bằng –2 B. Phần thực bẳng 5, phần ảo bằng 2
C. Phần thực bằng 5, phần ảo bằng –2i D. Phần thực bẳng 5, phần ảo bằng 2i
Câu 57. Cho hai số phức và . Tính môđun của số phức .
A. B. C. D.
Câu 58. Cho số phức . Số phức có môđun bằng
A. B. C. D.
Câu 59. Tìm số phức z thỏa mãn:
A. B. C. D.
Câu 60. Cho số phức z thỏa mãn: . Tìm môđun của .
1
z
1
3
1
4
3
25
4
25
−
1
3
1
4
−
3
5
4
5
−
52zi= −
z
1
2zi= +
2
43zi= −
12
zz−
12
25zz−=
12
23zz−=
12
22zz−=
12
2zz−=
23zi= +
w=z+2i
1w
=
2w =
29w =
5w =
( )(
)
2 1 42i iz i− ++=−
13zi=−−
13zi=−+
13zi= −
13
zi
= +
3
(1 3 )
1
i
z
i
−
=
−
z iz+

Bài tập trắc nghiệm số phức
Trang 11
A. B. C. D.
Câu 61. Cho số phức z thỏa mãn: . Xác định phần thực và phần ảo của z.
A. Phần thực – 2 ; Phần ảo 5i. B. Phần thực – 2 ; Phần ảo 5.
C. Phần thực – 2 ; Phần ảo 3. D. Phần thực – 3 ; Phần ảo 5i.
Câu 62. Cho số phức . Tìm phần thực, phần ảo của số phức
A. Phần thực bằng –2 và phần ảo bằng –3i B. Phần thực bằng –2 và phần ảo bằng –3
C. Phần thực bằng 2 và phần ảo bằng 3i D. Phần thực bằng 2 và phần ảo bằng 3
Câu 63. Cho số phức . Tính môđun của số phức
A. B. C. D.
Câu 64. Cho hai số phức: . Tìm số phức
A. B. C. D.
Câu 65. Cho số phức . Phần thực và phần ảo của số phức lần lượt là:
A.–3 và –7 B. 3 và –11 C. 3 và 11 D. 3 và –7
Câu 66. Cho hai số phức . Môđun của số phức bằng:
A.5 B. C. D. 3
Câu 67. Cho số phức .Tìm số phức ?
A. B. C. D.
Câu 68. Cho số phức . Tìm phần thực và phần ảo của số phức .
A. Phần thực bằng và phần ảo bằng B.Phần thực bằng và phần ảo bằng 3
C. Phần thực bằng và phần ảo bằng D. Phần thực bằng và phần ảo bằng
Câu 69. Cho hai số phức và . Tính môđun của số phức
A. B. C. D.
Câu 70. Cho số phức . Tìm số phức .
A. B. C. D.
Câu 71. Tìm phần thực và phần ảo của số phức
A. Phần thực bằng và phần ảo bằng B. Phần thực bằng và phần ảo bằng
C. Phần thực bằng 3 và phần ảo bằng D. Phần thực bằng 3 và phần ảo bằng 2.
Câu 72. Cho số phức . Tính ta được kết quả:
A. . B. . C. . D. .
82
83
42
43
2
(2 3 ) (4 ) (1 3 )iz iz i
− + + =−+
24
zi= +
w zi
= −
32
zi=−+
1zi+−
14zi+− =
11
zi+− =
15zi+− =
1 22zi+− =
12
2 5; 3 4z iz i
=+=−
12
.z zz
=
6 20zi= +
26 7zi
= +
6 20zi= −
26 7zi
= −
13zi=−+
23wiz= −
12
4 2; 2
z iz i= − =−+
12
zz
+
5 3
32zi= −
( )
23 21w i i z iz=−− + −
85
wi=−+
85wi= +
85wi= −
85wi=−−
63zi=−−
z
6−
3i−
6−
6
3
6
3i
1
12zi= +
2
5zi= −
12
zz−
12
1zz−=
12
7zz−=
12
5zz−=
12
7zz−=
23
zi= +
w = 2iz - z
87wi=−+
8wi=−+
47wi= +
87wi=−−
3 2.zi= +
3−
2.i−
3−
2.−
2.i
53zi= −
( )
2
1 zz++
22 33i−+
22 33i+
22 33i−
22 33i−−

Bài tập trắc nghiệm số phức
Trang 12
Câu 73. Cho hai số phức và . Kết luận nào sau đây là sai?
A. . B. . C. . D. .
Câu 74. Cho số phức . Trong các khẳng định dưới đây, khẳng định nào sai?
A. Số phức có phần thực bằng , phần ảo bằng . B. Số phức có phần thực bằng 8, phần ảo bằng
.
C. Môđun của bằng 10. D. Số liên hợp của là .
Câu 75. Thực hiện các phép tính
A. B. C. D.
Câu 76. Chọn mệnh đề sai trong các mệnh đề sau:
A. Cho x,y hai số phức thì số phức có số phức liên hợp
B. Cho x,y hai số phức thì số phức có số phức liên hợp
C. Cho x,y hai số phức thì số phức có số phức liên hợp
D. Số phức thì
Câu 77. Cho số phức z thỏa mãn z – (1– 9i) = (2+3i)z. Phần ảo của số phức z là:
A. –1 B. C. 2 D. –2
Câu 78. Trong các kết luận sau, kết luận nào là sai
A. Môđun của số phức z là một số thực B. Môđun của số phức z là một số thực không âm
C. Môđun của số phức z là một số phức D. Môđun của số phức z là một số thực dương
Câu 79. Số nào trong các số sau là số thực?
A.
( ) ( )
32 32ii+− −
B.
( ) ( )
2525ii+ +−
C.
( )
2
13i+
D.
2
2
i
i
+
−
Câu 80. Số nào trong các số sau là số thuần ảo :
A. B. C. D.
Câu 81. Đẳng thức nào trong các đẳng thức sau là đúng
A. B. C. D.
Câu 82. Đẳng thức nào trong các đẳng thức sau là đúng?
A. B. C. D.
Câu 83. Cho số phức z = 2 + 3i. Tìm phần thực phần ảo của số phức
1
1zi= +
2
1
zi= −
12
2zz−=
1
2
z
i
z
=
12
.2zz =
12
2
zz+=
(
)
24 3ui= −
u
8
6
−
u
i
u
u
86ui= +
33
22
i
−+
33
22
i+
33
22
i−
33
22
i−−
xy+
xy
+
xy−
xy−
xy
xy
z a bi= +
( )
( )
2
2 22
2z z ab+= +
6
5
( 2 3) ( 2 3)ii++ −
( 2 3).( 2 3)ii+−
2
(2 2 )i
+
23
23
i
i
+
−
1997
1i = −
2345
ii=
2005
1i =
2006
ii= −
8
(1 ) 16i+=−
8
(1 ) 16ii+=
8
(1 ) 16ii
+=−
8
(1 ) 16i+=
z

Bài tập trắc nghiệm số phức
Trang 13
A. Phần thực bằng 2 và phần ảo bằng –3. B. Phần thực bằng 2 và phần ảo bằng –3i.
C. Phần thực bằng 2 và phần ảo bằng 3. D. Phần thực bằng 2 và phần ảo bằng 3i.
Câu 84. Cho hai số phức z
1
= 1 – 2i và z
2
= 3 + 4i. Tính mô đun của
A. B. C. D.
Câu 85. Cho số phức z = 2 – i. Tìm sô phức
A. B. C. D.
Câu 86. Phần thực của
2zi=
là:
A. 2 B. 2i C. 0 D. 1
Câu 87. Số
zz
+
là
A. Sô thực B. Số thuần ảo C. 0 D. 1+2i
Câu 88. Nghiệm của phương trình
z
z
zi
=
+
là:
A.
0; 1zz i= = −
B.
0z =
C.
1zi= −
D.
0; 1zz= =
Câu 89. Môđun của
12i−
bằng:
A. 3 B. 1 C.
5
D. 2
Câu 90. Tìm số phức liên hợp của số phức
z a bi= +
A.
'
z a bi=−+
B.
'
z b ai= −
C.
'
z a bi=−−
D.
'
z a bi= −
Câu 91. Tìm phần ảo của số phức
z
thỏa mãn:
( )
( )
2
2 12zi i=+−
A.
2−
B.
2
C.
2
D.
2−
Câu 92. Cho số phức
2
( 2 ) (1 2 ).zii=+−
Tìm phần ảo của số phức
z
.
A.
2
B.
2−
C.
2.−
D.
2.
Câu 93. Rút gọn biểu thức
(2 )(3 )zi i i=−+
ta được:
A.
6z =
B.
17
zi= +
C.
2 5zi= +
D.
5zi=
Câu 94. Cho hai số phức
3
3
12
2 4 2(1 )
4 3 (1 ) ;
1
ii
z i iz
i
+− −
=−+− = ⋅
+
Tìm số phức
12
2. . ,zz
ω
=
A.
18 75. .i
ω
= −
B.
18 74. .i
ω
= +
C.
18 75. .i
ω
= +
D.
18 74. .i
ω
= −
Câu 95. Cho số phức z thỏa mãn:
(4 ) 3 4iz i−=−
. Điểm biểu diễn của z là:
A.
16 11
(; )
15 15
M −
B.
16 13
(; )
17 17
M −
C.
94
(; )
55
M −
D.
9 23
(; )
25 25
M −
Câu 96. Cho số phức
43zi= −
. Tìm phần thực và phần ảo của số phức z.
A. Phần thực bằng – 4 và phần ảo bằng –3i. B. Phần thực bằng – 4 và phần ảo bằng –3.
12
zz−
12
40zz−=
12
20zz−=
12
6zz−=
12
40
zz−=
w iz z= +
w 35
i= −
w 35i=−+
w 35i
= +
w 35
i=−−

Bài tập trắc nghiệm số phức
Trang 14
C. Phần thực bằng 4 và phần ảo bằng 3i. D. Phần thực bằng 4 và phần ảo bằng 3.
Câu 97. Cho hai số phức z
1
= 4 + 5i và z
2
= – 1 +2i . Tính môđun của số phức
A.
12
41.zz−=
B.
12
5.
zz
−=
C.
12
3 2.zz−=
D.
12
34.
zz−=
Câu 98. Cho số phức
32zi= +
. Tìm số phức
2.w iz z= +
A.
1 4.wi=−+
B.
9 2.
wi
= −
C.
4 7.
wi= +
D.
4 7.
wi= −
Câu 99. Cho
45zi=−+
Tìm phần thực, phần ảo của số phức
z
.
A. Phần thực bằng 4 và phần ảo bằng 5i. B. Phần thực bằng 4 và phần ảo bằng 5.
C. Phần thực bằng –4 và phần ảo bằng –5. D. Phần thực bằng –4 và phần ảo bằng –5i.
Câu 100. Cho hai số phức
12
3 2; 2 .z iz i= − =−+
Tìm mô đun của số phức :
12
.zz+
A.
12
5
zz
=
+
B.
12
2
zz
=
+
C.
12
13
zz
=
+
D.
12
2
zz
=
+
Câu 101. Cho số phức
2 3.
zi
= +
Tìm số phức
.w iz z= −
A.
35wi=−+
B.
53zi= +
C.
55zi=−+
D.
55zi= −
Câu 102. Số phức liên hợp của số phức
12zi= +
là
A.
12i−+
B.
12i−−
C.
2 i+
D.
12i−
Câu 103. Phần thực của số phức z thỏa mãn: là
A. 2 B. –3 C. –2 D. 3
Câu 104. Cho hai số phức
1
1zi= −
và
2
35zi
=−+
. Môđun của số phức
12 2
.w zz z= +
A.
130w =
B.
130w =
C.
112w =
D.
112w =
Câu 105. Cho số phức
3 2.zi= −
Tìm số phức
w iz z= +
A.
5 5.wi
=−−
B.
5 5.
wi= +
C.
3 7.wi= +
D.
77wi=−−
Câu 106. Cho số phức Z = 5 + 4i. Phần thực, phần ảo của số phức
Z
là:
A. Phần thực bằng 5, phần ảo bằng –4 B. Phần thực bằng 5, phần ảo bằng 4
C. Phần thực bằng –5, phần ảo bằng –4 D. Phần thực bằng –5, phần ảo bằng 4
Câu 107. Cho số phức z = (2 + i)(1 − i) + 1 + 3i . Môđun của z là:
A. 2 B. 2 C. D. 4
Câu 108. Cho số phức z thỏa mãn đẳng thức z + (1 + i) = 5 + 2i . Môđun của z là:
A. B. C. 2 D.
Câu 109. Giá trị của biểu thức
( )
8
1 i+
bằng:
A. 14 B. 15 C. 16 D. 17
Câu 110. Cho số phức z = 5 + 3i. Tìm phần thực và phần ảo của số phức
z
( ) ( )
( )
2
1 2 8 12
i iz i iz+ − = ++ +
5
2
13
2
z
10
2
2
5

Bài tập trắc nghiệm số phức
Trang 15
A. Phần thực bằng 5 và Phần ảo bằng –3. B. Phần thực bằng –5 và Phần ảo bằng 3.
C. Phần thực bằng 5 và Phần ảo bằng –3i. D. Phần thực bằng 5 và Phần ảo bằng 3.
Câu 111. Cho hai số phức
1
12
zi
= +
và
2
23zi=−+
. Tính môđun của số phức
12
.zz+
A.
12
26zz+=
. B.
12
5zz+=
. C.
12
1zz+=
. D.
12
2zz+=
.
Câu 112. Số phức liên hợp của
( )( )
1
1 32
3
zi i
i
=+ −+
+
là
A.
13 9
.
10 10
wi= −
B.
3
5.
10
wi
= −
C.
53 9
.
10 10
wi= −
D.
53 9
.
10 10
wi= +
Câu 113. Tìm phần thực, phần ảo của số phức z = i – (2 – 4i) + (3 – 2i) .
A. Phần thực bằng 3 và Phần ảo bằng –7i. B. Phần thực bằng 3 và Phần ảo bằng –7.
C. Phần thực bằng 3 và Phần ảo bằng 7i. D. Phần thực bằng 3 và Phần ảo bằng 7
Câu 114. Cho số phức và . Tính mô đun của số phức
A. . B. . C. . D. .
Câu 115. Cho số phức . Tìm số phức
A. w . B. w . C. w . D.w .
Câu 116. Cho số phức . Modul của số phức z là:
A.2 B.–3 C. D.13
Câu 117. Cho số phức , số phức liên hợp của số phức z là:
A. B. C.
D.
Câu 118. Tính ta được:
A.
B. C. D.
Câu 119. Phần thực của số phức bằng
A.0 B.1 C. D.
Câu 120. Cho số phức: . Tìm phần thực và phần ảo của số phức
A.Phần thực bằng –3 và phần ảo bằng 5 B. Phần thực bằng –3 và phần ảo bằng 4i
C. Phần thực bằng 3 và phần ảo bằng 4 D. Phần thực bằng –3 và phần ảo bằng 4
Câu 121. Cho hai số phức và . Tính môđun của số phức
A. B.
2
1
1
zi= +
2
32zi= −
12
.zz
12
. 26zz =
12
.6zz =
12
.6zz =
12
.2zz =
43zi= −
w2z iz= +
53i=−−
53i= +
33i= −
52i= −
23zi= −
13
13zi
= +
13zi
= − 3
zi=−−
13zi
=−+
3
zi= +
( ) ( )
32
12 3zi i=+ +−
38zi=−+
38zi=−−
38zi= −
38zi= +
30
(1 )i+
15
2
15
2−
35zi=−+
zi−
1
12zi= −
2
3zi= +
12
2zz−
12
2 26zz−=
12
2 41zz−=

Bài tập trắc nghiệm số phức
Trang 16
C.
D.
Câu 122. Cho số phức . Tìm số phức
A. B. C.
D.
Câu 123. Cho hai số phức: z
1
= 2 – 3i ; z
2
= –1 + i. Phần ảo của số phức w = 2z
1
– z
2
bằng:
A.–7 B. 5 C.7 D.–5
Câu 124. Phần ảo của số phức , biết số phức Z thỏa mãn : là
A. –1 B. 2 C. 1 D. –2
Câu 125. Cho hai số phức: . Tính .
A. i B.4i C. D.
Câu 126. Cho số phức . Tìm số phức .
A. w= 1+4i B. w=1–4i C. w=–15–4i D. w =15+4i
Câu 127. Cho số phức z = 1 –2i , phần ảo của số phức w = 2z + là :
A. –2 B. 2 C. 4 D. –4
Câu 128. Cho hai số phức z
1
=1 + 3i và z
2
= 2 – i . Khi đó | z
1
+ z
2
| bằng :
A. B. 5 C. D.
Câu 129. Cho số phức z = 4 – 3i +
. Khi đó bằng :
A. 20 – 8i B. 20 + 8i C.
D.
+
Câu 130. Cho số phức z = 1 – 5i. Tìm phần thực, phần ảo của số phức .
A. Phần thực bằng –1 và phần ảo bằng –5i. B. Phần thực bằng –1 và phần ảo bằng –5.
C. Phần thực bằng 1 và phần ảo bằng –5. D. Phần thực bằng 1 và phần ảo bằng –5i.
Câu 131. Cho số phức z thỏa . Tìm phần thực, phần ảo của số phức z.
A. Phần thực bằng 1 và phần ảo bằng 3i B. Phần thực bằng 1 và phần ảo bằng 3
C. Phần thực bằng –1 và phần ảo bằng –3i D. Phần thực bằng –1 và phần ảo bằng 3
Câu 132. Cho số phức . Phần thực, phần ảo của là
A.–5 và 2. B.–5 và 2i. C. 2 và –5. D. 5 và 2.
Câu 133. Cho hai số phức và . Môđun của số phức là
A. B. C. D.
Câu 134. Cho số phức z= 1+2i. Số phức là
A.1+i B. –1+i C.–1–i D. 1–i
Câu 135. Tìm mệnh đề sai trong các mệnh đề sau:
12
2 29zz−=
12
2 33
zz
−=
52zi= +
w iz z= −
33wi= −
33wi= +
33wi=−+
33wi=−−
1W Zi Z
=−+
( )
1 13 0iZ i+ −− =
12
1 3 ; z 3
zi i
=+=+
12
.
zz
23 4
i
+
3 1 ( 3 1)i++ −
1 23
1 3 ; z 2 ; z 3 4zi i i
=− =+=−
12 23
w zz zz= +
5
10
13
z
(1 ) 4 2iz i+=−
25zi= −
z
1
1zi= −
2
45zi= +
12
zz−
25
35
33
53
w iz z= +

Bài tập trắc nghiệm số phức
Trang 17
A. Số phức z = a + bi được biểu diễn bằng điểm M(a; b) trong mặt phẳng phức Oxy
B. Số phức z = a + bi có môđun là
C. Số phức z = a + bi = 0 ⇔
D. Số phức z = a + bi có số phức đối z’ = a – bi
Câu 136. Tìm mệnh đề sai trong các mệnh đề sau:
A. Số phức z = a + bi được biểu diễn bằng điểm M(a; b) trong mặt phẳng phức Oxy (đúng)
B. Số phức z = a + bi có môđun là (đúng)
C. Số phức z = a + bi = 0 ⇔ (đúng)
D. Số phức z = a + bi có số phức đối z’ = a – bi (Sai vì không có số phức đối)
Câu 137. Số phức z = bằng:
A. B. C. D.
Câu 138. Cho số phức z = 6 + 7i. Số phức liên hợp của z có điểm biểu diễn là:
A. (6; 7) B. (6; –7) C. (–6; 7) D. (–6; –7)
Câu 139. Trong các số phức sau, số thực là
A.
B.
C. D.
Câu 140. Số phức có mô đun là:
A. B. C. D.
Câu 141. Cho số phức: . Phần thực a và phần ảo b của lần lượt là
A. B. C. D.
Câu 142. Cho hai số phức: và . Modul của số phức: là
A. . B. . C. 20. D. 40.
Câu 143. Cho số phức z = a + bi. Khi đó số là
A. Một số thực B. 2 C. Một số thuần ảo D. i
Câu 144. Cho số phức
= 2 + 6,
= 1 + 2. Tính modun của số phức
22
ab+
0
0
a
b
=
=
22
ab+
0
0
a
b
=
=
34
4
i
i
−
−
16 13
17 17
i−
16 11
15 15
i−
94
55
i−
9 23
25 25
i−
(
)
( )
32 32ii+− −
(
) ( )
32 32ii+ +−
( ) (
)
12 12
ii+ +−+
( )
( )
52 52ii
+− −
( ) ( )
2
12 1z ii=+−
52z =
50z =
22
3
z =
10
3
z =
11 7zi=−+
z
11; 7.ab= = −
11; 7.ab=−=−
11; 7.ab
=−=
11; 7.ab
= =
1
48zi= −
2
2zi=−−
12
2.z zz=
45
5
( )
1
2
zz+

Bài tập trắc nghiệm số phức
Trang 18
A. 5 B. 6 C. 7 D. 8
Câu 145. Tìm mệnh đề sai trong các mệnh đề sau:
A. Số phức z = a + bi được biểu diễn bằng điểm M(a;b) trong mặt phẳng phức Oxy.
B. Số phức z = a + bi có môđun là .
C. Số phức z = a + bi = 0 ⇔ .
D. Số phức z = a + bi có số phức liên hợp là = – a – bi.
Câu 146. Cho số phức z = a + bi. Số phức z
2
có phần thực là :
A. a
2
+ b
2
B. a
2
– b
2
C. a + b D. a – b
Câu 147. Cho (x + 2i)
2
= yi (x, y ∈ R). Giá trị của x và y bằng
A. x = 1 và y = 4 hoặc x = –1 và y = –4. B. x = 3 và y = 12 hoặc x = –3 và y = –12.
C. x = 2 và y = 8 hoặc x = –2 và y = –8. D. x = 4 và y = 16 hoặc x = –4 và y = –16.
Câu 148. Cho số phức z = . Số phức 1 + z + z
2
bằng
A. . B. 2 – . C. 1. D. 0.
Câu 149. Tìm phần thực của số phức z thỏa mãn iz + 4 + 5i = i(6 + 3i)
A. 1 B. 7 C. 11 D. –1
Câu 150. Cho số phức z
1
= 1 – 3i, z
2
= 2 + i. Tìm số phức w =
A. 7i B. 5i C. – 4 – 7i D. – 7i
Câu 151. Cho số phức z = (2 + i)(1 – i) + 1 + 2i. Mô–đun của số phức z là
A.
B.
C.
D. 2
Câu 152. Gọi z
1
, z
2
là hai nghiệm phức của phương trình x
3
– 3x
2
+ 4x – 12 = 0. Tính
A. P = 0 B. P = 16 C. P = 4 D. P = – 4
Câu 153. Cho số phức z = –2 – 5i. Tìm phần thực và phần ảo của số phức
A. Phần thực bằng 2 và phần ảo bằng –5i B. Phần thực bằng –2 và phần ảo bằng 5i
C. Phần thực bằng 2 và phần ảo bằng –5 D. Phần thực bằng –2 và phần ảo bằng 5
Câu 154. Cho 2 số phức z
1
= –3i và z
2
= 3 – 5i. Tính môđun của số phức z
1
– z
2
:
A. B. C. D.
Câu 155. Cho (x + 2i)
2
= 3x + yi (x, y
∈
R). Giá trị của x và y bằng:
A. x = 1 và y = 2 hoặc x = 2 và y = 4 B. x = –1 và y = –4 hoặc x = 4 và y = 16
C. x = 2 và y = 5 hoặc x = 3 và y = –4 D. x = 6 và y = 1 hoặc x = 0 và y = 4
22
ab+
0
0
a
b
=
=
z
13
22
i−+
13
22
i−+
3i
12
2zz
−
22
42
17
5
12
2| | | |Pzz= −
z
12
| | 73zz−=
12
| | 13zz−=
12
| |3zz−=
12
| |5zz−=

Bài tập trắc nghiệm số phức
Trang 19
Câu 156. Modun của số phức bằng
A. 7 B. 3 C. 5 D. 2
Câu 157. Cho hai số phức và . Giá trị của biểu thức là
A. 0 B. 10 C. D. 100
Câu 158. Mô đun của số phức z thỏa mãn phương trình là
A. B. C. 1 D.
Câu 159. Cho số phức . Tìm phần thực và phần ảo của ?
A. Phần thực là –5, phần ảo là 2i. B. Phần thực là 5, phần ảo là 2.
C. Phần thực là –5, phần ảo là – 2. D. Phần thực là 2, phần ảo là –5.
Câu 160. Cho hai số phức và . Tính môđun của số phức ?
A. B. C. D.
Câu 161. Cho số phức . Tìm số phức
A. B. C. D.
Câu 162. Cho hai số phức và . Tìm phần thực và phần ảo của số phức .
A. Phần thực bằng 1 và phần ảo bằng 6. B. Phần thực bằng 1 và phần ảo bằng– 6.
C. Phần thực bằng –1 và phần ảo bằng 6. D. Phần thực bằng 6 và phần ảo bằng –1
Câu 163. Cho số phức . Modun của số phức z là:
A. B. C. D. 2
Câu 164. Tìm phần thực a và phần ảo b của số phức
A. B. C. D.
Câu 165. Tính
A. 8 + 14i B. 8 – 14i C. –8 + 13i D. 14i
Câu 166. Cho số phức , giá trị của là
A. 30 – 35i B. 30 + 35i C. 35 + 30i D. 35 – 30i
Câu 167. Cho số phức . Tìm phần thực và phần ảo ,mođun của số phức
A. Phần thực bằng –3 , phần ảo bằng –1, mođun
2
5 2 (1 )z ii=+ −+
1
3zi= +
2
2zi= −
1 12
z zz+
10−
( )( )
( )
( )
2 11 11 2 2zizii− ++ + −=−
2
3
3
2
1
2
52
zi=−+
z
1
23zi= −
2
12zi= −
12
zz−
12
34zz−=
12
26zz−=
12
2zz−=
12
2zz−=
43zi= −
( )
1w iz z
=+−
34wi
= +
32wi=−−
32wi= −
34wi=−+
1
23zi= +
2
1
zi= +
12
3zz
−
( )
35 4 2 1z ii= − +−
2 74
14 10i−
46
54
43 .
36
i
zi
i
+
=−+
+
73
,
15
a =
17
.
5
b = −
17
,
5
a
−
=
73
.
15
b =
73
,
15
a =
17
i.
5
b = −
73
,
15
a =
17
.
5
b =
( )( )
32 62
1
ii
z
i
−+
=
+
12
1 3, 2z iz i=+=−
(
)( )
121 2
23A zz z z=−+
3zi=−+
z
10z =

Bài tập trắc nghiệm số phức
Trang 20
B. Phần thực bằng –3, phần ảo bằng –2i mođun
C. Phần thực bằng 3 , phần ảo bằng i, mođun
D. Phần thực bằng 3 và phần ảo bằng 1, mođun
Câu 168. Cho số phức . Tìm môđun
A. B. C. D.
Câu 169. Cho số phức . Tìm số phức
A. B. C. D.
Câu 170. Tìm biết ?
A. B. C. D. 20
Câu 171. Gọi x, y là hai số thực thỏa: . Tính .
A. B. C. D.
Câu 172. Cho số phức . Tìm phần thực và phần ảo của số phức
A.Phần thực là –10 và phần ảo là B. Phần thực là –10 và phần ảo là
C. Phần thực là 10 và phần ảo là D. Phần thực là 10 và phần ảo là
Câu 173. Tìm số phức z thỏa :
A. B. C. D.
Câu 174. Cho số phức . Tính
A. B.
C. D.
Câu 175. Cho số phức . Tìm số phức
A. B. C. D.
Câu 176. Cho . Số phức liên hợp của z là:
A. B. C. D.
Câu 177. Cho thì bằng:
A. B. 5 C. D.
Câu 178. Tìm các số thực và y, biết:
13z =
10z =
10z =
12
2 ; z 1 3zi i=+=−
12
zz−
12
14zz−=
12
13zz−=
12
5zz−=
12
17zz−=
14zi= +
2.w z zi= +
79wi= +
69wi= +
33wi=−−
78wi=−+
z
( )( )
2
12 1z ii=+−
25
23
52
( ) ( )
2
35 2 42x iy i i−− −=−
2M xy= −
2
M =
0M =
1M =
2M = −
10 3zi
= −
z
3i−
3
3i−
3
( )
12 3iz z i+=−
11
44
zi= −
11
44
zi
=−+
11
88
zi=−+
11
88
zi= −
12
1 2; 1 5
z iz i=+ =−+
121
zzz+−
121
19zzz i+ − =−+
121
19zzz i+ − =−−
121
25zzz i+ − =−+
121
25zzz i+ − =−−
52zi= −
u z iz= −
33ui= +
73ui= −
33ui= −
73ui= +
12zi=−−
12
i
+
12i−+
2 i−
2 i+
( )( )
32 23 3 7
z i ii=+ − +−
z
27
19
29
x

Bài tập trắc nghiệm số phức
Trang 21
A. B. C. D.
Câu 179. Giá trị của biểu thức là:
A. 28 B. 56 C. 64 D. 72
Câu 180. Giá trị của biểu thức là:
A. –8 B. C. D. 1
Câu 181. Cho . Môđun của z bằng :
A. B. 1 C. 2 D. 3
Câu 182. Cho , ta có: bằng:
A. B. C. D.
Câu 183. Giá trị của biểu thức là:
A. B. C. D.
Câu 184. Cho số phức = .Tìm phần thực ,phần ảo của số phức .
A. Phần thưc bằng –2,phần ảo bằng B. Phần thưc bằng –2,phần ảo bằng
C. Phần thưc bằng 2,phần ảo bằng D. Phần thưc bằng 2,phần ảo bằng
Câu 185. Cho số phức phần thực phần ảo của lần lượt là :
A.3 và 2017 B.3 và 2017i C.3 và –2017 D.3 và –2017i
Câu 186. Cho khi đó bằng
A.10 B.8 C.6 D.7
Câu 187. Trong các khẳng định sau đây khẳng định nao đúng ?
A. B.
C.
D.
Câu 188. Cho số phức z thỏa mãn . Môđun của số phức w = là:
A.8 B. C.8 D.16
Câu 189. Cho hai số phức . Hai số phức khi:
( ) ( ) ( ) ( )
231 2 32 2 4 3x y x yi x y x y i+ + +− + = − + + − −
94
;
11 11
xy= =
94
;
11 11
xy
−
= =
94
;
11 11
xy
−
= =
94
;
11 11
xy
−−
= =
(
)
6
13Ai= +
3
13
22
Ni
=−+
1
8
−
1
8
23
zi= −
7
23zi= −
1
z
23i+
23
13 13
i+
23
13 13
i−
23
55
i+
( )
2016
1Mi= +
1008
2−
1008
2
1008
2
i
1008
2
i
−
z
24i
+
w zi= −
3i−
3.−
3.i−
3.
3 2017zi= −
z
12
3 4; 3 4
z iz i=+=−
12
|z z |+
2016
1i =
2017
1i =
2018
ii=
2019
1i = −
3
(1 3 )
1
i
z
i
−
=
−
z iz+
82
3
, ' ,( , , , )z a bi z c di a b c d R=+=+ ∈
'zz=

Bài tập trắc nghiệm số phức
Trang 22
A. B. C. D.
Câu 190. Điều kiện để số phức là số thuần ảo là
A.
B. C. D.
Câu 191. Trong các số phức sau, số phức nào có mô đun nhỏ nhất ?
A. B. C. D.
Câu 192. Cho
s
ố phức z thỏa mãn: .Tìm mô đun
s
ố phức
.
A.4 B. C. D. 5
Câu 193. Cho số phức . Tìm phần thực và phần ảo của số phức
A. Phần thực bằng 4 và phần ảo bằng –3 B. Phần thực bằng 4 và phần ảo bằng 3
C. Phần thực bằng 4 và phần ảo bằng 3i D. Phần thực bằng 4 và phần ảo bằng –3i.
Câu 194. Cho số phức thỏa mãn . Môđun của số phức z bằng:
A. B. C. D. .
Câu 195. Cho hai số phức . Tính tổng
A. B. C. D. .
Câu 196. Cho số phức thỏa mãn và . Tìm số phức
A. B. C. D. .
Câu 197. Số phức nghịch đảo của số phức là:
A. B. C. D. .
Câu 198. Cho số phức . Tìm phần thực và phần ảo của số phức
A. Phần thực bằng và phần ảo bằng B. Phần thực bằng và phần ảo bằng
C. Phần thực bằng và phần ảo bằng D. Phần thực bằng và phần ảo bằng
Câu 199. Cho hai số phức . Tính môđun của số phức .
A. B. C. D.
ac
bi di
=
=
ad
bc
=
=
ac
bd
=
=
ab
cd
=
=
3zi= −
13zi= −
32zi=−−
22zi
= +
(1 2 ) 7 4zi i+=+
2
zi
ω
= +
17
24
43zi
= +
z
z
(
)
1 24 0iz i
+ −− =
10z =
3z =
22z =
2z =
12
1 2; 4 2
z iz i=+=−
12
2Tz z= +
5T
=
35
T =
45T
=
55T
=
z
( )
2 10zi−+=
. 25zz=
z
5z =
34zi= −
5;34;34
z z iz i==+=−
34zi= +
13
22
zi
=−+
11 3
22
i
z
= −
1 13
22
i
z
=−−
113
22
i
z
=−+
11 3
22
i
z
= +
1
43
z
i
=
+
z
4
5
3
5
3
25
2
25
4
25
3
25
i
4
25
3
25
( )
2
12
3 2; 1 2z iz i=−=+
1
2
z
z
13
5
14
5
17
5
11
5

Bài tập trắc nghiệm số phức
Trang 23
Câu 200. Cho số phức . Tìm số phức
A. B. C. D.
Câu 201. Phần ảo và phần thực của số phức lần lượt là
A. B. C. D.
Câu 202. Cho hai số phức và . Tìm số phức liên hợp của số phức
.
A. B. C. D.
Câu 203. Cặp thỏa mãn biểu thức là:
A. B. C. D.
Câu 204. Cho số phức z = 5–2i. Số phức có phần ảo là
A. 29 B. 21 C. D.
Câu 205. Cho số phức . Tìm mệnh đề đúng trong các mệnh đề sau ?
A. z + = 2bi B. z – = 2a C. z. = a
2
– b
2
D.
Câu 206. Cho hai số phức z
1
= 2 + i, z
2
= 1 + 3i. Môđun của z
1
+ z
2
bằng bao nhiêu ?
A. 3 B. 4 C. 5 D. 6
Câu 207. Số viết dưới dạng a + bi thì a + b bằng bao nhiêu ?
A. 4 B. 25 C. 27 D. 17
Câu 208. Cho số phức thỏa mãn điều kiện: . Tính ?
A. B. C. D.
Câu 209. Nếu thì bằng:
A. B. C. D.
Câu 210. Cho số phức . Hỏi trong các phát biểu sau, phát biểu nào đúng?
A. là phần ảo
B. là mô–đun của z
C. Điểm biểu diễn số phức z trên mặt phẳng phức Oxy
D. có mô–đun khác nhau
45zi= −
2
i
w iz
z
+
= −
208 150
41 41
w = −
208 150
41 41
wi
=−−
208 150
41 41
wi= −
208 150
41 41
wi= +
10
(1 )
zi
= +
0; 32
0; 32
i
0; 32−
32; 0
1
52zi= −
2
34zi= −
1 2 12
2z .wz z z=++
54 26
wi= +
54 26wi
=−−
54 26wi= −
54 30wi= −
(
)
;xy
(2 3 1) ( 2 ) (3 2 2) (4 3)x y x yi x y x y i+ + +− + = − + + − −
94
;
11 11
94
;
11 11
−−
94
;
11 11
−
94
;
11 11
−
1
z
−
5
29
2
29
z a bi= +
z
z
z
2
2
zz=
100
43i+
z
23zz i+=+
21A iz i=++
1
2
3
5
zi=
2007
z
z
1
0
z−
,;z a bi a b=+∈
bi
22
ab+
( )
;M ab
;zz

Bài tập trắc nghiệm số phức
Trang 24
Câu 211. Số phức có mô–đun bằng và phần thực lớn hơn phần ảo 5 đơn vị. Biết z có phần thực
nhỏ hơn 2. Khi đó mô–đun có số phức có giá trị:
A. B. C. D.
Câu 212. Tổng của hai số phức liên hợp là:
A. Tổng của hai số phức liên hợp là một số thực
B. Tổng của hai số phức liên hợp là một số ảo
C. Tổng của hai số phức liên hợp là một số phức có đủ phần thực và ảo
D. Tích của hai số phức liên hợp là một số ảo
Câu 213. Với là hai số phức. Trong các khẳng định sau đây, khẳng định nào sai?
A. B.
C. với D.
Câu 214. Cho số phức z thỏa mãn điều kiện . Số phức có phần ảo bằng bao
nhiêu?
A. B. C. D.
Câu 215. Cho số phức . Xác định phần thực, phần ảo và tính mô–đun số phức
. Chọn đáp án đúng?
A. Số phức z có phần thực: –4, phần ảo: –3, mô–đun là 5
B. Số phức z có phần thực: 4, phần ảo: 3, mô–đun là 5
C. Số phức z có phần thực: –3, phần ảo: –4, mô–đun là 5
D. Số phức z có phần thực: 3, phần ảo: 4, mô–đun là 5
Câu 216. Tìm phần thực và phần ảo của số phức . Biết rằng . Phần thực và phần ảo
của số phức lần lượt là
A. B. C. D.
Câu 217. Số phức có mô–đun bằng:
A. B. C. D.
Câu 218. Tìm mô–đun của số phức:
A. B. C. D.
z
17
2wz= +
5
7
4
15
12
,zz
12 1 2
..zz z z=
12 1 2
zz z z+≥+
11
22
zz
zz
=
2
0z ≠
12 12
..zz zz
=
( )
1 13
iz i+ −=
1w zi z=−+
1−
2−
3
−
4−
( )( )
12 43 28z ii i= − − −+
z
z
(
)( )
12 2z ii= + −+
z
4; 3−−
4;3−
4; 3−
4;3
43zi= −
25
5
7
7
15
23
3
i
zi
i
+
=+−
−
170
3
z =
170
5
z =
170
5
z =
170
4
z =

Bài tập trắc nghiệm số phức
Trang 25
Câu 219. Tìm phần thực của số phức biết .
A. B. C. D.
Câu 220. Xét hai khẳng định sau đây:
(1) Số có phần thực bằng 1
(2) Bình phương của số có phần ảo bằng 7
Trong hai khẳng định trên
A. Cả 2 đều đúng B. Cả hai đều sai C. Chỉ có (1) đúng D.Chỉ có (2) đúng
Câu 221. Mondun của số phức bằng:
A. 1 B. 0 C. D. 2
Câu 222. Xét các phát biểu sau:
(1)
(2) Vì , nên ta nói là số phức liên hiệp của số
(3) Số đối của số là số
(4) Số đối của số bi là
Trong các câu trên, số phát biểu đúng là:
A. 1 B. 2 C. 3 D. 4
Câu 223. Xét các khẳng định sau:
(1) Với hai số phức tùy ý, ta có
(2) Với hai số phức tùy ý, ta có
Trong hai khẳng định trên
A. Chỉ có (1) đúng B. Chỉ có (2) đúng C. Cả hai đều đúng D. Cả hai đều sai
Câu 224. Số bằng:
A. B. C. 34 D. 25
Câu 225. Số phức có thể viết lại thành:
A. B. C. D. 4
3
2
.z zz
z
ω
= −+
12zi= −
31
5
−
32
5
−
33
5
−
32
5
( ) ( )
24 32ii i+− −−
(
)
23
i+
1zi= −
2
( )
( )
( ) (
)
00a bi a i bi a bi+ =+ −+ =−
( ) (
) ( )
( )
00a bi a bi i+ + − +− = +
(
) ( )
a bi
− +−
a bi+
( )
a bi
+
( )
a bi−+
( )
b i bi−=−
12
,zz
222
12 1 2
,zz z z= +
12
,zz
1
1
22
z
z
zz
=
(3 5 )(3 5 )ii+−
9 25i
+
23
i+
8
2
i
i
−
+
32
i−
23i+
1
2
2
i−

Bài tập trắc nghiệm số phức
Trang 26
Câu 226. Biểu thức có giá trị bằng
A. B. C. D.
Câu 227. Cho . Khi đó bằng?
A. Một số thuần ảo B. 1072 C. D. 20
Câu 228. Số nào sau đây là căn bậc 2 của
A.
B. C. D.
Câu 229. Xét các kết quả sau:
(1)
Trong ba kết quả trên, kết quả nào sai?
A. Chỉ sai B. Chỉ sai C. Chỉ sai D.Chỉ và sai
Câu 230. Tích số có giá trị bằng:
A. B. C. D.
Câu 231. Số phức có nghịch đảo bằng
A. B. C. D.
Câu 232. Xét các mệnh đề sau:
(1) Nếu thì là số thực.
(2) Giá trị tuyệt đối (hay mô–đun) của một số phức z bằng khoản cách OM, với M là điểm biểu diễn của z.
(3) Giá trị tuyệt đối (hay mô–đun)của một số phức z bằng số .
Chọn nhận định đúng trong các nhận định sau:
A. Cả ba câu đều đúng B.Chỉ có 1 câu đúng
C. Chỉ có 2 câu đúng D. Cả ba câu đều sai
Câu 233. Xét các kết quả sau :
Trong ba kết quả trên, kết quả nào sai ?
A. Chỉ (1) sai B. Chỉ (2) sai C. Chỉ (3) sai D. Chỉ (1) và (2) sai
Câu 234. Số nào sau đây bằng số
7 17
5
i
i
−
−
7
17
5
i+
3 i
+
22i−+
23i
−
172 30 , ' 172 30z iz i
=+==
.'zz
2 172
3
13
i
i
−
+
11
22
i
−
+
31
22
i
−
+
13
22
i
−
+
11
22
i
−
−
3
ii
=
( )
2
4
ii=
( )
3
( )
3
1 22ii+ =−+
( )
1
( )
2
( )
3
( )
1
( )
2
( )( )
33 23ii+−
68
i
−
68
i
+
33
i
−+
15 3i
−
45zt= −
45
41 41
i+
45
46 46
i+
25
27 27
i+
1
1
2
i+
zz=
z
.zz
( )
3
1 ii=
( )
4
2 ii=
( )
3
3 (1 ) 2 2ii+ =−+
( )( )
2 34?ii−+

Bài tập trắc nghiệm số phức
Trang 27
A. B. C. D.
Câu 235. Cho số phức . Môđun của số phức là:
A. B. C. D.
Câu 236. Tìm phần ảo của số phức , với n là số nguyên dương thỏa mãn
A. B. 64
C. 64i D. Không tồn tại phần ảo
Câu 237. Tìm modun của số phức z biết z không phải là số thực và thỏa mãn: .
A. B. C. Không tồn tại z D.
Câu 238. Cho hai số phức thỏa mãn: . So sánh hai số ta có
khẳng định sau:
A. B.
C. D. Không so sánh được
Câu 239. Cho . Các công thức sau, công thức nào sai:
A. B.
C. D.
Câu 240. Cho số phức z thỏa mãn: . Khẳng định nào sau đây đúng:
A. B. z có thể nhận giá trị là số thực hoặc số thuần ảo
C. Phần thực của z không lớn hơn 1 D. Đáp án B và C đều đúng
Câu 241. Cho số phức và và . Giá trị gần đúng phần
thực của số phức A là:
A. –16 B. 16 C. –26 D. 26
Câu 242. Cho các phát biểu về phép so sánh lớn hơn, bé hơn và bằng (>, < và =) như sau:
1. Ta có thể so sánh hai số thực bất kì
2. Ta có thể so sánh hai số phức bất kì
54
i
+
6 11i+
10 5i+
6
i+
( )
2
3zi= +
1
wz
z
= +
202 303
25 50
i−
303 202
25 50
i−
101
10
10201
100
2 23
3
n
i
z
i
−
=
−
(
)
42
log 3 log 9 3
nn− + +=
64 3−
( )
2
. 12
z z zz z+=
2
2z xi x=±−
{
}
0; 2z
∈
2z =
;ab
1ab= =
( )
;x abiy abiab
= ++ = + +
xy=
xy<
xy>
z a bi= +
z a bi= −
( )
2 22
2z a b abi=−+
( ) (
)
1
a b a bi
i
zz
++−
+
=
( )
2
1 22z i b ai+ =−+
3
zz=
1z =
( )
2
24 2
2,
i
x iy
x
+
=−=
27 2i
z
y
+
=
2 22
Ax y z=++

Bài tập trắc nghiệm số phức
Trang 28
3. Ta có thể so sánh hai số thuần ảo bất kì
4. Ta có thể so sánh môđun của hai số phức bất kì
Số phát biểu không đúng là:
A. 0 B. 4 C. 2 D. 1
Câu 243. Giả sử rằng nếu thì các căn bậc n ( cho trước) của w được biểu diễn trên mặt phẳng
phức bởi các đỉnh của một n–giác đều nội tiếp đường tròn tâm O bán kính R. Giá trị của R là;
A. B. Bình phương phần thực của
C. Giá trị tuyệt đối phần ảo của D. A, B và C đều sai
Câu 244. Cho số phức z thỏa mãn . Mô–đun của số phức là:
A. 3 B. 4 C. 5 D. 6
Câu 245. Xét các câu sau:
1. Nếu thì z là một số thực
2. Mô–đun của một số phức z bằng khoảng cách OM, với M là điểm biểu diễn z trong hệ tọa độ phức.
3. Mô–đun của một số phức z bằng số
Trong 3 câu trên:
A. Cả ba câu đều sai B. Chỉ có 1 câu đúng
C. Chỉ có 2 câu đúng D. Cả ba câu đều đúng
Câu 246. Cho tìm phần thực của số phức biết
A. 7 B. –50 C. 15 D. –10
Câu 247. Tìm số phức z để ta được:
A. z = 0 hay z = 1 B. z = 1 hay z = – i
C. z = 0 hay z = i D. z = 0, z = 1 + i hay z = 1 – i
Câu 248. Nếu thì
A. Bằng 0 B. Là số thuần ảo
C. Lấy mọi giá trị phức D. Lấy mọi giá trị thực
Câu 249. Tính số phức có giá trị bằng
A. B. C. D.
Câu 250. Cho số phức . Mô–đun của số phức z là:
0w ≠
3
n ≥
n
w
n
w
n
w
( )
( )
21 2
2 78
1
i
iz i
i
+
++ =+
+
1w zi= ++
zz=
.zz
2
1wz z= +−
w
( )( )
13 3
1
ii
z
i
−+
=
+
2
zz z
−=
1z =
2
1z
z
−
( )( )
14 25ii+−
22 3i+
22 3i−
18 3i−+
18 3i−−
92
zi= −

Bài tập trắc nghiệm số phức
Trang 29
A. B. C. 11 D. 7
Câu 251. Cho các số phức . Giả sử rằng , khi đó:
A. B. C. D. A, B và C đều sai
Câu 252. Cho số phức z thỏa mãn . Giá trị của là:
A. B. C. A và B đúng D. A và B sai
Câu 253. Chọn phát biểu không đúng
A. Số thực a âm hai căn bậc hai là và
B. Phương trình bậc n (với n là số nguyên dương) luôn có ít nhất một nghiệm phức
C. Phương trình bậc n (với n là số nguyên dương) có n nghiệm phức (không nhất thiết phân biệt)
D. Với một phương trình bất kì, nếu là một nghiệm của phương trình thì cũng là một nghiệm của nó.
Câu 254. Cho số phức z thỏa mãn . Tính
A. B. C. D.
Câu 255. Cho số phức z thỏa mãn . Tính tích phần thực và phần ảo của
A. 30 B. 3250 C. 70 D. 0
Câu 256. Cho số phức z thỏa mãn: (1).
Chọn đáp án sai?
A. z là số thuần ảo B. z có phần ảo là số nguyên tố
C. z có phần thực là số nguyên tố D. z có tổng phần thực và phẩn ảo là 5
Câu 257. Cho số phức z biết . Tìm tổng phần thực và phần ảo của z
A. B. C. D.
Câu 258. Tìm phần thực của số phức z, biết rằng
97
(1 2 ) 5 2
3
i
iz i
i
+
−− =−
−
A.
1−
B.
10
C.
1
D.
3
Câu 259. Tìm số phức z thỏa mãn :
( )( )
3 12 13zi i i− + +=
85
77
12
,zz
12 1
2zz z+=
12 2
2
zz z−<
12 2
2
zz z−=
12 2
2
zz z−>
7
1
2
z
z
z
−
+=
−
2zi
zi
+
−
170
10
2
2
ai−
ai
−−
0
z
∈
0
1
z
( )
( ) (
)
751 3 2z i i ii= − +− +
2.w zi=
6 24wi= +
6 24wi= −
3 12wi= −
3 12wi= +
( ) ( )
( )
3 4 32 47zi i i
= + −+ − −
.
zz
( )
( )
21 2
2 78
1
i
iz i
i
+
++ =+
+
( )
( )
2
1 21
2 (1)
2
ii
zz
i
−+
+=
−
42 2
15
−
22 4
5
−−
2 2 14
15
−−
2 2 14
5
−−

Bài tập trắc nghiệm số phức
Trang 30
A.
13
i+
B.
13i−
C.
14i+
D.
14i
−
Câu 260. Tìm số phức z biết:
( )
( )
(
)
23 2 1 2 1iz i i z
+ +−= +
?
A.
34i−+
B.
34i−
C.
34i+
D.
34
i−−

Bài tập trắc nghiệm số phức
Trang 31
B – HƯỚNG DẪN GIẢI
Câu 1. Cho
( )
; ' ' ' , , ', 'z x iy z x iy x y x y=+=+ ∈
. Tìm mệnh đề không đúng trong các mệnh đề sau:
A.
( ) ( )
'' 'z z x x iy y±=± + ±
B.
( )
.' ' ' ' 'z z xx yy i xy x y=−+ +
C.
22 22
'' ' '
''' ''
z xx yy x y xy
i
zxy xy
+−
= +
++
D. phương án B và C sai.
Hướng dẫn giải
Đáp án: D
Phân tích: Đề bài cho rằng tìm mệnh đề không đúng, do vậy ta sẽ đi xem xét từng phương án một,
* Với phương án A: Nhận thấy
(
) (
)
' ''z z x iy x iy
±=+ ± +
( ) (
)
''
x x y yi=± +±
. Vậy đây là phương án đúng.
* Với phương án B. Ta có:
( ) ( )
2
.' . ' '
' '' '
z z x iy x iy
xx ixy ix y i yy
=++
=++ +
( )
' yy' i ' '
xx xy x y= −+ +
. Vậy đây là phương án đúng.
* Với phương án C: Nhận thấy ở phần phương án mẫu số có dạng
22
''
xy+
nên ta sẽ nhân thêm số phức liên
hợp vào để tạo ra
22
''xy+
( )( )
( )( )
' iy'
' '' ''''
x iy x
z x iy
z x iy x iy x iy
+−
+
= =
+ +−
2
22 22 22
''' ' '' ' '
.
'' '' ''
xx ixy iyx i yy xx yy x y xy
i
xy xy xy
−+− + −
= = +
+ ++
Đây là phương án đúng
Vậy theo phương pháp loại trừ ta chỉ còn phương án D. Rõ ràng B và C đúng nhưng ở phương án D lại nói B và
C sai, do đó rõ ràng D là phương án không đúng, do vậy ta chọn D.
Câu 2. Số
( )
2345
iiii+++
bằng số nào dưới đây?
A. 0 B. i C. –i D. 2i
Hướng dẫn giải
Đáp án: A
Phân tích: Với bài toán này quý độc giả chỉ việc áp dụng công thức
2
1i = −
. Khi đó
2345
1 1. 1 0iiii i i+ + + =−− ++=
. Vậy đáp án của ta là A. Quý độc giả có thể chuyển máy tính sang dạng tính
toán bằng số phức để bấm cũng được. Tuy nhiên bài toán này nhẩm khá là nhanh mà quý độc giả không cần
tốn nhiều thời gian bấm máy tính.
Bài tập trắc nghiệm số phức
Trang 32
Câu 3. Tính
2009
i
A.
1−
B. 1 C.
i−
D.
i
Hướng dẫn giải
Đáp án: D
Phân tích: Ta thấy .
2009 2008
.
i ii=
.
(
)
1004
2
. 1.i i ii= = =
Ta sử dụng
2
1i = −
Câu 4. Tính
( )
( )
47 5 7
ii
− +− +
A.
11 12i−
B.
1 i−+
C.
12 11i+
D.
1−
Hướng dẫn giải
Đáp án: A
Lời giải: ta có
( )
( )
4 7 5 7 11 12ii i− +− + = −
Câu 5. Tìm phần thực, phần ảo của số phức sau
( ) ( ) ( )
4 23 5i ii−+ + − +
:
A. Số phức trên có phần thực là 1, phần ảo là
i
B. Số phức trên có phần thực là 1, phần ảo là –1
C. Số phức trên có phần thực là 1, phần ảo là 1 D. Số phức trên có phần thực là 1, phần ảo là
i−
Hướng dẫn giải
Đáp án: C
Ta có :
( ) (
) ( )
4 23 5i ii−+ + − +
1 i= +
Chú ý: Phần ảo không chứa i
Câu 6. Viết số phức
3
1
z
ở dạng chuẩn với
1zi
= +
A.
1
2
i
B.
11
44
i−−
C.
1
2
i−
D.
i
Hướng dẫn giải
Đáp án: B
Lời giải: Bấm máy tính ta được đáp án B.
( )
3
32
11
3 31
1
iii
i
=
+ ++
+
11
33 1 22ii i
= =
−− + + − +
2 11
8 44
i
i
+
= =−−
−
Câu 7. Cho
( )
; ' ' ', ,
z x iy z x iy x y=+=+ ∈
. Trong các mệnh đề sau mệnh đề nào sai ?
A.
( )
( )
'' 'z z x x iy y±=± + ±
B.
( )
. ' x' ' ' 'z z x yy i xy x y=−+ +
C.
22 22
'' ' '
.
''' ''
z xx yy x y xy
i
zxy xy
+−
= +
++
D.
( )
'' 'zz xxi yy+ = + + −+

Bài tập trắc nghiệm số phức
Trang 33
Hướng dẫn giải
Đáp án: D
Phân tích: Ta lần lượt đi xét từng mệnh đề một
Với A:
( ) ( ) ( ) ( )
' '' ' 'z z x iy x iy x x y y i±=+ ± + = ± + ±
đây là mệnh đề đúng
Với B:
( )
( )
.' . ' 'zz xyi xiy=++
2
' '' 'xx ixy ix y i yy=++ +
( )
' ' ''xx yy i xy x y=−+ +
đây là mệnh đề đúng.
Với C ta có:
( )(
)
( )
(
)
''
' ' iy' ' ' ' '
x iy x iy
z x iy
z x x iy x iy
+−
+
= =
+ +−
2
22 22 22
''' ' '' ' '
.
'' '' ''
xx ixy iyx i yy xx yy x y xy
i
xy xy xy
−+− + −
= = +
+ ++
đây là mệnh đề đúng
Câu 8. Tính
(
)(
)
53 35ii
+−
A.
15 15i−
B.
30 16i−
C.
25 30i+
D.
26 9i−
Hướng dẫn giải
Đáp án: B
Phân tích: Với bài toán này, bấm máy tính là cách làm nhanh nhất. Trước tiên, chuyển máy tính sang chế độ số
phức bằng cách ấn MODE → 2:CMPLX. Tiếp theo ấn biểu thức như trên và máy sẽ hiện luôn kết quả cho bạn
như sau:
Câu 9. Cho số phức z thỏa mãn
( )
1 . 14 2iz i+=−
. Tính tổng phần thực và phần ảo của
z
A. –4 B. 14 C. 4 D. –14
Hướng dẫn giải
Đáp án: B
Ta có:
( )
14 2
1 . 14 2 6 8 6 8
1
i
iz i z i z i
i
−
+ = − ⇔= =−⇒=+
+
Vậy tổng phần thực và phần ảo của
14z =
Câu 10. Cho số phức z thỏa mãn
( )
13 1iz i z− ++=−
. Môdun của số phức
w 13z 2i
= +
có giá trị bằng:

Bài tập trắc nghiệm số phức
Trang 34
A. –2 B.
26
13
C.
10
D.
4
13
−
Hướng dẫn giải
Đáp án: C
Ta có:
( ) ( )
( )( )
( )
2
2
1 23
1
13 1 5 23 1
23
23
ii
i
iz i z iz i z
i
−− +
−−
− ++= − ⇔ − =−−⇔ = =
−
+−
2
2323 15
13 2 1 3 1 9 10
13 13
iii i
z w zi i w
−− − − −
⇔= = ⇒ = + =−⇒ = +=
Câu 11. Cho số phức
( )( )
12 43 28z ii i
= − − −+
. Cho các phát biểu sau:
(1). Modun của z là một số nguyên tố
(2). z có phần thực và phần ảo đều âm
(3). z là số thuần thực
(4). Số phức liên hợp của z có phần ảo là 3i.
Số phát biểu sai là:
A. 1 B. 2 C. 3 D. 4
Hướng dẫn giải
Đáp án: A
Ta có:
(
)(
)
12 43 28 43
z ii i i= − − − + =−−
. Phần thực: –4, phần ảo: –3
( ) ( )
22
4 35z⇒ = − +− =
.
Câu 12. Cho số phức
( )
,z ax bi a b=+∈
, mệnh đề nào sau đây là không đúng?
A. Đối với số phức z , a là phần thực
B. Điểm
(
)
,M ab
trong một hệ tọa độ vuông góc của mặt phẳng phức được gọi là điểm biểu diễn số phức
z ax bi= +
C. Đối với số phức z , bi là phần ảo.
D. Số i được gọi là đơn vị ảo.
Hướng dẫn giải
Đáp án: C
Đây là một câu hỏi lí thuyết rất dễ gây hiểu lầm. Vì thế các bạn độc giả nên đọc kĩ từng mệnh đề để kết luận
xem mệnh đề nào đúng, mệnh đề nào sai.
Với mệnh đề thứ nhất và mệnh đề thứ 3 , ta cùng quay lại với trang 130 SGK cơ bản:
“ Đối với số phức
z ax bi= +
ta nói a là phần thực, b là phần ảo của z.”
Vậy ta có thể suy ra A đúng, C sai.

Bài tập trắc nghiệm số phức
Trang 35
Phân tích sai lầm: ở đây rất nhiều bạn nghĩ rằng câu C là đúng vì thế dẫn đến bối rối trong việc xét các câu còn
lại. Tuy nhiên các bạn độc giả nhớ kĩ rằng phần ảo chỉ có b mà ko có i . Các mệnh đề còn lại là đúng, tuy nhiên
các bạn nên đọc cả những mệnh đề đó và ghi nhớ luôn, vì chúng ta
đang trong quá trình ôn tập nên việc này là rất cần thiết.
Câu 13. Cho số phức
76zi= +
, tính mô đun của số phức
2
1
21
3
z
z
+
=
A.
3217
B.
85
C. 3127 D. 85
Hướng dẫn giải
Đáp án: A
Cách giải toán thông thường
( )
2
2
1
2. 7 6 1
98 168 72 1
33
i
ii
z
++
+++
= =
27 168
9 56
3
i
i
+
= = +
(do
2
1i
= −
)
Đến đây nhiều độc giả không nhớ kiến thức mô– đun là gì dẫn đến kết quả sai không đáng có như sau:
(Mô đun của z
1
) =
22
9 56 3127+=
=> Đán án C.
Vì thế quý độc giả cần nắm rõ các công thức: Mô đun của số phức z kí hiệu là
z
, có giá trị
22
z a bi a b=+= +
, hay chính độ dài của vectơ
OM
(với M là điểm biểu diễn số phức
z a bi= +
).
Cách bấm máy tính nhanh : Nếu bạn nào có tư duy nhẩm tốt thì có thể nhẩm nhanh theo cách trên, còn nếu tư
duy nhẩm không được tốt, các bạn có thể thao tác trên máy tính như sau: ( bởi vì nhiều khi thời gian các bạn
nhẩm còn nhanh hơn là thời gian cầm máy tính lên và bấm từng nút)
Bước 1: Ấn nút MODE trên máy tính, chọn chế độ phức 2: CMPLX bằng cách ấn nút số 2.
Bước 2: Nhập vào máy tính như sau
Từ đó ta tìm được số phức z
1
và đi tính mô đun số phức như cách 1.
Câu 14. Cho số phức
12
32, 65z iz i=+=+
. Tìm số phức liên hợp của số phức
12
56zz z= +
A.
51 40zi= +
B.
51 40zi= −
C.
48 37zi= +
D.
48 37zi= −
Hướng dẫn giải
Đáp án: B

Bài tập trắc nghiệm số phức
Trang 36
Các bước để làm dạng toán này như sau: Quý độc giả lần lượt thế
12
,zz
vào biểu thức z từ đó tìm được z.
( )
( )
5 3 2 6 6 5 51 40
zi i i= ++ +=+
Đến đây nhiều bạn vội vàn khoanh A, dẫn đến kết quả sai. Vì ở đây là tìm số phức liên hợp của z hứ không
phải tìm z. Vậy đáp án của ta là B.
Hoặc nhiều bạn bấm nhầm máy tính có thể ra các kết quả khác như C hoặc D. Vì vậy một lần nữa chị khuyên
các bạn cần hết sức cẩn thận khi đọc đề bài, khi tính toán.
Câu 15. Trong các kết luận sau, kết luận nào sai ?
A. Mô đun của số phức
( )
,z a bi a b=+∈
được tính bằng
22
z ab= +
B. Mô đun của số phức z (với z là khác 0) là một số thực dương.
C. Mô đun của số phức z là một số phức.
D. A và B đúng.
Hướng dẫn giải
Đáp án: C
Phân tích: Theo định nghĩa sách giáo khoa ta có:
Giả sử số phức
z a bi= +
được biểu diễn bởi điểm M(a;b) trên mặt phẳng tọa độ.
Độ dài vecto
OM
được gọi là mô đun của số phức z và kí hiệu là
z
.
Vậy
22
z OM a b= = +
.
Từ đây ta suy ra A, B đúng. Vậy đáp án là C.
Câu 16. Thu gọn biểu thức
2
( 2 3)
zi= +
ta được:
A.
11 6zi= −
B.
1zi=−−
C.
43zi
= +
D.
7 62zi=−+
Hướng dẫn giải
Đáp án: D
Sử dụng máy tính ở chế độ CMPLX. Nhập màn hình biểu thức
( )
2
23i+
và ấn “=” ta được kết quả
7 62zi=−+
Câu 17. Mô đun của số phức
6
5 2 (1 )z ii=+ −+
là :
A.
5 10
B.
61
C.
5
D.
55
Hướng dẫn giải
Đáp án: D

Bài tập trắc nghiệm số phức
Trang 37
Nhiều thí sinh tỏ ra lung túng trước biểu thức
( )
6
1 i+
, nếu như đây là bài tự luận thì các bước khai triển
biểu thức này khá dài và phức tạp, tuy nhiên chúng ta có thể sử dụng máy tính để có kết quả chính xác.
Một lưu ý là máy tính không thể tính được lũy thừa bậc 4 trở lên của một số phức. Do đó ta phải tính
gián tiếp qua 2 bước. Vì
( ) ( )
2
63
11ii
+=+
nên ta sẽ tính
( )
3
1 i+
trước rồi tính bình phương của giá trị vừa tìm
được.
Sử dụng máy tính Casio ta tính được
( ) ( ) ( )
3 62
1 22 1 22 8i i i ii+ =−+ ⇒ + =−+ =−
Vậy
(
)
6
52 1 52 (8)510z i i ii i=+−+ =+−− =+
22
5 10 125 5 5z⇒= + = =
Nhận xét: Một số sai lầm trong quá trình biến đổi có thể dẫn đến đáp án sai là B hoặc C. Nếu như sử dụng
phương pháp khai triển trực tiếp ra nháp thì bài toán này tốn khá nhiều thời gian khi đi thi, thí sinh có thể sẽ bị
không đủ thời gian làm những câu khác.
Câu 18. Tìm số nghịch đảo của
32
zi
= +
A.
32i−
B.
32i−+
C.
32
13 13
i
−
D.
32
13 13
i+
Hướng dẫn giải
Đáp án: C
Chú ý rằng hai số nghịch đảo của nhau là hai số có tích bằng 1
Do đó số nghịch đảo của số phức
32zi= +
là
1
11
32
z
zi
= =
+
Sử dụng máy tính Casio ta dễ dàng tính được
1
32
13 13
zi= −
Câu 19. Cho 3 số phức
1
13
22
zi
−
= +
;
2
3zi= +
và
3
12zi=−+
. Tìm môđun số phức
12 3
.z zz z= −
A. 4 B.
22
C.
2
D.
42
Hướng dẫn giải
Đáp án: B
Đây là một bài toán đơn giản, chỉ cần thực hiện các thao tác bấm máy tính, chúng ta cần tránh mất điểm ở
những câu dễ như thế này. Sử dụng máy tính thu được kết quả
22zi=−+
. Do đó đáp án B là chính xác.
Câu 20. Số đối của số phức
25zi= +
là:

Bài tập trắc nghiệm số phức
Trang 38
A.
25i−
B.
25i−+
C.
25i−−
D.
25
29 29
i−
Hướng dẫn giải
Đáp án: C
Chú ý rằng hai số được gọi là đối của nhau nếu tổng của chúng bằng 0, do đó số đối của số phức
25
zi
= +
phải
là
25
i
−−
Sai lầm thường gặp: nhầm lẫn giữa số đối và số phức liên hợp.
Câu 21. Phần ảo của số phức
2
23wz z
=−+
biết
3zi= −
là:
A. –4 B. –4i C. 4 D. 4i
Hướng dẫn giải
Đáp án: A
Biến đổi ta được kết quả sau
( ) ( )
2
2
2 3 3 23 3 5 4wz z i i i= − += − − − +=−
Vậy phần ảo của số phức w là –4
Câu 22. Các cặp số phức không là hai phân số liên hợp của nhau là:
A.
1; 1xy xy++ ++
B.
;xy xy
C.
;1xyxy
− −−
D.
;
xx
yi
yi
+
+
Hướng dẫn giải
Đáp án: D
Sử dụng công thức
ab ab+=+
ta thấy ngay các cặp (
1; 1
yxxy
++ ++
)và liên hợp với nhau
Bây giờ ta sẽ kiểm tra đáp án B và D
Ta thấy nếu z
1
và z
2
là 2 số phức liên hợp thì
12
zz
=
Ta có:
;
11
1
x xx
xx
y yi y
y
yi
= = =
+++
+
+
Rõ ràng:
1
xx
yi yi
yi
y
+≠ +⇒ ≠
+
+
;
xx
yi
yi
⇒
+
+
Không liên hợp

Bài tập trắc nghiệm số phức
Trang 39
Nhận xét: Có nhiều cách để kiểm tra 2 số phức liên hợp. Tùy từng biểu thức khác nhau để làm cho hiệu quả.
Ví dụ ở cặp
;xy xy
ta hoàn toàn có thể đặt phần thực phần ảo của các số phức x, y sau đó nhân ra. Tuy nhiên
nếu áp dụng cách này vào cặp
;
xx
yi
yi
+
+
thì rất mất nhiều thời gian tính toán.
Câu 23. Tìm modun của số phức z biết:
(
)
( )( )
(
)( )
2424
1
22
abbai
zz
abbai
+−
+=
+−
?
A. 2 B. 1 C. 0 D. 3
Hướng dẫn giải
Đáp án: B
Ta có:
( )
( )( )
(
) (
)
( )
(
)
( )
(
) ( )
(
)(
)
(
) (
)
( )
( )
( ) ( )
(
)
(
)
(
)(
)
22
22
22
22
2
2424
1
22
2424
2424
1
22
22
24 24
1
22
20 20
12
55
20
1 20
10 1
abbai
zz
ab bai
abbai
abbai
zz
ab bai
ab bai
ab ba
zz
ab ba
ab
zz
ab
zz
zz
zz
+−
+=
+ +−
+−
+−
⇒+= =
+ +−
+ +−
+ +−
⇒+ =
+ +−
+
⇒+ = =
+
⇒ + −=
⇒ − +=
⇒ −= ⇔ =
Câu 24. Tìm số phức
z
thỏa mãn
2 13
12
ii
z
ii
+ −+
=
−+
A.
22 4
25 25
i+
B.
22 4
25 25
i−
C.
22 4
25 25
i +
D.
22 4
25 25
i−+
Hướng dẫn giải
Đáp án: B
Ta có:
( )( )
( )
2
13 1
2 13
12
2
ii
ii
zz
ii
i
−+ −
+ −+
= ⇒=
−+
+
( )( )( )
2
13 1 2
22 4
25 25 25
ii i
i
−+ − −
= = +

Bài tập trắc nghiệm số phức
Trang 40
Sai lầm cơ bản: Ra đáp án của z mà khoanh luôn đáp án A, do không đọc kĩ đề bài là tìm
z
.
Câu 25. Tìm phần thực của số phức z biết:
2
10
z
z
z
+=
A. 10 B. 5 C. –5 D.
10
Hướng dẫn giải
Đáp án: B
Ta có:
( ) ( )
2
2.Re 10 Re 5
z
z zz z z
z
+ =+= = ⇒ =
.
Câu 26. Cho số phức
z a bi= +
thỏa mãn
2. 3 3z iz i+=+
. Tính giá trị biểu thức:
2016 2017
Pa b= +
A. 0 B. 2 C.
4032 2017
2017
33
5
−
D.
4032 2017
2017
33
5
−
−
Hướng dẫn giải
Đáp án: B
.
z a bi i z ia b=−⇒ =+
( ) ( ) ( )
2. 2 2 2z iz abi iab a b b ai⇒+ =+ + + = + + +
2016 2017
23
1 11 2
23
ab
ab P
ba
+=
⇒ ⇒==⇒ = + =
+=
Sai lầm thường gặp:
.
z abi iz iab=−⇒ =−
9
23
5
23 3
5
a
ab
ba
b
=
−=
⇒⇒
+=
= −
=> Đáp án C
Câu 27. Nếu
23zi= +
thì
z
z
bằng:
A.
56
2
11
i
i
+
−
B.
5 12
13
i+
C.
5 12
13
i−
D.
34
7
i−
Hướng dẫn giải
Đáp án: B
Vì
2 332zi i= +=+
nên
32zi= −
, suy ra
( )( )
32 32
3 2 5 12
3 2 9 4 13
ii
zi i
zi
++
++
= = =
−+

Bài tập trắc nghiệm số phức
Trang 41
Câu 28. Số nào trong các số phức sau là số thực
A.
( ) (
)
33ii
+− −
B.
( ) ( )
2 5 12 5ii+ +−
C.
( )( )
1 31 3ii+−
D.
2
2
i
i
+
−
Hướng dẫn giải
Đáp án: C
( )
( ) ( )
2
1 31 3 1 3 4ii i+ −=− =
Câu 29. Tập hợp các nghiệm của phương trình
z
z
zi
=
+
là:
A.
{ }
0;1 i−
B.
{ }
0
C.
{ }
1 i−
D.
{
}
0;1
Hướng dẫn giải
Đáp án: A
0
0
1
10
1
1
1
z
z
z
zz
zi
zi zi
zi
=
=
= ⇔− =⇔ ⇔
= −
++
=
+
Câu 30. Cho hai số phức
12
1 2; 2 3z iz i=+=−
. Tổng của hai số phức là
A.
3
i−
B.
3 i+
C.
35i−
D.
35i+
Hướng dẫn giải
Đáp án: A
12
12 23 3zz i i i+ =+ +− =−
Câu 31. Môđun của số phức
( )( )
12
12
ii
z
i
+−
=
+
là:
A. 2 B. 3 C.
2
D.
3
Hướng dẫn giải
Đáp án: C
Mô đun của số phức
( )( )
12
12
12
ii
z iz
i
+−
= =−⇒ =
+
Câu 32. Phần ảo của số phức z biết
( ) ( )
2
2 .1 2zi i=+−
là:
A.
2
B.
2−
C. 5 D. 3
Hướng dẫn giải
Đáp án: B
( )
( )
2
2 .1 2 5 2 5 2
z i i iz i= + − =+ ⇒=−

Bài tập trắc nghiệm số phức
Trang 42
Vậy phần ảo của z là:
2
−
Câu 33. Cho số phức
1
1
3
zi= −
. Tính số phức
3w iz z= +
.
A.
8
3
w =
B.
10
3
w =
C.
8
3
wi= +
D.
10
3
wi= +
Hướng dẫn giải
Đáp án: A
1
18
1
3
33
33
iz i
zi w
zi
=−+
=− ⇒ ⇒=
= −
Câu 34. Cho hai số phức
z a bi= +
và
' ''
z a bi= +
. Điều kiện giữa a,b,a’,b’ để
.'zz
là một số thực là:
A.
' '0aa bb+=
B.
' bb' 0aa −=
C.
ab' a'b 0+=
D.
ab' a'b 0−=
Hướng dẫn giải
Đáp án: C
(
)( ) ( )
. ' ' ' ' bb' ' 'z z a bi a b i aa ab a b i=+ + = −+ +
z.z’ là số thực khi
'' 0ab a b+=
Câu 35. Cho số phức
z x yi= +
, biết rằng
,xy∈
thỏa
( ) (
) ( ) (
)
32 21 1 5x y ix y i
− + + = +− −
. Tìm số
phức
( )
6w z iz= +
A.
17 17wi= +
B.
17wi= +
C.
1wi= −
D.
1 17wi= +
Hướng dẫn giải
Đáp án: A
Ta có
( ) ( ) ( ) ( )
3
23
2
32 21 1 5
4
34
3
x
x
x y ix y i
y
y
=
=
− + + = +− − ⇔ ⇔
=
=
Suy ra
34 34
23 23
z iz i=+ ⇒=−
, nên
3434
6 17 17
2323
w ii i
= +++ =+
Câu 36. Cho số phức
126zi=−−
. Tìm phần thực và phần ảo của số phức
z
.
A. Phần thực bằng
1−
và phần ảo bằng
26i−
B. Phần thực bằng
1
−
và phần ảo bằng
26
C. Phần thực bằng 1 và phần ảo bằng
26
D. Phần thực bằng
1−
và phần ảo bằng
26i
Hướng dẫn giải
Đáp án: B

Bài tập trắc nghiệm số phức
Trang 43
126 1 26
z iz i=−− ⇒ =−+
. Vậy phần thực bằng –1 và phần ảo bằng
26
.
Câu 37. Tính
ab+
biết rằng a, b là các số thực thỏa mãn
(
)
2017
13a bi i
+=+
A.
(
)
672
1 3 .8
ab+= +
B.
( )
671
1 3 .8
ab+= +
C.
( )
672
3 1 .8
ab+= −
D.
(
)
671
3 1 .8
ab+= −
Hướng dẫn giải
Đáp án: A
Ta có:
(
)
3
13 8i
+=−
và
2017 3.672 1
= +
Câu 38. Cho số phức
13zi
=−−
. Tìm phần thực và phần ảo của số phức
z
A. Phần thực bằng
1−
và phần ảo bằng 3. B. Phần thực bằng
1−
và phần ảo bằng
3i
C. Phần thực bằng 1 và phần ảo bằng 3. D. Phần thực bằng 1 và phần ảo bằng
3i
.
Hướng dẫn giải
Đáp án: A
13 13z iz i=−− ⇒ =−+
. Suy ra phần thực bằng –1 và phần ảo bằng 3.
Câu 39. Cho số phức
23zi= −
. Tìm số phức
1
zi
w
z
+
=
−
A.
1wi=−+
B.
71
55
wi=−−
C.
42
55
wi= +
D.
24
55
wi= −
Hướng dẫn giải
Đáp án: A
Ta có:
( )(
)
( )
2
2
24 13
2 3 2 4 10 10
1
2 3 1 1 3 10
13
ii
zi ii i i
wi
zi i i
++
++++ −+
= = = = = =−+
− −− −
+−
Câu 40. Cho số phức
2016 2017zi= −
. Tìm phần thực và phần ảo của số phức z.
A. Phần thực bằng 2016 và phần ảo bằng
2017i−
. B. Phần thực bằng 2016 và phần ảo bằng –2017.
C. Phần thực bằng 2017 và phần ảo bằng
2016i−
. D. Phần thực bằng 2016 và phần ảo bằng 2017.
Hướng dẫn giải
Đáp án: D
2016 2017 2016 2017z iz i= − ⇒= +
. Vậy Phần thực bằng 2016 và phần ảo 2017
Câu 41. Cho các số phức
12
1 2, 1 3z iz i=−=−
. Tính mô–đun của số phức
12
zz+
A.
12
5zz+=
B.
12
26zz+=
C.
12
29zz+=
D.
12
23zz+=
Hướng dẫn giải

Bài tập trắc nghiệm số phức
Trang 44
Đáp án: C
11
12 12
22
12 12
2 5 29
13 13
z iz i
zz i zz
z iz i
=−=+
⇒ ⇒+=+⇒ + =
=−=+
Câu 42. Thu gọn số phức
32 1
1 32
ii
z
ii
+−
= +
−+
ta được:
A.
23 61
26 26
zi= +
B.
23 63
26 26
zi= +
C.
15 55
26 26
zi= +
D.
26
13 13
zi= +
Hướng dẫn giải
Đáp án: C
3 2 1 15 55
1 3 2 26 26
ii
zi
ii
+−
=+=+
−+
Câu 43. Cho số phức
3
13
1
i
z
i
+
=
+
. Tìm phần thực và phần ảo của số phức
z
.
A. Phần thực bằng 2 và phần ảo bằng
2i−
B. Phần thực bằng 2 và phần ảo bằng
2−
C. Phần thực bằng 2 và phần ảo bằng
2i
D. Phần thực bằng 2 và phần ảo bằng 2
Hướng dẫn giải
Đáp án: B
( )
(
)
3
3
3
13
13 8
22 22
1 22
1
i
i
z iz i
ii
i
+
+−
= = = =+ ⇒=−
+ −+
+
Vậy phần tực bằng 2 và phần ảo bằng –2
Câu 44. Cho số phức z thỏa mãn:
(
) ( )
2
32 2 4iz i i+ +− =+
. Hiệu phần thực và phần ảo của số phức z là:
A. 1 B. 0 C. 4 D. 6
Hướng dẫn giải
Đáp án: B
( ) ( ) ( ) ( )
2
2
32 2 4 32 44 4 32 15iz i i iz i i i iz i+ + − = +⇔ + + − + = +⇔ + =+
( )( )
22
15 32
1 5 13 13
1
3 2 3 2 13
ii
ii
zz z i
i
+−
++
⇔= ⇔= ⇔= =+
++
Suy ra hiệu phần thực và phần ảo của z bằng 1 – 1 =0
Câu 45. Gọi x,y là hai số thực thỏa mãn biểu thức
32
1
x yi
i
i
+
= +
−
. Khi đó, tích số x.y bằng:
A.
.5xy=
B.
.5xy= −
C.
.1xy=
D.
.1xy= −
Hướng dẫn giải

Bài tập trắc nghiệm số phức
Trang 45
Đáp án: B
( )( )
2
32 5
32 32 1 33 2 2
32 1
1
xx
x yi
i x yi i i x yi i i i
yy
i
=+=
+
=+ ⇔+ = + −⇔+ =−+ − ⇔ ⇔
=−+ =−
−
Câu 46. Cho số phức
( )
14 3zi=−+
. Tìm phần thực và phần ảo của số phức
z
.
A. Phần thực bằng
11
−
và phần ảo bằng
4i
B. Phần thực bằng
11
−
và phần ảo bằng 4
C. Phần thực bằng
11−
và phần ảo bằng
4i
−
D. Phần thực bằng
11−
và phần ảo bằng
4−
Hướng dẫn giải
Đáp án: B
( )
1 4 3 11 4
ziz i=− + ⇒=−+
=> Phần thực bằng –11 và phần ảo bằng 4
Câu 47. Tìm mệnh đề sai trong các mệnh đề sau:
A. Số phức
z a bi= +
được biểu diễn bằng điểm M trong mặt phẳng phức Oxy.
B. Số phức
z a bi= +
có môđun là
2
ab+
C. Số phức
0
0
0
a
z a bi
b
=
=+=⇔
=
D. Số phức
z a bi= +
có số phức đối
' a biz = −
Hướng dẫn giải
Đáp án: D
Số phức đối của
z a bi= +
là số phức
'z z a bi=−=−−
nên D là đáp án của bài toán
Câu 48. Cho hai số phức
z a bi= +
và
z' a' b'i= +
. Số phức z.z’ có phần thực là:
A.
a a'+
B.
aa'
C.
aa' bb'−
D.
2bb'
Hướng dẫn giải
Đáp án: C
( )( ) ( ) ( )
2
. ' ' 'i . ' ' ' ' ' . ' ' a'bz z a bi a b a a ab i a bi bb i aa b b ab i=+ +=+ + + =− ++
Số phức z.z’ có phần thực là
( )
.' .'aa bb−
Câu 49. Phần thực của số phức
( )
2
z 23i
= +
A. –7 B.
62
C.
2
D. 3
Hướng dẫn giải
Đáp án: A
( )
2
2
2 3 2 62 9 7 62z i ii i= + = + + =−+
có phần thực là –7.
Câu 50. Cho số phức z thỏa
( ) ( )( )
2
12 34 2zi ii−=+ −
. Khi đó, số phức z là:

Bài tập trắc nghiệm số phức
Trang 46
A.
25z =
B.
5zi=
C.
25 50zi= +
D.
5 10zi= +
Hướng dẫn giải
Đáp án: D
( ) ( )( )
( )
( )
2
2
34 44
12 34 2
12
i ii
zi ii z
i
+ −+
− = + − ⇔=
−
( )
( )
22
22
3 16 1 2
5 10
12
ii
z zi
−+
⇔= ⇔=+
+
Câu 51. Cho hai số phức
3z a bi= −
và
( )
'2 ,z b ai a b=+∈
. Tìm a và b để
'6
zz i−=−
A.
3; 2
ab
=−=
B.
6; 4ab= =
C.
6; 5ab=−=
D.
4; 1ab= = −
Hướng dẫn giải
Đáp án: D
Ta có:
( )
'23z z a b b ai− = − +− −
*
26 4
'6
31 1
ab a
zz i
ba b
−= =
− = −⇔ ⇔
− −=− =−
Câu 52. Tính môđun của số phức
( )
2016
1zi= +
A.
1008
2
B.
1000
2
C.
2016
2
D.
1008
2−
Hướng dẫn giải
Đáp án: A
( ) ( ) ( )
( )
( )
( )
1008
252
2 2016 2 1008
1008 1008 1008 4 1008
1 2 1 1 2 2. 2. 2ii i i i i i+ =⇒+ = + = = = =
Mô đun:
1008
2z =
Câu 53. Tính A=3+2i+(6+i)(5+i).
A. 30+10i B. 32+13i C. 33+13i D. 33+12i
Hướng dẫn giải
Đáp án: B
A=3+2i+(6+i)(5+i)=3+2i+(6.5–1.1)+i(6.1+1.5)=3+2i+29+11i=32+13i.
Câu 54. Cho z=1–i, môđun của số phức 4z–1 là:
A. 2 B. 3 C. 4 D. 5
Hướng dẫn giải
Đáp án: D
4z–1=4(1–i)–1=3–4i, suy ra môđun bằng 5.

Bài tập trắc nghiệm số phức
Trang 47
Câu 55. Cho z=3+4i, tìm phần thực ảo của số phức :
A. Phần thực là , phần ảo là B. Phần thực là , phần ảo là
C. Phần thực là , phần ảo là D. Phần thực là , phần ảo là
Hướng dẫn giải
Đáp án: B
.
Câu 56. Cho số phức . Tìm phần thực và phần ảo của số phức
A. Phần thực bằng 5, phần ảo bằng –2 B. Phần thực bẳng 5, phần ảo bằng 2
C. Phần thực bằng 5, phần ảo bằng –2i D. Phần thực bẳng 5, phần ảo bằng 2i
Hướng dẫn giải
Đáp án: B
= 5 + 2i. Phần thực bằng 5, phần ảo bằng 2
Câu 57. Cho hai số phức và . Tính môđun của số phức .
A. B. C. D.
Hướng dẫn giải
Đáp án: A
= –2 + 4i,
Câu 58. Cho số phức . Số phức có môđun bằng
A. B. C. D.
Hướng dẫn giải
Đáp án: D
,
Câu 59. Tìm số phức z thỏa mãn:
A. B. C. D.
Hướng dẫn giải
Đáp án: D
.
1
z
1
3
1
4
3
25
4
25
−
1
3
1
4
−
3
5
4
5
−
( )
(
)
1 1 34 34 3 4
3 4 3 4 3 4 25 25 25
ii
i
z i ii
−−
= = = = −
+ −+
52zi= −
z
z
1
2
zi= +
2
43zi= −
12
zz−
12
25zz−=
12
23zz−=
12
22zz−=
12
2zz−=
12
zz−
22
12
( 2) 4 2 5zz−=−+=
23zi= +
w=z+2i
1
w =
2w =
29w =
5w =
w=z+2i=2-3i+2i=2+i
22
21 5w
= +=
( )( )
2 1 42i iz i− ++=−
13zi=−−
13zi=−+
13zi= −
13zi= +
13zi= +

Bài tập trắc nghiệm số phức
Trang 48
Câu 60. Cho số phức z thỏa mãn: . Tìm môđun của .
A. B. C. D.
Hướng dẫn giải
Đáp án: A
Câu 61. Cho số phức z thỏa mãn: . Xác định phần thực và phần ảo của z.
A. Phần thực – 2 ; Phần ảo 5i. B. Phần thực – 2 ; Phần ảo 5.
C. Phần thực – 2 ; Phần ảo 3. D. Phần thực – 3 ; Phần ảo 5i.
Hướng dẫn giải
Đáp án: B
z = –2+5i, suy ra Phần thực – 2 ; Phần ảo 5.
Câu 62. Cho số phức . Tìm phần thực, phần ảo của số phức
A. Phần thực bằng –2 và phần ảo bằng –3i B. Phần thực bằng –2 và phần ảo bằng –3
C. Phần thực bằng 2 và phần ảo bằng 3i D. Phần thực bằng 2 và phần ảo bằng 3
Hướng dẫn giải
Đáp án: D
Phần thực bằng 2 và phần ảo bằng 3
Câu 63. Cho số phức . Tính môđun của số phức
A. B. C. D.
Hướng dẫn giải
Đáp án: C
Câu 64. Cho hai số phức: . Tìm số phức
A. B. C. D.
Hướng dẫn giải
Đáp án: B
3
(1 3 )
1
i
z
i
−
=
−
z iz+
82
83
42
43
2
(2 3 ) (4 ) (1 3 )iz iz i
− + + =−+
24zi= +
w
zi
= −
23w zi i= −= +
32
zi=−+
1zi+−
14
zi+− =
11
zi+− =
15zi+− =
1 22zi+− =
13212zi ii i+−=−+ +−=−+
15zi+− =
12
2 5; 3 4
z iz i=+=−
12
.z zz
=
6 20zi= +
26 7zi= +
6 20zi= −
26 7zi= −
( ) ( )
12
. 2 5 . 3 4 26 7zz i i i=+ −=+
26 7zi= +

Bài tập trắc nghiệm số phức
Trang 49
Câu 65. Cho số phức . Phần thực và phần ảo của số phức lần lượt là:
A.–3 và –7 B. 3 và –11 C. 3 và 11 D. 3 và –7
Hướng dẫn giải
Đáp án: C
Câu 66. Cho hai số phức . Môđun của số phức bằng:
A.5 B. C. D. 3
Hướng dẫn giải
Đáp án: B
Câu 67. Cho số phức .Tìm số phức ?
A. B. C. D.
Hướng dẫn giải
Đáp án: A
Câu 68. Cho số phức . Tìm phần thực và phần ảo của số phức .
A. Phần thực bằng và phần ảo bằng B.Phần thực bằng và phần ảo bằng 3
C. Phần thực bằng và phần ảo bằng D. Phần thực bằng và phần ảo bằng
Hướng dẫn giải
Đáp án: B
Số phức liên hợp của z là , phần thực bằng –6, phần ảo bằng 3.
Câu 69. Cho hai số phức và . Tính môđun của số phức
A. B. C. D.
Hướng dẫn giải
Đáp án: C
Câu 70. Cho số phức . Tìm số phức .
A. B. C. D.
Hướng dẫn giải
Đáp án: A
13zi=−+
23wiz= −
13 13z iz i=−+ ⇒ =−− ⇒
( )
2 3 1 3 3 11wi i i= − −− = +
12
4 2; 2z iz i= − =−+
12
zz+
5
3
12 12
25zz i zz+ = −⇒ + =
32zi= −
( )
23 21w i i z iz=−− + −
85wi=−+
85wi
= +
85wi
= −
85wi=−−
32 32z iz i=−⇒=+⇒
( )( ) ( )
2 3 32 232 1 85wi i i i i i= − − + + − −=−+
63zi=−−
z
6−
3i−
6−
6
3
6
3i
63Zi
=−+
1
12zi= +
2
5zi= −
12
zz−
12
1zz−=
12
7zz−=
12
5zz−=
12
7zz−=
12
(1 2 ) (5 ) 4 3zz i i i− = + − − =−+
( )
2
2
12
4 35zz⇒−=− +=
23zi= +
w = 2iz - z
87wi=−+
8wi=−+
47wi= +
87wi=−−

Bài tập trắc nghiệm số phức
Trang 50
.
Câu 71. Tìm phần thực và phần ảo của số phức
A. Phần thực bằng và phần ảo bằng B. Phần thực bằng và phần ảo bằng
C. Phần thực bằng 3 và phần ảo bằng D. Phần thực bằng 3 và phần ảo bằng 2.
Hướng dẫn giải
Đáp án: D
Câu 72. Cho số phức . Tính ta được kết quả:
A. . B. . C. . D. .
Hướng dẫn giải
Đáp án: B
Ta có .
Suy ra .
Câu 73. Cho hai số phức và . Kết luận nào sau đây là sai?
A. . B. . C. . D. .
Hướng dẫn giải
Đáp án: A
Ta có . Suy ra . Do đó A sai.
Ta có . Do đó B đúng.
Ta có . Do đó C đúng.
Ta có Do đó D đúng.
Câu 74. Cho số phức . Trong các khẳng định dưới đây, khẳng định nào sai?
A. Số phức có phần thực bằng , phần ảo bằng . B. Số phức có phần thực bằng 8, phần ảo bằng
.
C. Môđun của bằng 10. D. Số liên hợp của là .
Hướng dẫn giải
Đáp án: B
Ta có , suy ra và .
2 3 2 (2 3 ) (2 3 ) 8 7z iwi i i i
= − ⇒ = + − − =−+
3 2.zi= +
3
−
2.i−
3
−
2.−
2.
i
53zi= −
( )
2
1 zz++
22 33
i−+
22 33i+
22 33i−
22 33i−−
53 53z iz i=− ⇒=+
( )
( ) ( ) ( ) ( )
2
2
1 1 5 3 5 3 6 3 16 30 22 33zz i i i i i++ =++ ++ =+ + + = +
1
1zi
= +
2
1zi= −
12
2zz−=
1
2
z
i
z
=
12
.2
zz =
12
2
zz+=
( ) ( )
12
1 12zz i i i− =+−−=
22
12
02 2zz−= +=
( )( )
1
2
11
12
1 22
ii
z
ii
i
zi
++
+
= = = =
−
(
)( )
12
1 1 11 2
zz i i= + − =+=
( ) ( )
12
1 1 2.zz i i+ =++−=
( )
24 3ui= −
u
8
6
−
u
i
u
u
86ui= +
( )
243 86u ii
= −=−
( )
2
2
8 6 10u = +− =
86ui= +

Bài tập trắc nghiệm số phức
Trang 51
Do đó B sai, các mệnh đề còn lại đều đúng.
Câu 75. Thực hiện các phép tính
A. B. C. D.
Hướng dẫn giải
Đáp án: B
Câu 76. Chọn mệnh đề sai trong các mệnh đề sau:
A. Cho x,y hai số phức thì số phức có số phức liên hợp
B. Cho x,y hai số phức thì số phức có số phức liên hợp
C. Cho x,y hai số phức thì số phức có số phức liên hợp
D. Số phức thì
Hướng dẫn giải
Đáp án: D
Ta có thì .
Câu 77. Cho số phức z thỏa mãn z – (1– 9i) = (2+3i)z. Phần ảo của số phức z là:
A. –1 B. C. 2 D. –2
Hướng dẫn giải
Đáp án: B
Ta biến đổi đưa về
Bấm Mt ta được
Câu 78. Trong các kết luận sau, kết luận nào là sai
A. Môđun của số phức z là một số thực B. Môđun của số phức z là một số thực không âm
C. Môđun của số phức z là một số phức D. Môđun của số phức z là một số thực dương
Hướng dẫn giải
Đáp án: C
PP loại trừ
Câu 79. Số nào trong các số sau là số thực?
A.
( )
( )
32 32ii+− −
B.
( )
( )
2525ii+ +−
C.
( )
2
13i+
D.
2
2
i
i
+
−
Hướng dẫn giải
33
22
i
−+
33
22
i+
33
22
i−
33
22
i
−−
xy+
xy
+
xy−
xy
−
xy
xy
z a bi
= +
( )
( )
2
2 22
2z z ab+= +
z a bi= +
22 2
z2za+=
6
5
19
13
i
z
i
−
=
−−
13 6
55
zi= +

Bài tập trắc nghiệm số phức
Trang 52
Đáp án: B
Sử dụng MTCT có được:
(
)
(
)
32 32 4
i ii
+− −=
( )
( )
2 5 2 54ii+ +− =
là số thực
( )
2
1 3 2 23ii+ =−+
2 1 22
33
2
i
i
i
+
= +
−
Câu 80. Số nào trong các số sau là số thuần ảo :
A. B. C. D.
Hướng dẫn giải
Đáp án: C
Bấm máy
Câu 81. Đẳng thức nào trong các đẳng thức sau là đúng
A. B. C. D.
Hướng dẫn giải
Đáp án: B
Bấm máy
Câu 82. Đẳng thức nào trong các đẳng thức sau là đúng?
A. B. C. D.
Hướng dẫn giải
Đáp án: D
Bấm máy
Câu 83. Cho số phức z = 2 + 3i. Tìm phần thực phần ảo của số phức
A. Phần thực bằng 2 và phần ảo bằng –3. B. Phần thực bằng 2 và phần ảo bằng –3i.
C. Phần thực bằng 2 và phần ảo bằng 3. D. Phần thực bằng 2 và phần ảo bằng 3i.
Hướng dẫn giải
Đáp án: A
Câu 84. Cho hai số phức z
1
= 1 – 2i và z
2
= 3 + 4i. Tính mô đun của
A. B. C. D.
Hướng dẫn giải
( 2 3) ( 2 3)ii
++ −
( 2 3).( 2 3)ii+−
2
(2 2 )
i+
23
23
i
i
+
−
1997
1i = −
2345
ii=
2005
1i =
2006
ii= −
8
(1 ) 16
i+=−
8
(1 ) 16
ii+=
8
(1 ) 16
ii
+=−
8
(1 ) 16i
+=
z
12
zz−
12
40zz−=
12
20zz−=
12
6zz−=
12
40zz
−=

Bài tập trắc nghiệm số phức
Trang 53
Đáp án: A
Câu 85. Cho số phức z = 2 – i. Tìm sô phức
A. B. C. D.
Hướng dẫn giải
Đáp án: C
Câu 86. Phần thực của
2zi=
là:
A. 2 B. 2i C. 0 D. 1
Hướng dẫn giải
Đáp án: C
2 02zi i= = +
. Phần thực của z là 0.
Câu 87. Số
zz+
là
A. Sô thực B. Số thuần ảo C. 0 D. 1+2i
Hướng dẫn giải
Đáp án: A
Giả sử
(, )
z a bi a b=+∈
2zz a+=
là số thực
Câu 88. Nghiệm của phương trình
z
z
zi
=
+
là:
A.
0; 1zz i= = −
B.
0z =
C.
1zi
= −
D.
0; 1zz= =
Hướng dẫn giải
Đáp án: A
Câu 89. Môđun của
12i−
bằng:
A. 3 B. 1 C.
5
D. 2
Hướng dẫn giải
Đáp án: C
Môđun của
12i−
bằng:
22
1 ( 2) 5+− =
Câu 90. Tìm số phức liên hợp của số phức
z a bi= +
A.
'
z a bi=−+
B.
'
z b ai= −
C.
'
z a bi=−−
D.
'
z a bi= −
12 12
2 6 40zz i zz− =−− ⇒ − =
w iz z= +
w 35i= −
w 35i
=−+
w 35i= +
w 35i=−−
( )
w 2 2 33
ii i i= − + += +
( )
( ) ( 1) 0 0; 1
z
z z i zz i z zz i z z i
zi
= ≠−⇔+=⇔+−=⇔= =−
+

Bài tập trắc nghiệm số phức
Trang 54
Hướng dẫn giải
Đáp án: D
Câu 91. Tìm phần ảo của số phức
z
thỏa mãn:
( )
( )
2
2 12zi i=+−
A.
2−
B.
2
C.
2
D.
2−
Hướng dẫn giải
Đáp án: A
Câu 92. Cho số phức
2
( 2 ) (1 2 ).zii=+−
Tìm phần ảo của số phức
z
.
A.
2
B.
2−
C.
2.
−
D.
2.
Hướng dẫn giải
Đáp án: A
Bấm máy tính
Câu 93. Rút gọn biểu thức
(2 )(3 )zi i i=−+
ta được:
A.
6z =
B.
17
zi= +
C.
2 5zi= +
D.
5zi=
Hướng dẫn giải
Đáp án: B
Bấm máy tính
Câu 94. Cho hai số phức
3
3
12
2 4 2(1 )
4 3 (1 ) ;
1
ii
z i iz
i
+− −
=−+− = ⋅
+
Tìm số phức
12
2. . ,zz
ω
=
A.
18 75. .i
ω
= −
B.
18 74. .i
ω
= +
C.
18 75. .i
ω
= +
D.
18 74. .i
ω
= −
Hướng dẫn giải
Đáp án: D
Bấm máy tính
Câu 95. Cho số phức z thỏa mãn:
(4 ) 3 4iz i−=−
. Điểm biểu diễn của z là:
A.
16 11
(; )
15 15
M −
B.
16 13
(; )
17 17
M −
C.
94
(; )
55
M −
D.
9 23
(; )
25 25
M −
Hướng dẫn giải
Đáp án: B
Ta có
3 4 16 13
(4 ) 3 4
4 17 17
i
iz i z i
i
−
− =− =>= = −
−
=>
16 13
(; )
17 17
M −
Câu 96. Cho số phức
43zi= −
. Tìm phần thực và phần ảo của số phức z.
A. Phần thực bằng – 4 và phần ảo bằng –3i. B. Phần thực bằng – 4 và phần ảo bằng –3.
(
) (
)
2
2 12 52 52
z i i iz i
= + − =+ ⇒=−

Bài tập trắc nghiệm số phức
Trang 55
C. Phần thực bằng 4 và phần ảo bằng 3i. D. Phần thực bằng 4 và phần ảo bằng 3.
Hướng dẫn giải
Đáp án: D
Ta có
43zi= +
⇒
Phần thực bằng 4 và Phần ảo bằng 3 ( không phải 3i)
Câu 97. Cho hai số phức z
1
= 4 + 5i và z
2
= – 1 +2i . Tính môđun của số phức
A.
12
41.zz−=
B.
12
5.zz−=
C.
12
3 2.zz−=
D.
12
34.zz−=
Hướng dẫn giải
Đáp án: D
Ta có
22
12 12
5 3 5 3 34
zz i zz− =+⇒ − = + =
Câu 98. Cho số phức
32zi= +
. Tìm số phức
2.w iz z
= +
A.
1 4.wi=−+
B.
9 2.wi= −
C.
4 7.wi= +
D.
4 7.wi= −
Hướng dẫn giải
Đáp án: A
Ta có
32zi= +
32zi⇒=−
( )
2 322 32 14w iz z i i i i⇒ = + = + + − =−+
.
Câu 99. Cho
45zi=−+
Tìm phần thực, phần ảo của số phức
z
.
A. Phần thực bằng 4 và phần ảo bằng 5i. B. Phần thực bằng 4 và phần ảo bằng 5.
C. Phần thực bằng –4 và phần ảo bằng –5. D. Phần thực bằng –4 và phần ảo bằng –5i.
Hướng dẫn giải
Đáp án: C
Ta có:
45 45z iz i=−+ ⇒ =−−
.
Phần thực bằng –4 và phần ảo bằng –5.
Câu 100. Cho hai số phức
12
3 2; 2 .z iz i
= − =−+
Tìm mô đun của số phức :
12
.zz+
A.
12
5
zz
=
+
B.
12
2
zz
=
+
C.
12
13
zz
=
+
D.
12
2
zz
=
+
Hướng dẫn giải
Đáp án: B
12
2
1
zz
i
= =
+
−
Câu 101. Cho số phức
2 3.zi
= +
Tìm số phức
.w iz z= −
A.
35wi=−+
B.
53zi= +
C.
55zi=−+
D.
55zi= −
Hướng dẫn giải
Đáp án: C
( ) ( )
55
23 23
w iz z i i
ii
= − = − =−+
+−

Bài tập trắc nghiệm số phức
Trang 56
Câu 102. Số phức liên hợp của số phức
12zi= +
là
A.
12i−+
B.
12i−−
C.
2
i
+
D.
12i−
Hướng dẫn giải
Đáp án: D
Số phức liên hợp của số phức
12
zi= +
là
12zi= −
Câu 103. Phần thực của số phức z thỏa mãn: là
A. 2 B. –3 C. –2 D. 3
Hướng dẫn giải
Đáp án: A
Ta có:
( ) ( ) ( ) ( ) ( )
(
)
( )(
)
2
1 2 8 12 24 12 8
8 12
8
12 8 23
12 5
i iz i iz iz iz i
ii
i
iz i z i
i
+ −=+++⇔+−+=+
+−
+
⇔ + = +⇔ = = = −
+
Vậy phần thực của
z
bằng
2
Câu 104. Cho hai số phức
1
1zi= −
và
2
35
zi
=−+
. Môđun của số phức
12 2
.w zz z= +
A.
130w =
B.
130w
=
C.
112
w =
D.
112w =
Hướng dẫn giải
Đáp án: A
Ta có:
( )( )
2 12
35 . 1 35 82z i zz i i i=−− ⇒ = − −− =−−
Khi đó:
( )
2
2
11 3 11 3 130w iw=−+⇒ = − + =
Câu 105. Cho số phức
3 2.
zi= −
Tìm số phức
w iz z= +
A.
5 5.wi=−−
B.
5 5.wi= +
C.
3 7.wi= +
D.
77
wi=−−
Hướng dẫn giải
Đáp án: B
Ta có:
Câu 106. Cho số phức Z = 5 + 4i. Phần thực, phần ảo của số phức
Z
là:
A. Phần thực bằng 5, phần ảo bằng –4 B. Phần thực bằng 5, phần ảo bằng 4
C. Phần thực bằng –5, phần ảo bằng –4 D. Phần thực bằng –5, phần ảo bằng 4
Hướng dẫn giải
Đáp án: A
( ) ( )
( )
2
1 2 8 12i iz i iz+ − = ++ +
w 55i
= +

Bài tập trắc nghiệm số phức
Trang 57
Phần thực 5, phần ảo –4
Câu 107. Cho số phức z = (2 + i)(1 − i) + 1 + 3i . Môđun của z là:
A. 2 B. 2 C. D. 4
Hướng dẫn giải
Đáp án: A
Ta có:
2 113 4 2
16 4 20 2 5
zi i i
z
= −+++ = +
= += =
Câu 108. Cho số phức z thỏa mãn đẳng thức z + (1 + i) = 5 + 2i . Môđun của z là:
A. B. C. 2 D.
Hướng dẫn giải
Đáp án: D
Gọi
z x yi z x yi=+ ⇒=−
, ta có
( )( )
1 52
52
2 52
25 2
21
x yi i x yi i
x yi x yi xi y i
x y xi i
xy x
xy
+ ++ − =+
⇔+ +− + +=+
⇔ ++ =+
+= =
⇔⇔
= =
,
ta có:
21
21 5z = +=
Câu 109. Giá trị của biểu thức
( )
8
1 i+
bằng:
A. 14 B. 15 C. 16 D. 17
Hướng dẫn giải
Đáp án: C
Ta có:
( ) ( )
( )
( )
4
4
82 4
2
1 1 1 2 2 16i i ii i
+ = + =++ = =
Câu 110. Cho số phức z = 5 + 3i. Tìm phần thực và phần ảo của số phức
z
A. Phần thực bằng 5 và Phần ảo bằng –3. B. Phần thực bằng –5 và Phần ảo bằng 3.
C. Phần thực bằng 5 và Phần ảo bằng –3i. D. Phần thực bằng 5 và Phần ảo bằng 3.
Hướng dẫn giải
Đáp án: A
53zi= −
Suy ra: Phần thực bằng 5 và Phần ảo bằng –3
5
2
13
2
z
10
2
2
5

Bài tập trắc nghiệm số phức
Trang 58
Câu 111. Cho hai số phức
1
12zi= +
và
2
23zi=−+
. Tính môđun của số phức
12
.zz+
A.
12
26zz+=
. B.
12
5zz+=
. C.
12
1
zz+=
. D.
12
2
zz+=
.
Hướng dẫn giải
Đáp án: D
12
1 2 ( 2 3) 1zz i i i
+ = − +−+ =−+
Suy ra
22
12
( 1) 1 2zz+ =−+=
Câu 112. Số phức liên hợp của
( )( )
1
1 32
3
zi i
i
=+ −+
+
là
A.
13 9
.
10 10
wi= −
B.
3
5.
10
wi= −
C.
53 9
.
10 10
wi= −
D.
53 9
.
10 10
wi= +
Hướng dẫn giải
Đáp án: C
Bấm máy tính được:
53 9
.
10 10
wi= −
Câu 113. Tìm phần thực, phần ảo của số phức z = i – (2 – 4i) + (3 – 2i) .
A. Phần thực bằng 3 và Phần ảo bằng –7i. B. Phần thực bằng 3 và Phần ảo bằng –7.
C. Phần thực bằng 3 và Phần ảo bằng 7i. D. Phần thực bằng 3 và Phần ảo bằng 7
Hướng dẫn giải
Đáp án: B
Tìm phần thực, phần ảo của số phức
z = i – (2 – 4i) + (3 – 2i) = i–2+4i+9–12i–4= 3–7i
Câu 114. Cho số phức và . Tính mô đun của số phức
A. . B. . C. . D. .
Hướng dẫn giải
Đáp án: A
Cho số phức và .
Khi đó
Câu 115. Cho số phức . Tìm số phức
A. w . B. w . C. w . D.w .
Hướng dẫn giải
Đáp án: D
2
2
1
1
zi= +
2
32
zi= −
12
.zz
12
. 26zz =
12
.6zz =
12
.6zz =
12
.2zz =
1
1zi
= +
2
32zi= −
12
.5zz i= +
12
. 25 1 26zz⇒ = +=
43zi= −
w2z iz= +
53i=−−
53i= +
33i= −
52i= −

Bài tập trắc nghiệm số phức
Trang 59
Cho số phức . Tìm số phức
Câu 116. Cho số phức . Modul của số phức z là:
A.2 B.–3 C. D.13
Hướng dẫn giải
Đáp án: C
Lời giải:
Câu 117. Cho số phức , số phức liên hợp của số phức z là:
A. B. C.
D.
Hướng dẫn giải
Đáp án: A
Lời giải: vậy
Câu 118. Tính ta được:
A.
B. C. D.
Hướng dẫn giải
Đáp án: B
Câu 119. Phần thực của số phức bằng
A.0 B.1 C. D.
Hướng dẫn giải
Đáp án: A
Câu 120. Cho số phức: . Tìm phần thực và phần ảo của số phức
A.Phần thực bằng –3 và phần ảo bằng 5 B. Phần thực bằng –3 và phần ảo bằng 4i
C. Phần thực bằng 3 và phần ảo bằng 4 D. Phần thực bằng –3 và phần ảo bằng 4
Hướng dẫn giải
Đáp án: D
Câu 121. Cho hai số phức và . Tính môđun của số phức
A. B.
C.
D.
43
zi= −
w 52i= −
23zi= −
13
22 2 2
2 ( 3) 13z ab= + = +− =
13zi
= +
13
zi
= −
3zi=−−
13
zi=−+
3
zi= +
z a bi= +
⇒
z a bi= −
13zi
= −
( ) ( )
32
12 3zi i=+ +−
38zi=−+
38zi=−−
38zi= −
38zi= +
( ) ( )
32
23 2
1 2 3 1 6 3.4 8 9 6
16 128 96 1 38
z i i i i i ii
i ii i
= + + − =+ + + +− +
=+ − − + − −=−−
30
(1 )
i+
15
2
15
2−
30 2 15 15 15 2 7 15
(1 ) ((1 ) ) (2 ) 2 . .( ) 2i i i ii i+=+ = = =−
35zi=−+
zi−
1
12zi= −
2
3zi= +
12
2zz−
12
2 26zz−=
12
2 41zz−=
12
2 29zz−=
12
2 33zz−=

Bài tập trắc nghiệm số phức
Trang 60
Hướng dẫn giải
Đáp án: B
Sử dụng máy tính tính số phức . Tính môdun
Câu 122. Cho số phức . Tìm số phức
A. B. C.
D.
Hướng dẫn giải
Đáp án: C
Câu 123. Cho hai số phức: z
1
= 2 – 3i ; z
2
= –1 + i. Phần ảo của số phức w = 2z
1
– z
2
bằng:
A.–7 B. 5 C.7 D.–5
Hướng dẫn giải
Đáp án: A
w = 2z
1
– z
2
= 5 – 7i
Câu 124. Phần ảo của số phức , biết số phức Z thỏa mãn : là
A. –1 B. 2 C. 1 D. –2
Hướng dẫn giải
Đáp án: A
Từ giả thiết
W = 1 – ( 2 – i )i + 2 + i = 2 – i
Phần ảo : –1
Câu 125. Cho hai số phức: . Tính .
A. i B.4i C. D.
Hướng dẫn giải
Đáp án: B
.
Câu 126. Cho số phức . Tìm số phức .
A. w= 1+4i B. w=1–4i C. w=–15–4i D. w =15+4i
Hướng dẫn giải
Đáp án: A
12
2 54zz i− =−−
( ) ( )
22
12
2 5 4 41zz− = − +− =
52
zi
= +
w iz z= −
33wi= −
33wi= +
33wi=−+
33wi=−−
( ) (
)
52 52 52 33z i w iz z i i i i= − ⇒ = − = − − + =−+
1
W Zi Z=−+
( )
1 13 0iZ i+ −− =
(
)
13
1 13 0 2
1
i
iZ i Z i
i
+
+ −− = ⇔ = = +
+
12
1 3 ; z 3
zi i=+=+
12
.zz
23 4
i+
3 1 ( 3 1)i++ −
12
. (1 3 )( 3 ) 4zz i i i=+ +=
1 23
1 3 ; z 2 ; z 3 4zi i i=− =+=−
12 23
w zz zz= +
12 23
(1 3 )(2 ) (2 )(3 4 )=1+4iw zz zz i i i i= + =− −+ + +

Bài tập trắc nghiệm số phức
Trang 61
Câu 127. Cho số phức z = 1 –2i , phần ảo của số phức w = 2z + là :
A. –2 B. 2 C. 4 D. –4
Hướng dẫn giải
Đáp án: A
w = 3 – 2i
Câu 128. Cho hai số phức z
1
=1 + 3i và z
2
= 2 – i . Khi đó | z
1
+ z
2
| bằng :
A. B. 5 C. D.
Hướng dẫn giải
Đáp án: D
Ta có:
Câu 129. Cho số phức z = 4 – 3i +
. Khi đó bằng :
A. 20 – 8i B. 20 + 8i C.
D.
+
Hướng dẫn giải
Đáp án: C
=
73
15
17
5
Câu 130. Cho số phức z = 1 – 5i. Tìm phần thực, phần ảo của số phức .
A. Phần thực bằng –1 và phần ảo bằng –5i. B. Phần thực bằng –1 và phần ảo bằng –5.
C. Phần thực bằng 1 và phần ảo bằng –5. D. Phần thực bằng 1 và phần ảo bằng –5i.
Hướng dẫn giải
Đáp án: C
Câu 131. Cho số phức z thỏa . Tìm phần thực, phần ảo của số phức z.
A. Phần thực bằng 1 và phần ảo bằng 3i B. Phần thực bằng 1 và phần ảo bằng 3
C. Phần thực bằng –1 và phần ảo bằng –3i D. Phần thực bằng –1 và phần ảo bằng 3
Hướng dẫn giải
Đáp án: B
Câu 132. Cho số phức . Phần thực, phần ảo của là
A.–5 và 2. B.–5 và 2i. C. 2 và –5. D. 5 và 2.
Hướng dẫn giải
Đáp án: A
5
10
13
12
32zz i
+=+
z
(1 ) 4 2iz i+=−
42
13 13
1
i
z iz i
i
−
= =− ⇒=+
+
25zi= −
z

Bài tập trắc nghiệm số phức
Trang 62
Phần thực bằng –5 và phần ảo bằng 2.
Câu 133. Cho hai số phức và . Môđun của số phức là
A. B. C. D.
Hướng dẫn giải
Đáp án: B
Cho hai số phức và . Môđun của số phức là
= –3–6i => =
Câu 134. Cho số phức z= 1+2i. Số phức là
A.1+i B. –1+i C.–1–i D. 1–i
Hướng dẫn giải
Đáp án: C
Cho số phức z= 1+2i. Số phức là
= i(1+2i)+1–2i= –1–i
Câu 135. Tìm mệnh đề sai trong các mệnh đề sau:
A. Số phức z = a + bi được biểu diễn bằng điểm M(a; b) trong mặt phẳng phức Oxy
B. Số phức z = a + bi có môđun là
C. Số phức z = a + bi = 0 ⇔
D. Số phức z = a + bi có số phức đối z’ = a – bi
Hướng dẫn giải
Đáp án: D
Câu 136. Tìm mệnh đề sai trong các mệnh đề sau:
A. Số phức z = a + bi được biểu diễn bằng điểm M(a; b) trong mặt phẳng phức Oxy (đúng)
B. Số phức z = a + bi có môđun là (đúng)
C. Số phức z = a + bi = 0 ⇔ (đúng)
D. Số phức z = a + bi có số phức đối z’ = a – bi (Sai vì không có số phức đối)
Câu 137. Số phức z = bằng:
A. B. C. D.
1
1zi= −
2
45zi= +
12
zz−
25
35
33
53
1
1zi
= −
2
45zi= +
12
zz−
12
zz−
12
zz−
35
w iz z
= +
w iz z= +
w iz z= +
22
ab+
0
0
a
b
=
=
22
ab
+
0
0
a
b
=
=
34
4
i
i
−
−
16 13
17 17
i−
16 11
15 15
i−
94
55
i−
9 23
25 25
i−

Bài tập trắc nghiệm số phức
Trang 63
Hướng dẫn giải
Đáp án: A
Ta có
Câu 138. Cho số phức z = 6 + 7i. Số phức liên hợp của z có điểm biểu diễn là:
A. (6; 7) B. (6; –7) C. (–6; 7) D. (–6; –7)
Hướng dẫn giải
Đáp án: B
Cho số phức z = 6 + 7i. Số phức liên hợp của z có điểm biểu diễn là:
Ta có
Câu 139. Trong các số phức sau, số thực là
A.
B.
C. D.
Hướng dẫn giải
Đáp án: B
Câu 140. Số phức có mô đun là:
A. B. C. D.
Hướng dẫn giải
Đáp án: A
Câu 141. Cho số phức: . Phần thực a và phần ảo b của lần lượt là
A. B. C. D.
Hướng dẫn giải
Đáp án: C
Câu 142. Cho hai số phức: và . Modul của số phức: là
A. . B. . C. 20. D. 40.
Hướng dẫn giải
Đáp án: D
2
3 4 (3 4 )(4 ) 12 3 16 4 16 13
4 17 17 17 17
i i i i ii
zi
i
− − + +− −
= = = = −
−
6 7 6 7 (6; 7)Z iZ i M=+⇒=− ⇒ −
( )
( )
32 32ii+− −
( ) (
)
32 32
ii+ +−
(
) ( )
12 12ii+ +−+
( )
( )
52 52ii+− −
(
) ( )
2
12 1z ii=+−
52z =
50z =
22
3
z =
10
3
z =
17 52z iz=+⇒=
11 7zi=−+
z
11; 7.ab= = −
11; 7.ab
=−=−
11; 7.
ab=−=
11; 7.
ab= =
11 7 11; 7z ia b=−+ ⇒=− =
1
48zi= −
2
2
zi=−−
12
2.z zz
=
45
5
22
22z iz i=−−⇒ =−+

Bài tập trắc nghiệm số phức
Trang 64
Câu 143. Cho số phức z = a + bi. Khi đó số là
A. Một số thực B. 2 C. Một số thuần ảo D. i
Hướng dẫn giải
Đáp án: A
z = a + bi =>
1
2
(
z + z
)
= a
Câu 144. Cho số phức
= 2 + 6,
= 1 + 2. Tính modun của số phức
A. 5 B. 6 C. 7 D. 8
Hướng dẫn giải
Đáp án: A
|
z
z
|
=
(2 + 1)
+ (6 2)
= 5
Câu 145. Tìm mệnh đề sai trong các mệnh đề sau:
A. Số phức z = a + bi được biểu diễn bằng điểm M(a;b) trong mặt phẳng phức Oxy.
B. Số phức z = a + bi có môđun là .
C. Số phức z = a + bi = 0 ⇔ .
D. Số phức z = a + bi có số phức liên hợp là = – a – bi.
Hướng dẫn giải
Đáp án: D
Số phức z = a + bi có số phức liên hợp = a – bi.
Câu 146. Cho số phức z = a + bi. Số phức z
2
có phần thực là :
A. a
2
+ b
2
B. a
2
– b
2
C. a + b D. a – b
Hướng dẫn giải
Đáp án: B
Khai triển biểu thức .
Câu 147. Cho (x + 2i)
2
= yi (x, y ∈ R). Giá trị của x và y bằng
A. x = 1 và y = 4 hoặc x = –1 và y = –4. B. x = 3 và y = 12 hoặc x = –3 và y = –12.
C. x = 2 và y = 8 hoặc x = –2 và y = –8. D. x = 4 và y = 16 hoặc x = –4 và y = –16.
Hướng dẫn giải
Đáp án: C
( )
( )
2
12
2 . 2 4 8 2 40 40 40z zz i i i z= = − −+ = ⇒ = =
( )
1
2
zz+
22
ab
+
0
0
a
b
=
=
z
z
( ) ( )
( )
22
2 2 22
22z a bi a abi bi a b abi=+ =+ + =−+

Bài tập trắc nghiệm số phức
Trang 65
Với x, y ∈ R, ta có
với x = 2 => y= 8; x = – 2 => y = –8.
Câu 148. Cho số phức z = . Số phức 1 + z + z
2
bằng
A. . B. 2 – . C. 1. D. 0.
Hướng dẫn giải
Đáp án: D
Ta có: .
Câu 149. Tìm phần thực của số phức z thỏa mãn iz + 4 + 5i = i(6 + 3i)
A. 1 B. 7 C. 11 D. –1
Hướng dẫn giải
Đáp án: A
Tìm Phần thực là 1.
Câu 150. Cho số phức z
1
= 1 – 3i, z
2
= 2 + i. Tìm số phức w =
A. 7i B. 5i C. – 4 – 7i D. – 7i
Hướng dẫn giải
Đáp án: B
Câu 151. Cho số phức z = (2 + i)(1 – i) + 1 + 2i. Mô–đun của số phức z là
A.
B.
C.
D. 2
Hướng dẫn giải
Đáp án: C
z = 4+i
Mô–đun của z bằng .
Câu 152. Gọi z
1
, z
2
là hai nghiệm phức của phương trình x
3
– 3x
2
+ 4x – 12 = 0. Tính
A. P = 0 B. P = 16 C. P = 4 D. P = – 4
Hướng dẫn giải
Đáp án: C
2
22
2
40
(x 2i) 4 4
4
4
x
x
yi x xi yi
yx
xy
= ±
−=
+ = ⇔ −+ = ⇔ ⇔
=
=
13
22
i−+
13
22
i
−+
3i
22
13 13 13133
11 () 0
22 22 22 42 4
zz i i i i++=−++−+ =++−−=
(6 3 ) 4 5
17
ii i
zi
i
+ −−
= = +
12
2
zz−
w 2(1 3 ) (2 ) 5i ii
= + − +=
22
42
17
5
17
12
2| | | |Pzz= −

Bài tập trắc nghiệm số phức
Trang 66
Phương trình có 2 nghiệm phức z
1
= 2i và z
2
= –2i
.
Câu 153. Cho số phức z = –2 – 5i. Tìm phần thực và phần ảo của số phức
A. Phần thực bằng 2 và phần ảo bằng –5i B. Phần thực bằng –2 và phần ảo bằng 5i
C. Phần thực bằng 2 và phần ảo bằng –5 D. Phần thực bằng –2 và phần ảo bằng 5
Hướng dẫn giải
Đáp án: D
nên Phần thực bằng –2 và phần ảo bằng 5.
Câu 154. Cho 2 số phức z
1
= –3i và z
2
= 3 – 5i. Tính môđun của số phức z
1
– z
2
:
A. B. C. D.
Hướng dẫn giải
Đáp án: B
z
1
– z
2
= –3 + 2i, do đó: .
Câu 155. Cho (x + 2i)
2
= 3x + yi (x, y
∈
R). Giá trị của x và y bằng:
A. x = 1 và y = 2 hoặc x = 2 và y = 4 B. x = –1 và y = –4 hoặc x = 4 và y = 16
C. x = 2 và y = 5 hoặc x = 3 và y = –4 D. x = 6 và y = 1 hoặc x = 0 và y = 4
Hướng dẫn giải
Đáp án: B
Cho (x + 2i)
2
= 3x + yi (x, y ∈ R). Giá trị của x và y bằng:
Giải: (x + 2i)
2
= 3x + yi x
2
– 4 + 4xi = 3x + yi
Câu 156. Modun của số phức bằng
A. 7 B. 3 C. 5 D. 2
Hướng dẫn giải
Đáp án: C
Trước hết, ta rút gọn số phức:
Vậy modun của số phức là 5.
Câu 157. Cho hai số phức và . Giá trị của biểu thức là
A. 0 B. 10 C. D. 100
Hướng dẫn giải
12
| |4zz
−=
z
25zi=−+
12
| | 73zz−=
12
| | 13zz−=
12
| |3zz
−=
12
| |5
zz−=
12
| | 13
zz−=
2
1; 4
43
4; 16
4
xy
xx
xy
xy
=−=−
−=
⇔⇔
= =
=
2
5 2 (1 )z ii=+ −+
2
52 (1 ) 52 2 5i i ii+−+ =+−=
1
3zi
= +
2
2zi= −
1 12
z zz+
10−

Bài tập trắc nghiệm số phức
Trang 67
Đáp án: B
Ta có:
Vậy .
Câu 158. Mô đun của số phức z thỏa mãn phương trình là
A. B. C. 1 D.
Hướng dẫn giải
Đáp án: A
Ta cần rút gọn biểu thức trước:
Đặt ta có:
Vậy modun của số phức cần tìm là: .
Câu 159. Cho số phức . Tìm phần thực và phần ảo của ?
A. Phần thực là –5, phần ảo là 2i. B. Phần thực là 5, phần ảo là 2.
C. Phần thực là –5, phần ảo là – 2. D. Phần thực là 2, phần ảo là –5.
Hướng dẫn giải
Đáp án: C
Phần thực là –5, phần ảo là 2.
Câu 160. Cho hai số phức và . Tính môđun của số phức ?
A. B. C. D.
Hướng dẫn giải
Đáp án: D
Câu 161. Cho số phức . Tìm số phức
A. B. C. D.
2
1 12
3 (3 )(2 ) 3 6 2 3 10z zz i i i i i i i+ = ++ + − = ++ + − − =
1 12
10z zz+=
( )
(
)
( )
(
)
2 11 11 2 2zizii
− ++ + −=−
2
3
3
2
1
2
2 (1 ) 1 (1 ) 1 2 2 2 (1 ) (1 ) 2zi izi i i zizi+−−+ −+−=− ⇔ ++ −=
z a bi z a bi=+ ⇒=−
2( )(1 ) ( )(1 ) 2 2 2 2( ) 1 ( ) 2abi i abi i a b abi b abi+ + + − − = ⇔ − + + +− − + =
1
0
3
3( ) ( ) 2
3( ) 2 1
3
a
ab
a b a bi
ab
b
=
+=
⇔ −++ =⇔ ⇔
−= −
=
22
1 1 22
3 3 93
−
+==
52zi
=−+
z
1
23zi= −
2
12zi= −
12
zz−
12
34zz−=
12
26zz−=
12
2zz−=
12
2zz−=
22
12 12
1 1 ( 1) 2zz i zz− = −⇒ − = +− =
43zi= −
( )
1w iz z=+−
34wi= +
32wi=−−
32wi
= −
34wi=−+

Bài tập trắc nghiệm số phức
Trang 68
Hướng dẫn giải
Đáp án: C
Câu 162. Cho hai số phức và . Tìm phần thực và phần ảo của số phức .
A. Phần thực bằng 1 và phần ảo bằng 6. B. Phần thực bằng 1 và phần ảo bằng– 6.
C. Phần thực bằng –1 và phần ảo bằng 6. D. Phần thực bằng 6 và phần ảo bằng –1
Hướng dẫn giải
Đáp án: C
Câu 163. Cho số phức . Modun của số phức z là:
A. B. C. D. 2
Hướng dẫn giải
Đáp án: A
Ta có: .
Câu 164. Tìm phần thực a và phần ảo b của số phức
A. B. C. D.
Hướng dẫn giải
Đáp án: A
Ta có: . Phần thực , phần ảo .
Câu 165. Tính
A. 8 + 14i B. 8 – 14i C. –8 + 13i D. 14i
Hướng dẫn giải
Đáp án: B
Sử dụng máy tính cầm tay
Câu 166. Cho số phức , giá trị của là
A. 30 – 35i B. 30 + 35i C. 35 + 30i D. 35 – 30i
Hướng dẫn giải
Đáp án: B
( )
1 32w iz z i= + −=−
1
23zi= +
2
1zi= +
12
3zz−
12
3 16zz i− =−+
( )
35 4 2 1z ii= − +−
2 74
14 10i−
46
14 10 2 74z iz=− ⇒=
54
43 .
36
i
zi
i
+
=−+
+
73
,
15
a =
17
.
5
b = −
17
,
5
a
−
=
73
.
15
b =
73
,
15
a =
17
i.
5
b = −
73
,
15
a =
17
.
5
b =
73 17
15 5
zi= −
73
15
a =
17
5
b = −
( )( )
32 62
1
ii
z
i
−+
=
+
12
1 3, 2z iz i=+=−
(
)( )
121 2
23A zz z z=−+

Bài tập trắc nghiệm số phức
Trang 69
Sử dụng máy tính cầm tay
Câu 167. Cho số phức . Tìm phần thực và phần ảo ,mođun của số phức
A. Phần thực bằng –3 , phần ảo bằng –1, mođun
B. Phần thực bằng –3, phần ảo bằng –2i mođun
C. Phần thực bằng 3 , phần ảo bằng i, mođun
D. Phần thực bằng 3 và phần ảo bằng 1, mođun
Hướng dẫn giải
Đáp án: A
Phần thực bằng –3 , phần ảo bằng –1, mođun
Câu 168. Cho số phức . Tìm môđun
A. B. C. D.
Hướng dẫn giải
Đáp án: D
Câu 169. Cho số phức . Tìm số phức
A. B. C. D.
Hướng dẫn giải
Đáp án: B
Câu 170. Tìm biết ?
A. B. C. D. 20
Hướng dẫn giải
Đáp án: A
Bấm máy
Câu 171. Gọi x, y là hai số thực thỏa: . Tính .
A. B. C. D.
Hướng dẫn giải
Đáp án: D
3zi=−+
z
10z =
13z =
10z =
10z
=
10z =
12
2 ; z 1 3zi i=+=−
12
zz−
12
14zz−=
12
13zz−=
12
5zz−=
12
17zz−=
12
17zz−=
14zi= +
2.w z zi= +
79wi= +
69wi= +
33wi=−−
78wi=−+
2 . 2(1 4 ) (1 4 ) 6 9w z zi i i i i= + = + +− =+
z
( )( )
2
12 1z ii=+−
25
23
52
( ) ( )
2
35 2 42x iy i i−− −=−
2M xy= −
2M =
0M =
1M =
2M = −

Bài tập trắc nghiệm số phức
Trang 70
Từ ĐK suy ra hệ
thay vào 2x–y=–2
Câu 172. Cho số phức . Tìm phần thực và phần ảo của số phức
A.Phần thực là –10 và phần ảo là B. Phần thực là –10 và phần ảo là
C. Phần thực là 10 và phần ảo là D. Phần thực là 10 và phần ảo là
Hướng dẫn giải
Đáp án: D
Số phức liên hợp của z là , phần thực là 10 , phần ảo là
Câu 173. Tìm số phức z thỏa :
A. B. C. D.
Hướng dẫn giải
Đáp án: B
(3 – 1 – 2i)z = i ⇔ ⇔
Câu 174. Cho số phức . Tính
A. B.
C. D.
Hướng dẫn giải
Đáp án: A
Vì :
Câu 175. Cho số phức . Tìm số phức
A. B. C. D.
Hướng dẫn giải
Đáp án: C
Vì :
Câu 176. Cho . Số phức liên hợp của z là:
33 4
54 2
xy
xy
−=
−+ =−
10
3
14
3
x
y
= −
⇔
= −
10 3zi
= −
z
3i−
3
3i−
3
10 3
i
+
3
( )
12 3iz z i+=−
11
44
zi= −
11
44
zi
=−+
11
88
zi=−+
11
88
zi
= −
22
i
z
i
=
−
(22) 22 1 1
44 8 4 4
ii i
zz i
+ −+
= ⇔= =−+
+
12
1 2; 1 5
z iz i=+ =−+
121
zzz+−
121
19zzz i+ − =−+
121
19zzz i+ − =−−
121
25zzz i+ − =−+
121
25zzz i+ − =−−
( ) ( ) ( )
121
12 15 12 19zzz i i i i+ − = + +−+ − − =−+
52zi= −
u z iz= −
33ui= +
73ui
= −
33ui= −
73ui= +
52 (52)52 5 233u ii i i i i=+− − =+−−=−
12zi=−−

Bài tập trắc nghiệm số phức
Trang 71
A. B. C. D.
Hướng dẫn giải
Đáp án: B
Câu 177. Cho thì bằng:
A. B. 5 C. D.
Hướng dẫn giải
Đáp án: D
.
Câu 178. Tìm các số thực và y, biết:
A. B. C. D.
Hướng dẫn giải
Đáp án: D
Câu 179. Giá trị của biểu thức là:
A. 28 B. 56 C. 64 D. 72
Hướng dẫn giải
Đáp án: C
Câu 180. Giá trị của biểu thức là:
A. –8 B. C. D. 1
Hướng dẫn giải
12
i+
12i−+
2
i−
2
i+
12
12
zizi
=−+
=−− ⇒
( )( )
32 23 3 7
z i ii=+ − +−
z
27
19
29
5 2 29z iz=−⇒=
x
( ) ( ) ( ) ( )
231 2 32 2 4 3x y x yi x y x y i+ + +− + = − + + − −
94
;
11 11
xy= =
94
;
11 11
xy
−
= =
94
;
11 11
xy
−
= =
94
;
11 11
xy
−−
= =
9
2 3 13 2 2 5 1
11
2 4 3 53 3 4
11
x
xy xy xy
x y xy x y
y
=
+ += − + −+ =
⇔⇔
−+ = − − − + =−
=
(
)
6
13Ai= +
(
)
(
)
( )
2
63
2
13 13 8 64Ai i
=+ =+ =−=
3
13
22
Ni
=−+
1
8
−
1
8

Bài tập trắc nghiệm số phức
Trang 72
Đáp án: C
Câu 181. Cho . Môđun của z bằng :
A. B. 1 C. 2 D. 3
Hướng dẫn giải
Đáp án: A
Câu 182. Cho , ta có: bằng:
A. B. C. D.
Hướng dẫn giải
Đáp án: B
Câu 183. Giá trị của biểu thức là:
A. B. C. D.
Hướng dẫn giải
Đáp án: D
Câu 184. Cho số phức = .Tìm phần thực ,phần ảo của số phức .
A. Phần thưc bằng –2,phần ảo bằng B. Phần thưc bằng –2,phần ảo bằng
C. Phần thưc bằng 2,phần ảo bằng D. Phần thưc bằng 2,phần ảo bằng
Hướng dẫn giải
Đáp án: D
Câu 185. Cho số phức phần thực phần ảo của lần lượt là :
A.3 và 2017 B.3 và 2017i C.3 và –2017 D.3 và –2017i
Hướng dẫn giải
(
)
( )
3
3
11
.1 3 . 8 1
28
Ni
−
=− − = −=
23
zi= −
7
( )
2
2
23 7
23
z
zi
= +− =
=−⇒
23
zi
= −
1
z
23i+
23
13 13
i+
23
13 13
i−
23
55
i+
1 1 23 2 3
2 3 13 13 13
i
i
zi
+
= = = +
−
( )
2016
1Mi= +
1008
2
−
1008
2
1008
2
i
1008
2
i
−
(
) ( )
(
)
1008
504
2 1008
1008 2 1008 1008
1 2 2. 2.12Mi i i
=+== ==
z
24
i
+
w zi= −
3i−
3.−
3.i−
3.
3 2017zi= −
z

Bài tập trắc nghiệm số phức
Trang 73
Đáp án: A
Câu 186. Cho khi đó bằng
A.10 B.8 C.6 D.7
Hướng dẫn giải
Đáp án: C
Bấm máy tính trực tiếp ra kết quả đáp án C
Câu 187. Trong các khẳng định sau đây khẳng định nao đúng ?
A. B.
C.
D.
Hướng dẫn giải
Đáp án: A
nên ta chọn được đáp án A
Câu 188. Cho số phức z thỏa mãn . Môđun của số phức w = là:
A.8 B. C.8 D.16
Hướng dẫn giải
Đáp án: A
suy ra
Câu 189. Cho hai số phức . Hai số phức khi:
A. B. C. D.
Hướng dẫn giải
Đáp án: C
Câu 190. Điều kiện để số phức là số thuần ảo là
A.
B. C. D.
Hướng dẫn giải
Đáp án: A
Câu 191. Trong các số phức sau, số phức nào có mô đun nhỏ nhất ?
3 2017 Re 3, Im 2017z iz z=+ ⇒= =
12
3 4; 3 4z iz i
=+=−
12
|z z |+
2016
1i =
2017
1i =
2018
ii=
2019
1i = −
*
41
1 42
()
43
14
n
i if n k
if n k
i kN
i if n k
if n k
= +
−=+
= ∈
−=+
=
3
(1 3 )
1
i
z
i
−
=
−
z iz+
82
3
3
(1 3 )
44 44;w 44 4 48
1
i
z iz i ii i
i
−
= =−+ ⇒ =−− =−+ + + =
−
8w =
, ' ,( , , , )z a bi z c di a b c d R=+=+ ∈
'zz
=
ac
bi di
=
=
ad
bc
=
=
ac
bd
=
=
ab
cd
=
=

Bài tập trắc nghiệm số phức
Trang 74
A. B. C. D.
Hướng dẫn giải
Đáp án: D
Câu 192. Cho
s
ố phức z thỏa mãn: .Tìm mô đun
s
ố phức
.
A.4 B. C. D. 5
Hướng dẫn giải
Đáp án: D
Suy ra: và
Vậy:
Câu 193. Cho số phức . Tìm phần thực và phần ảo của số phức
A. Phần thực bằng 4 và phần ảo bằng –3 B. Phần thực bằng 4 và phần ảo bằng 3
C. Phần thực bằng 4 và phần ảo bằng 3i D. Phần thực bằng 4 và phần ảo bằng –3i.
Hướng dẫn giải
Đáp án: A
Phần thực bằng 4 và phần ảo bằng –3
Câu 194. Cho số phức thỏa mãn . Môđun của số phức z bằng:
A. B. C. D. .
Hướng dẫn giải
Đáp án: A
Câu 195. Cho hai số phức . Tính tổng
A. B. C. D. .
Hướng dẫn giải
Đáp án: D
Câu 196. Cho số phức thỏa mãn và . Tìm số phức
A. B. C. D. .
Hướng dẫn giải
Đáp án: B
3zi= −
13zi= −
32zi=−−
22zi
= +
(1 2 ) 7 4zi i+=+
2zi
ω
= +
17
24
74
(1 2 ) 7 4 3 2
12
i
z i iz i
i
+
+ =+ ⇔= =−
+
32
zi= +
43zi= +
z
43zi= +
43
zi⇒=−
⇒
z
( )
1 24 0
iz i
+ −− =
10z =
3z =
22z =
2z =
24
3
1
i
zi
i
+
= = +
+
⇒
10z =
12
1 2; 4 2z iz i=+=−
12
2Tz z= +
5T =
35
T =
45T =
55
T =
12
5; 2 5zz= =
⇒
55
T =
z
( )
2 10zi−+=
. 25zz=
z
5z =
34zi= −
5;34;34z z iz i==+=−
34zi= +

Bài tập trắc nghiệm số phức
Trang 75
Gọi số phức có dạng
Ta có:
Từ (1) và (2) ta được:
Câu 197. Số phức nghịch đảo của số phức là:
A. B. C. D. .
Hướng dẫn giải
Đáp án: B
Câu 198. Cho số phức . Tìm phần thực và phần ảo của số phức
A. Phần thực bằng và phần ảo bằng B. Phần thực bằng và phần ảo bằng
C. Phần thực bằng và phần ảo bằng D. Phần thực bằng và phần ảo bằng
Hướng dẫn giải
Đáp án: D
Cho số phức . Tìm phần thực và phần ảo của số phức
Phần thực bằng và phần ảo bằng
Câu 199. Cho hai số phức . Tính môđun của số phức .
A. B. C. D.
z
( )
,z a bi a b R=+∈
z a bi⇒=−
( ) ( )
2 10 2 1 10z i a bi−+= ⇔−+− =
( ) ( )
( )
22
2 1 10 1ab⇔− +− =
. 25zz=
( )
22
25 2ab⇔+=
5, 0
3, 4
3, 4
ab
ab
ab
= =
= =
= = −
13
22
zi=−+
11 3
22
i
z
= −
1 13
22
i
z
=−−
113
22
i
z
=−+
11 3
22
i
z
= +
13 1 1 13
22 22
13
22
zi i
z
i
=−+ ⇒= =−−
−+
1
43
z
i
=
+
z
4
5
3
5
3
25
2
25
4
25
3
25
i
4
25
3
25
1
43
z
i
=
+
z
1 43 43
4 3 25 25 25 25
z iz i
i
= = − ⇒= +
+
4
25
3
25
( )
2
12
3 2; 1 2z iz i=−=+
1
2
z
z
13
5
14
5
17
5
11
5

Bài tập trắc nghiệm số phức
Trang 76
Hướng dẫn giải
Đáp án: A
Cho hai số phức . Tính môđun của số phức .
Câu 200. Cho số phức . Tìm số phức
A. B. C. D.
Hướng dẫn giải
Đáp án: C
Thực hiện bấm máy
Câu 201. Phần ảo và phần thực của số phức lần lượt là
A. B. C. D.
Hướng dẫn giải
Đáp án: D
. Phần ảo: 32; Phần thực: 0
Câu 202. Cho hai số phức và . Tìm số phức liên hợp của số phức
.
A. B. C. D.
Hướng dẫn giải
Đáp án: C
Câu 203. Cặp thỏa mãn biểu thức là:
A. B. C. D.
Hướng dẫn giải
Đáp án: A
( )
2
12
3 2; 1 2z iz i=−=+
1
2
z
z
( )
2
11
12
22
17 6 13
3 2; 1 2
25 25 5
zz
z iz i i
zz
=− =+ ⇒=−− ⇒ =
45
zi= −
2
i
w iz
z
+
= −
208 150
41 41
w = −
208 150
41 41
wi=−−
208 150
41 41
wi= −
208 150
41 41
wi= +
10
(1 )
zi
= +
0; 32
0; 32
i
0; 32−
32; 0
( )
5
10 2 5
(1 ) (1 ) (2 ) 32zi i i i=+=+ = =
1
52zi= −
2
34zi= −
1 2 12
2z .wz z z=++
54 26wi= +
54 26
wi
=−−
54 26wi= −
54 30wi= −
5 2 3 4 2(5 2 )(3 4 ) 54 26 54 26w i i i i iw i
=+ +− + − + = + ⇒ = −
( )
;
xy
(2 3 1) ( 2 ) (3 2 2) (4 3)x y x yi x y x y i+ + +− + = − + + − −
94
;
11 11
94
;
11 11
−−
94
;
11 11
−
94
;
11 11
−

Bài tập trắc nghiệm số phức
Trang 77
Ta có:
Câu 204. Cho số phức z = 5–2i. Số phức có phần ảo là
A. 29 B. 21 C. D.
Hướng dẫn giải
Đáp án: D
vì : ,phần ảo :
Câu 205. Cho số phức . Tìm mệnh đề đúng trong các mệnh đề sau ?
A. z + = 2bi B. z – = 2a C. z. = a
2
– b
2
D.
Hướng dẫn giải
Đáp án: D
Vì z + = 2a nên A sai. z – = 2bi nên B sai, z. = a
2
+ b
2
nên C sai,
Câu 206. Cho hai số phức z
1
= 2 + i, z
2
= 1 + 3i. Môđun của z
1
+ z
2
bằng bao nhiêu ?
A. 3 B. 4 C. 5 D. 6
Hướng dẫn giải
Đáp án: C
z
1
+ z
2
= 2 + i + 1 + 3i = 3 + 4i .
Câu 207. Số viết dưới dạng a + bi thì a + b bằng bao nhiêu ?
A. 4 B. 25 C. 27 D. 17
Hướng dẫn giải
Đáp án: A
4( 4 – 3i ) = 16 – 12i
Ta có : a + b = 16 –12 = 4.
Câu 208. Cho số phức thỏa mãn điều kiện: . Tính ?
A. B. C. D.
9
2 3 13 2 2 5 1
11
2 4 3 53 3 4
11
x
xy xy xy
x y xy x y
y
=
+ += − + −+ =
⇔⇔
−+ = − − − + =−
=
1
z
−
5
29
2
29
1
1 52
5 2 29 29
zi
i
−
= = +
−
2
29
z a bi= +
z
z
z
2
2
zz=
z
z
z
2
2 22 22 22 22
2a ( ) 4a
z ab bi ab b ab z= −+ = − + =+=
22
12
34 5zz⇒+= +=
100
43i+
23
100 100(4 3 ) 100(4 3 )
4 3 (4 3 )(4 3 ) 4 3
ii
i ii
−−
= = =
+ +− +
z
23zz i+=+
21
A iz i=++
1
2
3
5

Bài tập trắc nghiệm số phức
Trang 78
Hướng dẫn giải
Đáp án: C
Thủ thuật giải phương trình số phức (chứa )
Nhập Mode+2 (Cmplx) chuyển chế độ số phức
Cách nhập số phức liên hợp: Shift+2+2 “conjg” + “X”
Nhập , rồi bấm
(bấm nghĩa là gán )
Nhập rồi bấm calc:
Câu 209. Nếu thì bằng:
A. B. C. D.
Hướng dẫn giải
Đáp án: D
Câu 210. Cho số phức . Hỏi trong các phát biểu sau, phát biểu nào đúng?
A. là phần ảo
B. là mô–đun của z
C. Điểm biểu diễn số phức z trên mặt phẳng phức Oxy
D. có mô–đun khác nhau
Hướng dẫn giải
Đáp án: C
Số phức có là phần ảo A sai. Ta có suy ra B, D sai.
Câu 211. Số phức có mô–đun bằng và phần thực lớn hơn phần ảo 5 đơn vị. Biết z có phần thực
nhỏ hơn 2. Khi đó mô–đun có số phức có giá trị:
A. B. C. D.
Hướng dẫn giải
Đáp án: A
Gọi . Ta có (loại)
;zz
⇒
23XX i+ −−
:100 0,01 297 0,99Calc i i+ ⇒−
(
)
( )
1
33 1 0 1
1
x
x yi z i
y
=
⇒ − −− + = ⇔ ⇒ = +
=
Calc
100 0,01i+
100, 0.01xy= =
: 21A iX i++
1 "" 3iA++=⇒ =
zi=
2007
z
z
1
0
z−
( )
( )
2003
2007
2007 2
.z i ii i z
= = =−=−
,;z a bi a b=+∈
bi
22
ab+
( )
;M ab
;
zz
z a bi= +
b
⇒
22
z a bi z z a b=−→== +
z
17
2wz= +
5
7
4
15
( )
; ,2
z a bi a b R a=+ ∈<
22
14
17
41
5
aa
z ab
bb
ab
= =
= +=
⇔∪
=−=−
−=

Bài tập trắc nghiệm số phức
Trang 79
Suy ra
Suy ra
Câu 212. Tổng của hai số phức liên hợp là:
A. Tổng của hai số phức liên hợp là một số thực
B. Tổng của hai số phức liên hợp là một số ảo
C. Tổng của hai số phức liên hợp là một số phức có đủ phần thực và ảo
D. Tích của hai số phức liên hợp là một số ảo
Hướng dẫn giải
Đáp án: A
Câu 213. Với là hai số phức. Trong các khẳng định sau đây, khẳng định nào sai?
A. B.
C. với D.
Hướng dẫn giải
Đáp án: B
B sai ví dụ ta lấy
Câu 214. Cho số phức z thỏa mãn điều kiện . Số phức có phần ảo bằng bao
nhiêu?
A. B. C. D.
Hướng dẫn giải
Đáp án: A
Số phức có phần ảo bằng –1
Câu 215. Cho số phức . Xác định phần thực, phần ảo và tính mô–đun số phức
. Chọn đáp án đúng?
A. Số phức z có phần thực: –4, phần ảo: –3, mô–đun là 5
B. Số phức z có phần thực: 4, phần ảo: 3, mô–đun là 5
14zi
= −
2 34 5w z iw=+=− → =
2z a bi z a bi z z a=+⇒=−→+=
12
,zz
12 1 2
..
zz z z=
12 1 2
zz z z+≥+
11
22
zz
zz
=
2
0z ≠
12 12
..zz zz
=
1
12 2
12
1
,1
0
zi
z iz i z i
zz
= =
= =−⇒ =− =
+=
( )
1 13iz i
+ −=
1w zi z=−+
1
−
2−
3−
4−
( )
13
1 13 0 2
1
2
i
iz i z i
i
wi
+
+ −− = ↔ = = +
+
→=−
w
( )( )
12 43 28z ii i= − − −+
z

Bài tập trắc nghiệm số phức
Trang 80
C. Số phức z có phần thực: –3, phần ảo: –4, mô–đun là 5
D. Số phức z có phần thực: 3, phần ảo: 4, mô–đun là 5
Hướng dẫn giải
Đáp án: A
. Phần thực: –4, phần ảo: –3
Câu 216. Tìm phần thực và phần ảo của số phức . Biết rằng . Phần thực và phần ảo
của số phức lần lượt là
A. B. C. D.
Hướng dẫn giải
Đáp án: B
suy ra .
Vậy phần thực và phần ảo của số phức lần lượt là: –4; 3.
Câu 217. Số phức có mô–đun bằng:
A. B. C. D.
Hướng dẫn giải
Đáp án: B
Câu 218. Tìm mô–đun của số phức:
A. B. C. D.
Hướng dẫn giải
Đáp án: B
Ta có:
Câu 219. Tìm phần thực của số phức biết .
A. B. C. D.
( )( )
12 43 28 43z ii i i= − − − + =−−
( ) ( )
22
4 35z = − +− =
z
( )( )
12 2z ii= + −+
z
4; 3−−
4;3−
4; 3−
4;3
( )( )
12 2 43z i iz i= + −+ ⇔ =−−
43zi=−+
z
43zi= −
25
5
7
7
15
23
3
i
zi
i
+
=+−
−
170
3
z =
170
5
z =
170
5
z =
170
4
z =
( )
( )
(
)(
)
15 3
1 8 11 7
23 23
3 3 55 55
ii
zi i i i
ii
++
−
=+− =+− + = +
−+
22
11 7 170
55 5
z
= +=
3
2
.z zz
z
ω
= −+
12zi= −
31
5
−
32
5
−
33
5
−
32
5

Bài tập trắc nghiệm số phức
Trang 81
Hướng dẫn giải
Đáp án: B
Ta có
Phần thực là: ; phần ảo là:
Câu 220. Xét hai khẳng định sau đây:
(1) Số có phần thực bằng 1
(2) Bình phương của số có phần ảo bằng 7
Trong hai khẳng định trên
A. Cả 2 đều đúng B. Cả hai đều sai C. Chỉ có (1) đúng D.Chỉ có (2) đúng
Hướng dẫn giải
Đáp án: B
Số có phần thực bằng –1
có phần ảo bằng
Câu 221. Mondun của số phức bằng:
A. 1 B. 0 C. D. 2
Hướng dẫn giải
Đáp án: C
Câu 222. Xét các phát biểu sau:
(1)
(2) Vì , nên ta nói là số phức liên hiệp của số
(3) Số đối của số là số
(4) Số đối của số bi là
Trong các câu trên, số phát biểu đúng là:
A. 1 B. 2 C. 3 D. 4
Hướng dẫn giải
Đáp án: B
Câu (1) và câu (2) sai. Ta phải có:
32 6
55
i
ω
−
= +
32
5
−
6
5
( ) ( )
24 32ii i+− −−
(
)
23
i
+
(
) ( )
24 32 1
ii ii
+ − − − =−−
( )
2
2 3 7 62ii+ =−+
62
1zi= −
2
( ) (
)
( ) ( )
00a bi a i bi a bi+ =+ −+ =−
(
) ( ) ( )
( )
00a bi a bi i
+ + − +− = +
(
) ( )
a bi− +−
a bi+
( )
a bi+
( )
a bi−+
( )
b i bi
−=−
( ) ( ) ( ) ( )
(1) 0 0a bi a i bi a bi+ =+ ++ =+

Bài tập trắc nghiệm số phức
Trang 82
(2) vì , nên ta nói là số đối của
Câu 223. Xét các khẳng định sau:
(1) Với hai số phức tùy ý, ta có
(2) Với hai số phức tùy ý, ta có
Trong hai khẳng định trên
A. Chỉ có (1) đúng B. Chỉ có (2) đúng C. Cả hai đều đúng D. Cả hai đều sai
Hướng dẫn giải
Đáp án: A
Ta có (1) đúng, thật vậy, giả sử:
Khi đó: , nên:
Suy ra . Khai triển và thu gọn vế phải ta được
Vậy (1) đúng. Tuy nhiên, phải thêm điều kiện , ta viết:
Câu 224. Số bằng:
A. B. C. 34 D. 25
Hướng dẫn giải
Đáp án: C
Ta có:
Câu 225. Số phức có thể viết lại thành:
A. B. C. D. 4
Hướng dẫn giải
Đáp án: A
Ta có: .
( ) ( ) ( )
( )
00a bi a b i i+ + − +− = +
( )
(
)
a bi− +−
a bi+
12
,zz
222
12 1 2
,zz z z= +
12
,zz
1
1
22
z
z
zz
=
1 1 12 2 2
,z a bi z a bi=+=+
( ) ( )
12 1 2 12 12 1 2
z z aa bb ab ba i= −+−
( ) ( )
22
12 1 2 12 12 12
z z aa bb ab ba= − +−
( ) ( )
22
2
12 1 2 12 12 1 2
z z aa bb ab ba=− +−
(
) ( )
22
2 22
12 1 1 2 2 1 2
zz a b a b z z=+ +=
2
0z ≠
1
1 12
12 1 2
2
22
222 2
2
11
..
z
z zz
zz z z
zzz z
z
= = = =
(3 5 )(3 5 )ii+−
9 25i
+
23i
+
( )( ) ( )
2
3 5 3 5 9 25 9 25 1 9 25 34ii i+ − =− =− −=+ =
8
2
i
i
−
+
32
i−
23i
+
1
2
2
i−
( )( )
( )( )
82
8
32
21 2 2
ii
i
i
ii
−−
−
= = −
+ +−

Bài tập trắc nghiệm số phức
Trang 83
Câu 226. Biểu thức có giá trị bằng
A. B. C. D.
Hướng dẫn giải
Đáp án: D
Ta có:
Câu 227. Cho . Khi đó bằng?
A. Một số thuần ảo B. 1072 C. D. 20
Hướng dẫn giải
Đáp án: B
. Do đó:
Câu 228. Số nào sau đây là căn bậc 2 của
A.
B. C. D.
Hướng dẫn giải
Đáp án: A
Gọi số phức cần tìm là
Câu 229. Xét các kết quả sau:
(2)
Trong ba kết quả trên, kết quả nào sai?
A. Chỉ sai B. Chỉ sai C. Chỉ sai D.Chỉ và sai
7 17
5
i
i
−
−
7
17
5
i+
3 i
+
22i−+
23i
−
( )( )
( )( )
7 17 5
7 17 35 17 7 85 52 78
23
5 5 5 26 26
ii
i ii i
i
i ii
−+
− ++− −
= = = = −
− −+
172 30 , ' 172 30
z iz i=+==
.'zz
2 172
. ' 900 172 1072zz =+=
. ' . ' 1072zz zz= =
3
13
i
i
−
+
11
22
i
−
+
31
22
i
−
+
13
22
i
−
+
11
22
i
−
−
a bi+
22
22
1
2
1
0
2
3
2
21
1
13
2
1
2
a
b
ab
i
a bi a b abi i
ab
i
a
b
=
−
=
−=
−
+ = ⇔ − + =−⇔ ⇔
= −
+
=
−
=
3
ii=
( )
2
4
ii=
( )
3
( )
3
1 22ii+ =−+
( )
1
( )
2
( )
3
( )
1
( )
2

Bài tập trắc nghiệm số phức
Trang 84
Hướng dẫn giải
Đáp án: D
và sai, vì:
và
Ngoài ra, (3) đúng vì ta có:
Câu 230. Tích số có giá trị bằng:
A. B. C. D.
Hướng dẫn giải
Đáp án: D
Câu 231. Số phức có nghịch đảo bằng
A. B. C. D.
Hướng dẫn giải
Đáp án: A
Câu 232. Xét các mệnh đề sau:
(4) Nếu thì là số thực.
(5) Giá trị tuyệt đối (hay mô–đun) của một số phức z bằng khoản cách OM, với M là điểm biểu diễn của z.
(6) Giá trị tuyệt đối (hay mô–đun)của một số phức z bằng số .
Chọn nhận định đúng trong các nhận định sau:
A. Cả ba câu đều đúng B.Chỉ có 1 câu đúng
C. Chỉ có 2 câu đúng D. Cả ba câu đều sai
Hướng dẫn giải
Đáp án: A
Câu 233. Xét các kết quả sau :
Trong ba kết quả trên, kết quả nào sai ?
A. Chỉ (1) sai B. Chỉ (2) sai C. Chỉ (3) sai D. Chỉ (1) và (2) sai
Hướng dẫn giải
Đáp án: D
(1) Và (2) sai vì : và
( )
1
( )
2
33
.
i ii i= = −
( )
2
4
11i =−=
( )
3
23
1 13 3 22i iii i+ =+ + + =−+
( )(
)
33 23
ii
+−
68
i−
68
i+
33
i−+
15 3i−
45zt= −
45
41 41
i+
45
46 46
i+
25
27 27
i+
1
1
2
i+
zz=
z
.
zz
( )
3
1
ii=
( )
4
2 ii=
( )
3
3 (1 ) 2 2ii+ =−+
32
.i ii i= = −
( )
( )
2
2
42
ii= = −1 =1

Bài tập trắc nghiệm số phức
Trang 85
Ngoài ra, (3) đúng vì ta có :
Câu 234. Số nào sau đây bằng số
A. B. C. D.
Hướng dẫn giải
Đáp án: C
Ta có:
Câu 235. Cho số phức . Môđun của số phức là:
A. B. C. D.
Hướng dẫn giải
Đáp án: C
Ta có , suy ra
.
Do đó .
Câu 236. Tìm phần ảo của số phức , với n là số nguyên dương thỏa mãn
A. B. 64
C. 64i D. Không tồn tại phần ảo
Hướng dẫn giải
Đáp án: B
Ta có
( )
3
23
3 3 22i iii i1+ =1+ + + = − +
( )
( )
2 34?ii
−+
54
i+
6 11i
+
10 5i+
6 i+
(
)(
) (
)
( )
2
2 3 4 2.3 2. 4 .3 . 4
68 3 4 65 4 05
i i ii ii
iii i i
− + = + −−
= + − − = + + =1+
( )
2
3zi= +
1
wz
z
= +
202 303
25 50
i−
303 202
25 50
i−
101
10
10201
100
( )
2
3 86zi i=+=+
1 1 202 303
86
8 6 25 50
wz i i
zi
= += +− = −
+
22
202 303 101
25 50 10
w
= +=
2 23
3
n
i
z
i
−
=
−
( )
42
log 3 log 9 3
nn− + +=
64 3−

Bài tập trắc nghiệm số phức
Trang 86
Suy ra .
Ta có
Câu 237. Tìm modun của số phức z biết z không phải là số thực và thỏa mãn: .
A. B. C. Không tồn tại z D.
Hướng dẫn giải
Đáp án: D
Bài toán này chỉ cần lưu ý một số tính chất sau của số phức:
Khi đó ta có ngay:
Do đó, .
Sai lầm thường gặp: Đáp án A người ta không yêu cầu tìm z. Đáp án B sai do không loại trường hợp z thực.
Câu 238. Cho hai số phức thỏa mãn: . So sánh hai số ta có
khẳng định sau:
A. B.
C. D. Không so sánh được
Hướng dẫn giải
Đáp án: A
( ) ( )
(
)
( ) (
)
( )
(
)
( )( )
42
42
22
2
2
log 3 log 9 3 3
2.log 3 2log 9 6
1
2. log 3 log 9 6
2
log 3 9 6
3 9 64 6 27 64 0
7
13
n nn
nn
nn
nn
n n nn
n
n
− + += >
⇔ − + +=
⇔ −+ +=
⇔ − +=
⇔− += ⇔+−−=
=
⇔
= −
7n =
( )
7
7
7
2 23
3 2 cos sin
66
3
i
z ii
i
ππ
− −−
= = −= +
−
77
128 cos sin 64 3 64
66
ii
ππ
−−
= + =−+
( )
2
. 12z z zz z+=
2
2z xi x=±−
{ }
0; 2z ∈
2z =
2
; ;.
m
m
z z z z zz z= = =
( )
( )
( )
( )
( )
( )
22
2
32 2
. 12 12
120 2 3 60
0 0;
2
z z zz z z z z z
zz z zz z z
z z loai z
z
+=⇒ +=
⇒ + − =⇒ − + +=
=⇔= ∉
⇒
=
2z =
;ab
1ab= =
( )
;x abiy abiab= ++ = + +
xy=
xy<
xy>

Bài tập trắc nghiệm số phức
Trang 87
Do nên ta có thể đặt:
Khi đó ta có:
Rút gọn ta có:
;
Do đó, .
Câu 239. Cho . Các công thức sau, công thức nào sai:
A. B.
C. D.
Hướng dẫn giải
Đáp án: C
Kinh nghiệm: Với dạng toán này ta thực hiện từ những đáp án theo hình thức từ đơn giản đến phức tạp.
Ta thấy ngay khẳng định A, B là đúng. Thử với khẳng định D ta có:
nên khẳng định D là đúng. Đến đây ta có thể khoanh C ngay, ta thử kiểm
chứng xem???
Như vậy mẫu số sai.
Câu 240. Cho số phức z thỏa mãn: . Khẳng định nào sau đây đúng:
A. B. z có thể nhận giá trị là số thực hoặc số thuần ảo
C. Phần thực của z không lớn hơn 1 D. Đáp án B và C đều đúng
Hướng dẫn giải
Đáp án: D
Ta có:
1ab= =
cos sin ; cos sina A i Ab B i B
=+=+
( ) ( )
( )
( )
22
2
2
cos cos sin sin 1
cos cos sin sin sin sin
cos sin sin cos cos cos
x A B AB
ABABAB
y
AB A B A B
= + + ++
− −−
=
+ + ++
( ) (
)
3 2cos 2 sin sinx AB A B=+ −+ +
( )
( )
3 2cos 2 sin siny AB A B=+ −+ +
xy=
z a bi= +
z a bi= −
( )
2 22
2
z a b abi=−+
( ) (
)
1
a b a bi
i
zz
++−
+
=
( )
2
1 22z i b ai+ =−+
( ) ( )( )
2
1 2 22
z i a bi i b ai+ = + =−+
( )( ) (
) ( )
2
22
1
11
iabi ab abi
ii
z a bi a b
z
+ − ++−
++
= = =
++
3
zz=
1z =
3
33
0
1
z
zzzzzz
z
=
=⇔===⇔
=

Bài tập trắc nghiệm số phức
Trang 88
Như vậy khẳng định A sai.
Ta nhận thấy và đều thỏa mãn phương trình nên B là đúng.
Rõ ràng từ thì ta thấy ngay phần thực của z không lớn hơn 1 nên khẳng định C cũng đúng.
Câu 241. Cho số phức và và . Giá trị gần đúng phần
thực của số phức A là:
A. –16 B. 16 C. –26 D. 26
Hướng dẫn giải
Đáp án: C
Ta tính được , , và .
Câu 242. Cho các phát biểu về phép so sánh lớn hơn, bé hơn và bằng (>, < và =) như sau:
1. Ta có thể so sánh hai số thực bất kì
2. Ta có thể so sánh hai số phức bất kì
3. Ta có thể so sánh hai số thuần ảo bất kì
4. Ta có thể so sánh môđun của hai số phức bất kì
Số phát biểu không đúng là:
A. 0 B. 4 C. 2 D. 1
Hướng dẫn giải
Đáp án: C
Phát biểu 1 đúng, phát biểu 2 sai vì ta chỉ xét được hai số phức có bằng nhau hay không chứ không xét được số
nào lớn hơn hay bé hơn, phát biểu 3 sai vì lí do tương tự, phát biểu 4 đúng vì môđun của hai số phức bất kì là
hai số thực dương và ta hoàn toàn so sánh chúng được.
Câu 243. Giả sử rằng nếu thì các căn bậc n ( cho trước) của w được biểu diễn trên mặt phẳng
phức bởi các đỉnh của một n–giác đều nội tiếp đường tròn tâm O bán kính R. Giá trị của R là;
A. B. Bình phương phần thực của
C. Giá trị tuyệt đối phần ảo của D. A, B và C đều sai
Hướng dẫn giải
Đáp án: A
Tham khảo tại trang 207 và 208 SGK Giải Tích 12 – Nâng Cao.
Câu 244. Cho số phức z thỏa mãn . Mô–đun của số phức là:
1z =
zi=
0; 1zz= =
(
)
2
24 2
2,
i
x iy
x
+
=−=
27 2i
z
y
+
=
2 22
Ax y z=++
34
xi
= −
64 102
25 25
yi
= +
483 1313
145 290
zi
= −
26,5 33,3Ai≈− −
0w ≠
3
n ≥
n
w
n
w
n
w
( )
( )
21 2
2 78
1
i
iz i
i
+
++ =+
+
1w zi= ++

Bài tập trắc nghiệm số phức
Trang 89
A. 3 B. 4 C. 5 D. 6
Hướng dẫn giải
Đáp án: C
Ta có:
Câu 245. Xét các câu sau:
1. Nếu thì z là một số thực
2. Mô–đun của một số phức z bằng khoảng cách OM, với M là điểm biểu diễn z trong hệ tọa độ phức.
3. Mô–đun của một số phức z bằng số
Trong 3 câu trên:
A. Cả ba câu đều sai B. Chỉ có 1 câu đúng
C. Chỉ có 2 câu đúng D. Cả ba câu đều đúng
Hướng dẫn giải
Đáp án: D
Khẳng định A đúng vì:
Khẳng định B đúng vì:
Khẳng định C đúng vì:
Câu 246. Cho tìm phần thực của số phức biết
A. 7 B. –50 C. 15 D. –10
Hướng dẫn giải
Đáp án: B
Ta có:
( )
22
21 2
78
1
32
2
143
43 5
i
i
i
zi
i
w zi i
w
+
+−
+
= = +
+
= ++= +
⇒= +=
zz
=
.zz
;0z a bi z z a bi a bi b=+ =⇒+ =− ⇒=
22
z a bi z a b OM=+⇒= + =
( )( )
22
22
.
.
z a bi
z ab
z zz
z z a bi a bi a b
= +
= +
⇒=
=+ −=+
2
1wz z= +−
w
( )( )
13 3
1
ii
z
i
−+
=
+

Bài tập trắc nghiệm số phức
Trang 90
Câu 247. Tìm số phức z để ta được:
A. z = 0 hay z = 1 B. z = 1 hay z = – i
C. z = 0 hay z = i D. z = 0, z = 1 + i hay z = 1 – i
Hướng dẫn giải
Đáp án: D
Ta có:
Câu 248. Nếu thì
A. Bằng 0 B. Là số thuần ảo
C. Lấy mọi giá trị phức D. Lấy mọi giá trị thực
Hướng dẫn giải
Đáp án: B
Ta có:
( )( ) ( )
( )
(
)(
)
( )
( )
( )
2
2
13 3 68 1
68
17
1 1 11
1 1 17 17
50 7
Re 50
i i ii
i
zi
i i ii
w zz i i
i
w
−+ −−
−
= = = =−−
+ + +−
⇒ =−+ + =−+−− +−−
=−+
⇒=−
2
zz z−=
( ) ( ) ( )
( )
2
2
22
22
22
0
0
1; 1
22
0; 1
z z z a bi a bi a bi
bi a b abi
ab
ab
ba
b ab
zz i
−= ⇔ + − − = +
⇔ =−+
= =
−=
⇔⇔
= = ±
=
⇒= =±
1z =
2
1z
z
−

Bài tập trắc nghiệm số phức
Trang 91
Câu 249. Tính số phức có giá trị bằng
A. B. C. D.
Hướng dẫn giải
Đáp án: A
Bấm máy tính hoặc tính tay ta có:
Câu 250. Cho số phức . Mô–đun của số phức z là:
A. B. C. 11 D. 7
Hướng dẫn giải
Đáp án: A
Công thức modun là:
Câu 251. Cho các số phức . Giả sử rằng , khi đó:
A. B. C. D. A, B và C đều sai
Hướng dẫn giải
Đáp án: B
Gọi .
Ta có
( )
(
)
( )
( )
( )
(
)
(
)
( )
( )
( )
(
)
22
2
22
2
22
2
2
22 2 2 22
22
22 22
2
22
2
22
;1 1
12
1
1
12
1
1
12 2 1
11
1
1
21
z a bi z a b
a b abi
a bi
z
z a bi a bi
a b abi a bi
z
z a bi a bi
z
z
aab ab abab i
ab
aab bab i
z
z ab
z
bi a b
z
=+ =⇔+=
− −+
+−
−
⇒= =
++
− −+ −
−
⇒=
+−
−
⇒
−−+ + − −−
=
+
+−+ ++
−
⇒=
+
−
⇒ = +=
( )( )
14 25ii+−
22 3
i+
22 3
i−
18 3i
−+
18 3i−−
(
)( )
1 4 2 5 22 3ii i
+ −=+
92
zi= −
85
77
22
9 2 85z = +=
12
,zz
12 1
2zz z+=
12 2
2
zz z−<
12 2
2
zz z
−=
12 2
2
zz z−>
( )
12
, , ,,,z a bi z x yi a b x y=+=+ ∈
12 1
2zz z+=

Bài tập trắc nghiệm số phức
Trang 92
Câu 252. Cho số phức z thỏa mãn . Giá trị của là:
A. B. C. A và B đúng D. A và B sai
Hướng dẫn giải
Đáp án: C
Điều kiện
Ta có
Với , suy ra .
Với , suy ra .
Câu 253. Chọn phát biểu không đúng
A. Số thực a âm hai căn bậc hai là và
B. Phương trình bậc n (với n là số nguyên dương) luôn có ít nhất một nghiệm phức
C. Phương trình bậc n (với n là số nguyên dương) có n nghiệm phức (không nhất thiết phân biệt)
D. Với một phương trình bất kì, nếu là một nghiệm của phương trình thì cũng là một nghiệm của nó.
Hướng dẫn giải
Đáp án: D
Ta chọn phương án D. Chính xác là “Với một phương trình bất kì, nếu là một nghiệm của phương trình
cũng là một nghiệm của nó”. Tham khảo trang 194 và 195 SGK Giải Tích 12 – Nâng Cao.
( )
( )
( ) ( )
( )
( ) ( )
( )
( ) ( )
22
22
2 2 22
22
22
12 2
2
2
22
2
2
2
a x b y i a bi
ax by a b
x y a b ax by
ax by x y
a x b y i x yi
zz z
⇔ +++ = +
⇔+ ++ = +
⇔+ =+− −
⇔− +− = +
⇒ −+− = +
⇔−=
7
1
2
z
z
z
−
+=
−
2
zi
zi
+
−
170
10
2
2
2,z zi≠≠
( )( )
2
7
1 12 7
2
12
2 50
12
z
z zz z
z
zi
zz
zi
−
+= ⇔ + − = −
−
= +
⇔ − +=⇔
= −
12zi= +
2 1 4 11 7 170
1 3 10 10 10
zi i
i
i
zi
++
= =−+ =
−
−
12zi= −
2 1 11 2
1 22 2
zi
i
i
zi
+
= =−=
+
−
ai−
ai−−
0
z ∈
0
1
z
0
z ∈
0
z

Bài tập trắc nghiệm số phức
Trang 93
Câu 254. Cho số phức z thỏa mãn . Tính
A. B. C. D.
Hướng dẫn giải
Đáp án: A
Câu 255. Cho số phức z thỏa mãn . Tính tích phần thực và phần ảo của
A. 30 B. 3250 C. 70 D. 0
Hướng dẫn giải
Đáp án: D
Câu 256. Cho số phức z thỏa mãn: (1).
Chọn đáp án sai?
A. z là số thuần ảo B. z có phần ảo là số nguyên tố
C. z có phần thực là số nguyên tố D. z có tổng phần thực và phẩn ảo là 5
Hướng dẫn giải
Đáp án: A
Giả sử:
=> B, C, D đúng
Câu 257. Cho số phức z biết . Tìm tổng phần thực và phần ảo của z
( )( ) ( )
751 3 2
z i i ii= − +− +
2.w zi=
6 24wi
= +
6 24wi= −
3 12wi= −
3 12wi= +
( )( ) ( )
7 5 1 3 2 12 3
z i i ii i= − +− + = −
(
)
w 2 . 2 12 3 6 24zi i i i= = −=+
( ) ( )
( )
3 4 32 47zi i i
= + −+ − −
.zz
(
)
( )
( )
3 4 3 2 4 7 55 15zi i i i
= + −+ − − =− +
(
)( )
55 15 55 15 3250
zz i i=−+ −− =
( )
( )
21 2
2 78
1
i
iz i
i
+
++ =+
+
z a bi= +
( ) ( )
( )
21 2
1 2 78
1
i
i a bi i
i
+
⇔+ + + =+
+
( )( )
2
2
21 2 1
2 2 78
1
ii
a bi ai bi i
i
+−
⇔ + ++ + =+
+
2
2 37 3
2 2 1 2 2 78 32
2 18 2
ab a
a bi ai bi i i i i z i
ba b
−+= =
⇔ + + − +−+ − = + ⇔ ⇔ ⇒ = +
+ += =
( )
( )
2
1 21
2 (1)
2
ii
zz
i
−+
+=
−

Bài tập trắc nghiệm số phức
Trang 94
A. B. C. D.
Hướng dẫn giải
Đáp án: C
Câu 258. Tìm phần thực của số phức z, biết rằng
97
(1 2 ) 5 2
3
i
iz i
i
+
−− =−
−
A.
1−
B.
10
C.
1
D.
3
Hướng dẫn giải
Đáp án: C
Ta có:
97 7
(1 2 ) 5 2 (1 2 ) 7 1 3 ( ) 1
3 12
e
ii
iz i iz i z i R z
ii
++
− − = − ⇔ − = +⇔ = =+ ⇒ =
−−
Vậy đáp án đúng là C.
Sai lầm thường gặp: Không đọc kĩ đề tưởng là tìm z và thu được đáp án C.
Câu 259. Tìm số phức z thỏa mãn :
( )( )
3 12 13zi i i− + +=
A.
13i+
B.
13i−
C.
14i
+
D.
14i−
Hướng dẫn giải
Đáp án: C
Đặt z=a+bi;
( )
;ab∈
Ta có:
( )( )
3 1 2 1 3zi i i− + +=
( )( ) ( ) ( )
3 12 13 2 7 2 3 3abi i i i a b ab i i⇔⇔+ − + += − + + +− =
2 70 1
2 33 4
ab a
ab b
− += =
⇔⇔
+−= =
Vậy
14zi= +
Câu 260. Tìm số phức z biết:
( )( ) ( )
23 2 1 2 1iz i i z+ +−= +
?
A.
34i−+
B.
34i−
C.
34i+
D.
34i−−
42 2
15
−
22 4
5
−−
2 2 14
15
−−
2 2 14
5
−−
( )
(
)
( )
2
2
1 212
2 22
1 22
22
i ii
ii
a bi a bi
ii
− ++
−
++ − = =
−−
(
)
(
)
( )
2
2 22 2 4 22 42 2
3
45
i ii
a bi
i
+ + + +−
⇔ −= =
−
42 2 4 22
;
15 5
ab
− −−
⇔= =

Bài tập trắc nghiệm số phức
Trang 95
Hướng dẫn giải
Đáp án: B
Đặt z=a+bi;
( )
;
ab∈
Ta có
( )( ) ( )
23 2 1 2 1iz i i z+ +−= +
(
) ( ) ( )
( )
(
) ( ) (
)
23 1 2 2 1
237 321 2 2
i a b i i a bi
a b a b i a b a bi
+ −+ + = + +
−−+ + +
⇔
⇔ =−+ +
237 2
3 2 12
ab ab
a b ab
− −=−
⇔
+ += +
73
14
ab a
ab b
−= =
⇔⇔
+=− =−
Vậy z=3–4i
Đáp án đúng là B

Bài tập trắc nghiệm số phức
Trang 96
C – BÀI TẬP TỰ LUYỆN ( CÂU)
Câu 1: Biết rằng số phức
z x iy= +
thỏa
2
z 8 6i=−+
. Mệnh đề nào sau đây sai?
A.
22
xy 8
xy 3
−=−
=
B.
42
x8x90
3
y
x
+ −=
=
C.
x1 x 1
hay
y3 y 3
= = −
= = −
D.
22
x y 2xy 8 6i+ + =−+
Câu 2: Cho số phức
( )
( )
( )
z m 1 m 2 i, m R= −+ − ∈
. Giá trị nào của
m
để
z5≤
A.
2m6−≤ ≤
B.
6m2
−≤ ≤
C.
2m6≤≤
D.
m6
m2
≤−
≥
Câu 3: Viết số phức
( ) ( )
23
2 i 1 2i
3i
− +−
−
dưới dạng đại số:
A. 2i – 13 B. 2i – 11 C. – 11 – 14i D. 2i + 13
Câu 4: Tìm mệnh đề sai trong các mệnh đề sau:
A. Số phức
z a bi 0=+=
khi và chỉ khi
a0
b0
=
=
B. Số phức
z a bi
= +
được biểu diễn bởi điểm M(a; b) trong mặt phẳng phức Oxy.
C. Số phức
z a bi= +
có môđun là
22
ab+
D. Số phức
z a bi= +
có số phức đối
z' a bi= −
Câu 5: Cho số phức
z a bi,a,b R=+∈
và các mệnh đề. Khi đó số
( )
1
zz
2
+
là:
1) Điểm biểu diễn số phức
z
là
( )
M a;b
.
2) Phần thực của số phức
( )
1
zz
2
+
là
3) Môdul của số phức
2z z+
là
22
9a b+
4)
zz<
A. Số mệnh đề đúng là 2 B. Số mệnh đề đúng là 1
C. Số mệnh đề sai là 1 D. Cả 4 đều đúng
Câu 6: Mệnh đề nào sau đây sai.
A.
12 1 2
zz z z=⇔=
B.
z 0 z0=⇔=

Bài tập trắc nghiệm số phức
Trang 97
C. Tập hợp điểm biểu diễn số phức z thỏa mãn điều kiện
z 1
=
| là đường tròn tâm O, bán kính R = 1
D. Hai số phức bằng nhau khi và chỉ khi phần thực và phần ảo tương ứng bằng nhau
Câu 7: Cho hai số phức
1 2 3 12
z 4 3i, z 4 3i, z z .z= + =−+ =
. Lựa chọn phương án đúng:
A.
3
z 25
=
B.
2
31
zz=
C.
12 12
zz zz+=+
D.
12
zz=
Câu 8: Cho các số phức
3i 3i
z , z'
5 7i 5 7i
−+
= =
+−
. Trong các kết luận sau:
(I).
z z'+
là số thực,
(II).
z z'
−
là số thuần ảo,
(III).
z z'−
là số thực,
Kết luận nào đúng?
A. Cả I, II, III. B. Chỉ II. III. C. Chỉ III, I. D. Chỉ I, II.
Câu 9: Cho số phức
z1≠
. Xét các số phức
2009
2
2
ii
zz
z1
−
α= − +
−
và
3
2
zz
zz
z1
−
β= + +
−
. Khi đó
A.
,Rα β∈
B.
,βα
đều là số ảo C.
R,β∈ α
là số ảo D.
R,α∈ β
là số ảo
Câu 10: Cho số phức z =
13
i
22
−+
. Số phức 1 + z + z
2
bằng:
A.
13
i
22
−+
B. 2 -
3i
C. 1 D. 0
Câu 11: Giá trị biểu thức
2 3 2017
1 i i i ... i++ + + +
là:
A.
1i−
B.
i−
C.
i
D.
1i+
Câu 12: Đẳng thức nào đúng trong các đẳng thức sau:
A.
2018 1009
(1 i) 2 i+=
B.
2018 1009
(1 i) 2 i+=−
C.
2018 1009
(1 i) 2+=−
D.
2018 1009
(1 i) 2+=
Câu 13: Cho
12
z ,z ∈
và các đẳng thức:
1
1
1212 12121212
22
z
z
z.zz.z; ;zzzz;zzzz.
zz
= = +=+ −=−
Số đẳng thức đúng trong các đẳng thức trên là:
A. 1 B. 3 C. 4 D. 2
Câu 14: Đẳng thức nào sau đây là đẳng thức đúng?
A.
8
(1 i) 16+=−
B.
8
(1 i) 16+=
C.
8
(1 i) 16i+=
D.
8
(1 i) 16i+=−
Câu 15: Đẳng thức nào sau đây là đẳng thức đúng?
A.
2006
ii= −
B.
2345
ii=
C.
1997
i1= −
D.
2005
i1=
Câu 16: Số nào trong các số phức sau là số thuần ảo ?

Bài tập trắc nghiệm số phức
Trang 98
A.
( )
2
2 2i
+
B.
( )
(
)
2 3i 2 3i++ −
C.
( )
( )
2 3i . 2 3i+−
D.
3 2i
2 3i
+
−
Câu 17: Giá trị của
2 4 4k
1 i i ... i++++
với
*
kN∈
là
A.
2ki
B.
2k
C. 0 D. 1
Câu 18: Các số
x;y R
∈
thỏa mãn đẳng thức
(1 i)(x yi) (2y x)i 3 2i
− −+ −=−
. Khi đó tổng
x 3y
+
là:
A. - 7 B. - 1 C. 13 D. - 13
Câu 19: Cho số phức z = x + yi ; x, y
∈
thỏa mãn z
3
= 18 + 26i. Giá trị của
2021 2012
T (z 2) (4 z)=− +−
là:
A.
1007
2−
B.
1007
3
C.
1007
2
D.
1006
2
−
Câu 20: Các số nguyên dương n để số phức
n
13 3 9i
12 3 i
+
−
là số thực ? số ảo ? là:
A. n = 2 + 6k, k
∈
B. n = 2 + 4k, k
∈
C. n = 2k, k
∈
D. n = 3k, k
∈
Câu 21: Cho số phức
z 2i 3= +
khi đó
z
z
bằng:
A.
5 12i
13
−
B.
5 6i
11
+
C.
5 12i
13
+
D.
5 6i
11
−
Câu 22: Tính số phức
3
1i3
z
1i
+
=
+
:
A. 1 + i B. 2 + 2i C. 2 – 2i D. 1 – i
Câu 23: Cho
5
1i
z
1i
+
=
−
, tính
5678
zzzz+++
.
A. 4 B. 0 C. 3 D. 1
Câu 24: Tính giá trị
2 3 11
P i i i ... i=++++
là
A. −1 B. 0 C. 1 + i D. 1 – i
Câu 25: Tính
( ) ( )
2007
P 15i 13i= + −+
kết quả là
A.
2007
2i−
B.
2007i
C.
2007
2−
D.
2007
2i
Câu 26: Giá trị của biểu thức
105 23 20 34
A i i i –i= ++
là:
A.
2i
B. 2 C.
2i−
D.
2−
Câu 27: Nếu
z1=
thì
2
z1
z
−
A. Là số ảo B. Bằng 0 C. Lấy mọi giá trị phức D. Lấy mọi giá trị thực

Bài tập trắc nghiệm số phức
Trang 99
Câu 28: Số phức
16 8
1i 1i
z
1i 1i
+−
= +
−+
bằng:
A.
i
−
B. 2 C.
i
D.
2−
Câu 29: Biết số phức
ab
zi
cc
=−−
( với a, b, c là những số tự nhiên) thỏa mãn
( )
2
iz 1 3i z
z
1i
−+
=
+
. Khi đó giá
trị của a là:
A. - 45 B. 45 C. - 9 D. 9
Câu 30: Cho x, y là 2 số thực thỏa điều kiện:
x1 y1
x1 1i
+−
=
−+
là:
A.
x 1; y 1=−=
B.
x 1; y 2=−=
C.
x 1; y 3= = −
D.
x 1; y 3= =
Câu 31: Cho
12
z 2 3i; z 1 i=+=+
.
3
12
12
zz
T нn h :
(z z )
+
+
A.
85
B.
61
5
C. 85 D.
85
25
Câu 32: Cho hai số phức
12
z ax b, z cx d=+=+
và các mệnh đề sau:
(I)
22
1
1z
ab
z
=
+
; (II)
12 12
zz zz+=+
; (III)
12 12
zz zz−=−
.
Mệnh đề đúng là:
A. Chỉ (I) và (III) B. Cả (I), (II) và (III) C. Chỉ (I) và (II) D. Chỉ (II) và (III)
Câu 33: Tìm căn bậc hai của số phức
z 7 24i= −
A.
z 4 3i=−−
và
z 4 3i= +
B.
z 4 3i=−−
và
z 4 3i=−+
C.
z 4 3i
= −
và
z 4 3i= +
D.
z 4 3i= −
và
z 4 3i=−+
Câu 34: Cho
z 5 3i= −
. Tính
( )
1
zz
2i
−
ta được kết quả là:
A.
3i−
B. 0 C.
3−
D.
6i
−
Câu 35: Cho số phức
( )
z a bi, a, b=+∈
. Nhận xét nào sau đây luôn đúng?
A.
z2 a b≤+
B.
z2 a b≥+
C.
( )
z 2a b≥+
D.
( )
z 2a b≤+
Câu 36: Tìm các căn bậc 2 của số phức
1 9i
z 6i
1i
+
= −
−
A.
4i±
B.
2i±
C.
2±
D.
4±
Câu 37: Tính
( )
6
1i
−
ta được kết quả là:
A.
4 4i−−
B.
4 4i+
C.
8i
D.
4 4i−

Bài tập trắc nghiệm số phức
Trang 100
Câu 38: Giá trị của
2024
i
1i
−
là
A.
2024
1
2
−
B.
1012
1
2
C.
2024
1
2
D.
1012
1
2
−
Câu 39: Tính
7
3i
z
22
= +
ta được kết quả viết dưới dạng đại số là:
A.
3i
22
+
B.
13
i
22
+
C.
3i
22
−−
D.
13
i
22
−−
Câu 40: Tìm các căn bậc hai của - 9
A. - 3 B. 3 C. 3i D.
3i±
Câu 41: Cho
13
zi
22
=−+
. Tính
2
1zz
++
A. 2 B. - 2 C. 0 D. 3
Câu 42: Tìm số phức
12
z 2z ,ω= −
biết rằng:
11
z 1 2i, z 2 3i.
=+=−
A.
3 4i.ω=− −
B.
3 8i.ω=− +
C.
3 i.
ω= −
D.
5 8i.
ω= +
Câu 43: Tích 2 số phức
1
z 1 2i= +
và
i
z 3i= −
A. 5 B. 3 - 2i C. 5 - 5i D.
5 5i+
Câu 44: Tổng của hai số phức
3 i;5 7i+−
là
A.
8 8i+
B.
8 8i−
C.
8 6i−
D.
5 6i−
Câu 45: Các số thực x và y thỏa (2x + 3y + 1) + ( - x + 2y)i = (3x - 2y + 2) + (4x - y - 3)i là
A. Kết quả khác B.
9
x
11
4
y
11
= −
=
C.
9
x
11
4
y
11
=
= −
D.
9
x
11
4
y
11
=
=
Câu 46: Biết số phức
z 3 4i= −
. Số phức
25i
z
là:
A.
4 3i−+
B.
4 3i−−
C.
4 3i−
D.
4 3i+
Câu 47: Cho biết:
( ) ( ) ( ) ( )
3
34
1 i i 2i i 3 i 1 2 i= = + =−+
Trong ba kết quả trên, kết quả nào sai
A. Chỉ (3) sai B. Chỉ (2) sai C. Chỉ (1) và (2) sai D. Chỉ (1) sai
Câu 48: Tổng 2 số phức
1i
+
và
3i+

Bài tập trắc nghiệm số phức
Trang 101
A.
13+
B. 2i C.
1 3i++
D.
1 3 2i++
Câu 49: Cho 2 số phức
12
z 2 i, z 1 i=+=−
. Hiệu
12
zz−
A. 1 + i B. 1 C. 2i D. 1 + 2i
Câu 50: Tính
( )
3 4i (2 3i)+ −−
ta được kết quả:
A.
3i−
B.
5 7i+
C.
1 7i+
D.
1i−
Câu 51: Đẳng thức nào đúng
A.
4
(1 i) 4+=
B.
4
(1 i) 4i+=
C.
8
(1 i) 16+=−
D.
8
(1 i) 16+=
Câu 52: Cho số phức z = 2i + 3 khi đó
z
z
bằng:
A.
5 12i
z
13
+
=
−
B.
5 12i
z
13
−
=
−
C.
5 6i
z
11
+
=
D.
5 6i
z
11
−
=
Câu 53: Số
12 5i−
bằng:
A. - 12.5 B.
7
C. 13 D. `
Câu 54: Giá trị biểu thức (1 -
i3
)
6
bằng:
A. 64 B. 2
5
C. 2
4
D. Kết quả khác
Câu 55: Tính
1
2
z
z
, với ` và
2
z 2i= −
A. 1 - i B. - i C. 1 + i D. I
Câu 56: Giá trị ` bằng
A. i B. - 1 C. - i D. 1
Câu 57: Nghịch đảo của số phức
5 2i−−
là:
A. ` B. ` C. ` D.
Câu 58: Tìm cặp số thực
x, y
thỏa mãn: `
A.
1
xy
2
= =
B.
12
x ;y
33
= =
C.
xy0= =
D.
12
x ;y
33
=−=−
Câu 59: Giá trị biểu thức (1 + i)
10
bằng
A. i B. Kết quả khác C. – 32i D. 32i
Câu 60: Dạng đơn giản của biểu thức
(4 3i) (2 5i)− ++
là:
A. 1 + 7i B. 6 + 2i C. 6 – 8i D. 1 – 7i
Câu 61: Các căn bậc hai của 8 + 6i là
119
1
z 1 2i
= +
2008
i
52
i
29 29
−+
52
i
29 29
−
52
i
29 29
−+
( ) ( )
x 2y 2x y i 2x y x 2y i+ + − = ++ +

Bài tập trắc nghiệm số phức
Trang 102
A. Kết quả khác B.
1
2
3i
3i
β= −
β=−−
C.
1
2
3i
3i
β= +
β= −
D.
1
2
3i
3i
β= +
β=−−
Câu 62: Số nào sau đây bằng số
( )
( )
2 i 3 4i−+
A.
5 4i+
B.
6 11i+
C.
10 5i+
D.
6i+
Câu 63: Cho
( )( )
( )( )
2 i 1 2i 2 i 1 2i
z
2i 2i
+− −+
= +
−+
. Trong các két luận sau, kết luận nào đúng?
A.
22
z.z
5
=
B.
z
là số thuần ảo C.
z
∈
D.
z z 22+=
Câu 64: Thu gọn z = i + (2 – 4i) – (3 – 2i) ta được:
A. z = 5 + 3i
B. z = - 1 – 2i
C. z = 1 + 2i
D. z = - 1 – i
Câu 65: Thu gọn z = i(2 – i)(3 + i) ta được:
A.
z 2 5i= +
B.
z 5i=
C.
z6=
D.
z 1 7i= +
Câu 66: Kết quả của phép tính
(2 3i)(4 i)−−
là:
A. 6 - 14i B. - 5 - 14i C. 5 - 14i D. 5 + 14i
Câu 67: Số phức z =
( )
3
1i+
bằng:
A.
4 3i+
B.
3 2i−
C.
4 4i+
D.
2 2i
−+
Câu 68: Số phức z thỏa mãn: . là:
A.
3
z1 i
2
= +
B.
11
zi
22
= −
C.
13
zi
22
=−−
D.
13
zi
22
=−+
.
Câu 69: Số phức
3 4i
z
4i
−
=
−
bằng:
A.
16 11
zi
15 15
= −
B.
16 13
zi
17 17
= −
C.
94
zi
55
= −
D.
9 23
zi
25 25
= −
Câu 70: Thực hiện các phép tính sau: A =
4i
(2 3i)(1 2i)
3 2i
−
− ++
+
; .
A.
114 2i
13
−−
B.
114 2i
13
+
C.
114 2i
13
−
D.
114 2i
13
−+
Câu 71: Rút gọn biểu thức
z i (2 4i) (3 2i)=+− −−
ta được:
A.
z 1 2i
= +
B.
z –1– i
=
C.
z –1– i=
D.
z 5 3i= +
Câu 72: Rút gọn biểu thức
z i(2 i)(3 i)=−+
ta được:
A.
z6=
B.
z 1 7i= +
C.
z 2 5i= +
D.
z 5i=
Câu 73: Thực hiện các phép tính sau: B =
3 4i
(1 4i)(2 3i)
−
−+
.
( ) ( )( )
1 i z 2 3i 1 2i 7 3i+ +− + =+

Bài tập trắc nghiệm số phức
Trang 103
A.
3 4i
14 5i
+
−
B.
62 41i
221
−
C.
62 41i
221
+
D.
62 41i
221
−−
Câu 74: Kết quả của phép tính
(a bi)(1 i)+−
(a, b là số thực) là:
A.
ab(ba)i++ +
B.
a b (b a)i
++ −
C.
a b (b a)i−+ −
D.
a b (b a)i−++ −
Câu 75: Cặp số (x; y) thõa mãn điều kiện
(2x 3y 1) ( x 2y)i (3x 2y 2) (4x y 3)i+ + +− + = − + + − −
là:
A.
94
;
11 11
−−
B.
94
;
11 11
C.
49
;
11 11
−−
D.
49
;
11 11
Câu 76: Các số thực x, y thoả mãn: 3x + y + 5xi = 2y – 1 + (x – y)i là
A.
14
(x; y) ;
77
=
B.
24
(x; y) ;
77
= −
C.
14
(x; y) ;
77
= −
D.
14
(x; y) ;
77
=−−
Câu 77: Các số thực x, y thoả mãn:
2
x -y-(2y 4)i 2i+=
là:
A.
(x; y) ( 3; 3);(x; y) ( 3;3)=−=−
B.
(x; y) ( 3;3); (x; y) ( 3; 3)= = −
C.
(x; y) ( 3; 3); (x; y) ( 3; 3)= − =−−
D.
(x; y) ( 3;3); (x; y) ( 3; 3)= =−−
Câu 78: Thu gọn z =
( )
2
2 3i+
ta được:
A.
z 11 6i= −
B. z = - 1 - i C.
z 4 3i
= +
D. z = - 7 + 6
2i
Câu 79: Thu gọn z = (2 + 3i)(2 – 3i) ta được:
A.
z4=
B.
z 9i
= −
C.
z 4 9i= −
D.
z 13=
Câu 80: Cho hai số phức
12
z 1 2i; z 2 3i
=+=−
. Tổng của hai số phức là
A. 3 – 5i B. 3 – i C. 3 + i D. 3 + 5i
Câu 81: Tìm các số thực
x,y
thỏa mãn đẳng thức:
( ) (
)
3
x 3 5i y 1 2i 35 23i
+ + − =−+
A. (x; y) = ( - 3; - 4) B. (x; y) = ( - 3; 4) C. (x; y) = (3; - 4) D. (x; y) = (3; 4)
Câu 82: Tìm các căn bậc hai của số phức sau: 4 + 6 i
A. z
1
= 3 - i và z
2
= - 3 - i B. Đáp án khác
C. z
1
= - 3 + i và z
2
= 3 + i D. z
1
= 3 + i và z
2
= - 3 - i
Câu 83: Các căn bậc hai của số phức
117 44i−+
là:
A.
(
)
2 11i
±+
B.
( )
2 11i±−
C.
( )
7 4i±+
D.
( )
7 4i±−
Câu 84: Cho 2 số thực
x,y
thỏa phương trình:
2x 3 (1 2y)i 2(2 i) 3yi x++ − = − + −
. Khi đó:
2
x 3xy y− −=
A. - 3 B. 1 C. - 2 D. - 1
Câu 85: Cho số phức z thỏa mãn:
2
(3 2i)z (2 i) 4 i+ +− =+
. Hiệu phần thực và phần ảo của số phức z là:
A. 3 B. 1 C. 0 D. 2
5
5
5
5
5
5
5

Bài tập trắc nghiệm số phức
Trang 104
Câu 86: Cho các mệnh đề
2
i1= −
,
12
i1=
,
112
i1=
,
1122
i1=
. Số mệnh đề đúng là:
A. 3 B. 0 C. 1 D. 4
Câu 87: Tìm số nguyên x, y sao cho số phức
z x yi= +
thỏa mãn
3
z 18 26i= +
A.
x3
y1
=
= −
B.
x3
y1
= −
=
C.
x3
y1
=
=
D.
x1
y3
=
=
Câu 88: Xét số phức
1m
z (m R)
1 m(m 2i)
−
= ∈
−−
. Tìm m để
1
z.z
2
=
.
A.
m 0, m 1= =
B.
m1= −
C.
m1= ±
D.
m1=
Câu 89: Cho hai số phức
z
và
w
thoả mãn
z w1= =
và
1 z.w 0+≠
. Số phức
zw
1 z.w
+
+
là:
A. Số thực B. Số âm C. Số thuần ảo D. Số dương
Câu 90: Cho số phức
2017
1i
z
1i
+
=
−
. Khi đó
7 15
z.z .z
=
A.
i
−
B. 1 C.
i
D.
1−
Câu 91: Phần ảo của số phức z = 1 + (1 + i) + (1 + i)
2
+ (1 + i)
3
+ … + (1 + i)
20
bằng:
A. 2
10
B. 2
10
+ 1 C. 2
10
– 1 D. - 2
10
Câu 92: Trong các kết luận sau, kết luận nào sai?
A.
zz+
là một số thực B.
zz−
là một số ảo
C.
z.z
là một số thực D.
22
zz+
là một số ảo
Câu 93: Tổng i
k
+ i
k + 1
+ i
k + 2
+ i
k + 3
bằng:
A. i B. - i C. 1 D. 0
Câu 94: Số phức z = 8i viết dưới dạng lượng giác là:
A. z =
33
8 cos i sin
22
ππ
+
B. z =
8 cos isin
22
ππ
+
C. z =
( )
8 cos 0 isin 0+
D. z =
( )
8 cos isinπ+ π
Câu 95: Dạng lượng giác của số phức z =
2 cos isin
66
ππ
−
là:
A. z =
11 11
2 cos isin
66
ππ
+
B. z =
77
2 cos isin
66
ππ
+
C. z =
55
2 cos isin
66
ππ
+
D.
13 13
2 cos isin
66
ππ
+
Câu 96: Số phức nào dưới đây được viết dưới dạng lượng giác:

Bài tập trắc nghiệm số phức
Trang 105
A. 2
sin icos
55
ππ
+
B.
22
3 cos isin
33
ππ
+
C.
2 2 cos isin
55
−π −π
−+
D.
1
cos isin
27 7
ππ
+
Câu 97: Cho số phức z = - 1 - i. Argumen của z (sai khác k2π) bằng:
A.
4
π
B.
3
4
π
C.
5
4
π
D.
7
4
π
Câu 98: Cho số phức z = cosϕ + isinϕ. kết luận nào sau đây là đúng:
A.
( )
nn
z z n cos+= ϕ
B.
(
)
nn
z z 2cos n+= ϕ
C.
( )
nn
z z 2n cos+= ϕ
D.
(
)
nn
z z 2cos+= ϕ
Câu 99: Cho
( )
00
1
z 3 cos20 isin 20= +
,
( )
00
2
z 2 cos110 isin110=−+
. Tích z
1
. z
2
bằng:
A. 6(1 - 2i) B. 4i C. 6i D. 6(1 - i)
Câu 100: Cho
( )
00
1
z 8 cos100 isin100= +
,
( )
00
2
z 4 cos 40 isin 40= +
. Thương
1
2
z
z
bằng:
A. 1 + i
3
B.
( )
21 i 3−
C. 1 - i
3
D. 2(1 + i)
Câu 101: Mô đun của số phức
2
z z,ω= +
với
1i
(2 i).z 5 i
1i
−
++ =−
+
bằng:
A.
22
B.
42
C.
52
D.
32
Câu 102: Số nào trong các số sau là số thuần ảo ?
A.
( 2 3i) ( 2 3i)++ −
B.
2
(2 2i)+
C.
2 3i
2 3i
+
−
D.
( 2 3i).( 2 3i)+−
Câu 103: Biết rằng nghịch đảo của số phức
z
bằng số phức liên hợp của nó, trong các kết luận sau, kết luận
nào đúng ?
A.
|z| 1=
B.
z
là một số ảo C.
z∈
D.
|z| 1= −
Câu 104: Cho số phức
z
thỏa
|z 1 2i| |z|
−+ =
. Khi đó giá trị nhỏ nhất của
|z|
là:
A. 1 B.
5
C. 2 D.
5
2
Câu 105: Tìm các số phức a và b biết
ab 2
a.b 9
+=−
=
biết phần ảo của a là số dương.
A.
a 2 8i, b 2 8i=−+ =−+
B.
a 1 3i, b 1 3i=−+ =−+
C.
a 1 5i, b 1 5i=−+ =−+
D.
a 1 8i, b 1 8i=−+ =−+
Câu 106: Khi số phức
z
thay đổi tùy ý thì tập hợp các số
2z 2z+
là
A. Tập hợp các số thực dương B. Tập hợp tất cả các số thực

Bài tập trắc nghiệm số phức
Trang 106
C. Tập hợp tất cả các số phức không phải là số ảo D. Tập hợp các số thực không âm
Câu 107: Cho
z
là số phức khác 0 thỏa mãn
1
z
z
=
. Mệnh đề nào dưới đây là đúng
A.
z
là số thực B.
z
có mô đun bằng -1
C.
z
là số thuần ảo D.
z
có điểm biểu diễn nằm trên đường tròn
22
xy1+=
Câu 108: Cho số phức z thỏa mãn:
3(z 1 i) 2i(z 2)
+− = +
. Khi đó giá trị của
| z(1 i) 5 |++
là:
A. 4 B.
29
C. 5 D. 6
Câu 109: Cho z = m + 3i, z’ = 2 – (m +1)i. Giá trị nào của m sau đây để z.z’ là số thực ?
A. m = -2 hoặc m = 3 B. m = -1 hoặc m = 6 C. m = 2 hoặc m = -3 D. m = 1 hoặc m = 6
Câu 110: Số phức liên hợp của số phức
33
33
(2 i) (2 i)
z
(2 i) (2 i)
+ +−
=
+ −−
là:
A.
2
i
11
−
B.
2i+
C.
2i−
D.
2
i
11
Câu 111: Cho số phức z thỏa mãn điều kiện
(1 i)(z i) 2z 2i+ −+ =
. Mô đun của số phức
2
z 2z 1
w
z
−+
=
là:
A.
22
B.
5
C.
10
D.
25
Câu 112: Cho số phức z thỏa mãn
3
(1 3i)
z
1i
−
=
−
. Mô đun của số phức w =
z iz+
A.
16
B. 8 C.
83
D.
82
Câu 113: Cho số phức z, thỏa mãn điều kiện
2
(3 2i)z (2 i) 4 i+ +− =+
. Phần ảo của số phức
w (1 z)z
= +
là:
A.
2−
B.
2
C.
1
−
D.
0
Câu 114: Phần ảo của số phức z thỏa mãn
( )
2
z 3z 1 2i+=−
là:
A.
1−
B.
2−
C. 2 D.
1
Câu 115: Số phức z thỏa mãn
( ) ( )
( )
2
1 i 2 iz 8 i 1 2iz+ − = ++ +
có mô đun là
A.
1
B.
5
C.
17
D.
13
Câu 116: Cho số phức z thỏa
( ) ( )
2
1 i (2 i)z 8 i 1 2i z+ − = ++ +
. Phần thực của số phức z là:
A. 4 B. 3 C. 1 D. 2
Câu 117: Mô đun của số phưc
( )
3
z 1 4i 1 i=++−
là:
A.
5
B.
1
C.
2
D.
3
Câu 118: Cho số phức z thỏa mãn
2(1 2i)
(2 i)z 7 8i
1i
+
++ =+
+
. Mô đun của số phức
w zi1= ++

Bài tập trắc nghiệm số phức
Trang 107
A. 3 B. 4 C. 5 D. 6
Câu 119: Tìm mô đun của số phức z thỏa mãn:
(1 2i)(z i) 4i(i 1) 7 21i− ++ −=−
A.
z5=
B.
z 37=
C.
z 23=
D.
z9=
Câu 120: Cho số phức
z
thõa mãn điều kiện:
( ) ( )
( )
2
2 3i z 4 i z 1 3i− + + =−+
. Phần ảo của z là:
A. 5 B. 4 C. 3 D. 2
Câu 121: Số phức liên hợp của
1
z (1 i)(3 2i)
3i
=+ −+
+
là:
A.
53 9
zi
10 10
=−−
B.
53 9
zi
10 10
= −
C.
53 9
zi
10 10
= +
D.
53 9
zi
10 10
=−+
Câu 122: Cho số phức z thỏa mãn
3
(1 3i)
z
1i
−
=
−
. Mô đun của số phức w =
z iz+
A. 8 B.
16
C.
82
D.
83
Câu 123: Cho số phưc z thỏa điều
( )
( )
( )
( )
z z 1 i z z 2 3i 4 i+ ++ − + =−
. Phần ảo của là:
A.
1
2
B. 1
C.
2
D.
1
3
−
Câu 124: Tìm phần ảo của số phức z thỏa mãn:
(
)
( )
2
4 3i
1 z z 3 i 8 13i
2i 1
−
+− + =−
−
A. 2 B. 3 C. 1 D. 7
Câu 125: Cho
2
z
1i3
=
+
. Số phức liên hợp của z là:
A.
1i3−
B.
13
i
22
−
C.
13
i
22
+
D.
1i3+
Câu 126: Cho
2
w z z1= +−
tìm phần thực của số phức nghịch đảo của
w
biết:
(4 3i)(2 i)
z
5 4i
−+
=
−
A.
63
41
B.
3715
1681
C.
3715
1681
−
D.
34
41
Câu 127: Cho các nhận định sau (giả sử các biểu thức đều có nghĩa):
1) Số phức và số phức liên hợp của nó có mô đun bằng nhau
2) Với
z 2 3i= −
thì mô đun của z là:
z 2 3i= +
3) Số phức z là số thuần ảo khi và chỉ khi
zz= −
4) Tập hợp điểm biểu diễn số phức z thỏa mãn
zz1 2++=
là một đường tròn.
5) Phương trình:
3
z 3zi 1 0+ +=
có tối đa 3 nghiệm.

Bài tập trắc nghiệm số phức
Trang 108
Số nhận định đúng là:
A. 4 B. 2 C. 3 D. 5
Câu 128: Cho số phức z thỏa mãn
(3 i)z (2i 1)z 4i 3++++=
. Khi đó phần thực của số phức
z
bằng:
A. 5i B. -2 C. 2 D. -5
Câu 129: Số phức
2 3 20
z 1 i i i ... i=++ + + +
có phần thực và phần ảo là
A.
2−
và 0 B. 1 và 0 C.
0
và
2
D. 0 và 1
Câu 130: Nhận xét nào sau đây là sai ?
A. Mọi phương trình bậc hai đếu giải được trên tập số phức
B. Cho số phức
z a bi
= +
. Nếu
a, b
càng nhỏ thì mô đun của
z
càng nhỏ.
C. Mọi biểu thức có dạng
22
AB+
đều phân tích được ra thừa số phức.
D. Mọi số phức
z1≠−
và có mô đun bằng 1, có thể đặt dưới dạng:
1 ti
z
1 ti
+
=
−
, với
t ∈
.
Câu 131: Phát biểu nào sau đây là đúng:
A. Mọi số phức
z
và số phức liên hợp
z
của nó có bình phương bằng nhau.
B. Mọi số phức
z
và số phức liên hợp
z
của nó có căn bậc hai bằng nhau.
C. Mọi số phức
z
và số phức liên hợp
z
của nó có phần ảo bằng nhau.
D. Mọi số phức
z
và số phức liên hợp
z
của nó có mô đun bằng nhau.
Câu 132: Mô đun của
2iz−
bằng
A.
2z
B.
2z−
C.
2z
D. 2
Câu 133: Cho số phức z thỏa mãn:
( )
z 2i 1 z 10+− =
và có phần thực bằng 2 lần phần ảo của nó. Tìm môđun
của z ?
A.
5
z
2
=
B.
5
z
2
= −
C.
5
z
3
=
D.
5
z
2
=
Câu 134: Cho số phức
z a bi
= +
và số phức
z' a' b'i= +
. Số phức
z.z '
có phần ảo là:
A.
aa ' bb '+
B.
( )
2 aa ' bb'+
C.
ab' a 'b+
D.
ab a 'b '+
Câu 135: Số nào trong các số sau là số thuần ảo ?
A.
( )
2
2 2i+
B.
( ) ( )
2 3i 2 3i++ −
C.
( )( )
2 3i 2 3i+−
D.
2 3i
2 3i
+
−
Câu 136: Cho số phức z thỏa
( )
5z i
2i
z1
+
= −
+
. Tính mô đun của số phức
2
w 1zz=++
:

Bài tập trắc nghiệm số phức
Trang 109
A.
3 13
8
B.
13
C.
2
D.
2
Câu 137: Số nào trong cách số sau là số thực ?
A.
(
)
( )
2 i5 2 i5
+ +−
B.
( )
( )
3 2i 3 2i
+− −
C.
( )
2
1i3+
D.
2i
2i
+
−
Câu 138: Với mọi số ảo z, số
2
2
zz+
là
A. Số 0 B. Số thực âm C. Số thực dương D. Số ảo khác 0
Câu 139: Cho số phức z thỏa mãn
2
(2 3i).z (4 i).z (1 3i) 0− + + ++ =
. Gọi a, b lần lượt là phần thực và phần ảo
của số phức
z
. Khi đó
2a 3b+=
A. 11 B. 1 C.
19−
D.
4
Câu 140: Cho số phức z thỏa mãn
z i 3 2z−= −
. Mô đun của số phức
2i 1 iz++
bằng:
A. 1 B. C. D. 3
Câu 141: Cho
( )
z m 3i, z ' 2 m 1 i.=+ =−+
Giá trị nào của m đây để
z.z '
là số thực ?
A.
m1=
hay
m6=
B.
m2= −
hay
m3=
C.
m2=
hay
m3= −
D.
m1
= −
hay
m6=
Câu 142: Cho số phức z thỏa mãn
(
)
3iz 2 3i z 2 4i++ =+
. Mô đun của số phức
2iz
bằng:
A. 1 B.
22
C.
2
D. 2
Câu 143: Mô đun của số phức
22
x y i 2xy
z
x y 2i xy
++
−+
bằng:
A.
22
x 8y xy+−
B. Kết quả khác. C. 1 D.
22
2x 2y 3xy+−
Câu 144: Cho số phức
z 3i= +
. Số
*
nN∈
để
n
z
là số thực là
A.
*
n 4k 2, k N=+∈
B.
*
n6k,kN
= ∈
. C.
*
n 5k 1, k N=+∈
D.
*
n 3k 3, k N=+∈
Câu 145: Số nào trong các số sau là số thuần ảo:
A.
( )
( )
2 3i 2 3i
+−
B.
( )
2
2 2i+
C.
( ) ( )
2 3i 2 3i++ −
D.
2 3i
2 3i
−
+
Câu 146: Số phức
7 17i
z
5i
−
=
−
có phần thực là
A. 2 B. 3 C. 1 D. 4
5
2

Bài tập trắc nghiệm số phức
Trang 110
Câu 147: Số phức z thỏa mãn
iz 2 i 0+ −=
có phần thực bằng:
A. 4 B. 1 C. 3 D. 2
Câu 148: Số nào trong các số phức sau là số thuần ảo ?
A.
( ) ( )
7i 7i++ −
B.
( ) ( )
10 i 10 i−+ +
C.
( )
( )
5i7 5 i7− +−−
D.
( )
(
)
3i 3i
+ −−+
Câu 149: Phần thực và phần ảo của số (2 – i). i. (3 + i) lần lượt là:
A. 1 và 7 B. 1 và 0 C. 0 và 1 D. 1 và 3
Câu 150: Xét các câu sau:
1) Nếu
zz=
thì z là một số thực
2) Mô đun của một số phức z bằng khoảng cách OM, với M là điểm biểu diễn z.
3) Mô đun của một số phức z bằng số
z.z
Trong 3 câu trên:
A. Cả ba câu đều đúng B. Chỉ có 1 câu đúng C. Cả ba câu đều sai D. Chỉ có 2 câu đúng
Câu 151: Mô đun của số phức z thỏa mãn phương trình
(2z 1)(1 i) (z 1)(1 i) 2 2i− ++ + −=−
là:
A.
2
B.
22
3
C.
2
3
D. Đáp án khác
Câu 152: Cho số phức z thỏa:
( )
3
1 3i
z
1i
−
=
−
. Khi đó mô đun của số phức
z iz+
bằng:
A.
8
B.
82
C.
8−
D.
16
Câu 153: Khẳng định nào sau đây là sai
A. Trong tập hợp số phức, mọi số đều có số nghịch đảo
B. Căn bậc hai của mọi số thực âm là số phức
C. Phần thực và phần ảo của số phức z bằng nhau thì z nằm trên đường phân giác góc phần tư thứ nhất và góc
phần tư thứ ba
D. Hiệu hai số phức liên hợp là một số thuần ảo
Câu 154: Trong các khẳng định sau, khẳng định nào sau đây là không đúng
A. Tập hợp số thực là tập con của số phức
B. Nếu tổng của hai số phức là số thực thì cả hai số ấy đều là số thực
C. Hai số phức đối nhau có hình biểu diễn là hai điểm đối xứng nhau qua gốc tọa độ O
D. Hai số phức liên hợp có hình biểu diễn là hai điểm đối xứng nhau qua Ox
Câu 155: Ta có số phức z thỏa mãn
1 9i
z 5i
1i
+
= −
−
. Phần ảo của số phức z là:

Bài tập trắc nghiệm số phức
Trang 111
A. 0 B. 1 C. 3 D. 2
Câu 156: Những số vừa là số thuần ảo, vừa là số thực là:
A. Chỉ có số 0 B. Chỉ có số 1 C. 0 và 1 D. Không có số nào
Câu 157: Cho hai số phức
12
z 2 5i; z 3 4i=+=−
. Phần thực của số phức
12
z .z
là:
A. 26 B. 27 C. 25 D. 28
Câu 158: Phần ảo của số phức
2
z (1 2i).(2 i) .=−+
là:
A. -2 B. 2 C. 1 D. -1
Câu 159: Cho số phức z thỏa
2
(1 2i) .z z 4i 20+ += −
. Mô đun số z là:
A. 10 B. 5 C. 4 D. 6
Câu 160: Phần thực của số phức
23
z (3 2i) (2 i) .=− ++
là:
A. 7 B. 5 C. 8 D. 6
Câu 161: Số phức
z
thỏa mãn:
( )
z2zz 26i
+ +=−
có phần thực là:
A.
3
4
B.
1−
C.
2
5
D.
6−
Câu 162: Cho số phức
zi 3
= −
. Giá trị phần thực của
A. 0 B.
512−
C. Giá trị khác D. 512
Câu 163: Phần ảo của số phức z bằng bao nhiêu ? biết
2
z ( 2 i) (1 2i)=+−
A. 2 B. -2 C.
2.−
D.
2.
Câu 164: Biết hai số phức có tổng bằng 3 và tích bằng 4. Tổng mô đun của chúng bằng
A. 5 B. 10 C. 8 D. 4
Câu 165: Mô đun của số phức
2
z (1 2i)(2 i)=−+
là:
A.
55
B.
16 2
C.
52
D.
45
Câu 166: Phần ảo của số phức
2
z ( 2 i) (1 2i)=+−
bằng:
A.
2
−
B. 2 C.
2
D. 3
Câu 167: Cho số phức
( ) ( )
z 3 2 3i 4 2i 1= +− −
. Nhận xét nào sau đây về số phức liên hợp của z là đúng:
A.
z 10 i= −
B.
z 10 i= +
C.
( ) ( )
z 3 2 3i 4 2i 1= ++ −
D.
z i 10= −
Câu 168: Cho số phức
z 5 12i
=−−
. Khẳng định nào sau đây là sai:
A. Số phức liên hợp của z là
z 5 12i= −
B.
w 2 3i= −
là một căn bậc hai của z
C. Môđun của z là 13 D.
1
5 12
zi
169 169
−
=−+

Bài tập trắc nghiệm số phức
Trang 112
Câu 169: Cho số phức z thỏa mãn hệ thức
2i
(i 3)z (2 i)z
i
+
++ =−
. Mô đun của số phức
w zi= −
là:
A.
26
5
B.
6
5
C.
25
5
D.
26
25
Câu 170: Trong các kết luận sau, kết luận nào sai ?
A. Mô đun của số phức z là một số thực
B. Mô đun của số phức z là một số thực dương
C. Mô đun của số phức z là một số phức
D. Mô đun của số phức z là một số thực không âm
Câu 171: Mô đun của số phức
( )
3
z 5 2i 1 i=+−+
là:
A. 7 B. 3 C. 5 D. 2
Câu 172: Cho số phức
z 1i3= −
. Hãy xác định mệnh đề sai trong các mệnh đề sau:
A. z có một acgumen là
2
3
π
B.
z2=
C. A và B đều đúng D. z có dạng lượng giác là
55
z 2 cos isin
33
ππ
= +
Câu 173: Cho số phức z, thỏa mãn điều kiện
2
(3 2i)z (2 i) 4 i+ +− =+
. Phần ảo của số phức
w (1 z)z= +
là:
A. 0 B. 2 C. -1 D. - 2
Câu 174: Cho số phức
z 12 5i=−+
. Mô đun của số phức
z
bằng
A.
7
B.
17
C.
119
D.
13
Câu 175: Tìm mô đun của số phức z thỏa mãn:
(1 2i)(z i) 4i(i 1) 7 21i− ++ −=−
A.
z5=
B.
z 23=
C.
z9=
D.
z 37=
Câu 176: Cho số phức z thỏa mãn
2(1 2i)
(2 i)z 7 8i
1i
+
++ =+
+
. Mô đun của số phức
w zi1= ++
A. 3 B. 4 C. 5 D. 6
Câu 177: Số phức liên hợp của số phức
15
z (1 i)= +
là:
A.
z 128 128i=−−
B.
zi
= −
C.
z 128 128i= +
D.
z 128 128i= −
Câu 178: Phần thực của số phức
( )
30
1i
+
bằng:
A. 0 B. 1 C.
15
2
D.
15
2−
Câu 179: Cho hai số phức
12
z 1 2i; z 2 3i=+=−
. Xác định phần ảo của số phức
12
3z 2z−
A. 11 B. 12 C. 10 D. 13

Bài tập trắc nghiệm số phức
Trang 113
Câu 180: Cho số phức z thỏa
( ) ( )
2
1 i (2 i)z 8 i 1 2i z+ − = ++ +
. Phần thực của số phức z là:
A. 3 B. 1 C. 2 D. 4
Câu 181: Tìm phần phần ảo của số phức sau:
( ) ( ) ( ) (
)
2 3 20
1 1i 1i 1i ... 1i++++ ++ +++
A.
10
21−−
B.
10
21−
C.
10
21−+
D.
10
21+
Câu 182: Cho số phức
z 4 3i= −
. Phần thực và phần ảo của số phức
z
lần lượt là
A. -4 và -3 B. -4 và 3 C. 4 và -3 D. 4 và 3
Câu 183: Cho các số phức
12 3
z 1 i, z 3 4i, z 1 i=+=− =−
. Xét các phát biểu sau
1) Mô đun của số phức
1
z
bằng
2
.
2) Số phức
3
z
có phần ảo bằng
1
.
3) Mô đun của số phức
2
z
bằng
5
.
4) Mô đun của số phức
1
z
bằng mô đun của số phức
3
z
.
5) Trong mặt phẳng
Oxy
, số phức
3
z
được biểu diễn bởi điểm
M (1;1)
6)
123
3z z z+−
là một số thực.
Trong các phát biểu trên, có bao nhiêu phát biểu đúng ?
A.
2
B.
5
C.
3
D.
4
Câu 184: Cho số phức
z a bi;(a, b )
=+∈
. Trong 4 khẳng định sau, khẳng định nào sai ?
1)
( )
2
2 22
z z 2(a b )
+=−
2)
22
z.z a b= +
3) Phần ảo của
3
z
là
32
a 3a b
+
4) Phần thực của
3
z
là
23
3a b b−
A. (3) B. (4) C. (1) D. (2)
Câu 185: Cho số phức
1i
z
1i
−
=
+
. Phần thực và phần ảo của
2010
z
là:
A.
a 1, b 0= =
B.
a 0, b 1= =
C.
a 1, b 0=−=
D.
a 0, b 1= = −
Câu 186: Trong các kết luận sau, kết luận nào là sai ?
A. Mô đun của số phức
z
là một số thực âm. B. Mô đun của số phức
z
là một số phức.
C. Mô đun của số phức
z
là một số thực. D. Mô đun của số phức
z
là một số thực dương.
Câu 187: Cho số phức z thỏa mãn:
2
(3 2i)z (2 i) 4 i+ +− =+
. Hiệu phần thực và phần ảo của số phức z là:
A. 3 B. 1 C. 0 D. 2

Bài tập trắc nghiệm số phức
Trang 114
Câu 188: Cho số phức z thỏa mãn
3
(1 3i)
z
1i
−
=
−
. Mô đun của số phức w =
z iz+
A. 8 B.
83
C.
82
D.
16
Câu 189: Mô đun số phức
(1 i)(2 i)
z
1 2i
+−
=
+
là:
A.
6
|z|
26
=
B.
26
|z|
5
=
C.
26
|z|
5
=
D.
| z | 26
=
Câu 190: Cho số phức z thỏa mãn
( )
(
)
2
z 3 2i 1 i=−+
. Mô đun của số phức
w iz z= +
là:
A.
2 2.
B. 2 C. 1 D.
2.
Câu 191: Cho số phức
z x yi 1 (x, y )=+≠ ∈
. Phần ảo của số phức
z1
z1
+
−
là:
A.
(
)
2
2
xy
x1 y
+
−+
B.
(
)
2
2
2x
x1 y
−
−+
C.
( )
2
2
xy
x1 y−+
D.
( )
2
2
2y
x1 y
−
−+
Câu 192: Mô đun của số phức
( )
( )
( )
( )
2 3 19
z 1 1i 1i 1i .... 1i
=+−+− +− + +−
bằng:
A.
z 20=
B.
10
z2 1= +
C.
z1=
D.
10
z2 1= −
Câu 193: Cho số phức
z a bi.= +
Để
3
z
là một số thực, điều kiện của a và b là:
A.
b0=
và a bất kì hoặc
22
b 3a=
B.
b 3a
=
C.
22
b 5a=
D.
a0
=
và b bất kì hoặc
22
ba=

Bài tập trắc nghiệm số phức
Trang 114
MỤC LỤC
PHẦN 1. TÓM TẮT LÝ THUYẾT
PHẦN 2. SỐ PHỨC VÀ CÁC PHÉP TOÁN ( 453 CÂU)
A – BÀI TẬP ( 260 CÂU)
B – HƯỚNG DẪN GIẢI
C – BÀI TẬP TỰ LUYỆN ( 193 CÂU)
PHẦN 3. PHƯƠNG TRÌNH VÀ CÁC BÀI TẬP TÌM SỐ PHỨC THỎA MÃN ĐIỀU KIỆN (256 CÂU)
A – BÀI TẬP (130 CÂU)
B – HƯỚNG DẪN GIẢI
C – BÀI TẬP TỰ LUYỆN (126 CÂU)
PHẦN 4. BIỂU DIỄN HÌNH HỌC CỦA SỐ PHỨC, TÌM TẬP HỢP ĐIỂM (227 CÂU)
A – BÀI TẬP (138 CÂU)
B – HƯỚNG DẪN GIẢI
C – BÀI TẬP TỰ LUYỆN (89 CÂU)

Bài tập trắc nghiệm số phức
Trang 115
PHẦN 3. PHƯƠNG TRÌNH VÀ CÁC BÀI TẬP TÌM SỐ PHỨC THỎA MAN ĐIỀU KIỆN (256 CÂU)
A – BÀI TẬP ( 130 CÂU)
Câu 1. Cho phương trình
2
13 45 0zz− +=
. Nếu
0
z
là nghiệm của phương trình thì
00
zz+
bằng:
A. –13 B. 13 C. 45 D. –45
Câu 2. Cho phương trình
( )
2
25 64 0z iz i− − −− =
. Trong các số:
I. 2–3i II. 2+3i III. –2i IV. 2i
Những số nào là nghiệm của phương trình trên:
A. I, II B. I, III C. II, III D. II, IV
Câu 3. Tìm tất cả các nghiệm của
43 2
4 14 36 45 0zz z z− + − +=
, biết
2zi= +
là một nghiệm của
phương trình:
A.
1 23
2 ; 3; 3
z iz iz i=+= =−
B.
1 2 34
2 ; 2 3; 3; 3z iz iz iz i=+=− = =−
C.
1 2 34
2 ; 2 ; 3; 3z iz iz z i=+=−= =−
D.
123
2; 2; 3z iz iz i=+=−=
Câu 4. Tập hợp các nghiệm phức của phương trình
2
2
0zz+=
là:
A. Tập hợp mọi số ảo và số 0. B.
{ }
;0
i±
C.
{ }
;0i−
D.
{
}
0
Câu 5. Cho z
1
; z
2
; z
3
; z
4
là bốn nghiệm của phương trình
4
1
1
2
z
zi
−
=
−
. Tính giá trị của biểu thức
2222
1234
( 1)( 1)( 1)( 1)Tz z z z=++++
A.
17
9
B.
17
9
−
C. 425 D. –425
Câu 6. Giải phương trình
43 2
2 (1 ) 2z zi i z z i− +−+ + =
trên tập số phức. Tính tổng các nghiệm của
phương trình.
A. 2i B. 1 C.
1 i+
D. i
Câu 7. Gọi
1234
;;;zzzz
là nghiệm của phương trình
43 2
2 2 40zz z z− − − +=
Tính
2222
1234
1111
T
ZZZZ
=+++
A. 5 B.
5
4
C.
7
4
D.
9
4
Câu 8. Gọi
12
;
zz
là các nghiệm phức của phương trình
2
3 70zz+ +=
. Khi đó
44
12
Az z= +
có giá trị là
:
A. 23 B.
23
C. 13 D.
13
Câu 9. Giải phương trình trên tập số phức:
42
10zz+ +=
?

Bài tập trắc nghiệm số phức
Trang 116
A.
1 2 11
13 13 13 13
; ;;
2 2 22
i iii
z z zz
−− −+ − +
= = = =
B.
12
13 13
;
22
ii
zz
−− −+
= =
C.
11
13 13
;
22
ii
zz
−+
= =
D. Phương trình vô nghiệm
Câu 10. Cho phương trình
2
2 10 0zz++=
. Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình đã cho.
Khi đó giá trị biểu thức
22
12
Az z= +
bằng:
A.
4 10
B. 20 C.
3 10
D.
10
Câu 11. Gọi
12
,zz
là hai nghiệm của phương trình phức
( )
4
2
200
1
17
z
z
zi
−
+=
−
quy ước z
2
là số phức có phần
ảo âm. Tính
12
zz+
A.
12
5 42zz+=+
B.
12
1zz+=
C.
12
17zz+=
D.
12
105zz+=
Câu 12. Cho phương trình phức
3
zz
=
. Phương trình đã cho có bao nhiêu nghiệm ?
A. 1 nghiệm B. 3 nghiệm C. 4 nghiệm D. 5 nghiệm
Câu 13. Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình
2
2 10 0zz−+=
. Tính
22
12
Az z
= +
A.
20A =
B.
10A =
C.
30A =
D.
50A =
Câu 14. Phương trình (3–2i)z+4+5i=7+3i có nghiệm z bằng:
A. 1 B. i C. 1–i D. 0
Câu 15. Tính tổng các nghiệm của phương trình trên tập số phức:
A. 0 B. C. D.
Câu 16. Phương trình có 4 nghiệm phức, tổng môđun của bốn nghiệm bằng:
A. 0 B. C. D. 7
Câu 17. Kí hiệu là các nghiệm của phương trình . Khi đó tổng T = bằng
A. T = B. T =6 C. T = D. T = 4
Câu 18. Gọi là bốn nghiệm phức của phương trình .
Tổng bằng:
A.5 B. C. D.
Câu 19. Kí hiệu là bốn nghiệm phức của phương trình . Tính tổng
.
A. B. C. D.
4
80z −=
4
28
4
28
i
44
28 28i
+
42
7 10 0zz+ +=
22 25+
22
12
,zz
2
2 30zz+ +=
22
12
zz+
3
23
1234
,,,zz zz
42
2320zz− −=
1234
Tz z z z=+++
52
32
2
123
,,
4
à zz z zv
42
20 0zz+− =
12 34
22T zz zz= ++ +
4T =
25T
= +
4 35T
= +
6 35T
= +

Bài tập trắc nghiệm số phức
Trang 117
Câu 20. Giải phương trình trong tập số phức z
2
– (5 + 2i)z + 10i = 0
A. z = 5 2i B. z = 5, z = 2i C. z = 2, z = –5i D. z = –2 5i
Câu 21. Giải phương trình trong tập số phức z
2
– (5 + 2i)z + 10i = 0
A. z = 5 2i B. z = 5, z = 2i C. z = 2, z = –5i D. z = –2 5i
Câu 22. Nghiệm của phương trình trong tập số phức C là
A. B. C. D. Vô nghiệm
Câu 23. Kí hiệu z
1
, z
2
, z
3
là ba nghiệm phức của phương trình .
Tính tổng
A. B. C. D.
Câu 24. Nghiệm của phương trình trên tập số phức là
A. ; . B. ;
C. ; D. ; .
Câu 25. Giải phương trình sau trên tập số phức :
A. B.
C. D. x= 5i
Câu 26. Giải phương trình
20iz i+ −=
trên tập số phức.
A.
12zi= −
B.
2
zi= +
C.
12zi= +
D.
43zi= −
Câu 27. Gọi
12
,zz
là hai nghiệm phức của phương trình
2
2 4 30zz+ +=
. Giá trị của biểu thức
12
zz+
bằng
A.
2
B.
3
C.
23
D.
6
Câu 28. Kí hiệu z
1
, z
2
, z
3
và z
4
là bốn nghiệm phức của phương trình
42
2 63 0zz− −=
.
Tính tổng T = | z
1
| + | z
2
| + | z
3
| + | z
4
| .
A.
6.T =
B.
2 7.T =
C.
3 2 7.T = +
D.
6 2 7.T = +
Câu 29. Kí hiệu
1234
,,,zzzz
là bốn nghiệm của phương trình
42
4 77 0 .zz+ −=
Tính tổng
3
12 4
.Sz
zz z
=+++
A.
2 7 2 11S = +
B.
2 7 2 11S = −
C.
27S =
D.
2 11S =
Câu 30. Kí hiệu
12
,zz
lần lượt là hai nghiệm phức của phương trình
2
2 2 50zz− +=
. Giá trị của biểu
thức
22
12
11Az z=−+−
bằng:
2
2 20
zz+ +=
,ii
−
1 ,1
ii+ −−
1 ,1ii
−− −+
32
3 9 13 0zzz+ +−=
123
Tz z z=++
27T =
12T = −
1 13
T
= +
1 2 13
T = +
2
2 5 40xx− +=
1
57
44
xi
−
= +
2
57
44
xi
−
= −
1
57
44
xi
= +
2
57
44
xi= −
1
57
24
xi
= +
2
57
24
xi= −
1
37
44
xi
= +
2
37
44
xi= −
3 (2 3 )(1 2 ) 5 4
x ii i++ − =+
15xi= +
5
1
3
xi=−−
5
1
3
xi=−+

Bài tập trắc nghiệm số phức
Trang 118
A.
25
B.
5
C.
5
D.
25
Câu 31. Kí hiệu
123
,,zzz
và
4
z
là bốn nghiệm phức của phương trình
42
7 10 0zz
+ +=
. Tính tổng
1234
Tz z z z=+++
A. T = 14. B. T =
25
C. T =
22
+
25
D. T =2 +
22
Câu 32. Cho các số phức
z a bi= +
. Hãy lập phương trình bậc 2 với hệ số thực nhận
z
và
z
làm
nghiệm là:
A.
2 22
20
x bx a b− ++=
B.
2 22
20x ax a b+ ++=
C.
2 22
20x ax a b− ++=
D.
2 22
20x bx a b+ ++=
Câu 33. Gọi
1
z
và
2
z
lần lượt là nghiệm của phươngtrình:
2
2 50zz− +=
. Tính
12
zz= +
bằng:
A.
25
B. 10 C. 3 D. 6
Câu 34. Phương trình có nghiệm trên tập số phức là
A. B. C. D.
Câu 35. Nghiệm của phương trình
( ) ( )
2
2 22
36 2 363 0zz zzz z++ + ++− =
trên tập số phức là:
A.
6, 6, 1 5zi z i z i= =− =−+
và
15zi=−−
B.
3 3, 3 3, 1 5z z zi= + = − =−+
và
15zi=−−
C.
3 3, 3 3, 1 5z iz iz i= + = − =−+
và
15zi=−−
D.
6, 6, 1 5zi z i z i
= =−=+
và
15zi= −
Câu 36. Phương trình z
3
+ 1 = 0 có nghiệm là . Tính giá trị biểu thức
A.T = 0. B. T = 1. C. T =2. D. T = 3.
Câu 37. Nghiệm của phương trình là:
A. 8 – i B. 8 + i C. – 8 – i D. – 8 + i
Câu 38. Kí hiệu
1234
,,,zz zz
là bốn nghiệm phức của phương trình
42
60zz− −=
. Tính tổng
1234
Pz z z z=+++
.
A.
( )
22 3P = +
B.
( )
23P = +
C.
( )
32 3P = +
D.
( )
42 3P = +
Câu 39. Gọi z
1
, z
2
là hai nghiệm phức của phương trình z
2
– 4z + 9 = 0. Tổng P = |z
1
| + |z
2
| bằng:
A.3 B.6 C.18 D.4
14
3
i
z
=
12
3
i
z
=
15
3
i
z =
13
3
i
z =
123
,,zz z
222
123
Tz z z=++
( ) ( )
2 53 2zi i−= −
z =
z =
z =
z =

Bài tập trắc nghiệm số phức
Trang 119
Câu 40. Gọi là các nghiệm của phương trình . Tính giá trị biểu thức:
A. 10 B. 20 C. –10 D. 5
Câu 41. Kí hiệu z
1
, z
2
, z
3
, z
4
là bốn nghiệm phức của phương trình z
4
– z
2
– 12 = 0 . Khi đó tổng
T =
|
1
|
+
|
2
|
+
|
3
|
+
|
4
|
là :
A. 4 B. 2
√
3 C. 4+2
√
3 D. 2+ 2
√
3
Câu 42. Gọi z
1
và z
2
là hai nghiệm phức của phương trình: . Khi đó bằng:
A. 10 B. 7 C. 14 D. 21
Câu 43. Gọi
là các nghiệm của phương trình: . Giá trị của
là:
A. 1 B. C. D. 7
Câu 44. Gọi là ba nghiệm của phương trình . Khi đó bằng
A. S = 1 B. S = 4 C. S = 2 D. S = 3
Câu 45. Cho số phức z có phần ảo âm và thỏa mãn
2
3 50
zz− +=
. Tìm môđun của số phức
2 3 14
z
ω
= −+
.
A. 4 B.
17
C.
24
D. 5
Câu 46. Trong C, phương trình (2 – i) – 4 = 0 có nghiệm là:
A. z = B. z = C. z = D. z =
Câu 47. Trong C, phương trình z
4
– 6z
2
+ 25 = 0 có nghiệm là:
A. B. C. D. Vô nghiệm
Câu 48. Gọi và là hai nghiệm phức của phương trình: .Khi đó bằng:
A.10 B. 7 C. 14 D. 21
Câu 49. Gọi là hai nghiệm phức của phương trình: . Tìm số phức liên hợp của số
phức ?
A. . B. . C. . D. .
Câu 50. Tập nghiệm của phương trình: là
A. . B. . C. . D. .
12
, zz
2
2 50zz+ +=
22
1 2 12
4
A z z zz
=+−
2
4 70zz
+ +=
22
12
zz+
1234
,,,zz zz
42
60
zz
+ −=
1234
Tz z z z=+++
22 23+
22 23−
123
, z , zz
3
10z −=
123
S| || || |zz z=++
z
84
55
i−
48
55
i−
23
55
i+
73
55
i−
zi= ±
;5zizi=±=±
5zi= ±
1
z
2
z
2
4 70zz+ +=
22
12
zz+
12
,zz
2
2 30zz+ +=
( )( )
12
w 52iz z=−+
w 10 4i= +
w 10 4i=−−
w 10 4i= −
w 10 4i=−+
42
3 20zz+ +=
{ 1; 2}S =−−
{ ; 2}S ii=
{ ; ; 2; 2}S i ii i=−−
S = ∅

Bài tập trắc nghiệm số phức
Trang 120
Câu 51. Phương trình z
4
– z
2
– 6 = 0 có 4 nghiệm phức phân biệt. Khi đó tổng môđun của các nghiệm
phức trong phương trình là:
A. 4 B. C. D.
Câu 52. Trong C, phương trình (i+z)( – 2 + 3i) = 0 có nghiệm là:
A. B. C. D.
Câu 53. Gọi là hai nghiệm phức của phương trình . Tính ?
A. 10 B. 7 C. 14 D. 21
Câu 54. Gọi , là 2 nghiệm phức của phương trình . Tính giá trị của biểu thức sau
.
A. B. C. D.
Câu 55. Phương trình có bao nhiêu nghiệm phức với phần ảo âm?
A. 0 B. 1 C. 3 D. 2
Câu 56. Gọi là nghiệm của phương trình sau trên tập số phức:
.Khi đó, tổng có giá trị bằng
A. B. C. 0 D. 4
Câu 57. Nghiệm của phương trình là
A. –1 + i, 2 – i B. 1 + i, 2 + i C. –1 + i, 2 + i D. –1 – i, 3 – i
Câu 58. Phương trình
2
4 50xx+ +=
có nghiệm phức và tổng các mô đun của chúng là:
A.
22
B.
23
C.
25
D.
27
Câu 59. Kí hiệu là hai nghiệm của phương trình . Tính
A. B. C. D.
Câu 60. Gọi và là hai nghiệm của phương trình .Tính
A. B. C. D.
Câu 61. Nghiệm của phương trình: trên tập số phức là:
A. B. C. D.
23 22+
23
32
+
z
23
zi
zi
=
= −
2
53
zi
zi
=
= +
23
zi
zi
= −
= +
3
25
zi
zi
=
= −
12
;
zz
2
4 70zz
+ +=
22
12
zz+
1
z
2
z
2
2 50zz+ +=
22
12
Az z= +
25
A =
10A =
10A =
2 10A =
3
8
z =
1234
,,,zz zz
( ) ( )
2
2 22
36 2 363 0z z zz z z++ + ++− =
1234
zzzz+++
8−
4−
2
13 0
zz i− −+ =
;
12
zz
2
8 20 0zz++ =
12
11
zz
T
+
=
2
5
Ti
= −
8T = −
2
5
T = −
5
2
T = −
1
z
2
z
2
2 30zz++=
12
M zz= +
1
2
M = −
23
2
M = −
1
2
M =
23
2
M =
2 35 4ix x i+= +
23 14
29 29
i−
23 14
29 29
i
+
54i−
73i+

Bài tập trắc nghiệm số phức
Trang 121
Câu 62. Các nghiệm của phương trình: trên tập số phức là:
A. B. C. D.
Câu 63. Các nghiệm của phương trình: trên tập số phức là:
A. B. C. D.
Câu 64. Nghiệm của phương trình là
A. B.
C.
D.
Câu 65. Kí hiệu là hai nghiệm của phương trình , với có phần ảo âm. Tìm số
phức nghịch đảo của số phức .
A. B.
C. D.
Câu 66. Gọi là hai nghiệm của phương trình . Tính
A. B. C. D.
Câu 67. Số nghiệm của phương trình:
A. B. C. D.
Câu 68. Số lượng các số phức thỏa mãn có phần thực âm là
A. B. C. D.
Câu 69. Phương trình có hai nghiệm phức . Khẳng định nào sau đây sai:
A. B. là số phức liên hợp của
C. D.
Câu 70. Gọi là nghiệm phức có phần ảo âm của phương trình . Giá trị của
bằng
A. 3 B. 9 C. D.
Câu 71. Giải phương trình trên tập số phức. Tìm tập nghiệm S.
A. B. C. D.
Câu 72. Phương trình cho ta nghiệm :
2
2 3 20xx− +=
3535
;
44
ii−+
3737
;
44
ii−+
77
33
;
44
ii−+
77
33
;
22
ii
−+
4
40z −=
2; 2i±±
2±
2
i±
2; 2
i±±
2
20x
+=
2i±
2i±
2±
2
12
;
zz
2
2 3 40zz− +=
1
z
12
23wz z= −
1 3 5 23
146 146
i
w
= +
1 3 5 23
146 146
i
w
=−+
1 3 5 23
146 146
i
w
=−−
1 3 5 23
146 146w
=−+
12
,zz
2
3 60zz−+=
33
12
Az z= +
5,8075−
3 54
9
−+
3 54
9
+
−
3 54
9
−
( )
32
21 31 0z i z iz i
− + + +−=
1
2
3
4
z
3
1z =
0
1
2
3
2
2 26 0zz++=
12
,zz
12
. 26zz
=
1
z
2
z
12
2zz+=−
12
zz>
1
z
2
2 30zz+ +=
2
1
Az=
122−−
122−+
( )
2
34 5 10x ix i− + + −=
{ }
1; 3 2Si i=++
{ }
1
Si= +
{ }
32Si= +
{ }
1; 3 2;Si i i=++
(1 2 ) 3ix x i+=−

Bài tập trắc nghiệm số phức
Trang 122
A. B. C. D.
Câu 73. Gọi là các nghiệm phức của phương trình . Giá trị của biểu thức
là:
A. 1 B. –1 C. D.
Câu 74. Giải phương trình trên tập số phức:
A. B. C. D.
Câu 75. Gọi là các nghiệm phức của phương trình . Tính giá trị của biểu
thức:
A. B. C. D. 2
Câu 76. Căn bậc hai của số phức
4 65i
+
là:
A.
12
35, 35z iz i= − =−−
B.
12
3 5, 3 5z iz i= + =−−
C.
12
3 5, 3 5z iz i=+=−
D.
12
35, 35z iz i= + =−+
Câu 77. Một căn bậc hai của số phức là:
A. B. C. D.
Câu 78. Tìm căn bậc hai của mỗi số phức sau :
A. B. C. D.
Câu 79. Số nào sau đây là căn bậc 2 của:
A. 2 + i B. 2 – i C. 3 + i D. 3 – i
Câu 80. Số phức z thỏa mãn:
(
) ( ) ( )
3 2 41 2
iz i iz− − −= +
. Mô đun của z là :
A.
3
B.
5
C.
10
D.
3
4
Câu 81. Tính
z
biết:
5
(1 )(3 2 )
(2 )
iz
zii
i
=+ −−
+
A.
17
2
B.
17
C.
1
2
2
i+
D.
1
2
2
i−+
Câu 82. Cho số phức z thỏa mãn điều kiện
2 34zz i−=+
. Phát biểu nào sau đây là sai:
A. z có phần thực là –3 B.
4
3
zi+
có modun là
97
3
11
44
i−+
13i
+
1
2
i
1
2
2
i−
12
,zz
2
4 50zz− +=
( ) ( )
2011 2011
12
11Pz z=− +−
1006
2
1006
2−
32
10zzz+ ++=
{
}
1;
Si= −
{
}
1;
Si
=−±
{ }
0S
=
{ }
1;Si= ±
1234
;;;zzzz
42
5 40
zz
+ +=
1234
1111
1111
S
zzzz
=+++
−−−−
7
5
2
5
1
15 8zi= +
15 4i+
4 i−
4 i+
15 4i−
1 43i+
(2 3 )i±+
(3 3 )i±+
(2 3 )i±−
(3 2 )i±+
34i+

Bài tập trắc nghiệm số phức
Trang 123
C. z có phần ảo là
4
3
D. z có modun là
97
3
Câu 83. Tìm số phức z thỏa mãn điều kiện:
2
(1 3 )
1
iz i z
z
i
−
−+
=
+
A.
45 9
26 26
zi= −
B.
45 9
26 26
zi= +
C.
45 9zi= +
D.
45 9i−−
Câu 84. Tìm tất cả các số thực m biết
1 ( 2)
im
z
mm i
−
=
−−
và
2
.
2
m
zz
−
=
trong đó i là đơn vị ảo.
A.
0
1
m
m
=
=
B.
1m = −
C.
0
1
m
m
=
= −
D.
m∀
.
Câu 85. Cho hai số phức z
1
; z
2
thỏa mãn
1
1
2
2
iz +=
và
21
z iz=
. Tìm giá trị nhỏ nhất của biểu thức
12
zz−
A.
1
2
2
−
B.
1
2
2
+
C.
1
2
2
−
D.
1
2
2
+
Câu 86. Tìm số phức z thỏa mãn
13z =
và
2 21
z i zi+ − = +−
A.
32zi= ±
B.
32zi= −
C.
23i±
D.
32zi=±−
Câu 87. Cho số phức z thỏa mãn
2
2
1
zi
zi
+−
=
+−
. Tìm trung bình cộng giá trị nhỏ nhất và lớn nhất của
z
.
A.
3
B.
10 3±
C.
2 10
D.
10
Câu 88. Tính phần ảo của số phức z, biết
3
12z iz+=
và z có phần thực dương.
A.
2
B.
5
C.
1−
D.
i
−
Câu 89. Cho số phức z thỏa mãn
(
)
3 76i z iz i+ −=−
. Môđun của số phức z bằng:
A.
25
B. 25 C. 5 D.
5
Câu 90. Tìm phần ảo của số phức z biết:
1
1
z
z
−
+
là một số thực?
A. 1 B. 0 C. –1 D. 2
Câu 91. Tìm số phức z biết
2
. 29, 21 20zz z i= =−−
, phần ảo z là một số thực âm.
A.
25zi=−−
B.
25zi= −
C.
52zi= −
D.
52zi=−−
Câu 92. Cho số phức z thỏa mãn:
28zz i+=−
. Tìm số phức liên hợp của z.

Bài tập trắc nghiệm số phức
Trang 124
A.
15 8i−+
B.
15 6
i
−+
C.
15 2i−+
D.
15 7i
−+
Câu 93. Tìm phần thực, phần ảo của các số phức z, biết:
10
13
zz
z
+=
=
A. Phần thực bằng 5; phần ảo bẳng 12 hoặc bằng –12.
B. Phần thực bằng 5; phần ảo bẳng 11 hoặc bằng –12.
C. Phần thực bằng 5; phần ảo bẳng 14 hoặc bằng –12.
D. Phần thực bằng 5; phần ảo bẳng 12 hoặc bằng –1.
Câu 94. Tìm số phức
z
biết số phức z thỏa:
1
1
3
1
z
zi
zi
zi
−
=
−
−
=
+
A.
1zi= +
B.
1
zi= −
C.
1zi=−−
D.
1zi=−+
Câu 95. Cho số phức z thỏa mãn
( )
2 35z iz i++ =+
. Tính môđun của số phức z
A.
13
z =
B.
5z =
C.
13z =
D.
5z =
Câu 96. Cho số phức z thỏa
( )
23 19
z iz i−+ =−
. Khi đó
.zz
bằng:
A. 5 B. 25 C.
5
D. 4
Câu 97. Cho số phức z thỏa mãn
( )
2
1 2 4 20izz i+ += −
. Mô đun của z là:
A.
3z =
B.
4z =
C.
5z =
D.
6z =
Câu 98. Cho số phức z thỏa mãn điều kiện . Tính
A. 1 B. C. 3 D.
Câu 99. Biết rằng nghịch đảo của số phức z bằng số phức liên hợp của nó, trong các kết luận sau, kết
luận nào là đúng ?
A. B. C. z là số thuần ảo D.
Câu 100. Tìm số phức z thỏa mãn và là số thực
A. B.
C. D.
Câu 101. Nếu môđun của số phức z bằng r (r > 0) thì môđun của số phức
( )
2
1 iz−
bằng:
23zz i+=+
21A iz i=++
( )
2; 3;1−
5
zR∈
1z
=
1z = −
1z zi+= +
1
z
z
+
11 11
;
22 22
z iz i=+ =−−
11 11
;
22 22
z iz i=− =−+
11 11
;
33 33
z iz i=+ =−−
11 11
;
33 33
z iz i=− =−+

Bài tập trắc nghiệm số phức
Trang 125
A. 4r B. 2r C.
2r
D. r
Câu 102. Tìm số các số phức
z
thỏa mãn đồng thời hai điều kiện
2z =
và
2
z
là số thuần ảo.
A.
1
B.
2
C.
3
D.
4
Câu 103. Cho số phức z thỏa mãn hệ thức
2
( 3) (2 ) .
i
i z iz
i
+
++ =−
Tính mô đun của số phức .
A.
26
5
B.
6
5
C.
25
5
D.
26
25
Câu 104. Cho số phức Z thỏa mãn ( 1 + 2i)Z + ( 1 – 2 ) i = 1+ 3i . Khi đó mô đun của số phức Z là :
A. B. C. 11 D. 85
Câu 105. Số phức Z có mô đun nhỏ nhất sao cho : là:
A. B. C. D.
Câu 106. Trong các số phức z thỏa mãn điều kiện .Tìm số phức z có môđun nhỏ nhất.
A. B. C. D.
Câu 107. Số phức z nào sau đây có môđun nhỏ nhất thỏa :
A. B. z = –3 – 4i C. D.
Câu 108. Số phức thỏa là
A. B. C. D.
Câu 109. Cho số phức z thỏa mãn: . Tìm giá trị nhỏ nhất của ?
A. . B. . C. . D. .
Hướng dẫn giải
Câu 110. Cho số phức z = a + bi thỏa mãn . Tính S = a
2016
+ b
2017
A. S = 0 B. S = 2 C. S
D. S
Câu 111. Số phức z thoả là:
A. z = 7 + 7i B. z = 5 – 2i C. z = 2 + 5i D. z = 1 –2i
Câu 112. Cho số phức z thỏa mãn . Tìm mô đun của số phức z:
A. 100 B. 10 C. D. 3
w zi= −
Z
11
85
34ZZ i= −+
3
2
2
zi=−−
3
2
2
zi=−+
3
2
2
zi= +
3
2
2
zi
= −
24 2z izi
−− = −
1zi=−+
22zi
=−+
22zi
= +
32zi= +
| || 3 4|zz i= −+
7
3
8
zi= −
3
2
2
zi=−−
3
2
2
zi
= +
z
(
)
23 19z iz i
−+ =−
3zi=−−
z= 2
i−−
z=2 i−
z=2 i+
12
zi z i++ = −
z
1
2
−
2
2
2
1
2
2 33z iz i+=+
4032 2017
2017
33
5
−
= −
4032 2017
2017
33
5
−
=
2 18iz z i+ =−−
2
(1 ) (1 2 )
z iz i−+ =−
109

Bài tập trắc nghiệm số phức
Trang 126
Câu 113. Cho số phức z thỏa mãn . Tìm phần ảo của số phức
A. 6 B. 3 C. 5 D. 2
Câu 114. Cho số phức z thỏa mãn . Tìm số phức w biết
A. 2+3i B. 2–3i C. 6+6i D. 6–6i
Câu 115. Cho số phức z thỏa mãn: . Tìm số phức liên hợp của số phức w=7z–2
A. B. C. D.
Câu 116. Có bao nhiêu số phức z thỏa mãn điều kiện ?
A. 0 B. 1 C. 3 D. 2
Câu 117. Cho số phức z thỏa mãn . Modun của số phức là
A. 4 B. 9 C. 1 D. 2
Câu 118. Cho số phức thỏa mãn điều kiện . Tính môđun của
A. B. C. D.
Câu 119. Cho số phức thỏa mãn điều kiện . Phần thực và phần ảo của là:
A. 2 và –3 B. 2 và 3 C. –2 và 3 D. –3 và 2
Câu 120. Tìm số phức z có phần ảo khác 0, thỏa mãn và ?
A. B. C. D.
Câu 121. Tìm số phức z thỏa hệ thức ?
A. B. C. D.
Câu 122. Cho số phức z thỏa mãn điều kiện . Phát biểu nào sau đây sai?
A. z có phần thực là –3 B. có mô–đun
C. z có phần ảo là D. z có mô–đun
(1 ) (3 ) 2 6iz iz i− +− =−
w2 1z= +
(1 ) (3 ) 2 6iz iz i− +− =−
w2 2z= +
2
2
(1 ) 3 ( )
1
i
i z iz
i
++ =
−
42
w
77
i=−+
42
w
77
i
=−−
w 62i=−+
w 62i=−−
2
zz z= +
z
zi
zi
= −
+
2
1zz
ϖ
= ++
z
( )
2 31 1 9z iz i+−=−
z
12
13
12
2
z
( )
2 35z iz i++ =+
z
(2 ) 10zi
−+=
. 25zz=
43i+
43i−
34i+
34i−
2
2
2
zz
z
+=
=
3; 1 3zz i= = ±
2; 1 3
zz i=−=±
1; 1 3zz i=−=±
2; 2 3zz i
=−=±
2 34zz i
−=+
4
3
zi+
97
3
4
3
97
3

Bài tập trắc nghiệm số phức
Trang 127
Câu 123. Kí hiệu (qui ước là số có phần ảo của lớn hơn) là nghiệm của hệ phương trình
. Khi đó bằng:
A. B. C. D.
Câu 124. Biết rằng số phức z thỏa mãn là một số thực. Tìm giá trị nhỏ nhất của
A. 8 B. C. D.
Câu 125. Cho các số phức z thoả mãn . Tìm số phức z
để |z| đạt giá trị lớn nhất.
A. B.
C.
D.
Câu 126. Biết rằng và là một số thực khác 0, số phức liên hợp của số phức z là:
A. B. C. Không tồn tại z D. Không tồn tại
Câu 127. Tìm số phức z có môđun nhỏ nhất thỏa mãn điều kiện .
A. B. C. D.
Câu 128. Tìm phần thực của số phức z biết: .
A. 1 B. –1 C. 0 D. –4
Câu 129. Tìm số phức z có và đạt giá trị lớn nhất.
A. 1 B. –1 C. i D. –i
Câu 130. Cho số phức thỏa mãn . Tính giá trị biểu thức: .
A. 0 B. 2 C. D.
12
,zz
1
z
2
.1
8
21
27
zz
zz
=
+ −=
12
36zz+
65i+
65i−+
65i−−
65i−
( )
(
)
3 13
u z iz i= +− ++
z
2
22
2
2
( )
22zi i−+=
(
)
25 2 5
5 25
55
zi
+
+
= −
(
)
25 2 5
5 25
55
zi
+
+
= +
(
)
25 2 5
5 25
55
zi
−
+
= −
(
)
25 2 5
5 25
55
zi
−
+
= +
( )
11zi−+ =
2zi
−
12i+
12i−
z
23
iz zi−− + = −
36
55
i−
63
55
i−
9
5
9
5
2 34
zz i
+=+
1z =
zi+
z a bi
= +
2, 3 3z iz i+=+
2016 2017
Pa b= +
4032 2017
2017
33
5
−
4032 2017
2017
33
5
−
−

Bài tập trắc nghiệm số phức
Trang 128
B – HƯỚNG DẪN GIẢI
Câu 1. Cho phương trình
2
13 45 0
zz− +=
. Nếu
0
z
là nghiệm của phương trình thì
00
zz+
bằng:
A. –13 B. 13 C. 45 D. –45
Hướng dẫn giải
Đáp án: A
Phân tích: Đây là bài toán tìm nghiệm phương trình đơn giản, quý độc giả chỉ cần bấm máy tính là có đáp án:
phương trình có hai nghiệm
1
13 11
22
zi= +
và
2
13 11
22
zi= −
Hai nghiệm này là số phức liên hợp của nhau, do đó
00 12
13zz zz+=+=
.
Câu 2. Cho phương trình
( )
2
25 64 0
z iz i
− − −− =
. Trong các số:
I. 2–3i II. 2+3i III. –2i IV. 2i
Những số nào là nghiệm của phương trình trên:
A. I, II B. I, III C. II, III D. II, IV
Hướng dẫn giải
Đáp án: B
Phân tích: Với bài toán này ta đặt
( )
z x yi x=+∈
, khi đó phương trình
( ) ( )( )
2
25 64 0x yi i x yi i⇔ + − − + −− =
( )
2 22 2
2 22 5 5x xyi i y x yi xi yi⇔+ + − + − −
64 0
i−− =
( )
( )
22
2 25 25x y xyi x y y x i⇔−+ − +− +
64 0i−− =
22
256
xy xy⇔−−−−
( )
2 254 0xy y x i+ −+− =
22
2 5 60
2 2 5 40
xy xy
xy y x
− − − −=
⇔
− + −=
Rõ ràng đến đây việc giải hệ phương trình này mất khá nhiều thời gian như sau:
Cho nên ta nên thử từng đáp án rồi bằng cách bấm máy như sau:
Đầu tiên ta chuyển máy tính về chế độ tính toán với số phức bằng cách bấm
→
. Khi đó ta
nhập vào màn hình biểu thức phương trình như sau:
( )
2
25 64X iX i− − −−
Khi đó ấn và lần lưojt thử từng nghiệm, từ đó ta nhận được kết quả I và III là nghiệm của phương trình.
Với bài toán dạng này, tôi khuyên quý độc giả nên thử máy tính để tiết kiệm thời gian làm bài.

Bài tập trắc nghiệm số phức
Trang 129
Câu 3. Tìm tất cả các nghiệm của
43 2
4 14 36 45 0zz z z− + − +=
, biết
2zi= +
là một nghiệm của
phương trình:
A.
1 23
2 ; 3; 3z iz iz i=+= =−
B.
1 2 34
2 ; 2 3; 3; 3z iz iz iz i=+=− = =−
C.
1 2 34
2 ; 2 ; 3; 3z iz iz z i=+=−= =−
D.
123
2; 2; 3z iz iz i=+=−=
Hướng dẫn giải
Đáp án: C
Phân tích: Có một cách làm nhanh của bài toán như sau: do
2zi= +
nên có thể
2zi= −
cũng là một nghiệm
nên có thể phương trình sẽ có một nhân tử đó là:
2
4 50
zz
− +=
. Khi đó bấm máy tính để tìm nhân tử còn lại
như sau: Bấm vào máy tính biểu thức
43 2
2
4 14 36 45
45
XX X X
XX
−+ −+
−+
sau đó ấn CALC thì máy hiện X? ta nhập
100 = thì máy hiện
Ta phân tích
10009 10009=
, khi đó nhân tử còn lại sẽ là
2
9z +
. Vậy phương trình
( )( )
22
3
3
9 450
2
2
xi
zi
z zz
zi
zi
= −
=
⇔ + −+=⇔
= +
= −
Câu 4. Tập hợp các nghiệm phức của phương trình
2
2
0zz+=
là:
A. Tập hợp mọi số ảo và số 0. B.
{ }
;0i±
C.
{ }
;0i−
D.
{ }
0
Hướng dẫn giải
Đáp án: A
Phân tích:
Ta có
2
2
0zz+=
2 22 2 2 2
2 02 2 0a abi b i a b a abi⇔+ + ++=⇔ + =
( )
20a a bi⇔ +=
( do
2
1i = −
)
0
00
a
a bi z
=
⇔
+ =⇔=
Với
0a =
thì
0z bi
= +
là số thuần ảo.
Với
0z =
Vậy đáp án đúng là A.

Bài tập trắc nghiệm số phức
Trang 130
Nhiều độc giả gặp bài toán này sẽ thấy bối rối, và thử các giá trị B, C hoặc D vào thấy thảo mãn sẽ khoanh
ngay, đó là các kết quả sai. Vì thế các bạn cần giải ra xem kết quả rõ ràng như thế nào nhé.
Câu 5. Cho z
1
; z
2
; z
3
; z
4
là bốn nghiệm của phương trình
4
1
1
2
z
zi
−
=
−
. Tính giá trị của biểu thức
2222
1234
( 1)( 1)( 1)( 1)Tz z z z=++++
A.
17
9
B.
17
9
−
C. 425 D. –425
Hướng dẫn giải
Đáp án: A
Đây là một bài toán số phức ở mức độ vận dụng cao khá hay và khó. Để giải quyết cần sự tinh ý và cẩn thận
trong từng bước giải.
Từ phương trình
4
1
1
2
z
zi
−
=
−
, ta suy ra
44
(2 ) ( ) 0zi zi− −− =
Đặt
44
( ) (2 ) ( )fz zi zi= − −−
3
12 4
15( )( )( )( )zzzz zz zz=−−−−
Vì
(
)( )
2 22
2
1 1i z z i zizi=−⇒ + = − = − +
[ ]
1234
( )( )( )( )T z iz iz iz i⇒=−−−−
[ ]
1234
( )( )( )( )z iz iz iz i++++
[ ]
1234
( )( )( )( )T iziz iziz⇔= − − − −
[ ]
1234
( )( )( )( )iz iz iz iz
−− −− −− −−
() ( ) (). ( )
.
15 15 225
fi f i fi f i
T
−−
⇔= =
Tính các giá trị
( ); ( )fi f i−
4444
44
( ) (2 ) ( 1) ( 1) 5
( ) ( 2 ) ( 1) 85
fi i i i i i
f i ii i
= − −− = −− =
− =− − −−− =
5.85 17
225 9
T⇒= =
Nhận xét: Đối với bài toán này, có lẽ Casio hay Vinacal cũng “bó tay”. Một số bạn thì có hướng làm đúng
nhưng lại chọn đáp án C vì ngay từ đầu khi đặt F(z) đã không có hệ số 15 ở đâu.
Câu 6. Giải phương trình
43 2
2 (1 ) 2z zi iz z i− +−+ + =
trên tập số phức. Tính tổng các nghiệm của
phương trình.
A. 2i B. 1 C.
1 i+
D. i
Hướng dẫn giải
Đáp án: D
Bài tập trắc nghiệm số phức
Trang 131
SHIFT
SOLVE
Đây là một bài toán ở mức độ vận dụng cao, đòi hỏi kĩ năng biến đổi cũng như dự đoán của thí sinh. Điểm mấy
chốt của bài toán là phải thay
2
1
i = −
đúng lúc.
Phương trình đã cho
22 2 2
()()2()0
zzi zi zizi⇔ +− +− +=
(Thay
2z
bằng
2
2zi
−
)
22 2
( )( 2 ) 0z i z zi i⇔ + −+=
(Thay –1 bằng
2
i
)
2
22
(*)
( )( ) 0
zi
z iz i
zi
= −
⇔ + −=⇔
=
Đến đây nhận thấy nếu phương trình (*) vô nghiệm thì tổng các nghiệm bằng
i
, nếu phương trình (*) có
nghiệm thì sẽ có 2 nghiệm là đối hoặc liên hợp của nhau do đó tổng các nghiệm vẫn bằng
i
.
Vậy đáp án D là chính xác.
Câu 7. Gọi
1234
;;;
zzzz
là nghiệm của phương trình
43 2
2 2 40zz z z− − − +=
Tính
2222
1234
1111
T
ZZZZ
=+++
A. 5 B.
5
4
C.
7
4
D.
9
4
Hướng dẫn giải
Đáp án: D
Đây là bài toán yêu cầu cả kĩ năng sử dụng máy tính casio và kĩ năng biến đổi.
Sử dụng chức năng của máy tính ta tìm được 2 nghiệm thực của phương trình 1 và 2.
Ta suy ra được phương trình sẽ có phân tử là
( )( )
2
1 2 32x x xx− −=−+
Đến đây ta sử dụng kĩ thuật biến đổi, thêm bớt để tiếp tục
43 2
2 2 40zz z z− − − +=
43232 2
3 2 2 6 42 640zzzzzzzz⇔−++−++−+=
( )( )
22
32 220zz zz⇔ −+ ++=
22 2
1
2
11 1 1 9
1
1 2 (1 ) (1 ) 4
1
z
z
T
zi
ii
zi
=
=
⇔ ⇒=+ + + =
=−+
−+ −−
=−−
Câu 8. Gọi
12
;zz
là các nghiệm phức của phương trình
2
3 70zz+ +=
. Khi đó
44
12
Az z= +
có giá trị là
:
A. 23 B.
23
C. 13 D.
13

Bài tập trắc nghiệm số phức
Trang 132
Hướng dẫn giải
Đáp án: A
Sử dụng chức năng tìm nghiệm trên máy tính ta tính được
12
35 35
;
22 22
z iz i
−−
=+=−
Tuy nhiên máy tính không thể tính được lũy thừa bậc bốn của một số phức nên ta sẽ phải tính lần lượt.
Ta có
2
2
1
3 5 11 5 3
22 2 2
zi i
−−
= +=−
( )
2
2
42
11
11 5 3 23 53 3
22 22
zz i i
−
⇒= = − = +
Tương tự thì
4 44
2 12
23 53 3
23
22
z izz= − ⇒+=
Câu 9. Giải phương trình trên tập số phức:
42
10zz+ +=
?
A.
1 2 11
13 13 13 13
; ;;
2 2 22
i iii
z z zz
−− −+ − +
= = = =
B.
12
13 13
;
22
ii
zz
−− −+
= =
C.
11
13 13
;
22
ii
zz
−+
= =
D. Phương trình vô nghiệm
Hướng dẫn giải
Đáp án: A
Ta có
42
10zz+ +=
( )( )
22
1 - 1 0z z zz
+⇔ ++ =
⇔
2
2
10
10
zz
zz
−
+=
+=
+
Xét phương trình:
( )
2
1 =0 1zz++
Ta có
2
1 4 3 3i
∆= − = − =
=>Phương trình (1) có 2 nghiệm là:
12
13 13
;
22
ii
zz
−− −+
= =
Xét phương trình
2
- 10zz+=
(2)
=>Phương trình (2) có 2 nghiệm là:
34
13 13
;
22
ii
zz
−+
= =
Vậy phương trình có 4 nghiệm là:
12
13 13
;
22
ii
zz
−− −+
= =
;
34
13 13
;
22
ii
zz
−+
= =
Câu 10. Cho phương trình
2
2 10 0zz++=
. Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình đã cho.
Khi đó giá trị biểu thức
22
12
Az z= +
bằng:
A.
4 10
B. 20 C.
3 10
D.
10
Hướng dẫn giải

Bài tập trắc nghiệm số phức
Trang 133
Đáp án: B
Ta có
( )
(
)
22
1
2
2
13
2 10 0 1 3
13
zi
zz z i
zi
=−+
++=⇔+ = ⇔
=−−
Suy ra
(
)
( )
( )
22
2 22
22
2
12
1 3 1 3 10 10 20Az z
= + = −+ + −+− =+=
Câu 11. Gọi
12
,zz
là hai nghiệm của phương trình phức
( )
4
2
200
1
17
z
z
zi
−
+=
−
quy ước z
2
là số phức có phần
ảo âm. Tính
12
zz+
A.
12
5 42zz+=+
B.
12
1zz+=
C.
12
17zz+=
D.
12
105zz+=
Hướng dẫn giải
Đáp án: C
Ta có
(
)
2
4
2
.zz z=
suy ra
( )
4
2
2
z
z
z
=
. Khi đó ta được
( ) ( )
2
1
1 12
2
34
1 4 28 0 3 4 17
44
zi
z z i z i zz
zi
= −
⇔ +++ =⇔ ⇒ =+ ⇒ + =
=−+
Câu 12. Cho phương trình phức
3
zz=
. Phương trình đã cho có bao nhiêu nghiệm ?
A. 1 nghiệm B. 3 nghiệm C. 4 nghiệm D. 5 nghiệm
Hướng dẫn giải
Đáp án: D
Gọi
( )
,z a bi z a bi a b=+⇒=− ∈
. Thay vào phương trình ta được:
( ) ( )
32
3 2 23
23
22
22
0
0
0
1
3
33
1
3
0
31
31
a
b
a
b
a ab a
a ab a b b i a bi
a
ab b b
b
ab
ab
=
=
=
= ±
−=
− + − =−⇔ ⇔
= ±
−=
=
−=
−=−
Vậy phương trình phức đã cho có 5 nghiệm
Câu 13. Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình
2
2 10 0zz−+=
. Tính
22
12
Az z= +
A.
20A =
B.
10A =
C.
30A =
D.
50A =
Hướng dẫn giải

Bài tập trắc nghiệm số phức
Trang 134
Đáp án: A
Phương trình
( )
2
2 10 0 1
zz−+=
có nên (1) có hai nghiệm phức là và
Ta có:
Vậy
Câu 14. Phương trình (3–2i)z+4+5i=7+3i có nghiệm z bằng:
A. 1 B. i C. 1–i D. 0
Hướng dẫn giải
Đáp án: A
(3–2i)z+4+5i=7+3i (3–2i)z=3–2i .
Câu 15. Tính tổng các nghiệm của phương trình trên tập số phức:
A. 0 B. C. D.
Hướng dẫn giải
Đáp án: A
Tổng các nghiệm bằng 0.
Câu 16. Phương trình có 4 nghiệm phức, tổng môđun của bốn nghiệm bằng:
A. 0 B. C. D. 7
Hướng dẫn giải
Đáp án: B
Đặt , khi đó phương trình trở thành , suy ra phương trình có 4 nghiệm
phức là , tổng môđun 4 nghiệm là .
Câu 17. Kí hiệu là các nghiệm của phương trình . Khi đó tổng T = bằng
A. T = B. T =6 C. T = D. T = 4
Hướng dẫn giải
Đáp án: B
có nghiệm
Câu 18. Gọi là bốn nghiệm phức của phương trình .
Tổng bằng:
A.5 B. C. D.
Hướng dẫn giải
Đáp án: C
' 1 10 9 0∆= − =− <
1
13zi
= +
2
13zi= −
( )
( )
(
)
2 22
22
13 86 86 86 8620
Ai i i
= − =−− +−+ = − + + − + =
20A =
⇔
1z⇔=
4
80
z −=
4
28
4
28i
44
28 28i+
42
7 10 0zz+ +=
22 25+
22
2
tz=
2
7 10 0 2 5tt t t+ + = ⇔ =−∨=−
2, 5zi zi=±=±
22 25
+
12
,zz
2
2 30zz+ +=
22
12
zz+
3
23
2
2 30zz+ +=
1 2 12
1 2, 1 2,| | | | 3z iz i z z=−− =−+ = =
1234
,,,zz zz
42
2320zz− −=
1234
Tz z z z=+++
52
32
2

Bài tập trắc nghiệm số phức
Trang 135
Câu 19. Kí hiệu là bốn nghiệm phức của phương trình . Tính tổng
.
A. B. C. D.
Hướng dẫn giải
Đáp án: D
.
Câu 20. Giải phương trình trong tập số phức z
2
– (5 + 2i)z + 10i = 0
A. z = 5 2i B. z = 5, z = 2i C. z = 2, z = –5i D. z = –2 5i
Hướng dẫn giải
Đáp án: B
Câu 21. Giải phương trình trong tập số phức z
2
– (5 + 2i)z + 10i = 0
A. z = 5 2i B. z = 5, z = 2i C. z = 2, z = –5i D. z = –2 5i
Hướng dẫn giải
Đáp án: B
Câu 22. Nghiệm của phương trình trong tập số phức C là
A. B. C. D. Vô nghiệm
Hướng dẫn giải
Đáp án: C
Câu 23. Kí hiệu z
1
, z
2
, z
3
là ba nghiệm phức của phương trình .
Tính tổng
A. B. C. D.
Hướng dẫn giải
1
2
42
3
4
2
2
1
2320
2
1
2
z
z
zz
zi
zi
=
= −
− −=⇒ ⇒
=
= −
(
)
(
)
22
22
1234
11
2 2 32
22
Tz z z z
= + + + = +− + +− =
123
,,
4
à zz z zv
42
20 0zz+− =
12 34
22T zz zz= ++ +
4T =
25
T = +
4 35
T = +
6 35
T = +
42
20 0
zz+− =
(
)( )
22
5
5 40
2
zi
zz
z
= ±
⇔ + −=⇔
= ±
25 5 4 2 6 35T
⇒ = + ++=+
2
2 20zz+ +=
,ii−
1 ,1ii+ −−
1 ,1ii−− −+
( )
2
22
1
2 20 1
1
zi
zz z i
zi
=−+
+ +=⇔ + = ⇔
=−−
32
3 9 13 0zzz+ +−=
123
Tz z z=++
27T =
12T
= −
1 13T
= +
1 2 13T = +

Bài tập trắc nghiệm số phức
Trang 136
Đáp án: D
Kí hiệu z
1
;z
2;
z
3
là 3 nghiệm của phương trình: z
3
+ 3z
2
+ 9z – 13 = 0
Giải phương trình ta được 3 nghiệm : z
1
=1 ; z
2
= –2 – 3i ; z
3
= –2 +3i
Câu 24. Nghiệm của phương trình trên tập số phức là
A. ; . B. ;
C. ; D. ; .
Hướng dẫn giải
Đáp án: B
Tính . Phương trình có hai nghiệm phức và .
Câu 25. Giải phương trình sau trên tập số phức :
A. B.
C. D. x= 5i
Hướng dẫn giải
Đáp án: C
Câu 26. Giải phương trình
20iz i+ −=
trên tập số phức.
A.
12zi= −
B.
2zi
= +
C.
12zi= +
D.
43
zi= −
Hướng dẫn giải
Đáp án: C
PT đã cho tương đương với PT
2
12
i
zi
i
−+
= = +
.
Câu 27. Gọi
12
,zz
là hai nghiệm phức của phương trình
2
2 4 30zz+ +=
. Giá trị của biểu thức
12
zz+
bằng
A.
2
B.
3
C.
23
D.
6
Hướng dẫn giải
Đáp án: D
Bấm máy tính
1
1z⇒=
2
13z⇒=
3
13z
⇒=
123
1 2 13
zzz
⇒++=+
2
2 5 40xx− +=
1
57
44
xi
−
= +
2
57
44
xi
−
= −
1
57
44
xi= +
2
57
44
xi
= −
1
57
24
xi
= +
2
57
24
xi= −
1
37
44
xi
= +
2
37
44
xi= −
(
)
2
5 4.2.4 7
∆= − − =−
1
57
44
xi= +
2
57
44
xi= −
3 (2 3 )(1 2 ) 5 4x ii i
++ − =+
15xi
= +
5
1
3
xi=−−
5
1
3
xi=−+
( )
( )
54 23 12
3
i ii
x
+−+ −
=

Bài tập trắc nghiệm số phức
Trang 137
Câu 28. Kí hiệu z
1
, z
2
, z
3
và z
4
là bốn nghiệm phức của phương trình
42
2 63 0
zz− −=
.
Tính tổng T = | z
1
| + | z
2
| + | z
3
| + | z
4
| .
A.
6.
T =
B.
2 7.T
=
C.
3 2 7.T
= +
D.
6 2 7.T = +
Hướng dẫn giải
Đáp án: D
Ta có : .
Câu 29. Kí hiệu
1234
,,,
zzzz
là bốn nghiệm của phương trình
42
4 77 0 .
zz+ −=
Tính tổng
3
12 4
.Sz
zz z
=+++
A.
2 7 2 11S
= +
B.
2 7 2 11S = −
C.
27S =
D.
2 11S =
Hướng dẫn giải
Đáp án: A
Ta có:
2
42
2
7
7
4 77 0
11
11
z
z
zz
z
zi
= ±
=
+ −=⇔ ⇔
= −
= ±
3
12 4
2 7 2 11Sz
zz z
⇒= + + + = +
Câu 30. Kí hiệu
12
,zz
lần lượt là hai nghiệm phức của phương trình
2
2 2 50
zz− +=
. Giá trị của biểu
thức
22
12
11Az z=−+−
bằng:
A.
25
B.
5
C.
5
D.
25
Hướng dẫn giải
Đáp án: C
Giải phương trình
2
2 2 50zz− +=
tính được các nghiệm
12
13 13
;
22 22
z iz i=+=−
Tính
22
12
55
11 5
22
Az z= −+ − =+=
Câu 31. Kí hiệu
123
,,zzz
và
4
z
là bốn nghiệm phức của phương trình
42
7 10 0zz
+ +=
. Tính tổng
1234
Tz z z z=+++
A. T = 14. B. T =
25
C. T =
22
+
25
D. T =2 +
22
Hướng dẫn giải
Đáp án: C
Sử dụng máy tính ta được
2
42
2
3
9
2 63 0
7
7
z
z
zz
zi
z
= ±
=
− −=⇔ ⇔
= ±
= −

Bài tập trắc nghiệm số phức
Trang 138
12 34
2; 2; 5; 5
22 25
z iz i z iz i
T
==−==−
⇒= +
Câu 32. Cho các số phức
z a bi= +
. Hãy lập phương trình bậc 2 với hệ số thực nhận
z
và
z
làm
nghiệm là:
A.
2 22
20
x bx a b− ++=
B.
2 22
20x ax a b+ ++=
C.
2 22
20x ax a b
− ++=
D.
2 22
20x bx a b
+ ++=
Hướng dẫn giải
Đáp án: C
Sử dụng định lý vi ét ta được
Câu 33. Gọi
1
z
và
2
z
lần lượt là nghiệm của phươngtrình:
2
2 50zz− +=
. Tính
12
zz= +
bằng:
A.
25
B. 10 C. 3 D. 6
Hướng dẫn giải
Đáp án: A
1
2
2
12
2 50
12
zi
zz
zi
= −
− +=⇔
= +
12
5; 5zz= =
=>
12
zz= +
=
25
Câu 34. Phương trình có nghiệm trên tập số phức là
A. B. C. D.
Hướng dẫn giải
Đáp án: B
2
'13 2 2i∆= − =− =
1.2
1 21 2
33
ii
z
−±
= =
−
Câu 35. Nghiệm của phương trình
( ) ( )
2
2 22
36 2 363 0zz zzz z++ + ++− =
trên tập số phức là:
A.
6, 6, 1 5zi z i z i= =− =−+
và
15zi=−−
B.
3 3, 3 3, 1 5z z zi= + = − =−+
và
15zi=−−
C.
3 3, 3 3, 1 5z iz iz i= + = − =−+
và
15zi=−−
D.
6, 6, 1 5zi z i z i= =−=+
và
15zi= −
Hướng dẫn giải
14
3
i
z
=
12
3
i
z
=
15
3
i
z =
13
3
i
z =

Bài tập trắc nghiệm số phức
Trang 139
Đáp án: B
Đặt ta được
22
3
23 0
tz
t zt z
tz
= −
+−=⇔
=
Vậy
3 3, 3 3, 1 5z z zi= + = − =−+
và
15zi=−−
Câu 36. Phương trình z
3
+ 1 = 0 có nghiệm là . Tính giá trị biểu thức
A.T = 0. B. T = 1. C. T =2. D. T = 3.
Hướng dẫn giải
Đáp án: D
Phương trình z
3
+ 1 = 0 có nghiệm là .
Nên
Câu 37. Nghiệm của phương trình là:
A. 8 – i B. 8 + i C. – 8 – i D. – 8 + i
Hướng dẫn giải
Đáp án: A
Câu 38. Kí hiệu
1234
,,,zzzz
là bốn nghiệm phức của phương trình
42
60
zz
− −=
. Tính tổng
1234
Pz z z z
=+++
.
A.
( )
22 3P = +
B.
( )
23
P
= +
C.
( )
32 3P = +
D.
( )
42 3P = +
Hướng dẫn giải
Đáp án: A
2
42
2
2
22
60
3
3
3
zi
z zi
zz
z
z
z
=
=−=−
− −=⇔ ⇔
=
=
= −
. Vậy
( )
22 3P
= +
Câu 39. Gọi z
1
, z
2
là hai nghiệm phức của phương trình z
2
– 4z + 9 = 0. Tổng P = |z
1
| + |z
2
| bằng:
A.3 B.6 C.18 D.4
Hướng dẫn giải
Đáp án: B
2
36tz z=++
123
,,zz z
222
123
Tz z z=++
13 13
1
12 3
22
,,
ii
zz z
+−
=−= =
222
123
13 13
13
44 44
Tz z z
= + + =++++=
( ) ( )
2 53 2zi i−= −
z =
z =
z
=
z
=
2
(15 10 )(2 ) 30 15 20 10 40 5
8
(2 )(2 ) 5 5
i i i ii i
zi
ii
− + +−− −
= = = = −
−+

Bài tập trắc nghiệm số phức
Trang 140
=>|z
1
| + |z
2
| = = 6
Câu 40. Gọi là các nghiệm của phương trình . Tính giá trị biểu thức:
A. 10 B. 20 C. –10 D. 5
Hướng dẫn giải
Đáp án: C
Vậy . Chọn C
Câu 41. Kí hiệu z
1
, z
2
, z
3
, z
4
là bốn nghiệm phức của phương trình z
4
– z
2
– 12 = 0 . Khi đó tổng
T =
|
1
|
+
|
2
|
+
|
3
|
+
|
4
|
là :
A. 4 B. 2
√
3 C. 4+2
√
3 D. 2+ 2
√
3
Hướng dẫn giải
Đáp án: C
Câu 42. Gọi z
1
và z
2
là hai nghiệm phức của phương trình: . Khi đó bằng:
A. 10 B. 7 C. 14 D. 21
Hướng dẫn giải
Đáp án: C
Câu 43. Gọi
là các nghiệm của phương trình: . Giá trị của
là:
A. 1 B. C. D. 7
Hướng dẫn giải
Đáp án: B
Giải phương trình ta được
Câu 44. Gọi là ba nghiệm của phương trình . Khi đó bằng
12
2 5; 2 5z iz i=+=−
2 22 2
2 ( 5) 2 ( 5)+ + +−
12
, z
z
2
2 50zz+ +=
22
1 2 12
4
A z z zz=+−
11
2
2
2
12 12
2 50
12
12
z iz i
zz
zi
zi
=−+ =−−
+ +=⇔ ⇒
=−−
=−+
12
12
14 5 ; 14 5
14 5 ; 14 5
zz
zz
= += = +=
= += = +=
5 5 4. 5. 5 10A =+− =−
2
4 70zz+ +=
22
12
zz+
22
2
12
4 7 0 2 3 14zz z i zz+ + = ⇔ =−± ⇒ + =
1234
,,,zz zz
42
60zz+ −=
1234
Tz z z z=+++
22 23+
22 23−
42
60zz+ −=
12 3 4
2; 2; 3; 3z z zi z i= =−= =−
1234
22 23Tz z z z=+++= +
123
, z , zz
3
10z −=
123
S| || || |zz z=++

Bài tập trắc nghiệm số phức
Trang 141
A. S = 1 B. S = 4 C. S = 2 D. S = 3
Hướng dẫn giải
Đáp án: D
Gọi là ba nghiệm của phương trình . Tính tổng S=
=> S= 3
Câu 45. Cho số phức z có phần ảo âm và thỏa mãn
2
3 50zz− +=
. Tìm môđun của số phức
2 3 14z
ω
= −+
.
A. 4 B.
17
C.
24
D. 5
Hướng dẫn giải
Đáp án: D
(
)
2
2
3 4.5 11 11i
∆= − − =− =
Phương trình
2
3 11
2
3 50
3 11
2
i
z
zz
i
z
−
=
− +=⇔
+
=
Vì z có phần ảo âm nên
3 11 3 11
2 3 14 14 11
22
ii
zi
ω
−−
= ⇒ = −+ = −
Suy ra
14 11 5
ω
= +=
Câu 46. Trong C, phương trình (2 – i) – 4 = 0 có nghiệm là:
A. z = B. z = C. z = D. z =
Hướng dẫn giải
Đáp án: A
Ta có Pt tương đương
Câu 47. Trong C, phương trình z
4
– 6z
2
+ 25 = 0 có nghiệm là:
A. B. C. D. Vô nghiệm
123
, z , zz
3
10z −=
123
| || || |zzz
++
3
10z −=
2
( 1)( 1) 0z zz
− ++ =
2
1
10
z
zz
=
++=
1
13
2
13
2
z
i
z
i
z
=
−+
=
−−
=
z
84
55
i−
48
55
i−
23
55
i+
73
55
i−
4 4(2 ) 8 4 8 4
2 5 55 55
i
Z iZ i
i
+
= = =+ ⇒=−
−
zi= ±
;5zizi=±=±
5zi= ±

Bài tập trắc nghiệm số phức
Trang 142
Hướng dẫn giải
Đáp án: B
Trong C, phương trình z
4
+ 6z
2
+ 5 = 0 có nghiệm là:
Ta có
Vậy pt có nghiệm
Câu 48. Gọi và là hai nghiệm phức của phương trình: .Khi đó bằng:
A.10 B. 7 C. 14 D. 21
Hướng dẫn giải
Đáp án: C
Ta có
Câu 49. Gọi là hai nghiệm phức của phương trình: . Tìm số phức liên hợp của số
phức ?
A. . B. . C. . D. .
Hướng dẫn giải
Đáp án: B
Câu 50. Tập nghiệm của phương trình: là
A. . B. . C. . D. .
Hướng dẫn giải
Đáp án: C
Câu 51. Phương trình z
4
– z
2
– 6 = 0 có 4 nghiệm phức phân biệt. Khi đó tổng môđun của các nghiệm
phức trong phương trình là:
A. 4 B. C. D.
Hướng dẫn giải
Đáp án: B
22
1 ;5 5
z ziz zi=−⇔=± =−⇔=±
;5zizi=±=±
1
z
2
z
2
4 70
zz
+ +=
22
12
zz
+
22
2
1,2 1 2
4 7 0 2 3 14z z z iz z
+ + = ⇒ =−± ⇒ + =
12
,zz
2
2 30zz+ +=
( )
( )
12
w 52iz z=−+
w 10 4
i= +
w 10 4i=−−
w 10 4i= −
w 10 4i=−+
1
2
2
12
2 30
12
zi
zz
zi
=−−
+ +=⇔
=−+
( )( ) ( )
( )
( )
12
w 52 52 1 21 2 252 104 w 104iz z i i i i i i=− + =− −− −+ =− − =−+⇒=−−
42
3 20zz+ +=
{ 1; 2}S =−−
{ ; 2}S ii=
{ ; ; 2; 2}S i ii i=−−
S = ∅
22
42
22
2
22
2
3 20
1
zi
zi
zz
zi
zi
=−=
= ±
+ +=⇔ ⇔
=−=
= ±
23 22+
23
32+

Bài tập trắc nghiệm số phức
Trang 143
z
4
– z
2
– 6 = 0 . Do đó phương trình có 4 nghiệm phức
Vậy tổng mođun các nghiệm là .
Câu 52. Trong C, phương trình (i+z)( – 2 + 3i) = 0 có nghiệm là:
A. B. C. D.
Hướng dẫn giải
Đáp án: C
Trong C, phương trình (i+z)( – 2 + 3i) = 0 có nghiệm là: (i+z)( – 2 + 3i) = 0
Câu 53. Gọi là hai nghiệm phức của phương trình . Tính ?
A. 10 B. 7 C. 14 D. 21
Hướng dẫn giải
Đáp án: C
Ta có:
Với bài toán này, ta có thể sử dụng chức năng giải phương trình bậc 2 trên máy tính CASIO, ta có thể nhận
được kết quả và một cách nhanh chóng hơn.
Câu 54. Gọi , là 2 nghiệm phức của phương trình . Tính giá trị của biểu thức sau
.
A. B. C. D.
Hướng dẫn giải
Đáp án: B
Suy ra:
Câu 55. Phương trình có bao nhiêu nghiệm phức với phần ảo âm?
A. 0 B. 1 C. 3 D. 2
2
2
3
2
z
z
=
⇔
= −
1,2 3,4
3; 2z zi=±=±
1234
| || || || |2322zzzz+ + += +
z
23
zi
zi
=
= −
2
53
zi
zi
=
= +
23
zi
zi
= −
= +
3
25
zi
zi
=
= −
z
z
(
)
2
0
2, 3 2 3
)03
iz
a bi
zi zi
ab
i
zi
=−=−
=
⇔ ⇔⇔
= = = +
=
+
−− +
12
;zz
2
4 70zz+ +=
22
12
zz
+
22
2 22 2
12
23
4 4 3 ( 2) 3 2.( 4 3) 14
23
zi
zz z i zz
zi
=−+
+ + =−⇔ + = ⇔ ⇒ + = + =
=−−
1
z
2
z
1
z
2
z
2
2 50zz+ +=
22
12
Az z= +
25
A
=
10A =
10A =
2 10A =
1
2
2
12
2 50
12
zi
zz
zi
=−+
+ +=⇔
=−−
22
22
22 2 2
12
(1) 2 (1) (2) 10Az z= + =−+ +−+− =
3
8z =

Bài tập trắc nghiệm số phức
Trang 144
Hướng dẫn giải
Đáp án: B
Câu 56. Gọi là nghiệm của phương trình sau trên tập số phức:
.Khi đó, tổng có giá trị bằng
A. B. C. 0 D. 4
Hướng dẫn giải
Đáp án: A
Đặt
Phương trình trở thành:
Câu 57. Nghiệm của phương trình là
A. –1 + i, 2 – i B. 1 + i, 2 + i C. –1 + i, 2 + i D. –1 – i, 3 – i
Hướng dẫn giải
Đáp án: A
Câu 58. Phương trình
2
4 50xx+ +=
có nghiệm phức và tổng các mô đun của chúng là:
A.
22
B.
23
C.
25
D.
27
Hướng dẫn giải
Đáp án: C
22
4 5 0; ' 4 5 1xx i+ + = ∆= − =−=
12
2; 2x ix i
⇒ =−− =−+
Mô đun của
12
,xx
đều bằng
22
21 5+=
=> Tổng các môđun của x
1
và x
2
bằng
25
(
)
( )
32
8 2 24z z zz=⇔− ++
2
2
2
13
24
13
z
z
zi
zz
zi
=
=
⇔ ⇔ =−+
++
=−−
1234
,,,
zzzz
( ) ( )
2
2 22
36 2 363 0zz zzz z++ + ++− =
1234
zzzz+++
8−
4−
2
36
tz z=++
22
2z 3z 0 ( )( 3z) 0t t t zt+ − =⇔− + =
22
1,2
22
3,4
15
3 6 2 60
3
3 6 3 6 60
33
zi
tzzzzzz
tz
zz z zz
z
=−±
= + += + +=
⇔⇔ ⇔ ⇔
= −
+ +=− + +=
=−±
( )
(
)
(
)
( )
1234
151533338
zzzz i i+ + + =−+ +−− +−+ +−− =−
2
13 0
zz i− −+ =
2
1
2
(3 2 )
1
2
i
xi
xi
∆= −
=−+
= −

Bài tập trắc nghiệm số phức
Trang 145
Câu 59. Kí hiệu là hai nghiệm của phương trình . Tính
A. B. C. D.
Hướng dẫn giải
Đáp án: C
. Khi đó
Có thể dùng Viét nhanh hơn, nhưng không có cơ sở lí luận
Câu 60. Gọi và là hai nghiệm của phương trình .Tính
A. B. C. D.
Hướng dẫn giải
Đáp án: C
Vì : PT có hai nghiệm phức
Câu 61. Nghiệm của phương trình: trên tập số phức là:
A. B. C. D.
Hướng dẫn giải
Đáp án: A
Câu 62. Các nghiệm của phương trình: trên tập số phức là:
A. B. C. D.
Hướng dẫn giải
Đáp án: C
;
12
zz
2
8 20 0zz++ =
12
11
zz
T
+
=
2
5
Ti= −
8T = −
2
5
T = −
5
2
T
= −
2
42
8 20 0
42
zi
zz
zi
=−+
++=⇔
=−−
12
11 1 1 2
42 42 5zz i i
T
+= + =−
−+ −−
=
1
z
2
z
2
2 30zz++=
12
M zz= +
1
2
M = −
23
2
M
= −
1
2
M =
23
2
M =
2
2 30zz++=
2
23 23i∆=− =
1 23 1 23
;
44 44
z iz i=−+ =−−
12
11
22
M zz⇒ =+ =−=
2 35 4ix x i+= +
23 14
29 29
i−
23 14
29 29
i
+
54i−
73i+
(
)( )
34 52
3 4 23 14
5 2 29 29 29
ii
i
xi
i
−+ −−
−+
= = = −
−+
2
2 3 20xx− +=
3535
;
44
ii−+
3737
;
44
ii−+
77
33
;
44
ii−+
77
33
;
22
ii−+

Bài tập trắc nghiệm số phức
Trang 146
Có
Câu 63. Các nghiệm của phương trình: trên tập số phức là:
A. B. C. D.
Hướng dẫn giải
Đáp án: D
Câu 64. Nghiệm của phương trình là
A. B.
C.
D.
Hướng dẫn giải
Đáp án: A
Câu 65. Kí hiệu là hai nghiệm của phương trình , với có phần ảo âm. Tìm số
phức nghịch đảo của số phức .
A. B.
C. D.
Hướng dẫn giải
Đáp án: B
Kí hiệu là hai nghiệm của phương trình , với có phần ảo âm. Tìm số phức nghịch đảo
của số phức .
Câu 66. Gọi là hai nghiệm của phương trình . Tính
2
2 3 20xx− +=
7∆=−
37
4
37
4
i
x
i
x
−
=
⇒
+
=
4
40z −=
2; 2i±±
2±
2
i±
2; 2i±±
2
4
2
22
4
2
2
zz
z
z
zi
= = ±
=⇔⇔
= −
= ±
2
20x
+=
2i±
2i
±
2±
2
22
20 2 2x x xi+ = ⇔ =−⇔ =±
12
;zz
2
2 3 40zz− +=
1
z
12
23
wz z= −
1 3 5 23
146 146
i
w
= +
1 3 5 23
146 146
i
w
=−+
1 3 5 23
146 146
i
w
=−−
1 3 5 23
146 146w
=−+
12
;zz
2
2 3 40zz− +=
1
z
12
23wz z= −
1
2
12
2
3 23
1 3 5 23
44
2 3 40
2 3 146 146
3 23
44
zi
zz i
zz
zi
= −
− +=⇔ ⇒ =− +
−
= +
12
,zz
2
3 60zz−+=
33
12
Az z= +

Bài tập trắc nghiệm số phức
Trang 147
A. B. C. D.
Hướng dẫn giải
Đáp án: D
Câu 67. Số nghiệm của phương trình:
A. B. C. D.
Hướng dẫn giải
Đáp án: C
Thủ thuật chia số phức
Nhẩm . Suy ra phương trình có nghiệm
Tách bằng máy tính
Được kết quả:
Có 3 nghiệm
Câu 68. Số lượng các số phức thỏa mãn có phần thực âm là
A. B. C. D.
Hướng dẫn giải
Đáp án: C
Ta có
z có phần thực âm .
Câu 69. Phương trình có hai nghiệm phức . Khẳng định nào sau đây sai:
A. B. là số phức liên hợp của
5,8075−
3 54
9
−+
3 54
9
+
−
3 54
9
−
( )
3
3
33
1 2 12 1212
1 6 1 54 3
3( ) 3.
9
3 33
Az z zz zzzz
−+
=+= + − + = − =
(
)
32
21 31 0z i z iz i− + + +−=
1
2
3
4
0ABCD+++ =
1z
=
( )
32
21 3 1
: 1000
1
X i X iX i
calc X
X
− + + +−
+=
−
( ) ( )
22
998999 1999 1 2 1 1 2 1i z z z i z iz i− → − −− − = − + −+
( ) (
) ( )
( )
( )
(
)
( )
( )
32 2
2
2
2 1 3 1 1 12 1 0
1
1
12 1 0 12 4 1 1
z izizizz izi
z
zi
z iz i i i
zi
→ − + + +−= − − + −+ =
=
↔
= +
− + − + = ↔∆= − + − − + = ↔
=
z
3
1z =
0
1
2
3
( )
( )
33 2
1
1 10 1 1 0
13
22
z
z z z zz
z
=
=↔ −= ↔ − ++ = ↔
=−±
13
22
z↔=−±
2
2 26 0zz++=
12
,zz
12
. 26zz =
1
z
2
z

Bài tập trắc nghiệm số phức
Trang 148
C. D.
Hướng dẫn giải
Đáp án: D
Theo định lí Viete dễ thấy A, D đúng. B cũng đúng vì hai nghiệm luôn có dạng .
Câu 70. Gọi là nghiệm phức có phần ảo âm của phương trình . Giá trị của
bằng
A. 3 B. 9 C. D.
Hướng dẫn giải
Đáp án: A
Ta có
Suy ra . Do đó
Câu 71. Giải phương trình trên tập số phức. Tìm tập nghiệm S.
A. B. C. D.
Hướng dẫn giải
Đáp án: A
Câu 72. Phương trình cho ta nghiệm :
A. B. C. D.
Hướng dẫn giải
Đáp án: A
Phương trình tương đương với
Câu 73. Gọi là các nghiệm phức của phương trình . Giá trị của biểu thức
là:
A. 1 B. –1 C. D.
12
2zz+=−
12
zz>
1,2
2
bi
z
a
−± ∆
=
1
z
2
2 30zz+ +=
2
1
Az=
122−−
122−+
2
12
2 30
12
zi
zz
zi
=−+
+ +=⇔
=−−
1
12zi=−−
( )
2
1 2 1 22 3Ai i= −− =−+ =
( )
2
34 5 10x ix i
− + + −=
{ }
1; 3 2Si i=++
{ }
1Si= +
{ }
32Si= +
{ }
1; 3 2;Si i i=++
(
) ( )
( )
2
1
34 5 10 1 3 2 0
32
xi
x ix i x i x i
xi
= +
− + + −= ⇔ −− − − = ⇔
= +
(1 2 ) 3ix x i+=−
11
44
i−+
13i
+
1
2
i
1
2
2
i−
( )
23ix x i1+ = −
( )
( )
23 . .
22 2 2 2 4 4
ii
ii
i xix i
ii
− − −1
− 1 − 1 11
1+ − = − ⇔ = = = =− +
− + −1+
12
,zz
2
4 50zz− +=
( ) ( )
2011 2011
12
11
Pz z=− +−
1006
2
1006
2−

Bài tập trắc nghiệm số phức
Trang 149
Hướng dẫn giải
Đáp án: D
Cách 1: Bấm máy tính ta được .
Cách 2: Xét phương trình .
Ta có , suy ra .
Suy ra
Câu 74. Giải phương trình trên tập số phức:
A. B. C. D.
Hướng dẫn giải
Đáp án: B
Ta có:
Câu 75. Gọi là các nghiệm phức của phương trình . Tính giá trị của biểu
thức:
A. B. C. D. 2
Hướng dẫn giải
Đáp án: A
Giải phương trình ta được bốn nghiệm:
. Do đó ta có:
1
2
2
2
zi
zi
= +
= −
2
4 50zz− +=
2
'1i∆=−=
12
2, 2
z iz i=+=−
(
) (
)
( ) ( )
( )
( )
(
) ( )
( )
(
) (
)(
)
(
) (
)
( )
2011 2011 2011 2011
12
1005 1005
22
1005 1005
1005 1005
1005 1006
1 11 1
11 11
12 1 2
21 21
2 112
Pz z i i
ii ii
ii i i
ii ii
ii
= − + − =+ +−
=+ + +− −
=+ +− −
= +− −
= −−− =−
32
10zzz+ ++=
{ }
1;
Si= −
{
}
1;
Si=−±
{
}
0S =
{ }
1;Si= ±
(
)
( )
32 2
2
10 1 1 0
1
1
1
zzz z z
z
z
zi
z
zi
+ ++= ⇔ + + =
= −
= −
⇔ ⇔=
= −
= −
1234
;;;zzzz
42
5 40zz+ +=
1234
1111
1111
S
zzzz
=+++
−−−−
7
5
2
5
1
;2ii±±

Bài tập trắc nghiệm số phức
Trang 150
Câu 76. Căn bậc hai của số phức
4 65
i+
là:
A.
12
35, 35z iz i= − =−−
B.
12
3 5, 3 5
z iz i= + =−−
C.
12
3 5, 3 5z iz i=+=−
D.
12
35, 35z iz i= + =−+
Hướng dẫn giải
Đáp án: B
Bấm máy tính
Câu 77. Một căn bậc hai của số phức là:
A. B. C. D.
Hướng dẫn giải
Đáp án: C
Ta có:
Câu 78. Tìm căn bậc hai của mỗi số phức sau :
A. B. C. D.
Hướng dẫn giải
Đáp án: A
Gọi là một căn bậc hai của , ta có
Thay vào ta được
(nhận) (loại)
(
)(
)
( )
( )
11 1 1
1 1 12 12
2 2 227
1 1 12 12 2 5 5
S
ii i i
S
ii i i
=++ +
+− − +
= + =+=
+− − +
15 8zi= +
15 4i+
4 i−
4 i+
15 4i−
( )
( )
2
22
22
12
15 8 2
4; 1
15
4; 1
2 18
4; 4
z i a bi a b abi
ab
ab
ab
ab
w iw i
=+= + − − +
=−=−
−=
⇔⇔
= =
=
⇒ =−− = +
1 43i+
(2 3 )i±+
(3 3 )i±+
(2 3 )i±−
(3 2 )i±+
( )
,x iy x y
+∈
1 43i+
( )
( )
( )
22
2
22
11
2 1 43
232
xy
x iy x y xyi i
xy
−=
+ =−+ =+ ⇔
=
( )
( )(
)
23
2 03
yx
x
⇒= ≠
(
)
3
( )
1
2 42
2
12
1 12 0x xx
x
− =⇔−−=
2
4x
⇔=
2
3x = −

Bài tập trắc nghiệm số phức
Trang 151
* Với thì
* Với thì
Vậy căn bậc hai của là
Câu 79. Số nào sau đây là căn bậc 2 của:
A. 2 + i B. 2 – i C. 3 + i D. 3 – i
Hướng dẫn giải
Đáp án: A
Gọi số phức cần tìm là a +bi
Câu 80. Số phức z thỏa mãn:
( ) ( )
( )
3 2 41 2iz i iz− − −= +
. Mô đun của z là :
A.
3
B.
5
C.
10
D.
3
4
Hướng dẫn giải
Đáp án: C
Phân tích: Đặt
( )
;z x iy x y z x iy=+ ∈ ⇒=−
Vậy phương trình trở thành:
( ) (
) ( ) (
) ( )
3 2 . 41 2 .i x iy i i x iy− − − −= + +
( )
22
3 2 3 2 44 2 2x ix iy i y i x iy ix i y⇔ − − + −+ = + + +
( )
22
3 2 2 4 2 3 42 0x x i y i y ix iy i iy ix⇔ − + − − +− − + − − =
(
) ( )
4 3540xy i x y⇔ −− +− − + =
40 3
3 5 40 1
xy x
xy y
−−= =
⇔⇔
− − += =−
( )
2
2
3 3 1 10z iz⇒ = −⇒ = +− =
Câu 81. Tính
z
biết:
5
(1 )(3 2 )
(2 )
iz
zii
i
=+ −−
+
2x =
3y =
2x = −
3y = −
1 43i+
( )
23i
±+
34i+
34a bi i+= +
⇔
22
22
2
1
3
2 34
24
2
1
a
b
ab
a b abi i
ab
a
b
=
=
−=
−+ =+⇔ ⇔
=
= −
= −

Bài tập trắc nghiệm số phức
Trang 152
A.
17
2
B.
17
C.
1
2
2
i+
D.
1
2
2
i
−+
Hướng dẫn giải
Đáp án: A
Đặt
;,z a bi a b R=+∈
. Ta có:
5
(1 )(3 2 )
(2 )
iz
zii
i
=+ −−
+
5 (2 )( ) 5 (1 2 )( )
5 2 ( 2) 0 5 2 2 (1 2) 0
1
52 2 0
2
12 0
2
a bi i i i a bi a bi i i a bi
a bi i a b b ai a b ai
ab
a
a
b
⇔ + = +− − − ⇔ + = +− + −
⇔+=+−−+− =⇔−−+− =
−−=
=
⇔
−=
=
Vậy
22
17
2
z ab
= +=
Vậy đáp án đúng là A.
Câu 82. Cho số phức z thỏa mãn điều kiện
2 34zz i−=+
. Phát biểu nào sau đây là sai:
A. z có phần thực là –3 B.
4
3
zi+
có modun là
97
3
C. z có phần ảo là
4
3
D. z có modun là
97
3
Hướng dẫn giải
Đáp án: B
Đặt
( )
,, 2 2 2z x yi x y z x yi z x yi= + ∈ ⇒ = − ⇒− =− +
3
3
2 2 34 3 34
4
34
3
x
x
x yi x yi i x yi i
y
y
= −
−=
+−+ =+⇔−+ =+⇔ ⇔
=
=
Vậy
( )
2
2
4 4 97 97
33
3 3 93
z iz
=−+ ⇒ = − + = =
Câu 83. Tìm số phức z thỏa mãn điều kiện:
2
(1 3 )
1
iz i z
z
i
−
−+
=
+
A.
45 9
26 26
zi= −
B.
45 9
26 26
zi= +
C.
45 9zi= +
D.
45 9i−−
Hướng dẫn giải
Đáp án: A
Cách 1: Sử dụng máy tính fx–570VN PLUS.
Bài tập trắc nghiệm số phức
Trang 153
Nhập biểu thức trên vào, lưu ý:
+ Để biểu diễn mô đun số phức ta nhập SHIFT Abs
+ Để biểu diễn
z
trên máy tính cầm tay ta ấn SHIFT 2(CMPLX) máy sẽ hiện như sau:
Chọn 2: Conjg là biểu diễn số phức liên hợp của số phức.
Vậy biểu diễn biểu thức như sau:
Sau đó CALC rồi nhập từng giá trị vào: Thử vào ta được A là đáp án do kết quả bằng 0, máy hiện như sau:
Cách 2: Nhận thấy ở đây mẫu số đang ở dạng số phức, do đó chúng ta sẽ vẫn liên hợp để bài toán trở nên đơn
giản hơn.
Gọi
( , )z a bi a b=+∈
. Ta có:
2 22
(1 3 ) 4 ( 2 )
11
iz i z a b b a i
z ab
ii
− + −− + −
=⇔=+
++
22
[ 4 ( 2 ) ](1 )
2
a b b ai i
ab
−− + − −
⇔=+
22
3 3 (5 ) 2( )a b b ai a b⇔− − + − = +
22
50
3 3 2( )
ba
ab ab
−=
⇔
−− = +
2
0
45
5
26
26 9 0
9
26
ab
ab
a
bb
b
= =
=
= −
⇔⇔
+=
−
=

Bài tập trắc nghiệm số phức
Trang 154
Vậy ta chọn A.
Câu 84. Tìm tất cả các số thực m biết
1 ( 2)
im
z
mm i
−
=
−−
và
2
.
2
m
zz
−
=
trong đó i là đơn vị ảo.
A.
0
1
m
m
=
=
B.
1
m
= −
C.
0
1
m
m
=
= −
D.
m∀
.
Hướng dẫn giải
Đáp án: A
Phân tích: Vì z đang còn rất phức tạp, đặc biệt là dưới mẫu do đó chúng ta nghĩ ra việc làm đơn giản nó về
dạng chuẩn
( , )z a bi a b=+∈
sau đó tìm được
z
và thay vào biểu thức
.zz
Ta có
2 2 22
22 2 22
(1 )(1 2 ) (1 ) 2 (1 2 )
1 ( 2 ) (1 ) 4 (1 )
i m m m mi m m m i m m
z
mm i m m m
− − −− −− ++−+
= = =
−− −+ +
22
22 2 2
(1 ) (1 )
(1 ) 1 1
mmim m i
m mm
+ ++
= = +
+ ++
22
11
mi
z
mm
⇒= −
++
Như vậy:
2
22
2 11
. ( 2)
2 ( 1) 2
mm
zz m
m
−+
= ⇒ =−−
+
2
11
( 2)
12
m
m
⇔ =−−
+
32
0
20
1
m
m mm
m
=
⇔ − +=⇔
=
Câu 85. Cho hai số phức z
1
; z
2
thỏa mãn
1
1
2
2
iz +=
và
21
z iz=
. Tìm giá trị nhỏ nhất của biểu thức
12
zz−
A.
1
2
2
−
B.
1
2
2
+
C.
1
2
2
−
D.
1
2
2
+
Hướng dẫn giải
Đáp án: A
Phân tích: Bài toán này thực chất là dựa trên kiến thức “Biểu diễn hình học số phức”. Ta thấy nếu đặt
111
z x yi
= +
1; 1
(; )xy∈
. Khi đó điểm
1; 1
(;)Mx y
là điểm biểu diễn số phức z
1
thỏa mãn:
11 11
11
( )2 2
22
i x y i ix y++=⇔−+=
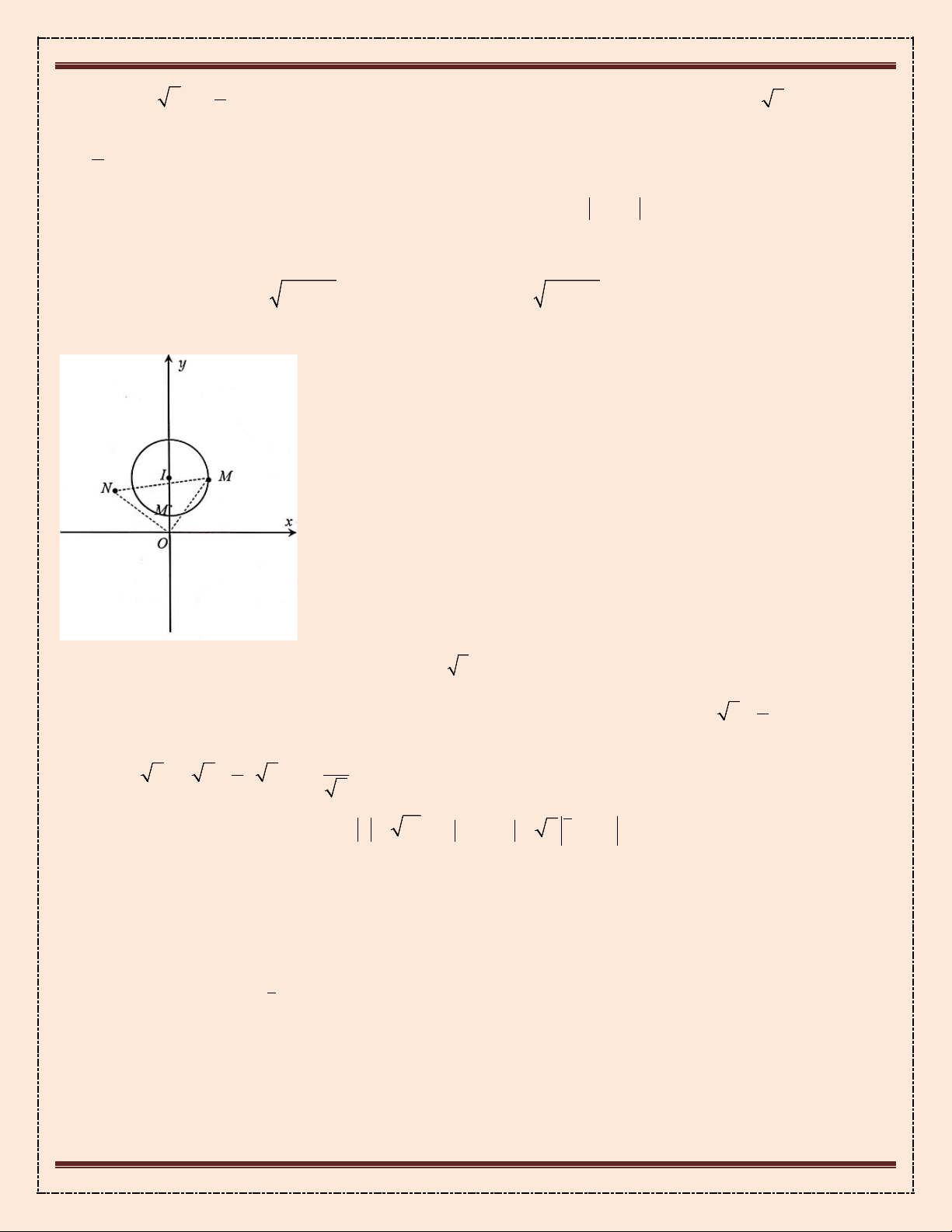
Bài tập trắc nghiệm số phức
Trang 155
22
11
1
( 2)
4
xy⇔+ − =
. Suy ra tập hợp các điểm M biểu diễn z
1
là đường tròn (C) có tâm
(0; 2)
I
và bán kính
1
2
R =
.
Khi đó nếu N là điểm biểu diễn của số phức z
2
thì việc tìm GTNN của
12
zz
−
là việc tìm GTNN của MN.
Theo đề thì
( )
2 1 1 1 11
;z iz y x i N y x= =−+ ⇒ −
là điểm biểu diễn z
2
. Ta nhận thấy rõ ràng
22
11 11 1 1
.0OM ON x y x y x y=+=⇒+
. Dễ nhận thấy OM=ON=
22
11
xy+
Ta có hình vẽ sau:
Do OMN là tam giác vuông cân tại O nên MN=OM
2
, do đó để MN nhỏ nhất thì OM nhỏ nhất. Dễ thấy, OM
nhỏ nhất khi M≡M’ (M’ là giao điểm của OI với đường tròn như hình vẽ). Tức là
1
0; 2
2
M
−
. Khi đó
11
2 2 22
2
2
MN OM
= =−=−
Câu 86. Tìm số phức z thỏa mãn
13z =
và
2 21z i zi+ − = +−
A.
32zi= ±
B.
32zi= −
C.
23
i±
D.
32
zi=±−
Hướng dẫn giải
Đáp án: C
Gọi
,( , )z a bi a b R z a bi=+ ∈ ⇒=−
Theo giả thiết:

Bài tập trắc nghiệm số phức
Trang 156
22
2
22 22
13
13
2 21
( 2) ( 1) 2 ( 1) ( 1)
13
3
9
2
2
( 2) ( 1) 2. ( 2) ( 1)
z
z
z i zi
a bi a bi
ab
a
a
b
b
ab ab
=
=
⇔
+ − = +−
+ + − = +− +
+=
= ±
=
⇔⇔
= −
= −
+ +− = + ++
Vậy
32zi=−−
hoặc
32zi= −
Đáp án đúng là C.
Câu 87. Cho số phức z thỏa mãn
2
2
1
zi
zi
+−
=
+−
. Tìm trung bình cộng giá trị nhỏ nhất và lớn nhất của
z
.
A.
3
B.
10 3±
C.
2 10
D.
10
Hướng dẫn giải
Đáp án: D
Phân tích:
Giả sử
(, )z x yi x y=+∈
. Từ giả thiết suy ra:
22 22
22
2
2 2 ( 1) 2 1 ( 1)
1
( 2) ( 1) 2( 1) ( 1)
( 3) 10
zi
x yi x yi
zi
x y xy
xy
+−
= ⇔ + + − = +− +
+−
⇔+ +− = + ++
⇔++ =
Tập hợp biểu diễn của z là đường tròn tâm
(0; 3)I −
, bán kính
10R =
Gọi M là điểm biểu diễn của z. Ta có:
10 3 10 3IM IO OM IM OI OM−≤≤+⇔−≤≤+
min
min
max
max
min max
10 3
10 3
( 10 3) 10 3)
10
22
z OM
z OM
zz
⇔=−
⇔=+
+
−+
⇒= =
Vậy đáp án đúng là D.
Sai lầm thường gặp: Không hiểu thế nào là trung bình cộng và nhầm tưởng sang tổng của hai số có thể gây ra
đáp án C.
Câu 88. Tính phần ảo của số phức z, biết
3
12z iz+=
và z có phần thực dương.
A.
2
B.
5
C.
1−
D.
i−
Hướng dẫn giải
Đáp án: C

Bài tập trắc nghiệm số phức
Trang 157
Ta có:
;( , )z x yi x y=+∈
33
32
3 2 23
23
12 ( ) 12
3 (1)
3 (3 12)
3 12 (2)
z i z x yi i x yi
x xy x
x xy x y y i x yi
xy y y
+=⇔+ +=−
−=
⇔− + −+ =−⇔
−+=−
Do
22
0 31x xy>⇒ = +
. Thế vào (2) ta được
23 3
3(3 1) 12 2 3 0(3)
y yy y y y+ − + =−⇔ ++=
Giải (3) ta được:
2
14yx
=−⇒ =
. Do
0x >
nên
2x =
Vậy
2 Im( ) 1zi z
= −⇒ =−
Đáp án đúng là C.
Câu 89. Cho số phức z thỏa mãn
( )
3 76
i z iz i+ −=−
. Môđun của số phức z bằng:
A.
25
B. 25 C. 5 D.
5
Hướng dẫn giải
Đáp án: D
Việc sử dụng máy tính Casio trong bài toán này duy nhất chỉ có thể ở bước thử lại đáp án. Để giải quyết bài
toán chúng ta cần giải phương trình đã cho theo phương pháp “cổ điển”:
Đặt
( )
;z a bi a b R=+∈
. Phương trình đã cho tương đương:
( )
3 76z iz z i+ −=−
( )
( )
3 .2 7 6a bi i bi i⇔ ++ =−
3 2 3 76a b bi i⇔−+ =−
327 1
36 2
ab a
bb
−= =
⇔⇔
=−=−
Suy ra mô đun số phức z là
22
12 5z = +=
Câu 90. Tìm phần ảo của số phức z biết:
1
1
z
z
−
+
là một số thực?
A. 1 B. 0 C. –1 D. 2
Hướng dẫn giải
Đáp án: B
Đặt z=a+bi;
( )
;ab∈
Ta có:
[
][ ]
22
11
11
1 1 ( 1)
a bi a bi
z a bi
z a bi a b
−+ +−
− −+
= =
+ ++ + +
Do
1
1
z
z
−
+
là số thực nên
22
2
00
( 1)
b
b
ab
=⇔=
++

Bài tập trắc nghiệm số phức
Trang 158
Câu 91. Tìm số phức z biết
2
. 29, 21 20zz z i
= =−−
, phần ảo z là một số thực âm.
A.
25zi=−−
B.
25zi= −
C.
52zi= −
D.
52zi=−−
Hướng dẫn giải
Đáp án: B
Đặt
( )
, ,0z a ib a b b
=+ ∈<
Ta có:
(
)
(
)
( )
22
22
2 22
. 29 1
21 2
2 21 20
2 20 3
zabi zza b
ab
z a b abi i
ab
=−⇒ = + =
−=−
= − + =−− ⇔
= −
(1) trừ (2), ta có
2
2 50b =
mà
0b <
nên
5b = −
Thay
5b
= −
vào (3) ta được
2a =
Vậy
25zi
= −
Câu 92. Cho số phức z thỏa mãn:
28
zz i+=−
. Tìm số phức liên hợp của z.
A.
15 8i−+
B.
15 6
i
−+
C.
15 2i−+
D.
15 7i−+
Hướng dẫn giải
Đáp án: A
Đặt
( )
22
,,z a bi a b z a b=+ ∈ ⇒= +
Khi đó
22 22
28 28 28z z i a bi a b i a a b bi i+=−⇔++ + =−⇔+ + +=−
22
15
2
8
8
a
a ab
b
b
= −
+ +=
⇔⇔
= −
= −
Vậy
15 8 15 8z iz i
=−−⇒=−+
Câu 93. Tìm phần thực, phần ảo của các số phức z, biết:
10
13
zz
z
+=
=
A. Phần thực bằng 5; phần ảo bẳng 12 hoặc bằng –12.
B. Phần thực bằng 5; phần ảo bẳng 11 hoặc bằng –12.
C. Phần thực bằng 5; phần ảo bẳng 14 hoặc bằng –12.
D. Phần thực bằng 5; phần ảo bẳng 12 hoặc bằng –1.
Hướng dẫn giải
Đáp án: A
Giả sử
( )
,
z x yi z x yi x y=+ ⇒=− ∈
Bài tập trắc nghiệm số phức
Trang 159
Theo đề ta có:
22
2 10
5
12
13
x
x
y
xy
=
=
⇔
= ±
+=
Câu 94. Tìm số phức
z
biết số phức z thỏa:
1
1
3
1
z
zi
zi
zi
−
=
−
−
=
+
A.
1zi= +
B.
1zi= −
C.
1zi=−−
D.
1zi=−+
Hướng dẫn giải
Đáp án: B
Đặt
z a bi= +
với
,ab∈
. Ta có:
( ) ( )
22
22
1
11 1 1 0
z
z zi a b a b ab
zi
−
=⇔ −= −⇔ − + = + − ⇔−=
−
( ) ( )
22
22
1
3
1 3 11
1
a
zi
ab ab b
b
zi
=
−
=⇔ +− =++ ⇔=⇒
=
+
. Vậy
1zi= −
Câu 95. Cho số phức z thỏa mãn
( )
2 35z iz i++ =+
. Tính môđun của số phức z
A.
13z =
B.
5z =
C.
13
z
=
D.
5z
=
Hướng dẫn giải
Đáp án: A
Gọi
( )
,z a bi a b=+∈
Ta có:
( ) (
)(
)
2 35 2 35
z i z i a bi i a bi i++ =+⇔+++ − =+
( ) ( )
33 2
2 2 35 3 35
53
ab a
a bi a b ai bi i a b a b i i
ab b
+= =
⇔++ ++− =+⇔ ++− =+⇔ ⇔
−= =−
(
)
2
2
2 3 2 3 13z iz
= − ⇒ = +− =
Câu 96. Cho số phức z thỏa
( )
23 19z iz i−+ =−
. Khi đó
.zz
bằng:
A. 5 B. 25 C.
5
D. 4
Hướng dẫn giải
Đáp án: A
Gọi
( )
,z a bi a b z a bi=+ ∈ ⇒=−
( ) ( )
( )( ) ( )
23 19 23 19 2 2 3 19a ai+3bz i z i a bi i a bi i a bi bi i−+ =−⇔ + −+ − =−⇔+− − + =−

Bài tập trắc nghiệm số phức
Trang 160
( ) ( )
31 2
3 3 3 19
33 9 1
a
ab a
a b bi i
ab b
−− = =
⇔− − +− + = − ⇔ ⇔
−+ =− =−
Suy ra
22
2 2 . 215z iz izz= −⇒ = +⇒ = + =
Câu 97. Cho số phức z thỏa mãn
( )
2
1 2 4 20izz i+ += −
. Mô đun của z là:
A.
3z =
B.
4z =
C.
5z =
D.
6
z
=
Hướng dẫn giải
Đáp án: C
Gọi
(
)
,
z a bi a b z a bi== ∈ ⇒=−
( )
( )
( ) ( )
2
2
1 2 4 20 1 4 4 4 20i z z i i i a bi a bi i+ += − ⇔+ + + + − = −
( )( ) ( )
2
3 4 4 20 3 3 4 4 20 4i a bi a bi i a bi ai bi a bi i⇔−+ + +− =− ⇔−− + + +−=−+
2 4 20 4
444 3
ab a
ab b
−− =− =
⇔⇔
−= =
Ta có
22
43 5z = +=
Câu 98. Cho số phức z thỏa mãn điều kiện . Tính
A. 1 B. C. 3 D.
Hướng dẫn giải
Đáp án: C
Đặt z = a + bi
Câu 99. Biết rằng nghịch đảo của số phức z bằng số phức liên hợp của nó, trong các kết luận sau, kết
luận nào là đúng ?
A. B. C. z là số thuần ảo D.
Hướng dẫn giải
Đáp án: B
Gọi z= a+bi
23zz i+=+
21A iz i=++
( )
2; 3;1−
5
z a bi⇒=−
( )
( )
23
23
1
1
zz i
a bi a bi i
a
b
+=+
⇔ + +− =+
=
⇔
=
213 3A iz i i
=+== =
zR∈
1z =
1z = −

Bài tập trắc nghiệm số phức
Trang 161
GPT:
Câu 100. Tìm số phức z thỏa mãn và là số thực
A. B.
C. D.
Hướng dẫn giải
Đáp án: A
Gọi , ta có :
Để thực thì
Xét hệ (1) và (2) có đáp số :
Câu 101. Nếu môđun của số phức z bằng r (r > 0) thì môđun của số phức
( )
2
1 iz−
bằng:
A. 4r B. 2r C.
2
r
D. r
Hướng dẫn giải
Đáp án: B
Giả sử
(, )z a bi a b=+∈
Môđun của số phức z bằng r (r > 0)
22
ab r⇒ +=
Số phức
( )
2
1 22i z b ai− =−+
Môđun của số phức
( )
2
1
iz−
bằng:
Câu 102. Tìm số các số phức
z
thỏa mãn đồng thời hai điều kiện
2z =
và
2
z
là số thuần ảo.
A.
1
B.
2
C.
3
D.
4
Hướng dẫn giải
22
1
11a bi a b z
a bi
=−⇔ + =⇔=
+
1z zi
+= +
1
z
z
+
11 11
;
22 22
z iz i=+ =−−
11 11
;
22 22
z iz i=− =−+
11 11
;
33 33
z iz i=+ =−−
11 11
;
33 33
z iz i=− =−+
( )
,,z a bi a b=+∈
( )
1 1z zi ab+= +⇔ =
22 22
11ab
z a bi a b i
z abi ab ab
+=++ =+ + −
++ +
1
z
z
+
( )
22
0 2
b
b
ab
−=
+
1
2
1
2
ab
ab
= =
= = −
2 2 22
( 2 ) (2 ) 2 2b a ab r− + = +=

Bài tập trắc nghiệm số phức
Trang 162
Đáp án: D
Đặt
, a,bz a bi=+∈
Ta có
22
22
21
1
0
ab a
b
ab
+= =±
⇔
= ±
−=
1 ; z=-1+i; z=-1-i; z=1-izi= +
Câu 103. Cho số phức z thỏa mãn hệ thức
2
( 3) (2 ) .
i
i z iz
i
+
++ =−
Tính mô đun của số phức .
A.
26
5
B.
6
5
C.
25
5
D.
26
25
Hướng dẫn giải
Đáp án: A
Bấm máy tính
Câu 104. Cho số phức Z thỏa mãn ( 1 + 2i)Z + ( 1 – 2 ) i = 1+ 3i . Khi đó mô đun của số phức Z là :
A. B. C. 11 D. 85
Hướng dẫn giải
Đáp án: B
Giả sử z = a + bi ; a,b ,
Từ giả thiết ( 1 + 2i)Z + ( 1 – 2 ) i = 1+ 3i
Ta có : ( 1 + 2i)( a+ bi ) + ( 1 – 2 ) i = 1+ 3i
Z= 9 + 2i
Câu 105. Số phức Z có mô đun nhỏ nhất sao cho : là:
A. B. C. D.
Hướng dẫn giải
Đáp án: C
Khi đó :
w zi= −
Z
11
85
∈
Z a bi
= −
Z
( )
a bi
−
41 9
4 ( 1) 1 3
13 2
ab a
a bb i i
bb
−= =
⇔− + + =+ ⇔ ⇔
+= =
34ZZ i= −+
3
2
2
zi=−−
3
2
2
zi=−+
3
2
2
zi= +
3
2
2
zi
= −
;,z x yi x y
=+∈
34 34z z i x yi x yi i
= −+ ⇔ + = − −+
( )
34x yi x y i⇔ + = −+ −
25 6
6 8 25 0
8
x
xy y
−
⇔+−=⇔=

Bài tập trắc nghiệm số phức
Trang 163
Ta có :
Số phức z có mô đun nhỏ nhất đạt được khi
Vậy
Câu 106. Trong các số phức z thỏa mãn điều kiện .Tìm số phức z có môđun nhỏ nhất.
A. B. C. D.
Hướng dẫn giải
Đáp án: C
Gọi
Ta có
Suy ra
Câu 107. Số phức z nào sau đây có môđun nhỏ nhất thỏa :
A. B. z = –3 – 4i C. D.
Hướng dẫn giải
Đáp án: C
Gọi z = a + bi => ;
–6a + 8b + 25 = 0(*)
Trong các đáp án, có đáp án A và C thỏa (*).
Ở đáp án A: |z| = 25/8 ; Ở đáp án C: |z| = 5/2.
Câu 108. Số phức thỏa là
A. B. C. D.
Hướng dẫn giải
Đáp án: C
Gọi z=a+bi
Ta có
( )
2
2
22
25 6 1 1 5
100 300 625 10 15 400
88 8 2
x
Zx x x x
−
=+ = − += −+≥
3
;2
2
xy= =
3
2
2
zi= +
24 2z izi−− = −
1
zi=−+
22zi=−+
22zi= +
32zi
= +
(, )z x iy x y=+∈
22
2 4 2 2 ( 4) ( 2) 4 1 1z izi x y ixy i xy xy−− = − ⇔ −+ − = + − ⇔+ =≤ + +
22
min
22 22 2 2z x y z khi z i
= +≥ ⇒ = =+
| || 3 4|zz i= −+
7
3
8
zi= −
3
2
2
zi=−−
3
2
2
zi
= +
z a bi= −
| || 3 4|zz i= −+
z
( )
23 19z iz i−+ =−
3zi=−−
z= 2 i−−
z=2 i−
z=2 i+
z a bi⇒=−
( )( ) ( ) ( )
23 19 3 3 3 19a bi i a bi i a b a b i i+ − + − = − ⇔− − +− + =−
31 2
33 9 1
ab a
ab b
−− = =
⇒⇒
−+ =− =−

Bài tập trắc nghiệm số phức
Trang 164
Câu 109. Cho số phức z thỏa mãn: . Tìm giá trị nhỏ nhất của ?
A. . B. . C. . D. .
Hướng dẫn giải
Đáp án: C
Gọi
Dấu = xảy ra khi và chỉ khi . Vậy Min|z| =
Câu 110. Cho số phức z = a + bi thỏa mãn . Tính S = a
2016
+ b
2017
A. S = 0 B. S = 2 C. S
D. S
Hướng dẫn giải
Đáp án: B
Gọi z = a +bi
S = a
2016
+ b
2017
= 2.
Câu 111. Số phức z thoả là:
A. z = 7 + 7i B. z = 5 – 2i C. z = 2 + 5i D. z = 1 –2i
Hướng dẫn giải
Đáp án: C
Gọi z = a + bi khi đó
Ta có:
12
zi z i++ = −
z
1
2
−
2
2
2
1
2
z x yi z x yi=+ ⇒=−
( )
(
)
(
)
(
)
( )
( )
( ) ( ) ( )
22 2 22 2
22
12 1 2 1 1 2
11 2 11 2 10 1
z i z i x yi i x yi i x y i x y i
x y xy x y xy xy yx
++ = − ⇔ + ++ = − − ⇔ + + + = − +
⇔ + ++ = ++ ⇔+ ++ =++ ⇔−−=⇔=−
2
2 2 22 2
1 11
(1) 21 2 21 2
2 22
zxx xxx xx x
= + − = + − += − += − + ≥
1
2
x =
2
2
2 33z iz i+=+
4032 2017
2017
33
5
−
= −
4032 2017
2017
33
5
−
=
2 33
2( ) 3 3
( 2 ) ( 2a) 3 3
3
1
2a 3
z iz i
abi iab i
ab b i i
a bi
ab
b
+=+
⇔+ + + =+
⇔+ ++ =+
+=
⇔ ⇔==
+=
2 18iz z i+ =−−
z a bi= −
212
2 18
28 5
ab a
iz z i
ab b
−=− =
+ =−− ⇔ ⇔
−=− =

Bài tập trắc nghiệm số phức
Trang 165
Vậy z = 2 + 5i.
Câu 112. Cho số phức z thỏa mãn . Tìm mô đun của số phức z:
A. 100 B. 10 C. D. 3
Hướng dẫn giải
Đáp án: C
Gọi
Ta có:
Câu 113. Cho số phức z thỏa mãn . Tìm phần ảo của số phức
A. 6 B. 3 C. 5 D. 2
Hướng dẫn giải
Đáp án: A
Gọi
Ta có:
=> Phần ảo của w là 6.
Câu 114. Cho số phức z thỏa mãn . Tìm số phức w biết
A. 2+3i B. 2–3i C. 6+6i D. 6–6i
Hướng dẫn giải
Đáp án: D
Gọi
Ta có:
2
(1 ) (1 2 )z iz i−+ =−
109
(, )z a bi z a bi a b R=+ =>=− ∈
2
(1 ) (1 2 ) (1 )( ) 3 4
(2 ) 3 4
10
3
10 3 | | 109
z i z i a bi i a bi i
b b ai i
a
b
z iz
−+ =− =>+ −+ − =−−
<=> − + − = − −
=
<=>
=
=>= + => =
(1 ) (3 ) 2 6iz iz i
− +− =−
w2 1z= +
(, )z a bi z a bi a b R=+ =>=− ∈
(1 ) (3 ) 2 6 (1 )( ) (3 )( ) 2 6
422 2
4 2 2 26
26 3
23 w 56
i z i z i i a bi i a bi i
ab a
a b bi i
bb
zi i
+ +− =−<=>+ + +− − =−
−= =
<=> − − = − <=> <=>
−=− =
<=> = + => = +
(1 ) (3 ) 2 6iz iz i− +− =−
w2 2z= +
(, )z a bi z a bi a b R=+ =>=− ∈

Bài tập trắc nghiệm số phức
Trang 166
Câu 115. Cho số phức z thỏa mãn: . Tìm số phức liên hợp của số phức w=7z–2
A. B. C. D.
Hướng dẫn giải
Đáp án: D
Gọi
Ta có:
Câu 116. Có bao nhiêu số phức z thỏa mãn điều kiện ?
A. 0 B. 1 C. 3 D. 2
Hướng dẫn giải
Đáp án: A
Gọi thay vào biểu thức ta có:
Ta thấy không thể nào tồn tại số thực z thỏa mãn điều kiện trên vì một bên là phần thực, một bên là phần ảo.
Câu 117. Cho số phức z thỏa mãn . Modun của số phức là
A. 4 B. 9 C. 1 D. 2
Hướng dẫn giải
Đáp án: C
Gọi
(1 ) (3 ) 2 6 (1 )( ) (3 )( ) 2 6
422 2
4 2 2 26
26 3
23 w 66 w 66
i z i z i i a bi i a bi i
ab a
a b bi i
bb
zi i i
+ +− =−<=>+ + +− − =−
−= =
<=> − − = − <=> <=>
−=− =
<=>=+=>=+=>=−
2
2
(1 ) 3 ( )
1
i
i z iz
i
++ =
−
42
w
77
i=−+
42
w
77
i=−−
w 62i=−+
w 62i=−−
(, )z a bi z a bi a b R=+ =>=− ∈
2
2
(1 ) 3 ( )
1
(1 )( ) 3 ( ) 2 2 (4 ) 2
4
20
42
7
w62 w62
42 2
77
7
i
i z iz
i
i a bi i a bi i a b a b i i
a
ab
zi i i
ab
b
++ =
−
<=> + + + − = − <=> + + + = −
= −
+=
−
<=> <=> <=> = + => = − + => = − −
+=−
=
2
zz z= +
( )
;;z a bi a b R=+∈
2 22
2a bi z a bi bi z bi bi z+= +−⇔= −⇔ =
z
zi
zi
= −
+
2
1zz
ϖ
= ++
z a bi z a bi=+ ⇒=−
( )
22
2 22
1
( ) 1 1 (2 ) 0
(2 1) 0
aa b
a bi a bi a b a ab b i
ab
−+=
− = + +⇔ − − + + + = ⇔
+=

Bài tập trắc nghiệm số phức
Trang 167
Từ phương trình 2, ta có 2 trường hợp:
Nếu (vô nghiệm)
Vậy modun của số phức là 1.
Câu 118. Cho số phức thỏa mãn điều kiện . Tính môđun của
A. B. C. D.
Hướng dẫn giải
Đáp án: B
Đặt , ta có:
Vậy .
Câu 119. Cho số phức thỏa mãn điều kiện . Phần thực và phần ảo của là:
A. 2 và –3 B. 2 và 3 C. –2 và 3 D. –3 và 2
Hướng dẫn giải
Đáp án: A
Đặt
Phương trình trở thành:
Suy ra: và . Giải ra được
Câu 120. Tìm số phức z có phần ảo khác 0, thỏa mãn và ?
A. B. C. D.
Hướng dẫn giải
Đáp án: C
2
0, 1 0b aa
= −+=
2
1 7 1 7 17 7
11 1
2 4 2 2 44 2
a b zz i i
−
= ⇒= ⇒ ++=−+ +−− =−
z
( )
2 31 1 9z iz i+−=−
z
12
13
12
2
z a bi= +
( )
,
ab∈
( )
( ) ( )( )
2 31 1 9 2 31 1 9z i z i a bi i a bi i+−=−⇔ ++− −=−
( ) ( )
5 3 3 19a b a bi i⇔ − +− − = −
531
39
ab
ab
−=
⇔
+=
2
3
a
b
=
⇔
=
22 22
2 3 13z ab= += +=
z
( )
2 35z iz i++ =+
z
(2 ) 10zi−+=
. 25zz=
43i+
43i−
34i+
34i−
( ) ( )
2
22
3
10 2
2 1 10
3, 4
34
5
5, 0( )
8 15 0
25
10 2
x
yx
x yi
xy
zi
x
xyl
xx
xy
yx
=
= −
−+− =
= =
⇔ ⇔ ⇔ ⇔=+
=
= =
−+=
+=
= −

Bài tập trắc nghiệm số phức
Trang 168
Câu 121. Tìm số phức z thỏa hệ thức ?
A. B. C. D.
Hướng dẫn giải
Đáp án: A
Giả sử
Vậy
Câu 122. Cho số phức z thỏa mãn điều kiện . Phát biểu nào sau đây sai?
A. z có phần thực là –3 B. có mô–đun
C. z có phần ảo là D. z có mô–đun
Hướng dẫn giải
Đáp án: B
Đặt
Khi đó phương trình đã cho trở thành
Vậy
Câu 123. Kí hiệu (qui ước là số có phần ảo của lớn hơn) là nghiệm của hệ phương trình
. Khi đó bằng:
A. B. C. D.
2
2
2
zz
z
+=
=
3; 1 3zz i= = ±
2; 1 3
zz i
=−=±
1; 1 3zz i
=−=±
2; 2 3
zz i=−=±
(
)
;,z x yi x y R=+∈
(
)
(
)
( )
(
) (
)
( )
22
2
2
2 22 22 22 2 3
2 23 3
24
2 2 4 6 24
1 13
4 4 6 4 2 4 8 24 16 0
20
z xy
z z x y x xy y x y x y xy x
xy
xx x x x
xy
=↔+=
+=↔−++ −=↔+ ++− +=
=→=±
↔ +− − + =↔ − + =↔
=−→ =
2; 1 3zz i
=−=±
2 34
zz i
−=+
4
3
zi
+
97
3
4
3
97
3
(
)
, 2 22z x yi x y R z x yi z x yi=+ ∈ →=−→−=−+
3
3
2 2 34 3 34
4
34
3
x
x
x yi x yi i x yi i
y
y
= −
−=
+−+ =+↔−+ =+↔ ↔
=
=
( )
2
2
4 4 97 97
33
3 3 93
z iz
=−+ → = − + = =
12
,zz
1
z
2
.1
8
21
27
zz
zz
=
+ −=
12
36zz+
65i+
65i−+
65i−−
65i−

Bài tập trắc nghiệm số phức
Trang 169
Hướng dẫn giải
Đáp án: D
Đặt suy ra . Khi đó ta được
suy ra .
Vậy: .
Câu 124. Biết rằng số phức z thỏa mãn là một số thực. Tìm giá trị nhỏ nhất của
A. 8 B. C. D.
Hướng dẫn giải
Đáp án: C
Giả sử , ta có:
Theo giả thiết
Cách 1: min min
Dấu “=” xảy ra khi
Vậy min
( )
,Rz x yi x y=+∈
z x yi= −
( )
(
)
( ) ( )
22
2
32
1
1
52
8
420
21
27
27
x yi x yi
yx
xx x
x yi x yi
+ −=
= −
⇔
−−+ =
+ + − −=
( )
2
2
2
2
3
3
5
5
3
9
2
13
3
12
25
5
144
3
x
x
y
y
x
x
l
y
y
=
=
=
=
⇔⇔
=
= −
= −
= −
12
25 25
,
33 33
zz
=+=−
12
36 65zz i+=−
( )
(
)
3 13
u z iz i= +− ++
z
2
22
2
2
(
)
,z x yi x y R
=+∈
( )
( )
( ) (
)
( )
22
3 13 3 1 1 3 4 4 62 4u z iz i x y i x y i x y x y xy i
= +− ++ = ++ − +− − = + + − + + − −
40u xy∈ ⇔−−=
z
2
z
( )
( )
22
2
22 2 2
4 2 8 16 2 2 8 8z xy y y y y y=+=+ += ++= + +≥
22yx=−⇒ =
z
min
2 2 22
z iz=−⇒ =

Bài tập trắc nghiệm số phức
Trang 170
Cách 2: Giả sử là điểm biểu diễn của z thì
Ta tìm được
Câu 125. Cho các số phức z thoả mãn . Tìm số phức z
để |z| đạt giá trị lớn nhất.
A. B.
C.
D.
Hướng dẫn giải
Đáp án: A
Gọi số phức Từ giả thiết ta có:
Để đạt giá trị lớn nhất, nhỏ nhất ta sẽ thấy điểm M ứng vói vị trí nhỏ nhất, điểm M’ứng với vị trí lớn nhất.
đường thẳng đi qua M,M’ cũng đi qua O và tâm I của đường tròn nên có phuương trình
Vậy số phức thoả mãn:
đạt giá trị lớn nhất khi:
đạt giá trị nhỏ nhất khi:
Câu 126. Biết rằng và là một số thực khác 0, số phức liên hợp của số phức z là:
A. B. C. Không tồn tại z D. Không tồn tại
Hướng dẫn giải
Đáp án: B
Gọi , suy ra
( )
;M xy
min
min
z OM OM d
⇔ ⇔⊥
( )
min
2; 2 2 2 2 2M z iz
−⇔=− ⇔ =
( )
22zi i−+=
(
)
25 2 5
5 25
55
zi
+
+
= −
(
)
25 2 5
5 25
55
zi
+
+
= +
( )
25 2 5
5 25
55
zi
−
+
= −
( )
25 2 5
5 25
55
zi
−
+
= +
;,z x yi x y=+∈
( ) (
) ( ) (
) ( )
22
2 2 2 1 2 1 2 4 1; 2zi i y x i x y I− + = ⇔− − + − = ⇔ − + + = ⇒ = −
z
2yx
= −
( ) ( )
( )
( )
22
25 2 5
5 25
,
1 24
55
2
25 2 5
5 25
,
55
xy
xy
yx
xy
−+
+
= =
− ++ =
⇒
= −
−−
−
= =
z
( )
25 2 5
5 25
55
zi
−+
+
= +
z
( )
25 2 5
5 25
,
55
zy i
−−
−
= =
( )
11zi−+ =
2zi−
12i+
12i−
z
( )
,z a bi a b=+∈

Bài tập trắc nghiệm số phức
Trang 171
là số thực khi và chỉ khi
Mặt khác,
(nhận)
Vậy .
Câu 127. Tìm số phức z có môđun nhỏ nhất thỏa mãn điều kiện .
A. B. C. D.
Hướng dẫn giải
Đáp án: A
Gọi
Ta có
Ta cần tìm z sao cho đạt giá trị nhỏ nhất.
Ta có
Do đó
Vậy .
Câu 128. Tìm phần thực của số phức z biết: .
A. 1 B. –1 C. 0 D. –4
Hướng dẫn giải
Đáp án: A
Đặt . Khi đó ta có:
( )
22z ia b i−=+−
00
2, 0
20 2
aa
z a ia
bb
≠≠
⇔ ⇒=+ ≠
−= =
( )
( ) ( )
22
11 1 1
1 11 1 0
zi a i
aa
− + = ⇔ −+ =
⇔−+=⇔− =
1
a⇔=
12 12z iz i=+ ⇒=−
23iz zi−− + = −
36
55
i−
63
55
i−
9
5
9
5
(
)
,z a bi a b
=+∈
(
)
( )
(
) (
) ( )
22 2
2
23 2 3 1
2 3 1 23
iz zi a b i a b i
a b a b ab
−− + = − ⇔ − − + = + −
⇔− ++ =+− ⇔= +
22
ab
+
( )
2
2
22 2
6 99
23 5
5 55
ab b b b
+= + += + +≥
(
)
9 6 3 36
min
5 5 5 55
ab b a z i
2
−
+2= ⇔ = ∧ = ⇒ = −
36
55
zi= −
2 34zz i
+=+
z a bi= +
( ) ( )
2 23
33 1
2 34
44
z z a bi a bi a bi
aa
zz i
bb
+=++ − =−
= =
+ =+⇔ ⇔
−= =−

Bài tập trắc nghiệm số phức
Trang 172
Do đó, phần thực của số phức z là 1.
Sai lầm thường gặp: Không phân biệt được đâu là phần thực của số phức z và có thể ghi đáp án D.
Câu 129. Tìm số phức z có và đạt giá trị lớn nhất.
A. 1 B. –1 C. i D. –i
Hướng dẫn giải
Đáp án: C
Đặt thì ;
Khi đó ta có:
Do đó, giá trị lớn nhất đạt được bằng 2 khi:
và
Câu 130. Cho số phức thỏa mãn . Tính giá trị biểu thức: .
A. 0 B. 2 C. D.
Hướng dẫn giải
Đáp án: B
Sai lầm thường gặp:
đáp án C
1z
=
zi+
z a bi= +
22
z ab= +
(
)
2
2
1zi a b+= + +
22
1 11z ab b=⇔ + =⇒≤
( )
2
2
22
1
2 1 2 2 2.1 2 2
zi a b
ab b b
+= + +
= + + += +≤ +≤
0; 1ab= =
zi=
z a bi= +
2, 3 3z iz i+=+
2016 2017
Pa b= +
4032 2017
2017
33
5
−
4032 2017
2017
33
5
−
−
.z a bi i z ia b=−⇒ =+
( ) ( ) ( )
2016 2017
2. 2 2 2
23
1 11 2
23
z iz abi iab a b b ai
ab
ab P
ba
⇒=+ =+ + + = + + +
+=
⇒ ⇒==⇒= + =
+=
9
23
5
23 3
5
z abi iz iab
a
ab
ba
b
=− ⇒ =−−
=
−=
⇒ ⇒⇒
+=
= −

Bài tập trắc nghiệm số phức
Trang 173
C – BÀI TẬP TỰ LUYỆN (126 CÂU)
Câu 1: Tổng tất cả các nghiệm phức của phương trình
2
z z0
+=
và
13
z 0,z 1,z i
22
= =−=±
A. - 1 B. 1 C.
3
D. 0
Câu 2: Gọi
12
z , z
là hai nghiệm phương trình
2
z 2z 8 0;+ +=
trong đó
1
z
có phần ảo dương. số phức
(
)
1 21
w 2z z z
= +
là:
A.
z 12 6i= +
B.
z 11 6i= −
C.
z 9 6i= −
D.
z 12 6i=−+
Câu 3: Tập hợp các nghiệm của phương trình
2
z 2 z 35 0+ −=
trên tập số phức là
A.
{ }
2 i,2 i−+
B.
{ }
2 3i, 2 3i
−+
C.
{ }
5,5−
D.
{ }
5i,5i−
Câu 4: Gọi
12
z ;z
là hai nghiệm của phương trình
2
z 2z 6 0.
− +=
Trong đó
1
z
có phần ảo âm. Giá trị biểu thức
1 12
M z 3z z
=+−
là.
A.
M 6 2 21.= +
B.
M 6 21 .
= +
C.
M 2 6 21 .= +
D.
M 2 21 6= −
Câu 5: Trong tập số phức
, phương trình
42
z 3z 2 0+ +=
có bao nhiêu nghiệm?
A. 0 B. 1 C. 2 D. 4
Câu 6: Tập nghiệm trong C của phương trình
32
z z z10+ ++=
là:
A.
{ }
1;1; i−
B.
{ }
i;i; 1−−
C.
{ }
1−
D.
{
}
i;i;1−
Câu 7: Tính
22
12
z 2z+
biết
12
z ,z
là nghiệm của phương trình
2
z 2z 17 0++=
A.
68
B.
51
C.
17
D.
34
Câu 8: Cho phương trình
2
z mz 2m 1 0− + −=
trong đó m là tham số phức; giá trị m để phương trình có hai
nghiệm
12
z ;z
thỏa mãn
22
12
z z 10+=−
.
A.
m 2 3i; m 2 3i.
=−=+
B.
m 1 2i;m 1 2i
=−=+
C.
m 1 3i; m 2 3i.=−=+
D.
m 1 3i; m 1 3i.=−=+
Câu 9: Cho phương trình
( )
2
z mz m 2 01,+ + +=
trên trường phức và m là tham số thực. Giá trị m để (1) có
hai nghiệm ảo
12
z ;z
trong đó z
1
có phần ảo âm và phần thực của số phức
12
z izϖ= +
bằng
1
.
2
A. Không có m B.
m2= −
C.
m1=
D.
m5= −

Bài tập trắc nghiệm số phức
Trang 174
Câu 10: Cho hệ phương trình
1
2
12
z1
z1
zz 3
=
=
+=
. Tính
12
zz−
A.
2
B.
3−
C.
1
D.
0
Câu 11: Trong tập số phức
, phương trình
3
z 10+=
có bao nhiêu nghiệm?
A. 1 B. 2 C. 3 D. 0
Câu 12: Phương trình
2
z 2z 6 0− +=
có các nghiệm
12
z ;z
. Khi đó giá trị của biểu thức
22
12
22
12
zz
F
zz
= +
là:
A.
2
9
B.
2
3
C.
2
3
−
D.
2
9
−
Câu 13: Gọi z
1
, z
2
, z
3
, z
4
là các nghiệm phức của phương trình
4
z1
1.
2z i
−
=
−
Giá trị của
2222
1 234
P (z 1)(z 1)(z 1)(z 1)=++++
là:
A.
17
9
B.
9
17
C.
17
8
D.
8
17
Câu 14: Với mọi số phức
z
, ta có
2
|z 1|+
bằng
A.
zz1
++
B.
z.zzz1
+++
C.
z.z 1+
D.
2
|z| 2|z| 1++
Câu 15: Trên tập số phức, giá trị của m để phương trình bậc hai z
2
+ mz + i = 0 có tổng bình phương hai
nghiệm bằng - 4i là:
A. m = 1 - i hoặc m = - 1 + i B. m = 1 + i
C. m = 1 - i D. m = - 1 + i
Câu 16: Các giá trị thực của m để phương trình sau có ít nhất một nghiệm thực z
3
+ (3 + i)z
2
- 3z - (m + i) = 0
là:
A. m = 1 hoặc m = 5 B. m = 1 C. m = 5 D. m = 4
Câu 17: Tìm số phức z thỏa mãn đồng thời hệ:
2
|z z| 2
|z| 2
+=
=
là:
A.
z 1; z 1 3i=−=±
B.
z 1; z 1 2i=−=±
C.
z1;z1 2i= = ±
D.
z1;z1 3i
= = ±
Câu 18: Nếu
z1=
thì
2
z1
z
−
A. Bằng
0
B. Là số ảo C. Lấy mọi giá trị phức D. Lấy mọi giá trị thực

Bài tập trắc nghiệm số phức
Trang 175
Câu 19: Tập hợp các nghiệm của phương trình
z
z
zi
=
+
là
A.
{0;1 i}−
B.
{0}
C.
{1 i}−
D.
{0; 1}
Câu 20: Tập hợp các nghiệm phức của phương trình
2
2
zz0+=
là
A.
{
}
i;0−
B. Tập hợp mọi số ảo C.
{ }
i; 0;i−
D.
{ }
0
Câu 21: Giá trị của các số thực b, c để phương trình z
2
+ bz + c = 0 nhận số phức z = 1 + i làm 1 nghiệm là:
A.
b2
c2
= −
=
B.
b2
c2
=
= −
C.
b1
c3
= −
=
D.
b4
c2
= −
=
Câu 22: Trên tập hợp số phức, phương trình
2
z 7z 15 0++=
có hai nghiệm
12
z ; z .
Giá trị biểu thức
1 2 12
z z zz++
là:
A.
22
B.
15
C.
7−
D.
8
Câu 23: Trên tập hợp số phức, phương trình
4
x 16 0+=
nhận giá trị nào dưới đây là nghiệm?
A.
11
i
22
+
B.
11
i
22
+
C.
1
2i
2
−+
D.
2 2i
−+
Câu 24: Giải phương trình
z z 2 4i+=+
có nghiệm là
A. −3 + 4i B. −4 + 4i C. −2 + 4i D. −5 + 4i
Câu 25: Số phức z thoả mãn hệ
z1
1
zi
z 3i
1
zi
−
=
−
−
=
+
là:
A.
z 1i=−−
B.
z1i= +
C.
z 1i= −
D.
z 1i=−+
Câu 26: Phương trình bậc hai
2
z (1 3i)z 2(1 i) 0+− − +=
có nghiệm là:
A.
12
z 2i, z 1 i=− =−+
B.
12
z 2i, z 1 i= =−+
C.
12
z 2i, z 1 i= =−−
D.
12
z 2i, z 1 i= = +
Câu 27: Số phức z thỏa mãn
( )
z 2 i 10−+=
và
z.z 25=
là:
A.
z 3 4i= −
hoặc
z5=
B.
z 3 4i= +
hoặc
z5=
C.
z 3 4i= −
hoặc
z5= −
D.
z 3 4i= +
hoặc
z5= −
Câu 28: Có bao nhiêu số phức z thỏa điều kiện:
( )
( )
2
2z 1 z 1 1 i z+ +−= −
?
A. 2 B. 3 C. 1 D. 4
Câu 29: Trong trường số phức phương trình
3
z 10+=
có mấy nghiệm?

Bài tập trắc nghiệm số phức
Trang 176
A. 3 B. 2 C. 1 D. 4
Câu 30: Tập hợp các nghiệm của pt
2
2
zz0
+=
A. Tập hợp mọi số ảo B.
i;0±
C. 0 D.
i;0−
Câu 31: Nghiệm của pt
3
z 80−=
là
A.
2; 1 3i; 1 3i−+ −−
B.
2; 1 3i; 1 3i− −+ −−
C.
2;1 3i;1 3i+−
D.
2;1 3i;1 3i−+ −
Câu 32: Phương trình
63
z 9z 8 0− +=
trên tập số phức C có bao nhiêu nghiệm.
A. 4 B. 2 C. 8 D. 6
Câu 33: Cho phương trình
32
z (2i 1)z (3 2i)z 3 0.− − + − +=
Trong số các nhận xét
1. Phương trình chỉ có một nghiệm thuộc tập hợp số thực
2. Phương trình chỉ có 2 nghiệm thuộc tập hợp số phức
3. Phương trình có hai nghiệm có phần thực bằng 0
4. Phương trình có hai nghiệm là số thuần ảo
5. Phương trình có ba nghiệm, trong đó có hai nghiệm là hai số phức liên hợp
Số nhận xét sai là:
A. 1 B. 2 C. 3
D. 4
Câu 34: Cho phương trình sau
( )
4
2
z i 4z 0++ =
Có bao nhiêu nhận xét đúng trong số các nhận xét sau:
1. Phương trình vô nghiệm trên trường số thực R
2. Phương trình vô nghiệm trên trường số phức
3. Phương trình không có nghiệm thuộc tập hợp số thực
4. Phương trình có bốn nghiệm thuộc tập hợp số phức
5. Phương trình chỉ có hai nghiệm là số phức
6. Phương trình có hai nghiệm là số thực
A. 1 B. 2 C. 3 D. 5
Câu 35: Phương trình
63
z 9z 8 0− +=
trên tập số phức có bao nhiêu nghiệm.
A. 4 B. 2 C. 8 D. 6
Câu 36: Giải phương trình sau:
( )
2
z 1 i z 18 13i 0+− − + =
A.
z 4 i , z 5 2i= − =−+
B.
z 4 i , z 5 2i= − =−−
C.
z 4 i , z 5 2i= − =−−
D.
z 4 i , z 5 2i= + =−+

Bài tập trắc nghiệm số phức
Trang 177
Câu 37: Phương trình
2
8z 4z 1 0− +=
có nghiệm là
A.
1
11
zi
44
= +
và
2
51
zi
44
= −
B.
1
11
zi
44
= +
và
2
13
zi
44
= −
C.
1
11
zi
44
= +
và
2
11
zi
44
= −
D.
1
21
zi
44
= +
và
2
11
zi
44
= −
Câu 38: Biết z
1
và z
2
là hai nghiệm của phương trình
2
2z 3z 3 0+ +=
. Khi đó, giá trị của
22
12
zz+
là:
A.
9
4
B.
9
4
−
C. 9 D. 4
Câu 39: Gọi
12
z ,z
là nghiệm phức của phương trình
2
z 2z 4 0
+ +=
.
22
12
Az z= +
bằng
A. 2 B.
7−
C.
8
D. 4
Câu 40: Gọi
12
z ,z
là hai nghiệm phức của phương trình
2
2z 4z 3 0
+ +=
. Giá trị của biểu thức
12
zz+
bằng
A.
2
B.
3
C.
23
D.
6
Câu 41: Hai số phức
4i
+
và
2 3i−
là nghiệm của phương trình:
A.
(
)
2
x 6 2i x 11 10i 0
−− +− =
B.
( )
2
x 11 10i x 6 2i 0
+ − +− =
C.
( )
2
x 6 2i x 11 10i 0+− +− =
D.
(
)
2
x 11 10i x 6 2i 0− − +− =
Câu 42: Giải phương trình
2
8z 4z 1 0− +=
trên tập số phức.
A.
11 11
z i hay z i
44 44
=−+ =−
B.
11 11
z i hay z i
44 44
=+ =−−
C.
11 11
z i hay z i
44 44
=+=−
D.
11 11
zihayzi
44 44
=−=−
Câu 43: Gọi
12
z ,z
là 2 nghiệm của phương trình
2
z 2iz 4 0− −=
. Khi đó môđun của số phức
12
w (z 2)(z 2)=−−
là
A. 4 B. 5 C. 6 D. 7
Câu 44: Phương trình
2
z az b 0+ +=
có một nghiệm phức là
z 1 2i= +
. Tổng 2 số
a
và
b
bằng
A. 0 B.
4−
C.
3−
D. 3
Câu 45: Nghiệm phương trình
4
zi
1
zi
+
=
−
là:
A.
z 0; z 1= =
B.
z 0; z 1= = −
C.
z 0; z 1= = ±
D. Đáp án khác.
Câu 46: Bộ số thực
( )
a; b;c
để phương trình
32
z az bz c 0+ + +=
nhận
z1i= +
và
z2=
là nghiệm.

Bài tập trắc nghiệm số phức
Trang 178
A.
( )
4;6; 4−−
B.
( )
4; 6; 4−
C.
( )
4; 6; 4−−−
D.
( )
4;6; 4
Câu 47: Giải phương trình sau trên tập hợp các số phức:
4z 3 7i
z 2i
zi
−+
= −
−
A.
z 1 2i= +
và
z 3 i.= −
B.
z 1 2i= −
và
z 3 i.= +
C.
z 1 2i= −
và
z 3 i.= −
D.
z 1 2i= +
và
z 3 i.= +
Câu 48: Môđun của số phức z – 2i bằng bao nhiêu? Biết z thỏa mãn phương trình
(z 2i)(z 2i) 4iz 0− −+ =
A.
2
B.
22
C.
3
D.
23
Câu 49: Tìm tất cả các nghiệm của
43 2
z 4z 14z 36z 45 0− + − +=
biết
z 2i= +
là một nghiệm
A.
z 2 i ; z 3i ; z 3i=+= =−
B.
z 2 i ; z 2 3i ; z 3i ; z 3i=+=− = =−
C.
z 2 i;z 2 i;z 3i;z 3i
=+=−= =−
D.
z 2 i;z 2 i;z 3i.=+=−=
Câu 50: Phương trình
2
(2 i)z az b 0; (a,b )+ + += ∈
có 2 nghiệm là
3i+
và
1 2i
−
. Khi đó
a =
?
A.
9 2i
−−
B.
15 5i+
C.
9 2i+
D.
15 5i
−
Câu 51: Số nghiệm phức
z
của phương trình
2
z z0+=
là:
A. 4 B. 3 C. 1 D. 2
Câu 52: Gọi z
1
, z
2
là các nghiệm phức của phương trình z
2
+
(1 – 3i)z - 2(1 + i) = 0. Khi đó
22
1 2 12
w z z 3z z=+−
là số phức có môđun là:
A.
2 13
B.
20
C. 2 D.
13
Câu 53: Gọi z
1,
z
2
là các nghiệm phức của phương trình
2
z 3z 7 0+ +=
Khi đó A
44
12
zz= +
có giá trị là:
A.
23
B. 23 C. 13 D.
13
Câu 54: Phương trình:
42
x 2x 24x 72 0+ − +=
trên tập số phức có các nghiệm là:
A.
2 i2
±
hoặc
2 2i 2−±
B.
2 i2±
hoặc
1 2i 2±
C.
2 i2±
D.
1 2i 2±
Câu 55: Số nghiệm của phương trình với ẩn số phức
z
:
2
2
4z 8 z 3 0+ −=
là:
A. 4 B. 3 C. 2 D. 1
Câu 56: Cho số phức z thỏa mãn
2
z 6z 13 0−+=
. Tính
6
z
zi
+
+
A. 4 B. 5 C. 6 D. Đáp án khác
Câu 57: Có bao nhiêu số phức thỏa mãn phương trình
2
2
zzz= +
:

Bài tập trắc nghiệm số phức
Trang 179
A.
0
. B.
1
. C.
3
. D.
2
.
Câu 58: Tìm hai số phức biết rằng tổng của chúng bằng 4 - i và tích của chúng bằng 5(1 - i). Đáp số của bài
toán là:
A.
z 3i
z 1 2i
= +
= −
B.
z 3 2i
z 5 2i
= +
= −
C.
z 3i
z 1 2i
= +
= −
D.
z1i
z 2 3i
= +
= −
Câu 59: Trong C, phương trình
( )( )
22
z i z 2iz 1 0+ − −=
có nghiệm là:
A.
( )
21 i
2
−
,
( )
2
1i
2
−+
, i B. 1 - i ; - 1 + i ; 2i
C.
( )
3
1 2i
2
−
;
(
)
3
2i
2
−+
; 4i D. 1 - 2i ; - 15i ; 3i
Câu 60: Cho phương trình z
3
+ az + bz + c = 0. Nếu z = 1 + i và z = 2 là hai nghiệm của phương trình thì a, b, c
bằng:
A.
a4
b6
c4
= −
=
= −
B.
a2
b1
c4
=
=
=
C.
a4
b5
c1
=
=
=
D.
a0
b1
c2
=
= −
=
Câu 61: Tìm số phức z biết
2z 3i z 5z 4z+−= +
A.
3
zi
2
=
B.
3
zi
2
= −
C.
3
z
2
=
D.
3
zi
2
= +
Câu 62: Tìm một số phức z thỏa điều kiện
z 3i
zi
−
+
là số thuần ảo với
A.
z 2i
=−+
B.
z 2i= +
C. Cả A và B đều đúng. D. Cả A và B đều sai.
Câu 63: Cho các nhận định sau (giả sử các biểu thức đều có nghĩa):
1) Số phức và số phức liên hợp của nó có môđun bằng nhau
2) Với
z 2 3i= −
thì môđun của z là:
z 2 3i= +
3) Số phức z là số thuần ảo khi và chỉ khi
zz= −
4) Tập hợp điểm biểu diễn số phức z thỏa mãn
zz1 2++=
là một đường tròn.
5) Phương trình:
3
z 3zi 1 0+ +=
có tối đa 3 nghiệm.
Số nhận định đúng là:
A. 4 B. 2 C. 3 D. 5
Câu 64: Tìm một số phức z thỏa
5 i3
z 10
z
+
− −=

Bài tập trắc nghiệm số phức
Trang 180
A.
z 1 3i
= −
B.
z 2 3i
= −
C. -2 D.
z 2 3i=−−
Câu 65: Tìm số phức z thỏa mãn
5iz
z (1 i)(3 2i)
2i
=+ −−
+
. Số phức z là:
A.
1
2i
2
−
B.
1 2i−
C.
1 2i+
D.
1
2i
2
+
Câu 66: Trong các số phức sau, số nào thỏa điều kiện
1
z z1
z
= = −
?
A.
z 2 i3= −
B.
13
zi
22
=−−
C.
z 2 i3= +
D.
13
zi
22
= −
Câu 67: Tìm số phức z có phần ảo gấp 3 lần phần thực đồng thời
( )
z 10 z z
= +
A.
0
và
2
B.
z 1 3i=−−
C.
z 2 6i
= +
D.
z 3 12i= +
Câu 68: Số phức z thỏa mãn
z 2z 3 2i+=−
là:
A.
1 2i−
. B.
1 2i+
. C.
2i−
. D.
2i+
.
Câu 69: Số phức z thỏa điều kiện
( )
z 2 i 10−+=
và
z.z 25
=
là:
A.
z5;z34i
= = +
B.
z 5; z 3 4i=−=+
C.
z5;z34i= = −
D.
z 5; z 3 4i=−=−
Câu 70: Tìm số phức z biết
2
(1 2i) z z 4i 20+ += −
A.
z 3 4i= −
B.
z 3 4i=−+
C.
z 3 4i= +
D.
z 3 4i=−−
Câu 71: Tìm số phức
12
2.z .z ,ω=
biết
3
3
12
2 4i 2(1 i)
z 4 3i (1 i) ; z
1i
+− −
=−+− = ⋅
+
A.
18 75.i.ω= −
B.
18 74.i.ω= +
C.
18 75.i.ω= +
D.
18 74.i.ω= −
Câu 72: Với mọi số ảo z, số
2
2
zz+
là
A. Số 0 B. Số thực âm C. Số ảo khác D. Số thực dương
Câu 73: Có bao nhiêu số phức z thỏa mãn
z.z2z194i+=−
A. 1 B. 2 C. 0 D. 3
Câu 74: Để
2
zzz−=
ta được kết quả:
A.
z0
=
hay
zi=
B. z = 2 hay
z1=
C.
z 0, z 1 i= = +
hay
z 1i= −
D.
z1=
hay
zi= −
Câu 75: Tìm số phức
z
biết:
2
z 3z (3 2i) (1 i)+=− +

Bài tập trắc nghiệm số phức
Trang 181
A.
5
z
3
=
B.
17 14i
z
4
+
=
C.
17 7
zi
44
= +
D.
17 7
zi
42
= +
Câu 76: Tìm số phức z thỏa mãn:
( )
( )
2
2 i z iz 2i 1 i 33 5i+ + − += −
A.
z 3 5i
= −
B.
z 3 5i=−+
C.
aa ' bb '+
D.
z 3 5i=−−
Câu 77: Có bao nhiêu số phức thỏa mãn
2
z z0+=
:
A. 1 B. 4. C. 3 D. 2
Câu 78: Số phức z thỏa mãn
z 2z 9 2i+=+
và
2z z 3 6i−=−
là:
A.
z 3 2i=−+
B.
z 3 2i= +
C.
z 3 2i=−−
D.
( ) ( )
2 3i 2 3i++ −
Câu 79: Tập hợp các nghiệm phức của phương trình
2
2
zz0+=
là:
A. Tập hợp số ảo B.
2 3i
2 3i
+
−
C.
{ }
0
D.
{ }
i;0−
Câu 80: Có bao nhiêu số phức z thỏa mãn
z (2 i) 10−+=
và
z.z 25
=
:
A. 1 B. 3 C. 2 D. 4.
Câu 81: Số phức
z
thỏa mãn:
( )
3 i z (1 2i)z 3 4i+ ++ =−
là:
A.
z 2 3i= +
B.
z 2 5i= +
C.
z 1 5i=−+
D.
z 2 3i=−+
Câu 82: Tìm số phức
z
biết:
z 2z 2 4i
+=−
A.
2
z 4i
3
=−+
B.
2
z 4i
3
= −
C.
2
z 4i
3
= +
D.
2
z 4i
3
=−−
Câu 83: Cho số phức z thỏa mãn
z z 6, z.z 25+= =
. Số giá trị của z thỏa mãn là:
A. 1 B. 2 C. 3 D. 4
Câu 84: Nghiệm của phương trình 2ix + 3 = 5x + 4 trên tập số phức là:
A.
23 14
i
29 29
−−
B.
23 14
i
29 29
−
C.
23 14
i
29 29
−+
D.
23 14
i
29 29
+
Câu 85: Số phức
z
thỏa
z 2z 3 i+=−
có phần ảo bằng:
A.
1
3
−
B.
1
3
C.
1−
D.
1
Câu 86: Cho số phức z thỏa mãn điều kiện (1 + i)(z – i) + 2z = 2i. khi đó môđun của số phức
2
z 2z 1
w
z
−+
=
là
A. 9 B. 10 C. 11 D. 12

Bài tập trắc nghiệm số phức
Trang 182
Câu 87: Cho số phức z thỏa:
2zz4i9++ =
. Khi đó, modun của
2
z
là
A. 25 B. 4 C. 16 D. 9
Câu 88: Cho số phức z thỏa mãn hệ thức
2i
(i 3)z (2 i)z
i
+
++ =−
. Môđun của số phức
w zi= −
là:
A.
25
5
B.
26
25
C.
26
5
D.
6
5
Câu 89: Số phức z thỏa mãn: . là:
A.
13
zi
22
=−+
. B.
11
zi
22
= −
C.
3
z1 i
2
= +
D.
13
zi
22
=−−
Câu 90: Phương trình
3
z8=
có bao nhiêu nghiệm phức với phần ảo âm
A. 1 B. 2 C. 3 D. 4
Câu 91: Biết rằng nghịch đảo của số phức z bằng số phức liên hợp của nó, trong các kết luận sau, kết luận nào
đúng ?
A.
z∈
B.
z1=
C.
z1= −
D. z là một số thuần ảo
Câu 92: số phức z thỏa mãn:
( ) (
) ( )
3 2i z 4 1 i 2 i z− − −= +
. Môđun của z là:
A.
10
B.
5
C.
3
D.
3
4
Câu 93: Số phức z thỏa
z (2 3i)z 1 9i−+ =−
là:
A.
z 3i=−−
B.
z 2i=−−
C.
z 2i= −
D.
z 2i= +
Câu 94: Phần thực của số phức z thỏa mãn
( ) (
) ( )
2
1 i 2 iz 8 i 1 2iz+ − = ++ +
là
A. -6 B. -3 C. 2 D. -1
Câu 95: Số phức z thõa mãn điều kiện
5 i3
z 10
z
+
− −=
là:
A.
1 3i vа 2 - 3i+
B. Đáp án khác C.
1 3i vа 2 - 3i−+
D.
1 3i vа 2 - 3i−+
Câu 96: Nghiệm của phương trình
3x (2 3i)(1 2i) 5 4i++ − =+
trên tập số phức là:
A.
5
1i
3
−
B.
5
1i
3
−+
C.
5
1i
3
+
D.
5
1i
3
−−
Câu 97: Số các số phức
z
thỏa hệ thức:
2
z z2+=
và
z2=
là:
A. 3 B. 1 C. 2 D. 4
( ) ( )( )
1 i z 2 3i 1 2i 7 3i+ +− + =+

Bài tập trắc nghiệm số phức
Trang 183
Câu 98: Gọi z là nghiệm phức có phần thực dương của phương trình:
( )
2
z 1 2i z 17 19i 0++ − + =
. Khi đó, giả
sử
2
z a bi= +
thì tích của a và b là:
A.
168−
B.
12
−
C.
240−
D.
5−
Câu 99: Số phức z thỏa mãn
2
| z | 2(z i)
2iz 0
z 1i
+
++ =
−
có dạng a+bi khi đó
a
b
bằng:
A.
1
5
B. -5
C. 5
D. -
1
5
Câu 100: Cho số phức z thoả mãn
4
zi
z1
−=
+
. Số phức
2
w z i(z 1)=++
có dạng a+bi khi đó
a
b
là:
A.
4
3
B.
4
3
−
C.
4
3
D.
4
3
−
Câu 101: Cho số phức z thỏa mãn:
(1 2i)(z i) 3z 3i 0+ −− + =
. Môđun của số phức
2
2z z 3i
w
z
++
=
là
m 106
26
.
Giá trị m là:
A. 3 B. 2 C. 1 D. 4
Câu 102: Tìm số phức z biết
( )
z 2 3i z 1 9i−+ =−
A. z = 2 + i B. z = - 2 - i C. z = - 2 + i D. z = 2 – i
Câu 103: Cho số phức
( )
n
z 1i= +
, biết
nN∈
và thỏa mãn
44
log (n 3) log (n 9) 3.−+ +=
Tìm phần thực của số phức z.
A.
a7=
B.
a0=
C.
a8=
D.
a8= −
Câu 104: Cho số phức z thỏa
2
(1 2i) .z z 4i 20+ += −
. Môđun số z là::
A. 4 B. 5 C. 10 D. 6
Câu 105: Tìm số phức z thỏa mãn
| z (2 i) | 10−+ =
và
z.z 25=
.
A. z = 3 + 4i; z = -5 B. z = 3 + 4i; z = 5 C. z = 3 - 4i; z = 5 D. z = -3 + 4i; z = 5
Câu 106: Cho số phức z thỏa mãn phương
(1 2i).z 1 2i.+=−
Phần ảo của số phức
2iz (1 2i).zω= + −
là:
A.
3
5
B.
4
5
C.
2
5
D.
1
5
Câu 107: Cho số phức z thỏa mãn
z
z2
1 2i
+=
−
. Phần thực của số phức w = z
2
– z là:
A. 3 B. 1 C. 2 D. 0

Bài tập trắc nghiệm số phức
Trang 184
Câu 108: Tìm số phức liên hợp của:
A.
53 9
zi
10 10
−
=−−
B.
53 9
zi
10 10
−
= +
C.
53 9
zi
10 10
−
=−+
D.
Câu 109: Cho số phức z thỏa
5(z i)
2i
z1
+
= −
+
. Tính môđun của số phức w = 1 + z + z
2
.
A. 1 B. 2 C.
13
D. 4
Câu 110: Cho số phức z thỏa mãn điều kiện
(1 i)(z i) 2z 2i+ −+ =
. Môđun của số phức
2
z 2z 1
w
z
−+
=
là:
A.
5
B.
22
C.
10
D.
25
Câu 111: Cho phương trình
( )
1 i z (2 i)z 3+ −− =
. Môđun của số phức
i 2z
w
1i
−
=
−
là ?
A.
122
4
B.
122
2
C.
122
5
D.
122
3
Câu 112: Tính môđun của số phức z biết rằng:
( )( )
(
)
( )
2z 1 1 i z 1 1 i 2 2i− ++ + −=−
A.
3
3
B. Đáp án khác C.
5
3
D.
2
3
Câu 113: Cho số phức
z
thỏa mãn điều kiện
z (2 i)z 13 3i+− =−
. Phần ảo của số phức
z
bằng
A.
2
B.
4
C.
3
D.
1−
Câu 114: Cho số phức
z
thỏa
(1 i)(z i) 2z 2i+ −+ =
. Môđun của số phức
2
1zz
w
1z
++
=
−
là
A.
5
B.
10
C.
13
D. 5
Câu 115: Môđun của số phức z thỏa mãn phương trình
(2z 1)(1 i) (z 1)(1 i) 2 2i− ++ + −=−
là:
A.
22
z
3
=
B.
2
z
3
=
C.
z2
=
D.
42
z
3
=
Câu 116: Cho số phức
z
thỏa mãn
(3 4i)z (1 3i) 12 5i+ +− = −
. Phần thực của số phức
2
z
bằng
A. 5 B. -4 C. 4 D. -3
Câu 117: Trong các số phức
z
thỏa mãn
z z 3 4i= −+
, số phức có môđun nhỏ nhất là:
A.
z 3 4i= +
B.
z 3 4i=−−
C.
3
z 2i
2
= −
D.
3
z 2i
2
= +
1
(1 )(3 2 )
3
zii
i
=+ −+
+
53 9
10 10
zi
= −

Bài tập trắc nghiệm số phức
Trang 185
Câu 118: Trong các số phức
z
thỏa mãn
(1 i)
z21
1i
+
+=
−
,
0
z
là số phức có môđun lớn nhất. Môdun của
0
z
bằng:
A. 1 B. 4 C.
10
D. 9
Câu 119: Cho số phức
z
thỏa
z i 1 z 2i+− = −
. Giá trị nhỏ nhất của
z
là
A.
1
2
B. 1 C.
2
D.
1
4
Câu 120: Tìm số phức z thoả mãn (z – 1)(
z
+ 2i) là số thực và môđun của z nhỏ nhất ?
A. z = 2i B.
42
zi
55
= +
C.
34
zi
55
= +
D.
1
z1 i
2
= +
Câu 121: Trong các số phức z thỏa mãn điều kiện
z 2 4i z 2i−− = −
. Tìm số phức z có môđun bé nhất.
A. z =2 + i B. z =3 + i C. z =2 + 2i D. z =1 +3 i
Câu 122: Trong số phức z thỏa mãn điều kiện
z 3i z 2 i+ = +−
, số phức z có môđun bé nhất là:
A.
z 1 2i
= −
B.
z 1 2i=−+
C.
12
zi
55
=−+
D.
12
zi
55
= −
Câu 123: Trong các số phức z thỏa mãn điều kiện
3
z 3 2i
2
−+ =
, số phức z có môđun nhỏ nhất là:
A.
3 78 9 13
z2 i
26
13
+
=++
B.
z 2 3i= −
C.
3 78 9 13
z2 i
26
13
−
=−+
D.
z 2 3i= +
Câu 124: Số phức z có modun nhỏ nhất thỏa mãn
| z 2 4i | | z 2i |−− = −
là số phức có môđun
A.
32
B.
42
C.
52
D.
22
Câu 125: Cho số phức z thỏa mãn:
z 4 3i 3.−+ =
Số phức z có môđun nhỏ nhất là:
A.
46
zi
55
= +
B.
5
z3 i
2
= +
C.
z 1 4i= −
D.
z 2 3i= +
Câu 126: Số phức
z
thay đổi sao cho
|z| 1=
thì giá trị bé nhất
m
và giá trị lớn nhất
M
của
|z i|−
là
A.
m 0, M 2= =
B.
m 0, M 2= =
C.
m 0, M 1= =
D.
m 1, M 2= =

Bài tập trắc nghiệm số phức
Trang 188
MỤC LỤC
PHẦN 1. TÓM TẮT LÝ THUYẾT
PHẦN 2. SỐ PHỨC VÀ CÁC PHÉP TOÁN ( 453 CÂU)
A – BÀI TẬP ( 260 CÂU)
B – HƯỚNG DẪN GIẢI
C – BÀI TẬP TỰ LUYỆN ( 193 CÂU)
PHẦN 3. PHƯƠNG TRÌNH VÀ CÁC BÀI TẬP TÌM SỐ PHỨC THỎA MÃN ĐIỀU KIỆN (256 CÂU)
A – BÀI TẬP (130 CÂU)
B – HƯỚNG DẪN GIẢI
C – BÀI TẬP TỰ LUYỆN (126 CÂU)
PHẦN 4. BIỂU DIỄN HÌNH HỌC CỦA SỐ PHỨC, TÌM TẬP HỢP ĐIỂM (227 CÂU)
A – BÀI TẬP (138 CÂU)
B – HƯỚNG DẪN GIẢI
C – BÀI TẬP TỰ LUYỆN (89 CÂU)

Bài tập trắc nghiệm số phức
Trang 189
PHẦN 4. BIỂU DIỄN HÌNH HỌC CỦA SỐ PHỨC, TÌM TẬP HỢP ĐIỂM (227 CÂU)
A – BÀI TẬP (138 CÂU)
Câu 1. Cho các số phức z thỏa mãn . Biết rằng tập hợp các điểm biểu diễn các số phức z là
một đường tròn. Tâm của đường tròn đó là:
A. B. C. D.
Câu 2. Tập hợp biểu diễn của số phức z
thỏa mãn: :
A. Là đường thẳng B. Là đường thẳng
B. Là đường thẳng D. Là đường thẳng
Câu 3. Tìm số phức z biết tập hợp các điểm biểu diễn của nó là đường tròn có bán kính bằng và z–
iz–1 là số thuần ảo.
A. B.
C.
D.
Câu 4. Gọi
1
z
là nghiệm phức có phần ảo âm của phương trình
2
2 30
zz+ +=
. Tọa độ điểm M biểu
diễn số phức
1
z
là:
A.
( 1; 2)
M −
B.
( 1; 2)M −−
C.
( 1; 2 )M
−−
D.
( 1; 2 )Mi−−
Câu 5. Cho các số phức z thỏa mãn
12z −=
. Biết rằng tập hợp các điểm biểu diễn các số phức
(1 3 ) 2w iz=++
là một đường tròn. Bán kính r của đường tròn đó là
A. r = 4. B. r = 8. C. r = 2. D. r = 16.
Câu 6. Số phức
53zi= −
có điểm biểu diễn là:
A.
( )
5; 3M −
B.
( )
3; 5N −
C.
( )
5;3P −
D.
( )
3; 5
Q −
Câu 7. Tìm
z
biết rằng z có phần thực bằng hai lần phần ảo và điểm biểu diễn của z nằm trên đường
thẳng
: 2 10 0d xy+− =
A.
25z =
B.
5z =
C.
23z =
D.
3z =
Câu 8. Tìm số phức z biết rằng điểm biểu diễn của z nằm trên đường tròn có tâm O, bán kính bằng 5 và
nằm trên đường thẳng
: 2 50dx y− +=
A.
34zi= −
B.
34zi= +
C.
43zi= +
D.
43zi= −
Câu 9. Cho
.4zz=
, tập hợp các điểm biểu diễn z có đồ thị là (đối với các đồ thị có gạch chéo thì tập
hợp điểm là cả phần gạch chéo và cả biên):
12 3zi
−+ =
I
( )
1; 2I −
( )
1; 2
I
( )
1; 2I −
(
)
1; 2I −−
( )
3 23z z iz+=+
3yx= −
3yx= −
3
yx
=
3
yx
=
5
12
2
zi
zi
=−+
= −
12
2
zi
zi
=−+
=−−
12
2
zi
zi
= +
=−−
12
2
zi
zi
= −
= −
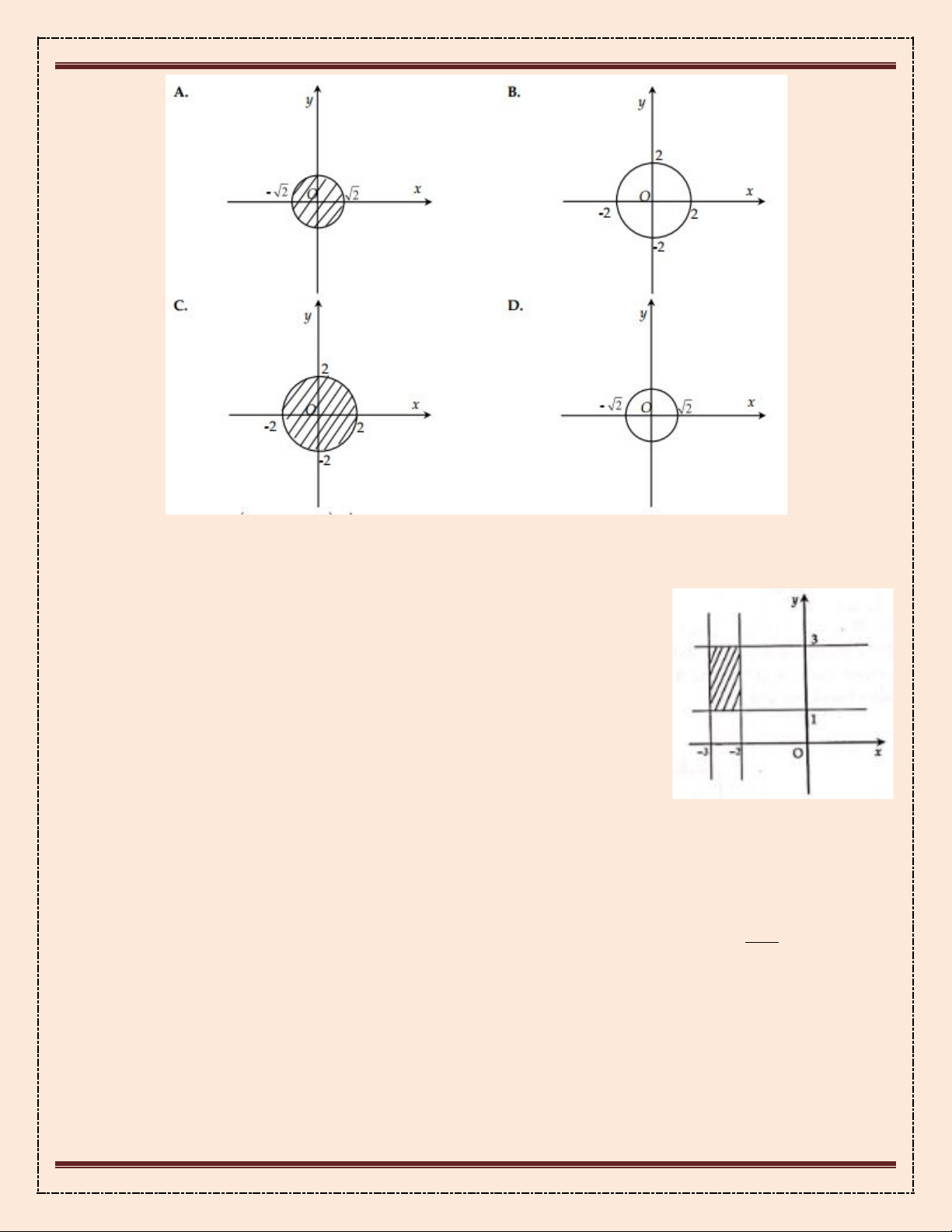
Bài tập trắc nghiệm số phức
Trang 190
Câu 10. Số phức thỏa mãn điều kiện nào thì có phần biểu diễn là phần gạch chéo trong hình vẽ (kể cả
biên) ?
A. Số phức z có phần thực thuộc đoạn
[
]
3; 2−−
trên trục Ox, phần ảo thuộc
đoạn
[
]
1; 3
trên trục Oy.
B. Số phức z có phần thực thuộc đoạn
[ ]
1; 3
trên trục Ox, phần ảo thuộc đoạn
[ ]
3; 2−−
trên trục Oy.
C. Số phức z có phần thực thuộc đoạn
[
]
3; 2−−
trên trục Oy, phần ảo thuộc
đoạn
[ ]
1; 3
trên trục Ox.
D. Số phức z có phần thực thuộc đoạn
(
)
3; 2−−
trên trục Ox, phần ảo thuộc
đoạn
( )
1; 3
trên trục Oy.
Câu 11. Xác định tập hợp các điểm biểu diễn số phức z trên mặt phẳng phức sao cho
1
zi−
là số thuần ảo.
A. Trục tung, bỏ điểm
( )
0;1
B. Trục hoành, bỏ điểm
( )
1; 0−
C. Đường thẳng
1y =
, bỏ điểm
( )
0;1
D. Đường thẳng
1x = −
, bỏ điểm
( )
1; 0−
Câu 12. Gọi A là điểm biểu diễn của số phức
32zi= +
và điểm B là điểm biểu diễn số phức
'23zi= +
.
Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hai điểm A và B đối xứng với nhau qua gốc tọa độ O.
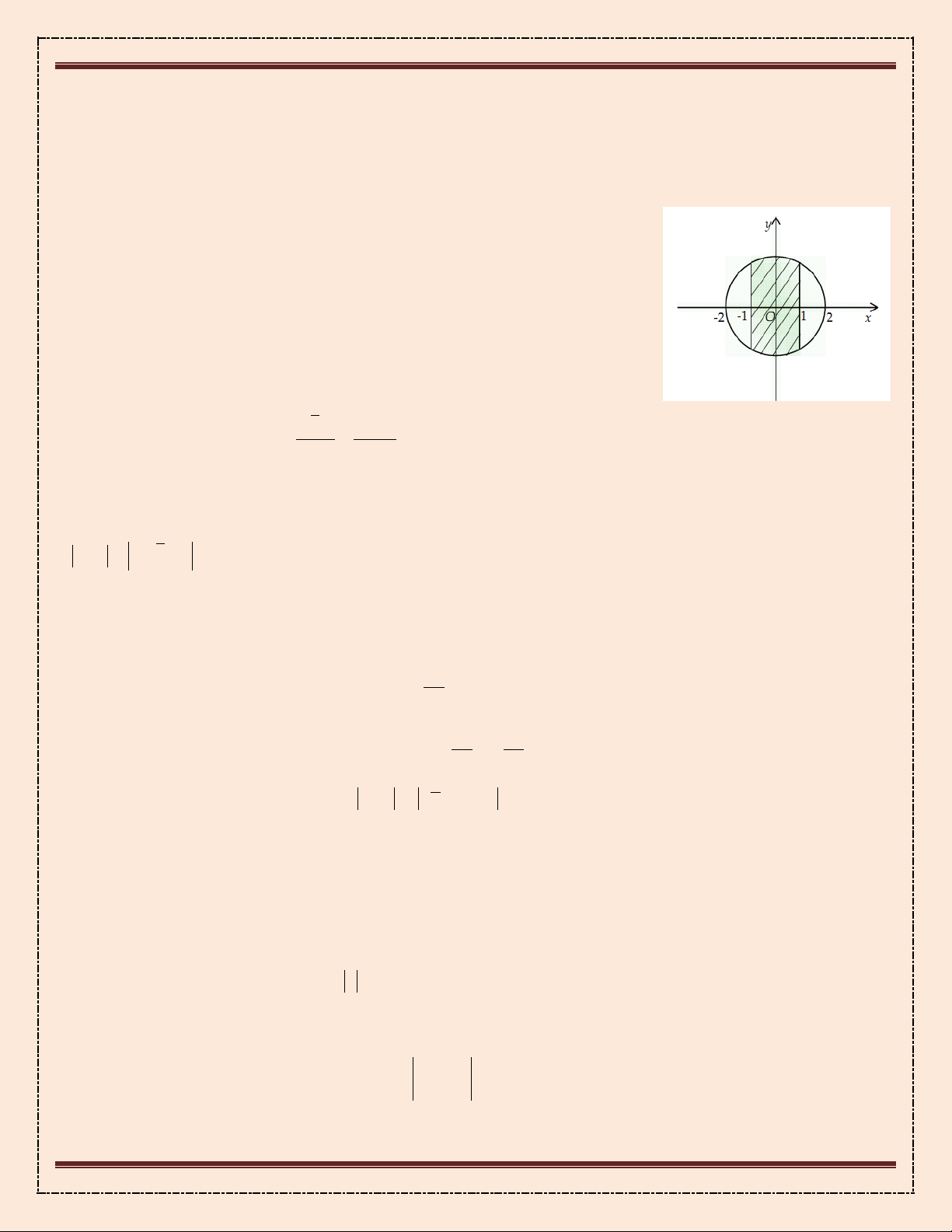
Bài tập trắc nghiệm số phức
Trang 191
B. Hai điểm A và B đối xứng với nhau qua trục tung.
C. Hai điểm A và B đối xứng nhau qua trục hoành
D. Hai điểm A và B đối xứng nhau qua đường thẳng
yx
=
Câu 13. Số phức thỏa mãn điều kiện vào thì có điểm biểu diễn ở phần gạch chéo?
A. Số phức có phần thực nằm trong
( )
1;1
−
và mô đun nhỏ hơn 2.
B. Số phức có phần thực nằm trong
[ ]
1;1−
và mô đun nhỏ hơn 2
C. Số phức có phần thực nằm trong
[ ]
1;1−
và mô đun không vượt quá 2.
D. Số phức có phần thực nằm trong
( )
1;1
−
và mô đun không vượt quá 2.
Câu 14. Cho số phức
67
13 5
zi
z
i
+
−=
+
, điểm nào sau đâu là điểm biểu diễn của số phức z:
A. M(0;1) B. N(1;1) C. P(–1;–1) D. Q(0,–1)
Câu 15. Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn hệ thức:
21 2
z zz−= −+
A. Tập hợp các điểm cần tìm là hai đường thẳng
0; 2xx= =
B. Tập hợp các điểm cần tìm là đường tròn
22
2xy+=
C. Tập hợp các điểm cần tìm là đường elip:
2
2
1
2
y
x +=
D. Tập hợp các điểm cần tìm là hai đường elip:
22
22
1; 1
22
yx
xy+ = +=
Câu 16. Cho số phức z thỏa mãn
1z −
=
26zz i−−
. Tập hợp các điểm biểu diễn của số phức là :
A. Đường tròn tâm
( )
1 ; 2
I
bán kính R=1 B. Đường thẳng có phương trình
5 60xy− −=
C. Đường thẳng có phương trình
6 12 0xy−+=
D. Đường thẳng có phương trình
3 60xy− −=
Câu 17. Cho các nhận định sau (giả sử các biểu thức đều có nghĩa) :
1) Số phức và số phức liên hợp của nó có mô đun bằng nhau.
2) Với
23zi= −
thì mô đun của z là:
23zi
= +
3) Số phức z là số thuần ảo
⇒
zz
−
= −
4) Tập hợp điểm biểu diễn số phức z thỏa mãn
12zz
−
++ =
là một đường tròn.
Số nhận định đúng là:

Bài tập trắc nghiệm số phức
Trang 192
A. 2 B. 3 C. 4 D. 1
Câu 18. Cho các điểm A,B,C trong mặt phẳng phức theo thứ tự được biểu diễn bởi các số
1 i
+
;
24i+
;
65i+
. Tìm số phức biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành :
A.
78i+
B.
38
i−+
C.
52i+
D.
32
i−+
Câu 19. Trên hệ trục tọa độ Oxy cho điểm
(3; 4)
A
biểu diễn số phức z. Phần ảo của số phức
w
z
z
=
là
A.
3
5
B.
4
5
C.
3
5
i
D.
4
5
i
Câu 20. Cho số phức z thỏa mãn
(1 )(3 2 ) 2 2z i ii+− − = +
. Điểm A là điểm biểu diễn số phức z trên hệ
tọa độ. Khoảng cách từ A đến đường thẳng (d) :
2 2 50
xy− +=
là :
A.
7
22
B.
7
4
C.
72
8
D.
7
2
Câu 21. Tập hợp các điểm biểu diễn số phức thỏa mãn
2
( )9ziz
−
+− =−
A. Hình tròn B. Đường tròn
C. Hai đường thẳng song song D. Đường thẳng
Câu 22. Cho số phức z thỏa mãn:
2 23 2 12z ii z− + = −−
. Tập hợp điểm biểu diễn cho số phức z là:
A.
20 16 47 0xy
− −=
B.
20 16 47 0xy+ +=
C.
20 16 47 0xy+ −=
D.
20 16 47 0xy
− +=
Câu 23. Gọi
,,
ABC
lần lượt là các điểm biểu diễn cho các số phức
12
1 3; 3 2z iz i=−+ =−−
;
3
4zi= +
.
Chọn kết luận đúng nhất:
A. Tam giác ABC cân B. Tam giác ABC vuông cân
C. Tam giác ABC vuông D. Tam giác ABC đều
Câu 24. Trên mặt phẳng Oxy tìm biểu diễn số phức z thỏa mãn :
( )
21z i iz
−=+
?
A. Hình tròn tâm I(0;–2) bán kính
22
B. Hình tròn tâm I(0;2) bán kính
22
C. Đường tròn tâm I(0;–2) bán kính
22
D. Đường tròn tâm I(0;2) bán kính
22
Câu 25. Trên mặt phẳng Oxy tìm biểu diễn số phức z thỏa mãn :
1 22zi≤− <
?
A. Hình tròn tâm I(0;2) bán kính 2.
B. Hình tròn tâm I(0;2) bán kính 1.
C. Hình tròn tâm I(0;2) bán kính 2 trừ đi phần trong hình tròn tâm I(0;2) bán kính 1.
D. Hình tròn tâm I(0;2) bán kính 2 trừ đi hình tròn tâm I(0;2) bán kính 1.
Câu 26. Miêu tả tập số phức z trên hệ tọa độ phức mà thỏa mãn
3 2 10zi+−=
là:

Bài tập trắc nghiệm số phức
Trang 193
A. Đường thẳng
3 2 100xy−=
B. Đường thẳng
2 3 100xy
−=
C. Đường tròn
( ) ( )
22
2 3 100xy
− ++ =
D. Đường tròn
( ) ( )
22
3 2 100
xy
− ++ =
Câu 27. Cho số phức z thỏa mãn
20iz i+ −=
. Tính khoảng cách từ điểm biểu diễn của z trên mặt phẳng
tọa độ Oxy đến điểm
( )
3; 4M −
.
A.
25
B.
13
C.
2 10
D.
22
Câu 28. Trong mặt phẳng với hệ tọa độ Oxy, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
(
)
2 15iz−+ − =
. Phát biểu nào sau đây là sai ?
A. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm
( )
1; 2I −
B. Tập hợp các điểm biểu diễn các số phức z là đường tròn có bán kính
5R =
C. Tập hợp các điểm biểu diễn các số phức z là đường tròn có đường kính bằng 10
D. Tập hợp các điểm biểu diễn các số phức z là hình tròn có bán kính
5R =
Câu 29. Trong mặt phẳng phức
( ) ( ) ( )
4;1 , 1;3 , 6; 0A BC−−
lần lượt biểu diễn các số phức
123
,,zz z
.
Trọng tâm G của tam giác ABC biểu diễn số phức nào sau đây?
A.
4
3
3
i+
B.
4
3
3
i−+
C.
4
3
3
i−
D.
4
3
3
i
−−
Câu 30. Trong mặt phẳng phức, tập hợp các điểm M biểu diễn số phức z biết
34
zz i= −+
là:
A. Elip
22
1
42
xy
+=
B. Parabol
2
4x
y =
C. Đường tròn
22
40xy+ −=
D. Đường thẳng
6 8 25 0x y+−=
Câu 31. Cho số phức z thỏa
3z =
. Biết rằng tập hợp số phức
wzi= +
là một đường tròn. Tìm tâm của
đường tròn đó.
A.
( )
0;1I
B.
( )
0; 1I −
C.
( )
1; 0I −
D.
( )
1; 0I
Câu 32. Biết điểm
( )
1; 2M −
biểu diễn số phức z trong mặt phẳng tọa độ phức. Tính môđun của số phức
2
w iz z= −
.
A.
26
B.
25
C.
24
D.
23
Câu 33. Cho số phức
1zi= +
. Tìm tập hợp các điểm biểu diễn số phức
32wzi= +
.
A. Tập hợp các điểm biểu diễn số phức w nằm trên đường tròn có phương trình
( ) ( )
22
3 11xy− ++ =
B. Điểm biểu diễn số phức w là điểm có tọa độ
( )
3; 1−−
C. Điểm biểu diễn số phức w là điểm có tọa độ
( )
3; 1−
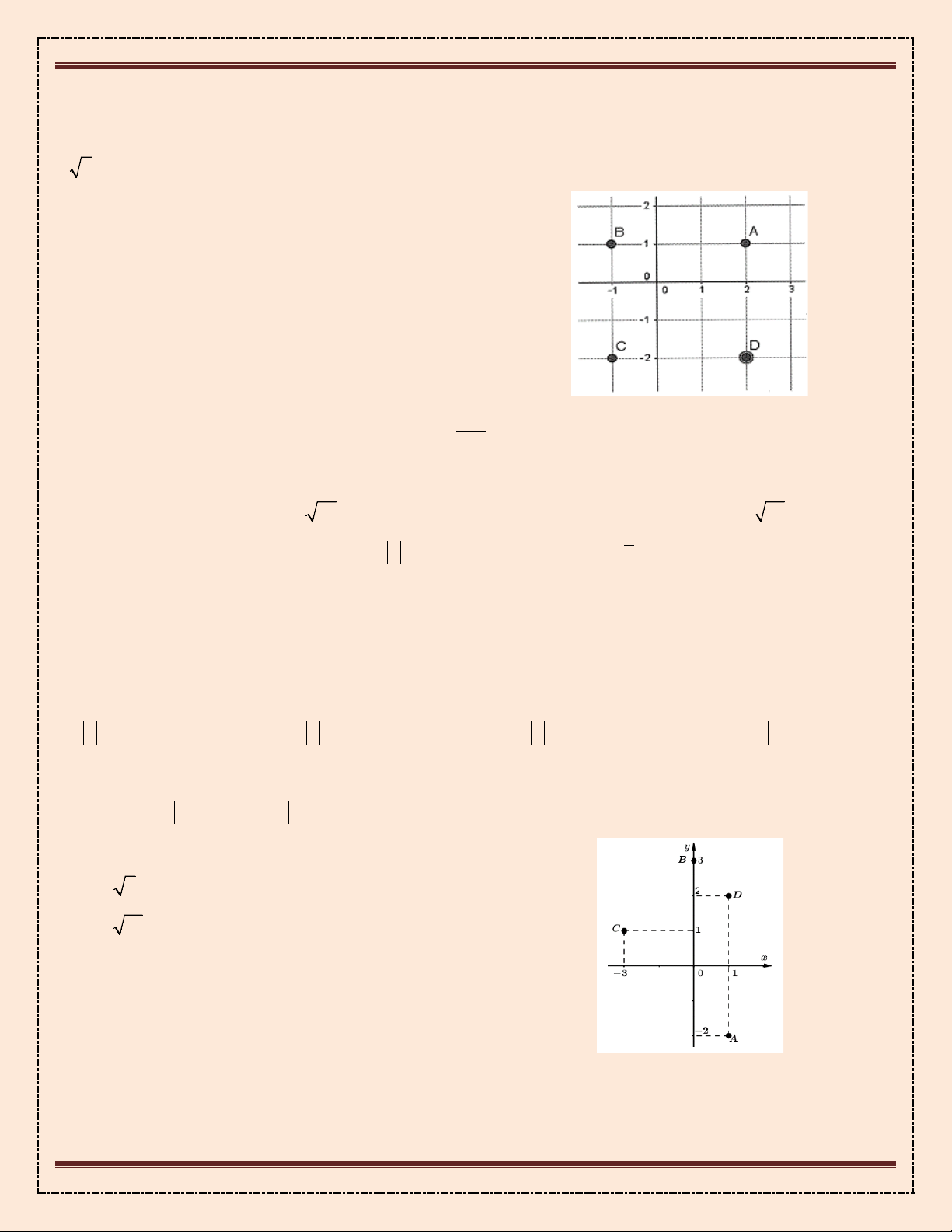
Bài tập trắc nghiệm số phức
Trang 194
D. Tập hợp các điểm biểu diễn số phức w nằm trên đường tròn có phương trình
( ) ( )
22
3 11xy+ ++ =
Câu 34. Trong hình dưới, điểm nào trong các điểm A, B, C, D biểu diễn cho số phức có môđun bằng
22
.
A. Điểm A
B. Điểm B
C. Điểm C
D. Điểm D
Câu 35. Cho số phức z thỏa mãn
( )
1
27
i
zi
i
+
=+−
. Hỏi khi biểu diễn số phức này trên mặt phẳng phức
thì nó cách gốc tọa độ khoảng bằng bao nhiêu ?
A. 9 B.
65
C. 8 D.
63
Câu 36. Cho các số phức z thỏa mãn
2z =
và số phức w thỏa mãn
( )
34 2iw i z i=−+
. Biết rằng tập hợp
các điểm biểu diễn các số phức w là một đường tròn. Tính bán kính r của đường tròn đó.
A.
5r
=
B.
10r =
C.
14r =
D.
20r =
Câu 37. Cho số phức z có tập hợp điểm biểu diễn trên mặt phẳng phức là đường tròn
(
)
22
: 25 0
Cx y
+−=
. Tính mô–đun của số phức z.
A.
3z =
B.
5z =
C.
2z =
D.
25z
=
Câu 38. Cho các số phức
1234
,,,zz zz
có các điểm biểu diễn trên mặt phẳng phức là A, B, C, D (như hình
bên). Tính
1234
Pzz zz= +++
A.
2P =
B.
5P =
C.
17P =
D.
3P =

Bài tập trắc nghiệm số phức
Trang 195
Câu 39. Trong mặt phẳng tọa độ, tập hợp điểm biểu diễn số phức z thỏa mãn
( )
1z i iz−= +
là một
đường tròn, đường tròn đó có phương trình là:
A.
22
2 2 10x
xy y
+ + + −=
B.
22
2 10xy y
+ + −=
C.
22
2 10xxy+ + −=
D.
22
2 10xxy
+ + +=
Câu 40. Tập hợp các điểm trong mặt phẳng Oxy biểu diễn các số phức z thỏa mãn
12
zi−+ =
là:
A. Đường tròn tâm
( )
1;1I
−
, bán kính 2 B. Đường tròn tâm
(
)
1; 1I −
, bán kính 2
C. Đường tròn tâm
( )
1; 1I −
, bán kính 4 D. Đường thẳng
2xy+=
.
Câu 41. Cho hai số phức z và z’ lần lượt được biểu diễn bởi hai vectơ
u
và
'u
. Hãy chọn câu trả lời sai
trong các câu sau:
A.
'uu+
biểu diễn cho số phức
z'z+
B.
'uu−
biểu diễn cho số phức
z'z−
C.
.'uu
biểu diễn cho số phức
z. 'z
D. Nếu
z a bi= +
thì
u OM=
, với
(
)
;M ab
Câu 42. Trong mặt phẳng phức gọi A, B, C là điểm biểu diễn số phức với . Biết tam
giác ABC vuông tại B. Tìm tọa độ của C ?
A. B. C. D.
Câu 43. Tập hợp biểu diễn số phức z thỏa là đường tròn có bán kính bằng:
A. 2 B. 6 C. 4 D. 8
Câu 44. Cho số phức thõa mãn . Gọi M là điểm biểu diễn cho số phức z. Tọa độ điểm
M là
A. (1; 2) B. (4; 1) C. (1; 4) D. (–1; –4)
Câu 45.
Tập hợp điểm biểu diễn số phức thỏa mãn là đường tròn tâm , bán kính
A.
B.
C.
D.
Câu 46. Điểm biểu diễn số phức:
( )( )
23 4
32
ii
z
i
−−
=
+
có tọa độ là:
A.
( )
1; 4−
B.
( )
1; 4−−
C.
( )
1; 4
D.
( )
1; 4−
Câu 47. Trong mp tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn: .
A. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(2, –1), bán kính R= .
B. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0, 1), bán kính R= .
C. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0, –1), bán kính R= .
,1 3 , 5i ia i++
a ∈
( )
3; 5C
−
( )
3; 5C
( )
2;5C
( )
2;5C
−
.4zz=
z
(1 ) 5 3iz i−=+
z
(4 3 ) 2zi−+ =
I
R
(4;3), 2IR=
(4; 3), 4IR−=
( 4;3), 4IR−=
(4; 3), 2IR−=
( )
1z i iz−= +
2
3
3
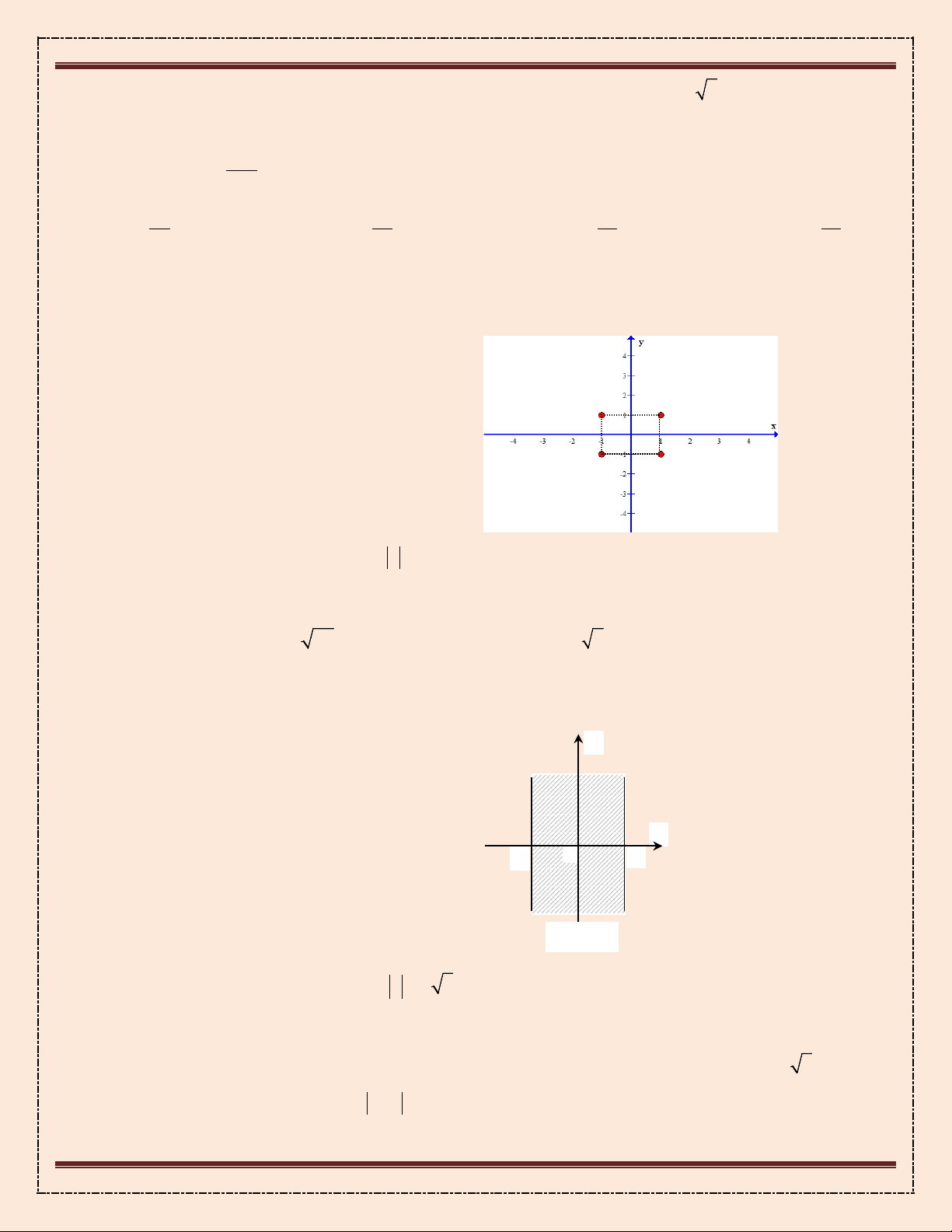
Bài tập trắc nghiệm số phức
Trang 196
D. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0, –1), bán kính R= .
Câu 48. Trong mặt phẳng tọa độ Oxy, gọi M là điểm biểu diễn cho số phức z = 3 – 4i; M’ là điểm biểu
diễn cho số phức . Tính diện tích tam giác OMM’.
A. . B. C. D.
Câu 49. Cho số phức z thỏa mãn . Điểm nào sau đây biểu diễn cho z trong các điểm M,
N, P, Q ở hình bên?
A. Điểm M
B. Điểm N
C. Điểm P
D. Điểm Q
Câu 50. Cho các số phức z thỏa mãn .Biết rằng tập hợp các điểm biểu diễn các số phức
là một đường tròn.Tính bán kính r của đường tròn đó.
A.20 B. C. D.7
Câu 51. Cho số phức z = a + bi; a,b ∈ R. Để điểm biểu diễn của z nằm trong dãi (–2;2)
(hình 1), điều kiện của a và b là:
A.
B.
C. và b ∈ R
D. a, b ∈ (–2; 2)
Câu 52. Cho các số phức z thỏa mãn . Biết rằng tập hợp các điểm biểu diễn các số phức
là một đường tròn. Tính bán kính r của đường tròn đó.
A. B. C. D.
Câu 53. Cho số phức thỏa mãn . Biết rằng tập hợp các điểm biểu diễn các số phức
là một đường tròn. Tâm của đường tròn đó là:
2
/
1
2
i
zz
+
=
'
25
4
OMM
S
∆
=
'
25
2
OMM
S
∆
=
'
15
4
OMM
S
∆
=
'
15
2
OMM
S
∆
=
(
)
13 2 4iz i+ +=−
2z =
( )
32 2w i iz=−+−
20
7
2
2
a
b
≥
≥
2
-2
a
b
≤−
≤
22a−< <
35z =
(2 )w iz i=−+
4r =
15r =
16r =
35r =
z
1zi+=
2wz i= −
y
2
O
x
-2
(H×nh 1)
P
N
Q
M
Bài tập trắc nghiệm số phức
Trang 197
A. . B. . C. . D. .
Câu 54. Xác định tập hợp các điểm biểu diễn số phức z trên mặt phẳng phức sao cho
zi
zi
−
+
là số thực
A. Đường tròn phương trình x
2
+ y
2
= 1 bỏ đi điểm (0; –1)
B. Hyperbol phương trình x
2
– y
2
= – 1 bỏ đi điểm (0; –1)
C. Trục tung bỏ đi điểm (0; –1)
D. Trục hoành bỏ đi điểm (0; –1)
Câu 55. Gọi A là điểm biểu diễn của số phức và B là điểm biểu diễn của số phức
A. Hai điểm A và B đối xứng với nhau qua trục hoành.
B. Hai điểm A và B đối xứng với nhau trục tung.
C. Hai điểm A và B đối xứng với nhau qua gốc tọa độ O.
D. Hai điểm A và B đối xứng với nhau qua đường thẳng y = x .
Câu 56. Trong mặt phẳng tọa độ các điểm A, B, C lần lượt biểu diễn các số phức ; ;
. Số phức biểu diễn trọng tâm G của tam giác ABC là:
A. B. C. D.
Câu 57. Trong mặt phẳng tọa độ Oxy, tập họp điểm biểu diễn số phức z, biết là đường tròn
có tâm I. Hoành độ tâm I có tọa độ là:
A. x
I
= –4 B. x
I
= –2 C. x
I
= 2 D. x
I
= 4
Câu 58. Cho số phức z thỏa mãn Hỏi điểm biểu diễn của z là điểm nào trong các điểm M,
N, P, Q ở hình bên ?
A. Điểm P
B. Điểm M
C. Điểm Q
D. Điểm N
Câu 59. Cho số phức z thỏa mãn
( )
12 8 .iz i+=+
Hỏi điểm biểu diễn của z là điểm nào
trong các điểm M, N, P, Q ở hình dưới đây?
( )
0; 1I −
( )
0; 3
I −
(
)
0;3
I
( )
0;1I
25
zi
= +
' 25zi=−+
1
3zi
= −
2
22
zi= −
3
5zi=−−
12zi=−−
2zi=−+
1zi=−−
1zi=−+
21zi−−=
( )
13
iz i−=+
M
N
P
Q
2
-1
-2
1
0
x
y
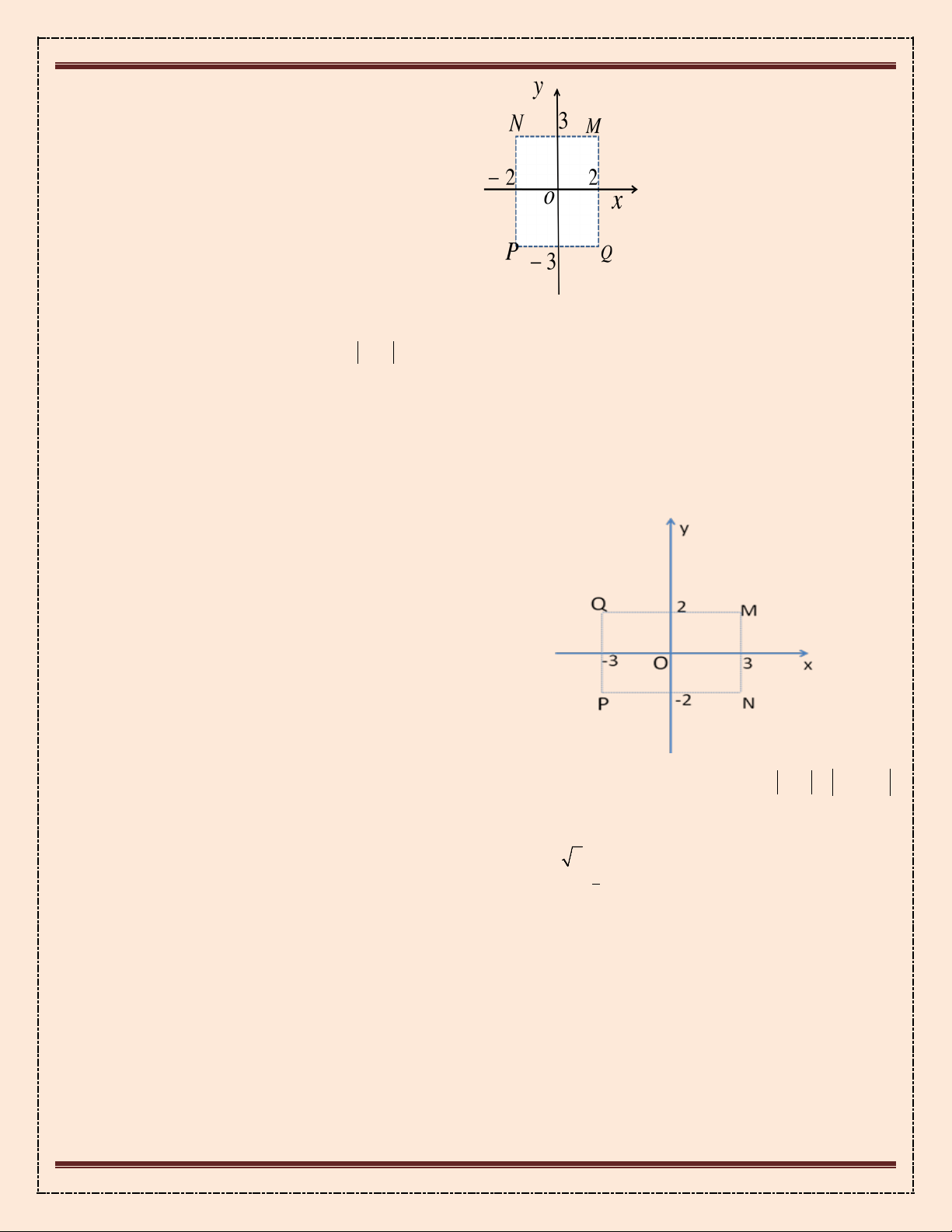
Bài tập trắc nghiệm số phức
Trang 198
A. Điểm P.
B. Điểm Q.
C. Điểm M.
D. Điểm N.
Câu 60. Cho số phức z thỏa mãn
12z −=
.Biết rằng tập hợp các điểm biểu diễn các số phức
2
w zi= −
là một đường tròn. Tìm bán kính r của đường tròn đó.
A. r = 2 B. r = 1 C. r = –2 D. r = 4
Câu 61. Cho số phức z thỏa mãn .Hỏi điểm biểu diễn của z là điểm nào trong các điểm
M,
N, P, Q ở hình bên ?
A. Điểm N
B. Điểm M
C. Điểm P
D. Điểm Q
Câu 62. Tập hợp các điểm trong mặt phẳng phức biểu diễn các số z thỏa mãn điều kiện:
( )
1
z i iz−= +
là đường tròn có bán kính là
A. R = 1 B. R = 2 C. R =
2
D. R = 4
Câu 63. Tập hợp các số phức z thoả mãn đẳng thức |z + 2 + i| = | – 3i| có phương trình là:
A. y = x + 1 B. y = – x + 1 C. y = –x – 1 D. y = x – 1
Câu 64. Cho số phức
z
thỏa mãn
(1) 3.iz i− =−−
Hỏi điểm biểu diễn của
z
là điểm nào trong các điểm
M, N, P, Q ở hình bên ?
( )
5
1
zi
i
= −
−
z
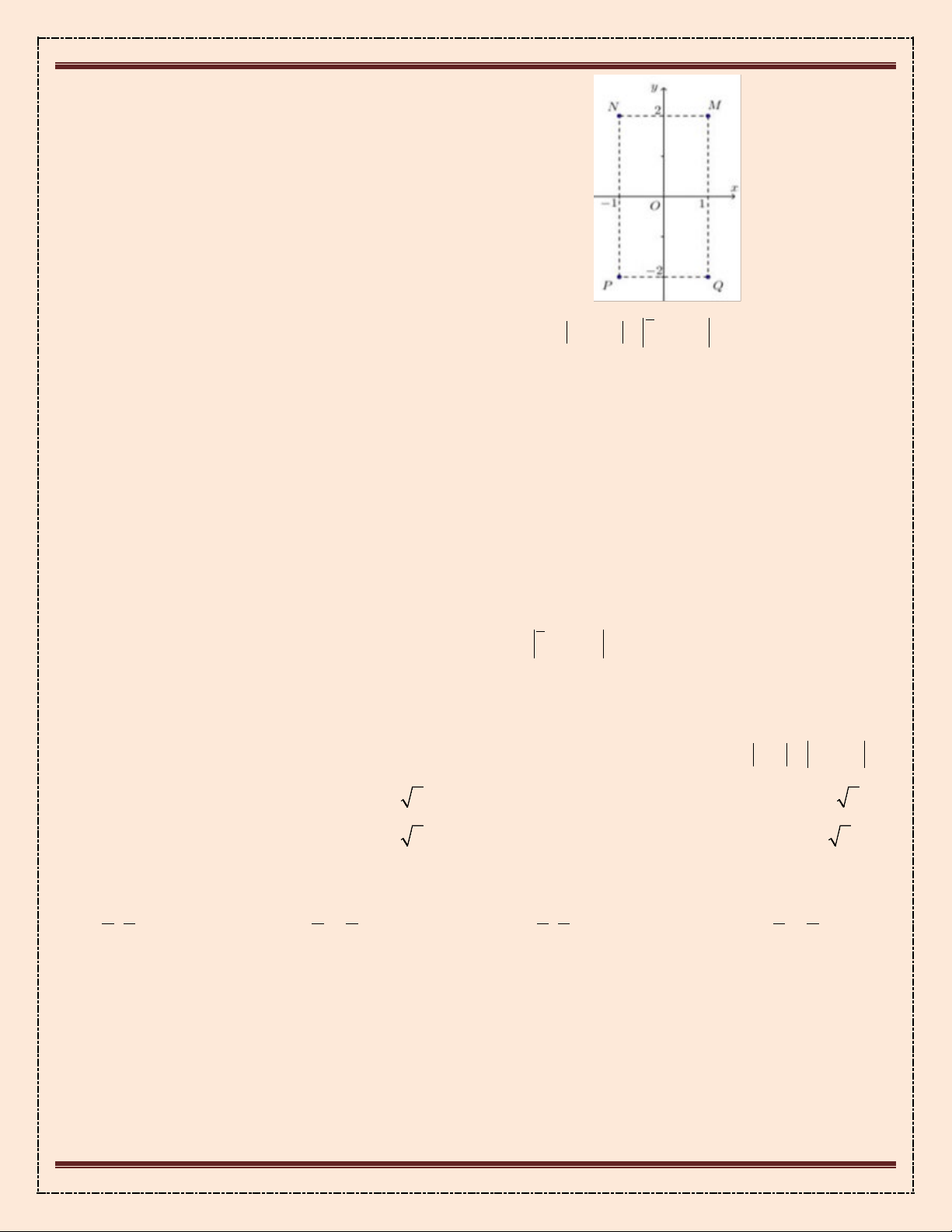
Bài tập trắc nghiệm số phức
Trang 199
A. Điểm P.
B. Điểm Q.
C. Điểm M.
D. Điểm N.
Câu 65. Tập hợp các điểm biểu diễn của số phức
z
thỏa mãn
1 12z iz i−+ = +−
là đường thẳng d:
A. 4x+2y+3=0. B. 2x+y=0. C. 3x–y–1=0. D.–4x+2y+3=0.
Câu 66. Trong không gian với hệ tọa độ Oxyz, cho 3 điểm M(2;0;0), N(0;–3;0), P(0;0;4). Nếu tứ giác
MNPQ là hình bình hành thì điểm Q có tọa độ:
A. (–2;–3;–4) B. (2;3;4) C. (–2;–3;4) D. (3;4;2)
Câu 67. Một vận động viên đẩy tạ theo quỹ đạo là một parabol có phương trình . Vị trí
quả tạ đang di chuyển xem như là một điểm trong không gian Oxy. Khi đó vị trí cao nhất của quả tạ là điểm
biểu diễn của số phức nào sau đây:
A. z . B. z . C. z . D.z .
Câu 68. Tập hợp các điểm biểu diễn số phức z thõa mãn là đường tròn có tâm I, bán kính
R :
A.I(4;3), R =2 B.I(4;–3), R =4 C.I(–4;3), R= 4 D.I(4; –3), R= 2
Câu 69. Trong mặt phẳng tọa độ Oxy, tập hợp điểm biểu diễn các số phức z thỏa mãn là:
A. Đường tròn tâm I (0;–1) và bán kính B. Đường tròn tâm I (0;–1) và bán kính
C. Đường tròn tâm I (–1;0) và bán kính D. Đường tròn tâm I (0;1) và bán kính
Câu 70. Điểm biểu diễn của số phức z thỏa : là:
A. B. C. D.
Câu 71. Gọi A là điểm biểu diễn của số phức Z = 1 + 2i và B là điểm biểu diễn của số phức Z’ = –1 + 2i.
Tìm mệnh đề đúng trong các mệnh đề sau :
A. Hai điểm A và B đối xứng nhau qua trục hoành
B. Hai điểm A và B đối xứng nhau qua trục tung
C. Hai điểm A và B đối xứng nhau qua gốc tọa độ O
D. Hai điểm A và B đối xứng nhau qua đường thẳng y = x
2
24
yx x=−+ +
13i= −
5 i= +
15i= +
3 i= −
43 2zi−+ =
( )
1z i iz−= +
22R =
2R =
22R =
2R =
2
(1 ) (1 2 )
iz i+=−
71
( ;)
22
−
71
(; )
22
−
71
(;)
22
71
(;)
22
−−

Bài tập trắc nghiệm số phức
Trang 200
Câu 72. Tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa là
A. B.
C. D.
Câu 73. Cho số phức . Điểm biểu diễn của số phức z là:
A. M(–1;3) B. M(–1;–3) C. M(1;–3) D. M(1;3)
Câu 74. Tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa
|
− 2
|
< 3 là
A. Đường tròn bán kính r = 3
B. Hình tròn bán kính r = 3 không kể đường tròn bán kính r = 3
C. Đường tròn bán kính r = 9
D. Hình tròn bán kính r = 9
Câu 75. Điểm biểu diễn của số phức z thỏa : là:
A. B. C. D.
Câu 76. Điểm biểu diễn của các số phức z = a + ai với , nằm trên đường thẳng có phương trình là:
A. y = 2x B. y = –x C. y = x+ 1 D. y = x
Câu 77. Tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa là
A. B.
C. D.
Câu 78. Trong mặt phẳng phức gọi A, B, C lần lượt là các điểm biểu diễn của các số phức
, , . Tam giác ABC là :
A. Một tam giác cân B. Một tam giác đều
C. Một tam giác vuông D. Một tam giác vuông cân
Câu 79. Cho số phức z thỏa và . Trong mặt phẳng phức, tập hợp điểm biểu
diễn số phức w là đường tròn tâm I, bán kính R là:
A. I(3;–4); R=2 B. I(4;–5); R=4 C. I(5;–7); R=4 D. I(7;–9) ; R=4
Câu 80. Cho số phức z thỏa mãn
. Hỏi điểm biểu diễn của z là điểm nào trong các điểm I,
J, K, H ở hình bên
( )
1 22iz i+ −=
( ) ( )
22
1 11
xy+ +− =
(
) (
)
22
1 11xy
+ ++ =
( ) ( )
22
1 11
xy− +− =
( ) ( )
22
1 11xy−++ =
( 1)( 2)z ii i=−+
2
(1 ) (1 2 )iz i
+=−
71
( ;)
22
−
71
(; )
22
−
71
(;)
22
71
(;)
22
−−
a ∈
( )
1 22iz i+ −=
( ) (
)
22
1 11xy+ +− =
( ) (
)
22
1 11
xy
+ ++ =
( ) ( )
22
1 11xy−+− =
( ) ( )
22
1 11xy−++ =
(1 )(2 i)
1
Zi=−+
2
13Zi= +
3
13
Zi=−−
34 2zi−+ =
21wz i= +−
( )
12 3
iz i−=+
Bài tập trắc nghiệm số phức
Trang 201
A. Điểm K
B. Điểm H
C. Điểm I
D. Điểm J
Câu 81. Cho số phức z thoả mãn (1–i)z+4–2i=0. Điểm biểu diễn của z có toạ độ là
A. (–3;–1) B. (–3;1) C. (3;–1) D. (3;1)
Câu 82. Tập hợp các điểm biểu diễn của số phức z thoả mãn điều kiện là đường tròn có
phương trình
A. B.
C. D.
Câu 83. Cho số phức z = a + a
2
i với a ∈ R. Khi đó điểm biểu diễn của số phức liên hợp của z nằm trên:
A. Đường thẳng y = 2x B. Đường thẳng y = –x + 1
C. Parabol y = x
2
D. Parabol y = –x
2
Câu 84. Gọi M là điểm biểu diễn số phức z trong mặt phẳng phức. Như thế, số được biểu diễn bởi
điểm
A. Đối xứng với M qua O B. Đối xứng với M qua Oy
C. Đối xứng với M qua Ox D. Không xác định được
Câu 85. Cho số phức z thỏa mãn và . Trong mặt phẳng phức, tập hợp điểm
biểu diễn số phức w là đường tròn có tâm I, bán kính R. Khi đó
A. B. C. D.
Câu 86. Cho phương trình: . Điểm biểu diễn của z trên mặt phẳng tọa độ là
A. . B. . C. . D. .
Câu 87. Số phức z = 2 − 3 có điểm biểu diễn là
A.(2; 3) B. (−2; −3) C.(2; −3) D. (−2; 3)
Câu 88. Tập hợp các điểm trong mặt phẳng biểu diễn số phức z thõa mãn điều kiện
|
− 1 + 2
|
= 4 là
A. Một đường thẳng B. Một đường tròn
C. Một hình chữ nhật D. Một hình vuông
x
y
H
K
J
I
-
1
5
-
7
5
7
5
1
5
1
3zi+=
22
( 1) 9xy+− =
22
( 1) 9xy++ =
2
( 1) 9xy− +=
22
( 1) 3xy++ =
z−
34 2zi
−+ =
w2 1zi= +−
(
)
I 3; 4 , 2R−=
( )
I 4; 5 , 4R−=
( )
I 5; 7 , 4R−=
( )
I 7; 9 , 4R−=
(1 4 ) 5 2iz i z−=−
43
;
55
−
43
;
55
34
;
55
34
;
55
−
Bài tập trắc nghiệm số phức
Trang 202
Câu 89. Tập hợp các điểm trong mặt phẳng phức biểu diễn cac số phức z thỏa mãn là
đường thẳng có phương trình là :
A.
B.
C.
D.
Câu 90. Điểm M trên hình vẽ là điểm biểu diễn của số phức nào sau đây:
A. (1 + i)z = 3 – i
B. (1 – i)z = 3 – i
C. (1 – i)z = 3 + i
D. (1 + i)z = 3 + i
Câu 91. Trong mặt phẳng phức, gọi A, B, C lần lượt là các điểm biểu diễn của các số phức
z
1
= (1 – i)(2 + i); z
2
= 1 + 3i; z
3
= –1 – 3i. Tam giác ABC là:
A. Tam giác cân B. Tam giác đều
C. Tam giác vuông D. Tam giác vuông cân
Câu 92. Tập hợp các điểm biểu diễn số phức z thỏa mãn là:
A. Một đường tròn bán kinh R=2
B. Hai đường tròn có tâm lần lượt O(2;1), O’(–2;–1)
C. Một hình hyperbol có phưng trình
D. Hai hình hyperbol có phương trình và
Câu 93. Tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa mãn
là:
A. Đường tròn tâm I(0;1), bán kính R=1 B. Đường tròn tâm , bán kính R=
C. Đường Parabol có phương trình
D. Đường Parabol có phương trình
Câu 94. Cho số phức z thỏa , biết tập hợp các điểm biểu diễn số phức z nằm trên đường
tròn tâm I có bán kính R. Tìm tọa độ I và R.
A. B. C. D.
Câu 95. Cho số phức , với x, y là hai số thực thỏa :
| 5| 6zz++=
1
2
x =
1
2
x = ±
1
2
y =
1
2
y
= ±
x
y
2
M
1
22
|z ( ) | 4z
−=
1
1
( ):y
2
H
x
=
1
1
( ):y
H
x
=
2
1
( ):yH
x
= −
2| | | 2 |zi zz i
−= −+
( 3;0)I
3
2
4
x
y =
2
4
y
x =
12 2zi−+ =
(1; 2), 2IR−=
( 1; 2), 4IR−=
( 2;1), 2IR−=
(1; 2), 4IR−=
z x yi= +
( ) ( )
( ) ( )
21 32 2 4x y ix y i++ − = + + +
Bài tập trắc nghiệm số phức
Trang 203
Điểm M trên mặt phẳng tọa độ biểu diễn cho z, tìm tọa độ M.
A. B. C. D.
Câu 96. Trên mặt phẳng toạ độ Oxy, tập hợp điểm biểu diễn các số phức z thoả mãn điều kiện
là :
A. B.
C. D.
Câu 97. Cho số phức z thỏa mãn .Hỏi điểm biểu diễn của z là điểm nào trong các điểm
M,N,P,Q ở hình bên ?
A. Điểm P
B. Điểm Q
C. Điểm M
D. Điểm N
Câu 98. Cho các số phức z thỏa mãn .Biết rằng tập hợp các điểm biểu diễn các số phức
là một đường tròn .Xác định tâm I và tính bán kính r của đường tròn đó
A. B. C. D.
Câu 99. Gọi M là điểm biểu diễn của số phức 3 +4i và N là điểm biểu diễn của số phức –3 +4i. Khẳng
định nào sau đây là đúng ?
A. Hai điểm M và N đối xứng với nhau qua trục hoành.
B. Hai điểm M và N đối xứng với nhau qua trục tung.
C. Hai điểm M và N đối xứng với nhau qua gốc toạ độ O.
D. Hai điểm M và N đối xứng với nhau qua đường thẳng y = x.
Câu 100. Tìm tọa độ điểm M biểu diễn của số phức trên mặt phẳng phức.
A. B. C. D.
Câu 101. Trên mặt phẳng phức cho . Biết rằng lần lượt biểu diễn các số phức ;
. Điểm biểu diễn số phức z sao cho vuông tại C. Khẳng định nào sau đây là đúng ?
A. B. C. D.
( )
1; 3M
( )
3;1M
( )
1; 3M −−
( )
3; 1M −−
(2)2zi i−+=
3 4 20xy+ −=
22
( 1) ( 2) 9
xy+ +− =
22
( 1) ( 2) 4xy
−++ =
2 10xy+ −=
( )
2 34iz i+=+
P
M
N
Q
34 2zi−+ =
21wz i= +−
(7; 9); 4Ir
−=
(4; 5); 4Ir
−=
(3; 4); 2Ir−=
( 7;9); 4Ir−=
1
23
z
i
=
−
( )
2; 3M −
23
;
13 13
M
( )
3; 2M −
( )
4; 1M −
ABC∆
,AB
1
22zi= −
2
24zi=−+
C
ABC∆
24zi= −
22zi=−+
24zi= +
22zi= −

Bài tập trắc nghiệm số phức
Trang 204
Câu 102. Cho số phức z thỏa mãn : =2. Biết rằng tập hợp các điểm biểu diễn của số phức z là
một đường tròn. Tìm tâm và bán kính r của đường tròn đó.
A. Tâm I(–1;1) và bán kính R = 2 B. Tâm I(1;1) và bán kính R = 4
C. Tâm I(1;–1) và bán kính R = 4 D. Tâm I(1;–1) và bán kính R = 2
Câu 103. Trên mặt phẳng tọa độ, tập hợp điểm biểu diễn số phức z thỏa mãn điều kiện là:
A. Đường tròn tâm O, bán kính bằng 2. B. Đường tròn tâm O, bán kính bằng .
C. Hình tròn tâm O, bán kính bằng 2. D. Hình tròn tâm O, bán kính bằng .
Câu 104. Cho số phức thõa mãn là nghiệm phương trình
Điểm M,N lần lượt biểu diễn cho trên Oxy khi đó độ dài MN bằng
A.4 B.2 C.5 D.3
Câu 105.
G
ọi
và
là các nghiệm của phương trình . Gọi M, N là các điểm biểu diễn
của
và
trên mặt phẳng phức. Khi đó độ dài của MN là:
A. B. C. D.
Câu 106. Trong mặt phẳng tọa độ Oxy, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
là
A. Đường tròn có phương trình . B. Đường thẳng có phương trình
C. Đường thẳng có phương trình D. Đường tròn có phương trình .
Câu 107. Cho số phức z thỏa mãn . Tìm tập hợp các điểm biểu diễn các số phức
là
A. Đường tròn có bán kính bằng B. Đường tròn có bán kính bằng
C. Đường tròn có bán kính bằng D. Đường tròn có bán kính bằng
Câu 108. Cho . Số phức z được biểu diển bởi điểm nào trong hình sau:
1
zi−+
2z ≤
2
2
12
,zz
2
2 50zz+ +=
12
,zz
1
z
2
z
2
4 90zz− +=
1
z
2
z
4MN =
5MN =
25MN = −
25MN =
1 (2 )z iz−−=
22
1
4
xyx+ +=
1
4
x =
1
4
y =
22
11
24
xy x++ =
19z +=
(2 3 ) 1w iz
=−+
9 13
9 11
3 11
9
2 10z =
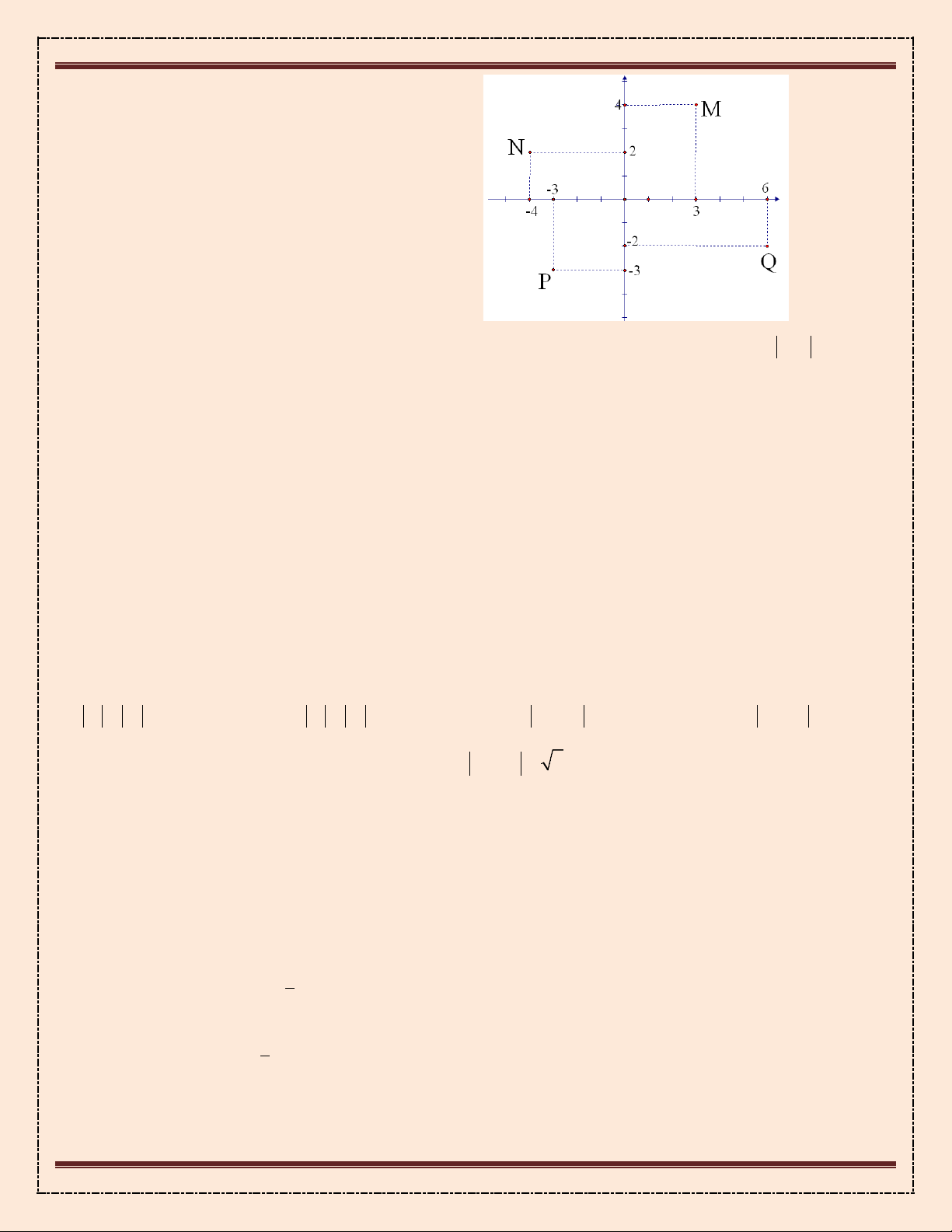
Bài tập trắc nghiệm số phức
Trang 205
A. P
B. M
C. N
D. Q
Câu 109. Tập hợp tất cả các điểm biểu diển số phức trên mặt phẳng tọa độ thỏa mãn là một
đường tròn. Gọi I là tâm của đường tròn này, tọa độ I là:
A. B. C. D.
Câu 110. Gọi A là điểm biểu diễn của số phức 5 +8i và B là điểm biểu diễn của số phức –5 +8i. Tìm mệnh
đề đúng trong các mệnh đề sau?
A. Hai điểm A và B đối xứng với nhau qua trục hoành.
B. Hai điểm A và B đối xứng với nhau qua trục tung.
C. Hai điểm A và B đối xứng với nhau qua gốc toạ độ O.
D. Hai điểm A và B đối xứng với nhau qua đường thẳng y = x.
Câu 111. Giả sử A, B theo thứ tự là điểm biểu diễn của các số phức z
1
, z
2
. Khi đó độ dài của véctơ
bằng
A.
B.
C.
D.
Câu 112. Tập hợp điểm biểu diễn số phức z, biết là
A. Điểm B. Đường thẳng C. Đường tròn D. Elip
Câu 113. Cho A và B lần lượt là điểm biểu diễn của z
1
= 1 – 3i và z
2
= 7 + 5i. Độ dài đoạn AB bằng:
A. 10 B. 9 C. 8 D. 7
Câu 114. Cho A ( –2 ; 3 ), B ( 4 ; –1 )là điểm biểu diễn của hai số phức z và z’. Phần ảo của số phức z.z’
bằng :
A. – 14 B. – 12 C. 12 D. 14
Câu 115. Cho biết z + 2i + 3 là số thuần ảo, tập hợp các điểm biểu diễn của z có phương trình là :
A. x + 2y + 3 = 0 B. x – 2y + 3 = 0 C. x – 2y – 3 = 0 D. x + 2y – 3 = 0
Câu 116. Cho biết z. = 4, tập hợp các điểm biểu diễn của z có phương trình là :
A. x
2
+ y
2
– 2 = 0 B. x
2
+ y
2
– 16 = 0 C. x
2
– y
2
– 4 = 0 D. x
2
+ y
2
– 4 = 0
z
1zi
−=
(0; 1)I −
(0;1)
I
(1; 0)I
( 1; 0)I −
AB
12
zz−
12
zz+
21
zz−
21
zz
+
34 2zi
+=
z
z

Bài tập trắc nghiệm số phức
Trang 206
Câu 117. Trong mặt phẳng phức, gọi A, B, C lần lượt là điểm biểu diễn các số phức
. Tam giác ABC là:
A. Tam giác vuông tại A B. Tam giác vuông tại B
C. Tam giác cân tại A D. Tam giác đều
Câu 118. Tập hợp điểm biểu diễn số phức thỏa mãn là số ảo là:
A. Đường tròn B. Đường thẳng
C. Đường thẳng D. Các đường thẳng trừ
Câu 119. Điểm nào sau đây biểu diễn số phức: ?
A. B. C. D.
Câu 120. Xét các điểm A, B, C trong mặt phẳng phức theo thứ tự biểu diễn các số ,
. Khi đó số phức biểu diễn bởi điểm D sao cho ABCD là hình vuông là:
A. B. C. D.
Câu 121. Trên mặt phẳng phức tập hợp điểm biểu diễn số phức z thỏa mãn: . Chọn đáp án
đúng?
A. Tập hợp điểm biểu diễn số phức là đường thẳng:
B. Tập hợp điểm biểu diễn số phức là đường tròn
C. Tập hợp điểm biểu diễn số phức là đường tròn
D. Tập hợp điểm biểu diễn số phức là đường tròn
Câu 122. Cho các số phức có điểm biểu diễn lần lượt là A, B, C, D, E trong mặt phẳng
phức tạo thành một ngũ giác lồi. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DE. Gọi I, J lần
lượt là trung điểm các đoạn MP và NQ. Biết I, J là điểm biểu diễn hai số phức và là số phức có
điểm biểu diễn là E. Tìm số phức ?
A. B. C. D.
Câu 123. Tập hợp điểm biểu diễn số phức thỏa điều kiện nằm trên đường tròn có tâm là:
A. B. C. D.
Câu 124. Tập hợp các điểm biểu diễn số phức z thỏa mãn là đường thẳng
. Tính ab+c:
(
) (
)
1 ,4 31,1 231
ii i++ + + +
z
2
z
22
1xy+=
yx=
yx= −
yx
= ±
(0;0)
O
12
.8zz i i+=−+
( )
8,1−
( )
4,8
( )
8, 1−
( )
4, 1−−
4
1
i
i −
( )( )
26
1 12,
3
i
ii
i
+
−+
−
1
i
−−
1
i+
1
i
−+
1
i−
11
zi−+ =
0xy+=
( ) (
)
22
1 19xy−++ =
(
) ( )
22
1 11xy
− ++ =
( ) ( )
22
2 24xy
− ++ =
12345
,,,,zzzzz
1 ,2ii−
45i
−
1
z
1
23zi= −
1
47
zi= −
1
87zi= −
1
82zi= −
z
12 1zi++ =
( )
1; 2I
( )
1; 2I −
( )
1; 2I −
( )
1; 2I −−
1 12z iz i−+ = +−
:0ax by c∆ + +=

Bài tập trắc nghiệm số phức
Trang 207
Chọn đáp án đúng:
A. 11 B. 9 C. 15 D. 6
Câu 125. Trong mặt phẳng Oxy là tọa độ ba điểm biểu diễn của số phức
. Tọa độ trực tâm của tam giác là:
A. B. C. D.
Câu 126. Trong mặt phẳng phức, các điểm biểu diễn tương ứng với các số 0,1, tạo thành:
A. Một hình vuông B. Một hình bình hành
B. Một hình chữ nhật D. Một hình khác.
Câu 127. Trên mặt phẳng phức, tập hợp các số sao cho là số thực được biểu diễn bởi:
A. Đường có phương trình
B. Đường có phương trình
C. Đường có phương trình
D. Nửa mặt phẳng bờ là Ox
Câu 128. Trong mặt phẳng xy cho tam giác MNP với alf ba điểm biểu diễn của các số phức
. Toạ độ tâm đường tròn ngoại tiếp tam giác MNP là:
A. B. C. D.
Câu 129. Trong mặt phẳng xy cho tam giác MNP với alf ba điểm biểu diễn của các số phức
. Toạ độ tâm đường tròn ngoại tiếp tam giác MNP là:
A. B. C. D.
Hướng dẫn giải
Đáp án: D
là tâm đườn tròn ngoại tiếp
Câu 130. Gọi P là điểm biểu diễn của số phức trong mặt phẳng phức.
Cho các mệnh đề sau :
(1) Môđun của là bình phương khoảng cách OP.
(2) Nếu P là biểu diễn của số thì khoảng cách từ O đến P bằng 7.
Chọn đáp án đúng :
,,MNP
1
5 6;zi=−+
23
z 4 ; 43iz i=−− = +
H
MNP
(3;1)
( 1; 3)−
(2; 3)
−
( 3; 2)
−
,2
i −
z x yi= +
2
z
0xy =
0x =
0
y =
,,MNP
12 3
1; 3 ; 5 5z z iz i==+==
( )
4; 2
( )
4; 2−
( )
4; 4−
( )
4; 2
−
,,
MNP
12 3
1; 3 ; 5 5z z iz i==+==
( )
4; 2
(
)
4; 2−
( )
4; 4
−
( )
4; 2
−
( ) ( ) ( )
1; 1, 3;1, 5; 5
M NP−−
( )
;I xy
MNP∆
( ) ( )
( ) ( )
( ) ( ) ( ) ( )
( )
22 22
22
22 2 2 2 2
1131
115 5
24
4; 2
52
xyx y
MI NI
MI PI
xyx y
xy x
I
xy y
− ++ =− +−
=
⇔
=
− ++ =− ++
+= =
⇔ ⇔−
−= =−
a bi+
a bi+
34i+

Bài tập trắc nghiệm số phức
Trang 208
A. Chỉ có (1) đúng B. Chỉ có (2) đúng C. Cả hai đều đúng D. Cả hai đều sai.
Câu 131. Trong mặt phẳng tọa độ Oxy, cho điểm M là điểm biểu diễn của số phức . Phương
trình đường trung trực của đoạn OM là :
A. B. C. D.
Câu 132. Cho các số phức z thỏa mãn phần trực thuộc và phần ảo thuộc đoạn .
Hỏi tập hợp các điểm biểu diễn số phức z.
A. Phần mặt phẳng giới hạn bởi đường thẳng và
B. Phần mặt phẳng giới hạn bởi đường thẳng và
C. Miền ngoài của hình chữ nhật có bốn đỉnh là
D. Miền trong của hình chữ nhật có bốn đỉnh là giao của .
Câu 133. Trên mặt phẳng phức, tập hợp các điểm biểu diễn số phức z mà cả phần thực và phần ảo của nó
đều thuộc đoạn là:
A. Tập các điểm nằm trên biên và bên trong hình tròn có tâm và bán kính
B. Tập các điểm nằm trên đoạn thẳng với
C. Tập các điểm nằm trên biên và bên trong hình vuông có bốn đỉnh
D. Tập các điểm thỏa mãn:
Câu 134. Miêu tả tập số phức z trên hệ tọa độ phức mà thỏa mãn là
A. Đường thẳng B. Đường thẳng
C. Đường tròn D. Đường tròn
Câu 135. Tập hợp các điểm biểu diễn số phức z trong hệ tọa độ vuông góc của mặt phẳng thỏa mãn
với phần thực không âm là:
A. Một hình tròn B. Một hình viên phân
C. Một hình vành khăn D. Một hình quạt
Câu 136. Bán kính của đường tròn biểu diễn số phức z thỏa mãn hệ thức trong mặt
phẳng phức là:
A. B. C. D.
Câu 137. Cho các số phức và . Gọi A, B, C, D lần lượt là các
điểm biểu diễn của . Hỏi tứ giác ABDC là hình gì?
42
zi= +
2 50xy+ +=
2 50xy
+−=
2 50xy− +=
2 50xy++=
[ ]
0;3
[ ]
2; 4−
3x
=
0x =
2y = −
4y =
0, 3, 2, 4.xxy y
= = =−=
0, 3, 2, 4
xxy y= = =−=
[ ]
2; 2−
( )
0;0
2
R =
0yx
+=
[ ]
2; 2x
∈−
( ) (
) (
) ( )
2; 2 ; 2; 2 ; 2; 2 ; 2; 2− − −−
( )
;xy
22
4xy
+≤
3 2 10zi
+−=
3 2 100xy−=
2 3 100xy−=
( ) ( )
22
2 3 100
xy− ++ =
(
)
( )
22
3 2 100xy− ++ =
23 4zi++ ≤
32 2 12z iz i+− = +−
29
9
29
3
29
9
23
9
1 23
24 , , 27 2z iz iz i=− =−=−
4
64zi= −
1234
,,,zz zz

Bài tập trắc nghiệm số phức
Trang 209
A. Hình vuông B. Hình chữ nhật C. Hình bình hành D. Hình thang
Câu 138. Tập hợp các điểm biểu diễn số phức z sao cho là một số thuần ảo. Là một đường
tròn tâm
Tính tổng a + b
A. 2 B. 1 C. –2 D. 3
Câu 139. Trong mặt phẳng tọa độ Oxy, cho ba điểm M,N, P là điểm biểu diễn của 3 số phức:
. Với giá trị nào của x thì tam giác MNP vuông tại P?
A. 1 và 2 B. 0 và 7 C. và D. 3 và 5
23
zi
u
zi
++
=
−
( )
;bIa
123
8 3; 1 4; 5z iz iz xi=+=+=+
1−
7−

Bài tập trắc nghiệm số phức
Trang 210
B – HƯỚNG DẪN GIẢI
Câu 1. Cho các số phức z thỏa mãn . Biết rằng tập hợp các điểm biểu diễn các số phức z là
một đường tròn. Tâm của đường tròn đó là:
A. B. C. D.
Hướng dẫn giải
Đáp án: A
Gọi số phức . Từ giả thiết ta có:
Câu 2. Tập hợp biểu diễn của số phức z
thỏa mãn: :
A. Là đường thẳng B. Là đường thẳng
B. Là đường thẳng D. Là đường thẳng
Hướng dẫn giải
Đáp án: A
Đặt suy ra . Khi đó ta được
Câu 3. Tìm số phức z biết tập hợp các điểm biểu diễn của nó là đường tròn có bán kính bằng và z–
iz–1 là số thuần ảo.
A. B.
C.
D.
Hướng dẫn giải
Đáp án: A
Gọi z=x+yi
Ta có hệ
Hệ có hai nghiệm (2 ; –1) và (–1 ;2)
12 3zi−+ =
I
( )
1; 2I −
(
)
1; 2I
( )
1; 2I −
( )
1; 2
I −−
;,z x yi x y
=+∈
( )
( ) ( ) ( )
22
1 2 3 1 2 3 1 2 9 1; 2x yi i x y i x y I+ −+ = ⇔ −+ + = ⇔ + + + = ⇒ −
(
)
3 23z z iz+=+
3yx
= −
3yx= −
3yx=
3yx
=
(
)
,z x yi x y R=+∈
z x yi= −
( )
22 22
42 2 3xyi xy xyi− = ++ +
( )
( )
22
22 2
22
22
2
0, 0
34
32
0, 0
3
3
xy x
xy
xy y
xy y
xy
yx
xy
+=
≥≤
⇔⇔
+=
+=−
≥≤
⇔ ⇔=−
=
5
12
2
zi
zi
=−+
= −
12
2
zi
zi
=−+
=−−
12
2
zi
zi
= +
=−−
12
2
zi
zi
= −
= −
22
5
1
xy
xy
+=
+=

Bài tập trắc nghiệm số phức
Trang 211
Câu 4. Gọi
1
z
là nghiệm phức có phần ảo âm của phương trình
2
2 30zz+ +=
. Tọa độ điểm M biểu
diễn số phức
1
z
là:
A.
( 1; 2)M −
B.
( 1; 2)
M −−
C.
( 1; 2 )
M −−
D.
( 1; 2 )
Mi−−
Hướng dẫn giải
Đáp án: C
+
1
2
2
12
2 30
12
zi
zz
zi
=−−
+ +=⇔
=−+
Câu 5. Cho các số phức z thỏa mãn
12z
−=
. Biết rằng tập hợp các điểm biểu diễn các số phức
(1 3 ) 2w iz=++
là một đường tròn. Bán kính r của đường tròn đó là
A. r = 4. B. r = 8. C. r = 2. D. r = 16.
Hướng dẫn giải
Đáp án: A
Gọi
( )
,z a bi a b R=+∈
và
( )
,w x yi x y R=+∈
Ta có :
22
1 2 ( 1) 4 (1)z ab
−=⇔ − + =
Từ
( )
( )
(13)2 13 2w i z x yi i a bi= + +⇒+ = + + +
32 3 1 3
3 3 3( 1)
x ab x a b
y ab y a b
= − + − = −−
⇔⇔
= + − = −+
Từ đó :
( )
2
22 2
( 3) ( 3) 4 1 16.
x y ab
− +− = − + =
(do (1))
Suy ra r = 4
Câu 6. Số phức
53zi= −
có điểm biểu diễn là:
A.
( )
5; 3M −
B.
( )
3; 5N −
C.
( )
5;3P −
D.
( )
3; 5Q
−
Hướng dẫn giải
Đáp án: A
Phân tích: Ta cùng nhắc lại kiến thức sách giáo khoa như sau:
Điểm biểu diễn số phức
( )
,z x yi x y=+∈
trong mặt phẳng vuông góc là điểm
(
)
;M xy
.
Vậy
( )
5; 3M −
chính là điểm biểu diễn số phức
53zi= −
. Đây là bài toán đơn giản, vì thế quý độc giả cần cẩn
thận trong tính toán, trong nhẩm.
Câu 7. Tìm
z
biết rằng z có phần thực bằng hai lần phần ảo và điểm biểu diễn của z nằm trên đường
thẳng
: 2 10 0d xy+− =
A.
25z =
B.
5z =
C.
23z =
D.
3z =

Bài tập trắc nghiệm số phức
Trang 212
Hướng dẫn giải
Đáp án: A
Phân tích: Số phức z có dạng
z x yi= +
theo đề bài ta có
24
2 10 2
xy x
xy y
= =
⇔
+= =
22 22
4 2 25z xy⇒= + = + =
.
Câu 8. Tìm số phức z biết rằng điểm biểu diễn của z nằm trên đường tròn có tâm O, bán kính bằng 5 và
nằm trên đường thẳng
: 2 50dx y− +=
A.
34zi= −
B.
34zi= +
C.
43zi= +
D.
43zi= −
Hướng dẫn giải
Đáp án: B
Phân tích: ta có thể đặt
( )
,yz x iy x=+∈
. Khi đó từ đề bài ta có:
( )
2
22
2
25
2 5 25
2 50
25
xy
yy
xy
xy
+=
− +=
⇔
− +=
= −
2
0
5
5 20 0
25
4
3
y
x
yy
xy
y
x
=
= −
−=
⇔
= −
=
=
.
Câu 9. Cho
.4
zz=
, tập hợp các điểm biểu diễn z có đồ thị là (đối với các đồ thị có gạch chéo thì tập
hợp điểm là cả phần gạch chéo và cả biên):
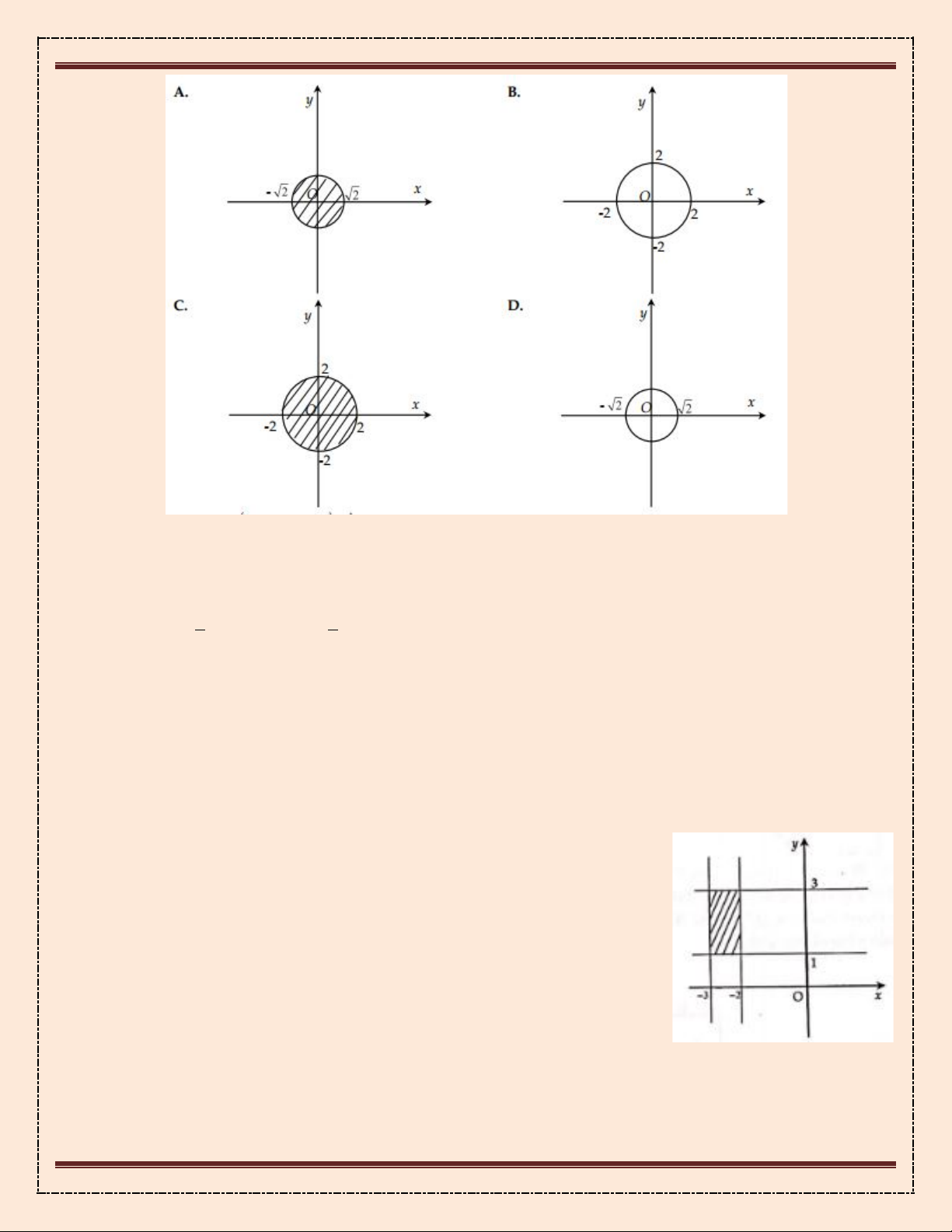
Bài tập trắc nghiệm số phức
Trang 213
Hướng dẫn giải
Đáp án: B
Phân tích: Bài toán yêu cầu tìm tập hợp các điểm biểu diễn của z , tức là liên quan đến x, y. Do vậy ta sẽ đặt
z x iy= +
, khi đó
z x iy= −
. Vậy
( )(
)
22
.z z x iy x iy x y
=+ −=+
Theo đề bài thì
22
4xy+=
. Nhận thấy đây là phương trình đường tròn tâm
(
)
0;0O
bán kính
2R =
. Vậy ta sẽ
chọn phương án B.
Ở đây có nhiều bạn sẽ nhầm sang bất phương trình nên đinh ninh chọn C là sai.
Câu 10. Số phức thỏa mãn điều kiện nào thì có phần biểu diễn là phần gạch chéo trong hình vẽ (kể cả
biên) ?
A. Số phức z có phần thực thuộc đoạn
[ ]
3; 2−−
trên trục Ox, phần ảo thuộc
đoạn
[ ]
1; 3
trên trục Oy.
B. Số phức z có phần thực thuộc đoạn
[ ]
1; 3
trên trục Ox, phần ảo thuộc đoạn
[ ]
3; 2−−
trên trục Oy.
C. Số phức z có phần thực thuộc đoạn
[ ]
3; 2−−
trên trục Oy, phần ảo thuộc
đoạn
[ ]
1; 3
trên trục Ox.
D. Số phức z có phần thực thuộc đoạn
( )
3; 2
−−
trên trục Ox, phần ảo thuộc
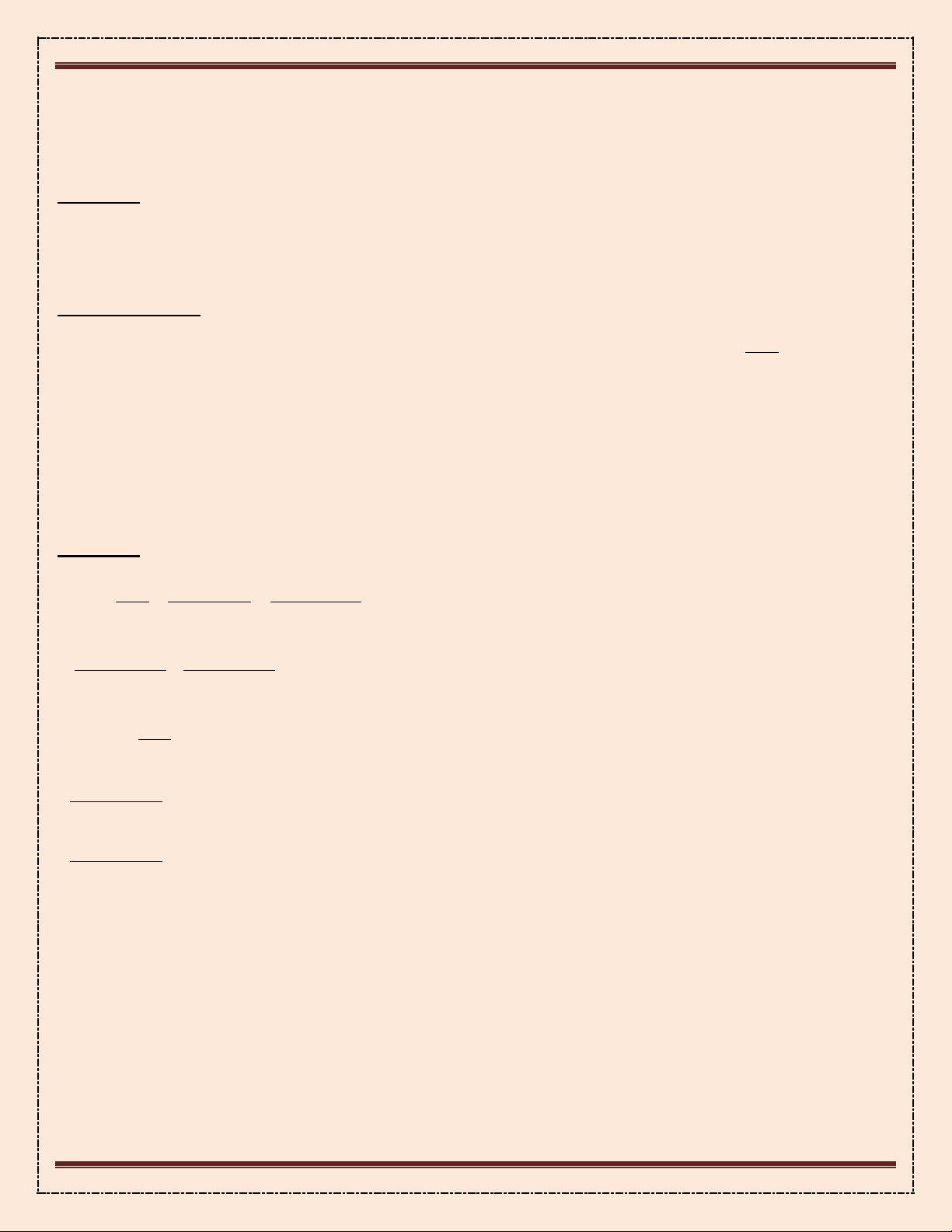
Bài tập trắc nghiệm số phức
Trang 214
đoạn
(
)
1; 3
trên trục Oy.
Hướng dẫn giải
Đáp án: A
Phân tích: Ta có số phức
(
)
.
z x yi x y=+∈
khi đó điểm
(
)
;
M xy
trong hệ tọa độ phẳng vuông góc là điểm
biểu diễn số phức z. Vậy khi đó ta thấy khi chiếu xuống trục Ox thì
32x− ≤ ≤−
tức là phần thực của z nằm
trong đoạn
[ ]
3; 2−−
, và ta thấy
13y≤
, khi đó phần ảo của z nằm trong đoạn
[ ]
1; 3
Phân tích sai lầm: Nhiều quý độc giả nhầm giữa phần thực và phần ảo nên chọn sai đáp án.
Câu 11. Xác định tập hợp các điểm biểu diễn số phức z trên mặt phẳng phức sao cho
1
zi
−
là số thuần ảo.
A. Trục tung, bỏ điểm
( )
0;1
B. Trục hoành, bỏ điểm
( )
1; 0−
C. Đường thẳng
1y
=
, bỏ điểm
(
)
0;1
D. Đường thẳng
1
x
= −
, bỏ điểm
( )
1; 0−
Hướng dẫn giải
Đáp án: A
Phân tích: Vì bài toán liên quan đến biểu diễn số phức nên ta sẽ đặt
( )
,z x iy x y=+∈
Khi đó
( )
( )
( )
2
2
1
11
1
1
x iy
z i x iy
xy
−−
= =
− +−
+−
( )
( )
22
22
1
11
xy
i
xy xy
−
= −
+− +−
Khi đó để
1
zi−
là số thuần ảo thì
( )
( )
2
2
2
2
0
1
0
11
0
1
x
xy
x
yy
xy
=
+−
=
⇔
−≠
≠
+−
Vậy đáp án của ta là A.
Câu 12. Gọi A là điểm biểu diễn của số phức
32zi= +
và điểm B là điểm biểu diễn số phức
'23zi= +
.
Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hai điểm A và B đối xứng với nhau qua gốc tọa độ O.
B. Hai điểm A và B đối xứng với nhau qua trục tung.
C. Hai điểm A và B đối xứng nhau qua trục hoành
D. Hai điểm A và B đối xứng nhau qua đường thẳng
yx
=
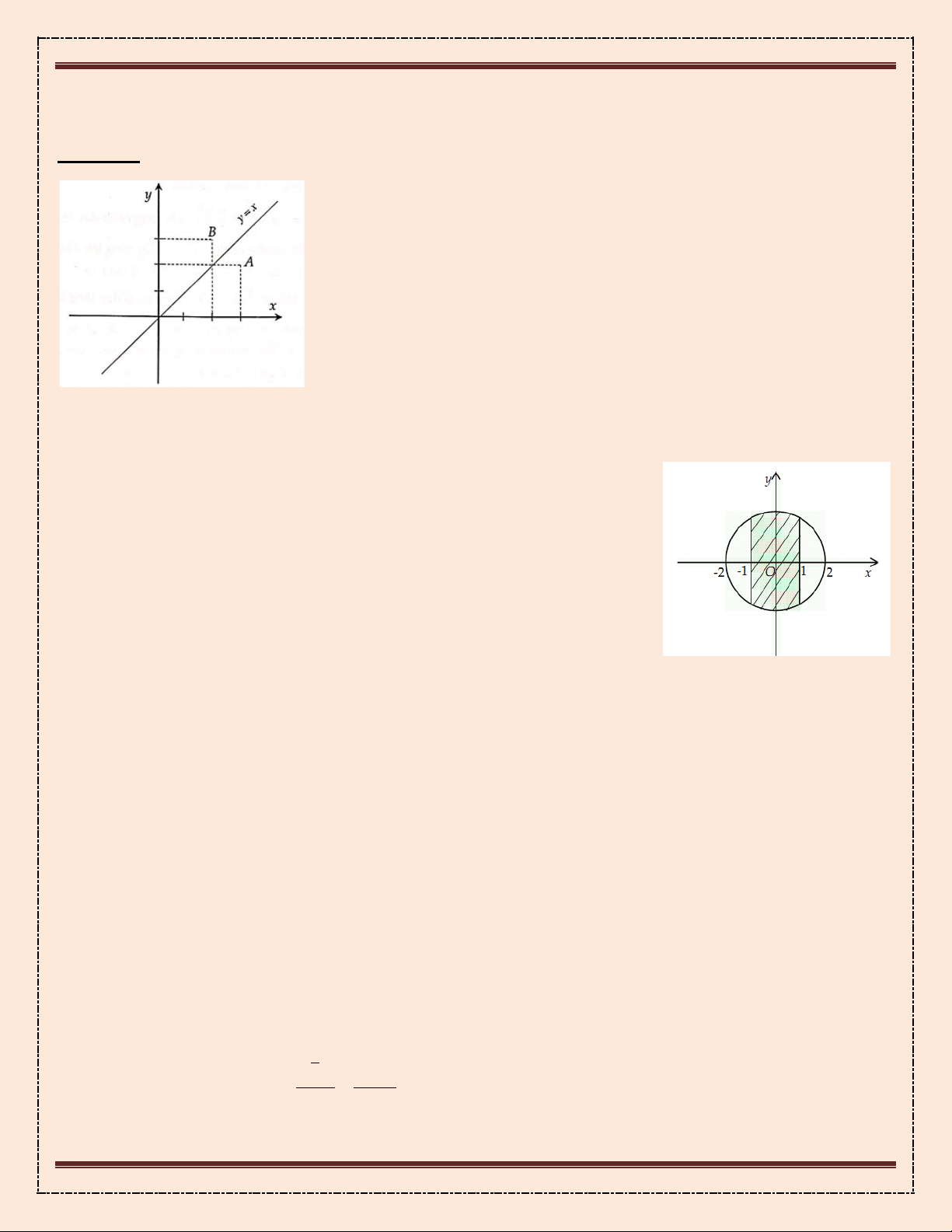
Bài tập trắc nghiệm số phức
Trang 215
Hướng dẫn giải
Đáp án: D
Phân tích: Ta có
( )
3; 2A
và
( )
2;3B
, ta có tọa độ hai điểm trên hình như sau:
Nhìn vào đồ thị ta thấy A, B, C là sai
Câu 13. Số phức thỏa mãn điều kiện vào thì có điểm biểu diễn ở phần gạch chéo?
A. Số phức có phần thực nằm trong
( )
1;1
−
và mô đun nhỏ hơn 2.
B. Số phức có phần thực nằm trong
[ ]
1;1−
và mô đun nhỏ hơn 2
C. Số phức có phần thực nằm trong
[ ]
1;1−
và mô đun không vượt quá 2.
D. Số phức có phần thực nằm trong
( )
1;1−
và mô đun không vượt quá 2.
Hướng dẫn giải
Đáp án: C
Phân tích:
Nhớ lại khái niệm về điểm biểu diễn số phức , cùng xem lại ở đáp án B , câu 26.
Vậy ở đây ta thấy nếu lấy một điểm bất kì trong phần gạch chéo là
( )
,M ab
thì
11
2
a
OM
−≤ ≤
≤
Vậy đáp án của chúng ta là C.
Phân tích sai lầm: Nhiều bạn không phân biệt được giữa các khái niệm “nhỏ hơn” và “không vượt quá”.
Ở đây ví dụ: không vượt quá 2 là bao gồm cả 2.
Còn nhỏ hơn 2 là không bao gồm 2.
Hoặc nhiều bạn quên không tính cả các điểm nằm trên đường tròn trong phần gạch chéo, và các điểm nằm trên
2 đường thẳng
1; 1xx=−=
trong phần gạch chéo. Dẫn đến khoanh vào các đáp án còn lại như A, B hoặc D.
Câu 14. Cho số phức
67
13 5
zi
z
i
+
−=
+
, điểm nào sau đâu là điểm biểu diễn của số phức z:
A. M(0;1) B. N(1;1) C. P(–1;–1) D. Q(0,–1)

Bài tập trắc nghiệm số phức
Trang 216
Hướng dẫn giải
Đáp án: B
Phân tích:
Gọi
(
, )
z a bi a b
=+∈
. Khi đó phương trình đã cho trở thành:
67
13 5
a bi i
a bi
i
−+
+− =
+
( )(1 3 ) 6 7
10 10 3 ( 3 ) 12 14
10 5
9 3 12 1
9 3 (11 3 ) 12 14
11 3 14 1
1
a bi i i
a bi a bi a b i b a i
ab a
a bi b a i
ba b
zi
−− +
⇔+ − = ⇔ + −+ + + = +
+= =
⇔ ++ + =+ ⇔ ⇔
+= =
⇒=+
Câu 15. Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn hệ thức:
21 2z zz
−= −+
A. Tập hợp các điểm cần tìm là hai đường thẳng
0; 2xx
= =
B. Tập hợp các điểm cần tìm là đường tròn
22
2xy+=
C. Tập hợp các điểm cần tìm là đường elip:
2
2
1
2
y
x +=
D. Tập hợp các điểm cần tìm là hai đường elip:
22
22
1; 1
22
yx
xy+ = +=
Hướng dẫn giải
Đáp án: A
Đặt
(, )z x yi x y=+∈
. Ta có:
21 2z zz−= −+
22 2 2
2 1 2 2 1 22
0
2 ( 1) 4 4 2 0
2
x yi x yi x yi x yi yi
x
x y y xx
x
⇔ +−=+−++⇔ −+ =+
=
⇔ −+ = + ⇔−=⇔
=
Vậy tập hợp các điểm cần tìm là 2 đường thẳng
0; 2xx= =
Đáp án đúng là A.
Câu 16. Cho số phức z thỏa mãn
1z −
=
26zz i−−
. Tập hợp các điểm biểu diễn của số phức là :
A. Đường tròn tâm
( )
1 ; 2I
bán kính R=1 B. Đường thẳng có phương trình
5 60xy− −=
C. Đường thẳng có phương trình
6 12 0xy−+=
D. Đường thẳng có phương trình
3 60xy− −=
Hướng dẫn giải
Đáp án: D

Bài tập trắc nghiệm số phức
Trang 217
Với
(, )z a bi a b R=+∈
thì theo đề bài ta sẽ có:
1 2( 3)
a bi a b i−+ = − +
( ) ( ) ( )
2 22
2
1 23a ba b⇔− +=− ++
2 22 2
21 44 49aa baa bb⇔−++=−++++
2 6 12 0
ab⇔− + + =
3 60xy⇔− −=
Vậy tập hợp các điểm biểu diễn số phức z là đường thẳng
3 60xy− −=
Câu 17. Cho các nhận định sau (giả sử các biểu thức đều có nghĩa) :
1) Số phức và số phức liên hợp của nó có mô đun bằng nhau.
2) Với
23zi= −
thì mô đun của z là:
23zi= +
3) Số phức z là số thuần ảo
⇒
zz
−
= −
4) Tập hợp điểm biểu diễn số phức z thỏa mãn
12zz
−
++ =
là một đường tròn.
Số nhận định đúng là:
A. 2 B. 3 C. 4 D. 1
Hướng dẫn giải
Đáp án: A
Các nhận định đúng là 1;3
Đáp án A đúng vì cả số phức và số phức liên hợp đều có mô đun là
22
ab+
Đáp án B sai vì mô đun của số phức
22
2 3 13
z = +=
còn
23i+
là số phức liên hợp của z
Đáp án C đúng vì
; ; ()z bi z bi bi bi z z= =− =−− ⇔ =−
Đáp án D sai. Với
(, )z a bi a b R=+∈
thì ta có
1 12 1z z a bi a bi a+ += + + − += +
1
2
1 2 12
3
2
a
zz a
a
=
⇒ ++= +=⇒
−
=
Như vậy tập hợp điểm biểu diễn số phức z là hai đường thẳng song song chứ không phải một đường tròn.
Câu 18. Cho các điểm A,B,C trong mặt phẳng phức theo thứ tự được biểu diễn bởi các số
1 i+
;
24i+
;
65i+
. Tìm số phức biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành :
A.
78i+
B.
38i−+
C.
52i+
D.
32i−+

Bài tập trắc nghiệm số phức
Trang 218
Hướng dẫn giải
Đáp án: A
Từ dữ kiện đề bài ta suy ra
(1;1); (2; 4); (6;5) (1;3)A B C AB⇒=
Đặt số phức z biểu diễn điểm D là
(, )z a bi a b R=+∈
thì
( , ) ( 6; 5)D a b CD a b=−−
Tứ giác ABDC là hình bình hành nên
AB CD=
61 7
78
53 8
aa
zi
bb
−= =
⇒ ⇔ ⇔=+
−= =
Sai lầm thường gặp: Nhầm chiều vecto:
AB DC=
dẫn đến lực chọn đáp án C.
Câu 19. Trên hệ trục tọa độ Oxy cho điểm
(3; 4)A
biểu diễn số phức z. Phần ảo của số phức
w
z
z
=
là
A.
3
5
B.
4
5
C.
3
5
i
D.
4
5
i
Hướng dẫn giải
Đáp án: B
Đây là một bài toán khá đơn giản, chỉ cần áp dụng các biến đổi thông thường.
Do
(3; 4)A
biểu diễn
z
nên suy ra
34
34 5 w
55
z iz i=+⇒=⇒=+
Câu 20. Cho số phức z thỏa mãn
(1 )(3 2 ) 2 2z i ii
+− − = +
. Điểm A là điểm biểu diễn số phức z trên hệ
tọa độ. Khoảng cách từ A đến đường thẳng (d) :
2 2 50xy− +=
là :
A.
7
22
B.
7
4
C.
72
8
D.
7
2
Hướng dẫn giải
Đáp án: A
Sử dụng máy tính casio ở chế độ CMPLX, bấm màn hình hiển thị
2 2 (1 )(3 2 )i ii+−− −
ấn = ta thu được kết
quả
17zi
= +
. Suy ra điểm
(1; 7)A
Khoảng cách cần tìm là
22
2.1 2.7 5
7
22
22
d
−+
= =
+
Câu 21. Tập hợp các điểm biểu diễn số phức thỏa mãn
2
( )9ziz
−
+− =−
A. Hình tròn B. Đường tròn
C. Hai đường thẳng song song D. Đường thẳng
Hướng dẫn giải

Bài tập trắc nghiệm số phức
Trang 219
Đáp án: C
Một vài thí sinh có thể theo “quán tính” khoanh ý A vì hầu như những bài trước về tập hợp biểu diễn đề là
đường tròn. Đây là một trường hợp khác các bạn cần cẩn thận kiểm tra.
Đặt
z a bi= +
với
;ab R∈
, suy ra
(2 1)z i z a bi i a bi b i+− = + +− + = +
( )
2
1
(2 1) 9
2
b
ziz b
b
=
⇒ +− =− + =−⇒
= −
Suy ra tập hợp biểu diễn số phức
z
sẽ là hai đường thẳng
1y =
và
2
y = −
. Chọn đáp án C
Câu 22. Cho số phức z thỏa mãn:
2 23 2 12z ii z
− + = −−
. Tập hợp điểm biểu diễn cho số phức z là:
A.
20 16 47 0xy− −=
B.
20 16 47 0xy+ +=
C.
20 16 47 0xy+ −=
D.
20 16 47 0xy− +=
Hướng dẫn giải
Đáp án: A
Ngoài cách biến đổi thông thường là đặt
( )
;z a bi a b R=+∈
sau đó biến đổi tương đương, ta cũng có thể thử
các đáp án bằng cách chọn một điểm trên mỗi đường rồi sau đó lấy số phức z mà điểm đó biểu diễn thay vào đề
bài kiểm tra lại.
Câu 23. Gọi
,,
ABC
lần lượt là các điểm biểu diễn cho các số phức
12
1 3; 3 2z iz i=−+ =−−
;
3
4zi= +
.
Chọn kết luận đúng nhất:
A. Tam giác ABC cân B. Tam giác ABC vuông cân
C. Tam giác ABC vuông D. Tam giác ABC đều
Hướng dẫn giải
Đáp án: C
Ta có tọa độ các điểm lần lượt là A(–1;3); B(–3;–2); C(4;1)
Tiếp theo ta tính các vecto tạo thành từ 3 điểm trên:
( ) ( ) ( )
2;5; 5;2; 7;3AB AC BC=−− = − =
Dễ dàng thấy rằng
.0AB AC =
và
22
2 5 29AB AC= = +=
Do đó tam giác ABC vuông cân tại A
Câu 24. Trên mặt phẳng Oxy tìm biểu diễn số phức z thỏa mãn :
( )
21z i iz−=+
?
A. Hình tròn tâm I(0;–2) bán kính
22
B. Hình tròn tâm I(0;2) bán kính
22
C. Đường tròn tâm I(0;–2) bán kính
22
D. Đường tròn tâm I(0;2) bán kính
22
Hướng dẫn giải
Đáp án: C
Đặt z=a+bi;
( )
;ab∈

Bài tập trắc nghiệm số phức
Trang 220
Ta có:
2 (1 i) z
zi−=+
(b 2)i (1 i)(a bi)a⇔+− = + +
22 22
22 2 2
22
22
(b 2)i a b (a b)i
(b 2) (a b) (a b)
4 42 2
44
( 2) 8
a
a
abab ab
ab b
ab
⇔ + − = −+ +
⇔ +− = − ++
⇔ + − += +
⇔++ =
⇔ ++ =
=>Tập biểu diễn các điểm M thỏa mãn đề bài là đường tròn tâm I(0;–2) bán kính
22
Sai lầm thường gặp: Nếu không để ý kỹ sẽ rất nhiều bạn bị nhầm lẫn giữa đáp án A và đáp án C
Câu 25. Trên mặt phẳng Oxy tìm biểu diễn số phức z thỏa mãn :
1 22zi≤− <
?
A. Hình tròn tâm I(0;2) bán kính 2.
B. Hình tròn tâm I(0;2) bán kính 1.
C. Hình tròn tâm I(0;2) bán kính 2 trừ đi phần trong hình tròn tâm I(0;2) bán kính 1.
D. Hình tròn tâm I(0;2) bán kính 2 trừ đi hình tròn tâm I(0;2) bán kính 1.
Hướng dẫn giải
Đáp án: D
Đặt z=a+bi;
( )
;ab∈
Ta có
Tập biểu diễn số phức z thõa mãn là hình tròn tâm I(0;2) bán kính (0;2) trừ đi phần trong của hình tròn tâm
I(0;2) bán kính 1
Sai lầm thường gặp: Nhiều bạn sẽ dễ bị nhầm giữa đáp án C và D
Câu 26. Miêu tả tập số phức z trên hệ tọa độ phức mà thỏa mãn
3 2 10
zi+−=
là:
A. Đường thẳng
3 2 100
xy−=
B. Đường thẳng
2 3 100
xy−=
C. Đường tròn
( ) ( )
22
2 3 100xy− ++ =
D. Đường tròn
( ) ( )
22
3 2 100xy− ++ =
Hướng dẫn giải
Đáp án: C
Mỗi số phức
z x yi= +
được biểu diễn bởi một điểm
( )
;xy
. Do đó ta có tập số phức z thỏa mãn là:
( ) ( )
22
3 2 10 2 3 100x i yi x y++−= ⇔ − + + =
Câu 27. Cho số phức z thỏa mãn
20iz i+ −=
. Tính khoảng cách từ điểm biểu diễn của z trên mặt phẳng
tọa độ Oxy đến điểm
( )
3; 4M −
.
Bài tập trắc nghiệm số phức
Trang 221
A.
25
B.
13
C.
2 10
D.
22
Hướng dẫn giải
Đáp án: C
Ta có:
( )
2
2
2 0 2 12
1
ii
i
iz i iz i z i
i
− −+
−+
+ −= ⇔ =−+→ = = =+
Suy ra điểm biểu diễn số phức z là
( )
1; 2A
Khi đó
(
) (
)
22
3 1 4 2 2 10AM = − +−− =
Câu 28. Trong mặt phẳng với hệ tọa độ Oxy, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
( )
2 15iz−+ − =
. Phát biểu nào sau đây là sai ?
A. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm
(
)
1; 2I −
B. Tập hợp các điểm biểu diễn các số phức z là đường tròn có bán kính
5R =
C. Tập hợp các điểm biểu diễn các số phức z là đường tròn có đường kính bằng 10
D. Tập hợp các điểm biểu diễn các số phức z là hình tròn có bán kính
5R =
Hướng dẫn giải
Đáp án: D
Gọi
( )
;z x yi x y=+∈
Theo giả thiết , ta có:
( ) ( )
( )
2 15 2 1 5i x yi y x i−+ + − = ⇔ −− + − =
(
) (
)
(
) ( )
22 2 2
2 1 5 1 2 25y x xy⇔ −− + − =⇔ − + + =
Vậy tập hợp điểm biểu diễn các số phức z là đường tròn tâm
( )
1; 2I −
, bán kính
5R =
Câu 29. Trong mặt phẳng phức
(
) ( )
( )
4;1 , 1;3 , 6;0
A BC
−−
lần lượt biểu diễn các số phức
123
,,zz z
.
Trọng tâm G của tam giác ABC biểu diễn số phức nào sau đây?
A.
4
3
3
i+
B.
4
3
3
i−+
C.
4
3
3
i
−
D.
4
3
3
i−−
Hướng dẫn giải
Đáp án: B
Trọng tâm của tam giác ABC là
4
3;
3
G
−
Vậy G biểu diễn số phức
4
3
3
zi=−+
Câu 30. Trong mặt phẳng phức, tập hợp các điểm M biểu diễn số phức z biết
34zz i= −+
là:

Bài tập trắc nghiệm số phức
Trang 222
A. Elip
22
1
42
xy
+=
B. Parabol
2
4xy =
C. Đường tròn
22
40xy+ −=
D. Đường thẳng
6 8 25 0x y+−=
Hướng dẫn giải
Đáp án: D
Đặt
( )
,z x yi x y=+∈
và
( )
;M xy
là điểm biểu diễn của z.
Ta có
( )( )
22
34 34 3 4
z xy
z i x iy i x y i
= +
−+ = − −+ = − −+
( )
(
)
22
34 3 4z ix y
⇒ −+ = − +−+
Vậy
( ) ( )
22
22
3 4 3 4 6 8 25 0zz i xy x y xy= −+ ⇔ + = − +−+ ⇔ + − =
Câu 31. Cho số phức z thỏa
3z =
. Biết rằng tập hợp số phức
wzi= +
là một đường tròn. Tìm tâm của
đường tròn đó.
A.
( )
0;1I
B.
( )
0; 1I −
C.
( )
1; 0I −
D.
( )
1; 0I
Hướng dẫn giải
Đáp án: A
Đặt
(
)
,,w x yi x y=+∈
suy ra
( ) ( )
11zxyizxyi
=+ − ⇒=− −
. Theo đề suy ra
(
) (
)
2
2
1 3 19xy i x y−− =⇔+− =
Vậy tập số phức cần tìm nằm trên đường tròn có tâm
( )
0;1I
Câu 32. Biết điểm
( )
1; 2M −
biểu diễn số phức z trong mặt phẳng tọa độ phức. Tính môđun của số phức
2
w iz z= −
.
A.
26
B.
25
C.
24
D.
23
Hướng dẫn giải
Đáp án: A
Vì điểm
( )
1; 2M −
biểu diễn z nên
12 12z iz i=−⇒=+
Do đó
( ) ( ) ( )
2
1 2 1 2 2 3 4 1 5 26wi i i i i i w= + − − =−+−−− =+ ⇒ =
Câu 33. Cho số phức
1zi= +
. Tìm tập hợp các điểm biểu diễn số phức
32wzi= +
.
A. Tập hợp các điểm biểu diễn số phức w nằm trên đường tròn có phương trình
( ) ( )
22
3 11xy− ++ =
B. Điểm biểu diễn số phức w là điểm có tọa độ
( )
3; 1−−
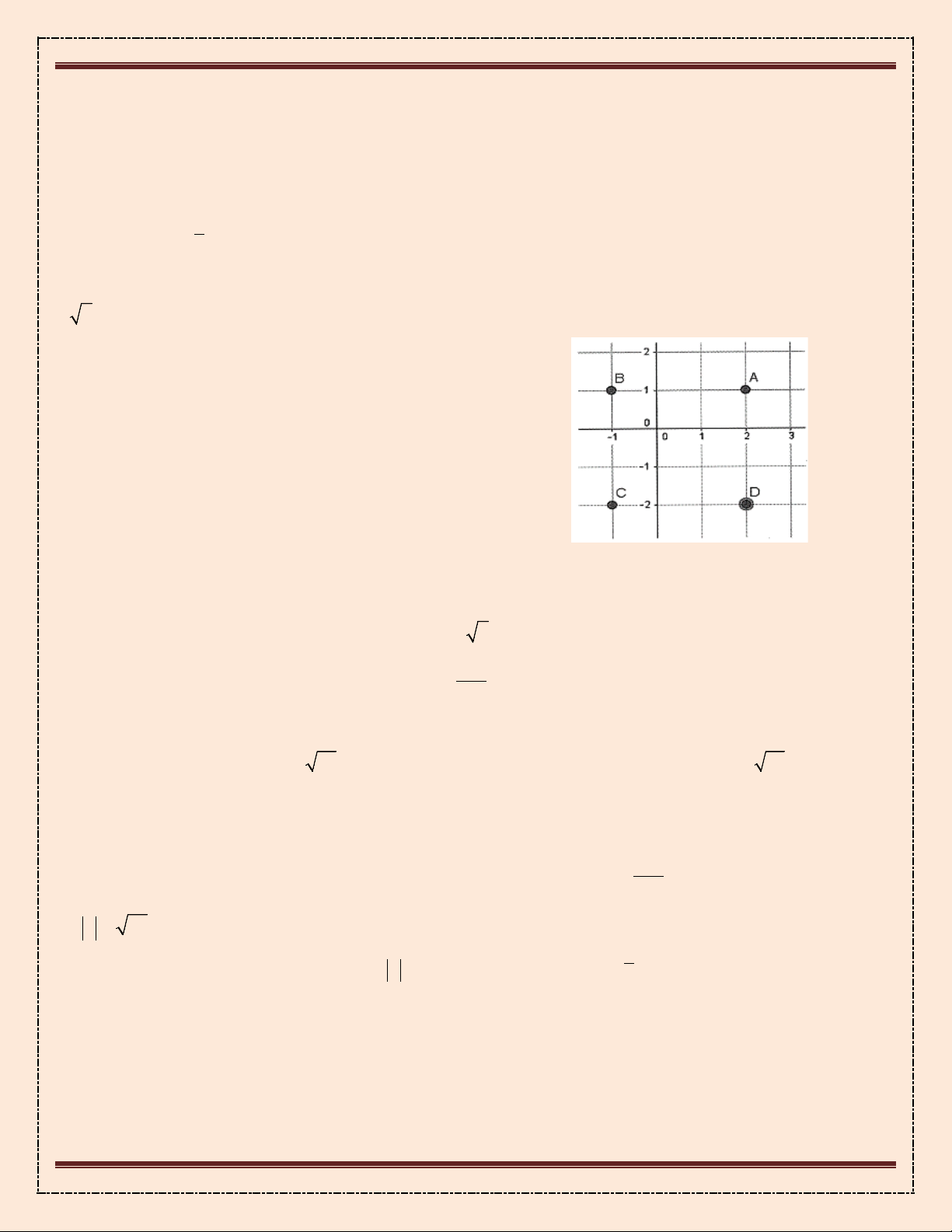
Bài tập trắc nghiệm số phức
Trang 223
C. Điểm biểu diễn số phức w là điểm có tọa độ
( )
3; 1
−
D. Tập hợp các điểm biểu diễn số phức w nằm trên đường tròn có phương trình
( ) ( )
22
3 11xy+ ++ =
Hướng dẫn giải
Đáp án: C
Ta có:
11z iz i=+⇒ =−
suy ra
3wi= −
. Nên điểm biếu diễn số phức w là điểm có tọa độ
( )
3; 1−
Câu 34. Trong hình dưới, điểm nào trong các điểm A, B, C, D biểu diễn cho số phức có môđun bằng
22
.
A. Điểm A
B. Điểm B
C. Điểm C
D. Điểm D
Hướng dẫn giải
Đáp án: D
D biểu diễn cho
22i+
. Số phức này có modun bằng
22
Câu 35. Cho số phức z thỏa mãn
( )
1
27
i
zi
i
+
=+−
. Hỏi khi biểu diễn số phức này trên mặt phẳng phức
thì nó cách gốc tọa độ khoảng bằng bao nhiêu ?
A. 9 B.
65
C. 8 D.
63
Hướng dẫn giải
Đáp án: B
Ở đây câu hỏi bài toán chính là tìm môđun của số phức z, ta có
( )
1
27 18
i
zi i
i
+
=+− =+
65z⇒=
Câu 36. Cho các số phức z thỏa mãn
2z =
và số phức w thỏa mãn
( )
34 2iw i z i=−+
. Biết rằng tập hợp
các điểm biểu diễn các số phức w là một đường tròn. Tính bán kính r của đường tròn đó.
A.
5r =
B.
10r =
C.
14r =
D.
20r =
Hướng dẫn giải
Đáp án: B
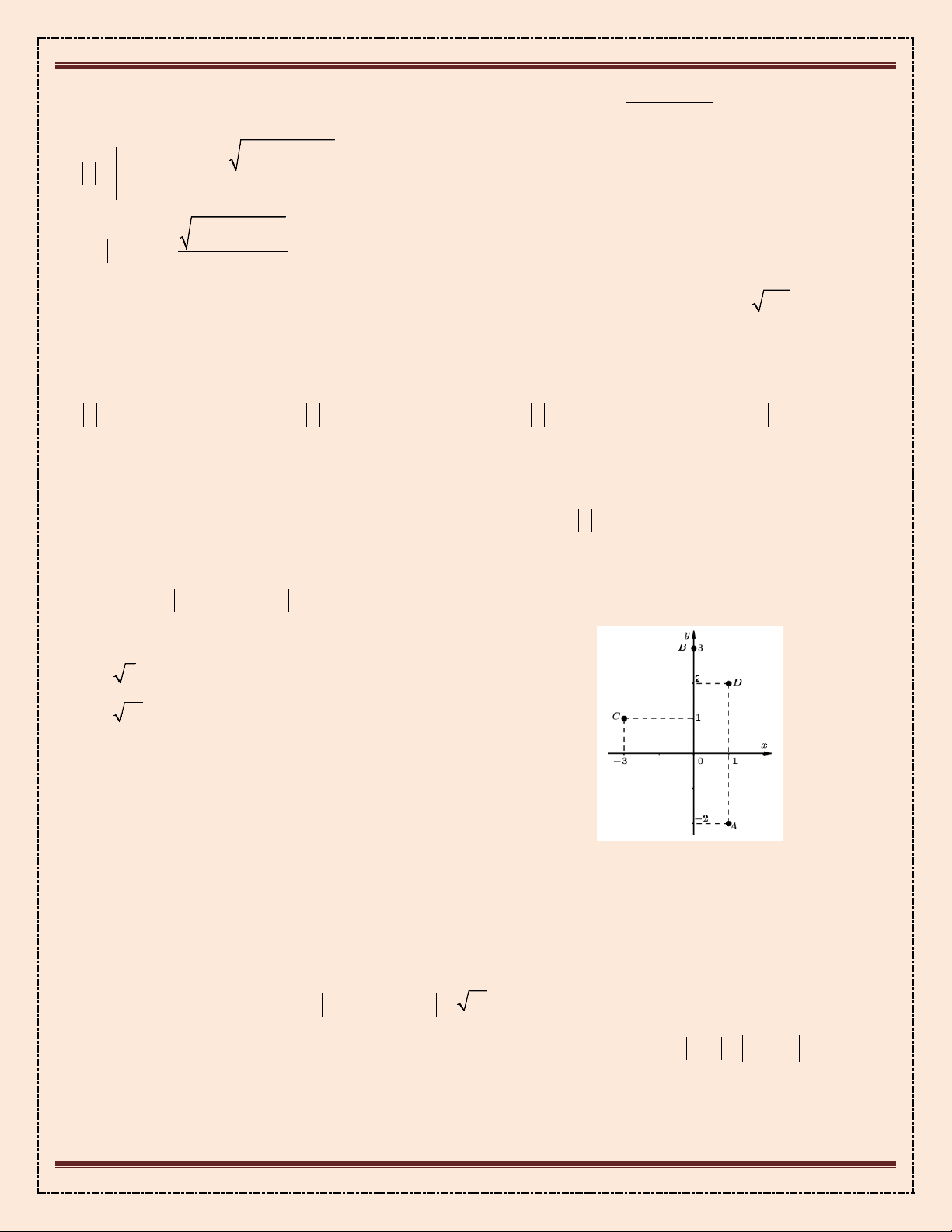
Bài tập trắc nghiệm số phức
Trang 224
(
) (
) ( ) ( )
(
)
2
34 2 34 2
34
yx i
w x yi iw ix yi iz i iz y x i z
i
+−
=+ ⇒ = − = − + ⇔ − =+ − ⇔=
−
( )
( )
2
2
2
2
34 5
xy
yx i
z
i
−+
+−
⇒= =
−
Ta có
(
)
( )
2
2
2
22
2
2 2 2 10
5
xy
z xy
−+
=⇔ =⇔− +=
Theo giả thiết tập hợp các điểm biếu diễn các số phức w là một đường tròn nên bán kính
2
10 10r = =
Câu 37. Cho số phức z có tập hợp điểm biểu diễn trên mặt phẳng phức là đường tròn
( )
22
: 25 0
Cx y+−=
. Tính mô–đun của số phức z.
A.
3z =
B.
5z =
C.
2z =
D.
25z =
Hướng dẫn giải
Đáp án: B
Đường tròn (C) có tâm và bán kính lần lượt là
( )
0;0 , 5IR
=
. Suy ra
5z =
Câu 38. Cho các số phức
1234
,,,zz zz
có các điểm biểu diễn trên mặt phẳng phức là A, B, C, D (như hình
bên). Tính
1234
Pzz zz= +++
A.
2
P =
B.
5P =
C.
17P =
D.
3P =
Hướng dẫn giải
Đáp án: C
Dựa vào hình vẽ suy ra
1 23 4
1 2, 3, 3 , 1 2z iz iz iz i=− = −+ =+
Khi đó
1234 1234
1 4 17zzzz i zzzz+++=−+⇒+++ =
Câu 39. Trong mặt phẳng tọa độ, tập hợp điểm biểu diễn số phức z thỏa mãn
(
)
1z i iz−= +
là một
đường tròn, đường tròn đó có phương trình là:
A.
22
2 2 10xxy y+ + + −=
B.
22
2 10xy y+ + −=

Bài tập trắc nghiệm số phức
Trang 225
C.
22
2 10x
xy+ + −=
D.
22
2 10x
xy+ + +=
Hướng dẫn giải
Đáp án: B
Đặt
(
) ( )
, ,;z x yi xy M xy=+∈
là điểm biểu di n của số phức trên mặt phẳng Oxy
(
)
( )
(
)
( )
11
z i iz x y i x y x yi
−= + ⇔ + − = − + +
( ) ( )
( )
2 22
2
1
x y xy xy⇔ +− = − ++
22
2 10xy y⇔ + + −=
Câu 40. Tập hợp các điểm trong mặt phẳng Oxy biểu diễn các số phức z thỏa mãn
12
zi−+ =
là:
A. Đường tròn tâm
( )
1;1
I
−
, bán kính 2 B. Đường tròn tâm
( )
1; 1
I
−
, bán kính 2
C. Đường tròn tâm
( )
1; 1I −
, bán kính 4 D. Đường thẳng
2
xy+=
.
Hướng dẫn giải
Đáp án: B
Gọi
( )
;z x yi x y=+∈
( ) ( )
12 12 1 12z i x yi i x y i−+ = ⇔ + −+ = ⇔ − + + =
(
) (
)
( ) (
)
22 22
112114
xy xy⇔ −++ =⇔− ++ =
Vậy tập hợp các điểm trong mặt phẳng Oxy biểu diễn các số phức z thỏa
12zi−+ =
là đường tròn tâm
( )
1; 1
I −
, bán kính bằng 2.
Câu 41. Cho hai số phức z và z’ lần lượt được biểu diễn bởi hai vectơ
u
và
'u
. Hãy chọn câu trả lời sai
trong các câu sau:
A.
'uu+
biểu diễn cho số phức
z'z+
B.
'uu−
biểu diễn cho số phức
z'z−
C.
.'uu
biểu diễn cho số phức
z. 'z
D. Nếu
z a bi= +
thì
u OM=
, với
( )
;M ab
Hướng dẫn giải
Đáp án: C
Ta có
.'uu
bằng một số, nên nó không thể biểu diễn cho
.'zz
Câu 42. Trong mặt phẳng phức gọi A, B, C là điểm biểu diễn số phức với . Biết tam
giác ABC vuông tại B. Tìm tọa độ của C ?
A. B. C. D.
Hướng dẫn giải
Đáp án: A
,1 3 , 5i ia i++
a ∈
(
)
3; 5C −
( )
3; 5C
( )
2;5C
( )
2;5C −

Bài tập trắc nghiệm số phức
Trang 226
Ta có
Tam giác ABC vuông tại B nên
Câu 43. Tập hợp biểu diễn số phức z thỏa là đường tròn có bán kính bằng:
A. 2 B. 6 C. 4 D. 8
Hướng dẫn giải
Đáp án: A
Giả sử z=x+iy .
Câu 44. Cho số phức thõa mãn . Gọi M là điểm biểu diễn cho số phức z. Tọa độ điểm
M là
A. (1; 2) B. (4; 1) C. (1; 4) D. (–1; –4)
Hướng dẫn giải
Đáp án: C
Câu 45.
Tập hợp điểm biểu diễn số phức thỏa mãn là đường tròn tâm , bán kính
A.
B.
C.
D.
Hướng dẫn giải
Đáp án: D
z = x + yi,
Tập hợp các điểm (x;y) là đường tròn I(4; –3), bán kinh R = 2
Câu 46. Điểm biểu diễn số phức:
( )( )
23 4
32
ii
z
i
−−
=
+
có tọa độ là:
A.
( )
1; 4
−
B.
( )
1; 4−−
C.
( )
1; 4
D.
( )
1; 4−
Hướng dẫn giải
Đáp án: B
( )( )
( )
( )( )
22
22
23 4 514 32
8 2 12 3 15 10 42 28
14
32 32 3 2 13
ii i i
iii iii
zi
ii
−− − −
−−+ −−+
= = = = =−−
++ +
Suy ra điểm biểu diễn của số phức z là
( )
1; 4−−
Câu 47. Trong mp tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn: .
(
)
( )
( )
0;1 , 1;3 , ;5A B Ca
( ) ( )( )
. 0 1 1 22 0 3BA BC a a= ⇔− − + − = ⇔ =−
.4zz=
(
)
(
)
22
4zz x iy x iy x y⇒=+ −=+=
z
(1 ) 5 3iz i−=+
53
(1 ) 5 3 1 4
1
i
iz i z i
i
+
− =+ ⇔= =+
−
z
(4 3 ) 2zi−+ =
I
R
(4;3), 2
IR=
(4; 3), 4IR−=
( 4;3), 4IR−=
(4; 3), 2IR−=
z x yi
= −
2 22
(4 3 ) 2 4 ( 3) 2 ( 4) ( 3) 2z i x yi x y
−+=⇔−−+=⇔−++=
( )
1z i iz−= +
Bài tập trắc nghiệm số phức
Trang 227
A. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(2, –1), bán kính R= .
B. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0, 1), bán kính R= .
C. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0, –1), bán kính R= .
D. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0, –1), bán kính R= .
Hướng dẫn giải
Đáp án: D
Đặt z = x+yi, biến đổi được phương trình x
2
+ (y+1)
2
= 2
Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0, –1), bán kính R= .
Câu 48. Trong mặt phẳng tọa độ Oxy, gọi M là điểm biểu diễn cho số phức z = 3 – 4i; M’ là điểm biểu
diễn cho số phức . Tính diện tích tam giác OMM’.
A. . B. C. D.
Hướng dẫn giải
Đáp án: A
M(3;–4), M'( ; – ). OM = 5; Phương trình MM': 4x+3y=0.
d(M',OM)= . Từ đó .
Câu 49. Cho số phức z thỏa mãn . Điểm nào sau đây biểu diễn cho z trong các điểm M,
N, P, Q ở hình bên?
A. Điểm M
B. Điểm N
C. Điểm P
D. Điểm Q
Hướng dẫn giải
Đáp án:
Điểm biểu diễn cho z
2
3
3
2
2
/
1
2
i
zz
+
=
'
25
4
OMM
S
∆
=
'
25
2
OMM
S
∆
=
'
15
4
OMM
S
∆
=
'
15
2
OMM
S
∆
=
7
2
1
2
5
2
'
25
4
OMM
S
∆
=
( )
13 2 4iz i+ +=−
( )
42
13 2 4 1
13
i
iz i z i
i
−−
+ + =−⇒ = =−+
+
( )
1;1Q −
P
N
Q
M
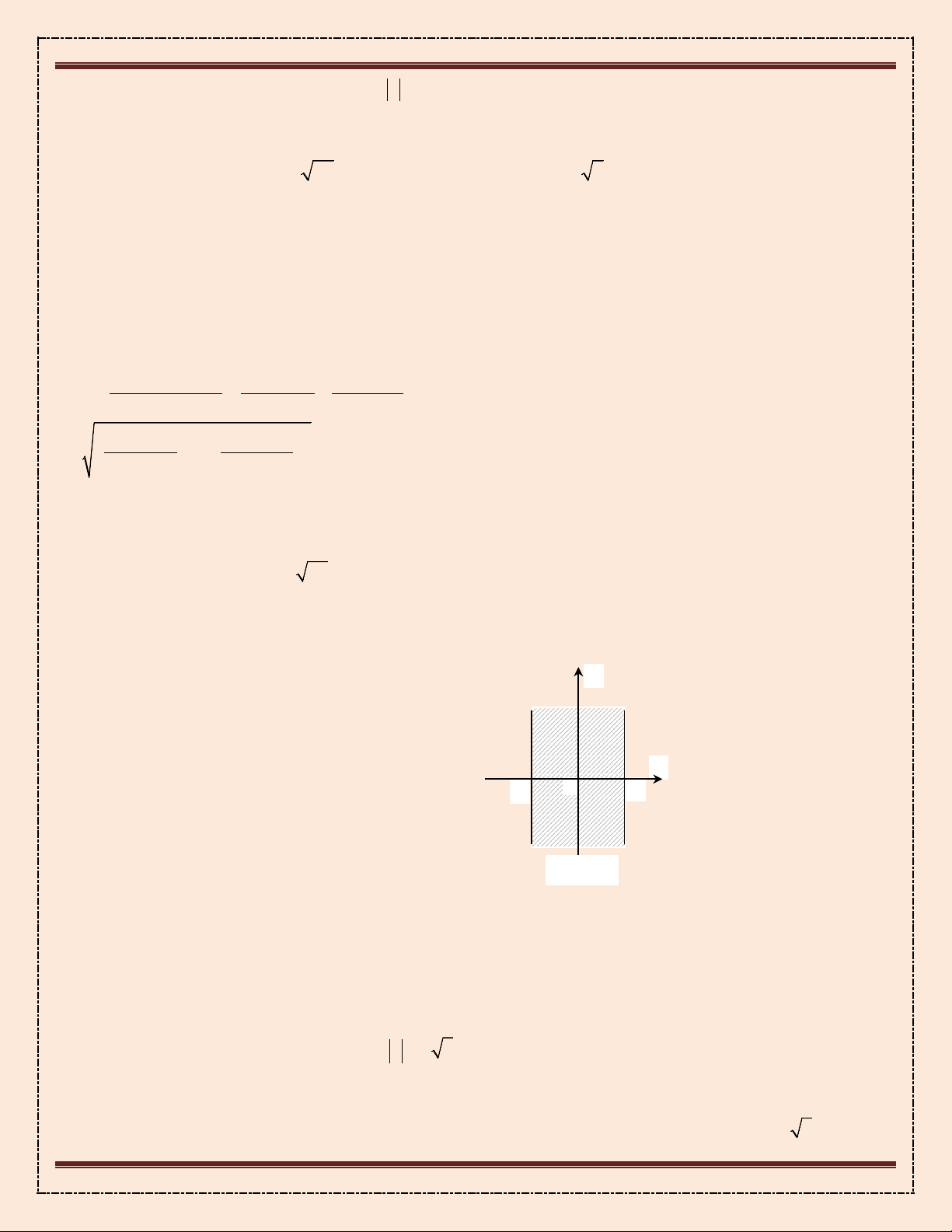
Bài tập trắc nghiệm số phức
Trang 228
Câu 50. Cho các số phức z thỏa mãn .Biết rằng tập hợp các điểm biểu diễn các số phức
là một đường tròn.Tính bán kính r của đường tròn đó.
A.20 B. C. D.7
Hướng dẫn giải
Đáp án: B
Đặt
Bán kính của đường tròn là
Câu 51. Cho số phức z = a + bi; a,b ∈ R. Để điểm biểu diễn của z nằm trong dãi (–2;2)
(hình 1), điều kiện của a và b là:
A.
B.
C. và b ∈ R
D. a, b ∈ (–2; 2)
Hướng dẫn giải
Đáp án: C
và b ∈ R
Câu 52. Cho các số phức z thỏa mãn . Biết rằng tập hợp các điểm biểu diễn các số phức
là một đường tròn. Tính bán kính r của đường tròn đó.
A. B. C. D.
2z =
( )
32 2
w i iz
=−+−
20
7
( )
,,w x yi x y=+∈
( )
( )
( )
( ) ( )
22
22
22
32 2
32 2
32
2 8 21
2 55
2 8 21
2
55
6 4 70
3 2 20
w i iz
x yi i i z
x yi
xy x y
zi
i
xy x y
xy xy
xy
=−+−
⇒+ =− + −
−+ +
−− + +
⇒= = +
−
−− + +
⇒ +=
⇒ + − + −=
⇒− ++ =
20
r
=
2
2
a
b
≥
≥
2
-2
a
b
≤−
≤
22a−< <
22a−< <
35z =
(2 )w iz i=−+
4r =
15r =
16r =
35r =
y
2
O
x
-2
(H×nh 1)

Bài tập trắc nghiệm số phức
Trang 229
Hướng dẫn giải
Đáp án: B
Câu 53. Cho số phức thỏa mãn . Biết rằng tập hợp các điểm biểu diễn các số phức
là một đường tròn. Tâm của đường tròn đó là:
A. . B. . C. . D. .
Hướng dẫn giải
Đáp án: B
Ta có .
Gọi . Suy ra .
Theo giả thiết, ta có
.
Vậy tập hợp các số phức là đường tròn tâm .
Câu 54. Xác định tập hợp các điểm biểu diễn số phức z trên mặt phẳng phức sao cho
zi
zi
−
+
là số thực
A. Đường tròn phương trình x
2
+ y
2
= 1 bỏ đi điểm (0; –1)
B. Hyperbol phương trình x
2
– y
2
= – 1 bỏ đi điểm (0; –1)
C. Trục tung bỏ đi điểm (0; –1)
D. Trục hoành bỏ đi điểm (0; –1)
Hướng dẫn giải
Đáp án: C
là số thực khi phần ảo bằng 0
Câu 55. Gọi A là điểm biểu diễn của số phức và B là điểm biểu diễn của số phức
A. Hai điểm A và B đối xứng với nhau qua trục hoành.
B. Hai điểm A và B đối xứng với nhau trục tung.
C. Hai điểm A và B đối xứng với nhau qua gốc tọa độ O.
(, )w x yi x y R=+∈
( )
2 12 1
( 1)
22 5
x y y xi
wi x y i
z
ii
+ −+ − −
− +−
⇒= = =
−−
22
22
2
2 1 2 2 ( 1)
45
555
xy yx x y
z
+− −− + −
=+==
22
( 1) 225
xy+− =
15r⇒=
z
1
zi+=
2wz i= −
( )
0; 1I −
( )
0; 3I
−
(
)
0;3I
( )
0;1I
22wz i zw i=− ⇔=+
( )
, w x yi x y
=+∈
(
)
2
z x yi=++
( )
21x yi i+ + +=
( ) ( ) ( )
22
22
3 1 3 1 31x yi x y x y⇔++ =⇔ ++ =⇔ + + =
2wz i= −
( )
0; 3I −
22
22
12
( 1)
xzi x y i
zi x y
− + −−
=
+ ++
22
2
0
( 1)
x
xy
−
⇔=
++
25zi= +
' 25zi=−+
Bài tập trắc nghiệm số phức
Trang 230
D. Hai điểm A và B đối xứng với nhau qua đường thẳng y = x .
Hướng dẫn giải
Đáp án: B
Ta có: . Dễ thấy A và B đối xứng nhau qua trục tung
Câu 56. Trong mặt phẳng tọa độ các điểm A, B, C lần lượt biểu diễn các số phức ; ;
. Số phức biểu diễn trọng tâm G của tam giác ABC là:
A. B. C. D.
Hướng dẫn giải
Đáp án: A
Ta có A(0;–3) ; B(2;–2); C(–5;–1) nên trọng tâm G(–1;–2)
Câu 57. Trong mặt phẳng tọa độ Oxy, tập họp điểm biểu diễn số phức z, biết là đường tròn
có tâm I. Hoành độ tâm I có tọa độ là:
A. x
I
= –4 B. x
I
= –2 C. x
I
= 2 D. x
I
= 4
Hướng dẫn giải
Đáp án: C
Đặt z=a+bi khi đó ta có
Câu 58. Cho số phức z thỏa mãn Hỏi điểm biểu diễn của z là điểm nào trong các điểm M,
N, P, Q ở hình bên ?
A. Điểm P
B. Điểm M
C. Điểm Q
D. Điểm N
Hướng dẫn giải
Đáp án: B
Cho z thỏa mãn: (1–i)z = 3 +i
Điểm biểu diễn M(1:2)
( ) ( )
2;5 , 2;5AB−
1
3zi
= −
2
22zi= −
3
5zi
=−−
12zi=−−
2zi
=−+
1zi=−−
1zi=−+
21zi
−−=
22
2 1 ( 2) ( 1) 1zi a b−−=⇒ − + − =
(
)
13
iz i−=+
3 (3 )(1 )
12
12
i ii
zi
i
+ ++
⇒= = =+
−
⇒
M
N
P
Q
2
-1
-2
1
0
x
y
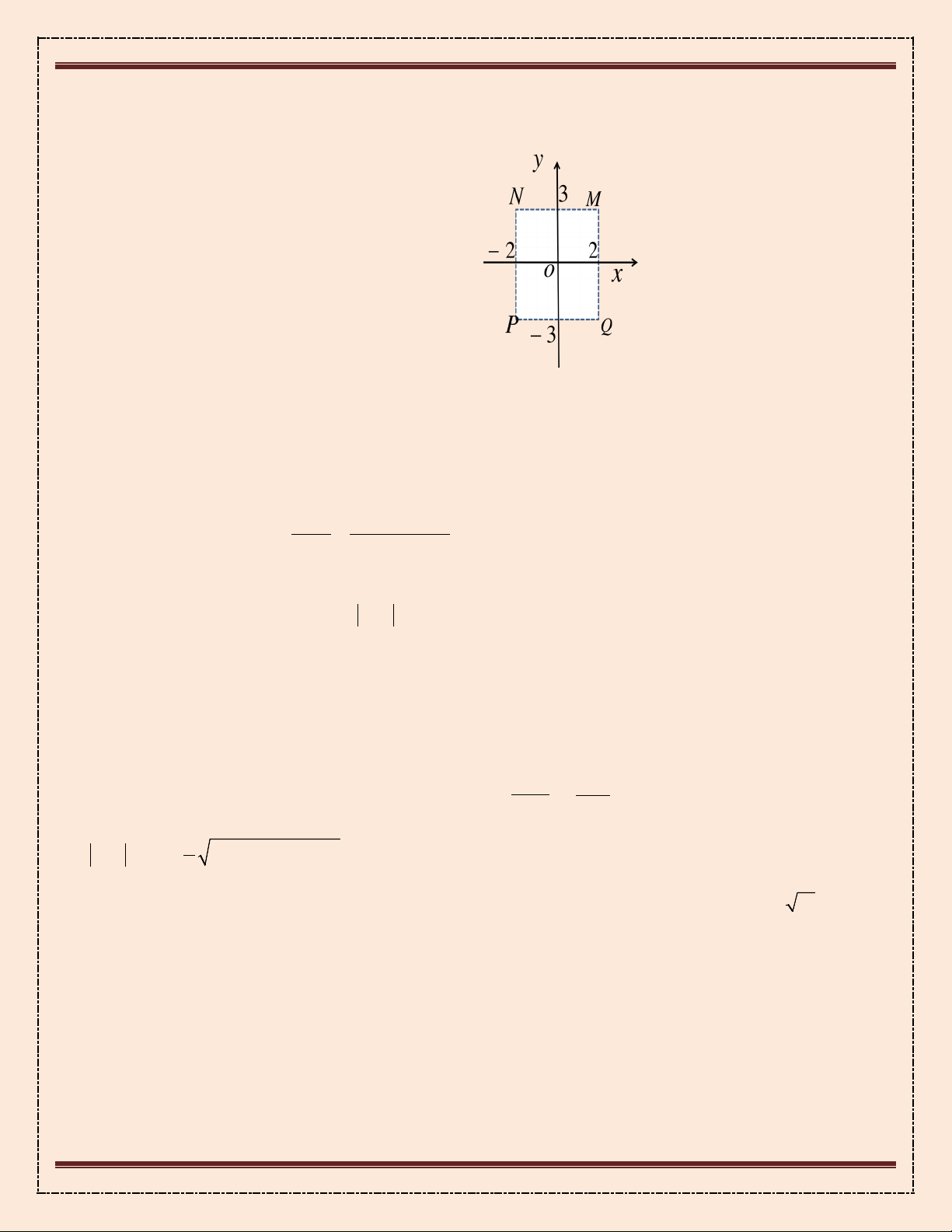
Bài tập trắc nghiệm số phức
Trang 231
Câu 59. Cho số phức z thỏa mãn
( )
12 8 .iz i+=+
Hỏi điểm biểu diễn của z là điểm nào
trong các điểm M, N, P, Q ở hình dưới đây?
A. Điểm P.
B. Điểm Q.
C. Điểm M.
D. Điểm N.
Hướng dẫn giải
Đáp án: B
Ta có :
( )
12 8iz i+=+
⇔
( )
( )
8 12
8
23
21 5
ii
i
zi
i
+−
+
= = = −
+
Vậy z được biểu diễn bởi điểm (2 ;–3), suy ra Q(2 ;–3).
Câu 60. Cho số phức z thỏa mãn
12z −=
.Biết rằng tập hợp các điểm biểu diễn các số phức
2w zi= −
là một đường tròn. Tìm bán kính r của đường tròn đó.
A. r = 2 B. r = 1 C. r = –2 D. r = 4
Hướng dẫn giải
Đáp án: D
Gọi
( )
2
,, 1
w a bi
ab Ri
= +
∈=−
;
Ta có:
2
1
1
2
2
a
b
w a bi z i
−
+
= + ⇒ −= +
Mà
Theo giả thiết, tập hợp các điểm biểu diễn các số phức
2w zi
= −
là một đường tròn nên ta có
16 4
r = =
Câu 61. Cho số phức z thỏa mãn .Hỏi điểm biểu diễn của z là điểm nào trong các điểm
M,
N, P, Q ở hình bên ?
( ) ( )
( ) ( )
22 22
1
1 2 2 16
21 21
2
z
ab ab
−=⇔ + =⇔ + =
−+ −+
( )
5
1
zi
i
= −
−
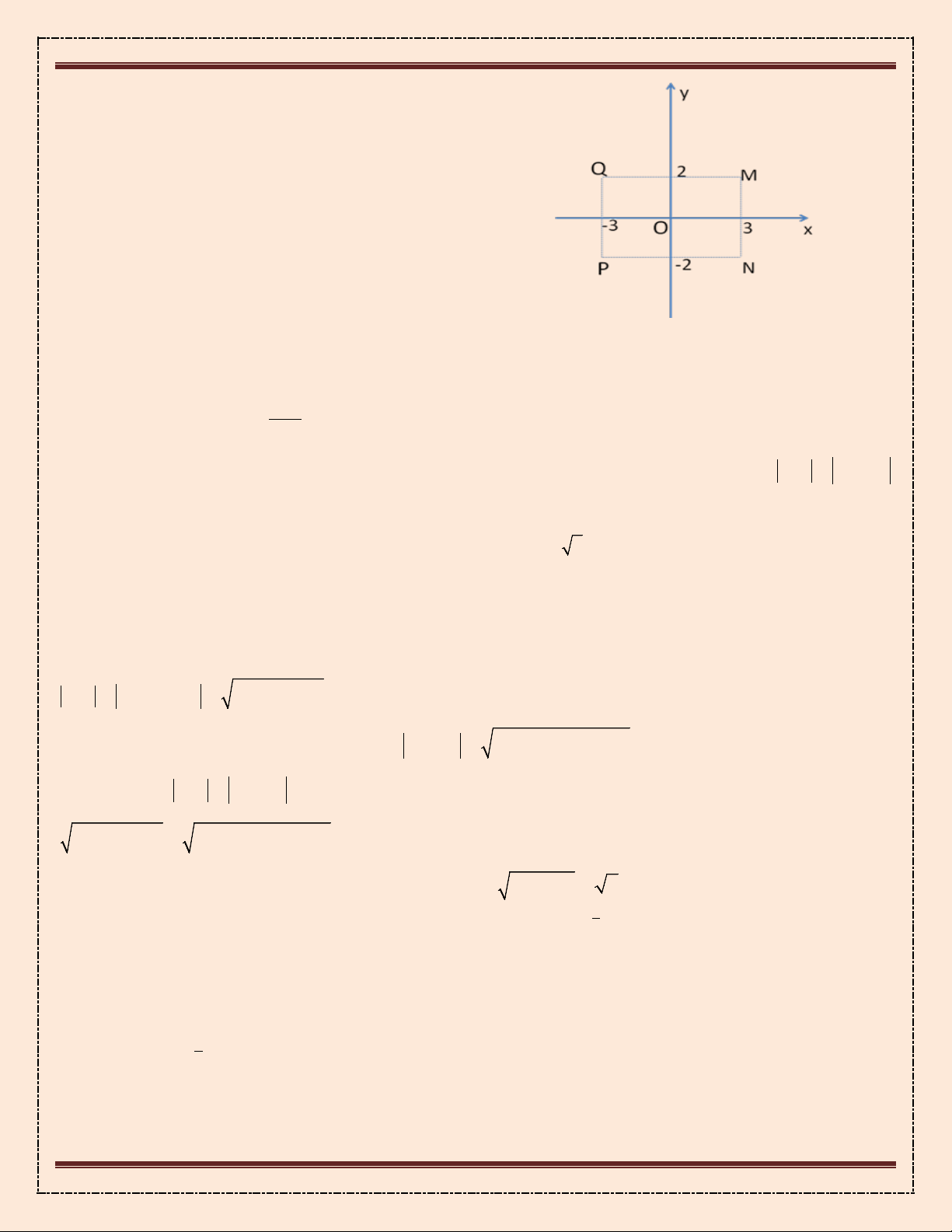
Bài tập trắc nghiệm số phức
Trang 232
A. Điểm N
B. Điểm M
C. Điểm P
D. Điểm Q
Hướng dẫn giải
Đáp án: B
Ta có:
( )
( )
5
5 32
3; 2
1
1
i
z i z iM
i
i
−
= −⇔ = = + ⇒
−
−
.
Câu 62. Tập hợp các điểm trong mặt phẳng phức biểu diễn các số z thỏa mãn điều kiện:
( )
1
z i iz−= +
là đường tròn có bán kính là
A. R = 1 B. R = 2 C. R =
2
D. R = 4
Hướng dẫn giải
Đáp án: C
Gọi
( )
;M xy
là điểm biểu diễn của số phức
(
)
;,z x iy x y
=+∈
trong mặt phẳng phức
( )
( )
2
2
11zi x y i x y−=+− = +−
( ) ( )( ) ( ) ( ) ( )
( ) ( )
22
11 1iz i x iy x y x yi iz x y x y+ =+ + =−++ ⇒+ = − ++
Theo giả thiết,
( )
1z i iz−= +
nên ta có:
( ) ( )
( )
2 22
2 22
1 2 1 0 (*)x y xy xy x y y+ − = − + + ⇔ + + −=
(*) là phương trình đường tròn tâm
( )
0; 1I −
bán kính
( )
2
112R = −− =
Câu 63. Tập hợp các số phức z thoả mãn đẳng thức |z + 2 + i| = | – 3i| có phương trình là:
A. y = x + 1 B. y = – x + 1 C. y = –x – 1 D. y = x – 1
Hướng dẫn giải
Đáp án: D
Gọi
z x yi z x yi=+ ⇒=−
, ta có
z
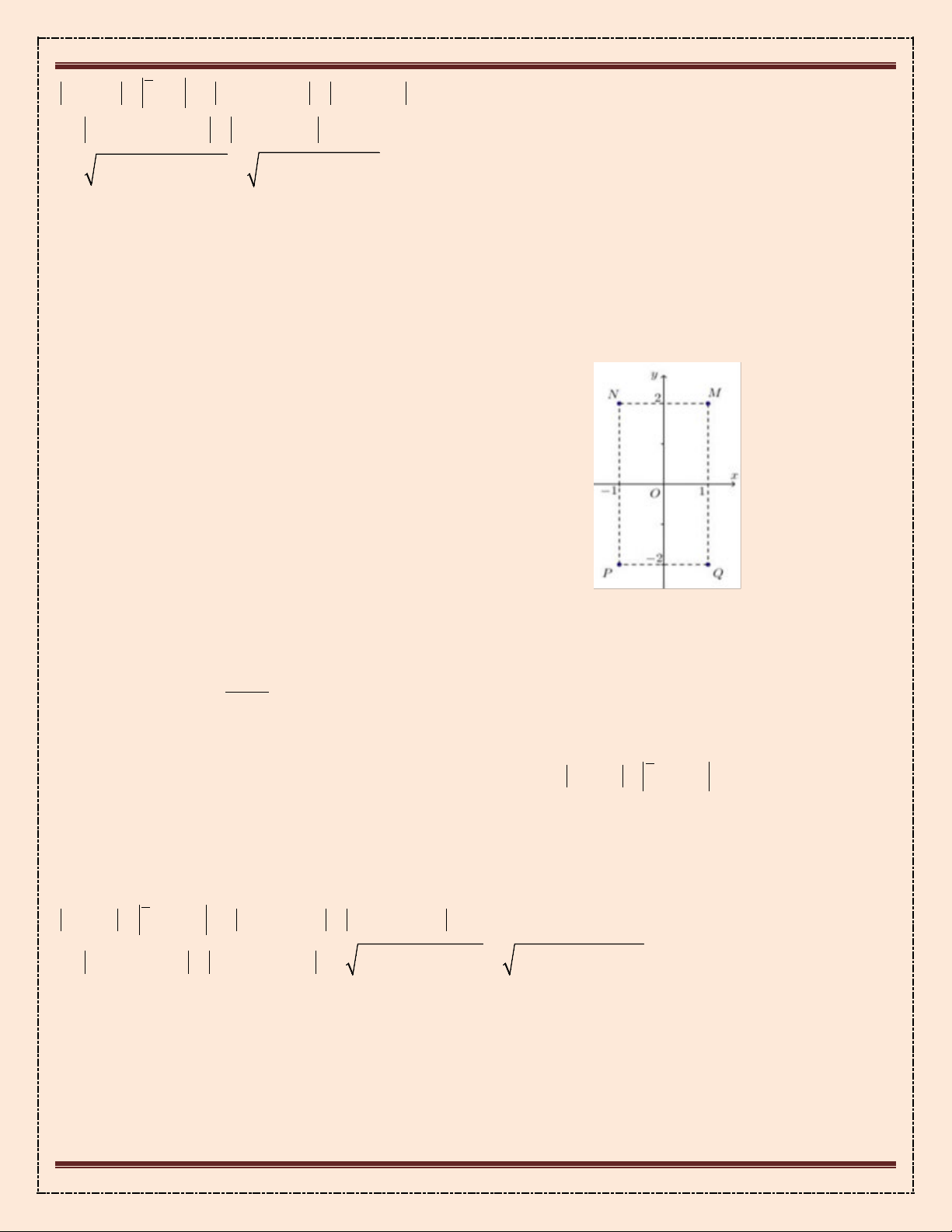
Bài tập trắc nghiệm số phức
Trang 233
( ) ( )
( )
( ) ( )
( )
( )
( ) ( ) ( )
2
22
2
22 2
2
2 2 22
23 2 3
21 3
21 3
21 3
44 21 69
1
z i z i x yi i x yi i
x y ixy i
x y xy
x y xy
x x y y xy y
yx
++= − ⇔ + ++= − −
⇔ +++ =−+
⇔ + + + = +− +
⇔+ ++ =++
⇔+++++=+++
⇔=−
Câu 64. Cho số phức
z
thỏa mãn
(1) 3.iz i− =−−
Hỏi điểm biểu diễn của
z
là điểm nào trong các điểm
M, N, P, Q ở hình bên ?
A. Điểm P.
B. Điểm Q.
C. Điểm M.
D. Điểm N.
Hướng dẫn giải
Đáp án: A
3
(1 ) 3 1 2
1
i
iz i z i
i
−−
− =−−⇔ = =−−
−
Điểm biểu diễn của z có tọa độ (–1;–2)
Câu 65. Tập hợp các điểm biểu diễn của số phức
z
thỏa mãn
1 12z iz i−+ = +−
là đường thẳng d:
A. 4x+2y+3=0. B. 2x+y=0. C. 3x–y–1=0. D.–4x+2y+3=0.
Hướng dẫn giải
Đáp án: A
( )
( )
22
22
1 12 1 12
1 ( 1) 1 ( 2) 1 ( 1) 1 ( 2)
z i z i a bi i a bi i
abiabi a b a b
−+ = +− ⇔ + −+ = − +−
⇔−++ =+−+ ⇔ − ++ = + ++
Biến đổi ta được:
4 2 30ab+ +=
suy ra đường thẳng d có PT
4 2 30xy+ +=
Câu 66. Trong không gian với hệ tọa độ Oxyz, cho 3 điểm M(2;0;0), N(0;–3;0), P(0;0;4). Nếu tứ giác
MNPQ là hình bình hành thì điểm Q có tọa độ:
A. (–2;–3;–4) B. (2;3;4) C. (–2;–3;4) D. (3;4;2)
Hướng dẫn giải

Bài tập trắc nghiệm số phức
Trang 234
Đáp án: B
Gọi tọa độ điểm Q(x;y;z)
Nếu tứ giác MNPQ là hình bình hành ta có
Vậy điểm Q(2;3;4)
Câu 67. Một vận động viên đẩy tạ theo quỹ đạo là một parabol có phương trình . Vị trí
quả tạ đang di chuyển xem như là một điểm trong không gian Oxy. Khi đó vị trí cao nhất của quả tạ là điểm
biểu diễn của số phức nào sau đây:
A. z . B. z . C. z . D.z .
Hướng dẫn giải
Đáp án: C
Parabol: y= có đỉnh I(1;5) là điểm biểu diễn cho số phức z
Câu 68. Tập hợp các điểm biểu diễn số phức z thõa mãn là đường tròn có tâm I, bán kính
R :
A.I(4;3), R =2 B.I(4;–3), R =4 C.I(–4;3), R= 4 D.I(4; –3), R= 2
Hướng dẫn giải
Đáp án: A
Lời giải: gọi số phức z = x+yi z = x– yi (x,y )
(1) là phương trình đường tròn có tâm I ( 4;3) , R =2
Câu 69. Trong mặt phẳng tọa độ Oxy, tập hợp điểm biểu diễn các số phức z thỏa mãn là:
A. Đường tròn tâm I (0;–1) và bán kính B. Đường tròn tâm I (0;–1) và bán kính
C. Đường tròn tâm I (–1;0) và bán kính D. Đường tròn tâm I (0;1) và bán kính
Hướng dẫn giải
Đáp án: B
Giả sử
MQ NP=
2
( 2; ; ) (0;3;4) 3
4
x
x yz y
z
=
⇔− = ⇔ =
=
2
24yx x
=−+ +
13i= −
5 i= +
15i= +
3 i= −
2
24xx−++
15i= +
43 2zi−+ =
⇒
∈
22
22
43 2 4(3 ) 2 8 1696 4
8 6 21 0(1)
x yi i x y i x x y y
xy xy
− −+ =⇔ −+ − = ⇔ − + +− + =
⇔+−−+=
( )
1z i iz−= +
22R =
2R =
22R =
2R =
(
)
,z a bi a b
=+∈
( )
( )
( ) ( )
1 ;1z i a b i iz a b a bi−= + − + = − + +
( ) ( )
2
2
1 12z i iz a b−= + ⇔ + + =

Bài tập trắc nghiệm số phức
Trang 235
Tập hợp điểm biểu diễn các số phức z thỏa mãn
là đường tròn tâm I(0;–1) và bán kính
Câu 70. Điểm biểu diễn của số phức z thỏa : là:
A. B. C. D.
Hướng dẫn giải
Đáp án: D
Câu 71. Gọi A là điểm biểu diễn của số phức Z = 1 + 2i và B là điểm biểu diễn của số phức Z’ = –1 + 2i.
Tìm mệnh đề đúng trong các mệnh đề sau :
A. Hai điểm A và B đối xứng nhau qua trục hoành
B. Hai điểm A và B đối xứng nhau qua trục tung
C. Hai điểm A và B đối xứng nhau qua gốc tọa độ O
D. Hai điểm A và B đối xứng nhau qua đường thẳng y = x
Hướng dẫn giải
Đáp án: B
Vì A ( 1 ; 2 ) ; B ( –1 ; 2 )
Hai điểm A và B đối xứng nhau qua trục tung
Câu 72. Tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa là
A. B.
C. D.
Hướng dẫn giải
Đáp án: C
Gọi z = x + yi ; x,y
Ta có ( 1 +i)z – 2i = ( 1 +i)(x + yi)–2i=x–y + (x+ y–2)i
Vậy đáp án câu C :
Câu 73. Cho số phức . Điểm biểu diễn của số phức z là:
A. M(–1;3) B. M(–1;–3) C. M(1;–3) D. M(1;3)
( )
1z i iz−= +
2R =
2
(1 ) (1 2 )
iz i
+=−
71
( ;)
22
−
71
(; )
22
−
71
(;)
22
71
(;)
22
−−
71
22
zi=−−
( )
1 22iz i+ −=
( ) ( )
22
1 11xy+ +− =
(
) (
)
22
1 11
xy+ ++ =
( ) ( )
22
1 11xy−+− =
( ) (
)
22
1 11xy−++ =
∈
( )
( ) ( )
22
22
1 2 2 2 2 444iz i x y x y x y x y+ − = − + +− = + − − +
( )
2 2 22
1 2 2 2 2 444 2 2210izi x y xy xy xy+ −= ⇔ + −−+= ⇔+−−+=
( ) ( )
22
1 11xy−+− =
( 1)( 2)z ii i=−+

Bài tập trắc nghiệm số phức
Trang 236
Hướng dẫn giải
Đáp án: B
Câu 74. Tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa
|
− 2
|
< 3 là
A. Đường tròn bán kính r = 3
B. Hình tròn bán kính r = 3 không kể đường tròn bán kính r = 3
C. Đường tròn bán kính r = 9
D. Hình tròn bán kính r = 9
Hướng dẫn giải
Đáp án: B
Câu 75. Điểm biểu diễn của số phức z thỏa : là:
A. B. C. D.
Hướng dẫn giải
Đáp án:
Câu 76. Điểm biểu diễn của các số phức z = a + ai với , nằm trên đường thẳng có phương trình là:
A. y = 2x B. y = –x C. y = x+ 1 D. y = x
Hướng dẫn giải
Đáp án: D
vì Z = a + ai với Điểm biểu diễn số phức Z có tọa độ là ( a; a ) thuộc đường thẳng y = x
Câu 77. Tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa là
A. B.
C. D.
Hướng dẫn giải
Đáp án: C
Gọi z = x + yi ; x,y
Ta có ( 1 +i)z – 2i = ( 1 +i)(x + yi)–2i=x–y + (x+ y–2)i
2
( 1)( 2) ( 2) 1 3 ( 1; 3)
z ii i ii i i M=−+= +−=−−⇒−−
22
( 2) 9
ab+− <
2
(1 ) (1 2 )iz i+=−
71
( ;)
22
−
71
(; )
22
−
71
(;)
22
71
(;)
22
−−
71
22
zi=−−
a ∈
a ∈
(
)
1 22iz i+ −=
(
) ( )
22
1 11xy+ +− =
(
) (
)
22
1 11xy
+ ++ =
( ) ( )
22
1 11xy−+− =
( ) ( )
22
1 11xy−++ =
∈
( ) ( ) ( )
22
22
1 2 2 2 2 444iz i x y x y x y x y+ − = − + +− = + − − +

Bài tập trắc nghiệm số phức
Trang 237
Vậy đáp án câu C :
Câu 78. Trong mặt phẳng phức gọi A, B, C lần lượt là các điểm biểu diễn của các số phức
, , . Tam giác ABC là :
A. Một tam giác cân B. Một tam giác đều
C. Một tam giác vuông D. Một tam giác vuông cân
Hướng dẫn giải
Đáp án: D
vì A( 3; –1 ) , B ( 1; 3 ) , C ( –1; –3)
Ta có BC
2
= AB
2
+ AC
2
và AB=AC vậy tam giác ABC vuông cân tại A
Câu 79. Cho số phức z thỏa và . Trong mặt phẳng phức, tập hợp điểm biểu
diễn số phức w là đường tròn tâm I, bán kính R là:
A. I(3;–4); R=2 B. I(4;–5); R=4 C. I(5;–7); R=4 D. I(7;–9) ; R=4
Hướng dẫn giải
Đáp án: D
Giả sử
Câu 80. Cho số phức z thỏa mãn
. Hỏi điểm biểu diễn của z là điểm nào trong các điểm I,
J, K, H ở hình bên
( )
2 2 22
1 2 2 2 2 444 2 2210izi x y xy xy xy+ −= ⇔ + −−+= ⇔+−−+=
(
) ( )
22
1 11
xy
− +− =
(1 )(2 i)
1
Zi=−+
2
13Zi
= +
3
13Zi=−−
20, 20, 40AB AC BC= = =
34 2zi−+ =
21wz i= +−
(, )
w x yi x y R=+∈
1 1 ( 1) ( 10
21
22 2
w i x yi i x y i
wz iz
−+ + −+ − + +
= +−⇒ = = =
( ) ( )
22
22
( 1) ( 1) 7 ( 9)
34 2 34 2 2
22
79
2 7 9 16
22
x yi x y i
zi i
xy
xy
−++ −++
−+ = ⇔ −+ = ⇔ =
−+
⇔ + =⇔− ++ =
( )
12 3iz i−=+
Bài tập trắc nghiệm số phức
Trang 238
A. Điểm K
B. Điểm H
C. Điểm I
D. Điểm J
Hướng dẫn giải
Đáp án: D
.
Điểm biểu diễn là J
Câu 81. Cho số phức z thoả mãn (1–i)z+4–2i=0. Điểm biểu diễn của z có toạ độ là
A. (–3;–1) B. (–3;1) C. (3;–1) D. (3;1)
Hướng dẫn giải
Đáp án: A
Cho số phức z thoả mãn (1–i)z+4–2i=0. Điểm biểu diễn của z có toạ độ là
(1–i)z+4–2i=0 (1–i)z = –4+2i z = –3–i
Câu 82. Tập hợp các điểm biểu diễn của số phức z thoả mãn điều kiện là đường tròn có
phương trình
A. B.
C. D.
Hướng dẫn giải
Đáp án: B
Tập hợp các điểm biểu diễn của số phức z thoả mãn điều kiện là đường tròn có phương trình:
Giả sử z=x+yi, x, y ∈ |R và M(x;y) là điểm biểu diễn của z
= 3
Câu 83. Cho số phức z = a + a
2
i với a ∈ R. Khi đó điểm biểu diễn của số phức liên hợp của z nằm trên:
A. Đường thẳng y = 2x B. Đường thẳng y = –x + 1
x
y
H
K
J
I
-
1
5
-
7
5
7
5
1
5
1
( )
3 17
12 3
12 5 5
i
iz i z i
i
+
− = +⇒ = = +
−
17
;
55
42
1
i
z
i
−+
=
−
3zi+=
22
( 1) 9xy+− =
22
( 1) 9xy++ =
2
( 1) 9xy− +=
22
( 1) 3xy++ =
3zi+=
3zi+=
( 1) 3xy i++ =
22
( 1)xy++
22
( 1) 9xy++ =

Bài tập trắc nghiệm số phức
Trang 239
C. Parabol y = x
2
D. Parabol y = –x
2
Hướng dẫn giải
Đáp án: D
vì Biêu diễn bằng điểm M(a, –a
2
) thỏa mãn phương trình y = –x
2
Câu 84. Gọi M là điểm biểu diễn số phức z trong mặt phẳng phức. Như thế, số được biểu diễn bởi
điểm
A. Đối xứng với M qua O B. Đối xứng với M qua Oy
C. Đối xứng với M qua Ox D. Không xác định được
Hướng dẫn giải
Đáp án: A
Câu 85. Cho số phức z thỏa mãn và . Trong mặt phẳng phức, tập hợp điểm
biểu diễn số phức w là đường tròn có tâm I, bán kính R. Khi đó
A. B. C. D.
Hướng dẫn giải
Đáp án: D
Câu 86. Cho phương trình: . Điểm biểu diễn của z trên mặt phẳng tọa độ là
A. . B. . C. . D. .
Hướng dẫn giải
Đáp án: A
Câu 87. Số phức z = 2 − 3 có điểm biểu diễn là
A.(2; 3) B. (−2; −3) C.(2; −3) D. (−2; 3)
Hướng dẫn giải
Đáp án: C
Câu 88. Tập hợp các điểm trong mặt phẳng biểu diễn số phức z thõa mãn điều kiện
|
− 1 + 2
|
= 4 là
A. Một đường thẳng B. Một đường tròn
C. Một hình chữ nhật D. Một hình vuông
Hướng dẫn giải
Đáp án: B
Gọi z = a + bi.
z−
34 2zi−+ =
w2 1zi= +−
( )
I 3; 4 , 2
R−=
( )
I 4; 5 , 4R−=
( )
I 5; 7 , 4R−=
(
)
I 7; 9 , 4
R−=
(1 4 ) 5 2iz i z−=−
43
;
55
−
43
;
55
34
;
55
34
;
55
−
( )
( )( )
(1 4 ) 5 2 (1 4 ) 2 5 (1 4 2) 5 (3 4 ) 5
534
5 15 20 3 4 4 3 4 3
;
34 34 34 25 5 5 5 55
iziz izzi i zi izi
ii
i ii
zi
i ii
− =− ⇔− + =⇔−+ =⇔− =
+
− −− −
⇔= = = = = + ⇒
− −+
Bài tập trắc nghiệm số phức
Trang 240
|
z − 1 + 2i
|
= 4 <=>
(
a − 1
)
2
+
(
b + 2
)
2
= 16
=> Tập các số phức thõa là đường tròn tâm I ( 1;2), bán kính R = 4
Câu 89. Tập hợp các điểm trong mặt phẳng phức biểu diễn cac số phức z thỏa mãn là
đường thẳng có phương trình là :
A.
B.
C.
D.
Hướng dẫn giải
Đáp án: B
Giả sử z = x + yi (x,y )
Vậy tập hợp các điểm cần tìm là đường thẳng
Câu 90. Điểm M trên hình vẽ là điểm biểu diễn của số phức nào sau đây:
A. (1 + i)z = 3 – i
B. (1 – i)z = 3 – i
C. (1 – i)z = 3 + i
D. (1 + i)z = 3 + i
Hướng dẫn giải
Đáp án: C
A. z = 1 – 2i B. z = 2 + i C. z = 1 + 2i D. z = 2 – i
Do đó M là điểm biểu diễn của số phức câu C
Câu 91. Trong mặt phẳng phức, gọi A, B, C lần lượt là các điểm biểu diễn của các số phức
z
1
= (1 – i)(2 + i); z
2
= 1 + 3i; z
3
= –1 – 3i. Tam giác ABC là:
A. Tam giác cân B. Tam giác đều
C. Tam giác vuông D. Tam giác vuông cân
Hướng dẫn giải
| 5| 6zz++=
1
2
x
=
1
2
x
= ±
1
2
y =
1
2
y = ±
R∈
| 5| 6
| 5| 6
|2 5| 6
1
2x 5 6
2
2x 5 6 1
2
zz
x yi x yi
x
x
x
++=
⇔ + +− +=
⇔ +=
=
+=
⇔⇔
+=−
= −
1
2
x = ±
x
y
2
M
1
Bài tập trắc nghiệm số phức
Trang 241
Đáp án: D
Trong mặt phẳng phức, gọi A, B, C lần lượt là các
điểm biểu diễn của các số phức
z
1
= (1 – i)(2 + i) , z
2
= 1 + 3i, z
3
= –1 – 3i. Tam giác
ABC là:
Ta có z
1
=3 – i => A(3; –1); z
2
= 1 + 3i => B(1; 3); z
3
= –1 – 3i => C(–1; –3)
=>Tam giác ABC vuông cân tại A
Câu 92. Tập hợp các điểm biểu diễn số phức z thỏa mãn là:
A. Một đường tròn bán kinh R=2
B. Hai đường tròn có tâm lần lượt O(2;1), O’(–2;–1)
C. Một hình hyperbol có phưng trình
D. Hai hình hyperbol có phương trình và
Hướng dẫn giải
Đáp án: D
Giả sử có điểm M(x;y) biểu diễn z trên mặt phẳng Oxy
Ta có:
Vậy tập hợp các điểm biểu diễn của z là hai đường hyperbol và
Câu 93. Tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa mãn
là:
A. Đường tròn tâm I(0;1), bán kính R=1 B. Đường tròn tâm , bán kính R=
C. Đường Parabol có phương trình
D. Đường Parabol có phương trình
20
20
40
AB
AC
BC
=
=
=
x
y
2
A
B
C
1
22
|z ( ) | 4z
−=
1
1
( ):y
2
H
x
=
1
1
( ):yH
x
=
2
1
( ):yH
x
= −
(; )z x yi x y R=+∈
22 222 2 2 2
22
2 ;() 2 () 4
1
|z ()|4 4| |4 | |1
1
z x xyi y z x xyi y z z xyi
y
x
z xy xy
y
x
=+ + =− +=>− =
=
=> − = <=> = <=> = <=>
−
=
1
1
( ):Hy
x
=
2
1
( ):Hy
x
= −
2| | | 2 |zi zz i
−= −+
( 3;0)I
3
2
4
x
y =
2
4
y
x =

Bài tập trắc nghiệm số phức
Trang 242
Hướng dẫn giải
Đáp án: C
Đặt và M(x;y) là điểm biểu diễn số phức z trên mặt phẳng phức.
Ta có:
Câu 94. Cho số phức z thỏa , biết tập hợp các điểm biểu diễn số phức z nằm trên đường
tròn tâm I có bán kính R. Tìm tọa độ I và R.
A. B. C. D.
Hướng dẫn giải
Đáp án: A
Đặt
Nên suy ra tập hợp các điểm biểu diễn số phức z là đường tròn tâm I(1; –2), bán kính R = 2
Câu 95. Cho số phức , với x, y là hai số thực thỏa :
Điểm M trên mặt phẳng tọa độ biểu diễn cho z, tìm tọa độ M.
A. B. C. D.
Hướng dẫn giải
Đáp án: A
Vậy
Nên điểm biểu diễn số phức z là M(1; 3)
Câu 96. Trên mặt phẳng toạ độ Oxy, tập hợp điểm biểu diễn các số phức z thoả mãn điều kiện
là :
A. B.
C. D.
Hướng dẫn giải
(; )z x yi x y R=+∈
2
22 2
2| | | 2 | 2|x (y 1)i| 2|(y 1) |
( 1) ( 1)
4
zi zz i i
x
xy y y
− = − + <=> + − = +
<=> + − = + <=> =
12 2zi
−+ =
(1; 2), 2IR−=
( 1; 2), 4IR
−=
( 2;1), 2IR−=
(1; 2), 4IR−=
( ) ( )
( ) ( )
22 22
12 12 ( 1)(2 )
122 12 2 12 4
z x yi z i x yi i x y i
zixyxy
= + ⇒ −+ = + −+ = − + +
⇒−+=⇔ − ++ =⇔− ++ =
z x yi= +
(
) (
)
(
) ( )
21 32 2 4x y ix y i
++ − = + + +
( )
1; 3M
( )
3;1M
( )
1; 3M −−
( )
3; 1M −−
( ) ( ) ( ) ( )
21 2 1
21 32 2 4
32 4 3
xx x
x y ix y i
yy y
+= + =
++ − = + + + ⇔ ⇔
−=+ =
13
zi= +
(2)2zi i−+=
3 4 20xy+ −=
22
( 1) ( 2) 9xy+ +− =
22
( 1) ( 2) 4xy− ++ =
2 10xy+ −=
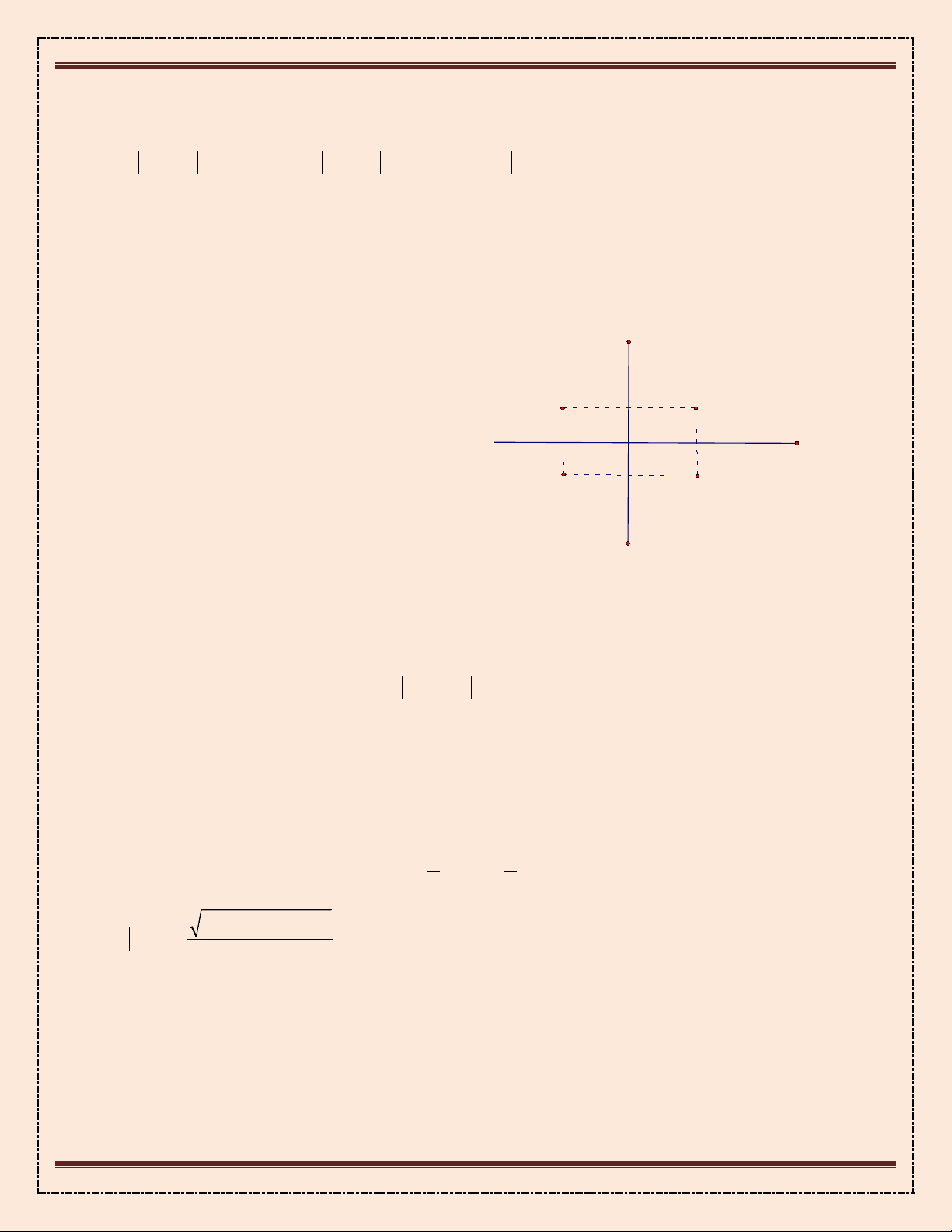
Bài tập trắc nghiệm số phức
Trang 243
Đáp án: C
Gọi
Vậy tập hợp điểm biểu diễn các số phức z thoả yêu cầu là đường tròn có phương trình .
Câu 97. Cho số phức z thỏa mãn .Hỏi điểm biểu diễn của z là điểm nào trong các điểm
M,N,P,Q ở hình bên ?
A. Điểm P
B. Điểm Q
C. Điểm M
D. Điểm N
Hướng dẫn giải
Đáp án: C
Câu 98. Cho các số phức z thỏa mãn .Biết rằng tập hợp các điểm biểu diễn các số phức
là một đường tròn .Xác định tâm I và tính bán kính r của đường tròn đó
A. B. C. D.
Hướng dẫn giải
Đáp án: D
Gọi ,ta có
Theo giả thuyết tập hợp các điểm biểu diễn các số phức là một đường tròn
Ta có
Câu 99. Gọi M là điểm biểu diễn của số phức 3 +4i và N là điểm biểu diễn của số phức –3 +4i. Khẳng
định nào sau đây là đúng ?
A. Hai điểm M và N đối xứng với nhau qua trục hoành.
( )
;,z x yi x y R=+∈
22
(2)2 ( )(2)2 ( 2)(1) 2
( 1) ( 2) 4
zii xyiii y xi
xy
−+=⇔ + −+=⇔−−+− =
⇔− ++ =
22
( 1) ( 2) 4xy
−++ =
( )
2 34iz i+=+
P
M
N
Q
( )
2 34 2
iz i z i+ =+ ⇒=+
34 2zi−+ =
21wz i= +−
(7; 9); 4Ir−=
(4; 5); 4Ir−=
(3; 4); 2Ir−=
( 7;9); 4Ir−=
w a bi= +
11
2 1 ( 1) ( 1)
22
wabiz iz a bi= + = +−⇔ = − + +
22
22
( 7) ( 9)
3 4 2 2 ( 7) ( 9) 16
2
ab
zi a b
− ++
−+ = ⇔ = ⇔ − + + =
21wz i= +−
22
( 7) ( 9) 16 (7; 9); 4a b Ir− ++ = ⇔ − =

Bài tập trắc nghiệm số phức
Trang 244
B. Hai điểm M và N đối xứng với nhau qua trục tung.
C. Hai điểm M và N đối xứng với nhau qua gốc toạ độ O.
D. Hai điểm M và N đối xứng với nhau qua đường thẳng y = x.
Hướng dẫn giải
Đáp án: B
Hai diểm biểu diễn có hoành độ đối nhau tung độ bằng nhau nên đối xứng nhau qua Oy.
Câu 100. Tìm tọa độ điểm M biểu diễn của số phức trên mặt phẳng phức.
A. B. C. D.
Hướng dẫn giải
Đáp án: B
Câu 101. Trên mặt phẳng phức cho . Biết rằng lần lượt biểu diễn các số phức ;
. Điểm biểu diễn số phức z sao cho vuông tại C. Khẳng định nào sau đây là đúng ?
A. B. C. D.
Hướng dẫn giải
Đáp án: C
A(2;–2) B(–2;4)
Thử lần lượt các điểm (2;–4) và (–2;2) không thỏa ĐK
Điểm (2;4) thỏa ĐK
Câu 102. Cho số phức z thỏa mãn : =2. Biết rằng tập hợp các điểm biểu diễn của số phức z là
một đường tròn. Tìm tâm và bán kính r của đường tròn đó.
A. Tâm I(–1;1) và bán kính R = 2 B. Tâm I(1;1) và bán kính R = 4
C. Tâm I(1;–1) và bán kính R = 4 D. Tâm I(1;–1) và bán kính R = 2
Hướng dẫn giải
Đáp án: D
Xét hệ thức: =2 (1)
Đặt z = x +yi (x, y ∈ R) ⇒ z – 1 + i = (x – 1) + (y + 1)i.
Khi đó (1) ⇔
1
23
z
i
=
−
( )
2; 3
M −
23
;
13 13
M
( )
3; 2M −
(
)
4; 1M −
23
13 13
zi
= +
ABC∆
,AB
1
22zi= −
2
24zi=−+
C
ABC
∆
24zi= −
22zi=−+
24zi= +
22zi= −
1zi
−+
1zi−+
22
( 1) ( 1) 2xy−++ =

Bài tập trắc nghiệm số phức
Trang 245
⇔ (x–1)
2
+ (y + 1)
2
= 4.⇒ Tập hợp các điểm M(z) trên mặt phẳng toạ độ biểu diễn số phức z thoả mãn (1) là
đường tròn có tâm tại I(1;–1) và bán kính R = 2.
Câu 103. Trên mặt phẳng tọa độ, tập hợp điểm biểu diễn số phức z thỏa mãn điều kiện là:
A. Đường tròn tâm O, bán kính bằng 2. B. Đường tròn tâm O, bán kính bằng .
C. Hình tròn tâm O, bán kính bằng 2. D. Hình tròn tâm O, bán kính bằng .
Hướng dẫn giải
Đáp án: C
,
Vậy tập hợp điểm biểu diễn số phức z là hình tròn tâm O, bán kính bằng 2
Câu 104. Cho số phức thõa mãn là nghiệm phương trình
Điểm M,N lần lượt biểu diễn cho trên Oxy khi đó độ dài MN bằng
A.4 B.2 C.5 D.3
Hướng dẫn giải
Đáp án: A
chọn A
Câu 105.
G
ọi
và
là các nghiệm của phương trình . Gọi M, N là các điểm biểu diễn
của
và
trên mặt phẳng phức. Khi đó độ dài của MN là:
A. B. C. D.
Hướng dẫn giải
Đáp án: D
Phương trình có hai nghiệm
Khi đó: .
Câu 106. Trong mặt phẳng tọa độ Oxy, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
là
A. Đường tròn có phương trình . B. Đường thẳng có phương trình
2z ≤
2
2
z x yi= +
22
;xy z x y∈⇒ = +
22
24z xy≤⇔ + ≤
12
,z
z
2
2 50zz+ +=
12
,zz
2
12
2 5 0 ; ( 1; 2), ( 1;2) MN 16 4
12
zi
zz M N
zi
=−−
+ += ⇔ −− − ⇒ = =
=−+
1
z
2
z
2
4 90zz− +=
1
z
2
z
4MN =
5MN =
25MN = −
25MN =
1 (2 )z iz−−=
22
1
4
xyx+ +=
1
4
x =
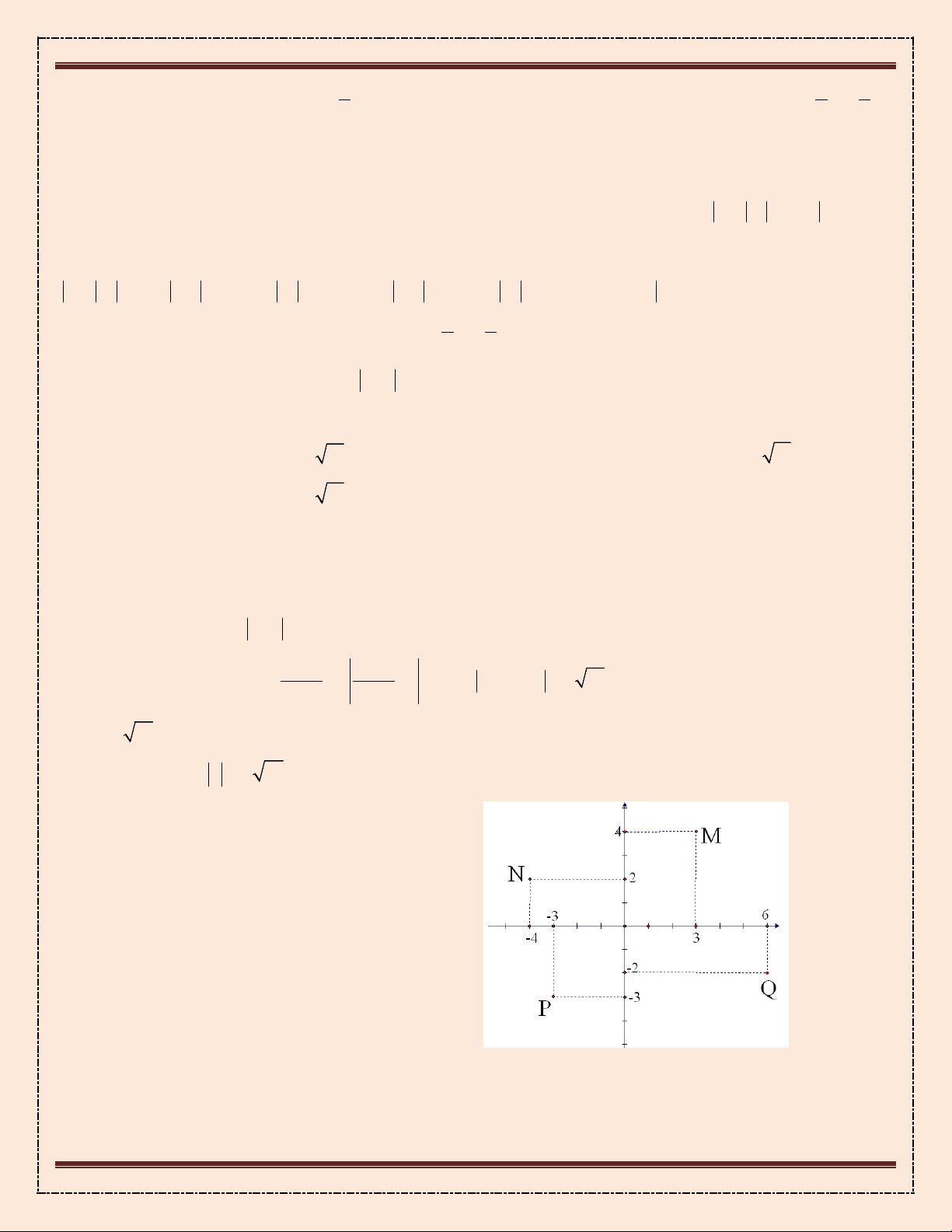
Bài tập trắc nghiệm số phức
Trang 246
C. Đường thẳng có phương trình D. Đường tròn có phương trình .
Hướng dẫn giải
Đáp án: D
Trong mặt phẳng tọa độ Oxy, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện là
Gọi . Ta có:
Câu 107. Cho số phức z thỏa mãn . Tìm tập hợp các điểm biểu diễn các số phức
là
A. Đường tròn có bán kính bằng B. Đường tròn có bán kính bằng
C. Đường tròn có bán kính bằng D. Đường tròn có bán kính bằng
Hướng dẫn giải
Đáp án: A
Cho số phức z thỏa mãn . Tìm tập hợp các điểm biểu diễn các số phức là
Ta có:
Câu 108. Cho . Số phức z được biểu diển bởi điểm nào trong hình sau:
A. P
B. M
C. N
D. Q
Hướng dẫn giải
Đáp án: D
1
4
y =
22
11
24
xy x++ =
1 (2 )
z iz
−−=
( )
;z x yi x y=+∈
22 2 2 22
1 (2 ) ( 1) (2 )( ) ( 1) (2 ) (2 )
11
( 1) (2 ) (2 )
24
z i z x yi i x yi x yi x y y x i
x y xy yx x y x
− − −+ − + −+ + + −
=⇔= ⇔=
⇔−+= + + − ⇔++ =
19z +=
(2 3 ) 1w iz=−+
9 13
9 11
3 11
9
19z +=
(2 3 ) 1w iz=−+
11
(2 3 ) 1 1 9 1 3 9 13
23 23
ww
w iz z w i
ii
−−
= − +⇒ = ⇒ + = ⇔ +− =
−−
9 13R⇒=
2 10z =

Bài tập trắc nghiệm số phức
Trang 247
Xét điểm Q là điểm biểu diễn của số phức
Câu 109. Tập hợp tất cả các điểm biểu diển số phức trên mặt phẳng tọa độ thỏa mãn là một
đường tròn. Gọi I là tâm của đường tròn này, tọa độ I là:
A. B. C. D.
Hướng dẫn giải
Đáp án: B
Giả sử
Ta có:
Vậy tâm I(0;1).
Câu 110. Gọi A là điểm biểu diễn của số phức 5 +8i và B là điểm biểu diễn của số phức –5 +8i. Tìm mệnh
đề đúng trong các mệnh đề sau?
A. Hai điểm A và B đối xứng với nhau qua trục hoành.
B. Hai điểm A và B đối xứng với nhau qua trục tung.
C. Hai điểm A và B đối xứng với nhau qua gốc toạ độ O.
D. Hai điểm A và B đối xứng với nhau qua đường thẳng y = x.
Hướng dẫn giải
Đáp án: B
Hai điểm A và B đối xứng với nhau qua trục tung: vì A(5;8), B(–5;8).
Câu 111. Giả sử A, B theo thứ tự là điểm biểu diễn của các số phức z
1
, z
2
. Khi đó độ dài của véctơ
bằng
A.
B.
C.
D.
Hướng dẫn giải
Đáp án: C
Vì
Câu 112. Tập hợp điểm biểu diễn số phức z, biết là
A. Điểm B. Đường thẳng C. Đường tròn D. Elip
Hướng dẫn giải
Đáp án: C
Gọi , ta có:
6 2 36 4 2 10z iz=− ⇒ = +=
z
1zi−=
(0; 1)I −
(0;1)
I
(1; 0)I
( 1; 0)I −
;,z x yi x y=+∈
22
1 ( 1) 1 ( 1) 1zi x y i x y−=⇔+− =⇔+− =
AB
12
zz
−
12
zz
+
21
zz−
21
zz
+
21
AB OB OA z z=−=−
34 2zi +=
z a bi= +
( ) ( )
22
3( ) 4 2 3a 3 4 2 4 3 3a 2a bi i i b b+ += ⇔ − += ⇔ − + =

Bài tập trắc nghiệm số phức
Trang 248
.
Câu 113. Cho A và B lần lượt là điểm biểu diễn của z
1
= 1 – 3i và z
2
= 7 + 5i. Độ dài đoạn AB bằng:
A. 10 B. 9 C. 8 D. 7
Hướng dẫn giải
Đáp án: A
z
1
= 1 – 3i A ( 1 ; –3 ), z
2
= 7 + 5i B ( 7 ; 5 )
= ( 6 ; 8 ) AB = = 10.
Câu 114. Cho A ( –2 ; 3 ), B ( 4 ; –1 )là điểm biểu diễn của hai số phức z và z’. Phần ảo của số phức z.z’
bằng :
A. – 14 B. – 12 C. 12 D. 14
Hướng dẫn giải
Đáp án: D
A ( –2 ; 3 ) z = –2 + 3i và B ( 4 ; –1 ) z’ = 4 – i
z.z’ = ( –2 + 3i)( 4 – i ) = –5 + 14i.
Câu 115. Cho biết z + 2i + 3 là số thuần ảo, tập hợp các điểm biểu diễn của z có phương trình là :
A. x + 2y + 3 = 0 B. x – 2y + 3 = 0 C. x – 2y – 3 = 0 D. x + 2y – 3 = 0
Hướng dẫn giải
Đáp án: A
Gọi z = x + yi = x –yi . Ta có : z + 2i + 3 = x + yi + 2i( x –yi ) + 3
= x + yi + 2ix – 2i
2
y + 3 = x + 2y + 3 + ( x + y )i. Vì là số thuần ảo nên : x + 2y + 3 = 0.
Câu 116. Cho biết z. = 4, tập hợp các điểm biểu diễn của z có phương trình là :
A. x
2
+ y
2
– 2 = 0 B. x
2
+ y
2
– 16 = 0 C. x
2
– y
2
– 4 = 0 D. x
2
+ y
2
– 4 = 0
Hướng dẫn giải
Đáp án: D
Gọi z = x + yi = x –yi. Ta có : z. = 4 ( x + yi )( x – yi) = 4 x
2
+ y
2
= 4 hay x
2
+ y
2
– 4 = 0.
Câu 117. Trong mặt phẳng phức, gọi A, B, C lần lượt là điểm biểu diễn các số phức
. Tam giác ABC là:
A. Tam giác vuông tại A B. Tam giác vuông tại B
C. Tam giác cân tại A D. Tam giác đều
Hướng dẫn giải
Đáp án: D
2
2
42
39
ab
+− =
⇒
⇒
AB
⇒
22
68
+
⇒
⇒
z
⇒
z
z
z
⇒
z
z
⇒
⇒
( )
( )
1 ,4 31,1 231ii i
++ + + +

Bài tập trắc nghiệm số phức
Trang 249
Ta có nên tam giác ABC là tam giác đều.
Câu 118. Tập hợp điểm biểu diễn số phức thỏa mãn là số ảo là:
A. Đường tròn B. Đường thẳng
C. Đường thẳng D. Các đường thẳng trừ
Hướng dẫn giải
Đáp án: D
Giả sử với
suy ra , vì là số ảo nên .
Vậy tập hợp các điểm thỏa yêu cầu bài toán là hai đường thẳng bỏ đi gốc tọa độ.
Câu 119. Điểm nào sau đây biểu diễn số phức: ?
A. B. C. D.
Hướng dẫn giải
Đáp án: A
có điểm biểu diễn là
Câu 120. Xét các điểm A, B, C trong mặt phẳng phức theo thứ tự biểu diễn các số ,
. Khi đó số phức biểu diễn bởi điểm D sao cho ABCD là hình vuông là:
A. B. C. D.
Hướng dẫn giải
Đáp án: A
Ta có
Gọi
Ta có ABCD là hình vuông thỏa mãn điều kiện cần
Chú ý: có thể dùng Casio để tính các phép toán về số phức trên (CMPLX) và bấm kí hiệu bằng các bấm Shift
rồi bấm Eng.
23AB BC CA= = =
z
2
z
22
1xy
+=
yx=
yx= −
yx
= ±
(0;0)O
z x yi
= +
,xy R∈
222
2z x y xyi
=−+
2
z
22
0
0
0
0
xy
xy
x
xy
y
= ±
−=
⇔
≠
≠
≠
xy
= ±
12
.8zz i i
+=−+
( )
8,1
−
( )
4,8
( )
8, 1
−
( )
4, 1−−
12
.8
zz i i+=−+
( )
8;1−
4
1
i
i −
( )( )
26
1 12,
3
i
ii
i
+
−+
−
1 i−−
1 i+
1 i−+
1 i−
(
) (
)( ) (
) (
) ( )
4 26
2 2 2; 2 ; 1 1 2 3 3;1 ; 2 0; 2 1;3
13
ii
i A i i i B i C AB
ii
+
= − → − − + = +→ = → → =
−−
( ) ( )
; ;2D x y DC x y
→ =−−
( )
1
1; 1
23
x
DC AB D
y
−=
= ↔ ↔ −−
−=
i

Bài tập trắc nghiệm số phức
Trang 250
Câu 121. Trên mặt phẳng phức tập hợp điểm biểu diễn số phức z thỏa mãn: . Chọn đáp án
đúng?
A. Tập hợp điểm biểu diễn số phức là đường thẳng:
B. Tập hợp điểm biểu diễn số phức là đường tròn
C. Tập hợp điểm biểu diễn số phức là đường tròn
D. Tập hợp điểm biểu diễn số phức là đường tròn
Hướng dẫn giải
Đáp án: C
Trên mặt phẳng phức tìm tập hợp điểm biểu diễn số phức z thỏa mãn:
Gọi số phức điểm biểu diễn trên mặt phẳng phức
Vậy tập hợp các điểm biểu diễn số phức z là đường tròn tâm , bán kính R = 1
Câu 122. Cho các số phức có điểm biểu diễn lần lượt là A, B, C, D, E trong mặt phẳng
phức tạo thành một ngũ giác lồi. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DE. Gọi I, J lần
lượt là trung điểm các đoạn MP và NQ. Biết I, J là điểm biểu diễn hai số phức và là số phức có
điểm biểu diễn là E. Tìm số phức ?
A. B. C. D.
Hướng dẫn giải
Đáp án: C
Ta có:
Mà do đó
Suy ra .
Câu 123. Tập hợp điểm biểu diễn số phức thỏa điều kiện nằm trên đường tròn có tâm là:
A. B. C. D.
Hướng dẫn giải
11zi−+ =
0xy+=
( ) ( )
22
1 19
xy− ++ =
( ) ( )
22
1 11xy
− ++ =
( ) ( )
22
2 24xy
− ++ =
11zi−+ =
( )
,R
z x yi x y=+∈
( )
;M xy
(
)
( ) ( )
22
1 1 1 1 1 1 11
z i x yi x y−+ =↔ −+ + =↔ − + + =
( )
1; 0I
12345
,,,,zzzzz
1 ,2ii
−
45i−
1
z
1
23zi
= −
1
47zi= −
1
87zi= −
1
82zi= −
( )
42IJ IQ IN
= +
0IM IP+=
IQ IN IM MQ IP PN MQ PN+ = + ++ = +
( )
1 11
2 22
AE BD DB AE= ++ =
( )
( )
40 1 4
8
4
7
42 1 5
A
A
A
A
x
x
IJ AE
y
y
−=−
=
=⇔⇔
= −
+=−
z
12 1zi++ =
( )
1; 2I
( )
1; 2I −
( )
1; 2I −
( )
1; 2I −−

Bài tập trắc nghiệm số phức
Trang 251
Đáp án: B
suy ra . Khi đó ta được .
Vậy tập hợp số phức nằm trên đường tròn có tâm .
Câu 124. Tập hợp các điểm biểu diễn số phức z thỏa mãn là đường thẳng
. Tính ab+c:
Chọn đáp án đúng:
A. 11 B. 9 C. 15 D. 6
Hướng dẫn giải
Đáp án: A
Giả sử: có điểm biểu diễn z trên mặt phẳng (Oxy)
Ta có:
Theo đề bài:
Vậy tập hợp các điểm biểu diễn của z là đường thẳng
Câu 125. Trong mặt phẳng Oxy là tọa độ ba điểm biểu diễn của số phức
. Tọa độ trực tâm của tam giác là:
A. B. C. D.
Hướng dẫn giải
Đáp án: D
Gọi là trực tâm , ta có
Câu 126. Trong mặt phẳng phức, các điểm biểu diễn tương ứng với các số 0,1, tạo thành:
A. Một hình vuông B. Một hình bình hành
B. Một hình chữ nhật D. Một hình khác.
Hướng dẫn giải
(
)
,Rz x yi x y=+∈
z x yi= −
(
)
(
)
(
) (
)
22
12 1 1 2 1
x yi x y++ − =⇔ + + − =
z
( )
1; 2I −
1 12z iz i−+ = +−
:0ax by c
∆ + +=
(
)
,z x yi x y=+∈
( )
;M xy
(
) ( ) (
) ( )
1 1 1; 12 1 2
z ix y iz ix y i
−+= − + + +− = + +− −
(
)
( )
( )
( )
22 2 2
1 12 1 1 1 2z iz i x y x y
−+ = +− ⇔ − + + = + +− −
( ) ( )
(
) ( )
222 2
22 22
1 1 1 2 21 21 21 4 4x y x y xx yy xx yy− + + = + + + ⇔ − ++ + += + ++ + +
4 2 30xy⇔ + +=
(
)
:4 2 3 0
xy∆ + +=
,,MNP
1
5 6;zi=−+
23
z 4 ; 43iz i=−− = +
H
MNP
(3;1)
( 1; 3)−
(2; 3)−
( 3; 2)−
( ) ( )
(
)
5;6 , 4; 1 , 4;3MN P− −−
( )
;H xy
MNP∆
( ) (
) ( )
5; 6 ; 8; 4 ; 4; 1MH x y NP NH x y=+− = =++
( )
( ) ( )
(
) ( )
( )
8 54 60
.0
9; 3 3; 2
9 43 10
.0
xy
MH NP
MP H
xy
NH MP
++ −=
=
= −⇒ ⇔ ⇒ −
+− +=
=
,2i −

Bài tập trắc nghiệm số phức
Trang 252
Đáp án: A
Các điểm tương ứng là:
Câu 127. Trên mặt phẳng phức, tập hợp các số sao cho là số thực được biểu diễn bởi:
A. Đường có phương trình
B. Đường có phương trình
C. Đường có phương trình
D. Nửa mặt phẳng bờ là Ox
Hướng dẫn giải
Đáp án: A
Ta có Như thế, là số thực khi và chỉ khi
Câu 128. Trong mặt phẳng xy cho tam giác MNP với alf ba điểm biểu diễn của các số phức
. Toạ độ tâm đường tròn ngoại tiếp tam giác MNP là:
A. B. C. D.
Hướng dẫn giải
Đáp án: D
là tâm đườn tròn ngoại tiếp
Câu 129. Gọi P là điểm biểu diễn của số phức trong mặt phẳng phức.
Cho các mệnh đề sau :
(1) Môđun của là bình phương khoảng cách OP.
(2) Nếu P là biểu diễn của số thì khoảng cách từ O đến P bằng 7.
Chọn đáp án đúng :
A. Chỉ có (1) đúng B. Chỉ có (2) đúng C. Cả hai đều đúng D. Cả hai đều sai.
Hướng dẫn giải
Đáp án: D
Phải sửa lại:
(1) Môđun của là khoảng cách OP
(2) Nếu P là biểu diễn của số thì khoảng cách từ O đến P bằng
( ) (
)
( )
( )
0;0 , 1;0 , 0;1 ; 2; 0
O ABC−
z x yi
= +
2
z
0xy =
0x =
0
y =
(
)
2
2 22
2.z x yi x y xyi=+ =−+
2
z
0xy =
,,MNP
12 3
1; 3 ; 5 5z z iz i
==+==
( )
4; 2
( )
4; 2−
( )
4; 4−
( )
4; 2
−
( )
(
) (
)
1; 1, 3;1, 5; 5
M NP−−
(
)
;I xy
MNP∆
(
)
( ) ( )
( )
( ) ( ) ( ) (
)
( )
22 22
22
22 2 2 2 2
1131
115 5
24
4; 2
52
xyx y
MI NI
MI PI
xyx y
xy x
I
xy y
− ++ =− +−
=
⇔
=
− ++ =− ++
+= =
⇔ ⇔−
−= =−
a bi+
a bi+
34
i+
a bi+
34i+
34 5i+=

Bài tập trắc nghiệm số phức
Trang 253
Câu 130. Trong mặt phẳng tọa độ Oxy, cho điểm M là điểm biểu diễn của số phức . Phương
trình đường trung trực của đoạn OM là :
A. B. C. D.
Hướng dẫn giải
Đáp án: B
Gọi là trung trực của đoạn OM
qua trung điểm I của và có vectơ pháp tuyến
:
Câu 131. Cho các số phức z thỏa mãn phần trực thuộc và phần ảo thuộc đoạn .
Hỏi tập hợp các điểm biểu diễn số phức z.
A. Phần mặt phẳng giới hạn bởi đường thẳng và
B. Phần mặt phẳng giới hạn bởi đường thẳng và
C. Miền ngoài của hình chữ nhật có bốn đỉnh là
D. Miền trong của hình chữ nhật có bốn đỉnh là giao của .
Hướng dẫn giải
Đáp án: D
Gọi . Từ giả thiết ta có nên suy ra tập hợp rất cả các điểm biểu diễn số phức z
là miền trong của hình chữ nhật có bốn đỉnh là giao của
Câu 132. Trên mặt phẳng phức, tập hợp các điểm biểu diễn số phức z mà cả phần thực và phần ảo của nó
đều thuộc đoạn là:
A. Tập các điểm nằm trên biên và bên trong hình tròn có tâm và bán kính
B. Tập các điểm nằm trên đoạn thẳng với
C. Tập các điểm nằm trên biên và bên trong hình vuông có bốn đỉnh
D. Tập các điểm thỏa mãn:
Hướng dẫn giải
Đáp án: C
Rõ ràng tập hợp các điểm là tập hợp các điểm nằm trên cạnh và nằm bên trong hình vuông có bốn đỉnh là:
.
Câu 133. Miêu tả tập số phức z trên hệ tọa độ phức mà thỏa mãn là
42zi
= +
2 50xy+ +=
2 50xy+−=
2 50xy− +=
2 50xy++=
( )
∆
( )
⇒∆
(
)
2;
OM ⇒Ι 1
(
)
4; 2n OM
= =
( )
⇒∆
( ) ( )
4 22 50042x y xy xy− + −1 = ↔ + −10 = 0 +−2 =⇔
[ ]
0;3
[ ]
2; 4−
3
x =
0
x
=
2
y = −
4
y =
0, 3, 2, 4.
xxy y= = =−=
0, 3, 2, 4xxy y
= = =−=
,,z x yi z y=+∈
03
24
x
y
≤≤
−≤ ≤
0, 3, 2, 4.xxy y
= = =−−
[
]
2; 2
−
( )
0;0
2
R =
0yx+=
[ ]
2; 2x
∈−
(
) ( ) (
) ( )
2; 2 ; 2; 2 ; 2; 2 ; 2; 2− − −−
( )
;xy
22
4xy+≤
( )
( ) ( ) ( )
2; 2 ; 2; 2 ; 2; 2 ; 2; 2− − −−
3 2 10zi+−=

Bài tập trắc nghiệm số phức
Trang 254
A. Đường thẳng B. Đường thẳng
C. Đường tròn D. Đường tròn
Hướng dẫn giải
Đáp án: C
Mỗi số phức được biểu diễn bởi một điểm . Do đó ta có tập số phức z thỏa mãn là:
Câu 134. Tập hợp các điểm biểu diễn số phức z trong hệ tọa độ vuông góc của mặt phẳng thỏa mãn
với phần thực không âm là:
A. Một hình tròn B. Một hình viên phân
C. Một hình vành khăn D. Một hình quạt
Hướng dẫn giải
Đáp án: B
Giả sử , suy ra , do đó . Vậy tập hợp điểm thỏa mãn yêu
cầu bài toán là phần hình giao nhau giữa hình tròn tâm , bán kính 4 và nửa mặt phẳng bờ là trục ảo
chứa các điểm có phần thực không âm. Do đó ta thu được một hình viên phân.
Câu 135. Bán kính của đường tròn biểu diễn số phức z thỏa mãn hệ thức trong mặt
phẳng phức là:
A. B. C. D.
Hướng dẫn giải
Đáp án: A
Gọi là điểm biểu diễn số phức
Ta có
Vậy tập hợp các điểm M là đường tròn , có tâm và bán kính là .
3 2 100xy−=
2 3 100xy−=
( ) ( )
22
2 3 100xy− ++ =
( ) ( )
22
3 2 100xy− ++ =
z x yi= +
( )
;xy
( ) ( )
22
3 2 10 2 3 100
x i yi x y
++−= ⇔ − + + =
23 4zi++ ≤
z x yi= +
( ) ( )
2 34
x yi+++ ≤
( ) ( )
22
2 3 16xy+ ++ ≤
( )
2; 3I −−
32 2 12z iz i+− = +−
29
9
29
3
29
9
23
9
(
)
;M xy
( )
,z x yi x y=+∈
32 2 12z iz i+− = +−
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
22 2 2
22
3 2 21 2 2
3 2 21 2 2
1 2 29
3 39
x yi x yi
xy x y
xy
⇔ ++ − = ++ −
⇔+ +− = + + −
⇔− +− =
22
1 2 29
3 39
xy
− +− =
12
;
33
29
3

Bài tập trắc nghiệm số phức
Trang 255
Câu 136. Cho các số phức và . Gọi A, B, C, D lần lượt là các
điểm biểu diễn của . Hỏi tứ giác ABDC là hình gì?
A. Hình vuông B. Hình chữ nhật C. Hình bình hành D. Hình thang
Hướng dẫn giải
Đáp án: D
Vì nên ACDB là hình thang.
Ta chọn phương án D.
Câu 137. Tập hợp các điểm biểu diễn số phức z sao cho là một số thuần ảo. Là một đường
tròn tâm
Tính tổng a + b
A. 2 B. 1 C. –2 D. 3
Hướng dẫn giải
Đáp án: C
Giả sử có điểm biểu diễn z trên mặt phẳng (Oxy)
Khi đó
Từ số bằng: ; u là số thuần ảo khi và chỉ khi:
Kết luận: Vậy tập hợp các điểm biểu diễn của z là một đường tròn tâm , bán kính , loại đi
điểm
Câu 138. Trong mặt phẳng tọa độ Oxy, cho ba điểm M,N, P là điểm biểu diễn của 3 số phức:
. Với giá trị nào của x thì tam giác MNP vuông tại P?
A. 1 và 2 B. 0 và 7 C. và D. 3 và 5
Hướng dẫn giải
Đáp án: B
Ta có 3 điểm
1 23
24 , , 27 2z iz iz i=− =−=−
4
64zi= −
1234
,,,zz zz
//AC BD
23zi
u
zi
++
=
−
( )
;bIa
( )
,z x yi x y=+∈
(
)
;
M xy
( )
(
) ( )
( )
2
2
23 1
23 2 3
1
1
x y ix y i
z i x yi i
u
zi x y i
xy
++ + − −
++ ++ +
= = =
− +−
+−
( )
22
2 2 3 22 1x y x y xy i+ + + −+ −+
(
)
( )
( )
( )
22
22
2
2
2
2
2 2 30
1 15
10
10
xy xy
xy
xy
xy
+ + + −=
+ ++ =
⇔
+− ≠
+− ≠
( )
1; 1I −−
5R
=
( )
0;1
123
8 3; 1 4; 5z iz iz xi=+=+=+
1−
7−
(
) ( ) ( )
8;3 , 1; 4 , 5;M N Px
( ) ( )
3; 3 , 4; 4MP x NP x⇒ −− = −

Bài tập trắc nghiệm số phức
Trang 256
Để vuông tại
MNP∆
( )( )
. 0 12 3 4 0 0; 7P MP NP x x x x
⇔ = ⇔− + − − = ⇔ = =

Bài tập trắc nghiệm số phức
Trang 257
C – BÀI TẬP TỰ LUYỆN (89 CÂU)
Câu 1: Tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng phức sao cho
(z 1)(z i)−−
là số thực.
A. Đường thẳng
x y10− +=
B. Đường tròn
22
x y xy0+ −−=
C. Đường tròn
22
x y xy0+ −+=
D. Đường thẳng
x y10−+ +=
Câu 2: Trong mặt phẳng phức, gọi A, B, C lần lượt là các điểm biểu diễn các số phức
1 23
z (1 i)(2 i), z 1 3i, z 1 3i= − + =+ =−−
. Tam giác ABC là:
A. Một tam giác đều. B. Một tam giác vuông (không cân).
C. Một tam giác vuông cân. D. Một tam giác cân (không đều).
Câu 3: Gọi M, N, P lần lượt là các điểm biểu diễn của các số phức 1 – i, 5 + 4i , 3 + i. Tìm số phức z biểu diễn
bởi điểm Q sao cho MNPQ là hình bình hành
A. 6i – 7 B. 7 + 6i C. 6 – 7i D. 6 + 7i
Câu 4: Xác định tập hợp các điểm biểu diễn số phức z trên mặt phẳng phức sao cho
1
zi−
là số thuần ảo.
A. Trục hoành, bỏ điểm (-1; 0) B. Đường thẳng x = -1, bỏ điểm (-1; 0)
C. Đường thẳng y = 1, bỏ điểm (0; 1). D. Trục tung, bỏ điểm (0; 1)
Câu 5: Trong mặt phẳng phức Oxy , cho ba điểm
A, B,C
biểu diễn cho 3 số phức
12 3
z 3 i,z 2 3i, z 1 2i
= + =−+ =−+
. Xác định độ lớn của số phức biểu diễn trọng tâm G của tam giác
ABC
A. 1 B. 5 C. 2 D. 3
Câu 6: Gọi M, N, P lần lượt là các điểm biểu diễn của các số phức 1 + i , 2 + 3i , 1 – 2i. Số phức z biểu diễn
bởi điểm Q sao cho
MN 3MQ 0+=
là:
A.
21
33
−
i B.
21
33
+
i C.
21
33
−+
i D.
21
33
−−
i
Câu 7: Tập hợp các điểm biểu diễn các số phức
z
thỏa mãn
z1i 1+− ≤
là
A. Đường tròn tâm
( )
I 1,1−
, bán kính
R1=
B. Đường tròn tâm
( )
I 1, 1−−
, bán kính
R1=
C. Hình tròn tâm
( )
I 1,1−
, bán kính
R1=
D. Hình tròn tâm
( )
I 1, 1−
, bán kính
R1=
Câu 8: Trong mặt phẳng phức cho tam giác ABC vuông tại C; Biết rằng A, B lần lượt biểu diễn các số phức:
21
z -2 4i,z 2 -2i=+=
. Khi đó, C biểu diễn số phức:
A.
z 2 4i= +
B.
z 2 2i=−−
C.
z 2 2i=−+
D.
z 2 4i= −
Câu 9: Cho các số phức:
21 3
z 1 3i;z 2 +2i;z 1 i=+ =− =−−
được biểu diễn lần lượt bởi các điểm A, B, C trên
mặt phẳng. Gọi M là điểm thỏa mãn:
AM AB AC= −
. Khi đó điểm M biểu diễn số phức:
A.
z 6i
=
B.
z 6i= −
C.
z 2=
D.
z 2= −
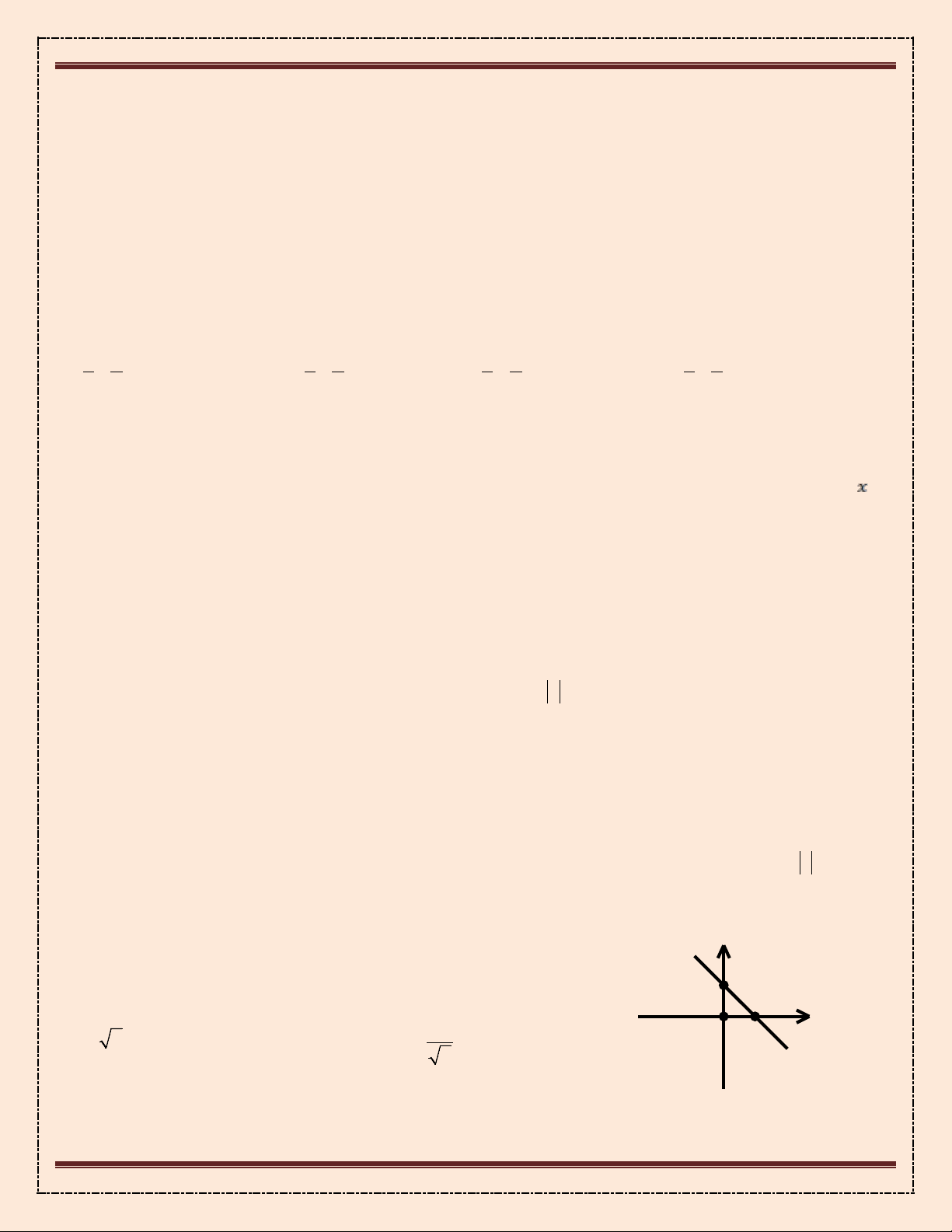
Bài tập trắc nghiệm số phức
Trang 258
Câu 10: Tromg mặt phẳng phức cho hai điểm A(4; 0), B(0; - 3). Điểm C thỏa mãn:
OC OA OB= +
. Khi đó
điểm C biểu diễn số phức:
A.
z 3 4i=−−
B.
z 4 3i= −
C.
z 3 4i=−+
D.
z 4 3i= +
Câu 11: Trong mặt phẳng Oxy cho điểm A biểu diễn số phức
1
z 1 2i= +
, B là điểm thuộc đường thẳng y = 2
sao cho tam giác OAB cân tại O. B biểu diễn số phức nào sau đây:
A.
z 1 2i=−+
B.
z 1 2i
= −
C.
z 2 i
= −
D.
z 3 2i= +
Câu 12: Cho 3 số phức i, 2 – 3i,
34−+
i có điểm biểu diễn trong mặt phẳng phức là A, B, C; Tìm số phức
biểu diễn trọng tâm G của tam giác ABC.
A.
12
33
+
i B.
12
33
−+
i C.
12
33
−
i D.
12
33
−−
i
Câu 13: Cho số phức
z 6 7i= +
. Số phức liên hợp của z có điểm biểu diễn là:
A.
(6; 7)
B.
(6; 7)−
C.
( 6; 7)−−
D.
( 6; 7)
−
Câu 14: Cho A, B, M lần lượt là điểm biểu diễn của các số phức - 4, 4i, x + 3i. Với giá trị thực nào của thì
A, B, M thẳng hàng?
A. x = - 2 B. x = 1 C. x = - 1 D. x = 2
Câu 15: Tập hợp các điểm biểu diễn của số phức z trong mặt phẳng Oxy biết
(1 i)z+
là số thực là:
A. Trục Ox B. Trục Oy
C. Đường thẳng
yx=
D. Đường thẳng
yx= −
Câu 16: Tập hợp các điểm M biểu diễn các số phức
z
thỏa mãn
z4
<
là
A. Đường tròn
B. Đường thẳng
C. Phần bên trong đường tròn có tâm là O và có bán kính R = 4
D. Đường hypebol
Câu 17: Tập hợp các điểm biểu diễn hình học của số phức z là đường thẳng ∆ như hình vẽ. Giá trị
z
nhỏ nhất
là:
A. 2 B. 1
C.
2
D.
1
2
O
y
x
1
1
Δ

Bài tập trắc nghiệm số phức
Trang 259
Câu 18: Gọi A, B, C lần lượt là điểm biểu diễn của các số phức z1 = 3 + 2i, z2 = 2 – 3i, z3 = 5 + 4i. Chu vi của
tam giác ABC là:
A. B. C. D.
Câu 19: Gọi A, B, C lần lượt là điểm biểu diển các số phức
1
4i
z,
1i
=
−+
( )( )
2
z 1 i 1 2i ,=−+
3
2 6i
z
3i
+
=
−
. Khi đó,
mệnh đề nào dưới đây là đúng.
A. A, B, C thẳng hàng B. Tam giác ABC là tam giác tù
C. Tam giác ABC là tam giác đều D. Tam giác ABC là tam giác vuông cân
Câu 20: Trong mặt phẳng phức, tập hợp các điểm biểu diễn của số phức z thỏa mãn điều kiện
z2 z2 5−++=
có dạng là:
A.
22
xy
1
25 9
94
+=
B.
22
xy9+=
C.
22
xy
1
9 25
49
+=
D.
22
x y 16
+=
Câu 21: Cho số phức với . Khi đó tập hợp các điểm M biểu diễn cho số phức trên
mặt phẳng Oxy là:
A. B.
C. D.
Câu 22: Tập hợp các điểm biểu diễn số phức z thỏa mãn:
z 2 z 2 10−++=
là:
A. Parabol B. Hình tròn C. Đường thẳng D. Elip
Câu 23: Cho biết có hai số phức z thỏa mãn
|z| 5=
và có phần thực bằng hai lần phần ảo. Hai điểm biểu diễn
của hai số phức đó:
A. Đối xứng nhau qua trục thực.
B. Cùng với gốc tọa độ tạo thành một tam giác vuông
C. Đối xứng nhau qua trục ảo.
D. Đối xứng nhau qua gốc tọa độ.
Câu 24: Tập hợp các số phức
( )
w 1 iz 1=++
với z là số phức thỏa mãn
|z 1| 1−≤
là hình tròn có diện tích là
A.
π
B.
3π
C.
4π
D.
2π
Câu 25: Cho số phức z = a + a
2
i với a ∈ R. Khi đó điểm biểu diễn của số phức liên hợp của z nằm trên:
A. Đường thẳng y = - x + 1 B. Parabol y = - x
2
C. Đường thẳng y = 2x D. Parabol y = x
2
Câu 26: Tìm tập hợp điểm biểu diễn số phức z thoả mãn
z2 iz+=−
26 2 2 58++
26 2 58++
22 2 2 56++
22 2 58
++
iz 1ϖ= +
| z 1 2i | 2−+ =
ϖ
22
(x 1) (y 2) 2− ++ =
22
(x 1) (y 3) 2− +− =
22
(x 3) (y 1) 2
− ++ =
22
(x 3) (y 1) 2
− +− =

Bài tập trắc nghiệm số phức
Trang 260
A.
4x 2y 3 0
− −=
B.
4x 2y 3 0− +=
C.
4x 2y 3 0+ +=
D.
4x 2y 3 0+ −=
Câu 27: Tập hợp các điểm biểu diễn số phức z thỏa mãn
z1i 2+− =
là
A. Đường tròn tâm (1; 2), bán kính R = 1. B. Đường tròn tâm ( - 1; 1), bán kính R = 2.
C. Đường tròn tâm (1; - 1), bán kính R = 2. D. Đường thẳng
xy2
−=
Câu 28: Trong mặt phẳng Oxy, tập hợp tất các điểm biểu diễn số phức z thỏa điều kiện:
( )
z 3 4i 2−− =
có
dạng
A.
( ) ( )
22
x3 y4 4− ++ =
B.
2x3y40+ +=
C.
( ) ( )
22
x4 y3 4− ++ =
D.
2x 3y 4 0− +=
Câu 29: Tập hợp các điểm biểu diễn cho số phức z thỏa mãn
( )
|z i| | 1 i z|−= +
là đường tròn có phương trình
A.
22
x y 2x 1 0+ − −=
B.
22
x y 2y 1 0+ − −=
C.
22
x y 2x 1 0+ + −=
D.
22
x y 2y 1 0+ + −=
Câu 30: Số phức z thỏa mãn
( )
z 2 i z 3 5i++ =+
có điểm biểu diễn M, thì
A. M nằm trong góc phần tư thứ nhất B. M nằm trong góc phần tư thứ hai.
C. M nằm trong góc phần tư thứ ba. D. M nằm trong góc phần tư thứ tư.
Câu 31: Xét các điểm A, B, C trong mặt phẳng phức theo thứ tự biểu diễn các số phức
4i
i1
−
, (1 – i)(2i + 1),
2 6i
3i
+
−
. Chọn khẳng định đúng trong các khẳng định sau:
A. Tam giác ABC có diện tích bằng 2 B. Tam giác ABC đều
C. Tam giác ABC vuông cân D. Tam giác ABC có chu vi bằng 4
Câu 32: Trong mặt phẳng Oxy, tập hợp các điểm M biểu diễn số phức z thỏa mãn điều kiện
z 3 2i 5−+ =
là:
A. Đường tròn tâm I( - 3;2) bán kính bằng 5 B. Đường tròn tâm I(3; - 2) bán kính bằng 5
C. Đường tròn tâm I( - 3; - 2) bán kính bằng 5 D. Đường tròn tâm I(3;2) bán kính bằng 5
Câu 33: Giả sử
12
z ,z
là hai nghiệm của phương trình
2
z 2z 5 0
− +=
và A, B là các điểm biểu diễn của
12
z ,z
.
Tọa độ trung điểm của đoạn thẳng AB là:
A.
( )
0,1
B.
( )
0, 1−
C.
( )
1,1
D.
( )
1, 0
Câu 34: Cho số phức z thỏa mãn
z 3 4i 2
−+ ≤
. Tập hợp các điểm biểu diễn của số phức z là:
A. Đường tròn tâm I(3; 4) bán kính R = 2 B. Đường tròn tâm I(3; - 4) bán kính R = 2
C. Hình tròn tâm I(3; - 4) bán kính R = 2 D. Hình tròn tâm I(3; 4) bán kính R = 2
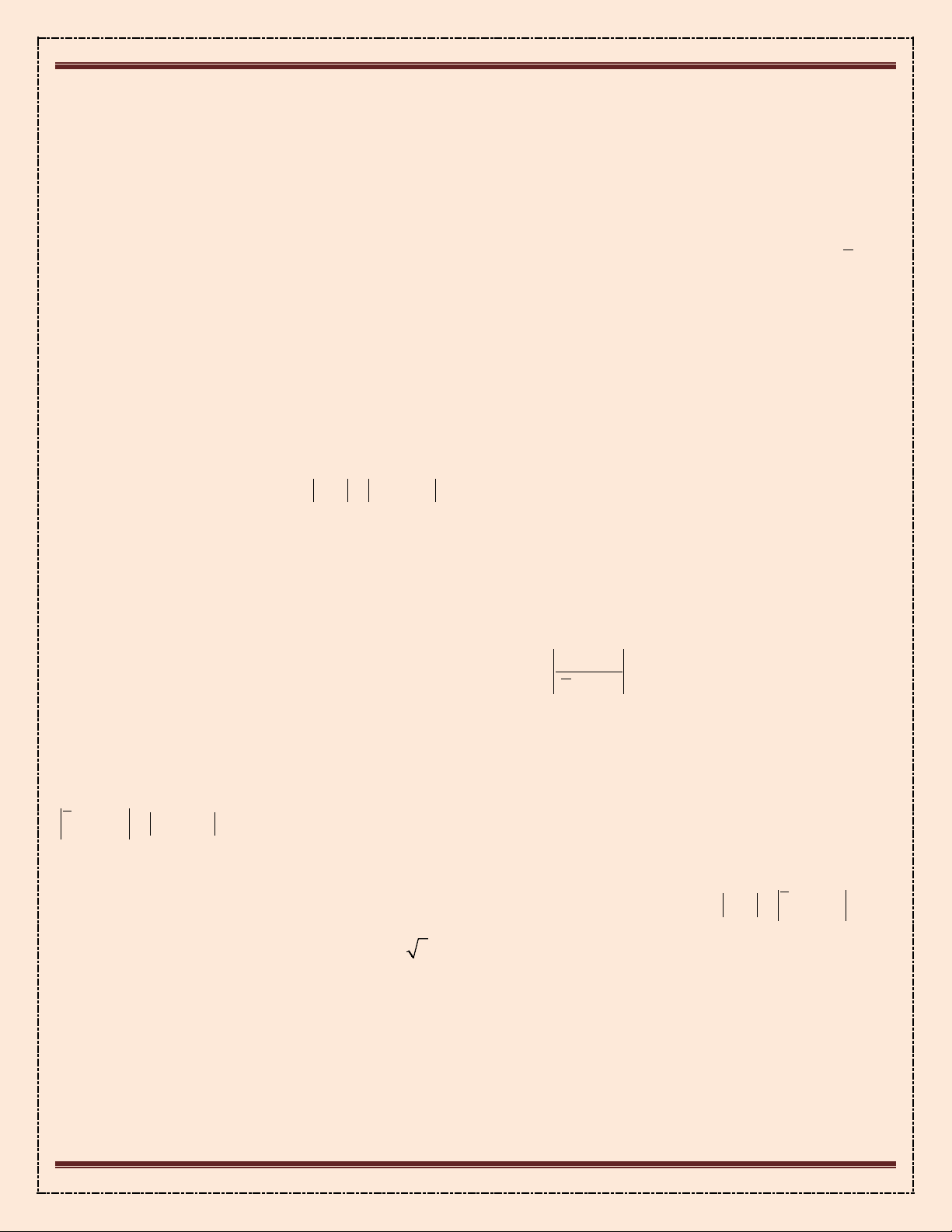
Bài tập trắc nghiệm số phức
Trang 261
Câu 35: Cho A, B, M lần lượt là điểm biểu diễn của các số phức
4; 4i; x 3i.−+
Với giá trị thực nào của
x
thì A,
B, M thẳng hàng:
A.
x1=
B.
x1= −
C.
x2= −
D.
x2=
Câu 36: Cho số phức z thỏa mãn
2
z
là số ảo. Tập hợp điểm biểu diễn số phức z là:
A. Đường thẳng B. Parabôn C. Elip D. Đường tròn
Câu 37: Trong mặt phẳng tọa độ Oxy. Giả sử điểm M biểu diễn số phức
z
, điểm N biểu diễn số phức
z
. Khi
đó:
A. Hai điểm M, N đối xứng nhau qua trục Oy B. Hai điểm M, N đối xứng nhau qua trục Ox.
C. Hai điểm M, N đối xứng nhau qua gốc tọa độ O. D. Tất cả đều sai.
Câu 38: Trong mặt phẳng phức, cho 3 điểm A, B, C biểu diễn các số phức
z 1 4i= +
,
z 2i= +
,
z 4i= +
. Tâm
đường tròn ngoại tiếp tam giác A, B, C biểu diễn số phức nào?
A.
z 2 3i= −
B.
z 3 3i= +
C.
z 2 3i= +
D.
z 4i= +
Câu 39: Cho số phức z thỏa mãn
z 1 z 2 3i−= −+
. Tập hợp các điểm biểu diễn của số phức z là:
A. Đường tròn tâm I(1; 2) bán kính R = 1
B. Đường thẳng có phương trình x - 5y - 6 = 0
C. Đường thẳng có phương trình 2x - 6y + 12 = 0
D. Đường thẳng có phương trình x - 3y - 6 = 0
Câu 40: Tập hợp các điểm biểu diễn số phức
z
biết
z
thỏa mãn:
z 2 3i
1
z4i
+−
=
−+
là:
A. Đường tròn tâm I( - 2;3) bán kính r = 1 B. Đường thẳng: 3x - y - 1 = 0
C. Đường thẳng: 3x + y - 1 = 0 D. Đường tròn tâm I( - 4;1) bán kính R = 1
Câu 41: Trong mặt phẳng Oxy, tập hợp các điểm M biểu diễn số phức z thỏa mãn điều kiện
z 3 2i z 1 3i−+ = −−
là:
A. Một Hyperbol B. Một đường tròn. C. Một parabol D. Một đường thẳng
Câu 42: Trong mặt phẳng phức tập hợp các điểm biểu diễn số phức
z x yi= +
thỏa mãn
zi z3i2−= − +
là
A. Đường tròn
( )
C
tâm
( )
I 0;1
, bán kinh
R3=
.
B. Đường thẳng D:
x 2y 3 0
+ +=
C. Đường tròn
( )
C
tâm
( )
I 2; 3−−
, bán kinh
R3=
.
D. Đường thẳng D:
y0=
.
Câu 43: Cho các điểm A, B, C trong mặt phẳng phức theo thứ tự được biểu diễn bởi các số:
1 i, 2 4i, 6 5i++ +
.
Tìm số phức biểu diễn điểm D sao cho tứ giác ABDC là hình bình hành:

Bài tập trắc nghiệm số phức
Trang 262
A.
3−
B.
7 8i
+
C.
3 8i−+
D.
5 2i
+
Câu 44: Tìm tập hợp các điểm biểu diễn số phức z thỏa mãn
z
2
zi
=
−
là:
A. bán kính
4
I 0;
3
bán kính
2
r
3
=
B. bán kính
( )
I 1; 0
bán kính
1
r
3
=
C. Đường tròn
( )
I 0;1
bán kính
2
r
3
=
D. bán kính
4
I 0;
3
bán kính
1
r
3
=
Câu 45: Tập hợp các điểm biểu diễn số phức z thỏa mãn các điều kiện sau đây, tập hợp nào là hình tròn:
A.
3iz z2
−+≤−
B.
z1i z
−+ =
C.
z 2i 3 i− ≤−
..
D.
z1i 2−+ =
Câu 46: Điểm
M ( 1; 3)−
là điểm biểu diễn của số phức:
A.
z 1 3i=−−
B.
z 1 3i
=−+
C.
z 2i= −
D.
z2=
Câu 47: Xét các điểm A, B, C trong mặt phẳng phức theo thứ tự biểu diễn lần lượt các số phức
( )(
)
12 3
4i 2 6i
z ,z 1 i 1 2i ,z
i1 3i
+
= =−+ =
−−
Nhận xét nào sau đây là đúng nhất
A. Ba điểm A, B, C thẳng hàng B. Tam giác ABC là tam giác vuông
C. Tam giác ABC là tam giác cân D. Tam giác ABC là tam giác vuông cân
Câu 48: Cho số phức z = 1 + bi , khi b thay đổi tập hợp các điểm biểu diễn số phức z trong mặt phẳng tọa độ là
A. Đường thẳng y - b = 0 B. Đường thẳng x - 1 = 0
C. Đường thẳng bx + y - 1 = 0 D. Đường thẳng x - y - b = 0
Câu 49: Cho các điểm A, B, C, D, M, N, P nằm trong mặt phẳng phức lần lượt biểu diễn các số phức
1 3i, 2 2i, 4 2i,1 7i, 3 4i,1 3i, 3 2i+ −+ −− − −+ − −+
Nhận xét nào sau đây là sai
A. Tứ giác ABCD là tứ giác nội tiếp
B. Hai tam giác ABC và MNP là hai tam giác đồng dạng
C. Hai tam giác ABC và MNP có cùng trọng tâm
D. A và N là hai điểm đối xứng nhau qua trục Ox
Câu 50: Cho A, B, C lần lượt là ba điểm biểu diễn số phức z
1
, z
2
, z
3
thỏa
123
zzz= =
Mệnh đề nào sau đây là đúng
A. O là trọng tâm tam giác ABC
B. O là tâm đường tròn ngoại tiếp tam giác ABC
C. Tam giác ABC là tam giác đều
D. Trọng tâm tam giác ABC là điểm biểu diễn số phức z
1
+ z
2
+ z
3

Bài tập trắc nghiệm số phức
Trang 263
Câu 51: Gọi M là điểm biểu diễn của số phức z = a + bi trong mặt phẳng phức. Khi đó khoảng cách OM bằng:
A. Môđun của a + bi B.
22
ab−
C.
ab+
D.
22
ab−
Câu 52: Cho số phức
z 6 7i= +
. Số phức liên hợp của z có điểm biểu diễn là:
A. (6; 7) B. (6; –7) C. (–6; 7) D. (–6; –7)
Câu 53: Cho số phức z = 5 – 4i. Số phức đối của z có điểm biểu diễn là:
A. ( - 5; - 4) B. (5; - 4) C. (5;4) D. ( - 5;4)
Câu 54: Số phức z = 2 – 3i có điểm biểu diễn là:
A. ( - 2;3) B. (2;3) C. ( - 2; - 3) D. (2; - 3)
Câu 55: Tọa độ điểm M biểu diễn cho số phức
z 3i
= +
A.
M( 3;i)
B.
M( 3;0)
C.
M(0; 3)
D.
M( 3;1)
Câu 56: Điểm biểu diễn của số phức
1
z
2 3i
=
−
là:
A. (3; –2) B.
23
;
13 13
C. (2; –3) D. (4; –1)
Câu 57: Gọi A là điểm biểu diễn của số phức z = 3 + 2i và B là điểm biểu diễn của số phức z’ = 2 + 3i. Tìm
mệnh đề đúng của các mệnh đề sau:
A. Hai điểm A và B đối xứng với nhau qua gốc tọa độ O
B. Hai điểm A và B đối xứng với nhau qua trục tung
C. Hai điểm A và B đối xứng nhau qua trục hoành
D. Hai điểm A và B đối xứng với nhau qua đường thẳng y = x
Câu 58: Trên mặt phẳng tọa độ Oxy, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
( )
zi 2 i 2−+=
là:
A.
( )
( )
22
x1 y2 4− ++ =
B.
x 2y 1 0
+ −=
C.
3x 4y 2 0+ −=
D.
( ) ( )
22
x1 y2 9+ +− =
Câu 59: Trong mặt phẳng tọa độ Oxy, tập hợp điểm M biểu diễn các số phức z thỏa mãn điều kiện
zi zi 4−+ +=
là một:
A. Đường tròn B. Đường Hypebol C. Đường elip D. Hình tròn
Câu 60: Gọi A là điểm biểu diễn của số phức z = 2 + 5i và B là điểm biểu diễn của số phức z’ = - 2 + 5i. Tìm
mệnh đề đúng trong các mệnh đề sau:
A. Hai điểm A và B đối xứng với nhau qua đường thẳng y = x
B. Hai điểm A và B đối xứng với nhau qua trục hoành
C. Hai điểm A và B đối xứng với nhau qua gốc tọa độ O

Bài tập trắc nghiệm số phức
Trang 264
D. Hai điểm A và B đối xứng với nhau qua trục tung
Câu 61: Tập hợp các điểm trong mặt phẳng phức biểu diễn số phức z thõa mãn điều kiện z
2
là số ảo là:
A. Trục ảo
B. 2 đường phân giác y = x và y = - x của các trục tọa độ
C. Đường phân giác của góc phần tư thứ nhất
D. Trục hoành
Câu 62: Phương trình
2
z 2z b 0− +=
có 2 nghiệm phức được biểu diễn trên mặt phẳng phức bởi hai điểm
A
và
B
. Tam giác
OAB
(với
O
là gốc tọa độ) đều thì số thực
b
bằng:
A. B, C, D đều sai B. 3 C. 2 D. 4
Câu 63: Cho số phức
z
thỏa mãn
z 3 4i 2−+ =
và
w 2z 1-i= +
. Trong mặt phẳng phức, tập hợp điểm biểu
diễn số phức
w
là đường tròn tâm
I
, bán kính
R
là
A.
I(3; 4), R 2−=
B.
I(4; 5), R 4−=
C.
I(5; 7),R 4−=
D.
I(7; 9),R 4
−=
Câu 64: Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện phần thực
bằng 3 lần phần ảo của nó là một
A. Parabol B. Đường tròn C. Đường thẳng D. Elip
Câu 65: Tập hợp điểm biểu diễn số phức
z
thỏa mãn
z (4 3i) 2−+ =
là đường tròn tâm
I
, bán kính
R
A.
I(4;3), R 2=
B.
I(4; 3), R 4−=
C.
I( 4;3), R 4−=
D.
I(4; 3), R 2−=
Câu 66: Trong mặt phẳng
Oxy,
gọi
A,B,C,D
lần lượt là bốn điểm biểu diễn các số phức
1 23 4
z 2 i, z 5i, z 3 2i, z 1 2i= − =− = − =−−
. Trong các khẳng định sau đây, khẳng định nào đúng?
A. Tam giác
ABC
vuông tại
A
B. Điểm
M (1; 2)
là trung điểm của đoạn thẳng
CD.
C. Tam giác
ABC
cân tại
B
.
D. Bốn điểm
A,B,C,D
nội tiếp được đường tròn.
Câu 67: Gọi A, B, C, D lần lượt là các điểm biểu diễn cho các số phức
1 2 34
z 7 3i, z 8 4i, z 1 5i, z 2i=−=+=+−
. Chọn kết luận
đúng nhất:
A. ABCD là hình bình hành. B. ABCD là hình vuông.
C. ABCD là hình chữ nhật. D. ABCD là hình thoi.
Câu 68: Gọi M, N, P lần lượt là các điểm biểu diễn cho các số phức
1 23
z 1 5i, z 3 i, z 6=+ =−=
. M, N, P là 3
đỉnh của tam giác có tính chất:
A. Vuông B. Vuông cân C. Cân D. Đều

Bài tập trắc nghiệm số phức
Trang 265
Câu 69: Giả sử M(z) là điểm trên mặt phẳng phức biểu diễn số phức z. Tìm tập hợp các điểm M(z) thỏa mãn
điều kiện: = 2
A. Đáp án khác B. (x + 1)
2
+ (y + 1)
2
= 4
C. (x - 1)
2
+ (y - 1)
2
= 4 D. (x - 1)
2
+ (y + 1)
2
= 4
Câu 70: Tập hợp các điểm M biểu diễn cho số phức z thoả mãn
z 5i z 5i 10− ++ =
là:
A. Đường tròn B. Đường elip C. Đường thẳng D. Đường parabol
Câu 71: Trong mặt phẳng phức, cho 3 điểm A, B, C lần lượt biểu diễn cho 3 số phức
2
12 3
z 1 i, z (1 i) , z a i, a =+ =+ =−∈
. Để tam giác ABC vuông tại B thì
a =
A. - 3 B. - 2 C. 3 D. - 4
Câu 72: Tập hợp điểm biễu diễn số phức z thoả
z 2i 3−=
là đường tròn tâm I. Tất cả giá trị m thoả khoảng
cách từ I đến d: 3x + 4y – m = 0 bằng
1
5
là?
A.
m 10;m 14= =
B.
m 10;m 12= =
C.
m 10;m 11= =
D.
m 12;m 13= =
Câu 73: Trong mặt phẳng phức, tập hợp điểm biểu diễn cho số phức
z
thỏa
z 3 2i 4+− =
là
A. Đường tròn tâm I( - 3;2), bán kính R = 4. B. Đường tròn tâm I(3; - 2), bán kính R = 16.
C. Đường tròn tâm I(3; - 2), bán kính R = 4. D. Đường tròn tâm I( - 3;2), bán kính R = 16.
Câu 74: Tập hợp các điểm biểu diễn số phức z thỏa mãn
z (3 4i) 2−− =
trong mặt phẳng Oxy là:
A. Đường thẳng
2x y 1 0+ +=
B. Đường tròn
22
(x 3) (y 4) 4− ++ =
C. B và C đều đúng.
D. Đường tròn
22
x y 6x 8y 21 0+−++=
Câu 75: Tập hợp điểm
M
biểu diễn số phức
z
thoả điều kiện:
z 1 i z 3 2i+− = +−
là:
A. Đường thẳng B. Elip C. Đoạn thẳng D. Đường tròn
Câu 76: Cho phương trình x
2
– 2x + 2 = 0. Gọi A và B lần lượt là các điểm biểu diễn các nghiệm của pt. Khi
đó diện tích tam giác OAB là:
A. 1đvdt B. 2đvdt C. đvdt D. đvdt
Câu 77: Trong mặt phức cho tam giác ABC vuông tại C; Biết rằng A, B lần lượt biểu diễn các số phức: z
1
= -
2 – 4i; z
2
= 2 – 2i. Khi đó có một điểm C biểu diễn số phức:
A. z = 2 – 4i B. z = - 2 + 2i C. z = 2 + 2i D. z = 2 – 2i
Câu 78: Trong mặt phẳng phức cho ba điểm A, B, C lần lượt biểu diễn các số phức
z
1
= 2; z
2
= 4 + i ; z
3
= - 4i. M là điểm sao cho:
OA OB OC 3OM 0++− =
. Khi đó M biểu diễn số phức:
A. z = 18 –i B. z = - 9 + 18i C. z = 2 – i D. z = - 1 + 2i
1zi−+
Bài tập trắc nghiệm số phức
Trang 266
Câu 79: Trong mặt phẳng Oxy cho điểm A biểu diễn số phức z
1
= 1 + 2i. B là điểm thuộc đường thẳng y = 2
sao cho tam giác OAB cân tại O. B biểu diễn số phức nào sau đây:
A. z = - 1 + 2i B. z = 1 – 2i C. z = - 1 – 2i D. z = 1 + 2i
Câu 80: Gọi M và M’ theo thứ tự là các điểm của mặt phẳng phức biểu diễn số phức z 0 và
1i
zz
2
+
=
. Tam
giác OMM’ là tam giác gì?
A. Tam giác vuông B. Tam giác cân C. Tam giác vuông cân D. Tam giác đều
Câu 81: Điểm biểu diễn của các số phức z = a + ai với a ∈ R, nằm trên đường thẳng có phương trình là:
A. y = x B. y = 2x C. y = 3x D. y = 4x
Câu 82: Cho số phức z = a - ai với a ∈ R, điểm biểu diễn của số phức đối của z nằm trên đường thẳng có
phương trình là:
A. y = 2x B. y = - 2x C. y = x D. y = - x
Câu 83: Cho số phức z = a + a
2
i với a ∈ R. Khi đó điểm biểu diễn của số phức liên hợp của z nằm trên:
A. Đường thẳng y = 2x B. Đường thẳng y = - x + 1
C. Parabol y = x
2
D. Parabol y = - x
2
Câu 84: Giả sử A, B theo thứ tự là điểm biểu diễn của các số phức z
1
, z
2
. Khi đó đọ dài của véctơ
AB
bằng:
A.
12
zz−
B.
12
zz+
C.
21
zz−
D.
21
zz+
Câu 85: Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thoả mãn điều kiện
zi 1−=
là:
A. Một đường thẳng B. Một đường tròn C. Một đoạn thẳng D. Một hình vuông
Câu 86: Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thoả mãn điều kiện z
2
là một số thực âm là:
A. Trục hoành (trừ gốc toạ độ O) B. Trục tung (trừ gốc toạ độ O)
C. Đường thẳng y = x (trừ gốc toạ độ O) D. Đường thẳng y = - x (trừ gốc toạ độ O)
Câu 87: Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thoả mãn điều kiện z
2
là một số ảo là:
A. Trục hoành (trừ gốc toạ độ O) B. Trục tung (trừ gốc toạ độ O)
-
2
x
y
O
(Hình 3)
-
3i
y
x
O
(Hình 2)
y
2
O
x
-
(Hình 1)

Bài tập trắc nghiệm số phức
Trang 267
C. Hai đường thẳng y = ±x (trừ gốc toạ độ O) D. Đường tròn x
2
+ y
2
= 1
Câu 88: Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thoả mãn điều kiện z
2
= (
z
)
2
là:
A. Trục hoành
B. Trục tung
C. Gồm cả trục hoành và trục tung
D. Đường thẳng y = x
Câu 89: Cho số phức z = x + yi. (x, y ∈ R). Tập hợp các điểm biểu diễn của z sao cho
zi
zi
+
−
là một số thực âm
là:
A. Các điểm trên trục hoành với - 1 < x < 1 B. Các điểm trên trục tung với - 1 < y < 1
C. Các điểm trên trục hoành với
x1
x1
≤−
≥
D. Các điểm trên trục tung với
y1
y1
≤−
≥
Bấm Tải xuống để xem toàn bộ.




