Áp dụng đẳng thức và bất đẳng thức mô đun tìm GTLN – GTNN của mô đun số phức Toán 12

Áp dụng đẳng thức và bất đẳng thức mô đun tìm GTLN – GTNN của mô đun số phức Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

48 24 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Số phức

Môn: Toán 12

Thông tin:

14 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
NHÓM TOÁN VD – VDC ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN
https://www.facebook.com/groups/toanvd.vdc Trang 1
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD - VDC
ÁP DỤNG ĐẲNG THỨC
VÀ BẤT ĐẲNG THỨC MÔ ĐUN
NĂM HỌC 2020 – 2021
Mỗi số phức, ở khía cạnh đại số, là nghiệm tương ứng duy nhất một tam thức bậc hai monic
hệ số thực có biệt thức âm. Nếu
z
là nghiệm của
2
()f x x ax b= + +
với
và
2
40ab = −
thì nghiệm còn lại sẽ gọi là liên hợp của nó. Tích hai nghiệm sẽ là
b
và là một
số không âm. Căn bậc hai của
b
gọi là module.
Ở khía cạnh hình học, mỗi số phức sẽ là cặp tọa độ của một vector, và độ lớn của vector đó
chính là module.
Module của số phức. Số phức liên hợp:
( )
,z a bi a b= +
thì module của
z
là
22
z a b=+
; Số phức liên hợp của
z
là
z a bi=−
Ta có: Phần thực của
z
là
Re
2
zz
z
+
=
, phần ảo của
z
là
Im
2
zz
z
−
=
;
1 2 1 2
zz z z=
,
2
z zz=
;
1 2 1 2
z z z z+ = +
,
1 2 1 2
zz z z=
,
zz=
;
1
1
22
z
z
zz
=
,
( )
11
2
2
2
0
zz
z
z
z

=


.
1/ Đẳng thức Mô - Đun
+
( )
22
2
22
1 2 1 2 1 2 1 2
..m z nz m z n z m n z z z z+ = + + +
với
,mn
và
12
,zz
.
+
22
2
2
1 2 1 2
12
2
22
z z z z
z z z z z

+−
+ + + = + +



với
12
,,z z z
.
+
2
1
1 2 1 2
12
z
z
z z z z
zz
+ = +
với
12
,zz
là các số phức khác
0
.
+Nếu
2
,,
0
40
a b c
a
b ac
= −
thì phương trình
2
0az bz c+ + =
có hai nghiệm phức không
thực
1,2
2
bi
z
a
−
=
. Dễ thấy
1 2 1 2
z z z z= =
.
2/ BĐT Mô - Đun
LÝ THUYẾT
I.
=I
NHÓM TOÁN VD – VDC ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN
https://www.facebook.com/groups/toanvd.vdc Trang 2
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
Lớp 7:
A B B C A C A B BC− +
.
Lớp 10:
a b a b a b− + +
.
Lớp 12:
1 2 1 2 1 2
z z z z z z− + +
.
+
1 2 1 2
z z z z z z+ + + −
. Đẳng thức xảy ra khi và chỉ khi
( )
( )
( )
( )
( )
( ) ( )
1 1 2
2 2 1
2
1 2 2
; 0;1
0
; 0; ; 0
z z k z z z z
kk
z z k z z z z
zz
z z k z z z z k k
+ = + + − −


+ = + + − −


+=
+ = + +
.
+
1 2 1 2
z z z z z z+ − + −
. Đẳng thức xảy ra khi và chỉ khi
( )
( )
( )
(
)
( )
( ) ( )
1 1 2
2 1 2
2
1 2 2
, ;0 1;
0
; 0; , 0
z z k z z z z
kk
z z k z z z z
zz
z z k z z z z k k
+ = + + − −


− +
+ = − − + +


+=
+ = + +
.
Câu 1:
Minh Hoạ-T4/N2021
Xét hai số phức
12
,zz
thỏa mãn
12
1, 2zz==
và
12
3zz−=
. Giá trị lớn nhất
12
35z z i+−
bằng
Ⓐ.
5 19−
. Ⓑ.
5 19+
. Ⓒ.
5 2 19−+
. Ⓓ.
5 2 19+
.
a Định hướng
Tất cả giả thiết của đề bài đều nói về Mô đun của số phức, chính vì thế ta xét:
2
12
m z nz+
.
Bằng tính toán ta có kết quả:
( )
22
2
22
1 2 1 2 1 2 1 2
..m z nz m z n z m n z z z z+ = + + +
. Trong đó
,mn
là các số thực và
12
,zz
là các số phức. Như vậy từ giả thiết ta sẽ tính được
12
3zz+
và
đưa bài toán đã cho về bài toán quen thuộc.
b Lời giải tham khảo
Lời giải
+
( )
22
2
1 2 1 2 1 2 1 2
3 . .z z z z z z z z= − = + − +
( )
1 2 1 2
5 . .z z z z= − +
( )
1 2 1 2
. . 2z z z z + =
;
( )
2
2
1 2 1 2 1 2 1 2
3 9 3 . . 19z z z z z z z z+ = + + + =
.
+Áp dụng bất đẳng thức mô đun, có:
( )
( )
1 2 1 2 1 2
3 5 3 5 3 5z z i z z i z z i+ − − + + − + + −
12
3951 519 5z z i+ − +−
.
MỘT SỐ VÍ DỤ
II.
=I
NHÓM TOÁN VD – VDC ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN
https://www.facebook.com/groups/toanvd.vdc Trang 3
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
+Vì đây là bài toán trắc nghiệm nên chọn B; Tuy nhiên
12
3 5 5 19z z i+ − = +
khi và chỉ khi
( )
12
,0
35
kk
z z k i
+ = −
12
3 19z z i + = −
Chọn B
Câu 2:
Minh Hoạ-L2/N2017
Xét các số phức
z
thỏa mãn
2 4 7 6 2z i z i+ − + − − =
. Gọi
,mM
lần lượt là giá trị nhỏ
nhất, giá trị lớn nhất của
1zi−+
. Giá trị của biểu thức
P m M=+
bằng
Ⓐ.
13 73+
. Ⓑ.
5 2 2 73
2
+
. Ⓒ.
5 2 73+
. Ⓓ.
5 2 73
2
+
.
a Định hướng
2 4 7 6 2z i z i+ − + − − =
( ) ( )
2 4 7 2 4 7z i z i z i z i + − + − + + = + − + − + +
sẽ
suy ra
( ) ( )
.z a x b x i=+
với
0;1x
.Đến đây ta có bài toán quen thuộc.
b Lời giải tham khảo
Lời giải
+
2 4 7 6 2z i z i+ − + − − =
( ) ( )
2 4 7 2 4 7z i z i z i z i + − + − + + = + − + − + +
( ) ( )
2 6 6 ; ,0 1z i x i x x + − = +
( ) ( )
2 6 1 6z x x i = − + + +
( ) ( )
1 3 6 2 6z i x x i − + = − + + +
2
72 12 13xx= − +
.
+Xét hàm số
( )
2
72 12 13, 0;1f x x x x= − +
, dễ thấy
( )
0;1
1 5 2
m in
12 2
f x f

==


;
( ) ( )
0;1
m ax 1 73f x f==
.Vậy
52
; 73
2
mM==
Chọn B
Câu 3:
Chuyên Thái Bình-L5/N2018
Cho số phức
z
thỏa mãn
( ) ( )
1 2 1 2 4 2i z i z+ + + + − =
. Gọi
,mn
lần lượt là giá trị lớn
nhất và giá trị nhỏ nhất của
z
. Đặt
w m ni=+
, giá trị của
2018
w
bằng
Ⓐ.
1009
2
. Ⓑ.
1009
4
. Ⓒ.
1009
5
. Ⓓ.
1009
6
.
a Định hướng
+Biến đổi giả thiết:
( ) ( )
1 2 1 2 4 2i z i z+ + + + − =
1 1 4z i z i + − + − + =
.
+Áp dụng BĐT:
1 2 1 2
z z z z+ +
dễ dàng tìm được
m
.
+Áp dụng
22
2
2
1 2 1 2
12
2
22
z z z z
z z z z z

+−
+ + + = + +



và
,ab
ta
NHÓM TOÁN VD – VDC ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN
https://www.facebook.com/groups/toanvd.vdc Trang 4
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
có :
( )
22
2a b a b+ +
tìm được
n
.
b Lời giải tham khảo
Lời giải
+
4 1 1 1 1 2z i z i z i z i z= + − + − + + − + − + =
2z
( )
1
. Đẳng thức ở
( )
1
xảy
ra khi
( ) ( )
1 1 , , 0
2
z i k z i k k
z
+ − = − +
=
( )
21zi = − +
2m=
.
+
4 1 1z i z i= + − + − +
22
2 1 1z i z i

+ − + − +

22
21zi= + −
2z
( )
2
. Đẳng thức ở
( )
2
xảy ra khi
11
2
z i z i
z
+ − = − +
=
( )
1zi = +
2n=
. Vậy
2018
1009
6w =
Chọn D
Câu 4:
THPT Đặng Thúc Hứa Nghệ An-Lần1 Năm 2018
Cho số phức
z
thỏa mãn điều kiện
5 1 3 3 1z i z i z i− = + − + − +
. Giá trị lớn nhất của
biểu thức
23zi−+
bằng
Ⓐ.
13
3
. Ⓑ.
1 13+
. Ⓒ.
9
. Ⓓ.
45
.
a Định hướng
+ Ta có:
2 2 2 2
1 3 1 2 1 2z i z i z i i

+ − + − + = − + −

.
+ Mặt khác:
5 1 3 3 1z i z i z i− = + − + − +
( )
( )
22
22
1 3 1 3 1z i z i + + − + − +
( )
2
20 5zi= − +
. Từ đó suy ra
25zi−
. Đến đây ta có bài toán quen thuộc.
b Lời giải tham khảo
Lời giải
+ Ta có:
2 2 2 2
1 3 1 2 1 2z i z i z i i

+ − + − + = − + −

; Từ đó
5 1 3 3 1z i z i z i− = + − + − +
( )
( )
22
22
1 3 1 3 1z i z i + + − + − +
( )
2
20 5zi= − +
. Suy ra
25zi−
.
+
( ) ( )
2 3 2 4 2 4z i z i i z i i− + = − + − + − + − +
2 5 2 5 4 5 + =
NHÓM TOÁN VD – VDC ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN
https://www.facebook.com/groups/toanvd.vdc Trang 5
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
2 3 4 5zi − +
( )
1
. Đẳng thức ở
( )
1
xảy ra khi
( )
1 3 1
13
25
,0
24
z i z i
zi
kk
z i k i
+ − − +
=
−=
− = − +
25zi = − +
. Vậy
m ax 2 3 4 5zi− + =
Chọn D
Câu 5
Chuyên Sư Phạm Hà Nội-L2/N2021
Xét các số phức
z
thỏa mãn
12z −=
. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị bé
nhất của biểu thức
2 2 3P z z= + + −
. Tổng
Mm+
bằng
Ⓐ.
14
. Ⓑ.
7
. Ⓒ.
45 3 35
5
+
. Ⓓ.
15 5 33
3
+
.
a Định hướng
+
( )
( )
2
2
kk
z z z w z w+ = + + −
( )
( )
( )
( )
2
2
k k k
z w z w z w z w z w z w= + + − + + − + + −
với
1;2k =
. Do đó nếu
( )
12
z w p z w− = −
với
p
thì sẽ tính được
2
2
12
a z z b z z+ + +
theo
zw+
và
k
zw−
(
,ab
). Khi đó dễ dàng tính được
M
.
+Nhìn vào kết luận, ta tìm cách làm xuất hiện hệ số
2
trước biểu thức
2z +
(Cân bằng hệ số)
bằng công thức
2
1
1 2 1 2
12
z
z
z z z z
zz
+ = +
với
12
,zz
là các số phức khác
0
nhưng không được.
Viết
( )
2 3 3P z z z= − − + − + −
ta dễ dàng tìm được
m
.
b Lời giải tham khảo
Lời giải
+Ta có
( )
( ) ( )
( )
( ) ( )
2
22
2
22
2 1 3 1 9 3 1 1 13 3 1 1
3 1 2 1 4 2 1 1 8 2 1 1
z z z z z z z
z z z z z z z
+ = − + = − + + − + − = + − + −
− = − − = − + − − + − = − − + −
suy
ra
22
2 2 3 3 50zz+ + − =
;
12
. 2 2 . 3 3
23
P z z= + + −
( )
22
14
2 2 3 3
23
zz

+ + + −


5 33
3
=
. Vì làm bài
trắc nghiệm nên dự đoán
5 33
3
M =
.
+
( )
2 3 3 2 3 0 5P z z z z z= − − + − + − − − + − + =
. Khi
3z =
thỏa mãn điều kiện đề
bài thì
5P =
. Vậy
5m =
Chọn D
c Bài tập tương tự
Cho số phức
z
thỏa mãn
1 2 2zi− − =
. Giá trị lớn nhất của biểu
NHÓM TOÁN VD – VDC ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN
https://www.facebook.com/groups/toanvd.vdc Trang 6
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
thức
1 5 4T z i z i= + − + − −
bằng
Ⓐ.
37
. Ⓑ.
35
. Ⓒ.
36
. Ⓓ.
42
.
Câu 6:
Sở Vĩnh Phúc-L2/N2018
Cho số phức
z
thoả mãn điều kiện
2 2 2zi− − =
. Gọi
,Mm
lần lượt là giá trị lớn nhất, giá
trị nhỏ nhất của biểu thức
3 2 3 4H z i z i= + − + − +
. Giá trị
Mm+
bằng
Ⓐ.
16 2
. Ⓑ.
11 2
. Ⓒ.
2 26 8 2+
. Ⓓ.
2 26 6 2+
.
a Định hướng
+ Tìm
m
khá đơn giản và rõ ràng áp dụng:
1 2 1 2
z z z z+ +
.
+ Ta đã biết:
22
2
2
1 2 1 2
12
2
22
z z z z
z z z z z

+−
+ + + = + +



, do đó ta có:
2 2 2 2
3 2 3 4 2 3 3z i z i z i i

+ − + − + = + + −

. Mặt khác biết
2 2 2zi− − =
, tìm
m ax zi+
là bài toán quen thuộc. Như vậy áp dụng BĐT :
,ab
,
( )
22
2a b a b+ +
là
có thể tìm được
M
.
b Lời giải tham khảo
Lời giải
+
3 2 3 4 3 2 3 4 6 2H z i z i z i z i= + − + − + − + − − + − =
( )
1
.
Đẳng thức ở
( )
1
xảy ra khi
( )
3 2 6 6 ; ,0 1
2 2 2
z i k i k k
zi
+ − = −
− − =
zi = −
.
+
22
2 3 2 3 4H z i z i

+ − + − +

22
4 3 3z i i

= + + −

2
2 18zi= + +
.
( ) ( )
2 2 2z i z i i+ = − − + +
2 2 2z i i − − + +
42=
. Suy ra
10 2H
( )
2
.
Đẳng thức ở
( )
2
xảy ra khi
( )
3 2 3 4
,0
2 2 2
2 2 2
z i z i
ll
z i l i
zi
+ − = − +
− − = +
− − =
43zi = +
.
+Vậy
6 2; 10 2mM==
Chọn A
Câu 7:
Đề tham khảo-2018
Xét các số phức
z x yi=+
(
,xy
) thỏa mãn
4 3 5zi− − =
. Khi biểu thức
1 3 1P z i z i= + − + − +
đạt giá trị lớn nhất, giá trị của
xy+
bằng
Ⓐ.
4
. Ⓑ.
6
. Ⓒ.
8
. Ⓓ.
10
.
a Định hướng
NHÓM TOÁN VD – VDC ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN
https://www.facebook.com/groups/toanvd.vdc Trang 7
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
+ Nhận thấy
( )
1 3 4 3 5z i z i+ − = − − +
,
( ) ( )
1 4 3 3 2z i z i i− + = − − + +
do đó không
tính được
22
1 3 1z i z i

+ − + − +
theo
43zi−−
(
,

là các số thực).
+ Tuy nhiên ta lại có
2 2 2 2
1 3 1 2 1 2z i z i z i i

+ − + − + = − + −

.
b Lời giải tham khảo
Lời giải
+
2 2 2 2
2 1 3 1 4 1 2P z i z i z i i
+ − + − + = − + −
2
25 zi= + −
( )
1
.
+
( ) ( )
4 3 4 2 4 3 4 2 3 5z i z i i z i i− = − − + + − − + + =
( )
2
. Đẳng thức ở
( )
2
xảy ra
khi
( )
,0
4 3 4 2
4 3 5
kk
z i k i
zi
− − = +
− − =
64zi = +
.
+ Từ
( )
1
và
( )
2
suy ra
10 2P
( )
3
. Đẳng thức ở
( )
3
xảy ra khi và chỉ khi đẳng thức ở
( )
1
và
( )
2
đồng thời xảy ra
64
1 3 1
zi
z i z i
=+
+ − = − +
64zi = +
Chọn D
Câu 8:
Sở GD&ĐT Quảng Nam-2018
Cho số phức
z
thỏa mãn
2z
. Giá trị nhỏ nhất của biểu
thức
2 1 2 1 4P z z z z i= + + − + − −
bằng
Ⓐ.
4 2 3+
. Ⓑ.
23+
. Ⓒ.
14
4
15
+
. Ⓓ.
7
2
15
+
.
a Định hướng
+Nhận thấy
zz−
là số thuần ảo. Coi
zz−
là một biến số và tìm cách giảm biến số trong
biểu thức
P
bằng BĐT
1 1 1 1 1 1 2z z z z z z z z+ + − = + + − + = + + − + − +
.Suy
ra
2 2 4P z z z z i Q − + + − − =
.
+Nếu đặt
( )
,,z x yi x y= +
thì
Q
là biểu thức chứa một biến
y
và ta có bàn toán quen
thuộc.
b Lời giải tham khảo
Lời giải
+Đặt
( )
,,z x yi x y= +
, ta có :
( )
2 1 1 4 2 2 4P z z z z i z z z z i= + + − + + − − − + + − −
NHÓM TOÁN VD – VDC ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN
https://www.facebook.com/groups/toanvd.vdc Trang 8
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
( )
2
2 2 1 2yy= + + −
.
+
( )
2
2 2 2
2 1 2 1 3 1 2y y y y


+ + − = + + + −



32yy + + −
3 2 2 3yy + + − = +
.
+Từ đó suy ra
( )
2 2 3P +
( )
1
.Khi
3
3
zi=
thỏa mãn
2z
thì
( )
2 2 3P =+
.Vậy
( )
m in 2 2 3P =+
Chọn A
Câu 9:
Face book - 2021
Cho số phức
z
thỏa mãn
2.zi−=
Biết biểu thức
T 3 2 4z i z i= + + − −
đạt giá trị nhỏ
nhất khi
( )
,.z x yi x y= +
Hiệu
xy−
bằng
Ⓐ.
3 6 13
17
−
. Ⓑ.
6 13 3
17
−
. Ⓒ.
3 6 13
17
+
. Ⓓ.
3 6 13
17
+
−
.
a Định hướng
+ Khai thác kết luận: Biểu thức
T 3 2 4z i z i= + + − −
đạt giá trị nhỏ nhất. Ta phải “cân
bằng hệ số” (làm xuất hiện thừa số
2
ở biểu thức
3zi+
) trước khi áp dụng bất đẳng thức
mô đun bằng đẳng thức sau:
2
1
1 2 1 2
12
z
z
z z z z
zz
+ = +
( )
1 2 1 2
, ; 0, 0z z z z
.
+Tổng quát bài toán:Cho trước hai số phức
12
,zz
thỏa mãn
1
12
0z
zz
và số thực dương
c
.Biết
số phức
z
thỏa mãn
zc=
.Tìm giá trị nhỏ nhất của
1
12
z
z z z z
c
− + −
.
b Lời giải tham khảo
Lời giải
+Ta có
( ) ( ) ( )
4
3 4 4
4
i z i
z i z i i z i i
z i i
−
+ = − + = − +
−
2 z=
;
( )
24T z i z= + + −
2 4 2 17z i z + + − =
( )
1
.
+Đẳng thức ở
( )
1
xảy ra khi
( ) ( )
4 , ,0 1
2
z k i k k
zi
= +
−=
4 8 13 1 2 13
17 17
zi
++
= +
.
+Vậy
3 6 13
17
xy
+
−=
Chọn C
NHÓM TOÁN VD – VDC ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN
https://www.facebook.com/groups/toanvd.vdc Trang 9
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
c Bài tập tương tự
Câu 1: Trong không gian với hệ tọa độ
O xyz
, cho mặt cầu
( ) ( ) ( )
22
2
: 1 4 8S x y z+ + − + =
và các
điểm
( ) ( )
3;0;0 , 4;2;1AB
.Gọi
M
là điểm thuộc mặt cầu
( )
S
. Giá trị nhỏ nhất của
2M A M B+
bằng
Ⓐ.
22
. Ⓑ.
62
. Ⓒ.
23
. Ⓓ.
63
.
Câu 2: Trong không gian cho tam giác
A BC
có
2 , , 120AB R A C R CA B= = =
.Gọi
M
là điểm
thay đổi thuộc mặt cầu tâm
B
bán kính
R
.Giá trị nhỏ nhất của
2M A M C+
là
Ⓐ.
4R
. Ⓑ.
6R
. Ⓒ.
19R
. Ⓓ.
27R
.
Câu 10:
Face book - 2021
Cho số phức
z
thỏa mãn
1z =
và
( )
2019
2021 2020
P 6 2 1z z z z= + + − +
. Gọi
;Mm
lần lượt
là giá trị lớn nhất; giá trị nhỏ nhất của biểu thức
P
. Giá trị của biểu thức
T M m=−
bằng
Ⓐ.
1
2
. Ⓑ.
1
. Ⓒ.
2
. Ⓓ.
4
.
a Định hướng
+
2
1
1 1 . 1z z zz z
z
= = = =
. Từ đó ta có :
2021 2020
2019
1
6 2 1P z z z
z
= + + − +
2020 2020
2020
1
6 2 1z z z
z
= + + − +
2020 2020 2020
6 2 1z z z= + + − +
.
+ Đặt
( )
2020
,z x yi x y= +
.Ta đưa về bài toán quen thuộc.
b Lời giải tham khảo
Lời giải
+
2
1
1 1 . 1z z zz z
z
= = = =
. Từ đó ta có :
2021 2020
2019
1
6 2 1P z z z
z
= + + − +
2020 2020
2020
1
6 2 1z z z
z
= + + − +
( )
2020 2020 2020
6 2 1z z z= + + − +
(Chú ý
( )
( )
2020
2020
2020
1
zz
z
==
).
+Đặt
( )
2020
,z x yi x y= +
, khi đó:
2020
2 2 2020
1x y z z+ = = =
22
1xy = −
11x −
.
+Ta có
( )
2 6 2 1P x x yi= + − + +
( )
2
2
2 6 2 1x x y= + − + +
( )
( )
2 2 1 6xx= − + +
NHÓM TOÁN VD – VDC ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN
https://www.facebook.com/groups/toanvd.vdc Trang 10
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
+Xét hàm số
( ) ( )
( )
2 2 1 6, 1;1f x x x x= − + + −
. Dễ thấy
( )
1;1
1
m in 3
2
f x f
−

= − =


;
( ) ( )
1;1
m ax 1 4f x f
−
==
Chọn B
Câu 11:
Lê Quý Đôn Lai Châu-L1/N2018
Cho hai số phức
12
,zz
thỏa mãn điều kiện
1 1 1
22z i z z i+ = − −
và
2
10 1zi− − =
. Giá trị
nhỏ nhất của biểu thức
12
zz−
bằng
Ⓐ.
10 1+
. Ⓑ.
3 5 1−
. Ⓒ.
101 1−
. Ⓓ.
101 1+
.
a Định hướng
+ Đặt
( )
1
;,z x yi x y= +
, khi đó từ
1 1 1
22z i z z i+ = − −
tính được
2
4
x
y =
. (Nếu đặt
2
z a bi=+
thì tính
a
theo
b
sẽ rất phức tạp).
+ Tìm cách kết nối kết luận
12
zz−
với giả thiết
2
10 1zi− − =
bằng:
12
zz−
+
2
10zi−−
1 2 2
10z z z i − + − −
( )
2
2
2
10 1
4
x
x

= − + −


.
b Lời giải tham khảo
Lời giải
+ Đặt
( )
1
;,z x yi x y= +
, khi
đó:
( ) ( )
2
22
2
1 1 1
2 2 2. 1 2 2
4
x
z i z z i x y y y+ = − − + − = − − =
2
1
4
x
z x i = +
.
+
12
zz−
+
2
10zi−−
1 2 2
10z z z i − + − −
( )
2
2
2
10 1
4
x
x

= − + −


( )
2
2
2
12
10 1 1
4
x
z z x

− − + − −


.
+ Xét hàm số
( )
2
2
2
( ) 10 1 ,
4
x
f x x x

= − + −


. Dễ thấy
( ) ( )
m in 4 45f x f==
.
+ Suy ra
12
3 5 1zz− −
( )
1
. Đẳng thức ở
( )
1
xảy ra khi
( )
1
1 2 2
12
44
,0
10
3 5 1
zi
kk
z z k z i
zz
=+
− = − −
− = −
1
2
44
50 2 5 5 5
55
zi
zi
=+
−+
=+
Chọn B
NHÓM TOÁN VD – VDC ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN
https://www.facebook.com/groups/toanvd.vdc Trang 11
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
Câu 12:
Chuyên Đại Học Vinh-L2/N2021
Cho các số thực
,bc
sao cho phương trình
2
0z bz c+ + =
có hai nghiệm phức
12
,zz
thỏa
mãn
1
4 3 1zi− + =
và
2
8 6 4zi− − =
. Mệnh đề nào sau đây đúng?
Ⓐ.
54bc+=
. Ⓑ.
5 12bc+ = −
. Ⓒ.
5 12bc+=
. Ⓓ.
54bc+ = −
.
a Định hướng
+Nếu
1
z
là số thực thì
( )
2
11
1 4 3 4 9z i z= − + = − +
. Điều này vô lý.
+Vì
1,2
z
là các nghiệm phức không thực của phương trình
2
0z bz c+ + =
nên
12
zz=
1 2 2
z z z = =
.
b Lời giải tham khảo
Lời giải
+Nếu
1
z
là số thực thì
( )
2
11
1 4 3 4 9 3z i z= − + = − +
. Điều này vô lý.
+Vì
1,2
z
là các nghiệm phức không thực của phương trình
2
0z bz c+ + =
nên
1 2 1 2 2
.z z z z z= = =
+Mặt khác:
11
1 4 3 4 3z i z i= − + − − +
1
46z
;
22
4 8 6 8 6z i z i= − − − − −
1
10z=−
1
6 14z
. Suy ra
1
6z =
.
+
11
4 3 4 3z i z i− + = − − +
khi và chỉ khi
( )
1
43z k i= − +
với
k
và
0k
. Từ đây dễ
dàng tính được
1
24 18
55
zi=−
;
2
24 18
55
zi=+
;
2
1 2 1
36c zz z= = =
và
12
48
5
b z z− = + =
Chọn A.
Nhận xét
Gọi
,AB
lần lượt là điểm biểu diễn các số phức không thực
12
,zz
trong mặt phẳng tọa độ
O xy
thì
A
đối xứng với
B
qua trục thực
Ox
. Từ đây ta có các bài toán mới bằng cách thay điều kiện
1
2
4 3 1
8 6 4
zi
zi
− + =
− − =
bởi điều kiện cho
A
thuộc đường tròn và
B
hoặc thuộc đường tròn; hoặc đoạn
thẳng; hoặc đường thẳng; hoặc parabol; hoặc hình thoi…Chú ý:
1,2
z
là các nghiệm phức không
thực của phương trình bậc hai hệ số thực.
Câu 13:
Chuyên Tuyên Quang-L3/N2021
Cho số phức
z
thỏa mãn
6z z z z− + +
. Giá trị nhỏ nhất của biểu thức
22
2 3 4 13P z i z i= − + + + −
bằng
Ⓐ.
156
. Ⓑ.
155
. Ⓒ.
146
. Ⓓ.
147
.
a Định hướng
NHÓM TOÁN VD – VDC ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN
https://www.facebook.com/groups/toanvd.vdc Trang 12
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
+Gọi
( )
;M x y
là điểm biểu diễn số phức
z x yi=+
trong mặt phẳng tọa độ
O xy
, khi đó từ
6z z z z− + +
M
nằm trong hình vuông.
+
22
2 1 5 3 8P z i i

= + − + − +

2
2 146MA=+
với
( )
1;5A −
. Như thế chỉ cần tìm giá trị
lớn nhất và giá trị nhỏ nhất của
MA
sẽ tìm được giá trị lớn nhất và giá trị nhỏ nhất của
P
.
b Lời giải tham khảo
Lời giải
+Trong mặt phẳng tọa độ
O xy
, gọi
( )
;M x y
là điểm biểu diễn số phức
z x yi=+
( )
,xy
.
Khi đó
6z z z z− + +
3xy +
M
không nằm ngoài hình vuông
EFG H
(hình
vẽ).
+
22
2 1 5 3 8P z i i

= + − + − +

2
2 146MA=+
với
( )
1;5A −
. Vì
0
90A FE
nên
22
5M A M F=
156P
. Khi
3zi=
thỏa mãn điều kiện bài toán thì
156P =
. Vậy
m in 156P =
Chọn A
c Bài tập tương tự
Câu 1: Cho số phức
z
thoả mãn
2
z z z z z+ + − =
. Giá trị lớn nhất của biểu thức
52P z i= − −
bằng
Ⓐ.
2 5 3+
. Ⓑ.
2 3 5+
. Ⓒ.
5 2 3+
. Ⓓ.
5 3 2+
.
Câu 2: Cho số phức
z
thỏa mãn
2
25z z z= + +
. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của
24zi−+
. Giá trị của
Mm+
bằng
Ⓐ.
4 4 2+
. Ⓑ.
82
. Ⓒ.
8
. Ⓓ.
3 4 2+
.
Câu 3: Cho số phức
z
thỏa mãn
2
32z z z+ = +
. Gọi
,Mm
lần lượt là giá trị lớn nhất, nhỏ nhất
của
13zi++
. Giá trị của
Mm+
bằng
Ⓐ.
3 13+
. Ⓑ.
4 13+
. Ⓓ.
2 13+
. Ⓓ.
5 13+
.
Câu 4: Gọi
S
là tập tất cả các số thực dương
m
để có bốn số phức
z
thỏa mãn hệ
2
zm
z z z z z
=
+ + − =
. Tổng bình phương các phần tử của
S
bằng
Ⓐ.
12
. Ⓑ.
17
. Ⓒ.
19
. Ⓓ.
22
.
NHÓM TOÁN VD – VDC ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN
https://www.facebook.com/groups/toanvd.vdc Trang 13
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
Câu 14:
Sở GD Hòa Bình-T5/N2021
Cho hai số phức
,zw
thỏa mãn
2z =
,
3 2 1wi− + =
. Giá trị lớn nhất của biểu thức
2
24H z zw= − −
bằng
Ⓐ.
16 2
. Ⓑ.
18 2
. Ⓒ.
18
. Ⓓ.
24
.
a Định hướng
+Không thể biến đổi giả thiết, do đó biến đổi kết
luận :
2
2 . 2
2
zz
H z zw z z z w
−
= − − = −
4
2
zz
w
−
=−
.
+Đến đây chúng ta tìm cách giảm biến bằng cách xét
1 3 2
42
H z z
w w i
−
− = − − − +
.
b Lời giải tham khảo
Lời giải
+Đặt
z x yi=+
với
,xy
thì
2
zz
yi
−
=
; Vì
2z =
nên
22
4xy+=
22y −
0 2 4y +
( )
2
2 16y +
.
+Ta có
2
2 . 2
2
zz
H z zw z z z w
−
= − − = −
4
2
zz
w
−
=−
1 3 2
42
H z z
w w i
−
− = − − − +
32
2
zz
w w i
−
− + − +
32
2
zz
i
−
= − +
( )
32yi= − + +
( )
2
9 2 5y= + +
24H
.
+Khi
2
18 14
55
zi
wi
=
=−
(thỏa mãn điều kiện đề bài) thì
24H =
.Vậy
max 24H =
Chọn D.
Nhận xét
Ta có thể tìm
minH
như sau
+
1 3 2
42
H z z
w w i
−
+ = − + − +
32
2
zz
w w i
−
− + − +
( )
2
92y= + +
3
8H
.
+Khi
2
22
zi
wi
=−
=−
(thỏa mãn điều kiện đề bài) thì
8H =
. Vậy
min 8H =
.
Biểu diễn hình học số phức : Trong mặt phẳng tọa độ
Oxy
, gọi
,MN
lần lượt biểu diễn số
phức
2
zz−
,
w
thì
2
zz
NM w
−
=−
. Rõ ràng điểm
M
thuộc đoạn thẳng
AB
với
(0; 2), (0;2)AB−
và
N
là điểm thuộc đường tròn
( )
C
có tâm
(3; 2)I −
, bán kính
1r =
.
NHÓM TOÁN VD – VDC ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN
https://www.facebook.com/groups/toanvd.vdc Trang 14
NHÓM TOÁN VD
– VDC
NHÓM TOÁN VD
– VDC
+Ta có
11NM IN MI NM MI IA+ − −
(Chú ý
IA AB⊥
).
+
1 1 max ;NM NI IM MI IA IB + = + +
.
| 1/14
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

NHÓM TOÁN VD – VDC
ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN NHÓM TOÁN VD - VDC
ÁP DỤNG ĐẲNG THỨC
VÀ BẤT ĐẲNG THỨC MÔ ĐUN NHÓ
NĂM HỌC 2020 – 2021 M TO ÁN I. LÝ THUYẾT VD =I –
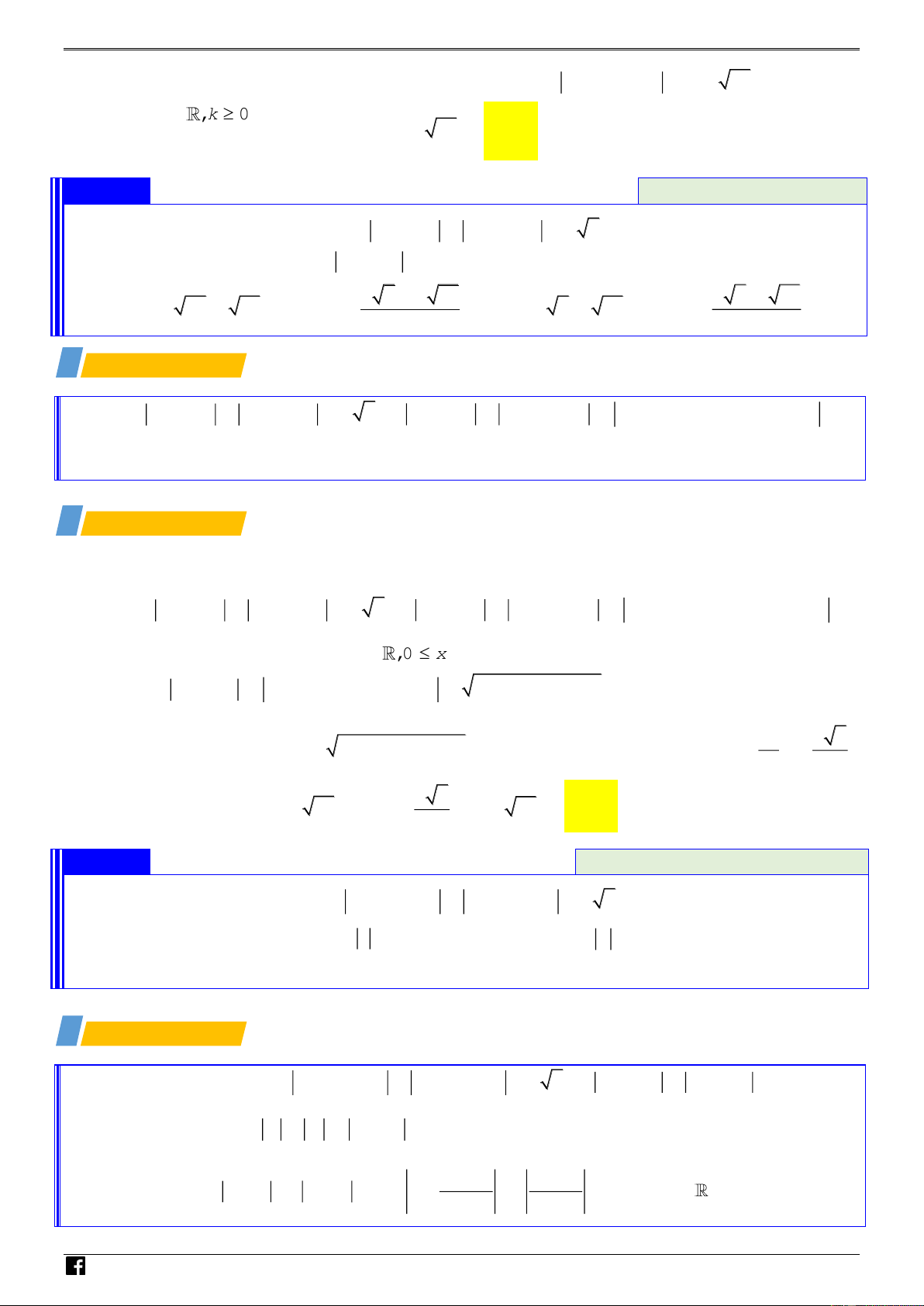
Mỗi số phức, ở khía cạnh đại số, là nghiệm tương ứng duy nhất một tam thức bậc hai monic V D
hệ số thực có biệt thức âm. Nếu zlà nghiệm của 2 ( f )
x = x + ax + b với , a b  và C 2
 = a − 4b  0 thì nghiệm còn lại sẽ gọi là liên hợp của nó. Tích hai nghiệm sẽ là b và là một
số không âm. Căn bậc hai của b gọi là module.
Ở khía cạnh hình học, mỗi số phức sẽ là cặp tọa độ của một vector, và độ lớn của vector đó chính là module.
Module của số phức. Số phức liên hợp:
z = a + b ( i , a b
) thì module của z là 2 2
z = a + b ; Số phức liên hợp của z là z + z z − z
z = a − bi Ta có: Phần thực của z là R ez =
, phần ảo của z là Im z = ; 2 2 z z zz = z z 2
, z = zz; z + z = z + z , zz = z z , z = z; 1 1 = , 1 2 1 2 1 2 1 2 1 2 1 2 z z 2 2 NHÓ  z z 1 1   = (z  0 . 2 ) z z M  2  2 TO ÁN
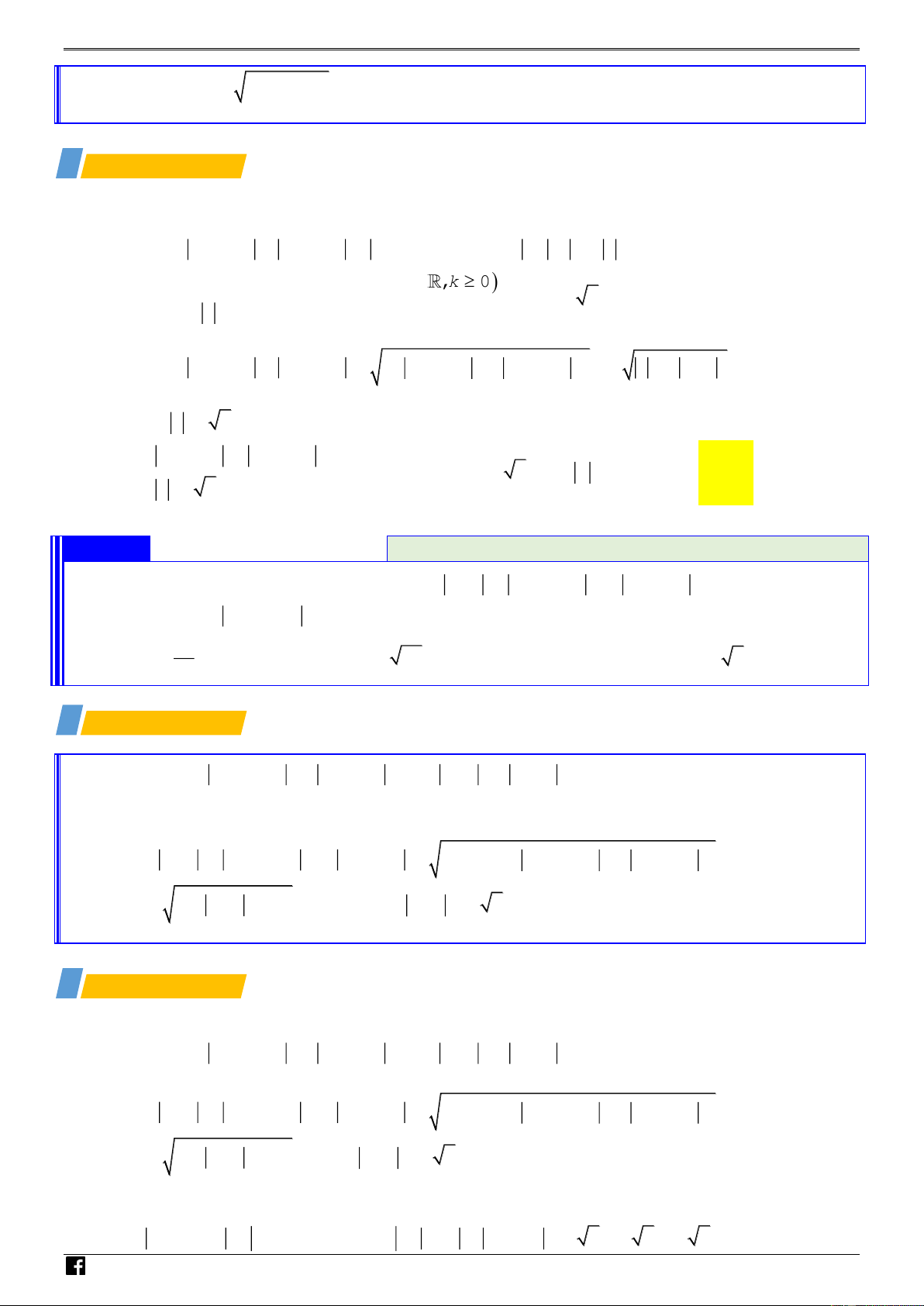
1/ Đẳng thức Mô - Đun VD 2 2 2 + 2 2 m z + nz
= m z + n z + m n z .z + z .z với m ,n  và z ,z  . 1 2 1 2 ( 1 2 1 2 ) 1 2 – 2 2 V  + −  2 2 z z z z D + 1 2 1 2 z + z + z + z = 2  z + +  với , z z ,z  . 1 2 1 2 C  2 2    z z + 2 1 z + z = z +
z với z ,z là các số phức khác 0 . 1 2 1 2 z z 1 2 1 2  , a , b c   +Nếu a   0 thì phương trình 2
az + bz + c = 0 có hai nghiệm phức không  2
 = b − 4ac  0  b −  i  thực z =
. Dễ thấy z = z z = z . 1,2 2a 1 2 1 2
2/ BĐT Mô - Đun
https://www.facebook.com/groups/toanvd.vdc Trang 1 NHÓM TOÁN VD – VDC
ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN
Lớp 7: A B − B C A C A B + B C .
Lớp 10: a − b a + b a + b .
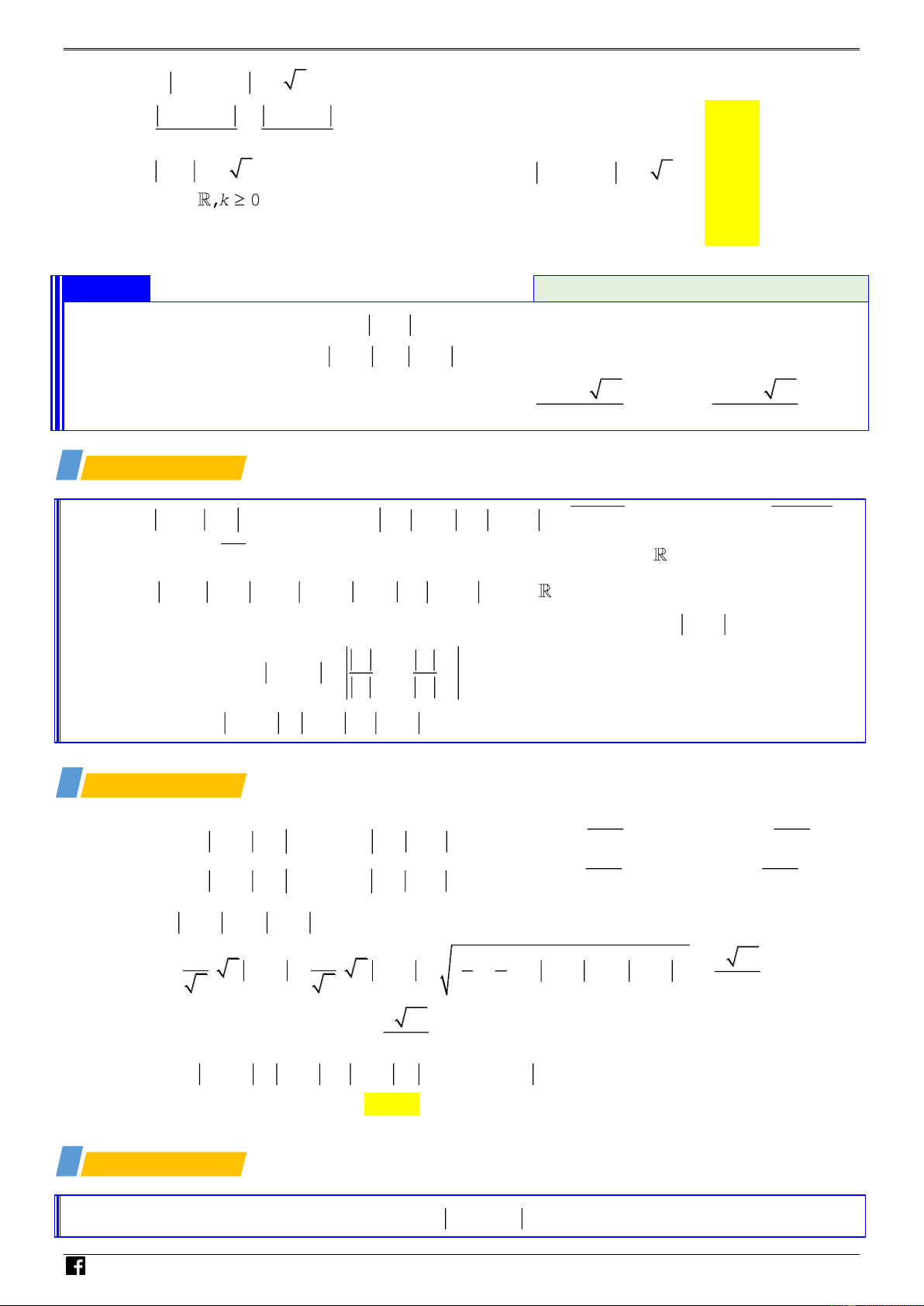
Lớp 12: z − z z + z z + z . 1 2 1 2 1 2 NHÓ
+ z + z + z + z z − z . Đẳng thức xảy ra khi và chỉ khi 1 2 1 2 M TO  z
 + z = k z + z + z − − z  1 ( 1 ) ( 2 ) 
(k  ;k  0; 1) ÁN  z
 + z = k z + z + z − − z  2  ( 2 ) ( 1 )  . VD  z  + z = 0 2  – z
+ z = k z + z ; z + z  0;k  ;k  0  1 ( 2 ) ( 2 ) VD
+ z + z − z + z z − z . Đẳng thức xảy ra khi và chỉ khi C 1 2 1 2  z
 + z = k z + z + z − − z  1 ( 1 ) ( 2 ) 
(k  ,k  ( ; − 0 1;+ ))  z
 + z = k z
− − z + z + z  2  ( 1 ) 2   .  z  + z = 0 2 z
+ z = k z + z ; z + z  0;k  ,k  0  1 ( 2 ) ( 2 ) II. MỘT SỐ VÍ DỤ =I Câu 1:
Minh Hoạ-T4/N2021
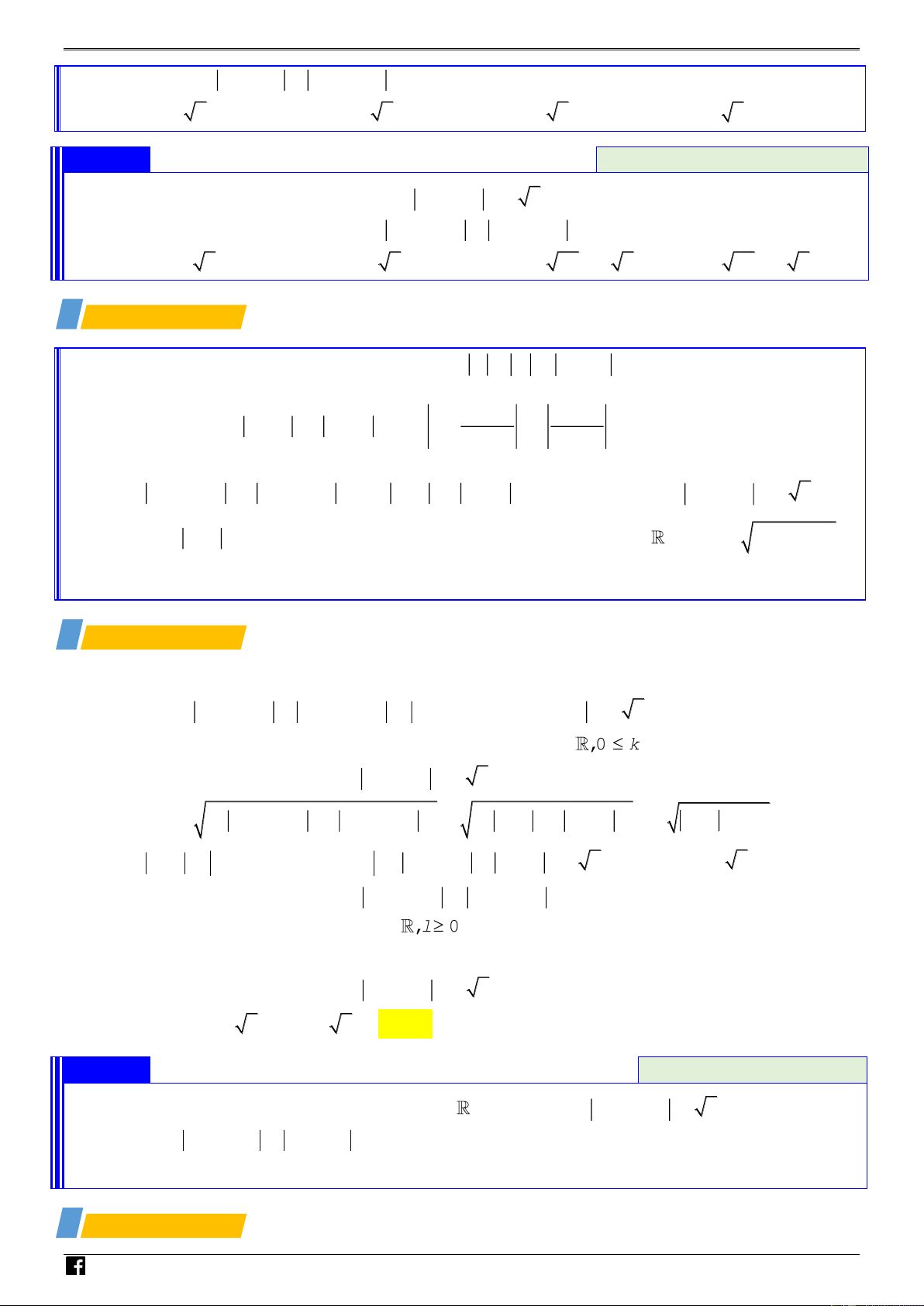
Xét hai số phức z ,z thỏa mãn z = 1,z = 2 và z − z = 3 . Giá trị lớn nhất 1 2 1 2 1 2 NHÓ
3z + z − 5i bằng 1 2 Ⓐ. 5 − 19 . Ⓑ. 5 + 19 . Ⓒ. −5 + 2 19 . Ⓓ. 5 + 2 19 . M TO a Định hướng ÁN VD 2
Tất cả giả thiết của đề bài đều nói về Mô đun của số phức, chính vì thế ta xét: m z + nz . 1 2 – 2 2 2 2 2 V
Bằng tính toán ta có kết quả: m z + nz
= m z + n z + m n z .z + z .z . Trong đó 1 2 1 2 ( 1 2 1 2 ) D C
m ,n là các số thực và z ,z là các số phức. Như vậy từ giả thiết ta sẽ tính được 3z + z và 1 2 1 2
đưa bài toán đã cho về bài toán quen thuộc.
b Lời giải tham khảo Lời giải 2 2 2 +3 = z − z
= z + z − z .z + z .z = 5 − (z .z + z .z  (z .z + z .z = 2 1 2 1 2 ) 1 2 1 2 ) ; 1 2 1 2 ( 1 2 1 2 ) 2 2
3z + z = 9 z
+ z + 3 z .z + z .z = 19 . 1 2 1 2 ( 1 2 1 2 )
+Áp dụng bất đẳng thức mô đun, có: 3z + z − 5
− i  3z + z + 5
− i  3z + z + 5 − i 1 2 ( 1 2) ( ) 1 2
 5 − 19  3z + z − 5i  5 + 9 1 . 1 2
https://www.facebook.com/groups/toanvd.vdc Trang 2 NHÓM TOÁN VD – VDC
ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN
+Vì đây là bài toán trắc nghiệm nên chọn B; Tuy nhiên 3z + z − 5i = 5 + 19 khi và chỉ khi 1 2 k   ,k  0 
 3z + z = i
− 19 Chọn B
3z + z = k 5 − i  1 2 1 2 ( ) NHÓ Câu 2:
Minh Hoạ-L2/N2017 M TO
Xét các số phức z thỏa mãn z + 2 − i + z − 4 − 7i = 6 2 . Gọi m ,M lần lượt là giá trị nhỏ ÁN
nhất, giá trị lớn nhất của z − 1 + i. Giá trị của biểu thức P = m + M bằng VD 5 2 + 2 73 5 2 + 73 Ⓐ. 13 + 73 . Ⓑ. . Ⓒ. 5 2 + 73 . Ⓓ. . – 2 2 V D a Định hướng C
z + 2 − i + z − 4 − 7i = 6 2  z + 2 − i + z
− + 4 + 7i = (z + 2 − ) i + ( z − + 4 + 7 ) i sẽ
suy ra z = a (x) + b(x).i với x  0; 
1 .Đến đây ta có bài toán quen thuộc.
b Lời giải tham khảo Lời giải
+ z + 2 − i + z − 4 − 7i = 6 2  z + 2 − i + z
− + 4 + 7i = (z + 2 − ) i + ( z − + 4 + 7 ) i
z + 2 − i= x(6 + 6 ) i (
; x  ,0  x  ) 1  z = ( 2
− + 6x) + (1 + 6x)i
z − 1 + i = ( 3 − + 6 ) x + (2 + 6 ) x i 2
= 72x − 12x + 13 . NHÓ  1  5 2 2
f x = 72x − 12x + 13,x  0;1 M +Xét hàm số ( )
 , dễ thấy m in f( ) x = f =   ; 0;  1 12  2 TO 5 2 ÁN
m ax f(x) = f( ) 1 = 73 .Vậy m =
;M = 73 Chọn B 0;  1 2 VD Câu 3: –
Chuyên Thái Bình-L5/N2018 VD
Cho số phức z thỏa mãn (1 + ) i z + 2 + (1 + )
i z − 2 = 4 2 . Gọi m ,n lần lượt là giá trị lớn C 2018
nhất và giá trị nhỏ nhất của z . Đặt w = m + ni, giá trị của w bằng Ⓐ. 1009 2 . Ⓑ. 1009 4 . Ⓒ. 1009 5 . Ⓓ. 1009 6 . a Định hướng
+Biến đổi giả thiết: (1 + ) i z + 2 + (1 + )
i z − 2 = 4 2  z + 1 − i + z − 1 + i = 4 .
+Áp dụng BĐT: z + z z + z dễ dàng tìm được m . 1 2 1 2 2 2  + −  2 2 z z z z +Áp dụng 1 2 1 2 z + z + z + z = 2  z + +  và  , a b  ta 1 2  2 2  
https://www.facebook.com/groups/toanvd.vdc Trang 3 NHÓM TOÁN VD – VDC
ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN có :a + b  ( 2 2
2 a + b ) tìm được n . NHÓ b Lời giải tham khảo M Lời giải TO
+ 4 = z + 1 − i + z − 1 + i z + 1 − i+ z − 1 + i = 2z z  2 ( ) 1 . Đẳng thức ở ( ) 1 xảy ÁN z  + 1 − i= k
(z − 1 + )i (,k  ,k  0) VD ra khi   z =  2 ( 1 − + ) i m = 2.  z = 2  – VD 2 2   + − + − +  2 2 C
+ 4 = z + 1 − i + z − 1 + i 2 z 1 i z 1 i = 2 z + i− 1    z  2 (2) . Đẳng thức ở (2) xảy ra khi
z + 1 − i = z − 1 + i    z =  (1 + ) i n = 2 2018 . Vậy 1009 w = 6 Chọn D z = 2  Câu 4:
THPT Đặng Thúc Hứa Nghệ An-Lần1 Năm 2018
Cho số phức z thỏa mãn điều kiện 5 z − i = z + 1 − 3i + 3 z − 1 + i . Giá trị lớn nhất của
biểu thức z − 2 + 3i bằng 13 Ⓐ. . Ⓑ. 1 + 13 . Ⓒ. 9 . Ⓓ. 4 5 . 3 NHÓ a Định hướng M 2 2 2 2 TO
+ Ta có: z + 1 − 3i + z − 1 + i = 2  z − i + 1 − 2i    . ÁN + Mặt khác: VD
5 z − i = z + 1 − 3i + 3 z − 1 + i  ( + )( 2 2 2 2 1 3
z + 1 − 3i + z − 1 + i ) – VD 2
= 20 z − i + 5 . Từ đó suy ra z − i  2 5 . Đến đây ta có bài toán quen thuộc. C ( )
b Lời giải tham khảo Lời giải 2 2 2 2
+ Ta có: z + 1 − 3i + z − 1 + i = 2  z − i + 1 − 2i    ; Từ đó
5 z − i = z + 1 − 3i + 3 z − 1 + i  ( + )( 2 2 2 2 1 3
z + 1 − 3i + z − 1 + i ) = ( 2
20 z − i + 5) . Suy ra z − i  2 5 . +
z − 2 + 3i = (z − ) i + ( 2 − + 4 )
i z − i + 2
− + 4i  2 5 + 2 5 = 4 5
https://www.facebook.com/groups/toanvd.vdc Trang 4 NHÓM TOÁN VD – VDC
ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN
z − 2 + 3i  4 5 ( ) 1 . Đẳng thức ở ( ) 1 xảy ra khi  z + 1 − 3i z − 1 + i =  1 3  NHÓ z − i = 2 5   z = 2
− + 5i. Vậy m ax z − 2 + 3i = 4 5 Chọn D k   ,k  0 M  TO z  − i= k  ( 2 − + 4 ) i ÁN VD Câu 5
Chuyên Sư Phạm Hà Nội-L2/N2021 –
Xét các số phức zthỏa mãn z − 1 = 2 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị bé VD
nhất của biểu thức P = z + 2 + 2 z − 3 . Tổng M + m bằng C 45 + 3 35 15 + 5 33 Ⓐ. 14. Ⓑ. 7 . Ⓒ. . Ⓓ. . 5 3 a Định hướng 2 2 2 + z + z
= z + w + z − w
= z + w + z − w + z + w z − w + z + w z − w k ( )( k ) ( )( k ) k ( ) ( k )2
với k = 1;2. Do đó nếu z − w = p z − w 1 ( 2
) với p  thì sẽ tính được 2 2 a z + z
+ b z + z theo z + w và z − w ( , a b
). Khi đó dễ dàng tính được M . 1 2 k
+Nhìn vào kết luận, ta tìm cách làm xuất hiện hệ số 2 trước biểu thức z + 2 (Cân bằng hệ số) z z bằng công thức 2 1 z + z = z +
z với z ,z là các số phức khác 0 nhưng không được. 1 2 1 2 z z 1 2 1 2 NHÓ Viết P = ( z
− − 2 + z − 3 ) + z − 3 ta dễ dàng tìm được m . M TO
b Lời giải tham khảo ÁN Lời giải 2 2 2 VD
z + 2 = (z − )
1 + 3 = z − 1 + 9 + 3 (z − 1 + z − )
1 = 13 + 3 (z − 1 + z −  )1 +Ta có  suy – 2 2 2 V
z − 3 = (z − )
1 − 2 = z − 1 + 4 − 2 
(z−1+ z− )1 = 8 − 2(z−1+ z− )1 D C 2 2
ra 2 z + 2 + 3 z − 3 = 50 ; 1 2  1 4  5 33 P = . 2 z + 2 + . 3 z − 3  +   ( 2 2
2 z + 2 + 3 z − 3 ) = . Vì làm bài 2 3  2 3  3 5 33
trắc nghiệm nên dự đoán M = . 3 + P = ( z
− − 2 + z − 3 ) + z − 3  z
− − 2 + z − 3 + 0 = 5 . Khi z = 3 thỏa mãn điều kiện đề
bài thì P = 5 . Vậy m = 5 Chọn D c Bài tập tương tự Cho số phức z thỏa mãn
z − 1 − 2i = 2 . Giá trị lớn nhất của biểu
https://www.facebook.com/groups/toanvd.vdc Trang 5 NHÓM TOÁN VD – VDC
ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN
thứcT = z + 1 − i + z − 5 − 4i bằng Ⓐ. 3 7 . Ⓑ. 3 5 . Ⓒ. 3 6 . Ⓓ. 4 2 . Câu 6: NHÓ
Sở Vĩnh Phúc-L2/N2018
Cho số phức z thoả mãn điều kiện z − 2 − i = 2 2 . Gọi M ,m lần lượt là giá trị lớn nhất, giá M TO
trị nhỏ nhất của biểu thức H = z + 3 − 2i + z − 3 + 4i. Giá trị M + m bằng ÁN Ⓐ. 16 2 . Ⓑ. 11 2 . Ⓒ. 2 26 + 8 2 .
Ⓓ. 2 26 + 6 2 . VD a Định hướng – V D
z + z z + z C
+ Tìm m khá đơn giản và rõ ràng áp dụng: . 1 2 1 2 2 2  + −  2 2 z z z z + Ta đã biết: 1 2 1 2 z + z + z + z = 2  z + +  , do đó ta có: 1 2  2 2   2 2 2 2
z + 3 − 2i + z − 3 + 4i = 2  z + i + 3 − 3i  
 . Mặt khác biết z − 2 − i = 2 2 , tìm
m ax z + i là bài toán quen thuộc. Như vậy áp dụng BĐT :  , a b  , a + b  ( 2 2 2 a + b ) là
có thể tìm được M . b Lời giải tham khảo Lời giải NHÓ
+ H = z + 3 − 2i + z
− + 3 − 4i z + 3 − 2i− z + 3 − 4i = 6 2 ( ) 1 . z
 + 3 − 2i= k
(6 − 6 )i;k  ,0  k  1 M Đẳng thức ở ( ) 1 xảy ra khi   z = i − . TO
z − 2 − i = 2 2  ÁN 2 2 2 2 2
+ H  2  z + 3 − 2i + z − 3 + 4i  = 4  z + i + 3 − 3i  = 2 z + i + 18 .     VD
z + i = (z − 2 − ) i + (2 + 2 )
i z − 2 − i + 2 + 2i = 4 2 . Suy ra H  10 2 (2) . – VD
z + 3 − 2i = z − 3 + 4i C  l   ,l 0 
Đẳng thức ở (2) xảy ra khi 
z = 4 + 3i.
z − 2 − i = ( l 2 + 2 ) i
z − 2 − i = 2 2 
+Vậy m = 6 2;M = 10 2 Chọn A Câu 7:
Đề tham khảo-2018
Xét các số phức z = x + yi ( , x y
) thỏa mãn z − 4 − 3i = 5 . Khi biểu thức
P = z + 1 − 3i + z − 1 + i đạt giá trị lớn nhất, giá trị của x + y bằng Ⓐ. 4 . Ⓑ. 6 . Ⓒ. 8 . Ⓓ. 10 . a Định hướng
https://www.facebook.com/groups/toanvd.vdc Trang 6 NHÓM TOÁN VD – VDC
ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN
+ Nhận thấy z + 1 − 3i = (z − 4 − 3 )
i + 5 , z − 1 + i = (z − 4 − 3 ) i + (3 + 2 ) i do đó không 2 2
tính được  z + 1 − 3i +  z − 1 + i theo z − 4 − 3i (, là các số thực). NHÓ 2 2 2 2
+ Tuy nhiên ta lại có z + 1 − 3i + z − 1 + i = 2  z − i + 1 − 2i    . M TO
b Lời giải tham khảo ÁN VD Lời giải – 2 2 2 2 2 V
+ P  2  z + 1 − 3i + z − 1 + i  = 4 z − i + 1 − 2i  = 2 5 + z − i ( ) 1 . D     C
+ z − i = (z − 4 − 3 ) i + (4 + 2 )
i z − 4 − 3i + 4 + 2i = 3 5 (2) . Đẳng thức ở (2) xảy ra  k   ,k  0  khi z
 − 4 − 3i= k(4 + 2 )
i z = 6 + 4i. 
z − 4 − 3i = 5  + Từ ( )
1 và (2) suy ra P  10 2 (3) . Đẳng thức ở (3) xảy ra khi và chỉ khi đẳng thức ở  = + ( ) z 6 4i
1 và (2) đồng thời xảy ra  
z = 6 + 4iChọn D
z + 1 − 3i = z − 1 + i Câu 8:
Sở GD&ĐT Quảng Nam-2018 Cho số phức z thỏa mãn z  2 . Giá trị nhỏ nhất của biểu NHÓ
thức P = 2 z + 1 + 2 z − 1 + z − z − 4i bằng M 14 7 Ⓐ + + 4 + 2 + TO . 4 2 3 . Ⓑ. 2 3 . Ⓒ. . Ⓓ. . 15 15 ÁN VD a Định hướng – − − V
+Nhận thấy z z là số thuần ảo. Coi z z là một biến số và tìm cách giảm biến số trong D z + + z − = z + + z − + = z + + z − +  z − z + C
biểu thức P bằng BĐT 1 1 1 1 1 1 2 .Suy ra
P  2 z − z + 2 + z − z − 4i = Q .
+Nếu đặt z = x + yi ( , , x y
) thì Q là biểu thức chứa một biến y và ta có bàn toán quen thuộc.
b Lời giải tham khảo Lời giải
+Đặt z = x + yi ( , , x y  ) , ta có :
P = 2 ( z + 1 + z
− + 1) + z − z − 4i  2 z − z + 2 + z − z − 4i
https://www.facebook.com/groups/toanvd.vdc Trang 7 NHÓM TOÁN VD – VDC
ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN = ( 2
2 2 y + 1 + y − 2 ).   + y + + y − = +  ( )2 2 2 2 2 1 2 1 3 y
 + 1 + y − 2  y + 3 + y − 2     NHÓ 
y + 3 + 2 − y = 2 + 3 . M TO 3 P  2 2 + 3 ( ) 1 z = i z P = 2 2 + 3 ÁN +Từ đó suy ra ( ) .Khi thỏa mãn 2 thì ( ).Vậy 3 VD
m in P = 2 (2 + 3) Chọn A – V D C Câu 9: Face book - 2021
Cho số phức z thỏa mãn z − i = 2. Biết biểu thức T = z + 3i + 2 z − 4 − i đạt giá trị nhỏ
nhất khi z = x + yi ( , x y
). Hiệu x − y bằng 3 − 6 13 6 13 − 3 3 + 6 13 3 + 6 13 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. − . 17 17 17 17 a Định hướng
+ Khai thác kết luận: Biểu thức T = z + 3i + 2 z − 4 − i đạt giá trị nhỏ nhất. Ta phải “cân
bằng hệ số” (làm xuất hiện thừa số 2 ở biểu thức z + 3i ) trước khi áp dụng bất đẳng thức z z
mô đun bằng đẳng thức sau: 2 1 z + z = z +
z (z ,z  ;z  0,z  0 . 1 2 1 2 ) 1 2 1 2 z z 1 2 NHÓ  z  0
+Tổng quát bài toán:Cho trước hai số phức z ,z thỏa mãn 1
và số thực dương c .Biết 1 2  M z z  1 2 TO z ÁN
số phức zthỏa mãn z = c.Tìm giá trị nhỏ nhất của 1 z − z + z − z . 1 2 c VD –
b Lời giải tham khảo VD C Lời giải 4i z − i
+Ta có z + 3i = (z − ) i + 4i = (z − )i +
(4 )i = 2 z ; T = 2( z + 4+i− z) z − i 4i
 2 z + 4 + i− z = 2 17 ( ) 1 . z  = k
(4 + )i (,k  ,0  k  ) 1 +Đẳng thức ở ( ) 1 xảy ra khi   z − i = 2  4 + 8 13 1 + 2 13  z = + i. 17 17 3 + 6 13 +Vậy x − y =  Chọn C 17
https://www.facebook.com/groups/toanvd.vdc Trang 8 NHÓM TOÁN VD – VDC
ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN
c Bài tập tương tự 2 2 Câu 1:
Trong không gian với hệ tọa độ O xyz, cho mặt cầu (S) (x + ) + (y − ) 2 : 1 4 + z = 8 và các NHÓ
điểm A (3;0;0) ,B (4;2; )
1 .Gọi M là điểm thuộc mặt cầu (S ) . Giá trị nhỏ nhất của
M A + 2M B bằng M TO Ⓐ. 2 2 . Ⓑ. 6 2 . Ⓒ. 2 3 . Ⓓ. 6 3 . ÁN Câu 2:
Trong không gian cho tam giác A BC có A B = 2R,A C = R,CA B = 120 .Gọi M là điểm VD
thay đổi thuộc mặt cầu tâm B bán kính R .Giá trị nhỏ nhất của M A + 2M C là – Ⓐ R R . 4R . Ⓑ. 6R . Ⓒ. 19 . Ⓓ. 2 7 . V D C Câu 10: Face book - 2021
Cho số phức z thỏa mãn z = 1 và = z + (z)2019 2021 2020 P + 6z − 2 z
+ 1 . Gọi M ;m lần lượt
là giá trị lớn nhất; giá trị nhỏ nhất của biểu thức P . Giá trị của biểu thức T = M − m bằng 1 Ⓐ. . Ⓑ. 1. Ⓒ. 2 . Ⓓ. 4 . 2 a Định hướng 2 1 1
+ z = 1  z = 1  . zz = 1  z = . Từ đó ta có : 2021 2020 P = z + + 6z − 2 z + 1 z 2019 z 1 2020 2020 = z z + + 6 − 2 z + 1 2020 2020 2020 = z + z + 6 − 2 z + 1 . 2020 z NHÓ + Đặt 2020 z = x + y ( i ,
x y  ).Ta đưa về bài toán quen thuộc. M TO ÁN b Lời giải tham khảo VD Lời giải – V 2 1 1 D
+ z = 1  z = 1  . zz = 1  z = . Từ đó ta có : 2021 2020 P = z + + 6z − 2 z + 1 2019 C z z 1 2020 2020 = z z + + 6 − 2 z + 1 2020 = z + ( 2020 z ) 2020 + 6 − 2 z + 1 (Chú ý 2020 z 1 = (z)2020 = ( 2020 z ). 2020 ) z +Đặt 2020 z = x + y ( i , x y  ), khi đó: 2020 2 2 2020 x + y = z = z = 1 2 2
x = 1 − y  1 −  x  1.
+Ta có P = 2x + 6 − 2 (x + ) 1 + yi = x + − (x + )2 2 2 6 2
1 + y = 2 (x − 2 (x + ) 1 ) + 6
https://www.facebook.com/groups/toanvd.vdc Trang 9 NHÓM TOÁN VD – VDC
ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN  1
+Xét hàm số f(x) = 2 (x − 2 (x + )
1 ) + 6,x  −1; 
1 . Dễ thấy m in f( ) x = f − = 3   ;  1 − ;  1  2 
m ax f(x) = f( )
1 = 4 Chọn B  1 − ;  1 NHÓ Câu 11:
Lê Quý Đôn Lai Châu-L1/N2018 M TO
Cho hai số phức z ,z thỏa mãn điều kiện 2 z + i = z − z − 2i và z − i− 10 = 1. Giá trị 1 2 1 1 1 2 ÁN
nhỏ nhất của biểu thức z − z bằng 1 2 VD Ⓐ. 10 + 1.
Ⓑ. 3 5 − 1. Ⓒ. 101 − 1. Ⓓ. 101 + 1 . – VD a Định hướng C 2 x
+ Đặt z = x + y ; i , x y
, khi đó từ 2 z + i = z − z − 2i tính được y = . (Nếu đặt 1 ( ) 1 1 1 4
z = a + bi thì tính a theo b sẽ rất phức tạp). 2
+ Tìm cách kết nối kết luận z − z với giả thiết z − i− 10 = 1 bằng: 1 2 2 2 2  xz − z 2
+ z − i− 10  z − z + z − i− 10 = (x − 10) + − 1 . 1 2 2 1 2 2   4  
b Lời giải tham khảo Lời giải NHÓ
+ Đặt z = x + y ; i , x y  , khi 1 ( ) M 2 2 2 2 x x 2 TO
đó:2 z + i = z − z − 2i  2. x + y − 1 = 2
− y − 2  y =  z = x + i. 1 1 1 ( ) ( ) 4 1 4 ÁN 2 2 VD 2  x
+ z − z + z − i− 10  z − z + z − i− 10 = (x − 10) + − 1 1 2 2 1 2 2   – 4   VD 2 2   C 2 x  −  − + − − z z x 10 1 1. 1 2 ( )   4   2 2 2  x+ Xét hàm số ( f ) x = (x − 10) + − 1 ,x    . Dễ thấy m in f( ) x = f( ) 4 = 45 . 4   z  = 4 + 4i 1
k  ,k  0 
+ Suy ra z − z  3 5 − 1 ( ) 1 . Đẳng thức ở ( ) 1 xảy ra khi  1 2
z − z = k z − i− 10 1 2 ( 2 ) 
z − z = 3 5 − 1  1 2 z  = 4 + 4i 1    50 − 2 5
5 + 5 Chọn B z  = + i 2  5 5
https://www.facebook.com/groups/toanvd.vdc Trang 10 NHÓM TOÁN VD – VDC
ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN Câu 12:
Chuyên Đại Học Vinh-L2/N2021 Cho các số thực ,
b c sao cho phương trình 2
z + bz + c = 0 có hai nghiệm phức z ,z thỏa 1 2 NHÓ
mãn z − 4 + 3i = 1và z − 8 − 6i = 4. Mệnh đề nào sau đây đúng? 1 2
Ⓐ. 5b + c = 4.
Ⓑ. 5b + c = 1 − 2 .
Ⓒ. 5b + c = 12.
Ⓓ. 5b + c = 4 − . M TO a Định hướng ÁN VD
+Nếu z là số thực thì 1 = z − 4 + 3i =
z − 4 + 9 . Điều này vô lý. 1 ( 1 )2 1 – VD
+Vì z là các nghiệm phức không thực của phương trình 2
z + bz + c = 0 nên 1,2 C
z = z z = z = z . 1 2 1 2 2
b Lời giải tham khảo Lời giải
+Nếu z là số thực thì 1 = z − 4 + 3i =
z − 4 + 9  3 . Điều này vô lý. 1 ( 1 )2 1
+Vì z là các nghiệm phức không thực của phương trình 2
z + bz + c = 0 nên 1,2
z = z z = z = z . 1 2 1 2 2
+Mặt khác: 1 = z − 4 + 3i z − 4
− + 3i  4  z  6 ; 1 1 1
4 = z − 8 − 6i z − 8
− − 6i = z − 10  6  z  14. Suy ra z = 6 . 2 2 1 1 1
+ z − 4 + 3i = z − 4
− + 3i khi và chỉ khi z = k 4 − + 3i
k  . Từ đây dễ 1 ( ) với k và 0 1 1 NHÓ 24 18 24 18 2 48
dàng tính được z = − i; z = +
i; c = zz = z = 36 và b − = z + z = 1 5 5 2 5 5 1 2 1 1 2 5 M Chọn A. TO Nhận xét ÁN
Gọi A,B lần lượt là điểm biểu diễn các số phức không thựcz ,z trong mặt phẳng tọa độ O xy thì 1 2 VD
A đối xứng với B qua trục thực O x. Từ đây ta có các bài toán mới bằng cách thay điều kiện –
z − 4 + 3i = 1 V  1 D 
bởi điều kiện cho A thuộc đường tròn và B hoặc thuộc đường tròn; hoặc đoạn
z − 8 − 6i = 4 C  2
thẳng; hoặc đường thẳng; hoặc parabol; hoặc hình thoi…Chú ý: z1,2 là các nghiệm phức không
thực của phương trình bậc hai hệ số thực. Câu 13:
Chuyên Tuyên Quang-L3/N2021
Cho số phức zthỏa mãn z − z + z + z  6 . Giá trị nhỏ nhất của biểu thức 2 2
P = z − 2 + 3i + z + 4 − 13i bằng Ⓐ. 156 . Ⓑ. 155 . Ⓒ. 146 . Ⓓ. 147 . a Định hướng
https://www.facebook.com/groups/toanvd.vdc Trang 11 NHÓM TOÁN VD – VDC
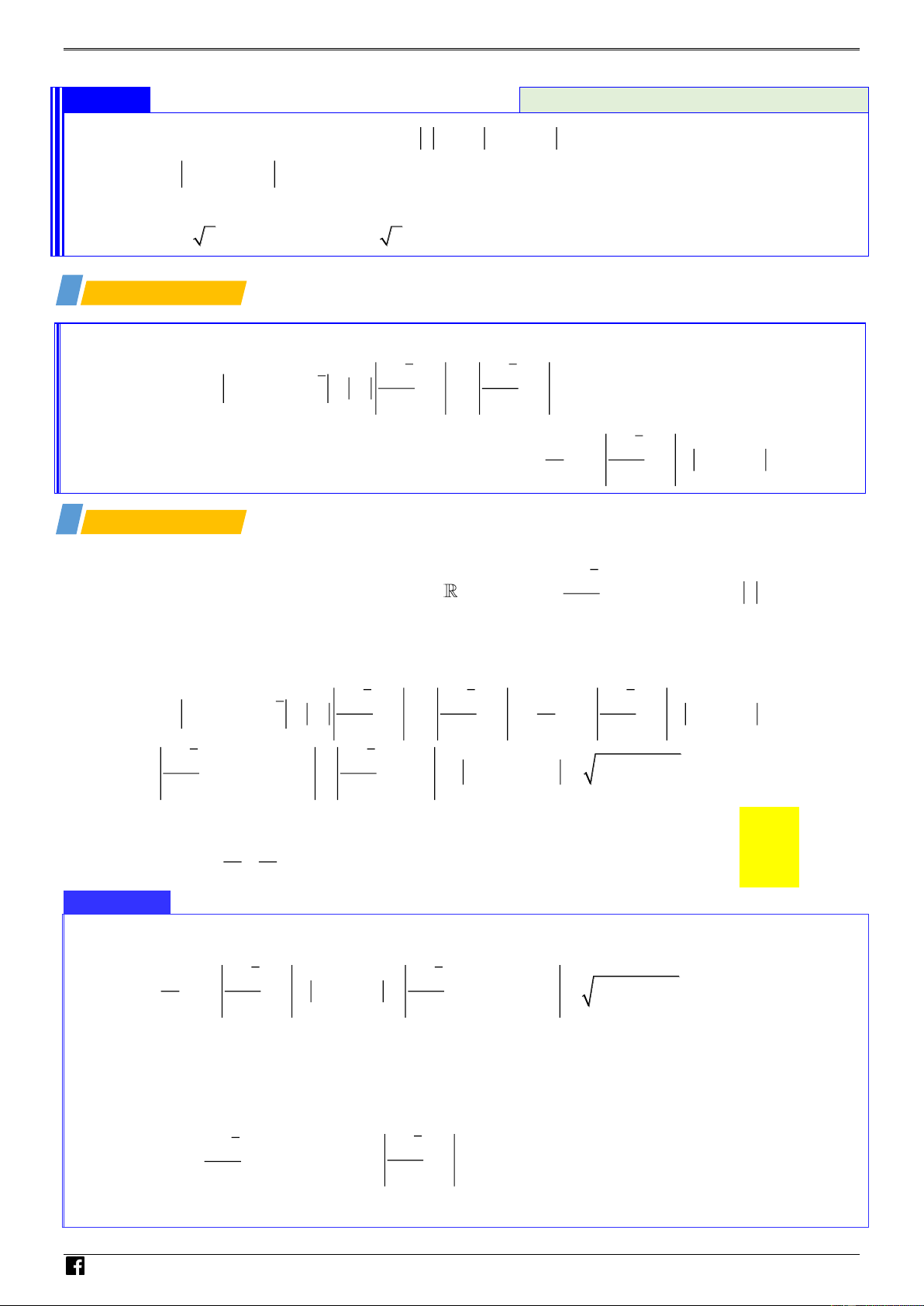
ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN +Gọi M ( ;
x y) là điểm biểu diễn số phức z = x + yitrong mặt phẳng tọa độ O xy , khi đó từ
z − z + z + z  6  M nằm trong hình vuông. 2 2
+ P = 2  z + 1 − 5i + −3 + 8i  2
= 2M A + 146 với A ( 1
− ;5) . Như thế chỉ cần tìm giá trị NHÓ  
lớn nhất và giá trị nhỏ nhất của M A sẽ tìm được giá trị lớn nhất và giá trị nhỏ nhất của P . M TO
b Lời giải tham khảo ÁN Lời giải VD
+Trong mặt phẳng tọa độ O xy , gọi M ( ;
x y) là điểm biểu diễn số phức z = x + yi ( , x y  ) . – V
Khi đó z − z + z + z  6  x + y  3  M không nằm ngoài hình vuông EFG H (hình DC vẽ). 2 2
+ P = 2  z + 1 − 5i + −3 + 8i  2 
 = 2M A + 146 với A ( 1 − ;5) . Vì 0 AFE  90 nên 2 2
M A M F = 5  P  156 . Khi z = 3i thỏa mãn điều kiện bài toán thì P = 156 . Vậy m in P = 156  NHÓ Chọn A
c Bài tập tương tự M TO Câu 1:
Cho số phức z thoả mãn 2
z + z + z − z = z . Giá trị lớn nhất của biểu thức ÁN
P = z − 5 − 2i bằng VD Ⓐ. 2 + 5 3 . Ⓑ. 2 + 3 5 . Ⓒ. 5 + 2 3 . Ⓓ. 5 + 3 2 . – VD Câu 2:
Cho số phức z thỏa mãn 2
z = 2 z + z + 5 . Gọi M ,m lần lượt là giá trị lớn nhất và giá trị C
nhỏ nhất của z − 2 + 4i . Giá trị của M + m bằng Ⓐ. 4 + 4 2 . Ⓑ. 8 2 . Ⓒ. 8 . Ⓓ. 3 + 4 2 . Câu 3:
Cho số phức z thỏa mãn 2
z + 3 = 2 z + z . Gọi M ,m lần lượt là giá trị lớn nhất, nhỏ nhất
của z + 1 + 3i. Giá trị của M + m bằng Ⓐ. 3 + 13 . Ⓑ. 4 + 13 . Ⓓ. 2 + 13 . Ⓓ. 5 + 13 . Câu 4:
Gọi S là tập tất cả các số thực dương m để có bốn số phức z thỏa mãn hệ  z = m  
. Tổng bình phương các phần tử của S bằng 2
z + z + z − z = z  Ⓐ. 12 . Ⓑ. 17 . Ⓒ. 19 . Ⓓ. 22 .
https://www.facebook.com/groups/toanvd.vdc Trang 12 NHÓM TOÁN VD – VDC
ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN Câu 14:
Sở GD Hòa Bình-T5/N2021
Cho hai số phức z, w thỏa mãn z = 2 , w − 3+ 2i =1. Giá trị lớn nhất của biểu thức NHÓ 2
H = z − 2zw − 4 bằng M TO Ⓐ. 16 2 . Ⓑ. 18 2 . Ⓒ. 18 . Ⓓ. 24. ÁN VD a Định hướng – V +Không thể biến đổi giả thiết, do đó biến đổi kết DC − − z z z z luận : 2
H = z − 2zw − . z z = 2z − w = 4 − w . 2 2 H z − z
+Đến đây chúng ta tìm cách giảm biến bằng cách xét −1 =
− w − w − 3+ 2i . 4 2
b Lời giải tham khảo Lời giải z − z +Đặt
z = x + yi với x, y  thì = yi ; Vì z = 2 nên 2 2 2 x + y = 4  2
−  y  2  0  y + 2  4  ( y + )2 2 16 . +Ta có z − z z − z H z − z NHÓ 2
H = z − 2zw − . z z = 2z − w = 4 − w  −1 =
− w − w − 3+ 2i 2 2 4 2 M z − z z − z TO 
− w + w − 3+ 2i = − 3+ 2i = 3
− + ( y + 2)i = + ( y + )2 9 2  5  H  24. 2 2 ÁN z = 2i VD  +Khi 
18 14 (thỏa mãn điều kiện đề bài) thì H = 24.Vậy max H = 24 Chọn D. w = − i –   5 5 V D Nhận xét C
Ta có thể tìm min H như sau H z − z z − z + +1 =
− w + w − 3+ 2i
− w + w − 3+ 2i = + ( y + )2 9 2  3  H  8 . 4 2 2 z = 2 − i +Khi 
(thỏa mãn điều kiện đề bài) thì H = 8 . Vậy min H = 8. w = 2 − 2i
Biểu diễn hình học số phức : Trong mặt phẳng tọa độ Oxy , gọi M , N lần lượt biểu diễn số z − z z − z phức , w thì NM =
− w . Rõ ràng điểm M thuộc đoạn thẳng AB với 2 2 ( A 0; 2
− ), B(0;2) và N là điểm thuộc đường tròn (C)có tâm I(3; 2
− ) , bán kính r =1.
https://www.facebook.com/groups/toanvd.vdc Trang 13 NHÓM TOÁN VD – VDC
ÁP DỤNG BĐT VÀ BĐT MÔ - ĐUN
+Ta có NM + IN MI NM MI −1 IA−1(Chú ý IA ⊥ AB).
+ NM NI + IM =1+ MI 1+ maxI ; A I B . NHÓ M TO ÁN VD – VDC NHÓ M TO ÁN VD – VDC
https://www.facebook.com/groups/toanvd.vdc Trang 14