Bài giảng 5 chương 4: Differentiation | Môn kinh tế vi mô

7/27/2020 lOMoAR cPSD| 47207194 Slide 4.1 Lecture 5 (24/03/2020) Chapter 4 Differentiation
• Section 4.1. The derivative of a function
• Section 4.2. Rules of differentiation
• Section 4.3. Marginal functions
• Section 4.4. Further rules of differentiation
Jacques, Mathematics for Economics and Business, 7th edition © Pearson Education Limited 2012 Slide 1.2 Section 4.1 The derivative of a function
Revisions of slopes of lines and curves and their geometric meaning,
estimating a derivative by measuring the slope of a tangent
and differentiating power functions Slide 4.3
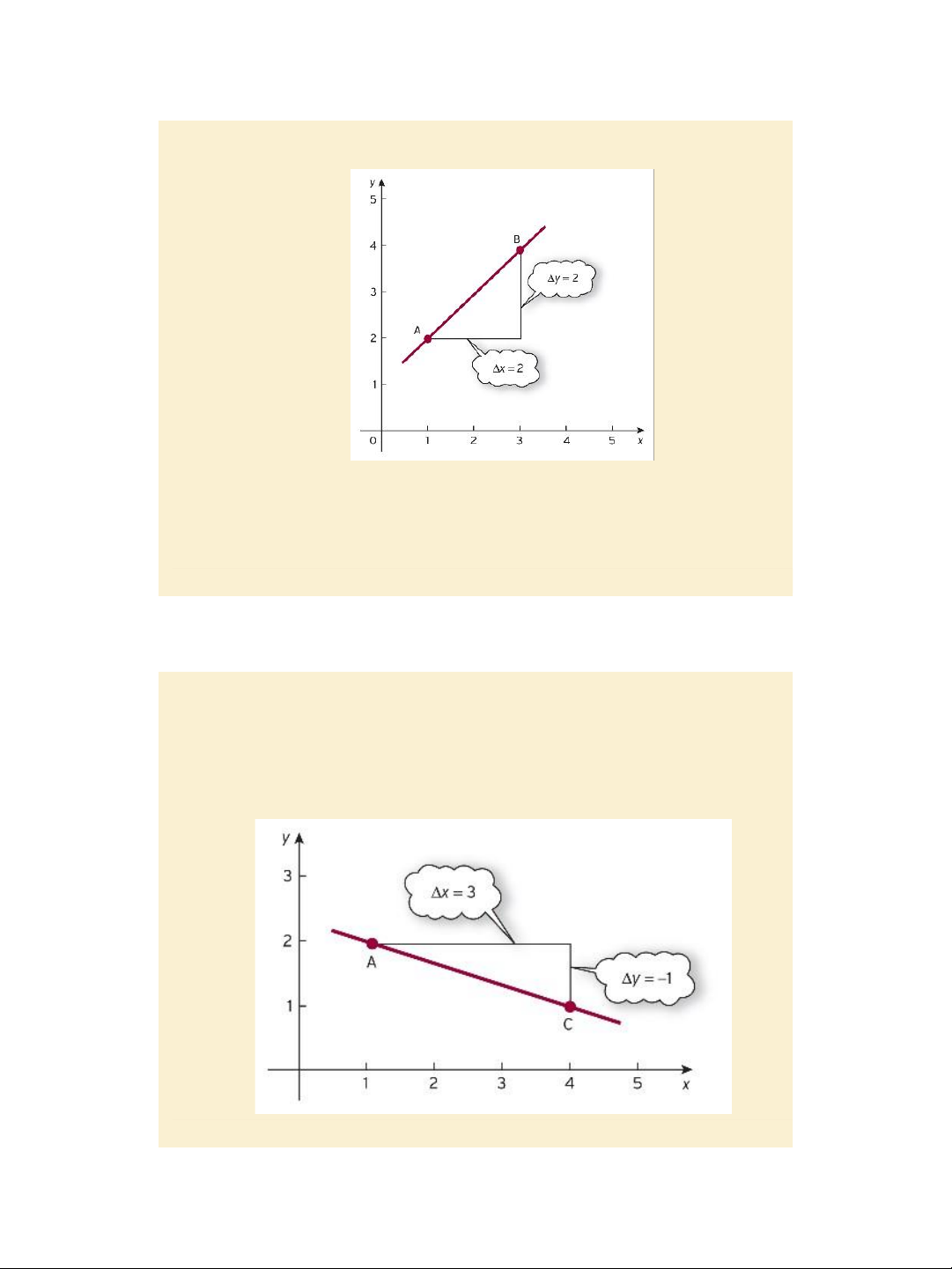
Jacques, Mathematics for Economics and Business , 7 th edition © Pearson Education Limited 2012 1 7/27/2020 lOMoAR cPSD| 47207194 Figure 4.1
Calculating the slope of a straight line:
Slope = ∆𝒚 > 0 (an uphill line), page 269 ∆𝒙
Jacques, Mathematics for Economics and Business, 7th edition © Pearson Education Limited 2012 Slide 4.4
Jacques, Mathematics for Economics and Business , 7 th edition © Pearson Education Limited 2012 2 7/27/2020 lOMoAR cPSD| 47207194 Figure 4.2
Calculating the slope of a straight line:
Slope = ∆𝒚 < 0 ( a downhill line), page 269 ∆𝒙 Slide 4.5 Figure 4.3
Calculating the slope of a straight line: ∆𝒚
Slope = = 0 ( a horizontal line), page 270 ∆𝒙
Jacques, Mathematics for Economics and Business, 7th edition © Pearson Education Limited 2012 Slide 4.6
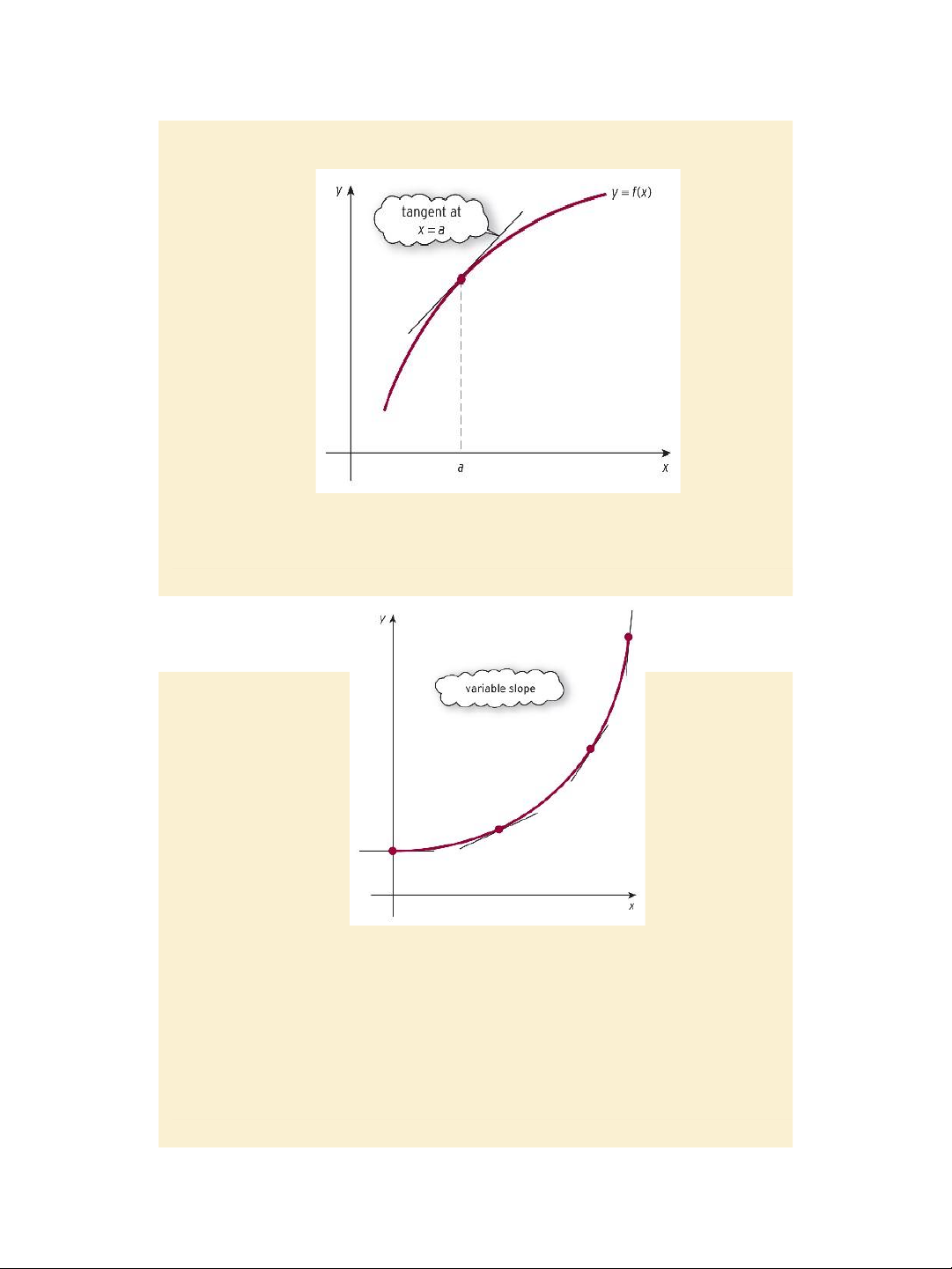
Jacques, Mathematics for Economics and Business , 7 th edition © Pearson Education Limited 2012 3 7/27/2020 lOMoAR cPSD| 47207194 Figure 4.4
The tangent at a point of a curve page 270 Slide 4.7 Figure 4.5
Variable slope: the curve becomes
steeper and steeper page 271
Jacques, Mathematics for Economics and Business, 7th edition © Pearson Education Limited 2012
Jacques, Mathematics for Economics and Business , 7 th edition © Pearson Education Limited 2012 4 7/27/2020 lOMoAR cPSD| 47207194 Slide 4.8 Figure 4.6 Constant slope for a straight line page 271 Slide 4.9 Figure 4.7
Estimating derivatives by measuring slopes
Example and practice problem, pages 272-273:
𝐝𝐲 ∆𝒚 𝒇 𝒙+𝟎.𝟓 −𝒇(𝒙−𝟎.𝟓) f’ (x)= = 𝐝𝐱 ∆𝒙 𝟏
Jacques, Mathematics for Economics and Business, 7th edition © Pearson Education Limited 2012
Jacques, Mathematics for Economics and Business , 7 th edition © Pearson Education Limited 2012 5 7/27/2020 lOMoAR cPSD| 47207194 Slide 1.10
Differentiation of power functions n then f’(x) = 𝒅𝒚 = nxn-1 If f(x) = x 𝒅𝒙
Example and practice pages 274-275 Key terms: page 277
Exercise 4.1*: Problems 3, 4, page 278 Slide 1.11 Section 4.2 Rules of differentiation
Revisions on rules of differentiation
𝑹𝒖𝒍𝒆 𝟏: 𝒉 𝒙 = 𝒄𝒇 𝒙 ⟹ 𝒉′ 𝒙 = 𝒄𝒇′ 𝒙
𝑹𝒖𝒍𝒆 𝟐: 𝒉 𝒙 = 𝒇 𝒙 ± 𝒈 𝒙 ⟹ 𝒉′ 𝒙 = 𝒇′ 𝒙 ± 𝒈′ 𝒙 Second order derivative
′′ 𝒙 = 𝒅𝒅𝒙𝟐𝒚𝟐 = 𝒇′(𝒙) ′ = 𝒅𝒙𝒅𝒅𝒚𝒅𝒙 𝒇
Jacques, Mathematics for Economics and Business , 7 th edition © Pearson Education Limited 2012 6 7/27/2020 lOMoAR cPSD| 47207194
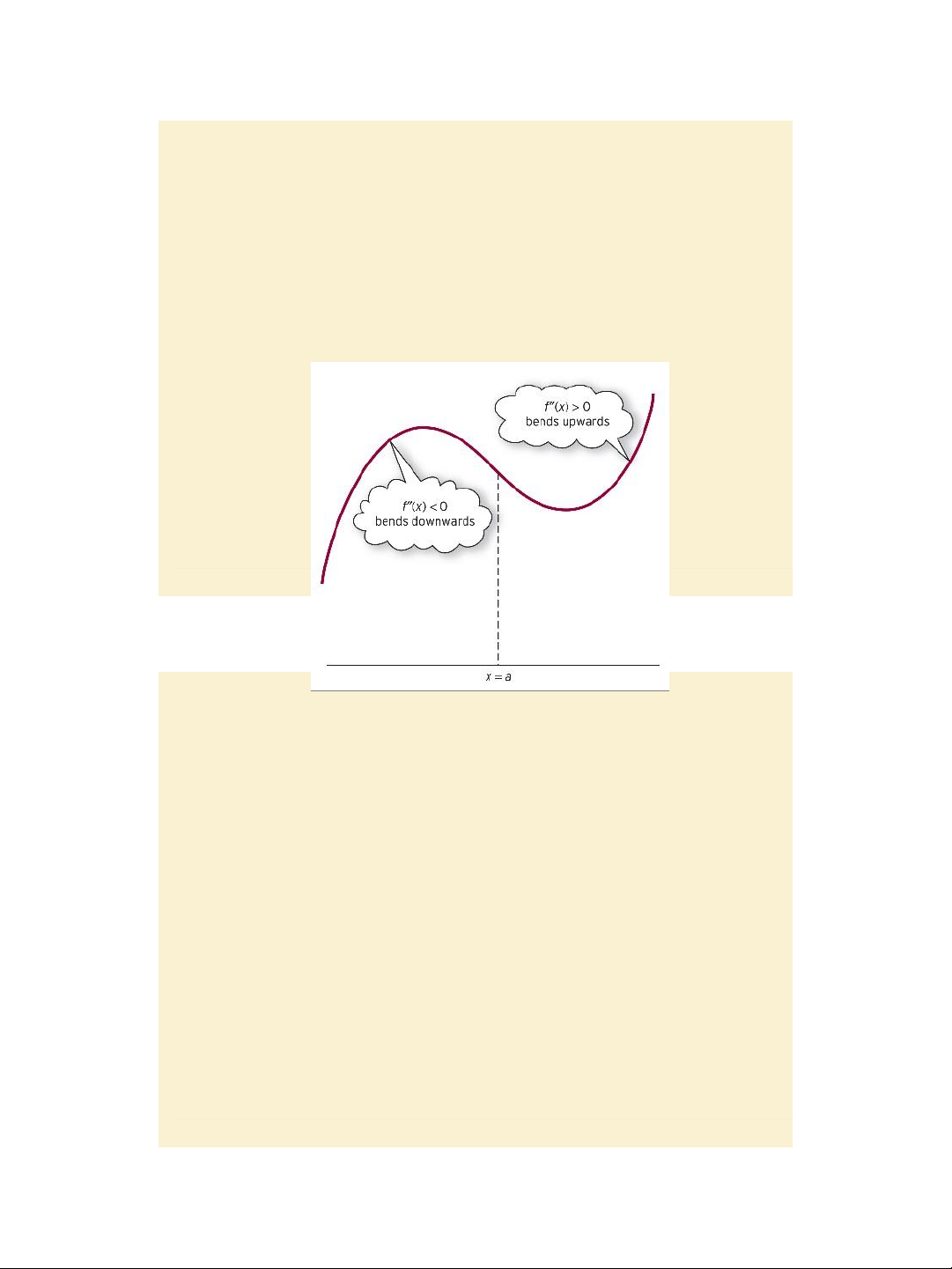
Jacques, Mathematics for Economics and Business, 7th edition © Pearson Education Limited 2012 Slide 4.12 Figure 4.11
Concavity and convexity page 285
Key terms: page 286, Exercise 4.2*: problems 2, 4, page 288 Slide 1.13 Section 4.3 Marginal functions
Marginal revenue and marginal cost
The relationship between marginal and average revenue
for monopoly and perfect competition
Jacques, Mathematics for Economics and Business , 7 th edition © Pearson Education Limited 2012 7 7/27/2020 lOMoAR cPSD| 47207194
Marginal product of labor
Marginal propensity to consume and to save
Jacques, Mathematics for Economics and Business, 7th edition © Pearson Education Limited 2012 Slide 4.14 Figure 4.12 Marginal revenue
𝑴𝑹 = 𝑻𝑹 ′ = 𝒅(𝑻𝑹) ≅ 𝚫 𝑻𝑹
𝚫𝑸 𝒇𝒐𝒓 𝒔𝒎𝒂𝒍𝒍 𝒄𝒉𝒂𝒏𝒈𝒆 𝒊𝒏 𝒅𝒆𝒎𝒂𝒏𝒅 𝑸: 𝚫𝑸 = 𝟏 𝒅𝑸
Example and practice problem, pages 290 - 291
Change in total revenue 𝚫 𝑻𝑹 ≅ 𝑴𝑹 × 𝚫𝑸
Example and practice problem, pages 291 - 292 Slide 4.15
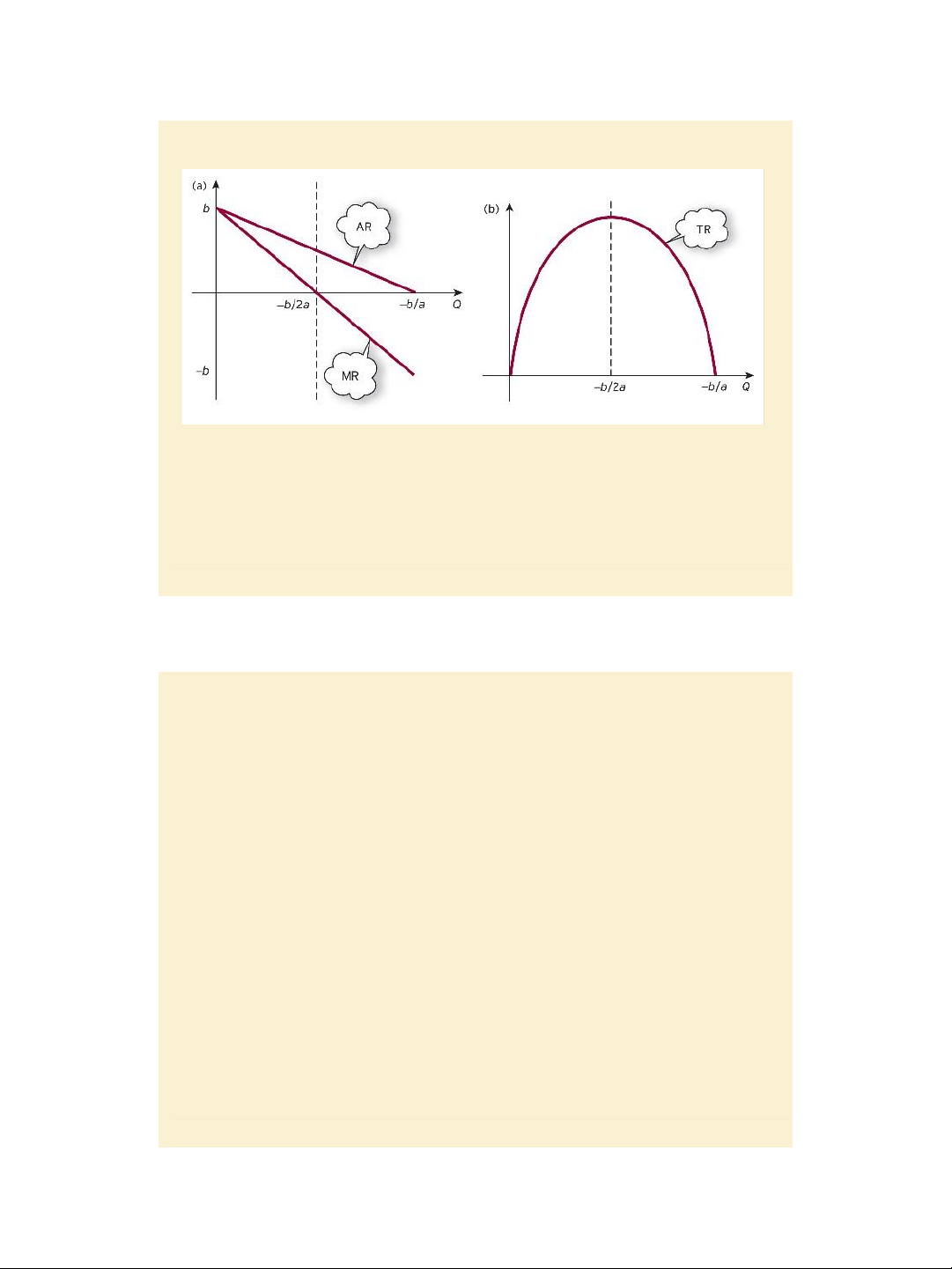
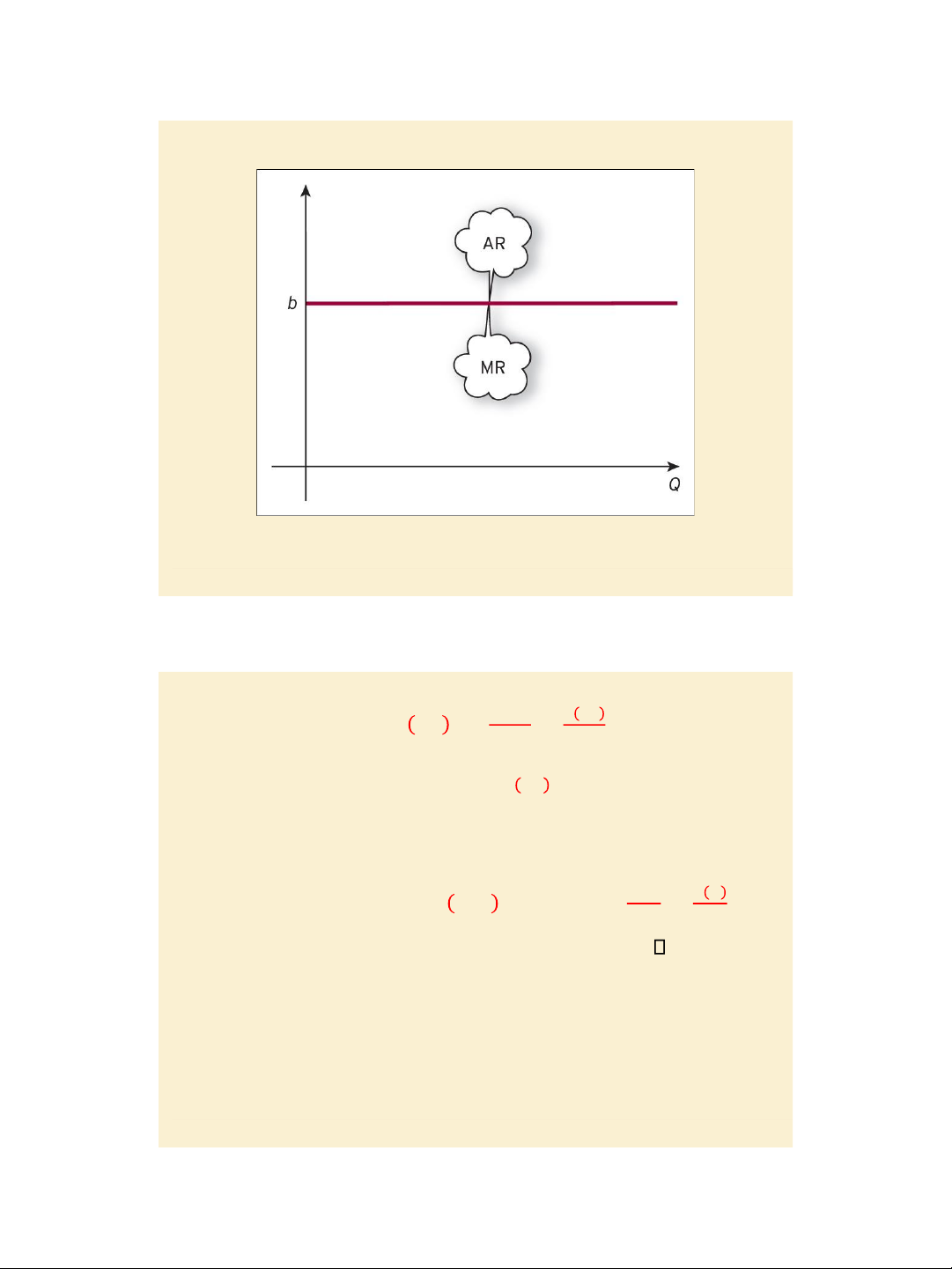
Jacques, Mathematics for Economics and Business , 7 th edition © Pearson Education Limited 2012 8 7/27/2020 lOMoAR cPSD| 47207194 Figure 4.13
The relationship between MR and Average revenue
Monopoly: P = aQ + b, TR = PQ = aQ2 + bQ, MR = 2aQ + b, AR = TR/Q =P
Example and practice problem, pages 293 - 294
Jacques, Mathematics for Economics and Business, 7th edition © Pearson Education Limited 2012 Slide 4.16
Jacques, Mathematics for Economics and Business , 7 th edition © Pearson Education Limited 2012 9 7/27/2020 lOMoAR cPSD| 47207194 Figure 4.14
The relationship between MR and Average Revenue
Perfect competition: P = b, TR = PQ = bQ, MR = b = P , AR = TR/Q =P, pages 295 - 296 Slide 4.17 Marginal cost
𝑴𝑪 = 𝑻𝑪 ′ = 𝒅(𝑻𝑪) 𝚫 𝑻𝑪 ≅ 𝒅𝑸 𝚫𝑸
for small change in demand Q: ΔQ = 1 Change
in total cost 𝚫 𝑻𝑪 𝑴𝑪 × 𝚫𝑸 ≅
Example and practice problem, page 296
Marginal product of labor
Production function 𝑸 = 𝒇 𝑲, 𝑳 ⟹ 𝑴𝑷𝑳 = 𝒅(𝑸) ≅ 𝒅𝑳 𝚫𝚫𝑳𝑸 for
small change in labor L: ΔL = 1 ⇒ MPL = (Q) Example, pages 297 – 299
Law of diminishing marginal productivity / returns “The
increase in output due to a 1 unit increase in labor will
Jacques, Mathematics for Economics and Business , 7 th edition © Pearson Education Limited 2012 10 7/27/2020 lOMoAR cPSD| 47207194
eventually decline, i.e. MPL will get smaller once the size of
workforce has reached a certain threshold level.”
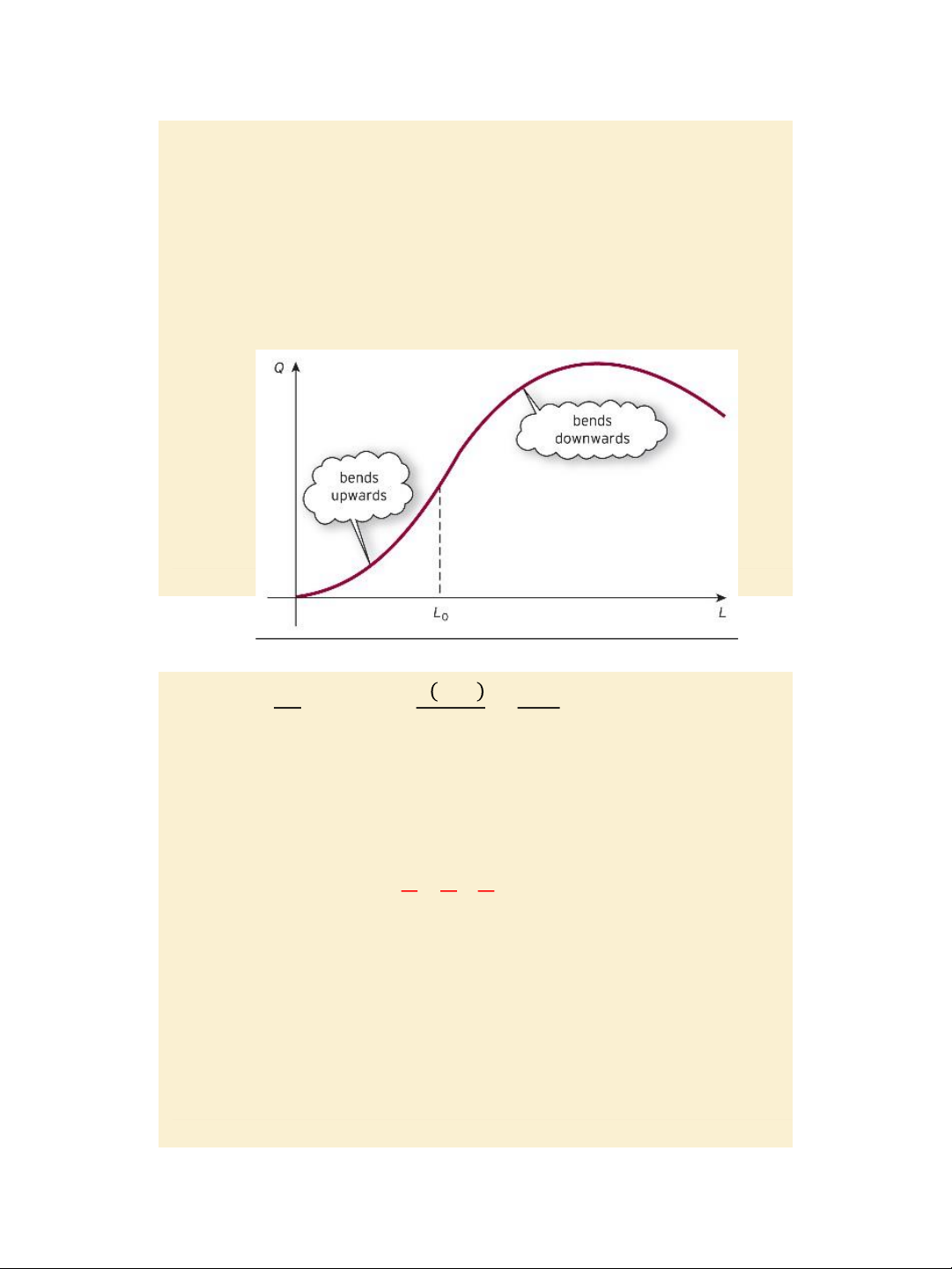
Jacques, Mathematics for Economics and Business, 7th edition © Pearson Education Limited 2012 Slide 4.18 Figure 4.15
The law of diminishing MP L 𝑑𝑄 𝑑 𝑀𝑃 𝑑 2 𝑄 𝑀𝑃 𝐿 𝐿 = ⟹ =
<0 𝑓𝑜𝑟 𝐿> 𝐿 𝑑𝐿 𝑑𝐿 𝑑𝐿 2 0
⇒ 𝑎𝑓𝑡𝑒𝑟 𝑡𝑕𝑟𝑒𝑠𝑡𝑕𝑜𝑙𝑑 𝐿0 𝑕𝑎𝑠 𝑏𝑒𝑒𝑛 𝑟𝑒𝑎𝑐𝑕𝑒𝑑, 𝑀𝑃𝐿 𝑤𝑖𝑙𝑙 𝑔𝑜 𝑑𝑜𝑤𝑛 Practice problem, page 299 Slide 4.19
Consumption and savings
Y= 𝐂 + 𝐒 ⇒ 𝒅𝒀 = 𝒅𝑪 + 𝒅𝑺 = 𝑴𝑷𝑪 + 𝑴𝑷𝑺 = 𝟏 𝒅𝒀 𝒅𝒀 𝒅𝒀
Example and practice problem, pages 299 – 300 Key terms: page 301,
Exercise 4.3*: problems 1, 2, 3, 5, 6, pages 302 - 303.
Jacques, Mathematics for Economics and Business , 7 th edition © Pearson Education Limited 2012 11 7/27/2020 lOMoAR cPSD| 47207194
Jacques, Mathematics for Economics and Business, 7th edition © Pearson Education Limited 2012 Slide 4.20 Section 4.4 Further rules of differentiation
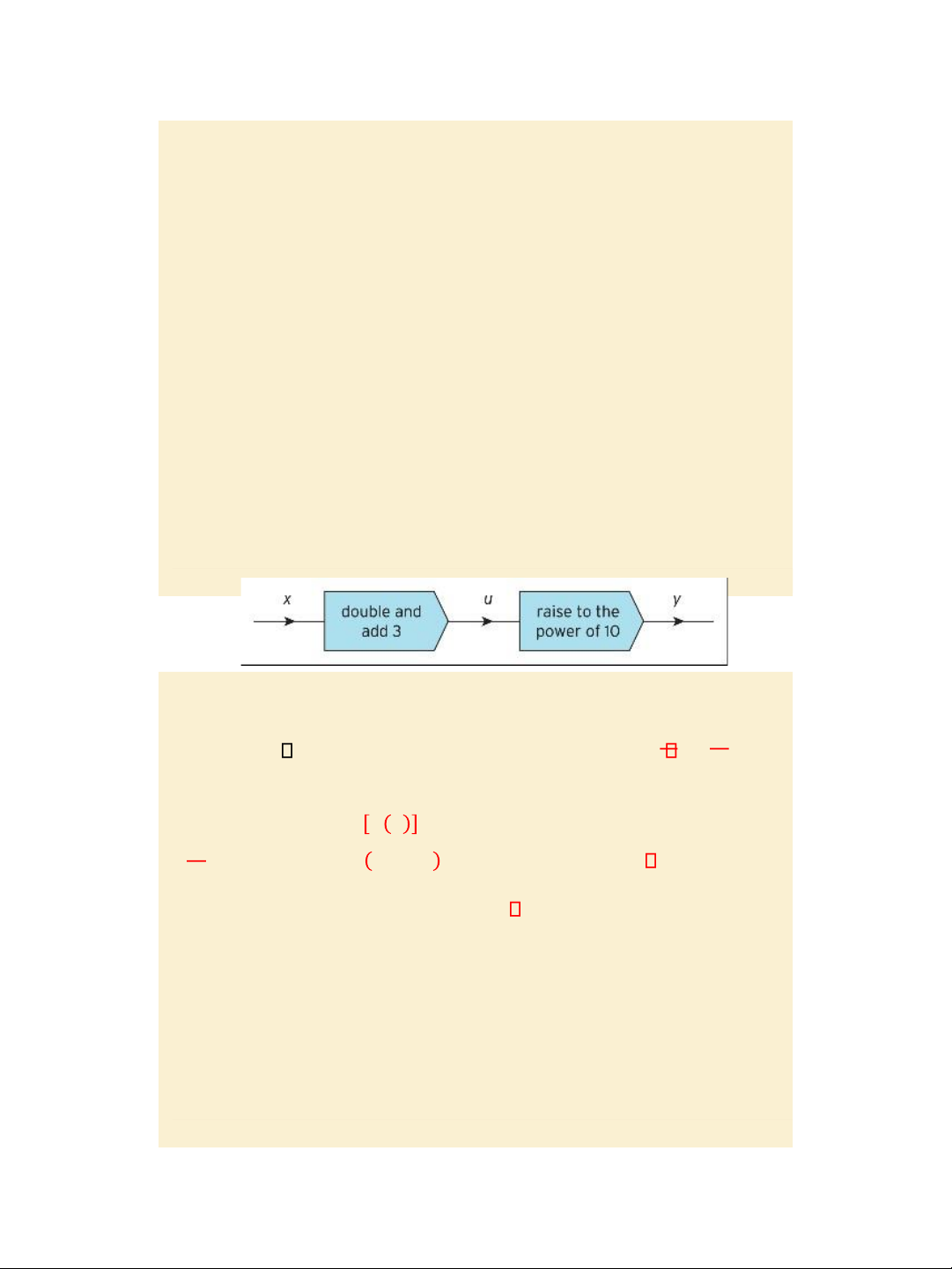
Differentiating functions using the chain rule, the product rule, and the quotient rule Figure 4.16.
The chain rule example, page 304: y = u10, u = 2x + 3 or: y =
(2x + 3)10 𝐲 = 𝐲 𝐮 𝐱 𝐔𝐬𝐢𝐧𝐠
𝐭𝐡𝐞 𝐜𝐡𝐚𝐢𝐧 𝐫𝐮𝐥𝐞 𝐝𝐲 = 𝐝𝐲 × 𝐝𝐱 𝐝𝐮
𝐝𝐮 9 × 2 = 20 2𝑥 + 3 9. The product rule: y= uv y’ = = 10𝑢 𝐝𝐱
u’v + v’u. The quotient rule: y= u/v y’ = (u’v - v’u) / v2. Example, page 306.
Exercise 4.4*: Problems 6, 7, page 313.
Jacques, Mathematics for Economics and Business , 7 th edition © Pearson Education Limited 2012 12