Bài giảng Chương 1: Các hệ thống số và mã số môn Kỹ thuật số | Trường Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

KHOA ĐIỆN – ĐIỆN TỬ
BỘ MÔN ĐIỆN TỬ CÔNG NGHIỆP – Y SINH
KỸ THUẬT SỐ (DIGI330163) CHƯƠNG 1
CÁC HỆ THỐNG SỐ VÀ MÃ SỐ
ThS. NGUYỄN TRƯỜNG DUY 28/08/2024 NỘI DUNG 2
➢ Giới thiệu các hệ thống số đếm
▪ Hệ thống số thập phân
▪ Hệ thống số nhị phân
▪ Hệ thống số bát phân
▪ Hệ thống số thập lục phân ➢ Các loại mã ▪ Mã BCD ▪ Mã Gray ▪ Mã ASCII ▪ Mã thừa 3
ThS. NGUYỄN TRƯỜNG DUY 28/08/2024 1.1 GIỚI THIỆU 3
Như chúng ta đã biết điện tử có thể phân thành hai nhóm đó là điện tử tương tự và điện
tử số. Điện tử tương tự như các thiết bị xử lý các đại lượng liên tục còn điện tử số như các
thiết bị xử lý tín hiệu rời rạc.
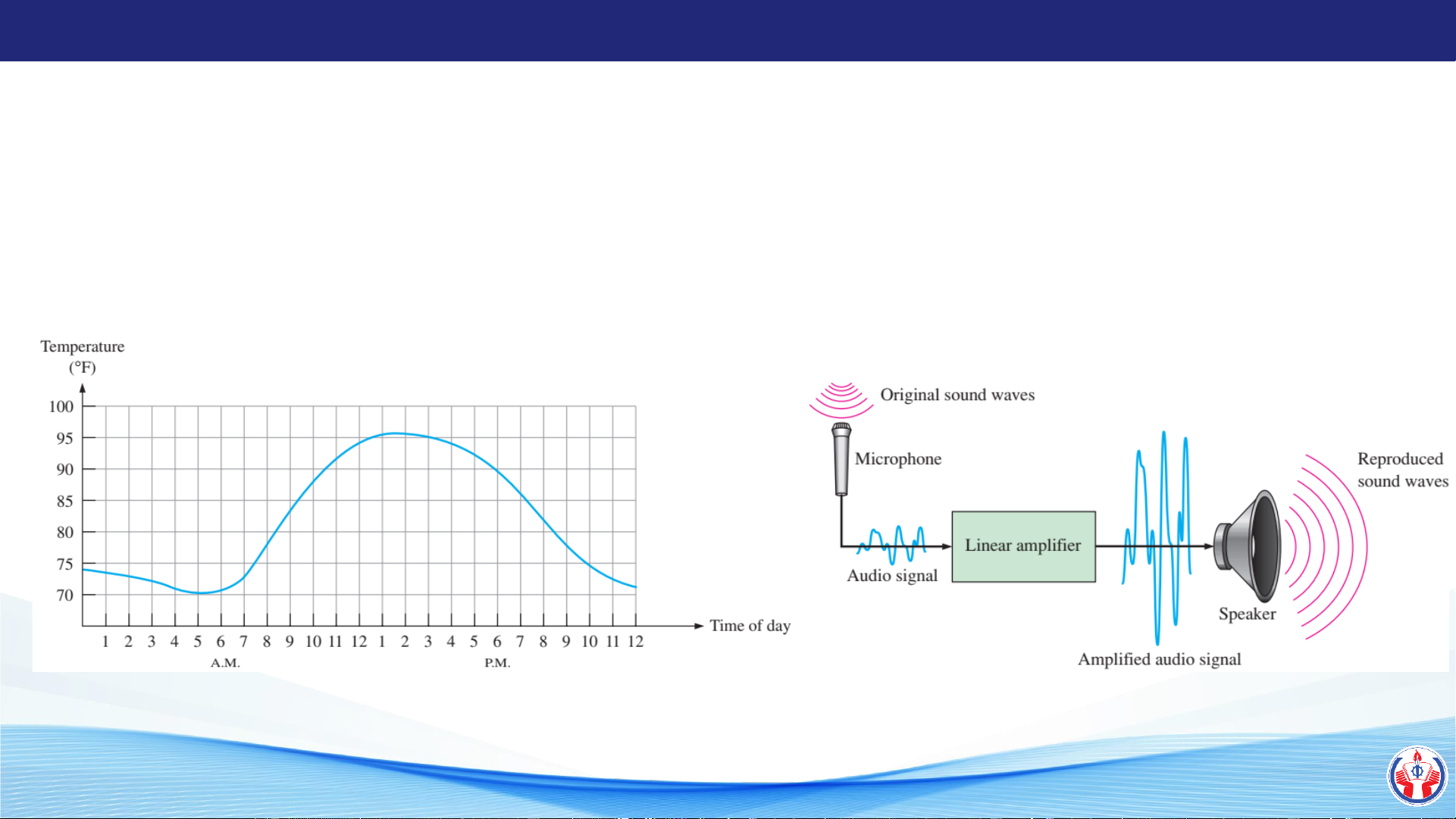
➢ Tín hiệu tương tự và hệ thống tương tự
Tín hiệu tương tự
Hệ thống tương tự
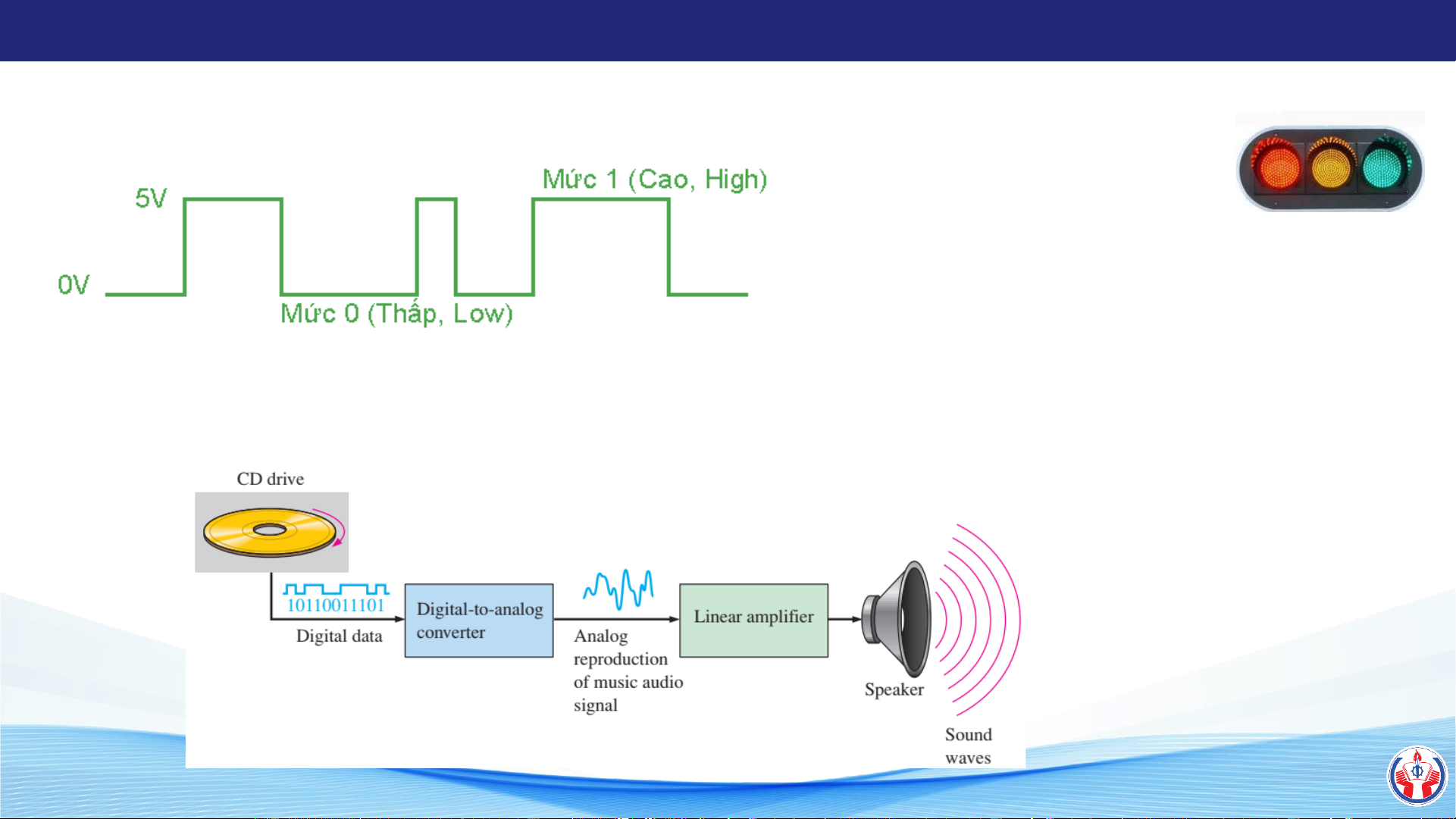
ThS. NGUYỄN TRƯỜNG DUY 28/08/2024 1.1 GIỚI THIỆU 4 ➢ Tín hiệu số
➢ Hệ thống điện tử số ▪ Đèn giao thông
▪ Bảng led quảng cáo ▪ Máy tính, …
➢ Hệ thống bao gồm cả tương tự và số
ThS. NGUYỄN TRƯỜNG DUY 28/08/2024 1.1 GIỚI THIỆU 5
➢ Ưu điểm của hệ thống số
▪ Hệ thống số dễ thiết kế hơn
▪ Thông tin được lưu trữ dễ dàng
▪ Độ chính xác cao hơn
▪ Các hoạt động có thể lập trình dễ dàng
▪ Các mạch điện tử số ít bị ảnh hưởng bởi nhiễu
▪ Nhiều mạch điện có thể tích hợp trên một IC
ThS. NGUYỄN TRƯỜNG DUY 28/08/2024 1.1 GIỚI THIỆU 6
➢ Những hạn chế của kỹ thuật số
▪ Hầu hết các đại lượng vật lý trong tự nhiên là các tín hiệu tương tự
▪ Để sử dụng kỹ thuật số điều khiển các đại lượng này với tín hiệu vào và
tín hiệu ra đều là tương tự cần thực hiện 3 bước sau:
1. Chuyển đổi các tín hiệu vào tương tự sang dạng tín hiệu số.
2. Xử lý dữ liệu số theo yêu cầu.
3. Chuyển đổi dữ liệu số sang dạng tín hiệu tương tự.
ThS. NGUYỄN TRƯỜNG DUY 28/08/2024
1.2 CÁC HỆ THỐNG SỐ ĐẾM 7
➢ Các hệ thống số chúng ta thường sử dụng bao gồm thập phân, nhị phân, bát phân và
thập lục phân. Trong số này quen thuộc nhất là hệ thống số thập phân.
➢ Các hệ thống số được phân loại theo cơ số của hệ thống số:
▪ Hệ thống số có cơ số 10 được gọi là hệ thống số thập phân (decimal number system)
▪ Hệ thống số có cơ số 2 gọi là hệ thống số nhị phân (binary number system)
▪ Hệ thống số có cơ số 8 gọi là hệ thống số bát phân (octal number system)
▪ Hệ thống số có cơ số 16 gọi là hệ thống số thập lục phân (hexadecimal number system).
ThS. NGUYỄN TRƯỜNG DUY 28/08/2024
1.2 CÁC HỆ THỐNG SỐ ĐẾM 8
➢ Hệ thống số thập phân (hệ cơ số 10)
Gồm 10 ký số: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Trọng số của mỗi ký số trong 1 số thập phân như sau:
…105 104 103 102 101 100. 10-1 10-2 10-3…
▪ Ký số tận cùng bên trái là ký số có trọng số lớn nhất MSD (Most Significant Digit).
▪ Ký số tận cùng bên phải là ký số có trọng số nhỏ nhất LSD (Least Significant Digit).
Với một hệ thống số bất kỳ có thể biểu diễn tổng quát như sau: n 1 − n−2 n 3 − 1 0 1 − 2 − −m a X + a X + a X
+...+ a X + a X + b X + b X +...+ b X n n 1 − n−2 2 1 1 2 m
ThS. NGUYỄN TRƯỜNG DUY 28/08/2024
1.2 CÁC HỆ THỐNG SỐ ĐẾM 9
➢ Hệ thống số nhị phân (hệ cơ số 2)
Gồm 2 ký số: 0 và 1
Trọng số của mỗi ký số trong 1 số nhị phân như sau:
…25 24 23 22 21 20. 2-1 2-2 2-3…
Ví dụ: Cho một số nhị phân: 1011.1012
Giá trị tương đương với số thập phân là:
1011.1012 = 123 + 022 + 121 + 120 +12-1 + 02-2 + 12-3
= 23 + 21 + 20 + 2-1 + 2-3
= 8 + 2 + 1 + 0.5 + 0.125 = 11.62510
ThS. NGUYỄN TRƯỜNG DUY 28/08/2024
1.2 CÁC HỆ THỐNG SỐ ĐẾM 10
➢ Hệ thống số nhị phân (hệ cơ số 2)
Trong hệ thống số nhị phân:
▪ Mỗi ký số (0 hoặc 1) được gọi là bit (0 hay 1).
▪ Bit tận cùng bên trái là bit có trọng số lớn nhất MSB (Most Significant Bit).
▪ Bit tận cùng bên phải là bit có trọng số nhỏ nhất LSB (Least Significant Bit).
Cách đếm các số nhị phân:
➢ Với 1 số nhị phân gồm n bit thì:
▪ Số trạng thái là 2n.
▪ Số thập phân tương ứng lớn nhất là: 2n – 1.
ThS. NGUYỄN TRƯỜNG DUY 28/08/2024
1.2 CÁC HỆ THỐNG SỐ ĐẾM 11
➢ Hệ thống số bát phân (hệ cơ số 8)
Gồm 8 ký số: 0, 1, 2, 3, 4, 5, 6, 7.
Trọng số của mỗi chữ số trong 1 số thập phân như sau:
…85 84 83 82 81 80. 8-1 8-2 8-3…
Ví dụ: Cho một số bát phân: 245.78
245.78 = 282 + 481 + 580 + 78-1
ThS. NGUYỄN TRƯỜNG DUY 28/08/2024
1.2 CÁC HỆ THỐNG SỐ ĐẾM 12
➢ Hệ thống số thập lục phân (hệ cơ số 16)
Gồm 16 ký số: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Trọng số của mỗi chữ số trong 1 số thập phân như sau:
…165 164 163 162 161 160. 16-1 16-2 16-3…
Ví dụ: Cho một số thập lục phân: 12C.7 16
12C.7H = 1162 + 2161 + 12160 + 716-1 = 300.437510
ThS. NGUYỄN TRƯỜNG DUY 28/08/2024
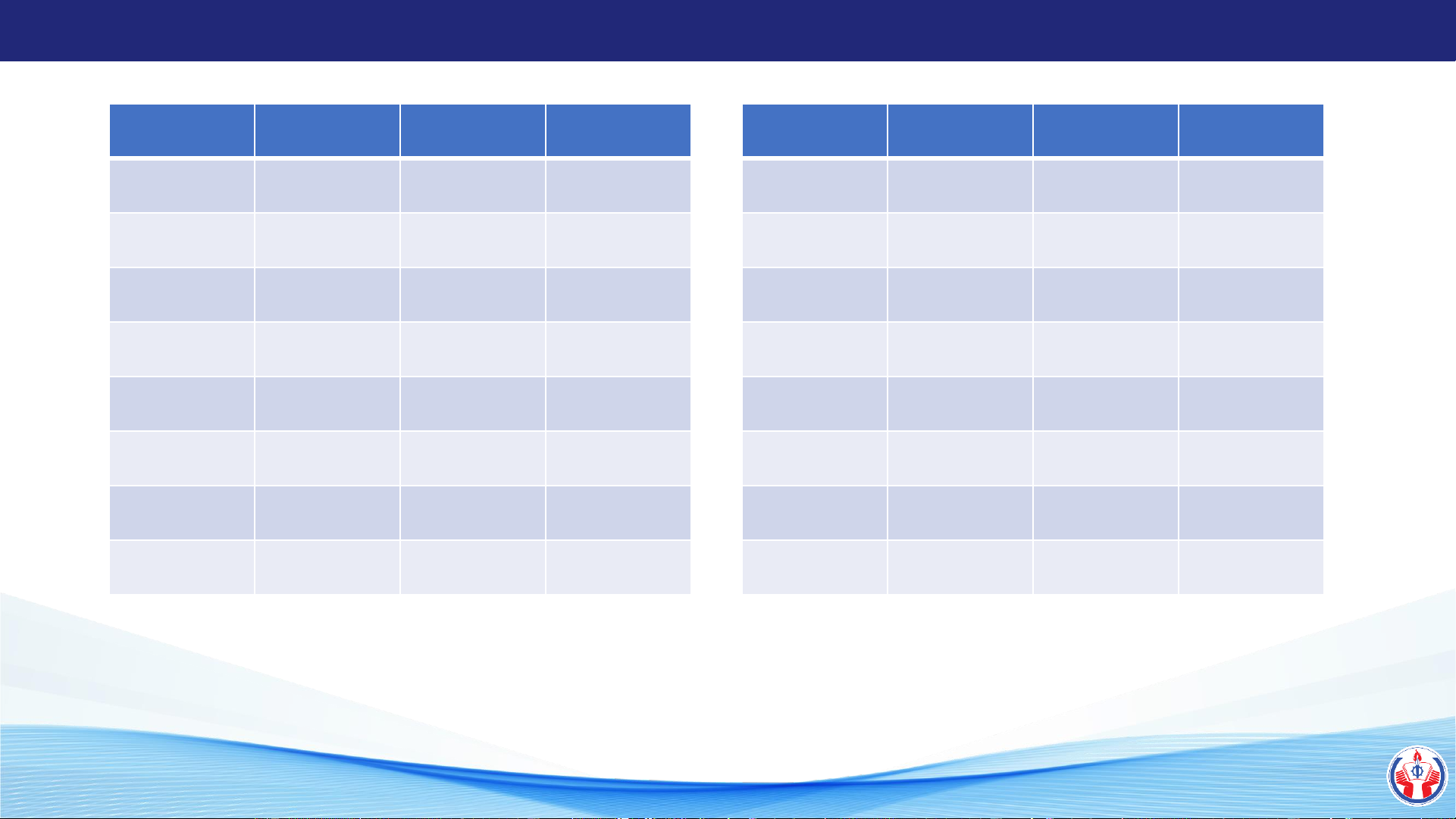
1.2 CÁC HỆ THỐNG SỐ ĐẾM 13 DEC Binary Octal Hex DEC Binary Octal Hex 0 0000 0 0 8 1000 10 8 1 0001 1 1 9 1001 11 9 2 0010 2 2 10 1010 12 A 3 0011 3 3 11 1011 13 B 4 0100 4 4 12 1100 14 C 5 0101 5 5 13 1101 15 D 6 0110 6 6 14 1110 16 E 7 0111 7 7 15 1111 17 F
ThS. NGUYỄN TRƯỜNG DUY 28/08/2024
1.3 CHUYỂN ĐỔI GIỮA CÁC HỆ THỐNG SỐ 14
➢ Chuyển từ hệ thống số có cơ số X sang thập phân
Công thức chuyển đổi như sau:
𝑮𝒊á 𝒕𝒓ị 𝒕𝒉ậ𝒑 𝒑𝒉â𝒏 = ෍ 𝑲ý 𝒔ố 𝒙 𝑪ơ 𝒔ố𝒕𝒓ọ𝒏𝒈 𝒔ố
Ví dụ: Chuyển đổi số nhị phân 1101101B thành thập phân Trọng số 6 5 4 3 2 1 0 Số nhị phân 1 1 0 1 1 0 1
1101101B = 1.26 + 1.25 + 0.24 + 1.23 + 1.22 + 0.21 + 1.20
= 64 + 32 + 8 + 4 + 1 = 10910
ThS. NGUYỄN TRƯỜNG DUY 28/08/2024
1.3 CHUYỂN ĐỔI GIỮA CÁC HỆ THỐNG SỐ 15
➢ Chuyển từ hệ thống số thập phân sang hệ thống số có cơ số X
❑ Đối với phần nguyên:
▪ Lấy số thập phân chia liên tục cho X cho đến khi kết quả bằng 0 và lấy số dư sau mỗi lần chia
▪ Số dư đầu tiên là LSD (LSB), số dư cuối cùng là MSD (MSB)
❑ Đối với phần lẻ:
▪ Lấy phần lẻ số thập phân nhân liên tục cho X và giữ phần nguyên sau mỗi
lần nhân (cho đến khi phần lẻ số thập phân bằng 0 hoặc lấy đủ số lẻ cần thiết)
▪ Phần nguyên đầu tiên là MSD (MSB), phần nguyên cuối cùng là LSD (LSB)
ThS. NGUYỄN TRƯỜNG DUY 28/08/2024
1.3 CHUYỂN ĐỔI GIỮA CÁC HỆ THỐNG SỐ 16
➢ Chuyển từ hệ thống số thập phân sang hệ thống số có cơ số X
Ví dụ: Chuyển 12 thành nhị phân 10
ThS. NGUYỄN TRƯỜNG DUY 28/08/2024
1.3 CHUYỂN ĐỔI GIỮA CÁC HỆ THỐNG SỐ 17
➢ Chuyển từ hệ thống số thập phân sang hệ thống số có cơ số X
Ví dụ: Chuyển 0.312510 thành nhị phân
ThS. NGUYỄN TRƯỜNG DUY 28/08/2024
1.3 CHUYỂN ĐỔI GIỮA CÁC HỆ THỐNG SỐ 18
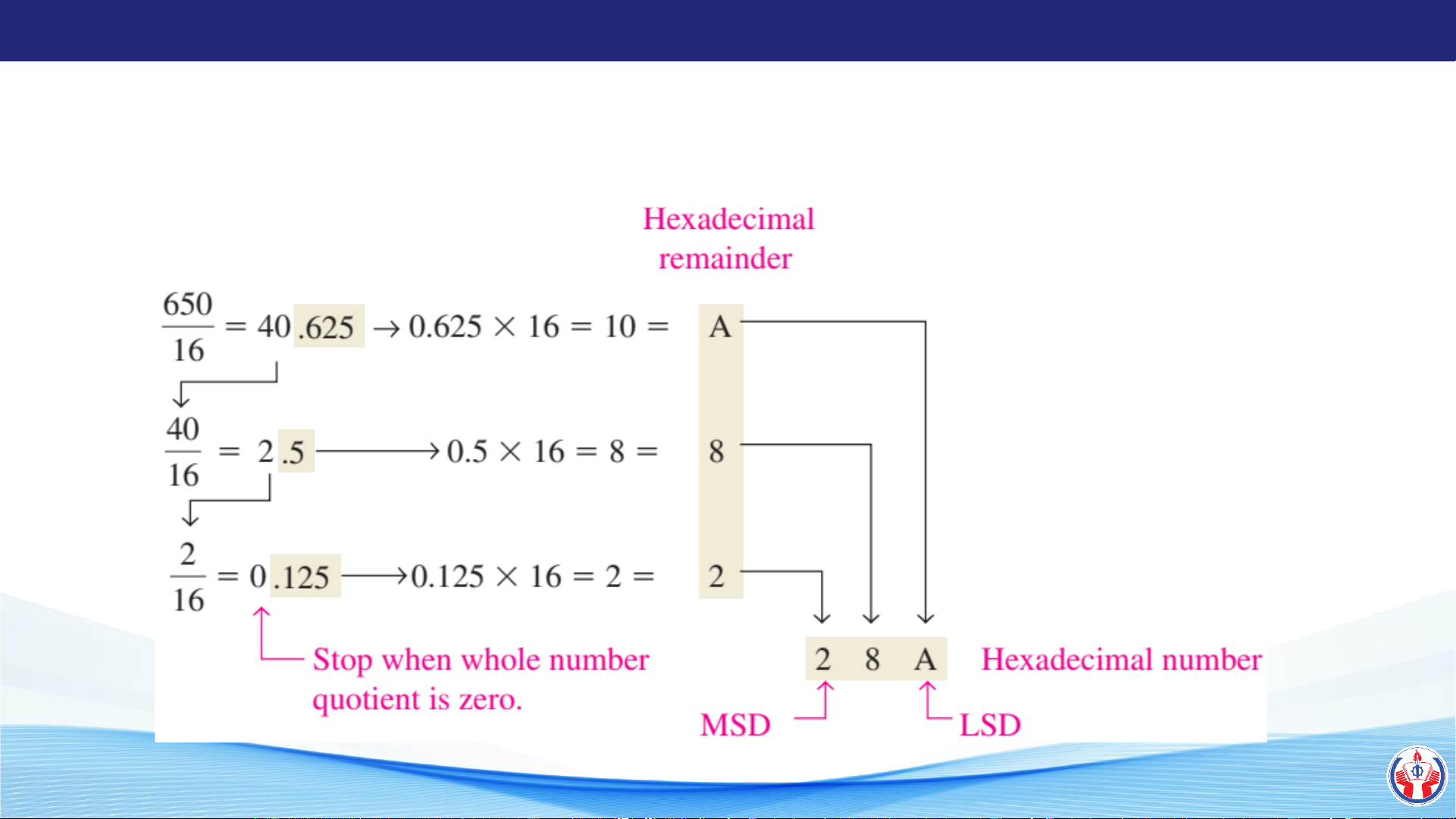
➢ Chuyển từ hệ thống số thập phân sang hệ thống số có cơ số X
Ví dụ: Chuyển 650 thành thập lục phân 10
ThS. NGUYỄN TRƯỜNG DUY 28/08/2024
1.3 CHUYỂN ĐỔI GIỮA CÁC HỆ THỐNG SỐ 19
➢ Chuyển từ hệ thống số thập phân sang hệ thống số có cơ số X
Ví dụ: Chuyển 359 thành bát phân 10
ThS. NGUYỄN TRƯỜNG DUY 28/08/2024
1.3 CHUYỂN ĐỔI GIỮA CÁC HỆ THỐNG SỐ 20
➢ Chuyển từ hệ thống số nhị phân sang thập lục phân
Phương pháp: bắt đầu từ phải sang trái tách số nhị phân thành từng nhóm 4
bit. Sau đó chuyển từng nhóm sang số Hex
Ví dụ: Chuyển 1100101001010111B và 111111000101101001B thành số Hex
ThS. NGUYỄN TRƯỜNG DUY 28/08/2024