Bài giảng chương 1: ma trận và các phép toán | Toán kinh tế

TRƯỜNG ĐẠI HỌC TÔN ĐỨC THẮNG KHOA TOÁN THỐNG KÊ Bộ môn Toán Kinh Tế CHƯƠNG 1
MA TRẬN VÀ CÁC PHÉP TOÁN
(Matrix and matrix operators)
GV: ThS. Phạm Thị Yến Anh
Email: phamthiyenanh@tdtu.edu.vn Chương 1.
MA TRẬN VÀ CÁC PHÉP TOÁN
1.1. Ma trận và các phép toán trên ma trận.
1.2. Phép khử Gauss-Jordan và hệ phương trình tuyến tính.
1.3. Định thức của ma trận.
1.4. Ma trận nghịch đảo.
1.5. Mô hình Input – Output Leontief.
1.6. Mô hình cân bằng thị trường. 2 12/02/2023
C01120 - CHAPTER 1. MATRIX AND MATRIX OPERATORS MA TRẬN (matrix) 3 12/02/2023
C01120 - CHAPTER 1. MATRIX AND MATRIX OPERATORS
MỘT SỐ VÍ DỤ MA TRẬN 8 x 8 4 12/02/2023
C01120 - CHAPTER 1. MATRIX AND MATRIX OPERATORS
MỘT SỐ VÍ DỤ MA TRẬN 1.048.576x16.384 5 12/02/2023
C01120 - CHAPTER 1. MATRIX AND MATRIX OPERATORS
1.1. MA TRẬN VÀ CÁC PHÉP TOÁN MA TRẬN (matrix)
Một ma trận A loại m x n là một bảng chữ
nhật gồm mxn số thực được viết thành m hàng
(dòng) n cột như sau: 6 12/02/2023
C01120 - CHAPTER 1. MATRIX AND MATRIX OPERATORS MA TRẬN (MATRIX)
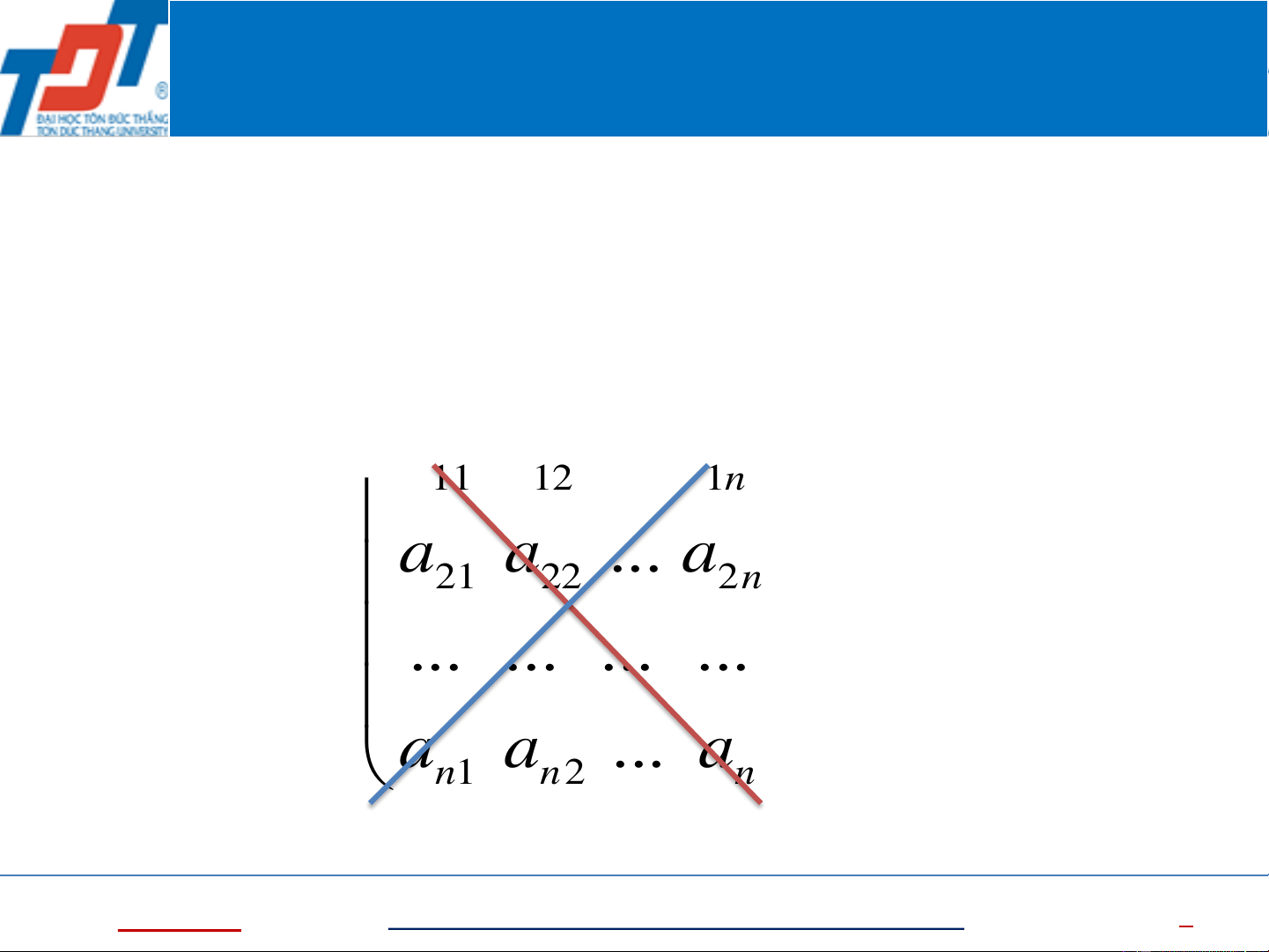
 a a ... a  11 12 1n Kí hiệu:  
𝑨 = (𝒂𝒊𝒋)𝒎𝒙𝒏 a a ... a 21 22 2n  
A   ... ... a ...  ij   Dòng i   a a ... a  1 m m2
mn mn
Cột j 𝑎𝑖𝑗 là phần tử của ma trận A nằm
ở giao điểm của dòng i cột j 7 12/02/2023
C01120 - CHAPTER 1. MATRIX AND MATRIX OPERATORS MA TRẬN (MATRIX) Ví dụ 1 −1 0 a/
là ma trận cấp 2x3 và có các 4 2 3 phần tử là
𝑎11 = 1; 𝑎12 = −1; 𝑎13 = 0 ;
𝑎21 = 4; 𝑎22 = 2; 𝑎23 = 3 1 2 b/
là ma trận cấp 2x2 và có các phần 4 3
tử: 𝑎11 = 1; 𝑎12 = 2; 𝑎21 = 4; 𝑎22 = 3 8 12/02/2023
C01120 - CHAPTER 1. MATRIX AND MATRIX OPERATORS MA TRẬN VUÔNG
• Khi m = n, bảng số thành hình vuông, ta có
ma trận vuông với n hàng n cột, ta gọi nó là ma trận cấp n  a a ... a  11 12 1n   a a ... a 21 22 2n  
A   ... ... ... ...    a a ... a  1 n n 2
nn  n  n Đường chéo phụ Đường chéo chính 12/02/2023
C01120 - CHAPTER 1. MATRIX AND MATRIX OPERATORS 9 MA TRẬN CHÉO 1 0 0 0 0 0    0 3 0 0 0 0    0 0 0 0 0 0    0 0 0 1 0 0    0 0 0 0 5 0      0 0 0 0 0 1 6 x 6
Ma trận chéo là ma trận vuông có các phần tử 10
nằm ngoài đường chéo chính bằng 0. MA TRẬN ĐƠN VỊ 1 0 0 0 0 0    0 1 0 0 0 0    0 0 1 0 0 0    0 0 0 1 0 0    0 0 0 0 1 0      0 0 0 0 0 1  6 x 6
Ma trận đơn vị là ma trận chéo có các phần tử nằm 11
trên đường chéo chính đều bằng 1. Ký hiệu In MA TRẬN TAM GIÁC
Ví dụ: 1 2 5 0 6 0    0 2 0 1 0 7    0 0 1 0 0 3    0 0 0 2 0 0    0 0 0 0 1 1       0 0 0 0 0 1 6 x 6
Ma trận tam giác trên là ma trận vuông có các phần 12
tử nằm phía dưới đường chéo chính đều bằng 0. MA TRẬN TAM GIÁC
Ma trận tam giác dưới là ma trận vuông có các
phần tử nằm phía trên đường chéo chính đều bằng 0.  1 0 0    2 0 0     2  3 5   3 x 3
Ma trận tam giác trên hay ma trận tam giác dưới gọi 13
chung là ma trận tam giác.
CÁC PHÉP TOÁN TRÊN MA TRẬN 1. PHÉP CHUYỂN VỊ
Cho ma traän A  (a ) ij mn
Ma traän chuyeån vò cuûa A kí hieäu laø T A  (a ) ji nm Ví dụ:  1 2 3   1 0 1   A  0 5  T    1 A    2 5 2    1 2 0    3   1 0 12/02/2023
C01120 - CHAPTER 1. MATRIX AND MATRIX OPERATORS 14
CÁC PHÉP TOÁN TRÊN MA TRẬN 2. HAI MA TRẬN BẰNG NHAU
Cho ma traän A  (a ) , B  (b ) ij mn ij mn
A  B  a  b ij ij 12/02/2023
C01120 - CHAPTER 1. MATRIX AND MATRIX OPERATORS 15
CÁC PHÉP TOÁN TRÊN MA TRẬN 2. HAI MA TRẬN BẰNG NHAU 1 3   y   2x 1 3y  Ví dụ: A  ; B       z 2t 
 z  3 t  2 x  0 2x 1 1  3   y  3  y  3   y  2 A  B     z  3  z 3  z  t   2  2t  2 t  2  12/02/2023
C01120 - CHAPTER 1. MATRIX AND MATRIX OPERATORS 16
CÁC PHÉP TOÁN TRÊN MA TRẬN
Cho ma traän A  (a ) , B  (b ) 3. PHÉP CỘNG ij mn ij mn (TRỪ)
C  A  B  (a b ) ij ij mn  1  3 2 1 0 1  Ví dụ: A    , B  0 1 1  1 2 0  2 3 2 3  0 3 3  2 3 1 A  B   A  B  1 3 1      1 1 1 2 3   23 12/02/2023
C01120 - CHAPTER 1. MATRIX AND MATRIX OPERATORS 17
CÁC PHÉP TOÁN TRÊN MA TRẬN 4. PHÉP NHÂN
Cho ma traän A  (a ) ,   VỚI SỐ THỰC ij mn A  (a ) ij mn Ví dụ 1:  1  3 2 A    ,   2  0 1 12 3  2 6 4 
A  2A     0 2 2 23 12/02/2023
C01120 - CHAPTER 1. MATRIX AND MATRIX OPERATORS 18
CÁC PHÉP TOÁN TRÊN MA TRẬN
Ví dụ 2: Một công ty sản xuất bàn và ghế tại 2 địa điểm khác nhau A, B.
Cho C là ma trận tổng chi phí sản xuất mỗi loại lần lượt tại A và B.  627 681 C  Bàn 135 150   Ghế
Địa điểm A Địa điểm B
Giả sử chỉ có 2 loại chi phí: chi phí lao động và chi phí
nguyên vật liệu. Chi phí lao động chiếm 2/3 tổng chi phí. Tính chi phí mỗi loại? 12/02/2023
C01120 - CHAPTER 1. MATRIX AND MATRIX OPERATORS 19
CÁC PHÉP TOÁN TRÊN MA TRẬN
a) Tìm ma trận chi phí lao động L đối với mỗi loại sản phẩm tại A và B ? 2 627 681  418 454 L  x      3 135 150  90 100 
b) Xác định ma trận chi phí nguyên vật liệu M ? 1 627 681 209 227 M  x      3 135 150  45 50  12/02/2023
C01120 - CHAPTER 1. MATRIX AND MATRIX OPERATORS 20