Bài giảng Chương 1 môn Truyền động điện tự động | Trường Đại học Bách Khoa Hà Nội

1.7.2.8. Chọn bộ điều chỉnh theo Ziegler-Nichols
1. Bộ điều chỉnh PID Gr(s) =Kp(1+ +Tds) (1.77)
Nếu e(t)- là tín hiệu vào của bộ điều chỉnh PID
u(t) -à tín hiệu ra của nó xác định bằng biểu thức: u(t)=Kp[e(t)+ ]
Phương tình (1.77) còn có thể viết như sau: Gr(s) =Kp+ +Kds (1.78)
Ở đây: Kp, Ti và Td là các thông số của bộ điều chỉnh. Trong đó Kp-hệ số tỷ lệ; Ti-thời gian tích phân; Td thời gian vi phân. Ki-hệ số tích phân, Kd-hệ số vi phân.
Lúc này các hệ số Kp, Ki, Kd là thông số của máy.
Lưu ý: PID hiện tại, thay vì điều chỉnh hệ số tỷ lệ ta điều chỉnh cả dải tỷ
lệ. Dải tỷ lệ này lại tỷ lệ với 1/Kp và có giá trị ví dụ 25% khi Kp=4. Hình 1.9 là sơ
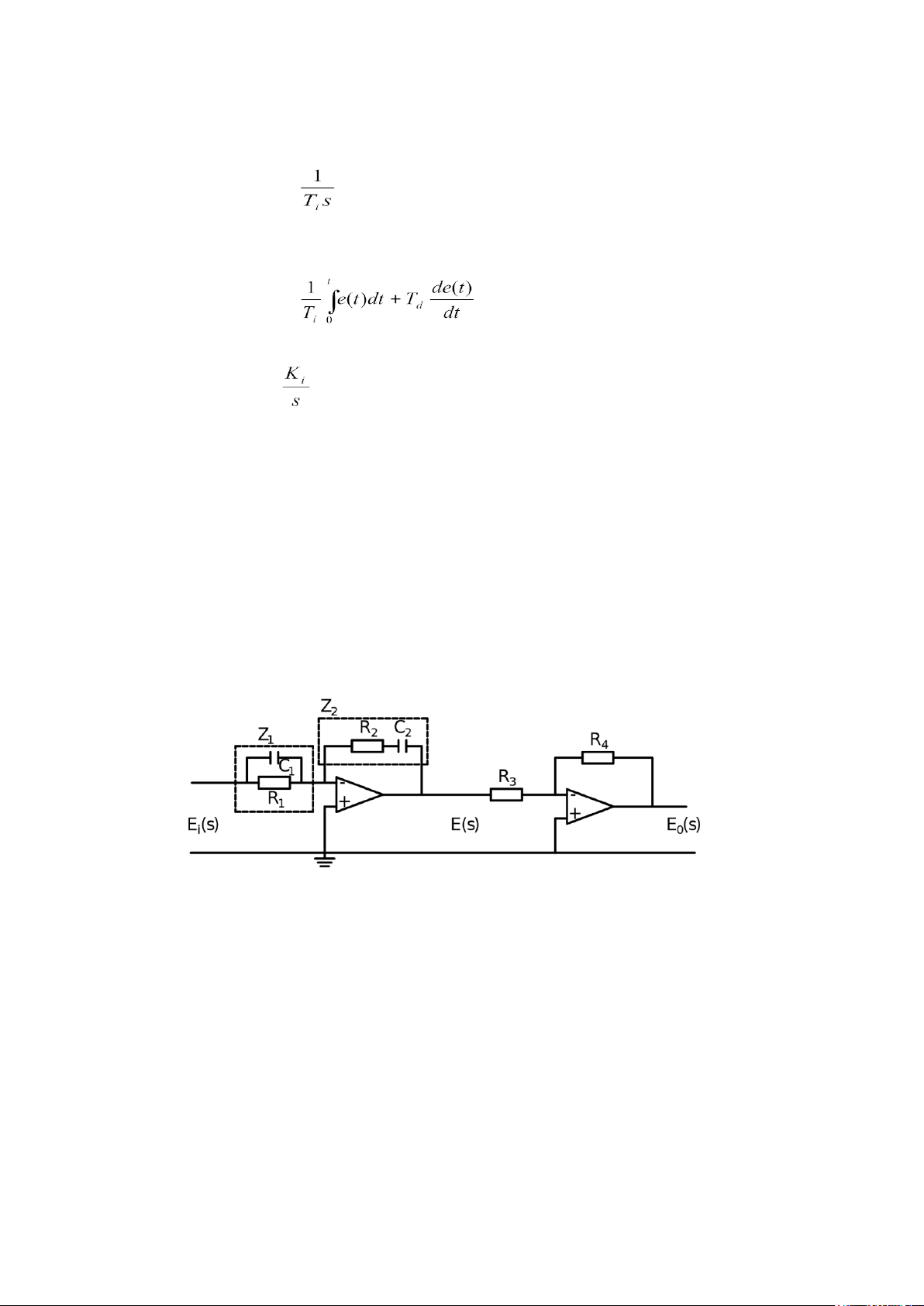
đồ bộ PID dùng khuyếch đại thuật toán.
Hàm truyền của hệ thống tính như sau: G r( s )= Trong đ ó Z 1 = ; Z 2 = Vậy G r( s )= L ư u ý rằng do đó ta có: = = Đặt: K ; T p= i= ; T d =
Các hệ số khuyếch đại của bộ PID có giá trị như sau: K ; K p= i= ; K d =
Chúng ta nhận thấy rằng mạch khuyếch đại thứ 2 hoạt động là một tín hiệu
ngược tác động như khuyếch đại điều chỉnh
Lựa chọn bộ điều chỉnh PID
Trên hình 1.10 biểu diễn hệ thống điều khiển dùng PID.
H. 1.10: Hệ thống điều chỉnh dùng PID
Nếu có mô hình toán của đối tượng, có thể áp dụng những kỹ thuật thiết
kế khác nhau để xác định thông số của bộ điều chỉnh PID.
Tuy nhiên nếu đối tượng rất phức tạp mô hình toán của nó không dễ xác
định thì ta không thể xác định các thông số của PID bằng giải tích, lúc này phải
áp dụng phương pháp thực nghiệm để xác định PID.
Quá trình lựa chọn các thông số của PID gọi là qui luật tính PID.
Ziegler và Nichols đã đề xuất qui tắc tính PID (tức là tìm các giá trị Kp,
Ti,Td) dựa trên đáp ứng thí nghiệm hoặc dựa trên giá trị.
Qui tắc Ziegler-Nichols trình bày sau đây rất thuận lợi khi mô hình toán
của đối tượng đã biết.
3. Qui tắc Ziegler-Nichols chọn thông số PID
Xác định hệ số khuyếch đại, hằng số thời gian tích phân và vi phân dựa
trên đáp ứng quá độ của đối tượng khi tín hiệu vào là tín hiệu đơn vị. Qui tắc
Ziegler- Nichols có 2 phương pháp.
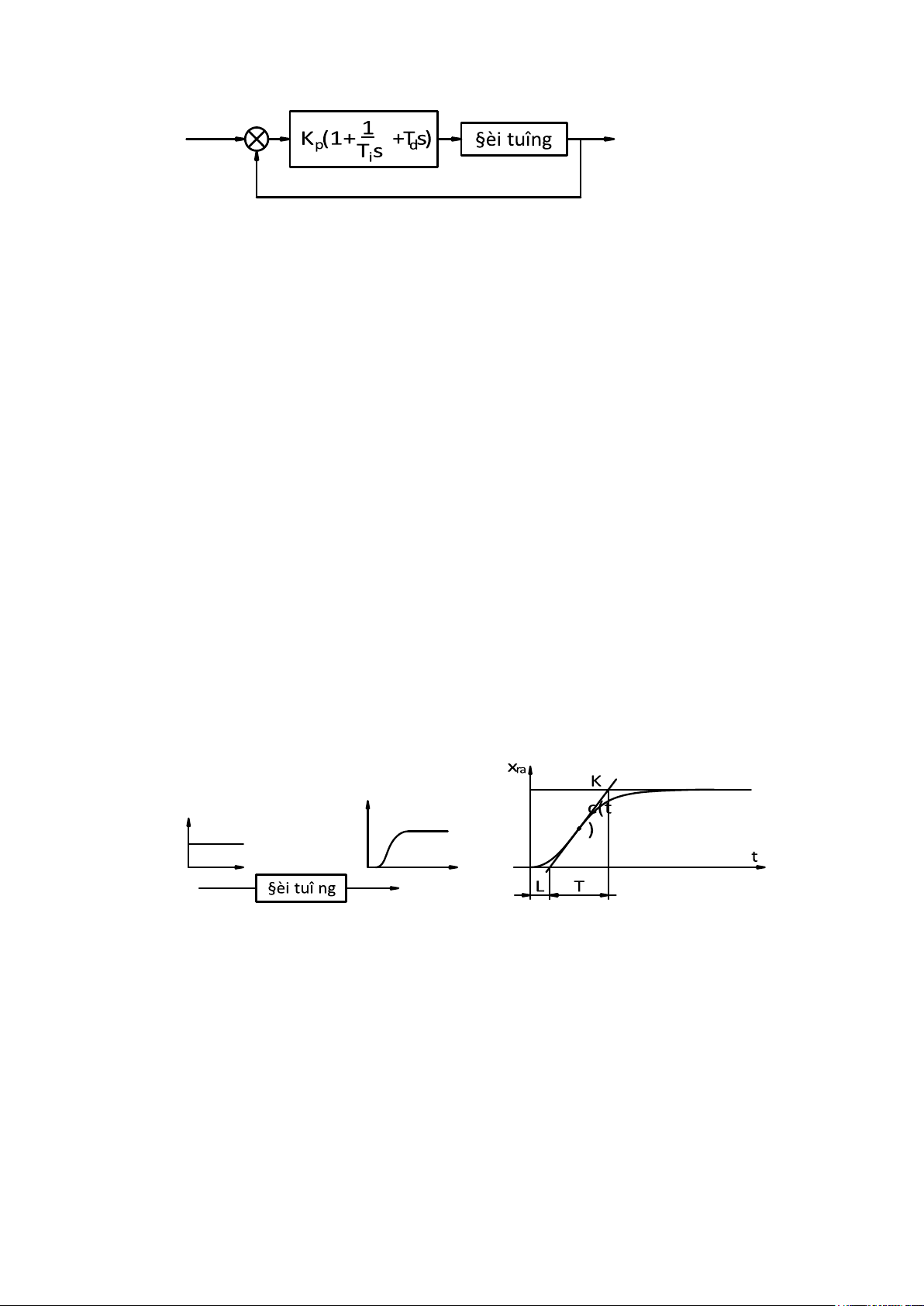
Phương pháp 1: áp dụng cho trường hợp tín hiệu đáp ứng có dạng chữ S, hình 1.12,
-Đường cong đáp ứng được bằng hàm mũ, hoặc mô phỏng đối tượng.
H. 1.12: Đối tượng và đặc tính có thể áp dụng phương pháp 1
-Đặc tính chữ S đặc trưng bằng 2 hằng số thời gian: thời gian chết L và hằng số thời gian T.
-Các đại lượng này xác định bằng tang của góc hợp bởi đường thằng đi qua
đường cong tại điểm tuyến tính và tiếp tuyến với nó, đồng thời cắt đường thằng c(t)=K (H.1.12).
-Hàm truyền C(s)/U(s) có thể tuyến tính bằng hệ tuyến tính bậc nhất có hàm truyền:
Zieglerr và Nichols đã xác định hàng loạt giá trị Kp, Ti, Td và cho ta biểu thức: G (1+ r(s)=Kp(1+ +Tds)=1,2 +0,5Ls) =0,6T.
Như vậy PID có một cực ở vùng gốc và 2 giá trị zero tại s=-1/L
Bảng 1.3: Phương pháp thứ nhất Ziegler và Nichols chọn các bộ điều chỉnh khi tín
hiệu vào là tín hiệu nhảy bậc đơn vị Loại bộ điều Kp Ti Td khiển P T/L 0 PI 0,9T/L 0 PID 2L 0,5L
Phương pháp thứ 2:
-đặt Ti= và Td=0, (chỉ sử dụng tính chất điều chỉnh tỷ lệ (xem h.1.13),
-Tăng Kp từ giá trị 0 tới giá trị tới hạn Kcr, tín hiệu ra phải dao động (nếu
với một Kp nào đó, không có dao động thì phương pháp này không áp dụng được).
Như vậy giá trị KCr và ứng với nó là chu kỳ Pcr được xác định (bằng thí
nghiệm hình 1.14). Lựa chọn các thông số của PID theo bảng 4
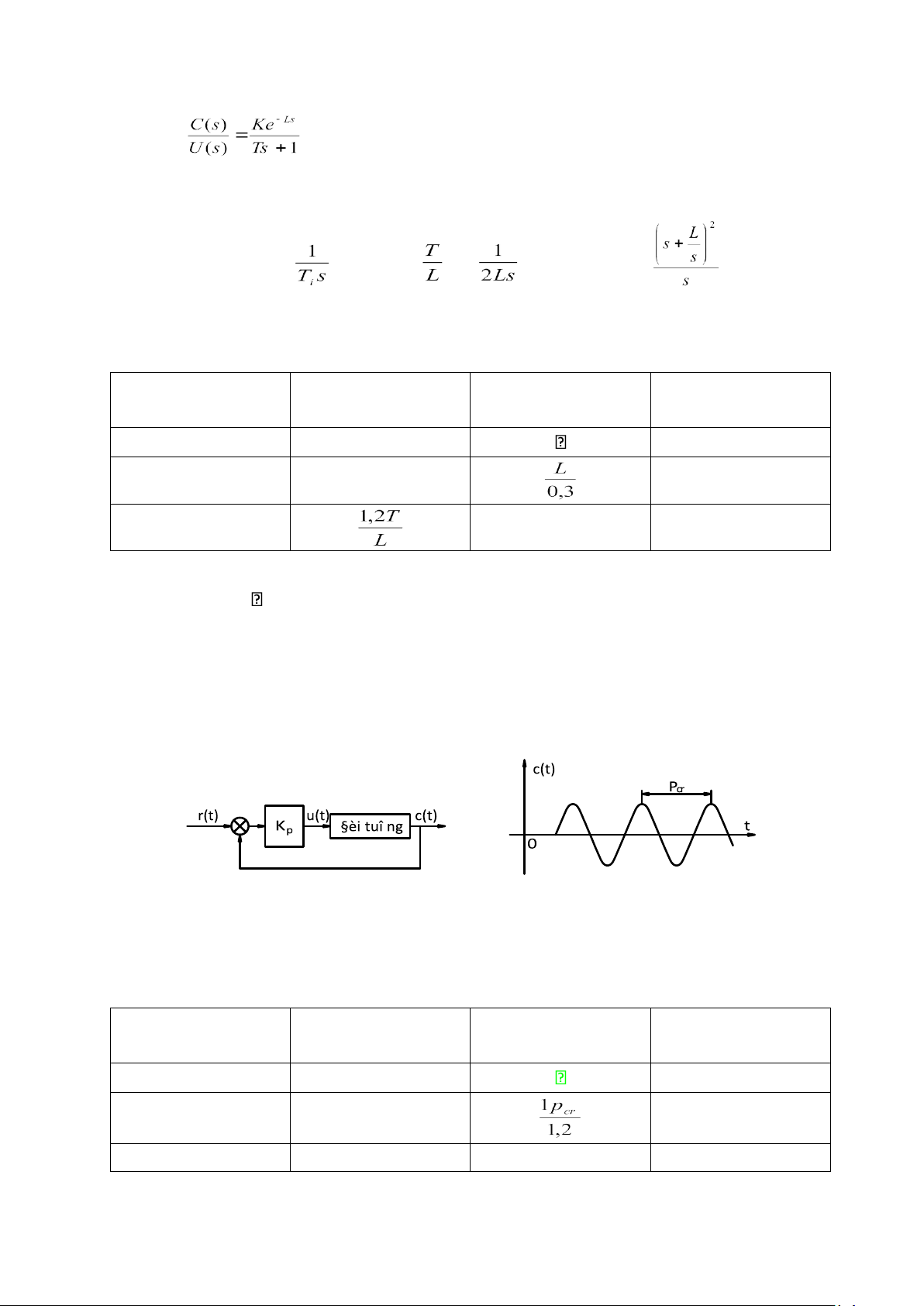
H. 1.13: Hệ thống điều chỉnh dùng PID H. 1.14: Chứa dao động với chu kỳ Pcr
Bảng 1.4: Phương pháp thứ hai Ziegler và Nichols chọn các bộ điều
chỉnh khi tính hiệu vào là tín hiệu nhảy bậc đơ n vị Loại bộ điều Kp Ti Td khiển P 0,5Kcr 0 PI 0,45Kcr 0 PID 0,6Kcr 0,5Pcr 0,125Pcr
Vậy PID chọn theo phương pháp 2 của Ziegler và Nichols có: Gr(s)=Kp(1+ +Tds)=0,6Kcr(1+ +0,125Pcrs) =0,075Kcrpcr( )
Như vậy PID có một cực ở vùng gốc và 2 giá trị zero tại s=-4/Pcr
Chú ý: Qui tắc chọn PID của Ziegler áp dụng cho hệ thống tự động khi đối
tượng không biết chính xác. Luật của Ziegler cũng có thể áp dụng cho các đối
tượng mà đặc tính động của nó đã biết.
-Nếu hàm truyền của đối tượng không biết, nhưng có thể tính được đáp
ứng của hàm đơn vị nhảy bậc, hoặc tính được Kcr hay Pcr thì ta có thể xác định
Kp, Ti và Td theo bảng 1.3 và 1.4.
- Một cách tổng quát, luật này có thể áp dụng cho đối tượng phức tạp
nhưng không chứa các khâu tích phân. Khi đối tượng chứa một khâu tích phân thì
phương pháp này có thể không áp dụng được. Ví dụ I: xét một đối tượng cụ thể sau: G(s)=
Phương pháp thứ nhất không áp dụng được, Do chứa khâu tích phân đáp
ứng không có dạng chữ S, và tăng theo thời gian.
Phương pháp thứ 2 cũng không áp dụng được vì không có dao động, để
kiểm tra ta xét ổn định của hệ thống: Phương trình đặc trưng có dạng:
s(s+1)(s+5)+Kp(s+2)(s+3)=0 Hoặc s3+(6+Kp)s2+(5+5Kp)s+6Kp=0 Ma trận Routh có dạng: s3 1 5+5Kp s2 6+Kp 6Kp s1 0 s0 6Kp
Hệ số ở cột tứ nhất đều dương cho mọi giá trị của Kp như vậy mạch kín
không xuất hiện dao động và vì vậy giá trị tới hạn của hệ số Kcr không xuất hiện
do đó phương pháp thứ 2 không áp dụng được
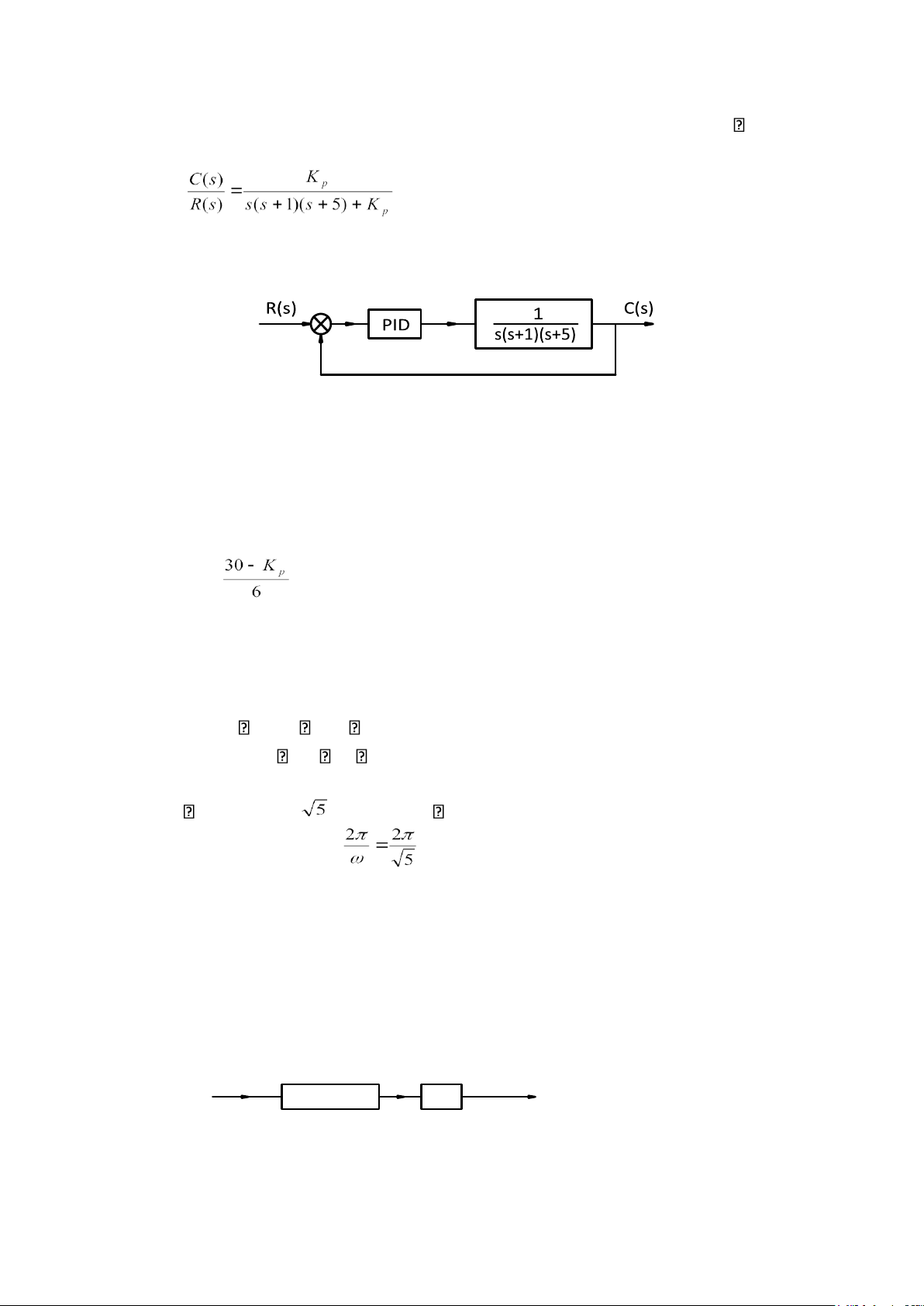
Ví dụ 2: Cho hệ thống hình vẽ 1.15 trong đó sử dụng bộ điều chỉnh PID hàm truyền của PID: Gc(s)=Kp(1+ +Tds)
Có nhiều phương pháp để lựa chọn PID ở đây sử dụng luật Ziegler-Nichols để chọn KP, Ti, Td .
Nếu sau khi chọn đáp ứng khi tín hiệu vào đơn vị có độ quá điều chỉnh
cực đại bằng 25% thì đạt, nếu px >40% sẽ chọn lại để px= 25%
Do có khâu tích phân, sử dụng qui tắc Ziegler-Nichols 2, đặt Ti= và Td=0.
Hàm truyền của hệ kín có dạng:
Giá trị Kp này làm cho hệ thống dao động , kiểm tra ổn định của hệ thống bằng định luật Rougth.
H. 1.15: PID điều khiển hệ thống
Phương trình đặc trưng: s3+6s2+5s+Kp=0 Ma trận Routh: s3 1 5 s2 6 Kp s1 s0 Kp
Nghiên cứu cột thứ nhất của ma trận Routh ta thấy dao động xảy ra khi
Kp=30 vậy Kcr =30, thay Kp=Kcr=30 ta có phương trình: s3+6s2+5s+30=0 Hay (j )3+6(j )2+(j )+30=0 Hoặc: 6(5- 2)+j (5- 2)=0
Từ phương trình này tìm tần số dao động : 2=5 hay = Do đó chu kỳ p = cr =2,81 Theo bảng 1.4 ta có:
Kp=0,6Kcr=18; Ti=0,5Pcr=1,405, Td=0,125Pcr=0,35124
1.8 Chỉ tiêu chất lượng trên mặt phẳng nghiệm phương trình đặc trưng.(đọc)
1.9. Tổng hợp hệ thống bằng phương pháp không gian trạng thái.
-Giả thiết hệ thống có tín hiệu điều khiển u và đáp ứng y (h.1.17) u x y=Cx X' = Ax+Bu C U(s) y(s) a) b)
H. 1.17: Sơ đồ khối hệ thống đơn biến a) Hệ thống hở b) Hệ thống kín Hàm truyền có dạng: G(s) = = (1.82)
Hàm này trong không gian trạng thái có thể biểu diễn bằng biểu thức: X’ =Ax+Bu (1.83a) Y = Cx (1.83b)
trong đó x-véc tơ trạng thái có kích thước n
A -ma trận vuông bậc n có các phần tử không đổi, không phụ thuộc vào thời gian.
B, C- tương ứng là ma trận cột (véc tơ) và ma trận hàng, có các phần tử
không đổi không phụ thuộc vào thời gian
Định nghĩa sau: Đối tượng (hoặc quá trình) điều khiển được là đối tượng,
nếu ta sử dụng những khoảng điều khiển giới hạn và không đổi, có thể đưa hệ
thống từ trạng thái ban đầu bất kỳ x0(x0≠0) tới trạng thái cuối cùng xk trong một
thời gian nhất định. Dễ dàng chứng minh được rằng quá trình viết bằng biểu thức
(1.83) là điều khiển được chỉ khi bậc của ma trận [B, AB,A2B....An-1B] (1.84) phải bằng n.
Giả thiết thêm rằng tất cả các thành phần x1, x2, ...xn của véc tơ trạng thái là đo được (h.1.17).
Tổng hợp hệ thống thực chất là chọn các hệ số khuyếch đại K = [k1, k2, kn] (1.85)
để sao cho với các giá trị đó, nghiệm của phương trình đặc trưng của hệ thống
kín phải nằm tại nửa trái của mặt phẳng phức, tức là hệ thống kín có tính chất đã cho (h.1.16b). Các bước thực hiện:
a. Chọn phương pháp mô hình trực tiếp song song hoặc lặp các thành phần của véc tơ trạng thái.
b. Xác định phương trình đặc trưng của hệ thống kín có các hệ số : c0,
c1, ......cn-1 là hàm các hệ số khuyếch đại k1, k2, kn
M(p) =pn+cn-1pn-1+....c1p+c0=0 (1.86)
Để lựa chọn các biến trạng thái bằng phương pháp mô hình trực tiếp, ta
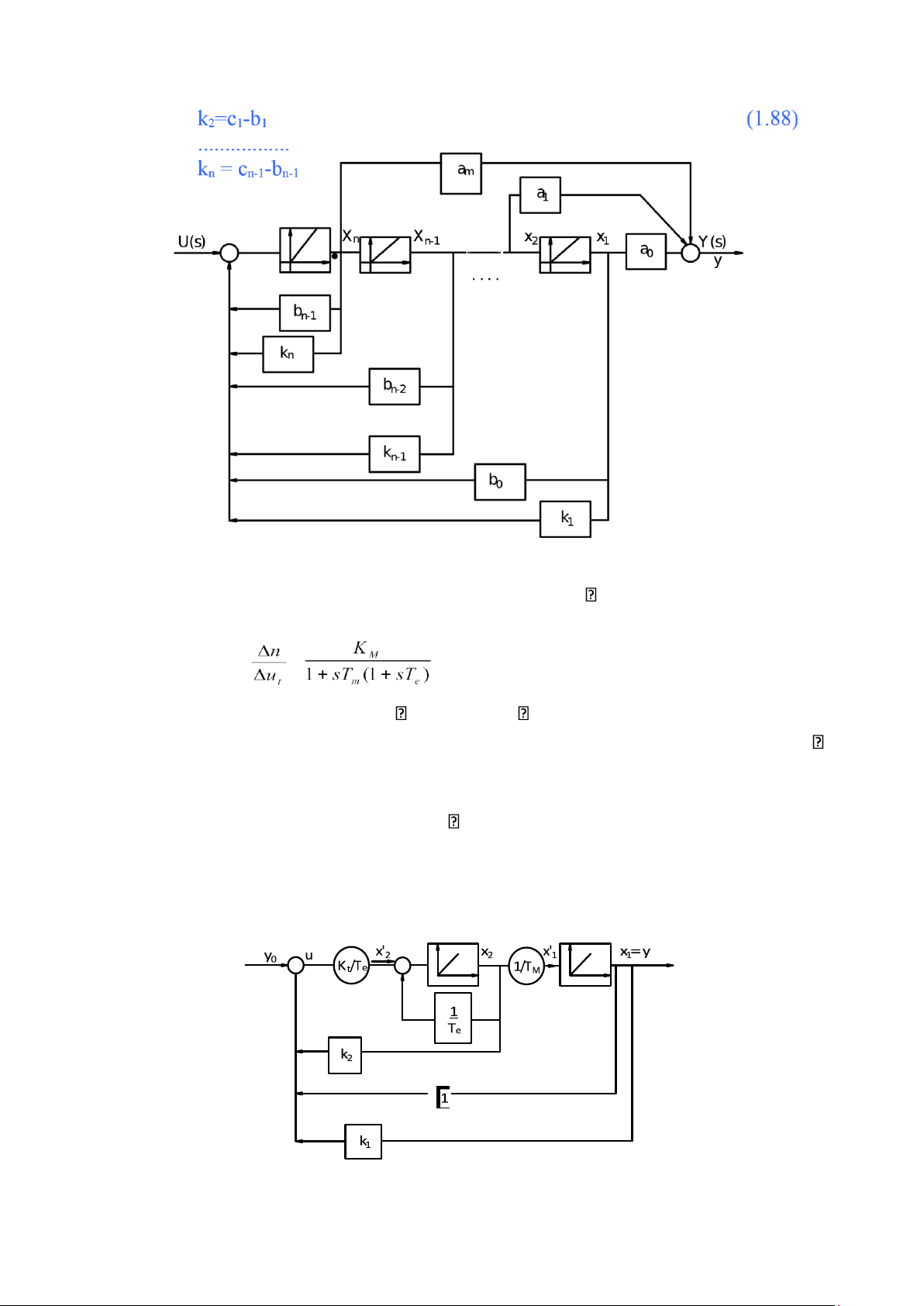
nhận sơ đồ biểu diễn trên h.1.18 trong đó c0 = b0+k1 c1 = b1+k2 (1.87) ............... cn-1=bn-1+kn
c. Từ những yêu cầu về các tính chất của hệ thống kín ta xác định
vị trí cácnghiệm s1, s2, ...sn của phương trình đặc trưng hệ thống kín
(1.83), rồi tính các hệ số c0, c1, ...cn-1
d. Đem so sánh các hệ số của lũy thừa s cùng bậc của phương trình đặc
trưng của hệ thống kín, sẽ xác định được giá trị các hệ số khuyếch đại k1, k2, ....kn
cần tìm. Với trường hợp khi thay đổi trạng thái áp dụng phương pháp trực tiếp nhận được k1 = c0-b0
H. 1.18: Sơ đồ các biến trạng thái của hệ thống hình 1.17b khi lập trình trực tiếp24
Ví dụ: động cơ một chiều kích từ độc lập có không đổi được biểu diễn
bằng hàm truyền với tín hiệu điều khiển như sau (m0=0). G(s)= = Trong đó K 2 M =1/ , Tm = TM/Kt
Động cơ có các thông số sau:Pđm = 40KW Uđm= 440V, nđm = 3000v/p,
=1, Tm =45ms,Te = 25ms, TM=450ms, Kt = 10.
Chúng ta muốn hệ thống có độ quá điều chỉnh không vượt giá trị 15% và
tần số dao động riêng không dập tắt 0 =2/Te.
Trên cơ sở sơ đồ biến trạng thái ta lựa chọn các véc tơ thành phần x1 = n; x2=it
Cần phải xác định các hệ số khuyếch đại k1, k2 như trên h.1.19 để cho hệ
thống kín có được tính chất trên.
H. 1.19: Sơ đồ biến trạng thái cho ví dụ trên Với
mục đích này ta xác định phương trình đặc trưng của hệ thống kín.
Đầu tiên ta xác định hàm truyền tương đương của hệ thống chứa trong
vòng phản hồi có hệ số khuyếch đại k2. G = 2(s)=
(1.89) hàm truyền hệ thống kín: G = 1(s) = (1.90)
Phương trình đặc trưng có dạng:
M(s) =s2TmTe+sTm(Ktk2+1)+k1+1=0 (1.91)
Đem chia 2 vế (1.91) cho TmTe được: 25 s2+s + = 0 (1.88)
Từ đặc tính biểu diễn mối quan hệ quá điều chỉnh px với hệ số tắt dần
[1] ta có khi px =15% thì có giá trị 0,5. Căn cứ vào những yêu cầu trên, hệ
thống dao động bậc 2 sẽ có dạng: s2+s2 0+ 20 = s2+2s. =0 (1.92)
So sánh các hệ số cùng bậc của phương trình (1.88) và (1.89) ta có: suy ra k2 = 1/Kt và suy ra k1 = 4 -1
Thay giá rị các thông số của động cơ điện vào các biểu thức trên ta có: k1= 4. -1 =6,2 k2= 1/10
Cần lưu ý rằng cách giải hệ thống trên đây là tĩnh và việc chỉnh định
bằng dịch chuyển các cực không đảm bảo hệ không tĩnh(astatyzm) và sai số ze
ro ở trạng thái ổn định .
1.10. Bù sai lệch tĩnh ở hệ hữu sai (đọc)
1.11. Bù sai lệch tĩnh, sai lệch tốc độ và gia tốc ở hệ vô sai cấp 1(đọc)
1.12.Cấu trúc hệ thống điều khiển (đọc)
quá giá trị cho phép khi khởi động hoặc hãm, điều đó cũng có thể do mô men tải tăng qúa mức. 26