Bài giảng Chương 5: Chuỗi Fourier môn Cơ sở kỹ thuật điện | Trường Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

KHOA ĐIỆN - ĐIỆN TỬ
BỘ MÔN CƠ SỞ KỸ THUẬT ĐIỆN
TOÁN ỨNG DỤNG CHO KỸ SƯ
CHƯƠNG 5: CHUỖI FOURIER FOURIER SERIES
TRỢ GIẢNG: LÊ QUANG SANG
CHƯƠNG 5: CHUỖI FOURIER 2 1. CHUỖI FOURIER
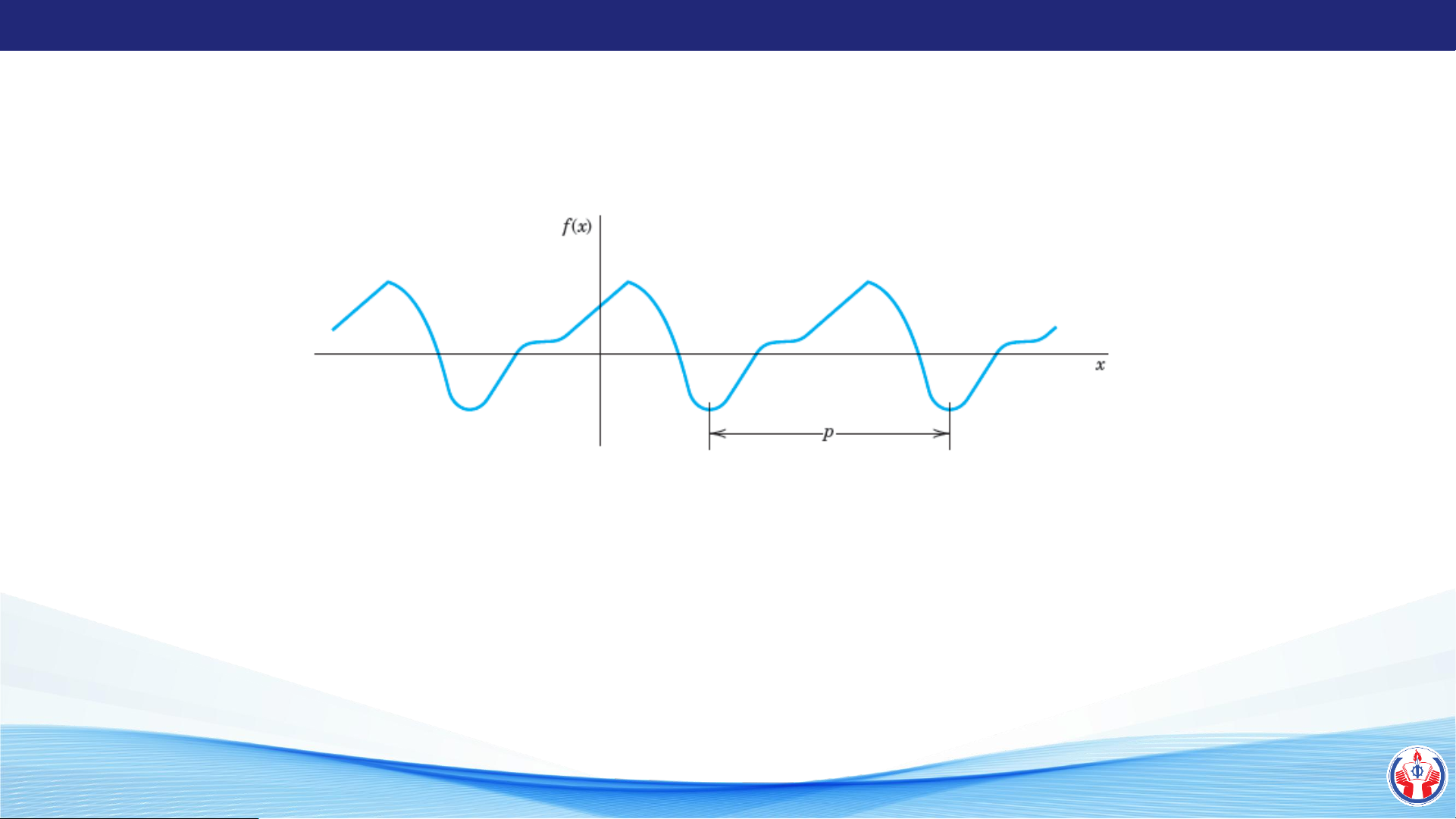
Một tín hiệu được gọi là tuần hoàn nếu thỏa mãn: 𝑓(x + np) = 𝑓(x)
Hàm f(x) tuần hoàn với chu kỳ p (period) LÊ QUANG SANG
CHƯƠNG 5: CHUỖI FOURIER 3 1. CHUỖI FOURIER
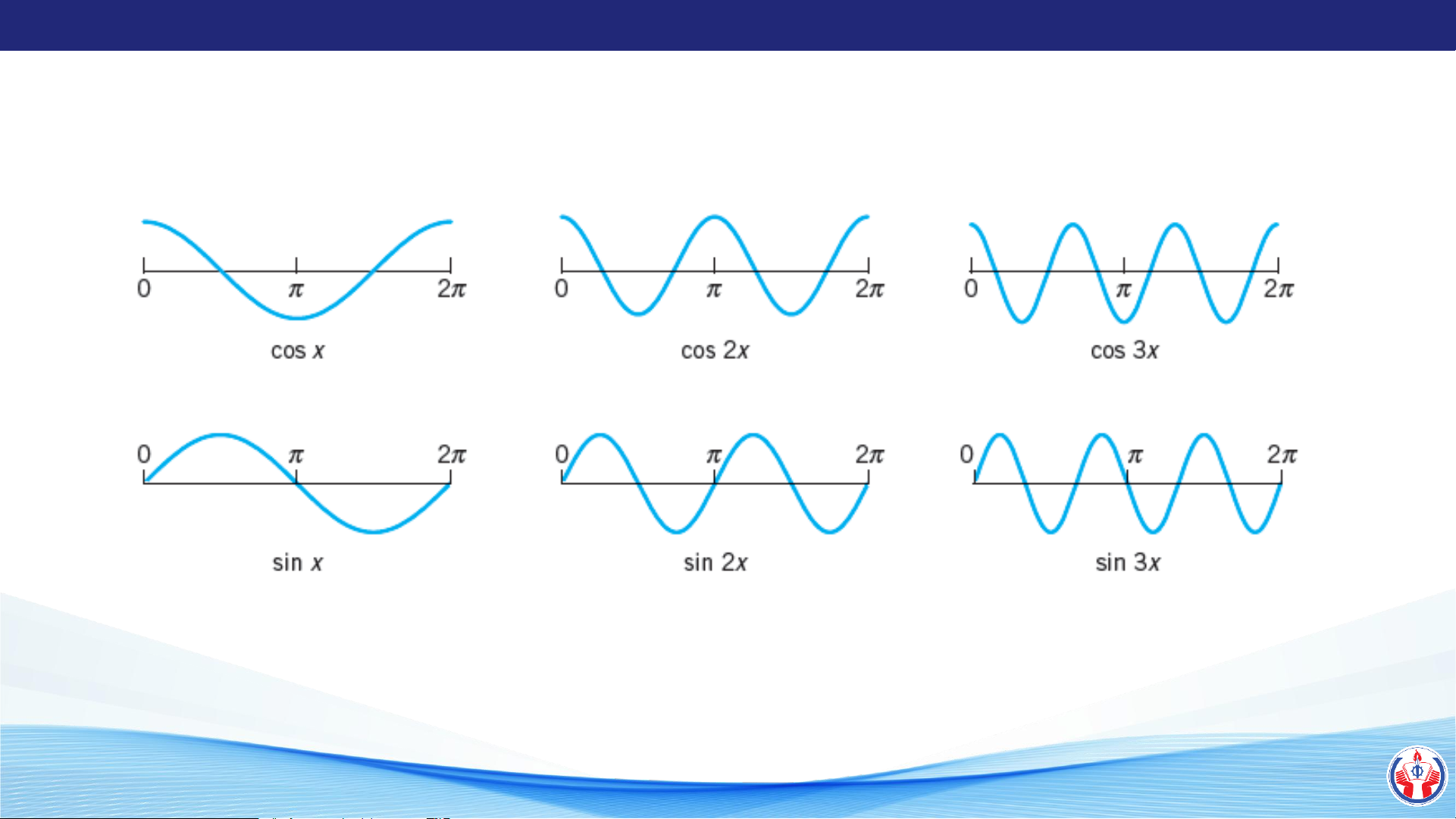
Một số hàm f(x) tuần hoàn với chu kỳ 2 như cos x, sin x, cos 2x, sin 2x,…, cos nx, sin nx
Các hàm cos, sin có chu kỳ 2 LÊ QUANG SANG
CHƯƠNG 5: CHUỖI FOURIER 4
2. CÔNG THỨC TÍNH NHANH 1 1 x cos nxdx = cos nx + x sin nx  2 n n 1 1 x sin nxdx = sin nx − x cos nx  2 n n 2 2x x 2 2 x cos nxdx = cos nx + ( − )sin nx  2 3 n n n 2 2x 2 x 2 x sin nxdx = sin nx + ( − ) cos nx  2 3 n n n LÊ QUANG SANG
CHƯƠNG 5: CHUỖI FOURIER 5
3. CÁCH XÁC ĐỊNH HÀM THÔNG QUA ĐỒ THỊ
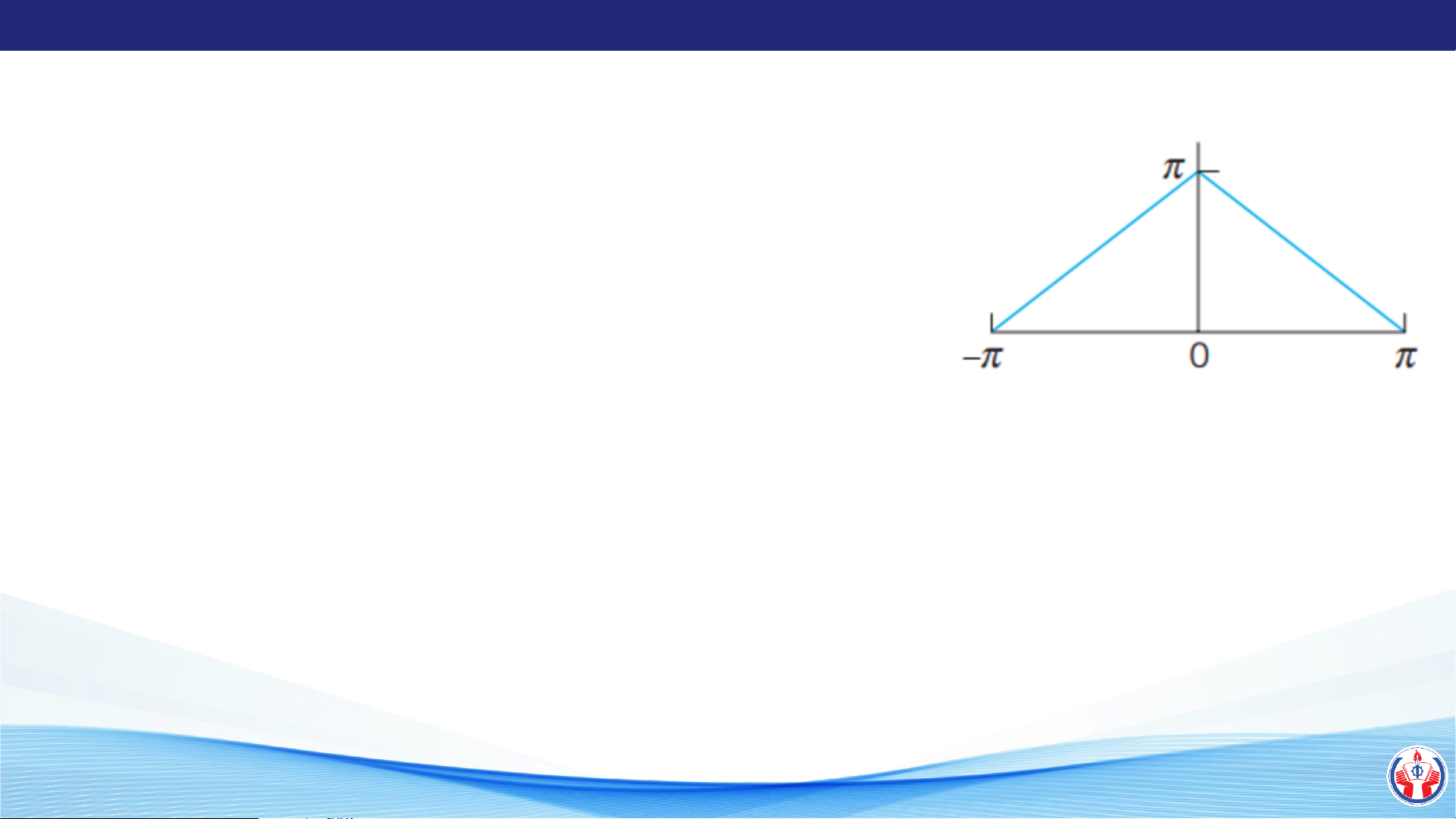
Xét đoạn từ - đến 0 0  =  − a + b a = 1  →    = 0a + b b = 
y = x +  -  x  0 Xét đoạn từ 0 đến  0  =  a + b a = 1 −  →  x +  −  x  0    = → f (x) = 0a + b b =   −x +  0  x  
y = −x +  0  x   LÊ QUANG SANG
CHƯƠNG 5: CHUỖI FOURIER 6
4. HÀM CÓ CHU KỲ P = 2𝝅
Các hàm f(x) tuần hoàn với chu kỳ 2 được biểu diễn dưới dạng chuỗi Fourier như sau: 
f (x) = a + (a cos nx + b sin nx) 0 n n n 1 =
Trong đó a , a , b gọi là các hệ số Fourier của hàm f(x) và được xác định bằng công thức: 0 n n   a = 1
f (x)dx a = 1 f x nxdx n 0   2   ( )cos − −  Với n = 1, 2, 3,… b = 1 f x nxdx n   ( )sin − LÊ QUANG SANG
CHƯƠNG 5: CHUỖI FOURIER 7
4. HÀM CÓ CHU KỲ P = 2𝝅 2 1 2
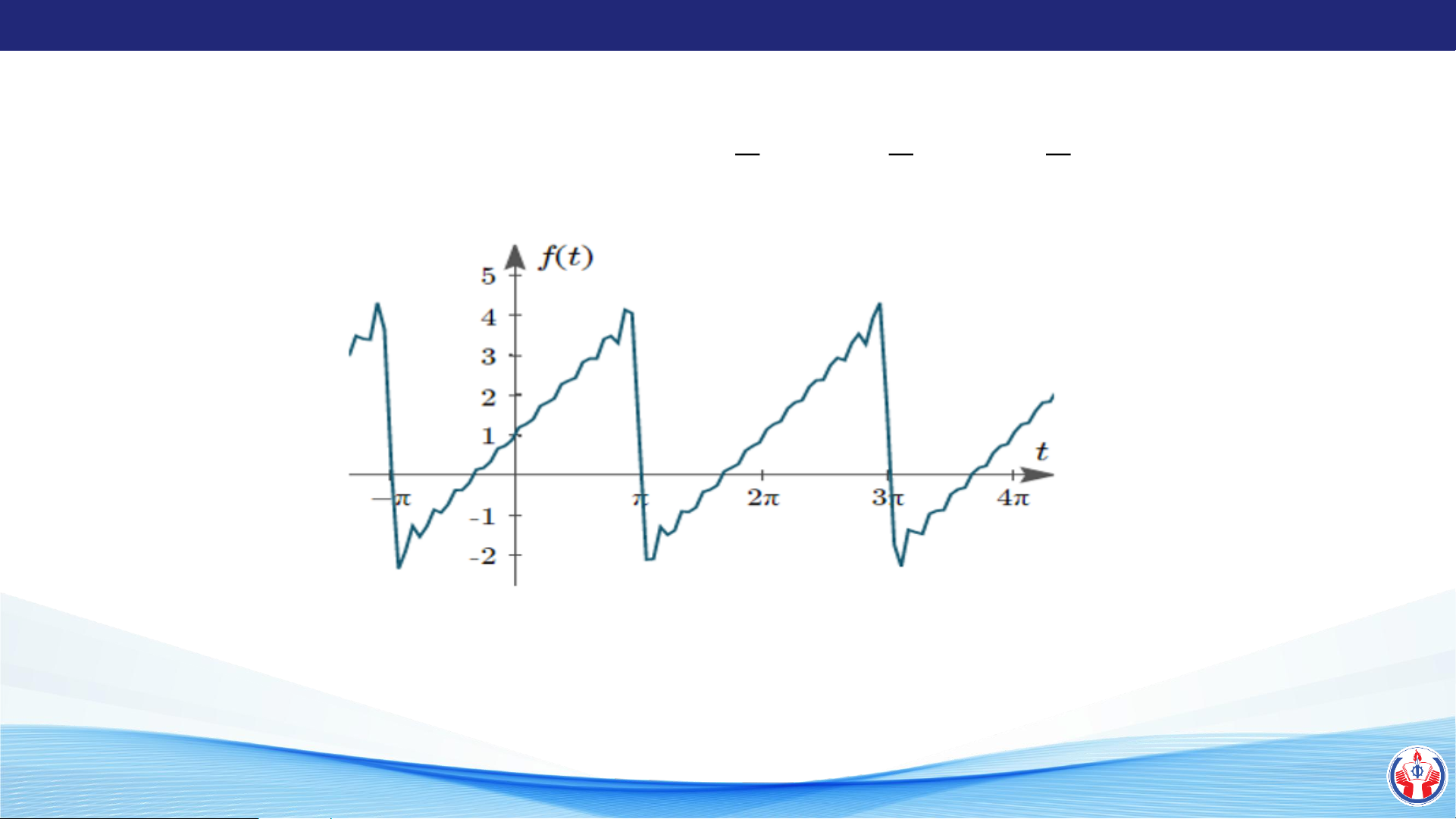
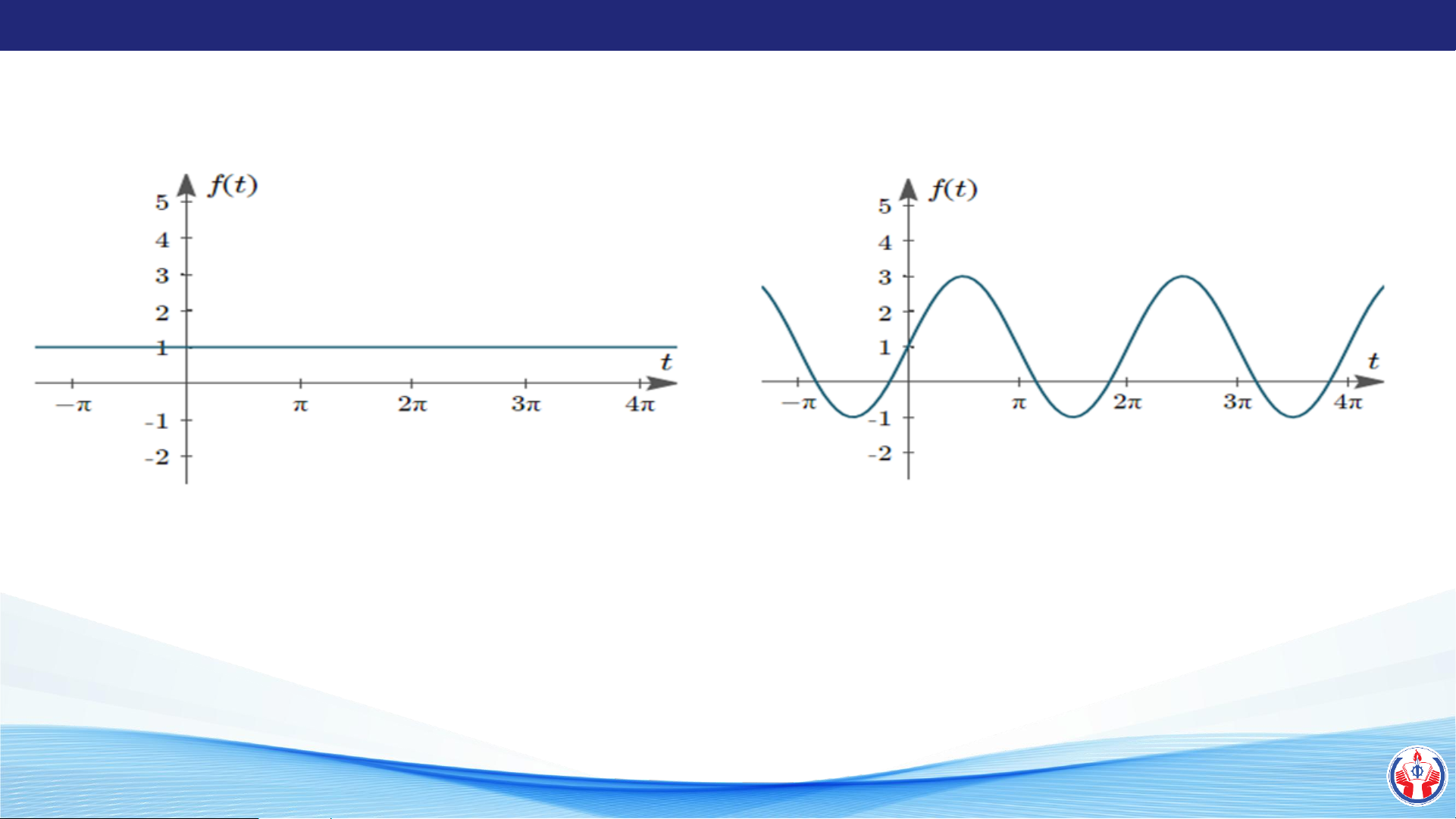
Ví dụ 1: Cho hàm f (t) = 1+ 2 sin t + sin 2t + sin 3t − sin 4t + sin 5t + ... 3 2 5 LÊ QUANG SANG
CHƯƠNG 5: CHUỖI FOURIER 8
4. HÀM CÓ CHU KỲ P = 2𝝅 f (t) = 1
Sự phát triển tín hiệu của hàm f(t)
f (t) = 1 + 2 sin t LÊ QUANG SANG
CHƯƠNG 5: CHUỖI FOURIER 9
4. HÀM CÓ CHU KỲ P = 2𝝅
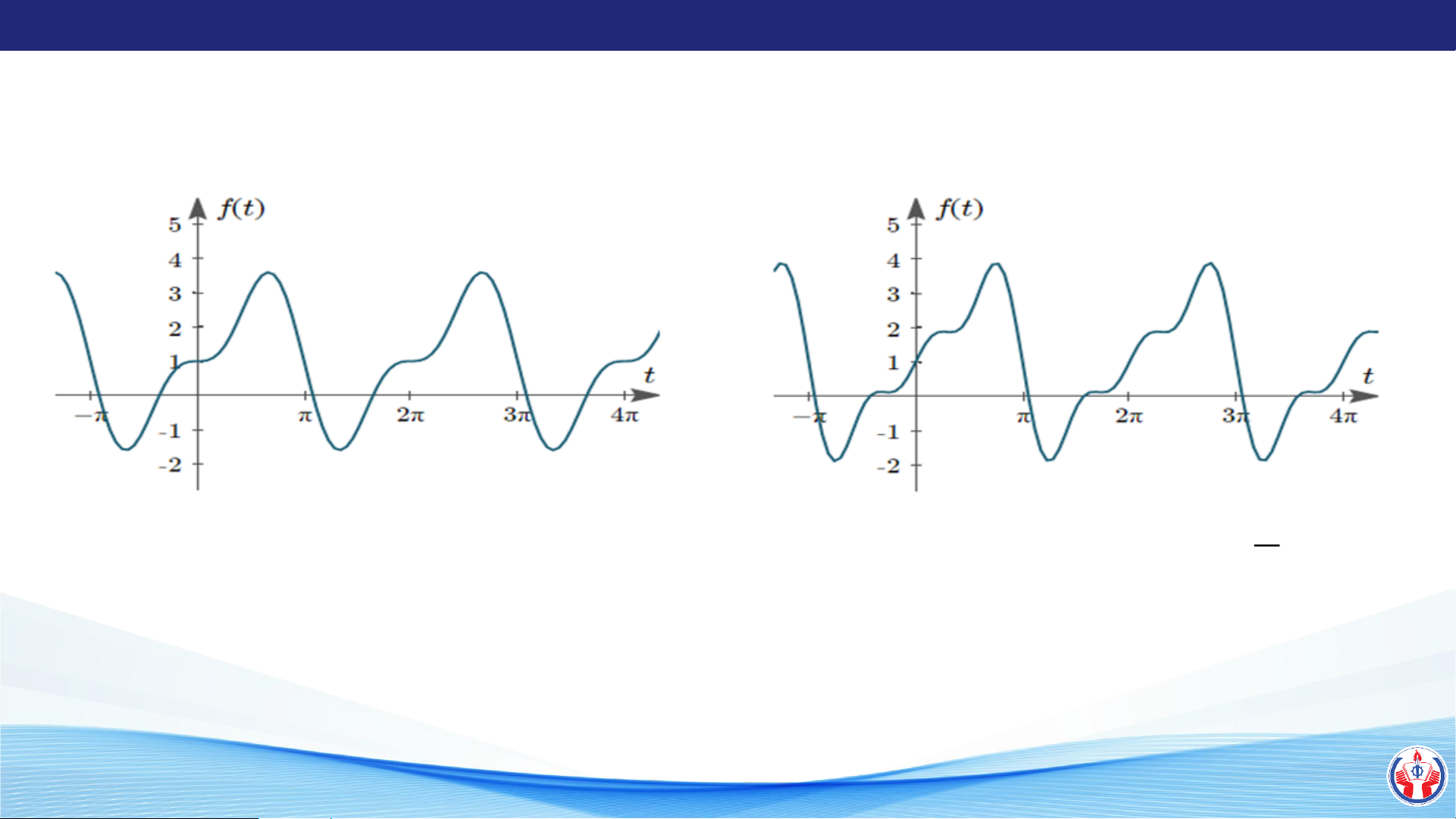
f (t) = 1 + 2 sin t + 2 sin 2t
f (t) = 1 + 2 sin t + sin 2t + sin 3t 3
Sự phát triển tín hiệu của hàm f(t) LÊ QUANG SANG
CHƯƠNG 5: CHUỖI FOURIER 10
4. HÀM CÓ CHU KỲ P = 2𝝅 2 1
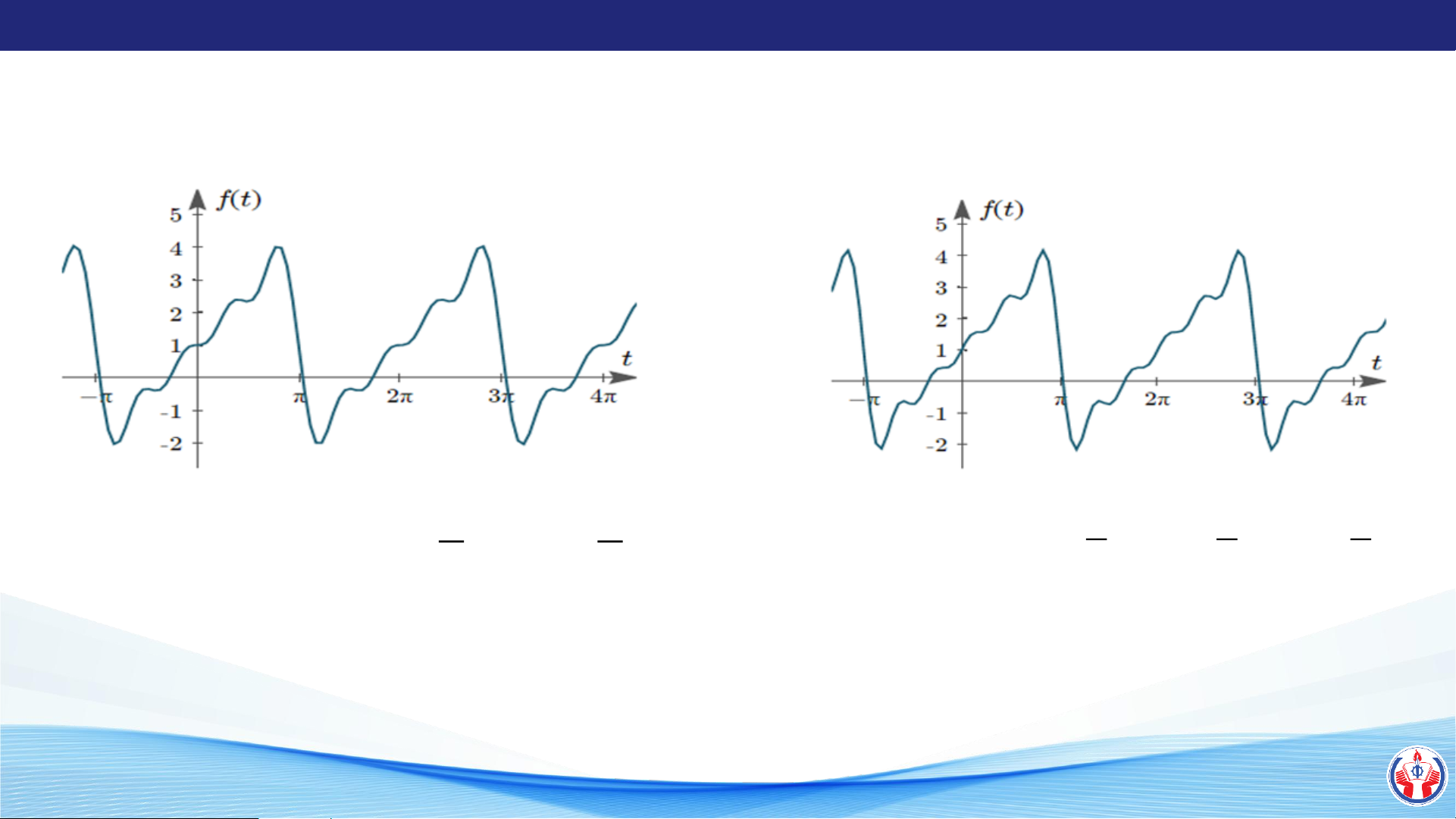
f (t) = 1 + 2 sin t + sin 2t + sin 3t − 2 1 2
sin 4t f (t) = 1+ 2sin t + sin 2t + sin 3t − sin 4t + sin 5t 3 2 3 2 5
Tín hiệu của hàm f(t) đến hài bậc 5 LÊ QUANG SANG
CHƯƠNG 5: CHUỖI FOURIER 11
4. HÀM CÓ CHU KỲ P = 2𝝅
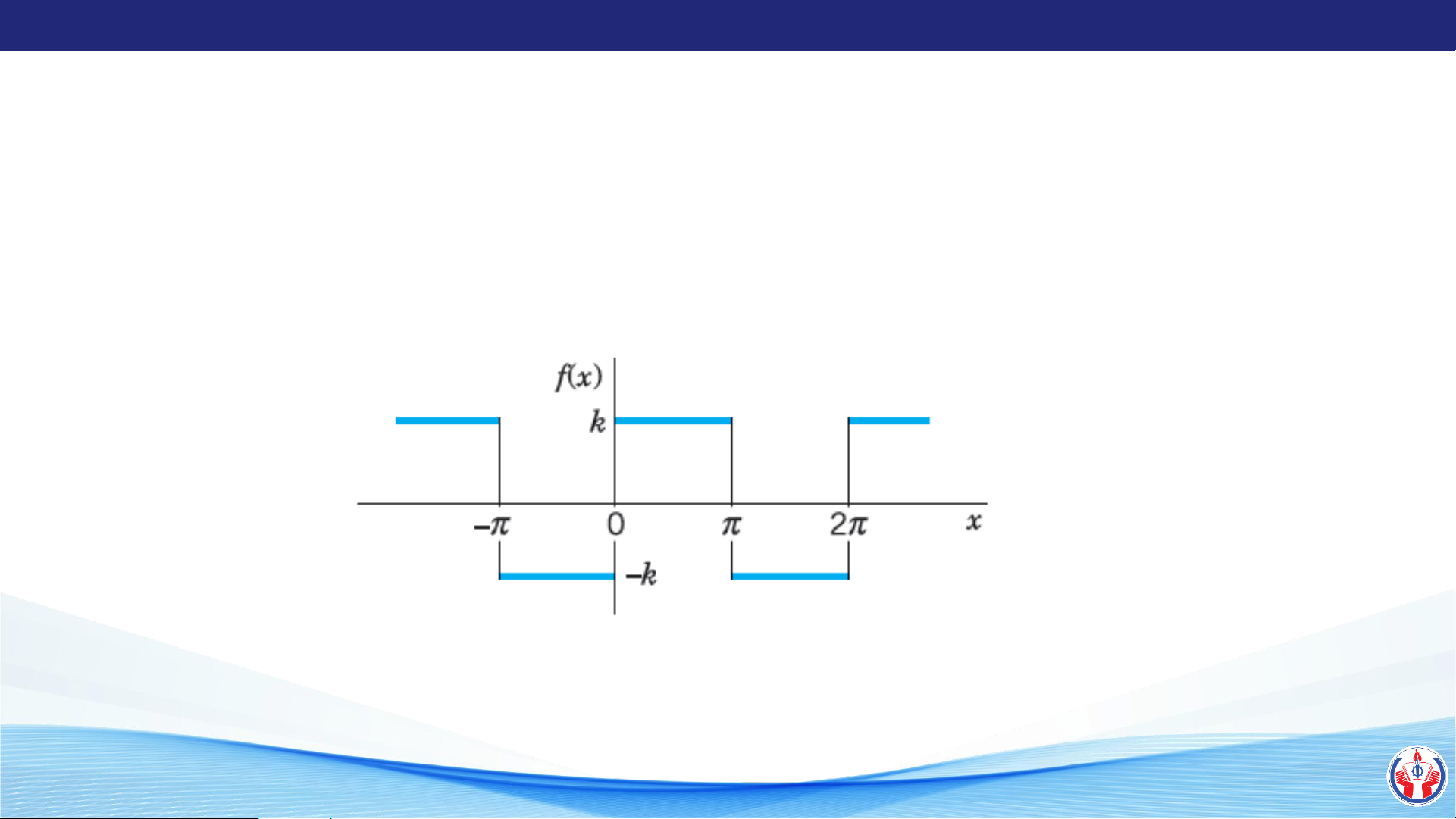
Ví dụ 2: Viết chuỗi Fourier của hàm sau −k  −  x  0 f (x +  f 2 ) = (x) =  f (x)  k 0  x  
Tín hiệu của hàm f(x) với chu kỳ 2𝜋 LÊ QUANG SANG
CHƯƠNG 5: CHUỖI FOURIER 12
4. HÀM CÓ CHU KỲ P = 2𝝅 Bước 1: Tìm 𝑎0  0  1 1   1 0  a = f (x)dx = kdx kdx kx kx 0 0   − +    = − +  =   2  2  −  0  − − 2 0  LÊ QUANG SANG
CHƯƠNG 5: CHUỖI FOURIER 13
4. HÀM CÓ CHU KỲ P = 2𝝅 Bước 2: Tìm 𝑎𝑛  0  1 1   a =
f (x) cos nxdx = k cos nxdx k cos nxdx n   − +      − − 0  0   
= 1 − sin nx + sin nx k k  =  0  n −  n 0   LÊ QUANG SANG
CHƯƠNG 5: CHUỖI FOURIER 14
4. HÀM CÓ CHU KỲ P = 2𝝅 Bước 3: Tìm 𝑏𝑛  0  1 1   b =
f (x)sin nxdx = k sin nxdx k sin nxdx n   − +      − − 0  0   
= 1  cosnx − cosnx  = k k k [cos 0 − cos(−  n ) − cos(  n ) +  cos 0]  n n n 0   −  = 2k (1− cos   n ) n LÊ QUANG SANG
CHƯƠNG 5: CHUỖI FOURIER 15
4. HÀM CÓ CHU KỲ P = 2𝝅
Bước 4: Viết chuỗi Fourier   4k n lẻ b = n n   0 n chẵn x = 4k x + 4k x + 4k x + 4k x + 4k f ( ) sin sin 3 sin 5 sin 7 sin 9x +      ... 3 5 7 9 LÊ QUANG SANG
CHƯƠNG 5: CHUỖI FOURIER 16
4. HÀM CÓ CHU KỲ P = 2𝝅
Ví dụ 3: Viết chuỗi Fourier của hàm sau −x  −  x  f (x +  f x = 0 2 ) = ( )  f (x)  x 0  x    0  Bước 1: Tìm 𝑎 1 1   0 a = f (x)dx = xdx xdx 0   − +  2     − 2 − 0  0   2 2  1 x x  = − +  =  2  2 2  2 −  0  LÊ QUANG SANG
CHƯƠNG 5: CHUỖI FOURIER 17
4. HÀM CÓ CHU KỲ P = 2𝝅 Bước 2: Tìm 𝑎𝑛  0  1 1   a =
f (x) cos nxdx = x cos nxdx x cos nxdx n   − +      − − 0  0   1 −  cos(nx) x sin(nx) cos(nx) x sin(nx) 2(cos(  n ) − =  − + +  = 1))   2 2 n n n n n 0   2 −   −  4 n lẻ a = n  2 n 0 n chẵn LÊ QUANG SANG
CHƯƠNG 5: CHUỖI FOURIER 18
4. HÀM CÓ CHU KỲ P = 2𝝅 Bước 3: Tìm 𝑏𝑛  0  1 1   b =
f (x)sin nxdx = x sin nxdx x sin nxdx n   − +      − − 0  0   1 − 
=  nx sin(nx) + x sin(nx) + nx sin(nx) − x sin(nx)  =  0  2 2 n n −  n n 0   LÊ QUANG SANG
CHƯƠNG 5: CHUỖI FOURIER 19
4. HÀM CÓ CHU KỲ P = 2𝝅
Bước 4: Viết chuỗi Fourier  4  1 1 1  f (x) = − cos x + cos 3x + cos 5x + cos 7x + 2   ...   9 25 49  LÊ QUANG SANG
CHƯƠNG 5: CHUỖI FOURIER 20
5. HÀM CÓ CHU KỲ P = 2L
Các hàm f(x) tuần hoàn với chu kỳ 2L được biểu diễn dưới dạng chuỗi Fourier như sau:    n  n 
f (x) = a + a cos x b sin x 0  +  n n  L L n=1  
Trong đó a , a , b gọi là các hệ số Fourier của hàm f(x) và được xác định bằng công thức: 0 n n 1 L 1 L  a = f (x)dx = n x a f x dx n 0   ( )cos 2L L − L − L L 1 L  Với n = 1, 2, 3,… = n x b f x dx n  ( )sin L − L L LÊ QUANG SANG