Chương 5 ĐIỀU TRA CHỌN MẪU VÀ ƯỚC LƯỢNG
( Survey sampling methods and Estimation )
Đặt vấn đề: - Tổng thể nghiên cứu trong thực tế có thể vô hạn hay hữu hạn song
không phải lúc nào cũng có thể hoặc cũng cần thu thập dữ liệu trên
toàn bộ tổng thể. Từ đó, điều tra chọn mẫu và ước lượng các tham
số của tổng thể chung từ tổng thể mẫu là các phương pháp chủ lực
trong thống kê thực hành.
- Về mặt phương pháp luận, lý thuyết mẫu là nội dung động nhất của
lý thuyết về khoa học thống kê.
Giải quyết vấn đề: Từ bản chất của phương pháp mẫu, có 2 nội dung cơ bản cần
giải quyết là chọn tổng thể mẫu và ước lượng kết quả.
Tài liệu tham khảo cho SV:
- Lyù thuyeát: giaùo trình Xaùc suaát thoáng keâ, Thoáng keâ öùng duïng, Kinh teá löôïng….
- ÖÙng duïng: caùc taøi lieäu höôùng daãn trong caùc cuoäc ñieàu tra choïn
maãu cuûa TCTK: www.gso.gov.vn vaø caùc taøi lieäu ñieàu tra thöïc teá cuûa caùc ñôn vò.
1. MỘT SỐ VẤN ĐỀ CH U NG VỀ ĐI
ỀU TRA CHỌN MẪU : 1.1.Khái niệm:
ĐTCM là điều tra không toàn bộ trên một số đơn vị của tổng thể và từ đó suy rộng
thành các đặc trưng của toàn bộ tổng thể.
Từ khái niệm trên, có 2 nội dung cơ bản cần giải quyết trong ĐTCM là:
-Chọn tổng thể mẫu: + phương pháp chọn mẫu
+ số lượng đơn vị tổng thể (kích thước mẫu) .
-Suy rộng kết quả ( ước lượng ): + phương pháp + công thức.
1.2. Ưu điểm và hạn chế (so với điều tra toàn bộ) Tiêu chí ĐTCM ĐT toàn bộ 1.Sai số: - Sai số chọn mẫu Có Không - Sai số do kê khai thấp hơn cao hơn (phi CM) 2.Chi phí: tiết kiệm hơn / 3.Tổ chức: nhanh gọn hơn / 4.Nội dung: có thể mở rộng / 5. Ứ n g dụng :
-Khi tổng thể không thể ĐT t.bộ.
- Cần thiết cho các nguồn
-Cần tổng hợp nhanh tài liệu. thông tin quan trọng. -Phúc tra,…
-ĐT nghiên cứu thị trường, ĐT xã hội hội học,…
1.3. Sai số trong ĐTCM .
Trong ĐTCM tồn tại 2 loại sai số: - Sai số do kê khai (nonsampling error)
- Sai số chọn mẫu ( sampling error : б )
1.4. Các ký hiệu thường dùng. Chỉ tiêu Tổng thể chung Tổng thể mẫu
1. Số đơn vị tổng thể N n 2. Các tham số θ θ’ -Số trung bình µ x -Tỉ lệ p p ˆ -Phương sai б2 s2 +của STB б 2 x s2x + của tỉ lệ б 2 p = p (1-p ) 2 = ˆ s p 1 ( ˆp) p −
2. CÁC PHƯƠNG PHÁP CHỌN MẪU ( Types of survey sampling methods) 2.1. Phân loại.
2.1.1. Căn cứ vào mức độ ngẫu nhiên khi chọn mẫu: 2 loại phương pháp
*Chọn mẫu phi ngẫu nhiên (có chủ đích) (non random sampling).
- Xuất hiện trước ( khoảng 300 năm trước)
- Xuất phát từ các nhà thống kê thực hành .
- Không coù luaän cöù chöùng minh.
* Chọn mẫu ngẫu nhiên (random sampling).
- Xuất hiện sau ( đầu thế kỷ 20)
- Do các nhà thống kê lý thuyết chứng minh.
- Có cơ sở khoa học (lý thuyết xác suất): ñònh lyù giôùi haïn trung taâm
(the central limit theorem)
Trong thực hành, thường chọn mẫu theo phương pháp kết hợp giữa ngẫu nhiên và
phi ngẫu (a mixture of random and non random sampling): chọn mẫu cả khối, chọn
mẫu nhiều giai đoạn (multi- stage sampling)
2.1.2. Căn cứ theo yếu tố xác suất khi chọn mẫu: 2 loại chọn mẫu.
*Chọn mẫu theo xác suất ( probability samples ).
*Chọn mẫu không theo xác suất ( nonprobability samples ).
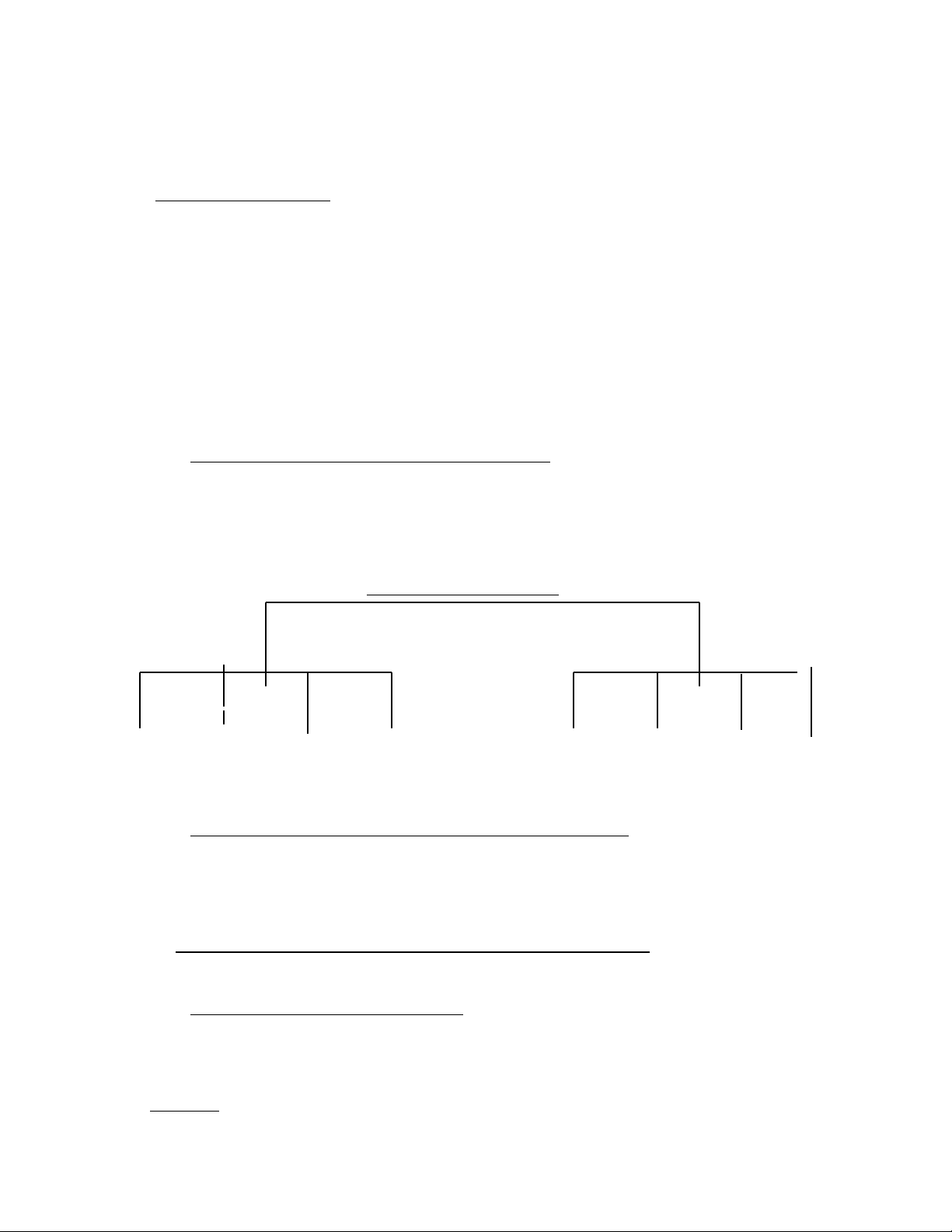
Các phương pháp chọn mẫu CM không theo XS CM theo XS
Judgment Quota Chunk Convenience Simple Systematic Stratified Cluster
Sample Sample Sample Sample Random Sample Sample Sample Sample
2.1.3. Căn cứ theo sự thay đổi của tổng thể khi chọn mẫu: 2 phương pháp
*Chọn hoàn lại (chọn lặp, chọn nhiều lần) (select with replacement)
*Chọn không hoàn lại (chọn không lặp, chọn một lần)(select without replacement)
2.2. Một số phương pháp chọn mẫu ngẫu nhiên thông dụng.
2.2.1. Chọn mẫu ngẫu nhiên đơn giản (simple random sample)
Là phương pháp hoàn toàn ngẫu nhiên, không qua một sự sắp xếp nào.
*Kỹ thuật: - rút thăm ( “ names in a hat”or Raffle method)
- quay số ( “lottery” method )
- dùng Bảng số ngẫu nhiên ( random number tables method)
*Ưu điểm: hoàn toàn ngẫu nhiên, bảo đảm tính khách quan.
*Hạn chế: -Không bảo đảm tính đại biểu khi tổng thể có cấu thành phức tạp.
-Khó đánh số thứ tự các đơn vị tổng thể khi tổng thể lớn.
*Áp dụng: khi giữa các đơn vị tổng thể không khác biệt lớn.
2.2.2 Chọn mẫu hệ thống (Systematic sample).
Trong choïn maãu ngaãu nhieân heä thoáng các đơn vị được chọn từ tổng thể chung một
cách tuần tự và có khoảng cách ( d ) đều nhau.
Bao gồm: - chọn mẫu hệ thống theo đường thẳng.
- chọn mẫu hệ thống xoay vòng.
*Kỹ thuật: -d : khoảng cách về thời gian, không gian, thứ hạng. N -Xác định d = n
-Chọn đơn vị đầu tiên một cách ngẫu nhiên, sau đó chọn các đơn vị còn
lại tuần tự có khoảng cách d. *Ưu điểm: - đơn giản.
- các đơn vị trải đều, từ đó tính đại diện có thể cao.
*Hạn chế: - có thể xuất hiện sai số hệ thống.
- khi d là số thập phân thì phải làm tròn số , từ đó khi ước lượng có thể bị chệch.
*Áp dụng: khi tổng thể có biến động tương đối đều theo thời gian, không gian,…
2.2.3. Chọn mẫu phân tổ (stratified sample)
Trong choïn maãu phaân toå, các đơn vị tổng thể chung được phân thành k tổ và tổng
thể mẫu được chọn từ các tổ của tổng thể chung.
Có 2 cách phân bổ số đơn vị mẫu chọn từ từng tổ:
- Phân bổ theo tỉ lệ (với số đơn vị mỗi tổ)
- Phân bổ không theo tỉ lệ( phân bổ Neyman)
*Kỹ thuật: - Phân tổ tổng thể chung thành k tổ.
- Chọn các đơn vị mẫu từ các tổ theo phương pháp phân bổ thích hợp.
+ Phân bổ theo tỉ lệ:
Ưu điểm: dễ thực hiện, từ đó được áp dụng phổ biến hơn trong thực tế.
Hạn chế: phụ thuộc vào sự phân tổ tổng thể chung. Nếu phân tổ phù hợp
với hiện tượng thì tính đại biểu sẽ cao. Nếu không, sẽ ngược lại.
+Phân bổ Neyman: phân bổ theo sự biến thiên trong nội bộ tổ ( độ lệch chuẩn)
Ưu điểm: tính đại diện rất cao.
Hạn chế: khi phải ước tính độ lệch chuẩn sẽ không bảo đảm có sự phân bố tốt nhất.
*Áp dụng: khi tổng thể chung lớn và cấu thành các khối theo loại hình, địa bàn,…
2.2.4. Chọn mẫu cả khối (cụm) (cluster sample)
Là chọn mẫu các khối, sau đó tiến hành điều tra toàn bộ trên các khối đã chọn.
*Kỹ thuật:- chọn mẫu các khối của tổng thể chung.
- điều tra toàn bộ trên từng khối . *Ưu điểm: nhanh gọn.
*Hạn chế: nếu giữa các khối có chênh lệch lớn thì tính đại diện thấp.
*Áp dụng: - trong từng khối của tổng thể chung khá chênh lệch.
- giữa các khối của tổng thể chung ít chênh lệch.
Ngoài ra, vài phương pháp khác như: chọn mẫu theo xác suất tỉ lệ với qui mô,
chọn mẫu nhiều giai đoạn ,….
3. SAI SỐ CHỌN MẪU (σ),PHẠM VI SAI SỐ CHỌN MẪU (ε) VÀ KÍCH
THƯỚC MẪU (n) TRONG ĐTCM NGẪU NHIÊN ĐƠN GIẢN.
3.1. Sai số chọn mẫu ( σ )
Là trung bình của các sai số chênh lệch giữa tham số của từng tổng thể mẫu có thể
được chọn khác nhau với tham số thật sự của tổng thể chung.
Trong tính toaùn, töøng cheânh leäch noùi treân giöõa töøng tham soá maãu vôùi tham soá
cuûa toång theå chung (θi’ - θ ) coù theå laø cheânh leäch + hay cheânh leäch - . Do vaäy, ta
phaûi bình phöông cheânh leäch vaø sau ñoù laáy caên baäc 2. Nhö vaäy, cuoái cuøng sai
soá choïn maãu ñöôïc tính laø ñoä leäch chuaån cuûa caùc soá trung bình maãu ( σ x ).
Töø ñoù, coù 2 noäi dung caàn xaùc ñònh laø:
* Từ N đơn vị tổng thể chung, số khả năng thiết lập tổng thể mẫu với n đơn vị là:
–Tröôøng hôïp chọn hoàn lại: 2 k = N n N!
- Tröôøng hôïp choïn không hoàn lại: k = C = N !
n (N − n)! TD: N = 4 , n =2 . Tổng thể chung: A B C D. Chọn có hoàn lại: 2 k = N = 2 4 = 16.
Các tổng thể mẫu coù thể chọn ñược là: AA AB AC AD BB BA BC BD CC CA CB CD DD DA DB DC.
→ Các tham số tương ứng cuûa caùc toång theå maãu laø: ' ' , ' 1 θ , 2 θ ,θ3,..., k θ ⇒ k Sai số.
→ Như vậy, Sai số chọn mẫu là sai số trung bình chọn mẫu (Sai số chuẩn: standard error : SE ) ∑k θ ' 2 ( ) i − θ SE = 1 = ξ k
Tuy nhieân, trong thöïc haønh ngöôøi ta chæ tieáp caän vôùi 1 toång theå maãu cuï theå vaø
sai soá choïn maãu ñöôïc tính nhö sau: 2 σ σ x = n
**Ngoaøi ra, Sai số chọn mẫu gồm hai loại:
-Sai số ngẫu nhiên: do các đơn vị được chọn ngẫu nhiên
-Sai số hệ thống: khi mẫu được chọn có chủ đích.
→ Nhìn chung , sai số chọn mẫu thường được hiểu là sai số ngẫu nhiên.
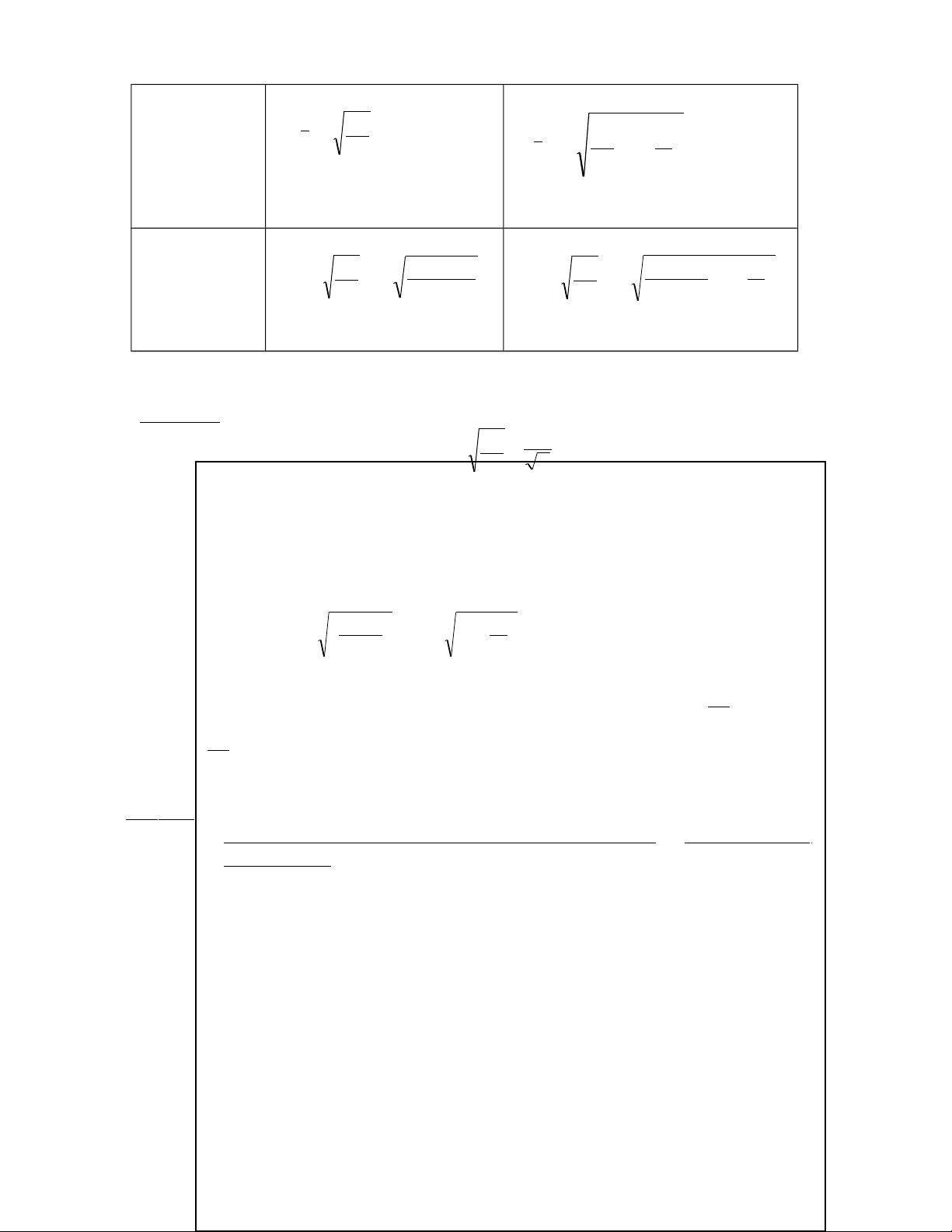
Công thức Sai số chọn mẫu trong chọn mẫu ngẫu nhiên đơn giản: CHỌN HOÀN CHỌN KHÔNG HOÀN 2 σ σ σ = = σ2  n  n n σ = 1−  n  N  Khi ước 2 σ 2 σ n Lượng σ x =   n σ x = 1 −  Soá trung n  N  bình Khi Ước 2 σ p 1 ( − p) 2 σ 1 ( p −p)  n  Lượng σp = = σ = 1 −  n n p = n n  N  Tỉ lệ T rong ñ o ù : 2 σ
++ Coâng thöùc sai soá choïn maãu σ σ = =
ñöôïc xaây döïng treân cô sôû choïn coù n n
hoaøn laïi. Trong thöïc teá, toång theå maãu coù n quan saùt thöôøng ñöôïc choïn khoâng hoaøn laïi
töø toång theå chung höõu haïn coù N phaàn töû. Töø ñoù, khi tính sai soá choïn maãu trong tröôøng
hôïp choïn khoâng hoaøn laïi caàn coù ñaïi löôïng Heä soá ñieàu chænh toång theå höõu haïn (finite
population correction factor : fpc) :
fpc =  N − n n   = 1−    N −1   N  n
++ Tröôøng hôïp choïn khoâng hoaøn, khi N rất lớn so n (thoâng thöôøng ≤ 0,05 ) N n thì ( 1-
) → 1 : có thể duøng coâng thöùc nhö choïn coù hoaøn laïi. N G hi chú :
Thông thường , khi tính Sai số chọn mẫu ta chưa biết 2
σ , thứ tự ưu tiên xử lý như sau:
1. Dùng phương sai lớn nhất của lần điều tra trước nếu có. Áp dụng
thích hợp với những hiện tượng không có sự thay đổi lớn trong quá trình phát triển.
2. Sử dụng phương sai của cuộc điều tra tương tự ở nơi khác. Áp dụng
nếu hiện tượng nghiên cứu ở nơi khaùc cũng có những đặc điểm và điều
kiện tương tự với hiện tượng nghiên cứu.
3. Tiến hành điều tra thí điểm để tính độ lệch tiêu chuẩn.
Nếu hiện tượng nghiên cứu có phân phối chuẩn thì có thể ước tính độ
lệch tiêu chuẩn theo khoảng biến thiên R.
Theo Qui tắc 3σ , nếu X~ N (µ, 2
σ ) thì hầu hết các giá trị của X sai
lệch với µ không quá 3 lần σ .
Ta có : R= (xmax - xmin) = (µ +3σ ) – (µ -3σ ) = 6σ R x x
⇒ σ = = max− min 6 6
4 . Dùng phương sai mẫu ( s2): ñöôïc söû duïng nhieàu nhaát trong thöïc haønh.
3.2. Phạm vi sai số chọn mẫu (ε )
Được xác định nhằm phục vụ cho việc suy rộng từ kết quả của tổng thể mẫu thành
kết quả của tổng thể chung.
ε phụ thuộc vào : + Sai số chọn mẫu σ
+ Độ tin cậy của tài liệu suy rộng ( 1 - α ) là xác suất đúng của
tài liệu suy rộng. Từ độ tin cậy mong muốn, xác định hệ số tin
cậy z. Độ tin cậy càng cao thì hệ số tin cậy càng lớn.  Công thức: ε = σ z 2 tröôøng hôïp chính: a. T
ổng thể có phân phối chuẩn + biết 2 σ * Ö
ớ c lượng 2 bên: 2 α α σ
ε = σ z 2 = z 2 n σ α α
 Khi ước lượng STB: ε σ x = z 2 x = z 2 n 1 ( p −p) α α
 Khi ước lượng tỉ lệ: ε σ n p = z 2 p ˆ = z 2 * Ö
ớ c lượng 1 bên : ε = σ z α b. T
ổng thể có phân phối chuẩn, n
< 30 + chưa biết 2 σ : ε = s t α * Ö
ớ c lượng 2 bên: ε = s tn-1, 2
* Öớ c lượng 1 bên : ε = s tn-1, α
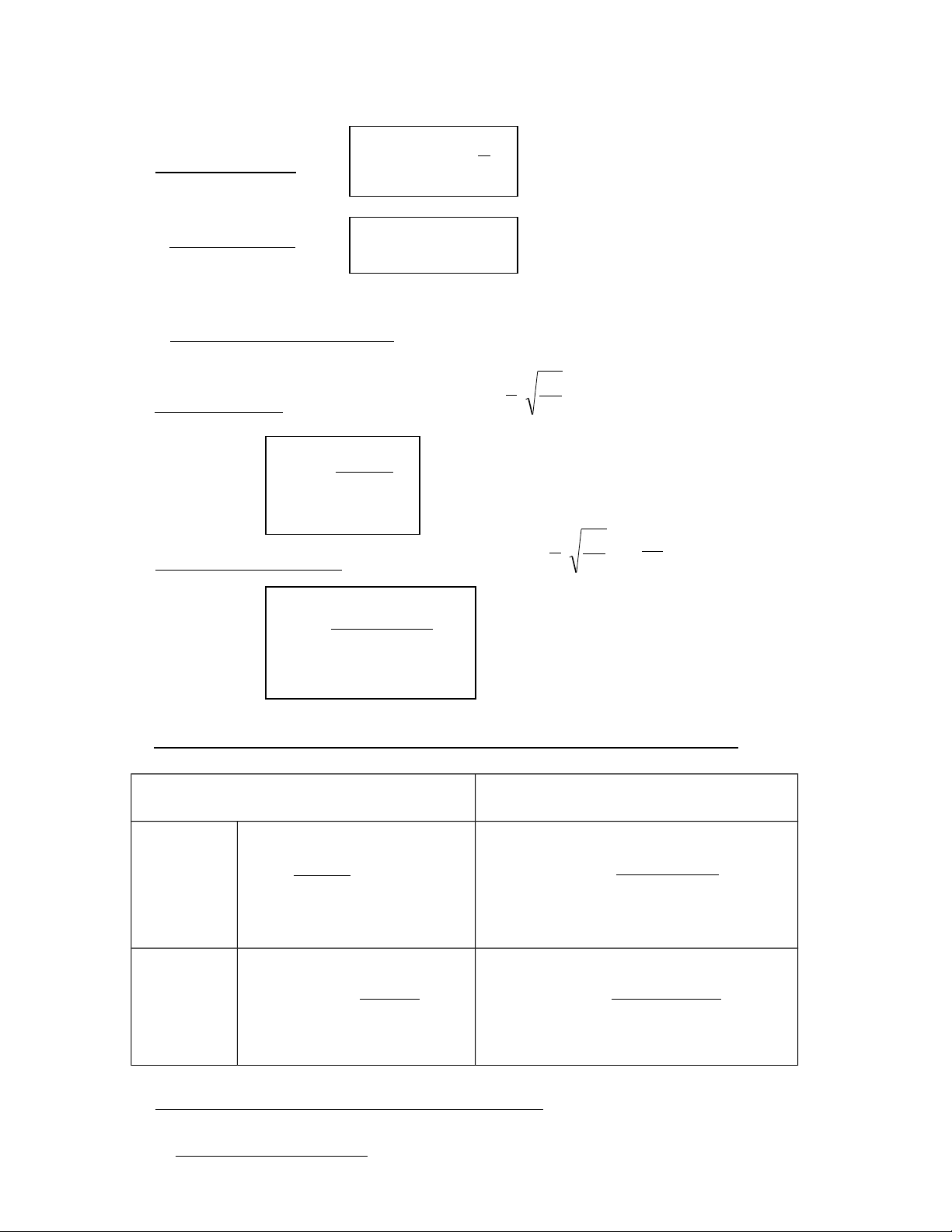
3.3. Xác định kích thước mẫu ( Estimating the sample size) 2 α σ a. C
hoïn hoaøn laïi : Từ công thức ε = z 2 n 2 2 z σ
 n = α/22 εx 2 α σ n
b. Choïn khoâng hoaøn laïi: Từ công thức ε = z 2 n (1- N ) 2 2 z σ N  n = α / 2 2 2 2 ε N + z x α / 2σ
Công thức xác định kích thước mẫu trong chọn mẫu ngẫu nhiên đơn giản: CHỌN HOÀN CHỌN KHÔNG HOÀN Khi ước 2 2 z 2 2 z σ N α / 2 σ α / 2 Lượng n = n = 2 ε 2 2 2 ε N + z σ STB x x α / 2 Khi Ước 2 z 2 α / 2 pq z pqN α / 2 Lượng n = 2 n = ε 2
ε N + z 2 pq Tỉ lệ p p α / 2
5. ƯỚC LƯỢNG ( Estimate) TRONG ĐTCM.
5.1. Khái niệm – Phân loại:
Trong ĐTCM, ước lượng là sự suy rộng từ kết quả các tham số của tổng thể mẫu
thành kết quả các tham số của tổng thể chung.
* Có 2 phương pháp ước lượng: - Ước lượng trực tiếp.
- Ước lượng gián tiếp.
Ước lượng trực tiếp là dùng 1 đặc trưng của tổng thể mẫu để ước lượng cùng đặc
trưng đó của tổng thể chung.Thí dụ, dùng trung bình mẫu x để ước lượng trung
bình của tổng thể µ ,….
Ước lượng gián tiếp là dùng 1 đặc trưng của tổng thể mẫu cùng các tham số có liên
quan để ước lượng 1 đặc trưng của tổng thể chung, thí dụ ước lượng hồi qui,…
Trong thực hành, chủ yếu dùng ước lượng trực tiếp. Có thể phân biệt các loại ước lượng trực tiếp sau:
*Căn cứ vào khoảng ước lượng: - Ước lượng điểm.
- Ước lượng khoảng.
* Căn cứ vào tổng thể ước lượng: - Ước lượng cho đơn vị tổng thể
- Ước lượng cho tổng thể
5.2. Ước lượng điểm.
Thoáng keâ toán chứng minh: E ( x ) = µ E ( p ˆ ) = p E (s2 ) = s2
Nghĩa là các tham số mẫu là ước lượng không chệch của các tham số chung.
Ước lượng điểm bò haïn cheá do phụ thuộc vào tổng thể mẫu cụ thể chọn được.
5.2. Ước lượng Khoảng.
Công thức: θ’- ε ≤ θ ≤ θ’ + ε
→ θ’- Z σ ≤ θ ≤ θ’ + Z σ Cuï theå: 2 2
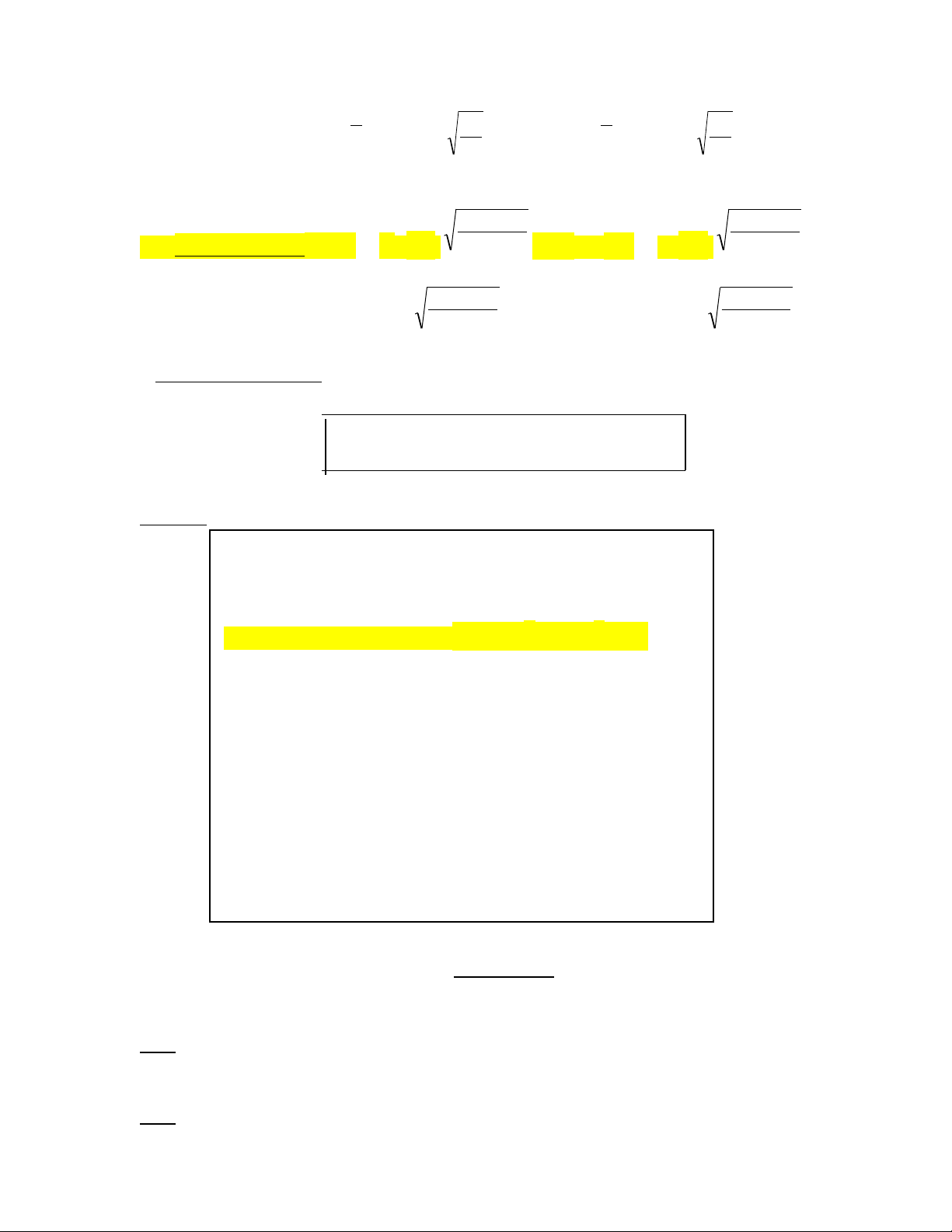
→ *Öôùc löôïng Soá trung bình: σ σ x - zα/2
≤ µ ≤ x + zα/2 n n 2 2 Hay: σ σ x - tn-1, α/2
≤ µ ≤ x + tn-1, α/2 n n p 1 ( − p) p 1 ( − p) p ˆ p ˆ
→ *Öôùc löôïng Tæ leä: - zα/2 n ≤ p ≤ + zα/2 n p 1 ( − p) p 1 ( − p) p ˆ p ˆ Hay: - t n n n-1, α/2
≤ p ≤ + tn-1, α/2
* Ước lượng tổng thể
(θ’- ε ) N ≤ θ N ≤ (θ’ + ε ) N
Ghi chú: Một số thuật ngữ: Độ tin cậy : 1- α (confidence level)
Hệ số tin cậy : z α/2, z α , tn-1, α/2 , tn-1, α.
(confidence Coefficient)
Khỏang tin cậy : θ’- ε ≤ θ ≤ θ’ + ε
(confidence interval)
Giới hạn tin cậy dưới : θ’ - ε (interval lower limit)
G/hạn tin cậy trên : θ’ + ε
(interval upper limit) BÀI TẬP
05.1: Hãy liên hệ thực tế để cho thí dụ về từng phương pháp chọn mẫu ngẫu nhiên thông dụng.
05.2: Chọn câu trả lời đúng nhất:
Câu 1: Một nhân viên tiếp thị qua điện thọai cài đặt để lưu lại trong máy tính của
công ty các số điện thọai tuần tự với khỏang cách 20 chọn từ danh mục các
cuộc điện đàm của công ty từ đầu đến cuối tháng 2/2009. Nhân viên trên đã
dùng phương pháp chọn mẫu ngẫu nhiên: a. Đơn giản. b. Hệ thống. c. Phân tổ. d. Cả khối. e. Phương pháp khác.
Câu 2: Khi kích thước tổng thể mẫu càng lớn thì có ảnh hưởng:
a. Giảm sai số chọn mẫu.
b. Tăng sai số do kê khai.
c. Không ảnh hưởng đến sai số trong điều tra TK. d. a, b, c đúng. e. a, b, c sai.
Câu 3:Trong thực hành, ước lượng các tham số của tổng thể chung chỉ từ tham số
của 1 tổng thể mẫu cụ thể:
a. Là sự hạn chế của phương pháp .
b. Là hạn chế đã được tính đến trong sai số chuẩn. c. a, b đúng. d. a, b sai.
Câu 4: Khi ước lượng trị số tối đa của số trung bình tổng thể chung là : a. Ước lượng 1 bên. b. Ước lượng bên trái.
c. Ước lượng bên phải.
Câu 5: Với cùng sai số chọn mẫu, Khỏang tịn cậy càng lớn thì:
d. Hệ số tin cậy càng lớn.
e. Độ tin cậy càng lớn. f. a, b đúng. g. a, b sai.
05.3: Hãy trả lời đúng (Đ) , sai (S) cho các câu sau:
a. _____ Tổng thể mẫu là một bộ phận của tổng thể chung được chọn ra để phân tích.
b. _____ Điều tra nghiên cứu thị trường chủ yếu là điều tra chọn mẫu.
c. _____ Kiểm kê kho định kỳ là ĐT chọn mẫu.
d. _____ Sai số do kê khai trong các phiếu ĐT chọn mẫu thường cao hơn trong ĐT tòan bộ.
05.4: Ñeå döï baùo moät soá chæ tieâu quan troïng lieân quan ñeán chieán löôïc taøi chính
naêm 2010 vaø naêm 2020 cuûa quoác gia, ngaønh taøi chính ñaõ keát hôïp vôùi
ngaønh thoáng keâ tieán haønh ñieàu tra choïn maãu veà thu nhaäp, tieát kieäm vaø ñaàu
tö cuûa daân cö ôû moät soá tænh thaønh. Thaønh phoá BMT coù 100.000 hoä gia ñình.
Yeâu caàu:1. Caàn ñieàu tra thöïc teá bao nhieâu hoä gia ñình trong tröôøng hôïp choïn coù
hoaøn laïi vaø choïn khoâng hoaøn laïi vôùi ñoä tin caäy 95%, phaïm vi sai soá
choïn maãu khoâng vöôït quaù 2,5% vaø đñộđlệch chuẩn của caùc laàn ñiều
tra trước laø 37%, 42%, 45%.
2. Biết rằng kết quả điều tra cho thấy 20% số hộ gia đình có thu nhập lớn
hơn thu nhập bình quân chung. Dựa vào kết quả điều tra chọn có hoàn
lại, hãy xác định sai số chọn mẫu khi suy rộng tỉ lệ chung.
05.5: Công ty TNHH Bánh kẹo Bình Tân có 500 công nhân, trong đó có 100 coâng
nhaân cùng thao tác đóng gói thành phẩm. Tổ kỹ thuật của công ty vừa cải
tiến SX để tăng năng suất lao động của CN đóng gói. Chọn ngẫu nhiên hoàn
lại 50 CN để theo dõi NSLĐ đóng gói. Kết quả như sau:
NSLĐ 1 CN (x: Số CN (f :người) kg/giờ) 20 – 30 14 30 – 40 17 40 – 50 11 50 – 60 8 Tổng 50 Y
êu cầu : 1. Hãy ước lượng NSLĐ bình quân một CN
đóng gói thành phẩm của công ty với độ tin cậy 98%.
2. Để phạm vi sai số chọn mẫu khi suy rộng NSLĐ bình quân không vượt
quá 3 kg với độ tin cậy 98%, cần chọn mẫu bao nhiêu CN?
3. NSLĐ trước cải tiến SX là 36,5
kg/người/giờ. Giả thiết rằng NSLĐ của CN
có phân phối chuẩn, với mức nghĩa 2%, có
thể kết luận NSLĐ sau cải tiến SX cao hơn
NSLĐ trước cải tiến không ?
05.6: Moät coâng ty baûo hieåm nghieân cöùu tình hình bò tai naïn cuûa nhöõng ngöôøi
haønh ngheà laùi xe nhaèm hoaïch ñònh phöông aùn thu phí baûo hieåm coù phaân
bieät theo lyù lòch haønh ngheà. Coâng ty tieán haønh khaûo saùt treân moät soá laùi xe
trong 3 naêm. Baûng thoáng keâ keát quaû nhö sau: Đã bị tai Chưa bị tai Tổng Độ tuổi nạn(%) nạn(%) cộng(%) < 20 0,48 7,52 8 21-30 0,45 14,55 15 31-65 0,98 48,02 49 66-99 1,12 26,88 28 Cộng 3,03 96,97 100
Yeâu caàu: 1. Laäp baûng tính tæ troïng nhoùm bò tai naïn vaø chöa bò tai naïn cuûa töøng
nhoùm tuoåi so vôùi toång soá quan saùt cuûa nhoùm tuoåi. Cho nhaän xeùt veà
tæ leä bò tai naïn theo caùc nhoùm tuoåi.
2. Öôùc löôïng tæ troïng ñaõ bò tai naïn cuûa nhoùm tuoåi 31-65 vôùi ñoä tin caäy
95%. Cho bieát coù 200 laùi xe ôû ñoä tuoåi naøy ñöôïc khaûo saùt.
Document Outline

• Chương 5 ĐIỀU TRA CHỌN MẪU VÀ ƯỚC LƯỢNG