


























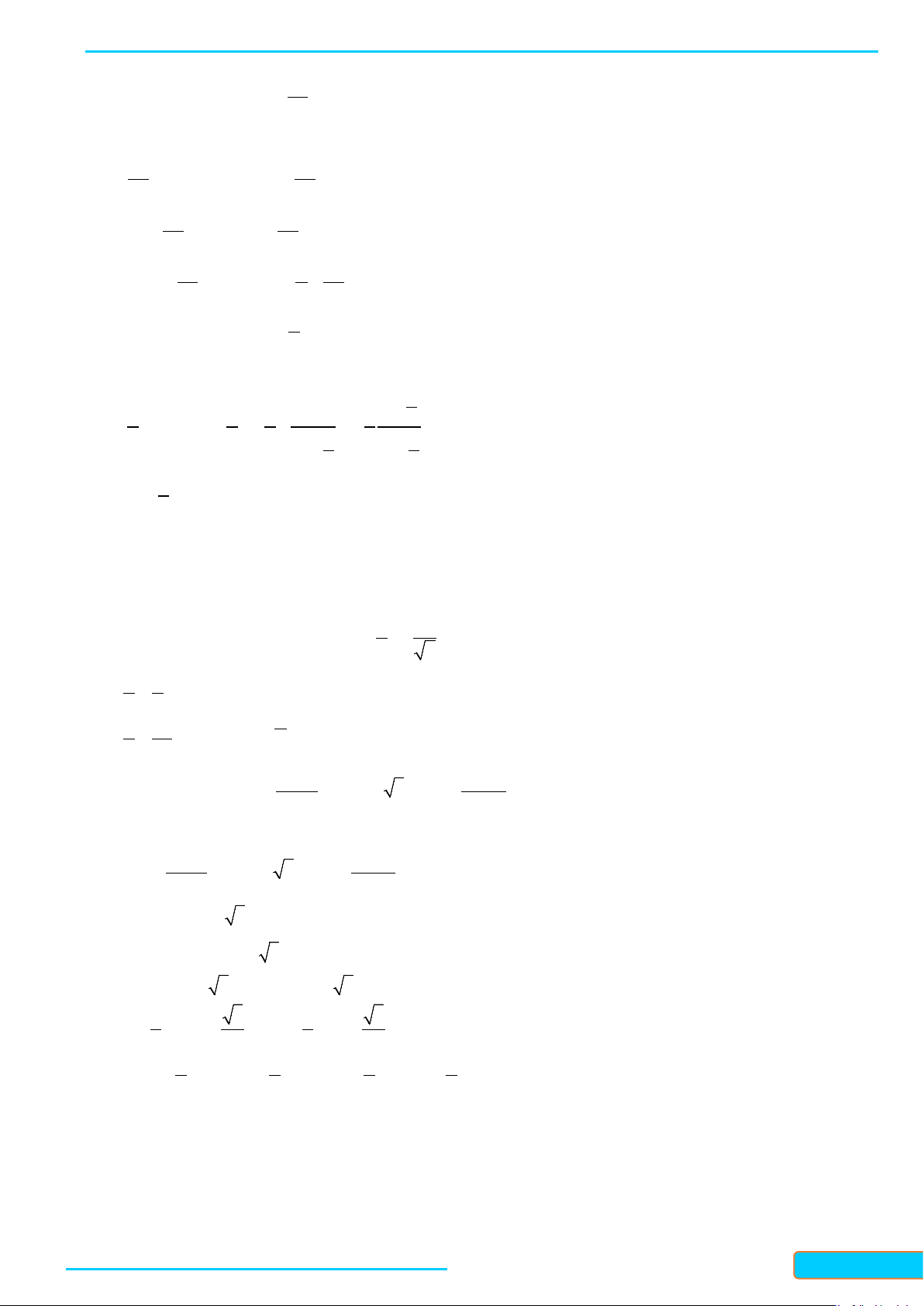



























































Preview text:
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com CHƯƠNG VII. ĐẠO HÀM
Trong chương này, chúng ta sẽ tìm hiểu những vấn đề sau: định nghĩa đạo hàm, ý nghĩa hình học của
đạo hàm; các quy tắc tính đạo hàm; đạo hàm bậc hai.
BÀI 1. ĐỊNH NGHĨA ĐẠO HÀM. Ý NGHĨA HÌNH HỌC CỦA ĐẠO HÀM
Tên lửa vũ trụ là phương tiện được chế tạo đặc biệt giúp con người thực hiện các sứ mệnh trong không
gian như: tiếp cận đến các hành tinh ngoài Trái Đất, vận chuyển con người và thiết bị lên vũ trụ,. (Hình 1).
Nếu quỹ đạo chuyển động của tên lửa được miêu tả bằng hàm số theo thời gian thì đại lượng nào biểu
thị độ nhanh chậm của chuyển động tại một thời điểm?
A. KIẾN THỨC CƠ BẢN CẦN NẮM
I. ĐẠO HÀM TẠI MỘT ĐIỂM
1. Các bài toán dẫn đến khái niệm đạo hàm
a) Bài toán tìm vận tốc tức thời
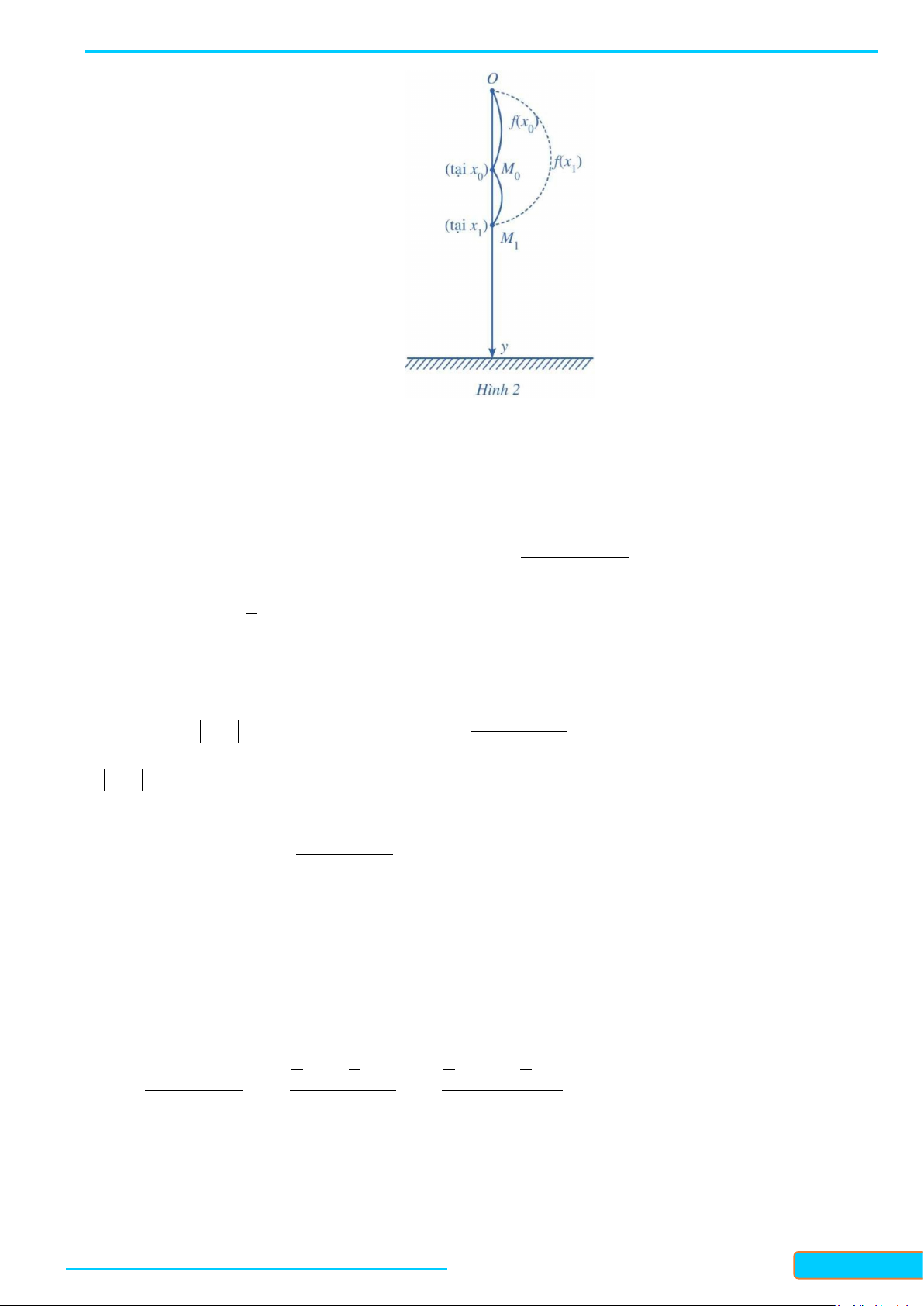
Từ vị trí O (ở một độ cao nhất định nào đó), ta thả một viên bi cho rơi tự do xuống đất và nghiên cứu
chuyển động của viên bi. Bằng việc chọn trục Oy theo phương thẳng đứng, chiều dương hướng xuống
đất, gốc O là vị trí ban đầu của viên bi, tức là tại thời điểm 0 giây, và bỏ qua sức cản không khí, ta nhận
được phương trình chuyển động của viên bi là y = f (x) 1 2
= gx ( g là gia tốc rơi tự do, 2
g ≈ 9,8m / s ). 2
Giả sử tại thời điểm x , viên bi ở vị trí M có y = f x ; tại thời điểm x , viên bi ở vị trí M có 0 ( 0) 0 0 1 1
y = f x . Khi đó, trong khoảng thời gian từ x đến x , quãng đường viên bi đi được 1 ( 1) 0 1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 1
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
là M M = f x − f x (Hình 2). Vậy vận tốc trung bình của viên bi trong khoảng thời gian đó là . 0 1 ( 1) ( 0)
Nếu x − x càng nhỏ thì tỉ số trên càng phản ánh chính xác hơn sự nhanh chậm của viên bi tại thời điểm 1 0
f (x − f x 1 ) ( 0)
x . Từ đó, người ta xem giới hạn của tỉ số
khi x dần x là vận tốc tức thời tại thời điểm 0 x − x 1 0 1 0 f x − f x
x của viên bi, kí hiệu là v(x . Nói cách khác, v(x = lim
. Giá trị v(x gọi là đạo hàm 0 ) 0 ) ( 1) ( 0) 0 ) 0 1 x → 0 x x − x 1 0
của hàm số y = f (x) 1 2
= gx tại thời điểm x . 2 0
b) Bài toán tìm cường độ tức thời
Điện lượng Q truyền trong dây dẫn là một hàm số của thời gian t , Q = Q(t). Cường độ trung bình trong
Q(t) − Q(t0 )
khoảng thời gian t − t được xác định bởi công thức . 0 t − t0
Nếu t − t càng nhỏ thì tỉ số này càng biểu thị chính xác hơn cường độ dòng điện tại thời điểm t . Người 0 0
ta đưa ra định nghĩa sau đây:
Q(t) − Q(t0 )
Giới hạn hữu hạn (nếu có) lim
được gọi là cường độ tức thời của dòng điện tại thời điểm t t→t 0 0 t − t0 .
2. Định nghĩa đạo hàm tại một điểm
Hoạt động 1. Tính vận tốc tức thời của viên bi tại thời điểm x =1s trong bài toán tìm vận tốc tức thời. 0 Lời giải
Vận tốc tức thời của viên bi tại thời điểm x =1s 0 1 2 1 2 1 2 1 gx − g.1 .9,5x − .9,8 − v( )
f (x ) f ( ) 1 1 1 1 2 2 2 2 1 = lim = lim = lim = 9,8(m / s) 1 x 1 → x −1 1 x 1 → x −1 1 x 1 → x −1 1 1 1
Trong trường hợp tổng quát, ta có định nghĩa sau:
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 2
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Cho hàm số y = f (x) xác định trên khoảng ( ;
a b) và điểm x ∈ ;
a b . Nếu tồn tại giới hạn hữu hạn 0 ( )
f (x) − f (x0 ) lim
thì giới hạn đó được gọi là đạo hàm của hàm số y = f (x) tại x và được kí hiệu là x→ 0 0 x x − x0
f ′(x hoặc y′ . 0 ) 0 x Nhận xét.
Trong định nghĩa trên, ta đặt: x
∆ = x − x và gọi x
∆ là số gia của biến số tại điểm x ; 0 0 y
∆ = f (x + x
∆ − f x và gọi y
∆ là số gia của hàm số ứng với số gia x ∆ tại điểm x . 0 ) ( 0) 0 f x + x ∆ − f x Khi đó, ta có: ( lim lim y f x ∆ ′ = = . 0 ) ( 0 ) ( 0) x ∆ →0 x ∆ →0 x ∆ x ∆
3. Cách tính đạo hàm bằng định nghĩa
Cho hàm số y = f (x) xác định trên khoảng (a;b) và điểm x thuộc khoảng đó. 0
Để tính đạo hàm f ′(x của hàm số y = f (x) tại x , ta lần lượt thực hiện ba bước sau: 0 ) 0 Bước 1. Xét x
∆ là số gia của biến số tại điểm x . Tính y
∆ = f (x + x ∆ − f x . 0 ) ( 0) 0 ∆
Bước 2. Rút gọn tỉ số y . x ∆ ∆
Bước 3. Tính lim y . x ∆ →0 x ∆ ∆
Kết luận: Nếu lim y = a thì f ′(x = a . 0 ) x ∆ →0 x ∆
Ví dụ 1. Tính đạo hàm của hàm số ( ) 1
f x = tại x = 2 bằng định nghĩa. x 0 Lời giải + Xét x
∆ là số gia của biến số tại điểm x = 2 . 0 2 − (2 + x ∆ ) −∆ Ta có: y 1 1 x ∆ = f (2 + x ∆ ) − f (2) = − = = . 2 + x ∆ 2 2(2 + x ∆ ) 2(2 + x ∆ ) Suy ra: y ∆ 1 − = . x ∆ 2(2 + x ∆ ) + Ta thấy: y ∆ 1 − 1 lim lim − = = . x ∆ →0 x ∆ →0 x ∆ 2(2 + x ∆ ) 4 − Vậy f ′( ) 1 2 = . 4
❓ Tính đạo hàm của hàm số f ( x) = 2x tại x = 3 bằng định nghĩa. 0 Lời giải + Xét x
∆ là số gia của biến số tại điểm x = 3. 0 Ta có: y ∆ = f (3+ x
∆ ) − f (3) = 2( x ∆ + 3) − 2.3 = 2 x ∆ .
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 3
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com ∆ Suy ra: y = 2 . x ∆ ∆
+ Ta thấy: lim y = lim 2 = 2 . x ∆ →0 x ∆ →0 x ∆ Vậy f ′(3) = 2 .
Ví dụ 2. Tính đạo hàm của hàm số ( ) 2
f x = x tại điểm x bất kì bằng định nghĩa. Lời giải + Xét x
∆ là số gia của biến số tại điểm x . Ta có: y
∆ = f (x + x
∆ ) − f (x) = (x + x ∆ )2 2 − x = x ∆ (2x + x ∆ ) . ∆
Suy ra: y = 2x + x ∆ . x ∆ ∆
+ Ta thấy: lim y = lim (2x + x ∆ ) = 2x . x ∆ →0 x ∆ →0 x ∆
Vậy f ′(x) = 2x .
❓ Tính đạo hàm của hàm số ( ) 3
f x = x tại điểm x bất kì bằng định nghĩa. Lời giải + Xét x
∆ là số gia của biến số tại điểm x . Ta có: y
∆ = f (x + x ∆ ) − f (x) = (x + x ∆ )3 3 2 2 3 − x = x x ∆ + x x ∆ + x ∆ = x ∆ ( 2 2 3 . 3. . . 3x + 3 . x x ∆ + x ∆ ) . ∆ Suy ra: y = ( 2 2 3x + 3 .x x ∆ + x ∆ ) . x ∆ ∆
+ Ta thấy: lim y = lim ( 2 2 3x + 3 .x x ∆ + x ∆ ) 2 = 3x . x ∆ →0 x ∆ →0 x ∆ Vậy f ′(x) 2 = 3x . Nhận xét. Hàm số ( ) 2
f x = x có đạo hàm tại mọi điểm x trên khoảng (−∞;+ ∞). Ta nói hàm số đó có đạo hàm trên
khoảng (−∞;+ ∞). Một cách tổng quát: Hàm số y = f (x) được gọi là có đạo hàm trên khoảng (a;b) nếu
nó có đạo hàm tại mọi điểm x trên khoảng đó.
4. Ý nghĩa vật lí của đạo hàm
Đạo hàm xuất hiện trong nhiều khái niệm vật lí. Chẳng hạn: Xét chuyển động thẳng xác định bởi phương
trình s = s(t) , với s = s(t) là một hàm số có đạo hàm. Như đã thấy trong bài toán mở đầu, vận tốc tức
thời của chuyển động tại thời điểm t là đạo hàm của hàm số tại t : v(t = s′ t 0 ) ( 0) 0 0
II.Ý NGHĨA HÌNH HỌC CỦA ĐẠO HÀM
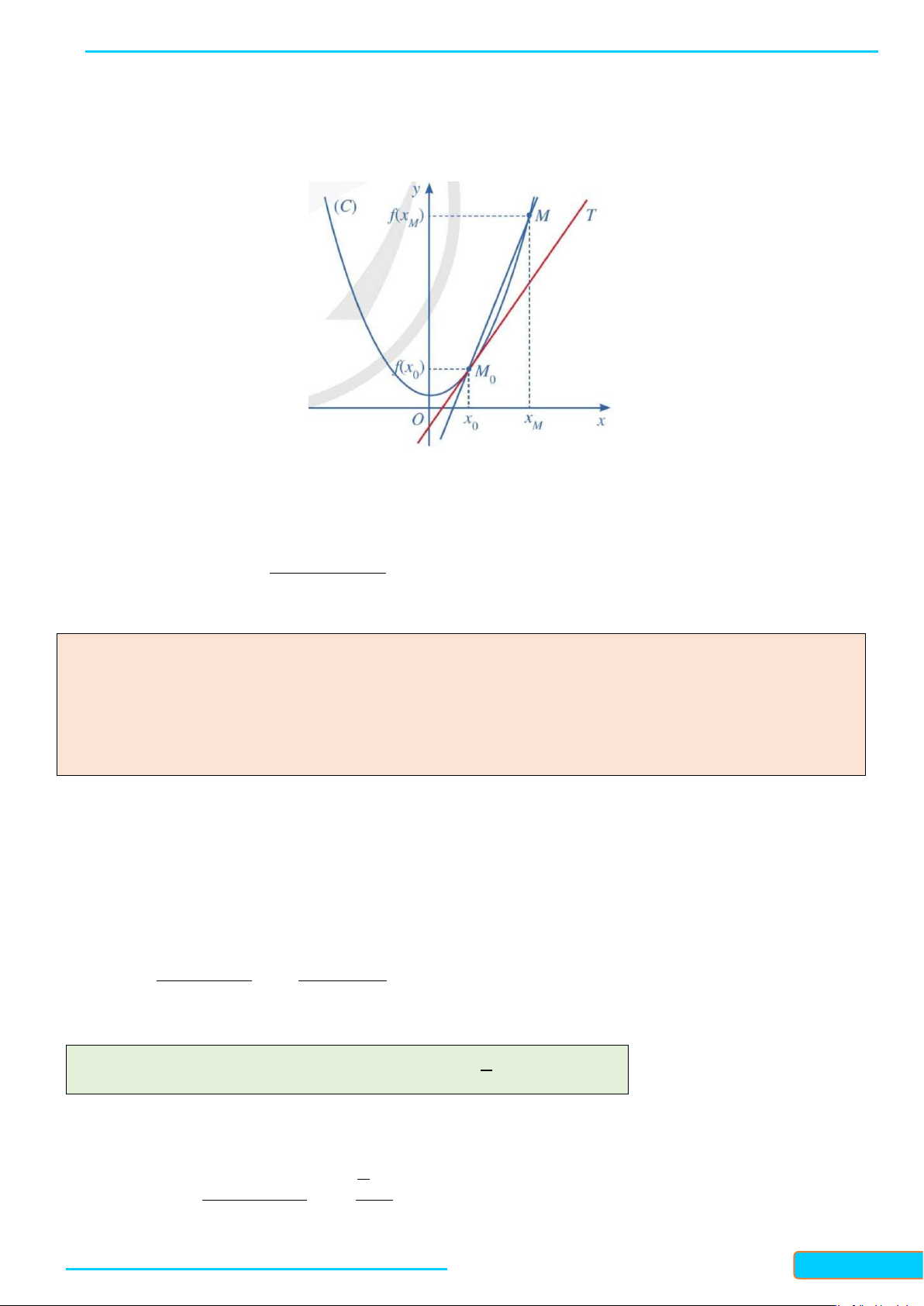
Cho hàm số y = f (x) có đồ thị (C), một điểm M cố định thuộc (C) có hoành độ x . Với mỗi điểm M 0 0
thuộc (C) khác M , kí hiệu x là hoành độ của điểm M và k là hệ số góc của cát tuyến M M . Giả sử 0 M M 0
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 4
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
tồn tại giới hạn hữu hạn k = lim k . Khi đó, ta coi đường thẳng 0
M T đi qua M và có hệ số góc k là M 0 0 0 M x → 0 x
vị trí giới hạn của cát tuyến M M khi điểm M di chuyển dọc theo (C) dần tới M . 0 0
Đường thẳng M T được gọi là tiếp tuyến của (C) tại điểm M , còn M được gọi là tiếp điểm (Hình 3). 0 0 0 Hình 3
a) Xác định hệ số góc k của tiếp tuyến M T theo x . 0 0 0
b) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm M . 0
f (x − f x M ) ( 0)
Ta có: k = lim k = = f ′ x . M lim 0 ( 0) M x → 0 x M x → 0 x x − x M 0
Như vậy ta có kết luận sau:
+ Đạo hàm của hàm số y = f (x) tại điểm x là hệ số góc của tiếp tuyến của đồ thị hàm số đó tại điểm 0 M x ; f x . 0 ( 0 ( 0))
+ Phương trình tiếp tuyến của đồ thị hàm số y = f (x) tại điểm M x ; f x là 0 ( 0 ( 0))
y = f ′(x x − x + f x . 0 ) ( 0 ) ( 0)
Ví dụ 3. Cho hàm số 2
y = −x có đồ thị (C).
a) Xác định hệ số góc của tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 3.
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm M (3;− 9) . Lời giải
a) Tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 3 có hệ số góc là: 2 2 ′( f x − f −x − − f 3) ( ) (3) ( 3) = lim = lim = lim(−x − 3) = 6 − . x→3 x→3 x→3 x − 3 x − 3
b) Phương trình tiếp tuyến của đồ thị (C) tại điểm M (3;− 9) là: y = 6 − (x − 3) + ( 9 − ) hay y = 6 − x + 9 .
❓ Viết phương trình tiếp tuyến của đồ thị hàm số 1
y = tại điểm N (1; ) 1 . x Lời giải
Tiếp tuyến của đồ thị tại điểm có hoành độ bằng 1 có hệ số góc là: 1 f (x f − − N ) ( ) 1 1 = lim x k k = = = − = f ′ N lim lim 1 1 0 ( ) xN 1 → xN 1 → x x − N 1 → x − N 1 1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 5
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Phương trình tiếp tuyến của đồ thị hàm số 1
y = tại điểm N (1; ) 1 là x y = −(x − ) 1 +1 = −x + 2
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1. Tìm số gia của hàm số 1. Phương pháp
• Số gia của hàm số y = f (x) tại điểm x0 là y ∆ = f (x0 + x ∆ ) − f (x0 ). • Chú ý rằng số gia y
∆ của hàm số là một hàm số của số gia biến số x. ∆
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Tìm số gia của hàm số y = f (x) 3 2
= x − 3x + 2 , biết rằng x =1; 0 x ∆ = − ,1 0 . Lời giải Ta có y
∆ = f (x + x ∆ − f x = f − f = − + − − + = . o ) ( ) (0,9) ( ) 3 2 3 2 1 0,9 3.0,9 2 (1 3.1 2) 0,229 0
Ví dụ 2: Tính số gia của hàm số y = 2x + 3 theo x và x ∆ . Lời giải y
∆ = f (x + x
∆ − f x = x + x ∆ + − x + = x ∆ o ) ( 2 o 3 2 3 2 0 ) ( ) ( 0 ) Ví dụ 3: ∆
Tính y của hàm số 3 2
y = 2x − 3x theo x và x ∆ . x ∆ Lời giải y
∆ = f (x + x
∆ − f x = x + x ∆ − x + x ∆ − x − x o ) ( ) 2( o )3 3( o )2 ( 3 2 2 3 0 0 0 ) = 2( 3 2 2 3 x + 3x x ∆ + 3x ( x ∆ ) + ( x ∆ ) ) −3( 2 2 x + 2x x ∆ + ( x ∆ ) ) −( 3 2 2x − 3x 0 0 0 0 0 0 0 ) = x ∆ ( 2 2 6x + 6x x ∆ + 3( x
∆ ) − 6x − 3 x ∆ 0 0 0 ) y ∆ x ∆ ( 2 2 6x + 6x x ∆ + 3( x
∆ ) − 6x − 3 x ∆ 0 0 0 ) Suy ra = 2 2 = 6x + 6x x ∆ + 3( x
∆ ) − 6x − 3 x ∆ . x ∆ x ∆ 0 0 0
Dạng 2. Tính đạo hàm bằng định nghĩa 1. Phương pháp
• Tính số gia của hàm số y ∆ = f (x0 + x ∆ ) − f (x0 ). • Lập tỉ y ∆ . x ∆ • Tính giới hạn y lim ∆ . x ∆ →0 x ∆
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Tính đạo hàm (bằng định nghĩa) của hàm số 2 y = 2x + x + 1 tại x . 0 = 2 Lời giải
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 6
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Cho x một số gia 0 = 2 x
∆ . Khi đó hàm số nhận một số gia tương ứng: y ∆ = f (x + x ∆ ) − f (x ) = 2(2 + x ∆ )2 + (2 + x ∆ ) +1−( 2 0 0 2.2 + 2 + 1) = x ∆ (9 + 2 x ∆ ) ∆y ∆x(9 + 2∆x) Ta có lim = lim = lim (9 + 2∆x) = 9 . ∆x→0 ∆x ∆x→0 ∆x ∆x→0 Vậy f'(2) = 9
Ví dụ 2: Tính đạo hàm (bằng định nghĩa) của mỗi hàm số sau tại các điểm đã chỉ ra 2 y = x + 3 tại ; x x ∀ ∈ Lời giải y ∆ f (x + x ∆ ) − f (x) ( x ∆ + x)2 2 + 3 − x + 3
Ta có: f ′(1) = lim = lim = lim x ∆ 0 → x ∆ x ∆ →0 x ∆ x ∆ →0 x ∆ ( x ∆ )2 2 2 + 2∆ .
x x + x + 3 − x + 3 ( x ∆ )2 + 2∆ .xx = lim = lim x ∆ →0 x ∆ x
∆ →0 ∆ .x( ( x ∆ )2 2 2 + 2∆ .
x x + x + 3 + x + 3) ∆ + x 2x 2 = lim x x = = . x ∆ →0 ( ( x ∆ )2 2 2 + 2∆ .
x x + x + 3 + x + 3) 2 2 2. x + 3 x + 3 3 2 x + x +1 −1
Ví dụ 3: Tính đạo hàm của hàm số khi x ≠ 0 f (x) = x tại x = 0 . 0 khi x = 0 Lời giải 3 2
Ta có : f (0) = 0 , do đó:
f (x) − f (0) x + x +1 −1 x +1 1 lim = lim = lim = . 2 x→0 x→0 x→0 3 2 x x x + x +1 +1 2 1 Vậy f (′0) = . 2 2 x + x khi x ≤1
Ví dụ 4: Tìm a,b để hàm số f (x) =
có đạo hàm tại x = 1. ax + b khi x >1 Lời giải Điều kiện cần: f (1) = 2
lim f (x) = lim ( 2 x + x = − − ) 2 x 1 → x 1 →
lim f (x) = lim (ax + b) = a + b x 1+ x 1+ → →
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 7
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Để hàm số f (x) có đạo hàm tại x = 1 thì f (x) liên tục tại x = 1
⇔ lim f (x) = lim f (x) = f (1) ⇔ a + b = 2 x 1+ x 1− → → Điều kiện đủ:
f (x) − f (1) 2 f (1− ′ ) = lim x + x − 2 = lim
= lim ( x + 2) = 3 x 1− → x −1 x 1− → x −1 x 1− →
f (x) − f (1)
f (x) − f (1)
ax + b − (a + b) f (1+ ′ ) − = ax a lim = lim = lim = lim = a x 1+ → x −1 x 1+ → x −1 x 1+ → x −1 x 1+ → x −1
Để hàm số f (x) có đạo hàm tại x = 1 thì f (1+ ′ ) = f (1− ′
) ⇔ a = 3⇒ b = 1 − .
Dạng 3. Ý nghĩa vật lý của đạo hàm 1. Phương pháp
. Vận tốc tức thời tại thời điểm t0 của chất điểm chuyển động với phương trình s = s (t) là
v(t = s' t 0 ) ( 0).
. Cường độ tức thời tại thời điểm t0 của một dòng điện với điện lượng Q = Q(t) là
I (t = Q' t 0 ) ( 0) .
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Một chất điểm chuyển động có phương trình chuyển động là:
s = f (t) 2
= t + 4t + 6 (t được tính bằng giây, s được tính bằng mét)
a) Tính đạo hàm của hàm số f (t) tại điểm t0 .
b) Tính vận tốc tức thời của chuyển động tại thời điểm t = 5. Lời giải 2 2 − + + − + + a) Ta có:
f (t) f (t t 4t 6 t 4t 6 0 ) ( 0 0 ) lim = lim
== lim(t + t + 4 = 2t + 4. 0 ) 0 t→t0 t→t t − t 0 t→t t − t 0 0 0
Vậy f '(t = 2t + 4 0 ) 0 .
b) Vận tốc tức thời của chuyển động tại thời điểm t = 5 là v = f = + = t '(5) 2.5 4 14 (m/s).
Ví dụ 2: Cho biết điện lượng trong một dây dẫn theo thời gian biểu thị bởi hàm số Q = 6t + 5 (t được
tính bằng giây, Q được tính bằng Coulomb). Tính cường độ của dòng điện trong dây dẫn tại thời điểm t =10. Lời giải
Vì Q '(t) = 6 ⇒ Cường độ của dòng điện trong dây dẫn tại thời điểm t =10 là I = Q = tt '(10) 6
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 8
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Dạng 4. Phương trình tiếp tuyến 1. Phương pháp
Phương trình tiếp tuyến của đồ thị hàm số y = f (x) tại điểm M0 (x0;y0 ) là:
y = f′(x0 )(x − x0 ) + f (x0 ).
Nếu tiếp tuyến có hệ số góc k thì ta giải phương trình f′(x0 ) = k tìm hoành độ tiếp điểm.
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Cho hàm số f (x) 2
= x + 5 có f ′(x) = 2 .x Viết phương trình tiếp tuyến với đồ thị của hàm số tại
điểm M có hoành độ x = 1. − 0 Hướng dẫn giải x = 1
− ⇒ f (x ) = (− )2 1 + 5 = 6 0 0 f ′(− ) 1 = 2 − .
Phương trình tiếp tuyến: y = 2 − (x + ) 1 + 6 .
Ví dụ 2: Phương trình tiếp tuyến của đồ thị hàm số = ( ) 4
y f x = x tại điểm có hoành độ bằng 1 − Hướng dẫn giải
Ta có: f ( ) = f ′(x) 3 1 1;
= 4x , do đó f ′(− ) 1 = 4. −
Phương trình tiếp tuyến cần tìm là y = 4 − (x + ) 1 +1 = 4 − x − 3.
Ví dụ 3: Viết phương trình tiếp tuyến của đồ thị hàm số = ( ) 3
y f x = x tại điểm mà tiếp điểm có tung độ bằng 1 − Hướng dẫn giải Ta có: Khi y = 1 − thì 3 x = 1 − , do đó x = 1. −
f (− ) = − f ′(x) 2 1 1;
= 3x , do đó f ′(− ) 1 = 3.
Phương trình tiếp tuyến cần tìm là y = 3(x + ) 1 −1 = 3x + 2.
Ví dụ 5: Viết phương trình tiếp tuyến của đồ thị hàm số = ( ) 4
y f x = x có hệ số góc bằng 4. Hướng dẫn giải Ta có: f ′(x) 3 = 4x .
Hệ số góc của tiếp tuyến bằng 4 nên 3
4x = 4 , do đó x =1; f ( ) 1 =1.
Phương trình tiếp tuyến cần tìm là y = 4(x − ) 1 +1 = 4x − 3.
C. GIẢI BÀI TẬP SÁCH GIÁO KHOA Bài 1.
Tính đạo hàm của hàm số f (x) 3
= 3x −1 tại điểm x =1 bằng định nghĩa. 0 Lời giải + Xét x
∆ là số gia của biến số tại điểm 1. Ta có: y ∆ = f (1+ x ∆ ) − f ( ) 1 = ( + x ∆ )3 − −( 3 − ) 2 3 = x ∆ + x ∆ + x ∆ = x ∆ ( 2 3 1 1 3.1 1 9. 9. 3 3. . 3+ 3. x ∆ + x ∆ ) .
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 9
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com ∆ Suy ra: y = ( 2 3. 3+ 3. x ∆ + x ∆ ). x ∆ ∆
+ Ta thấy: lim y = lim 3.( 2 3+ 3. x ∆ + x ∆ ) = 3.3 = 9. x ∆ →0 x ∆ →0 x ∆ Vậy f ′( ) 1 = 9 . Bài 2.
Chứng minh rằng hàm số f (x) = x không có đạo hàm tại điểm x = 0 , nhưng có đạo hàm tại 0
mọi điểm x ≠ 0 . Lời giải
Ta có: lim x = lim x = 0 = f (0) nên hàm số f (x) = x liên tục tại x = 0. x 0+ x 0+ → →
f (x) − f (0) x − 0 Ta có: lim = lim = lim x =1 x 0+ x 0+ x 0 x x + → → → x
f (x) − f (0) x − 0 lim = lim = lim −x = 1 − x 0− x 0− x 0 x x − → → → x
f (x) − f (0)
f (x) − f (0) Nên lim ≠ lim
nên hàm số không có đạo hàm tại x = 0 . x 0+ → x→0 x − x
Với mọi x ≠ 0 thì f (x) = x tồn tại đạo hàm •
x ∈(−∞,0) ⇒ f ′( x ) = 1 − •
x ∈(0,+∞) ⇒ f ′( x ) =1 Bài 3. Cho hàm số 2 y = 2
− x + x có đồ thị (C).
a) Xác định hệ số góc của tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 2.
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm M (2;− 6) . Lời giải
a) Tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 2 có hệ số góc là: 2 2 − x + x − ( 2 2.2 − + 2)
k = f ′ x = lim 0 ( 0) x→2 x − 2 2 2 − x + x + 6
−(x − 2)(2x + 3) = lim = lim = 7 − x→2 x→2 x − 2 x − 2
b) Phương trình tiếp tuyến của đồ thị (C) tại điểm M (2;− 6) là: y = 7
− (x − 2) − 6 => y = 7 − x + 8 Bài 4.
Giả sử chi phí C (USD) để sản xuất Q máy vô tuyến là C (Q) 2
= Q + 80Q + 3500.
a) Ta gọi chi phí biên là chi phí gia tăng để sản xuất thêm 1 sản phẩm từ Q sản phẩm lên Q +1
sản phẩm. Giả sử chi phí biên được xác định bởi hàm số C′(Q) . Tìm hàm chi phí biên.
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 10
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
b) Tìm C′(90) và giải thích ý nghĩa kết quả tìm được.
c) Hãy tính chi phí sản xuất máy vô tuyến thứ 100. Lời giải
a) Chi phí biên là chi phí gia tăng để sản xuất thêm 1 sản phẩm từ Q sản phẩm lên Q +1 sản
phẩm. Chi phí biên được xác định bởi hàm số C′(Q) ( 2
Q + 80Q + 3500) −( 2
(Q +1) + 80(Q + ) 1 + 3500)
=> C′(Q) = lim Q→Q 1 + Q − Q −1 ( 2
Q + 80Q + 3500) −( 2
Q + 2Q +1+ 80Q + 80 + 3500) C′(Q) = lim Q→Q 1 + 1 −
C′(Q) = lim (2Q + 80) Q→Q 1 +
b) C′(90) = 2.90 + 80 = 260(USD)
=> Ý nghĩa: Chi phí gia tăng để sản xuất thêm 1 sản phẩm từ 89 sản phẩm lên 90 sản phẩm là 260 (USD)
c) Chi phí sản xuất 101 máy vô tuyến là: C ( ) 2
101 =101 + 80.101+ 3500 = 21781(USD)
Chi phí sản xuất 100 máy vô tuyến là: C ( ) 2
100 =100 + 80.100 + 3500 = 21500(USD)
Chi phí sản xuất máy vô tuyến thứ 100 là C ( )
101 − C (100) = 281(USD)
D. BÀI TẬP TRẮC NGHIỆM
Câu 1: Tính số gia của hàm số 2
y x 2 tại điểm x 2 ứng với số gia x 1. 0 A. y 13. B. y 9. C. y 5. D. y 2. Lời giải Chọn C Ta có y
f x x
f x f 2 1 f 2 f 3 f 2 0 0 2 2 3 2 2 2 5.
Câu 2: Tính số gia của hàm số 3 2
y = x + x +1 tại điểm x ứng với số gia x ∆ = 1. 0 A. 2 y
∆ = 3x + 5x + 3. B. 3 2 y
∆ = 2x + 3x + 5x + 2. 0 0 0 0 0 C. 2 y
∆ = 3x + 5x + 2. D. 2 y
∆ = 3x − 5x + 2. 0 0 0 0
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 11
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Lời giải Chọn C Ta có y
∆ = f (x + x
∆ − f x = f x +1 − f x 0 ) ( 0) ( 0 ) ( 0) = (x + )3 1 + (x + )2 3 2 2
1 +1 − x + x +1 = 3x + 5x + 2. 0 0 0 0 0 0 2
Câu 3: Tính số gia của hàm số x y = tại điểm x = 1 − ứng với số gia . x ∆ 2 0 A. 1 y ∆ = ( x ∆ )2 − ∆ .x B. 1 y ∆ = ( x ∆ )2 − x ∆ . 2 2 C. 1 y ∆ = ( x ∆ )2 + x ∆ . 1 y ∆ = x ∆ + ∆ . x 2 D. ( )2 2 Lời giải Chọn A Ta có y
f x x
f x f 1 x f 1 0 0 1 x 2 1 12 x x 2 1 1 x 2 x . 2 2 2 2 2
Câu 4: Tính số gia của hàm số 2
y = x − 4x +1 tại điểm x ứng với số gia x ∆ là: 0 A. y ∆ = x ∆ ( x
∆ + 2x − 4 . B. y ∆ = 2x + ∆ . x 0 ) 0 C. y ∆ = x ∆ (2x − 4 x ∆ . D. y ∆ = 2x − 4∆ . x 0 ) 0 Lời giải Chọn A Ta có y
∆ = f (x + x
∆ ) − f (x ) = (x + x
∆ )2 − 4(x + x ∆ ) 2
+1 − x − 4x +1 0 0 0 0 0 0 = x ∆ ( x ∆ + 2x − 4 . 0 )
Câu 5: Tính số gia của hàm số 1
y = tại điểm x (bất kì khác 0 ) ứng với số gia . x ∆ x A. x ∆ ∆ y ∆ ∆ x x ∆ = B. x y ∆ = − C. y ∆ = − . D. y ∆ = . x(x + x ∆ ). x(x + x ∆ ). x + x ∆ x + x ∆ Lời giải Chọn B Ta có ( ) ( ) 1 1 x y f x x f x ∆ ∆ = + ∆ − = − = − x + x ∆ x x(x + x ∆ ) .
Câu 6: Tính tỷ số y
của hàm số y 3x 1 theo x và x . x A. y y y y 0. B. 1. C. 2. D. 3. x x x x Lời giải
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 12
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Chọn D Ta có y y f x x
f x 3x x
1 3x 1 3 x 3. x
Câu 7: Tính tỷ số y của hàm số 2
y x 1 theo x và x . x A. y y y y 0. B. x 2x. C. 2x x . D. x . x x x x Lời giải Chọn B Ta có y f x
x f x x x2
x x x x 2 2 1 1 2 y 2x . x x
Câu 8: Tính tỷ số y của hàm số 3
y 2x theo x và x . x A. y x x 3 3 2 2 y . B. x 2 2 . x x x C. y y x x x x 2 2 6 6 2 . D. x x x x 2 2 3 3 . x x Lời giải Chọn C Ta có y f x x
f x x x
3 x x x x x 2 x 3 3 2 2 2 6 6 2 y 2 6x 6x x 2 x 2 . x
Câu 9: Tính tỷ số y ∆ của hàm số 1
y = theo x và . x ∆ x ∆ x A. y ∆ 1 ∆ y ∆ y ∆ = B. y 1 = − . C. 1 = − . D. 1 = . x ∆ x(x + x ∆ ) . x ∆ x(x + x ∆ ) x ∆ x + x ∆ x ∆ x + x ∆ Lời giải Chọn B Ta có ( ) ( ) 1 1 x y f x x f x ∆ ∆ = + ∆ − = − = − x + x ∆ x x(x + x ∆ ) y ∆ 1 ⇒ = − x ∆ x(x + x ∆ ) .
Câu 10: Đạo hàm của hàm số ( ) 2
f x = x − x tại điểm x ứng với số gia x ∆ là: 0
A. lim ∆x + x ∆x − ∆x
B. lim(∆x + 2x −1 . 0 ) ∆x→ (( )2 2 . 0 0 ) ∆x→0
C. lim(∆x + 2x +1 .
D. lim ∆x + x ∆x + ∆x ∆x→ (( )2 2 . 0 0 ) 0 ) ∆x→0 Lời giải
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 13
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Chọn B Ta có y
∆ = f (x + x
∆ ) − f (x ) = (x + x
∆ )2 − (x + x ∆ ) − ( 2 x − x 0 0 0 0 0 0 ) ( )2 2 y x x x x ∆ = ∆ + ∆ − ∆ ⇒ = x ∆ + 2x −1. 0 0 x ∆ Khi đó ( lim y f x ∆ ′ = = lim x ∆ + 2x −1 . 0 ) ( 0 ) x ∆ →0 ∆ x ∆ →0 x
Câu 11: Trong các phát biểu sau, phát biểu nào sau đây là đúng?
A. Nếu hàm số y f x không liên tục tại x0 thì nó có đạo hàm tại điểm đó.
B. Nếu hàm số y f x có đạo hàm tại x0 thì nó không liên tục tại điểm đó.
C. Nếu hàm số y f x có đạo hàm tại x0 thì nó liên tục tại điểm đó.
D. Nếu hàm số y f x liên tục tại x0 thì nó có đạo hàm tại điểm đó. Lời giải Chọn C
Câu 12: Cho f là hàm số liên tục tại x . Đạo hàm của f tại x là: 0 0
A. f x . 0
B. f x h f x 0 0 . h C.
f x h f x 0 0 lim
(nếu tồn tại giới hạn). h0 h D.
f x h f x h 0 0 lim
(nếu tồn tại giới hạn). h0 h Lời giải Chọn C
Ta có Cho f là hàm số liên tục tại x . 0
Nếu tồn tại giới hạn (hữu hạn)
f x f x
f x f x0 0 lim
thì f x lim . 0 x x0 x x x x x x 0 0 0 Đặt
f x h f x 0 0
h x x f x lim . 0 0 h0 h
Câu 13: Cho hàm số y f x có đạo hàm tại x là f x . Mệnh đề nào sau đây sai? 0 0 A.
f x f x f x x f x 0 0 0
f x lim .
B. f x lim . 0 0 x x0 x x x 0 x 0 C.
f x h f x
f x x f x 0 0 0 0
f x lim .
D. f x lim . 0 0 h0 h x x0 x x0 Lời giải Chọn D Hàm số
f x f x0
y f x có đạo hàm tại x là f x f x lim . 0 0 0 x x0 x x0
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 14
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Đặt f x x f x
f x h f x 0 0 0 0 h x
x x f x lim lim . 0 0 x 0 h0 x h 3 4x khi x 0 Câu 14: Cho hàm số f x 4 . Tính f 0. 1 khi x 0 4
A. f 1 0 .
B. f 1 0 .
C. f 1 0 . D. Không tồn tại. 4 16 32 Lời giải Chọn B 3 4 x 1 Xét
f x f 0 2 4 4 4 x lim lim lim x 0 x 0 x 0 x 0 x 4x
2 4x2 4x x 1 1 lim lim lim . x 0
4x 2 4 x
x 0 4x 2 4 x x0 42 4 x 16 2 x 11 Câu 15: Cho hàm số f x khi x 0 . x
Tính f 0. 0 khi x 0
A. f 0 0.
B. f 01.
C. f 1 0 . D. Không tồn tại. 2 Lời giải Chọn C 2 x 1 1 0 2 Xét
f x f 0 x x 1 1 lim lim lim 2 x 0 x 0 x 0 x 0 x x
2x 1 1 2x 1 1 2 x 1 1 lim lim lim . x 0 2 x 2 x 1 x 0 2 1 x 2
x 1 x0 2 1 x 1 1 2 3 2
x 4x 3x Câu 16: Cho hàm số khi x 1
f x xác định trên \2 bởi f x 2
x 3x 2 . Tính f 1 . 0 khi x 1
A. f 3 1 . B. f 1 1. C. f 1 0. D. Không tồn tại. 2 Lời giải Chọn D 3 2 Xét
x 4x 3x x x 1 x 3 x x 3
lim f x lim lim lim 2. 2 x 1 x 1 x 1 x 3x 2 x 1 x 2 x 1 x 2
Ta thấy: lim f x f
1 . Do đó, hàm số không tiên tục tại điểm x 1. x 1
Vậy hàm số không tồn tại đạo hàm tại điểm x 1.
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 15
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 2 Câu 17: Cho hàm số f x x 1 khi x 0
. Khẳng định nào sau đây sai? 2 x khi x 0
A. Hàm số không liên tục tại x 0 .
B. Hàm số có đạo hàm tại x 2 .
C. Hàm số liên tục tại x 2 .
D. Hàm số có đạo hàm tại x 0 . Lời giải Chọn D
lim f x lim 2 x 1 1
Xét các giới hạn x0 x 0 .
lim f x lim 2 x 0 x0 x 0
Do lim f x lim f x nên hàm số không liên tục tại x 0 . x 0 x 0
Do đó, hàm số không có đạo hàm tại x 0 . 2 x khi x 2
Câu 18: Tìm tham số thực b để hàm số f x 2 x
có đạo hàm tại x 2.
bx 6 khi x 2 2 A. b 3. B. b 6. C. b 1.
D. b 6. Lời giải Chọn B
Để hàm số có đạo hàm tại x 2 trước tiên hàm số phải liên tục tại x 2 , tức là 2 x
lim f x lim f x 2 lim
bx 6 lim x 2 2b 6 4 b 6. x 2 x 2 x 2 2 x 2
Thử lại với b 6 , ta có 2 2 x x bx 10 6x 10 f x f 2 2 2 lim lim lim x 2 x 2 x 2 x 2 x 2 x 2
x 210 x 10 x lim lim 4; x 2 2x 2 x 2 2
f x f 2 2 x 4 lim lim 4. x 2 x 2 x 2 x 2 Vì
f x f 2
f x f 2 lim lim
nên hàm số có đạo hàm tại x 2. x 2 x 2 x 2 x 2 2 Câu 19: Cho hàm số f x mx 2x 2 khi x 0
. Tìm tất cả các giá trị của các tham số , m n sao cho nx 1 khi x 0
f x có đạo hàm tại điểm x 0 . A. Không tồn tại , m .
n B. m 2, . n
C. n 2, . m
D. m n 2. Lời giải Chọn C Ta có
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 16
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
f 02 f
x f 0 2 2
mx 2x 2 2 mx 2x lim lim lim
lim mx 2 2. x0 x 0 x 0 x 0 x 0 x x
f x f 0 nx 2 2 nx lim lim lim lim n n x0 x 0 x 0 x 0 x 0 x x
Hàm số có đạo hàm tại f x f 0
x 0 khi và chỉ khi tồn tại giới hạn lim x 0 x 0
f x f 0
f x f 0 lim lim n 2 . x 0 x 0 x 0 x 0 2 x Câu 20: Cho hàm số f x khi x 1 2
. Tìm tất cả các giá trị của các tham số ,a b sao cho f x ax
b khi x 1
có đạo hàm tại điểm x 1. A. 1
a 1, b . B. 1 1
a , b . C. 1 1
a , b . D. 1
a 1, b . 2 2 2 2 2 2 Lời giải Chọn A
Hàm số có đạo hàm tại x 1, do đó hàm số liên tục tại x 1. 1
a b . 1 2
f x f 1
ax b . a 1 b ax 1 lim lim lim lim a a x 1 x 1 x 1 x 1 x 1 x 1 x 1 Ta có 2 x 1 .
f x f 1 x 1 x 1 x 1 2 2 lim lim lim lim 1 x 1 x 1 x 1 x 1 x 1 2x 1 x 1 2
Hàm số có đạo hàm tại
f x f 1
f x f 1 x 1 lim lim a 1. 2 x 1 x 1 x 1 x 1 Từ 1 và 2 , ta có 1
a 1, b . 2
Câu 21: Một chất điểm chuyển động theo phương trình ( ) 2
s t = t , trong đó t > 0, t tính bằng giây và s(t)
tính bằng mét. Tính vận tốc của chất điểm tại thời điểm t = 2 giây. A. 2m/s. B. 3m/s. C. 4m/s. D. 5m/s. Lời giải Chọn C
Ta tính được s′(t) = 2t.
Vận tốc của chất điểm v(t) = s′(t) = 2t ⇒ v(2) = 2.2 = 4m/s.
Câu 22: Một viên đạn được bắn lên cao theo phương trình s(t) 2
= 196t − 4,9t trong đó t > 0, t tính bằng
giây kể từ thời điểm viên đạn được bắn lên cao và s(t) là khoảng cách của viên đạn so với mặt
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 17
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
đất được tính bằng mét. Tại thời điểm vận tốc của viên đạn bằng 0 thì viên đạn cách mặt đất bao nhiêu mét? A. 1690m. B. 1069m. C. 1906m. D. 1960m. Lời giải Chọn D
Ta tính được s′(t) =196 −9,8t.
Vận tốc của viên đạn v(t) = s′(t) =196 −9,8t ⇒ v(t) = 0 ⇔ 196 −9,8t = 0 ⇔ t = 20.
Khi đó viên đạn cách mặt đất một khoảng h = s( ) 2 20 =196.20 − 4,9.20 =1960m.
Câu 23: Một chất điểm chuyển động có phương trình s(t) 3 2
= t − 3t + 9t + 2 , trong đó t > 0, t tính bằng
giây và s(t) tính bằng mét. Hỏi tại thời điểm nào thì bận tốc của vật đạt giá trị nhỏ nhất? A. t =1s. B. t = 2s. C. t = 3s. D. t = 6s. Lời giải Chọn A
Ta tính được s′(t) 2
= 3t − 6t + 9.
Vận tốc của chất điểm v(t) = s′(t) = t − t + = (t − )2 2 3 6 9 3 1 + 6 ≥ 6. Dấu '' ′′ = xảy ra ⇔ t =1.
Câu 24: Vận tốc của một chất điểm chuyển động được biểu thị bởi công thức v(t) 2
= 8t + 3t , trong đó
t > 0, t tính bằng giây và v(t) tính bằng mét/giây. Tìm gia tốc của chất điểm tại thời điểm mà
vận tốc chuyển động là 11 é
m t / giây A. 2 6m/s . B. 2 11m/s . C. 2 14m/s . D. 2 20m/s . Lời giải Chọn C
Ta tính được v′(t) = 8+ 6t. Ta có v(t) 2
= 11 ⇔ 8t + 3t =11 ⇔ t =1 ( 0 t > ).
Gia tốc của chất điểm a(t) = v′(t) = + t ⇒ a( ) = v′( ) 2 8 6 1 1 = 8 + 6.1 =14m/s .
Câu 25: Một vật rơi tự do theo phương trình 1 2
s = gt , trong đó 2
g = 9,8m/s là gia tốc trọng trường. Tìm 2
vận tốc trung bình của chuyển động trong khoảng thời gian từ t (t = 5s) đến t + t ∆ với t ∆ = 0,001s. A. v = 49m/s.
B. v = 49,49m/s.
C. v = 49,0049m/s. D. v = 49,245m/s. tb tb tb tb Lời giải Chọn C
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 18
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 1 1 ( + ∆ )− ( ) g (t + t ∆ )2 2 − gt s t t s t Ta có 2 2 1 v = = = gt + g t ∆ = 49,0049m/s. tb t ∆ t ∆ 2
Câu 26: Tìm hệ số góc k của tiếp tuyến của parabol 2
y x tại điểm có hoành độ 1 . 2 A. k 0. B. k 1. C. 1 k . D. 1 k . 4 2 Lời giải Chọn B Vậy 1 k = y ′ = 1. 2
Câu 27: Viết phương trình tiếp tuyến của đường cong 3
y x tại điểm 1; 1 .
A. y 3x 4. B. y 1.
C. y 3x 2.
D. y 3x 2. Lời giải Chọn D
Ta tính được k y' 1 3. x 1 0
Ta có y 1. Suy ra phương trình tiếp tuyến y 1 3x
1 y 3x 2. 0 k 3
Câu 28: Viết phương trình tiếp tuyến của đường cong 1
y tại điểm có hoành độ bằng 1 . x
A. x y 2 0.
B. y x 2.
C. y x 2.
D. y x 2. Lời giải Chọn A
Ta tính được k y' 1 1.
Với x 1 y 1. 0 0 x 1 0
Ta có y 1. Suy ra phương trình tiếp tuyến y 1 1 x
1 y x 2. 0 k 1
Câu 29: Viết phương trình tiếp tuyến của đường cong 3
y = x tại điểm có tung độ bằng 8. A. y = 8. B. y = 12 − x +16.
C. y =12x − 24.
D. y =12x −16. Lời giải Chọn D
Với y = 8 ⇒ x = 2. 0 0
Ta tính được k = y′(2) =12.
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 19
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com x = 2 0
Ta có y = 8 . Suy ra phương trình tiếp tuyến y −8 =12(x − 2) ⇔ y =12x −16. 0 k = 12 Câu 30: Cho hàm số 3 2
y = x − 3x + 2. Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm với trục tung.
A. y = 2 .x B. y = 2. C. y = 0. D. y = 2. − Lời giải Chọn B Ta có : 2
x = 0; y = 2; y′ = 3x − 6x ⇒ k = y′ 0 = 0 0 0 ( ) x = 0 0
Ta có : y = 2. Suy ra phương trình tiếp tuyến cần tìm là: y = 2. 0 k = 0 Câu 31: Cho hàm số 3 2
y = x − 3x + 2. Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm với
đường thẳng y = 2. − A. y = 9 − x + 7; y = 2 − . B. y = 2. −
C. y = 9x + 7; y = 2 − .
D. y = 9x + 7; y = 2. Lời giải Chọn C x = 1 −
Phương trình hoành độ giao điểm : 3 2
y = x − 3x + 2 = 2 − ⇔ . x = 2 y = 2 − Với x = 1 − →
. Suy ra phương trình tiếp tuyến cần tìm là: y = 9x + 7. k = y′ (− )1 = 9 y = 2 − Với x = 2 →
. suy ra phương trình tiếp tuyến cần tìm là: y = 2. − k = y′ ( 2 − ) = 0 Câu 32: Cho hàm số 3 2
y = x − 3x + 2. Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song
song với đường thẳng y = 9x + 7.
A. y = 9x + 7; y = 9x − 25.
B. y = 9x − 25.
C. y = 9x − 7; y = 9x + 25.
D. y = 9x + 25. Lời giải Chọn B
Gọi M (x ; y là tọa độ tiếp điểm. 0 0 )
Ta tính được k = y′(x ) 2
= 3x − 6x . Do tiếp tuyến song song với đường thẳng y = 9x + 7 nên có 0 0 0 x = 1 − 2 0
k = 9 ⇔ 3x − 6x = 9 ⇔ . 0 0 x = 3 0
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 20
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com y = 2 − Với 0 x = 1 − →
. Phương trình tiếp tuyến cần tìm là: y = 9x + 7(loaii) (vì trùng với 0 k = 9 đường thẳng đã cho). y = 2 Với 0 x = 3 →
. Phương trình tiếp tuyến cần tìm là: y = 9x − 25. 0 k = 9 Câu 33: Cho hàm số 3 2
y = x − 3x + 2. Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến
vuông góc với đường thẳng 1 y = − .x 45
A. y = 45x −173; y = 45x + 83.
B. y = 45x −173.
C. y = 45x +173; y = 45x −83.
D. y = 45x −83. Lời giải Chọn A
Gọi M (x ; y là tọa độ tiếp điểm. 0 0 )
Ta tính được k = y′(x ) 2
= 3x − 6x . Do tiếp tuyến vuông góc với đường thẳng 1 y = − x nên 0 0 0 45 1 x = 5 có 2 0 k. − = 1
− ⇔ k = 45 ⇔ 3x − 6x = 45 ⇔ . 0 0 45 x = 3 − 0 y = 52 Với 0 x = 5 →
. Phương trình tiếp tuyến cần tìm là: y = 45x −173. 0 k = 45 y = 52 − Với 0 x = 3 − →
. Phương trình tiếp tuyến cần tìm là: y = 45x + 83. 0 k = 45
Câu 34: Viết phương trình tiếp tuyến của đường cong 1
y = biết hệ số góc của tiếp tuyến bằng 1 − . x 4
A. x + 4y −1 = 0; x + 4y +1 = 0.
B. x + 4y − 4 = 0; x + 4y + 4 = 0. C. 1 1
y = − x − 4; 4 y = − x + . D. 1 y = − x . 4 4 4 Lời giải Chọn B
Gọi M (x ; y là tọa độ tiếp điểm. Ta tính được k = y′( 1 x = − . 0 ) 0 0 ) 2 x0 Theo giả thiết ta có 1 1 1 2 k = − ⇔ −
= − ⇔ x = 4 ⇔ x = 2. ± 2 0 0 4 x 4 0 • Với 1
x = 2 → y = . Phương trình tiếp tuyến cần tìm là: 1
y = − (x − ) 1
2 + ⇔ x + 4y − 4 = 0. 0 0 2 4 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 21
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com • Với 1 x = 2 − → y = − . Phương trình tiếp tuyến cần tìm là: 0 0 2 1 y = − (x + ) 1
2 − ⇔ x + 4y + 4 = 0. 4 2 Câu 35: Cho hàm số 3 2
y = x − 3x + 2. Viết phương trình tiếp tuyến của đồ thị hàm số biết cosin góc tạo
bởi tiếp tuyến và đường thẳng ∆ : 4x − 3y = 0 bằng 3. 5 A. y = 2; 1 y = . B. y = 2; − 1 y = . C. y = 2; − 1 y = − . D. y = 2; 2 y = − . Lời giải Chọn D
Gọi M (x ; y là tọa độ tiếp điểm⇒ k = y′(x = 3x − 6x . 0 ) 2 0 0 ) 0 0
Phương trình tiếp tuyến d có dạng y + y = k x − x . 0 ( 0 )
Suy ra tiếp tuyến d có một vectơ pháp tuyến là n = −k d ( ) ;1 .
Đường thẳng ∆ có một vectơ pháp tuyến là n = − ∆ (4; 3). k = 0 4 − k − 3 Theo đề bài ta có: (d ) 3 cos , ∆ = = ⇒ 24 . 2 k +1 16 + 9 5 k = − 7 Với 24 2 24 k = −
⇒ 3x − 6x = − : vô nghiệm. 0 0 7 7 x = 0 Với 2 0
k = 0 ⇒ 3x − 6x = 0 ⇔ . 0 0 x = 2 0
• x = 0 ⇒ y = 2 ⇒ Phương trình tiếp tuyến cần tìm là: y − 2 = 0 ⇔ y = 2. 0 0
• x = 2 ⇒ y = 2
− ⇒ Phương trình tiếp tuyến cần tìm là: y + 2 = 0 ⇔ y = 2. − 0 0
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 22
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
BÀI 2. CÁC QUI TẮC TÍNH ĐẠO HÀM
Ta có thể tính đạo hàm của hàm số bằng cách sử dụng định nghĩa. Tuy nhiên, cách làm đó là không thuận
lợi khi hàm số được cho bằng những công thức phức tạp. Trong thực tiễn, để tính đạo hàm của một hàm
số ta thường sử dụng các quy tắc tính đạo hàm để đưa việc tính toán đó về tính đạo hàm của những hàm số sơ cấp cơ bản.
Đạo hàm của nhũng hàm số sơ cấp cơ bản là gì?
Làm thế nào để thực hiện đuợc các quy tắc tính đạo hàm?
A. KIẾN THỨC CƠ BẢN CẦN NẮM
I. ĐẠO HÀM CỦA MỘT SỐ HÀM SƠ CẤP CƠ BẢN
1. Đạo hàm của hàm số n
y = x (n∈,n >1)
a) Tính đạo hàm của hàm số 2
y = x tại điểm x bất kì bằng định nghĩa. 0
b) Dự đoán đạo hàm của hàm số n
y = x tại điểm x bất kì. Lời giải a) + Xét x
∆ là số gia của biến số tại điểm x . 0 Ta có: y
∆ = f (x + x
∆ − f x = (x + x ∆ )2 − ( 2 2 x = 2.x . x ∆ + x ∆ = x ∆ 2x + x ∆ . 0 0 ) 0 ( 0 ) 0 ) ( 0) Suy ra: y ∆ = (2x + x ∆ . 0 ) x ∆ + Ta thấy: lim y
∆ = lim (2x + x ∆ = 2x . 0 ) 0 x ∆ →0 x ∆ →0 x ∆
Vậy f ′(x = 2x . 0 ) 0
b) Dự đoán đạo hàm của hàm số n
y = x tại điểm x bất kì là: n n 1 y x
y′ n⋅ x − = ⇒ = Hàm số n
y = x (n∈,n >1) có đạo hàm tại mọi x∈ và ( n x )′ n 1 = nx − .
Nhận xét: Bằng định nghĩa, ta chứng minh được:
- Đạo hàm của hàm hằng bằng 0 : (c)′ = 0 với c là hằng số;
- Đạo hàm của hàm số y = x bằng 1: (x)′ =1.
Ví dụ 1. Cho hàm số 10
f (x) = x .
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 1
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
a) Tính đạo hàm của hàm số trên tại điểm x bất kì.
b) Tính đạo hàm của hàm số trên tại điểm x =1. 0 Lời giải
a) Ta có: f ′ x = ( 10 x )′ 9 ( ) = 10x .
b) Đạo hàm của hàm số tại điểm x =1 là: 9 f (′1) =10.1 =10. 0 1. Cho hàm số 22 y = x .
a) Tính đạo hàm của hàm số trên tại điểm x bất kì.
b) b) Tính đạo hàm của hàm số trên tại điểm x = 1 − . 0 Lời giải a) Ta có: 21 y′ = 22x
b) Đạo hàm của hàm số tại điểm x = 1 − là: f (− ) 21 ' 1 = 22⋅( 1 − ) = 22 − 0
2. Đạo hàm của hàm số y = x
Tính đạo hàm của hàm số y = x tại điểm x =1 bằng định nghĩa. 0 Lời giải
b) Với Δx là sõ gia của đối số x =1. 0
Khi đó hàm sỗ sỗ gia tương ứng:
Δy = f (1+ Δx) − f ( ) 1 = 1+ Δx − 1 f ′( ) Δy 1+ Δ Ta có: = lim = lim x − 1 1 Δx→0 Δx→0 Δx Δx 1+ Δx −1 = lim
Δx→0Δx( 1+ Δx + 1) Δ = lim x
Δx→0Δx( 1+ Δx + 1) 1 1 1 = lim = =
Δx→0 1+ Δx + 1 1 + 1 2
Hàm số y = x có đạo hàm tại mọi x∈, x > 0 và 1 ( x)′ = . 2 x
Ví dụ 2. Tính đạo hàm của hàm số f (x) = x tại điểm x = 4 0 Lời giải
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 2
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Ta có: 1 f (′x) = với x > 0 . 2 x
Vậy đạo hàm của hàm số trên tại điểm x = 4 là: 1 1 f (′4) = = . 0 2 4 4
2. Tính đạo hàm của hàm số f (x) = x tại điểm x = 9 . 0 Lời giải Ta có: 1 f (′x) = với x > 0 . 2 x
Vậy đạo hàm của hàm số trên tại điểm x = 9 là: 1 1 f (9 ′ ) = = . 0 2 9 6
3. Đạo hàm của hàm số lượng giác Sử dụng kết quả sin lim
x =1, tính đạo hàm của hàm số y = sin x tại điểm x bất kì bằng định nghĩa. x→0 x Lời giải
Giả sử Δx là số gia của đối số x . 0 Ta có: = ( Δx Δ Δ + Δ − = sin + Δ − sin = 2cos + sin x y f x x f x x x x x ; 0 ) ( 0) ( 0 ) 0 0 2 2 Δ sin x Δy Δx 2 = cos x + 0 Δx 2 Δx 2 Δ sin x Do đó Δy Δx 2 lim = limcos x + . 0 x ∆ →0 x ∆ →0 Δx 2 Δx 2 Δ sin x Vì 2 lim π = 1 nên Δy Δ lim limcos x = + = cos x . x ∆ →0 Δx 0 x ∆ →0 x ∆ →0 Δx 3 2 2
Vậy f ′(x = cos x . 0 ) 0
Hàm số y = sin x có đạo hàm tại mọi x∈ và (sin x)′ = cos x . π
Ví dụ 3. Tính đạo hàm của hàm số f (x) = sin x tại điểm x = . 0 3 Lời giải
Ta có: f (′x) = cos x . π
Đạo hàm của hàm số trên tại điểm x = là: 0 3
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 3
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com π π 1 f ′ = cos = . 3 3 2 π
3. Tính đạo hàm của hàm f (x) = sin x tại điểm x = . 0 2 Lời giải
Ta có: f (′x) = cos x . π
Đạo hàm của hàm số trên tại điểm x = là: 0 2 π π f ′ = cos = 0. 2 2
Bằng định nghĩa, tính đạo hàm của hàm số y = cos x tại điểm x bất kì. Lời giải
Giả sử Δx là số gia của đối số x . Ta có: = ( + ) − ( ) = ( + ) Δx Δ Δ Δ cos Δ − cos = 2 − sin + ⋅ sin x y f x x f x x x x x 2 2 Δx Δx Δx Δ 2 − sin + ⋅sin sin + ⋅ sin x x x Δy 2 2 2 2 = = − Δx Δx Δx 2 Δx Δ sin + ⋅ sin x x Δy 2 2 lim = lim− = s − inx Δx→0 Δx→0 Δx Δx 2
Vậy f ′(x) = si − nx .
Hàm số y = cos x có đạo hàm tại mọi x∈ và (cos x)′ = −sin x . π
Ví dụ 4. Tính đạo hàm của hàm số f (x) = cos x tại điểm x = . 0 6 Lời giải
Ta có: f (′x) = −sin x . π
Đạo hàm của hàm số trên tại điểm x = là: 0 6 π π 1 f ′ = − sin = − 6 6 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 4
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
4. Một vật dao động theo phương trình f (x) = cos x , trong đó x là thời gian tính
theo giây. Tính vận tốc tức thời của vật tại thời điểm x = 2( s) 0 Lời giải
Để tính vận tốc của vật dao động tại một thời điểm xác định, ta cần lấy đạo hàm của hàm f (x) theo x tại thời điểm đó
Có f ′(x) = si − nx
Đạo hàm của hàm số trên tại điểm x = 2( s) là: 0 ⇒ f ′(2) = si − n (2) π
Bằng định nghĩa, tính đạo hàm của hàm số y = tan x tại điểm x bất kì, x ≠ + kπ (k ∈) 2 Lời giải
Giả sử Δx là số gia của đối số x . 0
Δy = f (x + Δx − f x = tan x + Δx − tan x 0 ) ( 0) ( 0 ) 0 Ta có:
sin (x + Δx − x ; 0 0 ) sin Δx = =
cos(x + Δx .cos x
cos x + Δx .cos x 0 ) 0 ( 0 ) 0 Δy sin Δx =
Δx cos(x + Δx .cos x .Δx 0 ) 0 Do đó Δy sin Δ lim = lim x . x ∆ →0 x ∆ →0 Δx
cos(x + Δx .cos x Δ . x 0 ) 0 Vì sin lim x ∆ =1 nên Δy 1 1 lim = lim = . x ∆ →0 x ∆ x ∆ → Δ x
x ∆ → cos(x + Δx) 2 0 0 .cos x cos x 0 0 0 Vậy f ′( 1 x = . 0 ) 2 cos x0 π Hàm số y 1
= tan x có đạo hàm tại mọi x ≠ + kπ ,k ∈ và (tan x)′ = . 2 2 cos x π
Ví dụ 5. Tính đạo hàm của hàm số f (x) = tan x tại điểm x = . 0 4 Lời giải Ta có: 1 π f (x) x kπ ,k ′ = ≠ + ∈ . 2 cos x 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 5
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com π
Đạo hàm của hàm số trên tại điểm x = là: 0 4 π 1 f ′ = = 2 4 2 cos π 4 π
5. Tính đạo hàm của hàm số f (x) = tan x tại điểm x = − . 0 6 Lời giải Ta có: 1 π f (x) x kπ ,k ′ = ≠ + ∈ . 2 cos x 2 π
Đạo hàm của hàm số trên tại điểm x = − . là: 0 6 π 1 4 f ′ − = = 6 2 π 3 cos − 6
Bằng định nghĩa, tính đạo hàm của hàm số y = cot x tại điểm x bất kì, x ≠ kπ (k ∈) . Lời giải
Giả sử Δx là số gia của đối số x . 0
Δy = f (x + Δx − f x = cot x + Δx − cot x 0 ) ( 0) ( 0 ) 0 Ta có:
sin (x + Δx − x ; 0 0 ) sin Δx = − = −
sin (x + Δx .sin x
sin x + Δx .sin x 0 ) 0 ( 0 ) 0 Δy sin Δx = − Δx
sin (x + Δx .sin x .Δx 0 ) 0 Do đó Δy sin Δ lim = lim x − . x ∆ →0 x ∆ →0 Δx
sin (x + Δx .sin x Δ . x 0 ) 0 Vì sin lim x ∆ =1 nên Δy 1 − 1 lim lim − = = . x ∆ →0 x ∆ x ∆ → Δ x
x ∆ → sin (x + Δx) 2 0 0 .sin x sin x 0 0 0 Vậy f ′( 1 x − = . 0 ) 2 sin x0 1
Hàm số y = cot x có đạo hàm tại mọi x ≠ kπ ,k ∈ và (cot x)′ = − . 2 sin x π
Ví dụ 6. Tính đạo hàm của hàm số f (x) = cot x tại điểm x = . 0 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 6
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Lời giải Ta có: 1 f (′x) = −
(x ≠ kπ ,k ∈) . 2 sin x π
Đạo hàm của hàm số trên tại điểm x π = là: 1 f ′ = − = 1 − . 0 2 2 2 sin π 2 π
6. Tính đạo hàm của hàm số f (x) = cot x tại điểm x = − . 0 3 Lời giải Ta có: 1 f (′x) = −
(x ≠ kπ ,k ∈) . 2 sin x π
Đạo hàm của hàm số trên tại điểm x π = − là: 1 4 ′ − = − = − . 0 f 3 3 2 π 3 sin − 3
4. Đạo hàm của hàm số mũ x Sử dụng kết quả e −1 lim
= 1, tính đạo hàm của hàm số x
y = e tại điểm x bất kì bằng định x→0 x nghĩa. Lời giải
Giả sử Δx là số gia của đối số x . Ta có: ( ) ( ) ( x+Δ Δ Δ x ) x x ( x y f x x f x e e e e∆ = + − = − = − ) 1 Δ x y e ( x e∆ − ) 1 = Δx Δx ( x e∆ − ) 1 Do lim = 1 Δx→0 Δx Δ x y e ( x e∆ − ) 1 => lim = lim x = e Δx→0 Δx→0 Δx Δx Vậy ′( ) x f x = e . Hàm số x
y = e có đạo hàm tại mọi x ∈ và ( x ) x e ′ = e .
Một cách tổng quát, ta có định lí sau:
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 7
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Hàm số x
y = a (a > 0,a ≠ )
1 có đạo hàm tại mọi x ∈ và ( x )′ x a = a ln a .
Ví dụ 7. Tính đạo hàm của hàm số ( ) 2x
f x = tại điểm x =1. 0 Lời giải Ta có: ′( ) = 2x f x ln 2 .
Đạo hàm của hàm số trên tại điểm x =1 là: f ′( ) 1 1 = 2 ln 2 = 2ln 2 . 0
7. Tính đạo hàm của hàm số ( ) 10x f x = tại điểm x = 1 − . 0 Lời giải Ta có: ′( ) =10x f x ln10 .
Đạo hàm của hàm số trên tại điểm x = 1 − là: f ′( ) 1 − ln10 1 =10 ln10 = . 0 10
5. Đạo hàm của hàm số lôgarit ln (1+ x) Sử dụng kết quả lim
= 1, tính đạo hàm của hàm số y = ln x tại điểm x dương bất kì x→0 x bằng định nghĩa. Lời giải
Giả sử Δx là số gia của đối số x .
Ta có: Δy = f (x + Δx) − f (x) = ln(x + Δx) − ln(x) x + Δx Δx + Δy (x x) (x) ln ln 1 ln Δ ln x x + − = = = Δx Δx Δx Δx .x x Δ ln 1 x + lim x Do =1 Δx→0 Δx x Δ ln 1 x + Δy x 1 => lim = lim = Δx→0 Δx→0 Δx Δx . x x x
Hàm số y = ln x có đạo hàm tại mọi x dương và ( ) 1 ln x ′ = . x
Một cách tổng quát, ta có định lí sau:
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 8
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Hàm số y = log x a > a ≠ có đạo hàm tại mọi x dương và ( x ′ = . a ) 1 log a ( 0, ) 1 x ln a
Ví dụ 8. Tính đạo hàm của hàm số f (x) = ln x tại điểm x =1. 0 Lời giải
Ta có: f ′(x) 1 = (x > 0). x
Đạo hàm của hàm số trên tại điểm x =1 là: f ′( ) 1 1 = =1. 0 1
8. Tính đạo hàm của hàm số f (x) 1
= log x tại điểm x = . 0 2 Lời giải Ta có: f ′(x) 1 = (x > 0) . x ln10
Đạo hàm của hàm số trên tại điểm 1 x = là: 1 1 2 . 0 f ′ = = 2 2 1 ln10 .ln10 2
II. ĐẠO HÀM CỦA TỔNG, HIỆU, TÍCH, THƯƠNG VÀ ĐẠO HÀM CỦA HÀM HỢP
1. Đạo hàm của tổng, hiệu, tích, thương
Cho hai hàm số f (x), g (x) xác định trên khoảng ( ;
a b), cùng có đạo hàm tại điểm x ∈ ; a b . 0 ( )
a) Xét hàm số h(x) = f (x) + g (x), x∈(a;b) . So sánh: h(x + x ∆ − h x f (x + x ∆ − f x g x + x ∆ − g x 0 ) ( 0) ( 0 ) ( 0) 0 ) ( 0) lim và lim + lim x ∆ →0 x ∆ x ∆ →0 x ∆ →0 x ∆ x ∆
b) Nêu nhận xét về h′(x và f ′(x + g′ x . 0 ) ( 0) 0 ) Lời giải a) h(x + x ∆ − h x f x + x ∆ + g x + x
∆ − f x − g x 0 ) ( 0) ( 0 ) ( 0 ) ( ( 0) ( 0)) lim = lim ( ) 1 x ∆ →0 x ∆ →0 x ∆ x ∆ f (x + x ∆ − f x g x + x ∆ − g x 0 ) ( 0) ( 0 ) ( 0) lim + lim x ∆ →0 x ∆ →0 x ∆ x ∆
f (x + x ∆ − f x g x + x ∆ − g x 0 ) ( 0) ( 0 ) ( 0) = lim + x ∆ →0 x ∆ x ∆
f (x + x
∆ − f x + g x + x ∆ − g x 0 ) ( 0) ( 0 ) ( 0) = lim x ∆ →0 x ∆
f (x + x ∆ + g x + x
∆ − f x − g x 0 ) ( 0 ) ( ( 0) ( 0)) lim (2) x ∆ →0 x ∆
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 9
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com ( ) h x + x ∆ − h x f x + x ∆ − f x g x + x ∆ − g x 1 (2) ( 0 ) ( 0) ( 0 ) ( 0) ( 0 ) ( 0) => lim = lim + ilm x ∆ →0 x ∆ →0 x ∆ →0 x ∆ x ∆ x ∆
b) Nhận xét về h′(x và f ′(x + g′ x : h′(x = f ′ x + g′ x 0 ) ( 0) ( 0) 0 ) ( 0) 0 )
Nhận xét: Ta có: h′(x = f ′ x + g′ x , tức là đạo hàm của tổng thì bằng tổng các đạo hàm. 0 ) ( 0) ( 0)
Tương tự, ta cũng có các quy tắc tính đạo hàm của hiệu, tích, thương.
Cụ thể, ta có định lí sau:
Giả sử f = f (x), g = g (x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Ta có:
( f + g)′ = f ′+ g′;
( f − g)′ = f ′− g′ ; ′ ( ′ − ′
fg)′ = f g′ + fg′ ; f f g fg = g = g x ≠ 0 . 2 ( ( ) ) g g
Hệ quả: Cho f = f (x) là hàm số có đạo hàm tại điểm x thuộc khoảng xác định.
Nếu c là một hằng số thì (cf )′ = cf ′ . 1 ′ f ′ = − f = f x ≠ 0 . 2 ( ( ) ) f f
Ví dụ 9. Tính đạo hàm của mỗi hàm số sau: a) ( ) 3
f x = x + x . b) ( ) 4 2
g x = x − x . Lời giải a) f ′ x = ( 3 x )′ + (x)′ 2 ( ) = 3x +1. b) g′(x) = ( 4 x )′ −( 2 x )′ 3 = 4x − 2x .
9. Tính đạo hàm của hàm số f (x) = x x tại điểm x dương bất kì. Lời giải
f x = x x + x( x) 1 '( ) ' ' = x + .x 2 x
Ví dụ 10. Tính đạo hàm của hàm số: 2x +1 y = . x −1 Lời giải
2x +1 ′ (2x + ) 1 ′ (x − ) 1 − (2x + ) 1 (x − ) 1 ′ 2(x − ) 1 − (2x + ) 1 Ta có: 3 − = = = . x 1 − (x − )2 1 (x − )2 1 (x − )2 1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 10
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com π
10. Tính đạo hàm của hàm số f (x) = tan x + cot x tại điểm x = . 0 3 Lời giải
f '(x) = (tan x)'+ (cot x)' 1 1 = − 2 2 cos x sin x π ′ 1 1 8 => f = − = 3 2 π 2 π 3 cos sin 3 3
2. Đạo hàm của hàm hợp
Cho hàm số y = f (u) =
u u = g (x) 2 sin ; = x .
a) Bằng cách thay u bởi 2
x trong biểu thức sin u , hãy biểu thị giá trị của y theo biến số x .
b) Xác định hàm số y = f (g (x)). Lời giải a) Thay u bởi 2
x trong biểu thức sin u , giá trị của y theo biến số x là: y = f ( 2 x ) 2 = sin x
b) y = f (g (x)) = f ( 2 x ) = ( 2 sin x )
Giả sử hàm số u = g (x) xác định trên ( ;
a b) và lấy giá trị trên ( ;
c d)); y = f (u) là hàm số của
u , xác định trên ( ;cd ) và lấy giá trị trên . Khi đó, ta có thể lập được một hàm số mới xác định trên ( ;
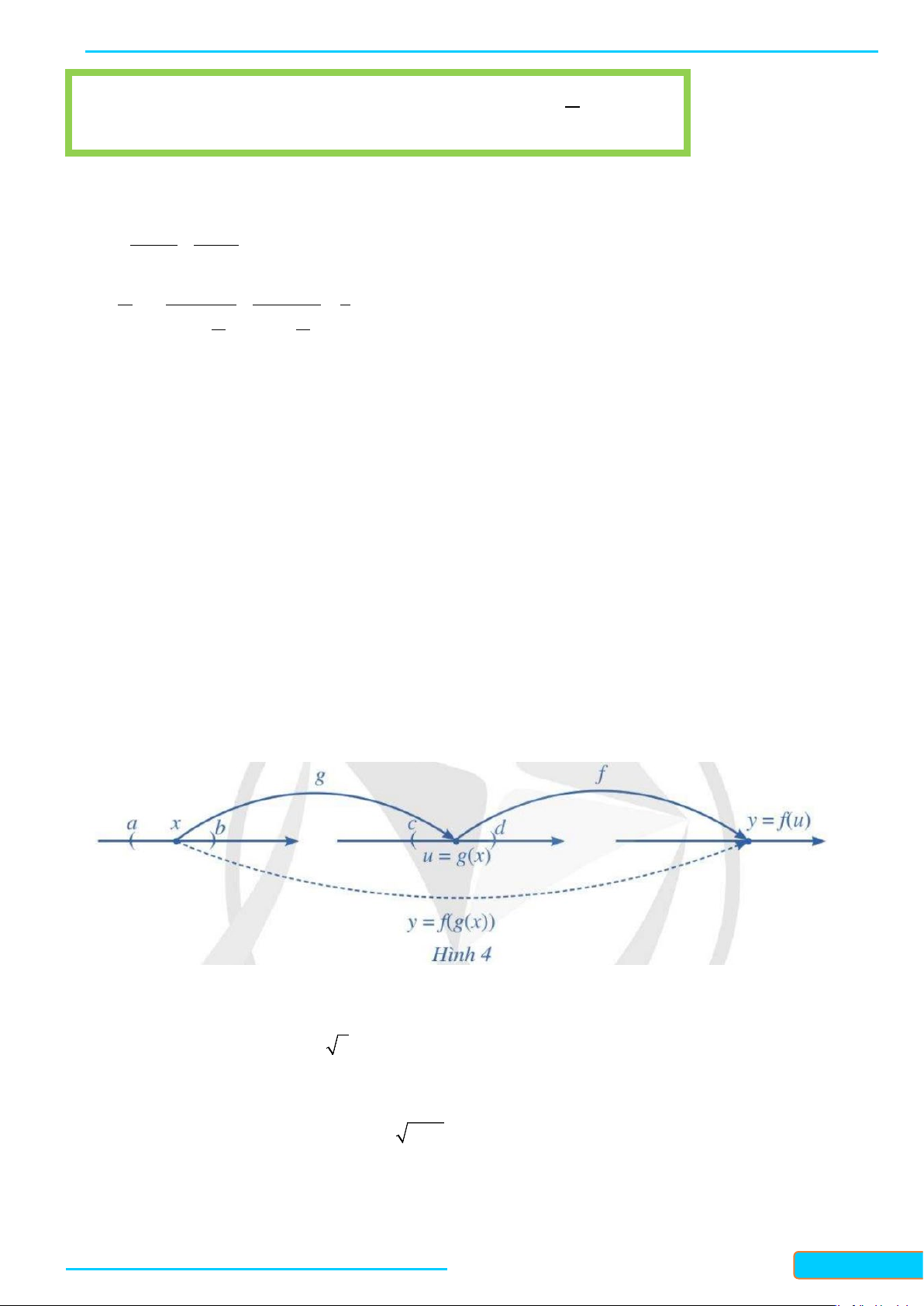
a b) và lấy giá trị trên theo quy tắc như Hình 4.
Hàm số y = f (g (x)) được gọi là hàm hợp của hai hàm số y = f (u),u = g (x).
Ví dụ 11. Cho hàm số y = f (u) = u và u = g (x) = x − 2 . Tìm hàm hợp y = f (g (x)) và tập xác định của nó. Lời giải
Ta có: y = f (g (x)) = f (x − 2) = x − 2 .
Hàm số trên xác định khi và chỉ khi x − 2 ≥ 0 hay x ≥ 2 . Tập xác định của hàm số đó là [2;+∞)
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 11
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
11. Hàm số y = log 3x +1 là hàm hợp của hai hàm số nào? 2 ( ) Lời giải
Hàm số y = log 3x +1 là hàm hợp của hai hàm số y = log u ,u = 3x +1 2 ( ) 2 ( )
Ví dụ 12. Mỗi hàm số sau đây là hàm hợp của hai hàm số nào?
a) y = sin (2x + 3) ;
b) y = 2sin x + 3. Lời giải
a) Đặt u = 2x + 3, ta có: y = sin u .
Vậy y = sin (2x + 3) là hàm hợp của hai hàm số y = sin u,u = 2x + 3.
b) Đặt u = sin x , ta có: y = 2u + 3. Vậy y = 2sin x + 3 là hàm hợp của hai hàm số
y = 2u + 3,u = sin x .
Cho hàm số u = g(x) có đạo hàm tại x và hàm số y = f (u) có đạo hàm tại u = g x . Xét 0 ( 0) 0
hàm hợp y = f (g(x)).
Ta có quy tắc tính đạo hàm của hàm hợp như sau:
Nếu hàm số u = g(x) có đạo hàm tại x là u′ và hàm số y = f (u) có đạo hàm tại u là y′ thì hàm x u
hợp y = f (g(x)) có đạo hàm tại x là y′ = y′ u′ . x u . x
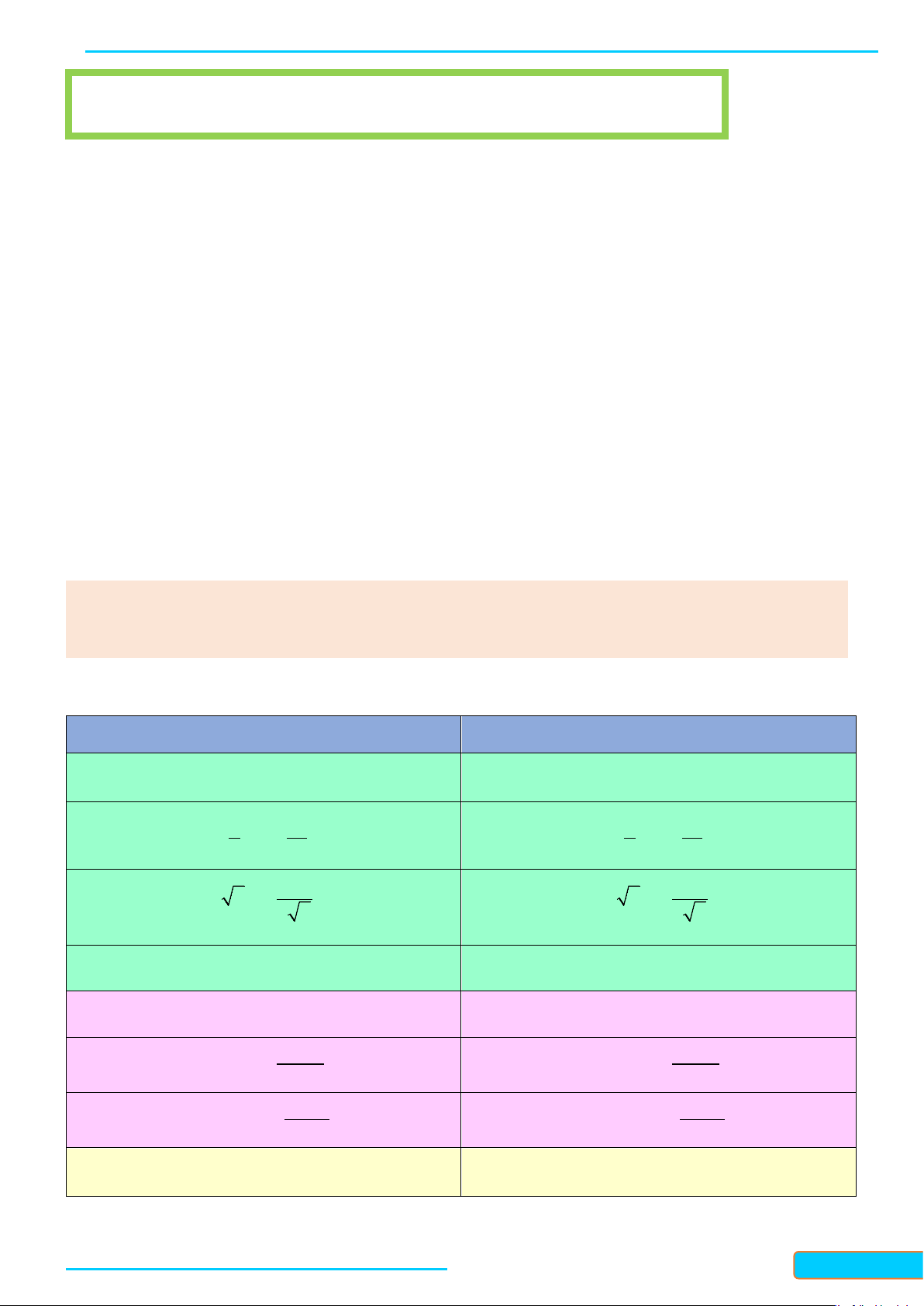
Nhận xét: Bảng đạo hàm của một số hàm số sơ cấp cơ bản và hàm hợp:
Đạo hàm của hàm số sơ cấp cơ bản thường gặp
Đạo hàm của hàm hợp ( ở đây u = u ( x) ( nx)′ n 1 = . n x − ( nu)′ n 1 = . n x − .u′ 1 ′ 1 ′ ′ = − 1 u = − 2 x x 2 u u ( ′ ′ x )′ 1 = u ( u) = 2 x 2 u
(sin x)′ = cos x
(sinu)′ = u .′cosu
(cos x)′ = −sin x (cosu)′ = u − .′sin u ( ′ x)′ 1 tan = ′ u (tanu) = 2 cos x 2 cos u ( ′ x)′ 1 cot = − ′ u (cotu) = − 2 sin x 2 sin u ( x)′ x e = e ( u)′ = . u e u′ e
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 12
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com ( x)′ x a = a .ln a ( u )′ = . u a
u′ a .ln u ( )′ 1 ′ ln x = ′ u (lnu) = x u ( ′ ′ x ′ = log u u = a ) 1 log ( a ) xln a u ln a
Ví dụ 13. Tìm đạo hàm của mỗi hàm số sau: a) 4 y = (3− 2x)
b) y = cos(4x + 5) . Lời giải
a) Đặt u = 3− 2x , ta có: 4
y = u . Khi đó: 3
y′ = u u′ = − . u 4 ; x 2
Theo công thức tính đạo hàm của hàm hợp, ta có: 3 3 3
y′ = y′ ⋅u′ = u − = − u = − − x x u x 4 .( 2) 8 8(3 2 ) .
b) Đặt u = 4x + 5, ta có y = cosu . Khi đó: y′ = − u u′ = . u sin ; x 4
Theo công thức tính đạo hàm của hàm hợp, ta có:
y′ = y′ u′ = − u = − u = − x + x u . x sin .4 4sin 4sin(4 5).
12. Tìm đạo hàm của mỗi hàm số sau: a) 3x 1 y e + =
b) y = log 2x − 3 3 ( ) Lời giải 3x 1 + ′ ′ 3x 1 + a) y ' = (e
) = (3x+ )1 .(e ) 3x 1 = 3e + ′ 2x 3 ′ − b) y′ = ( 2 log 2x − 3 = = 3 ( )) ( ) (
2x − 3)ln 3 (2x −3)ln 3
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1. Đạo hàm của hàm đa thức 1. Phương pháp
Chủ yếu ta dùng các công thức sau ( nx)' n 1 nx − = . (c)′ = ; (x)' 0 =1.
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 13
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
(u+v)′ =u′+v′
(u −v)′ = u′−v′
(uv)′ = u v′ + v u′
2. Các ví dụ rèn luyện kĩ năng Ví dụ 1: Cho hàm số 3 2
y = 2x − 3x − 5 . Tìm x để y′ = 0 Lời giải 3 2
y = 2x − 3x − 5 x = 0 2
⇒ y′ = 0 ⇔ 6x − 6x = 0 ⇔ x(x − ) 1 = 0 ⇔ . x = 1
Ví dụ 2: Cho hàm số 3 2
y = 3x + x +1. Giải bất phương trình y′ ≤ 0 . Lời giải 3 2 2
y = 3x + x +1⇒ y′ = 9x + 2x 2 2
y′ ≤ 0 ⇔ 9x + 2x ≤ 0 ⇔ − ≤ x ≤ 0. 9
Ví dụ 3: Cho hai hàm số f (x) 1 2 = x + 4 ; x g (x) 3 2
= 9x − x . Tìm x để f ′(x) = g′(x) 2 2 Lời giải
f ′(x) = x + 4; g′(x) = 9 − 3 .x
Do đó f ′(x) = g′(x) 5
⇔ 4x = 5 ⇔ x = . 4
Ví dụ 4: Cho hàm số f (x) 1 3
= mx − x . Tìm m để x = 1
− là nghiệm của bất phương trình f ′(x) < 2 3 Lời giải Ta có: f ′(x) 2
= m − x . Giá trị x = 1
− là nghiệm của bất phương trình f ′(x) < 2 khi và chỉ khi:
m −1< 2 ⇔ m < 3.
Dạng 2. Đạo hàm của hàm phân thức 1. Phương pháp
Ta thường sử dụng các công thức sau: ' u u v′ − v u ′ = v ≠ 0 2 ( ) v v ' ′ ' 1 u = − , u ≠ 0 . 2 ( ) u u
2. Các ví dụ rèn luyện kĩ năng x(1− 3x) Ví dụ 1: y = x +1 Lời giải x(1− 3x) (1−6x)(x + )1−1( 2 x − 3x ) 2 3x − − 6x +1 y = ⇒ y′ = = . x +1 (x + )2 1 (x + )2 1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 14
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Ví dụ 2: Tính đạo hàm của hàm số 2x + 3 y = 2x −1 Lời giải Dùng công thức nhanh: ax + b ad − bc y = ⇒ y′ = . cx + d (cx +d)2 Do đó, với 2x + 3 8 y = thì y′ = − . 2x −1 (2x − )2 1
Ví dụ 3: Tính đạo hàm của hàm số 1 y = 2 x +1 Lời giải ( 2x )1′ − + 2x y − ′ = = . (x + )21 (x + )2 2 2 1 2
Ví dụ 4: Tính đạo hàm của hàm số x +1 y = ? 2 x −1 Lời giải 2 2 x +1 x −1+ 2 2 y = = = 1+ 2 2 2 x −1 x −1 x −1 2( 2 x )1′ − − Do đó 4x y − ′ = = . (x − )21 (x − )2 2 2 1
Ví dụ 5: Tính đạo hàm của hàm số 1 y = 2 x + x −1 Lời giải ( 2x x )1′ − + − 2x − −1 y′ = = . (x +x− )21 (x +x− )2 2 2 1 2
Ví dụ 6: Tính đạo hàm của hàm số x + x + 3 y = 2 x + x −1 Lời giải 2 2 x + x + 3 x + x −1+ 4 4 y = = = 1+ . 2 2 2 x + x −1 x + x −1 x + x −1 4( 2 x x )1′ − + − 4 − (2x + ) 1 Do đó: y′ = = . (x +x− )21 (x +x− )2 2 2 1
Dạng 3. Đạo hàm của hàm chứa căn 1. Phương pháp
Ta thường dùng các công thức sau
Hàm số y = x có đạo hàm tại mọi x dương và ( x)' 1 = . 2 x
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 15
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Ngoài ra, đối với hàm hợp ( u )' 1 = 2 u
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Cho hàm số y = 4x − x . Tìm x để y′ = 0 ? Lời giải 1
y = 4x − x ⇒ y′ = 4 − 2 x 1 1 1 y′ = 0 ⇔ 4 −
= 0 ⇔ x = ⇔ x = . 2 x 8 64
Ví dụ 2: Tính đạo hàm của hàm số 3
y = x − x +1 Lời giải 2 1 y′ = 3x − . 2 x
Ví dụ 3: Cho hàm số f (x) 1 3 2
= x − 3 2x +18x − 7. Tìm x để f ′(x) ≤ 0 3 Lời giải
f ′(x) = x − x + = (x − )2 2 6 2 18 3 2 .
f ′(x) ≤ ⇔ (x − )2 0 3 2 ≤ 0 ⇔ x = 3 2.
Ví dụ 4: Cho hàm số f (x) = 1+ x . Tính f (3) + (x −3). f ′(3) ? Lời giải Ta có: f ′(x) 1 = ⇒ f ′( ) 1 3 = . 2 1+ x 4 + Lại có: f (3) x
= 2. Vậy f ( ) + (x − ) f ′( ) = + (x − ) 1 5 3 3 . 3 2 3 . = . 4 4
Ví dụ 5: Tính đạo hàm của hàm số: 1 y = ? 2 x +1 Lời giải −x 2 + − Ta có: x 1 x y′ = = . 2 x +1 (x + )3 2 1
Ví dụ 6: Tính đạo hàm của hàm số: 2 y = x x +1? Lời giải 2 + Ta có: 2 x 2x 1 y′ = x +1 + . x = . 2 2 x +1 x +1
Ví dụ 7: Tính đạo hàm của hàm số: 1+ x y = ? 1− x Lời giải
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 16
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com + − + + − Ta có: 1 1 x 1 2 2x 1 x 3 ′ = 1− + = . x y x = . 1− x
2 1− x 1− x 2 1− x 2 (1− x)3
Dạng 4. Tính đạo hàm của các hàm số lượng giác 1. Phương pháp
• Áp dụng quy tắc tính đạo hàm.
• Áp dụng các đạo hàm lượng giác cơ bản.
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Tính đạo hàm của hàm số y = tan 7x Hướng dẫn giải (7x)′ 7 y′ = = . 2 2 cos 7x cos 7x
Ví dụ 2: Tính đạo hàm của hàm số y = cos x Hướng dẫn giải (cos x)′ −sin x y′ = = . 2 cos x 2 cos x
Ví dụ 3: Tính đạo hàm của hàm số y = cos 2x Hướng dẫn giải (cos2x)′ 2 − sin 2x −sin 2x y′ = = = .
2 cos 2x 2 cos 2x cos 2x
Ví dụ 4: Tính đạo hàm của hàm số y = sin x Hướng dẫn giải (sin x)′ cos = sin x y x ⇒ y′ = = . 2 sin x 2 sin x
Ví dụ 5: Tính đạo hàm của hàm số y = sin 3x Hướng dẫn giải (sin3x)′ 3cos3x y′ = = .
2 sin 3x 2 sin 3x
Ví dụ 6: Tính đạo hàm của hàm số 2 y = tan 5x Hướng dẫn giải (5x)′ 10sin5 ′ = 2 tan 5 . x y x = . 2 3 cos 5x cos 5x π
Ví dụ 7: Tính đạo hàm của hàm số y cos 3x = − 3 Hướng dẫn giải π π ′ π π y = cos − 3x ⇒ y = − 3x . − sin − 3x = 3sin − 3x ′ . 3 3 3 3 π
Ví dụ 8: Tính đạo hàm của hàm số y sin 2x = − 2 Hướng dẫn giải
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 17
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com π y = sin
− 2x = cos 2x ⇒ y′ = 2 − sin 2 .x 2
Ví dụ 9: Tính đạo hàm của hàm số f (x) = 2sin 2x + cos 2x Hướng dẫn giải y 2(sin2x)′ (cos2x)′ ′ = + = 4cos2x − 2sin2x. Ví dụ 10: Cho ( ) 2 2 f x π
= cos x − sin x. Tính f′ 4 Hướng dẫn giải
Cách 1: Giải bằng tự luận Ta có f (x) 2 2
= cos x − sin x = cos 2 .
x Do đó f ′(x) = 2 − sin 2 . x π π Vậy f ′ = 2 − sin = 2. − 4 2
Cách 2: Giải nhanh bằng máy tính
Chuyển sang chế độ rad bằng cách ấn phím SHIFT MODE 4
Nhập vào màn hình d (cos(X) 2 (sin(X) 2 +
rồi ấn phím = ta được kết quả dx x π = 4
Ví dụ 11: Tính đạo hàm của hàm số 3 y = cos 4x Hướng dẫn giải 3 2 y = x ⇒ y′ = x ( x)′ 2 = x (− x) 2 cos 4 3cos 4 . cos 4 3cos 4 . 4sin 4 = 12 − cos 4 . x sin 4 . x π y ′ π
Ví dụ 12: Với y cos 2x = − thì
8 có giá trị bằng bao nhiêu? 4 π y ′ 3 Hướng dẫn giải
Cách 1: Giải bằng tự luận π π y = cos
− 2x ⇒ y = 2sin − 2x ′ 4 4 π π π π π 2π y = 2 sin − = 0; y = 2sin ′ ′ − ≠ 0 8 4 4 3 4 3 π y ′ 8 ⇒ = 0. π y ′ 4
Cách 2: Giải nhanh bằng máy tính
Chuyển sang chế độ rad bằng cách ấn phím SHIFT MODE 4
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 18
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com d π cos − 2X dx 4 x π = Nhập vào màn hình
8 rồi ấn phím = ta được kết quả d π cos − 2X dx 4 x π = 3
Ví dụ 13: Cho hàm số 5π π f (x) 2sin x = + . Tính f ′ . 6 6 Lời giải Ta có: ′ 5π ′ π f (x) 2cos x f = + ⇒ = 2 − 6 6
Ví dụ142: Cho hàm số 2 2
f (x) = cos x − sin x . Tính π f ′ . 4 Lời giải
Ta có: f (x) = cos 2x ⇒ f (′x) = 2 − sin 2 . x Do đó : π f ′ = 2 − . 4
Ví dụ 15: Cho hàm số π
y = f (x) = tan x + cot x . Tính f ′ . 4 Lời giải 1 1 tanx + cot x ′ − π Ta có: ( ) ( ) 2 2 cos x sin x f x = = ⇒ f ′ ′ = 0.
2 tanx + cot x 2 tanx + cot x 4
Dạng 5: Giải phương trình lượng giác ( f’ x) = 0 1. Phương pháp Tính đạo hàm ( f’ x)
Để giải phương trình f (’x) = 0, ta áp dụng cách giải các phương trình lượng giác cơ bản và một số
phương trình lượng giác thường gặp.
2. Các ví dụ rèn luyện kĩ năng Ví dụ 1: Cho hàm số π 1
y = sin − x . Giải phương trình y′ = 0 . 3 2 Hướng dẫn giải π 1 1 − π 1
y = sin − x ⇒ y′ = cos − x 3 2 2 3 2 π 1 π 1 y 0 cos x 0 x π k x π ′ = ⇔ − = ⇔ − = + π ⇔ = − − k2 , π k ∈ . 3 2 3 2 2 3
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 19
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Ví dụ 2: Cho hàm số 2π y = cos
+ 2x .Giải phương trình y′ = 0 . 3 Hướng dẫn giải 2π 2π y = cos + 2x ⇒ y′ = 2 − sin + 2x 3 3 2π 2 y 0 sin 2x 0 π ′ = ⇔ + = ⇔ + 2x = kπ 3 3 2π π k 2x k x π ⇔ = − + π ⇔ = − + ,k ∈ . 3 3 2
Ví dụ 3: Cho hàm số 2 x y = cot
, Giải phương trình y′ = 0 . 4 Hướng dẫn giải x cos 2 x x 1 1 1 4 y = cot ⇒ y′ = 2cot .− . = − 4 4 4 2 x 2 3 x sin sin 4 4 x
y′ = 0 ⇔ cos = 0 ⇔ x = 2π + k4 , π k ∈ . 4
Ví dụ 4: Giải phương trình: f′(x) = 0, biết f(x) = cosx −sinx + x. Hướng dẫn giải
Ta có: f′(x) = −sinx − cosx +1. Vậy: ′( ) π 1
f x = 0 ⇔ sin x + cosx = 1 ⇔ sinx + = 4 2 x π π + = + k2π x = k2π 4 4 ⇔ ⇔ π . π 3π x = + k2 x + = + k2 π π 2 4 4
Ví dụ 6: Cho hàm số ( ) sin3x cos3x f x = + cosx − 3 sinx +
. Tìm tập nghiệm của f′(x) = 0 3 3 Hướng dẫn giải Ta có: ( ) sin3x cos3x f x = + cosx − 3 sinx + 3 3
f′(x) = cos3x − sinx − 3(cosx − sin3x)
f′(x) = 0 ⇔ cos3x − sinx − 3(cosx − sin3x) = 0
⇔ cos3x + 3 sin3x = sin x + 3 cosx 1 3 1 3 ⇔ cos3x + sin3x = sin x + cosx 2 2 2 2
cos π cos3x sin π sin3x cos π sin x sin π ⇔ + = + cosx 3 3 3 3
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 20
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com π π
⇔ cos3x − = sinx + 3 3 π π π π
⇔ cos3x − = cos − x − = cos − x 3 2 3 6 π π π k 3x x k2 x π − = − + π = + 3 6 8 2 ⇔ ⇔ ; k ∈ . 3x π π x k2 − = − + + π x π = + kπ 3 6 12
Dạng 6. Tính đạo hàm 1. Phương pháp: ( xe)′ x = e ( xa)′ x = a .ln a ( ue)′ u = u e′ ( u a )′ u = u a ′ .ln a
Với mọi 0 < a ≠ 1 ( 1 x a ) 1 log ' = (ln x)' = . x ln a x ( u ' 1 loga u)' = (lnu)' = .u' u.ln a u
Ngoài ra ta có thể sử dụng MTCT để kiểm tra và thử đáp án
2. Các ví dụ rèn luyện lĩ năng
Ví dụ 1: Tính đạo hàm của hàm số y = log 2x − 2 . 3 ( ) Lời giải (2x − 2)' Ta có 1 y' = ( ) = − ( − ) . 2x 2 ln 3 x 1 ln 3
Ví dụ 2: Tính đạo hàm của hàm số x 1 y + = 2x Lời giải x 2 − (x + ) x 1 2 ln 2 1− (x + ) 1 ln 2 y' = = x x 4 2
Ví dụ 3: Tính đạo hàm của hàm số x + 2 y = ln (x + 2) x −1 Lời giải 3 − x + 2 1 3 − ln x + 2 ' 1 y = ln x + 2 + . = + 2 ( ) ( ) (x − )1 x −1 x + 2 (x − )2 1 x −1
Ví dụ 4: Cho hàm số ( ) 2 x f x x e− =
. Giải bất phương trình f ′(x) ≥ 0 Lời giải 2
f '(x) 2x − x 2 =
≥ 0 ⇔ 2x − x ≥ 0 ⇔ 0 ≤ x ≤ 2 x e
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 21
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
C. GIẢI BÀI TẬP SÁCH GIÁO KHOA
Bài 1. Cho u = u(x),v = v(x), w = (
w x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Phát
biểu nào sau đây là đúng? a) (u + v + )
w ′ = u′ + v′ + w′ b) (u + v − )
w ′ = u′ + v′ − w′;
c) (uv)′ = u v′′ ′ ′ d) u u =
với v = v(x) ≠ 0,v′ = v (′x) ≠ 0. v v′ Lời giải a) Đúng b) Đúng
c) Sai: => (uv)′ = u v′ + uv′ ′ ′ ′ d) Sai: u u v − uv => = 2 v v
Bài 2. Cho u = u(x),v = v(x), w = (
w x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Chứng minh rằng ( . u .v )
w ′ = u .′ .vw + u.v .′w + u. .vw′ . Lời giải Đặt . u v = a Có ( .
u v)′ = u v′ + uv′ ⇒ ( . u . v ) w = ( . a w)′ ′ = a '.w + .
a w' = (u v′ + uv′) w + u. .vw′ = u .′ .vw + u.v .′w + u. .vw′
Bài 3. Tìm đạo hàm của mỗi hàm số sau: a) 3 2
y = 4x − 3x + 2x +10; b) x +1 y = x −1 c) y = 2 − x x
d) y = 3sin x + 4cos x − tan x e) = 4x + 2 x y e
g) y = xln x Lời giải 3 2
a) y = 4x − 3x + 2x +10 2
y′ =12x − 6x + 2 x +1 b) y = x−1 y′ = (x + ) 1 1 ⋅ x −1 1 −x −1 2 − y′ = + = 2 2 x −1 (x −1) (x −1) c) y = 2 − x x
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 22
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
y′ = − x + (− x) 1 2 2 2 x 2 ′ = 2 x y − x − = 2 − x − x = 3 − x 2 x
d) y = 3sinx + 4cosx − tanx 1
y′ = 3cosx − 4sinx − 2 cos x e) = 4x + 2 x y e
′ = 4xln4 + 2 x y e g) y = ln x x y′ = lnx +1 Bài 4. Cho hàm số 3 2 ( ) 2 x f x + = .
a) Hàm số f (x) là hàm hợp của các hàm số nào?
b) Tìm đạo hàm của f (x) . Lời giải
a) Hàm số f (x) là hàm hợp của hai hàm số = 2u y ,u = 3x + 2 b) f ′(x) 3x+2 = 3⋅2 ⋅ln2
Bài 5. Tìm đạo hàm của mỗi hàm số sau: a) 2
y = sin 3x + sin x b) 2 1 log (2 1) 3 x y x − + = + + . 2 Lời giải a) 2 sin3x + sin x
y′ = 3cos3x + sin2x b) log (2 ) 2 1 1 3 x x − + + + 2 2 − x y + ′ = ( + − ⋅ ⋅ x + ) ( 2) 2 1 3 ln3 2 1 ln2
Bài 6. Viết phương trình tiếp tuyến của đồ thị mỗi hàm số sau: a) 3 2
y = x − 3x + 4 tại điểm có hoành độ x = 2 ; 0
b) y = ln x tại điểm có hoành độ x = e; 0 c) x
y = e tại điểm có hoành độ x = 0 . 0 Lời giải a) 3 2
y = x − 3x + 4 => f (2) = 0
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 23
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
y = f (x)′ 2 ' = 3x − 6x f (2)′ => = 0
Phương trình tiếp tuyến của đồ thị hàm số 3 2
y = x − 3x + 4 tại điểm có hoành độ x = 2 là: 0
y = 0.(x − 2) + 0 b)
y = ln x => f (e) =1 1 1
f (x)′ = => f (e)′ = x e
Phương trình tiếp tuyến của đồ thị hàm số y = ln x tại điểm có hoành độ x = elà: 0 1 = ( − ) +1 x y x e = e e c) x
y = e = f (′x)
=> f (0) = f ′(0) 0 = e =1
Phương trình tiếp tuyến của đồ thị hàm số x
y = e tại điểm có hoành độ x = 0 là: 0 y = x +1
Bài 7. Một viên đạn được bắn lên từ mặt đất theo phương thẳng đứng với tốc độ ban đầu v =196 m / s 0
(bỏ qua sức cản của không khí). Tìm thời điểm tại đó tốc độ của viên đạn bằng 0 . Khi đó viên đạn cách
mặt đất bao nhiêu mét (lấy 2 g = 9,8 m / s )? Lời giải Ta lần lượt có:
• Phương trình của viên đạn đi theo phương thẳng đứng được cho bởi : 1 2 2
y = − gt − v t <=> y = 4 − ,9t +196t 2 o
• Vận tốc viên đạn tại thời điểm t là : v = y ' = 9 − ,8t +196 Từ đó, ta nhận thấy:
• Thời điểm tại đó tốc độ của viên đạn bằng 0 được cho bởi: 9
− ,8t +196 = 0 ⇔ t = 20s
• Khi đó viên đạn cách mặt đất một khoảng cho bởi: 2 y = 4
− ,9.20 +196.20 =1960m
Bài 8. Cho mạch điện như Hình 5. Lúc đầu tụ điện có điện tích Q . Khi đóng khoá K , 0
tụ điện phóng điện qua cuộn dây; điện tích q của tụ điện phụ thuộc vào thời gian t
theo công thức q(t) = Q sinωt , trong đó ω là tốc độ góc. Biết rằng cường độ I(t) 0
của dòng điện tại thời điểm t được tính theo công thức I(t) = q (′t) . Cho biết 8 Q 10− = (C) và 6
ω =10 π (rad / s) . Tính cường độ của dòng điện tại thời điểm 0
t = 6( s) (tính chính xác đến 5 10− ( mA)) .0 Lời giải
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 24
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Cường độ của dòng điện tại t là :
I(t) = q (′t) = Q .ω.cosωt 0 Khi 8 Q 10− = (C) và 6
ω =10 π (rad / s) thì cường độ của dòng điện tại thời điểm t = 6( s) là : 0 8 − π
I(6) = q (′6) =10 .π.cos( 6 10 .π.6) = ( A) 10 ≈ 31,41593(mA)
D. BÀI TẬP TRẮC NGHIỆM
Câu 1: Cho hàm số f (x) 1 3 2
= x − 2 2x + 8x −1, có đạo hàm là f ′(x) . Tập hợp những giá trị của x 3
để f ′(x) = 0 là: A. { 2 − 2}. B. {2; 2}. C. { 4 − 2}. D. {2 2}. Lời giải Chọn D Ta có: f ′(x) 2
= x − 4 2x + 8 .
Phương trình f ′(x) 2
= 0 ⇔ x − 4 2x + 8 = 0 ⇔ x = 2 2 . Câu 2: Cho hàm số 3 2
y = 3x + x +1, có đạo hàm là y′. Để y′ ≤ 0 thì x nhận các giá trị thuộc tập nào sau đây? A. 2 ;0 − . B. 9 − ;0 . 9 2 C. 9 ; −∞ − ∪ 2 [0;+∞ ). D. ; −∞ − ∪ [0;+∞ ). 2 9 Lời giải Chọn A Ta có: 2
y′ = 9x + 2x . Do đó, 2 2 2
y ≤ 0 ⇔ y = 9x + 2x ≤ 0 ⇔ − ≤ x ≤ 0x ∈ − ;0 ′ ′ . 9 9
Câu 3: Tính đạo hàm của hàm số f (x) 4 3 2
= −x + 4x − 3x + 2x +1 tại điểm x = 1 − . A. f ′(− ) 1 = 4. B. f ′(− ) 1 =14. C. f ′(− ) 1 =15. D. f ′(− ) 1 = 24. Lời giải Chọn D
Ta có: f ′(x) 3 2 = 4
− x +12x − 6x + 2.
Suy ra f ′(− ) = − (− )3 + (− )2 1 4 1 12 1 − 6(− ) 1 + 2 = 24 .
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 25
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Câu 4: Cho hàm số 1 3
y = x − (2m + ) 2
1 x − mx − 4, có đạo hàm là y′. Tìm tất cả các giá trị của m để 3
y′ ≥ 0 với x ∀ ∈ . A. 1 m 1; ∈ − − . B. 1 m ∈ 1; − − . 4 4 C. m ( ] 1 ; 1 ; ∈ −∞ − ∪ − +∞ . D. 1 m ∈ 1; − . 4 4 Lời giải Chọn B Ta có: 2
y′ = x − 2(2m + ) 1 x − m .
Khi đó, y′ ≥ 0 với x ∀ ∈ 2
⇔ x − 2(2m + )
1 x − m ≥ 0 với x ∀ ∈ ⇔ ∆′ = ( m + )2 2 1 2
1 + m ≤ 0 ⇔ 4m + 5m +1≤ 0 ⇔ 1 − ≤ m ≤ − . 4 Câu 5: Cho hàm số 1 3
y = − mx + (m − ) 2
1 x − mx + 3, có đạo hàm là y′. Tìm tất cả các giá trị của m để 3
phương trình y′ = 0 có hai nghiệm phân biệt là x , x 1 2 thỏa mãn 2 2 x + x = 6 . 1 2 A. m = 1 − + 2 ; m = 1 − − 2. B. m = 1 − − 2.
C. m =1− 2 ; m =1+ 2. D. m = 1 − + 2. Lời giải Chọn A Ta có: 2
y′ = −mx + 2(m − ) 1 x − m .
Phương trình y′ = 0 có hai nghiệm phân biệt 2
⇔ −mx + 2(m − )
1 x − m = 0 có 2 nghiệm phân biệt m ≠ 0 m ≠ 0 ⇔ . ∆ = ( ⇔ ′ m − )2 2 1 1 − m > 0 m < 2 2(m − ) 1 + =
Khi đó, gọi x , x x x 1 2 ⇒ 1
2 là hai nghiệm phân biệt của phương trình m . x x = 1 1 2 2 m −1
Ta có: x + x = 6 ⇔(x + x ) ( ) 2 2 2 2 − 2x x = 6⇔ − 2 = 6 1 2 1 2 1 2 m 2
⇔ m + 2m −1 = 0 ⇔ m = 1 − ± 2 .
So với điều kiện thì m = 1
− ± 2 thỏa yêu cầu bài toán.
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 26
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Câu 6: Biết hàm số f (x) 3 2
= ax + bx + cx + d (a > 0) có đạo hàm f ′(x) > 0 với x
∀ ∈ . Mệnh đề nào sau đây đúng? A. 2
b − 3ac > 0. B. 2
b − 3ac ≥ 0. C. 2
b − 3ac < 0. D. 2
b − 3ac ≤ 0. Lời giải Chọn C
Ta có f ′(x) 2
= 3ax + 2bx + c . Vì a > 0 và f ′(x) > 0 với x
∀ ∈ nên ∆′ < 0 tức là 2
b − 3ac < 0 .
Câu 7: Biết hàm số f (x) 3 2
= ax + bx + cx + d (a < 0) có đạo hàm f ′(x) < 0 với x
∀ ∈ . Mệnh đề nào sau đây đúng? A. 2
b − 3ac > 0. B. 2
b − 3ac ≥ 0. C. 2
b − 3ac < 0. D. 2
b − 3ac ≤ 0. Lời giải Chọn C Ta có f ′(x) 2
= 3ax + 2bx + c . Vì a < 0 và f ′(x) < 0 với x
∀ ∈ nên ∆′ < 0 tức là 2
b − 3ac < 0
Câu 8: Tính đạo hàm của của hàm số y = (x − x )2 3 2 2 .
A. f ′(x) 5 4 3
= 6x − 20x +16x .
B. f ′(x) 5 3 = 6x +16x .
C. f ′(x) 5 4 3
= 6x − 20x + 4x .
D. f ′(x) 5 4 3
= 6x − 20x −16x . Lời giải Chọn A Ta có: y ( 3 2 x x )′ ′ = − ( 3 2 x − x ) = ( 2 x − x)( 3 2 x − x ) 5 4 3 2 2 2 2 3 4 2
= 6x − 20x +16x .
Câu 9: Cho hàm số y = ( x + )3 2 2
1 , có đạo hàm là y′. Để y′ ≥ 0 thì x nhận các giá trị nào sau đây?
A. Không có giá trị nào của .x B. (−∞;0]. C. [0;+∞). D. . Lời giải Chọn C Ta có: y ( x )′ ′ = + ( x + )2 =
x( x + )2 = x( x + )2 2 2 2 2 3 2 1 2 1 3.4 2 1 12 2 1 .
Do đó, y′ ≥ ⇔ x( x + )2 2 0 12 2 1 ⇔ x ≥ 0 .
Câu 10: Tính đạo hàm của hàm số y = ( − x )5 3 1 .
A. y′ = x ( − x )4 2 3 5 1 .
B. y′ = − x ( − x )4 2 3 15 1 .
C. y′ = − x ( − x )4 2 3 3 1 .
D. y′ = − x ( − x )4 2 3 5 1 . Lời giải Chọn B
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 27
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Ta có: y ( x )′ ′ = −
( − x )4 = (− x )( − x )4 = − x ( − x )4 3 3 2 3 2 3 5 1 1 5 3 1 15 1 .
Câu 11: Tính đạo hàm của hàm số y = (x − x )2016 3 2 2 . A. y′ = (x − x )2015 3 2 2016 2 . B. y′ = (x − x )2015 3 2 ( 2 2016 2
3x − 4x). C. y′ = ( 3 2 x − x )( 2 2016 2
3x − 4x). D. y′ = ( 3 2 x − x )( 2 2016 2
3x − 2x). Lời giải Chọn B Ta có: y (x x )′ ′ = − (x − x )2015 =
( x − x)(x − x )2015 3 2 3 2 2 3 2 2016 2 2 2016 3 4 2 .
Câu 12: Tính đạo hàm của hàm số y = ( 2
x − 2)(2x − ) 1 .
A. y′ = 4 .x B. 2
y′ = 3x − 6x + 2. C. 2
y′ = 2x − 2x + 4. D. 2
y′ = 6x − 2x − 4. Lời giải Chọn D Ta có: y ( 2 x
)′ ( x ) ( 2x )( x )′ ′ = − − + − −
= x( x − ) + ( 2 x − ) 2 2 2 1 2 2 1 2 2 1 2
2 = 6x − 2x − 4
Câu 13: Tính đạo hàm của hàm số f (x) = x(x − )
1 (x − 2)...(x − 2018) tại điểm x = 0 .
A. f ′(0) = 0.
B. f ′(0) = 2018 − !.
C. f ′(0) = 2018!.
D. f ′(0) = 2018. Lời giải Chọn C
Xét hàm số f (x) = f x f x f x ... f x n ≥ n∈ . n 1; 0 ( ) 1 ( ) 2 ( ) ( ) ( )
Bằng quy nạp, dễ dàng chứng minh được:
f (x) = f ′ ′
x f x ... f x + f x f ′ x f x + + f x f x f ′ x n ... n ... ... 0 ( ) 1 ( ) ( ) 0 ( ) 1( ) ( ) 0 ( ) 1 ( ) n ( )
Áp dụng công thức trên cho hàm số f (x) = x(x − )
1 (x − 2)...(x − 2018) và thay x = 0 với chú
ý f 0 = 0 ta được: 0 ( ) f ′(0) = (− ) 1 .( 2 − )...( 2018 − )+ 0.( 2 − )....( 2018 − )+ 0.(− ) 1 ...( 2017 − ) = 2018!.
Câu 14: Tính đạo hàm của hàm số f (x) = x(x + )
1 (x + 2)...(x + 2018) tại điểm x = 1004 − . A. f ′( 1004 − ) = 0. B. f ′( 1004 − ) =1004!. C. f ′( 1004 − ) = 1004 − !. D. f (− ) = ( )2 ' 1004 1004! . Lời giải Chọn D
Xét hàm số f (x) = f x f x f x ... f x n ≥ n∈ . n 1; 0 ( ) 1 ( ) 2 ( ) ( ) ( )
Bằng quy nạp, dễ dàng chứng minh được:
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 28
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
f (x) = f ′ ′
x f x ... f x + f x f ′ x f x + + f x f x
f ′ x . n ... n ... ... 0 ( ) 1 ( ) ( ) 0 ( ) 1( ) ( ) 0 ( ) 1 ( ) n ( )
Áp dụng công thức trên cho hàm số f (x) = x(x + )
1 (x + 2)...(x + 2018) và thay x = 1004 − với chú ý f 1004 − = 0 ta được 1004 ( ) f ′( 1004 − ) = ( 1004 − ).( 1004 − + ) 1 ...( 1004 − +1003). ( 1004 − +1005)...( 100 − 4 + 2018) = (− ) 1 .1.( 2 − ).2.....( 1004 − ).1004 = (1004 )2 ! .
Câu 15: Tính đạo hàm của hàm số ( ) 2x f x = tại điểm x = 1 − . x −1 A. f ′(− ) 1 =1. B. f ′(− ) 1 1 = − . C. f ′(− ) 1 = 2. − D. f ′(− ) 1 = 0. 2 Lời giải Chọn B TXĐ: D = \{ } 1 . − Ta có f ′(x) 2 1 = ⇒ f ′ 1 − = − 2 ( ) (x − )1 2 2
Câu 16: Tính đạo hàm của hàm số x + 2x − 3 y = . x + 2 2 2 2 A. 3 y′ + + + + + + = 1+ . B. x 6x 7 y′ = . C. x 4x 5 y′ = . D. x 8x 1 y′ = . (x + 2)2 (x + 2)2 (x + 2)2 (x + 2)2 Lời giải Chọn A Ta có 3 3 y = x − ⇒ y′ =1+ . x + 2 (x + 2)2 x(1−3x)
Câu 17: Tính đạo hàm của hàm số y = . x +1 2 2 2 A. 9 − x − 4x +1 − y′ − − + 1 6 = . B. 3x 6x 1 y′ = . C. 2 y′ =1− 6x . D. x y′ = . 2 (x +1) 2 (x +1) (x + )2 1 Lời giải Chọn B x( − x) 2 1 3 Ta có: x − 3x y = = x +1 x +1 ( 2
x 3x )′ (x ) 1 ( 2
x 3x )(x ) 1 ′ − + − − +
(1−6x)(x + )1−( 2 x − 3x ) 2 3 − x − 6x +1 ⇒ y′ = = = . (x + )2 1 (x + )2 1 (x + )2 1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 29
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 2
Câu 18: Cho hàm số ( ) 1−3x + x f x =
. Giải bất phương trình f ′(x) > 0. x −1 A. x∈ \{ } 1 . B. x∈ . ∅
C. x∈(1;+∞). D. x∈ . Lời giải Chọn A ( 2 1 3x x )′ (x ) 1 ( 2 1 3x x )(x ) 1 ′ − + − − − + −
Ta có: f ′(x) = (x − )2 1 ( 3
− + 2x)(x − ) 1 − ( 2 1− 3x + x ) 2 x − 2x + 2 = = . (x − )2 1 (x − )2 1 2 2 x − 2x + 2
x − 2x + 2 > 0
Bất phương trình f ′(x) > 0 ⇔ > 0 ⇔ ⇔ x ∈ \ 1 . 2 { } (x − )1 x ≠ 1 3
Câu 19: Cho hàm số ( ) x f x =
. Phương trình f ′(x) = 0 có tập nghiệm S là: x −1 A. 2 S 0; = . B. 2 S = − ;0. C. 3 S = 0; . D. 3 S = − ;0. 3 3 2 2 Lời giải Chọn C
( 3x)′ (x− ) 3
1 − x (x − )′ 2 1 3x (x − ) 3 3 2 1 − x Ta có ′( ) 2x − 3x f x = = = . (x − )2 1 (x − )2 1 (x − )2 1 x = 0 3 2
Phương trình f ′(x) 2x − 3x 3 2 = 0 ⇔
= 0 ⇔ 2x − 3x = 0 ⇔ . (x − )2 3 1 x = 2 2
Câu 20: Tính đạo hàm của hàm số 2 − x + x − 7 y = . 2 x + 3 2 2 A. 3
− x −13x −10 y′ − + + = x x 3 ′ ( B. y = . x + 3) . 2 2 (x +3)2 2 2 2 C. −x + 2x + 3 y′ − − − = 7x 13x 10 ′ ( D. y = . x + 3) . 2 2 (x +3)2 2 Lời giải Chọn C ( 2 2x x 7)′ ( 2 x 3) ( 2 x 3)′ − + − + − + ( 2 2 − x + x − 7) Ta có: y′ = ( x + 3)2 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 30
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com ( 4 − x + ) 2
1 (x + 3) − 2 .x( 2 2 − x + x − 7) 2 −x + 2x + 3 y′ = ( = x )2 2 2 2 (x + + 3) 3
Câu 21: Cho hàm số y = 2 − x + 3 .
x Tập nghiệm S của bất phương trình y′ > 0 là: A. S = ( ; −∞ +∞). B. 1 S ; = −∞ . C. 1 S = ;+∞ . D. S = . ∅ 9 9 Lời giải Chọn C Ta có 1 y = 2 −
x + 3x ⇒ y − ′ = + 3. x Do đó 1 − 1 1 y′ > 0 ⇔ + 3 > 0 ⇔ 3 > ⇔ x > x x 9
Câu 22: Tính đạo hàm của hàm số f (x) = x −1 tại điểm x =1. A. f ′( ) 1 1 = . B. f ′( ) 1 =1. C. f ′( ) 1 = 0. D. Không tồn tại. 2 Lời giải Chọn D Ta có f ′(x) 1 = . 2 x −1
Tại x =1 thì f ′(x) không xác định.
Câu 23: Tính đạo hàm của hàm số 2 y = 1− 2x . A. 1 y′ − − = . B. 4x y′ = . C. 2x y′ = . D. 2x y′ = . 2 2 1− 2x 2 1− 2x 2 1− 2x 2 1− 2x Lời giải Chọn C ( 2 1 2x )′ − − − Ta có 4x 2x y′ = = = . 2 2 2 2 1− 2x 2 1− 2x 1− 2x
Câu 24: Tính đạo hàm của hàm số 2 3
y = x − 4x . 2 2 2 A. x − 6x y′ − − = . B. 1 y′ x 12x x 6x = . C. y′ = . D. y′ = . 2 3 x − 4x 2 3 2 x − 4x 2 3 2 x − 4x 2 3 2 x − 4x Lời giải Chọn A 2 2 − − Ta có 2x 12x x 6x y′ = = . 2 3 2 3 2 x − 4x x − 4x
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 31
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Câu 25: Cho hàm số f (x) 2
= x − 2x. Tập nghiệm S của bất phương trình f ′(x) ≥ f (x) có bao nhiêu giá trị nguyên? A. 0 B. 1 C. 2 D. 3 Lời giải Chọn C ( 2x 2x)′ − − − Ta có f ′(x) 2x 2 x 1 = = = . 2 2 2
2 x − 2x 2 x − 2x x − 2x
Khi đó, f ′(x) ≥ f (x) x −1 2 ⇔ ≥ x − 2x 2 x − 2x 2 2 3− 5 3+ 5
⇔ x −1≥ x − 2x ⇔ x − 3x +1≤ 0 ⇔ ≤ x ≤ 2 2
Vì x ∈ ⇒ x = {1; }
2 ⇒ tập S có 2 giá trị nguyên.
Câu 26: Tính đạo hàm của hàm số f (x) = x x.
A. f ′(x) 1 = x.
B. f ′(x) 3 = x. C. ′( ) 1 x f x = . D. ′( ) x f x = x + . 2 2 2 x 2 Lời giải Chọn B ′
Ta có f ′(x) = x′ x + x ( x) 1 x 3 . . = x + . x = x + = x. 2 x 2 2
Câu 27: Tính đạo hàm của hàm số 2
y = x x − 2x. 2 2 2 A. 2x − 2 − − − − y′ 3x 4x 2x 3x 2x 2x 1 = . B. y′ = . C. y′ = . D. y′ = . 2 x − 2x 2 x − 2x 2 x − 2x 2 x − 2x Lời giải Chọn C 2 2 2 − − + − − Ta có 2 2x 2 x 2x x x 2x 3 ′ = − 2 + . x y x x x = = . 2 2 2 2 x − 2x x − 2x x − 2x
Câu 28: Tính đạo hàm của hàm số y = ( x − ) 2 2 1 x + x. 2 2 A. 2 4x −1 y′ − = 2 x + x − . B. 2 4x 1
y′ = 2 x + x + . 2 2 x + x 2 x + x 2 2 C. 2 4x −1 y′ + = 2 x + x + . D. 2 4x 1
y′ = 2 x + x + . 2 2 x + x 2 2 x + x Lời giải Chọn C
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 32
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com ′
Ta có y′ = ( x − )′ 2
x + x + ( x − ) ( 2 2 1 . 2 1 . x + x )
(2x − )1(2x + ) 2 1 2 2 4x −1 = 2. x + x + = 2 x + x + . 2 2 2 x + x 2 x + x
Câu 29: Tính đạo hàm của hàm số 1 y = . 2 x +1 A. x y′ = . B. x y′ = − . 2 2 (x +1) x +1 2 2 (x +1) x +1 2 C. x + y′ x(x 1) = . D. y′ = − . 2 2 2(x +1) x +1 2 x +1 Lời giải Chọn B ′ ′ 1 ′ − ( 2x +1) −( 2 x + ) 1 Ta có y′ = = = 2 2 2 x +1 x +1 2 x +1( 2 x + ) 1 −x = . 2 x +1( 2 x + ) 1
Câu 30: Tính đạo hàm của hàm số x −1 y = . 2 x +1 2 A. 2x + + − + y′ 1 x 2(x 1) x x 1 = . B. y′ = . C. y′ = . D. y′ = . 2 x +1 2 3 (x +1) 2 3 (x +1) 2 3 (x +1) Lời giải Chọn B ′ x (x )′ x (x )( x ) 2 2 2 x +1 − (x − − + − − + )1 1 . 1 1 1 2 Ta có x +1 y′ = ( = x +1)2 ( x +1)2 2 2 2 2
x +1− x + x 1+ x = ( = x ) . 3 2 3 2 (x + + 1) 1
Câu 31: Tính đạo hàm của hàm số 2x −1 y = . x + 2 A. 5 x + 2 + y′ = . . B. 1 5 x 2 y′ = . . . (2x − )2 1 2x −1 2 (2x − )2 1 2x −1 C. 1 x + 2 + y′ 1 5 x 2 = . . D. y′ = . . . 2 2x −1
2 (x + 2)2 2x −1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 33
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Lời giải Chọn D 1 2x 1 ′ − 1 5 x + 2 Ta có y′ = . = . . .
2x −1 x + 2 2 (x + 2)2 2x −1 2 x+2 2
Câu 32: Tính đạo hàm của hàm số x +1 y = . x A. 1 x 1 y 1 ′ = − 1 x . B. y′ = . 2 2 2 x +1 x 2 2 x +1 C. 1 x 1 y 1 ′ = + 1 x 1 . D. y′ = x − . 2 2 2 x +1 x 2 2 2 x +1 x Lời giải Chọn A 2 ′ + Ta có 1 x 1 1 x 1 y 1 ′ = = − . 2 2 2 x +1 x 2 x +1 x 2 x
Câu 33: Tính đạo hàm của hàm số 1 y = . x +1 − x −1 A. 1 y′ = − ( B. 1 y′ = .
x +1 + x −1) .2
2 x +1 + 2 x −1 C. 1 1 y′ = + . D. 1 1 y′ = + . 4 x +1 4 x −1 2 x +1 2 x −1 Lời giải Chọn C Ta có 1 x +1 + x −1 y = = . x +1 − x −1 2 1 ′
⇒ y′ = ( x + + x − ) 1 1 1 1 1 1 1 = + = + . 2
2 2 x +1 2 x −1 4 x +1 4 x −1 2 Câu 34: + +
Tính đạo hàm của hàm số f (x) 3x 2x 1 = tại điểm x = 0. 3 2 2 3x + 2x +1
A. f ′(0) = 0. B. f ′( ) 1 0 = . C. Không tồn tại. D. f ′(0) =1. 2 Lời giải Chọn B
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 34
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com ( ′ 2 3x + 2x + )′ 3 2
1 .2 3x + 2x +1 − ( 2 3x + 2x + ) 1 .( 3 2 2 3x + 2x +1)
Ta có f ′(x) = ( 2 3x + 2x +1)2 3 2 2 ( + ) 3 2 + + − ( 2 + + ) 9x + 4 6 2 2 3 2 1 3 2 1 x x x x x x 3 2 4 3 2 3x + 2x +1
9x + 6x − 9x + 8x + 4 = ( = x x )2 4( 3 2 3x + 2x + ) 3 2 3 2 1 3x + 2x + + + 1 2 3 2 1 ⇒ f ′( ) 4 1 0 = = . 8 2 3
Câu 35: Tính đạo hàm của hàm số a y =
( a là hằng số). 2 2 a − x 3 3 A. a x y′ a x = ( . B. y′ = . 2 2 a − x ) 2 2 a − x 2 2 a − x 3 3 a ( 2 3a − 2x) C. a x y′ = D. y′ = . 2( . 2 2 a − x ) 2 2 a − x 2( 2 2 a − x ) 2 2 a − x Lời giải Chọn A ′ 3 −a ( 2 2 a − x ) 3 −a ( 2 − x) 3 Ta có a x y′ = = = . 2 2 2 2 a − x 2 a − x .( 2 2 a − x ) ( 2 2 a − x ) 2 2 a − x π
Câu 36: Tính đạo hàm của hàm số y sin 3x = − . 6 π π A. y 3cos 3x ′ = − . B. y′ = 3 − cos − 3x. 6 6 π π C. y cos 3x ′ = − . D. y′ = 3 − sin − 3x. 6 6 Lời giải Chọn B π ′ π π Ta có y 3x .cos 3x 3.cos 3x ′ = − − = − − . 6 6 6 π
Câu 37: Tính đạo hàm của hàm số 1 2 y sin x = − − . 2 3 π π A. 2 y x cos x ′ = − 1 . B. 2 y′ = x cos − x. 3 2 3 π π C. 1 y xsin x ′ = − 1 . D. 2 y′ = x cos − x . 2 3 2 3
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 35
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Lời giải Chọn A π ′ π π π Ta có 1 2 2 y . 1 x .cos x ′ = − − − = − .( 2 − x) 2 2 .cos − x = . x cos − x . 2 3 3 2 3 3
Câu 38: Tính đạo hàm của hàm số y = ( 2
sin x − 3x + 2) . A. y′ = ( 2
cos x − 3x + 2).
B. y′ = ( x − ) ( 2 2
3 .sin x − 3x + 2).
C. y′ = ( x − ) ( 2 2
3 .cos x − 3x + 2).
D. y′ = −( x − ) ( 2 2
3 .cos x − 3x + 2). Lời giải Chọn C Ta có y ( 2 x x )′ ′ = − +
( 2x − x+ ) = ( x− ) ( 2 3 2 .cos 3 2 2
3 .cos x − 3x + 2).
Câu 39: Tính đạo hàm của hàm số 2
y = x tan x + x . A. 1
y′ = 2x tan x + . B. 1
y′ = 2x tan x + . 2 x x 2 2 C. x 1
y′ = 2x tan x + + . D. x 1
y′ = 2x tan x + + . 2 cos x 2 x 2 cos x x Lời giải Chọn C ′ ′ Ta có y (x ) x ( x)′ ′ = x + ( x ) 2 2 2 x 1 tan + tan . = 2x tan x + + . 2 cos x 2 x
Câu 40: Tính đạo hàm của hàm số 2 y = 2cos x . A. 2 y′ = 2 − sin x . B. 2 y′ = 4 − xcos x . C. 2 y′ = 2 − xsin x . D. 2 y′ = 4 − xsin x . Lời giải Chọn D Ta có y′ = − ( 2 x )′ 2 2 2 2. .sin x = 2.2 − .xsin x = 4 − xsin x . Câu 41: +
Tính đạo hàm của hàm số x 1 y = tan . 2 A. 1 y′ = . B. 1 y′ = . C. 1 y′ = − . D. 1 y′ = − . 2 x +1 2cos 2 x +1 cos 2 x +1 2cos 2 x +1 cos 2 2 2 2 Lời giải Chọn A
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 36
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com x +1 ′ ′ Ta có x +1 2 1 y′ = tan = = . 2 2 x +1 2 x + 1 cos 2cos 2 2
Câu 42: Tính đạo hàm của hàm số 2
y sin 2 x . A. 2x 2 2 x y cos 2 x . B. 2 y cos 2 x . 2 2 x 2 2 x C. x x 1 2 y cos 2 x . D. 2 y cos 2 x . 2 2 x 2 2 x Lời giải Chọn C 2 Ta có 2 x 2 x y 2 x 2 2 2 cos 2 x cos 2 x cos 2 x 2 2 2 2 x 2 x
Câu 43: Tính đạo hàm của hàm số y cos 2x 1 . A. sin 2x 1 x x y . B. sin 2 1 y .
C. y sin 2x 1. D. sin 2 1 y . 2x 1 2x 1 2 2x 1 Lời giải Chọn A 2x 1 ′ ′ +
Ta có y′ = −( x + ) ( ) sin 2x +1 2 1 sin 2x +1 = sin 2x +1 = − . 2 2x +1 2x +1
Câu 44: Tính đạo hàm của hàm số 2 y = cot x +1 . A. x y′ = − . B. x y′ = . 2 2 2 x +1.sin x +1 2 2 2 x +1.sin x +1 C. 1 y′ = − . D. 1 y′ = . 2 2 sin x +1 2 2 sin x +1 Lời giải Chọn A ( ′ x 2 x +1) 2 Ta có x +1 x y′ = − = − = − . 2 2 2 2 2 2 2 sin x +1 sin x +1 x +1.sin x +1
Câu 45: Tính đạo hàm của hàm số y = sin(sin x).
A. y′ = cos(sin x).
B. y′ = cos(cos x).
C. y′ = cos .xcos(sin x).
D. y′ = cos .xcos(cos x). Lời giải Chọn C
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 37
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Ta có: y = sin (sin x) ′ = (sin x)′ ′
.cos(sin x) = cos .xcos(sin x) .
Câu 46: Tính đạo hàm của hàm số y = cos(tan x). A. y′ = ( x) 1 sin tan ⋅ ⋅ B. y′ = − ( x) 1 sin tan ⋅ ⋅ 2 cos x 2 cos x
C. y′ = sin (tan x).
D. y′ = sin (tan x). Lời giải Chọn C Ta có y ( x)′ ′ = − ( x) 1 tan sin tan = − .sin tan x . 2 ( ) cos x
Câu 47: Tính đạo hàm của hàm số 2
y = 2sin x − cos 2x + x .
A. y′ = 4sin x + sin 2x +1.
B. y′ = 4sin 2x +1.
C. y′ = 4cos x + 2sin 2x +1.
D. y′ = 4sin x − 2sin 2x +1. Lời giải Chọn B
Ta có y 2.2(sin x)′ .sin x (2x)′ ′ = +
sin 2x +1 = 4cos xsin x + 2sin 2x +1
= 2sin 2x + 2sin 2x +1 = 4sin 2x +1 π π π
Câu 48: Tính đạo hàm của hàm số 2 y = sin − 2x + x − . 2 2 4 π π π π A. y′ = 2
− sin (π − 4x) + ⋅ B. y′ = 2sin − x cos − x + . 2 2 2 2 π π π C. y′ = 2sin − x cos − x + .x D. y′ = 2
− sin (π − 4x). 2 2 2 Lời giải Chọn A π π π 1− cos π − 4x 2 ( ) Ta có π π y = sin − 2x + x − = + x − 2 2 4 2 2 4 1 ( π π π x) 1 cos 4 x = − − + + − 2 2 2 4 π π ′ Suy ra 1 y′ = − (π − x) 1 cos 4 + x + − 2 2 2 4 1 = ( ′ π π
π − 4x) sin(π − 4x) + = 2
− sin (π − 4x) + . 2 2 2
Câu 49: Tính đạo hàm của hàm số 3
y = cos (2x − ) 1 . A. y′ = 3
− sin (4x − 2)cos(2x − ) 1 . B. 2
y′ = 3cos (2x − ) 1 sin (2x − ) 1 .
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 38
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com C. 2 y′ = 3 − cos (2x − ) 1 sin (2x − ) 1 . D. 2
y′ = 6cos (2x − ) 1 sin (2x − ) 1 . Lời giải Chọn A Ta có 3 y = ( x − ) ′ 2
cos 2 1 = 3cos (2x − ) 1 cos(2x − )1 ′ ′ = − ( x − ) 2 6sin 2 1 cos (2x − ) 1 = 3 − 2sin (2x − ) 1 cos(2x − ) 1 cos(2x − ) 1 = 3
− sin (4x − 2)cos(2x − )1.
Câu 50: Tính đạo hàm của hàm số 3
y = sin (1− x) . A. 3
y′ = cos (1− x). B. 3
y′ = −cos (1− x). C. 2 y′ = 3
− sin (1− x).cos(1− x). D. 2
y′ = 3sin (1− x).cos(1− x). Lời giải Chọn C Ta có 3 y′ = ( − x) ′ = ( − x) ′ 2 ( − x) = − ( − x) 2 sin 1 3. sin 1 .sin 1 3.cos 1 .sin (1− x).
Câu 51: Tính đạo hàm của hàm số 3
y = tan x + cot 2x . 2 A. 2
y′ = 3tan .xcot x + 2 tan 2 .x B. 3tan x 2 y′ = − + . 2 2 cos x sin 2x 2 C. 2 1
y′ = 3tan x − . D. 3tan x 2 y′ = − . 2 sin 2x 2 2 cos x sin 2x Lời giải Chọn D 2
Ta có y′ = ( 3 x + x)′ 2 = x( x)′ 2 3tan x 2 tan cot 2 3tan tan − = − 2 2 2 sin 2x cos x sin 2x Câu 52: +
Tính đạo hàm của hàm số sin x cos x y = . sin x − cos x 2 2 A. −sin 2x y′ − = . B. sin x cos x y′ = .
(sin x −cos x)2
(sin x −cos x)2 C. 2 − 2sin 2x y′ − = . D. 2 y′ = .
(sin x −cos x)2
(sin x −cos x)2 Lời giải Chọn D 2 sin π x + + π Ta có sin x cos x 4 y = = = − tan x + . sin x − cos x π 4 2 cos x − + 4
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 39
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com − Suy ra 1 1 2 y′ = − = − = . 2 π
cos x − sin x
(sin x −cos x)2 2 cos x + 4 2
Câu 53: Tính đạo hàm của hàm số 2 y = − . tan (1− 2x) A. 4x y′ − − − = . B. 4 y′ = . C. 4x y′ = . D. 4 y′ = . 2 sin (1− 2x) sin (1− 2x) 2 sin (1− 2x) 2 sin (1− 2x) Lời giải Chọn D 1 − 2 − (tan(1− 2x))′ 4. 2 cos (1− 2x) − Ta có 4 y′ = − = = . 2 tan (1− 2x) 2 tan (1− 2x) 2 sin (1− 2x)
Câu 54: Tính đạo hàm của hàm số cos 2x y = . 3x +1 2 − (3x + )
1 sin 2x − 3cos 2x 2 − (3x + )
1 sin 2x − 3cos 2x A. y′ = . B. y′ = . (3x + )2 1 3x +1 −(3x + )
1 sin 2x − 3cos 2x 2(3x + )
1 sin 2x + 3cos 2x C. y′ = . D. y′ = . (3x + )2 1 (3x + )2 1 Lời giải Chọn A
(cos2x)′ (3x )1 (3x )1′ + − + .cos2x 2 − (3x + )
1 sin 2x − 3cos 2x Ta có y′ = = . (3x + )2 1 (3x + )2 1
Câu 55: Cho f (x) 2
= 2x − x + 2 và g (x) = f (sin x) . Tính đạo hàm của hàm số g (x) .
A. g′(x) = 2cos 2x −sin .x
B. g′(x) = 2sin 2x + cos .x
C. g′(x) = 2sin 2x − cos .x D. /
g (x) = 2cos 2x + sin .x Lời giải Chọn C
Ta có g (x) = f ( x) 2
sin = 2sin x − sin x + 2 ⇒ g (x) = ( 2
2sin x − sin x + 2)′ ′ = 2.2sin .
x cos x − cos x = 2sin 2x − cos .x
Câu 56: Tính đạo hàm của hàm số
f x 5sin x 3cos x tại điểm x . 2 A. f 3. B. C. D. f 3. f 5. f 5. 2 2 2 2 Lời giải Chọn A
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 40
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Ta có f x5sin x 3cos x 5sin x 3cos x 5cos x 3sin x . Suy ra f
5cos 3sin 3 2 2 2
Câu 57: Tính đạo hàm của hàm số f x 3
2 sin 2x tại điểm x . 5 5 A. f 4. B. C. D. f 4. f 2. f 2. 5 5 5 5 Lời giải Chọn A Ta có f x 3 3 3 3
2 sin 2x 2 . 2x cos
2x 4 cos 2x 5 5 5 5 Suy ra 3 2 f 4 cos .
4 cos 4 5 5 5
Câu 58: Hàm số 4 x
f x x có đạo hàm là f x , hàm số gx 2x sin
có đạo hàm là gx. Tính giá 2 trị biểu thức f 1 P . g 1 A. 4 P . B. P 2. C. P 2. D. 4 P . 3 3 Lời giải Chọn B Ta có x x f x 3
4x và gx 2x sin 2 .cos . 2 2 2 Suy ra f 1 4 P 2. g 1 2 cos 2 2 Câu 59: Hàm số x
f x 4x có đạo hàm là f x , hàm số gx 4x sin
có đạo hàm là gx. Tính giá 4 trị biểu thức f 2 P . g2 A. P 1. B. 16 P . C. 16 P . D. 1 P . 16 17 16 Lời giải Chọn A Ta có x
f x 4 và gx 4 cos . 4 4 Suy ra f 2 4 P 1 g2 . 2 4 cos 4 4
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 41
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Câu 60: Hàm số f (x) = asin x + bcos x +1 có đạo hàm là f ′(x). Để f ′( ) 1 0 = và f π − = 1 thì giá 2 4
trị của a và b bằng bao nhiêu? A. 2 a = b = . B. 2 2 a = ; b = − . 2 2 2 C. 1 1 a = ; b = − . D. 1 a = b = . 2 2 2 Lời giải Chọn D f′( ) 1 0 = 2 Ta có /
f (x) = acos x − bsin x. Khi đó f π − = 1 4 1 1 1
a cos0 − bsin 0 = a = 2 b = 2 2 ⇔ ⇔ ⇔ . π π − + − + = 2 2 1 asin b cos 1 1 − a + b = 0 a = 4 4 2 2 2
Câu 61: Cho hàm số y = f (x) 2
− cos x với f (x) là hàm số liên tục trên . Trong các biểu thức dưới
đây, biểu thức nào xác định hàm số f (x) thỏa mãn y′(x) =1 với mọi x ∈ ? A. f (x) 1
= x + cos2x. B. f (x) 1 = x − cos2x. 2 2
C. f (x) = x −sin2x.
D. f (x) = x + sin2x. Lời giải Chọn A
Ta có y′(x) = f ′(x) + 2sin x cos x = f ′(x) + sin2x .
Suy ra y′(x) =1⇔ f ′(x) + sin2x =1⇔ f ′(x) =1−sin2x.
Đến đây ta lần lượt xét từng đáp án, ví dụ xét đáp án A ta có / f ′(x) 1 1
= x + cos2x = x + (cos x)/ / 2 =
1− sin 2x (thỏa mãn) 2 2 Câu 62: Cho hàm số 2
y = cos x + sin x. Phương trình y' = 0 có bao nhiêu nghiệm thuộc khoảng (0; ) π . A. 1 nghiệm. B. 2 nghiệm. C. 3 nghiệm. D. 4 nghiệm. Lời giải Chọn C y' = 2
− cosxsin x + cosx = cosx(1− 2sin x)
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 42
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com x π = + kπ 2 cosx = 0 y' = 0 π ⇔ 1 ⇔ x = + k2π ;(k ∈) sin x = 6 2 5 x π = + k2π 6 Vì π π 5π x∈(0; ) π ⇒ x∈ ; ;
. Vậy có 3 nghiệm thuộc khoảng (0; ) π 6 2 6
Câu 63: Cho hàm số y = (m +1)sinx + mcosx − (m + 2)x +1. Tìm giá trị của m để y' = 0 có nghiệm? A. m ≤ 1 − . B. m ≥ 2. C. 1 − ≤ m ≤ 3. D. m ≤ 2. − m ≥ 3 Lời giải Chọn A
y' = (m +1)cosx − msin x − (m + 2)
Phương trình y' = 0 ⇔ (m +1)cosx − msinx = (m + 2)
Điều kiện phương trình có nghiệm là 2 2 2 a + b ≥ c 2 2 2 2 m ≤ 1 −
⇔ (m +1) + m ≥ (m + 2) ⇔ m − 2m − 3 ≥ 0 ⇔ m ≥ 3
Câu 64: Cho hàm số ( ) cosx f x =
. Biểu diễn nghiệm của phương trình lượng giác f′(x) = 0 trên đường cos2x
tròn lượng giác ta được mấy điểm phân biệt? A. 1 điểm. B. 2 điểm. C. 3 điểm. D. 4 điểm. Lời giải Chọn B 1 −sin x. cos2x − cosx (−sin2x) f′(x) 2 cos2x sin x = = 3 cos2x cos2x f '(x) = 0 ⇔ x = k ,k π ∈ .
Ta biểu diễn được 2 điểm phân biệt trên đường tròn lượng giác.
Câu 65: Cho hàm số f (x) = −cosx + sinx − cos2x. Phương trình f′(x) =1 tương đương với phương trình nào sau đây? A. sinx = 0. B. sinx −1= 0. C. (sinx − ) 1 (cosx − ) 1 = 0. D. cosx = 0. Lời giải Chọn C
f ′(x) = sinx + cosx + 2sin2x
f′(x) =1⇔ sinx + cosx + 2sin2x =1 Đặt = + ( ≤ ) 2 t sinx cosx t 2 ⇒ sin2x = t −1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 43
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com t = 1 Khi đó phương trình 2 2t t 3 0 ⇔ + − = ⇔ 3 t = − (l) 2 x = k2π Với π t 1 sinx cosx 1 2 sin x 1 = ⇔ + = ⇔ + = ⇔ π ( k∈Z) 4 x = + k2π 2
Nghiệm trên cũng là nghiệm của phương trình (sinx − ) 1 (cosx − ) 1 = 0 .
Câu 66: Cho hàm số f (x) 3 cos x 3 = 2
+ sin x − 2cosx − 3sin x . Biểu diễn nghiệm của phương trình lượng 3
giác f′(x) trên đường tròn ta được mấy điểm phân biệt? A. 1 điểm. B. 2 điểm. C. 4 điểm. D. 6 điểm. Lời giải Chọn B ′( ) 3 3 f x = 2sin x − 3cos x f′(x) 3 3 3 3 = 0 ⇔ tan x = ⇔ tan x = . 2 2
Vậy có hai điểm biểu diễn nghiệm trên đường tròn lượng giác. Câu 67: Hàm số 2 x +x 1 y 8 + =
(6x +3)ln 2 là đạo hàm của hàm số nào sau đây? A. 2 1 8 + + = x x y B. 2 1 2 + + = x x y C. 2 3 3 1 2 + + = x x y D. 2 3 3 1 8 + + = x x y Lời giải Chọn A
Câu 68: Đạo hàm của hàm số x 1 y + = 9x 1− 2(x + ) 1− (x + ) A. 1 ln 3 1 ln 3 y ' = . B. y ' = . 2 3 x 2 3 x 1− 2(x + ) 1− 2(x + ) C. 1 ln 9 1 ln 3 y ' = . D. y ' = . 3x 3x Lời giải Chọn A (x ) 1 ′
+ .9x − (9x )′ .(x + ) 1
9x − 9x (x + ) 1 ln 9 1− 2(x + ) 1 ln 3 y′ = = = . 2x 2x 2 9 9 3 x
Câu 69: Cho hàm số y = log (2x +1) 3 , ta có: 1 2 A. 1 y′ = . B. y′ = . C. y′ = . D. 2 y′ = . 2x +1 (2x +1)ln 3 (2x +1)ln 3 2x +1 Lời giải Chọn C 1
Câu 70: Đạo hàm của hàm số y = là: log x 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 44
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com A. ' ln 2 x ln 2 x ln 2 y = − . B. ' ln 2 y = . C. 'y = − . D. 'y = . 2 x ln x 2 x ln x 2 log x 2 log x 2 2 Lời giải Chọn A log x ' ( )' 2 ln 2 y = − = − 2 2 ln x xln x
Câu 71: Kết quả tính đạo hàm nào sau đây sai?
A. (3x )′ = 3x ln3
B. (10x )′ =10x ln10 C. ( ′ 1 log x = D. ( 2x )′ 2 = x e e 3 ) xln3 Lời giải Chọn D
Ta có ( 2x )′ 2 = 2 x e
e , suy ra D sai.
Câu 72: Đạo hàm của hàm số y = (2x + ) 1 ln (1− x) là. A. ( − x) 2x +1 2ln 1 − .
B. 2xln (x − ) 1 . 1− x C. 2x +1 + + 2x . D. ( − x) 2x 1 2ln 1 + . 1− x 1− x Lời giải Chọn A y ( x )′ ′ = +
( − x)+( x + ) ( ( − x))′ = ( − x)+( x + ) 1 2 1 .ln 1 2 1 . ln 1 2.ln 1 2 1 . − (1− x) = ( − x) 2x +1 2ln 1 − 1− x x −1
Câu 73: Đạo hàm của hàm số y log = 2 là: ln x + − + − + − + −
A. xln x 1 x
B. xln x 1 x .
C. xln x 1 x .
D. xln x 1 x . x(x − ) . 1 ln 2
(x − )1ln xln 2 (x − )1ln 2 x(x − ) 1 ln 2.ln x Lời giải Chọn D ' x −1 + − Ta có: ' ln x
x ln x 1 x y = = x − x(x − ) . 1 1 ln 2.ln ln 2 x ln x
Câu 74: Cho hàm số ( ) 2 ` = 2x +a f x v a f ′( )
1 = 2ln2. Mệnh đề nào sau đây đúng? A. 2 − < a < 0
B. 0 < a <1 C. a >1 D. a < 2 − Lời giải Chọn A Ta có f (x) 2 x +a = x ⇒ f ( ) a 1 + a 1 2 .2 ln 2 1 = 2ln 2.2 = 2ln 2 ⇒ 2 + ′ ′ = 1⇒ a = 1 −
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 45
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Câu 75: Cho hàm số 1
y = ln . Hệ thức nào sau đây đúng? x A. y e + y' = 0 B. y e − y' = 0 C. y e .y' = 0 D. y 1 e .y' = 2 x Lời giải Chọn A / 1 Ta có 1 1 1 1 y ' = = = . x − = − y 1 , = ln x e
e = ⇒ y ' y + e = 0 2 1 x x x x x
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 46
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 47
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
BÀI 3. ĐẠO HÀM CẤP 2
A. KIẾN THỨC CƠ BẢN CẦN NẮM I. ĐỊNH NGHĨA 1. Xét hàm số 3 2
y = x − 4x + 5 . a) Tìm y′.
b) Tìm đạo hàm của hàm số y′. Lời giải a) Có 2
y′ = 3x −8x
b) y′′ = 6x −8
Giả sử hàm số y = f (x) có đạo hàm y′ = f ′(x) tại mọi điểm x∈( ; a b) . Nếu hàm số
y′ = f ′(x) tiếp tục có đạo hàm tại x thì ta gọi đạo hàm của y′ tại x là đạo hàm cấp hai của
hàm số y = f (x) tại x , kí hiệu là y′′ hoặc f ′′(x).
Ví dụ 1. Cho hàm số f (x) 4 2 = x − 4x + 3.
a) Tìm đạo hàm cấp hai của hàm số tại điểm x bất kì.
b) Tính đạo hàm cấp hai của hàm số tại điểm x = 1 − . 0 Lời giải
a) Ta có: f ′(x) 3
= 4x −8x và f ′′(x) 2 = 12x −8.
b) Ta có: f ′′(− ) = ⋅(− )2 1 12 1 −8 = 4 .
Ví dụ 2. Cho hàm số f (x) 1 = . x + 2
a) Tìm đạo hàm cấp hai của hàm số tại điểm x ≠ 2 − .
b) Tính đạo hàm cấp hai của hàm số tại điểm x = 2 . 0 Lời giải a) Với x ≠ 2 − , ta có: ′ ′ + f ′(x) 1 (x 2) 1 − = = − = x 2 +
(x + 2)2 (x + 2)2 − (x + 2)2 ′ ′ + f ′′(x) 1 2(x 2) 2 = = = = . ( x + 2)2 (x + 2)4
(x + 2)4 (x + 2)3 b) Ta có: f ′′( ) 2 1 2 = = . (2+ 2)3 32 Lời giải
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 1
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Ta có y′ = 3cos3x => y′ = 9s − in3x
II. Ý NGHĨA CƠ HỌC CỦA ĐẠO HÀM CẤP HAI 1
2. Một vật rơi tự do theo phương thẳng đứng có phương trình 2
s = gt , trong đó g là gia tốc rơi 2 tự do, 2 g ≈ 9,8 m / s .
a) Tính vận tốc tức thời v(t) tại thời điểm t = 4 s ;t = 4,1 s . 0 ( ) 1 ( ) b) Tính tỉ số v
∆ trong khoảng thời gian t∆ = t −t . t ∆ 1 0 Lời giải
a) v(t) = s′(t) = gt
Vận tốc tức thời v(t) tại thời điểm t = 4 s . 0 ( )
v(4) = 9,8.4 = 39,2(m / s)
Vận tốc tức thời v(t) tại thời điểm t = 4,1 s . 0 ( ) v(4, )
1 = 9,8.4,1 = 40,18(m / s) b) tỉ số v
∆ trong khoảng thời gian t∆ = t −t . t ∆ 1 0 v ∆
v(t − v t 1 ) ( o ) gt − gt 1 o = = = g t ∆ t − t t − t 1 o 1 o ∆
Tỉ số v gọi là gia tốc trung bình của chuyển động trong khoảng thời gian t ∆ . t ∆ v ∆
v′(t) = lim
= a(t) gọi là gia tốc tức thời của chuyển động tại thời điểm t . t ∆ →0 t ∆
Trong trường hợp tổng quát, ta có:
Đạo hàm cấp hai s′′(t) là gia tốc tức thời của chuyển động s = s(t) tại thời điểm t .
Ví dụ 3. Xét dao động điều hoà có phương trình chuyển động s(t) = Acos(ωt +ϕ), trong đó , A ω,ϕ là
các hằng số. Tìm gia tốc tức thời tại thời điểm t của chuyển động đó. Lời giải
Gọi v(t) là vận tốc tức thời của chuyển động tại thời điểm t , ta có:
v(t) = s (t) = Acos (ωt +ϕ) ′ ′ = −Aω sin (ωt +ϕ)
Gia tốc tức thời của chuyển động tại thời điểm t là:
s′′(t) = v′ (t) = −Aω (ωt +ϕ) ′ 2 sin = −Aω cos (ωt +ϕ)
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Tính đạo hàm cấp cao của hàm số y = f (x) 1. Phương pháp
Tính đạo hàm cấp 1: f’(x)
Tính đạo hàm cấp 2: ' f ' (x) = f '(x)
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 2
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Tính đạo hàm cấp hai của hàm số f (x) 4 5 2 = x − 3x − x + 4 5 Hướng dẫn giải f (x) 4 5 2
= x − 3x − x + 4 thì ′( ) 4
f x = 4x − 6x −1, do đó: ′′( ) 3 f x = 16x − 6. 5
Ví dụ 2: Tính đạo hàm cấp hai của hàm số y = cos2x Hướng dẫn giải y = cos2x thì y′ = 2 − sin2x. Do đó y′ = 4 − cos2x.
Ví dụ 3: Cho hàm số f (x) 1 3 1 2
= x + x −12x −1. Giải f ' (x) ≥ 0 3 2 Hướng dẫn giải f (x) 1 3 1 2
= x + x −12x −1 thì f ′(x) 2
= x + x −12; f ′′(x) = 2x +1. 3 2
Do đó f ′ (x) 1 ≥ 0 ⇔ x ≥ − . 2
Ví dụ 4: Cho hàm số 1 y = . Tính y′′? x +1 Hướng dẫn giải Ta có: 1 2 y′ = − ⇒ y′′ = . (x + )2 1 (x + )3 1
Ví dụ 5: Cho hàm số x − 3 y = . Tính = ( ′)2 M 2 y + (1− y).y′.′ x + 4 Hướng dẫn giải Ta có: 7 14 y′ = ⇒ y′′ = − (x + 4)2 (x + 4)3 Lại có x − 3 7 1− y = 1− = x + 4 x + 4 Vậy: = ( )2 + ( − ) 49 7 14 M 2 y 1 y .y = 2. + . ′ ′′ − = 0. ( + )4 x + 4 x 4 (x+4)3
Ví dụ 6: Cho hàm số 1 2 y = x + x +1. Tính 2 y′ − 2y.y′.′ 2 Hướng dẫn giải
Ta có: y′ = x +1⇒ y′ =1. Vậy: y′ − 2y.y′ = (x + )2 2 1 2 2 2
1 − 2 x + x +1.1= x + 2x +1− x − 2x − 2 = 1 − . 2
Ví dụ 7: Cho hàm số y = xsinx. Tính xy − 2(y′ −sinx) + xy′.′ Hướng dẫn giải
Ta có: y′ = sinx + cosx ⇒ y′ = cosx + (cosx − xsinx) = 2cosx − xsinx. Vậy: − ( ′ − ) 2 + ′′ = − ( + − ) 2 xy 2 y sin x xy
x sin x 2 sin x x cosx sin x + 2x cosx − x sin x = 0.
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 3
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Ví dụ 8: Cho hàm số y = Asin(ωx + ϕ).Tính 2 M = y′ + ω .y. Hướng dẫn giải Ta có: ′ = ω (ω +ϕ) 2 y A cos x
⇒ y′ = −Aω sin(ωx + ϕ) 2 2 ⇒ ′′ + ω = − ω (ω +ϕ) 2 y y A sin x + Aω sin(ωx + ϕ) = 0.
Ví dụ 9: Cho hàm số y = sin 2x − cos 2x . Giải phương trình y′ = 0. Hướng dẫn giải
Ta có: y′ = 2cos 2x + 2sin 2x ⇒ y′ = 4 − sin 2x + 4cos 2 . x Phương trình π y 0
4sin 2x 4cos 2x 0 sin 2x ′ = ⇔ − + = ⇔ − = 0 4 π π π
⇔ 2x − = kπ ⇔ x = + k ;k ∈ . 4 8 2 2
Ví dụ 10: Cho hàm số: = ( − 4) x y m + cos . x 2
Tìm m sao cho y′ ≤ 0 với mọi x ∈ . Hướng dẫn giải
Ta có: y′ = (m − 4) x −sin x ⇒ y′′ = m − 4 − cos x
y′′ ≤ 0 ⇔ m − 4 − cos x ≤ 0 ⇔ cos x ≥ m − 4(*) Vì cos x ≥ 1, − x ∀ ∈ .
Vậy bất phương trình (*) luôn nghiệm đúng x ∀ ∈ ⇔ 1
− ≥ m − 4 ⇔ m ≤ 3.
Ví dụ 11: Cho hàm số 3x − 2 y =
. Giải bất phương trình y′ > 0. 1− x Hướng dẫn giải Ta có: 1 2 y′ = ⇒ y′′ = . (1−x)2 (1−x)3 Vậy 2 y′′ > 0 ⇔
> 0 ⇔ 1− x > 0 ⇔ x < 1. (1−x)3 3 3 2 Ví dụ 12 : x + 3x + 2
ax + bx + cx + d
Hàm số f (x) = có f ( ′′ x) =
. Tính S = a − b + c − 2d . x −1 (x − )3 1 Lời giải 3 x + 3x + 2 Ta có : f (x) = = 2 6 x + x + 4 + . x −1 x −1 6
⇒ f (′x) = 2x +1− ( . x − )2 1 12 2(x − )3 1 +12 3 2
2x − 6x + 6x +10 ⇒ f ( ′′ x) = 2 + = = . (x − )3 1 (x − )3 1 (x − )3 1
⇒ a = 2, b = 6,
− c = 6, d =10 .
Do đó S = a − b + c − 2d = 6 − .
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 4
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Dạng 2: Ý nghĩa vật lý của đạo hàm cấp hai 1. Phương pháp
Ý nghĩa của đạo hàm cấp hai: Gia tốc tức thời (γ ) tại thời điểm t là đạo hàm cấp 2 của hàm số s = f (t) .
2. Các ví dụ rèn luyện kĩ năng
Câu 1: Một chất điểm chuyển động thẳng được xác định bởi phương trình : 3 2
s = t − 3t + 5t + 2 , trong đó
t tính bằng giây và s tính bằng mét. Tính gia tốc của chuyển động khi t = 3 . Lời giải
• Gia tốc chuyển động tại t = 3s là s ''(3)
• Ta có: s′(t) 2 = 3t − 6t + 5
• s′′(t) = t − ⇒ s′ ( ) 2 6 6 3 =12m / s .
Câu 2: Cho chuyển động thẳng xác định bởi phương trình 3 2 S = t
− + 3t + 9t , trong đó t tính bằng giây và
S tính bằng mét. Tính vận tốc của chuyển động tại thời điểm gia tốc triệt tiêu. Lời giải
• Vận tốc của chuyển động chính là đạo hàm cấp một của quãng đường: 2 v = S′ = 3 − t + 6t + 9
• Gia tốc của chuyển động chính là đạo hàm cấp hai của quãng đường: a = S′′ = 6 − t + 6
• Gia tốc triệt tiêu khi S′′ = 0 ⇔ t =1.
• Khi đó vận tốc của chuyển động là S′( ) 1 =12m/ s.
Câu 3: Một chất điểm chuyển động theo quy luật s(t) 3 2 = t
− + 6t với t là thời gian tính từ lúc bắt đầu
chuyển động, s(t) là quãng đường đi được trong khoảng thời gian t . Tính thời điểm t tại đó vận tốc
đạt giá trị lớn nhất. Lời giải
Ta có v(t) = s′(t) 2 = 3
− t +12t có đồ thị là Parabol, do đó v(t) 12 t − ⇔ = = 2. max 6 −
C. GIẢI BÀI TẬP SÁCH BÀI TẬP
Bài 1. Tìm đạo hàm cấp hai của mỗi hàm số sau: a) 1 y = . b) y = log x . c) 2x y = . 2x + 3 3 Lời giải a) 1 y = 2x + 3
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 5
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 2 1 y′ = − = 2 − ⋅ 2 2 4x +12x + 9 4x +12x + 9 8x +12 y′′ = 2.
− − (4x +12x+9)2 2 b) y = log x 3 1
y′ = x⋅ln3 ln3 1 => y′ = − = − 2 2 (x⋅ln3) x ⋅ln3 c) 2x y = y′ = 2xln2 x 2 => y′ = 2 (ln2)
Bài 2. Tính đạo hàm cấp hai của mỗi hàm số sau: a) 2
y = 3x − 4x + 5 tại điểm x = 2 − ; 0
b) y = log 2x +1 tại điểm x = 3; 3 ( ) 0 c) 4x 3 y e + = tại điểm x =1; 0 π d) π y sin 2x = + tại điểm x = ; 3 0 6 e) π y cos 3x = − tại điểm x = 0 . 6 0 Lời giải a) 2
y = 3x − 4x + 5 y′ = 6x − 4 y′ = 6 b) log 2x +1 3 ( ) 2 1 y′ = ( = ⋅ x + ) 2 2 1 ln3 (2x + )1ln3 2⋅ln3 4 y′′ 2. − => = − = 2 2 2 (2x +1) (ln3) (2x +1) ⋅ln3 Thay x = 3 0 => y ′( ) 4 3 − = 49⋅ln3 c) 4x 3 e +
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 6
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 4x+3 y′ = 4e 4x+3
=> y′′ =16e => y′′( ) 7 1 =16e d) π sin 2x + 3 π y′ 2cos 2x = + 3 π y′′ 4sin 2x => = − + 3 π 2π y′′ 4sin => = − 6 3 e) π y cos 3x = − 6 π y′ 3sin 3x = − − 6 π y′ 9cos 3x = − − 6 π y′ (0) 9cos = − − 6 Bài 3.
Một vật rơi tự do theo phương thẳng đứng có phương trình 1 2
s = gt , trong đó g là gia tốc rơi 2 tự do, 2 g ≈ 9,8 m / s .
a) Tính vận tốc tức thời của vật tại thời điểm t = 2 s . 0 ( )
b) Tính gia tốc tức thời của vật tại thời điểm t = 2 s . 0 ( ) Lời giải
a) v(t) = s′(t) = gt
Vận tốc tức thời v(t) tại thời điểm t = 2 s . 0 ( )
v(2) = 9,8.2 =19,6(m / s)
b) a(t) = v′(t) = g
Gia tốc tức thời của vật tại thời điểm t = 2 s . 0 ( ) a( ) = g = ( 2 2 9,8 m / s ) Bài 4.
Một chất điểm chuyển động theo phương trình s(t) 3 2
= t − 3t + 8t +1, trong đó t > 0, t tính
bằng giây và s(t) tính bằng mét. Tìm vận tốc tức thời, gia tốc tức thời của chất điểm:
a) Tại thời điểm t = 3(s) ;
b) Tại thời điểm mà chất điểm di chuyển được 7 ( m) .
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 7
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Lời giải
v(t) = s′(t) 2 = 3t − 6t + 8
a(t) = v′(t) = 6t − 6
a) vận tốc tức thời tại thời điểm t = 3(s) là: v( ) = s′( ) 2 3
3 = 3.3 − 6.3+ 8 =17(m / s)
Gia tốc tức thời của chất điểm tại thời điểm t = 3(s) là: a( ) 2
3 = 6.3− 6 =12(m / s )
b) Chất điểm di chuyển được 7 ( m) ⇒ s(t) 3 2
= t − 3t + 8t +1 = 7 ⇔ t =1(s)
vận tốc tức thời tại thời điểm t =1(s)là: v( ) 2
1 = 3.1 − 6.1+ 8 = 5(m / s)
Gia tốc tức thời của chất điểm tại thời điểm t =1(s)là: a( ) 2
1 = 6.1− 6 = 0(m / s ) Bài 5.
Một con lắc lò xo dao động điều hoà theo phương ngang trên mặt phẳng không ma sát như
Hình 7 , có phương trình chuyển động x = 4sin t , trong đó t tính bằng giây và x tính bằng centimét.
a) Tìm vận tốc tức thời và gia tốc tức thời của con lắc tại thời điểm t (s) . π
b) Tìm vị trí, vận tốc tức thời và gia tốc tức thời của con lắc tại thời điểm 2 t = (s). Tại thời 3
điểm đó, con lắc di chuyển theo hướng nào? Lời giải
a) Vận tốc tức thời của con lắc tại thời điểm t (s) là:
v(t) = x′ = 4cost
Gia tốc tức thời của con lắc tại thời điểm t (s) là:
a(t) = v′(t) = 4 − sin t
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 8
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com π b) Tại thời điểm 2 t = (s) 3 2π π x = 4 2 .sin = 2 3 (cm) 3 3 2π 2π v( ) = 4cos = 2( − cm / s) 3 3 2π 2π a( ) = 4 − sin = 2 − 3 ( 2 cm / s ) 3 3
D. BÀI TẬP TRẮC NGHIỆM
Câu 1: Đạo hàm cấp hai của hàm số ( ) 5 4
f x = 2x − +1 bằng biểu thức nào sau đây? x A. 3 4 40x 4 8 8 − . B. 3 40x + . C. 3 40x − . D. 3 40x + . 3 x 3 x 3 x 3 x Lời giải CHỌN C ( ) 5 4 f x 4 8 = 2x − +1 thì f′(x) 4 = 10x + , do đó f′ (x) 3 = 40x − . x 2 x 3 x
Câu 2: Đạo hàm cấp hai của hàm số y = sin2x bằng biểu thức nào sau đây? A. −sin2x. B. 4 − sin x. C. 4 − sin2x. D. 2 − sin2x. Lời giải CHỌN C
y = sin2x thì y′ = 2cos2x . Do đó y′ = 4 − sin2x . 2
Câu 3: Cho hàm số y = cos x. Tính y′′? A. y′ = 2 − cos2x. B. y′ = 4 − cos2x. C. y′ = 2cos2x. D. y′ = 4cos2x. Lời giải CHỌN A Ta có: y′ = 2
− cosxsin x = −sin2x ⇒ y′ = 2 − cos2x. 2 3
Câu 4: Cho hàm số y = 2x − x . Tính M = y .y′ +1. A. 1 2. − B. 0. C. 1. − D. . 2 2x − x Lời giải CHỌN B 1− x 1 1− x 2 ( )2 Ta có: y = ⇒ y = . 1. − 2x − x ′ ′ − 2 2x − x ( 2 2x x ) 2 2x − x − 1 − 3 3 = ( ⇒ y .y′′ = 1 − ⇒ y .y′′ +1 = 0 . 2 2x − x ) 2 2x − x
Câu 5: Cho hàm số f (x) = (x + )4 1 . Tính f ′ (2).
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 9
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com A. 27. B. 81. C. 96. D. 108. Lời giải CHỌN D
Ta có: ′( ) = ( + )3 ⇒ ′ ( ) = ( + )2 f x 4 x 1 f x
12 x 1 . Vậy f′′(2) =108. Câu 6: Cho hàm số 3 y = sin .
x Tính M = y′′ + 9 . y A. sinx. B. 6sinx. C. 6cosx. D. 6 − sin x. Lời giải CHỌN B Ta có: 2 2 3
y′ = 3sin x cosx ⇒ y′ = 6sin x cos x − 3sin x. Vậy: 2 3 3 = ′ + = − + = ( 2 2 M y
9y 6sin x cos x 3sin x 9sin x 6sin x cos x + sin x) = 6sinx. Câu 7: Cho hàm số 5 4
y = 3x − 5x + 3x − 2. Giải bất phương trình y′ < 0. A. x∈(−∞ ) ;1 \ { } 0 . B. x∈(1;+∞). C. x∈( 1; − ) 1 . D. x∈( 2; − 2). Lời giải CHỌN A Ta có: 4 3 3 2
y′ = 15x − 20x + 3 ⇒ y′ = 60x − 60x . 3 2 2 ′′ < ⇔ − < ⇔ ( − ) x < 1 y 0 60x 60x 0 60x x 1 < 0 ⇔ . x ≠ 0 Câu 8: Cho hàm số 1 y =
. Giải bất phương trình y′ < 0. (x + )3 1 A. x < 1. − B. x > 1. − C. x ≠1. D. Vô nghiệm. Lời giải CHỌN A Ta có: 3 − 12 y′ = ⇒ y′′ = . (x + )4 1 (x + )5 1 Vậy 12 y′′ < 0 ⇔
< 0 ⇔ x +1< 0 ⇔ x < 1 − . (x + )5 1
Câu 9: Cho hàm số = ( ) 2 2 − x + 3x y f x =
. Đạo hàm cấp 2 của f là: 1− x A. 1 y′′ 2 2 − 2 = 2 + . B. y′′ = . C. y′′ = . D. y′′ = . (1−x)2 (1−x)3 (1−x)3 (1−x)4 Lời giải CHỌN B 1 1 2(1− x)(− ) 1 2 y = 2x −1+ ⇒ y′ = 2 + ⇒ y′ = = . 1− x (1− x)2 (1− x)2 (1− x)3
Câu 10: Cho hàm số: = ( − ) 4 3 2 y 2 m x + 2x + 2mx + 2m −1.
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 10
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Tìm m để phương trình y′ = 0 có hai nghiệm phân biệt. A. 1 3 m 3 1 ∈− ; ∞ ∪ ;+∞ \ { } 2 . B. m∈− ;
∞ − ∪ ;+∞ \ { } 2 . 2 2 2 2 C. 3 1 m 1 3 ∈− ;
∞ − ∪− ;+∞ \ { } 2 . D. m∈− ; ∞ ∪ ;+∞ \ { } 2 . 2 2 2 2 Lời giải CHỌN D Ta có: ′ = ( − ) 3 2 + + ⇒ ′′ = ( − ) 2 y 4 2 m x 6x 4mx y 12 2 m x +12x + 4m.
Phương trình y′ = 0 có hai nghiệm phân biệt hay phương trình: ( − ) 2 3 2 m x + 3x + m = 0 có hai nghiệm phân biệt. m ≠ 2 1 2 − m ≠ 0 2 − m ≠ 0 m < ⇔ ⇔ ⇔ . 2 2 ∆ > 0 4m − 8m + 3 > 0 3 m > 2
Câu 11: Cho chuyển động thẳng xác định bởi phương trình 3 2 S = t − 3t
(t: tính bằng giây, s: tính bằng mét).
Khẳng định nào sau đây là đúng?
A. Vận tốc của chuyển động khi t = 3s là v =12m / s.
B. Vận tốc của chuyển động khi t = 3s là v = 24m / s.
C. Gia tốc của chuyển động khi t = 4s là 2 a =18m / s .
D. Gia tốc của chuyển động khi t = 4s là 2 a = 9m / s . Lời giải CHỌN C 3 2 2
S = t − 3t ⇒ v(t) = S′ = 3t − 6t ⇒ ( ) 2 v 3 = 3.3 −18 = 9(m / s). 3 2
S = t − 3t ⇒ a = S′′ = 6t − 6 2 ( a = 6.4 − 6 = 18 m / s . t=4s) ( )
Câu 12: Một chất điểm chuyển động thẳng xác định bởi phương trình: 3 2
S = t − 3t + 5t + 2 , trong đó t tính
bằng giây và S tính bằng mét. Gia tốc của chuyển động khi t = 3 là: A. ( 2 24 m / s ). B. ( 2 17 m / s ). C. ( 2 14 m / s ). D. ( 2 12 m / s ). Lời giải CHỌN D
Gia tốc của chuyển động khi t = 3 bằng S′′(3). ′( ) 2
S t = 3t − 6t + 5; S′′(t) = 6t − 6 nên ′ ( ) = − = ( 2 S 3 18 6 12 m / s ).
Câu 13: Cho chuyển động thẳng xác định bởi phương trình: 3 2
S = t − 3t − 9t + 2 (t: tính bằng giây, s tính bằng mét).
Khẳng định nào sau đây là đúng?
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 11
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
A. Vận tốc của chuyển động bằng 0 khi t = 0 hoặc t = 3.
B. Gia tốc của chuyển động tại thời điểm t =1 là 2 a =12m / s .
C. Gia tốc của chuyển động tại thời điểm t = 3 là 2 a =12m / s .
D. Gia tốc của chuyển động bằng 0 khi t = 0. Lời giải CHỌN C 3 2 S = t − 3t − 9t + 2 ⇒ v(t) 2 = S3t − 6t − 9 ( ) 2 2 t = 1 −
v t = 0 ⇔ 3t − 6t − 9 = 0 ⇔ t − 2t − 3 = 0 ⇔ t =3 3 2 S = t − 3t − 9t + 2 ⇒ a = S′′ = 6t − 6 2 ⇒ (a = 6.3 − 6 = 12 m / s . t=3s) ( )
Câu 14: Một chất điểm chuyển động thẳng xác định bởi phương trình: 3 2
S = t − 2t + 4t +1, trong đó t tính
bằng giây và S tính bằng mét. Gia tốc của chuyển động khi t = 2 là: A. ( 2 12 m / s ). B. ( 2 8 m / s ). C. ( 2 7 m / s ). D. ( 2 6 m / s ). Lời giải CHỌN B
Gia tốc của chuyển động khi t = 2 bằng S′′(2). ′( ) 2
S t = 3t − 4t + 4; S′′(t) = 6t − 4 nên ′ ( ) = − = ( 2 S 2 12 4 8 m / s ).
Câu 15: Phương trình chuyển động của một chất điểm được biểu thị bởi công thức S (t) 2 3
= 4 − 2t + 4t + 2t , trong đó t > 0 và t tính bằng giây (s) , S (t) tính bằng mét (m) . Tìm
gia tốc a của chất điểm tại thời điểm t = 5(s) . A. a = 68 .
B. a =115 .
C. a =100 .
D. a = 225 . Lời giải Chọn A
Theo ứng dụng đạo hàm của hàm số có:
v(t) = S′(t) 2 = 2
− + 8t + 6t và a(t) = v′(t) = 8 +12t ⇒ a( ) = ( 2 5
68 m / s ) .
Câu 16: Một vật chuyển động có phương trình 4 3 2
S = t −3t −3t + 2t +1 (m) , t là thời gian tính bằng giây.
Gia tốc của vật tại thời điểm t = s 3 là A. 2 48 m/s . B. 2 28 m/s . C. 2 18 m/s . D. 2 54 m/s . Lời giải Chọn A 4 3 2
S = f (t) = t − 3t − 3t + 2t +1 ⇒ 3 2
f '(t) = 4t − 9t − 6t + 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 12
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com ⇒ 2
a(t) = f '(t) =12t −18t − 6
Gia tốc của vật tại thời điểm t = s 3 là 2
a(3) =12.3 −18.3− 6= 2 48 m/s .
Câu 17: Một chất điểm chuyển động có phương trình 3 2 s = t
− + t + t + 4 ( t là thời gian tính bằng giây).
Gia tốc của chuyển động tại thời điểm vận tốc đạt giá trị lớn nhất là A. 6 . B. 0 . C. 2 . D. 4 . Lời giải Chọn B
Vận tốc của chất điểm có phương trình là: 2 v = s' = 3 − t + 2t +1. b − 1
Vận tốc của chất điểm đạt GTLN khi t = = . 2a 3
Gia tốc của chất điểm có phương trình là: s'' = 6 − t + 2 . 1
Tại thời điểm vận tốc đạt GTLN thì gia tốc bằng s '' = 0 . 3
Câu 18: Cho chuyển động thẳng xác định bởi phương trình 3 2
s(t) 2t 3t 4t, trong đó t được tính
bằng giây và s được tính bằng mét. Vận tốc tức thời của vật tại thời điểm gia tốc bằng không là
A. 2,5m / .s
B. 4m / .s
C. 2,5m / .s
D. 8,5m / .s Lời giải Chọn C
Ta có, gia tốc tức thời của chuyển động bằng: a(t) s(t) 12 t6. Thời điểm gia tốc bằng
không là: a(t) s(t) 12 t6 0 t 0,5.Vậy khi đó vận tốc tức thời của chuyển động bằng 2 5
v(t) s(t) 6t 6t 4 v(0,5) . vậy chọn C 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 13
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
BÀI TẬP CUỐI CHƯƠNG VII
Câu 1: Cho u = u(x),v = v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Phát biểu nào sau đây đúng?
A. (uv)' = u '.v' .
B. (uv)' = u.v'.
C. (uv)' = u '.v .
D. (uv)' = u '.v + v'.u . Lời giải Chọn D
Có (uv)′ = u v′ + uv
Câu 2: Cho u = u(x),v = v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Phát biểu nào sau đây đúng? ′ ′
A. u u ' − = u u v v u
với v = v(x) ≠ 0, v' = v'(x) ≠ 0 B. '. '. =
với v = v(x) ≠ 0 v v ' v v ′ ′
C. u u '.v − v'.u − = u u v v u
với v = v(x) ≠ 0 D. '. '. =
với v = v(x) ≠ 0 2 v v v v ' Lời giải Chọn C ′ ′ ′ Có u u v − uv = 2 v v
Câu 3: Tìm đạo hàm của mỗi hàm số sau: a) y = ( 2 x + x)( 3 2 x − 3x) ; b) 1 y = ; 2 − x + 5 c) y = 4x + 5 ;
d) y = sin .xcos x ; e) x y = xe ; f) 2 y = ln x . Lời giải a) y = ( 2 x + x)( 3 2 x − 3x)
y′ = (2x + 2)( 3 x − 3x) + ( 2 x + 2x)( 2 3x − 3) 4 2 3 4 2 3
y′ = 2x − 6x + 2x − 6x + 3x − 3x + 6x − 6x 4 3 2
y′ = 5x + 8x − 9x −12x b) 1 y = 2 − x + 5 2 y′ = 2 ( 2 − x + 5) c) y = 4x + 5
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 1
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 4 y′ = 2 4x + 5 d) y = sin c x osx 2 2
y′ = cos x − sin x e) x y = xe x x
y′ = e + xe g) 2 y = ln x 2 y′ = lnx x
Câu 4: Tìm đạo hàm cấp hai của mỗi hàm số sau: a) 4 3 2
y = 2x − 3x + 5x ; b) 2 y = ; 3− x
c) y = sin 2 .xcos x ; d) 2x 3 y e− + = e) y = ln (x + ) 1 f) = ln ( x y e + ) 1 . Lời giải 4 3 2
a) y = 2x − 3x + 5x 3 2
y′ = 8x − 9x +10x 2
y′′ = 24x −18x +10 b) 2 y = 3− x 2 y′ = 2 (3− x) 4(3− x) 4 y′′ = = 4 3 (3− x) (3− x) c) y = sin2 c x osx
y′ = 2cos(2x)⋅cosx + sin2x⋅( s − inx) y′′ = 4
− sin (2x)⋅cosx + 2cos(2x)⋅( s
− inx) + 2cos(2x)⋅( s
− inx) − sin2x⋅(cosx)
y′′ = cosx( 4
− sin (2x) − sin2x)⋅sinx⋅(2cos(2x) + 2cos(2x)) y′′ = 5
− sin (2x)⋅cosx − 4cos(2x)⋅sinx 2 − x+3 d) y = e 2 − x+3 y′ = 2 − e 2 − x+3 y ′ = 4e
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 2
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com e) y = ln (x + ) 1 1 y′ = x+11 y′′ = − 2 (x +1) g) = ln ( x y e + ) 1 x e y′ = xe +1 x 2x x e −e e y′′ = + = x e +1 ( xe + )2 1 ( xe + )2 1
Câu 5: Vận tốc của một chất điểm chuyển động được biểu thị bởi công thức v(t) 2
= 2t + t , trong đó
t > 0, t tính bằng giây và v(t) tính bằng m / s . Tìm gia tốc tức thời của chất điểm:
a) Tại thời điểm t = 3 (s) ;
b) Tại thời điểm mà vận tốc chất điểm bẳng 8 m/s . Lời giải
a(t) = v′(t) = 2t + 2
a) Gia tốc tức thời của chất điểm tại thời điểm t = 3 (s) là: a( ) = + = ( 2 3 2.3 2 8 m / s )
b) Vận tốc chất điểm bẳng 8 m/s v(t) 2 = 2t + t = 8 ⇔ t = 2(s)
Gia tốc tức thời của chất điểm tại thời điểm t = 2 (s) là: a( ) = + = ( 2 2 2.2 2 6 m / s )
Câu 6: Một con lắc lò xo dao động điều hòa theo phương ngang trên mặt phẳng không ma sát, có phương trình chuyển động 2π x 4cos πt = − +
3, trong đó t tính bằng giây và x tính bằng centimet. 3
a) Tìm vận tốc tức thời và gia tốc tức thời của con xắc lò xo tại thời điểm t = 3 (s) .
b) Tìm thời điểm mà vận tốc của con lắc bẳng 0 . Lời giải 2π v = x = 4 − π sin πt ′ − 3 2 2π a = v = 4 − π cos πt ′ − 3
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 3
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
a) Vận tốc tức thời của con xắc lò xo tại thời điểm t = 3 (s) là: 2π v 4π sin π.3 = − − = 2 − 3π (cm / s) 3
Gia tốc tức thời của con xắc lò xo tại thời điểm t = 3 (s) là: 2 2π 2 a = 4 − π cos3π − = 2 − π ( 2 cm / s ) 3
b) vận tốc của con lắc bẳng 0 => 2π 2π v = 4 − π sin πt − = 0 => t = s 3 3
BÀI TẬP TỔNG ÔN CHƯƠNG IX A. TRẮC NGHIỆM
Câu 1: Trong các phát biểu sau phát biểu nào là đúng?
A. Nếu hàm số y = f (x) không liên tục tại x thì nó có đạo hàm tại điểm đó. 0
B. Nếu hàm số y = f (x) có đạo hàm tại x thì nó không liên tục tại điểm đó. 0
C. Nếu hàm số y = f (x) có đạo hàm tại x thì nó liên tục tại điểm đó. 0
D. Nếu hàm số y = f (x) liên tục tại x thì nó có đạo hàm tại điểm đó. 0 Lời giải Chọn C
Nếu hàm số y = f (x) có đạo hàm tại x thì nó liên tục tại điểm đó còn nếu hàm số liên tục tại 0
điểm x thì nó chưa chắc có đạo hàm tại điểm đó. 0
Câu 2: Cho f là hàm số liên tục tại x . Đạo hàm của f tại x là: 0 0 A. f (x)
f (x + h − f x 0 ) ( ) B. . h
f (x + h − f x 0 ) ( ) C. lim
(nếu tồn tại giới hạn). h→0 h
f (x + h − f x − h 0 ) ( 0 ) D. lim
( nếu tồn tại giới hạn). h→0 h Lời giải Chọn C f x h f x f ′(x ) ( + )− ( ) = 0 lim . 0 h→0 h
Câu 3: Cho hàm số y = f (x) có đạo hàm tại x là f ′(x . Mệnh đề nào sau đây sai? 0 ) 0 f x − f x f x + x ∆ − f x
A. f ′(x = lim .
B. f ′(x = lim . 0 ) ( 0 ) ( 0) 0 ) ( ) ( 0) x→ 0 x x − x x ∆ →0 x ∆ 0
f x + h − f x
f x + x − f x
C. f ′(x = lim .
D. f ′(x = lim . 0 ) ( 0 ) ( 0) 0 ) ( 0 ) ( 0) h→0 h x→ 0 x x − x0
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 4
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Lời giải Chọn D f x − f x
f x + h − f x Ta có f ′(x lim , f x lim 0 ) ( ) ( 0) = ′( 0 ) ( 0 ) ( ) = x→x h→ 0 x − 0 x h 0
f x + ∆x − f x và f ′(x lim
là những khẳng định đúng. 0 ) ( 0 ) ( 0) = ∆x→0 ∆x
f x + x − f x
Khẳng định sai là f ′(x lim 0 ) ( 0 ) ( 0) = x→x0 x − x0 3− 4 − x khi x ≠ 0
Câu 4: Cho hàm số f (x) 4 = . Tính f ′(0). 1 khi x = 0 4 A. f ′( ) 1 0 = . B. f ′( ) 1 0 = . C. f ′( ) 1 0 = . D. Không tồn tại. 4 16 32 Lời giải Chọn D f x − f 0 x Ta có f (0) ( ) ( ) 3 − 4 − ′ = lim = lim
(không tồn tại giới hạn) x→0 x→ x − 0 0 4x
Do đó không tồn tại f ′(0) . 3 2
x − 4x + 3x Câu 5: Cho hàm số khi x ≠ 1
f (x) xác định trên \ { } 2 bởi f (x) 2
= x −3x + 2 . Tính f ′( ) 1 . 0 khi x =1 A. f ′( ) 3 1 = . B. f ′( ) 1 = 1. C. f ′( ) 1 = 0 . D. không tồn tại. 2 Lời giải Chọn D 3 2 f (x) x 4x 3x − f ( ) − + − 3 2 0 1 2 x − 3x + 2
x (x − 4x +3) x (x − ) 1 (x + x +3) lim = lim = lim = lim x→ x→ x→ x −1 x −1
(x − )1(x − )1(x −2) x→ (x− )2 0 0 1 1 1 (x − 2) x ( 2 x + x + 3) = lim → Khoâng toàn taïi. x 1 → ( x − ) 1 (x − 2) 2 x -1 khi x 0
Câu 6: Cho hàm số f (x) ≥ = 2
-x khi x < 0
Khẳng định nào sau đây sai?
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 5
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
A. Hàm số không liên tục tại x = 0.
B. Hàm số có đạo hàm tại x = 2.
C. Hàm số liên tục tại x = 2.
D. Hàm số có đạo hàm tại x = 0. Lời giải Chọn D
Ta có lim f (x) = f = − + (0) 1 x→0
Mặt khác lim f (x = do đó hàm số không liên tục tại điểm x = 0 nên hàm số không đạo − ) 0 x→0
hàm tại x = 0. 2 mx 2x 2 khi x 0
Câu 7: Cho hàm số f (x) + + > =
. Tìm tất cả các giá trị của các tham số m, n sao cho nx +1 khi ≤ 0
f (x) có đạo hàm tại điểm x = 0.
A. Không tồn tại m, n. B. m = 2,∀n .
C. n = 2,∀m .
D. m = n = 2 . Lời giải Chọn A
Ta có lim f (x) = f = lim f = + + = + (x) lim+ ( 2 mx 2x 2) 2 − (0) 1, x→0 x→0 x→0
Do đó hàm số không liên tục tại điểm x = 0 nên hàm số không thể có đạo hàm tại điểm x = 0. 2 x
Câu 8: Cho hàm số f (x) khi x ≤1 = 2
. Tìm tất cả các giá trị của các tham số ,
a b sao cho f (x)
ax + b khi > 1 có
đạo hàm tại điểm x = 1. A. 1
a = 1, b = − . B. 1 1 a = , b = . C. 1 1 a = , b = − . D. 1 a = 1, b = . 2 2 2 2 2 2 Lời giải Chọn A Ta có f = = = + = + − (x) f ( ) 1 lim 1 , lim f +
(x) lim+(ax b) a b x 1 → 2 x 1 → x 1 →
Hàm số liên tục tại điểm 1
x = 1 khi và chỉ khi lim f = = ⇔ + = −
(x) f ( )1 lim f+ (x) a b x 1 → x 1 → 2 x khi x 1
Mặt khác f (x) < ′
⇒ f ( −1 ) =1, f ( + ′ ′ 1 ) = a
ax khi x > 1 1 a = 1 a + b
Suy ra hàm số có đạo hàm tại điểm x 1 = = ⇒ 2 ⇔ 1 . 1 b a = − = 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 6
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com f ( x ∆ + ) 1 − f ( ) 1
Câu 9: Cho f (x) 2018 2 = x
−1009x + 2019x . Giá trị của lim bằng x ∆ →0 x ∆ A. 1009. B. 1008. C. 2018. D. 2019. Lời giải Chọn D f (∆x + ) 1 − f ( ) 1 Ta có lim = f ′( ) 1 ∆x→0 ∆x f (∆x + ) 1 − f ( ) 1
Mặt khác f ′(x) = 2017 2018x
− 2018x + 2019 suy ra lim = f ′( ) 1 = 2019 . ∆x→0 ∆x
Câu 10: Cho hàm số ( ) x f x = (
. Giá trị của f ′(0) là x − )
1 (x − 2)....(x − 2019) A. 1 − . B. 1 . C. 2019 − !. D. 2019!. 2019! 2019! Lời giải Chọn A x f x − f 0
x −1 x − 2 .... x − 2019 Ta có f ′(0) ( ) ( ) ( )( ) ( ) = lim = lim x→0 x→ x − 0 0 x 1 1 = lim = . x→0 (x − )
1 (x − 2)...(x − 2019) 2019 − !
Câu 11: Cho f (x) = x(x + )
1 (x + 2)(x + 3)...(x + n) với *
n∈ . Tính f ′(0) . n n +1
A. f ′(0) = 0 .
B. f ′(0) = n .
C. f ′(0) = n!. D. f ′(0) ( ) = . 2 Lời giải Chọn C f x − f 0
x x +1 ... x + n Ta có f ′(0) ( ) ( ) ( ) ( ) = lim = lim = lim (x + )
1 (x + 2)...(x + n) x→0 x→0 x→ x − 0 0 x = 1.2...n = n!.
Câu 12: Cho hàm số f (x) = x − 2 . Khẳng định nào sau đây là sai? A. f (2) = 0.
B. f (x) nhận giá trị không âm.
C. f (x) liên tục tại x = 2.
D. f (x) có đạo hàm tại x = 2. Lời giải Chọn D
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 7
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
x − 2 khi x ≥ 2 1 khi x > 2
Ta có f (x) = x − 2 =
⇒ f ′(x) =
−x + 2 khi x < 2 -1 khi x < 2
Do lim f (x) = lim f (x = nên hàm số liên tục tại điểm x = 2. + − ) 0 x→2 x→2 Mặt khác f ( + 2 ) ≠ f ( − ′
′ 2 ) nên hàm số không có đạo hàm tại điểm x = 2.
Câu 13: Cho hàm số y = f (x) có đạo hàm thỏa mãn f ′(6) = 2 Tính giá trị của biểu thức
f (x) − f (6) lim . x→6 x − 6 A. 2. B. 1 . C. 1 . D. 12. 3 2 Lời giải Chọn A
f (x) − f (6) Ta có lim = f ′(6) = 2. x→6 x − 6
2 f (x) − xf (2)
Câu 14: Cho hàm số y = f (x) có đạo hàm tại điểm x = 2 . Tìm lim . 0 x→2 x − 2 A. 0. B. f ′(2) .
C. 2 f ′(2) − f (2) .
D. f (2) − 2 f ′(2) . Lời giải Chọn C
2 f (x) − xf (2) x f
( x) − f (2) + 2 f
(x)− xf (x) lim = lim x→2 x→2 x − 2 x − 2
x f (x) − f (2) f (x)(2 − x) = lim + lim
= 2 f ′(2) + lim − f (x) = 2 f ′(2) − 2 f 2 . x 2 x 2 x 2 ( ) → → → x − 2 x − 2
Câu 15: Cho hàm số f (x) 1 3 2
= x − 2 2x + 8x −1, có đạo hàm là f '(x) . Tập hợp những giá trị của x để 3 f '(x) = 0 là { 2− 2} {2; 2} { 4− 2} {2 2} A. B. C. D. Lời giải Chọn D f (x) 2 '
= x − 4 2x + 8 ; f (x) 2 '
= 0 ⇔ x − 4 2x + 8 = 0 ⇔ x = 2 2 . Câu 16: Cho hàm số 3 2
y = 3x + x +1, có đạo hàm là y ' . Để y ' ≤ 0 thì x nhận các giá trị thuộc tập nào sau đây? A. 2 ;0 − B. 9 − ;0 9 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 8
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com C. 9 ; −∞ − ∪[0;+∞ 2 ) D. ; −∞ − ∪[0;+∞ ) 2 9 Lời giải Chọn A 2
y ' = 9x + 2x ; 2 2
y ' ≤ 0 ⇔ 9x + 2x ≤ 0 ⇔ − ≤ x ≤ 0. Vậy 2 S ;0 = − . 9 9
Câu 17: Tính đạo hàm của hàm số f (x) 4 3 2
= −x + 4x − 3x + 2x +1 tại điểm x = 1 − . A. f '(− ) 1 = 4 B. f '(− ) 1 =14 C. f '(− ) 1 =15 D. f '(− ) 1 = 24 Lời giải Chọn D
𝑓𝑓′(𝑥𝑥) = −4𝑥𝑥3 + 12𝑥𝑥2 − 6𝑥𝑥 + 2 ⇒ 𝑓𝑓′(−1) = 24. Câu 18: Cho hàm số 1 3
y = x − (2m + ) 2
1 x − mx − 4, có đạo hàm là y ' . Tìm tất cả các giá trị của m để 3
y ' ≥ 0 với x ∀ ∈ . A. 1 m 1; ∈ − − B. 1 m ∈ 1; − − 4 4 C. m ( ] 1 ; 1 ; ∈ −∞ − ∪ − +∞ D. 1 m ∈ 1; − 4 4 Lời giải Chọn B 2
y ' = x − 2.(2m + ) 1 x − m
Khi đó 𝑦𝑦′ ≥ 0; ∀𝑥𝑥 ∈ ℝ ⇔ 𝛥𝛥′ = (2𝑚𝑚 + 1)2 + 𝑚𝑚 ≤ 0 ⇔ 4𝑚𝑚2 + 5𝑚𝑚 + 1 ≤ 0 ⇔ −1 ≤ 𝑚𝑚 ≤ − 1 4 Vậy 1 m 1; ∈ − −
là giá trị thỏa mãn bài toán. 4
Câu 19: Biết hàm số f (x) 3 2
= ax + bx + cx + d (a > 0) có đạo hàm là f '(x) > 0 với x ∀ ∈ . Mệnh đề nào sau đây đúng? A. 2
b − 3ac > 0 B. 2 b − 3ac ≥ 0 C. 2
b − 3ac < 0 D. 2 b − 3ac ≤ 0 Lời giải Chọn C
𝑓𝑓′(𝑥𝑥) = 3𝑎𝑎𝑥𝑥2 + 2𝑏𝑏𝑥𝑥 + 𝑐𝑐 > 0; ∀𝑥𝑥 ∈ ℝ ⇔ � 𝑎𝑎 > 0 . 𝛥𝛥′ < 0 ⇔ � 𝑎𝑎 > 0
𝑏𝑏2 − 3𝑎𝑎𝑐𝑐 < 0 3
Câu 20: Hàm số y = x + x có đạo hàm bằng 2 3x +1 2 3x +1 2 3x + x 3 x + x A. 3 2 x + x B. 3 x + x C. 3 2 x + x D. 3 2 x + x
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 9
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Lời giải Chọn A ( 3x + x) 2 ' 3x +1 y ' = = 3 3
2 x + x 2 x + x .
Câu 21: Tính đạo hàm của hàm số y = ( x − )4 7 5
A. y = ( x − )3 ' 4 7 5
B. y = − ( x − )3 ' 28 7
5 C. y = − ( − x)3 ' 28 5 7
D. y = ( − x)3 ' 28 5 7 Lời giải Chọn C
y = ( x − ) ( x − )3 = ( x − )3 ' 4. 7 5 '. 7 5 28 7 5 .
Câu 22: Tính đạo hàm của hàm số y = ( − x )5 3 1
A. y = x ( − x )4 2 3 ' 5 1
B. y = − x ( − x )4 2 3 ' 15 1
C. y = − x ( − x )4 2 3 ' 3 1
D. y = − x ( − x )4 2 3 ' 5 1 Lời giải Chọn B
y = ( − x ) ( − x )4 = − x ( − x )4 3 3 2 3 ' 5. 1 '. 1 15 1 .
Câu 23: Tính đạo hàm của hàm số y = (x − x )2016 3 2 2
y ' = 2016(x − 2x )2015 3 2 y = (x − x )2015 3 2 ( 2 ' 2016 2 3x − 4x) A. B. y = (x − x )2015 3 2 ( 2 ' 2016 2 3x − 4x) y = ( 3 2 x − x )( 2 ' 2016 2 3x − 2x) C. D. Lời giải Chọn B y =
(x − x ) (x − x )2015 =
( x − x) (x − x )2015 3 2 3 2 2 3 2 ' 2016. 2 '. 2 2016. 3 4 . 2 .
Câu 24: Tính đạo hàm của hàm số f (x) = x(x − )
1 (x − 2)...(x − 2018) tại điểm x = 0 A. f '(0) = 0 B. f '(0) = 2018 − !
C. f '(0) = 2018!
D. f '(0) = 2018 Lời giải Chọn C
f '(x) = (x − )
1 (x − 2)...(x − 2018) + x(x − 2)...(x − 2018) +...+ x(x − ) 1 ...(x − 2017)
Suy ra f '(0) = (0 − )
1 .(0 − 2)....(0 − 2018) =1.2.3....2018 = 2018!.
Câu 25: Tính đạo hàm của hàm số f (x) = x(x + )
1 (x + 2)...(x + 2018) tại điểm x = 1004 −
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 10
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com A. f '( 1004 − ) = 0 B. f '( 1004 − ) =1004! C. f '( 1004 − ) = 1004 − ! D. f (− ) = ( )2 ' 1004 1004! Lời giải Chọn D
f '(x) = (x + )
1 (x + 2)...(x + 2018) + x(x + 2)...(x + 2018) +...+ x(x + ) 1 ...(x + 2017) f '( 1004 − ) = .x(x + )
1 .(x + 2)...(x +1003).(x +1005)...(x + 2018) Suy ra x= 1004 − = (− ) (− ) (− ) (− ) (− ) = ( )2
1004 . 1003 . 1002 ... 1 . 2 ...1003.1004 1004! . 2
Câu 26: Tính đạo hàm của hàm số x + 2x − 3 y = x + 2 2 2 2 A. 3 y ' + + + + + + = 1+ B. x 6x 7 y ' = C. x 4x 5 y ' = D. x 8x 1 y ' = (x + 2)2 (x + 2)2 (x + 2)2 (x + 2)2 Lời giải Chọn A
(2x + 2).(x + 2)−( 2x + 2x −3) 2 2 2
2x + 6x + 4 − x − 2x + 3 x + 4x + 7 y ' = = = (x + 2)2 (x + 2)2 (x + 2)2 .
Câu 27: Đạo hàm của hàm số 2 y = 3x + 4 là A. 1 y ' = B. ' x y = C. 6 ' x y = D. 3 ' x y = 2 2 3x + 4 2 3x + 4 2 3x + 4 2 3x + 4 Lời giải Chọn D ( 2 3x + 4)' 6x 3 ' = = = x y 2 2 2
2 3x + 4 2 3x + 4 3x + 4 .
Câu 28: Đạo hàm của hàm số y = ( x − ) 2 2 1 x + x là 2 6x + 2x −1 2 2 y ' = A. 8x + 4x −1 + y ' + + 4x 1 = B. 8x 4x 1 y ' = C. y ' = D. 2 2 x + x 2 2 x + x 2 2 x + x 2 2 x + x Lời giải Chọn D ( 2x + x ' 2 ) y ' = (2x − )
1 '. x + x + (2x − ) 1 . 2 2 x + x
(2x − )1.(2x + ) 2 2 2 1 2
2x + 2x + 4x −1 6x + 2x −1 = 2 x + x + = = 2 2 2 2 x + x 2 x + x 2 x + x .
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 11
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 3
Câu 29: Đạo hàm của hàm số 2 2 y x = − bằng x 2 2 A. 2 2 y ' 3 x = − 1 2 B. 2
y ' = 6 x − x − x 2 x x 2 2 C. 1 2 2 y ' 6 x 1 2 x = + − D. 2
y ' = 6 x − x − 2 x x x x Lời giải Chọn C ' 2 2 2 2 2 2 2 2 2 y ' 3 x x 3 2x x = − − = + − 2 x x x x .
Câu 30: Tính đạo hàm của hàm số 2x −1 y = x + 2 A. 5 x + 2 y ' + = . B. 1 5 x 2 y ' = . . (2x − )2 1 2x −1 2 (2x − )2 1 2x −1 C. 1 x + 2 + y ' 1 5 x 2 = . D. y ' = . . 2 2x −1
2 (x + 2)2 2x −1 Lời giải Chọn D ' − 5 2x 1 x + 2 (x + 2)2 1 5 x + 2 y ' = = = . . . 2x −1
2x −1 2 (x + 2)2 2x −1 2 2 x + 2 x + 2 Câu 31: Cho hàm số 2
y = x + x +1 . Mệnh đề nào sau đây đúng? A. 2
y ' x +1 = y B. 2
2y ' x +1 = y C. 2
y ' x +1 = 2y D. 2 2y x +1 = y ' Lời giải Chọn B ( + + x x ) 2 ' 2x x 1 x 2 1 1 + + + 2 2 2 2 x +1 x +1 y ' y y = = = = = 2 2 2 2y 2 2 x + x +1 y 2y x +1 2 x +1 Do đó 2
2y ' x +1 = y . 3
Câu 32: Cho hàm số ( ) x f x =
. Phương trình f '(x) = 0 có tập nghiệm S là x −1 A. 2 S 0; = B. 2 S = − ;0 C. 3 S = 0; D. 3 S = − ;0 3 3 2 2 Lời giải
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 12
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Chọn C 2 3 x = 0 3 2 ( ) 3x (x − ) 1 − x 2x − 3 ' x f x 0 = = = ⇔ . (x − )2 (x − )2 3 1 1 x = 2
Câu 33: Cho hàm số y = 2 −
x + 3x . Tập nghiệm S của bất phương trình y ' > 0 là A. S = ( ; −∞ +∞) B. 1 S ; = −∞ C. 1 S = ;+∞ D. S = ∅ 9 9 Lời giải Chọn C 1 1 − 1 − + 3 ' = 2. − + 3 = + 3 x y = > 0 2 x x x 1
⇔ 3 x >1 ⇔ x > . 9
Câu 34: Cho hàm số f (x) 2 = 5
− x +14x − 9 . Tập hợp các giá trị của x để f '(x) < 0 là A. 7 ; +∞ B. 7 ; −∞ C. 7 9 ; D. 7 1; 5 5 5 5 5 Lời giải Chọn C Điều kiện 2 9 5
− x +14x − 9 > 0 ⇔ 1< x < 5 Khi đó f (x) 7 ' < 0 ⇔ 5
− x + 7 < 0 ⇔ x > 5
Vậy tập nghiệm của bất phương trình là 7 9 ; . 5 5
f (x) − f (2)
Câu 35: Cho hàm số f (x) 2 3 2018
= x + x + x +...+ x . Tính lim x→2 x − 2 A. 2018 2017.2 +1 B. 2017 2019.2 +1 C. 2018 2017.2 −1 D. 2017 2018.2 +1 Lời giải Chọn A
f (x) − f (2) lim = f '(2) x→2 x − 2 2018 2019 Mặt khác ( ) 2 3 2018 1 = + + + ...+ = . − x x − x f x x x x x x = 1− x 1− x ( 2018 1− 2019x )(1− x)+( 2019 x − x ) 2018 2019 Do đó f (x) 2019.2 −1+ 2 − 2 ' = ⇒ f ' 2 = 2 ( ) (1− x) 1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 13
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com 2018 = 2017.2 +1.
Câu 36: Cho f (x) là hàm số thỏa mãn f ( ) 1 = f '( ) 1 =1. Giả sử ( ) 2
g x = x f (x) . Tính g '( ) 1 A. 0 B. 1 C. 2 D. 3 Lời giải Chọn D
g (x) = x f (x) 2 ' 2 .
+ x . f '(x) Suy ra g '( ) 1 = 2 f ( ) 1 + f '( ) 1 = 3.
Câu 37: Tính đạo hàm của hàm số y sin 3 x . 6 A. y 3cos 3 y x . B. ' 3cos 3x. 6 6 C. y cos 3 y x . D. ' 3sin 3x. 6 6 Lời giải Chọn B ′
y π 3x .cos π 3x 3.cos π 3x ′ = − − = − − . 6 6 6
Câu 38: Tính đạo hàm của hàm số 1 2 y sin x . 2 3 A. 2 y 1 x cos y x x . B. 2 cos x. 3 2 3 C. 1 y 1 x cos 3x. D. 2
y x cos x . 2 3 2 3 Lời giải Chọn A 1 ′ π 2 π 2 1 y x .cos x .( 2x) π 2 π 2 .cos x .xcos x ′ = − − − = − − − = − . 2 3 3 2 3 3
Câu 39: Tính đạo hàm của hàm số 2
y x tan x x . A. 1
y 2x tan x . B. 1
y 2x tan x . 2 x x 2 2 C. x 1 y x 1 2x tan x .
D. y 2x tan x . 2 cos x 2 x 2 cos x x Lời giải Chọn C
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 14
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com y (x )′ x ( x)′ ′ = + x + ( x) 2 2 2 ′ x 1 tan tan . = 2x tan x + + . 2 cos x 2 x
Câu 40: Tính đạo hàm của hàm số 2 y 2cos x . A. 2
y 2sin x . B. 2
y 4x cos x . C. 2
y 2xsin x . D. 2
y 4xsin x . Lời giải Chọn D y′ = − ( 2 x )′ 2 2 2 2. .sin x = 2.2 − .xsin x = 4 − .
x sin x .
Câu 41: Tính đạo hàm của hàm số x 1 y tan . 2 A. 1 y 1 1 1 y y y 2 x . B. 1 2cos 2 x . C. 1 cos 2 x . D. 1 2cos 2 x . 1 cos 2 2 2 2 Lời giải Chọn A x 1 ′ + x +1 ′ 2 1 y′ = tan = = . 2 2 x +1 2 x + 1 cos 2cos 2 2
Câu 42: Tính đạo hàm của hàm số 2
y sin 2 x . A. 2x 2 2 y x cos 2 x . B. 2 y cos 2 x . 2 2 x 2 2 x C. x 2 y x 1 cos 2 x . D. 2 y cos 2 x . 2 2 x 2 2 x Lời giải Chọn C ′ ′ + y′ = ( x 2 + x ) ( 2 2 2 2 ) 2 x 2 cos 2 + x = cos 2 + x = cos 2 + x . 2 2 2 2 + x 2 + x
Câu 43: Tính đạo hàm của hàm số y = cos 2x +1 . A. sin 2x +1 y′ x + x + = − . B. sin 2 1 y′ =
. C. y′ = −sin 2x +1 . D. sin 2 1 y′ = − . 2x +1 2x +1 2 2x +1 Lời giải Chọn A ′ ′ +
y′ = −( x + ) (2x )1 sin 2x +1 2 1 sin 2x +1 = sin 2x +1 = − . 2 2x +1 2x +1
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 15
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Câu 44: Tính đạo hàm của hàm số 2 y = cot x +1 . A. ′ = − x y . B. ′ = x y . 2 2 2 x +1sin x +1 2 2 2 x +1sin x +1 C. 1 y′ = − . D. 1 y′ = . 2 2 sin x +1 2 2 sin x +1 Lời giải Chọn A ( ′ x 2 x +1) 2 x +1 x y′ = − = − = − . 2 2 2 2 2 2 2 sin x +1 sin x +1 x +1.sin x +1
Câu 45: Tính đạo hàm của hàm số sin x + cos = x y . sin x − cos x 2 2 A. sin 2 ′ x − = − x y . B. sin cos ′ = x y .
(sin x −cos x)2
(sin x −cos x)2 C. 2 − 2sin 2 ′ = x y . D. 2 y′ = − .
(sin x −cos x)2
(sin x −cos x)2 Lời giải Chọn D 2 sin x π + Ta có sin x + cos x 4 y = =
= − tan x π + . sin x − cos x π 4 2 cos x − + 4 Suy ra 1 1 2 y − ′ = − = − = . 2 π
cos x − sin x
(sin x −cos x)2 2 cos x + 4 2
Câu 46: Tính đạo hàm của hàm số 2 y = − . tan (1− 2x) A. 4 y′ = . B. 4 y′ = − . C. 4 ′ = − x y . D. 4 y′ = − . 2 sin (1− 2x) sin (1− 2x) 2 sin (1− 2x) 2 sin (1− 2x) Lời giải Chọn A 1 − 2 − (tan(1− 2x))′ 4. 2 cos x(1− 2x) 4 y − ′ = − = = . 2 tan (1− 2x) 2 tan (1− 2x) 2 sin (1− 2x)
Câu 47: Tính đạo hàm của hàm số π
f (x) = 5sin x − 3cos x tại điểm x = . 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 16
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com A. π f ′ π π π = 3 . B. f ′ = 3 − . C. f ′ = 5 − . D. f ′ = 5 . 2 2 2 2 Lời giải Chọn A
f (x) (5sin x 3cos x)′ 5(sin x)′ 3(cos x)′ ′ = − = −
= 5cos x + 3sin x Suy ra f π ′ = 5cos π + 3sin π = 3. 2 2 2
Câu 48: Hàm số nào dưới đây thỏa mãn hệ thức 2
y′ + 2y + 2 = 0 ?
A. y = sin 2x .
B. y = tan 2x .
C. y = cos 2x .
D. y = cot 2x . Lời giải Chọn D Với 1
y = tan 2x ⇒ y′ = .2 2 cos 2x Do đó 2 2 2 4 y′ + 2y + 2 = + 2tan 2x + 2 = 2 2 cos 2x cos 2x Với 1 y −
= cot 2x ⇒ y − ′ = .2 suy ra 2 2 2 y′ + 2y + 2 =
+ 2cot 2x + 2 = 0 . 2 sin 2x 2 sin 2x
Câu 49: Cho f (x) 3
= sin ax , a > 0 . Tính f ′(π) . A. f ′(π) 2
= 2sin (aπ)cos(aπ) .
B. f ′(π) = 0 . C. f ′(π) 2 = 3a sin (aπ) . D. f ′(π) 2
= 3a sin (aπ)cos(aπ). Lời giải Chọn D f ′(x) 2
= sin (ax)(sin ax)′ 2 3
= 3sin (ax)(a cos ax) Câu 50: Cho hàm số 2
y = sin x . Mệnh đề nào dưới đây đúng?
A. 2 y + y = 2 sin 2x π ′ ′′ − .
B. 4y − y′′ = 2 . 4
C. 4y + y′′ = 2 .
D. 2 y′+ y′.tan x = 0 . Lời giải Chọn C
y′ = sinx .cosx = sin x, y′′ = cos x = ( 2 − sin x) 2 2 2 2 2 2 2 1 2 = 2 − 4 sin x Do đó 2 2
4y + y′′ = 4 sin x+ 2 − 4 sin x = 2 . Câu 51: Xét hàm số 1− cos x y =
khi x ≠ 0 và f (x) = 0 . Mệnh đề nào sau đây đúng? 2 x
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 17
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
A. f (x) là một hàm số lẻ.
B. f (x) là một hàm tuần hoàn chu kì 2π.
C. f (x) có đạo hàm tại x = 0 bằng 0.
D. f (x) không có đạo hàm tại x = 0 . Lời giải Chọn D
(− ) 1−cos(−x) 1−cosx y x = =
khi x ≠ 0 và f (0) = 0. Do đó, f (x) là một hàm số chẵn, (−x)2 2 x
f (x) không là hàm số tuần hoàn 2 2 2 x x sin sin − Mặt khác 1 cosx 2 1 2 1 lim y = lim = lim = lim
= nên hàm số không liên tục tại 2 2 x→0 x→0 x→0 x→0 x x 2 x 2 4 2 2
điểm x = 0 do đó f (x) không có đạo hàm tại x = 0 .
Câu 52: Đạo hàm của hàm số y = log 4x +1 là 3 ( ) 4 1 A. ln 3 y′ = . B. y′ = . C. y′ = . D. 4ln 3 y′ = . 4x +1 (4x + )1ln3 (4x + )1ln3 4x +1 Lời giải Chọn B (4x ) 1 ′ + 4 y′ = ( = . 4x + ) 1 ln 3 (4x + ) 1 ln 3
Câu 53: Đạo hàm của hàm số 2017x y = là x 1 x A. .2017x y x − ′ = . B. 2017x y′ = C. 2017 y′ = .
D. y′ = 2017 .ln 2017 . ln 2017 Lời giải Chọn D Ta có 2017x y′ = .ln 2017 .
Câu 54: Cho hàm số ( ) = ( + ) 1 x f x x
e . Tính f ′(0) A. 2e . B. 0 . C. 1. D. 2 Lời giải Chọn D Ta có: ( ) = ( + )
1 x ⇒ '( ) = ( + 2) x f x x e f x x
e ⇒ f '(0) = 2 .
Câu 55: Tính đạo hàm của hàm số = 3x y + log x . A. x 1 y′ = 3 ln3+ . B. 1 y′ = log x + . x ln10 3 x ln3
C. y′ = log x + ln3 x 3 . D. 1 ln y − ′ = . ln3
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 18
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Lời giải Chọn A = 3x y + log x . x 1 y′ = 3 ln 3+ . x ln10
Câu 56: Tìm tập xác định D của hàm số 2
y = 4 − log x . 2 A. D = [ 2; − 2] .
B. D = (0;16]. C. D = (0;4] . D. 1 D ;4 = . 4 Lời giải Chọn D x > 0 x > 0 x > 0 Hàm số có nghĩa ⇔ ⇔ ⇔ . 2 1 log x ≤ 4 2 − ≤ log x ≤ 2 ≤ x ≤ 4 2 2 4
Câu 57: Cho hàm số f x = ( 4 ( ) ln x + )
1 . Đạo hàm f ′( ) 1 bằng. A. 2 . B. ln 2 . C. 1. D. 1 . 2 2 Lời giải Chọn C 3 Ta có: ′( ) 4x f x = ⇒ f ′ 1 = 2 . 4 ( ) x +1
Câu 58: Tính đạo hàm của hàm số = ( 2 − 2 + 2)3x y x x .
A. ′ = ( − ) x + ( 2 2 2 3 − 2 + 2)3x y x x x ln 3 .
B. ′ = (2 − 2)3x y x ln 3. C. 2 ′ = .3x y x .
D. ′ = (2 − 2)3x y x . Lời giải Chọn A = ( − ) x + ( 2 ' 2 2 3 − 2 + 2)3x y x x x ln 3.
Câu 59: Đạo hàm của hàm số 1 y = là. 2x A. 2 x y − ′ = ln 2. B. 1 y′ = − . C. ln 2 y′ = − . D. 1 y′ = − . 2x 2x (2x)2 Lời giải Chọn C 1 − x − x ln 2 y = = 2 ⇒ y′ = 2 − .ln 2 = − . 2x 2x
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 19
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Câu 60: Tính đạo hàm của hàm số 1 2 x y − = . 1−x 1−x − A. 2 y′ = . B. ln 2 1 ′ − 2 = 2 −x y . C. ln 2 1 ′ = 2 −x y . D. y′′ = . 2 1− x 2 1− x 2 1− x 2 1− x Lời giải Chọn C ' = ( 1− )' 1−x − ln 2 1 .2 .ln 2 = 2 −x y x . 2 1− x
Câu 61: Tính đạo hàm của hàm số tan 2 x y = . tan x 1 − A. tan . x 2 y′ = . B. tan x 1 y tan .x2 − ′ = ln 2 . ln 2 tan x tan x C. 2 ln 2 y′ = . D. 2 ln 2 y′ = . 2 sin x 2 cos x Lời giải Chọn D Ta có: tan ′ = 2 x ln 2(tan )′ 1 tan = 2 x y x ln 2. 2 cos x
Câu 62: Cho hàm số = ( ) = ln(2.ex y f x
+ m) có f ′(− ) 3
ln 2 = . Mệnh đề nào dưới đây đúng? 2 A. m∈(1;3). B. m∈( 5; − 2 − ).
C. m∈(1;+∞) . D. m∈( ; −∞ 3) . Lời giải Chọn D
Điều kiện: 2.ex + m > 0 . x Ta có f ′(x) 2e = . 2ex + m −ln 2
Theo đề bài ta có f ′(− ) 3 ln 2 = 2e 3 1 3 1 ⇔ = ⇔ = ⇔ m = − . 2 −ln 2 2e + m 2 1+ m 2 3 Vậy m∈( ; −∞ 3) .
Câu 63: Cho hàm số = ( 2 ln x y
e + m ) . Với giá trị nào của m thì y′( ) 1 1 = . 2
A. m = .e
B. m = − .e C. 1 m = .
D. m = ± e. e Lời giải Chọn D x Ta có e ′ = ⇒ ′ 1 e y y = . x 2 ( ) 2 e + m e + m Khi đó y′( ) 1 e 1 2 1 = ⇔
= ⇔ 2e = e + m ⇔ m = ± e . 2 2 e + m 2
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 20
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com
Câu 64: Hàm số y = ( 2
ln x − 2mx + 4) có tập xác định D = khi các giá trị của tham số m là: A. m < 2. B. m < 2 − hoặc m > 2. C. m = 2 . D. 2
− < m < 2 . Lời giải Chọn D Hàm số y = ( 2
ln x − 2mx + 4) có tập xác định khi 2
x − 2mx + 4 > 0, x ∀ ∈ ( ) 1 ( ) a =1> 0 2 1 ⇔
⇔ m − 4 < 0 ⇔ 2 − < m < 2. ∆′ < 0
Câu 65: Ông Tú dự định gửi vào ngân hàng một số tiền với lãi suất 6,5% một năm. Biết rằng, cứ sau
mỗi năm số tiền lãi sẽ được nhập vào vốn ban đầu. Tính số tiền tối thiểu x (triệu đồng, x∈ )
ông Tú gửi vào ngân hàng để sau 3 năm số tiền lãi đủ mua một chiếc xe gắn máy giá trị 30 triệu đồng. A. 145 triệu đồng B. 154 triệu đồng C. 150 triệu đồng D. 140 triệu đồng Lời giải Chọn A 3
Theo công thức lãi kép, số tiền lãi ông Tú nhận được sau 3 năm là: 6,5 y x 1 = + − x 100 = ( )3 1,065 −1 x . Ta có: ( )3 1,065 30 −1 x = 30 ⇔ x = ≈144,27 triệu. (1,065)3 −1
Vậy ông Tú cần gửi ít nhất 145 triệu để sau 3 năm số tiền lãi đủ mua một chiếc xe gắn máy giá trị 30 triệu đồng.
Câu 66: Hàm số = log 4x − 2x y
+ m có tập xác định là 2 ( ) khi A. 1 m < . B. m > 0. C. 1 m ≥ . D. 1 m > . 4 4 4 Lời giải Chọn D
Điều kiện: 4x − 2x + m > 0 .
Hàm số đã cho có tập xác định là khi và chỉ khi 4x − 2x + m > 0 (*) x ∀ ∈ . Đặt 2x
t = với t > 0, khi đó bất phương trình (*) trở thành: 2t − t + m > 0 t ∀ > 0 . Xét hàm số ( ) 2
f t = t − t , t
∀ > 0 ta có f ′(t) = 2t −1; f ′(t) 1 = 0 ⇔ t = . 2
Lập bảng biến thiên ta tìm được f (t) 1 1 min = f = − . ( 0;+∞) 2 4
Để bất phương trình 2t − t + m > 0 , t ∀ > 0 thì 1 1
−m < − ⇔ m > . 4 4
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 21
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Cách khác: Trường hợp 1: 1
∆ = 1− 4m < 0 ⇔ m > thì 2
t − t + m > 0 t
∀ ∈ (thỏa mãn yêu cầu bài toán) 4 1 Trường hợp 2: 1
∆ = 0 ⇔ m = thì phương trình 2 1
t − t + = 0 ⇔ t = (không thỏa mãn yêu 4 4 2 cầu bài toán). b Trường hợp 3: 1
∆ > 0 ⇔ m < . Ta thấy − =1 > 0 nên phương trình 2
t − t + m = 0 không 4 a
thể có hai nghiệm âm. Tức là 2t − t + m không thề luôn dương với mọi t > 0. Vậy 1 m > . 4 B. TỰ LUẬN
Câu 67: Cho hàm số f (x) 2
= x − 2x . Giải bất phương trình f '(x) ≥ f (x) Lời giải
f '(x) ≥ f (x) 2x − 2 2 ⇔
> x − 2x (với 2
x − 2x > 0 ) 2 2 x − 2x x > 2 x > 2 x < 0 ⇔
⇔ x < 0 (vô nghiệm). 2 2
x −1 > x − 2x
0 > x − x +1
Câu 68: Cho hàm số y = f (x) có đạo hàm trên ℝ. Xét các hàm số g (x) = f (x) − f (2x) và
h(x) = f (x) − f (4x) . Biết rằng g '( )
1 =18 và g '(2) =1000 . Tính h'( ) 1 Lời giải
g '(x) = f '(x) − 2 f '(2x) và h'(x) = f '(x) − 4 f '(4x) f '( ) 1 − 2 f '(2) =18 f '( ) 1 − 2 f '(2) =18 Do g '( )
1 =18 và g '(2) =1000 nên ⇔ f ' (2) 2 f '(4) 1000 − = 2 f ' (2)− 4 f '(4) = 2000
Cộng vế theo vế ta được f '( )
1 − 4 f '(4) = 2018 ⇒ h'( ) 1 = 2018. Câu 69: Cho hàm số y = f (x) 1 = . Tính giá trị của biểu thức x + x +1 P = f '( )
1 + f '(2) +...+ f '(2018) Lời giải ( ) x +1 − x f x = = x +1 − x x +1− x Suy ra f (x) 1 1 1 1 1 ' = − = − − 2 x 1 2 x 2 x x 1 + +
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 22
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Khi đó 1 1 1 1 1 1 1 1 1 1− 2019 P − = − + − + ...+ − = − 1− = 2 1 2 2 3 2018 2019 2 2019 2 2019
Câu 70: Cho hàm số f (x) thỏa mãn '( ) b f x = ax + , f (− ) 1 = 2, f ( ) 1 = 4 , f '( ) 1 = 0 . 2 x 2 Viết ( ) ax b f x =
− + c . Tính abc 2 x Lời giải f '( ) 1 a b 0 = + = a = 1 Ta có f (− ) a b 5 1 = − + c = 2 ⇔ b = 1 − ⇒ abc = − . 2 1 − 2 5 ( )1 a b 4 c f c = = − + = 2 2 1 Câu 71: Cho 2 + y ax b
= x − 2x + 3 , y ' = . Khi đó giá trị .
a b bằng bao nhiêu? 2 x − 2x + 3 Lời giải (x −2x+3)' 2 2x − 2 x −1 y ' = = = 2 2 2
2 x − 2x + 3 2 x − 2x + 3 x − 2x + 3
Do đó a =1,b = 1 − ⇒ ab = 1 − .
Câu 72: Cho hàm số ( ) sin 4x cos 4 cos 3 sin x f x x x = + − +
. Tìm nghiệm của phương trình 4 4 π
f ′(x) = 0 thuộc 0; 2 Lời giải
( ) cos4 x 4. sin 4x 4 3 . f x sinx cosx − ′ = − − + 4 4
= cos 4 x− sinx− 3 cosx+ 3 sin 4x π π Khi đó f (x) 0
3 sin 4x cos 4 x sinx 3 cosx 2 sin 4x
2 sin x ′ = ⇔ + = + ⇔ + = + 6 3 π π 4x x k2 + = + + π π = + π 6 3 x k 18 ⇔ π π π l.2 4x + = − π π x + + 2 l. π x = + 6 3 10 5 π π π
Kết hợp x 0; x ; ∈ ⇒ = . 2 18 2
Câu 73: Tìm tất cả các giá trị thực của tham số m để hàm số y = ( 2
log x − 2mx + 4) có tập xác định là
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 23
BÀI GIẢNG TOÁN 11-CÁNH DIỀU
WEB: Toanthaycu.com Lời giải Điều kiện: 2
x − 2mx + 4 > 0 (*)
Để (*) đúng với mọi x∈ thì 2
∆′ = m − 4 < 0 ⇔ 2 − < m < 2.
Câu 74: Một người gửi số tiền 100 triệu đồng vào một ngân hàng với lãi suất 7% / năm. Biết rằng nếu
không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu (
người ta gọi đó là lãi kép). Để người đó lãnh được số tiền 250 triệu thì người đó cần gửi trong
khoảng thời gian ít nhất bao nhiêu năm? (nếu trong khoảng thời gian này không rút tiền ra và lãi suất không thay đổi). Lời giải
Ta có công thức tính = (1+ )n A a
r với A là số tiền gởi sau n tháng, a là số tiền gởi ban đầu, r là lãi suất. 6 6 250.10 100.10 (1 0,07)n = + 1,07n ⇔
= 2,5 ⇔ n = log 2,5 =13,542. 1,07
Câu 75: Cho hình vuông ABCD có diện tích bằng 36, AB là một vecto chỉ phương của đường thẳng
y = 0. Các điểm A , B , C lần lượt nằm trên đồ thị hàm số y = log x ; y = 2log x ; y = 3log x a a a . Tìm a . Lời giải
Do diện tích hình vuông là 36 cạnh bằng 6 Gọi A( ;
m log m ∈ y =
x B(m − 6;log m và C (m − 6;6 + log m a ) a ) a ) loga
Vì B(m − 6;log m ∈ y = x log m = m − (1) a 2loga ( 6) a ) 2loga
Vì C (m − 6;6 + log m ∈ y =
x 6 + log m = m − (2) a 3loga ( 6) a ) 3loga Giải ( )
1 m = 9 Thay vào (2) 6 a = 3 x
Câu 76: Cho hàm số f (x) 2 = . Tính f ( ) 1 19 0 f ... f + + + 2x + 2 10 10 Lời giải a b Với a 2 2
+ b = 2 , ta có f (a) + f (b) = + 2a + 2 2b + 2
2a.2b + 2.2a + 2a.2b + 2.2b a+b a a+b b + + + a b + + + = 2 2.2 2 2.2 4 2.2 4 2.2 ( = = = 1. 2a + 2)(2b + 2)
2a+b + 2.2a + 2.2b + 4
4 + 2.2a + 2.2b + 4
Do đó với a + b = 2 thì f (a) + f (b) =1.
Áp dụng ta được f ( ) 1 19 0 f ... f + + + 10 10 = f ( ) 1 19 2 18 9 11 0 + f + f + f + f + ...+ f + f + f ( ) 1 10 10 10 10 10 10 1 2 59 = + 9.1+ = . 3 4 6
Bản word đề và lời giải vui lòng lh Zalo: 0834332133 24
Document Outline
- Bài 7.1. Định nghĩa và ý nghĩa đạo hàm_Lời giải
- BÀI 1. ĐỊNH NGHĨA ĐẠO HÀM. Ý NGHĨA HÌNH HỌC CỦA ĐẠO HÀM
- A. KIẾN THỨC CƠ BẢN CẦN NẮM
- B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
- Dạng 1. Tìm số gia của hàm số
- 1. Phương pháp
- 2. Các ví dụ rèn luyện kĩ năng
- Dạng 2. Tính đạo hàm bằng định nghĩa
- 1. Phương pháp
- 2. Các ví dụ rèn luyện kĩ năng
- Dạng 3. Ý nghĩa vật lý của đạo hàm
- 1. Phương pháp
- 2. Các ví dụ rèn luyện kĩ năng
- Dạng 4. Phương trình tiếp tuyến
- 1. Phương pháp
- 2. Các ví dụ rèn luyện kĩ năng
- C. GIẢI BÀI TẬP SÁCH GIÁO KHOA
- BÀI 1. ĐỊNH NGHĨA ĐẠO HÀM. Ý NGHĨA HÌNH HỌC CỦA ĐẠO HÀM
- Bài 7.2_Quy tắc tính đạo hàm_Lời giải
- BÀI 2. CÁC QUI TẮC TÍNH ĐẠO HÀM
- A. KIẾN THỨC CƠ BẢN CẦN NẮM
- B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
- Dạng 1. Đạo hàm của hàm đa thức
- 1. Phương pháp
- 2. Các ví dụ rèn luyện kĩ năng
- Dạng 2. Đạo hàm của hàm phân thức
- 1. Phương pháp
- 2. Các ví dụ rèn luyện kĩ năng
- Dạng 3. Đạo hàm của hàm chứa căn
- 1. Phương pháp
- 2. Các ví dụ rèn luyện kĩ năng
- Dạng 4. Tính đạo hàm của các hàm số lượng giác
- 1. Phương pháp
- 2. Các ví dụ rèn luyện kĩ năng
- Dạng 5: Giải phương trình lượng giác
- 1. Phương pháp
- 2. Các ví dụ rèn luyện kĩ năng
- Dạng 6. Tính đạo hàm
- 1. Phương pháp:
- 2. Các ví dụ rèn luyện lĩ năng
- C. GIẢI BÀI TẬP SÁCH GIÁO KHOA
- D. BÀI TẬP TRẮC NGHIỆM
- BÀI 2. CÁC QUI TẮC TÍNH ĐẠO HÀM
- Bài 7.3_Đạo hàm cấp 2_Lời giải
- BÀI 3. ĐẠO HÀM CẤP 2
- A. KIẾN THỨC CƠ BẢN CẦN NẮM
- B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
- Dạng 1: Tính đạo hàm cấp cao của hàm số
- 1. Phương pháp
- 2. Các ví dụ rèn luyện kĩ năng
- Dạng 2: Ý nghĩa vật lý của đạo hàm cấp hai
- C. GIẢI BÀI TẬP SÁCH BÀI TẬP
- D. BÀI TẬP TRẮC NGHIỆM
- BÀI 3. ĐẠO HÀM CẤP 2
- Bài 7.4. ÔN TẬP CHƯƠNG 7_ĐẠO HÀM_LỜI GIẢI
- BÀI TẬP CUỐI CHƯƠNG VII
- BÀI TẬP TỔNG ÔN CHƯƠNG IX
- A. TRẮC NGHIỆM
- B. TỰ LUẬN




