lOMoAR cPSD| 45148588
DI TRUY陰N H窺C QU井N TH韻
I. Một số khái niệm cơ bản 1. Qu亥n th吋
Sự quần tụ số 8ông cá thể của một loài chiếm một không gian nhất 8ịnh và tồn tại qua
một th運i gian tương 8ối dài có 8ặc trưng về sinh thái và di truyền . Một quần tụ cá thể
như thế 8ược gọi là quần thể
Quần thể không phải là một tập hợp cá thể ngẫu nhiên , nhất th運i.
Mỗi quần thể là một cộng 8ồng lịch sử phát triển chung,có thành phần kiểu gen 8ặc trưng
và tương 8ối ổn 8ịnh.
Quần thể sinh sản vô tính khá 8ồng nhất về mặt di truyền.
Quần thể sinh sản hữu tính gồm các dạng sau:
✓ Quần thể tự phối 8iển bình
✓ Quần thế giao phối cận huyết
✓ Quần thể giao phối có lựa chọn
✓ Trong quần thể ngẫu phối diễn ra sự bắt cặp giao phối ngẫu nhiên của các cá thể
8ực cái trong quần thể . Ěây là dạng quần thể tồn tại phổ biến 荏 8ộng vật
2.T亥n số alen và t亥n số ki吋u gen
Mỗi quần thể 8ặc trưng bằng một vốn gen nhất 8ịnh.Vốn gen là toàn bộ thông tin di
truyền ,nghƿa là bao gồm các alen của tất cả các gen hình thành trong quá trình tiến hóa
mà quần thể có tại một th運i 8iểm xác 8ịnh.
Vốn gen bao gồm những kiểu gen riêng biệt, 8ược biểu hiện thành những kiểu hình nhất 8ịnh.
Tính 8ược tất cả các alen thuộc một gen nhất 8ịnh trong quần thể thì có thể tính 8ược
tần số của mỗi alen 8ối với gen này trong vốn gen.
Tần số tương 8ối của alen 8ược tính bằng tỉ lệ giữa số alen 8ược xét 8ến trong tổng số
các alen của 1 gen trong quần thể, hay bằng tỷ lệ phần trĕm số giao tử mang alen 8ó trong quần thể. Ví dụ :
Dưới 8ây là ví dụ về một 8ặc 8iểm 8ược chi phối b荏i một cặp allele nằm trên NST
thư運ng minh họa cho cách thức xác 8ịnh tần số của các allele trong quần thể.
Gen CCR5 chịu trách nhiệm mã hóa cho một receptor cytokin trên bề mặt tế bào,
receptor này 8óng vai trò như một 8iểm vào của các chủng virus gây suy giảm miễn dịch
荏 ngư運i (HIV) gây hội chứng suy giảm miễn dịch mắc phải (acquired
immunodeficiency syndrome, AIDS). Một 8ột biến mất 32 cặp nucleotide trong gen
CCR5 làm xuất hiện allele CCR5 mã hóa cho một protein không có chức nĕng do 8ã
bị thay 8ổi trong cấu trúc và bị chấm dứt sớm việc tổng hợp.
Những ngư運i 8ồng hợp tử về allele CCR5 ( CCR5/ CCR5) sẽ không có loại
receptor cytokin trên bề mặt tế bào và tạo nên khả nĕng 8ề kháng với HIV. Việc mất
chức nĕng của gene CCR5 là một 8ặc 8iểm lành tính và 8ược xác 8ịnh dựa trên khả
nĕng 8ề kháng với HIV. Allele bình thư運ng và allele 8ột biến mất 32 cặp base 1 lOMoAR cPSD| 45148588
CCR5 8ược phân biệt một cách dễ dàng qua phân tích gene bằng kỹ thuật PCR. Một
mẫu nghiên cứu trên 788 ngư運i Âu châu 8ã cung cấp số lượng thông tin
8ầy 8ủ về số cá thể 8ồng hợp hoặc dị hợp của 2 allele nói trên
Trên cơ s荏 tần số kiểu gen quan sát 8ược chúng ta có thể trực tiếp xác 8ịnh tần số của
của các allele một cách 8ơn giản thông qua việc 8ếm các allele. Khi chúng ta tính
toán tần số trong quần thể của một allele, chúng ta sẽ xem vốn gen (gene pool) như
là một tập hợp tất cả các allele 荏 một locus 8ặc hiệu trong toàn bộ quần thể. Ěối
với các locus trên NST thư運ng, kích cỡ của vốn gene 荏 một locus sẽ gấp 8ôi số cá thể
trong quần thể vì mỗi kiểu gen trên NST thư運ng sẽ gồm có hai allele, nghƿa là ngư運i
có kiểu gene CCR5/ CCR5 sẽ có 2 allele CCR5, và ngư運i có kiểu gen
CCR5/ CCR5 sẽ có 1 allele CCR5 CCR5.
Trong ví dụ này tần số của các allele CCR5 sẽ là:
(2 x 647 +1 x 134) / 788 x 2 = 0,906
Tương tự, ngư運i ta có thể tính toán 8ược tần số của allele CCR5 là 0,094, hoặc bằng
cách tính trực tiếp từ số cá thể:
(2 x 7 + 1 x 134) = 148 trong tổng số 1576 allele, hoặc 8ơn giản là lấy 1 trừ cho tần số
của allele CCR5: 1 - 0,906 = 0,094.
II. Quá trình di truy隠n trong qu亥n th吋 nội phối: -
Những quần thể nội phối 8iển hình là các quần thể thực vật tự thụ phấn , 8ộng vật tự thụ tinh. -
Nĕm 1903 ông W. Johannsen là ngư運i 8ầu tiên nghiên cứu cấu trúc của quần thể
bằng phương pháp di truyền. 8ối tượng nghiên cứu của ông là cây 8ậu tự thụ phấn phaseoles vustgaris. 2 lOMoAR cPSD| 45148588 -
Ông theo dõi sự di truyền về trọng lượng hạt và 8ã phân lập 8ược thành 2 dòng:
dòng hạt to ( trọng lượng trung bình là 518,7mg ) và dòng hạt nhỏ ( trung bình là
443,4mg ). Ěiều 8ó chứng tỏ quần thể gồm những cây khác nhau về mặt di truyền. -
Tiếp theo ông theo dõi sư di truyền riêng rẽ trong mỗi dòng hạt nặng và hạt nhẹ
thì không thấy dòng nào cho sự khác biệt nhau về trọng lượng hạt như trư運ng hợp trên.
Ěiều 8ó chứng tỏ sự khác nhau về trọng lượng hạt bên trong dòng ( thuần) không di truyền 8ược.
 Như vậy có thể rút ra nhận xét như sau: các quần thể thực vật tự thụ phấn gồm những
dòng có kiểu gen khác nhau. -
Tự phối hay giao phối gần (gọi chung là nội phối) làm cho quần thể dần dần bị
phân thành những dòng thuần có kiểu gen khác nhau. Trải qua nhiều thế hệ nội phối, các
gen 荏 trạng thái dị hợp chuyển sang trạng thái 8ồng hợp. Số thể dị hợp giảm dần, số 8ồng hợp tĕng dần. -
雲 quần thể tự phối hay tự thụ phấn diễn ra các kiểu tự phối cho ra những kết quả khác nhau.
Thế hệ bố mẹ ( P) Ō thế hệ con (F1) AA x AA Ō AA aa x aa Ō aa Aa x Aa Ō AA ; Aa ; aa -
Trong các công thức tự phối : AA x AA và aa x aa thì KG 荏 F1 , F2 … Fn vẫn
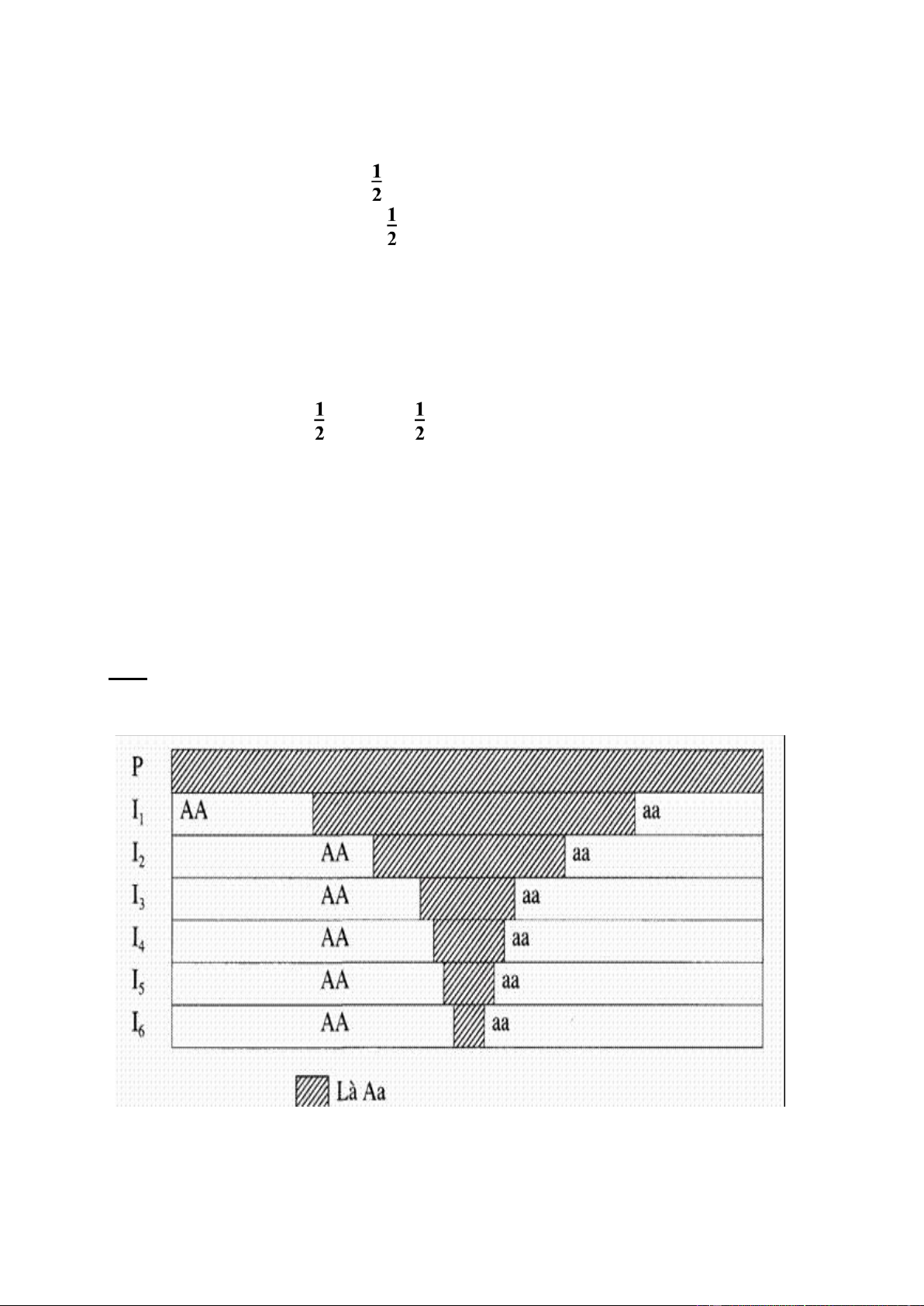
giống như 荏 thế hệ ban 8ầu. Còn khi một thể dị hợp tự thụ phấn tỉ lệ dị hợp thể sẽ giảm
dần sau mỗi thế hệ và quần thể dần 8ược 8ồng hợp tử hóa ( hình X.1) 3 lOMoAR cPSD| 45148588 -
Nếu gọi Ho là phần dị hợp tử trong quần thể ban 8ầu và Hn là phần dị hợp tử
trong quần thể thứ n , thì tỉ lệ dị hợp tử sau mỗi thế hệ bằng một nửa tỉ lệ dị hợp tử 荏
thế hệ trước 8ó,.nghiã là : Hn = Hn-1 Hn-1 = Hn-2 1 n
Hn = [ 2 ] Ho
- Trong quần thể , thành phần dị hợp thể Aa qua tự phối hay giao phối với nhau sẽ diễn
ra sự phân li, trong 8ó các thể 8ồng hợp trội AA và lặn aa 8ược tạo ra với tần số như
nhau trong mỗi thế hệ. do 8ó , quần thể kh荏i 8ầu với cấu trúc di truyền ( d , h , r ) dần
dần chuyển thành ( d + h ; 0 ; r + h ) , nghƿa là thành cấu trúc ( p ; 0 ; q ).
- Trong quá trình tự phối liên tiếp qua nhiều thế hệ, tần số tương 8ối của các alen không
thay 8ổi nhưng tần số tương 8ối các KG hay cấu trúc di truyền của quần thể thay 8ổi.
- Trong trư運ng hợp quần thể ban 8ầu gồm toàn cá thể dị hợp ( 0 ; 1 ; 0 ) sau n thế hệ 1 n
nội phối thì thành phần dị hợp tử là [ ] và 8ồng hợp tử tương ứng là: 2
2n-11 n - 1 = 1 - [ ] 2n 2
Giả sử rằng quần thể gồm ba kiểu gene AA, Aa và aa 8ược phân tách thành một tỷ lệ nội
phối (F) ta ước tính hệ số nội phối trong một quần thể tự nhiên bằng cách sử dụng biểu 4 lOMoAR cPSD| 45148588
thức về tần số các thể dị hợp 8ã cho 荏 trên. Qua 8ó ta có thể tìm ra biểu thức cho F như sau:
H = 2pq – 2Fpq = (1 – F)2pq Ō 1 – F = H/2pq Ō F = 1 – (H/2pq)
Trong 8ó : hệ số nội phối (F) tần số thể
dị hợp Aa tần số allen A và a (p và q ) từ
8ó suy ra ; tần số của AA, Aa, và aa tương ứng là : P = p2 + Fpq H = 2pq – 2Fpq Q = q2 + Fpq Với :q = 1 – p
Ví dụ, một quần thể thực vật gồm ba kiểu gene AA, Aa và aa với các tần số tương ứng
là P = 0,70, H = 0,04 và Q = 0,26. Ta có thể ước tính hệ số nội phối như sau :
Trước tiên, tính 8ược các tần số allele A và a (p và q ):
p = 0,70 + ½ (0,04) = 0,72 và q = 1 – p = 0,28
Vậy hệ số nội phối F = 1 – ( 0,04/2 x 0,72 x 0,28 ) = 0,901
III. Quá trình di truy隠n trong qu亥n th吋 ngẫu phối
1. Một số 8ặc trưng di truy隠n cơ bản
- Giao phối ngẫu nhiên (ngẫu phối) giữa các cá thể trong quần thể là nét 8ặc trưng
của quần thể giao phối. Ěây là hệ thống giao phối phổ biến nhất 荏 phần lớn 8ộng
thực vật. Trong quần thể ngẫu phối nổi lên mối quan hệ phụ thuộc lẫn nhau giữa các
cá thể về mặt sinh sản (giữa 8ực và cái, giữa bố mẹ và con). Vì vậy quần thể giao
phối 8ược xem là 8ơn vị sinh sản, 8ơn vị tồn tại của loài trong tự nhiên. Chính mối
quan hệ về sinh sản là cơ s荏 8ảm bảo cho quần thể tồn tại trong không gian và qua th運i gian.
- Quần thể giao phối nổi bậc 荏 8ặc 8iểm 8a hình. Quá trình giao phối là nguyên
nhân làm cho quần thể 8a hình về kiểu gen, do 8ó 8a hình về kiểu hình. Các cá thể 5 lOMoAR cPSD| 45148588
trong quần thể chỉ giống nhau 荏 những nét cơ bản, chúng khác nhau về nhiều chi tiết.
Chẳng hạn, nếu gọi r là số alen thuộc 1 gen (locut), còn n là số gen khác nhau,
trong 8ó các gen phân ly 8ộc lập, thì số kiểu gen khác nhau trong quần thể 8ược tính bằng công thức: [r(r + 1)]/2 Ví dụ:
Nếu r = 2, n = 1 thì có 3 kiểu gen, kết quả này tương ứng với công thức tổ hợp
của Menden là 3n. Nếu r = 4 và n = 2 thì có 100 KG khác nhau.
- Trong quần thể, các loài 8ộng, thực vật giao phối thì số gen trong kiểu gen của cá
thể rất lớn, số gen có nhiều alen cǜng không ít, vì thế quần thể rất 8a hình, khó mà
tìm 8ược 2 cá thể giống hệt nhau (trừ trư運ng hợp sinh 8ôi cùng trứng).
- Tuy quần thể là 8a hình nhưng 1 quần thể xác 8ịnh 8ược phân biệt với những
quần thể khác cùng loài 荏 những tần số tương 8ối các alen, các kiểu gen, các kiểu hình.
2. Ě鵜nh luật Hardy-Weinberg (viết tắt: H -W )
Nĕm 1908, nhà toán học ngư運i Anh G.N.Hardy và một bác sƿ ngư運i Ěức là W.
Weinberg 8ã 8ộc lập nghiên cứu, 8ồng th運i phát hiện ra quy luật phân bố các kiểu gen
và kiểu hình trong quần thể giao phối.
a. Nội dung 8鵜nh luật
Trong một quẩn thể ngẫu phối kích thước lớn, nếu như không có áp lực của các quá trình
8ột biến, di nhập cư, biến 8ộng di truyền và chọn lọc, thì tần số các alen 8ược duy trì ổn
8ịnh từ thế hệ này sang thế hệ khác và tần số các kiểu gen (của một gen gồm hai alen
khác nhau) là một hàm nhị thức của các tần số alen, 8ược biễu diễn bằng công thức sau:
( p + q )2 = p2 + 2pq + q2 = 1
Ví dụ trong trư運ng hợp 8ơn giản, gen A có 2 alen là A và a, thì trong quần thể có 3 kiểu
trên AA, Aa, aa. Giả sử các kiểu gen trong quần thể 荏 thế hệ xuất phát là: 0,64AA + 0,32Aa + 0,04aa = 1
Tần số tương 8ối của alen A là: 0,64 + 0,32/2 = 0,8
Tần số tương 8ối của alen a là: 0,04 + 0,32/2 = 0,2
Tần số của A so với a 荏 thế hệ xuất phát là: A/a = 0,8/0,2. Tỷ lệ này có nghƿa là trong
số các giao tử 8ực cǜng như giao tử cái, số giao tử mang alen A chiếm 80%, còn số giao
tử mang alen a chiếm 20%. Khi tổ hợp tử do các loại giao tử này tạo ra thế hệ tiếp theo như sau: 6 lOMoAR cPSD| 45148588 ƕ 0,8A 0,2a Ɣ 0,8A 0,64AA 0,16Aa 0,2a 0,16Aa 0,04aa
Tần số tương 8ối các kiểu gen 荏 thế hệ này là: 0,64AA + 0,32Aa + 0,04aa = 1 và tần
số tương 8ối các alen: A/a = 0,8/0,2. Trong các thế hệ tiếp theo tần số 8ó vẫn không thay 8ổi.
Tổng quát: Nếu một gen A có 2 alen: A với tần số p; a với tần số q thì ta có công thức: p2AA + 2pqAa + q2 aa = 1 .
Lưu ý rằng: p2 + 2pq + q2 = (p + q)2 = 1 => p + q = 1 => q = (1 - p)
Do 8ó, sự phân bố các kiểu trên còn có thể diễn 8ạt bằng: [pA + (1 - p) a]2 = 1. Nếu gen
A có số alen nhiều hơn 2, như: a1, a2, a3,... với các tần số tương ứng p, q, r,... thì sự phân
bố các kiểu trên trong quần thể sẽ tương ứng với sự triển khai biểu thức (p + q + r +...)2 =1.
Ě鵜nh luật Hardy-Weinberg chỉ áp dụng cho qu亥n th吋 giao phối và chỉ nghiệm
8úng trong những 8i隠u kiện sau:
- Có sự giao phối tự do, nghƿa là các cá thể có kiểu gen và kiểu hình khác nhau trong
quần thể 8ều giao phối 8ược với nhau, với xác suất ngang nhau. Ěây là 8iều kiện cơ bản nhất.
- Quần thể phải có số lượng cá thể 8ủ lớn.
- Các loại giao tử mang alen trội, lặn 8ược hình thành qua giảm phân với tỷ lệ ngang
nhau, có sức sống như nhau, tham gia vào thụ tinh với xác suất ngang nhau.
- Các cơ thể 8ồng hợp và dị hợp có sức sống ngang nhau, 8ược truyền gen cho các thế hệ sau ngang nhau.
- Không có áp lực của quá trình 8ột biến và quá trình chọn lọc tự nhiên hoặc áp lực 8ó là không 8áng kể.
- Quần thể 8ược cách ly với các quần thể khác, không có sự trao 8ổi gen. 7 lOMoAR cPSD| 45148588
b. Ch泳ng minh
雲 một quần thể Mendel, xét một locus autosome (gen trên NST thư運ng), gồm hai alen
A1 và A2 có tần số như nhau 荏 cả hai giới 8ực và cái. Ký hiệu p và q cho các tần số alen
nói trên (p + q =1). Cǜng giả thiết rằng các cá thể 8ực và cái bắt cặp ngẫu nhiên, nghƿa
là các giao tử 8ực và cái gặp gỡ nhau một cách ngẫu nhiên trong sự hình thành các hợp
tử. Khi 8ó tần số của một kiểu gen nào 8ó chính là bằng tích của các tần số hai alen
tương ứng. Xác suất 8ể một cá thể có kiểu gene A1A1 là bằng xác suất (p) của alne A1
nhận từ mẹ nhân với xác suất (p) của alen A1 nhận từ bố, hay p.p = p2. Tương tự, xác
suất mà một cá thể có kiểu gene A2A2 là q2. Kiểu gene A1A2 có thể xuất hiện theo hai
cách: A1 từ mẹ và A2 từ bố với tần số là pq, hoặc A2 từ mẹ và A1 từ bố cǜng với tần số
pq; vì vậy tần số của A1A2 là pq + pq = 2pq (Bảng 1).
Bảng 1. Các t亥n số H-W sinh ra từ sự k院t hợp ngẫu nhiên các giao tử Tần số giao tử cái p(A1) q(A2) Tần số p(A1) giao tử p2(A1A1) pq(A1A2) 8ực q(A2) pq(A1A2) q2(A2A2)
Ěiều chứng minh trên 8ược tóm tắt như sau:
* Quần thể ban 8ầu có 3 kiểu gen : A1A1 A1A2 A2A2 Tổng
Tần số các kiểu gen : P H Q 1
Tần số các alen : p = P + ½H ; q = Q + ½H *
Quần thể thế hệ thứ nhất sau ngẫu phối có :
Tần số các kiểu gen : (p + q)2 = p2 + 2pq + q2 = 1
Tần số các alen: f(A1) = p2 + ½(2pq) = p(p+q) = p
f(A2) = q2 + ½(2pq) = q(p+q) = q Nhận xỨt: 8 lOMoAR cPSD| 45148588
Từ chứng minh trên cho thấy các tần số alen 荏 thế hệ con giống hệt 荏 thế hệ ban 8ầu,
nghƿa là f(A1) = p và f(A2) = q. Do 8ó, các tần số kiểu gen 荏 thế hệ tiếp theo vẫn là p2,
2pq và q2 (giống như 荏 thế hệ thứ nhất sau ngẫu phối). Ěiều 8ó chứng tỏ rằng các tần
số kiểu gene 8ạt 8ược cân bằng chỉ sau một thế hệ ngẫu phối. Trạng thái ổn 8ịnh về
thành phần di truyền 8ược phản ánh bằng công thức H-W như vậy 8ược gọi là cân bằng
H-W (Hardy-Weinberg equilibrium).
c. T亥n số giao phối và sự ki吋m ch泳ng nguyên lý H-W
Nguyên lý H-W có thể 8ược chứng minh theo một cách khác dựa trên tần số của các
kiểu giao phối. Mặc dù nó cồng kềnh hơn phương pháp 8ã xét nhưng lại cho thấy rõ hơn
bằng cách nào các tần số H-W phát xuất từ quy luật phân ly của Mendel.
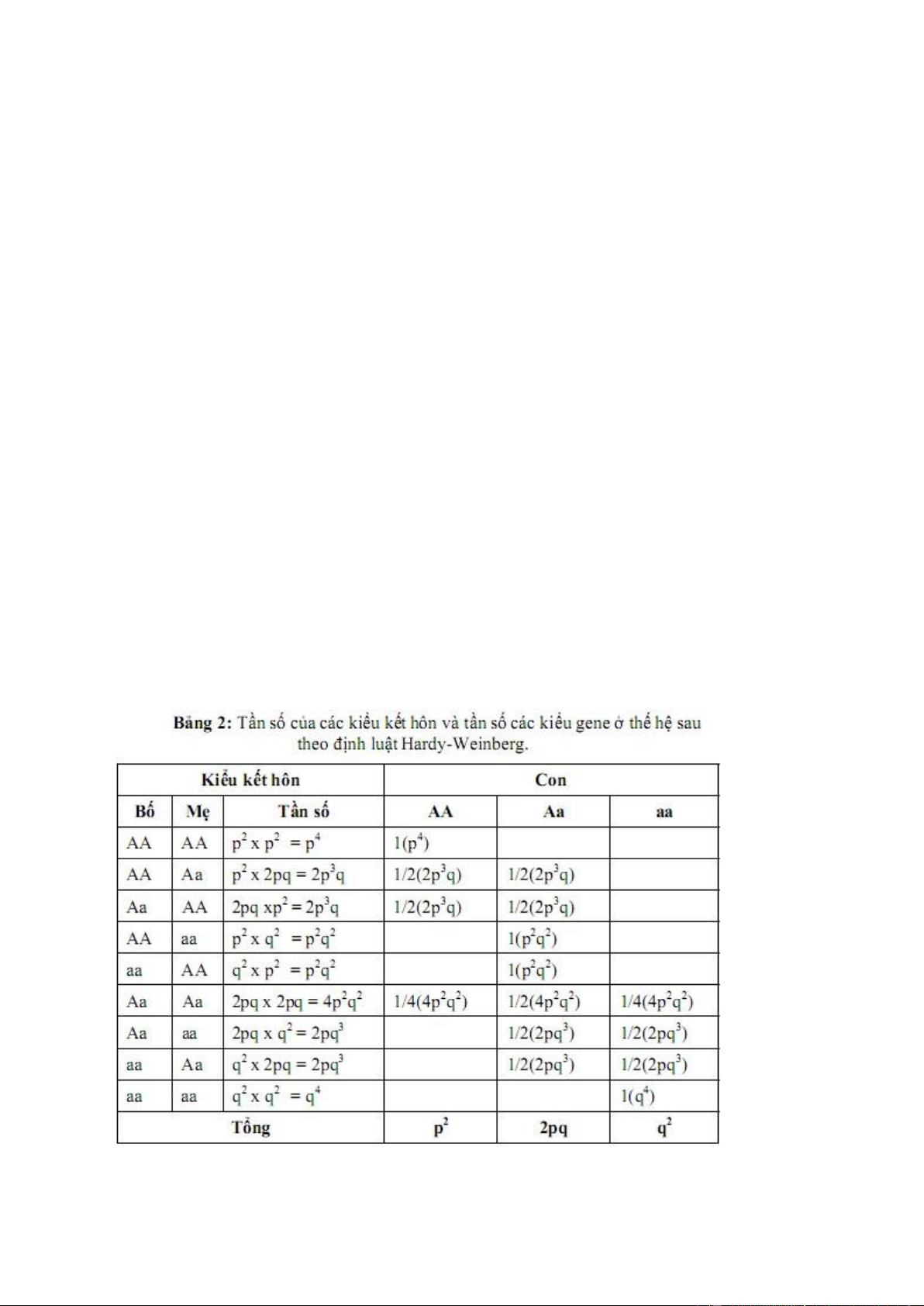
Xét cấu trúc giao phối của quấn thể ngẫu phối như trên ta thấy có tất cả là 9 kiểu giao
phối với tần số giao phối như 荏 Bảng 2.Vì tần số mỗi kiểu gen 荏 hai giới 8ược xem là
như nhau, nên một số kiểu giao phối thuận nghịch là tương 8ương vì vậy chỉ còn lại 6
kiểu giao phối khác nhau với tần số tương ứng. Bây gi運 ta xét các kiểu gen 8運i con
sinh ra từ mỗi kiểu giao phối và sau 8ó tìm tần số của mỗi kiểu gen trong toàn bộ 8運i
con, với giả thiết rằng tất cả các kiểu giao phối 8ều hữu thụ ngang nhau và tất cả các
kiểu gen 8ều có sức sống như nhau. Sau khi rút gọn ta 8ược các tần số kiểu gene 8運i
con tương ứng là p2 , 2pq và q2 (荏 dòng cuối cùng của bảng). Các trị số này chính là
các tần số cân bằng H-W (equilibrium frequencies) 8ạt 8ược sau một thế hệ ngẫu phối,
bất luận các tần số kiểu gene 荏 8運i bố mẹ như thế nào. 9 lOMoAR cPSD| 45148588
d. Các mệnh 8隠 và hệ quả
(1) Nếu như không có áp lực của các quá trình tiến hoá (8ột biến, di nhập cư, biến 8ộng
di truyền và chọn lọc), thì các tần số alen 8ược giữ nguyên không 8ổi từ thế hệ này sang
thế hệ khác. Ěây là mệnh 8ề chính của nguyên lý hay 8ịnh luật H-W. (2) Nếu sự giao
phối là ngẫu nhiên, thì các tần số kiểu gen có quan hệ với các tần số alen bằng công thức
8ơn giản: ( p+q )2 = p2 + 2pq + q2 =1.
(3) Hệ quả 1: Bất luận các tần số kiểu gen ban 8ầu (P, H, Q) như thế nào, miễn sao các
tần số alen 荏 hai giới là như nhau, chỉ sau một thế hệ ngẫu phối các tần số kiểu gen
8ạt tới trạng thái cân bằng (p2, 2pq và q2).
(4) Hệ quả 2: Khi quần thể 荏 trạng thái cân bằng thì tích của các tần số 8ồng hợp tử
bằng bình phương của một nửa tần số dị hợp tử, nghƿa là: p2.q2 = (2pq/2)2
Thật vậy, khi quần thể 荏 trạng thái cân bằng lý tư荏ng, ta có: H = 2pq
Biến 8ổi 8ẳng thức trên ta 8ược: pq = ½H
Bình phương cả hai vế, ta có: p2.q2 = (½H)2, trong 8ó H = 2pq. Như vậy 8ẳng thức này
cho thấy mối tương quan giữa các thành phần 8ồng hợp và dị hợp khi quần thể 荏 trạng
thái cân bằng lý tư荏ng. (5) Hệ quả 3:
✓ Tần số của các thể dị hợp không vượt quá 50% và giá trị cực 8ại này chỉ xảy ra
khi p = q = 0,5 Ō H = 2pq = 0,5. Lúc này các thể dị hợp chiếm một nửa số cá thể trong quần thể.
✓ Ěối với alen hiếm (tức có tần số thấp), nó chiếm ưu thế trong các thể dị hợp nghƿa
là tần số thể dị hợp cao hơn nhiều so với tần số thể 8ồng hợp về alen 8ó. Ěiều này
gây hậu quả quan trọng 8ối với hiệu quả chọn lọc.
e. Ý nghƿa 8鵜nh luật Hardy-Weinberg
Về thực tiễn, dựa vào công thức Hardy-Weinberg có thể từ tỷ lệ kiểu hình suy ra tỷ lệ
kiểu gen và tần số tương 8ối các alen, ngược lại, từ tần số tương 8ối của alen 8ã biết có
thể dự tính tỷ lệ các kiểu gen và kiểu hình. Nắm 8ược kiểu gen của một số quần thể có
thể dự 8oán tác hại của các 8ột biến gây chết, 8ột biến có hại, hoặc khả nĕng gặp những
8ồng hợp tử mang 8ột biến có lợi.
Về lý luận, 8ịnh luật Hardy-Weinberg giải thích vì sao trong tự nhiên có những quần thể
8ứng vững trạng thái ổn 8ịnh trong th運i gian dài. Trong tiến hoá, sự duy trì, kiên 8ịnh
những 8ặc 8iểm 8ạt 8ược có ý nghƿa quan trọng chứ không phải chỉ có sự phát sinh các
8ặc 8iểm mới mới có ý nghƿa. 10 lOMoAR cPSD| 45148588
f. 永ng dụng c栄a 8鵜nh luật Hardy-Weinberg
❖でng dụng chính cてa 8ịnh luật H-W trong di truyền y học là tư vấn di truyền cho
các bệnh di truyền gene lặn NST thường.
Ví dụ trong bệnh Phenylketonuria (PKU), tần số của ngư運i mắc bệnh 荏 trạng
thái 8ồng hợp sẽ 8ược xác 8ịnh chính xác trong quần thể qua chương trình sàng lọc
trên trẻ sơ sinh 荏 Ireland là 1/4.500, 8ịnh luật Hardy-Weinberg cho phép xác 8ịnh
tần số của những ngư運i dị hợp tử có biểu hiện hoàn toàn bình thư運ng: vì q =
1/4500 nên q = 0,015 p = 1 - 0,015 = 0,985 do 8ó 2pq = 0,029 # 0,03
Như vậy tần số của ngư運i dị hợp tử mang gene bệnh PKU 荏 quần thể ngư運i
Ireland là khoảng 3%, nghƿa là nguy cơ 8ể một ngư運i bố hoặc mẹ mang gene bệnh
trong một hôn nhân sẽ là khoảng 3%.
❖Tần số gene và kiểu gene trong trường hợp gene liên kết với NST giới tính X.
Ěối với gene nằm trên NST giới tính X thì 荏 ngư運i nữ sẽ có 3 kiểu gene khác nhau
trong khi 8ó 荏 ngư運i nam chỉ có 2 kiểu gene do NST Y không mang gene do 8ó việc
áp dụng 8ịnh luật Hardy - Weinberg có chút thay 8ổi. Lấy bệnh mù màu làm ví dụ với
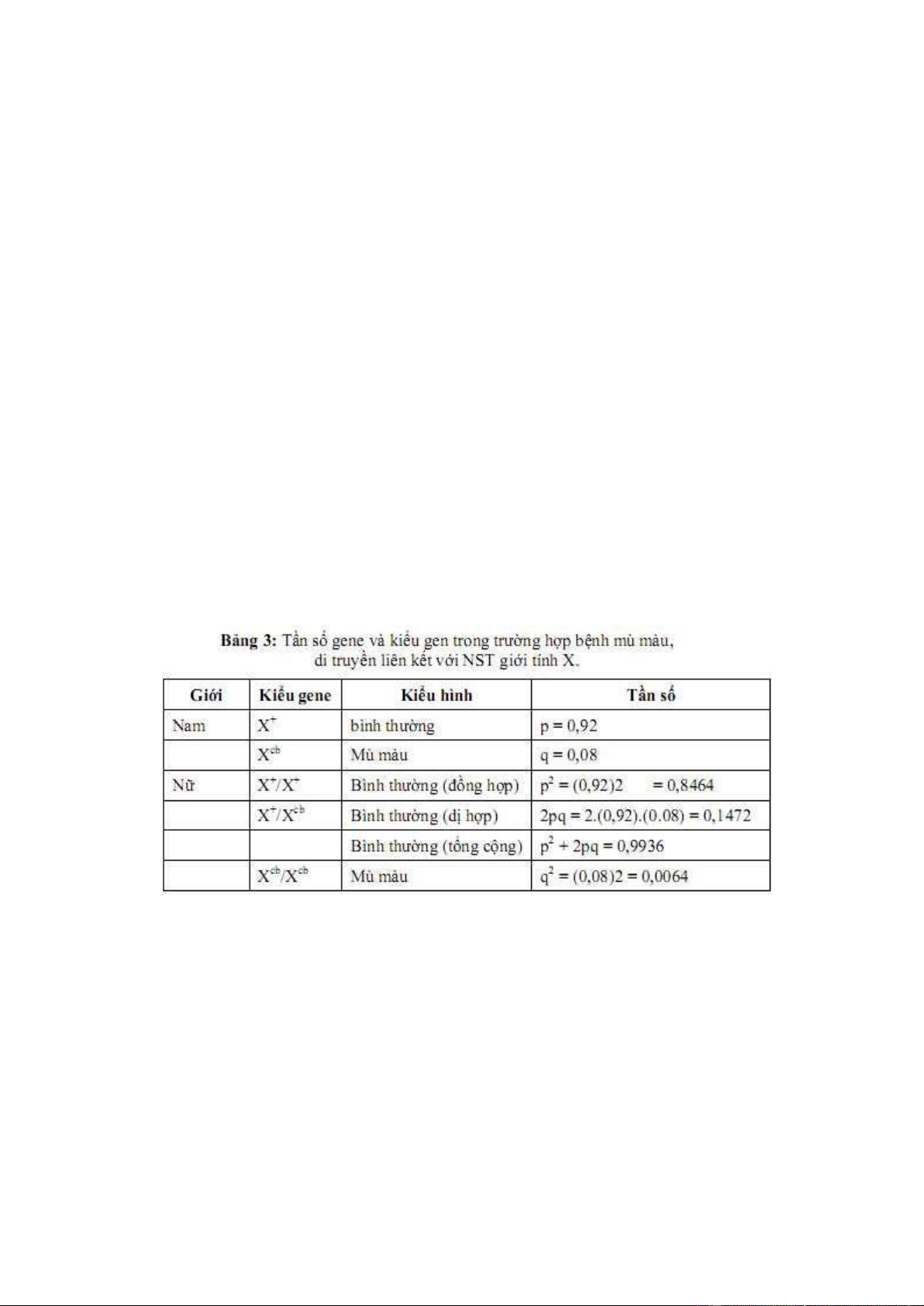
allele 8ột biến 8ược kí hiệu là cb và allele bình thư運ng 8ược kí hiệu là (+). Tần số của
các kiểu gene 8ược trình bày trong bảng 3.
Qua bảng 3 có thể nhận thấy tần số mắc bệnh mù màu 荏 ngư運i nữ thấp hơn nhiều so
với ngư運i nam, mặc dù tần số allele là như nhau 荏 cả hai giới. Chưa tới 1%
ngư運i nữ mắc bệnh mù màu nhưng tần số này 荏 ngư運i nam là 8%. Tần số
ngư運i nữ dị hợp mang gene bệnh là 15% những ngư運i này sẽ có nguy cơ sinh ra con trai mắc bệnh mù màu.
3. Ě鵜nh luật giao phối ổn 8鵜nh
Sự giao phối ngẫu nhiên giữa các cá thể trong quần thể là một cơ chế quan trọng 8ể tạo
ra sự cân bằng của quần thể về mặt di truyền. Như trong cấu trúc di truyền (0,1; 0,4; 11 lOMoAR cPSD| 45148588 0,5) nói trên 荏 trạng . Nếu như sự
ngẫu phối diễn ra thì cấu trúc di truyến của quần thể sẽ bị thay 8ổi. Tần số tương 8ối của
các alen trong quần thể là :
p(A) = d + h/2 = 0,1 + 0,4/2 = 0,3
q(a) = r + h/2 = 0,5 +0,4/2 = 0,7 hay q = 1 – 0,3 = 0,7
Từ các tần số tương 8ối của các alen ta dễ dàng xác 8ịnh 8ược thành phần di
truyền của quần thể 荏 thế hệ sau qua ngẫu phối: pA 0,3 qa 0,7 pA 0,3 0,09 AA 0,21 Aa qa 0,21 Aa 0,49 aa 0,7
Cấu trúc di truyền của quần thể mới 8ược tạo ra là: 0,09 AA : 0,42 Aa : 0,49 aa
Như vậy cấu trúc di truyền này 8úng theo công thức Hacdi-Vanbec: p2 : 2pq : q2
nghƿa là (0.3)2: 2(0.3 x 0.7): (0.7)2 2 2
2pq 2 → 0.09 x 0.049 = (0.42/2)2
Hoặc nó thòa mãn 8ẳng thức p q = ( ) 2
Tần số tương 8ối của các alen 荏 quần thể mới (0,09; 0,42; 0,49) xác 8ịnh 8ược là:
pA = 0,09 = 0,3 qn = 1- 0,3 = 0,7
Kết quả cho thấy tần số tương 8ối của các alen A và a 8ược duy trì ổn 8ịnh và nếu
sự ngẫu phối tiếp tục diễn ra thì cấu trúc di truyền của quần thể vẫn là 0,09AA : 0,42Aa
: 0,49aa. Từ 8ó ta thấy trạng thái cân bằng di truyền của quần thể 8ược duy trì ổn 8ịnh.
Tất nhiên 8iều 8ó 8ược nghiệm 8úng với nhiều 8iều kiện là cặp alen 8ược xét 8ến nằm
trên NST thư運ng, quần thể có số lượng lớn cá thể, không có quá trình chọn lọc và 8ột biến…
Như vậy, từ một quần thể có cấu trúc di truyền không cân bằng di truyền qua ngẫu
phối 8ã 8ạt 8ược trạng thái cân bằng di truyền ngay 荏 ngay thế hệ sau. Ěó là nội dung
của 8ịnh luật giao phối ổn 8ịnh do Prison nêu ra.
Sự thay 8ổi tương quan giữa các KG và các KH từ các quần hể ban 8ầu không 荏
trạng thái cân bằng di truyền sẽ bị thay 8ổi khi có sự ngẫu phối diễn ra và quần thể 8ạt 12 lOMoAR cPSD| 45148588
8ược trạng thái cân bằng. Từ 8ó cho thấy, trạng thái cân bằng di truyền 8ược tạo ra qua
ngẫu phối không phụ thuộc vào cấu trúc ban 8ầu của quần thể. Qua 8ó cần nhấn lại ngẫu
phối là một nhân tố quan trọng tạo ra và duy trì trạng thái cân bằng di truyền của quần thể.
4 . Sự cân bằng qu亥n th吋 với trường hợp các dãy alen
雲 mức 8ộ cá thể mỗi gen tồn tại thành từng cặp alen , nhưng trong quần thể mỗi gen có
thể có số alen khác nhau lớn hơn 2 vd như gen I quy 8ịnh nhóm máu 荏 ngư運i có 3 alen : IA , IB , IO.
Ěịnh luật Hacdi-Vanbec cǜng 8úng với trư運ng hợp dãy alen nếu như các 8iều kiện
nghiệm 8úng của nó 8ược 8ảm bảo.
Xét trư運ng hợp một gen có 3 alen kí hiệu : A1 , A2 , A3 với các tần số tương 8ối tương
ứng là :p, q , r , trong 8ó p + q + r =1. Cấu trúc di truyền của quần thể cân bằng là : p2
A1A1 + q2 A2A2 + r2 A3A3 + 2pq A1A2 + 2pr A1A3 + 2qr A2A3
荏 8ây tần số tương 8ối của các KG là số hạng triển khai bình phương của tổng tần số các alen : ( p + q + r )2
Nguyên tắc xác 8ịnh sự cân bằng trong quần thể ngay 荏 thế hệ thứ nhất do sự ngẫu phối
vối dãy alen cǜng như trư運ng hợp xét 1 gen với 2 alen khác nhau
VD : p(A1) = 0.3 ; q(A2 )= 0.5 ; r (A3 )= 0.2 qua sự kết hợp ngẫu nhiên của các giao tử
ta sẽ có 8ược tần số tương 8ối của các KG.
Quần thể có cấu trúc di truyền 荏 trạng thái cân bằng là :
0.09 A1A1 + 0.25 A2A2 + 0.44 A3A3 + 0.3 A1A2 + 0.12 A1A3 + 0.2 A2A3
VD : các alen qui 8ịnh nhóm máu ngư運i là IA , IB , IO ( gọi tắt là A, B ,O ) có các tần
số tương 8ối tương ứng là p , q , r . Cấu trúc chung của quần thể là
p2 AA + q2 BB + r2 OO + 2pq AB + 2pr AO + 2qr BO
Giả thuyết trong 1 quần thể ngư運i , tần số tương 8ối của các nhóm máu là A= 0.36 , B= 0.23, O= 0.33
Khi tính toán cấu trúc quần thể nói trên theo 8ịnh luật Hacdi- Vanbec , những số liệu về
KG , KH có thể dược viết dưới dạng sau : KH : A B AB O KG : AA + AO BB + BO AB OO
Tần số lí thuyết : p2 + 2pr q2 + 2qr 2pq r2
Tần số thực tế : 0.36 0.23 0.08 0.33
Tần số tương 8ối của các alen có thể xác 8ịnh như sau : r2 = 0.33 Ō r = 0.5744 13 lOMoAR cPSD| 45148588
q2 + 2pr + r2 = 0.23 + 0.33 = 0.56 Ō (q + r ) 2 = 0.56
Ōq + r = 0.7483 Ōq = 0.7483 – 0.5744 = 0.1739 Cǜng
tương tự : p2 + 2pr + r2 = 0.69 Ō (p + r ) = 0.69
Ō p + r = 0.8307 Ō p = 0.8307 – 0.5744 = 0.2563
5. Sự cân bằng c栄a qu亥n th吋 khi có sự khác nhau v隠 t亥n số gen ở các cơ th吋 8ực và cái
Ta xét trư運ng hợp một gen với 2 alen : A và a Giả thiêt rằng :
- Tần số tương 8ối của A của phần 8ực trong quần thể là p’ - Tần số tương 8ối của
a của phần 8ực trong quần thể là q’
- Tần số tương 8ối của A của phần cái trong quần thể là p’’
- Tần số tương 8ối của a của phần cái trong quần thể là q’’
Khi 8ó cấu trúc di truyền của quần thể 荏 thế hệ sau có thể nhận 8ược bằng cách nhân 2 nhị thức sau :
( p’A +q’a ) ( p’’A + q’’a ) = p’p’’AA+( p’q’’+p’’q’)Aa + q’q’’aa
Ěối với quần thể mới này có thể xác 8ịnh ngay 8ược giá trị mới của p và q ( kí hiệu là
pNvà qN )Cĕn cứ vào công thức xác 8ịnh tần số tương 8ối của gen dựa vào tần số tương
8ối của các thể 8ồng hợp trội , lặn và dị hợp ta có :
p N p ' p ' ' 1 ( p q' ' ' p ' 'q ' ) 2
Thay giá trị q= 1- p thì vế phải của dẳng thức có dạng : ' ' ' ' ' ' ' ' ' 1 p (1 p ) 1 p (1 p ) p N p p 2 2 p N p ' p ' ' 1
p ' 1 p ' p ' ' 1 p ' ' 1 p ' p ' ' 2 2 2 2 1 ' 1 p ' ' 1 ( p ' p ' ' ) p N p 2 2 2
Cǜng bằng cách tính tượng tự ta tính 8ược : ' ' ' q N 1 ( q q ) 2
Những công thức này bao hàm cả 8ịnh luât Hacdi- Vanbec xem như trư運ng hợp thuần
túy khi p’= p’’ và q’= q’’ . Từ kết quả trên quần thể có cấu trúc p2N AA 2 p N q N Aa q2N aa
Sự cân bằng của quần thể sẽ 8ạt 8ược ngay sau khi có sự ngẫu phối diễn ra cho thế hệ
sau ( 8ịnh luật giao phối ổn 8ịnh ) . 14 lOMoAR cPSD| 45148588
Ěể minh họa cho phần lý thuyết trên ta xét một ví dụ cụ thể sau 8ây : Giả
sử trong quần thể kh荏i 8ầu có :
P’= 0,8 ; q’= 0,2 ; p’’= 0,4 ; q’’= 0,6
Tương quan của tần số các kiểu gen 荏 thế hệ thứ nhất là :
( 0,8A+0,2a ) ( 0,4A+ 0,6a ) = 0,32AA+ 0,56Aa +0,12aa
Rõ ràng cấu trúc di truyền của quần thể mới này không 荏 trạng thái cân bằng , vì p 2pq 2 q2 2
. 雲 thế hệ thứ nhất này chủ yếu san bằng sự chênh lệch tần số của
2 mỗi alen 荏 phần cái và 8ực . Từ các công thức trên ta xác 8ịnh 8ược tần
số cân bằng của mỗi alen là : 1 1
p N (0 ,8 0 ,4 ) 0 ,6 ; q N (0 ,2 0 ,6 ) 0 ,4 2 2
Hoặc dựa vào cấu trúc di truyền của quần thể 荏 thế hệ thứ nhất theo phương pháp tính
tần số thông thư運ng ta cǜng xác 8ịnh tần số tương 8ối của mỗi alen : 1 0 ,56 p N d h 0 ,32 0 ,6 2 2 1 0 ,56 q N r h 0 ,12 0 ,4 2 2
Cấu trúc di truyền của quần thể 荏 thế hệ thứ hai là : 0,36AA +0,48Aa + 0,16aa Rõ ràng
cấu trúc di truyền của quần thể 8ã 8ạt 荏 trạng thái cân bằng , vì nó tuân theo công thức
Hacdi – Vanbec : p2 AA 2 pqAa q2 aa hay p q2 2 2pq 2 . 2 15