









































Preview text:
Tµi liÖu to¸n 12 n¨m häc 2018
1. HỆ TỌA ĐỘ TRONG KHÔNG GIAN
A.TÓM TẮT LÝ THUYẾT
1. Tọa độ của vectơ
a) Định nghĩa: u x; y; z u xi y j zk với i, j, k là các vectơ đơn vị, tương ứng trên các trục Ox, Oy, Oz .
b) Tính chất: Cho hai vectơ a a ;a ;a , b b ;b ;b và k là số thực tùy ý, ta có: 1 2 3 1 2 3 z
• a b a b ;a b ;a b . 1 1 2 2 3 3 k(0;0; )1
• a b a b ;a b ;a b . 1 1 2 2 3 3 j(0;1; )0
• k.a ka ;ka ;ka . 1 2 3 O y x a b (i1;0 ) ;0 1 1 • a b a b . 2 2 a b 3 3 a kb • a a a
a cùng phương b b 0 1 1 1 2 3 a kb
với b , b , b 0 . 2 2 b b b 1 2 3 1 2 3 a kb 3 3 • .
a b a .b a .b a .b . 1 1 2 2 3 3 • a b . a b 0
a .b a .b a .b 0 . 1 1 2 2 3 3 • 2 2 2 2
a a a a , suy ra 2 2 2 2
a a a a a . 1 2 3 1 2 3 • a b
a b a b a b cosa;b . 1 1 2 2 3 3 với a 0, b 0. 2 2 2 2 2 2 a . b
a a a . b b b 1 2 3 1 2 3
2. Tọa độ của điểm
a) Định nghĩa: M x; y; z OM x; y;z ( x : hoành độ, y tung độ, z cao độ).
Chú ý: Trong hệ tọa độ Oxyz , cho điểm M x; y;z ta có các khẳng định sau:
• M O M 0;0;0 .
• M Oxy z 0 , tức là M x; y;0.
• M Oyz x 0 , tức là M 0; y;z.
• M Oxz y 0 , tức là M x;0;z.
• M Ox y z 0 , tức là M x;0;0.
• M Oy x z 0 , tức là M 0; y;0.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 1 Tµi liÖu to¸n 12 n¨m häc 2018
• M Oz x y 0 , tức là M 0;0;z.
b) Tính chất: Cho bốn điểm không đồng phẳng Ax ; y ;z , B
x ; y ; z , C
x ; y ; z và Dx ; y ;z . D D D A A A B B B C C C
• AB x x ; y y ;z z . B A B A B A
• AB AB x x 2 y y 2 z z 2 . B A B A B A • Tọa độ trung điểm x x y y z z
I của đoạn thẳng AB là A B I ; A B ; A B . 2 2 2 • Tọa độ trọng tâm x x x y y y z z z
G của tam giác ABC là A B C G ; A B C ; A B C . 3 3 3 • Tọa độ trọng tâm x x x x y y y y z z z z
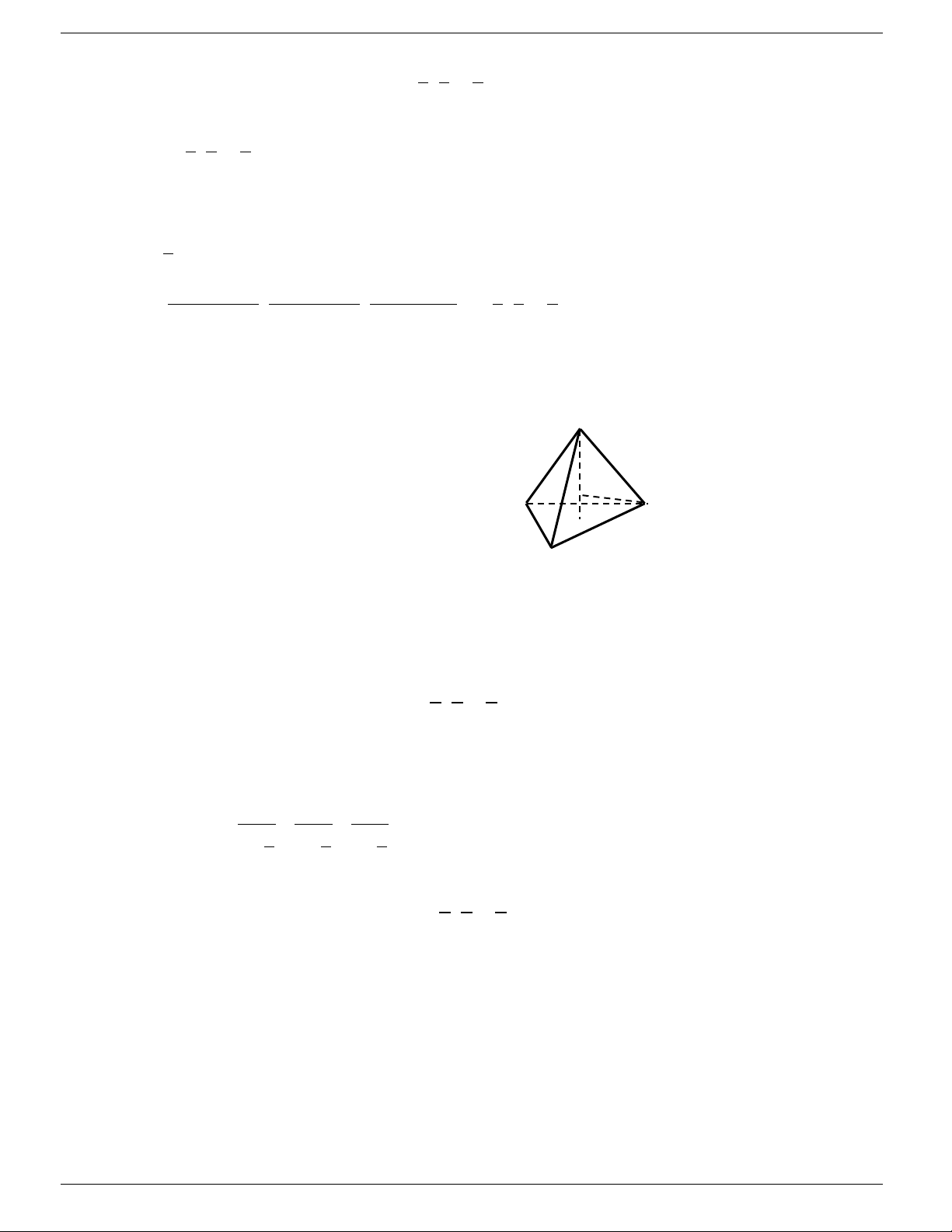
G của tứ diện ABCD là A B C D G ; A B C d ; A B C D . 4 4 4
3. Tích có hướng của hai vectơ
a) Định nghĩa: Trong không gian Oxyz , cho hai vectơ a a ;a ;a ,
b b ;b ;b . Tích có hướng của hai vectơ a và b là 1 2 3 1 2 3 một vectơ, kí hiệu là , a b và được xác định như sau:
a a a a a a 2 3 3 1 1 2 , a b ; ; .
a b a b ;a b a b ;a b a b 2 3 3 2 3 1 1 3 1 2 2 1
b b b b b b 2 3 3 1 1 2 b) Tính chất
• a cùng phương với b ,ab 0 . • , a b
vuông góc với cả hai vectơ a và b . • b,a a,b . • ,
a b a . b .sin a;b. c) Ứng dụng
• Xét sự đồng phẳng của ba vectơ: +) Ba véctơ a; ; b c đồng phẳng ,ab .c 0 .
+) Bốn điểm ,
A B, C, D tạo thành tứ diện AB,AC .AD 0 .
• Diện tích hình bình hành: S AB,AD . ABCD
• Tính diện tích tam giác: 1 S AB,AC . A BC 2
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 2 Tµi liÖu to¸n 12 n¨m häc 2018
• Tính thể tích hình hộp: V AB,AC .AD .
ABCD.A ' B 'C ' D '
• Tính thể tích tứ diện: 1 V AB, AC .AD . ABCD 6
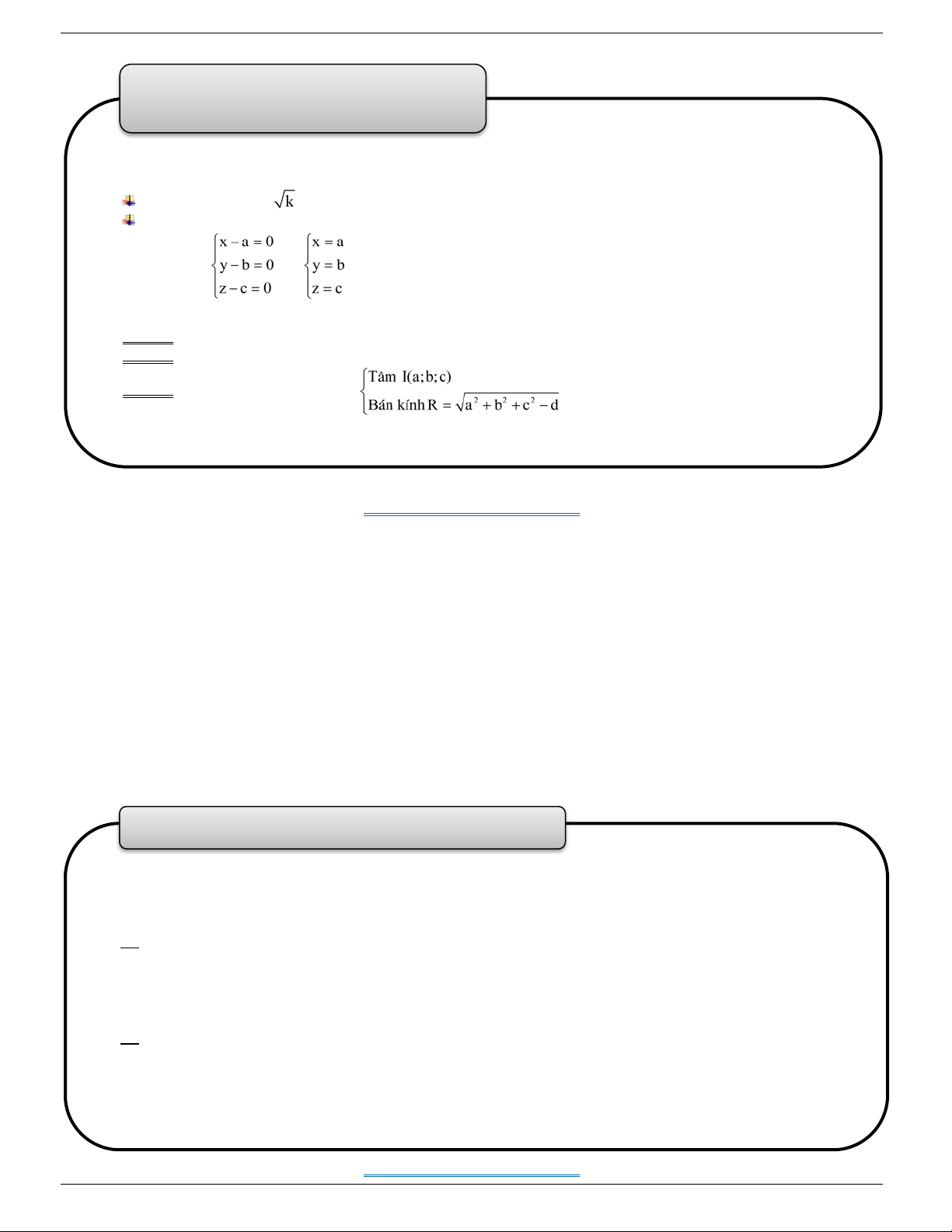
4. Phương trình mặt cầu
● Mặt cầu tâm I a;b;c, bán kính R có phương trìnhS x a2 y b2 z c2 2 : R . ● Xét phương trình 2 2 2
x y z 2ax 2by 2cz d 0 . * Ta có 2
x ax 2
y by 2 * 2 2
z 2cz d
2 2 2 2 2 2 . x a y b z c d
a b c tâm I ; a b ; c
Để phương trình * là phương trình mặt cầu 2 2 2
a b c d . Khi đó S có . 2 2 2
bán kính R a b c d tâm O 0;0;0
● Đặc biệt: S 2 2 2 2
: x y z R , suy ra S có . bán kính R
B.PHƯƠNG PHÁP GIẢI TOÁN
Vấn đề 1. CÁC ĐỊNH TỌA ĐỘ CỦA ĐIỂM, TỌA ĐỘ VECTƠ Phương pháp
Sử dụng các kết quả trong phần: Tọa độ của vectơ. Tọa độ của điểm.
Liên hệ giữa tọa độ vectơ và tọa độ hai điểm mút.
1. caùc ví duï minh hoïa
Ví dụ 1. Cho ba điểm A(1; 2; 3), B(3; 5; 4), C(3; 0; 5).
a. Chứng minh A, B, C là ba đỉnh của một tam giác.
b. Tính chu vi, diện tích của ∆ABC.
c. Tìm toạ độ điểm D để ABCD là hình bình hành và tính côsin góc giữa hai vectơ AC và BD .
d. Tính độ dài đường cao hA của ∆ABC kẻ từ A.
e. Tính các góc của ∆ABC.
f. Xác định toạ độ trực tâm H của ∆ABC.
g. Xác định toạ độ tâm đường tròn ngoại tiếp ∆ABC.
Ví dụ 2. Trong không gian Oxyz, cho bốn điểm A(5; 3; −1), B(2; 3; −4), C(1; 2; 0), D(3; 1; −2).
a. Tìm tọa độ các điểm A1, A2 theo thứ tự là các điểm đối xứng với điểm A qua mặt phẳng (Oxy) và trục Oy.
b. Chứng minh rằng A, B, C, D là bốn đỉnh của một hình tứ diện.
c. Tính thể tích khối tứ diện ABCD.
d. Chứng minh rằng hình chóp D.ABC là hình chóp đều.
e. Tìm tọa độ chân đường cao H của hình chóp D.ABC.
f. Chứng minh rằng tứ diện ABCD có các cạnh đối vuông góc với nhau.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 3 Tµi liÖu to¸n 12 n¨m häc 2018
g. Tìm tọa độ điểm I cách đều bốn điểm A, B, C, D.
Vấn đề 2. PHƯƠNG TRÌNH MẶT CẦU Phương pháp
Với phương trình cho dưới dạng chính tắc:(S): (x − a)2 + (y − b)2 + (z − c)2 = k, với k > 0 ta lần lượt có: Bá n kính bằng R = .
Tọa độ tâm I là nghiệm của hệ phương trình: ⇔ ⇒ I(a; b; c).
Với phương trình cho dưới dạng tổng quát ta thực hiện theo các bước: Bíc 1:
Chuyển phương trình ban đầu về dạng:(S): x2 + y2 + z2 − 2ax − 2by − 2cz + d = 0. (1) Bíc 2:
Để (1) là phương trình mặt cầu điều kiện là:a2 + b2 + c2 − d > 0. Bíc 3: Khi đó (S) có thuộ c tính: .
1. caùc ví duï minh hoïa
Ví dụ 1. Cho họ mặt cong (Sm) có phương trình:(Sm): (x − 2)2 + (y − 1)2 + (z − m)2 = m2 − 2m + 5.
a. Tìm điều kiện của m để (Sm) là một họ mặt cầu.
b. Tìm mặt cầu có bán kính nhỏ nhất trong họ (Sm).
c. Chứng tỏ rằng họ (Sm) luôn chứa một đường tròn cố định.
Ví dụ 2. Cho họ mặt cong (Sm) có phương trình:(Sm): x2 + y2 + z2 - 2m2x - 4my + 8m2 - 4 = 0.
a. Tìm điều kiện của m để (Sm) là một họ mặt cầu.
b. Chứng minh rằng tâm của họ (Sm) luôn nằm trên một Parabol (P) cố định trong mặt phẳng Oxy, khi m thay đổi.
c. Trong mặt phẳng Oxy, gọi F là tiêu điểm của (P). Giả sử đường thẳng (d) đi qua F tạo với chiều dương của trục
Ox một góc α và cắt (P) tại hai điểm M, N.
Tìm toạ độ trung điểm E của đoạn MN theo α.
Từ đó suy ra quỹ tích E khi α thay đổi.
Vấn đề 3. VIẾT PHƯƠNG TRÌNH MẶT CẦU
Phương phá p
Gọi (S) là mặt cầu thoả mãn điều kiện đầu bài. Chúng ta lựa chọn phương trình dạng tổng quát hoặc dạng chính tắc. Khi đó:
1. Muố n có phương trình dạng chính tắc, ta lập hệ 4 phương trình với bốn ẩn a, b, c, R, điều kiện R > 0. Tuy nhiên,
trong trường hợp này chúng ta thường chia nó thành hai phần, bao gồm:
Xác định bán kính R của mặt cầu.
Xác tâm I(a; b; c) của mặt cầu.
Từ đó, chúng ta nhận được phương trình chính tắc của mặt cầu.
2. Muố n có phương trình dạng tổng quát, ta lập hệ 4 phương trình với bốn ẩn a, b, c, d, điều kiện a2 + b2 + c2 − d > 0.
Chú ý: 1. Cần phải cân nhắc giả thiết của bài toán thật kỹ càng để lựa chọn dạng phương trình thích hợp.
2. Trong nhiều trường hợp đặc thù chúng ta còn sử dụng phương pháp quỹ tích để xác định phương trình mặt cầu.
1. caùc ví duï minh hoïa
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 4 Tµi liÖu to¸n 12 n¨m häc 2018
Ví dụ 1. Viết phương trình mặt cầu trong các trường hợp sau:
a. Đường kính AB với A(3; −4; 5), B(−5; 2; 1).
b. Tâm I(3; −2; 1) và đi qua điểm C(−2; 3; 1).
Ví dụ 2. Viết phương trình mặt cầu đi qua hai điểm A(1; 2; 2), B(0; 1; 0) và tâm I thuộc trục Oz.
Ví dụ 3. Viết phương trình mặt cầu đi qua ba điểm A(2; 1; 1), B(1; 1; 0), C(0; 2; 4) và có tâm nằm trên mặt phẳng (Oyz).
Ví dụ 4. Lập phương trình mặt cầu đi qua ba điểm A(2; 1; 1), B(1; 1; 0), C(0; 2; 4) và có bán kính bằng 5 .
Ví dụ 5. Cho bốn điểm A(1; 1; 1), B(1; 2; 1), C(1; 1; 2) và D(2; 2; 1).
a. Chứng tỏ rằng A, B, C, D không đồng phẳng. Tính thể tích tứ diện ABCD.
b. Lập phương trình mặt cầu ngoại tiếp tứ diện ABCD.
Ví dụ 6. Viết phương trình mặt cầu:
a. Có tâm I(2; 1; −6) và tiếp xúc với trục Ox.
b. Có tâm I(2; −1; 4) và tiếp xúc với mặt phẳng (Oxy).
c. Có tâm O(0; 0; 0) tiếp xúc với mặt cầu (T) có tâm I(3; –2; 4), bán kính bằng 1.
Ví dụ 7. Lập phương trình mặt cầu:
a. Có tâm nằm trên tia Ox, bán kính bằng 5 và tiếp xúc với mặt phẳng (Oyz).
b. Có bán kính bằng 2 và tiếp xúc với (Oxy) tại điểm M(3; 1; 0).
1i. Baøi taäp töï luaän töï luyeän Bài 1
1. Trong không gian với hệ tọa độ Oxyz cho ba véc tơ a 2i 3j 5k,
b 3j 4k, c i 2j
a) Xác định tọa độ các véc tơ a, ,
b c , x 3a 2b và tính x
b) Tìm giá trị của x để véc tơ y 2x 1; x ;3x
2 vuông góc với véc tơ 2b c
c) Chứng minh rằng các véc tơ a, ,
b c không đồng phẳng và phân tích véc tơ u 3;7;14 qua ba véc tơ a, , b c .
2. Trong không gian với hệ trục tọa độ Oxyz , cho các véc tơ a 2i 3j k, b i 2k,
c 2j 3k
a) Xác định tọa độ các véc tơ a, , b c
b) Tìm tọa độ véc tơ u 2a 3b 4c và tính u
c) Tìm x để véc tơ v (3x 1;x 2;3 x) vuông góc với b
d) Biểu diễn véc tơ x (3;1;7) qua ba véc tơ a, , b c . Bài 2
1. Cho hai véc tơ a,b có 0
a 2 3, b 3,(a,b ) 30 . Tính
a) Độ dài các véc tơ a b,5a 2b,3a 2b,
b) Độ dài véc tơ a,b , a, 3b , 5a, 2b .
2. Tìm điều kiện của tham số m sao cho a) Ba véc tơ
u(2;1; m),v(m 1; 2; 0),w(1; 1;2) đồng phẳng. b) (
A 1; 1;m),B(m; 3;2m 1),C(4; 3;1),D(m 3; m;2 m) cùng thuộc một mặt phẳng.
c) Góc giữa hai véc tơ a(2;m;2m 1),b(m;2;1) là 0 60 .
Bài 3 Cho tam giác ABC có B(1;1;1),C(2;3;5). Điểm A có tung độ là 1 , hình chiếu của điểm A trên BC là 3 7 K 1; ;3
và diện tích tam giác ABC là 49 S . 3 3
1. Tìm tọa độ đỉnh A biết A có hoành độ dương.
2. Tìm tọa độ chân đường vuông góc hạ từ B đến AC.
3. Tìm tọa độ tâm I của đường tròn ngoại tiếp và tọa độ trực tâm H của tam giác ABC.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 5 Tµi liÖu to¸n 12 n¨m häc 2018
4. Chứng minh HG 2GI với G là trọng tâm tam giác ABC.
Bài 4 Cho tứ diện ABCD có các cặp cạnh đối bằng nhau. Tọa độ các điểm (
A 2; 4;1),B(0; 4; 4),C(0; 0;1) và D có hoành độ dương.
1. Xác định tọa độ điểm D.
2. Gọi G là trọng tâm của tứ diện ABCD. Chứng minh rằng G cách đều các đỉnh của tứ diện.
3. Gọi M,N lần lượt là trung điểm của A ,
B CD. Chứng minh rằng MN là đường vuông góc chung của hai đường
thẳng AB và CD.
4. Tính độ dài các đường trọng tuyến của tứ diện ABCD. Tính tổng các góc phẳng ở mỗi đỉnh của tứ diện ABCD.
Bài 5 Trong không gian Oxyz cho bốn điểm ( A 0;2; 0), (
B 1; 0;3), C(0;2;0), D(3;2;1) .
1. Chứng minh rằng bốn điểm , A ,
B C,D không đồng phẳng;
2. Tính diện tích tam giác BCD và đường cao BH của tam giác BCD ;
3. Tính thể tích tứ diện ABCD và đường cao của tứ diện hạ từ A ;
4. Tìm tọa độ E sao cho ABCE là hình bình hành;
5. Tính cosin của góc giữa hai đường thẳng AC và BD ;
6. Tìm điểm M thuộc Oy sao cho tam giác BMC cân tại ;
7. Tìm tọa độ trọng tâm G của tứ diện ABCD và chứng minh , A G, ’
A thẳng hàng với A' là trọng tâm tam giác BCD .
Bài 6 Cho tam giác ABC có (
A 2; 3;1),B(1;2; 0),C(1;1; 2).
1. Tìm tọa độ chân đường vuông góc kẻ từ A xuống BC .
2. Tìm tọa độ H là trực tâm của tam giác ABC .
3. Tìm tọa độ I là tâm đường tròn ngoại tiếp của tam giác ABC .
4. Gọi G là trọng tâm của tam giác ABC . Chứng minh rằng các điểm G,H,I nằm trên một đường thẳng. Bài 7
Trong không gian với hệ tọa độ Đề Các vuông góc Oxyz cho tam giác đều ABC có (
A 5; 3;1),B(2; 3; 4) và điểm C
nằm trong mặt phẳng (Oxy) có tung độ nhỏ hơn 3 .
a) Tìm tọa độ điểm D biết ABCD là tứ diện đều.
b) Tìm tọa độ điểm S biết S , A S ,
B SC đôi một vuông góc. Bài 8
Trong không gian với hệ tọa độ Oxyz cho điểm A3;2;4
a) Tìm tọa độ các hình chiếu của A lên các trục tọa độ và các mặt phẳng tọa độ
b) Tìm M Ox,N Oy sao cho tam giác AMN vuông cân tại A
c) Tìm tọa độ điểm E thuộc mặt phẳng (Oyz) sao cho tam giác AEB cân tại E và có diện tích bằng 3 29 với B 1;4;4 . Bài 9
Trong không gian với hệ trục Oxyz cho ( A 4; 0; 0),
B(x ;y ; 0) với x ,y 0 thỏa mãn AB 2 10 và 0 AOB 45 . 0 0 0 0
a) Tìm C trên tia Oz sao cho thể tích tứ diện OABC bằng 8 .
b) Gọi G là trọng tâm A
BO và M trên cạnh AC sao cho AM x . Tìm x để OM GM .
1ii. Baøi taäp traéc nghieäm töï luyeän
Vấn đề 1. TỌA ĐỘ CỦA VECTƠ
B. a 2;3; 5 , b 3;4;0, c 0;2;0 .
Câu 1. Trong không gian với hệ tọa độ Oxyz , cho ba vectơ
C. a 2;3; 5 , b 0;3;4, c 1;2;0.
a 2i 3 j 5k , b 3 j 4k , c i 2 j .
D. a 2;3; 5 , b 1;3;4, c 1;2; 1 .
Khẳng định nào sau đây đúng?
Câu 2. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ
A. a 2;3; 5 , b 3;4;0, c 1 ;2;0. a 0;1;
3 và b 2;3;
1 . Nếu 2x 3a 4b thì tọa
độ của vectơ x là:
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 6 Tµi liÖu to¸n 12 n¨m häc 2018 A. 9 5 x
A. x 2a 3 .
B. x 2a 3 . 4; ; b c b c . B. 9 5 x 4; ; . 2 2 2 2
C. x 2a 3b c .
D. x 2a 3b c . C. 9 5 x 4; ; . D. 9 5 x 4; ; . 2 2 2 2
Câu 8. Trong không gian với hệ tọa độ Oxyz , cho ba vectơ
Câu 3. Trong không gian với hệ tọa độ
a 1;0;2, b 2 ;1; 3 , c 4;3 ;5 . Tìm hai số Oxyz , cho ba vectơ thực ta được: m , n sao cho . m a . n b c a 2;1;
3 , b 1;3;2 và c 3;2;4 . A. m 2; n 3.
B. m 2;
n 3. C. m 2; n 3.
x.a 5
Câu 9. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ
Gọi x là vectơ thỏa mãn: x.b 11 . Tọa độ của vectơ
a 2;m 1;
1 và b 1;3;2. Với những giá trị x.c 20
nguyên nào của m thì b2ab 4 ? x là: A.2;3;
1 . B. 2;3;2 . C. 3;2;2 . D. 1;3;2 . A. 4 . B. 4 . C. 2 . D. 2 .
Câu 10. Trong không gian với hệ tọa độ Oxyz , cho hai
Câu 4. Trong không gian với hệ tọa độ Oxyz , cho ba vectơ
vectơ u m;2;m
1 và v 0;m 2; 1 .
a 1;1;0 , b 1;1;0 và c 1;1; 1 .
Tất cả giá trị của m có thể có để hai vectơ u và v cùng
Trong các khẳng định sau, khẳng định nào sai? phương là:
A. m 1. B. m 0. C. m 1. D. m 2.
A. a 2. B. c 3. C. a . b
D. c . b
Câu 11. Trong không gian với hệ tọa độ Oxyz , để hai vectơ
Câu 5. Trong không gian với hệ tọa độ Oxyz , cho ba vectơ
a m;2;
3 và b 1;n;2 cùng phương, ta phải có:
a 1;1;0, b
1;1;0 và c 1;1; 1 . 1 3 3 2 m m m m A. 2 2 2 3 . B. . C. . D. .
Trong các khẳng định sau, khẳng định nào đúng? 4 4 2 4 n n n n 3 3 3 3 A. . a c 1 . B. ,
a b cùng phương.
Câu 12. Trong không gian với hệ tọa độ Oxyz , cho hai
vectơ a 2;1;2 và b 0; 2; 2 . Tất cả giá trị C. b c 2 cos , .
D. a b c 0 . 6 của
m để hai vectơ u 2a 3mb và v ma b vuông góc là:
Câu 6. Trong không gian với hệ tọa độ Oxyz , cho các vectơ p 3,2, 1 , q 1,1,2, r 2,1, 3 và A. 26 2 . B. 26 2 . 6 6 c 11,6,
5 . Khẳng định nào sau đây là đúng ? C. 26 2 . D. 2 .
A. c 3p 2q r .
B. c 2p 3q r . 6 6
Câu 13. Trong không gian với hệ tọa độ Oxyz , cho vectơ
C. c 2p 3q r .
D. c 3p 2q 2r .
u 1;1;2 và v 1;0;m . Tìm tất cả các giá trị của
Câu 7. Trong không gian với hệ tọa độ Oxyz , cho các vectơ
m để góc giữa hai vectơ u và v có số đo bằng 0 45 : a 2;3; 1 , b 1
;5;2, c 4;1;
3 và x 3,22, 5
Một học sinh giải như sau:
. Đẳng thức nào đúng trong các đẳng thức sau?
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 7 Tµi liÖu to¸n 12 n¨m häc 2018 Bước 1: u v 1 2m cos , . 2 6. m 1
Vấn đề 2. TỌA ĐỘ CỦA ĐIỂM
Bước 2: Góc giữa hai vectơ u và v có số đo bằng 0 45 nên suy ra
Câu 19. Trong không gian với hệ tọa độ Oxyz , cho bốn điểm A(2;0;0), B ( 0;2;0), C (
0;0;2) và D (2;2;2) . Gọi M , N 12m 1 2
12m 3. m 1 . *
lần lượt là trung điểm của AB và CD . Tọa độ trung 2 6. m 1 2
điểm I của MN là: Bước 3: Phương trình 1 1 m 2 6 A. I
; ;1 .B. I (1;1;0) . C. I (1;−1;2) . D. I (1;1; ) 1 .
* 1 2m2 2 2 m 2 1 m 4m 2 0 . 2 2 m 2 6
Câu 20. Trong không gian với hệ tọa độ Oxyz , cho hai
Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào? vectơ a = (1;1; 2 − ) , b = ( 3; − 0;− ) 1 và điểm A(0;2; ) 1 . Tọa A. Đúng B. Sai ở bước 1
độ điểm M thỏa mãn AM = 2a − b là: C. Sai ở bước 2
D. Sai ở bước 3
A. M (−5;1;2) .B. M (3;−2; )
1 .C. M (1;4;−2) .D. M (5;4;−2) .
Câu 14. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a Câu 21. Trong không gian với hệ tọa độ Oxyz , hình chiếu
và b thỏa mãn a 2 3, 3
b và a b 0 , 30 . Độ dài
của điểm M 1;3;
5 trên mặt phẳng Oxy có tọa độ
của vectơ 3a 2b bằng: là: A. 54. B. 54. C. 9. D. 6. A.1;3; 5 .
B.1;3;0. C.1;3;
1 . D.1;3;2.
Câu 15. Trong không gian với hệ tọa độ Oxyz , cho vectơ
Câu 22. Trong không gian với hệ tọa độ Oxyz , cho điểm
u 2;1;2 và vectơ đơn vị v thỏa mãn u v 4. M 3;2;
1 . Tọa độ điểm M ' đối xứng với M qua
Độ dài của vectơ u v bằng:
mặt phẳng Oxy là: A. 4 . B. 3 . C. 2 . D. 1.
A. M '3;2;
1 . B. M '3;2;
1 . C. M '3;2
1 . D. M '3;2; 1 .
Câu 16. Trong không gian với hệ tọa độ Oxyz , cho hai
vectơ a và b thỏa mãn a 2, 5
b và a b 0
, 30 . Câu 23. Trong không gian với hệ tọa độ Oxyz , cho điểm
M 2016;1;2017 . Hình chiếu vuông góc của điểm Độ dài của vectơ , a b bằng:
M trên trục Oz có tọa độ: A. 10 . B. 5 . C. 8 . D. 5 3 .
A.0;0;0 B.2016;0;0 C.0;1;0 D.0;02017
Câu 17. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a
Câu 24. Trong không gian với hệ tọa độ Oxyz , cho điểm
và b thỏa mãn a 2 3, 3
b và a b 0 , 30 . Độ dài A3;2;
1 . Tọa độ điểm A' đối xứng với A qua trục của vectơ 5 , a 2b bằng: Oy là: A. A. B. C. D. 3 3. B. A'3;2; 1 A'3;2 1 A'3;2; 1 A'3;2; 1 9. C. 30 3. D. 90.
Câu 18. Trong không gian với hệ tọa độ Oxyz , cho hai Câu 25. Trong không gian với hệ tọa độ Oxyz , cho điểm vectơ A1;2;
3 . Khoảng cách từ A đến trục Oy bằng:
u và v thỏa mãn u 2 , v 1 và u v 0 , 60 .
Góc giữa hai vectơ v và u v bằng: A. 10. B. 10. C. 2. D. 3. A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 .
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 8 Tµi liÖu to¸n 12 n¨m häc 2018
Câu 26. Trong không gian với hệ tọa độ Oxyz , cho điểm
C. D10;17;7
D. D10;17;7
M 3;1;2. Trong các phát biểu sau, phát biểu nào Câu 30. Trong không gian với hệ tọa độ Oxyz , cho sáu sai? điểm A1;2; 3 , B2;1; 1 , C 3;3;
3 , A', B ', C ' thỏa
A. Tọa độ hình chiếu của
M trên mặt phẳng xOy là
mãn A' A B ' B C 'C 0 . Nếu G ' là trọng tâm tam M '3;1;0 .
giác A' B 'C ' thì G ' có tọa độ là:
B. Tọa độ hình chiếu của M trên trục Oz là A. 4 1 2; ; B. 4 1 2; ; C. 4 1 2; ; D. 4 1 2; ; 3 3 3 3 3 3 3 3 M '0;0;2 .
Câu 31. Trong không gian với hệ tọa độ Oxyz , cho bốn
C. Tọa độ đối xứng của M qua gốc tọa độ O là
điểm M 2;3;
5 , N 4;7;9 , P 3;2; 1 và Q 1;8;12 M '3;1;2 .
. Bộ ba điểm nào sau đây là thẳng hàng?
D. Khoảng cách từ M đến gốc tọa độ O bằng 3 14. A. M, N,
P B. M , N, Q C. M , P, Q D. N, P, Q
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho điểm Câu 32. Trong không gian với hệ tọa độ Oxyz , cho ba
M 2;5;4. Trong các phát biểu sau, phát biểu nào điểm A2;1; 3 , B10;5
;3 và M 2m 1;2;n 2 . sai? Để ,
A B, M thẳng hàng thì giá trị của , m n là:
A. Tọa độ điểm M ' đối xứng với M qua mặt phẳng A. 3
m 1;n B. 3
m , n 1
yOz là M 2;5;4. 2 2
B. Tọa độ điểm M ' đối xứng với M qua trục Oy là C. 3
m 1, n D. 2 3
m ,n 2 3 2
M 2;5;4 .
Câu 33. Trong không gian với hệ tọa độ Oxyz , cho hai
C. Khoảng cách từ M đến mặt phẳng tọa xOz bằng điểm A1;3;
5 và B3;2;4. Điểm M trên trục Ox 5 . cách đều hai điểm ,
A B có tọa độ là:
D. Khoảng cách từ M đến trục Oz bằng 29. A. 3 M ;0;0 . B. 3 M
;0;0 . C. M 3;0;0 . D. M 3;0;0 . 2 2
Câu 28. Trong không gian với hệ tọa độ Oxyz , cho điểm M 1;2;
3 . Trong các phát biểu sau, phát biểu nào sai? Câu 34. Trong không gian với hệ tọa độ Oxyz , cho ba điểm A1;1;
1 , B1;1;0 , C 3;1; 1 . Điểm M trên
A. Tọa độ đối xứng của O qua điểm M là O '2;4;6.
mặt phẳng Oxz cách đều ba điểm ,
A B, C có tọa độ
B. Tọa độ điểm M ' đối xứng với M qua trục Ox là là: M '1;2; 3 . A. 5 7 0; ; . B. 7 5 ;0; . C. 5 7 ;0; . D. 6 6 ;0; . C. Khoảng cách từ
M đến mặt phẳng tọa yOz bằng 6 6 6 6 6 6 5 7 1.
Câu 35. Trong không gian với hệ tọa độ Oxyz , cho tam
D. Khoảng cách từ M đến trục Oy bằng 10.
giác ABC biết 1;0;2 , B2;1;
1 , C 1;2;2 . Tìm
Câu 29. Trong không gian với hệ tọa độ Oxyz , cho ba điểm
tọa độ trọng tâm G của tam giác ABC.
A3;4;2 , B5;6;2 , C 4;7; 1 . Tìm tọa độ điểm
A.G4;1; 1 B. 4 1 1 G ; ;
D thỏa mãn AD 2AB 3AC . 3 3 3
A. D10;17;7
B. D10;17;7 C. 1 1 G 2; ; D. 4 1 1 G ; ; 2 2 3 3 3
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 9 Tµi liÖu to¸n 12 n¨m häc 2018
Câu 36. Trong không gian với hệ tọa độ Oxyz , cho tam
A.C 4;5;2 . B.C 4;5;2 . C.C 4;5;2. D.C 4;5;2.
giác ABC có A(0;0; ) 1 , B ( 1; − 2 − ;0) , C (2;1;− )
1 . Khi đó Câu 43. Trong không gian với hệ tọa độ Oxyz , cho tam giác
tọa độ chân đường cao H hạ từ A xuống BC là:
ABC có A2;1;6 , B3;1;4 , C 5;1;0 . Trong
các khẳng định sau, khẳng định nào đúng? A. 5 14 8 4 H ;− ;− B. H ;1;1 19 19 19 9 tam giác ABC là C. 8 3 H 1;1;− D. H 1; ;1 A. Tam giác cân. B. Tam giác đều. 9 2 C. Tam giác vuông. D. Cả A và C.
Câu 37. Trong không gian với hệ tọa độ Oxyz , cho tam giác
ABC có A1;2; 1 , B2;1; 3 , C 4;7;
5 . Tọa độ Câu 44. Trong không gian với hệ tọa độ Oxyz , cho ba điểm
chân đường phân giác trong góc B của tam giác ABC
A1;2;0, B 1;0;
1 và C 0;1;2. Mệnh đề nào sau là: đây là đúng? A. Ba điểm ,
A B, C thẳng hàng. A. 2 11 ; ;1 B. 2 11 1 ; ; C. 11
;2;1 D.2;11; 1 3 3 3 3 3 3 B. Ba điểm ,
A B, C tạo thành tam giác cân.
Câu 38. Trong không gian với hệ tọa độ Oxyz , cho C. Ba điểm ,
A B, C tạo thành tam giác có một góc A2;1; 3 , B4;0; 1 , C 10;5
;3 . Độ dài đường phân bằng 0 60 .
giác trong góc B của tam giác ABC bằng: D. Ba điểm ,
A B, C tạo thành tam giác vuông. A. 2 3 B. 2 5 C. 2 D. 2 5 3
Câu 45. Trong không gian với hệ tọa độ Oxyz , cho các điểm A2;0;
1 , B0;2;0 và C 1;0;2. Mệnh đề nào sau đây
Câu 39. Trong không gian với hệ tọa độ Oxyz , cho tam giác đúng?
ABC có A0;4;0 , B5;6;0 , C 3;2;0. Tọa độ chân A. Ba điểm ,
A B, C thẳng hàng.
đường phân giác ngoài góc A của tam giác ABC là: A. B. Ba điểm ,
A B, C tạo thành tam giác cân ở A .
15;14;0 B. 15;4;0C. 15;4;0D. 15;14;0 C. Ba điểm ,
A B, C tạo thành tam giác cân ở B .
Câu 40. Trong không gian với hệ tọa độ Oxyz , cho ba
điểm M 2;3; 1 , N 1;1;
1 , P 1;m 1;2 . Với những D. Ba điểm ,
A B, C tạo thành tam giác vuông.
giá trị nào của m thì tam giác MNP vuông tại N ?
Câu 46. Trong không gian với hệ tọa độ Oxyz , cho các A. m 3
B. m 2
C. m 1
D. m 0 điểm ,
A B, C có tọa độ thỏa mãn OA i j k ,
Câu 41. Trong không gian với hệ tọa độ Oxyz , cho tam
OB 5i j k , BC 2i 8 j 3k . Tọa độ điểm D để giác ABC có đỉnh tứ giác
C 2;2;2 và trọng tâm G1;1;2.
ABCD là hình bình hành là:
Tìm tọa độ các đỉnh ,
A B của tam giác ABC , biết A A. D3;1;
5 B. D1;2;
3 C. D2;8;6
D. D3;9;4
thuộc mặt phẳng Oxy và điểm B thuộc trục cao.
Câu 47. Trong không gian với hệ tọa độ Oxyz , cho ba điểm
A. A1;1;0, B0;0;4 B. A1;1;0, B0;0;4
M 2;0;0 , N 0;3;0, P 0;0;4. Nếu MNPQ là hình
bình thành thì tọa độ của điểm Q là:
C. A1;0;
1 , B0;0;4 D. A4;4;0, B0;0; 1
A.2;3;4 B.3;4;2 C.2;3;4 D.2;3;4
Câu 42. Trong không gian với hệ tọa độ Oxyz , cho tam giác
ABC có A4;1;2 , B3;5;10 . Trung điểm cạnh Câu 48. Trong không gian với hệ tọa độ Oxyz , cho ba điểm
AC thuộc trục tung, trung điểm cạnh BC thuộc mặt A1;2;
1 , B3;1;2 , C 6;0;
1 . Trong các điểm sau đây,
phẳng Oxz . Tọa độ đỉnh C là:
điểm nào là đỉnh thứ tư của hình bình hành có ba đỉnh là ,
A B,C . M 4;3;2 ; N 2;1;0 ; P 2;1; 1
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 10 Tµi liÖu to¸n 12 n¨m häc 2018
A. Chỉ có điểm M
B. Chỉ có điểm N
C. Ba vectơ đôi một vuông góc với nhau
C. Chỉ có điểm P
D. Cả hai điểm M và N
D. Ba vectơ có độ lớn bằng nhau
Câu 49. Trong không gian với hệ tọa độ Oxyz , cho hình bình Câu 55. Trong không gian với hệ tọa độ Oxyz , trong các
hành OABD , có OA 1;1;0 và OB 1;1;0 với O là bộ ba vectơ ,
a b, c sau đây, bộ nào thỏa mãn tính chất
gốc tọa độ. Khi đó tọa độ của D là: , a b .c 0
(hay còn gọi là ba vectơ ,
a b, c đồng phẳng).
A. 0;1;0. B. 2;0;0. C. 1;0;
1 . D. 1;1;0. A. a 1;1;
1 , b 0;1;2, c 4;2; 3 .
Câu 50. Trong không gian với hệ tọa độ Oxyz , cho bốn điểm
A1;0;2, B2;1;
1 , C 1;2;2 và D4;57. Trọng
B. a 4;3;4,b 2;1;2, c 1;2; 1 .
tâm G của tứ diện ABCD có tọa độ là: C.
a 2;1;0, b 1;1;2, c 2;2; 1 .
A.2;1;2 B.8;2;8 C.8;1;2 D.2;1;2 D.
a 1;7;9, b 3;6;
1 , c 2;1;7.
Câu 51. Trong không gian với hệ tọa độ Oxyz , cho hình hộp Câu 56. Trong không gian với hệ tọa độ Oxyz , cho bốn
ABCD.A' B 'C ' D ' . Biết A2;4;0 , B4;0;0,
vectơ a 2,3, 1 ,
b 5,7,0 , c 3,2,4 và
C 1;4;7 và D '6;8;10. Tọa độ điểm B ' là:
d 4,12, 3.
A.10;8;6 B.6;12;0
C.13;0;17 D.8;4;10
Mệnh đề nào sau đây sai?
Vấn đề 3. TÍCH CÓ HƯỚNG CỦA HAI VECTƠ
A. d a b c
Câu 52. Trong không gian với hệ tọa độ Oxyz , cho hai
B. a , b , c là ba vectơ không đồng phẳng.
vectơ a và b khác 0 . Kết luận nào sau đây sai? C. D.
a b d c
2a 3b d 2c A. ,
a b a b sin
,ab B. ,a3b 3 a;b
Câu 57. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ
C. 2a,b 2 a,b D. 2 ,2 a b 2 , a b
a và b khác 0 . Gọi c ,ab
. Mệnh đề sau đây là
Câu 53. Trong không gian với hệ tọa độ Oxyz , cho hai đúng?
vectơ u và v khác 0 . Phát biểu nào sau đây là sai?
A. c cùng phương với a . A. , u v
có độ dài là u v cos , u v
B. c cùng phương với b . B. , u v 0 khi hai vecto ,
u v cùng phương
C. c vuông góc với hai vectơ a và b . C.
D. Cả A và B đều đúng. , u v
vuông góc với hai vecto , u v
Câu 58. Trong không gian với hệ tọa độ Oxyz , cho ba D. , u v là một vectơ
vectơ a 1;2;
1 , b 3;1;0 và c 1;5;2 .
Câu 54. Trong không gian với hệ tọa độ Oxyz , cho ba
Khẳng định nào sau đây là đúng? vectơ ,
a b và c khác 0 . Điều kiện cần và đủ để ba
A. a cùng phương với b . vectơ ,
a b, c đồng phẳng là:
B. a , b , c không đồng phẳng. A. . a . b c 0 B. , a b.c 0
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 11 Tµi liÖu to¸n 12 n¨m häc 2018
C. a , b , c đồng phẳng. D. a vuông góc b . A1;2; 1 , B5;0;
3 và C 7,2,2 . Tọa độ giao điểm M
của trục Ox với mặt phẳng đi qua điểm ,
A B, C là:
Câu 59. Trong không gian với hệ tọa độ Oxyz , cho ba vectơ
a 3;1;2 , b 1;2;m và c 5;1;7 . Giá trị
A. M 1;0;0 . B. M 1;0;0 .C. M 2;0;0. D. M 2;0;0. của m để c a,b là:
Câu 66. Trong không gian với hệ tọa độ Oxyz , cho bốn A. 1 B. 0 C. 1 D. 2 . điểm
Câu 60. Trong không gian với hệ tọa độ
A0;2; , B3;1; , C 4;3;0 và D1;2;m . Oxyz , cho ba 1 1 vectơ u = (2; 1; − )
1 , v = (m;3;− ) 1 và w = (1;2; )
1 . Để ba Tìm m để bốn điểm ,
A B, C, D đồng phẳng. Một học
vectơ đã cho đồng phẳng khi m nhận giá trị nào sau sinh giải như sau: đây?
Bước1: AB 3;1;
1 , AC 4;1;2, AD 1;0;m 2 A. −8 B. 4 C. − 7 D. − 8 . 3 3 1 1 1 3 3 1
Câu 61. Trong không gian với hệ tọa độ Oxyz , cho ba
Bước2: AB, AC ; ; 3;10; 1 1 2 2 4 4 1 vectơ
a 1;m;2, b m 1;2;
1 và c 0;m 2;2 . .
Để ba vectơ đã cho đồng phẳng khi m nhận giá trị nào
sau đây?
Suy ra AB, AC .AD 3 m 2 m 5. A. 2 Bước3: ,
A B, C, D đồngphẳng m B. 5 m
C. m 2 . D. m 0 . 5 2
AB, AC
.AD 0 m 5 0 m 5 .
Câu 62. Trong không gian với hệ tọa độ Oxyz , cho ba
Đáp án: m 5 .
vectơ a 2,0, 3 , b 0,4, 1 và c 2 m 2,m , 5 .
Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào?
Để ba vectơ đã cho đồng phẳng khi m nhận giá trị nào sau đây? A. Đúng B. Sai ở Bước 1.
A. m 2 hoặc m 4 B. m 2 hoặc m 4 C. Sai ở Bước 2. D. Sai ở Bước 3.
C. m 1 hoặc m 6
D. m 2 hoặc m 5
Câu 67. Trong không gian với hệ tọa độ Oxyz , cho tam
giác ABC . Tập hợp các điểm M thỏa mãn
Câu 63. Trong không gian với hệ tọa độ Oxyz , cho bốn
MA MB ,AC 0 là: điểm
A1;2;0, B1;0;
1 , C 0;1;2 và D0;m; p .
Hệ thức giữa m và p để bốn điểm ,
A B, C, D đồng
A. Đường thẳng qua C và song song với cạnh AB . phẳng là:
B. Đường thẳng qua trung điểm I của AB và song
A. 2m p 0 B. m p 1 C. m 2p 3 D. 2m 3p 0 song với cạnh AC .
Câu 64. Trong không gian với hệ tọa độ Oxyz , cho các điểm
C. Đường thẳng qua trung điểm I của AB và vuông góc với cạnh AC .
A0;0;4 , B2;1;0, C 1;4;0 và Da;b;0 . Điều kiện cần và đủ của ,
a b để hai đường thẳng AD và BC
D. Đường thẳng qua B và song song với cạnh AC .
cùng thuộc một mặt phẳng là:
Câu 68. Trong không gian với hệ tọa độ Oxyz , cho tam
A. 3a b 7 . B. 3a 5b 0 . C. 4a 3b 2 . D. a 2b 1.
giác ABC có A1;0;0 , B0;0; 1 , C 2;1; 1 . Diện tích
của tam giác ABC bằng:
Câu 65. Trong không gian với hệ tọa độ Oxyz , cho ba điểm
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 12 Tµi liÖu to¸n 12 n¨m häc 2018
ABCD với A2;1; 1 , B3;0; 1 , C 2;1; 3 , điểm D A. 7 B. 5 C. 6 D. 11 2 2 2 2
thuộc Oy và thể tích của tứ diện ABCD bằng 5 . Tọa
Câu 69. Trong không gian với hệ tọa độ Oxyz , cho tam
độ của đỉnh D là:
giác ABC có A1;0;0 , B0;0; 1 , C 2;1; 1 . Độ dài
A. D0;7;0 B. D0;8;0
đường cao kẻ từ A của tam giác ABC bằng:
C. D0;7;0 hoặc D0;8;0. A. 30 B. 15 C. 2 5 D. 3 6 5 5
D. D0;7;0 hoặc D0;8;0 .
Câu 70. Trong không gian với hệ tọa độ Oxyz , cho hai Câu 76. Trong không gian với hệ tọa độ Oxyz , cho tứ diện
điểm C 4;0;0 và B2;0;0. Tìm tọa độ điểm M thuộc
ABCD với A1;2;4 , B4;2;0 , C 3;2; 1 và
trục tung sao cho diện tích tam giác MBC bằng 3 . D1;1;
1 . Độ dài đường cao của tứ diện ABCD kẻ từ
A. M 0;3;0, M 0;2;0 . B. M 0;3;0, M 0;3;0. đỉnh D bằng:
C. M 0;4;0, M 0;3;0. D. M 0;3;0, M 0;1;0 . A. 3 B. 1 C. 2 D. 1 2
Câu 71: Trong không gian với hệ tọa độ Oxyz , cho ba điểm A1;2; 1 , B 2;1; 1 , C 0;1;2 .
Câu 77. Trong không gian với hệ tọa độ Oxyz , cho bốn
điểm A2;2;0 , B2;4;0, C 4;0;0 và D0;2;0 .
Gọi H a;b;c là trực tâm của tam giác ABC . Giá trị
Mệnh đề nào sau đây là đúng?
của a b c bằng: A. Bốn điểm ,
A B, C, D tạo thành tứ diện. A. 4 B. 5 C. 7 D. 6 B. Bốn điểm ,
A B, C, D tạo thành hình vuông.
Câu 72. Trong không gian với hệ tọa độ Oxyz , cho hình bình C. Bốn điểm ,
A B, C, D tạo thành hình chóp đều.
hành ABCD . Biết A2;1; 3 , B0;2; 5 , C 1;1; 3 . Diện
tích hình bình hành ABCD là:
D.Diện tích ABC
bằng diện tích DBC . A.
Câu 78. Trong không gian với hệ tọa độ Oxyz , cho bốn 2 87 B. 349 C. 87 D. 349 2
điểm A1;0;0 , B0;1;0, C 0;0; 1 và D1;1; 1 . Trong
Câu 73. Trong không gian với hệ tọa độ Oxyz , cho hình
các mệnh đề sau, mệnh đề nào sai?
bình hành ABCD với A1;0;
1 , B2;1;2 và giao điểm A. Bốn điểm ,
A B, C, D tạo thành một tứ diện. của hai đường chéo là 3 3 I ;0; . Diện tích của hình 2 2 B. Ba điểm ,
A B, D tạo thành tam giác đều.
bình hành ABCD bằng:
C. AB CD . A. 5 B. 6 C. 2 D. 3
D. Ba điểm B, C, D tạo thành tam giác vuông.
Câu 74. Trong không gian với hệ tọa độ Oxyz , cho tứ diện Câu 79. Cho hình hộp ABCD.A'B'C 'D' . Hãy xác định ba
ABCD với A1;0;0 , B0;1;0, C 0;0; 1 , D2;1; 1 .
vectơ nào sau đây đồng phẳng?
Thể tích của tứ diện ABCD bằng:
A. AA',BB ',CC '
B. AB, AD, AA' A.1 B. 2 C. 1 D. 1
2 3
C. AD, A' B ',CC '
D. BB ', AC, DD '
Câu 75. Trong không gian với hệ tọa độ Oxyz , cho tứ diện Câu 80. Trong không gian với hệ tọa độ Oxyz , cho hình
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 13 Tµi liÖu to¸n 12 n¨m häc 2018
hộp ABCD.A' B 'C ' D ' có A1;1;6 , B0;0;2, C. S 2 2 2 :
x y z 2x 6z 2 0 3
C 5;1;2 và D '2;1;
1 . Thể tích của khối hộp đã cho D. S :
x y z 2x 4 y 6z 2 0 4 2 2 2 bằng: A. 36 B. 38 C. 40 D. 42
Câu 85. Trong không gian với hệ tọa độ Oxyz , mặt cầu
tâm I 6,3,4 tiếp xúc với Ox có bán kính R bằng:
A. R 6 B. R 5 C. R 4 D. R 3
Vấn đề 4. PHƯƠNG TRÌNH MẶT CẦU
Câu 86. Trong không gian với hệ tọa độ Oxyz , Cho mặt
Câu 81. (ĐỀ MINH HỌA QUỐC GIA NĂM 2017) Trong
không gian với hệ tọa độ cầu S có phương trình Oxyz , cho mặt cầu 2 2 2 .
x y z 2x 4 y 6z 5 0
S x 2 y 2 z 2 : 1 2
1 9 . Tính tọa độ tâm I
và bán kính R của S.
Trong các số dưới đây, số nào là diện tích của mặt cầu S ?
A. I 1;2;
1 và R 3 . B. I 1;2; 1 và R 3 .
A. 12 B. 9
C. 36 D. 36
C. I 1;2;
1 và R 9 . D. I 1;2; 1 và R 9 .
Câu 87: Trong các phương trình sau, phương trình nào là
Câu 82. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu
phương trình của mặt cầu:
S có phương trình 2 2 2
x y z 2x 4 y 6z 2 0 A. 2 x + 2 y + 2
z −10xy − 8y + 2z −1 = 0
. Tính tọa độ tâm I và bán kính R của S. B. 2 x + 2 y + 2 3 3
3z − 2x − 6y + 4z −1 = 0
A. Tâm I 1;2;
3 và bán kính R 4 . C. 2 x + 2 y + 2 2 2
2z − 2x − 6 y + 4z + 9 = 0
B. Tâm I 1;2;
3 và bán kính R 4 .
D. x + ( y − z )2 2
− 2x − 4 ( y − z ) − 9 = 0
C. Tâm I 1;2;
3 và bán kính R 4 .
Câu 88. Trong không gian với hệ tọa độ Oxyz , giả sử tồn
D. Tâm I 1;2;
3 và bán kính R 16 . tại mặt cầu S có phương trình
Câu 83. Trong không gian với hệ tọa độ 2 2 2
Oxyz , mặt cầu nào
x y z 4x 8y 2az 6a 0 . Nếu S có
sau đây có tâm nằm trên trục Oz ?
đường kính bằng 12 thì a nhận những giá trị nào? A. S 2 2 2
: x y z 2x 4 y 2 0 . a 2 a 2 a 2 a 2 1 A. B. C. D. a 8 a 8 a 4 a 4 B. S 2 2 2
: x y z 6z 2 0 . 2
Câu 89. Trong không gian với hệ tọa độ Oxyz , giả sử tồn C. S 2 2 2
: x y z 2x 6z 0 . 3 tại mặt cầu S có phương trình 2 2 2
x y z 4x 2 y 2az 10a 0 . Với những giá D. S 2 2 2
: x y z 2x 4 y 6z 2 0 . 4
trị nào của a thì S có chu vi đường tròn lớn bằng 8
Câu 84. Trong không gian với hệ tọa độ Oxyz , mặt cầu ?
nào sau đây có tâm nằm trên mặt phẳng tọa độ Oxy? A. 1;1
1 B. 1;10 C. 1;1
1 D. 10;2 A. S 2 2 2 :
x y z 2x 4 y 2 0 1
Câu 90. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu B. S 2 2 2 :
x y z 4 y 6z 2 0 S có phương trình 2
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 14 Tµi liÖu to¸n 12 n¨m häc 2018 2 2 2
x y z 2m 2x 3my 6m 2z 7 0 . Gọi
C. x 2 y 2 z 2 1 4 2 9
R là bán kính của S, giá trị nhỏ nhất của R bằng:
D. x 2 y 2 z 2 1 4 2 81 A. 7 B. 377 C. 377 D. 377 7 4
Câu 95. Trong không gian với hệ tọa độ Oxyz , mặt cầu S
có tâm I 2;1;
1 , tiếp xúc với mặt phẳng tọa độ Oyz .
Câu 91. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu
Phương trình của mặt cầu S là:
S có phương trình 2 2 2
x y z 2x 4 y 6z 0 . 2 2 2
Mặt phẳng Oxy cắt S theo giao tuyến là một đường
A. x 2 y 1 z 1 4
tròn. Đường tròn giao tuyến này có bán kính r bằng:
B. x 2 y 2 z 2 2 1 1 1
A. r 5 B. r 2
C. r 6 D. r 4
C. x 2 y 2 z 2 2 1 1 4
Câu 92. Trong không gian với hệ tọa độ Oxyz , mặt cầu S có 2 2 2
tâm I 1;2;0, bán kính R 5 . Phương trình của mặt
D. x 2 y 1 z 1 2 cầu S là:
Câu 96. Trong không gian với hệ tọa độ Oxyz , mặt cầu S
A. S x 2 y 2 2 : 1
2 z 25 .
đi qua A0,2,0, B2;3; 1 , C 0,3; 1 và có tâm ở trên
mặt phẳng Oxz . Phương trình của mặt cầu S là:
B. S x 2 y 2 2 : 1 2 z 5 .
A. x y 2 z 2 2 6 4 9
C. S x 2 y 2 2 : 1
2 z 25 .
B. x y 2 2 2 3 z 16
D. S x 2 y 2 2 : 1 2 z 5 .
C. x y 2 z 2 2 7 5 26
Câu 93. Trong không gian với hệ tọa độ Oxyz , cho hai 2 2 điểm 2 A2;4; 1 , B 2; 2;
3 . Phương trình mặt cầu D. x
1 y z 3 14
đường kính AB là:
Câu 97. Trong không gian với hệ tọa độ Oxyz , mặt cầu S
A. x y 2 z 2 2 3 1 9
có bán kính bằng 2 , tiếp xúc với mặt phẳng Oyz và
có tâm nằm trên tia Ox . Phương trình của mặt cầu S
B. x y 2 z 2 2 3 1 9 là:
C. x y 2 z 2 2 3 1 3
A. S x 2 2 2 :
2 y z 4 .
D. x y 2 z 2 2 3 1 9
B. S x y 2 2 2 : 2 z 4 .
Câu 94. Trong không gian với hệ tọa độ Oxyz , mặt cầu S
C. S x 2 2 2 :
2 y z 4 .
có tâm I 1;4;2 và có thể tích V 972 . Khi đó
phương trình của mặt cầu S là:
D. S x y z 2 2 2 : 2 4 .
A. x 2 y 2 z 2 1 4 2 81
Câu 98. Trong không gian với hệ tọa độ Oxyz , cho các điểm
A2,0,0, B 0,4,0, C
0,0,4. Phương trình nào sau
B. x 2 y 2 z 2 1 4 2 9
đây là phương trình mặt cầu ngoại tiếp tứ diện OABC (
O là gốc tọa độ).
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 15 Tµi liÖu to¸n 12 n¨m häc 2018 A. 2 2 2
x y z 2x 4 y 4z 0
O 0;0;0, A 2;2; 3 , B 2;1;
1 , có bao nhiêu điểm nằm
trong mặt cầu S?
B. x 2 y 2 z 2 1 2 2 9 A. 0 B. 1 C. 2 D. 3
C. x 2 y 2 z 2 2 4 4 20
Câu 105. Trong không gian với hệ tọa độ Oxyz , cho điểm D. 2 2 2
x y z 2x 4 y 4z 9 A1;a;
1 và mặt cầu S có phương trình 2 2 2
x y z 2y 4z 9 0 . Tập các giá trị của a để
Câu 99. Trong không gian với hệ tọa độ Oxyz , cho ba
điểm A nằm trong khối cầu là?
điểm A1,0,0 , B0,2,0, C0,0, 3 . Tập hợp các điểm
M x, y, zthỏa mãn: 2 2 2
MA MB MC là mặt cầu có A. 1;
3 B. 1;3 bán kính là: C. 3; 1 D. ; 1 3;
A. R 2 B. R 2 C. R 3
D. R 3
Câu 106. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu
Câu 100. Trong không gian với hệ tọa độ Oxyz , mặt cầu có
S x y 2 z 2 2 : 4
1 36 . Vị trí tương đối của
phương trình nào sau đây đi qua gốc tọa độ?
mặt cầu S với mặt phẳng Oxy là: A. S 2 2 2
: x y z 2x 4 y 2 0 1
A. Oxy cắt S.
B. Oxy không cắt S. B. S 2 2 2
: x y z 4 y 6z 2 0 2
C. Oxy tiếp xúc S.
D. Oxy đi qua tâm S. C. S 2 2 2
: x y z 2x 6z 0 3
Câu 107. Trong không gian với hệ tọa độ Oxyz , cho mặt D. S 2 2 2
: x y z 2x 4 y 6z 2 0 2 2 2 4
cầu S:x
1 y 2 z 5 4 .
Câu 101. Trong không gian với hệ tọa độ Oxyz , cho mặt Mặt phẳng nào sau đây cắt mặt cầu S?
cầu S x 2 y 2 z 2 : 1 2 3 9 .
A. Oxy. B. Oyz . C. Oxz . D. Cả A, B, C.
Điểm nào sau đây nằm ngoài mặt cầu S?
Câu 108. Trong không gian với hệ tọa độ Oxyz , mặt cầu
A. M 1;2;
5 .B. N 0;3;2 . C. P 1;6;
1 .D. Q 2;4; 5 .
nào sau đây tiếp xúc với mặt phẳng tọa độ Oxy ?
Câu 102. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu
A.S :x 2
1 y z 22 2 2 1 S 2 2 2
: x y z 6x 4 y 2z 0 . Điểm nào sau đây 2 2 2 thuộc mặt cầu
B. S : x 1 y 3 z 1 2 2 S? 2 2 A. 2 M 0;1;
1 .B. N 0;3;2 . C. P 1;6;
1 . D. Q 1;2;0 .
C. S : x 1 y 1 z 1 3
Câu 103. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu
D. S : x y z 42 2 2 16 4
S x y 2 z 2 2 : 1
2 25 . Điểm nào sau đây nằm Câu 109. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu
bên trong mặt cầu S.
S x 2 y z 2 2 2 : 3
2 m 4 . Tập các giá trị của
A. M 3;2;4.B. N 0;2;2 . C. P 3;5;2.D. Q1;3;0. m để mặt cầu S tiếp xúc với mặt phẳng Oyz là:
Câu 104. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu
A. m 5 . B. m 5 . C. m 0 . D. m 2 . S 2 2 2
: x y z 2x 4 y 6z 0 . Trong ba điểm
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 16 Tµi liÖu to¸n 12 n¨m häc 2018
Câu 110. Trong không gian với hệ tọa độ Oxyz , cho mặt
B. S :x 2 2 2
1 y z 1 2 cầu S có phương trình
C. S : x 1 y 1 z 1 3 2 2 2
x y 2 2 2 2 2
5 z m 2m 6 . Tập các giá trị
của m để mặt cầu S cắt trục Oz tại hai điểm phân
D. S :x 2 1 y 2 3 z 2 1 2 4 biệt là:
Câu 113. Trong không gian với hệ tọa độ Oxyz , cho mặt
A. m 1. B. m 3 . C. 3 m 1. D. m 3 hoặc m 1 .
cầuS:x 2
1 y 2 z 2 2 3 14 và điểm
Câu 111. Trong không gian với hệ tọa độ Oxyz , cho mặt
A1;1;6 . Tìm trên trục Oz điểm B sao cho đường
cầu S có phương trình x 2 y 2 2 1 3 z 9 .
thẳng AB tiếp xúc với S.
Mệnh đề nào sau đây đúng ? A. 19 B0;0; . B. 19
B0;0; .C. 3 B0;0; .D. 3
B0;0; .
A.S tiếp xúc với trục Ox B. S không cắt trục Oy 3 3 19 19
C. S tiếp xúc với trục Oy D. S tiếp xúc với trục Oz Câu 114. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S 2 2 2
: x y z 4x 4 y 4z 0 và điểm
Câu 112. Trong không gian với hệ tọa độ Oxyz , mặt cầu
A4;4;0 .Tìm tọa độ điểm B thuộc S sao cho tam
nào sau đây tiếp xúc với hai trục tọa độ Oy và Oz ?
giác OAB đều (O là gốc tọa độ).
A. S :x 2
1 y z 22 2 2 1 B0;4;4 B0;4;4 B0;4;4 B0;4;4 A. . B. .C. .D. . B 4;0;4 B 4;0;4 B 4;0;4 B 4;0;4
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 17 Tµi liÖu to¸n 12 n¨m häc 2018
1. HỆ TOẠ ĐỘ TRONG KHÔNG GIAN
D¹ng to¸n 1: Tọa độ của điểm, vectơ và các yếu tố liên quan Phương pháp
Sử dụng các kết quả trong phần: Tọa độ của vectơ. Tọa độ của điểm.
Liên hệ giữa tọa độ vectơ và tọa độ hai điểm mút.
Tích có hướng của hai vectơ và các ứng dụng
ThÝ dô 1. Cho ba điểm A(1; 2; 3), B(3; 5; 4), C(3; 0; 5).
a. Chứng minh A, B, C là ba đỉnh của một tam giác.
b. Tính chu vi, diện tích của ∆ABC.
c. Tìm toạ độ điểm D để ABCD là hình bình hành và tính côsin góc giữa hai vectơ AC và BD .
d. Tính độ dài đường cao hA của ∆ABC kẻ từ A.
e. Tính các góc của ∆ABC.
f. Xác định toạ độ trực tâm H của ∆ABC.
g. Xác định toạ độ tâm đường tròn ngoại tiếp ∆ABC. Giải a. Ta có:
AB (2; 3; 1) và AC (2; −2; 2) ⇒ AB và AC không cùng phương.
Vậy, ba điểm A, B, C không thẳng hàng. b. Ta lần lượt có: CV∆ABC = AB + AC + BC = 2 2 2 2 2 2 2 2 2 + 3 + 1 + 2 + ( 2 − ) + 2 + ( 5 − ) + 1 = 14 + 12 + 26 . 1 1 1 S 2 2 2 ∆ ABC = AB, AC = |(8; −2; −10)| = 8 + ( 2) − + ( 1 − 0) = 42 . 2 2 2
c. Giả sử D(x; y; z), để ABCD là hình bình hành điều kiện là:
AB = DC ⇔ (2; 3; 1) = (3 − x; −y; 5 − z) 2 = 3 − x x = 1 ⇔ 3 = −y ⇔ y = 3 − ⇒ D(1; −3; 4). 1 = 5 − z z = 4 AB.BD 12 51
cos( AC , BD ) = = = . AB . BD 12. 68 17 d. Ta có: 1 2S 2 42 2 273 S ∆ ∆ABC = hA.BC ⇔ hA = ABC = = . 2 BC 26 13 e. Ta lần lượt có: AB.AC
cosA = = 0 ⇔ A = 900, AB . AC BA.BC 51 118
cosB = = và cosC = sinB = 2 1 − cos B = . BA . BC 13 13
f. Ta có thể lựa chọn một trong hai cách sau:
Cách 1: Giả sử H(x; y; z) là trực tâm ∆ABC, ta có điều kiện:
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 1 Tµi liÖu to¸n 12 n¨m häc 2018 AH ⊥ BC AH ⊥ BC
BH ⊥ AC ⇔ BH ⊥ AC
H ∈ (ABC)
Ba vect¬ AB, AC, AH ®ång ph¼ng AH.BC = 0 − − − − = (x 1; y 2; z 3).(0; 5; 1) 0 ⇔ BH.AC = 0 ⇔ (
x − 3; y − 5; z − 4).(2; − 2; 2) = 0
AB, AC.AH = 0
(8; − 2; −10).(x −1; y − 2; z − 3) = 0 5( − y − 2) + z − 3 = 0 5y − z = 7 x = 1 ⇔
2(x − 3) − 2(y − 5) + 2(z − 4) = 0 ⇔ x − y + z = 2 ⇔ y = 2 8
(x −1) − 2(y − 2) −10(z −3) = 0 4x − y − 5z = 13 − z = 3
Vậy, ta được trực tâm H(1; 2; 3).
Cách 2: Vì ∆ABC vuông tại A nên trực tâm H ≡ A, tức là H(1; 2; 3).
g. Ta có thể lựa chọn một trong hai cách sau:
Cách 1: Giả sử I(x; y; z) là tâm đường tròn ngoại tiếp ∆ABC, ta có: AI = BI 2 2 AI = BI 2 2 AI = BI AI = CI ⇔ 2 2 AI = CI ⇔ 2 2 AI = CI
I ∈ (ABC) AB, AC, AH ®ång ph¼ng AB, AC.AI = 0 2 2 2 2 2 2 (x
−1) + (y − 2) + (z − 3) = (x − 3) + (y − 5) + (z − 4) ⇔ 2 2 2 2 2 2 (x
−1) + (y − 2) + (z − 3) = (x − 3) + y + (z − 5) 4x − y −5z = 13 − 2x + 3y + z = 18 x = 3 ⇔ x − y + z = 5 ⇔ y = 5 / 2 . 4x − y −5z = 13 − z = 9 / 2 5 9
Vậy, ta được tâm đường tròn ngoại tiếp là I 3; ; . 2 2
Cách 2: Vì ∆ABC vuông tại A nên tâm I của đường tròn ngoại tiếp ∆ABC chính là trung điểm của BC, tức là 5 9 I 3; ; . 2 2
F Nhận xét: Như vậy, với bài toán trên (tam giác trong không gian) các em học sinh có thể ôn tập được hầu
hết kiến thức trong bài học "Hệ tọa độ trong không gian", và trong đó với các câu f), g):
Ở cách 1, chúng ta nhận được phương pháp chung để thực các yêu cầu của bài toán.
Ở cách 2, bằng việc đánh giá được dạng đặc biệt của ∆ABC chúng ta nhận được lời giải
đơn giản hơn rất nhiều.
ThÝ dô 2. Trong không gian Oxyz, cho bốn điểm A(5; 3; −1), B(2; 3; −4), C(1; 2; 0), D(3; 1; −2).
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 2 Tµi liÖu to¸n 12 n¨m häc 2018
a. Tìm tọa độ các điểm A1, A2 theo thứ tự là các điểm đối xứng với điểm A qua mặt phẳng
(Oxy) và trục Oy.
b. Chứng minh rằng A, B, C, D là bốn đỉnh của một hình tứ diện.
c. Tính thể tích khối tứ diện ABCD.
d. Chứng minh rằng hình chóp D.ABC là hình chóp đều.
e. Tìm tọa độ chân đường cao H của hình chóp D.ABC.
f. Chứng minh rằng tứ diện ABCD có các cạnh đối vuông góc với nhau.
g. Tìm tọa độ điểm I cách đều bốn điểm A, B, C, D. Giải a. Ta lần lượt:
Hình chiếu vuông góc của điểm A trên mặt phẳng (Oxy) là điểm E(5; 3; 0). Từ đó, vì E là trung điểm của AA1 nên A1(5; 3; 1).
Hình chiếu vuông góc của điểm A trên trục Oy là điểm F(0; 3; 0). Từ đó, vì F là trung điểm của AA2 nên A2(−5; 3; 1).
b. Ta có thể lựa chọn một trong hai cách sau:
Cách 1: Để chứng minh bốn điểm A, B, C, D không đồng phẳng ta sẽ đi chứng minh ba vectơ DA (2; 2; 1), DB
(−1; 2; −2), DC (−2; 1; 2) không đồng phẳng.
Giả sử trái lại, tức là ba vectơ DA , DB , DC đồng phẳng, khi đó sẽ tồn tại cặp số thức α, β sao cho: = −α − β 2 2
DA = α DB + β DC ⇔ 2 = 2α + β , vô nghiệm 1 = 2 − α + 2β
⇒ Ba vectơ DA , DB , DC không đồng phẳng.
Vậy, bốn điểm A, B, C, D là bốn đỉnh của một hình tứ diện.
Cách 2: Ta có DA (2; 2; 1), DB (−1; 2; −2), DC (−2; 1; 2), từ đó suy ra:
2 1 1 2 2 2 DA, DB.DC = .( 2 − ) + .1 + .2 = 27 ≠ 0 2 2 − 2 − 1 − 1 − 2
⇒ Ba véctơ DA , DB và DC không đồng phẳng.
Vậy, bốn điểm A, B, C, D là bốn đỉnh của một hình tứ diện.
1 9
c. Thể tích V của tứ diện ABCD được cho bởi V = DA, DB.DC = . 6 2 d. Ta lần lượt có: 2 2 2 DA = 2 + 2 + 1 = 3 2 2 2 DB = ( 1 − ) + 2 + ( 2 − ) = 3 ⇒ DA = DB = DC. 2 2 2 DC = ( 2 − ) + 1 + 2 = 3
Tương tự, ta cũng có AB = BC = CA = 3 2 .
Vậy, hình chóp D.ABC là hình chóp đều.
e. Ta có thể trình bày theo hai cách sau:
Cách 1: Giả sử H(x; y; z) là hình chiếu vuông góc của D lên mặt phẳng (ABC), ta có điều kiện: DH ⊥ AB DH ⊥ AB DH.AB = 0
DH ⊥ AC ⇔ DH ⊥ AC ⇔ DH.AC = 0
H ∈ (ABC)
Ba vect¬ AB, AC, AH ®ång ph¼ng AB, AC.AH = 0
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 3 Tµi liÖu to¸n 12 n¨m häc 2018 x + z = 1 x = 8/ 3 ⇔ 8 8 5
4x + y − z = 15 ⇔ y = 8 / 3 ⇒ H ; ; − . 3 3 3 x − 5y − z = 9 − z = 5 − / 3 8 8 5 Vậy, ta được H ; ; − . 3 3 3
Cách 2: Dựa theo kết quả câu d), ta suy ra chân đường cao H của hình chóp D.ABC chính là trọng tâm của ∆ABC, do đó:
1 OH = (OA + OB + OC) 3 + + + + + + ⇔ x x x y y y z z z 8 8 5 A B C A B C A B C H ; ; = ; ; − . 3 3 3 3 3 3
f. Với cặp cạnh AD và BC, ta có:
DA (2; 2; 1), BC (−1; −1; 4) ⇒ DA . BC = 0 ⇔ AD ⊥ BC.
Chứng minh tương tự, ta cũng có AB ⊥ CD và AC ⊥ BD.
Vậy, tứ diện ABCD có các cạnh đối vuông góc với nhau. D
g. Ta có thể trình bày theo hai cách sau:
Cách 1: Giả sử I(x; y; z) là tâm mặt cầu ngoại tiếp tứ diện ABCD, ta có: AI = BI 2 2 AI = BI I A B AI = CI ⇔ 2 2 AI = CI H AI = DI 2 2 AI = DI C 2 2 2 2 2 2 (x
− 5) + (y − 3) + (z +1) = (x − 2) + (y − 3) + (z + 4) ⇔ 2 2 2 2 2 2 (x
− 5) + (y − 3) + (z +1) = (x −1) + (y − 2) + z 2 2 2 2 2 2
(x − 5) + (y − 3) + (z + 1) = (x − 3) + (y −1) + (z + 2) x + z = 1 x = 5 / 2 ⇔ 5 7 3 4x + y − z = 15 ⇔ y = 7 / 2 ⇒ I ; ; − . 2 2 2 4x + 4y + 2z = 21 z = 3 − / 2
Cách 2: Dựa theo kết quả câu d), ta suy tâm I(x; y; z) thuộc DH sao cho ID = IB, tức là ta có: 2 2 2 2 2 2 (x
− 3) + (y −1) + (z + 2) = (x − 2) + (y − 3) + (z + 4) 2 2 DI = BI
⇔ x − 3 y −1 z + 2 = = DI // HI 8 8 5 x − y − z + 3 3 3 2x − 4y + 4z = 1 − 5 x = 5 / 2 ⇔ 5 7 3 5 x + y = 16 ⇔ y = 7 / 2 ⇒ I ; ; − . 2 2 2 x + z = 1 z = 3 − / 2
F Nhận xét: Như vậy, với bài toán trên (khối đa diện) các em học sinh đã ôn tập được các kiến thức trong
bài học "Hệ tọa độ trong không gian", và trong đó:
Ở câu b), chúng ta nhận được hai phương pháp để chứng minh bốn điểm không đồng
phẳng (tương ứng với ba vectơ không đồng phẳng) và thông thường chúng ta sử dụng
cách 2 trong bài thi. Và đặc biệt giá trị DA, DB.DC
được xác định rất nhanh và chính
xác với các em học sinh biết sử dụng máy tính Casio fx − 570MS.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 4 Tµi liÖu to¸n 12 n¨m häc 2018
Ở câu e), cách 1 trình bày phương pháp chung cho mọi dạng tứ diện và cách 2 được đề
xuất dựa trên dạng đặc biệt của tứ diện ABCD. Và các em học sinh cần nhớ thêm rằng
chúng ta còn có một cách chung khác bằng việc thực hiện theo các bước:
Bíc 1: Viết phương trình mặt phẳng (ABC).
Bíc 2: Viết phương trình đường thẳng (d) qua D và vuông góc với mặt phẳng (ABC).
Bíc 3: Khi đó, điểm H chính là giao điểm của đường thẳng (d) với mặt phẳng (ABC).
Hai cách sử dụng trong câu g) với ý tương tượng tự như câu e). Tuy nhiên, các em học
sinh cũng có thể thực hiện như sau:
Bíc 1: Viết phương trình mặt cầu (S) ngoại tiếp tứ diện ABCD (phương trình mặt cầu đi qua bốn điểm).
Bíc 2: Từ kết quả ở bước 1, chúng ta nhận được tọa độ tâm I.
D¹ng to¸n 2: Phương trình mặt cầu Phương pháp
Với phương trình cho dưới dạng chính tắc:
(S): (x − a)2 + (y − b)2 + (z − c)2 = k, với k > 0 ta lần lượt có: Bán kính bằng R = k .
Tọa độ tâm I là nghiệm của hệ phương trình: x − a = 0 x = a
y − b = 0 ⇔ y = b ⇒ I(a; b; c). z − c = 0 z = c
Với phương trình cho dưới dạng tổng quát ta thực hiện theo các bước:
Bíc 1: Chuyển phương trình ban đầu về dạng:
(S): x2 + y2 + z2 − 2ax − 2by − 2cz + d = 0. (1)
Bíc 2: Để (1) là phương trình mặt cầu điều kiện là: a2 + b2 + c2 − d > 0.
Bíc 3: Khi đó (S) có thuộc tính: T m © I(a;b;c) . 2 2 2 B k ¸n Ýnh R = a + b + c − d
ThÝ dô 1. Cho họ mặt cong (Sm) có phương trình:
(Sm): (x − 2)2 + (y − 1)2 + (z − m)2 = m2 − 2m + 5.
a. Tìm điều kiện của m để (Sm) là một họ mặt cầu.
b. Tìm mặt cầu có bán kính nhỏ nhất trong họ (Sm).
c. Chứng tỏ rằng họ (Sm) luôn chứa một đường tròn cố định. Giải
a. Để (Sm) một họ mặt cầu điều kiện là:
m2 − 2m + 5 > 0 ⇔ (m − 1)2 + 4 > 0, luôn đúng.
Vậy, với mọi m thì (Sm) luôn là phương trình của mặt cầu với: T m © I(2;1;m) . 2 B k ¸n Ýnh R = (m −1) + 4 b. Ta có:
R2 = (m - 1)2 + 4 ≥ 4 ⇒ Rmin = 2, đạt được khi m = 1.
Vậy, trong họ (Sm) mặt cầu (S1) có bán kính nhỏ nhất bằng 2.
c. Giả sử M(x0; y0; z0) là điểm cố định mà họ (Sm) luôn đi qua, ta có:
(x0 − 2)2 + (y0 − 1)2 + (z0 − m)2 = m2 − 2m + 5, ∀m
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 5 Tµi liÖu to¸n 12 n¨m häc 2018 ⇔ 2 2 2
2(1− z )m + (x − 2) + (y −1) + z − 5 = 0, m ∀ 0 0 0 0 1 − z = 0 z = 1 ⇔ 0 0 ⇔ . 2 2 2 (x
− 2) + (y −1) + z − 5 = 0 2 2 (x − 2) + (y −1) = 4 0 0 0 0 0
Vậy, họ (Sm) luôn chứa đường tròn (C) có tâm I0(2; 1; 1) và bán kính R0 = 2 nằm trong mặt phẳng (P0): z = 1.
F Chú ý: Thông qua lời giải câu c) các em học sinh hãy tổng kết để có được phương pháp thực hiện yêu cầu
"Chứng tỏ rằng họ mặt cầu (Sm) luôn chứa một đường tròn cố định".
ThÝ dô 2. Cho họ mặt cong (Sm) có phương trình:
(Sm): x2 + y2 + z2 - 2m2x - 4my + 8m2 - 4 = 0.
a. Tìm điều kiện của m để (Sm) là một họ mặt cầu.
b. Chứng minh rằng tâm của họ (Sm) luôn nằm trên một Parabol (P) cố định trong mặt phẳng
Oxy, khi m thay đổi.
c. Trong mặt phẳng Oxy, gọi F là tiêu điểm của (P). Giả sử đường thẳng (d) đi qua F tạo với
chiều dương của trục Ox một góc α và cắt (P) tại hai điểm M, N.
Tìm toạ độ trung điểm E của đoạn MN theo α.
Từ đó suy ra quỹ tích E khi α thay đổi. Giải
a. Ta có thể trình bày theo hai cách sau:
Cách 1: Biến đổi phương trình ban đầu về dạng:
(x − m2)2 + (y − 2m)2 + z2 = m4 − 4m2 + 4.
Từ đó, để phương trình đã cho là phương trình của mặt cầu điều kiện là:
m4 − 4m2 + 4 > 0 ⇔ (m2 − 2)2 > 0 ⇔ m2 − 2 ≠ 0 ⇔ m ≠ ± 2 .
Vậy, với m ≠ ± 2 thì (Sm) là phương trình của mặt cầu có: 2 T m © I(m ;2m;0) . 2 BkÝnh R = m − 2
Cách 2: Để (Sm) là một họ mặt cầu điều kiện cần và đủ là:
m4 + 4m2 - 8m2 + 4 > 0 ⇔ (m2 - 2)2 > 0 ⇔ m2 − 2 ≠ 0 ⇔ m ≠ ± 2 .
Vậy, với m ≠ ± 2 thì (Sm) là phương trình của mặt cầu có: 2 T m © I(m ;2m;0) . 2 BkÝnh R = m − 2 b. Ta có: 2 x = m 2 y = 4x Im: y = 2m ⇔ . z = 0 z = 0
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 6 Tµi liÖu to¸n 12 n¨m häc 2018
Vậy, trong mặt phẳng Oxy tâm Im luôn nằm trên Parabol (P): y2 = 4x.
c. Trong mặt phẳng Oxy, xét Parabol
(P): y2 = 4x, có tiêu điểm F(1; 0).
Phương trình đường thẳng (d) đi qua F tạo với chiều dương của trục Ox một góc α có dạng: qua F(1;0) (d): ⇔ (d): y = (x - 1)tanα. hÖ sè gãc k = tan α
Toạ độ giao điểm M, N của (P) và (d) là nghiệm của hệ phương trình: 2 y = 4x
⇒ x2tan2α - 2(tan2α + 2)x + tan2α = 0. (1) y = (x −1) tan α Ta có:
∆' = (tan2α + 2)2 - tan4α = 4tan2α + 4 > 0, ∀α
do đó (1) luôn có 2 nghiệm phân biệt.
Vậy (P) và (d) luôn cắt nhau tại hai điểm phân biệt M(xM; yM), N(xM; yM) có hoành độ thoả mãn: 2 2(tan α + 2) x + x = . M N 2 tan α
Gọi E(xE, yE) là trung điểm của đoạn MN, ta có: 2 tan α + 2 1 x = x = (x + x ) E 2 tan α E M N 2 ⇔ 2 1 2(tan α + 2) y = (x −1) tan α y = − 2 tan α E E E 2 2 tan α 2 tan α + 2 x = E ⇔ 2 α tan . (I) 2 y = E tan α
Khử α từ hệ (I) ta được 2 yE = 4xE - 2
Vậy, quĩ tích trung điểm E của đoạn MN thuộc Parabol (P1) cú phương trình y2 = 4x - 2 trong mặt phẳng Oxy.
F Nhận xét: Như vậy, với bài toán trên:
Ở câu a), việc trình bày theo hai cách chỉ có tính minh họa, bởi trong thực tế chúng ta
thường sử dụng cách 2.
Ở câu b), chúng ta sử dụng kiến thức về tam thức bậc hai.
Ở câu c), các em học sinh đã thấy được mối liên hệ giữa hình học giải tích trong mặt
phẳng với hình học giải tích trong không gian.
D¹ng to¸n 3: Viết phương trình mặt cầu Phương pháp
Gọi (S) là mặt cầu thoả mãn điều kiện đầu bài. Chúng ta lựa chọn phương trình dạng tổng quát hoặc dạng chính tắc. Khi đó:
1. Muốn có phương trình dạng chính tắc, ta lập hệ 4 phương trình với bốn ẩn a, b, c, R, điều kiện R > 0. Tuy
nhiên, trong trường hợp này chúng ta thường chia nó thành hai phần, bao gồm:
Xác định bán kính R của mặt cầu.
Xác tâm I(a; b; c) của mặt cầu.
Từ đó, chúng ta nhận được phương trình chính tắc của mặt cầu.
2. Muốn có phương trình dạng tổng quát, ta lập hệ 4 phương trình với bốn ẩn a, b, c, d, điều kiện a2 + b2 + c2 − d > 0.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 7 Tµi liÖu to¸n 12 n¨m häc 2018
F Chú ý: 1. Cần phải cân nhắc giả thiết của bài toán thật kỹ càng để lựa chọn dạng phương trình thích hợp.
2. Trong nhiều trường hợp đặc thù chúng ta còn sử dụng phương pháp quỹ tích để xác định phương trình mặt cầu.
ThÝ dô 1. Viết phương trình mặt cầu trong các trường hợp sau:
a. Đường kính AB với A(3; −4; 5), B(−5; 2; 1).
b. Tâm I(3; −2; 1) và đi qua điểm C(−2; 3; 1). Giải
a. Ta có thể trình bày theo các cách sau:
Cách 1: Mặt cầu (S) có: T©m I lµ trung ®iÓm AB T©m I( 1; − −1; 3) (S): AB ⇔ (S): B¸n kÝnh R = R = 29 2
⇔ (S): (x + 1)2 + (y + 1)2 + (z - 3)2 = 29. Cách 2: Ta có:
M(x; y; z) ∈ (S) ⇔ MA ⊥ MB ⇔ AM.BM = 0
⇔ (x − 3; y + 4; z − 5).(x + 5; y − 2; z − 1) = 0
⇔ (x − 3)(x + 5) + (y + 4)(y − 2) + (z − 5)(z − 1) = 0
⇔ x2 + y2 + z2 + 2x + 2y - 6z − 18 = 0.
Đó chính là phương trình mặt cầu (S) cần tìm. Cách 3: Ta có:
M(x; y; z) ∈ (S) ⇔ ∆MAB vuông tại M ⇔ AM2 + BM2 = AB2
⇔ (x − 3)2 + (y + 4)2 + (z − 5)2 + (x + 5)2 + (y − 2)2 + (z − 1)2 = 116
⇔ x2 + y2 + z2 + 2x + 2y - 6z − 18 = 0.
Đó chính là phương trình mặt cầu (S) cần tìm.
b. Ta có thể trình bày theo các cách sau:
Cách 1: Mặt cầu (S) có: T©m I T©m I(3;− 2;1) (S): ⇔ (S): § i qua C B¸n kÝnh R = IC = 5 2
⇔ (S): (x − 3)2 + (y + 2)2 + (z − 1)2 = 50.
Cách 2: Mặt cầu (S) có tâm I(3; −2; 1) có phương trình:
(x − 3)2 + (y + 2)2 + (z − 1)2 = R2.
Điểm C(−2; 3; 1) ∈ (S) điều kiện là:
(−2 − 3)2 + (3 + 2)2 + (1 − 1)2 = R2 ⇔ R2 = 50.
Vậy, phương trình mặt cầu (S) có dạng:
(x − 3)2 + (y + 2)2 + (z − 1)2 = 50.
Cách 3: Mặt cầu (S) có tâm I(3; −2; 1) có phương trình:
(S): x2 + y2 + z2 − 6x + 4y − 2z + d = 0.
Điểm C(−2; 3; 1) ∈ (S) điều kiện là:
4 + 9 + 1 + 12 + 12 − 2 + d = 0 ⇔ d = 36.
Vậy, phương trình mặt cầu (S): x2 + y2 + z2 − 6x + 4y − 2z + 36 = 0. Cách 4: Ta có:
M(x; y; z) ∈ (S) ⇔ IM = IA ⇔ IM2 = IA2
⇔ (x − 3)2 + (y + 2)2 + (z − 1)2 = 50.
Đó chính là phương trình mặt cầu (S) cần tìm.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 8 Tµi liÖu to¸n 12 n¨m häc 2018
F Nhận xét: Như vậy, với bài toán trên:
Ở câu a), với cách 1 chúng ta đi xác định tọa độ tâm I và tính bán kính R, từ đó sử dụng
công thức để nhận được phương trình chính tắc của mặt cầu (S). Các cách 2, cách 3
chúng ta đã sử dụng phương pháp quỹ tích để nhận được phương trình mặt cầu (S).
Ở câu b), cách 1 có ý tương tương tự như trong câu a). Các cách 2, cách 3 chúng ta đã sử
dụng các dạng phương trình có sẵn của mặt cầu và ở đó giá trị của tham số còn lại (R
hoặc d) được xác định thông qua điều kiện C thuộc (S). Cách 4 chúng ta sử dụng phương
pháp quỹ tích để nhận được phương trình mặt cầu (S).
ThÝ dô 2. Viết phương trình mặt cầu đi qua hai điểm A(1; 2; 2), B(0; 1; 0) và tâm I thuộc trục Oz. Giải
Ta có thể trình bày theo các cách sau:
Cách 1: Mặt cầu (S) có tâm I thuộc trục Oz suy ra I(0; 0; c) nên nó có dạng: x2 + y2 + (z − c)2 = R2.
• Điểm A(1; 2; 2) ∈ (S) nên:
1 + 4 + (2 − c)2 = R2 ⇔ (c − 2)2 + 5 = R2. (1)
• Điểm B(0; 1; 0) ∈ (S) nên:
1 + (−c)2 = R2 ⇔ c2 + 1 = R2. (2) Lấy (2) - (1), ta được: 4c − 8 = 0 ⇔ c = 2.
Thay c = 2 vào (2), ta được R2 = 5.
Vậy, phương trình mặt cầu (S) có dạng:
(S): x2 + y2 + (z − 2)2 = 5.
Cách 2: Mặt cầu (S) có tâm I thuộc trục Oz suy ra I(0; 0; c) nên nó có dạng:
x2 + y2 + z2 − 2cy + d = 0, với c 2 − d > 0.
Với các điểm A, B thuộc (S), ta có hệ phương trình: 9 − 4c + d = 0 c = 2 ⇔ . 1 + d = 0 d = 1 −
Vậy, phương trình mặt cầu (S) có dạng:
(S): x2 + y2 + z2 − 4z − 1 = 0.
Cách 3: Mặt cầu (S) có tâm I thuộc trục Oz suy ra I(0; 0; c).
Với các điểm A, B thuộc (S), ta có điều kiện là:
IA = IB ⇔ IA2 = IB2 ⇔ 1 + 4 + (2 − c)2 = 1 + (−c)2 ⇔ c = 2.
Vậy, phương trình mặt cầu (S) được cho bởi: T©m I(0;0;2) (S):
⇔ (S): x2 + y2 + (z − 2)2 = 5. B¸n kÝnh R = IA = 5
Cách 4: Mặt cầu (S) có tâm I thuộc trục Oz suy ra I(0; 0; c). Trung điể 1 3 m của AB là điểm M ; ; 1
, ta có điều kiện là: 2 2
IM ⊥ AB ⇔ IM ⊥ AB ⇔ IM.AB = 0 ⇔ 1 3 1 3 ; ; 1 − c ( 1 − ; −1; − 2) = 0 ⇔ −
− − 2(1− c) = 0 ⇔ c = 2. 2 2 2 2
Vậy, phương trình mặt cầu (S) được cho bởi:
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 9 Tµi liÖu to¸n 12 n¨m häc 2018 T©m I(0;0;2) (S):
⇔ (S): x2 + y2 + (z − 2)2 = 5. B¸n kÝnh R = IA = 5
F Chú ý: Ngoài bốn cách giải trên, để viết phương trình mặt cầu đi qua hai điểm A, B và có tâm thuộc
đường thẳng (d) chúng ta còn có thể thực hiện theo các bước sau:
Bíc 1: Mặt cầu (S) đi qua hai điểm A, B suy ra tâm I thuộc mặt phẳng (P) là mặt phẳng trung trực của AB. Ta có:
Qua E lµ trung ®iÓm cña AB (P): . vtpt AB
Bíc 2: Tâm {I} = (P) ∩ (d), nên toạ độ của I là nghiệm của hệ phương trình tạo bởi (d) và (P).
Bíc 3: Vậy, phương trình mặt cầu (S) được cho bởi: T m © I (S): . B n ¸ kÝnh R = IA
ThÝ dô 3. Viết phương trình mặt cầu đi qua ba điểm A(2; 1; 1), B(1; 1; 0), C(0; 2; 4) và có tâm nằm trên mặt phẳng (Oyz). Giải
Ta có thể trình bày theo các cách sau:
Cách 1: Giả sử mặt cầu (S) có phương trình:
(S): x2 + y2 + z2 − 2ax − 2by − 2cz + d = 0, với a 2 + b2 + c2 − d > 0.
Vì tâm I(a; b; c) thuộc mặt phẳng (Oxy) nên a = 0. (1)
Với các điểm A, B, C thuộc (S), ta có hệ phương trình:
6 − 4a − 2b − 2c + d = 0 2b + 2c − d = 6 b = 1 2 − 2a − 2b + d = 0
⇔ 2a + 2b − d = 2 ⇔ c = 2 . 20 − 4b −8c + d = 0 4b + 8c − d = 20 d = 0
Vậy, phương trình mặt cầu (S): x2 + y2 + z2 − 2y − 4z = 0.
Cách 2: Mặt cầu (S) có tâm I thuộc mặt phẳng (Oyz) suy ra I(0; b; c).
Với các điểm A, B, C thuộc (S), ta có điều kiện là: AI = BI = IC 2 2 AI = BI 2 2 2 2
4 + (b −1) + (c −1) = 1+ (b −1) + c ⇔ ⇔ 2 2 AI = CI 2 2 2 2
4 + (b −1) + (c −1) = (b − 2) + (c − 4) c = 2 c = 2 ⇔ ⇔ . b + 3c = 7 b = 1
Vậy, phương trình mặt cầu (S) được cho bởi: T©m I(2;1;0) (S):
⇔ (S): x2 + (y − 1)2 + (z − 2)2 = 9. B¸n kÝnh R = IA = 3
F Chú ý: Ngoài hai cách giải trên, để viết phương trình mặt cầu đi qua ba điểm A, B, C và có tâm thuộc mặt
phẳng (P) chúng ta còn có thể tận dụng được tính chất của ∆ABC để nhận được lời giải đơn giản hơn, cụ thể:
Bíc 1: Ta có:
Nếu ∆ABC đều thì tâm đường tròn ngoại tiếp ∆ABC là trọng tâm H của ∆ABC.
Nếu ∆ABC vuông tại A thì tâm đường tròn ngoại tiếp ∆ABC là trung điểm H của BC.
Bíc 2: Viết phương trình đường thẳng (d) qua H và vuông góc với với mặt phẳng (ABC).
Bíc 3: Tâm {I} = (P) ∩ (d), nên toạ độ của I là nghiệm của hệ phương trình tạo bởi (d) và (P).
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 10 Tµi liÖu to¸n 12 n¨m häc 2018
Bíc 4: Vậy, phương trình mặt cầu (S) được cho bởi: T©m I (S): . B¸n kÝnh R = IA
Chúng ta sẽ được thấy cách giải này trong phần đường thẳng.
ThÝ dô 4. Lập phương trình mặt cầu đi qua ba điểm A(2; 1; 1), B(1; 1; 0), C(0; 2; 4) và có bán kính bằng 5 . Giải
Ta có thể trình bày theo các cách sau:
Cách 1: Giả sử mặt cầu (S) có phương trình:
(S): x2 + y2 + z2 − 2ax − 2by − 2cz + d = 0,
ta có ngay a 2 + b2 + c2 − d = 5. (1)
Vì các điểm A, B, C thuộc (S), ta có hệ phương trình:
6 − 4a − 2b − 2c + d = 0 2a + 2b − d = 2 c = 2 − a 2 − 2a − 2b + d = 0 ⇔ a + c = 2 ⇔ b = 5a +1. (I) 20 − 4b −8c + d = 0 a − b − 4c = 9 − d = 12a
Thay (I) vào (1), ta được:
a 2 + (5a + 1)2 + (2 − a)2 − 12a = 5 ⇔ 27a2 − 6a = 0 ⇔ 2 a = 0 hoặc a = . 9 Khi đó:
Với a = 0 ta được b = 1, c = 2 và d = 0 nên:
(S1): x2 + y2 + z2 − 2y − 4z = 0. 2 19 16 8
Với a = ta được b = , c = vµ d = nên: 9 9 9 3 4 38 32 8 2 2 2 (S ) : x + y + z − x − y − z − = 0 . 2 9 9 9 3
Vậy, tồn tại hai mặt cầu (S1) và (S2) thỏa mãn điều kiện đầu bài.
Cách 2: Giả sử mặt cầu (S) với bán kính bằng 5 có phương trình:
(S): (x − a)2 + (y − b)2 + (z − c)2 = 5.
Vì các điểm A, B, C thuộc (S), ta có hệ phương trình: 2 2 2 (
2 − a) + (1 − b) + (1 − c) = 5 2 2 2 (1 − a) + (1 − b) + c = 5 2 2 2 (1 − a) + (1 − b) + c = 5 ⇔ a + c = 2 2 2 2 a + (2 − b) + (4 − c) = 5 a − b − 4c = 9 − 2 2 2 (1 − a) + (1 − b) + c = 5 2 2 2 (
1 − a) + 25a + (2 − a) = 5 ⇔ c = 2 − a ⇔ c = 2 − a b = 5a +1 b = 5a + 1 2 27a − 6a = 0 a = 0 ⇒ b =1, c = 2 vµ d = 0 ⇔ c = 2 − a ⇒ 2 19 16 8 . a = ⇒ b = , c = vµ d = b = 5a + 1 9 9 9 3 Khi đó:
Với a = 0, b = 1, c = 2 và d = 0 ta được:
(S1): x2 + y2 + z2 − 2y − 4z = 0.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 11 Tµi liÖu to¸n 12 n¨m häc 2018 2 19 16 8 Với a = , b = , c = vµ d = ta được: 9 9 9 3 4 38 32 8 2 2 2 (S ) : x + y + z − x − y − z − = 0 2 9 9 9 3
Vậy, tồn tại hai mặt cầu (S1) và (S2) thỏa mãn điều kiện đầu bài.
ThÝ dô 5. Cho bốn điểm A(1; 1; 1), B(1; 2; 1), C(1; 1; 2) và D(2; 2; 1).
a. Chứng tỏ rằng A, B, C, D không đồng phẳng. Tính thể tích tứ diện ABCD.
b. Lập phương trình mặt cầu ngoại tiếp tứ diện ABCD. Giải
a. Ta có AB (0; 1; 0), AC (0; 0; 1), AD (1; 1; 0) , suy ra:
AB, AC.AD
= (1; 0; 0)(1; 1; 0) = 1 ≠ 0
⇒ AB , AC , AD không đồng phẳng ⇔ A, B, C, D không đồng phẳng. Ta có:
1 1 V ABCD = AB, AC .AD = | đvtt. 6 6
b. Ta có thể trình bày theo các cách sau:
Cách 1: Giả sử mặt cầu (S) có tâm I(a; b; c), khi đó ta có điều kiện: IA = IB 2 2 IA = IB IA = IC ⇔ 2 2 IA = IC IA = ID 2 2 IA = ID 2 2 2 2 2 2 (x
−1) + (y −1) + (z −1) = (x −1) + (y − 2) + (z −1) ⇔ 2 2 2 2 2 2 (x
−1) + (y −1) + (z −1) = (x −1) + (y −1) + (z − 2) 2 2 2 2 2 2
(x −1) + (y −1) + (z −1) = (x − 2) + (y − 2) + (z −1) 2y = 3 ⇔ 3 3 3 3 2z = 3 ⇔ x = y = z = ⇒ I ; ; . 2 2 2 2 x + y − 3 = 0
Vậy, phương trình mặt cầu (S) được cho bởi: 3 3 3 T©m I ; ; 2 2 2 2 2 2 3 3 3 3 (S): ⇔ (S): x − + y − + z − = . 3 2 2 2 4 B¸n kÝnh R = IA = 2
Cách 2: Giả sử mặt cầu (S) có dạng:
(S): x2 + y2 + z2 - 2ax - 2by - 2cz + d = 0, điều kiện a2 + b2 + c2 - d ≥ 0.
Điểm A, B, C, D ∈ (S), ta được: 3
− 2a − 2b − 2c + d = 0 2a + 2b + 2c − d = 3
6 − 2a − 4b − 2c + d = 0 2a + 4b + 2c − d = 6 ⇔ 6 − 2a − 2b − 4c + d = 0 2a + 2b + 4c − d = 6
9 − 4a − 4b −2c + d = 0 4a + 4b + 2c − d = 9 3 a = b = c = ⇔
2 , thoả mãn điều kiện. d = 6
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 12 Tµi liÖu to¸n 12 n¨m häc 2018
Vậy, phương trình mặt cầu (S) có dạng:
(S): x2 + y2 + z2 - 3x − 3y - 3z + 6 = 0.
F Chú ý: Với câu b), ngoài hai cách giải trên, để viết phương trình mặt cầu đi qua bốn điểm không đồng
phẳng A, B, C, D (ngoại tiếp tứ diện ABCD) chúng ta còn có thể tận dụng được tính chất của tứ
diện ABCD để nhận được lời giải đơn giản hơn, cụ thể:
Trường hợp 1: Nếu DA = DB = DC thì:
Bíc 1: Xác định tâm I bằng cách:
Dựng đường cao DH⊥(ABC).
Dựng mặt phẳng trung trực (P) của DA.
Khi đó {I} = (DH) ∩ (P).
Bíc 2: Vậy, phương trình mặt cầu (S) được cho bởi: T©m I (S): . B¸n kÝnh R = IA
Trường hợp 2: Nếu DA⊥(ABC) thì:
Bíc 1: Xác định tâm I bằng cách:
Gọi K là tâm đường tròn ngoại tiếp ∆ABC.
Dựng đường thẳng (d) qua K và song song với DA (hoặc (d) ⊥ (ABC).
Dựng mặt phẳng trung trực (P) của DA.
Khi đó {I} = (d) ∩ (P).
Bíc 2: Vậy, phương trình mặt cầu (S) được cho bởi: T©m I (S): . B¸n kÝnh R = IA Trườ π
ng hợp 3: Nếu ACB =
ADB = thì mặt cầu ngoại tiếp DABC có tâm I là trung điểm AB 2 AB và bán kính R = . 2
Trường hợp 4: Nếu AD và BC có đoạn trung trực chung EF thì:
Bíc 1: Ta lần lượt:
Viết phương trình tham số của đường thẳng (EF) theo t.
Khi đó, mặt cầu ngoại tiếp tứ diện ABCD có tâm I ∈ EF (thỏa mãn phương trình tham số của EF).
Từ điều kiện IA2 = IC2 = R2 suy ra giá trị tham số t, từ đó nhận được tọa độ tâm I.
Bíc 2: Vậy, phương trình mặt cầu (S) được cho bởi: T©m I (S): . B¸n kÝnh R = IA
ThÝ dô 6. Viết phương trình mặt cầu:
a. Có tâm I(2; 1; −6) và tiếp xúc với trục Ox.
b. Có tâm I(2; −1; 4) và tiếp xúc với mặt phẳng (Oxy).
c. Có tâm O(0; 0; 0) tiếp xúc với mặt cầu (T) có tâm I(3; –2; 4), bán kính bằng 1. Giải
a. Gọi H1 là hình chiếu vuông góc của I lên Ox, ta có H1(2; 0; 0).
Để (S) tiếp xúc với trục Ox điều kiện là: R = d(I, Ox) = IH1 = 2 2 1 + ( 6 − ) = 37. Khi đó:
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 13 Tµi liÖu to¸n 12 n¨m häc 2018 T©m I(2;1;− 6) (S):
⇔ (S): (x - 2)2 + (y − 1)2 + (z + 6)2 = 37. B¸n kÝnh R = 37
b. Vì (S) tiếp xúc với mặt phẳng (Oxy) điều kiện là: R = d(I, (Oxy)) = 4. Khi đó: T©m I(2;−1;4) (S):
⇔ (S): (x - 2)2 + (y + 1)2 + (z − 4)2 = 16. B¸n kÝnh R = 4
c. Để (S) tiếp xúc với mặt cầu (T) có tâm I(3; –2; 4), bán kính bằng 1 điều kiện là: R +1 = OI R +1 = 29 R = 29 −1 ⇔ ⇔ . R −1 = OI R −1 = 29 R = 29 +1 Khi đó:
Với R = 29 −1 , ta được mặt cầu: T©m O(0;0;0) (S1): ⇔ (S ) : x + y + z = 29 −1 1 ( )2 2 2 2 . B¸n kÝnh R = 29 −1
Với R = 29 + 1 , ta được mặt cầu: T©m O(0;0;0) (S2): ⇔ (S ) : x + y + z = 29 + 1 2 ( )2 2 2 2 . B¸n kÝnh R = 29 +1
Vậy, tồn tại hai mặt cầu (S1), (S2) thỏa mãn điều kiện đầu bài.
F Nhận xét: Như vậy, qua bài toán trên chúng ta đã làm quen với việc viết phương trình mặt cầu tiếp xúc
với đường thẳng, mặt phẳng và mặt cầu. Cụ thể:
Mặt cầu (S) tâm I tiếp xúc với đường thẳng (d) khi: R = d(I, (d)).
Mặt cầu (S) tâm I tiếp xúc với mặt phẳng (P) khi: R = d(I, (P)).
Mặt cầu (S) tâm I tiếp xúc với mặt cầu (T) tâm T, bán kính RT khi: (S)vµ (T)tiÕp xóc ngoµi R + R = IT T ⇔ . (S)vµ (T)tiÕp xóc trong R − R = IT T
ThÝ dô 7. Lập phương trình mặt cầu:
a. Có tâm nằm trên tia Ox, bán kính bằng 5 và tiếp xúc với mặt phẳng (Oyz).
b. Có bán kính bằng 2 và tiếp xúc với (Oxy) tại điểm M(3; 1; 0). Giải
a. Giả sử mặt cầu (S) có tâm I(a; b; c) và bán kính R.
Từ giả thiết suy ra R = 5, ngoài ra:
(S) tiếp xúc với mặt phẳng (Oyz) điều kiện là: d(I, (Oyz)) = R ⇔ a = 5.
Tâm nằm trên tia Ox điều kiện là b = c = 0.
Vậy, phương trình mặt cầu (S) được cho bởi: T©m I(5;0;0) (S):
⇔ (S): (x - 5)2 + y2 + z2 = 25. B¸n kÝnh R = 5
b. Ta lần lượt đánh giá:
Mặt cầu (S) tiếp xúc với mặt phẳng (Oxy) tại điểm M(3; 1; 0) nên tâm I(3; 1; c). Vì R = 2 nên:
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 14 Tµi liÖu to¸n 12 n¨m häc 2018
IM = 2 ⇔ c = ±2 ⇒ I1(3; 1; 2) và I2(3; 1; −2). Khi đó:
Với tâm I1(3; 1; 2) ta được mặt cầu: T©m I (3;1;2) (S1): 1
⇔ (S1): (x - 3)2 + (y − 1)2 + (z − 2)2 = 4. B¸n kÝnh R = 2
Với tâm I2(3; 1; −2) ta được mặt cầu: T©m I (3;1;− 2) (S2): 2
⇔ (S2): (x - 3)2 + (y − 1)2 + (z + 2)2 = 4. B¸n kÝnh R = 2
Vậy, tồn tại hai mặt cầu (S1) và (S2) thỏa mãn điểu kiện đầu bài. BÀI TẬP TỰ LUẬN Bi 1
1. Trong không gian với hệ tọa độ Oxyz cho ba véc tơ
a 2i 3j 5k,
b 3j 4k, c i 2j
a) Xác định tọa độ các véc tơ a, ,
b c , x 3a 2b và tính x
b) Tìm giá trị của x để véc tơ y 2x 1; x ;3x
2 vuông góc với véc tơ 2b c
c) Chứng minh rằng các véc tơ a, ,
b c không đồng phẳng và phân tích véc tơ u 3;7;14 qua ba véc tơ a, , b c .
2. Trong không gian với hệ trục tọa độ Oxyz , cho các véc tơ
a 2i 3j k, b i 2k,
c 2j 3k
a) Xác định tọa độ các véc tơ a, , b c
b) Tìm tọa độ véc tơ u 2a 3b 4c và tính u
c) Tìm x để véc tơ v (3x 1;x 2; 3 x) vuông góc với b
d) Biểu diễn véc tơ x (3;1;7) qua ba véc tơ a, , b c . Bi 2
1. Cho hai véc tơ a,b có 0
a 2 3, b 3,(a,b ) 30 . Tính
a) Độ dài các véc tơ a b,5a 2b,3a 2b,
b) Độ dài véc tơ a,b , a,3b , 5a, 2b .
2. Tìm điều kiện của tham số m sao cho a) Ba véc tơ
u(2;1; m),v(m 1; 2; 0),w(1; 1;2) đồng phẳng. b) (
A 1; 1;m),B(m; 3;2m 1),C(4; 3;1),D(m 3; m;2 m) cùng thuộc một mặt phẳng.
c) Góc giữa hai véc tơ a(2;m;2m 1),b(m;2;1) là 0 60 .
Bi 3 Cho tam giác ABC có B(1;1;1),C(2;3;5). Điểm A có tung độ 1 7 là
, hình chiếu của điểm A trên BC là K 1; ; 3 và diện tích tam 3 3 49
giác ABC là S . 3
1. Tìm tọa độ đỉnh A biết A có hoành độ dương.
2. Tìm tọa độ chân đường vuông góc hạ từ B đến AC.
3. Tìm tọa độ tâm I của đường tròn ngoại tiếp và tọa độ trực tâm H của tam giác ABC.
4. Chứng minh HG 2GI với G là trọng tâm tam giác ABC.
Bi 4 Cho tứ diện ABCD có các cặp cạnh đối bằng nhau. Tọa độ các
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 15 Tµi liÖu to¸n 12 n¨m häc 2018 điểm (
A 2; 4;1),B(0; 4; 4),C(0; 0;1) và D có hoành độ dương.
1. Xác định tọa độ điểm D.
2. Gọi G là trọng tâm của tứ diện ABCD. Chứng minh rằng G cách đều các đỉnh của tứ diện.
3. Gọi M, N lần lượt là trung điểm của A ,
B CD. Chứng minh rằng MN là đường vuông góc chung của hai đường thẳng AB và CD.
4. Tính độ dài các đường trọng tuyến của tứ diện ABCD.
Tính tổng các góc phẳng ở mỗi đỉnh của tứ diện ABCD.
Bi 5 Trong không gian Oxyz cho bốn điểm ( A 0;2; 0), (
B 1; 0;3), C(0;2; 0), D(3;2;1) .
1. Chứng minh rằng bốn điểm , A ,
B C,D không đồng phẳng;
2. Tính diện tích tam giác BCD và đường cao BH của tam giác BCD ;
3. Tính thể tích tứ diện ABCD và đường cao của tứ diện hạ từ A ;
4. Tìm tọa độ E sao cho ABCE là hình bình hành;
5. Tính cosin của góc giữa hai đường thẳng AC và BD ;
6. Tìm điểm M thuộc Oy sao cho tam giác BMC cân tại ;
7. Tìm tọa độ trọng tâm G của tứ diện ABCD và chứng minh , A G, ’
A thẳng hàng với A' là trọng tâm tam giác BCD .
Bi 6 Cho tam giác ABC có (
A 2; 3;1),B(1;2; 0),C(1;1; 2).
1. Tìm tọa độ chân đường vuông góc kẻ từ A xuống BC .
2. Tìm tọa độ H là trực tâm của tam giác ABC .
3. Tìm tọa độ I là tâm đường tròn ngoại tiếp của tam giác ABC .
4. Gọi G là trọng tâm của tam giác ABC . Chứng minh rằng các điểm G, H, I nằm trên một đường thẳng. Bi 7
Trong không gian với hệ tọa độ Đề Các vuông góc Oxyz cho tam giác đều ABC có (
A 5; 3;1),B(2; 3; 4) và điểm C nằm
trong mặt phẳng (Oxy) có tung độ nhỏ hơn 3 .
a) Tìm tọa độ điểm D biết ABCD là tứ diện đều.
b) Tìm tọa độ điểm S biết S , A S ,
B SC đôi một vuông góc. Bi 8
Trong không gian với hệ tọa độ Oxyz cho điểm A3;2;4
a) Tìm tọa độ các hình chiếu của A lên các trục tọa độ và các mặt phẳng tọa độ
b) Tìm M Ox, N Oy sao cho tam giác AMN vuông cân tại A
c) Tìm tọa độ điểm E thuộc mặt phẳng (Oyz) sao cho tam giác AEB cân tại E và có diện tích bằng 3 29 với B 1;4;4 . Bi 9
Trong không gian với hệ trục Oxyz cho ( A 4; 0; 0),
B(x ;y ; 0) với 0 0 x ,y 0
thỏa mãn AB 2 10 và 0 AOB 45 . 0 0
a) Tìm C trên tia Oz sao cho thể tích tứ diện OABC bằng 8 .
b) Gọi G là trọng tâm A
BO và M trên cạnh AC sao cho AM x . Tìm x để OM GM . HƯỚNG DẪN GIẢI.
Vấn đề 1. CÁC ĐỊNH TỌA ĐỘ CỦA ĐIỂM, TỌA ĐỘ VECTƠ Bài 1
1. a) Ta có: a = (2; 3; 5 − ) , b = (0; 3; − 4), c = ( 1; − 2 − ; 0) Suy ra 3a = (6; 9; 1 − 5), 2b = (0; 6; − 8) ⇒ x = (6; 3; 7 − ) Do đó: 2 2 2 x = 6 + 3 + ( 7) − = 94
b) Ta có: 2b − c = (1; 4
− ; 8), nên y vuông góc với 2b − c khi và chỉ khi y ( b − ) 1 . 2
c = 0 ⇔ 1.(2x − 1) − 4.(−x) + 8(3x + 2) = 0 ⇔ x = − . 2 c) Cách 1: Ta có: , a b ( 3; 8; 6) ,ab = − − − ⇒ .c = 3 + 16 = 19 ≠ 0
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 16 Tµi liÖu to¸n 12 n¨m häc 2018 Nên ba véc tơ , a ,
b c không đồng phẳng.
Cách 2. Giả sử ba véc tơ , a ,
b c đồng phẳng. Khi đó tồn tại hai số thực ,
x y sao cho a = . x b + . y c (1) −y = 2
Mà xb + yc = (− ; y 3 − x − 2 ;
y 4x) nên (1) ⇔ 3
− x − 2y = 3 hệ này vô nghiệm. 4x = 5 − Vậy , a ,
b c không đồng phẳng.
Giả sử u = ma + nb + pc (2)
Do ma + nb + pc = (2m − ;
p 3m − 3n − 2 ; p 5
− m + 4n) nên (2) tương đương với 2m − p = 3
3m − 3n − 2p = 7 ⇔ m = 2, n = 1, − p = 1 5 − m + 4n = 14 −
Vậy u = 2a − b + c .
2. a) Ta có a = (2; 3; 1 − ), ( b = 1 − ; 0; 2), c = ( 0; 2; 3 − )
b) Ta có: u = 2a + 3b − 4c = (1; 2
− ;16) ⇒ u = 3 29 . 6
c) Ta có: v ⊥ b ⇔ . v b = 0 ⇔ 1
− (3x − 1) + 2(3 − x) = 0 ⇔ x = . 5 32 k = 11 k − p = 3 d) Giả sử: 1
x = k.a + .
p b + l.c ⇔ 3k + 2l = 2 ⇔ p = − 11
−k + 2p − 3l = 7 37 l = − 11 Vậy 32 1 37 x = a − b − c . 11 11 11 Bài 2 1. Do 0
a = 2 3, b = 3, ( , a b) = 30 nên ta có . a b = 9. a) Sử dụng công thức 2 2 2 2 2 ma + nb = (ma + n ) b
= m a + 2mn.ab + n b .
Ta tính được a + b = 39, 5a + 2b = 2 129, 3a − 2b = 6.
b) Sử dụng công thức ,
ma nb = m.n . a . b . si n( , ma nb). Với chú ý 0 0 0 ( , a 3b) = ( , a b) = 30 , (5 ,
a − 2b) = 180 − ( , a b) = 150 . 2. a) Ta có [ ] 2 u,v = ( 2
− m;− m − m;− m − 5) nên ba véc tơ đã cho đồng phẳng khi và chỉ khi [u,v].w = 0 hay − + − 2
2m.1 ( m − m).(−1) + (−m − 5).2 = 0 ⇔ 2
m − 3m − 10 = 0 ⇔ m = −2;m = 5.
Vậy giá trị cần tìm của m là m = 2; − m = 5. b) Ta có CA( 3
− ;− 4;m − 1),CB(4 − m;0;2 − 2m), CD(1 − m;3 + m;m − 1). Suy ra C
A,CB = (8(1 − m); (m −1)(m + 2); 4(m − 4)).
Vậy bốn điểm A,B,C,D đồng phẳng khi và chỉ khi CA ,CB .CD = 0, hay
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 17 Tµi liÖu to¸n 12 n¨m häc 2018 2
8(1 − m) + (m − 1)(m + 2)(3 + m) + 4(m − 1)(m − 4) = 0 2
⇔ (m − 1) (m + 18) = 0 ⇒ m = 1; m = 18. −
Vậy giá trị cần tìm của m là m = 1; m = 18. − a. b
c) Ta có cos(a, b) = nên a . b 0 2m + 2m + (2m −1).( 1 − ) 1 2m + 1 cos60 = ⇔ = 2 2 2 2 2 2
2 + m + (2m −1) . m + 2 + ( 1) − 2 2 2 5m − 4m + 5. m + 5 Với 1
m ≥ − , nên bình phương hai vế và rút gọn ta được 2 4 3 2 2 2
5m − 4m + 14m − 36m + 21 = 0 ⇔ (m − 1) (5m + 6m + 21) = 0 ⇔ m = 1
Giá trị cần tìm của m là m = 1. Bài 3 2S 14
1. Ta có BC(3;2;6) ⇒ BC = 7 nên ABC AK = = . BC 3 AK ⊥ BC Gọi 1 A x; ;z
thì AK (1 − x;2;3 − z). Do đó từ 14 suy ra 3 AK = 9 3 x + 6z = 25 3 x + 6z = 25 ⇔ (1 − x) + (3 − z)2 2 160 2 = 45 z − 318z + 405 = 0 9 Từ đó ta có 37 1 25 A − ; ; (loại) hoặc 1 5 A 5; ; (thỏa mãn). 15 3 5 3 3
2. Gọi L là chân đường vuông góc hạ từ B đến AC. 8 10
Ta có CL = tCA nên L 2 + 3t;3 − t;5 − t . 3 3 Do đó 8 10 8 10 BL 3 + 3t;2 − t;6 − t ,CA 3;− ; − nên 3 3 3 3 3 19 7 BL.CA = 0 ⇔ t = ⇒ L ; ;3 . 5 5 5 3 3 5 4 7 3. I ; ; , H 3; ; . 2 2 3 3 3 13 17 1 4 1 1 2 4. G 2; ; ⇒ HG 1; − ; − = 2GI − ; ; − . 9 9 9 9 2 18 9
Bài 4 A(2;4;1),B(0;4;4),C(0;0;1)
1. Gọi D(x; y;z). Từ DA = BC,DB = CA,DC = AB ta có hệ 2 2 2 x = 2(1 − y) (
x − 2) + (y − 4) + (z −1) = 25 2 2 2 12 − 4y
x + (y − 4) + (z − 2) = 20 ⇔ z = 3 2 2 2 x y (z 1) 13 + + − = 2 2 2 x + y + (z −1) = 13 166 144 52 Suy ra D(2;0;4), D − ; ; . Chọn điểm D(2;0;4). 61 61 61
2. Tọa độ trọng tâm của tứ diện là 5 G 1;2; . 2 Tính được 29 GA = GB = GC = GD = . 2
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 18 Tµi liÖu to¸n 12 n¨m häc 2018
Vậy G cách đều các đỉnh của tứ diện (là tâm mặt cầu ngoại tiếp tứ diện). 5 5 3. Ta có M 1;4; , N 1;0; ⇒ MN(0;− 4;0). 2 2
Do đó MN.AB = MN.CD = 0. Hay MN là đường vuông góc chung của hai đường thẳng AB và CD. 4. Gọi A ,′B ,C ′
,′D′ lần lượt là trọng tâm của các mặt đối diện. 2 29
Ta có AA′ = BB′ = CC′ = DD′ = . 3
5. Ba góc ở mỗi đỉnh của tứ diện là ba góc của một tam giác, nên tổng các góc ở mỗi đỉnh là 0 180 . Bài 5
1. Ta có BA = (1; 2; 3), BC = (1; 2 − ; 3),
BD = (4; 2; 4) , CD = (3; 4;1) 2 − 3 3 1 1 − 2 Suy ra , BC BD = ; ; = ( 1 − 4; 8;10) 2 4 4 4 4 2
Do đó BA. ,
BC BD = 32 ≠ 0 ⇒ A, B, , C D không đồng phẳng. 1 1 2. Ta có: 2 2 2 S , BC BD = = ( 1 − 4) + 8 + 10 = 3 10 B ∆ CD 2 2 1 2S 6 10 6 65 Vì ∆ S BH .CD BCD BH = = = . B ∆ = nên suy ra CD 2 CD 13 26
1 16 3. Ta có: V BA. , BC BD = = . ABCD 6 3 Gọi 3V 16 8 10
h = d( A, (BCD)) ABCD ⇒ h = = . S 15 B ∆ CD 3 10 4. Gọi E( ; x ; y ) z . x = 1 x = 1
ABCE là hình bình hành ⇔ CE = BA ⇔ y + 2 = 2 ⇔ y = 0 . z = 3 z = 3 Vậy E(1; 0; 3) . AC BD
5. Ta có: AC = (0; 4; − 0) ⇒ . AC BD = 8 − ⇒ (AC BD) . 8 1 cos , = = = . . AC BD 4.6 3
6. Ta có M ∈ Oy ⇒ M (0; ;
y 0) . Tam giác BM C cân tại 2 2
M ⇔ M C = M B 2 2 2 2 3 ⇔ ( 1) −
+ y + 3 = (y + 2) ⇔ y = . 2 Vậy 3 M 0; ; 0 . 2 2 2 1 1 1 2 2 1 3 1
7. Ta có: A ' ; 0; − , G ; ; −
⇒ AA ' = ; −2; − , AG = ; − ; − 3 3 2 2 2 3 3 2 2 2 2 2 − 2 − 4
4 Mà 3 3 = = = ⇒ AA ' =
AG ⇒ A, A ', G thẳng hàng. 1 3 − 1 3 3 − 2 2 2 Bài 6
1. Gọi K là chân đường vuông góc kẻ từ A xuống BC .
Khi đó: K ∈ BC AK ⊥ BC
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 19 Tµi liÖu to¸n 12 n¨m häc 2018
• K ∈ BC nên BK = t. , BC do đó
x + 1 = t(1 + 1) x = 2t − 1 K K
y − 2 = t(1 − 2) ⇒ y t t
⇒ K (2t − 1; 2 − t; − 2t) . K = 2 − ( ∈ ) K x − 0 = t(−2 − 0) x = − t K 2 K
• AK ⊥ BC ⇔ AK .BC = 0. Vì AK (2t − 3; − 1 − t; − 1 − 2t) nên 1 (2t − 3).2 + ( 1 − − t).( 1 − ) + ( 1 − − 2t).( 2 − ) = 0 ⇔ t = 3 Tọa độ điểm K cần tìm là 1 5 2
K − ; ; − . 3 3 3 2. Gọi H ( ; x ; y )
z là trực tâm tam giác ABC Ta có
AH (x − 2; y − 3; z − 1), BH (x + 1; y − 2; ) z , AB( 3;
− − 1; − 1), AC( 1;
− − 2; − 3), BC(2; − 1; − 2)
Tích có hướng của hai véc tơ AB, AC là 1 − 1 − 1 − 3 − 3 − 1 −
AB, AC = ; ; = (1; − 8; 5). 2 − 3 − 3 − 1 − 1 − 2 −
Vì H là trực tâm tam giác ABC nên
⊥ AH .BC = 0 AH BC
2x − y − 2z = 1 −
BH ⊥ CA ⇔ BH .CA = 0
⇔ x + 2y + 3z = 3
H ∈ ( ABC)
x − 8 y + 5z = 17
AB, AC .AH = 0 −
Giải hệ ta được 2 29 1 H ; ; − . 15 15 3 3. Gọi I ( ; x ; y ) z
là tâm đường tròn ngoại tiếp tam giác ABC . Ta có
AI (x − 2; y − 3; z − 1), BI (x + 1; y − 2; )
z , CI (x − 1; y − 1; z + 2).
Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên 2 2 AI = BI AI = BI
6x + 2y + 2z = 9 2 2 AI = CI ⇔ AI = CI
⇔ x + 2y + 3z = 4
I ∈ ( ABC)
x − 8 y + 5z = 17
AB, AC .AI = 0 −
Giải hệ ta được 14 61 1 I ; ; − . 15 30 3
4. Trọng tâm G của tam giác ABC có tạo độ thỏa mãn
2 − 1 + 1 3 + 2 + 1 1 + 0 − 2 2 1 G ; ; = ; 2; − 3 3 3 3 3 Do đó 8 1 4 1 H G ; ; 0 , GI ;
; 0 nên H G = 2GI , tức là ba điểm ,
G H , I nằm trên một đường 15 15 15 30 thẳng. Bài 7
Vì C ∈ (Ox ) y nên C( ; x ; y 0). Ta có AB( 3;
− 0; − 3), AC(x − 5; y − 3;1), BC(x − 2; y − 3; 4)
Tam giác ABC là tam giác đều nên AB = AC = , BC do đó 2 2 2 AC = AB
(x − 5) + (y − 3) + 1 = 18 ⇔ = 2 2 2 2 2 2 AC BC (x
− 5) + (y − 3) + 1 = (x − 2) + (y − 3) + 4
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 20 Tµi liÖu to¸n 12 n¨m häc 2018 2 (y − 3) = 1 x = 1; y = 4 ⇔ ⇔ . x = 1 x = 1; y = 2
Vì C có tung độ nhỏ hơn 3 nên C(1; 2; 0). a) Gọi D( ; x ; y ). z
Khi đó AD(x − 5; y − 3; z + 1), BD(x − 2; y − 3; z + 4), CD(x − 1; y − 2; ) z
Tam giác ABC là tam giác đều nên ABCD là tứ diện đều khi và chỉ khi AD = BD = CD = AB = 3 2. Ta có hệ phương trình 2 2 2 2 2 2
(x − 5) + ( y − 3) + (z + 1) = (x − 2) + ( y − 3) + (z + 4) 2 2 2 2 2 2
(x − 5) + (y − 3) + (z + 1) = (x − 1) + (y − 2) + z 2 2 2
(x − 5) + ( y − 3) + (z + 1) = 18 z = 1 − x z = 1 − x
⇔ y = 16 − 5x
⇔ y = 16 − 5x 2 2 2 2 (x
− 5) + (13 − 5x) + (2 − x) = 18 3x − 16x + 20 = 0 Giải phương trình 2
3x − 16x + 20 = 0 ta được 10 x = 2, x = . 3
Vậy tọa độ các điểm
D là D(2; 6; − 1) hoặc 10 2 7 D ; − ; − . 3 3 3 b) Gọi S( ; x ; y ).
z Ta có AS(x − 5; y − 3; z + 1), BS(x − 2; y − 3; z + 4), CS(x − 1; y − 2; ) z
SA, SB, SC đôi một vuông góc khi và chỉ khi = 2 . AS BS 0
(x − 5)(x − 2) + ( y − 3) + (z + 1)(z + 4) = 0 B .
S CS = 0 ⇔ (x − 2)(x − 1) + (y − 3)(y − 2) + (z + 4)z = 0 =
(x − 1)(x − 5) + ( y − 2)( y − 3) + ( z z + 1) = 0 . CS AS 0 2 2 2
x + y + z − 7x − 6 y + 5z = 23 −
x + y − 4z = 12 2 2 2
⇔ x + y + z − 3x − 5y + 4z = 8 − ⇔ 3 − x − 3z = 3 − 2 2 2 2 2 2
x + y + z − 6x − 5 y + z = 11 − x
+ y + z − 6x − 5y + z = 11 − y = 5z + 11
⇔ x = 1 − z 2 3z + 10z + 8 = 0 Giải phương trình 2
3z + 10z + 8 = 0 ta được 4 z = 2; − z = − . 3 Suy ra hai điểm S thỏa mãn là 7 13 4
S(3;1; − 2), S ; ; − . 3 3 3 Bài 8
a) Gọi A , A , A lần lượt là hình chiếu của A lên các trục , Ox ,
Oy Oz . B , B , B là hình chiếu của A lên 1 2 3 1 2 3
các mặt phẳng tọa độ (Ox ), y (Oy ), z (Ozx) . Ta có: A 3; 0; 0 , A 0; 2;
− 0 , A 0; 0; 4 và B 3; 2;
− 0 , B 3; 0; 4 , B 0; 2; − 4 1 ( ) 2 ( ) 3 ( ) 1 ( ) 2 ( ) 3 ( )
b) Do M ∈ Ox ⇒ M (m; 0; 0) , N ∈ Oy ⇒ N ( 0; n; 0)
Suy ra AM = (m − 3; 2; 4 − ), AN = ( 3; − n + 2; 4 − )
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 21 Tµi liÖu to¸n 12 n¨m häc 2018
AM .AN = 0
Tam giác AM N vuông cân tại A nên ta có 2 2 AM = AN 2(n + 2) + 16 m − 3 = (1) 3
− (m − 3) + 2(n + 2) + 16 = 0 3 ⇔ ⇔ 2 2 2 2 2 2 2 (m − 3) + 2 + ( 4 − ) = ( 3 − ) + (n + 2) + ( 4 − ) 2(n + 2) + 16 2 = (n + 2) + 5 (2) 3 Ta có: 2 2
(2) ⇔ 4(n + 2) + 64(n + 2) + 256 = 9(n + 2) + 45 32 3 231 + 22 + 3 231 n + 2 = n = 2 ⇔ + − + − = ⇔ 5 ⇔ 5 5(n 2) 64(n 2) 211 0 32 − 3 231 22 − 3 231 n + 2 = n = 5 5 189 + 6 231 m = ⇒ 5 . 189 − 6 231 m = 5
Vậy có hai bộ thỏa yêu cầu bài toán: 189 6 231 22 3 231 + + M ; 0; 0 , N 0; ; 0 hoặc 1 1 15 5 189 6 231 22 3 231 − − M ; 0; 0 , N 0; ; 0 . 2 2 15 5
c) Vì E ∈ (Oy ) z nên E (0; ; x y) Suy ra AE = ( 3;
− y + 2; z − 4), BE = (
1; y − 4; z + 4) AE, BE ⇒
= (8y + 6z − 8;4z + 8;10 − 4y) 2 2 2 2 AE = BE AE = BE
Nên từ giả thiết bài toán ta có:
⇔ 2 1
AE, BE = 3 29
AE, BE = 1044 2 2 2 2 2 2 2 4z + 1 AE
= BE ⇔ 9 + (y + 2) + (z − 4) = 1 + (y − 4) + (z + 4) ⇔ y = 3 2 AE BE =
⇔ ( y + z − )2 + z + + ( − y)2 2 , 1044 8 6 8 (4 8) 10 4 = 1044 2 2 50z − 16 ⇔ + ( − z + )2 26 16z 34 4 8 +
− 1044 = 0 ⇔ z = 2, z = − 3 3 25
• z = 2 ⇒ y = 3 nên E (0; 3; 2) • 34 37 37 34 z = − ⇒ y = − nên 0; − ; − . 25 25 25 25 Bài 9
Ta có: OA = (4; 0; 0),
OB = (x ; y ; 0) ⇒ OA.OB = 4x 0 0 0
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 22 Tµi liÖu to¸n 12 n¨m häc 2018 2 2
(x − 4) + y = 40 0 0
Theo giả thiết bài toán ta có hệ phương trình sau: 4x 0 1 = 2 2 2 4. x + y 0 0 2 x + 2 y − 8x = 24 0 0 0 2 y = 2 x ⇔ ⇔ 0 0 2x = 2 x + 2 y 2
x − 4x − 12 = 0 0 0 0 0 0 x = 6 ⇔ 0 ⇒ B (6;6;0) y = 6 0
a) Do C ∈ Oz ⇒ C(0; 0; m), 0 m > . Ta có: OA (4; 0; 0), OB (6; 6; 0) OA, OB = = ⇒ = (0; 0; 24)
và OC = (0; 0; m)
1 OA, OB ⇒ .OC = 24m ⇒ V
= .24m = 8 ⇔ m = 2 ⇒ C(0; 0; 2) . OABC 6 10 b) Ta có G
; 2; 0 , AM = x AC = ( 4 − ; x 0; 2x) 3 2 ⇒ M (4 − 4 ;
x 0; 2x) ⇒ OM = (4 − 4 ;
x 0; 2x); GM = − 4 ; x 2; 2x 3
2 2
⇒ OM ⊥ GM ⇔ OM .GM = 0 ⇔ (4 − 4x)( − 4x) + 4x = 0 3 2 56 8 2 7 ± 19 ⇔ 20x − x +
= 0 ⇔ 15x − 14x + 2 = 0 ⇔ x = . 3 3 15
ĐÁP ÁN TRẮC NGHIỆM
Câu 1. Dựa vào lý thuyết: x mi n j pk , suy ra x m;n; p. Chọn C. Câu 2. Ta có 3
2x 3a 4b x 2b a . Suy ra 9 5 x
4; ; . Chọn A. 2 2 2 2m n 3p 5 m 2 Câu 3. Đặt x , m , n p, ta có m 3n 2 p 11 n
3 x 2,3,2. Chọn B. 3
m 2n4p 20 p 2
Câu 4. Ta có a 110 2 ; c 111 3. Xét . a b
1 .11.1 0.0 0 , suy ra a .
b Vậy đáp án còn lại D là sai. Chọn D. . b c Câu 5. Ta có b c 1.1 1.1 0.1 2 cos , . Chọn C. 2 2 2 2 2 2 b . c 1 1 0 . 1 1 1 6
Câu 6. Kiểm trả các đáp án, ta thấy đáp án B đúng.
Thật vậy, ta có 2p 3q r 11,6,
5 c . Chọn B.
Câu 7. Ta có 2a 3b c 3,22, 5 . Chọn A. Câu 8. Ta có . m a .
n b m 2n;n;2m 3n .
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 23 Tµi liÖu to¸n 12 n¨m häc 2018 m 2n 4 m 2 Suy ra . m a . n b c n 3 . Chọn C. n 3
2m 3n 5 2
ab 3;2m5;4
Câu 9. Ta có
b2ab 6m20 . b 1;3;2 8 3m 10 2 Do đó m
b (2a b ) 4 6m 20 4 . 3 Chọn A. 3m 10 2 m 4 m 0 m 0
Câu 10. Ta có u và v cùng phương k : u kv
2 km 2 . Chọn B. k 1 m 1 k 3 m k.1 m
Câu 11. Để hai vectơ
a và b cùng phương 2 k : a kb 2
k.n . 4 3 k.2 n 3 Chọn B.
u4,23 2 ,m3 2m4
Câu 12. Ta có . v 2 ,
m m 2,2m 2
Do đó u v 4.2m 23 2mm 23 2m42m 2 0 26 2 2
9 2m 6m 6 2 0 m . Chọn A. 6
Câu 13. Sai ở Bước 3, do giải phương trình cơ bản A B mà không có điều kiện B 0. Chọn D. Câu 14. Ta có
a.b a . b .cosa,b 9. Sử dụng công thức:
ma nb ma nb2 2 2 2 2 m a 2 . mn ab n b
Ta tính được a b 2 2 3 2
3 .12 2.3.2.9 2 .9 36 6 . Chọn D. 2 2
u 3 u u 9
Câu 15. Theo giả thiết, ta có . 2 1 2
v 1v v 1 2 Từ 2 2
u v 4 , suy ra 16 u v u v 2uv . 2 2 2 2 Kết hợp 1 và 2 , ta được 2
2uv u v u v 9 1 4 6 .
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 24 Tµi liÖu to¸n 12 n¨m häc 2018 2 Khi đó 2 2
u v u v 2uv 9 16 4. Vậy u v 2. Chọn C.
Câu 16. Áp dụng công thức ,
a b a . b .sin
,ab, ta được 0 ,
a b 2.5.sin 30 5. Chọn B.
Câu 17. Chú ý rằng a b 0 a b 0 5 , 2 180 , 150 .
Sử dụng công thức ma,nb .
m n . a . b .sinma,nb , ta được a b 0 5 , 2 5.
2 .2 3.3.sin150 30 3. Chọn C. A
Câu 18. Vẽ tam giác đều ABC , gọi M là trung điểm BC . Ta chọn u ,
BA v BM thỏa mãn giả thiết bài toán.
Suy ra u v BABM MA .
Khi đó v uvBM MA 0 , , 90 . Chọn D. B M C
Câu 19. M là trung điểm của AB suy ra tọa độ điểm M (1;1;0) .
N là trung điểm của CD suy ra tọa độ điểm N (1;1;2) .
I là trung điểm của MN suy ra tọa độ điểm I (1;1; ) 1 . Chọn D.
Câu 20. Ta có 2a − b = (5;2;−3) . Gọi M x; y;z, suy ra AM = (x; y − 2;z − ) 1 . x 5 x 5 Theo giả thiết, suy ra y 2 2
y 4 . Chọn D. z 1 3 z 2
Câu 21. Áp dụng lý thuyết: Điểm M x ; y ;z có tọa độ hình chiếu trên các mặt phẳng Oxy, Oyz , Oxz lần lượt là 0 0 0 M x ; y ;0 , 0; M y ; z ,
M x ;0; z . Chọn B. 1 0 0 2 0 0 3 0 0
Câu 22. Áp dụng lý thuyết: Điểm M x ; y ;z có các điểm đối xứng qua các mặt phẳng tọa độ Oxy, Oyz , Oxz 0 0 0
lần lượt là M x ; y ;z , M x ; y ;z , M x ;y ;z . 1 0 0 0 2 0 0 0 3 0 0 0
Do đó điểm đối xứng của M 3;2;
1 qua mặt phẳng Oxy là M '3;2; 1 . Chọn A.
Câu 23. Áp dụng lý thuyết: Điểm M x ; y ;z có hình chiếu vuông góc lên các trục Ox, Oy, Oz lần lượt là 0 0 0
M x ;0;0 , M 0; y ;0 , M
0;0; z . Do đo hình chiếu vuông góc của M 2016;1;2017 trên trục Oz là Ox 0 Oy 0 Oz 0
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 25 Tµi liÖu to¸n 12 n¨m häc 2018
0;0;2017 . Chọn D.
Câu 24. Áp dụng lý thuyết: Điểm M x ; y ;z thì điểm đối xứng của M qua các trục Ox , Oy , Oz lần lượt là 0 0 0
M x ;y ;z , M x ; y ;z , M x ;y ; z . 1 0 0 0 2 0 0 0 3 0 0 0
Do đó điểm đối xứng của A3;2;
1 qua trục y 'Oy là A'3;2; 1 . Chọn C.
Câu 25. Khoảng cách từ Ax; y;z đến trục Ox , được tính theo công thức d A Ox 2 2 , y z .
Tương tự d A Oy 2 2 ,
x z và d A Oz 2 2 , x y . Do đó d ,
A Oy 1 9 10. Chọn B.
Câu 26. Khoảng cách từ M đến gốc tọa độ O bằng MO 9 1 4 14 . Chọn D.
Câu 27. Tọa độ điểm M ' đối xứng với M qua mặt phẳng yOz là M 2;5;4 . Chọn A.
Câu 28. Tọa độ điểm M ' đối xứng với M qua trục Ox là M '1;2; 3 . Chọn B.
Câu 29. Ta có AB 2;2;0, AC 1;3;
3 . Gọi Dx; y;z .
x 3 223 1 7 x 10 Theo giả thiết AD 2AB 3AC y 4 2.2 3.3 13
y 17 . Chọn A.
z 2 2.03 39 z 7
Câu 30. Gọi G 'x; y;z là trọng tâm của tam giác A'B'C' .
Ta có G ' A' G ' B ' G 'C ' 0 G ' A AA'G 'B BB'G 'C CC ' 0
G ' A G ' B G 'C A' A B ' B C 'C 0 .
Suy ra G ' cũng là trọng tâm của tam giác ABC nên có tọa độ 4 1 G 2; ; . Chọn C. 3 3
Câu 31. Ta có MN 2;10;14 , MQ 1;5;7 . Suy ra MN 2MQ. Do đó ba điểm M, N,
Q thẳng hàng. Chọn B.
Câu 32. Ta có AB 12;6;0, AM 2m3;3;n 1 . 2
m 3 12k 3 Để m ,
A B, M thẳng hàng * k : AM k AB 3 6k 2 . n 1 0.k n 1 Chọn B.
Câu 33. Gọi M a;0;0Ox .
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 26 Tµi liÖu to¸n 12 n¨m häc 2018
Theo giả thiết: MA MB a 2 1 3 2 5 a 2 3 2 42 3 2 2 a . 2 Suy ra 3 M ;0;0 . Chọn B. 2
Câu 34. Gọi M x;0;zOxz . 2 2 MA MB MA MB Yêu cầu bài toán 2 2 MA MC MA MC 1
x2 102 1 z2 1 x2 102 0 z2 x 5/6 . Chọn C.
x2 2 z2 x2 2 z2 z 7/6 1 1 0 1 3 1 0 1
Câu 35. Áp dụng công thức tìm tọa độ trọng tâm. Chọn B.
Câu 36. Gọi H x; y;z . Ta có AH x; y;z 1 , BC 3;3; 1 , BH
x 1; y 2; z. x.3 .
y 3 z 1 . 1 0
AH BC Yêu cầu bài toán 5 14 8
H ; ; . x 1 y 2 z 19 19 19 BC BH 3 3 1 Chọn A.
Câu 37. Gọi D là chân đường phân giác trong góc B của tam giác ABC Ta có BA DA
DC . Tính được BA 26 , BC 104 . BC Suy ra 26 DA
DC DC 2DA . 104
4 x 21 x x 2 /3 Gọi
Dx; y; z . Từ DC 2DA 7 y 22 y
y 11/3 . Chọn A. 5
z 21z z 1 Câu 38. Gọi DA BA
D là chân phân giác trong của góc B , ta có 3 1
DA DC . DC BC 15 5 Suy ra D0;0;
3 . Vậy BD 2 5 . Chọn B. Câu 39. Gọi AB
F là chân đường phân giác ngoài góc A của tam giác ABC , ta có FB .FC . AC
Tính được AB 5 5 , AC 3 5 . Suy ra 5
FB FC 3FB 5FC . 3 3
5 x 53 x x 15 Gọi
F x; y; z. Từ 3FB 5FC 3
6 y 52 y
y 4 . Chọn B. 3
0z 50z z 0
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 27 Tµi liÖu to¸n 12 n¨m häc 2018
Câu 40. Ta có NM 3;2;2 , NP 2;m2; 1 .
Tam giác MNP vuông tại N NM.NP 0 6 2m22 0 m 0 . Chọn D.
Câu 41. Giả sử Ax ; y ;0Oxy, B0;0;z Oz. A A B
Vì G1;1;2 là trọng tâm của tam giác ABC nên x 0 A 2 1 3 x 1 A y 0 2 1 A
y 1 A B . A 1;1;0, 0;0;4 3 z 4 0 z 2 B 2 B 3 Chọn B.
Câu 42. Gọi M là trung điểm của AC . Do M Oy nên M 0; y;0 .
Suy ra C 4;2y 1;2 .
Gọi N là trung điểm của BC , suy ra 7
N ; y 3;6 . 2
Do N Oxz nên y 3 0 y 3 C 4;5;2. Chọn A. Câu 43. Ta có 2 2 2
AB 125; AC 45;BC 80 . Do đó 2 2 2
AB CA CB ABC vuông tạiC . Chọn C.
AB 0;2; 1
Câu 44. Ta có
AB.AC 0 AB AC . Chọn D.
AC 1;1;2
Câu 45. Ta có AB 3;BC 3; AC 2 . Vậy tam giác cân ở B . Chọn C.
Câu 46. Ta có A1;1; 1 , B5;1; 1 và BC 2;8
;3 . Suy ra tọa độ điểm C 7;9;2 .
Gọi Dx; y;z . Vì ABCD là hình bình hành nên x x x x x 3 A C B CD BA
y y y y y 9 . Chọn D. A C B
z z z z z 4 A C B
Câu 47. Gọi Qx; y;z . Để MNPQ là hình bình hành thì MN QP
x x x x
x x x x P Q N M x 2 Q P M N
y y y y
y y y y y 3 . Chọn C. P Q N M Q P M N
z z z z
z z z z z 4 P Q N M Q P M N
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 28 Tµi liÖu to¸n 12 n¨m häc 2018
Câu 48. Ta có AB 2;3;
3 , MC 2;3; 3 .
Suy ra AB MC hay ABCM là hình bình hành. NA 3;1;
1 , BC 3;1;
1 . Suy ra NA BC hay NACB là hình bình hành. Chọn D.
Câu 19. Từ giả thiết, suy ra A1;1;0 và B1;1;0 . Gọi Dx; y;z . x x x x 2 B A Do
OABD là hình bình hành nên OD AB
y y y y 0 . Chọn B. B A
z z z z 0 B A
Câu 50. Áp dụng công thức tính tọa độ trọng tâm của tứ diện. Chọn D.
Câu 51. Gọi I là tâm của hình hộp nên I là trung điểm của của D ' B , suy ra I 5;4; 5 .
Và I cũng là trung điểm của AC ' , suy ra C '8;4;10. Gọi B 'x; y;z. x x x x x 13 B C' C Do
B 'C 'CB là hình bình hành nên C ' B ' CB y y y y
y 0 . Chọn C. B C ' C
z z z z z 17 B C ' C
Câu 52. Rõ ràng A đúng theo tính chất của tích có hướng.
Đặt a x; y;z,
b x '; y ';z '
x, y, z, x ', y ', z ' . Ta có 3
b 3x ';3y';3z ' , a 3b
3yz '3zy ';3xz '3zx ';3xy '3x ' y ● , a b
yz ' zy '; xz ' zx '; xy ' x ' y , a b
yz ' zy '; xz ' zx '; xy ' x ' y , a 3b 3 a;b . Do đó B đúng. 2
a 2x;2y;2z 2 , a b
2yz '2zy ';2xz '2zx ';2xy '2x ' y ● , a b
yz ' zy '; xz ' zx '; xy ' x ' y , a b
yz ' zy '; xz ' zx '; xy ' x ' y 2 , a b 2 , a b . Do đó C đúng.
Vậy đáp án sai là D. Chọn D.
Câu 53. Áp dụng lý thuyết về tính chất của tích có hướng, ta có ,
u v u v sin ,uv.
Vậy A là đáp án sai. Chọn A.
Câu 54. Chọn B.
Câu 55. Kiểm tra ta thấy chỉ có bộ B thỏa mãn.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 29 Tµi liÖu to¸n 12 n¨m häc 2018
Thật vậy, ta có a 4;3;4, b 2; 1;2 a,b 10;0;10. Suy ra ,
a b.c 10.1 0.2 10.1 0. Chọn B.
Câu 56. Nhận thấy ,
a b.c 35 0 nên ,
a b,c không đồng phẳng. a
b (7,10,1) Ta có
. Suy ra a b c d và d c a b d a b c . c
d (7,10,1)
Vậy chỉ có câu D là sai. Chọn D. (Bạn đọc có thể kiểm tra trực tiếp) c a
Câu 57. Dựa vào lý thuyết về tích có hướng của hai vectơ, suy ra . Chọn C. c b a,b 1;3;7 Câu 58. Ta có: , a b.c 0 . Suy ra ,
a b, c đồng phẳng. Chọn C. c 1;5;2 Câu 59. Ta có , a b m
4,3m 2,7. m 4 5 Để c a,b thì
m 1. Chọn A. 3m 2 1 Câu 60. Ta có: , u w = ( 3 − ; 1; − 5)
Để ba vectơ đồng phẳng thì 8 ,
u w.v = 0 ⇔ 3
− m − 3 − 5 = 0 ⇔ m = − . Chọn D. 3 a b 2 ,
m 4;2m 1; m m 2 Câu 61. Ta có ,
a b.c 5m 2 . c 0;m2;2 Để ba vectơ 2 ,
a b, c đồng phẳng thì a,b.c 0
5m 2 0 m . Chọn A. 5 , a b 12,2,8 Câu 62. Ta có 2 ,
a b .c 2m 12m 16 . c 2 m 2,m , 5 m 2 Để ba vectơ ,
a b, c đồng phẳng thì a,b.c 0 2
2m 12m 16 0 . Chọn A. m 4
Câu 63. Ta có AB 0;2;
1 , AC 1;1;2 , AD 1;m 2; p .
Suy ra AB, AC 5;1;2 .
Để bốn điểm ,
A B, C, D đồng phẳng khi AB, AC .AD 0
m 2 p 3 . Chọn C.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 30 Tµi liÖu to¸n 12 n¨m häc 2018
Câu 64. Ta có AB 2;1;4, AC 1;4;4,
AD a;b;4. Suy ra AB, AC 12;4;7 .
Để hai đường thẳng AD và BC cùng thuộc một mặt phẳng khi và chỉ khi bốn điểm ,
A B, C, D đồng phẳng
AB, AC
.AD 0 3a b 7 . Chọn A.
Câu 65. Gọi M x;0;0Ox . Mà M Ox ABC nên bốn điểm ,
A B, C, M đồng phẳng.
Ta có AB 4;2;4 , AC 6;0;
3 , AM x 1;2;
1 . Suy ra AB, AC 6;12;12 . Bốn điểm ,
A B, C, M đồng phẳng
AB, AC .AM 0 6 x
1 12212.1 0 x 1 M 1;0;0 . Chọn A.
Câu 66. Ta có AB 3;1;0 nên bài giải sai ở Bước 1. Chọn B.
Câu 67. Gọi I là trung điểm của AB , ta có MA MB 2MI .
Khi đó MA MB ,AC 0
2MI, AC 0 .
Suy ra MI cùng phương với AC . Chọn B. Câu 68. Diện tích 1 6 S , CA CB . Chọn C. A BC 2 2 Câu 69. Diện tích 1 6 S , CA CB . A BC 2 2 Độ dài đường cao 2S 6 30 AH . Chọn A. BC 5 5
Câu 70. Điểm M Oy nên M 0;m;0 . Ta có BM 2;m;0 , BC 2;0;0 .
Suy ra BM,BC
0;0;2m . Theo giả thiết 1 1 m 3 M 0;3;0 S 3
BM , BC 3 2m 3 . Chọn B. MBC 2 2 m 3 M 0;3;0.
AB 1;1;2
AH a 1;b 2;c 1 Câu 71: Ta có AC 1; 1; 3 AB,AC 1;5;2. và
BH a 2;b 1;c 1
BC 2;0; 1
Do H là trực tâm của tam giác
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 31 Tµi liÖu to¸n 12 n¨m häc 2018
AH.BC 0 2a 1 c 1 0 ABC
BH.AC 0 1 a 2 1 b 1 3c 1 0
AB, AC .AH 0 1 a
1 5b 22c 1 0
2a c 3 a 2 a b 3c 0 b
1 . Do đó a b c 4 . Chọn A. a
5b 2c 9 c 1
Câu 72. Ta có AB 2;3;8 , AC 1;0;6. Suy ra AB, AC 18;4; 3 .
Diện tích hình bình hành S AB,AC 349 . Chọn B. ABCD
Câu 73. Do ABCD là hình bình hành nên I là trung điểm của BD , suy ra D1;1; 1 . AB 1;1; 1 Ta có AB, AD 1;0; 1 .
AD 0;1;0
Diện tích của hình bình hành S AB AD . Chọn C. 2 2 2 , 1 0 1 2 ABCD
Câu 74. Áp dụng công thức 1 1 V AB.AC
.AD . Chọn C. 6 2
Câu 75. Gọi D0;b;0 .
1 b 7
Áp dụng công thức V
AB.AC .AD 5 4 b 1 2 30 . Chọn C. 6 b 8
Câu 76. Diện tích tam giác 1 25 S AB,AC . ABC 2 2
Thể tích tứ diện 1 25 V AB, AC .AD . ABCD 6 3
Suy ra độ dài đường cao ABC 3V h d D, ABCD 2 . Chọn C. S A BC
Câu 77. Ta có AB DC 4;2;0, BC 2;4;0 và AB.BC 0 .
Suy ra ABCD là hình vuông. Chọn B.
Câu 78. Ta có BC 2 , BD 2 , CD 2 . Suy ra tam giác BCD đều.
Vậy D là đáp án sai. Chọn D.
Câu 79. Nhận thấy ba vectơ AA', ', BB '
CC có giá cùng song song với mặt phẳng (BCC ' B ') nên ba vectưo
AA', ', BB '
CC đồng phẳng. Chọn A.
Câu 80. Do ABCD.A' B 'C ' D ' nên ta có A' D ' = BC , suy ra A'(7;0;−5) .
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 32 Tµi liÖu to¸n 12 n¨m häc 2018
Và AA' = BB ' nên suy ra B '(6;−1;− ) 1 .
Ta có BA 1;1;4, BC 5;1;4 và BB ' 6;1; 1 .
Thể tích khối hộp V BB ',BC
.BA 38 . Chọn B.
ABCD.A ' B 'C ' D ' Câu 81. Chọn A.
Câu 82. Ta có: S 2 2 2
: x y z 2x 4 y 6z 2 0
hay S x 2 y 2 z 2 : 1 2 3 16 .
Do đó mặt cầu Scó tâm I 1;2;
3 và bán kính R 4 . Chọn A.
Câu 83. Phương trình S 2 2 2
: x y z 6z 2 0 vắng x và y nên tâm mặt cầu này nằm trên trục Oz . 2
Ngoài ra ta có thể chuyển phương trình mặt cầu S về dạng: x y z 2 2 2
3 11 , suy ra tâm I 0;0; 3 Oz . 2 Chọn B.
Nhận xét: Trong phương trình mặt cầu, nếu vắng đồng thời hai hệ số của biến bậc nhất nào thì tâm của mặt cầu
nằm trên trục tọa độ không chứa tên của những biến đó.
Câu 84. Phương trình S 2 2 2
: x y z 2x 4 y 2 0 vắng z nên tâm của mặt cầu này nằm trên mặt phẳng Oxy. 1
Ngoài ra ta có thể chuyển phương trình mặt cầu S về dạng: 1
x 2 y 2 2 1
2 z 7 , suy ra tâm I 1;2;0Oxy . Chọn A.
Nhận xét: Trong phương trình mặt cầu, nếu vắng hệ số của biến bậc nhất nào thì tâm của mặt cầu đó nằm trên mặt
phẳng tọa độ không chứa tên của biến đó.
Câu 85. Bán kính R d I Ox 2 2 ,
y z 5 . Chọn B. I I
Câu 86. Ta có S 2 2 2
: x y z 2x 4 y 6z 5 0
hay S x 2 y 2 z 2 : 1 2 3 9
Do đó mặt cầu Scó bán kính R 3 . Diện tích mặt cầu là : 2
S 4R 36 . Chọn C.
Câu 87. Xét đáp án B, ta có 2 4 1 2 2 2 2 2 2
3x + 3y + 3z − 2x − 6y + 4z −1 = 0 ⇔ x + y + z − x − 2y + z − = 0 3 3 3 2 2 2 2 1 ⇔ x − + ( y − )2 2 1 1 2 2 1 + z + = + +1 + > 0 . Chọn B. 3 3 3 3 3
Câu 88. Ta có S 2 2 2
: x y z 4x 8y 2az 6a 0
hay S x 2 y 2 z a2 2 : 2 4
a 6a 20 0 .
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 33 Tµi liÖu to¸n 12 n¨m häc 2018
Do đó bán kính mặt cầu : 2
R a 6a 20 . a 2 Để 2 2
2R 12 R 6 a 6a 20 6 a 6a 16 0 . Chọn A. a 8
Câu 89. Ta có S 2 2 2
: x y z 4x 2y 2az 10a 0
hay x 2 y 2 z a2 2 2 1
a 10a 5 .
Để S là phương trình của mặt cầu 2
a 10a 5 0 . *
Khi đó mặt cầu S có bán kính 2
R a 10a 5 .
Chu vi đường tròn lớn của mặt cầu S là: 2
P 2R 2 a 10a 5 . Theo giả thiết: a 1 2 2 2
2 a 10a 5 8 a 10a 5 4 a 10a 11 0 . Chọn C. a 11
Câu 90. Ta có S 2 2 2
: x y z 2m 2x 3my 6m 2z 7 0 2 2
hay x m 2 3m y
z m 2 m 2 3m S : 1 3 1 7 1 3m 2 1 0 . 2 2 2 2 Suy ra bán kính m 2 3m m 2 49m R 7 1 3 1 8m 9 2 4 2 7 8 377 377 m . Chọn B. 2 7 49 7
Câu 91. Đường tròn giao tuyến của S với mặt phẳng Oxy có phương trình 2 2 2 2 2 x 1 y 2 z 3 14 x 1 y 2 5 . z 0 z 0
Từ phương trình ta thấy đường tròn giao tuyến có
tâm J 1,2,0Oxy và có bán kính r 5 . Chọn A.
Câu 92. Chọn C.
Câu 93. Mặt cầu đường kính AB có tâm là trung điểm của đoạn thẳng AB .
Suy ra tọa độ tâm mặt cầu cần tìm là 0;3; 1
Ta có AB 2 2 2 1 2 2 2 4
3 1 6 R AB 3 . 2
Do đó phương trình mặt cầu đường kính AB là x y 2 z 2 2 3 1 9 . Chọn D.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 34 Tµi liÖu to¸n 12 n¨m häc 2018
Câu 94. Gọi R 0 là bán kính mặt cầu S. Ta có 4 3 3
V R 972 R 729 R 9 . 3
Suy ra phương trình của mặt cầu S là x 2 y 2 z 2 1 4 2 81. Chọn A.
Câu 95. Bán kính mặt cầu: R d I,Oyz x 2 I .
Do đó phương trình mặt cầu cần tìm là x 2 y 2 z 2 2 1 1 4 . Chọn C.
Câu 96. Gọi tâm mặt cầu S là I a;0;bOxz. IA IB a
4b a22 9b 2 2 2 1 a
1 I 1;0; 3 Ta có . Chọn D. IA IC a
4 b a 9b 2 2 2 2 b 3 1 R 14
Câu 97. Gọi I a;0;0Ox với a 0 là tâm của S.
Theo giả thiết, ta có d I,Oyz R x 2 a 2. I
Vậy S x 2 2 2 :
2 y z 4 . Chọn C.
Câu 98. Gọi I a;b;c là tâm mặt cầu ngoại tiếp tứ diện OABC . a
b c a 22 2 2 2 2 2 2 2 b c IO IA 4a 4 0 a 1 Ta có IO IB a b c a b 42 2 2 2 2 2 2 2 c 8b 16 0 b 2 . 2 2 IO IC a
b c a b c 2 2 2 2 2 2 8c 16 0 c 2 4
Bán kính mặt cầu ngoại tiếp tứ diện OABC là 2 2 2
R IO 1 2 2 3 . Chọn B.
Cách nhanh. Ta thử tọa độ các điểm vào các phương trình. Cụ thể thấy tọa độ điểm O0;0;0 chỉ thỏa mãn B. Câu 99. Ta có
MA MB MC x 2 y z x y 2 z x y z 2 2 2 2 2 2 2 2 2 2 1 2 3
x y z x y z
x 2 y 2 z 2 2 2 2 2 4 6 12 0 1 2 3 2 .
Suy ra tập hợp các điểm M x, y, zthỏa mãn là mặt cầu có bán kính R 2 . Chọn B.
Câu 100. Phương trình S 2 2 2
: x y z 2x 6z 0 vắng hệ số tự do nên mặt cầu của nó đi qua gốc tọa độ O . 3 Chọn C.
Câu 101. Mặt cầu S có tâm I 1;2;
3 , bán kính R 3 .
Xét điểm P 1;6;
1 , ta có IP 2;4;4 . Suy ra IP 4 16 16 6 R .
Do đó điểm P nằm ngoài mặt cầu S. Chọn C.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 35 Tµi liÖu to¸n 12 n¨m häc 2018
Câu 102. Mặt cầu S có tâm I 3;2;
1 , bán kính R 14 .
Xét điểm M 0;1;
1 , ta có IM 3;1;2. Suy ra IM 9 1 4 14 R .
Do đó điểm M thuộc mặt cầu S. Chọn A
Câu 103. Mặt cầu S có tâm I 0;1;2 , bán kính R 5 .
Xét điểm Q , ta có IQ 1;2;2. Suy ra IQ 1 4 4 3 R .
Do đó điểm Q nằm bên trong mặt cầu S. Chọn D.
Câu 104. Ta có S 2 2 2
: x y z 2x 4 y 6z 0
hay S x 2 y 2 z 2 : 1 2 3 14 .
Suy ra S có tâm I 1;2;
3 và bán kính R 14 . Ta có OI 14 , R IA 1 ,
R IB 26 R .
Vậy trong ba điểm đã cho nhận thấy có một điểm A2;2;
3 thỏa mãn. Chọn B.
Câu 105. Ta có S 2 2 2
: x y z 2y 4z 9 0
hay S x y 2 z 2 2 : 1 2 14 .
Suy ra S có tâm I 0;1;2 và bán kính R 14 .
Điểm A nằm trong khối cầu IA R IA R 2 a2 2 2 2 1 1 3 14 a 1 2
a 2a 3 0 . Chọn D. a 3
Câu 106. Mặt cầu S có tâm I 0;4;
1 , bán kính R 6 .
Ta có d I,Oxy z 1 R
I 0;4;1 Oxy (do z 1 0 ). Chọn A. I và I
Câu 107. Mặt cầu S có tâm I 1;2;
5 , bán kính R 2 .
Ta có d I,Oxy z 5 ,
R d I,Oyz x 1 ,
R d I,Oxz y 2 R I I I .
Vậy chỉ có mặt phẳng Oyz cắt mặt cầu S. Chọn B.
Câu 108. Xét mặt cầu S : x y z 42 2 2
16 , có tâm I 0;04Oz và R 4 . 4
Ta có d I,Oxy z 4 R I . Chọn D.
Câu 109. Mặt cầu S có tâm I 3;0;2, bán kính 2
R m 4 .`
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 36 Tµi liÖu to¸n 12 n¨m häc 2018
Để S tiếp xúc với Oyz khi d I Oyz 2 ,
R x R 3 m 4 m 5. I Chọn B.
Câu 110. Mặt cầu S có tâm I 2; 5;0, bán kính 2
R m 2m 6 .
Để S cắt trục Oz tại hai điểm phân biệt khi d I Oz 2 2 ,
R x y R I I m 3 2 2
3 m 2m 6 m 2m 3 0 . Chọn D. m 1
Câu 111. Mặt cầu S có tâm I 1;3;0 , bán kính R 3 .
Nhận thấy d I Ox 2 2 ,
y z 3 R . Vậy S tiếp xúc với trục Ox . Chọn A. I I
Câu 112. Xét mặt cầu S :x 2 2 2
1 y z 1 có tâm I 1;0;0 , bán kính R 1 . 2
Ta có d I Oy 2 2 ,
x z 1 R và d I Oz 2 2 ,
x y 1 R . Chọn B. I I I I
Câu 113. Mặt cầu S có tâm I 1;2;
3 , bán kính R 14.
Ta có IA 2;1;
3 , suy ra IA 14 R nên A S.
Gọi B0;0;cOz là điểm cần tìm. Suy ra AB 1;1;c 6 .
Để tiếp xúc với S AB IA AB IA c 19 . 0 2 1 1 3 6 0 c . 3 Chọn A.
Câu 114. Giả sử Ba;b;cS.
B S 2 2 2 a
b c 4a4b4c 0
Theo giả thiết, ta có 2 2 2 2 2 O
A OB a
b c 32 . 2 2 OA AB
4 a2 4 b2 2 c 32
Giải hệ phương trình, ta tìm được hai nghiệm a;b;c là 0;4;4 hoặc 4;0;4 . Chọn D.
Gi¶ng d¹y: nguyÔn b¶o v¬ng - 0946798489 Page | 37
Document Outline
- BÀI 1. HỆ TỌA ĐỘ TRONG KHÔNG GIAN
- BÀI 1. ĐÁP ÁN HỆ TỌA ĐỘ TRONG KHÔNG GIAN




