














































































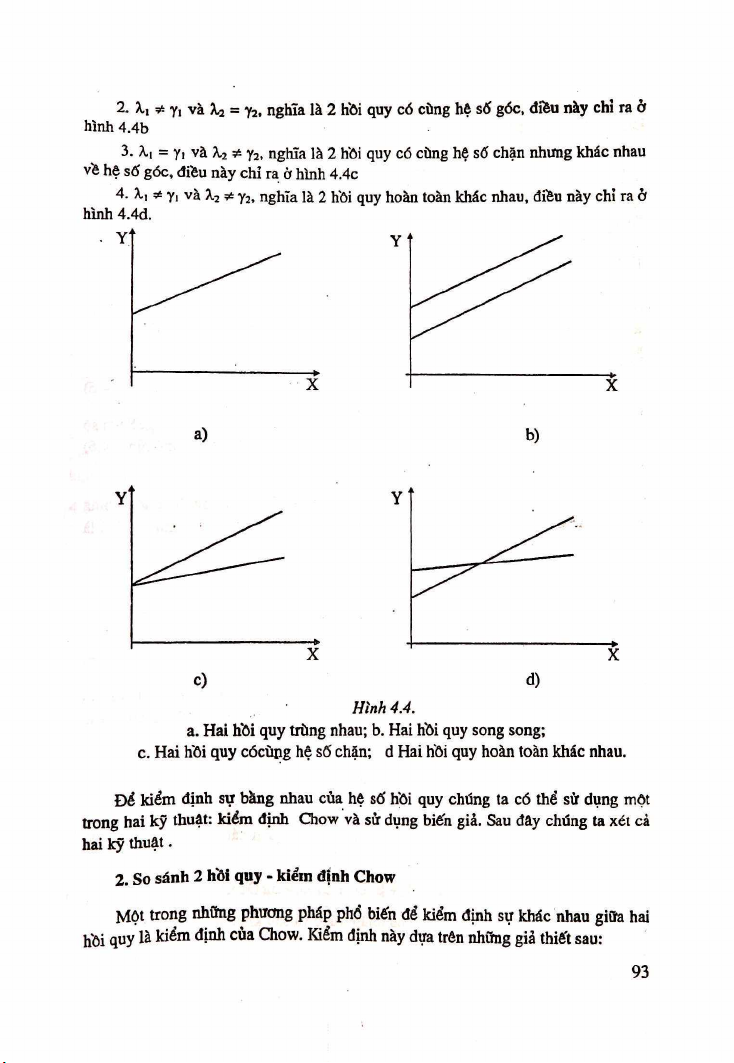






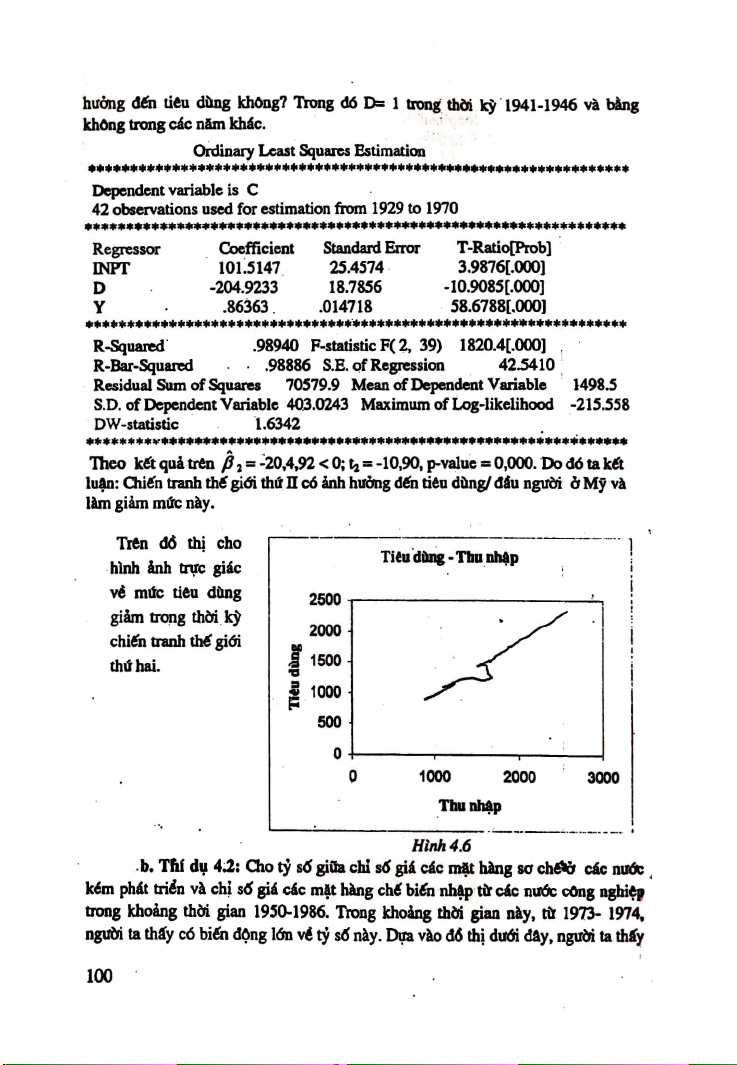
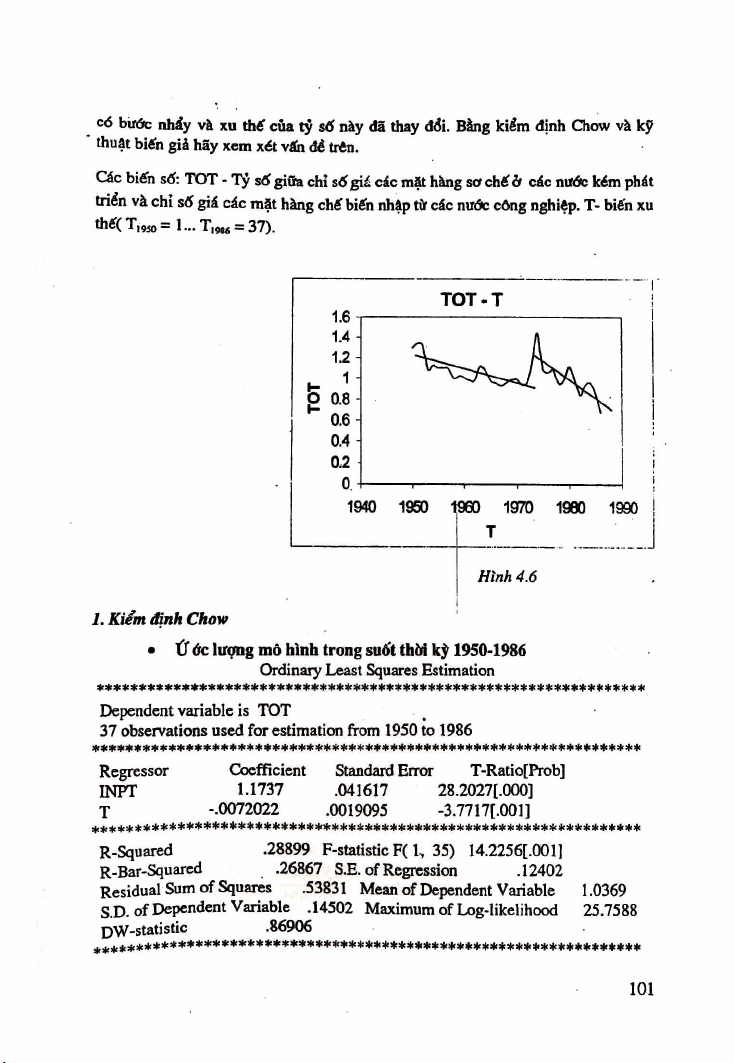






















Preview text:
PỜ N G Đ ẠI H Ọ C KINH T É Q U Ố C DÂN KHOA TOÁN KINH TÊ
BỌ MÔN ĐIÈU KHIÉN HỌC KINH TÉ NGUYỄN QUANG DONG BÀI G IẢ N G KINH TẾ LƯỢNG ■ í QTKD
NHÀ XUẤT BẢN ĐẠI HỌC KINH TẾ QUỐC DÂN
P G S . N G U Y Ê N Q U A N G D O N G BÀI GIẢNG KINH TÉ LƯỢNG
N H À X U Ấ T BẢ N Đ Ạ I H Ọ C K IN H T Ế Q U Ố C DÂN MỎ ĐẦU
L KINH T Ế LƯỢNG LÀ G ì?
Cho đến nay chua có một câu trả lời dược mọi người cùng chấp nhận cho câu
hỏi này .Thuật ngữ tiếng Anh "Econometrics" được ghép từ hai gốc từ "Econo" có
nghĩa là "Kinh tế” và Metrics có nghĩa là "Đo lưỉmg". Thuật ngữ này do giáo sư
kinh tế học người Na-Uy là A.K.Ragnar Frisch- giải thưởng Nobel về kinh tế học
(1969) cùng với J.Tinbergen, sử dụng lần đẳư tiên vào khoảng năm 1930.
Kinh tế lượng có nghĩa Ịà đo lường kinh tế. Mặc dù đo lưòmg kinh tế là một nội
dũng quan trọng của kinh tế lượng nhưng phạm vi của kinh tế lượng rộng hơn
nhiều.Điều đó được thể hiện thông qua một sô' định nghĩa sau đây:
- Kinh tế lượng bao gồm viộc áp dụng thống kê toán cho các số liệu kinh tế để
cùng cố về mặt thực nghiệm cho các mô hình do các nhà kinh tế toán đề xuất và
để tìm ra lòi giải bằng số.a)
- Kinh tế lượng có thể được định nghĩa như là sự [fhân tích vế lượng các vấn đẻ
kinh tế hiện thỉri dựa trên việc vận dụng đồng thời lý thuyết và thực tế được tỉiực
hiện bằng các phương pháp suy đoán thích hợp.<2)
- Kinh tế lượng có thể được xem như là một khoa học xã hội trong đó các công
cụ của lý thuyết kinh tế, toán học và suy đoán thống kê được ấp dụng để phân tích
cẳc vấn đề kinh tế.(3)
- Kinh tế lượng quan tâm đến việc xác định về thực nghiệm các luật kinh tế.<4)
TTiuật ngữ "Econometrics"" được dịch sang tiếng Việt là "Kinh tế lượng học''
hoặc "Đo lường kinh tế”, ngắn gọn hơn là "Kinh trắc". Có những định nghĩa, quan
niệm khác nhau về kinh tế lượng bắt nguồn từ thực tế: các nhà kinh tế lượng trước
hết và phần lớn họ là các nhà kinh tế có khả năng sử dụng lý thuyết kinh tế để cài
tiến việc phân tích thực nghiệm về các vấn dề mà họ đặt ra. Họ đồng thời là các
nhà kinh tế toán- m ổ hình hoấ lý thuyết kinh tế theo cách làm cho lý thuyết kinh
tế phù hợp với việc kiểm định giả thiết thống kê. Họ cũng là những nhà kế toán - '
tìm kiếm, thu thập các số liệu kinh tế, gắn các biến kinh tế lý thuyết với các biến
quan sát được. Họ cũng là các nhà thống kê thực hành- sử dụng kỹ thuật tính toán
để ước lượng các quan hệ kinh tế hoặc dự báo các hiện tượng kinh tế. (1) Gerhard Tinlner, Methodology of Mathematical Economics and
Econometrics, The University of Chicago Press,Chicago, 1968, p .74 .
(2) P-ASammuelson, T.C.Koopmans, and jp.N.Stone, " Report o f the Evaluative
Committee for Economelrica", Econome trica.vol 22, no. 2, April 1954,pp. 141-146.
(3) ArthurS.Goldherger, Economet lie Theoiy, John Wiley & Sons, Inc.
(4) HJheil, Principles o f Econometrics, John Wiley & Sons, Inc. 5 MỎ ĐẦU L KINH T Ế LƯỢNG LÀ GÌ?
Cho đến nay chưa có một câu trả lòi được mọi người cùng chấp nhậii cho câu
hòi này .Thuật ngữ tiếng Anh "Econometrics" được ghép từ hai gốc từ "Econo" có
nghĩa là "Kinh tế” và Metrics cổ nghĩa là "Đo lường". Thuật ngữ này do giáo sư
kinh tế học người Na-Uy là A.K,Ragnar Frisch- giải thường Nobel về kinh tế học
(1969) cùng với J.Tinbergen, sử dụng lần đầư tiên vào khoảng năm 1930.
. Kinh tế lượng có nghĩa Ịà do lường kinh tế. Mặc dù đo lường kinh tế là một nội
dũng quan trọng cùa kinh tế lượng nhưng phạm vi của kinh tế lượng rộng hớn
nhiều.Điều đó được thể hiện thông qua một sô' định nghĩa sau đây:
- Kinh tế lượng bao gồm việc áp dụng thống kê toán cho các số liệu kinh tế để
cùng cố về mặt thực nghiộm cho các mô hình do các nhà kinh tế toán đề xuất và
để tìm ra lời giải bằng số.(1>
- Kinh tế lượng có thể được định nghĩa như là sự ỊÍhân tích về lượng các vấn đề
kinh tế hiện thời dựa trên việc vận dụng đổng thời lý thuyết và thục tế được thực
hiện bằng các phương pháp suy đoán thích hợp.c)
- Kinh tế lượng có thể được xem như là một khoa học xã hội trong đó các công
cụ của lý thuyết kinh tế, toán học và suy đoán thống kê được áp dụng để phân tích
cẩc vấn đề kinh tế.<3)
- Kinh tế lượng quan tâm đến việc xác định về thực nghiệm các luât kinh tế.(4)
Thuật ngữ "Econometrics"" dược dịch sang tiếng Việt là “Kinh tế lượng học''
hoặc "Đo lưỉmg kinh tế", ngắn gọn hơn là "Kinh trăc". Có nhũng định nghĩa, quan
niệm khác nhau về kinh tế lượng bắt nguồn từ thực tế: các nhà kinh tế lượng trước
hết và phần lớn họ là các nhà kinh tế có khả năng sử dụng lý thuyết kinh tế để cài
tiến việc phân tích thực nghiệm về các vấn đề mà họ đặt ra. Họ đổng thời là các
nhà kinh tế toán- m ô hình hoá lý thuyết kinh tế theo cách làm cho lý thuyết kinh
tế phù hợp với việc kiểm định giả thiết thống kê. Họ cũng là những nhà kế toán - '
tìm kiếm, thu thập cấc số liệu kinh tế, gắn cac biến kinh tế lý thuyết với các biến
quan sất được. Họ cũng là các nhà thống kê thực hành- sử dụng kỹ thuật tính toán
để uớc lượng các quan hệ kinh tế hoặc dự báo các hiện tượng kinh tế. (1) Gerhard Tintner, Methodology of Mathematical Economics and
Econometrics, The University of Chicago Press,Chicago, 1968, p.74 .
(2) PASammuelson, T.C.Koopmans, and J^i.N.Slone, " Report o f the Evaluative
Committee for Econometrica", Econome tricaỳol 22, no. 2, April 1954,pp. 141-146.
(3) ArthurS.Goldherger, Economet ric Theory. John Wiley & Sons, Inc.
(4) H.Theil, Principles o f Econometrics, John Wiley & Sons, Inc. 5
Trên các lĩnh vực khác nhau, người ta có các quan niem khác nhau vể kinh tê'
lượng. Tuy vậy, theo các quan diổm trên thì kinh tế lượng la sư kết hợp các lý
thuyết kinh tế, kinh tế toán, thống kề kinh tế, thống kê toan nhưng nó vằii là 'ttộ1
môn độc lập vì những lý do sau đây:
- Các lý thuyết kinh tế thưòng nêu ra các giả thuyết hay cấc giả thiết. Phần lớn
các giả thuyết này nói về chất.
Ví dụ: kinh tế học vi mô khẳng định Tằng trong các điều kiện khác không thaỵ
đổi nếu giảm giá về một loại hàng hoá nào đó thì sẽ làm tăng lượng cẩu vé loại
hàng hoá này và ngựợc lại. Dù rằng lý thuyết kinh tố có khẳng định quan hệ
nghĩch biến giữa giá ca vá lượng cầu nhung lý thuyết này không đưa ra một số đo
bằng số vể quan hệ giữa chúng, không nói cho ta biết lượng cáu sẽ tăng hoặc
giảm bao nhiêu nếu ta giảm hoặc tăng một đơn vị giá cả. Các nhà kinh tế luợng sẽ
cho chúng ta ước lưạng bằng số vẻ các con số này.
- Nội dung chính của kinh tế toán là trình bày lý thuyết kinh tế dưới dạng toán
học (các phương tìn h và bất phương trình), nếu thiếu các mô hình toán học thì
khỡng thể đo hoặc kiểm tra bằng thực nghiệm lý thuyết kinh tế. Kinh tế lượng chù
yếu quan tâm đến kiểm đinh vẻ mặt thực nghiệm các lý thuyết kinh tế. Kinh tê'
lượng thường sử dụng các phương trình toán học do các nhà kinh tế toán đề
xuất và đặt cấc phương trình dưối dạng phù hợp để kiểm định bằng thực nghiệm. •
Thống kê kinh tế chủ yếu liên quan đẾn việc thu thập, xử lý và trình bày các
số liệu. Những số liệu này là nh&ng số liệu thô dối với Kinh tế lượng. Thống kê
kinh tế khổng đi xa hơn, khâng liên quan đến việc sử dụng số liệu để kiểm tra các giả thuyết kinh tế.
- Các số liệu kinh tế là các | ố liệu không phải do các cuộc thí nghiệm dem lại,
chúng nằm ngoài sự kiểm soát của tất cả mọi ngucri. Các số liệu về tiêu dùng, tiết
kiệm, giá cả,... do các cơ quan Nhà nước hoặc tư nhãn thu thập đều là các số liệu
phi thực nghiệm. Cấc số liệu này chứa sai số của phép đo. Kinh tế lượng phái sử
dụng các công cụ, phương pháp cùa thống kê toán để tìm ra bản chất của các số liệu thống kê.
n . PHƯƠNG PHÁP LUẬN CỦA KINH TẾ LƯỢNG
Phân tích kinh tế luạng được thực hiện theo các bước sau đây:
1. Nêu ra các giả thuyết hay giả thiết về các mối quan hệ giữa các biến kinh
tế. Chẳng hạn kinh tế vĩ mô khẳng định rằng mức tiêu dùng cua các hộ gia đình
phụ thuộc theo quan hộ cùng chiều vói thu nhập khả dụng của họ.
2. Thiết lập các mô hình toán học để mô tả mối quan hê giữa các biến số này Chẳng hạn: Y = p, + Pj X + u
trong đó, Y :CỊŨ tieu cho tiêu dùng của môt hộ gia đình,
X :Thu nhập khả dụng của hộ gia đình
P (:Hệ số chặn, p2: Hệ số góc, u: Yếu tố ngẫu nhiên. 6
Sự tồn tại của yếu tố ngẫu nhiên bắt nguồn từ mối quan hệ giữa các biến kinh
tế nói chung là không chính xác.
3. Thu thập số liệu: Để ước lượng các tham số của mô hình, cần phải thu thập
số liệu. Kinh tế lượng đòi hòi kích thước mẫu khá lớn.
4. Ước lượng các tham số cùa mô hình nhằm nhận được số đo về mức ảnh
hưởng cùa các biến với các số liệu hiện có. Các ước lượng này là các kiểm định
thực nghiệm cho lý thuyết kinh tế.
5. Phân tích kết quả: Dựa trên lý thuyết kinh tế để plĩkn tích và đánh giá kết
quả nhận được. Xét xem các kết quả nhận được có phù hợp với lý thuyết kinh tế
không, kiểm đinh các giả thiết thống kê về các ước lượng nhận được. Trong mô hình: Y= p, +p2X + u,
nếu ưổc lượng cùa p2 là số dương
và nhỏ hơn 1 thì ước lượng này là
hợp lý về mặt kinh tế. Trong trường
hợp ngược lại ( < 0 hoặc > 1) thì
khồng phù hợp vể mặt kinh tế. Khi
đó cần phải tìm ra một mô hình đúng.
Ngoài phân tích về mặt kinh tế
còn phải phân tích về kỹ thuật —
các yêu cầu về mặt toán học.
6. Dự báo Nếu như mồ hình phù
hợp vói lý thuyết kinh tế thì có thể sử
đụng mô hình để dự báo. Dự báo giá
trị trung bình hoặc dự báo giá trị cá biệt.
7. Ra quyết định: Để bào bảo tính
hiên thực của dự báo cần có các
chính sách, các giải pháp tương ứng.
Các bước trên đây có nhiệm vụ khác nhau trong quá trình phân tích một vấn đề kinh
tế và chúng được thực hiện theo một trình tự nhất định. Tìm ra bản chất một vấn đé
kinh tế là một việc không đơn giàn. Vì vậy, quá trình trên đây phải được thực hiện
nhiều lần như là các phép lặp cho đến khi chúng ta thu được một mô hình đúng. Có
thể minh họa quá trình phân tích kinh-tế lượng một vấn đề kinh tế bằng sơ đồ trên. 7
Những điểu nói tran đây cho thấy rõ nội dung nghiên cứu dối tương và mục
đích, cũng như công cụ và cách tiếp cận trong nghien cứu của bò môn khoa học
này. Chính vì vậy, từ khi ra đời đến nay kinh tế lưọng dã đem' lãi cho các nhà
kinh tế một công cụ do lường sắc bén để đo các quan he kmh t í Ngày nay.
phạm vi sử dụng của kinh tế lượng đs vượt quá phạm vi kinh tế đã ian sang các
lĩnh vực khác như xã hội học, vũ trụ học... Trong 30 năm gần day kinh tế lượng là
một bộ phận khững thể thiếu được trong chuông trình đào tạo các cán bộ kinh tế
của hầu hết các nước trên thế giới. Số các đáu sách YÍỂt VỀ kinh tế lứợng, bao
gồm các sách giáo khoa ở bậc đại học và sau đại học, các sách chuyên khảo,
cũng như các tài liêu thực hành, các chuyin san về Ịý thuyết và úng dụng kình tế
lượng, đã trà nên hết súc phong phú. Sự đòi hỏi phải phân tích định lượng các hiên
tượng kinh tế, kiểm định sự phù hợp và độ tin cậy cùa các giả thuyết trong quá
trình hoạch định chính sách vĩ mô cũng như ra các quyết định tác nghiệp, viẹc dự
báo và dự đoán có đô tin cậy cao..., tát cả đã làm cho kinh tế lưọng học có một
vai trò ngày càng quan trọng và bản than nó cũng khổng ngừng được phát triển
và hoàn thiện. Sự phát triển cùa máy tính điện tử đã làm ra răng sức mạnh của
kinh t i lượng. Điều đó, giúp các nhà kinh tế kiểm chúng được các lý thuyết kinh
tế có thích hợp hay không, dẫn tới những quyết định đúng đắn trong hoạt động
kinh doanh tác nghiệp và hoạch định các chính sách và chiến lược kinh tế xã hội.
Cùng với việc giảng dạy kinh tế vi mữ và kinh tế vĩ mô, thì kinh tế lượng là một
môn không thẻ thiếu đuọc. Nếu như kinh tế vĩ mô mô tả sự vạn động của toàn bộ
nền kinh tế, kinh tế vi mỡ mổ tả hành vi cùa người sản xuất và người tiều dùng,
thì kinh tế lucmg trang bị cho nhà kinh tế môt phương pháp lượng hoá và phân tích
sự vận động và các hành vi trên. Ba môn này sẽ trang bị những kiến thức cơ sở để
học sinh và các nhà kinh tế đi vào các chuyên ngành hẹp. 8 CHƯƠNG I
MA HÌNH HỐI QUY HAI BIẾN
MỘĨVẦi ĩư TƯỞNG Cơ BẢN
Hồi quy là một công cụ cơ bản của đo lường kinh tế. Phân tích hồi quy giải
quyết những vấn dề cụ thể gì, phân tích hôi quy khác với các phân tích khác như
thế nào, cơ sở thông tín để phân tích hồi quy là gì, vì sao phải xây dựng mô hlnh
h'ôi quy...? Các vấn dề trền và bản chất cùa chúng sẽ được đề cạp một cách vắn tắt trong chương này.
Thuật ngữ "Hồi quy" đã được Francis Galíon sử dụng vào nãm 1886. Trong
một bài báo nổi tiếng của mình, ông đã cho rằng có một xu hướng về chiều cao của
những đứa trê do cha mẹ cao không bình thường hoặc thấp không bình thường sinh
ra. Người ta gọi xu huống này là luật Galton. Trong bài báo của mình Galton dùng
cụin từ "regression to mediocrity" - quy về trung bình. Từ đó vấn đề hồi quy được
nhiều người quan tâm và hoàn thiện, các úng dụng của phân tích hồi quy dã có nội dung rộng hơn nhiều. 1.1. PHÂN TÍCH HỐI QUY
Phân tích hồi quy nghiên cứu mối liên hộ phụ thuộc cùa một biến (gọi là biến
phụ thuộc hay biến dược giải thích) với một hay nhiều biến khác (được gọi là (các)
biến độc lập hay giải thích) nhằm ước lượng và/ hoặc dự báo giá trị trung bình cùa
biến phụ thuộc với các giá trị đã biết của (các) biến độc lập.
Ta xem xét các thí dụ sau đây: T h í dụ 1.1 a.
Luật Galton Karl Pearson nghiên cứu sự phụ thuộc chiều cao cùa các cháu
trai vào chiều cao của bố những đứa trẻ này. Ông đã xây dựng được đồ thị chi ra
phân bố chiều cao cùa các cháu trai ứng với chiều cao cùa người cha. Qua mô hình này có thể thấy:
Thứ nhất, với chiều cao đã biết của người cha thì chiều cao của các cháu trai sẽ
là một khoảng, dao động quanh giá trị trung bình;
Thứ hai, chiều cao của cha tăng thì chiều cao của các cháu trai cũng tăng. Mô
hình này giải thích được điều mà Galton đặt ra và còn được đùng trong dự báo. 9 Hình 1.1.
Tiếp tục nghiên cứu vấn dề trên, Karl Pearson đã phát hiện ra rằng: chiều cao
trung bình cùa các cháu trai của nhóm bố cao nhỏ hơn chiều cao cùa bố và chiều
cao trung bình cùằ <^ác cháu trai của nhóm bố thấp lớn hơn chiêu cao của bố. Điều
này duơc thể hiên: h ệ \ố góc của đường thẳng trên hình 1.1 nhỏ hơn 1.
Trong thí dụ này, chíSụ cao của các cháu trai là biến phụ thuộc, chiều cao của
người bố là biến độc lập.
b. Một người nghiên cứu sự phụ thuộc của lượng cầu về một loạt hàng hóa vào
giá bản thân hàng hóa, thu nhập cùa nguời tiêu dùng và giá của những hàng hóa
khác cạnh tranh với hàng hóa này.
Trong trường hợp này, lượng cầu là biến phụ thuộc, giá cùa bản thân hàng hóa,
của các hàng hóa cạnh ưanh, và thu nhập của người tiêu dùng là các biến độc lập.
c. Một nhà kinh tế lao động nghiên cứu tỷ lệ thay đổi cùa tiền lương trong
quan hệ với tỷ lộ thất nghiêp đã đưa ra đồ thị ờ hình 1.2. Đường cong trên hình 1.2
được gọi là đường cong Phillips, trong đó: tỷ lê thay đổi của tiền lương là biến phụ
thuộc, tỳ lệ thất nghiệp - biến độc lập. Mô hình cho phép dự đoán đuợc sụ thay đổi
trung bình của tỷ lộ tiền luơng với một tỷ lệ thất nghiệp nhất định. ■ • I'
d. Trong điều kiện các yếu tố khác không thay đổi, tỷ lệ lạm phát càng cao thì
tỳ lê thu nhập của nhân dân được giữ dưới dạng tiền mặt càng ít.
0 5 thể minh họa điều đó bàng đồ thị ở hình 1.3. 10 Hình 1.2 Hình 1 3
Ta có thể đưa ra được rất nhiều ví dụ về sự phụ thuộc của một biến vào một
hoặc nhiều biến khác. Kỹ thuật phân tích hồi quy giúp ta nghiên cứu mối quan lỉệ như vậy giữa các biến.
Các ký hiệu: Y - biến phụ thuộc [hay biến được giải thích]
Xi - biến độc lập [hay biến giải thích] thứ i
Trong đó, biến phụ thuộc Y là đại lượng ngẫu nhiên, có quy luật phân bổ xác
suất, các biến độc lập Xị không phải là biến ngẫu nhiên, giá trị của chúng đã được cho trước.
Phân tích hồi quy giải quyết các vấn dề sau đây:
l ắ U6c lượng giá trị trung bình cùa biến phụ thuộc với giá trị đã cho cùa biến độc lập.
2. Kiểm định giả thiết vê bản chất cùa sự phụ thuộc.
3. Dự đoán giá trị trung bình của biến phụ thuộc khi biết giá trị cùa các biến độc lập.
4. Kết hợp các vấn đề trên.
Trong phân ưch hồi quy chúng ta phân biệt các quan hê sau đây:
1. Q ụan hệ thống kè và quan hệ hàm số
Vấn đề mấu chốt trong phân tích hồi quy là sự phụ thuộc thống kẻ cùa biến
phụ thuộc vào một hay nhiều biến giải thích. Biến phụ thuộc là đại lượng ngẫu
nhiên, có phân bố xác suất. Các biến giải thích thì giá trị cùa chúng đã biết. Biến
phụ thuộc là ngẫu nhiên vì có vô vàn nhân tố tác động đến nó mà trong mô hình ta 11
không đề cập đến được, úng với mỗi giá trị đã biết cùa biến độc lập có thổ có nhiêu
giá trị khác nhau cùa biến phụ thuộc. Trong quan hệ hàm sổ các biến không phải là
ngẫu nhiên, ứng với mỗi giá trị của biến dộc lập có một giá trị của biến phụ thuộc,
phân tích hồi quy không xét đến các quan hệ hàm sỗ. T hí dụ l ã
Sự phụ thuộc cùa năng suất một loại iúa trên một hecta vào nhiệt độ, lượng
mưa, dộ chiếu sáng, phân bón... là quan'hệ tỉiđng kê. Các biến: nhiêt độ, lượng
raua, độ chiếu sáng, phân bón là các biến độc lập. Năng suất tính trên 1 hecta là
biến phụ thuộc, là đại lượng ngẫu nhiên không thể dự báo một cách chính xác năng
su it của giống lúa này trên một hecta vì:
- Có sai số trong phép đo các biến này,
- Còn rất nhiều nhân tố khác cũng ảiih hưởng đến năng suất mà ta không th”
liệt kê ra và nếu có cũng khổng thể tách được ảnh hưởng cùa riêng từng nhần tố đến
. năng su it dù ràng chúng ta có đua thêm bao nhiêu biến giải thích khác.
Trong vật lý khi xét một động từ chuyển động dẫu, người ta có công thức: s= vểt
trong dó, s là độ dài quầng dường đi dược;
V là vận tốc trong một đơn vị thời gian; t là thời gian.
Đây là quan hộ hầm số, ứng với mỗi giá trị cùa vận lốc và thời gian ta chì có
một giá trị duy nhất cùa đọ dài quãng đuờng, phân tích hồi quy không xét các quan hệ này.
2. H àm hbi quy và quan hệ nhàn quả
Phân tích hồi quy nghiên cứu quan hệ giữa một biến phụ thuộc với một hoặc
nhiều biến độc lập khác. Điều này không đòi hỏĩgiữa biến độc lập và cá biến phụ
thuộc có mối quan hệ nhân quả. Nếu như quan hệ nhân quả tồn tại thi nó phải được
xác lập dựa trên các lý thuyết kinh tế khác. Thí dụ, luật cầu nói ràng trong điều kiện
các biến (điều kiện) khác không thay đổi thì nhu cầu về một loạt hàng hóa tỷ lộ
nghịch với giá của chính hàng hóa này hay íxong thí dụ 1.2 chúng ta có thể dự đoận
sản luựng dựa vào luợng mua và các biến khác, nhung không thổ chấp nhận dược
việc dự báo lượng mua bằng việc thay đổi sản luợng. 3. Hồi quy và tương quan
. Hồi quy và tuơng quan khác nhau về: mục đích'và kỹ thuật. Phân tích tương
quan trước hết là đo mức độ kết họp tuyến tính giữa hai biến. Ví dụ: Mức độ quan
hệ giữa nghiên thuốc lá và ung thư phổi, giữa kết quả thi môn thống kê và môn
toán. Nhung phân tích hồi quy lại ước lượng hoặc dự báo một biến ưên cơ sở giá trị'
đã cho của các biến khác. Về kỹ thuật trong phân tích hồi quy các biến không có
tính chất đối xứng. Biến phụ thuộc là đại lượng ngẫu nhiên. Các biến giải thích giá 12
trị của chúng đã được xác định. Trong phân tích tương quan, khổng có sự phan biệt
giữa các biến, chúng có tính chất đối xúng: r (X,Ỵ) = r (Y,X)
1.2 . BẢN CHẤT VÀ NGUỒN sô ' LIỆU CHO PHÂN TÍCH H ồ i QUY
Thành cồng của bất kỳ một sự phân tích kinh tế nào đều phụ thuộc việc vào sử
dụng các số liệu thích hợp và phụ thuộc vào phuơng pháp xử lý các số liệu dó. Do
vậy ở đây sẽ trình bày đôi nét về bản chất, nguồn gốc và những hạn chế của sổ liệu
mà chúng ta sẽ gặp phải trong phân tích kinh tế nói chung và phân tích hbi quy nói riêng. l ễ Các loại số liệu
Có ba loại số liệu: Các số liệu theo thời gian (chuỗi thời gian), các số liệu chéo
và các số liệu hỗn hợp của hai loại trên.
Các số liệu theo thời gian là các số liẹu được thu thập trong một thời kỳ nhất
định, ví dụ như các số liệu về GNP, số người thất nghiệp, lượng cung về tiền... Có
sđ liệu dược thu thập bàng tuần như lượng cung vầ tiền, cố số liệu thu thập hàng
tháng, quý, năm... Các số liệu này có thể đo đuợe bằng những con sổ như giá cà,
thu thập, nhung cũng có những số liệu khổng đo đuợc bằng con số, chúng là những
chì tiêu chất lượng như: nam hoặc nữ, có gia đình hay chưa có gia đình, có việc làm
hay chưa có việc làm, màu xanh hay màu trắng. Người ta gọi các biến loại này là
biến giả (dummy). Chúng cũng quan trọng nhu những biến số lượng khác.
Các số liêu chéo là các sơ liệu vè một hoặc nhiều biến được thu thập tại một
thời điểm ở nhiều địa phuong, đơn vị khác nhau: ví dụ nhu các số liệu về điều tra
dâu số vào 0 giờ ngăy 1/1/1992; các số liệu điều tra vồ vốn cơ bản cùa các xí
nghiệp dệt ngày 1A7/2006 ở Việt Nam. .. 4
Các số liệu hỗn hợp theo thòi gian và khổng gian: các số liêu về giá vàng hàng
ngày ò thành phố Hà Nội, Hồ Chí Minh, Hải Phòng, Nam Định.
2. Nguồn gốc các số liệu
Các số liệu có thể do các cơ quan nhà nước, các tổ chức quốc tế, các cống ty tư
nhân hay các cá nhăn thu thập. Chúng có thể là các số liệu thực nghiệm hoặc tehông
phải thực nghiệm. Các số liêu thực nghiệm thường đuợc thu thập trong khoa học tự
nhiên, một điều ưa viên muốn thu thập các số liệu ảnh hưởng cùa một số nhân tố
đến đối tượng nghiên cứu, anh ta dã giữ nguyên các yếu tố khác. Thí dụ, một kỹ su
nống nghiệp nghiên cúu khả năng chịu bệnh cùa một giống lúa mới. Anh ta tiến
hành thí nghiệm bằng cách trồng hai giổng lúa mới và cũ trên hai khu ruộng có độ
màu mỡ như nhau, thực hiện chế độ chăm sóc hai khu ruộng như nhau và theo dõi
sự phát triển của sâu bệnh trên hai khu ruộng Bày bằng cách gây cùng một loại
bệnh trên hai khu ruộng. Các số liệu thu được sẽ là các số liộu thực nghiệm. 13
Trong khoa học xã hội các số liẹu nối chung là các số liệu không phải do thực
nghiêm mà có. Các số liệu về GNP, số người thất nghiệp giá cổ phiếu... không nàm
dưới sự kiểm soát của kỹ thuật viên. Điều này thường gây ra những vấn trong việc tìm ra những nguyên nhân chính xác ảnh hưởng đến một tình huống
riêng biệt. Thí dụ: có phải lượng cung về tiền ảnh hưởng đến GDP hay còn có nguyên nhãn khác...?
3. Nhược điểm của các số liệu
Chất iượng của các số liêu thu được thường khổng tốt. Điều dó do các nguyên nhăn sau đay:
- Hầu hết các số liệu trong khoa học xã hội đều là các số liệu phi thục nghiệm.
Do vậy, có thể có sai số quan sát hoặc bỏ sót quan sát hoặc cả hai.
- Ngay với các số liệu đuợc thu thập bàng thục nghiệm cũng có sai số cùa phép đo.
- Trong các cuộc đíÊu tra bằng câu hỏi, vấn đề không nhận đuợc câu trả lòi
hoặc có trả lời nhưng khững trả lời hft các câu hỏi.
- Các mẫu đuợc thu thập trong các cuộc đíầu tra rất khác nhau vồ kích cỡ cho
nên rất khó khăn trong việc so sánh các kết quả giữa các đợt điều tra.
- Các số liệu kinh tế thường có sẵn ở múc tổng hạp cao, không cho phép đi sâu vào các đcm vị nhỏ.
- Ngoài ra còn có những số liệu thuộc bí mật quốc gia m à không phải ai cũng
cố thể sử dụng được.
Do vậy kết quả nghiên cứu sẽ phụ thuộc vào chất luợng của cáo số liệu được
sử dụng và phụ thuộc vào mỡ hình được lựa chọn (vâh dề này sẽ đuợc trình bày ở các chương sau).
1.3. MÔ HÌNH HỒI QUY TỔNG THỂ
Phần trên chúng ta nói phân tích hồi quy dặc biệt quan tâm đến ước lượng
hoặciđụ bấo giá trị trung bình của biến 'phụ thuộc trên cơ sở biết các giá trị của
biến độc lập. Ta xét các thí dụ giả định sau đây: Thí dụ 1.3
y : Chi tiêu cùa một gia đình trong một tuần tính bằng $
X : Thu nhập sau khi đã trừ thuế của một gia đình tính bàng $
Giả sử ổ n g ở một địa phương chỉ có cả thảy 60 gia đình, 60 gia dinh này được
chia thành 10 nhóm, chênh lệch về thu nhập của các nhóm gia đình từ nhóm này
sang nhóm tiếp theo đều bằng nhau. Ta có bảng số liêu sau đây: 14
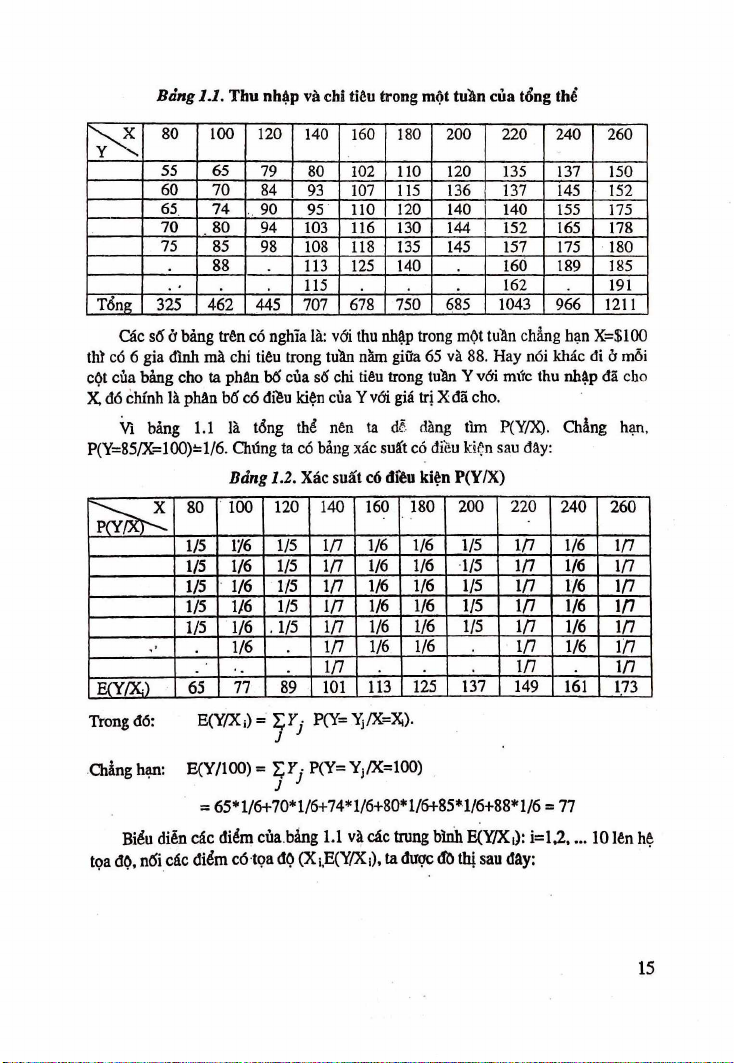
Bảng 1.1. T hu nhập và chi tiêu trong một tuần của tổng thé' 80 100 120 140 160 180 200 220 240 260 Y \ 55 65 79 80 102 110 120 135 137 150 60 70 84 93 107 115 136 137 145 152 65 74 90 95 110 120 140 140 155 175 70 80 94 103 116 130 144 152 165 178 75 85 98 108 118 135 145 157 175 180 88 113 125 140 160 189 185 115 162 191 _ĨỂĩĩS_ 325 462 445 707 678 750 685 1043 966 1211
Các số ở bảng trên có nghĩa là: với thu nhập trong một tuần chẳng hạn x=$100
thỉ có 6 gia đình mà chi tiêu trong tuần nằm giữa 65 và 88. Hay nói khác đi ờ mỗi
cột của bảng cho ta phân bố của số chi tiêu trong tuần Y với mức thu nhập đã cho
X, đó chính là phân bố có điều kiện của Y với giá trị X đã cho.
Vì bảng 1.1 là tổng thể nên ta dí đàng tìm P(Y/X). Chẳng hạn,
P(Y=85/X=100)-l/6. Chứng ta có bảng xác suất có điầu kiện sau đây:
Bảng 1.2. Xác suất cố đĩêu kiện P(Y/X) 80 100 120 140 160 180 200 220 240 260 1/5 1/6 1/5 1/7 1/6 1/6 1/5 1/7 1/6 1/7 1/5 1/6 1/5 1/7 1/6 1/6 1/5 1/7 1/6 1/7 1/5 1/6 1/5 1/7 1/6 1/6 1/5 1/7 1/6 1/7 1/5 1/6 1/5 1/7 1/6 1/6 1/5 1/7 1/6 1/7 1/5 1/6 . 1/5 1/7 1/6 1/6 1/5 1/7 1/6 1/7 1/6 1/7 1/6 1/6 1/7 1/6 1/7 1/7 1/7 1/7 E(Y/Xi) 65 77 89 101 113 125 137 149 161 173 Trong đó:
E(Y/Xi) = Ị Y: P(Y= Yj/X=X). 7 J Chẳng han:
E(Y/100) = 2 ; y , P(Y= Yj/X=100) 7 J
= 65* 1/6+70* 1/6+74* 1/6+80* 1/6+85* 1/6+88* 1/6 = 77
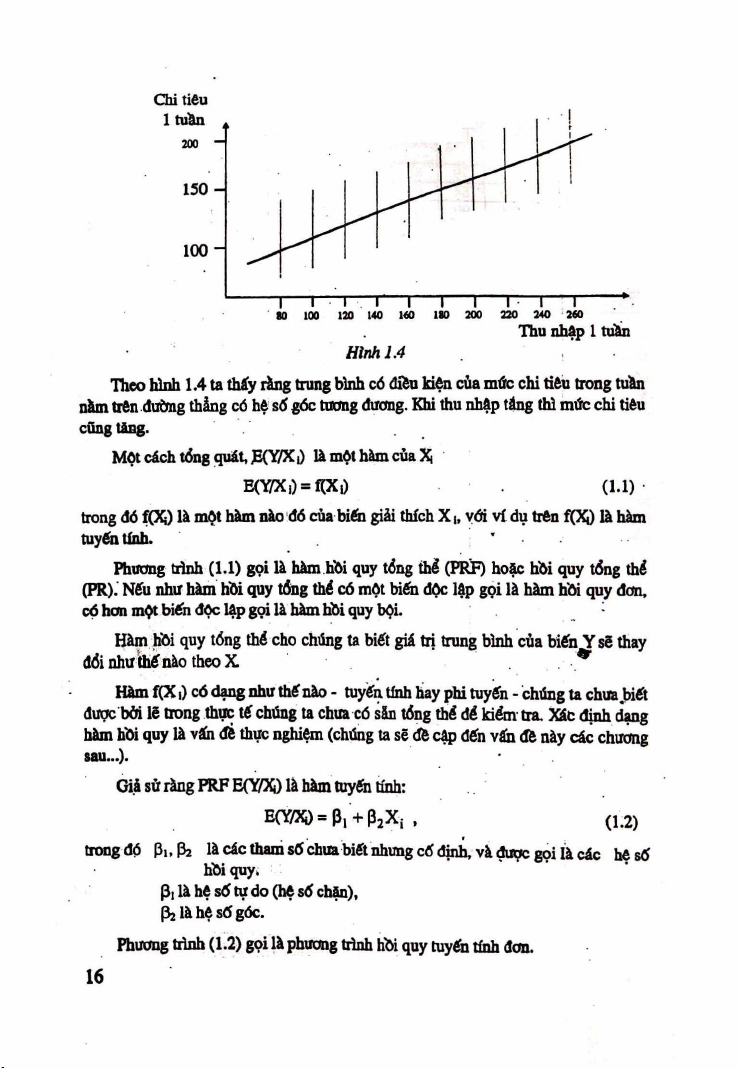
Biểu diễn các diổm của bảng 1.1 và các trung bình E(Y/X|): i= l,2 ,... 10 lên hộ
tọa độ, nối các điểm có tọa độ (Xi,E(Y/Xi), ta được đô thị sau đây: 15 Chi tiêu
Theo hình 1.4 ta thíy ràng trung bình có điều kiện của mức chi tiêu trong tuần
nàm trên đường thẳng có bệ số góc toong dương. Khi thu nhập táng thì múc chi tiêu cũng tảng.
Một cách tổng quát, Ẹ(Y/X i) là một hàm của Xị E (Y /X |) = Í(X |) ( 1 Ể1)
trong đó ỊỌĩi) là một hãm nào đó cùa biến giải thích XI, với ví dụ trên f(Xi) là hàm tuyến tính. '
Phuơng tìn h (1.1) gọi là hàm hồi quy tổng thể (PRP) hoặc hồi quy tổng thể
(PR). Nếu như hàm hồi quy tổng thể có một biến độc lạp gọi là hàm hồi quy don,
có hơn một biến độc lạp gọi là hàm hồi quy bội.
Hàm Ịiòi quy tổng thổ cho chúng ta biết giá trị trung bình của biến Y sẽ thay dổi như thế nào theo X *
Hàm f(X |) có dạng như thế nào - tuyến tính hay phi tuyín - chúng ta chua biết
được bởi lẽ trong thạc tế chúng ta chua có sẵn tổng thể để kiểm tra. Xác định riạnẹ
hàm hồi quy là vắn đè thục nghiệm (chúng ta sẽ đẽ cập đến vẫii đè này các chuỡng sau...).
Giả sử ràng PRF E(Y/Xi) là hàm tuyến tính: E 0 7 X D = p 1 + p 2X i , (lệ2)
trong đó Pi, P2 là các tham số chua biết nhung cố định, và đuợc gọi là các he số t ò i quy,
(3| là hộ số tự do (hê số chạn), P2 là hô số góc.
Phương trình (1.2) gọi là phuơng trình hồi quy tuyến tính đơn. 16 ■
Trong phân ứch hồi qủy chúng ta phải ước lượng giá trị trung bình cùa biến Y,
tức là ước lượng hàm hồi quy chẳng hạn dạng ( 1.2)ể Ở phương trình ( 1Ể2), giá trị
cùa các X ta đã biết, đo vậỵ việc uớc lượng ( 1.2) trở thành việc ước lượng các tham số chưa biết p Ẫ
và P2, trên cơ sở những quan sát của Y và X Phần này sẽ được trình bày ở chương II.
Thuật ngữ "tuyến tính" ở đâỵ được hiểu theo hai nghĩa: tuyến tính đối với
tham số và tuyến tính đối: với các biến. Thí dụ E07X) = Pi + P 2X j2 là hàm tuyến
tính đối vái tham sô' nhung không tuyến tính (phi tuyến) đối với biến; E(Y/X) =
p 1 + V pT Xi là hàm tuyến tính đối với biến nhưng phi tuyến đối vói tham số. Hàm
hồi quy tuyến tín tìu ô n luôn đuợọ hiểu là hồi quy tuyến tính đối với các tham số,
nó có thể hoặc không phải lặ tuyêh tính đô'i với biến. 1.4.
SAI S ố NGẪU NHIÊN VÀ BẢN CHẤT CỦA .NÓ
Giả sử chúng tạ đã có hàm hồi quy tổng thể E(Y/Xi); vì E(Y/JQ là giá trị trụng
bình của biến Y với giẩ Ị ậ X đã biết, cho nên các giá trị cá biột Ỵ không phải bao
giờ cung trùng với E(Y/X|). mà chúng xoay quanh E(Y/Xj).
Ký hiệu n là chênh lệch giữa giá trị cá biệt Yi và E(Y/X): ụ = Y , - E ( Y « ) h a ỹ : Yi= E(Y/Xi)+ Ui (1.3)
ụ là biến ngẳu nhiên, người ta gọi l í là yếu tố ngẫu nhiên (hoặc nhiễu) và (1.3)
đứcte gội PRF ngẫu nhiên.
Nếu như ECY/X) là tuyến tính đối với X thì Yi = /ổ, + P 1X l + ụ
Với thí đụ 1-3 và với x = $100 ta có Y| = 65 = pi + 100 P2 + U| Yj = 7 0 = 01 + 100 32 + u i Y3 = 74 = Pi + 100 pĩ + l ĩ Y4 = 80 = pi + 100 pj + l ĩ Ys = 85 = Pi + 100Pi + Ub yé = 88 = pĩ + 100 p2 + Từ (1.3) E(WJŨ) = E(E(Y/Xi) + E(UiyXi) E (Y /») = E(Y/Xi) + E(WXÌ) (1.4) -> E (U « ;) = 0.
Như vậy, nếu đường hồi quy của tổng thể đi qua các trung bình có điều kiên
cùa Y thì E Ó m = 0, trong trường hợp này (1.2) và (1.3) là như nhau. Nhung (1.3)
chi ra rằng ngoài các biến giải thích đã có trong mô hình còn có các yếu tố khác
ảnh hưởng đèn biến phụ thuộc Y. Nhung trung bình ảnh hưòng cùa các yếu tố này 17
đến biến phụ thuộc bằng 0 và do vậy không cần phải đua các yếu tố này vào mô hình.
Nhung cũng có thể nêu vấn dề: Các yếu tố này là những yếu tố nào và có thể
đua vào mô hình được không? Câu trả lời là: Chứng ta có thể xây dựng được mô
hình hồi quy bội, nhưng dù chúng ta có đưa vào bao nhiêu biến di chăng nữa thì
yếu tố l ỉ vẫn tôn tại vì một số lý do sau đây:
- Chúng ta có thể biết một cách chính xác biến giải thích X và biẾn phụ thuộc
Y nhung chúng ta không biết hoặc biết không rõ về các biến khác ảnh huởng đến
Y. Vì vậy, Ư, được sử dụng nhu yếu lố đại diộn cho tất cả các biến không có ưong mồ hình.
- Ngay cà khi biết các biến bị loại khỏi mô hình là các biến nào, khi đó
chúng ta có thể xây dựng mô hình hồi quy bội, nhưng có thể không có các số liệu cho các biến này.
- Ngoài các biến giải thích đã có trong mô hình còn có một sổ biến khác
nhung ảnh hưcmg của chúng đến Y rất nhỏ. Trong trường hợp này, chúng ta cũng sử
dụng yếu tố ngẫu nhiên l í đại diện cho chứng. Trong thí dụ đã tì n h bày ỏ phần
trên: số con trong gia đình, giới tính, tôn giáo..., cũng ảnh huởng đến chi tiêu trong
gia đình, u, đại diện cho chúng.
- Về mặt kỹ thuật và kinh tế, chúng ta muốn có một mô hình đơn giản nhất có
thể được. Nếu như chúng ta có thổ giải thích được hành vi của biến Y bằng một số
nhò nhất cấc biến giải thích và nếu nhu ta khOng biết tường minh những biến khác
là những biến nào có thể bị loại ra khỏi mô hình thì ta dùng yếu tô' Ư, để thay cho lất cả các biến này.
Trên đây là một vài iý do về sự tồn tại của n . U| giữ vai trò đặc biệt trong phân
tích hồi quy, chúng phải thỏa mãn những điều kiện nhất định thì việc phân tích trên
mô hình hồi quy mới có ý nghĩa. Sẽ là sai lầm nghiêm trọng nếu như sù dụng một
công cụ mà không biết những điều kiện để sử dụng nó có dược thỏa mãn hay
khôngế Trong phạm vi của cuốn sách này chúng tôi đặc biệt quan tâm đến những
điều kiộn để vận dụng mô hình. Tuy nhiên, trong thực tiễn nhũng điều kiên này
không phải bao giờ cũng được thỏa mãn và bạn đọc có thể tìm thấy cách phát hiện
và cách khác phục nếu như có một số giả thiết của mô hình khơng được thỏa mãn.
Những vấn đề này sẽ được trình bày dần dần trong các chương sau. 1.5. HÀM HỒI QUY MẪU
Ở phần phụ lục, chương n có trình bày sơ lược vê tổng thể và mẫu. vi sao phải
nghiên cứu mẫu. Ván dê ò đây cũng tương tự nhu vậy. Chúng ta không có tổng thổ,
hoặc có nhưng không thể nghiên cứu được toàn bộ tổng thể. Điều này có nghía là
chúng ta không thể xây dụng được hàm hồi quy tổng thể (PRF). Chung ta chì có
mẫu ngẫu nhiên được lấy từ tổng thể. Chúng ta muốn ước lượng PRF từ những
thông tin thu được trên mẫu ngẫu nhiên cùa các giá trị Y đối với các giá trị của X đa 18
biết. Một đíẽu chắc chắn rằng chúng ta không thể ước lượng một cách chính xác
PRF dựa trên mẫu ngẫu nhiên.
Hàm hồi quy được xây dựng trên cơ sở một mẫu ngẫu nhiên được gọi là hàm
hồi quy mẫu (SRF) hoặc hồi quy mẫu.
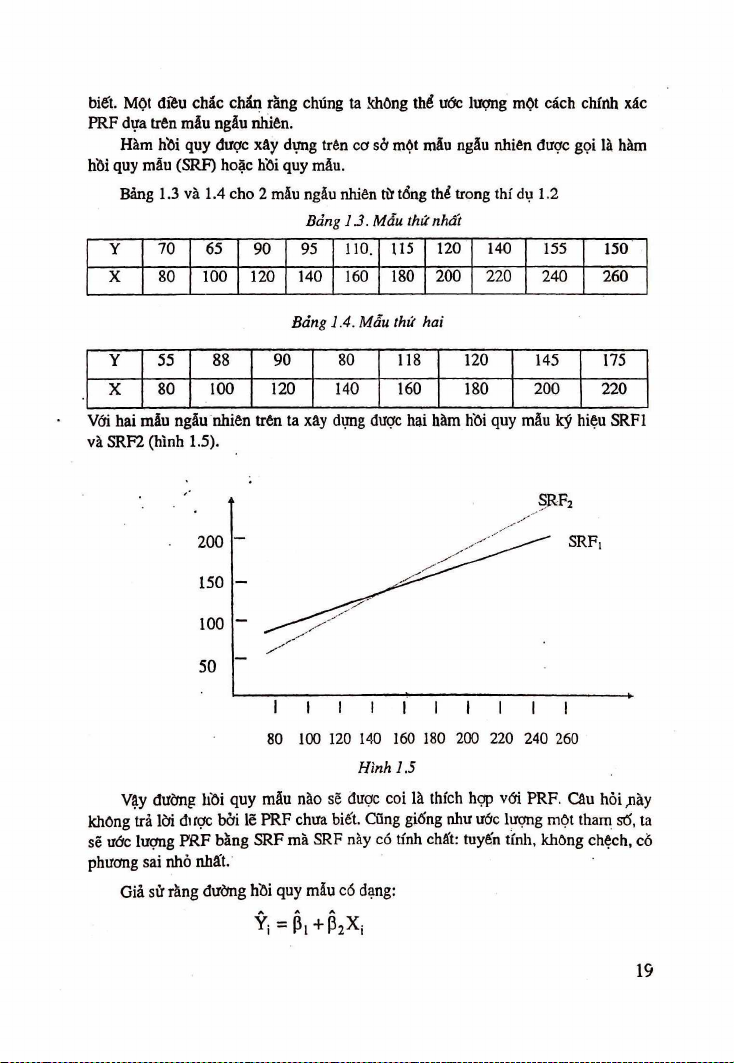
Bảng 1.3 và 1.4 cho 2 mẫu ngẫu nhiên từ tổng thể trong thí dụ 1.2
Bàng 13. Mẫu thứ nhất Y 70 65 90 95 110. U5 120 140 155 150 X 80 100 120 140 160 180 200 220 240 260
Bàng 1.4. Mẫu thứ hai Y 55 88 90 80 118 120 145 175 X 80 100 120 140 160 180 200 220
Với hai mẫu ngẫu nhiên trên ta xây dựng dược hai hàm h'ôi quy mẫu ký hiệu SRF1 và SRF2 (hình 1.5).
80 100 120 140 160 180 200 220 240 260 Hình 1.5
Vậy đuờng hồi quy mẫu nào sẽ được coi là thích hợp với PRF. Câu hỏi ,này
không trả lời được bời lẽ PRF chua biết. Cũng giống như ước lượng một tham sổ, ta
sẽ ước lượng FRF bằng SRF mà SRF này có tính chất: tuyến tính, không chệch, cỏ phương sai nhỏ nhất.
Giả sử rằng đường hồi quy m ỉu có dạng: Ỳ . - p . + M . 19
trong đó: Ỹj là uớc luợng cùa E(Y/X|)
Pị và p 2 là ước luạng của p! và P2
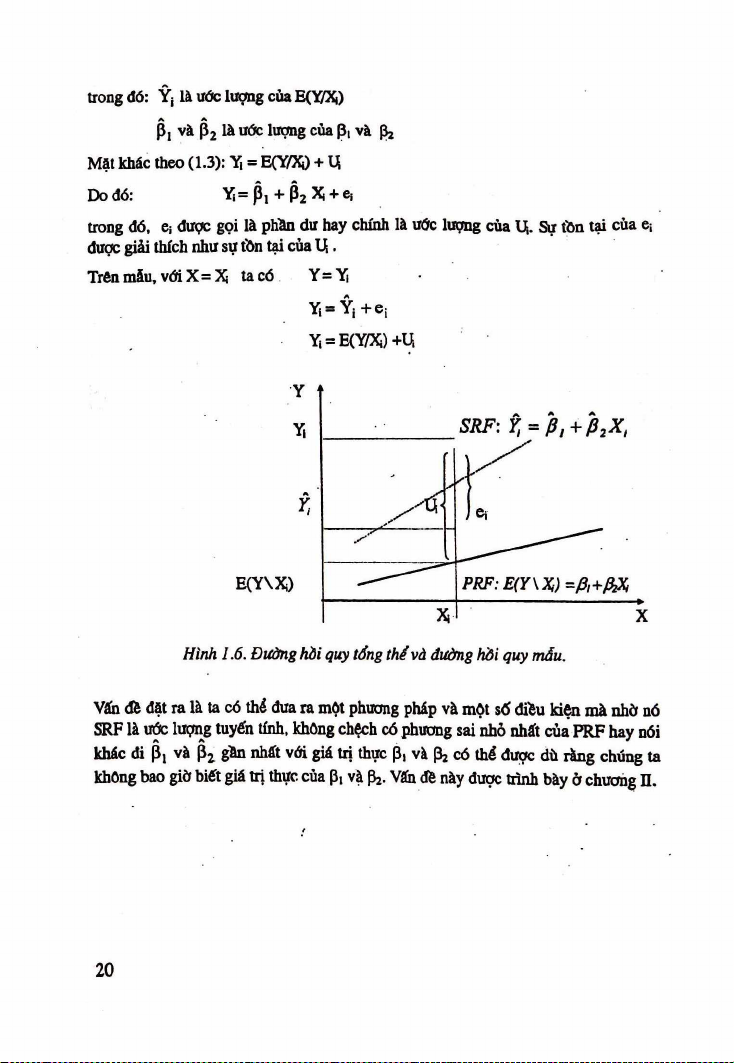
Mặt khác theo (1.3): Y| = E(Y/Xi) + u Do đó: Y! = + p 2 Xi + eị
trong đó, ei được gọi là phần du hay chính là uớc luọng của Uj. Sự tồn tại cùa e;
duợc giải thích nhu sự tồn tại của ụ .
Trên mảu, với X = Xi ta có Y = Ỵ Ỵ - Ỳ , + e | Ỵ - B C W O + ụ
Hình 1.6. Đường hòi quy tổng thề và đường hồi quy mẩu.
Ván dề đặt ra là ta có thể đưa ra một phương pháp và một số điều kiện m à nhờ nó
SRF là uớc lượng tuyến tính, không chệch có phuỡng sai nhỏ nhất của PRF hay nói khác đi và
gần nhất với giá trị thực p, và p2 có thể được dù rằng chúng ta
khổng bao giờ biết giá trị thực của Pi và
Văn dè này được trinh bày ở chương n. 20 CHƯƠNG 11 MÕ HÌNH HỔI QUY HAI BIÊN
ưức LUỰNG VÀ KIỂM ĐỊNH GIẢ THIẾT
Trong chương này sẽ trình bày vấn dề ướciuợng hàm hồi quy tổng thể PRF
một cách chính xác có thể được trên cơ sở hàm hồi quy mẫu. Có một số phương
pháp ước lượng hàm hồi quy mẫu, phương pháp thường dùng là phương pháp bình
phương nhỏ nhất OLS (Ordinary Least Square). Chúng ta sẽ trình bày phương pháp
này cho mô hình hai biến ở chương này, chương sau sẽ trình bày phương pháp OLS cho mô hình hồi quy bội.
2.1. PHUƠNG PHÁP BÍNH PHUONG n h ỏ n h ấ t
Phương pháp bình phương nhỏ nhất do nhà toán học Đức Carl Friedrich Gauss
đua ra. Sử dụng phương pháp này kèm theo một vài giả thiết, các ước lượng thu
được có tính chất đặc biệt, nhò đó mà phương pháp này là phương pháp mạnh nhít
và được nhiều người thích sử dụng.
1. Nội dung phưomg pháp bình phuomg nhỏ nhất
Giả sử E(YIXị) = pi + i32Xị là PRF
Khi đó giá trị quan sát Yj! Yi= E(YIXị) + l í = pi + P2X + l í Ỷị = P, + P 2X; làSRF Yi = p , + p 2X i + e i
Vấn dề là phải tìm ý( = P ị + P i X ,
Giả sử rang chúng ta có n cặp quan sát cùa Y và X, cặp quan sát thứ i có giá trị
tương ứng (Yi,Xj) : i = l , n . Ta phải tìm Yị sao cho nó càng gần với giá trị thực
của Yi có thể được, tức là phần dư
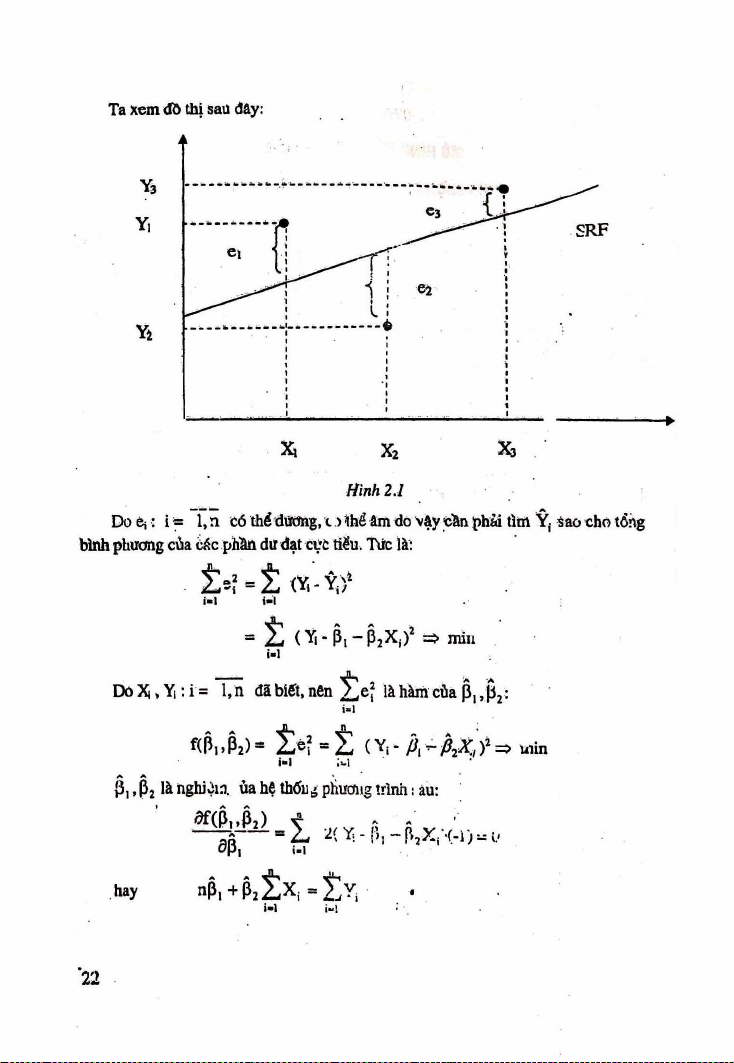
e, = Y ,-Ỷ 1= Ỵ Ì ậ 1 - ệ í X J càng nhỏ càng tốt. 21 Ta xem đồ thị sau đay: Hình 2.1
D o è j: i= l , n có th ể d tia n g .o ih ổ â m d o vậy cần phải tìm Ỳị sao cho tổng
bình phương của các phần dư đạt Cực tiểu. Tức là: Ỉ 2? = Ỉ n - Ỷ . ý i«l i-ì = ỉ
( Y ,- P , - p 2X f)2 => min iễl
D o X i,Y i:i = l ,n đãbiết.nên
l à h à r a c ù a P |,jj2ỉ i«l
f(P, p2)ề Ỉ*ỉ = È (Ỵ| - Â - fax, Ý => uin i-l ;-i
P , , ậ 2 là nghiộm. ủa hệ thỐLịị piìuơi.12 trìn h : áu: a f ( P „ ê , ) f .. a op, Ii-i s S - - = hay n P , + P 2Ỉ X j = Ị ] v »■1 i«l '22 ^
— = Ẻ 2 C Ỵ - P , - ệ , X iX-55) = 0 a p 2 i.1 hay
ệ w% x + p 2 ỉ X f , Ề Y,JÍ i=l h=l i**l
P t , P-Ị được tìm từ hệ phương tìn h sau: n Á + Á í J f i = í Y, . 1 =1 i-1
Á ẳ x+ Á ẳ x? = £ Y,Xi (2.1) M i-1 i»1
' Hệ phương trình (2.1) gọi là hộ phương trình chuẩn. Giải hệ phương trình trên ta được:
n Ỉ Y . X i - Í Ỉ X . Ỉ Y i
P 2 = — ------------------- V — = — - (2.2) n Ẻ X ? - Ỉ X , i , i«l \ i - l / P , = Ỹ - P 2X (2.3) Đặt Xi = X - X yi = Y i - Ỹ È y iX ị Khi đó P , = ----- (2.2)' Ỉ * ỉ i-l
P ,, P2 là các ước lượng của Pi và p2 được tính bằng phuơng pháp bình phương
nhò nhất - được gọi là các ước lượng bình phương nhỏ nhất.
2. Các tín h c h ấ t của các ước lượng bình phưong nhỏ n h ất
1. P i , p 2 được xác định một cách duy nhất ứng với n cặp quan sát (X|,Y1)
2. ậ | , p 2 là các ước lượng điểm của pi, p2 và là các đại lượng ngẫu nhiên,
với các mẫu khác nhau chúng có giá trị khác nhau.
Ỳ- = P, + P 2Xi - SRF có các tính chất sau đây:
1. SRF đí qua trung bình mẫu ( X , Y ), nghĩa là : Ỹ = p, + :ậ2 X 23 ,
f Giá trị trung binh của Ỹị bàng giá trị 'trung- bình cùạ cậc quan sát: Y = Ỹ .
3. Giá trị bung bình của các phần dứ: éị = 0 I . *-!'• L * -
4. Các phần du ei không tuơng quan với Ỷj tức lài Ỳ;ej = 0 i»l 5.
Các phần dư ei không tưong quan với Xi tức là :. e, Xl = 0 T hí dụ 2.1
Bảng sau đây cho số liệu về lãi suất (Ỷ) và tỷ lệ lạm phát(X) trong năm 1988
ở 9 nước Giả sử rằng sự phụ thuộc Ẹ(Y/X> ẹó dạng tụỵến tính dối vãi cả biến số và
tham số. Hãy ước lượng hàm hổi qụy và tính cầo đặc tnm g của nó._____________ _ Ệị?^1v3 ■ 66 ,3 - m . : 1 :S ® r -7,6 Ì X ậ k i p l i EN l l i s i ã ế - l s ề Ẻ 1 W | p § p .•4,4
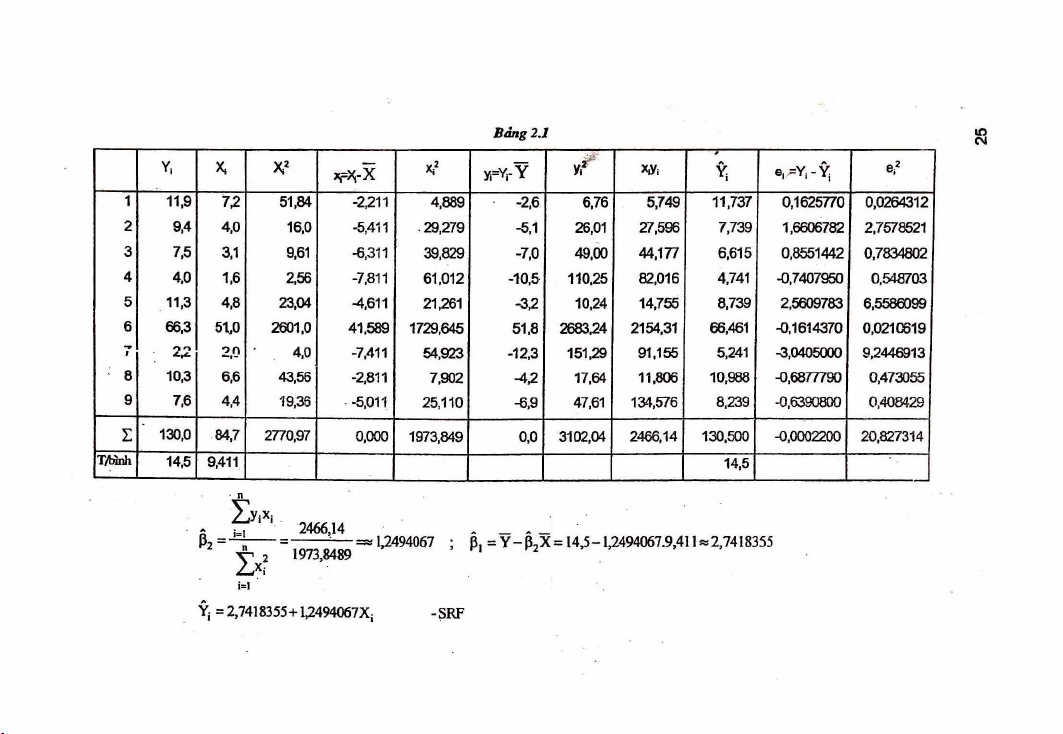
Quá trình tính toán được thể hiện trong bảng 2.1.
2.2. CÁC GIẢ THIẾT c ơ BẢN CỦA PHUƠNG PHÁP BÌNH PHUƠNG NHỎ NHẤT
Trong phân tích tò i quy, mục đích của chúng ta là ước lượng, dự bảo về tổng
thể, tức là ước lượng E(Y I X i) hay trong mô hình hồi quy tuyên tính, đơn là ước
lượng E0fl X i) = Pị + P2X1 • Pi và P2 tìm được bằng phương pháp bình phương
nhỏ nhất là cấc ước lượng điểm của Pi và p2. Chúng ta không biết được chất lượng
cùa các ước lượng này như thế nào. c h ít iưọng của các ước lượng phụ thuộc vào:
- Dạng hàm của mô hình được lựa chọn
- Phụ thuộc vào các Xi và Ui
- Phụ thuộc vào kích thựớc mẫu
Về dạng hàm của mô hình chúng ta sẽ đ& cập đến ờ chương, IX Ở đây chúng
ta sẽ nói về các giả thiết đổi với Xi và Ư,. Với các giả thiết này thì các uớc lượng
tìm được bàng phương pháp binh phuơng nhỏ nhất là các uớc lượng tuyến tính
không chệch, có phương sai nhỏ nhất. I
G iả thiết I: Biến (các biến) giải thíph là phi ngẫu nhiên, tức là cấc giá trị của
chúng là các số đã được xác định.
Giả thiết này không có gì mới, vì phân tích hồi quy đuơc đề cập [à phan tích
. hồi quy có điều kiện, phụ thuộc vào các giá trị X đã cho. 2+ Bảng 2.1 V, X, X,2 *ĩ ypYrY y f m V, e^Y.-Ỹị e,2 1 11,9 7,2 51,84 -2,211 4,889 -2,6 6,76 5,749 11,737 0,1625770 0,0264312 2 9,4 4,0 16,0 -5,411 . 29,279 -5,1 26,01 27,566 7,739 1,6606782 2,7578521 3 7,5 3.1 9,61 -6,311 39,829 -7,0 49,00 44,177 6,615 0,8551442 0,7834802 4 4.0 1.6 2,56 -7,811 61,012 -10,5 110,25 82,016 4,741 -0,7407950 0,548703 5 11,3 4,8 23,04 -4,611 21,261 -3,2 10,24 14,755 8,739 2,5609783 6,5586089 6 66,3 51,0 2601,0 41,589 1729,645 51,8 2683,24 2154,31 66,461 -0,1614370 0,0210619 1 2 2 20 4,0 -7,411 54,923 -12,3 151,29 91,155 5,241 -3,0405000 9,2446913 8 10,3 6,6 43,56 -2,811 7,902 -4,2 17,64 11,806 10,988 -0,6877790 0,473055 9 7,6 4,4 19,38 -5,011 25,110 -6,9 47,61 134,576 8,239 -0,6390800 0,408429 I 130,0 84,7 2770,97 0,000 1973,849 0,0 3102,04 2466,14 130,500 -0,0002200 20,827314 Tj/b5nh 14,5 9,411 14,5 ■ n Z y i xi - i=l w 2466,14 _ . p 2 = „------= _ =» 1,2494067 ;
B, = Y - B , X = 14,5-1,2494067.9,411*2,7418355 n V 2 1973,8489 1 2 p 2 X i=i
Ỷj = 2,7418355 + 1.2494067X, - SRF
Giả thiết 2: Kỳ vọng của yếu tó ngẫu nhiên u bằng khống, tức là E ( ự l X |) = 0
Giả thiết này có nghĩa là các yếu tố không có trong mô hình, ụ đại diện cho
chúng, không có ảnh hưởng hệ thống đến giá trị trang b'mh của Y.
VÔ mặt hình học giả thiết này được mô tả bàng dò thị (hình 2.2).
Đồ thị chỉ ra rằng với mõi giá trị của X, cắc giá trị có thể có của Y xoay quanh
giá trị trung binh. Phân bố của phần lớn hơn hay nhỏ hơn giá trị trung bình chính là
các lị , theo giả thiết này trung bình của các chênh lệch này bang 0 .
Chú ý: Giả thiết E(U I X.) - 0 kéo theo E(Y, I + P2 Xa . Y G iá trị trung bình P R F Hình 2.2 26
Giá thiết 3. Phương sai bằng nhau (phương sai thúần nhất) của các u (Homoscedasticity o f ụ ).
Var (Ui I Xi) = Var(Uj I X ị) = ơ2 V i* j
Giả thiết 3 có nghĩa là phân bô' có điểu kiộn của Y với giá trị đã cho của X có
phương sai bằng nhau, các giá trị cá biệt của y xoay quanh giá trị trung bình với phương sai như nhau.
Giả thiết 3 kéo theo Var(Yr IX ) = ơ2.
Về măt hình học có thể mô tả giả thiết này như hình 2.3.
Hình 2.4: Var (U I Xi) * Var (ƯJI x ; ) = ơ j : j
(Phương sai khống thuần nhất)
Giả thiết 4. Không cổ sự tương quan giữa các l í : Còv( l í , Uj) = 0 Vi * j Hình 2.5 a. Không tự tương quan; b. Tự tuơng quan dương; c. Tự tương quan âm 27
Giả thiết này có nghĩa là ụ là ngẫu nhiên. V6 mặt hình học có nghĩa là néu
như có một giá trị u nào đó lớn hơn (nhỏ hơn) giá trị trũng bình thì không có nghĩa
giá b ị khác cũng lớn han (nhỏ hơn) giá trị trung bình.
Giả thiết 5. LỊ và J í không tương quan với nhau: Cov(Ư,, Xi) = 0.
Trên đây đã đưa một số giả thiết cơ bản. Bạn đọc có thể đặt ván dề: vì sao
phải có các giả thiết này? Chứng được thực hiện như thế nào? Cấi gì sẽ xảy ra nếu
các giả thiết này không được thòạ mãn? Bằng cách nào biết được mô hình hồi quy
thỏa mãn tất cả các giả thiết này. Vấn dề mà bạn đưa ra thật lý thú nhưng không
thể giải đáp ngay trong chương này được. Chúng sẽ được giải đáp dàn dần ưong các chương sau. 2 .3 .
Đ ộ CHÍNH XÁC CỦA CÁC uớc LUỢNG BÌNH PHUƠNG NHỎ NHẤT
Theo phương pháp bình phương nhỏ nhát, các ước lucmg P ,, P 2 được xác định theo công thức: p , = Ỹ - P2 X ậ 2 = Ẻ Xi y, / £ X? ì-1 1-1
Các uớc lượng này là hàm của mẫu, là đại lượng ngảu nhiên, với các mẫu khác
nhau ta có các ước lượng khác nhauề Vi phương sai hay độ lệch chuẩn đặc trưng
cho độ phân tán của đại lượng ngảu nhiên, nên ta dùng chúng làm thước đo cho
chít lượng của uớc lượng.
Vài các giả thiết cùa phuong pháp bình phương nhỏ nhất, phương sai và đọ
lệch chuẩn cùa các ước lượng đuợc cho bời các cồng thức sau: v a r ( Ằ ) = ^ ~ ; se( P2 ) = ° pĩ M
V a r ( P ,) = — £ - ^ - < 7 . s e ( / ? ,) = <7 n í x f \ n Ỷ f Xĩ >=• 1 M trong đố, ơ 2 = Var(U)
se: sai số tiêu chuẩn (Standard error) 28 X| = J5- X
Trong các công thức trên ơ1 chua biết, ơ2 đuợc ưãc lượng bằn ..g. . ước lượng
k h ô n g c h ệ c h c ù a I 1Ó l à ớ = — — ; â = ỵ ỵ ^ n _ 2 )
là s a i s ô 't iê u c h u ẩ n c ù a
đường hổi quy (Standard error of regression). Nó chính là độ lệch tiêu chuẩn các
giá trị Yquanh đường hồi quy mẫu.
Các tính chất của các ước lượng bình phương nhỏ nhất được thể hiện qua định lý sau đây:
Định lý Gauss - Markov: Với các giả thiết 1-5 của phương pháp bình phương bé
nlĩất, các ước lượng bình phương nhò nhất là cấc 1tóc lượng tuyến tính, không chệch và
có phuơng sai nhổ nhất trong lớp các ước lượng tuyến tính không chệch.
Với các kết quả ở bảng 2.1, ta tính được:
ơ2 chưa biết nhưng có thể dùng ước lưcmg không chệch của nó là ờ 2. „ , £ , ơ2 2,9746993 Var( B, ) = —-— = - ■ — — » 0,001507055 ■V 2 1973,8489 M se( p j) = 0,0388208 „ 2>ỉ , 2770,97 Var ( P ,) = -
a = ------ —------- 2,9746993 « 0,464 Ỷ V 2 9.1973,8489 n Z / xi i«l se( P, ) *0,6811
2.4. HỆ SỐ r2 ĐO ĐỘ PHÙ HỢP CỦA HÀM H ỗ l QUY MẪU SPF Ta có Yi = Ỷj + Ci
Y i- Ỹ = Ỹ i - Ỹ + e,
= Ỷj - Ỹ + e, hay y, = ỹj+ e , . Z y? = ỉ
ỷ i + í e ĩ + 2 S ỷ ,e , |Ế=1 |ắ»l M = ỉ ý i +
e- + 0 . Vì ỹ, = P 2 Xi nên : i=l i=l 29
È y?*= N Ẻ x? + £ e? M jẵl i-1 Ký hiệu:
T S S = ẳ y? = ẳ Ơ I- Y )2 . i-l i-l
-T> TSS (Total Sum o f Squares) là tổng bình phương của tất cả cấc sai lộch giữa
các giá trị quan sát Yị với giẩ tri trung bình của chúng, ESS = £ (Ỷ,
Y )J = £ <Ỷ€ - Ỹ )2 = í
ỳ ] = P I Ỳ X?. j=l ịế| i-l i*l
ESS (Explained Sura of Squares) là tổng bình phương của tất eả các sai lệch
giữa các giá ư ị của biến phụ thuộc Y nhận được từ hàm ti&i quy mẫu với giá trị
trung bình của chúng (Ỳ - Ỹ ). Phần này đo độ chính xác của hàm hồi quy.
RSS = ỉ e? = Ỳ ơ i - % Ỷ i-l i-l
RSS (Residual Sum o f Squares) là tổng bình phương của tất cả các sai lệch
giữa các giá trị quan sất Y và các giá trị nhận được từ hàm hồi quy.
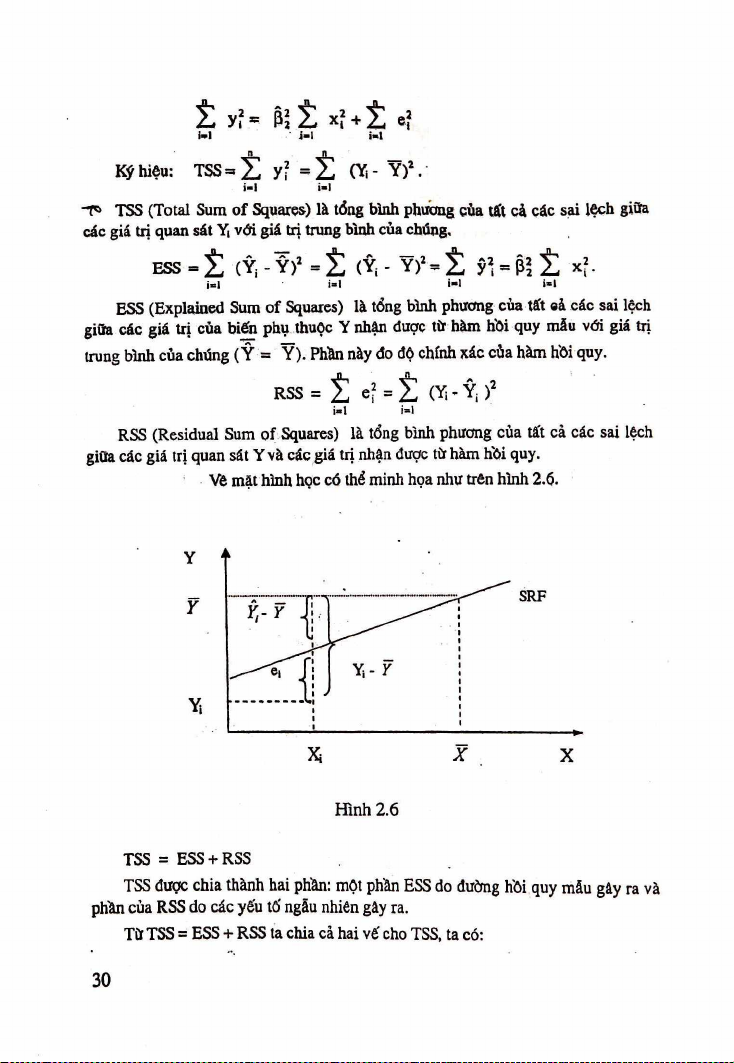
Vè mặt hình học có thể minh họa như trên hình 2.6. H ình 2.6 TSS = ESS + RSS
TSS được chia thành hai phần: một phần ESS do đường hồi quy mẫu gây ra và
phần cùa RSS do các yếu tố ngẫu nhiên gây ra.
Từ TSS = ESS + RSS ta chia cả hai vế cho TSS, ta có: 30 Ỳ ( Ỷ Ẵ- W Ỷ e ? E SS RSS £ r > M TSS + TSS Í ( Y ; - ỹ / ẻ ( Y , - W Iẳ»l i=I ẳ ( Ỹ i - Ỹ ) M ____ ESS RSS Đặt r 2 = — 2 — TSS — - TSS m - Ỹ ) i-1 W >? Pỉ£x? 1 I 1 i=l ĩ .I Ó n l W M Èy? — -ĩ i-I n A / i»l }§ /n- l s2 = 2 n 6 — sị I : r ỉ / A - 1 trong đó: S 2
X và Sy là phương sai mẫu của X và Y. Ỉ X iy ,- ( ỉ * ! * ) Mật khác P , = - 3 - — => r ’ w ỉ * ? p ìp i
r=j f l P =f S F ) B H i ?
Từ định nghĩa r2 chúng ta thấy r2 đo tỷ lộ hay sô' phần trãm của toàn bộ sai lệch cùa
Y vái giá trị trưng bình của chúng được giải thích bàng mô hình (hay biến độc lập), r2
được sư dụng để đo độ thích hợp cùa hàm hồi quy. Dễ đàng thấy được 0 < r2 < 1. Nếu
lấy căn bậc hai cùa r ta được r. r chính là hệ số tương quan mẫu, tuy nhiên dấu của r tuỳ
thuộc vào quan hệ cùng chiều hay ngược chiều giữa Y và X. 31
Các tính chái của hệ s ổ tương quan r
l ễ r có thé âm hoặc duơng, dấu cùa r phụ thuộc vào dấu của tử số, đó chính là
dấu cùa Cov(X,Y), hay là dấu của hệ só góc. 2 . -1 á r <; 1
3. r có tính chát đốì xúng r(X,Ỵ) = r(Y,X)
4ằ Nếu X' = a X + c ; Y = b V + a; a,b,c,d là các hằng số
a,b > 0 thì lỌC, Ỹ ) = r(X,Y)
5. Nếu X,Y độc lập với nhau thì r(X,Y) = 0; Điều ngược lại không đúng.
6. r đo sự phụ thuộc tuyến tính, nhung không có ý nghĩa trong việc định rõ
tính chất các quan hệ phi tu y ến .
7. r đo độ phụ thuộc tuyến tính giữa X và Y, vậy không đòi hỏi X,Y có mối quan hệ nhãn qui. 8 . r2 cQng có thể é tín u h rn b bằăng công thức m : ức:
[ ỉ ( v , - Ỹ ) (Ý, - ? ) " ( ỉ y , ỹ , ) r = i“l j»I i-1 i«l
Với các số ở bảng 4.1 ta cổ: 2 4 6 6 142 = 1” 0 ’9566
2.5. PHÀN B ố XÁC SUẤT CỦA Ui
Phần trên chúng ta đã trinh bày các ưởc lượng điểm của Pi và Pj thu đuợc
bằng pbuơng pháp bình phuong nhỏ nhít. Với các giả thiết cơ bản: E ( U ) = 0 Var ( I Ị ) = o 2 Cov (U , Uj) = 0 ( V i* j)
thi p , , P2 là các ước lượng tuyến tính không chêch có phương sai nhò nhất của Pi
và P í. Mục đích cùa phân tích hồi quy khôiig nhải chi là suy đoán về Pi và Pỉ hay
PRF mà còn phải kiểm tra bản chất của sự phụ thuộc, còn phải thực hiện các dự
đoán khác. Do vậy cần phải biết phân bố xác su it của p! và p 2. Các phân bố này
phụ thuộc vào phân bố cùa các Uj.
Bây giờ chúng ta đua them giả thiết. 32
G iả thiềt 6. Ụ có phân bố N(0, ơ3)
.Với các giả thiết trẽn, các ước lượng bình phương nhỏ nhất P ,, p 2 và ở 2 có
•các tính chất sau đây:
1. Chúng là các ước lượng không chệch 2. Có phuong sai cực tiểu
3. Khi số quan sát đù lớn thì các uớc lượng này xấp xỉ với giá trị thực của phân bố. 4. Pl
TO tính chất này suy ra z = —— — ~ N (0,1) ơ p, 5. p 2 ~ N (p 2 ,ơ? )
Từ tính chất này ta suy ra z = Ẽ3—Ẻ 1 „ K (0,1)
7. Trong các ước lượng không chệch cùa Pi, pj bất kể là tuyến tính hay phi
tuyến tính thì P ,, P2 có phương sai nhỏ nhít. 8 . Yi - N(Pi ■+ P2 , ơ2).
Với các tính chất trên chúng ta có thể tìm khoảng tin cậy và kiểm định giả
thiết về các tham số hồi quy.
2 .6 . K H O Ả N G T IN CẬY VÀ K lỂM đ ị n h g i ả t h i ế t VỀ .CÁC h ệ s ố H Ồ I QUY
Với các giả thiết 2-6 thì : p, ~ N (Pi, o | ) Pl p 2 ~ N ( Ị h , o ị ).. 2 _ trong dó : ơ * =
nhưng do ơ 2 chưa biết nên a ị và a ị cũng chua biết. Do vậy, phải dùng ước
lứợng không chệch cùa c 2 là ô 2 . Khi đó các thổng kề: 33 p , - P i p 2 - p 2 t = ■ >— v à t = — - J p f có phần bố T(n-2) và s e ( P ,) se(P 2) Ẳ
X2 = ( n - 2 ) - ? 7 ~ x 2( n - 2 ). Ơ
Do đó có thể tìm khoảng tin cậy, kiém định giả thiết cho các bệ số hồi quy và ƠJ.
1Ễ Khoảng tin cậy của Pi t = P l ~ ~ T (n -2 ) se (P i)
Với hộ số tín cậy 1 - a la tìm được tc/2 (n -2) thòa mãn. p ( - W ( t t-2) s < W (n -2)) = 1 - a . se(P ,)
Khoảng tin c&y (1 - a ) của Pi là:
(0 ! -ta /2 (n -2) s e ( Pj) ; p | + ta/2 ( n - 2) s e ( P , ) )
2. Kiểm định giả thiết đối với pỂ
Có thể đua ra giả thiết nào đó về pi, ciiẳng hạn Pi = p ị . Nếu giả thiết này (King thì: P i - P , t = - T (n -2 ). se (P ,) Ta có bảng sau đây:
Bảng 2 2 . Kiểm định giả thiết về pi Loại giả thiết Giả thiết Ho Giả thiết đối H| Miền bác bỏ Hai phía p i = p ; Pi * p ’ m > W n - 2 ) Phía phẫi t > t„ (n -2 ) p i s p ; Pi > P* Phía dái t < - t a ( n - 2 ) Pi £ P* P i< P * a thường nhò hơn 0,1
ta (n -2) đuợc xác định bởi p (t > ta (n -2)) = a , được cho trong bảng 2 phần phụ lục.
3. K hoảng tin cậy củ a Pi Dựa vào: t = - T ( n - 2) se(P 2)
do đó với hệ số tin cậy 1 - a , khoảng tin cậy cùa Pí được xác định bởi: 34 p 3 - i v
P ( - W ( n - 2 ) ắ i l i ^ - ắ t a ữ ( n - 2 ) ) = l - a • se (P j)
~ P( p 2 - ta/2 (n -2 ) se ( p 2) ổ Pj ^ p 2 + tan (n -2) se( P2)) = 1 - a .
4. Kiểm định giả thiết đối với Pj
Có thể đua ra giả thiết về giá trị thực của p2. chẳng hạn p2 = P*.
Nếu giả thiết này đúng thì . _ P2 - P 2 ' T (n -2) s e f lij)
Bđng 2.3. Kiểm định giả thiết v í Pi Loại giả thiết Giả thiết Ho Giả thiết đối H| Miên bác bỏ Hai phía p 2 = p ; P2 * pj 11 1 > taữ (n -2 ) Phía phải t > t„ (n -2 ) P2 > P2 Phía trái t < - U n -2 ) • p2 s p ; P 2 < P ;
Nếu như đua ra giả thiết P2 = (3 2 = 0 thì điều này có nghĩa là đua ra giả thiết
biến độc lập X không ảnh hưởng đến biến phụ thuộc Y, .khi các ti được tính bằng còng thức: se(Pị) se(Pi)
Với các số ở bảng 2.1, ta có thể tun khoảng tin cậy của Pi và (3j, cOng nhu
kiểm định- các giả thiết về tham số này.
Với a = 0,10 => (0,050 (n - 2) = to,050 (7) = 1,895 (theo bảng 2);
se(P ,) = 0,6811; se( P j ) = 0.0388
Khoảng tin cậy của Pi và p2 với hẹ số tin cậy 90% là: •
(P , -1,895 s e ( p ,); P, + 1,895 se(P,))
(2,7418335 - 1,895 . 0,6811 ; 2,741835 + 1,895 . 0,6811) hay (1,451149:4.0325195)
( fỳ2 -1,8*95 se ( p 2 ); P2 + 1,895 . se ( p 2 ))
(1,2494067 -1,895. 0,0388 ; 1,2494067 + 1,895. 0,0388) (1,17588; 1,3229327)
Có thể kiểm định giả thiết Ho : = PĨ = 0 35
Giả thiết Ho về mặt kinh tế túc là chúng ta đua ra giả thi£t biến X khổng ảnh
huởng đến Y, trong ví dụ cụ thể này nghĩa là nêu ra giả thiết ợ lệ lạm phát không
ảnh hũởng đến lãi suất ngân hàng.
Với a = 0,05, to,(B5 ơ ) = 2,365 (bảng 2) ■ Ễ i - g i 1,2494067 - 0 _ se(P 2) = 0 ,0 3 8 8 . t>to,cnj(7)
do đó ta bác bỏ giả thiết Ho và chip nhện Hi
6. Khoảng tin cậy đối với a2 XJ = ( n - 2 ) ^ - ~ x 2(n-2).
Do đó, khoảng tin cậy (1 - a ) của ơ2 đúợc xác định từ , ô 2 2 P ( X 1
( n - 2 ) ắ ( n - 2 ) ^ 7 á X « « (11- 2 ) ) = 1 - a p í í p i i £ l ^ s { z a / i ( n - 2 ) X i - * n ( n - 2 ) )
trong dóx*«(k) đuợc cho bởi bảng 4, phần phụ lục.
6. Kiểm định giả thiết đtfi VỚI ơ Bảng 2.4 Loại giả thiết Giả thiết Giả thiết đối Miền bác bỏ Ho H, Hai phía II a 2 * ơ ị
~~°~v • - > x l , i l » - 2 ) hoãc a O < n - 2)â* , 1 ^ X \ ~ m ! l \ n *) . <70ặ " b I Phía phải I ơ 2 > ơ ị ( n - 2)ôJ .
------J — > X Ỉ ( n - 2 ) ơ õ Phía tiái II o°L ơ 2 < o ị (n -,2 )ỡ l , . ... . í < x ỉ-« (n 2) <*0
Kiểm định giả thiết cho thí dụ 2.1
Phần trên đã tính đuợc ô 2 = 2,9740993
Có th í kiểm tra giả thiết: H0 : ơ í = ơ ị = 3 H , : ơ 2 * 3 36
CL = 0,05 => 5C
0,025 (n-2) — X 0.025 (7) = 16,0128; x20.975 (7) = 1,68987 ( n - 2 ) ô í 7.2,9746993 — 7 = — ------ = 2,3136 o j 32
2.7. KIỂM ĐỊNH SỰPHÙ HỢP CỦA HÀM H ồ i QUY, PHÂN TÍCH H ồ i QUY VÀ PHAN TÍCH PHUONG SAI
Phần này sẽ trình bày việc phân tích hồi quy theo quan điểm cùa phân tích
phương sai, nó cung cấp cho chúng ta một cách khác, hữu ích trong việc giải quyết
vấn dề phán đoán thống kê.Theo phần 2.5 chúng ta có: ị y ì - ị ỹ ú ị ' ! i-1 i-l i-1 = ÍM ỉ X? + £ e? i>1 i-1 hay TSS = ESS + RSS. Mặt khác:
r = ESS/TSS, nên ESS= I^TSS và RSS = (1 -r) TSS. ơ 2 Do P2 cổ phân bố N (Pj, nên P’ ' \ Iẽ x ỉ ~N(0,1) ơ V i-1 (P í " P ĩ ) 2 V ĩ 2 , ệ> và — - ỷ — 2 X ~ x ( 1) i.1 pỉ Do ( n - 2 ) p - = J^ - ~ x V 2 ) ( P i - P a ^ ỉ * ? ỉ e? (P2 - P 2f Z x? ---------
— / 1 : - ^ 7 - / (n -2) = — --------& — nên: F = -------- — / 1 : -*=4“ ' ơ t i / . ỉn! / ( n - 2)
hay F = --------- ——------- có phân bố F( 1, n-2).
Chứng ta kiểm định giả thiết: 37 H o: (32 = 0 H ,:p 2 * 0 P Ỉ Ẻ * ? Nếu F = - > Fg(l,n -2 ) Ơ .
thì bác bỏ gia’ thiết Ho, tức là bác bỏ giả thiết X không ảnh hưòng đến Ỳ. Trong đó a thường nhò han 0 ,1.. ■ r' ■ Mặt khác n ' Ti . . ' Ệ - 5 ? I 2 *Ỉ 2 '“ X' ESS / 1 _ T S S r 2 / 1 F = ỹ
= RSS / (n -2 ) _ ( l - r 2 ) T S S / ( n - 2 )
cho nên quá trình phân tích phương sai cho phép chúng ta đưa ra các phán đoán
thống kê về độ thích hợp của hàm hồi quy. Ta có thể đưa ra quá trình phan tích
phương sai một cách ngắn gọn bàng bảng sau đay: -
Bảng 2.5. Bảng phản tích phucmg sai cho mô hình hồi quy hai biến Nguồn biến thiên Tổng bình phương Bậc tự do Phuơng sai Từ hàm hồi quy 1 Plỉ *? (ESS)
Ẹ ỹ i = P Ỉ ằi-l iấ 1 Từ các yếu tố ngẫu t e? n -2 ^ e ‘ = ề ’ nhiên (RSS) i-l ( n - 2 ) T S S tvĩ n-1 i-l
Với thí dụ (2.1) a = 0,05 ; F a (l,n-2) = 5,59 (bảng 3) ta có: „ r 2 n - 2 0,9932 7 ' = 1 - r 2 ‘ 1
“ 1 - 0,9932 ■ 1 - 1022,04 F > F « (141-2)
do đó bác bỏ giả thiết P2 = 0 hay bác bố giả thiết r2 = 0
2.8. PHÂN TÍCH HỎI Q U Y VA D ự BÁO
Các phần trên đã trình bày phuơng pháp xây dựng một hàm hồi quy các đánh
giá và phán xét về các hệ sổ của hàm hồi quy. Tuy nhiên mục đích cuá chúng ta
không chỉ dùng tại đó. Có thể sử dụng hàm hồi quy để dụ báo. Có hai loại dự báo-
- Dự báo trung bình có điều kiện cùa Y với một giá trị X = Xb 38
- Dự báo giá trị cá biệt cùa Y với x = X)
- Dự báo giá trị trung bình.
Giả sử X = Xó ta muổn dự báo E(YlXo). Đường hồi quy mẫu cho ước lượng
điểm của E(WCo)-ễ Ỷ0 = P, + P2 Xo.
Ỷ0 là ước lượng không chộch có phuong sai nhò nhất của E(YIXo). Tuy nhiên .
Ỹ0 vẫn khấc so với giá tri thực của nó.
Ỳ0 có phân bổ chuẩn với kỳ vọng pi + p2 Xo , nên
var ( Ỳ0 ) = E (P , + p j X o - P . - f t X o)2
= E [ ( P , - P , ) + Xb( p j - f c )]2
= E [(P , - p , ) 1 + 2 J « P , - p i )( p 2 - p 2 ) + x ’ ( p 2 - p 2 ) 2]
Var (Ỷ , ) = E[( P, - p, )2] + E [X | ( p 2 - h )2]
+ 2 X E K P , - p , x p a - f t ) ]
= Var (P ,) + Xb2 Var ( P i) + 2 X) Cov ( P, , P2 ) Var(Ỳ0)
= V ar( Ỹ - P 2 X ) + Xo2 V ar( p 2 ) + 2X oC ov( P, , p 2 )
= — + X 2 V a r i f o + X ] Var(P1) + 2 X ữC o r{fi]J ì ) n
, ĩ L + T P - ? - + x i - 2 L - 2 X j Ị L Ị/> -1 ? íix =l íix =1 V \ 1 = q 2 ( l + (Xon- Z ) } ■ " ± * ỉ im1
Nhưngơ2 chưa biết, nôn ta sử dụng ước luọng không chệch cùa ơ 2 là ồ2, khi dộ: Ỷ0 - ( p , + p j X 0) t - ° ; ^ \ - ~T(n-2) se(Y 0)
Do đó khoảng tin cậy 1- a của E( Yl Xo):
P( Pi + p 2 ^0 ■ t d/ỉ(n-2) se ( Y0 ) ắ Pi + P2 Xo
á p i + p 2 Xo + 1 „ữ(n-2) s e ( Ý ó ) ) = 1 -a .
Ỳ0-1 a /2 (n-2) s e ( Ỳ0 ) ắ E(Y/Xo) < Ỷ0 + 1 a *(n-2) sè ( Ỷ, ) )
Thí d ụ : Hây dự báo mức lãi suất trung bình nếu tỷ lệ làm phát = 5%, 39 a = 0,1; c = 1.895. V ar(Ỷ 0 ) - ớ * [ - + . n
.= 0,3366 suyra se ( Ỳ0 ) = 0,58.. p, + P2 Xo
= 2,7418335 + 1,2494067 , 5 = 8,98,8867
7,889767 ắ E ( YIXo) 5 10,087967.
Dự báo giá trị các biệt:
NẾu chúng ta muốn dự báo giá trị riêng biộl V = Yò với X = Xd ■ khi đó ước
luọiig củà Yo là, Ỳ0 = p | + p 2 Xó
và Var ( Yo) = o2 [ 1+ — + ( x ^ -— ]: -t= ~ T (n -2 ). n se(J o ) i-l
• Khoảng tin cậy của Yo được xác định bởi:
P(Ỹ0 - t'c.a(n-2) se (Yo) í Y , í Ỹ 0 + t a«(n-2) se (Y0)i = l - .a
. Thí dụ: Hãy dự báo múc lãi suất nếu tỷ lê iạm phát Xỉ = 5%, a = 0,1. se (Y o) = 1,8184 • 8,988867 - 1,895 . 1,8184 ắ Yo £ 8,988867 + 1,895 . 1,8184 5,542999 ắYo ắ 12,434735
2.9. TRÌNH BẰY KẾT QUẢ PHÂN TÍCH H ồ i QUY
k ft quả phâii tích hồi quy có thể trình bày vắn tắt duứi dạng sau đây: Y . - P , + r2 • (se( ậi ) ) ( se(. P j )) Bạc tự do n - 2
t = ( p , / s e ( P , U P 2 / s e ( P 2) ) " : ễ.
Với các thông tin trênbưtìc đầu chúng ta có thể thục hiện đuọc một số phãn tích. 40 2.10. THÍ DỤ \ 1.
T h í dụ 2.2: Cho số liệu sau đây về năng suất (tạ / ha) cùa một loại cây
trổng và mức phân bón(tạ / ha) cho loại cây này tính trên một ha trong 10 năm từ
1988-1997. Hặy'uớc lượng mô hình hổi quy cua năng suất phụ thuộc mức phân
bón và trả lời các câu hòi sau đây:
a) H ãy giải thích ý nghĩa kinh tế của các hệ số nhận được.
b ) H ãy tính đ ộ lệch tiêu chuẩn của các Ị).
c) V ới m ức ý nghĩa 5% hãy cho biết m ức phân bón có ảnh hưởng đến
năng su ất loại cây này không?
d) H ãy tìm khoảng tin cậy 95% cho các hệ số hồi quy.
e) H ãy tính r 2 và giải thích ý nghĩa của kết quả nhận được.
f) V ới m ức phân bón là 20 tạ / ha, hãy dự báo giá trị trung bình và giá
trị c á b iệ t của năng suất vái hộ số tin cậy 95%.
i) Hãy đọc kết quả và giải thích các kết quả do MFIT3 đưa ra Năm Phân.bón(X) Năng suất(Y) Năm Phân bón(X) Năng suất(Y) 1990 6 40 1995 18 58 1991 10 44 1994 22 60 1992 12 46 1995 24 68 1993 14 48 1996 26 74 1994 16 52 1997 32 80
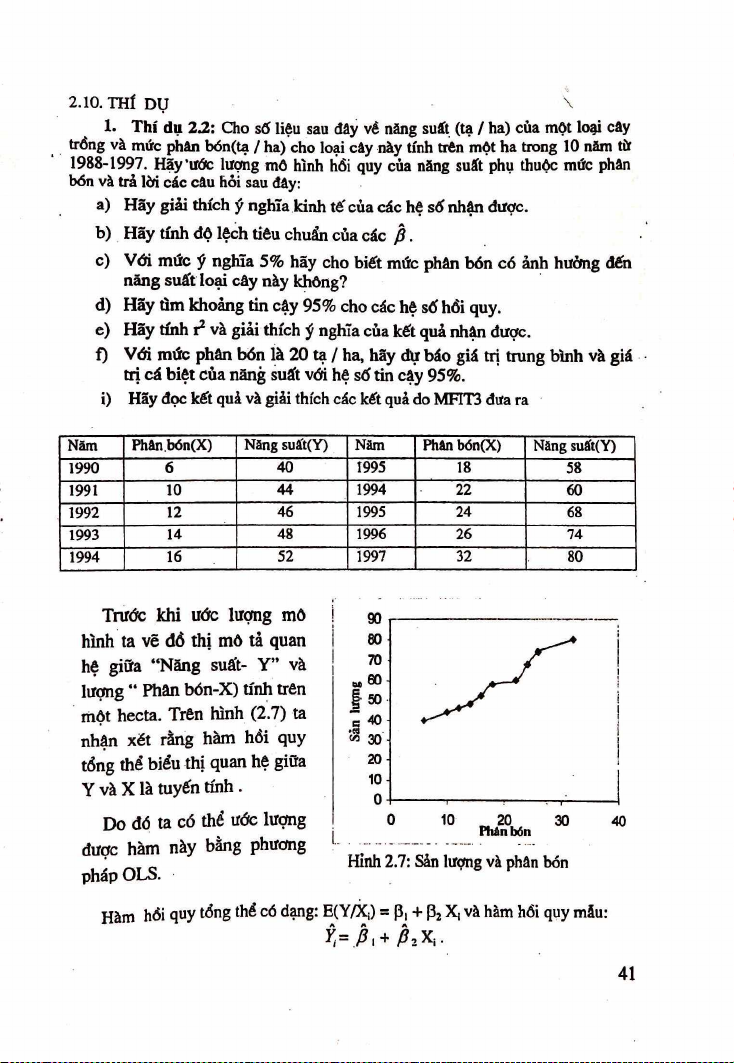
Trước k h i ước lượng m ồ ị 90
h ình ta vê đ ồ th ị m ô tả quan
hệ giữ a “ N ăng suất- Y ” và
lượng ‘ễ Phân bón-X ) tính trên
m ộ t hecta. T rên hình (2.7) ta
n h ận x é t rằng hàm hồi quy
tổng thể b iểu thị quan hệ giữa 20 10 Y và X là tuyến tính . 0
D o đó ta có thể ước lượng 0 10 _ 20 30 40 Phán bón
được hàm này bằng phương
Hình 2.7: Sản lượng và phân bón p háp OLS.
Hàm hổi quy tổng thể có dạng: E(Y/X|) = p, + p 2 X, và hàm hổi quy mẫu: Ỷ ^ P ^ P i X ; . 41
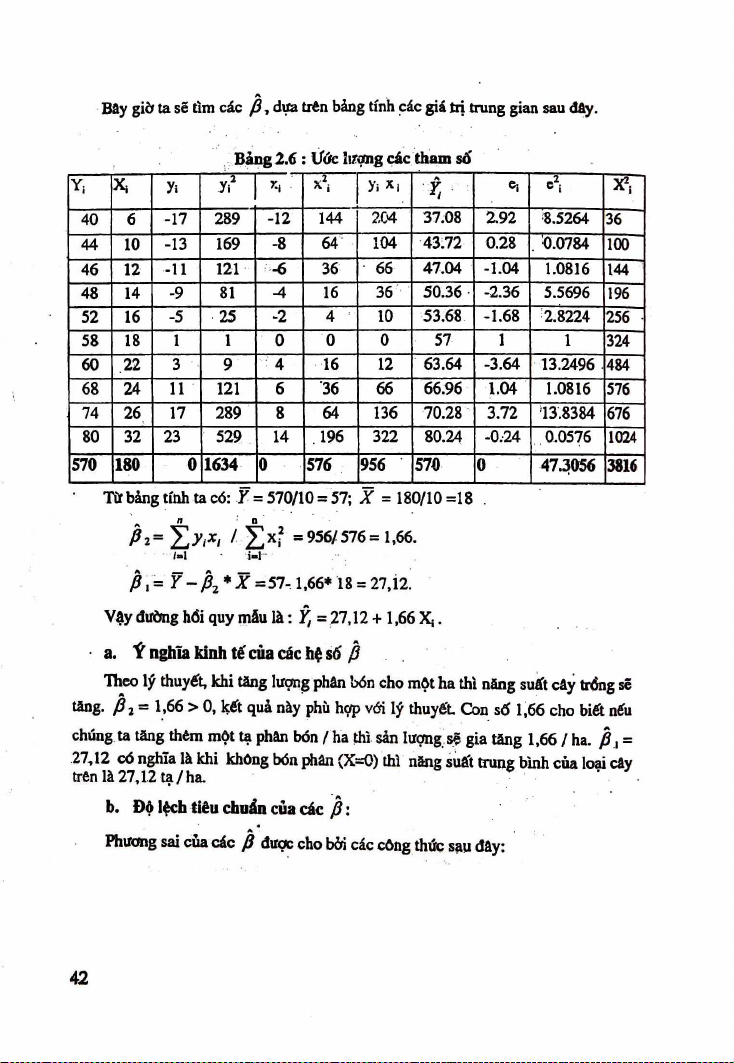
Bây giờ ta sẽ tìm các p , dựa trên bảng tính các giá trị trung gian sau đây.
Bảng 2.6 : ước ỉưạng các tham số Yi X* y> y* X, X2, >'ì X| ei * ẳ X1, 40 6 -17 289 -12 144 204 37.08 2.92 8.5264 36 44 10 -13 169 -8 64 104 43.72 0.28 . 0.0784 100 46 12 -11 121 -6 36 66 47.04 -1.04 1.0816 144 48 14 -9 81 ■4 16 36 50.36 -2.36 5.5696 196 52 16 -5 25 -2 4 10 53.68 -1.68 2.8224 256 58 18 1 1 0 0 0 57 1 1 324 60 22 3 9 4 16 12 63.64 -3.64 13.2496 484 68 24 11 121 6 36 66 66.96 1.04 1.0816 576 74 26 17 289 8 64 136 70.28 3.72 ‘13.8384 676 80 32 23 529 14 .196 322 80.24 -0.24 0.0576 1024 570 180 0 1634 0 576 956 57« 0 47.3Ơ56 3816
Từ bảng tính ta có: Y = 570/10 = 51; X = 180/10=18 .
P i = ỉ Ềy lx l / 2 X = 9 5 6 /5 7 6 = 1,66. M i-1
P , = Ỹ - P 2 * X = 57- 1,66* 18 = 27,12
Vậy đường hổi quy mẫu l à : Ỹ, = 27,12 + 1,66 X j.
a. Ỹ nghĩa kinh tế của các hệ số p
Theo lý thuyết, khi tàng lượng phân bón cho một ha thì năng suất cây trổng sẽ
tâng, p 2 = 1,66 > 0, kết quả này phù họp vối lý thuyết Con số 1,66 cho biết nếu
chúng ta tăng thêm một tạ phân bón / ha thì sản lượng sệ gia tăng 1,66 / ha. f i t =
27,12 cổ nghĩa là khi khổng bón phân (X—
0) thì năng suất trung bình của loai cây trên là 27,12 tạ /h a .
b. Độ lệch tiêu chuẩn của các ậ :
Phương sai của các p được cho bởi các cổng thức sạu đây: 42 V a r( yậ,) =
tức này ơ2 chưa biết, ước lương cùa nó là: ở 2 = —— = 47,3056 / 8 = 5,9132; n - 2
à = 2,432. Thay ở 2 vào các biểu thức trên và lấy căn bậc 2 ta có độ lệch tiêu chuẩn tương ứng: se ( P ,) =
2,432 = 1,98 ; se( /? 2) = 2,432/ V576 = 0,101; c.
M ức phán bón / h a có ảnh hưởng đến năng suất cùa loại cây trên
không? Để trả lời câu hỏi này, ta phải kiểm định giả thiết sau đây: Ho: 33 = 0 H| : P2 * 0.
t2 = (yố2 - Ị3j) / se(yỡ,J = (1,66-0) /0,101 = 16,43.
Với mức ỷ nghĩa 5%, ta có (0025(8) = 2,306. I tj I = 16,43 > 10025(8), do đó
giả thiết Ho bị bác bò. Điều này có nghĩa là lượng phân bón / ha có ảnh hưởng đến năng suất. d.
K hoảng tin cậy 95% cho các hệ số hồi quy:
Khoảng tin cậy của các hệ số hổi quy được cho bởi công thức sau:
( yỡi - 1 a/2 (n-2) se (p i) < P i< P i + 1 ờ/2 (n-2) se(yờj)) , i =1,2.
Khoảng tin cậy đối với Pi :
(2 7 4 2 - 2,306* 1,98 < p, < 27,12 - 2,306* 1,98) 22,55 < p , < 31,69
Khoảng tin cậy đối vối p2 :
(1 66 - 2,306* 0,101 < p2 < 1,66 - 2,306* 0,101 ) 1,43 < p ,< 1,89
e. H ệ số r 1: r2 = ESS/ TSS = (TSS- RSS) / TSS = (1- RSS/TSS) r3 = 1- 47,3056/1634 = 0,971.
Như vậy lượng phân bón giải thích xấp xỉ 97% sự biến thiên của năng suất. f
Dự báo giá trị trung binh và cá biệt khi mức phân bốn là = 20 tạ / ha:
Phương sai của giá trị trung bình: 43 VarCf0W
( - + (* ° X- ) = 5,9132 ( - L + g ^ j p L ) = 0,63238. n ^ x 2 M Se(ỷ0) = 0,795.'
Phương sai cùa giá trị cá biệt: Var(Y0)={ X ° ~ X )- ) = 6,54558 ; Se(Y0) = 2,558. " t/-1 x‘.
Một ước lượng điổm của năng suất khi mức phân bón là 20 tạ / ha.
ỷ0 = 27,12+ 1,66 * 20 = 60,32 to.o2í(8) = 2,306.
Khoảng tin cây 95% cho mức sản lượng trung bình là:
Ỳ0 - se( Ỹữ )t0,02s(8 ) < E(Y/ x„ = 20) < Ỵ 0 + se( Ỳ0 > ^ ( 8 )
60.32 - 0,795* 2,306 < E(Y/ Xo = 20) < 60,32 + 0,795* 2,306
58,468 Do vậy khoảng tín cậy 95% cho mức sân lượng cá biệt là:
Y0 - se(Yo)to,oj5(8) < Y0 < yo + se(Y0)t002J(8)
60.32 - 2,558* 2,306 < Y„ < 60,32 + 2,558* 2,306 54,421 < Y0< 66,218 Ị
hẵ K ết qu ả ước lượng mò hình này bằng M FIT3:
Ordinary Least Squares Estimation
>|B^^4c^Jfe3K3|r>|r3|c3^4c9^4c3fca#c9|(i|ca|e4(4«3|ca|cafca|c3fc3|e3fca|(ỉf«aÌ«4**l«*K:4«3|«*Ì(a|«4(3|c3|c>Ìe3Ì>4e>|e3Ìe3Ìe4e3f<4c9|eaiaica|caÌcỉfcafc Dependent variable is Y
10 observations used for estimation from 1 to 10
I|ti|(%^9fr4e9|c3|c9|c3#c3fc3|c3fc4c3|c4e9fe3fe3fe3ic3|<3|ca|e3|(3f(>|(4e4*3|cỉlc4c3fca|(3ieai(9fc3f(ỉfc3fcafc9ic3ic3ic4e3|e#cafv9#:3|c3ie9ic9|c3|e3|c3tea|eafe9f(ace Regressor Coefficient Standard Error T-Ratio[Prob] 1NPT 27.1250 1.9793 13.7046[.000] X 1.6597 0.10132 16.3808[.0C0] R-Squared
.97105 F-statistic F( 1, 8) 268.3312[.000] R-Bar-Squared .96743 S.E. of Regression 2.4317
Residual Sum of Squares 47.3056 Mean of Dependent Variable 57.00
S.D. of Dependent Variable 13.4743
Maximum o f Log-likelihood -21.9596 DW-statistic 1.7836 44 M ột số Uiuật ngữ:
Ordinary Least Squares Estimation: ước lượng bình phương nhồ nhất cổ điển
Dependent variable = Biến phụ thuộc Observation = 'Quan sát
Regressor = Biến độc lập; Các phần mềm kinh tế Iuọng đếu coi hệ số chặn
được nhân với một biến mà biến này chỉ có giá trị dùy nhất bằng 1. INPT là tên
thường được dùng cho iúến này. Nếu muốn, ta có thể dùng tên khác. Ở phương
pháp ma trận ta sẽ thấy tiện ích cùa vấn để này.
Coefficient = Hệ số - giá trị cùa các P tuong ứrtg với bộ số liệu dùng để uúc luọng;
Standard Error = Đ ộ lệch tiẻu chuẩn - các se( P )\
T-Ratió[Prob] = Tỳ số t[ Xác suất ] = p / se( P )[Prob];
[Prob] = p- value = P( I t(n-2) I > I p / se( p ) I). Có thể dựa vào giá trị này để
kiểm định giả th iế t: H o: Pi = 0 ; H | : (3ị * 0;
Nếu như a > p, suy ra a / 2 > p / 2 và t 0/2 < t p /2 thì Ho bị bác bỏ. Trường hợp
ngược lại, nếu a < p, suy ra t ạ / 2 > t , /2. Với t(n-2) < t p/2 thì t(n-2) cũng nhỏ hcm t
a n . Điều này có nghĩa là khổng có cơ sờ bằc bỏ H,. Như vậy nếu a > p thì Ho bị
bác bò, a < p thì không có cơ sà bác bỏ Ho. ■
Chú ý rằng p-value trong phâíi bố T, khi dùng MFTT3, được tính bằng công thức: JV-
value = P( I t(n-2) I > I y ồ /s e (/5 )|). Nếu chúng ta kiểm định một phía, ngWa là H,: p,
> 0 (hoặc Ị3ị < 0) đù cần so sánh a • với p/2 sau đó kết luận một cách tuơng tự.
R-Squared = r2; R-Bar-Squared = r đã hiộu chỉnh, được ký hiệu là :~ p .
Residual Sum o f Squares = RSS = Tổng bình phương của các phẩn dư.
S.D. o f Dependent Variable = Độ lệch tiêu chuẩn của biến phụ thuộc = ỵợrằ -ỹy F-statistic F( 1,
8) = 268.3312[.00Ọ]. Giá trị F (l,8) được tính bằng công thức 1ể^ * n Ệ2 • .ặ ■ P( 1 g) = —1— ■
- . Trong hổi quy hai biến giản đơn, giá trị này cũng bằng bình
phương của tỳ số t ứng với hê số góc, trong ví dụ này, ta có t2 = 16,3808. Bình
piiuỡng tị ta có (16.3808)2 = 268,3306. Kiểm định F ở đây là kiểm định một phía vì
Ho I3 - 0- Hj: r3 > 0. Do đó giá trị p-value được so sánh trực tiếp với a .
s E o f Regression = độ lệch tiêu chưẩii cùa hàm hồi quy - ờ .
Mean o f Dependent Variable = Trung bình cùa biến phụ thuộc. 45 2.
Thí dụ 2 3 : Cho kết quả ước lượng sau đây bằng MFIT3, trong đó Y- tổng
chi tiêu; X- thu nhập sau thuế trong khoảng thời gian (1986-1997) và cho X = 145; £ x,2 =4817. M
Ordinary Least Squares Estimation
************************************************************* Dependent variable is Ỵ
12 observations used for estimation from 1986 to 1997
*************************************************************** Regressor Coefficient Standard Eưor T-Ratio[Prob] : ENFT 2.1288 7.1641 ễ29715[.772] X . ' .86118 .048943 17.5955[.000]
****** I*.******************************************************** R-Squared .96871 F-statistic F( 1, 10)- 309.6016[.000] R-Bar-Squared .96558 S.E. of Regression 3.3951
Residual Sum of Squares 115.2685
Mean of Dependent Variable 127.0000
S.D. of Dependent Variable 18.3005 Maximum of Log-likclihood -30.6014 DW-statistic 1.7822 .
*************************************************************** a.
Hãy viết hàm h6 i quy m ỉu và cho biết kết quả ước lượng có phù hợp với lý
thuyết kinh tế không? Vì sáo?
b: Với mức ý righĩa 5%, phđn tiêu dùng không phụ thuộc vào thu nhập có khác không hay không?
c. Với m íc ý nghĩa 5%, thu nhập sau thuế có ảnh hường đến mức tiêu dùng hay không?
d. Hãy tìm khoảng tin cây 95% cho hệ số góc.
e. Cho mức thu nhập sau thuế ià 150, hãy dự báo giá trị trung bình và giá trị
cá biệt cùa mức tiêu dùng với hê số tin cậy 95%. 46
BÀI TẬP: CÁC KHÁI NIỆM VÀ MÔ HÌNH HỒI QUY HAI BIẾN
2.1. Hãy giải thích các khái niệm sau đây:
a. Hàm hổi quy tổng thể và hàm hổi quy mẫu.
b. Yếu tố ngẫu nhiên và phần dư.
c. Các hệ số hổi quy, ước lượng của các hệ số hồi quy. d. Tự tương quan.
e. Phương sai của sai số đồng đều. f. Hàm hổi quy tuyến tính.
2.2. Cho các mô hình sau đây, mỏ hình nào là tuyến tính đối vói tham số, mỏ hình
nào tuyến tính đối với các biến số, mô hình nào là tuyến tính đối với cả tham
số và cà biến số? M ô hình nào là mô hình hồi quy tuyến tính? a . Y = p, + p2 / X + U ; đ. Ln(Y) = Pi + Pj ln(X) + U; b. Y = p, + p ,ln (X ) + U; e. Ln(Y) = p, + p 2 / X + U; c .L n (Y )= 0i + p2 x + u .
2.3. Các mô hình sau đây có phải là mờ hình hổi quy tuyến tính?Vì sao? a. .Y = exp(|3| + p2 X + U).
b. ¥ = 1 /( 1 + exp(Pi + p 2 X + U)). c. Ln(Y) = p, + p2 / x + u d. Y = 3 , + p2í x + u
2.4. Hãy biến đổi các mô hình sau đây về mô hình hồi quy tuyến tính. a. Y = l / ( P , + Pi X);
b. Y = X / (P, + Pí X);
c. Y = 1 / ( 1 + exp(-Pi - p2 X)).
25. Cho các giả thiết ờ cột (1), hãy chì ra rang các giả thiêt ở cột (2) là tuơng đuong.
Các giả thiết cùa mô hình hổi quy cổ điển 0 ) (2) E(Ưi / Xi ) = 0 E(Y ./X i) = p , + p 2Xi
Cov(Ui, Uj) = 0 , i * j Cov(Yi, Ỵj) = 0, i * j Var(Uị / X |) = 0 Var( Yị / X i) = 0.
2.6. Trong mô hình Yi = Pi + Pí Xị + Uj.
a. Nếu ta nhân mỗi Xi vdi một hằng số, chẳng "hạn 10, khi đó các e và
các giá trị ý sẽ thay đổi? Hãy giải thích?
b. Nếu ta cộng vào mỗi X| với một hàng số thì các e và các giá trị Ỷ sẽ
thay đổi không? Hay giải thích? •47
2.7. Bảng duới đây cho cặp' biéh phụ thuỏc và độc lập. Trong mỗi trơông họp
cho biết quan hộ giSa hai biến li: cùng chiềui ngược chiẻu hay không xác định. Hãy giải thich. B iế n P h u th u ỏ c B iế n đ ò c lả p a. GNP Lẫi suất b. Tiết kiệm cá nhân Lãi suit c. Cẩu về tién GDP d. Sản lượng
Vốn cơ bản( hoăc lao động) e. Lượng cẩu vé xe máy ' Giá Xăng f.
Lượng điện tiêu thụ của G á ga hộ gia đình. .
2.8. Bảng sau dãy cho chuỗi thòi giạn về mức áSu dừng (Y) / đầU ' người và thu
nhập( X) / đầu nguời tính theo giá cố định (1980, dơn vị: 100.000 VNĐ) Song
thời kỳ từ 1971-1990 ò một địa phương . ’ . Năm Y X Nàm Y X 1971 48,34 52,02 1981 57,17 . 6 3 3 6 ! 1972 48,54 52,41 Ỉ982 60,84 67.42 1973 47,44 51,55 1983 60,73 67Ị86 1974 54,58 58,88 .1984 76,04 §3,39 1975 55,00 59,66 1985 76,42 84,26 1976 63,49 68,42 1986 69,34 77,41 1977 59,22 64,27 1987 61,75 70,08 1978 57,77 63,01 1988 68,78 77,44 1979 60,22 65,61 1989 67,07 75,79 1980 55,40 61,05 1990 72,94. 81,89
Từ bảng trèn tính đuợc: X
- 76,289; Y = 61,054; X;2 = 1961Ị1;
X* = 92520; y ỉ = 1414,7; I X! y€ = 1658,2. a. Hãy ub.
Hãy cho biết kết quả uớc lượng có phù bop với lỷ thuyết kinh tế không? V isao? c.
Hãy tính ESS, RSS, ước luọng của phương sai cùa u. d.
Vói hệ số tin cậy 95% hãy úm khoẻng tin cậy cùa các Kệ 'số hồi quý, e.
Với mức ý nghĩa 5% hãy kiểm định giả thiết p2 = 0. Tdr kết qúả nhân
được hãy nêu ý nghĩa vé m ặt kinh tế cùa kết luânT
g. Hãy tính và giải thích ý nghĩa của I1.-.
2.9. Quan sát ngẫu nhiên 10 người trong Ị tuẩn người ta có các .sđ liệu sau: 48 Thu nhập $ (X) 31 50 47 45 39 50 35 40 45 50 Chi tiêu $ (Y) 29 42 38 30 29 41 23 36 42 48 ắ' 10 10 10
Người ta tính được: = 547,6 ;
= 403,6 ; / . y Ị X I = 385,4 ; 1=1 /-I /=1 RSS = 132,3561. Cho a = 5%.
a. Bộ số liệu trên thuộc loại số liệu gì?
b. Ước lượng hàm hồi quy dạng tuyến tính: Y = pi + (32 X + u
c. Nâu ý nghĩa kinh tế của các hộ số hổi quy ước lượng dược. Các giá trị đó
có phù hợp với ly thuyết kinh tế không?
d. Tìm r bằng 2 cách ứng với 2 trường hợp: biết và không biết RSS. Giải thích ý nghĩa r2?
e. Có ý kiến cho rằng thu nhập không ảnh hưdng đến chi tiêu, bạn hãy nhận
xét về ý kiến này(thực hiện bằng 2 kiểm định: t và F).
f. Tim khoảng tin cậy 95% cho hệ số góc.
g. Trong các thời kỳ trước người ta vẫn đùng 80% thu nhập cho chi.tiỄu, có
thể kết luận rằng trong thời kỳ quan sát tỷ lệ này đã giảm hay không?
h. Hãy dự báo mức chi tiêu trung bình nếu thu nhập tuần là 42$.
2.10. Một công ty sản xuất một loại sản phẩm. Lượng sản phẩm (Q) mà cồng ty
sản xuất phụ thúộc vào giá sàn phẩm này trên thị trường (P). Dựa trên số liệu trong
27 tháng từ tháng 1 năm 2006 đến tháng 3 năm 2008, người ta ước lượng được mô
hình dưới đây. Cho a = 5%; Q tính bằng 1000 sản phẩm, p tính bằng nghi đồng!
Ordinary Least Squares Estimation
* * * * * * **** * * * * * **** **** * * * * ** * * * * * ** ** * * * * * * * * * * * * * * * * * * * * * * * * * Dependent variable is Q
27 observations used for estimation from 97M1 to 99M3
***************************************************************** Regressor Coefficient Standard Error T-Ratio[P-ob] p 0.389687 0.118694 3.283121 [C0028} INPT 10.31076 2.586328 3.986638 [0.0004]
***************************************************************** R -Squared 0.277958 F-statistic F( 1 ,2 5 ) 10.7788[.0027] R-Bar-Squared 0.25217 S.E. of Regression ' 3.989267
Residual Sum o f Squares 445.599 ■ Mean o f Dependent Variable 18.45833
S.D. of Dependent Variable 4.613 Maximum of Log-likelihood -83.04149 DW-statistic 2.409
a. Viết hàm hổi quỵ tổng thể', hầm hổi quy mẫu. 49
b. Hệ số chặn và hộ sổ góc đuạc ước lượng bằng bao nhiêu?
c. Cấc hộ số thu được từ hàm hồi quy m&ú có phù hợp lý thuyết kinh tế không?
d. Các hê sổ của mô hình có ý nghĩa thống kê không? Con số [Prob] cho biết điều gi?
e. Có thể nói rằng khi giấ thay đổi thì lttợng cung có thaỳ đổi không?
f. Hệ số xác định đo độ phù hợp cùa hầm hỏi quy bằng bao nhiêu, giá trị đó có ý nghĩa gì?
g. Hàm có thể coi là phù hợp khững?
h. Tìm ước lưạng điểm cho phuong sai y.ếú tố ngỉu nhiên L
Tồng bình phương phần dư bằng bao nhiêu? j. TSS và ESS bằng bao nhiêu?
k. Tìm khoảng tin cậy cho hẹ số chặn và hệ số góc của mô hình 1.
Khi giá tăng thêm 1 nghìn thì lượng cung thay đổi trung bình trọng khoảng nào?
m. Khi giá tăng 1 nghìn thì lượng cung tăng tối đa bao nhiêu?
n. Có thể nói khi giá giảm 1 nghìn .thì luợng cung giảm 0,5 đom vị được không?•
o. Tìm một ước lưọng diểnỊ cho lưọng cung khi giá là 10,5 nghìn đổng,
p. Tìm lượng cung trung bình và cá biệt khi giá là 10,55 nghìn đổng.
2.11. Một cơ quan nghiên cứu mối quan hệ giữa số đơn vị sản phẩm và các yếu tố
đẩu vào của quá trình sản xuất ở một số ca sở sản xuất đã đưa ra những mô hình
hồi quy. Lúc đầu người nghiẽn cứu chú trọng vào quản lý nguồn nhân lực nên đưa - ra mồ hình sau:
Với s là sản lucmg, L là lao động (người). Cho á =5%.
Ordinary Least Squares Estimation Ordinary Least Squares Estimation Dependent variable is s
20 observations used for estimation from 1 to 20 <• Regressor Coefficient Standard Error T-Ratio[Prob] INPT 34.4438 29.0219 1.1868[.251] L 19.2371 6.8786 2.7967[.012] R-Squared
.30290 F-statistic F( 1,18) 7.8213[.0'2] R-Bar-Squared .26417 S.E. of Regression 49.5267 Residual Sum o f Squares
44152.1 Mean of Dependent Variable 109.4666
S.D. o f Dependent Variable 57.7367 Maximum o f Log-likelihood -105 .3754 DW-statistic 0.7151
***************************************************************** 50
a. Viết hàm hồi quy tổng thể, hàm sổ đó và các tham số có ý nghĩa như thế nào?
b. Viết hàm hổi quy mẫu. Các hệ sô' cùa hàm hổi quy mẫu có phù hợp lý thuyết kinh tế không?
c. Theo lý thuyết thì khi không có lao động sẽ không có sản lượng, nhưng
trong hàm hổi quy mẫu thì khi không có lão động ước lượng điểm mức sản
lượng lại không bằng không. Trên thực tế gia trị đó có thể coi là bằng 0 hay không?
đ. Hộ số góc của mô hình có ý nghĩa thống kê không?
e. Hệ số xác định bằng bao nhiêu %, giá trị đó có ý nghĩa như thê' nào? f.
Có thể nói hàm hồi quy phù hợp không?
g. Tim ước lượng điểm và khoảng cho phương sai yếu tô' ngẫu nhiên.
h. RSS, TSS, ESS bằng bao nhiêu? i.
Tim khoảng tin cậy cho hê sô' chận của mô hình. j.
Khi doanh nghiệp thêm một lao động thì sàn lượng tăng trong khoảng nào?
k. Khi giảm bót 1 lao động thì sản lượng giảm tối đa bao nhiêu đơn vị? 1.
Có thể cho rằng khi bớt 1 lao động thì sản lượng giảm 30 đơn vị được không?
m. Nếu tăng 1 lao động thì sản lượng tăng nhiều hơn 20 đơn vị có đúng không?
n. Tim ước lượng điểm mức sản lượng với doanh nghiệp có 30 lao động.
o. Tìm mức sản lượng trung bình và cá biệt khi doanh nghiệp có 30 lao động? 51 CHƯƠNG in Hổi QUY Bội
Mô bình bồi qui hai biến duạc trình bày ở chuông n là một mô hình giản đem
nhái. Trong nhiẻu trường hợp mô hình này khống phù họp ví có nhièu biến tác
động đến biến phụ thuộc Y, nếu như chì dùng một bịến độc lập thì khổng thể giải
thích đuạc sự biến đổi cùa biến Y. Chẳng hạn khi nghiên cứu nhu cầu về một loại
hàng hóà nào đó (Y ), thì nhu cầu này phụ thuộc vào nhiều yếu tố, trước hết là: thu
nhập của người tiêu dùng, giá của bản thân bàng hóa, giá cùa các loại hàng hóa
thay thế tỊ*ng hóa này ... Do đó cần phải mở rộng mô hình hồi quy hai biến thành
mô hình có chứa nhiều biến hon, ờ đây là mô hình hồi quy bội 3 biến và sau đó sẽ
trình bày mỡ hình dưới dạng tổng quát có số biến độc lập bất kỳ bằngiphuong pháp ma trận.
3.1. MÔ HÌNH HỒI QUY BA BIẾN
Giống như bong mổ hình hai hiỄh, hằm hồi quy 3 biến của tổng thể PRF có dạng; E ( YI ) = Pi + p2 + P jX ỉ ( 3 .1 )
PRF là kỳ vọng cố điều kiên của biến Y với giá trị đã cho của các biến và Xj
Trong đó Y : Biến phụ thuộc; Xì, X j: Các biến độc lập.
Pi : Hệ số tự do ( hệ số chăn ), nó chính là giá trị trang bình cùa biỗh Y khiX j= X3 = 0.
p2 , p3 : Gọi là các hộ số hồi qui riêng.
Ỵ là giá trị của biến Y ở quan sát thứ i, khi đó:
Ỵ = E ( Yl Xa . X,,) + ự = p, + Pa Jfc + .p, Xji + ụ .
LỊ là yếu tố ngẫu nhiên, sự tồn tại cùa u đã được giải thích ở chương I.
3.2. CÁC GIẢ THIẾT CỦA MÔ HÌNH
- Các l í có kỳ vọng bằng 0 : E ( Ụ i Xa . Xj i ) = 0 ( V i )
- Khổng có sự tương quan giữa các Ư,: Cov ( ụ , Uj ) = 0 Vi * j
- Các 15 thuần n h ấ t: Vai ( U ) = a2
- Giữa các biến giải thích X2, X3 không có quan hệ tuyến tính
- u có phân bố N ( 0 , o 2).
Trong mô hình hồi quy bội có thêm một giả thiết mới - giả thiết thứ 4 - giữa
các biến Xị, x 3 không có quan hệ tuyến tính. Nếu I)hư X iJii có quan hộ tuyến tính
với nhau thì nguời ta nói răng có hiện tượng đa cộng tuyến. Chúng ta sẽ giải thích 52
một cách sơ lược về giả thiết này. ở chương V chúng ta sẽ giải thích sâu hơn. Các
giả thiết khác đã được nói ở chương II.
Vê mật hình thức, nếu như có hiện tuợng cộng tuyến giữa cắc biến giải thích
và trong mô hình có tất cả các biến này (hì chúng ta không thể tách được ảnh
hưởng cùa từng biến lên biến biến phụ thuộc Y. Thật vậy: Giả sử Xa = 3Xj| Khi đó Yi
= p, + & Xji + (3, X,, + Ụ = P, + 3 P Ĩ Xa + pjX ji + U
= Pi + ( 3 P2 + p3) x 3[ + Ụ Đặt
P3 = 3 P2 + P3 => Yi = (3] + P3 x 3i + Ư,
Như vậý trên thực tế ta có mô hình hai biến mà không phài là mô hình ba biến.
Uarc lượng mô hình này bằng phương pháp OLS ta tìm được p ' 1, P ’2 là ước lượng
cùa p, và p3 . p ’2 là ảnh hưởng kết hợp của Xj và x 3 lên Y. Chúng ta khống có
cách nào để tách riêng ra trong P ’2 bao nhiêu là p3.
Giả Ihiết 4 nói rằng hàm PRF chỉ chứa các biến giải thích mà chúng không
phải là hàm tuyến tính của một vài biến nào đó trong mô hình.
Ỹ nghĩa của các hệ số p2 và
E ( Y I X i i ^ i) = p 1 + pjX ii + P3X i .
= p2 . Điêu này có nghĩa là khi chúng ta giữ nguyên yếu tỐXí (Xì- ÕX2
constant) thì giá trị trung bình cùa biến phụ thuộc Y sẽ thay đổi (tẫng hoặc giảm tùy thuộc
vào dấu của P2 ) P2 đơn vị cho mỗi đơn vị tăng cùa yếu tố X2.
— — = P3 điẽu này có nghĩa là giá tri trung bình cùa biến Y tăng ( hoặc giảm) â X y
03 đơn vị cho mỗi đơn vị tăng của x 3. Nhu vậy các hộ số tíồi qui riêng ( hệ số góc) phản
ánh ảnh liuủng của một biến giải thích đổi vói giá trị trung bình cùa biến phụ thuộc khi giá
trị cùa biến giải thích khác chứa trong mô hỉnh không đổi.
3.3. u ớ c LUỢNG CÁC THAM s ố CỦA MÔ HÌNH Hồi QUY BA BIẾN
Để ước lượng các tham số của mô hình:
E ( YlXji, X31) = Pi + P2 Xji + P3 Xji 53
chúng ta sử dụng phuong pháp bình phương tối thiểu OLS, tư tưởng chính của
phuong pháp này đã được trình bày ở chương n . »i - ; •; '
Giả sử chúng ta có n quan sát, quan sát thứ i-có 3 giá tri ứng với Y, Xĩ,
vàX 3,k íh iệ u ( Ỵ ,J Q ỉí,Xal). ; ’ í .
Hàm hồi quy mẫu SRF được xây dụng tìm quan sất này có dạng: Yj = p, + p 2 Xái + P3 Xai
Trong đó Pi : i= l,2 ,3 là ước lượng tương ứng cùa P i: i=l,2,3. K hiđó Yi=p, +
Xii + p 3 X^ị + e,; e, là phần dư ứng với quan sát thứ i,
é, = Ya - ỹ | = Y, - Pi - P2 Pa
Phuơng pháp OLS tính giá trị cùa các tham số Pi , P2 , P3 sao cho:
RSS= £ ^ * = 1/ ( Ỵ - P, - P j X a - P j Xj , ) 2 =>min. A iBU A ,
Các tham số P ị, P2,P 3 đuợc tính từ hệ phương trình chuán sau đây: P . + p 2 X 2 + P3 x 3= Ỹ
P i £ x « + ậ , í X ị , + P x í X3ễ= z YịXa j»l i»l i«l i-1 i-| P, í *31+ P2Ỉ
x3j + p , ỉ XỈi = Ỳ Yi x3i. i«al i»l i»l i»l Trong đ ó : x , = ỉ
5 W n ; X 3= ỉ X a / n ; Ỹ = í Y , / n . Đặt :yi = Yị - Y ;
Xjj = Xj j “ X 2 í X j j = J ^ j - X3 .
Giải hệ phương trình ta đ u ợ c;
ậ , - Ỹ - p 2 x 2 - p , x 3
( ẻ >'‘*ỉ i M È xĨ ‘J - ( Ệ M i X ỷ ix2ixj i J P — 1-1 1=1 M W
( Ỹ j xì ‘) ( Ỳ j xh ) - ( Ỳ é Xĩ i x } i ) 2 i-l /-/ 1*1
ix3ỉ X ^ j x2j) “ ( £ y j* 2 i x3i) P _ _ i i ______ i-1 Ị-Ị______ ị-Ị______ 3 A
J L , r ~ ĩ -------------------
(zC XJ i X 2 X3i)_ ( 2 j X2iX3i)2 . » . w i-1 i-l
Pi . P2 . P3 dược gọi là các uớc lượng bình phưcmg nhỏ nhất. 54 T h í dụ 3.1
Bảng sau đây cho số liệu về doanh thu 0 0 , chi phí- cho quảng cáo (X2) tiền
lương của nhân viên tiếp thị (X3) của 12 công ty tu nhân (đơn vị 1.000.000 đ ) . Xây
dựng hàm hồi quy Ỵ phụ thuộc vào Xì, x 3. STT Y X, I X, X ,=x,- X , Xi— X, - X , 1 1 127 18 10 -2,417 -2,167 -14,333 2 149 25 11 4,583 -1,167 7,667 3 106 19 6 -1,417 -6,167 -35,333 4 163 24 16 3,583 3,833 21,667 5 102 15 7 -5,417 -5,167 -39,333 6 180 26 17 5,583 4,833 38,667 *7 161 25 14 4,583 1,833 19,667 8 128 16 12 -4,417 -.1667 -13,333 9 139 17 12 -3,417 -.167 -2,333 10 144 23 12 2,583 -,167 2,667 11 159 22 Ị4 1,583 1,833 17,667 12 138 15 .15 -5,417 2,833 -3,333 1696 245 146 0 0 0 STT Xi1 Xj- yx2 y*3 X2X3 y' 1 5,840 4,694 34.Ổ3Ộ ỈĨ.Ỗ5Ổ 5,236 ÌỎ5.444 2 21,007 1,361 35,139 -8,944 -5,347 58,778 - 3 2,007 38,028 50,056 217,889 8,736 1248,4 4 12,840 14,694 77,639 83,056 13,736 469,444 5 29,340 26,694 213,056 203,222 27,986 1547,1 6 31,174 23,3611 215,889 186,889 26,986 1495,1 7 21,007 3,361 90,139 36,056 8,403 386,778 8 19,507 ,028 58,889 2,222 ,736 177,778 9 11,674 ,028 7,9722 ,389 ,569 5,444 10 6,674 ,028 6,889 -,444 -.431 7,111 11 2,507 3,361 • 27,972 32,389 2,903 312,111 12 29,340 8,028 18,056 -9,444 -15,347 11,111 192.917 123,667 836,333 774,333 74,167 5924,7
Theo kết quà ở bảng trên đây ta có: Y =1696/12 = 141,3333.
x 2 = 245/ 12 = 20,4167 và X j =146/ 12 .= 12ÌÌ667.
Theo các công thức ( 3ế2 ): ’
8 3 6 ,3 3 3 3 -1 2 3 ,6 6 6 7 -7 7 4 ,3 3 3 3 -7 4 ,1 6 6 8 P 2 -
192,9167 • 123,6667 - (74.16668)2 ’
ậ = 4 7587. P, = 141,3333 - 2,5057 . 20,4167 - 4,7587 . 12,1667 = 32,2773. 55 Ỷ e, é*! 124,9673 2,0327 4,1319 147,2661 1,7339 3,0064 108,4383 -2.4383 5,9453 168,5530 -5,5539. 30,8450 103,1741 -1,1741 1,3785 178,3240 1,6760 0,2940 161,5422 -0,5422 0,2940 129,4732 -1,4732 2,1703 . 131,9790 7,0210 49,2944 147,0134 -3,0134 9,0806 154,0250 4,9750 24,7506 141,2436 -3,2436 10,5209 0 144,2269 PHUONG NHỎ NHẤT Phương sai và độ l
ộ Ịệch chuẩn của các ướ ư c ớ lượng
lượng bình phương nhồ nh nhắ t đuợc
cho bồi các công thúc: sau đ& đ y & : y Ỉ xỉi !■
v ar( ậ j ) = __ ;________ 2-2__________ — o 2
( Ỉ 4 X Ỉ 4 ) - (Jxj.xj, )2 £ x | , (1 - rẳ) i-1 i-l i-l Í_1
Trong đó r23 là hệ số tuơng quan mẫu giữa biến Xi và X j. se ( ) = -y/variPj) p l i-l v a r ( P 3 ) s — --------f
(TẨxi)( ỵ ixi ) - ( ỵ gxilx3l)ỉ W i- 1 M / „ !
s e ( P 3 ) = VvarCP3) ; co v ( p 2 , ậ 3 ) = ------------
ẳO - t Ề y í x ị J Ì x ỉ , 56 ( È x 2ix 3i) ’
Trong đó 123 là hệ số tướng quan giữa biến Xi và Xi .r ả = V 2 v ~ 2-i*2i Z j X3Ị
Trong các công thúc ưên ơ2 là phương sai c ủa Uị nhimg chưa biết, u&c lượng
không chêch của o 2 l à : ơ 2 = = ẼỄỄ. n - 3 n - 3
3 là số tham số của mô hình, trong trường hợp tổng quát nếu mô hình có k
t h a m s ố p ,, 02 ... pk thì Ớ 2 = ỉ e‘/ ' ( n - k Ỵ
Với các SỐ liệu ỏ thí dụ 3.1, ta có: ỡ
ik=144,2269/ 9 = 16,0252 n - 3 123,6667 » /----- - ĩ —
Var( p 2) = i 3 3 ^ 6 7 5 -16,0252 * 0,107959;Se( p 2)=1/v a r ( p 2) =0,32857
Var < p 3 ) = ĩ S ă r S ỉ •l 6 ’0 2 5 2 * ° ’16841 :Se( Â ) = # i ) = ° '41038 ■ 1o3j 0 , 0 / j
3.5. MÔ HÌNH HỒI QUY TUYẾN TÍNH K BIẾN-PHUƠNG PHÁP MA TRẬN
Phần này giới thiệu với bạn đọc mô hình hồi quy bội k biến bằng ngôn ngữ ma
trận. Với ngôn ngữ ma trận kết hợp với kỹ thuật tính toán cho phép chúng ta giải
quyết các ván dề cùa phân tích hồi quy một cách nhanh chóng, chính xác.
Hàm hồi quy tổng thể có dạng
Yj = Pi + piX* + Ể.. + pkXki + Uị
Trong đó (3| là hệ số tự đo (hộ số chặn).
Pj: j = 2 , k là các hệ số hồi quy riêng.
Giả sử chúng ta có n quan sát, mỗi quan sát gồm k giá trị (Ỵ, .....Xci)
Y| = Pi + pĩXíi +••• + PkXci + u, Yĩ = pi + PỉXáí + l i
Y„ = Pi + pỉXín + ... + PkXic, + IỊ, 'V , ' P r ' ' u , ' u 2 Ký hiệu: Y = Y , ; p = ; u = .Yn . .Pk. u ế . 57 1 * 2 1 x n .. ■ X u ' 1 X j 2 x 32 . ■ X ị^ x = Ị , x 2„ x 3n Khi dó ta có: Y = xp + U
Giả thiết 4 nói rằng giữa các biến độc lập không có quan hệ tuyến tính với
nhau, khi đó các cột của ma trận X lạ dộc lập tuyến tính. Do đó hạng của ma trận X
bằng sổ cột của ma trăn này tức là R(X) = k, ma trận X khổng suy biến.
T h í dụ 3.2. Với thí dụ 3.1 ta có ma trận X như sau: 1,0000 18,0000 10,0000 1,0000 25,0000 11,0000 1,0000 19,0000 , 6,0000 1,0000 24,0000 16,0000 uoooọ 15,0000 7,0000 1,0000 26,0000 17,0000 X = 1,0000 25,0000 14,0000 1,0000 16,0000 12,0000 1,0000 17,0000 12,0000 1,0000 23,0000 12,0000 1,0000 22,0000 14,0000 1,0000 15,0000 15,0000
3.6. UỞC LUỢNG CÁC THAM s ố - OLS
Hàm hồi qui mẫu SRF cố dạng Ỳ , = p , + M 2i + . . . + p k X ki
Y |= P i + P ị X jj + . . . + p k X kj + e i hay Y = x p + e Trong đó e = . = Y -X P
Các uớc lượng OLS duợc tìm bằng cách: 58
£ . 2 = 2 ( Ỵ - p, - p 2X 2i- . . . - p kX ki)2^ m i n i — 1 i*l ỵ e?
là tổng bình phương của các phần dư (RSS). i=j •
e'e = ị e ĩ = ( Y - X P )'( Y - x p ) = Y Y - P ,X Y -Y X P+ p 'x x p = Y Y - 2 p'X Y + p 'x 'x p = -2X Y + 2X x p X Y = x x p n £ * 2 i z x 3i ■- ZX/0 ' P . ' 1 * 2 , ■vị I ^ 2 i x 3 i 5 % p2 fo VCỵ I X t à 5 ^ / í: • Ằ . X X P • r 1 1 - i ' I X 2Ì x 22 "■ x 2 n y2 ■■ ► ?» 1 1 ^ 1 X' Y
Với giả th iế t4, X kỊiông suy biến, nên X ’X cũng không suy biến,iđo tíó tồn tai
(X *X) . Từ đó: p = ( X X) A Y.
Thí dụ: Vói ma trận X ở thí dụ 3.2, khi đó: '1 2 245 146' 2,440 -0,0884 -0,0454 X’ X = 245 5195 3055 ; ( x ' x ỵ ' = -0,0884 0,0067 -0,0040 146 3055 1900 -0,0454 -0,0040 0,0105 '1696 32,2773" X Y = 35463,048 : . ậ - 2,5057 21409,652 4,7587 59
3.7. MA TRẦN PHUONG SAI CỦA 3
Để kiểm định giả thiết, tìm khoảng tin cậy. cOng như thục hiện các suy luân
thống kê khấc cần phải tìm var(Pi), ỉ = 1, k và Cov( pi, P j ). Phuơng pháp ma
trận cho phép chúng ta tìm chúng một cách dễ dàng.
Ma trân hiệp phuơng sai của: > a r ( Ậ )
C ơ v í Ậ , ^ ) - CovCPv ếk) VarCpj) -
Cov(P2J k) C o v (P ) = C o v { P k , P ộ C o v ( ệ k J 2 ) - V a r ( p k )
Cov( ậ ) đuợc xác định nhu thế nào? ịì= (X 'V 'X 'Y Y = xp + u
P = (X 'X )lX'(Xp + Ụ) = p + ix'xr'x'u
ậ - P = ( x ' x ) ' ’x ' u
•Cov(p) = E i(P - P) (P - P) ] = E {[(x’x )'‘x ’u ][ ( x ’ x ) ’‘x ’u ] } ■
= E[(X'X) 'X u u ’X(XX’ )•*]=(X'X) ‘X E(UU')X(X'xy‘
= (X , X)‘IX o2IX (X 'X )' Cov(P) =Ơ 2(X 'JỘ '‘
Trong công thức trên (X X) ■' là ma ừận nghịch đảo cùa ma trận (X X ), a 2 là
Var (Ụ), nhung chua biết chúng ta phải dùng ưóc lược khổng chệch của o 2 là: * = £ e ‘ / ( n - k ) > . , e' e = ■-! er
= i-> ( Y i - Yi ) = Y ' Y - 2 Ỷ ' Y + Ỷ ' Y
= Ỷ' Y - 2 P ' X ' Y + P ' X' XP = Y ’ Y - P 'X 'Y . Với thí dụ 3.2 thì: 39,1009 -1,4164 - 0,72713' C ov(/ớ) = -1,41464 0,10796 - 0,064747 -0,72713 -0,064747 0,16841 60
3.8. CÁC TÍNH CHẤT CỦA UỚC LUỢNG BÌNH PHUDNG NHỎ NHẤT
Trong mô hlnh hồi quy bội các ước lượng binh phương nhỏ nhất có các tính
chất giống nhu trong mô hình 2 giản biến đơn. Ở đây chỉ nêu ra các tính chất, việc chứng minh các
tính chất này duợc .ựình bày trong phàn phụ
lục m .2 , sách ‘! Kinh tế lượng” - Nhà xuất bản Khoa học và Kỹ thuật, 2001. 'Để
đơn giản hoá dưới đây chỉ đưa ra các tính chất đổi với mô hình có hai biến độc lập.
Tuy nhiên những tính chất này đúng cho mô hình có sđ biến độc lập bất kỳ.
1. Đường hồi quy bội cùng đi qua điểm ( Y , x 2 , x 3) 2. Ỹ = Y 3. Ỳ e, = 0 i-l
4. Các phần dư eị không tương quan với Xa và x 3i, nghĩa là: ỉ Ci Xíi = 2 ^ e, x 3i = 0 i=l i=l
5. Các phần đưe-, không tương quan với Ỹ; : J ’ ei Ỳj = 0 i-1
6. Từ công thức se ( P2 ) và se ( ậ 3 ) ta thấy rằng nếu như giữa Xỉ và X, có
quan hệ tuyến tính quá chặt, Ĩ23 * ± 1 thỉ var( P j ) và var(p3) rất lớn. Do đó ta sẽ
khó khăn trong việc đoán nhận giá trị thực của p2 và p3. Vấn dề này sẽ được giải
thích dầy đủ hơn ở chương V.
7. Từ công thức xác định var( P2 ) và var(P3), la thấy chúng tỷ lệ thuận với ơ2
và Ĩ23, tỷ lệ nghịch .với J
[ X x 3i I ■ Như vậy sự biến thiền cùa Xịi càng lớn thì i-1 Vi=i /
var (Pj) càng nhỏ, hay Pj càng được ước lượng chính xác. 8. P2 , p 3 ■
là các ước lượng tuyến tính không chệch có phương sai nhỏ nhất
trong lớp các lượng tuyến tính không chệch cùa p2 và p3.
3.9. UỚC LUỢNG HỢP LÝ TỐI ĐA ( ML)
Với các giả thiết đã trinh bày ở (3.2) thì Yi ~ N(pi + P2X21 + ... + pk Xịti, ơ2) và
các ước lượng của Pi, p 2
Pk là .p ,,..... Pk thu được bằng OLS và ML là như
nhau Nhưng ước luợng của ơ2 từ ML: ỡ J = ỉ
ef / n là ước luợng chệch. Í«| . . 61
3.10.HỆSỐXÁCĐỊNHBỘIR2VÀHỆSỐXÁCĐỊNHBỘIĐÃH]ỆUCHÌNH r 2
Trong mô hình hồi quy hai biỗh, ỉ do độ thích hợp cùa hàm K6Ì qui. Nó chính là tỳ
lệ của toàn bộ sự biến đổi của biỗii phụ thuộc Y do biến giải thích X gâyia. Trong mô hình
hôi quy bội tỷ lệ cùa toàn bộ sự khác biệt cùa biến Ydo tất cả các biến giải thích X2. Xị, ....
Xk gây ra đuợc gọi là hệ số xác định bội, ký hiệu R2. I
Hẹ số xác định bôi R2 có Ihể tính bàng một trong hai cồng thức sau: '2 _ ESS T S S - R S S RSS R - T S S - TSS - TSS
Phần trước đã chúng minh e'e = S ẹ ? = Y Y - P'XY.~ 1=1
= ỵ e M - t ) = Ệ e ,(7 , - Â - A x v - . . ẵ- Â ^ ) M iềl
= ỵ e , ợ , - Ỹ - Ằ (X2, - X ) . . . - p k ( X ki - x u )) í-1
= Ỳ e, ( y , - Ỹ - & ( X 2i- X ) . . . - K w » - * » > ) / - I = ẳ
e ‘ (y< - Ấ X 2i - ' Ả * * ) = Ẻ - ° - /-1 1-1 A ■
s , ỵ i y i(y i-0 i* ĩi~ -0 * x iứ) Im I
= ấ *<>/ - Â Ê y . - x a - * Á ẳ y i * « /-I i-l i-1
TSS = ẳ y i = ẳ Yj2 - 2 I Ỵ Ỹ +n Ỹ 2 = Y Y - n Ỹ 2 . i=l i=l ESS = TSS - c*e = p X Y - n Y 2 p x Y - n Ỹ 2 Y Y - n Y 2
r ĩ = E S S _ = ị § c '2
Ẫ y l x 2 i + ^ l i
+ - + h I , y i x k i
= ras = ~ /p »l ĩ = Ằ , ~ 1y' 62 0
ắ R2 ắ 1. Nếu R2 = 1, có nghĩa là đường hồi quy giải thích 100% sự thay đổi
cùa Y . Nếu R3= o! có nghĩa là mô hình không giải thích sự lhay đổi nào cùa Y.
Một tính chất quan trọng của R2 là nó là hàm không giảm của số biến giải
thfch có Irong mô hình. Dẻ dàng thấy rằng J y? = ỉ
(Yi - Y Ý không phụ i-1 Í.I n
thuộc vào số biến giải thích trong mồ hình, nhưng X e í là hàm giảm của số này. i-1
Do đó, nếu tăng số biến giải thích trong mô hình thì R2 cũng tăng. Vấn đề đặt ra là
khi nào thì đưa thêm biến giải thích mới vào mô hình?
Không thể dùng R2 làm tiêu chuẩn để xem xét viộc đưa Ihêm hay không đưa
thêm một biến giải thích mới vào mô hình. Bởi vì R2 còn phụ thuộc vào sô' bậc tụ đo của 05 - Ỳ; Ý và
(Yị - Y )2 tương ứng là (n-k) và (n-1). Trong đó k là i-1 . Ỉ*1
số các tham số (kể cả hệ số chận) của mô hình.
Người ta dùng hẹ số xác định bội đã hiệu chình, ký hiộu R 2 dể cân nhắc khi
xem xét việc thêm biến giải thích mới vào mô hình. ___ ỉ e f / ( n - k ) „2
ị ý Ị Ị ( n - l ) s ị » - *
R 2 có các tính chất sau:
1. Nếu k > l, R 2 <, R2 < 1, điều này có nghĩa là nếu số biến giải thích tăng
lên thl R J tăng chậm hơn so với R2.
2. R2 £ 0, nhưng R 2 có thể âm. Như vậy khi R 2 còn tăng thì ta còn phài
đưa thêm biến mới. R 2 còn có thể tăng khi mà hệ số cùa biíỄn mới trong hàm hồi
quy khác không. Khi nào biết được hệ số cùa biến mới Xk trong hàm hồi qui khác không? Khi mà giả thiết: Ho : pk = 0 H , : p k * 0
bi bác bỏ trong đó Xk là biến chúng ta định đưa thềm vào mô hình. 63 _7 R SS J144,2269 Trong thí dụ 3 .2 : R = l — = 0 , 9 7 5 6 6
R 2 = l - C L - R 2) ^ - = 1-(1-0,97566)(12-1) / (12-3) = 0,97025 •• n - k 3.11. MA TRẬN TUDNG QUAN
Giả sử chúng ta có mô hình hồi quy bội:
Yi =pi +PjXjì + ... +pkXici + l ỉ
Kí hiệu Tiị là hộ số tuơng quan giữa biến thứ t và thứ j. Nếu t= l thì r,j là hẹ số
tương quan giữa các biến Y và biến X|. f e y 'x ' ) ; r , ( l ĩ ĩ i l ; n n ' r il n n ẳ x ỉ ẳ x Ị i i=I i=l i=l Ị=1 Trong đó: Xji = - X j
Dẻ dàng thấy rằng: r,j = Ij,; Tjj = 1. r13 •• ' rl l 1 rì2 rl3 ... r12 ■ r\k ' rlk r21 r22 r23 •" r2k r21 1 r23 " ể R = r2 k = & (S . . . 1 / t ì rk2 rk3 ể’ rk k . 1
3 . 1 2 . H Ệ S ố T U Ơ N G Q U A N R I Ê N G P H A N
Chúng ta dã biết hẹ sổ tương quan r đo múc độ phụ thuộc tuyến' tính giũa hai
biến. Đối' với mồ hình hồi quy 3 b iế n :
Yi = pi + PzJfcj + P3X31 + l í
Chúng ta địnti nghĩa r,M là hệ số tương quan giữa biến Y v à X ĩ trong khi Xi không đổi,
ri3,2 là hệ sổ tương quan riêng giữa biến Y và Xi trong khi Tỉi không đổi.
Ĩ23.I là hộ số tirong quan riêng giữa X2 và x3 trong khi Ykhông đổi.
Ta có thể dẽ dàng chỉ ra rằng: 64 rl2 ~ r13r23 r13 ~ r12r23 113.2 -
V (1 ~ r>3 )(1 — r23 ) ■\/(1_ r ằ ) ( 1~ rẳ ) r23 ~ rl2~r13 123,1 ='
V ( l - 4 ) ( l - r ,3)
Hộ số tương quan riêng đã được định nghĩa như trên được gọi là hệ số tương
quan bậc nhất. Từ “bậc” ờ đây ngụ ý chi số hạng sau dấu phảy vì thế Ĩ Ị 2 14 là hệ số
tương quan riêng bậc 2; còn ri2, Ĩ13 là các hệ số tương quan bậc không.
Giữa hệ số xác định bội và các hệ sổ tương quan bậc không và hộ số tương
quan bậc nhất có các mối liên hệ sau:
r 2 _ rn + Tầ ~ ^ r!2r13r23 1-4
rẩ + ( 1- r lỉ) ru,2 vâ R2 = r?3 + ( 1' r 13) r 12,3 ■
Ma trận R nói ỏ trên đuợc gọi là ma trận hệ số tương quan riêng cấp 0. 1 0,78228 0,90463] Với thí dụ 3.2, ta cò: R = 0,78228 1 0,48017 0,90463 0,48017 1
3.13. KIỂM ĐỊNH GIẢ THIỂT VÀ KHOẢNG TIN CÂY CỦA CÁC HỆ s ố H ồ i QUY RIÊNG -KIỂM ĐỊNH T
Với giả thiết u - N(0,ơ2) ta có thể kiểm định giả thiết, tìm khoảng tin cây cho các số hồi quy riêng. P ~ N (P,ơ2(XX) ■')
Thành pKần P i cổ phân bổ chuẩn với kỳ vọng. Pi và phương sai bằng ơ 2 nhan
với phần tử nằm trên dòng thứ i và cột i của ma trận (XX) ' 1 hay chỉnh là phần tử
thứ i trên đưímg chéo chính của ma ừận Cov( P ). Tuy nhiên do ơ2 chưa biết, nên
ta phải dùng ước lượng không chệch của ơ2 là: ô 2 = ẳ e ? / ( n - k ) i=l 65 Khi đó t = V
có phân bố t(n - k). Với tiêu chuẩn này có thể tìm khoảng tin
cậy kiểm định giả thiết v ỉ các hẹ số hồi quy rifing.
Khoảng tin cậy với hộ số tin cậy 1- a của Pi đuợc xác đ ịn h : 3 - P
P ( - tofl( n - k ) < - r - s T
< t« fl(n -k )) = 1 -a .D o đ ó : S e(P |)
( P i- t« fl(n ,-k )S e (P i) < P , < ậ i + t afl(n -k } S e (P i) ) , V i = 1 , * .
Chúng ta có thể kiểm định giả thiết Pi = pi
Tiêu chuẩn dùng để ldểm dinh:-1 = - ậ —Ệ^- — t(n - k) 5 e (Â )
Tùy theo cảc giả thiết Hi, chúng ta có các miền bác bỏ sau dây: B ả n g 3.1 Loại giả thiết Ho H, M iầnbấcbỏ Hai phía Pi = P>* Pi ^ pế* l t l > t o / 2(n - k ) Bên trái p. = £ )& * p i< p r t < - t B( n - k ) Bên phải p. = (Sft*) f t* p T t > t a ( n - k )
Nếu Pi* = 0, chúng ta muốD kiểm định biến độc lập Xi không ảnh hưòng đến biến phụ thuộc.
3.14. KIỂM ĐỊNH G IẢ THIẾT
Pí = p3 = ... = Pk = 0 hay R2 = 0
Chúng ta đã trinh bày kỹ thuẠt phan tích phucmg sai và mối quan hẹ giũa R2
v ì F. Bằng ngôn ngữ ma trận có thể trình bày tổng quát các vấn dề dó.
Bảng 3 3 . Phân tích phương sai cho mò hình hồi quy bội k biến Nguồn biến thiên Tổng bình phương Bậc tự do Phuangsai Từ hàm hồi quy (ESS) P 'X Y - n Y * k-1 P ' X ' Y - n Y l k - \ Phần dư (RSS) y 'y - p ' x 'y n - k Y ' Y - ệ ' X ' Y n - k Tổng Y Y - n Ỹ 2 n - 1 66 Do R2 = V Xh g Y Y - n Y 2
nên P 'X 'Y -n Y 2 = R2( Y 'Y - n Ỹ 2),
Y Y - p X Y = (1 - R2) (Y Y - n Y 2). Ta có bảng sau đây:
B àng 5J ề Phân tích phương sai đối vái R2 Nguôn biến thiên Tổng bình phương Bậc tự do Phương sai Từ hàm hồi quy R2( Y " Y - n Ỹ 2) k - 1 R 'i Y ' Y - n ĩ 1) (ESS) k - l Phần dư (1 - R 2) ( Y " Y - n Ỹ 2) n - k (1 - R 3)(Y' Y - n Ỹ J ) (RSS) n - k Tổng Y "Y - n Ỹ 2 rv- 1
Với giả thiết P ~ NCP.Ơ2) thì giả thiết
Ho: p2 = p3 = ... = pk = 0 ( hayR 2 = 0)
Hi: có ít nhất một pi * 0 ( hay R2 > 0 )
được kiểm định bàng tiêu chuẩn: ( P ' X Y - n Ỹ 2 ) / F = . . . . .
....... / - 1- - F ( ( k - l) ,( n - k ) )
( Y Y - ặếX ễY ) / / (n (n -k ) , ậ X Y - n Ỹ 2 R V ( k - l ) ° 0 R " Y Y - n Y 2 ’ n n " ( 1 - R ) / ( n - k ) '
Với tiêu chuẩn F cho phép kiểm định giả thiết:
H o:(32= p 3 = ... Pk = 0 ( hay R5 = 0 )
H,: Có ít nhất một Pi * 0 ( hay R2 > 0 ) Với thí dụ 3.2 : 67
F = 180,3545; F0.Ũ5(2 ,9) = 4,26. F > F0.05(2,9),_do dó giả.thiết Ho bị bác bỏ.
3.15. HỒI QUY CÓ Đ Ề U KIỆN RÀNG BUỘC — KlỂMĐỊNH F
Giả sử rằng chúng ta có hàm hồi quy
Y, = p 1 + p2Xi1 + . . . ;+pkXu + a '(*)
Bây giờ chúng ta kiểm định giả thiết: Ho: Pk-m+i'= Pk-nH-2 - - Pk = 0
Vớị.gịảithiệítnàythìhànihồi.quycó.dạng: .
. Ỵi = pi +. PíXai + — + Pk-mXic-m + y
(đuợc gọi là hàm hồi quy thu hẹp hay hầm hổi quy có điềụ kiên ràng buộc). Kíhiộu en;
Véctơptìàn dư tiỊrhàmh&qụy.có điếu kiện ràng buộc. :i euR :
Véctơ phần du từ hàm hồi quy ban đầu( không điều kiện ràng buộc), m:
SỔ biến bị loại khỏi mô hình ban đầu ( số điều kiện ràng buộc), n: SỐ quan sát.
Khi đố tiêu chuẩn kiểm định giả thiết Ho:
Nếu F > F„(m, n - k) thì giả thiết Hũ bị bác bỏ.
Đôi khi ta dùng cổng thúc sau đây: ( e Re R ~ e URe U R ) / m
(TSS - ESSịị) - (TSS Ẻ ~^ESSU„ ) / m ® U R ® Ư R k )
(TSS - ESSUR) Ị ( n - k )
(E SSịjR — ESS rị ) Ị ĩĩĩ
Chia t ả tử số và mẫu cho TSS, ta đuợc (TSS-ESSm)l(n-k>
" p _ ■ (R2u r - R2R)/m công thứcxút gọn: F= F(m, (n - k)).
i: ~ ạ - R 2u K )/(n -k )
'Cách trình bày như trên chì là truồng hop riêng của kiểm định “ tổ-hợp tuyến táih cùa
các hệ' SỐ hổi quy”, v a i giả thiét vể tổ họp tuyến tính cùa các hệ số hổi quy, có thé làm iittù 68,
công thức tính F qua các R2 sẽ không dùng được. Trong trường hợp này chúng ta phải
dùng công thức ban đẩu, tính F qua RSS. 3.16. D ựB Á O
Chúng ta cố thể sử dụng mô hình hồi quy vào dự báo: dự báo giá trị trung
bình và dự báo giá trị cá biệt ì x 2 ° Cho x° = X ?
Dự báo giá trị trung bình: E (Y IX0 )
Ỵ — pi + PỉXỉ + + Pk Xic = x p .
Với x = x ° ta có ( 7 o lX 0 ) = X°'p =>var(ỳolX o) = X0'var(p)X 0
v a r i f o i x f ) = ^ ' ( X ' X j Y vì v a r(P ) = ơ 2(X X r '
Nhưng ơ 2 chưa biết nên phải dùng ước lượng không chệch ớ 2 của nó : V a r ( ỹ l X ° ) = Ớ ^ Q Ó Q ' 1* 0 s e i ^ o i x 0 ) = V ^ x ' ^ x ' ^ - ' x 0
ỷ 0 - tyẠ n - k) se( Ỷ 0 IX0 ) 5 E(YI Xo)
ỉ f o + t ^ ( n - k) se ( ý 0 I x°)
Dự báo giá trị cá biệt
Yi = x 'p + e , =>var(YolX0 ) = var(Xỏ,p ) + ơ2
Var(Yo I x°) = ả 2[l+ X ° '( X X rlX0 ] se(Yo I x°) = ựvar(Yo|X0)
Ỳ 0 - t ^ ( n - k ) s e ( Y „ I X ° ) < (Y„I X °)ắ f o + ty t (n - k) se(Y0 1 x 0) .
Viêc trinh bày mô hình hồi quy bằng ngôn ngữ ma trận đã cung cấp cho
chúng ta một công nghệ mà nhờ đó có thổ sử dụng kỹ thuật tính toán, tự động hóa
toàn bô quá trình tính toán, phân tích và dự b á a 69
3.17. THÍ D Ụ -thí dụ 3.3
Chúng ta cố các biến số sau -đay: Y- sản lượng/ ha; Xj- phân h o í học/ ha; X) •
thuốc trừ sau / ha. Hãy ước lượng mố hình hổi quy tuyên tính theo tham stf và các
biến số của Y phụ thuộc v ìo x2 và X} và trả íỉri các cảu hỏi sau đây. Cho a = 5%.
a. Kết quả ước lượng cố phù hạp với thực tế không? HSy giải thích ý nghĩa
kinh tế của các hộ số nhận được.
b. Phân bón( thuốc trừ sâu) có ảnh huống đến năng suất cùa loại cay trổng trên hay không?
c. Hãy tìm khoảng tin cậy cho các hộ sổ hồi quy riêng.
d. Hãy giải thích nghĩa của hẹ số R2 nhận được.
e. Cả phan bón và thuổc trừ sau đéu khổng ảnh hường đến năng su it ?
g. Bạn cố thể bỏ biến x 3 ra khỏi mô hình dược khống vì sao?
h. Hãy ước lượng mô hình bằng phương pháp ma trận.
i. Phải chãng phân bón và thuốc trừ sâu đéu có ảnh huởng như nhau đền nang
suất giống cây tròng trên?
k. Hãy dự báo giá trị trung bình v ì cá biệt khi x 2 = 20; Xj = 15.
1. Hãy phân tích kết quả dựa trên tính toán bằng MFTT3 ễ'T
Để trả lòi được câu hỏi a trước bết phải ước lượng mỏ hlnh. Dựa vào bảng(33) ta tính được: n n n n ( Ỉ 4 ) ( Ỉ 4 ) - < X w 2 M /- 1 M / Ề1 .i.m / ị -] (956X504)ễ- (900)(524) _
----------------------------- T— = Ư,Ồ5. (576)(504) - (525) ", _E_, n n
i x 3i x 2 x 2 i) “ ( S y i x 2i x S x 2ỉx 3i) i«l 1*1 i.| 70 Bảng 3.3 Y x 2 X, y x2 X3 yx2 y*3 X2X2 V 2 X2 x32 Ỷ e e2 y2 40 6 4 -17 -12 -8 204 136 96 144 64 40.32 -0.32 0.1024 289 44 10 4 -13 -8 -8 104 104 64 64 64 42.92 1.08 1.1664 169 46 12 5 -11 -6 -7 66 77 42 36 49 45.33 0.67 0.4489 121 48 14 7 -9 -4 -5 36 45 20 16 25 48.85 -0.85 0.7225 81 52 16 9 -5 -2 -3 10 15 6 4 9 52.37 -0.37 0.1369 25 58 18 12 1 0 0 0 0 0 0 0 57 1 1 1 60 22 14 3 4 2 12 6 8 16 4 61.82 -1.82 3.3124 9 68 24 20 11 6 8 66 88 48 36 64 69.78 -1.78 3.1684 121 74 26 21 17 8 9 136 153 72 64 81 72.19 1.81 3.2761 289 80 32 24 23 14 12 322 276 168 196 144 79.42 0.58 0.3364 529 570 180 120 0 0 0 956 900 524 576 504 S70 0 13.67 1634 g
( 9 0 0 ) ( 5 7 6 ) - ( 9 5 6 X 5 2 4 ) Ps (576)(504) - (524)2 Ậ
y p * ,X2--P3. XJ = 57^-0,65* 18.U ,U -? 1 Z ^ 3 1,98.
Vậy hàm hồỊ quỵ mẫu: Ệ = 31,98'+ 0,65 X2 + Ịj ị JjXjj
a. Khi người;ta tãng phân; bón / ha và tăng thêm thuốc trừ sâu /Jia thì nâng suất
loại cây trên sệ tặng.; /3 2 và p.Ị đềụ d ư ơ n g .ch an ên .có th ể nồi rằng kết quả ước
lượng phù họp vổi thực tế. Tất nhiỀn điều ttên không có nghĩa là khi tăng phân bón(
thuổc trừ sâu) / ha đến vô cùng thì năng suất cũng, tăng như yậy. p 1 = 0,65 có
nghĩa là khi gia tang phân bốn /.há ỉ tấn till năhg suất trung bình / ha sẽ tăng 0,65
t á n ; v à / ? 3 = 1 ,1 1 c ố n g lũ á là k h i g ia t ă n g t iiu ố c t r ừ s â i T / ị h a 1 t ấ n t h ì n ă n g suât
trung bình / ha sẽ tàng 1,11 tán.
b. Để trả lòi câu, hòi nàỵ chúng ta phải kiểm định .các.gịả thiết:
Hq: Pi = 0 ;H |-: Pj 5* 0 vói i = 2,3
bằng kiểm định;t: tị S |/ Ị .ị / S e ị ậ i ) .
ở * = RSS/(n-k) = 13,6704/(10-3) = 1,95. ± A
v a r( p 2 ) = — -----— ; w -----------■crr ‘'
( Ẽ xl ) ( Ẹ * ỉ i ) - ( E xĩ i ^ y /ằ| /mí /-'
= (504)01.95)/ (57ố*504-524J) = 0,06.
se( P2 ) = y v a r ( P 2) = 054.
var < P i rv— Jsi . --- —&ỉ
( /L iX2 l)(5 ',Xìl ) - ( ^ X2lX3l)2 1*1 l - l 1.1
= ( 5 7 6 X 1 , 9 5 ) / ( 5 7 6 * 5 0 4 - 5 2 4 2) = 0 , 0 7 .
se ( P 3 ) = V var( P j ) = 0,27. 72 Từđó
t , = /ậ 2 / S c ( ^ j ) = 0,65 / 0,24 = 2,7và
t j = ^ 3/ S e ( /Ồ3) = 1,11 /0,27 = 4,11.
to.raí(7) = 2,365. t2 > W 7 ) ; *3 > t«02j(7 ) do đó giả thiết Ho bị bác bồ, thừa nhãn H|,
nghĩa phân bón( thuốc trừ sâu) ảnh hưởng đến năng suất giống cây trên.
c. Khoảng tin cậy cho các hệ số hổi quy riêng được cho bỏi công thức sau:
( Pi - torc (n - k) Se (Pi) < p ể < Pi + W ( n - k ) S e ( p i) ) ,V i = T J c .
( Â - t a f l ( n . - 3 ) S e ( Ẵ ) < p2 < p 2 + - 3) Se ( 0 2 ) )
0,65- 2,365*0,24 < P2 < 0,65+ 2,365*0,24 0 ,0824 < P2 < 1,2176
( /?3 - t„/2(n - 3) Se ( Â 3) <03 < /?3 + t a* ( n - 3 ) S e ( /Â3) )
1,11-2,365*0,27 < Pj < 1,11+2,365*0,27 0 .461 < p3 < 1,738
d. Hệ số xác định bội và hộ số xác định bội đã hiệu chinh.
R = 1- RSS/TSS = 1- 13,6704/ 1634 = 0,9916.
" F = 1 - ( l - R J ) (n - l)/(n -k ) = l - (1-0,9916) (10-1)/(10-3) = 0,9892.
e. Cả hai yếu tố phân bón và thuốc trừ sâu đều không cùng ảnh hường tới năng suất: H o: P2 = p 3 = 0 hay R2 = 0
H t : có ít nhất một trong hai hệ số khác 0 hay R2 > 0. p_ R ’ / Q c - l ) _ 0 , 9 9 1 6 / ( 3 - 1 ) (1 - R 2 ) / (n - k)
( 1 - 0 , 9 9 1 6 ) 7 ( 1 0 - 3 ) " ’
Trong khi đó F0i05(2,7) = 4,47, do đó Ho bị bác bỏ. Ta kết luận rằng có ít nhất môt
yếu tố ảnh hường đến nang suất.
g. 0 5 thể bò biến x3 ra khỏi mô hình được không?
Để trả lời câu hòi này cần phải dùng kiểm định hổi quy có điéu kiện Tàng
buộc. Ước lượng mồ hình có cả hai biến x , và Xj ta có R’-ur = 0,9916. Khi bỏ biến
X chúng ta thu được mô hình ở ví dụ 2.2, R2r = 0,971.
H o : p 3 = 0 ; H , : P j * 0 . 73 (J?2W - R * R ) /m
(0 ,9 9 1 6 - 0 ,9 7 1 )/!
( J L - R ' u r t / i n - k )
( l - 0 ắ9 9 1 6 ) / ( 1 0 - 3 ) ’ ẻ
Fftos<1.7) = 3.59. F > Fojb( 1,7), giả thiết Ho bị bác bỏ. 1. Phương pháp ma trận 1 6 4 1 10 4 1 12 5 1 14 7 ì 1 1 1 1 1 1 1 1 1 1 16 9 X'X=
6 10 12 14 16 18 22 24 26 32 118 12 4 4 5 7 9 12 14 20 21 24 1 22 14 1 24 20 1 26 21 1 32 24 10 180 120 180 3816 2684 120 2684 1944 ' 1.363 -0.177 0.1602' 570' (X’X)-'= -0.18 0.032 -0.033 X’Y = 11216 0.16 -0.03 0.0366 7740 31.98067
P = (X ,X )-'(X ’Y) =
0.6500Ĩ ,Y'Y = 34124. 1.10986
e ’e = RSS = Y'Y - ~p ’(X’Y) = 13,6704. .
ỡ 1 = R S S /(n -3 )= 1 3,6704/7= 1,952914.
• 2.662$ -Q.S456 0.3129
Cov( p ) = ở 1 (X’X)'1 = -0.3456 0.06258 - 0.065
0.3129 - 0.065 0.0715
TSS= Y’Y — n y 2 = 34124 - 10* 572 = 1643. 74
ESS = TSS-RSS= 1643- 13,6704= 1629,3296. R2 = 0,9916.
Các phần tử dọc đường chéo chính cùa ma trận Cov( P ) trên là phương sai của
các p tương ứng. Từ ma trận này biết được Cov( p i , P ) , chằng hạn Cọv( p J ,
P j) = -0,065 và tính được:
Vai?2- iổ 3) = Vai(yớ 3) + V a K ^ 3)-2C cA <^2, pỉ>
= 0,063 + 0,0715 - 2(-0,065) = 0,2645. SeCyffj-/?,) = 0,514.
Đến đây có đủ thổng tin để thực hiện các phin tích đã nói ò trẽn. i.
Phải chãng phán bốn và thuốc trừ sâu đều có ảnh hưỏng như nhau đến năng
suất giống cây trồng trên. Để trả lỀri, ta phải kiểm định giả thiết sau đây: Ho: (ì> =
Pj hay ỊỊí - p3 = 0 ; H,: p2 * p j .
t = ầ - Ề l Z Ì ẼỊ Z Ễ ủ = Ấ - 4 _ t(n_3) 5 e ( Â - Â ) ^ SeCp2 - p J t =
~ f t , - = - - ị — % = (0,65-1,11) /0 ,5 1 4 = - 0,895.
S c ( Â - Â ) S e ( Â - Â )
Trong trường hợp này ta chua cố đủ cơ sở để bác bỏ Ho vì to 025(7) = 2,36.
k. Dự b á o : Với x 2 = 20; x 3 = 15, một ước lượng điểm tương ứng là:
ỹ0= Ỷ (X, = 20; X, = 15) = 31,98 + 0,65*(20) + 1,11*(13) = 61,63.
Phương sai của giá trị trung bình:
Var(ý„1 x ° ) = o 2X°'(X'X)-'X° 2.6628 - 0.3456 0.3129 1
= (1 ,2 0 ,1 5 ) -0.3456 0.06258 - 0.065 20 = 0,308533 0.3129 - 0.065 0.0715 15 S e(ỹ0 l Ar 0 ) = 0 ^55.
Khoảng tin cậy 95% cho giá trị trung bình:
To - tỊ ị( n - k) sc (Ỷ 0 1 x ° ) á E(YI x>) í Ỷo + t ^ ( n - k) se (ý „ I x°)
61 63 - 2,365*(0,555) á E(YI Xo) á 61,63 + 2,365*(0,555)
60,317 <; E(YIXo) < 62,943
Phương sai cùa giá trị cá b iệ t: » . . Var(Yo Ix°) = Ớ t 1 + ]= var(KoI * ° ) + ố 2 75 = 0,308533+li95= 2.2585
Se(Yo I x°) = ýVar(Y0|X a) = 'I ^ íẽ'
Khoảng tin cậy cua giá trị cá biêt:
?0 - ty (n - k) se(Yo I x°) £ (Yo I x°) <; ỹ 0 +
■ ^íV ỷ Ũ ỊỴ Ị l^ o ) •
61,63 - 2,365*(2,2585) s E(Y I Xo) á 61,63 ị 2,365*(2,2585)
56,289 ắ EỌÍ IXo) ỉ 66,971 lệ
Dọa ơên kết quả tính bằng MFIT3, đối chiếu lại với các kết quả tính toái ờ trên.
Ordinary Ix a st Squares Estimation
Ạ*********************************************************** Dependent variable is Y
10 observations used for estimation from 1 to 1 0 1 Regressor Coefficient Standard Error Í T-Ratio[Prob] INPT 31.9807 " 1.6318 19,5985[.000] X2 _ .65005 f , .25016 . 2.5985[.036] X3 : 1.1099 : .26743 ■ - < u 501 [.004] R-Squared
.99163. F-statistic F( 2, 7) 4J4.8492[.000].
R-Bar-Squared .98924 S.É. of Regression 1.3975
Residual Sum of Squares 13.67Ọ4
Mean of Dependent Variable 57.0000
S.D. o f Dependent Variable 13-4743 Maximum o f Log-likelihood -15.7526 DW-statistic 2.1141
3.18. MỘT S ố DẠNG CỦA HAM H ồ i QUY
Mô Mnh hồi quy tuyến tính đuọc hiểu theo nghĩa tuyến tính đối với các tham
số. Nó có thể tuyến tính hoặc không tuyén tính đối với các biến. Dạng của hàm hồi
qui là một ván dồ quan trọng, một trong những nhân tố có tính chất quyết định đốì
với két quả nghiên cứu. Tuy vậy, ván đề "dạng cùa hàm hồi quy" lại không có một
cơ sở lý thuyết đủ mạnh để có. thể khlng định dạng cùa hàm hồi quy là dạng này
mà khOng phải là dạng khác. Dạng hàm của mô hình hồi quy là m ột vấn dề thạc nghiệm. , v y : f . . . V.,
Một trong những phưong pháp thuờng đuợe dùng-là biểu -diẻn c íc số liệu len
hộ tọa độ. Nếu như dô thị chỉ ra quan hệ giữa hai biến l à tuyến ttoh thì dạng .hỉm 76
của mô hình là tuyến tính, nếu quan hê được chì ra là hàm bạc 2,3 (phi tuyến)... thì
dạng hàm cùa mô hình được chọn một cách tương úng. Phương pháp này đuợc sử
dụng trong mô hình hồi quy giản đơn. Nó sẽ là không hữu ích nếu chúng ta có mô hình hồi quy bội.
Ở đây sẽ trình bày một số dạng hàm đơn giản mà hay gãp trong ứng dụng thực tiễn.
1. H àm có hệ số co giãn khống đổi - hàm Cobb - Douglas
Hàm Cobb - Douglas có dạng Y= p |X P2
Hàm này là phi tuyến đối với X và phi tuyến đối vãi tham số Ps- Tuy nhiên có
thể biến đổi về dạng tuyến tính đối với tham số. Lấy ln hai vế, ta có: lnY = ln 13, + p2 lnX Đặt (V = ln P i ; Y ' = lnY ■ X ' = lnX Ta có Ỵ ' = p,' + f e X '
Đây là mò bình giản đơn đã biết. Ta cố thể minh họa hàm ban dầu và hàm sau
khi biến dổi Y bằng dồ thị sau: Hình 3.1 Hình 3.2
Hàm Cobb - Douglas có thể mở rộng cho trữỉmg hợp có nhiều biến giải thích:
Y = p 1x > x 3p’ .. . x mp" Bằng phép biến đổi:
l n Y = l n P i + P 2 ln X j+ P 3 ln )Q + ... PolnXm
chúng ta dễ Hang có hàm tuyến tínỉi đối với các tham số. Trong hàm Cobb -
Douglas, hệ số co dãn cùa Y đối với X; bằng P i. 77 2. H àm có dạng: Ys= P ( l + r ) '
Hàm có dạng Y, = p (1+ r)‘, trong dó t là thời gian. Hàm này tbuờng dùng dể
do sự tăng trưởng của yếu tố Y| theo thời gian, r là tỷ lê tin g trường.
Ở năm (thời kỳ) t = 0, ta có Y0 = p , do đổ Y, = Yo (1 + r)‘
Biến dổi hàm về dạng tuyến tính đối với tham số:
lnY, = inY„ + t l n ( l + r ) Đạt
Y|' = In Y ,; Po = ln Yo; pi = In (1 + r) Khỉ đó Y |'= Ị3o + Pi t
Dẻ dàng ước luạng dược hàm này và từ đó tìm được Yo và r
3. Hàm dạng Hypecbol: Y = p , + — X
Hàm này là phi tuyến đối với X, nhưng tuyến tính đối với các tham số. Sau
đây là một số tniờng hợp quan trọng của hàm này
a) P i »p2 > 0, khi đó dồ thị có dạng: Y
Truờng hạp này có mức tiệm cận duới, dù X
có tảng đến d iu, Ykhông thể nhỏ han pi.
Hàm này thường được dùng khi phân
tích chi phí trung bình để sản xuất ra một sản phẩm. b) Pi >0, P2<0
Truờng hạp này cố múc tiệm cận
trên. Engel (Ỉ821 - 1896) khi nghiên
cúu mức chi tiẽu phụ thuộc vào thu
nhập đã đẽ xuất hãm này. 78
4. H àm có dạng đa thức: Y = p, + (5j X + Pj X2 + Ps X3
Hàm này thường được sử dụng để nghiên cứu quan hộ giữa chi phí và số lượng
sản phẩm được sảit xuất ra. Chẳng hạn Y - tổng chi phí, X - số lượng sản phẩm
đuợc sản xuất ra. Nếu như xây dựng được hàm này thì ta đễ dàng tìm được chi phí
trung bình và chi phí biên.
T C : Tổng chi phí; MC: Chi phí biên; AC: Chi phí trung bình.
Trôn đây đã trình bày một số dạng mô hình hồi quy. Tất nhiên rằng còn rất
nhiều dạng khác mà ở đây cũng chi giới thiệu được vằi mô hình giản đcm.Trong
thục tế để vân đụng mô hình này hay mô hình khác tnrớc hết phải hiểu đuợc mối
quan hộ giữa các biến, tính chất cùa các mô hình (các dạng hàm) muốn vận dụng. 79 BÀI TẬP
3.1. Hãỵ giải thích l õ : „
a. Hệ số hói quy riêng. .
b. Hệ số xác định bội và hệ số xáp định bội đã hiệu chình. c. Đa công tuyến. ’ ■
d. Kiểm định vể sự bằng không đổng thời , cùa tá t các hệ số>hổi quyứng với
biỂn độc lập và kiếm định riêng rê từng hệ số hổi quy.
3.2. Bảng' duới đây cho: Ỷ- Thu iibập/đầu nguìriOO tính bằng USD; X ,-T ỷ lệ
phẩn' trăm của' ladđộng nông nghiệp; X* - Số nănvtrung bình đừợc đào tạo đối vói
những người trên 25’tuổi. Cho a = 5%. '-'Ạ- -í-' ì •• •'-■■■■ n 1 2 3 4 5 6 7 8 9 10 i l 12 13 14 15 Y 6 8 8 7 .7 12 9 8 9 10 10 11 9 10 11 X, 9 10 8 7 10 4 5 5 6 8 7 4 9 5 8 Xí 8 13 11 10 12 16 10 10 12 14 12 16 14 10 12
Từ các số liệu trên tính được: Y = 9; X I = 7; X 2 = 12; ĨXii y-, =;-28; Zxa Ỵi =•
-Í2; Zxu Xa =-12; Sx2ii = 60; 2x2a = 74.
a. Giả thiết rằng; Ẹ(Y/ XÊt X , ) = Po + Pi x ,,+ P2X2 . Dựa vàomẫutrêivhãy tìm đườnghổi.quy mỉu.
b. Tim ước lưcmg phương sai ,của yếu tố ngẫu nhtèn. c. Tun
lượng phương sai của các hê số hổi quy mẫu.
d. Hãyikiểm định sự bằng không của từng hệ số hồi quy và ý rig h larủ t ra từ các kiểm định ấy.
e. Hãy tìm khoảng tíu cậy đối xứng cho các hệ sốhồi quy. f. Tim hệ số R2 và R2 .
g. Phải chăng cả hai yếu tố "Tỷ lệ lao dộng nông nghiệp" và "Số năm đuọc
đào tạo" đéu không cùng ảnh hưởng đến Thu nhập theo đẩu người. 3.3Ỗ
Trờ lại bài tập 2.11, chương n , khi hổi quy biến Sản lượng (S) theo Lao động
(L: nguòi), vì thấy hẹ số xác định (r* = 0,3029) cùa mô hình s phụ thuộc L và hê số
chặn khá nhỏ, nên người ta đưa thêm biến K là vốn (triệu đồng) vào và hổi quy
được mô hình duới đây. Cho a = 5%. 80
Ordinary Least Squares Estimation
****^^*^*^ + + + + + + ^ + + ^ ^ + + + ^++^^^ + ^JjfS|cỉị|í|Dependent variable is s
20 observations used for estimation from 1 to 20 Regressor Coefficient Standard Error T-Ratio[Prob] INPT -20.6583 22.0029 -,93889[.361] K 10.7720 2.1599 4.9874[.000] L 17.2232 4.5279 3.8038[.001] R-Squaréd
F-statistic F( 2, 17) 21.5343[.000] R-Bar-Squared .68369 S.E. of Regression 32.4717 Residual Sum of Squares
17925.0 Mean of Dependent Variable 109.4666
S.D. o f Dependent Variable 57.7367 Maximum of Log-likelihood -96.3610 DW-statistic 2.3574
a. Viết hàm hổỉ quy tổng thể, hồi quy mẫu.
b. Các ước lượng nhận đuợc có phù hợp về lý thuyết không?
c. Tìm ước lượng điểm mức sản lượng doanh nghiệp có 20 lao động, nguồn vốn 300 triệu đồng.
đ. Các giá trị ước lượng có ý nghĩa thống kê không?
e. Tính hệ số xác định bội bằng các cách. f.
Phải chăng các biến độc lập không giải thích được cho sự biến động của sản lượng?
g. Có thể nói vốn, lao động cùng tác động thuận chiều đến sản lượng không?
h. Khi lao động không đổi, nếu thêm vốn 1 triệu thì sàn lượng tang trong khoảng nào? j.
Có thể nói khi lao động không đổi, tăng vốn thêm 1 triệu thì sản lượng
tăng ít hơn 10 đơn vị được không? j.
Nguồn vốn không đổi, thêm 1 lao động thì sản lượng tăng có bằng 20 đơn vị không" k
Giá trị đ6 tối thiểu bằng bao nhiêu? lệ
Dùng liể m định thu hẹp hổi quy để xem xét có nên đưa thêm biến K vào
mô hình hay không nếu biết với mô hình s phụ thuộc L có hệ số chặn hệ sô'
xác định bằng 0.3029 và RSS bằng 44152.1
3 4 Với bài tập (3. 2), một người đưa ra dạng khác của mô hình và hổi quy được
kết quả sau, với LS, LK, LL làlogarit cơ sđ tự nhiên cùa các biến tươhg ứng. 81
Ordinary Least Squares Estimation Dependent variable is LS
20 observations used for estimation from 1 to 20
***************************************************************** Regressor Coefficient Standard Error T-Ratio[Prob] INPT 2.8749 .22746 12.6390[.000] - LK .52178 .093498 5.5806[.000] LL .68225 .14080 4.8457[.000] R-Squared
.78117 F-statistic F( 2, 17) 30.3438[.000] R-Bar-Squared .75543- S.E. of Regression .28222 Residual Sum of Squares
1.3540 Mean of Dependent Variable 4.5516
S.D. o f Dependent Variable .57067 Maximum of Log-likelihood -1.4523 DW-statístic 1.9062
Cho hiệp phương sai của các ước lượng úng với các biến LK và LL bằng 0,0127.
a. Viết hàm số kinh tế ban đầu với các biến S,K , L.
b. Viết hàm hổi quy mẫu. Cho biết ý nghĩa cùã các ước lượng nhận được.
c. Các uớc lượng nhận dưọc có phù hợp lý thuyết không?
d. Các biến giải thích giải thích được bao nhiêu phẩn ữăm sự biến động của biến phụ thuộc.
e. Kiểm định sự phù hạp của hàm hổi quy.
f. Khi lao động tăng 1 % thì sản lượng tăng trong khoảng'bao nhiêu%?
g. Khi vốn giảm 1% thì sản lượng giảm tối đa bao nhỉẽu %?
h. Nguổn vốn tăng lén bằng 1,2 lần so vdi trước thì sản lưcmg có tăng tưong úng bằng 1,2 lẩn kh0ng7 i.
Khi yếu tố khác không đổi, nếu nguổn vốn tăng lên t lần mà sản luợng tâng
nhỏ hon t lần thì ta nòi sản lưạng tăng chậm hon vói tăng nguổn vốn, nếu
sản lượng tăng lổn h MI t lẩn ta gọi là tăng nhanh hon so với tãng nguồn
vốn và bằng đúng t thì IỊỌÍ là tăng bằng với tăng nguồn vốn. Theo kết quả
hổi quy trên thì sản lượng tăng là nhanh, châm hay bằng so với tăng nguồn vốn?
k. Sản lượng tăng bằng vói tăng lao đông? 82 CHƯƠNG IV HỐI Q ur VỚI BIẾN GlÂ
Trong các mô hình hồi quy tuyến tính mà chúng ta đã xem xét lừ các chương
trước cho đến nay thì các biến giải thích đêu là các biến số lượng. Các biến đó có
thể nhận giá trị bằng số. Chẳng hạn, tiền lương cùa cán bộ, doanh số bán ra cùa
một cửa hàng, chi tiêu cho quảng cáo, cung tiền,... là những biến số iượng. Nhưng
trong thực tế có nhiều trường hợp các biến giải thích (hoặc thậm chí cả biến phụ
thuộc) là biến chất luợng. Trong chương này ta sẽ nghiên cứu hồi quy khi biến giải
thích là biến chất lượng.
4.1. BẢN CHẤT CỦA BIẾN GIẢ- MÔ HÌNH TRONG ĐÓ BIEN g iả i t h íc h LÀ BIẾN GIẢ
Biến chất lượng như đã nói ở ưên thường chi ra có hoặc không có một thuộc
tính nào đó, chẳng hạn nam hay nữ; khu vực tư nhân hay nhà nước... Vấn đề đạt ra
là làm thế nào để lượng hóa được những thuộc tính như vậy. Trong phân tích hồi
quy người ta sử dụng kỹ thuật gọi là kỹ thuật biến giả. Kỹ thuật này cho phép ta
lượng hóa đuợc nhũng thuộc tính nhu vậy. Chặng hạn để giải thích cho việc một số
thanh niên vào trường đại học, một số khấc thì không, chúng ta tạo rạ biến giả mà
nhận giá trị là 1 nếu thanh niên vào đại học và nhận giá trị là không nếu thanh niên
đó khồng vào đại học. Chúng ta cũng sẽ chì ra biến giả có thể được sử dụng như
thế nào trong phạm vi hồi quy để giải thích cho sự kiện là có những quan sát trong
phạm trù (thuộc tính) đã cho gắn với một tập các tham số h'ổi quy còn các quan sát
khác ưong phạm trù thứ 2 (hoặc thứ 3) lại gắn với những tham số hồi quy khác.
Biến giả được sử dụng trong mô hình hồi quy giống như biến số lượng thông thường.
Giả sử một công ty sử dụng 2 quá trình sản xuất (kí hiẹu quá trình sản xuất A
và quá trình sản xuất B) để sản xuất ra một loại sản phẩm. Giả sử sản phẩm thu
được từ mỗi một quá trình sản xuất là đại lượng ngẵii nhiên có phân phối chuẩn và
cí> kỳ vọng khác nhau nhưng phương sai như nhau. Chúng ta có thể biểu thị quá
t r ì n h sản xuất đ ồ như m ột phương trình h ồ i quy Y, = p, + PJ>, + u (4.1)
trong đó Yi là sản lượng sản phẩm gắn với quá trình thứ i.
0 là biến giả nhạn 1 trong 2 giá trị: 83
1 nếu sản lượng sản phẩm thu được từ quá trình sản xuất A. Di =
0 nếu sản lượng sản phẩm thu được từ quá trình sản xuất B.
Mô hình hồi quy trên đây giống như mo hình hồi quy 2 biến mà chúng ta gập
trước đây chi khác là biến số luợng X được thay bằng biến giả D. Cân cứ vào mô
hình này chúng ta có thể biết duợc sản lượng trung bình do quá ưình sản xuất A có
khác với sản lượng trung bình do quá trinh sản xuất B tạo ra hay khống?
Hệ số chặn Pi của hồi quy tuyến tính đo sin lượng trung bình gắn với quá
trình sản xuít B, trong khi đố độ dđc P2 của dL\'rug ìj'0i quy đo sự khác nhau vồ sản
lượng sinh ra do việc thay đổi từ quá trình sản xuất B đến quá trình sản xuất A
Điều nàý có thể thấy bằng cách lấy giá trị kỳ vọng cả 2 vế cùa phuong
trình(4.1) ứng với D| = 0 và D| = 1: E(Yj I Di = 0) =Pi E(Yi I Di = 1) =p! + p2
Kiểm định giả thiết Ho: pỉ = 0 cung cấp kiểm định về giả thiết là khổng có sụ
khác nhau v i sản lượng.do quá trình sản xuất A và B tạo ra. Điều này dẻ làm đuợc
như dã chi ra iruớc dây. •
Thù tục biến giả có thể dễ đàng m í rộr>ir cho’ trường li'ip biến định tín;) có
nhiều hen 2 phạm lrù. Chẳng hạn Uorig ilú dụ ò Irêa ta gi'ả thiết có 3 quá trìuh sản
xuất khác nhau có thể sử dụng á i sản xuất ra úi', pkíừn và ngnời ta hv vọng giải
thíc.1 cho vấn dề là sản lượng duợc sản xuất ra cho mỗi quá Irình có thể xhông Ẹhir
nhau. Trong trường hợp này ta sẽ đita v\o 2 biến giả là Di và D2. Chúng ta sẽ xét mô hình': Yi = Pi +P2D11 +P.1D21 + Ụ (4.2) trọng dó :
1 nếu sản lượng sàn phẩm thu được từ quá trình sản xiiất D] -
0 nếu sản lưọiig sàn phẩm.tlui được từ q -á trìnl khác. ■
1 nếu sản lượn3 ĩàn phẩm thu đuợc lir quá trình sả>.\ xu i: 'Jể I " O 2 - '
0 uếu sản iuợr<5 ràâ phếm thu ù u ạ c .ư quá trình khác.
, Nhu vậy 3 quá trình sản su it này Uược biểu tlụ dưới dụng Jác kếi hỢi sao ù a
các giá trị của các biến giả: ! Quá trìnii sản xuất D, Di i A 1 0 B 0 1 c 0 0 . 84
Bằng viộc lấy kỳ vọng cho mỗi một trong 3 trường hợp này chúng ta cố thể
giải thích kết quả hồi quy: E ( Ỵ I D ã= l ; . D ĩ = 0) =Pi + 0 2 ; E(Ỵ I D, = 0; Dj = 1) =p, + p3 E(Y |ID , = 0; D2 = 0)=(3,.
Hệ số chặn của hồi quy biểu thị giá trị kỳ vọng của sản lượng do quá trình sản
xuất c tạo ra. Hê số góc thứ nhất do sự thay đổi trung bình v'ê sản luợng do việc
chuyển từ quá trình sàn xuất c sang quá trình sản xuất A và hộ số góc thứ 2 tức là
p3 đo thay đổi trung bình về sản lượng khi thay đổi từ quá trình sản xuất c sang quá trình sản xuất B.
Kiểm định giả thiết Ho: P2 = 0 có nghĩa là không có sự khác nhau giữa quá
trinh sản xuất A và quá trình sản xuất c . Giả thiết Ho: P3 = 0 cũng có ý nghĩa
tương tự nhưng lại so sánh 2 quá trình sản xuất B và c.
Thí dụ: Để xem xét kết quả sản luợng do 2 quá trình sản xuất A và B có khấc
nhau hay không người ta tiến hành lấy một mẫu được cho trong bảng dưới đây.
Hãy phân tích kết quả tíồi qui thu được.
Dựa vào các k ít quả dưới đây ta thấy ràng sản lượng trung binh 1 ca của quá
trình sản xuất B ước lượng là 18000 kg = P i, còn sản lượng trung bình 1 ca đã
duọc ước luợng của quá trình sản xuất A là 21,280 kg = + P 2 . B ảng 4.1
Quá trình sản xuất A là 1, .Sản lượng trong 1 ca
quá trình sản xuất B là 0. hoạt động 1 2 2 ,0 0 19,0 0 18,0 1 2 1 ,0 0 18,5 1 21 0 1 20,5 , 0 17,0 0 17,5 1 2 1 ,2
Kết quả hồi quy như sau: Ỳj = 18 + 3,2 Di 85 (Se) = (0,44) (t) = (7,439) (p) =• (0,000)
R2 = 0.8737. p 2 có ý nghĩa về mặt thống kê, kết quả chỉ ra rang sản lượng trung bình cùa
2 quá trinh đó là khác nhau. Hôi quy trẽn có thể mô tả trên hình 4.1. 3i + p 2 PỆ ---------- Quá tiình Quá trình sản xuất B sản xuất A Hình 4.1
Trước khi chuyển sang mục sau ta cần một số chú ý:
l ề Để phân biệt 2 phạm trù nam hoặc nữ hay quá trình sản xuất À hoặc B
ngưỉri ta dùng một biến giả. Để phân biệt 3 phạm trù nguời ta dùng 2 biến giả. Một
cách tổng quát để phân biệt N phạm trù người ta dùng N -l biến giậ. Số biến giả
thấp hơn số phạm trù là 1 dể tránh tính đa cộng tuyến hoàn hảo. Để phãn biệt 3
quá trình sàn xuất A, B và c ta chỉ sử dụng 2 biến giả Di và E>2 nếu ta đua thêm 1
biến giả D3 nữa chảng hạn.
■ 1 nếu sản ỉượng săn phẩm thu được từ quá trình sản xuất c.
D3 = ' 0 nếu sản lượng sản phẩm thu được từ quá trình sản xuất khácế
Thì việc đua thêm Dj vào không cho thêm thôag tin mà lại gặp đa cộng
tuyến hoàn hảo (xem chương VI). Trong trường hợp này thì ước lượng bình phuơng
bé nhất cùa các tham số hồi quy không thể thu được. Có hiện tượng đa tuyến tính hoàn hảo vì: Dj = 1 - D ,-D 2 2.
Phạm trù đuợc gán giá trị 0 được coi li phạm trù cơ sở. Phạm trù được gọi là co sở
theo nghĩa việc so sánh đuợc tiến bành với phạm trù này. Như vậy trong mô Kinh trên quá
tình sản xuất c là phạm trù cơ sở, nghĩa là nếu ta uớc lượng hồi quy (4.2) vổi Di = ữ, P 2 =
0, thì chi có quá trinh sản xuất c, hệ số chăn sẽ là P |. 86
3 ể Hẹ số P 2 gắn với biến giả Dj được gọi là hộ sổ chặn chêch lệch, vì nó cho
biết giá trị của hệ sõ chặn của phạm trù nhận giá trị bằng 1 sẽ khác bao nhiêu với
hệ số chặn cùa phạm trù cơ sở.
4.2. HỒI QUY VỚI MỘT BIỂN LUỢNG VÀ MỘT BIẾN CHẤT
Trong mục này ta sẽ xét mô hình hồi quy chì có một biến lượng và một biến
chất vói sổ phạm trù nhiều hơn hoặc bàng 2. Trường hợp có nhiều biến lượng và
một biến chất thì thủ tục cũng được xét tương tự như ta sẽ làm dưới đây chỉ khác là
số biến luợng sẽ tăng lên. Để đễ theo dõi trong mục này ta chia ra, làm 2 trường
hợp: trường hợp 1 khi biến chất chỉ có hai phạm trù, trưcmg hợp 2 khi biến chất có nhiều hơn 2 phạm trù.
1. T rường hợp khi biến chất chỉ có 2 phạm trù
Trong trường hợp này, mô hình hồi qui sẽ đơn giản vì theo chú ý ở trên khi
biến chất có 2 phạm trù thì chì cần đạt 1 biến giả là đủ. Thí dụ ta xét mô hình sau: . Y, = p, + p2Di + p3JÍ + ụ (4.3) Trong đó:
Yj: Là tiền lương hàng tháng cùa một công nhân cơ khí i,
X i : bậc thợ cùa công nhân i,
D i = 1 nếu công nhân i làm việc trong khu vục tư nhân,
D I = 0 nếu công nhân i ỉàm việc trong khu vực quốc doanh.
Mô hình có một biến luọng đó là bậc thợ cùa người cổng nhân và một biến chất chỉ
lỗ cồng nhân đó làm việc thuộc khu vực nào. Nếu ta già thiết E(UÍ) = 0 ttó (4.3) có thể cho
ta thấy liệu tiền Iutmg của nguời công nhân làm việc ờ khu vực tư nhân có khác tiền lương
của người 'công nhân làm việc ở khu vục nhà nước không nếu các điều kiện khác không
thay đổi. Bằng'cách lấy kỳ vọng cả 2 vế (4.3) ta đuạc:
Tiền lương trung bình cùa nguời công nhân cơ khí làm việc trong khu vục nhà nuức: E(Yi I Xj, Di = 0) = Pi +p3Xj (4.3.1)
Tiên lương tu n g bình của người công nhân cơ khí làm việc trong khu vực tư nhân:
E(Yj I X , Di—1) - (Pi + P2) + IỈ3XÌ (4.3.2) 87 Hình 4.2
Hình 4.2 chỉ cho chúng ta thấy ràng tiền lương của công nhân cơ khí làm việc
trong khu vực tư nhân và nhà nước tính theo bậc thợ có cùng độ dốc p3 nhung lại
khác nhau về hệ số chặn. Nói một cách khác mô htah này giả thiết rằng mức tiền
lương trung bình của người công nhân ngành cơ khí làm việc ò khu vực tu nhân
khấc với mức tiền lương trung bình cùa công nhân cơ khí làm việc ở khu vục nhà
nước nhung tốc độ tăng luong trung bình theo bậc thì như nhau.
NẾU giả thiết về tốc đồ đã nêu trẽn là cố giá trị thì kiểm định giả thiết răng 2
hồi quy (4.3.1) và (4.3.1) có cùng bệ s6 chặn có thể tiến hìn h dễ dàng bằng cách
uớc lượng tò i quy (4.3) và chú rằng ý nghĩa về mặt thống kê của Pj đã được ước
lượng trẽn cơ sở của kiểm định t Nếu t chi ra rằng jj 2 là có ý nghĩa vầ mật thổng
kê thì chúng ta từ bỏ giả thiết Hũ là tiền lương của cổng nhằn cơ khí ở 2 khu vục kinh tế là như nhau.
2. Trường họp khi biến chất có nhiều hơn 2 phạm trù
Khi biến ch ít có nhiều hơn 2 phạm trù thì vấn dề cũng khổng phức tạp hon
nhiêu bởi vì theo chú ý ở trẽn nếu sô' phạm trù là N thì ta đưa vào mô hình hồi quy
N - 1 biến giả làm biến giải thích..
Thí dụ căn cứ vào số liệu chéo người ta muốn hồi quy thu nhập hàng năm của
một cán bộ giảng dạy đại học đối với tuổi nghề giảng dạy và vùng mà,anh ta giảng
dạy. Vì biến vùng là biến chất, trên thực tế chúng ta có thể căn cứ vào 3 vùng khác
nhau trong cả nước, là Bắc, Trung, Nam. Như vây trong trường hợp này, biến chất
của ta có 3 phạm trù, theo chú ý ờ trên ta sẽ đưa vào mồ hình hồi quy 2 biến giả.
Giả sử rằng cả 3 hồi quy có cùng độ dốc nhưng khác nhau hệ số chăn, chúng ta có mổ bình sau:
Yj = Pi + PjDiì +P3D2Ì + P4XÌ + l í (4.4)
Trong đó Y| thu nhập hàng Dăm cùa một giảng viên đại học
Xị: tuổi nghề của giảng viên
Ị l nếu giảng viên i thuộc một truỉrng đại học ở miền Bắc.
1 - I 0 nếu giảng viên thuộc một trường không phải ở miền Bắc
1 nếu giảng viên i thuộc một truờng dại học miền Nam.
0 nếu giảng viên thuộc một trưèmg không phải ở miền Nam.
Như vậy, ta coi giảng viên thuộc một trường đại học ở miên Trung là phạm trù
cơ sở, hệ số chặn chênh lệch p2 và
cho chúng ta biết hệ số chặn cùa các phạm
trù khác với hệ số chặn của phạm trù ca sà bao nhiêu. Chúng ta có thể tính được
. nếu giả thiết E(Ụ) = 0 thì từ (4.4) ta có:
Thu nhập tnmg bình cùa một cán bộ giảng dạy ờ một truờng đại học ở miên Thing:
E(Yi ID, = 0 ,D 2 = 0 , J i ) = p 1 + p4Xi (4.4.1)
Thu nhập trung bình cùa một cán bộ giảng dạy ở một trường đại học miên Bắc:
E(Yi I D, = 1, Da = 0, X,) = (p, + p2) + p4xi (4.4.2)
Thu nhập trung bình của mộl cán bộ giảng dạy ở trường đại học miền Nam:
E(Yi I D, = 0, Dj = 1, x ;) = (Pi + p3) + P,Xi (4.4.3)
Giả sử pi > 0 ta có minh họa sau:
Hình 4.3. Thu nhập của một cán bộ giảng dạy đại học trong
mối quan.hộ với tuổi ngh'ê và vùng mà anh ta giảng dạy.
Sau khi ước lượng hồi quy (4.4) chúng ta dễ thấy rằng liệu có sự khác nhau v'ê
thu nhập của cán bộ giảng dạy ở các miền khác nhau cùa đất nước không.
Thí dụ : Cãn cú vào số liệu chéo về doanh thu trên đầu người từ các tỉnh và
thu nhập quốc dân tính theo dâu người của các tình đó. Người ta muốn hồi qui
logarit R (log thu nhập/ngưòi) đối với logarit G (log thu nhập quốc dân/ngưòi) và
tính vùng của mỗi tỉnh. Theo cách phân chia đã biếl 1 tỉnh thuộc 1 trong 3 vùng
Bắc (N) Trung (Q hoặc Nam (S). Số liệu cho trong bảng 4.3. 89 Mô hình hồi quy l à :
L og Rị = Pi + P2D1Ì +P3D2Ì + P4 logG i + l í Trong đó: Log R: ln(thu nhập/người)
Log G: ln ( thu nhập quốc dân /người).
1 nếu tỉnh đó thuộc mièn Bắc D , i = 0
nếu tỉnh đó không phải là tỉnh miền Bác. 1
nếu tỉnh đó thuộc miền Nam ^ =
0 nếu tinh đó khổng phải là tinh miền Nam.
Kết quả hồi quy như sau: Bảng 4.3 Tinh Vùng G R Tinh Vùng G , R H.Gìang N 53099 15433 Q.Ngãi c 921501 51778 T.Q. N 1026246 32534 B.Định c 974381 71581 C.Bằng N 939592 25915 P.Yên c 1162995 69315 L.Sơn N 1105916 79225 K.Hoà c 2195192 204879 L.Châu N 1173320 27660 N.Thuận c 506939 44556 L.Cai N 819802 35570 B.Thuận c 1825380 105927 Y.Bái N 1506025 46Ữ10 K.Tum c 1181003 65642 B.Thái N 1565816 48172 G.Lai c 1024570 69518 S.La N 643444 29338 Đ.lắc c 1725293 83590 Q.Ninh . N 2195642 311755 L.ĐỔng c 1493055 107289 H.Bình N 2040215 72890 HCM s 4997041 962414 V.Phú N 1229249 74594 Đ.Nai s 2370994 239017 H.Bắc N 1021338 47667 VT-BR s 1991269 907834 H-Nội N 3631625 1062935 S.Bc s 1491414 192057 H.Phòng N 2070000 160291 T.Ninh s 1553681 204342 H.Tây N 1142000 45778 L.An s 1762790 147537 H.Himg N 1303451 105546 T. Giang s 1057203 109833 T.Bình N 1162747 51436 A. Giang s 1760437 142684 N.Hà N 1181747 53902 Đ.Tháp s 1370071 100655 N.Bình N 1062831 42545 B.Tre s 1532974 82319 T.Hoá c 1200650 102550 V.Long s 2021798 116666 Ng. An c 930844 59498 T.Vinh s 2024467 66530 H/Tĩnh c 910650 30163 Sóc trang s 1571656 84334 Q.Blnh c 992594 41673 Cần Thơ s 1760304 121340 Q.Trị c 943805 70579 K.Giang s 2329861 154636 T.T.Huế c 1009223 90856 M.Hải s 1736902 142079 QN-ĐN c 1367673 198297 90
logRi = -15,040082 - 0,42196 D, - 0,337541)2 + 1,94474 log G|
Ta có thể viết 3 phương trinh hồi quy: Miền Trung:
log Rị = -1 5 ,0 4 + 1,93 log Gi Miên Bắc:
log R| = -15,46 + l,91i log Gi Miền N am :
log Rị = - 15,83 + 1,9.') log G i.
Theo chú ý ở trên p2 cho ta biết log (doanh thu) thay dổi khi chuyển từ tình
miền Trung đến một tinh miền Bắc.
P 3 cho ta biết doanh thu thay đổi khi chuyển từ miền Trung đến một tình miền Nan*.
4.3. HỒI QUY VỚI MỘT BIỂN LUỢNG VÀ HAI BIẾN CHẤT
Trong mục này ta xét hồi quy với 1 biến lượng và 2 biến chất. Nguyên tắc đã
trình bày à trên duợc mở rộng cho trường hợp này. Số biến giả được đưa vào mô
hình hồi quy phụ thuộc vào số biến chất và các phạm trù mà mỗi biến chất có.
Thí dụ: Chúng ta hãy quay lại thí dụ vê thu nhập cùa một giảng viên đại học,
bây giờ chúng ta giả thiết thêm rằng giới tính của giảng viên cũng là nhân tổ quan
trọng để xác định thu nhập của giảng viên. Như vậy ta có 2 biến chất: - Vùng có 3 phạm trù
- Giới tính có 2 phạm trù. Mồ hình sẽ có dạng
Yi = P i +P2D11 + P3D2Ì +P4D3Ì +psX ị + Ư1 (4.5) trong đó:
Yi là thu nhập hàng nẫm của giảng viên đại học
Xi là tuổi nghề của giảng viên i.
1 nếu giảng viên thuộc tiirờng đại học miền Bắc.
D ii = • 0 nếu giảng viên không thuộc trường đại học miền Bắc.
1 nếu giảng viên thuộc trường đại học miền Nam. D 2i =
0 nếu giảng viên không thuộc trường đại học miền Nam.
• 1 nếu giảng viên là nam D 3i = 0 nếu giảng viên là nữ
Phạm trù cơ sở bây giờ ỉà giảng viên nữ thuộc một trường đại học miền Trung.
Già sử E(U) = 0 chúng ta có thể thu được kết quà sau bằng cách lấy kỳ vọng có
điều kiên cả 2 vế (4.5).
Thu nhập trung bình cùa 1 giảng viên nữ ở một truờng đại học miền Trung 91
E(Y, I D,= 0 , Dj = 0 , Dj = 0, x,).=p, + PsX;
Thu nhập trung bình của 1 giảng viên nam ở một truờng đại học miần Trung
E(Yi I D,= 0, E>2 = 0, D, = 1. Xi) = (Pi +P4) + p3x>
Thu nhập trung bình của 1 giảng viên nữ ở một truờng đại học miền'Bắc
E(Yi I D,= 1, D ĩ= 0, Ds = 1. Xi) =(pẵ +Pj) + PsX
Thu nhập trung bình của.l giản? viên nam ở một truờng đại học miền Bắc E(Ỵ I D,= 1,
= 0, D3 = 1, X,) =(P, +p2+ p4) + PsX,
Thu nhập trung bình cùa 1 giảng viên nữ ở một truờng đại học m iln Nam
E(Yi I D,= 0. I >2 = 1, Dj = 0, Xị) =(p, +p3) + p3X;
Thu nhập trung bình của 1 giảng viên nam ở một tniờng đại học miền Nam
E(Y, I D,= 0, Dj = 1, D, = 1, Xi) =(p, + p 3 + M + p 5X, 4.4. SO SÁNH HAI H ồ i QUY l ễT u tu d n g c ơ b ả n
Tất cả các mô hình hồi quy đã xét đến nay, chúng ta đốu giả thiết ràng biến
lượng ảnh hưởng đến hệ số cbặn nhưng khổng ảnh huởng đến hệ số góc các hồi
quy của I'.áe»nhóin con khác nhau. Nhung nếu hệ số góc khác nhau thì việc kiểm
định về tính* khác nhau của hệ số chặn sẽ ít có ý nghĩa. Một khía cạnh khác nữa là
các tập số liệu mà chúng ta sử dụng là các tập số liệu (fan nhưng liệu môt mô bình
đã cho có thổ áp dụng cho hai tập số hay không? Chẳng hạn khi nghiên cứu mối
q’lan hẹ giũa tiết kiẽm và thu nhập trước và sau chuyển đổi kinh tế cùa nước ta. Vì
thế chúng ta cần phát triển phương pháp chung để ứm xem liệu 2 hồi quy có khác
nhau hay không? Sự khác nhau nếu có thì ở hệ số chặn, hệ số góc híiy cả hai. Thí dụ: Ta có hồi quy:
Thời kỳ irước cải tổ:
Yi = Xi + XịXì + Uii (4.5a) với i = l,n, Thời kỳ sau cải tổ:
Yj = yi + Ỵ2*j + U i Cj = T T « 7 ) (4.5b)
t-ong đó X thu nhập; Yià tiết kiệm; Ưii, U i là các ĩihiẽu trong 2 hồi quy.
Có 4 khà năng xảy ra đối với 2 hồi quy này: I. X| =
và x 2 = 72, nghĩa là 2 hồi quy đòng nhất, írên đồ thị chúng chồng
khlt ìin nha-., điều ní.y chỉ ra ở hình 4 /m 92
2. Xi * 7i và Xa = 72, nghĩa là 2 hồi quy có cùng hộ số góc, điều này chì ra ở hình 4.4b 3. A., = Ỵ, và Ằ.2
y2, nghĩa là 2 hồi quy có cùng hệ số chặn nhung khác nhau
về hạ sổ góc, điều này chỉ rạ ờ hình 4 .4c
4. Xị * y, và X-2 * y2, nghĩa là 2 hồi quy hoàn toàn khác nhau, điều này chì ra ở hình 4.4d. Hình 4.4.
a. Hai hồi quy trùng nhau; b. Hai hồi quy song song;
c. Hai hồi quy cócùpg hệ số chặn; d Hai hồi quy hoàn toàn khác nhau.
Để kiểm định sự bằng nhau của hệ số hồi quy chúng ta có thể sử dụng một
trong hai kỹ thuật: kiểm định Chow và sử dụng biến già. Sau đay chúng ta xét cả hai kỹ th u ậ t.
2. So sánh 2 hồi quy - kiểin định Chow
Một trong những phucmg pháp phổ biến để kiểm định sự khác nhau giũa hai
hôi quy là kiểm định của Chow. Kiểm định này dựa trôn những giả thiết sau: 93
a. Các nhiễu H i và Uy có phân phối chuẩn có kỳ vọng bằng 0 và phuơng sai
khổng dổi và dều bàng ơ 2: Uii ~ N (0,ơ2) l i j - N ( 0 ,ơ 2).
b. Cấc Uii và XẶj có phân phối độc lập.
Với giả thiết đã cho thì thù tục kiểm định Chow là như sau:
Bước 1. Kết hợp tấi cả các quan sất của 2 thời kỳ lại ta được n = n, + n2 quan
sát rồi ước luợng hồi quy gộp. Mô hình gộp của (4.5a) và (4.5b) lúc này có thể viết dưới dạng: Y i= P ,+ (325Q + U (4.6)
Từ hồi quy này chúng ta thu đơợc tổng bình phuơng cấc phần dư là RSS với số
bậc tự do n, + n2 - k (trong đó k là số tham số duợc ước lượng, trong mô hình (4.6) tM k=2 .
Bướcĩ. uồc luợng riêng từng hồi quy (4.5a) và (4.5b) và thu được tổng bình
phuong các phần dư tuơng ứng từ mô hình (4.5a) là RSS| và tù mô hình (4.5b) là
R S S í và bậc tự do tucmg ứng n, - k và n2 - k.
Đặt RSS = RSS| +RSS2 với bậc tự do ni + n2 - 2k
Bước 3. Sử dụng tiêu chuẩn F như sau : n _ ( R S S - R S S " ) / k , A n s F = — 7/ --------- -T (4 -7) R S S / ( n , + n 2 - 2 k )
Với bậc tự do là k và ni + n2 -2k. Nếu giá trị F tính đuợc vượt giá trị F tới hạn
thì ta tù bỏ giả thiết rằng hai hồi quy là như nhau. Điều này có nghĩa là hai tập số
liệu là khổng gộp được.
3. So sánh hai hồi quy ■ thủ tục biến giả
Kiém định Chow cho phép ta so sánh 2 hồi quy. Sau dây ta sẽ trinh bày thù
tục biến g iỉ mà cũng sẽ cho ta gộp ỉất cả Di và n2 quan sát lại với nhau và uớc luợng hồi quy sau:
Yi= p ,+ Pj Dì + p3Xi + P«(D|Xi) + Ụ (4.8)
Giả sử Y| và Xị là tiết kiệm và thu nhập trước và sau khi chuyển đổi kinh tế. 94
0 đối với quan sát thuộc vào trước thời điểm chuyển đổi D , =
1 đối với quan sát thuộc vào sau thời điểm chuyển đổi.
Để thấy được ứng dụng của mô hình (4.8) ta lấy kỳ vọng có dĩèu kiện cả hai
vế cùa phương trình này với già thiết E(Ụ) = 0 chúng ta thu đurợc:
E(Yi I Di = 0, Xi) = Pi + P3XÌ (4.8a)
E(Y, ID, = 1. Xi) = O i + k ) + (P3 + PO X, (4.8b)
Với ỷ nghĩa các kí hiộu đã cho ờ trên ta có thể giải thích như sau:
(4.8a) là hàm tiết kiêm trung bình cho thời kỳ trước chuyển đổi kinh tế diễn
ra.(4.8b) là hàm tiết kiêm trung bình từ khi chuyển đổi kinh tế vê sau. Hai hàm này
hoàn toàn giống như hai hàm đã cho (4.5a) và (4.5b) cho nên uớc lượng (4.8) cũng
tương đứơng với việc uớc lượng hàm (4.5a) và (4.5b).
Trong (4.8) thì p2 chính là hệ số chặn biểu thị sự khác nhau cùa tiết kiệm giữa
2 thời kỳ còn (3* chính là hệ sô' độ dốc khác nhau nó chỉ ra rằng hệ số góc cùa hàm
tiết kiộm trước khi chuyển đổi khác với hộ số góc cùa thời kỳ từ khi chuyển đổi kinh tế là bao nhiều.
4.5. ẢNH HUỞNG CỦA TUƠNG TÁC GIỮA CÁC B Ế N g iả Chúng ta xét mô hình sau:
Y| = p!+ P2D2Ì + P3D 3Ì+ p4 Xj + t í (4.9)
trong đó: Ỵ là chi tiêu hàng năm v‘ê quần áo, X là thu nhập 1 nếu là nữ D2 = 0 nếu là nam 1 nếu là sinh viên d 3= 0 nếu là công nhân viên
Ngụ ý cùa mô hình trên đây là ảnh hưởng chênh lệch của biến giả giới tính D2
là hằng SỐ qua 2 tầng lớp sinh viên và công nhân viên và ảnh hường chênh .lệch D,
cũng là hàng số qua 2 giới. Điều này có nghĩa là nếu chi tiêu trung bình về quần áo
của nữ cao hơn của nam tw điều này cũng đúng với cả hai tầng lớp. Tương tự cõng
có thể nói ràng chì tiêu trung bình v'6 quần áo của sinh viên nhiều hơn cùa công
nhân viên thì đi'êu đó cũng đúng dù nó là nam hay tiữ. 95
Trong nhiều áp dụng thi giả thiết như vây khống duy trì đuọc. Nữ sinh có thể
tiêu dùng nhiều quần áo hcm nam công nhăn viên. Nói một cách khác có thể có ảnh
hường tương tác giữa 2 biến chất D2 và Dj và do đó ảnh huỏng của chúng lên frung
bình Y có thể không phải là phép cộng đem giản như trôn mà là nh ìn như mổ hình sau:
Y; = Pi + P2 P 21 + P j D j ì + P*(D2ìDjì) + PsXị + u (4.10)
Từ (4.10) ta thu được chi tiêu trung bình về quần áo cùa một nữ sinh sẽ là
E(YI D2 = 1, Dj = 1, Xi) = (Pi + p2 + + P4) + p 5x;
Trong dó p2 là ảnh hưồng chênh lệch của nfc, p 3 là ảnh hưởng chênh lệch cùa
sinh viên, còn p< là ảnh hưởng chẽnh lệch của nữ sinh. p4 cho ta biết chi tiêu trang
binh về quần áo của một nữ sinh khác khác với chi tiêu trung bình của nam và nữ
công nhân viên. Điều này cho biết sự tuơng tác giữa các biến giả làm thay đổi ảnh
hưởng cùa 2 thuộc tính đã đuợc xem xét 1 cách riêng rẽ như tbế nào.
Để kiểm dinh hệ số P4 - tuong tác của các biến giả - có ý nghiã về mặt thống
kẽ hay khổng, có thể kiểm định t.
4.6. SỬDỤNG BIẾN GIẢ TRONG PHÂN TÍCH MÙA
Như chúng ta đã biết nhiều chuỗi thời gian trong kinh tế có tính chất thời vụ rít rõ,
chẳng hạn doanh số bán của các cửa hàng bán quần áo vào 10 ngày trưóc lết hàng
năm, doanh số bán ra của cửa hàng văn phòng phẩm vào dầu năm h ọ c ,... Thông
thường người ta muốn loại nhãn tố mùa khỏi chuỗi thời gian để người ta cố thể tập
trung vào các thành phần khác của chuỗi thời gian nhu khuynh hướng tăng hoặc
giảm hoàn toàn đều đặn theo một thời kỳ thối gian dài. Quá trình loại thành phần
khỏi chuỗi thời gian thu được như vây gọi là chuỗi thời gian dã được điều chình
theo mùa. Có một số phương pháp điều chinh theo mùa của chuỗi thời gian, trong
mục này ta xét phương pbáp biến giả.
Hoàn toàn như đã trình bày ở trên việc đưa biến giả vào đề loại yếu tố kbỏi
chuỗi thời gian được thực hiện, dựa ưẽn các giả thiết: 1.
Yếu tố thòi vụ chỉ ảnh hưởng đến hệ số chặn của hồi qui, hoặc:
2. Yếu tố thòi vụ ảnh huởng đến cả hệ số góc. 96
Ung với mỗi giả thiết, mô hình được xem xét cũng khác nhau. Để thuận tiện trình bày, ta xét:
Nghiên cứu mối liên hệ giữa thu nhập với chi tiêu cho quần áo, dụng cụ gia
đình, người ta thu thập được một mẫu ngỉu nhiên kích thước n và cho ràng mỏi
một quí có thổ biểu thị mẫu theo mùa. Khi đó mô hình như sau:
Yi = P 1 + p2p 2i + 33D 3l+ p4D Ji + P 5X + IÍ (4.11) Trong đó:
Y| biểu thị chi tiêu của nguời tiêu đùng v ỉ các loại hàng nói trên .
Xj là thu nhập người tiêu dùng i
1 nếu quan sát nằm ồ quí 2 D2 = 0
nếu quan sát nằm ồ quí khác.
1 nếu quan sát nàm ở quí 3 Dj =
0 nếu quan sát nằm ở quí khác
1 nếu quan sát nấm ở quí 4 D 4 =
0 nếu quan sát nằm ở quí khác.
Trong mô hình trên la giả thiết biến có 4 phạm trù, nên ta dùng 3 biến giả,
phạm trù cơ sờ là quí I. N ha vậy nếu có ảnh hưởng theo' mùa của từng quí khác
nhau thì hê số chặn p2, 03 và p4 khác nhau có ý nghĩa v í mặt thống kê. Mỗi một hệ
sơ chặn cho ta biết chi tiêu trung bình ở mỗi quí khác vối quí I như thế nìo. Với giả
thiết E(Ụ) = 0 ta có: Chi tiêu trung bình về các khoản đã kể trền trong quí I là:
E(Y| I D2 = 0, E>3 - 0, D4 = 0, XI) = Pi + PsXị
chi tiêu trung bình v ỉ các khoản đã kể trên trong quí n là:
E(Yi I D2 = 1, D3 = 0, D4 = 0, Xị) = (pi +pĩ) +PsXi
chi tiêu trung bình về các khoản dã kể trên trong quỉ m là:
E(Yi I Eh = 0, Dj = 1 , ^ = 0, Xi) = (p ,+ p 3) + p 5X,
chi tiêu trung bình về các khoản đã kể trên trong quí IV là:
E(Y| I D2 = 0, D j = 0, D4 = 1, JQ) = (Pi +P4) + PsX
Bây giờ ta giả sử rằng có sự ảnh hưởng tương tác giữa mùa và thu nhập 16n chi
tiêu nói cách khác là có sự ảnh hưởng 16n cả hệ sổ góc của hồi qui. Sử dụng
phường pháp tương tự như tr đã tìn h bày ở trên ta di đến mô hình:
Yi= p, + 02 Díi + Pj D Ji+ p4 D« + p5Xi + p6(D,,Xi) +
+37(D3iXÍ) + Ps(D4jXi) + \jỊ (4.12) 97
Nhu vậy viộc phân tích thời vụ có thé sử dụng 2 mô hình (4.11) và (4.12). Tuy
nhiẽn mô lủnh (4.12) tổng quát hơn, để tránh sự khổng thích hợp ta nên sử dụng
mô hỉnh (4.12). Qua việc ước lượng hồi quy (4.12) chúng ta có thể biết được hẹ số
góc nào có ý nghĩa, hệ số góc nào khỗng có ý nghĩa.
4.7. HỒI QUY TUYẾN TÍNH TÙNG KHỨC
Hầu hết các mổ hình kinh tế luợng mà chúng ta nghiên cứu cho đến nay hần
tíết đều là các mô hình liên tục theo nghía là cả biến độc lập và biến phụ thuộc lấy
một s6 lớn giá trị và sự thay đổi nhỏ trong một biến này có ảnh hưởng do đuợc đến
biến khác. Điều này đã được cải biên khi chúng ta sừ dụng thù tục biến giả để giải
thíctì cho sụ khác nhau về hê số chăn hay độ dốQ hoặc cả hệ số chặn và độ dốc.
Bây giờ chúng ta mò rộng sự phân tích cho phép thay đổi độ dốc, nhưng hạn chế
ràng đoạn thẳng đuợc uớc lượng vẫn là liên tục. Thí dụ chi ra ở hình 4.5, mô hình
đúng là một mô hình liên tục hay có sự thay đổi về kết cấu. Y' A
Nếu chúng ta xẹm xét tiêu dùng của nước ta trước và san khi chuyển dổi thì
chúng ta thấy mỡ hình có dạng như hình 4.5.
ở đây cần nhấn mạnh rằng mộ hình đang xem xét khác với các mô hình có
biến già đă được bình bày trong mục truớc bời vì chúng ta giả thiết rằng không có
sự m ít liên tục hoặc sụ dịch chuyển trong múc tiêu dừng từ năm này qua năm
khác. Mô hình nhừ vậy chúng ta gọi là mô hình tuyến tính từng khúc, ở hình 4.5
mô hình gồm 2 đoạn. Chúng ta sẽ thấy mô hlnh có thể ước lượọg được bằng
phương pháp bình phương nhỏ nhất với việc sừ dụng biến giả thích hợp.
Để ước lượng mô hình đã cho trong hình 4.5, chúng ta giả thiết Ang tiêu dùng
nước ta trong 2 thời kỳ trước và sau chuyển đổi khác nhau. Gọi năm chuyển đổi
kinh tế (từ cơ chế kế hoạch sang cơ chế thị trường) là to. Ta xét mô hình sau:
Ỵ = p 1+(32X, + p3(Xt - X tt)Dl + U , (4.13)
Y,: tiêu d ù n g ; X: thu nhập 98
X ị : thu nhập trong năm bắt đầu chuyển giai đoạn từ cơ chế có kế hoạch
sa n g tơ chế thị trường. 1 nếu t > to
D| = • 0 nếu là giá trị khác cùa t
Với giả thiết E(U) = 0 chúng ta thấy ngay ràng: trung bình của tiẽu dùng trong
những năm trước khi chuyển đổi kinh tế là:
E(Y, I D| = 0, Xi) = Pi +(32X, (4.14) và vói D, = 1 thì ta có
E(Y, I D, = 1, X) = (B, - Pj X , ^ (P2 + P,)X, (4.15)
Vậy 02 cho độ đốc của đường hồi quy trước khi chuyển đỏi. (p 2 + pj) cho đô
dốc cùa đường hồi quy sau khi chuyển đổi.
Chú ý rằng không có sự gián đoạn vì
E(Yị ) = (3, + p2X ị , theo phương trình (4.14)
. = 0i-3.iXti) + (p3 + P3)X,0 = P i+ P2 X ,
Ta cũng chú ý rằng khi p3 = 0 Ihì phuong trình (4.13) sẽ trờ thành phương
tìn h của đường thẳng, vậy kiểm định p3 = 0 sẽ cung cấp cho ta kiểm định đơn giản
về sự thay đổi cấu trúc.
Nhung vấn dề sẽ như thế nào nếu mô hình có nhiều Ihay đổi vê cấu trúc ứng
vái to và t|, thi mô hình thich hợp sẽ là:
v,= (3, + p2X + pj(X, -x,0 )D| +p4(X, - xti )D2+U (4.16) trong đ ó r 1 nếu t > t| D2 =
0 nếu t nhận giá trị khác 1 nếu t > t„ d 4 =
0 nếu t nhận giá trị khác
Vậy phuơng trình c 10 mõi một ưong 3 giai đoạn là như sau: Pi + P2X; với 0 < t < t,, ECO = Pi - P3 X , ) + (p2 + pi) X v<^ to < t ^ t| Pi - P j^ („ ■ ) + (P2 + p 3 + P4) X| • vói t > t| . 4.8. THÍ D ự
a ẽT hì dụ 4.1: Cho mức tiêu dùng theo đẩu người và thu nhập sau thuế của
Mỹ trong thời kỳ 1929-1970. Trong thời gian này có xảy ra chiên tranh thế giđri thứ
hai từ 1941- 1946. Dựa vào kết quả sau đây hãy cho biết " chiến tranh" có ảnh 99
hưởng đên tiêu dùng không? Trong đó D= 1 trong thời kỳ 1941-1946 và bằng khổng trong các năm khác.
Ordinary Least Squares Estimation Dependent variable is c
42 observations used for estimation from 1929 to 1970 Regressor Coefficient Standard Error T-Ratio[Prob] INPT 101.5147 25.4574 3.9876[.000] D -204.9233 18.7856 -10.9085[.000] Y .86363 .014718 58.6788[.000] R-Squaied
.98940 F-statistic F( 2, 39) 1820.4[.000] R-Bar-Squared .98886 S.E. of Regression 42.5410 Residual Sum of Squares
70S79.9 Mean of Dependent Variable Ỉ498.S
S.D. of Dependent Variable 403.0243 Maximum of Log-likelihood -215.558 DW-statistic 1.6342
Theo kết quả trên p J = -20,4,92 < 0; tj = -10,90, p-value = 0,000. Do dó ta kết
luận: Chiến tranh thế giới thứ n có ảnh hưòng đến tíea dùng/ đẩu người ờ Mỹ và lim giảm mức này. Trên dồ thị cho hỉnh ảnh trực giác vẻ mức tiêu dùng giảm trong thời kỳ chiến tranh thế giới thứhaiằ b.
Thí dụ 4.2: Cho tỷ số giũa chỉ số giá các mạt hàng sơ ché*ờ các nước
kém phát triển và chì số giá các mặt hàng chế biến nhập từ các nuớc công nghiệp
trong khoảng thời gian 1950-1986. Trong khoảng thời gian này, từ 1973- 1974,
người ta thấy có biéh động lón vể tỳ số này. Dựa vào đổ thị dưới đây, người ta thấy 100
có bước nhẩy và xu thế của tỷ số này đã thay đổi. Bằng kiểm định Chow và kỹ
thuật biến giả hãy xem xét vấn đề trên.
Các biến sđ: TOT - Tỳ số giữa chỉ số giá các mặt hàng sơ chế ở các nước kém phát
triển và chì số giá các mặt hàng chế biến nhập từ các nước công nghiệp. T- biến xu
thế( T|950 — 1... T„ 86 = 37).
i ể Kiểm định Chow •
ú ớ c lượng m ô hình trong suốt thòi kỳ 1950-1986
Ordinary Least Squares Estimation Dependent variable is TOT
37 observations used for estimation from 1950 to 1986
9f( * * * * * * * * * * * ** * ** ** * *** *** ** * * * * * ** * *»H
* ** * * + ** * * * *** * ** +* * * * * * * * * Regressor Coefficient Standard Error T-Ratio[Prob] INPT 1.1737 .041617 28.2027[.000] T -.0072022 .0019095 -3.7717[.001]
***************************************************************** R-Squared
.28899 F-statistic F( 1, 35) 14.2256[.001] R -B ar-Squared .26867 S.E. of Regression .12402
R e s i d u a l Sum o f Squares
.53831 Mean of Dependent Variable 1.0369
S.D. of D ependent Variable .14502 Maximum of Log-likelihood 25.7588 D W -statistic .86906
***************************************************************** 101 •
ứ ớc lượng mô hình trong suốt thời kỳ 1950-1972
Ordinary Least Squares Estimation
****************************************************** *********** Dependent variable is TOT
23 observations used for estimation from 1950 to 1972 Regressor Coefficient Standard Eưor T-Ratio[Prob] INPT 1.2269 .031119 39.4271[.000] T -.014305 .0022696 -6.3031[.000] R-Squared
.65420 F-statistic F( 1, 21) 39.7295[.000] R-Bar-Squared .63774 S.E. of Regression .072199 Residual Sum of Squares
.10947 Mean of Dependent Variable 1.0553
S.D. of Dependent Variable .11996 Maximum of Log-likelihood 28.8621 DW-statistic .95185
* * * * * + afr 4* * * * * * * * * * * * * * a*e 4c $ 4c 4c * * % * * * * * * * * * * $ % * % sfc 4c 9fc * 3fc * * * * * * * * * % * * * * * •
ứ ớ c lượng mổ hình trong suốt thời kỳ 1973-1986
Ordinary Least Squares Estimation
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * ** * 9|( * * % * afc * % * % * 3fc * 9fc * * * * 3fc * afe * * * * * * Dependent variable is TOT
14 observations used for estimation from 1973 to 1986 Regressor Coefficient Standard Error T-Ratio[Prob] INFT 2.0906 .21450 9.7465[.000] T -.035538 .0069721 -5.0971L 000]
***************************************************************** R-Squared
.68405 F-statistic F( 1, 12) 25.9806[.000] R-Bar-Squared .65772 S.E. of Regression .10516 Residual Sum of Squares Mean of Dependent Variable 1.0067
S.D. o f Dependent Variable .17975 Maximum of Log-likelihood 12.7456 DW-statistic 2.2306
Theo các kết quả trên: RSS = 0,53831;
RSS =RSS, + RSS; = 0.10947 + 0,13271= 0.24218Ệ p _ (R S S - R S S ) / k (0,53832 - 0 ,2 4 2 1 8 )/2
~ R S S /(n l + n2 - 2 k ) ~ 0 ,2 4 2 1 8 /( 3 7 - 4 )
Fo,oj(2i33) = 3,3. F > Fũi0j(2,33) diều này chứng tỏ có thay đổi của hê số chăn hoặc
hệ số gốc hoặc cả hai. 102
2. K ỹ thuật biến giả
Các biến D = 1 trong thời kỳ từ 1973-1986; TD = T*D.
Ordinary Least Squares Estimation Dependent variable is TOT
37 observations used for estimation from 1950 to 1986 Regressor Coefficient Standard Eưor T-Ratio[Prob] INPT 1.2269 .036923 33.2293[.000] T -.014305 .0026929 '-5.3123[.000] D .86368 .17859 4.8361 [.000] TD -.021232 .0062856 -3.3779[.002] R-Squared .68013 F-statistic F( 3, 33) 23.3891 [.000] R-Bar-Squared .65105 S.E. of Regression .085665 Residual Sum of Squares
.24217 Mean of Dependent Variable 1.0369
S.D. of Dependent Variable .14502 Maximum of Log-likelihood 40.5362 DW-statistic 1.7080
Từ kết quả trên, các kiểm định t về hệ số của D và TD đéu cho biết chúng
khác không. Nghĩa là đã có đặ có thay đổi về hệ số chặn và hệ số góc.
v ể mặt kinh tế, phép kiểm định trên cho biết trong khoảng thời gian 37
năm 1950-1986, tỷ lệ giữa chỉ số giá các mặt hàng sơ chế ờ các nước kém phát
triển và chỉ số giá các măt hàng chế biến nhập từ các nước công nghiệp có xu
hướng giảm. Một đô la xuất các mặt hàng sơ chế ngày càng mua được ít hàng chế biến hơn. 103 BÀI TẬP
4.1. Các biến số sau đây là định lượng hay định tính: a. GDP
b. Khủng hoảng dầu mỏ 1973.
c. Xuất khẩu của Việt nam sang các nước ASIAN.
d. Thành viên cùa Tổ chức thương mại thế giới. WTO.
e. Cán bộ tốt nghiẹp ĐH. Kinh tế quóc dân.
f. Học sinh diện chỉnh sách.
4.2. Nghiện cứu sự biến động của lượng gas bán ra (Q: bình) phụ thuộc vào giá gas
(PG: nghìn đ/bình), có người cho rằng chất lưọng gas là quan trọng, người đố cho
rằng Trong những tháng đại lý nhộp binh gas mới thì lượng bán ra khổng giống vãi
nhãng tháng nhập bình gas cũ, do dó dã hổi quy mổ hình có các biến như sau:
D = 1 với những tháng nhập bình mới, D = 0 với những tháng khác, DPG = D*PG. Cho a = 5% .
Ordinary Least Squares Estimation Dependent variable is Q
27 observations used for estimation from 97M1 to 99M3
***************************************************************** Regressor Coefficient Standard Error T-Ratio[Prob] PG -7.0673 .20832 33.9252[.000] D 106.0104 98.5409 1.0758[.293] DPG .278299 .078845 2.6307[.012] INPT 2403.548 564.094 4.2609[.000] R-Squared .99252 F-statistic F( 3,23) 1016.28[.000] R-Bar-Squared .99154 S.E. of Regression 41.5680 Residual Sum o f Squares
39741.7 Mean of Dependent Variable 1831.4
S.D. of Dependent Variable 451.9370 Maximum of Log-likelihood -136.78 DW-statistic 1.9506
a. Viết hàm hồi quy tổng thể, hàm hồi quy mẫu cho từng trường họp tháng bán bình gas mới và cũ?
b. Tìm ước lượng điểm mức chênh lệch của hê số chặn trong 2 trường hợp trên.
c. Trong tháng bấn bình gas mới nếu giá gas là 110 nghìn thì ước luợng điểm
lượng bán là bao nhiéu? Với tháng bán bình cũ thì giá trị đó bằng bao nhiều?
d. Vẽ đổ thị cùa hàm hổi quy mẫu trong 2 trường hợp. 104
e. Các hệ số của mô hlnh có khác 0 một cách có ý nghĩa không?
f. Hệ số chặn của mô hình trong những tháng nhập bình mới và bình cO có thực sự khác nhau không?
g. Đổ thị thực tế của hàm hổi quy tổng thể có thể có dạng nhữ thế nào?
h. Khi cùng giảm giá 1 nghìn thì khả năng bán thẽm của những binh gas cũ
và mới chênh lệch nhau trong khoảng nào? i.
Một người cho rằng do binh ga luôn có giá cao và an toàn nên lượng bán
không chịu ảnh hưỏng của chất lượng bình gas mà chịu ảnh hưởng cùa việc
quàng cáo. Ajih ta cho ràng trong những tháng có quảng cáo tích cực thl
lượng bán tâng hơn so với những tháng khống tích cực quảng cáo. Hãy xây
dựng mô hình và nều cách kiểm tra. j.
NẾU m uốn xem xét ảnh hưồng đổng thời của cả việc tháng nhập bình gas
• mới hay cũ và có quảng cáo tích cực hay không thì phải xây dựng mô hình
và thực hiện các kiểm định như th ế nào?
4.3. M ột cơ quan nghiên cứu mối quan hê giữa sản lượng đầu ra cùa các cơ sờ sản
xuất và nguồn lực đầu vào (Vốn : K ; Lao động :L) cho rằng cơ sở sản xuất thuộc
sờ hữu nhà nước và không thuộc sở hữu nhà nước thì hiệu quả của nguồn vốn và
lao động không như nhau, do đó xem xét sự biến động của sàn lượng khống chì
phụ thuộc vào vốn và lao động mà còn cả yếu tố thuộc sở hữu nhà nưóc hay khổng.
Khi đặt thêm biến D: D =1 nếu cơ sở sản xuất không thuộc nhà nước v àD = 0 nếu
nguọc lại, và hổi quy mô hình sau với DL = D*L; DK = D*K. Cho a = 5%.
Ordinary Least Squares Estimation Dependent variable is s
20 observations used for estimation from 1 to 20
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * Regressor Coefficient Standard Error T-Ratio[Prob] INPT 19.0034 26.9511 .70511[.492] L 16.9695 6.4600 2.6268[. ] K 9.7180 3.3396 2.7482[. ] DL 5.7866 1.7489 3.3086[. ] DK 2.8915 1.7838 1.6209[.126]
***************************************************************** R-Squared
.79542 F-statistic F( 4,15) 14.5806[.000] R - B a r - S q u a r e d .74087 S.E. of Regression 29.3907
R e s i d u a l Sum o f Squares
12957.2 Mean of Dependent Variable 109.4666
s D. of D ependent Variable 57.7367 Maximum of Log-likelihood -93.1155 DW-statistic 2.4750
if**************************************************************** 105
a. Viết hàm hồi quy tổng thể. Người nghiên cứu xem xét yếu tố thuộc và
không thuộc sở hữu nhà nước tác động đến những hệ số hồi quy nào? Có
xem xét tác động đến hệ số chặn không?
b. Viết hàm hồi quy mẫu cho các cơ sở sản xuất thuộc sở hữu nhà nước và không thuộc nhà nước. : <■' !
c. T im ước lượng điểm của s in lượng của doanh nghiệp thuộc nhà nước và
khống thuộc nhà nuớc khi có 30 công nhãn và nguồn vốn 350 triộụ.
d. Tìm ước lượng điểm mức chênh lêch sản lượng c ù á c ơ số thuộc ivà khổng
thuộc sở hữu nhà nước khi thay đổi một lao động và nguổn vốn thay dổi 1 triệu.
e< Khi cùng thay đổi nguổn vốn, lao động khống đổi thì cơ sở thuộc và không
thuộc nhà nước mức sản lượng thay đổi có khác nhau khống? Nếu cùng
thay đổi lao động, vốn không đổi thì mức thay, đổi sản lượng trong hai
troâmg hợp trên có giống nhau không?
f. Việc đưa thêm biến giả vào có thực sự cán thiết và làm tăng ý nghĩa mô
hình khổng? Dùng kiểm định thu hẹp hổi quy để đua ra kết luận nếu biết
với mô hình s phụ thuộc vào K, L có hệ số chăn RSS bằng 17925,0
g. Nếu có người quan tâm khổng phải là việc cơ sở sản xuất đó thuộc hay
không thuộc sờ hữu nhà nưóe mà là cơ sờ sản xuất thuộc loại lớn (nguổn
vốn trên 1 tỷ) hay loại nhỏ (nguồn vốn dưới 1 tỷ) vì cho rằng cơ sở loại lớn
thì hiệu quả nguổn vốn và nguồn lao động lón hơn cơ sở loại nhỏ. Khi đó
muốn kiểm tra phải làm như thế nào.
h. Nếu muón xem xét tác động của cả yếu tố thuộc và không thuộc sở liữu
nhà nước và yếu tố cơ sờ lớn và nhỏ thì phải làm như thế nào ? 106 CHƯƠNG V BACỆNSĨOTẾH
Trong mô hình phân tích hồi quy bội, chúng la đã già thiết giữa các biến giải
thích của mô hình không có đa cộng tuyến. Nhưng già thiết đó bị vi phạm thì hận
quả sẽ như thế nào và làm th ế nào để phát hiện ra rằng giả thiết này bị vi phạm và
biộn pháp khắc phục nó. Đó là nội dung của chucmg này. Trựớc hết ta cần làm rõ
bản chất và nguyên nhân của đa cộng tuyến.
5.1. BẢN CHẤT CỦA ĐA CỘNG TUYẾN- ĐA CỘNG TUYẾN h o à n h ả o VÀ KHÔNG HOÀN HẢO
Tư tưởng đa cộng tuyến thấm sâu vào mọi khía cạnh của hồi quy bội. Lý do
làm cho “đa cộng tuyến” có ảnh hưởng lớn như vậy là vì khi ta nghiên cứu mối
quan hệ giữa biến Y và các biến giải thích Xi. ta gập quan hệ nào đó giữa các biến Xi vối nhau.
Trường hợp lý tưống là các biến Xí trong mô hủih hồi quy không có tương
quan với nhau; mỗi một biến Xi chứa một thông tin riêng về Y, thông tin không
chứa trong bất kỳ biến Xj khác. Trong thực hành, khi điều này xảy ra ta không gặp
hiện tượng đa cộng tuyến.
ở trường hợp ngược lại, chúng ta gặp đa cộng tuyến hoàn hảo. Giả sử ta phải
ước lượng hàm hồi quy gồm k biến giải thích Xi, X ỉ, x3..... Xk, Yi = P ,X M + p2Xa + .... + p à + ĩ ỉ
Đa cộng tuyến hoàn hảo xảy ra khi một biến giải thích được biểu diẽn dưới
dạng tổ hợp tuyến tính của các biến giải thích còn lại đối với mọi điểm cùa tập số
liệu. Hoặc có thể phất biểu: Đa cộng tuyến hoàn hảo giữa các biến giải thích X|,
X2, X )......Xk xảy ra nếu điều kiện sau được thỏa mãn:
l lX, + X2X2 + .........+ XkXk = 0 (5.1)
trong đó Xi, t a .........A.k, là các hằng số không (Tông thời bằng không.
Thuật ngữ đa cộng tuyến lần dầu tien được Ragnar Frisch sử dụng vào năm
1934 với nội đung trên. Tuy nhiên ngày nay, thuật ngữ này được sử dụng theo
nghĩa rộng hơn. Nó bao g‘ôm cả đa cộng tuyến hoàn hảo và trường hợp trong đó
các biến giải thích có tương quan với nhau theo nghĩa sau:
\) X ii + X ĩXìi + ....... + XkXiá + Vj-= 0 (5.2) 107
trong dó V| là sai số ngẫu nhiên.
Ta hãy minh họa tư tuởng trên bằng dồ thị như sau:
Các biến gidi thích X Biến phụ thuộc Y Các biỂn trục giao cho
thững tin từ những nguồn
độc lập. Không có cộng X, tuyến. Cộng tuyến hoàn toàn. Thông tin dông nhất Không cổ hôi quy. Xj X|
Múc độ cộng tuyến nìo dó * ^
giữa các biến X Những ván
dè hồi quy phụ thuộc v&o X, bạc của công tuyến. Tương quan ngược chiầu N x* giữa các biến X. Cộng tuyến mạnh. \ - - Hình 5.1
Giả sử ta xét mô hình hồi quy trẽn với hai biến giải thích (k = 3). Ta biểu thị
một biến cùng nội dung thông tin của nố bằng một vectơ trong mặt phẳng. Hai
biến khổng cộng tuyến biểu thi bởi 2 vectơ trục giao bong mặt phẳng. Đó là những
vectơ có cùng gốc và tạo thành gốc 90 độ. Các biến cộng tuyến hoàn toàn biểu thị
bằng 2 vectơ nằm trẽn cùng một dường thẳng. Các biến cổng tuyến khong hoằn
toàn nàm giữa hai cạc trên. Góc tucmg ứng giữa hai vecto sẽ hoặc nàm giũa 0 và 90
độ hoặc nằm giữa 90 độ và 180 độ. Gốc giữa các vecto càng gần 0 độ hoặc 180 độ
thì tính cộng tuyến càng lớn.
5.2. UỐC LUỢNG KHI c ó ĐA CỘNG TUYỂN HOÀN HẢO -
Sau đây chúng ta sẽ chỉ ra rằng khi có da cổng tuyến hoàn hảo thì các hê số
hồi quy là khổng xác định còn các sai số tiêu chuẩn là vổ hạn.Để đơn giản về mặt
trình bày, chúng ta xét mổ hình hồi quy 3 biến và chúng ta sẽ sử dụng dạng độ ìẹch ưong đó:
y, = Ỵ - Ỹ ; X, = Xi- X ; ( i = ũ õ (5.3) 108 (5.4) (5.5) (5.6) (5.7)
Giả sử X3| = XXĩi trong đó X là hằng sổ khác không, thay điều kiện này vào (5.6) ta được: % _ ( Y , y , XỊ, ) (
ỳ - Í Ắ ^ y ^ ^ X Ằ ỵ ^ x l ) (5.8)
( ' ỵ ẵ* ỉ i ) ( À ỵ í x ỉ i ) - ( * i ' ỵ l x ĩ i ) i
là biểu thúc khổng xác định, -niơng tự như vậy ta cũng có thể chi ra jj3 không xác định.
Vì sao chúng ta lại thu được kết quả như ở (5.8). Lưu ý đến ý nghĩa của ậ 2 có
thể giải thích điều đó. p 2 cho ta tốc độ thay đổi trung bình cùa Y khi X2 thay đổi 1
đơn vị còn x3 không đổi. Nhung khi Xj = XXì thì điều đó có nghĩa là không thể
tách ảnh huởng của Xỉ và X3 khỏi mảu đã cho. Trong kinh tế luợng thì điều này
phá hủy toàn bộ ý định tách ảnh hưởng riêng của từng biến lên biến phụ thuộc. Thí dụ: X31 =
, thay điều kiên này vào (5.5) ta được: yi =
I + Pj(ÀX2i) + Ci = ( P 2 + xp3)xji + ei = a x ji + ei
Trong đó ă = p2 + ^ p 3 .
Áp dụng công thức tính ước lượng cùa phưcmg pháp bình phương bé nhít thông thường ta được: â = (p J + X p 3) = 2J x 2i2
Như vậy dù a được ước lượng một cách duy nhất thì cững không thể xác định
dươc P và ệ>! từ một phương tìn h 2 ẩn. 109
Như vậy trong trường họp đa cộng tuyến hoàn hảo, chúng ta không thể nhận
được lời giải duy nhất cho các hẹ số hồi quy riêng, nhung trong khi đó ta lại có thể
nhận được lòi giải duy nhất cho tổ hợp tuyến tính của các hệ số này. Chú ý rằng
trong tiucmg đa cộng tuyến hoàn hảo thì phương sai và cấc sai số tiêu chuẩn của
các uớc lượng P i , P ì là vô hạn.
5.3. UỚC LUỢNG TRQNG TRUỠNG HỢP CÓ ĐA CỘNG TUYẾN KHÔNG HOÀN HẦO
Đa cộng tuyến hoàn hảo chỉ là trường hợp đặc biột hiếm xảy ra. Trong các số
liệu liên quan đến chuỗi thời gian, thường xảy ra đa cộng tuyến không hoàn hảo. XẾt mô hình (5.5).
Bây giờ chúng ta già thiết giữa X ì và X3 có cộng tuyến không hoàn toàn theongỉũa: . ' -V X31 = Xx2i + V|
trong đó \ *■ 0, Vị là nhiễu ngẫu nhiên sao cho X xjjV j = 0 .
Trong trường hợp này theo phương pháp bình phương bé nhất ta dẽ dàng thu
được các ước lượng P2 và . /?2 A
6 (i> , xvK ^ J ằĩj+ỵr*)-ỊẲỵ$ylx2l ,ỉ =
( 2 4 x ^ 2 4 + 2 > , 1) - ( ^ Z 4 )2 (5.9)
Trong truỉmg họp này khồng có lý đo gì đổ nói rằng (5.9) là không ước luợng đuọc.
5.4. HẬU QUẢ CỦA ĐA CỘNG TUYẾN
Trong trường hợp có tồn tại đa cộng tuyến gần hoàn hảo thì có thể gặp một số tình huống sau: 1.
Phương sai và hiệp phương sai của các ước lượng bình quân bé nhất lớn
Chúng ta xét mô hình (5.5), theo công thức tính phương sai và hiệp phương
sai của các ước luọng P i và p ì (chương hồi quy bội) ta có: v" < f o • ỵ ề = ĩ) (5' 10) 110 v à : COV(ậ2,p 3) = ------ - (5.12) (l — r23)'V^'X2i 2 j x 3i
Trong đó Ĩ23 là hệ số tương quan giữa X2, X3
Từ (5.10) và (5.11) ta thấy khi r23 tăng dăn đến 1 (nghĩa là cộng tuyến tăng)
thì phương sai của 2 ước lượng này tăng dần đến vô hạn. (5.12) chỉ ra ràng khi f23
tăng dần đến 1 thì cov( P 2. P 3) tăng về giá trị tuyệt đối.
2 . K hoảng tin cậy rộng hơn
Như ta đã biết trong chương tnrớc khoảng tin cậy 95% cho (32 và p3 khi ơ2 đã biết là:
Â2 ± 1,96se( P2) và p3 ± l,96se(p3) Trong đó:
s e ( Â ) = Vvar( Â ) - ~ f = T
Cho nên ta có thể viết lại các khoảng túi cậy 95% cho p2 là: P i + 1,96 (5.13) y23 ■Ị í xỉ, và cho P3 là: P i ± 1,96 (5.14) Í P
(5 13) và (5.14) chứng tỏ khi r23 càng gần tới 1 thì khoảng tin cậy cho các tham số càng rộng.
Do đó trong trường hợp có đa cộng tuyến gần hoàn hảo thì số liệu của mẫu có
thể thích hợp vối tập các giả thiết khác nhau. Vì thế xác suất chấp nhận giả thiết sai
tăng lên (tức là tăng sai lầm loại n). 111
3. Tỷ số t m ất ỷ nghĩa
Như dã b iã, khi kiểm định giả thiết H o: Pj = 0, chúng ta dã sử dụng tỷ số t =
Pj/seijjj) và đ a n so sánh gíà trị t dã đwjc uôc Iiwng với giá uị tới hạn t Nhung khi có đa
cộng tuyến gần hoàn hảo thì sai số tiêu chuẩn uớc lượng đuợc sẽ rất cao vì vậy làm cho d
số t nhỏ đi v í giá trị tuyé đối. Kít quả là sẽ làm tăng khả năng chấp nhận giả thiô Ho.
4. R2 cao nhung tì số t it ỷ nghĩa
Đế giải thích điều này. Ta hãy xét mổ hình hồi quy k biến như sau:. Yj = Pi +
+ p3Xái + ••••• + PfcXid + y
Trong trường hợp có đa cộng tuyến gần hoàn hảo, như đã chi ra ồ
trin, ta có thể tìm được một hoặc một số hệ số góc riêng là không có ý nglũa về
mặt thống kê trên cơ sở kiểm định t. Nhung trong khi đó R2 lại
có thể rất cao, nên bàng kiểm định F, chúng ta có thể bác bỏ giả thiết: Ho: P2 = P3
= ...... = pk = 0. Mâu thuẫn này cũng là tín hiệu của đa cộng tuyến.
s . C ác ước lượng bìn h phuong bé n h át và các sai số tiêu chuẩn của chúng
trỏ nên r ấ t nhạy đối với những thay đổi nhỏ trong số liệu
6. Dấu của các uớc lưọng của hệ số hồi quy có thể sai
Khi có đa cộng tuyến gần hoàn bảo thì có thể thu đuợc các ước lượng của các
hệ số hồi quy trái với điều chúng ta mong dại. Chẳng hạn lý thuyết kinh tế cho
rằng đối với hàng hóa bình thường khi thu nhập tâng, cầu hàng hóa lảng, nghĩa là
khi bồi quy thu nhập là một trong các biến giải thích, biến phụ thuôc là luợng cáu
của hàng hóa, nếu xảy ra hiện toọng đa cộng tuyến gần hoàn hảó thì uớc luợng của
hệ sổ của biến thu nhập có thể mang díu am - màu thuẫn với dĩèu ta mong đợi.
7. Thêm vào hay bớt đi các biỂn cộng tuyến với các biỂn khác, mỡ hình se
thay đổi v i độ lớn của các uớc lượng hoặc đấu của chúng
Tóm lại triệu chúng chù yếu của đa cộng tuyến mà ta đã nói ở trên là tăng sai
số tiêu chuẩn. Sai số tieu chuẩn cao hơn có ngụ ý rằng sự biến thiên của bẹ số hồi
quy từ mẫu này đến mẫu khác cao hơn do đó một sự thay đổi nhỏ trong số liệu
hoạc trong mô hình hồi quy (nhu thêm vào hoặc bớt di một biến) sẽ gay ra sự thay
đổi lớn của các hệ số.
Nhu vậy chúng ta đã biết đuợc một sổ bậu quả của đa cộng tuyến. Nhung dù
hậu quà như thế nào đi chăng nữa thì diều quan trọng là làm thế nào để thấy duợc
sự (Ồn tại của nó để ta có thể ngăn ngừa những bậu quà tai hại đối với thủ tục ước
lượng và sử dụng mổ ỉủnh hồi quy đổ dự đoán, điều khiển hoặc hiểu quá tiình liên
quan với nó. Sau đây sẽ trình bày một sổ phương pháp để phái hiện đa cộng tuyỂD
và mổ tả ỉỉhững triệu chứng chủ yếu của nó. 112
5.5. PHÁT HIỆN RA S ự T ồ N TẠI CỬA ĐA CỘNG TUYẾN Theo Kmanta thì ‘m
vấn dề vè đa cộng tuyến là vấn đê v í bậc chứ khống phải
yề loại”, nên việc phân biệt có ý nghĩa khống phải là có hay khống có đa cộng
tuyến mà là bậc khác nhau cùa chúng.
Vì đa cộng tuyến dề cập đến điều kiện cùa các biến giải thích mà được già
định là phi ngẫu nhiên, đó là đặc điểm cùa m ỉu chứ không phải cùa tổng thể.
Do đó chúng ta không kiểm định “tính đa cộng tuyến - mà nếu muốn chúng ta
có thể đo bậc của nó trong một mẫu bất kỳ.”
Sau đây là một vài quy tắc để đo mức đa cộng tuyến.
1. R 2 cao nhung tì số t tbấp
Trong trường hợp R2 cao (thuờng R2 > 0,8) mà tỳ số t thấp như trên đã chú Ỳ
đó chính là dấu hiộu của đa cộng tuyến.
2ẽ Tương q u an cáp giữa các biỂn giải thích cao
Nếu hộ số tương quan cặp giũa các biến giải thích cao (vượt 0,8) thi cố khả
năng cố tồn tại đa cộng tuyến. Tuy nhiên tiẽu chuẩn này thường khổng chính xác.
Có nhũng trường hợp tương quan cặp khổng cao nhung vẫn cố đã cộng tuyến. Thí
dụ, ta cố 3 biến giải thích Xi, "Xì, và X] nhu sau:
X , = ( 1 , 1 , 1 , 1 , 1 . 0 , 0 , 0 . 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 )
Xi - ( 0 , 0 , 0 , 0 , 0 , 1 , 1 , 1 , 1 . 1 , 0 ,0 ,0 ,0 ,0 , 0 ,0 ,0 ,0 ,0 )
X, = (1,1,1,1,1,1,1,14,1. 0,0,0,0,0, .0,0,0,0,0)
Rõ ràng x 3 = Xĩ + X| nghĩa là ta có đa cộng tuyến hoàn hảo, tuy nhiên tuơng quan cặp là: 1
Tiĩ = »1/3 ; r,3 = rjj = 0 ,5 9
Nhu vậy đa cộng tuyến xảy xa mà không có sự báo trước của tương quan cặp
nhưng dầu sao nó cOng cung cấp cho ta những kiểm tra tiên nghiệm có ích.
3ử Xem xét tương q u an riêng ‘
Vì vấn dề được dề cập đến dựa vào tương quan bạc khống. Farrar và Glauber
đã (fô nghị sừ dụng hộ số tirong quan riêng. Trong hồi quy cùa Y đối vói các biến
Xi Xì, x». Nếu tá nhận thấy ràng r2|,234 cao trong khi đó r2,2.34 ; r\ 3.24 ; r214,23 tucmg
đổi thấp thì điều dó có thể gợi ý rầng các biến Xj, Xí, và X* có tương quan cao và
ít nhất một trong các biến này là thừa.
Dù tương quan riêng rất có ích nhưng nó cũng khổng đảm bảo rằng sẽ cung
cấp cho ta hướng dẫn chính xác trong việc phát hiện ra đa cộng tuyến. 113 4. Hồi quy phụ
Một cách có thể tin cậy đuọc để đánh giá mức đọ cửa da cộng tuyến là hồi
quy phụ.HỒi quy phụ là hồi quy mỗi một biến giải thích X; theo các biến giải thích
còn lại. R2 được tính từ hồi quy này ta ký hiẹu R2|
Mối liền hệ giữa Fị và R*i: p _ R? / (k -2 )
i = ( 1 - R ? ) / ( n - k + 1 )
Fj tuấn theo phân phối F với k - 2 và n- k + 1 bậc tự do. Trong đó n là cở mẫu,
k là sổ biến giải thích kể cả hộ số chặn trong mô hình. R2; là hệ số xác định trong hồi quy cùa biến
theo các biến Xkhác. Nếu F| tính được vuợt điểm tới hạn Fi(k-
2, n-k+1) ở mức ý nghĩa đã cho thì có nghĩa là Xi có liên hộ tuyến tinh với các biến
Xkhác. Nếu Fj có nghĩa về mặt thống kê chúng, ta cũng vẫn phải quyết định liệu
biến Xj nào sẽ bị loại khỏi mổ bình. Một trở ngại củá kỹ thuật hồi quy phụ là gáoh
nặng tính toán. Nhưng ng&y nay nhiều chương trinh máy tính đã cổ thể đảm đương
đuợc công việc tính toán này.
5. N hân tử phóng đại phương sai
Một thước đo khác của hiện tượng đa cộng tuyến là nhân tử phóng đại
phương s a i gắn với biến 35, ký hiệu là VIF(Xj).
VIF(Xi) đuợc thiết lập trên cơ sở của fiệ số xác định R2j trong hồi quy của biẾn ■
Xj với các biến khác như sau: v n w = (5.15)
Nhìn vào công thức (5.15) có thể giải thích ỶIF(X) bằng tỳ số của phuong sai
thục của Pi trong hồi quy gốc của Y đối với các biến X và phuơng sai của uớc
lượng Pi trong hồi quy mà ở đó Xi Inrc giao với các biến khác.Ta coi tình huđng lý
tuởng là tinh huống mà trong đó các biếa độc lập khổng tương quan với nhau, và
VIF so sánh tình huống thực và tình, huống lý tưởng. Sụ so sánh này không có ích
nhiều và nó khổng cung c ỉp cho ta biết phải làm gì với tinh huống dó. Nố chỉ cho
bi£t rằng tình hỉnh là khổng lý tưỏng.
ĐỒ thị của mối liên hệ eủa R2i và VIF như chỉ ra ỏ hình 5.2 114 0 Hình 5.2
Như hình vẽ chỉ ra khi R2i tăng từ 0,9 đến 1 thì VIF tăng rất mạnh. Khi R2, = 1 thì VIF là vô hạn.
Có nhiều chương trình máy tính có thể cho biết VIF đối với các biến độc lập trong hồi quy. 6. Độ đo Theil
Khía cạnh chủ yếu của VIF chỉ xem xét đến tương quan qua lại giữa các biến
giải thích. Một độ đo mà xem xét lương quan cùa biến giải thích với biến được giải
thích là độ đo Theil. Độ đo Theil được định nghĩa nhu sau:
m = R2 - Ề ( R 2 - R Ì j ) 1=2
Trong đó R2 là hệ số xác định bội trong hồi quy của Y đối với các biến Xj, x 3,
.... Xk trong mô hình hồi quy:
Y j= Pi + p 2X2i + P3X31 + ....... + PkXki +Ui
R^i là hệ SỐ xác định bội trong mô hình hồi qui của tíiến Y đối với các biến X2 ,
x 3, ... ,X[.1, X +1....... X k '
Đại lượng R2 - J^2.| được gọi là "đóng góp tăng thêm vào" vào hệ số xác định
bội. Nếu X2, X3, ..... Xk không tương quan với nhau thì m = 0 vì những đóng góp
tăng thỗm đó cộng lại bằng R2 . Trong các trường hợp khác m có thể nhận giá trị âm hoặc dương lớn.
Đổ thấy đuợc độ đo này có ý nghĩa, chúng ta xét trường hợp mô hình có hai
biến giải thích Xj và x 3. Theo ký hiệu đã sử dụng ờ chương trước ta có:
m = R2 - (RJ - r212) - (R2 - r213)
Tỷ số t liê .1 hệ với tưcmg quan riêng r2!2.3 , r2i3,2
Trong phần hồi quy bội ta đã biết: R = r 12 + ( 1 - ^ 12) 1^13,2 R = r 13 + (1 - r2ij) ^123
Xhay 2 công thức này vào biểu thức xác định m ta đuợc: 115
m = R2 - [r2i2 + (1 - r212) r213,2 - r^id - [1*13 + (1 - 1* 13) r2i2j - r213 ]
= R2 - K1 - r212) I*1M + (1 - > , 3> r2!2,3 ] (5.17)
Công thức (5.17) cho ta biết điều gì? Để thấy được đíồu đó ta hãy đạt
1 - r*!2 = w2 ; 1 - r2!, = w3 và gọi là các tiọng số. Công thức (5.17) được viết lại duới dạn
m = R2 - [W2 r2|},2 + W3 r*I2jl
Như vậy độ do Theil bàng hiệu giữa bệ số xác định bội và tỏng có trọng số
của các hệ sổ tương quan riêng.
Thí dụ: Giả sử các hộ số tương quan giữa các biến Y và Xì, Xì là nhu sau: Y X í X a Y 1 , 0 0 0 , 9 5 0 , 9 5 * 0 , 9 5 1 , 0 0 . 0 , 9 7 X a 0 , 9 5 0 , 9 7 1 , 0 0
Để tính duợc độ do Theil ta phải tính đuợc R2 và 1*12,3 > r2!3,2 .Theo công thúc
đã biết ở chương hồi quy bội ta cố: Ị
- ị h i z l n h ú í (0.95-0,95 *0,97)2 ' -
(1 - r ỉĩ)(1 - r ả ) ( 1 - 0,9S2X I- 0.972 )
fa » = S i ư ;
r^ế3 - (0.95)2 = 0,9025 R *
= ĩ \ i + ( 1 - I * ,2) 1* 13* = ( 0 . 9 5 ) * + ( 1 - 0 , 9 5 2) 0 , 1 4 * 0,916
Vậy m = 0,916 - 2[1 - 0,9025]’0,14 = 0,888.
Do đó độ đo cùa Theil về mức độ đa cộng tuyến là 0,888.
Tuy nhiên chúng ta vẫn không thể trả lời dược câu hỏi ẵ‘tỉnh cộng tuyến có nghiêm trọng khững?”.
Nhu vậy trên đây chúng ta đã thảo luận một số độ đo đa cộng tuyến nhung tất
cả đều có ý nghĩa sử dụng hạn chế. Chúng chỉ cho ta những thổng báo rằng sự việc
không phải là lý tưởng.
Còn niột sổ độ đo nữa nhung liên quan đến giá trị riêng hoặc thống kẽ Bayes
chúng ta không trình bày ở đá y. 5.6. BIỆN PHÁP KHÁC PHỤC
Vân dề đặt ra là nếu đa cộng tuyến là nghiêm ưọng thì ta có thể lằm gì? cõng
như trong trường hợp trên, chúng ta cũng khống cố những biện pháp hoàn hảo bởi
vì đa cộng tuyến cơ bản là vấn đề mẫu. Tuy nhiên những quy tắc ngón tay cái có
thể đuợc áp dụng ở đây, còn sự thành cống lại.phụ thuộc vào tính nghiêm trọng của
vấn dề cộng tuyến. Sau đây ta xem xét một số phuơng pháp: U6
1. Sử dụng thông tin tién nghiêm
Một trong các cách tiếp cận để giải quyết vấn đê đa cộng tuyến là phải tận
dụng thông tin tiên nghiệm hoặc thông tin từ nguồn khác để ước lượng các hệ sổ riêng.
Thí dụ: Ta muốn ước lượng hàm sản xuất của một quá ừình sản xuất nào đó có dạng: Q, = AƯYkV * (5.17)
. Trong đó Q, là lượng sản phẩm được sản xuất thời kỳ t; L, lao động thòi kỳ t;
Ki vốn thời kỳ t; ụ là nhiễu; Ạ a , p là các tham số mà chúng ta cần ước lượng.
Lấy ln cả hai vế (5.17) ta được: InQ, = lnA + ctlnL, +PK, u, Đặt
lnQ, = Q \ ; InA = A* ; lnL, = L‘, ta được
Q*. = A* + txL*, + Ị3K*, + Ui (5.18)
Giả sử K và L có tương quan rất cao dĩ nhiên điều này sẽ dẫn đến phương sai
của các ước lượng cùa các hộ số co giãn của hàm sản xụất lớn.
Giả sử từ một ngùốn thông tin khác nào đó mà ta biết được lằng ngành công
nghiệp này thuộc ngành có lợi tức theo quy mô không đổi nghĩa là
a + p = 1. Với thông tin này, cách xử lý của chúng ta sẽ là thay p = 1 - a vào (5.18) và thu đuợc:
Q ’| = A* + a L \ + (1 -a)K*, + u, (5.19) Từ đó ta dược Q*. - K*| = A* + Đặt
Q*, - K*, = y , và L*| - K*| = z ”, ta được
Y , = A' + a Z \ + ut
Thông tin tiên nghiệm đã giúp chúng ta giảm số biến độc lập trong mô hình xuống còn 1 biến z \
Sau khi thu đuợc ước lượng à của a
thì P tính được từ điều kiên p = 1 - â
2. T h u th ập thêm số liệu hoẠc lấy thỀm m ẫu mới
Vì đa cộng tuyến là đặc trưng cùa mẫu nên có thể có mẫu khác- liên quari đến
cùng các biến ữong mẫu ban đàu mà cộng tuyến có thể không nghiêm trọng nữa.
Điều này chỉ có thể làm được khi chi phí cho việc lấy mẫu khác có thể chấp nhận được trong thực tế.
Đ ô i k h i c h ỉ c ầ n t h u t h ậ p t h ề m s ố l i ệ u , tă n g c ỡ m ẫ u c ó th ể là m g i ả m t ín h
nghiêm trọng cùa đa cộng tuyến. 117 3. Bỏ b ỉá i
Khi có hiện tượng đa cộng tuyến nghiêm trọng tỉử cách “ đơn giản nhất” là bỏ
biến cộng tuyến ra khỏi phương trình. Khi phải sử dụng biện pháp này thì cách thức tiến hành như sau:
Giả sử trong mô hình hồi quy của ta có Ylà biến được giải thích còn X2, Xa,....
là các biỂn giải thích. Chúng ta thấy rằng Xỉ tương quan chặt chẽ vói X3 . Khi đó
nhiều thông tin về Y chứa ở Xi thì cũng chứa ờ X3 . Vậy nếu ta bỏ một trong hai
biến Xị hoặc x 3 khỏi mô hình hồi quy, ta sẽ giải quyết được vấn đề đa cộng tuyến
nhung sẽ mất đi một số thững tin về Y.
Bằng phép so sánh R2 và R 2 trong các phép hồi quy khác nhau mà có và
khổng có một trong hai biên chúng ta có thể quyết định nền bỏ biến nào trong 2
biến x 2 và x 3 khõi mô hình.
Thí dụ: R2 đối với hồi quy của Yđối với tất cả cấc biến Xi, X2, ...,Xk là 0,94;
R2 khi loại biến Xí là 0,87 và R2 khi- loại X) là 0,92 ; Nhu vậy trong trường hợp này ta loại X a.
Chúng ta lưu ỷ một bạn chế của biẹn pháp này là trong các mỡ hình kinh tế cổ
nhâng trường hợp đòi hỏi nhất định phải có biến này hoặc biến khác ở trong mồ
hình. Trong những trường hạp như vậy việc loại bỏ 1 biến phải được cân nhác cẩn
thận giữa sai lệch khi bỏ một biến cộng tuyến với việc tăng phương sai của các uớc
luợng hộ số khi biến đó ở ưong mồ hình. Điều này sẽ đuợc xem xét ở chương XL
4. Sử dạng sai phân cấp một
Thù tục này đuợc trình bày trong chuơng v i n - “Tự tương quan”. Mặc dần
biện pháp này có thể giảm tương quan qua lại giữa các biến nhung chứng cũng có
thể dược sử dụng như một giải pháp cho v in dề đa cộng tuyến.
Thí dụ: Chúng ta có số liệu chuõi thời gian biểu thị liên hệ giữa biến Y và các
biến phụ thuộc Xi và X3 theo mô hĩnh sau: Y| = Pi + IW&I + P A + Ụ (5.20)
Trong đó t là thời gian. Phương trình trên đúng vói t thì cũng đúng với t - 1 nghĩa là:
Y|-1 - Pi + PXjM + P3X31-1 + IỊ-I (5.21)
Từ (5.20) và (5.21) ta đuợc:
Y| - Y|.1 = PỉCXii - Xỉ,.]) + P3CX3, + Xji-i) + I Ị - H-I (5.22) Đặt
y, = Y[ - Y|_1 ; X21 = Xj| - Xjt-|; X31 = Xìt + X31.1 ; ■ . V, = u - ụ . , . ta được: y, - P2X2, + £ 3X3, + V, (5.23) 118
Mô hình h'ôi quy dạng (5.23) thường làm giảm tính nghiêm trọng của đa cộng
tuyến vì dù x 2 và Xj có thể tương quan cao nhung không có lý do tiên nghiêm nà<>-
chắc chắn rằng sai phân cùa chúng cũng tương quan cao.
Tuy nhiên biến đổi sai p h in bậc nhất sinh ra một số vấn dề chẳng hạn như số
hạng sai số V| trong (5.23) có thể không thỏa mãn giả thiết của mô hình hồi quy
tuyến tính cổ điển là các nhiễu không tương quan. Vậy thì biện pháp sửa chữa này
có thể lại còn tồi tê hơn căn bệnh.
5. G iảm tưong quan trong hồi quy đa thức
N ét đặc biệt của hồi quy đa thức là các biến giải thích xuất hiện với lũy thừa
khác nhau trong mô hình h'ôi quy. Trong thực hành, để giảm tương quan trong hồi
quy đa thức, người ta thường sừ dụng dạng độ lệch (lệch so với giá trị trung bình).
Nếu viộc sử dụng dạng độ lệch mà vẫn không giảm da cộng tuyến thì người ta có
thể phải xem xét đến kỹ thuật “đa thức trục giao”.
6 . M ột số biện p h áp khác
N goài các biện pháp đã kể trên, người ta còn sử dụng một số biên pháp khác
nữa để cứu chữa căn bộnh Ị}ày như sau:
- Hồi quy thành phần chính.
- Sử dụng các ước lượng từ bên ngoài...
Nhưng tất cả các biện pháp đã trình bày ờ trên có thể làm giải pháp cho vấn
dề đa cộng tuyến như thế nào còn phụ thuộc vào bản chất của tập số liệu và tính
nghiêm trọng của vấn đề đa cộng tuyến. 7 /T h í dụ
Cho các biến số c - Tiêu dùng; Y- Thu nhập sau thuế; L- Tài sản dễ chuyển
thành tiền. Dựa trên 38 quan sắt, ta ước lượng được các m ô hình sau đây: c = -7 ,1 6 0 + 0,95213Y + e RJ = 0,9933 (5.24) (t) ( 1,93) (73,25)
C = -10,627 + 0,68166Y + 0.37252L + e R- = 0,9953. (5.25) (t) (-3,25) (9,60) (3,96) L = 9,307 + 0,76207 Y + e R2 = 0,9758 (5.26) (t) (1,8) (37,2)
(5 26) cho ta thấy giữa L và Y có tương quan khá cao với nhau. Điểu này chứng tỏ
có đa cộng tuyến. Nếu thay L trong (5.26) vào (5.25) sẽ được (5.24). Tuy nhiên
nếu chỉ nhìn vào (5.25) thì ta không phát hiện ra điều đó. Bởi vì các tỷ số t trong
(5 25) đều cao, dấu của các hệ số đều phù hợp. Dựa trên (5.24) và (5.25), bằng
kiểm định F, ta thấy không thể bỏ L đi được. 119
Bay giờ sẽ xem xét kỹ hon vắn dề này. Ta sẽ ước luợng lại mô hình (5.24),
(5.25) và (3.26) sau khi bỏ di hai quan sát cuổi cùng. Ta cồ ieết qúả sau đay:
c = -6,980 + 0,95145Y + e RJ = 0,9925 (5.27) (t) (-1,74) (67,04)
c = -13,391 +0,63258Y + 0,45065L + e RJ = 0,9951. (5.28) (t) (-3,71) (8,12) (4,24)
L = 9,307 + 0,76207 Y + e R2 = 0,9758 (5.29) (t) (2,69) (37,80)
Bằng cách so sánh từng hộ số (5.24) với (5.27); (5.25) với (5.28) và (5.26) với
(5.29), sẽ thấy ràng dù chỉ thay đổi chút ít số liệu nhung kết quả khác biệt rít
nhiều. Điẻu này cho thấy đa cộng tuyến ở đây là nghiêm trọng. 120 B À I TẬP
5.1. Hãy giải thích các văn đề sau:
a. Đ a cộng tuyến, đa công tuyến hoàn hảo và đa cộng tuyến không hoàn hào.
b. H àm hổi quy phụ, mục đích cua việc đust vào hàm hổi quy phụ là gì?
c. Hàm tổng chi phí có dạng: TCOST = p, + Pọ Q + PjQ2 + P„Q3. Trong hàm
này có chứa cả Q, Q2 và Q3 . Bạn có chó rằng có đa cộng tuyến trong mô hình này không?
5. 2. Vổri Q là lượng bán gas, PG là giá một blah gas, PE là giá điện sinh hoạt, PC là giá bếp gas.
a. Khi hổi quy Q phụ thuộc PG và hộ số chăn, có thể có hiện tượng đa cộng tuyến không? b. Cho mô hình [1]
[1] Ordinary Least Squares Estimation Dependent variable is Q
27 observations used for estimation from 97M1 to 99M3
***************************************************************** Regressor Coefficient Standard Error T-Ratio[Prob] INPT 1053.6 123.052 8.5615[.000] PG -6.9435 .626036 -11.09i2[.000] PC -.001737 .001815 -.95682[.349] PE 338.15 128.23 2.6371[.015]
**************************************************************** R-Squared .99406 F-statistic F( 3,23) 1284.9[.000]
Nghi ngờ trong mô hình [1]: Q phụ thuộc PG, PC, PE và hộ số chặn có thể có hiộn
tượng đá cộng tuyến, vì thống kê T của hệ số ứng với biến PC nhỏ mà R5 lớn. Hãy
nêu một cách kiểm tra hiện tượng đó.
c. Tiến hành hổi quy được kết quả sau đay:
[2] Ordinary Least Squares Estimation Dependent variable is PC
27 observations used for estimation from 97M1 to 99M3 Regressor Coefficient Standard Errol- T-Ratio[Prob] P E - 7 . 3 6 0 8 3 .6 7 3 0 - 2 .0 0 4 0 [ .0 5 6 ] p 5 .34168 .020910 16.3406[.000] TxJ-pT 5 5 5 .7 0 8 2 50.9517 10.9066[.000]
***************************************************************** R Sauared
.93617 F-statistic F( 2 ,2 4 ) 176.0110[.000]
**************************************************************** 121
d. Mô hình [2] nhằm mục đích gì?
e. Biến PC có phụ thuộc tuyến tính vào biến PE không? Có phụ thuộc tuyến tính vào biến PG không?
f. M ô hình [1] có khuyết tật đa cộng tuyến không? Đa cộng tuyến này là
hoàn hảo hay không hoàn hảo? Các ưóc luạng cua mô hình [1] còn là uớe lượng tốt nhất khổng?
g. Nêu một cách khắc phục đơn giản khuyết tật trong mô hình [1]
h. Khi bò biến PC khỏi mô hình [1], tiến hành hồi quy Q theo PG, PE có hê
số chận thu được R2 = 0,9821. Có nên bỏ biến PC không? i.
Để kiểm tra mô hình Q phụ thuộc PG, PE và hệ số chặn có khuyết tạt
không, người ta hồi quy PG theo PE có hệ số chặn thu được hệ số xác định
bằng 0,1215. Mô hình đó dùng để làm gì, có kết luận gì thu dược? j.
Khi hổi quy mô hình : Q phụ thuộc PG, D, DPG có hệ số chặn với D là
biến giả nhận giá trì bằng 1 nếu là tháng đại lý bán bình gas mới, D = 0
với các thấng bán bình gas cũ, DPG = D*PG. Các biến D và DPG cố thể
có quan hệ cộng tuyến với nhau hay không?
5.3. Với s là sản lượng của một cơ sở sản xuít, K là nguổn vốn, L là lao động, D là
biến giả với D = 1 nếu cơ sờ sản xuất khổng thuộc sò hữu nhà nước và D = 0 nếu
cơ sở thuộc sỏ hữu nhà nước, a = 5%.
a. Khi hổi quy mô hình: s phụ thuộc L có hệ số chận có thể có hiện tuọng đa cộng tuyến không?
b. Khi hổi quy mô hình [1]:
[1] Ordinary Least Squares Estimation * * % % * * * %
% * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * %
* * * * * * * sệt * * * * * * * 4c Dependent variable is s
20 observations used for estimation from 1 to 20 Regressor Coefficient Standard Eưor T-Ratio[Prob] INFT -20.6583 22.0029 -,93889[.361] K 10.7720 ế 2.1599 4.9874[.000] L 17.2232 4.5279 3.8038[.00I] R-Squared .71699
F-statistic F ( 2 , 17) 21.5343[.C00]
***************************************************************** 122
Nếu nghi ngờ mô hình [1] trên có hiện tượng đa cộng tuyến, hãy nêu m ột cách kiểm định.
c. Cho biết bàng kết quả hồi quy [2] dưới đây dùng để làm gì? Kết luận gì thu
được về hiện tượng đa cộng tuyến trong mô hình [1]?
[2] O rdinary L east Squares Estimation D ependent variable is K
20 observations used for estim ation from 1 to 20 R egressor Coefficient Standard Error T-Ratio[Prob] L .18696 .07589 2.4634[.024] INPT 5.1153 13.4659 -37987[ế708]
***************************************************************** R-Squared
.254482 F-statistic F( 1,18) 6.1443[.024]
d. Khi hổi quy s phụ thuộc vào L, K, T có hệ số chặn, trong đó T là biến số
công nghệ, người ta thu được hệ số của T bằng 5.8332 vói độ lệch chuẩn
bằng 4.9235. Biến số T đua vào có ý nghĩa không?
e. Nghi ngờ trong mô hình nói ờ câu (d) có hiện tượng đa cộng tuyến, người
ta hổi quy T theo L, K có hệ số chặn thu được R2 bằng 0,6213. Kết quả đó
cho biết điều gì? Khi đó có nên đưa biến T vào mô hình không? f.
Nếu muốn kiểm tra mô hình LS phụ thuộc vào LL, LK - L. là logarit cơ
số tự nhiên của các biến tương ứng - có hệ số chặn, để biết có hiện tượng
đa cộng tuyến hay không, ta co thể làm thế nào?
g. Khi hổi quy LK theo LL có hệ số chận thu được ước lượng hệ số góc bằng
1,928 và độ lệch ehuẩn bằng 1,437. Kết quả đó dùng để làm gì, kết luận gì thu được.
h. Khi đặt biến DL = D*L với D là biến giâ, khi đó D và DL có quan hộ cộng tuyến không? 123

