Bài giảng Mối quan hệ Giữa Đạo Hàm Và Liên Tục Vi Phân Đạo Hàm Cấp Cao | Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

Bài giảng Mối quan hệ Giữa Đạo Hàm Và Liên Tục Vi Phân Đạo Hàm Cấp Cao | Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh. Tài liệu gồm 1 trang giúp bạn tham khảo, củng cố kiến thức và ôn tập đạt kết quả cao trong kỳ thi sắp tới. Mời bạn đọc đón xem!

15 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Toán cao cấp 1 - TCC

Trường: Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

Thông tin:

1 trang 3 tuần trước

Tác giả:

Profile Phạm Thị Huyền
0
0
0
0
( ) ( )
'( ) lim
xx
f x f x
fx
xx
→
−
=
−
hoặc
00
00
00
( ) ( )
'( ) lim lim ( )
xx
f x x f x
y
f x x x x
xx
→ →
+ −
= = = −

( )' ' ' 'u v w u v w+ − = + −
( )' . 'ku k u=
(k: hằng số)
( . )' '. '.u v u v v u=+
'
2
'. '.u u v v u
vv
−

=


'
2
1'u
uu

=−


' ' '
.
x u x
y y u=
( )' 0C =
(C: hằng số)
( )' 1x =
1
( )' .
nn
x n x
−
=
'
2
11
xx

=−


( )
1
'
2
x
x
=
(sin )' cosxx=
(cos )' sinxx= −
2
1
(tan )'
cos
x
x
=
2
1
(cot )'
sin
x
x
= −
00
( ) '( )v t s t=
0 0 0
( ) '( ) ''( )a t v t s t==
00
( ) '( )I t Q t=
0 0 0
(( )')yxy x x y= − +
0
x
0
x
0
x
0
x
0
x
QUI
TẮC
TÍNH
ĐẠO
HÀM
2
3
4
5
6
7
1
ĐẠO
HÀM
CỦA
CÁC
HÀM
SỐ SƠ
CẤP
CƠ
BẢN
ĐỊNH NGHĨA
MQH GIỮA ĐẠO
HÀM VÀ LIÊN TỤC
2
1
3
4
VI PHÂN
ĐẠO HÀM CẤP CAO
1
2
3
4
5
6
7
8
9
00
( ) '( ).df x f x x=
'dy y dx=
(3)
'' ( ')'; ( '')'...y y y y==
( )
++

++
=

++

++
a b a c b c
xx
d e d f e f
ax bx c
dx ex f
dx ex f
2
2
22
2
  
2
  
.
( )

+−
=

+

+
ax b ad bc
cx d
cx d
2
.
( )

+ + + + −
=

+

+
ax bx c adx aex be dc
dx e
dx e
22
2
2
.
Đạo
hàm
theo u
tương
tự đạo
hàm
theo x
có
nhân
thêm
u’
| 1/1
| | Tải xuống

Có thể bạn quan tâm:

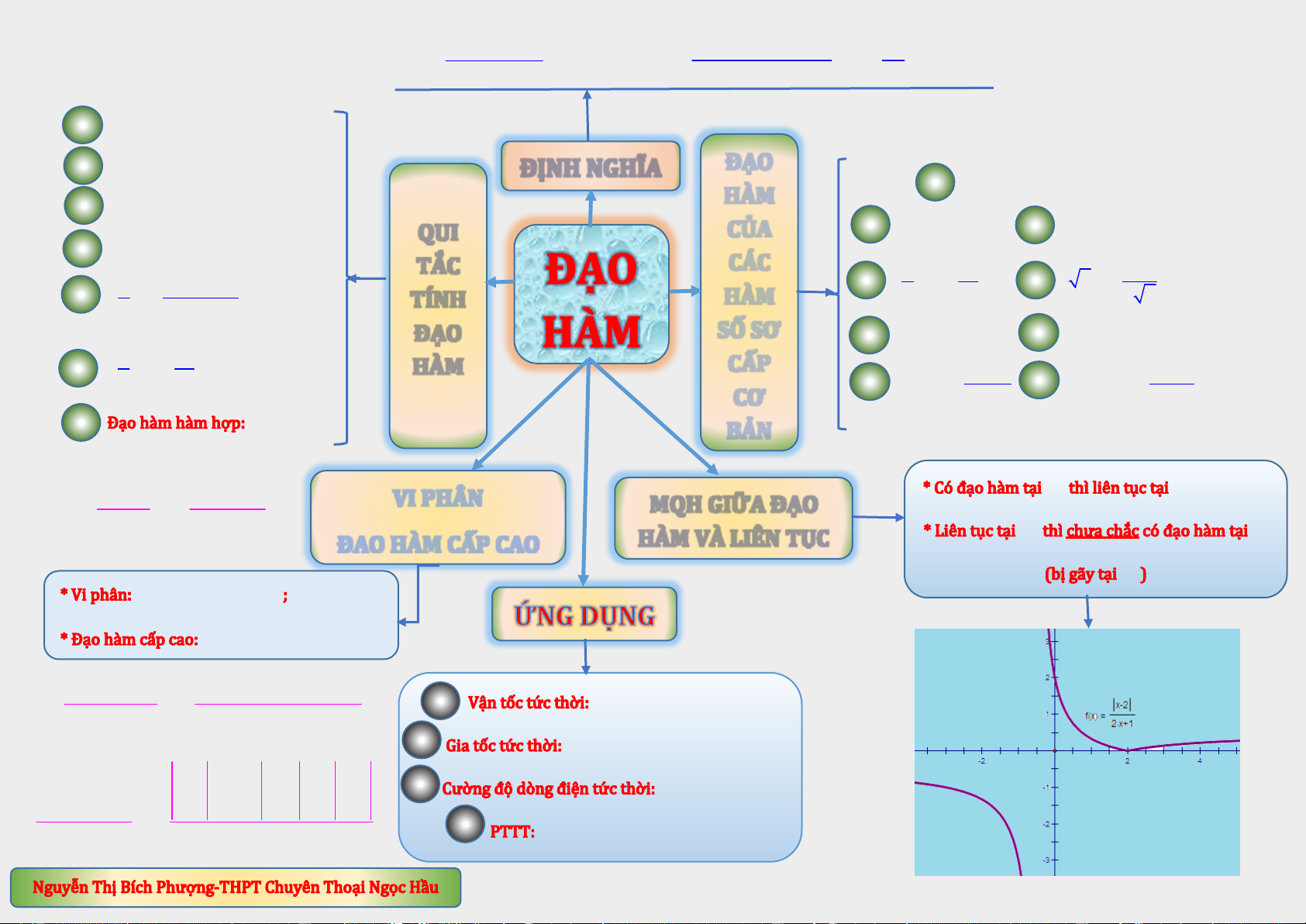
Preview text:

f (x) − f (x ) f (x + x  ) − f (x ) y  0 f '(x ) = lim hoặc 0 0 f '(x ) = lim = lim ( x  = x − x ) 0 0 0 x→ − x  →0 x  →0   0 x x x x x 0 1 (u + v − )
w ' = u '+ v '− w' 2
(ku) ' = k.u ' (k: hằng số) ĐẠO ĐỊNH NGHĨA
1 (C) ' = 0 (C: hằng số) Đạo HÀM 3 ( .
u v) ' = u '.v + v '.u hàm 2 (x) ' = 1 3 n n 1 (x ) ' . n x − = QUI CỦA theo u ( . u . v ) w ' = u '. . v w + . u v '.w + . u . v w' 4 tương ' TẮC CÁC  1  1 tự đạo '  u
u '.v − v '.u 4 = −   5 ( x ) 1 ' = hàm 5 =   2 HÀM x x 2 x TÍNH 2  v v theo x ĐẠO SỐ SƠ
6 (sin x) ' = cos x
7 (cos x) ' = −sin x có '  1  u ' nhân 6 = −   HÀM CẤP 2  1 1 thêm u u 8 (tan x) ' =
9 (cot x) ' = − 2 CƠ cos x 2 sin x u’ ' ' ' 7 y = y .u x u x BẢN x xax + b  0 0 ad − bc VI PHÂN   = . MQH GIỮA ĐẠO cx + d 2   (cx +d) x x 0 0 HÀM VÀ LIÊN TỤC ĐẠO HÀM CẤP CAO x 0
df (x ) = f '(x ). x
dy = y 'dx 0 0 (3)
y ' = ( y ') '; y = (y ')'... 2 
ax + bx + c adx 2 + a
2 ex + be − dc   = . 1
v(t ) = s '(t ) 0 0 dx +  e  ( 2 dx + e ) 2
a(t ) = v '(t ) = s ' (t ) 0 0 0 a b a c b c 2 3 x + 2 x +
I (t ) = Q '(t ) 0 0 2   + +  d e d f e f ax bx c   = . 4 2 2 2 y = y ( ' x (
) x − x ) + y
dx + ex + f 0 0 0  
(dx +ex + f )