
























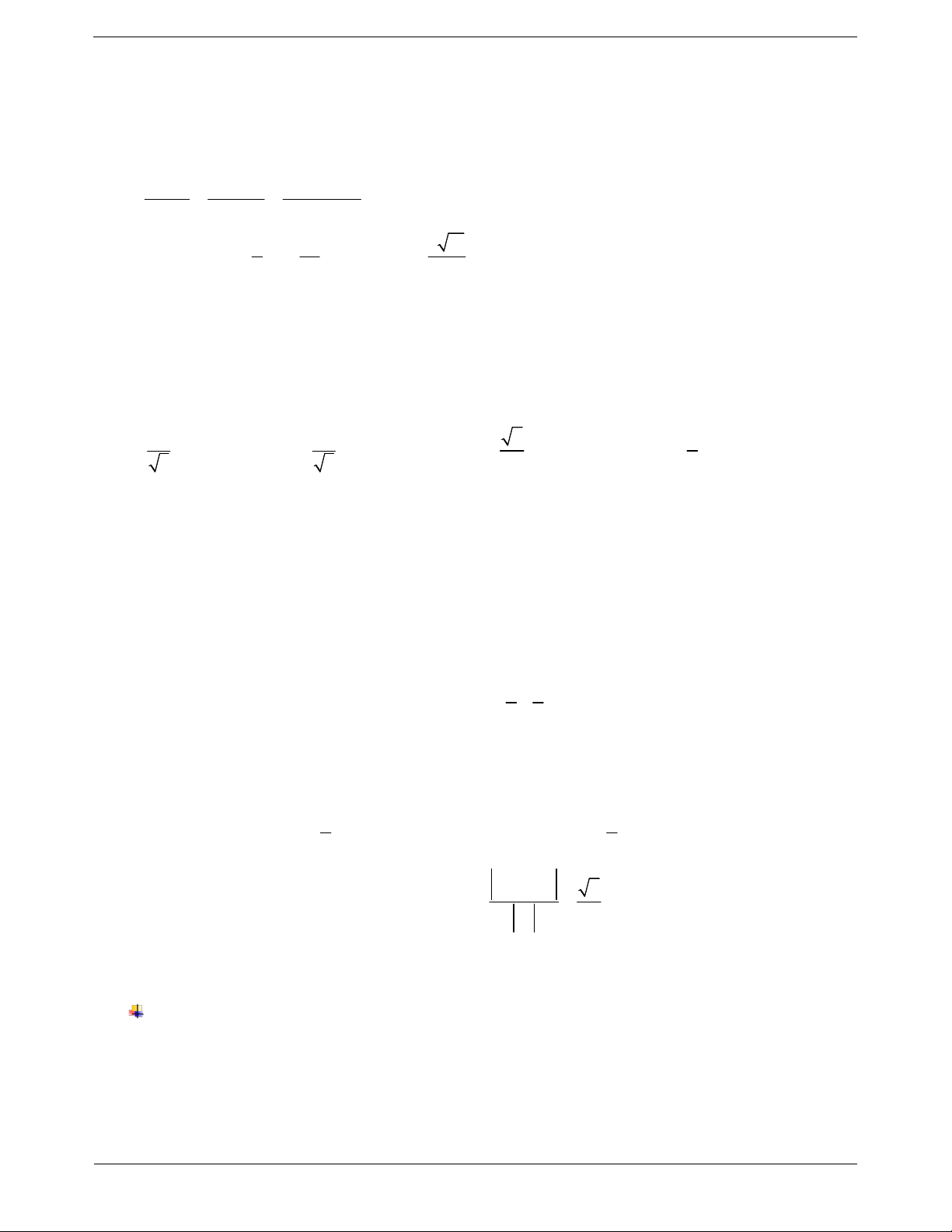









Preview text:
CHUYÊN ĐỀ 7. PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN Oxyz
BÀI 3. PHƯƠNG TRÌNH ĐƯỜNG THẲNG Mục tiêu Kiến thức
+ Nắm vững khái niệm vectơ chỉ phương của đường thẳng, góc giữa hai đường thẳng, góc giữa
đường thẳng và mặt phẳng.
+ Trình bày và vận dụng được các công thức tính khoảng cách, góc.
+ Trình bày được cách viết phương trình tham số của đường thẳng.
+ Trình bày được các vị trí tương đối của hai đường thẳng, của đường thẳng và mặt phẳng và của
đường thẳng với mặt cầu. Vận dụng được các công thức để xét vị trí tương đối của hai đường
thẳng; của đường thẳng với mặt phẳng và của đường thẳng với mặt cầu. Kĩ năng
+ Biết cách viết phương trình tham số, phương trình chính tắc của đường thẳng.
+ Biết cách tính khoảng cách, tính góc.
+ Biết cách xét vị trí tương đối của hai đường thẳng, vị trí tương đối của đường thẳng với mặt
phẳng và vị trí tương đối của đường thẳng với mặt cầu. TOANMATH.com Trang 1 I. LÍ THUYẾT TRỌNG TÂM
1. Phương trình đường thẳng
Vectơ chỉ phương của đường thẳng Chú ý:
Cho đường thẳng . Vectơ u 0 gọi là vectơ chỉ phương của + Nếu u là vectơ chỉ phương của
đường thẳng nếu giá của nó song song hoặc trùng với .
thì k.u k 0 cũng là vectơ chỉ
Cho đường thẳng đi qua M x ; y ; z và có vectơ chỉ 0 0 0 phương của . phương là u a; ; b c .
+ Nếu đường thẳng đi qua hai điểm
A, B thì AB là một vectơ chỉ phương.
Phương trình tham số của đường thẳng
Cho đường thẳng có phương trình
Phương trình tham số của đường thẳng có dạng (1) thì x x at u 0 +
;a ;bc là một vectơ chỉ
y y bt , t (1) 0 phương của . z z ct 0 + Với điểm M thì
M x at; y bt; z ct trong đó t 0 0 0
là một giá trị cụ thể tương ứng với từng điểm M. Phương trình chính tắc Nếu a, ,
b c 0 thì phương trình chính tắc của đường thẳng có dạng x x y y z z 0 0 0 2 a b c 2. Khoảng cách
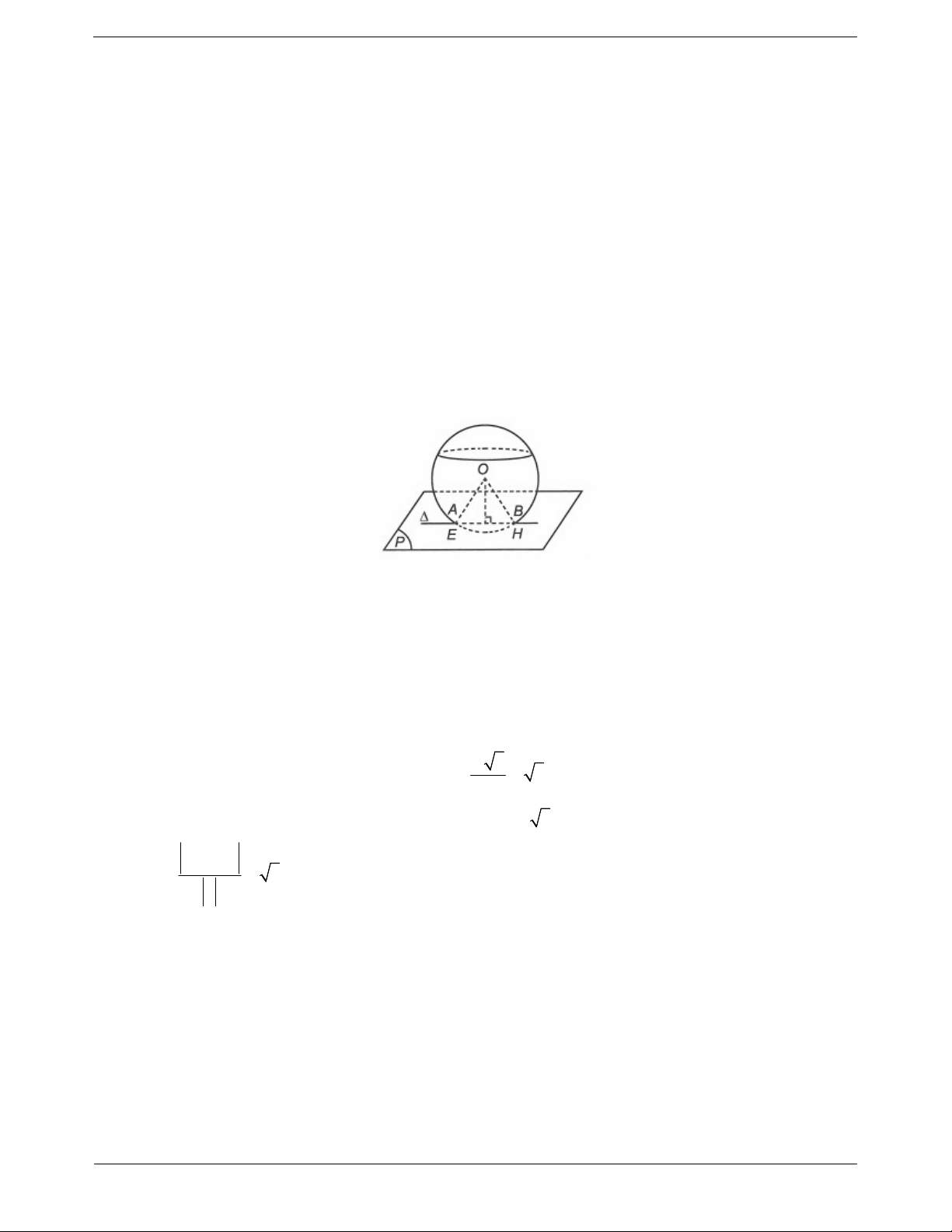
Khoảng cách từ điểm đến đường thẳng
Cho đường thẳng đi qua M , có vectơ chỉ phương u và điểm M . Khi đó để tính khoảng cách từ 0
M đến ta có các cách sau: MM ,u
Cách 1: Sử dụng công thức: d M ,d 0 . u Cách 2:
+ Lập phương trình mặt phẳng P đi qua M vuông góc với .
+ Tìm giao điểm H của P với .
+ Khi đó độ dài MH là khoảng cách cần tìm. Cách 3:
+ Gọi N d , suy ra tọa độ N theo tham số t . TOANMATH.com Trang 2 + Tính 2 MN theo t .
+ Tìm giá trị nhỏ nhất của tam thức bậc hai.
Khoảng cách giữa hai đường thẳng chéo nhau
Cho hai đường thẳng chéo nhau đi qua M có vectơ chỉ phương u và đi qua M có vectơ chỉ 0 0
phương u . Khi đó khoảng cách giữa hai đường thẳng và được tính theo các cách sau:
u,u.M M
Cách 1: Sử dụng công thức: d , 0 0 . u,u
Cách 2: Tìm đoạn vuông góc chung MN . Khi đó độ dài MN là khoảng cách cần tìm.
Cách 3: Lập phương trình mặt phẳng P chứa qua và song song với . Khi đó khoảng cách cần tìm
là khoảng cách từ một điểm bất kì trên đến P . 3. Vị trí tương đối
Vị trí tương đối giữa hai đường thẳng
Trong không gian Oxyz, hai đường thẳng x x y y z z 0 0 0 d : đi qua M x ; y ; z có 1 0 0 0 1 a b c vectơ chỉ phương u ; a ; b c , và 1 x x y y z z 0 0 0 d : đi qua M x ; y ; z có 2 0 0 0 2 a b c
vectơ chỉ phương u a ;b ;c . 2
Để xét vị trí tương đối của d và d , ta sử dụng 1 2 phương pháp sau: Phương pháp hình học a a a
Ta có thể dùng phương pháp đại số để xét vị 1 2 3 u / /u + d trùng d 1 2 b b b 1 2 1 2 3
trí tương đối: Dựa vào số nghiệm của hệ M d 1 2 M d 1 2
phương trình các đường thẳng. u ,u 0
Chú ý trường hợp vô nghiệm 1 2 + d / /d 1 2
hoặc u , M M 0
+ Nếu u ;u cùng phương thì d //d . 1 2 1 2 1 1 2
+ Nếu u ;u không cùng phương thì d ; d a a a 1 2 1 2 1 2 3 u | u 1 2 b b b chéo nhau. 1 2 3 M d 1 2 M d 1 2 u ,u 0 1 2 + d cắt d 1 2
u ,u .M M 0 1 2 1 2 TOANMATH.com Trang 3
+ d chéo d u ,u .M M 0 1 2 1 2 1 2
Vị trí tương đối giữa đường thẳng và mặt phẳng
Trong không gian Oxyz, cho mặt phẳng Phương pháp đại số
: Ax By Cz D 0 có vectơ pháp tuyến Xét hệ phương trình x x at 1 0 x x at 0 n ; A ; B C d y y y y bt 2 0 và đường thẳng : bt đi qua 0 z z ct z z ct 3 0 0
Ax By Cz D 0 4
M x ; y ; z có vectơ chỉ phương u a b c . d ; ; 0 0 0
Để xét vị trí tương đối của d và ta sử dụng phương
Thay (1), (2), (3) vào (4), ta được pháp sau:
A x at B y bt C z ct D 0 * 0 0 0 Phương pháp hình học u n
+) Nếu phương trình (*) vô nghiệm t thì Nếu d thì d . M x ; y ; z d // . 0 0 0 u n
+) Nếu phương trình (*) có nghiệm t duy Nếu d thì d // . M x ; y ; z
nhất thì d cắt . 0 0 0 Nếu u và n u k n k
+) Nếu phương trình (*) có vô số nghiệm t d cùng phương . d với 0 thì d . thì d .
Chú ý: Để tìm điểm chung của đường thẳng Nếu u .n 0 u và n d ; d
không cùng phương thì d
d và mặt phẳng ta giải phương trình (*), cắt .
sau đó thay giá trị t vào phương trình tham số của d để tìm ; x y; z
Vị trí tương đối giữa đường thẳng và mặt cầu
Trong không gian Oxyz, cho đường thẳng và mặt cầu x x at 0
có phương trình lần lượt là: d : y y bt , t và 0 z z ct 0
S x a2 y b2 z c2 2 : R .
Để xét vị trí tương đối của d và ta sử dụng phương pháp sau: Phương pháp hình học Phương pháp đại số
Bước 1: Tìm khoảng cách từ tâm I của S đến d .
thay x, y, z từ phương trình tham số của d vào Bước 2:
phương trình S , khi đó ta được phương trình TOANMATH.com Trang 4
+ Nếu d I,d R thì d không cắt S .
bậc hai theo t . Biện luận số giao điểm của d
+ Nếu d I,d R thì d tiếp xúc S .
và S theo số nghiệm của phương trình bậc hai theo t .
+ Nếu d I,d R thì d cắt S .
Chú ý: Để tìm điểm chung của đường thẳng và
mặt cầu ta giải phương trình bậc hai theo t ,
sau đó thay giá trị của t vào phương trình
tham số của d để tìm ; x y; z. 4. Góc
Chú ý: Góc giữa hai đường thẳng là góc nhọn.
Góc giữa hai đường thẳng
Trong không gian Oxyz, cho hai đường thẳng d , d 1 2
lần lượt có các vectơ pháp tuyến là u ,u . 1 2
Góc giữa d và d bằng hoặc bù với góc giữa u và 1 2 1 u . 2 u .u
Ta có: cos d ,d cosu ,u 1 2 . 1 2 1 2 u . u 1 2
Góc giữa đường thẳng và mặt phẳng
Chú ý: Góc giữa đường thẳng và mặt phẳng là
Trong không gian Oxyz, cho đường thẳng d có vectơ góc nhọn.
chỉ phương u và mặt phẳng có vectơ pháp tuyến d n .
Góc giữa đường thẳng d và mặt phẳng bằng
góc giữa đường thẳng d với hình chiếu d của nó trên . u n Ta có: d u n . sin , cos , d . d u . n d TOANMATH.com Trang 5 SƠ ĐỒ HỆ THỐNG HÓA Đi qua M x ; y ; z và có 0 0 0 0
vectơ chỉ phương là u a; ; b c u Tham số: Chính tắc: Phương trình x x at Nếu a, , b c 0 thì 0 đường thẳng y y bt , t x x y y z z 0 0 0 0 z z a b c ct 0 ĐƯỜNG THẲNG Khoảng cách từ điểm Hai đường thẳng d , d 1 2
M đến đường thẳng u / /u u / /u 1 2 1 2 MM u d d , ; d / /d ; 1 2 1 2 d M , M 0 d M d 1 2 1 2 u
Khoảng
d cắt d u ,u 0; u ,u .M M 0 1 2 1 2 1 2 1 2 cách Khoảng cách 2 đường
d chéo d u ,u .M M 0
thẳng chéo nhau , 1 2 1 2 1 2
u,u.M M d , 0 0
Vị trí Đường thẳng d và mặt phẳng u,u
tương d u n ;M x y z d ; ; 0 0 0 đối
d // u n ; M x y z d ; ; 0 0 0 Giữa hai đường thẳng d và d
d cắt u .n 0 u n d , , d cosd ,d cos u ,u 1 2 không cùng phương 1 2 Góc
Đường thẳng d và mặt cầu S I, R Góc giữa đường thẳng d không cắt
d và mặt phẳng S d I,d R
d tiếp xúc S d I, d R
sin d, cosu ,n d
d cắt S d I,d R TOANMATH.com Trang 6 II. CÁC DẠNG BÀI TẬP
Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng
Bài toán 1: Xác định vectơ chỉ phương của đường thẳng Ví dụ mẫu
Ví dụ 1. Trong không gian với hệ tọa độ Oxyz, vectơ nào là một vectơ chỉ phương của đường thẳng có x 1 3y 3 z phương trình ? 3 2 1 3 2 A. a 3; ;1 . B. a 9;2; 3 . C. a 3;2; 1 . D. a 3; ;1 . 2 3 Hướng dẫn giải x 1 3y 3 z x 1 y z 3 Ta có . 3 2 1 9 2 3
Vậy một vectơ chỉ phương của đường thẳng là a 9;2; 3 . Chọn B.
Ví dụ 2. Trong không gian Oxyz, cho đường thẳng vuông góc với mặt phẳng có phương trình
x 2z 3 0 . Một vectơ chỉ phương của là: A. a 1;0;2 . B. b 2; 1 ;0. C. v1;2;3 . D. u 2;0; 1 . Hướng dẫn giải
Vì vuông góc với mặt phẳng nên vectơ chỉ phương của là vectơ pháp tuyến của mặt phẳng . Chọn A.
Ví dụ 3. Trong không gian với hệ tọa độ Oxyz, cho OA 2i 3 j 5k; OB 2
j 4k . Tìm một vectơ chỉ
phương của đường thẳng AB . A. u 2;5; 1 . B. u 2;3; 5 . C. u 2 ;5; 1 . D. u 2;5;9 . Hướng dẫn giải
Ta có OA 2i 3 j 5k A 2;3; 5 ;
OB 2 j 4k B 0; 2 ;4 . Suy ra AB 2 ; 5 ; 1 .
Suy ra đường thẳng AB có một vectơ chỉ phương là u 2;5; 1 . Chọn A.
Bài toán 2: Viết phương trình đường thẳng khi tìm được một vectơ chỉ phương và điểm thuộc đường thẳng Phương pháp giải TOANMATH.com Trang 7
Đường thẳng d đi qua điểm M x ; y ; z và có vectơ chỉ phương a a ;a ;a có phương trình 1 2 3 0 0 0 0 x x a t 0 1
tham số là y y a t t . 0 2 z z a t 0 3
Đường thẳng d đi qua hai điểm A, B: Một vectơ chỉ phương của d là AB .
Đường thẳng d đi qua điểm M x ; y ; z và song song với đường thẳng cho trước: Vì d // nên 0 0 0 0
vectơ chỉ phương của cũng là vectơ chỉ phương của d .
Đường thẳng d đi qua điểm M x ; y ; z và vuông góc với mặt phẳng P cho trước: Vì d P 0 0 0 0
nên vectơ pháp tuyến của P cũng là vectơ chỉ phương của d .
Đường thẳng d là giao tuyến của hai mặt phẳng P , Q .
Cách 1: Tìm một điểm và một vectơ chỉ phương
Tìm toạ độ một điểm A d bằng cách giải hệ phương trình mặt phẳng của P , Q với việc chọn giá trị cho một ẩn.
Tìm một vectơ chỉ phương của d : a n , n . P Q
Cách 2: Tìm hai điểm A, B thuộc d rồi viết phương trình đường thẳng đi qua hai điểm đó.
Đường thẳng d đi qua điểm M x ; y ; z và vuông góc với hai đường thẳng d , d : Vì d d , d d 0 0 0 0 1 2 1 2
nên một vectơ chỉ phương của d là: u u ,u . 1 d d2 Ví dụ mẫu
Ví dụ 1. Trong không gian Oxyz, phương trình chính tắc của đường thẳng đi qua điểm M 2; 1 ;3 và có
vectơ chỉ phương u 1;2;4 là x 1 y 2 z 4 x 1 y 2 z 4 A. . B. . 2 1 3 2 1 3 x 2 y 1 z 3 x 2 y 1 z 3 C. . D. . 1 2 4 1 2 4 Hướng dẫn giải
Phương trình chính tắc của đường thẳng đi qua điểm M 2; 1
;3 và có vectơ chỉ phương u 1;2;4 là x 2 y 1 z 3 . 1 2 4 Chọn D.
Ví dụ 2. Trong không gian Oxyz, cho điểm A1;2;3 và mặt phẳng P có phương trình
3x 4 y 7z 2 0 .
Đường thẳng đi qua A và vuông góc với mặt phẳng P có phương trình là TOANMATH.com Trang 8 x 3 t x 1 3t A. y 4 2t t .
B. y 2 4t t . z 7 3 t z 3 7 t x 1 3t x 1 4t
C. y 2 4t t .
D. y 2 3t t . z 3 7 t z 3 7 t Hướng dẫn giải
Gọi u là vectơ chỉ phương của đường thẳng thỏa mãn yêu cầu bài toán.
Ta có vectơ pháp tuyến của mặt phẳng P : n . P 3; 4 ;7 x 1 3t P u n P 3; 4;7 Vì
nên phương trình tham số của là y 2 4t t . A A1;2;3 z 3 7 t Chọn B.
Ví dụ 3. Cho điểm A1;2;3 và hai mặt phẳng P : 2x 2y z 1 0, Q : 2x y 2z 1 0 .
Phương trình đường thẳng d đi qua A song song với cả P và Q là x 1 y 2 z 3 x 1 y 2 z 3 A. . B. . 1 1 4 1 2 6 x 1 y 2 z 3 x 1 y 2 z 3 C. . D. . 1 6 2 5 2 6 Hướng dẫn giải
Mặt phẳng P có một vectơ pháp tuyến là n . P 2;2; 1
Mặt phẳng Q có một vectơ pháp tuyến là n Q 2;1;2
Đường thẳng d có một vectơ chỉ phương là u . d
Do đường thẳng d song song với P và Q nên u n d P
u n ,n . d P Q 5;2; 6 u n d Q
Suy ra đường thẳng d đi qua A1;2;3 và có vectơ chỉ phương u . d 5; 2 ; 6 x 1 y 2 z 3
Phương trình chính tắc của d là . 5 2 6 Chọn D.
Ví dụ 4. Trong không gian Oxyz, cho tam giác ABC với A1;4;
1 , B 2;4;3, C 2;2; 1 . Phương
trình tham số của đường thẳng đi qua điểm A và song song với BC là TOANMATH.com Trang 9 x 1 x 1 x 1 x 1 A. y 4 t B. y 4 t C. y 4 t D. y 4 t z 1 2 t z 1 2 t z 1 2 t z 1 2 t Hướng dẫn giải
Gọi là đường thẳng đi qua điểm A và song song với BC . Ta có: BC 0; 2 ;4 .
Do song song với BC nên một vectơ chỉ phương của là u 0;1;2 . x 1
Vậy phương trình tham số của đường thẳng là y 4 t . z 1 2 t Chọn A.
Ví dụ 5. Đường thẳng là giao tuyến của hai mặt phẳng x z 5 0 và x 2 y z 3 0 thì có phương trình là x 2 y 1 z x 2 y 1 z A. . B. . 1 3 1 1 2 1 x 2 y 1 z 3 x 2 y 1 z 3 C. . D. . 1 1 1 1 2 1 Hướng dẫn giải
Mặt phẳng P có vectơ pháp tuyến là n 1;0;1 . 1
Mặt phẳng Q có vectơ pháp tuyến là n 1; 2 ;1 . 2
Ta có n , n 2;2;2 . 1 2
Gọi u là một vectơ chỉ phương của thì u n và u n . 1 2
Suy ra u cùng phương với n , n . Chọn u 1;1; 1 1 2
Lấy M 2;1;3 thuộc mặt phẳng P và Q .
Đường thẳng đi qua M 2;1;3 có một vectơ chỉ phương u 1;1; 1 . x 2 y 1 z 3
Vậy phương trình là: . 1 1 1 Chọn C.
Ví dụ 6. Trong không gian Oxyz, cho tam giác ABC có A2;1; 1 , B 2;3;
1 và C 0;1;3 . Gọi d là
đường thẳng đi qua tâm đường tròn ngoại tiếp tam giác ABC và vuông góc với mặt phẳng ABC .
Phương trình đường thẳng d là x 1 y 1 z 2 x 1 y z A. . B. . 1 1 1 1 1 1 TOANMATH.com Trang 10 x y 2 z x 1 y z C. . D. . 2 1 1 1 1 1 Hướng dẫn giải
Ta có AB 4;2;2 AB 16 4 4 2 6 . AC 2; 2
;4 AC 4 4 16 2 6 . BC 2; 4
; 2 BC 4 16 4 2 6 .
Vậy tam giác ABC đều nên tâm đường tròn ngoại tiếp là trọng tâm G 0;1; 1 .
Ta có AB, AC 12;12;12 121;1; 1 .
Đường thẳng d đi qua G 0;1;
1 và có vectơ chỉ phương cùng phương với AB, AC , do đó chọn u 1;1; 1. x t
Phương trình đường thẳng d là y 1 t . z 1 t
Với t 1, ta có điểm A1;0;0 d .
Vậy đường thẳng d đi qua A1;0;0 và có vectơ chỉ phương u 1;1; 1 . Chọn B.
Ví dụ 7. Trong không gian Oxyz, cho hai M 1;2;3, N 3;4;5 và mặt phẳng P : x 2y 3z 14 0 .
Gọi là đường thẳng thay đổi nằm trong mặt phẳng P , các điểm H, K lần lượt là hình chiếu vuông
góc của M , N trên . Biết rằng khi MH NK thì trung điểm của HK luôn thuộc một đường thẳng d
cố định, phương trình của đường thẳng d là x t x t x t x 1 A. y 13 2t . B. y 13 2t . C. y 13 2t . D. y 13 2t . z 4 t z 4 t z 4 t z 4 t Hướng dẫn giải
Gọi I là trung điểm của HK .
Do MH NK nên HMI KNI IM IN . Khi đó I thuộc mặt phẳng Q là mặt phẳng trung trực của đoạn MN . 1
Ta có Q đi qua trung điểm của MN là điểm J 2;3;4 và nhận n MN 1;1; 1 làm vectơ pháp 2
tuyến nên có phương trình là Q : x y z 9 0 . x y z
Mà I A P . Suy ra I d P Q 9 0 : x 2y 3z 14 0
Tìm được 0;13;4 d và vectơ chỉ phương của d là 1; 2 ; 1 . TOANMATH.com Trang 11 x t Vậy d : y 13 2t . z 4 t Chọn A.
Ví dụ 8. Trong không gian Oxyz. Cho điểm E 1;1; 1 , mặt cầu S 2 2 2
: x y z 4 và mặt phẳng
P: x 3y 5z 3 0 . Gọi là đường thẳng đi qua E , nằm trong P và cắt S tại hai điểm , A B sao
cho OAB là tam giác đều. Phương trình tham số của là x 1 2t x 1 4t x 1 2t x 1 t A. y 1 t . B. y 1 3t . C. y 1 t . D. y 1 t . z 1 t z 1 t z 1 t z 1 2 t Hướng dẫn giải Gọi u a; ;
b c là một vectơ chỉ phương của với 2 2 2 a b c 0 . Ta có n . P 1;3;5
Vì P nên u n u.n 0 a 3b 5c 0 a 3b 5c . (1) P P
Mặt cầu S có tâm O 0;0;0 và bán kính R 2 .
Gọi H là hình chiếu vuông góc của O trên AB R 3
Ta có OAB là tam giác đều cạnh R nên OH 3 . 2
Suy ra khoảng cách từ O đến đường thẳng bằng OH 3 . u,OE Khi đó 3 u
a b2 b c2 c a2 2 2 2 3 a b c
a b c2 0 a b c 0 (2)
Thay (1) vào (2) ta được:
3b 5c b c 0 b c a 2c .
Thay c 1 thì b 1 và a 2 .
Ta được một vectơ chỉ phương của là u 2;1; 1 TOANMATH.com Trang 12 x 1 2t
Vậy phương trình của đường thẳng là y 1 t . z 1 t Chọn C.
Bài toán 3: Viết phương trình đường thẳng bằng phương pháp tham số hóa Phương pháp giải
Viết phương trình đường thẳng d đi qua điểm M x ; y ; z , vuông góc và cắt đường thẳng . 0 0 0 0
Cách 1: Gọi H là hình chiếu vuông góc của M trên đường thẳng . Khi đó H , M H u . Khi 0 0
đó đường thẳng d là đường thẳng đi qua M , H . 0
Cách 2: Gọi P là mặt phẳng đi qua M và vuông góc với d . Q là mặt phẳng đi qua M và chứa 0 0
d . Khi đó d P Q
Viết phương trình đường thẳng d đi qua điểm M x ; y ; z và cắt hai đường thẳng d , d . 0 0 0 0 1 2
Cách 1: Gọi M d d, M d d . Suy ra M , M , M thẳng hàng. Từ đó tìm được M , M và 1 1 2 2 0 1 2 1 2
suy ra phương trình đường thẳng d .
Cách 2: Gọi P là mặt phẳng đi qua M và chứa d ; Q là mặt phẳng đi qua M và chứa d . 0 1 0 2
Khi đó d P Q . Do đó một vectơ chỉ phương của d có thể chọn là u n ,n . P Q
Đường thẳng d nằm trong mặt phẳng P và cắt cả hai đường thẳng d ,d : Tìm các giao điểm 1 2
A d P , B d P . Khi đó d chính là đường thẳng AB . 1 2
Đường thẳng d song song với và cắt cả hai đường thẳng d ,d : Viết phương trình mặt phẳng P 1 2
song song với và chứa d , mặt phẳng Q song song với và chứa d . Khi đó d P Q . 1 2
Đường thẳng d là đường vuông góc chung của hai đường thẳng d , d chéo nhau: 1 2 MN d
Cách làm: Gọi M d , N d . Từ điều kiện
1 , ta tìm được M , N . Viết phương trình đường 1 2 MN d2
thẳng MN chính là đường vuông góc chung của d , d . 1 2 Ví dụ mẫu
Ví dụ 1. Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng P : x y z 1 0 và đường thẳng x 4 y 2 z 1 d :
. Phương trình đường thẳng d là hình chiếu vuông góc của d trên mặt phẳng 2 2 1 P là x y 2 z 1 x y 2 z 1 A. . B. . 5 7 2 5 7 2 TOANMATH.com Trang 13 x y 2 z 1 x y 2 z 1 C. . D. . 5 7 2 5 7 2 Hướng dẫn giảii x 4 2t
Đường thẳng d có phương trình tham số là y 2 2t t . z 1 t
Lấy điểm M d P M 4 2t;2 2t; 1
td . Thay đổi tọa độ điểm M vào phương trình
mặt phẳng P ta được: 4 2t 2 2t 1 t 0 t 2 . Suy ra M 0;2; 1 .
Do đó d P M 0;2; 1 . Lấy A4;2;
1 d . Gọi H là hình chiếu vuông góc của A lên mặt phẳng P .
Đường thẳng AH đi qua A4; 2 ; 1 và nhận n
làm vectơ chỉ phương nên AH có P 1;1; 1 x 4 t1 phương trình là y 2 t t . 1 1 z 1 t1
Suy ra H 4 t ;2 t ;1 t . 1 1 1
Thay tọa độ H vào phương trình mặt phẳng P được 2 10 8 1
4 t 2 t 1 t 1 0 t H ; ; . 1 1 1 1 3 3 3 3
MH là hình chiếu của d lên mặt phẳng P , MH đi qua M 0;2; 1 và nhận 10 14 4 2 x y 2 z 1 MH ; ;
5;7;2 là vectơ chỉ phương nên có phương trình là . 3 3 3 3 5 7 2 Chọn B. x 1 y 1 z x 2 y z 3
Ví dụ 2. Cho các đường thẳng d : và đường thẳng d : . Phương trình 1 1 2 1 2 1 2 2
đường thẳng đi qua A1;0;2 , cắt d và vuông góc với d là 1 2 x 1 y z 2 x 1 y z 2 A. . B. . 2 2 1 4 1 1 x 1 y z 2 x 1 y z 2 C. . D. . 2 3 4 2 2 1 Hướng dẫn giải
Gọi I d , I 1 t,1 2t,t AI t;2t 1;t 2 là một vectơ chỉ phương của . 1 Do u
là một vectơ chỉ phương của đường thẳng d và d . d 1; 2; 2 2 2 2
Suy ra AI.ud 0 t 2 2t 1 2 t 2 0 3t 6 0 t 2 . 2 TOANMATH.com Trang 14 x 1 y z 2 Vậy AI 2;3; 4
. Phương trình đường thẳng cần tìm là . 2 3 4 Chọn C.
Ví dụ 3. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P :3x y 2z 0 và hai đường thẳng x 1 y 6 z x 1 y 2 z 4 d : và d : . 1 1 2 1 2 3 1 4
Đường thẳng vuông góc với P cắt cả hai đường thẳng d và d có phương trình là 1 2 x 2 y 1 z x 5 y z 4 A. . B. . 3 1 2 3 1 2 x 2 y 8 z 1 x 1 y 2 z 2 C. . D. . 3 1 2 3 1 2 Hướng dẫn giải x 1 t x 1 y 6 z d :
y 6 2t , t 1 1 2 1 z t M d M 1 t;6 2t;t . 1 x 1 3t x 1 y 2 z 4 d :
y 2 t , t 2 3 1 4 z 4 4t
N d N 1 3t ; 2 t ; 4 4t . 1
MN 2 t 3t ; 4 2t t ; 4 t 4t .
P :3x y 2z 0 có vectơ pháp tuyến n3;1; 2 .
Đường thẳng d vuông góc với P cắt cả hai đường thẳng d tại M và cắt d tại N suy ra 1 2 2 3 3 2 t t k t
MN kn 4 2t t k t 1 4t 4t 2 k k 1 t 2 M 1;2;2
Do d P nên u n . d P x 1 3s
Phương trình đường thẳng d là y 2 s ; s . z 2 2 s x y z Chọn s A 2 1 1 2;1;0 d d : . 3 1 2 Chọn A. TOANMATH.com Trang 15 x y z 2
Ví dụ 4. Viết phương trình đường thẳng d qua A1;2;3 cắt đường thẳng d : và song 1 2 1 1
song với mặt phẳng P : x y z 2 0. x 1 t x 1 t x 1 t x 1 t A. y 2 t . B. y 2 t . C. y 2 t . D. y 2 t . z 3 t z 3 z 3 z 3 t Hướng dẫn giải Do d d B B 2 ; m ;
m m 2 AB 2m 1;m 2; m 1 . 1
d song song với mặt phẳng P nên A . B n 0 1 m m m m AB . P 2
1 1. 2 1 0 1 1; 1 ;0 x 1 t
Vậy phương trình đường thẳng y 2 t . z 3 Chọn C.
Ví dụ 5. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 2x y z 10 0 , điểm A1;3;2 và x 2 y 1 z 1 đường thẳng d : . 2 1 1
Tìm phương trình đường thẳng cắt P và d lần lượt tại M và N sao cho A là trung điểm của MN . x 6 y 1 z 3 x 6 y 1 z 3 A. . B. . 7 4 1 7 4 1 x 6 y 1 z 3 x 6 y 1 z 3 C. . D. . 7 4 1 7 4 1 Hướng dẫn giải
Ta có N d N 2 2t;1 t;1 t .
A là trung điểm của MN M 4 2t;5 t;3 t.
Mà M P nên tọa độ M thỏa phương trình P , ta được:
24 2t 5 t 3 t 10 0 t 2 N 6; 1 ;3,M 8;7; 1 . Suy ra MN 14;8; 2 . 1
Đường thẳng đi qua hai điểm M và N nên có một vectơ chỉ phương u NM 7;4; 1 nên có 2 x 6 y 1 z 3 phương trình là . 7 4 1 Chọn A. TOANMATH.com Trang 16
Ví dụ 6. Trong không gian tọa độ Oxyz, cho điểm A3;3;3 thuộc mặt phẳng : 2x 2y z 15 0
và mặt cầu S x 2 y 2 z 2 : 2 3 5 100 .
Đường thẳng qua A , nằm trên mặt phẳng cắt S tại M , N . Để độ dài MN lớn nhất thì phương
trình đường thẳng là x 3 y 3 z 3 x 3 y 3 z 3 A. . B. . 1 4 6 16 11 1 0 x 3 5t x 3 y 3 z 3 C. y 3 . D. . 1 1 3 z 3 8 t Hướng dẫn giải
Mặt cầu S có tâm I 2;3;5 và bán kính R 10.
Mặt phẳng có vectơ pháp tuyến n 2;2; 1 .
Gọi H , K lần lượt là hình chiếu vuông góc của I lên và mặt phẳng .
IK nên phương trình đường thẳng IK đi qua I và vuông góc với mặt phẳng là x 2 2t y 3 2t . z 5 t x 2 2t y 3 2t
Tọa độ điểm K là nghiệm hệ phương trình K 2;7;3. z 5 t
2x 2y z 15 0
Vì nên IH IK . Do đó IH nhỏ nhất khi H trùng với K .
Để MN lớn nhất thì IH phải nhỏ nhất.
Khi đó đường thẳng cần tìm đi qua A và K . Ta có AK 1;4;6 . x 3 y 3 z 3
Đường thẳng có phương trình là: . 1 4 6 Chọn A.
Ví dụ 7. Trong không gian Oxyz, cho ABC có A2;3;3 , phương trình đường trung tuyến kẻ từ B là x 3 y 3 z 2 x 2 y 4 z 2 d :
, phương trình đường phân giác trong của góc C là : . 1 2 1 2 1 1
Đường thẳng AB có một vectơ chỉ phương là A. u 2;1; 1 . B. u 1; 1 ;0. C. u 0;1; 1 . D. u 1;2; 1 . Hướng dẫn giải TOANMATH.com Trang 17 x 2 2t
Ta có phương trình tham số của là: y 4 t C 2 2t;4 t;2 t . z 2 t 7 t 5 t
Gọi M là trung điểm của AC nên M 2 t; ; . 2 2 7 t 5 t t 3 2 2 3 2 2 t 1 1 t 1 t Vì M d nên t 1. 1 2 1 1 4 2 Suy ra C 4;3; 1 .
Phương trình mặt phẳng P đi qua A và vuông góc với là: 2x y z 2 0.
Gọi H là giao điểm của P và H 2;4;2 . Gọi
A là điểm đối xứng với A qua đường phân giác , suy ra H là trung điểm A A A 2;5; 1 . Do
A BC nên đường thẳng BC có vectơ chỉ phương là C
A 2;2;0 2 1 ;1;0 . x 4 t
Suy ra phương trình của đường thẳng BC là y 3 t . z 1
Vì B BM BC B 2;5; 1 A .
Đường thẳng AB có một vectơ chỉ phương là AB 0;2; 2 20;1; 1 . Chọn C. x 1 y 2 z
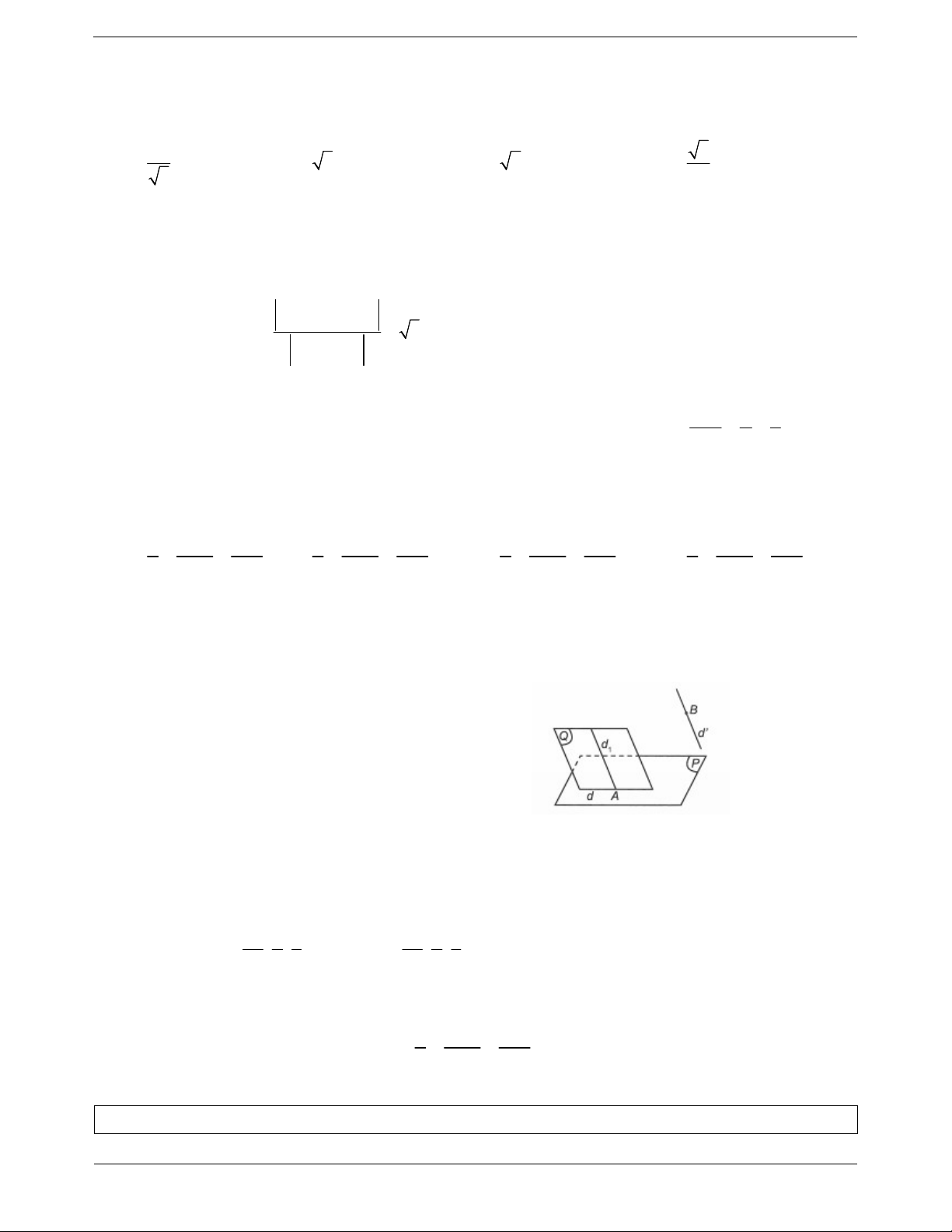
Ví dụ 8. Trong không gian hệ tọa độ Oxyz, cho đường thẳng : và hai điểm 2 1 1 A4;2;4, B0;0; 2
. Gọi d là đường thẳng song song và cách một khoảng bằng 5 , gần đường
thẳng AB nhất. Đường thẳng d cắt mặt phẳng Oxy tại điểm nào dưới đây? 2 14 A. 2;1;0 . B. ; ;0 . C. 3;2;0 . D. 0;0;0 . 3 3 Hướng dẫn giải x 4t
Phương trình tham số của đường thẳng AB có dạng: y 2 t . z 2 6 t
Để đường thẳng d thỏa mãn bài toán thì ta có hình vẽ tương ứng TOANMATH.com Trang 18
Đoạn vuông góc chung của hai đường thẳng AB và là MN với M 0; 5 ; 1 , N 3;1; 1 .
Để d gần đường thẳng AB nhất thì d phải đi qua điểm D nằm trên đoạn MN mà
DN d d, 5, MN 3 5 . Do đó MN 3DN D 2;1; 1 .
Vectơ chỉ phương của đường thẳng d là u . d 2; 1 ; 1 x 2 2t
Suy ra phương trình tham số của d là y 1 t z 1 t x 0
Đường thẳng d cắt Oxy tại điểm có z 1 t 0 t 1 . y 0
Vậy giao điểm của d và Oxy là 0;0;0 . Chọn D.
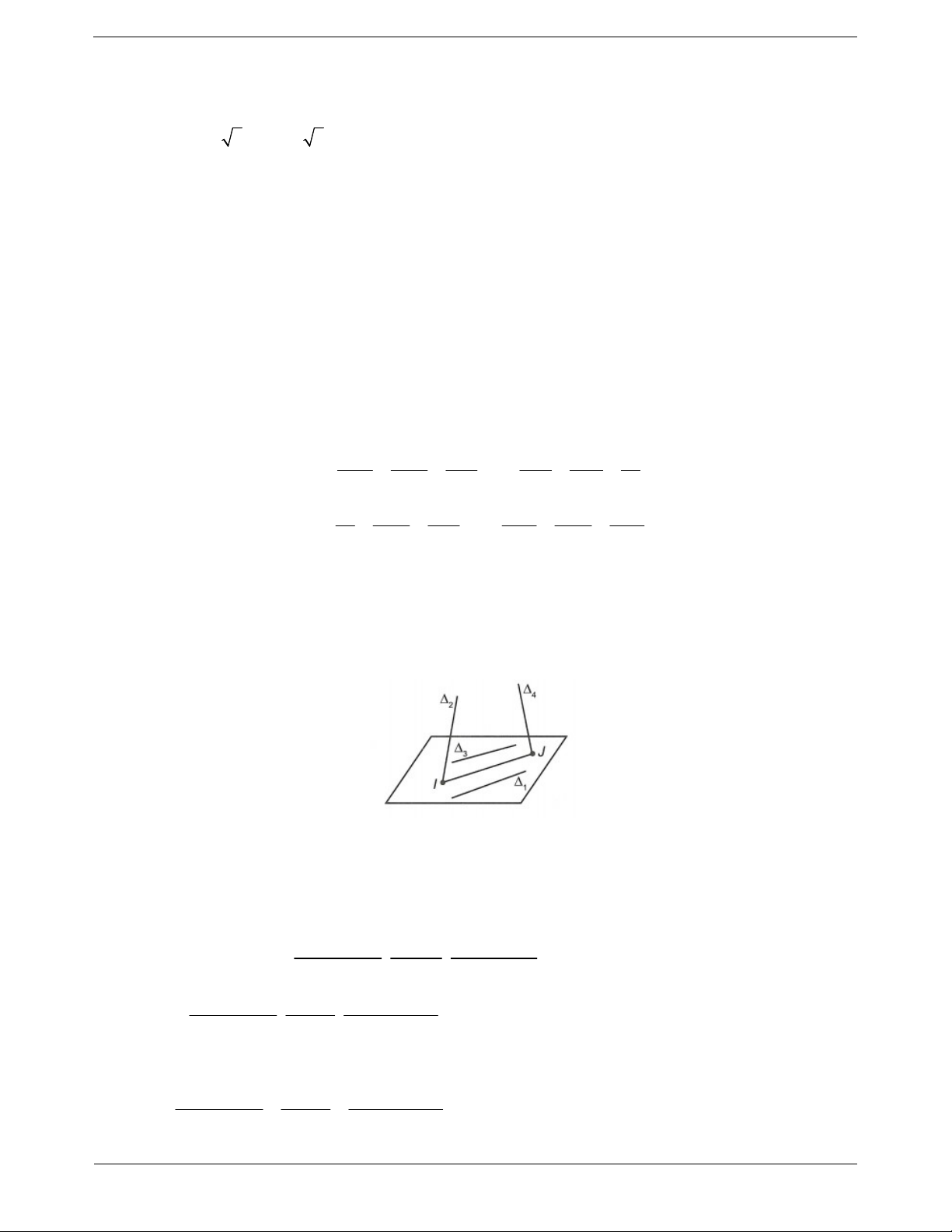
Ví dụ 9. Trong không gian với hệ tọa độ Oxyz, cho bốn đường thẳng x 2 y 2 z 1 x 1 y 1 z : ; : 1 2 1 1 1 1 2 1 x y 2 z 1 x 5 y a z b : ; : 3 4 1 1 1 1 3 1
Biết không tồn tại đường thẳng nào trong không gian mà cắt được đồng thời cả bốn đường thẳng trên. Giá
trị của biểu thức T a 2b bằng A. 2. B. 3. C. 2. D. 3. Hướng dẫn giải Ta có: // . 1 3
Gọi P là mặt phẳng chứa và P : x 2y z 3 0 . 3 1
Gọi I P I 0; 1 ;1 . 2
2a b 22 3b 24 2a 7b 8 Gọi J P J ; ; . 4 6 6 6 2
a b 22 3b 18 2a 7b 14 IJ ; ; . 6 6 6
Để thỏa mãn yêu cầu bài toán thì IJ phải cùng phương với u 1; 1 ; 1 . 1 2
a b 22 3b 18 2a 7b 14 Suy ra a 2b 2 . 6 6 6 Chọn A. TOANMATH.com Trang 19
Bài tập tự luyện dạng 1 Bài tập cơ bản
Câu 1: Trong không gian Oxyz, vectơ nào sau đây là vectơ chỉ phương của đường thẳng x 1 y 2 z : 1 1 2 A. u 1; 2 ;0 . B. u 2 ;2;4 . C. u 1;1;2 . D. u 1 ; 2;0 .
Câu 2: Trong không gian Oxyz, đường thẳng qua hai điểm M 2
;1;2, N 3;1;0 có vectơ chỉ phương là A. u 1;0;2 . B. u 5; 2 ; 2 . C. u 1 ;0; 2 . D. u 5;0;2 . x 1 y 2 z 1
Câu 3: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : nhận vectơ u là 2 1 2
vectơ chỉ phương. Giá trị a b bằng A. 8. B. 8. C. 4. D. 4.
Câu 4: Trong không gian Oxyz, đường thẳng d đi qua điểm E 1;0;2 và có vectơ chỉ phương
a 3;1;7. Phương trình của đường thẳng d là x 1 y z 2 x 1 y z 2 A. . B. . 3 1 7 3 1 7 x 1 y z 2 x 1 y z 2 C. . D. . 1 1 3 1 1 3
Câu 5: Trong không gian Oxyz, cho E 1;0;2 và F 2;1;5 . Phương trình đường thẳng EF là x 1 y z 2 x 1 y z 2 A. . B. . 3 1 7 3 1 7 x 1 y z 2 x 1 y z 2 C. . D. . 1 1 3 1 1 3 x 1 y 2 z 2
Câu 6: Trong hệ tọa độ Oxyz, cho đường thẳng d :
. Phương trình nào sau đây là 1 2 3
phương trình tham số của d ? x 1 x 1 t x 1 t x 1 A. y 2 t . B. y 2 2t . C. y 2 2t . D. y 2 t . z 2 3 t z 1 3 t z 2 3 t z 1 t
Câu 7: Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng P : 2x y 2z 9 0 và đường thẳng x 1 y 3 z 3 d : . 1 2 1
Phương trình tham số của đường thẳng đi qua A0;1;4 vuông góc với d và nằm trong P là x 5t x 2t x t x t A. y 1 t . B. y t . C. y 1 . D. y 1 2t . z 4 5 t z 4 2 t z 4 t z 4 t TOANMATH.com Trang 20
Câu 8: Trong không gian tọa độ Oxyz, gọi d là giao tuyến của hai mặt phẳng : x 3y z 0 và
: x y z 4 0. Phương trình tham số của đường thẳng d là x 2 t x 2 t x 2 t x 2 t A. y 2 . B. y t . C. y t . D. y t . z 2 2 t z 2 2 t z 2 2 t z 2 2 t
Câu 9: Trong không gian Oxyz, cho mặt phẳng :3x y z 0 và đường thẳng x 3 y 4 z 1 :
. Phương trình của đường thẳng d nằm trong mặt phẳng , cắt và vuông góc 1 2 2
với đường thẳng là x 2 2t x 1 4t x 4 t x 1 4t A. y 2 5t . B. y 5 t . C. y 5 . D. y 5t . z 17 t z 3 7 t z 7 3 t z 3 7 t x 1 y 3 z 1
Câu 10: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : và mặt phẳng 3 4 1
P:2x y 2z 12 0. Viết phương trình đường thẳng d là hình chiếu vuông góc của đường thẳng d trên mặt phẳng P . x 1 y 2 z 3 x 1 y 4 z 3 A. d : . B. d : . 2 1 2 3 4 1 x y 4 z 2 x 1 y 4 z 2 C. d : . D. d : . 3 1 1 3 4 1 x 1 t x 2 y 2 z 3
Câu 11: Trong không gian Oxyz, cho hai đường thẳng d :
, d : y 1 2t và điểm 1 2 2 1 1 z 1 t
A1;2;3 . Đường thẳng đi qua điểm A , vuông góc với d và cắt d có phương trình là 1 2 x 1 y 2 z 3 x 1 y 2 z 3 A. . B. . 1 3 1 1 3 1 x 1 y 2 z 3 x 1 y 2 z 3 C. . D. . 1 3 5 1 3 5 x 1 y 1 z
Câu 12: Trong không gian Oxyz, cho điểm M 2;1;0 và đường thẳng d : . Phương 2 1 1
trình đường thẳng đi qua điểm M cắt và vuông góc với đường thẳng d là x 2 y 1 z x 2 y 1 z A. . B. . 1 4 1 1 4 1 x 2 y 1 z x 2 y 1 z C. . D. . 2 4 1 1 4 2 x 2 y 2 z x 2 y 1 z
Câu 13: Trong không gian Oxyz, cho hai đường thẳng d : ; d : . 1 2 1 1 1 1 2 3
Phương trình đường thẳng cắt d , d lần lượt tại A và B sao cho AB nhỏ nhất là 1 2 TOANMATH.com Trang 21 x t x 2 t x 1 t x 2 t A. y 3 2t . B. y 1 2t . C. y 1 2t . D. y 1 2t . z 2 t z t z 2 t z t Bài tập nâng cao
Câu 14: Trong không gian Oxyz, gọi d là đường thẳng đi qua điểm A1; 1
; 2, song song với mặt phẳng x 1 y 1 z
P : 2x y z 3 0 , đồng thời tạo với đường thẳng :
một góc lớn nhất. Phương 1 2 2
trình đường thẳng d là x 1 y 1 z 2 x 1 y 1 z 2 A. . B. . 4 5 3 4 5 3 x 1 y 1 z 2 x 1 y 1 z 2 C. . D. . 4 5 3 4 5 3
Câu 15: Trong không gian tọa độ Oxyz, cho mặt cầu S có phương trình
x 2 y 2 z 2 2 1
3 20 , mặt phẳng có phương trình: x 2y 2z 1 0 và đường thẳng x y 2 z 4 có phương trình:
. Viết phương trình đường thẳng nằm trong mặt phẳng , vuông 1 2 3
góc với đường thẳng , đồng thời cắt mặt cầu S theo dây cung có độ dài lớn nhất. x 3t x 1 3t x 2 2t x 1 2t A. : y 2 . B. : y 1 .
C. : y 1 5t . D. : y 1 5t . z 4 t z 1 t z 3 4 t z 1 4 t
Câu 16: Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A2;1; 2 , B5;1;
1 và mặt cầu S có phương trình 2 2 2
x y z 6 y 12z 9 0 . Xét đường thẳng d đi qua A và tiếp xúc với S sao cho
khoảng cách từ B đến d nhỏ nhất. Phương trình của đường thẳng d là x 2 x 2 x 2 2t x 2 t A. y 1 t . B. y 1 4t . C. y 1 2t . D. y 1 4t . z 2 2 t z 2 t z 2 t z 2 t x y z 3
Câu 17: Trong không gian Oxyz, cho đường thẳng d :
và mặt cầu S có phương trình: 2 2 1
x 2 y 2 z 2 3 2
5 36 . Gọi là đường thẳng đi qua A2;1;3 , vuông góc với đường thẳng d
và cắt S tại hai điểm có khoảng cách lớn nhất. Khi đó đường thẳng có một vectơ chỉ phương là
u 1;a;b. Giá trị của ab bằng 1 A. 4. B. 2. C. . D. 5. 2
Câu 18: Đường thẳng đi qua điểm M 3;1;
1 , nằm trong mặt phẳng : x y z 3 0 và tạo với x 1
đường thẳng d : y 4 3t một góc nhỏ nhất thì phương trình của đường thẳng là z 3 2 t TOANMATH.com Trang 22 x 1 x 8 5t x 1 2t x 1 5t A. y t. B. y 3 4t . C. y 1 t . D. y 1 4t . z 2t z 2 t z 3 2t z 3 2t
Câu 19: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC biết A2;1;0, B3;0;2,C 4;3; 4 .
Phương trình đường phân giác trong của góc A là x 2 x 2 x 2 t x 2 t A. y 1 t . B. y 1 . C. y 1 . D. y 1 . z 0 z t z 0 z t
Câu 20: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A1;1;2, B 2 ;3; 1 ,C 3; 1 ;4.
Phương trình đường cao của tam giác ABC kẻ từ đỉnh B là x 2 t x 2 t x 2 t x 2 t A. y 3 t . B. y 3 . C. y 3 t . D. y 3 t . z 1 t z 1 t z 1 t z 1 t
Dạng 2: Các vấn đề về góc
Bài toán 1. Góc giữa đường thẳng và mặt phẳng Phương pháp giải Cho đường thẳng
Ví dụ: Trong không gian với hệ trục tọa độ Oxyz cho x y x x y y z z 3 2 z 0 0 0 :
và mặt phẳng đường thẳng : và mặt phẳng a b c 2 1 1
: Ax By Cz D 0.
:3x 4y 5z 8 0.
Gọi là góc giữa hai mặt phẳng và Tính góc tạo bởi và . ta có công thức: Hướng dẫn giải Aa Bb Cc
có vectơ chỉ phương u 2;1; . sin 1 2 2 2 2 2 2 A B C . a b c
có vectơ pháp tuyến n 3;4;5. Chú ý: ,
A B,C và a,b, c không đồng thời bằng 0. Ta có: sin , cos ,nu 3.2 4.1 5.1 3 . 2 2 2 2 2 2 3 4 5 . 2 1 1 2 Suy ra , 60. Ví dụ mẫu TOANMATH.com Trang 23 x 3 y 1 z 2
Ví dụ 1: Trong không gian Oxyz, cho hai đường thẳng : và mặt phẳng 1 1 4
P: x y 2z 6 0 . Biết cắt mặt phẳng P tại ,
A M thuộc sao cho AM 2 3 . Tính khoảng
cách từ M tới mặt phẳng P . A. 2 . B. 2. C. 3 . D. 3. Hướng dẫn giải x 3 y 1 z 2 Đường thẳng :
có vectơ chỉ phương u 1;1;4 . 1 1 4
Mặt phẳng P : x y 2z 6 0 có vectơ chỉ phương n 1;1; 2 . u n P u n . 1 sin , cos , sin u . n 3 Suy ra d M 1 , MH M . A sin 2 3. 2 . 3 Chọn B.
Bài toán 2: Góc giữa hai đường thẳng Phương pháp giải Cho hai đường thẳng:
Ví dụ: Trong không gian Oxyz, cho hai đường thẳng x x y y z z 0 0 0 : 1 a b c x 1 y 2 z 3 x y z 3 1 2 : ; : . 1 2 x x y y z z 2 1 2 1 1 4 0 0 0 : 2 a b c
Tính góc giữa hai đường thẳng trên.
Gọi là góc giữa hai đường thẳng và . 2 1 Hướng dẫn giải aa bb cc
Vectơ chỉ phương của là u 2 ;1;2 . 1 Ta có: cos . 1 2 2 2 2 2 2
a b c . a b c
Vectơ chỉ phương của là u 1;1;4 . 2 2 u .u
cos , cosu ,u 1 2 1 2 1 2 u . u 1 2 2.11.1 2. 4 2
2 1 2 . 1 1 4 2 2 2 2 2 9 2 . 3.3 2 2
Vậy góc giữa hai đường thẳng đã cho là 45 . Ví dụ mẫu TOANMATH.com Trang 24
Ví dụ 1. Trong không gian Oxyz, cho đường thẳng d là giao tuyến của hai mặt phẳng
P : x z.sin cos 0; Q : y z.cos sin 0; 0; . 2
Góc giữa d và trục Oz là: A. 30 . B. 45 . C. 60 . D. 90 . Hướng dẫn giải
Mặt phẳng P có vectơ pháp tuyến là n . P 1;0;sin
Mặt phẳng Q có vectơ pháp tuyến là n . Q 0;1;cos
d là giao tuyến của P và Q nên vectơ chỉ phương của d là: u n ,n . d P Q sin ;cos ; 1
Vectơ chỉ phương của Oz là u . Oz 0;0; 1 0.sin 0.cos 1.1 1 Suy ra cos d,Oz d,Oz 45 . 2 2 2 2
sin cos 1 . 0 0 1 2
Vậy góc giữa d và trục Oz là 45. Chọn B.
Ví dụ 2. Trong không gian Oxyz, d là đường thẳng đi qua điểm A1; 1
;2, song song với mặt phẳng x 1 y 1 z
P : 2x y z 3 0 , đồng thời tạo với đường thẳng :
một góc lớn nhất. Phương 1 2 2
trình đường thẳng d là x 1 y 1 z 2 x 1 y 1 z 2 A. . B. . 4 5 3 4 5 3 x 1 y 1 z 2 x 1 y 1 z 2 C. . D. . 4 5 3 4 5 3 Hướng dẫn giải
Mặt phẳng P : 2x y z 3 0 có một vectơ pháp tuyến là n . P 2;1; 1 x 1 y 1 z Đường thẳng :
có một vectơ chỉ phương là u . 1; 2;2 1 2 2
Giả sử đường thẳng d có vectơ chỉ phương là u . d
Do 0 d, 90 mà theo giả thiết d tạo góc lớn nhất nên d, 90 ud u . Lại có d // P nên u
d nP . Do đó chọn u d
u , nP 4;5;3 . x 1 y 1 z 2
Vậy phương trình đường thẳng d là . 4 5 3 Chọn D. TOANMATH.com Trang 25 x 2 y 1 z 2
Ví dụ 3. Trong không gian Oxyz, cho đường thẳng d : và mặt phẳng 4 4 3
P:2x y 2z 1 0 . Đường thẳng đi qua E2;1;2, song song với P có một vectơ chỉ phương
u ;m ;n 1, đồng thời tạo với d góc bé nhất. Tính 2 2 T m n . A. T 5 . B. T 4 . C. T 3. D. T 4 . Hướng dẫn giải
Mặt phẳng P có vectơ pháp tuyến là n 2;1;2; đường thẳng d có vectơ chỉ phương là v 4;4;3.
// P u n 2m n 2 0 n 2m 2 . . u v 4m 4n 3 Mặt khác ta có: cos ;d u v m n 1. 4 4 2 2 2 2 2 3 4m 5 1 4m 52 2 1 16m 40m 25 . 415m 8m 5 . . 2 2 2 41 5m 8m 5 41 5m 8m 5 Vì 0 ,d90 nên
,d bé nhất khi và chỉ khi cos ,d lớn nhất. 2 2 16t 40t 25 7 2t 90t Xét hàm số f t f t . 2 5t 8t 5 2 5t 8t 52 Bảng biến thiên: 5 x 0 4 f 0 + 0 16 5 5 f 16 0 5
Dựa vào bảng biến thiên ta có: max f t f 0 5. Suy ra
,d bé nhất khi m 0n 2. Do đó 2 2 T m n 4. Chọn D.
Bài tập tự luyện dạng 2 Bài tập cơ bản TOANMATH.com Trang 26 x 2 y 1 z 1
Câu 1: Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d : và mặt phẳng 1 2 3
:x 2y 3z 0. Gọi là góc giữa đường thẳng d và mặt phẳng . Khi đó góc bằng A. 0 . B. 45 . C. 90 . D. 60 . x 1 y 2 z 3
Câu 2: Trong không gian Oxyz, cho hai đường thẳng : và 1 2 1 2 x 3 y 1 z 2 :
. Góc giữa hai đường thẳng , bằng 2 1 1 4 1 2 A. 30 . B. 45 . C. 60 . D. 135 . x 2 y 1 z 3 x 5 y 3 z 5
Câu 3: Trong không gian Oxyz, hai đường thẳng d : và d : tạo 1 1 2 1 2 1 2 m
với nhau góc 60 , giá trị của tham số m bằng 3 1 A. m 1. B. m . C. m . D. m 1. 2 2 Bài tập nâng cao
Câu 4: Trong không gian Oxyz, cho mặt cầu S x 2 y z 2 2 : 1 2 4 và đường thẳng x 2 t d : y t . z m 1 t
Tổng tất cả các giá trị thực của tham số m để d cắt S tại hai điểm phân biệt , A B và các mặt phẳng
tiếp diện của S tại ,
A B tạo với nhau một góc lớn nhất bằng A. 1,5. B. 3. C. 3. D. 2,25. Dạng 3: Khoảng cách
Bài toán 1: Khoảng cách từ một điểm đến đường thẳng Phương pháp giải
Ví dụ: Trong không gian với hệ tọa độ Oxyz, cho x 1 y 2 z 2 đường thẳng d : . 1 2 2
Tính khoảng cách từ M 2 ;1; 1 tới d .
Cho đường thẳng đi qua điểm M x ; y ; z Hướng dẫn giải 0 0 0 0 A d AM u
và có vectơ chỉ phương u a; ;
b c. Khi đó Ta có 1;2; 2 3; 1; 1 , 1;2; 2 .
Khoảng cách từ điểm M đến đường thẳng d là:
khoảng cách từ điểm M đến được tính bởi 1 AM;u công thức: d M d 5 2 ; . u 3 M M ;u d M , 0 1 . 1 u TOANMATH.com Trang 27 Ví dụ mẫu
Ví dụ 1. Viết phương trình đường thẳng d đi qua điểm A1;1; 1
cho trước, nằm trong mặt phẳng
P: 2x y z 2 0 và cách điểm M 0;2; 1 một khoảng lớn nhất. x 1 y 1 z 1 x 1 y 1 z 1 A. . B. . 1 3 1 1 3 1 x 1 y 1 z 1 x 1 y 1 z 1 C. . D. . 1 3 1 1 3 1 Hướng dẫn giải
Ta gọi B là hình chiếu của M lên đường thẳng d khi đó MB MA . Suy ra MB
MA nên đường thẳng d đi qua điểm A và vuông góc với MA . max
Đồng thời đường thẳng d nằm trong mặt phẳng P nên ta có u M , A n . d P 1;3; 1 Chọn C.
Ví dụ 2. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A2;1; 2 , B5;1; 1 và mặt cầu S 2 2 2
: x y z 6y 12z 9 0 . Xét đường thẳng d đi qua A và tiếp xúc với S sao cho khoảng
cách từ B đến d nhỏ nhất. Phương trình của đường thẳng d là x 2 x 2 x 2 2t x 2 t A. y 1 t . B. y 1 4t . C. y 1 2t . D. y 1 4t . z 2 2 t z 2 t z 2 t z 2 t Hướng dẫn giải Mặt cầu S 2 2 2
: x y z 6y 12z 9 0 có tâm I 0;3;6 bán kính R 6 .
IA 6 R AS , IB 3 10 R nên B nằm ngoài S . TOANMATH.com Trang 28
Đường thẳng d đi qua A và tiếp xúc với S nên d nằm trong mặt phẳng P tiếp xúc với mặt cầu S tại A .
Mặt phẳng P đi qua A và nhận IA làm vectơ pháp tuyến có phương trình là x 2y 2z 0 .
Gọi H là hình chiếu của B lên P thì tọa độ của H 4; 1 ; 1 .
Ta có: d B;d d ; B P BH .
Vậy khoảng cách từ B đến d nhỏ nhất khi d đi qua H . Ta có u AH . d 2;2; 1 x 2 2t
Suy ra phương trình đường thẳng d là: y 1 2t . z 2 t Chọn C.
Bài toán 2: Khoảng cách giữa hai đường thẳng chéo nhau Phương pháp giải
Trong không gian Oxyz, cho hai đường thẳng Ví dụ: Trong không gian Oxyz, tính khoảng cách
chéo nhau: có vectơ chỉ phương u a; ;
b c và giữa hai đường thẳng 1 x 1 4t
đi qua M x ; y ; z ; có vectơ chỉ phương 0 0 0 0 2 x 1 y 2 z d : và d : y 1 2t , t . 1 2 1 1 2
u a ;b ;c và đi qua M x ; y; z . z 2 2t 0 0 0 0 Hướng dẫn giải
Đường thẳng d đi qua điểm M 1; 2 ;0 và có một 1
vectơ chỉ phương u 2;1;1 . 1
Đường thẳng d đi qua điểm N 1;1;2 và có một
Khi đó khoảng cách giữa và được tính bởi 2 1 2
vectơ chỉ phương u 4;2; 2 . 2 u,u.M M
công thức d , 0 0 . 1 2 u,u
Do u cùng phương với u và M d nên d //d . 1 2 2 1 2 u MN
Nếu // ( u và u cùng phương và M ) , 1 2 1 2 0 2
Suy ra d d ;d d N;d 1 . 1 2 1 u
thì d , d M , 1 1 2 0 2
Ta có MN 0;1;2, u, MN 3;4;2 . u , MN 32 42 2 1 2 174 Suy ra . u 2 2 2 6 1 1 1 174 Vậy d d ;d . 1 2 6 Ví dụ mẫu TOANMATH.com Trang 29
Ví dụ 1. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A1;1;0, B 2;1; 1 ,C 0;1;2, D 1; 1 ; 1 .
Khoảng cách giữa AB và CD là 1 3 A. . B. 3 . C. 6 . D. . 3 2 Hướng dẫn giải AB 1;0; 1 Ta có AB,CD 2;2; 2 . CD 1; 2 ; 1
AB,CD. AC Suy ra d AB,CD 3 . AB,CD Chọn B. x 1 y z
Ví dụ 2. Cho phương trình mặt phẳng P : 2x y z 3 0 , đường thẳng d : và điểm 1 2 1 A0;2;
1 . Viết phương trình đường thẳng d đi qua A , nằm trong P sao cho khoảng cách d và d đạt giá trị lớn nhất. x y 2 z 1 x y 2 z 1 x y 2 z 1 x y 2 z 1 A. . B. . C. . D. . 1 7 9 1 7 9 1 7 9 1 7 9 Hướng dẫn giải
Gọi d là đường thẳng đi qua A và song song với d . 1 x t
Phương trình của d là: y 2 2t . 1 z 1 t
Trên đường thẳng d lấy điểm B 1;0;0. 1
Gọi Q là mặt phẳng chứa d và d . 1
Ta có d d, d d d ,Q d B,Q.
Do d cố định cho nên d d, d d B,Q d B,d . 1 1
Đẳng thức xảy ra khi và chỉ khi n
BH trong đó H là hình chiếu của B lên d . Q 1 2 2 1
5 2 1 Ta tìm được H ; ; nên BH ; ; n . Q 5 ;2; 1 3 3 3 3 3 3 Ta có u n ;n . d P Q 1;7;9 x y 2 z 1
Vậy phương trình của đường thẳng d là . 1 7 9 Chọn A.
Lưu ý : Vì đường thẳng d đi qua A nên ta có thể loại đáp án bằng cách thay tọa độ điểm A vào các đáp TOANMATH.com Trang 30 án trong bài
Bài tập tự luyện dạng 3 Bài tập cơ bản
Câu 1: Trong không gian Oxyz, cho điểm P ; a ;
b c . Khoảng cách từ điểm P đến trục tọa độ Oy bằng A. 2 2 a c . B. b . C. b . D. 2 2 a c . x 1 y 2 z 3
Câu 2: Trong không gian Oxyz, khoảng cách giữa đường thẳng d : và mặt phẳng 2 2 3
P: x 2y 2z 5 0 bằng 16 5 A. . B. 2. C. . D. 3. 3 3 x 7 y 5 z 9
Câu 3: Trong không gian Oxyz, khoảng cách giữa hai đường thẳng d : và 1 3 1 4 x y 4 z 18 d : bằng 2 3 1 4 A. 30. B. 20. C. 25. D. 15. Bài tập nâng cao
Câu 4: Trong không gian Oxyz, cho hai điểm M 2 ;2; 1 , A1;2; 3 và đường thẳng x 1 y 5 z d :
. Tìm vectơ chỉ phương u của đường thẳng qua M , vuông góc với đường thẳng 2 2 1
d đồng thời cách điểm A một khoảng nhỏ nhất. A. u 2;2; 1 . B. u 3;4; 4 . C. u 2;1;6 . D. u 1;0;2 . x y z
Câu 5: Phương trình đường thẳng d đi qua O và vuông góc với 1 1 : và cách điểm 2 1 2
M 3;1;0 một khoảng nhỏ nhất là x y z x y z x y z x y z A. . B. . C. . D. . 1 7 14 10 5 9 13 9 5 13 17 14 1 0
Dạng 4: Vị trí tương đối
Bài toán 1: Vị trí tương đối giữa đường thẳng và mặt phẳng Phương pháp giải
Trong không gian Oxyz, xét đường thẳng có vectơ chỉ phương là a a ;a ;a và đi qua 1 2 3
M x ; y ; z và mặt phẳng : Ax By Cz D 0 có vectơ pháp tuyến n ; A ; B C . 0 0 0 0 cắt .
a n 0 Aa Ba Ca 0 . 1 2 3 a n Aa Ba Ca // . 0 0 1 2 3 . M P Ax By Cz D 0 0 0 0 0 TOANMATH.com Trang 31 a n Aa Ba Ca . 0 0 1 2 3 M P Ax By Cz D 0 0 0 0 0
a và n cùng phương a : a : a A: B : C . 1 2 3
Ta có thể biện luận vị trí tương đối dựa vào số nghiệm của phương trình đường thẳng và mặt phẳng . Ví dụ mẫu x 1 y z 5
Ví dụ 1. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : và mặt phẳng 1 3 1
P:3x 3y 2z 6 0.
Mệnh đề nào dưới đây đúng?
A. d cắt và không vuông góc với P .
B. d song song với P .
C. d vuông góc với P . D. d nằm trong P . Hướng dẫn giải
Đường thẳng d nhận u 1;3;
1 làm một vectơ chỉ phương.
Mặt phẳng P nhận n 3; 3
;2 làm một vectơ pháp tuyến. Do .
u n 0 và hai vectơ này không cùng phương nên đường thẳng d cắt và không vuông góc với P . Chọn A.
Ví dụ 2. Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng có phương trình x 2 y 1 z 1 d :
và mặt phẳng P x my 2 : m
1 z 7 0 với m là tham số thực. Tìm m sao 1 1 1
cho đường thẳng d song song với mặt phẳng P . m 1 A. m 1. B. m 1. C. . D. m 2 . m 2 Hướng dẫn giải
Đường thẳng d có vectơ chỉ phương là u 1;1;
1 và mặt phẳng P có vectơ pháp tuyến là n 2 1; ; m m 1 . m d // P 1 2 2
u n u.n 0 1 m m 1 0 m m 2 0 m 2
Thử lại ta thấy với m 2 thì d P (loại). Vậy m 1. Chọn B. x 1 y 2 z 3
Ví dụ 3. Trong không gian Oxyz, cho đường thẳng d : và mặt phẳng 2 4 1
: x y 2z 5 0, mệnh đề nào dưới đây là đúng? TOANMATH.com Trang 32 A. d // . B. d .
C. d cắt và không vuông góc với . D. d . Hướng dẫn giải x 1 2t
Ta có d : y 2 4t , t . z 3 t x 1 2t 1 y 2 4t 2 Xét hệ phương trình: z 3 t 3 x y 2z 5 0 *
Thay (1), (2), (3) vào (*) ta được 1 2t 2 4t 23 t 5 0 .
Phương trình này có vô số nghiệm.
Do đó, đường thẳng d nằm trong mặt phẳng . Chọn B. x 12 y 9 z 1
Ví dụ 4. Tọa độ giao điểm M của đường thẳng d : và mặt phẳng 4 3 1
P:3x 5y z 2 0 là A. 1;0; 1 . B. 0;0;2 . C. 1;1;6 . D. 12;9; 1 . Hướng dẫn giải
Gọi M 4t 12;3t 9;t 1 d .
Ta có M P 34t 12 53t 9 t 1 2 0 t 3. Suy ra M 0;0;2. Chọn B.
Ví dụ 5. Trong không gian Oxyz, cho hai mặt phẳng
P: x 2y z 1 0, Q: 2x y z 2 0 x y 1 z 1 x y 2 z 1
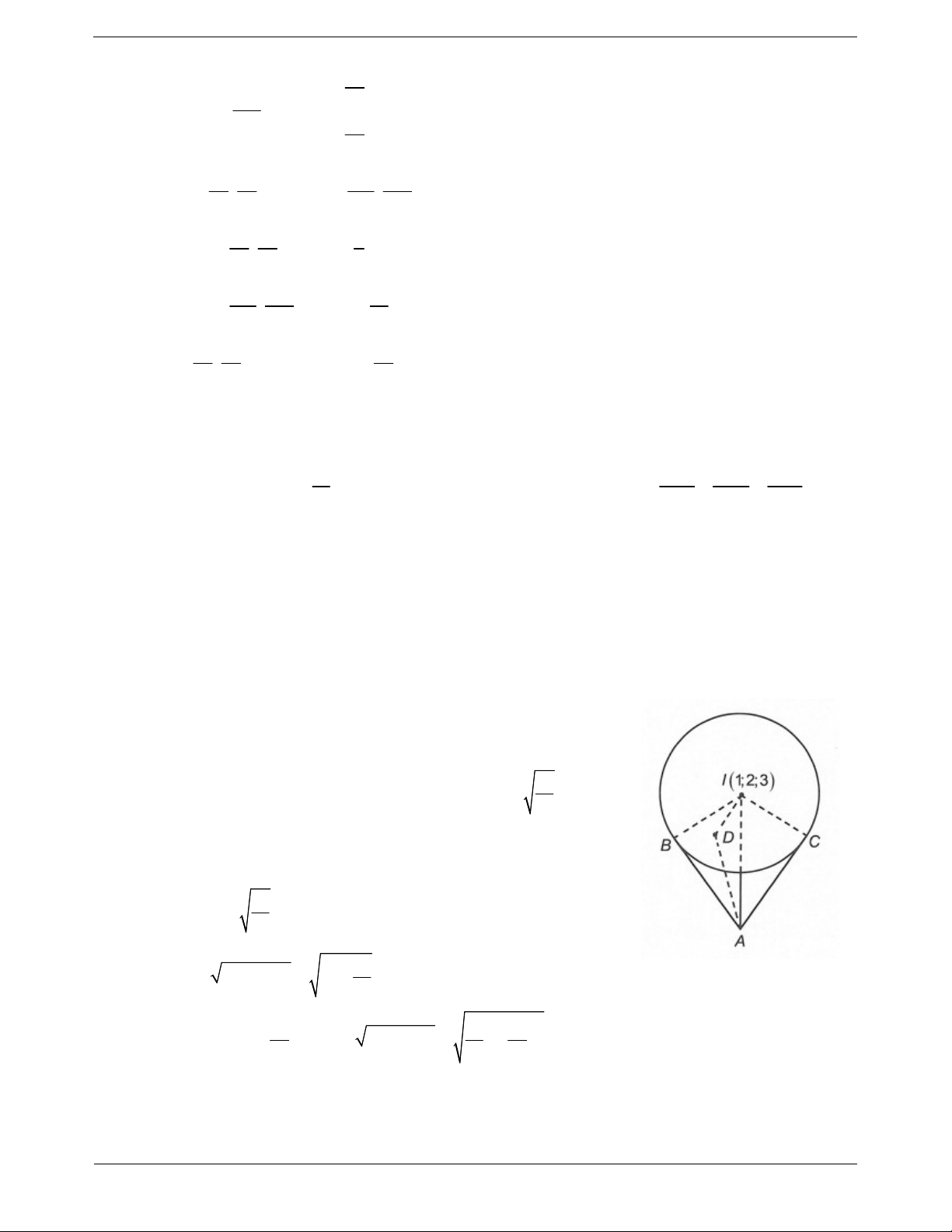
và hai đường thẳng : , : . 1 2 2 1 2 1 1 2
Đường thẳng song song với hai mặt phẳng P,Q và cắt , tương ứng tại H, K . Độ dài đoạn 1 2 HK bằng 8 11 11 A. . B. 5 . C. 6. D. . 7 7 Hướng dẫn giải Ta có u n , n . P Q 1 ;1; 3 TOANMATH.com Trang 33
Gọi H 2t;1 t;1 2t; K ; m 2 ; m 1 2m
HK m 2t;1 m t;2 2m 2t .
Vì song song với 2 mặt phẳng P,Q nên HK ku nên m 2t 1 m t 2 2m 2t . 1 1 3 2 3 8 11 Tính ra được m ; t . Suy ra HK . 7 7 7 Chọn A.
Ví dụ 6. Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng P 2 m m x 2 m y m 2 : 2 2 1
2 z m m 1 0 luôn chứa đường thẳng cố định khi m thay
đổi. Khoảng cách từ gốc tọa độ đến là? 1 2 2 2 A. . B. . C. . D. . 3 3 3 3 Hướng dẫn giải Ta có: 2 m m x 2 m y m 2 2 2 1
2 z m m 1 0, m 2 m 2x y 1 m2x z
1 4x y 2z 1 0, m 2x y 1 0 2x y 1 0 y z 2x z 1 0 2x z 1 0 2x y 1 0 4x y 2z 1 0 t 1 x 2 2
Vậy P luôn chứa đường thẳng cố định: y t z t 1 1
Đường thẳng đi qua A ;0;0
và có vectơ chỉ phương u ;1;1 . 2 2 O , A u 2
Vậy khoảng cách từ gốc tọa độ đến là: d ; O . u 3 Chọn C.
Bài toán 2: Vị trí tương đối giữa hai đường thẳng Phương pháp giải TOANMATH.com Trang 34 x x y y z z
Trong không gian Oxyz, cho hai đường thẳng 0 0 0 d : đi qua M x ; y ; z có 1 0 0 0 1 a b c x x y y z z vectơ chỉ phương u ; a ; b c và 0 0 0 d :
đi qua M x; y; z có vectơ chỉ phương 2 0 0 0 1 2 a b c u a ;b ;c . 2
Để xét vị trí tương đối của d và d , ta sử dụng phương pháp sau: 1 2 a a a 1 2 3 u / /u +) d trùng d 1 2 b b b . 1 2 1 2 3 M d 1 2 M d 1 2 u ,u 0 a a a 1 2 3 1 2 u / /u +) d //d 1 2 b b b . 1 2
hoặc 1 2 3 u , M M 0 M d 1 1 2 1 2 M d 1 2 u ,u 0 1 2 +) d cắt d 1 2
. u ,u .M M 0 1 2 1 2
+) d chéo d u ,u .M M 0 . 1 2 1 2 1 2 Ví dụ mẫu
Ví dụ 1. Trong không gian tọa độ Oxyz, cho hai đường thẳng x 1 y 1 z 2 x 3 y 9 z 2 d : và d : m 0 2 2 1 1 2 1 4 8 m
Tập hợp các giá trị m thỏa mãn d //d có số phần tử là: 1 2 A. 1. B. 0. C. 3. D. 2. Hướng dẫn giải
Đường thẳng d đi qua A1; 1
; 2 và có vectơ chỉ phương là u 1;2;1 . 1 1
Đường thẳng d đi qua B 3; 9 ; 2
và có vectơ chỉ phương là u 2 4;8; m . 2 2
Đường thẳng d //d khi và chỉ khi u cùng phương với u và hai đường thẳng d và d không trùng 1 2 1 2 1 2 nhau. 3 1 9 1 2 2 Vì
nên B nằm trên đường thẳng d . 1 2 1 1
Do đó hai đường thẳng này luôn có điểm chung là B nên hai đường thẳng không thể song song. Chọn B.
Ví dụ 2. Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng x 1 t x 2 2t
d : y 2 3t và d: y 2 t z 3t z 1 3t TOANMATH.com Trang 35
Tìm tọa độ giao điểm M của d và d . A. M 0;1;4 . B. M 1 ;0;4 . C. M 4;0; 1 . D. M 0;4; 1 . Hướng dẫn giải
Tọa độ giao điểm M của d và d ứng với t và t là nghiệm của hệ phương trình: 1 t 2 2t t 2t 1 t 1
2 3t 2 t 3
t t 4 . t 1 3 t 1 3t t 3t 2 Vậy M 0;1;4 . Chọn A.
Ví dụ 3. Trong không gian tọa độ Oxyz, xét vị trí tương đối của hai đường thẳng x 1 y 1 z x 3 y 3 z 2 : , : 1 2 2 2 3 1 2 1 A. song song với . B. chéo với . 1 2 1 2 C. cắt . D. trùng với . 1 2 1 2 Hướng dẫn giải 2 2 Vì
nên vectơ chỉ phương u 2; 2;3 của đường thẳng không cùng phương với vectơ chỉ 1 1 2 1 phương u 1 ; 2 ;1 của . 2 2
Suy ra chéo với hoặc cắt . 1 2 1 2 Lấy M 1; 1 ;0 , N 3;3; 2
. Ta có MN 2;4;2 . 1 2
Khi đó u ,u .MN 0 . 1 2
Suy ra u ,u , MN đồng phẳng. 1 2 Vậy cắt . 1 2 Chọn C.
Bài toán 3: Vị trí tương đối giữa đường thẳng và mặt cầu Phương pháp giải x x a t 1
Ví dụ 1: Trong không gian với hệ tọa độ Oxyz, cho 0 1
Cho đường thẳng d : y y a t 2 và mặt 0 2
mặt cầu S x y z 2 2 2 : 2 25 và đường z z a t 3 0 3 x 2 2t
cầu S x a2 y b z c2 2 2 :
R có tâm thẳng d có phương trình y 2 3t z 3 2t I ; a ; b c, bán kính R .
Chứng minh d luôn cắt S tại hai điểm phân biệt. Hướng dẫn giải
Bước 1: Tính khoảng cách từ tâm I của mặt cầu TOANMATH.com Trang 36
S đến đường thẳng d là
Mặt cầu S có tâm I 0;0;2 và bán kính R 5 . IM .a
Đường thẳng d đi qua M 2 ;2;3 và có vectơ h d I, d 0 a
chỉ phương là u 2;3;2 . IM ,u Ta có h d I, d 3 . u
Bước 2: So sánh d I, d với bán kính R của Vì h R nên d cắt mặt cầu S tại hai điểm phân mặt cầu: biệt.
Nếu d I,d R thì d không cắt S .
Nếu d I,d R thì d tiếp xúc S .
Nếu d I,d R thì d cắt S tại hai điểm
phân biệt M , N và MN vuông góc với
đường kính (bán kính) mặt cầu S . Phương pháp đại số
Ví dụ 2: Trong không gian Oxyz, mặt cầu
Thế (1), (2), (3) vào phương trình S và rút gọn S x y z 2 2 2 :
2 17 cắt trục Oz tại hai
đưa về phương trình bậc hai theo t * . điểm ,
A B . Tìm độ dài đoạn AB .
Nếu phương trình (*) vô nghiệm thì d Hướng dẫn giải không cắt S .
Gọi M là giao điểm của S với trục Oz .
Nếu phương trình (*) có một nghiệm thì d Ta có M Oz nên M 0;0;t . tiếp xúc S .
Mà M S nên t 2 2 2 0 0 2 17
Nếu phương trình (*) có hai nghiệm thì d t 2 t 2 17
2 17 t 2 17 .
cắt S tại hai điểm phân biệt M , N . t 2 17
Chú ý: Để tìm tọa độ M , N ta thay giá trị t vào Suy ra tọa độ các giao điểm là A0;0; 2 17,
phương trình đường thẳng d . B 0;0; 2
17 AB 2 17 . Ví dụ mẫu
Ví dụ 1. Trong không gian tọa độ Oxyz, cho điểm A0;0; 2
và đường thẳng có phương trình là x 2 y 2 z 3 . 2 3 2
Phương trình mặt cầu tâm A , cắt tại hai điểm B và C sao cho BC 8 là
A. x 2 y 2 z 2 2 3 1 16 . B. x y z 2 2 2 2 25 . TOANMATH.com Trang 37 C. x 2 2 2 2 y z 25 . D. x y z 2 2 2 2 16 . Hướng dẫn giải
Gọi S là mặt cầu tâm A0;0; 2
và có bán kính R .
Đường thẳng đi qua M 2
;2;3 có vectơ chỉ phương u 2;3;2 .
Gọi H là trung điểm BC nên AH BC . M . A u Ta có AH d , A . u MA 2; 2 ; 2 2 2 1 7 2 10 Với M . A u 7;2;10 AH 3 . u 2;3;2 2 2 2 2 3 2
Bán kính mặt cầu S là: 2 2 2 2
R AB AH HB 3 4 5 .
Vậy phương trình mặt cầu S là: x y z 2 2 2 2 25 . Chọn B.
Ví dụ 2. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S x 2 y 2 z 2 : 1 1 2 9 và điểm M 1;3;
1 . Biết rằng các tiếp điểm của các tiếp tuyến kẻ từ M tới mặt cầu đã cho luôn thuộc một đường
tròn C có tâm J a; ; b c .
Giá trị 2a b c bằng 134 116 84 62 A. . B. . C. . D. . 25 25 25 25 Hướng dẫn giải
Ta có mặt cầu S có tâm I 1; 1
; 2 và bán kính R 3.
Khi đó IM 5 R M nằm ngoài mặt cầu. x 1
Phương trình đường thẳng MI là x 1 4t . z 23t Tâm J ; a ;
b c nằm trên MI nên J 1;1 4t;2 3t .
Xét MHI vuông tại H có 2 2
MI 5; IH 3 MH MI HI 4 . M 1;3; 1 Mặt khác
MJ 4 4t2 33t2 . J
1;1 4t; 2 3t 16 2 MJ.MI MH MJ 5
t2 t2 256 4 4 3 2 25 TOANMATH.com Trang 38 9 t 369 2 25 25t 50t 0 . 25 41 t 25 11 23 139 7 3 Suy ra J 1; ; hoặc J 1; ; . 25 25 25 25 11 23 9 +) Với J 1; ;
thì IJ IM (nhận). 25 25 5 139 73 41 +) Với J 1; ; thì IJ IM (loại). 25 25 5 11 23 84 Vậy J 1; ; nên 2a b c . 25 25 25 Chọn C.
Ví dụ 3. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S có phương trình là x 4 y 4 z 4
x 2 y 2 z 2 14 1 2 3
và đường thẳng d có phương trình . Gọi 3 3 2 2
A x ; y ; z , x 0 là điểm nằm trên đường thẳng d sao cho từ A kẻ được ba tiếp tuyến đến mặt cầu 0 0 0 0
S có các tiếp điểm B,C,D sao cho ABCD là tứ diện đều.
Giá trị của biểu thức P x y z là 0 0 0 A. 6. B. 16. C. 12. D. 8. Hướng dẫn giải
Gọi I là tâm mặt cầu thì I 1;2;3 .
Gọi O là giao điểm của mặt phẳng BCD và đoạn AI . 14
Vì theo giả thiết AB AC AD và IB IC ID nên AI 3
vuông góc với mặt phẳng BCD tại O . Khi đó O là tâm đường tròn ngoại tiếp BCD . 14 Đặt AI x x . 3 14 Ta có 2 2 2 AB AI IB x 3 2 14 14 14 2 2 2 IB I . O IA OI OB IB IO 3x 3 3x 2 2 2 2 BD OB OD 2O . B OD.cos120 3OB TOANMATH.com Trang 39 14 196
BD 3OB BD 3OB 3. 2 3 9x
Do ABCD là tứ diện đều nên 14 14 196 14 196 2 2 AB BD x 3 x 14 2 2 3 3 9x 3 3x 14 2 x 4 2 3x 56x 196 0 3 x 14 . 2 x 14
A d nên A4 3t;4 2t;4 t . Suy ra AI
t 2 t 2 t 2 14 4 3 1 4 2 2 4 3 14 t 0 A4;4;4 t 1 1 . t 2 A 2 ;0;2
Do x 0 nên điểm A có tọa độ A4;4;4 . 0 Suy ra P 12. Chọn C.
Ví dụ 4. Trong không gian với hệ tọa độ Oxyz, cho ba điểm P,Q, R lần lượt di động trên ba trục tọa độ 1 1 1 1
Ox,Oy,Oz (không trùng với gốc tọa độ O ) sao cho
. Biết mặt phẳng PQR luôn 2 2 2 OP OQ OR 8 1 3
tiếp xúc với mặt cầu S cố định. Đường thẳng d thay đổi nhưng luôn đi qua M ; ;0 và cắt 2 2 S tại hai điểm ,
A B phân biệt. Diện tích lớn nhất của AOB là A. 15 . B. 5 . C. 17 . D. 7 . Hướng dẫn giải
Gọi H là hình chiếu vuông góc của điểm O trên mặt phẳng PQR . 1 1 1 1 1 1 Dễ thấy OH 2 2 . 2 2 2 2 2 OH OP OQ OR OH 8
Khi đó PQR luôn tiếp xúc với mặt cầu S tâm O , bán kính R 2 2 . TOANMATH.com Trang 40 1 3 Ta có OM
0 1 R nên điểm M nằm trong mặt cầu S . 4 4 1
Gọi I là trung điểm của AB , do OAB cân tại O nên S OI.AB . O AB 2
Đặt OI x . Vì OI OM nên 0 x 1 và 2 AB 2 8 x . 1 Ta có 2 2 2 4 S .
x 2 8 x x 8 x 8x x . O AB 2 Xét hàm số f x 2 4 8x x , 0 x 1. Vì f x x 2
4 4 x 0 với mọi x0;
1 nên f x f 1 7 .
Suy ra diện tích của OAB lớn nhất bằng 7 đạt được khi M là trung điểm của AB . Chọn D.
Bài tập tự luyện dạng 4 Bài tập cơ bản
Câu 1: Trong không gian Oxyz, cho đường thẳng d đi qua điểm M và nhận vectơ a làm vectơ chỉ
phương và đường thẳng d đi qua điểm M và nhận vectơ a làm vectơ chỉ phương. Điều kiện để đường
thẳng d song song với đường thẳng d là a ka ,k 0 a ka ,k 0 a a a ka ,k 0 A. . B. . C. . D. . M d M d M d M d x 1 y 2 z 2
Câu 2: Cho đường thẳng d : và điểm A1;2;
1 . Tìm bán kính của mặt cầu có tâm I 1 2 1
nằm trên d , đi qua A và tiếp xúc với mặt phẳng P : x 2y 2z 1 0 . A. R 2 . B. R 4 . C. R 1 . D. R 3 . x 1 y 2 z 2
Câu 3: Cho đường thẳng d :
. Phương trình mặt cầu tâm I 1;2; 1 cắt d tại các 3 2 2 điểm , A B sao cho AB 2 3 là
A. x 2 y 2 z 2 1 2 1 25
B. x 2 y 2 z 2 1 2 1 4 .
C. x 2 y 2 z 2 1 2 1 9 .
D. x 2 y 2 z 2 1 2 1 16 .
Câu 4: Trong không gian Oxyz, cho hai mặt cầu S :x 2 1 y 2
1 z 22 16 và S : x 1 y 2 z 1 9 2 2 2 2 1
cắt nhau theo giao tuyến là một đường tròn tâm là I ; a ;
b c. Giá trị a b c bằng 7 1 10 A. . B. . C. . D. 1. 4 4 3 Bài tập nâng cao
Câu 5: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng TOANMATH.com Trang 41 P 2 m x 2
m m y m 2 : 1 2 2 1 4
2 z m 2m 0 luôn chứa một đường thẳng cố định khi m
thay đổi. Đường thẳng d đi qua M 1;1;
1 vuông góc với và cách O một khoảng lớn nhất có vectơ chỉ phương u 1 ; ;
b c . Giá trị của T b c bằng A. 12. B. 9. C. 11. D. 10.
Câu 6: Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm A3;0;0, B0;2;0,C 0;0;6 và D 1;1;
1 . Kí hiệu d là đường thẳng đi qua D sao cho tổng khoảng cách từ các điểm , A B,C đến d lớn
nhất. Hỏi đường thẳng d đi qua điểm nào dưới đây? A. M 1 ; 2 ; 1 . B. N 5;7;3 . C. P 3;4;3 . D. Q 7;13;5. x 3 y 1 z 2
Câu 7: Trong không gian Oxyz, cho đường thẳng :
. Có tất cả bao nhiêu giá trị thực 1 3 1
của m để phương trình 2 2 2
x y z x my m 2 4 2 2
1 z m 2m 8 0 là phương trình của một mặt
cầu S sao cho có duy nhất một mặt phẳng chứa và cắt S theo giao tuyến là một đường tròn có bán kính bằng 1? A. 1. B. 6. C. 7. D. 2.
Câu 8: Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm M 6;0;0, N 0;6;0, P 0;0;6 . Hai mặt
cầu có phương trình S 2 2 2
: x y z 2x 2 y 1 0 và S : x y z 8x 2y 2z 1 0 cắt 2 2 2 2 1
nhau theo đường tròn C . Hỏi có bao nhiêu mặt cầu có tâm thuộc mặt phẳng chứa C và tiếp xúc với
ba đường thẳng MN, NP, PM ? A. 1. B. 3. C. Vô số. D. 4.
Câu 9: Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A2;1;3, B6;5;5 . Gọi S là mặt cầu
đường kính AB . Mặt phẳng P vuông góc với AB tại H sao cho khối nón đỉnh A và đáy là hình tròn
tâm H (giao của mặt cầu S và mặt phẳng P ) có thể tích lớn nhất, biết rằng P : 2x by cz d 0 với b, , c d . Tính S b c d . A. S 18 . B. S 18 . C. S 12 . D. S 24 .
Dạng 5: Một số bài toán cực trị Ví dụ mẫu
Ví dụ 1: Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm M 2 ;2;
1 , A1;2;3 và đường x 1 y 5 z thẳng d :
. Tìm một vectơ chỉ phương u của đường thẳng đi qua M , vuông góc với 2 2 1
đường thẳng d đồng thời cách điểm A một khoảng bé nhất. A. u 2;2; 1 . B. u 1;7; 1 . C. u 1;0;2 . D. u 3;4; 4 . Hướng dẫn giải TOANMATH.com Trang 42
Xét P là mặt phẳng qua M và P d .
Mặt phẳng P qua M 2 ; 2 ;
1 và có vectơ pháp tuyến n u 2;2; 1 nên có phương trình: P d
2x 2 y z 9 0 .
Gọi H , K lần lượt là hình chiếu của A lên P và .
Khi đó AK AH const nên AK đạt giá trị nhỏ nhất khi và chỉ khi K H .
Đường thẳng AH đi qua A1;2; 3
và có vectơ chỉ phương u 2;2; 1 nên AH có phương trình d x 1 2t
tham số là y 2 2t . z 3t
Vì H AH nên H 1 2t;2 2t; 3 t .
Lại H P nên 21 2t 22 2t 3
t 9 0 t 2 H 3; 2 ; 1 . Vậy u HM . 1;0;2 Chọn C.
Ví dụ 2: Trong không gian Oxyz, cho mặt cầu S có phương trình 2 2 2
x y z 4x 2 y 2z 3 0 và
điểm A5;3;2 . Một đường thẳng d thay đổi luôn đi qua A và luôn cắt mặt cầu tại hai điểm phân biệt M , N .
Tính giá trị nhỏ nhất của biểu thức S AM 4AN . A. S 30 . B. S 20 . C. S 5 34 9 . D. S 34 3. min min min min Hướng dẫn giải
Mặt cầu S có tâm I 2;1; 1 , bán kính R 2 2 2 2 1 1 3 3.
Ta có: AI 2 2 2 2 5 1 3 1 2
34 R nên A nằm ngoài mặt cầu S .
Ta lại có: S AM 4AN .
Đặt AM x, x 34 3; 34 3 . 25 Mà 2 2
AM .AN AI R 34 9 25 AN . AM Do đó: 100 S f x x
với x 34 3; 34 3 x . TOANMATH.com Trang 43 2 100 x 100 Ta có: f x 1
0 với x 34 3; 34 3 2 x x . Do đó: min
f x f 34 3 5 34 9 . 343; 343 Dấu “=” xảy ra ,
A M , N , I thẳng hàng và AM 34 3; AN 34 3. Chọn C.
Ví dụ 3: Trong không gian Oxyz, cho hai điểm A9;6;1
1 , B 5;7;2 và điểm M di động trên mặt cầu
S x 2 y 2 z 2 : 1 2 3 36 .
Giá trị nhỏ nhất của AM 2MB bằng A. 105 . B. 2 26 . C. 2 29 . D. 102 . Hướng dẫn giải
Mặt cầu S x 2 y 2 z 2 : 1 2
3 36 có tâm I 1;2;3 và bán kính R 6 . Ta có IA 12 2R .
Gọi E là giao điểm của IA và mặt cầu S suy ra E là trung điểm của IA nên E 5;4;7 .
Gọi F là trung điểm của IE suy ra F 3;3;5 . IF IM 1 Xét MIF và AIM có AIM chung và . IM IA 2 MA AI
Suy ra MIF# AIM c.g.c 2 MA 2MF . MF MI
Do đó AM 2MB 2MF MB 2BF 2 29 (theo bất đẳng thức tam giác).
Dấu “=” xảy ra khi M là giao điểm FB và mặt cầu S . Chọn C.
Bài tập tự luyện dạng 5 Bài tập cơ bản
Câu 1: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A2;2;4, B3;3; 1 và đường thẳng x 5 y 2 z d :
. Xét M là điểm thay đổi thuộc d , giá trị nhỏ nhất của 2 2 2MA 3MB bằng 2 1 1 A. 14. B. 160. C. 4 10 D. 18. TOANMATH.com Trang 44
Câu 2: Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A1;0;3; B3;1;3; C 1;5; 1 . Gọi
M x ; y ; z thuộc mặt phẳng tọa độ Oxy sao cho biểu thức T 2 MA MB MC có giá trị nhỏ 0 0 0
nhất. Giá trị của x y bằng 0 0 8 8 A. x y . B. x y . C. x y 2 . D. x y 2 . 0 0 5 0 0 5 0 0 0 0 Bài tập nâng cao
Câu 3: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A1;2;3, B2; 2 ;
1 và mặt phẳng có
phương trình 2x 2 y z 9 0 . Gọi M là điểm thay đổi trên mặt phẳng sao cho M luôn nhìn
đoạn AB dưới một góc vuông. Xác định phương trình đường thẳng MB khi MB đạt giá trị lớn nhất. x 2 t x 2 2t x 2 t x 2 t A. y 2 2t . B. y 2 t . C. y 2 . D. y 2 t . z 1 2t z 1 2t z 1 2t z 1
Câu 4: Cho mặt cầu S x 2 y 2 z 2 : 2 1
3 9 và hai điểm A1;1;3, B21;9; 1 3 . Điểm M ; a ;
b c thuộc mặt cầu S sao cho 2 2
3MA MB đạt giá trị nhỏ nhất.
Khi đó giá trị của biểu thức T . a . b c bằng A. 3. B. 8. C. 6. D. 18 . ĐÁP ÁN
Dạng 1. Xác định vectơ chỉ phương và viết phương trình đường thẳng 1-B 2-B 3-B 4-B 5-B 6-C 7-C 8-C 9-B 10-B 11-D 12-D 13-A 14-D 15-D 16-C 17-D 18-B 19-C 20-B
Dạng 2. Các vấn đề về góc 1-C 2-B 3-A 4-C Dạng 3. Khoảng cách 1-A 2-A 3-C 4-D 5-D
Dạng 4. Vị trí tương đối 1-A 2-D 3-D 4-D 5-C 6-B 7-D 8-C 9-B
Dạng 5. Một số bài toán cực trị 1-B 2-C 3-C 4-B TOANMATH.com Trang 45




